郑振龙jiangyi16
金融工程复习资料要点郑振龙

金融工程复习资料1、什么是金融工程?答:金融工程是指综合运用现代金融学、工程方法和信息技术,运用各种基础性和衍生性的证券,设计、开发和应用新型的金融产品,以达到创造性解决金融问题、管理风险的根本目标的学科技术。
2、金融工程的作用?答:主要有三大作用:1)变幻无穷的新产品:构造出无穷多种新产品,满足不同市场状况下的特定需求。
使金融产品的内涵和外延、品种与数量都无时不处于变化和拓展当中,这方面为市场参与这提供了更多不同风险收益特征的投资工具,使市场趋于完全,风险管理更容易实现;另一方面,使得套利更容易进行、有助于减少定价偏误。
2)更具准确性、时效性和灵活性的低成本风险管理:推动了现代风险度量技术的发展;衍生证券是风险分散与对冲的最佳工具(1、成本优势;2、更高的准确性;3、很大的灵活性)3)【弊】风险放大与市场波动:衍生证券的高杠杆性质使得投资者只需动用少量资金,就可操作数倍乃至于数十倍自有资金的金融衍生品交易。
使得投机成本低廉,大大增加了投机者的数量、规模和投机冲动。
本质上,以放大风险换取高回报。
(水能载舟、亦能覆舟)3、金融工程的根本目的:解决金融问题金融工程的主要内容:设计、定价与风险管理(===核心)4、金融工程运用的主要工具有哪些基本类型?答:金融工程运用的主要工具有两大类:基础性证券与金融衍生证券。
基础性证券包括股票和债券(银行的存贷款也属于基础性证券)。
金融衍生证券包括远期、期货、互换和期权四类。
所以金融工程的主要工具主要有6种,分别是股票、债券、远期、期货、互换和期权。
【小概念】远期:是指双方约定在未来的某一确定时间,按确定价格买卖一定数量的某种标的金融资产的合约。
期货:一般指期货合约,就是指由期货交易所统一制定的、规定在将来某一特定的时间和地点交割一定数量标的物的标准化合约。
互换:两个或两个以上当事人按照商定条件,在约定时间内交换一系列现金流的合约。
期权:指赋予其购买者在规定期限内按双方约定的价格购买或出售一定数量某种标的资产的权利的合约。
郑振龙金融工程PPT FE13讲义资料

451000 40.351000 11.5% 40.351000
➢ 期权投资收益率为
45 60200 40 60200 746.3% 0.67 60200
Copyright © 2012 Zheng, Zhenlong & Chen, Rong
7
案例 13.2 :期权的杠杆效应 (cont.)
28
蝶式差价组合( Butterfly Spreads ) (cont.)
蝶式差价组合由四份具有相同期限、不同协议价格的 同种期权头寸组成。
若 X1 < X2 < X3 ,且 X2 = ( X1 + X3 )/2 ,则蝶式差价组合有 如下四种:
Copyright © 2012 Zheng, Zhenlong & Chen, Rong
包括标的资产与期权的组合、期权与期权的组合。 只要期权协议价格足够多,组合种类是无限的。 分析方法:
➢ Payoff 和 profit 分布图 ➢ 盈亏状况分析表
Copyright © 2012 Zheng, Zhenlong & Chen, Rong
14
标的资产与期权的组合
(a)标的资产多头与看涨期权空头的组合
10
案例 13.3 :期权的其他作用 (cont.)
2007 年 8 月 31 日以 38.5 美元的价格买入 1000 股 GE 股票,同时卖出 10 份 9 月 22 日到期、执行价格为 40 美元的 GE 看涨期权,期权费收入 350 美元。假如 9 月22 日到期前 GE 股票价格未能高于 40 美元,多头不 执行期权,则 C 无需履行自己卖出 GE 股票的义务, 保留手中股票,同时尽享 350 美元期权费。当然,如 果 9 月 22 日到期前 GE 股票价格高过 40 美元,C 就必 须以 40 美元卖出手中股票,但其实际卖出价是 40.35 美元。
金融工程第三版(郑振龙)课后习题答案

第1章7.该说法是正确的。
从图1.3中可以看出,如果将等式左边的标的资产多头移至等式右边,整个等式左边就是看涨期权空头,右边则是看跌期权空头和标的资产空头的组合。
9. ()5%4.82⨯=元1000012725.21e⨯10. 每年计一次复利的年利率=(1+0.14/4)4-1=14.75%连续复利年利率= 4ln(1+0.14/4)=13.76%。
11. 连续复利年利率=12ln(1+0.15/12)=14.91%。
12. 12%连续复利利率等价的每季度支付一次利息的年利率=4(e0.03-1)=12.18%。
因此每个季度可得的利息=10000×12.8%/4=304.55元。
第2章1、2007年4月16日,该公司向工行买入半年期美元远期,意味着其将以764.21人民币/100美元的价格在2007年10月18日向工行买入美元。
合约到期后,该公司在远期合约多头上的盈亏=10000(752.63764.21)115,800⨯-=-。
矚慫润厲钐瘗睞枥庑赖。
2、收盘时,该投资者的盈亏=(1528.9-1530.0)×250=-275美元;保证金账户余额=19,688-275=19,413美元。
若结算后保证金账户的金额低于所需的维持保证金,即19,688(S P5001530)25015,750&指数期货结算价时+-⨯<(即S&P500指数期货结算价<1514.3时),交易商会收到追缴保证金通知,而必须将保证金账户余额补足至19,688美元。
聞創沟燴鐺險爱氇谴净。
3、他的说法是不对的。
首先应该明确,期货(或远期)合约并不能保证其投资者未来一定盈利,但投资者通过期货(或远期)合约获得了确定的未来买卖价格,消除了因价格波动带来的风险。
本例中,汇率的变动是影响公司跨国贸易成本的重要因素,是跨国贸易所面临的主要风险之一,汇率的频繁变动显然不利于公司的长期稳定运营(即使汇率上升与下降的概率相等);而通过买卖外汇远期(期货),跨国公司就可以消除因汇率波动而带来的风险,锁定了成本,从而稳定了公司的经营。
郑振龙金融工程 FE5ppt课件

19:38
最新版整理ppt
1
股票头寸与短期国库券头寸
股票头寸 ⇐⇒ 短期国库券头寸
➢ 股票多头 + 股指期货空头 = 短期国库券多头 ➢ 股票多头 = 短期国库券多头 + 股指期货多头
构造短期国库券多头等价于将系统性风险降为零。
➢ 若r f r , 外汇远期贴水; ➢ 若r f r , 外汇远期升水。
19:38
最新版整理ppt
1
理解 ERA
合约本质
当前约定未来某个时点的远期升贴水幅度,是远期的远期。从 实物交割的角度来看,也可以理结算
19:38
最新版整理ppt
1
ERA 的定价:实物交割 I
第五章 股指期货、外汇远期、 利率远期与利率期货
19:38
目录
股票指数期货
外汇远期
远期利率协议
利率期货
利率风险管理
19:38
最新版整理ppt
1
股票指数期货概述 I
股票指数
➢ 运用统计学中的指数方法编制而成的、反映股市中总体股价 或某类股票价格变动和走势情况的一种相对指标。
课后阅读:上证综指与沪深300指数对派发红利的处 理有何不同?
➢ 管理系统性风险 ➢ 多为交叉套期保值
19:38
最新版整理ppt
1
最小方差套期保值比率 I
一元线性回归方程 rHabrG
CAPM Beta 系数
R Hrf (R Mrf)
rirM 2
rirM
ri
rM
rM
最小方差套期保值份数
N VH
VG
19:38
必下载原版无删减教师专用郑振龙金融工程第三章教学

本章将要用到的符号主要有: T:远期和期货合约的到期时间,单位为年。 t:现在的时间,单位为年。变量T 和t 是从合约生效之 前的某个日期开始计算的,T-t 代表远期和期货合约中 以年为单位的距离到期时间的剩余时间。 S:远期(期货)标的资产在时间t时的价格。 ST:远期(期货)标的资产在时间T时的价格(在t时刻 这个值是个未知变量)。 K:远期合约中的交割价格。 f:远期合约多头在t时刻的价值,即t时刻的远期价值。
3
远期价格是指使远期合约签订时价值为零的交割价格。 远期价格是理论上的交割价格。关于远期价格的讨论也 要分远期合约签订时和签订后两种情形。
- 一份公平合理的远期合约在签订的当天应使交 割价格等于远期价格。如果实际交割价格不等于这个理 论上的远期价格,该远期合约价值对于多空双方来说就 都不为零 ,实际上隐含了套利空间。
,Ser同(T 时t) 得到
的本Ie利r(收T 入t) 。最终套利者在T时刻可实现无风险利
润
K (S I 。 )er(T t)
23
如果 K (S I )er(Tt) ,即交割价格低于远期理论价格。则 套利者可以进行反向操作:借入标的资产卖掉,得到现 金收入S以无风险利率贷出,同时买入一份交割价为K 的远期合约。在T时刻,套利者可得到贷款本息收
5
当无风险利率恒定且所有到期日都相同时,交割日相同 的远期价格和期货价格应相等。
当标的资产价格与利率呈正相关时,期货价格高于远期 价格。
- 这是因为当标的资产价格上升时,期货价格通常也会随
之升高,期货合约的多头将因每日结算制而立即获利,并可按高于 平均利率的利率将所获利润进行再投资。而当标的资产价格下跌时, 期货合约的多头将因每日结算制而立即亏损,但是可按低于平均利 率的利率从市场上融资以补充保证金。相比之下,远期合约的多头 将不会因利率的变动而受到上述影响。在此情况下,期货多头比远 期多头更具吸引力,期货价格自然就大于远期价格。
(完整版)金融工程复习提纲—郑振龙第四版

1.金融工程:开发设计新式工具和实行金融手段一、根本目的:解决金融问题二、主要内容:设计、订价与风险管理三、主要工具:基础产品与金融衍生产品四、技术手段:现代金融学、数理和工程方法与信息技术五、作用:促使金融业创新与发展2.推进金融工程发展的重要要素:日趋动乱的全世界经济环境、鼓舞金融创新的制度环境、金融理论和技术的发展创新、信息技术的进步、市场追求效率的结果。
3.套期保值者、套利者和谋利者。
他们有不一样的参加目的,他们的行为都对市场发挥侧重要作用。
套保者的操作是为了转移和管理已有头寸的风险裸露,他是衍生证券市场产生和发展的原动力。
套利者则是经过发现现货和衍生证券价钱之间的不合理关系,经过同时操作,获得低风险或无风险的套利利润。
他的参加有益于市场效率的提升。
4. 一年复利一次:FV=A*( 1+r)^t一年复利 m 次FV = A×e rT若二者相等则:1+r1=( 1+r/m ) ^m=e^rr 连续复利年利率=mln ( 1+rm/m ),当 m=1 时, r=ln ( 1+r1 )5.远期合约:规定在未来的某一时间以确立的价钱交易一种确立产品的合约买方、多方、多头:未来将买入标的物的一方卖方、空方、空头:未来将卖出标的物的一方作用:确立标的财产未来某时辰的价钱,除去价钱风险注意: 1.远期合约不可以带来确立盈余; 2.是多头两方的零和游戏6.常有的金融远期合约:远期利率协议、远期外汇协议、远期股票合约1.远期利率协议 FRA:某一时辰开始,借贷一笔数额确立、特定钱币表示的名义本金的协议。
1*4 远期利率( r1*4 )表示 1 个月后开始的限期为三个月的远期利率2.远期外汇协议 FXA:某一时间按商定汇率买卖必定金额的某种外汇的合约。
本金不行交割远期 NDF:指不交割名义本金,只交割规定汇率与实质汇率的差额。
3.远期股票合约:某一特准期间按特订价钱交托必定数目单个股票或一揽子股票的协议7.远期市场的交易体制:分别的场外交易,非标准化合约优势:灵巧弊端: 1.市场效率低; 2.流动性较差; 3.违约风险相对较高8.金融期货合约:指在交易所交易的、协议两方商定在未来某一个日期按预先确立的条件(交割价钱、交割地址、交割方式)买入或卖出必定标准数目的特定金融工具的标准化协议。
金融基础知识——厦门大学郑振龙教授的演讲

基础的金融知识-来自厦门大学郑振龙教授的演讲演讲人:厦门大学郑振龙教授今天非常高兴第一次能到西南财经大学来演讲。
西南财经大学在国内金融界大家知道是非常著名的,这里有很多高手,所以今天我讲的有不对的地方大家尽管可以指出来。
金融工程这个东西是非常枯燥的,大家都知道一大堆的数学模型和编程的任务,今天在这里交流主要是交流一些思想。
我觉得很多人把金融工程简单的理解成一种数学和计算机,实际上,如果要比数学和计算机,我们在座的各位都比不上数学系和计算机系的。
那么为什么他们的金融工程做的不如我们,肯定是其中缺乏一个金融思想。
所以在这里更多的给大家交流一下思想上的体会。
数学的东西涉及得很少,而是在思想上同大家进行的交流。
金融工程是一个新的学科,这个学科出现以后对传统的金融学有很大的冲击。
所以我们实际上是从一个比较新的角度来重新认识金融问题。
首先看一下什么叫金融。
我是1982年入学念本科的,现在已经20多年过去了,老师教我,就是资金融通,简称金融,现在不知道老师如何教你们的。
实际上现在这样的理解是非常的狭窄的,金融按照定义来划分可以分为MANETARY ECONOMICS 和FINANCIAL ECONOMICS。
金融经济学实际上是新金融。
国外的金融同国内的金融区别很大,这个大家应该很熟悉,我就不多讲了。
金融经济学是研究在不确定条件下,将资产沿着时间和空间两个维度进行最优配置的决策科学,所以是非常微观的,在国外属于管理学的范畴。
简单来说就是关于时间和风险的经济学。
那么对于时间经济学,大家知道主要是研究利率——货币在时间上的价值。
所以大家研究利率水平决定和利率期限结构等内容。
有了这两样东西后,我们就可以将现金流沿着时间轴在不同时点之间自由转换。
有了即期期限结构我们就可以有远期期限结构,所有沿着时间维度上的现金流我们就可以比较。
不然今天的100元钱同100年前、100年后的一百元钱差距多大我们根本不能无法度量。
另外一个是风险经济学,涉及到风险的识别、风险的管理以及风险的定价,如果能对风险进行度量就能将风险价值转化成确定性价值。
16《猫》郑振铎

5、“妻听见了,也匆匆地跑下来,看了 死鸟,很难过,便道:‘不是这猫咬 死的还有谁?它常常对鸟笼望着,我 早就叫张婶要小心了。张婶!你为什 么不小心?’” 妻子的话表现了什么?
妻子的话照应了上文猫对鸟笼凝望 一事,小猫蒙冤。
8、“隔了几天,李嫂在楼下叫道:‘猫, 猫?又来吃鸟了。’同时我看见一只 黑猫飞快的逃过露台,嘴里衔着一只 黄鸟。 ”这个情节的设置起到了怎样 的作用?
3、“我坐在藤椅上看着他们,可以微笑 着消耗过一二小时的光阴,那时太阳 光暖暖的照着,心上感着生命的新鲜 与快乐。” 如何理解这句话所表达的 意思?表达了作者怎样的思想感情?
【1】由于小猫的活泼可爱,家里人 都很喜欢它,它也陪伴家人度过许多 快乐的时光,给生活增添了许多乐趣。
【2】表达了我对小猫的喜爱之情。
从内容上看,真相大白,原来花 白猫蒙受了冤屈,同时也为下文写 “我”的自责做了铺垫。
9、“想到它的无抵抗的逃避,益使我感 到我的暴怒,我的虐待,都是针,刺 我的良心的针!”这句话使用了什么 修辞手法?有什么表达效果?
比喻;
将原来对猫的暴怒、虐待比作刺 “我”” 的良心的针,生动形象地表达 了“我”发现真相后内心的悔恨愧疚。
犯罪嫌疑人:___那__只__丑___猫_______
犯罪嫌疑人作案的可能性:
1、案发前的表现:对黄鸟似乎特别注意,常常 跳__在__桌__子__上___,__对__鸟__笼__凝__望着。
2、案发后的表现:躺在露台板上晒太阳,态度很 _安__详__,__嘴__里__好__像__还__在__吃___着什么。
污wū涩sè 一缕lǚ 怅chàng然 红绫líng 畏wèi罪潜qián逃 屋wū脊jǐ 忧yōu郁yù
怂sǒng恿yǒng 蜷quán伏 诅zǔ骂 惩chéng戒jiè 虐nüè待 叮dīng嘱zhǔ 凝níng望wàng
金融工程.郑振龙(全套课件560P)

由于期初的组合应该等于看涨期权的价值,即有N S0-B=c0,把N和B 代入本式中,得到看涨期权的价值 公式
c0=[pcu+(1-p)cd]e-r(T-t) 其中p=(er(T-t)S0-Sd)/(Su-Sd)=(er(T-t)-d)/(u-d) 。
无套利分析(包括其应用状态价格定价技术) 的过程与结果同市场参与者的风险偏好无关。
2021/4/13
34
状态价格定价法的应用
假设某股票符合我们上面提到的两种市 场状态,即期初价值是S0,期末价值是S1, 这里S1只可能取两个值:一是S1=Su=uS0,u >1,二是S1= Sd=dS0,d<1。我们现在想 要确定的是依附于该股票的看涨期权的 价值是多少?
13
无套利的价格是什么?
无套利均衡的价格必须使得套利者处于 这样一种境地:他通过套利形成的财富 的现金价值,与他没有进行套利活动时 形成的财富的现金价值完全相等,即套 利不能影响他的期初和期末的现金流量 状况。
2021/4/13
14
例子
假设现在6个月即期年利率为10%(连续 复利,下同),1年期的即期利率是12%。 如果有人把今后6个月到1年期的远期利 率定为11%,试问这样的市场行情能否 产生套利活动?
资产多头看跌期权多头看涨期权多头资产多头看涨期权空头看跌期权空头资产空头看涨期权多头看跌期权多头资产空头看跌期权空头看涨期权空头第三章金融远期和期货市场概述金融远期合约forwardcontracts是指双方约定在未来的某一确定时间按确定的价格买卖一定数量的某种金融资产的合约
金融工程
2021/4/13
2021/4/13
7
金融理论的发展与金融工程
金融工程_第二版_郑振龙__课后习题和答案整理(华北电力大学)

第二章金融工程的基本分析方法习题1、假定外汇市场美元兑换马克的即期汇率是1美元换1.8马克,美元利率是8%,马克利率是4%,试问一年后远期无套利的均衡利率是多少?2、银行希望在6个月后对客户提供一笔6个月的远期贷款。
银行发现金融市场上即期利率水平是:6个月利率为9.5%,12个月利率为9.875%,按照无套利定价思想,银行为这笔远期贷款索要的利率是多少?3、假如英镑与美元的即期汇率是1英镑=1.6650美元,远期汇率是1英镑=1.6600美元,6个月期美远与英镑的无风险年利率分别是6%和8%,问是否存在无风险套利机会?如存在,如何套利?4、一只股票现在价格是40元,该股票一个月后价格将是42元或者38元。
假如无风险利率是8%,用无风险套利原则说明,执行价格为39元的一个月期欧式看涨期权的价值是多少?5、条件同题4,试用风险中性定价法计算题4中看涨期权的价值,并比较两种计算结果。
6、一只股票现在的价格是50元,预计6个月后涨到55元或是下降到45元。
运用无套利定价原理,求执行价格为50元的欧式看跌期权的价值。
7、一只股票现在价格是100元。
有连续两个时间步,每个步长6个月,每个单步二叉树预期上涨10%,或下跌10%,无风险利率8%(连续复利),运用无套利原则求执行价格为100元的看涨期权的价值。
8、假设市场上股票价格S=20元,执行价格X=18元,r=10%,T=1年。
如果市场报价欧式看涨期权的价格是3元,试问存在无风险的套利机会吗?如果有,如何套利?9、股票当前的价格是100元,以该价格作为执行价格的看涨期权和看跌期权的价格分别是3元和7元。
如果买入看涨期权、卖出看跌期权,再购入到期日价值为100 的无风险债券,则我们就复制了该股票的价值特征(可以叫做合成股票)。
试问无风险债券的投资成本是多少?如果偏离了这个价格,市场会发生怎样的套利行为?习题解答:1、按照式子:(1+8%)美元=1.8×(1+4%)马克,得到1美元=1.7333马克。
金融工程讲义课件.pptx

主要内容
▪ 金融工程-- 概念与技术 ▪ 金融工程--理论与实体工具 ▪ 金融工程--模型与应用
金融工程--概念
▪ 金融工程 ▪ 金融风险管理 ▪ 金融产品与策略 ▪ 金融工程(思想、技术--方案、产品)
金融工程-- 技术
▪ 无风险套利、均衡分析技术
• 金融工程的基本思想与核心技术
▪ 组合、分解技术
▪ 金融工程的概念有狭义和广义两种。狭义的金融工程主要是指利用先进的数 学及通讯工具,在各种现有基本金融产品的基础上,进行不同形式的组合分 解,以设计出符合客户需要并具有特定P/L(Price List)性的新的金融产 品。而广义的金融工程则是指一切利用工程化手段来解决金融问题的技术开 发,它不仅包括金融产品设计,还包括金融产品定价、交易策略设计、金融 发展历程:
▪ 描述型金融学 分析型金融学
金融工程学
金融行为学
▪ 定性分析 定性分析+定量分析 创造性 +工程化 金融学+行为学
金融伦理(可持续发展)
金融技术含量 金融心理/习惯
附1. 金融工程与现代金融学的发展
现代金融学的基本结构框架
附2. 金融工程的数学基础
《金融工程》
中南财经政法大学
新华金融保险学院
张 金 林 博士 教授
2005年9月 武汉
教学安排
▪ 上课内容1-8讲 ▪ 时间安排:教学8周。
(8周授课、1周座谈) ▪ 成绩:作业30%、期末70%。
参考书目
▪ 1. 《金融工程学》格利茨 著 唐旭译 ▪ 2. 《金融工程原理》宋蓬明 著 清华大学出版社 ▪ 3. 《金融工程学》陈松南 著 复旦大学出版社 ▪ 4. 《 金融工程》郑振龙 主编 ▪ 5. 《全球资产与负债管理建模》津巴等著
金融工程(第二版)郑振龙Chapter 4课件

当价格的上升可能对投资者造成不利影响的时候,选 择多头套期保值;
价格的下跌可能对投资者造成不利影响的时候,选择 空头套期保值。
17
在1单位现货空头用n单位期货多头进行套期保值的情形下,投资者的 整个套期保值收益可以表达为
nG 1G 0(H 1H 0)
最优套期保值比率就是使得套期保值收益对被套期保值的资产价格的
H 0 H 1 G 1 G 0 H 0 G 0 H 1 G 1 b 0 b 1 (4.1)
在1单位现货多头而用1单位期货空头进行套期保值的情形下,投 资者的整个套期保值收益可以表达为
( H 1 H 0 ) G 0 G 1 H 1 G 1 H 0 G 0 b 1 b 0 (4.2)
4
什么是完美的套期保值? 若远期(期货)的到期日、标的资产和交易金额等条 件的设定使得远期(期货)与现货都能恰好匹配,从 而能够完全消除价格风险时,我们称这种能够完全消 除价格风险的套期保值为“完美的套期保值”。
而不完美的套期保值 ,则是指那些无法完全消除价格 风险的套期保值 。通常不完美的套期保值是常态 。
21
22
二、运用远期与期货进行投机
远期(期货)与其标的资产价格变动的风险源是相同的, 因此投机既可以通过远期(期货)实现,也可以通过现货实现。 然而,远期(期货)具有进入成本低、高杠杆效应等优势,这 使得远期(期货)成为更好的投机途径。
但值得注意的是:高杠杆可能会使得一个小比例的价 格变化带来放大的收益,但也可能导致一个小比例的价格变 化带来放大的亏损,这是衍生产品高杠杆效应的双刃剑本质。 (案例4.4 沪深300指数期货仿真交易杠杆效应)
期货市场的多头对现货市场进行套期保值。担心价 格上涨的投资者会运用多头套期保值的策略,其主 要目的是锁定未来买入价格。 (案例4.1) (二)空头套期保值 空头套期保值也称卖出套期保值,即通过进入远期或 期货市场的空头对现货市场进行套期保值。担心价 格下跌的投资者会运用空头套期保值的策略,其主 要目的是锁定未来卖出价格。 (案例4.2)
郑振龙《金融工程》笔记和课后习题详解-期权与期权市场【圣才出品】

第九章期权与期权市场9.1复习笔记一、期权的定义与种类所谓期权,是指赋予其购买者在规定期限内按双方约定的价格(简称执行价格)购买或出售一定数量某种资产(称为标的资产)的权利的合约。
1.看涨期权与看跌期权按期权买者的权利划分,期权可分为看涨期权和看跌期权。
所谓看涨期权,就是赋予了多方未来按约定价格买入某种资产的权利。
未来如果价格上涨,多方将执行这个权利;如果价格下跌,多方有权放弃这个权利。
而期权费,就是购买这个权利所支付的费用。
所谓看跌期权,就是赋予了多方未来按约定价格卖出某种资产的权利。
未来如果价格下跌,多方将执行这个权利;如果价格上涨,多方有权放弃这个权利。
而期权费,就是购买这个权利所支付的费用。
期权是一种金融合约,是买卖双方关于未来某种权利的协议。
其协议要素包括:买卖双方、约定的权利、约定期限、执行价格、约定交易数量和期权价格(期权费)等。
在期权交易中存在着双重的买卖关系:对期权本身的购买和出售形成了期权的多方和空方。
对于期权的多方来说,期权合约赋予他的只有权利,而没有任何义务。
对期权的出售者来说,他只有履行合约的义务,而没有任何权利。
期权的其他一些要素包括期限、执行价格和交易数量等。
期权买方只能在合约所规定的时间内行使其权利,一旦超过期限仍未执行即意味着自愿放弃了这一权利。
执行价格是指期权合约所规定的、期权买方在行使其权利时实际执行的买卖标的资产的价格。
交易数量则指每份期权合约可以交易的股票数量。
2.欧式期权与美式期权按期权多方执行期权的时限划分,期权可分为欧式期权和美式期权。
欧式期权的多方只有在期权到期日才能执行期权(即行使买进或卖出标的资产的权利),而美式期权允许多方在期权到期前的任何时间执行期权。
3.期权合约的标的资产按期权合约标的资产划分,金融期权合约可分为股票期权、股价指数期权、期货期权、利率期权、信用期权、货币期权(外汇期权)及互换期权等。
股票期权是指以单一股票作为标的资产的期权合约,一般是美式期权。
2022届高考数学第一轮总复习人教版理科讲义:16-理数第十六章
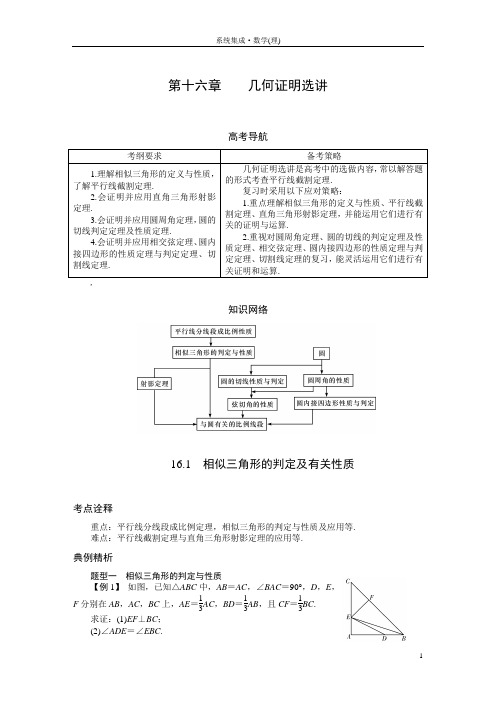
第十六章几何证明选讲高考导航考纲要求备考策略1.理解相似三角形的定义与性质,了解平行线截割定理.2.会证明并应用直角三角形射影定理.3.会证明并应用圆周角定理,圆的切线判定定理及性质定理.4.会证明并应用相交弦定理、圆内接四边形的性质定理与判定定理、切割线定理.几何证明选讲是高考中的选做内容,常以解答题的形式考查平行线截割定理.复习时采用以下应对策略:1.重点理解相似三角形的定义与性质、平行线截割定理、直角三角形射影定理,并能运用它们进行有关的证明与运算.2.重视对圆周角定理、圆的切线的判定定理及性质定理、相交弦定理、圆内接四边形的性质定理与判定定理、切割线定理的复习,能灵活运用它们进行有关证明和运算.,知识网络16.1相似三角形的判定及有关性质考点诠释重点:平行线分线段成比例定理,相似三角形的判定与性质及应用等.难点:平行线截割定理与直角三角形射影定理的应用等.典例精析题型一相似三角形的判定与性质【例1】如图,已知△ABC中,AB=AC,∠BAC=90°,D,E,F分别在AB,AC,BC上,AE=13AC,BD=13AB,且CF=13BC.求证:(1)EF⊥BC;(2)∠ADE=∠EBC.【思路分析】先判定两个三角形相似,再由两个三角形相似的性质可证明. 【证明】设AB =AC =3a (a >0),则AE =BD =a ,CF =2a . (1)CE CB =2a 32a =23,CF CA =2a 3a =23, 又因为∠C 为公共角,故△BAC ∽△EFC .由∠BAC =90°,得∠EFC =90°,所以EF ⊥BC .(2)由(1)得EF =2a ,故AE EF =a 2a =22. 又AD BF =2a 22a =22,所以AE FE =AD FB.又因为∠DAE =∠BFE =90°,所以△ADE ∽△FBE ,所以∠ADE =∠EBC .【方法归纳】对于两三角形间角、边长、高、中线长、面积等的比例关系,经常利用两三角形的相似比来解决,所以判定两三角形相似是关键.【举一反三】1.如图所示,已知P A 与⊙O 相切,A 为切点,过点P 的割线交圆于B ,C 两点,弦CD ∥AP ,AD ,BC 相交于点E ,F 为CE 上一点,且DE 2=EF ·CE .(1)求证:CE ·BE =EF ·EP ;(2)若CE ∶BE =3∶2,DE =3,EF =2,求P A 的长.【解析】(1)证明:因为DE 2=EF ·CE ,所以DE CE =EF ED, ∠DEC =∠FED ,所以△DEF ∽△CED ,所以∠EDF =∠C .又因为CD ∥AP ,所以∠P =∠C ,所以∠EDF =∠P ,又∠DEF =∠PEA ,所以△EDF ∽△EP A , 所以AE FE =EP ED,所以AE ·ED =EF ·EP . 又因为AE ·DE =CE ·BE ,所以CE ·BE =EF ·EP .(2)因为DE 2=EF ·CE ,DE =3,EF =2,所以CE =92. 因为CE ∶BE =3∶2,所以BE =3.由(1)可知:CE ·BE =EF ·EP ,解得EP =274. 所以BP =EP -BE =154. 因为P A 是⊙O 的切线,所以P A 2=PB ·PC ,所以P A 2=154×⎝⎛⎭⎫274+92,解得P A =1534. 题型二 探求几何结论【例2】如图,在梯形ABCD 中,点E ,F 分别在AB ,CD 上,EF ∥AD ,假设EF 做上下平行移动.(1)若AE EB =12,求证:3EF =BC +2AD ; (2)若AE EB =23,试判断EF 与BC ,AD 之间的关系,并说明理由; (3)请你探究一般结论,即若AE EB =m n,那么你可以得到什么结论? 【思路分析】题中有三条平行线,可考虑平行线分线段成比例定理,并作AH ∥DC ,利用定理求解即可,由(1)(2)两种特殊情况猜想一般情况的结论并证明.【解析】如图,过点A 作AH ∥CD 分别交EF ,BC 于点G ,H .(1)证明:因为AE EB =12,所以AE AB =13, 又EG ∥BH ,所以EG BH =AE AB =13,即3EG =BH , 又EG +GF =EG +AD =EF ,从而EF =13(BC -HC )+AD , 所以EF =13BC +23AD ,即3EF =BC +2AD . (2)EF 与BC ,AD 的关系式为5EF =2BC +3AD ,理由和(1)类似.(3)因为AE EB =m n ,所以AE AB =m m +n, 又EG ∥BH ,所以EG BH =AE AB ,即EG =m m +nBH . EF =EG +GF =EG +AD =m m +n(BC -AD )+AD , 所以EF =m m +n BC +n m +nAD , 即(m +n )EF =mBC +nAD .【方法归纳】在相似三角形中,平行辅助线是常作的辅助线之一;探求几何结论可按特殊到一般的思路去获取.【举一反三】2.如右图,正方形ABCD 的边长为1,P 是CD 边上的中点,点Q 在线段BC 上,设BQ =k ,是否存在这样的实数k ,使得以Q ,C ,P 为顶点的三角形与△ADP 相似?若存在,求出k 的值;若不存在,请说明理由.【解析】设存在满足条件的实数k ,则在正方形ABCD 中,∠D =∠C =90°,由Rt △ADP ∽Rt △QCP 或Rt △ADP ∽Rt △PCQ 得AD QC =DP CP 或AD PC =DP CQ ,由此解得CQ =1或CQ =14. 从而k =0或k =34. 题型三 解决线的位置或数量关系【例3】如图,在△ABC 中,点D 是AC 的中点,点E 是BD 的中点,延长AE 交BC 于点F ,则BF FC的值为. 【思路分析】利用线段中点作辅助线构造平行直线,根据平行线分线段成比例定理求解.【解析】如图,过点D 作DM ∥AF 交BC 于点M .因为点E 是BD 的中点,所以在△BDM 中,BF =FM ,又点D 是AC 的中点,所以在△CAF 中,CM =MF ,所以BF FC =BF FM +MC =12. 【方法归纳】对于有关线段的位置或数量关系,应利用两三角形全等或相似证明角相等,再证两直线平行或线段相等.【举一反三】3.如图,AB ∥EF ∥CD ,已知AB =20,CD =80,BC =100,则EF = 16 .【解析】因为AB ∥CD ,所以AB CD =AE EC =2080=14,由AE EC =14,得EC AC =45. 又因为EF ∥AB ,所以EF AB =EC CA ,即EF =EC CA ·AB =45×20=16.体验高考 (2015广东)如图,已知AB 是圆O 的直径,AB =4,EC 是圆O 的切线,切点为C ,BC =1.过圆心O 作BC 的平行线,分别交EC 和AC 于点D 和点P ,则OD = .【解析】8.易得AC =42-12=15,由OP ∥BC ,且O 为AB 的中点,可知CP =12AC =152,OP =12BC =12, ∠CPO =∠ACB =90°,所以∠CPD =90°.因为EC 是切线,所以∠DCP =∠CBA ,从而△CPD ∽△BCA ,故CP BC =DP AC, 所以DP =152.故OD =DP +OP =152+12=8. 【举一反三】(2015江苏)如图,在△ABC 中,AB =AC ,△ABC 的外接圆⊙O 的弦AE 交BC 于点D .求证:△ABD ∽△AEB .【证明】因为AB =AC ,所以∠ABD =∠C .又因为∠C =∠E ,所以∠ABD =∠E ,又∠BAE 为公共角,所以△ABD ∽△AEB .16.2 直线与圆的位置关系考点诠释重点:与圆有关的若干定理及其应用,并将其运用到立体几何中.难点:对平面截圆柱、圆锥所得的曲线为圆、椭圆、双曲线、抛物线的证明途径与方法. 典例精析题型一 切线的判定和性质的运用【例1】如图,P A 切⊙O 于点A ,割线PBC 经过圆心O ,OB =PB =1,OA 绕点O 逆时针旋转60°到OD ,则PD = .【思路分析】利用切线的性质及余弦定理可求解.【解析】7.如图,连接AB ,因为P A 切⊙O 于点A ,B 为PO 中点,所以AB =OB =OA ,所以∠AOB =60°,所以∠POD =120°.在△POD 中,由余弦定理得PD 2=PO 2+DO 2-2PO ·DO ·cos ∠POD =4+1-4×⎝⎛⎭⎫-12=7, 所以PD =7.【方法归纳】圆的切线常见的几种应用:(1)通过圆的切线可以找出弦切角与所夹的弧所对的圆周角;(2)可以得到直角,从而注意运用射影定理,直角三角形斜边上的中线等于斜边的一半;(3)圆的切线要注意切线定理的使用,可以构造相似三角形,计算线段的长度等. 【举一反三】1.如图,AB 是圆O 的直径,直线CE 与圆O 相切于点C ,AD ⊥CE 于点D ,若圆O 的面积为4π,∠ABC =30°,则AD 的长为 1 .【解析】CD 是圆O 的切线,所以∠ABC =∠ACD =30°,因为圆的面积是4π,从而圆的半径是2,所以在直角三角形ACD 中,AC =2,所以AD =1.题型二 四点共圆问题【例2】如图,圆O 与圆P 相交于A ,B 两点,圆心P 在圆O 上,圆O 的弦BC 切圆P 于点B ,CP 及其延长线交圆P 于D ,E 两点,过点E 作EF ⊥CE ,交CB 的延长线于点F .(1)求证:B ,P ,E ,F 四点共圆;(2)若CD =2,CB =22,求出由B ,P ,E ,F 四点所确定的圆的直径.【思路分析】(1)要证B ,P ,E ,F 四点共圆,先证四边形BPEF 的对角互补,由条件易证得;(2)利用切割线定理及三角形相似求出PF 的长,即为所求圆的直径.【解析】(1)证明:如图,连接PB .因为BC 切圆P 于点B ,所以PB ⊥BC .又因为EF ⊥CE ,所以∠PBF +∠PEF =180°,所以B ,P ,E ,F 四点共圆.(2)因为B ,P ,E ,F 四点共圆,且EF ⊥CE ,PB ⊥BC ,所以此圆的直径就是PF .因为BC 切圆P 于点B ,且CD =2,CB =22,所以由切割线定理得CB 2=CD ·CE ,得CE =4,DE =2,BP =1.又因为Rt △CBP ∽Rt △CEF ,所以EF ∶BP =CE ∶CB ,得EF = 2.在Rt △FEP 中,PF =PE 2+EF 2=3,即由B ,P ,E ,F 四点确定的圆的直径为 3.【方法归纳】判断四点共圆有以下几种方法:(1)如果四个点与一定点的距离相等,那么这四个点共圆;(2)如果一个四边形的一组对角互补,那么这个四边形的四个顶点共圆;(3)如果一个四边形的一个外角等于它的内对角,那么这个四边形的四个顶点共圆;(4)如果两个三角形有公共边,公共边所对的角相等且在公共边的同侧,那么这两个三角形的四个顶点共圆.【举一反三】2.如图,AB 是⊙O 的直径,CB 与⊙O 相切于点B ,E为线段CB 上一点,连接AC ,AE 分别交⊙O 于D ,G 两点,连接DG 并延长交CB 于点F .(1)求证:C ,D ,G ,E 四点共圆.(2)若F 为EB 的三等分点且靠近点E ,EG =1,GA =3,求线段CE的长.【解析】(1)如图,连接BD ,则∠AGD =∠ABD ,又∠ABD +∠DAB =90°,∠C +∠CAB =90°,所以∠C =∠ABD ,所以∠C =∠AGD ,所以∠C +∠DGE =180°,所以C ,E ,G ,D 四点共圆.(2)因为EG ·EA =EB 2,EG =1,GA =3,则EB =2,又F 为EB 的三等分点,所以EF =23,FB =43, 又因为FG ·FD =FE ·FC =FB 2,所以FC =83,CE =2. 题型三 圆中有关定理的综合应用【例3】如图,过点P 的直线与⊙O 相交于A ,B 两点.若P A =1,AB =2,PO =3,则⊙O 的半径等于 .【思路分析】取AB 的中点C ,连接OB ,OC ,利用圆的半径、弦心距、半弦长之间的关系求解.【解析】 6.如图,取AB 的中点C ,连接OB ,OC ,则OC ⊥AB ,且CB =1,CP =2,OC =OP 2-CP 2= 5.所以圆O 的半径为OB =OC 2+CB 2= 6.【方法归纳】对于圆中的弦长、切线长问题,一般可用相交弦定理、切割线定理或割线定理来求解.有关角的问题则用圆周角定理、弦切角定理等来解决.【举一反三】3.如图,直线PQ 与⊙O 相切于点A ,AB 是⊙O 的弦,∠P AB 的平分线AC 交⊙O 于点C ,连接CB ,并延长与直线PQ相交于点Q ,若AQ =6,AC =5.(1)求证:QC 2-QA 2=BC ·QC ;(2)求弦AB 的长.【解析】(1)证明:因为PQ 与⊙O 相切于点A ,由切割线定理得QA 2=QB ·QC =(QC -BC )QC ,所以QC 2-QA 2=BC ·QC .(2)由(1)可知,QA 2=QB ·QC =()QC -BC QC .因为PQ 与⊙O 相切于点A ,所以∠P AC =∠CBA .因为∠P AC =∠BAC ,所以∠BAC =∠CBA ,所以AC =BC =5,又已知AQ =6,所以QC =9.由∠QAB =∠ACQ 知,△QAB ∽△QCA ,所以AB CA =QA QC ,所以AB =103. 体验高考(2015新课标Ⅱ)如图,O 为等腰三角形ABC 内一点,⊙O 与△ABC 的底边BC 交于M ,N 两点,与底边上的高AD 交于点G ,且与AB ,AC 分别相切于E ,F两点.(1)证明:EF ∥BC ;(2)若AG 等于⊙O 的半径,且AE =MN =23,求四边形EBCF 的面积.【解析】(1)证明:由于△ABC 是等腰三角形,AD ⊥BC ,所以AD是∠CAB 的平分线.又因为⊙O 分别与AB ,AC 相切于点E ,F ,所以AE =AF ,故AD ⊥EF .从而EF ∥BC .(2)由(1)知,AE =AF ,AD ⊥EF ,故AD 是EF 的垂直平分线.又EF 为⊙O 的弦,所以O 在AD 上.连接OE ,OM ,则OE ⊥AE .由AG 等于⊙O 的半径得AO =2OE ,所以∠OAE =30°.因此△ABC 和△AEF 都是等边三角形.因为AE =23,所以AO =4,OE =2.因为OM =OE =2,DM =12MN =3,所以OD =1. 于是AD =5,AB =1033. 所以四边形EBCF 的面积为12×⎝⎛⎭⎫10332×32-12×(23)2×32=1633.【举一反三】(2015新课标Ⅰ)如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.(1)若D为AC的中点,证明:DE是⊙O的切线;(2)若OA=3CE,求∠ACB的大小.【解析】(1)证明:如图,连接AE,由已知得,AE⊥BC,AC⊥AB.在Rt△AEC中,由已知得,DE=DC,故∠DEC=∠DCE.连接OE,则∠OBE=∠OEB.又∠ACB+∠ABC=90°,所以∠DEC+∠OEB=90°,故∠OED=90°,即DE是⊙O的切线.(2)设CE=1,AE=x.由已知得,AB=23,BE=12-x2.由射影定理可得,AE2=CE·BE,所以x2=12-x2,即x4+x2-12=0.解得x=3,所以∠ACB=60°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十六章 套利行为套利(Arbitrage )是保证各种金融产品(如现货、远期、期权和互换)、各种期限结构(如即期利率期限结构、远期利率期限结构、附息票债券到期收益率期限结构、远期汇率期限结构等)、各地金融市场保持高度相关性的重要途径和力量,是效率市场(Efficient Markets )的必要条件,也是金融工程学的另一重要运用领域。
第一节 套利的基本原理套利是指利用一个或多个市场存在的各种价格差异,在不冒任何损失风险且无需投资者自有资金的情况下有可能赚取利润的交易策略(或行为)。
由此可见,判断一个交易策略是不是严格的套利策略,有3条标准:①没有自有资金投入,所需资金通过借款或卖空获得;②没有损失风险,最糟糕的情况是终点又回到起点,套利者的最终结果(已扣掉借款利息)还是零;③存在正的赚钱概率。
这意味着套利的最终结果可能没赚钱,但只要事前存在赚钱的概率且不存在亏钱的概率就可以了。
套利是利用资产定价的错误、价格联系的失常,以及市场缺乏有效性的其它机会,通过买进价格被低估的资产,同时卖出价格被高估的资产来获取无风险利润的交易策略。
套利是市场无效率的产物,而套利的结果则促使市场效率的提高,因此套利对社会的正面效应远超过负面效面,我们应予充分鼓励和肯定。
套利有五种基本的形式:空间套利、时间套利、工具套利、风险套利和税收套利。
一、空间套利最明显和最直观的套利形式是空间套利(或称地理套利),它是指在一个市场上低价买进某种商品,而在另一市场上高价卖出同种商品,从而赚取两个市场间差价的交易行为。
空间套利是最早的套利形式之一,也是大多数经营活动的主要形式。
例如,X 股票同时在A 、B 两个证交所上市,但X 在A 市场的价格为每股10元,而在B 市场的价格仅为每股8元,于是可以通过在B 市场买入X 股票,然而转托管到A 市场,再在A 市场卖出。
这样,扣除手续费和佣金后将获得较丰厚的无风险利润。
从上例可以看出,只要两个市场的价差超过套利活动将产生的相关费用,套利活动就有利可图。
然而,套利活动买低卖高的结果将使低价市场的价格上升和高价市场的价格回落,直到两个市场的价差小于相关费用,此时两个市场价格处于相对均衡状态,并可用下式表示: ε+=j i P P (16.1) 其中,P i 和P j 分别表示 i 市场和j 市场的价格,ε表示在由相关费用(C )确定的区间内变动的随机数,且:C C ≤≤-ε。
式(16.1)就是著名的一价定律。
一价定律可以推广到不同货币的情形。
如果i 市场的价格用货币 i 表示,j 市场的价格用货币j 表示用货币i 表示的每单位货币j 的汇率用E i ,j 表示,ε以货币i 表示,则一价定律等式变为: ε+=j i j i E P P , (16.2)二、时间套利时间套利是指同时买卖在不同时点交割的同种资产,它包括现在对未来的套利和未来对未来的套利。
我们在第十二章曾详细论述了各种远期和期货价格与现货价格之间的平价关系公式,通过这些公式,可以推导出不同期限的远期(或期货)价格对远期(或期货)价格的平价关系公式 。
只要现实中现货和远期、期货价格的关系偏离这些平价关系的幅度超过手续费和税收,就可进行时间套利。
远期、期货价格与现货价格之间的关系可用持有成本(Carry Cost )来总结。
持有成本等于标的资产的存储成本加上融资购买标的资产所支付的利息,再减去资产的收益。
如果用F i (t,T )表示t 时刻i 市场某种标的资产T 时刻到期的远期或期货价格,P i (t)表示t 时刻标的资产在i 市场的现货价格,G i (t,T)表示T -t 期间的持有成本,则t 时刻现货价格与T 时刻到期的远期或期货价格的均衡条件为:),()(),(T t G t P T t F i i i += (16.3) 同样,用T *代替T (其中,T *>T ),则有:),()(),(**T t G t P T t F i i i += (16.4) 将式(16.3)代入(16.4),并令),(),(),(**T t G T t G T T G i i i -=,得:),(),(),(**T T G T t F T t F i i i += (16.5) 正如式(16.1)和(16.2)是空间的均衡条件一样,式(16.3)至(16.5)是时间的均衡条件。
当式(16.3)至(16.5)的等式不成立时,就会产生套利机会(忽略交易费用),如果等式左边大于右边,套利者可买进现货同时卖出远期或期货,或者买进较近期的远期或期货,同时卖出较远期的远期或期货。
如果等式左边小于右边,则可进行相反的操作,从而获得无风险利润。
套利活动的结果将使式(16.3)至(16.5)成立,此时市场处于时间均衡状态。
将式(16.2)代入(16.3)可得到一个更一般的既可解释空间又可解释时间价格关系的均衡条件:ε++=),()()(),(,T t G t E t P T t F i j i j i (16.6)其中,C C ≤≤-ε三、工具套利工具套利就是利用同一标的资产的现货及各种衍生证券的价格差异,通过低买高卖来赚取无风险利润的行为。
从第12和13章关于衍生证券定价的分析中,我们看到各种衍生证券的价格部分或全部取决于标的资产现货价格、利率、期限(或时间)、波动率等变量,当这些变量值已知时,我们就可推导出各种衍生证券价格之间的关系。
我们还看到,远期利率的期限结构取决于即期利率的期限结构,而不同期限的利率期货价格中也隐含着远期利率期限结构,即期和远期利率期限结构又决定了汇率的期限结构。
可以说,各种金融工具之间的价格联系是多渠道且紧密的,它们之间普遍存在着或简单或复杂的平价关系。
当这种平价关系被打破时,市场就提供了工具套利的机会。
更有甚者,同类金融工具之间也可进行工具套利,以期权为例,看涨期权与看跌期权之间、不同期限的看涨期权或看跌期权之间都存在着价格联系,都存在着套利的可能性。
工具套利是各种套利形式中最振奋人心的一种。
在这种套利形式中,多种资产或金融工具组合在一起,形成一种或多种与原来有着截然不同性质的金融工具,这正是创造复合金融工具的过程。
这个过程反过来也成立。
一项金融工具可以分解成一系列的金融工具,且每一个都有着与原来的金融工具不同的特性,金融工具的组合和分解正是金融工程的主要运用。
四、风险套利风险套利是指利用风险定价上的差异,通过买低卖高赚取无风险利润的交易行为。
根据高风险高收益原则,风险越高,所要求的风险补偿就越多。
根据资本资产定价模型,风险可分为系统性风险(用β衡量)和非系统性风险,非系统性风险可以通过分散化组合予以抵消,因此只存在系统性风险才能获得风险报酬,且两者之间有一个严密的平价关系。
如果现实生活中各种风险资产的定价偏离了这个平价公式,就存在风险套利机会。
保险是风险套利的一个生动的例子。
保险公司为许多面临较高风险的公司和个人提供保险,即前者为后者承担风险,作为回报,后者要向前者支付保险费,作为前者承担风险的报酬。
保险公司通过把这些风险集中起来,将使各个风险中所含的非系统性风险互相抵消,以而大大降低了风险总量。
这样,保险公司就可通过收取相对较高的保险费,并投资于风险水平与所保风险总水平相当的资产而获得风险套利的利润。
五、税收套利税收套利是指利用不同投资主体、不同证券、不同收入来源在税收待遇上存在的差异所进行的套利交易。
在我国,个人证券买卖的资本利得可以免税,而法人单位则要按本单位的所得税率纳税,且法人单位的所得税率有很大差别,有的33%,有的15%。
对于股票和公司债券的现金股利,用未分配利润和盈余公积金派送的股票红利、利息,个人和单位均要纳税。
对于国债的利息,个人和单位均可免税。
第二节 套利实例在本章第一节中,我们论述了几种主要的套利类型及其原理,本节我们将着重讨论花样最多、难度较大的时间套利和工具套利。
为表述方便起见,我们假定:1.没有交易费用和税收;2.套利者可按无风险利率自由借贷;3.套利者均可按市场中间价格买卖资产。
一、基于远期和期货合约的套利基于远期和期货合约的套利属于时间套利,它是利用远期和期货价格与标的资产现货价格的差异来进行套利。
(一)股价指数期货套利股价指数可以近似看作是支付连续收益率的资产,股价指数期货价格与股价指数现货价格之间必须保持如下关系,否则就存在套利机会:))((t T q r Se F --=如果))((t T q r Se F -->,投资者就可以通过购买股价指数中的成份股票,同时卖出指数期货合约来获得无风险套利利润。
相反,如果))((t T q r Se F --<,投资者就可以通过卖空股价指数中的成份股票,同时买入指数期货合约来获得无风险套利利润。
由于买卖成份股需要花费较长的时间,而市场行情是瞬间万变的,因此在实践中人们大多利用计算机程序进行自动交易。
即一旦指数现货与期货的平价关系被打破时,电脑会根据事先设计好的程序进行套利交易。
应该注意的是,由于指数套利涉及的买卖较多,在某些极端的情况下,由于行情变化过快,即使运用程序交易也无法避免某些风险。
例如,在发生金融恐慌时,股票价格飞速下降,此时即使期货价格低于现货价格,通过买入指数期货卖出成份股现货进行的套利活动也可能因为卖出委托的迟延而给套利者带来风险。
事实上,1987年10月19日“黑色星期一”美国股市发生大崩盘的当天收市时,S&P500指数为225.06点,而12月份交割的S&500指数期货价格却只有201.50点,比现货价格低23.56点。
而在第二天纽约证交所对程序交易买行了临时性限制措施后,12月份的指数期货价格价格最多时比现货价格低了18%。
例 16.1假设S&P500指数现在的点数为1000点,该指数所含股票的红利收益率预计为每年5%(连续复利),3个月期S&P500指数期货的市价为950点,3个月期无风险连续复利年利率为10%,请问如何进行套利?在本例中,))((t T q r SeF --<,因此投资者可以通过卖空成份股买入指数期货来套利,其具体步骤为:①确定套利的金额(假定为1000万美元);②按各成份股在指数中所占权重卖空成份股,总计金额为1000万美元;③将卖空成份股所得款项1000万美元按无风险利率贷出3个月;④买入20份3个月期S&P500指数期货①;⑤3个月后收回贷款本金,其利息收入为:1000万32.25)1(25.01.0=-⨯e 万美元⑥3个月后按市价买回成份股,平掉股票的空仓,假设此时指数现货点数为S T ,则股票现货盈亏为: 1000)10001000(⨯-T S 万 ⑦3个月后按指数现货点数(S T )对期货头寸进行结算,其盈亏为:20500)950(⨯⨯-T S⑧此次套利套利的总盈亏为:25.32万+1000万-1万⨯S T +1万⨯S T -950万=75.32万美元(二)外汇远期和期货套利据式(12.12),外汇远期或期货汇率与现货汇率之间必须保持如下平价关系,否则就存在套利机会:))((t T r r fSe F --= 如果))((t T r r f Se F -->,套利者就可以通过买入外汇现货,卖出外汇远期或期货来获取无风险利润。
