押题试卷(一)答案
最新部编人教版小学五年级语文上册第三单元名校押题试卷1(附答案)

麻雀自夸
麻雀蹲在矮树上,()地对着蓝天白云间盘旋的隼说:“我现在就读的鸟类运动学校是一所著名的学府,它曾培养出时速300多千米的飞行冠军尖尾燕,每小时能跑70多千米的长跑冠军鸵鸟,还有飞越过地球南北极的远飞冠军燕鸥.......
隼叹息道:“唉!你的学习环境太好了,真令我羡慕!”
麻雀得意极了,他又()地说:“我的老师苍鹰更棒了,他是鸟类著名的短飞冠军,曾打破世界纪录,时速达600多千米。”
19 习作表达
请将喜欢的一个故事进行缩写,不超过400字。
参考答案
1.根据拼音写词语
sǎo zi qīn mì zhǎng bèi chē liàng
jiān yù zhēn guì xī han yóu yǒng
【答案】嫂子亲密长辈车辆
监狱珍贵稀罕游泳
【详解】本题主要考查对词语的拼写能力。解答本题,首先读一读拼音,知道要写什么词语,然后写出正确的词语,写完后读一读,看看是否正确。注意掌握生字的结构和易错点。书写时要注意“嫂、辆、狱、稀、游”容易写错。书写时要注意这些字的笔画、结构。要做到规范、正确和美观。
本题要搭配的四字词语是动宾结构的短语,动宾结构由动词和名词组成。
4.把词语补充完整
()开眼笑()中不足()盆大雨无()无束
()不舍富丽堂()狂风()号成家()业
【答案】①.眉②.美③.倾④.拘⑤.恋恋⑥.皇⑦.怒⑧.立
【详解】考查了补写词语,只要平时注意积累和识记,做起来就不难。书写时要注意同音字、形近字的区别,不要把字写错误,要依据词语的意思来写。
3.读一读,选一选
遵守()保守()独占()遭受()败坏()开辟()等待()
A.惩罚B.秘密C.家产D.诺言E.荒地F.时机G.门风
人教版数学小升初押题试卷(含答案)

2022年小升初冲刺模拟测试数学试题学校________ 班级________ 姓名________ 成绩________(时间:90分钟满分:100分)第Ⅰ卷客观题一、单选题(共8题;共8分)1.因为大圆的半径:小圆的半径=3:2,所以大圆的面积与小圆的面积比是()A. 3:2B. 6:4C. 2:3D. 9:42.酒泉到兰州的实际距离是735km,在一幅地图上量得这两地之间的距离是3.5cm,这幅地图的比例尺是( )A. 1:2100000B. 1:21000000C. 3.5:7353.把一块圆柱形的钢锭熔铸成与它等底的圆锥,高将()。
A. 扩大到原来的3倍B. 扩大到原来的6倍C. 缩小到原来的13 D. 缩小到原来的164.一个圆柱与一个圆锥的底面积和体积都相等。
已知圆柱的高是4dm,圆锥的高是()dm。
A. 12B. 4C. 85.加工一个零件,甲单独做要14小时完成,乙单独做要15小时完成,甲、乙两人工作效率的最简比是()。
A. 14: 15B. 15: 14C. 4:5D. 5:46.将一个长方体切4刀,正好可以切成若干个小正方体(如图),增加的表面积是原来长方体表面积的()。
A. 43B. 45C. 547.如图,从A到B沿大圆周走比较近,还是沿小圆周走比较近?正确答案是()。
A. 沿大圆周走近B. 沿小圆周走近C. 一样近8.有8瓶水,其中7瓶质量相同,另一瓶是盐水,比其他的水略重一些。
至少称()次能保证找出这瓶盐水。
A. 2B. 3C. 4D. 5二、判断题(共8题;共8分)9.圆柱的体积比圆锥的体积多2倍。
()10.如果3A=4B(A≠0,B≠0),那么A、B成正比例。
( )11.a是非零自然数,如果a=4b,则a和b的最小公倍数是b。
()12.半径是2cm的圆的周长和面积相等。
()13.统计图的优点是使人们更直接、更容易地在图上得到信息。
()14.小明用一张长方形彩纸剪正方形.他先剪出了一个尽可能大的正方形,然后发现剩下的纸恰好能剪成四个完全相同的小正方形.那么,每个小正方形的面积可能相当于大正方形面积的14,也可能相当于大正方形面积的116.()15.一个圆的周长是9.42米,剪成两个半圆后每个半圆的周长是4.71米.()16.一种商品先提价10%,后再打九折出售,现价和原价相同。
人教版2024年中考语文押题预测试卷及答案

…○………………内………………○………………装………………○………………订………………○………………线………………○…………………○………………外………………○………………装………………○………………订………………○………………线………………○………………… 学校:______________姓名:_____________班级:_______________考号:______________________人教版2024年语文中考押题预测试卷及答案(满分:120分 时间:150分钟)题号 一 二 三 四 五 附加题 总分 分数第一部分 积累与运用(共24分)一、(完成1-5题,共16分)1.(2分)下列词语中,每对加点字的读音都相同的一项是( ) A .勾当./锐不可当. 炽.热/旗帜.鲜明 B .咀嚼./味同嚼.蜡 咆.哮/刨.根问底 C .钦差./参.差不齐 粗犷./心旷.神怡 D .挑.衅/挑.拨离间 抵.挡/坦荡如砥.2.(2分)下列词语中,没有错别字的一项是( ) A .吝啬 锋芒毕露 娇媚 格物至知 B .狼藉 和颜悦色 闲遐 藏污纳垢 C .诀别 震聋发聩 伫立 画龙点睛 D .旁骛 坦荡如砥 灌输 雷霆万钧3.(2分)下列句子中画线成语使用恰当的选项是( )A .为我们的文学事业呕心沥血的人,为我国人民革命明哲保身的人,他们的英名和业绩是永存的。
B .我们真诚地希望孙颖莎夺取世界冠军之后再接再厉,不断带给人们惊喜。
C .榜样们在日常生活中凡事都首当其冲,工作中都迎难而上,公益活动也会带头参加。
D .学习了他的先进事迹后,我们每一个青年都应该追本溯源,看看自己做得如何。
4.(2分)下列句子中没有语病....的一项是( ) A .一个人的生活阅历越丰富,越有助于自身对经典文学作品的价值作深入思考和逐步了解。
B .一个人能否成为真正的阅读爱好者,关键在于青少年时期是否培养阅读的兴趣。
2020年河南省中考原创押题数学试卷(一)含答案解析

2020 年河南省中考原创押题数学试卷(一)一、选择题:本大题共 8小题,每小题 3 分,共 24分 1.下面的数中,与﹣ 2 的和为 0 的是( )A .B .﹣C .2D .﹣ 22.下列计算正确的是( )A .2 +4 =6B .=4 C . ÷ =3 D .=﹣33.发展工业是强国之梦的重要举措,如图所示零件的左视图是( )4.股票每天的涨、 跌幅均不能超过 10%,即当涨了原价的 10%后,便不能再涨, 叫做涨停;当跌了原价的 10% 后,便不能再跌,叫做跌停.已知一只股票某天跌停,之后两天时间又6.小明是我校手工社团的一员, 他在做折纸手工, 如图所示在矩形 ABCD 中,AB=6 ,BC=8 ,点 E 是 BC 的中点,点 F 是边 CD 上的任意一点, △ AEF 的周长最小时, 则 DF 的长为( )7.如果一组数据 a 1,a 2,⋯,a n 的方差是 2,那么一组新数据 2a 1+1,2a 2+1,⋯,2a n +1 的方差是( )8.如图,矩形 ABCD 中, AB=3 ,BC=4,动点 P 从 A 点出发,按 A →B →C 的方向在 AB 和 BC 上移动,记PA=x ,点D 到直线 PA 的距离为 y ,则 y 关于 x 的函数图象大致是 ( )则 x 满足的方程是(2B .(1+x )2=C . 1+2x=D1+2x=5.正比例函数 y=6x 的图象与反比例函数 A .第一象限 B .第二象限 C .第三象限 D .第一、三象限A . 2B . 3C . 4D .8C .涨回到原价.若这两天此股票股价的平均增长率为 x , y= 的图象的交点位于(2 A .(1+x )2二、填空题:每小题 3 分,共 21 分9.若实数 a 、b 满足| 3a ﹣1|+ b 2=0,则 a b 的值为 _____11.不等式组 的非负整数解是 ______12.点动成线,线动成面,面动成体,在 Rt △ABC 中,∠ C=90°,AC=3 ,BC=4 ,将△ ABC 饶边 AC 所在的直线旋转一周得到圆锥,则该圆锥的表面积是 _______ .213.反比例函数 的图象经过点 P ( a ,b ),其中 a 、b 是一元二次方程 x 2+kx +4=0 的两根,那么点 P 的坐标是 _____ .214.如图,把抛物线 y= x 2平移得到抛物线 m ,抛物线 m 经过点 A (﹣ 6,0)和原点 O (0, 20),它的顶点为 P ,它的对称轴与抛物线 y= x 2交于点 Q ,则图中阴影部分的面积为 _____ .15.如图 1,两个等边△ ABD ,△ CBD 的边长均为 1,将△ ABD 沿AC 方向向右平移到△ 的位置,得到图 2,则阴影部分的周长为 .三、解答题:本大题共 8 小题,共 75分17.如图,在正方形 ABCD 内有一点 P 满足 AP=AB , PB=PC ,连接 AC 、 PD . 求证:(1)△APB ≌△DPC ;(2)∠ BAP=2 ∠ PAC .10.请写出一个二元一次方程组A ′B ′D 16.化简求值:A.,其中 a=18.如图所示,小明在自家楼顶上的点 A 处测量建在与小明家楼房同一水平线上邻居的电梯的高度,测得电梯楼顶部 B 处的仰角为 45 °,底部 C 处的俯角为 26°,已知小明家楼房的 高度 AD=15 米,求电梯楼的高度 BC (结果精确到 0.1 米)(参考数据: sin26°≈0.44,cos26°≈0.90, tan26°≈ 0.49)19.最近两年雾霾对我国北方大部分地区影响较严重, 其中和越来越多的汽车尾气排放有极大的关系.据报道,历经一百天的调查研究,我市 PM2.5 的源解析已经通过专家论证,各 种调查显示,机动车为PM2.5的最大来源,一辆车每行驶 20 千米平均向大气里排放 0.035 千克污染物, 校环保志愿小分队从环保局了解到我市 100 天的空气质量等级情况, 并制成统 计图和表:空气质量等级 优 良轻度污染中度污染重度污染 严重污染天数(天) 10 a12825 b(1)表中 a=______ ,b=_,图中严重污染部分对应的圆心角n= _____ ;(2)请你根据 “2020 年我市 100天空气质量等级天数统计表 ”计算 100 天内重度污染和严重 污染出现的概率共是多少?(3)小明是社区环保志愿者,他和同学们调查了机动车每天的行驶路程,了解到每辆车每 天平均出行 25 千米,已知我市 2020 年机动车保有量已突破 200 万辆,请你通过计算, 估计 2020 年我市一天中出行的机动车至少要向大气里排放多少千克污染物?20.如图,已知, A (0,4),B (﹣ 3,0), C (2,0),D 为 B 点关于 AC 的对称点,反比 例函数 y= 的图象经过 D 点. (1)证明四边形 ABCD 为菱形; (2)求此反比例函数的解析式;3)已知在y= 的图象(x>0)上一点N,y 轴正半轴上一点M ,且四边形ABMN 是平克)是销售单价x(元)的一次函数,且当x=60 时,y=80;x=50 时,y=100 .在销售过程中,每天还要支付其他费用450 元.(1)求出y 与x 的函数关系式,并写出自变量x 的取值范围.2)求该公司销售该原料日获利w(元)与销售单价x (元)之间的函数关系式.3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?22.王老师在组织一次数学教学中,扁拟了如下问题串【原题初探】如图 1 所示,在四边形延长线于点F,求ABCD 中,AD∥BC,E为CD 边的中点,连接AE 并延长交BC的S四边形ABCD= S△ADE ;变式猜想】如图 2 所示,在已知锐角∠ AOB 内有一定点P,过点P 任意作一条直线MN ,分别交射线OA,OB 于点M,N,小明在将直线MN 绕着点P 旋转的过程中发现,△ MON 的面积存在最小值,试问当MN 在什么位置时,△ MON 的面积最小【拓展应用】如图3所示,一块四边形土地OABC ,其中OA 边长60米,AB 边长30 米,C点到OA 边的距离为45 米,使用测角器测得∠ AOC=45 °,OA⊥AB,OC⊥BC,机井P距离OA,AB 均是20米,过机井P画一条分割线将这块地分成两块四边形地块(与四边形土地OABC )的一组对边相交),则其中以点O 为顶点的四边形地块的最大面积为_________ .23.如图,抛物线y=ax2﹣x﹣2(a≠0)的图象与x轴交于A、B 两点,与y轴交于C点,已知 B 点坐标为(4,0).(1)求抛物线的解析式;(2)试探究△ ABC 的外接圆的圆心位置,并求出圆心坐标;(3)若点M 是线段BC 下方的抛物线上一点,求△ MBC 的面积的最大值,并求出此时M 点的坐标.30 元.物价部门规定其销售单价不高于每千克60元,不低于每千克30 元.经市场调查发现:日销售量y (千2020 年河南省中考原创押题数学试卷(一)参考答案与试题解析一、选择题:本大题共8小题,每小题 3 分,共24分1.下面的数中,与﹣ 2 的和为0 的是()A.B.﹣C.2 D.﹣2..﹣..﹣【考点】相反数.【分析】设这个数为x,根据题意可得方程x+(﹣2)=0,再解方程即可.【解答】解:设这个数为x ,由题意得:x+(﹣2)=0 ,x﹣2=0,x=2,故选:C.2.下列计算正确的是()A.2 +4 =6 B.=4 C.÷ =3 D .=﹣3【考点】实数的运算.【分析】 A 、根据合并二次根式的法则即可判定;B、根据二次根式的乘法法则即可判定;C、根据二次根式的除法法则即可判定;D、根据二次根式的性质即可判定.【解答】解:A、2 +4 不是同类项不能合并,故 A 选项错误;B、=2 ,故 B 选项错误;C、÷ =3,故 C 选项正确;D、=3,故 D 选项错误.故选:C.3.发展工业是强国之梦的重要举措,如图所示零件的左视图是(【考点】简单组合体的三视图.【分析】根据从左边看得到的图形是左视图,可得答案.【解答】解:从左边看是一个矩形平均分成 2 个,故选:C.4.股票每天的涨、跌幅均不能超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10% 后,便不能再跌,叫做跌停.已知一只股票某天跌停,之后两天时间又涨回到原价.若这两天此股票股价的平均增长率为x,则x 满足的方程是()22A .(1+x )=B.(1+x)2=C.1+2x=D1+2x=【考点】由实际问题抽象出一元二次方程.【分析】股票一次跌停就跌到原来价格的90%,再从90%的基础上涨到原来的价格,且涨幅只能≤10%,所以至少要经过两天的上涨才可以.设平均每天涨x,每天相对于前一天就上涨到1+x.【解答】解:设平均每天涨x .则90%(1+x)2=1,即(1+x)2= ,,故选 B .5.正比例函数y=6x 的图象与反比例函数y= 的图象的交点位于()A .第一象限B .第二象限C .第三象限D .第一、三象限考点】反比例函数与一次函数的交点问题.分析】根据反比例函数与一次函数的交点问题解方程组标,然后根据交点坐标进行判断.所以正比例函数y=6x 的图象与反比例函数y= 的图象的交点坐标为(故选: D .6.小明是我校手工社团的一员,他在做折纸手工,如图所示在矩形ABCD 中,AB=6 ,BC=8 ,点 E 是BC 的中点,点F 是边CD 上的任意一点,△ AEF 的周长最小时,则DF的长为()3 D. 4轴对称-最短路线问题.如图作点E关于直线CD的对称点E′,连接AE ′与直线CD交于点F.此时△AEF 的周长最小.由CF∥ AB ,推出CF:AB=CE ′:BE′=1:3,求出CF即可解决问题.【解答】解:如图作点E关于直线CD的对称点E′,连接AE ′与直线CD交于点F.此时△解答】解:考点】分析】1,6),(﹣1,﹣6).即可得到两函数的交点坐解方程组AEF 的周长最小.∴CF :AB=CE ′:BE ′=1: 3, ∴CF=2,∴DF=CD ﹣ CF=4. 故选 D .7.如果一组数据 a 1,a 2,⋯,a n 的方差是 2,那么一组新数据 2a 1+1,2a 2+1,⋯,2a n +1 的方差是( )A .2B .3C .4D . 8【考点】 方差.【分析】 设已知数据的平均数为 ,根据数据的方差列出关系式, 进而求出新数据的平均数, 得出方差即可.【解答】 解:∵一组数据 a 1,a 2,⋯,a n 的方差是 2,平均数为 , ∴S 2= [ ( a 1﹣ ) 2+(a 2﹣ )2+⋯+(a n ﹣ )2]=2, ∵2a 1+1,2a 2+1,⋯,2a n +1 的平均数为 2 +1,∴S ′2= [ ( 2a 1+1﹣ 2 ﹣1)2+(2a 2+1﹣2 ﹣1)2+⋯+(2a n +1﹣2 ﹣1)2]=2×22=8, 故选: D8.如图,矩形 ABCD 中, AB=3 ,BC=4,动点 P 从 A 点出发,按 A →B →C 的方向在 AB 和 BC 上移动,记PA=x ,点D 到直线 PA 的距离为 y ,则 y 关于 x 的函数图象大致是 ( )【考点】 动点问题的函数图象.【分析】 ① 点 P 在 AB 上时,点 D 到AP 的距离为 AD 的长度, ② 点 P 在 BC 上时,根据 同角的余角相等求出∠ APB= ∠PAD ,再利用相似三角形的列出比例式整理得到 y 与 x 的关 系式,从而得解.【解答】 解:① 点 P 在 AB 上时, 0≤ x ≤ 3,点 D 到 AP 的距离为 AD 的长度,是定值4; ② 点P 在 BC 上时, 3<x ≤5,∵∠ APB +∠BAP=90 °, ∠PAD+∠BAP=90 °,CF ∥ AB ,∴∠ APB= ∠PAD,又∵∠ B=∠ DEA=90 °,∴△ ABP ∽△ DEA ,=,纵观各选项,只有 B 选项图形符合.故选:B.二、填空题:每小题 3 分,共21 分9.若实数a、b 满足| 3a﹣1|+ b2=0,则a b的值为 1 .【考点】非负数的性质:偶次方;非负数的性质:绝对值.【分析】根据非负数的性质列式求出a、b的值,然后代入代数式,根据任何非0 数的0次幂等于 1 进行计算即可得解.【解答】解:根据题意得,3a﹣1=0,b=0,解得a= ,b=0,b0a = ()=1.故答案为:1.10.请写出一个二元一次方程组此题答案不唯一,如:,使它的解是【考点】二元一次方程组的解.【分析】根据二元一次方程解的定义,可知在求解时,应先围绕x=2,y= ﹣ 1 列一组算式,然后用x,y 代换即可列不同的方程组.答案不唯一,符合题意即可.【解答】解:此题答案不唯一,如:,① +② 得:2x=4 ,解得:x=2 ,将x=2 代入① 得:y=﹣1,∴一个二元一次方程组的解为:故答案为:此题答案不唯一,如:11.不等式组的非负整数解是0【考点】一元一次不等式组的整数解.【分析】先求出不等式组中每个不等式的解集,然后求出其公共解集,最后求其非负整数解即可.【解答】解:由不等式1﹣x>0得x<1,由不等式3x>2x﹣4得x>﹣4,所以其解集为﹣4< x< 1,则不等式组的非负整数解是0.故答案为:0.12.点动成线,线动成面,面动成体,在Rt△ABC 中,∠ C=90°,AC=3 ,BC=4 ,将△ ABC 饶边AC 所在的直线旋转一周得到圆锥,则该圆锥的表面积是36πcm2.【考点】圆锥的计算.【分析】先利用勾股定理计算出AB=5 ,由于以AC 所在直线为轴,把△ ABC 旋转 1 周所得的圆锥的底面圆的半径为4,母线长为5,则可利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式计算圆锥的侧面积,然后加上底面积即可得到圆锥面积.【解答】解:∵∠ C=90°,AC=3 ,BC=4 ,∴AB==5,以AC 所在直线为轴,把△ ABC 旋转 1 周所得的圆锥的底面圆的半径为 4 ,母线长为5,所以圆锥的全面积=π?42+ ?2π?4?5=36π(cm2).故答案为36πcm2.213.反比例函数的图象经过点P(a,b),其中a、b是一元二次方程x2+kx+4=0 的两根,那么点P的坐标是(﹣2,﹣2).【考点】待定系数法求反比例函数解析式;根与系数的关系.【分析】先根据点P(a,b)是反比例函数的图象上的点,把点P 的坐标代入解析式,得到关于a、b、k 的等式ab=k;又因为a、b 是一元二次方程x2 +kx+4=0 的两根,得到a+b= ﹣k,ab=4,根据以上关系式求出a、 b 的值即可.【解答】 解:把点 P ( a , b )代入 y= 得, ab=k , 因为 a 、 b 是一元二次方程 x 2+kx+4=0 的两根,根据根与系数的关系得:14.如图,把抛物线 y= x 2平移得到抛物线 m ,抛物线 m 经过点 A (﹣ 6,0)和原点 O (0,故答案为:|=| =∴S=| ﹣3| ×| a+b= ﹣k , ab=4 ,,解得2,﹣ 2).0),它的顶点为 P ,它的对称轴与抛物线 y= x 2 交于点 Q ,则图中阴影部分的面积为【考点】 二次函数图象与几何变换.【分析】 根据点 O 与点 A 的坐标求出平移后的抛物线的对称轴,然后求出点 点 P 作 PM ⊥ y 轴于点 M ,根据抛物线的对称性可知阴影部分的面积等于矩形 然后求解即可.【解答】 解:过点 P 作 PM ⊥y 轴于点 M ,∵抛物线平移后经过原点 O 和点 A (﹣ 6, 0), ∴平移后的抛物线对称轴为 x= ﹣ 3,得出二次函数解析式为: y= ( x+3)2+h , 将(﹣ 6, 0)代入得出:0= (﹣ 6+3)2+h ,解得: h= ﹣ ,P 的坐标,过 NPMO 的面积,∴点 P 的坐标是(﹣ 3,﹣ ),根据抛物线的对称性可知,阴影部分的面积等于矩形NPMO 的面积,于是有:点 P 的坐标是(﹣15.如图 1,两个等边△ ABD ,△CBD 的边长均为 1,将△ ABD 沿 AC 方向向右平移到△ A ′B ′D 的位置,得到图 2,则阴影部分的周长为 2 .分析】 根据两个等边△ ABD ,△ CBD 的边长均为 1,将△ ABD 沿 AC 方向向右平移到△A 'B 'D '的位置,得出线段之间的相等关系,进而得出OM+MN +NR +GR+EG+OE=A ′D ′+CD=1 +1=2,即可得出答案.【解答】 解:∵两个等边△ ABD ,△ CBD 的边长均为 1,将△ ABD 沿 AC 方向向右平移到 △A ′B ′D ′的位置,∴A ′M=A ′N=MN ,MO=DM=DO ,OD ′=D ′E=OE ,EG=EC=GC ,B ′G=RG=RB ′, ∴OM+MN +NR +GR+EG+OE=A ′D ′+CD=1+1=2;故答案为: 2.三、解答题:本大题共 8 小题,共 75分【考点】 分式的化简求值.【分析】 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形, 约分得到最简结果,将 a 与 b 的值代入计算即可求出值.16.化简求值:17.如图,在正方形 ABCD 内有一点 P 满足 AP=AB , PB=PC ,连接 AC 、PD . 求证:(1)△APB ≌△DPC ;(2)∠ BAP=2 ∠ PAC .【考点】 正方形的性质;全等三角形的判定与性质.【分析】(1)AP=AB ,PB=PC ,∴∠ ABC ﹣∠ PBC=∠ DCB ﹣∠ PCB ,即∠ ABP= ∠DCP , 因此可证得两三角形全等.(2)有( 1)∠ CAD=45 °,△ PAD 为等边三角形,可求得∠ BAP=30 °∠PAC=∠PAD ﹣∠CAD=15 °,因此可证的结论.【解答】( 1)解:∵四边形 ABCD 是正方形,∴∠ ABC= ∠DCB=90 °. ∵PB=PC ,∴∠ PBC= ∠PCB .∴∠ ABC ﹣∠ PBC= ∠DCB ﹣∠ PCB ,即∠ ABP= ∠ DCP . 又∵ AB=DC , PB=PC , ∴△ APB ≌△ DPC .(2)证明:∵四边形 ABCD 是正方形, ∴∠ BAC= ∠ DAC=45 °. ∵△ APB ≌△ DPC ,∴ AP=DP . 又∵ AP=AB=AD ,∴ DP=AP=AD . ∴△ APD 是等边三角形. ∴∠ DAP=60 °.∴∠ PAC=∠ DAP ﹣∠ DAC=15 °. ∴∠ BAP= ∠ BAC ﹣∠ PAC=30 °. ∴∠ BAP=2 ∠PAC .18.如图所示,小明在自家楼顶上的点 A 处测量建在与小明家楼房同一水平线上邻居的电梯的高度,测得电梯楼顶部 B 处的仰角为 45 °,底部 C 处的俯角为 26°,已知小明家楼房的 高度 AD=15 米,求电梯楼的高度 BC (结果精确到 0.1 米)(参考数据: sin26°≈0.44,cos26°≈0.90, tan26°≈ 0.49)考点】 解直角三角形的应用 - 仰角俯角问题.a=时,原式 =b==﹣6.【分析】首先过点 A 作AE ⊥BC 于E,可得四边形ADCE 是矩形,即可得CE=AD=15 米,然后分别在Rt△ ACE 中,AE= 与在Rt△ABE 中,BE=AE ?tan45°,即可求得BE 的长,继而求得电梯楼的高度.【解答】解:过点 A 作AE ⊥BC 于E,∵AD ⊥CD ,BC⊥CD,∴四边形ADCE 是矩形,∴CE=AD=15 米,在Rt△ACE 中,AE= = ≈30.6(米),在Rt△ABE 中,BE=AE ?tan45°=30.6(米),∴BC=CE+BE=15+30.6=45.6(米).答:电梯楼的高度BC 为45.6 米.19.最近两年雾霾对我国北方大部分地区影响较严重,其中和越来越多的汽车尾气排放有极大的关系.据报道,历经一百天的调查研究,我市PM2.5 的源解析已经通过专家论证,各种调查显示,机动车为PM2.5 的最大来源,一辆车每行驶20 千米平均向大气里排放0.035千克污染物,校环保志愿小分队从环保局了解到我市100 天的空气质量等级情况,并制成统计图和表:空气质量等级优良轻度污染中度污染重度污染严重污染天数(天)10a12825b(1)表中a=25 ,b=20,图中严重污染部分对应的圆心角n= 72° ;(2)请你根据“2020 年我市100天空气质量等级天数统计表”计算100 天内重度污染和严重污染出现的概率共是多少?(3)小明是社区环保志愿者,他和同学们调查了机动车每天的行驶路程,了解到每辆车每天平均出行25 千米,已知我市2020 年机动车保有量已突破200 万辆,请你通过计算,估计2020 年我市一天中出行的机动车至少要向大气里排放多少千克污染物?【考点】扇形统计图;用样本估计总体;概率公式.【分析】(1)根据优的天数和所占的百分比求出总天数,再乘以良和严重污染所占的百分比,求出a,b,再用360°乘以严重污染所占的百分比求出严重污染部分对应的圆心角的度数;(2)用重度污染和严重污染所占的百分比相加即可得出答案; (3)根据题意和用样本估计总体的方法,列出算式,求解即可.【解答】 解:( 1)根据题意,得: a=100× 25%=25(天), 严重污染所占的百分比是: 1﹣10%﹣25%﹣12%﹣8%﹣25%=20% , b=100×20%=20(天),n=360°× 20%=72 °,故答案为: 25, 20,72°;(2)100 天内重度污染和严重污染出现的频率为 × 100%=45% ;(3)根据题意,得: 200×10000× 0.035× =87500(千克),答:估计 2020 年我市一天中出行的机动车至少要向大气里排放 87500 千克污染物.20.如图,已知, A (0,4),B (﹣ 3,0), C (2,0),D 为 B 点关于 AC 的对称点,反比 例函数 y= 的图象经过 D 点. (1)证明四边形 ABCD 为菱形; (2)求此反比例函数的解析式;(3)已知在 y= 的图象( x >0)上一点 N ,y 轴正半轴上一点 M ,且四边形 ABMN 是平由 D 为 B 点关于 AC 的对称点,可得 AB=AD , BC=DC ,即可证得 AB=AD=CD=CB ,继而 证得四边形 ABCD 为菱形;(2)由四边形 ABCD 为菱形,可求得点 D 的坐标, 然后利用待定系数法,即可求得此反比 例函数的解析式;(3)由四边形 ABMN 是平行四边形,根据平移的性质,可求得点 N 的横坐标,代入反比 例函数解析式,即可求得点 N 的坐标,继而求得 M 点的坐标. 【解答】 解:(1)∵A (0,4),B (﹣ 3,0),C (2,0), ∴OA=4 ,OB=3 ,OC=2 , ∴AB==5,BC=5 , ∴AB=BC ,0), C ( 2, 0),利用勾股定理可求得 AB=5=BC ,又∵D 为 B 点关于 AC 的对称点, ∴AB=AD , CB=CD , ∴AB=AD=CD=CB , ∴四边形ABCD 为菱形;2)∵四边形 ABCD 为菱形,(3)∵四边形 ABMN 是平行四边形, ∴AN ∥BM ,AN=BM , ∴AN 是 BM 经过平移得到的,∴首先 BM 向右平移了 3 个单位长度, ∴N 点的横坐标为 3, 代入 y= 得 y=21.鄂州市化工材料经销公司购进一种化工原料若干千克,价格为每千克 30 元.物价部门规定其销售单价不高于每千克 60元,不低于每千克 30 元.经市场调查发现: 日销售量 y (千 克)是销售单价 x (元)的一次函数,且当 x=60 时, y=80; x=50 时, y=100 .在销售过程 中,每天还要支付其他费用 450 元.( 1)求出 y 与 x 的函数关系式,并写出自变量 x 的取值范围. (2)求该公司销售该原料日获利 w (元)与销售单价 x (元)之间的函数关系式.(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元? 【考点】 二次函数的应用.【分析】(1)根据 y 与 x 成一次函数解析式,设为 y=kx +b ,把 x 与y 的两对值代入求出 k 与b 的值,即可确定出 y 与 x 的解析式,并求出 x 的范围即可;(2)根据利润 =单价×销售量列出 W 关于 x 的二次函数解析式即可; (3)利用二次函数的性质求出 W 的最大值,以及此时 x 的值即可. 【解答】 解:( 1)设 y=kx +b ,根据题意得 ,解得: k=﹣2, b=200, ∴y= ﹣2x+200(30≤x ≤60);(2)W=(x ﹣30)(﹣2x+200)﹣ 450=﹣2x 2+260x ﹣6450=﹣2(x ﹣65)2+2000; (3)W= ﹣2(x ﹣ 65)2+2000, ∵30≤x ≤60,∴x=60 时,w 有最大值为 1950 元,∴当销售单价为 60元时,该公司日获利最大,为 1950 元.﹣ 4=∴ M 点的纵坐标为:∴D 点的坐标为( 5, 4),反比例函数 y= 的图象经过 D 点,∴k=20 ,∴反比例函数的解析式为:∴ M 点的坐标为:22.王老师在组织一次数学教学中,扁拟了如下问题串【原题初探】如图1所示,在四边形ABCD 中,AD∥BC,E为CD边的中点,连接AE 并延长交BC的延长线于点F,求证:S 四边形ABCD= S△ADE ;【变式猜想】如图 2 所示,在已知锐角∠ AOB 内有一定点P,过点P 任意作一条直线MN ,分别交射线OA,OB 于点M,N,小明在将直线MN 绕着点P 旋转的过程中发现,△ MON 的面积存在最小值,试问当MN 在什么位置时,△ MON 的面积最小【拓展应用】如图3所示,一块四边形土地OABC ,其中OA 边长60米,AB 边长30米,C点到OA 边的距离为45 米,使用测角器测得∠ AOC=45 °,OA⊥AB,OC⊥BC,机井P距离OA,AB 均是20米,过机井P画一条分割线将这块地分成两块四边形地块(与四边形土地OABC )的一组对边相交),则其中以点O 为顶点的四边形地块的最大面积为1000m2.【考点】几何变换综合题.【分析】【原题初探】:根据可以求得△ ADE ≌△ FCE ,就可以得出S△ADE=S△FCE就可以得出结论;【变式猜想】:根据问题情境的结论可以得出当直线旋转到点P是MN 的中点时S△MON最小,过点M 作MG∥OB 交EF于G.由全等三角形的性质可以得出结论;【拓展应用】:当过点P的直线l与四边形OABC 的另一组对边CB、OA分别交M、N,延长CB 交x轴于T,由B、C的坐标可得直线BC 的解析式,就可以求出T的坐标,从而求出△OCT 的面积,再由问题迁移的结论可以求出最大值,通过比较就可以求出结论.【解答】解:【原题初探】证明:∵ AD ∥BC,∴∠ ADE= ∠ FCE,在△ ADE 与△ FCE 中,,∴△ ADE≌△ FCE,∴S△ADE =S△ FCE,∴S四边形ABCD =S四边形ABCE+S△ADE =S四边形ABCE +S△ FCE=S△ABF;【变式猜想】当直线旋转到点P是MN 的中点时S△MON最小,如图( 1),过点 P 的另一条直线 EF 交 OA 、OB 于点 E 、F ,设 PF <PE ,过点 M 作 MG ∥OB 交 EF 于 G ,由方法探究可以得出当 P 是 MN 的中点时 S 四边形 MOFG =S △MON .∵S 四边形 MOFG <S △EOF , ∴S △MON <S △EOF ,∴当点 P 是 MN 的中点时 S △MON 最小; 【拓展应用】 ① 如图 3 ,当过点 P 的直线 l 与四边形 OABC 的一组对边 OC 、AB 分别交于点 M 、N ,延长 OC 、AB 交于点 D ,∵OA 边长 60 米,使用测角器测得∠ AOC=45 °, OA ⊥AB , ∴△ OAD 是等腰直角三角形, ∴S △ AOD = AO 2= × 602=1800由变式猜想的结论可知,当 PN=PM 时,△ MND 的面积最小, ∴四边形 ANMO 的面积最大. 作 PP 1⊥ OA ,MM 1⊥OA ,垂足分别为 P 1,M 1, ∴M 1P 1=P 1A=20 , ∴OM 1=M 1M=20 , ∴MN ∥OA ,当过点 P 的直线 l 与四边形 OABC 的另一组对边 CB 、OA 分别交 M 、N ,延长 CB 交 x 轴 于T ,过点 C 作 CH ⊥OA , ∴CH=45 . ∵∠ COA=45 °,∴△ CHA 为等腰直角三角形, ∴OC=45 , ∵OC ⊥BC ,∴△OCT 是等腰直角三角形,2∴S △OCT = OC 2=2025, OT=90由问题迁移的结论可知,当 PM=PN 时,△ MNT 的面积最小, ∴四边形 CMNO 的面积最大. ∴NP 1=M 1P 1,MM 1=2PP 1=40,∴S 四边形 OANM=S △OMM1+S 四边形 ANMM1 × 20× 20+20× 40=1000② 如图 4 ,∴ TM 1=40∴OM 1=OT ﹣TM 1=50.∵AT=AB=30 ,∴AM 1=TM 1﹣AT=40 ﹣30=10,∵AP 1=20 ,∴P1N=P1M1=AP1=AM 1=20﹣10=10,∴NT=P 1N+AP1+AT=10+20+30=60∴S△MNT = ×40×60=1200,∴S四边形OCMN =2025 ﹣1200=725< 1000.∴综上所述:截得四边形面积的最大值为1000(m2),故答案为1000m2.23.如图,抛物线y=ax2﹣x﹣2(a≠0)的图象与x轴交于A、B 两点,与y轴交于C点,已知 B 点坐标为(4,0).(1)求抛物线的解析式;(2)试探究△ ABC 的外接圆的圆心位置,并求出圆心坐标;(3)若点M 是线段BC 下方的抛物线上一点,求△ MBC 的面积的最大值,并求出此时M(1)该函数解析式只有一个待定系数,只需将 B 点坐标代入解析式中即可.(2)首先根据抛物线的解析式确定 A 点坐标,然后通过证明△ ABC 是直角三角形来推导出直径AB 和圆心的位置,由此确定圆心坐标.(3)△ MBC 的面积可由 S △MBC = BC ×h 表示,若要它的面积最大,需要使 h 取最大值, 即点 M 到直线 BC 的距离最大,若设一条平行于 BC 的直线,那么当该直线与抛物线有且 只有一个交点时,该交点就是点M .方法二:(1)略. (2)通过求出 A ,B ,C 三点坐标,利用勾股定理或利用斜率垂直公式可求出 AC ⊥ BC ,从 而求出圆心坐标.(3)利用三角形面积公式, 过 M 点作 x 轴垂线, 水平底与铅垂高乘积的一半, 得出△ MBC 的面积函数,从而求出 M 点.【解答】 方法一:解:(1)将 B ( 4,0)代入抛物线的解析式中,得:0=16a ﹣ × 4﹣ 2,即: a= ;(2)由( 1)的函数解析式可求得: A (﹣ 1,0)、C (0,﹣ 2);∴OA=1 ,OC=2,OB=4 ,即: OC 2=OA ?OB ,又: OC ⊥AB ,∴△ OAC ∽△ OCB ,得:∠ OCA= ∠OBC ;∴∠ ACB= ∠OCA+∠OCB=∠OBC+∠OCB=90 °,∴△ ABC 为直角三角形, AB 为△ABC 外接圆的直径;所以该外接圆的圆心为 AB 的中点,且坐标为: ( , 0). 3)已求得: B (4, 0)、C ( 0,﹣ 2),可得直线 BC 的解析式为: y= x ﹣设直线 l ∥BC ,则该直线的解析式可表示为: y= x+b ,当直线 l 与抛物线只有一个交点时, 可列方程:2 x +b= x y= x ﹣ 4. x ﹣2,即: x 2﹣2x ﹣2﹣ b=0,且△ =0;∴4﹣4×﹣ 2﹣b ) =0,即 b= ﹣ 4;∴直线 l :∴抛物线的解析式为:所以点M 即直线l 和抛物线的唯一交点,有:即M(2,﹣3).过M点作MN⊥x轴于N,S△BMC =S梯形OCMN+S△MNB ﹣S△OCB= ×2×(2+3)+ ×2×3﹣× 2× 4=4.方法二:∴K AC×K BC=﹣1,∴ AC⊥BC,∴△ ABC 是以AB 为斜边的直角三角形,△外接圆的圆心坐标为(,0).(3)过点M 作x 轴的垂线交BC ′于H,∵B(4,0),C(0,﹣2),∴l BC:y= x﹣2,设H(t,t﹣2),M(t,t2﹣t﹣2),22 ∴S△ MBC = ×(H Y﹣M Y)(B X﹣C X)= ×(t﹣2﹣t2+ t+2)(4﹣0)=﹣t2+4t,∴当t=2 时,S有最大值4,∴M(2,﹣3).1)略.∴A(﹣1,0),B(4,0).C(0,﹣2),∴K AC= =﹣2,K BC= = ,ABC 的外接圆的圆心是AB 的中点,△ ABC 的2020 年9 月20 日。
2024贵州省中考一模押题预测卷化学试卷及答案

2024年中考第一次模拟考试(贵州卷)化学(考试时间:60分钟试卷满分:100分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
可能用到的相对原子质量:H-1C-12N-14O-16Na-23P-31S-32Ca-40一、单项选择题(本大题共7小题,每小题2分,共14分。
每小题只有一个选项符合题意,请将符合题意的选项用2B铅笔填涂在答题卡相应位置)1.下列图示的实验操作正确的是()A.点燃酒精灯B.滴加液体C.读液体体积D.闻药品气味2.有一位同学暑假去西藏发生了严重的高原反应,医生让他吸入了一种气体后,症状得到缓解。
此气体可能是()A.氧气B.氮气C.稀有气体D.二氧化碳3.小李同学用pH计测得生活中一些物质的pH如下表所示。
下列说法正确的是()物质肥皂水牙膏西瓜汁洁厕灵pH10.28.5 5.8 1.4A.牙膏显酸性B.西瓜汁的酸性比洁厕灵的酸性强C.肥皂水使紫色石蕊溶液显红色D.蚊虫叮咬处可涂抹牙膏或肥皂水4.金银花作为常见的中药材,具有清热解毒、消炎退肿等功效,其有效成分之一是绿原酸(C16H18O9)。
下列有关绿原酸的说法正确的是()A.绿原酸分子由碳、氢、氧三个元素组成B.绿原酸中碳元素的质量分数最大C.绿原酸的相对分子质量是354gD.绿原酸中碳、氢、氧元素的质量比为16:18:95.在生活生产中碳单质的应用广泛。
下列有关含碳物质的性质或用途正确的是()A.活性炭具有吸附性B.木炭常温下化学性质很活泼C.金刚石用作电极D.石墨用作钻探机钻头6.从生活走进化学,让化学服务于健康生活。
下列说法错误的是()A.老年人骨质疏松可服用含CaCO3的钙片B.贫血病患者需服用葡萄糖酸锌C.胃酸过多患者可服用含Al(OH)3的药物D.坏血病患者可服用维生素C片7.三种金属X、Y、Z相互之间的反应关系如下①Y+H2SO4——YSO4+H2↑,Z和H2SO4不反应②Z+2XNO3——Z(NO3)2+2X则X、Y、Z的金属活动性顺序为()A.X>Y>Z B.X>Z>Y C.Y>X>Z D.Y>Z>X二、非选择题(本大题共7小题,共46分)8.(6分)铼被誉为“超级金属”,铼及其合金被广泛应用到航空航天领域。
主管护师押题试卷1

押题试卷(一)一、A型题:每一道考试题下面有A、B、C、D、E五个备选答案。
请从中选择一个最佳答案。
1.急性肾炎水肿部位最早多由下列哪一部位开始A.眼睑B.面部C.腰部D.胫前区E.踝部∙隐藏答案∙收藏本题∙错题反馈正确答案:A2.流行病的流行过程必须具备哪三个环节A.病原体,环境,易感人群B.病原体,环境,传染源C.传染源,传播途径,易感人群D.病原体,传播途径,易感人群E.传染源,传播途径,环境∙隐藏答案∙收藏本题正确答案:C3.容易引起急性肾衰的损伤是A.严重挤压伤B.广泛擦伤C.严重撕裂伤D.多处刺伤E.冻伤∙隐藏答案∙收藏本题∙错题反馈正确答案:A4.下列哪种叙述最符合类风湿性关节炎的定义A.是一种病因不明的关节炎B.是一种感染后引起的自身免疫性关节炎C.是一种慢性对称性多关节炎为主要表现的系统性自身免疫性疾病D.是一种以手足关节病变为主要表现的系统性自身免疫性疾病E.是一种以脊柱关节病变为主要表现的系统性自身免疫性疾病∙隐藏答案∙收藏本题正确答案:C5.造成再生障碍性贫血最主要的原因是A.造血原料不足B.进行性贫血加重C.长期服用氯霉素D.骨髓造血功能衰竭E.急性大量失血∙隐藏答案∙收藏本题∙错题反馈正确答案:D6.心室颤动首选的治疗措施是A.心内注射肾上腺素B.同步电复律C.非同步电复律D.静脉注射苯妥英钠E.胺碘酮静注∙隐藏答案∙收藏本题正确答案:C7.急性心肌梗死急性期发生的室性早搏的治疗应给予A.维拉帕米静滴B.心律平静滴C.胺碘酮静滴D.利多卡因静滴E.溴苄胺∙隐藏答案∙收藏本题∙错题反馈正确答案:D8.Ⅲ度房室传导阻滞,心室率为35次/分的患者,首选的治疗方法是A.洋地黄B.异丙肾上腺素C.麻黄素D.阿托品E.安装人工心脏起搏器∙隐藏答案∙收藏本题正确答案:E9.心脏瓣膜病变中,最多见的是A.二尖瓣病变B.三尖瓣病变C.主动脉瓣病变D.肺动脉瓣病变E.联合瓣膜病变∙隐藏答案∙收藏本题∙错题反馈正确答案:A10.风心病哪类严重瓣膜损害可导致左心室射血受阻,引起左心室排血量显著降低,出现心绞痛、眩晕,甚至猝死A.二尖瓣狭窄B.二尖瓣关闭不全C.主动脉瓣狭窄D.主动脉瓣关闭不全E.肺动脉瓣关闭不全∙隐藏答案∙错题反馈正确答案:C11.治疗上呼吸道感染的措施,下列哪项不妥A.适当休息B.体温超过39℃时物理降温C.呼吸道隔离,防止交叉感染D.多饮水E.常规应用抗生素治疗∙隐藏答案∙收藏本题∙错题反馈正确答案:E12.慢性支气管炎急性发作期患者的主要治疗是A.吸氧B.控制感染C.解痉、平喘D.祛痰E.镇咳∙隐藏答案∙错题反馈正确答案:B13.剧烈频繁的呕吐可引起A.代谢性酸中毒B.代谢性碱中毒C.呼吸性酸中毒D.呼吸性碱中毒E.混合型酸中毒∙隐藏答案∙收藏本题∙错题反馈正确答案:B14.确诊慢性胃炎最可靠的检查方法是A.活组织检查B.纤维胃镜检查C.胃肠钡餐检查D.胃液分析E.血清学检查∙隐藏答案∙错题反馈正确答案:B15.甲亢患者的饮食应给予A.高蛋白、高热量、高维生素B.高蛋白、高热量、高盐C.高热量、低蛋白、低盐D.高热量、低蛋白、高盐E.低热量、低蛋白、高维生素∙隐藏答案∙收藏本题∙错题反馈正确答案:A16.消化性溃疡患者节律性疼痛变为持续性,进食或服用制酸药后长时间不能缓解,并向肩背部放射时,可能是发生了A.癌变B.出血C.胃底静脉曲张D.幽门梗阻E.穿孔∙收藏本题∙错题反馈正确答案:E17.胃、十二指肠溃疡急性穿孔的疼痛特点是A.上腹隐痛B.上腹刀割样疼痛C.上腹烧灼样痛D.上腹胀裂样痛E.上腹阵发性绞痛∙隐藏答案∙收藏本题∙错题反馈正确答案:B18.最容易发生嵌顿和绞窄的疝是A.股疝B.脐疝C.腹股沟斜疝D.白线疝E.腹股沟直疝∙收藏本题∙错题反馈正确答案:A19.患者李某,大叶性肺炎,做青霉素皮试时呈阳性,值班护士的处理措施哪项不对A.通知医生,选用其他药物B.在体温单、床头卡上注明青霉素阳性标记C.告知患者及家属D.严格交班E.以后用青霉素之前一定要做皮试∙隐藏答案∙收藏本题∙错题反馈正确答案:E20.胃肠道手术,术前禁食的主要目的是A.避免手术困难B.避免手术后腹胀C.预防麻醉中呕吐造成窒息D.防止术后吻合口瘘E.早期恢复肠蠕动∙收藏本题∙错题反馈正确答案:C21.手术人员无菌技术不正确的是A.帽子必须完全盖住头发B.先穿无菌手术衣再戴无菌手套C.每桶苯扎溴铵溶液最多可供40人次泡手D.戴无菌手套时,已消毒手指不能接触手套背侧部E.肘部触及有菌物后可继续手术,但应注意该处不再接触无菌区∙隐藏答案∙收藏本题∙错题反馈正确答案:E22.高渗性脱水的常见原因是A.急性肠梗阻B.感染性休克C.肺炎高热D.慢性十二指肠瘘E.挤压综合征∙收藏本题∙错题反馈正确答案:C23.低渗性脱水的常见原因是A.急性肠梗阻B.感染性休克C.肺炎高热D.慢性十二指肠瘘E.挤压综合征∙隐藏答案∙收藏本题∙错题反馈正确答案:D24.破伤风最早累及的肌肉是A.膈肌B.面肌C.四肢肌D.颈项肌E.咀嚼肌∙收藏本题∙错题反馈正确答案:E25.急性腹膜炎患者发生休克的主要原因是A.剧烈腹痛B.毒素吸收及血容量减少C.呼吸循环功能不全D.大量呕吐失液E.胃肠道渗出液刺激∙隐藏答案∙收藏本题∙错题反馈正确答案:B26.急性梗阻性化脓性胆管炎的最常见的梗阻因素是A.胆管狭窄B.胆管扭转C.胆道蛔虫D.胆管结石E.胆道肿瘤∙收藏本题∙错题反馈正确答案:D27.易引起感染的骨折是A.开放性骨折B.闭合性骨折C.完全骨折D.不完全骨折E.稳定性骨折∙隐藏答案∙收藏本题∙错题反馈正确答案:A28.不完全骨折是A.粉碎性骨折B.楔行骨折C.嵌插骨折D.青枝骨折E.横行骨折∙收藏本题∙错题反馈正确答案:D29.终末血尿提示出血部位在A.前尿道B.后尿道C.肾脏D.输尿管E.膀胱∙隐藏答案∙收藏本题∙错题反馈正确答案:B30.脓尿镜检时每高倍视野可见脓球A.1个以上B.2个以上C.3个以上D.4个以上E.5个以上∙收藏本题∙错题反馈正确答案:E31.患者,男性,43岁。
2022年河南省三甲名校原创押题试卷一道德与法治

2022年河南省三甲名校原创押题试卷一道德与法治1、20.个性和集体融合起来,不会失去个性;相反,只有在集体中,个性才能得到高度的觉醒和完善。
对这句话理解不正确的是()[单选题] *A.个性的形成和发展离不开周围的环境B.集体生活不利于学生的个性发展(正确答案)C.集体为学生的个性发展提供了条件和可能D.在集体中学习他人的优点,有利于完善个性2、在发展中国特色社会主义过程中,法治和德治的关系表述正确的是[单选题] *法治比德治更重要德治比法治更重要法治是德治的前提法治和德治相互联系、相辅相成、相互促进(正确答案)3、【单选题】马克思主义道德观认为,道德是反映()的特殊意识形态。
[单选题]*A.社会政治关系(正确答案)B.社会经济关系C.社会文化关系D.社会舆论关系4、【单选题】人生态度是指人们通过生活实践形成的对人生问题的一种( )心理倾向和精神状态。
[单选题] *A.稳定的(正确答案)B.平衡的C.长期的D.短期的5、下列正确的人生价值评价是()[单选题] *B.一个人只要尽心尽力,尽职尽责,他的人生价值就是值得肯定。
(正确答案)C.贡献越大人生价值越大D.精神贡献价值大于物质贡献价值A.能力越大人生价值越大6、【单选题】2018年5月2日,习近平在北京大学师生座谈会上的讲话指出:“青年是国家的希望,民族的未来。
我衷心希望,每一个青年都成为社会主义建设者和接班人,不辱时代使命,不负人民期望。
”习近平给广大青年提出四点希望,其中作为一个人立德之源、立功之本的是()。
[单选题] *A.爱国(正确答案)B.励志C.求真D.力行7、【单选题】为什么人服务是道德的核心问题,社会主义道德的核心是()。
[单选题] *A.为政党服务B. 为人民服务(正确答案)C.为军队服务D.为群众服务8、4. ()是个体的人生活动对社会、他人所具有价值。
[单选题] *A人生的自我价值B人生的社会价值(正确答案)C人生目的D人生价值9、【单选题】()是一个国家和民族在新的历史条件下形成和发展的。
2023年普通高等学校招生全国统一考试语文押题卷(一)及答案

2023年普通高等学校招生全国统一考试押题卷(一)语文本试卷满分150分,考试时间150分钟。
一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5小题,17分)阅读下面的文字,完成1~5题。
材料一:习近平总书记在党的二十大报告中首次阐明:“中国式现代化,是中国共产党领导的社会主义现代化,既有各国现代化的共同特征,更有基于自己国情的中国特色。
”中国式现代化是人口规模巨大的现代化、全体人民共同富裕的现代化、物质文明和精神文明相协调的现代化、人与自然和谐共生的现代化、走和平发展道路的现代化。
归根结底,中国式现代化打下了中华文化自信自强的烙印,是引领中国建设实践的文明新形态。
世界百年未有之大变局和大国博弈背景下,文化作为立场与价值的作用愈加凸显。
文化立场的实质是价值选择,是文化建设的出发点和落脚点,不仅体现为明确的主体性观念、意识和态度,也深层次地关涉文化发展的场域延展与坐标指向。
习近平总书记多次强调要“坚守中华文化立场”,这就要求必须以中华文化的主体性、独特性,深化中华文化自觉、提振中华文化自信、推进中华文化自强,更加自觉地在文化实践中,巩固中华文化一脉相承、守正创新的核心理念、精神品格及立场坐标,将文化创新创造转化为中国特色社会主义文化发展道路的政治智慧、精神标识与价值塑造。
现阶段,我们要坚守中华文化立场,提炼展示中华文明的精神标识和文化精髓,加快构建中国话语和中国叙事体系,加强国际传播能力建设,全面提升国际传播效能,形成同我国综合国力和国际地位相匹配的国际话语权。
(摘编自蔡劲松《以文化自信自强谱写中国式现代化文化长卷》,有删改) 材料二:中华创世神话学术高地建设工程以学理上能贯通、学术上集大成为学术目标,通过历时五年的辛勤工作,首次对中华创世神话进行了全面的学术梳理和探索研究,填补了国内相关研究领域的空白。
考古学研究早已证明人类文明起源并非一种模式,中华文明起源具有独特的路径。
对中华创世神话的分析既是建立中国特色人类文明起源叙事,从而完善人类文明起源叙事的尝试,也是与以古希腊罗马神话为代表的西方文明起源叙事的平等对话。
2020年河北省中考数学押题试卷(一)
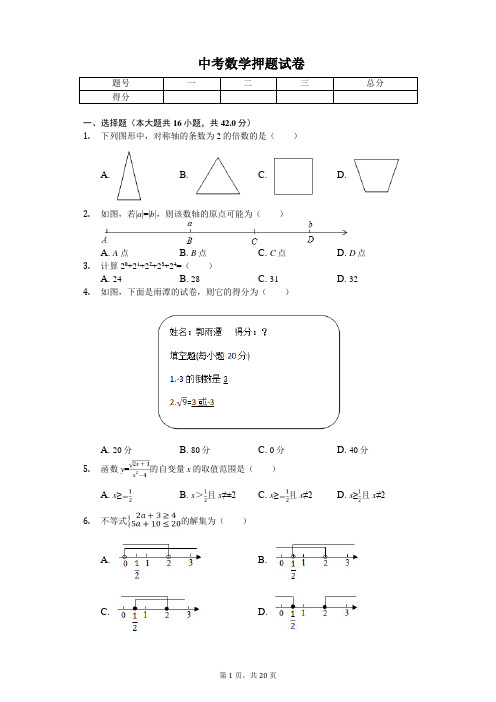
中考数学押题试卷题号一二三总分得分一、选择题(本大题共16小题,共42.0分)1.下列图形中,对称轴的条数为2的倍数的是()A. B. C. D.2.如图,若|a|=|b|,则该数轴的原点可能为()A. A点B. B点C. C点D. D点3.计算20+21+22+23+24=()A. 24B. 28C. 31D. 324.如图,下面是雨潭的试卷,则它的得分为()A. 20分B. 80分C. 0分D. 40分5.函数y=的自变量x的取值范围是()A. x≥B. x>且x≠±2C. x≥且x≠2D. x≥且x≠26.不等式的解集为()A. B.C. D.7.如图在⊙O中,AB为直径,C为圆上一点,连接CO并延长CO交⊙O于点D.则四边形ABCD为()A. 正方形B. 菱形C. 矩形D. 梯形8.如图,反比例函数y1=(k1>0)和y2=(k2<0)中,作直线x=10,分别交x轴,y1=(k1>0)和y2=(k2<0)于点P,点A,点B,若=3,则=()A. B. 3 C. -3 D.9.若=1,a与b互为倒数,ab>0,a+b>0,则代数式(a+b)2-ab=()A. 1B. -1C. 0D. 210.如图,在平面直角坐标系中,四边形OBCD是菱形,OB=OD=1,∠BOD=60°将菱形OBCD绕点O旋转任意角度,得到菱形OB1C1D1,则点C1的纵坐标的最小值为()A. B. -1 C. - D. 111.如表为昱乾初二学年的年级排名.若添加数据9后,该组数据的平均数增加了,则昱乾的八下三调考试级名为()考试八下一调八下二调八下三调八下期末年级排名66?4A. 26B. 19C. 1D. 3812.如图所示,在平面直角坐标系中,直线y1=2x+4分别与x轴,y轴交于A,B两点,以线段OB为一条边向右侧作矩形OCDB,且点D在直线y2=-x+b上,若矩形OCDB 的面积为20,直线y1=2x+4与直线y2=-x+b交于点P.则P的坐标为()A. (2,8)B.C.D. (4,12)13.星期天,鹤翔骑电动车回老家看望奶奶,速度为20km/h.当他行驶了40千米后发现忘记带课本了,于是给奶奶打电话,同时自己按原速返回.奶奶30分钟后骑自行车从家出发,1小时后与鹤翔相遇.鹤翔与奶奶之间的距离y(km)与时间x(h)的关系如图所示.则奶奶骑车的速度为()A. 10km/hB. 45km/hC. 40km/hD. 80km/h14.如图所示,抛物线L:y=ax2+bx+c(a<0)的对称轴为x=5,且与x轴的左交点为(1,0),则下列说法正确的有()①C(9,0);②b+c>-10;③y的最大值为-16a;④若该抛物线与直线y=8有公共交点,则a的取值范围是a≤.A. ①②③④B. ①②③C. ①③④D. ①④15.如图,在正方形ABCD中,AB=1,P是边BC上的一个动点,由点B开始运动,运动到C停止.连接AP,以AP为直角边向右侧作等腰直角三角形,另一个顶点为Q.则点P从B运动到C的过程中,点Q的运动路径长为()A. πB.C.D. 116.如图,在平面直角坐标系中,正六边形的边长为1,且有一个顶点与原点重合,现将该六边形沿x轴向右翻转(无滑动),且每次旋转60°.则翻转2020次后,点P 的运动路径长为()A. 2019π+3B. (449+)πC. (449+)πD. π+2019二、填空题(本大题共3小题,共10.0分)17.一元二次方程x2+x-12=0的根为______.18.如图,在正方形ABCD中,AC=,E,F分别是边AD,CD上的点,且AE=DF.AF,DE交于点O,P为AB的中点,则OP=______.19.一个含30度角的三角板和一个含45度角的三角板按如图所示的方式拼接在一起,经测量发现,AC=CE=,取AB中点O,连接OF.∠FCE在∠ACB内部任意转动(包括边界),则CE在运动过程中扫过的面积为______,在旋转过程中,线段OF的最小值为______.三、解答题(本大题共7小题,共68.0分)20.(1)若a+b=3,2a-b=3,求代数式a2b2+4a++b的值.(2)解方程:x2-4x-60=0.21.期末考试结束后,数学老师对本班的数学成绩进行了统计.根据图中信息回答下列问题.(1)该班级的人数为______,D等级的学生有______人.并根据数据补全统计图.(2)若规定80以上为及格,求该班级的及格率.(3)若在各个分数段的人数这一组数据上,再添加一个数据a(a为正整数),该组数据的中位数没有改变,请直接写出a的值.22.规定一种新的运算△:a△b=a(a+b)+a-b.例如,1△2=1×(1+2)+1-2=2.(1)10△12=______.(2)若x△3=-7,求x的值.(3)求代数式-2x△4的最小值.23.在Rt△ABC中,AB=8,BC=6,点P从点A出发,速度为4个单位每秒,同时点Q从点C出发,以v个单位每秒的速度向B运动.当有一个点到达点B时,点P,Q同时停止运动.设运动时间为t.(1)若v=2,t=1,求△PQB的面积.(2)若在运动过程中,PQ始终平行于AC,求v的值.24.问题探究.【情景导入】在物理学中,自由落体下落的距离s与下落时间t的平方成正比.若忽略空气阻力,则s与t满足函数关系s=2,g表示重力加速度,看作一个定值.如表是一次试验的记录,根据如表,求g的值,并求出s与t的关系式.s/m520125t/s125【尝试探索】如图所示,一个重力为的物体在理想环境下做自由落体运动,后落地.求下落点到地面的距离s.【实际应用】若鹤翔从顶楼(30楼)跳下,忽略一切影响因素,假设他做自由落体运动,每层楼高3m,在他开始运动的同时,消防员恰好赶到,则消防员铺设气垫至少需要10秒,则鹤翔能否得以生存?(结果取整数)25.【问题背景】(1)如图1,⊙O与∠P的两边分别切与A,B两点.求证:PA=PB.【深入探究】(2)在(1)的条件下,若∠APB=60°,连接PO,以PO为一条边向上作等边三角形POQ,连接AO,AQ.求证:AO=AQ.(3)若在(1)的条件下,以OP为斜边向上作等腰直角三角形POQ,取OP中点M,连接MB,MQ,BQ,求证:∠MQB=∠MBQ.【拓展延伸】在(3)的条件下,连接AO,AQ,探索AO,AQ,AP之间的数量关系.26.【情景导入】(1)如图1,在平面直角坐标系中,直线AB与y轴交于点A,与x轴交于点B,与直线y=8交于点C.求点C的坐标.【尝试探究】(2)①在(1)的条件下,若P是直线y=6上一点,且△PBC是等腰三角形,求点P的坐标.②若确定点P的坐标为(2,6),直线AB可在平面内任意平移.当△PBC是等腰三角形时,求点C的坐标.【延伸拓展】在(1)的条件下,若△PBC为直角三角形,且∠BPC=90°,连接AP,请直接写出sin∠PAC的最大值.答案和解析1.【答案】C【解析】解:A、图形有一条对称轴,不符合题意;B、图形有三条对称轴,不符合题意;C、图形有四条对称轴,符合题意;D、图形有一条对称轴,不符合题意;故选:C.根据轴对称图形的概念、对称轴的概念解答.本题考查的是轴对称图形的概念,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴.2.【答案】C【解析】解:因为|a|=|b|,所以该数轴的原点可能为点C.故选:C.由|a|=|b|可知:数b的绝对值等于数a的绝对值,可得该数轴的原点.本题考查数轴的特点和绝对值性质,是需要熟练掌握的内容.本题考查数轴的特点和绝对值性质,是需要熟练掌握的内容.本题考查数轴的特点和绝对值性质,是需要熟练掌握的内容.3.【答案】C【解析】解:原式=1+2+4+8+16=31故选:C.根据零指数幂的意义以及实数的运算法则即可求出答案.本题考查实数运算,解题的关键是熟练运用实数运算法则,本题属于基础题型.4.【答案】C【解析】解:∵-3的倒数是-,∴第1题不正确;∵的算术平方根是3,∴第2题不正确,∴雨潭的得分为0分.故选:C.首先根据:求一个整数的倒数,就是写成这个整数分之一,可得:-3的倒数是-;然后根据算术平方根的含义和求法,可得:的算术平方根是3.此题主要考查了算术平方根的含义和求法,以及倒数的含义和求法,要熟练掌握.5.【答案】C【解析】解:由题意得:2x+1≥0,且x2-4≠0.解得:x≥且x≠2.故选:C.根据二次根式被开方数大于等于0和分式的分母不为0回答即可.本题主要考查了函数自变量的取值范围问题,明确二次根式被开方数大于等于0和分式的分母不为0是解题的关键.6.【答案】C【解析】解:,解①得a≥,解②得a≤2,∴不等式组的解集为≤a≤2,在数轴上表示为,故选:C.分别解出两个不等式,然后确定两个不等式的解集的公共部分.本题考查了解一元一次不等式组,解不等式组应遵循的原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.7.【答案】C【解析】解:∵AB,CD是直径,∴∠ADB=∠ACD=90°,∠CAD=∠CBD=90°,∴四边形ABCD是矩形.故选:C.利用圆周角定理以及矩形的判定方法即可解决问题.本题考查圆周角定理,矩形的判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.8.【答案】C【解析】解:∵点A在反比例函数y1=y1=(k1>0)的图象上,点B在反比例函数y2=(k2<0)的图象上,且=3,∴k1=OP•PA,k2=-OP•BP,∴==-3,故选:C.根据已知条件得到k1=OP•PA,k2=-OP•BP,代入于是得到结论.本题考查了反比例函数图象上点的坐标特征、反比例函数系数k的几何意义、正确的理解题意是解题的关键.9.【答案】C【解析】解:∵=1,a与b互为倒数,∴=1,ab=1,∴a+b=1,∴(a+b)2-ab=1-1=0.故选:C.直接将已知变形进而得出a+b,ab的值,即可得出答案.此题主要考查了有理数的乘法,正确将已知变形是解题关键.10.【答案】C【解析】解:如图,连接OC,过点C作CE⊥x轴,∵四边形OBCD是菱形,∴OD∥BC,∴∠BOD=∠CBE=60°,且CE⊥OB于E,∴BE=BC=,CE=,∴OC===∴当点C1在y轴上时,点C1的纵坐标有最小值为-,故选:C.如图,连接OC,过点C作CE⊥x轴,由直角三角形的性质可求BE=BC=,CE=,由勾股定理可求OC的长,即可求解.本题考查了菱形的性质,等边三角形的判定和性质,旋转的性质,勾股定理等知识,求出OC的长是本题的关键.11.【答案】C【解析】解:设昱乾的八下三调考试级名为x,依题意有(6+6+x+4+9)÷5=(6+6+x+4)÷4+,解得x=1.故昱乾的八下三调考试级名为1.故选:C.设昱乾的八下三调考试级名为x,根据平均数的计算公式由等量关系列出方程求解即可.考查了算术平均数,平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.12.【答案】C【解析】解:∵直线y1=2x+4分别与x轴,y轴交于A,B两点,∴B(0,4),∴OB=4,∵矩形OCDB的面积为20,∴OB•OC=20,∴OC=5,∴D(5,4),∵D在直线y2=-x+b上,∴4=-5+b,∴b=9,∴直线y2=-x+9,解得,∴P(,),故选:C.由直线y1=2x+4求得OB=4,根据解析式面积求得D(5,4),代入y2=-x+b求得解析式,然后联立解析式,解方程组即可求得.本题考查了两条直线平行或相交问题,主要考查了待定系数法求一次函数的解析式,一次函数图象上点的坐标特征.13.【答案】A【解析】解:设奶奶骑车的速度为x千米/时,根据题意可得:40=20×1.5+xx=10∴设奶奶骑车的速度为10千米/时,故选:A.设奶奶骑车的速度为x千米/时,由图象可得鹤翔1.5小时的路程+奶奶1小时的路程=40km,列出方程,即可求解.本题考查了一次函数的应用,理解图象是本题的关键.14.【答案】B【解析】解:∵抛物线L:y=ax2+bx+c(a<0)的对称轴为x=5,且与x轴的左交点为(1,0)∴抛物线L与x轴的交点C为(9,0)故①正确;∵抛物线L与x轴的左交点为(1,0)∴a+b+c=0∴b+c=-a>0>-10故②正确;∵抛物线L:y=ax2+bx+c(a<0)的对称轴为x=5∴-=5,即b=-10a又∵a+b+c=0∴c=9a∴==-16a故③正确;若该抛物线与直线y=8有公共交点,则有8≤-16a,∴a≤-故④错误.故选:B.利用图象信息以及二次函数的性质一一判断即可.本题考查二次函数的图象与系数的关系、抛物线与x轴的交点等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.15.【答案】C【解析】解:如图,延长AD到M,使得DM=AD,连接CM,则点Q运动轨迹是线段CM.作QN⊥BC于N,∵PA=PQ,∠APQ=90°,∴∠APB+∠QPN=90°,∠QPN+∠PQN=90°,∴∠APB=∠PQN,在△ABP和△PNQ中,,∴△ABP≌△PNQ,∴AB=PN=BC,PB=NQ,∴PB=CN=QN,∴∠QCN=45°,∴点Q在线段CM上,点Q的运动轨迹是线段CM,CM=CD=.故选:C.如图,延长AD到M,使得DM=AD,连接CM,则点Q运动轨迹是线段CM.只要证明△ABP≌△PNQ,CN=QN即可解决问题.本题考查正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、轨迹等知识,解题的关键是学会添加常用辅助线,构造全等三角形,属于中考常考题型.16.【答案】C【解析】【分析】根据正六边形的特点,每6次翻转为一个循环组循环,求出每次循环的路径即可解决问题本题考查的是正多边形和圆,涉及到坐标与图形变化-旋转,正六边形的性质,确定出最后点P所在的位置是解题的关键,难点在于作辅助线构造出直角三角形.【解答】解:∵正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,∴每6次翻转为一个循环,∵2020÷6=336余数为4每一个循环的路径=++++=π+π,∴2020次后,点P的运动路径长为336(π+π)+++=(449+)π,故选:C.17.【答案】x1=3,x2=-4【解析】解:∵x2+x-12=0,∴(x-3)(x+4)=0,则x-3=0或x+4=0,解得x1=3,x2=-4.故答案为:x1=3,x2=-4.利用因式分解法求解可得.本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.18.【答案】【解析】解:∵四边形ABCD是正方形,∴AD=AB,∠D=∠EAB=90°,AC=AB,∴AB=AC=×=1,在△ADF和△BAE中,,∴△ADF≌△BAE(SAS),∴∠DAF=∠ABE,∵∠DAF+∠BAO=90°,∴∠ABE+∠BAO=90°,∴∠AOB=90°,∵P为AB的中点,∴OP=AB=;故答案为:.证明△ADF≌△BAE(SAS),得出∠DAF=∠ABE,证出∠AOB=90°,由直角三角形斜边上的中线性质即可得出答案.本题考查了正方形的性质、全等三角形的判定与性质以及直角三角形斜边上的中线性质等知识;证明三角形全等是解题的关键.19.【答案】-1【解析】解:连接OC.在Rt△ABC中,∵∠ACB=90°,∠A=30°,AC=,∴BC=AC•tan30°=1,∴AB=2BC=2,∵OA=OB,∴OC=AB=1,在Rt△EFC中,∵∠CEF=90°,CE=EF=,∴CF=CE=,∴CE在运动过程中扫过的面积==π,∵OF≥CF-OC,∴OF≥-1,∴OF的最小值为-1.故答案为π,-1.利用扇形面积公式,两点之间线段最短即可解决问题.本题考查轨迹,扇形的面积等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.20.【答案】解:(1)∵a+b=3,2a-b=3,∴a=2,b=1,∴a2b2+4a++b=22×12+4×2++1=4×1+8++1=4+8++1=13+;(2)∵x2-4x-60=0∴(x-10)(x+6)=0∴x-10=0或x+6=0解得,x1=10,x2=-6.【解析】(1)根据a+b=3,2a-b=3,可以求得a、b的值,然后代入所求式子,即可求得所求式子的值;(2)根据因式分解的方法可以解答此方程.本题考查因式分解的应用、二次根式的化简求值、解二元一次方程,解答本题的关键是明确它们各自的解答方法.21.【答案】100人 5(1)该班级的人数为45÷45%=100(人),D等级人数为100×(1-15%-45%-35%)【解析】解:=5(人),A组人数为100×15%=15(人),C组人数为100×35%=35(人),补全图形如下:故答案为:100人,5;(2)该班级的及格率为45%+15%=60%;(3)∵原分数段人数的数据为5、15、35、45,∴中位数为=25,若要使中位数不发生改变,则需添加数据25,即a=25.(1)先有B分数段人数及其所占比例求出总人数,再用总人数乘以各分数段对应的百分比求出对应人数,从而得解;(2)将80以上即A、B组百分比相加即可得;(3)根据中位数的概念求解可得.本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题,本题根据B 组的人数与所占的百分比求解是解题的关键,也是本题的突破口.22.【答案】218【解析】解:(1)∵a△b=a(a+b)+a-b,∴10△12=10×(10+12)+10-12=218.(2)∵x△3=-7,∴x(x+3)+x-3=-7,∴x2+4x+4=0,解得x=-2.(3)∵a△b=a(a+b)+a-b,∴-2x△4=-2x(-2x+4)-2x-4=4x2-10x-4=(2x-2.5)2-10.25∴2x-2.5=0,即x=1.25时,-2x△4的最小值是-10.25.故答案为:218.(1)根据:a△b=a(a+b)+a-b,求出10△12的值是多少即可.(2)若x△3=-7,则x(x+3)+x-3=-7,据此求出x的值是多少即可.(3)根据:a△b=a(a+b)+a-b,可得:-2x△4=-2x(-2x+4)-2x-4,据此求出-2x△4的最小值是多少即可.此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.23.【答案】解:(1)∵AB=8,BC=6,点P从点A出发,速度为4个单位每秒,v=2,t=1∴AP=4×1=4,CQ=2×1=2∴PB=8-4=4,BQ=6-2=4∴△PQB的面积为:PB×BQ÷2=4×4÷2=8.答:△PQB的面积为8.(2)∵PQ始终平行于AC∴△BPQ∽△BAC∴=∵PQ始终平行于AC∴不妨取t=1∴=解得:v=3答:v的值为3.【解析】(1)先分别用含t的式子表示出PB、BQ,再根据直角三角形的面积公式计算即可;(2)先由PQ始终平行于AC得出△BPQ∽△BAC,从而根据相似三角形的性质列出比例式,取t=1代入,解出v即可.本题考查了相似三角形的判定与性质在几何动点问题中的应用,熟练掌握相关判定定理与性质定理是解题的关键.24.【答案】解:【情景导入】由题可得5=g×12,解得g=10,∴s与t的关系式为s=5t2 .【尝试探索】当t=10时,s=5×100=500m,即下落点到地面的距离为500m;【实际应用】当s=30×3=90时,90=5t2,解得t≈4,(负值已舍去)∵10s>4s,∴不能得以生存.【解析】【情景导入】依据表格中的数据进行计算,即可得到g的值,进而得到s与t 的关系式;【尝试探索】依据t的值为10,即可得到s的值;【实际应用】依据楼高s的值,即可得到t的值,进而得出结论.本题主要考查了二次函数的应用,解此类题的关键是通过题意,确定出二次函数的解析式,实际问题中自变量x的取值要使实际问题有意义.25.【答案】解:【问题背景】(1)连接OA,OB,OP,∵PA、PB是切线,∴PA⊥OA,PB⊥OB,∴∠PAO=∠PBO=90°,在Rt△PAO和Rt△PBO中,,∴Rt△PAO≌Rt△PBO(HL),∴PA=PB;【深入探究】(2)∵Rt△PAO≌Rt△PBO,∴∠APO=∠BPO,∵∠APB=60°,∴∠APO=∠BPO=30°,∵△POQ是等边三角形,∴∠OPQ=60°,PO=PQ,∴∠APQ=∠APO=30°,且PO=PQ,∴PA垂直平分OQ,∴AO=AQ;(3)如图3,连接OB,∵PB是⊙O是切线,∴PB⊥OB,且点M是OP的中点,∴BM=PO,∵△OPQ是等腰直角三角形,且点M是OP的中点,∴QM=OP,∴QM=BM,∴∠MQB=∠MBQ;拓展延伸】AO+AQ=AP,理由如下:过点Q作QH⊥AQ交AP于点H,∴∠AQH=∠PQO=90°,∴∠AQO=∠PQH,∵∠QPO+∠QOP=90°,∠AOP+∠APO=90°,∴∠APQ+∠APO=∠APO+∠AOQ,∴∠APQ=∠AOP,且∠AQO=∠PQH,QP=OQ,∴△AOQ≌△HPQ(ASA)∴QH=AQ,AO=PH,∴AH=AQ,∵AP=PH+AH,∴AO+AQ=AP.【解析】【问题背景】(1)连接OA,OB,OP,由“HL”可证Rt△PAO≌Rt△PBO,可得PA=PB;【深入探究】(2)由全等三角形的性质和等边三角形的性质,可证PA垂直平分OQ,可得AO=AQ;(3)连接OB,由直角三角形的性质和等腰直角三角形的性质可得MB=QM=OP,由等腰三角形的性质可得结论;【拓展延伸】过点Q作QH⊥AQ交AP于点H,由“ASA”可证△AOQ≌△HPQ,可得QH=AQ,AO=PH,由直角三角形的性质可得AH=AQ,即可得AO+AQ=AP.本题是圆的综合题,考查了圆的有关知识,全等三角形的判定和性质,等腰直角三角形的性质,直角三角形的性质,添加恰当辅助线是本题的关键.26.【答案】解:(1)点A、B的坐标分别为:(0,-4)、(3,0),将点A、B的坐标代入一次函数表达式:y=kx+b并解得:直线AB的表达式为:y=x-4,当y=8时,x=9,故点C(9,8);(2)设点P(m,6),而点B、C的坐标分别为:(3,0)、(9,8),PB2=(m-3)2+36,PC2=(m-9)2+4,BC2=100,当PB=PC时,(m-3)2+36=(m-9)2+4,解得:m=当PB=BC时,同理可得:m=11或-5;当PC=BC时,同理可得:m=9±4;综上,P(9-4,6)或P(9+4,6)或P(11,6)或P(-5,6)或P();(3)设直线平移了m个单位,则点B、C的坐标为:(3+m,0)、(9+m,8),而点P(2,6);PB2=(m+1)2+36,PC2=(m+7)2+4,BC2=100,当PB=PC时,同理可得:m=-;当PB=BC时,同理可得:m=7或-9;当PC=BC时,同理可得:m=-7;综上,C(4+2,8)或C(2-,8)或C(16,8)或C(0,8)或C(,8);(4)如下图,点P在以BC的中点R(6,4)为圆心的圆上,当直线AP(P′)与圆R相切时,sin∠PAC有最大值,圆的半径为5,即HP′=5,而AH=10,sin∠PAC==.【解析】(1)点A、B的坐标分别为:(0,-4)、(3,0),将点A、B的坐标代入一次函数表达式即可求解;(2)分PB=PC、PB=BC、PC=BC分别求解即可;(3)分PB=PC、PB=BC、PC=BC分别求解即可;(4)如下图,点P在以BC的中点R(6,4)为圆心的圆上,当直线AP(P′)与圆R 相切时,sin∠PAC有最大值,即可求解.本题考查的是一次函数综合运用,涉及到一次函数的性质、等腰三角形和直角三角形的性质、圆的基本知识等,其中(2)(3),要注意分类求解,避免遗漏.。
中学教师资格证《心理学》(题库)考前押题试卷一

中学教师资格证《心理学》(题库)考前押题试卷一[单选题]1.请问下列哪项动机属于社会性动机?()(江南博哥)A.繁衍后代B.获取食物C.逃避危险D.参与交往参考答案:D参考解析:根据需要的不同性质,可将动机分为生理性动机和社会性动机。
人在成长的过程中要逐渐社会化,为得到社会的认同,同时也满足自己的社会文化需要,就会产生各种社会性动机,如工作动机、交往动机、成就动机、成长动机等。
社会性动机推动人们从事社会活动,参与社会团体,并在其中获得认可、地位与成功感。
[单选题]2.引导学生分辨勇敢和鲁莽、谦让和退缩是属于刺激()。
A.获得B.消退C.分化D.泛化参考答案:C参考解析:刺激分化,指的是通过选择性强化和消退使有机体学会对条件刺激和与条件刺激相类似的刺激做出不同的反应。
例如,为了使狗能够区分开圆形和椭圆形光圈,如果只在圆形光圈出现时才给予食物强化,而在呈现椭圆形光圈时则不给予强化,那么狗便可以学会只对圆形光圈做出反应而不理会椭圆形光圈。
在实际的教育和教学过程中,也经常需要对刺激进行分化,如引导学生分辨勇敢和鲁莽、谦让和退缩,要求学生区别重力和压力、质量和重量等。
[单选题]3.个人用来回答事物是什么、为什么和怎么样的知识叫()。
A.理性知识B.陈述性知识C.感性知识D.程序性知识参考答案:B参考解析:陈述性知识也称描述性知识,是个人能用言语进行直接陈述的知识。
这类知识主要用来回答事物是什么、为什么和怎么样的问题,可用来区别和辨别事物。
目前学校教学传授的主要是这类知识。
[单选题]4.不属于元认知策略的是()。
A.计划策略B.学习策略C.监控策略D.调节策略参考答案:B参考解析:学习策略是指学习者为了提高学习的效果和效率,有目的有意识地制定的有关学习过程的复杂的方案。
一般而言,学习策略可分为认知策略、元认知策略和资源管理策略。
由此可知学习策略包括元认知策略。
[单选题]5.依据学习内容的不同为划分标准,一般可以把学习分为哪三类?()A.知识学习、意义学习和命题学习B.意义学习、发现学习和机械学习C.命题学习、接受学习和发现学习D.技能学习、知识学习和社会规范学习参考答案:D参考解析:根据学习的内容,可将学习分为:①知识学习:知识是客观事物的特征与联系在人脑中的主观表征,可以表现为概念、命题、图式等不同形式,分别标志着对事物反映的不同广度与深度;②技能学习:指通过学习而形成合乎法则的活动方式,有心智技能与操作技能两种;③社会规范的学习:即把外在的行为要求转化为主体内在的行为需要的内化过程。
2024海南省中考一模押题预测卷道法试卷及答案

2024年中考第一次模拟考试(海南卷)道德与法治(考试时间:60分钟试卷满分:100分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题:本大题共16小题,每小题3分,共48分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.借助手机里美颜相机、美图秀秀等自拍软件的神效,生活中的一些人常沉迷于把自己的照片修饰得光艳完美,但照片中的美图和现实中的真相总是有着一定的差距。
这启发我们正确认识自我应做到()A.只看优点B.忽略缺点C.全面客观D.悦纳自己2.2022年 3月21日是“世界睡眠日”,中国的主题是:良好睡眠,健康同行。
下列做法不符合健康睡眠规律的是()A.尽量避免在卧室里放置过多的电器B.不困不睡,不累不息C.保持每天8小时左右的睡眠时间D.保持头北脚南的睡觉方向3.脑科学研究表明:男性喜欢运用大脑中的灰质思考,灰质中富含大量的神经元,而女性则擅长用大脑中的白质思考,白质包含更多神经元之间的连接体,这种差异导致了男女在思考方式上的不同。
这一研究成果说明男女生正常交往可以()A.学习对方长处B.消除性别差异C.扩大交往范围D.把握交往分寸4.2023年2月,《党和国家机构改革方案》审议通过。
此次机构改革除了组建“中央科技委员会”加强党中央对科技工作的集中统一领导外,还重新组建科学技术部,整体承担中央科技委员会办事机构职责。
这一改革旨在()①进一步理顺科技领导和管理体制,适应发展变局②坚持依法行政,减少政府部门对科技工作的干预③加强权力的监督和制约,遏制科技领域腐败现象④加快实现更高水平科技自立自强,建设科技强国A.①②B.①④C.②③D.③④5.2023年7月7日,一名男乘客在高铁上被熊孩子揪头发弹脑壳,男子找其家长理论,遭家长怒吼:“他还是小孩,弹你又怎样?莫非你还要和小孩计较?”该家长的言行()①文明素养有所欠缺②没有做到换位思考③应该受到刑罚处罚④应该做到诚信待人A.①②B.①④C.②③D.③④6.公民最基本、最重要的权利是()A.选举权B.人身自由C.物质帮助权D.监督权7.党的十八大以来,我国加大反腐力度,“老虎”“苍蝇”一起打,开展“天网行动”,抓捕外逃贪官。
人教版小升初语文押题试卷(含答案)

一、选择题。
(20分)1.下列词语中音、形、义完全正确的一组是( )。
A.帐篷.(péng ) 波滔汹涌 发奋图强 波澜.壮阔(波浪) B.草棚.(péng ) 惊恐万状 寸步不让 若有所悟.(明白) C.烦躁.(zào ) 天经地义 唇枪舌剑 大名鼎鼎..(一种容器) D.缝隙.(xì) 浮想连翩 恼羞成怒 脱颖.而出(尖子) 2.依次填入下列各句横线上的汉字,正确的一组是( )。
①实践、认识、再实践、再认识……以________无穷。
②他是被_____迫而跟随别人做坏事的。
③琳琳优美的演唱,贏得全场观众一片喝_______。
④瞧她那_____得意相,一定又有什么高兴事。
A.至 协 采 副B.致 胁 彩 付C.至 胁 彩 副D.致 协 采 付3.下面按褒义词、中性词、贬义词分类完全正确的一组是( )①千钧一发 ②贪生怕死 ③奋不顾身 ④理想 ⑤想象 ⑥妄想 ⑦武断⑧果断 ⑨结果A.③⑤⑥/①④⑨/②⑦⑧B.③④⑧/①⑤⑨/②⑥⑦C.③④⑧/①②⑥/⑤⑦⑨D.①⑦⑧/③⑤⑨/②④⑥ 4.下列词句中加点字解释错误的是第( )个。
①秉.烛夜游 秉:拿着,持。
②若.隐若现 若:好像。
③童孙未解..供耕织 未解:不懂得。
④渔者得而并禽.之 禽:指飞禽。
5.判断下面一段文字依次运用的修辞手法,正确的一项是( )。
我们应当心胸开阔如海,应该乐于助人,与人为善,试想如果心眼比针尖还小,事事斤斤计较个人得失,怎么能与同学们相处得好呢?A.明喻 夸张 设问B.夸张 暗喻 反问C.明喻 夸张 反问D.夸张 暗喻 设问6.下面一段话的标点符号正确的一项是( )为什么瓜秧开了花不结瓜 是水浇得不够 是肥施得不足 还是土壤根本不行 一位雷达兵懂一些农业知识 他找到了答案 西瓜开了花要授粉A.? ? ? ?,一 !B. ?、、?,,。
C.?,,?,:。
D. ,,,?。
—。
7.下列诗句中咏梅的诗句是( )。
人教版2024年中考语文押题预测试卷及答案

语文试题 第1页(共20页) 语文试题 第2页(共20页)人教版2024年语文中考押题预测试卷及答案(满分:120分 时间:150分钟)一、积累与运用(20分)班级开展以“陪伴”为主题的学习活动,小雨和小雯特邀你参与。
1.(2分)小雨的学习从朗读开始,请你选出下面语句朗读处理不合适的一项( )A.朗读要读准字音,小雨这样读加点的字:当你沐浴.(yù)后,湿发披在两肩,穿过金色花的林阴.(yīn),走到做祷.(dǎo)告的小庭院时,你会嗅到这花香,却不知道这香气是从我身上来的。
B.小雨想展示“我”无比悔恨的心情,他这样处理重音:看着三轮车远去,也绝.没有想到那竟.是永远的诀别。
C.小雨想表现“我”矛盾的心理,他这样处理语调(“↗”“↘”“→”分别表示语调的上扬、下降和延长):我想拆散一家人,分成两路,各得其所↘,终→不愿意↗。
D.小雨希望读出诗人对幸福自由生活的向往以及对这种幸福生活必将到来的坚信不疑,他这样处理节奏:那隔着河的/牛郎织女,/定能够/骑着牛儿/来往。
/我想/他们此刻,/定然在/天街/闲游。
2.(2分)陪伴让人不再孤单。
小雯写了个“单”字,请你分别加上偏旁组成新的汉字,填入相应方框内。
A.金□脱壳B.鸡毛□子C. □精竭虑D.□食壶浆 3.(2分)人们常用“鱼水之交”来形容刘备与诸葛亮之间的亲密关系。
小雨看到南阳卧龙岗武侯祠有一副楹联,觉得联中两个词“启”和“佐”值得反复吟咏。
请你将这两个词还原到楹联中。
上联:纵论三分天下,审势画策□先主 下联:长怀一统江山,辅国连治□后人4.(3分)在下面横线处续写两个句子,使之与前后文构成一组排比句。
陪伴,如春风拂面,轻柔而温暖; , ;, ;如冬雪纷飞,纯净而静谧。
它用不离不弃的坚守,诠释了什么是情深意长;它用始终如一的相随,演绎了什么是风雨同舟。
陪伴,是生命中最美的风景,是心灵深处最真的情愫。
5.(3分)下列句子组成语段,顺序排列正确的一项是( )①都说陪伴是最长情的告白②它无情地检验爱情,凶狠地喜新厌旧 ③陪伴是最好的爱④时间是世界上最温柔的洪水猛兽⑤爱一个人不是谁说了算,而是能不能一世相伴 ⑥可以抵世间所有的坚硬,温暖生命所有的岁月 ⑦的确,世上最好的爱,是陪伴A.①②④⑤⑥⑦③B.②①⑦⑥④⑤③C.③⑥①⑦④②⑤D.⑦②⑥③①④⑤6.(8分)小雯以“陪伴”为主题辑录了一组古诗词。
广东省初中学业水平考试 语文押题卷(一)(含答案)

广东省初中学业水平考试语文押题卷(一)本试卷共8页,22小题,满分120分。
考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的准考证号、姓名、考场号和座位号填写在答题卡上。
用2B铅笔在“考场号”和“座位号”栏相应位置填涂自己的考场号和座位号。
将条形码粘贴在答题卡“条形码粘贴处”。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
一、积累运用(29分)1.默写古诗文。
(共10分。
答对一句得1分,满分不超过10分)(1)偶然乘兴,步过东冈。
,燕儿舞,蝶儿忙。
(秦观《行香子》)(2)而或长烟一空,,浮光跃金,,渔歌互答,此乐何极!(范仲淹《岳阳楼记》)(3)停杯投箸不能食,。
[李白《行路难》(其一)](4)沉舟侧畔千帆过,,今日听君歌一曲,。
(刘禹锡《酬乐天扬州初逢席上见赠》)(5)相见时难别亦难,,春蚕到死丝方尽,。
(李商隐《无题》)(6)戏文中有“惟愿取,年年此夜,人月双清”,使人想起苏轼《水调歌头》中“但愿人长久,”的美好祝愿。
(7)古人写诗词,比较喜欢运用“化用”这一文学修辞方法。
如陆游的《游山西》中的“,。
”就是化用(宋)强彦文《残句》中的“远山初见疑无路,曲径徐行渐有村”;(宋)曾几《苏秀道中》的“不愁屋漏床床湿,且喜溪流岸岸深”就是化用杜甫的《茅屋为秋风所破歌》中的“ _,雨脚如麻未断绝”两句。
2.对于李白的《渡荆门送别》,清人沈德潜曾评价说:“诗中无送别意,题中‘送别’二字可删。
”从全诗来看,你同意他这种说法吗?为什么?(2分)阅读下面的文字,完成3~5题。
2024年陕西省初中学业水平考试押题卷物理试卷含答案解析

2024年陕西省初中学业水平考试·押题卷物理试卷含答案解析一、单选题(共30 分)1. “中国环流三号”是我国目前设计参数最高、规模最大的核聚变大科学装置。
下列能源的产生与“中国环流三号”的设计原理相同的是()A.地热能B.潮汐能C.风能D.太阳能【答案】D【解析】中国环流三号”是利用核聚变产生能量的装置。
A.地热能是由地壳抽取的天然热能,这种能量来自地球内部的熔岩,故A不符合题意;B.潮汐能是从海水面昼夜间的涨落中获得的能量,故B不符合题意;C.地球表面大量空气流动所产生的动能就是风能,故C不符合题意;D.太阳能是太阳内部核聚变产生的,故D符合题意。
故选D。
2. 陕北说书以其特有的方言韵调,在说唱中讲述当地的风土人情和民俗文化。
下列说法正确的是()A.艺人发出的声音是由舌头振动产生的B.艺人说书使用话筒是为了提高声音的响度C.艺人发出的声音在空气中的传播速度为3.0×108m/sD.禁止现场观众大声交谈是在人耳处减弱噪声【答案】B【解析】A.表演者发出的声音是由声带振动产生的,故A错误;B.艺人使用话筒是为了提高声音的大小,即声音的响度,故B正确;C.声音在15℃的空气中的传播速度是340m/s,故C错误;D.禁止现场观众大声交谈是在声源处减弱噪声,故D错误。
故选B。
3. 下列现象中,关于物态变化的相关描述不正确的是()A.壶口冒“白气”是壶嘴喷出的水蒸气B.铁熔化的条件之一是温度必须达到铁的熔点C.“雾凇”的形成是一种凝华现象D.冰凌熔化需要吸热【答案】A【解析】【分析】(1)“白气”是水蒸气遇冷液化形成的液态小水滴;(2)晶体熔化的条件:温度达到熔点且持续吸热;(3)物质由气态直接变成固态的过程叫凝华;(4)物质由固态变成液态的过程叫熔化,熔化吸热。
A.壶口冒“白气”是壶嘴喷出的水蒸气遇冷液化成的小水滴,故A错误,符合题意;B.铁熔化的条件之一是温度必须达到铁的熔点,故B正确,不符合题意;C.“雾凇”是空气中的水蒸气遇冷直接凝华形成的冰晶,故C正确,不符合题意;D.冰凌熔化需要吸热,温度不变,故D正确,不符合题意。
《证券投资基金基础知识》押题试卷(一)试题及答案

《证券投资基金基础知识》押题试卷(一)试题及答案1.证券投资基金及其管理人应向投资者和潜在投资者披露的信息不包括()。
[单选题] *A. 影响证券投资基金价值的重大事件B. 基金投资策略C. 对投资组合收取的各项费用D. 针对特定投资者的信息(正确答案)答案解析:证券投资基金及其管理人应向投资者和潜在投资者披露影响证券投资基金价值的重大事件,此种披露应能帮助投资者了解该证券投资基金的性质及其风险与收益的关系,从而使投资者在评估基金业绩时不单纯注重收益,而对收益可能导致的风险也给予关注。
披露的内容还包括对基金投资策略的披露及对投资组合收取的各项费用的披露。
2.在风险偏好一定的情况下,( )的Tb值对应的投资组合对投资者的吸引力更大。
[单选题] *A. 较大(正确答案)B. 较小C. 无法判断D. 不变答案解析:在风险偏好一定的情况下,较大的Tb值对应的投资组合对投资者的吸引力更大。
3.下列关于房地产投资信托基金特点,描述错误的是()。
[单选题] *A. 流动性强B. 抵补通货膨胀效应C. 风险较低D. 信息不对称程度较高(正确答案)答案解析:房地产投资信托(基金),是指通过发行受益凭证或者股票来进行募资,并将这些资金投资到房地产或者房地产抵押贷款的专门投资机构。
房地产投资信托是一种资产证券化产品,可以采取上市的方式在证券交易所挂牌交易。
房地产投资信托基金的主要收益来自稳定的股息和证券价格增值。
房地产投资信托基金具有以下特点:①流动性强;②抵补通货膨胀效应;③风险较低;④信息不对称程度较低。
4.常用来作为平均收益率的无偏估计的指标是()。
[单选题] *A. 时间加权收益率B. 加权平均收益率C. 几何平均收益率D. 算术平均收益率(正确答案)答案解析:算术平均收益率即计算各期收益率的算术平均值,一般可以用作对平均收益率的无偏估计,因此它更多地被用于对将来收益率的估计。
5.下列关于QFII基金托管人资格的规定,错误的是()。
2022年全国高校体育单招考试语文卷模拟试题一(含答案解析)

2022年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试押题试卷语文(一)一、语文知识∶本大题共10小题,每小题4分,共 40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列各组词语加点的字,读音全部相同的一项是()A.语塞.堵塞.闭门塞.听B.呐.喊木讷.寡言纳.闷C.款识.赏识.博闻强识.D.绯.闻妄自菲.薄氛.围2.下列各组词语中,书写完全正确的一项是()A.梦魇老两口名门旺族 B 污诟度假村寸草春晖C.福祉流线形论资排辈D.贻误万户侯泾渭分明3.依次填入下列句中横线处的词语,最恰当的一项是()音乐无处不在,无时不有。
音乐人生的酸甜苦辣,表达生活的喜怒哀乐。
不管你是什么年龄,无论你走到哪里,只要你重新听到那熟悉的旋律,就会那颗的_ _心,引起你久久的怀念。
A.诠释感动敏锐B.解释触动敏感C. 解释感动敏锐D.诠释触动敏感4.下列各句中加点熟语使用不恰当的一项是()A.世界上热点问题不少,按下葫芦起了瓢.......。
解决这些问题要得理又得法,一味示强施压不行,外部武力干预更要不得,政治解决是唯一出路。
B.在这次跳高比赛中,甲运动员鲤鱼跳龙门.....,消极应战,告别比赛。
C.上届乒乓球赛的冠军,这次却被一个名不见经传.....的小将打败,爆出了本届比赛的最大冷门。
D.做事情要未雨绸缪,不可临渴掘井,要知道"船到江心补漏迟......."啊,你要早做打算。
5.下列各句中加点成语使用恰当的一项是()A.在评价某些历史人物时,我们不能只是简单地对他们盖棺论定....,还应该特别注意研究他们的人生经历和思想变化轨迹。
B.户籍制度改革牵扯到住房、医疗、教育、就业等方方面面的利益,绝不可能一挥而就....。
C.最美的是小镇的春天,草长莺飞,风声鹤唳....,走进小镇就如同置身于世外桃源,来此旅游的人一定会被这里的美丽景色深深吸引。
D.长安汽车的H5一月份销量继续在同类车中领先,达到3.6万辆,这惊鸿一瞥....的数字背后,折射的是国产车的质量越来越值得人们的信赖。
2024年普通高等学校招生全国统一考试数学(新高考I卷)押题密卷(含答案)

试卷类型:A2024年普通高等学校招生全国统一考试 押题密卷2数学 新高考I 卷注意事项:1. 答题前,考生务必用黑色字迹钢笔或签字笔将自己的姓名、考生号、考场号和座位号填写在答题卡上.用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上.将条形码横贴在答题卡右上角“条形码粘贴处”.2. 作答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上. 3. 非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4. 考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设集合A ={3,2a },B ={a ,b },若A ∩B ={2},则A ∪B =A .{1,2,3}B .{2,3,4}C .{1,2,4}D .{2,3,5}2. 设复数z 的共轭复数为 z ,则下列一定为纯虚数的是A .z +zB .z -zC .z ·zD .zz̅3. 设α,β是两个不同平面,直线m ⊂α,直线n ⊂β,则A .m ⊥β是m ⊥n 的充分条件B .m //n 是α//β的必要条件C .m ⊥β是m ⊥n 的必要条件D .m ⊥n 是α⊥β的必要条件4. 已知随机变量ξi 的分布列如表所示(i =1,2).若0<p 1<12<p 2<23,则A .E (ξ1)<E (ξ2),D (ξ1)<D (ξ2)B .E (ξ1)<E (ξ2),D (ξ1)>D (ξ2)C .E (ξ1)>E (ξ2),D (ξ1)<D (ξ2)D .E (ξ1)>E (ξ2),D (ξ1)>D (ξ2)5. 已知sin(θ+π)<0,cos(θ-π)>0,则A .tan θ2<cot θ2B .tan θ2>cot θ2C .sin θ2<cos θ2D .sin θ2>cos θ26. 已知数列{a n }的前n 项和为S n ,且对于任意n ∈N *,都有a n a n +1<0,a n S n 恒为定值c(c >0),则A .|a 2|<|a 3|<|a 4|B .|a 3|<|a 2|<|a 4|C .|a 3|<|a 4|<|a 2|D .|a 4|<|a 3|<|a 2|7. 设非负实数x ,y ,2x =3y ,则A .2x =3yB .2x >3yC .2x <3yD .无法比较2x 与3y 的大小8. 已知F 1,F 2是椭圆与双曲线的公共焦点,P 是它们的一个公共点,且|PF 1|<|PF 2|,PF 1的垂直平分线经过点F 2,若椭圆的离心率为e 1,双曲线的离心率为e 2,则 e 12-2e 2的最小值是 A .2 B .-2 C .6D .-6二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9. 掷骰子5次,分别记录每次骰子出现的点数,根据这5次的统计结果,下列选项中有可能出现点数1的是 A .中位数:3,众数:2 B .平均数:4,中位数:5 C .极差:4,平均数:2D .平均数:4,众数:510.已知函数f (x )=x 4-x 2+x -1,则A .f(x)有两个零点B .f(x)有唯一极值C .过坐标原点可作曲线y =f (x )的一条切线D .曲线y =f (x )上存在三条互相平行的切线11.如图,与圆柱底面成60°的平面α截此圆柱,其截面图形为椭圆.已知该圆柱底面半径为2,则 A .椭圆的离心率为√32B .椭圆的长轴长为 8√33C .椭圆的面积为32πD .椭圆内接三角形面积的最大值为 6√3三、填空题:本题共3小题,每小题5分,共15分.12.在△ABC 中,C ≠π2,若cos A =sin B ,则A 的取值范围是_________.13.已知a ,b ,c 成等差数列,点P (-1,0)到直线l :ax +by +c =0的距离为 2√2 ,则直线l 的倾斜角是_________.14.设点P 是边长为2的正△ABC 的三边上的动点,则 P A ⃗⃗⃗⃗ ·(PB ⃗⃗⃗⃗⃗ +PC⃗⃗⃗⃗⃗ )的取值范围是_________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤. 15.(满分13分)已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,a =6,b +12cos B =2c . (1)求A 的大小;(2)请在下列三个条件中选择一个作为已知条件,使△ABC 存在,并解决问题: M 为△ABC 内一点,AM 的延长线交BC 于点D ,求△ABC 的面积.①M 为△ABC 的外心,AM =4; ②M 为△ABC 的垂心,MD =√3 ; ③M 为△ABC 的内心,AD =3√3 .16.(满分15分)图形的被覆盖率是指,图形被覆盖部分的面积与图形的原面积之比.通常用字母C 表示.如图所示,边长为1的正三角形被n (n ∈N *)层半径相等的圆覆盖,最下面一层与正三角形底边均相切,每一层相邻两圆外切,层与层相邻的圆相外切,且每一层两侧的圆与正三角形两边相切.记覆盖的等圆层数为n 时,等圆的半径为a n .图中已给出n 等于1,2,10时的覆盖情形.(1)写出a 1,a 2的值,并求数列{a n }的通项公式;(2)证明:此正三角形的被覆盖率低于91%.(参考数据:π≈3.14,√3≈1.73)17.(满分15分)设ξ为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,ξ=0;当两条棱平行时,ξ的值为两条棱之间的距离;当两条棱异面时,ξ=1.(1)求概率P(ξ=0);(2)求ξ的分布列,并求其数学期望E(ξ).18.(满分17分)如图,已知抛物线E:y2=x与圆M:(x-4)2+y2=r2(r>0)相交于A、B、C、D四个点.(1)求r的取值范围;(2)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标.19.(满分17分)已知函数f(x)=(x-a)(e x-a),a≥0.(1)当a=0时,讨论f(x)的单调性;(2)证明:f(x)有唯一极小值点x0,并求f(x0)的最大值.2024年普通高等学校招生全国统一考试 押题密卷2数学 参考答案单项选择题 1.A 2.B 3.A 4.D 5.B6.C7.C8.B多项选择题 9.BCD对于A ,中位数是3,则这5个数从小到大排列后,第3个数是3,第1、2个数是2才能使众数为2,故第1个数不是1,故A 不正确,对于B ,有可能出现点数1,例如1,2,5,6,6; 对于C ,有可能出现点数1,例如1,1,1,2,5; 对于D ,有可能出现点数1,例如1,4,5,5,5; 故选BCD.10.ACD对于A ,()32()(1)1f x x x x =−++,对于函数322()1,()32g x x x g x x x +=′=++, 令gg ′(xx )<0⇒−23<xx <0,令gg ′(xx )>0⇒xx <−23或xx >0,所以函数gg (xx )在(−23,0)上单调递减,在(−∞,−23)和(0,+∞)上单调递增,则函数gg (xx )在xx =−23,xx =0处分别取极大值和极小值, 由gg (0)>0,知gg (xx )只有一个零点,所以ff (xx )有两个零点,故A 正确;对于B ,假设B 成立,设切点坐标为�xx 0,ff (xx 0)�,切线方程为()()342000004211y xx x x x x x =−+−+−+−,即()34200042131y xx x x x =−+−+−,∴4200310x x −+−=,但显然4200310x x −+−<,故B 错误; 对于C ,32()421,()122f x x x f x x ′=′+′=−−, 令ff ″(xx )<0⇒−√66√6,令ff ″(xx )>0⇒xx <−√66或xx >√66,所以函数()f x ′在(上单调递减,在(−∞,−√66)和(√66,+∞)上单调递增,∴函数()f x ′在x =处分别取到极大值和极小值,由0f >′知()f x ′只有一个零点,ff (xx )有一个极值点,故C 正确; 对于D ,若D 正确,则存在实数m 使得3()421f x x x m ′=−+=有三个不同的根, 即函数yy =4xx 3−2xx +1mm 3个交点,由选项C 可知,,m f f∈ ′′,故D 正确.故选ACD. 11.AD对于A ,bb =rr =2,aa =rrcccccc 60°=2124,所以cc =√aa 2−bb 2=√16−4=2√3,所以离心率ee =ccaa =2√34=√32,所以A 正确;对于B ,长轴长2248a =×=,所以B 不正确;对于C ,椭圆的面积SS =ππaabb =2×4ππ=8ππ,所以C 不正确; 对于D ,椭圆方程为xx 2aa 2+yy 2bb 2=1,椭圆内接三角形一个顶点在长轴左顶点,另两点在直线xx =mm (mm >0)上,此时另两点的距离为:2bb �1−mm 2aa2,三角形的面积为:12(aa +mm )⋅2bb �1−mm 2aa 2=bb ⋅�(aa +mm )(aa +mm )�1−mm aa ��1−mm aa�=aabb √3⋅��1+mmaa��1+mm aa ��3−3mm aa ��1+mm aa � ≤aabb √3��1+mm aa +1+mm aa +3−3mm aa +1+mm aa 4�4=aabb√3×94=3√3bbcc4 当且仅当1+mm aa=3−3mm aa,即mm =aa2时,取等号.∴SS3√3aabb 43√3×4×24√3△mmaaxx,所以D 正确,故选AD . 填空题 12.�0,ππ4�因为ssss ss BB >0,ccccss AA =ssss ss BB ,所以ccccss AA >0,所以AA <ππ2. 若BB <ππ2,由ccccss AA =ssss ss BB ,可得ssss ss (ππ2−AA )=ssss ss BB ,由正弦函数在(0,ππ2)的单调性可得,BB =ππ2−AA ,则CC =ππ2,原题设不成立; 若π2B >,同理可得BB =AA +ππ2,由AA +BB <ππ,解得π(0,)4A ∈.故答案为(0,ππ4).13.ππ4∵a ,bb ,cc 成等差数列,2b a ∴=+,即cc =2bb −aa ,点PP (−1,0)到直线ll :aaxx +bbyy +cc =0,=,两边平方化简可得(aa +bb )2=0,即bb =−aa ,则直线ll 的斜率为1ab−=,故直线的倾斜角是ππ4,故答案为ππ4.14.�−98,2�根据题意,以AABB 中点为坐标原点,建立如图所示的平面直角坐标: 正三角形AABBCC 的边长为2,则AA (−1,0),BB (1,0),CC�0,√3�,点PP 是AABBCC 三边上的动点,�����⃗=(−1−tt,0),PPBB�����⃗=(1−tt,0),PPCC�����⃗=�−tt,√3�则PPAA�����⃗⋅�PPBB�����⃗+PPCC�����⃗�所PPAA=(−1−tt,0)⋅�(1−tt,0)+�−tt,√3��=(−1−tt)⋅(1−2tt)=2�tt+14�2−98,(−1≤tt≤1)所以当tt=−14时取得最小值为−98;当tt=1时取得最大值为2. ②,当PP在线段CCBB上时,直线CCBB的方程为yy=−√3xx+√3,设PP�mm,−√3mm+√3�,(0≤mm≤1),�����⃗=�−1−mm,√3mm−√3�,PPBB�����⃗=�1−mm,√3mm−√3�,PPCC�����⃗=�−mm,√3mm�,则PPAA�����⃗⋅�PPBB�����⃗+PPCC�����⃗�所PPAA=�−1−mm,√3mm−√3�⋅��1−mm,√3mm−√3�+�−mm,√3mm��=�−1−mm,√3mm−√3�⋅�1−2mm,2√3mm−√3�=8�mm−12�2,(0≤mm≤1)所以当mm=12时取得最小值为0;当mm=1或mm=0时取得最大值为2. ③,当PP在线段AACC上时,直线AACC的方程为yy=√3xx+√3,设PP�ss,√3ss+√3�,(−1≤ss≤0),�����⃗=�−1−ss,−√3ss−√3�,PPBB�����⃗=�1−ss,−√3ss−√3�,PPCC�����⃗=�−ss,−√3ss�,则PPAA�����⃗⋅�PPBB�����⃗+PPCC�����⃗�,所PPAA=�−1−ss,−√3ss−√3�⋅��1−ss,−√3ss−√3�+�−ss,−√3ss��,=�−1−ss,−√3ss−√3�⋅�1−2ss,−2√3ss−√3�,=8�ss+58�2−98,(−1≤ss≤0),所以当ss=−58时取得最小值为−98;当ss=0时取得最大值为2.�����⃗⋅�PPBB�����⃗+PPCC�����⃗�的取值范围为�−98,2�,综上可知,PPAA解答题15.(1)在△AABBCC 中,由余弦定理得ccccss BB =aa 2+cc 2−bb 22aacc,又因为aa =6,12cos 2b B c +=, 所以2221222a c b b c ac+−+⋅=,整理得2236b c bc +−=.在△AABBCC 中,由余弦定理得22362cos b c bc A +−=,所以bbcc =2bbcc ccccss AA , 即ccccss AA =12又因为AA ∈(0,ππ),所以AA =ππ3.(2)选①,设△AABBCC 的外接圆半径为R ,则在△AABBCC 中,由正弦定理得62sin sin 3BCR A π===,即R =因为MM 为外心,所以AAMM =2√3,与AAMM =4盾,故不能选①. 选②,因为MM 为△AABBCC 的垂心,所以222BMDMBD ACB ACB πππ∠=−∠=−−∠=∠, 又MMMM =√3,所以在△MMBBMM中,tan BD MD BMD ACB =⋅∠=∠,同理可得CDABC =∠,又因为6BD CD +=6ABC ACB ∠∠=,即tan tan ABC ACB ∠+∠又因为在△AABBCC中,tan()tan ABC ACB BAC ∠+∠=−∠=所以tan tan 1tan tan ABC ACBABC ACB∠+∠=−∠∠tan tan 3ABC ACB ∠∠=,故ttaass ∠AABBCC ,tan ACB ∠为方程xx 2−2√3xx +3=0两根,即tan tan ABC ACB ∠=∠因为∠AABBCC ,∠AACCBB ∈(0,ππ),所以3ABC ACB π∠=∠=,所以△AABBCC 为等边三角形, 所以SS △AAAAAA =12×62×√32=9√3.选③,因为MM 为△AABBCC 的内心,所以∠BBAAMM =∠CCAAMM =12∠BBAACC =ππ6, 由SS △AAAAAA =SS △AAAAAA +SS △AAAAAA , 得111sin sin sin 232626bc c AD b ADπππ=⋅+⋅, 因为AAMM =3√3,所以1()2b c =+,即3bc b c +=,由(1)可得2236b c bc +−=,即(bb +cc )2−3bbcc =36,所以2()33609bc bc −−=, 即(9)409bc bc+−=, 又因为bbcc >0,所以bbcc =36,所以SS ΔΔAAAAAA =12bbcc ssss ss ππ3=12×36×√32=9√3.16.(1)由题意得,1a =,2a =当覆盖的等圆有ss 层时,最下面一层的圆有ss 个,相邻两圆的圆心距为2aa nn ,最左边与最右边的两圆的圆心距为()21n n a −.又最左边与最右边的两圆的圆心在三角形底边上投影与底边最近顶点距离之和为n ,则()211n n n a −+=,∴n a =.(2)证明:被覆盖面积()211π2n n n S a +==2S =.被覆盖率120.9050.91S C S =<≈<, ∴对任意的层数ss ,此正三角形的被覆盖率CC 低于91%.17.(1)若两条棱相交,则交点必为正方体8个顶点中的1个,过任意1个顶点恰有3条棱,所以共有8C 32对相交棱,因此P(ξ=0)=232128C C =8×366=411.(2)若两条棱平行,则它们的距离为1或√2,其中距离为√2的共有6对,故P(ξ=√2)=2126C =111, 于是P(ξ=1)=1-P(ξ=0)-P(ξ=√2)=1-411-111=611, 所以随机变量ξ的分布列是 ξ1√2P(ξ)411611111因此E(ξ)=1×611+√2×111=6+√211.18.(1)联立方程组与,可得,所以方程由两个不等式正根由此得到解得,所以r的范围为(2)不妨设E与M的四个交点坐标分别为设直线AC,BD的方程分别为,解得点p的坐标为设t=,由t=及(1)可知由于四边形ABCD为等腰梯形,因而其面积将代入上式,并令,得求导数,令,解得当时,,当,;当时,当且仅当时,由最大值,即四边形ABCD的面积最大,故所求的点P的坐标为()19.(1)当aa=0时,()e x=,f x x则ff′xx,令ff ′(xx )=0,得xx =−1, 则ff (xx )在(−∞,−1)上单调递减,在(−1,+∞)上单调递增.(2)由ff (xx )=(xx −aa )(ee xx −aa ),得()f x ′=e ()e (1)e x x x a x a x a a −+−=−+−, 令()(1)e x G x x a a =−+−,得()G x ′=(2)e x x a −+. 令()0G x ′=,则xx =aa −2, 所以()f x ′在(−∞,aa −2)上单调递减,在(aa −2,+∞)上单调递增, 易知()e a f a a ′=−,设函数()e x H x x =−, 令()e 10x H x ′−,可得xx =0,则()e x H x x =−在(−∞,0)上单调递减,在(0,+∞)上单调递增, 又HH (0)=1>0,故()e 0x H x x =−>在RR 上恒成立,故()e 0a f a a ′=−>,又2(2)e 0a f a a −′−=−−<, 所以存在0(2,)x a a ∈−,使得()00f x ′=. 又当(,2)x a ∈−∞−时,易知()0f x ′<,故ff (xx )有且仅有一个极小值点xx 0.因为()00f x ′=,所以()0001e 0e 1x x x a +≥+,即xx 0≥−1, 则ff (xx 0)=�xx 0−(xx 0+1)ee xx 0ee xx 0+1��ee xx 0−(xx 0+1)ee xx 0ee xx 0+1�=−ee xx 0(ee xx 0−xx 0)2(ee xx 0+1)2设()()22e e ()e 1x x x x g x −=−+,求导得()g x ′=()()23e e e (1)e 2e 1x x x x x x x x −++−− −+. 设2()e (1)e 2x x h x x x =++−−,求导得2()2e (2)e 1x x h x x ′=++−,注意到ℎ′(xx )在[−1,+∞)上单调递增,且�ℎ′(−1)=2ee −2+ee −1−1<0ℎ′(0)=3>0, 所以存在cc ∈(−1,0),使得()0h c ′=,从而()h x 在(−1,cc )上单调递减,在(,)c +∞上单调递增, 又(0)0h =,2(1)e 10h −−=−<,ee xx −xx >0,所以当−1≤xx <0时,gg′(xx )>0;当xx >0时,()0g x ′<. 所以gg (xx )在(−1,0)上单调递增,在(0,+∞)上单调递减,则()01(0)4f x g ≤=−, 即ff (xx 0)的最大值为−14.。
【中考卷】湖南省2021届中考生物考前押题卷(一)含答案与解析

………………○………………内………………○………………装………………○………………订………………○………………线………………○…………………………○………………外………………○………………装………………○………………订………………○………………线………………○…………… 学校:______________姓名:_____________班级:_______________考号:______________________湖南省2021届中考考前押题卷(一)生 物注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
5.考试范围:中考全部内容。
一、选择题(每小题2分,共50分)1.生物能够表现出非生物所不具有的生命现象。
下列古诗描述的现象中,不包含生命现象的是( ) A.种豆南山下,草盛豆苗稀 B.离离原上草,一岁一枯荣 C.夜来风雨声,花落知多少D.床前明月光,疑是地上霜2.在观察菜豆植株的不同结构时选取实验材料不正确的是( ) A.观察气孔——叶表皮 B.观察子房——雄蕊 C.观察根毛——根尖D.观察子叶——种子3.刚收获的小麦种子堆积久了会发热,与此现象有关的细胞结构主要是( ) A.细胞质B.线粒体C.叶绿体D.液泡4.下列有关银杏的描述中,错误的是( ) A. 银杏是一种古老的裸子植物 B. 银杏的果实就是我们通常说的“白果” C. “白果”是银杏的种子D. 银杏是一种高大的乔木5.从同一株植物上剪下两根长势相近的枝条,进行如图处理。
将装置放在适宜条件下,数小时后发现甲装置塑料袋壁上的水珠比乙多。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
•34.What’s the last step of constructing a working solar still?A.Dig a hole of a certain size.B.Put the cup in place.C.Weight the sheet’s center down.D.Cover the hole with the plastic sheet.35.When a solar still works, drops of water come into the cup from _________.A.the plastic tubeB.outside the holeC.the open airD.beneath the sheet第二节(共5小题;每小题2分,满分10分)根据短文内容,从短文后的选项中选出能填入学科&网空白处的最佳选项。
选项中有两项为多余选项。
If anyone had told me three years ago that I would be spending most of my weekends camping, I would have laughed heartily. Campers, in my eyes, were people who enjoyed insects bites, ill-cooked meals, and uncomfortable sleeping bags. They had nothing in common with me. 36 . The friends who introduced me to camping thought that it meant to be a pioneer.37 We sleepin a tent, cooked over an open fire, and walked a long distance to take the shower and use the bathroom. This brief visit with Mother Nature cost me two days off from work, recovering from a bad case of sunburn and the doctor`s bill for my son’s food poisoning. I was, nevertheless, talked into going on another fun-filled holiday in the wilderness.38Instead, we had a pop-up camper with comfortable beds and an air conditioner. My nature-loving friends had remembered to bring all the necessities of life. 39 We have done a lot of it since. Recently, we bought a twenty-eight-foot travel trailer complete with a bathroom and a built-in TV set. There is a separate bedroom, a modern kitchen with a refrigerator. The trailer even has matching carpet and curtains. 40 It must be true that sooner or later, everyone finds his or her way back to nature. I recommend that you find your way in style.A. Thistimetherewasnotent.B. Thingsaregoingtobeimproved.C. Thetriptheytookmeonwasaroughone.D. Iwastolearnalotaboutcampingsincethen,however.E. ImustsaythatIhavecertainlycometoenjoycamping.F. After the trip, my family became quite interested in camping.G. There was no shade as the trees were no more than 3 feet tall.第三部分语言知识运用(共两节,满分45分)第一节完形填空(共20小题;每小题1.5分,满分30分) 阅读下面的短文,从短文后各题所给的A、B、C和D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
While high school does not generally encourage students to explore new aspects of life,college sets the stage for that exploration. I myself went through this41 process and found something that has changed my42 atcollege for the better:I discovered ASL-American Sign Language(美式手语). I never felt an urge to43any sign language before.My entire family is hearing,and so are all my friends.The44 language were enough in all my interactions(交往).Little did I know that I would discover my45 for ASL. 8 The 46 began during my first week at college. I watched as the ASL Club 47their translation of a song. Both the hand movements and the very48 of communicating without speaking 49 me. What I saw was completely unlike anything I had experienced in the 50.This newness just left me51 more. After that, feeling the need to52further, I decided to drop in on one of ASL club’s meetings. I only learned how to 53 the alphabet that day. Yet instead of being discouraged by my 54 progress,I was excited. I then made it a point to 55 those meetings and learn all I could. The following term, I 56 an ASL class. The professor was deaf and any talking was57. I soon realized that the silence was not unpleasant.58, if there had been any talking, it would have59 us to learn less. Now, I appreciate the silence and the 60 way of communication it opens.41. A. searching B. planning C. natural D. formal42. A. progress B. experience C. major D. opinion43. A. choose B. read C. learn D. create44. A. official B. foreign C. body D. spoken45. A. love B. concern C. goal D. request46. A. meeting B. trip C. story D. task47. A. recorded B. performed C. recited D. discussed48. A. idea B. amount C. dream D. reason49. A. disturbed B. supported C. embarrassed D. attracted50. A. end B. past C. course D. distance51. A. showing B. acting C. saying D. wanting52. A. exercise B. explore C. express D. explain53. A. print B. write C. sign D. count54. A. slow B. steady C. normal D. obvious55. A. chair B. sponsor C. attend D. organize56. A. missed B. passed C. gave up D. registered for57. A. prohibited B. welcomed C. ignored D. repeatedstly B.Thus C.Instead D.However59.A.required B.caused C.allowed D.expected60.A.easy B.popular C.quick D.new第二节(共10小题;每小题1.5分,满分15分)阅读下面短文,在空白处填入1个适当的单词或括号内单词的正确形式。
There has been a recent trend in the food service industry toward lower fat content and less salt. This trend, which was started by the medical community(医学界) 61 a method of fighting heart disease, has had some unintended side 62 (effect) such as overweight and heart disease—the very thing the medical community was trying to fight. Fat and salt are very important parts of a diet. They are required 63 (process) the food that we eat, to recover from injury and for several other bodily functions. When fat and salt 64 (remove) from food, the food tastes as if it is missing something. As 65 result, people will eat more food to try to make up for that something missing. Even 66 (bad), the amount of fast food that people eat goes up. Fast food 67 (be) full of fat and salt; by 68 (eat) more fast food people will get more salt and fat than they need in their diet.Having enough fat and salt in your meals will reduce the urge to snack(吃点心) between meals and will improve the taste of your food. However, be 69 (care) not to go to extremes. Like 9 anything, it is possible to have too much of both, 70 is not good for the health.第四部分写作(共两节,满分35分) 第一节短文改错(共10小题;每小题l分,满分10分) 假定英语课上老师要求同桌之间交换修改作文,请你修改你同桌写的以下作文。
