第4章时间序列分析
spss教程第四章---时间序列分析

第四章时间序列分析由于反映社会经济现象的大多数数据是按照时间顺序记录的,所以时间序列分析是研究社会经济现象的指标随时间变化的统计规律性的统计方法。
.为了研究事物在不同时间的发展状况,就要分析其随时间的推移的发展趋势,预测事物在未来时间的数量变化。
因此学习时间序列分析方法是非常必要的。
本章主要内容:1. 时间序列的线图,自相关图和偏自关系图;2. SPSS 软件的时间序列的分析方法−季节变动分析。
§4.1 实验准备工作§4.1.1 根据时间数据定义时间序列对于一组示定义时间的时间序列数据,可以通过数据窗口的Date菜单操作,得到相应时间的时间序列。
定义时间序列的具体操作方法是:将数据按时间顺序排列,然后单击Date →Define Dates打开Define Dates对话框,如图4.1所示。
从左框中选择合适的时间表示方法,并且在右边时间框内定义起始点后点击OK,可以在数据库中增加时间数列。
图4.1 产生时间序列对话框§4.1.2 绘制时间序列线图和自相关图一、线图线图用来反映时间序列随时间的推移的变化趋势和变化规律。
下面通过例题说明线图的制作。
例题4.1:表4.1中显示的是某地1979至1982年度的汗衫背心的零售量数据。
试根据这些的数据对汗衫背心零售量进行季节分析。
(参考文献[2])表4.1 某地背心汗衫零售量一览表单位:万件解:根据表4.1的数据,建立数据文件SY-11(零售量),并对数据定义相应的时间值,使数据成为时间序列。
为了分析时间序列,需要先绘制线图直观地反映时间序列的变化趋势和变化规律。
具体操作如下:1. 在数据编辑窗口单击Graphs→Line,打开Line Charts对话框如图4.2.。
从中选择Simple单线图,从Date in Chart Are 栏中选择Values of individual cases,即输出的线图中横坐标显示变量中按照时间顺序排列的个体序列号,纵坐标显示时间序列的变量数据。
时间序列分析
第四章时间序列分析【案例导入】1在同行业中,路口煤矿自2000年以来的生产经营状况一直不错,尤其自2005年以来正经历着快速的发展。
然而,2007年5月,煤矿出现了渗水和倒塌事故,尽管没有造成人员伤亡,却导致生产停顿,一直到同年8月份才恢复正常生产。
幸运的是该煤矿办理了相关保险,然而与固定资产索赔不同的是,停业期间的收入损失很难确定,致使保险索赔工作陷入僵持状态。
此时,煤矿收入的历史资料为解决这一问题提供了依据,即根据表4-1的时序资料,煤矿确定了收入增长的长期趋势,并测算出5~7月可能实现的收入,最终为保险索赔奠定了基础,也为保险公司所接受。
单位:万元些历史资料,可以发现收入的变动趋势,即收入随时间增长或下降的趋势。
对这些资料的进一步观察,可以显示出收入的长期趋势,进而做出较好的推断。
从某种角度上看,这种方法就是观察现象发展的历史“足迹”,即过去是这样“走”的,则今后也许仍然会这样“走”。
通过上述方法有利于我们判断现象的未来发展,显然是一种预测思路。
通过本章学习,要明确时间序列的概念、作用、种类和编制原理,掌握各种动态分析指标的涵义、计算方法和应用条件;掌握动态趋势分析中长期趋势的测定与季节变动规律的计算和分析方法,以便在今后的实际工作中,运用这些方法进行统计分析。
本章的重点是时间序列的水平指标和速度指标,以及这些指标的计算和运用;难点是时间序列的各种趋势分析方法和预测模型。
第一节时间序列的概念和种类一、时间序列的概念社会经济现象总是随着时间的推移而变动的。
任何一个企业管理部门或研究机构或国家机关,要掌握社会活动或经济活动的变化过程及其发展趋势,就必须及时掌握和分析有关的时间序列资料。
所谓时间序列,亦称时间数列或动态数列,是社会经济指标的数值按时间顺序排列而形成的一种数列。
它反映社会经济现象发展变化的过程和特点,是研究现象发展变化的趋势和规律以及对未来状态进行科学预测的重要依据。
表4-2是某市社会劳动者、国内生产总值、第三产业比重和社会劳动生产率依时间顺序排列形成的数列,即为时间序列。
时间序列分析第四章ARMA模型的特性 王振龙第二版

4.1 格林函数和平稳性
一、线性常系数差分方程及其解的一般形式 先回忆线性常系数微分方程及其解的结构:
y(t ) a0 y(t ) u(t )
可转化为
y(t ) u(t ) y(t 1) a0 1 a0 其中 a0
将上述方程中的近似号改为等号,实数t改为自然数k, a0’就用a0表示,则得到一阶线性常系数差分方程
它的特征方程为: n an1 n1 ... a1 a0 0
设特征方程有不相等n个根
1, 2 ,..., n
k C ii i 1 n
则齐次方程的通解为:y (k )
若特征方程有一个l 重根,不妨设为 1 ... l 则齐次方程的通解为:
y(k ) (C1 C2 k ... Cl k l 1 )1k Ci ik
1 1 2 1 , C2 , C1 C2 1 C1 1 2 2 1 C1 C2 于是 X t at 1 1 B 1 2 B
j j j j C1 (1B) C2 (2 B) at C11 C22 at j j 0 j 0 j 0 G j at j
即:
X a
j 0
j 1 t j
k
t
t k 1
ak
上式右端是驱动函数at 的线性组合,显示了系统对现在以 及过去扰动的记忆
若
1 1,则
随着 j 的增大而缓慢减小,表明系统的记忆较强;
1j
若
1 0 ,则
随着 j 的增大而急剧减小,表明系统的记忆较弱; 客观地描述了系统的动态性
第四章 混沌时间序列分析及相空间重构

Lyapunov Exponents
f
• Quantifies separation in time between trajectories, assuming rate of growth (or decay) is exponential in time, as: n
1 i lim ln( eig J(p)) n n p 0
估计吸引子维数的算法,需要大量的数据点作为输入,当这些点的 输入被选择为最大化的包含吸引子信息情况下,输入数据点的数量可以减 少。(由Holzfuss和Mayer—kress 1986年提出) 重构相空间所需要解决的关键问题,就是确定重构维数m。 在重构相空间维数未知的情况下,可用以下方法获得: 令 nr 为重构空间的维数。首先把nr (或m)设置为1,计算重构吸引子 的维数Dcap,然后增加 nr (或m)的大小,并重复计算重构吸引子的维数 Dcap,直到Dcap不再改变为止(如曹书p103),最后的Dcap是正确的相 关维数,产生正确的Dcap的最小 nr (m) 即重构空间的最小维数m.
Time delay embedding
Differs from traditional experimental measurements
Provides detailed information about degrees of freedom beyond the scalar measured Rests on probabilistic assumptions - though not guaranteed to be valid for any particular system Reconstructed dynamics are seen through an unknown “smooth transformation” Therefore allows precise questions only about invariants under “smooth transformations” It can still be used for forecasting a time series and “characterizing essential features of the dynamics that produced it”
时间序列分析方法第04章预测

时间序列分析方法第04章预测在本章当中我们讨论推测的一样概念和方法,然后分析利用),(q p ARMA 模型进行推测的问题。
§4.1 预期原理利用各种条件对某个变量下一个时点或者时刻时期内取值的判定是推测的重要情形。
为此,需要了解如何确定推测值和度量推测的精度。
4.1.1 基于条件预期的推测假设我们能够观看到一组随机变量t X 的样本值,然后利用这些数据推测随机变量1+t Y 的值。
专门地,一个最为简单的情形确实是利用t Y 的前m 个样本值推测1+t Y ,现在t X 能够描述为:},,,{11+--=m t t t t Y Y Y X假设*|1t t Y +表示依照t X 关于1+t Y 做出的推测。
那么如何度量推测成效呢?通常情形下,我们利用缺失函数来度量推测成效的优劣。
假设推测值与真实值之间的偏离作为缺失,那么简单的二次缺失函数能够表示为(该度量也称为推测的均方误差):2*|11*|1)()(t t t t t Y Y E Y MSE +++-=定理4.1 使得推测均方误差达到最小的推测是给定t X 时,对1+t Y 的条件数学期望,即:)|(1*|1t t t t X Y E Y ++=证明:假设基于t X 对1+t Y 的任意推测值为:)(*|1t t t X g Y =+那么此推测的均方误差为:21*|1)]([)(t t t t X g Y E Y MSE -=++对上式均方误差进行分解,能够得到:)]}()|()][|({[2)]()|([)]|([)]}()|([)]|({[)(111212112111*|1t t t t t t t t t t t t t t t t t t t t X g X Y E X Y E Y E X g X Y E X Y E Y E X g X Y E X Y E Y E Y MSE --+-+-=-+-=++++++++++ 其中交叉项的数学期望为(利用数学期望的叠代法那么):0)]}()|()][|({[111=--+++t t t t t t X g X Y E X Y E Y E 因此均方误差为:21211*|1)]()|([)]|([)(t t t t t t t t X g X Y E X Y E Y E Y MSE -+-=++++为了使得均方误差达到最小,那么有:)|()(1t t t X Y E X g +=现在最优推测的均方误差为:211*|1)]|([)(t t t t t X Y E Y E Y MSE +++-= End我们以后经常使用条件数学期望作为随机变量的推测值。
第4章平稳时间序列预测

101,96,97.2万元 请确定该超市第二季度每月销售额的预测值.
解: 预测值计算
X t 10 0.6 X t 1 0.3 X t 2 t , t ~ N (0,36) x1 101, x2 96, x3 97.2
四月份: 五月份: 六月份:
方法
第四章 平稳时间序列预测
预测
平稳时间序列预测的定义 利用平稳时间序列{Xt ,t=0,±1,±2,…}在时刻t及以 前时刻 t-1,t-2,…的所有信息,对 Xt+l(l>0)进行估计, 相应的预测量记为
ˆ l , 称为预测步长,t称为预 X t l
测的原点.
第四章 平稳时间序列预测
ห้องสมุดไป่ตู้
第一节 正交投影预测
统计人数 预测人数
ˆ 2002 104 110 6 2002 x2002 x ˆ 2003 108 100 8 2003 x2003 x ˆ 2004 105 109 4 2004 x2004 x
ˆ2004 (1) 100 0.8 2004 0.6 2003 0.2 2002 109.2 x ˆ2004 (2) 100 0.6 2004 0.2 2003 96 x ˆ2004 (3) 100 0.2 2004 100.8 x ˆ2004 (4) 100 x ˆ2004 (5) 100 x
与预测图(预测1999-2003)
例2:MA(q)模型的预测
已知某地区每年常驻人口数量近似服从MA(3)模型 (单位:万人):
X t 100 t 0.8t 1 0.6 t 2 0.2 t 3 , 25
时间序列分析基于r第2版

时间序列分析基于r第2版《时间序列分析基于R第2版》(Time Series Analysis and Its Applications: With R Examples, 2nd Edition)是由Shumway和Stoffer合著的一本经典时间序列分析教材。
该书详细介绍了时间序列分析的理论和实践应用,并使用R语言进行实例演示和编程实现。
以下是《时间序列分析基于R第2版》的主要内容概述:第1章:时间序列分析简介介绍时间序列分析的基本概念和应用领域,并概述本书的内容和使用R语言进行时间序列分析的优势。
第2章:时间序列的基本特性介绍时间序列的基本特性,包括平稳性、自相关性和白噪声等概念,并通过实例演示如何使用R进行时间序列数据的可视化和描述性统计分析。
第3章:时间序列的线性模型介绍时间序列的线性模型,包括自回归模型(AR)、滑动平均模型(MA)和自回归滑动平均模型(ARMA)等,并通过R语言实现模型的参数估计和预测。
第4章:时间序列的谱分析介绍时间序列的谱分析方法,包括周期图和功率谱密度估计等,并通过R语言实现谱分析方法的应用和结果可视化。
第5章:时间序列的非线性模型介绍时间序列的非线性模型,包括ARCH、GARCH和非线性AR模型等,并通过R语言实现模型的参数估计和预测。
第6章:时间序列的状态空间模型介绍时间序列的状态空间模型,包括线性状态空间模型和非线性状态空间模型,并通过R语言实现模型的参数估计和预测。
第7章:多变量时间序列分析介绍多变量时间序列分析的方法,包括向量自回归模型(VAR)、向量误差修正模型(VEC)和协整模型等,并通过R语言实现模型的参数估计和预测。
第8章:季节性和周期性时间序列介绍季节性和周期性时间序列的分析方法,包括季节性自回归移动平均模型(SARMA)和周期性自回归移动平均模型(PARMA)等,并通过R语言实现模型的参数估计和预测。
第9章:时间序列的预测介绍时间序列的预测方法,包括简单指数平滑、Holt线性趋势模型和ARIMA模型等,并通过R语言实现模型的参数估计和预测。
No.11-第4章-时间序列模型的参数估计与检验

所示,拟合AR(2)模型 t对 X t3 和 t对 t1 的散点图如图2、3所示。图1
有微弱的负相关趋势,说明AR(1)不是适应模型,而图2、3看不出有相关 趋势,说明AR(2)是适应模型。
图1
图2
图3
(2)估计相关系数法
1 j m
检验统计量
T
nm
ˆ j j a jj Q(~)
~ t(n m)
取检验水平 ,可得检验的拒绝域为
t t1 2 n m
小结:时间序列模型的检验
当我们对模型进行识别并估计出模型参数之后,所得到的时间序列模型 是否可用,还需要进行检验。
模型是否适用,可以检验残差序列是否为白噪声序列。 参数是否合适,可以构造统计量做假设检验,以使模型结构更为精简、 有效。 检验通过之后就可以利用所得到的模型进行预测和预报了。
(*)
令
Xt Xt ˆ1Xt1 ˆ2 Xt2 ˆp Xtp
于是(*)可以写成:
X~t t 1t1 2t2 qtq
构成一个MA模型。按照估计MA模型参数的方法,可以得到 1,2, ,q
以及
2
的估计值。
需要说明的是,在上述模型的平稳性、识别与估计的讨论中, ARMA(p,q)模型中均未包含常数项。
然后利用Yule Walker方程组,求解模型参数的估计值 ˆ1,ˆ2,...,ˆp
ˆ1 ˆ0 ˆ1
ˆ2
ˆ1
ˆ0
ˆ
p
ˆ
p 1
ˆ p2
ˆ p1 1 ˆ1
ˆ
p
时间序列分析-基于R(第四章作业)
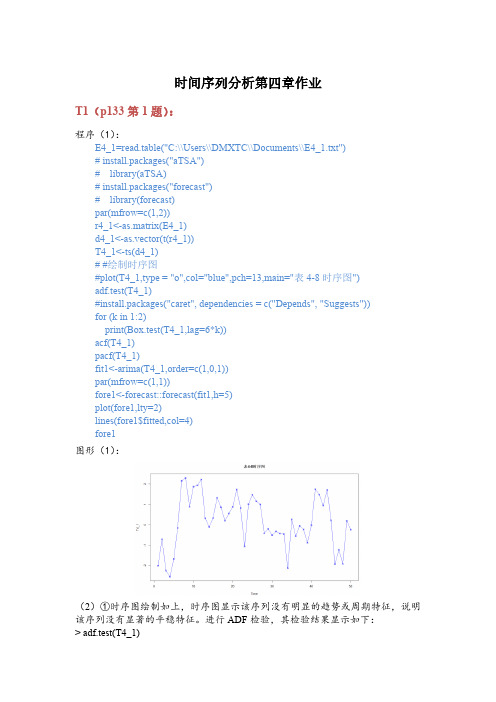
时间序列分析第四章作业T1(p133第1题):程序(1):E4_1=read.table("C:\\Users\\DMXTC\\Documents\\E4_1.txt")# install.packages("aTSA")# library(aTSA)# install.packages("forecast")# library(forecast)par(mfrow=c(1,2))r4_1<-as.matrix(E4_1)d4_1<-as.vector(t(r4_1))T4_1<-ts(d4_1)# #绘制时序图#plot(T4_1,type = "o",col="blue",pch=13,main="表4-8时序图")adf.test(T4_1)#install.packages("caret", dependencies = c("Depends", "Suggests"))for (k in 1:2)print(Box.test(T4_1,lag=6*k))acf(T4_1)pacf(T4_1)fit1<-arima(T4_1,order=c(1,0,1))par(mfrow=c(1,1))fore1<-forecast::forecast(fit1,h=5)plot(fore1,lty=2)lines(fore1$fitted,col=4)fore1图形(1):(2)①时序图绘制如上,时序图显示该序列没有明显的趋势或周期特征,说明该序列没有显著的平稳特征。
进行ADF检验,其检验结果显示如下:> adf.test(T4_1)Augmented Dickey-Fuller Testalternative: stationaryType 1: no drift no trendlag ADF p.value[1,] 0 -3.60 0.01[2,] 1 -3.19 0.01[3,] 2 -3.30 0.01[4,] 3 -3.20 0.01Type 2: with drift no trendlag ADF p.value[1,] 0 -3.65 0.0100[2,] 1 -3.23 0.0256[3,] 2 -3.44 0.0165[4,] 3 -3.48 0.0148Type 3: with drift and trendlag ADF p.value[1,] 0 -3.70 0.0340[2,] 1 -3.29 0.0833[3,] 2 -3.64 0.0388[4,] 3 -3.94 0.0193----Note: in fact, p.value = 0.01 means p.value <= 0.01检验结果显示,该序列所有ADF检验统计量的P值均小于显著性水平(α=0.05),所以可以确定该系列为平稳序列;②对平稳序列进行纯随机性检验,其检验结果如下:Box-Pierce testdata: T4_1X-squared = 25.386, df = 6, p-value = 0.0002896Box-Pierce testdata: T4_1X-squared = 31.153, df = 12, p-value = 0.001867结果显示6阶和12阶延迟的LB统计量的P值都小于显著性水平(α=0.05),所以可以判断该系列为平稳非白噪声序列。
应用时间序列分析课件第四章

第 4 章 非平稳序 列的确定性分析 褚为娟 4.1 时间序列的分 解 4.2 确定性因素分 解 4.3 趋势分析 4.4 季节效应分析 4.5 综合分析 4.6 X − 11 过程
确定性因素分解缺点: (1) 循环因素和趋势因素的影响难以严格分开(观察期不够 长); (2) 交易日影响没有被考虑(经济现象) 改进:(观察期不够长时) 长期趋势(Trend)、 交易日因素(Day)、 季节性变化(Season)、 随机波动(Immediate) 常用的模型: (1) (2) 加法模型 : xt = Tt + Dt + St + It ; 乘法模型 : xt = Tt · Dt · St · It ;
线性拟合
第 4 章 非平稳序 列的确定性分析 褚为娟 4.1 时间序列的分 解 4.2 确定性因素分 解 4.3 趋势分析 4.4 季节效应分析 4.5 综合分析 4.6 X − 11 过程
使用场合: 长期趋势呈现出线形特征 模型结构: xt = a + bt + It E(It ) = 0, Var(It ) = σ 2 {It } 为随机波动,Tt = a + bt 为消除随机波动的影响后序列 的长期趋势。
Wold 分解定理说明任何平稳序列都可以分解为确定性序列 和随机序列之和。 它是现代时间序列分析理论的灵魂,是 构造ARMA模型拟合平稳序列的理论基础。 Cramer 分解定理是Wold分解定理的理论推广, 它说明任何 一个序列的波动都可以视为同时受到了 确定性影响和随机 性影响的综合作用。 平稳序列要求这两方面的影响都是稳 定的, 而非平稳序列产生的机理就在于它所受到的这两方 面的影响至少有一方面是不稳定的。
趋势拟合法
第 4 章 非平稳序 列的确定性分析 褚为娟 4.1 时间序列的分 解 4.2 确定性因素分 解 4.3 趋势分析 4.4 季节效应分析 4.5 综合分析 4.6 X − 11 过程
概率与数理统计第4章时间序列分析

概率与数理统计第4章时间序列分析第4章时间序列分析[引例]某酿酒公司⽣产⼀种红葡萄酒,这种红葡萄酒颇受市场欢迎,其销售量稳步上升(表4-1),对公司盈利起到重要作⽤。
表4-1 某酿酒公司红葡萄酒销售量单位:件——资料来源:国际通⽤MBA教材配套案例《管理统计案例》机械⼯业出版社1999.3 本章⼩结1.时间序列是把同⼀现象在不同时间上的观察数据按时间先后顺序排列起来所形成的数列,它是动态分析的基础。
时间序列的分析有指标分析和构成因素分析两类。
时间序列的影响因素可归结为长期趋势、季节变动、循环变动和不规则变动等四种,常以乘法模型为基础来进⾏时间序列的分解和组合。
2.⽔平分析指标主要有平均发展⽔平、增减量(逐期、累计)和平均增减量。
不同类型的时间序列计算平均发展⽔平的⽅法有所不同。
累计增减量等于相应逐期增减量之和。
平均增减量是观察期内各个逐期增减量的平均数。
速度分析指标有发展速度、增减速度、平均发展速度和平均增减速度。
定基发展速度也即发展总速度,它等于相应时期内各环⽐发展速度的连乘积。
增减速度等于发展速度减1。
平均发展速度是环⽐发展速度的平均数,其计算⽅法通常采⽤⼏何平均法。
平均增减速度等于平均发展速度减1。
3. 长期趋势的分析⽅法主要有平滑法(移动平均、指数平滑法)和⽅程拟合法。
移动平均关键在于选择平均项数;能消除序列中的季节影响(平均项数与季节周期长度必须⼀致)。
指数平滑法是关键在于确定平滑系数。
⽅程拟合法通常采⽤最⼩⼆乘法来估计趋势⽅程中的参数。
4. 季节⽐率的测定⽅法:原资料平均法和趋势剔除法。
原资料平均法适⽤于⽔平趋势的季节序列;趋势剔除法适⽤于有明显上升(或下降)趋势的季节序列。
当没有季节因素影响时,季节⽐率为1或100%。
序列的季节调整即以原始数据除以对应季节的季节⽐率,⽬的是从时间序列中去掉季节影响,便于分析其它成分。
5.利⽤分析⼯具库中的“移动平均”、“指数平滑法”、“回归”或图表中的添加趋势线功能,可以测定时间序列的长期趋势。
第4章_时间序列分析

校级精品课程《统计学》习题第四章时间序列一、单项选择题1.时间序列是()A.分配数列B.分布数列C.时间数列D.变量数列2.时期序列和时点序列的统计指标()。
A.都是绝对数B.都是相对数C.既可以是绝对数,也可以是相对数D.既可以是平均数,也可以是绝对数3.时间序列是( )。
A.连续序列的一种B.间断序列的一种C.变量序列的一种D.品质序列的一种4.最基本的时间序列是( )。
A.时点序列B.绝对数时间序列C.相对数时间序列D.平均数时间序列5.为便于比较分析,要求时点序列指标数值的时间间隔( )。
A.必须连续B.最好连续C.必须相等D.最好相等6.时间序列中的发展水平( )。
A.只能是总量指标B.只能是相对指标C.只能是平均指标D.上述三种指标均可7.在平均数时间序列中各指标之间具有( )。
A.总体性B.完整性C.可加性D.不可加性8.序时平均数与一般平均数相比较()。
A.均抽象了各总体单位的差异B.均根据同种序列计算C.序时平均数表明现象在某一段时间内的平均发展水平,一般平均数表明现象在规定时间内总体的一般水平D.严格说来,序时平均数不能算作平均数9.序时平均数与一般平均数的共同点是( )。
A.两者均是反映同一总体的一般水平B.都是反映现象的一般水平C.两者均可消除现象波动的影响D.都反映同质总体在不同时间的一般水平10.时期序列计算序时平均数应采用( )。
A.加数算术平均法B.简单算术平均法C.简单算术平均法D.加权算术平均数11.间隔相等连续时点序列计算序时平均数,应采用( )。
A.简单算术平均法B.加数算术平均法C.简单序时平均法D.加权序时平均法12.由间断时点序列计算序时平均数,其假定条件是研究现象在相邻两个时点之间的变动为( )。
A.连续的B.间断的C.稳定的D.均匀的13.时间序列最基本速度指标是( )。
A.发展速度B.平均发展速度C.增减速度D.平均增减速度14.用水平法计算平均发展速度应采用( )。
第四章 时间序列

a a a a a1 a2 f1 2 3 f 2 n 1 n f n 1 2 2 全年平均人数 a 2 f
426 430 430 430 430 435 435 438 438 410 410 4ห้องสมุดไป่ตู้0 420 424 2 1 3 1 2 2 1 2 2 2 2 2 2 2 427(人) 2 1 3 1 2 2 1
计算该企业第一季度平均每月的计划完成程度。 解:该企业第一季度平均每月的计划完成程度
a (5100 6180 8640 ) / 3 6640 c 104.84% (5000 6000 8000 ) / 3 6333 .3 b
例:某企业某年第二季度职工人数资料如下表:
日 期
全部职工人数(人) b 非生产人员占全部人数的% c 非生产人员(人) (a=bc)
(二)由相对数列计算序时平均数 基本
相对数列的 (c ) 序时平均数 公式:
分子数列的序时平均数 (a ) 分母数列的序时平均数 (b )
即:
a c b
例:某企业某年第一季度各月的有关统计资料如下表:
月份 计划产量(件) b a 实际产量(件) 计划完成程度(%)c 一月份 5000 5100 102 二月份 6000 6180 103 三月份 8000 8640 108
13.99 13.17
资料来源:《安徽统计年鉴2012》.
(三)平均数列
例:安徽省历年城镇非私营单位在岗职工平均工资 年份 职工平均工 资(元) 2006 17949 2007 2008 2009 2010 2011
22180 26363 29659
34341 40640
资料来源:《安徽统计年鉴2012》.
管理统计学4 第四章 时间序列

星蓝海学习网
4.2序时平均数和平均发展速度
4.2.2相对数的序时平均数和平均数的序时平均数
库存周转速度属于相对数,该相对数的分母为时点数。从年度上看,年周转速度应等 于年销售量与年平均库存量的比值。因此,先平均后对比是计算相对数序时平均的基 本方法。 平均数序时平均数的计算与相对数的序时平均数的计算方法相同,也是先平均后对比。
管理统计学 [第四版]
星蓝海学习网
第四章 时间序列分析
星蓝海学习网
案例导入
近年来,中国房地产发展繁荣,房价更是水涨船高。下表是国家统计局对十 年来广东省商品房年销售价格的统计数。
年份 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 售价 4443 4853 5914 5953 6513 7486 7879 8112 9090 9083
4.1 发展水平和发展速度分析
4.1.2 发展水平和增长量
发展水平 发展水平是指时间数列上指标的具体数值。 发展水平的指标形式可以是绝对数,也可以是相对数或平均数。 增长量 为了分析上方便,就把作为研究对象的发展水平称为报告期水平,把要对比的基础水 平则称为基期水平。 用报告期水平减去基期水平,就等于增长量。其中,当基期水平为上期水平时,就称 为逐期增长量;当基期水平为某个时期的固定发展水平(X0)时,就称为累计增长量。 逐期增长量:X1-X0、X2-X1、X3-X2、…Xn-Xn-1 。 累计增长量:X1-X0、X2-X0、X3-X0、…Xn-X0。 二者的关系:(Xn-X0)= (X1 -X0)+(X2-X1)+(X3-X2)+…(Xn-Xn-1)。
时间序列分析

时间序列分析时间序列分析是一种统计学方法,用于分析时间序列数据的模式、趋势和周期性。
它可以帮助我们了解随着时间推移,数据如何变化,并预测未来的发展趋势。
本文将介绍时间序列分析的基本概念、常用方法和实际应用。
一、时间序列分析的基本概念时间序列是按照时间顺序排列的一系列数据点。
它可以是连续的,例如每天的股票价格,也可以是离散的,例如每个月的销售量。
时间序列分析旨在通过观察数据中的模式和趋势,揭示数据背后的规律和关系。
二、时间序列分析的常用方法1. 描述统计法描述统计法用于计算数据的统计指标,如平均值、标准差和相关系数。
这些指标可以帮助我们了解数据的分布情况和相关性。
2. 组件分析法组件分析法将时间序列分解为趋势、季节和随机成分。
趋势表示长期的变化趋势,季节表示重复出现的周期性变化,随机成分表示无法通过趋势和季节解释的随机波动。
通过对组成部分的分析,可以更好地理解时间序列的内在规律。
3. 平稳性检验法平稳性是时间序列分析的基本假设之一。
平稳时间序列的统计特性不随时间变化而改变。
平稳性检验可以通过观察时间序列的趋势、自相关图和单位根检验等方法进行。
4. 预测方法时间序列分析的一个重要应用是预测未来的数值。
常用的预测方法包括移动平均法、指数平滑法和ARIMA模型等。
这些方法基于过去的数据,通过建立模型来预测未来的趋势和周期性。
三、时间序列分析的实际应用时间序列分析在各个领域都有广泛的应用。
在金融领域,它可以用于股票价格的预测和风险管理;在经济学领域,它可以用于 GDP 的预测和经济政策制定;在气象学领域,它可以用于天气预报和气候变化研究。
除了上述领域外,时间序列分析还用于交通流量预测、销售预测、生态学研究等。
通过对历史数据的分析,我们可以更好地理解和预测未来的发展趋势,为决策提供依据。
结论时间序列分析是一种强大的工具,可以帮助我们理解时间序列数据中的模式和趋势。
通过对数据的描述统计、组件分析和预测,我们可以揭示数据背后的规律,并用于实际问题的解决。
第4章时间数列分析

本章主要内容
第一节 时间数列的种类和编制方法 第二节 时间数列的传统分析指标 第三节 长期趋势的测定 第四节 季节变动、循环变动和剩余变动的测定 第五节 时间数列预测方法
第一节 时间数列的种类和编制方法
一、时间数列的概念 时间数列是统计数据(指标数值)按时间顺序排列而形
成的数列,又称时间序列或动态数列。
计量单位相同的总 量指标
Y=T·S·C·I
是对原数列指标增 加或减少的百分比
3.变动因素的分解: (1)加法模型用减法。例:T=Y-(S+C+I) (2)乘法模型用除法。例:T=Y/(S·C·I)
二、长期趋势(T)的测定
(一)修匀法:基本目的就是消除影响事物变化的非基本因素
1、随手法 2、时距扩大法和序时平均法 时距扩大法是按较长的时距将原数列加以归并,以消除季节变动 和偶然因素的影响。只适用于时期数列。 序时平均法是分段计算序时平均数,以消除季节变动和偶然因素 的影响。适用于时期数列和时点数列。
c1
a1 b1
;
c2
a2 ; b2
;c an ቤተ መጻሕፍቲ ባይዱn
ca b
a、b均为时期数列时
ca
aN
a
cb
b
bN
b
b
a、b均为时点数列时
ca b
a1 2
a2
b1 2
b2
aN 1
aN 2
bN 1
bN 2
a 1a c
N1 N1
a为时期数列、b为时点数列时
ca b
a1 a2
b1 2
b2
aN 1 aN N
例
bN
bN 1 2
二、时间数列种类
第四章_ 统计学时间序列分解法和趋势外推法

拟合优度指标: 评判拟合优度的好坏一般使用标准误差来作 为优度好坏的指标:
SE ( y yˆ)2 n
回总目录 回本章目录
n
n
Q(b0 , b1, b2 ) ( yt yˆt )2 ( yt b0 b1t b2t 2 )2 最小值
t 1
t 1
即:
y nb0 b1 t b2 t 2 ty b0 t b1 t 2 b2 t3
t 2 y b0
t 2 b1
t 3 b2
时序 (t)
23 24 25 26 27 28 29 30 31 32
总额 ( yt ) 1163.6 1271.1 1339.4 1432.8 1558.6 1800.0 2140.0 2350.0 2570.0 2849.4
回总目录 回本章目录
(1)对数据画折线图分析,以社会商品零售总额为 y轴,年份为x轴。
回总目录 回本章目录
(2)从图形可以看出大致的曲线增长模式,较符合 的模型有二次曲线和指数曲线模型。但无法
确
定哪一个模型能更好地拟合该曲线,则我们 将
分别对该两种模型进行参数拟合。
适用的二次曲yˆt 线 模b0型 b为1t: b2t 2
适用的指数曲线模yˆt 型 a为ebt:
回总目录 回本章目录
(3)进行二次曲线拟合。首先产生序列 t2 ,然后 运用普通最小二乘法对模型各参数进行估计。得 到估计模型为:
生长曲线趋势外推法: 皮尔曲线预测模型 :
yˆt a b ln t
yt
1
L aebt
龚珀兹曲线预测模型 : yˆt kabt
回总目录 回本章目录
三、趋势模型的选择
图形识别法: 这种方法是通过绘制散点图来进行的,即将 时间序列的数据绘制成以时间t为横轴,时序观察 值为纵轴的图形,观察并将其变化曲线与各类函 数曲线模型的图形进行比较,以便选择较为合适 的模型。
西南财经大学向蓉美、王青华《统计学》第三版——第4章:时间序列分析
§4.1 时间序列反映某种现象的统计数值按时间先后顺序排列 起来所形成的数列。
任何一个时间数列,都具备两个基本要素:一是现象所 属的时间,称为时间要素;一是反映现象在不同时间上数量 表现的统计数据,称为数据要素.
时间 指标数值
t1 t2 t3 …tn y1 y2 y3 …yn
年末总人口 (万人)
96259 98705 114333 121121 122389 123626 124761 125786 126743 127627 128453 129227 129988 130756 131448 132129 132802 133450 134091 134735 135404
年份
1978 1980 1990 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012
国内生产总值 (亿元)
3645.2 4545.6 18547.9 60793.7 71176.6 78973.0 84402.3 89677.1 99214.6 109655.2 120332.7 135822.8 159878.3 183084.8 211923.5 257305.6 314045.4 340902.8 401512.8 473104.0 519322.0
人口自然增长率 (‰)
12.00 11.87 14.39 10.55 10.42 10.06 9.14 8.18 7.58 6.95 6.45 6.01 5.87 5.89 5.28 5.17 5.08 4.87 4.79 4.79 4.95
城镇居民家庭人均可支 配收入(元)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⒉计算相对数时间数列的序时平均数
基本公式
ai 若时间数列ci bi
a 则: c b
⑴ a、b均为时期数列时
a a N a cb c b b N b b
a 1 ca
【例】 某化工厂某年一季度利润计划完成情况如下
月 份 一 二 三
计划利润(万元)
利润计划完成程度(﹪)
指标 国民总收入(亿元) 国内生产总值(亿元) 第一产业增加值(亿元) 2012年 516810.05 519470.1 52373.63 2011年 468562.38 473104.05 47486.21 2010年 399759.54 401512.8 40533.6 2009年 340319.95 340902.81 35226
第四章
时间数列 指标小结
时间数列分析
第一节 时间数列及分析方法概述 第二节 时间数列的水平指标分析 第三节 时间数列的速度指标分析 第四节 时间数列分析
第一节 时间数列及分析方法概述
一、时间数列的概念 二、时间数列的分类
三、编制时间数列应注意的问题
四、时间数列分析方法及作用
第一节 时间数列及分析方法概述 一、时间数列的概念
160722.23 26660.98 173595.98 30015.05
157638.78
135239.95 22398.83 148038.04 25607.53
二、时间数列的分类
时间数列按照所列入指标数值的不同可分为:
绝对数动态数列 相对数动态数列 平均数动态数列
时期数列 时点数列
人 均 粮 食 消 费 量 ( 公 斤 ) ? ?
a1
一季 度初
二季 度初
90天
a2
三季 度初
90天
a3
次年一 季度初
180天
a4
a1 a2 2
a2 a3 2
a3 a4 2
a2 a3 a3 a4 a1 a2 1 1 2 2 2 2 11 2
a2 a3 a N 1 a N a1 a2 f1 f2 f N 1 2 2 一般有: 2 f1 f 2 f N 1
②由间断时点数列计算
一季 度初 二季 度初 三季 度初
每隔一段时间登 记一次,表现为 期初或期末值
※间隔相等 时,采用简单序时平均法
a1
a1 a2 2
a2
a2 a3 2
a3
a3 a4 2
四季 度初
a4
次年一 季度初
a5
a4 a5 2
a1 aNa5 aa a4 a5 a1 a2 a2 a3 a3 14 a2 a a1 a a4 2N 3 2 2 2 2 2 2 2 2 一般有:a 4 N 1 5 1
②该企业第二季度的月平均劳动生产率:
c a 10000 12.6 14.6 16.3 3 2200 b 2000 2000 2200 4 1 2 2 6904 .76元 人
③该企业第二季度的劳动生产率:
C
a
b
12.6 14.6 16.310000 2200 2000 2000 2200 4 1
按所选基期的不同,分为:
a a , a a , , a a 逐期增长量 1 0 2 1 n n1 两相邻累计增长量之
计增长量。
差等于相应时期的逐 a1 a0 , a2 a0各逐期增长量之和 ,, an a0 累计增长量 等于相应时期的累 期增长量。
⒉ ai a0 ai 1 a0 ai ai 1
200
125
300
120
400
150
因为
求该厂一季度的计划平均完成程度。 利润计划
实际利润 a c b 计划利润 完成程度
所以,该厂一季度的计划平均完成程度为 :
a cb 1.25 200 1.2 300 1.5 400 c 134.4﹪ b b 200 300 400
⑵ a、b均为时点数列时
aN a1 a2 a N 1 N 1 a 2 2 c bN b b1 b2 bN 1 N 1 2 2
⑶ a为时期数列、b为时点数列时
a1 a2 a N 1 a N N a c bN 1 b b1 b2 bN N 2 2
注意时间的长短应统一; 总体范围应该一致; 指标的经济内容应该相同; 指标的计算方法和计量单位应该一致。
四、时间数列分析方法及作用
时间数列分析常用方法有:指标分析法和成分分析法 时间数列对于现象发展动态分析具有十分重要的意义,其主要作 用可概括为以下几个方面: 第一,时间数列可以反映现象发展变化过程和历史情况; 第二,利用时间数列计算动态分析指标,可以反映现象发展变化 的方向、速度、趋势和规律。 第三,利用时间数列对现象发展变化趋势与规律的分析,可以进 行动态预测。 第四,将多个时间数列纳入同一模型中研究,可以揭示现象之间 相互联系的程度及动态演变关系。
a
i 1 m i 1
m
i
fi
i
f
【例】某企业5月份每日实有人数资料如下:
日 期 实有人数 1~9日 10~15日 16~22日 23~31日 780 784 786 783
解
af a f
780 9 784 6 786 7 783 9 783(人) 9679
基期水平 最初水平 中间水平 最末水平 报告期水平
( N 项数据)
或: a0 , a1 , , an1 , an
( n+1 项数据)
二、平均发展水平
→平均发展水平是对不同时期的发展水平求平均数,统
计上又叫序时平均数。
(一)一般平均数与序时平均数的区别 (二)序时平均数的计算方法
⒈计算绝对数时间数列的序时平均数 ⑴由时期数列计算,采用简单算术平均法 ⑵由时点数列计算 ①由连续时点数列计算 ②由间断时点数列计算 ⒉计算相对数时间数列的序时平均数 3.平均发展水平计算总结
2
20714 .28元 人 N c
2
三、增长量
又称增长水平,它是报告期水平与基期水 平之差,反映报告期比基期增长的水平。说明 社会经济现象在一定时期内所增长的绝对数量。
其计算公式为:
增长水平=报告期水平-基期水平
设时间数列中各 期发展水平为:
a0 , a1 , , an1 , an
【例】某商业企业1999年第二季度某商品库存 资料如下,求第二季度的月平均库存额 时间 库存量(百件) 3月末 4月末 5月末 6月末 66 72 64 68
解:第二季度的月平均库存额为:
66 68 72 64 2 67.67百件 a 2 4 1
※间隔不相等 时,采用加权序时平均法
【例】 某地区1999年社会劳动者人数资料如下 单位:万人
时间 社会劳动者 人数 1月 1日 362 5月31日 390 8月31日 416 12月31日 420
解:则该地区该年的月平均人数为: 362 390 390 416 416 420 5 3 4 2 2 2 a 53 4 396.75万人
第二节 时间数列的水平分析指标 属于现象发展的水平分析指标有:
一、发展水平 二、平均发展水平 三、增长量
四、平均增长量。
一、
发展水平
发展水平 指时间数列中每一项指标数值
它表示现象在某一时间上所达到的一种数量状态。
它是计算其他时间数列分析指标的基础。
设时间数列中各期发展水平为:
a1 , a2 , , aN 1 , aN
解:①第二季度各月的劳动生产率:
c1 四月份: 12.6 10000 元 人 6300 2000 2000 2
14.6 10000 c2 6952 .4元 人 五月份: 2000 2200 2
16.3 10000 c3 7409 .1元 人 六月份: 2200 2200 2
计算的依据不同:前者是根据变量数列
计算的,后者则是根据时间数列计算的; 说明的内容不同:前者表明总体内部各 单位的一般水平,后者则表明整个总体在 不同时期内的一般水平。
⑴由时期数列计算,采用简单算术平均法
a1 a2
aN 1 a N
a
a1 a2 a N a N
a
i 1
平均发展水平计算总结
时期 数列 序 时 总量指标 平 均 方 法 相对指标 、平均指 标 连续 时点 间断 时点 简单算术平均
间隔相等 简单算术平均
间隔不等 加权算术平均 间隔相等 两次简单平均
时点 数列
间隔不等 先简单后加权
视情况选用:先平均再相除、先加总再 相除、加权算术平均、加权调和平均等
一般平均数与序时平均数的区别:
第二产业增加值(亿元)
工业增加值(亿元) 建筑业增加值(亿元) 第三产业增加值(亿元) 人均国内生产总值(元)
235161.99
199670.66 35491.34 231934.48 38459.47
220412.81
188470.15 31942.66 205205.02 35197.79
187383.21
?
时期数列特点: 数列中各个指标值是可加的;
数列中每个指标值的大小随着时期的长
短而变动;
数列中每个指标值通常是通过连续不断
的登记而取得。
时点数列特点:
数列中各个指标值是不能相加的; 数列中每个指标值的大小与时间间隔
的长短没有直接关系;
数列中每个指标值通常是按期登记一
