应用时间序列分析第4章答案解析
时间序列分析基于R——习题答案

第一章习题答案略第二章习题答案2。
1(1)非平稳(2)0.0173 0.700 0.412 0.148 -0。
079—0。
258—0。
376(3)典型的具有单调趋势的时间序列样本自相关图2。
2(1)非平稳,时序图如下(2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图2.3(1)自相关系数为:0。
2023 0。
013 0。
042 —0。
043 -0。
179-0.251 -0.094 0.0248 —0.068 -0。
072 0.0140.109 0.217 0.3160。
0070-0。
025 0。
075 -0.141 -0。
204 -0。
245 0。
066 0。
0062 -0.139 -0.0340。
206 -0.010 0.080 0。
118(2)平稳序列(3)白噪声序列2。
4,序LB=4.83,LB统计量对应的分位点为0.9634,P值为0。
0363.显著性水平=0.05列不能视为纯随机序列。
2。
5(1)时序图与样本自相关图如下(2) 非平稳 (3)非纯随机2。
6(1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2)) (2)差分序列平稳,非纯随机第三章习题答案3。
1 ()0t E x =,21() 1.9610.7t Var x ==-,220.70.49ρ==,220φ=3.2 1715φ=,2115φ=3。
3 ()0t E x =,10.15() 1.98(10.15)(10.80.15)(10.80.15)t Var x +==--+++10.80.7010.15ρ==+,210.80.150.41ρρ=-=,3210.80.150.22ρρρ=-=1110.70φρ==,2220.15φφ==-,330φ=3。
4 10c -<<, 1121,1,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩3.5 证明:该序列的特征方程为:32--c 0c λλλ+=,解该特征方程得三个特征根:11λ=,2c λ=3c λ=-无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
时间序列分析-王燕-习题4答案(2)

6、方法一:趋势拟合法income<-scan('习题4.6数据.txt')ts.plot(income)由时序图可以看出,该序列呈现二次曲线的形状。
于是,我们对该序列进行二次曲线拟合:t<-1:length(income)t2<-t^2z<-lm(income~t+t2)summary(z)lines(z$fitted.values, col=2)方法二:移动平滑法拟合选取N=5income.fil<-filter(income,rep(1/5,5),sides=1)lines(income.fil,col=3)7、(1)milk<-scan('习题4.7数据.txt')ts.plot(milk)从该序列的时序图中,我们看到长期递增趋势和以年为固定周期的季节波动同时作用于该序列,因此我们可以采用乘积模型和加法模型。
在这里以加法模型为例。
z<-scan('4.7.txt')ts.plot(z)z<-ts(z,start=c(1962,1),frequency=12)z.s<-decompose(z,type='additive') //运用加法模型进行分解z.1<-z-z.s$seas //提取其中的季节系数,并在z中减去(因为是加法模//型)该季节系数ts.plot(z.1)lines(z.s$trend,col=3)z.2<-ts(z.1)t<-1:length(z.2)t2<-t^2t3<-t^3r1<-lm(z.2~t)r2<-lm(z.2~t+t2)r3<-lm(z.2~t+t2+t3)summary(r1)summary(r2)summary(r3) ##发现3次拟合效果最佳,故选用三次拟合ts.plot(z.2)lines(r3$fitt,col=4)pt<-(length(z.2)+1) : (length(z.2)+12)pt1<-pt ##预测下一年序列pt2<-pt^2pt3<-pt^3pt<-matrix(c(pt1,pt2,pt3),byrow=T,nrow=3)/*为预测时间的矩阵。
应用回归分析,第4章课后习题参考答案

第4章违背基本假设的情况思考与练习参考答案4.1 试举例说明产生异方差的原因。
答:例4.1:截面资料下研究居民家庭的储蓄行为Y i=β0+β1X i+εi其中:Y i表示第i个家庭的储蓄额,X i表示第i个家庭的可支配收入。
由于高收入家庭储蓄额的差异较大,低收入家庭的储蓄额则更有规律性,差异较小,所以εi的方差呈现单调递增型变化。
例4.2:以某一行业的企业为样本建立企业生产函数模型Y i=A iβ1K iβ2L iβ3eεi被解释变量:产出量Y,解释变量:资本K、劳动L、技术A,那么每个企业所处的外部环境对产出量的影响被包含在随机误差项中。
由于每个企业所处的外部环境对产出量的影响程度不同,造成了随机误差项的异方差性。
这时,随机误差项ε的方差并不随某一个解释变量观测值的变化而呈规律性变化,呈现复杂型。
4.2 异方差带来的后果有哪些?答:回归模型一旦出现异方差性,如果仍采用OLS估计模型参数,会产生下列不良后果:1、参数估计量非有效2、变量的显著性检验失去意义3、回归方程的应用效果极不理想总的来说,当模型出现异方差性时,参数OLS估计值的变异程度增大,从而造成对Y的预测误差变大,降低预测精度,预测功能失效。
4.3 简述用加权最小二乘法消除一元线性回归中异方差性的思想与方法。
答:普通最小二乘估计就是寻找参数的估计值使离差平方和达极小。
其中每个平方项的权数相同,是普通最小二乘回归参数估计方法。
在误差项等方差不相关的条件下,普通最小二乘估计是回归参数的最小方差线性无偏估计。
然而在异方差的条件下,平方和中的每一项的地位是不相同的,误差项的方差大的项,在残差平方和中的取值就偏大,作用就大,因而普通最小二乘估计的回归线就被拉向方差大的项,方差大的项的拟合程度就好,而方差小的项的拟合程度就差。
由OLS 求出的仍然是的无偏估计,但不再是最小方差线性无偏估计。
所以就是:对较大的残差平方赋予较小的权数,对较小的残差平方赋予较大的权数。
时间序列分析基于R——习题答案
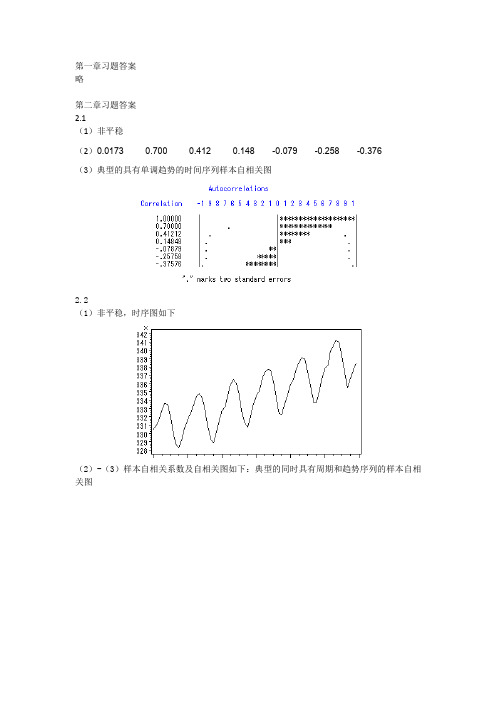
第一章习题答案略第二章习题答案2.1(1)非平稳(2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376(3)典型的具有单调趋势的时间序列样本自相关图2.2(1)非平稳,时序图如下(2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图2.3(1)自相关系数为:0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118(2)平稳序列(3)白噪声序列2.4,序列LB=4.83,LB统计量对应的分位点为0.9634,P值为0.0363。
显著性水平=0.05不能视为纯随机序列。
2.5(1)时序图与样本自相关图如下(2) 非平稳 (3)非纯随机 2.6(1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2)) (2)差分序列平稳,非纯随机第三章习题答案3.1 ()0t E x =,21() 1.9610.7t Var x ==-,220.70.49ρ==,220φ= 3.2 1715φ=,2115φ=3.3 ()0t E x =,10.15() 1.98(10.15)(10.80.15)(10.80.15)t Var x +==--+++10.80.7010.15ρ==+,210.80.150.41ρρ=-=,3210.80.150.22ρρρ=-=1110.70φρ==,2220.15φφ==-,330φ=3.4 10c -<<, 1121,1,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩3.5 证明:该序列的特征方程为:32--c 0c λλλ+=,解该特征方程得三个特征根:11λ=,2c λ=3c λ=-无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
第四章时间序列作业答案

第四章动态数列一、判断题1.若将某地区社会商品库存额按时间先后顺序排列,此种动态数列属于时期数列。
()2.定基发展速度反映了现象在一定时期内发展的总速度,环比发展速度反映了现象比前一期的增长程度。
()3.平均增长速度不是根据各期环比增长速度直接求得的,而是根据平均发展速度计算的。
()4.用水平法计算的平均发展速度只取决于最初发展水平和最末发展水平,与中间各期发展水平无关。
()5.平均发展速度是环比发展速度的平均数,也是一种序时平均数。
()6.季节变动,是指某些现象由于受自然因素和社会条件的影响,在一年之内比较有规律的变动。
7.按月平均法是一种考虑长期趋势影响的测定季节变动的方法。
8.某公司连续四个季度销售收入增长率分别为9%、12%、20%和18%,其环比增长速度为0.14%1、×2、×3、√4、√5、√6、√7、×8、×二、单项选择题1.根据时期数列计算序时平均数应采用()。
A.几何平均法B.加权算术平均法C.简单算术平均法D.首末折半法2.下列数列中哪一个属于动态数列()。
A.学生按学习成绩分组形成的数列B.工业企业按地区分组形成的数列C.职工按工资水平高低排列形成的数列D.出口额按时间先后顺序排列形成的数列3.已知某企业1月、2月、3月、4月的平均职工人数分别为190人、195人、193人和201人。
则该企业一季度的平均职工人数的计算方法为()。
4.说明现象在较长时期内发展的总速度的指标是()。
A、环比发展速度 B.平均发展速度 C.定基发展速度 D.环比增长速度5.已知各期环比增长速度为2%、5%、8%和7%,则相应的定基增长速度的计算方法为()。
A.(102%×105%×108%×107%)-100%B.102%×105%×108%×107%C.2%×5%×8%×7%D.(2%×5%×8%×7%)-100%6.定基增长速度与环比增长速度的关系是()。
(完整word版)时间序列分析基于R__习题答案及解析
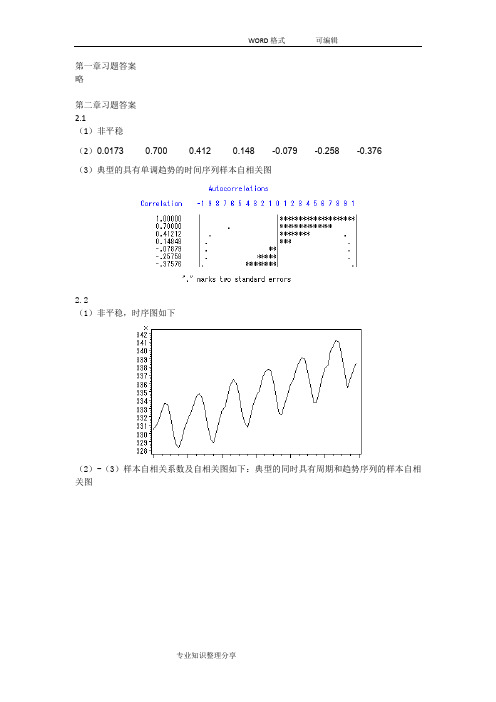
第一章习题答案略第二章习题答案2.1(1)非平稳(2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376(3)典型的具有单调趋势的时间序列样本自相关图2.2(1)非平稳,时序图如下(2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图2.3(1)自相关系数为:0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118(2)平稳序列(3)白噪声序列2.4,序列LB=4.83,LB统计量对应的分位点为0.9634,P值为0.0363。
显著性水平=0.05不能视为纯随机序列。
2.5(1)时序图与样本自相关图如下(2) 非平稳 (3)非纯随机 2.6(1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2)) (2)差分序列平稳,非纯随机第三章习题答案3.1 ()0t E x =,21() 1.9610.7t Var x ==-,220.70.49ρ==,220φ= 3.2 1715φ=,2115φ=3.3 ()0t E x =,10.15() 1.98(10.15)(10.80.15)(10.80.15)t Var x +==--+++10.80.7010.15ρ==+,210.80.150.41ρρ=-=,3210.80.150.22ρρρ=-=1110.70φρ==,2220.15φφ==-,330φ=3.4 10c -<<, 1121,1,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩3.5 证明:该序列的特征方程为:32--c 0c λλλ+=,解该特征方程得三个特征根:11λ=,2c λ=3c λ=-无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
应用时间序列分析习题答案

应用时间序列分析习题答案第二章习题答案2.1(1)非平稳(2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376(3)典型的具有单调趋势的时间序列样本自相关图2.2(1)非平稳,时序图如下(2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图2.3(1)自相关系数为:0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.0100.080 0.118(2)平稳序列(3)白噪声序列2.4LB=4.83,LB统计量对应的分位点为0.9634,P 值为0.0363。
显著性水平=0.05,序列不能视为纯随机序列。
2.5(1)时序图与样本自相关图如下(2)非平稳(3)非纯随机2.6(1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2))(2)差分序列平稳,非纯随机第三章习题答案 3.1 解:1()0.7()()tt t E x E xE ε-=⋅+0)()7.01(=-t x E 0)(=t x E t t x ε=-)B 7.01(t t t B B B x εε)7.07.01()7.01(221 +++=-=- 229608.149.011)(εεσσ=-=t x Var49.00212==ρφρ 022=φ3.2 解:对于AR (2)模型:⎩⎨⎧=+=+==+=+=-3.05.02110211212112011φρφρφρφρρφφρφρφρ 解得:⎩⎨⎧==15/115/721φφ3.3 解:根据该AR(2)模型的形式,易得:0)(=tx E原模型可变为:t t t t x x x ε+-=--2115.08.02212122)1)(1)(1(1)(σφφφφφφ-+--+-=t x Var2)15.08.01)(15.08.01)(15.01()15.01(σ+++--+==1.98232σ⎪⎩⎪⎨⎧=+==+==-=2209.04066.06957.0)1/(1221302112211ρφρφρρφρφρφφρ ⎪⎩⎪⎨⎧=-====015.06957.033222111φφφρφ3.4 解:原模型可变形为:t t x cB B ε=--)1(2由其平稳域判别条件知:当1||2<φ,112<+φφ且112<-φφ时,模型平稳。
时间序列分析参考答案

时间序列分析参考答案时间序列分析参考答案时间序列分析是一种研究随时间变化的数据模式和趋势的统计方法。
它可以帮助我们理解数据的变化规律,预测未来的趋势,以及制定相应的决策。
在本文中,我们将探讨时间序列分析的基本概念、方法和应用。
一、时间序列分析的基本概念时间序列是按照时间顺序排列的一系列数据观测值。
它可以是连续的,比如每天的股票价格,也可以是离散的,比如每月的销售额。
时间序列分析的目标是找出数据中的模式和趋势,以便进行预测和决策。
时间序列分析的基本概念包括趋势、季节性和周期性。
趋势是指数据在长期内的整体变化方向,可以是上升、下降或平稳。
季节性是指数据在一年中周期性重复出现的变化模式,比如节假日销售额的增长。
周期性是指数据在较长时间内出现的波动,通常周期长度大于一年。
二、时间序列分析的方法时间序列分析的方法包括描述性分析、平稳性检验、模型建立和预测等。
描述性分析是对时间序列数据进行可视化和统计分析,以了解数据的基本特征。
常用的描述性分析方法包括绘制折线图、直方图和自相关图等。
折线图可以显示数据的整体趋势和季节性变化,直方图可以展示数据的分布情况,自相关图可以帮助我们发现数据的相关性。
平稳性检验是判断时间序列数据是否具有平稳性的方法。
平稳性是指数据的均值和方差在时间上保持不变。
常用的平稳性检验方法包括单位根检验和ADF检验等。
模型建立是根据时间序列数据的特征,选择合适的模型来描述数据的变化规律。
常用的模型包括AR模型、MA模型和ARMA模型等。
AR模型是自回归模型,表示当前观测值与过去观测值之间的线性关系;MA模型是移动平均模型,表示当前观测值与过去观测值的误差之间的线性关系;ARMA模型是自回归移动平均模型,综合考虑了自回归和移动平均的效果。
预测是利用已知的时间序列数据,通过建立模型来预测未来的观测值。
常用的预测方法包括滚动预测、指数平滑法和ARIMA模型等。
滚动预测是指根据当前观测值和过去观测值的模型,逐步预测未来的观测值;指数平滑法是基于历史数据的加权平均值,对未来的观测值进行预测;ARIMA模型是自回归移动平均差分整合模型,可以处理非平稳的时间序列数据。
【分享】应用时间序列分析课后答案

【分享】应用时间序列分析课后答案在学习应用时间序列分析这门课程时,课后答案对于我们巩固知识、检验学习成果以及发现自身的不足之处都具有重要的意义。
下面,我将为大家分享一下这门课程的课后答案,并结合答案对一些重点和难点问题进行分析和讲解。
首先,让我们来看看第一章的课后答案。
第一章主要介绍了时间序列分析的基本概念和方法,包括时间序列的定义、分类以及平稳性的概念等。
在课后习题中,有这样一道题:“请解释什么是时间序列,并举例说明。
”答案是:“时间序列是按时间顺序排列的一组数据。
例如,某地区每天的气温记录、股票市场每天的收盘价、某工厂每月的产量等都是时间序列。
”通过这道题,我们可以更清晰地理解时间序列的概念,并且能够将其与实际生活中的例子相结合,加深对知识的理解。
另一道题是:“判断一个时间序列是否平稳的方法有哪些?”答案为:“常见的方法有观察序列的均值、方差是否随时间变化;自相关函数是否只与时间间隔有关,而与时间起点无关等。
”这道题帮助我们掌握了判断时间序列平稳性的关键要点。
第二章主要讲解了时间序列的模型,如 AR 模型、MA 模型和ARMA 模型等。
比如,有这样一道习题:“请简述 AR(1)模型的表达式和特点。
”答案是:“AR(1)模型的表达式为 Xt =φXt-1 +εt,其中φ 为自回归系数,εt 为白噪声。
其特点是当前值主要由前一期的值和随机扰动项决定。
”通过这个答案,我们能够明确 AR(1)模型的数学形式和基本特征。
还有一道题是:“比较 AR 模型和 MA 模型的异同。
”答案从模型的表达式、参数含义、适用情况等方面进行了详细的比较,让我们对这两种模型有了更全面的认识。
第三章涉及时间序列的预测方法。
像“简述时间序列预测的基本步骤”这道题,答案是:“首先对时间序列进行平稳性检验和预处理;然后选择合适的模型进行拟合;接着对模型进行参数估计和诊断检验;最后利用模型进行预测。
”这个答案为我们提供了一个清晰的预测流程框架。
应用时间序列第四章习题解答1-4

t x x x x x t 1 t (1 ) t 1 (1 ) t 1 (1 ) t 1 ……○ t t t t t t
令 A lim
t
t x t
1 式两端取极限,得: ○
lim
t
(2)
ˆ21 x 20 x20 (1 ) x19 (1 )2 x18 … (1 )19 x1 x
0.4 13 0.4 0.6 11 0.4 0.62 10 … 0.4 0.619 10 11.79240287
t x x lim (1 ) lim t 1 t t t t
即 A (1 ) A
lim
t
xt A 1。 t
另解:根据指数平滑的定义有(1)式成立, (1)式等号两边同乘 (1 ) 有(2)式成立
t t (t 1) (1 ) (t 2) (1 ) 2 (t 2) (1 )3 (1) x t (1 ) x t (1 ) (t 1) (1 ) 2 (t 2) (1 )3 (2)
1 1 ˆ21 ( x20 x19 x18 x17 x16 ) (13 11 10 10 12) 11.2 解:(1) x 5 5
1 1 ˆ22 ( x ˆ21 x20 x19 x18 x17 ) (11.2 13 11 10 10) 11.04 x 5 5
a
6 25 6 4 0.16 。 25 25
b a 0.4
4. 现有序列 xt t , t 1, 2,… ,使用平滑系数为 的指数平滑法
概率与数理统计第4章时间序列分析

概率与数理统计第4章时间序列分析第4章时间序列分析[引例]某酿酒公司⽣产⼀种红葡萄酒,这种红葡萄酒颇受市场欢迎,其销售量稳步上升(表4-1),对公司盈利起到重要作⽤。
表4-1 某酿酒公司红葡萄酒销售量单位:件——资料来源:国际通⽤MBA教材配套案例《管理统计案例》机械⼯业出版社1999.3 本章⼩结1.时间序列是把同⼀现象在不同时间上的观察数据按时间先后顺序排列起来所形成的数列,它是动态分析的基础。
时间序列的分析有指标分析和构成因素分析两类。
时间序列的影响因素可归结为长期趋势、季节变动、循环变动和不规则变动等四种,常以乘法模型为基础来进⾏时间序列的分解和组合。
2.⽔平分析指标主要有平均发展⽔平、增减量(逐期、累计)和平均增减量。
不同类型的时间序列计算平均发展⽔平的⽅法有所不同。
累计增减量等于相应逐期增减量之和。
平均增减量是观察期内各个逐期增减量的平均数。
速度分析指标有发展速度、增减速度、平均发展速度和平均增减速度。
定基发展速度也即发展总速度,它等于相应时期内各环⽐发展速度的连乘积。
增减速度等于发展速度减1。
平均发展速度是环⽐发展速度的平均数,其计算⽅法通常采⽤⼏何平均法。
平均增减速度等于平均发展速度减1。
3. 长期趋势的分析⽅法主要有平滑法(移动平均、指数平滑法)和⽅程拟合法。
移动平均关键在于选择平均项数;能消除序列中的季节影响(平均项数与季节周期长度必须⼀致)。
指数平滑法是关键在于确定平滑系数。
⽅程拟合法通常采⽤最⼩⼆乘法来估计趋势⽅程中的参数。
4. 季节⽐率的测定⽅法:原资料平均法和趋势剔除法。
原资料平均法适⽤于⽔平趋势的季节序列;趋势剔除法适⽤于有明显上升(或下降)趋势的季节序列。
当没有季节因素影响时,季节⽐率为1或100%。
序列的季节调整即以原始数据除以对应季节的季节⽐率,⽬的是从时间序列中去掉季节影响,便于分析其它成分。
5.利⽤分析⼯具库中的“移动平均”、“指数平滑法”、“回归”或图表中的添加趋势线功能,可以测定时间序列的长期趋势。
应用回归分析-第4章课后习题参考答案

第4章违背基本假设的情况思考与练习参考答案4.1 试举例说明产生异方差的原因。
答:例4.1:截面资料下研究居民家庭的储蓄行为Y i=β0+β1X i+εi其中:Y i表示第i个家庭的储蓄额,X i表示第i个家庭的可支配收入。
由于高收入家庭储蓄额的差异较大,低收入家庭的储蓄额则更有规律性,差异较小,所以εi的方差呈现单调递增型变化。
例4.2:以某一行业的企业为样本建立企业生产函数模型Y i=A iβ1K iβ2L iβ3eεi被解释变量:产出量Y,解释变量:资本K、劳动L、技术A,那么每个企业所处的外部环境对产出量的影响被包含在随机误差项中。
由于每个企业所处的外部环境对产出量的影响程度不同,造成了随机误差项的异方差性。
这时,随机误差项ε的方差并不随某一个解释变量观测值的变化而呈规律性变化,呈现复杂型。
4.2 异方差带来的后果有哪些?答:回归模型一旦出现异方差性,如果仍采用OLS估计模型参数,会产生下列不良后果:1、参数估计量非有效2、变量的显著性检验失去意义3、回归方程的应用效果极不理想总的来说,当模型出现异方差性时,参数OLS估计值的变异程度增大,从而造成对Y的预测误差变大,降低预测精度,预测功能失效。
4.3 简述用加权最小二乘法消除一元线性回归中异方差性的思想与方法。
答:普通最小二乘估计就是寻找参数的估计值使离差平方和达极小。
其中每个平方项的权数相同,是普通最小二乘回归参数估计方法。
在误差项等方差不相关的条件下,普通最小二乘估计是回归参数的最小方差线性无偏估计。
然而在异方差的条件下,平方和中的每一项的地位是不相同的,误差项的方差大的项,在残差平方和中的取值就偏大,作用就大,因而普通最小二乘估计的回归线就被拉向方差大的项,方差大的项的拟合程度就好,而方差小的项的拟合程度就差。
由OLS 求出的仍然是的无偏估计,但不再是最小方差线性无偏估计。
所以就是:对较大的残差平方赋予较小的权数,对较小的残差平方赋予较大的权数。
时间序列分析(张能福)第四章

第一节模型的识别单变量时间序列的Box-Jenkins 模型识别方法主要是根据样本自相关和偏自相关函数的截尾和拖尾性来判断序列所适合的模型。
平稳序列的自相关函数和偏自相关函数的统计特性对非零均值序列的处理计算样本均值,将每一序列值减去样本均值。
将序列均值作为一未知参数处理。
例如AR 模型例:,Xt 的均值是多少?判定在m步之后截尾的做法是:判定在n步之后截尾的做法是:拖尾:即被负指数控制收敛于零。
若序列自相关函数和偏自相关函数无以上特征,而是出现缓慢衰减或周期性衰减情况,则说明序列不是平稳的。
例:见演示试验。
第二节模型的定阶自相关函数和偏自相关函数定阶法自相关函数和偏自相关函数不但可以用来进行模型的识别,同样也可以用来进行AR 模型和MA 模型的定阶。
该方法对ARMA 模型定阶较为困难,同时,用该方法定的阶数也只能作为初步参考值。
残差方差定阶法残差方差定阶法借用了统计学中多元回归的原理。
假定模型是有限阶的自回归模型,如果选择的阶数小于真正的阶数,则是一种不足拟合,因而剩余平方和必然偏大,残差方差也将偏大;如果选择的阶数大于真正的阶数,则是一种过度拟合,残差方差并不因此而显著减小。
AR 、MA 、ARMA 三种模型的残差方差估计式分别为:F检验定阶法基本过程:对N个独立的观察值,建立回归模型:若舍弃后面S个因子,另建一个回归模型:检验舍弃的回归因子对Y的影响是否显著,等价于检验原假设:最佳准则函数定阶法对于AR 模型,AIC 函数可取:BIC 定阶理论上AIC 准则不能给出模型阶数的相容估计,即当样本趋于无穷大时,由AIC 准则选择的模型阶数不能收敛到其真值(通常比真值高)。
另一个定阶选择是BIC 准则:对于AR 模型:还可以定义其它类型的准则函数,如自回归移动平均模型的参数矩估计:将模型分成两个部分,先对AR 部分应用YULE-WALKER 方程,计算得到剩余序列,对剩余序列应用MA 模型的参数估计方法。
【分享】应用时间序列分析课后答案

【分享】应用时间序列分析课后答案在学习应用时间序列分析这门课程的过程中,课后答案对于我们巩固知识、检验理解程度以及发现问题和不足都有着至关重要的作用。
今天,我就来和大家分享一下我整理的应用时间序列分析课后答案,希望能对正在学习这门课程的朋友们有所帮助。
首先,让我们来了解一下什么是时间序列分析。
简单来说,时间序列分析是一种用于研究随时间变化的数据的统计方法。
它可以帮助我们揭示数据中的趋势、季节性、周期性等特征,并进行预测和建模。
在课程的第一章,通常会介绍时间序列的基本概念和表示方法。
课后答案中,对于一些关键概念的理解问题,比如时间序列的平稳性、白噪声等,会有详细的解释和说明。
以平稳性为例,答案会指出平稳时间序列的均值和方差不随时间变化,自相关函数只与时间间隔有关等重要特征,并通过具体的例子来帮助我们加深理解。
第二章可能会涉及到时间序列的模型。
常见的模型如自回归模型(AR)、移动平均模型(MA)以及自回归移动平均模型(ARMA)。
课后答案会给出这些模型的数学表达式、参数估计方法以及适用场景。
比如,在解释 AR 模型时,答案会说明如何通过 YuleWalker 方程来估计参数,以及如何判断模型的阶数。
当学习到时间序列的预测方法时,课后答案会展示具体的预测步骤和计算过程。
例如,使用简单的移动平均法进行预测,答案会清晰地列出计算每个预测值的算式,并对预测结果的准确性进行评估和分析。
在时间序列的季节性分析这部分内容中,课后答案会介绍如何识别季节性模式,以及如何通过季节性调整来消除季节性影响。
对于一些复杂的季节性模型,如乘积季节模型,答案会提供详细的建模思路和参数估计方法。
另外,关于时间序列的平稳化处理也是一个重要的知识点。
课后答案会讲解常见的平稳化方法,如差分法、对数变换等,并通过实际数据演示这些方法的效果。
除了理论知识的答案,一些课后习题还会要求我们运用所学知识进行实际数据分析。
这时候,答案不仅会给出最终的分析结果,还会展示详细的数据处理过程和使用的统计软件代码。
人大版应用时间序列分析(第5版)习题答案
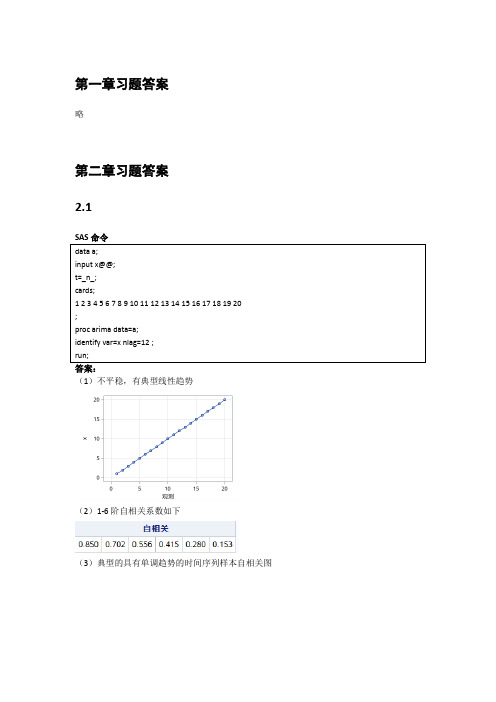
第一章习题答案略第二章习题答案2.1答案:(1)不平稳,有典型线性趋势(2)1-6阶自相关系数如下(3)典型的具有单调趋势的时间序列样本自相关图2.2答案:(1)不平稳(2)延迟1-24阶自相关系数(3)自相关图呈现典型的长期趋势与周期并存的特征2.3答案:(1)1-24阶自相关系数(2)平稳序列(3)非白噪声序列2.4计算该序列各阶延迟的Q统计量及相应P值。
由于延迟1-12阶Q统计量的P值均显著大于0.05,所以该序列为纯随机序列。
2.5答案(1)绘制时序图与自相关图(2)序列时序图显示出典型的周期特征,该序列非平稳(3)该序列为非白噪声序列2.6答案(1)如果是进行平稳性图识别,该序列自相关图呈现一定的趋势序列特征,可以视为非平稳非白噪声序列。
如果通过adf检验进行序列平稳性识别,该序列带漂移项的0阶滞后P值小于0.05,可以视为平稳非白噪声序列(2)差分后序列为平稳非白噪声序列2.7答案(1)时序图和自相关图显示该序列有趋势特征,所以图识别为非平稳序列。
(2)单位根检验显示带漂移项0阶延迟的P值小于0.05,所以基于adf检验可以认为该序列平稳(3)如果使用adf检验结果,认为该序列平稳,则白噪声检验显示该序列为非白噪声序列如果使用图识别认为该序列非平稳,那么一阶差分后序列为平稳非白噪声序列2.8答案(1)时序图和自相关图都显示典型的趋势序列特征(2)单位根检验显示该序列可以认为是平稳序列(带漂移项一阶滞后P值小于0.05)(3)一阶差分后序列平稳第三章习题答案 3.10101()0110.7t E x φφ===--() 221112() 1.96110.7t Var x φ===--() 22213=0.70.49ρφ==()12122221110.490.7=0110.71ρρρφρρ-==-(4) 3.21111222211212(2)7=0.515111=0.30.515AR φφφρφφφρφρφφφ⎧⎧⎧=⎪=⎪⎪⎪--⇒⇒⎨⎨⎨⎪⎪⎪=+=+⎩⎩⎪⎩模型有:,2115φ=3.312012(1)(10.5)(10.3)0.80.15()01t t t t t tt B B x x x x E x εεφφφ----=⇔=-+==--,22121212()(1)(1)(1)10.15=(10.15)(10.80.15)(10.80.15)1.98t Var x φφφφφφ-=+--+-+--+++=()1122112312210.83=0.70110.150.80.70.150.410.80.410.150.70.22φρφρφρφρφρφρ==-+=+=⨯-==+=⨯-⨯=() 1112223340.70.15=0φρφφφ====-()3.41211110011AR c c c c c ⎧<-<<⎧⎪⇒⇒-<<⎨⎨<±<⎪⎩⎩() ()模型的平稳条件是 1121,21,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩() 3.5证明:该序列的特征方程为:320c c λλλ--+=,解该特征方程得三个特征根:11λ=,2λ=3λ=无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
应用时间序列分析习题答案解析

第二章习题答案2.1(1)非平稳(2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376(3)典型的具有单调趋势的时间序列样本自相关图2.2(1)非平稳,时序图如下(2)- (3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图2.3(1) 自相关系数0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 --0.034 0.206 -0.010 0.080 0.1182)平稳序列3)白噪声序列 2.4LB=4.83 ,LB 统计量对应的分位点为 0.9634 ,P 值为 0.0363 。
显著性水平 =0.05,序列不能视为纯随机序列。
2.51)时序图与样本自相关图如下2) 非平稳3)非纯随机2.6(1)平稳,非纯随机序列(拟合模型参考: ARMA(1,2) )(2)差分序列平稳,非纯随机 第三章习题答案 3.1 解:E(x t ) 0.7 E(x t1) E( t )3.2解:对于 AR (2)模型:1 1 02 1 1 2 10.52 1 121 1 20.3解得:17/152 1/153.3解:根据该 AR(2)模型的形式,易得: E(x t ) 0原模型可变为: x t 0.8x t 1 0.15x t 2t(1 0.7B) x ttx t (1 10.7B) 1t 22(1 0.7B 0.72B 2)Var(x t ) 1 22 2 1.9608 21 0.492 210 0.49 22 0(1 0.7)E(x t )E(x t ) 0Var ( x t )12(1 2)(1 1 2)(1 1 2 )(1 0.15)(1 0.15)(1 0.8 0.15)(1 0.80.15)22=1.98231 1 /(12 ) 0.69572 1 1 2 0 0.40663 1 2 2 1 0.2209 11 122 2330.69570.153.4 解:原模型可变形为: 2(1 B cB 2)x tt由其平稳域判别条件知:当 | 2 | 1, 21 且2 1 1时, 模型平稳。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河南大学:姓名:汪宝班级:七班学号:1122314451 班级序号:68 5:我国1949年-2008年年末人口总数(单位:万人)序列如表4-8所示(行数据).选择适当的模型拟合该序列的长期数据,并作5期预测。
解:具体解题过程如下:(本题代码我是做一问写一问的)1:观察时序图:data wangbao4_5;input x@@;time=1949+_n_-1;cards;54167 55196 56300 57482 58796 60266 61465 6282864653 65994 67207 66207 65859 67295 69172 7049972538 74542 76368 78534 80671 82992 85229 8717789211 90859 92420 93717 94974 96259 97542 98705100072 101654 103008 104357 105851 107507 109300 111026112704 114333 115823 117171 118517 119850 121121 122389123626 124761 125786 126743 127627 128453 129227 129988130756 131448 132129 132802;proc gplot data=wangbao4_5;plot x*time=1;symbol1c=black v=star i=join;run;分析:通过时序图,我可以发现我国1949年-2008年年末人口总数(随时间的变化呈现出线性变化.故此时我可以用线性模型拟合序列的发展.X t=a+b t+I t t=1,2,3,…,60E(I t)=0,var(I t)=σ2其中,I t为随机波动;X t=a+b就是消除随机波动的影响之后该序列的长期趋势。
2:进行线性模型拟合:proc autoreg data=wangbao4_5;model x=time;output out=out p=wangbao4_5_cup;run;proc gplot data=out;plot x*time=1 wangbao4_5_cup*time=2/overlay ;symbol2c=red v=none i=join w=2l=3;run;分析:由上面输出结果可知:两个参数的p值明显小于0.05,即这两个参数都是具有显著非零,4:模型检验又因为Regress R-square=total R-square=0.9931,即拟合度达到99.31%所以用这个模型拟合的非常好。
5:结论所以本题拟合的模型为:X t=-2770828+1449t+I t t=1,2,3,…,60E(I t)=0,var(I t)=σ26:作5期预测proc forecast data=wangbao4_5 method=stepar trend=2 lead=5out=out outfull outest=est;id t;var x;proc gplot data=out;plot x*time=_type_/href=2008;symbol1i=none v=star c=black;symbol2i=join v=none c=red;symbol3i=join v=none c=black l=2;symbol4i=join v=none c=black l=2;run;6:爱荷华州1948-1979年非农产品季度收入数据如表4——9所示(行数据),选择适当的模型拟合该序列的长期趋势。
解:具体做题过程如下:(本题代码我是做一问写一问的)1、绘制时序图data wangbao4_6;input x@@;time=_n_;cards;601 604 620 626 641 642 645 655 682 678 692 707736 753 763 775 775 783 794 813 823 826 829 831830 838 854 872 882 903 919 937 927 962 975 9951001 1013 1021 1028 1027 1048 1070 1095 1113 1143 1154 1173 1178 1183 1205 1208 1209 1223 1238 1245 1258 1278 1294 1314 1323 1336 1355 1377 1416 1430 1455 1480 1514 1545 1589 1634 1669 1715 1760 1812 1809 1828 1871 1892 1946 1983 2013 2045 2048 2097 2140 2171 2208 2272 2311 2349 2362 2442 2479 2528 2571 2634 2684 2790 2890 2964 3085 3159 3237 3358 3489 3588 3624 3719 3821 3934 4028 4129 4205 4349 4463 4598 4725 4827 4939 5067 5231 5408 5492 5653 5828 5965;proc gplot data=wangbao4_6;plot x*time;symbol c=black v=star i=join;run;分析;可知时序图显示该序列有明显的曲线递增趋势。
尝试使用修正指数型模型进行迭代拟合:t t bc a x +=+Єt , t=1,2,…,1282、拟合模型proc nlin method =gauss; model x=a+b*c**time;parameters a=0.1 b=0.1 c=1.1; output predicted =xhat out =out; run ;NLIN 过程输出以下六方面信息: (1)迭代过程(2)收敛状况(本次迭代收敛)(3)估计信息摘要(4)主要统计量(5)参数信息摘要得到的拟合模型为:t 0307.12.1128.604ε+⨯+=tt x t=1,2,…,128(6)近似相关矩阵3、拟合效果为了直观看出拟合效果,我们可以将原序列值和拟合值联合作图:proc gplot data =out; plot x*t=1 xhat*t=2/overlay ; symbol1 c =black v =star i =join; symbol2 c =red v =none i =join;分析:由上图图我们可以看出,原序列值和拟合值很接近,拟合效果较好。
综合以上的分析,我们可以选择模型:t 0307.12.1128.604ε+⨯+=t t x 来拟合该序列的长期趋势。
拟合效果很不错。
8: 某城市1980年1月至1995年8月每月屠宰生猪的数量(单位:头)如表4—11所示(行数据),选择适当的模型拟合该序列的发展,并预测1995年9月至1997年9月该城市的生猪屠宰量。
解:具体解题过程如下:(本题代码我是做一问写一问的) ata wangbao4_8; input x@@;time=_n_;cards;76378 71947 33873 96428 105084 95741 110647 100311 94133 103055 90595 101457 76889 81291 91643 96228 102736 100264 103491 97027 95240 91680 101259 109564 76892 85773 95210 93771 98202 97906 100306 94089 102680 77919 93561 117062 81225 88357 106175 91922 104114 109959 97880 105386 96479 97580 109490 110191 90974 98981 107188 94177 115097 113696 114532 120110 93607 110925 103312 120184 103069 103351 111331 106161 111590 99447 101987 85333 86970 100561 89543 89265 82719 79498 74846 73819 77029 78446 86978 7587869571 75722 64182 77357 63292 59380 78332 72381 55971 6975085472 70133 79125 85805 81778 86852 69069 79556 88174 6669872258 73445 76131 86082 75443 73969 78139 78646 66269 7377680034 70694 81823 75640 75540 82229 75345 77034 78589 7976975982 78074 77588 84100 97966 89051 93503 84747 74531 9190081635 89797 81022 78265 77271 85043 95418 79568 103283 95770 91297 101244 114525 101139 93866 95171 100183 103926 102643 108387 97077 90901 90336 88732 83759 99267 73292 78943 94399 9293790130 91055 106062 103560 104075 101783 93791 102313 82413 83534 109011 96499 102430 103002 91815 99067 110067 101599 97646 104930 88905 89936 106723 84307 114896 106749 87892 100506;proc gplot data=wangbao4_8;plot x*time=1;symbol1c=red i=join v=star;run;proc arima data=wangbao4_8;identify var=x;run;1:时序图与平稳性判别分析:上图是数据对应的时序图,从图上曲线分析来看,数据并没有周期性或者趋向性规律,并且每月的生猪的屠宰量大约在80000上下波动。
所以由该序列图我可以认为它是个平稳的数列。
即可以用第三章的AR模型或MA 模型或ARMA模型进行拟合。
