2019年秋人教版八年级数学上13.3等腰三角形强化训练含答案

合集下载

人教版八年级上册数学《等腰三角形》同步训练含答案

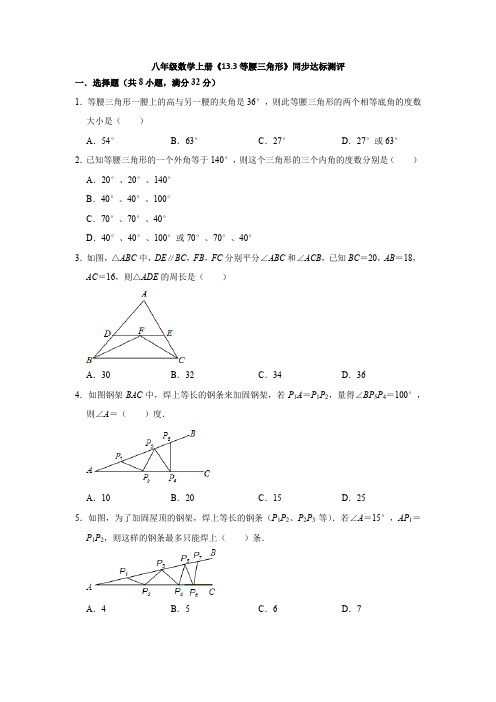
八年级数学上册《13.3等腰三角形》同步达标测评一．选择题（共8小题，满分32分）1．等腰三角形一腰上的高与另一腰的夹角是36°，则此等腰三角形的两个相等底角的度数大小是（）A．54°B．63°C．27°D．27°或63°2．已知等腰三角形的一个外角等于140°，则这个三角形的三个内角的度数分别是（）A．20°、20°、140°B．40°、40°、100°C．70°、70°、40°D．40°、40°、100°或70°、70°、40°3．如图，△ABC中，DE∥BC，FB，FC分别平分∠ABC和∠ACB，已知BC＝20，AB＝18，AC＝16，则△ADE的周长是（）A．30B．32C．34D．364．如图钢架BAC中，焊上等长的钢条来加固钢架，若P1A＝P1P2，量得∠BP5P4＝100°，则∠A＝（）度．A．10B．20C．15D．255．如图，为了加固屋顶的钢架，焊上等长的钢条（P1P2、P2P3等）．若∠A＝15°，AP1＝P1P2，则这样的钢条最多只能焊上（）条．A．4B．5C．6D．76．如图，AB＝BC＝CD＝DE＝EF＝FG，则∠A的范围是（）A．0°＜∠A＜15°B．0°＜∠A＜18°C．0°＜∠A＜20°D．0°＜∠A＜22.5°7．如图，已知∠MON＝30°，点A1、A2、A3…在射线ON上，点B1、B2、B3…在射线OM 上；△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形．若OA1＝1，则△A2021B2021A2022的边长为（）A．4044B．4046C．22020D．220218．如图，直线AB⊥CD，垂足为O，点P在∠BOC的平分线上，点E在直线AB上，且△EOP是等腰三角形，则这样的点P有（）A．1个B．2个C．3个D．4个二．填空题（共7小题，满分28分）9．如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作等边△ABC和等边△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．则下列结论：①AD＝BE；②PQ∥AE；③AP＝BQ；④DE＝DP．其中正确的是．10．如图，△ABC是等边三角形，BD平分∠ABC，点E在BC的延长线上，且CE＝1，∠E＝30°，则BC＝．11．如图，在第1个△A1BC中，∠B＝30°，A1B＝CB；在边A1B上任取一点D，延长CA1到A2，使A1A2＝A1D，得到第2个△A1A2D；在边A2D上任取一点E，延长A1A2到A3，使A2A3＝A2E，得到第3个△A2A3E，…按此做法继续下去，则第n个三角形中以A n为顶点的底角度数是．12．如图，在△ABC中，AB＝AC，∠BAD＝30°，AE＝AD，则∠EDC的度数是．13．已知等腰三角形一腰上的高与另一腰的夹角为30°，则这个等腰三角形顶角为°．14．如图，线段OP的一个端点O在直线a上，以OP为一边画等腰三角形，并且使另一个顶点在直线a上，这样的等腰三角形能有个．15．如果△ABM和△ACN分别是以△ABC的边AB、AC为边的形外等边三角形，MC交BN 于P，连P A，则∠APN＝．三．解答题（共9小题，满分60分）16．如图，在△ABC中，已知AD平分∠BAC，过AD上一点P作EF⊥AD，交AB于E、交AC于F，交BC延长线于M，则有正确结论：∠M＝（∠ACB﹣∠B）．请说明理由．17．如图，在△ABC中，∠B＝60°，延长BC到D，延长BA到E，使AE＝BD，连接CE、DE，使EC＝DE，求证：△ABC是等边三角形．18．如图，已知△ABC中，AB＝AC，DE⊥AB，DF⊥AC，BG⊥AC．求证：DE+DF＝BG．19．如图，已知∠EAC是△ABC的外角，AD平分∠EAC，AD∥BC，点F为BC中点．求证：AF⊥BC．20．如图，在等腰△ABC中，AB＝AC，BD为∠ABC平分线，延长BC到点E，使CE＝CD，作DH⊥BE于H，求证：H为BE的中点．21．已知：如图，在等边三角形ABC的三边上，分别取点D，E，F，使AD＝BE＝CF．求证：△DEF是等边三角形．22．如图，已知△ABC是等边三角形，E是AC延长线上一点，选择一点D，使得△CDE是等边三角形，如果M是线段AD的中点，N是线段BE的中点，求证：△CMN是等边三角形．23．如图，等边△ABC的边长为12cm，D为AC边上一动点，E为AB延长线上一动点，DE 交CB于点P，点P为DE中点（1）求证：CD＝BE；（2）若DE⊥AC，求BP的长．24．如图，过等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，且P A＝CQ，连PQ交AC边于D．（1）求证：PD＝DQ；（2）若△ABC的边长为1，求DE的长．参考答案一．选择题（共8小题，满分32分）1．解：在三角形ABC中，设AB＝AC，BD⊥AC于D．①若是锐角三角形，∠A＝90°﹣36°＝54°，底角＝（180°﹣54°）÷2＝63°；②若三角形是钝角三角形，∠BAC＝36°+90°＝126°，此时底角＝（180°﹣126°）÷2＝27°．所以等腰三角形底角的度数是63°或27°．故选：D．2．解：（1）当40°角是顶角时，另两个底角度数为70°，70°；（2）当40°角是底角时，另两个角度数为40°，100°．故选：D．3．解：∵DE∥BC，∴∠BFD＝∠FBC，∠EFC＝∠BCF，∵FC分别平分∠ABC和∠ACB，∴∠DBF＝∠FBC，∠ECF＝∠BCF，∴∠BFD＝∠DBF，∠EFC＝∠ECF，∴DF＝DB，EF＝EC，∵△ADE的周长＝AD+AE+DE，DE＝DF+EF，∴△ADE的周长＝AD+BD+AE+EC＝AB+AC，∵AB＝18，AC＝16，∴△ADE的周长＝34．故选：C．4．解：∵AP1＝P1P2，P1P2＝P2P3，P3P4＝P2P3，P3P4＝P4P5，∴∠A＝∠P1P2A，∠P2P1P3＝∠P2P3P1，∠P3P2P4＝∠P3P4P2，∠P4P3P5＝∠P4P5P3，∴∠P3P5P4＝4∠A，∵∠P3P5P4+∠BP5P4＝180°，∠BP5P4＝100°，∴∠P3P5P4＝80°，∴∠A＝20°．故选：B．5．解：∵∠A＝∠P1P2A＝15°∴∠P2P1P3＝30°，∠P1P3P2＝30°∴∠P1P2P3＝120°∴∠P3P2P4＝45°∴∠P3P2P4＝45°∴∠P2P3P4＝90°∴∠P4P3P5＝60°∴∠P3P5P4＝60°∴∠P3P4P5＝60°∴∠P5P4P6＝75°∴∠P4P6P5＝75°∴∠P4P5P6＝30°∴∠P6P5P7＝90°，此时就不能在往上焊接了，综上所述总共可焊上5条．故选：B．6．解：采用排除法：①∵AB＝BC＝CD＝DE＝EF＝FG，当∠A＝15°，∴∠BCA＝∠A＝15°，∴∠CBD＝∠BDC＝∠BCA+∠A＝15°+15°＝30°，∴∠BCD＝180°﹣（∠CBD+∠BDC）＝180°﹣60°＝120°，∴∠ECD＝∠CED＝180°﹣∠BCD﹣∠BCA＝180°﹣120°﹣15°＝45°，∴∠CDE＝180°﹣（∠ECD+∠CED）＝180°﹣90°＝90°，∴∠EDF＝∠EFD＝180°﹣∠CDE﹣∠BDC＝180°﹣90°﹣30°＝60°，∴∠FGE＝∠GEF＝∠EFD+∠A＝60°+15°＝75°，即此时符合；①当∠A＝18°时，同法求出∠FEG＝∠FGE＝90°，此时△FEG不存在，此时不符合，同样，当∠A取大于18°的角都不符合，当∠A＝小于18°的数时，△FEG存在，即选项A、C、D错误，只有选项B正确；故选：B．7．解：∵△A1B1A2是等边三角形，∴A1B1＝A2B1，∵∠MON＝30°，∴OA1＝A1B1＝1，∴A2B1＝1，∵△A2B2A3、△A3B3A4是等边三角形，∴A1B1∥A2B2∥A3B3，B1A2∥B2A3，∴A2B2＝2B1A2，B3A3＝2B2A3，∴A3B3＝4B1A2＝4，A4B4＝8B1A2＝8，A5B5＝16B1A2＝16，以此类推：△A2021B2021A2022的边长为22020．故选：C．8．解：如图，①当OP＝OE时，这样的点E由2个，②当PE＝OE时，这样的点E由1个，③当OP＝PE时，这样的点E由1个，∴这样的点P有4个，故选：D．二．填空题（共7小题，满分28分）9．解：∵等边△ABC和等边△CDE，∴AC＝BC，CD＝CE，∠ACB＝∠ECD＝60°，∴180°﹣∠ECD＝180°﹣∠ACB，即∠ACD＝∠BCE，在△ACD与△BCE中，，∴△ACD≌△BCE（SAS），∴AD＝BE，故①小题正确；∵△ACD≌△BCE（已证），∴∠CAD＝∠CBE，∵∠ACB＝∠ECD＝60°（已证），∴∠BCQ＝180°﹣60°×2＝60°，∴∠ACB＝∠BCQ＝60°，在△ACP与△BCQ中，，∴△ACP≌△BCQ（ASA），∴AP＝BQ，故③小题正确；PC＝QC，∴△PCQ是等边三角形，∴∠CPQ＝60°，∴∠ACB＝∠CPQ，∴PQ∥AE，故②小题正确；∵AD＝BE，AP＝BQ，∴AD﹣AP＝BE﹣BQ，即DP＝QE，∠DQE＝∠ECQ+∠CEQ＝60°+∠CEQ，∠CDE＝60°，∴∠DQE≠∠CDE，故④小题错误．综上所述，正确的是①②③．故答案为：①②③．10．解：∵△ABC是等边三角形，∴∠ABC＝∠ACB＝60°，BA＝BC，∵BD平分∠ABC，∴∠DBC＝∠E＝30°，BD⊥AC，∴∠BDC＝90°，∴BC＝2DC，∵∠ACB＝∠E+∠CDE，∴∠CDE＝∠E＝30°，∴CD＝CE＝1，∴BC＝2CD＝2，故答案为211．解：∵在△CBA1中，∠B＝30°，A1B＝CB，∴∠BA1C＝＝75°，∵A1A2＝A1D，∠BA1C是△A1A2D的外角，∴∠DA2A1＝∠BA1C＝×75°；同理可得∠EA3A2＝（）2×75°，∠F A4A3＝（）3×75°，∴第n个三角形中以A n为顶点的内角度数是（）n﹣1×75°．故答案为：（）n﹣1×75°．12．解：设∠EDC＝x，∠B＝∠C＝y，∠AED＝∠EDC+∠C＝x+y，又因为AD＝AE，所以∠ADE＝∠AED＝x+y，则∠ADC＝∠ADE+∠EDC＝2x+y，又因为∠ADC＝∠B+∠BAD，所以2x+y＝y+30，解得x＝15，所以∠EDC的度数是15°．故答案是：15°．13．解：当高在三角形内部时（如图1），顶角是60°；当高在三角形外部时（如图2），顶角是120°．故答案为：60或120．14．解：△AOP，△BOP，△COP，△DOP就是所求的三角形．15．解：∵△ABM和△ACN都是等边三角形，∴AB＝AM，AN＝AC，∠BAM＝∠CAN＝60°，∴∠BAM+∠BAC＝∠CAN+∠BAC，即∠CAM＝∠BAN，在△ABN与△AMC中，，∴△ABN≌△AMC（SAS），∴∠ANP＝∠ACP，又∵∠AEN＝∠PEC（对顶角相等），∵∠AEP＝∠NEC（对顶角相等），∴∠APN＝∠ACN＝60°．故答案为：60°．三．解答题（共9小题，满分60分）16．证明：∵EF⊥AD，AD平分∠BAC，∴∠1＝∠2，∠APE＝∠APF＝90°，又∵∠AEF＝180°﹣∠1﹣∠APE，∠AFE＝180°﹣∠2﹣∠APF，∴∠AEF＝∠AFE，∵∠CFM＝∠AFE，∴∠AEF＝∠AFE＝∠CFM，∵∠AEF＝∠B+∠M，∠MFC＝∠ACB﹣∠M，∴∠B+∠M＝∠ACB﹣∠M，即：∠M＝（∠ACB﹣∠B）．17．证明：延长BD至F，使DF＝BC，连接EF，∵EC＝ED，∴∠ECD＝∠EDC，∴∠ECB＝∠EDF，∴△ECB≌△EDF（SAS），∴BE＝EF，∠B＝60°，∴△BEF为等边三角形，∴BE＝BF，∵AE＝BD，∴DF＝AB，BC＝DF，∴AB＝BC，∴△ABC是等边三角形．18．证明：连接AD．则△ABC的面积＝△ABD的面积+△ACD的面积，AB•DE+AC•DF＝AC•BG，∵AB＝AC，∴DE+DF＝BG．19．证明：∵AD∥BC，∴∠EAD＝∠B，∠DAC＝∠C，∵AD平分∠EAC，∴∠EAD＝∠DAC，∴∠B＝∠C，∴AB＝AC，∵点F为BC中点，∴AF⊥BC．20．证明：∵AB＝AC，∴∠ABC＝∠SCB，∵BD平分∠ABC，∴∠ABD＝∠CBD，∵CE＝CD，∴∠CDE＝∠E，∵∠ACB＝∠E+∠CDE＝2∠DBC，∴∠DBC＝∠E，∴△BDE为等腰三角形，BD＝ED，∵DH垂直于BE，∴H为BE中点（三线合一）．21．证明：∵△ABC是等边三角形，∴AB＝BC＝AC，∵AD＝BE＝CF，∴AF＝BD，在△ADF和△BED中，，∴△ADF≌△BED（SAS），∴DF＝DE，同理DE＝EF，∴DE＝DF＝EF．∴△DEF是等边三角形．22．证明：∵△ABC是等边三角形，△CDE是等边三角形，M是线段AD的中点，N是线段BE的中点，∴∠ACB＝∠ECD＝60°，∴∠ACB+∠BCD＝∠ECD+∠BCD，即∠ACD＝∠BCE，在△ACD和△BCE中，，∴△ACD≌△BCE，∴AD＝BE，AM＝BN；∴AC＝BC，∠CAD＝∠CBE，AM＝BN，∴△AMC≌△BNC（SAS），∴CM＝CN，∠ACM＝∠BCN；又∵∠NCM＝∠BCN﹣∠BCM，∠ACB＝∠ACM﹣∠BCM，∴∠NCM＝∠ACB＝60°，∴△CMN是等边三角形．23．（1）证明：作DF∥AB交BC于F，如图所示：∵△ABC是等边三角形，∴∠A＝∠ABC＝∠C＝60°，∵DF∥AB，∴∠CDF＝∠A＝60°，∠DFC＝∠ABC＝60°，∠DFP＝∠EBP，∴△CDF是等边三角形，∴CD＝DF，∵点P为DE中点，∴PD＝PE，在△PDF和△PEB中，，∴△PDF≌△PEB（AAS），∴DF＝BE，∴CD＝BE；（2）解：∵DE⊥AC，∴∠ADE＝90°，∴∠E＝90°﹣∠A＝30°，∴AD＝AE，∠BPE＝∠ACB﹣∠E＝30°＝∠E，∴BP＝BE，由（1）得：CD＝BE，∴BP＝BE＝CD，设BP＝x，则BE＝CD＝x，AD＝12﹣x，∵AE＝2AD，∴12+x＝2（12﹣x），解得：x＝4，即BP的长为4．24．（1）证明：如图，过P做PF∥BC交AC于点F，∴∠AFP＝∠ACB，∠FPD＝∠Q，∠PFD＝∠QCD ∵△ABC为等边三角形，∴∠A＝∠ACB＝60°，∴∠A＝∠AFP＝60°，∴△APF是等边三角形；∵AP＝PF，AP＝CQ，∴PF＝CQ∴△PFD≌△QCD，∴PD＝DQ．（2）△APF是等边三角形，∵PE⊥AC，∴AE＝EF，△PFD≌△QCD，∴CD＝DF，DE＝EF+DF＝AC，∵AC＝1，DE＝．。

2019人教新版八年级数学上 13.3 等腰三角形同步练习卷包含答案

13.3 等腰三角形一．选择题（共8小题）1．下列三角形：①有两个角等于60°；②有一个角等于60°的等腰三角形；③三个外角（每个顶点处各取一个外角）都相等的三角形；④一腰上的中线也是这条腰上的高的等腰三角形．其中是等边三角形的有（）A．①②③B．①②④C．①③D．①②③④2．如图，△ABC、△ADE中，C、D两点分别在AE、AB上，BC与DE相交于F点．若BD＝CD ＝CE，∠ADC+∠ACD＝114°，则∠DFC的度数为何？（）A．114 B．123 C．132 D．1473．如图，网格中的每个小正方形的边长为1，A、B是格点，以A、B、C为等腰三角形顶点的所有格点C的个数为（）A．7个B．8个C．9个D．10个4．如图所示，△ABC是等边三角形，且BD＝CE，∠1＝15°，则∠2的度数为（）A．15°B．30°C．45°D．60°5．如图，已知△ABC中，AB＝AC，AD＝AE，∠BAE＝30°，则∠DEC等于（）A．7.5°B．10°C．15°D．18°6．如图所示，在△ABC中，AB＝AC，∠BAD＝α，且AE＝AD，则∠EDC＝（）A．αB．αC．αD．α7．如图，在△ABC中，AB＝20cm，AC＝12cm，点P从点B出发以每秒3cm的速度向点A运动，点Q从点A同时出发以每秒2cm的速度向点C运动，其中一个动点到达端点时，另一个动点也随之停止运动，当△APQ是以PQ为底的等腰三角形时，运动的时间是（）A．2.5秒B．3秒C．3.5秒D．4秒8．如图，已知AB＝A1B，A1B1＝A1A2，A2B2＝A2A3，A3B3＝A3A4…，若∠A＝70°，则∠A n﹣1A n B n的度数为（）﹣1A．B．C．D．二．填空题（共3小题）9．等腰三角形一腰上的高与另一腰的夹角为20°，则顶角的度数是．10．如图，在△ABC中，AB＝AC，点E在CA延长线上，EP⊥BC于点P，交AB于点F，若AF ＝2，BF＝3，则CE的长度为．11．如图，△ABC是边长为3的等边三角形，△BDC是等腰三角形，且∠BDC＝120°．以D 为顶点作一个60°角，使其两边分别交AB于点M，交AC于点N，连接MN，则△AMN的周长为．三．解答题（共8小题）12．如图，△ABC是等腰三角形，D，E分别是腰AB及AC延长线上的一点，且BD＝CE，连接DE交底BC于G．求证GD＝GE．13．如图所示，△ABC中，AB＝BC，DE⊥AB于点E，DF⊥BC于点D，交AC于F．（1）若∠AFD＝155°，求∠EDF的度数；（2）若点F是AC的中点，求证：∠CFD＝∠B．14．等边△ABC中，点P在△ABC内，点Q在△ABC外，且∠ABP＝∠ACQ，BP＝CQ，问△APQ 是什么形状的三角形？试说明你的结论．15．如图，已知D是△ABC的边BC上的一点，CD＝AB，∠BDA＝∠BAD，AE是△ABD的中线．（1）若∠B＝60°，求∠C的值；（2）求证：AD是∠EAC的平分线．16．已知：在△AOB和△COD中，OA＝OB，OC＝OD．（1）如图①，若∠AOB＝∠COD＝60°，求证：①AC＝BD②∠APB＝60°．（2）如图②，若∠AOB＝∠COD＝α，则AC与BD间的等量关系式为，∠APB的大小为（直接写出结果，不证明）17．如图，在△ABC中，AB＝AC＝2，∠B＝40°，点D在线段BC上运动（D不与B、C重合），连接AD，作∠ADE＝40°，DE交线段AC于E．（1）当∠BDA＝115°时，∠BAD＝°；点D从B向C运动时，∠BDA逐渐变（填“大”或“小”）；（2）当DC等于多少时，△ABD≌△DCE，请说明理由；（3）在点D的运动过程中，△ADE的形状也在改变，判断当∠BDA等于多少度时，△ADE是等腰三角形．18．如图1，已知线段AB的长为2a，点P是AB上的动点（P不与A，B重合），分别以AP、PB为边向线段AB的同一侧作正△APC和正△PBD．（1）当△APC与△PBD的面积之和取最小值时，AP＝；（直接写结果）（2）连接AD、BC，相交于点Q，设∠AQC＝α，那么α的大小是否会随点P的移动而变化？请说明理由；（3）如图2，若点P固定，将△PBD绕点P按顺时针方向旋转（旋转角小于180°），此时α的大小是否发生变化？（只需直接写出你的猜想，不必证明）19．如图，在Rt△ABC中，∠C＝90°，∠A＝60°，AB＝12cm，若点P从B点出发以2cm/秒的速度向A点运动，点Q从A点出发以1cm/秒的速度向C点运动，设P、Q分别从B、A同时出发，运动时间为t秒．解答下列问题：（1）用含t的代数式表示线段AP，AQ的长；（2）当t为何值时△APQ是以PQ为底的等腰三角形？（3）当t为何值时PQ∥BC？参考答案一．选择题（共8小题）1．解：①两个角为60度，则第三个角也是60度，则其是等边三角形，故正确；②这是等边三角形的判定2，故正确；③三个外角相等则三个内角相等，则其是等边三角形，故正确；④根据线段的垂直平分线的性质．可以证明三边相等，故正确．所以都正确．故选：D．2．解：∵BD＝CD＝CE，∴∠B＝∠DCB，∠E＝∠CDE，∵∠ADC+∠ACD＝114°，∴∠BDC+∠ECD＝360°﹣114°＝246°，∴∠B+∠DCB+∠E+∠CDE＝360°﹣246°＝114°，∴∠DCB+∠CDE＝57°，∴∠DFC＝180°﹣57°＝123°，故选：B．3．解：如图所示，以A为圆心，AB长为半径画弧，则圆弧经过的格点C3、C8、C7即为点C 的位置；以B为圆心，AB长为半径画弧，则圆弧经过的格点C1、C2、C6、C4、C5即为点C的位置；作线段AB的垂直平分线，垂直平分线没有经过格点．故以A、B、C为等腰三角形顶点的所有格点C的个数为8个．故选：B．4．解：在△ABD和△BCE中，，∴△ABD≌△BCE，∴∠1＝∠CBE，∵∠2＝∠1+∠ABE，∴∠2＝∠CBE+∠ABE＝∠ABC＝60°．故选：D．5．解：∵AC＝AB，∴∠B＝∠C，∵∠AEC＝∠B+∠BAE＝∠B+30°＝∠AED+α，∴∠B＝∠C＝∠AED+α﹣30°，∵AE＝AD，∴∠AED＝∠ADE＝∠C+α，即∠AED＝∠AED+α﹣30°+α，∴2α＝30°，∴α＝15°，∠DEC＝α＝15°，故选：C．6．解：根据题意：在△ABC中，AB＝AC∴∠B＝∠C∵AE＝AD∴∠ADE＝∠AED，即∠B+∠α﹣∠EDC＝∠C+∠EDC化简可得：∠α＝2∠EDC∴∠EDC＝α．故选：A．7．解：设运动的时间为x，在△ABC中，AB＝20cm，AC＝12cm，点P从点B出发以每秒3cm的速度向点A运动，点Q从点A同时出发以每秒2cm的速度向点C运动，当△APQ是等腰三角形时，AP＝AQ，AP＝20﹣3x，AQ＝2x即20﹣3x＝2x，解得x＝4．故选：D．8．解：∵在△ABA1中，∠A＝70°，AB＝A1B，∴∠BA1A＝70°，∵A1A2＝A1B1，∠BA1A是△A1A2B1的外角，∴∠B1A2A1＝＝35°；同理可得，∠B2A3A2＝17.5°，∠B3A4A3＝×17.5°＝，∴∠A n﹣1A n B n﹣1＝．故选：C．二．填空题（共3小题）9．解：此题要分情况讨论：当等腰三角形的顶角是钝角时，腰上的高在外部．根据三角形的一个外角等于与它不相邻的两个内角的和，即可求得顶角是90°+20°＝110°；当等腰三角形的顶角是锐角时，腰上的高在其内部，故顶角是90°﹣20°＝70°．故答案为：110°或70°．10．证明：在△ABC中，∵AB＝AC，∴∠B＝∠C，∵EP⊥BC，∴∠C+∠E＝90°，∠B+∠BFP＝90°，∴∠E＝∠BFP，又∵∠BFP＝∠AFE，∴∠E＝∠AFE，∴AF＝AE，∴△AEF是等腰三角形．又∵AF＝2，BF＝3，∴CA＝AB＝5，AE＝2，∴CE＝7．11．解：∵△BDC是等腰三角形，且∠BDC＝120°∴∠BCD＝∠DBC＝30°∵△ABC是边长为3的等边三角形∴∠ABC＝∠BAC＝∠BCA＝60°∴∠DBA＝∠DCA＝90°延长AB至F，使BF＝CN，连接DF，在Rt△BDF和Rt△CND中，BF＝CN，DB＝DC∴△BDF≌△CDN，∴∠BDF＝∠CDN，DF＝DN∵∠MDN＝60°∴∠BDM+∠CDN＝60°∴∠BDM+∠BDF＝60°，∠FDM＝60°＝∠MDN，DM为公共边∴△DMN≌△DMF，∴MN＝MF∴△AMN的周长是：AM+AN+MN＝AM+MB+BF+AN＝AB+AC＝6．三．解答题（共8小题）12．证明：过E作EF∥AB交BC延长线于F．∵AB＝AC，∴∠B＝∠ACB，∵EF∥AB，∴∠F＝∠B，∵∠ACB＝∠FCE，∴∠F＝∠FCE，∴CE＝EF，∵BD＝CE，∴BD＝EF，在△DBG与△GEF中，，∴△DGB≌△EGF（AAS），∴GD＝GE．13．解：（1）∵∠AFD＝155°，∴∠DFC＝25°，∵DF⊥BC，DE⊥AB，在Rt△EDC中，∴∠C＝90°﹣25°＝65°，∵AB＝BC，∴∠C＝∠A＝65°，∴∠EDF＝360°﹣65°﹣155°﹣90°＝50°．（2）连接BF∵AB＝BC，且点F是AC的中点，∴BF⊥AC，∠ABF＝∠CBF＝∠ABC，∴∠CFD+∠BFD＝90°，∠CBF+∠BFD＝90°，∴∠CFD＝∠CBF，∴∠CFD＝∠ABC．14．解：△APQ为等边三角形．证明：∵△ABC为等边三角形，∴AB＝AC．在△ABP与△ACQ中，∵，∴△ABP≌△ACQ（SAS）．∴AP＝AQ，∠BAP＝∠CAQ．∵∠BAC＝∠BAP+∠PAC＝60°，∴∠PAQ＝∠CAQ+∠PAC＝60°，∴△APQ是等边三角形．15．（1）解：∵∠B＝60°，∠BDA＝∠BAD，∴AB＝AD，∵CD＝AB，∴CD＝AD，∴∠DAC＝∠C，∴∠BDA＝∠DAC+∠C＝2∠C，∵∠BAD＝60°，∴∠C＝30°；（2）证明：延长AE到M，使EM＝AE，连接DM，在△ABE和△MDE中，，∴△ABE≌△MDE，∴∠B＝∠MDE，AB＝DM，∵∠ADC＝∠B+∠BAD＝∠MDE+∠BDA＝∠ADM，在△MAD与△CAD，，∴△MAD≌△CAD，∴∠MAD＝∠CAD，∴AD是∠EAC的平分线．16．解：（1）①证明：∵∠AOB＝∠COD＝60°，∴∠AOB+∠BOC＝∠COD+∠BOC，∴∠AOC＝∠BOD．在△AOC和△BOD中，，∴△AOC≌△BOD（SAS），∴AC＝BD；②证明：∵△AOC≌△BOD，∴∠OAC＝∠OBD，∴∠OAC+∠AOB＝∠OBD+∠APB，∴∠OAC+60°＝∠OBD+∠APB，∴∠APB＝60°；（2）AC＝BD，∠APB＝α．17．解：（1）∠BAD＝180°﹣∠ABD﹣∠BDA＝180°﹣40°﹣115°＝25°；从图中可以得知，点D从B向C运动时，∠BDA逐渐变小；故答案为：25°；小．（2）∵∠EDC+∠EDA+∠ADB＝180°，∠DAB+∠B+∠ADB＝180°，∠B＝∠EDA＝40°，∴∠EDC＝∠DAB．∵∠B＝∠C，∴△ABD≌△DCE．∴当DC＝AB＝2时，△ABD≌△DCE．（3）∵AB＝AC，∴∠B＝∠C＝40°，①当AD＝AE时，∠ADE＝∠AED＝40°，∵∠AED＞∠C，∴此时不符合；②当DA＝DE时，即∠DAE＝∠DEA＝（180°﹣40°）＝70°，∵∠BAC＝180°﹣40°﹣40°＝100°，∴∠BAD＝100°﹣70°＝30°；∴∠BDA＝180°﹣30°﹣40°＝110°；③当EA＝ED时，∠ADE＝∠DAE＝40°，∴∠BAD＝100°﹣40°＝60°，∴∠BDA＝180°﹣60°﹣40°＝80°；∴当∠ADB＝110°或80°时，△ADE是等腰三角形．18．解：（1）设AP的长是x，则BP＝2a﹣x，∴S△APC+S△PBD＝x•x+（2a﹣x）•（2a﹣x）＝x2﹣ax+a2，当x＝﹣＝﹣＝a时△APC与△PBD的面积之和取最小值，故答案为：a；（2）α的大小不会随点P的移动而变化，理由：∵△APC是等边三角形，∴PA＝PC，∠APC＝60°，∵△BDP是等边三角形，∴PB＝PD，∠BPD＝60°，∴∠APC＝∠BPD，∴∠APD＝∠CPB，∴△APD≌△CPB，∴∠PAD＝∠PCB，∵∠QAP+∠QAC+∠ACP＝120°，∴∠QCP+∠QAC+∠ACP＝120°，∴∠AQC＝180°﹣120°＝60°；（3）此时α的大小不会发生改变，始终等于60°．理由：∵△APC是等边三角形，∴PA＝PC，∠APC＝60°，∵△BDP是等边三角形，∴PB＝PD，∠BPD＝60°，∴∠APC＝∠BPD，∴∠APD＝∠CPB，∴△APD≌△CPB，∴∠PAD＝∠PCB，∵∠QAP+∠QAC+∠ACP＝120°，∴∠QCP+∠QAC+∠ACP＝120°，∴∠AQC＝180°﹣120°＝60°．19．解：（1）∵Rt△ABC中，∠C＝90°，∠A＝60°，∴∠B＝30°．又∵AB＝12cm，∴AC＝6cm，BP＝2t，AP＝AB﹣BP＝12﹣2t，AQ＝t．（2）∵△APQ是以PQ为底的等腰三角形，∴AP＝AQ，即12﹣2t＝t，解得t＝4，即当t＝4秒时△APQ是等腰三角形．（3）∵当AQ：AC＝AP：AB时，有PQ∥BC，∴t：6＝（12﹣2t）：12，解得t＝3．即当t＝3秒时，PQ∥BC．。

人教版八年级上册数学 13.3 等腰三角形同步习题(含答案)

13.3 等腰三角形同步习题一．选择题1．等腰三角形的两边长为3和7，则其周长为（）A．17B．13C．13或17D．以上都不对2．等腰三角形的两边长分别为3cm和7cm，则周长为（）A．13cm B．17cm C．13cm或17cm D．11cm或17cm 3．在△ABC中，∠A：∠B：∠C＝1：2：3，最小边BC＝4cm，则最长边AB的长为（）A．8cm B．6cm C．cm D．5cm4．在△ABC中，AB＝AC，若∠A＝40°，则∠C为（）A．40°B．70°C．40°或70°D．100°5．如图，在△ABC中，AB＝AC，点D，点E分别是BC，AC上一点，且DE⊥AD，若∠BAD＝55°，∠B＝50°，则∠DEC的度数为（）A．125°B．120°C．115°D．110°6．如图，将边长为7cm的等边△ABC沿边BC向右平移5cm得到△A'B'C'，则四边形AA'C'B 的周长为（）A．30cm B．31cm C．32cm D．33cm7．如图，在△ABC中，D、E分别为AB、AC边上的点，DA＝DE，DB＝BE＝EC．若∠ABC ＝130°，则∠C的度数为（）A．20°B．22.5°C．25°D．30°8．△ABC中，AB＝AC，∠BAC＝120°，BC＝2，D为BC的中点，AE＝AB，则△EBD 的面积为（）A．B．C．D．9．如图，在△ABC中，AB＝AC，点D，E在边BC上，∠BAD＝∠CAE，若BC＝15，DE ＝6，则CE的长为（）A．3.5B．4.5C．5D．5.510．如图，在等边△ABC中，BC＝4，D，E分别是AB，AC的中点，EF⊥BC于点F，连接DF．则DF等于（）A．2B．3C．D．2二．填空题11．如图，AD、BE是等边△ABC的两条高线，AD、BE交于点O，则∠AOB＝度．12．等腰三角形周长为20cm，则腰长xcm的取值范围是．13．在等腰三角形ABC中，BC边上的高恰好等于BC边长的一半，则∠BAC等于．14．如图，在△ABC中，AE＝DE＝BD，AD＝EC，∠1＝17°，则∠EBC的度数是．15．如图，点C为线段AB上一点，且CB＝2，分别以AC、BC为边，在AB的同一侧作等边△ACD和等边△CBE，连接DE，AE，∠CDE＝30°，则△ADE的面积为．三．解答题16．如图，在△ABC中，AB＝AC，D是三角形内一点，连接AD，BD，CD，∠BDC＝90°，∠DBC＝45°．（1）求证：∠BAD＝∠CAD；（2）求∠ADB的度数．17．如图，在△ABC中，点D，E分别在边AC，AB上，BD与CE交于点O，给出下列三个条件：①∠EBO＝∠DCO；②BE＝CD；③OB＝OC．（1）上述三个条件中，由哪两个条件可以判定△ABC是等腰三角形？（用序号写出所有成立的情形）（2）请选择（1）中的一种情形，说明你的理由．参考答案1．A2．B3．A4．B5．C6．B7．D8．B9．B10．C11．120．12．5＜x＜1013．90°或75°或15°14．56°15．416．（1）证明：∵∠BDC＝90°，∠DBC＝45°，∴∠BCD＝180°﹣∠BDC﹣∠DBC＝45°，∴∠DBC＝∠BCD，∴DB＝DC．在△ABD与△ACD中，，∴△ABD≌△ACD（SSS），∴∠BAD＝∠CAD；（2）解：∵△ABD≌△ACD（SSS），∴∠ADB＝∠ADC，∵∠ADB+∠ADC+∠BDC＝360°，∠BDC＝90°，∴∠ADB＝（360°﹣90°）＝135°．17．解：（1）由①②或①③可以判定△ABC是等腰三角形；（2）由①②判定△ABC是等腰三角形，理由如下：在△BOE和△COD中，∵∠EBO＝∠DCO，BE＝CD，∠BOE＝∠COD，∴△BOE≌△COD，∴OB＝OC，∴∠OBC＝∠OCB，∴∠OBC+∠EBO＝∠OCB+∠DCO，即：∠ABC＝∠ACB，∴AB＝AC，即△ABC是等腰三角形．①③判定△ABC是等腰三角形，理由如下：∵OB＝OC，∴∠OBC＝∠OCB，又∵∠EBO＝∠DCO，∴∠OBC+∠EBO＝∠OCB+∠DCO，即：∠ABC＝∠ACB，∴AB＝AC，即△ABC是等腰三角形．。

人教版八年级数学上册 13.3 等腰三角形课时训练(含答案)

人教版八年级数学上册13.3 等腰三角形课时训练一、选择题1. 以下列各组数据为边长，可以构成等腰三角形的是()A．1，1，2 B．1，1，3C．2，2，1 D．2，2，52. 如图，在Rt△ABC中，∠BCA＝90°，∠A＝30°，CD⊥AB，垂足为D，则AD 与BD的长度之比为()A．2∶1 B．3∶1 C．4∶1 D．5∶13. 如图，在等腰三角形中，若∠1＝110°，则∠2的度数为()A．35°B．70°C．110°D．35°或55°4. 如图，已知直线l垂直平分线段AB，P是l上一点，已知P A＝1，则PB()A．等于1 B．小于1C．大于1 D．最小为15. 如图，在△ABC中，∠C＝90°，∠B＝30°，AC＝3，P是BC边上的动点，则AP的长可能是()A．2 B．5.2 C．7.8 D．86. 具备下列条件的三角形为等腰三角形的是链接听P27例1归纳总结() A．有两个角分别为20°，120°B．有两个角分别为40°，80°C．有两个角分别为30°，60°D．有两个角分别为50°，80°7. 如图，在△ABC中，AB＝AC，AD，CE分别是△ABC的中线和角平分线．若∠CAD＝20°，则∠ACE的度数是()A．20°B．35°C．40°D．70°8. 如图，AC＝AD，BC＝BD，则有()A．CD垂直平分ABB．AB垂直平分CDC．AB与CD互相垂直平分D．CD平分∠ACB9. 下列条件不能得到等边三角形的是()A．有两个内角是60°的三角形B．有一个角是60°的等腰三角形C．腰和底相等的等腰三角形D．有两个角相等的等腰三角形10. 如图，在△ABC中，∠BAC＝72°，∠C＝36°，∠BAC的平分线AD交BC于点D，则图中有等腰三角形()A．0个B．1个C．2个D．3个二、填空题11. 如图，等腰三角形ABC中，AB＝AC＝12，∠A＝30°，则△ABC的面积等于________．12. 等腰三角形的两边长分别为6 cm，13 cm，其周长为________ cm.13. 如图，在△ABC中，AB＝AC，E为BC的中点，BD⊥AC，垂足为D.若∠EAD ＝20°，则∠ABD＝________°.14. 如图所示，OP平分∠AOB，∠AOP＝15°，PC∥OA，PD⊥OA于点D，PC ＝4，则PD＝________.15. 如图所示，在△ABC中，DE是AC的垂直平分线，AE=5 cm，△ABD的周长为18 cm，则△ABC的周长为.三、解答题16. 如图，在等边三角形ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF⊥DE，交BC的延长线于点F.求证：DF＝2DC.17. 如图，已知Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，∠BAC的平分线分别交BC，CD于点E，F.求证：△CEF是等腰三角形．18. 如图，上午8时，一条船从海岛A出发，以15海里/时的速度向正北方向航行，上午10时到达海岛B处，从A，B望灯塔C，测得∠NAC＝30°，∠NBC＝60°.(1)求海岛B到灯塔C的距离；(2)这条船继续向正北方向航行，在什么时间小船与灯塔C的距离最短？19. 已知:如图所示，锐角三角形ABC 的两条高BD ，CE 相交于点O ，且OB=OC.(1)求证:△ABC 是等腰三角形;(2)判断点O 是否在∠BAC 的平分线上，并说明理由.20. 如图①，在△ABC 中，AB ＝AC ，P 为底边BC 上一点，PE ⊥AB ，PF ⊥AC ，CH ⊥AB ，垂足分别为E ，F ，H .易证PE ＋PF ＝CH .证明过程如下：连接AP .∵PE ⊥AB ，PF ⊥AC ，CH ⊥AB ，∴S △ABP ＝12AB ·PE ，S △ACP ＝12AC ·PF ，S △ABC ＝12AB ·CH . 又∵S △ABP ＋S △ACP ＝S △ABC ， ∴12AB ·PE ＋12AC ·PF ＝12AB ·CH . ∵AB ＝AC ，∴PE ＋PF ＝CH .如图②，若P 为BC 延长线上的点，其他条件不变，PE ，PF ，CH 之间又有怎样的数量关系？请写出你的猜想，并加以证明．人教版八年级数学上册13.3 等腰三角形课时训练-答案一、选择题1. 【答案】C2. 【答案】B[解析] ∵在Rt△ABC中，∠BCA＝90°，∠A＝30°，CD⊥AB，∴2BD＝BC，2BC＝AB.∴AB＝4BD.∴AD∶BD＝3∶1.3. 【答案】A4. 【答案】A5. 【答案】B[解析] 根据垂线段最短，可知AP的长不能小于3.∵在△ABC中，∠C＝90°，∠B＝30°，AC＝3，∴AB＝6.∴AP的长不能大于6.6. 【答案】D7. 【答案】B8. 【答案】B9. 【答案】D[解析] 有两个内角是60°的三角形，有一个角是60°的等腰三角形，腰和底相等的等腰三角形均可以得到等边三角形，而有两个角相等的等腰三角形不能得到等边三角形．10. 【答案】D[解析] ∵∠BAC＝72°，∠C＝36°，∴∠ABC＝72°.∴∠BAC＝∠ABC.∴CA＝CB.∴△ABC是等腰三角形．∵∠BAC的平分线AD交BC于点D，∴∠DAB＝∠CAD＝36°.∴△ACD 是等腰三角形．∵∠ADB ＝∠CAD ＋∠C ＝72°，∴∠ADB ＝∠B.∴AD ＝AB. ∴△ADB 是等腰三角形．二、填空题11. 【答案】36[解析] 过点B 作BD ⊥AC 于点D.∵∠A ＝30°，AB ＝12，∴在Rt △ABD 中，BD ＝12AB ＝12×12＝6. ∴S △ABC ＝12AC·BD ＝12×12×6＝36.12. 【答案】32[解析] 由题意知，应分两种情况：(1)当腰长为6 cm 时，三角形的三边长为6 cm ，6 cm ，13 cm ，6＋6＜13，不能构成三角形；(2)当腰长为13 cm 时，三角形的三边长为6 cm ，13 cm ，13 cm ，能构成三角形，周长＝2×13＋6＝32(cm)．13. 【答案】50[解析] ∵AB ＝AC ，E 为BC 的中点，∴∠BAE ＝∠EAD ＝20°.∴∠BAD ＝40°，又∵BD ⊥AC ，∴∠ABD ＝90°－∠BAD ＝90°－40°＝50°.14. 【答案】2[解析] 过点P 作PE ⊥OB 于点E.∵∠AOP ＝∠BOP ，PD ⊥OA ，PE ⊥OB ， ∴PE ＝PD.∵∠BOP ＝∠AOP ＝15°，∴∠AOB ＝30°. ∵PC ∥OA ，∴∠BCP ＝∠AOB ＝30°. ∴在Rt △PCE 中，PE ＝12PC ＝12×4＝2. ∴PD ＝PE ＝2.故答案是2.15. 【答案】28 cm三、解答题16. 【答案】证明：∵△ABC 是等边三角形，∵DE∥AB，∴∠EDC＝∠B＝60°，∠DEC＝∠A＝60°.∵EF⊥DE，∴∠DEF＝90°.∴∠F＝90°－∠EDC＝30°.∵∠ACB＝∠EDC＝∠DEC＝60°，∴△EDC是等边三角形．∴DE＝DC.∵∠DEF＝90°，∠F＝30°，∴DF＝2DE＝2DC.17. 【答案】证明：∵∠ACB＝90°，∴∠B＋∠BAC＝90°.∵CD⊥AB，∴∠CAD＋∠ACD＝90°.∴∠ACD＝∠B.∵AE是∠BAC的平分线，∴∠CAE＝∠EAB.∵∠EAB＋∠B＝∠CEF，∠CAE＋∠ACD＝∠CFE，∴∠CFE＝∠CEF. ∴CF＝CE.∴△CEF是等腰三角形．18. 【答案】解：(1)∵∠NBC＝60°，∠NAC＝30°，∴∠ACB＝30°.∴AB＝BC.∵AB＝15×2＝30(海里)，∴BC＝30 海里，即从海岛B到灯塔C的距离为30海里．(2)过点C作CP⊥AB于点P，则线段CP的长为小船与灯塔C的最短距离．∵∠NBC＝60°，∠BPC＝90°，∴∠PCB＝90°－60°＝30°.∴PB＝12BC＝15海里．∵15÷15＝1(时)，∴这条船继续向正北方向航行，在上午11时小船与灯塔C 的距离最短．19. 【答案】解:(1)证明:∵OB=OC ， ∴∠OBC=∠OCB.∵锐角三角形ABC 的两条高BD ，CE 相交于点O ， ∴∠BEC=∠CDB=90°.∵∠BEC+∠BCE+∠ABC=∠CDB+∠DBC+∠ACB=180°， ∴180°-∠BEC-∠BCE=180°-∠CDB-∠DBC ， ∴∠ABC=∠ACB ，∴AB=AC ，∴△ABC 是等腰三角形. (2)点O 在∠BAC 的平分线上.理由:连接AO 并延长交BC 于点F .在△AOB 和△AOC 中，∴△AOB ≌△AOC (SSS)，∴∠BAF=∠CAF ， ∴点O 在∠BAC 的平分线上.20. 【答案】解：PE ＝PF ＋CH.证明如下：连接AP.∵PE ⊥AB ，PF ⊥AC ，CH ⊥AB ，∴S △ABP ＝12AB·PE ，S △ACP ＝12AC·PF ，S △ABC ＝12AB·CH.∵S △ABP ＝S △ACP ＋S △ABC ， ∴12AB·PE ＝12AC·PF ＋12AB·CH. ∵AB ＝AC ，∴PE ＝PF ＋CH.。

人教版数学八年级上册13.3 等腰三角形同步练习(解析版)

人教版数学八年级上册13.3：等腰三角形同步练习一．选择题（共15小题）1．在Rt△ABC中，∠C＝90°，∠B＝30°，斜边AB的长为2cm，则AC长为（）A．4 cm B．2 cm C．1 cm D．cm2．一个等腰三角形但不是等边三角形，它的角平分线、高线、中线总数共（）条．A．9B．7C．6D．33．如图，△ABC是等边三角形，AE⊥BC于E，AD⊥CD于D，AB∥CD，则图中60°的角有（）A．3个B．4个C．5个D．6个4．下列判断不正确的是（）A．等腰三角形的两底角相等B．等腰三角形的两腰相等C．等边三角形的三个内角都是60°D．两个内角分别为120°、40°的三角形是等腰三角形5．在△ABC中，∠ACB＝90°，∠B＝30°，CD⊥AB于D，若AC＝6，则BD等于（）A．6B．3C．9D．126．等腰三角形的对称轴，最多可以有（）A．1条B．3条C．6条D．无数条7．等腰三角形两边的长分别为2cm和5cm，则这个三角形的周长是（）A．9cm B．12cmC．9cm或12cm D．在9cm或12cm之间8．如图，在△ABC中，AB＝AC，D为BC的中点，E为AC边上一点，且AE＝AD，∠BAC ＝40°，则∠EDC的度数是（）A．10°B．20°C．30°D．40°9．一个三角形有两条边相等，这个三角形一边等于5cm，一边等于10cm，则另一边等于（）A．5cm B．10cm C．15cm D．12cm10．如图，△ABC是等腰三角形，AD是底边BC上的高线，DE⊥AB于E，DF⊥AC于F，图中除AB＝AC外，相等的线段共有（）A．1对B．2对C．3对D．4对11．等腰三角形一腰上的高与底边所夹的角为a，则这个等腰三角形的顶角为（）A．a B．90°﹣a C．12a D．2a12．等腰三角形的底角为a，则a的取值范围是（）A．a≤45°B．0°＜a＜90°C．45°＜a＜90°D．0°≤a＜90°13．如图，在等边三角形ABC中，三条中线AE，BD，CF相交于点O，则等边三角形ABC 中，从△BOF到△COD需要经过的变换是（）A．轴对称变换B．旋转变换C．平移变换D．相似变换14．如果以4cm长的线段为底组成一个等腰三角形，腰长x的取值范围是（）A．x＞4cm B．x＞2cm C．x≥4cm D．x≥2cm15．等腰三角形周长是32cm，一边长为10cm，则其他两边的长分别为（）A．10cm，12cm B．11cm，11cmC．11cm，11cm或10cm，12cm D．不能确定二．填空题（共6小题）16．若等腰三角形的一腰上的高与另一腰的夹角等于50°，则其顶角的度数为．若等腰三角形的一腰上的高与底边的夹角等于50°，则其顶角的度数为．17．一个等腰三角形的腰长为3cm，则底边长的取值范围是．18．如图，AB＝AC，∠A＝100°，AB∥CD，则∠BCD＝度．19．等腰三角形的顶角与底角的度数之比为4：1，则它的各内角度数为．20．△ABC中，∠A：∠B：∠C＝1：2：3，AB＝10，则BC＝．21．（1）等腰三角形的一个角为100°，那么另外两个角分别为．（2）等腰三角形的一个角为50°，则底角是．三．解答题（共9小题）22．已知等腰三角形的周长为28cm，其中的一边长是另一边长的倍，求这个等腰三角形各边的长．23．如图，已知AB＝AC，D为BC边中点，你能说出AD与BC的位置关系吗？请说明理由．24．如图，△ABC是等腰三角形，且AB＝AC，试作出BC边上的中线和高以及∠A的平分线，从中你发现了什么？与其他同学进行交流．25．如图，在△ABC中，AB＝AC，∠C＝2∠A，BD平分∠ABC．请找出图中其他的等腰三角形，并选择其中的一个说明理由．26．已知D是等腰△ABC底边BC上的一个点，DE⊥AB于E，DF⊥AC于F，当D点在什么位置时，DE＝DF，并加以证明．27．如图，AD是等腰△ABC顶角的外角的平分线，那么AD与BC平行吗？为什么？28．如图，在△ABC中，AD平分∠BAC，G是CA延长线上一点，GE∥AD交AB于F．交BC于E，试判断△AGF的形状并加以证明．29．如图，在等腰△ABC中，AB＝AC，AD是BC边上的高，点E、F分别是边AB、AC上的点，且EF∥BC．（1）试说明△AEF是等腰三角形；（2）试比较DE与DF的大小关系，并说明理由．30．已知：如图，△ABC中，AB＝AC，D是BC延长线上一点，E是AC延长线上一点，且DE∥AB，求证：ED＝EC．人教版数学八年级上册13.3：等腰三角形同步练习参考答案一．选择题（共15小题）1．在Rt△ABC中，∠C＝90°，∠B＝30°，斜边AB的长为2cm，则AC长为（）A．4 cm B．2 cm C．1 cm D．cm【解答】解：∵∠C＝90°，∠B＝30°，∴AB＝2AC，∵AB＝2cm，∴AC＝AB＝1cm，故选：C．2．一个等腰三角形但不是等边三角形，它的角平分线、高线、中线总数共（）条．A．9B．7C．6D．3【解答】解：由于任意一个三角形都有三条角平分线、三条高线、三条中线，而等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合，所以一个等腰三角形但不是等边三角形，它的角平分线、高线、中线总数共7条．故选：B．3．如图，△ABC是等边三角形，AE⊥BC于E，AD⊥CD于D，AB∥CD，则图中60°的角有（）A．3个B．4个C．5个D．6个【解答】解：∵△ABC是等边三角形，∴∠ABC＝∠ACB＝∠CAB＝60°∵AB∥CD，∴∠ACD＝∠CAB＝60°，∵AD⊥CD，∴∠DAB＝90°，∵AE⊥BC，∴∠BAE＝∠CAE＝30°，∴∠DAE＝60°∴图中60°的角有5个，故选：C．4．下列判断不正确的是（）A．等腰三角形的两底角相等B．等腰三角形的两腰相等C．等边三角形的三个内角都是60°D．两个内角分别为120°、40°的三角形是等腰三角形【解答】解：A、等腰三角形的两底角相等，正确，故本选项错误；B、等腰三角形的两腰相等，正确，故本选项错误；C、等边三角形的三个内角都是60°，正确，故本选项错误；D、两个内角分别为120°、40°的三角形的第三个内角为20°，不是等腰三角形，故本选项正确．故选：D．5．在△ABC中，∠ACB＝90°，∠B＝30°，CD⊥AB于D，若AC＝6，则BD等于（）A．6B．3C．9D．12【解答】解：∵∠ACB＝90°，CD⊥AB，∴∠ACD＝∠B＝30°，∵AC＝6，∴AD＝AC＝×6＝3，AB＝2AC＝2×6＝12，∴BD＝AB﹣AD＝12﹣3＝9．故选：C．6．等腰三角形的对称轴，最多可以有（）A．1条B．3条C．6条D．无数条【解答】解：等腰三角形为等边三角形时对称轴最多，可以有3条．故选：B．7．等腰三角形两边的长分别为2cm和5cm，则这个三角形的周长是（）A．9cm B．12cmC．9cm或12cm D．在9cm或12cm之间【解答】解：当腰长是2cm时，因为2+2＜5，不符合三角形的三边关系，应排除；当腰长是5cm时，因为5+5＞2，符合三角形三边关系，此时周长是12cm．故选：B．8．如图，在△ABC中，AB＝AC，D为BC的中点，E为AC边上一点，且AE＝AD，∠BAC ＝40°，则∠EDC的度数是（）A．10°B．20°C．30°D．40°【解答】解：∵在△ABC中，D为BC中点，AB＝AC，∴AD⊥BC，AD是∠BAC的角平分线，又∵AD＝AE，∠BAC＝40°，∴∠ADE＝80°∴∠EDC＝∠ADC﹣∠ADE＝90°﹣80°＝10°．故选：A．9．一个三角形有两条边相等，这个三角形一边等于5cm，一边等于10cm，则另一边等于（）A．5cm B．10cm C．15cm D．12cm【解答】解：当第三边是5cm时，则5+5＝10，不能构成三角形，当另一边长是10cm时，能构成三角形．故选：B．10．如图，△ABC是等腰三角形，AD是底边BC上的高线，DE⊥AB于E，DF⊥AC于F，图中除AB＝AC外，相等的线段共有（）A．1对B．2对C．3对D．4对【解答】解：∵△ABC是等腰三角形，AD是底边BC上的高线，∴BD＝CD，∠BAD＝∠CAD，∵DE⊥AB，DF⊥AC，∴DE＝DF，∠BED＝∠DFC＝90°，在Rt△BED和Rt△CFD中，，∴Rt△BED≌Rt△CFD（HL），∴BE＝CF，∵AB＝AC，∴AE＝AF．故图中除AB＝AC外，相等的线段共有4对．故选：D．11．等腰三角形一腰上的高与底边所夹的角为a，则这个等腰三角形的顶角为（）A．a B．90°﹣a C．12a D．2a【解答】解：如图，AB＝AC，BD是腰AC的高，则∠DBC＝α∴∠C＝90°﹣α∴∠A＝180°﹣2（90°﹣α）＝2α故选：D．12．等腰三角形的底角为a，则a的取值范围是（）A．a≤45°B．0°＜a＜90°C．45°＜a＜90°D．0°≤a＜90°【解答】解：∵等腰三角形的底角为a，且三角形的内角和等于180°，∴0°＜2a＜180°，∴0°＜a＜90°．故选：B．13．如图，在等边三角形ABC中，三条中线AE，BD，CF相交于点O，则等边三角形ABC 中，从△BOF到△COD需要经过的变换是（）A．轴对称变换B．旋转变换C．平移变换D．相似变换【解答】解：∵△BOF与△COD是关于OE的轴对称图形，∴从△BOF到△COD需要经过轴对称变换．故选A14．如果以4cm长的线段为底组成一个等腰三角形，腰长x的取值范围是（）A．x＞4cm B．x＞2cm C．x≥4cm D．x≥2cm【解答】解：此等腰三角形的底为4cm，则有2x＞4，解得x＞2，故选：B．15．等腰三角形周长是32cm，一边长为10cm，则其他两边的长分别为（）A．10cm，12cm B．11cm，11cmC．11cm，11cm或10cm，12cm D．不能确定【解答】解：当该边是腰时，底边是32﹣20＝12cm，则另外两边是10cm，12cm；当该边是底时，则腰的长为：（32﹣10）÷2＝11cm，则另外两边是11cm，11cm；经检验，两种情况都符合三角形的三边关系．故选：C．二．填空题（共6小题）16．若等腰三角形的一腰上的高与另一腰的夹角等于50°，则其顶角的度数为40°或140°．若等腰三角形的一腰上的高与底边的夹角等于50°，则其顶角的度数为100°．【解答】解：（1）①当为锐角三角形时可以画图，高与右边腰成50°夹角，由三角形内角和为180°可得，顶角为40°；②当为钝角三角形时可画图，此时垂足落到三角形外面，因为三角形内角和为180°，由图可以看出等腰三角形的顶角的补角为40°，三角形的顶角为140°．（2）如图，①顶角是钝角时，∠B＝90°﹣50°＝40°，则顶角＝180°﹣2×40°＝100°，是钝角，符合；②顶角是锐角时，∠B＝90°﹣50°＝40°，∠A＝180°﹣2×40°＝100°，是钝角，不符合．故答案为：40°或140°；100°．17．一个等腰三角形的腰长为3cm，则底边长的取值范围是0＜底边＜6cm．【解答】解：∵3﹣3＝0，3+3＝6cm，∴底边的取值范围是0＜底边＜6cm．故答案为：0＜底边＜6cm．18．如图，AB＝AC，∠A＝100°，AB∥CD，则∠BCD＝40度．【解答】解：∵AB＝AC∴∠B＝∠ACB＝（180﹣∠A）＝40°∵AB∥CD∴∠BCD＝∠B＝40°．故填40．19．等腰三角形的顶角与底角的度数之比为4：1，则它的各内角度数为120°，30°，30°．【解答】解：设等腰三角形的各角为4x，x，x∵4x+x+x＝180°∴x＝30°∴三个内角分别是120°，30°，30°．故填120°，30°，30°．20．△ABC中，∠A：∠B：∠C＝1：2：3，AB＝10，则BC＝5．【解答】解：由∠A：∠B：∠C＝1：2：3，可设∠A＝x°，则∠B＝2x°，∠C＝3x°．∵∠A+∠B+∠C＝180°，∴x+2x+3x＝180，∴x＝30，∴∠A＝30°，∠B＝60°，∠C＝90°，∴BC＝AB＝×10＝5．故答案为5．21．（1）等腰三角形的一个角为100°，那么另外两个角分别为40°，40°．（2）等腰三角形的一个角为50°，则底角是50°，65°．【解答】解：（1）∵等腰三角形的一个角为100°∴两底角的和＝180°﹣100°＝80°又∵等腰三角形的两底角相等∴两底角都为40°．（2）当50°的角是底角，则底角就为50°；当50°的角是顶角，则两底角的和等于130°，所以底角等于65°．故填40°，40°；50°，65°．三．解答题（共9小题）22．已知等腰三角形的周长为28cm，其中的一边长是另一边长的倍，求这个等腰三角形各边的长．【解答】解：设等腰三角形的一边长为xcm，则另一边长为xcm，则等腰三角形的三边有两种情况：xcm，xcm，xcm或xcm，xcm，xcm，则有：①x+x+x＝28，得x＝8cm，所以三边为：8cm、8cm、12cm；②x+x+x＝28，得x＝7cm，所以三边为7cm、10.5cm、10.5cm．因此等腰三角形的三边的长为：8cm，8cm，12cm或7cm，10.5cm，10.5cm．23．如图，已知AB＝AC，D为BC边中点，你能说出AD与BC的位置关系吗？请说明理由．【解答】解：AD⊥BC．理由如下：∵AB＝AC，D为BC边中点，∴AD⊥BC．24．如图，△ABC是等腰三角形，且AB＝AC，试作出BC边上的中线和高以及∠A的平分线，从中你发现了什么？与其他同学进行交流．【解答】解：如图，过点A作AD⊥BC于点D，在Rt△ABD和Rt△ACD中，∵AB＝AC，AD＝AD，∴Rt△ABD≌Rt△ACD（HL）∴BD＝CD，即AD也是中线，∴∠BAD＝∠CAD，即AD又是高线，所以等腰三角形底边上的中线、高以及顶角的角平分线重合．25．如图，在△ABC中，AB＝AC，∠C＝2∠A，BD平分∠ABC．请找出图中其他的等腰三角形，并选择其中的一个说明理由．【解答】解：△ABD、△BCD．理由：∵在△ABC中，AB＝AC，∠C＝2∠A，∴∠ABC＝∠C＝2∠A，∵∠A+∠ABC+∠C＝180°，∴∠A+2∠A+2∠A＝180°，解得：∠A＝36°，∴∠ABC＝∠C＝72°，∵BD平分∠ABC，∴∠ABD＝∠DBC＝36°，∴∠A＝∠ABD＝36°，∠BDC＝∠C＝72°，∴△ABD与△BCD是等腰三角形．26．已知D是等腰△ABC底边BC上的一个点，DE⊥AB于E，DF⊥AC于F，当D点在什么位置时，DE＝DF，并加以证明．【解答】解：当D是BC中点时DE＝DF，理由：∵AB＝AC，∴∠B＝∠C；∵∠BED＝∠CFD＝90°，BD＝CD；∴△BDE≌△CDF；∴DE＝DF．27．如图，AD是等腰△ABC顶角的外角的平分线，那么AD与BC平行吗？为什么？【解答】解：AD∥BC．∵△ABC是等腰三角形，∴∠B＝∠C，又∵∠EAC是△ABC的一个外角，∴∠EAC＝∠B+∠C＝2∠B，∵AD是等腰△ABC顶角的外角的平分线，∴2∠DAC＝∠EAC，∴∠C＝∠DAC，∴AD∥BC（内错角相等，两直线平行）．28．如图，在△ABC中，AD平分∠BAC，G是CA延长线上一点，GE∥AD交AB于F．交BC于E，试判断△AGF的形状并加以证明．【解答】解：△AGF是等腰三角形；理由：∵GE∥AD，∴∠G＝∠CAD，∠BAD＝∠GF A，∵AD平分∠BAC，∴∠CAD＝∠BAD，∴∠G＝∠GF A，∴AG＝AF，∴△AGF是等腰三角形．29．如图，在等腰△ABC中，AB＝AC，AD是BC边上的高，点E、F分别是边AB、AC上的点，且EF∥BC．（1）试说明△AEF是等腰三角形；（2）试比较DE与DF的大小关系，并说明理由．【解答】解：（1）∵EF∥BC，∴∠AEF＝∠B，∠AFE＝∠C．又∵AB＝AC，∴∠B＝∠C，∴∠AEF＝∠AFE，∴AE＝AF，即△AEF是等腰三角形；（2）DE＝DF．理由如下：∵AD是等腰三角形ABC的底边上的高，∴AD也是∠BAC的平分线．又∵△AEF是等腰三角形，∴AG是底边EF上的高和中线，∴AD⊥EF，GE＝GF，∴AD是线段EF的垂直平分线，∴DE＝DF．30．已知：如图，△ABC中，AB＝AC，D是BC延长线上一点，E是AC延长线上一点，且DE∥AB，求证：ED＝EC．【解答】证明：∵AB＝AC，∴∠B＝∠ACB，∵AB∥ED，∴∠B＝∠D，∴∠ACB＝∠D，又∵∠ACB＝∠ECD，∴∠ECD＝∠D，∴ED＝EC．。

人教版八年级数学上册同步练习 13.3 等腰三角形同步练习及答案.doc

第13章《轴对称》同步练习（§13.3）班级学号姓名得分一、填空题（每题3分，共30分）1．等腰三角形的一个角是110°,则它的底角为_______°．2．等腰三角形的腰长是6，则底边长3，周长为______________________．3．等腰三角形一个底角为50°，则此等腰三角形顶角为________________________． 4．在△ABC 中，AB =AC ，点D 在AC 边上，且BD =BC =AD ，则∠A = °．5．已知直线yy ′⊥xx ′，垂足为O ，则图形①与图形_____成轴对称 6．等腰三角形一腰上的中线把这个三角形的周长分成15㎝和12㎝，则这个三角形的底边长为㎝．7．腰长为12㎝，底角为15°的等腰三角形的面积为． 8．到三角形各顶点距离相等的点是三角形的交点． 9．在直角坐标系内有两点A （-1，1）、B （2，3），若M 为x 轴上一点，且MA +MB 最小，则M 的坐标是________，MA +MB =________．10．等腰三角形的周长为13cm,其中一边长为5cm,则该等腰三角形的腰边长为_____cm.．二、选择题（每题3分，共24分）11．点M （1，2）关于原点对称的点的坐标为（）A ．（—1，2）B ．（－1，－2）C ．（1，－2）D ．（2，－1）12．下列说法正确的是（）A ．等腰三角形的高、中线、角平分线互相重合B ．顶角相等的两个等腰三角形全等C ．等腰三角形一边不可以是另一边的二倍D ．等腰三角形的两个底角相等13．已知∠AOB =30°，点P 在∠AOB 的内部，P 1与P 关于OB 对称，P 2与P关于OA 对称，则P ，P 1，P 2三点构成的三角形是（） A ．直角三角形 B ．钝角三角形C ．等腰三角形D ．等边三角形14．如图，DE 是∆ABC 中AC 边的垂直平分线，若BC =8厘米，AB =10厘米，则∆EBC 的周长为（）厘米 A ．16 B ．28 C ．26 D ．18 15．等腰三角形的对称轴，最多可以有（）A ．1条B ．3条C ．6条D ．无数条① y ′③②x ′Oxy （第5题）（第14题）E DABC16．下列判断不正确的是（）A ．等腰三角形的两底角相等B ．等腰三角形的两腰相等C ．等边三角形的三个内角都是60°D ．两个内角分别为120°、40°的三角形是等腰三角形 17．下列轴对称图形中对称轴最多的是（）A ．等腰直角三角形；B ．正方形；C ．有一个角为60°的等腰三角形；D ．圆18．如图，∠A =15°，AB =BC =CD =DE =EF ，则∠FEM =（）A ．45°B ．60°C ．75°D ．90°三、解答题（共46分）19．（7分）已知，如图ΔABC 中，AB ＝AC ，D 点在BC 上，且BD ＝AD ，DC ＝AC ．将图中的等腰三角形全都写出来．并求∠B 的度数．20．（7分）如图，在⊿ABC 中，∠ABC 和∠ACB 的平分线交于点O ，过O 点作EF ∥BC ，交AB 于E ，交AC 于F ，BE =5cm ，CF =3cm ，求EF 的长．21．（8分）如图，已知P 点是∠AOB 平分线上一点，PC，（1）∠PCD =∠PDC 吗？为什么？（2）OP 是CD 的垂直平分线吗？为什么？NMEFCBAD （第18题）BC D22．（8分）已知：如图，AD 平分∠BAC ，DE ⊥AB ，DF ⊥AC ，DB =DC ，求证：△ABC 是等腰三角形．23．（8分）如图，已知直线MN 与MN 同侧两点A 、B 求作：点P ，使点P 在MN 上，且∠APM ＝∠BPN24．（8分）如图，在⊿ABC 中，∠ACB =90，DE是AB 的垂直平分线，∠CAE ：∠EAB =4：1．求∠B 的度数．D A C BEC参考答案一、填空题1．35 2．15 3．80°4．36°5．②6．7或11 7．36 8．线段中垂线9．)0,41(，5 10．5或4二、选择题11．B 12．D 13．D 14．D 15．B 16．D 17．D 18．C三、解答题19．⊿ABC，⊿ADB，⊿ADC ，∠B=36°20．EF=8㎝21．（1）利用角平分线性质得PC=PD，所以∠PCD=∠PDC （2）成立22．略23．略24．15°。

人教版八年级上册数学《等腰三角形》同步训练附答案

人教版八年级数学上册《13.3等腰三角形》同步训练1．如图，△ABC是等边三角形，△BCD是等腰三角形，且BD＝CD，过点D作AB的平行线交AC于点E，若AB＝8，DE＝6，则BD的长为（）A．6B．C．D．2．求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形．已知：如图，∠CAE是△ABC的外角，∠1＝∠2，AD∥BC．求证AB＝AC．以下是排乱的证明过程：①又∠1＝∠2，②∴∠B＝∠C，③∵AD∥BC，④∴∠1＝∠B，∠2＝∠C，⑤∴AB＝AC．证明步骤正确的顺序是（）A．③→②→①→④→⑤B．③→④→①→②→⑤C．．①→②→④→③→⑤D．①→④→③→②→⑤3．如图，△ABC是等边三角形，AD是BC边上的中线，点E在AD上，且DE＝BC，则∠AFE＝（）A．100°B．105°C．110°D．115°4．如图，已知△ABC是等边三角形，D是BC边上的一个动点（异于点B、C），过点D作DE⊥AB，垂足为E，DE的垂直平分线分别交AC、BC于点F、G，连接FD，FE．当点D在BC边上移动时，有下列三个结论：①△DEF一定为等腰三角形；②△CFG一定为等边三角形；③△FDC可能为等腰三角形．其中正确的有（）A．0个B．1个C．2个D．3个5．如图，在Rt△ABC中，∠A＝90°，CM平分∠ACB交AB于点M，过点M作MN∥BC 交AC于点N，且MN平分∠AMC，若AN＝2，则BC的长为（）A．12B．16C．20D．86．如图，AB∥CD，CB平分∠ACD，点E在AB上，DE⊥CB，垂足为F，连接AF则下列结论中错误的是（）A．AB＝AC B．∠AFC＝∠DC．∠AEF+∠D＝180°D．∠AFC＞∠FCD7．如果一个等腰三角形的两边长为2和5，那么这个三角形的周长是（）A．9B．12C．9或12D．不确定8．若等腰三角形的一个内角比另一个内角大30°，则这个等腰三角形的底角度数是（）A．50°B．80°C．50°或70°D．80°或40°9．若等腰三角形一边长9cm，另一边长4cm，则它的周长为（）A．22cm B．17cm C．22cm或17cm D．22cm或19cm 10．等腰三角形一边长9cm，另一边长4cm，它的第三边是（）cm．A．4 B．9 C．4或9 D．大于5且小于1311．下列对△ABC的判断，错误的是（）A．若∠A：∠B：∠C＝1：2：3，则△ABC是直角三角形B．若AB＝BC，∠C＝50°，则∠B＝50°C．若AB＝BC，∠A＝60°，则△ABC是等边三角形D．若∠A＝20°，∠C＝80°，则△ABC是等腰三角形12．已知等腰三角形的周长为19，一边长为8，则此等腰三角形的底边长为（）A．3B．8C．3或8D．8或5.513．若等腰三角形的顶角是大于60°的锐角，则底角度数的取值范围是（）A．x＜60°B．x≤60°C．45°＜x＜60°D．45°≤x＜60°14．△ABC中，∠BAC＝∠BCA，AD平分∠BAC，DE∥AC，下列说法正确的是（）A．∠B＝36°B．∠ADB＝108°C．∠ADB＝3∠EDA D．∠AED＝3∠B 15．等腰三角形的两边长为3和8，则这个等腰三角形的周长是（）A．14B．19C．14或19D．2016．如图，在△ABC中，AB＝AC，尺规作图：（1）分别以B，C为圆心，BC长为半径作弧，两弧交于点D；（2）作射线AD，连接BD，CD．则下列结论中错误的是（）A．∠BAD＝∠CAD B．△BCD是等边三角形C．AD垂直平分BC D．S四边形ABDC＝AD⋅BC17．如图，在△ABC中，AB＝AC，AC的垂直平分线l交BC于点D．若∠BAD＝78°，则∠B的度数是（）A．34°B．30°C．28°D．26°18．如图，在△ABC中，AB＝AC，以点C为圆心，CB长为半径画弧，交AB于点B和点D，再分别以点B，D为圆心，大于BD长为半径画弧，两弧相交于点M，作射线CM 交AB于点E．若AE＝5，BE＝1，则EC的长度是（）A．B．C．9D．19．如图，在等腰△ABD中，∠A＝32°，取大于AB的长为半径，分别以点A，B为圆心作弧相交于两点，过此两点的直线交AD边于点E（作图痕迹如图所示），连接BE，BD，则∠EBD的度数为．20．如图，在△ABC中，AB＝AC，以点B为圆心，BC长为半径画弧交AC于点C和点D，再分别以点C和点D为圆心，大于DC长为半径画弧，两弧相交于点F，作射线BF交AC于点E．若∠A＝40°，则∠EBC＝度．21．如图，在边长为2的等边三角形ABC中，D，E分别为AB，BC的中点，EF⊥AC于点F，G为EF的中点，连接DG，则DG的长为．22．如图，在△ABC中，AB＝AC，∠B＝35°，D是BC边上的动点，连接AD，若△ABD 为直角三角形，则∠DAC的度数为．23．已知等腰三角形的一个内角为110°，则等腰三角形的底角的度数为．24．用三根木棒首尾相连围成一个等腰三角形，其中两根木棒的长度分别为3cm和6cm，则第三根木棒长为cm．25．如图，在△ABC中，AB＝AC，AD平分∠BAC交BC于点D，BC＝16cm，则BD＝cm．26．如图，在平面直角坐标系中，点A的坐标为（0，2），点B的坐标为（4，0），在y轴上取一点C使△ABC为等腰三角形，符合条件的C点有个．27．如图，在△ABC中，AB＝AC，∠BAC＝108°，AC的中垂线交BC于点D，交AC于点E，连接AD，则图中等腰三角形有个．28．如图，在△ABC中，以点B为圆心，BA长为半径画弧，交BC边于点D，连接AD．若∠B＝40°，∠C＝32°，求∠DAC的度数．29．如图，已知△ABC中，AB＝AC，∠ABC、∠ACB的平分线交于点E，直线AE交BC于点D，说明AD⊥BC的理由．30．若关于x，y的二元一次方程组的解都是正数．（1）求a的取值范围；（2）若此方程组的解是一个等腰三角形的一条腰和底边的长，且这个等腰三角形的周长为12，求a的值．31．如图，在△ABC中，D是三角形内一点，连接DA、DB、DC，且∠1＝∠2，∠3＝∠4，求证：AB＝AC．参考答案1．解：连接AD交BC于点O，取AC中点N，连接ON，如图，∵△ABC是等边三角形，∴AB＝AC＝BC＝8，∠ABC＝60°，∵△BCD是等腰三角形，∴BD＝DC，∴AD垂直平分BC，∴BO＝CO＝4，∵AN＝CN，∴ON＝AB＝4，ON∥AB，∵AB∥DE，∴ON∥DE，∴OD＝AO，∴AO＝4，∴OD＝2，在Rt△BOD中，BD＝＝2．故选：B．2．解：∵③AD∥BC，∴④∠1＝∠B，∠2＝∠C，∵①∠1＝∠2，∴②∠B＝∠C，∴⑤AB＝AC，故证明步骤正确的顺序是③→④→①→②→⑤，3．解：∵△ABC是等边三角形，∴∠BAC＝60°，∵AD是BC边上的中线，∴∠BAD＝BAC＝30°，AD⊥BC，BD＝CD＝BC，∴∠CDE＝90°，∵DE＝BC，∴DE＝DC，∴∠DEC＝∠DCE＝45°，∴∠AEF＝∠DEC＝45°，∴∠AFE＝180°﹣∠BAD﹣∠AEF＝180°﹣30°﹣45°＝105°，故选：B．4．解：∵DE的垂直平分线分别交AC、BC于点F、G，∴FE＝FD，∴△DEF一定为等腰三角形，故①正确；∵DE⊥AB，DE⊥FG，∴AB∥FG，∴∠FGC＝∠B＝60°，又∵△ABC是等边三角形，∴∠C＝60°，∴△CFG中，∠C＝∠CFG＝∠CGF，∴△CFG一定为等边三角形；故②正确；∵∠FDC＞∠FGC＝60°，∠C＝60°，∠CFD＜∠CFG＝60°，∴△FDC不可能为等腰三角形．故③错误；5．解：∵CM平分∠ACB交AB于点M，∴∠NCM＝∠BCM，∵MN∥BC∴∠NCM＝∠BCM＝∠NMC，∵MN平分∠AMC，∴∠AMN＝∠NMC＝∠B，∴∠ACB＝2∠B，NM＝NC，∴∠B＝30°；∵AN＝2，∠AMN＝∠B＝30°，∴MN＝2AN＝4，∴NM＝NC＝4，∴AC＝AN+NC＝6，∴BC＝2AC＝12，故选：A．6．解：∵AB∥CD，∴∠B＝∠BCD，∠AEF+∠D＝180°，故C选项正确；∵CB平分∠ACD，∴∠ACB＝∠BCD，∴∠ACB＝∠B，∴AC＝AB，故A选项正确；∵DE⊥CB，∴∠CFD＝90°，∴∠D+∠BCD＝90°，假如∠AFC＝∠D，则∠CAF＝∠CFD＝90°，而∠CAF不一定是90°，∴∠AFC与∠D不一定相等，故B选项错误；∵∠AFC是△ABF的外角，∴∠AFC＞∠B，∵∠B＝∠FCD，∴∠AFC＞∠FCD，故D选项正确，故选：B．7．解：∵2+2＝4＜5，∴腰的长不能为2，只能为5，∴等腰三角形的周长＝2×5+2＝12，故选：B．8．解：在△ABC中，设∠A＝x，∠B＝x+30°，分情况讨论：当∠A＝∠C为底角时，2x+（x+30°）＝180°，解得x＝50°，底角∠A＝50°；当∠B＝∠C为底角时，2（x+30°）+x＝180°，解得x＝40°，底角∠B＝70°．故这个等腰三角形的底角的度数为50°或70°．故选：C．9．解：①当腰为4cm时，三边为4cm，4cm，9cm，∵4+4＜9，∴不符合三角形的三边关系定理，此种情况舍去；②当腰为9cm时，三边为4cm，9cm，9cm，此时符合三角形的三边关系定理，此时等腰三角形的周长是4cm+9cm+9cm＝22cm，故选：A．10．解：①当腰为4cm时，三边为4cm，4cm，9cm，∵4+4＜9，∴不符合三角形的三边关系定理，此种情况舍去；②当腰为9cm时，三边为4cm，9cm，9cm，此时符合三角形的三边关系定理，所以三角形的第三边为9cm，故选：B．11．解：A．若∠A：∠B：∠C＝1：2：3，则∠A＝30°，∠B＝60°，∠C＝90°，所以△ABC是直角三角形，故此选项正确，不符合题意；B．若AB＝BC，∠C＝50°，则∠A＝∠C＝50°，∠B＝100°，故此选项错误，符合题意；C．若AB＝BC，∠A＝60°，则∠A＝∠C＝60°，∠B＝60°，所以△ABC是等边三角形，故此选项正确，不符合题意；D．若∠A＝20°，∠C＝80°，则∠B＝80°，∠C＝∠B＝80°，所以△ABC是等腰三角形，故此选项正确，不符合题意．故选：B．12．解：本题可分两种情况：①当腰长为8时，底边长＝19﹣2×8＝3；经检验，符合三角形三边关系；②底边长为8，此时腰长＝（19﹣8）÷2＝5.5，经检验，符合三角形三边关系；因此该等腰三角形的底边长为3或8．故选：C．13．解：设等腰三角形的底角为x°，则顶角为（180°﹣2x），由题意可得：60°＜180°﹣2x＜90°，∴45°＜x＜60°，∴底角度数的取值范围是45°＜x＜60°，故选：C．14．解：设∠CAD＝x°，∵AD平分∠BAC，∠BAC＝∠BCA，∴∠BCA＝∠BAC＝2x°，∵DE∥AC，∴∠BDE＝∠BCA＝2x°，∠ADE＝∠CAD＝x°，∴∠ADB＝∠BDE+∠ADE＝2x°+x°＝3x°，即∠ADB＝3∠EDA，故选：C．15．解：①若3是腰，则另一腰也是3，底是8，但是3+3＜8，故不构成三角形，舍去．②若3是底，则腰是8，8．3+8＞8，符合条件．成立．故周长为：3+8+8＝19．故选：B．16．解：根据作图方法可得BC＝BD＝CD，∵BD＝CD，∴点D在BC的垂直平分线上，∵AB＝AC，∴点A在BC的垂直平分线上，∴AD是BC的垂直平分线，故C结论正确；∴O为BC中点，∴AO是△BAC的中线，∵AB＝AC，∴∠BAD＝∠CAD，故A结论正确；∵BC＝BD＝CD，∴△BCD是等边三角形，故B结论正确；∵四边形ABDC的面积＝S△BCD+S△ABC＝BC•DO+BC•AO＝BC•AD，故D选项错误，故选：D．17．解：∵AB＝AC，∴∠B＝∠C，∵AC的垂直平分线l交BC于点D，∴AD＝DC，∴∠DAC＝∠C，∵∠ADB＝∠DAC+∠C＝2∠C，∴∠ADB＝2∠B，∵∠BAD＝78°，∴∠B+∠ADB+∠BAD＝∠B+2∠B+78°＝180°，∴∠B＝34°，故选：A．18．解：由作法得CE⊥AB，则∠AEC＝90°，AC＝AB＝BE+AE＝5+1＝6，在Rt△ACE中，CE＝＝，故选：A．19．解：∵AD＝AB，∠A＝32°，∴∠ABD＝∠ADB＝（180°﹣∠A）＝74°，由作图可知，EA＝EB，∴∠ABE＝∠A＝32°，∴∠EBD＝∠ABD﹣∠ABE＝74°﹣32°＝42°，故答案为：42°．20．解：∵AB＝AC，∠A＝40°，∴∠ACB＝（180°﹣40°）÷2＝70°，由题意可知，BC＝BD，∴∠BDC＝∠ACB＝70°，∴∠CBD＝180°﹣70°×2＝40°，由题意可知，BF平分∠DBC，∴∠EBC＝∠CBD＝20°．故答案为：20．21．解：连接DE，∵在边长为2的等边△ABC中，D，E分别为AB，BC的中点，∴DE是△ABC的中位线，∴DE＝1，且DE∥AC，BD＝BE＝EC＝1，∵EF⊥AC于点F，∠C＝60°，∴∠FEC＝30°，∠DEF＝∠EFC＝90°，∴FC＝EC＝，故EF＝＝＝，∵G为EF的中点，∴EG＝，∴DG＝＝，故答案为：．22．解：如图，∵AB＝AC，∠B＝35°，∴∠B＝∠C＝35°，∴∠BAC＝110°，当∠BAD＝90°时，∠DAC＝110°﹣90°＝20°；当∠ADB＝90°时，∵AB＝AC，AD⊥BC，∴∠DAC＝∠BAD＝55°．故答案为：20°或55°．23．解：∵等腰三角形的一个内角是110°，∴等腰三角形的顶角为110°，∴等腰三角形的底角为35°，故答案为：35°．24．解：组成等腰三角形的两根木棒的长度分别为3cm和6cm，根据三角形三边关系可得，组成等腰三角形的第三根木棒长为6cm，故答案为：6．25．解：∵AB＝AC，AD平分∠BAC交BC于点D，∴BD＝DC＝BC，∵BC＝16cm，故答案为：8．26．解：观察图形可知，若以点A为圆心，以AB为半径画弧，与y轴有2个交点，但其中一个与B点重合，故此时符合条件的点由1个；若以点B为圆心，以AB为半径画弧，与y轴有2个交点；线段AB的垂直平分线与y轴有1个交点；∴符合条件的C点有：1+2+1＝4（个），故答案为：4．27．解：∵AB＝AC，∠BAC＝108°，∴△ABC是等腰三角形，∠B＝∠C＝（180°﹣∠BAC）÷2＝36°，∵AC的中垂线交BC于点D，交AC于点E，∴AD＝CD，∴△ADC是等腰三角形，∠DAC＝∠C＝36°，∴∠BAD＝∠BAC﹣∠DAC＝72°，∠ADB＝∠DAC+∠C＝72°，∴∠BAD＝∠ADB，∴△BAD是等腰三角形．故图中等腰三角形有3个．故答案为：3．28．解：∵∠B＝40°，∠C＝32°，∴∠BAC＝180°﹣∠B﹣∠C＝108°，由作图可知：BA＝BD，∴∠BAD＝∠BDA＝（180°﹣∠B）÷2＝70°，∴∠DAC＝∠BAC﹣∠BAD＝38°．29．证明：∵AB＝AC，∴∠ABC＝∠ACB，∵BE平分∠ABC，CE平分∠ACB，∴∠EBC＝，，∴∠EBC＝∠ECB，∴EB＝EC，∴AE垂直平分BC，∴AD⊥BC．30．解：（1）解得，∵若关于x、y的二元一次方程组的解都为正数，∴，解得：a＞1；（2）∵二元一次方程组的解是一个等腰三角形的一条腰和一条底边的长，这个等腰三角形的周长为12，∴2（a﹣1）+a+2＝12，解得：a＝4，∴x＝3，y＝6，故3，3，6不能组成三角形，∴2（a+2）+a﹣1＝12，解得：a＝3，∴x＝2，y＝5，故2，5，5能组成等腰三角形，∴a的值是3．31．证明：∵∠1＝∠2，∴DB＝CD，在△ABD和△ACD中，，∴△ABD≌△ACD（SAS），∴AB＝AC．。

人教版八年级数学上册 13.3 等腰三角形课后训练(含答案)

课后训练基础巩固1．若等腰三角形底角为72°，则顶角为()．A．108°B．72°C．54°D．36°2．如图，在△ABC中，AB＝AC，AD＝BD＝BC，则∠C＝()．A．72°B．60°C．75°D．45°3．若等腰三角形的周长为26 cm，一边为11 cm，则腰长为()．A．11 cm B．7.5 cmC．11 cm或7.5 cm D．以上都不对4．下列三角形：①有两个角等于60°的三角形；②有一个角等于60°的等腰三角形；③三个外角(每个顶点处各取一个外角)都相等的三角形；④一腰上的中线也是这条腰上的高的等腰三角形．其中是等边三角形的有()．A．①②③B．①②④C．①③D．①②③④5．如图所示，已知∠1＝∠2，要使BD＝CD，还应增加的条件是()．①AB＝AC②∠B＝∠C③AD⊥BC④AB＝BCA．①B．①②C．①②③D．①②③④6．如图所示，在△ABC中，∠ACB＝90°，∠B＝30°，CD⊥AB于点D，若AD＝2，则AB＝__________.能力提升7．如图，在△ABC中，AB＝AC，BD和CD分别是∠ABC和∠ACB的平分线，EF过D点，且EF∥BC，图中等腰三角形共有()．A．2个B．3个C．4个D．5个8．如图所示的正方形网格中，网格线的交点称为格点．已知A、B是两格点，如果C 也是图中的格点，且使得△ABC为等腰三角形，则点C的个数是()．A．6 B．7 C．8 D．99．如图，D是△ABC中BC边上一点，AB＝AC＝BD，则∠1和∠2的关系是()．A．∠1＝2∠2 B．∠1＋∠2＝90°C．180°－∠1＝3∠2 D．180°＋∠2＝3∠110．如图，△ABC中，AB＝AC，∠C＝30°，DA⊥BA于A，BC＝4.2 cm，则AD＝__________.11．如图，若B、D、F在AN上，C、E在AM上，且AB＝BC＝CD，EC＝ED＝EF，∠A＝20°，则∠FED＝__________.12．如图，点E，F在BC上，BE＝CF，∠A＝∠D，∠B＝∠C，AF与DE交于点O.(1)求证：AB＝DC；(2)试判断△OEF的形状，并说明理由．13．(综合应用)如图所示，∠AOP＝∠BOP＝15°，PC∥OA，PD⊥OA，若PC＝4，求PD的长．14．如图所示，在△ABC中，AB＝AC，点E在CA的延长线上，且∠AEF＝∠AFE.求证：EF⊥BC.(第14题图) (第15题图)15．如图，在△ABC中，∠ACB＝45°，∠A＝90°，BD是∠ABC的角平分线，CH⊥BD，交B D的延长线于H，求证：BD＝2CH.16．(实际应用题)如图，某船上午11时30分在A处观测岛B在东偏北30°，该船以10海里/时的速度向东航行到C处，再观测海岛在东偏北60°，且船距海岛40海里．(1)求船到达C点的时间；(2)若该船从C点继续向东航行，何时到达B岛正南的D处？参考答案1．D点拨：等腰三角形两底角相等，所以顶角为36°，故选D.2．A点拨：设∠A＝x，由已知可知，∠BDC＝∠C＝∠ABC＝2∠A＝2x，因为∠A＋∠ABC＋∠C＝180°，所以x＋2x＋2x＝180°.解得x＝36°，所以∠C＝72°，故选A.3．C点拨：边长为11 cm的边长可能是腰，也可能是底，所以要分两种情况讨论．一种情况腰长为11 cm；另一种情况底边为11 cm，此时腰长为7.5 cm，两种情况都成立，故选C.4．D点拨：①②为判定定理，③每个外角都相等，则都是120°，所以每个内角都是60°，④一腰上的中线也是这条腰上的高，说明这条线段所在的直线是这条腰的垂直平分线，所以腰等于底，也是等边三角形，四个都成立，故选D.5．C点拨：①②说明△ABC为等腰三角形，由“三线合一”可知BD＝CD，由③能得到△ABD≌△ACD，所以BD＝CD，④不能得到BD＝CD，故选C.6．8点拨：由题意可知，在Rt△ACD和Rt△ABC中，∠ACD＝∠B＝30°，所以AC＝2AD，AB＝2AC.所以AB＝4AD＝4×2＝8.7．D点拨：由题意知，AB＝AC，AE＝AF，BE＝DE，CF＝DF，BD＝CD，所以所有的三角形都是等腰三角形，共有5个，故选D.8．C点拨：如图，共有8个格点．注意3和8也是，故选C.9．D点拨：因为AB＝BD，所以∠B＝180°－2∠1，∠C＝∠1－∠2.因为AB＝AC，所以∠B＝∠C.所以180°－2∠1＝∠1－∠2，整理得180°＋∠2＝3∠1，故选D.10．1.4 cm点拨：由已知可以推出∠B＝∠CAD＝∠C＝30°，AD＝DC，∠C＝30°，DA⊥BA于A，所以BD＝2AD.所以BC＝3DC＝3AD＝4.2(cm)．所以AD＝1.4 cm.11．20°点拨：运用一个外角等于和它不相邻的内角，及等腰三角形两底角相等可求出∠FED＝20°.12．(1)证明：∵BE＝CF，∴BE＋EF＝CF＋EF，即BF＝CE.又∵∠A＝∠D，∠B＝∠C，∴△ABF≌△DCE(AAS)．∴AB＝DC.(2)解：△OEF为等腰三角形，理由如下：∵△ABF≌△DCE，∴∠AFB＝∠DEC.∴OE＝OF.∴△OEF为等腰三角形．13．解：如图，过P作PE⊥OB，垂足为E.∵∠AOP ＝∠BOP ＝15°，PD ⊥OA ，∴PD ＝PE .∵PC ∥OA ，∴∠CPO ＝∠AOP ＝15°.∴∠BCP ＝∠BOP ＋∠CPO ＝30°，在Rt △CPE 中，∠BCP ＝30°，∴PE ＝114 2.22PC =⨯=. ∴PD ＝PE ＝2.14．证明：如图，过A 作AD ⊥BC ，垂足为D ，∵AB ＝AC ，∴∠BAD ＝12BAC ∠. ∵∠AEF ＝∠AFE ， ∠BAC ＝∠AEF ＋∠AFE ， ∴∠EF A ＝12BAC ∠. ∴∠EF A ＝∠BAD .∴EF ∥AD ，∴EF ⊥BC .15．证明：如图，延长CH 、BA 交于点E .∵CH ⊥BD ，BD 是∠ABC 的角平分线， ∴∠CHB ＝∠EHB ＝90°，∠CBH ＝∠EBH . 又∵BH ＝BH ，∴△CBH ≌△EBH .∴CH ＝EH .∴CE ＝2CH .∵∠ACB ＝45°，∠CAB ＝90°，∴∠ABC ＝45°，∴∠ACB ＝∠ABC .∴AC ＝AB .∵∠CAB ＝∠CAE ＝90°，∴∠E ＋∠ECA ＝90°.∵CH ⊥BD ，∴∠E ＋∠EBH ＝90°.∴∠ECA ＝∠EBH .∴△ECA ≌△DBA .∴CE ＝BD .∴BD ＝2CH .16．解：(1)∵∠A ＝30°，∠BCD ＝60°， ∴∠ABC ＝30°.∴∠A ＝∠ABC .∴AC ＝BC ＝40(海里),40÷10＝4(小时)．答：船到达C 点的时间是15时30分．(2)在Rt△BCD中，∠CBD＝30°，∴CD＝1122BC ×40＝20(海里),20÷10＝2(小时)．答：该船在17时30分到达D处．。

人教版数学八年级上册：13.3 等腰三角形同步练习(附答案)

13．3等腰三角形13．3.1等腰三角形第1课时等腰三角形的性质知识点1等边对等角1．若等腰三角形的顶角为40°，则它的底角度数为()A．40° B．50° C．60° D．70°2．如图，AB∥CD，点E在线段BC上，CD＝CE.若∠ABC＝30°，则∠D为() A．85°B．75°C．60°D．30°3．如图1是一把园林剪刀，把它抽象为图2，其中OA＝OB.若剪刀张开的角为30°，则∠A ＝．4．如图，在△ABC中，∠B＝90°，AB＝BD，AD＝CD，求∠CAD的度数．5．如图，在△ABC中，AB＝AC，D是△ABC内一点，且BD＝DC.求证：∠ABD＝∠ACD.知识点2等腰三角形“三线合一”6．如图，△ABC中，AB＝AC，D是BC中点，下列结论中不正确的是() A．∠B＝∠CB．AD⊥BCC．AD平分∠BACD．AB＝2BD7．如图，在△ABC中，AB＝AC，AD⊥BC，垂足为D.若BD＝2 cm，则CD＝cm.第7题图第8题图8．如图，在△ABC中，AB＝AC，D为BC中点，∠BAD＝35°，则∠C的度数为．9．如图，在△ABC中，AB＝AC，AD是BC边上的中线，BE⊥AC于点E.求证：∠CBE ＝∠BAD.10．已知等腰三角形的一个外角为130°，则它的顶角的度数为．11．如图，在△ABC中，AB＝AC，BD⊥AC于点D，∠A＝50°，则∠DBC的度数为．12．如图，在△ABC中，AB＝AC，∠A＝30°，AB的垂直平分线l交AC于点D，则∠CBD 的度数为()A．30° B．45°C．50°D．75°第12题图第13题图13．如图，在△ABC中，AB＝AC，点E在BC边上，在线段AC的延长线上取点D，使得CD＝CE，连接DE，CF是△CDE的中线．若∠FCE＝52°，则∠A的度数为() A．38° B．34°C．32° D．28°14．如图，在△ABC中，AB＝BC，∠ABC＝110°，AB的垂直平分线DE交AC于点D，连接BD，则∠ABD＝．第14题图第15题图15．如图，在△ABC中，点D在BC边上，BD＝AD＝AC，E为CD的中点．若∠CAE＝16°，则∠B＝．16．如图，点D，E在△ABC的边BC上，AB＝AC，BD＝CE.求证：AD＝AE.17．如图，在△ABC中，AC＝BC，∠ACB＝90°，点D是AB的中点，点E是AB边上一点，直线BF垂直于直线CE于点F，交CD于点G.求证：AE＝CG.第2课时等腰三角形的判定知识点1等角对等边1．如图，在△ABC中，∠B＝∠C，AB＝5，则AC的长为()A．2B．3C．4D．52．在△ABC中，∠A和∠B的度数如下，能判定△ABC是等腰三角形的是() A．∠A＝50°，∠B＝70°B．∠A＝70°，∠B＝40°C．∠A＝30°，∠B＝90°D．∠A＝80°，∠B＝60°3．如图，已知OC平分∠AOB，CD∥OB，则△COD 等腰三角形．(填“是”或“不是”)第3题图第4题图4．如图，在△ABC中，BD⊥AC，∠A＝50°，∠CBD＝25°，若AC＝5 cm，则AB＝．5．如图，在△ABC中，AD平分∠BAC，点D是BC的中点，DE⊥AB于点E，DF⊥AC 于点F.求证：△ABC是等腰三角形．6．如图，△ABC的边AB的延长线上有一个点D，过点D作DF⊥AC于F，交BC于E，且BD＝BE，求证：△ABC为等腰三角形．知识点2用尺规作等腰三角形7．已知等腰三角形的底边长为a，顶角的平分线长为b，求作这个等腰三角形．8．如图，已知点P是射线ON上一动点(即P可在射线ON上运动)，∠AON＝45°，当∠A ＝时，△AOP为等腰三角形．9．如图，在△ABC中，∠B＝∠C＝40°，D，E是BC上的两点，且∠ADE＝∠AED＝80°，则图中共有等腰三角形()A．6个B．5个C．4个D．3个第9题图第10题图10．如图，在△ABC中，BP平分∠CBA，AP平分∠CAB，且DE∥AB，若CB＝12，AC ＝18，则△CDE的周长是．11．如图，AD平分∠BAC，AD⊥BD，垂足为D，DE∥AC.求证：△BDE是等腰三角形．12．如图，在△ABC中，AB＝AC，∠BAC＝36°，CD是∠ACD的平分线，交AB于点D，过点A作AE∥BC，交CD的延长线于点E.(1)求∠ADC的度数；(2)求证：AE＝AC；(3)试问△ADE是等腰三角形吗？请说明理由．13．如图，OA平分∠BAC，∠1＝∠2.求证：△ABC是等腰三角形．参考答案第1课时等腰三角形的性质1．D 2．B 3．75°．4．解：∵△ABC 中，∠B ＝90°，AB ＝BD ，AD ＝CD ，∴∠BAD ＝∠ADB ＝45°，∠DCA ＝∠CAD. ∴∠BDA ＝2∠CAD ＝45°. ∴∠CAD ＝22.5°. 5．证明：∵AB ＝AC ，∴∠ABC ＝∠ACB. ∵BD ＝CD ，∴∠DBC ＝∠DCB.∴∠ABC －∠DBC ＝∠ACB －∠DCB ，即∠ABD ＝∠ACD. 6．D 7．2 8．55°．9．证明：∵AB ＝AC ，∴∠ABD ＝∠C.又∵AD 是BC 边上的中线， ∴AD ⊥BC.∵BE ⊥AC ，∴∠BEC ＝∠ADB ＝90°. ∴∠C ＋∠CBE ＝∠ABD ＋∠BAD ＝90°. ∴∠CBE ＝∠BAD. 10．50°或80°． 11．25°． 12．B 13．D 14．35°． 15．37°．16．证明：∵AB ＝AC ，∴∠B ＝∠C.在△ABD 和△ACE 中，⎩⎪⎨⎪⎧AB ＝AC ，∠B ＝∠C ，BD ＝CE ，∴△ABD ≌△ACE(SAS )． ∴AD ＝AE.17．证明：∵点D 是AB 中点，AC ＝BC ，∠ACB ＝90°，∴CD ⊥AB ，∠ACD ＝∠BCD ＝45°，∠CAD ＝∠CBD ＝45°. ∴∠CAE ＝∠BCG. 又∵BF ⊥CE ，∴∠CBG ＋∠BCF ＝90°. 又∵∠ACE ＋∠BCF ＝90°， ∴∠ACE ＝∠CBG.在△AEC 和△CGB 中， ⎩⎪⎨⎪⎧∠CAE ＝∠BCG ，AC ＝CB ，∠ACE ＝∠CBG ， ∴△AEC ≌△CGB(ASA )． ∴AE ＝CG.第2课时等腰三角形的判定1．D 2．B 3．是4．5__cm ．5．证明：∵AD 平分∠BAC ，DE ⊥AB 于点E ，DF ⊥AC 于点F ，∴DE ＝DF.∵点D 是BC 的中点， ∴BD ＝CD.在Rt △BDE 和Rt △CDF 中，⎩⎪⎨⎪⎧BD ＝CD ，DE ＝DF ， ∴Rt △BDE ≌Rt △CDF(HL )． ∴∠B ＝∠C.∴AB ＝AC ，即△ABC 为等腰三角形． 6．证明：∵DF ⊥AC ，∴∠DFA ＝∠EFC ＝90°. ∴∠A ＝∠EFC －∠D ， ∠C ＝∠DFA －∠CEF. ∵BD ＝BE ， ∴∠BED ＝∠D. ∵∠BED ＝∠CEF ， ∴∠D ＝∠CEF. ∴∠A ＝∠C.∴△ABC 为等腰三角形． 7．解：①作线段AB ＝a ；②作线段AB 的垂直平分线MN ，与AB 交于点D ； ③以点D 为圆心，b 为半径画弧，交MN 于点C ； ④连接AC ，BC ，则△ABC 就是所求作的三角形． 8．45°或67.5°或90° 9．C 10．30．11．证明：∵DE ∥AC ，∴∠CAD ＝∠ADE.∵AD 平分∠BAC ， ∴∠CAD ＝∠DAE. ∴∠ADE ＝∠DAE. ∵AD ⊥BD ，∴∠DAE ＋∠B ＝90°， ∠ADE ＋∠BDE ＝90°. ∴∠B ＝∠BDE.∴BE ＝DE ，即△BDE 是等腰三角形． 12．解：(1)∵AB ＝AC ，∠BAC ＝36°，∴∠B ＝∠ACB ＝12(180°－∠BAC )＝72°.∵CD 是∠ACB 的平分线， ∴∠DCB ＝12∠ACB ＝36°.∴∠ADC ＝∠B ＋∠DCB ＝72°＋36°＝108°. (2)证明：∵CD 是∠ACB 的平分线， ∴∠BCE ＝∠ACE. ∵AE ∥BC ， ∴∠BCE ＝∠E. ∴∠ACE ＝∠E. ∴AE ＝AC.(3)△ADE 是等腰三角形．理由：∵AE ∥BC ， ∴∠EAB ＝∠B ＝72°.∵∠B ＝72°，∠DCB ＝36°，∴∠ADE ＝∠BDC ＝180°－72°－36°＝72°. ∴∠EAD ＝∠ADE. ∴AE ＝DE.∴△ADE 是等腰三角形． 13．证明：过点O 作OD ⊥AB 于点D ，OE ⊥AC 于点E ，则△BOD 和△COE 都是直角三角形．∵OA 平分∠BAC ，OD ⊥AB ，OE ⊥AC ， ∴OD ＝OE. ∵∠1＝∠2， ∴OB ＝OC.∴Rt △BOD ≌Rt △COE(HL )． ∴∠ABO ＝∠ACO.又∵∠1＝∠2，∴∠ABC＝∠ACB.∴AB＝AC.∴△ABC是等腰三角形．。

人教版八年级上册数学习题133答案

.人教版八年级上册数学习题13.3答案1．(1) 35度，35°；(2) 解：当80°的角是等腰三角形的一个底角时，那么等腰三角形的另一个底角为80°，根据三角形的角和定理可以求出顶角为180°-80°-80°=20°；当80°的角是等腰三角形的顶角时，那么它的两个底角相等，均为1/2（°-80°）=50°．综上，等腰三角形的另外两个角是20°，80°或50°，50°．2.3．解：∵五角星的五个角都是顶角为36°的等腰三角形，∴每个底角的度数是1/2×（°- 36°）=72°．∴∠AMB=°-72°108°．4．资料Word. 5．证明：CE//DA,∴∠A=∠CEB.6.7．8．已知：如图13 -3-29所示，点P是直线AB上一点，求作直线CD，使CD⊥AB于点P.资料Word.F,，AB于点E作法：(1)以点P为圆心作弧交，CC两弧相交于点，过大于E(2)分别以点，F为圆心，1/2EF的长为半径作弧，CD为所求直线．，则直线P作直线CD．解：他们的判断是对的．理由：因为等腰三角形底边上的中线和底边上的高9 重合．10．资料Word.11.12.资料Word.13．解：等腰三角形两底角的平分线相等，两腰上的中线相等，两腰上的高相等．以等腰三角形两腰上的高相等为例进行证明．已知：在△ABC中，AB=AC，BD⊥AC，CE⊥AB，垂足分别为点D，E求证：BD=CE.14．资料Word.15.解：如图13-3-31所示，作∠BAC的平分线AD交BC于点D，过点D作DE ⊥AB于点E,则△ADC≌△ADE≌△BDE.人教版八年级上册数学第91页复习题答案1．解：除了第三个图形，其余的都是轴对称图形．找对称轴略．2．解：如图13-5-22所示．资料Word.3．证明：连接BC，∵点D是AB的中点，CD⊥AB，∴AC= BC.同理，AB=BC，∴AC=AB．4．解：点A与点B关于x轴对称；点B与点E关于y轴对称；点C与点E不关于x轴对称，因为它们的纵坐标分别是3，-2，不互为相反数．5．解：∠D=25°，∠E=40°，∠DAE=115°．6．7．8．解：等边三角形有3条对称轴，形有4条对称轴，正五边形有5条对称轴，正六边形右6条对称轴，正八边形有8条对称轴，正n边形有n条对称轴．资料Word.轴；x(4)的对称轴是是平移. (1)的对称轴是y轴；9．解：(1)(4)是轴对称；(2)(3)(3)个单位长度得到图形Ⅱ；再向左平移5I先向下平移3个单位长度，(2)中图形3个单位长度得到图形Ⅱ．I先向右平移5个单位长度，再向下平移中图形，于点EAB，ACABC是△的角平分线，DE，DF分别垂直于10．证明：因为AD，ADF≌Rt△，所以Rt△ADEDA=DA，F，所以DE= DF∠DEA= ∠DFA= 90°．又因为EF. 垂直平分，所以AD所以AE=AF是等边三角形，证明：∵△ABC11. °，∠B=∠C=60AB=BC=AC∴，/A= AD= BE=CF，又∵BD=CE=AF.∴CFF,. ≌△ADF≌△BED∴△．∴DF=ED=FE 是等边三角形．△DEF即所示，正五边形的每一如图13 - 5-235个点为正五边形的5个顶点，12.解：这都是等腰三角形．同理，ABEABD，△△ABC两点为例，，，以108个角为°AB △，.其他任意三点组成的三角形也都是等腰三角形资料Word.点拨：由正五边形的各边都相等，各角都为108°，各对角线都相等可联想到本题结论．13.14.资料Word.15．解：如图13-5-24所示，作点A关于MN的对称点A′，再作点B关于L 的对称点B′，连接A'B'，交MN于点C，交L于点D，则A一C一D一B是牧马人定的最短路径．资料Word。

人教版八年级数学上册13.3等腰三角形(包含答案 )

13.3等腰三角形知识要点：1.等腰三角形的性质（1）等腰三角形的两个底角相等（简写成“等边对等角”）．（2）等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合（简写成“三线合一”）．2.等腰三角形的判定（1）有两边相等的三角形是等腰三角形；（2）如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”）．3.等边三角形的概念：三边都相等的三角形是等边三角形．4.一在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半一、单选题1．将一张正方形纸片按如图1，图2所示的方向对折，然后沿图3中的虚线剪裁得到图4，将图4的纸片展开铺平，再得到的图案是（）A．B．C．D．【答案】B2．如图，在△ABC中，点D，E分别是边AB，AC的中点，AF△BC，垂足为点F，△ADE ＝30°，DF＝2，则△ABF的周长为（）A．B．C．D．【答案】D3．如图，△ABC中△ACB＝90°,CD是AB边上的高，△BAC的角平分线AF交CD于E，则△CEF必为（）A．等腰三角形B．等边三角形C．直角三角形D．等腰直角三角形【答案】A4．如图，梯形ABCD中，AD△BC，△B＝30°，△BCD＝60°，AD＝2，AC平分△BCD，则BC长为( )．A．4B．6C．D．【答案】B5．如果过三角形重心的一条直线将该三角形分成两个直角三角形，则该三角形一定是（）A．锐角三角形B．钝角三角形C．等腰三角形D．等边三角形【答案】C6．如图，有一底角为35°的等腰三角形纸片，现过底边上一点，沿与腰垂直的方向将其剪开，分成三角形和四边形两部分，则四边形中，最大角的度数是（）A．110°B．125°C．140°D．160°【答案】B7．如图,矩形ABCD中,AB=7,BC=4,按以下步骤作图：以点B为圆心,适当长为半径画弧,交AB,BC于点E,F;再分别以点E,F为圆心,大于12EF的长为半径画弧,两弧在△ABC内部相交于点H,作射线BH,交DC于点G,则DG的长为( )A．1B．112C．3D．212【答案】C8．如图，已知AB△CD，BC平分△ABE，△C=32°，则△BED的度数是（）A．32°B．16°C．49°D．64°【答案】D9．若等腰三角形的周长为18cm，其中一边长为4cm，则该等腰三角形的底边长为（）A．10B．7或10C．4D．7或4【答案】C10．如图，在Rt△ABC中，△C＝90°，D是AB的中点，E在边AC上，若D与C关于BE成轴对称，则下列结论：△△A＝30°；△△ABE是等腰三角形；△点B到△CED 的两边距离相等．其中正确的有（）A．0个B．1个C．2个D．3个【答案】D11．等腰三角形的顶角为150°,则它的底角为( )A．30°B．15°C．30°或15°D．50°【答案】B12．下列说法错误的是( )A．等腰三角形底边上的高所在直线是它的对称轴；B．等腰三角形底边上的中线所在直线是它的对称轴；C．等腰三角形顶角的平分线所在直线是它的对称轴；D．等腰三角形的一内角平分线所在直线是它的对称轴.【答案】D二、填空题13．如图，等边△ABC中，AD是中线，AD=AE，则△EDC = ______________【答案】15°14．如图，△ABC中，AB =AC，DE是AB的中垂线，△BCD的周长是14，BC = 5，那么AB =_________.【答案】915．等腰三角形周长为40，以一腰为边作等边三角形，其周长为45，则等腰三角形的底边长为_________【答案】1016．等边三角形的周长是30厘米，则边长为_______.【答案】10厘米17．等腰三角形的腰长为10,则底边长m的取值范围是_____.【答案】0＜m＜2018．等腰三角形的一个角是50°,则它的底角为__________°.【答案】50或65．19．等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的腰长为_____cm.【答案】5三、解答题20．如图所示，在△ABC中，△B＝90°，AB＝BC，BD＝CE，M是AC边的中点，求证△DEM 是等腰三角形．证明：连接BM ，∵AB ＝BC ，AM ＝MC ，∵BM∵AC ，且∵ABM ＝∵CBM ＝12∵ABC ＝45°， ∵AB ＝BC ，所以∵A ＝∵C ＝1802ABC ︒-∠＝45°， ∵∵A ＝∵ABM ，所以AM ＝BM ，∵BD ＝CE ，AB ＝BC ，∵AB －BD ＝BC －CE ，即AD ＝BE ，在∵ADM 和∵BEM 中，,45,,AD BE A EBM AM BM =⎧⎪∠=∠=︒⎨⎪=⎩∵∵ADM∵∵BEM （SAS ），∵DM ＝EM ，∵∵DEM 是等腰三角形．21．如图所示，在△ABC中，AB＝AC，D是BC边上的点，DE△AB，DF△AC，垂足分别为点E、F，△BAC＝120°．求证：12DE DF BC+=．证明：∵AB=AC，∵BAC=120°，∵∵B=∵C=30°，∵DE∵AB，DF∵AC，垂足为E，F，∵DE=12BD，DF=12DC，∵DE+DF=12BD+12DC=12（BD+DC）=12BC．∵DE+DF=12 BC．22．如图:已知在△ABC中,AB=AC,AE△BC,试说明AE平分△DAC.证明：∵AB=AC，∵∵B=∵C，∵AE∵BC，∵∵DAE=∵B，∵CAE=∵C，∵∵DAE=∵EAC，∵AE平分∵DAC．23．如图，已知AB=AC，D是AB上一点，DE△BC于E，ED的延长线交CA的延长线于F，那么△ADF是等腰三角形吗?为什么?【答案】∵ADF是等腰三角形，理由见解析.∵ADF是等腰三角形，理由如下：∵AB=AC，∵∵B=∵C（等边对等角），∵DE∵BC于E，∵∵FEB=∵FEC=90°，∵∵B+∵EDB=∵C+∵EFC=90°，∵∵EFC=∵EDB（等角的余角相等），∵∵EDB=∵ADF（对顶角相等），∵∵EFC=∵ADF，∵∵ADF是等腰三角形．24．如图，在△ABC中，AB=AC，△ABC和△ACB的平分线交于点O.(1) 结合图形，请你写出你认为正确的结论；(2) 过O作EF△BC交AB于E，交AC于F. 请你写出图中所有等腰三角形，并探究EF、BE、FC之间的关系；(3) 若AB≠AC，其他条件不变，图中还有等腰三角形吗？若有，请写出所有的等腰三角形，若没有，请说明理由；线段EF、BE、FC之间，上面探究的结论是否还成立？【答案】（1）结论：∵ABO=∵CBO=∵ACO=∵BCO，理由如下：∵AB=AC，∵∵ABC=∵ACB．∵OB平分∵ABC，OC平分∵ACB，∵∵ABO=∵CBO=∵ACO=∵BCO．（2）等腰三角形有：∵ABC、∵AEF，∵BEO，∵COF，∵BOC；EF、BE、FC之间的关系EF=BE+CF，理由如下：由（1）可得，∵ABC、∵BOC是等腰三角形；∵EF∵BC，∵∵ABC=∵AEF，∵AFE=∵ACB,∵∵ABC=∵ACB，∵∵AEF=∵AFE，∵AE=AF,即∵AEF是等腰三角形；∵BO平分∵ABC，∵∵EBO=∵OBC；∵EF∵BC，∵∵OBC=∵EOB，∵∵EBO=∵EOB；∵EO=BE，∵∵BEO是等腰三角形；同理可得OF=FC，∵∵COF是等腰三角形；∵EO+OF=BE+FC，即EF=BE+CF．（3）图中的等腰三角形有：∵BEO，∵COF ；结论仍然成立，理由如下：∵BO平分∵ABC，∵∵EBO=∵OBC；∵EF∵BC，∵∵OBC=∵EOB，∵∵EBO=∵EOB；∵EO=BE，人教版八年级数学上册13.3等腰三角形（包含答案）∵∵BEO是等腰三角形；同理可得OF=FC，∵∵COF是等腰三角形；∵EO+OF=BE+FC，即EF=BE+CF．11/ 11。

人教版八年级数学上册 13.3 等腰三角形同步训练(含答案)

人教版八年级数学上册13.3 等腰三角形同步训练一、选择题1. 如图，等腰三角形的对称轴是()A．直线l1B．直线l2C．直线l3D．直线l42. 如图，AC＝AD，BC＝BD，则有()A．CD垂直平分ABB．AB垂直平分CDC．AB与CD互相垂直平分D．CD平分∠ACB3. 已知等腰三角形的一个角等于42°，则它的底角为()A．42°B．69°C．69°或84°D．42°或69°4. 已知实数x、y满足|x－4|＋y－8＝0，则以x、y的值为两边长的等腰三角形的周长是()A. 20或16B. 20C. 16D. 以上答案均不对5. 如图，AD是△ABC的中线，下列条件中不能推出△ABC是等腰三角形的是()A．∠BAD＋∠B＝∠CAD＋∠C B．AB－BD＝AC－CDC．AB＋BD＝AC＋CD D．AD＝BC6. 如图，∠AOB＝50°，OM平分∠AOB，MA⊥OA于点A，MB⊥OB于点B，则∠MAB等于()A．50°B．40°C．25°7. 如图，△ABC是等边三角形，DE∥BC.若AB＝10，BD＝6，则△ADE的周长为()A．4 B．12 C．18 D．308. 如图，在五边形ABCDE中，AB＝AC＝AD＝AE，且AB∥ED，∠EAB＝120°，则∠BCD的度数为()A．150°B．160°C．130°D．60°9. 如图所示的正方形网格中，网格线的交点称为格点. 已知A，B是两格点，如果C也是图中的格点，且使得△ABC为等腰三角形．．．．．，那么符合题意的点C的个数是()A. 6B. 7C. 8D. 910. “三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角．这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在点O相连并可绕点O转动，点C固定，OC＝CD＝DE，点D，E可在槽中滑动．若∠BDE＝75°，则∠CDE的度数是()A．60°B．65°C．75°D．80°二、填空题11. 如图，在△ABC中，AB＝AC，D是AC上一点，且BC＝BD.若∠CBD＝46°，则∠A＝________°.12. 如图，直线a∥b，△ABC的顶点C在直线b上，边AB与直线b相交于点D.若△BCD是等边三角形，∠A＝20°，则∠1＝________．13. 一个等腰三角形的一边长是2，一个外角是120°，则它的周长是________．14. 如图所示，在△ABC中，DE是AC的垂直平分线，AE=5 cm，△ABD的周长为18 cm，则△ABC的周长为.15. 如图，BO平分∠CBA，CO平分∠ACB，MN过点O且MN∥BC，设AB＝12，AC＝18，则△AMN的周长为________．16. 如图，在△ABC中，若AB＝AC＝8，∠A＝30°，则S△ABC＝________．三、解答题17. 如图，在△ABC中，AB＝BD，根据图中的数据，求∠BAC的度数．18. 如图，在△ABC中，O是边AC上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交△ABC的外角平分线于点F.探究线段OE与OF的数量关系，并说明理由．19. 如图，已知Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，∠BAC的平分线分别交BC，CD于点E，F.求证：△CEF是等腰三角形．人教版八年级数学上册13.3 等腰三角形同步训练-答案一、选择题1. 【答案】A2. 【答案】B3. 【答案】D[解析] 在等腰三角形中，当一个锐角在未指明为顶角还是底角时，一定要分类讨论．①42°的角为等腰三角形的底角；②42°的角为等腰三角形的顶角，则底角为(180°－42°)÷2＝69°.所以底角为42°或69°.4. 【答案】B【解析】∵|x－4|＋y－8＝0，∴x－4＝0，y－8＝0，解得x＝4，y＝8.分两种情况讨论：①当4为腰时，根据三角形三边关系知4＋4＝8，∴这样的等腰三角形不存在；②当8为腰时，则有4＋8>8，这样能够组成等腰三角形，∴此三角形的周长是8＋8＋4＝20.5. 【答案】D[解析] 由∠BAD＋∠B＝∠CAD＋∠C可得∠ADB＝∠ADC，又∠ADB＋∠ADC＝180°，所以∠ADB＝∠ADC＝90°，又BD＝DC，由垂直平分线的性质可得AB ＝AC.由等式的性质，根据AB －BD ＝AC －CD ，AB ＋BD ＝AC ＋CD ，又BD ＝CD ，均可得AB ＝AC.选项D 不能得到AB ＝AC.6. 【答案】C[解析] ∵OM 平分∠AOB ，MA ⊥OA 于点A ，MB ⊥OB 于点B ，∴∠AOM ＝∠BOM ＝25°，MA ＝MB.∴∠OMA ＝∠OMB ＝65°.∴∠AMB ＝130°.∴∠MAB ＝12×(180°－130°)＝25°.故选C.7. 【答案】B[解析] ∵△ABC 为等边三角形，∴∠A ＝∠B ＝∠C ＝60°.∵DE ∥BC ，∴∠ADE ＝∠B ＝60°，∠AED ＝∠C ＝60°.∴△ADE 为等边三角形．∵AB ＝10，BD ＝6，∴AD ＝AB －BD ＝10－6＝4.∴△ADE 的周长为4×3＝12.8. 【答案】A[解析] ∵AB ∥ED ，∴∠E ＝180°－∠EAB ＝180°－120°＝60°. 又∵AD ＝AE ，∴△ADE 是等边三角形．∴∠EAD ＝60°.∴∠BAD ＝∠EAB －∠EAD ＝120°－60°＝60°.∵AB ＝AC ＝AD ，∴∠B ＝∠ACB ，∠ACD ＝∠ADC.在四边形ABCD 中，∠BCD ＝∠B ＋∠ADC ＝12(360°－∠BAD)＝12×(360°－60°)＝150°. 故选A. 9. 【答案】C10. 【答案】D[解析] ∵OC ＝CD ＝DE ，∴∠O ＝∠ODC ，∠DCE ＝∠DEC. ∴∠DCE ＝∠O ＋∠ODC ＝2∠ODC. ∵∠O ＋∠OED ＝3∠ODC ＝∠BDE ＝75°， ∴∠ODC ＝25°.∵∠CDE ＋∠ODC ＝180°－∠BDE ＝105°， ∴∠CDE ＝105°－∠ODC ＝80°.二、填空题11. 【答案】46[解析] ∵BC＝BD，∠CBD＝46°，∴∠C＝∠BDC＝12(180°－46°)＝67°.∵AB＝AC，∴∠ABC＝∠C＝67°.∴∠A＝46°.12. 【答案】40°[解析] 如图．∵△BCD是等边三角形，∴∠BDC＝60°.∵a∥b，∴∠2＝∠BDC＝60°.由三角形的外角性质和对顶角的性质可知，∠1＝∠2－∠A＝40°.13. 【答案】6[解析] 已知三角形的一外角为120°，则相邻内角度数为60°，那么含有60°角的等腰三角形是等边三角形．已知等边三角形的一边长为2，则其周长为6.14. 【答案】28 cm15. 【答案】30[解析] ∵MN∥BC，∴∠MOB＝∠OBC.∵∠OBM＝∠OBC，∴∠MOB＝∠OBM.∴MO＝MB.同理NO＝NC.∴△AMN的周长＝AM＋MO＋AN＋NO＝AM＋MB＋AN＋NC＝AB＋AC＝30.16. 【答案】16[解析] 如图，过点C作CD⊥AB，垂足为D，则△ADC是含30°角的直角三角形，那么DC＝12AC＝4，∴S△ABC＝12AB·DC＝12×8×4＝16.三、解答题17. 【答案】解：∵∠ADB＝30°＋40°＝70°，AB＝BD，∴∠BAD＝∠ADB＝70°.∴∠BAC＝∠BAD＋∠CAD＝100°.18. 【答案】解：OE＝OF.理由：∵MN∥BC，∴∠OEC＝∠BCE，∠OFC＝∠DCF.∵CE平分∠ACB，CF平分∠ACD，∴∠OCE＝∠BCE，∠OCF＝∠DCF.∴∠OEC＝∠OCE，∠OFC＝∠OCF.∴OE＝OC，OC＝OF.∴OE＝OF.19. 【答案】证明：∵∠ACB＝90°，∴∠B＋∠BAC＝90°.∵CD⊥AB，∴∠CAD＋∠ACD＝90°.∴∠ACD＝∠B.∵AE是∠BAC的平分线，∴∠CAE＝∠EAB.∵∠EAB＋∠B＝∠CEF，∠CAE＋∠ACD＝∠CFE，∴∠CFE＝∠CEF. ∴CF＝CE.∴△CEF是等腰三角形．。

人教版八年级数学上册 13.3 等腰三角形同步练习卷含答案

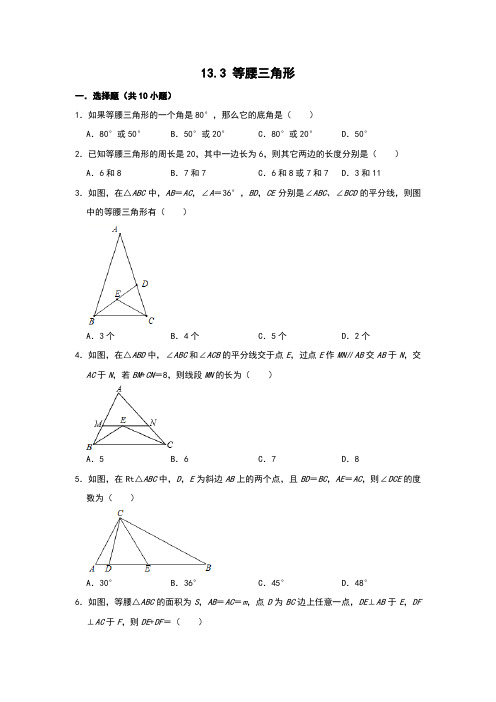
13.3 等腰三角形一．选择题（共10小题）1．如果等腰三角形的一个角是80°，那么它的底角是（）A．80°或50°B．50°或20°C．80°或20°D．50°2．已知等腰三角形的周长是20，其中一边长为6，则其它两边的长度分别是（）A．6和8 B．7和7 C．6和8或7和7 D．3和113．如图，在△ABC中，AB＝AC，∠A＝36°，BD，CE分别是∠ABC、∠BCD的平分线，则图中的等腰三角形有（）A．3个B．4个C．5个D．2个4．如图，在△ABD中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥AB交AB于N，交AC于N，若BM+CN＝8，则线段MN的长为（）A．5 B．6 C．7 D．85．如图，在Rt△ABC中，D，E为斜边AB上的两个点，且BD＝BC，AE＝AC，则∠DCE的度数为（）A．30°B．36°C．45°D．48°6．如图，等腰△ABC的面积为S，AB＝AC＝m，点D为BC边上任意一点，DE⊥AB于E，DF ⊥AC于F，则DE+DF＝（）A．B．C．D．7．如图，在△ABC中，AB＝3cm、AC＝4cm、BC＝5cm，在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画的条数为（）A．3 B．4 C．5 D．68．如图，已知每个小方格的边长为1，A，B两点都在小方格的格点（顶点）上，请在图中找一个格点C，使△ABC是以AB为腰的等腰三角形，这样的格点C有（）A．3个B．4个C．5个D．6个9．如果等腰三角形的周长20cm，那么这个等腰三角形腰长x的取值范围是（）A．x≥5cm B．5cm≤x＜10cm C．x＜10cm D．5cm＜x＜10cm 10．如图，∠AOB＝120°，OP平分∠AOB，且OP＝2．若点M，N分别在OA，OB上，且△PMN 为等边三角形，则满足上述条件的△PMN有（）A．2个B．3个C．4个D．无数个二．填空题（共11小题）11．在等腰△ABC中，一腰上的高与另一腰的夹角为26°，则底角的度数为．12．如图，在△ABC中，AC＝BC，点D在BC边上，∠BAD+∠C＝90°，点E在AC边上，∠AED＝2∠BAD，若BD＝16，CE＝7，则DE的长为．13．在△ABC中，AB＝AC，BC＝10，AB的垂直平分线与AC的垂直平分线分别交BC于点D，E，且DE＝4，则AD+AE的值为．14．等腰三角形周长为17cm，一腰上的中线将三角形分为两个三角形，这两个三角形的周长差为4cm，则此等腰三角形的底边长为．15．等腰三角形的一个外角等于100°，则这个等腰三角形顶角的度数为．16．△ABC中，AB＝AC＝5，S△ABC＝7.5，则BC的长为．17．我们知道，经过三角形一顶点和此顶点所对边上的任意一点的直线，均能把三角形分割成两个三角形，（1）如图，在△ABC中，∠A＝25°，∠ABC＝105°，过B作一直线交AC于D，若BD把△ABC分割成两个等腰三角形，则∠BDA的度数是．（2）已知在△ABC中，AB＝AC，过顶点和顶点对边上一点的直线，把△ABC分割成两个等腰三角形，则∠A的最小度数为．18．如图，线段AB＝a，点P是AB中垂线MN上的一动点，过点P作直线CD∥AB．若在直线CD上存在点Q使得△ABQ为等腰三角形，且满足条件的点Q有且只有3个，则PM的长为．19．如图，在△ABC中，AC＝BC，∠ACB＝100°，点D在线段AB上运动（D不与A，B重合），连接CD，作∠CDE＝40°，DE交BC于点E．若△CDE是等腰三角形，则∠ADC的度数是．20．已知如图等腰△ABC，AB＝AC，∠BAC＝120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP＝OC，下面的结论：①∠APO+∠DCO＝30°；②∠APO＝∠DCO；③△OPC是等边三角形；④AB＝AO+AP．其中正确的序号是．三．解答题（共5小题）21．（1）如图，在△ABC中，AB＝AC，∠A＝36°，BD平分∠ABC交AC于D．请说明△BDC 是等腰三角形；（2）在（1）的条件下请设计四个不同的方案，将△ABC分割成三个等腰三角形，请直接画出示意图并标出每个等腰三角形顶角度数；（3）若有一个内角为36°的三角形被分割成两个等腰三角形，则原三角形中最大内角的所有可能值为．22．数学课上，张老师举了下面的例题：例1：等腰△ABC中，∠A＝110°，求∠B的度数；例2：等腰△ABC中，∠A＝40°，求∠B的度数．爱思考的小敏发现，∠A的度数不同，得到∠B的度数的个数也可能不同．如果在等腰△ABC中，设∠A＝x°，当∠B有三个不同的度数时，请你探索x的取值范围．参考答案一．选择题（共10小题）1．解：根据题意，一个等腰三角形的一个角等于80°，①当这个角是底角时，即该等腰三角形的底角的度数是80°，②当这个角80°是顶角，设等腰三角形的底角是x°，则2x+80°＝180°，解可得，x＝50°，即该等腰三角形的底角的度数是50°；故选：A．2．解：当腰为6时，另一腰也为6，则底为20﹣2×6＝8，∵6+6＝12＞8，∴三边能构成三角形．当底为6时，腰为（20﹣6）÷2＝7，∵7+7＞6，∴三边能构成三角形．故选：C．3．解：共有5个．∵AB＝AC∴△ABC是等腰三角形；∵BD、CE分别是∠ABC、∠BCD的角平分线∴∠EBC＝∠ABC，∠ECB＝∠BCD，∵△ABC是等腰三角形，∴∠EBC＝∠ECB，∴△BCE是等腰三角形；∵∠A＝36°，AB＝AC，∴∠ABC＝∠ACB＝（180°﹣36°）＝72°，又BD是∠ABC的角平分线，∴∠ABD＝∠ABC＝36°＝∠A，∴△ABD是等腰三角形；同理可证△CDE和△BCD是等腰三角形．故选：C．4．解：∵∠ABC、∠ACB的平分线相交于点E，∴∠MBE＝∠EBC，∠ECN＝∠ECB，∵MN∥BC，∴∠EBC＝∠MEB，∠NEC＝∠ECB，∴∠MBE＝∠MEB，∠NEC＝∠ECN，∴BM＝ME，EN＝CN，∴MN＝ME+EN，即MN＝BM+CN．∵BM+CN＝8，∴MN＝8，故选：D．5．解：设∠DCE＝x，∠ACD＝y，则∠ACE＝x+y，∠BCE＝90°﹣∠ACE＝90°﹣x﹣y．∵AE＝AC，∴∠ACE＝∠AEC＝x+y，∵BD＝BC，∴∠BDC＝∠BCD＝∠BCE+∠DCE＝90°﹣x﹣y+x＝90°﹣y．在△DCE中，∵∠DCE+∠CDE+∠DEC＝180°，∴x+（90°﹣y）+（x+y）＝180°，解得x＝45°，∴∠DCE＝45°．故选：C．6．解：如图所示：连接AD，∵AB＝AC＝m，△ABC的面积是S，∴AB•DE+AC•DF＝S，∵AB＝AC＝m，∴DE+DF＝，故选：B．7．解：如图所示：BC＝3，AC＝4，AB＝5，∵32+42＝52，∴△ABC是直角三角形，∠ACB＝90°．当CD1＝AC＝4，CD3＝AD3，BA＝BD4＝3，AB＝AD2＝3，D5A＝AB，BD6＝CD，故能得到符合题意的等腰三角形6个．故选：D．8．解：当AB为腰时，分别以A、B点为顶点，以AB为半径作圆，可找出格点点C的个数有6个；故使△ABC是以AB为腰的等腰三角形的格点C有6个．故选：D．9．解：∵等腰三角形的腰长为xcm，周长20cm，∴底边为（20﹣2x）cm，∴20﹣2x＞0且2x＞20﹣2x，解得x＜10且x＞5．∴腰长x的取值范围是 5cm＜x＜10cm．故选：D．10．解：如图在OA、OB上截取OE＝OF＝OP，作∠MPN＝60°．∵OP平分∠AOB，∴∠EOP＝∠POF＝60°，∵OP＝OE＝OF，∴△OPE，△OPF是等边三角形，∴EP＝OP，∠EPO＝∠OEP＝∠PON＝∠MPN＝60°，∴∠EPM＝∠OPN，在△PEM和△PON中，，∴△PEM≌△PON（ASA）．∴PM＝PN，∵∠MPN＝60°，∴△PNM是等边三角形，∴只要∠MPN＝60°，△PMN就是等边三角形，故这样的三角形有无数个．故选：D．二．填空题（共11小题）11．解：①∵AB＝AC，∠ABD＝26°，BD⊥AC，∴∠A＝64°，∴∠ABC＝∠C＝（180°﹣64°）÷2＝58°．②∵AB＝AC，∠ABD＝26°，BD⊥AC，∴∠BAC＝26°+90°＝116°∴∠ABC＝∠C＝（180°﹣116°）÷2＝32°．故答案为：58°或32°．12．解：设∠C＝2α，∵∠BAD+∠C＝90°，∴∠BAD＝90°﹣2α，∵AC＝BC，∴∠B＝∠BAC＝90°﹣α，∴∠CAD＝α，作∠ADF＝∠DAE＝α交AE于F，∴∠DFE＝2α，AF＝DF，∵∠AED＝2∠BAD＝180°﹣4α，∴∠EDF＝2α，∴∠EFD＝∠EDF＝∠C，∴EF＝DE，DF＝CD，∴AF＝CD，∴CF＝BD＝16，∵CE＝7，∴EF＝DE＝9，故答案为：9．13．解：∵AB、AC的垂直平分线分别交BC于点D、E，∴AD＝BD，AE＝CE，∴AD+AE＝BD+CE，∵BC＝10，DE＝4，当BD与CE无重合时，如图1，AD+AE＝BD+CE＝BC﹣DE＝10﹣4＝6，当BD与CE有重合时，如图2，AD+AE＝BD+CE＝BC+DE＝10+4＝14，综上所述，AD+AE＝6或14．故答案为：6或14．14．解：如图所示，等腰△ABC中，AB＝AC，点D为AC的中点，设AB＝AC＝x，∵点D为AC的中点，∴AD＝CD＝AB，BC＝17﹣（AB+AC）＝17﹣2x．①当△ABD的周长大于△BCD的周长时，∵AB+AD+BD﹣（BC+CD+BD）＝4，∴AB﹣BC＝4，即x﹣（17﹣2x）＝4，解得x＝7，17﹣2x＝3，7，7，3能够组成三角形，符合题意；②当△BCD的周长大于△ABD的周长时，∵BC+CD+BD﹣（AB+AD+BD）＝4，∴BC﹣AB＝4，即17﹣2x﹣x＝4，解得x＝，17﹣2x＝，，，能够组成三角形，符合题意．综上所述，这个等腰三角形的底边长为3或，故答案为：3或，15．解：当100°的角是顶角的外角时，顶角的度数为180°﹣100°＝80°；当100°的角是底角的外角时，底角的度数为180°﹣100°＝80°，所以顶角的度数为180°﹣2×80°＝20°；所以这个等腰三角形顶角的度数为80°或20°．故答案为80°或20°．16．解：若△ABC是锐角三角形时，过点C作CD⊥AB于点D，过点A作AE⊥BC于点E，∵AB•CD＝，∴CD＝3，∴由勾股定理可知：AD＝4，∴BD＝1，∴BC＝，若△ABC是钝角三角形时，同理可求出得BC＝3，故答案为：或317．解：（1）根据题意得DA＝DB，∴∠ABD＝∠A＝25°，∴∠BDA＝180°﹣25°×2＝130°．故答案为：130°；（2）如图所示：AB＝AC，AD＝BD，BC＝CD，∵AD＝BD，∴∠ABD＝∠A，∵BC＝CD，∴∠CBD＝∠CDB＝2∠A，∴∠ABC＝∠ABD+∠CBD＝3∠A，∵AB＝AC，∴∠C＝∠ABC＝3∠A，∵∠A+∠ABC+∠C＝180°，∴∠A＝．故答案为：．18．解：如图所示，分别以A，B为圆心，AB长为半径画弧，①当直线CD经过两弧的交点时，直线CD与两弧共有3个交点G1，G2，G3，此时满足△GAB是等腰三角形的点G有且只有3个，△PAB是等边三角形，∴PM＝a；②当直线CD与两弧均相切时，直线CD与两弧、直线MN共有3个交点G1，G2，G3，此时满足△GAB是等腰三角形的点G有且只有3个，∴PM＝AG1＝AB＝a，故答案为：a或a．19．解：分三种情况：①当CD＝DE时，∴∠DCE＝∠DEC＝70°，∴∠ADC＝∠B+∠DCE＝110°，②当DE＝CE时，∵∠CDE＝40°，∴∠DCE＝∠CDE＝40°，∴∠ADC＝∠DCE+∠B＝80°．③当EC＝CD时，∠BCD＝180°﹣∠CED﹣∠CDE＝180°﹣40°﹣40°＝100°，∵∠ACB＝100°，∴此时，点D与点A重合，不合题意．综上所述，若△ADC是等腰三角形，则∠ADC的度数为80°或110°．故答案为：80°或110°．20．解：①如图1，连接OB，∵AB＝AC，AD⊥BC，∴BD＝CD，∠BAD＝∠BAC＝×120°＝60°，∴OB＝OC，∠ABC＝90°﹣∠BAD＝30°∵OP＝OC，∴OB＝OC＝OP，∴∠APO＝∠ABO，∠DCO＝∠DBO，∴∠APO+∠DCO＝∠ABO+∠DBO＝∠ABD＝30°；故①正确；②由①知：∠APO＝∠ABO，∠DCO＝∠DBO，∵点O是线段AD上一点，∴∠ABO与∠DBO不一定相等，则∠APO与∠DCO不一定相等，故②不正确；③∵∠APC+∠DCP+∠PBC＝180°，∴∠APC+∠DCP＝150°，∵∠APO+∠DCO＝30°，∴∠OPC+∠OCP＝120°，∴∠POC＝180°﹣（∠OPC+∠OCP）＝60°，∵OP＝OC，∴△OPC是等边三角形；故③正确；④如图2，在AC上截取AE＝PA，连接PB，∵∠PAE＝180°﹣∠BAC＝60°，∴△APE是等边三角形，∴∠PEA＝∠APE＝60°，PE＝PA，∴∠APO+∠OPE＝60°，∵∠OPE+∠CPE＝∠CPO＝60°，∴∠APO＝∠CPE，∵OP＝CP，在△OPA和△CPE中，，∴△OPA≌△CPE（SAS），∴AO＝CE，∴AB＝AC＝AE+CE＝AO+AP；故④正确；本题正确的结论有：①③④，故答案为①③④．三．解答题（共5小题）21．解：（1）∵AB＝AC，∵∠A＝36°，∴∠C＝∠ABC＝72°．∵BD平分∠ABC交AC于D，∴∠ABD＝∠DBC＝36°，∵∠A＝∠ABD＝36°，∴∠BDC＝∠A+∠ABD＝36°+36°＝72°＝∠C，∴△BDC是等腰三角形；（2）如图方案1，做∠B的角平分线BD交AC于点D，作∠BDC得角平分线DE交BC于点E，∵∠A＝36°，∴∠C＝∠ABC＝72°，∴∠DBC＝36°，∠BDC＝72°，∴∠EDG＝∠BDE＝36°，∴△ABD，△BDE，△DEC为等腰三角形；如图方案2，做∠B的角平分线BF交AC于点F，作∠C得角平分线CM交BF于点M，∵∠A＝36°，∴∠ACB＝∠ABC＝72°，∴∠FBC＝∠ABF＝36°，∠FCM＝∠MCB＝72°，∴∠CFM＝∠CMF＝72°，∴△ABF，△BMC，△CMF为等腰三角形；如图方案3，做∠C的角平分线CN交AB于点N，作∠BNC得角平分线NP交BC于点P，∵∠A＝36°，∴∠ACB＝∠ABC＝72°，∴∠BCN＝∠ACN＝36°，∠BNC＝∠B＝72°，∴∠BNP＝∠PNC＝36°，∠NPB＝72°，∴△ANC，△NPC，△BNP为等腰三角形；如图方案4，作∠B的角平分线BD交AC于点D，作∠BDE＝∠BDC交AB于点E，∵∠A＝36°，∴∠ACB＝∠ABC＝72°，∴∠BCD＝∠BDE＝∠BED＝72°，∠AED＝108°，∴∠A＝∠ADE＝36°，∴△AED，△BDE，△BCD为等腰三角形；（3）①原三角形是锐角三角形，最大角是72°的情况如图所示：∠ABC＝∠ACB＝72°，∠A＝36°，AD＝BD＝BC；②原三角形是直角三角形，最大角是90°的情况如图所示：∠ABC＝90°，∠A＝36°，AD＝CD＝BD；③原三角形是钝角三角形，最大角是108°的情况如图所示：④原三角形是钝角三角形，最大角是126°的情况如图所示：∠ABC＝126°，∠C＝36°，AD＝BD＝BC；⑤原三角形是钝角三角形，最大角是132°的情况如图所示：∠C＝132°，∠ABC＝36°，AD＝BD，CD＝CB．综上，原三角形最大内角的所有可能值为72°，90°，108°，132°，126°．故答案为：72°，90°，108°，132°，126°．22．解：例题1：根据三角形内角和定理，∵∠A＝110°＞90°，∠B＝∠C＝35°；例题2：若∠A为顶角，则∠B＝（180°﹣∠A）÷2＝70°；若∠A为底角，∠B为顶角，则∠B＝180°﹣2×40°＝100°；若∠A为底角，∠B为底角，则∠B＝40°；故∠B＝50°或20°或80°；问题：分两种情况：①当90≤x＜180时，∠A只能为顶角，∴∠B的度数只有一个；②当0＜x＜90时，若∠A为顶角，则∠B＝（）°；若∠A为底角，∠B为顶角，则∠B＝（180﹣2x）°；若∠A为底角，∠B为底角，则∠B＝x°．当≠180﹣2x且180﹣2x≠x且≠x，即x≠60时，∠B有三个不同的度数．综上所述，可知当0＜x＜90且x≠60时，∠B有三个不同的度数．。

人教版八年级数学上册 13.3等腰三角形同步练习(包含答案)

13.3等腰三角形知识要点：1.应用“三线合一”性质的前提条件是在等腰三角形中，且必须是底边上的中线、底边上的高和顶角平分线，若是一腰上的高与中线就不一定重合．2.等腰三角形是轴对称图形，顶角平分线（或底边上的高、底边上的中线）所在的直线是它的对称轴．3.等边三角形的性质：等边三角形的三个内角都相等，并且每一个角都等于60°4.一在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．一、单选题1．已知等腰三角形的周长为10，一边长为4，则此等腰三角形的腰长为( )A．2B．3C．4D．3或4【答案】D2．如图，在△ABC中，AB=AC，△A=36°，BE平分△ABC，CD平分△ACB，CD交BE 于点F，那么图中的等腰三角形共有( )个.A．6B．7C．8D．9【答案】C3．如果一个三角形的一内角平分线垂直于对边，那么这个三角形是( )A．等腰三角形B．等边三角形C．锐角三角形D．不能确定【答案】A4．在Rt△ABC中，△C=90°，△B=30°，则( )A．AB=2AC B．AC=2AB C．AB=AC D．AB=3AC【答案】A5．已知一个等腰三角形的一边长为5,另一边长为7,则这个等腰三角形的周长为( ) A．12 B．17 C．17或19 D．19【答案】C6．如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE△AB,DF△AC,垂足分别为E,F.则下列结论:△AD上任意一点到点C,B的距离相等;△AD上任意一点到边AB,AC的距离相等;△BD=CD,AD△BC;△△BDE=△CDF.其中正确的个数为（）A．4B．3C．2D．1【答案】A7．下列能判定△ABC为等腰三角形的是( )A．△A＝30°，△B＝60° B．△A＝50°，△B＝80°C．△A＝2△B＝80° D．AB＝3，BC＝6，周长为13【答案】B8．如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点.若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为()A．6 B．8 C．10 D．12【答案】C9．如图，AD△BC，D是BC的中点，那么下列结论错误的是()A．△ABD△△ACD B．△B＝△C C．△ABC是等腰三角形D．△ABC是等边三角形【答案】D10．如图，在△ABC中，△ACB=90°，BE平分△ABC，ED△AB与点D，△A=30°，AE=6cm，那么CE等于（）A．4cm B．2cm C．3cm D．1cm【答案】C11．如图，在△ABC中，△A＝45°，△B＝30°，CD△AB，垂足为D，AD＝1，则BD的长为()A．√2B．2 C．√3D．3【答案】C12．等边三角形的边长为2，则该三角形的面积为（）A．4√3B．2√3C．√3D．3【答案】C13．如图，AB＝AC，△BAC＝120°，AB的垂直平分线交BC于点D，那么△ADC的度数为（）A．120° B．30° C．60° D．80°【答案】C14．已知A和B两点在线段EF的中垂线上，且△EBF＝100°，△EAF＝70°，则△AEB等于( )A．95° B．15° C．95°或15° D．170°或30°【答案】C二、填空题15．等腰△ABC中，若△A=30°，则△B=________．【答案】30°或75°或120°16．已知等腰△ABC的腰AB=AC=10cm，底边BC=12cm，则△A的平分线的长是______cm．【答案】817．已知等腰三角形的周长为13，其中一边长为3，其它两边的长为____________【答案】5，518．在直角三角形中，最长边为10 cm，最短边为5 cm，则这个三角形中最小的内角为__________度.【答案】3019．如图，在Rt△ABC中，△C=90°，△A=30°，AB的垂直平分线交AC于点E，垂足为D，BE平分△ABC，若AE=2，则CE的长为______．【答案】120．已知等腰△ABC的两边长a、b满足（a-2）2+|b-4|=0，则等腰△ABC的周长为______ ．【答案】10三、解答题21．如图，等边三角形ABC的边长是10cm，求：（1）高AD的长（2）S△ABC（结果保留根号）【答案】2∵等边三角形三线合一的性质，∵D 为BC 中点，BD=DC=5cm ，∵AD∵BC ，=，∵∵ABC 的面积为211•10cm 22S BC AD ==⨯⨯=22．如图,在△ABC 中,△A=30°,AC=2√3,△B=60°，求点C 到AB 的距离和△ABC 的面积.【答案】√3，2√3.过点C 作CD∵AB,则∵ADC=90°,因为∵A=30°,AC=2√3,所以CD=√3,在∵ABC 中,因为∵A=30°,∵B=60°,所以∵ACB=90°,在Rt∵ABC 中,设BC=x,则AB=2x,因为AB 2=BC 2+AC 2,所以(2x)2=x 2+(2√3)2,x=2,所以S ∵ABC =12AC·BC=12×2√3×2=2√3.23．已知：如图，在△ABC 中，△A=30°，△ACB=90°，M 、D 分别为AB 、MB 的中点. 求证：CD△AB.∵∵ACB =90°，M 为AB 中点，∵CM 12=AB =BM ． ∵∵ACB =90°，∵A =30°，∵CB 12=AB =BM ，∵CM =CB ．∵D为MB的中点，∵CD∵BM，即CD∵AB．24．如图，在△ABC中，△ACB＝90°，CD△AB于点D，AF平分△CAB，交CD于点E，交BC于点F，若AF＝BF，求证：△CEF是等边三角形．证明：如图，∵AF是∵BAC的平分线，∵∵CAB=2∵1=2∵2，∵AF=BF，∵∵2=∵B，∵∵ACB=90°，∵∵B+∵CAB=90°，即∵B+2∵1=∵B+2∵2=90°，∵∵B=∵1=∵2=30°，∵∵4是∵ABF的外角，∵∵4=∵2+∵B=60°，∵CD是AB边上的高，∵∵2+∵3=90°，∵∵3=60°，∵∵5=∵3，∵∵4=∵5=60°，∵∵CEF是等边三角形．。

2018-2019人教版数学八年级上册 13.3《等腰三角形》同步测试题(含答案及解析)

ᦙᦙ 中， ᦙ 䁪 ᦙ，AB 的垂直平分线 MN 交 AC 1 . 如图，在于 D 点.若 BD 平分 ᦙᦙ，则䁪______ .
ᦙᦙ 中， ᦙ 䁪 ᦙ 䁪 1 ，ᦙᦙ 䁪 1 ，D 是 AB 的中点， . 如图，在 ᦙ 于点 E，则 DE 的长是______．过点 D 作 ′‸
三、计算题（本大题共 4 小题，共 24.0 分） ᦙᦙ 中， ᦙ 䁪 ᦙ，D，E，F 分别为 AB，BC，CA 1. 如图，上的点，且 ᦙ′ 䁪 ᦙ‸， ′‸ 䁪 ᦙ 1 求证： ᦙ′‸≌ ᦙ‸ ；若䁪，求 ‸′ 的度数．
四、解答题（本大题共 2 小题，共 16.0 分） ᦙᦙ 中， ‸ ᦙᦙ 于 E， ‸ 䁪 ᦙ‸，D 是 AE 上的一点，且 ′‸ 䁪 ᦙ‸， ⸵. 如图 1，在连接 BD，CD．
1 试判断 BD 与 AC 的位置关系和数量关系，并说明理由；如图 2，若将 ′ᦙ‸ 绕点 E 旋转一定的角度后，试判断 BD 与 AC 的位置关系和数量关系是否发生变化，并说明理由；如图 3，若将中的等腰直角三角形都换成等边三角形，其他条件不变．试猜想 BD 与 AC 的数量关系，请直接写出结论；你能求出 BD 与 AC 的夹角度数吗？如果能，请直接写出夹角度数；如果不能，请说明理由．
四边形 ABCD 是边长为 6 的正方形，点 E 在边 AB 上， 1 . 如图， ᦙ‸ 䁪，过点 E 作 ‸ ᦙᦙ，分别交 BD，CD 于 G，F 两点.若 M，N 分别是 DG，CE 的中点，则 MN 的长为
A. 3 B. C. 1 D. 4
二、填空题（本大题共 10 小题，共 30.0 分） ᦙᦙ 中， ᦙᦙ 䁪 ᦙ， ᦙ 䁪 1 ， ᦙ 䁪， 11. 如图，在 ᦙ‸ ′ 于 E， AD 平分 ᦙ ᦙ，交 BC 于点 D，则 ᦙ‸ 䁪 ______ ．

人教版八年级数学上册第十三章轴对称13.3 等腰三角形13.3.1等腰三角形的性质同步练习含答案

第十三章轴对称 13.3 等腰三角形 13.3.1 等腰三角形的性质1. 等腰三角形的一个内角是50°，则这个三角形的底角的大小是( ) A．65°或50° B．80°或40°C．65°或80° D．50°或80°2. 等腰三角形有一个角是90°，则另两个角分别是( )A．30°，60° B．45°，45°C．45°，90° D．20°，70°3. 如图，在△ABC中，AB=AC，过点A作AD∥BC，若∠1=70°，则∠BAC的大小为( )A．40° B．30° C．70° D．50°4. 如图，等腰三角形ABC中，AB=AC,BD平分∠ABC, ∠A=36°, 则∠1的度数为( )A．36° B．60° C．72° D．108°5. 等腰三角形的两边长分别为2和5，则它的周长是( )A．30 B．20 C．18 D．126. 等腰三角形一个底角为75°,它的另外两个角为____ __.7. 等腰三角形一个角为36°,它的另外两个角为____________________.8. 等腰三角形一个角为120°,它的另外两个角为_ ___ __.9. 在△ABC中， AB=AC，AB的垂直平分线与AC所在的直线相交得的锐角为50°，则底角的大小为___________．10. 如图，AB＝AC，若∠B＝35°，则x的值为____.11．如图，AB∥CD，AB＝AC，∠ABC＝70°，则∠ACD＝____.12．如图，△ABC中，AB＝AC，BD⊥AC于D，∠ABC＝72°，则∠ABD＝____.13．如图，在△ABC中，AB＝AC，D为BC的中点，∠BAD＝35°，则∠C的度数为____.14. 判断正(√;X)(1) 等腰三角形的顶角一定是锐角. ( )(2) 等腰三角形的底角可能是锐角或者直角、钝角都可以. ( )(3) 钝角三角形不可能是等腰三角形. ( )(4) 等腰三角形的顶角平分线一定垂直底边. ( )(5) 等腰三角形的角平分线、中线和高互相重合. ( )(6) 等腰三角形底边上的中线一定平分顶角. ( )15. 如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求△ABC各角的度数.16. 如图，在△ABC中，AB=AD=DC，∠BAD=26°，求∠B和∠C的度数.17. 如图，△ABC中，D是BC上一点，AC＝AD＝DB，∠BAC＝102°，求∠ADC的度数．18. 已知点D、E在△ABC的边BC上，AB＝AC.(1)如图①，若AD＝AE，求证：BD＝CE；(2)如图②，若BD＝CE，F为DE的中点，求证：AF⊥BC.答案：1---5 ABACD6. 75°, 30°7. 72°,72°或36°,108°8. 30°，30°9. 70°或20°10. 70°11. 40°12. 54°13. 55°14. (1) X(2) X(3) X(4) √(5) X(6) √15. 解：∵AB=AC，BD=BC=AD，∴∠ABC=∠C=∠BDC，∠A=∠ABD.设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,从而∠ABC= ∠C= ∠BDC=2x,于是在△ABC中，有∠A+∠ABC+∠C=x+2x+2x=180 ° ，解得x=36 ° ，在△ABC中，∠A=36°，∠ABC=∠C=72°.16. 解：∵AB=AD=DC ∴ ∠B= ∠ADB，∠C= ∠DAC设∠C=x，则∠DAC=x，∠B= ∠ADB= ∠C+ ∠DAC=2x，在△ABC中，根据三角形内角和定理，得2x+x+26°+x=180°，解得x=38.5°.∴ ∠C= x=38.5°，∠B=2x=77°.17. 解：设∠B＝∠BAD＝x，则∠ADC＝2x＝∠C，∴x＋2x＋102°＝180°，x＝26°，∴∠ADC＝52°.18. 证明：(1)如图①，过A作AG⊥BC于G.∵AB＝AC，AD＝AE，∴BG＝CG，DG＝EG，∴BG－DG＝CG－EG，∴BD＝CE；(2)∵BD＝CE，F为DE的中点，∴BD＋DF＝CE＋EF，∴BF＝CF.∵AB＝AC，∴AF⊥BC.。

人教版数学八年级上册13.3等腰三角形专项练习含答案

八年级上册13.3等腰三角形专项练习（含答案）（满分：100分）班级：姓名：学号：成绩:、选择题（每小题3分，共36分）1、如右图所示，在4ABC中，AB=AC , D是BC的中点，下列结论中不正确的是（）B、AD^BCC、AD 平分/BACD、/B = /C2、如图，等腰4ABC的周长为21 ,底边BC = 5, AB的垂直平分线DE交AB于点D,交AC于点E,则aBEC 的周长为（）A. 13B. 14C. 15D. 163、如图，在正三角形犯。

中，。

，町f分别是肥/。

，岫上的点，DE L AC ,EFL AB ,FD1BC，则△口£尸的面积与△血的面积之比等于（）C.布：2D.招：3A. 1 ：3B. 2 ： 3,AB=BC=CD=DE=EF , WJ/DEF 等于（C: 70° D: 6005、若等腰三角形腰上的高是腰长的一半，则这个等腰三角形的底角是（）A: 750或15 ° B: 75° C: 15° D : 75 ° A30 °6、如图，在Rt△肥C中，二91，艮0是工C的垂直平分线，交NC于点。

，交8c于点E •已知」朋月二1。

二则NC的度数为（）A•狗B- 40° C- 5/D- 6T7、某小区现有一块等腰直角三角形形状的绿地，腰长为100米，直角顶点为A .小区物业管委会准备把它分割成面积相等的两块，有如下的分割方法：方法一：在底边BC上找一点D,连接AD作为分割线；方法二：在腰AC上找一点D,连接BD作为分割线；方法三：在腰AB上找一点D,作DE //BC,交AC于点E, DE作为分割线；方法四：以顶点A为圆心，AD为半径作弧，交AB于点D,交AC于点E,弧DE作为分割线.这些分割方法中分割线最短的是（）方法一方法二方法三方法四A.方法一B.方法二C.方法三D.方法四8、等腰三角形一腰上的高与另一腰的夹角为60,，则顶角的度数为（）A. 30° B . 30° 或150 0 C . 60r曲50r D.61或120r9、如图所示，BEX AC 于点D,且AD=CD, BD = ED,若/ABC = 54° ,则/=（）A.25B.27C.30D.4510、等腰直角三角形的一个底角的度数是A3a B- 4? C 60° D- 9伊11、已知AABC是等边三角形，点D、E分别在AC、1BC边上，且AD=CE,AE与BD交于点F,则/AFD的度数为（）A.60 0B.45°C.750D. 70 °12、如图，△施中,儿5=乂。

八年级数学上册13.3 等腰三角形强化训练含答案

作品编号：4862354798562348112533学校：兽古上山市名扬镇装载小学* 教师：葛蝇给* 班级：朱雀捌班*等腰三角形基础训练1．若一个等腰三角形的两边长分别为2和5，则它的周长为(A ) A. 12 B. 9 C. 12或9 D. 9或72．如果三角形满足一个角是另一个角的3倍，那么我们称这个三角形为“智慧三角形”．下列各组数据中，能作为一个智慧三角形三边长的一组是(D )A. 1，2，3B. 1，1， 2C. 1，1，3D. 1，2， 33．等腰三角形一腰上的高与另一腰的夹角为30°，则顶角度数为(D ) A. 60° B. 120°C. 60°或150°D. 60°或120°4．下面给出的几种三角形：①有两个角为60°的三角形；②三个外角都相等的三角形；③一边上的高也是这边上的中线的等腰三角形；④有一个角为60°的等腰三角形．其中一定是等边三角形的有(B )A. 4个B. 3个C. 2个D. 1个(第5题图)5．如图，在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，过点O 作EF ∥BC 交AB 于点E ，交AC 于点F ，过点O 作OD ⊥AC 于D ，下列四个结论：①EF ＝BE ＋CF ；②∠BOC ＝90°＋12∠A ；③点O 到△ABC 各边的距离相等；④设OD ＝m ，AE ＋AF ＝n ，则S △AEF ＝mn . 其中正确的结论是( A )A. ①②③B. ①②④C. ②③④D. ①③④(第6题图)6．如图，在△ABC 中，D ，E 分别是AC ，AB 上的点，BD 与CE 交于点O .给出下列三个条件：①∠EBO ＝∠DCO ；②∠BEO ＝∠CDO ；③BE ＝CD .上述三个条件中，哪两个条件组合可判定△ABC 是等腰三角形(用序号写出一种情形)：①③或②③．7．在△ABC 中，AB ＝22，BC ＝145°，以AB 为一边作等腰直角三角形ABD ，使∠ABD ＝90°，连结CD ，则线段CD 的长为__5或13__．(第8题图)8．如图，在△ABC 中，AB ＝AC ，D 为CA 延长线上一点，DE ⊥BC ，交线段AB 于点F .请找出一组相等的线段(AB ＝AC 除外)并加以证明．解：AD ＝AF .证明如下： ∵AB ＝AC ，∴∠B ＝∠C . ∵DE ⊥BC ，∴∠B ＋∠BFE ＝∠C ＋∠D ＝90°， ∴∠BFE ＝∠D . ∵∠BFE ＝∠DF A ， ∴∠DF A ＝∠D ， ∴AF ＝AD .拓展提高(第9题图)9．如图，△ABC 是等边三角形，点P 是∠ABC 的平分线BD 上一点，PE ⊥AB 于点E ，线段BP 的垂直平分线交BC 于点F ，垂足为Q .若BF ＝2，则PE 的长为(B )A. 2B. 3C. 23D. 310．已知等腰△ABC 中，AD ⊥BC 于点D ，且AD ＝12BC ，则△ABC 底角的度数为(D )A. 45°B. 75°C. 60°D. 45°或75°11．在平面直角坐标系中，点A (2，2)，B (32，32)，动点C 在x 轴上，若以A ，B ，C 三点为顶点的三角形是等腰三角形，则点C 的个数为(B )A. 2B. 3C. 4D. 512．如图，等腰△ABC 纸片(AB ＝AC )可按图中所示方法折成一个四边形，点A 与点B 重合，点C 与点D 重合，则在原等腰△ABC 中，∠B ＝72度．(第12题图)(第13题图)13．如图，在四边形ABCD 中，AD ∥BC ，∠ABC 与∠DCB 的平分线相交于点H ，过H 作AD 的平分线交AB 于E ，交CD 于F .若BE ＝3，CF ＝2，则EF ＝__5__．14．如图，已知∠AOB ＝α，在射线OA ，OB 上分别取点OA ＝OB 1，连结AB 1，在B 1A ，B 1B 上分别取点A 1，B 2，使B 1B 2＝B 1A 1，连结A 1B 2，…，按此规律下去，记∠A 1B 1B 2＝θ1，∠A 2B 2B 3＝θ2，…，∠A n B n B n ＋1＝θn ，则：(1)θ1＝180°＋α2；(2) θn ＝()2n －1·180°＋α2n．,(第14题图))15．在如图所示的钢架中，焊上等长的13根钢条来加固钢架．若AP 1＝P 1P 2＝P 2P 3＝…＝P 13P 14＝P 14A ，则∠A 的度数是__12°__．,(第15题图))16．如图，∠BOC ＝9°，点A 在OB 上，且OA ＝1，按下列要求画图：以点A 为圆心，1为半径向右画弧交OC 于点A 1，得第1条线段AA 1；再以点A 1为圆心，1为半径向右画弧交OB 于点A 2，得第2条线段A 1A 2；再以点A 2为圆心，1为半径向右画弧交OC 于点A 3，得第3条线段A 2A 3； ……这样画下去，直到得第n 条线段，之后就不能再画出符合要求的线段了，则n ＝__9__．,(第16题图))17．如图，已知点A (3，0)，B (0，4)，C 为x 轴上一点． (1)画出等腰三角形ABC . (2)求出C 点的坐标．,(第17题图))解：(1)如解图．,(第17题图解))(2)①当A 是顶点时，C 1(－2，0)，C 2(8，0)， ②当B 是顶点时，C 3(－3，0)③当C 是顶点时，C 4⎝⎛⎭⎫－76，0.(第18题图)18．如图，在△ABC 中，AD ⊥BC ，垂足为D ，BE ⊥AC ，垂足为E ，M 为AB 边的中点，连结ME ，MD ，ED .(1)求证：△MED 为等腰三角形． (2)求证：∠EMD ＝2∠DAC .解：(1)证明：∵M 为AB 边的中点，AD ⊥BC ，BE ⊥AC ，∴ME ＝12AB ，MD ＝12AB ，∴ME ＝MD ，∴△MED 为等腰三角形．(2)∵ME ＝12AB ＝MA ，∴∠MAE ＝∠MEA ， ∴∠BME ＝2∠MAE .同理，MD ＝12AB ＝MA ，∴∠MAD ＝∠MDA ， ∴∠BMD ＝2∠MAD ，∴∠EMD ＝∠BME －∠BMD ＝2∠MAE －2∠MAD ＝2∠DAC .(第19题图)19．如图，已知点D 为等腰直角△ABC 内一点，∠CAD ＝∠CBD ＝15°，E 为AD 延长线上的一点，且CE ＝CA .(1)求证：DE 平分∠BDC .(2)若点M 在DE 上，且DC ＝DM ，求证：ME ＝BD . 解：(1)证明：∵△ABC 为等腰Rt △， ∴AC ＝BC ，∠CAB ＝∠CBA ＝45°. ∵∠CAD ＝∠CBD ＝15°，∴∠BAD ＝∠ABD ＝45°－15°＝30°，∴BD ＝AD . 又∵CA ＝CB ，∴△BDC ≌△ADC (SAS )． ∴∠DCA ＝∠DCB .又∵∠ACB ＝90°，∴∠DCA ＝∠DCB ＝45°.∵∠BDE ＝∠ABD ＋∠BAD ＝30°＋30°＝60°，∠EDC ＝∠DAC ＋∠DCA ＝15°＋45°＝60°， ∴∠BDM ＝∠EDC .∴DE 平分∠BDC .(第19题图解)(2)如解图，连结MC .∵DC ＝DM ，且∠MDC ＝60°， ∴△MDC 是等边三角形， ∴CM ＝CD .又∵∠EMC＝180°－∠DMC＝180°－60°＝120°，∠ADC＝180°－∠MDC＝180°－60°＝120°，∴∠EMC＝∠ADC.又∵CE＝CA，∴∠DAC＝∠CEM＝15°.∴△ADC≌△EMC(AAS)．∴ME＝AD＝BD.。

2019年秋人教版八年级上册数学13.3.1等腰三角形课后练习

2019年秋人教版八年级上册数学13.3.1等腰三角形课后练习一、单选题1．如图，在△ABC 中，AB=AC ，BD=BC ，AD=DE=EB ，则△A 是（）A ．30B ．45C ．36D ．202．如图，在△ABC 中，AD △BC ，垂足为D ，AD ＝BD ＝CD ，则下列结论错误的是( )A ．AB AC = B ．AD 平分BAC ∠ C ．AB BC = D ．90BAC ∠=o3．如图，在△ABC 中，△A =36°，AB =AC ，CD 是△ACB 的角平分线．若在边AC 上截取CE =CB ，连接DE ，则图中等腰三角形共有（）A ．2个B ．3个C ．4个D ．5个4．如果等腰三角形的周长为16，那么这个等腰三角形腰长x 的取值范围是（）A ．x ＞3B ．x ＜6C ．3＜x ＜6D ．4＜x ＜85．已知等腰三角形的两边长分别为4和9，则此三角形的周长是（）A ．17B ．22C ．17或22D ．126．如图，下列条件不能推出△ABC 是等腰三角形的是（）A ．△B ＝△C B ．AD △BC ，△BAD ＝△CADC．AD△BC，BD＝CD D．AD△BC，△BAD＝△ACD7．如图：Rt△ABC 中，AC＝BC，△ACB＝90°，D 为BC 边中点，CF△AD 交AD 于E，交AB 于F，BE交AC 于G，连DF，下列结论：△AC＝AF，△CD＋DF＝AD，△△ADC＝△BDF，△CE＝BE，△△ BED＝45°，其中正确的有（）A．5 个B．4 个C．3 个D．2 个8．如图，在△ABC中，AB＝AC，直线l1△l2，且分别与△ABC的两条边相交，若△1＝40°，△2＝23°，则△C的度数为（）A.40°B.50°C.63°D.67°二、填空题9．在△ABC中，AB＝AC，若△A－△B＝30°则△A＝_____，△B＝_____.10．如图，点D为△ABC的边AB上一点，若△1=△2，AB=7，AC=3，则△ACD的周长为______．11．等腰三角形一腰上的高与另一腰的夹角为30° ，则顶角的度数是__________12．在平面直角坐标系中，点A与点B的坐标分别是A(1,0)和B(5,0).以线段AB为底边作高为2的等腰三角形ABC，则顶点C的坐标为______.13．如图，D 为△ABC 的AC 边上的一点，△A＝△DBC＝36°，△C＝72°，则图中共有等腰三角形____个.14．如图，在等腰Rt ABC ∆中，90︒∠=C ，点F 是AB 的中点，且2AC =，将一块直角三角板的直角顶点放在点F 处，始终保持该直角三角板的两直角边分别与AC 、BC 相交，交点分别为D 、E ，则CD CE +的值为____.三、解答题15．已知等腰三角形的两条边长分别是a 、b ，满足()2a b 2a 2b 70-+++-=，求这个等腰三角形的周长. 16．如图，在△ABC 中，AB =AC ，DE 垂直平分AB ．（1）若AB =AC =10cm ，BC =6cm ，求△BCE 的周长；（2）若△A =40°，求△EBC 的度数．17．如图，在四边形ABCD 中，AD △BC ，E 为CD 的中点，连接AE 、BE ，BE △AE ，延长AE 交BC 的延长线于点F . 求证：△ABF 是等腰三角形．18．如图，在△ABC 中，BA ＝BC ，D 在边CB 上，且DB ＝DA ＝AC（1）填空：如图1，△B ＝ °，△C ＝ °；（2）如图2，若M 为线段BC 上的点，过M 作MH△AD ，交AD 的延长线于点H ，分别交直线AB 、AC 与点N 、E．△求证：△ANE是等腰三角形；△线段BN、CE、CD之间的数量关系是．19．已知在△ABC和△ABD中，△DAB＝△ABC＝90°，AD＝AB＝CB，BD＝6cm，F为线段BD上一动点，以每秒1cm 的速度从B匀速运动到D，过F作直线FQ△AF，且FQ＝AF，点Q在直线AF的右侧，设点F运动时间为t（s）．（1）当△ABF为等腰三角形时，t＝；（2）当F点在线段BO上时，过Q点作QH△BD于点H，求证：△AOF△△FHQ；（3）当F点在线段OD上运动的过程中，△ABQ的面积是否变化？若不变，求出它的值．参考答案1．B 2．C 3．D 4．D 5．B 6．D 7．D 8．C 9．80°，50° 10．10 11．60°或120°. 12．(3,2)(3,−2). 13．3 14．215．解∵()2a b2a2b70-+++-=，∵+20270a ba b-=⎧⎨+-=⎩，解得13ab=⎧⎨=⎩，当b为底边，a为腰时，112<+，此种情况不成立；当a为底边，b为腰时，这个等腰三角形的周长为：1+3+3=7.16．解（1）∵DE垂直平分AB，∵EA=EB，∵AB=AC=10cm，BC=6cm，∵∵BCE的周长=BC+CE+BE=BC+CE+AE=BC+AC=10cm+6cm=16cm.（2）∵AB=AC，∵A=40°，∵∵ABC=∵C=70°，∵EA=EB，∵A=40°，∵∵A=∵ABE=40°，∵∵EBC=∵ABC-∵ABE=70°-40°=30°.17．解∵AD∵BC，∵∵ADC=∵ECF，∵E是CD的中点，∵DE=EC．在∵ADE与∵FCE中，ADC ECFDE ECAED CEF∠∠⎧⎪⎨⎪∠∠⎩＝＝＝，∵∵ADE∵∵FCE（ASA），∵AE=EF，∵BE∵AE，∵∵ABF是等腰三角形．18．解：（1）∵BA＝BC，∵∵BCA＝∵BAC，∵DA＝DB，∵∵BAD＝∵B，∵AD＝AC，∵∵ADC＝∵C＝∵BAC＝2∵B，∵∵DAC＝∵B，∵∵DAC+∵ADC+∵C＝180°，∵2∵B+2∵B+∵B＝180°，∵∵B＝36°，∵C＝2∵B＝72°，故答案为：36；72；（2）∵在∵ADB中，∵DB＝DA，∵B＝36°，∵∵BAD＝36°，在∵ACD中，∵AD＝AC，∵∵ACD＝∵ADC＝72°，∵∵CAD＝36°，∵∵BAD＝∵CAD＝36°，∵MH∵AD，∵∵AHN＝∵AHE＝90°，∵∵AEN＝∵ANE＝54°，即∵ANE是等腰三角形；∵CD＝BN+CE．证明：由∵知AN＝AE，又∵BA＝BC，DB＝AC，∵BN＝AB﹣AN＝BC﹣AE，CE＝AE﹣AC＝AE﹣BD，∵BN+CE＝BC﹣BD＝CD，即CD＝BN+CE19．解：（1）∵∵BAD＝90°，AB＝AD，∵∵ABD＝∵ADB＝45°，若AB＝AF时，即点F与点D重合，∵BF＝BD＝6cm，∵t＝6＝6s，1若BF＝AF时，∵∵ABF＝∵BAF＝45°，∵∵AFB＝90°，∵AF∵BD，且AB＝AD∵BF＝DF＝3cm，∵t＝3＝3s，1故答案为：3s或6s；（2）如图1，∵∵DAB＝∵ABC＝90°，AD＝AB＝CB，∵∵ABD＝∵ADB＝45°，∵BAC＝∵ACB＝45°，∵∵AOB＝90°，∵AF∵FQ，QH∵BD，∵∵AFQ＝∵FHQ＝90°，∵∵QFH+∵FQH＝90°，∵AFO+∵QFH＝90°，∵∵AFO＝∵FQH，AF＝FQ，∵AOF＝∵FHQ＝90°∵∵AOF∵∵FHQ（AAS）；（3）不变，理由如下：如图2，过点Q作QH∵BD，∵∵DAB＝∵ABC＝90°，AD＝AB＝CB，∵∵ABD＝∵ADB＝45°，∵BAC＝∵ACB＝45°，∵∵AOB＝90°，∵AF∵FQ，QH∵BD，∵∵AFQ＝∵FHQ＝90°，∵∵QFH+∵FQH＝90°，∵AFO+∵QFH＝90°，∵∵AFO＝∵FQH，AF＝FQ，∵AOF＝∵FHQ＝90°∵∵AOF∵∵FHQ（AAS）∵OF＝QH＝t﹣3，∵S∵ABQ＝S∵AOF+S∵AFQ﹣S∵BFQ＝12BF×AO+12×AF2﹣12×BF×QH，∵S∵ABQ＝12×t×3+12[32+（t﹣3）2]﹣12×t×（t﹣3）＝9，故∵ABQ的面积不发生变化．。

2019年秋人教版八年级数学上13.3等腰三角形强化训练含答案

人教版八年级上册数学《等腰三角形》同步训练含答案

2019人教新版八年级数学上 13.3 等腰三角形 同步练习卷 包含答案

人教版八年级上册数学 13.3 等腰三角形 同步习题(含答案)

人教版 八年级数学上册 13.3 等腰三角形 课时训练(含答案)

人教版数学八年级上册13.3 等腰三角形同步练习(解析版)

人教版八年级数学上册同步练习 13.3 等腰三角形 同步练习及答案.doc