2009年成人高考专升本数学试题及答案

高等数学试卷-00023 2009年10月真题及答案

全国2009年10月高等教育自学考试高等数学（工本）试题课程代码：00023一、单项选择题（本大题共5小题，每小题3分，共15分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1. 向量a ={-1，-3，4}与x 轴正向的夹角α满足（）A. 0<1<α<2πB. α=2π C. 2π<α<π D. α=π2. 设函数f (x , y )=x +y, 则点（0，0）是f (x ,y )的（）A. 极值点B. 连续点C. 间断点D. 驻点3. 设积分区域D ：x 2+y 2≤1, x ≥0, 则二重积分⎰⎰D ydxdy 的值（） A. 小于零B. 等于零C. 大于零D. 不是常数 4. 微分方程xy ′+y =x +3是（）A. 可分离变量的微分方程B. 齐次微分方程C. 一阶线性齐次微分方程D. 一阶线性非齐次微分方程 5. 设无穷级数∑∞=1n p n收敛，则在下列数值中p 的取值为（）A. -2B. -1C. 1D. 2二、填空题（本大题共5小题，每小题2分，共10分）请在每小题的空格中填上正确答案。

错填、不填均无分。

6. 已知向量a ={3，0，-1}和b ={1，-2，1} 则a -3b =___________.7. 设函数z =2x 2+y 2，则全微分dz=___________.8. 设积分区域D 由y =x , x =1及y =0所围成，将二重积分⎰⎰Ddxdy y x f ),(化为直角坐标下的二次积分为___________. 9. 微分方程y ″+3y =6x 的一个特解y *=___________.10. 无穷级数14332232323232+++++n nΛ+…的和为___________. 三、计算题（本大题共12小题，每小题5分，共60分）11. 求过点（-1，-2，3）并且与直线223-=-=z y x 垂直的平面方程. 12. 求曲线x =t , y =t 2, z =t 3在点（1，1，1）处的切线方程.13. 求函数f (x , y , z )=xy 2+yz 2+zx 2在点P （1，2，1）处的梯度.14. 设方程e z -x 2y +z =3确定函数z =z (x , y ), 求xz ∂∂. 15. 计算二重积分⎰⎰--Dy x dxdy e 22，其中积分区域D ：x 2+y 2≤2. 16. 计算三重积分⎰⎰⎰Ωxdxdydz ，其中积分区域Ω是由x =0, y =0, z =0及x +y +z =1所围成.17. 计算对坐标的曲线积分⎰++C dy x y xdx )(, 其中C 为从点（1，0）到点（2，1）的直线段.18. 计算对面积的曲面积分⎰⎰∑xyzdS ，其中∑为球面x 2+y 2+z 2=a 2(a >0). 19. 求微分方程(1+x )dx -(1+y )dy =0的通解.20. 求微分方程y ″+ y ′-12y =0的通解.21. 判断级数∑∞=+⋅13)1(2n n n n 的敛散性. 22. 求幂级数∑∞=12n n n x 的收敛区间. 四、综合题（本大题共3小题，每小题5分，共15分）23. 求函数f (x , y )=x 3+3xy 2-15x -12y 的极值点.24. 求曲面z=22y x +(0≤z ≤1)的面积.25. 将函数f (x )=ln(1+x )展开为x 的幂级数.。

2009年成人高考专升本数学试题及答案

试介绍成人高等学校招生全国统一考试（简称“成人高考”）是为我国各类成人高等学校选拔合格新生以进入更高层次学历教育的入学考试。

考试分专科起点升本科(简称专升本)、高中起点升本科（简称高起本）和高职（高专）三个层次。

全国成人高等学校招生统一考试成人高等教育属国民教育系列，列入国家招生计划，国家承认学历，参加全国招生统一考试，各省、自治区统一组织录取。

成考教材成考用书除了大纲全国统一以外，教材辅导书试题集都没有做统一规定。

考生在选择教材时应谨慎。

选择辅导书、习题集时要看看出书组织单位是否是合法的法人，编写小组是否有正式的名称，出版社、出版单位最好选正规的单位。

购书时应该到大书店或者各区县成考办购买以防盗版、假冒伪劣辅导资料回家害人，选择辅导书不能贪多也不可贪便宜。

一般而言，高中起点升专(本)科的教材就分为人民教育出版社、高等教育出版社，还有人大出版社和成教出版社出版等，专升本教材则由中央广播电视大学出版社、人民教育出版社、高等教育出版社出版等。

具了解，如果上辅导班的话高中起点的教材用人民教育出版社的，专升本的教材用电大版高教版的比较多。

但是如果是自学呢？最好用高教版的教材。

授课方式成人高考的授课方式大体分为脱产、业余及函授三种形式，考生应根据自身的情况来选择适合自己的学习形式。

业余：业余授课方式一般在院校驻地招收学生，安排夜晚或双休日上课，所以，适合在职考生报考。

脱产：年龄较小或者想进入大学校门体验大学生活的考生可选择脱产的形式。

脱产学习就是在校内进行全日制学习方式，其管理方式与普通高校一样，对学生有正常的、相对固定的授课教室、管理要求，有稳定的寒暑假期安排。

注：2008年起，普通高校停止招收成人脱产班。

函授：该种学习形式也适合上班族人，业余时间少的考生。

函授教学主要以有计划、有组织、有指导的自学为主，并组织系统的集中面授。

函授教学的主要环节有：辅导答疑、作业、试验、实习、考试、课程设计、毕业设计及答辩。

2009年成人高考专升本高数二试题

2009年成人高考专升本高数二试题一、选择题:1～10小,每小题4分,共40分. 1. 2tan(1)lim 1x x x →-=-A . 0B . tan1C .4πD . 22. 设2sin ln 2y x x =++，则y '= A . 2sin x x -+B . 2cos x x +C . 12cos 2x x ++D . 2x3. 设函授()ln xf x e x =,则(1)f '= A . 0B .1C . eD . 2e4. 函授()f x 在[]0,2上连续,且在(0,2)内()f x '＞0，则下列不等式成立的是 A . (0)f ＞(1)f ＞(2)f B . (0)f ＜(1)f ＜(2)f C . (0)f ＜(2)f ＜(1)fD . (0)f ＞(2)f ＞(1)f5. (2)x x e dx +=⎰A . 2xx e C ++B . 22x x eC ++ C . 2xx xe C ++D .22x x xe C ++6.12011d dx dx x =+⎰ A . 21dx x+ B .211x+ C .4πD . 07. 若22()x x f x e dx e C =+⎰,则()f x =A . 2xB . 2xC . 2xeD . 18. 设函数tan()z xy =,则z x∂=∂ A . 2cos ()x xy -B . 2cos ()xxyC .2cos ()yxyD .2cos ()yxy -9. 设函数()z f u =,22u x y =+且()f u 二阶可导，则2zx y∂=∂∂A . 4()f u ''B . 4()xf u ''C . 4()yf u ''D .4()xyf u ''10. 任意三个随机事件A ，B ，C 中至少有一个发生的事件可表示为( ) A . A B C ⋃⋃ B . A B C ⋃⋂ C . A B C ⋂⋂ D .A B C ⋂⋃二、填空题:11～20小题,每小4分,共40分.11. 22343lim 3x x x x x→-+=- . 12. 1lim 13xx x →∞⎛⎫-= ⎪⎝⎭. 13. 设函数223,1()2,11,1x x f x x x x ⎧+<⎪==⎨⎪->⎩，则0(lim ())x f f x →= .14. 已知3y ax =在1x =处的切线平行于直线21y x =-,则a = . 15. 函数sin y x x =,则y ''= .16. 曲线52108y x x =-+的拐点坐标00(,)x y = . 17.xdx ⎰= .18. 3x e dx =⎰ . 19.1ln exdx x=⎰. 20. 设函数2ln()z x y =+,则全微分dz = .三、解答题: 21～28题,共70分.解答应写出推理、演算步骤. 21. (本小题满分8分)求311ln lim1x x xx →-+-. 22. (本小题满分8分)设函数sin xy e =,求.dy23. (本小题满分8分)计算1ln xdx x +⎰.24. (本小题满分8分)计算arcsin xdx ⎰.25. (本小题满分8分)有10件产品,基中8件是正品,2件是次品,甲、乙两人先后各抽取一件产品,求甲先抽到正品的条件下,乙抽到正品的概率. 26. (本小题满分10分)求函数22()f x x x=-的单调区间、极值、凹凸区间和拐点. 27. (本小题满分10分) (1)求在区间[]0,π上的曲线sin y x =与x 轴所围成图形的面积.S （2）求（1）中的平面图形绕x 轴旋转一周所得旋转体的体积V . 28. (本小题满分10分)求函数222482z x y x y =++-+的极值.09年试题参考答案和评分参考一、选择题：每小题4分，共40分。

2009专升本之高等数学答案

2009年福建省高职高专升本科入学考试高等数学试卷答案一、单项选择题1.C;2.B;3.A;4.B;5.A;6.D;7.D;8.D;9.C; 10A 。

二、填空题 11.2; 12.12; 13.211x+; 14.13(3cos sin )d x e x x x --+; 15. 33±; 16.94; 17.212±; 18.4;19.6; 20.112212x xC e C e -+。

三、计算题 21.解：2222222(arctan )11limlim()lim1().222421x x x x x x xxxπππ→+∞→+∞→+∞+==⋅=+⋅=+原式22.解：0ln(12)2(00)lim ()limlim 2x x x x x f f x xx+++→→→++====,01(00)lim ()lim (2sin)2x x f f x x x--→→-==+=,(0)2f =,(00)(00)(0)2f f f +=-== ,()f x ∴在点0x =处连续.23.解：211((ln ))ln 111; .1(ln ))2222ln t t dydyt t t dy t dt dx dx t t t dxt dt t=='+-====∴=='-⋅24.解：方程两边对x 求导：;y yy e xe y ''=+⋅ 整理得：;1yyey xe'=-222222223;(1)()(2)1.(1)(1)(1)(1)yyyy y y y yyyyyyyyy yee e d y dy e y xe e e xe y ee y exe xedxdxxe xe xe xe +⋅''''⋅--⋅--⋅+⋅--=====----25.解：令2sin ,()22x t t ππ=-<<，则2cos dx tdt =，∴原式=222111142cos csccot 4sin 2cos 444x tdt tdt t C C t tx-==-+=-⋅+⋅⎰⎰.26.解：1111222220213arccos arccos 11.66621x xxd x x dx x xπππ-=-=-⋅=--=+--⎰⎰原式27.解：1212(2,1,3),(1,3,1),213(8,1,5),131ij kn n s n n =-=-=⨯=-=--取方向向量所以直线方程为211815x y z -+-==-.28.解：()tan , ()sec P x x Q x x ==，tan tan ln cos ln cos 21(sec )(sec )cos (sec )cos cos (sec )cos (tan )sin cos xdx xdx x xy e xe dx C e xe dx C x x dx C xx xdx C x x C x C x--⎰⎰∴=+=+=⋅+=+=+=+⎰⎰⎰⎰通解又由00x y==知0C =，所以特解sin y x =.四、应用题29.解：设围成圆形的铁丝长为x ，则另一段为a x -，总面积为S ， 2222()()()(),2444x a x xx a S x πππ--=+=+211()2(),44222x x a a S x x ππ-'=+⋅=+- 令()0S x '=得唯一驻点11, (),122a x S x πππ''==++且11()0,122a S πππ''=+>+∴总面积在1a x ππ=+处取得最小值，从而围成正方形的铁丝长为1aπ+，围成圆形的铁丝长为1a ππ+时，总面积最小。

2009年成人高考高中起点升专科、本科《数学》(理科)试卷及详解【圣才出品】

15．圆
（r＞0，θ为参数）与直线 x－y＝0 相切，则 r＝（）．
A．
B．
C．2 D．4 【答案】A
【解析】消去圆的参数方程中的参数，有（x－1）2＋（y＋1）2＝r2，圆心为（1，
7 / 12
圣才电子书十万种考研考证电子书、题库视频学习平台

－1）．因为圆和 x－y＝0 相切，应有

17．某人打靶，每枪命中目标的概率都是 0.9，则 4 枪中恰有 2 枪命中目标的概率为（）．
A．0.0486 B．0.81 C．0.5 D．0.0081 【答案】A 【解析】所求概率应为
A．{x|－1≤x＜1}
B．
C．{x|－1＜x≤1}
D．
【答案】B
【解析】解不等式 3x ＋ 1 ≥ 0 ，得
，集合 B ＝ {x|x ＜ 1} ，所以
．
2．设 z＝1＋2i，i 为虚数单位，则
A．－2i
B．2i
C．－2
D．2
【答案】D
【解析】z＝1＋2i，则
，所以
（）．
1 / 12
圣才电子书十万种考研考证电子书、题库视频学习平台

2009 年成人高考高中起点升专科、本科《数学》（理科）试卷及详解
－、选择题：本大题共 17 小题，每小题 5 分，共 85 分。在每小题给出的四个选项中，
只有一项是符合题目要求的。
1．集合 A 是不等式 3x＋1≥0 的解集，集合 B＝{x|x＜1}，则集合 A∩B＝（）．
3 / 12
圣才电子书十万种考研考证电子书、题库视频学习平台

B．甲是乙的充分条件，但不是乙的必要条件 C．甲不是乙的充分条件，也不是乙的必要条件 D．甲是乙的充分必要条件【答案】D 【解析】由于 y＝2x 是（－∞，＋∞）内的增函数，所以 2a＞2b 等价于 a＞b，亦即甲是乙的充分必要条件．

2009年江苏专转本(高等数学)真题试卷(题后含答案及解析)

2009年江苏专转本（高等数学）真题试卷(题后含答案及解析)题型有：1. 选择题 2. 填空题 4. 解答题 5. 综合题 6. 证明题选择题在每小题给出的四个选项中，只有一项是符合要求的。

1．已知：则常数a，b的取值分别为( )A．z=-1，b=-2B．a=-2，b=0C．a=-1，b=0D．a=-2，b=-1正确答案：A解析：由已知得+ax+b=0，4+2a+b=0，+a=4+a=3解得a=-1，b=-2．2．已知函数f(x)=则x=2为f(x)的( )A．跳跃间断点B．可去间断点C．无穷间断点D．震荡间断点正确答案：B解析：由于，所以x=2为f(x)的可去间断点．3．设函数在点x=0处可导，则常数a的取值范围为( )A．0＜a＜1B．0＜a≤1C．a＞1D．a≥1正确答案：C解析：由已知f(x)在点x=0处可导,则存在，所以a-1＞0，即a＞1．4．曲线的渐近线的条数为( )A．1B．2C．3D．4正确答案：B解析：两条，一条垂直渐近线，一条水平渐近线．5．设F(x)=ln(3x+1)是函数f(x)的一个原函数，则f’(2x+1)dx=( )A．B．C．D．正确答案：D解析：由已知f(x)=F’(x)=，则∫f’(2x+1)dx=∫f’(2x+1)d(2x+1)=f(2x+1)+C=6．设a为非零常数，则数项级数( )A．条件收敛B．绝对收敛C．发散D．敛散性与a有关正确答案：C解析：，故原级数发散．填空题7．已知，则常数C=_____．正确答案：ln2解析：所以C=ln2．8．设函数φ(x)=∫02xtetdt，则φ’(x)=______．正确答案：4xe2x解析：利用变上限积分求导，φ’(x)=2xe2x.2=4xe2x．9．已知向量a=(1，0，-1)，b=(1，-2，1)，则a+b与a的夹角为_____．正确答案：解析：利用向量夹角公式10．设函数z=z(x，y)由方程xz2+yz=1所确定，则_______．正确答案：解析：隐函数求导，方程两边对x求导，得z2+x.2z.zx+zx.y=0，整理得zx=11．若幂级数(a＞0)的收敛半径为，则常数a=______．正确答案：2解析：根据所给幂级数an=(2n-1) 收敛半径R=所以a=2．12．微分方程(1+x2)ydx-(2-y)xdy=0的通解为_____．正确答案：2ln｜y｜-y=ln｜x｜+x2+C解析：这是一个可分离变量的常微分方程，分离变量得，化简得(+x)dx=(-1)dy．两边积分得2ln｜y｜-y=ln｜x｜++C 解答题解答时应写出推理、演算步骤。

2009年成人高考专升本高等数学一考试真题及参考答案

一、一、选择题：每小题4分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求。

第1题参考答案：A第2题参考答案：B第3题参考答案：D第4题参考答案：C第5题参考答案：B 第6题参考答案：A 第7题参考答案：D 第8题参考答案：B 第9题参考答案：C第10题参考答案：C二、填空题：本大题共10小题。

每小题4分，共40分，将答案填在题中横线上。

第11题第12题参考答案：0第13题第14题第15题第16题第17题第18题过点M0(1,-1,0)且与平面x-y+3z=1平行的平面方程为___.参考答案：(x-1)-(y+1)+3z=0(或x-y+3z=2) 因平面x-y+3z=1的法向量n={1，-1，3}，又因所求平面与平面x-y+3z=1平行，所以所求平面的法向量也为n，故所求平面的方程为(x-1)-(y+1)+3z=0（或x-y+3z=2）.第19题参考答案：4第20题设y=f(x)可导，点x0=2为f(x)的极小值点，且f(2)=3.则曲线y=f(x)在点(2,3)处的切线方程为___.参考答案：y=3 因x0=2为f(x)的极小值点，所以f′(2)=0,即f(x)在点(2，3)处的切线的斜率为0，故此切线方程为y=3.三、解答题：本大翘共8个小题，共70分。

解答应写出推理，演算步骤。

第21题第22题设y=xsinx,求y′.参考答案：y=xsinx y′=x′sinx+x(sinx)′(4分) =sinx+xcosx.（8分）第23题第24题第25题第26题第27题第28题。

2009年成人高考专升本高等数学二考试真题及参考答案

一、选择题：每小题4分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求。

第1题
参考答案：B
第2题
参考答案：B
第3题
参考答案：C
第4题
参考答案：B
第5题
参考答案：A 第6题
参考答案：D 第7题
参考答案：A 第8题
参考答案：C 第9题
参考答案：D
第10题
参考答案：A
二、填空题：本大题共10个小题，每小题4分，共40分，把答案填写在题中横线上。

第11题
参考答案：2/3
第12题
参考答案：
第13题
参考答案：8
第14题
参考答案：2/3
第15题
参考答案：2cosx-xsinx 第16题
参考答案：(1,-1)
第17题
参考答案：
第18题
参考答案：
第19题
参考答案：1/2
第20题
参考答案：
三、解答题：共70分。

解答应写出推理、演算步骤。

第21题
第22题
第23题
第24题
第25题有10件产品，其中8件是正品，2件是次品，甲、乙两人先后各抽取一件产品，求甲先抽到正品的条件下，乙抽到正品的概率.
第26题
第27题(1)求在区间[0，π]上的曲线y=sinx与x轴所围成图形的面积S;
(2)求(1)中的平面图形绕x轴旋转一周所得旋转体的体积V
第28题。

2009年成人高等学校招生全国考试数学(理工农医类)

2009年成人高等学校招生全国统一考试数学(理工农医类)1．答案必须答在答题卡上指定的位置，答在试卷上无效。

2．在本试卷中，tana 表示角a 的正切，cota 表示角a 的余切．一、选择题：本大题共17小题，每小题5分，共85分．在每小题给出的四个选项中，只有一项是符合题目要求的；将所选项前的字母填涂在答题卡相应题号的信息点上。

(1)集合A 是不等式310x +≥的解集，集合{}|x 1B x =，则集合A ∩B=(A){}|-11x x ≤(B)1|-13x x ⎧⎫≤⎨⎬⎩⎭ (C){}|-11x x ≤(D)1|-13x x ⎧⎫≤⎨⎬⎩⎭ (2)设Z=l+2i ，i 为虚数单位，则Z Z +=(A)-2i(B)2i(C)-2(D)2(3)函数1(1)1y x x =≠-+的反函数为 (A)1()y x x R =+∈(B)1()x x R -∈ (c)11(0)y x x =+≠(D)11(0)y x x=-≠ (4)函数y=log 2(x 2-3x+2)的定义域为(A){}|x 2x (B){}|x 3x (c){}|x 1x 2x 或(D){}|x 1x -(5)如果04πθ，则(A)cos θ<sin θ(B)sin θ<tan θ(C)tan θ<cos θ(D)cos θ<tan θ(6)下列函数中，在其定义域上为减函数的是（A ）212x y ⎛⎫= ⎪⎝⎭（B ）y=2x （C ）12x y ⎛⎫= ⎪⎝⎭（D ）y=x 2(7)设甲：22a b ，乙：ab ，则（A ）甲是乙的必要条件，但不是乙的充分条件（B ）甲是乙的充分条件，但不是乙的必要条件（C）甲不是乙的充分条件，也不是乙的必要条件（D）甲是乙的充分必要条件（8）直线x+2y+3=0经过（A）第一、二、三象限（B）第二、三象限（C）第一、二、四象限（D）第一、三、四象限（9）若θ为第一象限角，且sinθ-cosθ=0,则sinθ+cosθ=（A）2（B）22（C）23（D）24(10)正六边形中，由任意三个顶点连线构成的三角形的个数为（A）6（B）20（C）120（D）720（11）向量a=(1,2)，b=(-2,1)，则a与b的夹角为（A）300（B）450（C）600（D）900（12）l为正方体的一条棱所在的直线，则该正方体各条棱所在的直线中，与l异面的共有（A）2条（B）3条（C）4条（D）5条（13）若（1+x）n展开式中的第一、二项系数之和为6，则r=（A）5（B）6（C）7（D）8（14）过点（1，2）且与直线2x+y-3=0平行的直线方程为（A）2x+y-5=0（B）2y-x-3=0（C）2x+y-4=0（D）2x-y=0(15)x=1+rcos,y=-1+rcos,θθ⎧⎨⎩(0r,θ为参数)与直线x-y=0相切，则r=（A）2（B）3（C）2（D）4(16)若三棱锥的本个侧面都是边长为1的等边三角形，则该三棱锥的高为（A）22（B）33（C）63（D）12（17）某人打耙，每枪命中目标的概率都是0.9，则4枪中恰有2枪命中目标的概率为（A）0.0486（B）0.81（C）0.5（D）0.0081二、填空题；本大题共4小题，每小题4分，共16分．把答案写在答题卡相应题号后。

2009年成考专升本高数真题及答案

破碎场设备台帐
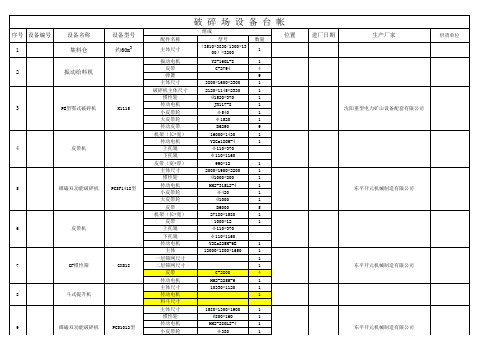
序号设备编号 1 设备名称集料仓设备型号约60m3
组成配件名称主体尺寸振动电机皮带弹簧主体尺寸破碎机主体尺寸惯性轮传动电机小皮带轮大皮带轮传动皮带机架（长*宽）传动电机上托辊下托辊皮带（宽*厚）主体尺寸惯性轮传动电机小皮带轮大皮带轮皮带机架（长*宽）皮带上托辊下托辊传动电机主体一层筛网尺寸二层筛网尺寸皮带传动电机主体尺寸传动电机料斗尺寸主体尺寸惯性轮传动电机小皮带轮型号（3510*3830/1300*13 00）*3200 Y2-160L-8 C-2794 3800*1600*2300 2120*1145*2330 Ø1520*370 JR117-8 φ 540 φ 1520 D6290 16000*1430 Y2Ga180M-4 φ 110*370 φ 110*1160 990*12 2000*1900*2200 Ø1000*200 HM2-315L2-4 φ 420 Ø1000 D6000 27180*1580 1000*12 φ 110*370 φ 110*1160 Y2Ga225M-6E 12000*1800*1650 数量 1 1 4 9 1 1 1 1 1 1 9 1 1
位置
进厂日期
生产厂家
供货单位
2
振动给料机
3
PE型鄂式破碎机
K1115
沈阳重型电力矿山设备配套有限公司
4
皮带机
5
碓磕双功能破碎机
PCSF1418型
1 1 1 1 1 1 5 1 1
东平开元机械制造有限公司
6
皮带机
7
GF惯性筛
GXS18
C-2800 HM2-225M-6 10330*1120

09年专升本高数真题答案

共 10 页，第 1 页2009年河南省普通高等学校选拔优秀专科毕业生进入本科阶段学习考试高等数学答案及【解析】析一、选择题（每小题2分，共计60分）1.答案D.【解析】：注意函数的定义范围、解析式，应选D.2.答案C.【解析】:，()ln(f x x -=-()()ln(ln(ln10f x f x x x +-=-++==，选C.()()f x f x -=-3．答案D.【解析】：，，应选D.11lim 11x x x +→-=-11lim 11x x x -→-=--4.答案C.【解析】：由等价无穷小量公式，应选C.5.答案B.【解析】：是的可去间断点,应选B.00e 1lim ()lim 1x x x f x x→→-==⇒0=x )(x f 6. 答案D.【解析】：，应选D.(1)(1)1lim(1)1(1)222x f f x f f x →--''==-⇒=-7.答案D.【解析】：，，应选D.1(3)21()2f x x -=(4)()f x =3214x --8.答案A.共 10 页，第 2 页【解析】：，应选A.0d 2cos 20d sin y t k x x x t =⇒=⇒==切9.答案B.【解析】:由得d e ()e d x xf x x -⎡⎤=⎣⎦，2d e ()d(e )e ()e ()e e x x x x x xf x f x C f x C --⎡⎤=⇒=+⇒=+⎣⎦把代入得,所以,应选B.(0)0f =1C =-2()e e x x f x =-10.答案A.【解析】:根据可导与连续的关系知，应选A.11.答案A.【解析】: ，，应选A.34486y x x '=-+212480(2,2)y x x ''=-<⇒∈-12. 答案B.【解析】: ，，应选B.e lim 0x x x →-∞=0e lim xx x→=∞13.答案D.【解析】: 根据极值点与驻点的关系和第二充分条件，应选D.14. 答案A.【解析】:根据连续函数在闭区间上的性质及的条件,在对应的开区间内至少有一个最值,()()f a f b =应选A.15.答案B.【解析】: ,应选B.()1()ln f x x x '==⇒21()f x x'=-16.答案C.【解析】: =,应选C.2221(1)(1)(1)2xf x dx f x d x -=---⎰⎰221(1)2x C --+17.答案D.【解析】: 根据定积分的保序性定理，应有，应选D.22(1)x e dx x dx ≥+⎰⎰18.答案C.共 10 页，第 3 页【解析】:因,考察积分的可加性有1ln ,1|ln |ln ,1x x x ex x e⎧-≤≤⎪=⎨⎪≤≤⎩，应选C.1111ln ln ln eeeex dx xdx xdx =-+⎰⎰⎰19．答案C.【解析】:由广义积分性质和结论可知:是的积分,收敛的,应选C.21(ln )edx x x +∞⎰2p =20.答案C.【解析】:根据方程的特点是抛物面,又因两个平方项的系数相等,从而方程在空间直角220x y z +-=坐标系中表示的曲面是旋转抛物面,应选C.21.答案D.【解析】:,应选D.0(,)2a b a b a b π=⇒⊥⇒= :22.答案A.【解析】:因,直线在平面内或平行但直线不在平面{}2,7,3s =-- {}4,2,20n s n s n =--⇒⋅=⇒⊥⇒内.又直线上点不在平面内.故直线与平面的位置关系是平行但直线不在平面内,应选A.(3,4,0)--23.答案B.【解析】:原式00(,)(,)(,)(,)limlim h h f a h b f a b f a h b f a b h h→→+---=-00(,)(,)(,)(,)limlim 2(,)x h h f a h b f a b f a h b f a b f a b h h→-→+---'=+=-应选B.24．答案D 【解析】：，应选D 22()()()()2()()()x y x y d x y x y d x y xdy ydx z dz x y x y x y +-+-+--=⇒==---25．答案D.【解析】:积分区有{(,)|0,0(,)|0,02x y y a x r r a πθθ⎧⎫≤≤≤≤=≤≤≤≤⎨⎬⎩⎭(,)ady f x y dx⎰共 10 页，第 4 页,应选D.20(cos ,sin )ad f r r rdr πθθθ=⎰⎰26.答案A.【解析】: 由格林公式知, ，(3)(2)228LDx y dx x y dy d S σ∆-+-=-=-=-⎰⎰⎰:应选A.27.答案C.【解析】: 根据可分离变量微分的特点,可化为220x y xdx e dy y++=知,应选C.22y x ye dy xe dx -=-28.答案A.【解析】: 由级数收敛的性质知,收敛,其他三个一定发散,应选A.110nn u ∞=∑29.答案C.【解析】: 根据可知,23ln(1),1123x x x x x +=-+--<≤ ,应选C.23ln(1),1123x x x x x -=-----≤< 30.答案B.【解析】: 令,级数化为,问题转化为:处收敛,确定处是否收敛.1x t -=1(1)nn n a x ∞=-∑1n n n a t ∞=∑2t =-1t =由阿贝尔定理知是绝对收敛的,故应选B.二、填空题（每小题2分，共30分）31.答案：.⎪⎭⎫ ⎝⎛≠≠-21,121x x x x 【解析】：.()1[()](1,)1()122f x x f f x x x f x x ==≠≠--32.答案：.21共 10 页，第 5 页【解析】：.2211cos ()1cos 2220sin 00()1cos 12limlim lim sin 2x x f x x x x x x x x f x x x x x x --→→→-==============:::33.答案：.2ln 【解析】：因，2223()221lim 12lim lim 1lim 1x xa axa x ax x a x x a a x a a x a e x x e x a e a a x x ⋅→∞-→∞→∞⋅--→∞⎛⎫⎛⎫++ ⎪ ⎪+⎛⎫⎝⎭⎝⎭==== ⎪-⎝⎭⎛⎫⎛⎫- ⎪- ⎪⎝⎭⎝⎭所以有 .38a e =ln 2a ⇒=34.答案：.1=a 【解析】：函数在内处处连续，当然在处一定连续，又因为(,)-∞+∞0x =，所以.0sin lim ()lim1;(0)x x xf x f a x→→===0lim ()(0)1x f x f a →=⇒=35.答案：.043=+-y x 【解析】：因.2231340(1)3x y k y x y x =''=⇒==⇒-+=+36.答案：.1=ξ【解析】：.(2)(0)()2121120f f f x x ξξ-'=-⇒-=⇒=-37.答案：.⎪⎭⎫⎝⎛41,0【解析】：,应填或或或.1()100,4f x x ⎛⎫'=<⇒∈ ⎪⎝⎭10,4⎛⎫ ⎪⎝⎭10,4⎡⎤⎢⎥⎣⎦10,4⎡⎫⎪⎢⎣⎭10,4⎛⎤⎥⎝⎦38.答案：.7【解析】：.222200()()()()2(2)(2)(0)7xf x dx xdf x xf x f x dx f f f ''''''==-=-+=⎰⎰⎰39.答案：.{}12,8,4-【解析】：因向量与共线,可设为，b a b{},2,3k k k -,所以.5649564a b k k k k ⋅=⇒++=⇒={}4,8,12b =- 40.答案：.()222212y xe x ++共 10 页，第 6 页【解析】：.22222222222(12)x y x y x y z z z e xe x e x x+++∂∂=⇒=⇒=+∂∂41.答案：.()0,0【解析】：.40(,)(0,0)40fx y xx y f x y y∂⎧=+=⎪∂⎪⇒=⎨∂⎪=-=∂⎪⎩42．答案：0.【解析】：利用对称性知其值为0或.232420cos sin 0Dx yd d r dr πσθθθ==⎰⎰⎰⎰43.答案：.()⎰⎰102,yydx y x f dy 【解析】：积分区域,{{}2(,)|01,(,)|01,D x y x x y x y y y x y =≤≤≤≤=≤≤≤≤则有.21100(,)(,)yxydx f x y dy dy f x y dx =⎰⎰⎰44.答案：.xx x xe e C e C y ---+=41231【解析】：的通解为，根据方程解的结构,原方程的通解为230y y y '''--=312x x y C e C e -=+.31214x x x y C e C e xe --=+-45.答案：.1332+-n n 【解析】：当时,.2n ≥3321(1)331n n n u S S n n n n -=-=--=-+三、计算题（每小题5分，共40分）46．求.011lim 1x x x e →⎛⎫- ⎪-⎝⎭ 【解析】：20001111lim lim lim1(1)x x x x x x x e x e x x e x e x →→→----⎛⎫-== ⎪--⎝⎭.0011lim lim 222x x x e x x x →→-===47.设是由方程确定的隐函数，求.()y y x =ln sin 2xy e y x x +=dxdy共 10 页，第 7 页【解析】：方程两边对求导得x ()ln 2cos 2xy ye xy y x x x''++= 即 ()ln 2cos 2xy e x y xy y y x x x x ''+++= 2(ln )2cos 2xy xy x e x x y x x e xy y'+=--所以 .dydx=22cos 2ln xy xy x x e xy y y x e x x --'=+ 48.已知，求.2()x xf x dx e C -=+⎰1()dx f x ⎰【解析】：方程两边对求导得2()x xf x dx e C -=+⎰x ，即，2()2xxf x e-=-22()xe f x x--=所以.211()2x xe f x =- 故22111()24x xdx xe dx xde f x =-=-⎰⎰⎰ .222211114448x x x x xe e dx xe e C =-+=-++⎰49.求定积分.44|(1)|x x dx --⎰【解析】：4014441|(1)||(1)||(1)||(1)|x x dx x x dx x x dx x x dx---=-+-+-⎰⎰⎰⎰ 01441(1)(1)(1)x x dx x x dx x x dx-=-+-+-⎰⎰⎰ 014322332401322332x x x x x x -⎛⎫⎛⎫⎛⎫=-+-+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.641164118843323332=++-+--+=50.已知求全微分.22xxy y z e +-=dz 【解析】：因,222222()(2)x xy y x xy y x z ex xy y e x y x+-+-∂'=+-=+∂共 10 页，第 8 页,222222()(2)x xy y x xy y y ze x xy y e x y y+-+-∂'=+-=-∂且它们在定义域都连续，从而函数可微，并有22xxy y z e +-=.z zdz dx dy x y∂∂=+∂∂22[(2)(2)]x xy y e x y dx x y dy +-=++-51.求，其中区域由直线围成.(2)Dx y d σ+⎰⎰D ,2,2y x y x y ===【解析】：积分区域如图所示：D 把看作Y 型区域，且有D (,)|02,2y D x y y x y ⎧⎫=≤≤≤≤⎨⎬⎩⎭故有22(2)(2)yy Dx y d dy x y dxσ+=+⎰⎰⎰⎰.2222025()4y y x xy dy y dy =+=⎰⎰230510123y ==52.求微分方程的通【解析】.22x y xy xe -'-=【解析】：这是一阶线性非齐次微分方程，它对应的齐次微分方程的通【解析】为，20y xy '-=2x y Ce =设原方程的【解析】为代入方程得,2()x y C x e =22()x x C x e xe -'= 即有，22()x C x xe -'=所以 ,222222211()(2)44x x x C x xe dx e d x e C ---==--=-+⎰⎰ 故原方程的通【解析】为.2214x x y e Ce -=-+53.求幂级数的收敛区间（考虑区间端点）.212nn n n x ∞=∑【解析】：这是标准缺项的幂级数，考察正项级数，212nn n n x ∞=∑x y→=2yx因,221112lim lim 22n n n n n nu n x l x u n ++→∞→∞+==⨯= 当，即是绝对收敛的；212x l =<||x <212n n n n x ∞=∑ 当，即是发散的；212x l =>||x >212n n n n x ∞=∑ 当，即化为，显然是发散的。

2009年成人高考专科起点升本科《高等数学(二)》真题及详解【圣才出品】

D．2x2＋xex＋C
十万种考研考证电子书、题库视频学习平台
【答案】A
【解析】根据丌定积分加法原则
．
6．
（）．
A．
B． C． D．0 【答案】D 【解析】因为定积分
是个常数，故对其求导为 0．
7．若 A．2x B．x2 C． D．1 【答案】A 【解析】由
，则
＝（）．
（1）（2）
9 / 10
圣才电子书十万种考研考证电子书、题库视频学习平台

28．求函数 z＝x2＋2y2＋4x－8y＋2 的极值．（本题满分 10 分）
解：令
，得
，，且 A＝2＞0，所以 f（－2，2）＝－10 为极小值．
10 / 10
，得
3 / 10
，故
．
圣才电子书十万种考研考证电子书、题库视频学习平台

8．设函数 z＝
，则（）．
A．
B．
C．
D．【答案】C
【解析】
．
9．设函数 z＝
，u＝x2＋y2 且
二阶可导，则
（）．
A．4 B．4x C．4y D．4xy 【答案】D
【
解
析
】
，
．
10．任意三个随机事件 A、B、C 中至少有一个发生的事件可表示为（）． A．A∪B∪C
21．计算
（本题满分 8 分）
解：由洛必达法则得
22．设函数 y＝esinx，求 dy．（本题满分 8 分）
7 / 10
圣才电子书

解：
十万种考研考证电子书、题库视频学习平台
则
23．计算解：
（本题满分 8 分）
24．计算解：

2009年成考专升本高数真题及答案

/cctvchildren/dongmanshijie/videopage/index.shtmlLXGIWYL = 一般武器KJKSZPJ = 暴力武器UZUMYMW‘= 超级武器HESOYAM = 恢复生命值, 防弹衣, $250kOSRBLHH = 增加两颗警星ASNAEB = 清除警星(偷渡和闯如军事基地无效) AFZLLQLL = 好天气ICIKPYH = 非常好的天气ALNSFMZO = 变阴暗天气AUIFRVQS = 下雨的天气CFVFGMJ = 雾深的天气YSOHNUL = 时间过的更快PPGWJHT = 快速游戏LIYOAAY = 慢速游戏AJLOJYQY = 暴动BAGOWPG = 街上的人见了你都逃跑(胆大者会向你开枪) FOOOXFT = 行人拥有武器AIWPRTON = 坦克CQZIJMB = 破旧的车JQNTDMH = 农场工人的车PDNEJOH = 赛车1VPJTQWV = 赛车2AQTBCODX = 葬礼车KRIJEBR = 环座型贵宾车UBHYZHQ = 垃圾车RZHSUEW = 高尔夫车CPKTNWT = 附近所有车爆炸XICWMD = 看不见的汽车PGGOMOY = 完美的处理SZCMAWO = 自杀ZEIIVG = 所有的红绿灯变绿灯YLTEICZ = 攻击性的驾驶员LLQPFBN = 粉红的交通(所有车变粉红色) IOWDLAC = 黑色的交通(所有车变黑色) AFSNMSMW = 船可以飞BTCDBCB = 肥胖JYSDSOD = 强壮值全满KVGYZQK = 薄的ASBHGRB = Elvis 在各处BGLUAWML = Peds 用武器攻击你, 火箭发射者CIKGCGX = 海滩党MROEMZH = 各处一组成员BIFBUZZ = 团队控制街道AFPHULTL = 忍者主题BEKKNQV = 所有丑女被你吸引BGKGTJH = 交通是便宜的汽车GUSNHDE = 交通是快速的汽车RIPAZHA = 汽车会飞JHJOECW = 未知JUMPJET = 战斗机Spawn HydraKGGGDKP = 水翼船Spawn Vortex HovercraftJCNRUAD = 非常的繁荣COXEFGU = 所有的汽车有Nitro All Cars Have Nitro(氮气) BSXSGGC = 未知Cars Float Away When HitXJVSNAJ = 总是午夜的OFVIAC = 橘色天空21:00MGHXYRM = 雷雨CWJXUOC = 沙暴LFGMHAL = 跳的更高BAGUVIX = 无限健康CVWKXAM = 无限氧气AIYPWZQP = 降落伞YECGAA = 火箭飞行器JetpackAEZAKMI = 不被通缉LJSPQK = 警星全满IAVENJQ = 百万打洞器AEDUWNV = 不会饥饿IOJUFZN = 暴动模态PRIEBJ = 玩趣屋主题MUNASEF = 肾上腺素模态WANRLTW = 无限弹药, 没有再装填OUIQDMW = 当驾驶的时候可以在车内使用准星瞄准攻击THGLOJ = 交通畅通FVTMNBZ = 交通是国家车辆SJMAHPE = 补充每一个子弹BMTPWHR = 国家车辆和Peds,拿天生的2个卡车用具ZSOXFSQ = 补充每一个(火箭筒)OGXSDAG = 最大威望Max RespectEHIBXQS = 最大性感Max Sex AppealVKYPQCF = Taxis 车可以跳舞NCSGDAG = 武器熟练度全满VQIMAHA = 更好的驾驶技能OHDUDE = 猎人(Ah-64阿帕奇战斗机)AKJJYGLC = 四轮摩托车AMOMHRER = 超长拖粪车EEGCYXT = 推土机URKQSRK = 杂技飞机Spawn Stunt PlaneAGBDLCID = 越野型大脚车回答者：爲楽谁 - 护国法师十五级发消息加为好友12-15 00:43 圣安地列斯的秘籍：LXGIWYL = 一般武器KJKSZPJ = 暴力武器UZUMYMW = 超级武器HESOYAM = 恢复生命值, 防弹衣, $250kOSRBLHH = 增加两颗警星ASNAEB = 清除警星(偷渡和闯如军事基地无效)AFZLLQLL = 好天气ICIKPYH = 非常好的天气ALNSFMZO = 变阴暗天气AUIFRVQS = 下雨的天气CFVFGMJ = 雾深的天气YSOHNUL = 时间过的更快PPGWJHT = 快速游戏LIYOAAY = 慢速游戏AJLOJYQY = 暴动BAGOWPG = 街上的人见了你都逃跑(胆大者会向你开枪)FOOOXFT = 行人拥有武器AIWPRTON = 坦克CQZIJMB = 破旧的车JQNTDMH = 农场工人的车PDNEJOH = 赛车1VPJTQWV = 赛车2AQTBCODX = 葬礼车KRIJEBR = 环座型贵宾车UBHYZHQ = 垃圾车RZHSUEW = 高尔夫车CPKTNWT = 附近所有车爆炸XICWMD = 看不见的汽车PGGOMOY = 完美的处理SZCMAWO = 自杀ZEIIVG = 所有的红绿灯变绿灯YLTEICZ = 攻击性的驾驶员LLQPFBN = 粉红的交通(所有车变粉红色) IOWDLAC = 黑色的交通(所有车变黑色) AFSNMSMW = 船可以飞BTCDBCB = 肥胖JYSDSOD = 强壮值全满KVGYZQK = 薄的ASBHGRB = Elvis 在各处BGLUAWML = Peds 用武器攻击你, 火箭发射者CIKGCGX = 海滩党MROEMZH = 各处一组成员BIFBUZZ = 团队控制街道AFPHULTL = 忍者主题BEKKNQV = 所有丑女被你吸引BGKGTJH = 交通是便宜的汽车GUSNHDE = 交通是快速的汽车RIPAZHA = 汽车会飞JHJOECW = 未知JUMPJET = 战斗机Spawn HydraKGGGDKP = 水翼船Spawn Vortex HovercraftJCNRUAD = 非常的繁荣COXEFGU = 所有的汽车有Nitro All Cars Have Nitro(氮气) BSXSGGC = 未知Cars Float Away When HitXJVSNAJ = 总是午夜的OFVIAC = 橘色天空21:00MGHXYRM = 雷雨CWJXUOC = 沙暴LFGMHAL = 跳的更高BAGUVIX = 无限健康CVWKXAM = 无限氧气AIYPWZQP = 降落伞YECGAA = 火箭飞行器JetpackAEZAKMI = 不被通缉LJSPQK = 警星全满IAVENJQ = 百万打洞器AEDUWNV = 不会饥饿IOJUFZN = 暴动模态PRIEBJ = 玩趣屋主题MUNASEF = 肾上腺素模态WANRLTW = 无限弹药, 没有再装填OUIQDMW = 当驾驶的时候可以在车内使用准星瞄准攻击THGLOJ = 交通畅通FVTMNBZ = 交通是国家车辆SJMAHPE = 补充每一个子弹BMTPWHR = 国家车辆和Peds,拿天生的2个卡车用具ZSOXFSQ = 补充每一个(火箭筒)OGXSDAG = 最大威望Max RespectEHIBXQS = 最大性感Max Sex AppealVKYPQCF = Taxis 车可以跳舞NCSGDAG = 武器熟练度全满VQIMAHA = 更好的驾驶技能OHDUDE = 猎人(Ah-64阿帕奇战斗机)AKJJYGLC = 四轮摩托车AMOMHRER = 超长拖粪车EEGCYXT = 推土机URKQSRK = 杂技飞机Spawn Stunt PlaneAGBDLCID = 越野型大脚车操作类AJLOJYQY = 行人互相攻击BAGOWPG = 行人都来攻击你FOOOXFT = 行人全副武装BLUESUEDESHOES = 行人变成猫王BGLUAWML = 行人用武器攻击你，路上只有军人，牛仔，帮派成员。

专升本高等数学(一)真题2009年

______． [答案] 4． [解题指导] 本题考查的知识点为二重积分的性质：
，其中σ为区域D的面积．由于积分区域D是边长为2的正方形，其面积为4，可知
． 20．设y=f(x)可导，点x0=2为f(x)的极小值点，且f(2)=3．则曲线y=f(x)
在点(2，3)处的切线方程为______． [答案] y=3． [解题指导] 本题考查的知识点为：极值的必要条件、切线方程．由于y=f(x)可导，点x0=2为f(x)的极值点，由极值的必要条件知
．因此
解法2
． 17．设z=sin(y-x2)，则
=______． [答案] COS(y-x2)． [解题指导] 本题考查的知识点为偏导数运算．求
时，只需将x认定为常量．z=sin(y-x2)，因此
． 18．过点M0(1，-1，0)且与平面x-y+3z=1平行的平面方程为______． [答案] (x-1)-(y+1)+3z=0(或x-y+3z=2)． [解题指导] 本题考查的知识点为平面方程．已知平面π1：x-y+3z=1的法线向量n1=(1，-1，3)．所求平面π与π1，平
[答案] B [解题指导] 本题考查的知识点为复合函数求导运算，在某点处的导数值．
故选B． 6．设f(x)为连续函数，
( )． A．f(2x) B．2f(x) C．-f(2x) D．-2f(x) [答案] A [解题指导] 本题考查的知识点为可变上限积分求导：若f(x)为连续函
数，则F'(x)=
=( )． A．2x+1 B．2xy+1 C．x2+1 D．2xy [答案] B．
[解题指导] 本题考查的知识点为偏导数计算．求时，只需将y认定为常量，依一元函数求导法则运算．由于z=x2y+x-3，因此

2009年河南专升本高数真题+答案解析

2009河南省普通高等学校选拔优秀专科毕业生进入本科阶段学习考试高等数学试卷一、选择题（每小题2 分，共50 分） 1．下列函数相等的是（）A ．2,x y y x x==B ．y y x ==C ．2,y x y ==D ．,y x y =【答案】D【解析】由函数相等的定义知D 正确．2．下列函数中为奇函数的是（） A ．()2x xe ef x -+=B ．()tan f x x x =C ．()ln(f x x =+D ．()1x f x x=- 【答案】C【解析】对于C ，()ln(f x x -=-+==)()x f x =-=-，故C 为奇函数．3．11lim1x x x →--的值是（） A ．1 B ．1- C ．0 D ．不存在【答案】D 【解析】1111lim lim 111x x x x x x ++→→--==--，1111lim lim 111x x x x x x --→→--==---，由于1111lim lim 11x x x x x x +-→→--≠--，因此极限不存在．4．当0x →时，下列无穷小中与x 等价的是（）A ．22x x -B C ．ln(1)x +D ．2sin x【答案】C【解析】由题意可知00ln(1)lim lim 1x x x xxx →→+==，故选C ．5．设1()x e f x x -=，则0x =是()f x 的（）A ．连续点B ．可去间断点C ．跳跃间断点D ．无穷间断点【答案】B【解析】由于001lim ()lim 1x x x e f x x →→-==，但()f x 在0x =处无定义，因此0x =是()f x 的可去间断点．6．设函数()f x 可导，且0(1)(1)lim12x f f x x→--=-，则(1)f '=（）A ．2B ．1-C ．1D ．2-【答案】D 【解析】00(1)(1)(1)(1)(1)lim2lim 22x x f x f f f x f x x→→----'===--．7．设函数()f x 具有四阶导数，且()f x ''=(4)()f x =（）AB C ．1D ．3214x --【答案】D【解析】()f x ''=()f x '''=3(4)21()4fx x -=-．8．曲线sin 2cos x t y t=⎧⎨=⎩在4t π=对应点处的法线方程为（）A．x =B ．1y =C ．1y x =+D ．1y x =-【答案】A【解析】切线的斜率为44()2cos 20()sin t t y t t k x t tππ=='==-='，因此法线方程为4cos t x tπ===．9．已知()x xd e f x e dx -⎡⎤=⎣⎦，且(0)0f =，则()f x =（）A ．2x x e e +B ．2x x e e -C ．2x x e e -+D ．2x x e e --【答案】B【解析】对等式两边积分()x xd e f x e dx -⎡⎤=⎣⎦⎰⎰，得()x x e f x e C -=+，所以2()x x f x e Ce =+．因为(0)0f =，所以1C =-，因此2()x x f x e e =-，故选B ．10．函数在某点处连续是其在该点处可导的（）A ．必要条件B ．充分条件C ．充要条件D ．无关条件【答案】A【解析】根据可导与连续的关系知选A ．11．曲线42246y x x x =-+的凸区间为（）A ．(2,2)-B ．(,0)-∞C ．(0,)+∞D ．(,)-∞+∞【答案】A【解析】34486y x x '=-+，21248y x ''=-，由0y ''<，得22x -<<，因此曲线的凸区间为(2,2)-．12．曲线xe y x =（）A ．仅有水平渐进线B ．既有水平渐进线，又有垂直渐近线C ．仅有垂直渐近线D ．既无水平渐进线，又无垂直渐近线【答案】B【解析】lim 0x x e x →-∞=，0lim x x e x →=∞，故曲线xe y x=既有水平渐进线，又有垂直渐近线．13．下列说法正确的是（） A ．函数的极值点一定是函数的驻点 B ．函数的驻点一定是函数的极值点C ．二阶导数非零的驻点一定是极值点D ．以上说法都不对【答案】C【解析】由极值的第二判定定理，知C 正确．14．设()f x 在[],a b 上连续，且不是常数函数，若()()f a f b =，则在(,)a b 内（） A ．必有最大值或最小值 B ．既有最大值又有最小值C ．既有极大值又有极小值D ．至少存在一点ξ，使得()0f ξ'=【答案】A【解析】根据极值的判定定理、最大值最小值定理和罗尔定理，知A 选项正确．15．若()f x 的一个原函数是ln x ，则()f x '=（）A ．1xB ．21x-C ．ln xD ．ln x x【答案】B【解析】因为1()(ln )f x x x '==，所以21()f x x'=-．16．若2()f x dx x C =+⎰，则2(1)xf x dx -=⎰（）A ．222(1)x C --+B ．222(1)xC -+C ．221(1)2x C --+D ．221(1)2x C -+【答案】C【解析】由题意知，因为2()f x dx x C =+⎰，则2222211(1)(1)(1)(1)22xf x dx f x d x x C -=---=--+⎰⎰．17．下列不等式中不成立的是（）A ．22211ln ln xdx xdx >⎰⎰B ．220sin xdx xdx ππ<⎰⎰C ．22ln(1)x dx xdx +<⎰⎰D ．22(1)x e dx x dx <+⎰⎰【答案】D【解析】对于D ，222001x xe dx ee ==-⎰，222001(1)42x dx x x ⎛⎫+=+= ⎪⎝⎭⎰，应有2200(1)xe dx x dx >+⎰⎰，故D 选项错误．18．1ln ee xdx =⎰（）A ．111ln ln eexdx xdx +⎰⎰B ．111ln ln eexdx xdx -⎰⎰C ．111ln ln eexdx xdx -+⎰⎰D ．111ln ln eexdx xdx --⎰⎰【答案】C【解析】1111111ln (ln )ln ln ln eeeeeexdx x dx xdx xdx xdx =-+=-+⎰⎰⎰⎰⎰．19．下列广义积分中收敛的是（）A ．lnex dx x+∞⎰B ．1ln edx x x+∞⎰C ．21ln edx x x+∞⎰D ．e+∞⎰【答案】C【解析】对于C 选项，22111ln 1ln ln ln eee dx d x x x x x+∞+∞+∞==-=⎰⎰，故收敛．20．方程220x y z +-=在空间直角坐标系中表示的是（）A ．球面B ．圆锥面C ．旋转抛物面D ．圆柱面【答案】C【解析】由旋转抛物面的定义知选C ．21．设{}1,1,,2=-a ，{}2,0,1=b ，则a 与b 的夹角为（）A ．0B ．6π C ．4π D ．2π 【答案】D【解析】1210210⋅=-⨯+⨯+⨯=a b ，所以a 与b 的夹角为2π，故选D ．22．直线34:273x y zL ++==--与平面:4223x y z π--=的位置关系是（） A ．平行但直线不在平面上 B ．直线在平面上C ．垂直D ．相交但不垂直【答案】A【解析】因为直线L 的方向向量(2,7,3)=--s ，平面的法向量为(4,2,2)=--n ，则 24(7)(2)3(2)0⋅=-⨯+-⨯-+⨯-=s n ．又点(3,4,0)--不在平面上，所以直线与平面平行．23．设(,)f x y 在点(,)a b 处有偏导数，则0(,)(,)limh f a h b f a h b h→+--=（）A ．0B ．2(,)x f a b 'C ．(,)x f a b 'D ．(,)y f a b '【答案】B【解析】由题意知，00(,)(,)(,)(,)lim2lim 2(,)2x h h f a h b f a h b f a h b f a h b f a b h h→→+--+--'==．24．函数x yz x y+=-的全微分为（）A ．22()()xdx ydy x y --B ．22()()ydy xdx x y --C ．22()()ydx xdy x y --D ．22()()xdy ydx x y --【答案】D 【解析】22()z y x x y ∂-=∂-，22()z x y x y ∂=∂-，故22()()xdy ydx dz x y -=-．25．00(,)ady f x y dx ⎰化为极坐标形式为（）A ．20(cos ,sin )ad f r r rdr πθθθ⎰⎰B ．2cos 0(cos ,sin )d f r r rdr πθθθθ⎰⎰C ．sin 2(cos ,sin )a d f r r rdr πθθθθ⎰⎰D ．20(cos ,sin )ad f r r rdr πθθθ⎰⎰【答案】D【解析】令cos x r θ=，sin y r θ=，可知02πθ≤≤，0r a ≤≤，故化为极坐标形式为200(cos ,sin )ad f r r rdr πθθθ⎰⎰．26．设L 是以(1,0)A -、(3,2)B -、(3,0)C 为顶点的三角形区域的边界，方向为ABCA ，则(3)(2)Lx y dx x y dy -+-=⎰（）A ．8-B ．0C ．8D ．20【答案】A【解析】由格林公式，知1(3)(2)224282L Dx y dx x y dy dxdy -+-=-=-⨯⨯⨯=-⎰⎰⎰．27．下列微分方程中，可分离变量的方程是（） A ．tan dy y ydx x x=+B ．22()20x y dx xydy +-=C ．220x y xdx e dy y++=D ．2x dyy e dx+= 【答案】C【解析】由可分离变量的方程形式，知选项C 正确．28．若级数1n n u ∞=∑收敛，则下列级数中收敛的是（）A ．110n n u∞=∑B ．1(10)n n u ∞=+∑C ．110n nu ∞=∑D ．1(10)n n u ∞=-∑【答案】A【解析】由无穷级数的基本性质知，1n n u ∞=∑收敛必有110nn u ∞=∑收敛．29．函数()ln(1)f x x =-的幂级数展开式为（） A ．23...,1123x x x x +++-<≤B ．23...,1123x x x x -+--<≤C ．23...,1123x x x x -----≤<D ．23...,1123x x x x -+-+-≤<【答案】C【解析】由幂级数展开公式，得()ln(1)f x x =-=23...,1123x x x x -----≤<．30．级数0(1)n n n a x ∞=-∑在点1x =-处收敛，则此级数2x =处（）A ．条件收敛B ．绝对收敛C ．发散D ．无法确定【答案】B【解析】由阿贝尔定理知级数在2x =处绝对收敛，故选B ．二、填空题（每小题 2分，共 30分） 31．已知()1xf x x=-，则[]()f f x =________．【答案】12xx- 【解析】[]()1()1()1211xf x xx f f x x f x x x-===----．32．当0x →时，()f x 与1cos x -等价，则0()lim sin x f x x x→=________．【答案】12【解析】由题意可知，()f x 与1cos x -等价，则00()1cos 1lim lim sin sin 2x x f x x x x x x →→-==．33．若2lim 8xx x a x a →∞+⎛⎫= ⎪-⎝⎭，则a =________．【答案】ln2【解析】333233lim lim 1lim 18x a ax xx a x aa x x x x a a a e x a x a x a -⋅⋅-→∞→∞→∞+⎛⎫⎛⎫⎛⎫=+=+== ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭，故ln2a =．34．设函数sin ,0(),0xx f x x a x ⎧≠⎪=⎨⎪=⎩在(,)-∞+∞内处处连续，则a =________．【答案】1【解析】因为()f x 在(,)-∞+∞内处处连续，所以0sin lim 1x xa x→==．35．函数31xy x=+在(2,2)点处的切线方程为________．【答案】1433y x =+【解析】23(1)y x '=+，所以切线斜率13k =，又因为过点(2,2)，所以切线方程为1433y x =+．36．函数2()2f x x x =--在区间[]0,2上使用拉格朗日中值定理时，结论中的ξ=________．【答案】1【解析】由拉格朗日中值定理，知存在(0,2)ξ∈，使得()()(2)(0)()12f b f a f f f b a ξ--'===-，()21f x x '=-，当1x =时，有(1)1f '=，故1ξ=．37．函数()f x x =________．【答案】10,4⎛⎫⎪⎝⎭【解析】()1f x '=，令()0f x '<，解得104x <<．38．已知(0)2f =，(2)3f =，(2)4f '=，则2()xf x dx ''=⎰________．【答案】7【解析】2222()()()2(2)()8(2)(0)7xf x dx xf x f x dx f f x f f '''''=-=-=-+=⎰⎰．39.设向量b 与{}1,2,3=-a 共线，且56⋅=a b ，则=b ________．【答案】{}4,8,12-【解析】由a 与b 共线，知λ=b a ，由1456λλ⋅=⋅==a b a a ，知4λ=，故{}4,8,12=-b ．40．设22x y z e+=，则22zx∂=∂________．【答案】222(42)xy x e ++【解析】222x y z xe x+∂=∂，222222222222(42)x y x y x y z e x xe x e x +++∂=+⋅=+∂．41．函数22(,)22f x y x xy y =+-的驻点为________．【答案】(0,0)【解析】4x f x y =+，4y f x y =-，令0x f =，0y f =，得驻点为(0,0)．42．设区域D 为229x y +≤，则2Dx yd σ=⎰⎰________．【答案】0【解析】令cos x r θ=，sin y r θ=，知232323334cos sin cos sin 0Dx yd d r rdr d r dr ππσθθθθθθ=⋅==⎰⎰⎰⎰⎰⎰．43．交换积分次序后，10(,)xdx f x y dy =⎰________．【答案】【解析】由题意知积分区域为01xx y ≤≤⎧⎪⎨≤≤⎪⎩，交换积分次序后，积分区域为201y y x y ≤≤⎧⎨≤≤⎩，故2110(,)(,)yxydx f x y dy dy f x y dx =⎰⎰⎰．44．已知14x y xe -=-是微分方程23x y y y e -'''-+=的一个特解，则该方程的通解为________．【答案】31214x x x y C e C e xe --=+-（12,C C 为任意常数）【解析】由题知，齐次方程所对应的特征方程为2230r r --=，解得11r =-，23r =，故对应的齐次方程的通解为312x x y C e C e -=+，又知特解为14x y xe -=-，故通解为31214x x x y C e C e xe --=+-（12,C C 为任意常数）．45．已知级数1n n u ∞=∑的部分和3n S n =，则当2n ≥时，n u =________．【答案】2331n n -+【解析】当2n ≥时，3321(1)331n n n u S S n n n n -=-=--=-+．三、计算题（每小题5 分，共40 分） 46．求011lim 1x x x e →⎛⎫- ⎪-⎝⎭．【答案】【解析】200000111111lim lim lim lim lim 1(1)222x x x x x x x x x x e x e x e x x e x e x x x →→→→→-----⎛⎫-===== ⎪--⎝⎭．47．设 ()y f x =是由方程ln sin 2xy e y x x +=确定的隐函数，求dydx．【答案】22cos2ln xy xyx x xye yx e x x--+ 【解析】方法一方程两边同时对x 求导得()ln 2cos2xy ye y xy y y x x''+++=，故 22cos2ln xy xy dy x x xye yy dx x e x x--'==+．方法二令(,)ln sin 2xy F x y e y x x =+-，则22cos 2ln xy x xy y F dyx x xye y dx F x e x x--=-=+．48．已知2()x xf x dx e C -=+⎰，求1()dx f x ⎰．【答案】21142x x e C ⎛⎫--+ ⎪⎝⎭【解析】等式两边对x 求导，得2()2x xf x e -=-，则211()2x xe f x =-，故 ()222211111()4442x x x x dx xde xe e dx x e C f x ⎛⎫=-=--=--+ ⎪⎝⎭⎰⎰⎰．49．求44(1)x x dx --⎰．【答案】1293【解析】40142224401(1)()()()x x dx x x dx x x dx x x dx ---=---+-⎰⎰⎰⎰32041132x x -⎛⎫=- ⎪⎝⎭32101132x x ⎛⎫-- ⎪⎝⎭32411132x x ⎛⎫+- ⎪⎝⎭1293=．50．已知22x xy y z e +-=，求全微分dz ．【答案】[]22(2)(2)xxy y e x y dx x y dy +-++-【解析】22(2)x xy y z x y e x+-∂=+∂，22(2)x xy y zx y e y +-∂=-∂，则[]22(2)(2)x xy y dz e x y dx x y dy +-=++-．51．求 (2)Dx y dxdy +⎰⎰，其中D 由y x =，2y x =，2y =围成．【答案】103【解析】由题意可知，积分区域D 为02y ≤≤，2yx y ≤≤，222002510(2)(2)43yy Dx y dxdy dy x y dx y dy +=+==⎰⎰⎰⎰⎰．52．求微分方程22x y xy xe -'-=的通解．【答案】2214x x y e Ce -=-+【解析】方程为一阶非齐次线性微分方程，其中()2P x x =-，2()x Q x xe -=，则方程的通解为222()()(2)(2)21()4P x dx P x dx x dx x dx x x x y e Q x e dx C e xe e dx C e e C ------⎛⎫⎡⎤⎡⎤⎰⎰⎰⎰=+=+=-+ ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭⎰⎰ 2214x x e Ce -=-+．53．求幂级数212nnn n x ∞=∑的收敛区间（考虑端点）．【答案】(【解析】令2t x =，则级数为12nn n n t ∞=∑，因为11121limlim 22n n n n n na n a n ++→∞→∞+=⋅=，所以12n n n n t ∞=∑的收敛半径为2，则212n n n nx ∞=∑，又当x =1n n ∞=∑发散，故所求幂级数的收敛域为(．四、应用题（每小题7 分，共 14 分）54．靠一堵充分长的墙边，增加三面墙围成一矩形场地，在限定场地面积为642m 的条件下，问增加的三面墙各长多少时，其总长最小．【答案】三面墙的长度分别为，和【解析】设与已知墙面平行的墙的长度为x m ，则另两面墙的长为64xm ，故三面墙的总长为128(0)l x x x=+>．令212810l x '=-=，解得唯一驻点x =又32560l x''=>，故当x =m 时，l 取值最小，此时，三面墙的长度分别为，和．55．设D 是由曲线()y f x =与直线0y =，3y =围成的区域，其中2,2()6,2x x f x x x ⎧≤=⎨->⎩，求D 绕y 轴旋转一周所生成的旋转体的体积．【答案】1172π 【解析】由题意得3322332300011117(6)(6)322y V y dy dy y y πππππ=--=---=⎰⎰．五、证明题（6 分） 56．设1()()()xx a bF x f t dt dt f t =+⎰⎰，其中函数()f x 在闭区间[],a b 上连续，且()0f x >．证明在开区间(,)a b 内，方程满()0F x =有唯一的实根．【解析】因为()F x 在[],a b 上连续，()0f x >，且1()0()a bF a dt f t =<⎰，()()0b a F b f t dt =>⎰，所以方程()0F x =在(,)a b 内有根，又因为1()()0()F x f x f x '=+>，所以()F x 在(,)a b 内单调，故至多有一个实根．综上，在开区间(,)a b 内，方程满()0F x =有唯一的实根．。

2009年河南专升本高数真题+答案解析

2009河南省普通高等学校选拔优秀专科毕业生进入本科阶段学习考试高等数学试卷一、选择题（每小题2 分，共50 分） 1．下列函数相等的是（）A ．2,x y y x x==B ．y y x ==C ．2,y x y ==D ．,y x y =【答案】D【解析】由函数相等的定义知D 正确．2．下列函数中为奇函数的是（） A ．()2x xe ef x -+=B ．()tan f x x x =C ．()ln(f x x =+D ．()1x f x x=- 【答案】C【解析】对于C ，()ln(f x x -=-+==)()x f x =-=-，故C 为奇函数．3．11lim1x x x →--的值是（） A ．1 B ．1- C ．0 D ．不存在【答案】D 【解析】1111lim lim 111x x x x x x ++→→--==--，1111lim lim 111x x x x x x --→→--==---，由于1111lim lim 11x x x x x x +-→→--≠--，因此极限不存在．4．当0x →时，下列无穷小中与x 等价的是（）A ．22x x -B C ．ln(1)x +D ．2sin x【答案】C【解析】由题意可知00ln(1)lim lim 1x x x xxx →→+==，故选C ．5．设1()x e f x x -=，则0x =是()f x 的（）A ．连续点B ．可去间断点C ．跳跃间断点D ．无穷间断点【答案】B【解析】由于001lim ()lim 1x x x e f x x →→-==，但()f x 在0x =处无定义，因此0x =是()f x 的可去间断点．6．设函数()f x 可导，且0(1)(1)lim12x f f x x→--=-，则(1)f '=（）A ．2B ．1-C ．1D ．2-【答案】D 【解析】00(1)(1)(1)(1)(1)lim2lim 22x x f x f f f x f x x→→----'===--．7．设函数()f x 具有四阶导数，且()f x ''=(4)()f x =（）AB C ．1D ．3214x --【答案】D【解析】()f x ''=()f x '''=3(4)21()4fx x -=-．8．曲线sin 2cos x t y t=⎧⎨=⎩在4t π=对应点处的法线方程为（）A．x =B ．1y =C ．1y x =+D ．1y x =-【答案】A【解析】切线的斜率为44()2cos 20()sin t t y t t k x t tππ=='==-='，因此法线方程为4cos t x tπ===．9．已知()x xd e f x e dx -⎡⎤=⎣⎦，且(0)0f =，则()f x =（）A ．2x x e e +B ．2x x e e -C ．2x x e e -+D ．2x x e e --【答案】B【解析】对等式两边积分()x xd e f x e dx -⎡⎤=⎣⎦⎰⎰，得()x x e f x e C -=+，所以2()x x f x e Ce =+．因为(0)0f =，所以1C =-，因此2()x x f x e e =-，故选B ．10．函数在某点处连续是其在该点处可导的（）A ．必要条件B ．充分条件C ．充要条件D ．无关条件【答案】A【解析】根据可导与连续的关系知选A ．11．曲线42246y x x x =-+的凸区间为（）A ．(2,2)-B ．(,0)-∞C ．(0,)+∞D ．(,)-∞+∞【答案】A【解析】34486y x x '=-+，21248y x ''=-，由0y ''<，得22x -<<，因此曲线的凸区间为(2,2)-．12．曲线xe y x =（）A ．仅有水平渐进线B ．既有水平渐进线，又有垂直渐近线C ．仅有垂直渐近线D ．既无水平渐进线，又无垂直渐近线【答案】B【解析】lim 0x x e x →-∞=，0lim x x e x →=∞，故曲线xe y x=既有水平渐进线，又有垂直渐近线．13．下列说法正确的是（） A ．函数的极值点一定是函数的驻点 B ．函数的驻点一定是函数的极值点C ．二阶导数非零的驻点一定是极值点D ．以上说法都不对【答案】C【解析】由极值的第二判定定理，知C 正确．14．设()f x 在[],a b 上连续，且不是常数函数，若()()f a f b =，则在(,)a b 内（） A ．必有最大值或最小值 B ．既有最大值又有最小值C ．既有极大值又有极小值D ．至少存在一点ξ，使得()0f ξ'=【答案】A【解析】根据极值的判定定理、最大值最小值定理和罗尔定理，知A 选项正确．15．若()f x 的一个原函数是ln x ，则()f x '=（）A ．1xB ．21x-C ．ln xD ．ln x x【答案】B【解析】因为1()(ln )f x x x '==，所以21()f x x'=-．16．若2()f x dx x C =+⎰，则2(1)xf x dx -=⎰（）A ．222(1)x C --+B ．222(1)xC -+C ．221(1)2x C --+D ．221(1)2x C -+【答案】C【解析】由题意知，因为2()f x dx x C =+⎰，则2222211(1)(1)(1)(1)22xf x dx f x d x x C -=---=--+⎰⎰．17．下列不等式中不成立的是（）A ．22211ln ln xdx xdx >⎰⎰B ．220sin xdx xdx ππ<⎰⎰C ．22ln(1)x dx xdx +<⎰⎰D ．22(1)x e dx x dx <+⎰⎰【答案】D【解析】对于D ，222001x xe dx ee ==-⎰，222001(1)42x dx x x ⎛⎫+=+= ⎪⎝⎭⎰，应有2200(1)xe dx x dx >+⎰⎰，故D 选项错误．18．1ln ee xdx =⎰（）A ．111ln ln eexdx xdx +⎰⎰B ．111ln ln eexdx xdx -⎰⎰C ．111ln ln eexdx xdx -+⎰⎰D ．111ln ln eexdx xdx --⎰⎰【答案】C【解析】1111111ln (ln )ln ln ln eeeeeexdx x dx xdx xdx xdx =-+=-+⎰⎰⎰⎰⎰．19．下列广义积分中收敛的是（）A ．lnex dx x+∞⎰B ．1ln edx x x+∞⎰C ．21ln edx x x+∞⎰D ．e+∞⎰【答案】C【解析】对于C 选项，22111ln 1ln ln ln eee dx d x x x x x+∞+∞+∞==-=⎰⎰，故收敛．20．方程220x y z +-=在空间直角坐标系中表示的是（）A ．球面B ．圆锥面C ．旋转抛物面D ．圆柱面【答案】C【解析】由旋转抛物面的定义知选C ．21．设{}1,1,,2=-a ，{}2,0,1=b ，则a 与b 的夹角为（）A ．0B ．6π C ．4π D ．2π 【答案】D【解析】1210210⋅=-⨯+⨯+⨯=a b ，所以a 与b 的夹角为2π，故选D ．22．直线34:273x y zL ++==--与平面:4223x y z π--=的位置关系是（） A ．平行但直线不在平面上 B ．直线在平面上C ．垂直D ．相交但不垂直【答案】A【解析】因为直线L 的方向向量(2,7,3)=--s ，平面的法向量为(4,2,2)=--n ，则 24(7)(2)3(2)0⋅=-⨯+-⨯-+⨯-=s n ．又点(3,4,0)--不在平面上，所以直线与平面平行．23．设(,)f x y 在点(,)a b 处有偏导数，则0(,)(,)limh f a h b f a h b h→+--=（）A ．0B ．2(,)x f a b 'C ．(,)x f a b 'D ．(,)y f a b '【答案】B【解析】由题意知，00(,)(,)(,)(,)lim2lim 2(,)2x h h f a h b f a h b f a h b f a h b f a b h h→→+--+--'==．24．函数x yz x y+=-的全微分为（）A ．22()()xdx ydy x y --B ．22()()ydy xdx x y --C ．22()()ydx xdy x y --D ．22()()xdy ydx x y --【答案】D 【解析】22()z y x x y ∂-=∂-，22()z x y x y ∂=∂-，故22()()xdy ydx dz x y -=-．25．00(,)ady f x y dx ⎰化为极坐标形式为（）A ．20(cos ,sin )ad f r r rdr πθθθ⎰⎰B ．2cos 0(cos ,sin )d f r r rdr πθθθθ⎰⎰C ．sin 2(cos ,sin )a d f r r rdr πθθθθ⎰⎰D ．20(cos ,sin )ad f r r rdr πθθθ⎰⎰【答案】D【解析】令cos x r θ=，sin y r θ=，可知02πθ≤≤，0r a ≤≤，故化为极坐标形式为200(cos ,sin )ad f r r rdr πθθθ⎰⎰．26．设L 是以(1,0)A -、(3,2)B -、(3,0)C 为顶点的三角形区域的边界，方向为ABCA ，则(3)(2)Lx y dx x y dy -+-=⎰（）A ．8-B ．0C ．8D ．20【答案】A【解析】由格林公式，知1(3)(2)224282L Dx y dx x y dy dxdy -+-=-=-⨯⨯⨯=-⎰⎰⎰．27．下列微分方程中，可分离变量的方程是（） A ．tan dy y ydx x x=+B ．22()20x y dx xydy +-=C ．220x y xdx e dy y++=D ．2x dyy e dx+= 【答案】C【解析】由可分离变量的方程形式，知选项C 正确．28．若级数1n n u ∞=∑收敛，则下列级数中收敛的是（）A ．110n n u∞=∑B ．1(10)n n u ∞=+∑C ．110n nu ∞=∑D ．1(10)n n u ∞=-∑【答案】A【解析】由无穷级数的基本性质知，1n n u ∞=∑收敛必有110nn u ∞=∑收敛．29．函数()ln(1)f x x =-的幂级数展开式为（） A ．23...,1123x x x x +++-<≤B ．23...,1123x x x x -+--<≤C ．23...,1123x x x x -----≤<D ．23...,1123x x x x -+-+-≤<【答案】C【解析】由幂级数展开公式，得()ln(1)f x x =-=23...,1123x x x x -----≤<．30．级数0(1)n n n a x ∞=-∑在点1x =-处收敛，则此级数2x =处（）A ．条件收敛B ．绝对收敛C ．发散D ．无法确定【答案】B【解析】由阿贝尔定理知级数在2x =处绝对收敛，故选B ．二、填空题（每小题 2分，共 30分） 31．已知()1xf x x=-，则[]()f f x =________．【答案】12xx- 【解析】[]()1()1()1211xf x xx f f x x f x x x-===----．32．当0x →时，()f x 与1cos x -等价，则0()lim sin x f x x x→=________．【答案】12【解析】由题意可知，()f x 与1cos x -等价，则00()1cos 1lim lim sin sin 2x x f x x x x x x →→-==．33．若2lim 8xx x a x a →∞+⎛⎫= ⎪-⎝⎭，则a =________．【答案】ln2【解析】333233lim lim 1lim 18x a ax xx a x aa x x x x a a a e x a x a x a -⋅⋅-→∞→∞→∞+⎛⎫⎛⎫⎛⎫=+=+== ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭，故ln2a =．34．设函数sin ,0(),0xx f x x a x ⎧≠⎪=⎨⎪=⎩在(,)-∞+∞内处处连续，则a =________．【答案】1【解析】因为()f x 在(,)-∞+∞内处处连续，所以0sin lim 1x xa x→==．35．函数31xy x=+在(2,2)点处的切线方程为________．【答案】1433y x =+【解析】23(1)y x '=+，所以切线斜率13k =，又因为过点(2,2)，所以切线方程为1433y x =+．36．函数2()2f x x x =--在区间[]0,2上使用拉格朗日中值定理时，结论中的ξ=________．【答案】1【解析】由拉格朗日中值定理，知存在(0,2)ξ∈，使得()()(2)(0)()12f b f a f f f b a ξ--'===-，()21f x x '=-，当1x =时，有(1)1f '=，故1ξ=．37．函数()f x x =________．【答案】10,4⎛⎫⎪⎝⎭【解析】()1f x '=，令()0f x '<，解得104x <<．38．已知(0)2f =，(2)3f =，(2)4f '=，则2()xf x dx ''=⎰________．【答案】7【解析】2222()()()2(2)()8(2)(0)7xf x dx xf x f x dx f f x f f '''''=-=-=-+=⎰⎰．39.设向量b 与{}1,2,3=-a 共线，且56⋅=a b ，则=b ________．【答案】{}4,8,12-【解析】由a 与b 共线，知λ=b a ，由1456λλ⋅=⋅==a b a a ，知4λ=，故{}4,8,12=-b ．40．设22x y z e+=，则22zx∂=∂________．【答案】222(42)xy x e ++【解析】222x y z xe x+∂=∂，222222222222(42)x y x y x y z e x xe x e x +++∂=+⋅=+∂．41．函数22(,)22f x y x xy y =+-的驻点为________．【答案】(0,0)【解析】4x f x y =+，4y f x y =-，令0x f =，0y f =，得驻点为(0,0)．42．设区域D 为229x y +≤，则2Dx yd σ=⎰⎰________．【答案】0【解析】令cos x r θ=，sin y r θ=，知232323334cos sin cos sin 0Dx yd d r rdr d r dr ππσθθθθθθ=⋅==⎰⎰⎰⎰⎰⎰．43．交换积分次序后，10(,)xdx f x y dy =⎰________．【答案】【解析】由题意知积分区域为01xx y ≤≤⎧⎪⎨≤≤⎪⎩，交换积分次序后，积分区域为201y y x y ≤≤⎧⎨≤≤⎩，故2110(,)(,)yxydx f x y dy dy f x y dx =⎰⎰⎰．44．已知14x y xe -=-是微分方程23x y y y e -'''-+=的一个特解，则该方程的通解为________．【答案】31214x x x y C e C e xe --=+-（12,C C 为任意常数）【解析】由题知，齐次方程所对应的特征方程为2230r r --=，解得11r =-，23r =，故对应的齐次方程的通解为312x x y C e C e -=+，又知特解为14x y xe -=-，故通解为31214x x x y C e C e xe --=+-（12,C C 为任意常数）．45．已知级数1n n u ∞=∑的部分和3n S n =，则当2n ≥时，n u =________．【答案】2331n n -+【解析】当2n ≥时，3321(1)331n n n u S S n n n n -=-=--=-+．三、计算题（每小题5 分，共40 分） 46．求011lim 1x x x e →⎛⎫- ⎪-⎝⎭．【答案】【解析】200000111111lim lim lim lim lim 1(1)222x x x x x x x x x x e x e x e x x e x e x x x →→→→→-----⎛⎫-===== ⎪--⎝⎭．47．设 ()y f x =是由方程ln sin 2xy e y x x +=确定的隐函数，求dydx．【答案】22cos2ln xy xyx x xye yx e x x--+ 【解析】方法一方程两边同时对x 求导得()ln 2cos2xy ye y xy y y x x''+++=，故 22cos2ln xy xy dy x x xye yy dx x e x x--'==+．方法二令(,)ln sin 2xy F x y e y x x =+-，则22cos 2ln xy x xy y F dyx x xye y dx F x e x x--=-=+．48．已知2()x xf x dx e C -=+⎰，求1()dx f x ⎰．【答案】21142x x e C ⎛⎫--+ ⎪⎝⎭【解析】等式两边对x 求导，得2()2x xf x e -=-，则211()2x xe f x =-，故 ()222211111()4442x x x x dx xde xe e dx x e C f x ⎛⎫=-=--=--+ ⎪⎝⎭⎰⎰⎰．49．求44(1)x x dx --⎰．【答案】1293【解析】40142224401(1)()()()x x dx x x dx x x dx x x dx ---=---+-⎰⎰⎰⎰32041132x x -⎛⎫=- ⎪⎝⎭32101132x x ⎛⎫-- ⎪⎝⎭32411132x x ⎛⎫+- ⎪⎝⎭1293=．50．已知22x xy y z e +-=，求全微分dz ．【答案】[]22(2)(2)xxy y e x y dx x y dy +-++-【解析】22(2)x xy y z x y e x+-∂=+∂，22(2)x xy y zx y e y +-∂=-∂，则[]22(2)(2)x xy y dz e x y dx x y dy +-=++-．51．求 (2)Dx y dxdy +⎰⎰，其中D 由y x =，2y x =，2y =围成．【答案】103【解析】由题意可知，积分区域D 为02y ≤≤，2yx y ≤≤，222002510(2)(2)43yy Dx y dxdy dy x y dx y dy +=+==⎰⎰⎰⎰⎰．52．求微分方程22x y xy xe -'-=的通解．【答案】2214x x y e Ce -=-+【解析】方程为一阶非齐次线性微分方程，其中()2P x x =-，2()x Q x xe -=，则方程的通解为222()()(2)(2)21()4P x dx P x dx x dx x dx x x x y e Q x e dx C e xe e dx C e e C ------⎛⎫⎡⎤⎡⎤⎰⎰⎰⎰=+=+=-+ ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭⎰⎰ 2214x x e Ce -=-+．53．求幂级数212nnn n x ∞=∑的收敛区间（考虑端点）．【答案】(【解析】令2t x =，则级数为12nn n n t ∞=∑，因为11121limlim 22n n n n n na n a n ++→∞→∞+=⋅=，所以12n n n n t ∞=∑的收敛半径为2，则212n n n nx ∞=∑，又当x =1n n ∞=∑发散，故所求幂级数的收敛域为(．四、应用题（每小题7 分，共 14 分）54．靠一堵充分长的墙边，增加三面墙围成一矩形场地，在限定场地面积为642m 的条件下，问增加的三面墙各长多少时，其总长最小．【答案】三面墙的长度分别为，和【解析】设与已知墙面平行的墙的长度为x m ，则另两面墙的长为64xm ，故三面墙的总长为128(0)l x x x=+>．令212810l x '=-=，解得唯一驻点x =又32560l x''=>，故当x =m 时，l 取值最小，此时，三面墙的长度分别为，和．55．设D 是由曲线()y f x =与直线0y =，3y =围成的区域，其中2,2()6,2x x f x x x ⎧≤=⎨->⎩，求D 绕y 轴旋转一周所生成的旋转体的体积．【答案】1172π 【解析】由题意得3322332300011117(6)(6)322y V y dy dy y y πππππ=--=---=⎰⎰．五、证明题（6 分） 56．设1()()()xx a bF x f t dt dt f t =+⎰⎰，其中函数()f x 在闭区间[],a b 上连续，且()0f x >．证明在开区间(,)a b 内，方程满()0F x =有唯一的实根．【解析】因为()F x 在[],a b 上连续，()0f x >，且1()0()a bF a dt f t =<⎰，()()0b a F b f t dt =>⎰，所以方程()0F x =在(,)a b 内有根，又因为1()()0()F x f x f x '=+>，所以()F x 在(,)a b 内单调，故至多有一个实根．综上，在开区间(,)a b 内，方程满()0F x =有唯一的实根．。

2009年成考专升本高数真题及答案

一、填空题（6'530⨯=分）1．已知(1,1,2)A -和(2,2,1)B ，则向量AB 的模=_____________112．过点(1,2,3)且与平面240x y z -+-=垂直的直线方程为______ 123121x y z ---==- 3．由抛物线2y x =与直线230x y --=所围的图形面积为_______ 3234．设222(,,)23f x y z x y z =++，则(1,1,1)gradf =_______________ {}2,4,65．(,)(1,2)lim 2x y y x y →=-______________ 23- 6．级数()11n n x n ∞=-∑的收敛区间为________________ [)0,2二、计算题（8'324⨯=分）1．2D xy dxdy ⎰⎰，其中(){},01,2D x y x x y x =≤≤<≤．解：2D xy dxdy ⎰⎰=5121220073x x dx xy dy x dx =⎰⎰⎰ 23=2222.()L x y ds +⎰,其中L 为圆周()cos ,sin 0x a t y a t t π==≤≤．解：()22242220()cos sin L x y ds a a t t dt π+=+⎰⎰ 5a π=3.()()L x y dx x y dy ++-⎰，其中L 是抛物线y x =上从点()1,1到()4,2的一段弧．解：()12y x x''==，()411()()2L x y dx x y dy x x x x dx x ⎡⎤++-=++-⎢⎥⎣⎦⎰⎰ =32241122x x x +- =13 三、判别级数134n n n ∞=⎛⎫ ⎪⎝⎭∑的收敛性．（8分）解：()133lim 1/44n nn n n +→∞⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭133lim 144n n n →∞+==< 所以原级数收敛。

2009年成人高考试卷(一)

题号一二三总分1～1011～151415161617181920211～21分数2009年数学复习大纲说明：本套试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分．考试时间：120分钟．第Ⅰ卷（选择题，共50分）1、选择题（下列各题选项中只有一个选项是正确的，请将正确的选项填入表格的答案栏中. 5分×10＝50分）1. 如果集合X={0}，那么　( )A．0X B．{0}∈X C． φ∈X D．{0}X2. 如果S={1，2，3，4，5}，M={1，3，4}，N={2，4，5}，那么(C S M)∩N等于　（）A．φ B．{1，3} C．(4) D．{2，5}3. 不等式的解集为 ( )A． B． C． D．4. 经过两点（3，－2）、（0，－４）的直线方程是（）A．2x+3y+12=0 B．2x-3y-12=0 C．3x+2y+12=0 D．3x-2y-12=05. 从原点向圆作两条切线，则这两条切线的夹角的大小为（）A． B． C． D．6. 在等比数列，已知，，则＝（）A．15 B．20 C．25 D．307. 将5本不同的书全发给4名同学，每名同学至少有一本书的概率是（）A． B． C． D．8. 由直线上的一点向圆引切线，则切线长的最小值为（）A．1 B． C． D．9. 已知|a|=1,|b|=,且(a-b)与a垂直，则a与b的夹角是（）A．60° B． 30° C． 135° D．４５°10. 曲线y=4x－x3在点(－1,－3)处的切线方程是（）A． y=7x+4 B． y=7x+2 C． y=x－4 D． y=x－2题号12345678910答案第Ⅱ卷（非选择题，共100分）2、填空题（把答案填写在题中的横线上。

5分×5＝25分）11. 已知函数f(x)的图象与函数的图象关于直线y=x对称，则f(9)=__ __.12. 若sin= -,则cos 2= .13. 设实数x,y满足条件则的最大值是_ _.14. 已知，则＝ .15. 某市的3个区共有高中学生20000人，且3个区的高中学生人数之比为2：3：5，现要用分层抽样方法从所有学生中抽取一个容量为200的样本，这3个区应抽取的人数分别为 .三、解答题（本大题共6个小题，共75分。