第6-1章_相关与回归分析习题解答2
统计学课后习题答案-相关分析与回归分析

、 单项选择题1. 相关分析是研究变量之间的 A. 数量关系 C •因果关系2. 在相关分析中要求相关的两个变量3. 下列现象之间的关系哪一个属于相关关系?A. 播种量与粮食收获量之间关系 C •圆半径与圆面积之间关系 D. 单位产品成本与总成本之间关系 4. 正相关的特点是A •两个变量之间的变化方向相反 C. 两个变量之间的变化方向一致 5. 相关关系的主要特点是两个变量之间A. 存在着确定的依存关系 C. 存在着严重的依存关系 B. 存在着不完全确定的关系 D. 存在着严格的对应关系6.当自变量变化时 , 因变量也相应地随之等量变化 ,则两个变量 之间存在着A. 直线相关关系B.负相关关系C.曲线相关关系 D.正相关关系 7. 当变量 X 值增加时 ,变量 Y 值都随之下降 ,则变量 X 和 Y 之间存 在着 A. 正相关关系 C.负相关关系D.曲线相关关系8. 当变量 X 值增加时 ,变量 Y 值都随之增加 ,则变量 X 和 Y 之间存 在着 A. 直线相关关系 B.负相关关系 C.曲线相关关系 D.正相关关系9. 判定现象之间相关关系密切程度的最主要方法是 A. 对现象进行定性分析 B.计算相关系数C.编制相关表 D.绘制相关图10. 相关分析对资料的要求是A. 自 变量不是随机的,因变量是随机的B. 两个变量均不是随机的C. 自变量是随机的,因变量不是随机的D. 两个变量均为随机的 11. 相关系数第七章相关分析与回归分析B.变动关系D. 相互关系的密切程度 A. 都是随机变量C. 都不是随机变量B. 自变量是随机变量 D. 因变量是随机变量B •圆半径与圆周长之间关系B.两个变量一增一减 D. 两个变量一减一增 B.直线相关关系A.既适用于直线相关,又适用于曲线相关B.只适用于直线相关C.既不适用于直线相关,又不适用于曲线相关D.只适用于曲线相关12.两个变量之间的相关关系称为C. 不相关D.负相关B.-1w rw 0 D. r=0 ,则相关系数 B.愈趋近于0D. 愈小于 1 ,则相关系数 B.愈趋近于0D. 愈小于116. 相关系数越接近于- 1,表明两变量间C. 负相关关系越强 D.负相关关系越弱17. 当相关系数 r=0 时 , A. 现象之间完全无关 B.相关程度较小 B. 现象之间完全相关D.无直线相关关系18. 假设产品产量与产品单位成本之间的相关系数为 -0.89,则说明这两个变量之间存在A.高度相关 B.中度相关 C. 低度相关D.显著相关19. 从变量之间相关的方向看可分为 A. 正相关与负相关 B.直线相关和曲线相关C. 单相关与复相关D.完全相关和无相关20. 从变量之间相关的表现形式看可分为 A. 正相关与负相关 B.直线相关和曲线相关C. 单相关与复相关D.完全相关和无相关21. 物价上涨 ,销售量下降 ,则物价与销售量之间属于 A. 无相关 B.负相关 C.正相关D.无法判断22. 配合回归直线最合理的方法是 A.随手画线法 B.半数平均法 C.最小平方法D.指数平滑法A.单相关B.复相关 13. 相关系数的取值范围是 A.-1W r < 1C.OW rw 114. 两变量之间相关程度越强 A.愈趋近于1 C.愈大于115. 两变量之间相关程度越弱 A.愈趋近于1 A. 没有相关关系B. 有曲线相关关系23.在回归直线方程y= a+ bx 中 b 表示A.当x增加一个单位时,y增加a的数量B.当y增加一个单位时,x增加b的数量C.当x增加一个单位时,y的平均增加量D.当y增加一个单位时,x的平均增加量24.计算估计标准误差的依据是A.因变量的数列C.因变量的回归变差25.估计标准误差是反映A.平均数代表性的指标B.因变量的总变差D.因变量的剩余变差B.相关关系程度的指标C.回归直线的代表性指标D.序时平均数代表性指标26.在回归分析中 ,要求对应的两个变量A.都是随机变量B.不是对等关系C.是对等关系D.都不是随机变量27.年劳动生产率(千元)和工人工资(元)之间存在回归方程 y=10+70x, 这意味着年劳动生产率每提高一千元时,工人工资平均A.增加70元B.减少70元C.增加80元D.减少80元28.设某种产品产量为 1000件时,其生产成本为 30000元,其中固定成本6000元,则总生产成本对产量的一元线性回归方程为:A.y=6+0.24xB.y=6000+24xC.y=24000+6xD.y=24+6000x29.用来反映因变量估计值代表性高低的指标称作A.相关系数G剩余变差B.回归参数D.估计标准误差、多项选择题1.下列现象之间属于相关关系的有A.家庭收入与消费支出之间的关系B.农作物收获量与施肥量之间的关系C.圆的面积与圆的半径之间的关系D.身高与体重之间的关系2.直线相关分析的特点是A.相关系数有正负号C.只有一个相关系数E.年龄与血压之间的关系B.两个变量是对等关系D. 因变量是随机变量3.从变量之间相互关系的表现形式看,相关关系可分为A.正相关B.负相关C.直线相关D.曲线相关E.单相关和复相关4.如果变量 x 与 y 之间没有线性相关关系,则A.相关系数r=0B.相关系数r=1C.估计标准误差等于0D.估计标准误差等于1E.回归系数b=05.设单位产品成本(元)对产量(件)的一元线性回归方程为y=85-5.6x,则B.单位成本与产量之间存在着正相关C.产量每增加1千件,单位成本平均增加 5.6元D.产量为 1 千件时,单位成本为 79.4 元E.产量每增加1千件,单位成本平均减少 5.6元6.根据变量之间相关关系的密切程度划分,可分为A.不相关B.完全相关C.不完全相关D.线性相关E.非线性相关16用最小平方法配合的回归直线 A . (y-y c )=最小值 C. (y-y c )2=最小值 E.(y-y c )2=最大值D.计算相关系数 8•当现象之间完全相关的A.0B.— 1E.计算估计标准误差 ,相关系数为C.1D.0.5E. — 0.59•相关系数r =0说明两个变量之间是 A •可能完全不相关 B •可能是曲线相关 C.肯定不线性相关 D.肯定不曲线相关E. 高度曲线相关 10下列现象属于正相关的有A. 家庭收入愈多,其消费支出也愈多B. 流通费用率随商品销售额的增加而减少D. 生产单位产品耗用工时,随劳动生产率的提高而减少E. 工人劳动生产率越高,则创造的产值就越多 11直线回归分析的特点有 A •存在两个回归方程 B •回归系数有正负值C. 两个变量不对等关系D. 自变量是给定的,因变量是随机的E. 利用一个回归方程,两个变量可以相互计算 12直线回归方程中的两个变量C. 必须确定哪个是自变量,哪个是因变量D. 一个是随机变量,另一个是给定变量E. 一个是自变量,另一个是因变量13. 从现象间相互关系的方向划分,相关关系可以分为 A.直线相关 B.曲线相关 D. 负相关 E.单相关14. 估计标准误差是A. 说明平均数代表性的指标B. 说明回归直线代表性指标C. 因变量估计值可靠程度指标D. 指标值愈小,表明估计值愈可靠C.正相关Ar D.r(x x)(y y)B rL xyC.rL xyL yyL xy LXX(X X)(y y) Er■(X X)2 (y y)2n xy x y、n x 2 ( x)2 、n y 2 ( y)217 方程 y c=a+bx,必须满足以下条件B. (y-y c)=02A.这是一个直线回归方程B.这是一个以X为自变量的回归方程C.其中a是估计的初始值D.其中b是回归系数E.y c是估计值18直线回归方程y c=a+bx中的回归系数bA.能表明两变量间的变动程度B.不能表明两变量间的变动程度C.能说明两变量间的变动方向D.其数值大小不受计量单位的影响E.其数值大小受计量单位的影响19相关系数与回归系数存在以下关系A.回归系数大于零则相关系数大于零B.回归系数小于零则相关系数小于零C.回归系数等于零则相关系数等于零D.回归系数大于零则相关系数小于零E.回归系数小于零则相关系数大于零20配合直线回归方程的目的是为了A.确定两个变量之间的变动关系B.用因变量推算自变量C.用自变量推算因变量D.两个变量相互推算E.确定两个变量之间的相关程度21若两个变量x和y之间的相关系数r=1,则A.观察值和理论值的离差不存在B.y的所有理论值同它的平均值一致C.x和y是函数关系D.x与y不相关E.x与y是完全正相关22.直线相关分析与直线回归分析的区别在于A.相关分析中两个变量都是随机的;而回归分析中自变量是给定的数值,因变量是随机的B.回归分析中两个变量都是随机的;而相关分析中自变量是给定的数值,因变量是随机的C.相关系数有正负号;而回归系数只能取正值D.相关分析中的两个变量是对等关系;而回归分析中的两个变量不是对等关系E.相关分析中根据两个变量只能计算出一个相关系数;而回归分析中根据两个变量只能计算出一个回归系数三、填空题1.__________________________________________________ 研究现象之间相关关系称作相关分析。
相关与回归分析(10)

18
2.2 相关系数的特征及判别标准
【例】根据下列数据,计算变量 x 、y 的
相关系数。
序 人均收入 恩格尔系数 序 人均收入 恩格尔系数
号
x
y
号
x
y
1 280
0.683
6
670
0.602
2 320
0.675
7
790
0.544
3 370
0.662
8
880
0.490
4 530
0.649
9
910
0.505
5.813
x2
78400 102400 152100 280900 422500 448900 624100 774400 828100 1102500
4814300
y2
0.466489 0.455625 0.438244 0.421201 0.321489 0.362404 0.295936 0.240100 0.255025 0.190096
0
x
2021/2/4
第六章 相关与回归分析
34
参数、的最小二乘法估计(OLS估计)
2021/2/4
第六章 相关与回归分析
35
3.2 一元线性回归模型的参数估计 最小二(平方)乘法:
Q βˆ 1 , βˆ 2 yi βˆ 1 βˆ 2xi 2
整
理得Q : 2
这两种分析的联系是,它们是研究现象之间相互依存关系的 两个不可分割的方面。在实际工作中,一般先进行相关分析, 由相关系数或相关指数的大小决定是否需要进行回归分析。
2021/2/4
第六章 相关与回归分析
30
一元线性回归模型
第6章相关分析与回归分析

(二)散点图(相关图)
用直角坐标系的横轴代表变量x ,纵轴代表变量y ,将两
个变量间相对应的变量值用坐标点的形式描绘出来,用 以表明相关点分布状况的图形。
70
根据上 65
例资料 60
绘制的
55
相关图
50
Y
2020/7/24
45 200
400
600
800
X
1000
1200
x与y关系散点图的主要类型
函数关系往往通过相关关系表现出来。把影响因变量变 动的因素全部纳入方程,这时的相关关系就有可能转化 为函数关系。 相关关系经常可以用一定的函数形式去近似地描述。
2020/7/24
(二)相关关系与因果关系
因果关系∈相关关系; 现象之间是因果关系同时是相关关系,但是相关关系不 一定是因果关系。 统计只能说明现象间有无数量上的关系,不能说明谁因 谁果。 例:有数据显示世界各国平均每人拥有电视机数x及居民 预期寿命y之间有很强的正相关,可否认为电视机很多的 国家,居民预期寿命比较长?
▪ 收入水平(y)与受教育程度(x)之间的关系
2020/7/24
相关关系的特点:yx(1)变量间关系不能用函数关系 精确表达;
(2)一个变量的取值不能由另一 个变量唯一确定;
(3)当变量 x 取某个值时,变量 y 的取值可能有几个;
(4)各观测点分布在直线附近。
2020/7/24
函数关系与相关关系的联系
线性形式,即当一个变量变动一个单位时,另一 个变量也按一个大致固定的增(减)量变动,就 称为线性相关。
非线性相关:当变量间的关系不按固定比例变
化时,就称之为非线性相关。
2020/7/24
4. 按研究变量的多少 单相关:两个变量之间的相关,称为单相关。 复相关:一个变量与两个或两个以上其他变量
回归分析第1章课后习题参考答案

第一章回归分析概述习题参考答案1.1 变量间的统计关系和函数关系有什么区别?(1)确定性关系或函数关系:研究的是确定现象非随机变量间的关系。
(2)统计依赖或相关关系:研究的是非确定现象随机变量间的关系。
1.2 相关分析和回归分析的区别与联系?相关分析和回归分析的联系是:它们通常都是基于两正态连续变量的假设,都是处理两变量间相互关系的统计方法,通常两种方法不同时出现;二者的区别是作为相互关系分析的方法,相关分析是通过提供一个相关系数来考察两变量间的联系程度,而回归分析则是重在建立两变量间的函数关系式,因此通常可以先考察相关系数的显著型,如果显著则可以进一步考虑建立变量间的回归方程。
此外,相关分析和回归分析又各有一些具体方法用于处理不同的情况,如相关分析还包括等级相关、质量相关和品质相关,回归分析还包括非线性回归等。
(其余区别在课本第四页最上面那段)1.3 线性回归模型中随机误差项ε的意义是什么?引入随机误差 使得变量之间的关系描述为一个随机方程,因而我们可以借助数学方法研究自变量和因变量之间的关系。
由于客观经济现象是错综复杂的,随机误差项可以概述表示由于人们的认识以及其他客观原因的局限而没有考虑到的种种偶然因素。
引入随机项扰动的理由如下:第一,表示被解释变量Y与解释变量X的不确定性关系第二,模型不可能包含所有变量,次要变量要省略;第三,确定模型数学形式肯定会有误差;第四,样本数据会有测量误差;第五,一些随机因素无法选入模型。
1.4 线性回归方程的基本假设是什么?假设1、解释变量X(x1 ,x2,…,xp)是确定性变量,不是随机变量;假设2、随机误差项ε具有零均值、等方差和序列不相关性:E(εi)=0 i=1,2, …Var (εi)=σ2 i=1,2, …,nCov(εi,εj)=0 i≠j i,j= 1,2, …,n假设3 ε服从零均值同方差、零协方差的正态分布。
εi ~N(0, σ2 ) i=1,2, …,n假设4、样本容量的个数多于解释变量的个数,即:n>p假设5、随机误差项ε与解释变量X之间不相关:Cov(Xi, εi)=0 i=1,2, …,n(在课本第7页到第8页)1.6收集整理数据包括哪些内容?在课本第10到12页1.7构造回归理论模型的基本根据是什么?(1)散点图(2)实际问题背景的理论及方法建模技术原理(3)经验公式1.8至于回归模型建立之后为什么要检验?是因为我们不明确这个模型是否真正揭示了被解释变量与解释变量之间的关系,因而用此模型区做预测、控制和分析时不够慎重的。
第6-1章_相关与回归分析习题解答2

相关与回归分析思考与练习一、判断题1.产品的单位成本随着产量增加而下降,这种现象属于函数关系。
答:错。
应是相关关系。
单位成本与产量间不存在确定的数值对应关系。
2.相关系数为0表明两个变量之间不存在任何关系。
答:.错。
相关系数为零,只表明两个变量之间不存在线性关系,并不意味着两者间不存在其他类型的关系。
3.单纯依靠相关与回归分析,无法判断事物之间存在的因果关系。
答:对,因果关系的判断还有赖于实质性科学的理论分析。
4.圆的直径越大,其周长也越大,两者之间的关系属于正相关关系。
答:错。
两者是精确的函数关系。
5.总体回归函数中的回归系数是常数,样本回归函数中的回归系数的估计量是随机变量。
答:对。
6.当抽取的样本不同时,对同一总体回归模型估计的结果也有所不同。
答:对。
因为,估计量属于随机变量,抽取的样本不同,具体的观察值也不同,尽管使用的公式相同,估计的结果仍然不一样。
二、选择题1.变量之间的关系按相关程度分可分为:b 、c 、da.正相关;b. 不相关;c. 完全相关;d.不完全相关; 2.复相关系数的取值区间为:aa. 10≤≤R ;b.11≤≤-R ;c.1≤≤∞-R ;d.∞≤≤-R 1 3.修正自由度的决定系数a 、b 、da.22R R ≤; b.有时小于0 ; c. 102≤≤R ;d.比2R 更适合作为衡量回归方程拟合程度的指标 4.回归预测误差的大小与下列因素有关:a 、b 、c 、da 样本容量;b 自变量预测值与自变量样本平均数的离差c 自变量预测误差;d 随机误差项的方差三、问答题1.请举一实例说明什么是单相关和偏相关?以及它们之间的差别。
答:例如夏季冷饮店冰激凌与汽水的消费量,简单地就两者之间的相关关系进行考察,就是一种单相关,考察的结果很可能存在正相关关系,即冰激凌消费越多,汽水消费也越多。
然而,如果我们仔细观察,可以发现一般来说,消费者会在两者中选择一种消费,也就是两者之间事实上应该是负相关。
统计学第六章课后题与答案解析

文档来源为:从网络收集整理.word版本可编辑.欢迎下载支持.第六章、单项选择题1.下面的函数关系是()A现代化水平与劳动生产率圆周的长度决定于它的半径C家庭的收入和消费的关系亩产量与施肥量2.相关系数r的取值范围B -1C -1< r < +13.年劳动生产率x(干元)和工人工资y=10+70x,这意味着年劳动生产率每提高1千元时,工人工资平均()A增加70元 B 减少70元C增加80元D减少80元4.若要证明两变量之间线性相关程度高, 则计算出的相关系数应接近于A +1B -1C 0.5 D5.回归系数和相关系数的符号是一致的, 其符号均可用来判断现象A线性相关还是非线性相关 B 正相关还是负相关C完全相关还是不完全相关 D 单相关还是复相关6.某校经济管理类的学生学习统计学的时间(X)与考试成绩(y)之间建立线性回归方程? =a+bx。
经计算,方程为? =200— 0.8X,该方程参数的计算()Aa值是明显不对的值是明显不对的C a值和b值都是不对的D a 值和b值都是正确的7.在线性相关的条件下, 自变量的均方差为2,因变量均方差为5,而相关系数为0.8 时,则其回归系数为:()A 8B 0.32C 2D 12&进行相关分析,要求相关的两个变量A都是随机的C一个是随机的,一个不是随机的随机或不随机都可以都不是随机的9.下列关系中,属于正相关关系的有A合理限度内,施肥量和平均单产量之间的关系B产品产量与单位产品成本之间的关系C商品的流通费用与销售利润之间的关系D流通费用率与商品销售量之间的关系10.相关分析是研究 ( )A变量之间的数量关系变量之间的变动关系C变量之间的相互关系的密切程度 D 变量之间的因果关系11.在回归直线 y c=a+bx ,b<0,则x与y之间的相关系数()A r=0B r=lC 0< r<1D -1< r <012.当相关系数 r=0 时,表明 (A现象之间完全无关 B 相关程度较小C现象之间完全相关 D 无直线相关关系13.下列现象的相关密切程度最高的是 ( )A某商店的职工人数与商品销售额之间的相关系数0.87B流通费用水平与利润率之间的相关系数为-0.94C商品销售额与利润率之间的相关系数为0.51D商品销售额与流通费用水平的相关系数为-0.8114.估计标准误差是反映 ( )A平均数代表性的指标相关关系的指标C回归直线方程的代表性指标D序时平均数代表性指标二、多项选择题1.下列哪些现象之间的关系为相关关系( )A 家庭收入与消费支出关系B 圆的面积与它的半径关系C广告支出与商品销售额关系D商品价格一定,商品销售与额商品销售量关系2.相关系数表明两个变量之间的( )A因果关系 C变异程度 D 相关方向 E 相关的密切程度3.对于一元线性回归分析来说( )A两变量之间必须明确哪个是自变量,哪个是因变量B回归方程是据以利用自变量的给定值来估计和预测因变量的平均可能值C 可能存在着 y 依 x 和 x 依 y 的两个回归方程D回归系数只有正号4.可用来判断现象线性相关方向的指标有( )A相关系数 B 回归系数 C 回归方程参数a D 估计标准误5.单位成本 ( 元)依产量 (千件 )变化的回归方程为 y c=78- 2x ,这表示 ( ) A产量为1000件时,单位成本 76元B产量为1000件时,单位成本 78元C产量每增加1000件时,单位成本下降 2元D产量每增加1000件时,单位成本下降 78元6.估计标准误的作用是表明 ( )A样本的变异程度回归方程的代表性C估计值与实际值的平均误差D样本指标的代表性7.销售额与流通费用率,在一定条件下,存在相关关系,这种相关关系属于A完全相关 B 单相关 C 负相关 D 复相关8.在直线相关和回归分析中 ( )A据同一资料, 相关系数只能计算一个B据同一资料, 相关系数可以计算两个C据同一资料, 回归方程只能配合一个D据同一资料, 回归方程随自变量与因变量的确定不同,可能配合两个9.相关系数 r 的数值 ( )A可为正值 B 可为负值 C 可大于1 D 可等于-110.从变量之间相互关系的表现形式看,相关关系可分为A正相关 B 负相关 C直线相关 D 曲线相关11.确定直线回归方程必须满足的条件是 ( )A现象间确实存在数量上的相互依存关系B 相关系数 r 必须等于 1C y与x必须同方向变化D现象间存在着较密切的直线相关关系12.当两个现象完全相关时,下列统计指标值可能为A r=1B r=0C r=-1D S y=013.在直线回归分析中,确定直线回归方程的两个变量必须是A一个自变量,一个因变量均为随机变量C对等关系一个是随机变量,一个是可控制变量14.配合直线回归方程是为了A确定两个变量之间的变动关系用因变量推算自变量C用自变量推算因变量两个变量都是随机的15.在直线回归方程中 ( )A在两个变量中须确定自变量和因变量 B 一个回归方程只能作一种推算C要求自变量是给定的,而因变量是随机的。
《应用回归分析》课后题答案解析

(8) t
1
2
/ Lxx
1
Lxx
2
其中
1 n2
n i1
ei 2
1 n2
n i1
( yi
2
yi )
0.0036 1297860 8.542 0.04801
t /2 1.895
t 8.542 t /2
接受原假设 H 0: 1 0, 认为 1 显著不为 0,因变量 y 对自变量 x 的一元线性回归成立。
( yi
2
yi )
1 n-2
n i=1
( yi
( 0 1
2
x))
=
1 3
( 10-(-1+71))2 (10-(-1+7 (20-(-1+7 4))2 (40-(-1+7
2))2 (20-(-1+7 5))2
3))2
1 16 9 0 49 36
3
110 / 3
1
330 6.1
《应用回归分析》部分课后习题答案
第一章 回归分析概述
变量间统计关系和函数关系的区别是什么 答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量 唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另 外一个变量的确定关系。
回归分析与相关分析的联系与区别是什么 答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。区别有 a. 在回归分析中,变量 y 称为因变量,处在被解释的特殊地位。在相关分析中,变 量 x 和变量 y 处于平等的地位,即研究变量 y 与变量 x 的密切程度与研究变量 x 与变量 y 的密切程度是一回事。b.相关分析中所涉及的变量 y 与变量 x 全是随机 变量。而在回归分析中,因变量 y 是随机变量,自变量 x 可以是随机变量也可以 是非随机的确定变量。C.相关分析的研究主要是为了刻画两类变量间线性相关的 密切程度。而回归分析不仅可以揭示变量 x 对变量 y 的影响大小,还可以由回归 方程进行预测和控制。
《应用回归分析》课后题答案[整理版]
![《应用回归分析》课后题答案[整理版]](https://img.taocdn.com/s3/m/603529c1f242336c1eb95eca.png)
《应用回归分析》课后题答案[整理版] 《应用回归分析》部分课后习题答案第一章回归分析概述 1.1 变量间统计关系和函数关系的区别是什么, 答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。
1.2 回归分析与相关分析的联系与区别是什么, 答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x 对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3 回归模型中随机误差项ε的意义是什么, 答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么,答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2….Cov(εi,εj)=,σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.1.5 回归变量的设置理论根据是什么,在回归变量设置时应注意哪些问题,答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系。
统计学原理-第六章--相关与回归分析习题

A+1 B 0 C 0.5 D [1]5.回归系数和相关系数的符号是一致的,其符号均可用来判断现象( )A线性相关还是非线性相关B正相关还是负相关C完全相关还是不完全相关D单相关还是复相关6.某校经济管理类的学生学习统计学的时间()与考试成绩(y)之x间建立线性回归方程y c=a+b。
经计算,方程为y c=200—0.8x,该方程参数x的计算( )A a值是明显不对的B b值是明显不对的C a值和b值都是不对的 C a值和6值都是正确的7.在线性相关的条件下,自变量的均方差为2,因变量均方差为5,而相关系数为0.8时,则其回归系数为:( )A 8B 0.32C 2D 12.58.进行相关分析,要求相关的两个变量( )A都是随机的B都不是随机的C一个是随机的,一个不是随机的D随机或不随机都可以9.下列关系中,属于正相关关系的有( )A合理限度内,施肥量和平均单产量之间的关系B产品产量与单位产品成本之间的关系C商品的流通费用与销售利润之间的关系D流通费用率与商品销售量之间的关系10.相关分析是研究( )A变量之间的数量关系B变量之间的变动关系C变量之间的相互关系的密切程度D变量之间的因果关系11.在回归直线y c=a+bx,b<0,则x与y之间的相关系数( )A =0B =lC 0<<1D -1<<0r r r r12.在回归直线yc=a+bx中,b表示( )A当x增加一个单位,,y增加a的数量B当y增加一个单位时,x增加b的数量C当x增加一个单位时,y的均增加量D当y增加一个单位时,x的平均增加量13.当相关系数r=0时,表明( )A现象之间完全无关B相关程度较小C现象之间完全相关D无直线相关关系14.下列现象的相关密切程度最高的是( )A某商店的职工人数与商品销售额之间的相关系数0.87B流通费用水平与利润率之间的相关关系为-0.94C商品销售额与利润率之间的相关系数为0.51D商品销售额与流通费用水平的相关系数为-0.8115.估计标准误差是反映( )A平均数代表性的指标B相关关系的指标C回归直线的代表性指标D序时平均数代表性指标三、多项选择题1.下列哪些现象之间的关系为相关关系( )A家庭收入与消费支出关系B圆的面积与它的半径关系C广告支出与商品销售额关系D单位产品成本与利润关系E在价格固定情况下,销售量与商品销售额关系2.相关系数表明两个变量之间的( )A线性关系B因果关系C变异程度D相关方向E相关的密切程度3.对于一元线性回归分析来说( )A两变量之间必须明确哪个是自变量,哪个是因变量B回归方程是据以利用自变量的给定值来估计和预测因变量的平均可能值C可能存在着y依x和x依y的两个回归方程D回归系数只有正号E 确定回归方程时,尽管两个变量也都是随机的,但要求自变量是给定的。
回归分析练习题及参考答案
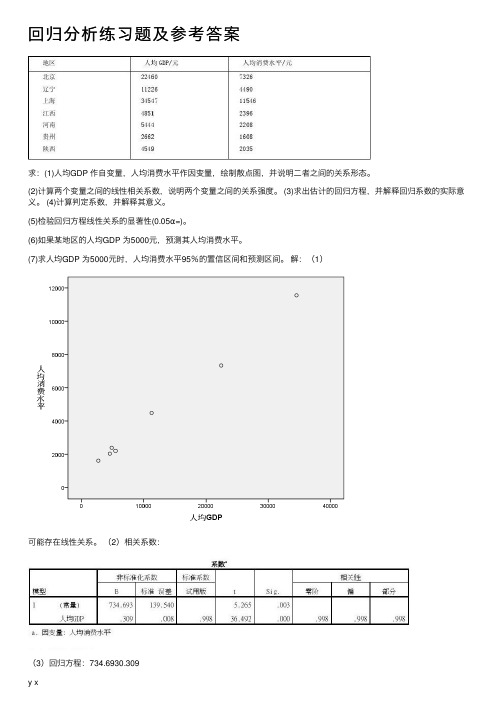
回归分析练习题及参考答案求:(1)⼈均GDP 作⾃变量,⼈均消费⽔平作因变量,绘制散点图,并说明⼆者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归⽅程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
(5)检验回归⽅程线性关系的显著性(0.05α=)。
(6)如果某地区的⼈均GDP 为5000元,预测其⼈均消费⽔平。
(7)求⼈均GDP 为5000元时,⼈均消费⽔平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:(3)回归⽅程:734.6930.309y x=+回归系数的含义:⼈均GDP没增加1元,⼈均消费增加0.309元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型⾮标准化系数标准化系数t 显著性B 标准误Beta1 (常量)734.693 139.540 5.265 0.003⼈均GDP(元)0.309 0.008 0.998 36.492 0.000 a. 因变量: ⼈均消费⽔平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%⼈均GDP对⼈均消费的影响达到99.6%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
模型摘要模型R R ⽅调整的R ⽅估计的标准差1 .998(a) 0.996 0.996 247.303a. 预测变量:(常量), ⼈均GDP(元)。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(5)F 检验:回归系数的检验:t 检验注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型⾮标准化系数标准化系数t 显著性B 标准误 Beta1(常量) 734.693 139.540 5.2650.003 ⼈均GDP (元)0.3090.0080.99836.4920.000a. 因变量: ⼈均消费⽔平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(6)某地区的⼈均GDP 为5000元,预测其⼈均消费⽔平为 734.6930.30950002278.693y =+?=(元)。
资源包 7相关与回归分析习题答案

章后习题参考答案第七章相关与回归分析1.单项选择题(1)A,(2)C,(3)D,(4)B,(5)A2.多项选择题(1)AB,(2)BE,(3)ABE,(4)BD,(5)ABCDE3.判析题(1)×,(2)√,(3)√,(4)√,(5)×4.简答题(1)什么是相关分析?相关分析的主要内容是什么?相关分析是研究现象之间是否存在某种依存关系,并对具体有依存关系的现象探讨其相关方向以及相关程度,是研究随机变量之间的关系的一种统计方法。
相关分析的内容:①确定现象之间有无相关关系②确定相关关系的表现形式③判定相关关系的密切程度和方向(2)什么是回归分析?回归分析的主要内容是什么?回归分析就是对具有相关关系的两个或两个以上变量之间的数量变化关系进行测定,建立因变量和自变量之间数量变动关系的数学表达式(回归方程),以便利用自变量的数值去估计或预测因变量数值的统计分析方法。
①根据研究的目的和现象之间的内在联系,确定自变量和因变量②确定回归分析模型的类型及数学表达式③对回归分析模型进行评价和诊断④根据给定的自变量数值推断因变量的数值(3)相关分析和回归分析有什么关系?①回归分析与相关分析的区别从广义上来说,相关分析包括回归分析,从狭义上说,相关分析与回归分析又有一定的区别。
狭义的相关分析和回归分析的区别主要有以下三个方面:第一,在相关分析中涉及的变量不存在自变量和因变量的划分问题,变量之间的关系是对等的;而在回归分析中,则必须根据研究对象的性质和研究分析的目的,对变量进行自变量和因变量的划分。
因此,在回归分析中,变量之间的关系是不对等的。
第二,在相关分析中所有的变量都必须是随机变量;而在回归分析中,自变量是给定的,因变量才是随机的。
第三,相关分析主要是通过一个指标即相关系数来反映变量之间相关密切程度的大小,由于变量之间是对等的,因此相关系数是惟一确定的;而在回归分析中,对于互为因果关系的两个变量,则有可能存在两个回归方程。
第6章回归分析与相关分析(2)-逐步回归

第6章 逐步回归分析现在我们知道,多元线性回归不仅仅是普通的线性代数运算,其间存在伪因果和共线性等诸多问题。
解决问题的办法已经开发了不少,著名的有前进(forward )法、后退(backward )法、剔除(remove )法、逐步(stepwise )回归法等。
目前看来效率较高、最受人们青睐的方法是逐步回归法。
§6.1逐步回归的基本原理多元逐步回归方法的基本思路在于,自动地从大量的可供选择的变量中选取最重要的变量,据以建立回归分析的预测或者解释模型。
变量选取的根据是自变量对因变量作用程度的大小:保留作用程度大的变量,剔除作用小的变量。
是否选取一个变量,定量判据就是相关系数。
假定有m 个自变量,1个因变量(用y 表示),则全部变量(包括自变量和因变量)之间的相关系数矩阵可以表作⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=yy ymy y my mmm m y my m R R R R R R R R R R R R R R R R L L M MOM ML L 2121222*********R , 根据相关系数定义一个自变量“贡献”系数jjjy j R R P 2=,按照贡献系数的大小决定一个自变量的去留。
式中P j 表示第j 个自变量对因变量的贡献系数,R jy 表示第j 个自变量与因变量的相关系数,R jj 表示相关系数矩阵对角线上第j 行第j 列元素(j =1,2,…,m )。
由于逐步回归分析是对自变量逐步进行的,每次计算都有一个贡献系数,第l 步计算的贡献系数表示为)1(2)1()(][−−=l jj l jy l j R R P .在逐步回归分析过程中,我们不仅要引入贡献最大的自变量,同时要考虑剔除贡献最小的因变量。
因此,变量的存留与否又涉及到统计判据——F 检验。
设定一个显著性水平α,查F 检验表,或者在数学或者统计分析软件中查出F 检验的临界值F α。
当然,也可以根据自己对系统的认识和建模的需要自己设定一个临界值。
回归分析参考答案

回归分析参考答案回归分析参考答案回归分析是一种常用的统计方法,用于研究变量之间的关系。
它可以帮助我们理解和预测变量之间的依赖关系,并且在实际应用中具有广泛的应用场景。
本文将介绍回归分析的基本概念、方法和应用,并提供一些参考答案,以帮助读者更好地理解和运用回归分析。
一、回归分析的基本概念回归分析是一种用于研究因变量和自变量之间关系的统计方法。
它基于一组观测数据,通过建立数学模型来描述因变量与自变量之间的关系,并用统计方法对模型进行估计和推断。
回归分析的目标是通过自变量的变化来预测因变量的值。
在回归分析中,因变量是我们想要预测或解释的变量,而自变量是我们用来解释因变量变化的变量。
回归分析可以分为简单线性回归和多元回归两种类型。
简单线性回归是指只有一个自变量和一个因变量的情况,而多元回归则是指有多个自变量和一个因变量的情况。
二、回归分析的方法回归分析的方法主要包括建模、参数估计和模型评估三个步骤。
1. 建模:在回归分析中,我们需要选择适当的模型来描述因变量和自变量之间的关系。
常见的模型包括线性模型、非线性模型和广义线性模型等。
选择合适的模型需要根据具体问题和数据特点来决定。
2. 参数估计:在建立模型之后,我们需要对模型的参数进行估计。
参数估计的方法有最小二乘法、最大似然估计和贝叶斯估计等。
最小二乘法是一种常用的参数估计方法,它通过最小化观测值与模型预测值之间的差异来估计参数。
3. 模型评估:在参数估计之后,我们需要对模型进行评估,以确定模型的拟合程度和预测能力。
模型评估的指标包括残差分析、方差分析和回归系数的显著性检验等。
通过这些指标,我们可以判断模型是否合理,并对模型进行改进。
三、回归分析的应用回归分析在实际应用中具有广泛的应用场景。
下面将介绍一些常见的应用领域和相应的参考答案。
1. 经济学:回归分析在经济学中常用于研究经济变量之间的关系。
例如,我们可以使用回归分析来研究收入和消费之间的关系,以及利率和投资之间的关系。
相关与回归分析

3.按相关的方向可划分为: 正相关,负相关
(1)正相关:两个相关现象间,当一个变量的 数值增加(或减少)时,另一个变量的数值也 随之增加(或减少),即同方向变化。 例如收入与消费的关系。 (2)负相关:当一个变量的数值增加(或减少) 时,而另一个变量的数值相反地呈减少(或增 加)趋势变化,即反方向变化。 例如物价与消费的关系。
y
x
3.相关关系举例
相关关系的例子
商品的消费量(y)与居民收入(x)之间的关系
商品的消费量(y)与物价(x)之间的关系
商品销售额(y)与广告费支出(x)之间的关系
粮食亩产量(y)与施肥量(x1) 、降雨量(x2) 、温 度(x3)之间的关系 收入水平(y)与受教育程度(x)之间的关系
2.按相关的形式可划分为: 线性相关,非线性相关
(1)当两种相关现象之间的关系大致呈现为 线性关系时,称之为线性相关。 (2)当两种相关现象之间的关系不表现为直 线关系,而是近似于某种曲线方程的关系, 则这种相关关系称为非线性相关。
(1)
(2)
(3)
(4)
图中()、()为线性相关,()、()为非线性相关。 1 2 3 4
完成量(小时)
20 50 20 30 50 20 50 40 20 80 40 20 50 80 30 单位成本(元/小时) 16 16 18 16 15 18 15 14 16 14 15 16 14 15 15
整理后有
完成量(小时)
20 20 20 20 20 20 20 20 20 30 30 30 30 30 40 单位成本(元/小时) 15 16 16 16 16 18 18 18 18 15 15 15 16 16 14
六章节相关与回归分析

学
1. 相关分析中,变量 x、 变量 y 处于平等地位。
回归分析中, y 为因变量,处在被解释的地位; x 为自变量,用于解释和预测因变量的变化。
2. 2. 相关分析中所涉及的变量 x 和 y 都是随机变 量;回归分析中,因变量y 是随机变量,自变量 x 可以是随机变量,也可以是非随机的确定变量 。
F检验与T检验的一致性: F=t的平方
6 - 38
统
计 学
三、回归预测
1. 回归预测是根据自变量 x 的取值来估计或 预测因变量 y 的取值;
2. 估计或预测的类型
点估计,给定x=xo,因变量y对应的点估计 为: yˆ0 a+bx0
区间估计: [yˆ0,yˆ0+]
3. 3. 相关分析主要描述两个变量之间相关关系的 密切程度;回归分析揭示变量之间数量变动的统 计规律性(不仅可以由回归方程揭示变量 x 对变量 y
的平均影响大小,还可以进行预测和控制 )。
6 - 18
统
计 学
回归模型的类型
回归模型(方程)——来表达变量之间的平 均数量关系的数学模型。该模型中包含:
y
离差分解图
x
6 - 31
统
计
离差平方和的分解
学
1. 从图上看有:总变差=回归变差+剩余变差
y y y ˆ y + y y ˆ
2. 两端平方后求和有:
n
n
n
yiy2 y ˆiy2+ yiy ˆ2
i 1
i 1
i 1
{ { {
总变差平方和 (SST)
回归平方和 (SSR)
残差平方和 (SSE)
记为: SST = SSR + SSE 或 Lyy =U+Q
相关和回归分析练习题

课本例题:对某10户居民家庭的年可支配收入和消费支出进行调查,得到的原始资料如下, 单位:千元居民家庭编号1 2 3 4 5 6 7 8 9 10 可支配收入25 18 60 45 62 88 92 99 75 98 消费支出 20 15 40 30 42 60 65 70 53 78 (1) 计算居民可支配收入与消费支出之间的相关系数,判断这两个变量之间是否显著相关;(P223)(2) 建立居民消费支出对居民可支配收入的一元线性回归方程,并解释回归系数的经济意义;(P227)(3) 计算拟合系数2R , 解释其意义;(P230)(4) 当居民可支配收入为120千元时,利用回归方程预测相应的消费支出。
(P232)相关系数的计算222222()()()()()()i i i i XX Y Y XY nXY r X n X Y n Y X X Y Y ---==⋅---⋅-∑∑∑∑∑∑ 参数1ˆβ和0ˆβ的估计122ˆXY nXY X nX β-=-∑∑ 01ˆˆY X ββ=- 拟合系数的计算2222222211222ˆˆˆ()()](()[)ii i i X n X Y n Y y x R y y ββ===--∑∑∑∑∑∑2,,X XX ∑∑ 2,,Y Y Y ∑∑ XY ∑ 1、 解:22()()()()i i i i X X Y Y r XX Y Y --=-⋅-∑∑∑ 21025,152711,128.125Y Y Y ===∑∑,129559.16ni i i X Y ==∑2195.56,5822.3334,24.445X X X ===∑∑变量X 的离差平方和2222()1041.86()92i i X X X n x X -==-=∑∑∑, 变量Y 的离差平方和2222()21382.8()75i i Y Y Y n y Y -==-=∑∑∑变量X 和Y 离差乘积项的和()()4503.305i i i i X x y X X Y Y Y nXY =--=-=∑∑∑ 22()()4503.3050.95401041.869221382.875()()i i i i XX Y Y r X X Y Y --===⨯-⋅-∑∑∑ 2.解:(1) 2199.5,7667.15,24.9375Y YY ===∑∑,1107610.4ni i i X Y ==∑ 22670,1587328,333.75X XX ===∑∑ 12241027.275ˆ0.0589696215.5XY nXY X nX β-===-∑∑ 00ˆˆ24.93780.0589333.75 5.2700Y X ββ=-=-⨯= 样本回归方程为ˆ 5.27000.0589i iY X =+ (2)变量X 的离差平方和222696215.5,i i x X nX =-=∑∑ 变量Y 的离差平方和2222692.1188i i y Y nY =-=∑∑22221ˆˆ()0.0589696215.52415.3178i i yx β==⨯=∑∑ 222ˆ2415.31780.89812692.1188ii y R y ===∑∑,表明自变量能解释因变量89.81%左右的变动,模型的拟合效果较好。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相关与回归分析思考与练习一、判断题1.产品的单位成本随着产量增加而下降,这种现象属于函数关系。
答:错。
应是相关关系。
单位成本与产量间不存在确定的数值对应关系。
2.相关系数为0表明两个变量之间不存在任何关系。
答:.错。
相关系数为零,只表明两个变量之间不存在线性关系,并不意味着两者间不存在其他类型的关系。
3.单纯依靠相关与回归分析,无法判断事物之间存在的因果关系。
答:对,因果关系的判断还有赖于实质性科学的理论分析。
4.圆的直径越大,其周长也越大,两者之间的关系属于正相关关系。
答:错。
两者是精确的函数关系。
5.总体回归函数中的回归系数是常数,样本回归函数中的回归系数的估计量是随机变量。
答:对。
6.当抽取的样本不同时,对同一总体回归模型估计的结果也有所不同。
答:对。
因为,估计量属于随机变量,抽取的样本不同,具体的观察值也不同,尽管使用的公式相同,估计的结果仍然不一样。
二、选择题1.变量之间的关系按相关程度分可分为:b 、c 、da.正相关;b. 不相关;c. 完全相关;d.不完全相关; 2.复相关系数的取值区间为:aa. 10≤≤R ;b.11≤≤-R ;c.1≤≤∞-R ;d.∞≤≤-R 1 3.修正自由度的决定系数a 、b 、da.22R R ≤; b.有时小于0 ; c. 102≤≤R ;d.比2R 更适合作为衡量回归方程拟合程度的指标 4.回归预测误差的大小与下列因素有关:a 、b 、c 、da 样本容量;b 自变量预测值与自变量样本平均数的离差c 自变量预测误差;d 随机误差项的方差三、问答题1.请举一实例说明什么是单相关和偏相关?以及它们之间的差别。
答:例如夏季冷饮店冰激凌与汽水的消费量,简单地就两者之间的相关关系进行考察,就是一种单相关,考察的结果很可能存在正相关关系,即冰激凌消费越多,汽水消费也越多。
然而,如果我们仔细观察,可以发现一般来说,消费者会在两者中选择一种消费,也就是两者之间事实上应该是负相关。
两者之间的单相关关系出现正相关是因为背后还有天气等因素的影响,天气越热,两种冷饮的消费量都越多。
如果设法将天气等因素固定不变,单纯考察冰激凌与汽水的消费量,则可能出现负相关关系。
像这种假定其他影响因素不变专门考察其中两个因素之间的关系就成为偏相关。
2.讨论以下几种场合,回归方程t t t t u X X Y +++=33221βββ中回归系数的经济意义和应取的符号。
(1)Y t 为商业利润率;X 2t 为人均销售额;X 3t 为流通费用率。
(2)Y t 为粮食销售量;X 2t 为人口数;X 3t 为人均收入。
(3)Y t 为工业总产值;X 2t 为占用的固定资产;X 3t 为职工人数。
(4)Y t 为国内生产总值;X 2t 为工业总产值;X 3t 为农业总产值。
答:(1)02>β,03<β人均销售额越大,企业利润越高,故此商业利润率越高,从而商业利润率与人均销售额呈正相关关系;而流通费用率越高,反映商业企业的经营成本越高,其商业利润率就越低。
(2)02>β,03>β人口数量越多,对粮食的消费量就越大;人均收入越多,对粮食的购买力就越强,故此这两个变量皆与粮食销售量呈正相关关系。
(3)02>β,03>β固定资产和职工人数是两大生产要素,数量越多,说明生产要素越密集,工业总产值就越高,所以它们与工业总产值的关系为正相关。
(4)01>β,02>β,03>β因为国内生产总值包括三次产业,所以工业总产值、农业总产值和全部的国内生产总值为正相关关系,同时即便某些特殊地区没有工业和农业,仍然有国内生产总值,所以,01>β。
四、计算题1.设销售收入X为自变量,销售成本Y为因变量。
现根据某百货公司12个月的有关资料计算出以下数据:(单位:万元) ∑-2)(X X t =425053.73 ; X = 647.88; ∑-2)(Y Y t = 262855.25 ; Y = 549.8; ∑--))((X XY Y tt= 334229.09(1) 拟合简单线性回归方程,并对方程中回归系数的经济意义做出解释。
(2) 计算决定系数和回归估计的标准误差。
(3) 对β2进行显著水平为5%的显著性检验。
(4)假定明年1月销售收入为800万元,利用拟合的回归方程预测相应的销售成本,并给出置信度为95%的预测区间。
解:(1)7863.073.42505309.334229)())((ˆ22==---=∑∑X X X X Y Y tt tβ3720.4088.647*7863.08.549ˆˆ21=-=-=X Y ββ (2)∑∑∑----=2222)()(]))(([Y Y X X X X Y Y r tttt999834.025.262855*73.42505309.3342292== 6340.43)()1(222=--=∑∑Y Y r et0889.222=-=∑n eS te(3)0:,0:2120≠=ββH H003204.073.4250530889.2)(2ˆ2==-=∑X X S S teβ4120.245003204.07863.0ˆ22ˆ2ˆ===βββS t228.2)10()2(05.02/==-t n t αt 值远大于临界值2.228,故拒绝零假设,说明2β在5%的显著性水平下通过了显著性检验。
(4)41.669800*7863.03720.40=+=f Y (万元)1429.273.425053)88.647800(12110089.2)()(11222=-++=--++=∑X X X X n S S t f e f所以,Y f 的置信度为95%的预测区间为:3767.241.6690667.1*228.214.696)2(2/±=±=-±f e f S n t Y α所以,区间预测为: 18.46764.466≤≤f Y2. 对9位青少年的身高Y 与体重X 进行观测,并已得出以下数据:i13.54Y =∑ ,∑=9788.22Y2i,i472X=∑,228158i X =∑,803.02i iX Y =∑要求:(1)以身高为因变量,体重为自变量,建立线性回归方程;(2)计算残差平方和决定系数;(3)计算身高与体重的相关系数并进行显著性检验;(自由度为7,显著水平为0.05的t 分布双侧检验临界值为2.365。
)(4)对回归系数2ˆβ进行显著性检验。
解:(1)2222)())())((ˆ∑∑∑∑∑∑∑--=---=tttttt tttX X N Y X Y X N X X X X Y Y β0273.0472*47228158*9472*54.1302.803*9=--=0727.09/472*0273.09/54.13ˆˆ21=-=-=X Y ββ(2)决定系数:9723.0)()(]))(([2222=----=∑∑∑Y Y X XX X Y Y r ttt t残差平方和0722.0)()1(222=--=∑∑Y Y r e t(3)身高与体重的相关系数:9861.09723.02===R r不同时为零和211210:,0:ββββH H ==1016.022=-=∑n eS te检验统计量9134.245)(ˆ2222=-=∑etS X X F β)2(2,1-=-N t F NF 值远大于临界值2.365,故拒绝零假设,说明回归方程在5%的显著性水平下通过了显著性检验。
(4)0:,0:2120≠=ββH H0005.03404.2220273.0)(2ˆ2==-=∑X XS S teβ6.540005.00273.0ˆ22ˆ2ˆ===βββS t365.2)7()2(05.02/==-t n t αt 值远大于临界值2.365,故拒绝零假设,说明2β在5%的显著性水平下通过了显著性检验。
资料来源:厦门市统计局网站,其中人均储蓄根据储蓄额与人口数推算。
试根据该表的资料,(1) 拟合以下形式的消费函数:Y t =β1+β2X 1t +β3X 2t +U t (2) 计算随机误差项的标准差估计值、修正自由度的决定系数,并对整个回归方程进行显著性检验。
(3) 假设某一居民家庭人均可支配收入为12,000元,人均储蓄为40000元,试预测其人均消费支出,并给出置信度为95%的预测区间。
解:(1)回归分析的EXCEL 操作步骤为:步骤一:首先将数据粘贴导入EXCEL 数据表中。
步骤二:进行回归分析选择“工具” →“数据分析” →“回归”,在该窗口中选定自变量和因变量的数据区域,最后点击“确定”完成操作:得到回归分析的输出结果见下图。
因此回归方程为:t t t X X Y 210245.05879.00116.1596-+=(2)随机误差项的标准差估计值为:S =369.3716,修正的决定系数为:9633.02=R 。
不同时为零和、32113210:,0:ββββββH H ===F=145.4606远大于F 统计量的临界值4.10,说明回归方程在5%的显著性水平下通过检验。
(3)预测 点估计值为:158.963140000*0245.012000*5879.00116.1596=-+=f C使用EXCEL 进行区间估计步骤如下: 步骤一:构造工作表步骤二:为方便后续步骤书写公式,定义某些单元格区域的名称首先,定义F6、F7、F8的名称:选定E6:F8区域,然后执行菜单命令“插入”→“名称”→“指定”,在调出的对话框中选中“最左列”,单击“确定”:其次,定义B2:D13的名称:先选定该区域,然后执行然后执行菜单命令“插入”→“名称”→“定义”:调出“定义名称”对话框,输入名称“X ”,单击“确定”。
最后,采用同样方法,将B15:D15定义为“Xf ”,将F2:F4定义为“B ”。
步骤三:计算点预测值f C在F6中输入公式“=MMULT(Xf,B)”,按回车键即可。
步骤四:计算t 临界值在F7中输入公式“=TINV(1-0.95,12-3)”,按回车键即可。
步骤五:计算预测估计误差的估计值f e S在F5中输入公式:“=MMULT(MMULT(Xf,MINVERSE(MMULT(TRANSPOSE(X),X))),TRANSPOSE(Xf))”然后按“Ctrl+Shift+Enter ”组合键即可。
再计算f e S ,在F8中输入公式“=369.3716*SQRT(1+F5)”。
369.3716为回归估计标准差。
步骤六:计算置信区间上下限在F9、F10中分别输入公式“=Cf-t 临界值*Sef ”和“=Cf+t 临界值*Sef ”。
