第三章题解
计算机组成原理—习题解答(第三章)

Copyright ©2012 Computer Organization Group. All rights reserved.
第三章 3.10
题解:
⑴ 64K×32位 / 16K×8位 = 4×4 = 16片; ⑵ 见下页; ⑶ 8ms / 128 = 62.5us,刷新周期为62.5us,128个刷新周期; ⑷ 分散式对存储器刷新一遍用时128×0.5us×2=128us,在8ms
题解: 1ms(1000us)内必须刷新64次,每次刷新时间为1/4us ,则1ms内16us用于刷新,比例为1.6%。 或者, 1ms中包含的存取周期数为:1ms/250ns=4000个
Copyright ©2012 Computer Organization Group. All rights reserved.
第三章 3.10
A6~0行 A13~7列
A6~0 刷新
A14
A15 -RAS
REF
A6~0 地址 -WE 多路 选择 -RAS0 器
-RAS1
片 选 译 -RAS2 码 器 2:4 -RAS3
-CAS
A6~0 -WE
16KX8 DRAM
16KX8 DRAM
第三章 3.6
3.6若用1M×1位的DRAM芯片构成1M×16位的主存储器 ,芯片内部存储元排列成正方形阵列,其刷新最大间隔时 间为4ms。则采用异步刷新时,两次刷新操作应相隔多长 时间?4ms时间内共需多少个刷新周期?
题解: 刷新定时信号的周期时间为: 4ms/1024 = 3.9us; ; 4ms时间内共需1024个刷新周期。
题解:
(1) 寻址范围=64K / (32/8) = 16K字;存储容量为16K×32bit。 (2) 字地址与字节地址的分配:(大端方式)
第三章 信道与信道容量 习题解答

,
,求
,
,
和
;
(2) 求该信道的信道容量及其达到信道容量时的输入概率分布。
解:
(1)先写出
:
根据公式
计算联合概率:
信宿端符号分布概率:
根据公式
计算:
3
求各熵: 信源熵:
比特/消息
信宿熵:
比特/消息
可疑度:
平均互信息量: 噪声熵: (2)二元对称离散信道的信道容量:
比特/消息 比特/消息
比特/秒
信源等概分布时(
解:设下标 1为原状况,下标 2为改变后状况。由
可得:
,
倍
如果功率节省一半则
倍 ,为 了 使 功 率 节 省 一 半 又 不 损 失 信 息 量 I,根 据
,可以: (1) 加大信道带宽 W,用带宽换取信噪比
,
,
7
缺点是对设备要求高。 (2) 加大传输时间 T,用传输时间换取信噪比,同理可得:
缺点是传输速度降低了。
噪声熵:
(5)平均互信息量:
2.有一个生产 A、B、C、D四种消息的信源其出现的概率相等,通过某一通信系统传输时,B和 C无误,A 以 1/4概率传为 A,以 1/4概率误传为 B、C、D,而 D以 1/2概率正确传输,以 1/2概率误传为 C,
(1)试求其可疑度?(2)收到的信号中哪一个最可靠?(3)散布度为多少? 解:(1)
,
将各数据代入: 解得:
如果
则
将各数据代入: 解得:
14.在理想系统中,若信道带宽与消息带宽的比为 10,当接收机输入端功率信噪比分别为 0.1和 10时,试
比较输出端功率信噪比的改善程度,并说明
与
之间是否存在阀值效应。
化工原理答案-第三章习题答案-150

第三章习题解答3-1 某圆柱形固定床填充的催化剂直径为p d ,高为h ,试求等体积的当量直径及球形度。
解:h d d e 2p 346ππ=,32p 23h d d e = ()p 312p p 2322218)24(23d h h d h d d h d P P +=⋅⋅+⨯⎪⎭⎫ ⎝⎛=πππφ3-2 求20mm×20mm×25mm 的长方体颗粒的体积当量直径,表面积当量直径,比表面积当量直径及形状系数。
解:体积当量直径:mm V d ev 7.262520206633=⨯⨯⨯==ππ表面积当量直径:mm Sd es 8.282)252020202020(=⨯⨯+⨯+⨯==ππ比表面积当量直径:mm S V a d ea 1.232)252020202020(252020666=⨯⨯+⨯+⨯⨯⨯⨯=== 形状系数:86.08.287.26222222=====es ev es ev P s d d d d S S ππφ 3-3 由边长皆为2mm 的立方体,直径和高度均为2mm 的圆柱体及直径为3mm 的球体各10kg 组成的均匀颗粒床层,床层直径为0.2m ,高度为 1 m 。
已知颗粒的密度皆为1900kg/m 3,求床层的空隙率和颗粒的平均比表面积。
解: 床层体积:3220314.012.044m h d V b =⨯⨯==ππ颗粒体积:30158.01900310m V P =⨯= 床层空隙率:497.00314.00158.00314.0=-=-=bpb V V V ε 颗粒的平均比表面积:3球柱立a a a a ++=-13000002.0002.0002.06002.0002.0-=⨯⨯⨯⨯=m a 立 1223000002.0)002.0(4002.02)002.0(4-=⨯⨯⋅+⨯⨯=m a πππ柱 1322000003.066003.0003.0-==⨯⨯=m a ππ球 11 2.67676232000300030003---==++=++=mm m a a a a 球柱立 3-4 某形状近似球形的微小固体颗粒,其沉降运动处于斯托克斯定理区,试计算(1)该颗粒在20℃与200℃的常压空气中的沉降速度之比为多少?(2)该颗粒在20℃与50℃的水中的沉降速度之比为多少?[(1)1.44,(2)0.55]解:(1)20℃空气的粘度s Pa ⋅⨯=-51081.1μ,200℃空气的粘度s Pa ⋅⨯=-5'106.2μ,因沉降速度处于斯托克斯定律区,ρρ>>p ,故()()()()44.11081.1106.2181855''''22'=⨯⨯=--=--=--μρρμρρμρρμρρs s s s t t g d gd u u (2)20℃水的粘度s Pa ⋅⨯=-3101μ,50℃水的粘度s Pa ⋅⨯=-3'1055.0μ,因沉降速度处于斯托克斯定律区,并考虑到液体的密度随温度变化很小,故()()()()55.01011055.0181833'''''22'=⨯⨯=≈--=--=--μμμρρμρρμρρμρρs s p p p p t t g d g d u u 无论是气体还是液体,温度的改变主要是通过粘度的变化而影响沉降速度。
新版化工原理习题答案第三章-非均相混合物分离及固体流态化-题解

第三章非均相混合物分离及固体流态化1.颗粒在流体中做自由沉降,试计算(1)密度为2 650 kg/m\直径为0.04 mm的球形石英顆粒在20 °C空气中自由沉降,沉降速度是多少?(2)密度为2 650 kg/m;,,球形度 0 = 0.6的非球形颗粒在20 £清水中的沉降速度为0. 1 m/ s,颗粒的等体积当量直径是多少?(3)密度为7 900 kg/m\克径为6.35 mm的钢球在密度为1 600 kg/n?的液体中沉降150 mm所需的时间为7.32 s,液体的黏度是多少?解:(1)假设为滞流沉降,则:18“查附录 20 °C 空气 p = 1.2O5kg/m\ //= 1.81 x IO'5Pa • s ,所以,“,=¥的吧:鵲眷吟9%沖276m方核算流型:=1.205X0.1276X004X10-=034<11.81X10'5所以,原假设正确,沉降速度为0. 1276 m/so(2)采用摩擦数群法4xl.81xl0-5 (2650-1.205)x9.81 $3x1.20 宁 xOf依0 = 0.6, ^Re"1 =431.9,查出:Re x =^A = o.3,所以:」O.3xl.81xlO-5in5 *d、= ------------- = 4.506 x 10 m = 45屮nc 1.205x0」(3)假设为滞流沉降,得:1/ = --------⑻,其中u{ = h/0 =0.15/7.32 m/s = 0.02(M9 m/s将已知数据代入上式得:J).00635'(7900J 600)5lp a s = 6.757Pa.s 18x0.02049核算流型n odu. 0.00635 x 0.02049 x 1600 n AOAO t -Re =匕_- = ----------------------- = 0.03081 < 1// 6.7572.用降尘室除去气体中的固体杂质,降尘室长5 m,宽5 m,高4.2 m,固体杂质为球形颗粒,密度为3000 kg/m\气体的处理量为3000 (标准)m7h o试求理论上能完全除去的最小颗粒直径。
习题解析控制工程

60°
45°
(3)
0
[s]
Re
2024/9/30
n=2s-1
20
Im
[s]
3.13
0
Re
0<<1
Im [s]
0
Re
-1<<0
2024/9/30
Im
[s]
0
Re
=1
Im [s]
0
Re
=-1
21
3.14
Gs
s2
9 s
9
s2
2
32 1
3s
32
6
n 31 /
0.167
s
M p 58.8%
t p 1.06s
xo t 10 t 0.1 0.1e10t
单位阶跃响应: (上式旳一阶导数)
xou t 10 1 e10t
单位脉冲响应:
(上式旳二阶导数或xou(t)旳一阶导数)
xoi t 100e10t
2024/9/30
8
系统旳闭环传递函数为:
3.8
GB
s
1
K 0G s K1Gs
15
3.11 内部局部闭环传递函数:
GB1s
s
2 n
2n
K
f n2
整个系统旳闭环传递函数:
GB
s
1
1 s
GB1s
1 s
GB1
s
s2
2 n
2 n
K
f
2 n
s
2 n
2024/9/30
16
GB s s2
n2
2 n
K
f
2 n
s
第三章 习题解答-2.0
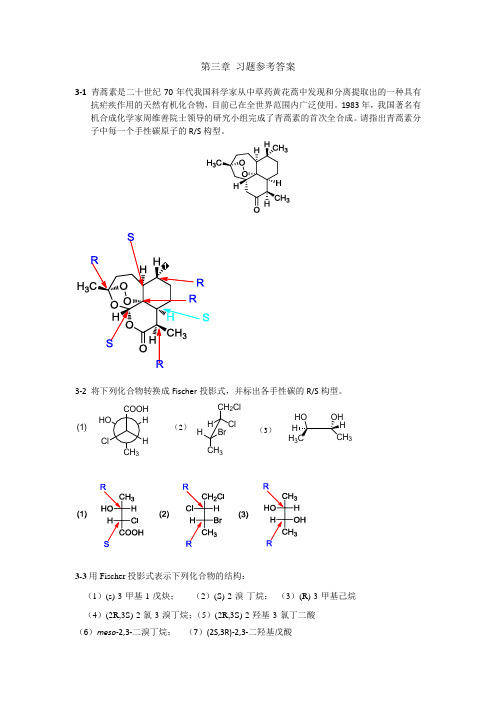
第三章 习题参考答案3-1 青蒿素是二十世纪70年代我国科学家从中草药黄花蒿中发现和分离提取出的一种具有抗疟疾作用的天然有机化合物,目前已在全世界范围内广泛使用。
1983年,我国著名有机合成化学家周维善院士领导的研究小组完成了青蒿素的首次全合成。
请指出青蒿素分子中每一个手性碳原子的R/S 构型。
3-2 将下列化合物转换成Fischer 投影式,并标出各手性碳的R/S 构型。
(2)(3)3BrHCH 3HClCH 2ClH 3H 3(1)3-3用Fischer 投影式表示下列化合物的结构:(1)(s)-3-甲基-1-戊炔; (2)(S)-2-溴-丁烷; (3)(R)-3-甲基己烷 (4)(2R,3S)-2-氯-3-溴丁烷;(5)(2R,3S)-2-羟基-3-氯丁二酸 (6)meso -2,3-二溴丁烷; (7)(2S,3R)-2,3-二羟基戊酸本题答案不唯一。
在画Fisher投影式时,习惯把含碳原子的基团放在竖键上,并把命名时编号最小的碳原子放在上端。
以下是较为符合习惯的Fisher投影式。
3-4下列化合物中哪些有手性?(1)、(3)、(5)、(7)、(9)无手性(2)、(4)、(6、)(8)、(10)有手性3-5长尾粉蚧壳虫信息素A是雌性长尾粉蚧壳虫(一种植物害虫)分泌的性激素,其外消旋体目前已被人工合成,并商业化用于农田害虫的控制和诱杀。
最近,化学家通过全合成途径确定了天然长尾粉蚧壳虫信息素的绝对构型(J. Org. Chem. 2013, 78, 6281−6284)。
通过全合成方法分别得到了A的2种立体异构体,发现其中的(S)-(+)-异构体具有吸引雄性长尾粉蚧壳虫的活性,而它的对映体(R)-( )-A则无此生物活性。
此结果表明雌性长尾粉蚧壳虫分泌的天然长尾粉蚧壳虫信息素为(S)-A。
商业化使用的外消旋体与纯的(S)-对映体生物活性相似,说明(R)-A对(S)-A的生物活性无抑制作用。
写出(R)-A和(S)-A的结构式。
第三章部分习题解答
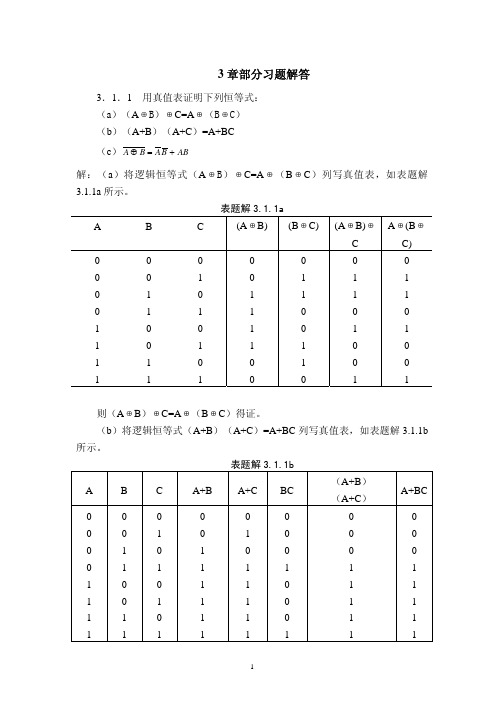
(b) ( A + B)(AB ) = AAB + BAB = AB
(c) ABC(B + C ) = ( A + B + C )(B + C ) = C + B( A + B ) = C + AB
(d) A + ABC + ABC + CB + CB = A(1 + BC + BC) + C(B + B ) = A + C
L3 = A3 ⊕ C
可分别用异或门、三态门设计逻辑电路,如图题解 3.4.4a、b 所示。
图题解 3.4.4
7
3.4.7 某雷达站有 3 部雷达 A、B、C,其中 A 和 B 功率消耗相等,C 的 功率是 A 的两倍。这些雷达由两台发电机 X 和 Y 供电,发电机 X 的最大输出功 率等于雷达 A 的功率消耗,发电机 Y 的最大输出功率是 X 的 3 倍。要求设计一 个逻辑电路,能够根据各雷达的启动和关闭信号,以最节约电能的方式启、停 发电机。
X = ABC + ABC + ABC + ABC = AB ⊕ C + B A ⊕ C
Y =AB+C 由逻辑表达式可设计出最节约电能的发电机启、停方式的逻辑电路,如图 题解 3.4.7b 所示。
表题解 3.4.7
A
B
C
X
Y
0
0
0
0
0
0
0
1
0
1
0
1
0
1
0
0
1
1
0
1
1
0
0
1
0
第三章习题解答

第三章 语法分析
对产生式V′→ε |[E] 有:FIRST(ε)∩FIRST(‘[’]= Φ; FIRST(‘[’)∩FOLLOW(V′)={[}∩{#,+,]}=Φ;
对E′→ε | +E 有:FIRST(ε)∩FIRST(‘+’)= Φ; FIRST(‘+’)∩FOLLOW(E′)={+}∩{ ] }=Φ。 故文法G[V′]为LL(1)文法。
第三章 语法分析 表3-12 习题3.24的SLR(1)分析表
状态
ACTION
GOTO
b
d
i
#
T
E
H
0
r3
s3
1
2
1
acc
2
s4
3
r2
4
r6
s6
r6
5
5
s7
r1
6
r4
r4
7
s8
8
r5
r5
第三章 语法分析
序号 状态栈 符号栈 产生式 输入串
10
#
E→ε bibi# 归约 r3
2 02
#E
bibi# 移进
第三章 语法分析
表3-8 优先关系表
a
b
c
a
⋖⋗
⋖≡
⋗
b
⋖
⋖⋗
≡
c
⋗
⋗
由于表中的优先关系不唯一,故文法G[S]不是算符优 先文法。
第三章 语法分析 (4) 消除文法G[S]的左递归: S→aSb | P P→bPc | bQc Q→aQ′ Q′→aQ′| ε 提取公共左因子后得到文法G′[S]: S→aSb | P P→bP′ P′→Pc | Qc Q→aQ′ Q′→aQ′| ε
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2007.4
Discrete Math. SLZ 经济学院
6
(4) f: NN, f (n) = n mod 4 Sol: f (n) = {0, 1, 2, 3}。非单非满 (5) f: IN, f (x) = |3n| + 2。 Sol: 偶函数,非单射。Min f(x) =2, 1无像源,非满射 (6) f: N2N, f(m, n) = mn。 N2 二维空间。 Sol: f (4, 1) = 41 = 4 = 22 = f (2, 2) , 所以非单射;
2007.4
Discrete Math. SLZ 经济学院
11
10. 设A和B都是有限集, |A| = |B| = n, 试证明由A 到B的函数, 如果它是单射, 则它必是满射。反 之亦真。
Proof: (反证)已知 f: AB是单射, 假设f 不是满射, 则B中至少有一个元素没有像源, 即A中元素至 多只有n-1个像, 但|A| = n, 所以A中至少有两个 元素对应同一个像, 这与f 是单射相矛盾。故f 是满射。
2007.4
Discrete Math. SLZ 经济学院
14
建立双射f: [0, 1] [a, b], f (x) = (b-a)x + a
所以 [a, b] ~ [0,1] = C
建立双射f: (0, 1) (a, b), f (x) = (b-a)x + a
所以 (a, b) ~ (0, 1) = C
(5) {‹|x|, x› | xR}
Sol: (1) 可以 (2) 可以 (3) 可以
(4) 可以
(5) 不可以 |x|有两个象, x和-x
2007.4
Discrete Math. SLZ 经济学院
1
2. 设f 和g是函数, 证明 f g dom f dom g, 且对所有x dom f, f(x) = g(x)。
2007.4
Discrete Math. SLZ 经济学院
7
7. 设|S| = n, 试证明任何从S到S的函数, 如果它是满 射, 则它必是单射。反之亦真。
Proof: 设f 是从S到S的任意函数, y1, y2, x1, x2S, f(x1)=y1, f(x2)=y2 若f 是满射,每个yS 均有原象, 且当y1 y2时, x1x2。 所以f 是单射。
= { (x, g(x)) | x dom g } =g
2007.4
Discrete Math. SLZ 经济学院
3
4. 设f, g, h都是实数集R上的函数, f(x) = 2x–1, g(x) = x + 4, h(x) = x/3。 求: fog, gof, hof, fo(hog), go(hof)。
Sol: f (0) = res7(0) = 0; f (1) = res7(3) = 3; f (2) = res7(6) = 6; f (3) = res7(9) = 2; f (4) = res7(12) = 5; f (5) = res7(15) = 1; f (6) = res7(18) = 4。 可见f 既是单射, 又是满射, 故是双射。
Proof: 因为 f = { (x, f(x)) | x dom f } g = { (x, g(x)) | x dom g }
f g 对任意 (x, f(x)) f, x dom f 有 (x, f(x)) g, x dom g
(x, f(x)) f (x, f(x)) g 且 (x dom f x dom g)
Proof: 因为hgf = (hg) f = h(gf )是满射, 所以hg和 h是满射
因为gf h = g(f h) = (gf )h是满射, 所以g和 gf 均是满射。
因为f hg = f (hg) = (f h)g是单射, 所以hg和 g均是单射。
所以g 和hg都是双射, hg的逆函数(hg)-1: AB也是双射
(hg)-1(hgf ) = ((hg)-1(hg))f = IBf = f , (hg)-1和hgf 均是满 射, 所以f 是满射;
(f hg) (hg)-1= f ((hg)(hg)-1) = f IA = f , f hg和(hg)-1均是单射, 所以f 是单射;因此f 是双射。
所以g-1和f-1 也是双射, 于是
2007.4
Discrete Math. SLZ 经济学院
9
(2) 若gf 是单射且f 是满射, 则g 是单射。
Proof: b1, b2B, b1≠b2, 因为f 是满射, 必有 a1, a2A, 使得 f (a1) = b1, f (a2) = b2 , 因为b1≠b2,所以 a1≠a2 , 又因为g是BC的函数, 所以有c1, c2C, 使得 g (b1) = c1, g (b2) = c2 。由合成函数定义
思考题解
1. 下列关系可以定义函数吗?
(1) {‹a, x›, ‹b, y›, ‹0, 1›, ‹Panda, Peris›}
(2) {‹a, ‹b, c››, ‹b, ‹c, d››, ‹d, ‹a, d››}
(3) {‹0, ‹b, c››, ‹1, ‹b, c››}
(4) {‹x, |x|› | xR}
2
即h为单射。
Discrete Math. SLZ 经济学院
15
13. 下面集合A的势是什么? (1) {(p, q) | p, q都是整数};
Sol: 令 f : A B = {p/q}, f (p, q) = p/q, f 为双射, 所以A~B, |B|= 0, 故A的势为0 。
(2) {(p, q) | p, q都是有理数}; (3) A由所有圆心在x轴上, 半径为1的单位圆组成
反之, 已知 f: AB是满射, 假设f 不是单射, 则A
中至少有两个元素对应同一个像, 即A在B中至
多有n-1个像, 这与f 是满射相矛盾。
2007.4
故f 是单射。Discrete Math. SLZ 经济学院
12
11. 设有函数f : AB, g: BC, h: CA, 且hgf 和gf h是满射, f hg是单射, 试证明g, f, h都是双射
反之,若f 是单射, f(x1)=y1, f(x2)=y2 则x1x2时, y1y2。 |S| = n, 所以有n个不同的象,故为满射。
2007.4
Байду номын сангаас
Discrete Math. SLZ 经济学院
8
8. 设f:AB,BC是两个函数,证明: (1) 若gf 是满射且g 是单射,则f 是满射。 Proof: bB, 因为g是由B到C的函数,
Sol: f (x) = (x - 3)2 - 29, f (4) = f (2) = -28, 非单射; min f (x) = -29, 即当像< -29时无像源, 非满射。 (3) f: N+N, f(x) = log n。
Sol: 不是函数。 若 f: N+R, 则因为logn 单调递升,故单射; 但fD是离散的N, logn 不连续, 非满射。
g f (a1) = g(b1) = c1, g f (a2) = g(b2) = c2, 因为g f是单射, 由a1≠a2 可知c1≠c2 , 即g(b1) ≠ g(b2), 故g是单射。
2007.4
Discrete Math. SLZ 经济学院
10
9 f: Z7Z7, f (n) = res7(3n), 判断f 是否单射、满 射和双射。 res7(3n)表示3n被7除后的余数。
作g: [0, 1)(0, 1)单射为g (x)= x/2 + 1/4 , 则 (0, 1) ~ [0, 1) 作f: (0, 1)[0, 1]单射为f (x)= x 作g: [0, 1](0, 1)单射为g (x)= x/3 + 1/4 , 则 (0, 1) ~ [0, 1] 作f: [0, 1](0, 1]单射为f (x)= x/2 + 1/2 作g: (0, 1][0, 1]单射为g (x)= x, 则[0, 1] ~ (0, 1] ~是可传递的, (0, 1) ~ [0, 1) ~ (0, 1] ~ [0, 1]
f-1(f hg)g-1 = (f-1f )h(gg-1)= IAhIB = h, f-1, f hg, g-1均是单射, 所以h 是单射; 因此h 是双射。
2007.4
Discrete Math. SLZ 经济学院
13
12. 证明(0, 1), [0, 1), [0, 1], (0, 2), (–∞, +∞)等势。 Proof: 用Bernstein 定理: 作f: (0, 1)[0, 1)单射为f (x)= x,
2007.4
Discrete Math. SLZ 经济学院
4
5. 设A = {0, 1}, B = {a, b, c}。写出A到B的所有函
数和它们的像集, 指出哪些是单射、满射和双射
Sol: R1={(0, a), (1, a)}, {a}, R2={(0, a), (1, b)}, {a, b},单射 R3={(0, a), (1, c)}, {a, c},单射 R4={(0, b), (1, a)}, {a, b},单射 R5={(0, b), (1, b)}, {b}, R6={(0, b), (1, c)}, {b, c},单射 R7={(0, c), (1, a)}, {a, c},单射 R8={(0, c), (1, b)}, {b, c},单射 R9={(0, c), (1, c)}, {c}, |B||A| = 32 = 9 , 无满射和双射。
nN, 像源(n, 1),使f (n, 1) = n1 = n, 满射。 (7) f: (2U)2(2U)2(二维), f (A, B) = (A∪B, A∩B) Sol: A, B2U, f (A, B) = (A∪B, A∩B)
