自动控制原理_胡寿松_第二版_课后答案_第二章_参考答案
胡寿松自动控制原理课后习题答案

1 请解释下列名字术语:自动控制系统、受控对象、扰动、给定值、参考输入、反馈。
解:自动控制系统:能够实现自动控制任务得系统,由控制装置与被控对象组成; 受控对象:要求实现自动控制得机器、设备或生产过程扰动:扰动就是一种对系统得输出产生不利影响得信号、如果扰动产生在系统内部称为内扰;扰动产生在系统外部,则称为外扰。
外扰就是系统得输入量。
给定值:受控对象得物理量在控制系统中应保持得期望值参考输入即为给定值、反馈:将系统得输出量馈送到参考输入端,并与参考输入进行比较得过程。
2请说明自动控制系统得基本组成部分。
解:作为一个完整得控制系统,应该由如下几个部分组成:①被控对象: 所谓被控对象就就是整个控制系统得控制对象;②执行部件: 根据所接收到得相关信号,使得被控对象产生相应得动作;常用得执行元件有阀、电动机、液压马达等。
③给定元件: 给定元件得职能就就是给出与期望得被控量相对应得系统输入量(即参考量);④比较元件: 把测量元件检测到得被控量得实际值与给定元件给出得参考值进行比较,求出它们之间得偏差、常用得比较元件有差动放大器、机械差动装置与电桥等。
⑤测量反馈元件:该元部件得职能就就是测量被控制得物理量,如果这个物理量就是非电量,一般需要将其转换成为电量。
常用得测量元部件有测速发电机、热电偶、各种传感器等;⑥放大元件: 将比较元件给出得偏差进行放大,用来推动执行元件去控制被控对象。
如电压偏差信号,可用电子管、晶体管、集成电路、晶闸管等组成得电压放大器与功率放大级加以放大。
⑦校正元件: 亦称补偿元件,它就是结构或参数便于调整得元件,用串联或反馈得方式连接在系统中,用以改善系统得性能、常用得校正元件有电阻、电容组成得无源或有源网络,它们与原系统串联或与原系统构成一个内反馈系统。
3请说出什么就是反馈控制系统,开环控制系统与闭环控制系统各有什么优缺点?解:反馈控制系统即闭环控制系统,在一个控制系统,将系统得输出量通过某测量机构对其进行实时测量,并将该测量值与输入量进行比较,形成一个反馈通道,从而形成一个封闭得控制系统;开环系统优点:结构简单,缺点:控制得精度较差;闭环控制系统优点:控制精度高,缺点:结构复杂、设计分析麻烦,制造成本高、4 请说明自动控制系统得基本性能要求。
《自动控制原理》 胡寿松 习题答案(附带例题课件)

二、本课程实验的基本理论与实验技术知识
采用 MATLAB 软件上机进行实验,就是利用现代计算机硬件和计算机软件技术,以数字仿真技术为核 心,实现对自动控制系统基本理论和分析方法的验证以及控制系统设计。 通过上机实验,使学生在 MATLAB 软件的基本使用、编程调试、仿真实验数订人:杨志超 大纲审定人:李先允 制订日期:2005 年 6 月
5
《自动控制原理》电子教案
《自动控制原理》课程实验教学大纲
一、实验教学目标与基本要求
《自动控制原理》 课程实验通过上机使用 MATLAB 软件, 使学生初步掌握 MATLAB 软件在控制理论中的 基本应用,学会利用 MATLAB 软件分析控制系统,从而加深对自动控制系统的认识,帮助理解经典自动控 制的相关理论和分析方法。 通过本课程上机实验, 要求学生对 MATLAB 软件有一个基本的了解, 掌握 MATLAB 软件中基本数组和矩阵的表示方法,掌握 MATLAB 软件的基本绘图功能,学会 MATLAB 软件中自动控制理论 常用函数的使用,学会在 MATLAB 软件工作窗口进行交互式仿真和使用 M_File 格式的基本编程方法,初步 掌握利用 MATLAB 软件进行控制系统设计,让学生得到撰写报告的基本训练。
4.频率法反馈校正的基本原理和方法(选讲)
(七)非线性控制系统 了解非线性系统与线性系统的区别,了解非线性特性和非线性系统的主要特征,学会非线性系统的描 述函数分析方法,了解非线性系统的相平面分析法(选讲) 。
3
《自动控制原理》电子教案
1. 非线性系统的基本概念 2. 典型非线性特性、非线性系统的主要特征 3. 描述函数定义、应用条件和求取方法 4. 应用描述函数分析非线性系统的稳定性 5. 非线性系统自激振荡分析和计算 6. 介绍非线性系统相平面分析法(选讲)
《自动控制原理》胡寿松习题答案附带例题课件

采用 MATLAB 软件上机进行实验,就是利用现代计算机硬件和计算机软件技术,以数字仿真技术为核 心,实现对自动控制系统基本理论和分析方法的验证以及控制系统设计。
通过上机实验,使学生在 MATLAB 软件的基本使用、编程调试、仿真实验数据的获取、整理、分析以 及实验报告的撰写等基本技能得到训练。
二、教学基本要求
本课程采用时域法、根轨迹法和频率特性法对自动控制系统的性能进行分析和设计,学完本课程应达
到以下基本要求。
1.掌握负反馈控制原理 掌握负反馈控制原理,能够分析负反馈控制系统的调节过程并画出相应的控制系统方框图。了解控制
系统的基本构成和分类。
2.熟悉建立控制系统数学模型的方法 熟悉用拉氏变换法求解线性系统微分方程的基本方法。掌握控制系统传递函数、动态结构图建立和简
2.绘制1800 根轨迹的基本法则 3.绘制 00 根轨迹的基本法则
4.广义根轨迹 5.非最小相位系统的根轨迹 6.用根轨迹法分析系统性能 (五)频率法 了解频率特性的基本概念,频率特性的几何表示方法,熟悉典型环节的对数频率特性曲线(Bode 图) 绘制和极坐标曲线(Nyquist 曲线),掌握系统开环对数频率特性曲线的绘制,了解系统开环极坐标曲线绘 制的一般方法,熟悉开环对数频率特性低频段、中频段、高频段的特征,学会运用奈奎斯特稳定判据判断 闭环系统的稳定性,掌握系统稳定裕度的基本概念和计算方法,了解系统性能和开环频率特性的关系。 1.频率特性的基本概念和几何表示 2.典型环节的频率特性 3.控制系统开环对数频率特性和极坐标曲线的绘制 4.最小相位系统传递函数的确定 5.奈奎斯特稳定判据和 Bode 图上的稳定判据 6.稳定裕度的基本概念和计算方法 7.频率特性与系统性能的基本关系 (六)控制系统性能的校正 了解校正装置和校正方法,熟悉串联超前校正、串联滞后校正的基本原理和方法。了解频率法反馈校 正的基本原理和方法(选讲)。 1.控制系统校正的基本概念和一般方法 2.频率法串联超前校正的基本原理和方法 3.频率法串联滞后校正的基本概念和方法
《自动控制原理》+胡寿松+习题答案(附带例题课件)

用电技术专业方向)
先修课程: 高等数学、大学物理、积分变换、电路、数字电子技术、模拟电子技术
一、课程性质、目的和任务
本课程为电气工程及其自动化专业的主要专业基础课程之一,目的是使学生掌握负反馈控制原理、控
制系统数学模型的建立和系统性能分析、设计的基本方法,培养学生分析和设计自动控制系统性能的基本
能力并能满足其它后续专业课程对自动控制理论知识的需要。
制系统的性能。了解开环零、极点对系统性能的影响。
5.熟悉频率分析法分析控制系统性能的方法 熟悉典型环节频率特性的求取以及频率特性曲线,掌握系统开环对数频率特性曲线、极坐标曲线绘制
的基本方法。了解根据开环对数频率特性曲线分析闭环系统性能的方法。熟悉用奈奎斯特稳定判据判断系
1
《自动控制原理》电子教案
统稳定性的方法。掌握稳定裕度的计算方法。 6.熟悉控制系统校正的方法 了解串联超前校正、串联滞后校正的校正装置设计的基本原理和方法。 7.熟悉非线性控制系统的分析方法 了解非线性控制系统的特点和常见非线性特性。熟悉非线性控制系统的描述函数法。
熟悉系统微分方程的建立,拉氏变换及其应用。掌握系统传递函数的定义及求取,系统动态结构图 的建立及其简化以及系统不同传递函数的定义及求取。
1.控制系统微分方程的建立 2.非线性数学模型的线性化 3.控制系统的传递函数 4.典型环节的传递函数 5.控制的动态结构图及变换 6.信号流图及梅逊公式 7.反馈控制系统的传递函数 (三)自动控制系统的时域分析法 熟悉控制系统的时域指标,一阶系统的单位阶跃响应、斜坡响应以及性能指标的求取。掌握典型二阶 系统的单位阶跃响应以及性能指标的求取。掌握劳斯稳定判据分析系统的稳定性方法。熟悉控制系统稳态 误差分析以及稳态误差、误差系数的求取。 1. 控制系统性能指标的定义 2.一阶系统性能分析 3.二阶系统性能分析 4. 欠阻尼二阶系统的时域分析和指标计算 5. 高阶系统的时域分析、闭环主导极点和高阶系统的降阶
《自动控制原理》第二版课后习题答案
7
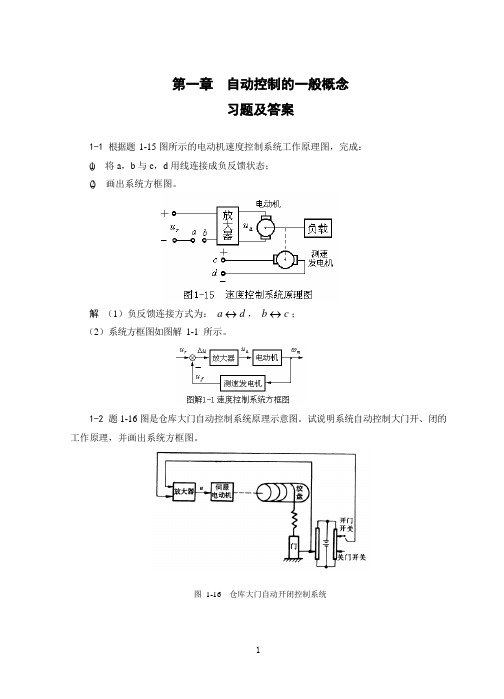
输出驱动 Z 轴直流伺服马达带动切削刀具连同刀具架跟随触针运动,当刀具位置与触针位置 一致时,两者位置偏差为零,Z 轴伺服马达停止。系统中,刀具是被控对象,刀具位置是被 控量,给定量是由模板确定的触针位置。系统方框图如图解 1-9 所示。最终原料被切割加工 成模板的形状。
图 1-16 仓库大门自动开闭控制系统
1
解 当合上开门开关时,电桥会测量出开门位置与大门实际位置间对应的偏差电压,偏 差电压经放大器放大后,驱动伺服电动机带动绞盘转动,将大门向上提起。与此同时,和大 门连在一起的电刷也向上移动,直到桥式测量电路达到平衡,电动机停止转动,大门达到开 启位置。反之,当合上关门开关时,电动机带动绞盘使大门关闭,从而可以实现大门远距离 开闭自动控制。系统方框图如图解 1-2 所示。
试分析系统的工作原理,指出系统的被控对象、被控量和给定量,画出系统的方框图。
图 1-18 导弹发射架方位角控制系统原理图
解 当导弹发射架的方位角与输入轴方位角一致时,系统处于相对静止状态。
当摇动手轮使电位器 P1的滑臂转过一个输入角 i 的瞬间,由于输出轴的转角 o i , 于是出现一个误差角 e i o , 该 误 差 角通过 电 位器 P1、 P2 转 换 成 偏 差 电 压 ue
2e2t单位阶跃输入时有rs依题意4e2t27已知系统传递函数3s2且初始条件为c01dt2ct2e2t28求图230所示各有源网络的传递函数根据运算放大器虚地概念可写出cs29某位置随动系统原理框图如图231所示已知电位器最大工作角度q3303018011根据运算放大器的特性可分别写出两级放大器的放大系数为3010210飞机俯仰角控制系统结构图如图232所示试求闭环传递函数q211已知系统方程组如下
胡寿松自控习题答案 第二章习题解答

(2)
iC 2
=
uC1
+ iC1R R
K 2 x0 = f (x& − x&0 )
消去中间变量 x,可得系统微分方程
f (K1
+
K
2
)
dx0 dt
+
K1K2 x0
=
K1 f
dxi dt
对上式取拉氏变换,并计及初始条件为零,得系统传递函数为
X 0 (s) =
fK1s
X i (s) f (K1 + K2 )s + K1K2
③图 2—57(c):以 x0 的引出点作为辅助点,根据力的平衡原则,可列出如下原始方程:
u0
= (iC
+ iR1 )R2
=
C
duC dt
+
uC R1
R2
=
C
d
(ui −
dt
u0
)
+
ui
− u0 R1
R2
整理得:
CR2
du0 dt
+ C
R2 R1
+ 1u0
= CR2
dui dt
+C
R2 R1ui − u0 = uC1 (1)
iC1
=
C1
duC1 dt
K
=
1
K2
( f1 s + 1)( f 2 s + 1) + f1
K 1
K2
K2
所以图 2-58(a)的电网络与(b)的机械系统有相同的数学模型。 2—4 试分别列写图 2-59 中个无源网络的微分方程式。
解:(a) :列写电压平衡方程:
自动控制原理-胡寿松-第二章

G(s)
C(s) R(s)b0 s m a Nhomakorabea s n
b1sm1 a1sn1
bm1s bm an1s an
bm
(1s
1)(
2 2
s
2
222s 1)
式中, i
an (T1s 1)(T22s2 22T2s
、T j 称为时间常数;
1)
(is 1)
(2) t≥0 时 f(t)是分段连续的
(3) ∫ ∞ f(t)e -st dt <∞
0
f(t)的拉氏变换为:
F(s)=∫
∞ 0
f(t)e-stdt
记作 F(s)=L[f(t)]
拉氏反变换为:
f(t)=L-1 [F(s)]
第一节控制系统的时域数学模型
2.常用函数的拉氏变换
(3()1(6))单单指位位数斜阶函坡数跃函函数e-数att I(t)
(Tjs 1)
m
K bm
K*
(zi )
i
为传递系数或增益。
an
n
( p j )
j 1
第二节控制系统的复数域数学模型
三、 典型环节的传递函数
不同的物理系统,其结构差别很大。但若 从系统的数学模型来看,一般可将自动控制系 统的数学模型看作由若干个典型环节所组成。 研究和掌握这些典型环节的特性将有助于对系 统性能的了解。
第二节控制系统的复数域数学模型
1.比例环节
放大倍数
微分拉氏方反程变: 换得c(:t)=Kr(t) c(取t)=拉K氏变换:
单位阶跃响应曲线
得传递函数: Gcr(((tts)))
K
自动控制原理_胡寿松_第二版_答案全解

自动控制原理_胡寿松_第二版_答案全解第二章控制系统数学模型练习及参考答案自动控制原理胡守松第二版课后解答2-2由牛顿第二运动定律,不管重力如何,都可以得到组织上述公式的拉普拉斯变换是通过注意运动从静止开始,即初始条件都为零而获得的所以传递函数是(2)取上弹簧和阻尼器之间的辅助点a,将点a的位移设定为x,方向向下;在作品的下半部分。
导出点作为辅助点B。
根据弹簧力和阻尼力平衡的原则,从点A和点B可分别列出下列原始方程:通过消除中间变量x,可以得到系统的微分方程。
对上述公式进行拉普拉斯变换,并考虑零的初始条件,系统传递函数为(3)以引出点为辅助点,根据力平衡原理,可列出以下原始方程:按项移位排序的系统微分方程对上述公式进行拉普拉斯变换,注意运动从静止开始,即那么系统传递函数是2-3(b)取k1和f1之间的辅助点A,设定点A的位移为X,方向向下;根据力平衡原理,可以列出以下原始方程:因此2-6解决方案:2-7解决方案:2-8解决方案:2-9解决方案:2-10解决方案:系统结构图如下:系统的传递函数是:2-11解决方案:(a)(b)(c)(d)(e)(f)2-12解决方案:第三章线性系统的时域分析练习和参考答案3-1解决方案:3-2溶液:3-3溶液:3-4解决方案:3-5解决方案:3-6解决方案:3-7解决方案:3-8解决方案:3-9解决方案:勒鲁斯的表格如下: 系统不稳定性3-10解决方案:(略) 3-11解决方案:系统的特征方程为: 简化;勒鲁斯的表格如下:。
自动控制原理第二版课后答案第二章精选全文完整版

x kx ,简记为
y kx 。
若非线性函数有两个自变量,如 z f (x, y) ,则在
平衡点处可展成(忽略高次项)
f
f
z xv
|( x0 , y0 )
x y |(x0 , y0 )
y
经过上述线性化后,就把非线性关系变成了线性 关系,从而使问题大大简化。但对于如图(d)所示的 强非线性,只能采用第七章的非线性理论来分析。对于 线性系统,可采用叠加原理来分析系统。
Eb (s) Kbsm (s)
Js2 m(s) Mm fsm(s)
c
(s)
1
i
m
(s)
45
系统各元部件的动态结构图
传递函数是在零初始条件下建立的,因此,它只 是系统的零状态模型,有一定的局限性,但它有现 实意义,而且容易实现。
26
三、典型元器件的传递函数
1. 电位器
1 2
max
E
Θs
U s
K
U
K E
max
27
2. 电位器电桥
1
2
E
K1p1
K1 p 2
U
Θ 1
s
Θ
K1 p
Θ 2
s
U s
28
3.齿轮
传动比 i N2 N1
G2(s)
两个或两个以上的方框,具有同一个输入信号,并 以各方框输出信号的代数和作为输出信号,这种形
式的连接称为并联连接。
41
3. 反馈连接
R(s)
-
C(s) G(s)
H(s)
一个方框的输出信号输入到另一个方框后,得 到的输出再返回到这个方框的输入端,构成输 入信号的一部分。这种连接形式称为反馈连接。
胡寿松自动控制原理课后习题答案

1请解释下列名字术语:自动控制系统、受控对象、扰动、给定值、参考输入、反馈。
解:自动控制系统:能够实现自动控制任务的系统,由控制装置与被控对象组成;受控对象:要求实现自动控制的机器、设备或生产过程扰动:扰动是一种对系统的输出产生不利影响的信号。
如果扰动产生在系统内部称为内扰;扰动产生在系统外部,则称为外扰。
外扰是系统的输入量。
2电;一般需要⑥放大元件:将比较元件给出的偏差进行放大,用来推动执行元件去控制被控对象。
如电压偏差信号,可用电子管、晶体管、集成电路、晶闸管等组成的电压放大器和功率放大级加以放大。
⑦校正元件:亦称补偿元件,它是结构或参数便于调整的元件,用串联或反馈的方式连接在系统中,用以改善系统的性能。
常用的校正元件有电阻、电容组成的无源或有源网络,它们与原系统串联或与原系统构成一个内反馈系统。
3请说出什么是反馈控制系统,开环控制系统和闭环控制系统各有什么优缺点?解:反馈控制系统即闭环控制系统,在一个控制系统,将系统的输出量通过某测量机构对其进行实时测量,并将该测量值与输入量进行比较,形成一个反馈通道,从而形成一个封闭的控制系统;开环系统优点:结构简单,缺点:控制的精度较差;4解:(1(2(32-1图2-1习题2-1质量-弹簧-摩擦系统示意图解:显然,系统的摩擦力为dtt dx f)(,弹簧力为)(t kx ,根据牛顿第二运动定律有 移项整理,得系统的微分方程为2-2试列写图2-2所示机械系统的运动微分方程。
解:由牛顿第二运动定律,不计重力时,得 整理得2-3(1(2(3解:(1(2)f ((3)(f 2-4(1(2(3))1()(2+=s s s F 解:(1)112()(2)(5)25s F s s s s s --==+++++(2)226211()(3)3s F s s s s s s --==++++ (3)22225115()(1)1s s s F s s s s s -+-==+++图2-2习题2-2机械系统示意图2-5试分别列写图2-3中各无源网络的微分方程(设电容C上的电压为)(tuc ,电容1C上的电压为)( 1tuc,以此类推)。
胡寿松自控习题答案 第二章习题解答
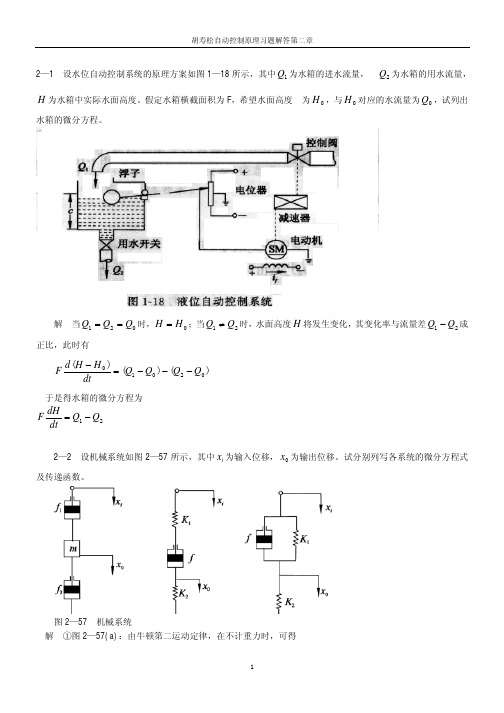
1 (T2 s + 1) U 0 ( s) Z2 C2 s (T1 s + 1)(T2 s + 1) = = = 所以: R1 1 U i ( s) Z1 + Z 2 R1C 2 s + (T1 s + 1)(T2 s + 1) + (T2 s + 1) T1 s + 1 C 2 s
即 F − F0 = K 1 ( y − y 0 )
其中 K 1 = = 12.65 × 1.1y 0 dy y= y
0
dF
0.1
0.1 = 13.915 × 1.1y 0
2-8 设晶闸管三相桥式全控整流电路的输入量为控制角,输出量为空载整流电压,它们之间的关系为:
ed = E d 0 cos α
xi (0) = x0 (0) = 0
则系统传递函数为
X 0 (s) fs + K 1 = X i ( s ) fs + ( K 1 + K 2 )
2-3 试证明图2-58(a)的电网络与(b)的机械系统有相同的数学模型。
2
胡寿松自动控制原理习题解答第二章
图 2-58
电网络与机械系统
1 C1 s R1 R1 1 解:(a):利用运算阻抗法得: Z 1 = R1 // = = = 1 C1 s R1C1 s + 1 T1 s + 1 R1 + C1 s R1
& (t ) + x(t ) = t ; (1) 2 x
解:对上式两边去拉氏变换得: (2s+1)X(s)=1/s2→ X ( s ) =
《自动控制原理》-胡寿松-002-自动控制原理-第二章ppt

2-0 预备知识—牢记一些典型时域数学模型
1.电容 2 .电感 3弹簧弹性力 4 阻尼器 5 牛顿定律 6 电机 7 二阶方程的通解
4
§2.1 傅里叶变换与拉普拉斯变换
▪ 傅里叶 变换 自学
5
拉氏变换及其性质
1.定义 X (s) x(t )est dt 0 记 X(s) = L[x(t)]
24
2.2 时域模型 - 微分方程
2.2.1. 建立系统或元件微分方程的步骤
I. 确定元件输入量和输出量
II. 根据物理或化学定律,列出元件的原始方 程
III. 在可能条件下,对各元件的原始方程进行 适当简化,略去一些次要因素或进行线性 化处理
IV. 消去中间变量,得到描述元件输入和输出 关系的微分方程
t
0
t
0
t0
0
t
A
解: x(t) = x1(t) + x2(t) =A1(t) A1(t t0 )
X (s) A A et0s A (1 et0s )
ss
s
13
例2-7 求e at 的拉氏变换。
解:
X (s) eat est dt
1
e(as)t
1
0
as
0 sa
X (s) L 1(t )eat 1 sa 例2-8 求e 0.2 t 的拉氏变换。 解:
论: (1) D(s) = 0无重根。
16
X (s) c1 c2
cn
n
ci
(s p1 ) (s p2 )
(s pn ) i1 (s pi )
式中ci 是待定常数,称为X(s)在极点si 处的留数。
ci
lim(s
自动控制原理 (胡寿松 著) 科学出版社 课后答案

《自动控制原理》习题参考答案 第1章
1.7.2 基础部分 1. 答:开环控制如:台灯灯光调节系统。 其工作原理为:输入信号为加在台灯灯泡两端的电压,输出信号为灯 泡的亮度,被控对象为灯泡。当输入信号增加时,输出信号(灯泡的亮度)增加,反之亦然。 闭环控制如:水塔水位自动控制系统。 其工作原理为:输入信号为电机两端电压,输出信号为水塔水位,被控 对象为电机调节装置。当水塔水位下降时,通过检测装置检测到水位下降,将此信号反馈至 电机,电机为使水塔水位维持在某一固定位置增大电机两端的电压,通过调节装置调节使水 塔水位升高。反之亦然。 2. 答:自动控制理论发展大致经历了几个阶段: 第一阶段:本世纪 40~60 年代,称为“经典控制理论”时期。 第二阶段:本世纪 60~70 年代,称为“现代控制理论”时期。 第三阶段:本世纪 70 年代末至今,控制理论向“大系统理论”和“智能控制”方向 发展。 3. 答:开环控制:控制器与被空对象之间只有正向作用而没有反馈控制作用,即系统的输 出量与对控制量没有影响。 闭环控制:指控制装置与被空对象之间既有正向作用,又有反向联系控制的过程。 开环控制与闭环控制的优缺点比较: 对开环控制系统来说,由于被控制量和控制量之间没有任何联系,所以对干扰造成的 误差系统不具备修正的能力。 对闭环控制系统来说,由于采用了负反馈,固而被控制量对于外部和内部的干扰都不 甚敏感,因此,有不能采用不太精密和成本低廉的元件构成控制质量较高的系统。 4. 答:10 线性定常系统; (2)非线性定常系统; (3)非线性时变系统; (4)非线时变系统; 1.7.3 提高部分 1.答:1)方框图:
kh da w. co m
40( S + 20) 系统在扰动作 S + 20 × 40 K1 + 20
自动控制原理第版(胡寿松)课后答案-全文可读

2-15
(2-11题~2-15题) (b)
32
k3
3
2-17(a) (c) (e) 2-18(a)
(b) 2-19与2-17同 2-21(a)
(2-17题~2-21题) (b)
(d) (f)
2-20与2-18同
(b)
2-22(a) (b) 9个单独回路:
6对两两互不接触回路: L1L2 L1L3 L2L3 L7L2 L8L2 L9L2 三个互不接触回路1组: L1L2L3
4条前向通路及其余子式: P1=G1G2G3G4G5G6 ,Δ1=1 ; P2=G7G3G4G5G6 , Δ2=1 ; P3=-G7H1G8G6 ,Δ3=1+G4H2 ; P4=G1G8G6 , Δ4=1+G4H2 ;
(c)
(d)
(e)
(f)
3-1 3-2 (2) 3-3 (1) 3-4 3-5
3-6 3-8 (a)
(Ts+1)寄生因子不影响系统稳定性,且因为它为非主导极点 所以也不太影响动态性能,但附加极点有增大阻尼的作用。
(7-3题~7-10题)
7-3 (1) e(nT)=10(2n-1)
(2)
7-4 (1) 7-5 (1)
(2) (2)
7-7
7-8 (1)
(2)
(3)
7-9 (a)
(b)
7 - 1 0( a )
(2)
-2
- 0.404
-2
- 3.29
-21.13
(4-11题~4-12题)
s1= - 9.98 s2,3= - 2.46
-4
系统始终不稳定!
时稳定
( - 8.47
自动控制原理 胡寿松习题答案

《自动控制原理》课程教学大纲
课程编号:
课程名称:自动控制原理
英文名称:Automatic Control Theory
课程类型::专业基础必修课
总 学 时:64 讲课学时:56
上机学时:8
学 时:64
学 分:4
适用对象:电气工程及其自动化专业(电力系统及自动化、电力系统继电保护、电网监控技术、供
熟悉系统微分方程的建立,拉氏变换及其应用。掌握系统传递函数的定义及求取,系统动态结构图 的建立及其简化以及系统不同传递函数的定义及求取。
1.控制系统微分方程的建立 2.非线性数学模型的线性化 3.控制系统的传递函数 4.典型环节的传递函数 5.控制的动态结构图及变换 6.信号流图及梅逊公式 7.反馈控制系统的传递函数 (三)自动控制系统的时域分析法 熟悉控制系统的时域指标,一阶系统的单位阶跃响应、斜坡响应以及性能指标的求取。掌握典型二阶 系统的单位阶跃响应以及性能指标的求取。掌握劳斯稳定判据分析系统的稳定性方法。熟悉控制系统稳态 误差分析以及稳态误差、误差系数的求取。 1. 控制系统性能指标的定义 2.一阶系统性能分析 3.二阶系统性能分析 4. 欠阻尼二阶系统的时域分析和指标计算 5. 高阶系统的时域分析、闭环主导极点和高阶系统的降阶
二、本课程实验的基本理论与实验技术知识
采用 MATLAB 软件上机进行实验,就是利用现代计算机硬件和计算机软件技术,以数字仿真技术为核 心,实现对自动控制系统基本理论和分析方法的验证以及控制系统设计。
通过上机实验,使学生在 MATLAB 软件的基本使用、编程调试、仿真实验数据的获取、整理、分析以 及实验报告的撰写等基本技能得到训练。
2
《自动控制原理》电子教案
自动控制原理(胡寿松)课后习题答案详解
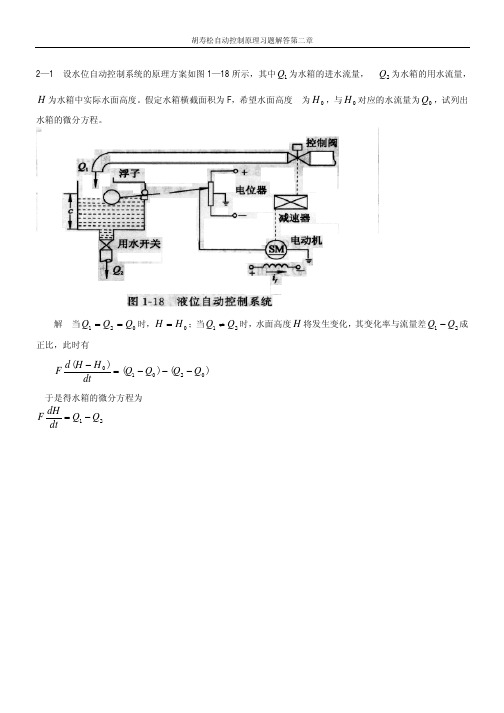
=
0.04 s 2
1 + 0.24s
+1
C (s)
=
0.04 s 2
10 6s + 10
R(s) 1 + G(s)H (s) 1 + 20 10
6s + 10 20s + 5
E(s) =
10
=
10
R(s) 1 + G(s)H (s) 1 + 20 10
6s + 10 20s + 5
=
(6s
200(20s + 5) + 10)(20s + 5) +
200
=
200(20s + 5) 120s 2 + 230s + 250
U 0 (s) + U i (s) R0
U1 (s) R0
U 2 (s) R0
式(1)(2)(3)左右两边分别相乘得
9
胡寿松自动控制原理习题解答第二章
U0 (s)
= − Z1 Z 2 R2 即
U 0 (s) + U i (s) R0 R0 R0
U 0 (s) + U i (s) = − R03
U0 (s)
正比,此时有
F
d(H − dt
H0)
=
(Q1
−
Q0 )
−
(Q2
−
Q0 )
于是得水箱的微分方程为
F
dH dt
= Q1 − Q2
胡寿松自动控制原理习题解答第二章
图 2-58 电网络与机械系统
1
解:(a):利用运算阻抗法得: Z1
=
R1
自动控制原理胡寿松 第2章

一些系统和元件的微分方程
如何理解晶闸管电路微分方程中,输出较输入滞后?
du2 R1C1 u2 u1 ——阻容网络 dt dua ua Kui ——晶闸管电路 dt
两个系统具有相似的微分方程 阻容网络u1输入后,由于电容的存在,u2要经过一段时间 的电容充电后才等于u1。类似的,ua与ui之间也存在滞后 关系。
(s2 3s 1)U2 (s) U1(s)
U 2 ( s)
对(13)做部分分式展开得:
(12) (13)
U1 ( s ) 1 s 2 3s 1 s( s 2 3s 1)
2 2 1 53 5 U 2 (s) 53 5 s 3 5 3 5 s s 2 2
T j ( j 1, 2,..., n)
—放大系数或增益
—时间常数
五.零极点对输出的影响: 1 极点与自由运动模态
C (S ) K R( S ) ( s a)( s b)
假设输入为单位阶跃信号,即r(t)=1(t),则可求输出如下:
K K K K 1 ab a(b a) b(a b) C (s) ( s a)( s b) s s sa s b
写成微分方程,得到该RC网络的数学模型,为一个二阶线性微分C2 R2C2 ) 2 u2 u1 dt dt
当u1(t)=1(t)时,其拉普拉斯变化式为U1(s)=1/s。设R1=R2=1Ω,
(11)
C1=C2=1F,并假设初始电压u2(0)=0V.对(11)两端求拉普拉斯变换,得
1 uc1 (i1 i2 )dt C1
(2) (3) (4) (5)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章
控制系统的数学模型习题及参考答案
自动控制原理胡寿松第二版
课后答案
2-2 由牛顿第二运动定律,在不计重力时,可得
整理得
将上式拉氏变换,并注意到运动由静止开始,即初始条件全部为零,可得
于是传递函数为
②其上半部弹簧与阻尼器之间,取辅助点A,并设A点位移为x,方向朝下;而在其下半部工。
引出点处取为辅助点B。
则由弹簧力与阻尼力平衡的原则,从A和B两点可以分别列出如下原始方程:
消去中间变量x,可得系统微分方程
对上式取拉氏变换,并计及初始条件为零,得系统传递函数为
③以引出点作为辅助点,根据力的平衡原则,可列出如下原始方程:
移项整理得系统微分方程
对上式进行拉氏变换,并注意到运动由静止开始,即
则系统传递函数为
2-3
(b)以k1和f1之间取辅助点A,并设A点位移为x,方向朝下;根据力的平衡原则,可列出如下原始方程:
所以
2-6解:
2-7 解:
2-8 解:
2-9解:
2-10解:
系统的结构图如下:
系统的传递函数为:
2-11 解:(a)
(b)
(c)
(d)
(e)
(f)
2-12 解:。
