习题 1-8
气象气候1至8章复习题

⽓象⽓候1⾄8章复习题⽓象学与⽓候学复习题第⼀、⼆章⼀、选择题1、300千⽶以上⼤⽓层⽓温达1000℃以上,其中运⾏的⼈造卫星不会烧毁,原因()a 卫星与⼤⽓处于相对静⽌的状态b 卫星在⼤⽓中⾼速运动,能很好地散热c该层⼤⽓稀薄,卫星从中吸收的及与之摩擦产⽣的热量有限d该层⼤⽓密度很⼤,有利于卫星散热2、关于⼤⽓层中的臭氧,正确的说法是()a 只有臭氧层有臭氧b 臭氧在⼤⽓层中均匀分布 c臭氧能⼤量吸收太阳辐射中的紫外线 d臭氧层分布在对流层中,所以与⼈类关系很密切3、当地⾯热量由盈余转为亏损时()a 太阳辐射最强b 地⾯辐射最强c ⼤⽓辐射最强d ⽓温最⾼4、层具有⽆线电波的反射能⼒。
()a 中间层 b平流层c暖层 d散逸层5、关于等温线与等⾼线的对应关系,正确的是()a 等⾼线数值越⼤,等温线数值越⼤b 等⾼线数值越⼤,等温线数值越⼩c等⾼线数值越⼤,等温线越稀疏 d同⼀海拔⾼度上,⽓温相等7、当天空出现青蓝⾊时,说明⼤⽓中的微粒直径是()a⼤于⼊射波的波长 b⼩于⼊射波的波长c等于⼊射波的波长 d与⼊射波的波长⽆关8、“⼤⽓保温效应”中起作⽤的是()a⽔b⼤⽓逆辐射c⼆氧化碳d尘埃9、关于⽓温空间分布,正确的说法是()a ⽓温由南向北逐渐降低b ⽓温从⼭麓向⼭顶降c 夏季⼤陆⽓温⽐同纬度海洋低d 冬季⼤陆⽓温⽐同纬度的海洋⾼10、夏半年,北半球的太阳辐射量最多的地区是()。
a.⾚道b.20°----25°Nc.30°N----25°Nd.副热带11、在⼲洁空⽓中能够强烈吸收和放射长波辐射的⽓体成分是:()A、氮⽓;B、氧⽓;C、臭氧;D、⼆氧化碳。
12、在低纬度对流层顶的⾼度是:()A、8-9公⾥;B、10-11公⾥;C、11-12公⾥;D、17-18公⾥。
13、⼀天中⼤⽓逆辐射最强的时刻在:()A、太阳⾼度最⼤时;B、12-13时;C、⽓温最⾼时;D、云量最多时。
管理会计习题
第二章【习题1】某企业生产的甲产品1—8月份的产量及总成本资料见下表,要求:(1)采用高低点法进行成本习性分析;(2)采用回归直线法进行成本习性分析。
【习题2】某企业的设备维修费属于混成成本,资料如下表所示:要求:(1)用高低点法分解设备维修费。
(2)用回归直线法分解设备维修费。
假设下一年度1月份的机器工作小时为15小时,预测设备的维修费是多少?第三章【习题1】某企业本期有关成本资料如下:单位直接材料成本为10元,单位直接人工成本为5元,单位变动性制造费用为7元,固定性制造费用总额为4 000元,单位变动性销售管理费用为4元,固定性销售管理费用为1 000元。
期初存货量为零,本期产量为1 000件,销量为600件,单位售价为40元。
要求:分别按两种成本法的有关公式计算下列指标:(1)单位产品成本。
(2)期间成本。
(3)销货成本。
(4)营业利润。
【习题2】某厂只生产一种产品,第1年、第2年的生产量分别是30 000件和24 000件,销售量分别是20 000件和30 000件,存货计价采用先进先出法,产品销价15元。
在生产成本中,每件产品变动成本为5元,固定制造费用每年为180 000元,销售及管理费用假定是固定费用,每年为25 000元。
要求:(1)分别采用变动成本法和完全成本法编制第1年和第2年的损益表。
2)具体说明这两年分别采用两种成本计算方法确定的税前利润发生差异的原因。
第四章【习题1】某企业只生产一种E产品,单价30元,2007年实现销售收入120000元,变动成本率60%,实现利润28000元。
假定2008年销售单价不变,变动成本率仍然为60%。
要求:(1)预测2008年的保本销售量。
(2)若2008年将销售量提高15%,则可获得多少利润?【习题2】公司本年度发生变动成本20 000元,边际贡献率为60%,销售利润率为20%。
要求:(1)计算本年度的利润。
(2)计算本年度的安全边际额。
财务管理第1—8章习题

财务管理第1—8章习题习题2-1:某人将100元存入银行,年利率2%,求5年后的终值。
习题2-2:某人为5年后能从银行取出500元,在年利率2%的情况下,目前应存入银行的金额是多少?习题2-3某人希望在5年末取得本利和20000元,则在年利率为2%、单利计息的方式下,此人现在应当存入银行()。
A.18114元B.18181.82元C.18004元D.18000元习题2-4某项投资4年后可得收益40000元,单利计算,按年利率6℅计算,其现值应该为多少?习题2-5某人将100元存入银行,复利年利率为2%,求5年后的终值。
习题2-6:某人为了5年后能从银行取出100元,在复利年利率2%的情况下,求当前应存入金额。
习题2-7某人目前向银行存入1000元。
在银行存款年利率为2%,在复利计息的方式下,5年后此人可以从银行取出()。
A.1100元B.1104.1元C.1204元D.1106.1元习题2-8(作业1)某人拟购房,开发商提出两种方案,一是一次性付款80万元,另一方案是5年后付款100万元,若目前的银行贷款利率是7℅,怎么选择合适的付款方式?习题2-9某人进行一项投资,预计6年后会获得收益880元。
在年利率为5%的情况下,这笔收益的现值为()。
A.4466.62元B.656.66元C.670.56元D.4455.66元习题2-10请查表确定年利率为8%时,9年期的复利现值系数和复利终值系数为多少?习题2-11甲某拟存入一笔资金以备三年后使用。
假定银行三年期存款年利率为5%,甲某三年后需用的资金总额为34500元,则在单利计息情况下,目前需存入得资金为()元。
A30000B29803.04C32857.14D31500习题2-12某公司拟发行面值为1000元、不计复利、5年后一次还本付息、票面利率为10%的债券。
已知发行时资金市场的年利率为12%,(P/F,10%,5)=0.6209,(P/F,12%,5)=0.5674,该公司债券的发行价格为()元。
《弹性力学》习题库解读

例2.7.1
图示矩形截面水坝,其右侧受静水压 力,顶部受集中力作用。试写出水坝 的应力边界条件。 左侧面: x h
l 1, m 0
fx f y 0
x f x 0, f y p( x) p0 l
代入边界条件公式,有
y
l
C
x 0 xy (1) 0 y (1) yx 0 p( x)
xy y 0
0
x y y0 p( x) p0 l
例 2.6.3
沿 z 向均不变化,只有平面应力分量 x , y , xy ,且
仅为 x,y 的函数的弹性力学问题,因此,此问题是 平面应力问题。
例 2.1.2
(本章习题2-1) 如图2-14,试分析说明,在不受任何面力作 用的空间体表面附近的薄层中,其应力状态接近 于平面应力的情况。
x 答:在不受任何面力作用的空间体表面附近的薄层 z Oy
2 2
B
0
°
1 0 (0 σ x ) 2
x
0
A
x 2 0
例 2.3.1
(1)求主应力的大小及方向
x 2 0 , y 0, xy 0
1 x y x y 2 xy 2 2 2
中,可以认为在该薄层的上下表面都无面力,且在 薄层内所有各点都有 z zx zy 0,只存在平 面应力分量 x , y , xy ,且它们不沿z方向变化,仅 为x、y的函数。可以认定此问题是平面应力问题。 图 2-14
例 2.1.3
如图所示的几种受力体是否是平面问题?若是, 则是平面应力问题,还是平面应变问题?
八下政治第一课练习题

一、选择(1—8题为单选题,9—12题为多选题)1.朱德同志有诗云:“锦绣山河收拾好,万民尽做主人翁。
”这里的“民”是指()A.公民B.人民C.农民D.国民2.在全国各地进行的基层人大代表换届选举中,具有选举权和被选举权的我国公民必须是()①年满18周岁②没有被夺政治权利③具有中华人民共和国国籍④具有参加选举的文化知识A.①②③B.②③④C.①②④D.①③④3.作家张某撰写了一部长篇小说,他利用小说的形式诽谤全国劳模杨某的行为构成诽谤罪,受到法律应有的制裁。
这一案例说明了()①言论自由不是无限制的绝对自由②滥用言论自由损害他人的合法权益是法律所不允许的③法律限制公民的言论自由(文学创作自由)④法律保护公民的人格和名誉不受侵犯A.①②③B.②③④C.①②④D.①③④4.十届全国人大一次会议议案组共收到议案1000多件。
这些议案,反映了来自基层广大人民群众的意见和建议。
这表明,我国的代表联系群众制度能有效地保障我国公民行使的权利()A.出版自由B.结社自由C.批评和建议D.集会自由5.公民和人民的区别是()A.人民享有政治权利,公民不享受有政治权利B.人民是政治概念,公民是法律概念C.人民享有权利多,公民享有权利少D.人民参与国家管理,公民不参与国家管理6.在我国,享受权利的主体极为广泛,公民享受权利的范围极其广泛,这表明了我国公民权利的()A.平等性B.广泛性C.一致性D.真实性7.下列人员中,不属于我国公民的有()A.长期在我国工作的外国人B.具有中国国籍长期在外国工作的人C.具有中国国籍未满18周岁的人D.具有中国国籍的残废人8.我国的国家性质是()A.人民代表参政议政的国家B.人民民主专政的社会主义国家C.社会主义公有制D.全体公民当家作主的国家9.18世纪法国资产阶级启蒙思想家孟德思鸠指出:“自由是做法律所许可的一切事情的权利;如果一个公民能够做法律做禁止的事情,他就不再有自由了,因为他人也同样会有这个权利。
《高等数学》 详细上册答案(一--七)

2014届高联高级钻石卡基础阶段学习计划《高等数学》上册(一----七)第一单元、函数极限连续使用教材:同济大学数学系编;《高等数学》;高等教育出版社;第六版;同济大学数学系编;《高等数学习题全解指南》;高等教育出版社;第六版;核心掌握知识点:1.函数的概念及表示方法;2.函数的有界性、单调性、周期性和奇偶性;3.复合函数、分段函数、反函数及隐函数的概念;4.基本初等函数的性质及其图形;5.极限及左右极限的概念,极限存在与左右极限之间的关系;6.极限的性质及四则运算法则;7.极限存在的两个准则,会利用其求极限;两个重要极限求极限的方法;8.无穷小量、无穷大量的概念,无穷小量的比较方法,利用等价无穷小求极限;9.函数连续性的概念,左、右连续的概念,判断函数间断点的类型;10.连续函数的性质和初等函数的连续性,闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),会用这些性质.天数学习时间学习章节学习知识点习题章节必做题目巩固习题(选做)备注第一天2h第1章第1节映射与函数函数的概念函数的有界性、单调性、周期性和奇偶性复合函数、反函数、分段函数和隐函数初等函数具体概念和形式,函数关系的建立习题1-14(3) (6)(8),5(3)★,9(2),15(4)★,17★4(4)(7),5(1),7(2),15(1)本节有两部分内容考研不要求,不必学习:1. “二、映射”;2. 本节最后——双曲函数和反双曲函数第二天3h1章第2节数列的极限数列极限的定义数列极限的性质(唯一性、有界性、保号性)习题1-21(2) (5)(8)★3(1)1. 大家要理解数列极限的定义中各个符号的含义与数列极限的几何意义;2. 对于用数列极限的定义证明,看懂即可。
第1章第3节函数的极限函数极限的概念函数的左极限、右极限与极限的存在性函数极限的基本性质(唯一性、局部有界性、局部保号性、不等式性质,函数极限与数列极限的关系等)习题1-32,4★3,1. 大家要理解函数极限的定义中各个符号的含义与函数极限的几何意义;2. 对于用函数极限的定义证明,看懂即可。
财务管理例题1-8章

财务管理例题1-8章(总26页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--财务管理例题第三章 价值、收益与风险例1:某公司于年初存入银行10000元,期限为5年,年利率为5%,则到期时的本利和为:F=10000×(1+5%×5) =12500(元)单利终值)1(n i P F ⋅+⨯=例2:某公司打算在3年后用60000元购置新设备,目前的银行利率为5%,则公司现在应存入:P=60000/(1+5%×3)=(元)单利现值)1/(n i F P ⋅+= n i P I ⋅⋅=例:某人拟在3年后获得本利和50000元,假设投资报酬率为5%,他现在应投入多少元(43192)例3:某公司将100000元投资于一项目,年报酬率为6%,1年后的本利和为:F=100000 ×(1+6%×1)=106000(元)若一年后公司并不提取现金,将106000元继续投资于该项目,则第2年年末的本利和为:F=100000×(1+6%)×(1+6%) =100000×2%)61(+=112360(元)例4:某人存入银行1000元,年利率8%,则5年后可取出多少钱?F=58%)(11000+⨯)(3.1469元=例5:某人为了5年后能从银行取出10000元,求在年利率2%的情况下当前应存入的金额。
F=5%)21/(10000+)(9057元= 例6:将例4改为每季复利一次,求FF=45)4/%81(1000⨯+⨯20%)21(1000+⨯=)(9.1485元= 如果要得到相当于这个金额的F 值,在每年复利一次的条件下年利率应该是多少?F=5)1(1000i +⨯= →=+5i)(1=查表可知:假定i 和(F/P,i,5)之间呈线性关系,则 4693.14859.1%84693.15386.1%8%9--=--x%24.8≈x课堂即时练习之一1.张先生要开办一个餐馆,于是找到十字路口的一家铺面,向业主提出要承租三年。
化工原理王志魁第五版习题解答:第一章 流体流动

第一章流体流动流体静力学【1-6】如习题1-6附图所示,有一端封闭的管子,装入若干水后,倒插入常温水槽中,管中水柱较水槽液面高出2m ,当地大气压力为101.2kPa 。
试求:(1)管子上端空间的绝对压力;(2)管子上端空间的表压;(3)管子上端空间的真空度;(4)若将水换成四氯化碳,管中四氯化碳液柱较槽的液面高出多少米?解管中水柱高出槽液面2m ,h=2m 水柱。
(1)管子上端空间的绝对压力绝p 在水平面11'-处的压力平衡,有.绝绝大气压力1012001000981281580 (绝对压力)ρ+==-⨯⨯=p gh p Pa (2)管子上端空间的表压表p 表绝 -大气压力=8158010120019620 =-=-p p Pa(3)管子上端空间的真空度真p ()真表=-=-1962019620 p p Pa-=(4)槽内为四氯化碳,管中液柱高度'h 'cclhh ρρ=4水常温下四氯化碳的密度,从附录四查得为/ccl kg m ρ=431594 '.h m ⨯==10002125 1594【1-7】在20℃条件下,在试管内先装入12cm 高的水银,再在其上面装入5cm 高的水。
水银的密度为/313550kg m ,当地大气压力为101kPa 。
试求试管底部的绝对压力为多少Pa 。
解水的密度/3水=998ρkg m ()....331011001213550005998981117410=⨯+⨯+⨯⨯=⨯p Pa【1-8】如习题1-8附图所示,容器内贮有密度为/31250kg m 的液体,液面高度为3.2m 。
容器侧壁上有两根测压管线,距容器底的高度分别为2m 及1m ,容器上部习题1-6附图空间的压力(表压)为29.4kPa 。
试求:(1)压差计读数(指示液密度为/31400kg m );(2)A 、B 两个弹簧压力表的读数。
解容器上部空间的压力.29 4(表压)=p kPa 液体密度/31250ρ=kg m ,指示液密度/301400ρ=kg m (1)压差计读数R=?在等压面''1111上-=p p ()()()()().'...p p h R g p p h g R g p h R g p h g R g Rg ρρρρρρρρ=+-++=+-++++++=+++-=11000 321 32212222 0()0因g 0,故0ρρ-≠=R (2)().....A p p g Paρ=+-=⨯+⨯⨯=⨯333212941022125098156410().....333222941012125098144110ρ=+-=⨯+⨯⨯=⨯B p p g Pa【1-9】如习题1-9附图所示的测压差装置,其U 形压差计的指示液为水银,其他管中皆为水。
操作系统(1~8章的课后习题答案)

1.1:存储程序式计算机的主要特点是:集中顺序过程控制(1)过程性:模拟人们手工操作(2)集中控制:由CPU集中管理(3)顺序性:程序计数器1.2:a:批处理系统的特点:早期批处理有个监督程序,作业自动过渡直到全部处理完,而脱机批处理的特点:主机与卫星机并行操作。
b:分时系统的特点:(1):并行性。
共享一台计算机的众多联机用户可以在各自的终端上同时处理自己的程序。
(2):独占性。
分时操作系统采用时间片轮转的方法使一台计算机同时为许多终端上同时为许多终端用户服务,每个用户的感觉是自己独占计算机。
操作系统通过分时技术将一台计算机改造为多台虚拟计算机。
(3):交互性。
用户与计算机之间可以进行“交互会话”,用户从终端输入命令,系统通过屏幕(或打印机)将信息反馈给用户,用户与系统这样一问一答,直到全部工作完成。
c:分时系统的响应比较快的原因:因为批量操作系统的作业周转时间较长,而分时操作系统一般采用时间片轮转的方法,一台计算机与许多终端设备连接,使一台计算机同时为多个终端用户服务,该系统对每个用户都能保证足够快的响应时间,并提供交互会话功能。
1.3:实时信息处理系统和分时系统的本质区别:实时操作系统要追求的目标是:对外部请求在严格时间范围内做出反应,有高可靠性和完整性。
其主要特点是资源的分配和调度首先要考虑实时性然后才是效率。
此外,实时操作系统应有较强的容错能力,分时操作系统的工作方式是:一台主机连接了若干个终端,每个终端有一个用户在使用。
用户交互式地向系统提出命令请求,系统接受每个用户的命令,采用时间片轮转方式处理服务请求,并通过交互方式在终端上向用户显示结果。
用户根据上步结果发出下道命。
分时操作系统将CPU 的时间划分成若干个片段,称为时间片。
操作系统以时间片为单位,轮流为每个终端用户服务。
每个用户轮流使用一个时间片而使每个用户并不感到有别的用户存在。
分时系统具有多路性、交互性、“独占”性和及时性的特征。
党课1~8章练习题

党课1~8章练习题党课第一章一、单选题,共50题,每题1.25分1.新技术革命以_C_为标志。
A.哥白尼发表《天体运行论》B.牛顿创立了万有引力C.瓦特发明了蒸汽机2.巴黎公社采取的带有无产阶级专政性质的措施主要有:_B_。
①公社人员由民主选举产生②没收逃亡资本家的工厂,交给工人合作社管理③取消旧的国家机器,建立工人阶级自己的国家机构④工职人员年薪不得超过熟练工人的工资。
A.①②B.②C.③④3.卡尔•马克思_B_年5月5日出生于德国莱茵省摩塞尔河畔特里尔城的一个犹太律师家庭。
A.1838年B.1818年C.1828年4.《共产党宣言》由_C_篇序言和正文组成。
A.九B.八C.七5.世界上第一个无产阶级政党的第一部组织章程,是_C_。
A.国际工人协会共同章程B.俄国社会民主工党章程C.共产主义者同盟章程6.巴黎公社是国际工人运动史上的伟大创举,主要表现在_C_。
A.废除了旧的军队、警察、法庭、议会B.规定公职人员的工资不得超过一个熟练工人的工资C.建立工人阶级自己的军队、治安、司法、立法机构7.恩格斯认为,就表述未来社会新纪元的核心思想而言,除了这一命题没有更合适的了。
这一命题是:_A_。
A.每个人的自由发展是一切人的自由发展的条件。
B.共产党人可以把自己的理论概括为一句话:消灭私有制。
C.共产主义革命就是同传统的所有制关系实行最彻底的决裂。
8.三大工人运动斗争内容不仅仅局限于要求改善生活条件和劳动条件等经济领域,而是由__斗争发展为_B_斗争。
A.政治、经济B.经济、政治C.内部、外部9.欧洲三大工人运动不包括_A_。
A.意大利B.英国C.法国10.马克思、恩格斯与1845-1846年合作撰写了_A_。
A.《德意志意识形态》B.《神圣家族》C.《共产党宣言》11.“党章的基本思想是职能的划分”。
这是_A_在俄国社会民主工党第二次代表大会上对党章的阐述。
A.列宁B.斯大林C.赫鲁晓夫12.马克思、恩格斯指出商品价值是由工人劳动创造的,资本家的利润是工人劳动创造的剩余价值,工人的工资仅仅是工人创造的价值的一部分,从而创立了_C_。
24点练习题库(1-10)

75 1、3、3、8
76 1、3、3、9
77 1、3、3、10
78 1、3、4、4
79 1、3、4、5
80 1、3、4、6
81 1、3、4、7
82 1、3、4、8
83 1、3、4、9
84 1、3、4、10
85 1、3、5、6
86 1、3、5、7
87 1、3、5、8
88 1、3、5、9
89 1、3、5、10
51 1、2、4、10
52 1、2、5、5
53 1、2、5、6
54 1、2、5、7
55 1、2、5、8
56 1、2、5、9
57 1、2、5、10
58 1、2、6、6
59 1、2、6、7
60 1、2、6、8
61 1、2、6、9
62 1、2、6、10
63 1、2、7、7
64 1、2、7、8
65 1、2、7、9
136 1、5、6、8
137 1、5、6、9
138 1、5、6、10
139 1、5、7、8
140 1、5、7、9
141 1、5、7、10
142 1、5、8、8
143 1、5、8、9
144 1、5、8、10
24点练习题(1-10)
方法一
方法二
完成日期:
姓名: 得分:
方法三
第 6 页,共 24 页
整理:数学郝老师
99 1、3、8、8
100 1、3、8、9
101 1、3、8、10
102 1、3、9、9
103 1、3、9、10
104 1、3、10、10
105 1、4、4、4
106 1、4、4、5
107 1、4、4、6
人教版小学二年级上册数学第一至八单元练习题

人教版小学二年级上册数学第一至八单元练习题第一单元长度单位练习题姓名________一、填空题1、我们学过的长度单位有()和()。
2、要知道物体的长度用()来量。
3、量比较长的物体可以用()作单位,量比较短的物体可以用()作单位。
如测量数学课本的长度应该用()作单位,测量楼房的高度应该用()作单位。
4、拿一条线,把两头拉紧,就成了一条()。
5、线段的特征:线段是()的,有()个端点,可以量出()。
6、1厘米1厘米地数,数()次是5厘米,数()次是8厘米。
7、小红今年上二年级,她的身高是125()。
8、在直尺上,从刻度“0”到刻度“5”是()厘米,从刻度“7”到刻度“10”是()厘米,从刻度“6”到刻度“13”是()厘米。
9、在米尺上,从刻度“0”到刻度“100”是()厘米,也就是()。
10、画一条8厘米长的线段,从尺子的()刻度开始画起,画到()的地方。
11、三角形是由()条线段围成的,正方形是由()条线段围成的。
12、看一看,填一填。
这个回形针长( )厘米这支铅笔长( )厘米13、1米=()厘米 500厘米=()米18厘米+4厘米=()厘米 45米+5米=()米40厘米-7厘米=()厘米 36米+9米=()米80厘米+20厘米=()米 4米=()厘米二、在括号里填上“米”或“厘米”。
1、一支粉笔的长是7()。
2、铅笔盒长是23( )3、教室宽8( )4、一棵树高3( )5、回形针长3()6、操场长80( )7、手掌宽7( ) 8、毛巾宽29( )9、教学楼高10( ) 10、妈妈的身高165( )11、铅笔长11( ) 12、教室门高2( )13、一张床长2( ) 14、茶杯高10( )15、黑板长3( ) 16、小刀长5( )17、电视屏幕宽29( ) 18、电视塔高120( )19、课桌的长大约是80() 20、窗户的高大约是2()21、图钉的长是1() 22、语文书长21()23、红领巾最长的边长50() 24、筷子长15()25、一本书厚1() 26、课桌的高70()27、操场一周长400( ) 28、一座大桥长约是40()29、哥哥的身高1()28() 30、小军身高120()31、一辆公交车长约7() 32、讲台高90()33、小兰一步的长大约是45( ) 34、校园里旗杆的高大约是15( ) 35、《新华字典》厚约5() 36、数学书长约26(),宽约18()37、一根香蕉长15() 38、足球场长90(),宽45()39、量一量。
通信原理教程+樊昌信+课后习题答案第一章至第八章

第一章习题习题1.1 在英文字母中E 出现的概率最大,等于0.105,试求其信息量。
解:E 的信息量:()()b 25.3105.0log E log E 1log 222E =-=-==P P I习题1.2 某信息源由A ,B ,C ,D 四个符号组成,设每个符号独立出现,其出现的概率分别为1/4,1/4,3/16,5/16。
试求该信息源中每个符号的信息量。
解:b A P A P I A 241log )(log )(1log 222=-=-==b I B 415.2163log 2=-=b I C 415.2163log 2=-= b I D 678.1165log 2=-=习题1.3 某信息源由A ,B ,C ,D 四个符号组成,这些符号分别用二进制码组00,01,10,11表示。
若每个二进制码元用宽度为5ms 的脉冲传输,试分别求出在下列条件下的平均信息速率。
(1) 这四个符号等概率出现; (2)这四个符号出现概率如习题1.2所示。
解:(1)一个字母对应两个二进制脉冲,属于四进制符号,故一个字母的持续时间为2×5ms 。
传送字母的符号速率为Bd 100105213B =⨯⨯=-R 等概时的平均信息速率为b 2004log log 2B 2B b ===R M R R(2)平均信息量为符号比特977.1516log 165316log 1634log 414log 412222=+++=H则平均信息速率为 b 7.197977.1100B b =⨯==H R R习题1.4 试问上题中的码元速率是多少?解:311200 Bd 5*10B B R T -===习题1.5 设一个信息源由64个不同的符号组成,其中16个符号的出现概率均为1/32,其余48个符号出现的概率为1/96,若此信息源每秒发出1000个独立的符号,试求该信息源的平均信息速率。
解:该信息源的熵为96log 961*4832log 321*16)(log )()(log )()(22264121+=-=-=∑∑==i i i i Mi i x P x P x P x P X H=5.79比特/符号因此,该信息源的平均信息速率 1000*5.795790 b/s b R mH === 。
物理学简明教程马文蔚第1至8章课后习题答案详解
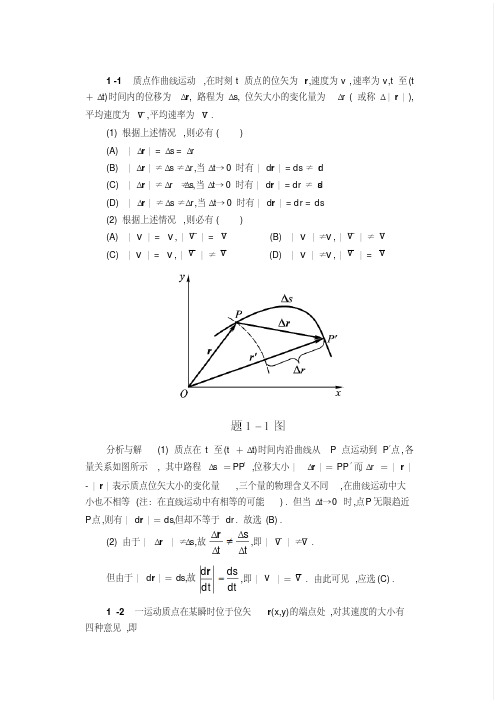
1 -1质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v,t 至(t +Δt)时间内的位移为Δr , 路程为Δs, 位矢大小的变化量为Δr ( 或称Δ|r |),平均速度为v ,平均速率为v .(1) 根据上述情况,则必有()(A) |Δr |= Δs = Δr(B) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= ds ≠ d r(C) |Δr |≠ Δr ≠ Δs,当Δt →0 时有|d r |= dr ≠ d s(D) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= dr = ds(2) 根据上述情况,则必有()(A) |v |= v ,|v |= v (B) |v |≠v ,|v |≠v(C) |v |= v ,|v |≠ v (D) |v |≠v ,|v |= v分析与解(1) 质点在t 至(t +Δt)时间内沿曲线从P 点运动到P ′点,各量关系如图所示, 其中路程Δs =PP ′, 位移大小|Δr |=PP ′,而Δr =|r |-|r |表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注:在直线运动中有相等的可能).但当Δt →0 时,点P ′无限趋近P 点,则有|d r |=ds,但却不等于dr .故选(B).(2) 由于|Δr |≠Δs,故t st ΔΔΔΔr ,即|v |≠v .但由于|d r |=ds,故t st d d d d r ,即|v |=v .由此可见,应选(C).1 -2一运动质点在某瞬时位于位矢r (x,y)的端点处,对其速度的大小有四种意见,即(1)t r d d ;(2)t d d r;(3)t s d d ;(4)22d d d d t y t x.下述判断正确的是()(A) 只有(1)(2)正确(B) 只有(2)正确(C) 只有(2)(3)正确(D) 只有(3)(4)正确分析与解t rd d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率.通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量;t d d r表示速度矢量;在自然坐标系中速度大小可用公式t sd d v 计算,在直角坐标系中则可由公式22d d d d t yt x v 求解.故选(D).1 -3一个质点在做圆周运动时,则有()(A) 切向加速度一定改变,法向加速度也改变(B) 切向加速度可能不变,法向加速度一定改变(C) 切向加速度可能不变,法向加速度不变(D) 切向加速度一定改变,法向加速度不变分析与解加速度的切向分量a t起改变速度大小的作用,而法向分量a n 起改变速度方向的作用.质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的.至于a t是否改变,则要视质点的速率情况而定.质点作匀速率圆周运动时, a t恒为零;质点作匀变速率圆周运动时,a t为一不为零的恒量,当a t改变时,质点则作一般的变速率圆周运动.由此可见,应选(B).1 -4质点的运动方程为23010t t x 和22015t t y ,式中x,y 的单位为m,t 的单位为s。
工程图学习题答案一.ppt

k
l
(3) 作一直线平行于AB,与CD、EF均相交。
′ ′
′
′
′
(2) 过点A作一直线,使其平行于直线DE;作直线AC与直线 DE相交,其交点距H面为20mm。
′
c
′ ′
c
(4) 作∠ABC的等分角线。
′
′
′
181h,
第二章 点、直线和平面
2-18 过点A作线段与CD相交于B,且使AB实长为30mm。 2-19 判别AB与BC是否垂直。
第三章 直线与平面、平面与平面的相对位置
3-5 △ABC平行于△DEF,点M属于△ABC,作出其正面投影。 3-6 判别已知两平面是否平行。
a
′
c ′ ′
b
′
′ ′
′
′
′
′
′
181h,
第三章 直线与平面、平面与平面的相对位置
3-7 求直线与平面的交点,并判别可见性。
3-8 求两平面的交线,并判别可见性。
3-19 求平行两直线AB、CD间的距离。
(1)
′ ′
′ ′
′ ′
3-20 完成下题。
已知点S,直线AB、CD的投影,试过S作一条直线 SK1K2 分别与直线 AB、CD相交于K 1、K 2 点。
′
k′2
′
k1′
′
′ ′
′
′
k2
k1
(2)
181h,
第三章 直线与平面、平面与平面的相对位置
3-21 以线段AB为底作等腰三角形,使定点C属于直线MN。3-22 以点A为顶点作等边 ABC,使底边BC属于直线MN。
3-28 在直线MN上确定一点K,使其与两平行直线AB、 CD等距。
人教版六年级数学上册全册同步练习题汇总--附答案

人教版六年级数学上册1--8单元同步练习题 第一单元 分数乘整数的意义及计算方法1. 填空。
(1)8+8+8+8用乘法算式表示为( )。
(2)27+27+27+27用乘法算式表示为( )。
(3)17×4=( )+( )+( )+( )=( )(4)213+213+213=( )×( )=()()() =()2. 列式计算(1)3个17的和是多少?______________________________________ (2)4个116的和是多少?______________________________________ 3. 直接写出结果。
38×4= 35×1= 9×23= 58×24= 715×20= 25×10=答案1. (1)8×4(2)2 7×4(3)1717171747(4)213 32×3136132.(1)17×3=37(2)116×4=143. 3235 6 152834整数乘分数的意义1. 判断。
(1)49×7=49×7=463 ( ) (2)3个35的和,与3和35的和同样大。
( )(3)1千米的34等于3千米的14。
( )2. 在( )里填上”>”“<”或“=”。
15×35 ( )15 16×34 ( )205×34 ( )5 5×34 ( ) 34 45×4 ( ) 45 45×4 ( )4 45×3 ( ) 45 14×2 ( ) 12×4 3. 解决问题。
(1)一堆煤,每天用去它的18,3天用去它的几分之几?(2)一张长方形铁皮,长是6米,宽是12米,这张铁皮的面积是多少平方米?(3)一个漏水的水龙头每小时滴水112桶,3小时滴水多少桶?一天呢?答案1. (1)× (2)× (3)√2. < < < > > < > <3. (1) 18×3=38 答:3天用去它的38(2)6×12=3(平方米)答:这张铁皮的面积是3平方米。
1-8高等数学课后习题答案

习题1-81. 研究下列函数的连续性, 并画出函数的图形:(1)⎩⎨⎧≤<-≤≤=21 210 )(2x x x x x f ; 解 已知多项式函数是连续函数, 所以函数f (x )在[0, 1)和(1, 2]内是连续的.在x =1处, 因为f (1)=1, 并且1lim )(lim 211==--→→x x f x x , 1)2(lim )(lim 11=-=++→→x x f x x . 所以1)(lim 1=→x f x , 从而函数f (x )在x =1处是连续的. 综上所述,函数f (x )在[0, 2]上是连续函数.(2)⎩⎨⎧>≤≤-=1|| 111 )(x x x x f . 解 只需考察函数在x =-1和x =1处的连续性.在x =-1处, 因为f (-1)=-1, 并且)1(11lim )(lim 11-≠==---→-→f x f x x , )1(1lim )(lim 11-=-==++-→-→f x x f x x , 所以函数在x =-1处间断, 但右连续.在x =1处, 因为f (1)=1, 并且1lim )(lim 11==--→→x x f x x =f (1), 11lim )(lim 11==++→→x x x f =f (1), 所以函数在x =1处连续.综合上述讨论, 函数在(-∞, -1)和(-1, +∞)内连续, 在x =-1处间断, 但右连续.2. 下列函数在指出的点处间断, 说明这些间断点属于哪一类, 如果是可去间断点, 则补充或改变函数的定义使它连续:(1)23122+--=x x x y , x =1, x =2; 解 )1)(2()1)(1(23122---+=+--=x x x x x x x y . 因为函数在x =2和x =1处无定义, 所以x =2和x =1是函数的间断点.因为∞=+--=→→231lim lim 2222x x x y x x , 所以x =2是函数的第二类间断点; 因为2)2()1(lim lim 11-=-+=→→x x y x x , 所以x =1是函数的第一类间断点, 并且是可去间断点. 在x =1处, 令y =-2, 则函数在x =1处成为连续的.(2)x x y tan =, x =k , 2ππ+=k x (k =0, ±1, ±2, ⋅ ⋅ ⋅); 解 函数在点x =k π(k ∈Z)和2ππ+=k x (k ∈Z)处无定义, 因而这些点都是函数的间断点.因∞=→xx k x tan lim π(k ≠0), 故x =k π(k ≠0)是第二类间断点; 因为1tan lim 0=→x x x , 0tan lim 2=+→x x k x ππ(k ∈Z), 所以x =0和2ππ+=k x (k ∈Z) 是第一类间断点且是可去间断点. 令y |x =0=1, 则函数在x =0处成为连续的;令2 ππ+=k x 时, y =0, 则函数在2ππ+=k x 处成为连续的. (3)xy 1cos 2=, x =0;解 因为函数xy 1cos 2=在x =0处无定义, 所以x =0是函数x y 1cos 2=的间断点. 又因为xx 1cos lim 20→不存在, 所以x =0是函数的第二类间断点.(4)⎩⎨⎧>-≤-=1 31 1x x x x y , x =1. 解 因为0)1(lim )(lim 11=-=--→→x x f x x . 2)3(lim )(lim 11=-=++→→x x f x x , 所以x =1是函数的第一类不可去间断点.3. 讨论函数x x x x f nn n 2211lim )(+-=∞→的连续性, 若有间断点, 判别其类型.解 ⎪⎩⎪⎨⎧<=>-=+-=∞→1|| 1|| 01|| 11lim )(22x x x x x x x x x f n nn . 在分段点x =-1处, 因为1)(lim )(lim 11=-=---→-→x x f x x , 1lim )(lim 11-==++-→-→x x f x x , 所以x =-1为函数的第一类不可去间断点. 在分段点x =1处, 因为1lim )(lim 11==--→→x x f x x , 1)(lim )(lim 11-=-=++→→x x f x x , 所以x =1为函数的第一类不可去间断点.4. 证明: 若函数f (x )在点x 0连续且f (x 0)≠0, 则存在x 0的某一邻域U (x 0), 当x ∈U (x 0)时, f (x )≠0.证明 不妨设f (x 0)>0. 因为f (x )在x 0连续, 所以0)()(lim 00>=→x f x f x x , 由极限的局部保号性定理, 存在x 0的某一去心邻域)(0x U, 使当x ∈)(0x U时f (x )>0, 从而当x ∈U (x 0)时, f (x )>0. 这就是说, 则存在x 0的某一邻域U (x 0), 当x ∈U (x 0)时, f (x )≠0.5. 试分别举出具有以下性质的函数f (x )的例子:(1)x =0, ±1, ±2, 21±, ⋅ ⋅ ⋅, ±n , n 1±, ⋅ ⋅ ⋅是f (x )的所有间断点, 且它们都是无穷间断点;解 函数x x x f ππcsc )csc()(+=在点x =0, ±1, ±2, 21±, ⋅ ⋅ ⋅, ±n , n 1±, ⋅ ⋅ ⋅处是间断的且这些点是函数的无穷间断点.(2)f (x )在R 上处处不连续, 但|f (x )|在R 上处处连续;解 函数⎩⎨⎧∉∈-=Q Q x x x f 1 1)(在R 上处处不连续, 但|f (x )|=1在R 上处处连续.(3)f (x )在R 上处处有定义, 但仅在一点连续.解 函数⎩⎨⎧∉-∈=QQ x x x x x f )(在R 上处处有定义, 它只在x =0处连续.。
一年级1一8单元基础知识通关必刷题

一年级1一8单元基础知识通关必刷题第一单元:生活中的数1、知识点:认识0-20的数,会用这些数进行简单的计数和比较大小。
2、重点:理解0-20每个数字的含义和用法。
3、难点:掌握10-20数字的计数方法。
4、练习题:比较0-20数字的大小,进行简单的加减法。
第二单元:比较5、知识点:掌握比较大小、多少、长短、高矮、轻重等基本比较方法。
6、重点:理解比较的意义和方法。
7、难点:运用比较的方法解决实际问题。
8、练习题:比较两个物体的长短、高矮、轻重等。
第三单元:位置与顺序9、知识点:认识上下、前后、左右等基本方向,会用这些方向描述物体的位置。
10、重点:理解位置和顺序的意义,能正确判断和描述物体的位置。
11、难点:掌握描述物体位置的方法。
12、练习题:描述教室中学生的位置,判断相对位置的改变。
第四单元:认识物体与图形13、知识点:认识常见的立体图形和平面图形,能正确区分两者。
14、重点:理解图形的基本特征和形状。
15、难点:掌握图形的拼接和组合方法。
16、练习题:拼接和组合简单的立体图形和平面图形。
第五单元:分类与统计17、知识点:按照一定的标准进行分类,会进行简单的统计。
18、重点:理解分类和统计的意义和方法。
19、难点:掌握分类和统计的基本技巧。
20、练习题:对一组物体进行分类并统计数量。
第六单元:加减法基础21、知识点:掌握5以内数的加减法运算,会解决简单的加减法问题。
22、重点:理解加减法的意义和方法。
23、难点:运用加减法解决实际问题。
24、练习题:进行5以内数的加减法运算,解决简单的加减法问题。
第七单元:认识钟表25、知识点:认识时钟和分钟表,能正确读出时间。
26、重点:理解时钟和分钟表的基本结构和功能。
27、难点:掌握时间的读取和时间的计算方法。
28、练习题:读取不同的时钟和分钟表时间,计算时间的差值。
第八单元:调查与记录知识点:能够进行简单的调查和记录,会制作简单的统计表。
重点是理解调查和记录的意义和方法难点是掌握调查和记录的基本技巧。
三年级下册数学1到8例题

三年级下册数学1到8例题
很抱歉,由于不知道你使用的是哪个版本的教材,我无法提供具体的三年级下册数学1 到8 例题。
不过,我可以为你提供一般三年级下册数学可能会涵盖的内容,希望对你有所帮助:
1. 除法:学习两位数除以一位数的除法,理解除法的意义。
2. 乘法:学习两位数乘以一位数和两位数乘以两位数的乘法。
3. 面积:学习计算长方形和正方形的面积。
4. 分数:初步认识分数,会读、写简单的分数。
5. 小数:初步认识小数,会读、写小数,理解小数的意义。
6. 数据收集与整理:学习收集、整理数据,并用图表表示数据。
7. 轴对称图形:认识轴对称图形,能在方格纸上画出简单的轴对称图形。
8. 平移和旋转:认识平移和旋转现象,并能在方格纸上画出简单图形平移后的图形。
这些只是一般三年级下册数学可能会涵盖的内容,具体的内容和例题可能因教材版本和教学要求而有所不同。
如果你能提供更具体的信息,我可以为你提供更准确的帮助。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
函数的连续性
习题 1-8
1. (1) 解
x →1+
讨论下列函数的连续性. 并画出函数的图形:
⎧ x3 + 1, 0 ≤ x < 1, ⎪ f ( x) = ⎨ ⎪ ⎩3 − x, 1 ≤ x ≤ 2;
(2)
⎧ ⎪ x − 1, f ( x) = ⎨ 2 ⎪ ⎩ 1− x ,
x < 0, x ≥ 0.
x → 0+
lim f ( x) = lim+ 1 − x 2 = 1 = f (0) ; lim− f ( x) = lim− ( x − 1) = −1 ≠ f (0) ,
x →0 x →0 x →0
故 x = 0 是 f ( x) 的跳跃间断点. 如图 1.6.
y 2 1 O
图 1.5
y
1 1
(1) 易知 f ( x) 在 [0, 1) 和 (1, 2] 上连续, 在 x = 1 点处,
x →1
x →1 x →1
lim f ( x) = lim+ (3 − x) = 2 = f (1) ; lim− f ( x) = lim− ( x3 + 1) = 2 = f (1) ,
故 f ( x) 在 x = 1 处也连续, 即函数在定义域 [1, 2] 上连续. 如图 1.5. (2) 函数定义域为 [−1, 1] , 易知函数在 [−1, 0) 和 (0, 1] 上连续, 在 x = 0 点处,
证 由 f ( x) 在 x = x0 连 续 , 故 ∀ε > 0 , ∃ δ > 0 , 当 x − x0 < δ 时 , 恒 有
f ( x) − f ( x0 ) < ε , 故
f ( x) − f ( x0 ) ≤ f ( x) − f ( x0 ) < ε ,
即 f ( x) 在 x0 也连续.
−1 1 2 x
O
x
−1
图 1.6
2. 指出下列函数的间断点及其类型, 如果是可去间断点, 则补充或改变函数 的定义使之连续: (1)
1 y = sin ; x
y= x2 − 1 ; x − 3x + 2
2
(2)y=arcFra bibliotekin x ; x
x > 0, x ≤ 0.
(3)
(4)
2 ⎧ ⎪ x + 1, f ( x) = ⎨ ⎪ ⎩ 2 − x,
4. 讨论函数 f ( x) = lim
1 − x2n x 的连续性, 若有间断点, 判断其类型. n →∞ 1 + x 2 n
解
⎧− x 当 x > 1, ⎪ 1 − x2n 易知 f ( x) = lim x = ⎨0 当 x = 1, 2 n n →∞ 1 + x ⎪ ⎩ x 当 x < 1,
n →∞
lim n[ln(1 + n) − ln n] = 1 .
1 lim ( − x ) x →∞ 1 tan x e
(6)
x →∞
lim (
x − 1 cot x 1 ( − x )( − ) = lim (1 − ) x →∞ x x
1
cot x
1 x)
=
= e−1 .
7. 设函数
⎧ 1+ x −1 , x > 0, ⎪ x ⎪ ⎪ f ( x) = ⎨b, x = 0, ⎪ arcsin ax ⎪ , x < 0. ⎪ ⎩ 2x
函数在 x = 1 和 x = 2 处无定义.
1
x2 − 1 x +1 = lim = −2 , 所以 x = 1 是函数的可去间断点, 补充定义 x →1 x 2 − 3 x + 2 x →1 x − 2 y (1) = −2 , 则函数连续;
因为 lim 因为 lim
x2 − 1 = ∞ , 所以 x = 2 是无穷间断点. x→2 x 2 − 3x + 2
x →−1+
在 x = −1 处 , 跳跃间断点;
lim f ( x) = lim + x = −1 ,
x →−1
x →−1−
lim f ( x) = lim − (− x) = 1 , 所以 x = −1 为
x →−1
在 x = 1 处 , lim+ f ( x) = lim+ (− x) = −1 , lim− f ( x) = lim− x = 1 , 所以 x = 1 为跳跃间
x 2 +1 −2 x 2 ⋅ 2 x 2 +1
=e
lim
x →∞
−2 x 2 x 2 +1
= e−2 .
3
(5)
1 1 因为 lim x[ln(1 + x) − ln x] = lim ln(1 + ) x = ln lim (1 + ) x = 1 , 所以 x →∞ x →∞ x →∞ x x
lim f ( x) = lim−
x →0
arcsin ax a = = f (0) = b , 故 a = 2b = 1 . 2x 2
4
2 x +1 2 e x
=e
x →∞
lim
2 x +1 x2
= e0 = 1 . = [lim(1 + 2 tan
x →0
2 1 2 x ]2 2 tan x)
lim(1 + 2 tan x)
x →0
2
cot 2 x
= e2 .
(4)
x2 − 1 2 2 − lim ( 2 ) x = lim (1 − 2 ) x →∞ x + 1 x →∞ x +1
x →0 x →0 x →0 x →0
(4)
因为 lim+ f ( x) = lim+ ( x 2 + 1) = 1 ; lim− f ( x) = lim− (2 − x) = 2 , 所以 x = 0 是函
数的跳跃间断点.
3. 设函数 f ( x) 在点 x0 处连续, 证明它的绝对值 f ( x) 亦在点 x0 处连续.
2
2
2+ x x2 + 2 + x2 − x
x →+∞
= lim
x →+∞
2 +1 x 2 1 1+ 2 + 1− x x
=
1 . 2 (4) lim x+2−2 x−2 1 1 = lim = lim = . x → 2 ( x − 2)( x + 2 + 2) x→2 x + 2 + 2 x−2 4
(6)
x →+∞
= lim
x x +1 + x
x →+∞
= lim
1 1+ 1 +1 x
x →+∞
=
1 . 2
6. 计算下列极限: (1)
(3) tan 2 x lim ; x →0 x lim(1 + 2 tan 2 x)cot x ;
x →0
2
(2) (4)
x →∞
lim
2 x +1 2 e x
;
x →∞
lim (
x 2 − 1 x2 ) ; x2 + 1
x − 1 cot x . ) x
1
(5)
解
n →∞
lim n [ln(1 + n) − ln n] ; lim tan 2 x 2x = lim = 2. x →0 x x
(6)
x →∞
lim (
(1) lim
x →0
(2) (3)
x →∞
x →1 x →1 x →1 x →1
断点. 5. (1)
计算下列极限: lim sin(2 x − 1) ;
x →1
(2)
lim ln(tan x) ;
x→ π 4
(3)
x →+∞
lim ( x 2 + 2 − x 2 − x ) ;
(4)
lim
x→2
x+2−2 ; x−2
1 − 1) . x
(5)
解 (1) 函数在 x = 0 处无定义, 且当 x → 0 时, 函数值在 −1 和 1 之间无限次的 变动, 称 x = 0 是函数的振荡间断点.
(2)
连续. (3)
因为 lim
arcsin x = 1 , 所以 x = 0 是可去间断点, 补充定义 y (0) = 1 , 则函数 x →0 x
x→2
(5)
1 1 x 2 sin x = lim x = lim x sin 1 = 0 . lim x →0 sin 2 x x →0 x →0 2 2x x x 2 sin
lim x( 1 + 1 x +1 − 1) = lim x( − 1) = lim x ( x + 1 − x ) x →+∞ x →+∞ x x
解
1 x ; lim x →0 sin 2 x x 2 sin (1) lim sin(2 x − 1) = sin1 .
x →1
(6)
x →+∞
lim x( 1 +
2
(2)
π lim ln(tan x) = ln(tan ) = 0 . π 4 x→
4
(3)
x →+∞
lim ( x + 2 − x − x ) = lim
试求 a 、 b , 使 f ( x) 处处连续. 解 f ( x) 处处连续, 则必在 x = 0 处连续, 故
