南京市金陵中学2011 届高三第四次模拟考试
江苏省金陵中学2011届高三高考模拟试卷(化学)

江苏省金陵中学2011届高三高考模拟试卷化 学可能用到的相对原子质量:H -1 C -12 N -14 O -16 Na -23 Mg -24 S -32 Al -27 Cl -35.5 K -39 Ca-40 Fe -56 Cu —64 Ba —137 Mn -55 一、选择题(本题包括8小题,每题3分,共24分。
每小题只有一个选项符合题意)1.据国外媒体报道,“火星快车”号和“金星快车”号探测器日前分别在火星和金星大气层中发现了一种非常特殊的气态化合物。
这种化合物的存在不但会导致金星上的温室效应被成倍的放大,而且可能会在火星上也诱发温室效应的产生。
它的结构式为:16O=C=18O )。
下列说法正确的是 A .16O 与18O 为同种核素 B .16O=C=18O 与16O=C=16O 互为同位素 C .16O=C=18O 的化学性质与16O=C=16O 几乎相同D .用 16O=C=18O 与Na216O2反应生成的氧气中含18O2.下列文字表述与反应方程式对应且正确的是A .溴乙烷的消去反应:CH3CH2Br浓硫酸 △C2H4↑ + HBrB .FeO 在空气中受热,迅速被氧化:6FeO + O2 △2Fe3O4C .粗硅的制取:SiO2 + C高温Si + CO2D .示踪原子法研究乙酸与乙醇酯化反应:3.设NA 为阿伏加德罗常数,下列有关说法正确的是 A .1molNH4NO3晶体中含有NH4+数为NA 个 B .1molC20H42分子中含有的共价键数目为62NAC .电解精炼铜过程中,电路中每通过NA 个电子,阳极溶解铜32gD . 标准状况下,2.24LCCl4和CH2O 的混合物中含有NA 个碳原子4.A 、B 、C 、D 、E 五种短周期元素,其原子序数逐渐增大。
元素A 的单质是密度最小的气体,元素B 的单质存在两种以上同素异形体,且其中一种是自然界中硬度最大的单质,元素D 的最外层电子数是次外层电子数的三倍。
江苏省金陵中学、海安市高级中学、南京外国语中学高三第四次模拟考试地理试题(word版)

南京市金陵中学、海安高级中学、南京外国语学校高三第四次模拟考试地理试题一、选择题。
(一)单项选择题从 2017 年 4 月 5 日起,全球 8 座射电望远镜连续进行了数天的联合观测,随后又经过 2 年的数据分析才一睹黑洞的真容。
这颗黑洞位于代号为 M87 的星系当中,距离地球 5300 万光年之遥,质量相当于 60 亿颗太阳。
北京时间 2019 年 4 月 10 日 21 点整,天文学家在布鲁塞尔(比利时)、圣地亚哥(智利)、上海、台北、东京(日本)、华盛顿(美国)六大都市同时召开全球新闻发布会,宣布首次直接拍摄到黑洞的照片。
完成下列小题。
1. 照片公布时,地球上 4 月 10 日与 4 月 11 日的范围之比约为 ( )A. 5:4B. 1:5C. 23:1D. 5:72. 从 2017 年 4 月 5 日起往后三个月内,下列说法正确的是( )A. 地球公转速度逐渐加快B. 华盛顿昼渐长夜渐短C. 圣地亚哥正午太阳高度逐渐减小D. 日出时上海东方明珠日影朝向西南【答案】1. C 2. D下图为我国某地所测得的等高线地形图。
根据图中信息,完成下列小题。
3. 图中甲、乙、丙、丁四地中,最容易出现泥石流灾害的是( )A. 甲B. 乙C. 丙D. 丁4. 上图中湖泊附近有一瀑布,瀑布落差32 米,图中湖泊湖面与图示区域最高点之间的相对高度最有可能为( )A. 520 米B. 514 米C. 532 米D. 540 米【答案】3. C 4. A下图为某地锋面气旋示意图。
读图,完成下列小题。
5. 图中( )A. 该天气系统位于北半球B. 低压中心位于锋线西侧C. 锋面自西北向东南移动D. 甲地风向可能为西北风6. 此时( )A. 受地形影响丁地风力大于乙地B. 受纬度影响乙地气温高于甲地C. 甲、丙两地受锋面影响多阴雨天D. 丙、丁两地气流以上升运动为主【答案】5. D 6. A读某地区地质剖面图,完成下列小题。
江苏省南京市金陵中学高考物理四模试卷

SYS201310282021一、选择题详细信息1. 难度:中等某物体在运动过程中,如果()A.机械能不守恒,则其运动状态一定变化B.所受的合外力恒定不变,它一定是做直线运动C.所受合外力不为零,它的动能一定变化D.做匀加速直线运动,它的机械能可能守恒SYS20131028202详细信息2. 难度:中等一个质点由静止开始沿直线运动,速度随位移变化的图线如图所示,关于质点的运动下列说法正确的是()A.质点做匀速直线运动B.质点做匀加速直线运动C.质点做加速度逐渐增大的加速运动D.质点做加速度逐渐减小的加速运动SYS20131028202详细信息3. 难度:中等半导体指纹传感器:在一块半导体基板上阵列了10万金属颗粒,传感器阵列的每一点是一个金属电极,充当电容器的一极,其外面是绝缘的表面.手指贴在其上与其构成了电容器的另一极,由于手指指纹深浅不同,嵴和峪与半导体电容感应颗粒形成的电容值大小不同,其工作过程是通过对电容感应颗粒预先充电到某一参考电压,然后对每个电容的放电电流进行测量,设备将采集到不同的数值汇总,也就完成了指纹的采集,则()A.指纹的嵴处与半导体基板上对应的金属颗粒距离近,电容小B.指纹的峪处与半导体基板上对应的金属颗粒距离远,电容小C.对每个电容感应颗粒都充电至某一参考电压时,在手指靠近时,各金属电极电量减小D.对每个电容感应颗粒都充电至某一参考电压时,在手指远离时,各金属电极均处于充电状态SYS20131028202详细信息4. 难度:中等有两个电源1和2,电动势和内电阻分别为E1、r1和E2、r2,阻值R相同的两个电阻分别接到两电源两端时,电阻R消耗的电功率分别是P1、P2,则()A.若E1>E2,r1=r2,不论R大小如何,一定是P1>P2B.若E1=E2,r1>r2,不论R大小如何,一定是P1>P2C.若E1>E2,r1>r2,不论R大小如何,不可能P1=P2D.若E1=kE2,r1=kr2(k≠1),不论R大小如何,一定是P1=P2 SYS20131028202详细信息5. 难度:中等如图所示,一半径为R的均匀带正电圆环水平放置,环心为O点,质量为m的带正电的小球从O点正上方h高的A点静止释放,并穿过带电环,关于小球从A到A关于O的对称点A′过程加速度(a)、重力势能(EpG)、机械能(E)、电势能(Ep电)随位置变化的图象一定错误的是(取O点为坐标原点且重力势能为零,向下为正方向,无限远电势为零)()A.B.C.D.SYS20131028202详细信息6. 难度:中等一颗科学资源探测卫星的圆轨道经过地球两极上空,运动周期为T=1.5h,某时刻卫星经过赤道上A城市上空.已知:地球自转周期T(24h),地球同步卫星轨道半径r,万有引力常量为G,根据上述条件()A.可以计算卫星绕地球运动的圆轨道半径B.可以计算地球的质量C.可以计算地球表面的重力加速度D.可以断定,再经过12h卫星第二次到达A城市上空SYS20131028202详细信息7. 难度:中等某同学自制变压器,在做副线圈时,将外表涂有绝缘层的导线对折后并在一起在铁芯绕n2圈,导线的两个端头为a、b,从导线对折的中点引出了一个c接头,连线成如图所示的电路(线圈电阻不计).已知原线圈匝数为n1,原线圈的输入电压为u1=Usint,则下列结论正确的是()A.K打到b时,V表读数为B.K打到b时,R中电流为零C.K打到c时,V表读数为D.K打到c时,R的电功率为SYS20131028202详细信息8. 难度:中等如图所示,在水平地面上O点正上方不同高度的A、B两点分别水平抛出一小球,如果两球均落在同一点C上,则两小球()A.落地的速度大小可能相等B.落地的速度方向可能相同C.落地的速度大小不可能相等D.落地的速度方向不可能相同SYS20131028202详细信息9. 难度:中等一对平行金属板长为L,两板间距为d,质量为m,电荷量为e的电子从平行板右侧以速度v沿两板的中线不断进入平行板之间,两板间所加交变电压uAB如图所示,交变电压的周期T=,已知所有电子都能穿过平行板,且最大偏距的粒子刚好从极板的边缘飞出,不计重力作用,则()A.所有电子都从右侧的同一点离开电场B.所有电子离开电场时速度都是vC.t=0时刻进入电场的电子,离开电场时动能最大D.t=时刻进入电场的电子,在两板间运动时最大侧位移为SYS201310282022二、解答题详细信息10. 难度:中等利用气垫导轨探究弹簧的弹性势能与形变量的关系,在气垫导轨上放置一带有遮光片的滑块,滑块的一端与轻弹簧贴近,弹簧另一端固定在气垫导轨的一端,将一光电门P固定在气垫导轨底座上适当位置(如图甲),使弹簧处于自然状态时,滑块向左压缩弹簧一段距离,然后静止释放,与光电门相连的光电计时器可记录遮光片通过光电门时的挡光时间,可计算出滑块离开弹簧后的速度大小.实验步骤如下:①用游标卡尺测量遮光片的宽度d;②在气垫导轨上通过滑块将弹簧压缩x1,滑块静止释放.由光电计时器读出滑块第一次通过光电门时遮光片的挡光时间t1;③利用所测数据求出滑块第一次通过光电门时的速度v和动能mv2;④增大弹簧压缩量为x2、x3、…重复实验步骤②③,记录并计算相应的滑块动能mv2,如下表所示:弹簧压缩量x(cm)0.5 1.0 1.5 2.0 2.5 3.0x2 0.25 1.00 2.25 4.00 6.25 9.000.49m 1.95m 4.40m 7.82m 12.22m 17.60m 动能mv2(1)测量遮光片的宽度时游标卡尺读数如图乙所示,读得d= ______ cm;(2)在两坐标系中分别作出mv2-x和mv2-x2图象;(3)由机械能守恒定律,Ep=mv2,根据图象得出结论是 ______ .SYS20131028202详细信息11. 难度:中等测量一未知电阻的阻值.(1)某同学首先用多用电表粗测电阻的大小,将多用表选择开关置于×10Ω挡,调零后,将红黑表笔分别接电阻两端,发现指针读数如图甲所示,则所测阻值为______ Ω.(2)接着该同学计划用VA法准确测量电阻的阻值,提供的实验器材有:8V直流电源;电压表(0~10V,内阻约20kΩ);电流表(0~50mA,内阻约10Ω);滑动变阻器(0~20Ω,1A);开关和导线.请根据实验要求和提供的器材,参考下面未完全连接好的实物电路在下面虚线方框内画出实验电路图(图乙),并完成下面实物电路(图丙)未连接的导线.(3)在上述(2)的实验中,连接好电路后,闭合开关,发现电流表和电压表皆没有读数,该同学用多用电表检查电路故障.他的操作如下:选用多用电表的直流电压挡,将红、黑表笔分别接在:电源正负极间;变阻器电阻丝的两端;电流表“-”接线柱和电压表“+”接线柱之间,结果多用电表的指针均发生偏转,则可能是连接 ______ 之间的导线发生了断路.(4)实验中移动变阻器滑动头,记下多组电流表、电压表读数(U,I),然后在坐标纸上作出UI图线,图线的 ______ 大小表示待测电阻阻值.在这个实验中,测量值 ______ 真实值.(填“>”“=”或“<”)SYS20131028202详细信息12. 难度:中等选做题:请从A、B和C三小题中选定两小题作答,如都作答,则按A、B两小题评分.A.(选修模块33)(1)下列说法正确的是 ______ .A.当两个分子间的分子势能增大时,分子间作用力一定减小B.大量分子的集体行为是不规则的,带有偶然性C.晶体和非晶体在一定的条件下可以转化D.人类利用能源时,是将高品质的能量释放出来并最终转化为低品质的内能(2)一定质量的理想气体,体积由V1压缩至V2,第一次是经过一个等温过程,最终气体压强是p1、气体内能是E1;第二次是经过一个等压过程,最终气体压强是p2、气体内能是E2;则p1 ______ p2,E1 ______ E2.(填“>”“=”或“<”)(3)当把一滴用酒精稀释过的油酸滴在水面上时,油酸就在水面上散开,油酸分子就立在水面上,形成单分子层油膜,现有按酒精与油酸的体积比为m:n 配制好的油酸酒精溶液置于容器中,还有一个装有约2cm深水的浅盘,一支滴管,一个量筒.现用滴管从量筒中取V体积的溶液,让其自由滴出,全部滴完共为N滴.①用滴管将一滴油酸酒精溶液滴入浅盘,待油酸薄膜稳定后,将薄膜轮廓描绘在坐标纸上,如图甲所示.(已知坐标纸上每个小方格面积为S,求油膜面积时,半个以上方格面积记为S,不足半个舍去)则油膜面积为 ______ .②求出估算油酸分子直径的表达式.B.(选修模块34)(1)下列说法正确的是 ______ .A.测定某恒星特定元素发出光的频率,对比地球上该元素的发光频率,可以推算该恒星远离地球的速度B.无线电波没有偏振现象C.红外线比无线电波更容易发生干涉和衍射现象D.在一个确定的参考系中观测,运动物体上物理过程的时间进程跟物体运动速度有关(2)在“研究单摆周期与摆长的关系”实验中,摆的振幅不要太大,摆线要细些、伸缩性要小,线的长度要尽量 ______ (填“长些”或“短些”).悬点要固定,摆长是悬点到 ______ 的距离.(3)如图乙,为一圆柱中空玻璃管,管内径为R1,外径为R2,R2=2R1.一束光线在圆柱横截面内射向玻璃管,为保证在内壁处光不会进入中空部分,问入射角i应满足什么条件?C.(选修模块35)(1)存在下列事实:①一对高能的γ光子相遇时可能产生一对正负电子;②一个孤立的γ光子不论其频率多高都不可能产生一对正负电子;③一个高能的γ光子经过重核附近时可能产生一对正负电子;④原子核发生变化时,只发射一些特定频率的γ光子.关于上述事实下列说法正确的是(电子质量me,光在真空中速度为c,普朗克常量为h) ______ .A.事实①表明,微观世界中的相互作用,只要符合能量守恒的事件就一定能发生B.事实②说明,动量守恒定律和能量守恒定律是自然界的普遍规律C.事实③中,由于外界重核的参与,系统动量不守恒,而γ光子的频率需满足ν≥D.事实④中表明,原子核的能级也是不连续的(2)本身不是易裂变材料,但是一种增殖材料,它能够吸收慢中子变成,然后经过 ______ 次 ______ 衰变转变为易裂变材料铀的同位素.(3)如图丙为通过某光电管的光电流与两极间电压的关系,当用光子能量为4.5eV的蓝光照射光电管的阴极K时,对应图线与横轴的交点U1=-2.37V.(以下计算结果保留两位有效数字)①求阴极K发生光电效应的极限频率.②当用光子能量为7.0eV的紫外线持续照射光电管的阴极K时,测得饱和电流为0.32μA,求阴极K单位时间发射的光电子数.SYS20131028202详细信息13. 难度:中等如图甲所示,水平天花板下悬挂一光滑的轻质的定滑轮,跨过定滑轮的质量不计的绳(绳承受拉力足够大)两端分别连接物块A和B,A的质量为m,B的质量m是可以变化的,当B的质量改变时,可以得到A加速度变化图线如图乙所示,不计空气阻力和所有的摩擦,A加速度向上为正.(1)求图乙中a1、a2和m1的大小.(2)根据牛顿定律和运动学规律,证明在A和B未着地或与滑轮接触时,AB 系统机械能守恒.(3)若m=0.8kg,m=1.2kg,AB开始都在离水平地面H=0.5m处,由静止释放AB,且B着地后不反弹,求A上升离水平地面的最大高度.(g取10m/s2)SYS20131028202详细信息14. 难度:中等如图所示,在坐标系xOy第二象限内有一圆形匀强磁场区域(图中未画出),磁场方向垂直xOy平面.在x轴上有坐标(-2l,0)的P点,三个电子a、b、c以相等大小的速度沿不同方向从P点同时射入磁场区,其中电子b射入方向为+y方向,a、c在P点速度与b速度方向夹角都是θ=.电子经过磁场偏转后都垂直于y轴进入第一象限,电子b通过y轴Q点的坐标为y=l,a、c到达y轴时间差是t.在第一象限内有场强大小为E,沿x轴正方向的匀强电场.已知电子质量为m、电荷量为e,不计重力.求:(1)电子在磁场中运动轨道半径和磁场的磁感应强度B.(2)电子在电场中运动离y轴的最远距离x.(3)三个电子离开电场后再次经过某一点,求该点的坐标和先后到达的时间差△t.SYS20131028202详细信息15. 难度:中等如图所示存在范围足够大的磁场区,虚线OO′为磁场边界,左侧为竖直向下的匀强磁场,磁感应强度为B1,右侧为竖直向上的磁感应强度为B2的匀强磁场区,B1=B2=B.有一质量为m且足够长的U形金属框架MNPQ平放在光滑的水平面上,框架跨过两磁场区,磁场边界OO′与框架的两平行导轨MN、PQ垂直,两导轨相距L,一质量也为m的金属棒垂直放置在右侧磁场区光滑的水平导轨上,并用一不可伸长的绳子拉住,绳子能承受的最大拉力是F,超过F绳子会自动断裂,已知棒的电阻是R,导轨电阻不计,t=0时刻对U形金属框架施加水平向左的拉力F让其从静止开始做加速度为a的匀加速直线运动.(1)求在绳未断前U形金属框架做匀加速运动t时刻水平拉力F的大小;绳子断开后瞬间棒的加速度.(2)若在绳子断开的时刻立即撤去拉力F,框架和导体棒将怎样运动,求出它们的最终状态的速度.(3)在(2)的情景下,求出撤去拉力F后棒上产生的电热和通过导体棒的电量.。
南京市金陵中学2011届高三第四次模拟考试

南京市金陵中学2011届高三第四次模拟考试南京市金陵中学2011届高三第四次模拟考试语文试题一、语言文字运用(15分)1. 下列加点的字,每对读音都不同相的一组是(3分)( )A. 着重/着手成春露脸/抛头露面枝蔓/顺蔓摸瓜B. 当权/安步当车场院/公共场所亟待/亟来问讯C. 标识/博闻强识处所/穴居野处靓丽/靓妆丽服D. 淬火/心力交瘁朔漠/溯游而上挟持/狭路相逢2. 下列各句中没有语病的一项是(3分)( )A. 九部门强调,严禁任何单位和个人在食品生产经营中使用食品剂以外的任何化学物质,严禁在农产品种植、加工、收购、运输中使用违禁药物或其他可能危害人体健康的物质。
B. 要成为世界一流大学,清华人应将目光从论文、课题、经费这些指标,向全面理顺教学和科研的关系,解决存在于我国高校中的重科研、轻教学的问题影响高校建设,切实重视人才培养。
C. 如何让富人不再只想着投资移民,让穷人尽快摆脱贫困,让全国的百姓真正走向共同富裕,这显然需要国家从宏观政策方面做出调整。
D. 随着药家鑫一案在西安市中级人民法院开审,更多人表现出了对案件发展走向的疑虑和担忧,但其辩护律师说,药家鑫的成长道路没有污点,且有自首情节,希望法庭从宽量刑。
3. 根据下面一段文字,概括说明什么是放线菌(不超过40个字)。
(4分)放线菌的细胞一般呈分枝丝状,因此,过去曾认为它是介于细菌与真菌之间的微生物。
随着电子显微镜的广泛应用和一系列其他技术的发展,越来越多的证据表明,放线菌无非是一类具有丝状分枝细胞的细菌。
放线菌一般分布在含水量较低、有机物丰富和呈微碱性的土壤环境中。
泥土所特有的泥腥味,主要就是由放线菌产生的。
放线菌主要以孢子繁殖。
据研究,在每克土壤中,放线菌的孢子数一般在一千万左右。
放线菌与人类的关系极为密切。
根据1978年的统计,在当时已发现的5 128种抗生素中,有3 165种为各种放线菌所产生。
另外,它们在自然界物质循环和提高土壤肥力等方面也有着重要作用。
江苏省南京市金陵中学、海安高级中学、南京外国语学校高三第四次模拟考试物理试题

南京市金陵中学、江苏省海安高级中学、南京外国语学校高三年级第四次模拟考试物理试题一、单项选择题:本题共5小题,每小题3分,共计15分,每小题只有一个选项符合题意。
1. 为了纪念物理学家对科学的贡献,许多物理量的单位是用物理学家的名字来命名的,下列属于基本单位的是()A. 牛顿B. 焦耳C. 库仑D. 安培【答案】D【点睛】解决本题的关键熟记单位制中的七个基本单位以及对应的物理量。
2. 如图所示,一个质量为的半球形物体放在倾角为的斜面上静止不动.若用通过球心的水平推力作用在物体上,物体仍静止在斜面上,斜面仍相对地面静止.已知,,取,则()A. 地面对斜面的弹力不变B. 物体对斜面的作用力增加C. 物体受到斜面的摩擦力增加D. 地面对斜面的摩擦力增加【答案】A【解析】以整体为研究对象,力F的是水平的,所以不影响竖直方向的受力,地面对斜面的弹力大小不变,故A正确;没有施加力F时根据平衡条件A受斜面作用力与重力等大反向,即大小为40N,根据牛顿第三定律物体A 对斜面的作用力为40N反向向下.施加力F后物体A对斜面的作用力如图:,可以看出物体对斜面的作用力不是增加10N,故B错误;没有施加力F时,对物体受力分析:根据平衡条件:f=mgsinθ=4×10×0.6=24N施加力F后,对物体受力分析,如图:根据平衡条件,在斜面方向:f′+Fcosθ=mgsinθ代入数据解得:f′=16N故物体受到斜面的摩擦力减少:=24N﹣16N=8N,故C错误;以整体为研究对象,水平方向增加了10N的力F,根据平衡条件得地面对斜面的摩擦力增加10N.故D错误。
故选:A。
【点睛】对没有施加力F时的半球进行受力分析,根据平衡条件求出物体受到的摩擦力;以整体为研究对象求出地面对斜面的摩擦力,然后进行比较.3. 如图所示,匝矩形闭合导线框处于磁感应强度大小为的水平匀强磁场中,线框面积为电阻为。
线框绕垂直于磁场的轴以角速度匀速转动,并与理想变压器原线圈相连,原副线圈匝数之比为,变压器副线圈接入一只额定电压为.电阻为的灯泡,灯泡正常发光。
江苏省南京市金陵中学2011届高三第四次模拟考试(英语)word版.pdf

南京市金陵中学2011届高三第四次模拟考试 英 语 注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),共五部分。
满分120分,考试时间120分钟。
2. 答题前,考生务必将学校、班级、姓名写在密封线内。
第Ⅰ卷(选择题,共85分) 第一部分:听力(共两节,满分 20分) 第一节(共5小题;每小题1分,满分5分) 听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A. £19.15.B. £9.15.C. £9.18. 答案是B。
( )1. What are they probably talking about?A. An apartment.B. A park.C. Food. ( )2. What is the woman doing?A. Asking for directions.B. Giving directions.C. Shopping. ( )3. What can we know about Jeffrey?A. He is a trouble maker.B. He is talkative.C. He is strict. ( )4. What is the probable relationship between the two?A. Manager and secretary.B. Teacher and student.C. Doctor and patient. ( )5. How would the man describe himself now?A. Fat.B. Slim.C. Wonderful. 第二节(共15小题;每小题1分,满分15分) 听下面5段对话或独白。
南京金陵中学2011届高考数学模拟预测试卷(1)

南京金陵中学2011年高考数学预测卷1一.填空题:本大题共14小题,每小题5分,共计70分.1.若复数z =1-m i(i 为虚数单位,m ∈R ),2z =-2i ,则复数z 的虚部为 . 2.若{}n a 为等差数列,n S 是其前n 项的和,且11S =223π,则6tan a 的值为 . 3.已知集合A =| 089n n n παα⎧⎫=∈⎨⎬⎩⎭,,Z ≤≤,若从A 中任取一个元素作为直线l 的倾斜角,则直线l 的斜率小于零的概率是 .4.函数()f x =2ln x x -的单调递增区间为 .5.某射击运动员在四次射击中分别打出了10,x ,10,8环的成绩,已知这组数据的平均数为9,则这组数据的标准差是 .6.如图正方形格子中,向量a -b = (用向量1e 和2e 表示).7.如图所示程序框图中,输出的数是 .8.如图,在正方体1111ABCD A B C D -中,给出以下四个结论:①1D C ∥平面11A ABB ;②11A D 与平面1BCD 相交;③AD ⊥平面1D DB ;④平面1BCD ⊥平面11A ABB .其中正确结论的序号是 .9.在△ABC 中,∠C 为直角,且AB BC ⋅ +BC CA ⋅ +CA AB ⋅=-25,则AB 的长为 .10.设函数()f x =||x x a -,若对于任意的1x ,2x ∈[2,)+∞,1x ≠2x ,不等式1212()()f x f x x x -->0恒成立,则实数a 的取值范围是 .11.如图,点P 是单位圆上的一个动点,它从初始位置0P (单位圆与x 轴的一个交点)开始沿单位圆按逆时针方向运动角α02πα⎛⎫<< ⎪⎝⎭到达点1P ,然后继续沿单位圆按逆时针方向运动3π到达点2P ,若的点2P 横坐标是45-,则cos α的值等于 .12.已知平面区域D 由A(1,3),B(5,2),C(3,1)为顶点的三角形内部和边界组成.若在区域D 上有无穷多个点(x ,y)可使目标函数z =x +my 取得最小值,则实数m = .13.已知有公共焦点的椭圆与双曲线中心在原点,焦点在x 轴上,左、右焦点分别为1F ,2F ,且它们在第一象限的交点为P ,△12PF F 是以1PF 为底边的等腰三角形.若1PF =10,双曲线的离心率的取值范围为(1,2),则该椭圆的离心率的取值范围是 .14.下列数阵称为“森德拉姆筛”,其特点是每行每列都是等差数列,则表中数字2010共出现 次.2 3 4 5 6 7 … 3 5 7 9 11 13 … 4 7 10 13 16 19 … 5 9 13 17 21 25 … 6 11 16 21 26 31 … 7 13 19 25 31 37 … … … … … … … …二.填空题:本大题共6小题,共计70分.请在指定区域内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)设函数()f x =m ·n ,其中向量m =(2,2cos x ),n =2x ,2cos x ),x ∈R . (1)求()f x 的最大值与最小正周期;(2)在△ABC 中,a ,b ,c 分别是A ,B ,C 的对边,()f A =4,a b +c =3(b >c),求b ,c 的值.16.如图,在四棱锥P -ABCD 中,底面ABCD 是正方形,侧面PAD ⊥底面ABCD ,且PA ⊥PD ,E ,F 分别为PC ,BD 的中点.(1)EF ∥平面PAD ; (2)EF ⊥平面PDC .17.某单位有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产业结构,调整出x (x ∈*N )名员工从事第三产业,调整后他们平均每人每年创造利润为310500x a ⎛⎫- ⎪⎝⎭万元(a >0),剩下的员工平均每人每年创造的利润可以提高0.2x%.(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?(2)在(1)的条件下,若调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则a 的取值范围是多少?18.在平面直角坐标系xOy 中,已知直线l :-y +3+=0和圆1C :2x +2y +8x +F =0.若直线l 被圆1C 截得的弦长为(1)求圆1C 的方程;(2)设圆1C 和x 轴相交于A ,B 两点,点P 为圆1C 上不同于A ,B 的任意一点,直线PA ,PB 交y 轴于M ,N 两点.当点P 变化时,以MN 为直径的圆2C 是否经过圆1C 内一定点?请证明你的结论; (3)若△RST 的顶点R 在直线x =-1上,点S ,T 在圆1C 上,且直线RS 过圆心1C ,∠SRT =30︒,求点R 的纵坐标的范围.19.已知数列{}n a 的前n 项的和n S 满足:n S =(1)1n aa a --(a 为常数,且a≠0,a≠1). (1)求{}n a 的通项公式; (2)设nb =2nnS a +1,若数列{}n b 为等比数列,求a 的值; (3)在满足条件(2)的情形下,设n c =2-11111n n a a +⎛⎫+ ⎪+-⎝⎭,数列{}n c 的前n 项的和为n T .求证:n T <13.20.在区间D 上,如果函数()f x 为增函数,而函数1()f x x为减函数,则称函数()f x 为“弱增函数”.已知函数()f x =1(1)判断函数()f x 在区间(0,1]上是否为“弱增函数”;(2)设1x ,2x ∈[0,)+∞,且1x ≠2x ,证明:21()()f x f x -<121||2x x -; (3)当x ∈[0,1]时,不等式1-≤1-bx 恒成立,求实数a ,b 的取值范围.参考答案一.填空题1.1.解析:2z =2(1i)m -=1+22i m -2mi =1-2m -2mi =-2i ,所以m =1. 2.解析:由1a +11a =2a +10a =…=5a +7a =62a ,可得11S =611a ,所以6a =23π,6tan a= 3.49.解析:A =280999πππ⎧⎫⎨⎬⎩⎭ ,,,,倾斜角α的可取值共9个,斜率小于零的只能为钝角,共4个.4.(2,+∞).解析:/()f x =1-2x =2x x-,解/()f x >0,得x >2,所以()f x 的增区间是(2,+∞). 5.1.解析:由10+x +10+8=36,得x =8,则这组数据的方差为1(1111)4+++=1.6.-1e +32e .解析:设向量a 的起始点为A ,终点为B ,向量b 的起始点C ,则a -b =AC=-1e +32e .7.16.解析:a =1,b =12;a =2,b =22=4;a =3,b =42=16.8.(1)(4).解析:因为1D C ∥1A B ,且1A B 在平面11A ABB 内,所以1D C ∥平面11A ABB ,故(1)正确;因为11A D 在平面1BCD 内,故(2)错误;AD 与平面1D DB 所成角∠ADB =45︒,故(3)错误;BC ⊥平面11A ABB ,且BC 在平面1BCD 内,故平面1BCD ⊥平面11A ABB ,故(4)正确.9.5.解析:因为∠C 直角,所以BC CA ⋅ =0,于是AB BC ⋅ +CA AB ⋅ =-25,则(AB BC ⋅ +)CA =-25,即AB BA ⋅=-25,故2AB =25,AB =5.10.(,2]-∞.解析:由题意()f x =||x x a -在[2,)+∞上单调递增.解法1:首先可以分类讨论:(1)当a≤2时,那么x ∈[2,)+∞时,()f x =x(x -a)=2x -ax ,此时2a<2,()f x 在[2,)+∞上递增是明显的;(2)当a >2时,那么x ∈[a ,)+∞时,()f x =x(x -a)=2x -ax ,也是递增的,而在(2,a)内()f x 必定有递减的区间,综上可知a≤2. 解法2:当x ∈[2,)+∞时,()f x =|x(x -a)|,画出()f x 的函数图象可知,()f x 的图象与x 轴的交点为(0,0),(a ,0),于是只有当a≤2时,()f x 在[2,)+∞上单调递增. 11.解析:由题意知cos 3πα⎛⎫+ ⎪⎝⎭=45-,sin 3πα⎛⎫+ ⎪⎝⎭=35,所以cos α=cos 33ππα⎛⎫+- ⎪⎝⎭=cos cos 33ππα⎛⎫+ ⎪⎝⎭+sin sin 33ππα⎛⎫+ ⎪⎝⎭.12.1.解析:依题意,令z =0,可得直线x +my =0的斜率为1m-,结合可行域可知当直线x +my =0与直线AC 平行时,线段AC 上的任意一点都可使目标函数z =x +my 取得最小值,而直线AC 的斜率为-1,所以m =-1.13.12(,)35.解析:如图,设椭圆的半长轴长,半焦距分别为1a ,c ,双曲线的半实轴长,半焦距分别为2a ,c ,1PF =m ,2PF =n ,则1222102m n a m n a m n c +=⎧⎪-=⎪⎨=⎪⎪=⎩,,,,得1255a c a c =+⎧⎨=-⎩,,.问题转化为1<5c c -<2,求5c c +的取值范围.设5c c -=x ,则c =51x x +,所以5c c +=21x x +=12-142x +.因为1<x <2,所以12-16<12-142x +<12-110,即13<12-142x +<25.14.6.解析:第i 行第j 列的数记为ij A .那么每一组i 与j 的解就是表中一个数.因为第一行数组成的数列1{}j A (j =1,2,…)是以2为首项,公差为1的等差数列,所以1j A =2+(j -1)×1=j +1,所以第j 列数组成的数列1{}j A (i =1,2,…)是以j +1为首项,公差为j 的等差数列,所以ij A =j +1+(i -1)×j =ij +1.令ij A =ij +1=2010,即ij =2009=1×2009=7×287=41×49=49×41=287×7=2009×1,故表中2010共出现6次.二.简答题15.解:(1)()f x =m ·n =24cos x +2x =4sin 26x π⎛⎫+ ⎪⎝⎭+2,所以()f x 的最大值是6,最小正周期T =π.(2)由()f A =4,得A =3π,有余弦定理cos A =2222b c a bc +-,a bc =2.又因为b +c=3,b >c ,所以b =2,c =1. 16.证明:(1)连结AC ,在△CPA 中,因为E ,F 分别为PC ,BD 的中点,所以EF ∥PA .而PA ⊂平面PAD ,EF ⊄平面PAD ,所以直线EF ∥平面PAD . (2)因为平面PAD ⊥平面ABCD ,平面PAD 平面ABCD =AD ,CD ⊂平面ABCD ,且CD ⊥AD ,所以CD ⊥PA .又因为PA ⊥PD ,且CD ,PD ⊂平面PDC ,所以PA ⊥平面PDC .而EF ∥PA ,所以EF ⊥平面PDC . 17.解:(1)由题意,得10(1000-x)(1+0.2x %)≥10×1000,即2x -500x≤0,又x >0,所以0<x≤500.即最多调整500名员工从事第三产业.(2)从事第三产业的员工创造的年总利润为310500x a x ⎛⎫- ⎪⎝⎭万元,从事原来产业的员工的年总利润为110(1000)1500x x ⎛⎫-+ ⎪⎝⎭万元,则310500x a x ⎛⎫- ⎪⎝⎭≤110(1000)1500x x ⎛⎫-+ ⎪⎝⎭,所以ax -23500x ≤1000+2x -x -21500x ,所以ax≤22500x +1000+x ,即a≤2500x +1000x +1恒成立.因为2500x +1000x ≥4,当且仅当2500x =1000x,即x =500时等号成立,所以a≤5,又a >0,所以0<a≤5.所以a 的取值范围为(0,5].18.证明:(1)圆1C :2(4)x ++2y =16-F .由题意,可得2+2⎝⎭=16-F ,所以F =12,所以圆1C 的方程为2(4)x ++2y =4.(2)设P(0x ,0y )(0y ≠0),则20(4)x ++20y =4.又A(-6,0),B(-2,0),所以PA l :y =06y x +(x +6),M(0,0066y x +),PB l :y =002y x +(x +1),N(0,0022y x +).圆2C 的方程为2x +2000062622y y x x y ⎛⎫+ ⎪++ ⎪-⎪⎪⎝⎭=200062622y y x x ⎛⎫- ⎪++ ⎪ ⎪⎪⎝⎭.化简得2x +2y -(0066y x ++0022y x +)y -12=0,令y =0,得x=±(-0)在圆1C 内,所以当点P 变化时,以MN 为直径的圆2C 经过圆1C 内一定点(-0).(3)设R(-1,t),作1C H ⊥RT 于H ,设1C H =d ,由于∠1C RH =30︒,所以1RC =2d .由题意d≤2,所以1RC ≤4,所以A 的纵坐标的范围为[. 19.(1)解:因为1S =1(1)1a a a --,所以1a =a .当n≥2时,n a =n S -1n S -=1n aa a --11n a a a --,所以1nn a a -=a ,即{}n a 是等比数列.所以n a =1n a a -⋅=n a . (2)解:由(1)知,n b =2(1)1n naa a a⋅--+1=(31)2(1)n n a a a a a ---,若{}n b 为等比数列,则有22b =13b b ,而1b =3,2b =32a a +,3b =22322a a a ++,故232()a a +=223223a a a ++⋅,解得a =13,再将a =13代入,得n b =3n 成立,所以a =13.(3)证明:由(2)知,n a =1()3n ,所以n c =2-11()3n +-111()3n +-=1-331n n ++1-11331n n ++-=131n+-1131n +-,由131n +<13n ,1131n +->113n +得131n +-1131n +-<13n -113n +,所以n c <13n -113n +,从而nT =1c +2c +…+n c <13-213+(213-313)+…+(13n -113n +)=13-113n +<13.20.(1)解:显然()f x 在区间上为增函数(0,1],因为1()f x x=1(1x -=1x,所以1()f x x在区间(0,1]上为减函数.所以()f x 在区间(0,1]上为“弱减函数”. (2)证明:证法1:要证21()()f x f x -<121||2x x -,不妨设0≤1x <2x ,由()f x =1[0,)+∞单调递增,得2()f x >1()f x ,那么只要证2()f x -1()f x <211()2x x -,即证2()f x -212x <1()f x -112x .令()g x =()f x -12x ,则问题转化为只要证明()g x =()f x -12x 在[0,)+∞单调递减即可.事实上,()g x =()f x -12x =112x ,当x ∈[0,)+∞时,/()g x-12≤0,所以()g x =()f x -12x 在[0,)+∞单调递减,故命题成立. 证法2:21()()f x f x -=|-, 因为1x ,2x ∈[0,)+∞,且1x ≠2x>2,所以21()()f x f x -<121||2x x -.(3)解:当x ∈[0,1]时,不等式1--bx 恒成立. 当x =0时,不等式显然成立;当x ∈(0,1]时,等价于1()1()a f x xb f x x ⎧⎪⎪⎨⎪⎪⎩≥≤恒成立.由(1)知1()f x x 为减函数,11()f x x <12,所以a≥12且b≤1。
南京金陵中学2011届高考数学模拟预测试卷(2)

南京金陵中学2011年高考数学预测卷2一.填空题:本大题共14小题,每小题5分,共计70分.1.命题“若一个数是负数,则它的平方数正数”的逆命题是 .2.设全集U ={1,3,5,7},集合M ={1,a -5},M ⊆U ,U M ð={5,7},则实数a = . 3.某工厂生产了某种产品3000件,它们来自甲、乙、丙三条生产线.为检查这批产品的质量,决定采用分层抽样的方法进行抽样.若从甲、乙、丙三条生产线抽取的个数分别为a ,b ,c ,且a ,b ,c 构成等差数列,则乙生产线生产了 件产品.4.若()f x =sin()4a x π++3sin()4x π-是偶函数,则实数a = . 5.从分别写有0,1,2,3,4五张卡片中取出一张卡片,记下数字后放回,再从中取出一张卡片.两次取出的卡片上的数字之和恰好等于4的概率是 .6.如右图,函数y =()f x 的图象在点P 处的切线方程,y =-x +5,在(3)f -/(3)f = .7.定义某种新运算⊗:S =a ⊗b 的运算原理如图所示,则5⊗4-3⊗6= .8.如图,四边形ABCD 中,若AC =,BD =1,则AB DC AC BD ⋅(+)(+)= .9.有三个球和一个正方体,第一个球与正方体的各个面相切,第二个球与正方体的各条棱相切,第三个球过正方体的各个顶点,则这三个球的表面积之比为 .10.若A ,B ,C 为△ABC 的三个内角,则4A +1B C+的最小值为 . 11.双曲线2222x y a b-=1(a >0,b >0)的左、右焦点分别是1F ,2F ,过1F 作倾斜角30︒的直线交双曲线右支于M 点,若2MF 垂直于x 轴,则双曲线的离心率e = .12.在平面直角坐标系中,点集A ={( x ,y) |2x +2y ≤1},B ={( x ,y) | x≤4,y≥0,3x -4y≥0},则点集Q ={( x ,y) |x =1x +2x ,y =1y +2y ,(1x ,1y )∈A ,(2x ,2y )∈B}所表示的区域的面积为 . 13.已知函数()f x =3x +2(1)a x -+3x +b 的图象与x 轴有三个不同交点,且交点的横坐标分别可作为抛物线、双曲线、椭圆的离心率,则实数a 的取值范围是 .14.定义函数()f x =[[]]x x ,其中[]x 表示不超过x 的最大整数, 如:[1.5]=1,[ 1.3]-=-2.当x ∈[0,)n (n ∈*N )时,设函数()f x 的值域为A ,记集合A 中的元素个数为n a ,则式子90n a n+的最小值为 .二.填空题:本大题共6小题,共计70分.请在指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分14分)在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,且A ,B ,C 成等差数列.(1)若AB BC ⋅ =32-,b a +c 的值;(2)求2sin sin A C -的取值范围. 16.(本小题满分14分)如图,四面体ABCD 中,O ,E 分别为BD ,BC 的中点,CA =CB =CD =BD =2,AB =AD(1)求证:AO ⊥平面BCD ;(2)求点E 到平面ACD 的距离. 17.(本小题满分14分)如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC ,该曲线段为函数y =sin()A x ωϕ+(A >0,ω>0,2π<ϕ<π),x ∈[-3,0]的图象,且图象的最高点为B(-1,)到CD ;赛道的后一部分为以O 圆心的一段圆弧 DE. (1)求ω,ϕ的值和∠DOE 的值;(2)若要在圆弧赛道所对应的扇形区域内建一个“矩形草坪”,如图所示,矩形的一边在道路AE 上,一个顶点在扇形半径OD 上.记∠POE =θ,求当“矩形草坪”的面积最大时θ的值. 18.(本小题满分16分)在直角坐标系xOy 中,直线l 与x 轴正半轴和y 轴正半轴分别相交于A ,B 两点,△AOB 的内切圆为圆M .(1)如果圆M 的半径为1,l 与圆M 切于点C (32,1),求直线l 的方程;(2)如果圆M 的半径为1,证明:当△AOB 的面积、周长最小时,此时△AOB 为同一个三角形;(3)如果l 的方程为x +y -20,P 为圆M 上任一点,求2PA +2PB +2PO 的最值. 19.(本小题满分16分)已知数列{}n a 满足1a =0,2a =2,且对任意m ,n ∈*N 都有21m a -+21n a -=12m n a +-+22()m n -. (1)求3a ,5a ;(2)设n b =21n a +-21n a -( n ∈*N ),证明:{}n b 是等差数列;(3)设n c =(1n a +-n a )1n q -( q≠0,n ∈*N ),求数列的前n 项的和n S .20.(本小题满分16分)对于函数y =()f x ,x ∈(0,)+∞,如果a ,b ,c 是一个三角形的三边长,那么()f a ,()f b ,()f c 也是一个三角形的三边长, 则称函数()f x 为“保三角形函数”.对于函数y =()g x ,x ∈[0,)+∞,如果a ,b ,c 是任意的非负实数,都有()g a ,()g b ,()g c 是一个三角形的三边长,则称函数()g x 为“恒三角形函数”.(1)判断三个函数“1()f x =x ,2()f x 3()f x =23x (定义域均为x ∈(0,)+∞)”中,那些是“保三角形函数”?请说明理由;(2)若函数()g x =2211x kx x x ++-+,x ∈[0,)+∞是“恒三角形函数”,试求实数k 的取值范围;(3)如果函数()h x 是定义在(0,)+∞上的周期函数,且值域也为(0,)+∞,试证明:()h x 既不是“恒三角形函数”,也不是“保三角形函数”.参考答案一.填空题1.若一个数的平方是正数,则它是负数.解析:因为一个命题的逆命题是将原命题的条件与结论进行交换,因此逆命题为:“若一个数的平方是正数,则它是负数”. 2.8.解析:由a -5=3,得a =8.3.1000.解析:因为a ,b ,c 构成等差数列,根据分层抽样的原理,所以甲、乙、丙三条生产线生产的产品数也成等差数列,其和为3000件,所以乙生产线生产了1000件产品. 4.-3.解析:由()f x 是偶函数可知,()f x -=()f x 对任意的x ∈R 恒成立,即sin()4a x π-++3sin()4x π--=sin()4a x π++3sin()4x π-,化简得2a =-6,a =-3.5.15.解析:从0,1,2,3,4五张卡片中取出两张卡片的结果有5×5=25种,数字之和恰好等于4的结果有(0,4),(1,3),(2,2),(3,1),(4,0),所以数字和恰好等于4的概率是P =15. 6.3.解析:函数y =()f x 的解析式未知,但可以由切线y =-x +5的方程求出(3)f =2,而/(3)f =k 切=-1,故(3)f -/(3)f =3.7.1.解析:由题意知5⊗4=5×(4+1)=25,3⊗6=6×(3+1)=24,所以5⊗4-3⊗6=1. 8.2.解析:AB DC AC BD ⋅ (+)(+)=AC CB DB BC AC BD ⋅ (+++)(+)=AC DB AC BD ⋅(+)(+)=AC BD AC BD ⋅(-)(+)=22AC BD - =2.9.1︰2︰3.解析:不妨设正方体的棱长为1,则这三个球的半径依次为12,从而它们的表面积之比为1︰2︰3. 10.9π.解析:因为A +B +C =π,且(A +B +C)·(4A +1B C +)=5+4·B C A ++AB C+≥5+9,因此4A +1B C +≥9π,当且仅当4·B C A +=AB C+,即A =2(B +C)时等号成立.11解析:如图,在Rt △12MF F 中,∠12MF F =30︒,12F F =2c ,所以1MF =2cos30c︒,2MF =2tan 30c ⋅︒.所以2a =1MF -2MF ,故e =ca12.18+π.解析:如图所示,点集Q 是由三段圆弧以及连接它们的三条切线围成的区域,其面积为:OPQ S ∆+OABP S +PCDQ S +OFEQ S +π=12×4×3+(3+4+5)×1+π=18+π.13.(-3,-2).解析:由题意知,三个交点分别为(1,0),(1x ,0),(2x ,0),且0<1x <1<2x .由(1)f =0可知b =-a -3,所以()f x =3x +2(1)a x -+3x +b =(x -1)(2x +ax +a +3),故2x +ax+a +3=0的两根分别在(0,1),(1,+∞)内.令()g x =2x +ax +a +3,则(0)0(1)0g g >⎧⎨<⎩,,得-3<a <-2.14.13.解析:当x ∈[0,1)时,()f x =[[]]x x =[0]x ⋅=0;当x ∈[1,2)时,()f x =[[]]x x =[1]x ⋅=[]x =1;当x ∈[2,3)时,再将[2,3)等分成两段,x ∈[2,5)2时,()f x =[[]]x x =[2]x ⋅=[2]x =4;x ∈5[2,3)时,()f x =[[]]x x =[2]x ⋅=[2]x =5.类似地,当x ∈[3,4)时,还要将[3,4)等分成三段,又得3个函数值;将[4,5)等分成四段,得4个函数值,如此下去.当x ∈[0,)n (n ∈*N )时,函数()f x 的值域中的元素个数为n a =1+1+2+3+4+…+(n -1)=1+(1)2n n -,于是90n a n +=2n +91n -12=1182()2n n+-12,所以当n =13或n =14时,90n a n+的最小值为13. 二.简答题15.解:(1)因为A ,B ,C 成等差数列,所以B =3π.因为AB BC ⋅ =32-,所以cos()ac B π-=32-,所以12ac =32,即ac =3.因为b 2222cos b a c ac B =+-,所以22a c ac +-=3,即2()3a c a c +-=3.所以2()a c +=12,所以a +c =.(2)2sin sin A C -=22sin()sin 3C C π--=1sin )sin 2C C C +-C .因为0<C <23πC ∈(.所以2sin sin A C -的取值范围是(.16.(1)证明:连结OC .因为BO =DO ,AB =AD ,所以AO ⊥BD .因为BO =DO ,CB =CD ,所以CO ⊥BD .在△AOC 中,由已知可得AO =1,CO 而AC =2,所以22AO CO +=2AC ,所以∠AOC =90︒,即AO ⊥OC .因为BD OC =O ,所以AO ⊥平面BCD .(2)解:设点E 到平面ACD 的距离为h .因为E ACD V -=A CDE V -,所以13ACD h S ∆⋅=13AO ⋅CDE S ∆⋅.在△ACD 中,CA =CD =2,ADACD S ∆=12AO =1,CDES ∆⋅=2122,所以h =CDE ACD AO S S ∆∆⋅1.所以点E 到平面ACD. 17.解:(1)依题意,得A=,4T =2,因为T =2πω,所以ω=4π,所以y =sin()4x πϕ+.当x =-1时,)4πϕ-+=,由2π<ϕ<π,得4πϕ-+=2π,所以ϕ=34π.又x =0时,y =OC =3,因为CDCOD =6π,从而∠DOE =3π.(2)由(1)可知OD =OP=,“矩形草坪”的面积S=)θ2sin )θθ+=2cos sin )θθθ-=112cos 2)22θθ+-=)6πθ+- 其中0<θ<3π,所以当26πθ+=2π,即θ=6π时,S 最大.18.解:(1)由题可得MC kl k=.所以l :y=+1.(2)设A(a ,0),B(0,b) (a >2,b >2),则l :bx +ay -ab =0.由题可得M (1,1).所以点M 到直线l 的距离d=1,整理得(a -2)(b -2)=2,即ab -2(a +b)+2=0.于是ab +2=2(a +b)≥a b≥6+a =b =2时,ab =6+所以面积S =12ab ≥3+△AOB 为直角边长为2L =a +b+(22(2=6+△AOB 为直角边长为2腰直角三角形.所以此时的△AOB 为同一个三角形.(3)l 的方程为x +y -20,得A(20),B(0,2,M :2(1)x -+2(1)y -=1,设P(m ,n)为圆上任一点,则2(1)m -+2(1)n -=1,2m +2n =2(m +n)-1,2(1)m -+2(1)n -=1≥2(2)2m n +-,2≤m +n≤22PA +2PB +2PO =23m +23n -(4++n)+22(2=(9+)-(2)(m +n).当m +n =2222max ()PA PB PO ++=(9+)-(2)( 2=17+m =n =1m +n =2时,222min ()PA PB PO ++=(9+)-(2)( 2=9+m =n =119.(1)解:由题意,令m =2,n =1,可得3a =22a -1a +2=6,再令m =3,n =1,可得5a =32a -1a +8=20.(2)证明:当n ∈*N 时,由已知(以n +2代替m)可得23n a ++21n a -=212n a ++8,于是[2(1)1n a ++-2(1)1n a +-]-(21n a +-21n a -)=8,即1n b +-n b =8.所以{}n b 是公差为8的等差数列.(3)解:由(1)(2)可知{}n b 是首项1b =3a -1a =6,公差为8的等差数列,则n b =8n -2,即21n a +-21n a -=8n -2.另由已知(令m =1)可得,n a =212n a --2(1)n -.那么1n a +-n a =21212n n a a +---2n +1=822n --2n +1=2n ,于是n c =12n nq -. 当q =1时,n S =2+4+6+…+2n =n (n +1).当q≠1时,n S =2·0q +4·1q +6·2q +…+2n·1n q -,两边同乘以q ,可得n qS =2·1q +4·2q +6·3q +…+2n·nq .上述两式相减,得(1)n q S -=212(1)n q q q-++++ -2n nq =121nq q-⋅--2n n q =11(1)21n n q nq q +-++⋅-,所以n S =12(1)12(1)n nq n q q +-++⋅-. 综上所述,n S =12(1)1(1)12 1.(1)n n n n q nq n q q q ++=⎧⎪-++⎨⋅≠⎪-⎩,,, 20.(1)解:对于1()f x =x ,它在(0,)+∞上是增函数,不妨设a≤b≤c ,则1()f a ≤1()f b ≤1()f c ,因为a +b >c ,所以1()f a +1()f b =a +b >c =1()f c ,故1()f x 是“保三角形函数”.对于2()f x(0,)+∞上是增函数,,不妨设a≤b≤c ,则2()f a ≤2()f b ≤2()f c ,因为a +b >c ,所以2()f a +2()f b2()f c ,故2()f x 是“保三角形函数”.对于3()f x =23x ,取a =3,b =3,c =5,显然a ,b ,c 是一个三角形的三边长,但因为3()f a +3()f b =223(33)⨯+<235⨯=3()f c ,所以3()f a ,3()f b ,3()f c 不是三角形的三边长,故3()f x 不是“保三角形函数”.(2)解:解法1:因为()g x =1+2(1)1k xx x +-+,所以当x =0时,()g x =1;当x >0时,()g x =1+111k x x++-.①当k =-1时,因为()g x =1,适合题意.②当k >-1时,因为()g x =1+111k x x ++-≤1=k +2,所以()g x ∈(1,2]k +.从而当k1时,()g x ∈[1,2]k +.由1+1>k +2,得k <0,所以-1<k <0.③当k <-1时,因为()g x =1+11k x x ++-≥1k +2,所以()g x ∈[2k +,1),从而当k >-1时,所以()g x ∈[2k +,1].由20(2)(2)1k k k +>⎧⎨+++>⎩,得,k >32-,所以32-<k <-1.综上所述,所求k 的取值范围是(32-,0).解法2:因为/()g x =2222(2)(1)(1)(21)(1)x k x x x kx x x x +-+-++--+=22(1)(1)(1)(1)k x x x x ++---+, ①当k =-1时,因为()g x =1,适合题意.②当k >-1时,可知()g x 在[0,1)上单调递增,在(1,)+∞上单调递减,而(0)g =1,(1)g =k +2,且当x >1时,()g x >1,所以此时()g x ∈[1,2]k +. ③当k <-1时,可知()g x 在[0,1)上单调递减,在(1,)+∞上单调递增,而(0)g =1,(1)g =k +2,且当x >1时,()g x <1,所以此时()g x ∈[2k +,1].(以下同解法1) (3)证明: ①因为()h x 的值域是(0,)+∞,所以存在正实数a ,b ,c ,使得()h a =1,()h b =1,()h c =2,显然这样的()h a ,()h b ,()h c 不是一个三角形的三边长,故()h x 不是“恒三角形函数”.②因为()h x 的最小正周期为T(T >0),令a =b =m +kT ,c =n ,其中k ∈*N ,且k >22n mT-,则a +b >c ,又显然b +c >a ,c +a >b ,所以a ,b ,c 是一个三角形的三边长.但因为()h a =()h b =()h m =1,()h c =()h n =2,所以()h a ,()h b ,()h c 不是一个三角形的三边长.故()h x 也不是“保三角形函数”.(说明:也可以先证()h x 不是“保三角形函数”,然后根据此知()h x 也不是“恒三角形函数”.)。
江苏省南京市金陵中学高三数学第四次模拟考试

南京市金陵中学2011届高三第四次模拟考试数学注意事项:1. 本试卷满分160分,考试时间120分钟.2. 答题前,考生务必将自己的学校、班级、姓名写在密封线内. 一、 填空题:本大题共14小题,每小题5分,共计70分.1. 在复平面内,复数-3+i 和1-i 对应的点间的距离为________.2. 命题:“若a ,b ,c 成等比数列,则b 2=ac ”及其逆命题、否命题、逆否命题中正确的个数是________.3. 右图是一个算法流程图,则输出的S 的值是________.4. 用半径为R 的半圆形铁皮卷成一个圆锥桶,那么这个圆锥的高是________.5. 为了调查高中学生眼睛高度近视的原因,某学校研究性学习小组用分层抽样的方法从全校三个年级的高度近视眼患者中,抽取若干人组成样本进行深入研究,有关数据见下表(单位:人):人都来自高三年级的概率是________.6. 双曲线x 2-y 24=1的渐近线被圆x 2+y 2-6x -2y +1=0所截得的弦长为________. 7. 在共有2 013项的等差数列{a n }中,有等式(a 1+a 3+…+a 2 013)-(a 2+a 4+…+a 2 012)=a 1 007成立;类比上述性质,在共有2 011项的等比数列{b n }中,相应的有等式________成立.8. 已知向量p 的模是2,向量q 的模为1,p 与q 的夹角为π4,a =3p +2q ,b =p -q ,则以a 、b 为邻边的平行四边形的长度较小的对角线的长是________.9. 若x ,y 满足不等式组⎩⎪⎨⎪⎧x -y +5≥0,x ≤3,x +y -k ≥0,且z =2x +4y 的最小值为-6,则k 的值为________.10. 已知等差数列{a n }和{b n }的前n 项和分别为S n ,T n ,且S n T n =n2n -1对任意n ∈N *恒成立,则a 10b 5的值为________. 11. 已知A ={x |1≤x ≤2},B ={x |x 2+2x +a ≥0},A ,B 的交集不是空集,则实数a 的取值范围是________.12. 定义在R 上的函数f (x )的图象过点M (-6,2)和N (2,-6),对任意正实数k ,有f (x +k )<f (x )成立,则当不等式|f (x -t )+2|<4的解集为(-4,4)时,实数t 的值为________.13. 平面四边形ABCD 中,AB =3,AD =DC =CB =1,△ABD 和△BCD 的面积分别为S ,T ,则S 2+T 2的最大值是________.14. 在直角坐标系xOy 中,点P (x P ,y P )和点Q (x Q ,y Q )满足⎩⎪⎨⎪⎧x Q =y P +x P ,y Q =y P -x P ,按此规则由点P 得到点Q ,称为直角坐标平面的一个“点变换”.此变换下,若OQOP=m ,∠POQ =θ,其中O 为坐标原点,则y =m sin(x +θ)的图象在y 轴右边第一个最高点的坐标为________.二、 解答题:本题共6小题,共计90分.解答时应写出必要的文字说明、证明过程或演算步骤.15. (本小题满分14分)已知函数f (x )=3sin 2x +sin x cos x -32(x ∈R ).(1) 若x ∈⎝⎛⎭⎫0,π2,求f (x )的最大值; (2) 在△ABC 中,若A <B ,f (A )=f (B )=12,求BCAB的值.16. (本小题满分14分)已知在直四棱柱ABCDA 1B 1C 1D 1中,底面ABCD 为直角梯形,且满足AD ⊥AB ,BC ∥AD ,AD =16,AB =8,BB 1=8,E ,F 分别是线段A 1A ,BC 上的点.(1) 若A 1E =5,BF =10,求证:BE ∥平面A 1FD . (2) 若BD ⊥A 1F ,求三棱锥A 1AB 1F 的体积.17. (本小题满分14分)省环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数f (x )与时刻x (时)的关系为f (x )=⎪⎪⎪⎪x x 2+1-a +2a +23,x ∈,其中a 是与气象有关的参数,且a ∈],若取每天f (x )的最大值为当天的综合放射性污染指数,并记作M (a ).(1) 令t =xx 2+1,x ∈,求t 的取值范围;(2) 省政府规定,每天的综合放射性污染指数不得超过2,试问:目前市中心的综合放射性污染指数是否超标?18. (本小题满分16分)已知椭圆C :x 2a 2+y 2b2=1(a >b >0),⊙O :x 2+y 2=b 2,点A ,F 分别是椭圆C 的左顶点和左焦点,点P 是⊙O 上的动点.(1) 若P (-1,3),P A 是⊙O 的切线,求椭圆C 的方程;(2) 是否存在这样的椭圆C ,使得P APF是常数?如果存在,求C 的离心率,如果不存在,说明理由.19. (本小题满分16分)已知函数f (x )=12ax 2-(2a +1)x +2ln x (a 为正数).(1) 若曲线y =f (x )在x =1和x =3处的切线互相平行,求a 的值; (2) 求f (x )的单调区间;(3) 设g (x )=x 2-2x ,若对任意的x 1∈(0,2],均存在x 2∈(0,2],使得f (x 1)<g (x 2),求实数a 的取值范围.(本小题满分16分)设数列{a n }满足:a 1=1,a 2=2,a n +2=a n (a 2n +1+1)a 2n +1(n ≥1,n ∈N *). (1) 求证:数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a n +1a n +1a n 是常数列; (2) 求证:当n ≥2时,2<a 2n -a 2n -1≤3; (3) 求a 2 011的整数部分.南京市金陵中学2011届高三第四次模拟考试数学附加题 注意事项:1. 附加题供选修物理的考生使用.2. 本试卷共40分,考试时间30分钟.3. 答题前,考生务必将自己的学校、班级、姓名写在密封线内.21. 【选做题】本题包括A 、B 、C 、D 四小题,只能选做2题,每小题10分,共计20分.解答时应写出必要的文字说明、证明过程或演算步骤.A. 选修41:几何证明选讲如图,设AB 为⊙O 的任意一条不与直线l 垂直的直径,P 是⊙O 与l 的公共点,AC ⊥l ,BD ⊥l ,垂足分别为C ,D ,且PC =PD .求证:(1) l 是⊙O 的切线;(2) PB 平分∠ABD.B. 选修42:矩阵与变换已知点A 在变换T :]→]=]的作用后,再绕原点逆时针旋转90°,得到点B .若点B 坐标为(-3,4),求点A 的坐标.C. 选修44:坐标系与参数方程求曲线C 1:⎩⎨⎧x =2t 2+1,y =2tt 2+1被直线l :y =x -12所截得的线段长.D. 选修45:不等式选讲已知a 、b 、c 是正实数,求证:a 2b 2+b 2c 2+c 2a 2≥b a +c b +ac.【必做题】第22题、第23题,每小题10分,共计20分.解答时应写出必要的文字说明、证明过程或演算步骤.22. (本小题满分10分)如图,在四棱锥OABCD 中,底面ABCD 是边长为1的菱形,∠ABC =45°,OA ⊥底面ABCD ,OA =2,M 为OA 的中点.(1) 求异面直线AB 与MD 所成角的大小;(2) 求平面OAB 与平面OCD 所成二面角的余弦值.23. (本小题满分10分)已知构成某系统的元件能正常工作的概率为p (0<p <1),且各个元件能否正常工作是相互独立的.今有2n (n 大于1)个元件可按如图所示的两种联结方式分别构成两个系统甲、乙. (1) 试分别求出系统甲、乙能正常工作的概率p 1,p 2;(2) 比较p 1与p 2的大小,并从概率意义上评价两系统的优劣.南京市金陵中学2011届高三第四次模拟考试数学参考答案及评分标准 1. 25 2. 2 3. -9 4. 32R 5. 126. 47. a 1·a 3·a 5…a 2 011a 2·a 4·a 6…a 2 010=a 1 006 8. 29 9. 0 10. 1917 11. 12. 2 13. 78 14. ⎝⎛⎭⎫π4,2 15. (1) f (x )=3(1-cos2x )2+12sin2x -32=12sin2x -32cos2x =sin ⎝⎛⎭⎫2x -π3.(4分) ∵0<x <π2,∴-π3<2x -π3<2π3.(6分)∴当2x -π3=π2时,即x =5π12时,f (x )取最大值1.(7分)(2) ∵f (x )=sin ⎝⎛⎭⎫2x -π3,x 是三角形的内角,则0<x <π,-π3<2x -π3<5π3. 令f (x )=12,得sin ⎝⎛⎭⎫2x -π3=12, ∴2x -π3=π6或2x -π3=5π6.解得x =π4或x =7π12.(9分)由已知,A ,B 是△ABC 的内角,A <B 且f (A )=f (B )=12,∴A =π4,B =7π12.∴C =π-A -B =π6.(11分)由正弦定理,得BC AB =sin Asin C =sinπ4sinπ6=2212= 2.(14分)16. (1) 过E 作EG ∥AD 交A 1D 于G ,连接GF . ∵A 1E A 1A =58,∴EG AD =58,∴EG =10=BF . ∵BF ∥AD ,EG ∥AD ,∴BF ∥EG .∴四边形BFGE 是平行四边形. ∴BE ∥FG .(4分)又FG ⊂平面A 1FD ,BE ⊄平面A 1FD , ∴BE ∥平面A 1FD .(6分)(2) ∵在直四棱柱ABCDA 1B 1C 1D 1中,A 1A ⊥平面ABCD ,BD ⊂平面ABCD ,∴A 1A ⊥BD . 由已知,BD ⊥A 1F ,AA 1∩A 1F =A 1, ∴BD ⊥平面A 1AF . ∴BD ⊥AF .(8分)∵梯形ABCD 为直角梯形,且满足AD ⊥AB ,BC ∥AD ,∴在Rt △BAD 中,tan ∠ABD =ADAB =2.在Rt △ABF 中,tan ∠BAF =FB AB =BF8.∵BD ⊥AF ,∴∠ABD +∠BAF =π2,∴BF 8=12,BF =4.(10分) ∵在直四棱柱ABCDA 1B 1C 1D 1中,A 1A ⊥平面ABCD ,∴平面AA 1B 1B ⊥平面ABCD , 又平面ABCD ∩平面AA 1B 1B =AB ,∠ABF =90°,∴FB ⊥平面AA 1B 1B ,即BF 为三棱锥F A 1B 1A 的高.(12分) ∵∠AA 1B 1=90°,AA 1=BB 1=8,A 1B 1=AB =8, ∴S △AA 1B 1=32.∴V 三棱锥A 1AB 1F =V 三棱锥F A 1B 1A =13×S △AA 1B 1×BF =1283.(14分)17. (1) 当x =0时,t =0;(2分)当0<x ≤24时,1t =x +1x .对于函数y =x +1x ,∵y ′=1-1x2,∴当0<x <1时,y ′<0,函数y =x +1x 单调递增,当1<x ≤24时,y ′>0,函数y =x +1x单调递增,∴y ∈.综上,t 的取值范围是].(5分)(2) 当a ∈]时,f (x )=g (t )=|t -a |+2a +23=⎩⎨⎧3a -t +23,0≤t ≤a ,t +a +23,a ≤t ≤12.(8分)∵g (0)=3a +23,g ⎝⎛⎭⎫12=a +76,g (0)-g ⎝⎛⎭⎫12=2a -12. 故M (a )=⎩⎨⎧g ⎝⎛⎭⎫12,0≤a ≤14,g (0),14<a ≤12=⎩⎨⎧a +76,0≤a ≤14,3a +23,14<a ≤12.(10分)当且仅当a ≤49时,M (a )≤2,(12分)故a ∈]时不超标,a ∈⎝⎛49,1]时超标.(14分)18. (1) ∵P (-1,3)在⊙O :x 2+y 2=b 2上, ∴b 2=4.(2分)又∵P A 是⊙O 的切线,∴P A ⊥OP ,∴OP →·AP →=0, 即(-1,3)·(-1+a ,3)=0,解得a =4.∴椭圆C 的方程为x 216+y 24=1.(5分)(2) 设F (c,0),c 2=a 2-b 2,设P (x 1,y 1),要使得P APF是常数,则有(x 1+a )2+y 21=λ,λ是常数. 即b 2+2ax 1+a 2=λ(b 2+2cx 1+c 2),(8分)比较两边,b 2+a 2=λ(b 2+c 2),a =λc ,(10分) 故cb 2+ca 2=a (b 2+c 2),即ca 2-c 3+ca 2=a 3, 即e 3-2e +1=0,(12分)(e -1)(e 2+e -1)=0,符合条件的解有e =5-12,即这样的椭圆存在,离心率为5-12.(16分)19. f ′(x )=ax -(2a +1)+2x (x >0).(1) f ′(1)=f ′(3),解得a =23.(4分)(2) f ′(x )=(ax -1)(x -2)x (x >0).①当0<a <12时,1a >2,在区间(0,2)和⎝⎛⎭⎫1a ,+∞上,f ′(x )>0; 在区间⎝⎛⎭⎫2,1a 上,f ′(x )<0, 故f (x )的单调递增区间是(0,2)和⎝⎛⎭⎫1a ,+∞,单调递减区间是⎝⎛⎭⎫2,1a .(6分) ②当a =12时,f ′(x )=(x -2)22x≥0,故f (x )的单调递增区间是(0,+∞).(8分)③当a >12时,0<1a<2,在区间⎝⎛⎭⎫0,1a 和(2,+∞)上,f ′(x )>0;在区间⎝⎛⎭⎫1a ,2上,f ′(x )<0,故f (x )的单调递增区间是⎝⎛⎭⎫0,1a 和(2,+∞),单调递减区间是⎝⎛⎭⎫1a ,2.(10分) (3) 由已知,在(0,2]上有f (x )max <g (x )max .(11分) 由已知,g (x )max =0,由(2)可知,①当0<a ≤12时,f (x )在(0,2]上单调递增,故f (x )max =f (2)=2a -2(2a +1)+2ln2 =-2a -2+2ln2,∴-2a -2+2ln2<0,解得a >ln2-1,ln2-1<0,故0<a ≤12.(13分)②当a >12时,f (x )在⎝⎛0,1a ]上单调递增,在]上单调递减, 故f (x )max =f ⎝⎛⎭⎫1a =-2-12a-2ln a . 由a >12可知ln a >ln 12>ln 1e=-1,2ln a >-2,-2ln a <2,∴-2-2ln a <0,f (x )max <0,(15分) 综上所述,a >0.(16分)20. (1) 易知,对一切n ≥1,a n ≠0,由a n +2=a n (a 2n +1+1)a 2n +1,得a n +2a n +1+1a n +1=a n +1a n +1a n. 依次利用上述关系式,可得a n +1a n +1a n =a n a n -1+1a n -1=a n -1a n -2+1a n -2=…=a 2a 1+1a 1=21+11=1, 从而数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a n +1a n +1a n 是常数列.(4分) (2) 由(1)得a n +1=a n +1a n.又a 1=1,∴可知数列{a n }递增,则对一切n ≥1,有a n ≥1成立,从而0<1a 2n≤1.(6分)当n ≥2时,a 2n =⎝⎛⎭⎫a n -1+1a n -12=a 2n -1+1a 2n -1+2, 于是a 2n -a 2n -1=1a 2n -1+2, ∴2<a 2n -a 2n -1≤3.(8分)(3) 当n ≥2时,a 2n =a 2n -1+1a 2n -1+2, ∴a 2n =1a 2n -1+…+1a 21+a 21+2(n -1). a 21=1,a 22=4,则当n ≥3时,a 2n =1a 2n -1+…+1a 21+a 21+2(n -1) =1a 2n -1+…+1a 22+1+1+2(n -1)=1a 2n -1+…+1a 22+2n >2n .a 22 011=1a 22 010+…+1a 21+2(2 011-1)+1>4 021 >3 969=632,(10分a 22 011=1a 22 010+…+1a 21+2(2 011-1)+1 =4 021+1a 21+…+1a 22 010<4 020+11+14+16+…+12×2 010=4 022+12⎝⎛⎭⎫12+13+…+12 010 =4 022+12⎝⎛⎭⎫140+141+…+1199+⎝⎛⎭⎫1200+1201+…+12 010]<4 022+12⎝⎛⎭⎫140+140+…+140+⎝⎛⎭⎫1200+1200+…+1200]= 4 022+12⎝⎛⎭⎫12×38+140×160+…+1200×1 811<4 022+12(19+4+10)<4 039<4 096=642.(14分)∴63<a 2 011<64,即a 2 011的整数部分为63.(16分)南京市金陵中学2011届高三第四次模拟考试数学附加题参考答案及评分标准21. A: (1) 连接OP ,∵AC ⊥l ,BD ⊥l ,∴AC ∥BD .又OA =OB ,PC =PD ,∴OP ∥BP ,从而OP ⊥l .∵P 在⊙O 上,∴l 是⊙O 的切线.(6分)(2) 连接AP ,∵l 是⊙O 的切线,∴∠BPD =∠BAP .又∠BPD +∠PBD =90°,∠BAP +∠PBA =90°,∴∠PBA =∠PBD ,即PB 平分∠ABD .(10分)B :]]=].(6分)设A (a ,b ),则由]]=],得⎩⎪⎨⎪⎧-b =-3,a +2b =4, ∴⎩⎪⎨⎪⎧a =-2,b =3,即A (-2,3).(10分) C :C 1:⎩⎨⎧x =2t 2+1,①y =2t t 2+1,②②①得t =y x ,代入①,化简得x 2+y 2=2x . 又x =2t 2+1≠0,∴C 1的普通方程为(x -1)2+y 2=1(x ≠0).(6分) 圆C 1的圆心到直线l :y =x -12的距离 d =⎪⎪⎪⎪1-0-122=122. 所求弦长为21-d 2=142.(10分) D :由⎝⎛⎭⎫a b -b c 2+⎝⎛⎭⎫b c -c a 2+⎝⎛⎭⎫c a -a b 2≥0,得2⎝⎛⎭⎫a 2b 2+b 2c 2+c 2a 2-2⎝⎛⎭⎫a b +b c +c a ≥0,∴a 2b 2+b 2c 2+c 2a 2≥b a +c b +a c.(10分) 22. 作AP ⊥CD 于点P ,分别以AB 、AP 、AO 所在直线为x 、y 、z 轴建立坐标系,则A (0,0,0),B (1,0,0),P ⎝⎛⎭⎫0,22,0,D ⎝⎛⎭⎫-22,22,0,O (0,0,2),M (0,0,1).(1) AB →=(1,0,0),MD →=⎝⎛⎭⎫-22,22,-1, 则cos 〈AB →,MD →〉=-12,故AB 与MD 所成角为π3.(4分) (2) OP →=⎝⎛⎭⎫0,22,-2,OD →=⎝⎛⎭⎫-22,22,-2,设平面OCD 的法向量n =(x ,y ,z ),则n ·OP →=0,n ·OD →=0,即⎩⎨⎧ 22y -2z =0,-22x +22y -2z =0,取z =2,则n =(0,4,2).(6分)易得平面OAB 的一个法向量为m =(0,1,0),cos 〈n ,m 〉=223,(9分) 故平面OAB 与平面OCD 所成二面角的平面角余弦值为223.(10分) 23. (1) p 1=p n (2-p n ),(2分)p 2=p n (2-p )n .(4分)(2) (用二项式定理证明)p 2-p 1=p n {n -2+n }=p n {-2+}=p n >0.(10分)说明:作差后化归为用数学归纳法证明:(2-p )n >2-p n 也可。
江苏省海安高级中学、南京外国语学校、金陵中学高三第
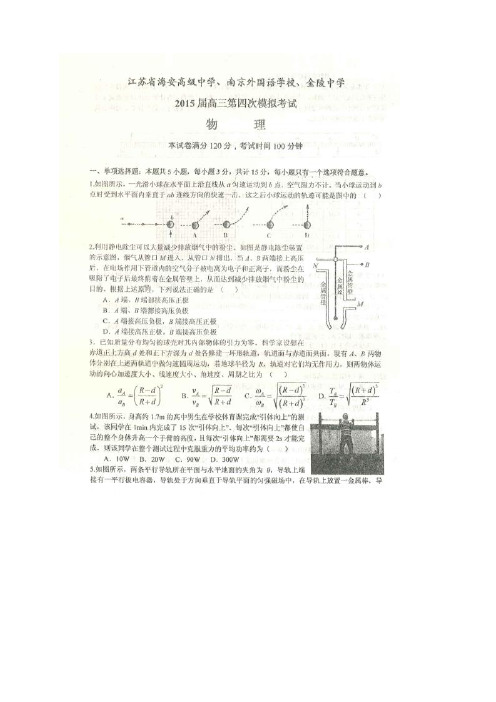
更正:15.(16分)如图所示,L1、L2为两平行的直线,间距为d。
L1下方和L2上方的空间有垂直于纸面向里的匀强磁场,且磁感应强度均为B。
现有一质量为m、电荷量为+q的粒子,以速度v从L1上的M点入射两线之间的真空区域,速度方向与L1成θ=30°角。
不计粒子所受的重力,试求:(1)粒子从M点出发后,经过多长时间第一次回到直线L1上?
(2)若在直线L1、L2之间的平面内,存在与图示速度方向垂直斜向上场强为E的匀强电场,则粒子经过多长时间第一次到达直线L2?
(3)若直线L1、L2之间无电场,v满足什么条件时,粒子恰好能回到M点?。
南京金陵中学2011年高考数学预测卷3

南京金陵中学2011年高考数学预测卷3(满分160分,考试时间120分钟)一、填空题:本大题共14小题,每小题5分,共计70分.1.已知集合P ={ x | x (x -1)≥0},Q ={ x | y =ln(1)x -},则P Q = . 2.高三(1)班共有56人,学号依次为1,2,3,…,56,现用系统抽样的办法抽取一个容量为4的样本,已知学号为6,34,48的同学在样本中,那么还有一个同学的学号应为 .3.已知i 是虚数单位,m ∈R ,且2i 1i m -+是纯虚数,则20112i 2i m m -⎛⎫⎪+⎝⎭= .4.若直线l 过点A (-2,-3),且与直线3x +4y -3=0垂直,则直线l 的方程为 . 5.设正项等比数列{}n a 的前n 项和为n S ,且10302S +10S =1020(21)S +,则数列{}n a 的公比 .6.设函数()f x =234x x --,x ∈[-3,6],则对任意0x ∈[-3,6],使0()f x ≤0的概率为 .7.下图伪代码运行输出的n 的值是 .8.点A 在曲线C :2x +2(2)y +=1上,点M (x ,y )在平面区域22020210x y x y y -+⎧⎪+-⎨⎪-⎩,,≥≤≥上,则AM 的最小值是 .9.设定义在R 上的函数()f x =11|1|1 1.x x x ⎧≠⎪-⎨⎪=⎩,,,若关于x 的方程2()f x +()bf x +c =0有3个不同的实数解1x ,2x ,3x ,则1x +2x +3x = .1While 111If mod(4)0then 1End if 1End while Print Endj n j j j j n n j j n ←←←+=←+←+,≤10.设△ABC 的BC 边上的高AD =BC ,a ,b ,c 分别表示角A ,B ,C 对应的三边,则b c +cb的取值范围是 . 11.给出下列命题,其中正确的命题是 (填序号).①若平面α上的直线m 与平面β上的直线n 为异面直线,直线l 是α与β的交线,那么l 至多与m ,n 中的一条相交;②若直线m 与n 异面,直线n 与l 异面,则直线m 与l 异面; ③一定存在平面γ同时与异面直线m ,n 都平行.12.在△ABC 中,AH 为BC 边上的高,tan 2C =12,则过点C ,以A ,H 为焦点的双曲线的离心率为 .13.若不等式a +21x x -≥2log 2x在x ∈(12,2)上恒成立,则实数a的取值范围为 .14.如图放置的等腰直角三角形ABC 薄片(∠ACB =90︒,AC =2)沿x 轴滚动,设顶点A (x ,y )的轨迹方程是y =()f x ,则()f x 在其相邻两个零点间的图象与x 轴所围区域的面积为 .二、填空题:本大题共6小题,共计70分.请在指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分14分)已知点A (3,0),B (0,3),C (cos α,sin α),α∈322ππ⎛⎫ ⎪⎝⎭,. (1)若AC =BC,求角α的值;(2)若AC BC ⋅ =-1,求22sin sin 21tan ααα++的值.16.(本小题满分14分)如图,在四棱锥P -ABCD 中,底面ABCD 是菱形,∠BAD =60︒,AB =2,P A =1,P A ⊥平面ABCD ,E 是PC 的中点,F 是AB 的中点.(1)求证:BE ∥平面PDF ;(2)求证:平面PDF ⊥平面P AB ; (3)求三棱锥P -DEF 的体积.如图,在边长为10的正三角形纸片ABC 的边AB ,AC 上分别取D ,E 两点,使沿线段DE 折叠三角形纸片后,顶点A 正好落在边BC 上(设为P ),在这种情况下,求AD 的最小值.18.(本小题满分16分)已知F 是椭圆1C :2222x y a b=1的右焦点,点P 是椭圆1C 上的动点,点Q 是圆2C :2x +2y =2a 上的动点.(1)试判断以PF 为直径的圆与圆2C 的位置关系; (2)在x 轴上能否找到一定点M ,使得QFQM=e (e 为椭圆的离心率)?若存在,求出点M 的坐标;若不存在,请说明理由.已知函数()f xa ≠0且a ≠1.(1)试就实数a 的不同取值,写出该函数的单调增区间;(2)已知当x >0时,函数在(0上单调递减,在)+∞上单调递增,求a 的值并写出函数的解析式;(3)记(2)中的函数图象为曲线C ,试问是否存在经过原点的直线l ,使得l 为曲线C 的对称轴?若存在,求出直线l 的方程;若不存在,请说明理由.20.(本小题满分16分)已知数列{}n a 满足1n a ++n a =4n -3(n ∈*N ). (1)若数列{}n a 是等差数列,求1a 的值; (2)当1a =2时,求数列{}n a 的前n 项和n S ;(3)若对任意n ∈*N ,都有2211n n n n a a a a ++++≥5成立,求1a 的取值范围.参考答案1.(1,)+∞.解析:P =(-∞,0] [1,)+∞,Q =(1,)+∞,所以P Q =(1,)+∞. 2.20.解析:采用系统抽样,所抽出的样本成等差数列,故另一个同学的学号应是20. 3.i .解析:因为2i 1im -+=(2i)(1i)2m --=(2)(2)i2m m --+是纯虚数,所以m =2.故20112i 2i m m -⎛⎫⎪+⎝⎭=201122i 22i -⎛⎫ ⎪+⎝⎭=()2011i -=3i -=i .4.4x -3y -1=0.解析:依题意直线l 的斜率为43,由点斜式方程得直线l 的方程为4x -3y -1=0.5.12.解析:设数列{}n a 的公比为q ,因为10302S +10S =1020(21)S +,所以1030202()S S -=2010()S S -,由此可得101020102()S S q -=2010()S S -,所以10q =1012⎛⎫⎪⎝⎭.又因为{}n a 是正项等比数列,所以q =12. 6.59.解析:函数()f x =234x x --=(x +1)(x -4),因此当x ∈[-1,4]时,()f x ≤0,所以对任意0x ∈[-3,6],使0()f x ≤0的概率为4(1)6(3)----=59.7.3.8.32.解析:曲线C 是圆2x +2(2)y +=1;不等式组的可行域如图阴影部分所示,A 点为(0,-1),当M 为(0,12)时,AM 最短,长度是32.9.3.解析:易知()f x 的图象关于直线x =1对称.2()f x +()bf x +c =0必有一根使()f x =1,不妨设为1x ,而2x ,3x 关于直线x =1对称,于是1x +2x +3x =3.10.[2.解析:因为BC 边上的高AD =BC =a ,.所以ABC S ∆=212a =1sin 2bc A ,所以sin A =2a bc .又因为cos A =2222b c a bc +-=212b c a c b bc ⎛⎫+- ⎪⎝⎭,所以b c +cb=2cos A +sin A b c +c b ≥2,所以b c +cb∈[2. 11.③.解析:①是错误的,因为l 可以与m ,n 都相交;②是错误的,因为m 与l 可以异面、相交或平行;③是正确的,因为只要将两异面直线平移成相交直线,两相交直线确定一个平面,此平面就是所求的平面.12.2.解析:如图所示,由tan 2C =12,得tan C =22tan21tan 2CC -=43.由题可知AH ⊥BC ,以A ,H 为焦点的双曲线的离心率e =AHAC CH-.由于△AHC 为直角三角形,且tan C =AHCH=43,可设AH =4a ,CH =3a ,则AC =5a ,所以离心率e =AH AC CH -=453aa a-=2.13.a ≥1.解析:不等式即为a ≥21x x --+2log 2x,在x ∈(12,2)上恒成立.而函数()f x =21x x --+2log 2x =112112x x x x⎧<<⎪⎪⎨⎪<⎪⎩,,,≤的图象如图所示,所以()f x 在(12,2)上的最大值为1,所以a ≥1.14.2+4π.解析:作出点A 的轨迹中相邻两个零点间的图象,如图所示.其轨迹为两段圆弧,一段是以C 为圆心,CA 为半径的四分之一圆弧;一段是以B 为圆心,BA 为半径,圆心角为34π的圆弧.其与x 轴围成的图形的面积为12×22×2π+12×2×2+12×2×34π=2+4π. 15.解析:(1)解法1:由题意知AC =(cos α-3,sin α),BC=(cos α,sin α-3).由AC =BC ,化简整理得cos α=sin α.因为α∈322ππ⎛⎫⎪⎝⎭,,所以α=54π. 解法2:因为AC =BC,所以点C 在直线y =x 上,则cos α=sin α.因为α∈322ππ⎛⎫⎪⎝⎭,,所以α=54π. (2)由AC BC ⋅=-1,得(cos α-3)cos α+sin α(sin α-3)=-1,即sin α+cos α=23.所以2(sin cos )αα+=1+2sin cos αα=49,即2sin cos αα=59-. 所以22sin sin 21tan ααα++=2sin cos αα=59-.16.解析:(1)取PD 的中点为M ,连结ME ,MF ,因为E 是PC 的中点,所以ME是△PCD 的中位线.所以ME ∥CD ,ME =12CD .又因为F 是AB 的中点,且由于ABCD 是菱形,AB ∥CD ,AB =CD ,所以ME ∥FB ,且ME =FB .所以四边形MEBF 是平行四边形,所以BE ∥MF .连结BD ,因为BE ⊄平面PDF ,MF ⊂平面PDF ,所以BE ∥平面PDF . (2)因为P A ⊥平面ABCD ,DF ⊂平面ABCD ,所以DF ⊥P A .连结BD ,因为底面ABCD 是菱形,∠BAD =60︒,所以△DAB 为正三角形. 因为F 是AB 的中点,所以DF ⊥AB .因为P A ,AB 是平面P AB 内的两条相交直线,所以DF ⊥平面P AB . 因为DF ⊂平面PDF ,所以平面PDF ⊥平面P AB .(3)因为E 是PC 的中点,所以点P 到平面EFD 的距离与点C 到平面EFD 的距离相等,故P DEF V -=C DEF V -=E DFC V -,又DFC S ∆=12×2E 到平面DFC 的距离h =12PA =12,所以E DFC V -=1312. 17.解析:显然A ,P 两点关于折线DE 对称,连结DP ,图(2)中,设∠BAP =θ,∠BDP =2θ.再设AD =x ,所以DP =x ,DB =10-x .在△ABC 中,∠APB =180︒-∠ABP -∠BAP =120︒-θ.在△BDP 中,由正弦定理知sin BD BPD ∠=sin DP DBP ∠,即10sin(1202)x θ-︒-=sin 60x︒,所以x因为0︒≤θ≤60︒,所以0︒≤120︒-2θ≤120︒,所以当120︒-2θ=90︒,即θ=15︒时,sin(1202)θ︒-=1.此时x 30,且∠ADE =75︒.所以AD 的最小值为30.18.解析:(1)取PF 的中点记为N ,椭圆的左焦点记为1F ,连结ON ,则ON 为1PFF ∆的中位线,所以ON =112PF .又由椭圆的定义可知,1PF +PF =2a ,从而1PF =2a -PF ,故ON =112PF =1(2)2a PF -=a -12PF .所以以PF为直径的圆与圆2C 内切.(2)设椭圆的半焦距为c ,M (x ,0),Q (0x ,0y ),F (c ,0),由QFQM=e ,得2QF =22e QM ,即20()x c -+20y =2200[()]e x x y -+.把20x +20y =2a 代入并化简整理,得202()c e x x -+22e a+22e x -2a -2c =0,要此方程对任意的Q (0x ,0y )均成立,只要2c e x -=0即可,此时x=2ce=2a c .所以x 轴上存在点M ,使得QF QM =e ,M 的坐标为(2a c ,0).19.解析:(1)①当a <0时,函数()f x 的单调增区间为(0),(0; ②当0<a <1时,函数()f x 的单调增区间为(-∞,0),(0,)+∞;③当a >1时,函数()f x 的单调增区间为(-∞,,)+∞.(2)由题设及(1)且a >1,解得a =3,因此函数解析式为()f xx ≠0). (3)假设存在经过原点的直线l 为曲线C 的对称轴,显然x ,y 轴不是曲线C 的对称轴,故可设l :y =kx (k ≠0).设P (p ,q )为曲线C 上的任意一点,///()P p q ,与P (p ,q )关于直线l 对称,且p ≠/p ,q ≠/q ,则/P 也在曲线C 上,由此得/2q q +=/2p p k +⋅,//q q p p --=1k -,且q ,/q /,整理得k 1k -,解得k k =所以存在经过原点的直线y 及y =为曲线C 的对称轴. 20.解析:(1)若数列{}n a 是等差数列,则n a =1a +(n -1)d ,1n a +=1a +nd . 由1n a ++n a =4n -3,得(1a +nd )+[1a +(n -1)d ]=4n -3,即2d =4,12a -d =-3,解得d =2,1a =12-.(2)由1n a ++n a =4n -3(n ∈*N ),得2n a ++1n a +=4n +1(n ∈*N ). 两式相减,得2n a +-n a =4.所以数列{}21n a -是首项为1a ,公差为4的等差数列. 数列{}2n a 是首项为2a ,公差为4的等差数列. 由2a +1a =1,1a =2,得2a =-1.所以n a =2=2125=2n n k n n k -⎧⎨-⎩,,(k ∈Z ).①当n 为奇数时,n a =2n ,1n a +=2n -3.n S =1a +2a +3a +…+n a =(1a +2a )+(3a +4a )+…+(2n a -+1n a -)+n a=1+9+…+(4n -11)+2n =1(1411)22n n -⨯+-+2n =22352n n -+.②当n 为偶数时,n S =1a +2a +3a +…+n a =(1a +2a )+(3a +4a )+…+(1n a -+n a )==1+9+…+(4n -7) =2232n n-.所以n S =22235=21223=22n n n k n n n k ⎧-+-⎪⎪⎨-⎪⎪⎩,,(k ∈Z ).(3)由(2)知,n a =1122=2123=2n a n k n a n k -+-⎧⎨--⎩,,(k ∈Z ).①当n 为奇数时,n a =2n -2+1a ,1n a +=2n -1-1a .由2211n n n n a a a a ++++≥5,得21a -1a ≥24n -+16n -10. 令()f n =24n -+16n -10=24(2)n --+6. 当n =1或n =3时,max ()f n =2,所以21a -1a ≥2. 解得1a ≥2或1a ≤-1.②当n 为偶数时,n a =2n -3-1a ,1n a +=2n +1a .由2211n n n n a a a a ++++≥5,得21a +13a ≥24n -+16n -12. 令()g n =24n -+16n -12=24(2)n --+4. 当n =2时,max ()g n =4,所以21a +13a ≥4. 解得1a ≥1或1a ≤-4.综上所述,1a 的取值范围是(-∞,4][2- ,)+∞.。
金陵中学高三四模三校联考地理参考答案

联考参考答案一.选择题(60分)(一)DACAB BBCBD CABDA CAD(二)BD AD CD AB AC AD BC BC二.综合题(60分)27.(1)风沙、春旱、寒潮 (任意二点,2分)(2)地形:北高南低,东高西低;以山地和高原为主。
(2分)气候:季风气候为主;南北气候有差异(大部分地区为温带季风气候,半岛南端为亚热带季风气候。
);与我国同纬度地区相比,气候的大陆性减弱,海洋性增强。
(2分)(3)有利方面:朝鲜有廉价的土地和劳动力;韩国有资金和技术设备;靠近朝韩边界,市场广阔;临近仁川港,交通运输便利。
(3分)不利方面:受两国关系的影响大。
(1分)(4)培育优良品种;改进栽培技术,提高单位面积产量和水果品质;使用有机肥和病虫害生物综合防治技术,发展生态农业;扩大宣传,打造品牌;开发苹果加工产品,延长产业链,增加附加值;保护生态环境等。
(任意三点,3分)28(1)东部多,西部少(1分)地形大气环流(季风)(2分)(2)海南:纬度低,冬季气温较高;青海:海拔高,夏季气温较低(2分)化肥和农药的大量使用造成环境污染;占用林地,造成生态破坏,水土流失加剧,生物多样性减少。
(2分)(3)地理位置优越,位于我国南部沿海地区,邻近港澳和东南亚;地处东亚到印度洋的国际航海线上,对外交通便利;地处热带,独特的气候条件有利于发展热带特色农业和旅游业;海洋资源丰富;国家政策支持;产业基础较好等(任意四点,4分)(4)跨海轮渡扩容:工程难度较小;一次性投资较少;可根据需要及时调整运力,设备利用率高,经济效益好。
新建跨海大桥:我国已经具备建设跨海大桥的工程技术和经济实力;经过跨海大桥的通行速度快,耗时短;对经济发展和人员往来的促进作用强;受天气影响较小。
新建跨海隧道:我国已经具备建设跨海大桥的工程技术和经济实力;经过跨海大桥的通行速度快,耗时短;对经济发展和人员往来的促进作用强;几乎不受天气影响。
(任选一个方案,观点1分,对应的理由2分)29.(1)伊利运河联通了五大湖和纽约港口的水运,促进了五大湖和纽约的经济联系;纽约城市的服务范围扩大(港口腹地增大);运河修建促使城市人口迅速增长,城市化进程加快。
江苏省南京市金陵中学2011届高三第四次模拟考试(英语).pdf

义务教育课程标准实验教科书 浙江版《数学》八年级上册 5.2 不等式的基本性质 复习回顾等式的性质: 1.若a=b, b=c,则a, c之间的关 系是 ; 2. 若a=b,则a+c b+c , a-c b-c;3. 若a=b,且若c≠0,则ac bc. a=c===等式性质1,2,3 合作学习 1、若a<b、bb a+c>b+c b a b+c a+c c c b-c a-c b a c c 把a>b表示在数轴上, 不妨设c>0 ∴a+c>b+c ∴a-c>b-c 如果a>b,那么a+c>b+c,a-c>b-c; 如果a<b,那么a+c<b+c,a-c<b-c. 观察:用“”填空,并找一找其中的规律. 8__12 8×4__12×48÷4__12÷4 8×(-4)__12×(-4) 8÷(-4)__12÷(-4) (-4)__(-6) (-4)×2__(-6)×2 (-4)÷2__(-6)÷2 (-4)×(-2)__(-6)×(-2) (-4)÷(-2)__(-6)÷(-2) < < < < < > > > > > 想一想:从上面的变化,你发现了什么? 当不等式的两边同乘同一个正数时,不等号的方向____;而乘同一个负数时,不等号的方向_____. 改变 不变 不等式的两边都乘(或都除以)同一个正数,所得的不等式仍成立; 不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得的不等式成立. 即:如果a>b,且c>0, 那么ac>bc, 即:如果a>b,且c<0, 那么ac< bc, (不等号方向不变) (不等号方向改变) 不等式的基本性质: 性质3:不等式的两边都乘(或都除以)同一个正数,所得到的不等式仍成立; 不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得到的不等式成立. 性质1:若a<b,b<c,则a<c。
南京市金陵中学高三年级第四次模拟考试

C. A trainer C. In the afternoon. C. A movie. 南京市金陵中学、江苏省海安高级中学、南京外国语学校2017届高三年级第四次模拟考试英语 本试卷分选择题和非选择题两部分。
满分120分,考试用时120分钟。
注意事项:答题前〃考生务必将自己的学校、姓名、考试号写在答题纸上。
考试结束后,将答题纸 交回。
第一部分听力(共两节,满分20分>做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案 转涂到答題卡上。
第•一节(共S 小题;每小题1分,满分5分)听下面5段对话a 每段对话后有一个小题,从题中所给的A 、B 、C 三个选项中选出最 佳选项•并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题 和阅读下一小题。
每段对话仅读一遍。
1. What is the man?A. A weather forecaster.B. A pilot.2. What, does the man imply?A. The woman should go onplaying chess.B. He wants to play chess with thewoman.C. The woman is weak in playingchess.3. Why does the man stop his talk withthe woman?A. He isn't interested in her words*B. He is expecting another call.C. He is angry with her,4. When will Steven arrive in Cairo? A. In the morning. B. Atnoon. 5. What are the speakers talking about? A. A story. B. A textbook.第二节(共15小題;每小題1分,满分1S 分)听下面5段对话或独白。
江苏省南京市金陵中学2011届高三生物第四次模拟考试

某某市金陵中学2011届高三第四次模拟考试生物注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分120分,考试时间100分钟。
2. 答题前,考生务必将自己的学校、班级、某某写在密封线内。
第Ⅰ卷(选择题共55分)一、单项选择题(本题包括20小题,每小题2分,共40分。
每小题只有一个选项最符合题意。
)1. 下列关于生物大分子的叙述错误的是( )A. 氨基酸的空间结构和种类决定了蛋白质功能B. 在小麦细胞中由A、G、T、U四种碱基参与构成的核苷酸的种类有6种C. 质量相同的糖原和脂肪完全氧化分解所释放的能量是不同的D. 细胞中氨基酸种类和数量相同的蛋白质不一定是同一种蛋白质2. 关于酶与ATP的叙述正确的是( )A. RNA聚合酶催化的底物是RNAB. 蔗糖酶能使蔗糖水解为两分子的葡萄糖,水解产物与斐林试剂反应产生砖红色沉淀C. 叶绿体和线粒体中均可以产生ATP,并用于物质的运输、细胞的分裂等各种生命活动D. 酶的形成需要消耗ATP,ATP的形成需要酶的催化3. 有关细胞生命历程的说法不正确的是( )A. 细胞生长,核糖体的数量增加,物质交换效率增强B. 细胞分化,核遗传物质没有发生改变,但mRNA有变化C. 细胞癌变,细胞膜上的糖蛋白减少,多个基因发生突变D. 细胞凋亡,相关基因活动加强,有利于个体的生长发育4. 下列有关实验方法的叙述正确的是( )A. 利用血球计数板可以统计培养液中的酵母菌数量B. 调查人类遗传病时应选择发病率较高的单基因遗传病来调查如白化病、系统性红斑狼疮、色盲等C. 在绿叶中色素分离的纸层析结果中,叶绿素a条带最宽,可见其在层析液中溶解度最大D. 可用标志重捕法调查棉蚜的种群密度5. 农科所技术员研究温度对某蔬菜新品种产量的影响,将实验结果绘制成如下曲线。
据此提出以下结论,你认为合理的是( )A. 光合作用酶的最适温度高于呼吸作用酶的最适温度B. 光照越强,该蔬菜新品种的产量越高C. 阴影部分表示5~35 ℃时蔬菜的净光合速率小于零D. 温室栽培该蔬菜时温度最好控制在25~30 ℃6. 右图是减数第一次分裂形成的子细胞,下列有关说法正确的是( )A. 与该细胞活动关系密切的激素是雄性激素B. 该细胞中有2条染色体、3个DNA分子C. 若①有基因B,②上相应位点的基因b是由基因突变导致的D. 该细胞分裂结束产生4个精细胞7. S型肺炎双球菌菌株是人类肺炎和小鼠败血症的病原体,而R型菌株却无致病性。
江苏省南京市金陵中学届高三化学第四次模拟考试【会员独享】

南京市金陵中学2011届高三第四次模拟考试化学注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)。
满分120分,考试时间100分钟。
2. 答题前,考生务必将自己的学校、班级、姓名写在密封线内,并认真核对。
可能用到的相对原子质量:H —1 C —12 N —14 O —16 Na —23 S —32 Fe —56Cu —64 Zn —65第Ⅰ卷(选择题 共40分)单项选择题(本题包括8小题,每小题2分,共计16分。
每小题只有一个选择符合题意)1. “绿色化学”又称环境无公害化学。
下列叙述符合“绿色化学”原则的是( )A. 绿色化学的核心是利用化学原理对工业生产造成的环境污染进行治理B. 用聚苯乙烯等塑料代替木材生产包装盒、快餐盒等,以减少木材使用C. 研制新型杀虫剂,使它只对目标昆虫有毒杀作用而对其他昆虫无害D. 现代石油化工采用银作催化剂,将乙烯直接氧化生产环氧乙烷符合“原子经济”2. 下列有关化学用语以及化学基本概念的表述中正确的一组是( )A. 过氧乙酸(CH 3COOOH)与羟基乙酸(HOCH 2COOH)所含官能团相同,两者互为同分异构体B. 日本福岛核电站泄露的放射性核素131 53Ⅰ和137 55Cs ,前者比后者少4个中子C. 亚硫酸氢钠和碳酸氢钠的电离方程式都表示为NaHRO 3 Na ++HRO -3(R =C 或S)D. 次氯酸的结构式为HOCl ,过氧化氢的电子式为H +[ OO ]2-H +3. 下列说法正确的是( )A. 氯水和过氧化钠都具有漂白作用,其漂白原理相似B. 硅和二氧化硅都是重要的半导体材料C. 蛋白质和油脂的水解都是由高分子化合物生成小分子化合物的过程D. MgO 和Al 2O 3在工业上用于制作耐高温材料,也用于电解法冶炼镁、铝金属4. 下列离子方程式不正确的是( )A. 用稀硫酸除去铜绿:4H ++Cu 2(OH)2CO 3===2Cu 2++CO 2↑+3H 2OB. 将Na 2O 2固体投入H 218O 中:2H 218O +2Na 2O 2===4OH -+4Na ++18O 2↑C. 向NH 4Al(SO 4)2溶液中滴入Ba(OH)2溶液恰好使SO 2-4完全沉淀:2Ba 2++NH +4+Al 3++2SO 2-4+4OH -===Al(OH)3↓+NH 3·H 2O +2BaSO 4↓D. 向Na 2FeO 4溶液中加入稀硫酸产生氧气:4FeO 2-4+20H +===4Fe 3++3O 2↑+10H 2O5. 设N A 为阿伏加德罗常数的值,下列叙述正确的是( )A. 20mL 10mol·L -1的浓硝酸或浓硫酸与足量铜加热反应转移电子数均为0.2N AB. 0.1mol 的白磷(P 4)或甲烷中所含的共价键数均为0.4N AC. 在精炼铜或电镀铜的过程中,当阴极析出铜32g 转移电子数均为N AD. 标准状况下,2.24L Cl 2通入足量H 2O 或NaOH 溶液中转移的电子数均为0.1N AA. SO 2气体的还原性较强,不能使其通过浓硫酸干燥B. 滴定管洗净后经蒸馏水润洗,即可注入标准液进行滴定C. 用图1装置吸收多余的HCl 气体D. 用图2装置检验溴乙烷发生消去反应生成乙烯8. 由短周期元素组成的中学常见物质A、B、C、D、E、X,存在下图转化关系(部分生成物和反应条件略去)。
江苏省南京市2011届高三英语模拟训练(4).pdf

淮安市开明中学 初中数学七年级上册 (苏科版) 4.3用方程解决问题(5) 丢番图被认为是代数学的鼻祖,但历史上没有一本 正式的著作里留下他完整的生平,甚至连他的国籍 都没有明确的记载. 然而有趣的是,他竟然有一个 墓志铭,上面镌刻着他的一些情况: “他生平的六分之一是幸福的童年. 再活十二分之一,颊上长出了细细须. 又过了生命的七分之一才结婚. 再过5年他感到很幸福,得了一个儿子. 可是这孩子光辉灿烂的生命只有他父亲的一半. 儿子死后,老人在悲痛中活了4年,结束了尘世 的生涯.” 你知道丢番图去世时的年龄是多少吗? 将一批会计报表输入电脑,甲单独做需 20h完成,乙单独做需12h完成.现在先由 甲单独做4h,剩下的部分由甲、乙合作完成。
甲、乙两人合作的时间是多少? 1、某下水管道工程由甲、乙两个工程队单独 铺设分别需要10天、15天完成。
如果两队从 两端同时施工
2天,然后由乙队单独施工,还需多少天完成? 2 甲、乙两水管往水池中注水,单独打开甲管用20h可注满一池水,单独打开乙水管40h可注满一池水。
现单独打开甲管8h后,乙管也开始工作,问再需要多少时间可注满水池? 现有甲、乙两项工程,甲工程的工作量是 乙工程的工作量的2倍,甲组有19人,乙组有14人(假设人均工作效率相同),怎样调配两组的人数才能使两项工程同时开工又同时完工呢? 两枝同样长但粗细不同的蜡烛,点完一根 粗蜡烛要2h而一根细蜡烛只能燃1h,一次晚上 停电了,小静同时点燃了这两枝蜡烛看书, 来电后同时熄灭,小静发现粗蜡烛长是细蜡烛 的2倍,问停电了多少分钟? 2. 2枝一样高的蜡烛,同时点燃后, 第一枝蜡烛每小时缩短8cm,第二枝蜡烛每小时缩短6cm. 2h后,第二枝蜡烛的高度是第一枝蜡烛的1.5倍。
求这2枝蜡烛原来的高度.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
年级 高度近视眼患者人数抽取人数高一 18 x高二 36 2 高三54y南京市金陵中学2011届高三第四次模拟考试数 学 I 试 题锥体的体积公式:V 锥体=13Sh ,其中S 是锥体的底面面积,h 是高. 一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡...相应的位置上....... 1.在复平面内,复数-3+i 和1-i 2.命题:“若a ,b ,c 成等比数列,则b 2=ac 否命题、逆否命题中正确的个数是 ▲ . 3.右图是一个算法流程图,则输出的S 的值是 ▲ .4.用半径为R 圆锥的高是 ▲ .5.为了调查高中学生眼睛高度近视的原因,某学校研究性学习小组用分层抽样的方法从全校三个年级 的高度近视眼患者中,抽取若干人组成样本进 行深入研究,有关数据见右表(单位:人): 若从高一与高三抽取的人选中选2人进行跟踪式家访调研,则这2人都来自高三年级的概率是 ▲ .(第3题图)6.双曲线x 2-y 24=1的渐近线被圆x 2+y 2-6x -2y +1=0所截得的弦长为 ▲ .7.在共有2013项的等差数列{a n }中,有等式(a 1+a 3+…+a 2013)-(a 2+a 4+…+a 2012)=a 1007成立;类比上述性质,在共有2011项的等比数列{b n }中,相应的有等式 ▲ 成立. 8.已知向量p 的模是2,向量q 的模为1,p 与q 的夹角为π4,a =3p +2q ,b =p -q ,则以a 、b 为邻边的平行四边形的长度较小的对角线的长是 ▲ .9.若x ,y 满足不等式组îïíïìx -y +5≥0,x ≤3,x +y -k ≥0,且z =2x +4y 的最小值为-6,则k 的值为 ▲ .10.已知等差数列{a n }和{b n }的前n 项和分别为S n ,T n ,且S n T n =n2n -1对任意n ÎN *恒成立,则a 10b 5的值为 ▲ . 11.已知A ={x |1≤x ≤2},B ={x |x 2+2x +a ≥0},A ,B 的交集不是空集,则实数a 的取值范围是 ▲ .12.定义在R 上的函数f (x )的图象过点M (-6,2)和N (2,-6),对任意正实数k ,有f (x +k )<f (x )成立,则当不等式| f (x -t )+2|<4的解集为(-4,4)时,实数t 的值为 ▲ . 13.平面四边形ABCD 中,AB =3,AD =DC =CB =1,△ABD 和△BCD 的面积分别为S ,T ,则S 2+T 2的最大值是 ▲ .14.在直角坐标系xOy 中,点P (x P ,y P )和点Q (x Q ,y Q )满足îíìx Q =y P +x P ,y Q =y P -x P,按此规则由点P 得到点Q ,称为直角坐标平面的一个“点变换”.此变换下,若OQOP =m ,∠POQ =q ,其中O 为坐标原点,则y =m sin(x +q )的图象在y 轴右边第一个最高点的坐标为 ▲ .二、解答题:本题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分14分)已知函数f (x )=3sin 2x +sin x cos x -32x ÎR ). (1)若x Î(0,π2),求f (x )的最大值;(2)在△ABC 中,若A <B ,f (A )=f (B )=12,求BCAB的值.16.(本小题满分14分)已知在直四棱柱ABCD -A 1B 1C 1D 1中,底面ABCD 为直 角梯形,且满足AD ⊥AB ,BC ∥AD ,AD =16,AB =8,BB 1=8.E ,F 分别是线段A 1A ,BC 上的点.(1)若A 1E =5,BF =10,求证:BE ∥平面A 1FD .(2)若BD ⊥A 1F ,求三棱锥A 1-AB 1F 的体积.17.(本小题满分14分)省环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数f (x )与时刻x (时)的关系为f (x )=|x x 2+1-a |+2a +23,x Î[0,24],其中a 是与气象有关的参数,且a Î[0,12],若用每天f (x )的最大值为当天的综合放射性污染指数,并记作M (a ).(1)令t =xx 2+1,x Î[0,24],求t 的取值范围;(2)省政府规定,每天的综合放射性污染指数不得超过2,试问目前市中心的综合放射性污染指数是否超标? 18.(本小题满分16分)已知椭圆C :x 2a 2+y 2b2=1(a >b >0),⊙O :x 2+y 2=b 2,点A ,F 分别是椭圆C 的左顶点和左焦点.点P 是⊙O 上的动点.(1)若P (-1,3),P A 是⊙O 的切线,求椭圆C (2)是否存在这样的椭圆C ,使得P APF 是常数?如果存在,求C 的离心率;如果不存在,说明理由. 19.(本小题满分16分)已知函数f (x )=122-(2a +1)x +2ln x (a 为正数). (1)若曲线y =f (x )在x =1和x =3处的切线互相平行,求a 的值; (2)求f (x )的单调区间;(3)设g (x )=x 2-2x ,若对任意x 1Î(0,2],均存在x 2Î(0,2],使得f (x 1)<g (x 2),求实数a 的取值范围.(第16题图) B DB 1120.(本小题满分16分)设数列{a n }满足:a 1=1,a 2=2,a n +2=a n (a 2n +1+1)a 2n +1(n ≥1,n ÎN *). (1)求证:数列{a n +1a n +1a n}是常数列;(2)求证:当2≥n 时,2<a 2n -a 2n -1≤3;(3)求a 2011的整数部分.B (第22题图) 数 学 Ⅱ(附 加 题)21.【选做题】本题包括A 、B 、C 、D 四小题,请选定其中两题,并在相应的答..............题区域内作答.......若多做,则按作答的前两题评分. 解答时应写出文字说明、证明过程或演算步骤.A .选修4-1:几何证明选讲 (本小题满分10分)如图,设AB 为⊙O 的任一条不与直线l 垂直的直径,P 是⊙O与l 的公共点,AC ⊥l ,BD ⊥l ,垂足分别为C ,D ,且PC =PD求证:(1)l 是⊙O 的切线;(2)PB 平分∠ABD .B .选修4-2:矩阵与变换 (本小题满分10分)已知点A 在变换:T :ëéûùx y →ëéûùx'y'=ëéûùx +2y y 作用后,再绕原点逆时针旋转90°,得到点B .若点B 坐标为(-3,4),求点A 的坐标. C .选修4-4:坐标系与参数方程 (本小题满分10分)求曲线C 1:îíìx =2t 2+1,y =2t t 2+1.被直线l :y =x -12所截得的线段长. D .选修4-5:不等式选讲 (本小题满分10分)已知a 、b 、c 是正实数,求证:a 2b 2+b 2c 2+c 2a 2≥b a +c b +ac.【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域.......内作答.解答时应写出文字说明、证明过程或演算步骤.22.(本小题满分10分)如图,在四棱锥O -ABCD 中,底面ABCD 是边长为1的菱形,∠ABC =45°,OA ⊥底面ABCD ,OA =2,M 为OA 的中点. (1)求异面直线AB 与MD 所成角的大小;(2)求平面OAB 与平面OCD 所成二面角的余弦值.23.(本小题满分10分)已知构成某系统的元件能正常工作的概率为p (0<p <1),且各个元件能否正常工作是相互独立的.今有2n (n 大于1)个元件可按下图所示的两种联结方式分别构成两个系统甲、乙.(1)试分别求出系统甲、乙能正常工作的概率p 1,p 2;(2)比较p 1与p 2的大小,并从概率意义上评价两系统的优劣.系统甲系统乙南京市金陵中学2011届高三第四次模拟考试数 学 I 试 题 评 分 细 则1.2 5 2.2 3.-9 4.32R 5.12 6.4 7.a 1·a 3·a 5…a 2011a 2·a 4·a 6…a 2010=a 10068.29 9.0 10.1917 11.[-8,+∞) 12.2 13.78 14.(π4,2)15.(1)f (x )=3(1-cos2x )2+12sin2x -32=12sin2x -32cos2x =sin(2x -π3). ………4分∵0<x <π2,∴-π3<2x -π3<2π3. ……………………………6分∴当2x -π3=π2时,即x =5p12时,f (x )的最大值为1.……………………………7分(2)∵f (x )=sin(2x -π3),x 是三角形的内角,则0<x <p ,-π3<2x -π3<5π3.令f (x )=12,得sin(2x -π3)=12,∴2x -π3=π6,或2x -π3=5π6,解得x =π4,或x =7p 12. ……………………………9分由已知,A ,B 是△ABC 的内角,A <B 且f (A )=f (B )=12,∴A =π4,B =7p12.∴C =p -A -B =π6. ……………………………11分由正弦定理,得BC AB =sin Asin C =sin π4sin π6=2212=2. ……………………………14分 16.(1)过E 作EG ∥AD 交A 1D 于G ,连结GF . ∵A 1E A 1A =58,所以EG AD =58,∴EG =10=BF . ∵BF ∥AD ,EG ∥AD ,∴BF ∥EG . ∴四边形BFGE 是平行四边形.∴BE ∥FG .…………………………………4分 又FG Ì平面A 1FD ,BE Ë平面A 1FD ,∴BE ∥平面A 1FD . …………………………………6分(2)∵在直四棱柱ABCD -A 1B 1C 1D 1中,A 1A ⊥面ABCD ,BD Ì面ABCD ,∴A 1A ⊥BD . 由已知,BD ⊥A 1F ,AA 1∩A 1F =A 1,∴BD ⊥面A 1AF .∴BD ⊥AF . ………………………………8分BDB 11∵梯形ABCD 为直角梯形,且满足AD ⊥AB ,BC ∥AD , ∴在Rt △BAD 中,tan ∠ABD =ADAB =2. 在Rt △ABF 中,tan ∠BAF =FB AB =BF8.∵BD ⊥AF ,∴∠ABD +∠BAF =π2,∴BF 8=12,BF =4. ………………10分 ∵在直四棱柱ABCD -A 1B 1C 1D 1中,A 1A ⊥面ABCD ,∴面AA 1B 1B ⊥面ABCD ,又面ABCD ∩面AA 1B 1B =AB ,∠ABF =90°, ∴FB ⊥面AA 1B 1B ,即BF 为三棱锥F -A 1B 1A 的高. ………………12分 ∵∠AA 1B 1=90°,AA 1=BB 1=8,A 1B 1=AB =8,∴S △AA 1B 1=32.∴V 三棱锥A 1-A B 1F =V 三棱锥F -A 1B 1A =13×S △AA 1B 1×BF =1283. ………………14分 17.(1)当x =0时,t =0; ………………2分当0<x ≤24时,1t=x +1x .对于函数y =x +1x ,∵y ′=1-1x 2,∴当0<x <1时,y ′<0,函数y =x +1x 单调递增,当1<x ≤24时,y ′>0,函数y =x +1x单调递增,∴y Î[2,+∞).∴1t Î(0,12].综上,t 的取值范围是[0,12]. ………………5分(2)当a Î[0,12]时,f (x )=g(t )=|t -a |+2a +23=îíì3a -t +23,0≤t ≤a ,t +a +23,a ≤t ≤12.………………8分 ∵g(0)=3a +23,g(12)=a +76,g(0)-g(12)=2a -12.故M (a )=îíìg(12),0≤a ≤14,g(0),14<a ≤12=îíìa +76,0≤a ≤14,3a +23,14<a ≤12. ………………10分当且仅当a ≤49M (a )≤2, ………………12分故a Î[0,49]时不超标,a Î(49,1]时超标. ………………14分18.(1)∵P (-1,3)在⊙O :x 2+y 2=b 2,∴b 2=4. ……………………………2分又∵P A 是⊙O 的切线,∴P A ⊥OP ,∴→OP ·→AP =0,即(-1,3)·(-1+a ,3)=0,解得a =4.∴椭圆C 的方程为x 216+y 24=1. ……………………………5分(2)设F (c ,0),c 2=a 2-b 2,设P (x 1,y 1),要使得P APF 是常数,则有(x 1+a )2+y 12=l [(x 1+c )2+y 12],l 是常数.即b 2+2ax 1+a 2=l (b 2+2cx 1+c 2), ……………………………8分 比较两边, b 2+a 2=l (b 2+c 2),a =l c , ……………………………10分 故cb 2+ca 2=a (b 2+c 2),即ca 2-c 3+ca 2=a 3,即e 3-2 e +1=0, ……………………………12分 (e -1)( e 2+e -1)=0,符合条件的解有e =5-12即这样的椭圆存在,离心率为5-12. ……………………………16分 19.f ′(x )=ax -(2a +1)+2x(x >0).(1)f ′(1)=f ′(3),解得a =23 ……………………………4分(2)f ′(x )=(ax -1)(x -2)x (x >0). ①当0<a <12时,1a>2,在区间(0,2)和(1a,+∞)上,f ′(x )>0;在区间(2,1a )上f ′(x )<0,故f (x )的单调递增区间是(0,2)和(1a ,+∞),单调递减区间是(2,1a . ……6分 ②当a =12时,f ′(x )=(x -2)22x ≥0,故f (x )的单调递增区间是(0,+∞). ………8分 ③当a >12时,0<1a <2,在区间(0,1a )和(2,+∞)上,f ′(x )>0;在区间(1a ,2)上f ′(x )<0,故f (x )的单调递增区间是(0,1a )和(2,+∞),单调递减区间是(1a,2). ……10分(3)由已知,在(0,2]上有f (x )max <g(x )max . ……………………………11分 由已知,g(x )max =0,由(2)可知, ①当0<a ≤12f (x )在(0,2]上单调递增,故f (x )max =f (2)=2a -2(2a +1)+2ln2=-2a -2+2ln2,∴-2a -2+2ln2<0,解得a >ln2-1,ln2-1<0,故0<a ≤12. ……13分②当a >12时,f (x )在(0,1a 上单调递增,在[1a ,2]上单调递减,故f (x )max =f (1a =-2-12a-2ln a .由a >12可知ln a >ln 12ln 1e=-1,2ln a >-2,-2ln a <2,∴-2-2ln a <0,f (x )max <0, ……………………………15分 综上所述,a >0. ……………………………16分20.(1)易知,对一切n ≥1,a n ≠0,由a n +2=a n (a 2n +1+1)a 2n +1,得a n +2a n +1+1a n +1=a n +1a n +1a n.依次利用上述关系式,可得a n +1a n +1a n =a n a n -1+1a n -1=a n -1a n -2+1a n -2=…=a 2a 1+1a 1=21+11=1,从而数列{a n +1a n +1a n}是常数列; ……………………………4分 (2)由(1)得a n +1=a n +1a n.又a 1=1,∴可知数列{a n }递增,则对一切n ≥1,有a n ≥1成立,从而0<1a n 2≤1. ……………………………6分当2≥n 时,a n 2=(a n -1+1a n -1)2=a 2n -1+1a 2n -1+2, 于是a n 2-a 2n -1=1a 2n -12, ∴ 2<a 2n -a 2n -1≤3; ……………………………8分(3)当2≥n 时,a n 2=a 2n -1+1a 2n -1+2, ∴a 2n =1 a 2n -1+…+1a 21+a 21+2(n -1).a 21=1,a 22=4,则当n ≥3时,a 2n =1 a 2n -1+…+1a 21+a 21+2(n -1)=1 a 2n -1+…+1a 22+1+1+2(n -1)=1a 2n -1+…+1a 22+2n >2n .a 22011=1 a 22010+…+1a 21+2(2011-1)+1>4021>3969=632, ……………………10分 a 22011=1 a 22010+…+1a 21+2(2011-1)+1=4021+1a 21+…+1 a 22010<4020+11+14+16+…+12×2010=4022+12(12+13+ (12010)=4022+12[(12+13+…+139)+(140+141+…+1199)+(1200+1201+…+12010)]<4022+12[(12+12+…+12)+(140+140+…+140)+(1200+1200+…+1200)]=4022+12(12×38+140×160+…+1200×1811)<4022+12+4+10)<4039<4096=642. ……………………14分∴63<a 2011<64,即a 2011的整数部分为63. ……………………16分数 学 Ⅱ(附 加 题)评 分 细 则 21-A :证明:(1)连结OP ,∵AC ⊥l ,BD ⊥l ,∴AC ∥BD .又OA =OB ,PC =PD ,∴OP ∥BD ,从而OP ⊥l . ∵P 在⊙O 上,∴l 是⊙O 的切线. ……………………6分(2)连结AP ,∵l 是⊙O 的切线,∴∠BPD =∠BAP .又∠BPD +∠PBD =90o ,∠BAP +∠PBA =90o ,∴∠PBA =∠PBD ,即PB 平分∠ABD . ……………………10分 21-B :解:ëéûù0 -11 0 ëéûù1 20 1=ëéûù0 -11 2. ……………………6分设A (a ,b ),则由ëéûù0 -11 2 ëêéûúùa b =ëêéûúù-3 4,得îíì-b =-3,a +2b =4, ∴îíìa =-2,b =3,即A (-2,3). ……………………10分 21-C :解:C 1:îíìx =2t 2+1,①y =2t t 2+1,②.②①得t =y x ,代入①,化简得x 2+y 2=2x . 又x =2t 2+1≠0,∴C 1的普通方程为(x -1)2+y 2=1(x ≠0).……………………6分 圆C 1的圆心到直线l :y =x -12的距离d =|1-0-12|2=122所求弦长=21-d 2=142. ……………………10分 21-D :证明:由èæøöa b -b c 2+ èæøöb c -c a 2+ èæøöc a -a b 2≥0,得 2(a 2b 2+b 2c 2+c 2a 2)-2(a b +b c +c a )≥0,∴a 2b 2+b 2c 2+c 2a 2≥b a +c b +a c.……………………10分22.解:作AP ⊥CD 于点P ,分别以AB 、AP 、AO 所在直线为x 、y 、z 轴建立坐标系,则A (0,0,0),B (1,0,0),P (0,22,0),D (-22,22,0),O (0,0,2),M (0,0,1). (1)AB →=(1,0,0),MD →=(-22,22,-1),则cos →→>=-1,故AB 与MD 所成角为π3. (2)OP →=(0,22,-2),OD →=(-22,22,-2), 设平面OCD 法向量n =(x ,y ,z ),则n ·OP →=0,n ·即îíì22y -2z =0-22x +22y -2z =0,取z =2,则n =(0,4,2). ……………………6分 易得平面OAB 的一个法向量为m =(0,1,0),cos <n ,m >=223, ……………………9分 故平面OAB 与平面OCD 所成二面角的平面角余弦值为223.………………10分 23.解:(1)p 1=p n (2-p n ), ……………………2分p 2=p n (2-p )n ; ……………………4分(2)(用二项式定理证明)p 2-p 1=p n {[1+(1-p )]n -2+[1-(1-p )]n=p n {[1+C 1n (1-p )+C 2n (1-p )2+C 3n (1-p )3+…+C nn (1-p )n ]-2+[1-C 1n (1-p )+C 2n (1-p )2-C 3n (1-p )3+…+(-1)n C n n (1-p )n ]}=p n [C 2n (1-p )2+C 4n (1-p )4+…]>0. …………………10分说明:作差后化归为用数学归纳法证明:(2-p )n >2-p n 也可.。
