中考微资料二
2024年江苏省淮安市盱眙县实验初级中学中考模拟考试二化学试卷

2024年江苏省淮安市盱眙县实验初级中学中考模拟考试二化学试卷一、选择题1.下列物质属于纯净物的是A.自来水B.石灰水C.矿泉水D.蒸馏水2.华夏造物历史悠久,《天工开物》中记载的下列造物过程涉及化学变化的是A.炼生铁B.晒海盐C.钉木舟D.织衣布3.下列物质属于无机材料的是A.橡胶轮胎B.蚕丝被C.玻璃瓶D.塑料盆4.下列净水方法中,净化程度最高的是A.蒸馏B.消毒C.吸附D.沉淀5.图所示为配制稀硫酸并制备氢气的实验,下列装置和实验操作正确并规范的是A.量取浓硫酸B.稀释浓硫酸C.制取氢气D.收集氢气6.三氟化氮(NF3)是一种优良的等离子蚀刻气体,用NF3蚀刻硅片时的产物均为气体,在芯片表面没有任何残留物。
该反应的微观示意图如下,下列有关说法正确的是A.该反应四种物质中只有一种单质B.该反应前后原子数目发生了改变C.反应物甲与乙粒子个数比为4:3D.物质丙与丁质量比为26:77.下列实验方案不能达到实验目的的是A .AB .BC .CD .D8.如图为4NH Cl 、NaCl 的溶解度曲线,下列有关说法正确的是A .NaCl 的溶解度一定小于4NH Cl 的溶解度B .1T ℃时,NaCl 、4NH Cl 两饱和溶液中溶质的质量质量分数相等C .除去4NH Cl 中的NaCl ,可用蒸发结晶D .将50℃时4NH Cl 饱和溶液100g 冷却至0℃,析出晶体等于21g 9.下列图像不能正确反映对应变化关系的是A .加热高锰酸钾制取氧气过程中剩余固体的质量B .一定温度下,向接近饱和的氯化钾溶液中加入氯化钾固体C .在密闭容器中用足量红磷燃烧测定空气中氧气的含量D .向等质量的铁粉和镁粉中分别加入足量的稀盐酸10.金-钒-氧团簇()234AuVO AuVO AuVO 、、催化除去CO 的反应过程如图所示(开尔文温度,常用符号K 表示),下列叙述正确的是A .催化剂在化学反应前后的性质和质量不变B .存在反应432AuVO CO AuVO CO +=+C .反应℃和反应℃是同一个反应D .除去28gCO 需要消耗216gO二、填空与简答11.中国传统节日,形式多样、内容丰富,是中华民族悠久的历史文化的一个组成部分。
2024成都中考数学第一轮专题复习之第三章 微专题 二次函数图象与系数a,b,c的关系 (含答案)

2024成都中考数学第一轮专题复习之第三章 微专题 二次函数图象与系数a ,b ,c 的关系1. (2023贵州)已知二次函数y =ax 2+bx +c 的图象如图所示,则点P (a ,b )所在的象限是( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限第1题图2. 如图,二次函数y =ax 2+bx +c 的图象与x 轴相交于A (-1,0),B 两点,对称轴是直线x =1,下列说法正确的是( )第2题图A. a >0B. b >0C. 点B 的坐标为(4,0)D. 当x >-1时,y 的值随x 值的增大而增大 3. (2023日照)在平面直角坐标系xOy 中,抛物线y =ax 2+bx (a ≠0)满足⎩⎪⎨⎪⎧3a +b >0a +b <0,已知点(-3,m ),(2,n ),(4,t )在该抛物线上,则m ,n ,t 的大小关系为( )A. t <n <mB. m <t <nC. n <t <mD. n <m <t4. (2023凉山州)已知抛物线y =ax 2+bx +c (a ≠0)的部分图象如图所示,则下列结论中正确的是( )第4题图A. abc <0B. 4a -2b +c <0C. 3a +c =0D. am 2+bm +a ≤0(m 为实数)5. (2023恩施州改编)如图,在平面直角坐标系xOy 中,O 为坐标原点,抛物线y =ax 2+bx +c (a ≠0)的对称轴为x =1,与x 轴的交点为(x 1,0),(x 2,0),其中一个交点为位于(2,0),(3,0)两点之间.下列结论正确的是( )A. 2a +b >0B. bc <0C. a >-13c D. -3<x 1·x 2<0第5题图6. 如图,二次函数y =ax 2+bx +c 的图象关于直线x =1对称,与x 轴交于A (x 1,0),B (x 2,0)两点,若-2<x 1<-1,则下列结论正确的是( )第6题图A. 3a +2b >0B. b 2<a +c +4acC. a >b >cD. a(m+1)(m-1)<b(1-m)7. 二次函数y=ax2+bx+c(a≠0)的图象如图所示.下列结论正确的是()第7题图A. 10a+3b+c>0B. a+b>am2+bmC. 3a+c<0D. 若ax21+bx1=ax22+bx2且x1≠x2,则x1+x2=4参考答案与解析1. D 【解析】由二次函数的图象开口方向向上,对称轴在y 轴的右侧,知a >0,x =-b 2a>0,∴b <0,∴P (a ,b )在第四象限.2. B 【解析】A.由图可知:抛物线开口向下,a <0,故选项A 错误,不符合题意;B.∵抛物线开口向下,∴a <0.∵抛物线的对称轴是直线x =-b 2a=1,∴b =-2a >0,故选项B 正确,符合题意;C.由A (-1,0),抛物线的对称轴是直线x =1可知,点B 的坐标为(3,0),故选项C 错误,不符合题意;D.∵抛物线的对称轴是直线x =1,开口向下,∴当x >1时,y 随x 的增大而减小,x <1时,y 随x 的增大而增大,故选项D 错误,不符合题意,故选B.3. C 【解析】∵当x =0时,y =ax 2+bx =0,∴抛物线恒过(0,0)点.∵⎩⎪⎨⎪⎧3a +b >0a +b <0 ,∴9a+3b >0,∴当x =3时,y =ax 2+bx =9a +3b >0,当x =1时,y =ax 2+bx =a +b <0,∴抛物线开口向上,∴抛物线的对称轴在直线x =12 与x =32之间.∵点(-3,m )到对称轴的距离在72 到92 之间,点(2,n )到对称轴的距离在12 到32 之间,点(4,t )到对称轴距离在52 到72 之间,∴n <t <m .4. C 【解析】∵抛物线开口向上,与y 轴交于负半轴,∴a >0,c <0.∵抛物线的对称轴为直线x =1,∴-b 2a=1,∴b =-2a <0,∴abc >0,故A 选项错误,不符合题意;∵当x =4时,y >0,抛物线的对称轴为直线x =1,∴当x =-2时,y >0,∴4a -2b +c >0,故B 选项错误,不符合题意;∵当x =3时,y =0,抛物线的对称轴为直线x =1,∴当x =-1时,y =0,∴a -b +c =0,又∵b =-2a ,∴3a +c =0,故C 选项正确,符合题意;∵抛物线的对称轴为直线x =1,且抛物线开口向上,∴抛物线的最小值为a +b +c =a -2a +c =-a +c ,∴am 2+bm +c ≥-a +c ,∴am 2+bm +a ≥0,故D 选项错误,不符合题意.5. D 【解析】∵抛物线y =ax 2+bx +c (a ≠0)的对称轴为直线x =1,∴-b 2a=1,∴b =-2a ,∴2a +b =0,故A 错误;∵抛物线开口向下,与y 轴交于正半轴,∴a <0,b =-2a >0,c >0,∴bc >0,故B 错误;∵抛物线y =ax 2+bx +c (a ≠0)的对称轴为直线x =1,x =3时y <0,∴x =-1时,y <0,即a -b +c <0,∴a -(-2a )+c <0,∴a <-13c ,故C 错误;∵抛物线与x 轴的交点为(x 1,0),(x 2,0),∴x 1,x 2为方程ax 2+bx +c =0的两个根,由函数图象与x 轴交点可知-1<x 1<0,2<x 2<3,∴-3<x 1·x 2<0,故D 正确.6. C 【解析】∵二次函数y =ax 2+bx +c 的图象关于直线x =1对称,∴其对称轴为直线x=1,即-b 2a=1,∴b =-2a ,∴3a +2b =3a -4a =-a .由图象可知该抛物线开口向上,∴a >0,∴3a +2b =-a <0,故A 错误;∵抛物线与x 轴有两个交点,∴Δ=b 2-4ac >0.由图象结合题意可知当x =-1时,y <0,∴a -b +c <0,∴a +c <b .∵a >0,∴b =-2a <0,∴a +c <0,∴b 2-4ac >a +c ,即b 2>a +c +4ac ,故B 错误;∵抛物线开口向上,与y 轴的交点在x 轴下方,∴a >0,c <0,∴a >c ,由②可知a -b +c <0,b =-2a ,∴3a +c <0,∴c <-3a ,∴b >c ,∴a >b >c ,故C 正确;由图象可知当x =1时,y 有最小值,且为a +b +c .∵a (m +1)·(m -1)-b (1-m )=am 2+bm -a -b =am 2+bm +c -(a +b +c ),又∵对于任意实数m ,都有y m ≥y =a +b +c ,∴am 2+bm +c -(a +b +c )≥0,即a (m +1)(m -1)-b (1-m )≥0,∴a (m +1)(m -1)≥b (1-m ),故D 错误.7. C 【解析】∵对称轴是直线x =1,与x 轴交点在(3,0)左边,∴9a +3b +c <0,∵图象开口向下,∴a <0,∴10a +3b +c <0,故A 错误;∵对称轴是直线x =1,图象开口向下,∴x =1时,函数最大值是a +b +c ,∴m 为任意实数时a +b +c ≥am 2+bm +c ,∴a +b ≥am 2+bm ,故B 错误;∵对称轴是直线x =1,∴-b 2a=1,b =-2a .由图可知抛物线与x 轴交点在(3,0)左边,∴由对称得另一个交点在(-1,0)右边,得a -b +c <0,∴3a +c <0,故C 正确;∵ax 21 +bx 1=ax 22 +bx 2,∴ax 21 +bx 1-ax 22 -bx 2=0,∴a (x 1+x 2)(x 1-x 2)+b (x 1-x 2)=0,∴(x 1-x 2)[a (x 1+x 2)+b ]=0.∵x 1≠x 2,∴a (x 1+x 2)+b =0,∴x 1+x 2=-b a.∵b =-2a ,∴x 1+x 2=2,故D 错误.。
人教版初中数学中考考点系统复习 方法技巧微专题(二) 反比例函数中的面积问题模型

1
第11题 图
-12
对点训练
-8
第3题 图
8
第4题 图
模型3 两点一垂线 模型展示
S△ABM=|k|
S△
模型解读 过正比例函数与反比例函数的一个交点作坐标轴的垂
线,两交点与垂足构成的三角形的面积等于|k|.
对点训练
D
A.k
B.k2
C.2
D.3
第5题 图
C A.k1=-6 B.k1=-3 C.k2=-6 D.k2=-12
第一轮 中考考点系统复习
第三章 函数及其图象 方法技巧微专题(二) 反比例函数中的
面积问题模型
模型1 一点.3
B.2
D.1
第1题 图
3
第2题 图
模型2 一点两垂线 模型展示
S四边形
模型解读 过反比例函数图象上一点作两条坐标轴的垂线,垂线与
坐标轴所围成的矩形面积等于|k|.
点)所构成的三角形面积,若两交点在同一支上,用减法; 若两交点分别在两支上,用加法.
对点训练
A.-12
C
B.-8
C.-6
D.-4
第8题 图
第9题 图
模型6 两曲一平行
模型解读 两条双曲线上的两点的连线与一条坐标轴平行,求这两
点与原点或坐标轴围成的图形面积,结合k的几何意义求解.
对点训练 13
第6题 图
模型4 两点两垂线 模型展示
S△APP'=2|k|
S▱
模型解读 过反比例函数与正比例函数的交点作两条坐标轴的垂
线,两交点与两垂足(或两垂线的交点)连线围成的图形面 积等于2|k|.
对点训练 8
模型5 两点和一点 S△AOB=S△COD-S△AOC-S△BOD
微专题二手拉手模型2021安徽中考数学高分分项突破方法分析模型应用PPT课件

AC 2
如解图,将△AED绕点A旋转,当点E落在线段CD上时,
∠AEC=∠ADB=90°,
∴BD= AB2 AD2
52
5 2
2
5 2
3.
第2题解图
AB=DB ABE=DBC , BE=BC
∴△ABE≌△DBC(SAS). ∴∠EAB=∠CDB. ∴∠AHD=∠ABD=60°;
(2)如解图,过B作AH、DC的垂线,
垂足分别为点M、N.
∵△ABE≌△DBC,
∴S△ABE=S△DBC.
即 1 AE·BM= 1 CD·BN.
22ຫໍສະໝຸດ 又∵AE=CD,结论 等)
模型应用 1. 如图,△ABD与△BCE都为等边三角形,连接AE与CD,延长AE交CD于
点H. (1)求证:∠AHD=60°; (2)连接HB,求证:HB平分∠AHC.
第1题图
证明:(1)∵∠ABE=∠ABD-∠EBD, ∠DBC=∠EBC-∠EBD,∠ABD=∠EBC=60°, ∴∠ABE=∠DBC. 在△ABE和△DBC中,
连接BD、CE,∠EAC=∠DAB.
(1)求证:△ABC∽△ADE;
(2)求证:△BAD∽△CAE; (3)已知BC=4,AC=3,AE=32 .将△AED绕点A旋转, 当点E落在线段CD上时,求BD的长.
第2题图
(1)证明:∵∠EAC=∠DAB, ∴∠CAB=∠EAD, ∵∠ACB=∠AED=90°, ∴△ABC∽△ADE;
微专题系列二
微专题 手拉手模型
(2016、2015、2014年23题, 2011年22题)
模型一 共顶点两等腰三角形,旋转后产生全等三角形
(2016、2015、2014年23题)
初中化学中考复习 专题2 课本基础实验及其创新-备战2020年中考科学探究题型特训(解析版)
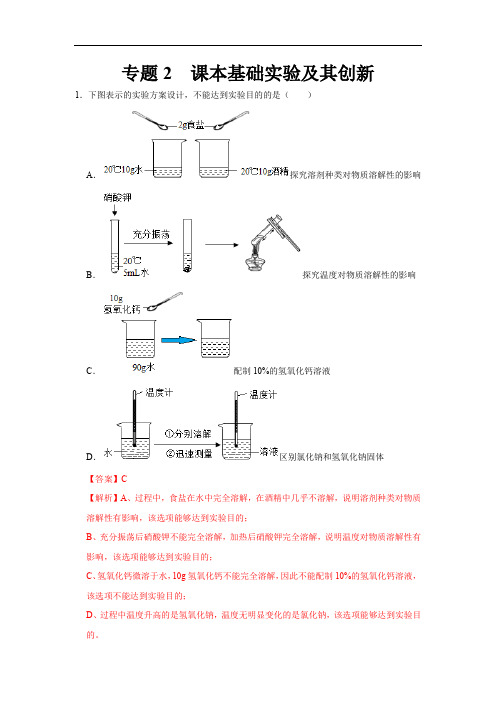
专题2 课本基础实验及其创新1.下图表示的实验方案设计,不能达到实验目的的是()A.探究溶剂种类对物质溶解性的影响B.探究温度对物质溶解性的影响C.配制10%的氢氧化钙溶液D.区别氯化钠和氢氧化钠固体【答案】C【解析】A、过程中,食盐在水中完全溶解,在酒精中几乎不溶解,说明溶剂种类对物质溶解性有影响,该选项能够达到实验目的;B、充分振荡后硝酸钾不能完全溶解,加热后硝酸钾完全溶解,说明温度对物质溶解性有影响,该选项能够达到实验目的;C、氢氧化钙微溶于水,10g氢氧化钙不能完全溶解,因此不能配制10%的氢氧化钙溶液,该选项不能达到实验目的;D、过程中温度升高的是氢氧化钠,温度无明显变化的是氯化钠,该选项能够达到实验目的。
2.下列实验操作、现象与结论一致的是()选项实验操作现象结论A向收集满CO2的软塑料瓶中加入约三分之一体积的水,旋紧瓶盖,振荡塑料瓶变瘪CO2能与水反应B点燃某气体,在火焰上方罩一个干冷的烧杯烧杯内壁有无色液体产生该气体不一定是氢气C将带火星的木条伸入某气体的集气瓶中木条熄灭该气体一定不含氧气D向某无色溶液中滴入紫色石蕊试液溶液变红该溶液一定是酸溶液【答案】B【解析】A、向收集满CO2的软塑料瓶中加入约三分之一体积的水,旋紧瓶盖,振荡,塑料瓶变瘪,不能说明CO2能与水反应,也可能是二氧化碳溶于水造成的,故选项实验操作、现象与结论不一致。
B、点燃某气体,在火焰上方罩一个干冷的烧杯,烧杯内壁有无色液体产生,该气体不一定是氢气,也可能是甲烷等气体,故选项实验操作、现象与结论一致。
C、将带火星的木条伸入某气体的集气瓶中,木条熄灭,不能该气体一定不含氧气,也可能是含有氧气的空气等,故选项实验操作、现象与结论不一致。
D、向某无色溶液中滴入紫色石蕊试液,溶液变红,该溶液不一定是酸溶液,也可能是硫酸氢钠等盐溶液,故选项实验操作、现象与结论不一致。
3.下列实验中,能达到相应实验目的的是()A.探究质量守恒定律B.探究燃烧的一个条件:温度达到可燃物的着火点C.探究甲烷组成含有氢、氧元素D.收集干燥的氢气【答案】B【解析】A、稀硫酸和氯化钠不能反应,不能用来验证质量守恒定律,该选项不能达到实验目的;B、过程中木屑燃烧,说明温度达到可燃物的着火点时才能够燃烧,该选项能够达到实验目的;C、过程中烧杯内壁出现水珠,说明反应生成水,进一步说明甲烷中含有氢元素,不能判断是否含有氧元素,该选项不能达到实验目的;D、可以用浓硫酸吸收水蒸气,但是不能用该装置收集氢气,该选项不能达到实验目的。
九年级数学中考一轮复习 微专题二讲义:圆的基本性质

微专题二:圆的基本性质【知识点扫描】1. 圆上各点到圆心的距离都等于.2. 圆是轴对称图形,任何一条直径所在的直线都是它的;圆又是对称图形,是它的对称中心.3. 垂直于弦的直径平分,并且平分;平分弦(不是直径)的垂直于弦,并且平分.4. 在同圆或等圆中,如果两个圆心角,两条弧,两条弦,两条弦心距,两个圆周角中有一组量,那么它们所对应的其余各组量都分别.5. 同弧或等弧所对的圆周角,都等于它所对的圆心角的.6. 半圆(或直径)所对的圆周角是,90°的圆周角所对的弦是.7.圆内接四边形的对角.8.圆的周长为,1°的圆心角所对的弧长为,n°的圆心角所对的弧长为,弧长公式为 .9.圆的面积为,1°的圆心角所在的扇形面积为,n°的圆心角所在的扇形面积为S= ×πr2 = = .10.圆锥的侧面积公式:S=rlπ.(其中为的半径,为的长);圆锥的全面积:S全=S侧+S底=πrl+πr2.【难点突破】重难点1垂径定理及其应用一.选择题:1.如图,AB是⊙O的直径,弦CD⊙AB于点G,点F是CD上一点,且满足CF:FD =3:7,连接AF并延长交⊙O于点E,连接AD、DE,若CF=3,AF=3,给出下列结论:⊙FG=2;⊙5 tanE;⊙495DEFS=;其中正确的是( )A. ⊙⊙B. ⊙⊙C. ⊙⊙D.⊙⊙⊙二、填空题:1.在半径为1的⊙O中,两条弦AB,AC的长分别为3和2,则弧BC的长度为.三、解答题:1.已知:如图,AB是圆O的直径,CD是圆O的弦,AB⊙CD,E为垂足,AE=CD=8,F是CD延长线上一点,连接AF交圆O于G,连接AD、DG.(1)求圆O的半径;(2)求证:⊙ADG⊙⊙AFD;(3)当点G是弧AD的中点时,求⊙ADG得面积与⊙AFD的面积比.重难点2圆周角定理及其推论一、选择题1. 如图,抛物线与x轴交于A、B两点,以线段AB为直径的半圆与抛物线在第二象限的交点为C,与y轴交于D点,设⊙BCD=α,则的值为()A.sin2α B.cos2α C.tan2α D.tan﹣2α2.如图,点C为⊙ABD外接圆上的一点(点C不在上,且不与点B,D重合),且⊙ACB=⊙ABD=45°,若BC=8,CD=4,则AC的长为()A.8.5B.5C.4D.二、填空题1.如图,⊙O是⊙AB C的外接圆,AD⊙B C于D,CE⊙AB于E,AD交CE于H点,交⊙O于N,OM⊙B C于M,BF为⊙O的直径,下列结论:⊙四边形AH CF为平行四边形;⊙AH=2OM,⊙BF=2F C;⊙DN=DH;其中正确的有______(第1题) (第2题)2.如图,在平面直角坐标系中,已知点A (0,2)、B(0,2+m)、C(0,2-m)(m>0),点P 在以D(4,6)为圆心,1 为半径的圆上运动,且始终满足⊙BPC=90°,则m的最大值是3.如图,AB,BC是⊙O的弦,⊙B=60°,点O在⊙B内,点D为上的动点,点M,N,P 分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是三.解答题1.请完成以下问题:(1)如图1,=,弦AC与半径OD平行,求证:AB是⊙O的直径;(2)如图2,AB是⊙O的直径,弦AC与半径OD平行.已知圆的半径为r,AC=y,CD=x,求y与x的函数关系式.2.如图,已知等腰直角三角形ABC ,点P 是斜边BC 上一点(不与B ,C 重合),PE 是⊙ABP 的外接圆⊙O 的直径.(1)求证:⊙APE 是等腰直角三角形; (2)若⊙O 的直径为2,求PC 2+PB 2的值.3.如图1,已知四边形ABCD 内接于圆0,AD=BC ,延长AB 到E ,使BE=AB ,连接EC ,F 是EC 的中点,连接BF(1)若圆0的半径为3,⊙DAB=120°,求劣弧BD 的长; (2)如图2,连接BD ,求证:BF=21BD ; (3)如图3,G 是BD 的中点,过B 作AE 的垂线交圆0于点P ,连接PG ,PF ,求证:PG=PF图1 图2 图34.如图1,圆O的两条弦AC、BD交于点E,两条弦所成的锐角或者直角记为⊙α(1)点点同学通过画图和测量得到以下近似数据:的度数30.2°40.4°50.0°61.6°的度数55.7°60.4°80.2°100.3°⊙α的度数43.0°50.2°65.0°81.0°猜想:、、⊙α的度数之间的等量关系,并说明理由﹒(2)如图2,若⊙α=60°,AB=2,CD=1,将以圆心为中心顺时针旋转,直至点A与点D 重合,同时B落在圆O上的点,连接CG﹒⊙求弦CG的长;⊙求圆O的半径.重难点3 三角形的外接圆及圆内接四边形 一、选择题1.如图,点A 的坐标为A (8,0),点B 在y 轴正半轴上,且AB=10,点P 是⊙AOB 外接圆上一点,且⊙BOP=45°,则点P 的坐标为( )A .(7,7)B .(7,7)C .(5,5)D .(5,5)2.如图所示,四边形ABCD 中,DC⊙AB ,BC=2,AB=AC=AD=3.则BD 的长为( ) A.13 B.5 C.23 D.243.如图,⊙ABC 内接于圆O ,延长AO 交BC 于点P ,交圆O 于点D ,连结OB ,OC ,BD ,DC ( )A .若AB=AC ,则BC 平分ODB .若OCBD ,则CD :AB=:3C .若⊙ABO=30°,则OC BDD .若BC 平分OD ,则AB=AC二.填空题1.在⊙ABC 中,45AB =5AC =,11BC =,则⊙ABC 的外接圆半径为____________2、如图,⊙ABC内接于⊙O,其外角平分线AD交⊙O于D,DM⊙AC于M,下列结论中正确的是.⊙DB=DC;⊙AC+AB=2CM;⊙AC﹣AB=2AM;⊙S⊙ABD=S⊙ABC.重难点4弧长及扇形面积的有关计算一.选择题1.如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为()A.π﹣1B.2π﹣1C.2π﹣2D.π﹣2二.填空题1、如图,一根长为a的竹竿AB斜靠在墙上,竹竿AB的倾斜角为α,当竹竿的顶端A下滑到点A'时,竹竿的另一端B向右滑到了点B',此时倾斜角为β.(1)线段AA'的长为.(2)当竹竿AB滑到A'B'位置时,AB的中点P滑到了P',位置,则点P所经过的路线长为(两小题均用含a,α,β的代数式表示)2、如图,△ABC中,D为BC的中点,以D为圆心,BD长为半径画一弧交AC于E点,若∠A=60°,∠B=100°,BC=4,则扇形BDE的面积为_ __3、如图,AB为半圆O的直径,C为AO的中点,CD⊙AB交半圆与点D,以C为圆心,CD为半径画弧DE交AB于E点,若AB=4cm,则图中阴影部分面积为cm2.三、简答题1、在⊙O中,己知弦BC所对的圆周角⊙BAC与圆心角⊙BOC互补.(1)求⊙BOC的度数.(2)若⊙O的半径为4,求弦BC和劣弧BC组成的弓形面积.。
2024年中考数学复习课件---微专题2 二次函数的增减性、最值问题

确的是( C
A.y1<y2<y3
C.y2<y1<y3
)
B.y1<y3<y2
D.y2<y3<y1
1
2
微专题2 二次函数的增减性、最值问题
返回类型清单
2.已知二次函数y=ax2+4ax+c(a<0)的图象经过A(-5,y1),B(-3,y2),
微专题2
二次函数的增减性、最值问题
微专题2
二次函数的增减性、最值
问题
类
型
清
单
类型一
根据对称性和增减性比较函数值
类型二
当对称轴确定求最值或取值范围
类型三
对称轴不确定,求最值或取值范围
微专题2 二次函数的增减性、最值问题
类型一
返回类型清单
根据对称性和增减性比较函数值
方法指导
1.解析式已知时,用代入法比较,将各点的橫坐标代入解析式,求出
数).当自变量x的值满足-1≤x≤2时,与其对应的函数值y随x的
增大而增大,则m的取值范围是 m≤-1
.
6
7
其在-1≤x≤2的最小值为-4,则m的值为
0
.
3
4
5
微专题2 二次函数的增减性、最值问题
返回类型清单
5.(2022·遵义桐梓县一模改编)如图,抛物线y=x2-2x-3与x轴交于
点A,B,交y轴于点C.当m-1≤x≤m时,函数有最小值2m,求m的值.
解:∵y=x2-2x-3=(x-1)2-4,∴抛物线顶点坐标为(1,-4).
对称轴在自
2024成都中考数学第一轮专题复习之第三章 微专题 二次函数综合题 知识精练(含答案)

2024成都中考数学第一轮专题复习之第三章微专题二次函数综合题知识精练类型一线段问题1.(2023重庆A卷节选)如图,在平面直角坐标系中,抛物线y=ax2+bx+2过点(1,3),且交x轴于点A(-1,0),B两点,交y轴于点C.(1)求抛物线的表达式;(2)点P是直线BC上方抛物线上的一动点,过点P作PD⊥BC于点D,过点P作y轴的平行线交直线BC于点E,求△PDE周长的最大值及此时点P的坐标.第1题图2.(2023济宁节选)如图,直线y=-x+4交x轴于点B,交y轴于点C,对称轴为x=32的抛物线经过B,C两点,交x轴负半轴于点A.P为抛物线上一动点,点P的横坐标为m,过点P作x轴的平行线交抛物线于另一点M,作x轴的垂线PN,垂足为N,直线MN交y轴于点D.(1)求抛物线的解析式;(2)若m<32,设直线MN交直线BC于点E,是否存在这样的m值,使MN=2ME?若存在,求出此时m的值;若不存在,请说明理由.第2题图类型二面积问题3.(2023安徽)在平面直角坐标系中,点O是坐标原点,抛物线y=ax2+bx(a≠0)经过点A(3,3),对称轴为直线x=2.(1)求a,b的值;(2)已知点B,C在抛物线上,点B的横坐标为t,点C的横坐标为t+1.过点B作x轴的垂线交直线OA于点D,过点C作x轴的垂线交直线OA于点E.(ⅰ)当0<t<2时,求△OBD与△ACE的面积之和;(ⅱ)在抛物线对称轴右侧,是否存在点B,使得以B,C,D,E为顶点的四边形的面积为32若存在,请求出点B的横坐标t的值;若不存在,请说明理由.类型三等腰三角形存在性问题4.(2023青海省卷节选)如图,二次函数y=-x2+bx+c的图象与x轴相交于点A和点C(1,0),交y轴于点B(0,3).(1)求此二次函数的解析式;(2)二次函数图象的对称轴上是否存在点M,使得△AMB是以AB为底边的等腰三角形?若存在,请求出满足条件的点M的坐标;若不存在,请说明理由.第4题图类型四直角三角形存在性问题5.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)与x轴,y轴分别交于点A(4,0),B(0,-4),对称轴是直线x=1,点P为平面内一点.(1)求抛物线的函数表达式;(2)若点P为y轴右侧抛物线上一点,其横坐标为t,过点P分别作AB和y轴的垂线,垂足分别为点E,F,PF交AB于点G,当△PEG≌△BFG时,求t的值;(3)若P是抛物线对称轴上的点,将抛物线y=ax2+bx+c先向左平移4个单位,再向上平移3个单位,得到新的抛物线y1,抛物线y1与y轴交于点M,点N为抛物线y1的顶点,当△PMN 为直角三角形时,直接写出所有符合条件的点P的纵坐标.第5题图备用图类型五特殊四边形存在性问题6.(2023邵阳节选)如图,在平面直角坐标系中,抛物线y=ax2+x+c经过点A(-2,0)和点B(4,0),且与直线l:y=-x-1交于D,E两点(点D在点E的右侧),点M为直线l上的一动点,设点M的横坐标为t.(1)求抛物线的解析式;(2)抛物线与y轴交于点C,点R为平面直角坐标系上一点,若以B,C,M,R为顶点的四边形是菱形,请求出所有满足条件的点R的坐标.第6题图类型六相似三角形问题7.(2023随州节选)如图,平面直角坐标系xOy中,抛物线y=ax2+bx+c过点A(-1,0),B(2,0)和C(0,2),连接BC,点P(m,n)(m>0)为抛物线上一动点,过点P作PN⊥x轴交直线BC于点M,交x轴于点N.(1)直接写出....抛物线和直线BC的解析式;(2)当P点在运动过程中,在y轴上是否存在点Q,使得以O,P,Q为顶点的三角形与以B,C,N为顶点的三角形相似(其中点P与点C相对应),若存在,直接写出....点P和点Q的坐标;若不存在,请说明理由.第7题图类型七角度问题x2+bx+c经过点A(-4,0),B(2,0),与y轴8.如图,在平面直角坐标系中,抛物线y=12交于点C,作直线A C.(1)求抛物线的函数表达式;(2)点M是直线AC下方抛物线上的一个动点,连接MA,MC,BC,求四边形ABCM面积的最大值及此时点M的坐标;(3)若点D是抛物线的顶点,点P是抛物线上的一个动点,是否存在点P,使得∠ACP=∠CAD,若存在,请直接写出点P的坐标;若不存在,请说明理由.第8题图参考答案与解析1.解:(1)将点(1,3),(-1,0)代入抛物线y=ax2+bx+2,+b+2=3,-b+2=0,=-12,=32,∴该抛物线的表达式为y=-12x2+32x+2;(2)∵当x=0时,y=2,∴C(0,2).∵当y=0时,x=-1或x=4,∴B(4,0),∴OC=2,OB=4,BC=25.∵直线BC过点B(4,0),C(0,2),∴直线BC的函数表达式为y=-12x+2.∵PD⊥BC,PE∥y轴,∴∠PDE=∠BOC=90°,∠PED=∠BCO,∴△PDE∽△BOC,∴DEOC=PEBC=PDBO,∴DE2=PE25=PD4,∴DE=55PE,PD=255PE.设P(m,-12m2+32m+2),则E(m,-12m+2)(0<m<4).∴PE=-12m2+32m+2-(-12m+2)=-12(m-2)2+2.∵-12<0,∴当m=2时,PE有最大值,最大值为2,∴△PDE 周长的最大值为DE +PD +PE =55PE +255PE +PE =655+2.此时点P 的坐标为(2,3).2.解:(1)在直线y =-x +4中,当x =0时,y =4,当y =0时,x =4,∴B (4,0),C (0,4).由题可设抛物线的解析式为y =a (x -32)2+k (a ≠0),把B (4,0),C (0,4)(4-32)2+k =0,(0-32)2+k =4,=-1,=254,∴抛物线的解析式为y =-(x -32)2+254=-x 2+3x +4;(2)存在,理由如下:∵点A 是抛物线y =-x 2+3x +4与x 轴的另一个交点,∴点A (-1,0).①当-1<m <32时,点P 在x 轴的上方,∵MN =2ME ,∴点E 为线段MN 的中点,∴点E 的横坐标为x E =3-m +m 2=32,纵坐标y E =y M +y N 2=-m 2+3m +42∴点E 的坐标为(32,-m 2+3m +42).又∵点E 在直线BC :y =-x +4上,代入得m 2-3m +1=0,解得m 1=3+52(舍去),m 2=3-52.②当m =-1时,P 点即A 点,此时点E 与点M 重合,不合题意.③当m <-1时,点P 在x 轴下方,点E 在射线NM 上.设线段MN 的中点是点F (32,-m 2+3m +42).∵MN =2ME ,∴M 为EF 的中点,∴点M 的横坐标为x m =3-m =x E +x F 2=x E +322.纵坐标为y m =-m 2+3m +4=y E +y F 2=y E +-m 2+3m +422.∴点E 的坐标为(92-2m ,-3m 2+9m +122).又∵点E 在y =-x +4上,∴代入得-3m 2+9m +122=2m -12,即3m 2-5m -13=0,解得m 1=5+1816(舍去),m 2=5-1816.综上,存在m 使MN =2ME ,m =3-52或m =5-1816. 3.解:(1)-b 2a=2,a +3b =3,=-1=4;(2)(i)如解图①,延长BD 与x 轴交于点M ,延长CE 与x 轴交于点N ,过点A 作AF ⊥CE 于点F ,第3题解图①由(1)知抛物线的解析式为y =-x 2+4x ,由题意知直线OA 的解析式为y =x ,∴B (t ,-t 2+4t ),C (t +1,-(t +1)2+4(t +1)),D (t ,t ),E (t +1,t +1),∴OM =t ,BD =-t 2+3t ,CE =-(t +1)2+3(t +1),AF =-t +2,∵0<t <2,∴1<t +1<3,∴S △OBD +S △ACE=12OM ·BD +12CE ·AF=12t ·(-t 2+3t )+12[-(t +1)2+3(t +1)]·(-t +2)=2.(ii)存在.如解图②,当点B 在点D 上方,即2<t <3时,过点D 作DQ ⊥EC 于点Q ,第3题解图②∵BD ∥EC ,∴四边形DBEC 为梯形,则S 四边形DBEC =12(BD +EC )·DQ =12(-t 2+3t +t 2-t -2)·1=t -1,当S 四边形DBEC =32时,可得t -1=32,解得t =52;当点D 在点B 上方,即t >3时,如解图③,过点D 作DQ ⊥EC 于点Q ,第3题解图③此时S 四边形DBCE =12(BD +EC )·DQ =12(t 2-3t +t 2-t -2)·1=t 2-2t -1,令t 2-2t -1=32,解得t 1=142+1<3,t 2=-142+1<3,均舍去.综上所述,t 的值为52.4.解:(1)∵点C (1,0)和点B (0,3)是二次函数y =-x 2+bx +c 图象上的两点,把点C (1,0)和点B (0,3)1+b +c =0,=3,=-2,=3,∴二次函数的解析式为y =-x 2-2x +3;(2)存在.如解图,连接AB ,作线段AB 的垂直平分线交对称轴于点M ,连接AM ,BM ,过点M 作MG ⊥y 轴于点G .设点M (-1,y ),对称轴与x 轴交于点Q ,则QM =y ,BG =3-y .∵△AMB 是等腰三角形,∴AM =BM ,则AM 2=BM 2,∴在Rt △AQM 中,AM 2=AQ 2+MQ 2=22+y 2.在Rt △BMG 中,BM 2=MG 2+BG 2=12+(3-y )2∴22+y 2=12+(3-y )2,解得y =1,∴点M 的坐标为(-1,1).第4题解图5.解:(1)∵抛物线过点B (0,-4),∴c =-4,即抛物线的函数表达式为y =ax 2+bx -4.将点A (4,0)代入y =ax 2+bx -4中,得16a +4b -4=0.∵抛物线的对称轴是直线x =1,∴-b 2a=1,a +4b -4=0,-b 2a=1,=12,=-1,∴抛物线的函数表达式为y =12x 2-x -4;(2)∵PE ⊥AB ,PF ⊥y 轴,∴∠PEG =∠BFG =90°.∵∠PGE =∠BGF ,∴△PEG ∽△BFG .∵A (4,0),B (0,-4),∴OA =OB =4,∴△OAB 是等腰直角三角形,∴∠OBA =45°.∵PF ⊥y 轴,∴△BFG 是等腰直角三角形,∴∠BGF =45°,∴∠PGE =45°∵PE ⊥AB ,∴△PEG 是等腰直角三角形,∴PG =2EG .当△PEG ≌△BFG 时,∴EG =FG ,∴PG =2FG .由A (4,0),B (0,-4)可知直线AB 的函数表达式为y =x -4,∴P (t ,12t 2-t -4),G (12t 2-t ,12t 2-t -4),∴PG =t -(12t 2-t )=-12t 2+2t ,FG =12t 2-t ,∴-12t 2+2t =2(12t 2-t ),解得t =0(舍去)或t =22;第5题解图(3)当△PMN 为直角三角形时,所有符合条件的点P 的纵坐标为-256或73或3+174或3-174.【解法提示】∵y =12x 2-x -4=12(x -1)2-92,∴y 1=12(x -1+4)2-92+3=12(x +3)2-32=12x 2+3x +3,∴N (-3,-32).令x =0,则y 1=3,∴M (0,3).∵抛物线y 的对称轴为直线x =1,点P 在抛物线对称轴上,∴设P (1,m ),∴PN 2=(1+3)2+(m +32)2,MN 2=1174,PM 2=12+(m -3)2.∵△PMN 为直角三角形,∴需要分以下三种情况:①当∠MNP =90°时,MN 2+PN 2=PM 2,1174+(1+3)2+(m +32)2=12+(m -3)2,解得m =-256;②当∠PMN =90°时,PM 2+MN 2=PN 2,12+(m -3)2+1174=(1+3)2+(m +32)2,解得m =73;③当∠MPN =90°时,PM 2+PN 2=MN 2,12+(m -3)2+(1+3)2+(m +32)2=1174,解得m =3+174或m =3-174.综上所述,当△PMN 为直角三角形时,所有符合条件的点P 的纵坐标为-256或73或3+174或3-174.6.解:(1)∵抛物线y =ax 2+x +c 经过A ,B 两点,a -2+c =0a +4+c =0,=-12,=4,∴抛物线的解析式为y =-12x 2+x +4;(2)∵抛物线与y 轴交于点C ,∴当x =0时,y =4,即C (0,4).∵B (4,0),M (t ,-t -1),∴BC =42+42=42,BM 2=(t -4)2+(-t -1)2=2t 2-6t +17,CM 2=t 2+(t +5)2=2t 2+10t +25,①如解图①,当BC 为对角线时,MB =CM ,∴2t 2-6t +17=2t 2+10t +25,解得t =-12,∴M (-12,-12).R -12=4+0,R -12=4+0,R =92,R =92,∴R (92,92);②当CM 为对角线时,如解图②,∵四边形BMRC 为菱形,∴BM =BC ,∴2t 2-6t +17=(42)2,解得t =3-392或t =3+392,∴-t -1=-3-392-1=-5+392或-t -1=-3+392-1=-5-392,∴M (3-392,-5+392)或M (3+392,-39-52).由菱形的性质可得,R +4=3-392+0,R +0=-5+392+4,或R +4=3+392+0,R +0=-5-392+4,解得R =-5-392,R =3+392,或R =-5+392,R =3-392,∴R (-5-392,3+392)或R (-5+392,3-392);③当BM 为对角线时,如解图③,即四边形CMRB 是菱形,点R 的坐标即为四边形BMRC 为菱形时,点M 的坐标,∴R (3-392,-5+392)或R (3+392,-39-52).综上所述,点R 的坐标为(3-392,-5+392)或(3+392,-39-52)或(-5-392,3+392)或(-5+392,3-392)或(92,92).图①图②图③第6题解图7.解:(1)抛物线的解析式为y =-x 2+x +2,直线BC 的解析式为y =-x +2;【解法提示】(1)∵抛物线过点A (-1,0),B (2,0),∴抛物线的解析式为y =a (x +1)·(x -2),将点C (0,2)的坐标代入上式,得2=-2a ,∴a =-1.∴抛物线的解析式为y =-(x +1)(x -2),即y =-x 2+x +2.设直线BC 的解析式为y =kx +t ,将点B (2,0),C (0,2)的坐标代入上0=2k +t2=t k =-1t 2.∴直线BC 的解析式为y =-x +2;(2)存在.P (2,2),Q (0,2-1)或P (13+13,7+139),Q (0,4-2139)或P (1+3,-1-3),Q (0,1)或P (1+5,-3-5),Q (0,-2).【解法提示】∵点P 与点C 相对应,∴△POQ ∽△CBN 或△POQ ∽△CNB .①若点P 在点B 左侧,则∠CBN =45°,BN =2-m ,CB =22.当△POQ ∽△CBN ,即∠POQ =45°时,直线OP 的解析式为y =x ,∴-m 2+m +2=m ,解得m =2或m =-2(舍去).∴OP 2=(2)2+(2)2=4,即OP =2.∴OP BC =OQ BN ,即222=OQ 2-2,解得OQ =2-1.∴P (2,2),Q (0,2-1).当△POQ ∽△CNB ,即∠PQO =45°时,当点Q 在点P 上方时,PQ =2m ,OQ =-m 2+m +2+m =-m 2+2m +2,∴PQ CB =OQ NB ,即2m 22=-m 2+2m +22-m,解得m =1+5(舍去)或m =1-5(舍去).当点Q 在点P 下方时,PQ =2m ,直线QP 的解析式为y =x -m 2+2.∴OQ =m 2-2,∴PQ CB =OQ NB,即2m 22=m 2-22-m,解得m =13+13或m =1-133(舍去),∴OQ =-4+2139,∴P (13+13,7+139),Q (0,4-2139).②若点P 在点B 右侧,则∠CBN =135°,BN =m -2.当△POQ ∽△CBN ,即∠POQ =135°时,直线OP 的解析式为y =-x ,∴-m 2+m +2=-m ,解得m =1+3或m =1-3(舍去),∴OP =2m =2+6,∴OP BC =OQ BN ,即2+622=OQ 3-1,解得OQ =1.∴P (1+3,-1-3),Q (0,1).当△POQ ∽△CNB ,即∠PQO =135°时,PQ =2m ,OQ =|-m 2+m +2+m |=m 2-2m -2.∴PQ CB =OQ NB ,即2m 22=m 2-2m -2m -2,解得m =1+5或m =1-5(舍去).∴P (1+5,-3-5),Q (0,-2).综上所述,P (2,2),Q (0,2-1)或P (13+13,7+139),Q (0,4-2139)或P (1+3,-1-3),Q(0,1)或P(1+5,-3-5),Q(0,-2).8.解:(1)∵抛物线y=12x2+bx+c经过点A(-4,0),B(2,0),-4b+c=0,2b+c=0,=1,=-4,∴抛物线的函数表达式为y=12x2+x-4;(2)在y=12x2+x-4中,令x=0,得y=-4,∴点C(0,-4).设直线AC的函数表达式为y=kx+c,将A(-4,0),C(0,-4)代入,=-4k+c,4=c,=-1,=-4,∴直线AC的函数表达式为y=-x-4.如解图①,过点M作ME⊥x轴于点E,交AC于点F,设点M的坐标为(d,12d2+d-4),则点F的坐标为(d,-d-4),∴MF=(-d-4)-(12d2+d-4)=-12d2-2d.∵A(-4,0),B(2,0),C(0,-4),∴OA=4,AB=6,OC=4,∴S△ABC=12AB·OC=12×6×4=12,S△ACM=12MF·OA=12×(-12d2-2d)×4=-d2-4d=-(d+2)2+4.当d=-2时,S△ACM取得最大值,为4.∴四边形ABCM面积的最大值=12+4=16,此时点M的坐标为(-2,-4);第8题解图①(3)存在点P,点P的坐标为(-5,72)或(-103,-169).【解法提示】如解图②,过点D 作DG ⊥x 轴于点G ,过点P 作PH ⊥y 轴于点H ,则∠DGA =∠CHP =90°.由题意得点D (-1,-92),设P (m ,12m 2+m -4),∴DG =92,AG =3,CH =12m 2+m -4-(-4)=12m 2+m ,PH =-m ,分两种情况讨论:①当点P 在直线AC 上方时,记为P 1,设过点P 1作P 1H ⊥y 轴的点H 为H 1,∵∠ACP 1=∠CAD ,∴P 1C ∥AD ,易得∠DAG =∠CP 1H 1.又∵∠DGA =∠CH 1P 1=90°,∴△DAG ∽△CP 1H 1,∴DG CH 1=AG P 1H 1,即9212m 2+m =3-m ,解得m =0(舍去)或m =-5,∴点P 1(-5,72);②当点P 在直线AC 下方时,记为P 2,设过点P 2作P 2H ⊥y 轴的点H 为H 2,∵OA =OC =4,∴∠OAC =∠OCA .∵∠ACP 2=∠CAD ,∴∠OAC +∠CAD =∠OCA +∠ACP 2,即∠DAG =∠P 2CH 2.又∵∠DGA =∠P 2H 2C =90°,∴△DAG ∽△P 2CH 2,∴DG P 2H 2=AG CH 2,即92-m =312m 2+m ,解得m =0(舍去)或m =-103,∴点P 2(-103,-169).综上所述,存在点P,点P的坐标为(-5,72)或(-103,-169).第8题解图②。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动词时态讲与练一般现在I __________TV every night. He ____________TV every night.一般过去I _____________TV last night.一般将来I________________ TV tomorrow evening.I________________ TV tomorrow evening.现在进行I_______________ TV now.过去进行I_________________ TV at that moment.现在完成I________________ TV already.过去完成I________________ TV by eleven last night.否定句或疑问句一般现在主语+ don’t/doesn’t +动原Do/Does +主语+动原一般过去主语+ didn’t +动原Did +主语+ 动原一般将来主语+ won’t + 动原Will +主语+ 动原现在进行主语+ am not /isn’t/aren’t +VingAm/ Is/ Are +主语+Ving过去进行主语+ wasn’t/ weren’t + VingWas/ Were +主语+Ving现在完成主语+ hasn’t/ haven’t+过去分词Have/ Has +主语+过去分词过去完成主语+ hadn’t +过去分词Had +主语+过去分词(一).一般现在时时间状语(时态标志)A:频率副词:always ;usually;often;sometimes; once a week, twice a year,etc. B: in the + 一天三段C: every + 时间名词D: on + 一周七天或一周七天+ 一天三E:on + 一周七天的复数= every + 一周七天用法1.表示经常性或习惯性的动作。
I leave home for school at 7 every morning.His father always takes a walk after supper2.表示目前的状态、能力、性格、个性。
I don't want so much. He works in an office.His father likes dumplings very much.3.用于表示客观真理,客观存在,科学事实;格言或警句中The earth moves around the sun. Shanghai lies in the east of China.Light travels faster than sound. Pride goes before a fall.【注意】此用法如果出现在宾语从句中,即使主句是过去时,从句谓语也要用一般现在时。
Columbus proved that the earth _______ (be)round.4.在时间状语从句或条件状语从句中,一般现在时代替一般将来时。
I'll help you as soon as you have problem.Tell Xiao Li about it if you meet him.1.We’ll go camping if it________ (be) fine tomorrow.2.We __________ (leave) until her mother__________ (come) back next week.3.If it ______(rain), we won’t go to the park.应用一般现在时各语气的基本句型结构思考--- 将下列变为否定句和一般疑问句They clean their classroom every day.________________________________ ____________________________ She helps her mother on weekends.________________________________ ______________________________ 用所给动词的正确形式填空1.My parents ______(work) five days a week.2.Li Lei ______(go) to work on foot.3.The sun _______(rise) in the east.4. A bike__________ (not run) as fast as a car.5.We __________(not like) such a kind of men.6._____ leaves_______ (fall) in winter?7.______ the sun ______(go) down in the west?8.What ____you usually _____(do) on Sundays?9.How often ____you _____(watch) TV?(二).现在进行时时间状语(时态标志)A:now;right now;at this moment etc.B: 句首提示词:Look! Listen!C:前句: It’s + 时刻。
下句马上叙述一个动作。
用法1. 表示说话者说话时正发生或者进行的动作;它注重现在正在进行的动作,而不管动作从什么时间开始,到什么时间结束。
What are you doing now?I am looking for my key.Listen! How wonderfully the girl __________(sing).Look! The children __________ (play) happily.The students ___________ (have) an exam at the moment.2.表示目前一段时间内正在进行的动作(但说话时这个动作不一定在进行)。
The students are preparing for the examination this week .We_______ (get) ready for the Art Festive these days.They ____________ (study) hard this term.The workers ___________(pick) apples on the farm these days.【注意】有些动词一般不可以用于进行时态①表示状态的动词,尤其是静态动词,如:be, have (有)②表示认识、知觉和情感的动词,如:know(知道), think(认为), hear(听见), find(发现), see(看见), like(喜欢), want(想要), wish(希望), prefer (更喜欢)等。
I am not having so much money now. WI don’t have so much money now.R1.We __________(have) a meeting now.2.Look! The boy ________(cry) hard. He ________(look) for his mother.3.Tom ___________(not read) now. He _________(help) his parents.4. --What ____ you_______ (do) these day?--I __________(write) an important article.5.--____you _______(cook) in the kitchen, mum?I am so hungry.--No, I ___________(wash) the clothes(三).一般将来时时间状语(时态标志)A: tomorrow / + 一天三段B: next + 时间名词C: in + 一段时间D: the day after tomorrow / the week after next / the month…/ the year….E: at once, later on, soon, in a moment, from now onF: 凡是说话时没到来的年,月,日,时刻用法1. 表示将来的动作或状态I’ll attend the meeting tomorrow.He will visit us next month.They will be back in two days.--It’s a secret between us. Don’t tell anybody. --Sure, I________.A. doB. don’tC. willD. won’t2.表示打算,计划; 已决定最近或将来要作的某事I am going to Beijing next week.--What are you going to do next week?-- I am going to listen to music.Look at the clouds. There is going to be a storm3. 动词“go, come, leave, arrive, stay,start, begin, fall, die”等多用进行结构即将发生的事。
We are leaving for London.The meeting is starting right now.The old man is dying.注:在条件状语从句中,一般用will表将来.We __________(come) if he invites us.They __________(have) a picnic if it doesn’t rain tomorrow.1.We ______________(have) a sports meeting next week.2.His parents_____________ (be) back in three weeks.3.___they ____________(do) the cleaning soon?4.They _____________(not discuss) it until the manager comes back.5. Please get ready. The train_________ (arrive)6.He _________(not go) swimming if it rains tomorrow.阅读理解(一)1.From the passage, we can't know where ________ will be held.A.Jay Chou's concert B.the painting showC.the fashion show D.the magic show2.Both Jay Chou's concert and the fashion show will last for ________.A.one month B.4 hours C.3 hours D.2 hours3.All the activities will take place in ________.A.September B.August C.July D.June4.Aifei may be a ________.A.singer B.painter C.magic performer D.fashion designer5.A ticket to the magic show is ________ yuan more expensive than that to the art show.A.30 B.40 C.100 D.150阅读理解(二)Even in early times, people could realize the importance of dreams and knew that dreams gave meaning to life. Every great achievement has been the result of years of dreaming. If a person has a dream and holds fast to it, he or she will find a way to bring it into reality(现实).Children do not have much experience or knowledge. However, they are natural dreamers. We should not laugh at them for being naive. With their rich imagination, they will come up with fantastic dreams. History is full of examples. Many great men were dreamers when they were children. One such dreamer was Thomas Edison. He used to be ostracized(排斥)when he was in primary school, but his achievements were greater than everyone else's in his time.Teenagers and young people should also be encouraged to dream. The world is full of successful teenagers and young people. They dreamt big and their dreams changed their lives and even the world. Steve Jobs and Bill Gates are the good examples. They have developed technology and brought great progress to human besides making money for themselves. Older people should believe that it is never too late to dream and that human mind is never too old to make dreams turn into reality. Colonel Saunders realized his dreams at the age of 67 and set up the biggest fried chicken company (KFC) in the world.To dream is a wonderful ability which can lead to wonderful results. Olympic records were broken by players who were brave enough to dream. No one is too young or too old to dream and to make dreams come true.6.People who ________ could probably realize their dreams.A.find a way to dream B.dream and hold fast to themC.get the meaning of life D.have very good school results7.Young people should be encouraged to dream because ________.A.their dreams are naturalB.they are greater than everyone elseC.they have much knowledgeD.their dreams might change the world8.What does the example of Colonel Saunders show us?A.Setting up a big company is a wonderful ability.B.Developing technology can bring great progress.C.Even older people can make their dreams come true.D.People should be brave enough to dream when they are young.9.The underlined word “naive” in the passage means “________” in Chinese.A.逆反的 B.幼稚的 C.调皮的 D.冲动的10.The best title (题目) for the passage is ________.A.From Dream to Reality B.Good Examples of Dreams C.Achievements in History D.A List of Successful Dreamers世界各地自然灾难频发:地震、干旱、火山喷发、洪涝…假如你是校学生会主席,请你以雪深灰的名义,根据所提供的要点提示项全校学生发出倡议:号召大家保护环境,共同维护我们的美好家园。
