高考数学专题突破 (23)
新高考数学复习专题突破练习题附解析(共13专题)

突破1.1 空间几何体的结构【基础巩固】1.如图,最左边的几何体由一个圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得,现用一个竖直的平面去截这个几何体,则截面图形可能是()A.①②B.②③C.③④D.①⑤【答案】B【解析】当截面过旋转轴时,圆锥的轴截面为等腰三角形,此时①符合条件;当截面不过旋转轴时,圆锥的轴截面为双曲线的一支,此时⑤符合条件.故截面图形可能是①⑤,选D.2.如图,一竖立在水平地面上的圆锥形物体的母线长为,一只小虫从圆锥的底面圆上的点出发,绕圆锥表面爬行一周后回到点处,若该小虫爬行的最短路程为,则圆锥底面圆的半径等于()A.B.C.D.【答案】C【方法点晴】本题主要考查了圆锥的有关计算及圆锥的侧面展开的应用,着重考查了求立体图形中两点之间的曲线段的最短线路长,解答此类问题一般应把几何体的侧面展开,展开在一个平面内,构造直角三角形,从而求解两点间的线段的长度,用到的知识为:圆锥的弧长等于底面周长,本题的解答中圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥的底面周长,扇形的半径等于圆锥的母线长,体现了“化曲面为平面”的思想方法.3.如图所示的几何体是由下列哪个平面图形绕虚线旋转一周得到的()A.B.C.D.【答案】A【解析】由题意知,该几何体是圆锥与圆台的组合体,所以该组合体是由直角三角形和直角梯形的组成的平面图形绕虚线旋转一周所得.故选A.4.下列关于棱柱的说法中,错误的是()A.三棱柱的底面为三角形B.一个棱柱至少有五个面C.若棱柱的底面边长相等,则它的各个侧面全等D.五棱柱有5条侧棱、5个侧面,侧面为平行四边形【答案】C【解析】n棱柱具体特征:底面为n边形,共3n条棱,(n+2)个面,其中n个侧面,2个底面,侧面为平行四边形,侧棱长相等.因为n棱柱底面为n边形,故A对;因为底面最少为三角形,故3个侧面,2个底面,共5个面,故B对;根据n棱柱特征,D对;而底面边长与侧棱长度不一定相等,故各个侧面不全等,故C错误.故选C.5.下列说法正确的是()A.棱柱的底面一定是平行四边形B.底面是矩形的平行六面体是长方体C.棱柱被平面分成的两部分可以都是棱柱D.棱锥的底面一定是三角形【答案】C【解析】对于选项A,棱柱的底面为任意的四边形即可,故错误.对于选项B,底面是矩形的直平行六面体才是长方体,故错误.对于选项D,三棱锥的底面一定是三角形,故错误.故选C.6.下列几何体不是简单旋转体()A.圆柱B.圆台C.球D.棱柱【答案】D【解析】在A中,圆柱是矩形绕着它的一条边旋转而成的,故圆柱是简单旋转体;在B中,圆台是直角梯形绕直角腰所在的直线旋转而成的,故圆台是简单旋转体;在C中,球是半圆绕着直径旋转而成的,故球是简单旋转体;在D中,棱柱不是旋转体.故选D.7.下列命题中,错误的是()A.圆柱的轴截面是过母线的截面中面积最大的一个B.用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台C.圆台的所有平行于底面的截面都是圆D.圆锥所有的轴截面是全等的等腰三角形【答案】B【解析】对于A,圆柱的轴截面是过母线的截面中面积最大的一个,为2r l,A正确;对于B,用一个平行于底面的平面截棱锥,底面与截面之间的部分组成的几何体叫棱台,∴B错误;对于C,圆台的所有平行于底面的截面都是圆,C正确;对于D,圆锥所有的轴截面都是全等的等腰三角形,D正确.故选B.8.如图所示的几何体是由下面哪一个平面图形旋转而形成的()A.B.C.D.【答案】A【解析】∵几何体是一个圆柱、两个圆台和一个圆锥的组合体,∴它是由A选项中的平面图形旋转而成的.故选A.9.下列叙述中正确的是()A.圆柱是将矩形旋转一周所得到的几何体B.棱柱中两个相互平行的平面一定是棱柱的底面C.过圆锥侧面上的一点有无数条母线D.球面上四个不同的点有可能在同一平面内【答案】D【解析】在A中,圆柱是将矩形以矩形的一条对角线为轴,旋转所得的就不是圆柱,故A错;在B中,棱柱的定义是,有两个面互相平行,其余各面都是四边形,相邻的公共边互相平行,有这些面围成的几何体是棱柱,棱柱中两个相互平行的平面不一定是棱柱的底面,故B错误;在C中,两点确定一条直线,圆锥过圆锥侧面上的一点只有一条母线,故C错误;在D中,球面上四个不同的点有可能在同一平面内,故D正确.故选D.10.如图所示,是由等腰梯形、矩形、半圆、圆、倒三角形对接形成的平面轴对称图形,若将它绕轴l旋转180°后形成一个组合体,下面说法不正确的是()A.该组合体可以分割成圆台、圆柱、圆锥和两个球体B.该组合体仍然关于轴l对称C.该组合体中的圆锥和球只有一个公共点D.该组合体中的球和半球只有一个公共点【答案】A【解题必备】考查简单组合体的构成,就必须要明白该组合体是由简单几何体拼接、截去还是挖去一部分而成的,因此,要仔细观察简单组合体的组成,并充分结合柱、锥、台、球的几何结构特征进行识别.【能力提升】11.正方形绕其一条对角线所在直线旋转一周,所得几何体是()A.圆柱B.圆锥C.圆台D.两个共底的圆锥【答案】D【思路点拨】本题考查旋转体的结构特征,熟练掌握旋转体的定义及旋转体的结构特征是解答本题的关键.12.有下列三组定义:①有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱;②用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台;③有一个面是多边形,其余各面都是三角形的几何体是棱锥.其中正确定义的个数为()A.0 B.1C.2 D.3【答案】B【思路点拨】从结构特征出发:棱台上、下两个底面平行且相似;棱锥侧面都是三角形且有一个公共顶点;棱柱上、下两个底面平行且侧面都是平行四边形,从而可快速得解.13.如图所示,在长方体中,则在长方体表面上连接两点的所有曲线长度的最小值为__________.14.一个几何体的三视图如图所示,则组成该几何体的简单几何体为().A.圆柱与圆台B.圆柱与四棱台C.四棱柱与四棱台D.四棱柱与圆台【解析】由三视图可得该几何体是一个组合体,由几何体上部的三视图均为矩形可知上部是四棱柱,由下部的三视图中有两个梯形可得下部是四棱台,故组成该几何体的简单几何体为四棱柱与四棱台,故选C . 15.将正方体(如图①)截去两个三棱锥,得到如图②所示的几何体,则该几何体的侧(左)视图为( ).【答案】B【解析】还原正方体后,将D 1,D ,A 三点分别向正方体右侧面作垂线.D 1A 的射影为C 1B ,且为实线,B 1C 被遮挡应为虚线.【高考真题】16.(2019全国II 文16)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.(本题第一空2分,第二空3分.)【解析】:该半正多面体共有888226+++=个面,设其棱长为x ,则221x x x ++=,解得21x =. 17.(2017年全国Ⅰ卷)某多面体的三视图如图所示,其中正(主)视图和侧(左)视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( ).A.10B.12C.14D.16【解析】观察三视图可知该多面体是由直三棱柱和三棱锥组合而成的,且直三棱柱的底面是直角边边长为2的等腰直角三角形,侧棱长为2.三棱锥的底面是直角边边长为2的等腰直角三角形,高为2,如图所示.因此该多面体的各个面中有两个梯形,且这两个梯形全等,梯形的上底长为2,下底长为4,高为2,故这些梯形的面积之和为2××(2+4)×2=12.故选B.【答案】B18.(2017年全国Ⅱ卷)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为().A.90πB.63πC.42πD.36π【解析】由几何体的三视图可知,该几何体是一个圆柱被一个平面截去上面虚线部分所得,如图所示.将圆柱补全,并将圆柱从点A处水平分成上下两部分.由图可知,该几何体的体积等于上部分圆柱体积的加上下部分圆柱的体积,所以该几何体的体积V=π×32×4+π×32×6×=63π.故选B.【答案】B20.(2015年全国Ⅰ卷)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正(主)视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=().A.1B.2C.4D.8【解析】如图,该几何体是一个半球与一个半圆柱的组合体,球的半径为r,圆柱的底面半径为r,高为2r,则表面积S=·4πr2+πr2+4r2+πr·2r=(5π+4)r2.又S=16+20π,∴(5π+4)r2=16+20π,∴r2=4,r=2,故选B.【答案】B突破1.2 空间几何体的三视图与直观图【基础巩固】1.(2018河北衡水压轴卷一)如图,在长方体1111ABCD A B C D -中,点E 、F 分别为11B C 、11C D 的中点,则四棱锥11A B EFD -的正视图与侧视图分别为 ( )A.②,③B.④,②C.②,①D.②,④ 【答案】.D【解析】由三视图的投影规则知,几何体在侧面11DCC D 上的投影为一直角三角形(直角在左边),AF 的投影为一虚线,1AB 的投影为一实线,故正视图为②;几何体在侧面11BCC B 上的投影为一直角三角形(直角在右边),AE 的投影为虚线,1AD 的投影为实线,故侧视图为④.故选D.2.若某三棱柱截去一个三棱锥后所剩几何体的三视图如图所示,则所截去的三棱锥的外接球的表面积等于 ( )A .34πB .32πC .17πD .172π 【答案】A【解析】由三视图知几何体是底面为边长为3,4,5的三角形,高为5的三棱柱被平面截得的,如图所示:截去的三棱锥是长方体的一个角,AB ⊥AD ,AD ⊥AC ,AC ⊥AB ,所以将三棱锥补成长方体,其外接球相同,外接球的直径为长方体的体对角线,半径为:222113343422++=,外接球的表面积为:21434342ππ⎛⎫⨯= ⎪⎝⎭故选A .3.某几何体的正视图和侧视图如图1所示,它的俯视图的直观图是''''A B C D ,如图2所示.其中24A'B'A'D'==,则该几何体的表面积为( )A .1612+πB .168+πC .1610+πD .8π【答案】A【解析】由俯视图的直观图得俯视图为边长为4的正方形,所以几何体为底面为半圆(半径为2),高为4的半圆柱,其表面积为214π244+2π21612π2⨯⨯+⨯⨯⨯=+,选A. 4.(2020·四川省成都市树德中学高三二诊(理))2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为43π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋中心(球心)与蛋巢底面的距离为( )A .22B .32C .212+ D .312+ 【答案】D【解析】设四个支点所在球的小圆的圆心为O ',球心为O ,由题意,球的体积为43π,即24433R ππ=可得球O 的半径为1,又由边长为2的正方形硬纸,可得圆O '的半径为12,利用球的性质可得222131()22O O '=-=,又由O '到底面的距离即为侧面三角形的高,其中高为12,所以球心到底面的距离为3131222++=。
空间点、直线、平面之间的位置关系5题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测

专题32空间点、直线、平面之间的位置关系5题型分类1.基本事实1:过不在一条直线上的三个点,有且只有一个平面.基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.基本事实4:平行于同一条直线的两条直线平行.2.“三个”推论推论1:经过一条直线和这条直线外一点,有且只有一个平面.推论2:经过两条相交直线,有且只有一个平面.推论3:经过两条平行直线,有且只有一个平面.3.空间中直线与直线的位置关系异面直线:不同在任何一个平面内,没有公共点.4.空间中直线与平面、平面与平面的位置关系图形语言符号语言公共点直线与平面相交a ∩α=A 1个平行a ∥α0个在平面内a ⊂α无数个平面与平面平行α∥β0个相交α∩β=l 无数个5.等角定理如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补.6.异面直线所成的角(1)定义:已知两条异面直线a ,b ,经过空间任一点O 分别作直线a ′∥a ,b ′∥b ,我们把直线a ′与b ′所成的角叫做异面直线a 与b 所成的角(或夹角).(2),π2.常用结论1.过平面外一点和平面内一点的直线,与平面内不过该点的直线是异面直线.2.分别在两个平行平面内的直线平行或异面.(一)共面、共线、共点问题的证明(1)共面:先确定一个平面,然后再证其余的线(或点)在这个平面内.(2)共线:先由两点确定一条直线,再证其他各点都在这条直线上.(3)共点:先证其中两条直线交于一点,再证其他直线经过该点(1)E ,F ,G ,H 四点共面;(1)证明E ,F ,G ,H 四点共面;(2)证明GE ,FH ,1BB 相交于一点.1-3.(2024高三·全国·专题练习)如图所示,在正方体(1)求证:1CE D F DA ,,三线交于点(2)在(1)的结论中,G 是D (二)(1)点、直线、平面位置关系的判定,注意构造几何体(长方体、正方体)模型来判断,常借助正方体为模型.(2)求异面直线所成角的方法方法解读平移法将异面直线中的某一条平移,使其与另一条相交,一般采用图中已有的平行线或者作平行线,形成三角形求解补形法在该几何体的某侧补接上同样一个几何体,在这两个几何体中找异面直线相应的位置,形成三角形求解题型2:空间位置关系的判断都相交,则直线A .2GH EF=C .直线EF ,GH 是异面直线2-3.【多选】(2024·湖北荆门A .若l αβ= ,A α∈B .若A ,B ,C 是平面C .若A α∈且B α∈,则直线D .若直线a α⊂,直线2-4.(2024·上海长宁·二模)如图,已知正方体则下列命题中假命题为(A .存在点P ,使得PQ ⊥B .存在点P ,使得//PQ AC .直线PQ 始终与直线CC(1)直线AF 与直线DE 相交;(2)直线CH 与直线DE 平行;(3)直线BG 与直线DE 是异面直线;(4)直线CH 与直线BG 成3-2.(2024高三·全国·课后作业)已知正四面体小为.3-3.(2024高三·河北·学业考试)如图直线1A E 与BF 所成角的大小为3-4.(2024高一下·北京·期末)如图,等腰梯形112BC CD DA AB ====,则直线3-5.(2024高三·全国·对口高考)线段AB 的两端分别在直二面角CD αβ--的两个面αβ、内,且与这两个面都成30︒角,则直线AB 与CD 所成的角等于.(三)空间几何体的切割(截面)问题(1)作截面应遵循的三个原则:①在同一平面上的两点可引直线;②凡是相交的直线都要画出它们的交点;③凡是相交的平面都要画出它们的交线.(2)作交线的方法有如下两种:①利用基本事实3作交线;②利用线面平行及面面平行的性质定理去寻找线面平行及面面平行,然后根据性质作出交线.A .177B .134-2.(2024·河南·模拟预测)在正方体确的个数为()①//MN 平面11AAC C ;②MN①异面直线1D D与AF所成角可以为②当G为中点时,存在点③当E,F为中点时,平面④存在点G,使点C与点则上述结论正确的是(A.①③B.②④4-5.(2024·新疆·二模)已知在直三棱柱BC=,432AC=,如图所示,若过的面积为()(四)等角定理的应用空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.一、单选题-如图所示,则直线PC()1.(2024高三·北京·学业考试)四棱锥P ABCDA.与直线AD平行B.与直线AD相交C .与直线BD 平行D .与直线BD 是异面直线2.(2024·广东)若直线1l 和2l 是异面直线,1l 在平面α内,2l 在平面β内,l 是平面α与平面β的交线,则下列命题正确的是A .l 与1l ,2l 都相交B .l 与1l ,2l 都不相交C .l 至少与1l ,2l 中的一条相交D .l 至多与1l ,2l 中的一条相交3.(2024高一·全国·课后作业)若直线l 在平面α外,则l 与平面α的公共点个数为()A .0B .0或1C .1D .24.(2024·上海·模拟预测)如图,正方体1111ABCD A B C D -中,P Q R S 、、、分别为棱1AB BC BB CD 、、、的中点,连接11A S B D 、,对空间任意两点M N 、,若线段MN 与线段11A S B D 、都不相交,则称M N 、两点可视,下列选项中与点1D 可视的为()A .点PB .点QC .点RD .点B5.(2024高二上·四川乐山·期末)若直线l 与平面α有两个公共点,则l 与α的位置关系是()A .l ⊂αB .//l αC .l 与α相交D .l α∈6.(2024高二上·上海静安·阶段练习)设A B C D 、、、是某长方体四条棱的中点,则直线AB 和直线CD 的位置关系是().A .相交B .平行C .异面D .无法确定7.(2024高三·全国·专题练习)如果两条异面直线称为“一对”,那么在正方体的十二条棱中共有异面直线()A.12对B.24对C.36对D.48对8.(2024高三·全国·专题练习)三棱柱各面所在平面将空间分成不同部分的个数为()A.18B.21C.24D.279.(2024高一·全国·课后作业)平面α上有三个不共线点到平面β距离相等,则平面α与平面β的位置关系是()A.相交B.平行C.垂直D.相交或平行10.(2024高一·全国·课前预习)下列命题中正确的是()A.一个平面内三条直线都平行于另一平面,那么这两个平面平行B.如果一个平面内所有直线都平行于另一个平面,那么这两个平面平行C.平行于同一直线的两个平面一定相互平行D.如果一个平面内有几条直线都平行于另一平面,那么这两个平面平行G N M H分别是正三棱柱(两底面为正三角形的直棱柱)的顶点或11.(2024高三·全国·专题练习)如图中,,,,GH MN是异面直线的图形有()所在棱的中点,则表示直线,A.①③B.②③C.②④D.②③④12.(2024高三上·内蒙古赤峰·阶段练习)已知直线l和平面α,若lα∥,Pα∈,则过点P且平行于l的直线().A.只有一条,不在平面α内B.只有一条,且在平面α内C.有无数条,一定在平面α内D.有无数条,不一定在平面α内13.(2024高三·全国·专题练习)将图(1)中的等腰直角三角形ABC沿斜边BC的中线AD折起得到空间四面体ABCD,如图(2),则在空间四面体ABCD中,AD与BC的位置关系是()A .相交且垂直B .相交但不垂直C .异面且垂直D .异面但不垂直14.(2024高三上·吉林长春·期末)如图,在底面为正方形的棱台1111ABCD A B C D -中,E 、F 、G 、H 分别为棱1CC ,1BB ,CF ,AF 的中点,对空间任意两点M 、N ,若线段MN 与线段AE 、1BD 都不相交,则称点M 与点N 可视,下列选项中与点D 可视的为()A .1B B .FC .HD .G15.(2024·全国)在正方体1111ABCD A B C D -中,P 为11B D 的中点,则直线PB 与1AD 所成的角为()A .π2B .π3C .π4D .π616.(上海市曹杨中学2023-2024学年高二上学期期中数学试题)如图,在正方体1111ABCD A B C D -中,点P 是线段11A C 上的动点,下列与BP 始终异面的是()A .1DDB .AC C .1AD D .1B C17.(2024·福建福州·三模)在底面半径为1的圆柱1OO 中,过旋转轴1OO 作圆柱的轴截面ABCD ,其中母线AB =2,E 是弧BC 的中点,F 是AB 的中点,则()A .AE =CF ,AC 与EF 是共面直线B .AE CF ≠,AC 与EF 是共面直线C .AE =CF ,AC 与EF 是异面直线D .AE CF ≠,AC 与EF 是异面直线18.(2024高二下·广西桂林·期中)已知直线m ⊂平面α,则“平面α∥平面β”是“m ∥β”的A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件19.(2024·新疆阿克苏·一模)已知M ,N ,P 是正方体1111ABCD A B C D -的棱AB ,1AA ,1CC 的中点,则平面MNP 截正方体1111ABCD A B C D -所得的截面是()A .三角形B .四边形C .五边形D .六边形20.(2023届上海春季高考练习)如图,P 是正方体1111ABCD A B C D -边11AC 上的动点,下列哪条边与边BP 始终异面()A .1DDB .AC C .1AD D .1B C21.(2024高二上·浙江杭州·期末)已知空间三条直线,,l m n ,若l 与m 异面,且l 与n 异面,则()A .m 与n 异面B .m 与n 相交C .m 与n 平行D .m 与n 异面、相交、平行均有可能22.(2024高三·全国·专题练习)下列命题中正确的个数为()①若ABC ∆在平面α外,它的三条边所在的直线分别交α于P Q R 、、,则P Q R 、、三点共线.②若三条直线a b c 、、互相平行且分别交直线l 于、、A B C 三点,则这四条直线共面;③空间中不共面五个点一定能确定10个平面.A .0B .1C .2D .323.(2024高三·全国·专题练习)下列结论正确的是()A .两个平面α,β有一个公共点A ,就说α,β相交于过A 点的任意一条直线.B .两两相交的三条直线最多可以确定三个平面.C .如果两个平面有三个公共点,则这两个平面重合.D .若直线a 不平行于平面α,且a ⊄α,则α内的所有直线与a 异面.24.(2024高三·全国·专题练习)给出下列说法:①梯形的四个顶点共面;②三条平行直线共面;③有三个公共点的两个平面重合;④三条直线两两相交,可以确定1个或3个平面.其中正确的序号是()A .①B .①④C .②③D .③④25.(2024·上海浦东新·一模)已知直线l 与平面α相交,则下列命题中,正确的个数为()①平面α内的所有直线均与直线l 异面;②平面α内存在与直线l 垂直的直线;③平面α内不存在直线与直线l 平行;④平面α内所有直线均与直线l 相交.A .1B .2C .3D .426.(2024高一·全国·课后作业)直线l 是平面α外的一条直线,下列条件中可推出//l α的是A .l 与α内的一条直线不相交B .l 与α内的两条直线不相交C .l 与αD .l 与α内的任意一条直线不相交27.(2024高三下·上海·阶段练习)如图所示,正三棱柱111ABC A B C -的所有棱长均为1,点P 、M 、N 分别为棱1AA 、AB 、11A B 的中点,点Q 为线段MN 上的动点.当点Q 由点N 出发向点M 运动的过程中,以下结论中正确的是()A .直线1C Q 与直线CP 可能相交B .直线1C Q 与直线CP 始终异面C .直线1C Q 与直线CP 可能垂直D .直线1C Q 与直线BP 不可能垂直28.(2024高三下·上海浦东新·阶段练习)已知正方体1111ABCD A B C D -中,M ,N ,P 分别是棱11A D ,11D C ,AB 的中点,Q 是线段MN 上的动点,则下列直线中,始终与直线PQ 异面的是()A .1AB B .1BC C .1CAD .1DD 29.(2024高一上·全国·专题练习)M ∈l ,N ∈l ,N ∉α,M ∈α,则有A .l ∥αB .l ⊂αC .l 与α相交D .以上都有可能30.(2024高三上·重庆沙坪坝·期中)在棱长为3的正方体1111ABCD A B C D -中,点Р是侧面11ADD A 上的点,且点Р到棱1AA 与到棱AD 的距离均为1,用过点Р且与1BD 垂直的平面去截该正方体,则截面在正方体底面ABCD 的投影多边形的面积是()A .92B .5C .132D .831.(2024高三下·上海闵行·阶段练习)在棱长为2的正方体1111ABCD A B C D -中,E ,F 分别为AB ,BC 的中点,对于如下命题:①异面直线1DD 与1B F ②点P 为正方形1111D C B A 内一点,当//DP 平面1B EF 时,DP 的最小值为322;③过点1D ,E ,F 的平面截正方体1111ABCD A B C D -所得的截面周长为1B BEF -的所有顶点都在球O 的表面上时,球O .则正确的命题个数为()A .1B .2C .3D .432.(2024高三·全国·对口高考)如图,正方体1111ABCD A B C D -的棱长为P 在对角线1BD 上,过点P 作垂直于1BD 的平面α,记这样得到的截面多边形(含三角形)的周长为y ,设BP x =,则当[]1,5x ∈时,函数()y f x =的值域为()A .36,66⎡⎤⎣⎦B .6,26⎡⎣C .(6D .(0,36二、多选题33.(2024高一下·辽宁营口·阶段练习)有下列命题:①经过三点确定一个平面;②梯形可以确定一个平面;③两两相交的三条直线最多可以确定三个平面;④如果两个平面有三个公共点,则这两个平面重合.其中正确命题是()A .①B .②C .③D .④34.(2024高一下·江苏苏州·阶段练习)下列命题中错误的是()A .空间三点可以确定一个平面B .三角形一定是平面图形C .若A ,B ,C ,D 既在平面α内,又在平面β内,则平面α和平面β重合D .四条边都相等的四边形是平面图形35.(2024·河北廊坊·模拟预测)我们知道,平面几何中有些正确的结论在空间中不一定成立.下面给出的平面几何中的四个真命题,在空间中仍然成立的有()A .平行于同一条直线的两条直线必平行B .垂直于同一条直线的两条直线必平行C .一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补D .一个角的两边分别垂直于另一个角的两边,那么这两个角相等或互补36.(2024高一下·陕西西安·期中)如图所示,在正方体1111ABCD A B C D -中,M ,N 分别为棱11C D ,1C C 的中点,则下列四个结论正确的是()A .直线AM 与1CC 是相交直线B .直线AM 与BN 是平行直线C .直线BN 与1MB 是异面直线D .直线AM 与1DD 是异面直线37.(2024高一·全国·课后作业)下列结论中正确的是()A .若两个平面有一个公共点,则它们有无数个公共点B .若已知四个点不共面,则其中任意三点不共线C .若点A 既在平面α内,又在平面β内,则α与β相交于b ,且点A 在b 上D .任意两条直线不能确定一个平面38.(2024高三·全国·专题练习)如图,已知正方体1111ABCD A B C D -的棱长为2,设P ,Q 分别为11A B ,1DD 的中点,则过点P ,Q 的平面α截正方体所得截面的形状可能为()A .三角形B .四边形C .五边形D .六边形39.(2024高一下·湖北武汉·期末)当三个平面都平行时,三个平面可将空间分成4个部分,那么三个平面还可将空间分成()部分.A .5B .6C .7D .840.(2024高三下·山东日照·阶段练习)如图,正方体1111ABCD A B C D -的棱长为1,线段11B D 上有两个动点E 、F ,且12EF =,则下列结论中正确的是()A .线段11B D 上存在点E 、F 使得//AE BF B .//EF 平面ABCDC .AEF △的面积与BEF △的面积相等D .三棱锥A -BEF 的体积为定值三、填空题41.(2024高三·全国·专题练习)给出下列四个命题:①平面外的一条直线与这个平面最多有一个公共点;②若平面α内的一条直线a 与平面β内的一条直线b 相交,则α与β相交;③若一条直线和两条平行线都相交,则这三条直线共面;④若三条直线两两相交,则这三条直线共面.其中真命题的序号是.42.(2024高一下·全国·课后作业)已知直线MN ⊥平面α于N ,直线NP MN ⊥,则NP 与平面α的关系是.43.(2024高一·全国·课后作业)如图,把下列图形的点、线、面的关系,用集合的语言表述:(1);(2);(3).44.(2024高一下·黑龙江齐齐哈尔·期末)已知空间中两个角α,β,且角α与角β的两边分别平行,若70α=︒,则β=.45.(2024高二下·上海虹口·期末)在空间,如果两个不同平面有一个公共点,那么它们的位置关系为.46.(2024高三下·重庆渝中·阶段练习)空间四边形的对角线互相垂直且相等,顺次连接这个四边形各边中点,所组成的四边形是.47.(2024高二上·上海徐汇·阶段练习)如图,在长方体ABCD -A 1B 1C 1D 1中,(1)直线A 1B 与直线D 1C 的位置关系是;(2)直线A 1B 与直线B 1C 的位置关系是;(3)直线D 1D 与直线D 1C 的位置关系是;(4)直线AB 与直线B 1C 的位置关系是.48.(2024高二上·上海徐汇·阶段练习)设A ∠和B ∠的两边分别平行,若45A ∠=︒,则B ∠的大小为.49.(2024高一·全国·课后作业)“直线l 与平面α没有公共点”是“l α∥”的条件.50.(2024高一下·全国·课后作业)在底面为正六边形的六棱柱中,互相平行的面视为一组,则共有组互相平行的面,与其中一个侧面相交的面共有个.52.(2024高一·全国·单元测试)若直线a 与平面α内无数条直线平行,则a 与α的位置关系是.53.(2024高二上·上海奉贤·阶段练习)如图,将正方体沿交于一顶点的三条棱的中点截去一小块,八个顶“阿基米德多面体”,则异面直线AB 与CD 所成角的大小是四、解答题54.(2024高一·全国·课后作业)已知:l ⊂α,D α∈,∈A l ,B l ∈,C l ∈,D l ∉.求证:直线,,AD BD CD 共面于α.55.(2024高一·全国·课后作业)如图,ABCD 为空间四边形,点E ,F 分别是AB ,BC 的中点,点G ,H 分别在CD ,AD 上,且13DH AD =,13DG CD =.(1)求证:E ,F ,G ,H 四点共面;(2)求证:EH ,FG 必相交且交点在直线BD 上.56.(2024高一下·北京·期末)如图,在正方体1111ABCD A B C D -中,E 是棱1CC 上一点,且1:1:2CE EC =.(1)试画出过1,,D A E 三点的平面截正方体1111ABCD A B C D -所得截面α;(2)证明:平面1D AE 与平面ABCD 相交,并指出它们的交线.57.(2024高一·全国·课后作业)如图所示是一个三棱锥,欲过点P 作一个截面,使得截面与底面平行,该怎样在侧面上画出截线?58.(2024高一·全国·课后作业)59.(2024高一下·全国·课后作业)在直三棱柱ABC -A 1B 1C 1中,E ,F 分别为A 1B 1,B 1C 1的中点.求证:平面ACC 1A 1与平面BEF 相交.60.(2024高一上·安徽亳州·期末)如图所示,在正方体ABCD -A 1B 1C 1D 1中,E 、F 分别是AB 和AA 1的中点.求证:(1)E ,C ,D 1,F 四点共面;(2)CE ,D 1F ,DA 三线共点.61.(2024高三·全国·专题练习)如图,在空间四边形ABCD 中,,,,E F G H 分别在,,,AB AD BC CD 上,EG 与FH 交于点P ,求证:,,P A C 三点共线.62.(2024高二·全国·课后作业)如图所示,在正方体1111ABCD A B C D -中,,E F 分别是AB 和1AA 的中点,求证:四边形1FECD 为平面图形.63.(2024高一·全国·专题练习)如图所示,在空间四边形ABCD 中,E ,F 分别为AB ,AD 的中点,G ,H 分别在BC ,CD 上,且::1:2BG GC DH HC ==.求证:(1)E 、F 、G 、H 四点共面;(2)EG 与HF 的交点在直线AC 上.64.(2024高二·上海·专题练习)如图所示,在正方体1111ABCD A B C D -中.画出平面11ACC A 与平面1BC D 及平面1ACD 与平面1BDC 的交线.65.(2024高一·全国·专题练习)如图,直升机上一点P 在地面α上的正射影是点A (即PA ⊥α),从点P 看地平面上一物体B (不同于A ),直线PB 垂直于飞机玻璃窗所在的平面β.求证:平面β必与平面α相交.66.(2024高一·全国·专题练习)如图,已知平面,αβ,且l αβ= ,设在梯形ABCD 中,AD BC ∕∕,且,AB CD αβ⊂⊂.求证:,,AB CD l 共点.67.(2024高一下·河南信阳·期中)如图,在正方体1111ABCD A B C D -中,E ,F 分别是1,AB AA 上的点,且12,2A F FA BE AE ==.(1)证明:1,,,E C D F 四点共面;(2)设1D F CE O ⋂=,证明:A ,O ,D 三点共线.68.(2024高一下·陕西西安·期中)(1)已知直线a b ∥,直线l 与a ,b 都相交,求证:过a ,b ,l 有且只有一个平面;(2)如图,在空间四边形ABCD 中,H ,G 分别是AD ,CD 的中点,E ,F 分别是边AB ,BC 上的点,且13CF AE FB EB ==.求证:直线EH ,BD ,FG 相交于一点.。
2023年高考数学二轮复习 第1部分 专题突破 专题1 培优点2 对数平均不等式、切线不等式

由对数平均不等式知 ln
x1-x2 x1-ln
x2>
x1x2=1,
又x2>x1>0, ∴x1-x2<0,ln x1-ln x2<0,
∴0<ln
x1-ln x1-x2
x2<1,
∴fxx11- -xf2x2=-2+alnxx11--xl2n x2<-2+a,
即证原不等式成立.
考点二
以泰勒公式为背景的切线不等式
(1)当a>0时,求函数f(x)的单调递增区间;
f(x)的定义域为(0,+∞), f′(x)=ax-(2a+1)+2x=ax-1xx-2, 当 0<1a<2,即 a>12时,在0,1a和(2,+∞)上,f′(x)>0,f(x)单调递增;
当1a=2,即 a=12时,f′(x)≥0,f(x)在(0,+∞)上单调递增; 当1a>2,即 0<a<12时,在(0,2)和1a,+∞上,f′(x)>0,f(x)单调递增. 综上所述,当 a>12时,f(x)的单调递增区间为0,1a和(2,+∞);
即eex≥x,ex≥ex,当 x=1 时等号成立,
即e-ln x≥e(-ln x),
所以1x≥e(-ln x), 即 ln x≥-e1x,当 x=1e时等号成立,
所以
exln
x+e2x≥ex-e1x+e2x=eexx >1(等号不同时成立).
方法二 由(1)知,f(x)=exln x+2eexx, 从而 f(x)>1 等价于 xln x>exx-2e. 设函数g(x)=xln x,则g′(x)=1+ln x.
构造函数 f(t)=2ln t-t+1t (t>1), 则 f′(t)=2t -1-t12=-t-t212<0,
同角三角函数的基本关系和诱导公式5题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测

专题17同角三角函数的基本关系和诱导公式5题型分类一、同角三角函数基本关系1、同角三角函数的基本关系(1)平方关系:22sin cos 1αα+=.(2)商数关系:sin tan ()cos 2k απααπα=≠+;【记忆口诀】奇变偶不变,符号看象限,说明:(1)先将诱导三角函数式中的角统一写作2n πα⋅±;(2)无论有多大,一律视为锐角,判断2n πα⋅±所处的象限,并判断题设三角函数在该象限的正负;(3)当n 为奇数是,“奇变”,正变余,余变正;当n 为偶数时,“偶不变”函数名保持不变即可.注:1、利用22sin cos 1αα+=可以实现角α的正弦、余弦的互化,利用sin tan cos =aa a可以实现角α的弦切互化.2、“sin cos sin cos sin cos αααααα+-,,”方程思想知一求二.222(sin cos )sin cos 2sin cos 1sin 2ααααααα+=++=+222(sin cos )sin cos 2sin cos 1sin 2ααααααα-=+-=-22(sin cos )(sin cos )2αααα++-=(一)同角求值(1)若已知角的象限条件,先确定所求三角函数的符号,再利用三角形三角函数定义求未知三角函数值.(2)若无象限条件,一般“弦化切”.(二)诱导求值与变形(1)诱导公式用于角的变换,凡遇到与2π整数倍角的和差问题可用诱导公式,用诱导公式可以把任意角的三角函数化成锐角三角函数.(2)通过2,,2πππ±±±等诱导变形把所给三角函数化成所需三角函数.(3)2,,2παβππ±=±±±等可利用诱导公式把,αβ的三角函数化(三)同角三角函数基本关系式和诱导公式的综合应用)利用同角三角函数关系式和诱导公式求值或化简时,关键是寻求条件、结论间的联系,灵活使用公式(π(四)三角恒等式的证明三角恒等式的证明中涉及到同角三角函数基本关系,和角公式,差角公式,二角公式,辅助角公式等基本知识点,理解和掌握这些基本知识点是解答该类问题的基础和关键原式得证【点睛】本题考查了利用同角三角函数关系证明三角函数恒等式,属于基础题.5-4.(2024高三·全国·专题练习)(1)求证:tan 2αsin 2α=tan 2α-sin 2α;(2)已知tan 2α=2tan 2β+1,求证:2sin 2α=sin 2β+1.【答案】(1)证明见解析;(2)证明见解析.【分析】(1)将22sin 1cos αα=-代入左式,化简即可得到右式.(2)将sin tan cos ααα=,sin tan cos βββ=代入条件,通分化简得到2212cos cos αβ=,即2cos 2α=cos 2β,然后由22sin cos 1αα+=,将余弦化成正弦即可证得结论.【详解】解析:(1)tan 2αsin 2α=tan 2α(1-cos 2α)=tan 2α-tan 2αcos 2α=tan 2α-sin 2α,则原等式得证.(2)因为tan 2α=2tan 2β+1,所以22sin cos αα+1=222sin 1cos ββ⎛⎫+ ⎪⎝⎭,即2212cos cos αβ=,从而2cos 2α=cos 2β,于是2-2sin 2α=1-sin 2β,也即2sin 2α=sin 2β+1,则原等式得证.一、单选题1.(2024·全国·模拟预测)已知2cos tan sin 5xx x =+,则cos2x =()A .13B .79C .23D .59【答案】B【分析】利用三角函数的基本关系式得到关于sin x 的方程,再利用倍角公式即可得解.【详解】因为2cos tan sin 5x x x =+,又sin tan cos xx x=,所以sin 2cos cos sin 5x xx x =+,则222cos sin 5sin x x x =+,即2222sin sin 5sin x x x -=+,则23sin 5sin 20x x +-=,即()()3sin 1sin 20x x -+=,所以1sin 3x =或sin 2x =-(舍去),所以217cos212sin 1299x x =-=-⨯=.故选:B.2.(2024·四川巴中·模拟预测)勾股定理,在我国又称为“商高定理”,最早的证明是由东汉末期数学家赵爽在为《周髀算经》作注时给出的,他利用了勾股圆方图,此图被称为“赵爽弦图”.“赵爽弦图”是由四个全等的直角三角形和中间的一个小正方形组成的大正方形图案(如图所示),若在大正方形内随机取一点,该点落在小正方形内的概率为917,则“赵爽弦图”里的直角三角形中最小角的正弦值为()A .217B C .217D 【答案】D【分析】设正方形的边长1,较小的角为θ,则中间小正方形的边长为cos sin θθ-,由题意可得29(cos sin )17θθ-=,显然可得π04θ<<,即可得到cos sin 0θθ>>,从而求出sin θ.【详解】设正方形的边长1,较小的角为θ,则中间小正方形的边长为cos sin θθ-,由题意可得29(cos sin )17θθ-=,显然π04θ<<,所以cos sin 0θθ>>,所以cos sin 17θθ-=,又229cos sin 2cos sin 17θθθθ+-=,所以2cos si 8n 17θθ=,所以22225(cos sin )cos sin 2cos sin 17θθθθθθ+==++,所以cos sin 17θθ+=,所以sin 17θ=.故选:D3.(2024·全国·模拟预测)已知2π2cos 53θ⎛⎫-= ⎪⎝⎭,则19π13π2sin cos 105θθ⎛⎫⎛⎫-++= ⎪ ⎪⎝⎭⎝⎭()A .2-B .2C .23-D .23【答案】A【分析】利用已知的三角函数值,利用换元法,结合三角函数的诱导公式,可得答案.【详解】令25m πθ=-,则22,cos 53m m πθ=+=,从而19π13π19π2π2π13π2sin cos 2sin cos 10510555m m θθ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-++=-++++ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦3π2sin cos(3π)3cos 22m m m ⎛⎫=-++=-=- ⎪⎝⎭.故选:A.4.(2024·山西·模拟预测)已知α为锐角,且cos 6πα⎛⎫+= ⎪⎝⎭,则tan 3πα⎛⎫-= ⎪⎝⎭()A.2B.CD.2【答案】D【分析】注意到πππ632αα⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭,利用同角三角函数的关系求角π6α+的正弦,再利用诱导公式求角π3α-的正弦、余弦,从而得到π3α-的正切.【详解】因为α为锐角,所以ππ2π,663α⎛⎫+∈ ⎪⎝⎭且πcos 6α⎛⎫+= ⎪⎝⎭,所以22πsin 06ππsin cos 166ααα⎧⎛⎫+> ⎪⎪⎪⎝⎭⎨⎛⎫⎛⎫⎪+++= ⎪ ⎪⎪⎝⎭⎝⎭⎩得πsin 6α⎛⎫+= ⎪⎝⎭由诱导公式得ππππsin sin cos 3266ααα⎡⎤⎛⎫⎛⎫⎛⎫-=-+=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦ππcos sin 363αα⎛⎫⎛⎫-=+=⎪ ⎪⎝⎭⎝⎭.所以πsin π33tan π32cos 3ααα⎛⎫- ⎪⎛⎫⎝⎭-== ⎪⎛⎫⎝⎭- ⎪⎝⎭.故选:D5.(2024高三上·安徽合肥·阶段练习)已知角α为钝角,且角(02π)θθ<<终边上有一点()sin ,cos P αα-,则角θ=()A .πα+B .π2α+C .2πα-D .3π2α-【答案】B【分析】利用三角函数的诱导公式及三角函数的定义即可求解.【详解】点()sin ,cos P αα-,由诱导公式可化为ππcos ,sin 22P αα⎛⎫⎛⎫⎛⎫++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,由三角函数的定义知,π2π2k θα=++,又因为α为钝角,02πθ<<,所以π2θα=+.故选:B.6.(2024高三上·宁夏银川·阶段练习)在平面直角坐标系中,在()1,3P 在角α终边上,则()()()3333sin πcos ππsin cos 2αααα++-⎛⎫--- ⎪⎝⎭的值为()A .1327B .1427C .1427-D .1413【答案】B【分析】根据三角函数的定义求角α的三角函数值,再利用诱导公式化简求值.【详解】因为点()1,3P 在角α终边上,则1x =,3y =,所以tan 3yxα==,()()()333333333sin πcos πsin cos 1114π227sin sin 2tan sin cos 2ααααααααα++---==+⎛⎫----- ⎪⎝⎭.故选:B7.(2024高三上·四川成都·期中)已知角α的顶点与坐标原点重合,始边与x 轴的正半轴重合,若角α的终边与23π角的终边相同,则sin()cos(2)3sin()2παπαπα+--=+()A1B1C.1D.1-【答案】C【分析】利用三角函数定义求得tan α=,再利用诱导公式化简即可.【详解】由题意得2tan tanπ3α==sin(π)cos(2π)sin cos sin cos sin cos tan 113ππcos cos sin()sin 22ααααααααααααα+------+====+=+-⎛⎫+-+ ⎪⎝⎭,故选:C.8.(2024·全国·模拟预测)已知直线:2310l x y +-=的倾斜角为θ,则()πsin πsin 2θθ⎛⎫-⋅-= ⎪⎝⎭()A .613B .613-C .25D .25-【答案】A【分析】根据直线一般方程可求得2tan 3θ=-,再利用诱导公式及同角三角函数之间的基本关系可得其结果.【详解】由直线l 的方程为2310x y +-=,得斜率2tan 3k θ==-,则()πsin cos sin πsin sin cos 21θθθθθθ-⋅⎛⎫-⋅-=-⋅= ⎪⎝⎭22222sin cos tan 63sin cos tan 113213θθθθθθ-⋅-====++⎛⎫-+ ⎪⎝⎭;故选:A .9.(2024·陕西宝鸡·一模)已知4ππsin 2sin 36αα⎛⎫⎛⎫-=+⎪ ⎪⎝⎭⎝⎭,则πsin 23α⎛⎫+= ⎪⎝⎭()A .34-B .34C .45-D .45【答案】C【分析】先利用诱导公式对已知条件化简得ππcos 2sin 66αα⎛⎫⎛⎫-+=+ ⎪ ⎪⎝⎭⎝⎭;再利用同角三角函数基本关系求出2π1sin 65α⎛⎫+= ⎪⎝⎭;最后利用二倍角公式即可求解.【详解】4π3πππsin sin cos 3266ααα⎡⎤⎛⎫⎛⎫⎛⎫-=-+=-+⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦.由4ππsin 2sin 36αα⎛⎫⎛⎫-=+⎪ ⎪⎝⎭⎝⎭可得:ππcos 2sin 66αα⎛⎫⎛⎫-+=+ ⎪ ⎪⎝⎭⎝⎭.因为22ππsin cos 166αα⎛⎫⎛⎫+++= ⎪ ⎪⎝⎭⎝⎭,所以2π1sin 65α⎛⎫+= ⎪⎝⎭.所以2ππππ4sin 22sin cos 4sin 36665αααα⎛⎫⎛⎫⎛⎫⎛⎫+=++=-+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.故选:C.10.(2024·全国·模拟预测)已知(ππtan cos 3cos 44ααα⎛⎫⎛⎫+=-- ⎪ ⎪⎝⎭⎝⎭,则cos2α=()AB.2C .12-D .1-【答案】B 【分析】由诱导公式和同角三角函数关系得到(πtan 3tan 4αα⎛⎫=-+ ⎪⎝⎭,再利用正切和角公式得到方程,求出tan 1α=,利用余弦二倍角,齐次化求出答案.【详解】因为ππππcos sin sin 4244ααα⎛⎫⎛⎫⎛⎫-=-+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以(ππtan cos 3sin 44ααα⎛⎫⎛⎫+=-+ ⎪ ⎪⎝⎭⎝⎭,故(πtan 3tan 4αα⎛⎫=-+ ⎪⎝⎭,因为πtan tanπtan 14tan π41tan 1tan tan 4ααααα++⎛⎫+== ⎪-⎝⎭-,所以(tan 1tan 31tan ααα+=--,故)(2tan 21tan 30αα-+-=,解得tan 1α=,所以)()2222222211cos sin 1tan cos2cos sin 1tan 11ααααααα---=====+++-故选:B .11.(2024·全国·模拟预测)已知圆22:(1)(1)1C x y -+-=,过点()3,2P ,作圆C 的两条切线,切点分别为,A B ,则tan ACB ∠=()A .43-B .43C .12-D .34【答案】A【分析】设切线的方程为2(3)y k x -=-,求得圆心C到切线的距离1d ==,求得k 的值,得到4tan 3APB ∠=,结合180APB ACB ∠+∠=︒,即可求解.【详解】由题意知,圆22:(1)(1)1C x y -+-=的圆心为(1,1)C ,半径1r =,且切线PA ,PB 的斜率都存在,设切线的方程为2(3)y k x -=-,即320kx y k --+=,因为直线与圆相切,所以圆心C到切线的距离1d =,解得10k =或2k =43,所以4tan 3APB ∠=,在四边形APBC 中,因为90APC ABC ∠=∠= ,可得180APB ACB ∠+∠=︒,所以4tan tan(180)tan 3ACB APB APB ∠=-∠=-∠=-.故选:A .12.(2024·河南郑州·模拟预测)已知tan 2θ=,则3πsin sin 2θθ⎛⎫+= ⎪⎝⎭()A .35B .12C .12-D .25-【答案】D【分析】利用诱导公式,平方关系和商关系即可求解.【详解】3πsin sin sin cos 2θθθθ⎛⎫+=- ⎪⎝⎭222sin cos tan 2sin cos tan 15θθθθθθ=-=-=-++.故选:D13.(2024·陕西西安·二模)已知π5cos 513α⎛⎫-= ⎪⎝⎭,则7πsin 10α⎛⎫-= ⎪⎝⎭()A .513-B .513C .-1213D .1213【答案】A 【分析】因为7πππ1052αα⎛⎫-=-- ⎪⎝⎭,由诱导公式可得选项.【详解】7ππππ5sin sin cos 1052513ααα⎛⎫⎛⎫⎛⎫-=--=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选:A.14.(2024·广东深圳·模拟预测)已知π4sin 35α⎛⎫+= ⎪⎝⎭,则5πcos 6α⎛⎫+ ⎪⎝⎭的值为()A .35-B .35C .45-D .45【答案】C 【分析】根据5πππ623αα⎛⎫+=++ ⎪⎝⎭,借助于诱导公式,即可求得结果.【详解】5πππcos cos 623αα⎡⎤⎛⎫⎛⎫+=++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ sin 3πα⎛⎫=-+ ⎪⎝⎭45=-,5πcos 6α⎛⎫∴+ ⎪⎝⎭的值为45-,故选:C15.(2024高三上·陕西西安·阶段练习)若1sin 3A =,则()sin 6A π-的值为()A .13B .13-C.3-D.3【答案】B【分析】本题考查诱导公式的基础运用,套用公式即可.【详解】利用诱导公式可得()()1sin 6sin sin 3A A A π-=-=-=-,故选:B.16.(2024高三上·陕西西安·阶段练习)若()1sin 2πα+=-,则cos α的值为()A .12±B .12CD.【答案】D【分析】先化简已知得1sin =2α,再求cos α的值.【详解】由()1sin 2πα+=-得1sin =2α,所以α在第一、二象限,所以cos =2α=±.故选:D.17.(2024·贵州贵阳·模拟预测)已知πsin sin 2θθ⎛⎫-+= ⎪⎝⎭,则tan θ=()A.B .1-C .1D【答案】B【分析】利用诱导公式以及同角三角函数的平方关系可得出关于sin θ、cos θ的方程组,求出这两个量的值,即可求得tan θ的值.【详解】因为πsin sin sin cos 2θθθθ⎛⎫-+=-= ⎪⎝⎭,由题意可得22sin cos sin cos 1θθθθ⎧-=⎪⎨+=⎪⎩sin 2cos 2θθ⎧=⎪⎪⎨⎪=-⎪⎩,因此,sin tan 1cos θθθ==-.故选:B.18.(2024高一下·湖南长沙·阶段练习)已知1sin cos 5αα+=,且()0,πα∈,sin cos αα-=()A .75±B .75-C .75D .4925【答案】C【分析】将已知等式两边平方,利用三角函数的基本关系求得2sin cos αα的值,结合α的范围确定sin α与cos α的正负,再利用完全平方公式及三角函数的基本关系可求得sin cos αα-的值.【详解】因为1sin cos 5αα+=,两边平方得()21sin cos 12sin cos 25αααα+=+=,故242sin cos 025αα=-<,所以sin α与cos α导号,又因为0πα<<,所以sin 0α>,cos 0α<,所以7sin cos 5αα-====.故选:C.19.(2024高三下·重庆渝中·阶段练习)已知θ是三角形的一个内角,且满足sin cos 5θθ-=,则tan θ=()A .2B .1C .3D .12【答案】A【分析】利用平方关系可求得42sin cos 5θθ=,可解得29(sin cos )5θθ+=,再结合θ是三角形的一个内角即可得sin ,cos θθ==tan 2θ=.【详解】将sin cos θθ-=两边同时平方可得112sin cos 5θθ-=,即42sin cos 5θθ=;所以29(sin cos )12sin cos 5θθθθ+=+=若sin +cos θθ=,解得sin θθ==,这与θ是三角形的一个内角矛盾,所以sin +cos θθ=,解得sin θθ==,此时求得tan 2θ=.故选:A.20.(2024高三上·北京·阶段练习)在平面直角坐标系xOy 中,角α与角β均以Ox 为始边,它们的终边关于直线y x =对称,若4sin 5α=,则cos β=()A .45-B .45C .35-D .35【答案】B【分析】根据题意利用任意角的三角函数的定义,结合诱导公式可求得结果.【详解】因为平面直角坐标系xOy 中,角α与角β均以Ox 为始边,它们的终边关于直线y x =对称,所以ππ,Z 24k k αβ+=+∈,即π2π,Z 2k k αβ+=+∈,所以π2π,Z 2k k βα=-+∈,因为4sin 5α=,所以π4cos cos 2πsin (Z)25k k βαα⎛⎫=-+==∈ ⎪⎝⎭,故选:B21.(2024·辽宁抚顺·模拟预测)已知(),0,a βπ∈,则“tan tan 1αβ=”是“2a πβ+=”的()A .充要条件B .既不充分也不必要条件C .充分不必要条件D .必要不充分条件【答案】D【分析】根据诱导公式的逆运用以及由三角函数的概念即可判断其充分性,由2a πβ+=代入tan α化简计算即可判断其必要性,从而得出结论.【详解】若tan tan 1αβ=,则1tan ta 2n tan παββ⎛⎫==- ⎪⎝⎭,故()2k k παπβ=+-∈Z ,即()2k k παβπ+=+∈Z .又()0,2αβπ+∈,故0k =或1k =,充分性不成立;若2παβ+=,即2παβ=-,所以1tan tan 2tan παββ⎛⎫=-= ⎪⎝⎭,所以tan tan 1αβ=,所以必要性成立.故选:D .22.(2024·陕西榆林·二模)已知π7π1cos cos 12125αα⎛⎫⎛⎫+++= ⎪ ⎪⎝⎭⎝⎭,则2πc 23os +α⎛⎫ ⎪⎝⎭=()A .2325-B .2325C .2425-D .2425【答案】C【分析】利用诱导公式和倍角公式化简求值.【详解】7ππππcos cos sin 1212212ααα⎛⎫⎛⎫⎛⎫+=++=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,由π7π1cos cos 12125αα⎛⎫⎛⎫+++= ⎪ ⎪⎝⎭⎝⎭,有ππ1cos sin 12125αα⎛⎫⎛⎫+-+= ⎪ ⎪⎝⎭⎝⎭,两边平方得π11sin 2625α⎛⎫-+= ⎪⎝⎭,则π24sin 2625α⎛⎫+= ⎪⎝⎭,故2ππππ24cos 2+=cos 2+=sin 2=225366ααα⎛⎫⎛⎫⎛⎫+-+-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选:C.23.(2024高三上·北京海淀·阶段练习)已知α为第二象限的角,且3cos 5α=-,则()sin πα-的值为()A .45B .45-C .35-D .35【答案】A【分析】先根据平方关系求出sin α,再利用诱导公式即可得解.【详解】因为α为第二象限的角,且3cos 5α=-,所以4sin 5α=,所以()4sin πsin 5αα-==.故选:A.24.(2024高一上·山西太原·阶段练习)已知π02α<<,且π1sin 34α⎛⎫-= ⎪⎝⎭,则5πsin 6α⎛⎫-= ⎪⎝⎭()A .4B .14-C .4D .14【答案】C【分析】根据角的范围及正弦值求出余弦值,进而利用诱导求出答案.【详解】因为π02α<<,所以ππ36π3α-<-<,又π1sin 34α⎛⎫-= ⎪⎝⎭,所以πcos 3α⎛⎫-== ⎪⎝⎭45πππππs 62in c 3sin cos os 33αααα⎛⎫⎛⎫⎛⎫⎛⎫-=+-=-=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.故选:C25.(2024·全国·模拟预测)已知π1tan 22θ⎛⎫+= ⎪⎝⎭,则()33sin 2cos sin πθθθ+=+()A .35B .56C .56-D .35-【答案】D【分析】结合诱导公式与同角三角函数的基本关系运算即可得.【详解】由题意得πsin cos 12πsin 2cos 2θθθθ⎛⎫+ ⎪⎝⎭==-⎛⎫+ ⎪⎝⎭,则tan 2θ=-,故()()33333322sin 2cos sin 2cos sin 2cos sin πsin sin sin cos θθθθθθθθθθθ+++==-+-+333323sin 2cos tan 2823sin sin cos tan tan 825θθθθθθθθ++-+=-=-=-=-++--.故选:D.26.(2024高三上·云南昆明·阶段练习)若π2αβ+=sin αβ+=tan α=()A.2BC .1D【答案】B【分析】由诱导公式可得出sin cos βα=,根据已知条件可得出关于sin α、cos α的方程组,解出这两个量的值,结合同角三角函数的商数关系可求得tan α的值.【详解】因为π2αβ+=,则π2βα=-,πsin sin cos 2αβαααα⎛⎫+=+-=+= ⎪⎝⎭联立22cos sin cos 1αααα+=+=⎪⎩sin cos αα⎧=⎨⎪=⎪⎩因此,sin tan cos 3ααα==故选:B.27.(2024高三上·四川成都·阶段练习)已知角α的终边过点()1,3,则πcos(π)cos()2αα-++的值是()A.B.C.D【答案】A【分析】利用三角函数定义,结合诱导公式计算得解.【详解】由角α的终边过点()1,3,得r =,31sin r r αα====,所以πcos(π)cos()cos sin 210105αααα-++=--=--=-.故选:A28.(2024高三上·安徽·阶段练习)在平面直角坐标系xOy 中,设角α的顶点与原点O 重合,始边与x 轴的非负半轴重合,若角α的终边过点()4,3P -,则()3πsin 2cos π22αα⎛⎫++-= ⎪⎝⎭()A .1425-B .1425C .1725-D .1725【答案】A【分析】根据任意角的三角函数的定义可得sin α,再利用诱导公式、二倍角公式运算求解.【详解】由题意得,5OP ==,则3sin 5α=-,则()3πsin 2cos π2cos 2cos 22cos 22ααααα⎛⎫++-=--=- ⎪⎝⎭()22314212sin 212525α⎡⎤⎛⎫=--=-⨯-⨯-=-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦.故选:A .29.(2024高三上·安徽·期中)已知()sin ,cos P θθ是角π3-的终边上一点,则tan θ=()A .B .C D 【答案】B【分析】由三角函数的定义可得sin ,cos θθ,进而由商数关系可求tan θ.【详解】因为()sin ,cos P θθ是角π3-的终边上一点,所以π1πcos sin ,sin cos 3232θθ⎛⎫⎛⎫-==-==- ⎪ ⎪⎝⎭⎝⎭,则sin tan cos 3θθθ==,故选:B.30.(2024高三上·安徽·期中)已知角θ的顶点在坐标原点,始边与x 轴的非负半轴重合,终边经过点()2,4P -,则()cos 2cos 2πθπθ⎛⎫--+= ⎪⎝⎭()A .5-B .5-C .0D .5【答案】C【分析】根据终边上的点可求得:sinθ=cos θ=,再结合三角函数诱导公式从而求解.【详解】因为:r OP ==(O 为坐标原点),所以:由三角函数的定义,得sin θ==cos θ==所以:()cos 2cos sin 2cos 02πθπθθθ⎛⎫--+=+= ⎪⎝⎭.故C 项正确.故选:C.31.(2024高一上·江苏常州·阶段练习)若π1cos()63α+=,则5π5πcos()sin()63αα--+=()A .0B .23C.13+D.13-【答案】A【分析】利用整体代换法与诱导公式化简求值即可.【详解】依题,令π6t α+=,则15ππsin ,ππ366t t αα⎛⎫=-=-+=- ⎪⎝⎭,5π3ππ3π3262t αα+=++=+,所以5π5πcos()sin()63αα--+3π=cos(π)sin()2t t --+cos cos 0t t =-+=.故选:A32.(2024高三上·重庆永川·期中)已知π0,2θ⎛⎫∈ ⎪⎝⎭,π2tan tan 43θθ⎛⎫+=- ⎪⎝⎭,则πcos cos 22π4θθθ⎛⎫- ⎪⎝⎭=⎛⎫+ ⎪⎝⎭()A .12-B .35-C .3D .53【答案】B【分析】由条件π2tan tan 43θθ⎛⎫+=- ⎪⎝⎭化简求得tan 3θ=,将所求式子利用三角恒等变换化简再根据同角三角函数关系式转化为正切求得结果.【详解】由π2tan tan 43θθ⎛⎫+=- ⎪⎝⎭,即tan 12tan 1tan 3θθθ+=--,又π0,2θ⎛⎫∈ ⎪⎝⎭,解得tan 3θ=,()()22πcos cos2sin cos sin2sin cos sinπsin cos4θθθθθθθθθθθ⎛⎫-⎪-⎝⎭∴==-+⎛⎫+⎪⎝⎭2222222sin cos sin tan tan333sin cos tan1315θθθθθθθθ---====-+++.故选:B.33.(2024高一下·山东潍坊·阶段练习)下列化简正确的是()A.()tanπ1tan1+=-B.()()sincostan360ααα-=-C.()()sinπtancosπααα-=+D.()()()cosπtanπ1sin2πααα---=-【答案】B【分析】应用诱导公式以及同角三角函数的基本关系对四个选项验证即可.【详解】对于A,由诱导公式得,()tanπ1tan1+=,故A错误;对于B,()()sin sin sincossintantan360cos aααααααα--===-- ,故B正确;对于C,()()sinπsintancosπcosααααα-==-+-,故C错误;对于D,()()()()()sincoscosπtanπcos tan cos1sin2πsin sinαααααααααα⋅----==-=---,故D错误.故选:B.二、多选题34.(2024·辽宁·模拟预测)设α为第一象限角,π1cos83α⎛⎫-=⎪⎝⎭,则()A.5π1sin83α⎛⎫-=-⎪⎝⎭B.7π1cos83α⎛⎫+=-⎪⎝⎭C.13πsin83α⎛⎫-=-⎪⎝⎭D.πtan8α⎛⎫-=-⎪⎝⎭【答案】BD【分析】首先由题意得π8α-是第一象限角,所以πsin 83α⎛⎫-=⎪⎝⎭,再利用诱导公式和同角三角函数关系式对选项逐个计算确定正确答案.【详解】由题意得π2π2π,Z 2k k k α<<+∈,则ππ3π2π2π,Z 888k k k α-<-<+∈,若π8α-在第四象限,则ππ1cos cos 8423α⎛⎫->=⎪⎝⎭,所以π8α-也是第一象限角,即πsin 8α⎛⎫-=⎪⎝⎭5πππππ1sin sin cos cos 828883αααα⎛⎫⎛⎫⎛⎫⎛⎫-=+-=-=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,A 项错误;7πππ1cos cos πcos 8883ααα⎛⎫⎛⎫⎛⎫+=-+=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,B 项正确;13π3ππππ1sin sin cos cos 828883αααα⎛⎫⎛⎫⎛⎫⎛⎫-=+-=--=--=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,C 项错误;πsin ππ8tan tan 2π88cos 8αααα⎛⎫- ⎪⎛⎫⎛⎫⎝⎭-=--=-=- ⎪ ⎪⎛⎫⎝⎭⎝⎭- ⎪⎝⎭项正确.故选:BD.35.(江苏省宜兴中学、泰兴中学、泰州中学2023-2024学年高一上学期12月联合质量检测数学试卷)质点P 和Q 在以坐标原点O 1的圆O 上逆时针作匀速圆周运动,同时出发.P 的角速度大小为2rad /s ,起点为圆O 与x 轴正半轴的交点,Q 的角速度大小为5rad /s ,起点为角π3-的终边与圆O 的交点,则当Q 与P 重合时,Q 的坐标可以为()A .2π2πcos ,sin 99⎛⎫ ⎪⎝⎭B .ππcos ,sin 99⎛⎫- ⎪⎝⎭C .5π5πcos ,sin 99⎛⎫-- ⎪⎝⎭D .ππcos ,sin 99⎛⎫- ⎪⎝⎭【答案】ACD【分析】由题意列出重合时刻t 的表达式,进而可得Q 点的坐标,通过赋值对比选项即可得解.【详解】点Q 的初始位置1Q ,锐角1π3Q OP ∠=,设t 时刻两点重合,则π522π(N)3t t k k -∈=+,即π2π(N)93k t k +∈=,此时点ππcos 5,sin 533Q t t ⎛⎫⎛⎫⎛⎫-+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,即2π10π2π10πcos ,sin 9393k k Q ⎛⎫⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭⎝⎭,(N)k ∈,当0k =时,2π2πcos ,sin 99Q ⎛⎫ ⎪⎝⎭,故A 正确;当1k =时,32π32πcos ,sin 99Q ⎛⎫ ⎪⎝⎭,即5π5πcos ,sin 99Q ⎛⎫-- ⎪⎝⎭,故C 正确;当2k =时,9,62π62πcos sin 9Q ⎛⎫ ⎪⎝⎭,即ππcos ,sin 99Q ⎛⎫- ⎪⎝⎭,故D 正确;由三角函数的周期性可得,其余各点均与上述三点重合,故B 错误,故选:ACD.36.(2024高一下·河南焦作·阶段练习)已知角,A B ,C 是锐角三角形ABC 的三个内角,下列结论一定成立的有()A .()sin sinBC A +=B .sin cos 22A B C +⎛⎫= ⎪⎝⎭C .()cos cos A B C +<D .sin cos A B<【答案】ABC【分析】根据三角形内角和及诱导公式,三角函数单调性一一判定选项即可.【详解】由题易知()()πsin sin πsin 2A B C A B C B C A A π⎛⎫++=<⇒+=-= ⎪⎝⎭、、,πsin sin cos 222A B C C +-⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,()()cos cos πcos 0cos A B C C C +=-=-<<,即A 、B 、C 结论成立.对于D ,由锐角三角形知,2A B π+>,得ππ022B A <-<<,因此πsin sin cos 2A B B ⎛⎫>-= ⎪⎝⎭,所以错误.故选:ABC37.(2024高一下·河北沧州·阶段练习)在△ABC 中,下列关系式恒成立的有()A .()sin sin ABC +=B .cos sin 22A B C +⎛⎫= ⎪⎝⎭C .()sin 22sin20A B C ++=D .()cos 22cos20A B C ++=【答案】ABC【分析】结合三角形的内角和定理和诱导公式,准确运算,即可求解.【详解】对于A 中,由()()sin sin sin A B C C π+=-=,所以A 正确;对于B 中由cos cos sin 2222A B C C π+⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭,所以B 正确;对于C 中,由()()()sin 22sin2sin 2sin2sin 2sin2A B C A B C C Cπ⎡⎤⎡⎤++=++=-+⎣⎦⎣⎦()sin 22sin2sin2sin20C C C C π=-+=-+=,所以C 正确;对于D 中,()cos(22)cos2cos 2cos2cos[2()]cos2A B C A B C C Cπ⎡⎤++=++=-+⎣⎦()cos 22cos2cos2cos22cos2C C C C C π=-+=+=,所以D 错误.故选:ABC.38.(2024高一上·江苏无锡·阶段练习)下列结论正确的有()A .sin cos 63ππαα⎛⎫⎛⎫+=- ⎪ ⎪⎝⎭⎝⎭B .52cos sin 063ππθθ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭C .()()22sin 15cos 751αα-++=D .()()22sin 15sin 751αα-++=【答案】ABD【解析】本题可通过诱导公式将sin 6απ⎛⎫+ ⎪⎝⎭转化为cos 3πα⎛⎫- ⎪⎝⎭,A 正确,然后通过诱导公式将5cos 6πθ⎛⎫+⎪⎝⎭转化为2sin 3πθ⎛⎫-- ⎪⎝⎭,B 正确,最后根据()()sin 15cos 75 αα-=+以及同角三角函数关系判断出C 错误以及D 正确.【详解】A 项:sin sin cos cos 63332πππππαααα⎛⎫⎛⎫⎛⎫⎛⎫+=+-=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,A 正确;B 项:因为522cos sin sin sin 6333ππππθθπθθ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=-+=---=-- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,所以52cos sin 063ππθθ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭,B 正确;C 项:因为()()()sin 15sin 75cos 752πααα⎡⎤-=-+=+⎢⎥⎣⎦,所以()()()222sin 15cos 752cos 751ααα-++=+≠,C 错误;D 项:()()()()2222sin 15sin 75cos 75sin 751αααα-++=+++=,D 正确,故选:ABD.【点睛】关键点点睛:本题考查诱导公式以及同角三角函数关系的应用,考查的公式有sin cos 2παα⎛⎫+= ⎪⎝⎭、()cos cos αα=-、sin cos 2παα⎛⎫-= ⎪⎝⎭、22cos sin 1αα+=等,考查化归与转化思想,是中档题.39.(2024高一上·黑龙江齐齐哈尔·期末)已知下列等式的左右两边都有意义,则下列等式恒成立的是()A .cos 1sin 1sin cos x xx x-=+B .221sin 12tan sin cos tan x x x x x++=C .()()sin 53cos 37x x -=+D .()()sin 60cos 480x x -=+【答案】ABC【分析】对于A 、B ,由同角三角函数的基本关系进行化简证明即可,对于C 、D ,由诱导公式进行化简证明即可.【详解】对于A ,()()()()()22cos 1sin cos 1sin cos 1sin cos 1sin 1sin 1sin 1sin 1sin cos cos x x x x x x x x x x x x x x----====++--,故A 正确;对于B ,()2222222sin cos sin 1sin cos 2sin 12tan sin cos sin cos sin cos tan x x x x x x x x x x x x x x+++++===,故B 正确;对于C ,()()()sin 53sin 9037=cos 37x x x ⎡⎤-=-++⎣⎦,故C 正确;对于D ,()()()()cos 480=cos 0=cos 18060=cos 0126x x x x -⎡⎤++---⎣⎦,故D 错误.故选:ABC.三、填空题40.(2024·全国)若π10,,tan 22⎛⎫∈= ⎪⎝⎭θθ,则sin cos θθ-=.【答案】5-【分析】根据同角三角关系求sin θ,进而可得结果.【详解】因为π0,2θ⎛⎫∈ ⎪⎝⎭,则sin 0,cos 0θθ>>,又因为sin 1tan cos 2θθθ==,则cos 2sin θθ=,且22222cos sin 4sin sin 5sin 1+=+==θθθθθ,解得sin θ=或sin θ=(舍去),所以sin cos sin 2sin sin -=-=-=-θθθθθ故答案为:5-.41.(2024高一上·福建莆田·阶段练习)已知tan α=-2απ<<π,那么sin cos 1αα=+.【分析】由同角三角函数关系及已知条件求得1sin 33αα==-,代入目标式求值即可.【详解】由tan α=-2απ<<π,则1sin 33αα==-,所以sin cos 1αα=+.42.(2024高三·全国·对口高考)若sin cos 2sin cos x xx x-=+,求sin cos x x 的值为.【答案】310-/0.3-【分析】由已知求出tan 3x =-,再将sin cos x x 化为22sin cos sin cos x xx x+,利用齐次式法求值,即得答案.【详解】由sin cos 2sin cos x xx x-=+可得sin cos 2(sin cos ),sin 3cos x x x x x x -=+∴=-,因为cos 0x =不适合sin cos 2sin cos x xx x-=+,故cos 0x ≠,所以tan 3x =-,故222sin cos tan 33sin cos sin cos tan 19110x x x x x x x x -====-+++,故答案为:310-43.(2024高三上·江西南昌·阶段练习)若4tan 3θ=,则sin cos sin cos θθθθ-=+.【答案】17【分析】分式上下同除以cos θ,化弦为切,代入4tan 3θ=求值即可.【详解】4tan 3θ= ,sin 411sin cos tan 11cos 3sin 4sin cos tan 1711cos 3θθθθθθθθθθ----∴====++++.故答案为:17.44.(2024·上海浦东新·模拟预测)已知sin cos αα、是关于x 的方程2320x x a -+=的两根,则=a .【答案】56-【分析】先通过根与系数的关系得到sin ,cos αα的关系,再通过同角三角函数的基本关系即可解得.【详解】由题意:Δ41202sin cos 3sin cos 3a a αααα⎧⎪=-≥⎪⎪+=⎨⎪⎪=⎪⎩,所以13a ≤,所以()224sin cos 12sin cos 139a αααα+=+=+=,即650a +=,解得56a =-.故答案为:56-.45.(2024高三·全国·专题练习)已知1sin cos 4αα-=,则33sin cos αα-=.【答案】47128【分析】由立方差公式,得()()3322sin cos sin cos sin cos sin cos αααααααα-=-++.将1sin cos 4αα-=两边平方,解得15sin cos 32αα=,代入即可得解.【详解】由题知()()3322sin cos sin cos sin cos sin cos αααααααα-=-++,因为1sin cos 4αα-=,两边平方有112sin cos 16αα-=,所以15sin cos 32αα=,所以()3311547sin cos 1432128αα-=⨯+=.故答案为:47128.46.(2024高三上·安徽合肥·阶段练习)已知23sin 2m m α-=+,1cos 2m m α+=-+,且α为第二象限角,则()()sin 2024πcos 2023π2021πcos 2ααα+++=⎛⎫+ ⎪⎝⎭.【答案】73-/123-【分析】由已知可求出m 的取值范围,由同角三角函数的平方关系求出m 的值,可求出tan α的值,再利用诱导公式结合弦化切可求得所求代数式的值.【详解】因为23sin 2m m α-=+,1cos 2m m α+=-+,且α为第二象限角,则2302102m m m m -⎧>⎪⎪+⎨+⎪-<⎪+⎩,解得2m <-或32m >,因为22222223151010sin cos 12244m m m m m m m m αα-+-+⎛⎫⎛⎫+=+-== ⎪ ⎪++++⎝⎭⎝⎭,整理可得22730m m -+=,即()()2130m m --=,解得12m =(舍)或3m =,所以,233sin 25m m α-==+,14cos 25m m α+=-=-+,所以,sin 353tan cos 544ααα⎛⎫==⨯-=- ⎪⎝⎭,因此,()()sin 2024πcos 2023πsin cos 147112021πsin tan 33cos 2ααααααα+++-==-+=--=--⎛⎫+ ⎪⎝⎭.故答案为:73-.47.(2024·全国·模拟预测)若()223ππ1cos cos 714f x x x ⎡⎤⎤⎛⎫⎛⎫=--++ ⎪ ⎪⎢⎥⎥⎝⎭⎝⎭⎣⎦⎦,则()f x 的最大值为,()f x 的最小值为.【答案】91【分析】借助诱导公式将函数式转化,再利用两点间的距离公式将数转化为形,利用形的直观来求最值.【详解】因为πππ3π3πcos sin sin sin 1421477x x x x ⎛⎫⎛⎫⎛⎫⎛⎫+=--=-=-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,=,此式可看作点(到点3π3πcos ,sin 77x x ⎡⎤⎛⎫⎛⎫--⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦的距离.而点3π3πcos ,sin 77x x ⎡⎤⎛⎫⎛⎫-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦的轨迹是圆221+=m n .又点(到圆心()0,0的距离为2,所以()f x 的最大值()()2max 219f x =+=,()f x 的最小值()()2min 211f x =-=.故答案为:9;1【点睛】将所给函数式展开必将陷入命题人的圈套,此时要整体把握目标,借助诱导公式将函数式转化,再利用两点间的距离公式将数转化为形,利用形的直观来求最值,既简单又节省时间.本题不仅要求学生具备扎实的基本功,具有整体把握目标的能力,还对学生分析问题和解决问题的能力、逻辑推理能力、运算求解能力等要求较高.48.(2024·四川绵阳·三模)已知π,π2θ⎛⎫∈ ⎪⎝⎭,()sin π3θ+=-,则tan θ=.【答案】【分析】根据诱导公式以及同角关系即可求解.【详解】由()sin π3θ+=-得sin 3θ=,由π,π2θ⎛⎫∈ ⎪⎝⎭可得cos θ=-,故sin tan cos θθθ==故答案为:2-49.(2024·山西阳泉·三模)已知πsin 6α⎛⎫+= ⎪⎝⎭ππ,44α⎛⎫∈- ⎪⎝⎭,则πsin 3α⎛⎫-=⎪⎝⎭.【分析】整体法诱导公式结合同角三角函数关系求出答案.【详解】因为ππ,44α⎛⎫∈- ⎪⎝⎭,所以ππ5π,61212α⎛⎫+∈- ⎪⎝⎭,故πcos 06α⎛⎫+> ⎪⎝⎭,所以πcos 6α⎛⎫+= ⎪⎝⎭ππππsin sin cos 3266ααα⎡⎤⎛⎫⎛⎫⎛⎫-=-+=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦50.(2024·浙江温州·二模)已知tan x =,则23sin 2sin cos x x x -=.【分析】利用同角三角函数的关系化简23sin 2sin cos x x x -为齐次式,再代入tan x =.【详解】因为tan x =,所以2222223sin 2sin cos 3tan 2tan 3sin 2sin cos sin cos 1tan x x x x xx x x x x x---==++、()2231⨯-==+51.(2024·黑龙江哈尔滨·二模)已知tan 2θ=,则1sin 2cos 2θθ+的值是.【答案】5【分析】利用正弦、余弦的二倍角公式以及弦化切的公式先化简,在将tan 2θ=代入即可.【详解】因为tan 2θ=,所以2211sin 2cos 22sin cos cos sin θθθθθθ=++-2222cos sin 2sin cos cos sin θθθθθθ+=+-221tan 2tan 1tan θθθ+=+-221252212+==⨯+-,故答案为:5.52.(2024高三·全国·专题练习)已知()7sin cos 0π13ααα+=<<,则tan α=.【答案】125-【分析】由同角三角函数的平方关系和商数关系,并分析三角函数值的正负即可求解.【详解】解:已知7sin cos 13αα+=①,则()2sin cos 12sin cos 69491αααα+=+=,60sin cos 0169αα=-<,0πα<< ,sin 0α∴>,则cos 0α<,sin cos 0αα->,17sin cos13αα∴-===②,联立①②,得12sin 13α=,5cos 13α=-12tan 5α∴=-,故答案为:125-.53.(2024高三上·湖南衡阳·期中)已知sin cos 3αα-=-,则sin 2α=.【答案】79【分析】sin cos 3αα-=-平方,结合同角三角函数平方关系即正弦二倍角公式求解.【详解】sin cos αα-=两边平方得:()22sin cos 12sin cos 1sin 29ααααα-=-=-=,解得:7sin 29α=.故答案为:7954.(2024·全国·模拟预测)已知π1sin 35α⎛⎫-= ⎪⎝⎭,则cos 6α5π⎛⎫-=⎪⎝⎭.【答案】15/0.2【分析】由三角函数的诱导公式化简可得.【详解】由题可得5π5ππππ1cos cos cos sin 663235αααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-=-=--=-= ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦.故答案为:1555.(2024高三上·内蒙古包头·阶段练习)若πtan 4θ⎛⎫+= ⎪⎝⎭πtan 4θ⎛⎫-=⎪⎝⎭.【答案】【分析】以π4θ+为整体,根据诱导公式运算求解.【详解】由题意可得:πππ1tan tanπ442tan 4θθθ⎡⎤⎛⎫⎛⎫-=+-=-=- ⎪ ⎪⎢⎥⎛⎫⎝⎭⎝⎭⎣⎦+ ⎪⎝⎭故答案为:56.(2024高一下·黑龙江佳木斯·开学考试)已知()1sin 535α︒-=,且27090α-︒<<-︒,则()sin 37α︒+=.【答案】【分析】设53βα︒=-,37γα︒=+,则90βγ︒+=,90γβ︒=-,从而将所求式子转化成求cos β的值,利用α的范围确定cos β的符号.【详解】设53βα︒=-,37γα︒=+,那么90βγ︒+=,从而90γβ︒=-.于是()sin sin 90cos γββ︒=-=.因为27090α︒︒-<<-,所以143323β︒︒<<.由1sin 05β=>,得143180β︒︒<<.所以cos β===所以()sin 37sin 5αγ︒+==-.故答案为:57.(2024高一上·新疆乌鲁木齐·期末)已知角α的终边与单位圆221x y +=交于点1,2⎛⎫⎪⎝⎭y P ,则3πsin 2α⎛⎫-= ⎪⎝⎭.【答案】12-/-0.5【分析】根据任意角三角比的定义和诱导公式求解.【详解】因为角α的终边与单位圆221x y +=交于点1,2⎛⎫⎪⎝⎭y P ,所以||1r OP ==13π12sin cos 212x r αα⎛⎫-=-=-=-=- ⎪⎝⎭,故答案为:12-.58.(2024高一·全国·课后作业)若角α的终边落在直线y x =上,则co 3si 22n s παπα⎛⎫⎛⎫++= ⎪ ⎪⎝⎭⎝⎭-.【分析】化简得到3sin cos cos sin 22ππαααα⎛⎫⎫⎪⎪-++=--⎝⎭⎝⎭,考虑角α为第一或第三象限角两种情况,计算得到答案.【详解】因为角α的终边落在直线y x =上,所以角α为第一或第三象限角,3sin cos cos sin 22ππαααα⎛⎫⎛⎫⎪ ⎪-++=--⎝⎭⎝⎭,当角α为第一象限角时,cos sin αα==,cos sin αα--==当角α为第三象限角时,cos sin αα==cos sin 22αα--=+=或.四、解答题59.(2024高三·全国·专题练习)已知角α的终边落在直线2y x =上.求(1)4sin 2cos 5sin 3cos αααα-+的值;(2)25sin 3sin cos 2ααα+-的值.【答案】(1)613(2)165【分析】由角α的终边落在直线2y x =上可得tan 2α=,再根据同角函数的关系求解即可.【详解】(1)由角α的终边落在直线2y x =上可得tan 2α=则原式=4tan 28265tan 310313αα--==++;(2)原式222225sin 3sin cos 5tan 3tan 20616222sin cos tan 155αααααααα+++=-=-=-=++.60.(2024高一下·安徽·期中)已知角θ的顶点为坐标原点O ,始边为x 轴的非负半轴,终边与单位圆相交于点P (),x y ,若点P 位于x 轴上方且12x y +=.(1)求sin cos θθ-的值;(2)求44sin cos θθ+的值.【答案】(2)2332【分析】(1)根据cos sin θθ+,cos sin θθ-,cos sin θθ三个直接的关系,可得sin cos θθ-.(2)由4422sin cos 12sin cos θθθθ+=-可得.【详解】(1)由三角函数的定义,1cos sin 2θθ+=,sin 0θ>,两边平方,得221cos sin 2sin cos 4θθθθ++=则32sin cos 04θθ=-<,sin 0θ>,cos 0θ<,所以sin cos 0θθ->,sin cos2θθ-=.(2)由(1)知,3sin cos 8θθ=-,4422222923sin cos (sin cos )2sin cos 126432θθθθθθ+=+-=-⨯=.。
高考数学专题突破:数学方法(特殊解法)

高考数学专题突破:数学方法(特殊解法)一.知识探究:1.换元法解数学题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化,这叫换元法。
换元的实质是转化,关键是构造元和设元,理论依据是等量代换,目的是变换研究对象,将问题移至新对象的知识背景中去研究,从而使非标准型问题标准化、复杂问题简单化,变得容易处理。
换元法又称辅助元素法、变量代换法。
通过引进新的变量,可以把分散的条件联系起来,隐含的条件显露出来,或者把条件与结论联系起来。
或者变为熟悉的形式,把复杂的计算和推证简化。
它可以化高次为低次、化分式为整式、化无理式为有理式、化超越式为代数式,在研究方程、不等式、函数、数列、三角等问题中有广泛的应用。
换元的方法有:局部换元、三角换元、均值换元等。
局部换元又称整体换元,是在已知或者未知中,某个代数式几次出现,而用一个字母来代替它从而简化问题,当然有时候要通过变形才能发现。
例如解不等式:4x+2x-2≥0,先变形为设2x=t(t>0),而变为熟悉的一元二次不等式求解和指数方程的问题。
三角换元,应用于去根号,或者变换为三角形式易求时,主要利用已知代数式中与三角知识中有某点联系进行换元。
如求函数y=x+1-x的值域时,易发现x∈[0,1],设x=sin2α ,α∈[0,π2 ],问题变成了熟悉的求三角函数值域。
为什么会想到如此设,其中主要应该是发现值域的联系,又有去根号的需要。
如变量x、y适合条件x2+y2=r2(r>0)时,则可作三角代换x=rcosθ、y=rsinθ化为三角问题。
均值换元,如遇到x+y=S形式时,设x=S2+t,y=S2-t等等。
我们使用换元法时,要遵循有利于运算、有利于标准化的原则,换元后要注重新变量X围的选取,一定要使新变量X围对应于原变量的取值X围,不能缩小也不能扩大。
如上几例中的t>0和α∈[0,π2 ]。
2.待定系数法要确定变量间的函数关系,设出某些未知系数,然后根据所给条件来确定这些未知系数的方法叫待定系数法,其理论依据是多项式恒等,也就是利用了多项式f(x)≡g(x)的充要条件是:对于一个任意的a值,都有f(a)≡g(a);或者两个多项式各同类项的系数对应相等。
高考数学二轮专题突破辅导与测试基本初等函数函数与方程及函数的应用公开课一等奖课件省赛课获奖课件

c=log2.11.5<log2.12.1=1,
因此 c<a<b.
(2)选项A,由于函数在区间上为增函数,由单调性定义可
知(x1-x2)[f(x1)-f(x2)]>0,故A错误;选项B,由函数图像的凸
凹性可知f
x1+x2 2
>
fx1+fx2 2
,故B错误;选项C,令g(x)=
fx x
=
ln x x
=exx在(-∞,0),(0,1)上为减函数,在(1,+∞)上为增函数,故 C
错误;同理,令 h(x)=xex,则 h′(x)=ex+xex=(1+x)ex,所以
h(x)=xex 在(-∞,-1)上为减函数,在(-1,+∞)上为增函数,
故 D 错误.
答案:B
——————————规律·总结————————————
2.已知函数 f(x)=2xx+-112,,xx∈∈210,,212.,
若存在 x1,x2,当 0≤x1<x2<2
时,f(x1)=f(x2),则 x1f(x2)的取值范围是_____.
x1+12=2x2-1,
解析:作出函数
f(x)的图像,由图知
22-12≤x1<12,
21≤x2<1.
所以
x1f(x2)
1 x
图像交点的个数,在同一坐标系中画出两个
函数图像如图所示:
由图可知共有6个交点,故函数F(x)=xf(x)-1的零点 个数为6.
(3)由x2-3≥x-1解得x≤-1或x≥2,所以f(x)=
|x-1|,x≤-1或x≥2, x2-3,-1<x<2.
函数y=f(x)-c恰有两个零点,即函
数y=f(x),y=c的图像恰有两个交点,作出函数y=f(x),y=c
2022-2023学年度高考数学专题突破《数列通项公式的多种妙解方式》含十六大经典题型附答案解析

数列通项公式的多种妙解方式经典题型一:观察法经典题型二:叠加法经典题型三:叠乘法经典题型四:待定系数法经典题型五:同除以指数经典题型六:取倒数法经典题型七:取对数法经典题型八:已知通项公式a n 与前n 项的和S n 关系求通项问题经典题型九:周期数列经典题型十:前n 项积型经典题型十一:“和”型求通项经典题型十二:正负相间讨论、奇偶讨论型经典题型十三:因式分解型求通项经典题型十四:其他几类特殊数列求通项经典题型十五:双数列问题经典题型十六:通过递推关系求通项(2022·全国·高考真题)记S n 为数列a n 的前n 项和,已知a 1=1,S n a n 是公差为13的等差数列.(1)求a n 的通项公式;(2)证明:1a 1+1a 2+⋯+1a n<2.【解析】(1)∵a 1=1,∴S 1=a 1=1,∴S 1a 1=1,又∵S n a n 是公差为13的等差数列,∴S n a n =1+13n -1 =n +23,∴S n =n +2 a n 3,∴当n ≥2时,S n -1=n +1 a n -13,∴a n =S n -S n -1=n +2 a n 3-n +1 a n -13,整理得:n -1 a n =n +1 a n -1,即a n a n -1=n +1n -1,∴a n =a 1×a 2a 1×a 3a 2×⋯×a n -1a n -2×a n a n -1=1×31×42×⋯×n n -2×n +1n -1=n n +1 2,显然对于n =1也成立,∴a n 的通项公式a n =n n +1 2;(2)1a n =2n n +1 =21n -1n +1 , ∴1a 1+1a 2+⋯+1a n=21-12 +12-13 +⋯1n -1n +1 =21-1n+1<2(2022·全国·高考真题(理))记S n为数列a n的前n项和.已知2S nn+n=2a n+1.(1)证明:a n是等差数列;(2)若a4,a7,a9成等比数列,求S n的最小值.【解析】(1)因为2S nn+n=2a n+1,即2S n+n2=2na n+n①,当n≥2时,2S n-1+n-12=2n-1a n-1+n-1②,①-②得,2S n+n2-2S n-1-n-12=2na n+n-2n-1a n-1-n-1,即2a n+2n-1= 2na n-2n-1a n-1+1,即2n-1a n-2n-1a n-1=2n-1,所以a n-a n-1=1,n≥2且n∈N*,所以a n是以1为公差的等差数列.(2)由(1)可得a4=a1+3,a7=a1+6,a9=a1+8,又a4,a7,a9成等比数列,所以a72=a4⋅a9,即a1+62=a1+3⋅a1+8,解得a1=-12,所以a n=n-13,所以S n=-12n+nn-12=12n2-252n=12n-2522-6258,所以,当n=12或n=13时S n min=-78.类型Ⅰ观察法:已知数列前若干项,求该数列的通项时,一般对所给的项观察分析,寻找规律,从而根据规律写出此数列的一个通项.类型Ⅱ公式法:若已知数列的前项和与a n的关系,求数列a n的通项a n可用公式a n=S1,(n=1)S n-S n-1,(n≥2)构造两式作差求解.用此公式时要注意结论有两种可能,一种是“一分为二”,即分段式;另一种是“合二为一”,即a1和a n合为一个表达,(要先分n=1和n≥2两种情况分别进行运算,然后验证能否统一).类型Ⅲ累加法:形如a n+1=a n+f(n)型的递推数列(其中f(n)是关于n的函数)可构造:a n-a n-1=f(n-1)a n-1-a n-2=f(n-2)...a2-a1=f(1)将上述m2个式子两边分别相加,可得:a n=f(n-1)+f(n-2)+...f(2)+f(1)+a1,(n≥2)①若f(n)是关于n的一次函数,累加后可转化为等差数列求和;②若f(n)是关于n的指数函数,累加后可转化为等比数列求和;③若f(n)是关于n的二次函数,累加后可分组求和;④若f(n)是关于n的分式函数,累加后可裂项求和.类型Ⅳ累乘法:形如a n +1=a n ⋅f (n )a n +1a n=f (n )型的递推数列(其中f (n )是关于n 的函数)可构造:a n a n -1=f (n -1)a n -1a n -2=f (n -2)...a 2a 1=f (1)将上述m 2个式子两边分别相乘,可得:a n =f (n -1)⋅f (n -2)⋅...⋅f (2)f (1)a 1,(n ≥2)有时若不能直接用,可变形成这种形式,然后用这种方法求解.类型Ⅴ构造数列法:(一)形如a n +1=pa n +q (其中p ,q 均为常数且p ≠0)型的递推式:(1)若p =1时,数列{a n }为等差数列;(2)若q =0时,数列{a n }为等比数列;(3)若p ≠1且q ≠0时,数列{a n }为线性递推数列,其通项可通过待定系数法构造等比数列来求.方法有如下两种: 法一:设a n +1+λ=p (a n +λ),展开移项整理得a n +1=pa n +(p -1)λ,与题设a n +1=pa n +q 比较系数(待定系数法)得λ=q p -1,(p ≠0)⇒a n +1+q p -1=p a n +q p -1 ⇒a n +q p -1=p a n -1+qp -1 ,即a n +q p -1 构成以a 1+qp -1为首项,以p 为公比的等比数列.再利用等比数列的通项公式求出a n +qp -1 的通项整理可得a n .法二:由a n +1=pa n +q 得a n =pa n -1+q (n ≥2)两式相减并整理得a n +1-a na n -a n -1=p ,即a n +1-a n 构成以a 2-a 1为首项,以p 为公比的等比数列.求出a n +1-a n 的通项再转化为类型Ⅲ(累加法)便可求出a n .(二)形如a n +1=pa n +f (n )(p ≠1)型的递推式:(1)当f (n )为一次函数类型(即等差数列)时:法一:设a n +An +B =p a n -1+A (n -1)+B ,通过待定系数法确定A 、B 的值,转化成以a 1+A +B 为首项,以A m n =n !n -m !为公比的等比数列a n +An +B ,再利用等比数列的通项公式求出a n +An +B 的通项整理可得a n .法二:当f (n )的公差为d 时,由递推式得:a n +1=pa n +f (n ),a n =pa n -1+f (n -1)两式相减得:a n +1-a n =p (a n -a n -1)+d ,令b n =a n +1-a n 得:b n =pb n -1+d 转化为类型Ⅴ㈠求出 b n ,再用类型Ⅲ(累加法)便可求出a n .(2)当f (n )为指数函数类型(即等比数列)时:法一:设a n +λf (n )=p a n -1+λf (n -1) ,通过待定系数法确定λ的值,转化成以a 1+λf (1)为首项,以A m n =n !n -m !为公比的等比数列a n +λf (n ) ,再利用等比数列的通项公式求出a n +λf (n ) 的通项整理可得a n .法二:当f (n )的公比为q 时,由递推式得:a n +1=pa n +f (n )--①,a n =pa n -1+f (n -1),两边同时乘以q 得a n q =pqa n -1+qf (n -1)--②,由①②两式相减得a n +1-a n q =p (a n -qa n -1),即a n +1-qa na n -qa n -1=p ,在转化为类型Ⅴ㈠便可求出a n .法三:递推公式为a n +1=pa n +q n (其中p ,q 均为常数)或a n +1=pa n +rq n (其中p ,q , r 均为常数)时,要先在原递推公式两边同时除以q n +1,得:a n +1q n +1=p q ⋅a n q n +1q ,引入辅助数列b n (其中b n=a n q n),得:b n +1=p q b n +1q 再应用类型Ⅴ㈠的方法解决.(3)当f (n )为任意数列时,可用通法:在a n +1=pa n +f (n )两边同时除以p n +1可得到a n +1p n +1=a n p n +f (n )p n +1,令an p n =b n ,则b n +1=b n +f (n )pn +1,在转化为类型Ⅲ(累加法),求出b n 之后得a n =p n b n .类型Ⅵ对数变换法:形如a n +1=pa q (p >0,a n >0)型的递推式:在原递推式a n +1=pa q 两边取对数得lg a n +1=q lg a n +lg p ,令b n =lg a n 得:b n +1=qb n +lg p ,化归为a n +1=pa n +q 型,求出b n 之后得a n =10b n.(注意:底数不一定要取10,可根据题意选择).类型Ⅶ倒数变换法:形如a n -1-a n =pa n -1a n (p 为常数且p ≠0)的递推式:两边同除于a n -1a n ,转化为1a n =1a n -1+p 形式,化归为a n +1=pa n +q 型求出1a n的表达式,再求a n ;还有形如a n +1=ma n pa n +q 的递推式,也可采用取倒数方法转化成1a n +1=m q 1a n +mp形式,化归为a n +1=pa n +q 型求出1a n的表达式,再求a n .类型Ⅷ形如a n +2=pa n +1+qa n 型的递推式:用待定系数法,化为特殊数列{a n -a n -1}的形式求解.方法为:设a n +2-ka n +1=h (a n +1-ka n ),比较系数得h +k =p ,-hk =q ,可解得h 、k ,于是{a n +1-ka n }是公比为h 的等比数列,这样就化归为a n +1=pa n +q 型.总之,求数列通项公式可根据数列特点采用以上不同方法求解,对不能转化为以上方法求解的数列,可用归纳、猜想、证明方法求出数列通项公式a n .(1)若数列{a n }的前n 项和为S n ,通项公式为a n ,则a n =S 1,n =1S n -S n -1,n ≥2,n ∈N ∗注意:根据S n 求a n 时,不要忽视对n =1的验证.(2)在数列{a n }中,若a n 最大,则a n ≥a n -1a n ≥a n +1 ,若a n 最小,则a n≤a n -1a n ≤a n +1 .经典题型一:观察法1.(2022·全国·高三专题练习)数列a n 的前4项为:12,15,18,111,则它的一个通项公式是( )A.12n -1B.12n +1C.13n -1D.13n +1【答案】C【解析】将12,15,18,111可以写成13×1-1,13×2-1,13×3-1,13×4-1,所以a n 的通项公式为13n -1;故选:C2.(2022·全国·高三专题练习(文))如图所示是一个类似杨辉三角的递推式,则第n 行的首尾两个数均为( )A.2nB.2n -1C.2n +2D.2n +1【答案】B【解析】依题意,每一行第一个数依次排成一列为:1,3,5,7,9,⋯,它们成等差数列,通项为2n -1,所以第n 行的首尾两个数均为2n -1.故选:B3.(2022·全国·高三专题练习)“一朵雪花”是2022年北京冬奥会开幕式贯穿始终的一个设计理念,每片“雪花”均以中国结为基础造型构造而成,每一朵雪花都闪耀着奥运精神,理论上,一片雪花的周长可以无限长,围成雪花的曲线称作“雪花曲线”,又称“科赫曲线”,是瑞典数学家科赫在1901年研究的一种分形曲线,如图是“雪花曲线”的一种形成过程:从一个正三角形开始,把每条边分成三等份,然后以各边的中间一段为底边分划向外作正三角形,再去掉底边,反复进行这一过程.若第一个正三角形(图①)的边长为1,则第5个图形的周长为___________.【答案】25627【解析】由题意知下一个图形的边长是上一个图形边长的13,边数是上一个图形的4倍,则周长之间的关系为b n =13⋅4⋅b n -1=43b n -1,所以{b n }是公比为q =43的等比数列,而首项b 1=3,所以b n =3⋅43n -1,当n =5时,“雪花”状多边形的周长为b 5=25627.故答案为:25627经典题型二:叠加法4.(2022·全国·高三专题练习)在数列{a n }中,已知a 1=1p ,a n +1=a n na n +1,p >0,n ∈N *.若p =1,求数列{a n }的通项公式.【解析】由题意,a n +1=a n na n +1 ,得:1a n +1-1a n=n ,运用累加法:1a 2-1a 1+1a 3-1a 2+⋯+1a n -1a n -1=1+2+⋯+n -1=n n -1 2,n ≥2∴1a n -1a 1=n n -1 2,即1a n =n n -1 2+p ,n ≥2 ,当p =1时,a n =2n 2-n +2,n ≥2 ,当n =1时,a n =1成立,所以a n =2n 2-n +25.(2022·全国·高三专题练习)已知数列a n 满足a n +1n +1-a n n =1n n +1n ∈N *,且a 1=1,求数列a n 的通项公式;【解析】因为a n +1n +1-a n n =1n n +1=1n -1n +1,所以a n n -a n -1n -1=1n -1-1n n ≥2 ,a n -1n -1-a n -2n -2=1n -2-1n -1,⋯a 22-a 11=1-12,所以累加可得a n n -a 1=1-1nn ≥2 .又a 1=1,所以a n n =2n -1n,所以a n =2n -1n ≥2 .经检验,a 1=1,也符合上式,所以a n =2n -1.6.(2022·全国·高三专题练习)已知数列a n 中,a 1=1中,a n +1=a n +n (n ∈N *)中,则a 4=________,a n =________.【答案】 7n 2-n +22【解析】依题意,n ∈N *,n ≥2,a n -a n -1=n -1,而a 1=1,则a n =a 1+(a 2-a 1)+(a 3-a 2)+⋯+(a n -a n -1)=1+1+2+⋯+(n -1)=1+1+n -12⋅n -1 =n 2-n +22,而a 1=1满足上式,所以a n =n 2-n +22,a 4=42-4+22=7.故答案为:7;n 2-n +22经典题型三:叠乘法7.(2022·全国·高三专题练习)在数列a n 中,a n +1=nn +2a n (n ∈N *),且a 1=4,则数列a n 的通项公式a n =________.【答案】8n n +1【解析】由a n +1=n n +2a n ,得a n +1a n =nn +2,则a 2a 1=13,a 3a 2=24,a 4a 3=35,⋮a n a n -1=n -1n +1n ≥2 ,累乘得a n a 1=13×24×35×⋯×n -3n -1×n -2n ×n -1n +1=2n n +1,所以a n =8n n +1.故答案为:8n n +1 .8.(2022·全国·高三专题练习)设a n 是首项为1的正项数列,且(n +2)a n +12-na n 2+2a n +1a n =0(n ∈N *),求通项公式a n =___________【答案】2n (n +1)【解析】由(n +2)a n +12-na n 2+2a n +1a n =0(n ∈N *),得[(n +2)a n +1-na n ](a n +1+a n )=0,∵a n >0,∴a n +1+a n >0,∴(n +2)a n +1-na n =0 ,∴a n +1a n =nn +2,∴a n =a 1⋅a 2a 1⋅a 3a 2⋅a 4a 3⋅⋅⋅⋅⋅a n a n -1=1×13×24×35×⋅⋅⋅×n -2n ×n -1n +1=2n (n +1)(n ≥2),又a 1=1满足上式,∴a n =2n (n +1).故答案为:2n (n +1).9.(2022·全国·高三专题练习)数列a n 满足:a 1=23,2n +2-1 a n +1=2n +1-2 a n n ∈N * ,则a n 的通项公式为_____________.【答案】a n =2n2n -1 2n +1-1【解析】由2n +2-1 a n +1=2n +1-2 a n 得,a n +1a n =2n +1-22n +2-1=2⋅2n -12n +2-1,则a n a n -1⋅a n -1a n -2⋅a n -2a n -3⋅⋅⋅a 2a 1=2⋅2n -1-12n +1-1⋅2⋅2n -2-12n -1⋅2⋅2n -3-12n -1-1⋅⋅⋅2⋅21-123-1=2n -1⋅32n +1-1 2n -1,即a n a 1=3⋅2n -12n -1 2n +1-1 ,又a 1=23,所以a n =2n 2n -1 2n +1-1.故答案为:a n =2n2n -1 2n +1-1.经典题型四:待定系数法10.(多选题)(2022·广东惠州·高三阶段练习)数列a n 的首项为1,且a n +1=2a n +1,S n 是数列a n 的前n 项和,则下列结论正确的是( )A.a 3=7 B.数列a n +1 是等比数列C.a n =2n -1 D.S n =2n +1-n -1【答案】AB【解析】∵a n +1=2a n +1,可得a n +1+1=2a n +1 ,又a 1+1=2∴数列a n +1 是以2为首项,2为公比的等比数列,故B 正确;则a n +1=2n ,∴a n =2n -1,故C 错误;则a 3=7,故A 正确;∴S n =21-2n1-2-n =2n +1-n -2,故D 错误.故选:AB .11.(2022·河南安阳·三模(文))已知数列a n 满足a n +1=2a n +12,且前8项和为506,则a 1=___________.【答案】32【解析】由题意得:∵a n +1=2a n +12∴a n +1+12=2a n +12 ,即a n +1+12a n +12=2∴数列a n +12 是以a 1+12为首项,2为公比的等比数列,记数列a n +12 的前n 项和为T n T 8=a 1+12 (1-28)1-2=a 1+12+a 2+12+a 3+12+⋯+a 8+12=(a 1+a 2+a 3+⋯a 8)+12×8=506+4=510解得:a 1=32故答案为:3212.(2022·河北衡水·高三阶段练习)已知数列a n 的前n 项和为S n ,且满足2S n +n =3a n ,n ∈N *.(1)求数列a n 的通项公式;(2)若b n =a 2n ,求数列b n 的前10项和T 10.【解析】(1)当n =1时,2S 1+1=3a 1,即2a 1+1=3a 1,解得a 1=1;当n ≥2时,∵2S n +n =3a n ,∴2S n -1+n -1=3a n -1,两式作差得2a n +1=3a n -3a n -1,即a n =3a n -1+1,a n +12=3a n -1+12,∴a n +12a n -1+12=3,又a 1+12=32,∴数列a n +12 是以32为首项,3为公比的等比数列,∴a n +12=32×3n -1=3n 2,a n =3n 2-12=123n -1 .(2)∵b n =a 2n ,则T 10=b 1+b 2+b 3+⋯+b 10=a 2+a 4+⋯+a 20=1232-1 +34-1 +⋯+320-1=1232+34+⋯+320 -10=12321-910 1-9-10 =911-8916.13.(2022·全国·高三专题练习)设数列a n 满足a 1=2,a n -2a n -1=2-n n ∈N * .(1)求证:a n -n 为等比数列,并求a n 的通项公式;(2)若b n =a n -n ⋅n ,求数列b n 的前n 项和T n .【解析】(1)因为a 1=2,a n -2a n -1=2-n n ∈N * ,所以a n =2a n -1+2-n ,即a n -n =2a n -1-n -1又a 1-1=2-1=1,所以a n -n 是以1为首项,2为公比的等比数列,所以a n -n =1×2n -1,所以a n =2n -1+n (2)由(1)可得b n =a n -n ⋅n =n ×2n -1,所以T n =1×20+2×21+3×22+⋯+n ×2n -1①,所以2T n =1×21+2×22+3×23+⋯+n ×2n ②,①-②得-T n =1+1×21+1×22+1×23+⋯+1×2n -1-n ×2n即-T n =1-2n1-2-n ×2n ,所以T n =n -1 ×2n +1;14.(2022·全国·高三专题练习)在数列a n 中,a 1=5,且a n +1=2a n -1n ∈N * .(1)证明:a n -1 为等比数列,并求a n 的通项公式;(2)令b n =(-1)n ⋅a n ,求数列b n 的前n 项和S n .【解析】(1)因为a n +1=2a n -1,所以a n +1-1=2a n -1 ,又a 1-1=4,所以a n +1-1a n -1=2,所以a n -1 是以4为首项,2为公比的等比数列.故a n -1=4×2n -1,即a n =2n +1+1.(2)由(1)得b n =(-1)n⋅2n +1+1 ,则b n =2n +1+1,n =2k ,k ∈N *-2n +1+1 ,n =2k -1,k ∈N* ,①当n =2k ,k ∈N *时,S n =-22-1 +23+1 -24+1 +⋯+-2n -1 +2n +1+1 =-22+23-24+25+⋯-2n +2n +1=22+24+⋯+2n =432n -1 ;②当n =2k -1,k ∈N *时,S n =S n +1-b n +1=432n +1-1 -2n +2+1 =-2n +2+73,综上所述,S n =432n -1 ,n =2k ,k ∈N*-2n +2+73,n =2k -1,k ∈N *经典题型五:同除以指数15.(2022·广东·模拟预测)已知数列a n 中,a 1=5且a n =2a n -1+2n -1n ≥2,n ∈N ∗ ,b n =a n -1n +1(1)求证:数列b n 是等比数列;(2)从条件①n +b n ,②n ⋅b n 中任选一个,补充到下面的问题中并给出解答.求数列______的前n 项和T n .注:如果选择多个条件分别解答,按第一个解答计分.【解析】(1)因为a 1=5且a n =2a n -1+2n -1n ≥2,n ∈N ∗ ,所以当n ≥2时,a n -1=2a n -1-1 +2n ,所以a n -12n =a n -1-12n -1+1,即a n -12n -a n -1-12n -1=1所以a n -12n 是以a 1-12=2为首项,1为公差的等差数列,所以a n -12n =2+n -1 ×1=n +1,所以a n =n +1 2n+1,b n =a n -1n +1=n +1 2n+1-1n +1=2n因为b 1=a 1-11+1=2,n ≥2时,b n b n -1=2n 2n -1=2所以数列b n 是以2为首项,2为公比的等比数列.(2)选①:因为b n =2n ,所以n +b n =n +2n ,则T n =(1+2)+2+22 +3+23 +⋅⋅⋅+n +2n=1+2+3+⋅⋅⋅+n +2+22+23+⋅⋅⋅+2n=12n n +1 +21-2n 1-2=n 22+n2+2n +1-2选②:因为b n =2n ,所以nb n =n ⋅2n,则T n =1×21+2×22+⋅⋅⋅+n ×2n (i )2T n =1×22+2×23+⋅⋅⋅+n ×2n +1(ii )(i )-(ii )得-T n =1×21+22+23+⋅⋅⋅+2n -n ×2n +1T n =n ×2n +1-21-2n 1-2=n ×2n +1-2n +1+2=n -1 2n +1+216.(2022·全国·高三专题练习)已知数列a n 满足a 1=1,a n +1=2a n +3n ,求数列a n 的通项公式.【解析】由a n +1=2a n +3n 两边同除以3n +1得a n +13n +1=23⋅a n 3n +13,令b n =a n 3n ,则b n +1=23b n +13,设b n +1+λ=23(b n +λ),解得λ=-1,b n +1-1=23(b n -1),而b 1-1=-23,∴数列{b n -1}是以-23为首项,23为公比的等比数列,b n -1=-23 n ,得a n =3n -2n17.(2022·全国·高三专题练习)在数列a n 中,a 1=1,S n +1=4a n +2,则a 2019的值为( )A.757×22020B.757×22019C.757×22018D.无法确定【答案】A【解析】∵a 1=1,S n +1=4a n +2,∴S 2=a 1+a 2=4a 1+2,解得a 2=5.∵S n +1=4a n +2,∴S n +2=4a n +1+2,两式相减得,a n +2=4a n +1-4a n ,∴a n +2-2a n +1=2a n +1-2a n ,∴a n +1-2a n 是以a 2-2a 1=3为首项,2为公比的等比数列,∴a n +1-2a n =3×2n -1,两边同除以2n +1,则a n +12n +1-a n 2n=34,∴a n 2n 是以34为公差,a 121=12为首项的等差数列,∴a n 2n =12+n -1 ×34=3n -14,∴a n =3n -14×2n =3n -1 ×2n -2,∴a 2019=3×2019-1 ×22017=757×22020.故选:A .经典题型六:取倒数法18.(2022·全国·高三竞赛)数列a n 满足a 1=p ,a n +1=a 2n +2a n .则通项a n =______.【答案】p +1 2n -1-1【解析】∵a n =a 2n -1+2a n -1,∴a n +1=a n -1+1 2=a n -2+1 22=⋯=a 1+1 2n -1=p +1 2n -1.即a n =p +1 2n -1-1.故答案为p +1 2n -1-119.(2022·全国·高三专题练习)已知数列a n 满足a 1=12,且a n +1=a n 3a n +1,则数列a n =__________【答案】13n -1【解析】由a n +1=a n 3a n +1两边取倒数可得1a n +1=1a n +3,即1a n +1-1a n=3所以数列1a n 是等差数列,且首项为2,公差为3,所以1a n=3n -1,所以a n =13n -1;故答案为:13n -120.(2022·全国·高三专题练习)数列a n 满足a n +1=a n 1+2a nn ∈N ∗,a 1=1,则下列结论错误的是( )A.2a 10=1a 3+1a 17B.21an是等比数列C.2n -1 a n =1D.3a 5a 17=a 49【答案】D 【解析】由a n +1=a n 1+2a n ,且a 1=1,则a 2=a 12a 1+1>0,a 3=a 21+2a 2>0,⋯,以此类推可知,对任意的n ∈N ∗,a n >0,所以,1a n +1=1+2a n a n =1a n +2,所以1a n +1-1a n =2,且1a 1=1,所以,数列1a n 是等差数列,且该数列的首项为1,公差为2,所以,1a n =1+2n -1 =2n -1,则2n -1 a n =1,其中n ∈N ∗,C 对;21a n +121a n=21an +1-1a n=22=4,所以,数列21an是等比数列,B 对;由等差中项的性质可得2a 10=1a 3+1a 17,A 对;由上可知a n =12n -1,则3a 5a 17=3×12×5-1×12×17-1=199,a 49=12×49-1=197,所以,3a 5a 17≠a 49,D 错.故选:D .21.(2022·全国·高三专题练习)已知数列a n 满足a 1=1,a n +1=a n 4a n +1,(n ∈N *),则满足a n >137的n 的最大取值为( )A.7 B.8C.9D.10【答案】C【解析】因为a n +1=a n 4a n +1,所以1a n +1=4+1a n ,所以1a n +1-1a n =4,又1a 1=1,数列1a n是以1为首项,4为公差的等差数列.所以1a n =1+4(n -1)=4n -3,所以a n =14n -3,由a n >137,即14n -3>137,即0<4n -3<37,解得34<n <10,因为n 为正整数,所以n 的最大值为9;故选:C 经典题型七:取对数法22.(2022·湖南·长郡中学高三阶段练习)若在数列的每相邻两项之间插入此两项的积,形成新的数列,再把所得数列按照同样的方法不断构造出新的数列.现对数列1,2进行构造,第一次得到数列1,2,2;第二次得到数列1,2,2,4,2;依次构造,第n n ∈N * 次得到的数列的所有项的积记为a n ,令b n =log 2a n ,则b 3=___________,b n =___________.【答案】 143n +12【解析】设第n 次构造后得到的数列为1,x 1,x 2,⋯,x k ,2.则a n =2x 1x 2⋯x k ,则第n +1次构造后得到的数列为1,x 1,x 1,x 1x 2,x 2,⋯,x k -1x k ,x k ,2x k ,2.则a n +1=4x 1x 2⋯x k 3=4×a n 2 3=12a 3n ,∴b n +1=log 2a n +1=log 212a 3n=-1+3b n ,∴b n +1-12=3b n -12 ,又∵b 1=log 222=2,∴数列b n -12 是以32为首项,3为公比的等比数列,∴b n -12=32×3n -1=3n 2,b n =3n +12,b 3=14.故答案为:14;3n +1223.(2022·全国·高三专题练习(文))英国著名物理学家牛顿用“作切线”的方法求函数零点时,给出的“牛顿数列”在航空航天中应用广泛,若数列x n 满足x n +1=x n -f x nf x n,则称数列x n 为牛顿数列.如果函数f x =2x 2-8,数列x n 为牛顿数列,设a n =ln x n +2x n -2,且a 1=1,x n >2.数列a n 的前n 项和为S n ,则S n =______.【答案】2n -1【解析】∵f x =2x 2-8,∴f x =4x ,又∵x n +1=x n -f x n f x n=x n -2x n 2-84x n =x n 2+42x n ,∴x n +1+2=x n +2 22x n ,x n +1-2=x n -222x n,∴x n +1-2x n +1-2=x n +2x n -2 2,又x n >2∴ln x n +1+2x n +1-2=ln x n +2x n -2 2=2ln x n +2x n -2 ,又a n =ln x n +2x n -2,且a 1=1,所以a n +1=2a n ,∴数列a n 是首项为1,公比为2的等比数列,∴a n 的前n 项和为S n ,则S n =1×1-2n1-2=2n -1.故答案为:2n -1.经典题型八:已知通项公式a n 与前n 项的和S n 关系求通项问题24.(2022·江苏南通·高三开学考试)从条件①2S n =n +1 a n ,②a 2n +a n =2S n ,a n >0,③S n +S n -1=a n n ≥2 ,中任选一个,补充到下面问题中,并给出解答.已知数列a n 的前n 项和为S n ,a 1=1,___________.(1)求a n 的通项公式;(2)设b n =a n +1+12n +1,记数列b n 的前n 项和为T n ,是否存在正整数n 使得T n >83.【解析】(1)若选择①,因为2S n =n +1 a n ,n ∈N *,所以2S n -1=na n -1,n ≥2,两式相减得2a n =n +1 a n -na n -1,整理得n -1 a n =na n -1,n ≥2,即a n n =a n -1n -1,n ≥2,所以a n n 为常数列,而a n n =a 11=1,所以a n =n ;若选择②,因为a 2n +a n =2S n n ∈N *,所以a 2n -1+a n -1=2S n -1n ≥2 ,两式相减a 2n -a 2n -1+a n -a n -1=2S n -2S n -1=2a n n ≥2 ,得a n -a n -1 a n +a n -1 =a n +a n -1n ≥2 ,因为a n >0,∴a n +a n -1>0,∴a n -a n -1=1n ≥2 ,所以a n 是等差数列,所以a n =1+n -1 ×1=n ;若选择③,由S n +S n -1=a n n ≥2 变形得,S n +S n -1=S n -S n -1,所以S n +S n -1=S n +S n -1 S n -S n -1 ,由题意知S n >0,所以S n -S n -1=1,所以S n 为等差数列,又S 1=a 1=1,所以S n =n ,S n =n 2,∴a n =S n -S n -1=2n -1n ≥2 ,又n =1时,a 1=1也满足上式,所以a n =2n -1;(2)若选择①或②,b n =n +1+12n +1=n +22n +1,所以T n =3×12 2+4×12 3+5×12 4+⋯+n +2 ×12n +1,所以12T n =3×12 3+4×12 4+5×12 5+⋯+n +2 ×12n +2,两式相减得12T n =3×12 2+12 3+12 4+⋯+12 n +1-n +2 ×12n +2=34+181-12n -1 1-12-n +2 ×12 n +2=1-n +42n +2,则T n =2-n +42n +1,故要使得T n >83,即2-n +42n +1>83,整理得,n +42n +1<-23,当n ∈N *时,n +42n +1>0,所以不存在n ∈N *,使得T n >83.若选择③,依题意,b n =a n +1+12n +1=n +12n,所以T n =2×12+3×12 2+4×12 3+⋯+n +1 ×12n,故12T n =2×12 2+3×12 3+4×12 4+⋯+n +1 ×12 n +1,两式相减得:12T n =1+12 2+12 3+⋯+12 n -n +1 ×12 n +1=1+141-12n -1 1-12-n +1 ×12 n +1=32-n +32n +1,则T n =3-n +32n ,令T n =3-n +32n >83,则n +32n <13,即2n -3n -9>0,令c n =2n -3n -9,则c 1=-10<0,当n ≥2时,c n +1-c n =2n +1-3n +1 -9-2n -3n -9 =2n -3>0,又c 4<0,c 5>0,故c 2<c 3<c 4<0<c 5<c 6⋯,综上,使得T n >83成立的最小正整数n 的值为5.25.(2022·河南省上蔡第一高级中学高三阶段练习(文))记各项均为正数的等比数列a n 的前n 项和是S n ,已S n =a n +43a n +1-4n ∈N * .(1)求a n 的通项公式;(2)求数列na n 的前n 项和T n .【解析】(1)设等比数列a n 的公比为q .因为S n =a n +43a n +1-4n ∈N * ,所以当n =1时,a 1=a 1+43a 2-4,解得a 2=3;当n =2时,a 1+a 2=a 2+43a 3-4,则a 1=43a 3-4.因为a n 是等比数列,所以a 1a 3=a 22,即43a 3-4 a 3=9,整理得4a 23-12a 3-27=0,解得a 3=-32(舍去)或a 3=92.所以q =a 3a 2=32,a 1=a 2q=2,所以a n =2×32n -1.(2)由(1)得na n =2n ×32 n -1,所以T n =2×1+2×32+3×32 2+⋯+n -1 × 32 n -2+n ×32 n -1①则32T n =2×1×32+2×32 2+3×32 3+⋯+ n -1 ×32 n -1+n ×32 n ②①-②得-T n 2=2×1+32+32 2+323+⋯+ 32 n -1 -2n ×32 n=2×1-32 n1-32-2n ×32 n =-4+4-2n ×32 n ,所以T n =4n -8 ×32n+8.26.(2022·全国·高三专题练习)设数列{a n }的前n 项和为S n ,a n +1=-S n S n +1n ∈N * ,a 1=1. 求证:数列1S n是等差数列.【解析】∵-S n S n +1=a n +1=S n +1-S n ,S 1=1≠0,则S n ≠0,所以-1=S n +1-S nS n S n +1,有1S n +1-1S n=1,所以数列1S n 是以1为首项,1为公差的等差数列.经典题型九:周期数列27.(2022·上海中学高二期末)数列{x n }满足x n +1=x n -x n -1,n ≥2,n ∈N *,x 1=a ,x 2=b ,则x 2019=_________.【答案】b -a .【解析】由题干中递推公式,可得:x 1=a ,x 2=b ,x 3=x 2-x 1=b -a ,x 4=x 3-x 2=b -a -b =-a ,x 5=x 4-x 3=-a -(b -a )=-b ,x 6=x 5-x 4=-b -(-a )=a -b ,x 7=x 6-x 5=a -b -(-b )=a ,x 8=x 7-x 6=a -(a -b )=b ,x 9=x 8-x 7=b -a ,⋯∴数列{x n }是以6为最小正周期的周期数列.∵2019÷6=336⋯3,∴x 2019=x 3=b -a .故答案为b -a .28.(2022·全国·高三专题练习)数列{a n }满足a 1=2,a 2=11-a 1,若对于大于2的正整数n ,a n =11-a n -1,则a 102=__________.【答案】12【解析】由题意知:a 2=11-2=-1,a 3=11--1 =12,a 4=11-12=2,a 5=11-2=-1,故{a n }是周期为3的周期数列,则a 102=a 3×34=a 3=12.故答案为:12.29.(2022·河南·模拟预测(文))设数列a n 满足a n +1=1+a n 1-a n ,且a 1=12,则a 2022=( )A.-2 B.-13C.12D.3【答案】D【解析】由题意可得:a 2=1+a 11-a 1=1+121-12=3,a 3=1+a 21-a 2=1+31-3=-2,a 4=1+a 31-a 3=1+-2 1--2 =-13,a 5=1+a 41-a 4=1-131+13=12=a 1,据此可得数列a n 是周期为4的周期数列,则a 2022=a 505×4+2=a 2=3.故选:D30.(2022·全国·高三专题练习)设数列a n 的通项公式为a n =-1 n 2n -1 ⋅cos n π2+1n ∈N * ,其前n 项和为S n ,则S 120=( )A.-60 B.-120C.180D.240【答案】D【解析】当n =4k -3,k ∈N *时,cos n π2=0,a 4k -3=1;当n =4k -2,k ∈N *时,cosn π2=-1,a 4k -2=2×4k -2 -1 ×-1 +1=-8k +6;当n =4k -1,k ∈N *时,cos n π2=0,a 4k -1=1;当n =4k ,k ∈N *时,cos n π2=1,a 4k =2×4k -1+1=8k .∴a 4k -3+a 4k -2+a 4k -1+a 4k =1+-8k +6 +1+8k =8,∴S 120=1204×8=240.故选:D 经典题型十:前n 项积型31.(2022·全国·高三专题练习)设数列a n 的前n 项积为T n ,且T n =2-2a n n ∈N * .(1)求证数列1T n 是等差数列;(2)设b n =1-a n 1-a n +1 ,求数列b n 的前n 项和S n .【解析】(1)因为数列a n 的前n 项积为T n ,且T n =2-2a n n ∈N * ,∴当n =1时,T 1=a 1=2-2a 1,则a 1=23,1T 1=32.当n ≥2时,T n =2-2T n T n -1⇒1=2T n -2T n -1,∴1T n -1T n -1=12,所以1T n 是以1T 1=32为首项,12为公差的等差数列;(2)由(1)知数列1T n =n +22,则由T n =2-2a n 得a n =n +1n +2,所以b n =1n +2 n +3=1n +2-1n +3,所以S n =13-14 +14-15 +⋯+1n +2-1n +3 =13-1n +3=n 3n +9.32.(2022·全国·高三专题练习)记T n 为数列a n 的前n 项积,已知1T n +3a n=3,则T 10=( )A.163B.154C.133D.114【答案】C 【解析】n =1,T 1=43,T n =a 1a 2a 3⋯a n ,则a n =T n T n -1(n ≥2),代入1T n +3a n =3,化简得:T n -T n -1=13,则T n =n +33,T 10=133.故选:C .33.(2022·全国·高三专题练习)记S n 为数列a n 的前n 项和,b n 为数列S n 的前n 项积,已知2S n +b n =2,则a 9=___________.【答案】1110【解析】因为b n =S 1∙S 2∙⋯S n ,所以b 1=S 1=a 1,b n -1=S 1∙S 2∙⋯S n -1(n ≥2),S n =b nb n -1(n ≥2), 又因为2S n +b n =2,当n =1时,得 a 1=23,所以b 1=S 1=a 1=23, 当n ≥2时, 2×b nb n -1+b n =2,即2b n =2b n -1+1,所以2b n 是等差数列,首项为2b 1=3,公差d =1, 所以2b n=3+(n -1)×1=n +2,所以b n =2n +2,满足 b 1=23,故b n =2n +2,即S 1∙S 2∙⋯S n =2n +2,所以S 1∙S 2∙⋯S n -1=2n +1(n ≥2),两式相除得:S n =n +1n +2,所以S n -1=nn +1(n ≥2),所以a n =S n -S n -1=n +1n +2-n n +1=1(n +1)(n +2),所以a 9=111×10=1110.故答案为:1110.经典题型十一:“和”型求通项34.(2022·山西·太原市外国语学校高三开学考试)在数列a n 中,a 1=1,且n ≥2,a 1+12a 2+13a 3+⋯+1n -1a n -1=a n .(1)求a n 的通项公式;(2)若b n =1a n a n +1,且数列b n 的前项n 和为S n ,证明:S n <3.【解析】(1)因为n ≥2,a 1+12a 2+13a 3+⋯+1n -1a n -1=a n ,所以当n ≥3,a 1+12a 2+13a 3+⋯+1n -2a n -2=a n -1,两式相减,得1n -1a n -1=a n -a n -1,即nn -1a n -1=a n ,当n =2时,a 2=a 1=1,所以当n ≥3时,a n a n -1=nn -1,所以当n ≥3时,a n =a n a n -1×a n -1a n -2×⋯×a 3a 2×a 2=n n -1×n -1n -2×⋯×32×1=n2,当n =2时,上式成立;当n =1时,上式不成立,所以a n =1,n =1n2,n ≥2.(2)证明:由(1)知b n =1,n =14n (n +1),n ≥2当n ≥2时,b n =4n (n +1)=41n -1n +1 ,所以当n =1,S 1=1<3;当n ≥2时,S n =1+412-13 +413-14 +⋯+41n -1n +1=1+412-13+13-14+⋯+1n -1n +1 =1+412-1n +1 =3-4n +1<3.综上,S n <3.35.(2022·全国·高三专题练习)数列a n 满足a 1∈Z ,a n +1+a n =2n +3,且其前n 项和为S n .若S 13=a m ,则正整数m =( )A.99 B.103C.107D.198【答案】B【解析】由a n +1+a n =2n +3得a n +1-(n +1)-1=-a n -n -1 ,∴a n-n-1为等比数列,∴a n-n-1=(-1)n-1a1-2,∴a n=(-1)n-1a1-2+n+1,a m=(-1)m-1a1-2+m+1,∴S13=a1+a2+a3+⋯+a12+a13=a1+2×(2+4+⋯+12)+3×6=a1+102,①m为奇数时,a1-2+m+1=a1+102,m=103;②m为偶数时,-a1-2+m+1=a1+102,m=2a1+99,∵a1∈Z,m=2a1+99只能为奇数,∴m为偶数时,无解,综上所述,m=103.故选:B.36.(2022·黑龙江·哈师大附中高三阶段练习(理))已知数列a n的前n项和为S n,若S n+1+S n=2n2n∈N*,且a1≠0,a10=28,则a1的值为A.-8B.6C.-5D.4【答案】C【解析】对于S n+1+S n=2n2,当n=1时有S2+S1=2,即a2-2=-2a1∵S n+1+S n=2n2,∴S n+S n-1=2(n-1)2,(n≥2)两式相减得:a n+1+a n=4n-2a n+1-2n=-a n-2(n-1),(n≥2)由a1≠0可得a2-2=-2a1≠0,∴a n+1-2na n-2(n-1)=-1(n≥2)即a n-2(n-1)从第二项起是等比数列,所以a n-2(n-1)=a2-2(-1)n-2,即a n=a2-2(-1)n-2+2(n-1),则a10=a2-2+18=28,故a2=12,由a2-2=-2a1可得a1=-5,故选C.经典题型十二:正负相间讨论、奇偶讨论型37.(2022·河南·高二阶段练习(文))数列a n满足a1=1,a n+a n+1=3n n∈N*,则a2018=__________ _.【答案】3026【解析】∵a n+a n+1=3n,∴a n+1+a n+2=3n+1,得a n+2-a n=3,∵a1=1,a n+a n+1=3n n∈N*,∴a1+ a2=3⇒a2=2,所以a n的偶数项构成等差数列,首项为2,公差为3,∴a2018=a2+1008×3=2+3024= 3026.故答案为:302638.(2022·全国·高三专题练习)已知数列a n中,a1=1,a2=2,a n+2=-1n+1a n+2,则a18a19=( )A.3B.113C.213D.219【答案】D【解析】当n为奇数时,a n+2-a n=2,即数列a n中的奇数项依次构成首项为1,公差为2的等差数列,所以,a19=1+10-1×2=19,当n为偶数时,a n+2+a n=2,则a n+4+a n+2=2,两式相减得a n+4-a n=0,所以,a18=a4×4+2=a2=2,故a18a19=219,故选:D.39.(2022·广东·高三开学考试)已知数列a n满足a1=3,a2=2,a n+2=a n-1,n=2k-1 3a n,n=2k .(1)求数列a n的通项公式;(2)求数列a n的前2n项的和S2n.【解析】(1)当n为奇数时,a n+2-a n=-1,所以所有奇数项构成以a1=3为首项,公差为-1的等差数列,所以a n=3+(n-1)⋅-12=7-n2,当n为偶数时,a n+2=3a n,所以所有偶数项构成以a2=2为首项,公比为3的等比数列,所以a n=2×(3)n-2=2×3n-22,所以a n=7-n2,n=2k-1 2×3n-22,n=2k ;(2)S2n=a1+a2+⋯+a2n=a1+a3+a5+⋯+a2n-1+a2+a4+⋯+a2n=3n+(-1)⋅n(n-1)2+21-3n1-3=(7-n)n2+3n-1=-12n2+72n+3n-1.40.数列{a n}满足a n+2+(-1)n+1a n=3n-1,前16项和为540,则a2= .【解析】解:因为数列{a n}满足a n+2+(-1)n+1a n=3n-1,当n为奇数时,a n+2+a n=3n-1,所以a3+a1=2,a7+a5=14,a11+a9=26,a15+a13=38,则a1+a3+a5+a7+a9+a11+a13+a15=80,当n为偶数时,a n+2-a n=3n-1,所以a4-a2=5,a6-a4=11,a8-a6=17,a10-a8=23,a12-a10=29,a14-a12=35,a16-a14=41,故a4=5+a2,a6=16+a2,a8=33+a2,a10=56+a2,a12=85+a2,a14=120+a2,a16=161+a2,因为前16项和为540,所以a2+a4+a6+a8+a10+a12+a14+a16=540-80=460,所以8a2+476=460,解得a2=-2.故答案为:-2.41.(2022•夏津县校级开学)数列{a n}满足a n+2+(-1)n a n=3n-1,前16项和为508,则a1= .【解析】解:由a n+2+(-1)n a n=3n-1,当n为奇数时,有a n+2-a n=3n-1,可得a n-a n-2=3(n-2)-1,⋯a3-a1=3⋅1-1,累加可得a n-a1=3[1+3+⋯+(n-2)]-n-12=(n-1)(3n-5)4;当n为偶数时,a n+2+a n=3n-1,可得a4+a2=5,a8+a6=17,a12+a10=29,a16+a14=41.可得a2+a4+⋯+a16=92.∴a 1+a 3+⋯+a 15=416.∴8a 1+14(0+8+40+96+176+280+408+560)=416,∴8a 1=24,即a 1=3.故答案为:3.经典题型十三:因式分解型求通项42.(2022秋•安徽月考)已知正项数列{a n }满足:a 1=a ,a 2n +1-4a 2n +a n +1-2a n =0,n ∈N *.(Ⅰ)判断数列{a n }是否是等比数列,并说明理由;(Ⅱ)若a =2,设a n =b n -n .n ∈N *,求数列{b n }的前n 项和S n .【解析】解:(Ⅰ)∵a 2n +1-4a 2n +a n +1-2a n =0,∴(a n +1-2a n )(a n +1+2a n +1)=0,又∵数列{a n }为正项数列,∴a n +1=2a n ,∴①当a =0时,数列{a n }不是等比数列;②当a ≠0时,an +1a n=2,此时数列{a n }是首项为a ,公比为2的等比数列.(Ⅱ)由(Ⅰ)可知:a n =2n ,∴b n =2n +n ,∴S n =(21+22+⋯+2n)+(1+2+⋯+n )=2(1-2n )1-2+n (1+n )2=2n +1-2+n (n +1)2.43.(2022•怀化模拟)已知正项数列{a n }满足a 1=1,2a 2n -a n -1a n -6a 2n -1=0(n ≥2,n ∈N *)设b n =log 2a n .(1)求b 1,b 2b 3;(2)判断数列{b n }是否为等差数列,并说明理由;(3){b n }的通项公式,并求其前n 项和为S n .【解析】解:(1)a 1=1,2a 2n -a n -1a n -6a 2n -1=0,a n >0,可得(2a n +3a n -1)(a n -2a n -1)=0,则a n =2a n -1,数列{a n }为首项为1,公比为2的等比数列,可得a n =2n -1;b n =log 2a n =n -1,b 1=0,b 2b 3=1×2=2;(2)数列{b n }为等差数列,理由:b n +1-b n =n -(n -1)=1,则数列{b n }为首项为0,公差为1的等差数列;(3)b n =log 2a n =log 22n -1=n -1,前n 项和为S n =12n (0+n -1)=n 2-n2.44.(2022秋•仓山区校级月考)已知正项数列{a n }满足a 1=2且(n +1)a 2n +a n a n +1-na 2n +1=0(n ∈N *)(Ⅰ)证明数列{a n }为等差数列;(Ⅱ)若记b n =4a n a n +1,求数列{b n }的前n 项和S n .【解析】(I )证明:由(n +1)a 2n +a n a n +1-na 2n +1=0(n ∈N *),变形得:(a n +a n +1)[(n +1)a n -na n +1]=0,由于{a n }为正项数列,∴a n +1a n =n +1n,利用累乘法得:a n =2n (n ∈N *)从而得知:数列{a n }是以2为首项,以2为公差的等差数列.(Ⅱ)解:由(Ⅰ)知:b n=42n∙2(n+1)=1n(n+1)=1n-1n+1,从而S n=b1+b2+⋯+b n=1-1 2+12-13+13-15+⋯+1n-1-1n+1=1-1n+1=n n+1.经典题型十四:其他几类特殊数列求通项45.(2022·全国·高三专题练习)在数列{a n}中,已知各项都为正数的数列{a n}满足5a n+2+4a n+1-a n=0.(1)证明数列{a n+a n+1}为等比数列;(2)若a1=15,a2=125,求{a n}的通项公式.【解析】(1)各项都为正数的数列{a n}满足5a n+2+4a n+1-a n=0,得a n+1+a n+2=15(a n+1+a n),即a n+1+a n+2 a n+a n+1=15所以数列{a n+a n+1}是公比为15的等比数列;(2)因为a1=15,a2=125,所以a1+a2=625,由(1)知数列{a n+a n+1}是首项为625,公比为15的等比数列,所以a n+a n+1=625×15n-1,于是a n+1-15n+1=-an-15 n=(-1)n a1-15,又因为a1-15=0,所以a n-15 n=0,即a n=15 n.46.(2022·湖北·天门市教育科学研究院模拟预测)已知数列a n满足a1=1,a2=6,且a n+1=4a n-4a n-1, n≥2,n∈N*.(1)证明数列a n+1-2a n是等比数列,并求数列a n的通项公式;(2)求数列a n的前n项和S n.【解析】(1)因为a n+1=4a n-4a n-1,n≥2,n∈N*所以a n+1-2a n=2a n-4a n-1=2(a n-2a n-1)又因为a2-2a1=4所以a n+1-2a n是以4为首项,2为公比的等比数列.所以a n+1-2a n=4×2n-1=2n+1变形得a n+12n+1-a n2n=1所以a n2n是以a12=12为首项,1为公差的等差数列所以a n2n=12+n-1=n-12,所以a n=(2n-1)2n-1(2)因为T n=1×20+3×21+5×22+⋅⋅⋅+(2n-1)2n-1⋯①所以2T n=1×21+3×22+5×23+⋅⋅⋅+(2n-1)2n⋯②①-②得:-T n=1+22+23+⋅⋅⋅+2n-1-(2n-1)2n=1+22(1-2n-1)1-2-(2n-1)2n所以T n=(2n-1)2n-2n+1+3=(2n-3)2n+347.(2022·内蒙古·赤峰红旗中学松山分校模拟预测(理))设数列{a n}的前n项和为S n,满足2S n=a2n+1a n n∈N*,则下列说法正确的是( )A.a2021⋅a2022<1B.a2021⋅a2022>1C.a2022<-22022D.a2022>22022【答案】A【解析】因为数列{a n}的前n项和为S n,满足2S n=a2n+1a n n∈N*,。
高考数学二轮复习专题突破—基本初等函数、函数的应用(含解析)

高考数学二轮复习专题突破—基本初等函数、函数的应用一、单项选择题1.(2021·陕西西安月考)函数f (x )=xx 2-1−12的零点个数是( ) A.1 B.2C.3D.42.(2021·福建泉州一模)已知a=32,b=√3√2,c=ln3ln2,则( ) A.a>b>c B.c>b>a C.c>a>bD.a>c>b3.(2021·浙江绍兴二模)函数f (x )=log a x+ax (a>1)的图象大致是( )4.(2021·湖北十堰期中)已知关于x 的方程9x -2a ·3x +4=0有一个大于2log 32的实数根,则实数a 的取值范围为( ) A.(0,52)B.(52,4)C.(52,+∞)D.(4,+∞)5.(2021·山东潍坊二模)关于函数f (x )={2x -a,0≤x <2,b-x,x ≥2,其中a ,b ∈R ,给出下列四个结论:甲:6是该函数的零点;乙:4是该函数的零点;丙:该函数的零点之积为0;丁:方程f (x )=52有两个根.若上述四个结论中有且只有一个结论错误,则该错误结论是( ) A.甲B.乙C.丙D.丁6.(2021·湖南师大附中期末)已知函数f(x)={lnx,x≥1,-ln(2-x),x<1,则方程(x-1)f(x)=1的所有实根之和为()A.2B.3C.4D.17.(2021·福建厦门期末)已知函数f(x)={|log3x|,0<x≤√3,1−log3x,x>√3,若关于x的方程f2(x)+mf(x)+112=0有6个解,则实数m的取值范围为()A.(-1,0)B.-1,-√33C.-1,-23D.-23,-√33二、多项选择题8.(2021·江苏扬州期末)17世纪初,约翰·纳皮尔为了简化计算发明了对数.对数的发明是数学史上的重大事件,恩格斯曾经把笛卡儿的坐标系、纳皮尔的对数、牛顿和莱布尼兹的微积分共同称为17世纪的三大数学发明.我们知道,任何一个正实数N可以表示成N=a×10n(1≤a<10,n∈Z)的形式,两边取常用对数,则有lg N=n+lg a,现给出部分常用对数值(如下表),则下列说法正确的有()A.310在区间(104,105)内B.250是15位数C.若2-50=a×10m(1≤a<10,m∈Z),则m=-16D.若m32(m∈N*)是一个35位正整数,则m=129.(2021·北京延庆模拟)同学们,你们是否注意到?自然下垂的铁链;空旷的田野上,两根电线杆之间的电线;峡谷的上空,横跨深涧的观光索道的钢索.这些现象中都有相似的曲线形态.事实上,这些曲线在数学上常常被称为悬链线.悬链线的相关理论在工程、航海、光学等方面有广泛的应用.在恰当的坐标系中,这类函数的表达式可以为f(x)=a e x+b e-x(其中a,b是非零常数,无理数e=2.718 28…),对于函数f(x),下列说法正确的是()A.如果a=b,那么函数f(x)为奇函数B.如果ab<0,那么f(x)为单调函数C.如果ab>0,那么函数f(x)没有零点D.如果ab=1,那么函数f(x)的最小值为210.(2021·海南第四次模拟)已知k>0,函数f(x)={-ln(k-x),x<0,ln(k+x),x>0,则()A.f(x)是奇函数B.f(x)的值域为RC.存在k,使得f(x)在定义域上单调递增D.当k=12时,方程f(x)=1有两个实数根三、填空题11.(2021·北京通州区一模)已知函数f(x)={x2+2x,x≤t,lnx,x>t(t>0)有两个零点,且其图象过点(e,1),则常数t的一个取值为.12.(2021·山东济宁期末)已知函数f(x)=e x+x2+ln(x+a)与函数g(x)=e x+e-x+x2(x<0)的图象上存在关于y轴对称的点,则实数a的取值范围为.答案及解析1.B 解析 令f (x )=xx 2-1−12=0,即x 2-2x-1=0,解得x=1±√2,经检验x=1±√2是方程f (x )=0的解,故f (x )有两个零点.故选B . 2.C 解析 a=32,b=√3√2=√62,则a>b ,因为a-c=32−ln3ln2=3ln2−2ln32ln2=ln8−ln92ln2<0,所以a<c ,所以b<a<c.故选C .3.A 解析 令g (x )=x+ax ,由于a>1,所以g (x )在区间(0,√a )上单调递减,在区间(√a ,+∞)上单调递增,故f (x )在区间(0,√a )上单调递减,在区间(√a ,+∞)上单调递增,对照题中选项中的图象,知A 选项正确.4.C 解析 令t=3x ,因为方程9x -2a·3x +4=0有一个大于2log 32的实数根,即x>2log 32,则t>32log 32=4,所以函数f (t )=t 2-2at+4有一个大于4的零点,所以f (4)=42-8a+4<0,解得a>52,即实数a 的取值范围是(52,+∞).故选C .5.B 解析 若甲是错误的结论,则由乙正确可得b=4,由丙正确得a=1,此时丁不正确,不符合题意;若乙是错误的结论,则由甲正确可得b=6,由丙正确得a=1,此时丁也正确,符合题意;若丙或丁是错误的结论,则甲和乙不可能同时正确,不符合题意,故选B .6.A 解析 当x>1时,2-x<1,所以f (2-x )=-ln[2-(2-x )]=-ln x=-f (x ),当x<1时,2-x>1,所以f (2-x )=ln(2-x )=-f (x ),当x=1时,f (1)=0,所以函数f (x )的图象关于点(1,0)对称.显然x=1不是方程的根,当x ≠1时,原方程可变为f (x )=1x-1,画出函数y=f (x )和y=1x-1的图象(如图所示).由图知,二者仅有两个公共点,设为点A (x 1,y 1),B (x 2,y 2),因为函数y=f (x )和y=1x-1的图象都关于点(1,0)对称,所以点A ,B 关于点(1,0)对称,所以x 1+x 22=1,即x 1+x 2=2.故选A .7.D 解析 令f (x )=t ,则原方程可化为t 2+mt+112=0,画出函数f (x )的图象(如图).由图象可知,若关于x 的方程f 2(x )+mf (x )+112=0有6个解,则关于t 的方程t 2+mt+112=0必须在区间0,12上有两个不相等的实根,由二次方程根的分布得{ 112>0,Δ=m 2-13>0,14+12m +112>0,-m 2∈(0,12),解得m ∈-23,-√33.故选D . 8.ACD 解析 对A,令x=310,则lg x=lg 310=10lg 3=4.77,所以x=104.77∈(104,105),A 正确;对B,令y=250,则lg y=lg 250=50lg 2=15.05,所以y=1015.05∈(1015,1016),则250是16位数,B 错误;对C,令z=2-50,则lg z=lg 2-50=-50lg 2=-15.05,又因为2-50=a×10m (1≤a<10,m ∈Z ),所以10-15.05=a×10m ,则10-15.05-m =a ∈[100,101),所以m=-16,C 正确;对D,令k=m 32,则lg k=lg m 32=32lg m ,因为m 32(m ∈N *)是一个35位正整数,所以34<32lg m<35,则3432<lg m<3532,即1.063<lg m<1.094,所以m=12,D 正确.故选ACD .9.BC解析对A,当a=b时,f(x)=a e-x+a e x,此时f(-x)=a e x+a e-x=f(x),故f(x)为偶函数.故A 错误.对B,当ab<0时,若a>0,b<0,则函数y=a e x在其定义域上单调递增,函数y=be x在其定义域上也单调递增,故函数f(x)=a e x+be x在其定义域上单调递增;若a<0,b>0,则函数y=a e x在其定义域上单调递减,函数y=be x 在其定义域上也单调递减,故函数f(x)=a e x+be x在其定义域上单调递减.综上,如果ab<0,那么f(x)为单调函数.故B正确.对C,当a>0,b>0时,函数f(x)=a e x+b e-x≥2√ae x·be-x=2√ab>0,当a<0,b<0时,函数f(x)=-(-a e x-b e-x)≤-2√(-ae x)·(-be-x)=-2√ab<0.综上,如果ab>0,那么函数f(x)没有零点.故C正确.对D,由ab=1,得b=1a.当a<0,b<0时,函数f(x)=--a e x-1ae-x≤-2√(-ae x)·(-1ae-x)=-2;当a>0,b>0时,函数f(x)=a e x+1a e-x≥2√ae x·1ae-x=2.故ab=1时,函数f(x)没有最小值.故D错误.10.AC解析当x>0时,f(-x)=-ln(k+x)=-f(x),当x<0时,f(-x)=ln(k-x)=-f(x),所以f(x)是奇函数,故选项A正确;当x>0时,f(x)=ln(k+x)单调递增,且f(x)>ln k,当x<0时,f(x)=-ln(k-x)单调递增,且f(x)<-ln k,f(x)的值域为(-∞,-ln k)∪(ln k,+∞),若k≥1,ln k≥0,此时f(x)的值域不包含0,且f(x)在定义域上单调递增,故选项B错误,选项C正确;对于选项D,若k=12,ln k=-ln 2,而ln 2<1,由前面的分析可知,方程f(x)=1在区间(-∞,0)上没有实数根,在区间(0,+∞)上有一个实数根,故选项D错误.11.2(答案不唯一)解析由x2+2x=0可得x=0或x=-2,由ln x=0可得x=1,因为函数f(x)={x2+2x,x≤t,lnx,x>t(t>0)有两个零点,且其图象过点(e,1),所以e>t≥1.所以t可取2.12.(-∞,e)解析由题意得,g(-x)=f(x)在区间(0,+∞)上有解,即e-x=ln(x+a)在区间(0,+∞)上有解,所以函数y=e-x与函数y=ln(x+a)的图象在区间(0,+∞)上有交点.如图,函数y=ln(x+a)的图象是由函数y=ln x的图象左右平移得到的,当y=ln x的图象向左平移至使y=ln(x+a)的图象经过点(0,1)时,函数y=e-x与函数y=ln(x+a)的图象交于点(0,1),将点(0,1)的坐标代入e-x=ln(x+a),有1=ln(0+a),得a=e,所以,若函数y=ln x的图象往左平移a个单位长度,且a≥e时,则函数y=e-x与函数y=ln(x+a)的图象在区间(0,+∞)上无交点.将函数y=ln x的图象向右平移时,函数y=e-x与y=ln(x+a)的图象在区间(0,+∞)上恒有交点.所以a<e,即a∈(-∞,e).。
广东省佛山市顺德区容山中学2024届高考数学试题二轮专题突破卷

广东省佛山市顺德区容山中学2024届高考数学试题二轮专题突破卷注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置. 3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效. 5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.如图,正方体1111ABCD A B C D -中,E ,F ,G ,H 分别为棱1AA 、1CC 、11B C 、11A B 的中点,则下列各直线中,不与平面1ACD 平行的是( )A .直线EFB .直线GHC .直线EHD .直线1A B2.若集合{}10A x x =-≤≤,01xB x x ⎧⎫=<⎨⎬-⎩⎭,则A B =( )A .[)1,1-B .(]1,1-C .()1,1-D .[]1,1-3.已知0x >,a x =,22xb x =-,ln(1)c x =+,则( )A .c b a <<B .b a c <<C .c a b <<D .b c a <<4.已知数列{}n a 的通项公式是221sin 2n n a n π+⎛⎫= ⎪⎝⎭,则12312a a a a +++⋅⋅⋅+=( ) A .0B .55C .66D .785.音乐,是用声音来展现美,给人以听觉上的享受,熔铸人们的美学趣味.著名数学家傅立叶研究了乐声的本质,他证明了所有的乐声都能用数学表达式来描述,它们是一些形如sin a bx 的简单正弦函数的和,其中频率最低的一项是基本音,其余的为泛音.由乐声的数学表达式可知,所有泛音的频率都是基本音频率的整数倍,称为基本音的谐波.下列函数中不能与函数0.06sin180000y t =构成乐音的是( ) A .0.02sin 360000y t =B .0.03sin180000y t =C .0.02sin181800y t=D .0.05sin 540000y t =6.已知集合{}|1A x x =>-,集合(){}|20B x x x =+<,那么A B 等于( )A .{}|2x x >-B .{}1|0x x -<<C .{}|1x x >-D .{}|12x x -<<7.已知平面α,β,直线l 满足l α⊂,则“l β⊥”是“αβ⊥”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .即不充分也不必要条件8.中国古典乐器一般按“八音”分类.这是我国最早按乐器的制造材料来对乐器进行分类的方法,最先见于《周礼·春官·大师》,分为“金、石、土、革、丝、木、匏(páo )、竹”八音,其中“金、石、木、革”为打击乐器,“土、匏、竹”为吹奏乐器,“丝”为弹拨乐器.现从“八音”中任取不同的“两音”,则含有打击乐器的概率为( ) A .314B .1114C .114D .279.已知函数22log ,0()22,0x x f x x x x ⎧>=⎨++≤⎩,方程()0f x a -=有四个不同的根,记最大的根的所有取值为集合D ,则“函数()()()F x f x kx x D =-∈有两个零点”是“12k >”的( ). A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件10.已知斜率为2的直线l 过抛物线C :22(0)y px p =>的焦点F ,且与抛物线交于A ,B 两点,若线段AB 的中点M 的纵坐标为1,则p =( )A .1BC .2D .411.已知函数()1f x +是偶函数,当()1,x ∈+∞时,函数()f x 单调递减,设12a f ⎛⎫=- ⎪⎝⎭,()3b f =,()0c f =,则a b c 、、的大小关系为() A .b a c <<B .c b d <<C .b c a <<D .a b c <<12.执行如图所示的程序框图,若输出的结果为11,则图中的判断条件可以为( )A .1?S >-B .0?S <C .–1?S <D .0?S >二、填空题:本题共4小题,每小题5分,共20分。
(参考答案)2023高考数学难点突破2(2):解析几何

2023高考数学难点突破专题训练(2)解析几何★应知应会椭圆的基本量1. 如图(1),过椭圆的一个焦点且与长轴垂直的弦AB=________,称为通径.图(1)图(2)2. 如图(2),P为椭圆上的点,F1,F2为椭圆的两个焦点,且∠F1PF2=θ,则△F1PF2的面积为________.3. 椭圆上的点到焦点距离的最大值为________,最小值为________.4. 设P,A,B是椭圆上不同的三点,其中A,B关于原点对称,则直线P A与PB的斜率之积为定值________.1. 2b2a 2. b2·tanθ2 3. a+c a-c 4. -b2a2直线与椭圆1. 直线与圆锥曲线的位置关系的判断将直线方程与圆锥曲线方程联立,消去一个变量得到关于x(或y)的一元方程:ax2+bx +c=0(或ay2+by+c=0).(1) 若a≠0,可考虑一元二次方程的判别式Δ,有:①Δ>0直线与圆锥曲线________;②Δ=0直线与圆锥曲线________;③Δ<0直线与圆锥曲线________.2. 圆锥曲线的弦长设斜率为k(k≠0)的直线l与圆锥曲线C相交于A(x1,y1),B(x2,y2)两点,则AB=________.1. (1) ①相交②相切③相离2. 1+k2|x2-x1|=1+1k2|y2-y1|双曲线的基本量运算1. 过双曲线的一个焦点且与实轴垂直的弦的长为________.2. 如图,P 为双曲线上的点,F 1,F 2为双曲线的两个焦点,且∠F 1PF 2=θ,则△F 1PF 2的面积为________.3. 焦点到渐近线的距离为________.4. 设P ,A ,B 是双曲线上的三个不同的点,其中A ,B 关于原点对称,则直线P A 与PB 的斜率之积为________.1. 2b 2a2. b 2tan θ2 3. b 4. b 2a 2 抛物线设AB 是过抛物线y 2=2px (p >0)焦点F 的弦,若A (x 1,y 1),B (x 2,y 2),则:(1) x 1x 2=p 24,y 1y 2=-p 2; (2) AF =p 1-cos α ,BF =p 1+cos α ,弦长AB =x 1+x 2+p =2p sin 2α(α为弦AB 的倾斜角);(3) 1F A +1FB =2p; (4) 以弦AB 为直径的圆与准线相切;(5) 以AF 或BF 为直径的圆与y 轴相切;(6) 过焦点弦的端点的切线互相垂直且交点在准线上.直线与圆锥曲线1. 已知椭圆C :x 2a 2 +y 2b 2 =1(a >b >0)上任意一点M (除短轴端点外)与短轴两端点B 1,B 2的连线分别与x 轴交于P ,Q 两点,O 为椭圆的中心,则OP ·OQ =a 2.2. 已知椭圆C :x 2a 2 +y 2b 2 =1(a >b >0)上任意一点M (除短轴端点外)与短轴两端点B 1,B 2的连线的斜率分别为k 1,k 2,则k 1k 2=-b 2a 2 . 3. 过抛物线y 2=2px (p >0)的焦点F 作直线交抛物线于A ,B 两点,且A (x 1,y 1),B (x 2,y 2),则x 1x 2=p 24,y 1y 2=-p 2. 4. 过抛物线y 2=2px (p >0)的顶点O 作两条互相垂直的直线交抛物线于A ,B 两点,则直线AB 过定点(2p ,0).。
立体几何中截面问题-高考数学微专题突破含详解

立体几何中截面问题-高考数学微专题突破一、单选题1.下列命题错误的是( )A .圆柱的轴截面是过母线的截面中面积最大的一个B .圆锥的轴截面是所有过顶点的截面中面积最大的一个C .圆台的所有平行于底面的截面都是圆D .圆锥所有的轴截面都是等腰三角形2.一正四面体木块如图所示,点P 是棱VA 的中点,过点P 将木块锯开,使截面平行于棱VB 和AC ,则下列关于截面的说法正确的是( ).A .满足条件的截面不存在B .截面是一个梯形C .截面是一个菱形D .截面是一个三角形3.已知正方体1111ABCD A B C D -,直线1AC ⊥平面α,平面α截此正方体所得截面中,正确的说法是( )A .截面形状可能为四边形B .截面形状可能为五边形C .截面面积最大值为D .截面面积最大值为24.球O 的截面把垂直于截面的直径分成1:3O 的体积为( )A .16πB .163πC .323πD .5.如图,在棱长为2的正方体1111ABCD A B C D -中,11A B 的中点是P ,过点1A 作与截面1PBC 平行的截面,则该截面的面积为( )A .B .C .D .46V ABC -中,40AVB BVC CVA ︒∠=∠=∠=,过点A 作截面则截面AEF ,则截面AEF 的周长的最小值为( )A B .2 C .3 D .47.已知正方体1111ABCD A B C D -的棱长为2,1AC ⊥平面α.平面α截此正方体所得的截面有以下四个结论:①截面形状可能是正三角形①截面的形状可能是正方形①截面形状可能是正五边形①截面面积最大值为则正确结论的编号是( )A .①①B .①①C .①①D .①① 8.已知长方体1111ABCD A B C D -各个顶点都在球面上,8AB AD ==,16AA =,过棱AB 作该球的截面,则当截面面积最小时,球心到截面的距离为( )A .3B .4C .5D .69.过半径为2的球O 表面上一点A 作球O 的截面,若OA 与该截面所成的角是30,则截面的面积是( )A .πB .2πC .3πD .10.直三棱柱111ABC A B C -中,若22BC AB ==,1AA AC ==M 是11B C 中点,过AM 作这个三棱柱的截面,当截面与平面ABC 所成的锐二面角最小时,这个截面的面积为( )A .2BC D11.在直三棱柱111ABC A B C -中,M 是1BB 上的点,3AB =,4BC =,5AC =,17CC =,过三点A 、M 、1C 作截面,当截面周长最小时,截面将三棱柱分成的两部分的体积比为( ).A .34B .45C .910D .101112.已知球O 是正三棱锥P ABC -的外接球,3,AB PA ==点E 在线段AC 上,且3AC AE =,过点E 作球O 的截面,则所得截面中面积最小的截面圆的面积是( ) A .2π B .π C .94π D .74π 13.下列说法正确的是A .平行于圆锥某一母线的截面是等腰三角形B .平行于圆台某一母线的截面是等腰梯形C .过圆锥顶点的截面是等腰三角形D .过圆台上底面中心的截面是等腰梯形14.已知圆锥的底面半径和高相等,侧面积为,过圆锥的两条母线作截面,截面为等边三角形,则圆锥底面中心到截面的距离为( )A B C .2 D 15.用一个平面截半径为25cm 的球,截面面积是2225cm π,则球心到截面的距离是( )A .5cmB .10cmC .15cmD .20cm 16.如图1-1-4所示的几何体:将它们按截面的形状分成两类时,下面分类方法正确的是( )A .截面可能是圆和三角形两类B .截面可能是圆和四边形两类C .截面可能是圆和五边形两类D .截面可能是三角形和四边形两类 17.在侧棱长为的正三棱锥中,,过 作截面,则截面的最小周长为( )A .B .4C .6D .1018.如图,三棱柱111ABC A B C -的所有棱长都为4,侧棱1AA ⊥底面ABC ,P ,Q ,R 分别在棱1AA ,AB ,11B C 上,2AP AQ ==,13B R =,过P ,Q ,R 三点的平面将三棱柱分为两部分,下列说法错误的是( )A.截面是五边形B .截面面积为C .截面将三棱柱体积平分D .截面与底面所成的锐二面角大小为π3 19.过正四面体ABCD 的顶点A 作一个形状为等腰三角形的截面,且使截面与底面BCD 所成的角为75︒,这样的截面有( )A .6个B .12个C .16个D .18个 20.如图,正四棱锥S ABCD -的所有棱长都等于a ,过不相邻的两条棱,SA SC 作截面SAC ,则截面的面积为A .232a B .2a C .212a D .213a 21.棱长为a 的正方体,过上底面两邻边中点和下底面中心作截面,则截面图形的周长等于( )A .2a + BC +D +b 22.在棱长为2的正方体1111ABCD A B C D -中,M 是棱11A D 的中点,过1C ,B ,M 作正方体的截面,则这个截面的面积为( )A .35B .35C .92D .98 23.棱锥被平行于底面的平面所截,当截面分别平分棱锥的侧棱、侧面积、体积时,相应截面面积为S 1、S 2、S 3,则( )A .S 1<S 2<S 3B .S 1>S 2>S 3C .S 2<S 1<S 3D .S 2>S 1>S 324.一个正方体内接于一个球,过球心作一个截面,如图所示,则截面的可能图形是( )A .①①①B .①①C .①①①D .①①① 25.如图是某几何体的三视图,则过该几何体顶点的所有截面中,最大截面的面积是( )A .2BCD .126.如图是某几何体的三视图,则过该几何体顶点的所有截面中,最大的截面面积是( )A .2BC .4D .32π 27.已知球O 是正三棱锥A BCD -的外接球,底边3BC =,侧棱AB =E 在线段BD 上,且3BD DE =,过点E 作球O 的截面,则所得截面圆面积的取值范围是( )A .5,44ππ⎡⎤⎢⎥⎣⎦B .[]2,4ππC .9,44ππ⎡⎤⎢⎥⎣⎦D .11,44ππ⎡⎤⎢⎥⎣⎦28.如图所示,在棱长为 6的正方体1111ABCD A B C D -中,点,E F 分别是棱1111,C D B C 的中点,过,,A E F 三点作该正方体的截面,则截面的周长为( )A .18+B .C .D .10++二、多选题 29.正方体1111ABCD A B C D -的棱长为2,已知平面1AC α⊥,则关于α截此正方体所得截面的判断正确的是( )A .截面形状可能为正三角形B .截面形状可能为正方形C .截面形状可能为正六边形D .截面面积最大值为30.如图所示,有一正四面体形状的木块,其棱长为a ,点P 是ACD △的中心.劳动课上,需过点P 将该木块锯开,并使得截面平行于棱AB 和CD ,则下列关于截面的说法中正确的是( )A .截面与侧面ABC 的交线平行于侧面ABDB .截面是一个三角形C .截面是一个四边形D .截面的面积为24a 31.如图,已知四棱锥P ABCD -所有棱长均为4,点M 是侧棱PC 上的一个动点(不与点,P C 重合),若过点M 且垂直于PC 的截面将该四棱锥分成两部分,则下列结论正确的是( )A .截面的形状可能为三角形、四边形、五边形B .截面和底面ABCD 所成的锐二面角为4πC .当1PM =时,截面的面积为D .当2PM =时,记被截面分成的两个几何体的体积分别为()1212,>V V V V ,则123=V V32.如图,设正方体1111ABCD A B C D -的棱长为2,E 为11A D 的中点,F 为1CC 上的一个动点,设由点A ,E ,F 构成的平面为α,则( )A .平面α截正方体的截面可能是三角形B.当点F 与点1C 重合时,平面α截正方体的截面面积为C .点D 到平面α D .当F 为1CC 的中点时,平面α截正方体的截面为五边形33.正方体的截面可能是( )A .钝角三角形B .直角三角形C .菱形D .正六边形三、双空题34.正方体1111ABCD A B C D -的棱长为1,点K 在棱11A B 上运动,过,,A C K 三点作正方体的截面,若K 为棱11A B 的中点,则截面面积为_________,若截面把正方体分成体积之比为2:1的两部分,则11A K KB =_______35.正方体1111ABCD A B C D -的棱长为2,点K 在棱11A B 上运动,过,,A C K 三点作正方体的截面,若K 与1B 重合,此时截面把正方体分成体积之比为(01)λλ<<的两部分,则λ=______;若K 为棱11A B 的中点,则截面面积为________.36.正方体1111ABCD A B C D -的棱长为2,M ,N ,E ,F 分别是11A B ,AD ,11B C ,11C D 的中点,则过EF 且与MN 平行的平面截正方体所得截面的面积为______,CE 和该截面所成角的正弦值为______.37.已知三棱锥P ABC -的四个顶点都在球O 的表面上,PA ⊥平面ABC ,6PA =,AB =2AC =,4BC =,则球O 的表面积为________;若D 是AB 的中点,过点D 作球O 的截面,则截面面积的范围是________.四、填空题38.如图所示,在棱长为2的正方体1111ABCD A B C D -中,11A B 的中点是P ,过点1A 作与截面1PBC 平行的截面,则截面的面积为__________.39.过半径为2的球O 表面上一点A 作球O 的截面,截面的面积为3π,则球心O 到该截面的距离为______40.已知正方体1111ABCD A B C D -的棱长为2,直线1AC ⊥平面α.平面α截此正方体所得截面有如下四个结论:①截面形状可能为正三角形;①截面形状可能为正方形;①截面形状不可能是正五边形;①截面面积最大值为其中所有正确结论的编号是______.41.体积为12的四面体ABCD 中,E F G 、、分别是棱AB BC AD 、、上的点,且2AE EB =,BF FC =,2AG GD =.过点E F G 、、作截面EFHG ,且点C 到此截面的距离为1.则此截面的面积是______.42.已知圆锥的底面半径和高相等,侧面积为4π,过圆锥的两条母线作截面,截面为等边三角形,则圆锥底面中心到截面的距离为____.43.在侧棱长为S ABC -中,40ASB BSC CSA ∠=∠=∠=︒,过点A 作截面AEF ,则截面最小的周长为______.44.过正四面体ABCD 的顶点A 作一个形状为等腰三角形的截面,且使截面与底面BCD 所成的角为75。
专题 排列组合专题突破训练(练习)2023届高考数学二轮复习专题

排列组合专题突破排列组合专项突破一(两个计数原理)1..将“福”“禄”“寿”填入到如图所示的4×4小方格中,每格内只填入一个汉字,且任意的两个汉字即不同行也不同列,则不同的填写方法有()A.288种B.144种C.576种D.96种2.里约奥运会期间,小赵常看的6个电视频道中有2个频道在转播奥运比赛.若小赵这时打开电视,随机打开其中一个频道,若在转播奥运比赛,则停止换台,否则就进行换台,那么,小赵所看到的第三个电视台恰好在转播奥运比赛的不同情况有()A.6种B.24种C.36种D.42种3.现安排一份5天的工作值班表,每天有一个人值日,共有5个人,每个人都可以值多天或不值班,但相邻两天不能同一个人值班,则此值日表共有多少种不同的排法.() A.1 080B.1 280 C.1 440D.2 5604.甲、乙等五名志愿者被分配到上海世博会中国馆、英国馆、澳大利亚馆、俄罗斯馆四个不同的岗位服务,每个岗位至少一名志愿者,则甲、乙两人各自独立承担一个岗位工作的分法共有种.(用数字作答)排列组合专项突破二(排数问题)1.从1,3,5三个数中选两个数字,从0,2两个数中选一个数字,组成没有重复数字的三位数,其中奇数的个数为()A.6B.12C.18D.242.从2,3,4,5,6,7,8,9这8个数中任取2个不同的数分别作为一个对数的底数和真数,则可以组成不同对数值的个数为()A.56B.54C.53D.523.4张卡片的正、反面分别写有0与1,2与3,4与5,6与7,将其中3张卡片排放在一起,可组成个不同的三位数.4.某公司安排甲、乙、丙、丁4人去上海、北京、深圳出差,每人仅出差一个地方,每个地方都需要安排人出差,若不安排甲去北京,则不同的安排方法共有() A.18种B.20种C.24种D.30种5.数学与文学有许多奇妙的联系,如诗中有回文诗“儿忆父兮妻忆夫”,既可以顺读也可以逆读.数学中有回文数,如343,12 521等.两位数的回文数有11,22,33,……,99共9个,则在三位数的回文数中偶数的个数是()A.40 B.30C.20D.10排列组合专项突破三(分类问题)1.如果一条直线与一个平面垂直,那么称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是()A.48B.18C.24D.362.某同学有同样的画册2本,同样的集邮册3本,从中取出4本赠送给4为朋友,每位朋友1本,则不同的赠送方法共有()A.4种B.10种C.18种D.20种3.某地环保部门召集6家企业的负责人座谈,其中甲企业有2人到会,其余5家企业各有1人到会,会上有3人发言,则发言的3人来自3家不同企业的可能情况的种数为() A.15 B.30C.35D.424.满足a,b∈{-1,0,1,2},且关于x的方程ax2+2x+b=0有实数解的有序数对(a,b)的个数为()A.14 B.13 C.12 D.105.从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有______种.排列组合专项突破四(涂色问题)1. 如图,给7条线段的5个端点染色,要求同一条线段的两个端点不能同色,现有4种不同的颜色可供选择,则不同的染色方法种数有()A.24B.48C.96D.1202.现有5种不同颜色的染料,要对如图所示的四个不同区域进行涂色,要求有公共边的两个区域不能使用同一种颜色,则不同的涂色方法的种数是()A.120 B.140C.240 D.2603.用红、黄、蓝,紫四种颜色随机地给正四面体的四个顶点染色,则“恰有一个面上的三个顶点同色”的概率为()A.12B.13C.14D.3164.如图,用五种不同的颜色给图中的O,A,B,C,D,E六个点涂色(五种颜色不一定用完),要求每个点涂一种颜色,且图中每条线段的两个端点涂不同的颜色,则不同的涂法种数是()A. 480B. 720C. 1080D. 12005.用黑白两种颜色随机地染如图所示表格中6个格子,每个格子染一种颜色,并且从左到右数,不管数到哪个格子,总有黑色格子不少于白色格子的染色方法种数为(用数字作答).排列组合专项突破五(相邻不相邻问题)1.七人并排站成一行,如果甲、乙两人必须不相邻,那么不同的排法种数是()A.3 600 B.1 440 C.4 820 D.4 8002.把5件不同的产品摆成一排,若产品A与产品B相邻,且产品A与产品C不相邻,则不同的摆法有________种.3.现有2门不同的考试要安排在5天之内进行,每天最多进行一门考试,且不能连续两天有考试,那么不同的考试安排方案种数是( )A .12B .6C .8D .164.张、王夫妇各带一个小孩儿到上海迪士尼乐园游玩,购票后依次入园,为安全起见,首尾一定要排两位爸爸,另外两个小孩要排在一起,则这6个人的入园顺序的排法种数是( ) A .12 B .24 C .36 D .485.A 家庭有一对夫妻和两个女儿,B 家庭有一对夫妻和两个儿子,共8人,一起去游乐场游玩,坐在共有8个座位的一排座位上,A 家庭的两个女儿要相邻,B 家庭的两个儿子要相邻,并且为了安全起见,两位爸爸要坐在两端.那么这8人的排座方法种数为 . 6.在大课间风采展示中,某班级准备了2个舞蹈,2个独唱,1个小品,共5个节目.要求相同类型的节目不能相邻,那么节目的不同演出顺序共有___________种,7.北京APEC 峰会期间,有2位女性和3位男性共5位领导人站成一排照相,则女性领导人甲不在两端,3位男性领导人中有且只有2位相邻的站法有( )A .12种B .24种C .48种D .96种排列组合专项突破六(分组分配问题)1.从5名大学毕业生中选派4人到甲、乙、丙三个贫困地区支援,要求甲地区2人,乙、丙地区各一人,则不同的选派方法总数为( )A .40B .60C .100D .1202.党的十九大报告提出“乡村振兴战略”,要“推动城乡义务教育一体化发展,高度重视农村义务教育为了响应报告精神,某师范大学5名毕业生主动申请到某贫困山区的乡村小学工作.若将这5名毕业生分配到该山区的3所乡村小学,每所学校至少分配1人最多分配2人,则分配方案的总数为 .3.把标号为1,2,3,4的四个小球分别放入标号为1,2,3,4的四个盒子中,每个盒子只放一个小球,则1号球不放入1号盒子的方法共有( )A .18种B .9种C .6种D .3种4.数学活动小组由12名同学组成,现将这12名同学平均分成四组分别研究四个不同课题,且每组只研究一个课题,并要求每组选出1名组长,则不同的分配方案有( )A.C 312C 39C 36A 33A 44种 B .C 312C 39C 3634种 C.C 312C 39C 36A 4443种 D .C 312C 39C 3643种5.将6本不同的书分给甲、乙、丙、丁4个人,每人至少1本的不同分法共有________种.(用数字作答)6.(多选)下列说法正确的是( )A .4只相同的小球放入3个不同的盒子,共有12种不同放法B .五名学生争夺四项比赛的冠军(冠军不并列),则获得冠军的可能性有54种C .将4封信投入到3个信箱中,共有64种不同的投法D .用0,1,…,9十个数字可以组成没有重复数字的三位偶数328个。
空间几何体的结构特征、表面积与体积6题型分类-备战2025年高考数学一轮专题复习考点突破和专题检测
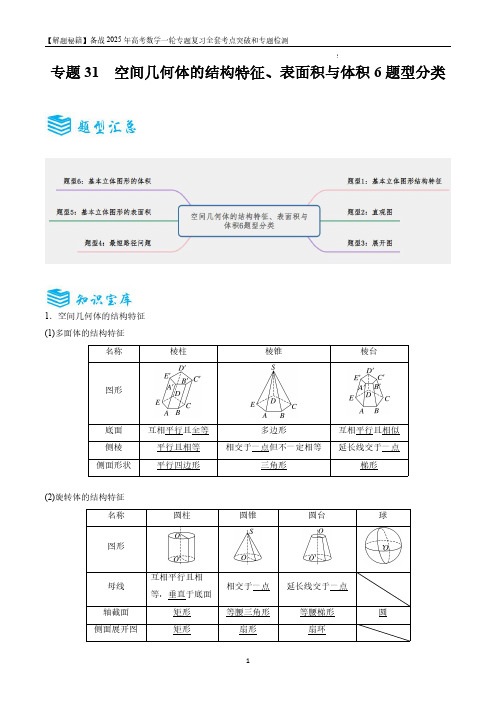
专题31空间几何体的结构特征、表面积与体积6题型分类1.空间几何体的结构特征(1)多面体的结构特征(2)旋转体的结构特征名称圆柱圆锥圆台球图形母线互相平行且相等,垂直于底面相交于一点延长线交于一点轴截面矩形等腰三角形等腰梯形圆侧面展开图矩形扇形扇环2.直观图(1)画法:常用斜二测画法.(2)规则:①原图形中x 轴、y 轴、z 轴两两垂直,直观图中x ′轴、y ′轴的夹角为45°或135°,z ′轴与x ′轴和y ′轴所在平面垂直.②原图形中平行于坐标轴的线段,直观图中仍分别平行于坐标轴,平行于x 轴和z 轴的线段在直观图中保持原长度不变,平行于y 轴的线段,长度在直观图中变为原来的一半.3.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧=2πrl S 圆锥侧=πrlS 圆台侧=π(r 1+r 2)l4.柱、锥、台、球的表面积和体积常用结论1.与体积有关的几个结论(1)一个组合体的体积等于它的各部分体积的和或差.(2)底面面积及高都相等的两个同类几何体的体积相等(祖暅原理).2.直观图与原平面图形面积间的关系:S 直观图=24S 原图形,S 原图形=22S 直观图.(一)1.空间几何体结构特征的判断技巧(1)说明一个命题是错误的,只要举出一个反例即可.(2)在斜二测画法中,平行于x轴的线段平行性不变,长度不变;平行于y轴的线段平行性不变,长度减半.(3)在解决空间折线(段)最短问题时一般考虑其展开图,采用化曲为直的策略,将空间问题平面化.2.多面体表面展开图可以有不同的形状,应多实践,观察并大胆想象立体图形与表面展开图的关系,一定先观察立体图形的每一个面的形状.3.最大路径问题:大胆展开,把问题变为平面两点间线段最短问题.2-2.(2024高一下·上海奉贤·期末)如图,23O A O B ''''==,,则AB 的长度为2-3.(2024高一上·山东济宁·阶段练习)有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示).ABC ∠=2-4.(2024高二上·宁夏石嘴山·正方形,则原来图形的面积是3-3.(2024·安徽黄山·一模)如图,以AD为斜边的等腰直角三角形,为.题型4:最短路径问题4-1.(2024高三·全国·专题练习)如图,一竖立在地面上的圆锥形物体的母线长为面圆上的点P出发,绕圆锥爬行一周后回到点为().A .153B .323527πC .128281πD .8334-2.(2024高一下·河南开封·期中)如图,已知正四棱锥S ABCD -的侧棱长为23,侧面等腰三角形的顶角为30︒,则从A 点出发环绕侧面一周后回到A 点的最短路程为()A .26B .23C .6D .64-3.(2024·辽宁·三模)盲盒是一种深受大众喜爱的玩具,某盲盒生产厂商要为棱长为4cm 的正四面体魔方设计一款正方体的包装盒,需要保证该魔方可以在包装盒内任意转动,则包装盒的棱长最短为()A .6cmB .26cmC .46cmD .6cm4-4.(2024高一下·湖北武汉·期中)如图,一个矩形边长为1和4,绕它的长为4的边旋转二周后所得如图的一开口容器(下表面密封),P 是BC 中点,现有一只妈蚁位于外壁A 处,内壁P 处有一米粒,若这只蚂蚁要先爬到上口边沿再爬到点P 处取得米粒,则它所需经过的最短路程为()A .2π36+B .2π16+C .24π36+D .241π+4-5.(2024高一·全国·课后作业)如图所示,在正三棱柱111ABC A B C -中,2AB =,12AA =,由顶点B 沿棱柱侧面(经过棱1AA )到达顶点1C ,与1AA 的交点记为M ,则从点B 经点M 到1C 的最短路线长为()A.22B.25C.4D.45(二)基本立体图形的表面积的体积1.(1)多面体的表面积是各个面的面积之和.(2)旋转体的表面积是将其展开后,展开图的面积与底面面积之和.(3)组合体的表面积求解时注意对衔接部分的处理.2.空间几何体的体积的常用方法公式法规则几何体的体积,直接利用公式割补法把不规则的几何体分割成规则的几何体,或者把不规则的几何体补成规则的几何体等体积法通过选择合适的底面来求几何体体积的一种方法,特别是三棱锥的体积A.27 722+三模)陀螺起源于我国,最早出土的石制陀螺是在山西夏县发现的新石器时代遗址A .()1441213π+C .()1081213π+5-4.(2024·河北·模拟预测)棱台)建筑物为方亭.”1111ABCD A B C D -的正四棱台(如图所示)面边长的3倍.已知方亭的体积为A .2380m B .2400m C .2450m 5-5.(2024高三下·海南海口·期中)如图是一个圆台形的水杯,圆台的母线长为分别为4cm 和2cm .为了防烫和防滑,该水杯配有一个皮革杯套,包裹住水杯杯和杯套的厚度忽略不计,则此杯套使用的皮革的面积为(A .238πcmB .2124πcm 3C .2140πcm 3D .248πcm A .242B .246-4.(2024·浙江·模拟预测)如图是我国古代量粮食的器具为20cm 和10cm ,侧棱长为56cm .约可装()31000cm 1L =()A .1.5LB .1.7LC .2.3LD .2.7L6-5.(2024高三上·广西·阶段练习)在棱长为2的正方体1111ABCD A B C D 内,放入一个以1AC 为铀线的圆柱,且圆柱的底面所在平面截正方体所得的截面为三角形,则该圆柱体积的最大值为.一、单选题1.(2024高三下·安徽·阶段练习)已知几何体,“有两个面平行,其余各面都是平行四边形”是“几何体为棱柱”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2.(2024高三·全国·对口高考)设有三个命题;甲:底面是平行四边形的四棱柱是平行六面体;乙:底面是矩形的平行六面体是长方体;丙:直四棱柱是平行六面体.以上命题中真命题的个数为()A .0个B .1个C .2个D .3个3.(2024高二上·安徽合肥·阶段练习)如图所示,观察四个几何体,其中判断正确的是()A .是棱台B .是圆台C .不是棱柱D .是棱锥4.(2024·西藏拉萨·一模)位于徐州园博园中心位置的国际馆(一云落雨),使用现代科技雾化“造云”,打造温室客厅,如图,这个国际馆中3个展馆的顶部均采用正四棱锥这种经典几何形式,表达了理性主义与浪漫主义的对立与统一.其中最大的是3号展馆,其顶部所对应的正四棱锥底面边长为19.2m ,高为9m ,则该正四棱锥的侧面面积与底面面积之比约为()13.16≈)A .2B .1.71C .1.37D .15.(2024高三下·湖南长沙·阶段练习)为了给热爱朗读的师生提供一个安静独立的环境,某学校修建了若干“朗读亭”.如图所示,该朗读亭的外形是一个正六棱柱和正六棱锥的组合体,正六棱柱两条相对侧棱所在的轴截面为正方形,若正六棱锥的高与底面边长的比为2:3,则正六棱锥与正六棱柱的侧面积的比值为()A .8B C .19D .1276.(2024·甘肃张掖·模拟预测)仿钧玫瑰紫釉盘是收藏于北京故宫博物院的一件明代宣德年间产的瓷器.该盘盘口微撇,弧腹,圈足.足底切削整齐.通体施玫瑰紫釉,釉面棕眼密集,美不胜收.仿钧玫瑰紫釉盘的形状可近似看成是圆台和圆柱的组合体,其口径为15.5cm ,足径为9.2cm ,顶部到底部的高为4.1cm ,底部圆柱高为0.7cm ,则该仿钧玫瑰紫釉盘圆台部分的侧面积约为()(参考数据:π的值取3 4.6≈)A .2143.1cmB .2151.53cmC .2155.42cmD .2170.43cm 7.(2024·广东梅州·三模)在马致远的《汉宫秋》楔子中写道:“毡帐秋风迷宿草,穹庐夜月听悲笳.”毡帐是古代北方游牧民族以为居室、毡制帷幔.如图所示,某毡帐可视作一个圆锥与圆柱的组合体,圆锥的高为4,侧面积为15π,圆柱的侧面积为18π,则该毡帐的体积为()A .39πB .18πC .38πD .45π8.(2024高三上·广东河源·开学考试)最早的测雨器记载见于南宋数学家秦九韶所著的《数书九章》(1247年).该书第二章为“天时类”,收录了有关降水量计算的四个例子,分别是“天池测雨”、“圆罂测雨”、“峻积验雪”和“竹器验雪”.如图“竹器验雪”法是下雪时用一个圆台形的器皿收集雪量(平地降雪厚度=器皿中积雪体积除以器皿口面积),已知数据如图(注意:单位cm ),则平地降雪厚度的近似值为()A .91cm 12B .31cm 4C .95cm 12D .97cm 129.(2024高一下·陕西宝鸡·期末)盲盒是一种深受大众喜爱的玩具,某盲盒生产厂商要为棱长为2cm 的正四面体魔方设计一款正方体的包装盒,需要保证该魔方可以在包装盒内任意转动,则包装盒的棱长最短为()A 6cmB .26cmC .6cmD .6cm10.(2024高二下·安徽·阶段练习)我们知道立体图形上的最短路径问题通常是把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.请根据此方法求函数()2222,313130,0)f x y x x y y x xy y x y =-+-+-+>>的最小值()A 2B 3C 6D .2311.(2024·全国)已知圆锥PO 3O 为底面圆心,PA ,PB 为圆锥的母线,120AOB ∠=︒,若PAB 934)A .πB 6πC .3πD .36π12.(2024·全国)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔1485m .时,相应水面的面积为21400km .;水位为海拔1575m .时,相应水面的面积为21800km .,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔1485m .上升到1575m .时,增加的水量2.65≈)()A .931.010m ⨯B .931.210m ⨯C .931.410m ⨯D .931.610m ⨯13.(2024高一·全国·课后作业)若一个正方体的体对角线长为a ,则这个正方体的全面积为()A .22a B .2C .2D .214.(2004·重庆)如图,棱长为5的正方体无论从哪一个面看,都有两个直通的边长为1的正方形孔,则这个有孔正方体的表面积(含孔内各面)是()A .258B .234C .222D .21015.(2024高一下·贵州黔西·期末)端午节吃粽子是中华民族的传统习俗.地区不同,制作的粽子形状也不同,黔西南州最出名的就是鲜肉的灰色粽子,其形状接近于正三棱锥(如图).若正三棱锥的底面边长为2,高为1,则该三棱锥的侧面积为()AB .C .D .16.(2024·河南·模拟预测)在正四棱锥P ABCD -中,AB =,若正四棱锥P ABCD -的体积是8,则该四棱锥的侧面积是()AB .C .D .17.(2024高三上·辽宁·期末)已知四棱台的上、下底面分别是边长为2和4的正方形,侧面均为腰长为4的等腰梯形,则该四棱台的表面积为()A .10+B .34C .20+D .6818.(2024高三上·广东·阶段练习)“李白斗酒诗百篇,长安市上酒家眠”,本诗句中的“斗”的本义是指盛酒的器具,后又作为计量粮食的工具,某数学兴趣小组利用相关材料制作了一个如图所示的正四棱台来模拟“斗”,用它研究“斗”的相关几何性质,已知该四棱台的上、下底的边长分别是2、4,高为1,则该四棱台的表面积为()A .B .32C .20+D .20+19.(2024高三上·湖北·开学考试)已知正四棱台上底面边长为2,下底面边长4,高为3,则其表面积为()A .36B .20C .20+D .4820.(2024高一下·全国·课后作业)已知一个圆柱的侧面展开图是一个正方形,则这个圆柱的全面积与侧面积的比是()A .122ππ+B .144ππ+C .12ππ+D .142ππ+21.(2024·广东湛江·二模)如图,将一个圆柱()*2n n ∈N 等分切割,再将其重新组合成一个与圆柱等底等高的几何体,n 越大,重新组合成的几何体就越接近一个“长方体”.若新几何体的表面积比原圆柱的表面积增加了10,则圆柱的侧面积为()A .10πB .20πC .10πnD .18π22.(2024·福建)以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于A .2πB .πC .2D .123.(2024高三上·全国·阶段练习)已知圆锥的底面半径为2,高为)A .4πB .12πC .16πD .π324.(2024·四川成都·二模)若圆锥的表面积为12π,底面圆的半径为2,则该圆锥的高为()A .4B .C .2D25.(2024高三上·河南·阶段练习)佛兰德现代艺术中心是比利时洛默尔市的地标性建筑,该建筑是一座全玻璃建筑,整体成圆锥形,它利用现代设计手法令空间与其展示的艺术品无缝交融,形成一个统一的整体,气势恢宏,美轮美英.佛兰德现代艺术中心的底面直径为8m ,侧面积为2229m ,则该建筑的高为()A .26mB .28mC .30mD .36m26.(2024高三上·河南·开学考试)圆台1OO 轴截面面积为1:2,母线与底面所成角为60 ,则圆台侧面积为()A .B .C .6πD .9π27.(2024高二上·江苏镇江·开学考试)已知圆台的上下底面半径分别为2和5,且母线与下底面所成为角的正切值为43,则该圆台的表面积为()A .59πB .61πC .63πD .64π28.(2024·甘肃兰州·模拟预测)攒尖是中国古建筑中屋顶的一种结构形式,常见的有圆形攒尖、三角攒尖、图所示是某研究性学习小组制作的三台阁仿真模型的屋顶部分,它可以看作是不含下底面的正四棱台和正三棱柱的组合体,已知正四棱台上底、下底、侧棱的长度(单位:dm )分别为2,6,4,正三棱柱各棱长均相等,则该结构表面积为()A .28dmB .244dmC .248dmD .28dm29.(2024高三上·黑龙江哈尔滨·期中)正三棱柱侧面的一条对角线长为2,且与底面成30︒角,则此三棱柱的体积为()A B .14C D 30.(2008·四川)若三棱柱的一个侧面是边长为2的正方形,另外两个侧面都是有一个内角为060的菱形,则该棱柱的体积等于A B .C .D .31.(2024高三上·河南焦作·开学考试)把过棱锥的顶点且与底面垂直的直线称为棱锥的轴,过棱锥的轴的截面称为棱锥的轴截面.现有一个正三棱锥、一个正四棱锥、一个正六棱锥,它们的高相等,轴截面面积的最大值也相等,则此正三棱锥、正四棱锥、正六棱锥的体积之比为()A .91::34B .91::38C .98D .3232.(2024·广东深圳·二模)设表面积相等的正方体、正四面体和球的体积分别为1V 、2V 和3V ,则()A .123V V V <<B .213<<V V V C .312V V V <<D .321V V V <<33.(2024·河南郑州·模拟预测)《九章算术·商功》:“斜解立方,得两堑堵,斜解堑堵,其一为阳马,其一为鳖臑”.意思是一个长方体沿对角面斜解(图1),得到一模一样的两个堑堵(图2),再沿一个堑堵的一个顶点和相对的棱斜解(图2),得一个四棱锥称为阳马(图3),一个三棱锥称为鳖臑(图4).若长方体的体积为V ,由该长方体斜解所得到的堑堵、阳马和鳖臑的体积分别为1V ,2V ,3V ,则下列等式错误的是()A .123V V V V ++=B .122V V =C .232V V =D .236VV V -=34.(2024高三下·浙江杭州·阶段练习)已知矩形ABCD 中,2AB =,4BC =,E 是AD 的中点,沿直线BE 将△ABE 翻折成△A BE ',则三棱锥A BDE '-的体积的最大值为()A .3B C D .335.(2024·全国)正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为()A .20+B .C .563D .336.(2024高一下·江苏连云港·阶段练习)在《九章算术⋅商功》中将正四面形棱台体(棱台的上、下底面均为正方形)称为方亭.在方亭1111ABCD A B C D -中,1122AB A B ==,四个侧面均为全等的等腰梯形且面积之和为)A .72B .76C D 37.(2024高三上·山西运城·期中)已知一个正四棱台的上下底面边长为1、3,则棱台的体积为()A .B .3C .12D .1338.(2024·河南·模拟预测)光岳楼,又称“余木楼”“鼓楼”“东昌楼”,位于山东省聊城市,在《中国名楼》站台票纪念册中,光岳楼与鹳雀楼、黄鹤楼、岳阳楼、太白楼、滕王阁、蓬莱阁、镇海楼、甲秀楼、大观楼共同组成中国十大名楼.其墩台为砖石砌成的正四棱台,如图所示,光岳楼的墩台上底面正方形的边长约为32m ,下底面正方形的边长约为34.5m ,高的4倍比上底面的边长长4m ,则光岳楼墩台的体积约为()A .39872.75mB .39954.75mC .39988.45mD .39998.25m 39.(四川省仁寿第一中学校(北校区)2023-2024学年高三上学期9月月考文科数学试题)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()A .πB .π2C .3π4D .π440.(2024高三上·江苏苏州·开学考试)若某圆柱体的底面半径与某球体的半径相等,圆柱体与球体的体积之比和它们的表面积之比的比值相等,则该圆柱体的高与球体的半径的比值为()A .54B .43C .32D .241.(2024·河南·模拟预测)圆锥的高为2,其侧面展开图的圆心角为2π3,则该圆锥的体积为().A .π4B .π3C .π2D .2π642.(2024高三上·福建厦门·阶段练习)已知母线长为5的圆锥的侧面积为15π,则这个圆锥的体积为()A .12πB .16πC .24πD .48π43.(2024高三下·河南开封·阶段练习)木桶作为一种容器,在我国使用的历史已经达到了几千年,其形状可视为一个圆台.若某圆台形木桶上、下底面的半径分别为20cm,13cm ,母线长为25cm ,木板厚度忽略不计,则该木桶的容积为()A .314225πcm 3B .34552πcmC .320725πcm 3D .36632πcm 44.(2024高三上·福建厦门·阶段练习)用一个平行于圆锥C 底面的平面截该圆锥得到一个圆台,若圆台上底面和下底面半径之比为23,则该圆台与圆锥C 的体积之比为()A .58B .1727C .1927D .34二、多选题45.(2024·全国)如图,四边形ABCD 为正方形,ED ⊥平面ABCD ,,2FB ED AB ED FB ==∥,记三棱锥E ACD -,F ABC -,F ACE -的体积分别为123,,V V V ,则()A .322V V =B .31V V =C .312V V V =+D .3123V V =46.(2024·福建·模拟预测)等腰梯形的上下底边之比为13,若绕该梯形的对称轴旋转一周所得几何体的表面积为16π,则该梯形的周长可能为()A .B .8C .D .1647.(2024·河南·模拟预测)如图,正三棱柱111ABC A B C -的底面边长为1,高为3,F 为棱1AA 的中点,,D E 分别在棱11,BB CC 上,且满足1A D DE EA ++取得最小值.记四棱锥111A B C ED -、三棱锥1,F A DE A DEF --的体积分别为123,,V V V ,则()A .123334V V V ++<B .23V V =C .1223V V =D .123V V V =+48.(2024高三上·湖南·5)A .该正方体的体积为5B 556C .该正方体的表面积为30D .该正方体的外接球的表面积为15π三、填空题49.(2024·辽宁锦州·模拟预测)已知用斜二测画法画梯形OABC 的直观图O A B C ''''如图所示,3O A C B ''''=,C E O A ''''⊥,8OABC S =,//CD y '''轴,22C E ''=D ¢为O A ''的三等分点,则四边形OABC 绕y 轴旋转一周形成的空间几何体的体积为.50.(2024高三·全国·对口高考)若正ABC 用斜二测画法画出的水平放置图形的直观图为A B C ''' ,当A B C ''' 3ABC 的面积为.51.(2024高三下·上海宝山·开学考试)我们知道一条线段在“斜二测”画法中它的长度可能会发生变化的,现直角坐标系平面上一条长为4cm 线段AB 按“斜二测”画法在水平放置的平面上画出为A B '',则A B ''最短长度为cm (结果用精确值表示)52.(2024高三·全国·阶段练习)如图,梯形ABCD 是水平放置的一个平面图形的直观图,其中=45∠ ABC ,1AB AD ==,DC BC ⊥,则原图形的面积为.53.(2024高三上·上海普陀·期中)2022年4月16日,神舟十三号载人飞船返回舱在东风着陆场预定区域成果着陆.如图,在返回过程中使用的主降落伞外表面积达到1200平方米,若主降落伞完全展开后可以近似看着一个半球,则完全展开后伞口的直径约为米(精确到整数)54.(2024高一下·四川成都·阶段练习)已知圆锥的底面半径为1,其侧面展开图为一个半圆,则该圆锥的体积为.55.(2024·安徽·模拟预测)如图,在三棱锥P -ABC 的平面展开图中,CD AB ∥,AB AC ⊥,22AB AC ==,CD =,cos BCF ∠65=,则三棱锥-P ABC 外接球表面积为.56.(2024·安徽马鞍山·模拟预测)已知三棱锥P -ABC 的底面ABC 为等边三角形.如图,在三棱锥P -ABC的平面展开图中,P ,F ,E 三点共线,B ,C ,E 三点共线,cos PCF ∠=PC =,则PB =.57.(2024高三上·山西大同·阶段练习)如图,在三棱锥-P ABC 的平面展开图中,1AC =,AB AD ==AB AC ⊥,AB AD ⊥,30CAE ∠=︒,则三棱锥-P ABC 的外接球的表面积为.58.(2024高三·河北·专题练习)如图,正方体1111ABCD A B C D -的棱长为a ,点E 为1AA 的中点,在对角面11BB D D 上取一点M ,使AM ME +最小,其最小值为59.(2024高三上·四川成都·开学考试)如图一个正六棱柱的茶叶盒,底面边长为10cm ,高为20cm ,则这个茶叶盒的表面积为2cm .60.(2024高二上·上海黄浦·阶段练习)若长方体的对角线的长为9cm ,其长、宽、高的和是15cm ,则长方体的全面积是.61.(2024·全国·模拟预测)正四棱锥P -ABCD 的各条棱长均为2,则该四棱锥的表面积为.62.(2024高三·全国·专题练习)一个正三棱台的上、下底面边长分别是3cm 和6cm ,高是32cm .则三棱台的斜高为;三棱台的侧面积为;表面积为.63.(2024高三·全国·专题练习)若矩形的周长为36,矩形绕它的一条边旋转形成一个圆柱,求圆柱侧面积的最大值为.64.(2024高二上·北京海淀·期中)若一个圆锥的轴截面是等边三角形,其面积为是.65.(2024高三上·全国·专题练习)某地球仪上北纬030纬线的长度为12()cm π,该地球仪的半径是cm ,表面积是cm2.66.(2024·全国)已知圆O 和圆K 是球O 的大圆和小圆,其公共弦长等于球O 的半径,32OK =,且圆O 与圆K 所在的平面所成的一个二面角为60 则球O 的表面积等于.67.(2009年普通高等学校招生全国统一考试理科数学(全国卷Ⅱ))设OA 是球O 的半径,M 是OA 的中点,过M 且与OA 成45 角的平面截球O 的表面得到圆C .若圆C 的面积等于74π,则球O 的表面积等于68.(2024·全国)用平面α截半径为R 的球,如果球心到截面的距离为2R ,那么截得小圆的面积与球的表面积的比值为.69.(2024高三上·广东广州·阶段练习)陀螺是中国民间较早的娱乐工具之一,也称陀罗,图l 是一种木陀螺,可近似地看作是一个圆锥和一个圆柱的组合体,其直观图如图2所示,其中A 是圆锥的顶点,B ,C 分别是圆柱的上、下底面圆的圆心,且1AB =,3AC =,底面圆的半径为1,则该陀螺的表面积是.70.(2024高三·全国·专题练习)如图,八面体的每一个面都是正三角形,并且4个顶点A ,B ,C ,D 在同一个平面内.如果四边形ABCD 是边长为30cm 的正方形,那么这个八面体的表面积是2cm .71.(2024高三上·天津北辰·阶段练习)已知一个圆柱的高是底面半径的2倍,且其上、下底面的圆周均在球面上,若球的体积为23,则圆柱的体积为.72.(2024高三上·云南昆明·、则该圆锥的体积为.73.(2024·浙江嘉兴·模拟预测)已知圆锥的底面半径为1,侧面积为2π,则此圆锥的体积是.74.(2024高三上·广东广州·阶段练习)已知圆锥的底面半径为2,侧面展开图是一个圆心角为120°的扇形.把该圆锥截成圆台,已知圆台的下底面与该圆锥的底面重合,圆台的上底面半径为1,则圆台的体积为.。
高考数学专题突破:劣构性考题含详解

高考数学专题突破:劣构性考题1.已知圆C 的圆心在直线30x y +-=上,且过点()1,3,()2,2. (1)求圆C 的方程;(2)若圆C 与直线:0l x y m -+=交于A ,B 两点,______,求m 的值.从下列三个条件中任选一个补充在上面问题中并作答:条件①:120ACB ∠=︒;条件①:圆上一点P 到直线的最大距离为32;条件①:12CA CB ⋅=-.2.已知函数()2cos cos f x x x x a ωωω=+,其中02ω<<,再从条件①、条件①、条件①这三个条件中选择两个作为已知.条件①:()102f =;条件①:()f x 的最小正周期为π;条件①:()f x 的图象经过点,16π⎛⎫⎪⎝⎭.(1)求()f x 的解析式; (2)求()f x 的单调递增区间.3.集合{}2230A x x x =+-<,{}23B x x =-<,{}2,C x m x m m =<<-∈R .(1)求A B .(2)现有三个条件:①B C C =,①B C =∅,①条件p :x C ∈,q :x B ∈,若p 是q 的充分不必要条件,在这三个条件中任选一个填到横线上,并解答本题.选择多个条件作答时,按第一个选择给分.已知______,求实数m 的取值范围.4.在①()2log f x x =,()244g x x x =-+,①()244f x x x =-+,()2log g x x =,两个条件中任选一个,补充到下面问题的横线中,并求解该问题. 已知函数___________(填序号即可). (1)求函数()()y f g x =的解析式及定义域; (2)解不等式()()1f g x ≤.5.在①直线l :210x +=是抛物线C 的准线;①F 是椭圆()22103142x y p p p +=>的一个焦点;①()0,1B ,对于C 上的点A ,AB AF +;在以上三个条件中任选一个,填到下面问题中的横线处,并完成解答.已知抛物线C :()220y px p =>的焦点为F ,满足_____. (1)求抛物线C 的标准方程;(2)()2,D y 是抛物线C 上在第一象限内的一点,直线l ':y x m =+与C 交于M ,N 两点,若DMN 的面积为2m ,求m 的值.6.悬索桥(如图)的外观大漂亮,悬索的形状是平面几何中的悬链线.1691年莱布尼兹和伯努利推导出某链线的方程为e e 2x xccc y ⎛⎫=+ ⎪⎝⎭,其中c 为参数.当1c =时,该方程就是双曲余弦函数()e e cosh 2x xx -+=,类似的我们有双曲正弦函数()e e sinh 2x x x --=.(1)从下列三个结论中选择一个进行证明,并求函数()()cosh 2sinh y x x =+的最小值; ①()()22cosh sinh 1x x -=⎡⎤⎡⎤⎣⎦⎣⎦; ①()()()sinh 22sinh cosh x x x =; ①()()()22cosh 2cosh sinh x x x =+⎡⎤⎡⎤⎣⎦⎣⎦.(2)求证:,4x ππ⎡⎤∀∈-⎢⎥⎣⎦,()()cosh cos sinh sin x x >.7.已知集合{}135A x a x a =+≤≤-,集合{}21log 4B x x =≤≤ (1)当4a =时,求()R A B ⋂;(2)若 ,求实数a 的取值范围.在①()R A B ⋂=∅;①“x A ∈”是“x B ∈”的充分条件;①()A A B ⊆这三个条件中任选一个,补充到本题第(2)问的横线处,并解答. 注:如果选择多个条件分别解答,按第一个解答计分.8.已知等差数列{an }的前n 项和为Sn ,数列{bn }满足:点(n ,bn )在曲线y =322x上,a 1=b 4,___,数列{1nS }的前n 项和为Tn . 从①S 4=20,①S 3=2a 3,①3a 3﹣a 5=b 2这三个条件中任选一个,补充到上面问题的横线上并作答.(1)求数列{an },{bn }的通项公式; (2)是否存在正整数k ,使得Tk >1516,且bk >18?若存在,求出满足题意的k 值;若不存在,请说明理由.9.已知0a >且1a ≠,给出下列四个函数: ①()11x f x a-=+;①()log 3a g x x =+;①()2h x x -=;①()tan x x ϕ=.从中任选一个函数,回答下列问题: (1)求所选函数的定义域和值域; (2)写出所选函数的两条性质.注意:如果选多个函数作答,则按第一个函数的答案给分.10.设数列{}n a 的前n 项和为n S ,11a =,__________.给出以下三个条件: ①数列{}n a 为等比数列,数列1{}n S a +也为等比数列;①点1(,)n n S a +在直线1y x =+上;①1121222n n n n a a a na -++++=在这三个条件中任选一个,补充在下面的问题中,并解答. (1)求数列{}n a 的通项公式; (2)设21231log log n n n b a a ++=⋅, 求数列{}n b 的前n 项和n T11.已知函数()()3sin 03,2f x x πωϕωϕ⎛⎫=+<<< ⎪⎝⎭,现有下列3个条件:①相邻两个对称中心的距离是2π;①312f π⎛⎫= ⎪⎝⎭;①06f π⎛⎫-= ⎪⎝⎭.(1)请选择其中两个条件,求出满足这两个条件的函数()f x 的解析式; (2)将(1)中函数()f x 的图像向右平移4π个单位长度,再把横坐标缩小为原来的23(纵坐标不变),得到函数()g x 的图像,请写出函数()g x 的解析式,并求其单调递减区间.12.设ABC 的内角A ,B ,C 的对边分别为22,,,6,36a b c a b bc c =-+=. (1)求A ;(2)从以下三个条件:①8b =;①sin B =①AC 边上的高112BH =中选择一个作为已知条件,使三角形存在且唯一确定,并求ABC 的面积.13.在①9a c ;①b =题(如果多选,以选①评分).在ABC 中,内角A ,B ,C 的对边分别是a ,b ,c ,已知sin cos c B b A =+. (1)求角B ;(2)若10BA BC ⋅=,且______,求ABC 的周长.14.在①2cos cos c a Ab B-=,①222222()tan )b c a A a c b +-=+-, ①2cos 2cos 22sin sin 2cos A C A C B ++=,三个条件中选一个填在下面试题的横线上,并加以解析. 在ABC 中,A ,B ,C 所对的边分别为a ,b ,c ,且满足___________. (1)求角B ;(2)若ABC 为锐角三角形且cos cos 1a B b A +=,求c 的值及ABC 面积的取值范围.15.已知点()()2,0P t t >在抛物线E :()220y px p =>上.有下列三个条件:①点P 到抛物线E 的焦点F 的距离为4;①点()1,6A -,记E 上动点B 到直线2px =-的距离为d ,且d AB +的最小值为 ①点P 到,02p ⎛⎫⎪⎝⎭的距离比点P 到y 轴距离大2.请选择其中一个条件解答下列问题: (1)求p 与t 的值;(2)直线l 与抛物线E 交于M ,N 两点,记直线PM 的斜率为1k ,直线PN 的斜率为2k ,当128k k +=时,直线l 是否过定点?若是,求出定点坐标;若不是,请说明理由. 16.在①2cos a B c =;①向量(),m a b c =-,(),n a b c b =-+,m n ⊥;①tan tan A B +=问题:在ABC 中,a ,b ,c 分别是内角A ,B ,C 的对边,已知a =3c =,D 为AC 边的中点,若______,求BD 的长度.注:如果选择多个条件分别解答,按第一个解答计分.17.在二项式2nx ⎫⎪⎭的展开式中,______.给出下列条件:①若展开式前三项的二项式系数的和等于37;①若展开式中第3项与第2项的二项式系数之比为7:2; ①所有偶数项的二项式系数的和为128.试在上面三个条件中选择一个补充在上面的横线上,并且完成下列问题:(1)求2nx ⎫⎪⎭展开式中x 的系数;(2)写出2nx ⎫⎪⎭展开式中二项式系数最大的项(不需要说明理由).注:如果选择多个条件分别解答,按第一个解答计分.18.已知底面为菱形的四棱锥P ABCD -中,PAD △是等边三角形,平面PAD ⊥平面ABCD ,E ,F 分别是棱PC ,AB 上的点.(1)从下面①①①中选取两个作为条件,证明另一个成立;①F 是AB 的中点;①E 是PC 的中点;①BE ∥平面PFD .(只需选择一种组合进行解答即可)(2)若2AD =,60DAB ∠=︒,PE EC =,求三棱锥P BDE -的体积.19.如图,直四棱柱1111ABCD A B C D -中,底面ABCD 是边长为1的正方形,点E 在棱1BB 上.(1)求证:11AC DE ⊥;(2)从条件①、条件①、条件①这三个条件中选择两个作为已知,使得1DB ⊥平面11EA C ,并给出证明.条件①:E 为1BB 的中点;条件①:1//BD 平面11EA C ;条件①:11DB BD ⊥. (3)在(2)的条件下,求平面11EA C 与平面11DA C 夹角的余弦值. 20.在①737S b a =;①353b S S =-;①1882a S b =,这三个条件中任选一个,补充在下面问题中.已知{}n a 是公差为1的等差数列,n S 为数列{}n a 的前n 项和,{}n b 是正项等比数列,111a b ==, ;()nn na c n Nb *=∈,试比较n c 与1n c +的大小,并说明理由. 21.已知圆C 的方程为2222230x y x y +---=. (1)求圆C 的圆心及半径;(2)是否存在直线l 满足:经过点(2,1)A -,且_________________ ?如果存在,求出直线l 的方程;如果不存在,请说明理由.从下列三个条件中任选一个补充在上面问题中并作答: 条件①:被圆C 所截得的弦长最长; 条件①:被圆C 所截得的弦长最短; 条件①:被圆C 所截得的弦长为8.注:如果选择多个条件分别作答,按第一个解答计分.22.在①原点到直线l 的距离取得最大值,①直线l 在x 轴上的截距是在y 轴上的截距的4倍这两个条件中任选一个,补充在下面的问题中并作答. 已知直线l 过点(2,1)P -.(1)当__________时,求直线l 的方程;(2)若直线l 与圆22(1)(1)1x y -+-=相切,求直线l 的方程. 注:如果选择多个条件分别解答,按第一个解答计分.23.已知点()0,1A ,________,从条件①、条件①、条件①中选择一个作为已知条件补充在横线处,并作答. (1)求直线1l 的方程;(2)求直线2l :220x y 关于直线1l 的对称直线的方程. 条件①:点A 关于直线1l 的对称点B 的坐标为()2,1-;条件①:点B 的坐标为()2,1-,直线1l 过点()2,1且与直线AB 垂直; 条件①点C 的坐标为()2,3,直线1l 过点()2,1且与直线AC 平行.注:如果选择多个条件分别解答,按第一个解答计分.24.在①[]2,0x ∃∈-,①[]2,0x ∀∈-这两个条件中任选一个,补充到下面问题中的横线上,并求解问题.已知函数()22f x x x a =+-.(1)若命题:“______,()0f x ≥”为真命题,求实数a 的取值范围;(2)当1a >时,求关于x 的不等式()()()2111f x a x a x a ≥++--+的解集.注:如选择多个条件分别解答,按第一个解答计分.25.给出条件①()f x 的最小值为0,①()0f x ≥.从这两个条件中任选一个,补充到下面问题中的横线上,并求解该问题.已知函数()222f x x ax =-+.(1)若命题:“R x ∀∈,__________.”为真命题,求实数a 的取值集合; (2)若()f x 在区间[]0,2内恰有两个不同的零点,求实数a 的取值范围. 注:如果选择多个条件分别解答,按第一个解答计分.26.北京2022年冬奥会将于2022年2月4日在北京和张家口开幕,运动员休息区本着环保、舒适、温馨这一出发点,进行精心设计,如图,在四边形ABCD 休闲区域,四周是步道,中间是花卉种植区域,为减少拥堵,中间穿插了氢能源环保电动步道AC ,2D B ∠=∠,且1AD =,3CD =,cos B =(1)求氢能源环保电动步道AC 的长; (2)若___________;求花卉种植区域总面积.从①π3BCA ∠=,①=BC . 注:如果选择多个条件分别解答,按第一个解答计分.27.网球比赛胜1局需得若干分,而每胜1球可得1分.甲、乙两人进行网球比赛,比赛进行到最后阶段,根据规则,有以下两种计分方式可供选择:①长盘制:先净胜2局者胜出比赛,要求:A .先得4分且净胜2分者胜1局,若分数为3平时,一方须净胜2分;B .球员轮流发一局球,直到比赛结束.①短盘制(俗称抢七):1局定胜负,要求:C .先得7分且净胜2分者胜1局,若分数为6平时,一方须净胜2分;D .一方球员发第1个球,对方发第2,3个球,然后双方轮流发两个球,直到比赛结束.请选择一种计分方式回答下列问题:假设甲发球时甲得分的概率为12,乙发球时甲得分的概率为13,各球的结果相互独立,若甲先发球.(1)求甲先得2分的概率;(2)求前5个球,甲得到4分的概率.我选择第___________种计分方式(填①或①,如果选择多个方式分别解答,按第一个解答计分) 28.已知函数()()2,1,12x bg x x x a+=∈-+,从下面三个条件中任选一个条件,求出,a b 的值,并解答后面的问题①已知函数()24f x x ax =-+,若()1f x +在定义域[]1,1b b -+上为偶函数;①已知函数()()0,1x f x a b a a =+>≠在[]1,2上的值域为[]2,4;①已知函数()3f x b x a=+-,满足()()220f x f x -++=(1)证明()g x 在()1,1-上的单调性 (2)解不等式()()120g t g t -+<29.如图,在三棱锥A BCD -中,BCD △是边长为2的等边三角形,AB AC =,O 是BC 的中点,OA CD ⊥.(1)证明:平面ABC ⊥平面BCD ;(2)若E 是棱AC 上的一点,从①2CE EA =;①二面角E BD C --大小为60︒;①A BCD -30.中心在原点的双曲线E 焦点在x 轴上且焦距为4,请从下面3个条件中选择1个补全条件,并完成后面问题: ①该曲线经过点()2,3A ;①该曲线的渐近线与圆22840x x y -++=相切;①点P 在该双曲线上,1F 、2F 为该双曲线的焦点,当点P 的纵坐标为32时,恰好12PF PF ⊥.(1)求双曲线E 的标准方程;(2)过定点()1,1Q 能否作直线l ,使l 与此双曲线相交于1Q 、2Q 两点,且Q 是弦12Q Q 的中点?若存在,求出l 的方程;若不存在,说明理由.31.在①点M 为椭圆C 上顶点时,12MF F △面积为①椭圆C 过点,①离心率e ,这三个条件中任选一个,补充在下面(横线处)问题中,解决下面两个问题.设椭圆2222:1(0)x y C a b a b+=>> 的左、右焦 点分别为1F ,2F ,直线:l y x m=+与椭圆C 交于A ,B 两点,以AB 为底边作等腰三角形,顶点为P (-3,2). 已知椭圆C 的短轴长为4,________.(1)求椭圆C 的方程; (2)求m 的值和△P AB 的面积.答案第1页,共38页参考答案:1.(1)()()22121x y -+-=(2)12m =± 【解析】 【分析】(1)根据圆心在过点()1,3,()2,2的线段的中垂线上,同时圆心圆心在直线30x y +-=上,可求出圆心的坐标,进而求得半径,最后求出其标准方程;(2)选①利用用垂径定理可求得答案,选①根据圆上一点P 到直线的最大距离为d r +可求得答案,选①先利用向量的数量积可求得120ACB ∠=︒,解法就和选①时相同. (1)由题意可知,圆心在点()1,3()2,2的中垂线上,该中垂线的方程为10x y -+=,于是,由3010x y x y +-=⎧⎨-+=⎩,解得圆心()1,2,圆C 的半径1R所以,圆C 的方程为()()22121x y -+-=; (2)①,因为120ACB ∠=︒,1CA CB ==,所以圆心C 到直线l 的距离1cos602d CA =⋅︒=,则12d ==,解得1m =, ①,圆上一点P 到直线的最大距离为32,可知圆心C 到直线l 的距离12d =.则1211d ==+,解得1m = ①,因为12CA CB ⋅=-,所以1cos 2CA CB ACB ⋅⋅∠=-,得120ACB ∠=︒,又1CA CB ==,所以圆心C 到直线l 的距离1cos602d CA =⋅︒=, 则12d ==,解得1m = 2.(1)条件选择见解析,()sin 26f x x π⎛⎫+ ⎝=⎪⎭;(2)单调递增区间为,36k k ππππ⎡⎤-++⎢⎥⎣⎦,Z k ∈.【解析】 【分析】(1)利用三角恒等变换化简得出()1sin 262f x x a πω⎛⎫=+++ ⎪⎝⎭.选择①①:由()102f =可求得a 的值,由正弦型函数的周期公式可求得ω的值,可得出函数()f x 的解析式;选择①①:由正弦型函数的周期公式可求得ω的值,由16f π⎛⎫= ⎪⎝⎭可求得a 的值,可得出函数()f x 的解析式; 选择①①:由()102f =可求得a 的值,由16f π⎛⎫= ⎪⎝⎭结合02ω<<可求得ω的值,可得出函数()f x 的解析式; (2)解不等式222262k x k πππππ-+≤+≤+,Z k ∈可得出函数()f x 的单调递增区间.(1)解:()1cos 212sin 2262x f x x a x a ωπωω+⎛⎫=+=+++ ⎪⎝⎭. 选择①①:因为()1012f a =+=,所以12a =-, 又因为()f x 的最小正周期为22ππω=,所以1ω=,所以()sin 26f x x π⎛⎫+ ⎝=⎪⎭;选择①①:因为()f x 的最小正周期为22ππω=,所以1ω=,则()1sin 262x a f x π⎛⎫+++ ⎪⎝⎭=, 又因为11162f a π⎛⎫=++= ⎪⎝⎭,所以12a =-,所以()sin 26f x x π⎛⎫+ ⎝=⎪⎭;选择①①:因为()1012f a =+=,所以12a =-,所以()sin 26f x x πω⎛⎫=+ ⎪⎝⎭.又因为sin 1636f ππωπ⎛⎫⎛⎫=+= ⎪⎪⎝⎭⎝⎭,所以()2Z 362k k πωπππ+=+∈, 所以16Z k k ω=+∈,,又因为02ω<<,所以1ω=,所以()sin 26f x x π⎛⎫+ ⎝=⎪⎭.(2)解:依题意,令222262k x k πππππ-+≤+≤+,Z k ∈,解得36k x k ππππ-+≤≤+,Z k ∈,所以()f x 的单调递增区间为,36k k ππππ⎡⎤-++⎢⎥⎣⎦,Z k ∈.3.(1){}11A B x x ⋂=-<< (2)答案见解析 【解析】 【分析】(1)先求出集合A ,根据集合的交集运算求得答案;(2)若选①,则可得C B ⊆,考虑C 为空集情况,列出相应的不等式组求解; 若选①,根据B C =∅,考虑C 为空集情况,列出相应的不等式组求解; 若选①,可知C B ,考虑C 为空集情况,列出相应的不等式组求解; (1)()()2230130x x x x +-<⇔-+<,解得31x -<< , ①{}31A x x =-<<.23323x x -<⇔-<-<,解得15x -<<,①{}15B x x =-<<. ①{}11A B x x ⋂=-<<. (2)选①:①B C C =,①C B ⊆.当C =∅,即21m m m ≥-⇒≥时,满足题意;当C ≠∅,即21m m m <-⇒<时,{m ≥−12−m ≤5⇒m ≥−1. 综上,[)1,m ∈-+∞.选①:当C =∅,即21m m m ≥-⇒≥时,满足题意;当C ≠∅,即21m m m <-⇒<时,21m -≤-或5m ≥,m ∈∅. 综上,[)1,m ∈+∞.选①:由题意得C B,当C =∅,即21m m m ≥-⇒≥时,满足题意;当C ≠∅,即21m m m <-⇒<时,{m ≥−12−m ≤5⇒m ≥−1, 当1m =- 时,满足C B , 综上,[)1,m ∈-+∞.4.(1)条件选择见解析,答案见解析; (2)条件选择见解析,答案见解析. 【解析】 【分析】(1)根据所选方案,直接求出()()y f g x =的解析式,根据对数的真数大于零可求得函数()()y f g x =的定义域;(2)根据所选方案,结合二次不等式和对数函数的单调性可得出原不等式的解集. (1)解:若选①,()()()22log 44y f g x x x ==-+,由2440x x -+>,解得2x ≠,故函数()()y f g x =定义域为()(),22,-∞+∞;若选①,()()()222log 4log 4y f g x x x ==-+,易知函数()()y f g x =定义域为()0,∞+. (2)解:若选①,由(1)知,()22log 441x x -+≤,因为2log y x =在()0,∞+上单调递增,且21log 2=,所以20442x x <-+≤,解得22x ≤<或22x <≤.所以不等式()()1f g x ≤的解集为)(22,22⎡+⎣;若选①,由(1)知,()222log 4log 41x x -+≤,令2log x t =,即2430t t -+≤,解得13t ≤≤,即21log 3x ≤≤,因为2log y x =在()0,∞+上单调递增,且21log 2=,23log 8=,所以28x ≤≤. 所以不等式()()1f g x ≤的解集为[]28,. 5.(1)22y x =(2)1-1- 【解析】 【分析】(1)选条件①,由准线方程得参数p ,从而得抛物线方程;选条件①,由椭圆的焦点坐标与抛物线焦点坐标相同求得p 得抛物线方程; 选条件①,由F ,A ,B三点共线时,AB AF FB +==p 得抛物线方程;(2)求出D 点坐标,由点到直线距离公式求得D 到直线MN 的距离,设()11,M x y ,()22,N x y ,直线方程代入抛物线方程,判别式大于0保证相交,由韦达定理得1212,x x x x +,由弦长公式得弦长MN ,再计算出三角形的面积后可解得m .(1)选条件①:由准线方程为12x =-知1p =,所以抛物线C 的方程为22y x =.选条件①:因为抛物线()220y px p =>的焦点坐标为,02p ⎛⎫ ⎪⎝⎭所以由已知得椭圆2213142x yp p +=的一个焦点为,02p ⎛⎫ ⎪⎝⎭.所以231424p p p -=,又0p >,所以1p =,所以抛物线C 的方程为22y x =.选条件①:由题意可知得,当F ,A ,B三点共线时,AB AF FB +==1p =,所以抛物线C 的方程为22y x =. (2)把()2,D y 代入方程22y x =,可得()2,2D ,设()11,M x y ,()22,N x y ,联立22y x m y x=+⎧⎨=⎩,消去y 可得()22220x m x m +-+=,由()222240m m ∆=-->,解得12m <, 又知1222x x m +=-,212x x m =,所以12MN x =-==由()2,2D 到直线l '的距离为d ==212DMN S m =△,2210m m m =⇒+-=,解得1m =-1m =-经检验均满足0∆>,所以m 的值为1-1-6.(1)条件选择见解析,证明见解析,函数()()cosh 2sinh y x x =+的最小值为78; (2)证明见解析. 【解析】 【分析】(1)利用双曲正、余弦函数的定义,结合指数运算可证得①①①成立,令()e e sinh R 2x xt x --==∈,利用二次函数的基本性质可求得函数()()cosh 2sinh y x x =+的最小值;(2),4x ππ⎡⎤∀∈-⎢⎥⎣⎦,将所证不等式等价转化为cos cos sin sin e e e e x x x x --+>-,分[],0x π∈-、0,4x π⎛⎤∈ ⎥⎝⎦两种情况讨论,利用指数函数的单调性结合正余弦函数的性质可证得结论成立. (1)证明:选①,()()22222222c 1e e e 2osh sin e h e e 2e e 2244x x x x x x x x x x ----⎛⎫⎛⎫+-+-⎡⎤⎡⎤⎣⎦⎣⎦⎪++-=-=-= ⎪⎝⎭⎝⎭; 选①,()()()()()22e e e e e e sinh 222sinh cosh 222x x x x x x x x x ----+-==⨯=⨯;选①,()()()222222e e e e e e cosh 2cosh sinh 222x x x x x x x x x ---⎛⎫⎛⎫++-⎡⎤⎡⎤==+=+ ⎪ ⎪⎣⎦⎣⎦⎝⎭⎝⎭. ()()22e e e e cosh 2sinh 22x x x x y x x --+-=+=+,令()e e sinh 2x xt x --==,因为函数e 2x y =、e 2xy -=-均为R 上的增函数,故函数()sinh y x =也为R 上的增函数,故()e e sinh R 2x x t x --==∈,则222e e 24x x t -+-=,所以()2cosh 221x t =+, 所以22177212488y t t t ⎛⎫=++=++≥ ⎪⎝⎭,当且仅当14t =-时取“=”,所以()()cosh 2sinh y x x =+的最小值为78.(2)证明:,4x ππ⎡⎤∀∈-⎢⎥⎣⎦,()()cos cos sin sin e e e ecosh cos sinh sin 22x x x xx x --+->⇔>cos cos sin sin e e e e x x x x --⇔+>-,当[],0x π∈-时,cos cos e e 0x x -+>,sin 0sin x x ≤≤-,所以sin sin e e x x -≤, 所以sin sin e e 0x x --≤,所以cos cos sin sin e e e e x x x x --+>-成立;当0,4x π⎛⎤∈ ⎥⎝⎦时,则022x x ππ<≤-<,且正弦函数sin y x =在0,2π⎛⎫ ⎪⎝⎭上为增函数,cos sin sin 2x x x π⎛⎫=-≥ ⎪⎝⎭,所以cos sin e e x x ≥,sin cos e 0e x x ---<<,所以cos cos sin sin e e e e x x x x --+>-成立,综上,,4x ππ⎡⎤∀∈-⎢⎥⎣⎦,()()cosh cos sinh sin x x >.7.(1)(){25R A B x x ⋂=≤<或}716x <≤ (2)7a ≤ 【解析】 【分析】(1)根据集合的补集与交集定义运算即可;(2)选①①①中任何一个,都可以转化为A B ⊆,讨论A =∅与A ≠∅求解即可. (1)化简集合{}21log 4B x x =≤≤有{}216B x x =≤≤ 当4a =时,{}57A x x =≤≤,则{5R A x x =<或}7x > 故(){25R A B x x ⋂=≤<或}716x <≤ (2)选①①①中任何一个,都可以转化为A B ⊆(①)当A =∅时,135a a +>-,即3a <时, A B ⊆ (①)当A ≠∅时,若A B ⊆,则 135123516a a a a +≤-⎧⎪+≥⎨⎪-≤⎩,解得37a ≤≤综上(①)(①),实数a 的取值范围是7a ≤. 8.(1)条件选择见解析;an =2n ,bn =25﹣n . (2)不存在,理由见解析. 【解析】 【分析】(1)把点(n ,bn )代入曲线y =322x 可得到bn =25﹣n ,进而求出a 1,设等差数列{an }的公差为d ,选①S 4=20,利用等差数列的前n 项和公式可求出d ,从而得到an ; 若选①S 3=2a 3,利用等差数列的前n 项和公式可求出d ,从而得到an ; 若选①3a 3﹣a 5=b 2,利用等差数列的通项公式公式可求出d ,从而得到an ; (2)由(1)可知Sn =1()2n n a a +=n (1+n ),1n S =111n n -+,再利用裂项相消法求出Tn=1﹣11n +,不等式51151116128k k -⎧->⎪⎪+⎨⎪>⎪⎩无解,即不存在正整数k ,使得Tk >1516,且bk >18.(1)解:①点(n ,bn )在曲线y =322x 上,①322=n n b =25﹣n ,①a 1=b 4=25﹣4=2, 设等差数列{an }的公差为d , 若选①S 4=20,则S 4=43422⨯⨯+d =20,解得d =2, ①an =2+2(n ﹣1)=2n ;若选①S 3=2a 3,则S 3=a 1+a 2+a 3=2a 3,①a 1+a 2=a 3, ①2+2+d =2+2d ,解得d =2, ①an =2+2(n ﹣1)=2n ;若选①3a 3﹣a 5=b 2,则3(a 1+2d )﹣(a 1+4d )=25﹣2=8, ①2a 1+2d =8,即2×2+2d =8,①d =2, ①an =2+2(n ﹣1)=2n ; (2)解:由(1)可知Sn =1()2n n a a +=(22)2n n +=n (1+n ),①1n S =1(1)+n n =111n n -+, ①Tn =(1﹣12)+(1231-)+……+(111n n -+)=1﹣11n +, 假设存在正整数k ,使得Tk >1516,且bk >18, ①51151116128k k -⎧->⎪⎪+⎨⎪>⎪⎩,即158k k >⎧⎨<⎩,此不等式无解,①不存在正整数k ,使得Tk >1516,且bk >18. 9.(1)答案见解析; (2)答案见解析. 【解析】 【分析】(1)利用指数型函数,对数型函数,幂函数及正切函数的性质求解;(2)利用函数的对称性及过定点求解①①;利用幂函数和正切函数的单调性及奇偶性求解①①. (1)选①,()11x f x a-=+的定义域为R ;当1a >时,11x a -≥,所以()f x 的值域为[)2,+∞; 当01a <<时,101x a -<≤,所以()f x 的值域为(]1,2; 选①,()log 3a g x x =+的定义域为{}3x x ≠-;值域为R ;选①,()2h x x -=的定义域为{}0x x ≠;值域为()0,∞+;选①,()tan x x ϕ=的定义域为,Z 2x x k k ππ⎧⎫≠+∈⎨⎬⎩⎭;值域为R ;(2)选①,()11x f x a-=+的图象关于直线1x =对称;()11x f x a-=+的图象过定点()1,2.选①,()log 3a g x x =+的图象关于直线3x =-对称;()log 3a g x x =+过定点()4,0-和()2,0-.选①,()2h x x -=是偶函数;()2h x x -=在(),0∞-上为增函数,在()0,∞+上为减函数.选①,()tan x x ϕ=在(),Z 22k k k ππππ⎛⎫-+∈ ⎪⎝⎭上为增函数;()tan x x ϕ=是奇函数.10.(1)12n na(2)()()3234212n n n +-++ 【解析】 【分析】(1)选①时,根据等比数列的性质,求出公比,即可求解答案;选①时,利用1,n n S a +之间的关系式,采用两式相减的方法求得结果;选①时,再写出()121211112222n n n n n a a a a n ----+++=≥这个递推式,和原递推式相减,可求得结果. (2)写出n b 的表达式,采用裂项求和的方法解得答案. (1)若选①,则22,2,2q q q +++成等比, 则22(2)2(2)q q q +=++ , 即得 2q 或 0q =(舍去) ,故 12n na ;若选①,由点1(,)n n S a +在直线1y x =+上, 得11n n a S +=+,()112n n a S n -=+≥, 两式相减化简得()122n n a a n +=≥, 验证212a a = 适合上式, 故12n na ;若选①,由121111222n n n n n a a a a +-+++=, 可知()121211112222n nn n n a a a a n ----+++=≥,两式相减化简得()122n n a n a +=≥ 验证212a a =适合上式, 故12n n a ;(2)由(1)知12n n a则()1111222n b n n n n ⎛⎫==- ⎪++⎝⎭,则121111111112324352n n T b b b n n ⎛⎫=+++=-+-+-+- ⎪+⎝⎭()()1111323122124212n n n n n +⎛⎫=+--=- ⎪++++⎝⎭ 11.(1)()3sin 23f x x π⎛⎫=+ ⎪⎝⎭(2)()3sin 36g x x π⎛⎫=- ⎪⎝⎭,()2252,9393k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ 【解析】 【分析】(1)根据题意,结合周期公式,选择相应的条件,代入函数解析式即可求解;(2)根据图象变换规则即可得到函数()g x 的解析式,利用整体法结合正弦函数的单调性即可求解. (1)选①①,因为相邻两个对称中心的距离为2T, 所以22T π=,得T π=.由2T πω=,得2ω=.由312f π⎛⎫= ⎪⎝⎭,得22122k ππϕπ⨯+=+,k Z ∈,则23k πϕπ=+,k Z ∈,因为2πϕ<,所以3πϕ=,所以()3sin 23f x x π⎛⎫=+ ⎪⎝⎭.选①①,因为相邻两个对称中心的距离为2T,所以22T π=,得T π=.由2T πω=,得2ω=.由06f π⎛⎫-= ⎪⎝⎭,得26k πϕπ⎛⎫-⨯+= ⎪⎝⎭,k Z ∈,则3k πϕπ=+,k Z ∈,因为2πϕ<,所以3πϕ=,所以()3sin 23f x x π⎛⎫=+ ⎪⎝⎭.选①①,由题意121264n πππω⎛⎫⎛⎫--=+⨯ ⎪ ⎪⎝⎭⎝⎭或()321264n n Z πππω⎛⎫⎛⎫--=+⨯∈ ⎪ ⎪⎝⎭⎝⎭, 即1244n ππω⎛⎫=+⨯ ⎪⎝⎭或()3244n n Z ππω⎛⎫=+⨯∈ ⎪⎝⎭,得82n ω=+或()86n n Z ω=+∈.因为03ω<<, 所以2ω=.由06f π⎛⎫-= ⎪⎝⎭,得26k πϕπ⎛⎫-⨯+= ⎪⎝⎭,k Z ∈,则3k πϕπ=+,k Z ∈,因为2πϕ<,所以3πϕ=,所以()3sin 23f x x π⎛⎫=+ ⎪⎝⎭.(2)将函数()f x 的图象向右平移4π个单位长度,可得3sin 26y x π⎛⎫=- ⎪⎝⎭的图像,再将横坐标缩小为原来的23(纵坐标不变),得到函数()3sin 36g x x π⎛⎫=- ⎪⎝⎭的图象.由()3232262k x k k Z πππππ+≤-≤+∈, 得()22529393k k x k Z ππππ+≤≤+∈, 所以函数()g x 的单调递减区间为()2252,9393k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦. 12.(1)π3A =(2)选第①个条件;【解析】 【分析】(1)利用余弦定理即可求出A ;(2)选第①个条件,这样的三角形不存在;选第①个条件,先利用正弦定理,余弦定理求出边长c ,即可求出ABCS ;选第①个条件:先求出边长c =2236b bc c -+=判断出这样的三角形有两个. (1)因为6a =,2236b bc c -+=,所以222b bc c a -+=.所以222b c a bc +-=,所以2221cos 22b c a A bc +-==. 又0πA <<,所以π3A =. (2)选第①个条件:8b =.由2236b bc c -+=可得:20828c c -=+,因为28428480∆=-⨯=-<,所以无解,这样的三角形不存在. 选第①个条件:sin B =. 由正弦定理,得sin sin a bA B=,所以6sin 4sin a B b A ===. 由2236b bc c -+=,得24200c c --=.解得2c =+2c =-.因此(11sin 4222ABC S bc A ==⨯⨯+=△选第①个条件:AC 边上的高112BH =.在ABH 中,由sin BH A AB =,所以11sin BH AB A ===,即c = 代入2236b bc c -+=得:21303b +=,解得:b =或b =,这样的三角形有两个. 13.(1)3B π=(2)答案见解析 【解析】 【分析】(1)由正弦定理的边化角公式结合三角恒等变换得出3B π=;(2)选①:由数量积公式得出20ac ,再由余弦定理得出b ,进而得出ABC 的周长;选①:由数量积公式得出20ac ,再由余弦定理得出10a c +=,进而得出ABC 的周长 (1)①sin cos c B b A =+①sin sin sin cos C A B B A =+ ①()sin sin sin cos A B A B B A +=+即sin cos cos sin sin sin cos A B A B A B B A +=+①sin cos sin A B A B =又因为sin 0A >sin B B =,即tan B =①0B π<<,①3B π=(2)选①①10BA BC ⋅=,①cos103BA BC π=,即①20ac由余弦定理得()22222cos 38132021b a c ac B a c ac =+-=+-=-⨯=即b =所以ABC 的周长为9a b c ++=选①①10BA AC ⋅=,①cos103BA BC π=,即①20ac由余弦定理得()22222cos 3b a c ac B a c ac =+-=+-,(()22320a c =+-⨯,所以10a c +=所以ABC 的周长为10a b c ++=+14.(1)3B π=;(2)1;. 【解析】 【分析】(1)选条件①,利用正弦定理边化角变形计算即得;选条件①,利用余弦定理变形计算即得;选条件①,利用二倍角的余弦公式结合余弦定理计算作答.(2)利用给定条件结合正弦定理求出c 并表示出a ,再列出面积的函数关系即可推理计算作答. (1)选条件①,在ABC 中,由正弦定理得2sin sin cos sin cos C A AB B-=, 即2sin cos sin cos cos sin C B A B A B -=,则2sin cos sin cos cos sin sin()sin C B A B A B A B C =+=+=,而sin 0C >,有1cos 2B =,又0B π<<,所以3B π=.选条件①,在ABC中,由余弦定理得2cos tan cos bc A A B =,即sin cos b A B =,由正弦定理得sin sin sin B A B A =,而sin 0A >,则tan B 0B π<<, 所以3B π=.选条件①,则有22212sin 12sin 2sin sin 22sin A C A C B -+-+=-,即222sin sin sin sin sin A C B A C +-=,在ABC 中,由正弦定理得222a cb ac +-=,由余弦定理得2221cos 22a cb B ac +-==,又0B π<<,所以3B π=.(2)设ABC 外接圆半径为R ,则由正弦定理有:2sin 2sin()2sin cos 2cos sin cos cos 1c R C R A B R A B R A B a B b A ==+=+=+=,由(1)及正弦定理得1sin()sin sin 1322sin sin sin 2c C C Cc A a C C C π+==== ABC的面积13sin 28tan S ac B C===, 因ABC 是锐角三角形,则022032C C πππ⎧<<⎪⎪⎨⎪<-<⎪⎩,即62C ππ<<,有tan C >,10tan C<<S <<所以ABC面积的取值范围是. 15.(1)4p =;4t = (2)定点(1,3)- 【解析】 【分析】(1)选①:由焦半径公式列方程可得解,选①:由||||||d AB BF AB AF +=+≥,列式可以求解; 选①:根据抛物线定义可得22p=,进而得解. (2)设直线l x ty m =+,与抛物线联立,由128k k +=,得1288844y y +=++,代入韦达定理求解即可. (1)选①:根据抛物线定义得: ||242pPF =+=,解得4p =, 则28y x =,将点()()2,0P t t >代入得:216t =,解得4t =; 选①:||||||d AB BF AB AF +=+≥== 当且仅当,,A B F (B 在AF 之间)三点共线时,取等号. 解得4p =,则28y x =,将点()()2,0P t t >代入得:216t =,解得4t =; 选①:点P 到,02p ⎛⎫⎪⎝⎭的距离等于到准线2p x =-的距离,点P 到,02p ⎛⎫⎪⎝⎭的距离比点P 到y 轴距离大2,则22p=,解得4p =, 则28y x =,将点()()2,0P t t >代入得:216t =,解得4t =. (2)直线l 与抛物线E 交于M ,N 两点,所以斜率显然不为0,设为x ty m =+, 设1122(,),(,)M x y N x y ,联立直线与抛物线:28x ty my x =+⎧⎨=⎩,得:2880y ty m --=,所以21212Δ6432088t m y y t y y m ⎧=+>⎪+=⎨⎪=-⎩,直线PM 的斜率为11211114482428y y y k x y --===-+-,同理直线PN 的斜率为2284k y =+,所以由128k k +=,得1288844y y +=++, 整理得:12123()80y y y y +++=,代入121288y y t y y m +=⎧⎨=-⎩得:82480m t -++=,整理得:31m t =+,所以直线l :31(3)1x ty m ty t t y =+=++=++过定点(1,3)-. 16.答案不唯一,具体见解析. 【解析】 【分析】选①,由正弦定理边化角,由余弦定理求出cos C ,再借助余弦定理计算作答. 选①,由向量关系结合余弦定理求出角C ,再由正弦定理求角A 即可计算作答. 选①,切化弦求出角C ,由正弦定理求出角A ,再借助余弦定理计算作答. 【详解】若选①:在ABC 中,因2cos a B c =,由正弦定理得2sin cos sin A B C =,而()sin sin C A B =+,即有2sin cos sin cos cos sin A B A B A B =+,整理得()sin 0A B -=, 又A B ππ-<-<,则0A B -=,即A B =,有b a ==2221cos 22a b c C ab +-==-,在BCD △中,由余弦定理2222124BD C =+-=⎝⎭,所以BD =若选①:由m n ⊥,得0m n ⋅=,即()()()0a a b b c c b -+-+=,整理得2220a ab c b --+=,在ABC 中,由余弦定理得:2221cos 22a b c C ab +-==,而0C π<<,则3C π=,由正弦定理得3sin3π=,即1sin 2A =,由a =3c =可得:03A C π<<=, 则6A π=,有2ππ=--=B A C,因此有b ,又D 为斜边AC 中点,所以2bBD ==若选①:依题意,sin cos cos sin cos cos A B A B A B +=()sin A B C +=,在ABC 中,()sin sin C A B =+,于是得tan C =23C π=,由正弦定理得:32sin 3π,解得1sin 2A =,由a =3c =可得:203A C π<<=,则有6A π=,从而有ππ6B A C,即b a =在BCD △中,由余弦定理得:2222124BD C =+-=⎝⎭,所以BD = 17.(1)112 (2)21120x - 【解析】 【分析】(1)根据所选条件求出n 的值,即可得到二项式展开式的通项,即可求出展开式中x 的系数;(2)根据展开式的二项式系数的特征,得到第5项的二项式系数取得最大,再根据通项计算可得; (1)解:因为2nx ⎫⎪⎭展开式中第1r +项的二项式系数为rn C ,若选①,则01237n n n C C C ++=,即(1)1372n n n -++=,即2720n n +-=,即(9)(8)0n n +-=.解得8n =或9n =-(舍去)若选①:则21:7:2n nC C =,解得8n =; 若选①:则12128n -=,解得8n =;综上可得2nx ⎫⎪⎭即为82x ⎫⎪⎭则展开式的通项为()838218822rrrr rr r T C C x x --+⎛⎫=-=- ⎪⎝⎭,令8312r -=解得2r =,所以()22382112T C x x =-=,故展开式中x 的系数为112;(2)解:因为82x ⎫⎪⎭展开式中一共含有9项,故第5项二项式系数最大,()44225821120T C x x --=-=,即展开式中二项式系数最大的项为21120x -;18.(1)证明见解析 (2)12【解析】 【分析】(1)分①①⇒①,①①⇒①,①①⇒①三种情况讨论,根据线面平行的判定定理及性质定理证明即可;(2)取AD 的中点G ,连接PG ,根据面面垂直的性质得到PG ⊥平面ABCD ,再根据1122P BDE B PDE B PDC P BCD V V V V ----===计算可得;(1)解:(1)①①⇒①,因为F 是AB 的中点,E 是PC 的中点,取PD 的中点M ,连接ME ,MF ,则//ME CD ,且1=2ME CD ,又四边形ABCD 为菱形,所以//BF DC 且1=2BF DC ,所以//BF EM 且=BF EM ,所以四边形BEMF 为平行四边形,所以//BE FM ,BE ⊄平面PDF ,FM ⊂平面PDF ,所以//BE 平面PDF ;(2)①①⇒①,取PD 的中点M ,连接ME 、MF ,因为E 是PC 的中点,所以//ME CD ,且1=2ME CD ,又//BF CD ,所以//BF ME ,因为//BE 平面PDF ,平面BEMF平面PDF MF =,BE ⊂平面BEMF ,所以//BE MF ,所以四边形BEMF 为平行四边形,所以=BF ME ,即12BF CD =,所以F 是AB 的中点;(3)①①⇒①,取DC 的中点N ,连接NB 、NE ,因为F 是AB 的中点,所以//BF DN 且BF DN =,所以BNDF 为平行四边形,所以//BN DF ,因为BN ⊄平面PDF ,DF ⊂平面PDF ,所以//BN 平面PDF ,又//BE 平面PDF ,BE BN B =,,BE BN ⊂平面BEN ,所以平面PDF //平面BEN ,因为平面BEN平面PCD EN =,平面PDF平面PCD PD =,所以//EN PD ,所以E 是PC 的中点;(2)解:取AD 的中点G ,连接PG ,因为APD △为等边三角形,所以PG AD ⊥,又平面PAD ⊥平面ABCD ,平面PAD 平面ABCD AD =,所以PG ⊥平面ABCD ,又2AB BC CD AD PA PD ======,所以2sin 60PG =⨯︒=122sin 602BCDS=⨯⨯⨯︒=E 是PC 的中点,所以1111122232P BDE B PDE B PDC P BCD V V V V ----====⨯=19.(1)证明见解析; (2)答案见解析;. 【解析】 【分析】(1)连结BD ,11B D ,由直四棱柱的性质及线面垂直的性质可得111BB AC ⊥,再由正方形的性质及线面垂直的判定、性质即可证结论.(2)选条件①①,设1111AC B D O ⋂=,连结OE ,1BD ,由中位线的性质、线面垂直的性质可得1DB OE ⊥、111AC DB ⊥,再由线面垂直的判定证明结论;选条件①①,设1111AC B D O ⋂=,连结OE ,由线面平行的性质及平行推论可得1DB OE ⊥,由线面垂直的性质有111AC DB ⊥,再由线面垂直的判定证明结论;(3)构建空间直角坐标系,求平面11EA C 、平面11DA C 的法向量,应用空间向量夹角的坐标表示求平面11EA C 与平面11DA C 夹角的余弦值. (1)连结BD ,11B D ,由直四棱柱1111ABCD A B C D -知:1BB ⊥平面1111A B C D ,又11A C ⊂平面1111A B C D ,所以111BB AC ⊥,又1111A B C D 为正方形,即1111A C B D ⊥,又1111B D BB B ⋂=, ①11A C ⊥平面11D DBB ,又DE ⊂平面11D DBB , ①11AC DE ⊥. (2)选条件①①,可使1DB ⊥平面11EA C .证明如下:设1111AC B D O ⋂=,连结OE ,1BD ,又E ,O 分别是1BB ,11B D 的中点, ①1//OE BD .又11DB BD ⊥,所以1DB OE ⊥.由(1)知:11A C ⊥平面11D DBB ,1DB ⊂平面11D DBB ,则111AC DB ⊥. 又11A C OE O ⋂=,即1DB ⊥平面11EA C .选条件①①,可使1DB ⊥平面11EA C .证明如下: 设1111AC B D O ⋂=,连结OE .因为1//BD 平面11EA C ,1BD ⊂平面11D DBB ,平面11D DBB ⋂平面11EA C OE =, 所以1//BD OE ,又11DB BD ⊥,则1DB OE ⊥.由(1)知:11A C ⊥平面11D DBB ,1DB ⊂平面11D DBB ,则111AC DB ⊥. 又11A C OE O ⋂=,即1DB ⊥平面11EA C . (3)由(2)可知,四边形11D DBB为正方形,所以1DD BD = 因为DA ,DC ,1DD 两两垂直,如图,以D 为原点,建立空间直角坐标系D xyz -,则()0,0,0D,(1A,(1B,(1C,E ⎛ ⎝⎭,(1D ,所以()111,1,0AC =-,(1DA =. 由(1)知:平面11EA C的一个法向量为(1DB =.设平面11DA C 的法向量为{,,}n x y z =,则11100n A C x y n DA x ⎧⋅=-+=⎪⎨⋅==⎪⎩,令x =()2,2,1n =-.。
2023年高考数学二轮复习第二篇经典专题突破专题三立体几何第1讲空间几何体

第二篇 专题三 第1讲一、选择题1.如图,△A ′B ′C ′是水平放置的△ABC 的斜二测直观图,其中O ′C ′=O ′A ′=2O ′B ′,则以下说法正确的是( C )A .△ABC 是钝角三角形B .△ABC 是等腰三角形,但不是直角三角形 C .△ABC 是等腰直角三角形D .△ABC 是等边三角形【解析】根据题意,将△A ′B ′C ′还原成原图,如图,原图中,则有OC =OA =OB , 则△ABC 是等腰直角三角形; 故选C.2.如图,半径为R 的球的两个内接圆锥有公共的底面.若两个圆锥的体积之和为球的体积的38,则这两个圆锥的高之差的绝对值为( D )A .R2B .2R3C .4R3D .R【解析】设球的球心为O ,半径为R ,体积为V ,上面圆锥的高为h (h <R ),体积为V 1,下面圆锥的高为H (H >R ),体积为V 2,两个圆锥共用的底面的圆心为O 1,半径为r .由球和圆锥的对称性可知h +H =2R ,|OO 1|=H -R .∵V 1+V 2=38V ,∴13πr 2h +13πr 2H =38×43πR 3, ∴r 2(h +H )=32R 3.∵h +H =2R ,∴r =32R .∵OO 1垂直于圆锥的底面,∴OO 1垂直于底面的半径,由勾股定理可知R 2=r 2+|OO 1|2, ∴R 2=r 2+(H -R )2,∴H =32R ,∴h =12R ,则这两个圆锥的高之差的绝对值为R ,故选D.3.已知一个圆锥的侧面积是底面积的2倍,记该圆锥的内切球的表面积为S 1,外接球的表面积为S 2,则S 1S 2等于( C )A .12B .13C .14D .18【解析】如图,由已知圆锥侧面积是底面积的2倍,不妨设底面圆半径为r ,l 为底面圆周长,R 为母线长,则12lR =2πr 2, 即12·2π·r ·R =2πr 2, 解得R =2r ,故∠ADC =30°,则△DEF 为等边三角形, 设B 为△DEF 的重心,过B 作BC ⊥DF ,则DB 为圆锥的外接球半径,BC 为圆锥的内切球半径, 则BC BD =12,∴r 内r 外=12,故S 1S 2=14. 4.如图所示,在正方体ABCD -A 1B 1C 1D 1中,动点E 在BB 1上,动点F 在A 1C 1上,O 为底面ABCD 的中心,若BE =x ,A 1F =y ,则三棱锥O -AEF 的体积( B )A .与x ,y 都有关B .与x ,y 都无关C .与x 有关,与y 无关D .与y 有关,与x 无关【解析】由已知得V 三棱锥O -AEF =V 三棱锥E -OAF =13S △AOF ·h (h 为点E 到平面AOF 的距离).连接OC ,因为BB 1∥平面ACC 1A 1, 所以点E 到平面AOF 的距离为定值. 又AO ∥A 1C 1,OA 为定值, 点F 到直线AO 的距离也为定值, 所以△AOF 的面积是定值,所以三棱锥O -AEF 的体积与x ,y 都无关.5.在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( C )A .2π3B .4π3C .5π3D .2π【解析】如图,过点C 作CE 垂直AD 所在直线于点E ,梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径, 线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径,ED 为高的圆锥, 该几何体的体积为V =V 圆柱-V圆锥=π·AB 2·BC -13·π·CE 2·DE =π×12×2-13π×12×1=5π3.6.如图,在三棱锥V -ABC 中,∠AVB =∠BVC =∠CVA =60°,VA =VB =VC ,若三棱锥V -ABC 的内切球O 的表面积为6π,则此三棱锥的体积为( D )A .63B .183C .62D .182【解析】连接VO ,并延长交底面ABC 于点E ,连接AE ,并延长交BC 于D ,∵在三棱锥V -ABC 中,∠AVB =∠BVC =∠CVA =60°,VA =VB =VC , ∴三棱锥V -ABC 是正四面体,∴E 是△ABC 的重心,∴VE ⊥平面ABC , ∵三棱锥V -ABC 的内切球O 的表面积为6π, ∴4πr 2=6π,解得球O 的半径r =OE =62, 设AB =a ,则AE =23AD =23a 2-⎝⎛⎭⎫a 22=3a 3,VE =a 2-⎝⎛⎭⎫3a 32=63a , ∴AO =VO =63a -62, ∵OE ⊥AE ,∴AE 2+OE 2=AO 2,∴⎝⎛⎭⎫3a 32+⎝⎛⎭⎫622=⎝⎛⎭⎫63a -622, 解得a =6,∴VE =63×6=26, ∴此三棱锥的体积为V =13S △ABC ·VE =13×12×6×6×sin 60×26=18 2.故选D.7.如图所示,某几何体由底面半径和高均为5的圆柱与半径为5的半球对接而成,在该封闭的几何体内部放入一个小圆柱体,且小圆柱体的上、下底面均与外层圆柱的底面平行,则小圆柱体积的最大值为( B )A .2 000π9B .4 000π27C .81πD .128π【解析】小圆柱的高分为上、下两部分,上部分的高同大圆柱的高相等,为5,下部分深入底部半球内.设小圆柱下部分的高为h (0<h <5),底面半径为r (0<r <5).由于r ,h 和球的半径构成直角三角形,即r 2+h 2=52, 所以小圆柱的体积V =πr 2(h +5)=π(25-h 2)(h +5)(0<h <5),把V 看成是关于h 的函数,求导得V ′=-π(3h -5)(h +5). 当0<h <53时,V ′>0,V 单调递增;当53<h <5时,V ′<0,V 单调递减. 所以当h =53时,小圆柱的体积取得最大值.即V max =π⎝⎛⎭⎫25-259×⎝⎛⎭⎫53+5=4 000π27,故选B. 二、填空题8.如图,在正三棱柱ABC -A 1B 1C 1中,AB =4,AA 1=6.若E ,F 分别是棱BB 1,CC 1上的点,则三棱锥A -A 1EF 的体积是.【解析】因为在正三棱柱ABC -A 1B 1C 1中, AA 1∥BB 1,AA 1⊂平面AA 1C 1C ,BB 1⊄平面AA 1C 1C , 所以BB 1∥平面AA 1C 1C ,从而点E 到平面AA 1C 1C 的距离就是点B 到平面AA 1C 1C 的距离, 作BH ⊥AC ,垂足为点H ,由于△ABC 是正三角形且边长为4,所以BH =23,从而三棱锥A -A 1EF 的体积VA -A 1EF =VE -A 1AF =13S △A 1AF ·BH =13×12×6×4×23=8 3.9.已知直四棱柱ABCD -A 1B 1C 1D 1的棱长均为2,∠BAD =60°.以D 1为球心,5为半径的球面与侧面BCC 1B 1的交线长为2. 【解析】如图,设B 1C 1的中点为E ,球面与棱BB 1,CC 1的交点分别为P ,Q , 连接DB ,D 1B 1,D 1P ,D 1E ,EP ,EQ ,由∠BAD =60°,AB =AD ,知△ABD 为等边三角形, ∴D 1B 1=DB =2,∴△D 1B 1C 1为等边三角形, 则D 1E =3且D 1E ⊥平面BCC 1B 1,∴E 为球面截侧面BCC 1B 1所得截面圆的圆心, 设截面圆的半径为r ,则r =R 2球 -D 1E 2=5-3= 2. 又由题意可得EP =EQ =2,∴球面与侧面BCC 1B 1的交线为以E 为圆心的圆弧PQ . 又D 1P =5,∴B 1P =D 1P 2-D 1B 21 =1, 同理C 1Q =1,∴P ,Q 分别为BB 1,CC 1的中点, ∴∠PEQ =π2,知PQ ︵的长为π2×2=2π2,即交线长为2π2.10.(2020·浙江)已知圆锥的侧面积(单位:cm 2)为2π,且它的侧面展开图是一个半圆,则这个圆锥的底面半径(单位:cm)是__1__.【解析】如图,设圆锥的母线长为l ,底面半径为r ,则圆锥的侧面积S 侧=πrl =2π, 即r ·l =2.由于侧面展开图为半圆, 可知12πl 2=2π,可得l =2,因此r =1.11.在如图所示的斜截圆柱中,已知圆柱的底面直径为40 cm ,母线长最短50 cm ,最长80 cm ,则斜截圆柱的侧面面积S =__2 600π__cm 2.【解析】将题图所示的相同的两个几何体对接为圆柱,则圆柱的侧面展开图为矩形.由题意得所求侧面展开图的面积S =12×(π×40)×(50+80)=2 600π(cm 2).12.如图,已知正方体ABCD -A 1B 1C 1D 1的棱长为1,P 为BC 的中点,过点A ,P ,C 1的平面截正方体所得的截面为M ,则截面M 的面积为2.【解析】如图,取A 1D 1,AD 的中点分别为F ,G . 连接AF ,AP ,PC 1,C 1F ,PG ,D 1G ,AC 1,PF . ∵F 为A 1D 1的中点,P 为BC 的中点,G 为AD 的中点,∴AF =FC 1=AP =PC 1=52,PG CD ,AF D 1G . 由题意可知CD C 1D 1,∴PG C 1D 1, ∴四边形C 1D 1GP 为平行四边形, ∴PC 1D 1G ,∴PC 1AF , ∴A ,P ,C 1,F 四点共面, ∴四边形APC 1F 为菱形. ∵AC 1=3,PF =2,过点A ,P ,C 1的平面截正方体所得的截面M 为菱形APC 1F ,∴截面M 的面积S =12AC 1·PF =12×3×2=62.三、解答题13.(2021·浙江高三期末)如图是一个以A 1B 1C 1为底面的直三棱柱被一平面所截得到的几何体,截面为ABC ,已知A 1B 1=B 1C 1=2,∠A 1B 1C 1=90°,AA 1=5,BB 1=4,CC 1=3,求:(1)该几何体的体积; (2)该几何体的表面积.【解析】 (1)把几何体ABC -A 1B 1C 1补成直棱柱A 1B 1C 1-ADE , 如图,作C 作与底面平行的截面CMN ,则截得两个直棱柱,则AM =2,BN =BD =1,CE =2, S △A 1B 1C 1=12×2×2=2,V ADE -MNC =2×2=4,VMNC -A 1B 1C 1=2×3=6,所以VABC -A 1B 1C 1=6+4×12=8;(也可求出四棱锥C -ABNM 的体积为2)(2)A 1C 1=22,因此SABB 1A 1=12×(5+4)×2=9,SBB 1C 1C =12×(4+3)×2=7,SCC 1A 1A =12×(3+5)×22=82,又AC =22+(22)2=23, BC =22+12=5=AB ,等腰三角形ABC 的底边AC 上的高为h =(5)2-(3)2=2,S△ABC=12×23×2=6,所以所求表面积为S=2+6+9+7+82=18+82+ 6.。
两条直线的位置关系9题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测(解析版)

专题39两条直线的位置关系9题型分类1.两条直线的位置关系直线l 1:y =k 1x +b 1,l 2:y =k 2x +b 2,l 3:A 1x +B 1y +C 1=0,l 4:A 2x +B 2y +C 2=0(其中l 1与l 3是同一条直线,l 2与l 4是同一条直线)的位置关系如下表:位置关系l 1,l 2满足的条件l 3,l 4满足的条件平行k 1=k 2且b 1≠b 2A 1B 2-A 2B 1=0且A 1C 2-A 2C 1≠0垂直k 1·k 2=-1A 1A 2+B 1B 2=0相交k 1≠k 2A 1B 2-A 2B 1≠02.三种距离公式(1)两点间的距离公式①条件:点P 1(x 1,y 1),P 2(x 2,y 2).②结论:|P 1P 2|=(x 2-x 1)2+(y 2-y 1)2.③特例:点P (x ,y )到原点O (0,0)的距离|OP |=x 2+y 2.(2)点到直线的距离点P (x 0,y 0)到直线l :Ax +By +C =0的距离d =|Ax 0+By 0+C |A 2+B 2.(3)两条平行直线间的距离两条平行直线l1:Ax+By+C1=0与l2:Ax+By+C2=0间的距离d=|C1-C2| A2+B2.常用结论1.直线系方程(1)与直线Ax+By+C=0平行的直线系方程是Ax+By+m=0(m∈R且m≠C).(2)与直线Ax+By+C=0垂直的直线系方程是Bx-Ay+n=0(n∈R).(3)过直线l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0的交点的直线系方程为A1x+B1y+C1+λ(A2x+B2y+C2)=0(λ∈R),但不包括l2.2.五种常用对称关系(1)点(x,y)关于原点(0,0)的对称点为(-x,-y).(2)点(x,y)关于x轴的对称点为(x,-y),关于y轴的对称点为(-x,y).(3)点(x,y)关于直线y=x的对称点为(y,x),关于直线y=-x的对称点为(-y,-x).(4)点(x,y)关于直线x=a的对称点为(2a-x,y),关于直线y=b的对称点为(x,2b-y).(5)点(x,y)关于点(a,b)的对称点为(2a-x,2b-y).(一)判断两条直线位置关系的注意点(1)斜率不存在的特殊情况.(2)可直接利用直线方程系数间的关系得出结论.,根据两直线平行和垂直时,其斜率间的关系得出方程组,解之可求得点(二)利用距离公式应注意的点(1)点P(x0,y0)到直线x=a的距离d=|x0-a|,到直线y=b的距离d=|y0-b|.(2)两条平行线间的距离公式要把两条直线方程中x,y的系数化为相等.∴PB l 的倾斜角为π6,PA l 的倾斜角为∴直线l 的倾斜角的取值范围是故选:D作B 关于直线:3l x y --则直线AB '和直线l 的交点即为设D 为l 上异于P 的一点,则故DA DB DA DB -=-故||||||PA PB -最大,即此时设(,)B a b ',则432b a a b -⎧=⎪⎪⎨⎪⨯-⎪⎩作C 关于直线:3l x y --则直线AC '和直线l 的交点即为设E 为l 上异于P 的一点,则故EC EA EC EC +=+故||||+PA PC 最小,即此时设(,)C m n ',则43332n m m -⎧=⎪⎪-⎨+⎪⨯⎪⎩故直线AC '方程为19x +即即1126(,)77P ;5-4.(2024高三下·江西2430x y -+=上一动点,则A .5B 【答案】B【分析】求点()0,2A -关于直线论两点之间线段最短可求5-5.(2024高二下·上海浦东新且1PQ l ⊥,点()3,3A --,【答案】310322+【分析】作出图象,易知l 然后在l 上,直线1l ,2l 之间找点由此求解.【详解】易知12l l //,作出图象如下,过直线:3l y x =-,过P 作直线//PC QB ,与直线l 交于点C ,易知四边形PCBQ 为平行四边形,故PC QB =,且B 到直线2l 的距离等于C 到1l 的距离,设(,3)C t t -,则3230122t t +-++-=,解得32t =或12t =-(舍),所以33,22C ⎛⎫- ⎪⎝⎭,而AP PQ QB AP PQ PC ++=++,且2(1)332222PQ --===(定值),故只需求出||||AP PC +的最小值即可,显然223331033222AP PC AC ⎛⎫⎛⎫+≥=--+-+= ⎪ ⎪⎝⎭⎝⎭,故AP PQ QB ++的最小值为310322+.故答案为:310322+.5-6.(2024高三下·河南·阶段练习)已知函数()()()ln 11f x a x a =++∈R 的图象恒过定点A ,圆22:4O x y +=上的两点()11,P x y ,()22,Q x y 满足()PA AQ λλ=∈R,则11222727x y x y +++++的最小值为()A .25B .75+C .155-D .3025-【答案】C 【分析】设直线l 为270x y ++=.取圆O 的弦PQ 的中点为E ,求出其轨迹方程,求出E 到直线l 距离的最小值.过P 、E 、Q 分别作直线l 的垂线,垂足分别为M 、R 、N ,将11222727x y x y +++++转化为25ER ,即可求其最小值.【详解】由题可知A 为(0,1),且P 、A 、Q 三点共线,设弦PQ 的中点为E (x ,y ),连接OE ,则OE ⊥PQ ,即OE ⊥AE ,∴0OE AE ⋅=,由此可得E 的轨迹方程为2+−122=14,【点睛】本题需充分利用数形结合思想进行简答,直线的距离公式联系在一起,数形结合求解最值5-7.(2024高三下·上海宝山·开学考试)如图,平面上两点2MN=,且使PM MN++【答案】99, 44骣÷ç÷ç÷ç桫【点睛】本小题主要考查两点间距离公式的应用,考查对称性,考查化归与转化的数学思想方法,考查数形结合的数学思想方法,属于中档题(三)对称问题的求解策略(1)解决对称问题的思路是利用待定系数法将几何关系转化为代数关系求解.(2)中心对称问题可以利用中点坐标公式解题,两点轴对称问题可以利用垂直和中点两个条件列方程组解题.求直线l关于直线0l对称的直线'lCA.35B.【答案】C【分析】求点A关于y轴的对称点6-3.(2024高二上·四川遂宁A .(1,4)-C .(3,4)--【答案】C 【分析】因点A 与点B 关于直线对称,则【详解】设(),A x y ,因点A 垂直,则212022112x y y x ++⎧++=⎪⎧⎪⇒⎨⎨-⎩⎪=⎪-⎩即点A 坐标为(3,4)--.则直线的对称点为(四)一、单选题1.(2024高二上·浙江·期中)已知点(,2)(0)a a >到直线:30l x y -+=的距离为1,则a 等于()AB.2C1D1+【答案】C【分析】根据点到直线得距离公式即可得出答案.1=.解得1a =-1a =-0a >,1a ∴=-故选:C.2.(2024高二上·黑龙江哈尔滨·期末)已知两条直线1:3460l x y -+=,2:3440l x y --=,则这两条直线之间的距离为()A .2B .3C .5D .10【答案】A【分析】由两平行线距离公式求解即可.【详解】这两条直线之间的距离为2d ==.故选:A3.(2024高二·全国·课后作业)求直线x +2y -1=0关于直线x +2y +1=0对称的直线方程()A .x +2y -3=0B .x +2y +3=0C .x +2y -2=0D .x +2y +2=0【答案】B【分析】结合两平行线间的距离公式求得正确选项.【详解】设对称直线方程为20x yc ++=,=,解得3c =或1c =-(舍去).所以所求直线方程为230x y ++=.故选:B4.(2024高二·全国·课后作业)直线0ax by c ++=关于直线0x y -=对称的直线为()A .0ax by c -+=B .0bx ay c -+=C .0bx ay c ++=D .0bx ay c +-=【答案】C【分析】根据两直线关于对称直线对称的概念即可求解【详解】解:设所求直线上的任意一点为(,)M x y 则M 关于直线0x y -=对称点为(,)N y x 点N 在直线0ax by c ++=上∴(,)N y x 满足直线方程,即0ay bx c ++=∴直线0ax by c ++=关于直线0x y -=对称的直线为0bx ay c ++=故选:C5.(2024·浙江温州·三模)已知直线12:0,:10l x y l ax by +=++=,若12l l ⊥,则a b +=()A .1-B .0C .1D .2【答案】B【分析】根据给定的条件,利用两直线的垂直关系列式计算作答.【详解】因为直线12:0,:10l x y l ax by +=++=,且12l l ⊥,则110a b ⋅+⋅=,所以0a b +=.故选:B6.(2024·安徽蚌埠·三模)已知直线1l :210ax y ++=,2l :()30a x y a --+=,则条件“1a =”是“12l l ⊥”的()A .充分必要条件B .充分不必要条件C .必要不充分条件D .既不必要也不充分条件【答案】B 【分析】根据两直线垂直的性质,可得()312a a ⎛⎫-⨯-=- ⎪⎝⎭,求出a 的值,即可判断.【详解】若12l l ⊥,则()312a a ⎛⎫-⨯-=- ⎪⎝⎭,解得1a =或2a =.故1a =是12l l ⊥的充分不必要条件.故选:B7.(2024高二上·全国·课后作业)直线220x y ++=与420ax y +-=互相垂直,则这两条直线的交点坐标为()A .()1,4-B .()0,2-C .()1,0-D .0,12⎛⎫ ⎪⎝⎭【答案】C【分析】由两直线垂直可得2a =-,联立解方程组可得交点坐标.【详解】易知直线220x y ++=的斜率为2-,由两直线垂直条件得直线420ax y +-=的斜率142a -=,解得2a =-;联立2202420x y x y ++=⎧⎨-+-=⎩,解得10x y =-⎧⎨=⎩;即交点为()1,0-故选:C.8.(2024高二下·四川广元·期中)若直线2mx ny +=过点()2,2A ,其中m ,n 是正实数,则12m n+的最小值是()A .3B .3+C .92D .5【答案】B 【分析】由点A 在直线上可知1m n +=【详解】因为直线2mx ny +=过点(2,2)A ,所以222m n +=,由m 和n 都是正实数,所以1m n +=,0m >,0n >.所以()12122123n m m n m n m n m n⎛⎫+=++=+++≥+ ⎪⎝⎭当2n m m n =时取等号,即1m =,2n =-所以12m n+的最小值是3+故选:B .9.(2024高二上·全国·课后作业)若直线230x y --=与420x y a -+=,则a 的值为()A .4B 6C .4或16-D .8或16-【答案】C【分析】将直线230x y --=化为4260x y --=,再根据两平行直线的距离公式列出方程,求解即可.【详解】将直线230x y --=化为4260x y --=,则直线230x y --=与直线420x y a -+=之间的距离d ==,即|6|10a +=,解得4a =或16a =-,所以a 的值为4a =或16a =-.故选:C10.(2024高二上·全国·课后作业)抛物线214y x =的焦点关于直线10x y --=的对称点的坐标是()A .(2,1)-B .(1,1)-C .11,44⎛⎫- ⎪⎝⎭D .11,1616⎛⎫- ⎪⎝⎭【答案】A【分析】求出抛物线214y x =焦点坐标为(0,1)F ,设(0,1)F 关于直线10x y --=的对称点的坐标是(,)F m n ',列出关于,m n 的方程组求解即可.【详解】抛物线214y x =即24x y =,其焦点坐标为(0,1)F ,设(0,1)F 关于直线10x y --=的对称点的坐标是(,)F m n ',则1110011022n m m n -⎧⨯=-⎪⎪-⎨++⎪--=⎪⎩,解得21m n =⎧⎨=-⎩,则(2,1)F '-,故选:A .11.(2024·四川)设m R ∈,过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于点(,)P x y ,则PA PB +的取值范围是A.B.C.D.【答案】B【详解】试题分析:易得(0,0),(1,3)A B .设(,)P x y ,则消去m 得:2230x y x y +--=,所以点P 在以AB 为直径的圆上,PA PB ⊥,所以222||||10PA PB AB +==,令,PA PB θθ==,则)4PA PB πθθθ+==+.因为0,0PA PB ≥≥,所以02πθ≤≤.所以sin()124πθ≤+≤PA PB ≤+≤选B.法二、因为两直线的斜率互为负倒数,所以PA PB ⊥,点P 的轨迹是以AB 为直径的圆.以下同法一.【考点定位】1、直线与圆;2、三角代换.12.(2024·全国)点(0,﹣1)到直线()1y k x =+距离的最大值为()A .1B CD .2【答案】B【分析】首先根据直线方程判断出直线过定点(1,0)P -,设(0,1)A -,当直线(1)y k x =+与AP 垂直时,点A 到直线(1)y k x =+距离最大,即可求得结果.【详解】由(1)y k x =+可知直线过定点(1,0)P -,设(0,1)A -,当直线(1)y k x =+与AP 垂直时,点A 到直线(1)y k x =+距离最大,即为||AP =故选:B.【点睛】该题考查的是有关解析几何初步的问题,涉及到的知识点有直线过定点问题,利用几何性质是解题的关键,属于基础题.13.(2024·北京东城·二模)已知三条直线1:220l x y -+=,2:20l x -=,3:0+=l x ky 将平面分为六个部分,则满足条件的k 的值共有()A .1个B .2个C .3个D .无数个【答案】C【分析】考虑三条直线交于一点或3l 与1l 或2l 平行时,满足条件,求出答案.【详解】当三条直线交于一点时,可将平面分为六个部分,联立1:220l x y -+=与2:20l x -=,解得22x y =⎧⎨=⎩,则将22x y =⎧⎨=⎩代入3:0+=l x ky 中,220k +=,解得1k =-,当3:0+=l x ky 与1:220l x y -+=平行时,满足要求,此时2k =-,当3:0+=l x ky 与2:20l x -=平行时,满足要求,此时0k =,综上,满足条件的k 的值共有3个.故选:C14.(2024高二上·辽宁沈阳·阶段练习)两直线方程为1:3260l x y --=,22:0x y l --=,则1l 关于2l 对称的直线方程为()A .3240x y --=B .2360x y +-=C .2340x y --=D .3260x y --=【答案】C【分析】根据题意,设所求直线上任一点M (x ,y )且M 关于直线22:0x y l --=的对称点1(M x ',1)y ,利用轴对称的性质列出方程组解出用x 、y 表示1x 、1y 的式子,再由点M '在直线3260x y --=上代入,化简即得所求对称直线方程;【详解】设所求直线上任一点(,)M x y ,M 关于直线20x y --=的对称点1(M x ',1)y ,则111112022y y x x x x y y -⎧=-⎪-⎪⎨++⎪--=⎪⎩,解出112(*)2x y y x =+⎧⎨=-⎩ 点M '在直线3260x y --=上,∴将(*)式代入,得3(2)2(2)60y x +---=,化简得2340x y --=,即为1l 关于2l 对称的直线方程.故选:C15.(2024高一下·海南·期末)设,,a b c 分别是ABC V 中,,A B C ∠∠∠所对边的边长,则直线sin 0A x ay c ⋅++=与sin sin 0bx B y C -⋅+=的位置关系是()A .平行B .重合C .垂直D .相交但不垂直【答案】C【分析】根据直线方程确定斜率,利用三角形边角关系及直线垂直的判定判断两直线的位置关系即可.【详解】由题设,sin 0A x ay c ⋅++=的斜率为sin Aa-,sin sin 0bx B y C -⋅+=的斜率为sin b B ,又sin sin b aB A =,则1sin sin b BA a ⋅=--,即两直线垂直.故选:C16.(2024高三下·江西·开学考试)费马点是指三角形内到三角形三个顶点距离之和最小的点.当三角形三个内角均小于120°时,费马点与三个顶点连线正好三等分费马点所在的周角,即该点所对的三角形三边的张角相等且均为120°.根据以上性质,.则(,)F x y =的最小值为()A .4B.2+C.3+D.4+【答案】B【分析】根据题意作出图形,证明出三角形ABC 为等腰直角三角形,作出辅助线,找到费马点,求出最小值.【详解】由题意得:(,)F x y 的几何意义为点E 到点()(),1,1,0,2A B C 的距离之和的最小值,因为AB =CB =4AC ==,所以222AB CB AC +=,故三角形ABC 为等腰直角三角形,,取AC 的中点D ,连接BD ,与AO 交于点E ,连接CE ,故122BD AC ==,AE CE =,因为3CO AO =,所以30CAO ∠=︒,故120AEC ∠=︒,则120BEC AEB ∠=∠=︒,故点E 到三角形三个顶点距离之和最小,即(,)F x y 取得最小值,因为122AD CD AC ===,所以cos 303AD AE ==︒,同理得:3CE =,3DE =,2BE BD DE =-=-,故(,)F x y 的最小值为22333AE CE BE ++=++-=+故选:B17.(2024·贵州毕节·模拟预测)直线()()1:11l x a y a a R ++=-∈,直线21:2l y x =-,下列说法正确的是()A .R a ∃∈,使得12l l ∥B .R a ∃∈,使得12l l ⊥C .R a ∀∈,1l 与2l 都相交D .R a ∃∈,使得原点到1l 的距离为3【答案】B 【分析】对A ,要使12l l ∥,则12k k ∥,所以1112a -=-+,解之再验证即可判断;对B ,要使12l l ⊥,121k k ×=-,1112a -=-+,解之再验证即可判断;对C ,当1a =时,1l 与2l 重合,即可判断;对D ,根据点到直线距离列方程即可判断.【详解】对A ,要使12l l ∥,则12k k ∥,所以1112a -=-+,解之得1a =,此时1l 与2l 重合,选项A 错误;对B ,要使12l l ⊥,121k k ×=-,11112a ⎛⎫⎛⎫-⋅-=- ⎪ ⎪+⎝⎭⎝⎭,解之得32a =-,所以B 正确;对C ,()1:11l x a y a ++=-过定点()2,1-,该定点在2l 上,但是当1a =时,1l 与2l 重合,所以C 错误;对D ,3d ==,化简得2820170a a -+=,此方程0∆<,a 无实数解,所以D错误.故选:B.18.(2024·全国)如果直线2y ax =+与直线3y x b =-关于直线y x =对称,那么()A .1,63a b ==B .1,63a b ==-C .3,2a b ==-D .3,6a b ==【答案】A【分析】由题意在2y ax =+上任取一点(0,2),其关于直线y x =的对称点在3y x b =-上,代入可求出b ,然后在3y x b =-上任取一点,其关于直线y x =的对称点在2y ax =+上,代入可求出a .【详解】在2y ax =+上取一点(0,2),则由题意可得其关于直线y x =的对称点(2,0)在3y x b =-上,所以06b =-,得6b =,在36y x =-上取一点(0,6)-,则其关于直线y x =的对称点(6,0)-在2y ax =+上,所以062a =-+,得13a =,综上1,63a b ==,故选:A19.(2024高一·全国·课后作业)已知ΔA 的顶点()2,1B ,()6,3C -,其垂心为()3,2H -,则其顶点A 的坐标为A .()19,62--B .()19,62-C .()19,62-D .()19,62【答案】A【分析】由垂心的定义可知AH BC ⊥,BH AC ⊥;根据垂直时斜率乘积为1-可知4AH k =,5AC k =,利用两点连线斜率公式可构造出方程组求得结果.【详解】H 为ΔA 的垂心AH BC ∴⊥,BH AC⊥又311624BC k -==---,211325BH k -==---∴直线,AH AC 斜率存在且4AH k =,5AC k =设(),A x y ,则243356AH AC y k x y k x -⎧==⎪⎪+⎨-⎪==⎪+⎩,解得:1962x y =-⎧⎨=-⎩()19,62A ∴--本题正确选项:A【点睛】本题考查根据直线与直线垂直的位置关系求解参数的问题;关键是能够利用垂心的性质得到直线与直线的垂直关系.20.(2024高三·全国·课后作业)若动点A ,B 分别在直线l 1:x +y -7=0和l 2:x +y -5=0上移动,则AB 的中点M 到原点的距离的最小值为()A .B .C .D .【答案】A【解析】先求出点M 所在直线的方程为l :x +y +m =0,再求出m 的值和原点到直线l 的距离即得解.【详解】依题意知AB 的中点M 的集合为与直线l 1:x +y -7=0和l 2:x +y -5=0距离都相等的直线,则M 到原点的距离的最小值为原点到该直线的距离.设点M 所在直线的方程为l :x +y +m =0,所以|m +7|=|m +5|,所以m =-6,即l :x +y -6=0.根据点到直线的距离公式得M=.故选:A.【点睛】本题主要考查平行线间的距离和点到直线的距离的计算,意在考查学生对这些知识的理解掌握水平.21.(2024高二上·湖北·阶段练习)在等腰直角三角形ABC 中,3AB AC ==,点P 是边AB 上异于A B 、的一点,光线从点P 出发,经BC CA 、反射后又回到点P ,如图,若光线QR 经过ABC V 的重心,则AP =()A .32B .34C .1D .2【答案】C【分析】根据题意,建立坐标系,设点P 的坐标,可得P 关于直线BC 的对称点1P 的坐标,和P 关于y 轴的对称点2P 的坐标,由1P ,Q ,2RP四点共线可得直线的方程,由于过ABC V 的重心,代入可得关于a 的方程,解之可得P 的坐标,进而可得AP 的值,即可得答案.【详解】根据题意,建立如图所示的坐标系,可得(3,0)B ,(0,3)C ,故直线BC 的方程为3x y +=,又由(0,0)A ,(3,0)B ,(0,3)C ,则ABC V 的重心为(1,1),设(,0)P a ,其中0<<3a ,点P 关于直线BC 的对称点1(,)P x y ,则有03220(1)1a x y y x a++⎧+=⎪⎪⎨-⎪⨯-=-⎪-⎩,解得33x y a =⎧⎨=-⎩,即1(3,3)P a -,易得P 关于y 轴的对称点2(,0)P a -,由光的反射原理可知1P ,Q ,R ,2P 四点共成直线QR 的斜率33ak a-=+,故直线QR 的方程为3()3ay x a a-=++,由于直线QR 过ABC V 的重心(1,1),代入化简可得20a a -=,解得:1a =或0(a =舍),即(1,0)P ,故1AP =,故选:C .22.(2024高一上·湖南长沙·开学考试)如下图,一次函数4y x =+的图象与x 轴,y 轴分别交于点A ,B ,点(2,0)C -是x 轴上一点,点E ,F 分别为直线4y x =+和y 轴上的两个动点,当CEF △周长最小时,点E ,F 的坐标分别为()A .53,22E ⎛⎫- ⎪⎝⎭,(0,2)F B .(2,2)E -,(0,2)F C .53,22E ⎛⎫- ⎪⎝⎭,20,3F ⎛⎫ ⎪⎝⎭D .(2,2)E -,20,3F ⎛⎫⎪⎝⎭【答案】C【分析】作C 关于y 轴的对称点G ,作C 关于4y x =+的对称点D ,连接DG 交y 轴于F ,交AB 于E ,有++=++=EC FC EF ED FG EF DG ,即此时CEF △周长最小,求出D 点坐标,可得直线DG 方程,与4y x =+联立求出E 点坐标,令0x =可得F 点坐标.【详解】作(2,0)C -关于y 轴的对称点(2,0)G ,作(2,0)C -关于4y x =+的对称点(,)D a b ,连接DG 交y 轴于F ,交AB 于E ,所以,==FG FC EC ED ,此时CEF △周长最小,即++=++=EC FC EF ED FG EF DG ,由(2,0)C -,直线AB 方程为4y x =+,所以122422ba b a ⎧=-⎪⎪+⎨-⎪=+⎪⎩,解得42a b =-⎧⎨=⎩,所以(4,2)D -,可得直线DG 方程为022042--=---y x ,即1233y x =-+,由41233y x y x =+⎧⎪⎨=-+⎪⎩,解得5232x y ⎧=-⎪⎪⎨⎪=⎪⎩,所以53,22E ⎛⎫- ⎪⎝⎭,令0x =可23y =,所以20,3F ⎛⎫⎪⎝⎭.故选:C.23.(2024高二上·广东深圳·期中)过定点A 的动直线0x ky +=和过定点B 的动直线210kx y k --+=交于点M ,则MA MB +的最大值是()A.B .3CD【答案】C【分析】求出A ,B 的坐标,并判断两直线垂直,推出点M 在以AB为直径的圆上,求得||AB =,即225MA MB +=,结合基本不等式即可求得答案.【详解】由题意知0x ky +=过定点(0,0)A ,动直线210kx y k --+=即(2)10k x y --+=过定点(2,1)B ,对于直线0x ky +=和动直线210kx y k --+=满足1(1)0k k ⨯+⨯-=,故两直线垂直,因此点M 在以AB为直径的圆上,||AB ==则225MA MB +=,所以22222()22()10MA MB MA MB MA MB MA MB +++=+≤=,当且仅当MA MB ==故MA MB +,故选:C24.(2024高二下·陕西西安·期末)设m ∈R ,过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于点(),P x y ,则PA PB ⋅的最大值是()AB C .5D .10【答案】C【分析】先求出两条直线经过的定点,然后根据两条直线的位置关系可判断它们垂直,从而PA PB ⊥,在利用勾股定理和基本不等式求解.【详解】显然0x my +=过定点(0,0)A 30mx y m --+=可化成(1)3y m x =-+,则经过定点()1,3B ,根据两条直线垂直的一般式方程的条件,1(1)0m m ⨯+⨯-=,于是直线0x my +=和直线30mx y m --+=垂直,又P 为两条直线的交点,则PA PB ⊥,又AB =222102PA PB AB PA PB +==≥⋅,则5PA PB ⋅≤,当PA PB ==PA PB ⋅的最大值是5.故选:C25.(河北省张家口市2023-2024学年高二上学期期末数学试题)已知0x y +=,则)AB .CD .【答案】C【分析】设点(,)P x y 为直线0x y +=上的动点,题意可转化成求(,)P x y 与()1,1的距离和(,)P x y 与()2,0的距离之和的最小值,求出1(1)M ,关于直线0x y +=的对称点)1(1M '--,,故PM PN PM PN M N''+=+≥=,即可求出答案【详解】设点(,)P x y 为直线0x y +=上的动点,可看作(,)P x y 与()1,1的距离和(,)P x y 与()2,0的距离之和,设点()()1,12,0M N ,,则点()1,1M '--为点1(1)M ,关于直线0x y +=的对称点,故PM PM '=,且M N ==',所以P M PN =+PM PN M N ''=+≥=,当且仅当,,P M N '三点共线时,取等号,.故选:C26.(2024·贵州·模拟预测)已知,x y +∈R ,满足22x y +=,则x 的最小值为()A .45B .85C .1D 【答案】B【分析】先求出点O 关于线段22x y +=的对称点C C PO P ==.根据几何意义,结合图象,即可得出取最小值时,点P 的位置,进而得出答案.【详解】如图,过点O 作点O 关于线段22x y +=的对称点C ,则PO PC =.设()00,C x y ,则有()0000212222y x x y ⎧⨯-=-⎪⎪⎨⎪⨯+=⎪⎩,解得008545x y ⎧=⎪⎪⎨⎪=⎪⎩,所以84,55C ⎛⎫⎪⎝⎭.设(),P x y,则PO =C PO P ==,又,x y +∈R ,所以点P 到y 轴的距离为x ,所以,x 可视为线段22x y +=上的点(),P x y 到y 轴的距离和到84,55C ⎛⎫⎪⎝⎭的距离之和.过P 作PD x ⊥轴,过点C 作CH x ⊥轴,显然有PD PC CH +≥,当且仅当,,C P H 三点共线时,和有最小值.则CH 即为最小值,CH 与线段AB 的交点1P ,即为最小值时P 的位置.因为85CH =,所以x 的最小值为85.故选:B .27.(2024·上海静安·二模)设直线1:220l x y --=与2l 关于直线:240l x y --=对称,则直线2l 的方程是()A .112220x y +-=B .11220x y ++=C .5110x y +-=D .10220x y +-=【答案】A【分析】根据三条直线交于一点,再利用点关于直线的对称点公式,求直线2l 上一点,即可求解.【详解】联立220240x y x y --=⎧⎨--=⎩,得20x y =⎧⎨=⎩,取直线1:220l x y --=上一点()0,1-,设点()0,1-关于直线:240l x y --=的对称点为(),a b ,则112124022b a a b +⎧=-⎪⎪⎨-⎪⨯--=⎪⎩,解得:1211,55a b ==-,直线2l 的斜率112k =-,所以直线2l 的方程为()1122y x =--,整理为:112220x y +-=.故选:A28.(2024高三·北京·+的最小值所属区间为()A .[10,11]B .(11,12]C .(12,13]D .前三个答案都不对【答案】C【分析】利用代数式的几何意义可求最小值.【详解】如图,设(,0),(0,),(9,2),(3,3)P x Q y A B --.根据题意,设题中代数式为M,则||||||||13M AP PQ QB AB =++≥==,等号当P ,Q 分别为直线AB 与x 轴,y 轴交点时取得.因此所求最小值为13.故选:C.29.(2024·北京)在平面直角坐标系中,记d 为点()cos ,sin P θθ到直线20x my --=的距离,当θ、m 变化时,d 的最大值为A .1B .2C .3D .4【答案】C【分析】P 为单位圆上一点,而直线20x my --=过点()2,0A ,则根据几何意义得d 的最大值为1OA +.【详解】22cos sin 1θθ+=∴Q ,P 为单位圆上一点,而直线20x my --=过点()2,0A ,所以d 的最大值为1213OA +=+=,选C.【点睛】与圆有关的最值问题主要表现在求几何图形的长度、面积的最值,求点到直线的距离的最值,求相关参数的最值等方面.解决此类问题的主要思路是利用圆的几何性质将问题转化.二、多选题30.(2024高二下·江苏南京·期末)已知动点,A B 分别在直线1:3460l x y -+=与2:34100l x y -+=上移动,则线段AB 的中点P 到坐标原点O 的距离可能为()A B .75C D 【答案】CD【分析】根据直线平行可得P 在直线:3480l x y -+=上运动,即可根据点到直线的距离公式即可求解.【详解】解: 动点,A B 分别在直线13460l x y -+=:与234100l x y -+=:上移动,又线段AB 的中点为P ,21//l l ,P ∴在直线:3480l x y -+=上运动,O ∴到直线l 的距离85d ==.P ∴到坐标原点O 的距离大于等于85.故选:CD .31.(24-25高二上·全国·单元测试)已知两条直线1l ,2l 的方程分别为34120x y ++=与8110ax y +-=,下列结论正确的是()A .若12//l l ,则6a =B .若12//l l ,则两条平行直线之间的距离为74C .若12l l ⊥,则323a =D .若6a ≠,则直线1l ,2l 一定相交【答案】AD【分析】根据两直线平行求出a 的值,可判断A 选项;利用平行线间的距离公式可判断B 选项;根据两直线垂直求出a 的值,可判断C 选项;根据两直线相交求出a 的范围,可判断D 选项.【详解】两条直线1l ,2l 的方程分别为34120x y ++=与8110ax y +-=,它们不重合,若12//l l ,则438a =⨯,得6a =,检验符合,故A 选项正确;若12//l l ,由A 选项可知,2l :68110x y +-=,直线1l 的方程可化为68240x y ++=,72=,故B 选项不正确;若12l l ⊥,则3480a +⨯=,得323a =-,故C 选项不正确;由A 选项知,当6a =时,12//l l ,所以若6a ≠,则直线1l ,2l 一定相交,故D 选项正确.故选:AD.32.(24-25高二上·全国·课后作业)已知直线l10y -+=,则下列结论正确的是()A .直线l的一个法向量为)B .若直线m:10x +=,则l m ⊥C.点)到直线l 的距离是2D.过()2与直线l40y --=【答案】CD【分析】对于A :根据直线方向向量与斜率之间的关系分析判断;对于B :根据直线垂直分析判断;对于C :根据点到直线的距离公式运算求解;对于D :根据直线平行分析求解.【详解】对于A ,因为直线l10y -+=的斜率k =11=≠-,可知)不为直线l 的一个法向量,故A 错误;对于B ,因为直线m:10x +=的斜率3k '=,且11kk '=≠-,所以直线l 与直线m 不垂直,故B 对于C,点)到直线l 的距离2d =,故C 正确;对于D ,过()2与直线l平行的直线方程是2y x -=-40y --=,故D 正确.故选:CD.33.(2024高二下·江西南昌·阶段练习)已知曲线e 2xy =和直线:240l x y --=,则()A .曲线上与直线l 平行的切线的切点为e 1,2⎛⎫⎪⎝⎭B .曲线上与直线l 平行的切线的切点为10,2⎛⎫⎪⎝⎭C .曲线上的点到直线l D.曲线上的点到直线l 的最短距离为(3e 5+【答案】BC【分析】根据导数得出切线斜率求切点判断A,B,再结合点到直线距离求出最短距离判断C,D.【详解】设与直线122y x =-平行的直线和e 2xy =相切,则斜率为12k =.因为e 2x y =,所以e 2x y '=,令e 122x k ==,可得切点为10,2⎛⎫ ⎪⎝⎭,故A 错误,B 正确;则点10,2⎛⎫ ⎪⎝⎭到直线240x y --=的距离就是曲线e 2xy =上的点到直线240x y --=的最短距离,C 正确,D 错误.故选:BC.34.(福建省莆田第三中学,励志学校2023-2024学年高二上学期期中联考数学试卷)以下四个命题叙述正确的是()A .直线210x y -+=在x 轴上的截距是1B .直线0x ky +=和2380x y ++=的交点为P ,且P 在直线10x y --=上,则k 的值是12-C .设点(,)M x y 是直线20x y +-=上的动点,O 为原点,则OM 的最小值是2D .直线()12:310:2110L ax y L x a y ++=+++=,,若12//L L ,则3a =-或2【答案】BC【分析】求出直线的横截距判断k 判断B ;求出点到直线的距离判断C ;验证判断D.【详解】对于A ,直线210x y -+=在x 轴上的截距是12-,A 错误;对于B ,由238010x y x y ++=⎧⎨--=⎩解得12x y =-⎧⎨=-⎩,即(1,2)P --,则120k --=,解得12k =-,B 正确;对于C,依题意,min OM =C 正确;对于D ,当2a =时,直线12:2310,:2310L x y L x y ++=++=重合,D 错误.故选:BC三、填空题35.(2024高二·全国·课后作业)已知(),6A a ,()2,B b -,点()2,3P 是线段AB 的中点,则a b +=.【答案】6【分析】利用中点坐标公式可求得,a b ,由此可得结果.【详解】由中点坐标公式知:222a -=,632b +=,解得:6a =,0b =,6a b ∴+=.故答案为:6.36.(2024高二·江苏·假期作业)已知点(),4M x -与点()2,3N 间的距离为x =.【答案】9或5-【分析】根据两点间的距离公式列方程求解即可.【详解】由MN =得MN ==即24450x x --=,解得9x =或5-.故答案为:9或5-.37.(2024高三上·河北廊坊·阶段练习)与直线:2310l x y -+=关于点()4,5对称的直线的方程为.【答案】23130x y -+=【分析】根据直线关于点对称方程的特点可设直线方程,在利用点到两条直线的距离相等即可求解直线方程.【详解】解:直线:2310l x y -+=关于点()4,5对称的直线的方程可设为230x y m -+=,其中1m ≠又()4,5点到直线:2310l x y -+=与到直线230x y m -+=的距离相等76m -=,所以13m =或1m =(舍).故所求直线方程为:23130x y -+=.故答案为:23130x y -+=.38.(2024高一·全国·课后作业)已知直线l 与直线1:1l y =及直线2:70l x y +-=分别交于点P ,Q .若PQ 的中点为点()1,1M -,则直线l 的斜率为.【答案】23-【分析】由点,P Q 关于点M 对称,运算可得解.【详解】解:设(),1P a ,则()2,3Q a --.由点Q 在直线2l 上,得2370a -+-=,2a =-.故()2,1P -.所以直线l 的斜率为()1121k --=--,所以23k =-故答案为23-【点睛】本题考查了点关于点对称问题,属基础题.39.(2024高二上·辽宁大连·阶段练习)设点A 在x 轴上,点B 在y 轴上,AB 的中点是1(2)P -,,则AB 等于【答案】【解析】根据点A 在x 轴上,点B 在y 轴上,且AB 的中点是1(2)P -,,利用中点坐标公式得到A ,B 的坐标,再利用两点间的距离公式求解.【详解】因为点A 在x 轴上,点B 在y 轴上,且AB 的中点是1(2)P -,,所以(40),(02),,-A B ,所以=AB 故答案为:【点睛】本题主要考查两点间的距离公式和中点坐标公式的应用,属于基础题.40.(2024高三上·黑龙江哈尔滨·期中)点()0,1-到直线()2y k x =+的距离的最大值是.【分析】直线()2y k x =+恒过点()2,0A -,根据几何关系可得,点()0,1B -到直线()1y k x =+的距离的最大值为||AB .【详解】因为直线()2y k x =+恒过点()2,0A -,记()0,1B -,直线()2y k x =+为直线l ,则当AB l ⊥时,此时点()0,1B -到直线()1y k x =+的距离最大,∴点()0,1-到直线()1y k x =+距离的最大值为:AB =.41.(2024高二上·江苏南通·期中)已知点A 在x 轴上,点B 在y 轴上,线段AB 的中点M 的坐标为()2,1-,则线段AB 的长度为.【答案】25【分析】利用直角三角形的几何性质得出2AB OM =,利用两点间的距离公式可求得结果.【详解】在平面直角坐标系中,AO BO ⊥,则ABO 为直角三角形,且AB 为斜边,故()22222125AB OM ==+-=.故答案为:542.(2024高二·全国·课堂例题)已知点()2,1A ,()3,4B ,()2,1C --,则ABC V 的面积为.【答案】5【分析】利用两点间距离公式求出一边长,再根据两点式求出该边所在直线的方程,利用点到直线的距离公式求高,进而求得三角形面积.【详解】设AB 边上的高为h ,则h 就是点C 到AB 所在直线的距离.易知()()22324110AB -+-.由两点式可得AB 边所在直线的方程为124132y x --=--,即350x y --=.点()2,1C --到直线350x y --=的距离()()()2232151031h ⨯----==+-所以ABC V 的面积为111010522ABC S AB h =⨯⨯=⨯△.故答案为:543.(2024·云南保山·一模)已知坐标原点为O ,过点()P 2,6作直线()2mx 4m n y 2n 0(m,-++=n 不同时为零)的垂线,垂足为M ,则OM 的取值范围是.【答案】5⎡+⎣【分析】根据题意,将直线变形为()()2420m x y n y ---=,分析可得该直线恒过点()4,2,设()4,2Q ,进而分析可得点M 的轨迹是以PQ 为直径的圆,其方程为()()22345x y -+-=,据此分析可得答案.【详解】根据题意,直线()2420mx m n y n -++=,即()()2420m x y n y ---=,则有2402x y y -=⎧⎨=⎩,解可得42x y =⎧⎨=⎩,则直线l 恒过点()4,2.设()4,2Q ,又由MP 与直线垂直,且M 为垂足,则点M 的轨迹是以PQ 为直径的圆,其方程为()()22345x y -+-=,所以55OM -≤+;即OM 的取值范围是5⎡+⎣;故答案为5⎡+⎣.【点睛】此类问题为“隐形圆问题”,常规的处理办法是找出动点所在的轨迹(通常为圆),常见的“隐形圆”有:(1)如果,A B 为定点,且动点M 满足()1MA MB λλ=≠,则动点M 的轨迹为圆;(2)如果ΔA 中,BC 为定长,A 为定值,则动点A 的轨迹为一段圆弧.特别地,当2A π=,则A 的轨迹为圆(除去,B C );(3)如果,A B 为定点,且动点M 满足22MA MB λ+=(λ为正常数),则动点M 的轨迹为圆;44.(2024高二上·全国·课后作业)已知点(),2P a 、()2,3A --、()1,1B ,且PA PB =,则a =.【答案】92-【分析】利用平面内两点间的距离公式可得出关于a 的等式,解之即可.【详解】已知点(),2P a 、()2,3A --、()1,1B ,且PA PB =,92a =-.故答案为:92-.45.(2024高二上·安徽六安·期中)已知两直线1110a x b y +-=和2210a x b y +-=的交点为(1,2)P ,则过111(,),Q a b 222(,)Q a b 两点的直线方程为.【答案】210x y +-=【分析】根据两直线1110a x b y +-=和2210a x b y +-=的交点列方程,对比后求得直线12Q Q 的方程.【详解】依题意两直线1110a x b y +-=和2210a x b y +-=的交点为(1,2)P ,所以112212210,210,a b a b Q Q +-=+-=,在直线210x y +-=上,所以过111(,),Q a b 222(,)Q a b 两点所在直线方程为210x y +-=.故答案为:210x y +-=46.(2024高三上·上海青浦·阶段练习)在平面直角坐标系xOy 中,若动点(,)P a b 到两直线1:l y x =和2:2l y x =-+,则22a b +的最大值为.【答案】8【分析】由已知可知两直线12l l ⊥,取P 在12,l l 的右侧时,分别过P 作两直线的垂线,结合几何性质确定P 点轨迹,即可求得22a b +的最大值,其他位置同理可得.【详解】若动点(),P a b 到两直线1:l y x =和2:2l y x =-+12,l l 交点为()121,1,,T l l 的斜率分别为1,1-,则12l l ⊥,P 在12,l l 的右侧时,过P 分别向12,l l 引垂线,垂足分别为Q R 、,那么PQ PR +过P 作y 轴的平行线,与12,l l 交点为C B 、如图,则,PQ TR PR RB ==,所以TR RB +其它位置同理,那么点P 轨迹为正方形ABCD ,当P 在()2,2C 时,PO 取得最大值222||a b PO +=取得最大值8.故答案为:8.。
2019年高考数学考纲解读与热点难点突破专题23分类讨论思想、转化与化归思想(热点难点突破)文(含解析)

2.设函数 f(x)=32xx,-x1≥,1x,<1, 则满足 f(f(a))=2f(a)的 a 的取值范围是(
)
A.23,1 B.[0,1] C.23,+∞ Df(a)得 f(a)≥1.
当 a<1 时,有 3a-1≥1,
ln x,x>0,
7.已知函数 f(x)=mx,x<0,
若 f(x)-f(-x)=0 有四个不同的实根,则 m 的取值范围是( )
A.(0,2e) C.(0,1)
B.(0,e)
D.0,1e
8.已知函数 f(x)=x(ex-e-x)-cos x 的定义域为[-3,3],则不等式 f(x2+1)>f(-2)的解集为( ) A.[- 2,-1] B.[- 2, 2] C.[- 2,-1)∪(1, 2] D.(- 2,-1)∪(1, 2) 答案 C 解析 因为 f(-x)=-x(e-x-ex)-cos(-x)=x(ex-e-x)-cos x=f(x),所以函数 f(x)为偶函数,令 g(x) =xex-e1x,易知 g(x)在[0,3]上为增函数,令 h(x)=-cos x,易知 h(x)在[0,3]上为增函数,故函数 f(x)=x(ex-e-x)-cos x 在[0,3]上为增函数,所以 f(x2+1)>f(-2)可变形为 f(x2+1)>f(2),所以 2<x2 +1≤3,解得- 2≤x<-1 或 1<x≤ 2,故不等式 f(x2+1)>f(-2)的解集为[- 2,-1)∪(1, 2]. 9.已知函数 f(x)=ax+b(a>0,a≠1)的定义域和值域都是[-1,0],则 a+b=________.
解得a=12, b=-2,
所以 a+b=-32.
10.设
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
章末复习学习目标 1.梳理本章知识,构建知识网络.2.掌握命题的等价性与充要条件的判定及其有关的应用.3.会解决有一些逻辑联结词与量词的简单的综合性问题.1.四种命题及其关系(1)四种命题(2)四种命题间的逆否关系(3)四种命题的真假关系两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.2.充分条件与必要条件(1)如果p⇒q,那么称p是q的充分条件,q是p的必要条件.(2)分类:①充要条件:p⇒q且q⇒p,记作p⇔q;②充分不必要条件:p⇒q且q⇏p.③必要不充分条件:p⇏q且q⇒p.④既不充分又不必要条件:p⇏q且q⇏p.3.全称命题与特称命题(1)全称命题与特称命题真假的判断方法①判断全称命题为真命题,需严格的逻辑推理证明,判断全称命题为假命题,只需举出一个反例.②判断特称命题为真命题,需要举出正例,而判断特称命题为假命题时,要有严格的逻辑证明.(2)含有一个量词的命题否定的关注点全称命题的否定是特称命题,特称命题的否定是全称命题.否定时既要改写量词,又要否定结论.4.简易逻辑联结词“且、或、非”的真假判断可以概括为口诀:“p与綈p”一真一假,“p或q”一真即真,“p且q”一假就假.1.“所有奇数都是质数”的否定“至少有一个奇数不是质数”是真命题.(√)2.命题“若p,则q”与命题“若綈p,则綈q”的真假性一致.(×)3.已知命题p:存在x∈R,x-2>0,命题q:对于任意x∈R,x2>x,则命题p或(綈q)是假命题.(×)题型一命题及其关系例1(1)有下列命题:①“若x+y>0,则x>0且y>0”的否命题;②“矩形的对角线相等”的否命题;③“若q≤1,则x2+2x+q=0有实根”的逆否命题;④不等边三角形的三个内角相等.其中是真命题的是()A.①②③B.②③④C.①③④D.①③考点四种命题的真假判断题点利用四种命题的关系判断真假答案 D(2)设a,b,c是非零向量,已知命题p:若a·b=0,b·c=0,则a·c=0;命题q:若a∥b,b∥c,则a∥c.则下列命题中真命题是()A.p或q B.p且qC.(綈p)且(綈q) D.p或(綈q)考点“p或q”形式的命题题点判断“p或q”形式命题的真假答案 A解析由向量数量积的几何意义可知,命题p为假命题;命题q中,当b≠0时,a,c一定共线,故命题q是真命题.故p或q为真命题.反思感悟 1.互为逆否命题的两命题真假性相同.2.“p与綈p”一真一假,“p或q”一真即真,“p且q”一假就假.跟踪训练1命题“若x2>1,则x<-1或x>1”的逆否命题是()A.若x2>1,则-1≤x≤1B.若-1≤x≤1,则x2≤1C.若-1<x<1,则x2>1D.若x<-1或x>1,则x2>1考点四种命题题点四种命题概念的理解答案 B解析条件与结论交换位置,并且分别否定.题型二充分条件与必要条件命题角度1充分条件与必要条件的判断例2(1)设x∈R,则“x2-3x>0”是“x>4”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件(2)已知a,b是实数,则“a>0且b>0”是“a+b>0且ab>0”的()A.充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件 考点 四种条件 题点 识别四种条件 答案 (1)B (2)C解析 (1)∵x 2-3x >0⇏x >4, x >4⇒x 2-3x >0,故x 2-3x >0是x >4的必要不充分条件. (2)∵a >0且b >0⇔a +b >0且ab >0,∴a >0且b >0是a +b >0且ab >0的充要条件. 反思感悟 条件的充要关系的常用判断方法 (1)定义法:直接判断若p 则q ,若q 则p 的真假.(2)等价法:利用A ⇒B 与綈B ⇒綈A ,B ⇒A 与綈A ⇒綈B ,A ⇔B 与綈B ⇔綈A 的等价关系,对于条件或结论是否定式的命题,一般运用等价法.(3)利用集合间的包含关系判断:若A ⊆B ,则A 是B 的充分条件或B 是A 的必要条件;若A =B ,则A 是B 的充要条件.跟踪训练2 使a >b >0成立的一个充分不必要条件是( ) A .a 2>b 2>0 B .12log a >12log b >0C .ln a >ln b >0D .x a >x b 且x >0.5考点 四种条件 题点 识别四种条件 答案 C解析 设条件p 符合条件,则p 是a >b >0的充分条件,但不是a >b >0的必然结果,即有“p ⇒a >b >0,a >b >0⇏p ”.A 选项中,a 2>b 2>0⇏a >b >0,有可能是a <b <0,故A 不符合条件;B 选项中,12log a >12log b >0⇔0<a <b <1⇏a >b >0,故B 不符合条件;C 选项中,ln a >ln b >0⇔a >b >1⇒a >b >0,而a >b >0⇏a >b >1,符合条件;D 选项中,x a >x b 且0<x <1时a <b ;x >1时a >b ,无法得到a ,b 与0的大小关系,故D 不符合条件.命题角度2 充分条件与必要条件的应用例3 设命题p :实数x 满足x 2-4ax +3a 2<0,其中a >0,命题q :实数x 满足⎩⎪⎨⎪⎧x 2-x -6≤0,x 2+2x -8>0.(1)若a =1,且p 且q 为真,求实数x 的取值范围; (2)若綈p 是綈q 的充分不必要条件,求实数a 的取值范围. 考点 充分、必要条件与充要条件的综合应用 题点 由四种条件求参数的范围解 (1)由x 2-4ax +3a 2<0得(x -3a )(x -a )<0. 又a >0,所以a <x <3a ,当a =1时,1<x <3, 即p 为真命题时,实数x 的取值范围是1<x <3.由⎩⎪⎨⎪⎧ x 2-x -6≤0,x 2+2x -8>0,解得⎩⎪⎨⎪⎧-2≤x ≤3,x <-4或x >2.即2<x ≤3.所以q 为真时,实数x 的取值范围是2<x ≤3.若p 且q 为真,则⎩⎨⎧1<x <3,2<x ≤3⇔2<x <3,所以实数x 的取值范围是(2,3).(2)方法一 綈p 是綈q 的充分不必要条件, 即綈p ⇒綈q 且綈q ⇏綈p .设綈p :A ={x |x ≤a 或x ≥3a },綈q :B ={x |x ≤2或x >3}, 则A B .所以0<a ≤2且3a >3,即1<a ≤2. 所以实数a 的取值范围是(1,2].方法二 因为綈p 是綈q 的充分不必要条件,所以q 是p 的充分不必要条件, 则{x |2<x ≤3}{x |a <x <3a },所以⎩⎪⎨⎪⎧a ≤2,3a >3,解得1<a ≤2.所以实数a 的取值范围是(1,2].反思感悟 利用条件的充要性求参数的范围(1)解决此类问题一般是把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的关系列出关于参数的不等式求解.(2)注意利用转化的方法理解充分必要条件:若綈p 是綈q 的充分不必要(必要不充分、充要)条件,则p 是q 的必要不充分(充分不必要、充要)条件.跟踪训练3 已知命题:p :2x 2-9x +a <0,q :2<x <3且綈q 是綈p 的必要条件,求实数a 的取值范围.考点 充分、必要条件与充要条件的综合应用 题点 由四种条件求参数的范围 解 ∵綈q 是綈p 的必要条件, ∴q 是p 的充分条件, 令f (x )=2x 2-9x +a ,则⎩⎪⎨⎪⎧f (2)≤0,f (3)≤0,解得a ≤9, ∴实数a 的取值范围是(-∞,9]. 题型三 逻辑联结词与量词的综合应用例4 已知p :任意x ∈⎣⎡⎦⎤14,12,2x <m (x 2+1),q :函数f (x )=4x +2x +1+m -1存在零点,若“p 且q ”为真命题,则实数m 的取值范围是__________. 答案 ⎝⎛⎭⎫45,1解析 由2x <m (x 2+1),可得m >2xx 2+1,又x ∈⎣⎡⎦⎤14,12时,⎝ ⎛⎭⎪⎫2x x 2+1max=45, 故当p 为真时,m >45;函数f (x )=4x +2x +1+m -1=(2x +1)2+m -2, 令f (x )=0,得2x =2-m -1,若f (x )存在零点, 则2-m -1>0,解得m <1,故当q 为真时,m <1.若“p 且q ”为真命题,则实数m 的取值范围是⎝⎛⎭⎫45,1.反思感悟 解决逻辑联结词与量词的综合应用问题首先理解逻辑联结词的含义,掌握简单命题与含有逻辑联结词的命题的真假关系.其次要善于利用等价关系,如:p 真与綈p 假等价,p 假与綈p 真等价,将问题转化,从而谋得最佳解决途径.跟踪训练4 已知命题p :“任意x ∈[0,1],a ≥e x ”,命题q :“存在x ∈R ,x 2+4x +a =0”,若命题“p 且q ”是真命题,则实数a 的取值范围是________. 考点 逻辑联结词与量词的综合应用 题点 由复合命题的真假求参数范围 答案 [e,4]解析 p :a ≥e ,q :a ≤4,∵p 且q 为真命题,∴p 与q 均为真, 则e ≤a ≤4.转化与化归思想的应用典例 已知函数f (x )=x 2,g (x )=⎝⎛⎭⎫12x -m .(1)若对任意x 1∈[-1,3],x 2∈[0,2],使得f (x 1)≥g (x 2)成立,求实数m 的取值范围; (2)若对任意x 2∈[0,2],存在x 1∈[-1,3],使得f (x 1)≥g (x 2)成立,求实数m 的取值范围. 解 (1)由题设知,f (x 1)min ≥g (x 2)max ,∵f (x )在[-1,0]上是减少的,在(0,3]上是增加的,∴f(x1)min=f(0)=0,又∵g(x)在[0,2]上是减少的,∴g(x2)max=g(0)=1-m,∴有0≥1-m,得m≥1,∴m的取值范围为[1,+∞).(2)由题设知,f(x1)max≥g(x2)max,∴有f(3)≥g(0),即9≥1-m,∴m的取值范围是[-8,+∞).[素养评析]从中我们可以看到面对形同质不同的问题,要善于从已有的问题或概念本身出发去加以辨析和研究,将抽象的问题具体化,如此才能更为准确地把握问题的内涵.1.若p是真命题,q是假命题,则()A.p且q是真命题B.p或q是假命题C.綈p是真命题D.綈q是真命题答案 D解析根据“且”“或”“非”命题的真假判定法则知D正确.2.已知命题p:0<a<4,q:函数y=ax2-ax+1的值恒为正,则p是q的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件考点充分、必要条件与充要条件的综合应用题点识别四种条件答案 A解析∵函数y=ax2-ax+1的值恒为正,∴①当a=0时y=1恒成立,②⎩⎪⎨⎪⎧a >0,Δ=a 2-4a <0,∴0<a <4,综上可得q :0≤a <4, 故{a |0<a <4}{a |0≤a <4}.3.已知命题p :对任意x ∈R ,总有2x >0;q :“x >1”是“x >2”的充分不必要条件,则下列命题为真命题的是( ) A .p 且q B .(綈p )且(綈q ) C .(綈p )且q D .p 且(綈q )考点 “p 且q ”形式的命题 题点 判断“p 且q ”形式命题的真假 答案 D解析 根据指数函数的性质可知,对任意x ∈R ,总有2x >0成立,即p 为真命题,“x >1”是“x >2”的必要不充分条件,即q 为假命题,则p 且(綈q )为真命题. 4.对任意x ∈[-1,2],x 2-a ≥0恒成立,则实数a 的取值范围是________. 考点 全称命题题点 由全称命题的真假求参数的范围 答案 (-∞,0]解析 由x 2-a ≥0,得a ≤x 2,故a ≤(x 2)min ,得a ≤0. 5.已知p :x 2+2x -3>0;q :13-x>1.若“(綈q )且p ”为真命题,求x 的取值范围. 考点 “p 且q ”形式的命题题点 已知p 且q 命题的真假求参数范围 解 因为“(綈q )且p ”为真,所以q 假p 真. 而当q 为真命题时,有x -2x -3<0,即2<x <3,所以当q 为假命题时有x ≥3或x ≤2; 当p 为真命题时,由x 2+2x -3>0,解得x >1或x <-3,由⎩⎪⎨⎪⎧x >1或x <-3,x ≥3或x ≤2,解得x <-3或1<x ≤2或x ≥3.所以x 的取值范围为(-∞,-3)∪(1,2]∪[3,+∞)1.否命题和命题的否定是两个不同的概念(1)否命题是将原命题的条件否定作为条件,将原命题的结论否定作为结论构造一个新的命题.(2)命题的否定只是否定命题的结论,常用于反证法.若命题为“若p ,则q ”,则该命题的否命题是“若綈p ,则綈q ”;命题的否定为“若p ,则綈q ”.2.四种命题的三种关系,互否关系,互逆关系,互为逆否关系,只有互为逆否关系的命题是等价命题.3.判断p 与q 之间的关系时,要注意p 与q 之间关系的方向性,充分条件与必要条件方向正好相反,不要混淆.4.注意常见逻辑联结词的否定一些常见逻辑联结词的否定要记住,如:“都是”的否定“不都是”,“全是”的否定“不全是”,“至少有一个”的否定“一个也没有”,“至多有一个”的否定“至少有两个”.。
