长沙市一中专练--函数基本知识过关(二)
长沙市长沙市第一中学必修第一册第二单元《一元一次函数,方程和不等式》测试卷(有答案解析)

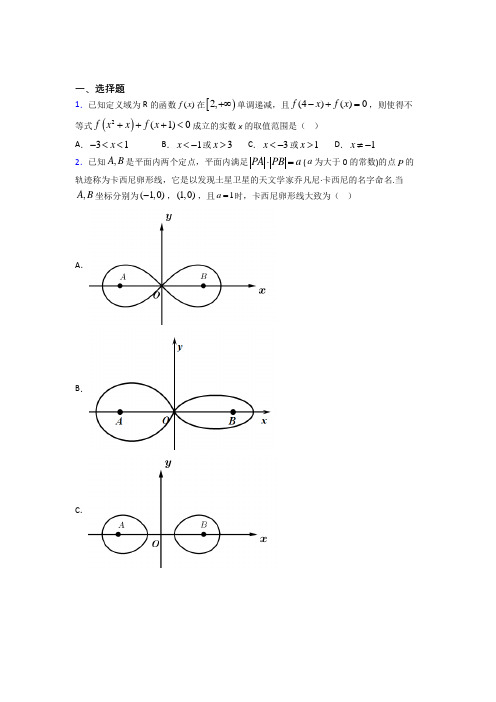
一、选择题1.已知0a >,0b >,2ab =,则42a b +的最小值为( )A .B .4C .D .82.已知正数x ,y 满足2021x y xy +=,则2120x y+的最小值为( ) A .2B .3C .4D .53.某单位计划今明两年购买某物品,现有甲、乙两种不同的购买方案,甲方案:每年购买的数量相等;乙方案:每年购买的金额相等,假设今明两年该物品的价格分别为1p 、2p ()12p p ≠,则这两种方案中平均价格比较低的是( )A .甲B .乙C .甲、乙一样D .无法确定4.若,a b ∈R ,且0ab >,则下列不等式中恒成立的是( )A .222a b ab +>B .a b +≥C .11a b +>D .2b aa b+≥ 5.已知正实数x ,y ,a 满足2x y axy +=,若2x y +的最小值为3,则实数a 的值为( ) A .1B .3C .6D .96.若正数a ,b 满足21a b +=,则下列说法正确的是( ) A .ab 有最大值12B .224a b +有最小值12C .ab 有最小值18 D .224a b +有最大值147.已知2x >,那么函数42y x x =+-的最小值是( ) A .5B .6C .4D .88.若,a b 为实数,且2a b +=,且33a b +的最小值为( )A .18B .6C .D .9.下列命题中是真命题的是( )A .y =的最小值为2;B .当a >0,b >0时,114a b++; C .若a 2+b 2=2,则a +b 的最大值为2;D .若正数a ,b 满足2,a b +=则11+4+22a b +的最小值为12.10.若不等式220ax bx ++>的解集是1123x x ⎧⎫-<<⎨⎬⎩⎭,则a b -=( )A .4-B .14C .10-D .1011.已知a≥0,b≥0,且a+b=2,则 ( ) A .ab≤ B .ab≥ C .a 2+b 2≥2D .a 2+b 2≤312.已知0x >,0y >,23x y +=,则23x yxy+的最小值为( )A .322-B .221C 21D 21参考答案二、填空题13.有一块直角三角形空地ABC ,2A π∠=,250AB =米,160AC =米,现欲建一矩形停车场ADEF ,点D 、E 、F 分别在边AB 、BC 、CA 上,则停车场面积的最大值为________平方米. 14.当1x >时,11x x +-的最小值为___________. 15.已知实数0a >,0b >2是2a 与2b 的等比中项,则13a b+的最小值是______. 16.设x >0,y >0,x +2y =4,则(4)(2)x y xy++的最小值为_________.17.已知a R ∈且11a>,则关于x 的不等式()2log 570a x x -+>的解集为______. 18.已知函数121()22x x f x +-+=+,如果对任意t ∈R ,f (3t 2+2t )+f (k 2﹣2t 2)<0恒成立,则满足条件的k 的取值范围是_____.19.若ad bc ≠,则()()2222a b cd ++__________()2ac bd +.(选“≥”、“≤”、“>”、“<”其一填入)20.已知a ,b 均为正实数,且1a b +=,则231a ab+的最小值为__________,此时a 的值为__________.三、解答题21.设函数2()(1)()f x x m x m m R =-++∈. (1)求不等式()0f x <的解集;(2)若当[0,4]x ∈时,不等式()40f x +>恒成立,求m 的取值范围.22.已知0,0x y >>,且440x y +=. (1)求xy 的最大值;(2)求11x y+的最小值.23.已知函数2()(,)f x x bx c b c =++∈R ,且()0f x ≤的解集为[1,2]-. (1)求函数()f x 的解析式;(2)设函数()f x 在[,1]x t t ∈+上的最小值为()g t ,求()g t 的表达式.24.已知不等式2320ax x -+>的解集为{1,x x <或}x b >, (1)求实数,a b 的值;(2)解关于x 的不等式2()0cx ac b x ab ++>-()c R ∈.25.已知函数()()()224f x x a x a R =-++∈.(1)解关于x 的不等式()42f x a ≤-;(2)若对任意的[]0,4x ∈,()10f x a ++≥恒成立,求实数a 的取值范围.26.(1)已知01x <<,求函数()(33)f x x x =-的最大值: (2)已知关于x 的不等式210ax bx a +-<的解集为122x x ⎧⎫-<<⎨⎬⎩⎭,求a ,b 的值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】由于0a >,0b >且2ab =,则利用基本不等式可得428a b +=≥=≥,从而可得答案【详解】因为0a >,0b >且2ab =,所以428a b +=≥==≥,当且仅当2a b =时,即1a =,2b =时取等号. 故选:D. 【点睛】关键点点睛:该题考查的是有关利用基本不等式求最值的问题,正确解题的关键是要明确等号成立的条件.2.C解析:C 【分析】 由已知得20211y x +=,再202121202120x y x y y x ⎛⎫⎛⎫+=++ ⎪ ⎪⎝⎭⎝⎭,运用基本不等式可得选项. 【详解】由2021x y xy +=得20211y x+=,2021202122224212021202120x y x y x y y x y x ⎛⎫⎛⎫+=++=++≥+=+= ⎪ ⎪⎝⎭⎝⎭, 当且仅当20212120x y y x=且20211y x +=,即42,40x y ==.时,等号成立. 故选:C. 【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件: (1)“一正二定三相等”“一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.3.B解析:B 【分析】分别计算出两种方案的平均价格,然后利用作差法可得出结论. 【详解】对于甲方案,设每年购买的数量为x ,则两年的购买的总金额为12p x p x +, 平均价格为121222p x p x p p x ++=; 对于乙方案,设每年购买的总金额为y ,则总数量为12y yp p +, 平均价格为12121222p p yyy p p p p =++.因为()()()()221212121212121212420222p p p p p p p p p p p p p p p p +--+-==>+++,所以,12121222p p p p p p +>+. 因此,乙方案的平均价格较低. 故选:B. 【点睛】方法点睛:比较法是不等式性质证明的理论依据,是不等式证明的主要方法之一,作差法的主要步骤为:作差——变形——判断正负.在所给不等式是积、商、幂的形式时,可考虑比商4.D解析:D 【分析】利用基本不等式的性质来逐一判断正误即可. 【详解】对于A ,222a b ab +≥,当且仅当a b =时,等号成立,故A 错误;对于B 、C ,虽然0ab >,只能说明,a b 同号,若,a b 都小于0时,则不等式不成立,故B ,C 错误;对于D ,0ab >,,0b a a b∴>,2b aa b ∴+≥,当且仅当a b =时,等号成立,故D 正确; 故选:D. 【点睛】易错点睛:本题考查基本不等式的相关性质,利用基本不等式求最值时,要注意其必须满足的三个条件:一正、二定、三相等,考查学生的逻辑推理能力,属于基础题.5.B解析:B 【分析】利用“乘1法”与基本不等式的性质即可得出. 【详解】因为正实数x ,y ,a 满足2x y axy +=, 所以21a y x+=,所以121122192(2)()(5)(5,x y x y x y a y x a y x a a+=⨯++=++≥+= 当且仅当22x y y x =且21a y x+=时取等号,由题意可得93a=, 解得3a =,故选:B 【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件: (1)“一正二定三相等”“一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.6.B解析:B 【分析】利用基本不等式分析22,4ab a b +的最值,注意取等条件的分析,由此得到结果. 【详解】因为21a b +=,所以12a b =+≥18ab ≤,取等号时11,24a b ==, 所以ab 有最大值18,所以A ,C 错误; 又因为()22211241414824a b ab b a ab =+-=-≥-⨯=+,取等号时11,24a b ==, 所以224a b +有最小值12,所以B 正确,D 错误, 故选:B. 【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件: (1)“一正二定三相等”“一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.7.B解析:B 【分析】根据基本不等式可求得最小值. 【详解】∵2x >,∴442+24+2622y x x x x =+=+-≥==--,当且仅当422x x =--,即4x =时等号成立.∴y 的最小值是6. 故选:B . 【点睛】本题考查用基本不等式求最值,利用基本不等式求最值时,要注意其必须满足的三个条件:(1)“一正二定三相等”“一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.8.B解析:B 【分析】根据基本不等式可知33a b +≥,结合条件求解出33a b +的最小值. 【详解】因为233236a b a b ++≥=⋅=,取等号时1a b ==,所以33a b +的最小值为6, 故选:B. 【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件: (1)“一正二定三相等”“一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.9.B解析:BCD 【分析】利用基本不等式分别判断A 、B 、D 选项,C 选项可设,a b αα==,利用三角函数的值域求范围. 【详解】A 选项,222x +≥0>,∴2y =≥==,即221x +=±时成立,又222x ≥+,故A 错;B 选项,当a >0,b >0时,1124a b +++≥⨯=,当且仅当1a b =⎧=,即1a b ==时等号成立,B 正确;C选项,设,a b αα==,则2sin 24a b πααα⎛⎫+==+≤ ⎪⎝⎭,C 正确;D 选项,2a b +=,()212192a b ⎡⎤⎛⎫∴+++= ⎪⎢⎥⎝⎭⎣⎦, 则()121252229291111++4+22442+2242a b a b a b a b a b ⎛⎫+ ⎪⎡⎤+⎛⎫⎛⎫+++=⨯++ ⎪ ⎪ ⎪⎢⎥++⎝⎭⎝=+⎣+⎭⎦ ⎪⎝⎭251942⎛ ≥⨯+= ⎝⎭,当且仅当122422a b a b ++=++且2a b +=时等号成立,解得1a b ==,故D 正确. 故选:BCD 【点睛】本题考查基本不等式的应用、利用三角函数的值域求范围,注意取等号的条件,属于中档题.10.C解析:C 【分析】由题意可知方程220ax bx ++=的根为11,23-,结合根与系数的关系得出12,2a b =-=-,从而得出-a b 的值.【详解】由题意可知方程220ax bx ++=的根为11,23- 由根与系数的关系可知,11112,2323b a a-+=--⨯=解得12,2a b =-=-即12210a b -=-+=-故选:C 【点睛】本题主要考查了根据一元二次不等式的解集求参数的值,属于中档题.11.C解析:C 【解析】 选C.由≥得ab≤=1,当且仅当a=b=1时,等号成立.又a 2+b 2≥2ab ⇒2(a 2+b 2)≥(a+b)2⇒a 2+b 2≥2,当且仅当a=b=1时,等号成立.12.B解析:B 【分析】把要求的式子变形为21x y y x++,再利用基本不等式求得它的最小值. 【详解】已知0x >,0y >,23x y +=,则22223(2)222121221x y x x y y x xy y x y x yxy xy xy y x y x+++++===+++=, 当且仅当222x y = 时,即当323x =-,且632y -,等号成立, 故23x y xy+的最小值为122+故选:B . 【点睛】本题考查基本不等式的运用,考查常数代换法,注意最值取得的条件,考查运算能力,属于中档题.二、填空题13.【分析】设米米根据可得出利用基本不等式可求得的最大值即为所求【详解】设米米则即整理可得由基本不等式可得当且仅当时即当时等号成立因此停车场面积的最大值为平方米故答案为:【点睛】易错点睛:利用基本不等式 解析:10000【分析】设AD x =米,AF y =米,根据tan DE CF ACABC BD EF AB∠===可得出16254000x y +=,利用基本不等式可求得xy 的最大值,即为所求.【详解】设AD x =米,AF y =米,则250BD AB AD x =-=-,160CF AC AF y =-=-,tan DE CF AC ABC BD EF AB ∠===,即160160250250y y x x -==-,整理可得16254000x y +=, 由基本不等式可得400016252162540x y x y xy =+≥⨯=,10000xy ∴≤,当且仅当162516254000x y x y =⎧⎨+=⎩时,即当12580x y =⎧⎨=⎩时,等号成立.因此,停车场面积的最大值为10000平方米. 故答案为:10000. 【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件: (1)“一正二定三相等”“一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.14.【分析】化简得到结合基本不等式即可求解【详解】由可得则当且仅当时即等号成立所以的最小值为故答案为:【点睛】利用基本不等式求最值时要注意其满足的三个条件:一正二定三相等:(1)一正:就是各项必须为正数 解析:3【分析】 化简得到111111x x x x +=-++--,结合基本不等式,即可求解. 【详解】由1x >,可得10x ->,则11111(1)13111x x x x x x +=-++≥-⋅=---, 当且仅当111x x -=-时,即2x =等号成立, 所以11x x +-的最小值为3. 故答案为:3.【点睛】利用基本不等式求最值时,要注意其满足的三个条件:“一正、二定、三相等”: (1)“一正”:就是各项必须为正数;(2)“二定”:就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”:利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.15.【分析】由是与的等比中项求得化简结合基本不等式即可求解【详解】由题意实数是与的等比中项可得得所以当且仅当时即时等号成立所以的最小值是故答案为:【点睛】本题主要考查了利用基本不等式求最值以及等比中项公解析:4+【分析】2a 与2b 的等比中项,求得1a b +=,化简13133()()4b a a b a b a b a b+=++=++,结合基本不等式,即可求解. 【详解】由题意,实数0a >,0b >2a 与2b 的等比中项,可得2222a b a b +=⨯=,得1a b +=,所以13133()()44b a a b a b a b a b +=++=++≥+=当且仅当3b a a b =时,即1322a b ==,时,等号成立,所以13a b+的最小值是4+.故答案为:4+【点睛】本题主要考查了利用基本不等式求最值,以及等比中项公式的应用,其中解答中熟记等比中项公式,合理利用“1”的代换,结合基本不等式求解是解答的关键,着重考查推理与运算能力,属于中档题.16.9【分析】将分式展开利用基本不等式求解即可【详解】又x +2y =4即当且仅当等号成立故原式故填9【点睛】本题考查基本不等式求最值考查等价变换思想与求解能力注意等号成立条件解析:9【分析】将分式展开,利用基本不等式求解即可【详解】(4)(2)82416161x y xy x y xy xy xy xy xy++++++===+又x +2y =4≥即2xy ≤,当且仅当2,1x y ==等号成立,故原式9≥ 故填9【点睛】本题考查基本不等式求最值,考查等价变换思想与求解能力,注意等号成立条件 17.【分析】先由且得到利用对数函数的单调性将不等式转化为求解【详解】因为且所以在上递减因为不等式所以即解得所以不等式的解集是故答案为:【点睛】本题主要考查对数不等式的解法和一元二次不等式的解法还考查了运 解析:()2,3【分析】先由a R ∈且11a >,得到01a <<,利用对数函数的单调性,将不等式()2log 570a x x -+> ,转化为22570571x x x x ⎧-+>⎨-+<⎩求解. 【详解】因为a R ∈且11a>, 所以01a <<,log a y x =在 ()0,∞+上递减,因为不等式()2log 570log 1a a x x -+>= , 所以22570571x x x x ⎧-+>⎨-+<⎩,即 22570560x x x x ⎧-+>⎨-+<⎩, 解得 23x <<,所以不等式的解集是()2,3,故答案为:()2,3【点睛】本题主要考查对数不等式的解法和一元二次不等式的解法,还考查了运算求解的能力,属于中档题.18.k<-1或k>1【分析】利用定义先求出函数为单调减函数与奇函数然后化简得到然后利用不等式得恒成立条件求出答案【详解】对于函数定义域为且所以为奇函数且对求导可得则在时为减函数可得利用为奇函数化简得利用 解析:k <-1或k >1.【分析】利用定义,先求出函数()f x 为单调减函数与奇函数,然后化简()()2223220f t t f k t ++-<得到222t t k --<,然后利用不等式得恒成立条件求出答案【详解】对于函数()f x ,定义域为R ,且()12122x x f x ---+-=+1122222xx x x +-+=+()12122x x f x +-==-+,所以,()f x 为奇函数,且对()f x 求导可得()'0f x <,则()f x 在x ∈R 时为减函数, ()()2223220f t t f k t ++-<,可得()()222322f t t f k t +<--,利用()f x 为奇函数 化简得()()222322f t t f t k +-<,利用()f x 在x ∈R 时为减函数,得222322t t t k +->,化简得222t t k --<恒成立,令()22g t t t =--,则有()2max g t k <,而()()max 11g t g =-=,所以21k <,得到1k >或1k <-答案:1k >或1k <-【点睛】本题考查函数的单调性、奇偶性以及不等式的恒成立问题,属于中档题19.>【分析】作差分析差的正负即可求解【详解】因为又所以所以故答案为:>【点睛】本题主要考查了比较法判断两个式子的大小考查了运算能力属于中档题解析:>【分析】作差,分析差的正负即可求解.【详解】因为()()()22222a b c d ac bd ++-+ ()()2222222222222a c a d b c b d a c b d acbd +=+++-+22222b c a d abcd =+- 20(bc ad )=-≥,又ad bc ≠所以2()0bc ad ->所以()()22222()a b c d ac bd ++>+, 故答案为:>【点睛】本题主要考查了比较法判断两个式子的大小,考查了运算能力,属于中档题.20.6【分析】首先由条件变形为化简后利用基本不等式求最小值【详解】所以当时等号成立即解得:所以即的最小值为6此时故答案为:6;【点睛】本题考查基本不等式求最值重点考查转化思想计算能力属于基础题型本题的关 解析:613【分析】 首先由条件变形为()222331a a b a ab ab+++=,化简后利用基本不等式求最小值. 【详解】 1a b +=,()21a b ∴+= 所以()222223314242a a b a a b ab a b ab ab ab b a +++++===++,44a b b a +≥=, 当4a b b a =时,等号成立,即120,0a b b a a b +=⎧⎪=⎨⎪>>⎩,解得:12,33a b ==, 所以231426a ab+≥+=, 即231a ab+的最小值为6,此时13a =. 故答案为:6;13【点睛】本题考查基本不等式求最值,重点考查转化思想,计算能力,属于基础题型,本题的关键是利用()21a b =+变形,化简. 三、解答题21.无22.无23.无24.无25.无26.无。
函数的基本性质练习题目(精华)

高一数学------函数的基本性质一、、知识点:本 章 知 识 结 构1、集合的概念集合是集合论中的不定义的原始概念,教材中对集合的概念进行了描述性说明:“一般地,把一些能够确定的不同的对象看成一个整体,就说这个整体是由这些对象的全体构成的集合(或集)”。
理解这句话,应该把握4个关键词:对象、确定的、不同的、整体。
对象――即集合中的元素。
集合是由它的元素唯一确定的。
整体――集合不是研究某一单一对象的,它关注的是这些对象的全体。
确定的――集合元素的确定性――元素与集合的“从属”关系。
不同的――集合元素的互异性。
2、有限集、无限集、空集的意义有限集和无限集是针对非空集合来说的。
我们理解起来并不困难。
我们把不含有任何元素的集合叫做空集,记做Φ。
理解它时不妨思考一下“0与Φ”及“Φ(空集)与{Φ}(集合中含有一个元素,即空集)”的关系。
几个常用数集N (自然数集)、N*(正整数集)、N +(正整数集)、Z (整数集)、Q (有理数集)、R (实数集) 3、集合的表示方法(1)列举法的表示形式比较容易掌握,并不是所有的集合都能用列举法表示,同学们需要知道能用列举法表示的三种集合:①元素不太多的有限集,如{0,1,8}②元素较多但呈现一定的规律的有限集,如{1,2,3,…,100} ③呈现一定规律的无限集,如 {1,2,3,…,n ,…} ●注意a 与{a}的区别:a 表示一个元素,{a}表示一个集合 ●注意用列举法表示集合时,集合元素的“无序性”。
(2)特征性质描述法的关键是把所研究的集合的“特征性质”找准,然后适当地表示出来就行了。
但关键点也是难点。
学习时多加练习就可以了。
另外,弄清“代表元素”也是非常重要的。
如{x|y =x 2}, {y|y =x 2}, {(x ,y )|y =x 2}是三个不同的集合。
4、集合之间的关系●注意区分“从属”关系与“包含”关系 “从属”关系是元素与集合之间的关系。
长沙市长沙市第一中学必修一第二单元《函数》测试卷(有答案解析)

一、选择题1.已知函数22()2(2)f x x a x a =-++,23()2(2)8g x x a x a =-+--+.设()(){1max ,H x f x =}()g x .()()(){}2min ,H x f x g x =(其中{}max ,p q 表示p ,q中较大值,{}min ,p q 表示p ,q 中较小值),记()1H x 的最小值为A ,()2H x 的最大值为B ,则A B -=( ) A .16-B .16C .8aD .816a -2.已知函数()y f x =是定义在R 上的单调函数,()0,2A ,()2,2B -是其函数图像上的两点,则不等式()12f x ->的解集为( ) A .()1,3 B .()(),31,-∞-⋃+∞ C .()1,1-D .()(),13,-∞+∞3.对于每个实数x ,设()f x 取24y x =-+,41y x =+,2y x =+三个函数值中的最小值,则()f x ( ) A .无最大值,无最小值 B .有最大值83,最小值1 C .有最大值3,无最小值D .有最大值83,无最小值 4.已知函数f (x )的定义域为R ,满足f (x )=2f (x +2),且当x ∈[2-,0) 时,19()4f x x x =++,若对任意的m ∈[m ,+∞),都有1()3f x ≤,则m 的取值范围为( ) A .11,5⎡⎫-+∞⎪⎢⎣⎭ B .10,3⎡⎫-+∞⎪⎢⎣⎭C .)5,2⎡-+∞⎢⎣ D .11,4⎡⎫-+∞⎪⎢⎣⎭5.已知,a t 为正实数,函数()22f x x x a =-+,且对任意[]0,x t ∈,都有()f x a ≤成立.若对每一个正实数a ,记t 的最大值为()g a ,若函数()g a 的值域记为B ,则下列关系正确的是( ) A .2B ∈B .12B ∉C .3B ∈D .13B ∉6.高斯函数属于初等函数,以大数学家约翰·卡尔·弗里德里希·高斯的名字命名,其图形在形状上像一个倒悬着的钟,高斯函数应用范围很广,在自然科学、社会科学、数学以及工程学等领域都能看到它的身影,设x ∈R ,用[]x 表示不超过x 的最大整数,则[]y x =称为高斯函数,例如:[]3.14-=-,[]4.84=.则函数21()122x xf x ⎡⎤=-⎢⎥+⎣⎦的值域为( ) A .{}0,1B .{}1,1-C .{}1,0-D .{}1,0,1-7.已知函数()3221x f x x =-+,且()()20f a f b ++<,则( ) A .0a b +<B .0a b +>C .10a b -+>D .20a b ++<8.已知的2()(1)()f x x x x ax b =+++图象关于直线1x =对称,则()f x 的值域为( ) A .[]4,-+∞B .9,4⎡⎫-+∞⎪⎢⎣⎭C .9,44⎡⎤-⎢⎥⎣⎦D .[]0,49.设二次函数2()()f x x bx b =+∈R ,若函数()f x 与函数(())f f x 有相同的最小值,则实数b 的取值范围是( ) A .(,2]-∞B .(,0]-∞C .(,0][2,)-∞+∞D .[2,)+∞10.对x R ∀∈,用()M x 表示()f x ,()g x 中较大者,记为()()()max{,}M x f x g x =,若()()2{3,1}M x x x =-+-,则()M x 的最小值为( )A .-1B .0C .1D .411.已知函数的定义域为R ,且对任意的12,x x ,且12x x ≠都有()()()12120f x f x x x -->⎡⎤⎣⎦成立,若()()2211f x f m m +>--对x ∈R 恒成立,则实数m 的取值范围是( ) A .(1,2)- B .[1,2]-C .(,1)(2,)-∞-+∞D .(,1][2,)-∞-+∞12.已知函数()113sin 22f x x x ⎛⎫=+-+ ⎪⎝⎭,则122018201920192019f f f ⎛⎫⎛⎫⎛⎫++⋅⋅⋅+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭( ) A .2018 B .2019 C .4036D .4038二、填空题13.定义在R 上的减函数()f x 满足(0)4f =,且对任意实数x 都有()(2)4f x f x +-=,则不等式|()2|2f x -<的解集为____________.14.若函数()y f x =的定义域是[0,2],则函数()g x =______. 15.已知1()1x f x x +=-,则135199()()()()100100100100f f f f ++++=______________16.已知定义在 +R 上的函数 ()f x 同时满足下列三个条件:① ()31f =-;②对任意x y +∈R , 都有 ()()()f xy f x f y =+;③ 1x > 时 ()0f x <,则不等式()()612f x f x <-- 的解集为___________.17.如图,是某个函数的图象,则该函数的解析式y =__________;18.若函数()f x 满足()()1f x f x =-,()()13f x f x +=--当且仅当(]1,3x ∈时,()3log f x x =,则()57f =______.19.已知函数()2(1)mf x m m x =--是幂函数,且()f x 在(0,)+∞上单调递增,则实数m =________.20.函数()()122x x f x x N +⎡⎤⎡⎤=-∈⎢⎥⎢⎥⎣⎦⎣⎦的值域为_______(其中[]x 表示不大于x 的最大整数)三、解答题21.已知函数()1f x x x=+. (1)请判断函数()f x 在()0,1和()1,+∞内的单调性,并用定义证明在()0,1的单调性.(2)当11,42x ⎡⎤∈⎢⎥⎣⎦时,210x ax -+≥恒成立,求实数a 的取值范围. 22.已知二次函数()2f x ax bx c =++.(1)若集合(){}{}|12A x f x x ===,,且()02f =. ①求函数()f x 的解析式; ②画出函数()y f x =的图象,并讨论函数y a =和函数()y f x =的图象的公共点个数;(2)若a =1,c =0,求函数()f x 在区间[]22-,上的最小值. 23.已知函数()x af x x+=(a 为常数),其中()0f x <的解集为()4,0-. (1)求实数a 的值;(2)设()()g x x f x =+,当()0x x >为何值时,()g x 取得最小值,并求出其最小值. 24.已知函数()y f x =的定义域为D ,如果存在区间[],a b D ⊆,使得[]{}[]|(),,,=∈=y y f x x a b a b ,则称区间,a b 为函数()y f x =的一个和谐区间.(1)直接写出函数3()f x x =的所有和谐区间; (2)若区间[]0,m 是函数3()22=-f x x 的一个和谐区间,求实数m 的值; (3)若函数2()2()=-+∈f x x x m m R 存在和谐区间,求实数m 的取值范围. 25.已知二次函数2()1(0)f x ax x a =++>. (1)求函数()f x 在区间[4,2]--的最大值()M a ; (2)若关于x 的方程()0f x =有两个实根1x 、2x ,且121,1010x x ⎡⎤∈⎢⎥⎣⎦,求实数a 的最大值.26.已知函数2()2(1)4f x x k x =+-+.(Ⅰ)若函数()f x 在区间[2,4]上具有单调性,求实数k 的取值范围; (Ⅱ)若()0f x >对任意的[1,2]x ∈恒成立,求实数k 的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【分析】根据()()22()244,()2412f x x a a g x x a a =----=-+-+,由()(){1max ,H x f x =}()g x .()()(){}2min ,H x f x g x =,得到max ()412B g x a ==-+,min ()44A f x a ==--求解.【详解】因为函数22()2(2)f x x a x a =-++,23()2(2)8g x x a x a =-+--+, 所以()()22()244,()2412f x x a a g x x a a =----=-+-+, 如图所示:当2x a =+时,()()44f x g x a ==--, 当2=-x a 时,()()412f x g x a ==-+, 因为max ()412g x a =-+,所以()()2max ()412H x g x g x a ≤≤=-+, 因为min ()44f x a =--,所以()()1min ()44H x f x f x a ≥≥=--, 所以44,412A a B a =--=-+, 所以16A B -=-, 故选:A 【点睛】方法点睛:(1)识别二次函数的图象主要从开口方向、对称轴、特殊点对应的函数值这几个方面入手.(2)用数形结合法解决与二次函数图象有关的问题时,要尽量规范作图,尤其是图象的开口方向、顶点、对称轴及与两坐标的交点要标清楚,这样在解题时才不易出错.2.D解析:D 【分析】根据题意可得出(0)2,(2)2f f ==-,从而得出()f x 在R 上为减函数,从而根据不等式()12f x ->得,(1)(2)f x f -<或(1)(0)f x f ->,从而得出12x ->或10x -<,解出x 的范围 【详解】解:由题意得(0)2,(2)2f f ==-, 因为函数()y f x =是定义在R 上的单调函数, 所以()f x 在R 上为减函数,由()12f x ->,得(1)2f x ->或(1)2f x -<-, 所以(1)(0)f x f ->或(1)(2)f x f -<, 所以10x -<或12x ->, 解得1x <或3x >,所以不等式()12f x ->的解集为()(),13,-∞+∞,故选:D 【点睛】关键点点睛:此题考查函数单调性的应用,考查绝对值不等式的解法,解题的关键是把()12f x ->转化为(1)(0)f x f ->或(1)(2)f x f -<,再利用()f x 在R 上为减函数,得10x -<或12x ->,考查数学转化思想,属于中档题 3.D解析:D 【分析】作出函数()f x 的图象,结合图象可得出结论. 【详解】由已知可得(){}min 24,41,2f x x x x =-+++,作出函数()f x 的图象如下图所示:函数()f x 的图象如上图中的实线部分,联立224y x y x =+⎧⎨=-+⎩,解得2383x y ⎧=⎪⎪⎨⎪=⎪⎩,由图象可知,函数()f x 有最大值83,无最小值. 故选:D. 【点睛】关键点点睛:本题考查函数最值的求解,解题的关键就是结合函数()f x 的定义,进而作出函数()f x 的图象,利用图象得出结论.4.D解析:D 【分析】求出[2,0)x ∈-时,()f x 的值域,满足1()3f x ≤,根据函数的定义,[0,2)x ∈时,满足1()3f x ≤,同时可得0x ≥时均满足1()3f x ≤,然后求得[4,2)x ∈--时的解析式,解不等式1()3f x ≤得解集,分析后可得m 的范围. 【详解】[2,0)x ∈-时,19()4f x x x =++在[]2,1--上递增,在[1,)-+∞上递减,1(),4f x ⎛⎤∈-∞ ⎥⎝⎦,满足1()3f x ≤,当[0,2)x ∈时,2[2,0)x -∈-,11()(2)[,)28f x f x =-∈-∞,满足满足1()3f x ≤, 按此规律,2x ≥时,()f x 均满足1()3f x ≤, 当[4,2)x ∈--时,29()2(2)2(2)22f x f x x x =+=++++,由2912(2)223x x +++≤+, 解得1043x -≤≤-或1124x -≤<-,当101134x -<<-时,1()3f x >. 因此当114x ≥-时,都有1()3f x ≤, 所以114m ≥-. 故选:D . 【点睛】关键点点睛:本题考查函数不等式恒成立问题,解题关键是依照周期函数的性质,根据函数的定义求出()f x 在[2,22)k k +(k ∈N )满足1()3f x ≤,在[2,0)-上直接判断,求出[4,2)--上的解析式,确定1()3f x ≤的范围,此时有不满足1()3f x ≤的x 出现,于是可得结论m 的范围.5.A解析:A【分析】根据函数的特征,要对t 进行分类讨论,求出t 的最大值,再根据a 是正实数,求出()g a 的值域即可判断答案. 【详解】 解:2()2f x x x a =-+∴函数()f x 的图象开口向上,对称轴为1x =①01t <时,()f x 在[0,]t 上为减函数,()(0)max f x f a ==,2()()2min f x f t t t a ==-+ 对任意的[0x ∈,]t ,都有()[f x a ∈-,]a . 22a t t a ∴-≤-+,即2220t t a -+≥,当()()22424120a a ∆=--⨯=-≤,即12a ≥时,01t <,当()()22424120a a ∆=--⨯=->,即102a <<时,11t ≤ ②1t >时,()f x 在[0,1]上为减函数,在[1,]t 上为增函数,则()()11min f x f a a ==-≥-,2(){(0),()}{,2}max f x max f f t max a t t a a ==-+≤,12a ∴≥,且22t t a a -+,即12t < t 的最大值为()g a综上可得,当12a ≥时(]0,2t ∈ 当102a <<时,()0,1t ∈ ∴函数()g a 的值域为(]0,2故选:A . 【点睛】二次函数、二次方程与二次不等式统称“三个二次”,它们常结合在一起,有关二次函数的问题,数形结合,密切联系图象是探求解题思路的有效方法.一般从:①开口方向;②对称轴位置;③判别式;④端点函数值符号四个方面分析.6.C解析:C 【分析】先求出函数()21122x x f x =-+的值域,再根据题干中要求即可得出()21122x xf x ⎡⎤=-⎢⎥+⎣⎦的值域. 【详解】()21121111=122122212x x x x xf x +-=--=-+++, ()121,x +∈+∞,()10,112x∴∈+, ()11,012x∴-∈-+, 1111,21222x ⎛⎫∴-∈- ⎪+⎝⎭, 即函数()21122x xf x =-+的值域为11,22⎛⎫- ⎪⎝⎭, 由高斯函数定义可知:函数()21122x xf x ⎡⎤=-⎢⎥+⎣⎦的值域为{}1,0- 故选:C. 【点睛】方法点睛:“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种,然后根据此新定义去解决问题,有时还需要用类比的方法去理解新的定义,这样有助于对新定义的透彻理解.但是,透过现象看本质,它们考查的还是基础数学知识,所以说“新题”不一定是“难题”,掌握好三基,以不变应万变才是制胜法宝.7.A解析:A 【分析】求得函数的单调性,构造奇函数利用单调性得解 【详解】由函数单调性性质得:3y x =,21xy =+在R 上单调递增所以()3221x f x x =-+在R 上单调递增, 令函数()()321121x x g x f x x -=+=-+,()()0g x g x +-=则函数()g x 为奇函数,且在R 上单调递增,故()()20f a f b ++<()()g a g b ⇔<-0a b a b ⇔<-⇔+<. 故选:A 【点睛】构造奇函数利用单调性是解题关键.8.B解析:B 【分析】结合函数对称性与解析式可知1,0-是零点,则2,3也是零点,由对应关系求出解析式,利用换元法和二次函数性质即可求解【详解】因为函数()()()21f x x x x ax b =+++有两个零点1-,0,又因为其图象关于直线1x =对称,所以2,3也是函数()f x 的两个零点,即()()()()123f x x x x x =+⋅--,所以()()()22223f x x x x x =---,令()222111t x x x =-=--≥-,则()()223933124y t t t t t t ⎛⎫=-=-=--- ⎭≥⎪⎝,所以94y ≥-,即()f x 的值域为9,4∞⎡⎫-+⎪⎢⎣⎭. 故选:B 【点睛】关键点睛:本题考查函数对称性的应用,换元法的应用,函数值域的求解,解题关键在于:(1)若函数对称轴为x a =,则有()()f a x f a x +=-; (2)换元法求解函数值域必须注意新元取值范围.9.C解析:C 【分析】由于参数b 的不确定性,可进行分类讨论,再结合二次函数对称轴和最值特点求解即可. 【详解】当0b =时,()2f x x =,()[)0,f x ∈+∞,()()[)0,ff x ∈+∞,符合题意;当0b <时,22()24b f b x x ⎛⎫=+ ⎪⎝-⎭,对称轴为02b x =->,画出大致图像,令()t f x =,min 0t <,则()()()f f x f t =,[)min,t t∈+∞,显然能取到相同的最小值,符合;当0b >时,对称轴为b x 02=-<,()2min 24b b f x f ⎛⎫=-=- ⎪⎝⎭,令()t f x =,2,4b t ⎡⎫∈-+∞⎪⎢⎣⎭,要使()f x 与函数()f t 有相同的最小值,则需满足:242b b -≤-,解得[2,)b ∈+∞综上所述,则b ∈(-∞,0]∪[2,+∞)故选:C.【点睛】本题解题关键是对二次函数对称轴进行分类讨论,同时结合最值与对称轴的关系解决问题. 10.C解析:C【分析】根据定义求出()M x 的表达式,然后根据单调性确定最小值.【详解】由23(1)x x -+=-解得:1x =-或2x =, 2(1)3x x -≥-+的解集为1x ≤-或2x ≥,2(1)3x x -<-+的解为12x -<<,∴2(1),12()3,12x x x M x x x ⎧-≤-≥=⎨-+-<<⎩或, ∴2x ≤时,()M x 是减函数,2x >时,()M x 是增函数,∴min ()(2)1M x M ==.故选:C .【点睛】关键点点睛:本题考查新定义函数,解题关键是确定新定义函数的解析式,根据新定义通过求最大值得出新函数的解析式,然后根据分段函数研究新函数的性质.11.A解析:A【分析】由函数的单调性列x 的不等式求解即可.【详解】由()()()12120f x f x x x -->⎡⎤⎣⎦,则函数()f x 在R 上为增函数,由()()2211f x f m m +>--对x ∈R 恒成立,故22min 1(1)m m x --<+,即211m m --<解得12m -<<. 故选:A.【点睛】本题考查函数的单调性,考查恒成立问题,是基础题12.A解析:A【分析】根据函数解析式可验证出()()12f x f x +-=,采用倒序相加法可求得结果.【详解】()11113sin 22f x x x ⎛⎫-=-+-+ ⎪⎝⎭,()()12f x f x ∴+-=, 令122018201920192019S f f f ⎛⎫⎛⎫⎛⎫=++⋅⋅⋅+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 则201712019201922018019S f f f ⎛⎫⎛⎫⎛⎫=++⋅⋅⋅+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 两式相加得:222018S =⨯,2018S ∴=.故选:A .【点睛】本题考查倒序相加法求和的问题,解题关键是能够根据函数解析式确定()()1f x f x +-为常数. 二、填空题13.【分析】由绝对值不等式可知利用中x 的任意性得再利用函数的单调性解不等式即可【详解】因为任意实数都有且令则故不等式解得即又函数为上的减函数解得故不等式的解集为故答案为:【点睛】方法点睛:本题考查了解抽 解析:(0,2)【分析】由绝对值不等式可知0()4f x <<,利用()(2)4f x f x +-=中x 的任意性得(2)0f =,再利用函数的单调性解不等式即可.【详解】因为任意实数x 都有()(2)4f x f x +-=,且(0)4f =,令2x =,则(2)(0)4f f +=,故(2)0f =不等式|()2|22()22f x f x -<⇒-<-<,解得0()4f x <<,即(2)()(0)f f x f << 又函数()f x 为R 上的减函数,解得02x <<,故不等式|()2|2f x -<的解集为(0,2)故答案为:(0,2)【点睛】方法点睛:本题考查了解抽象不等式,要设法把隐性划归为显性的不等式求解,方法是: (1)把不等式转化为[][]()()f g x f h x >的模型;(2)判断函数()f x 的单调性,再根据函数的单调性将不等式的函数符号“f ”脱掉,得到具体的不等式(组)来求解,但要注意奇偶函数的区别.14.【分析】根据抽象函数的定义域的求法结合函数列出不等式组即可求解【详解】由题意函数的定义域是即则函数满足解得即函数的定义域是故答案为:【点睛】求抽象函数定义域的方法:已知函数的定义域为求复合函数的定义 解析:31,2⎛⎤ ⎥⎝⎦【分析】 根据抽象函数的定义域的求法,结合函数()g x =. 【详解】由题意,函数()y f x =的定义域是[0,2],即02x ≤≤, 则函数()g x =021210x x ≤-≤⎧⎨->⎩,解得312x <≤, 即函数()g x =31,2⎛⎤ ⎥⎝⎦. 故答案为:31,2⎛⎤ ⎥⎝⎦. 【点睛】求抽象函数定义域的方法:已知函数()f x 的定义域为[],a b ,求复合函数()[]f g x 的定义域时:可根据不等式()a g x b ≤≤解得x ,则x 的取值范围即为所求定义域;已知复合函数()[]f g x 的定义域为[],a b ,求函数()f x 的定义域,求出函数()y g x =([,])x a b ∈的值域,即为()y f x =的定义域.15.100【分析】分析得出得解【详解】∴故答案为:100【点睛】由函数解析式得到是定值是解题关键解析:100【分析】分析得出(2)()2f x f x -+=得解.【详解】1()1x f x x +=- 211211(2)()2f x f x x x x x -+∴-+=++=--- ∴135199()()()()100100100100f f f f ++++ 1199319799101[()()][()()][()()]100100100100100100f f f f f f =+++++ 250100=⨯=故答案为:100.【点睛】由函数解析式得到(2)()2f x f x -+=是定值是解题关键.16.【分析】用赋值法由已知得到把转化为即再用定义法证明在上为减函数利用单调性可得答案【详解】因为对任意有令得所以令则所以可等价转化为即设当时则所以所以在上为减函数故由得得又所以原不等式的解集为故答案为:解析:()13, 【分析】用赋值法由已知得到()()()9332f f f =+=-,把()()612f x f x <--转化为()()61(9)f x f x f <-+,即()()699f x f x <-,再用定义法证明()f x 在(0,)+∞上为减函数,利用单调性可得答案.【详解】因为对任意12,(0,)x x ∈+∞,有()()()f xy f x f y =+,令x y ==f f f =+,得()231f f ==-,所以12f =-, 令3x y ==,则()()()9332f f f =+=-,所以()()612f x f x <--可等价转化为()()61(9)f x f x f <-+,即()()699f x f x <-, 设120x x <<,12,(0,)x x ∈+∞,当1x > 时 ()0f x <,则()()()22211111·x x f x f x f f x f x x x ⎛⎫⎛⎫==+< ⎪ ⎪⎝⎭⎝⎭, 所以()12()f x f x >,所以()f x 在(0,)+∞上为减函数,故由()()699f x f x <-, 得699x x >-,得3x <,又1x >,所以原不等式的解集为(1,3).故答案为:(1,3)【点睛】思路点睛:确定抽象函数单调性解函数不等式的基本思路:第一步(定性)确定函数在给定区间上的单调性和奇偶性;第二步(转化)将函数不等式转化为不等式类似()()f M f N <等形式;第三步(去)运用函数的单调性“去掉”函数的抽象符号f “”,转化成一般的不等式或不等式组;第四步(求解)解不等式或不等式组确定解集.17.【分析】根据分段函数图象用待定系数法求解即可【详解】当时设函数为当时解得;当时设函数为当时时解得所以故答案为:【点睛】本题考查利用函数图象求解析式考查待定系数法是基础题 解析:2,0139,1322x x y x x ≤<⎧⎪=⎨-+≤≤⎪⎩ 【分析】根据分段函数图象,用待定系数法求解即可.【详解】当01x ≤<时,设函数为y kx =,当1x =时2y =,解得2k =;当13x ≤≤时,设函数为y ax b =+,当1x =时3y =,3x =时0y =,解得32a =-,92b =. 所以2,0139,1322x x y x x ≤<⎧⎪=⎨-+≤≤⎪⎩. 故答案为:2,0139,1322x x y x x ≤<⎧⎪=⎨-+≤≤⎪⎩ 【点睛】本题考查利用函数图象求解析式,考查待定系数法,是基础题.18.2【分析】根据函数满足的关系可得是以6最小正周期的周期函数根据代入解析式即可【详解】根据已知条件进而有于是显然则是以6最小正周期的周期函数∵当时则故答案为:2【点睛】本题以抽象函数为载体研究抽象函数 解析:2【分析】根据函数满足的关系可得()f x 是以6最小正周期的周期函数,根据()()573f f =代入解析式即可.【详解】根据已知条件()()()()113f x f x f x f x ⎧=-⎪⎨+=--⎪⎩, 进而有()()()()()1133f x f x f x f x f x =-=+-=⎡⎤⎡⎤⎣⎦⎣⎦---=-+,于是()()3+=-f x f x ,显然()()()()()6333f x f x f x f x f x +=++=-⎡⎤⎡⎤+=--⎦⎦=⎣⎣,则()f x 是以6最小正周期的周期函数,∵当(]1,3x ∈时()f x x =,则()()()57693332f f f =⨯+===.故答案为:2.【点睛】本题以抽象函数为载体,研究抽象函数的结构特征,且挖掘暗含条件,巧妙地对复合函数的连续变形,体现了数学抽象,数学化归等关键能力与学科素,属于中档题. 19.2【分析】由函数是幂函数求得或结合幂函数的性质即可求解【详解】由题意函数是幂函数可得即解得或当时函数此时在上单调递增符合题意;当时函数此时在上单调递减不符合题意故答案为:【点睛】本题主要考查了幂函数 解析:2【分析】由函数()2(1)mf x m m x =--是幂函数,求得2m =或1m =-,结合幂函数的性质,即可求解.【详解】由题意,函数()2(1)mf x m m x =--是幂函数, 可得211m m --=,即220m m --=,解得2m =或1m =-,当2m =时,函数()2f x x =,此时()f x 在(0,)+∞上单调递增,符合题意; 当1m =-时,函数()1f x x -=,此时()f x 在(0,)+∞上单调递减,不符合题意, 故答案为:2.【点睛】本题主要考查了幂函数的定义及图像与性质的应用,其中解答中熟记幂函数的定义,结合幂函数的图象与性质进行判定是解答的关键,着重考查运算能力.20.【分析】由题设中的定义可对分区间讨论设表示整数综合此四类即可得到函数的值域【详解】解:设表示整数①当时此时恒有②当时此时恒有③当时此时恒有④当时此时此时恒有综上可知故答案为:【点睛】此题是新定义一个 解析:{}0,1【分析】由题设中的定义,可对x 分区间讨论,设m 表示整数,综合此四类即可得到函数的值域【详解】解:设m 表示整数.①当2x m =时,1[0.5]2x m m +⎡⎤=+=⎢⎥⎣⎦,[]2x m m ⎡⎤==⎢⎥⎣⎦. ∴此时恒有0y =.②当21x m =+时,1[1]12x m m +⎡⎤=+=+⎢⎥⎣⎦,[0.5]2x m m ⎡⎤=+=⎢⎥⎣⎦. ∴此时恒有1y =.③当221m x m <<+时,21122m x m +<+<+0.52x m m ∴<<+ 10.512x m m ++<<+ 2x m ⎡⎤∴=⎢⎥⎣⎦,12x m +⎡⎤=⎢⎥⎣⎦∴此时恒有0y =④当2122m x m +<<+时,22123m x m +<+<+0.512x m m ∴+<<+ 11 1.52x m m ++<<+ ∴此时2x m ⎡⎤=⎢⎥⎣⎦,112x m +⎡⎤=+⎢⎥⎣⎦∴此时恒有1y =.综上可知,{}0,1y ∈.故答案为:{}0,1.【点睛】此题是新定义一个函数,根据所给的规则求函数的值域,求解的关键是理解所给的定义,一般从函数的解析式入手,要找出准确的切入点,理解[]x 表示数x 的整数部分,考察了分析理解,判断推理的能力及分类讨论的思想 三、解答题21.(1)()f x 在()0,1内单调递减,在()1,+∞内单调递增,证明见解析;(2)5,2⎛⎤-∞ ⎥⎝⎦. 【分析】(1)由单调性的定义证明;(2)分离参数不等式变形为211x a x x x+≤=+在11,42x ⎡⎤∈⎢⎥⎣⎦时恒成立,然后由函数的单调性得右边的最小值即可得结论.【详解】(1)()f x 在()0,1内单调递减,在()1,+∞内单调递增.任取()12,0,1x x ∈且12x x <,()()12121211f x f x x x x x ⎛⎫⎛⎫-=--- ⎪ ⎪⎝⎭⎝⎭ ()121211x x x x ⎛⎫=-- ⎪⎝⎭()1212121x x x x x x ⎛⎫-=- ⎪⎝⎭. 因为1201x x ,所以120x x -<,1201x x <<,所以1210x x -<,因为()()120f x f x ->,即()()12f x f x >,因此,函数()y f x =在()0,1上是单调减函数.(2)由210x ax -+≥在11,42x ⎡⎤∈⎢⎥⎣⎦时恒成立, 得211x a x x x+≤=+在11,42x ⎡⎤∈⎢⎥⎣⎦时恒成立, 由(1)知,函数()1f x x x =+在11,42x ⎡⎤∈⎢⎥⎣⎦为减函数, 所以当12x =时,()1f x x x =+取得最小值, ()min 1522f x f ⎛⎫== ⎪⎝⎭, 所以52a ≤, 因此,实数a 的取值范围是5,2⎛⎤-∞ ⎥⎝⎦. 【点睛】方法点睛:本题考查用定义证明函数的单调性,考查不等式恒成立问题,解决不等式恒成立的常用方法是用分离参数法转化为求函数的最值.在不能分离参数时,可直接引入函数,利用分类讨论思想求得函数的最值,由最值满足的不等关系得出参数范围. 22.(1)①2()22f x x x =-+,②见解析;(2)2min 42,4(),44442,4b b b f x b b b -≥⎧⎪⎪=--<<⎨⎪+≤-⎪⎩. 【分析】(1)①先求得2c =;{1A =,2}说明()0f x x -=两根为1,2.利用韦达定理求a ,b ,从而可得解析式;②写成分段函数形式,再利用二次函数图象与性质求解. (2)根据对称轴位置,分三种情况讨论,分别利用二次函数的性质求解即可.【详解】(1)①(0)2f =,2c ∴={1A =,2},2(1)20ax b x ∴+-+=有两根为1,2. 由韦达定理得,212112a b a ⎧=⨯⎪⎪⎨-⎪=+⎪⎩,∴12a b =⎧⎨=-⎩ 2()22f x x x ∴=-+②函数()2222,022,0x x x y f x x x x ⎧-+≥==⎨-+<⎩, 函数()y f x =的图象如图,同一坐标系内画出函数y a =的图象,由图可知,当1a <时,函数y a =和函数()y fx =的图象的公共点个数为0;当1a =或2a >时,函数y a =和函数()y f x =的图象的公共点个数为2;当12a <<时,函数y a =和函数()y f x =的图象的公共点个数为4;当2a =时,函数y a =和函数()y f x =的图象的公共点个数为3;(2)a =1,c =0,函数2()f x x bx =+,当2,42b b -≤-≥时,()min ()242f x f b =-=-; 当22,442b b -<-<-<<时,2min ()24b b f x f ⎛⎫=-=- ⎪⎝⎭;当2,42b b -≥≤-时,()min ()242f x f b ==+; 综上,2min42,4(),44442,4b b b f x b b b -≥⎧⎪⎪=--<<⎨⎪+≤-⎪⎩ 【点睛】方法点睛:二次函数在闭区间上的最值主要有三种类型:轴定区间定、轴动区间定、轴定区间动,不论哪种类型,解决的关键是考查对称轴与区间的关系,当含有参数时,要依据对称轴与区间的关系进行分类讨论.23.(1)4a =;(2)当2x =时,()g x 取得最小值为5.【分析】(1)利用不等式的解集,推出对应方程的根,然后求解a .(2)化简函数的解析式,利用基本不等式转化求解函数的最值即可.【详解】(1)因为()00x a f x x +<⇔<的解集为()4,0-, 故()0x a f x x+==一个根为-4, 404a -+=- 得4a =(2)()()441x g x x f x x x x x +=+=+=++ 因为0x >,所以4115x x ++≥=, 当且仅当4x x=,即2x =时取等号; 所以当2x =时,()g x 取得最小值为5.【点睛】在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧,使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用,否则会出现错误.24.(1) 1.0,0,1,[]1,1-;(2)4m =或2;(3)904≤<m . 【分析】(1)本题可令3x x =,解得0x =或±1,然后根据函数()3f x x =的单调性以及“和谐区间”定义即可得出结果;(2)本题首先可将函数转化为()342,23342,23x x f x x x ⎧-≥⎪⎪=⎨⎪-+<⎪⎩,然后令322x x -=,解得45x =或4,最后绘出函数图像,结合函数图像即可得出结果; (3)讨论1a b <≤或1a b ≤<或1a b <<,根据二次函数的性质确定函数的单调区间,再由单调性求出函数的值域,根据题干,函数的新定义即可求解.【详解】解:(1)函数()3f x x =是增函数,定义域为R , 令3x x =,解得0x =或±1,故函数()3f x x =的所有“和谐区间”为[]1,0-、0,1、[]1,1-. (2)因为()322f x x =-, 所以()342,23342,23x x f x x x ⎧-≥⎪⎪=⎨⎪-+<⎪⎩, 因为[]()0,0m m >为函数()322f x x =-的一个“和谐区间”, 所以可令322x x -=,解得45x =或4, 如图所示,绘出函数图像:结合“和谐区间”的定义易知,当4x =时满足题意,因为()02f =,所以当2m =时,()min max 2,()0f x f x ==,满足题意,故m 的值为4或2.(3)①当1a b <≤时,()f x 在,a b 上时单调递减函数,由题意有()()f a b f b a =⎧⎨=⎩, 2222a a m b b b m a⎧-+=⎨-+=⎩得1a b +=,因为1a b <≤,所以110,122≤<<≤a b , 且221-+=-a a m a ,即210-+-=a a m,解得1122+=≥a 舍去,或1122=<a,112=-=b a . 由211(0)2=-++≤<m a a a , 得514m ≤<,所以当514m ≤<时,和谐区间为⎣⎦. ②1a b ≤<时,()f x 在,a b 上时单调递增函数,由题意有()()f a a f b b=⎧⎨=⎩,所以,a b 是方程22-+=x x m x 的两个不等实根. 因为3a b +=,又1a b ≤<,得2b ≤,因而有3122≤<<≤a b , 故方程2()30=-+=g x x x m 在31,2⎡⎫⎪⎢⎣⎭和3,22⎛⎤ ⎥⎝⎦内各有一个实根,即302≤<且322<≤, 解得924≤<m , 故当924≤<m时,和谐区间为3322⎡+⎢⎣⎦. ③当1a b <<时,min ()(1)11==-=<f x f m a ,得2m < 当12a b +≤时,即2a b +≤,则max ()()==f x f a b ,得22-+=a a m b , 又1a m =-,得2331=-+>b m m ,得 2m >或1m <,又由2222+=-+≤a b m m 及2m <,解得01m ≤<,此时和谐区间为21,33⎡⎤--+⎣⎦m m m . 当12+≥a b 时,即2a b +≥,则max ()()==f x f b b ,得22-+=b b m b ,解得32=b .若32-=b ,则由2m <知3122-+=-+<a b m ,舍去;若=b,12+=-≥a b m ,解得904≤≤m , 又2m <,所以02m ≤<,此时和谐区间为31,2⎡+-⎢⎣⎦m , 综上,所求范围是904≤<m . 【点睛】关键点点睛:本题考查函数新定义,能否结合题意明确函数新定义的含义是解决本题的关键,在解决函数类的问题时,合理利用函数图像可以给解题带来很大帮助,考查数形结合思想,是中档题. 25.(1)141,061163,6a a a a ⎧-<≤⎪⎪⎨⎪->⎪⎩;(2)14. 【分析】(1)根据对称轴的位置讨论两种情况:113,322-≤-->-a a,分别根据二次函数的单调性求出最大值即可得结果; (2)设11221,,1010⎡⎤==∈⎢⎥⎣⎦x x t t x x ,由韦达定理可得 211(1)2==+++t a t t t,利用函数的单调性可得实数a 的最大值.【详解】(1)对称轴12x a =-,[4,2],0∈-->x a 二次函数开口向上, ①当132-≤-a ,即106a <≤时:()(2)41=-=-M a f a , ②当132->-a ,即16a >时:()(4)163=-=-M a f a , 综上所述,141,06()1163,6a a M a a a ⎧-<≤⎪⎪=⎨⎪->⎪⎩.(2)由题知:方程210ax x ++=的两个根分别为1x x =、2x x =,由韦达定理知:121x x a ⋅=①,121x x a+=-②, 又已知121,1010⎡⎤=∈⎢⎥⎣⎦x t x ,③ 联立12121x x a x tx ⎧+=-⎪⎨⎪=⎩,得121,(1)(1)--==++t x x t a t a , 带入121x x a⋅=知:221(1)=+⋅t t a a , 即211(1)2==+++t a t t t ,其中1,1010⎡⎤∈⎢⎥⎣⎦t . 当1t =时,分母12t t++取得最小值4,所以a 得最大值为14. 【点睛】 本题考查二次函数图像、对称轴、最值的基本关系,清楚一元二次方程根与系数的关系的处理,对“对勾函数”的单调性、最值的理解是解题的关键.26.(1)(,3][1,)-∞-⋃-+∞(2)()1,-+∞【分析】(1)根据二次函数对称轴与区间关系,即可求解;(2)分离参数可得42(1)4k x ->--,求出44y x =--的最大值即可求解. 【详解】(1)由函数2()2(1)4f x x k x =+-+知, 函数()f x 图象的对称轴为1x k =-.因为函数()f x 在区间[]2,4上具有单调性,所以12k -≤或14k -≥,解得3k ≤-或1k ≥-,所以实数k 的取值范围为(,3][1,)-∞-⋃-+∞.(2) 因为()0f x >对任意的[1,2]x ∈恒成立, 所以可得42(1)k x x ->--对任意的[1,2]x ∈恒成立,因为44()44y x x x =--=-+≤-=-,当且仅当2x =时等号成立, 即max 4y =-,所以只需2(1)4k ->-,解得1k -<,所以实数k 的取值范围为()1,-+∞.【点睛】关键点睛:不等式在某区间上恒成立求参数的取值范围,一般需要分离参数,转化为求最值问题,往往可以利用函数单调性或均值不等式求最值,即可求出答案,本题中利用了均值不等式,特别注意等号是否能取到,否则不能用均值不等式求最值.。
高一数学《函数的基本性质》知识点及对应练习(详细答案)

函数的基本性质一、函数的有关概念1.函数的概念:设A、B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数.记作:y=f(x),x∈A.其中,x 叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合{f(x)| x∈A }叫做函数的值域.概念重点疑点:对于定义域中任何x,都有唯一确定的y=f(x)与x相对应。
即在直角坐标系中的图像,对于任意一条x=a(a是函数的定义域)的直线与函数y=f(x)只有一个交点;例1、下列对应关系中,x为定义域,y为值域,不是函数的是()A.y=x²+x³B.y=C.|y|=xD.y=8x解:对于|y|=x,对于任意非零x,都有两个y与x对应,所以|y|=x不是函数。
图像如下图,x=2的直线与|y|=x的图像有两个交点。
故答案选C例2、下列图象中表示函数图象的是()解析:对于任意x=a的直线,只有C选项的图形与x=a的直线只有一个交点,即对于定义域中任何x,都有唯一确定的y=f(x)与x相对应。
故选C。
注意:1、如果只给出解析式y=f(x),而没有指明它的定义域,则函数的定义域即是指能使这个式子有意义的实数的集合;2、函数的定义域、值域要写成集合或区间的形式.定义域补充:能使函数式有意义的实数x 的集合称为函数的定义域,求函数的定义域时列不等式组的主要依据是:(1)分式的分母不等于零; (2)偶次方根的被开方数不小于零;(3)对数式的真数必须大于零;(4)指数、对数式的底必须大于零且不等于1. (5)如果函数是由一些基本函数通过四则运算结合而成的.那么,它的定义域是使各部分都有意义的x 的值组成的集合.(6)指数为零底不可以等于零 (7)实际问题中的函数的定义域还要保证实际问题有意义.(注意:求出不等式组的解集即为函数的定义域。
第三章 函数的概念与性质单元检测试卷(基础过关)(解析版)

第三章 函数的概念与性质 单元检测试卷(基础过关)一、单选题1.已知幂函数()y f x =的图象过点()4,2,则14f ⎛⎫= ⎪⎝⎭( ) A.116B.12C.1D.2【答案】B【解析】设()f x x α=,将点(4,2)代入得4=2α,解得12α=,则()12f x x =,所以12111442f ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,答案为B.2.已知函数()248f x x kx =--在[)5,+∞上单调递增,则实数k 的取值范围是( )A.(),40-∞B.(],40-∞C.()40,+∞D.[)40,+∞ 【答案】B【解析】函数y =4x 2﹣kx ﹣8的对称轴为:x 8k = ∵函数在[)5,+∞上单调递增 ∴8k ≤5 ∴k ≤40 故选B.3.若定义在R 的奇函数f (x )在(,0)-∞单调递减,且f (2)=0,则满足(10)xf x -≥的x 的取值范围是( ) A .[)1,1][3,-+∞ B .3,1][,[01]-- C .[1,0][1,)-⋃+∞ D .[1,0][1,3]-⋃【答案】D【解析】因为定义在R 上的奇函数()f x 在(,0)-∞上单调递减,且(2)0f =, 所以()f x 在(0,)+∞上也是单调递减,且(2)0f -=,(0)0f =, 所以当(,2)(0,2)x ∈-∞-⋃时,()0f x >,当(2,0)(2,)x ∈-+∞时,()0f x <,所以由(10)xf x -≥可得:0210x x <⎧⎨-≤-≤⎩或0012x x >⎧⎨≤-≤⎩或0x = 解得10x -≤≤或13x ≤≤,所以满足(10)xf x -≥的x 的取值范围是[1,0][1,3]-⋃, 故选:D.4.已知()f x 是定义在[2b ,1]b -上的偶函数,且在[2b ,0]上为增函数,则(1)(2)f x f x -的解集( ) A.21,3⎡⎤-⎢⎥⎣⎦B.11,3⎡⎤-⎢⎥⎣⎦C.[]1,1-D.1,13⎡⎤⎢⎥⎣⎦【答案】B 【解析】解:()f x 是定义在[2b ,1]b -上的偶函数,210b b ∴+-=, 1b ∴=-,()f x 在[2-,0]上为增函数,()f x ∴在[0,2]上为减函数,距离对称轴越远,函数值越小,由(1)(2)f x f x -可得|1||2|x x -,且()2214x x -≥,且222x -,212x --解得113-x, 故不等式的解集为11,3⎡⎤-⎢⎥⎣⎦.故选:B .5.函数()221,13,1x x f x x x x ⎧-≤=⎨-->⎩,则()13f f ⎛⎫⎪ ⎪⎝⎭的值为( ) A.1516B.2716-C.89D.1516【答案】C【解析】∵函数f (x )221131x x x x x ⎧-≤=⎨--⎩,,>,∴f (3)=9﹣3﹣3=3,∴1133f =()f (13f ())=f (13)=1﹣(13)2=89. 故选:C .6.已知()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =,则(1)(2)(3)(50)f f f f ++++=( )A .50-B .0C .2D .50【答案】C【解析】因为()f x 是定义域为(,)-∞+∞的奇函数,且(1)(1)f x f x -=+,所以(1)(1)(3)(1)(1)4f x f x f x f x f x T +=--∴+=-+=-∴=, 因此(1)(2)(3)(50)12[(1)(2)(3)(4)](1)(2)f f f f f f f f f f ++++=+++++,因为(3)(1)(4)(2)f f f f =-=-,,所以(1)(2)(3)(4)0f f f f +++=,(2)(2)(2)(2)0f f f f =-=-∴=,从而(1)(2)(3)(50)(1)2f f f f f ++++==,选C.7.已知函数()21010x x f x x ⎧+≤=⎨>⎩,,,若()()423f x f x >--,则实数x 的取值范围是( )A.()1,-+∞ B.()1-∞-, C.()14-, D.()1-∞,【答案】C【解析】因为函数()21010x x f x x ⎧+≤=⎨>⎩,,且()()423f x f x >--,函数()f x 的图象如图:由图可知:当230x ->,即32x >时,40x -<,即4x <, 所以342x <<,当230x -≤即32x ≤时,423x x -<-即1x >-,所以312x -<≤,综上所述: 实数x 的取值范围是14x -<<. 故选:C.8.若()f x 满足对任意的实数a 、b 都有()()()f a b f a f b +=且()12f =,则(2)(4)(6)(2018)(1)(3)(5)(2017)f f f f f f f f ++++=( )A.1008B.2018C.2014D.1009【答案】B【解析】因为对任意的实数a 、b ,都有()()()f a b f a f b +=⋅,且(1)2f =, 所以(2)(1)(1)f f f =⋅,即(2)(1)2(1)f f f ==, 同理(4)(3)(1)f f f =⋅,即(4)(1)2(3)f f f ==; (6)(5)(1)f f f =⋅,即(6)(1)2(5)f f f ==; (2018)(2017)(1)f f f =⋅,即(2018)(1)2(2017)f f f ==;故(2)(4)(6)(2018)2(1)(3)(5)(2017)f f f f f f f f =====,则(2)(4)(6)(2018)100922018(1)(3)(5)(2017)f f f f f f f f ++++=⨯=,故选:B. 二、多选题9.已知a b c === )A.a b >B.c b >C.b c >D.b a >【答案】AC【解析】a b c ===()()()7577035577570142722322128,5525a b ========,()57010257749c ===,,a c a b ∴>>,又()()2270147270105255(78125),77(16807)b c ======,b c ∴>,a b c ∴>>.故选:AC. 10.函数2()xf x x a=+的图像可能是( ) A. B. C. D.【答案】ABC【解析】由题可知,函数2()xf x x a=+, 若0a =,则21()x f x x x==,选项C 可能; 若0a >,则函数定义域为R ,且(0)0f =,选项B 可能; 若0a <,则x a ≠-A 可能, 故不可能是选项D , 故选:ABC.11.对于定义在R 上的函数()f x ,下述结论正确的是( ) A.若()f x 是奇函数,则(0)0f =B.若函数(1)f x -的图象关于直线1x =对称,则()f x 为偶函数C.若对任意()1212,x x R x x ∈≠,有()()12120f x f x x x -<-,则()f x 是R 上的减函数D.若函数()f x 满足(2)(1)(0)(1)(2)f f f f f -<-<<<,则()f x 是R 上的增函数 【答案】ABC【解析】对于A 选项,由于函数()f x 是定义在R 上的奇函数,故()00f =,所以A 选项正确. 对于B 选项,()1f x -图像向左平移一个单位得到()f x 的图像,而()1f x -关于直线1x =对称,故()f x 关于0x =对称,也即()f x 为偶函数,故B 选项正确. 对于C 选项,根据减函数的定义可知,C 选项正确.对于D 选项,()()()()()21012f f f f f -<-<<<只是函数的部分函数值,无法确定函数是递增函数递减,故D 选项错误. 故选ABC.12.若函数()12f x x x a =+++的最小值为3,则实数a 的值可能为( ) A.1- B.4-C.5D.8【答案】BD【解析】当12a--,即2a 时,有31,,2()1,1,231, 1.a x a x a f x x a x x a x ⎧----⎪⎪⎪=+--<<-⎨⎪++-⎪⎪⎩易得,当2a x =-时,min ()1322a af x f ⎛⎫=-=-= ⎪⎝⎭,可得8a =. 当12a ->-,即2a <时,有31,,2()1,1,231, 1.a x a x a f x x a x x a x ⎧++>-⎪⎪⎪=--+--⎨⎪---<-⎪⎪⎩易得,当2a x =-时,min ()1322a a f x f ⎛⎫=-=-+= ⎪⎝⎭,可得4a =-.综上可得,所求a 的值为4-或8. 故选:BD三、填空题 13.若{}{}|02,|12A x x B x x =<<=≤<,则=A B ⋃____________.【答案】【解析】根据所给集合都是无限数集,利用数轴表示出集合,找出并集14.在幂函数y x α=的图象上任取两个不同的点()11,x y ,()22,x y ,若2121y y x x --是定值,则α=______.【答案】1或0 【解析】2121y y x x --表示两点()11,x y ,()22,x y 之间的斜率是定值,故幂函数y x α=的图象是直线,故1α=或0, 故答案为1或0.15.函数()f x 同时满足:①对于定义域上的任意x ,恒有()()0f x f x +-=;②对于定义域上的任意12,x x .当12x x ≠,恒有()()12120f x f x x x -<-.则称函数()f x 为“理想函数”,则下列三个函数中:(1)()1f x x=, (2)()2f x x =,(3)()22{0x x f x xx -≥=<. 称为“理想函数”的有 (填序号)【答案】(3) 【解析】∵函数f (x )同时满足①对于定义域上的任意x ,恒有f (x )+f (−x )=0; ②对于定义域上的任意1x ,2,x 当12x x ≠时,恒有()()12120f x f x x x -<-,则称函数f (x )为“理想函数”,∴“理想函数”既是奇函数,又是减函数,在(1)中,()1f x x=是奇函数,但不是增函数,故(1)不是“理想函数”; 在(2)中,()2f x x =,是偶函数,且在(−∞,0)内是减函数,在(0,+∞)内是增函数,故(2)不是“理想函数”; 在(3)中,()22,0 ,0x x f x x x ⎧-≥=⎨<⎩是奇函数,且是减函数,故(3)能被称为“理想函数”.故答案为(3).16.若函数()()()()2R f x a x x a =+-∈是偶函数,则a =_____,值域为________.【答案】2 (],4-∞【解析】()()2()2(2)2f x a x x x a x a =+-=-+-+,定义域为R .2()(2)2f x x a x a -=---+.因为()f x 为偶函数,所以()()f x f x -=. 所以20a -=,即2a =.2()4f x x =-+,因为20x -≤,所以244x -+≤.即值域为(],4-∞. 故答案为:2;(],4-∞ 四、解答题17.函数()2f x x -= ,(1)证明函数的奇偶性(2)判断函数在()-0∞,上单调性,并证明. 【答案】(1)证明见解析;(2)函数()f x 在()-0∞,上单调递增,证明见解析. 【解析】(1)函数()f x 为偶函数.()221f x x x-==的的定义域为{}0x x ≠ ()()2211()f x f x x x-===- 即函数()f x 为偶函数(2)函数()f x 在()-0∞,上单调递增 证明如下:任取12,x x ∈()-0∞,,且12x x < ()()()()222121211222222212121211=x x x x x x f x f x x x x x x x -+-∴-=-= ()1212,-0x x x x ∈∞<,且, ,故210x x ->,21+0x x < ()()212122120x x x x x x -+∴<即()()12f x f x <则函数()f x 在()-0∞,上单调递增18.已知函数())11f x a a =≠-. (1)若0a >,求()f x 的定义域;(2)若()f x 在区间(]0,1上是减函数,求实数a 的取值范围. 【答案】(1)3,a⎛⎤-∞ ⎥⎝⎦(2)()(],01,3-∞【解析】(1)当0a >且1a ≠时,由30ax -≥得3x a ≤,即函数()f x 的定义域是3,a ⎛⎤-∞ ⎥⎝⎦.(2)当10a ->即1a >时,令3t ax =-要使()f x 在(]0,1上是减函数,则函数3t ax =-在(]0,1上为减函数,即0a -<,并且且310a -⨯≥,解得13a;当10a -<即1a <时 ,令3t ax =-要使()f x 在(]0,1上是减函数,则函数3t ax =-在(]0,1为增函数,即0a -> 并且310a -⨯≥,解得0a <综上可知,所求实数a 的取值范围是()(],01,3-∞.19.已知函数()223mx f x x n+=+是奇函数,且()523f =.(1)求实数m 和n 的值;(2)判断函数()f x 在(],1-∞-上的单调性,并加以证明.【答案】(1)2m =,0n =;(2)(],1-∞-上为增函数,证明见解析 【解析】(1)∵()f x 是奇函数, ∴()()f x f x -=-.即222222333mx mx mx x n x n x n+++=-=-++--, 比较得n n =-,0n =.又()523f =, ∴42563m +=,解得2m =,即实数m 和n 的值分别是2和0. (2)函数()f x 在(],1-∞-上为增函数.证明如下:由(1)知()22222333x x f x x x+==+, 设121x x <≤-, 则()()()1212122113f x f x x x x x ⎛⎫-=-- ⎪⎝⎭()121212(1)23x x x x x x -⋅-=, ()12203x x -<,120x x >,1210x x ->, ∴()()120f x f x -<, ∴()()12f x f x <,即函数()f x 在(],1-∞-上为增函数. 20.设函数 ()11221x f x =-+, Ⅰ 证明函数 ()f x 是奇函数;Ⅱ 证明函数 ()f x 在 (),-∞+∞ 内是增函数; Ⅲ 求函数 ()f x 在 []1,2 上的值域.【答案】(1)见解析(2)见解析(3)13,610⎡⎤⎢⎥⎣⎦. 【解析】(1)首先确定定义域为R ,然后由()()f x f x -=- 即可证得结论; (2)利用增函数的定义证明函数的增函数即可;(3)利用(2)中函数的单调性结合函数的定义域可得函数 ()f x 在 []1,2 上的值域为13,610⎡⎤⎢⎥⎣⎦.(1) 由题意,得 x ∈R ,即函数的定义域关于原点对称,()()()111212221121222111221,x x xxx x f x f x -=-=-++-=+=-++=- 所以函数 ()f x 为奇函数.(2) 设 1x ,2x 是 (),-∞+∞ 内任意两实数,且 12x x <,则()()()()12121212111122122122.2121x x x x x x f x f x -=--+++-=++ 因为 12x x <,所以 12220x x -<,所以 ()()120f x f x -<,所以函数 ()f x 在 (),-∞+∞ 内是增函数.(3) 因为函数 ()f x 在 (),-∞+∞ 内是增函数,所以函数 ()f x 在 []1,2 上也是增函数, 所以 ()()min 116f x f ==,()()max 3210f x f ==,所以函数 ()f x 在 []1,2 上的值域为 13,610⎡⎤⎢⎥⎣⎦. 21.某商场以每件42元的价格购进一种服装,根据试营销量得知,这种服装每天的销售量0,()t t t N >∈(件)与每件的销售价4268,()x x x N <<∈(元)之间可看成一次函数关系:3204t x =-+.(1)写出商场每天卖这种服装的销售利润y (元)与每件的销售价x (元)之间的函数关系式(每天的销售利润是指所卖出服装的总销售额与购进这些服装所花费金额的差).(2)商场要想每天获得最大的销售利润,每件的销售价定为多少最为合适?最大销售利润为多少?【答案】(1)233308568(4268,)y x x x x N =-+-<<∈;(2)每件的销售价定为55元时,最大销售利润为507元【解析】(1)由题意得,每天的销售利润y (元)与每件的销售价x (元)之间的函数关系式为(42)y x =-2(3204)33308568(4268,)x x x x x N -+=-+-<<∈.(2)由(1)得23(55)507(4268,)y x x x N =--+<<∈,则当55x =时,max 507y =.即当每件的销售价定为55元时,每天可获得最大的销售利润,最大销售利润为507元. 22.已知函数()2f x x bx c =++. (1)若()()g x xf x =是奇函数,求b 的值;(2)若2b a =-,58a c -=,且()20f x >对任意的实数x 都成立,求a 的取值范围; (3)对于任意的[]12,1,1x x ∈-,总有()()124f x f x -≤,求b 的取值范围. 【答案】(1)0;(2)1,52⎛⎫ ⎪⎝⎭;(3)[]22-,. 【解析】(1)()()0g x g x -+=,220bx =由对任意x 恒成立,所以0b =.(2)依题意: ()()2425208a f x x a x -=+-+>, 令20x t =≥, 则()()288250h t t a t a =+-+->, 当对称轴202a --≤时, ()050h a =->,[)2,5a ∈, 当对称轴202a -->时, ∆<0,1,32a ⎛⎫∈ ⎪⎝⎭,则1,22a ⎛⎫∈ ⎪⎝⎭, 综上:1,52⎛⎫ ⎪⎝⎭.(3)法1:取11x =,21x =-,可得()()114f f --≤,24b ≤,所以[]2,2b ∈-,[]1,12b-∈-.函数()f x 在区间[]1,1-上的最小值2b f ⎛⎫- ⎪⎝⎭最大值为在()1f 或()1f -,所以 ()()142142b f f b f f ⎧⎛⎫--≤⎪⎪⎝⎭⎪⎨⎛⎫⎪---≤ ⎪⎪⎝⎭⎩,解得:[]2,2b ∈-.法2:分四种情况进行讨论, 当12b-≤-时,即2b ≥时, ()f x 在[]1,1-上单调增, ()()1124f f b --=≤,2b ≤,2b =, 当12b-≥时,即2b ≤-时, ()f x 在[]1,1-上单调减, ()()1124f f b --=-≤,2b ≥-,2b =-, 当()1,02b-∈-,即()0,2b ∈时 ()()max 1f x f =,()min 2b f x f ⎛⎫=- ⎪⎝⎭,()211422b b f f ⎛⎫⎛⎫--=+≤ ⎪ ⎪⎝⎭⎝⎭,得[]6,2b ∈-,∴()0,2b ∈. 当()0,12b-∈,即()2,0b ∈-时 ()()max 1f x f =-,()min 2b f x f ⎛⎫=- ⎪⎝⎭,()211422b b f f ⎛⎫⎛⎫---=-≤ ⎪ ⎪⎝⎭⎝⎭, 得[]2,6b ∈-,∴()2,0b ∈-. 综上,[]2,2b ∈-.。
长沙市长沙市第一中学数学 二次函数单元测试题(Word版 含解析)

长沙市长沙市第一中学数学二次函数单元测试题(Word版含解析)一、初三数学二次函数易错题压轴题(难)1.如图,抛物线y=﹣x2+bx+c与x轴交于A,B两点,其中A(3,0),B(﹣1,0),与y轴交于点C,抛物线的对称轴交x轴于点D,直线y=kx+b1经过点A,C,连接CD.(1)求抛物线和直线AC的解析式:(2)若抛物线上存在一点P,使△ACP的面积是△ACD面积的2倍,求点P的坐标;(3)在抛物线的对称轴上是否存在一点Q,使线段AQ绕Q点顺时针旋转90°得到线段QA1,且A1好落在抛物线上?若存在,求出点Q的坐标;若不存在,请说明理由.【答案】(1)2y x2x3=-++;3y x=-+;(2)(﹣1,0)或(4,﹣5);(3)存在;(1,2)和(1,﹣3)【解析】【分析】(1)将点A,B坐标代入抛物线解析式中,求出b,c得出抛物线的解析式,进而求出点C 的坐标,再将点A,C坐标代入直线AC的解析式中,即可得出结论;(2)利用抛物线的对称性得出BD=AD,进而判断出△ABC的面积和△ACP的面积相等,即可得出结论;(3)分点Q在x轴上方和在x轴下方,构造全等三角形即可得出结论.【详解】解:(1)把A(3,0),B(﹣1,0)代入y=﹣x2+bc+c中,得93010b cb c-++=⎧⎨--+=⎩,∴23bc=⎧⎨=⎩,∴抛物线的解析式为y=﹣x2+2x+3,当x=0时,y=3,∴点C的坐标是(0,3),把A(3,0)和C(0,3)代入y=kx+b1中,得11303k bb+=⎧⎨=⎩,∴113kb=-⎧⎨=⎩∴直线AC的解析式为y=﹣x+3;(2)如图,连接BC,∵点D是抛物线与x轴的交点,∴AD=BD,∴S△ABC=2S△ACD,∵S△ACP=2S△ACD,∴S△ACP=S△ABC,此时,点P与点B重合,即:P(﹣1,0),过B点作PB∥AC交抛物线于点P,则直线BP的解析式为y=﹣x﹣1①,∵抛物线的解析式为y=﹣x2+2x+3②,联立①②解得,1xy=-⎧⎨=⎩或45xy=⎧⎨=-⎩,∴P(4,﹣5),∴即点P的坐标为(﹣1,0)或(4,﹣5);(3)如图,①当点Q在x轴上方时,设AC与对称轴交点为Q',由(1)知,直线AC的解析式为y=﹣x+3,当x=1时,y=2,∴Q'坐标为(1,2),∵Q'D=AD=BD=2,∴∠Q'AB=∠Q'BA=45°,∴∠AQ'B=90°,∴点Q'为所求,②当点Q在x轴下方时,设点Q(1,m),过点A1'作A1'E⊥DQ于E,∴∠A1'EQ=∠QDA=90°,∴∠DAQ+∠AQD=90°,由旋转知,AQ=A1'Q,∠AQA1'=90°,∴∠AQD+∠A1'QE=90°,∴∠DAQ=∠A1'QE,∴△ADQ ≌△QEA 1'(AAS ),∴AD =QE =2,DQ =A 1'E =﹣m ,∴点A 1'的坐标为(﹣m +1,m ﹣2),代入y =﹣x 2+2x +3中,解得,m =﹣3或m =2(舍),∴Q 的坐标为(1,﹣3),∴点Q 的坐标为(1,2)和(1,﹣3).【点睛】本题考查的是二次函数的综合题,涉及解析式的求解,与三角形面积有关的问题,三角形“k ”字型全等,解题的关键是利用数形结合的思想,设点坐标并结合几何图形的性质列式求解.2.在平面直角坐标系中,抛物线22(0)y ax bx a =++≠经过点(2,4)A --和点(2,0)C ,与y 轴交于点D ,与x 轴的另一交点为点B .(1)求抛物线的解析式;(2)如图1,连接BD ,在抛物线上是否存在点P ,使得2PBC BDO ∠=∠?若存在,请求出点P 的坐标;若不存在,请说明理由;(3)如图2,连接AC ,交y 轴于点E ,点M 是线段AD 上的动点(不与点A ,点D 重合),将CME △沿ME 所在直线翻折,得到FME ,当FME 与AME △重叠部分的面积是AMC 面积的14时,请直接写出线段AM 的长. 【答案】(1)22y x x =-++;(2)存在,(23,209)或(103,529-);(3)5或 【解析】【分析】(1)根据点A 和点C 的坐标,利用待定系数法求解;(2)在x 轴正半轴上取点E ,使OB=OE ,过点E 作EF ⊥BD ,垂足为F ,构造出∠PBC=∠BDE ,分点P 在第三象限时,点P 在x 轴上方时,点P 在第四象限时,共三种情况分别求解;(3)设EF 与AD 交于点N ,分点F 在直线AC 上方和点F 在直线AC 下方时两种情况,利用题中所给面积关系和中线的性质可得MN=AN ,FN=NE ,从而证明四边形FMEA 为平行四边形,继而求解.【详解】解:(1)∵抛物线22(0)y ax bx a =++≠经过点A (-2,-4)和点C (2,0),则44220422a b a b -=-+⎧⎨=++⎩,解得:11a b =-⎧⎨=⎩, ∴抛物线的解析式为22y x x =-++;(2)存在,理由是:在x 轴正半轴上取点E ,使OB=OE ,过点E 作EF ⊥BD ,垂足为F ,在22y x x =-++中,令y=0,解得:x=2或-1,∴点B 坐标为(-1,0),∴点E 坐标为(1,0),可知:点B 和点E 关于y 轴对称,∴∠BDO=∠EDO ,即∠BDE=2∠BDO ,∵D (0,2),∴=,在△BDE 中,有12×BE ×OD=12×BD ×EF ,即2×EF ,解得:,∴,∴tan ∠BDE=EF DF =453555÷=43, 若∠PBC=2∠BDO ,则∠PBC=∠BDE ,∵BD=DE=5,BE=2,则BD 2+DE 2>BE 2,∴∠BDE 为锐角,当点P 在第三象限时,∠PBC 为钝角,不符合;当点P 在x 轴上方时,∵∠PBC=∠BDE ,设点P 坐标为(c ,22c c -++),过点P 作x 轴的垂线,垂足为G ,则BG=c+1,PG=22c c -++,∴tan ∠PBC=PG BG =221c c c -+++=43, 解得:c=23, ∴22c c -++=209, ∴点P 的坐标为(23,209);当点P 在第四象限时,同理可得:PG=22c c --,BG=c+1,tan ∠PBC=PG BG =221c c c --+=43, 解得:c=103, ∴22c c -++=529-,∴点P 的坐标为(103,529-), 综上:点P 的坐标为(23,209)或(103,529-);(3)设EF 与AD 交于点N ,∵A (-2,-4),D (0,2),设直线AD 表达式为y=mx+n ,则422m n n -=-+⎧⎨=⎩,解得:32m n =⎧⎨=⎩, ∴直线AD 表达式为y=3x+2,设点M 的坐标为(s ,3s+2),∵A (-2,-4),C (2,0),设直线AC 表达式为y=m 1x+n 1,则11114202m n m n -=-+⎧⎨=+⎩,解得:1112m n =⎧⎨=-⎩, ∴直线AC 表达式为y=x-2,令x=0,则y=-2,∴点E 坐标为(0,-2),可得:点E 是线段AC 中点,∴△AME 和△CME 的面积相等,由于折叠,∴△CME ≌△FME ,即S △CME =S △FME ,由题意可得:当点F 在直线AC 上方时,∴S △MNE =14S △AMC =12S △AME =12S △FME , 即S △MNE = S △ANE = S △MNF ,∴MN=AN ,FN=NE ,∴四边形FMEA 为平行四边形,∴CM=FM=AE=12AC=221442+22∵M (s ,3s+2),∴()()2223222s s -++=, 解得:s=45-或0(舍), ∴M (45-,25-), ∴AM=22422455⎛⎫⎛⎫-++-+ ⎪ ⎪⎝⎭⎝⎭=6105,当点F 在直线AC 下方时,如图,同理可得:四边形AFEM 为平行四边形,∴AM=EF ,由于折叠可得:CE=EF ,∴AM=EF=CE=22,综上:AM 61022 【点睛】 本题是二次函数综合题,涉及到待定系数法,二次函数的图像和性质,折叠问题,平行四边形的判定和性质,中线的性质,题目的综合性很强.难度很大,对学生的解题能力要求3.如图,抛物线()21y x a x a =-++与x 轴交于,A B 两点(点A 位于点B 的左侧),与y 轴的负半轴交于点C .()1求点B 的坐标.()2若ABC 的面积为6.①求这条抛物线相应的函数解析式.②在拋物线上是否存在一点,P 使得POB CBO ∠=∠?若存在,请求出点P 的坐标;若不存在,请说明理由.【答案】(1)(1,0);(2)①223y x x =+-;②存在,点P 的坐标为1133313++⎝⎭或53715337-+-⎝⎭. 【解析】【分析】(1)直接令0y =,即可求出点B 的坐标;(2)①令x=0,求出点C 坐标为(0,a ),再由△ABC 的面积得到12(1−a)•(−a)=6即可求a 的值,即可得到解析式;②当点P 在x 轴上方时,直线OP 的函数表达式为y=3x ,则直线与抛物线的交点为P ;当点P 在x 轴下方时,直线OP 的函数表达式为y=-3x ,则直线与抛物线的交点为P ;分别求出点P 的坐标即可.【详解】解:()1当0y =时,()210,x a x a -++= 解得121,.x x a ==点A 位于点B 的左侧,与y 轴的负半轴交于点,C∴点B 坐标为()1,0.()2①由()1可得,点A 的坐标为(),0a ,点C 的坐标为()0,,0,a a <1,AB a OC a ∴=-=- ABC 的面积为6,()()116,2a a ∴--⋅= 123,4a a ∴=-=.0,a < 3a ∴=-22 3.y x x =+-②点B 的坐标为()1,0,点C 的坐标为()0,3-,∴设直线BC 的解析式为3,y kx =-则03,k =-3k ∴=.,POB CBO ∠=∠∴当点P 在x 轴上方时,直线//OP 直线,BC∴直线OP 的函数解析式3,y x =为则23,23,y x y x x =⎧⎨=+-⎩1112x y ⎧=⎪⎪∴⎨⎪=⎪⎩(舍去),2212x y ⎧+=⎪⎪⎨⎪=⎪⎩∴点的P坐标为1322⎛⎫+ ⎪ ⎪⎝⎭; 当点P 在x 轴下方时,直线'OP 与直线OP 关于x 轴对称,则直线'OP 的函数解析式为3,y x =-则23,23,y x y x x =-⎧⎨=+-⎩1152x y ⎧-=⎪⎪∴⎨⎪=⎪⎩舍去),2252x y ⎧-=⎪⎪⎨⎪=⎪⎩∴点P'的坐标为⎝⎭综上可得,点P 的坐标为⎝⎭或⎝⎭【点睛】本题考查二次函数的图象及性质,一次函数的性质,熟练掌握二次函数的图象及性质,结合数形结合的思想和分类讨论的思想解题是解本题的关键.4.在平面直角坐标系中,将函数2263,(y x mx m x m m =--≥为常数)的图象记为G . (1)当1m =-时,设图象G 上一点(),1P a ,求a 的值;(2)设图象G 的最低点为(),o o F x y ,求o y 的最大值;(3)当图象G 与x 轴有两个交点时,设右边交点的横坐标为2,x 则2x 的取值范围是 ;(4)设1112,,2,16816A m B m ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭,当图象G 与线段AB 没有公共点时,直接写出m 的取值范围.【答案】(1)0a =或3a =-;(2)118;(3)21136x -<<-;(4)18m <-或116m >- 【解析】【分析】(1)将m=-1代入解析式,然后将点P 坐标代入解析式,从而求得a 的值;(2)分m >0和m ≤0两种情况,结合二次函数性质求最值;(3)结合二次函数与x 轴交点及对称轴的性质确定取值范围;(4)结合一元二次方程根与系数的关系确定取值范围.【详解】解:(1)当1m =-时,()22613y x x x =++≥ 把(),1P a 代入,得22611a a ++=解得0a =或3a =-(2)当0m >时,,(3)F m m -此时,0o y m =-<当0m ≤时,2223926=2()22y x mx m x m m m =-----∴239,22F m m m ⎛⎫--⎪⎝⎭此时,229911=()22918m m m ---++ ∴0y 的最大值118=综上所述,0y 的最大值为118(3)由题意可知:当图象G 与x 轴有两个交点时,m >0当抛物线顶点在x 轴上时,22=4(6)42()=0b ac m m -=--⨯⨯-△ 解得:m=0(舍去)或29m =-由题意可知抛物线的对称轴为直线x=32m 且x ≥3m∴当图象G 与x 轴有两个交点时,设右边交点的横坐标为x 2,则x 2的取值范围是21136x -<<- (4)18m <-或116m >- 【点睛】本题属于二次函数综合题,考查了二次函数的性质,不等式等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,学会用转化的思想思考问题,属于中考压轴题.5.定义:对于已知的两个函数,任取自变量x 的一个值,当0x ≥时,它们对应的函数值相等;当0x <时,它们对应的函数值互为相反数,我们称这样的两个函数互为相关函数.例如:正比例函数y x =,它的相关函数为(0)(0)x x y x x ≥⎧=⎨-<⎩. (1)已知点()5,10A -在一次函数5y ax =-的相关函数的图像上,求a 的值; (2)已知二次函数2142y x x =-+-. ①当点3,2B m ⎛⎫ ⎪⎝⎭在这个函数的相关函数的图像上时,求m 的值; ②当33x -≤≤时,求函数2142y x x =-+-的相关函数的最大值和最小值. (3)在平面直角坐标系中,点M 、N 的坐标分别为1,12⎛⎫-⎪⎝⎭、9,12⎛⎫⎪⎝⎭,连结MN .直接写出线段MN 与二次函数24y x x n =-++的相关函数的图像有两个公共点时n 的取值范围.【答案】(1)1;(2)①22- ;②max 432y =,min 12y =-;(3)31n -<≤-,514n <≤【解析】 【分析】(1)先求出5y ax =-的相关函数,然后代入求解,即可得到答案;(2)先求出二次函数的相关函数,①分为m <0和m ≥0两种情况将点B 的坐标代入对应的关系式求解即可; ②当-3≤x <0时,y=x 2-4x+12,然后可 此时的最大值和最小值,当0≤x≤3时,函数y=-x 2+4x-12,求得此时的最大值和最小值,从而可得到当-3≤x≤3时的最大值和最小值; (3)首先确定出二次函数y=-x 2+4x+n 的相关函数与线段MN 恰好有1个交点、2个交点、3个交点时n 的值,然后结合函数图象可确定出n 的取值范围. 【详解】解:(1)根据题意,一次函数5y ax =-的相关函数为5,(0)5,(0)ax x y ax x -≥⎧=⎨-+<⎩,∴把点()5,10A -代入5y ax =-+,则(5)510a -⨯-+=,∴1a =;(2)根据题意,二次函数2142y x x =-+-的相关函数为2214,(0)214,(0)2x x x y x x x ⎧-+-≥⎪⎪=⎨⎪-+<⎪⎩,①当m <0时,将B (m ,32)代入y=x 2-4x+12得m 2-4m+1322=,解得:m=2 当m≥0时,将B (m ,32)代入y=-x 2+4x-12得:-m 2+4m-12=32,解得:或m=2.综上所述:m=2-或m=2+或m=2- ②当-3≤x <0时,y=x 2-4x+12,抛物线的对称轴为x=2,此时y 随x 的增大而减小, ∴当3x =-时,有最大值,即2143(3)4(3)22y =--⨯-+=,∴此时y的最大值为432.当0≤x≤3时,函数y=-x2+4x12-,抛物线的对称轴为x=2,当x=0有最小值,最小值为12 -,当x=2时,有最大值,最大值y=72.综上所述,当-3≤x≤3时,函数y=-x2+4x12-的相关函数的最大值为432,最小值为12-;(3)如图1所示:线段MN与二次函数y=-x2+4x+n的相关函数的图象恰有1个公共点.∴当x=2时,y=1,即-4+8+n=1,解得n=-3.如图2所示:线段MN与二次函数y=-x2+4x+n的相关函数的图象恰有3个公共点.∵抛物线y=x2-4x-n与y轴交点纵坐标为1,∴-n=1,解得:n=-1.∴当-3<n≤-1时,线段MN与二次函数y=-x2+4x+n的相关函数的图象恰有2个公共点.如图3所示:线段MN与二次函数y=-x2+4x+n的相关函数的图象恰有3个公共点.∵抛物线y=-x 2+4x+n 经过点(0,1), ∴n=1.如图4所示:线段MN 与二次函数y=-x 2+4x+n 的相关函数的图象恰有2个公共点.∵抛物线y=x 2-4x-n 经过点M (12-,1), ∴14+2-n=1,解得:n=54. ∴1<n≤54时,线段MN 与二次函数y=-x 2+4x+n 的相关函数的图象恰有2个公共点. 综上所述,n 的取值范围是-3<n≤-1或1<n≤54. 【点睛】本题主要考查的是二次函数的综合应用,解答本题主要应用了二次函数的图象和性质、函数图象上点的坐标与函数解析式的关系,求得二次函数y=-x 2+4x+n 的相关函数与线段MN 恰好有1个交点、2个交点、3个交点时n 的值是解题的关键.6.已知二次函数y =ax 2+bx +c (a ≠0).(1)若b =1,a =﹣12c ,求证:二次函数的图象与x 轴一定有两个不同的交点; (2)若a <0,c =0,且对于任意的实数x ,都有y ≤1,求4a +b 2的取值范围;(3)若函数图象上两点(0,y 1)和(1,y 2)满足y 1•y 2>0,且2a +3b +6c =0,试确定二次函数图象对称轴与x 轴交点横坐标的取值范围. 【答案】(1)见解析;(2)240a b +≤ ;(3)12323b a <-<【解析】 【分析】(1)根据已知条件计算一元二次方程的判别式即可证得结论; (2)根据已知条件求得抛物线的顶点纵坐标,再整理即可;(3)将(0,y 1)和(1,y 2)分别代入函数解析式,由y 1•y 2>0,及2a +3b +6c =0,得不等式组,变形即可得出答案. 【详解】解:(1)证明:∵y =ax 2+bx+c (a≠0), ∴令y =0得:ax 2+bx+c =0 ∵b =1,a =﹣12c , ∴△=b 2﹣4ac =1﹣4(﹣12c )c =1+2c 2, ∵2c 2≥0,∴1+2c 2>0,即△>0,∴二次函数的图象与x 轴一定有两个不同的交点; (2)∵a <0,c =0,∴抛物线的解析式为y =ax 2+bx ,其图象开口向下, 又∵对于任意的实数x ,都有y≤1,∴顶点纵坐标214b a-≤,∴﹣b 2≥4a , ∴4a+b 2≤0;(3)由2a+3b+6c =0,可得6c =﹣(2a+3b ), ∵函数图象上两点(0,y 1)和(1,y 2)满足y 1•y 2>0, ∴c (a+b+c )>0, ∴6c (6a+6b+6c )>0,∴将6c =﹣(2a+3b )代入上式得,﹣(2a+3b )(4a+3b )>0, ∴(2a+3b )(4a+3b )<0, ∵a≠0,则9a 2>0, ∴两边同除以9a 2得,24()()033b b a a ++<, ∴203403b a b a ⎧+<⎪⎪⎨⎪+>⎪⎩或203403b a b a ⎧+>⎪⎪⎨⎪+<⎪⎩,∴4233b a -<<-,∴二次函数图象对称轴与x轴交点横坐标的取值范围是:12 323ba<-<.【点睛】本题考查了抛物线与x轴的交点、抛物线与一元二次方程的关系及抛物线与不等式的关系等知识点,熟练掌握二次函数的性质是解题的关键.7.如图,在平面直角坐标系中,二次函数y=﹣x2+6x﹣5的图象与x轴交于A、B两点,与y轴交于点C,其顶点为P,连接PA、AC、CP,过点C作y轴的垂线l.(1)P的坐标,C的坐标;(2)直线1上是否存在点Q,使△PBQ的面积等于△PAC面积的2倍?若存在,求出点Q 的坐标;若不存在,请说明理由.【答案】(1)(3,4),(0,﹣5);(2)存在,点Q的坐标为:(92,﹣5)或(212,﹣5)【解析】【分析】(1)利用配方法求出顶点坐标,令x=0,可得y=-5,推出C(0,-5);(2)直线PC的解析式为y=3x-5,设直线交x轴于D,则D(53,0),设直线PQ交x轴于E,当BE=2AD时,△PBQ的面积等于△PAC的面积的2倍,分两种情形分别求解即可解决问题.【详解】解:(1)∵y=﹣x2+6x﹣5=﹣(x﹣3)2+4,∴顶点P(3,4),令x=0得到y=﹣5,∴C(0,﹣5).故答案为:(3,4),(0,﹣5);(2)令y=0,x2﹣6x+5=0,解得:x=1或x=5,∴A (1,0),B (5,0), 设直线PC 的解析式为y =kx +b ,则有534b k b =-⎧⎨+=⎩,解得:35k b =⎧⎨=-⎩,∴直线PC 的解析式为:y =3x ﹣5, 设直线交x 轴于D ,则D (53,0),设直线PQ 交x 轴于E ,当BE =2AD 时,△PBQ 的面积等于△PAC 的面积的2倍, ∵AD =23, ∴BE =43, ∴E (113,0)或E ′(193,0), 则直线PE 的解析式为:y =﹣6x +22, ∴Q (92,﹣5), 直线PE ′的解析式为y =﹣65x +385, ∴Q ′(212,﹣5), 综上所述,满足条件的点Q 的坐标为:(92,﹣5)或(212,﹣5);【点睛】本题考查抛物线与x 轴的交点、二次函数的性质等知识,解题的关键是熟练掌握待定系数法,学会用转化的思想思考问题,属于中考常考题型.8.如图1所示,抛物线223y x bx c =++与x 轴交于A 、B 两点,与y 轴交于点C ,已知C点坐标为(0,4),抛物线的顶点的横坐标为72,点P是第四象限内抛物线上的动点,四边形OPAQ是平行四边形,设点P的横坐标为m.(1)求抛物线的解析式;(2)求使△APC的面积为整数的P点的个数;(3)当点P在抛物线上运动时,四边形OPAQ可能是正方形吗?若可能,请求出点P的坐标,若不可能,请说明理由;(4)在点Q随点P运动的过程中,当点Q恰好落在直线AC上时,则称点Q为“和谐点”,如图(2)所示,请直接写出当Q为“和谐点”的横坐标的值.【答案】(1)2214433y x x=-+;(2)9个;(3)33,22或44,;(4)33【解析】【分析】(1)抛物线与y轴交于点C,顶点的横坐标为72,则472223cb,即可求解;(2)APC∆的面积PHA PHCS S S,即可求解;(3)当四边形OPAQ是正方形时,点P只能在x轴的下方,此时OAP为等腰直角三角形,设点(,)P x y,则0x y+=,即可求解;(4)求出直线AP 的表达式为:2(1)(6)3y m x,则直线OQ的表达式为:2(1)3y m x ②,联立①②求出Q的坐标,又四边形OPAQ是平行四边形,则AO的中点即为PQ的中点,即可求解.【详解】解:(1)抛物线与y轴交于点C,顶点的横坐标为72,则472223cb,解得1434bc,故抛物线的抛物线为:2214433y x x=-+;(2)对于2214433y x x =-+,令0y =,则1x =或6,故点B 、A 的坐标分别为(1,0)、(6,0);如图,过点P 作//PH y 轴交AC 于点H ,设直线AC 的表达式为:y kx b =+ 由点A (6,0)、C (0,4)的坐标得460b kb,解得423b k, ∴直线AC 的表达式为:243y x =-+①, 设点2214(,4)33P x x x ,则点2(,4)3H x x ,APC ∆的面积221122146(44)212(16)22333PHAPHCSSSPH OA x x x x x,当1x =时,10S =,当6x =时,0S =, 故使APC ∆的面积为整数的P 点的个数为9个;(3)当四边形OPAQ 是正方形时,点P 只能在x 轴的下方, 此时OAP 为等腰直角三角形,设点(,)P x y ,则0x y +=, 即2214433yx x x ,解得:32x =或4, 故点P 的坐标为3(2,3)2或(4,4)-; (4)设点2214(,4)33P m m m ,为点(6,0)A ,设直线AP 的表达式为:y kx t =+,由点A ,P 的坐标可得260214433kt kmt m m ,解之得:2(1)326(1)3km tm∴直线AP 的表达式为:2(1)(6)3ym x , //AP OQ ,则AP 和OQ 表达式中的k 值相同,故直线OQ的表达式为:2(1)3y mx②,联立①②得:2(1)3243y m xy x,解得:446mmyx,则点6(Qm,44)m,四边形OPAQ是平行四边形,则AO的中点即为PQ的中点,如图2,作QC x⊥轴于点C,PD x⊥轴于点D,∴OC AD=,则有,66mm,解得:33m,经检验,33m是原分式方程得跟,则633m,故Q的横坐标的值为33±.【点睛】本题考查的是二次函数综合运用,涉及到一次函数的性质、平行四边形正方形的性质、面积的计算等,能熟练应用相关性质是解题的关键.9.在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.(1)求这个二次函数的关系解析式;(2)求直线AC 的函数解析式; (3)点P是直线AC 上方的抛物线上一动点,是否存在点P ,使△ACP 的面积最大?若存在,求出点P 的坐标;若不存在,说明理由;【答案】(1)y=﹣23x 2﹣43x+2;(2)223y x =+;(3)存在,(35,22-) 【解析】【分析】(1)直接用待定系数法即可解答;(2)先确定C 点坐标,设直线AC 的函数解析式y=kx+b ,最后用待定系数法求解即可;(3)连接PO ,作PM⊥x 轴于M ,PN⊥y 轴于N ,然后求出△ACP 面积的表达式,最后利用二次函数的性质求最值即可.【详解】解:(1)∵抛物线y=ax 2+bx+2过点A (﹣3,0),B (1,0), ∴093202a b a b =-+⎧⎨=++⎩解得2343a b ⎧=-⎪⎪⎨⎪=-⎪⎩, ∴二次函数的关系解析式为y=﹣23x 2﹣43x+2; (2)∵当x=0时,y=2,∴C (0,2)设直线AC 的解析式为y kx b =+,把A 、C 两点代入得 0=32k b b -+⎧⎨=⎩ 解得232k b ⎧=⎪⎨⎪=⎩ ∴直线AC 的函数解析式为223y x =+; (3)存在.如图: 连接PO ,作PM⊥x 轴于M ,PN⊥y 轴于N设点P 坐标为(m ,n ),则n=224233m m --+),PN=-m ,AO=3 当x=0时,y=22400233-⨯-⨯+=2,∴点C 的坐标为(0,2),OC=2∵PAC PAO PCO ACO S S S S =+-212411322()3223322m m m ⎛⎫=⨯⋅--++⨯⋅--⨯⨯ ⎪⎝⎭ =23m m --∵a=-1<0∴函数S △PAC =-m 2-3m 有最大值∴b 当m=()33212-=--⨯- ∴当m=32-时,S △PAC 有最大值n=222423435223332322m m ⎛⎫--+=-⨯-⨯+= ⎪⎝⎭ ∴当△ACP 的面积最大时,P 的坐标为(35,22-). 【点睛】 本题是二次函数压轴题,综合考查了二次函数的图象与性质、待定系数法、二次函数极值等知识点,根据题意表示出△PAC 的面积是解答本题的关键.10.如图,已知顶点为M (32,258)的抛物线过点D (3,2),交x 轴于A ,B 两点,交y 轴于点C ,点P 是抛物线上一动点.(1)求抛物线的解析式;(2)当点P 在直线AD 上方时,求△PAD 面积的最大值,并求出此时点P 的坐标; (3)过点P 作直线CD 的垂线,垂足为Q ,若将△CPQ 沿CP 翻折,点Q 的对应点为Q '.是否存在点P ,使Q '恰好落在x 轴上?若存在,求出点P 的坐标;若不存在,说明理由.【答案】(1)213222y x x =-++;(2)最大值为4,点P (1,3);(3)存在,点P的坐标为(13,93132-+). 【解析】【分析】 (1)用待定系数法求解即可;(2)由△PAD 面积S =S △PHA +S △PHD ,即可求解;(3)结合图形可判断出点P 在直线CD 下方,设点P 的坐标为(a ,213222a a -++),当P 点在y 轴右侧时,运用解直角三角形及相似三角形的性质进行求解即可.【详解】解:(1)设抛物线的表达式为:y =a (x ﹣h )2+k =a (x ﹣32)2+258, 将点D 的坐标代入上式得:2=a (3﹣32)2+258, 解得:a =﹣12, ∴抛物线的表达式为:213222y x x =-++; (2)当x =0时,y =﹣12x 2+32x +2=2, 即点C 坐标为(0,2), 同理,令y =0,则x =4或﹣1,故点A 、B 的坐标分别为:(﹣1,0)、(4,0),过点P 作y 轴的平行线交AD 于点H ,由点A 、D 的坐标得,直线AD 的表达式为:y =12(x +1), 设点P (x ,﹣12x 2+32x +2),则点H (x ,12x +12), 则△PAD 面积为:S =S △PHA +S △PHD =12×PH ×(x D ﹣x A )=12×4×(﹣12x 2+32x +2﹣12x 12-)=﹣x 2+2x +3, ∵﹣1<0,故S 有最大值,当x =1时,S 有最大值,则点P (1,3);(3)存在满足条件的点P ,显然点P 在直线CD 下方,设直线PQ 交x 轴于F ,点P 的坐标为(a ,﹣12a 2+32a +2),当P 点在y 轴右侧时(如图2),CQ =a ,PQ =2﹣(﹣12a 2+32a +2)=12a 2﹣32a , 又∵∠CQ ′O +∠FQ ′P =90°,∠COQ ′=∠Q ′FP =90°, ∴∠FQ ′P =∠OCQ ′,∴△COQ ′∽△Q ′FP ,'''Q C Q P CO FQ =,即213222'a a a Q F-=, ∴Q ′F =a ﹣3,∴OQ ′=OF ﹣Q ′F =a ﹣(a ﹣3)=3,CQ =CQ ′22223213CO OQ +=+= 此时a 13P 139313-+). 【点睛】此题考查了二次函数的综合应用,综合考查了翻折变换、相似三角形的判定与性质,解答此类题目要求我们能将所学的知识融会贯通,属于中考常涉及的题目.。
长沙市长沙市第一中学必修第一册第三单元《函数概念与性质》测试卷(有答案解析)
一、选择题1.已知定义域为R 的函数()f x 在[)2,+∞单调递减,且(4)()0f x f x -+=,则使得不等式()2(1)0f x x f x +++<成立的实数x 的取值范围是( ) A .31x -<<B .1x <-或3x >C .3x <-或1x >D .1x ≠-2.已知,A B 是平面内两个定点,平面内满足PA PB a ⋅=(a 为大于0的常数)的点P 的轨迹称为卡西尼卵形线,它是以发现土星卫星的天文学家乔凡尼·卡西尼的名字命名.当,A B 坐标分别为(1,0)-,(1,0),且1a =时,卡西尼卵形线大致为( )A .B .C .D .3.若奇函数()f x 在区间[]3,6上是增函数,且在区间[]3,6上的最大值为7,最小值为-1,则()()263f f -+-的值为( ) A .5B .-5C .13D .-134.设函数21,2()7,2x x f x x x ⎧-≤⎪=⎨-+>⎪⎩,若互不相等的实数a ,b ,c 满足()()()f a f b f c ==,则222a b c ++的取值范围是( ) A .()8,9 B .()65,129C .()64,128D .()66,1305.函数2()1sin 12xf x x ⎛⎫=-⎪+⎝⎭的图象大致形状为( ). A . B .C .D .6.已知函数()x xf x e e -=-,则不等式()()2210f x f x +--<成立的一个充分不必要条件为( ) A .()2,1- B .()0,1 C .1,12⎛⎫-⎪⎝⎭D .()1,1,2⎛⎫-∞-+∞ ⎪⎝⎭7.已知定义在R 上的偶函数()f x 满足:当0x ≥时,()2x f x =,且(2)(3)f x af x +≤-对一切x ∈R 恒成立,则实数a 的取值范围为( )A .1,32⎡⎫+∞⎪⎢⎣⎭B .1,32⎛⎤-∞ ⎥⎝⎦C .[32,)+∞D .(0,32]8.已知奇函数()f x 在区间[]2,3上单调递增,则()f x 在区间[]3,2--上( ) A .单调递增,且最大值为()2f - B .单调递增,且最大值为()3f - C .单调递减,且最大值为()2f -D .单调递减,且最大值为()3f -9.函数()32241x xxx y -=+的部分图像大致为( )A .B .C .D .10.下列函数中,是奇函数且在()0,∞+上单调递增的是( ) A .y x =B .2log y x =C .1y x x=+D .5y x =11.设函数()f x 的定义域为R ,()()112f x f x +=,当(]0,1x ∈时,()()1f x x x =-.若存在[),x m ∈+∞,使得()364f x =有解,则实数m 的取值范围为( ) A .1,2⎛⎤-∞ ⎥⎝⎦B .3,2⎛⎤-∞ ⎥⎝⎦C .9,4⎛⎤-∞ ⎥⎝⎦D .11,4⎛⎤-∞ ⎥⎝⎦ 12.定义在R 上的奇函数()f x 满足()10f =,且对任意的正数a 、b (ab ),有()()0f a f b a b -<-,则不等式()202f x x -<-的解集是( )A .()()1,12,-+∞B .()(),13,-∞-+∞C .()(),13,-∞+∞D .()(),12,-∞-+∞13.函数()23f x x =-( )A .3⎡⎤⎣⎦B .[]1,5C .2,3⎡⎣D .3⎡⎣14.已知()f x 是R 上的奇函数,且对x ∈R ,有()()2f x f x +=-,当()0,1x ∈时,()21x f x =-,则()2log 41f =( )A .40B .2516 C .2341D .412315.下列函数中,既是偶函数又在(0,+∞)上单调递增的是 ( )A .2x y =B .2yx C .2log y x = D .21y x =+二、填空题16.已知函数()f x 为定义在R 上的奇函数,且对于12,[0,)x x ∀∈+∞,都有()()()221112210x f x x f x x x x x ->≠-,且(3)2f =,则不等式6()f x x>的解集为___________.17.已知定义域为N 的函数()y f x =满足()()()2,105,10x x f x f f x x -≥⎧⎪=⎨+<⎪⎩,则()5f =___________.18.已知函数()y f x =,对任意x ∈R ,都有()()1f x f x a ⋅+=(a 为非零实数),且当[)0,1x ∈时,()2xf x =,则()2021f =___________.19.设2,0()1,0x x f x x -⎧≤=⎨>⎩,则满足()()1 2f x f x +<的实数x 的取值范围是__________.20.设非零实数a ,b 满足224a b +=,若函数21ax by x +=+存在最大值M 和最小值m ,则M m -=_________.21.研究函数())f x a b c =<<<,得到如下命题:①此函数图象关于y 轴对称;②此函数存在反函数;③此函数在()0,a 上为增函数;④此函数有最大值ab c+和最小值0; 你认为其中正确的是_______(写出所有正确的编号).22.定义在()1,1-上的函数()3sin f x x x =--,如果()()2110f a f a -+->,则实数a 的取值范围为______.23.已知()f x 是定义域为R 的奇函数,满足()()3f x f x =+,若()21f =-,则()2020f =______.24.已知函数()()22,0log 11,0ax x f x a x x -≤⎧⎪=⎨⎡⎤++>⎪⎣⎦⎩的值域为[)2,-+∞,则实数a 的取值范围是________.25.如果方程24x +y |y |=1所对应的曲线与函数y =f (x )的图象完全重合,那么对于函数y =f (x )有如下结论:①函数f (x )在R 上单调递减;②y =f (x )的图象上的点到坐标原点距离的最小值为1; ③函数f (x )的值域为(﹣∞,2];④函数F (x )=f (x )+x 有且只有一个零点. 其中正确结论的序号是_____.26.已知甲、乙两地相距150 km ,某人开汽车以60 km/h 的速度从甲地到达乙地,在乙地停留一小时后再以50 km/h 的速度返回甲地,把汽车距甲地的距离s 表示为时间t 的函数,则此函数的表达式为__________.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】由(4)()0f x f x -+=得到()f x 关于(2,0)对称,再由()f x 在[)2,+∞单调递减得到()f x 在R 上单调递减,利用单调性可得答案. 【详解】(4)()0f x f x -+=,则()f x 关于(2,0)对称,因为()f x 在[)2,+∞单调递减,所以()f x 在R 上单调递减, 所以(1)(3)f x f x +=--,由()2(1)0f x x f x +++<得()2(3)0f x x f x +--<, 所以()2(3)f x x f x +<-,所以23x x x +>-,解得1x >或3x <-. 故选:C . 【点睛】思路点睛:利用函数的单调性和奇偶性比较函数值大小的思路: (1)先根据奇偶性将自变量转变至同一单调区间; (2)根据单调性比较同一单调区间内的函数值的大小关系;(3)再结合奇偶性即可判断非同一单调区间的函数值大小,由此得到结果.2.A解析:A 【分析】设(,)P x y 1=,代0x =排除C 、D ,通过奇偶性排除B. 【详解】 解:设(,)P x y因为PA PB a ⋅=,,A B 坐标分别为(1,0)-,(1,0),且1a =1=当0x =时,上式等式成立,即点(0,0)满足PA PB a ⋅=,故排除C 、D.当x -代替x 1== 即图形关于y 轴对称,排除B. 故选:A. 【点睛】应用函数奇偶性可解决的四类问题及解题方法(1)求函数值:将待求值利用奇偶性转化为已知区间上的函数值求解;(2)求解析式:先将待求区间上的自变量转化到已知区间上,再利用奇偶性求解,或充分利用奇偶性构造关于()f x 的方程(组),从而得到()f x 的解析式;(3)求函数解析式中参数的值:利用待定系数法求解,根据()()0f x f x ±-=得到关于待求参数的恒等式,由系数的对等性得参数的值或方程(组),进而得出参数的值; (4)画函数图象和判断单调性:利用奇偶性可画出另一对称区间上的图象及判断另一区间上的单调性.3.D解析:D 【分析】先利用条件找到()31f =-,(6)7f =,再利用()f x 是奇函数求出(3)f -,(6)f -代入即可. 【详解】由题意()f x 在区间[]3,6上是增函数, 在区间[]3,6上的最大值为7,最小值为1-, 得()31f =-,(6)7f =,()f x 是奇函数,(3)2(6)(3)2(6)12713f f f f ∴-+-=--=-⨯=-.故答案为:13-. 【点睛】本题主要考查利用函数的单调性求最值,关键点是利用函数的奇偶性先求函数值,着重考查了推理与运算能力,属于基础题.4.D解析:D 【分析】画出函数()f x 的图象,不妨令a b c <<,则222a b +=.结合图象可得67c <<,从而可得结果. 【详解】画出函数()f x 的图象如图所示.不妨令a b c <<,则1221a b -=-,则222a b +=. 结合图象可得67c <<,故67222c <<. ∴66222130a b c <++<. 故选:D . 【点睛】数形结合是根据数量与图形之间的对应关系,通过数与形的相互转化来解决数学问题的一种重要思想方法,.函数图象是函数的一种表达形式,它形象地揭示了函数的性质,为研究函数的数量关系提供了“形”的直观性.归纳起来,图象的应用常见的命题探究角度有:确定方程根的个数; 求参数的取值范围; 求不等式的解集; 研究函数性质.5.B解析:B 【分析】首先判断函数的奇偶性,再判断0πx <<时,函数值的正负,判断得选项. 【详解】因为2()1sin 12x f x x ⎛⎫=- ⎪+⎝⎭,所以12()sin 12xx f x x -=⋅+, ()()()2221sin 1sin 1212x x xf x x x -⎛⎫⨯⎛⎫-=--=-- ⎪ ⎪++⎝⎭⎝⎭()()21221sin 12x x x ⎛⎫+- ⎪=-- ⎪+⎝⎭221sin 1sin 1212xx x x ⎛⎫⎛⎫=--=- ⎪ ⎪++⎝⎭⎝⎭()f x =,所以函数是偶函数,关于y 轴对称,排除C ,D , 令()0f x =,则21012x-=+或sin 0x =,解得()x k k Z π=∈,而0πx <<时,120x -<,120x +>,sin 0x >,此时()0f x <.故排除A.故选:B . 【点睛】思路点睛:函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置. (2)从函数的单调性,判断图象的变化趋势; (3)从函数的奇偶性,判断图象的对称性; (4)从函数的特征点,排除不合要求的图象.6.B解析:B 【分析】根据解析式可判断出()f x 是定义在R 的增函数且是奇函数,不等式可化为()()221f x f x <+,即得221x x <+,解出即可判断.【详解】可得()f x 的定义域为R ,x y e =和x y e -=-都是增函数,()f x ∴是定义在R 的增函数,()()x x f x e e f x --=-=-,()f x ∴是奇函数,则不等式()()2210f x f x +--<化为()()()2211f xf x f x <---=+,221x x ∴<+,解得112x -<<,则不等式成立的充分不必要条件应是1,12⎛⎫- ⎪⎝⎭的真子集, 只有B 选项满足. 故选:B. 【点睛】本题考查利用函数的单调性和奇偶性解不等式,解题的关键是判断出()f x 是增函数且是奇函数,从而将不等式化为()()221f xf x <+求解.7.C解析:C 【分析】根据题意,可得()f x 的解析式,分别求得当23x -≤≤时,3x >时,2x <-时,(2)f x +和(3)f x -的表达式,结合题意,即可求得a 的范围,综合即可得答案.【详解】由题意知:2,0()2,0x x x f x x -⎧≥=⎨<⎩当23x -≤≤时,20,30x x +≥-≥,所以2322x x a +-≤⋅,所以212x a -≥, 因为23x -≤≤,所以215max (2)232x a -≥==;当3x >时,20,30x x +>-<, 所以2(3)22x x a +--≤⋅,所以5232a ≥=; 当2x <-时,20,30x x +<-> 所以(2)322x x a -+-≤⋅,所以51232a -≥=, 综上32a ≥. 故选:C 【点睛】解题的关键是根据题意求得()f x 的解析式,分类讨论,将(2)f x +和(3)f x -进行转化,考查分类讨论的思想,属中档题.8.A解析:A【分析】利用函数单调性的定义结合奇函数的基本性质可判断函数()f x 在区间[]3,2--上的单调性,进而可得出函数()f x 在区间[]3,2--上的最值. 【详解】任取1x 、[]23,2x ∈--且12x x <,即1232x x -≤<≤-,所以,2123x x ≤-<-≤, 因为函数()f x 在区间[]2,3上单调递增,则()()21f x f x -<-, 因为函数()f x 为奇函数,则()()21f x f x -<-,()()12f x f x ∴<, 因此,函数()f x 在区间[]3,2--上为增函数,最大值为()2f -,最小值为()3f -.故选:A. 【点睛】方法点睛:利用定义证明函数单调性的方法:(1)取值:设1x 、2x 是所给区间上的任意两个值,且12x x <;(2)作差变形:即作差()()12f x f x -,并通过因式分解、配方、有理化等方法,向有利于判断符号的方向变形;(3)定号:确定差()()12f x f x -的符号; (4)下结论:判断,根据定义得出结论. 即取值→作差→变形→定号→下结论.9.A解析:A 【分析】研究函数奇偶性和区间(的函数值的正负,利用排除法即得结果. 【详解】函数()33222()4122x x xxxx x x y f x ---===++,定义域为R , 对于任意的自变量x ,()333222()()222222x x x x x xx x x x x xf x f x -------===++-=-+++,故函数()y f x =是奇函数,图象关于原点中心对称,故CD 错误;又(32()2222x x xxx x x x x y f x ----===++,故(x ∈时,00,0,202x x x x x ->+>-+>,,即()0y f x =<,故A 正确,B 错误. 故选:A. 【点睛】思路点睛:函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势;(3)从函数的奇偶性,判断图象的对称性;(4)从函数的特征点,排除不合要求的图象.10.D解析:D【分析】对四个选项一一一判断:A 、B 不是奇函数,C 是奇函数,但在()0,∞+上不单调.【详解】对于A : y =()0,∞+上单调递增,但是非奇非偶,故A 错误;对于B :2log y x =为偶函数,故B 错误;对于C :1y x x =+在(0,1)单减,在(1,+∞)单增,故C 错误; 对于D :5y x =既是奇函数也在()0,∞+上单调递增,符合题意.故选:D【点睛】四个选项互不相关的选择题,需要对各个选项一一验证.11.D解析:D【分析】根据()()112f x f x +=,可知()()112f x f x =-,可得函数解析式并画出函数图象,由图象可得m 的取值范围.【详解】根据()()112f x f x +=,可知()()112f x f x =-, 又当(]0,1x ∈时,()()110,4f x x x ⎡⎤=-∈⎢⎥⎣⎦, 所以(]1,2x ∈时,(]10,1x -∈,()()111(1)(1)20,228f x f x x x ⎡⎤=-=--∈⎢⎥⎣⎦, (]2,3x ∈时,(]11,2x -∈,()()111(1)(2)30,4416f x f x x x ⎡⎤=-=--∈⎢⎥⎣⎦, (]3,4x ∈时,(]12,3x -∈,()()111(1)(3)40,2832f x f x x x ⎡⎤=-=--∈⎢⎥⎣⎦,即3()64f x <恒成立, 可画出函数图象,当(]2,3x ∈时,13(2)(3)464x x --=,解得94x =或114x =, 故若存在[),x m ∈+∞,使得()364f x =有解,则实数114m ≤, 故选:D. 12.C解析:C【分析】易知函数()f x 在()0,∞+上单调递减,令2t x =-,将不等式()0f t t<等价为()00t f t >⎧⎨<⎩或()00t f t <⎧⎨>⎩,进一步求出答案. 【详解】∵对任意的正数a 、b (a b ),有()()0f a f b a b-<-, ∴函数()f x 在()0,∞+上单调递减,∴()f x 在(),0-∞上单调递减.又∵()10f =,∴()()110f f -=-=令2t x =-所以不等式()0f t t <等价为()00t f t >⎧⎨<⎩或()00t f t <⎧⎨>⎩∴1t >或1t <-,∴21x ->或21x -<-,∴3x >或1x <,即不等式的解集为()(),13,-∞⋃+∞.故选:C.【点睛】本题考查抽象函数的单调性和奇偶性以及不等式的知识点,考查逻辑思维能力,属于基础题.13.A解析:A 【详解】由()()2223682x 31x 3f x x x x =---+-=----,知2680x x -+-≥,解得[]2,4.x ∈令()2t 231x 3x =----,则()21x 323x t --=--.,即为()2y 1x 3=--和y 23x t =--两函数图象有交点,作出函数图象,如图所示:由图可知,当直线和半圆相切时t 最小,当直线过点A(4,0)时,t 最大.3t114-=+,解得35t =±35t =-当直线过点A(4,0)时,2430t ⨯--=,解得t 5=.所以t 35,5⎡⎤∈⎣⎦,即() 35,5f x ⎡⎤∈⎣⎦.故选A.14.C解析:C【分析】由已知得(4)()f x f x +=,由对数函数性质估计出2log 41(5,6)∈,然后利用已知条件把自变量变小为2log 416(1,0)-∈-,再由奇函数定义可求得函数值.【详解】25log 416<<,()()()()()2222f x f x f x f x f x +=-⇒++=-+=⎡⎤⎣⎦, 故()()()()2222log 41log 414log 4166log 41f f f f =-=--=-.∵()26log 410,1-∈,故()26log 41264236log 412114141f --=-=-=. 故选:C .【点睛】本题考查求函数值,方法是由已知条件得出函数的周期性,利用周期性和已知等式把函数自变量变小到(1,0)-上,然后由奇函数定义变到(0,1)上,从而由已知解析式求得函数值.15.D解析:D【解析】根据基本初等函数的性质知,符合条件的是21y x =+,因为满足2()1()f x x f x -=+=,且在(0,)+∞上是增函数,故选D.二、填空题16.【分析】令可得是上的增函数根据为奇函数可得为偶函数且在上是减函数分类讨论的符号将变形后利用的单调性可解得结果【详解】令则对于都有所以是上的增函数因为函数为定义在R 上的奇函数所以所以所以是定义在R 上的 解析:(3,0)(3,)-⋃+∞【分析】令()()g x xf x =,可得()g x 是[0,)+∞上的增函数,根据()f x 为奇函数可得()g x 为偶函数,且在(,0)-∞上是减函数,分类讨论x 的符号,将6()f x x >变形后,利用()g x 的单调性可解得结果.【详解】令()()g x xf x =,则对于12,[0,)x x ∀∈+∞,都有211221()()0()g x g x x x x x ->≠-, 所以()g x 是[0,)+∞上的增函数,因为函数()f x 为定义在R 上的奇函数,所以()()f x f x -=-,所以()()()()g x xf x xf x g x -=--==,所以()g x 是定义在R 上的偶函数,所以()g x 在(,0)-∞上是减函数,当0x >时,6()f x x>化为()63(3)xf x f >=,即()(3)g x g >,因为()g x 是[0,)+∞上的增函数,所以3x >, 当0x <时,6()f x x>化为()6xf x <,因为()f x 为奇函数,且(3)2f =,所以(3)(3)2f f -=-=-,所以()6xf x <化为()3(3)(3)g x f g <--=-,因为()g x 在(,0)-∞上是减函数,所以30x -<<, 综上所述:6()f x x>的解集为(3,0)(3,)-⋃+∞. 故答案为:(3,0)(3,)-⋃+∞ 【点睛】关键点点睛:构造函数()()g x xf x =,利用()g x 的奇偶性和单调性求解是解题关键. 17.9【分析】判断自变量的范围根据分段函数的解析式逐步求解即可解答过程要注意避免出现计算错误【详解】由题知故答案为:9【点睛】方法点睛:对于分段函数解析式的考查是命题的动向之一这类问题的特点是综合性强对 解析:9【分析】判断自变量的范围,根据分段函数的解析式,逐步求解即可,解答过程要注意避免出现计算错误.【详解】由题知,()()()2,105,10x x f x f f x x -≥⎧⎪=⎨+<⎪⎩, ()()()()()()()510,555101028f f f f f f f <∴=+==-=,()()()()()()(85)13811321128190,1f f f f f f f +<∴===-==-=, 故答案为:9.【点睛】方法点睛:对于分段函数解析式的考查是命题的动向之一,这类问题的特点是综合性强,对抽象思维能力要求高,因此解决这类题一定要层次清楚,思路清晰. 当出现(())f f a 的形式时,应从内到外依次求值.18.【分析】推导出函数是周期为的周期函数可得出再由可求得结果【详解】当时则对任意都有(为非零实数)则由可得所以函数是周期为的周期函数因此故答案为:【点睛】方法点睛:函数的三个性质:单调性奇偶性和周期性在 解析:a【分析】推导出函数()f x 是周期为2的周期函数,可得出()()20211f f =,再由()01f =可求得结果.【详解】当[)0,1x ∈时,()2x f x =,则()0021f ==, 对任意x ∈R ,都有()()1f x f x a ⋅+=(a 为非零实数),则()()10f f a ⋅=,()1f a ∴=,由()()1f x f x a ⋅+=可得()()21f x f x a +⋅+=,()()2f x f x ∴+=,所以,函数()f x 是周期为2的周期函数,因此,()()20211f f a ==.故答案为:a .【点睛】方法点睛:函数的三个性质:单调性、奇偶性和周期性,在高考中一般不会单独命题,而是常将它们综合在一起考查,其中单调性与奇偶性结合、周期性与抽象函数相结合,并结合奇偶性求函数值,多以选择题、填空题的形式呈现,且主要有以下几种命题角度;(1)函数的单调性与奇偶性相结合,注意函数的单调性及奇偶性的定义,以及奇、偶函数图象的对称性.(2)周期性与奇偶性相结合,此类问题多考查求值问题,常利用奇偶性及周期性进行交换,将所求函数值的自变量转化到已知解析式的函数定义域内求解;(3)周期性、奇偶性与单调性相结合,解决此类问题通常先利用周期性转化自变量所在的区间,然后利用奇偶性和单调性求解.19.【分析】画出图像结合图像判断题出函数的单调性即可求解【详解】作出函数的图像如图满足解得故答案为:【点睛】方法点睛:该不等式的求解利用的是函数的单调性用数形结合法解决更为直观解析:(),0-∞【分析】画出2,0()1,0x x f x x -⎧≤=⎨>⎩图像,结合图像判断题出函数的单调性,即可求解(1)(2)f x f x +<.【详解】作出函数2,0()1,0x x f x x -⎧≤=⎨>⎩的图像如图,满足(1)(2)f x f x +<2021x x x <⎧∴⎨<+⎩,解得0x <. 故答案为:(),0-∞.【点睛】方法点睛:该不等式的求解利用的是函数的单调性,用数形结合法解决更为直观. 20.2【分析】化简得到根据和得到解得答案【详解】则则即故即即故答案为:2【点睛】本题考查了函数的最值意在考查学生的计算能力和转化能力利用判别式法是解题关键解析:2【分析】化简得到20yx ax y b -+-=,根据0∆≥和224a b +=得到2222b b y -+≤≤,解得答案.【详解】 21ax b y x +=+,则20yx ax y b -+-=,则()240a y y b ∆=--≥, 即22440y yb a --≤,224a b +=,故224440y yb b -+-≤,()()22220y b y b -+--≤⎡⎤⎡⎤⎣⎦⎣⎦,即2222b b y -+≤≤,即22,22b b m M -+==, 2M m -=.故答案为:2.【点睛】本题考查了函数的最值,意在考查学生的计算能力和转化能力,利用判别式法是解题关键. 21.①④【分析】直接利用函数的定义域和函数的奇偶性判断①②进一步利用函数的单调性和函数的对称轴的应用求出函数的最值和单调区间从而判定③④【详解】解:函数由于整理得则:由于函数为偶函数函数的图象关于y 轴对解析:①④【分析】直接利用函数的定义域和函数的奇偶性判断①②,进一步利用函数的单调性和函数的对称轴的应用求出函数的最值和单调区间从而判定③④.【详解】解:函数()(0)||||f x a b c x b x c =<<<++-, 由于220a x -≥,整理得a x a -≤≤.则:()||||f x x b x c b c==++-+. 由于函数为偶函数,函数的图象关于y 轴对称,所以函数不存在反函数,存在反函数的函数的前提该函数具有单调性.故①正确②错误.因为22y a x =-在()0,a 上为减函数,所以()f x 在()0,a 上为减函数,故故③错误;可知()f x 在[],0a -单调递增,()0,a 单调递减,且为偶函数,则()f x 在0x =出取得最大值a b c+,在x a =±处取得最小值0,故④正确. 故答案为:①④.【点睛】本题考查函数性质的应用,属于基础题. 22.【分析】先得出函数是奇函数且是减函数从而得到结合函数的定义域从而求出的范围【详解】解:是奇函数又是减函数若则则解得:或由解得:综上:故答案为:【点睛】本题考查了函数的奇偶性函数的单调性的应用属于中档题解析:(【分析】先得出函数是奇函数且是减函数,从而得到211a a -<-,结合函数的定义域,从而求出a 的范围.【详解】解:()3sin (3sin )()f x x x x x f x -=-=-+=-,是奇函数, 又()3cos 0f x x '=-+<,是减函数,若2(1)(1)0f a f a -+->,则2((1))1f a f a -->,则211a a -<-,解得:1a >或2a <-,由2111111a a -<-<⎧⎨-<-<⎩,解得:0a <<,综上:1a <<故答案为:(.【点睛】本题考查了函数的奇偶性,函数的单调性的应用,属于中档题.23.1【分析】首先根据题中所给的条件判断出函数的最小正周期结合奇函数的定义求得结果【详解】因为所以函数是以3为周期的周期函数且是定义域为的奇函数所以故答案为:1【点睛】该题考查的是有关函数的问题涉及到的 解析:1【分析】首先根据题中所给的条件,判断出函数的最小正周期,结合奇函数的定义,求得结果.【详解】因为()()3f x f x =+,所以函数()f x 是以3为周期的周期函数,且是定义域为R 的奇函数,所以(2020)(67432)(2)(2)1f f f f =⨯-=-=-=,故答案为:1.【点睛】该题考查的是有关函数的问题,涉及到的知识点有函数奇偶性与周期性的综合应用,属于简单题目.24.【分析】根据题意分析函数的单调性结合函数的最小值为可得出关于实数的不等式组由此可求得实数的取值范围【详解】由于函数的值域为则函数在区间上单调递减或为常值函数函数在区间上单调递增或为常值函数①若函数在 解析:[)1,0-【分析】根据题意分析函数()y f x =的单调性,结合函数()y f x =的最小值为2-可得出关于实数a 的不等式组,由此可求得实数a 的取值范围.【详解】由于函数()()22,0log 11,0ax x f x a x x -≤⎧⎪=⎨⎡⎤++>⎪⎣⎦⎩的值域为[)2,-+∞, 则函数()2f x ax =-在区间(],0-∞上单调递减或为常值函数,函数()()2log 11f x a x =++⎡⎤⎣⎦在区间()0,∞+上单调递增或为常值函数.①若函数()2f x ax =-在区间(],0-∞上单调递减,则0a <,此时()()02f x f ≥=-, 且此时函数()()2log 11f x a x =++⎡⎤⎣⎦在区间()0,∞+上单调递增或为常值函数, 则10a +≥,解得1a ≥-,当0x >时,()()22log 11log 10f x a x =++≥=⎡⎤⎣⎦, 即当10a -≤<时,函数()y f x =的值域为[)2,-+∞;②若函数()2f x ax =-在区间(],0-∞为常值函数,则0a =,当0x ≤时,()2f x =-,当0x >时,()()22log 1log 10f x x =+>=,即当0a =时,函数()y f x =的值域为{}()20,-+∞,不合乎题意.综上所述,实数a 的取值范围是[)1,0-.故答案为:[)1,0-.【点睛】本题考查利用分段函数的值域求参数,要结合题意分析函数的单调性,考查分析问题和解决问题的能力,属于中等题. 25.②④【分析】根据题意画出方程对应的函数图象根据图像判断函数单调性值域最值以及函数零点个数的判断数形结合即可选择【详解】当y≥0时方程y|y|=1化为(y≥0)当y <0时方程y|y|=1化为(y <0)解析:②④【分析】根据题意,画出方程对应的函数图象,根据图像判断函数单调性、值域、最值以及函数零点个数的判断,数形结合即可选择.【详解】当y ≥0时,方程24x +y |y |=1化为2214x y +=(y ≥0), 当y <0时,方程24x +y |y |=1化为2214x y -=(y <0). 作出函数f (x )的图象如图:由图可知,函数f (x )在R 上不是单调函数,故①错误;y =f (x )的图象上的点到坐标原点距离的最小值为1,故②正确;函数f (x )的值域为(﹣∞,1],故③错误;双曲线2214x y -=的渐近线方程为y 12=±, 故函数y =f (x )与y =﹣x 的图象只有1个交点,即函数F (x )=f (x )+x 有且只有一个零点,故④正确.故答案为:②④.【点睛】本题考查函数单调性、值域以及零点个数的判断,涉及椭圆和双曲线的轨迹绘制,以及数形结合的数学思想,属综合中档题.26.【分析】算出该人从甲地到乙地所用时间和从乙地返回到甲地所用时间即可得到本题函数的定义域将其分为三段再结合各个时间段上该人的运动状态可得汽车离甲地的距离距离(千米)与时间(小时)的函数表达式【详解】根解析:60,0 2.5,150,2.5 3.5,32550,3.5 6.5t t s t t t ≤≤⎧⎪=<<⎨⎪-≤≤⎩【分析】算出该人从甲地到乙地所用时间和从乙地返回到甲地所用时间,即可得到本题函数的定义域,将其分为三段,再结合各个时间段上该人的运动状态,可得汽车离甲地的距离距离s (千米)与时间t (小时)的函数表达式.【详解】根据题意此人运动的过程分为三个时段,当0 2.5t ≤≤时,60s t =;当2.5 3.5t <<时,150s =;当3.5 6.5t ≤≤时,()15050 3.532550t t t =--=-.综上所述,60,0 2.5,150,2.5 3.5,32550,3.5 6.5.t t s t t t ≤≤⎧⎪=<<⎨⎪-≤≤⎩故答案为60,0 2.5,150,2.5 3.5,32550,3.5 6.5.t t s t t t ≤≤⎧⎪=<<⎨⎪-≤≤⎩【点睛】本题考查分段函数应用题,求函数表达式,着重考查基本初等函数的应用和分段函数的理解等知识,属于基础题.。
湖南省长沙县实验中学函数的概念与基本初等函数多选题试题含答案

湖南省长沙县实验中学函数的概念与基本初等函数多选题试题含答案一、函数的概念与基本初等函数多选题1.已知函数()()()sin 0f x x ωϕω=+>满足()01()12f x f x +=-=0,且()f x 在()00,1x x +上有最小值,无最大值.则下列说法正确的是()A .01()12f x +=- B .若00x =,则()sin 26f x x ππ⎛⎫=-⎪⎝⎭C .()f x 的最小正周期为3D .()f x 在()0,303上的零点个数最少为202个 【答案】AC 【分析】由题意知()00,1x x +在一个波谷的位置且有对称性,有01()12f x +=-且23πω=,进而可判断A 、B 、C 的正误,又[0,303]上共有101个周期,最多有203个零点,最少有202个零点,进而可知()0,303零点个数最少个数,即知D 的正误. 【详解】由()01()12f x f x +=-=0,且()f x 在()00,1x x +上有最小值,无最大值,∴()00,1x x +在一个波谷的位置且有对称性,即01()12f x +=-,002(1)()3x x πωϕωϕω++-+==, ∴()f x 的最小正周期为23T πω==,故A 、C 正确,B 错误;在[0,303]上共有101个周期,若每个周期有两个零点时,共有202个零点,此时区间端点不为零点;若每个周期有三个零点时,共有203个零点,此时区间端点为零点; ∴()0,303上零点个数最少为201个,即每个周期有三个零点时,去掉区间的两个端点,故D 错误. 故选:AC. 【点睛】关键点点睛:由条件推出()00,1x x +在一个波谷的位置且有对称性,可确定01()2f x +及最小正周期,再由正弦函数的性质判断()0,303上零点个数,进而确定最少有多少个零点.2.对于定义在R 上的函数()f x ,若存在正实数a ,b ,使得()()f x a f x b +≤+对一切x ∈R 均成立,则称()f x 是“控制增长函数”.在以下四个函数中是“控制增长函数”的有( ) A .()xf x e =B .()f x =C .()()2sin f x x=D .()sin f x x x =⋅【答案】BCD 【分析】假设各函数是“控制增长函数”,根据定义推断()()f x a f x b +≤+对一切x ∈R 恒成立的条件,并判断,a b 的存在性,即可得出结论. 【详解】对于A. ()()f x a f x b +≤+可化为22()()11x a x a x x b ++++≤+++,22ax a a b ≤--+0a >,不等式在x ∈R 上不恒成立,所以2()1f x x x =++不是“控制增长函数”;对于B. ()()f x a f x b +≤+可化为,b ≤,即2||||2x a x b +≤++恒成立.又||||x a x a +≤+,故只需保证2||||2x a x b +≤++.20,2a b b b->≥ ,当220a b -≤时,b ≤恒成立,()f x ∴=“控制增长函数”;对于C.()21()sin 1,()()2f x x f x a f x -≤=≤∴+-≤,2b ∴≥时,a 为任意正数,()()f x a f x b +≤+恒成立, ()2()sin f x x ∴=是“控制增长函数”;对于D. ()()f x a f x b +≤+化为,()sin()sin x a x a x x b ++≤+,令2a π= ,则(2)sin sin ,2sin x x x x b x b ππ+≤+≤,当2b π≥时,不等式()sin()sin x a x a x x b ++≤+恒成立,()sin f x x x ∴=⋅是“控制增长函数”.故选:BCD 【点睛】本题考查了新定义的理解,函数存在成立和恒成立问题的研究.我们可先假设结论成立,再不断寻求结论成立的充分条件,找得到就是“控制增长函数”.如果找出了反例,就不是“控制增长函数”.3.已知函数()()2214sin 2x xe xf x e -=+,则下列说法正确的是( )A .函数()y f x =是偶函数,且在(),-∞+∞上不单调B .函数()y f x '=是奇函数,且在(),-∞+∞上不单调递增C .函数()y f x =在π,02⎛⎫- ⎪⎝⎭上单调递增D .对任意m ∈R ,都有()()f m f m =,且()0f m ≥【答案】AD 【分析】由函数的奇偶性以及函数的单调性即可判断A 、B 、C 、D. 【详解】 解:对A ,()()222114sin =2cos 2xx xx e x e f x x e e-+=+-,定义域为R ,关于原点对称,()2211=2cos()2cos()()x x x xe ef x x x f x e e --++---=-=,()y f x ∴=是偶函数,其图像关于y 轴对称,()f x ∴在(),-∞+∞上不单调,故A 正确;对B ,1()2sin xxf x e x e '=-+, 11()2sin()=(2sin )()x xx xf x e x e x f x e e --''-=-+---+=-, ()f x '∴是奇函数,令1()2sin xxg x e x e =-+, 则1()+2cos 2+2cos 0x xg x e x x e '=+≥≥, ()f x '∴在(),-∞+∞上单调递增,故B 错误;对C ,1()2sin x x f x e x e'=-+,且()'f x 在(),-∞+∞上单调递增, 又(0)0f '=,π,02x ⎛⎫∴∈- ⎪⎝⎭时,()0f x '<,()y f x ∴=在π,02⎛⎫- ⎪⎝⎭上单调递减,故C 错误;对D ,()y f x =是偶函数,且在(0,)+∞上单调递增,()()f m f m ∴=,且()(0)0f m f ≥=,故D 正确.故选:AD. 【点睛】用导数求函数的单调区间或判断函数的单调性问题时应注意如下几方面: (1)在利用导数讨论函数的单调区间时,首先要确定函数的定义域; (2)不能随意将函数的2个独立的单调递增(或递减)区间写成并集形式;(3)利用导数解决含参函数的单调性问题时,一般将其转化为不等式恒成立问题,解题过程中要注意分类讨论和数形结合思想的应用.4.已知定义在R 上的函数()f x 的图象连续不断,若存在常数()t t R ∈,使得()()0f x t tf x ++=对任意的实数x 成立,则称()f x 是回旋函数.给出下列四个命题中,正确的命题是( )A .常值函数()(0)f x a a =≠为回旋函数的充要条件是1t =-;B .若(01)x y a a =<<为回旋函数,则1t >;C .函数2()f x x =不是回旋函数;D .若()f x 是2t =的回旋函数,则()f x 在[0]4030,上至少有2015个零点. 【答案】ACD 【分析】A.利用回旋函数的定义即可判断;B.代入回旋函数的定义,推得矛盾,判断选项;C.利用回旋函数的定义,令0x =,则必有0t = ,令1x =,则2310t t ++=,推得矛盾;D.根据回旋函数的定义,推得()()22f x f x +=-,再根据零点存在性定理,推得零点的个数. 【详解】A.若()f x a =,则()f x t a +=,则0a ta +=,解得:1t =-,故A 正确;B.若指数函数()01xy a a =<<为回旋函数,则0x t x a ta ++=,即0t a t +=,则0t <,故B 不正确;C.若函数()2f x x =是回旋函数,则()220x t tx ++=,对任意实数都成立,令0x =,则必有0t = ,令1x =,则2310t t ++=,显然0t =不是方程的解,故假设不成立,该函数不是回旋函数,故C 正确;D. 若()f x 是2t =的回旋函数,则()()220f x f x ++=,对任意的实数x 都成立,即有()()22f x f x +=-,则()2f x +与()f x 异号,由零点存在性定理得,在区间(),2x x +上必有一个零点,可令0,2,4,...20152x =⨯,则函数()f x 在[]0,4030上至少存在2015个零点,故D 正确. 故选:ACD 【点睛】本题考查以新定义为背景,判断函数的性质,重点考查对定义的理解,应用,属于中档题型.5.已知直线2y x =-+分别与函数x y e =和ln y x =的图象交于点()()1122,,,A x y B x y ,则下列结论正确的是( ) A .122x x +=B .122x x e e e +>C .1221ln ln 0x x x x +<D .122e x x >【答案】ABC 【分析】根据互为反函数的性质可得()()1122,,,A x y B x y 的中点坐标为()1,1,从而可判断A ;利用基本不等式可判断B 、D ;利用零点存在性定理以及对数的运算性质可判断C. 【详解】函数xy e =与ln y x =互为反函数, 则xy e =与ln y x =的图象关于y x =对称,将2y x =-+与y x =联立,则1,1x y ==,由直线2y x =-+分别与函数xy e =和ln y x =的图象交于点()()1122,,,A x y B x y ,作出函数图像:则()()1122,,,A x y B x y 的中点坐标为()1,1, 对于A ,由1212x x +=,解得122x x +=,故A 正确; 对于B ,12121222222x x x x x x e e e e e e e +≥=+⋅==, 因为12x x ≠,即等号不成立,所以122x x e e e +>,故B 正确;对于C ,将2y x =-+与xy e =联立可得2x x e -+=,即20x e x +-=,设()2xf x e x =+-,且函数为单调递增函数,()010210f =+-=-<,112211320222f e e ⎛⎫=+-=-> ⎪⎝⎭,故函数的零点在10,2⎛⎫ ⎪⎝⎭上,即1102x <<,由122x x +=,则212x <<, 122112211ln ln ln lnx x x x x x x x +=- ()1222122ln ln ln 0x x x x x x x <-=-<,故C 正确;对于D,由12x x +≥,解得121x x ≤, 由于12x x ≠,则121x x <,故D 错误; 故选:ABC 【点睛】本题考查了互为反函数的性质、基本不等式的应用、零点存在性定理以及对数的运算性质,考查了数形结合的思想,属于难题.6.若定义在R 上的函数()f x 满足()()0f x f x ,当0x <时,23()22f x x ax a =++(a ∈R ),则下列说法正确的是( )A .若方程()2af x ax =+有两个不同的实数根,则0a <或48a << B .若方程()2af x ax =+有两个不同的实数根,则48a << C .若方程()2af x ax =+有4个不同的实数根,则8a > D .若方程()2af x ax =+有4个不同的实数根,则4a > 【答案】AC 【分析】由题知()f x 是R 上的奇函数,则由0x <时的解析式可求出()f x 在R 上的解析式.先讨论特殊情况0x =为方程的根,则可求出0a =,此时方程化为()0f x =,而函数()f x 为R 上的减函数,则方程仅有一个根.当0x ≠时,由分段函数分类讨论得出0x <时,1(1)2(1)a x x =-+++-+,0x >时,4242a x x =-++-.利用数形结合思想,画出图象,则可得知方程()2af x ax =+不同的实数根个数分别为2个和4时,参数a 的取值范围. 【详解】 因为()()0f x f x 所以()()f x f x -=-,所以()f x 是R 上的奇函数,(0)0f =, 当0x >时,0x -<,23()22f x x ax a -=-+, 所以23()()22f x f x x ax a =--=-+-, 综上2232,02()0,032,02x ax a x f x x x ax a x ⎧++<⎪⎪==⎨⎪⎪-+->⎩,若0x =是方程()2af x ax =+的一个根, 则0a =,此时()2af x ax =+,即()0f x =, 而22,0()0,0,0x x f x x x x ⎧<⎪==⎨⎪->⎩,在R 上单调递减,当0a =时,原方程有一个实根. 当0x <时,23222a x ax a ax ++=+, 所以20x ax a ++=,当1x =-时不满足,所以21(1)21(1)x a x x x =-=-++++-+, 当0x >时,23222ax ax a ax -+-=+, 所以220x ax a -+=,当2x =时不满足,所以242422x a x x x ==-++--,如图:若方程()2af x ax =+有两个不同的实数根,则0a <或48a <<; 若方程()2af x ax =+有4个不同的实数根,则8a >. 故选:AC 【点睛】关键点点睛:本题的关键是将方程()2af x ax =+进行参数分离,再借助数形结合法,求出对应的参数的取值范围.7.已知函数()22,1,1x x f x x x -≥⎧=⎨<⎩,若存在实数a ,使得()()f a f f a ⎡⎤=⎣⎦,则a 的个数不是( ) A .2 B .3C .4D .5【答案】ABD 【分析】令()f a t =,即满足()f t t =,对t 进行分类讨论,结合已知函数解析式代入即可求得满足题意的t ,进而求得a. 【详解】令()f a t =,即满足()f t t =,转化为函数()1y f t =与2y t =有交点,结合图像由图可知,()f t t =有两个根0t =或1t = (1)当1t =,即()1f a =,由()22,1,1a a f a a a -≥⎧=⎨<⎩,得1a =±时,经检验均满足题意; (2)当0t =,即()0f a =,当1a ≥时,()20f a a =-=,解得:2a =;当1a <时,()20f a a ==,解得:0a =;综上所述:共有4个a . 故选:ABD . 【点睛】方法点睛:已知函数有零点(方程有根)求参数值(取值范围)常用的方法:(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围; (2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图像,利用数形结合的方法求解8.狄利克雷是德国著名数学家,是最早倡导严格化方法的数学家之一,狄利克雷函数()1,0,x Q f x x Q ∈⎧=⎨∉⎩(Q 是有理数集)的出现表示数学家对数学的理解开始了深刻的变化,从研究“算”到研究更抽象的“概念、性质、结构”.关于()f x 的性质,下列说法正确的是( )A .函数()f x 是偶函数B .函数()f x 是周期函数C .对任意的1x R ∈,2x ∈Q ,都有()()121f x x f x +=D .对任意的1x R ∈,2x ∈Q ,都有()()121f x x f x ⋅= 【答案】ABC 【分析】利用函数奇偶性的定义可判断A 选项的正误;验证()()1f x f x +=,可判断B 选项的正误;分1x Q ∈、1x Q ∉两种情况讨论,结合函数()f x 的定义可判断C 选项的正误;取20x =,1x Q ∉可判断D 选项的正误.【详解】对于A 选项,任取x Q ∈,则x Q -∈,()()1f x f x ==-; 任取x Q ∉,则x Q -∉,()()0f x f x ==-.所以,对任意的x ∈R ,()()f x f x -=,即函数()f x 为偶函数,A 选项正确; 对于B 选项,任取x Q ∈,则1x Q +∈,则()()11f x f x +==; 任取x Q ∉,则1x Q +∉,则()()10f x f x +==.所以,对任意的x ∈R ,()()1f x f x +=,即函数()f x 为周期函数,B 选项正确; 对于C 选项,对任意1x Q ∈,2x ∈Q ,则12x Q x +∈,()()1211f x x f x +==; 对任意的1x Q ∉,2x ∈Q ,则12x x Q +∉,()()1210f x x f x +==. 综上,对任意的1x R ∈,2x ∈Q ,都有()()121f x x f x +=,C 选项正确; 对于D 选项,取20x =,若1x Q ∉,则()()()12101f x x f f x ⋅==≠,D 选项错误. 故选:ABC. 【点睛】关键点点睛:本题解题的关键在于根据已知函数的定义依次讨论各选项,分自变量为无理数和有理数两种情况讨论,对于D 选项,可取1x Q ∉,20x =验证.二、导数及其应用多选题9.若存在常数k 和b ,使得函数()F x 和()G x 对其公共定义域上的任意实数x 都满足:()F x kx b ≥+和()G x kx b ≤+恒成立,则称此直线y kx b =+为()F x 和()G x 的“隔离直线”.已知函数()22x f x =(x ∈R ),()12g x x =(0x <),()ln h x e x =,(e 为自然对数的底数),则( )A .()()()m x f x g x =-在0x ⎛⎫∈ ⎪⎝⎭内单调递减 B .()f x 和()g x 之间存在“隔离直线”,且b 的最小值为2- C .()f x 和()g x 之间存在“隔离直线”,且k 的取值范围是[]2,1-D .()f x 和()g x 之间存在唯一的“隔离直线”,方程为2ey =-【答案】BD 【分析】对于A :令()()()m x f x g x =-,利用导数可确定()m x 单调性,进而作出判断; 对于B 和C :利用二次函数的性质以及不等式恒成立的知识求出b 、k 的范围,进而作出判断;对于选项D :根据隔离直线过()f x 和()h x 的公共点,可假设隔离直线为2e y kx =-;可得到222x ekx ≥-,再利用恒成立得出k 的值,最后尝试利用导数证明()2eh x ≤-,进而作出判断. 【详解】对于A ,()()()2122x m x f x g x x =-=-, ()322121022x m x x x x+'∴=+=>, 当x ⎛⎫∈ ⎪⎝⎭时,()0m x '>,()m x ∴单调递增,故A 错误; 对于B ,C ,设()f x ,()g x 的隔离直线为y kx b =+,22x kx b ≥+对任意x ∈R 恒成立,即2220x kx b --≥对任意x ∈R 恒成立,所以21480k b ∆=+≤,所以0b ≤,又12kx b x ≤+对任意(),0x ∈-∞恒成立,即22210kx bx +-≤对任意(),0x ∈-∞恒成立,因为0b ≤,所以0k ≤且21480b k ∆=+≤,所以22k b ≤-且22b k ≤-,4248k b b ≤≤-,解得20k -≤≤,同理20b -≤≤, 所以b 的最小值为2-,k 的取值范围是[]2,0-, 故B 正确,C 错误; 对于D ,函数()f x 和()h x的图象在x =∴若存在()f x 和()h x 的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为k,则隔离直线方程为(2e y k x -=,即2e y kx =-,则222x ekx ≥-(x ∈R),得2220x kx e -+≥对x ∈R 恒成立,则()24420k e ∆=-≤,解得k =,此时隔离直线方程为:2ey =-,下面证明()2e h x ≤-, 令()()ln 22e e G x h x e x =--=--(0x >),则()x G x x'=,当x =()0G x '=;当0x <<()0G x '<;当x >()0G x '>;∴当x =()G x 取到极小值,也是最小值,即()0min G x G==,()()02e G x h x ∴=--≥在()0,∞+上恒成立,即()2eh x ≤-,∴函数()f x 和()h x存在唯一的隔离直线2ey =-,D 正确. 故选:BD . 【点睛】关键点睛:本题考查导数中的新定义问题的求解;解题关键是能够充分理解“隔离直线”的定义,将问题转化为根据不等式恒成立求解参数范围或参数值、或不等式的证明问题,属于难题.10.设函数3()(,)f x x ax b a b R =++∈,下列条件中,使得()y f x =有且仅有一个零点的是( )A .1,2a b ==B .3,3a b =-=-C .0,2a b ><D .0,0a b <>【答案】ABC 【分析】求导2()3f x x a '=+,分0a ≥和0a <进行讨论,当0a ≥时,可知函数单调递增,有且只有一个零点;当0a <时,讨论函数的单调性,要使函数有一个零点,则需比较函数的极大值与极小值与0的关系,再验证选项即可得解. 【详解】3()f x x ax b =++,求导得2()3f x x a '=+当0a ≥时,()0f x '≥,()f x ∴单调递增,当x →-∞时,()f x →-∞;当x →+∞时,()f x →+∞;由零点存在性定理知,函数()f x 有且只有一个零点,故A ,C 满足题意;当0a <时,令()0f x '=,即230x a +=,解得13ax -=-,23a x -= 当x 变化时,()'f x ,()f x 的变化情况如下表:x,3a ⎛⎫--∞- ⎪ ⎪⎝⎭3a-- ,33a a ⎛⎫--- ⎪ ⎪⎝⎭3a- ,3a ⎛⎫-+∞ ⎪ ⎪⎝⎭()'f x+-+()f x极大值 极小值故当3ax -=-,函数()f x 取得极大值2333333a a a a a a f a b b ⎛⎫-----=-+=-+ ⎪ ⎪⎝⎭, 当3a x -=,函数()f x 取得极小值2333333a a a a a a f a b b ⎛⎫-----=++=+ ⎪ ⎪⎝⎭又当x →-∞时,()f x →-∞;当x →+∞时,()f x →+∞; 要使函数()f x 有且只有一个零点,作草图或则需00f f ⎧⎛<⎪ ⎪⎝⎨⎪<⎪⎩,即00b b ⎧<⎪⎪<,即0b <<,B 选项,3,3a b =-=-,满足上式,故B 符合题意;则需00f f ⎧⎛>⎪ ⎪⎝⎨⎪>⎪⎩,即00b b ⎧>⎪⎪>,即0b >>,D 选项,0,0a b <>,不一定满足,故D 不符合题意; 故选:ABC 【点睛】思路点睛:本题考查函数的零点问题,如果函数()y f x =在区间[,]a b 上的图像是连续不断的一条曲线,并且有()()0f a f b <,那么,函数()y f x =在区间(),a b 内有零点,即存在(),c a b ∈,使得()0f c =,这个c 也就是方程()0f x =的根,考查学生的逻辑推理与运算能力,属于较难题.。
长沙市必修一第二单元《函数》测试题(有答案解析)

一、选择题1.令[]x 表示不超过x 的最大整数,例如,[]3.54-=-,[]2.12=,若函数()[][]32f x x x =-,则函数()f x 在区间[]0,2上所有可能取值的和为( )A .1B .2C .3D .42.已知函数()f x =的定义域为R ,则实数m 的取值范围是( )A .04m ≤≤B .04m <≤C .04m ≤<D .04m <<3.已知函数()32f x x =-,2()2g x x x =-,(),()()()(),()()g x f x g x F x f x f x g x ≥⎧=⎨<⎩,则( )A .()F x 的最大值为3,最小值为1B .()F x 的最大值为2C .()F x 的最大值为7-,无最小值D .()F x 的最大值为3,最小值为-14.若函数()f x =在[]1,3-上具有单调性,则实数a 的可能取值是( )A .4-B .5C .14D .235.已知函数f (x )满足f (x -1)=2f (x ),且x R ∈,当x ∈[-1,0)时,f (x )=-2x -2x +3,则当x ∈[1,2)时,f (x )的最大值为( ) A .52B .1C .0D .-16.设0a >且1a ≠,函数221x x y a a =+-在区间[]1,1-上的最大值是14,则实数a 的值为( ) A .13或2 B .2或3C .12或2 D .13或3 7.已知函数()f x 是R 上的单调函数,且对任意实数x ,都有()21213xf f x ⎡⎤+=⎢⎥+⎣⎦成立,则()2020f 的值是( ) A .202021-B .202021+C .202020202121+-D .202020202121-+8.如果()()211f x mx m x =+-+在区间(]1-∞,上为减函数,则m 的取值范围( ) A .103⎛⎤⎥⎝⎦,B .103⎡⎤⎢⎥⎣⎦,C .103⎡⎫⎪⎢⎣⎭,D .103⎛⎫ ⎪⎝⎭,9.已知函数()f x 是奇函数,()f x 在(0,)+∞上是减函数,且在区间[,](0)a b a b <<上的值域为[3,4]-,则在区间[,]b a --上( )A .有最大值4B .有最小值-4C .有最大值-3D .有最小值-310.函数f (x )=x 2+2ln||2x x的图象大致为( ) A . B .C .D .11.若函数32()21f x ax x x =+++在(1,2)上有最大值无最小值,则实数a 的取值范围为( ) A .34a >-B .53a <-C .5334a -<<- D .5334a -≤≤- 12.若函数()()12311ax f x x a x x ⎧>⎪=⎨⎪-+≤⎩是R 上的减函数,则实数a 的取值范围是( )A .2,13⎛⎫⎪⎝⎭B .3,14⎡⎫⎪⎢⎣⎭C .23,34⎛⎤⎥⎝⎦D .2,3⎛⎫+∞⎪⎝⎭二、填空题13.已知1()1x f x x +=-,则135199()()()()100100100100f f f f ++++=______________14.已知存在[1,)x ∈+∞,不等式2212a x x x ≥-+成立,则实数a 的取值范围是__________.15.函数222421x x y x ++=+的值域为_________. 16.已知函数()()14f x a ax =--[]0,2上是减函数,则实数a 的取值范围是_____.17.已知函数y =f (n),满足f (1)=2,且f (n+1)=3f (n),n ∈N + .则f (3)=____________. 18.设函数f (x )满足:对任意的x 1,x 2∈R 都有(x 1-x 2)[f (x 1)-f (x 2)]>0,则f (-3)与f (-π)的大小关系是________.19.已知函数()2(1)mf x m m x =--是幂函数,且()f x 在(0,)+∞上单调递增,则实数m =________.20.若函数2()f x x k =+,若存在区间[,](,0]a b ⊆-∞,使得当[,]x a b ∈时,()f x 的取值范围恰为[,]a b ,则实数k 的取值范围是________.三、解答题21.已知函数2()7f x x mx m =++-,m R ∈.(1)若()f x 在区间[2,4]上单调递增,求m 的取值范围; (2)求()f x 在区间[1,1]-上的最小值()g m ;22.在①()()121f x f x x +=+-,②()()11f x f x +=-且()03f =,③()2f x ≥恒成立且()03f =这三个条件中任选一个,补充在下面的问题中,并作答.问题:已知二次函数()f x 的图象经过点()1,2,_________. (1)求()f x 的解析式; (2)求()f x 在[]1,4-上的值域.23.已知函数2()21,[1,3]f x ax bx x =++∈(,a b ∈R 且,a b 为常数) (1)若1a =,求()f x 的最大值;(2)若0a >,1b =-,且()f x 的最小值为4-,求a 的值. 24.已知函数()2mf x x x=++(m 为实常数). (1)当4m =时,试判断函数在[)2,+∞上的单调性,并用定义证明; (2)设0m <,若不等式()f x kx ≤在1[,1]2x ∈有解,求实数k 的取值范围. 25.已知函数()21ax bf x x +=+是()1,1-上的奇函数,且12.25f ⎛⎫= ⎪⎝⎭ (1)求()f x 的解析式;(2)判断()f x 的单调性,并加以证明;(3)若实数t 满足()()10f t f t ++>,求t 的取值范围. 26.已知函数2()2(1)4f x x k x =+-+.(Ⅰ)若函数()f x 在区间[2,4]上具有单调性,求实数k 的取值范围; (Ⅱ)若()0f x >对任意的[1,2]x ∈恒成立,求实数k 的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题1.B 解析:B 【分析】根据[]x 表示不超过x 的最大整数,分5种情况讨论,分别求出[]x 和[2]x 的值,即可以计算()3[][2]f x x x =-的函数值,相加即可得答案. 【详解】因为[]x 表示不超过x 的最大整数,所以: 当102x <时,有021x <,则[]0x =,则3[]0x =,[2]0x =,此时()0f x =, 当112x <时,有122x <,则[]0x =,则3[]0x =,[2]1x =,此时()1f x =-, 当312x <时,有223x <,则[]1x =,则3[]3x =,[2]2x =,此时()1f x =, 当322x <时,有324x <,则[]1x =,则3[]3x =,[2]3x =,此时()0f x =, 当2x =时,24=x ,则[]2x =,则3[]6x =,[2]4x =,此时()2f x =, 函数()f x 在区间[0,2]上所有可能取值的和为011022-+++=; 故选:B . 【点睛】结论点睛:分类讨论思想的常见类型(1)问题中的变量或含有需讨论的参数的,要进行分类讨论的; (2)问题中的条件是分类给出的;(3)解题过程不能统一叙述,必须分类讨论的;(4)涉及几何问题时,由几何元素的形状、位置的变化需要分类讨论的.2.C解析:C 【分析】由题意可知,对任意的x ∈R ,210mx mx ++>恒成立,然后分0m =和0m ≠,结合题意可得出关于实数m 的不等式组,由此可解得实数m 的取值范围. 【详解】由题意可知,对任意的x ∈R ,210mx mx ++>恒成立. 当0m =时,则有10>,合乎题意; 当0m ≠时,则有240m m m >⎧⎨∆=-<⎩,解得04m <<. 综上所述,04m ≤<. 故选:C. 【点睛】结论点睛:利用二次不等式在实数集上恒成立,可以利用以下结论来求解:设()()20f x ax bx c a =++≠①()0f x >在R 上恒成立,则00a >⎧⎨∆<⎩;②()0f x <在R 上恒成立,则00a <⎧⎨∆<⎩;③()0f x ≥在R 上恒成立,则00a >⎧⎨∆≤⎩; ④()0f x ≤在R 上恒成立,则00a <⎧⎨∆≤⎩.3.C解析:C 【分析】在同一坐标系中先画出()f x 与()g x 的图象,然后根据定义画出()F x ,就容易看出()F x 有最大值,无最小值,解出两个函数的交点,即可求得最大值. 【详解】在同一坐标系中先画出()f x 与()g x 的图象,如图然后根据定义画出()F x ,就容易看出()F x 有最大值,无最小值. 由图象可知,当0x <时,()y F x =取得最大值, 所以由232||2x x x -=-得27x =+或27x =-.结合函数图象可知当27x =-时,函数()F x 有最大值727-,无最小值. 故选:C .【点睛】关键点睛:本题主要考查了函数的图象,以及利用函数求最值,解答本题的关键是在同一坐标系中画出()f x 与()g x 的图象,根据图象得出函数的最值,由232||2x x x -=-得27x =+或27x =-.解析:C 【分析】令函数()218g x x ax =-++,则只需使当[]1,3x ∈-时,()0g x ≥且单调,然后针对()3210a g ⎧≥⎪⎨⎪-≥⎩或()1230ag ⎧≤-⎪⎨⎪≥⎩两种情况讨论求解. 【详解】由题意可设()218g x x ax =-++,则当[]1,3x ∈-时,()218g x x ax =-++单调,且()0g x ≥恒成立,因为()218g x x ax =-++的对称轴方程为2a x =, 则()3210a g ⎧≥⎪⎨⎪-≥⎩或()1230ag ⎧≤-⎪⎨⎪≥⎩,解得617a ≤≤或32a --≤≤,即[][]6,173,2a ∈--,则只有14满足题意. 故选:C . 【点睛】本题考查根据复合函数的单调性求参数的取值范围,解答时注意不仅要使原函数在所给区间上单调,且必须使原函数在所给区间上有意义.5.B解析:B 【分析】 首先设[)1,2x ∈,利用函数满足的关系式,求函数的解析式,并求最大值.【详解】 设[)1,2x ∈,[)21,0x -∈-,()()()222222323f x x x x x ∴-=----+=-++,()()()()211214f x f x f x f x -=--=-=⎡⎤⎣⎦, ()()()()2211122311444f x f x x x x ∴=-=-++=--+, [)1,2x ∈,()f x ∴在区间[)1,2单调递减,函数的最大值是()11f =.故选:B 【点睛】思路点睛:一般利用函数的周期,对称性求函数的解析式时,一般求什么区间的解析式,就是将变量x 设在这个区间,根据条件,转化为已知区间,再根据关系时,转化求函数()f x 的解析式.解析:D 【分析】本题首先可以令x t a =,将函数转化为()212y t =+-并判断出函数的单调性,然后分为01a <<、1a >两种情况进行讨论,根据最大值是14进行计算,即可得出结果. 【详解】令x t a =(0a >、1a ≠),则()222112y t t t =+-=+-, 因为0a >,所以0x t a =>,函数()212y t =+-是增函数, 当01a <<、[]1,1x ∈-时,1,t a a⎡⎤∈⎢⎥⎣⎦,此时2max11214y a ⎛⎫=+-= ⎪⎝⎭,解得13a =或15-(舍去);当1a >、[]1,1x ∈-时,1,t a a⎡⎤∈⎢⎥⎣⎦,此时()2max 1214y a =+-=,解得3a =或5-(舍去), 综上所述,实数a 的值为13或3, 故选:D. 【点睛】本题考查根据函数的最值求参数,能否通过换元法将函数转化为二次函数是解决本题的关键,考查二次函数单调性的判断和应用,考查分类讨论思想,考查计算能力,是中档题.7.D解析:D 【分析】采用换元法可构造方程()21213t f t t =-=+,进而求得()f x 解析式,代入2020x =即可得到结果. 【详解】由()f x 是R 上的单调函数,可设()221xf x t +=+,则()13f t =恒成立, 由()221x f x t +=+得:()221x f x t =-+,()21213t f t t ∴=-=+,解得:1t =, ()22112121x x xf x -∴=-=++,()2020202021202021f -∴=+. 故选:D . 【点睛】本题考查函数值的求解问题,解题关键是能够采用换元的方式,利用抽象函数关系式求解得到函数的解析式.8.B解析:B 【分析】当m =0时,()f x =1x -,符合题意.当0m ≠时,由题意可得0112m m m>⎧⎪-⎨≥⎪⎩,求得m 的范围.综合可得m 的取值范围.【详解】当0m =时,()1f x x =-+,满足在区间(]1-∞,上为减函数; 当0m ≠时,由于()()211f x mx m x =+-+的对称轴为12mx m-=,且函数在区间(]1-∞,上为减函数, 则0112m m m>⎧⎪-⎨≥⎪⎩,解得103m <≤.综上可得,103m ≤≤. 故选:B 【点睛】要研究二次型函数单调区间有关问题,首先要注意二次项系数是否为零.当二次项系数不为零时,利用二次函数的对称轴来研究单调区间.9.B解析:B 【分析】根据奇函数的性质,分析()f x 在对称的区间上单调性相同,即可找出最大值与最小值. 【详解】∵()f x 是奇函数,在(0,)+∞上是减函数,∴()f x 在(,0)-∞上也是减函数,即在区间[,](0)a b a b <<上递减. 又∵()f x 在区间[,](0)a b a b <<上的值域为[3,4]-, ∴()()4,3,f a f b ==-根据奇函数的性质可知()()4,3,f a f b -=--=且在区间[,]b a --上单调递减, ∴()f x 在区间[,]b a --上有最大值3,有最小值-4. 故选:B. 【点睛】本题考查了奇函数的单调性和值域特点,如果性质记不熟,可以将大致图像画出.本题属于中等题.10.B解析:B 【分析】利用奇偶性排除选项C 、D ;利用x →+∞时,()f x →+∞,排除A,从而可得结论. 【详解】 ∵f (-x )=( -x )2+2ln||2()x x --=x 2+2ln||2x x=f (x ), ∴f (x )是偶函数,其图象关于y 轴对称,排除C,D ; 又x →+∞时,()f x →+∞,排除A, 故选B . 【点睛】本题通过对多个图象的选择考查函数的图象与性质,属于中档题.这类题型也是近年高考常见的命题方向,该题型的特点是综合性较强、考查知识点较多,但是并不是无路可循.解答这类题型可以从多方面入手,根据函数的定义域、值域、单调性、奇偶性、特殊点以及0,0,,x x x x +-→→→+∞→-∞时函数图象的变化趋势,利用排除法,将不合题意的选项一一排除.11.C解析:C 【详解】分析:函数()3221f x ax x x =+++在()1,2上有最大值无最小值,则极大值在()1,2之间,一阶导函数有根在()1,2,且左侧函数值小于0,右侧函数值大于0,列不等式求解 详解:f ′(x )=3ax 2+4x +1,x ∈(1,2).a =0时,f ′(x )=4x +1>0,函数f (x )在x ∈(1,2)内单调递增,无极值,舍去. a ≠0时,△=16﹣12a . 由△≤0,解得43a ≥,此时f ′(x )≥0,函数f (x )在x ∈(1,2)内单调递增,无极值,舍去.由△>0,解得a 43<(a ≠0),由f ′(x )=0,解得x 123a--=,x 2=.当403a <<时,x 1<0,x 2<0,因此f ′(x )≥0,函数f (x )在x ∈(1,2)内单调递增,无极值,舍去.当a <0时,x 1>0,x 2<0,∵函数f (x )=ax 3+2x 2+x +1在(1,2)上有最大值无最小值,∴必然有f ′(x 1)=0,∴123a-<2,a <0.解得:53-<a 34-<. 综上可得:53-<a 34-<. 故选:C .点睛:极值转化为最值的性质:若()[]f x x a,b ∈在上有唯一的极小值,且无极大值,那么极小值为()f x 的最小值;若()[]f x x a,b ∈在上有唯一的极大值,且无极小值,那么极大值为()f x 的最大值;12.C解析:C 【分析】由函数是R 上的减函数,列出不等式,解出实数a 的取值范围. 【详解】因为()f x 是R 上的减函数,故023033a a a a>⎧⎪-<⎨⎪-≥⎩,故2334a <≤,故选:C 【点睛】本题考查函数的单调性的应用,考查分段函数,属于中档题.二、填空题13.100【分析】分析得出得解【详解】∴故答案为:100【点睛】由函数解析式得到是定值是解题关键解析:100 【分析】分析得出(2)()2f x f x -+=得解. 【详解】1()1x f x x +=- 211211(2)()2f x f x x x x x -+∴-+=++=--- ∴135199()()()()100100100100f f f f ++++ 1199319799101[()()][()()][()()]100100100100100100f f f f f f =+++++250100=⨯=故答案为:100.【点睛】由函数解析式得到(2)()2f x f x -+=是定值是解题关键.14.【分析】问题转化为即可由令问题转化为求的最大值根据二次函数的性质求出的最大值从而求出的范围即可【详解】若存在不等式成立即即可由令问题转化为求的最大值而的最大值是2故故故答案为:【点睛】方法点睛:本题解析:1[,)2+∞【分析】问题转化为22()2min x a x x -+即可,[1,)x ∈+∞,由22211221x x x x x=-+-+,令221()1f x x x=-+,[1,)x ∈+∞,问题转化为求()f x 的最大值,根据二次函数的性质求出()f x 的最大值,从而求出a 的范围即可. 【详解】若存在[1,)x ∈+∞,不等式2212a x x x -+成立,即22()2min x a x x -+即可,[1,)x ∈+∞,由22211221x x x x x=-+-+,令221()1f x x x =-+,[1,)x ∈+∞,问题转化为求()f x 的最大值, 而2117()2()48f x x=-+,[1,)x ∈+∞的最大值是2, 故221()22min x x x =-+,故12a, 故答案为:1[,)2+∞ 【点睛】方法点睛:本题考查函数的有解问题, 一般通过变量分离,将不等式有解问题转化为求函数的最值问题:()f x m >有解max ()f x m ⇔>;()f x m <有解min ()f x m ⇔<.15.【分析】将函数变形为关于的方程分析二次项的系数并结合与的关系求解出的取值范围从而值域可求【详解】因为所以所以当即时此时;当即时此时所以综上可知:所以的值域为故答案为:【点睛】易错点睛:利用判别式法求 解析:[]0,4【分析】将函数变形为关于x 的方程,分析二次项的系数并结合∆与0的关系求解出y 的取值范围,从而值域可求. 【详解】因为222421x x y x ++=+,所以222+42yx y x x +=+,所以()22420y x x y -++-=, 当20y -=,即2y =时,此时0x =;当20y -≠,即2y ≠时,此时()216420y ∆=--≥,所以[)(]0,22,4y ∈,综上可知:[]0,4y ∈,所以222421x x y x ++=+的值域为[]0,4, 故答案为:[]0,4. 【点睛】易错点睛:利用判别式法求解函数值域需要注意的事项: (1)原函数中分子分母不能约分; (2)原函数的定义域为实数集R .16.【分析】根据f (x )定义在02上且4﹣ax≥0即可得出a≤2然后讨论:①1<a≤2时满足条件;②a=1时不合题意;③0<a <1时不合题意;④a=0时不合题意;⑤a <0时满足条件这样即可求出实数a 的取 解析:012a a <<≤或【分析】根据f (x )定义在[0,2]上,且4﹣ax≥0,即可得出a≤2,然后讨论:①1<a≤2时,满足条件;②a=1时,不合题意;③0<a <1时,不合题意;④a=0时,不合题意;⑤a <0时,满足条件,这样即可求出实数a 的取值范围. 【详解】∵f (x )定义在[0,2]上;∴a >2时,x=2时,4﹣ax <0,不满足4﹣ax≥0; ∴a≤2;①1<a≤2时,a ﹣1>0;∴()(1f x a =-[0,2]上是减函数; ②a=1时,f (x )=0,不满足在[0,2]上是减函数; ∴a≠1;③0<a <1时,a ﹣1<0; ∵[0,2]上是减函数;∴()(1f x a =-[0,2]上是增函数; ∴0<a <1不合题意;④a=0时,f (x )=﹣2,不满足在[0,2]上是减函数; ∴a≠0;⑤a <0时,a ﹣1<0;[0,2]上是增函数;∴()(1f x a =-[0,2]上是减函数; ∴综上得,实数a 的取值范围为012a a <<≤或. 故答案为012a a <<≤或. 【点睛】考查函数定义域的概念,函数单调性的定义及判断.17.18【分析】根据递推关系式依次求f(2)f(3)【详解】因为f(n+1)=3f(n)所以【点睛】本题考查根据递推关系求函数值考查基本求解能力解析:18 【分析】根据递推关系式依次求f (2) ,f (3). 【详解】因为f (n+1)=3f (n),所以(2)3(1)6,(3)3(2)18.f f f f ==== 【点睛】本题考查根据递推关系求函数值,考查基本求解能力.18.f(-3)>f(-π)【解析】由得是上的单调递增函数又解析:f (-3)>f (-π)【解析】由()()1212()[]0x x f x f x >-- 得()f x 是R 上的单调递增函数,又3(3)()f f ππ>∴>--,-- .19.2【分析】由函数是幂函数求得或结合幂函数的性质即可求解【详解】由题意函数是幂函数可得即解得或当时函数此时在上单调递增符合题意;当时函数此时在上单调递减不符合题意故答案为:【点睛】本题主要考查了幂函数解析:2 【分析】由函数()2(1)mf x m m x =--是幂函数,求得2m =或1m =-,结合幂函数的性质,即可求解. 【详解】由题意,函数()2(1)mf x m m x =--是幂函数,可得211m m --=,即220m m --=,解得2m =或1m =-,当2m =时,函数()2f x x =,此时()f x 在(0,)+∞上单调递增,符合题意;当1m =-时,函数()1f x x -=,此时()f x 在(0,)+∞上单调递减,不符合题意,故答案为:2. 【点睛】本题主要考查了幂函数的定义及图像与性质的应用,其中解答中熟记幂函数的定义,结合幂函数的图象与性质进行判定是解答的关键,着重考查运算能力.20.【分析】根据二次函数的单调性得出是上的减函数从而有整理得即关于的方程在区间内有实数解记由二次函数的单调性和零点存在定理建立不等式组可求得范围【详解】∵函数是上的减函数∴当时即两式相减得即代入得由且得解析:31,4⎡⎫--⎪⎢⎣⎭【分析】根据二次函数的单调性得出2()f x x k =+是(,0]-∞上的减函数,从而有()()f a bf b a=⎧⎨=⎩,整理得22a k b b k a⎧+=⎨+=⎩,即关于a 的方程210a a k +++=,在区间11,2⎡⎫--⎪⎢⎣⎭内有实数解,记2()1h a a a k =+++,由二次函数的单调性和零点存在定理建立不等式组,可求得范围.【详解】∵函数2()f x x k =+是(,0]-∞上的减函数,∴当[,]x a b ∈时,()()f a bf b a=⎧⎨=⎩,即22a k bb k a ⎧+=⎨+=⎩, 两式相减得22a b b a -=-,即(1)b a =-+,代入2a k b +=得210a a k +++=, 由0a b <≤,且(1)b a =-+得112a -≤<-, 故关于a 的方程210a a k +++=,在区间11,2⎡⎫--⎪⎢⎣⎭内有实数解, 记2()1h a a a k =+++,所以函数()h a 在11,2⎡⎫--⎪⎢⎣⎭上单调递减,则()10102h h ⎧-≥⎪⎨⎛⎫-< ⎪⎪⎝⎭⎩,即()()221110111022k k ⎧-+-++≥⎪⎨⎛⎫⎛⎫-+-++<⎪ ⎪ ⎪⎝⎭⎝⎭⎩,解得31,4k ⎡⎫∈--⎪⎢⎣⎭, 故答案为:31,4⎡⎫--⎪⎢⎣⎭.【点睛】关键点点睛:在解决二次函数的值域问题,关键在于得出二次函数的对称轴与区间的关系,也即是判断出二次函数在区间上的单调性.三、解答题21.(1)[4,)-+∞;(2)226,27(),2246,2m m m m g m m m -≤-⎧⎪+-⎪=--<<⎨⎪-≥⎪⎩. 【分析】(1)计算二次函数的对称轴,然后根据单调性可得122m -≤,计算即可. (2)分类讨论112m -≤-,1112m -<-<,112m -≥,分别计算即可. 【详解】(1)由题可知,函数2()7f x x mx m =++-()m R ∈开口向上,对称轴的方程为2mx =-,若使得函数()f x 在[2,4]上单调递增, 则满足122m -≤,解得4m ≥-,即实数m 的取值范围[4,)-+∞. (2)①当112m -≤-即2m ≥时, 函数()y f x =在区间[1,1]-单调递增,所以函数()y f x =的最小值为()(1)6g m f =-=-; ②当1112m -<-<,即22m -<<时, 函数()y f x =在区间11,2m ⎡⎤--⎢⎥⎣⎦单调递减,在区间1,12m ⎡-⎤⎢⎥⎣⎦上单调递增, 所以函数()y f x =的最小值为21()724m g m f m m ⎛⎫=-=-+- ⎪⎝⎭; ③当112m -≥即2m ≤-时, 函数()y f x =在区间[1,1]-单调递减,所以函数()y f x =的最小值为()(1)26g m g m ==-,综上可得,函数的最小值为226,27(),2246,2m m m m g m m m -≤-⎧⎪+-⎪=--<<⎨⎪-≥⎪⎩. 【点睛】结论点睛:二次函数在区间上的最值问题:(1)动轴定区间;(2)定轴动区间;(3)动轴动区间;对本题属于动轴动区间问题需要讨论对称轴与所给区间位置关系. 22.(1)()223x x x f =-+;(2)[]2,11.【分析】(1)若选①:利用待定系数法并结合()f x 的图象经过点()1,2求解二次函数()f x 的解析式;若选②:根据对称轴方程以及()03f =并结合()f x 的图象经过点()1,2求解二次函数()f x 的解析式;若选③:根据已知条件判断出()1,2为图象的最低点,由此分析出对称轴,则二次函数的解析式可求;(2)根据(1)得到()f x 的解析式,然后利用配方法和整体替换的方法求解出()212x -+的取值范围,则()f x 在[]1,4-上的值域可求.【详解】 解:若选①,(1)设()()20f x ax bx c a =++≠,则()()()()221112f x a x b x c ax a b x a b c +=++++=+++++. 因为()()121f x f x x +=+-,所以()22221ax a b x a b c ax bx c x +++++=+++-,所以221a a b =⎧⎨+=-⎩,解得1a =,2b =-.因为()f x 的图象经过点()1,2,所以()1122f a b c c =++=-+=,所以3c =. 故()223x x x f =-+.若选②,(1)设()()20f x ax bx c a =++≠,则()f x 图象的对称轴方程为2bx a=-.由题意可得()()120312b a fc f a b c ⎧-=⎪⎪==⎨⎪=++=⎪⎩,解得123a b c =⎧⎪=-⎨⎪=⎩.故()223x x x f =-+.若选③,(1)()()20f x ax bx c a =++≠.因为()03f =,所以3c =.因为()()21f x f ≥=,所以()13212f a b b a ⎧=++=⎪⎨-=⎪⎩,解得1a =,2b =-.故()223x x x f =-+.(2)由(1)可知()()222312f x x x x =-+=-+. 因为14x -≤≤,所以213x -≤-≤,所以()2019x ≤-≤,所以()221211x ≤-+≤. 即()f x 在[]1,4-上的值域为[]2,11. 【点睛】方法点睛:求解函数解析式常用的方法有:(1)换元法:适用于求解已知()()f g x 的解析式求解()f x 的解析式的类型; (2)待定系数法:适用于已知函数的类型求解函数解析式,如已知函数为一次函数可设()()0f x kx b k =+≠或已知函数为二次函数可设()()20f x ax bx c a =++≠;(3)方程组法:适用于已知()(),f x f x -组成的方程求解()f x 的解析式或已知()1,f x f x ⎛⎫⎪⎝⎭组成的方程求解()f x 的解析式的类型.23.(1)答案见解析;(2)19. 【分析】(1)讨论2b -<和2b -≥两种情况根据二次函数性质求解; (2)讨论11a ≤,113a<<和13a ≥三种情况结合二次函数的单调性求解.【详解】(1)1a =时,2()21f x x bx =++,对称轴为x b =-,二次函数()f x 的图象开口向上,当2b -<,即2b >-时,max ()(3)106f x f b ==+; 当2b -≥,即2b ≤-时,max ()(1)22f x f b ==+.(2)2()21f x ax x =-+,对称轴为1x a=,二次函数()f x 的图象开口向上, 当11a≤,即1a ≥时,()f x 在[]1,3单调递增,()()min 114f x f a ==-=-,解得3a =-,不符合;当113a <<,即113a <<时,2min 112()14f x f a a a a ⎛⎫⎛⎫==⋅-+=- ⎪ ⎪⎝⎭⎝⎭,解得15a =,不符合;当13a ≥,即103a <≤时,()f x 在[]1,3单调递减,()()min 3954f x f a ==-=-,解得19a =,符合,综上,19a =.【点睛】思路点睛:求二次函数在闭区间[],a b 的最值的思路; (1)二次函数开口向上时,求函数的最大值,讨论对称轴和2a b+的大小求解; (2)二次函数开口向上时,求函数的最小值,讨论对称轴在(]()[),,,,,a a b b -∞+∞三个区间的范围求解.24.(1)增函数;证明见解析;(2)当23m ≤-时,[)45,k m ∈++∞; 当203-<<m 时, [)3,k m ∈++∞ 【分析】(1)用函数单调性的定义进行证明得解; (2)参变分离得到221m k x x++≤,再换元转化为二次函数求最值得解. 【详解】(1)()f x 为[)2,+∞上的增函数 证明如下:任取[)12,2,x x ∈+∞,且12x x < 则()121212121212444()()x x f x f x x x x x x x x x --=-+-=- 21120,4x x x x ->>所以12()()f x f x <;所以()f x 为[)2,+∞上的增函数 (2)由()f x kx ≤,得2mx kx x++≤ 212[,1],12m x k x x∈∴++≤令1t x =,[]2211()21()1,(1,2)g t mt t m t t m m =++=++-∈ 则1[,1]2x ∈有解,当且仅当[]min ()(1,2)k g t t ≥∈0m <当132m ->即203-<<m 时,min ()(1)3g t g m ==+ 当1302m <-≤即23m ≤-时,min ()(2)45g t g m ==+ 综上, 当23m ≤-时,[)45,k m ∈++∞. 当203-<<m 时, [)3,k m ∈++∞ 【点睛】函数不等式恒成立问题通常转化为函数最值问题,注意对参数进行讨论. 25.(1)()2xf x x x=+,()1,1x ∈-;(2)()f x 在()1,1-上递增,证明见解析;(3)1,12⎛⎫ ⎪⎝⎭.【分析】(1)由奇偶性知()00f =,进而结合1225f ⎛⎫=⎪⎝⎭待定系数求解即可得函数解析式; (2)()f x 在()1,1-上递增,利用函数单调性的定义证明即可;(3)由奇偶性将问题转化为()()1f t f t ->-,再根据单调性解不等式111111t t t t -<-<⎧⎪-<<⎨⎪->-⎩即可. 【详解】解:(1)因为函数()21ax bf x x +=+是()1,1-上的奇函数,12.25f ⎛⎫= ⎪⎝⎭所以()0,0012122152514b f a bf =⎧⎪⎧=⎪⎪+⇒⎨⎨⎛⎫== ⎪⎪⎪⎝⎭⎩+⎪⎩,解得10a b =⎧⎨=⎩, ∴ ()2xf x x x=+,()1,1x ∈-. (2)()f x 在()1,1-上递增,证明如下: 任取()12,1,1x x ∈-,且12x x >,则()()()()()()221221121222221212111111x x x x x x f x f x x x x x +-+-=-=++++ ()()()()()()2212121212122222121211111x x x x x x x x x x x x x x ---+-==++++, ∵()12,1,1x x ∈-,∴1210x x ->, 又12x x >,∴ 120x x ->, ∴()()120f x f x ->,∴ ()()12f x f x >,即()f x 在()1,1-上递增. (3)()()10f t f t -+>可化为()()1f t f t ->-,∴111021111112112t t t t t t t t ⎧⎪-<-<<<⎧⎪⎪-<<⇒-<<⇒<<⎨⎨⎪⎪->-⎩⎪>⎩.∴t 的取值范围1,12⎛⎫⎪⎝⎭.【点睛】(1)本题是函数性质的综合运用,在解题中要熟练掌握函数奇偶性、单调性的的判定及性质,对于单调性的证明要掌握规范的解题步骤.(2)在解含“f ”号得不等式时,首先根据函数的性质把不等式转化为()()()()f g x f h x >的形式,然后根据函数的单调性去掉“f ”号,转化为具体的不等式(组),此时要注意()g x 与()h x 的取值应在外层函数的定义域内. 26.(1)(,3][1,)-∞-⋃-+∞(2)()1,-+∞ 【分析】(1)根据二次函数对称轴与区间关系,即可求解;(2)分离参数可得42(1)4k x ->--,求出44y x =--的最大值即可求解. 【详解】 (1)由函数2()2(1)4f x x k x =+-+知,函数()f x 图象的对称轴为1x k =-.因为函数()f x 在区间[]2,4上具有单调性,所以12k -≤或14k -≥,解得3k ≤-或1k ≥-,所以实数k 的取值范围为(,3][1,)-∞-⋃-+∞.(2) 因为()0f x >对任意的[1,2]x ∈恒成立, 所以可得42(1)k x x ->--对任意的[1,2]x ∈恒成立,因为44()44y x x x =--=-+≤-=-,当且仅当2x =时等号成立, 即max 4y =-,所以只需2(1)4k ->-,解得1k -<,所以实数k 的取值范围为()1,-+∞.【点睛】关键点睛:不等式在某区间上恒成立求参数的取值范围,一般需要分离参数,转化为求最值问题,往往可以利用函数单调性或均值不等式求最值,即可求出答案,本题中利用了均值不等式,特别注意等号是否能取到,否则不能用均值不等式求最值.。
2020春长沙市一中高二寒假自主学习:函数(答案)【精选】.docx

函 数班级________姓名__________学号_________一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选择中,只有一个是符合题目要求的.)1.下列函数在其定义域上既是奇函数又是增函数的是( )A .1y x =-B .12xy ⎛⎫= ⎪⎝⎭C .3y x = D .2log y x =【答案】C【解析】A .1y x =-在定义域上既不是增函数,也不是减函数;B .12xy ⎛⎫= ⎪⎝⎭在定义域上既不是偶函数,也不是奇函数;C .3y x =在其定义域上既是奇函数又是增函数;D .2log y x =在定义域上既不是偶函数,也不是奇函数,故选C . 2.2327lg0.01+=( ) A .11 B .7 C .0 D .6 【答案】B【解析】222327lg0.013lg1927-+=+=-=,故选B .3.设p :0<x <1,q :2x ≥1,则p 是q 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 【答案】A【解析】由题知,2x ≥1⇒x ≥0,∵(0,1)⊂[0,+∞),∴满足p ⇒q ,但q ⇏p ,选A .4.若函数()20{ ln 0x x f x x x ≤=>,则1f f e ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭(其中e 为自然对数的底数)=( ) A .1e B .12C .2-D .ln2e 【答案】B【解析】由题意得11ln1f e e⎛⎫==- ⎪⎝⎭,∴()111122f f f e -⎛⎫⎛⎫=-== ⎪ ⎪⎝⎭⎝⎭.选B .5.函数()ln 2xy x =+的定义域为( )A .()2-+∞,B .()()211--⋃-+∞,,C .112⎛⎫⎪⎝⎭, D .()()11-∞-⋃+∞,, 【答案】B 【解析】函数()ln 2xy x =+中有:()20{ 20x ln x +>+≠,解得2x >-且1x ≠-,即定义域为()()211--⋃-+∞,,,故选C . 6.已知函数14log y x =与y kx =的图象有公共点A ,且A 点的横坐标为2,则k =( )A .12-B .12C .14-D .14【答案】C【解析】当2x =时,141log 22y ==-,∴122k -=,14k =-,故选C . 7.设0.6 1.50.60.6,0.6, 1.5a b c ===,则,,a b c 的大小关系是( )A .b a c <<B .a c b <<C .a b c <<D .b c a << 【答案】A【解析】函数y =0.6x 为减函数,故0.60.6a => 1.50.6b =,函数y =x 0.6在(0,+∞)上为增函数,故0.60.6a =<0.61.5c =,故b <a <c ,故选A . 8.函数1lg1y x =-的大致图象为( ) A . B . C . D .【答案】C【解析】由题意得,函数1lg1y x =-的关于1x =对称,排成B 、D ; 当1x >时,函数1lg1y x =-为单调递减函数,排成A ,故选C . 9.若函数()24x f x a =--存在两个零点,且一个为正数,另一个为负数,则a 的取值范围为( )A .()0,4B .()0,+∞C .()3,4D .()3,+∞ 【答案】C【解析】如图,若()24x f x a =--存在两个零点,且一个为正数,另一个为负数,则()34a ∈,,故选C .10.已知函数()()()ln 2ln 4f x x x =++-,则错误..的是( ) A .()f x 在()2,1-单调递增 B .()f x 在()1,4单调递减C .()y f x =的图象关于直线1x =对称D .()y f x =的图象关于点()1,0对称 【答案】D【解析】由函数()()()ln 2ln 4f x x x =++-,可得函数满足20{ 40x x +>->,解得24x -<<,又函数()()()()2ln 2ln 4ln 28f x x x x x =++-=-++, 设()228u x x x =-++,其开口向下,且对称轴为1x =,∴函数()u x 在()2,1x ∈-上单调递增,在()1,4x ∈上单调递减,根据复合函数的单调性可得()f x 在()2,1x ∈-上单调递增,在()1,4x ∈上单调递减, 且函数()f x 的图象关于直线1x =对称,故选D .11.设函数f (x )={(x −a )2−1,x ≤1,lnx ,x >1, 若f (x )≥f (1)恒成立,则实数a 的取值范围为( )A .[1,2]B .[0,2]C .[1,+∞)D .[2,+∞) 【答案】A 【解析】∵f (x )={(x −a )2−1,x ≤1,lnx ,x >1,若f (x )≥f (1)恒成立,∴f (1)是f (x )的最小值,由二次函数性质可得对称轴a ≥1,由分段函数性质得(1−a )2−1≤ln1,得0≤a ≤2,综上,1≤a ≤2,故选A .12.已知()f x 是定义在R 上恒不为零的单调递减函数.对任意,x y R ∈,都有()f x y +=()()f x f y ,集合()()()(){}22,|1 A x y f x f y f =>,()(){},|45 1 B x y f x ay =+-=,若A B ⋂=∅,则实数a 的取值范围为( )A .[]3,3-B .(][)--33+∞⋃∞,,C .[]22-, D .314⎡⎤--⎢⎥⎣⎦,【答案】A【解析】∵()f x 是定义在R 上恒不为零的单调递减函数.对任意,x y ∈R ,都有()()()f x y f x f y +=,()()()(){}()()(){}2222,|1 ,|1 A x y f x f y f x y f x y f =>=+> ()22={,|1}x y x y +<,令0x y ==,得()()()000f f f =,即()01f =,则()(){}()()(){}(){},|45 1 ,|450 ,|450 B x y f x ay x y f x ay f x y x ay =+-==+-==+-=,若A B ⋂=∅,则直线450x ay +-=与圆221x y +=最多有一个公共点,22514a-≥+,即29a ≤,解得33a -≤≤.二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上.) 13.函数()()2log 34f x x =-的定义域是__________. 【答案】3,4⎛⎫-∞ ⎪⎝⎭【解析】要使函数()()2log 34f x x =-有意义,则340x -<,解得34x <,函数()()2log 34f x x =-的定义域是3,4⎛⎫-∞ ⎪⎝⎭,故答案为3,4⎛⎫-∞ ⎪⎝⎭.14.如图,已知函数()f x 的图象为折线ACB (含端点,A B ),其中()()()4,0,40,0,4A B C -,,则不等式()()2log 2f x x >+的解集是__________. 【答案】[)4,2-【解析】在同一坐标系中作出函数()y f x =和()2log 2y x =+的图象,易知当2x =时,()()2log 22f x x =+=,∴不等式()()2log 2f x x >+的解集是[)4,2-.15.函数()223,{ ,x x x af x x x a-->=-≤当0a =时,()f x 的值域为______;当()f x 有两个不同零点时,实数a 的取值范围为______. 【答案】[)4,-+∞(),1-∞-或[)0,3【解析】当0a =时,由0x >,可得()()22g x 23144,x x x =--=--≥-由0x ≤,可得()h x x 0=-≥,∴当0a =时,()f x 的值域为[)4,-+∞;要使()f x 有两个不同零点,分两种情况:(1)()2g x 23x x =--,x a >有一个零点且()h x x x a =-≤,有一个零点,则()()20{03230h a a a g a a a =-≤⇒≤<=--<;(2)()2g x 23x x =--,x a >有两个零点且()h x x x a =-≤,没有零点,则()()20{1230h a a a g a a a =->⇒<-=-->,综合(1)、(2)可知当()f x 有两个不同零点时,实数a 的取值范围为(),1-∞-或[)0,3故答案为[)4,-+∞,(),1-∞-或[)0,3.16.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”为:设x R ∈,用[]x 表示不超过x 的最大整数,则[]y x =称为高斯函数,例如:[]2.13-=-,[]3.13=,已知函数()121123x xf x +=-+,则函数[]y x =的值域是__________. 【答案】{}1,0,1-【解析】()()1221221152123123312xx x x xf x ++-=-=-=-+++.()()()225215121,,0,2,2,0,,121231223x x x x⎛⎫+∈+∞∈-∈--∈- ⎪+++⎝⎭. []x 表示不超过x 的最大整数,∴{}521,0,1312x ⎡⎤-∈-⎢⎥+⎣⎦,故答案为{}1,0,1-.三、解答题(本大题共4小题,共40分.解答应写出文字说明、证明过程或演算步骤.) 17.(6分)根据已知条件,求函数的解析式.(1)已知()f x 为一次函数,且()94f f x x ⎡⎤=+⎣⎦,求()f x 的解析式. (2)下图为二次函数2y ax bx c =++的图像,求该函数的解析式. 【答案】(1)()31f x x =+或()32f x x =--;(2)()224233f x x x =-- 【解析】(1)∵()f x 为一次函数,∴设()f x kx b =+,∴()()294f f x k kx b b k x kb b x ⎡⎤=++=++=+⎣⎦,∴29{ 4k kb b =+=,∴3{1k b ==或3{2k b =-=-,∴()31f x x =+或()32f x x =--.(2)如图所示,二次函数过()1,0-,()3,0,()0,2-三点,∴代入得0{930 2a b c a b c c -+=++==-,解得234{ 32a b c ==-=-,∴()224233f x x x =--.18.(10分)已知二次函数()f x 满足()()--1=-1f x f x ,其图象过点(0,1),且与x 轴有唯一交点.(1)求()f x 的解析式;(2)设函数()g x =()(2)f x a x -+,求()g x 在[1,2]上的最小值()h a . 【答案】(1)f (x )=x 2+2x +1;(2)ℎ(a )={2−a , a ≤2,−14a 2+1, 2<a <4,5−2a , a ≥4.【解析】(1)设二次函数f (x )的解析式为f (x )=ax 2+bx +c (a ≠0),∵f(−x−1)=f(x−1),∴函数对称轴为x=−b2a =−x−1+x−12=−1.∵图象过点(0,1),∴c=1,∵函数f(x)的图象与x轴有唯一交点,∴Δ=b2−4ac=0,∴a=1,b=2,c=1,∴f(x)=x2+2x+1.(2)g(x)=f(x)−(2+a)x=x2−ax+1,函数图象对称轴为x=a2,且开口向上,当a2≤1时,即a≤2时,函数f(x)在[1,2]上单调递增,∴g(x)min=g(1)=2−a;当1<a2<2时,即2<a<4时,f(x)在[1,a2]上单调递减,在[a2,2]上单调递增,∴g(x)min=g(a2)=−14a2+1;当a2≥2即a≥4时,函数f(x)在[1,2]上单调递减,∴g(x)min=g(2)=5−2a,∴h(a)={2−a, a≤2,−14a2+1, 2<a<4,5−2a, a≥4.19.(12分)已知函数f(x)=x2+ax−b(a,b∈R).(1)若b=−1,且函数f(x)有零点,求实数a的取值范围;(2)当b=1−a时,解关于x的不等式f(x)≤0;(3)若正数a,b满足a+4b≤3,且对于任意的x∈[1,+∞),f(x)≥0恒成立,求实数a,b的值.【答案】(1) (−∞,−2]∪[2,+∞);(2) a<2时[−1,1−a];a=2时{−1};a>2时[1−a,−1];(3)a=1,b=2;【解析】(1) b=−1时,f(x)=x2+ax+1,由函数f(x)有零点,可得Δ=a2−4≥0,即a≤−2或a≥2;(2) b=1−a时,f(x)=x2+ax+a−1=(x+1)(x+a−1),当−1<1−a即a<2时,f(x)≤0的解集为[−1,1−a],当−1=1−a即a=2时,f(x)≤0的解集为{−1},当−1>1−a即a>2时,f(x)≤0的解集为[1−a,−1];(3)二次函数f(x)开口响上,对称轴x=−a2,由a>2可得f(x)在[1,+∞)单调递增,x∈[1,+∞)时f(x)≥0恒成立,当且仅当f(1)≥0,即1+a−b≥0,即a≥b−1,由a+4b ≤3,可得a≤3−4b,则b−1≤3−4b,由b>0可得b2−4b+4≤0,即(b−2)2≤0,则b=2,此时1≤a ≤1,则a =1.20.(12分)经市场调查,某商品在过去的100天内的销售量(单位:件)和价格(单位:元)均为时间t (单位:天)的函数,且销售量满足()f t =()60,160{ ,1150,611002t t t t t +≤≤∈-≤≤N ,价格满足()g t =()2001100,t t t -≤≤∈N .(1)求该种商品的日销售额()h t 与时间t 的函数关系;(2)若销售额超过16610元,商家认为该商品的收益达到理想程度,请判断该商品在哪几天的收益达到理想程度?【答案】(1)()h t =()()2214012000,160,{ 125030000,61100,2t t t t N t t t t N -++≤≤∈-+≤≤∈,(2)天数为第53,54,…60,61天,共9天. 【解析】 (1)由题意知,当1t 60,t ≤≤∈N 时,()h t =()()f t g t ⋅=()()60200t t +⋅- =214012000t t -++,当61t 100,t ≤≤∈N 时,()h t = ()()f t g t ⋅=()1150t 200t 2⎛⎫-⋅- ⎪⎝⎭=21250300002t t -+, 所求函数关系()h t =()()2214012000,160,{ 125030000,61100,2t t t t N t t t t N -++≤≤∈-+≤≤∈.(2)当160,t t ≤≤∈N 时,()h t =214012000t t -++=()27016900t --+, ∴函数()h t 在[]1,60上单调递增,∴()max h t = ()60h =16800 (元), 当61100,t t ≤≤∈N 时,()h t =21250300002t t -+=()2125012502t --, ∴函数()h t 在[]61,100上单调递减,∴()max h t = ()61h =16610.5 (元).若销售额超过16610元,当61100t ≤≤时,函数单调递减,故只有第61天满足条件. 当160t ≤≤时,经计算()5316611h =满足条件,又函数()h t 在[]1,60上单调递增, ∴第53,54,…,60天,满足条件,即满足条件的天数为第53,54,…60,61天,共9天.。
长沙市长沙市第一中学八年级数学下册第十九章《一次函数》经典练习(培优练)

一、选择题1.点()1,A a y 、()22,B a y 都在一次函数0)(2y ax a a =-+≠的图象上,则1y 、2y 的大小关系是( )A .12y y >B .12y y =C .12y y <D .不确定 2.一次函数y=-3x-2的图象和性质,表述正确的是( )A .y 随x 的增大而增大B .函数图象不经过第一象限C .在y 轴上的截距为2D .与x 轴交于点(-2,0)3.已知函数(0)y kx k =≠中y 随x 的增大而减小,则一次函数23y kx k =+的图象大致是( )A .B .C .D .4.已知A B ,两地相距240千米.早上9点甲车从A 地出发去B 地,20分钟后,乙车从B 地出发去A 地.两车离开各自出发地的路程y (千米)与时间x (小时)的函数关系如图所示,则下列描述不正确的是( )A .甲车的速度是60千米/小时B .乙车的速度是90千米/小时C .甲车与乙车在早上10点相遇D .乙车在12:00到达A 地5.若实数k 、b 满足0k b +=,且k b >,则一次函数y kx b =+的图象可能是( )A .B .C .D . 6.若直线y =kx+b 经过第一、二、四象限,则函数y =bx -k 的大致图像是( ) A . B . C . D . 7.下列图形中,表示一次函数y =mx +n 与正比例函数y =mnx (m ,n 为常数,且mn≠0)的图象的是( )A .B .C .D .8.在平面直角坐标系中,横坐标和纵坐标都是整数的点叫整点,已知直线()1:20l y mx m =+<与直线2:4l y x =-,若两直线与y 轴围成的三角形区域内(不含三角形的边)有且只有三个整点,则m 的取值范围是( )A .21m -<<-B .21m -≤<-C .322m -≤<-D .322m -<≤- 9.如图,已知直线1:2l y x =,过点()0,1A 作y 轴的垂线交直线l 于点B ,过点B 作直线l 的垂线交y 轴于点C ,过点C 作y 轴的垂线交直线l 于点D ,则点D 的坐标为( )A .()10,5B .()0,10C .()0,5D .()5,10 10.关于一次函数2y x b =-+(b 为常数),下列说法正确的是( )A .y 随x 的增大而增大B .当4b =时,直线与坐标轴围成的面积是4C .图象一定过第一、三象限D .与直线32y x =-相交于第四象限内一点 11.如图,在平面直角坐标系中点A 的坐标为()0,6,点B 的坐标为3,52⎛⎫- ⎪⎝⎭,将AOB 沿x 轴向左平移得到A O B ''',若点B '的坐标为19,52⎛⎫-⎪⎝⎭,点A '落在直线y kx =上,则k 的值为( )A .43-B .34-C .34D .611- 12.火车匀速通过隧道时,火车在隧道内的长度y (米)与火车行驶时间x (秒)之间的关系用图像描述如图所示,有下列结论:①火车的速度为30米/秒;②火车的长度为120米;③火车整体都在隧道内的时间为35秒;④隧道长度为1200米.其中正确的结论是( )A .①②③B .①②④C .③④D .①③④ 13.关于x 的一次二项式ax+b 的值随x 的变化而变化,分析下表列举的数据,若ax+b =11,则x 的值是( )A .3B .﹣5C .6D .不存在 14.关于函数(3)y k x k =-+,给出下列结论:①当3k ≠时,此函数是一次函数;②无论k 取什么值,函数图象必经过点(1,3)-;③若图象经过二、三、四象限,则k 的取值范围是0k <;④若函数图象与x 轴的交点始终在正半轴,则k 的取值范围是03k <<.其中正确结论的序号是( )A .①②③B .①③④C .②③④D .①②③④ 15.已知,整数x 满足1266,1,24x y x y x -≤≤=+=-+,对任意一个x ,p 都取12,y y 中的大值,则p 的最小值是( )A .4B .1C .2D .-5二、填空题16.已知关于x ,y 的二元一次方程组1,mx y y nx -=⎧⎨=⎩的解是1,2x y =⎧⎨=⎩则直线1y mx =-与直线y nx =的交点坐标是______; 17.已知直线2y ax a =-+(a 为常数)不经过第四象限,则a 的取值范围是________. 18.已知一次函数y kx b =+的图象与直线1y x =-+平行,且经过点(8,2),那么b 的值是________.19.已知一次函数(2) 3y m x m =-+-的图象经过第一、二、四象限,则化简=__________.20.如果直线y=2x+3与直线y=3x ﹣2b 的交点在y 轴上,那么b 的值为___.21.已知直线22y x =-与x 轴交于A ,与y 轴交于B ,若点C 是坐标轴上的一点,且AC AB =,则点C 的坐标为________.22.直线y =12x ﹣1向上平移m 个单位长度,得到直线y =12x+3,则m =_____. 23.已知一次函数5y x m =+的图象与正比例函数y kx =的图象交于点(2,4)(,k m -是常数),则关于x 的方程5x kx m =-的解是________.24.某一列动车从A 地匀速开往B 地,一列普通列车从B 地匀速开往A 地,两车同时出发,设普通列车行驶的时间为x (小时),两车之间的距离为y (千米),如图中的折线表示y 与x 之间的函数关系.根据图像进行探究,图中t 的值是__.25.在平面直角坐标系中,Rt ABO 的顶点B 在x 轴上,90∠=︒ABO ,AB OB =,点()10,8C 在AB 边上,D 为OB 的中点,P 为边OA 上的动点(不与,O A 重合).下列说法正确的是________(填写所有正确的序号).①当点P 运动到OA 中点时,点P 到OB 和AB 的距离相等;②当点P 运动到OA 中点时,APC DPO ∠=∠;③当点P 从点O 运动到点A 时,四边形PCBD 的面积先变大再变小;④四边形PCBD 的周长最小时,点P 的坐标为5050,77⎛⎫ ⎪⎝⎭.26.已知一次函数12y kx k =-(k 是常数)和21y x =-+.(1)无论k 取何值,12y kx k =-(k 是常数)的图像都经过同一个点,则这个点的坐标是_______;(2)若无论x 取何值,12y y >,则k 的值是_______.三、解答题27.我市全民健身中心面向学生推出假期游泳优惠活动,活动方案如下.方案一:购买一张学生卡,每次游泳费用按六折优惠;方案二:不购买学生卡,每次游泳费用按八折优惠.设某学生假期游泳x (次),按照方案一所需费用为1y (元),且11y k x b =+;按照方案二所需费用为2y (元),且22y k x =.其函数图象如图所示.(1)求y 1关于x 的函数关系式,并直接写出单独购买一张学生卡的费用和购买学生卡后每次游泳的费用;(2)求打折前的每次游泳费用和k 2的值;(3)八年级学生小明计划假期前往全民健身中心游泳8次,应选择哪种方案所需费用更少?说明理由.28.已知1y +与3x -成正比例,且5x =时,8y =,(1)求y 与x 之间的函数解析式;(2)当6y =-时,求x 的值.29.某校801班师生共45人前往某景区游览,该景区窗口票价标明:成人票每张30元,学生票享受六折优惠.(1)若老师有x 名,801班师生景区游览的门票总费用为y 元,请用x 的代数式表示y . (2)若师生门票总费用y 不超过858元,问至少有几名学生.30.为了加强公民的节水意识,某地规定用水收费标准如下:每户每月用水量不超过36m 时,水费按每立方米1.1元收费,超过36m 时,超过部分每立方米按1.6元收费,设每户每月用水量为3m x ,应缴水费为y 元.(1)写出y 与x 之间的函数表达式;(2)如果有两户家庭某月份需缴纳水费为5.5元和9.8元时,求这两户家庭这个月的用水量分别是多少?。
长沙市长郡中学必修一第二单元《函数》测试卷(答案解析)

一、选择题1.如果函数()y f x =在区间I 上是增函数,而函数()f x y x=在区间I 上是减函数,那么称函数()f x 在区间I 上为“缓增函数”,区间I 为()f x 的“缓增区间”.若函数()224f x x x =-+是区间I 上的“缓增函数”,则()f x 的“缓增区间”I 为( )A .[)1,+∞B .[)2,+∞C .[]0,1D .[]1,22.已知函数(1)f x +为偶函数,当0x >时,23()f x x x =+,则(2)f -=( ) A .4-B .12C .36D .803.已知函数()f x 的定义域是[]2,3-,则()23f x -的定义域是( ) A .[]7,3-B .[]3,7-C .1,32⎡⎤⎢⎥⎣⎦D .1,32⎡⎤-⎢⎥⎣⎦4.对任意[]1,1a ∈-,函数()()2442f x x a x a =+-+-的值恒大于零,则x 的取值范围是( ) A .13x <<B .1x <或3x >C .12x <<D .1x <或2x >5.若定义运算,,b a b a b a a b≥⎧*=⎨<⎩,则函数()()()2242g x x x x =--+*-+的值域为( ) A .(],4-∞B .(],2-∞C .[)1,+∞D .(),4-∞6.已知函数()f x 的定义域为R ,()0f x >且满足()()()f x y f x f y +=⋅,且()112f =,如果对任意的x 、y ,都有()()()0x y f x f y ⎡⎤--<⎣⎦,那么不等式()()234f x f x -⋅≥的解集为( )A .(][),12,-∞+∞ B .[]1,2 C .()1,2 D .(],1-∞7.已知函数()y f x =的定义域为[]0,4,则函数0(2)y x =-的定义域是( ) A .[1,5]B .((1,2)(2,5) C .(1,2)(2,3]⋃D .[1,2)(2,3]⋃8.已知函数()f x 是奇函数,()f x 在(0,)+∞上是减函数,且在区间[,](0)a b a b <<上的值域为[3,4]-,则在区间[,]b a --上( ) A .有最大值4 B .有最小值-4 C .有最大值-3 D .有最小值-39.函数sin sin 122xxy =+的部分图象大致是( )A .B .C .D .10.函数f (x )=x 2+2ln||2x x的图象大致为( ) A . B .C .D .11.函数2log xy x x=的大致图象是( ) A . B . C . D .12.已知函数f x ()满足当4x ≥时,f x ()=12x⎛⎫ ⎪⎝⎭;当4x <时,1f x f x =+()(),则22log 3f +()=A .124 B .112C .18D .38二、填空题13.设函数()x f x e =()g x mx =,若对于[]10,1x ∀∈,总[]21,2x ∃∈,使得()()12f x g x >恒成立,则实数m 的取值范围是_________.14.函数y x =+______.15.对于任意的1,32m ⎡⎤∈⎢⎥⎣⎦,不等式224t mt m +>+恒成立,则实数t 的取值范围是________________.16.定义域为R 的函数()f x 满足(2)2()f x f x +=,当[0,2)x ∈时,2 1.5,[0,1)()0.5,[1,2)x x x x f x x -⎧-∈⎪=⎨-∈⎪⎩,若[4,2)x ∈--时,1()42t f x t ≥-恒成立,则实数t 的取值范围是______.17.若233()1x x f x x -+=-,()2g x x =+,求函数()()y f g x =的值域________.18.设函数()y f x =是定义在R 上的偶函数,2()()g x f x x =-,若函数()y g x =在区间[0,)+∞上是严格增函数,则不等式2(1)(1)2f x f x x +->+的解集为___________.19.设()f x 是定义在R 上的偶函数,且()f x 在[)0,+∞上是减函数,若()()21f m f m ->,则实数m 的取值范围是__________20.若函数234y x x =--的定义域为[0,]m ,值域为25[,4]4--,则m 的取值范围______.三、解答题21.已知二次函数()2(f x ax bx c a R =++∈且2a >-),(1)1f =,且对任意的x ∈R ,(5)(3)f x f x -+=-均成立,且方程()42f x x =-有唯一实数解.(1)求()f x 的解析式;(2)若当(10,)x ∈+∞时,不等式()2160f x kx k +--<恒成立,求实数k 的取值范围;(3)是否存在区间[],()m n m n <,使得()f x 在区间[],m n 上的值域恰好为[]6,6m n ?若存在,请求出区间[],m n ,若不存在,请说明理由. 22.已知函数()22mf x x x=-. (1)当1m =时,判断()f x 在()0,∞+上的单调性,并用定义法加以证明. (2)已知二次函数()g x 满足()()2446g x g x x =++,()13g =-.若不等式()()g x f x >恒成立,求m 的取值范围.23.已知函数()222f x x ax =++,[]5,5x ∈-.(1)当1a =-时,求函数()f x 的最大值和最小值;(2)求实数a 的取值范围,使()y f x =在区间[]5,5-上是单调函数. (3)求函数()f x 的最小值()g a 的表达式,并求()g a 的最大值.24.(1)已知函数()f x =,求()f x 的定义域; (2)已知函数1()2f x x x=-+,依据函数单调性的定义证明()f x 在(0,)+∞上单调递减,并求该函数在[1,3]上的值域.25.设函数()()2288f x x x ax a R x x=++-+∈. (1)若函数()f x 为偶函数,求实数a 的值; (2)若关于x 的不等式()16f x x ≤-在区间0,上有解,求实数a 的取值范围.26.已知a R ∈,奇函数()f x 与偶函数()g x 的定义域均为(,0)(0,)-∞+∞,且满足()()2af xg x x x-=+-. (1)分别求()f x 和()g x 的解析式: (2)若对任意[1,),()()0x f x g x ∞∈++>恒成立,试求实数a 的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】 求得()42f x x x x=+-,利用双勾函数的单调性可求出函数()f x x 的单调递减区间,并求出函数()f x 的单调递增区间,取交集可得出()f x 的“缓增区间”. 【详解】由二次函数的基本性质可知,函数()224f x x x =-+的单调递增区间为[)1,+∞.设()()42f x g x x x x==+-,则函数()g x 在区间(]0,2上为减函数,在区间[)2,+∞上为增函数,下面来证明这一结论.任取1x 、[)22,x ∈+∞且12x x >,即122x x >≥,()()()1212121212444422g x g x x x x x x x x x ⎛⎫⎛⎫⎛⎫-=+--+-=-+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()()()()21121212121244x x x x x x x x x x x x ---=-+=,122x x >≥,则120x x ->,124x x >,所以,()()12g x g x >,所以,函数()g x 在区间[)2,+∞上为增函数,同理可证函数()g x 在区间(]0,2上为减函数. 因此,()f x 的“缓增区间”为[)(][]1,0,21,2I =+∞=.故选:D. 【点睛】关键点点睛:本题考查函数的新定义,求解本题的关键在于理解“缓增区间”的定义,结合二次函数和双勾函数的单调性求对应函数的单调区间.2.D解析:D 【分析】首先根据函数(1)f x +为偶函数,得到(1)(1)f x f x +=-+,所以有(2)(4)f f -=,结合题中所给的函数解析式,代入求得结果. 【详解】∵函数(1)f x +为偶函数,所以图象关于y 轴对称,即(1)(1)f x f x +=-+, 构造(2)(31)(31)(4)f f f f -=-+=+=,而40>, 所以23(4)4+4=16(14)80f =⨯+=. 故选:D. 【点睛】思路点睛:该题考查的是有关函数的问题,解题思路如下: (1)根据函数(1)f x +为偶函数,得到(1)(1)f x f x +=-+; (2)根据(1)(1)f x f x +=-+,得到(2)(4)f f -=; (3)结合当0x >时,23()f x x x =+,将4x =代入求得结果.3.C解析:C 【分析】由2233x -≤-≤解得结果即可得解. 【详解】因为函数()f x 的定义域是[]2,3-,所以23x -≤≤, 要使()23f x -有意义,只需2233x -≤-≤,解得132x ≤≤。
长沙市必修一第二单元《函数》检测题(含答案解析)

一、选择题1.下列函数中,在其定义域内既是奇函数又是减函数的是( )A .1y x=B .y =C .2x y =D .||y x x =-2.已知2()25x f x +=-,()()20g x ax a =+>,若对任意的[]11,2x ∈-,存在[]00,1x ∈,使()()10g x f x =,则a 的取值范围是( )A .1(0,]2B .1[,3]2C .[)3,+∞D .(]0,33.对于每个实数x ,设()f x 取24y x =-+,41y x =+,2y x =+三个函数值中的最小值,则()f x ( ) A .无最大值,无最小值 B .有最大值83,最小值1 C .有最大值3,无最小值D .有最大值83,无最小值 4.已知,a t 为正实数,函数()22f x x x a =-+,且对任意[]0,x t ∈,都有()f x a ≤成立.若对每一个正实数a ,记t 的最大值为()g a ,若函数()g a 的值域记为B ,则下列关系正确的是( ) A .2B ∈B .12B ∉C .3B ∈D .13B ∉5.设0a >且1a ≠,函数221x x y a a =+-在区间[]1,1-上的最大值是14,则实数a 的值为( )A .13或2 B .2或3C .12或2 D .13或3 6.若()f x 是偶函数,其定义域为(,)-∞+∞,且在[0,)+∞上是减函数,则(1)f -与2(22)f a a ++的大小关系是( )A . 2(1)(22)f f a a ->++B .2(1)(22)f f a a -<++C .2(1)(22)f f a a -≥++D . 2(1)(22)f f a a -≤++7.已知()f x 在[],x a b ∈的最大值为M ,最小值为m ,给出下列五个命题:( ) ①若对任何[],x a b ∈都有()p f x ≤,则p 的取值范围是(],m -∞. ②若对任何[],x a b ∈都有()p f x ≤,则p 的取值范围是(],M -∞. ③若关于x 的方程()p f x =在区间[],a b 有解,则p 的取值范围是[],m M . ④若关于x 的不等式()p f x ≤在区间[],a b 有解,则p 的取值范围是(],m -∞. ⑤若关于x 的不等式()p f x ≤在区间[],a b 有解,则p 的取值范围是(],M -∞.A .4B .3C .2D .1 8.已知53()1f x ax bx =++且(5)7,f =则(5)f -的值是( ) A .5-B .7-C .5D .79.若函数()f x =0,,则实数m 的取值范围是( ) A .()1,4 B .()(),14,-∞⋃+∞C .(][)0,14,+∞ D .[][)0,14,+∞10.设f (x )、g (x )、h (x )是定义域为R 的三个函数,对于以下两个结论:①若f (x )+g (x )、f (x )+h (x )、g (x )+h (x )均为增函数,则f (x )、g (x )、h (x )中至少有一个增函数; ②若f (x )+g (x )、f (x )+h (x )、g (x )+h (x )均是奇函数,则f (x )、g (x )、h (x )均是奇函数, 下列判断正确的是( ) A .①正确②正确B .①错误②错误C .①正确②错误D .①错误②正确11.已知函数f x ()满足当4x ≥时,f x ()=12x⎛⎫ ⎪⎝⎭;当4x <时,1f x f x =+()(),则22log 3f +()=A .124 B .112C .18D .3812.定义{},,max a b c 为,,a b c 中的最大值,设()28,,63⎧⎫=-⎨⎬⎩⎭h x max x x x ,则()h x 的最小值为( ) A .1811B .3C .4811D .4二、填空题13.已知实数0a ≠,函数()2,12,1x a x f x x a x +<⎧=⎨-+≥⎩,若()()11f a f a -=+,则a 的取值范围是___________.14.已知函数y =f (n),满足f (1)=2,且f (n+1)=3f (n),n ∈N + .则f (3)=____________. 15.设奇函数()f x 的定义域为[]5,5-,若当[]0,5x ∈时,()f x 的图象如图,则不等式()0xf x <的解集是___________.16.若()f x 是定义在R 上的以3为周期的奇函数,且()20f =,则方程()0f x = 在区间()0,6内的解的个数的最小值是__________ .17.若函数()f x 满足()()1f x f x =-,()()13f x f x +=--当且仅当(]1,3x ∈时,()3log f x x =,则()57f =______.18.已知函数()4f x x a a x=-++,若当[]1,4x ∈时,()5f x ≤恒成立,则实数a 的取值范围是______. 19.下列给出的命题中:①若()f x 的定义域为R ,则()()()g x f x f x =+-一定是偶函数;②若()f x 是定义域为R 的奇函数,对于任意的x ∈R 都有()(2)0f x f x +-=,则函数()f x 的图象关于直线1x =对称;③某一个函数可以既是奇函数,又是偶函数;④若1()2ax f x x +=+在区间(2,)-+∞上是增函数,则12a >; 其中正确的命题序号是__________.20.已知函数2262()2x ax x f x a x x⎧-+⎪=⎨>⎪⎩,≤,,是R 上的减函数,则a 的取值范围为______.三、解答题21.已知函数()221x f x x=+. (1)求()122f f ⎛⎫+⎪⎝⎭,()133f f ⎛⎫+ ⎪⎝⎭的值; (2)求证:()1f x f x ⎛⎫+ ⎪⎝⎭是定值; (3)求()()11120202320202f f f f f ⎛⎫⎛⎫⎛⎫+++⋅⋅⋅++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的值. 22.已知函数()()(),f x x x a a R g x x =-∈= (1)若0a =,试写出函数()f x 的单调区间;(2)记()()()F x g x f x =⋅,若()F x 为偶函数,求实数a 的值; (3)当1a >时,记()()()G x f x g x =+,试求函数()G x 在区间[]1,2上的最大值.23.(1)已知)1fx =-()f x 的表达式.(2)已知()f x 是偶函数,()g x 是奇函数,且2()()2f x g x x x +=+-,求()f x ,()g x 的表达式.24.定义在()0,∞+的函数()f x ,满足()()()f mn f m f n =+,且当1x >时,()0f x >.(1)求证:()()m f f m f n n ⎛⎫=- ⎪⎝⎭(2)讨论函数()f x 的单调性,并说明理由; (3)若()21f =,解不等式()()333f x f x +->. 25.已知a R ∈,函数2()25f x x ax =-+.(1)若不等式()0f x >对任意的x ∈R 恒成立,求实数a 的取值范围; (2)若1a >,且函数()f x 的定义域和值域都是[1,]a ,求实数a 的值; (3)函数()f x 在区间[1,1]a +的最大值为()g a ,求()g a 的表达式. 26.已知函数2()2(1)4f x x k x =+-+.(Ⅰ)若函数()f x 在区间[2,4]上具有单调性,求实数k 的取值范围; (Ⅱ)若()0f x >对任意的[1,2]x ∈恒成立,求实数k 的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】利用奇函数的定义和常见基本初等函数的性质,对选项逐一判断即可. 【详解】 选项A 中,函数1y x =,由幂函数性质知1y x=是奇函数,且其在()(),0,0,-∞+∞两个区间上递减,不能说在定义域内是减函数,故错误;选项B 中,函数y =[)0,+∞,不对称,故不具有奇偶性,,且在定义域内是增函数,故错误;选项C 中,指数函数2x y =,22x x -≠,且22x x -≠-,故不是奇函数,故错误;选项D 中,函数22,0,0x x y x x x x ⎧-≥=-=⎨<⎩,记()y f x =,当0x >时,0x -<,故22(),()f x x f x x =--=,故()()f x f x -=-,当0x =时,(0)0f =,故()()f x f x -=-,当0x <时,0x ->,故22(),()f x x f x x =-=-,故()()f x f x -=-,综上,()y f x =是奇函数,又0x ≥时,2()f x x =-是开口向下的抛物线的一部分,是减函数,由奇函数性质知()y f x =在定义域R 上是减函数,故正确. 故选:D. 【点睛】本题解题关键是熟练掌握常见的基本初等函数的性质,易错点是分段函数奇偶性的判断,分段函数必须判断定义域内的每一段均满足()()f x f x -=-(或()()f x f x -=)才能判定其是奇函数(或偶函数).2.A解析:A 【分析】根据指数函数的性质求出()f x 在[0,1]上的值域A ,利用一次函数的单调性求出()g x 在[1,2]-上的值域B ,由题得B A ⊆,再根据集合的包含关系即可求解.【详解】2()25x f x +=-,[]00,1x ∈,()()min 01f x f ∴==-,()()max 13f x f ==, ∴()f x 在[0,1]上的值域为[]1,3A =-,又()2(0)g x ax a =+>在[1,2]-上单调递增,∴()g x 在[1,2]-上的值域为[]2,22B a a =-++,由题意可得B A ⊆,021223a a a >⎧⎪∴-+≥-⎨⎪+≤⎩,解得102a <≤.故选:A 【点睛】本题考查函数的单调性求值域、集合的包含关系求参数的取值范围.探讨方程()()0f x g m -=解的存在性,通常可将方程转化为()()f x g m =,通过确认函数()f x 或()g m 的值域,从而确定参数或变量的范围3.D解析:D【分析】作出函数()f x 的图象,结合图象可得出结论. 【详解】由已知可得(){}min 24,41,2f x x x x =-+++,作出函数()f x 的图象如下图所示:函数()f x 的图象如上图中的实线部分,联立224y x y x =+⎧⎨=-+⎩,解得2383x y ⎧=⎪⎪⎨⎪=⎪⎩,由图象可知,函数()f x 有最大值83,无最小值. 故选:D. 【点睛】关键点点睛:本题考查函数最值的求解,解题的关键就是结合函数()f x 的定义,进而作出函数()f x 的图象,利用图象得出结论.4.A解析:A 【分析】根据函数的特征,要对t 进行分类讨论,求出t 的最大值,再根据a 是正实数,求出()g a 的值域即可判断答案. 【详解】 解:2()2f x x x a =-+∴函数()f x 的图象开口向上,对称轴为1x =①01t <时,()f x 在[0,]t 上为减函数,()(0)max f x f a ==,2()()2min f x f t t t a ==-+ 对任意的[0x ∈,]t ,都有()[f x a ∈-,]a . 22a t t a ∴-≤-+,即2220t t a -+≥,当()()22424120a a ∆=--⨯=-≤,即12a ≥时,01t <,当()()22424120a a ∆=--⨯=->,即102a <<时,11t ≤ ②1t >时,()f x 在[0,1]上为减函数,在[1,]t 上为增函数,则()()11min f x f a a ==-≥-,2(){(0),()}{,2}max f x max f f t max a t t a a ==-+≤,12a ∴≥,且22t t a a -+,即12t < t 的最大值为()g a综上可得,当12a ≥时(]0,2t ∈ 当102a <<时,()0,1t ∈ ∴函数()g a 的值域为(]0,2故选:A . 【点睛】二次函数、二次方程与二次不等式统称“三个二次”,它们常结合在一起,有关二次函数的问题,数形结合,密切联系图象是探求解题思路的有效方法.一般从:①开口方向;②对称轴位置;③判别式;④端点函数值符号四个方面分析.5.D解析:D 【分析】本题首先可以令x t a =,将函数转化为()212y t =+-并判断出函数的单调性,然后分为01a <<、1a >两种情况进行讨论,根据最大值是14进行计算,即可得出结果. 【详解】令x t a =(0a >、1a ≠),则()222112y t t t =+-=+-, 因为0a >,所以0x t a =>,函数()212y t =+-是增函数, 当01a <<、[]1,1x ∈-时,1,t a a⎡⎤∈⎢⎥⎣⎦,此时2max11214y a ⎛⎫=+-= ⎪⎝⎭,解得13a =或15-(舍去);当1a >、[]1,1x ∈-时,1,t a a⎡⎤∈⎢⎥⎣⎦,此时()2max 1214y a =+-=,解得3a =或5-(舍去), 综上所述,实数a 的值为13或3, 故选:D. 【点睛】本题考查根据函数的最值求参数,能否通过换元法将函数转化为二次函数是解决本题的关键,考查二次函数单调性的判断和应用,考查分类讨论思想,考查计算能力,是中档题.6.C解析:C 【分析】由()f x 是偶函数,可知(1)(1)f f -=,故只需比较(1)f 与2(22)f a a ++的大小即可,而2222(1)11a a a ++=++≥,再结合函数()f x 的单调性,即可得(1)f 与2(22)f a a ++大小关系.【详解】因为()f x 是偶函数,所以(1)(1)f f -=,又2222(1)11a a a ++=++≥,()f x 在[0,)+∞上是减函数,所以2(22)(1)f a a f ++≤,即2(22)(1)f a a f ++≤-. 故选:C 【点睛】关键点点睛:本题主要考查利用函数的单调性比较大小,关键是借助函数的奇偶性,将要比较的函数值对应的自变量转化到同单调区间上,并且比较它们的大小,再利用单调性作出判断.7.B解析:B 【分析】这是一个对不等式恒成立,方程或不等式解集非空的理解,概念题.对各个选项分别加以判断,在①②中,得出①正确②错误,④⑤中得出⑤正确④错误,而不难发现③是一个真命题,由此可得正确答案. 【详解】对任何x ∈[a ,b]都有()p f x ≤,说明p 小于等于()f x 的最小值,①是正确的; 由于①正确,所以②是一个错误的理解,故不正确;关于x 的方程p =f (x )在区间[a ,b ]上有解,说明p 应属于函数f (x )在[a ,b ]上的值域[m ,M ]内,故③是正确的;关于x 的不等式p ≤f (x )在区间[a ,b ]上有解,说明p 小于或等于的最大值,所以④是错误的,而⑤是正确的 正确的选项应该为①③⑤ 故选: B.【点睛】关键点点睛:本题考查了命题的真假判断与应用,属于基础题.不等式或方程解集非空,只要考虑有解;而不等式恒成立说明解集是一切实数,往往要考虑函数的最值了.8.A解析:A 【解析】()()53531,1f x ax bx f x ax bx =++∴-=--+,()()()()2,552f x f x f f +-=∴+-=,()5275f -=-=-,故选A. 9.D解析:D 【分析】令t =()0,t ∈+∞()0,+∞,记函数()22(2)1g x mx m x =+-+的值域为A ,则()0,A +∞⊆,进而分0m =和0m ≠两种情况,分别讨论,可求出m 的取值范围. 【详解】令t =1y t=的值域为0,,根据反比例函数的性质,可知()0,t ∈+∞()0,+∞, 记函数()22(2)1g x mx m x =+-+的值域为A ,则()0,A +∞⊆,若0m =,则()41g x x =-+,其值域为R ,满足()0,A +∞⊆;若0m ≠,则00m >⎧⎨∆≥⎩,即()24240m m m >⎧⎪⎨--≥⎪⎩,解得4m ≥或01m <≤. 综上所述,实数m 的取值范围是[][)0,14,+∞.故选:D.10.D解析:D 【分析】可举出反例判断①错误;根据奇偶性的性质可判断②正确,结合选项可得答案. 【详解】①错误,可举反例:21()31xx f x x x ⎧=⎨-+>⎩, 230()30121x x g x x x x x +⎧⎪=-+<⎨⎪>⎩,0()20x x h x x x -⎧=⎨>⎩,均不是增函数;但()()f x g x +、()()f x h x +、()()g x h x +均为增函数; 故①错误; ②()()f x g x +,()()f x h x +,()()g x h x +均是奇函数;()()()()[()()]2()f x g x f x h x g x h x f x ∴+++-+=为奇函数;()f x ∴为奇函数;同理,()g x ,()h x 均是奇函数; 故②正确. 故选:D . 【点睛】本题考查增函数的定义,一次函数和分段函数的单调性,举反例说明命题错误的方法,以及奇函数的定义与性质,知道()f x 和()g x 均是奇函数时,()()f x g x ±也是奇函数.11.A解析:A 【分析】根据232log 34<+<,()()222log 33log 3f f +=+可得,又有23log 34+> 知,符合4?x >时的解析式,代入即得结果. 【详解】因为函数f x ()满足当4x ≥时,f x ()=12x⎛⎫ ⎪⎝⎭; 当4x <时,1f x f x =+()(),所()()()()22222log 3log 121log 12log 24f f f f +==+=以=21log 242=124,故选A . 【点睛】本题主要考查分段函数的解析式、对数的运算法则,意在考查灵活应用所学知识解答问题的能力,属于中档题.12.C解析:C 【分析】首先根据题意画出()h x 的图象,再根据图象即可得到()h x 的最小值. 【详解】 分别画出2yx ,83y x =,6y x =-的图象, 则函数()h x 的图象为图中实线部分.由图知:函数()h x 的最低点为A ,836y x y x ⎧=⎪⎨⎪=-⎩,解得1848,1111⎛⎫⎪⎝⎭A .所以()h x 的最小值为4811. 故选:C. 【点睛】本题主要考查根据函数的图象求函数的最值,考查了数形结合的思想,属于中档题.二、填空题13.【分析】本题首先可讨论的情况此时然后根据函数的解析式求出和通过即可求出的值最后讨论的情况此时通过得出此时无解即可得出结果【详解】若则因为函数所以因为所以解得若则因为函数所以因为所以无解综上所述的取值解析:32⎧⎫⎨⎬⎩⎭【分析】本题首先可讨论0a >的情况,此时11a -<、11a +>,然后根据函数()f x 的解析式求出()1f a -和()1f a +,通过()()11f a f a -=+即可求出a 的值,最后讨论0a <的情况,此时11a ->、11a +<,通过()()11f a f a -=+得出此时a 无解,即可得出结果. 【详解】若0a >,则11a -<,11a +>, 因为函数()2,12,1x a x f x x a x +<⎧=⎨-+≥⎩,所以1212f aa a a ,1121f a a a a ,因为()()11f a f a -=+,所以21a a ,解得32a =, 若0a <,则11a ->,11a +<,因为函数()2,12,1x a x f x x a x +<⎧=⎨-+≥⎩,所以11213f aa a a ,12123f a a a a ,因为()()11f a f a -=+,所以1323a a ,无解,综上所述,32a =,a 的取值范围是32⎧⎫⎨⎬⎩⎭, 故答案为:32⎧⎫⎨⎬⎩⎭. 【点睛】本题考查分段函数的相关问题的求解,在分段函数求函数值的时候,要把自变量代入到所对应的解析式中是解本题的关键,考查分类讨论思想,考查计算能力,是中档题.14.18【分析】根据递推关系式依次求f(2)f(3)【详解】因为f(n+1)=3f(n)所以【点睛】本题考查根据递推关系求函数值考查基本求解能力解析:18 【分析】根据递推关系式依次求f (2) ,f (3). 【详解】因为f (n+1)=3f (n),所以(2)3(1)6,(3)3(2)18.f f f f ==== 【点睛】本题考查根据递推关系求函数值,考查基本求解能力.15.【分析】由奇函数的图象关于原点对称便可得出f (x )在-50上的图象这样根据f (x )在上的图象便可得出xf (x )<0的解集【详解】奇函数图象关于原点对称作出在的图象如下:由得或由图可知或的解集为【点睛 解析:[)(]5,22,5--【分析】由奇函数的图象关于原点对称便可得出f (x )在[-5,0]上的图象,这样根据f (x )在[]5,5-上的图象便可得出xf (x )<0的解集.【详解】奇函数图象关于原点对称,作出()f x 在[]5,5-的图象如下:由()0xf x <得()00x f x <⎧⎨>⎩或()00x f x >⎧⎨<⎩,由图可知52x -≤<-或25x <≤,()0xf x ∴<的解集为[)(]5,22,5--.【点睛】本题考查函数奇偶性、函数图象的综合,解题关键是根据函数奇偶性作出函数图象,利用数形结合思想求解,属于中等题.16.7【解析】由函数的周期为3可得因为若则可得出又根据为奇函数则又可得出又函数是定义在R 上的奇函数可得出从而在中令得出又根据是定义在R 上的奇函数得出从而得到即故从而共7个解解析:7 【解析】由函数的周期为3可得(3)()f x f x +=,因为(2)0f =, 若(0,6)x ∈,则可得出(5)=(2)0f f =, 又根据()f x 为奇函数,则(-2)=-(2)0f f =, 又可得出(4)=(1)(-2)=0f f f =,又函数()f x 是定义在R 上的奇函数,可得出(0)0f =, 从而(3)=(0)0f f =,在(3)()f x f x +=中, 令32x =-,得出33()()22f f -=,又根据()f x 是定义在R 上的奇函数,得出33()-()22f f -=, 从而得到33()-()22f f =,即3()02f =, 故933()(+3)()=0222f f f ==,从而93()()=(4)(1)(3)(5)(2)022f f f f f f f ======,共7个解.17.2【分析】根据函数满足的关系可得是以6最小正周期的周期函数根据代入解析式即可【详解】根据已知条件进而有于是显然则是以6最小正周期的周期函数∵当时则故答案为:2【点睛】本题以抽象函数为载体研究抽象函数解析:2 【分析】根据函数满足的关系可得()f x 是以6最小正周期的周期函数,根据()()573f f =代入解析式即可. 【详解】根据已知条件()()()()113f x f x f x f x ⎧=-⎪⎨+=--⎪⎩, 进而有()()()()()1133f x f x f x f x f x =-=+-=⎡⎤⎡⎤⎣⎦⎣⎦---=-+, 于是()()3+=-f x f x ,显然()()()()()6333f x f x f x f x f x +=++=-⎡⎤⎡⎤+=--⎦⎦=⎣⎣, 则()f x 是以6最小正周期的周期函数, ∵当(]1,3x ∈时()f x x =,则()()()57693332f f f =⨯+===.故答案为:2. 【点睛】本题以抽象函数为载体,研究抽象函数的结构特征,且挖掘暗含条件,巧妙地对复合函数的连续变形,体现了数学抽象,数学化归等关键能力与学科素,属于中档题.18.【分析】对分段讨论去绝对值计算求解【详解】当时可得当时符合题意;当时则不符合题意;当时此时不符合题意综上的取值范围是故答案为:【点睛】本题考查函数不等式的恒成立问题解题的关键是对分段讨论求解 解析:(],1-∞【分析】对a 分段讨论去绝对值计算求解. 【详解】当1a ≤时,()44f x x a a x x x=-++=+,可得当[]1,4x ∈时,()45f x ≤≤,符合题意;当14a <<时,()42,14,4a x x a xf x x a x x ⎧-+≤<⎪⎪=⎨⎪+≤≤⎪⎩,则()1325f a =+>,不符合题意;当4a ≥时,()42f x a x x=-+,此时()13211f a =+≥,不符合题意, 综上,a 的取值范围是(],1-∞. 故答案为:(],1-∞. 【点睛】本题考查函数不等式的恒成立问题,解题的关键是对a 分段讨论求解.19.①③④【分析】①根据奇偶函数的定义判断;②利用抽象函数的对称性判断;③通过特殊函数判断;④通过分离常数转化为熟悉的函数判断【详解】①函数的定义域为所以函数的定义域也是即所以函数是偶函数故①正确;②对解析:①③④ 【分析】①根据奇偶函数的定义判断;②利用抽象函数的对称性判断;③通过特殊函数判断;④通过分离常数,转化为熟悉的函数判断. 【详解】①函数()f x 的定义域为R ,所以函数()g x 的定义域也是R ,()()()g x f x f x -=-+,即()()g x g x -=,所以函数()g x 是偶函数,故①正确;②对应任意的x ∈R ,都有()()20f x f x +-=,即函数()f x 关于()1,0对称,并不关于1x =对称,故②不正确;③函数0y =既是偶函数又是奇函数,故③正确; ④()()212112222a x a ax af x a x x x ++-+-===++++,若函数在()2,-+∞上单调递增,则120a -<,解得:12a >,故④正确. 故答案为:①③④ 【点睛】方法点睛:函数的对称性包含中心对称和轴对称,一般判断的方法包含:1.若对函数()y f x =的定义域内的任一自变量x 的值都有()()2f x f a x =-,则()y f x =的图象关于x a =成轴对称;若对函数()y f x =的定义域内的任一自变量x 的值都有()()22f x b f a x =--,则()y f x =的图象关于(),a b 成中心对称;20.2【分析】由已知利用分段函数的性质及二次函数与反比例函数的单调性可求【详解】解;是上的减函数解可得故答案为:【点睛】本题主要考查了分段函数的单调性的应用二次函数及反比例函数性质的应用是求解问题的关键解析:[2,209] 【分析】由已知利用分段函数的性质及二次函数与反比例函数的单调性可求. 【详解】解;226,2(),2x ax x f x a x x⎧-+⎪=⎨>⎪⎩是R 上的减函数,∴204462a a a a ⎧⎪⎪>⎨⎪⎪-+⎩, 解可得,2029a. 故答案为:202,9⎡⎤⎢⎥⎣⎦【点睛】本题主要考查了分段函数的单调性的应用,二次函数及反比例函数性质的应用是求解问题的关键,属于中档题.三、解答题21.(1)()1212f f ⎛⎫+= ⎪⎝⎭,()1313f f ⎛⎫+= ⎪⎝⎭;(2)证明见解析;(3)2019. 【分析】(1)根据函数解析式,直接计算,即可得出结果;(2)根据函数解析式,计算1f x ⎛⎫⎪⎝⎭,得出()12f x f x ⎛⎫+= ⎪⎝⎭即可; (3)根据(2)的结论,可直接得出结果. 【详解】 (1)()221x f x x=+ ()22221124122121255112f f ⎛⎫ ⎪⎛⎫⎝⎭∴+=+=+= ⎪+⎝⎭⎛⎫+ ⎪⎝⎭,()222113913313131010113f f ⎛⎫ ⎪⎛⎫⎝⎭+=+=+= ⎪+⎝⎭⎛⎫+ ⎪⎝⎭; (2)证明:()22222222211111111111x x x x f f x x x x x x x ⎛⎫ ⎪+⎛⎫⎝⎭+=+=+== ⎪++++⎝⎭⎛⎫+ ⎪⎝⎭, ()1f x f x ⎛⎫+ ⎪⎝⎭∴是定值;(3)()()()111232020232020f f f f f f ⎛⎫⎛⎫⎛⎫++++⋅⋅⋅++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()()()111232020232020f f f f f f ⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫=++++⋅⋅⋅++ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦111=++⋅⋅⋅+ 2019=.22.(1)()f x 的单调增区间为(),-∞+∞,无单调递减区间;(2)0a =;(3)()()2max1,13422,3a a G x a a ⎧+⎪<≤=⎨⎪->⎩. 【分析】(1)0a =时,求出()f x 的解析式,可得函数的单调区间; (2)由函数是偶函数,利用特值列出方程解出实数a 的值;(3)化简函数()G x ,按1a >,12a <≤,23a <≤和3a >四种情况,分别判断对称轴和区间端点的关系,判断出单调性得出最值. 【详解】(1)0a =时,()22,0,0x x f x x x x x ⎧≥==⎨-<⎩,则()f x 在R 上单调递增,即函数()f x 的单调增区间为(),-∞+∞,无单调递减区间; (2)()()()2F x g x f x x x a =⋅=-,()F x 为偶函数,()()11F F ∴-=,即11a a --=-,平方解得0a =检验0a =时,()f x x x =,符合题意,故0a =;(3)()()()()()221,1,x a x x aG x f x g x x x a x x a x x a ⎧--≥⎪=+=-+=⎨-++<⎪⎩若1a >,当x a ≥时,对称轴为102a x -=<恒成立; 当x a <时,对称轴为12a x a +=<恒成立;若12a <≤,当x a ≥时,1012a -<≤;当x a <时,13122a +≤≤; 又[]1,2x ∈,此时()()()2max 111,224a G x G G a a G a +⎧+⎫+⎛⎫⎛⎫===⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎩⎭ 若23a <≤,当x a ≥时,11122a -<≤;当x a <时,31222a +<≤; 又[]1,2x ∈,此时()()2max 1124a a G x G ++⎛⎫==⎪⎝⎭若3a >,当x a ≥时,112a ->;当x a <时,122a +>; 又[]1,2x ∈,此时()()max 222G x G a ==- 综上,()()2max 1,13422,3a a G x a a ⎧+⎪<≤=⎨⎪->⎩【点睛】关键点点睛:本题考查分段函数的单调性,奇偶性和最值,考查二次函数的性质,解决本题的关键点是分情况讨论二次函数的对称轴与区间端点的关系,从而确定出函数的单调性和最值,考查学生分类讨论思想和计算能力,属于中档题.23.(1)2()43(1)f x x x x =-+≥;(2)2()2f x x =-,()g x x =. 【分析】(1)利用换元法求解析式即可;(2)根据函数奇偶性的性质利用方程组法即可求求()f x ,()g x 的表达式.【详解】 (1)由)1f x =-,令11t =≥,()21,1t x t =-=-,所以()()()2212143f t t t t t =---=-+,故()f x 的表达式为:2()43(1)f x x x x =-+≥;(2)由()f x 是偶函数,()g x 是奇函数, 得()()()(),f x f x g x g x -=-=-, 又由2()()2f x g x x x +=+-,(1) 得2()()2f x g x x x +-=---, 即2()()2f x g x x x =---,(2) 解(1)(2)联立的方程组得:2()2f x x =-,()g x x =,所以()f x ,()g x 的表达式为:2()2f x x =-,()g x x =.【点睛】关键点睛:利用换元法求解析式,根据函数奇偶性的定义利用方程组法是解决本题的关键. 24.(1)见解析;(2)见解析;(3)3023x x ⎧⎫<<⎨⎬⎩⎭【分析】(1)由()m f m f n n ⎛⎫=⋅⎪⎝⎭,结合题意即可得结果; (2)利用函数单调性的定义证明即可;(3)将原不等式等价转化为()()324f x f x +>,结合定义域和单调性即可得结果. 【详解】解:(1)由题可得()()m m f m f n f f n n n ⎛⎫⎛⎫=⋅=+ ⎪ ⎪⎝⎭⎝⎭, 即()()m f f m f n n ⎛⎫=- ⎪⎝⎭;(2)任取1x ,()20,x ∈+∞,且12x x <,则211x x >, 由(1)得:()()22110x f x f x f x ⎛⎫-=> ⎪⎝⎭,即()()21f x f x >,()f x ∴在()0,∞+上是增函数;(3)()21f =,()()()2224f f f ∴=+=,()()()3428f f f =+=,()()333f x f x +->, ()()()338f x f x f +>+, ()()324f x f x +>,又()f x 在()0,∞+上为增函数,30,240,324,x x x x +>⎧⎪∴>⎨⎪+>⎩, 解得:0323x <<,故不等式()()333f x f x +->的解集为3023x x ⎧⎫<<⎨⎬⎩⎭. 【点睛】关键点点睛:本题解题的关键是利用()m f m f n n ⎛⎫=⋅ ⎪⎝⎭,再结合题意,即可判断函数单调性和解不等式.25.(1)(a ∈;(2)2;(3)()g a 262,26,2a a a a ->⎧=⎨-⎩. 【分析】(1)利用二次函数的性质列出关系式求解即可.(2)根据二次函数定义域和值域之间的关系进行判断即可. (3)对对称轴分类讨论,得到最大值. 【详解】解:(1)a R ∈,函数2()25f x x ax =-+.开口向上,不等式()0f x >对任意的x ∈R 恒成立,可得:24200a -<,解得(a ∈.(2)函数2()25f x x ax =-+的对称轴为x a =,则函数在[1,]a 上为减函数,函数的值域为[1,]a ,∴()1f a =,即22251a a -+=,即24a =, 解得2a =-(舍)或2a =.(3)函数2()25f x x ax =-+的对称轴为x a =,开口向上,①当12a a +,即2a 时,()f x 在区间[1,1]a +上的最大值为2(1)6f a a +=-; ②2a >时,()f x 在区间[1,1]a +上的最大值为(1)f 62a =-.所以()g a 262,26,2a a a a ->⎧=⎨-⎩. 【点睛】方法点睛:求二次函数的最值或值域时,关键在于确定二次函数的对称轴与所求的区间的关系,也即是二次函数在所求区间上的单调性,利用单调性求得值域. 26.(1)(,3][1,)-∞-⋃-+∞(2)()1,-+∞ 【分析】(1)根据二次函数对称轴与区间关系,即可求解; (2)分离参数可得42(1)4k x ->--,求出44y x =--的最大值即可求解. 【详解】(1)由函数2()2(1)4f x x k x =+-+知,函数()f x 图象的对称轴为1x k =-.因为函数()f x 在区间[]2,4上具有单调性,所以12k -≤或14k -≥,解得3k ≤-或1k ≥-,所以实数k 的取值范围为(,3][1,)-∞-⋃-+∞.(2) 因为()0f x >对任意的[1,2]x ∈恒成立, 所以可得42(1)k x x ->--对任意的[1,2]x ∈恒成立,因为44()44y x x x =--=-+≤-=-,当且仅当2x =时等号成立, 即max 4y =-,所以只需2(1)4k ->-,解得1k -<,所以实数k 的取值范围为()1,-+∞.【点睛】关键点睛:不等式在某区间上恒成立求参数的取值范围,一般需要分离参数,转化为求最值问题,往往可以利用函数单调性或均值不等式求最值,即可求出答案,本题中利用了均值不等式,特别注意等号是否能取到,否则不能用均值不等式求最值.。
长沙市必修一第二单元《函数》测试题(含答案解析)

一、选择题1.如果函数()y f x =在区间I 上是增函数,而函数()f x y x=在区间I 上是减函数,那么称函数()f x 在区间I 上为“缓增函数”,区间I 为()f x 的“缓增区间”.若函数()224f x x x =-+是区间I 上的“缓增函数”,则()f x 的“缓增区间”I 为( )A .[)1,+∞B .[)2,+∞C .[]0,1D .[]1,22.已知函数()32f x x =-,2()2g x x x =-,(),()()()(),()()g x f x g x F x f x f x g x ≥⎧=⎨<⎩,则( )A .()F x 的最大值为3,最小值为1B .()F x的最大值为2 C .()F x的最大值为7-,无最小值 D .()F x 的最大值为3,最小值为-13.已知函数()y f x =是定义在R 上的单调函数,()0,2A ,()2,2B -是其函数图像上的两点,则不等式()12f x ->的解集为( ) A .()1,3 B .()(),31,-∞-⋃+∞ C .()1,1-D .()(),13,-∞+∞4.已知函数(2)f x 的定义域为3(0,)2,则函数(13)f x -的定义域是( ) A .21(,)33-B .11(,)63-C .(0,3)D .7(,1)2-5.已知函数()31,03,0x x x f x e x ⎧<⎪=⎨⎪≥⎩,则()()232f x f x ->的解集为( )A .()(),31,-∞-⋃+∞B .()3,1-C .()(),13,-∞-+∞ D .()1,3-6.定义{},min ,,a a b a b b a b≤⎧=⎨>⎩,若函数{}2()min 33,|3|3f x x x x =-+--+,且()f x 在区间[,]m n 上的值域为37,44⎡⎤⎢⎥⎣⎦,则区间[,]m n 长度的最大值为( ) A .1B .74C .114D .727.已知,a t 为正实数,函数()22f x x x a =-+,且对任意[]0,x t ∈,都有()f x a ≤成立.若对每一个正实数a ,记t 的最大值为()g a ,若函数()g a 的值域记为B ,则下列关系正确的是( ) A .2B ∈B .12B ∉C .3B ∈D .13B ∉8.对x R ∀∈,用()M x 表示()f x ,()g x 中较大者,记为()()()max{,}M x f x g x =,若()()2{3,1}M x x x =-+-,则()M x 的最小值为( )A .-1B .0C .1D .49.已知函数224()3f x x x=-+,()2g x kx =+,若对任意的1[1,2]x ∈-,总存在2[1x ∈,使得12()()g x f x >,则实数k 的取值范围是( ).A .1,12⎛⎫ ⎪⎝⎭B .12,33⎛⎫- ⎪⎝⎭C .1,12⎛⎫-⎪⎝⎭D .以上都不对10.如果()()211f x mx m x =+-+在区间(]1-∞,上为减函数,则m 的取值范围( ) A .103⎛⎤ ⎥⎝⎦,B .103⎡⎤⎢⎥⎣⎦,C .103⎡⎫⎪⎢⎣⎭,D .103⎛⎫ ⎪⎝⎭,11.已知定义在R 上的奇函数()y f x =,当0x ≥时,22()f x x a a =--,若对任意实数x 有()()f x a f x -≤成立,则正数a 的取值范围为( ) A .)1,4⎡+∞⎢⎣B .)1,2⎡+∞⎢⎣C .(10,4⎤⎥⎦D .(10,2⎤⎥⎦12.已知函数()f x 的定义域为R ,对任意的 12,x x <都有1212()(),f x f x x x -<-且(3)4,f =则(21)2f x x ->的解集为( )A .(2,)+∞B .(1,)+∞C .(0,)+∞D .(1,)-+∞二、填空题13.函数()()2325f x kx k x =+--在[)1+∞,上单调递增,则k 的取值范围是________. 14.函数1,1()32,12x a x f x a x x ⎧+>⎪=⎨⎛⎫-+≤ ⎪⎪⎝⎭⎩是R 上的单调递增函数,则实数a 取值范围为________.15.函数2()2f x x x =-,()1g x ax =+(0a >),若对任意的[]12,2x ∈-,存在[]22,2x ∈-,使12()()f x g x =,则a 的取值范围是___________.16.已知函数f (x )满足2f (x )+f (-x )=3x ,则f (x )=________. 17.若函数2(21)1,0()(2),0b x b x f x x b x x -+->⎧=⎨-+-≤⎩,满足对任意12x x ≠,都有1212()()0f x f x x x ->-成立,那么b 的取值范围是_____.18.已知()()21353m f x m m x+=++是幂函数,对12,(0,)x x ∈+∞且12x x ≠有()()12120f x f x x x ->-,若,a b ∈R ,0a b +<,0ab <,则()()f a f b +________0(填>,<).19.若函数()log (3)4,1(43)41,1a x x f x a x a x ++≥-⎧=⎨-+-<-⎩且满足对任意的实数m n ≠都有()()0f m f n m n-<-成立,则实数a 的取值范围____.20.下列给出的命题中:①若()f x 的定义域为R ,则()()()g x f x f x =+-一定是偶函数;②若()f x 是定义域为R 的奇函数,对于任意的x ∈R 都有()(2)0f x f x +-=,则函数()f x 的图象关于直线1x =对称;③某一个函数可以既是奇函数,又是偶函数;④若1()2ax f x x +=+在区间(2,)-+∞上是增函数,则12a >; 其中正确的命题序号是__________.三、解答题21.已知函数2()f x x bx c =++的图象经过坐标原点,且()1y f x =+为偶函数. (1)求函数()f x 的解析式;(2)求证:对于任意的[0,4]x ∈,总有24()2x f x x -≤≤;(3)记函数|()2|y f x x m =--在区间[]0,4的最大值为()G m ,直接写出()G m 的最小值. 22.设函数12ax y x +=-. (1)当1a =时,在区间[)(]2,22,6-⋃上画出这个函数的图像;(2)是否存在整数a ,使该函数在[4,)+∞上是严格减函数,且当4x ≥时,都有4y ≤,如果存在,求出所有符合条件的a ,若不存在,请说明理由. 23.已知函数()f x x x a =-,a ∈R ,()21g x x =-.(1)当1a =-时,解不等式()()f x g x ≥;(2)当4a >时,记函数()f x 在区间[]0,4上的最大值为()F a ,求()F a 的表达式. 24.已知二次函数()2()f x ax bx a b R =+∈、满足:①()()11f x f x +=-;②对一切x ∈R ,都有()f x x ≤.(1)求()f x ;(2)是否存在实数(),m n m n <使得()f x 的定义域为[],m n 、值域为[]3,3m n ,如果存在,求出m ,n 的值;如果不存在,说明理由.25.定义在[]1,1-上的奇函数()f x ,当10x -≤<时,23()6x x xf x +=.(1)求()f x 在[]1,1-上的解析式;(2)求()f x 的值域; (3)若实数a 满足1()()0a f f a a-+<,求实数a 的取值范围. 26.已知函数()()20,,f x ax bx c a b c R =++>∈满足1(0)()1f f a==. (1)求()f x 表达式及其单调区间(不出现b ,c );(2)设对任意[]12,1,3x x ∈,()()128f x f x -≤恒成立,求实数a 的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】 求得()42f x x x x=+-,利用双勾函数的单调性可求出函数()f x x 的单调递减区间,并求出函数()f x 的单调递增区间,取交集可得出()f x 的“缓增区间”. 【详解】由二次函数的基本性质可知,函数()224f x x x =-+的单调递增区间为[)1,+∞.设()()42f x g x x x x==+-,则函数()g x 在区间(]0,2上为减函数,在区间[)2,+∞上为增函数,下面来证明这一结论.任取1x 、[)22,x ∈+∞且12x x >,即122x x >≥,()()()1212121212444422g x g x x x x x x x x x ⎛⎫⎛⎫⎛⎫-=+--+-=-+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()()()()21121212121244x x x x x x x x x x x x ---=-+=,122x x >≥,则120x x ->,124x x >,所以,()()12g x g x >,所以,函数()g x 在区间[)2,+∞上为增函数,同理可证函数()g x 在区间(]0,2上为减函数.因此,()f x 的“缓增区间”为[)(][]1,0,21,2I =+∞=.故选:D. 【点睛】关键点点睛:本题考查函数的新定义,求解本题的关键在于理解“缓增区间”的定义,结合二次函数和双勾函数的单调性求对应函数的单调区间.2.C解析:C 【分析】在同一坐标系中先画出()f x 与()g x 的图象,然后根据定义画出()F x ,就容易看出()F x 有最大值,无最小值,解出两个函数的交点,即可求得最大值. 【详解】在同一坐标系中先画出()f x 与()g x 的图象,如图然后根据定义画出()F x ,就容易看出()F x 有最大值,无最小值. 由图象可知,当0x <时,()y F x =取得最大值, 所以由232||2x x x -=-得27x =+或27x =-.结合函数图象可知当27x =-时,函数()F x 有最大值727-,无最小值. 故选:C .【点睛】关键点睛:本题主要考查了函数的图象,以及利用函数求最值,解答本题的关键是在同一坐标系中画出()f x 与()g x 的图象,根据图象得出函数的最值,由232||2x x x -=-得27x =+或27x =-.3.D解析:D 【分析】根据题意可得出(0)2,(2)2f f ==-,从而得出()f x 在R 上为减函数,从而根据不等式()12f x ->得,(1)(2)f x f -<或(1)(0)f x f ->,从而得出12x ->或10x -<,解出x 的范围 【详解】解:由题意得(0)2,(2)2f f ==-, 因为函数()y f x =是定义在R 上的单调函数, 所以()f x 在R 上为减函数,由()12f x ->,得(1)2f x ->或(1)2f x -<-, 所以(1)(0)f x f ->或(1)(2)f x f -<, 所以10x -<或12x ->, 解得1x <或3x >,所以不等式()12f x ->的解集为()(),13,-∞+∞,故选:D 【点睛】关键点点睛:此题考查函数单调性的应用,考查绝对值不等式的解法,解题的关键是把()12f x ->转化为(1)(0)f x f ->或(1)(2)f x f -<,再利用()f x 在R 上为减函数,得10x -<或12x ->,考查数学转化思想,属于中档题 4.A解析:A 【分析】先求出函数()f x 的定义域(0,3),再求出函数(13)f x -的定义域. 【详解】函数(2)f x 的定义域为3(0,)2,则302x <<,所以023x << 所以函数()f x 的定义域为(0,3),则0133x <-<解得2133x -<< 函数(13)f x -的定义域为21(,)33- 故选:A 【点睛】对于抽象函数定义域的求解方法:(1)若已知函数()f x 的定义域为[]a b ,,则复合函数()()f g x 的定义域由不等式()a g x b ≤≤求出;(2)若已知函数()()f g x 的定义域为[]a b ,,则()f x 的定义域为()g x 在[]x a b ∈,上的值域.5.B解析:B 【分析】先分析分段函数的单调性,然后根据单调性将关于函数值的不等式转化为关于自变量的不等式,从而求解出解集. 【详解】 因为313yx =在R 上单调递增,所以313y x =在(),0-∞上单调递增, 又因为xy e =在R 上单调递增,所以xy e =在[)0,+∞上单调递增,且0311003e =>=⋅,所以()f x 在R 上单调递增, 又因为()()232f x f x ->,所以232xx ->,解得()3,1x ∈-,故选:B. 【点睛】思路点睛:根据函数单调性求解求解关于函数值的不等式的思路: (1)先分析出函数在指定区间上的单调性;(2)根据单调性将函数值的关系转变为自变量之间的关系,并注意定义域; (3)求解关于自变量的不等式,从而求解出不等式的解集.6.B解析:B 【分析】根据定义作出函数()f x 的解析式和图象,根据函数值域,求出对应点的坐标,利用数形结合进行判断即可. 【详解】其中(1,1)A ,(3,3)B , 即()233,133313x x x f x x x x ⎧--=⎨-+⋅<<⎩或,当3()4f x =时,当3x 或1x 时,由33|3|4x --=,得9|3|4x -=,即34C x =或214G x =,当7()4f x =时,当13x <<时,由27334x x -+=,得52E x =,由图象知若()f x 在区间[m ,]n 上的值域为3[4,7]4,则区间[m ,]n 长度的最大值为537244E C x x -=-=, 故选:B . 【点睛】 利用数形结合思想作出函数的图象,求解的关键是对最小值函数定义的理解.7.A解析:A 【分析】根据函数的特征,要对t 进行分类讨论,求出t 的最大值,再根据a 是正实数,求出()g a 的值域即可判断答案. 【详解】 解:2()2f x x x a =-+∴函数()f x 的图象开口向上,对称轴为1x =①01t <时,()f x 在[0,]t 上为减函数,()(0)max f x f a ==,2()()2min f x f t t t a ==-+ 对任意的[0x ∈,]t ,都有()[f x a ∈-,]a . 22a t t a ∴-≤-+,即2220t t a -+≥,当()()22424120a a ∆=--⨯=-≤,即12a ≥时,01t <,当()()22424120a a ∆=--⨯=->,即102a <<时,11t ≤ ②1t >时,()f x 在[0,1]上为减函数,在[1,]t 上为增函数,则()()11min f x f a a ==-≥-,2(){(0),()}{,2}max f x max f f t max a t t a a ==-+≤,12a ∴≥,且22t t a a -+,即12t < t 的最大值为()g a综上可得,当12a ≥时(]0,2t ∈ 当102a <<时,()0,1t ∈ ∴函数()g a 的值域为(]0,2故选:A . 【点睛】二次函数、二次方程与二次不等式统称“三个二次”,它们常结合在一起,有关二次函数的问题,数形结合,密切联系图象是探求解题思路的有效方法.一般从:①开口方向;②对称轴位置;③判别式;④端点函数值符号四个方面分析.8.C解析:C 【分析】根据定义求出()M x 的表达式,然后根据单调性确定最小值. 【详解】由23(1)x x -+=-解得:1x =-或2x =,2(1)3x x -≥-+的解集为1x ≤-或2x ≥,2(1)3x x -<-+的解为12x -<<,∴2(1),12()3,12x x x M x x x ⎧-≤-≥=⎨-+-<<⎩或,∴2x ≤时,()M x 是减函数,2x >时,()M x 是增函数,∴min ()(2)1M x M ==. 故选:C . 【点睛】关键点点睛:本题考查新定义函数,解题关键是确定新定义函数的解析式,根据新定义通过求最大值得出新函数的解析式,然后根据分段函数研究新函数的性质.9.C解析:C 【分析】根据题意得1min 2min ()()g x f x >,再分别求函数的最小值即可得答案. 【详解】解:∵x ∈,∴2[1,3]x ∈, ∴224()3[1,2]f x x x =-∈+. 当0k >时,()[2,22]g x k k ∈-++,所以只需满足:12k <-+,解得01k <<; 当0k =时,()2g x =.满足题意.当0k <时,()[22,2]g x k k ∈-++,所以只需满足:122k <+,解得102k >>-. ∴1,12k ⎛⎫∈- ⎪⎝⎭.故选:C . 【点睛】结论点睛:本题考查不等式的恒成立与有解问题,可按如下规则转化:一般地,已知函数()[],,y f x x a b =∈,()[],,y g x x c d =∈(1)若[]1,x a b ∀∈,[]2,x c d ∀∈,总有()()12f x g x <成立,故()()2max min f x g x <; (2)若[]1,x a b ∀∈,[]2,x c d ∃∈,有()()12f x g x <成立,故()()2max max f x g x <; (3)若[]1,x a b ∃∈,[]2,x c d ∃∈,有()()12f x g x <成立,故()()2min min f x g x <;(4)若[]1,x a b ∀∈,[]2,x c d ∃∈,有()()12f x g x =,则()f x 的值域是()g x 值域的子集 .10.B解析:B 【分析】当m =0时,()f x =1x -,符合题意.当0m ≠时,由题意可得0112m m m>⎧⎪-⎨≥⎪⎩,求得m 的范围.综合可得m 的取值范围.【详解】当0m =时,()1f x x =-+,满足在区间(]1-∞,上为减函数; 当0m ≠时,由于()()211f x mx m x =+-+的对称轴为12mx m-=,且函数在区间(]1-∞,上为减函数, 则0112m m m>⎧⎪-⎨≥⎪⎩,解得103m <≤.综上可得,103m ≤≤. 故选:B 【点睛】要研究二次型函数单调区间有关问题,首先要注意二次项系数是否为零.当二次项系数不为零时,利用二次函数的对称轴来研究单调区间.11.C解析:C 【分析】由于22()f x x a a =--有绝对值,分情况考虑2x a ≥和2x a <,再由()y f x =是奇函数画出图象,再根据()()f x a f x -≤考虑图象平移结合图形可得答案. 【详解】由题得, 当0x ≥时,22()f x x a a =--,故写成分段函数222222,0(),x a a x a f x x a a x a ⎧-+-≤≤=⎨-->⎩,化简得222,0()2,x x a f x x a x a ⎧-≤≤=⎨->⎩, 又()y f x =为奇函数,故可画出图像:又()f x a -可看出()y f x =往右平移a 个单位可得,若()()f x a f x -≤恒成立,则222(2)a a a ≥--,即24a a ≤,又a 为正数,故解得104a <≤. 故选:C . 【点睛】本题主要考查绝对值函数对分段函数的转换,图象的平移,属于中档题.12.A解析:A 【分析】由题可得[][]1122()()0f x x f x x ---<,可构造函数()()F x f x x =-是R 上的增函数,原不等式可转化为()()213F x F ->,再结合增函数的性质可求出答案. 【详解】 由题意,[][]121211221122()()()()()()0f x f x x x f x x f x x f x x f x x -<-⇔-<-⇔---<, 因为12,R x x ∈且12,x x <所以函数()()F x f x x =-是R 上的增函数.()3(3)31F f =-=,因为(21)2(21)(21)1f x x f x x ->⇔--->,所以()()213F x F ->, 则213x ->,解得2x >. 故选:A. 【点睛】本题考查了函数的单调性的应用,构造函数()()F x f x x =-是解决本题的关键,属于中档题.二、填空题13.【分析】根据函数的解析式分和两种情况讨论利用一次二次函数的性质即可求解【详解】由已知函数在上单调递增可得当时函数在上单调递减不满足题意;当时则满足解得综上所述实数的取值范围是故答案为:【点睛】本题主解析:25⎡⎫+∞⎪⎢⎣⎭, 【分析】根据函数的解析式,分0k =和0k ≠两种情况讨论,利用一次、二次函数的性质,即可求解. 【详解】由已知函数()()2325f x kx k x =+--在[)1+∞,上单调递增可得, 当0k =时,函数()25f x x =--在[)1+∞,上单调递减,不满足题意; 当0k ≠时,则满足03212k k k>⎧⎪-⎨-≤⎪⎩,解得25k ≥,综上所述,实数k 的取值范围是25⎡⎫+∞⎪⎢⎣⎭,. 故答案为:25⎡⎫+∞⎪⎢⎣⎭,. 【点睛】本题主要考查了函数单调性的应用,其中解答中熟记一次函数、二次函数的图象与性质是解答的关键,着重考查了分类讨论思想,以及推理与计算能力,属于基础题.14.【分析】根据指数函数和一次函数的性质得出关于的不等式组即可求解【详解】由题意函数是上的单调递增函数可得解得即实数取值范围故答案为:【点睛】利用函数的单调性求解参数的取值范围:根据函数的单调性将题设条解析:8[,6)3【分析】根据指数函数和一次函数的性质,得出关于a 的不等式组,即可求解. 【详解】由题意,函数1,1()32,12x a x f x a x x ⎧+>⎪=⎨⎛⎫-+≤ ⎪⎪⎝⎭⎩是R 上的单调递增函数, 可得13021322a a a a ⎧⎪>⎪⎪->⎨⎪⎪+≥-+⎪⎩,解得863a ≤<,即实数a 取值范围8[,6)3.故答案为:8[,6)3. 【点睛】利用函数的单调性求解参数的取值范围:根据函数的单调性,将题设条件转化为函数的不等式(组),即可求出参数的值或范围;若分段函数是单调函数,则不仅要保证在各区间上单调性一致,还要确保在整个定义域内是单调的.15.【分析】求出在上的值域再求出在上的值域由可得的范围【详解】所以又所以时因为对任意的存在使所以解得故答案为:【点睛】结论点睛:本题考查不等式的恒成立与有解问题可按如下规则转化:一般地已知函数(1)若总解析:7,2⎡⎫+∞⎪⎢⎣⎭【分析】求出()f x 在[2,2]-上的值域A ,再求出()g x 在[2,2]-上的值域B ,由A B ⊆可得a 的范围. 【详解】2()2f x x x =-2(1)1x =--,[2,2]x ∈-,所以()[1,8]f x ∈-,又0a >,所以[2,2]x ∈-时,()1[21,21]g x ax a a =+∈-++, 因为对任意的[]12,2x ∈-,存在[]22,2x ∈-,使12()()f x g x =,所以211218a a -+≤-⎧⎨+≥⎩,解得72a ≥.故答案为:7,2⎡⎫+∞⎪⎢⎣⎭. 【点睛】结论点睛:本题考查不等式的恒成立与有解问题,可按如下规则转化:一般地,已知函数()[],,y f x x a b =∈,()[],,y g x x c d =∈ (1)若[]1,x a b ∀∈,[]2,x c d ∀∈,总有()()12f x g x <成立,故()()2max min f x g x <; (2)若[]1,x a b ∀∈,[]2,x c d ∃∈,有()()12f x g x <成立,故()()2max max f x g x <; (3)若[]1,x a b ∃∈,[]2,x c d ∃∈,有()()12f x g x <成立,故()()2min min f x g x <; (4)若[]1,x a b ∀∈,[]2,x c d ∃∈,有()()12f x g x =,则()f x 的值域是()g x 值域的子集 .16.【分析】因为2f(x)+f(-x)=3x①所以将x 用-x 替换得2f(-x)+f(x)=-3x②解上面两个方程即得解【详解】因为2f(x)+f(-x)=3x①所以将x 用-x 替换得2f(-x)+f(x) 解析:3x【分析】因为2f (x )+f (-x )=3x ,①,所以将x 用-x 替换,得2f (-x )+f (x )=-3x ,②,解上面两个方程即得解. 【详解】因为2f (x )+f (-x )=3x ,①所以将x 用-x 替换,得2f (-x )+f (x )=-3x ,② 解由①②组成的方程组得f (x )=3x . 故答案为3x 【点睛】本题主要考查函数的解析式的求法,意在考查学生对该知识的理解掌握水平,属于基础题.17.【分析】由已知得出单调增然后由及可得结论【详解】因为对任意都有成立所以为单调递增函数因此故答案为:【点睛】本题考查分段函数的单调性分段函数在定义域内单调需满足分段函数的所有段同单调及相邻段端点处的函 解析:[1,2]【分析】由已知1212()()0f x f x x x ->-得出单调增,然后由2210,02b b -->≥及10b -≥可得结论. 【详解】因为对任意12x x ≠,都有()()12120f x f x x x ->-成立,所以()f x 为单调递增函数,因此21020210b b b ->⎧⎪-⎪≥⎨⎪-≥⎪⎩,12b ∴≤≤. 故答案为:[1,2].. 【点睛】本题考查分段函数的单调性,分段函数在定义域内单调,需满足分段函数的所有段同单调及相邻段端点处的函数值满足相应的大小关系.18.【分析】先根据是幂函数求出的值再根据且有得出为增函数进而得到函数解析式再根据函数的奇偶性即可求解【详解】解:是幂函数解得:或当时当时又对且时都有在上单调递增易知的定义域为且为上的奇函数且在上单调递增 解析:<【分析】先根据()()21353m f x m m x+=++是幂函数,求出m 的值,再根据12,(0,)x x ∈+∞且12x x ≠有()()12120f x f x x x ->-,得出()f x 为增函数,进而得到函数解析式,再根据函数的奇偶性即可求解. 【详解】 解:()()21353m f x m m x +=++是幂函数,23531m m +∴+=,解得:23m =-或1m =-, 当23m =-时,()13f x x =,当1m =-时,()01f x x ==,又对12,(0,)x x ∈+∞且12x x ≠时,都有()()12120f x f x x x ->-,()f x ∴在(0,)+∞上单调递增, ()13f x x∴=,易知()f x 的定义域为R ,且()()()1133f x x x f x -=-=-=-,()f x ∴为R 上的奇函数,且在R 上单调递增, 0a b <+, a b ∴<-,()()()f a f b f b ∴<-=-,()()0f a f b ∴+<.故答案为:<. 【点睛】关键点点睛:本题解题的关键是利用幂函数以及单调性得出函数的解析式.19.【分析】根据对任意实数都有成立得出在R 上单调递减从而得出解出a 的范围即可【详解】函数对任意的实数都有成立得在R 上单调递减∴故答案为:【点睛】关键点点睛:依函数单调性的定义得函数在R 上单调递减利用分段解析:324a ≤<. 【分析】根据对任意实数m n ≠,都有()()0f m f n m n-<-成立,得出()f x 在R 上单调递减,从而得出()()()4300143141log 134a a a a a ⎧-<⎪<<⎨⎪-⋅-+-≥-++⎩,解出a 的范围即可.【详解】函数()f x 对任意的实数m n ≠,都有()()0f m f n m n-<-成立,得()f x 在R 上单调递减,∴()()()4300143141log 134a a a a a ⎧-<⎪<<⎨⎪-⋅-+-≥-++⎩3430142a a a a ⎧<⎪⎪⎪⇒<<⇒≤<⎨⎪⎪≥⎪⎩.故答案为:324a ≤<. 【点睛】关键点点睛:依函数单调性的定义得函数在R 上单调递减,利用分段函数的单调性求解.20.①③④【分析】①根据奇偶函数的定义判断;②利用抽象函数的对称性判断;③通过特殊函数判断;④通过分离常数转化为熟悉的函数判断【详解】①函数的定义域为所以函数的定义域也是即所以函数是偶函数故①正确;②对解析:①③④ 【分析】①根据奇偶函数的定义判断;②利用抽象函数的对称性判断;③通过特殊函数判断;④通过分离常数,转化为熟悉的函数判断. 【详解】①函数()f x 的定义域为R ,所以函数()g x 的定义域也是R ,()()()g x f x f x -=-+,即()()g x g x -=,所以函数()g x 是偶函数,故①正确;②对应任意的x ∈R ,都有()()20f x f x +-=,即函数()f x 关于()1,0对称,并不关于1x =对称,故②不正确;③函数0y =既是偶函数又是奇函数,故③正确; ④()()212112222a x a ax af x a x x x ++-+-===++++,若函数在()2,-+∞上单调递增,则120a -<,解得:12a >,故④正确. 故答案为:①③④ 【点睛】方法点睛:函数的对称性包含中心对称和轴对称,一般判断的方法包含:1.若对函数()y f x =的定义域内的任一自变量x 的值都有()()2f x f a x =-,则()y f x =的图象关于x a =成轴对称;若对函数()y f x =的定义域内的任一自变量x 的值都有()()22f x b f a x =--,则()y f x =的图象关于(),a b 成中心对称; 三、解答题21.(1)2()2f x x x =-;(2)证明见解析;(3),2()4,2m m G m m m -<-⎧=⎨--≥-⎩,()G m 的最小值为2. 【分析】(1)由题意得,(0)0f =,再由偶函数的图象关于y 轴对称,求得,b c ,可得出函数的解析式;(2)原问题等价于对于任意的[0,4]x ∈,总有4()20f x x -≤-≤,令222()224(2)4g x x x x x x x =--=-=--,求得()2f x x -的范围,即可得证;(3)2|(2)4||()2|y f x x x m m =----=-,讨论m 的大小并结合二次函数的图象进行分析; 【详解】(1)由题意得,(0)0f =,即0c,所以2()f x x bx =+,()22+2+++(+1)(+1)(1+1)f x x b x x b x b =+=,因为()1y f x =+为偶函数,所以202b+-=,即2b =-, 所以2()2f x x x =-;(2)对于任意的[0,4]x ∈,总有24()2x f x x -≤≤等价于对于任意的[0,4]x ∈,总有4()20f x x -≤-≤,令222()224(2)4g x x x x x x x =--=-=--,则当[][]0,4,()4,0x g x ∈∈-,即对于任意的[0,4]x ∈,总有4()20f x x -≤-≤,故得证;(3)2|(2)4||()2|y f x x x m m =----=-,当4m ≤-时,由(2),因为对于任意的[0,4]x ∈,总有4()20f x x -≤-≤,则此时2(2)40x m ---≥,即有2(2)4,y x m =---,故0x =或4时,y 有最大值,即()G m m =-;当42m -<<-时,如图,由图,可得此时在0x =或4时,y 有最大值,即()G m m =-; 当2m ≥-时,如图或,由图,可得此时在2x =时,y 有最大值,即()4G m m =--, 综上,2()4,2m m G m m m -<-⎧=⎨--≥-⎩;当2m <-时,()2G m >,当2m ≥-时,()2G m ≥, 故()G m 的最小值为2. 【点睛】方法点睛:解决关于二次函数在某区间上的值域时,注意讨论二次函数的对称轴与区间的位置关系,再根据二次函数的单调性得出最值. 22.(1)答案见解析;(2)存在0a =或1. 【分析】(1)直接作出图象即可;(2)利用分离常数的方法结合反比例函数的单调性得出a 的范围,化简4y ≤将恒成立问题转化为求最值得出a 的范围,再由a 是整数求值即可. 【详解】(1)当1a =时,1233=1222x x y x x x +-+==+---(2)存在0a =或1符合题意.()212112=222a x a ax ay a x x x -++++==+--- 函数在[4,)+∞上是严格减函数,则120a +>,解得12a >-当4x ≥时,都有124ax y x =-≤+,等价于49ax x ≤-,即min 94a x ⎛⎫≤- ⎪⎝⎭又94y x =-在[)4,+∞上单调递增,则97444a ≤-= 故a 的取值范围是1724a -<≤,a 为整数,则符合条件的a 有0,1. 【点睛】关键点点睛:本题考查函数的图象,考查函数单调性的应用,以及函数的恒成立问题,解决本题的关键是将当4x ≥时,都有4y ≤进行去分母化简,并分离参变量,将不等式恒成立转化为函数的最值问题,结合反比例函数的单调性求出参数的范围,考查了学生逻辑思维能力和计算能力,属于中档题.23.(1){}1x x ≥-;(2)()2,484416,8a x F a a a ⎧<<⎪=⎨⎪-≥⎩【分析】(1)由1a =-,得211x x x +≥-,进而分1x ≥-和1x <-两种情况,分别解不等式,进而可求出原不等式的解集;(2)由[]0,4x ∈,且4a >,可得()2f x x ax =-+,进而结合二次函数的性质,分类讨论,可求出()f x 在区间[]0,4上的最大值的表达式. 【详解】(1)当1a =-时,()1f x x x =+,则211x x x +≥-.①当1x ≥-时,不等式为221x x x +≥-,解得1x ≥-,所以1x ≥-; ②当1x <-时,不等式为221x x x --≥-,解得112x ≤≤-,所以解集为空集. 综上,不等式的解集为{}1x x ≥-.(2)因为[]0,4x ∈,且4a >,所以()()2f x x a x x ax =-=-+,①当48a <<时,242a <<,则()224a aF a f ⎛⎫== ⎪⎝⎭;②当8a ≥时,42a≥,则()()4416F a f a ==-.综上()2,48{4416,8a a F a a a <<=-≥.【点睛】方法点睛:“动轴定区间”型二次函数最值的方法: (2)根据对称轴与区间的位置关系,进行分类讨论;(2)根据二次函数的单调性,分别讨论参数在不同取值下的最值,必要时需要结合区间端点对应的函数值进行分析. 24.(1)21()2f x x x =-+;(2)存在,40m n =-⎧⎨=⎩. 【分析】(1)由(1)(1)f x f x +=-,得到20b a +=,再由()f x x ≤恒成立,列出方程组,求得,a b 的值,得到函数的解析式;(2)假设存在()m n m n <、,根据题意得到[],m n 必在对称轴的左侧,且()f x 在[],m n 单调递增,列出方程组,即可求解. 【详解】(1)因为22(1)(1)(1)(2)f x a x b x ax a b x a b +=+++=++++,22(1)(1)(1)(2)f x a x b x ax a b x a b -=-+-=-+++,由()()11f x f x +=-可知,20a b +=,由于对一切x ∈R ,都有()f x x ≤即2()(1)0f x x ax b x -=+-≤,于是由二次函数的性质可得()()21400*a b a <⎧⎪⎨∆=--⨯≤⎪⎩由()*知()210b -≤,而()210b -≥,所以()210b -=即1b =,将1b =代入20a b +=得12a =-, 所以21()2f x x x =-+; (2)因为221111()(1)2222f x x x x =-+=--+≤, 若存在满足条件的实数(),m n m n <则必有132n ≤,解得16n ≤, 又因为()f x 在(],1-∞上单调递增,所以()f x 在[],m n 上单调递增.所以()()33fm m fn n ⎧=⎪⎨=⎪⎩,22132132m m mn n n ⎧-+=⎪⎪⎨⎪-+=⎪⎩,解得40m n =-⎧⎨=⎩或04m n =⎧⎨=-⎩,因为m n <,所以40m n =-⎧⎨=⎩, 故存在40m n =-⎧⎨=⎩满足条件.【点睛】关键点点睛:本题主要考查了二次函数的图象与性质的应用,其中解答中熟记二次函数的图象与性质,以及根据函数的值域判断出函数在[,]m n 上的单调性是解答的关键,着重考查了分析问题和解答问题的能力,属于中档试题.25.(1)23,106()0,0(23),01x xxx x x f x x x ⎧+-≤<⎪⎪⎪==⎨⎪-+<≤⎪⎪⎩;(2) [){}(]5,202,5--;(3)1,12⎛⎤⎥ ⎝⎦. 【分析】(1)利用函数为奇函数有()()f x f x -=-求(0,1]x ∈上的解析式,且(0)0f =即可得()f x 的解析式;(2)根据(1)所得解析式及对应定义域即可求其值域;(3)讨论10a -≤<、01a <<、1a =时不等式成立,结合()f x 的区间单调性即可求得a 的取值范围.【详解】(1)由题意,令(0,1]x ∈,则[1,0)x -∈-,即23()236x x x x xf x ---+-==+, 又∵()()f x f x -=-,有(0,1]x ∈时,()(23)x xf x =-+,∴23,106()0,0(23),01x xxx x x f x x x ⎧+-≤<⎪⎪⎪==⎨⎪-+<≤⎪⎪⎩.(2)由(1)解析式知:()f x 在[1,0)-和(0,1]上递减,对应值域分别为(2,5]、[5,2)--,则有:()f x 的值域[){}(]5,202,5--.(3)1()()0a f f a a -+<,即1()(1)f a f a<-,有[1,0)(0,1]a ∈-,∴当10a -≤<时,11a a >-,解得12a +<-或12a >,无解;当01a <<时,11a a >-,解得a <a >1a <<; 当1a =时,1()(1)5(1)(0)0f a f f f a==-<-==成立;∴综上有1,1]2a ∈. 【点睛】关键点点睛:首先利用函数奇偶性求函数解析式,并依据所得解析式和定义域求值域,再由函数不等式,结合区间单调性,在区间[1,0)(0,1]-⋃上讨论参数使不等式成立,求参数范围.26.(1)()21f x ax x =-+,减区间为1,2a ⎛-∞⎫ ⎪⎝⎭,递增区间为1,2a ⎛⎫+∞ ⎪⎝⎭;(2)50,4⎛⎤⎥⎝⎦. 【分析】 (1)由()101a f f ⎛⎫ ⎪⎝⎭==,整理得()21f x ax x =-+,结合二次函数的性质,即可求解;(2)把“对任意[]12,1,3x x ∈,()()128f x f x -≤恒成立”转化为()()max min 8f x f x -≤在[]1,3上恒成立,结合二次函数的图象与性质,分类讨论,即可求解.【详解】(1)由()101a f f ⎛⎫⎪⎝⎭==,可得()11(0)()f x a x x a -=--,整理得()21f x ax x =-+,因为0a >,则函数()21f x ax x =-+开口向上,对称轴方程为12x a=, 所以()f x 单调递减区间为1,2a ⎛-∞⎫ ⎪⎝⎭,()f x 单调递增区间为1,2a ⎛⎫+∞ ⎪⎝⎭. (2)因为“对任意[]12,1,3x x ∈,()()128f x f x -≤恒成立”, 即()()max min 8f x f x -≤在[]1,3上恒成立,由(1)知函数()21f x ax x =-+,①当12a ≥时,函数()f x 在区间[]1,3上单调递增可得()()()()max min 31828f x f x f f a -=-=-≤,解得54a ≤,即1524a ≤≤;②当106a <≤时,函数()f x 在区间[]1,3上单调递减 可得()()()()max min 13288f x f x f f a -=-=-≤,解得34a ≥-,即106a <≤; ③当1162a <<时,函数()f x 在区间11,2a ⎡⎤⎢⎥⎣⎦单调递减,在区间1,32a ⎡⎤⎢⎥⎣⎦单调递增, 可得()()(){}max max 1,3f x f f =,()min 1124f x f a a ⎛⎫==-⎪⎝⎭则()()112118243113932824f f a a a f f a a a ⎧⎛⎫-=-+≤≤ ⎪⎪⎪⎝⎭⎨⎛⎫⎪-=-+≤≤ ⎪⎪⎝⎭⎩,解得1162a <<,综上所述:实数a 的取值范围是50,4⎛⎤ ⎥⎝⎦.【点睛】由 恒成立求参数取值范围的思路及关键:一般有两个解题思路:一时分离参数法;二是不分离参数,采用最值法;两种思路都是将问题归结为求函数的最值,至于用哪种方法,关键是看参数是否能分离,两种思路的依据为:()a f x ≥恒成立max ()a f x ⇔≥,()a f x ≤恒成立max ()a f x ⇔≤.。
湖南省长沙市第一中学2023届高三二模数学试题(高频考点版)

一、单选题二、多选题三、填空题四、解答题1. 数列的前2017项的和为( )A.B.C.D.2. 已知函数在点处的切线为,动点在直线上,则的最小值是A .4B .2C.D.3.若函数的定义域为集合,则( )A.B.C.D.4. 已知复数满足,则在复平面内对应的点的坐标为( )A.B.C.D.5. 若函数取最小值时,则( )A.B.C.D.6. 将函数的图象向左平移个单位,得到新函数的一条对称轴为,则的值不可能是( )A.B.C.D.7. (多选)平面上点P 与不共线的三点A 、B 、C满足关系:,则下列结论错误的是( )A .P 在CA上,且B .P 在AB上,且C .P 在BC上,且D .P 点为的重心8. 以下四个命题中正确的是( )A .8道四选一的单选题,随机猜结果,猜对答案的题目数B .两个随机变量的线性相关性越强,则相关系数的绝对值越接近于1C.在某项测量中,测量结果服从正态分布(),若在内取值的概率为0.4,则在内取值的概率为0.2D .对分类变量X 与Y 的随机变量的观测值k 来说,k 越小,判断“X 与Y 有关系”的把握程度越大9.正三棱锥的顶点都在球O 的球面上,底面ABC 的边长为6,当球O的体积最小时,三棱锥的体积为______.10. 函数在处的瞬时变化率为______.11.若,,则 .12. 一个长方体的8个顶点坐标分别为,,,,,,,.则这个长方体外接球的球心坐标______.13.已知(1)化简,并求的值;湖南省长沙市第一中学2023届高三二模数学试题(高频考点版)湖南省长沙市第一中学2023届高三二模数学试题(高频考点版)(2)若,求的值.14. 连续投掷一颗骰子两次,求第一次不出现6点且第二次出现5点的概率.15. 最近国际局势波云诡谲,我国在某地区进行军事演练,如图,是三个军事基地,为一个军事要塞,在线段上.已知,,到,的距离分别为5km,.以点为坐标原点,直线为轴,建立平面直角坐标系如图所示,位于第一象限.(1)求两个军事基地的长;(2)若要塞正北方向距离要塞10km处有一处正在进行爆破试验,爆炸波生成时的半径为(参数为大于零的常数),爆炸波开始生成时,一飞行器以的速度自基地A开往基地,问参数控制在什么范围内时,爆炸波不会波及到飞行器的飞行.16. 已知M={x|2≤x≤5},N={x|a+1≤x≤2a﹣1}.(1)若M⊆N,求实数a的取值范围;(2)若M⊇N,求实数a的取值范围.。
湘教版高中数学必修第一册课后习题 第3章 函数的概念与性质 3.1.3 简单的分段函数 (2)

3.1.3 简单的分段函数必备知识基础练1.若f(x)={x -3,x ≥10,f (f (x +6)),x <10,则f(5)的值为( )A.8B.9C.10D.112.已知f(x)=|x|,g(x)=x 2,设h(x)={f (x ),f (x )≤g (x ),g (x ),f (x )>g (x ),则函数h(x)的大致图象是( )3.函数f(x)={2x ,0≤x ≤1,2,1<x <2,3,x ≥2的值域是( )A.RB.[0,2]∪{3}C.[0,+∞)D.[0,3]4.(江西名校联盟高一期末)已知函数y={x 2+1,x ≤0,2x ,x >0,若f(a)=10,则a 的值是( ) A.3或-3B.-3或5C.-3D.3或-3或55.设函数f(x)={(x +1)2,x <1,4x,x ≥1,则f(f(8))= ,使得f(a)≥4a的实数a 的取值范围是 .6.某市有甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲俱乐部每小时5元,乙俱乐部按月计费,一个月中30小时以内(含30小时)90元,超过30小时的部分每小时2元;某公司准备下个月从这两家俱乐部中选择一家开展活动,其活动时间不少于15小时,也不超过40小时.设在甲家开展活动x(15≤x≤40)小时的收费为f(x)元,在乙家开展活动x 小时的收费为g(x)元.(1)试分别写出f(x)和g(x)的解析式. (2)选择哪家比较合算?请说明理由.关键能力提升练7.设函数f(x)={12x -1,x ≥0,1x,x <0,若f(a)=a,则实数a 的值为( )A.±1B.-1C.-2或-1D.±1或-28.已知函数f(x)={x 2,x ≤1,x +4x-3,x >1,则f(x)的值域是( ) A.[1,+∞) B.[0,+∞) C.(1,+∞)D.[0,1)∪(1,+∞)9.(多选题)已知f(x)=x,g(x)=x 2-2x,且F(x)={g (x ),f (x )≥g (x ),f (x ),f (x )<g (x ),则F(x)的最值情况是( ) A.有最大值3 B.有最小值-1 C.无最小值D.无最大值10.设集合A=0,12,B=[12,1],函数f(x)={x +12,x ∈A ,2-2x ,x ∈B ,已知m ∈A,且f(f(m))∈A,则实数m 的取值范围是 .11.《中华人民共和国个人所得税》规定,公民月工资、薪金所得不超过5 000元的部分不纳税,超过5 000元的部分为全月纳税所得额,此项税款按下表分段累计计算:(1)已知张先生的月工资、薪金所得合计为10 000元,问他当月应缴纳多少个人所得税?(2)设王先生的月工资、薪金所得合计为x 元,当月应缴纳个人所得税为y 元,写出y 与x 的函数关系式.(3)已知李先生一月份应缴纳个人所得税为303元,那么他当月的工资、薪金所得合计为多少? 答案:1.A 由题意知,f(5)=f(f(11))=f(8)=f(f(14))=f(11)=8.故选A.2.D 当f(x)≤g(x),即|x|≤x 2时,解得x≤-1或x≥1或x=0,故h(x)={|x |,x ≤-1或x ≥1或x =0,x 2,-1<x <1且x ≠0,故h(x)的大致图象为D.3.B 当0≤x≤1时,0≤2x≤2,即0≤f(x)≤2;当1<x<2时,f(x)=2;当x≥2时,f(x)=3.综上可知f(x)的值域为[0,2]∪{3}.4.B 若a≤0,则f(a)=a 2+1=10,∴a=-3(a=3舍去);若a>0,则f(a)=2a=10,∴a=5.综上可得,a=5或a=-3,故选B.5.94 (-∞,1] 因为f(x)={(x +1)2,x <1,4x,x ≥1,所以f(8)=48=12,因此f(f(8))=f12=12+12=94.当a<1时,f(a)≥4a 可化为(a+1)2≥4a,即(a-1)2≥0显然恒成立,所以a<1;当a≥1时,f(a)=4a ≥4a,解得a=1.综上,a 的取值范围为(-∞,1].6.解(1)由题意可知f(x)=5x,15≤x≤40, g(x)={90,15≤x ≤30,30+2x ,30<x ≤40.(2)由5x=90,解得x=18, 即当15≤x<18时,f(x)<g(x); 当x=18时,f(x)=g(x); 当18<x≤40时,f(x)>g(x).所以当15≤x<18时,选甲家比较合算; 当x=18时,两家一样合算; 当18<x≤40时,选乙家比较合算.7.B 当a≥0时,有12a-1=a,解得a=-2(不满足条件,舍去);当a<0时,有1a=a,解得a=1(不满足条件,舍去)或a=-1.所以实数a 的值是-1.故选B. 8.B 由f(x)={x 2,x ≤1,x +4x-3,x >1,知当x≤1时,x 2≥0; 当x>1时,x+4x-3≥2√x ·4x-3=4-3=1,当且仅当x=4x,即x=2时等号成立.综上,f(x)的值域是[0,+∞).故选B.9.CD 由f(x)≥g(x)得0≤x≤3;由f(x)<g(x),得x<0或x>3,所以F(x)={x 2-2x ,x ∈[0,3],x ,x ∈(-∞,0)⋃(3,+∞).作出函数F(x)的图象如图,可得F(∈A,∴0≤m<12,f(m)=m+12∈12,1.∴f(f(m))=2-2m+12=1-2m.∵f(f(m))∈A,∴0≤1-2m<12,则14<m≤12. ∵0≤m<12,∴14<m<12.∴m 的取值范围是14,12.11.解(1)赵先生应交税为1500×3%+3000×10%+500×20%=445(元). (2)y 与x 的函数关系式为y={0,0≤x ≤5000,(x -5000)×3%,5000<x ≤6500,45+(x -6500)×10%,6500<x ≤9500,345+(x -9500)×20%,9500<x ≤14000.(3)李先生一月份缴纳个人所得税为303元,故必有6500<x≤9500,从而303=45+(x-6500)×10%,解得x=9080.所以王先生当月的工资、薪金所得为9080元.。
长沙市长沙市第一中学中考数学二次函数和几何综合专题

长沙市长沙市第一中学中考数学二次函数和几何综合专题一、二次函数压轴题1.若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数()211(1)x y x x x ⎧-≤-⎪=⎨⎪->-⎩的图象与性质.列表:描点:在平面直角坐标系中,以自变量x 的取值为横坐标,以相应的函数值y 为纵坐标,描出相应的点,如图所示.()1如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;()2研究函数并结合图象与表格,回答下列问题:①点()15,A y -,27,2B y ⎛-⎫ ⎪⎝⎭,15,2C x ⎛⎫ ⎪⎝⎭,()2,6D x 在函数图象上,则1y ______2y ,1x ______2x ;(填“>”,“=”或“<”)②当函数值2y =时,求自变量x 的值;③在直线1x =-的右侧的函数图象上有两个不同的点()33,P x y ,()44,Q x y ,且34y y =,求34x x +的值;④若直线y a =与函数图象有三个不同的交点,求a 的取值范围.2.小明对函数2(0)y a x bx c a =++≠的图象和性质进行了探究.已知当自变量x 的值为0或4时,函数值都为3-;当自变量x 的值为1或3时,函数值都为0.探究过程如下,请补充完整.(1)这个函数的表达式为 ; (2)在给出的平面直角坐标系中,画出这个函数的图象并写出这个函数的--条性质: ; (3)进一步探究函数图象并解决问题:①直线y k =与函数2y a x bx c =++有三个交点,则k = ;②已知函数3y x =-的图象如图所示,结合你所画的函数图象,写出不等式2a x bx c ++3x ≤-的解集: .3.如图,抛物线213222y x x =-++与x 轴交于点A B 、,与y 轴交于点C ,点D 与点C 关于x 轴对称,点P 的坐标为()0m ,,过点P 作x 轴的垂线l 交抛物线于点Q .(1)求点A 、点B 、点C 的坐标;(2)当点P 在线段OB 上运动时,直线l 交BD 于点M ,试探究当m 为何值时,四边形CQMD 是平行四边形;(3)在点P 的运动过程中,是否存在点Q ,使BDQ △是以BD 为直角边的直角三角形?若存在,求出点Q 的坐标;若不存在,请说明理由.4.在数学拓展课上,九(1)班同学根据学习函数的经验,对新函数y=x 2﹣2|x|的图象和性质进行了探究,探究过程如下:(初步尝试)求二次函数y=x 2﹣2x 的顶点坐标及与x 轴的交点坐标;(类比探究)当函数y=x 2﹣2|x|时,自变量x 的取值范围是全体实数,下表为y 与x 的几组对应值.x … ﹣3 ﹣52 ﹣2 ﹣1 0 1 2 523 … y … 3 54 0 ﹣1 0 ﹣1 0 54 3 …①根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请你画出该函数图象的另一部分;②根据画出的函数图象,写出该函数的两条性质.(深入探究)若点M (m ,y 1)在图象上,且y 1≤0,若点N (m+k ,y 2)也在图象上,且满足y 2≥3恒成立,求k 的取值范围.5.综合与探究如图,抛物线26y ax bx =+-与x 轴相交于A ,B 两点,与y 轴相交于点C ,()2,0A -,()4,0B ,直线l 是抛物线的对称轴,在直线l 右侧的抛物线上有一动点D ,连接AD ,BD ,BC ,CD .(1)求抛物线的函数表达式:(2)若点D 在x 轴的下方,当BCD △的面积是92时,求ABD △的面积; (3)在直线l 上有一点P ,连接AP ,CP ,则AP CP +的最小值为______;(4)在(2)的条件下,点M 是x 轴上一点,点N 是抛物线上一动点,是否存在点N ,使得以点B ,D ,M ,N 为顶点的四边形是平行四边形,若存在,请直接写出点N 的坐标;若不存在,请说明理由.6.如图,抛物线2:L y ax bx c =++经过(1,0),(0,3),(5,3)A B C -三点,该抛物线的顶点为D .(1)求该抛物线L 的表达式和点D 的坐标;(2)抛物线L '与抛物线L 关于直线BC 对称,P 是抛物线L 的B 、M 段上的一点,过点P 作y 轴的平行线交抛物线L '与点Q ,点P 、Q 关于抛物线L 的对称轴对称点分别为M 、N .试探究是否存在一点P ,使得四边形PQNM 为正方形?若存在,求出点P 的横坐标;若不存在,请说明理由.7.综合与探究如图,已知二次函数()220y ax bx a =++≠的图像与x 轴交于1,0A ,B 两点,与y 轴交于点C ,直线122y x =-+经过B ,C 两点 (1)求二次函数的解析式;(2)点P 是线段 BC 上一个动点,过点P 作x 轴的垂线于点Q ,交抛物线于点D ,当点Q 是线段PD 的中点时,求点P 的坐标;(3)在(2)的条件下,若点M 是直线BC 上一点,N 是平面内一点,当以P ,D ,M ,N 为顶点的四边形是菱形时,请直接写出点N 的坐标.8.已知抛物线()2n n n y x a b =--+(n 为正整数,且120n a a a ≤<<<)与x 轴的交点为(0,0)A 和()1,0,2n n n n A c c c -=+.当1n =时,第1条抛物线()2111=--+y x a b 与x 轴的交点为(0,0)A 和1(2,0)A ,其他以此类推.(1)求11,a b 的值及抛物 线2y 的解析式.(2)抛物线n y 的顶点n B 的坐标为(_______,_______);以此类推,第(1)n +条抛物线1n y +的顶点1n B +的坐标为(______,_______);所有抛物线的顶点坐标(,)x y 满足的函数关系式是_________.(3)探究以下结论:①是否存在抛物线n y ,使得△n n AA B 为等腰直角三角形?若存在,请求出抛物线n y 的解析式;若不存在,请说明理由.②若直线(0)=>x m m 与抛物线n y 分别交于点12,,,n C C C ,则线段12231,,,n n C C C C C C -的长有何规律?请用含有m 的代数式表示.9.综合与探究如图,已知直线y mx n =+与抛物线2y x bx c =++分别相交于A 、B 两点,1,0A ,()0,3B -,点C 是抛物线与x 轴的另一个交点(与A 点不重合).(1)求抛物线的解析式及直线y mx n =+的解析式;(2)求ABC 的面积;(3)在抛物线的对称轴上,是否存在点M ,使ABM 周长最短?若不存在,请说明理由;若存在,求出点M 的坐标.(4)如果对称轴上有一动点H ,在平面内是否存在点N ,使A 、B 、H 、N 四点构成矩形?若存在,直接写出N 点的坐标;若不存在,请说明理由10.如图,抛物线24y ax bx =++交x 轴于(3,0)A -,(4,0)B 两点,与y 轴交于点C ,AC ,BC .M 为线段OB 上的一个动点,过点M 作PM x ⊥轴,交抛物线于点P ,交BC 于点Q .(1)求抛物线的表达式;(2)过点P 作PN BC ⊥,垂足为点N .设M 点的坐标为(,0)M m ,请用含m 的代数式表示线段PN 的长,并求出当m 为何值时PN 有最大值,最大值是多少?(3)试探究点M 在运动过程中,是否存在这样的点Q ,使得以A ,C ,Q 为顶点的三角形是等腰三角形.若存在,请求出此时点Q 的坐标;若不存在,请说明理由.二、中考几何压轴题11.如图l ,在正方形ABCD ABCD 中,8AB =AB=8,点E E 在AC AC 上,且22AE =22AE =E 点作EF AC ⊥于点E ,交AB 于点F ,连接CF ,DE .(问题发现)(1)线段DE与CF的数量关系是________,直线DE与CF所夹锐角的度数是___________;(拓展探究)(2)当AEF绕点A顺时针旋转时,上述结论是否成立?若成立,请写出结论并结合图2给出证明;若不成立,请说明理由;(解决问题)(3)在(2)的条件下,当点E到直线AD的距离为2时,请直接写出CF的长.12.如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.(1)观察猜想:图1中,线段PM与PN的数量关系是,位置关系是;(2)探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.13.如图,四边形ABCD是正方形,点O为对角线AC的中点.(1)问题解决:如图①,连接BO ,分别取CB ,BO 的中点P ,Q ,连接PQ ,则PQ 与BO 的数量关系是_____,位置关系是____;(2)问题探究:如图②,AO E ∆'是将图①中的AOB ∆绕点A 按顺时针方向旋转45︒得到的三角形,连接CE ,点P ,Q 分别为CE ,BO '的中点,连接PQ ,PB .判断PQB ∆的形状,并证明你的结论;(3)拓展延伸:如图③,AO E ∆'是将图①中的AOB ∆绕点A 按逆时针方向旋转45︒得到的三角形,连接BO ',点P ,Q 分别为CE ,BO '的中点,连接PQ ,PB .若正方形ABCD 的边长为1,求PQB ∆的面积.14.如图1,在菱形ABCD 中,4,120AD B ︒=∠=,点E ,F 分别是AC ,AB 上的点,且1,232AE AD AF ==,猜想:①DE CF的值是_______; ②直线DE 与直线CF 所成的角中较小的角的度数是_______.(2)类比探究:如图2,将绕AEF ∆点A 逆时针旋转,在旋转的过程中,(1)中结论是否成立,就图2的情形说明理由.(3)拓展延伸:在AEF ∆绕点A 旋转的过程中,当,,D E F 三点共线时,请直接写出CF 的长. 15.折纸是一种许多人熟悉的活动.近些年,经过许多人的努力,已经找到了多种将正方形折纸的一边三等分的精确折法,下面探讨其中的一种折法:(综合与实践)操作一:如图1,将正方形纸片ABCD对折,使点A与点D重合,点B与点C重合,再将正方形纸片ABCD展开,得到折痕MN;操作二:如图2,将正方形纸片ABCD的右上角沿MC折叠,得到点D的对应的点为D′;操作三:如图3,将正方形纸片ABCD的左上角沿MD′折叠再展开,折痕MD′与边AB交于点P;(问题解决)请在图3中解决下列问题:(1)求证:BP=D′P;(2)AP:BP=;(拓展探究)(3)在图3的基础上,将正方形纸片ABCD的左下角沿CD′折叠再展开,折痕CD′与边AB 交于点Q.再将正方形纸片ABCD过点D′折叠,使点A落在AD边上,点B落在BC边上,然后再将正方形纸片ABCD展开,折痕EF与边AD交于点E,与边BC交于点F,如图4.试探究:点Q与点E分别是边AB,AD的几等分点?请说明理由.16.定义:有一组邻边相等且对角互补的四边形叫做等补四边形.(问题理解)(1)如图1,点A、B、C在⊙O上,∠ABC的平分线交⊙O于点D,连接AD、CD.求证:四边形ABCD是等补四边形;(拓展探究)(2)如图2,在等补四边形ABCD中,AB=AD,连接AC,AC是否平分∠BCD?请说明理由;(升华运用)(3)如图3,在等补四边形ABCD中,AB=AD,其外角∠EAD的平分线交CD的延长线于点F.若CD=6,DF=2,求AF的长.17.△ABC 中,∠BAC=α°,AB=AC ,D 是BC 上一点,将AD 绕点A 顺时针旋转α°,得到线段AE ,连接BE .(1)(特例感知)如图1,若α=90,则BD+BE 与AB 的数量关系是 .(2)(类比探究)如图2,若α=120,试探究BD+BE 与AB 的数量关系,并证明.(3)(拓展延伸)如图3,若α=120,AB=AC=4,BD=332,Q 为BA 延长线上的一点,将QD 绕点Q 顺时针旋转120°,得到线段QE ,DE ⊥BC ,求AQ 的长.18.在ABC ∆中,BD AC ⊥于点D ,点Р为射线BD 上任一点(点B 除外)连接AP ,将线段PA 绕点Р顺时针方向旋转α︒,ABC α=∠,得到PE ,连接CE .(1)(观察发现)如图1,当BA BC =,且60ABC ∠=︒时,BP 与CE 的数量关系是___________,BC 与CE 的位置关系是___________.(2)(猜想证明)如图2,当BA BC =,且90ABC ∠=︒时,(1)中的结论是否成立?若成立,请予以证明;若不成立,请说明理由.(请选择图2,图3中的一种情况予以证明或说理)(3)(拓展探究)在(2)的条件下,若8AB =,52AP =,请直接写出CE 的长. 19.(1)(操作)如图,请用尺规作图确定圆的圆心P ,保留作图痕迹,不要求写作法;(2)(探究)如图,若(1)中的圆P 的半径为2,放入平面直角坐标系中,使它与x 轴,y 轴分别切于点B 和C ,点A 的坐标为()8,0,过点A 的直线与圆P 有唯一公共点D (与B 不重合)时,求点D 的坐标;(3)(拓展)如图3,点M 从点()8,0A 出发,以每秒1个单位的速度沿x 轴向点O 运动,同时,点N 从原点O 出发,以每秒1个单位的速度沿y 轴向上运动,设运动时间为t (08s t <<),过点M ,N ,O 三点的圆,交第一象限角平分线OG 于点E ,当t 为何值时,MN 有最小值,求出此时OMEN S 四边形,并探索在变化过程中OMEN S 四边形的值有变化吗?为什么?20.(1)(问题发现)如图①,正方形AEFG 的两边分别在正方形ABCD 的边AB 和AD 上,连接CF . 填空:①线段CF 与DG 的数量关系为______;②直线CF 与DG 所夹锐角的度数为_______.(2)(拓展探究)如图②,将正方形AEFG 绕点A 逆时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请利用图②进行说明.(3)(解决问题)如图③,在正方形ADBC 中,AD AC =,点M 为直线BC 上异于B ,C 的一点,以AM 为边作正方形AMEF ,点N 为正方形AMEF 的中心,连接CN ,若4,2AC CM ==,直接写出CN 的长.【参考答案】***试卷处理标记,请不要删除一、二次函数压轴题1.A解析:(1)见解析;(2)①<,<;②x=3或x=-1;③2;④02a <<【分析】(1)根据函数图像的画法,从左至右依次连接个点,即可解决;(2)①根据A 点与B 点的横坐标,判断两点所在的函数图像,然后根据函数的性质解决即可;根据C 点与D 点的纵坐标,判断两点所在的函数图像,然后结合函数图像解决即可. ②当2y =时,判断其所在的函数图像,然后结合函数解析式计算解决即可.③由图可知13x -≤≤时,所以两点在函数1y x =-的图像上,然后根据函数的对称性解决即可.④结合函数图像,y a =与函数图象有三个不同的交点,可知必须与两函数图像分别相交才可以,据此解决即可; 【详解】解:()1如图所示:()()125,A y -①,27,2B y ⎛-⎫ ⎪⎝⎭,A 与B 在1y x=-上,y 随x 的增大而增大, 12y y ∴<;15,2C x ⎛⎫ ⎪⎝⎭,()2,6D x , C 与D 在1y x =-上,观察图象可得12x x <;②当2y =时,12x =-,1(2x ∴=-不符合); 当2y =时,21x =-,3x ∴=或1x =-;()33,P x y ③,()44,Q x y 在1x =-的右侧,13x ∴-≤≤时,点关于1x =对称,34y y =,342x x ∴+=;④由图象可知,当y a =与分段函数分别相交时才会有三个不同的交点,观察函数图像y >0,且y <2,故a 的取值范围为02a <<.2.(1)243y x x --=;(2)如图所示,见解析;性质:函数的图象关于直线=2x 对称;或:当0x =或4时,函数有最小值3-;(3)①1;②0x =或35x ≤≤.【分析】(1)将0x =,3y =-;4x =,3y =-;1x =,0y =代入2||(0)y a x bx c a =++≠,得到:3c =-,4b =-,1a =,即可求解析式为2|4|3y x x =--;(2)描点法画出函数图象,函数关于2x =对称;(3)①从图象可知:当2x =时,1y =,1k =时直线y k =与函数2|4|3y x x =--有三个交点;②3y x =-与243y x x =--的交点为0x =或5x =,结合图象,2|4|33y x x x =---≤的解集为35x ≤≤.【详解】解:(1)将0x =,3y =-;4x =,3y =-;1x =,0y =代入2||(0)y a x bx c a =++≠, 得到:3164310c a b c a b c ⎧=-⎪++=-⎨⎪++=⎩,解得143a b c =⎧⎪=-⎨⎪=-⎩ 2|4|3y x x ∴=--,故答案为2|4|3y x x =--.(2)如图:函数关于直线2x =对称,(3)①当2x =时,1y =,1k ∴=时直线y k =与函数2|4|3y x x =--有三个交点,故答案为1;②3y x =-与243y x x =--的交点为0x =或5x =或x=3,结合图象,2|4|33y x x x =---≤的解集为0x =或35x ≤≤,故答案为0x =或35x ≤≤.【点睛】本题类比函数探究过程探究绝对值函数与不等式组关系;能够准确的画出函数图象,从函数图象中获取信息,数形结合解题是关键.3.C解析:(1)1,04,00,2B C A -(),(),()(2)当2m =,四边形CQMD 是平行四边形(3)存在,点Q 的坐标为3,2(),()8,18- ,()1,0-【分析】(1)根据函数解析式列方程即可;(2)根据平行四边形的判定,用含未知数的值表示QM 的长度,从而可求解;(3)设Q 点的坐标为213,222⎛⎫-++ ⎪⎝⎭m m m ,分两种情况讨论:①当∠QBD=90时,由勾股定理可得:222BQ BD DQ +=,②当∠QDB=90时,由勾股定理可得:222BQ BD DQ =+,可解出m 的值.【详解】(1)令0x =,则2y =,C 点的坐标为(0,2);令0y =,则2130222x x =-++ 解得121,4x x =-=,点A 为(-1,0);点B 为(4,0) ∴1,04,00,2B C A -(),(),()(2)如图1所示:点C 与点D 关于x 轴对称,点()0,2D -,设直线BD 的解析式为2y kx =-,将()4,0B 代入得:420k -= 解得12k = ∴直线BD 的解析式为:122y x =- ∵//QM DC∴当=QM DC 时,四边形CQMD 是平行四边形设Q 点的坐标为213,222⎛⎫-++ ⎪⎝⎭m m m ,则1,22M m m ⎛⎫- ⎪⎝⎭ ∴2131224222m m m ⎛⎫-++--= ⎪⎝⎭解得12m = 20m =(不合题意,舍去)∴当2m =,四边形CQMD 是平行四边形(3)存在,设Q 点的坐标为213,222⎛⎫-++ ⎪⎝⎭m m m ∵BDQ △是以BD 为直角边的直角三角形∴①当∠QBD=90时,由勾股定理可得:222BQ BD DQ +=即()22222213134220222222m m m m m m ⎛⎫⎛⎫-+-+++=+-+++ ⎪ ⎪⎝⎭⎝⎭ 解得13m = 24m =(不合题意,舍去)∴Q 点的坐标为3,2()②当∠QDB=90时,由勾股定理可得:222BQ BD DQ =+即()22222213134220222222m m m m m m ⎛⎫⎛⎫-+-++=++-+++ ⎪ ⎪⎝⎭⎝⎭ 解得18m = 21m =-Q 点的坐标为()8,18- ()1,0-综上所述:点Q 的坐标为3,2(),()8,18- ,()1,0-.【点睛】本题考查了一次函数和抛物线的综合问题,解题的关键在于拿出函数解析式,会用含未知数的代数式表示出关键的点的坐标和线段的长度.4.【初步尝试】(0,0),(2,0);【类比探究】①如图所示:②函数图象的性质:1.图象关于y 轴对称;2.当x 取1或﹣1时,函数有最小值﹣1;【深入探究】k≤﹣5或k≥5.【详解】【分析】【初步尝试】利用配方法将y=x 2﹣2x 化为顶点式,可得顶点坐标,令y=0,解方程x 2﹣2x=0,求出x 的值,即可得到抛物线与x 轴的交点坐标;【类比探究】①根据表中数据描点连线,即可得到该函数图象的另一部分;②根据画出的图象,结合二次函数的性质即可写出该函数的两条性质;【深入探究】根据图象可知y 1≤0时,﹣2≤m≤2;y 2≥3时,m+k≤﹣3或m+k≥3,根据不等式的性质即可求出k 的取值范围.【详解】【初步尝试】∵y=x 2﹣2x=(x ﹣1)2﹣1,∴此抛物线的顶点坐标为(1,﹣1);令y=0,则x 2﹣2x=0,解得x 1=0,x 2=2,∴此抛物线与x 轴的交点坐标为(0,0),(2,0);【类比探究】①如图所示:②函数图象的性质:图象关于y 轴对称;当x 取1或﹣1时,函数有最小值﹣1;【深入探究】根据图象可知,当y 1≤0时,﹣2≤m≤2,当y 2≥3时,m+k≤﹣3或m+k≥3,则k≤﹣5或k≥5,故k 的取值范围是k≤﹣5或k≥5.【点睛】本题考查了二次函数的图象和性质,二次函数图象上点的坐标特征,利用数形结合思想解题是关键.5.A解析:(1)233642y x x =--;(2)454;(3)134)存在,点N 的坐标为:1514⎛⎫⎪⎝⎭或1514⎛⎫⎪⎝⎭或151,4⎛⎫--⎪⎝⎭【分析】(1)把A、B两点坐标代入26y ax bx=+-可得关于a、b的二元一次方程组,解方程组求出a、b的值即可得答案;(2)过D作DG x⊥轴于G,交BC于H,根据抛物线解析式可得点C坐标,利用待定系数法可得直线BC的解析式,设233,642D x x x⎛⎫--⎪⎝⎭,根据BC解析式可表示出点H坐标,即可表示出DH的长,根据△BCD的面积列方程可求出x的值,即可得点D坐标,利用三角形面积公式即可得答案;(3)根据二次函数的对称性可得点A与点B关于直线l对称,可得BC为AP+CP的最小值,根据两点间距离公式计算即可得答案;(4)根据平行四边形的性质得到MB//ND,MB=ND,分MB为边和MB为对角线两种情况,结合点D坐标即可得点N的坐标.【详解】(1)∵抛物线26y ax bx=+-与x轴相交于A,B两点,()2,0A-,()4,0B,∴426016460a ba b--=⎧⎨+-=⎩,解得:3432ab⎧=⎪⎪⎨⎪=-⎪⎩,∴抛物线的解析式为:233642y x x=--.(2)如图,过D作DG x⊥轴于G,交BC于H,当0x=时,6y=-,∴()0,6C-,设BC的解析式为y kx b=+,则640bk b=-⎧⎨+=⎩,解得326kb⎧=⎪⎨⎪=-⎩,∴BC的解析式为:362y x=-,设233,642D x x x⎛⎫--⎪⎝⎭,则3,62H x x⎛⎫-⎪⎝⎭,∴2233336632424DH x x x x x⎛⎫=----=-+⎪⎝⎭,∵BCD△的面积是92,∴1922DH OB ⨯=, ∴213943242x x ⎛⎫⨯⨯-+= ⎪⎝⎭, 解得:1x =或3,∵点D 在直线l 右侧的抛物线上,∴153,4D ⎛⎫- ⎪⎝⎭, ∴ABD △的面积11154562244AB DG ⨯=⨯⨯=;(3)∵抛物线26y ax bx =+-与x 轴相交于A ,B 两点,∴点A 与点B 关于直线l 对称,∴BC 为AP +CP 的最小值,∵B (4,0),C (0,-6),∴AP +CP 的最小值=BC 2246+213故答案为:213(4)①当MB 为对角线时,MN //BD ,MN =BD ,过点N 作NE ⊥x 轴于E ,过当D 作DF ⊥x 轴于F ,∵点D (3,154-), ∴DF =154, 在△MNE 和△BDF 中,NEM DFB NMB DBF MN BD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△MNE ≌△BDF ,∴DF =NE =154, ∵点D 在x 轴下方,MB 为对角线,∴点N 在x 轴上方,∴点N 纵坐标为154,把y =154代入抛物线解析式得:215336442x x =--, 解得:1114x =-,2114x =+,∴1N (114-,154),2N (114+,154)如图,当BM 为边时,MB //ND ,MB =ND ,∵点D (3,154-), ∴点N 纵坐标为154-, ∴233156424x x --=-, 解得:11x =-,23x =(与点D 重合,舍去), ∴3N (1-,154-),综上所述:存在点N ,使得以点B ,D ,M ,N 为顶点的四边形是平行四边形,点N 的坐标为:15114,4⎛⎫ ⎪⎝⎭或15114,4⎛⎫ ⎪⎝⎭或151,4⎛⎫-- ⎪⎝⎭. 【点睛】本题考查的是二次函数的综合,首先要掌握待定系数法求解析式,其次要添加恰当的辅助线,灵活运用面积公式和平行四边形的判定和性质,应用数形结合的数学思想解题. 6.D解析:(1)215322y x x =-++,点D 的坐标为549,28⎛⎫ ⎪⎝⎭;(2)存在,7292-. 【分析】(1)将(1,0),(0,3),(5,3)A B C -三点坐标代入2y ax bx c =++,利用待定系数法可求出抛物线L 的表达式,再由抛物线对称轴公式可求出点D 的坐标;(2)根据题意可求得抛物线L '的表达式,设点P 的横坐标为m ,则可由已知分别表示出点Q 、M 、N 的坐标,利用正方形的性质则可列出方程,求解后即可得出点P 的横坐标.【详解】解:(1)将(1,0),(0,3),(5,3)A B C -代入2y ax bx c =++得:032553a b c c a b c -+=⎧⎪=⎨⎪++=⎩, 解得12523a b c ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩, ∴该抛物线L 的表达式为:215322y x x =-++; ∵抛物线的顶点为D ,∴当522b x a =-=时,2155549()322228y =-⨯+⨯+=, ∴点D 的坐标为549,28⎛⎫ ⎪⎝⎭; (2)存在;如图所示:∵抛物线L '与抛物线L 关于直线BC 对称,(0,3)B ,∴12a =, 设抛物线L '的表达式为2132y x bx =++, 将(5,3)C 代入得52b =-, ∴抛物线L '的表达式为215322y x x =-+ 设点P 的横坐标为m ,∵PQ ∥y 轴,则Q 的横坐标为m , ∵点P 、Q 关于抛物线L 的对称轴对称点分别为M 、N .∴M 、N 的横坐标为5-m .∴PM =5-m -m =5-2m .∵点P 的纵坐标为215322-++m m ,点Q 的纵坐标为215322m m -+, ∴PQ =(215322-++m m )-(215322m m -+)=25m m -+, 当PM =PQ 时,四边形PQNM 为正方形,∴2525m m m -=-+解得m = ∵P 是抛物线L 的B 、M 段上的一点,∴m <5-m ,解得m <52.∴m .∴点P 【点睛】本题考查了二次函数的图象与性质,熟练掌握待定系数法及二次函数的图象与性质是解题的关键.7.B解析:(1)215222y x x =-+;(2)P (2,1);(3)21N ⎛- ⎝,1N ⎛- ⎝,()0,0N ,1811,55N ⎛⎫ ⎪⎝⎭【分析】(1)求出点B ,带入求解即可;(2)设,22t P t ⎛⎫-+ ⎪⎝⎭,(),0Q t ,()215,20<<422D t t t t ⎛⎫-+ ⎪⎝⎭,根据中点的性质列式计算即可;(3)根据菱形的性质分类讨论即可;【详解】(1)令1202x -+=,解得:4x =, ∴()4,0B ,令0x =,则2y =,∴()0,2C ,把1,0A ,()4,0B 代入()220y ax bx a =++≠中,∴2016420a b a b ++=⎧⎨++=⎩, ∴12a =,52b =-, ∴215222y x x =-+; (2)设,22t P t ⎛⎫-+ ⎪⎝⎭,(),0Q t ,()215,20<<422D t t t t ⎛⎫-+ ⎪⎝⎭,∵Q 为PD 中点,∴2115-2202222t t t ⎛⎫++-+=⨯ ⎪⎝⎭, ∴213402t t -+=, ∴12t =,24t =(舍),∴()2,1P ;(3)①如图,由题意可得:PD 为菱形的边,,PM DN 为菱形的对角线,//,PD MN 2,PD MN DM ===由(2)可得:()2,1P ,()2,1D -,2,PD ∴=设22,1M m m -+⎛⎫ ⎪⎝⎭,1,42N m m ⎛⎫-+ ⎪⎝⎭, 由2DM =可得:()221234,2m m ⎛⎫-+-+= ⎪⎝⎭ 整理得:()()51820,m m --=解得:1218,2,5m m == 检验:2m =不合题意舍去,取18,5m =1811811,,,.5555M N ⎛⎫⎛⎫∴ ⎪ ⎪⎝⎭⎝⎭如图,PD 为菱形的边, //,PD MN 2,PD MN DN ===同理可得:4225,1555N ⎛- ⎝或452521.N ⎛- ⎝⎭②如图,当PD 为对角线时,由()2,1P ,()2,1D -,()()4,0,0,0,B O可得:,M B 重合,,N O 重合时,四边形PMDN 为菱形,()0,0.N ∴ 综上:4225,1555N ⎛- ⎝,425,1555N ⎛- ⎝,()0,0N ,1811,55N ⎛⎫ ⎪⎝⎭; 【点睛】本题主要考查了二次函数综合,结合菱形的判定与性质、等腰三角形的性质和一元二次方程的求解是解题的关键.8.C解析:(1)1111a b =⎧⎨=⎩ ;y 2 =−(x−2)2+4;(2)(n ,n 2 );[(n +1),(n +1)2 ];y =x 2;(3)①存在,理由见详解;②C 1n -C n =2m .【分析】(1)1(2,0)A ),则1c =2,则2c =2+2=4,将点A 、1A 的坐标代入抛物线表达式得:()2112110=-0(-2-)a b a b ⎧-+⎪⎨=-+⎪⎩,解得:1111a b =⎧⎨=⎩ ,则点2A (4,0),将点A 、2A 的坐标代入抛物线表达式,同理可得:2a =2,2b =4,即可求解;(2)同理可得:3a =3,3b =9,故点n B 的坐标为(n ,2n ),以此推出:点1n B +[(n +1),(n +1)2],故所有抛物线的顶点坐标满足的函数关系式是:y =2x ,即可求解; (3)①△AAnBn 为等腰直角三角形,则AAn 2 =2ABn 2,即(2n )2=2(n 2+4n ),即可求解;②y 1n c -=−(m−n +1)2+(n−1)2,y n c =−(m−n )2+n 2,C 1n -C n = y n c −y 1n c -,即可求解.【详解】解:(1)1(2,0)A ,则1c =2,则2c =2+2=4,将点A 、1A 的坐标代入抛物线表达式得: 2112110=()0(2)a b a b ⎧--+⎨=---+⎩,解得:1111a b =⎧⎨=⎩, 则点2A (4,0),将点A 、2A 的坐标代入抛物线表达式,同理可得:2a =2,2b =4;故y 2 =−(x−2a )2+2b =−(x−2)2+4;(2)同理可得:3a =3,3b =9,故点n B 的坐标为(n ,2n ),以此推出:点1n B + [(n +1),(n +1)2],故所有抛物线的顶点坐标满足的函数关系式是:y =2x ;故答案为:(n ,n 2 );[(n +1),(n +1)2];y =x 2;(3)①存在,理由:点A (0,0),点An (2n ,0)、点n B (n ,n 2 ),△AAnBn 为等腰直角三角形,则AAn 2 =2ABn 2,即(2n )2=2(n 2 +n 4), 解得:n =1(不合题意的值已舍去),抛物线的表达式为:y =−(x−1)2 +1;②y 1n c -=−(m−n +1)2+(n−1)2,y n c =−(m−n )2+n 2,C 1n -C n =y n c −y 1n c -=−(m−n )2+n 2 +(m−n +1)2−(n−1)2=2m .【点睛】本题考查的是二次函数综合运用,这种找规律类型题目,通常按照题设的顺序逐次求解,通常比较容易.9.A解析:(1)33y x =-,223y x x =+-;(2)6;(3)存在点M 使ABM 周长最短,其坐标为()1,2--;(4)存在,10,3⎛⎫ ⎪⎝⎭,72,3⎛⎫-- ⎪⎝⎭,()2,1-,()2,2- 【分析】(1)把A 、B 两点的坐标分别代入抛物线2y x bx c =++和直线y mx n =+中,解之即可; (2)由图可知,12ABC S AC OB =⋅,所以只需求出AC ,OB 的长即可,因为C 点为抛物线与x 轴的一个交点,令y=0即可求出C 点坐标,根据已知可得A 点坐标,从而得到AC 的长,根据已知得到B 点坐标,可得OB 的长,从而求出ABC 的面积;(3)由题意知,A 、C 关于对称轴对称,则可知MA MC =,故当B 、M 、C 三点在同一条直线上时MB MC +最小,此时ABM 的周长最小,连接BC 交对称轴于点M ,则M 即为满足条件的点,设直线BC 的解析式为y kx m =+,将B ,C 的坐标代入即可求出该解析式,令x=-1,即可求出点M 的坐标;(4)在平面内是否存在点N ,使A 、B 、H 、N 四点构成矩形,求N 点坐标时,需分情况讨论,当HB ⊥AB 时,根据互相垂直的两直线的斜率之积为-1,互相平行的两直线的斜率相等求出直线HB ,直线HN ,直线AN 的解析式,根据N 点为直线HN 和直线AN 的交点,联立方程组解之即可;同理可得当HA ⊥AB 时,N 点的坐标;而当AB 为对角线时,可得HA ⊥AB ,从而可求出直线AH 的解析式,设H 点坐标为()1,y -,根据△AHB 为直角三角形,利用勾股定理求出H 点的坐标,然后在利用互相垂直的两直线的斜率之积为-1,互相平行的两直线的斜率相等求出N 点的坐标.【详解】解:(1)把A 、B 两点的坐标分别代入2y x bx c =++得103b c c ++=⎧⎨=-⎩, 解得23b c =⎧⎨=⎩, ∴抛物线解析式为223y x x =+-.把A 、B 两点的坐标分别代入y mx n =+得03m n n +=⎧⎨=-⎩, 解得33m n =⎧⎨=-⎩, ∴直线y mx n =+的解析式为33y x =-.(2)由(1)得,抛物线解析式为223y x x =+-,令0y =得2023x x =+-,解得11x =,23x =-,()3,0C ∴-,∵1,0A ,∴4AC =,∵()0,3B -,∴OB=3,1143622ABC S AC OB ∴=⋅=⨯⨯=; (3)()222314y x x x =+-=+-,∴抛物线的对称轴为1x =-, A 、C 关于对称轴对称,MA MC ∴=,MB MA MB MC ∴+=+,∴当B 、M 、C 三点在同一条直线上时MB MC +最小,此时ABM 的周长最小 ∴连接BC 交对称轴于点M ,则M 即为满足条件的点,设直线BC 的解析式为y kx m =+,直线BC 过点()0,3B -,()3,0C -,303k m m -+=⎧∴⎨=-⎩,解得13k m =-⎧⎨=-⎩, ∴直线BC 的解析式3y x =--,当1x =-时,2y =-,()1,2M ∴--,∴存在点M 使ABM 周长最短,其坐标为()1,2--.(4)存在,①当HB ⊥AB 时,如图所示由(1)得直线AB 的解析式为33y x =-,∵HB ⊥AB ,∴设直线HB 的解析式为13y x b =-+,将B(0,-3)代入得 3b =-,∴直线HB 的解析式为133y x =--, 当x=-1时,y=13-×(-1)-3=83-, ∴H 点的坐标为81,3⎛⎫-- ⎪⎝⎭, ∵四边形ABHN 为矩形,∴HN ∥AB ,AN ∥HB ,∴设直线HN 的解析式为y=3x+m ,把H 点坐标代入,得3×(-1)+m=83-, 解得m=13, ∴直线HN 的解析式为y=3x+13, ∴设直线AN 的解析式为13y x n =-+,把A 点坐标代入,得103n -+=, 解得n=13, ∴设直线AN 的解析式为1133y x =-+, ∵N 点为直线HN 和直线AN 的交点, ∴1331133y x y x ⎧=+⎪⎪⎨⎪=-+⎪⎩解得013x y =⎧⎪⎨=⎪⎩, ∴N 点坐标为10,3⎛⎫ ⎪⎝⎭. ②当HA ⊥AB 时,如图由(1)得直线AB 的解析式为33y x =-,∵HA ⊥AB ,∴设直线HA 的解析式为13y x b =-+,将A(1,0)代入得13-+b=0, 解得b=13, ∴直线HA 的解析式为1133y x =-+, 当x=-1时,()1121333y =-⨯-+=, ∴H 点的坐标为21,3⎛⎫- ⎪⎝⎭, ∵四边形ABNH 是矩形,∴AB ∥NH ,BN ∥AH ,∴设直线HN 的解析式为y=3x+m ,把H 点坐标代入,得()2313m =⨯-+, 解得m=113, ∴设直线HN 的解析式为y=3x+113, ∴设直线BN 的解析式为13y x n =-+,把B 点坐标代入,得 n=-3,∴设直线BN 的解析式为133y x =--, ∵N 点为直线HN 和直线BN 的交点,∴1133133y x y x ⎧=+⎪⎪⎨⎪=--⎪⎩解得273x y =-⎧⎪⎨=-⎪⎩, ∴N 点坐标为72,3⎛⎫-- ⎪⎝⎭. ③当AB 为对角线时,如图设H 点坐标为()1,y -,∵四边形AHBN 为矩形,∴△AHB 为直角三角形,∠AHB=90°,∴AH 2+BH 2=AB 2,即()()()2222111313y y --+++--=+-⎡⎤⎡⎤⎣⎦⎣⎦, 解得121,2y y =-=-,∴H 点坐标为(-1,-1),(-1,-2),(a )当H 点坐标为(-1,-1)时,设直线AH 的解析式为y=kx+b ,把A ,H 点坐标代入,得 01k b k b +=⎧⎨-+=-⎩解得1212k b ⎧=⎪⎪⎨⎪=-⎪⎩, ∴直线AH 的解析式为1122y x =-, ∵AH ∥BN , ∴设直线BN 的解析式为12y x b =+,把B 点坐标代入,得b=-3,∴直线BN 的解析式为132y x =-,∵AN ⊥BN ,∴设直线AN 的解析式为y=-2x+m ,把A 点坐标代入,得-2+m=0,解得m=2,∴直线AN 的解析式为y=-2x+2,∵N 点为直线AN 与BN 的交点, ∴22132y x y x =-+⎧⎪⎨=-⎪⎩ 解得22x y =⎧⎨=-⎩, ∴N 点坐标为(2,-2);(b )当H 点坐标为(-1,-2)时,设直线AH 的解析式为y=kx+b ,把A ,H 点坐标代入,得02k b k b +=⎧⎨-+=-⎩ 解得11k b =⎧⎨=-⎩, ∴直线AH 的解析式为y=x-1,∵AH ∥BN ,∴设直线BN 的解析式为y=x+n ,把B 点坐标代入,得n=-3,∴直线BN 的解析式为y=x-3,∵AN ⊥BN ,∴设直线AN 的解析式为y=-x+m ,把A 点坐标代入,得-1+m=0,解得m=1,∴直线AN 的解析式为y=-x+1,∵N 点为直线AN 与BN 的交点,∴13y x y x =-+⎧⎨=-⎩ 解得21x y =⎧⎨=-⎩, ∴N 点坐标为(2,-1).综上所述,存在点N ,使A 、B 、H 、N 四点构成矩形,N 点坐标为10,3⎛⎫ ⎪⎝⎭ 72,3⎛⎫-- ⎪⎝⎭ ()2,1- ()2,2-.【点睛】本题为二次函数的综合运用,涉及待定系数法,轴对称的性质,勾股定理,三角形的面积等知识.在(2)中求得点C 是解题的关键,在(3)中确定出M 点是解题的关键,在(4)中分情况讨论是解题的关键.10.A解析:(1)211433y x x =-++;(2)2PN =,当2m =时,PN 有最大值,最大值为3. (3)满足条件的点Q 有两个,坐标分别为:()1,3Q,Q ⎝⎭. 【分析】(1)将点A 、B 的坐标代入解析式中求解即可;(2)由(1)求得点C 坐标,利用待定系数法求得直线BC 的解析式,然后用m 表示出PN ,再利用二次函数的性质即可求解;(3)分三种情况:①AC=CQ ;②AC=AQ ;③CQ=AQ ,分别求解即可.【详解】解:(1)将(3,0)A -,(4,0)B 代入24y ax bx =++,得934016440a b a b -+=⎧⎨++=⎩,解之,得1313a b ⎧=-⎪⎪⎨⎪=⎪⎩. 所以,抛物线的表达式为211433y x x =-++.(2)由211433y x x =-++,得(0,4)C . 将点(4,0)B 、(0,4)C 代入y kx b =+,得404k b b +=⎧⎨=⎩,解之,得14k b =-⎧⎨=⎩. 所以,直线BC 的表达式为:4y x =-+.由(,0)M m ,得211,433P m m m ⎛⎫-++ ⎪⎝⎭,4(),Q m m -+. ∴221114443333PQ m m m m m =-+++-=-+ ∵OB OC =,∴45ABC OCB ∠=∠=︒.∴45PQN BQM ∠=∠=︒.∴2214sin 4533PN PQ m m ⎫=︒=-+=⎪⎝⎭.22)63m =--+.∵0< ∴当2m =时,PN.(3)存在,理由如下:由点(3,0)A -,(0,4)C ,知5AC =.①当AC CQ =时,过Q 作QE y ⊥轴于点E ,易得222222[4(4)]2CQ EQ CE m m m =+=+--+=,由2225m =,得152m =252m = 此时,点5285222Q ⎛- ⎝⎭; ②当AC AQ =时,则5AQ AC ==.在Rt AMQ △中,由勾股定理,得22[(3)](4)25m m --+-+=.解之,得1m =或0m =(舍)此时,点()1,3Q ;③当CQ AQ =时,由2222[(3)](4)m m m =--+-+,得252m =(舍). 综上知所述,可知满足条件的点Q 有两个,坐标分别为:()1,3Q ,52852Q -⎝⎭. 【点睛】本题是一道二次函数与几何图形的综合题,解答的关键是认真审题,找出相关条件,运用待定系数法、数形结合法等解题方法确定解题思路,对相关信息进行推理、探究、发现和计算.二、中考几何压轴题11.(1),;(2)结论仍然成立,证明详见解析;(3)的长为或.【分析】(1)延长DE 交CF 的延长线于点N ,由正方形的性质可得和均为等腰直角三角形,因此,易证,由相似三角形的性质即可得到,由三角形的解析:(1)2CF DE ,45︒;(2)结论仍然成立,证明详见解析;(3)CF 的长为5或413【分析】。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二基本初等函数题型1:指数运算例1.(1) 计算:220.53334[(3)(5)(0.008)89---+÷110.2522(0.02)(0.32)]0.0625-⨯÷=________;(2)化简:41233322338(4a a b ab a--÷+=________.练习1) 已知0a >化为分数指数幂的形式为________.练习2) 0110.753270.064160.018-⎛⎫--++= ⎪⎝⎭________.例2.若11223x x -+=,则22332223x x x x--+-=+-________.练习3) 已知实数x 满足13x x -+=,则22x x -+=______题型2:对数运算 例3.计算(1) 2(lg2)lg2lg50lg25+⋅+=________; (2) 3948(log 2log 2)(log 3log 3)+⋅+=________;(3) 2lg5lg8000(lg 11lg600lg0.036lg0.122⋅+=--________.练习4) 计算:1122log sin15log cos15︒+︒=________.例4.(2log 9)⋅(3log 4)=________练习5) 552log 10log 0.25+=______题型3:简单的指数、对数方程例5.设关于x 的方程1420()x x b b +--=∈R .(1) 若方程有实数解,求实数b 的取值范围;(2) 当方程有实数解时,讨论方程实根的个数,并求出方程的解.练习6) 方程14230x x +--=的解是________.例6.方程2log (1)x -=22log (1)x -+的解为________.练习7) 已知函数2log (0)()2(0)x x x f x x >⎧=⎨⎩…,若1()2f a =,则实数a 的值为________题型4:指数函数的图象与性质例7.若函数|1|1()2x y m -=+的图象与x 轴有公共点,则m 的取值范围是________练习8) 函数2()23x f x x -=+-的零点个数是________.练习9) 函数(0,1)x y a a a a =->≠的图象可能是()A .B .C .D .例8.设函数|1||1|()2x x f x +--=,求使()f x…x 的取值范围.练习10) 指数函数x y b a =⋅在[,2]b 上的最大值与最小值的和为6,则a =________.题型5:对数函数的概念与性质 1.定义域例9.(1)函数y =________(2) 设2()lg 2x f x x +=-,则2()()2x f f x+的定义域为_________练习11) 函数()()ln 1f x x -的定义域是________.练习12) 函数2lg(21)y x =++的定义域是_________2.函数值例10.设1233e ,2()log (1),2x x f x x x -⎧<⎪=⎨-⎪⎩…,则((2))f f 的值为________.练习13) 设f (x )是定义在R 上的奇函数,当x <0时,f (x )=x +e x (e 为自然对数的底数),则()ln6f 的值为________.3.求参数的范围例11.已知212()log (23)f x x ax =-+在区间(,1]-∞内是增函数,求实数a 的取值范围.练习14) 设01a <<,函数2()log (22)x x a f x a a =--,则使()0f x <的取值范围是_______题型6:函数的图象及应用 1.指数对数函数的图象例12.当a >1时,函数y =log a x 和y =(1-a )x 的图象只可能是( )2.图象的应用例13.函数()2ln f x x x =--在定义域内的零点个数为______________3.综合应用例14.已知函数()log (a f x ax =(0a >,1a ≠为常数).(1) 求函数f (x )的定义域;(2) 若a =2,试确定函数f (x )的单调性. (3) 若函数y =f (x )是增函数,求a 的取值范围.练习16) 已知01a <<,01x y <<…,且log log 1a a x y ⋅=,那么xy 的取值范围是_______题型7:幂函数概念及性质 1.幂函数的图象 例15.画出函数323xy x -=-的图象,试分析其性质(包括定义域、值域、单调区间、奇偶性、对称性).练习17) 已知函数223()n n f x x -++=(2,)n k k =∈N 的图象在[0,)+∞上单调递增,则n =________.2.幂函数的性质例16.已知幂函数2()m f x x +=是定义在区间[1,]m -上的奇函数,则(1)f m +=______练习18) 已知幂函数()f x x α=,当1x >时,恒有()f x x <,则α的取值范围是_______练习19) 已知幂函数()y f x =的图象过点1(,2,则4log (2)f 的值为_________题型8:抽象函数问题例17.函数()f x 的定义域为D :{|0}x x ≠,且满足对于任意12,x x D ∈,有1212()()()f x x f x f x ⋅=+.(1) 求(1)f 的值;(2) 判断()f x 的奇偶性并证明;(3) 如果(4)1f =,(31)(26)3f x f x ++-…,且()f x 在(0,)+∞上是增函数,求x 的取值范围.练习20) 已知定义域为R 的偶函数()f x 在(,0]-∞上是减函数,且1()22f =,则不等式(2)2x f >的解集为________.例18.设函数()f x 在(,)-+∞∞上满足(2)(2)f x f x -=+,(7)(7)f x f x -=+,且在闭区间[0,7]上,只有(1)(3)0f f ==.(1) 试判断函数()y f x =的奇偶性;(2) 试求方程()0f x =在闭区间[-2005,2005]上的根的个数,并证明你的结论.题型9:函数的图象 例19.函数y =1-11x -的图象是( )练习21) 将函数2()log (1)f x x =+的图象向左平移1个单位,再将图象上的所有点的纵坐标伸长到原来的2倍(横坐标不变),得到函数()y g x =的图象. (1) 求函数()y g x =的解析式和定义域; (2) 求函数()(1)()y F x f x g x ==--的最大值.例20.已知函数2()4f x x =-,()y g x =是定义在R 上的奇函数,当0x >时,2()log g x x =,则函数()()f x g x ⋅的大致图象为( )题型10:函数图象的应用例21.设2()|2|f x x =-,若0a b <<,且()()f a f b =,则ab 的取值范围是_______练习22) 函数1()ln 1f x x x =--的零点的个数是_______题型11:函数的综合问题例22.设函数1()7,02()0xx f x x ⎧-<⎪=…,若()1f a <,则实数a 的取值范围是________________例23.已知()f x 是定义在R 上的奇函数,满足33()()22f x f x -+=+,当3(0,)2x ∈时,2()l n (1)f x x x =-+,则函数()f x 在区间[0,6]上的零点个数是______练习24) 偶函数f (x )满足f (x -1)=f (x +1),且在x ∈[0,1]时,f (x )=x ,则关于x 的方程f (x )=1()10x ,在x ∈[0,4]上解的个数是_________练习25)若定义在R 上的偶函数()f x 满足(2)f x +()f x =,且当[0,1]x ∈时,()f x x =,则方程3()log f x x =的解个数是_______练习26) 已知2log 3log a =+2log 9log b =-3log 2c =,则a ,b ,c 的大小关系是___________例25.定义在(,0)(0,)-+∞∞上的函数()f x ,如果对于任意给定的等比数列{}n a ,{()}n f a 仍是等比数列,则称()f x 为“等比函数”.现有定义在(,0)(0,)-+∞∞上的如下函数:①()2x f x =;②2()log f x x =;③2()f x x =;④()l n 2xf x =,则其中是“等比函数”的()f x 的序号为________.练习27) 函数()f x 的定义域为A ,若12,x x A ∈且12()()f x f x =时总有12x x =,则称()f x 为单函数.例如,函数()1f x x =+()x ∈R 是单函数.下列命题:①函数2()2()f x x x x =-∈R 是单函数;②函数2log ,2()2,2x x f x x x ⎧=⎨-<⎩…是单函数;③若()f x 为单函数,12,x x A ∈且12x x ≠,则12()()f x f x ≠;④函数()f x 在定义域内某个区间D 上具有单调性,则()f x 一定是单函数.其中的真命题是________(写出所有真命题的编号).。
