(华师大版)九年级数学下:第27章《圆》全章导学案(40页)
华师大版九年级数学下册第27章: 圆 小结和复习教学案

小结与复习【学习目标】1.使学生对本章知识系统化、网络化 2.使学生掌握圆章基本题型、基本解题技巧 【自学互助】本章知识图解(学生根据图解自主复习相关知识并相互交流补充)【展示互导】例1:如图,⊙O 是△ABC 的外接圆,弦CM ⊥AB ,CN 是直径,F 是AB 的中点.求证:(1)CF 平分∠NCM ;(2)AN BM .B例2:如图,AB=AC,O是BC的中点,⊙O与AB相切于点D,求证:AC与⊙O相切.例3:如图,M是AB的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,.(1)求圆心到弦MN的距离;(2)求∠ACM的度数.C例4:如图,点O在∠APB的平分线上,⊙O与PA相切于点C.(1)求证:直线PB与⊙O相切;(2)PO的延长线与⊙O交于点E,若⊙O的半径为3,PC=4,求弦CE的长.例5:如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10cm,母线OE(OF)长为10cm,在母线OF上的点A处有一块爆米花的残渣,且FA=2cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,求此蚂蚁爬行的最短距离.例6:线段AB与⊙O相切于点C,连接OA、OB,OB交⊙O于点D,已知OA=OB=6cm,,求:(1)⊙O的半径;(2)圆中阴影部分面积.PB AACA基础演练:1.如图1,⊙O 中弦AB 、CD 相交于点P ,若∠A=30°,∠APD=70°,则∠B=_______.2.已知:⊙O 的半径为13cm ,弦AB ∥CD ,AB=24,CD=10cm ,则AB 、CD 之间的距离为_______. 3.已知两圆的半径分别是4和6,圆心距为7,则这两圆的位置关系为_______.4.如图4,⊙O 半径OA=10cm ,弦AB=16cm ,P 为AB 上一动点,则点P 到圆心O 的最短距离是_______. 5.如图5,在Rt △ABC 中,∠C=90°,∠B=30°,BC=4cm ,以点C 为圆心,以2cm 的长为半径作圆,则⊙C 与AB 的位置关系是_______.6.如图6,AB 是⊙O 的弦,半径OA=2,∠AOB=120°,则弦AB 的长为_______.7.如图7,△ABC 内接于圆O ,∠BAC=120°,AB=AC=4,BD 为⊙O 的直径,则BD=_______. 8.如图8,AB 切⊙O 于点A ,BO 交⊙O 于点C ,点D 是CMA 上异于点C 、A 的一点,若∠ABO=32°,则∠ADC的度数为_______.9.如图945°的扇AOB内部作一个正方形CDEF,使点C在OA上,点D、E在OB上,点F在AB上,则S阴=_______.(结果保留π)10.将一个底面半径为5cm,母线长为12cm的圆锥形纸筒沿一条母线剪开并展平,所得的侧面展开图的圆心角是_______.能力提升:1.已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.(1)如图①若AB=2,∠P=30°,求AP的长(结果保留根号);(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.2、“五一”节,小贾和同学一起到游乐场游玩大型摩天轮,摩天轮的半径为20m,匀速转动一周需要12min,小贾乘坐最底部的车厢(离地面0.5m).(1)经过2min后小贾到达点Q,此时他离地面多高?(2)在摩天轮转动的过程中,小贾将有多长时间连续保持在离地面不低于30.5m 的空中?3、如图,在Rt △ABC 中,∠C=90°,O 为直角边BC 上一点,以O 为圆心,OC 为半径的圆P 合好与斜边AB 相切于点D ,与BC 交于另一点E . (1)求证:△AOC ≌△AOD ;(2)若BE=1,BD=3,求⊙O 的半径及图中阴影部分的面积S .E4、如图,△ABC 内接于半圆,AB 是直径,过A 作直线MN ,若∠MAC=∠ABC . (1)求证:MN 是半圆的切线;(2)设D 是弧AC 的中点,连结BD 交AC 于G ,过D 作DE⊥AB 于E ,交AC 于F .求证:FD =FG . (3)若△DFG 的面积为4.5,且DG=3,GC=4,试求△BCG 的面积.5、如图所示,⊙O 半径为1,点P 是⊙O 上一点,弦AB 垂直平分线段OP ,点D 是弧APB 上的任一点(与端点A 、B 不重合),DE ⊥AB 于点E ,以点D 为圆心,DE 的长为半径作⊙D ,分别过点A 、B 作⊙D 的切线,两条切线相交于点C . (1)求弦AB 的长;(2)判断∠ACB 是否为定值,若是,求∠ACB 的大小; 否则,说明理由.(3)记△ABC 的面积为S,若2S DE ,求△ABC 的周长.A。
2023年华师大版九年级数学下册第二十七章《圆幂定理》导学案
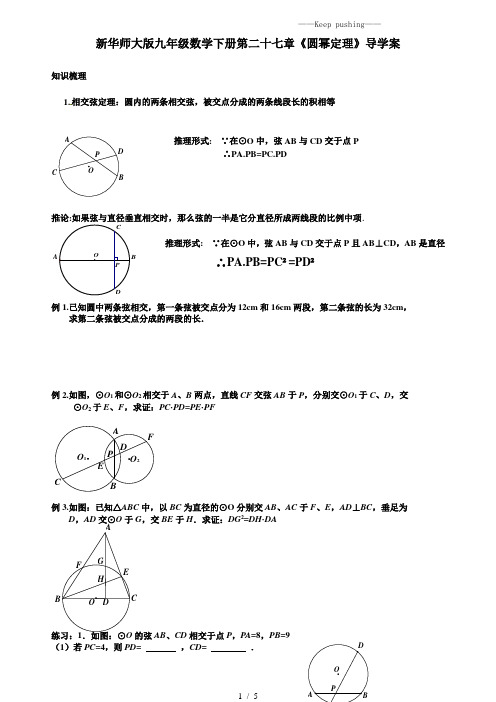
O C B P D A 新华师大版九年级数学下册第二十七章《圆幂定理》导学案知识梳理1.相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等推理形式: ∵在⊙O 中,弦AB 与CD 交于点P ∴PA.PB=PC.PD推论:如果弦与直径垂直相交时,那么弦的一半是它分直径所成两线段的比例中项.推理形式: ∵在⊙O 中,弦AB 与CD 交于点P 且AB ⊥CD ,AB 是直径 ∴PA.PB=PC ²=PD ²例1.已知圆中两条弦相交,第一条弦被交点分为12cm 和16cm 两段,第二条弦的长为32cm ,求第二条弦被交点分成的两段的长.例2.如图,⊙O 1和⊙O 2相交于A 、B 两点,直线CF 交弦AB 于P ,分别交⊙O 1于C 、D ,交⊙O 2于E 、F ,求证:PC ·PD =PE ·PF例3.如图:已知△ABC 中,以BC 为直径的⊙O 分别交AB 、AC 于F 、E ,AD ⊥BC ,垂足为D ,AD 交⊙O 于G ,交BE 于H .求证:DG 2=DH ·DA练习:1.如图:⊙O 的弦AB 、CD 相交于点P ,PA =8,PB =9(1)若PC =4,则PD = ,CD = .O P D C O 2O 1E F C BP D A G H E F O D AO P D C B A O B P A O C B D A (2)若PC =PD ,则CD = .(3)若PC :PD =2:3,则PC = ,PD = .(4)若CD =18(PC<P D ),则PC = ,PD = .2.已知:如图AB 是⊙O 的弦,P 是AB 上一点,AB =11,PA =3,OP =5,则⊙O 的半径是 .3.已知:如图点C 为弧AB 的中点,点D 为弦AB 的中点,CD =1,AB =6,则⊙O 的直径是 .4.已知:如图AB 是直径,CD ⊥AB 于点P ,PB =4,CD =12, 则PC = ,PA = ,OP = ,AC .5.已知:P 为CD 的中点,AB 为⊙O 的直径,F 为AB 延长线上一点,AB 与CD 相交于P ,PE ⊥DF , 求证:AP ·PB =DE ·DF中考链接1.如图⊙O 的弦BA 、CD 交于点P ,CP =2,DP =6,AB =10,则以AP 、BP 的长为根的一元二次方程 ( )A .x 2+8x +12=0B .x 2+10x +12=0C .x 2-10x +12=0D .x 2-10x +16=02.如图,AB 是⊙O 的弦,P 是BA 上一点,PO =5,PB =6,PA =4,则⊙O 的半径为3.如图,⊙O 的半径OA 与BC 相交于点D ,若OD =AD =3,BD :DC =2:3,则BC =4. 如图,AB 是⊙O 的直径,CD ⊥OB 于P ,弦EF 经过点P ,CD =46,AB =11,EP :PF =2:3, 求PB 和EF 的长.E O C B P D5.如图,⊙O 过点C 且与⊙C 相交于A 、B ,⊙O 的弦CD 交AB 于点E .求证:CA 2=CE 2+AE ·BE .6.已知A 为⊙O 上一点,B 为⊙A 与OA 的交点,⊙A 与⊙O 的半径分别为r 、R ,且r <R .(1)如图1,过点B 作⊙A 的切线与⊙O 交于M 、N 两点,求证:AM ·AN =2R r ;(2)如图2,若⊙A 与⊙O 交于E 、F ,C 是弧EBF 上任意一点,过点C 作⊙A 的切线与⊙O 交于P 、Q 两点,试问AP ·AQ =2R r 是否成立,并证明你的结论.切割线定理:推理形式:∵在⊙O 中,PC 是切线PB 是割线 ∵在⊙O 中,PB,PD 是割线 ∴PC ²=PA.PB ∴PA.PB=PC.PD例1.已知:如图7-159,PA 切圆于A ,BC 为圆直径,∠BAD=∠P ,PA=15cm ,PB=5cm .求 BD 的长. A B CP例2.如图所示,已知⊙O1和⊙O2相交于A,B两点,过A点作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E,DE与AC相交于点P.(1)求证:AD∥EC;(2)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长例3.(·新课标全国Ⅰ卷)如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.(1)证明:DB=DC;(2)设圆的半径为1,BC=3,延长CE交AB于点F,求△BCF外接圆的半径练习1.(·天津卷)如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于点D.过点C作BD的平行线与圆相交于点E,与AB相交于点F,AF=3,FB=1,EF=32,则线段CD的长为______2.(·重庆卷)如图,在△ABC中,∠ACB=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则DE的长为________3.如图,梯形ABCD内接于⊙O,AD∥BC,过B引⊙O的切线分别交DA、CA的延长线于E、F.(1)求证:AB2=AE·BC;(2)已知BC=8,CD=5,AF=6,求EF的长4.如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.(1)求证:FB=FC;(2)求证:FB2=FA·FD;(3)若AB是△ABC外接圆的直径,∠EAC=120°,BC=6 cm,求AD的长.5.如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB,AD⊥CD.(1)求证:OC∥AD;(2)若AD=2,AC=5,求AB的长.教师的职务是‘千教万教,教人求真’;学生的职务是‘千学万学,学做真人’。
(华师大版)九年级数学下:第27章《圆》全章导学案(40页)

学校_______ 班级_______小组_______ 姓名________小组评价______教师评价_____27.1 圆的认识第1课时 27.1.1 圆的基本元素【学习目标】1.理解圆的两种定义,理解并掌握弦、直径、弧、优弧、劣弧、半圆、等圆、等弧、圆心角等基本概念,能够从图形中识别;2.理解“直径与弦”、“半圆与弧”、“等弧与长度相等的弧”等模糊概念;3.能应用圆的有关概念解决问题.【学习重难点】重点:理解圆的定义,并掌握圆的基本元素,能从图形中识别;难点:理解“直径与弦”、“半圆与弧”、“等弧与长度相等的弧”等模糊概念;【学法指导】通过生活中圆形物体的感性认识,并自己动手操作画图,理解圆的定义,通过阅读教材理解圆的相关概念并在图中识别,澄清相关概念,并能用相关概念来解决问题.【自学互助】一、自学教材P36-37(图1)(一)知识链接1.自己回忆一下,小学学习过圆的哪些知识?2.结合生活实际,说说生活中有哪些物体是圆形的?并思考圆有什么特征?(二)根据以下题目自主学习并完成1.理解圆的定义:(自己动手画圆)(1)描述性定义:____________________________________________________。
从圆的定义中归纳:①圆上各点到定点(圆心O)的距离都等于____ __;②到定点的距离等于定长的点都在____ _.(2)集合性定义:__________________________________________________。
(3)圆的表示方法:以O点为圆心的圆记作______,读作______.(4)要确定一个圆,需要两个基本条件,一个是______,另一个是_____,其中_____ 确定圆的位置,______确定圆的大小.2.圆的相关概念:(1)弦、直径;(2)弧及其表示方法;(3)等圆、等弧。
如图1,弦有线段,直径是,最长的弦是,优弧有;劣弧有。
华师大版数学九年级下册第27章 章目标总览教案与反思

第27章圆满招损,谦受益。
《尚书》怀辰学校陈海峰组长教材简析本章的内容有:圆的认识、与圆有关的位置关系、圆中的计算问题、正多边形和圆.在对圆的初步认识的基础上,通过画圆引入圆的有关概念,通过类比点和线、线和线的位置关系学习点和圆、直线和圆的位置关系,进一步学习正多边形和圆、弧长和扇形面积,进而学会用圆的有关知识解决一些实际问题.在中考中,本章是考查的重点,主要考查圆的基本性质、与圆有关的位置关系、圆的有关计算.教学指导【本章重点】圆的定义、对称性和有关性质;切线的性质及判定定理;弧长、扇形的面积及有关计算等.【本章难点】同圆或等圆中弧、弦、圆心角之间的关系;垂径定理及其推论;正多边形和圆.【本章思想方法】1.体会和掌握类比的学习方法.如:通过与点和线位置关系的类比,学习点和圆的位置关系.2.体会数形结合思想:在点和圆的位置关系、直线和圆的位置关系,以及圆的运动、与圆有关的实际问题中,都需要与直观地图形结合起来,通过“数”“形”转化.因此,本章应突出数形结合思想,体会数形结合思想的作用.3.体会分类讨论思想:在圆中有的问题没有给出图形(如:弦所对的弧、弦所对的圆周角、点到圆的最大或最小距离等问题),根据题设条件可以画出符合题意的几种图形,因此在解决这些问题时,要注意分类讨论,防止漏解.课时计划27.1 圆的认识 4课时27.2 与圆有关的位置关系 4课时27.3 圆中的计算问题 2课时27.4 正多边形和圆 1课时【素材积累】司马迁写《史记》汉朝司马迁继承父业,立志著述史书。
他游历各地,阅读了大量书籍。
不料正在他着手编写《史记》时,遭到了李陵之祸的株连。
但他矢志不渝,忍辱负重,身受腐刑,幽而发愤,经过十余年的艰苦奋斗,终于写成了鸿篇巨著——《史记》。
2020春华师版九年级数学下册 第27章 全章教学设计

点和圆的位置关系教学目标1.理解不在同一直线上的三个点确定一个圆并掌握它的运用. 2.了解三角形的外接圆和三角形外心的概念. 3.了解反证法的证明思想.教学重点:不在同一直线上的三个点确定一个圆其它们的运用. 教学难点:讲授反证法的证明思路. 教学过程 一、情境引入探究1、经过平面内的已知点A探究2、经过平面内的两个点A 、B 这些圆有什么特点?为什么?探究3、经过平面内的三个点A 、B 、C 能作多少个圆?(1)若三个点共线,则无法作出满足条件的圆; (2)若三个点不共线,则可以作出唯一的一个圆。
作法:①连接AB 、AC ;②分别作AB 、AC 的垂直平分线12,l l,1l 与2l 交于点O ③ 以点O 为圆心,OA 为半径作⊙O ;∴⊙O 即为所求。
二、新课讲解不在同一直线上的三个点确定一个圆. 经过三角形的三个顶点的圆叫做三角形的外接圆.外接圆的圆心是三角形三条边垂直平分线的交点,这个点叫做这个三角形的外心.三角形外心的性质:三角形的外心到三个顶点的距离相等。
三角形的外心的位置因三角形的形状而改变,分四个小组作图找出三角形的外心的位置(4个小组分别作:锐角三角形、直角三角形、钝角三角形和等腰三角形)结论:锐角三角形的外心在三角形内;直角三角形的外心是斜边的中点;钝角三角形的外心在三角形外。
说明:设置等腰三角形一组,是用来说明研究三角形的外心的位置不能按边分。
三、课堂反馈1、经过平面上的两点可以作无数个圆,这些圆的圆心在这两点所连线段的垂直平分线上;经过平面内的三个点可以作0个或1个圆。
2、下列说法:①一个圆仅有一个内接三角形;②等腰三角形的外心在三角形内;③弦是圆的一部分;④作三角形任意两边的垂直平分线的交点就是这个三角形的外心;其中正确的有④ .3、(2007株洲)已知△ABC的三边长分别为6cm,8cm,10cm,则这个三角形的外接圆的面积为25 cm2.4、(2007山东)青岛国际帆船中心要修建一处公共服务设施,使它到三所运动员公寓A、B、C的距离相等。
2020年华师大版九年级数学下册第二十七章《圆的认识(1)》导学案

新华师大版九年级数学下册第二十七章《圆的认识(1)》导学案【学习目标】1、认识圆、弦、弧、圆心角等概念,2、深刻认识圆的两要素。
【重难点预测】重点:圆中的基本概念的认识。
难点:对等弧概念的理解。
【学案使用说明和学法指导】课前完成【知识链接】【知识链接】【自主学习】1、请同学们画一个圆,并从画圆的过程中阐述圆是如何形成的。
2、由以上的画圆和解答问题的过程中,让同学们思考圆的位置是由什么决定的?圆的大小又是由什么决定的?圆的圆心决定圆的,半径决定圆的,因此,圆的两要素是3、在右图中,认识圆的有关概念(1)圆的表示这个以点O为圆心的圆叫作“圆O”,记作“”。
(2)弦、半径、直径线段AB、BC、AC都是圆O中的弦,线段OA、OB、OC都是圆的,线段AC为圆的 .弦AB、BC、AC都是(选填“线段”、“射线”、“直线”),端点都在(选填“圆上”、“圆内”、“圆外”)(3)弧、半圆、劣弧、优弧、等弧弧的符号:“⌒”备注(教师复备栏及学生笔记栏)曲线BC、BAC 都是圆中的圆弧,简称弧,分别记为BC ︵、BAC ︵,直径所对的弧是半圆。
其中像弧BC ︵这样小于半圆周的圆弧叫做 ,像弧BAC ︵.这样的大于半圆周的圆弧叫做 。
优弧与劣弧的区分标准是 。
能够重合的两段弧叫做等弧 (4)圆心角圆心角是以 为顶点的角。
∠AOB 、∠AOC 、∠BOC 就是圆心角。
【合作探究】1、同学们想一想,如何在操场上画出一个很大的圆?说说你的方法。
2、任意画一个圆,表示出这个圆,并写出一条弦、半径、直径、弧、劣弧、优弧,一个圆心角。
总结知识点:圆⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧圆心角劣弧优弧弧)弦(最长弦元素半径圆心两要素:【当堂检测】 一、填空题1、写出右图中的所有的弦、圆心角、优弧、劣弧。
2、矩形的四个顶点在以为圆心,以为半径的圆上。
二、判断题1、直径是弦(),弦是直径()2、直径是圆中最长的弦()3、半圆是弧(),弧是半圆()4、半径相等的两个圆是等圆()5、长度相等的两段弧是等弧(),能够重合的两段弧是等弧()三、操作题根据下列条件作圆(1)以定点O为圆心,作半径等于2cm的圆;(2)以定点O为圆心作圆,使其通过另一点P。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学校_______ 班级_______小组_______ 姓名________小组评价______教师评价_____27.1 圆的认识第1课时 27.1.1 圆的基本元素【学习目标】1.理解圆的两种定义,理解并掌握弦、直径、弧、优弧、劣弧、半圆、等圆、等弧、圆心角等基本概念,能够从图形中识别;2.理解“直径与弦”、“半圆与弧”、“等弧与长度相等的弧”等模糊概念;3.能应用圆的有关概念解决问题.【学习重难点】重点:理解圆的定义,并掌握圆的基本元素,能从图形中识别;难点:理解“直径与弦”、“半圆与弧”、“等弧与长度相等的弧”等模糊概念;【学法指导】通过生活中圆形物体的感性认识,并自己动手操作画图,理解圆的定义,通过阅读教材理解圆的相关概念并在图中识别,澄清相关概念,并能用相关概念来解决问题.【自学互助】一、自学教材P36-37(图1)(一)知识链接1.自己回忆一下,小学学习过圆的哪些知识?2.结合生活实际,说说生活中有哪些物体是圆形的?并思考圆有什么特征?(二)根据以下题目自主学习并完成1.理解圆的定义:(自己动手画圆)(1)描述性定义:____________________________________________________。
从圆的定义中归纳:①圆上各点到定点(圆心O)的距离都等于____ __;②到定点的距离等于定长的点都在____ _.(2)集合性定义:__________________________________________________。
(3)圆的表示方法:以O点为圆心的圆记作______,读作______.(4)要确定一个圆,需要两个基本条件,一个是______,另一个是_____,其中_____ 确定圆的位置,______确定圆的大小.2.圆的相关概念:(1)弦、直径;(2)弧及其表示方法;(3)等圆、等弧。
如图1,弦有线段,直径是,最长的弦是,优弧有;劣弧有。
【展示互导】活动1.学生展示自主学习内容并相互交流活动2.判断下列说法是否正确,为什么?(1)直径是弦.( ) (2)弦是直径.( ) (3)半圆是弧.( ) (4) 弧是半圆.( )(5) 等弧的长度相等.( ) (6) 长度相等的两条弧是等弧.( )活动3.⊙O 的半径为2㎝,弦AB 所对的劣弧为圆周长的61,则∠AOB = ,AB = 活动4.已知:如图2,OA OB 、为⊙O 的半径,C D 、分别为OA OB 、的中点,求证:(1);A B ∠=∠ (2)AE BE =活动4.如图,AB 为⊙O 的直径,CD 是⊙O 中不过圆心的任意一条弦,求证:AB >CD 。
【质疑互究】通过自学和同学展示你还有哪些困惑或新的思考:【检测互评】1.教材P37练习1、2题2.下列说法正确的有( )①半径相等的两个圆是等圆; ②半径相等的两个半圆是等弧;③过圆心的线段是直径; ④ 分别在两个等圆上的两条弧是等弧. A. 1个 B. 2个 C. 3个 D. 4个3.如图3,点A O D 、、以及点B O C 、、分别在一条直线上,则圆中有 条弦.4. ⊙O 的半径为3cm ,则⊙O 中最长的弦长为5.如图4,在ABC ∆中,90,40,ACB A ∠=︒∠=︒以C 为圆心,CB 为半径的圆交AB 于ED CB A (图2)DC ABE (图3)点D ,求ACD 的度数.【总结提升】1、知识小结(1)圆的两种定义:① ;② .(2)什么是弦、直径、弧、半圆、优弧、劣弧、等圆、等弧? (3)同圆或等圆的半径有什么性质?2、拓展提升已知:如图,AB 是⊙O 的直径,CD 是⊙O 的弦,AB ,CD 的延长线交于E ,若AB =2DE , ∠E =18°,求∠C 及∠AOC 的度数.学校_______ 班级_______小组_______ 姓名________小组评价______教师评价_____第2课时 27.1.2 圆的对称性(1)【学习目标】1、经历探索圆的中心对称性及有关性质的过程2、理解圆的中心对称性及有关性质3、会运用圆心角、弧、弦之间的关系解决有关问题 【学习重难点】重点:理解圆的中心对称性及有关性质难点:运用圆心角、弧、弦之间的关系解决有关问题 【学法指导】通过观察、动手操作、合作交流等方法探索圆中的圆心角、弦、弧之间的关系,运用圆心角、弧、弦之间的关系解决有关问题。
【自学互助】1、自学教材p37-38内容2、按照下列步骤进行小组活动:⑴在两张透明纸片上,分别作半径相等的⊙O 和⊙O '⑵在⊙O 和⊙O '中,分别作相等的圆心角∠AOB 、∠'''B O A ,连接AB 、''B A⑶将两张纸片叠在一起,使⊙O 与⊙O '重合(如图)⑷固定圆心,将其中一个圆旋转某个角度,使得OA 与OA '重合在操作的过程中,你有什么发现?___________________________3、上面的命题反映了在同圆或等圆中,圆心角、弧、弦的关系,对于这三个量之间的关系,你还有什么思考?你能够用文字语言把你的发现表达出来吗?4、圆心角、弧、弦之间的关系: ___________________________________________________________________。
5、试一试:如图,已知⊙O 、⊙O '半径相等,AB 、CD 分别是⊙O 、⊙O '的两条弦填空: (1)若AB=CD ,则 ,(2)若AB= CD ,则 ,(3)若∠AOB=∠CO 'D ,则 ,6、在圆心角、弧、弦这三个量中,角的大小可以用度数刻画,弦的大小可以用长度刻画,那么如何来刻画弧的大小呢?弧的大小:圆心角的度数与它所对的弧的度数相等 【展示互导】活动1.学生展示自主学习内容并相互交流活动2. 如图,AB 、AC 、BC 都是⊙O 的弦,∠AOC=∠BOC ,∠ABC 与∠BAC 相等吗? 为什么?O(O ’)B ’A ’BA O ’D CO BA ︵ ︵【质疑互究】通过自学和同学展示你还有哪些困惑或新的思考:【检测互评】1、教材P39练习1、2题2、画一个圆和圆的一些弦,使得所画图形满足下列条件: (1)是中心对称图形,但不是轴对称图形;(2)既是轴对称图形,又是中心对称图形。
3、如图,在⊙O 中, , ∠1=30°,则∠2=_______ 4、一条弦把圆分成1:3两部分,则劣弧所对的圆心角为________。
5、⊙O 中,直径AB ∥CD 弦,︒=⋂60度数AC ,则∠BOD=______。
6、 在⊙O 中,弦AB 的长恰好等于半径,弦AB 所对的圆心角为7、如图,AB 是直径,BC ︵=CD ︵=DE ︵,∠BOC =40°,∠AOE 的度数是 。
【总结提升】 1、知识小结(1)在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别_________;(2)圆心角的度数与它所对的弧的度数________。
2、拓展提升(1)已知,如图,AB 是⊙O 的直径,M,N 分别为AO,BO 的中点,CM ⊥AB,DN ⊥AB,垂足分别为M,N 。
求证:AC=BD(2)已知,如图,在⊙O 中,弦AD BC =, 你能用多种方法证明AB CD =吗?学校_______ 班级_______小组_______ 姓名________小组评价______教师评价_____第3课时 27.1.2 圆的对称性(2)【学习目标】OBACC1 2 A BDO AC =BD OBACMDNEOB A CD(图)1.理解圆的轴对称性;2.掌握垂径定理及其推论,能用垂径定理及其推论进行有关的计算和证明. 【学习重难点】 重点:“垂径定理”及其应用 难点:垂径定理的题设和结论以及垂径定理的证明 【学法指导】本节课的学习中通过动手操作、观察、猜想、归纳、验证得出相关结论,并加以应用.【自学互助】1、自主学习教材P39-40相关内容2. 阅读教材p39“试一试”内容,按下面的步骤做一做:(如图1)第一步,在一张纸上任意画一个⊙O ,沿圆周将圆剪下,作⊙O 的一条弦AB ; 第二步,作直径CD ,使CD AB ⊥,垂足为E ; 第三步,将⊙O 沿着直径折叠. 你发现了什么?归纳:(1)图1是 对称图形,对称轴是 .(2)相等的线段有 ,相等的弧有 . 【展示互导】活动1:(1)如图2,怎样证明“自主学习2”得到的第(2)个结论. 叠合法证明:(2)垂径定理:垂直于弦的直径 弦,并且 的两条弧. 定理的几何语言:如图2 CD 是直径(或CD 经过圆心),且CD AB ⊥____________,____________,_____________∴(3)推论:_________________________________________________________________. 活动2 :垂径定理的应用如图3,已知在⊙O 中,弦AB 的长为8cm ,圆心O 到AB 的距离(弦心距)为3cm ,求⊙O 的半径.(分析:可连结OA ,作OC AB ⊥于C ) 解:【质疑互究】 通过自学和同学展示你还有哪些困惑或新的思考: 【检测互评】1.教材p40练习1,2题2.圆的半径为5cm ,圆心到弦AB 的距离为4cm ,则_____AB cm =.3.如图5,AB 是⊙O 的直径, CD 为弦,CD AB ⊥于E ,则下列结论中不成立的是( )(图1)CABDEOB A O(图3) CABDEO(图2)A.COE DOE ∠=∠B.CE DE =C.OE BE =D. BDBC = 3. 如图6,CD 为⊙O 的直径,AB ⊥CD 于E ,DE =8cm ,CE =2cm ,则AB =______cm .【总结提升】 1、知识小结(1)垂径定理是 ,定理有两个条件,三个结论。
(2)定理可推广为:在五个条件①过圆心,②垂直于弦,③平分弦,④平分弦所对的优弧⑤平分弦所对的劣弧中,知 推 。
2、方法小结:(1)在运用垂径定理解决问题是辅助线的常用作法:连半径,过圆心向弦作垂线段。
(2)如图4,根据垂径定理和勾股定理,“半弦、半径、弦心距”构成直角三角形,则r d a 、、的关系为,知道其中任意两个量,可求出第三个量. 3、拓展提升(1)已知:如图7,AB 是⊙O 的直径,弦CD 交AB 于E 点,BE =1,AE =5,∠AEC =30°,求CD 的长.(2)如图9,⊙O 中,直径AB =15cm ,有一条长为9cm 的动弦CD 在上滑动(点C 与A ,点D 与B 不重合),CF ⊥CD 交AB 于F ,DE ⊥CD 交AB 于E . (1)求证:AE =BF ;(2)在动弦CD 滑动的过程中,四边形CDEF 的面积是否为定值? 若是定值,请给出证明并求这个定值;若不是,请说明理由.学校_______ 班级_______小组_______ 姓名________小组评价______教师评价_____第4课时 27.1.2 圆的对称性(3)【学习目标】1.熟练掌握垂径定理及其推论;2.能用垂径定理及其推论进行有关的计算和证明,进一步应用垂径定理解决实际问题. 【学习重难点】(图5) C A BD E O (图6) (图7) dr aO (4) (图9)重点:“垂径定理及其推论”及其在实际问题中的应用难点:分清垂径定理及其推论的题设和结论、垂径定理及其在实际问题中的应用 【学法指导】本节课学习中通过对比理解垂径定理及其推论,应用中善于将实际问题转化为数学问题,培养建模思想和提高分析问题、解决问题的能力。
