最新北师大版七年级数学复习专题1整理
北师大版七年级下册数学期末全册单元重点题型复习

解: 画图略.过C点作渠岸的垂线所得垂线段
就是开沟的位置,原因: 直线外一点与直线
上各点连接的所有线段中,垂线段最短.
返回
性质2 平行线的性质 11. (中考·雅安)如图,已知AB∥CD,直线EF交AB于
点E,交CD于点F,且EG平分∠FEB,∠1=50°, 则∠2等于( D ) A. 50° B. 60° C. 70° D. 80°
1=(32-1)(32+1)(34+1)·…·(364+1)+1=3128-1
+1
=3128.
因为3128=(34)32=8132,
返回
公式2 完全平方公式 10.计算下列各式: (1)(3a+b-2)(3a-b+2);
解: 原式=[3a+(b-2)][3a-(b-2)]=(3a)2-(b-2)2 =9a2-b2+4b-4; (2)(中考·重庆)2(a+1)2+(a+1)(1-2a).
月份/月 平均价格/(元/kg)
月份/月 平均价格/(元/kg)
1
23456
4.6
4.8 4.8 5.0 4.8 4.4
7
8 9 10 11 12
4.0
3.8 3.6 3.6 3.8 4.0
(1)表中列出的是哪两个变量之间的关系? 哪个是自变 量,哪个是因变量?
解: 表中列出的是该地区大米的平均价格与月份两 个变量之间的关系,月份是自变量,大米的平 均价格是因变量.
z2=x2+2xy+y2+2xz+2yz+z2.
返回
只本
北师大版七年级下册数学 供 课
精品配套课件
免件 费来
交源
流于
使网
用络
第二章 相交线与平行线
全章热门考点整合应用
考点 1 三个概念
北师大版七年级下册数学(全册知识点考点梳理、重点题型分类巩固练习)(基础版)(家教、补习、复习用)

北师大版七年级下册数学全册知识点梳理及重点题型巩固练习幂的运算(基础)【学习目标】1. 掌握正整数幂的乘法运算性质(同底数幂的乘法、幂的乘方、积的乘方);2. 能用代数式和文字语言正确地表述这些性质,并能运用它们熟练地进行运算. 【要点梳理】要点一、同底数幂的乘法性质+⋅=m n m n a a a (其中,m n 都是正整数).即同底数幂相乘,底数不变,指数相加.要点诠释:(1)同底数幂是指底数相同的幂,底数可以是任意的实数,也可以是单项式、多项式.(2)三个或三个以上同底数幂相乘时,也具有这一性质,即mnpm n pa a a a++⋅⋅=(,,m n p 都是正整数).(3)逆用公式:把一个幂分解成两个或多个同底数幂的积,其中它们的底数与原来的底数相同,它们的指数之和等于原来的幂的指数。
即m n m n a a a +=⋅(,m n 都是正整数).要点二、幂的乘方法则()=m n mn a a (其中,m n 都是正整数).即幂的乘方,底数不变,指数相乘.要点诠释:(1)公式的推广:(())=m n p mnp a a (0≠a ,,,m n p 均为正整数)(2)逆用公式: ()()nmmnm n aa a ==,根据题目的需要常常逆用幂的乘方运算能将某些幂变形,从而解决问题. 要点三、积的乘方法则()=⋅n n n ab a b (其中n 是正整数).即积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.要点诠释:(1)公式的推广:()=⋅⋅nnnnabc a b c (n 为正整数).(2)逆用公式:()nn na b ab =逆用公式适当的变形可简化运算过程,尤其是遇到底数互为倒数时,计算更简便.如:1010101122 1.22⎛⎫⎛⎫⨯=⨯= ⎪ ⎪⎝⎭⎝⎭要点四、注意事项(1)底数可以是任意实数,也可以是单项式、多项式.(2)同底数幂的乘法时,只有当底数相同时,指数才可以相加.指数为1,计算时不要遗漏.(3)幂的乘方运算时,指数相乘,而同底数幂的乘法中是指数相加.(4)积的乘方运算时须注意,积的乘方要将每一个因式(特别是系数)都要分别乘方. (5)灵活地双向应用运算性质,使运算更加方便、简洁. (6)带有负号的幂的运算,要养成先化简符号的习惯. 【典型例题】类型一、同底数幂的乘法性质1、计算:(1)234444⨯⨯;(2)3452622a a a a a a ⋅+⋅-⋅;(3)11211()()()()()n n m n m x y x y x y x y x y +-+-+⋅+⋅+++⋅+. 【答案与解析】 解:(1)原式234944++==.(2)原式34526177772222a a a a a a a +++=+-=+-=.(3)原式11211222()()()()2()n n m n m n m n m n m x y x y x y x y x y +++-++-+++=+++=+++=+.【总结升华】(2)(3)小题都是混合运算,计算时要注意运算顺序,还要正确地运用相应的运算法则,并要注意区别同底数幂的乘法与整式的加减法的运算法则.在第(2)小题中a 的指数是1.在第(3)小题中把x y +看成一个整体. 举一反三: 【变式】计算:(1)5323(3)(3)⋅-⋅-;(2)221()()p p p x x x +⋅-⋅-(p 为正整数); (3)232(2)(2)n ⨯-⋅-(n 为正整数). 【答案】解:(1)原式532532532103(3)333333++=⋅-⋅=-⋅⋅=-=-. (2)原式22122151()p p p p p p p x x x x x +++++=⋅⋅-=-=-. (3)原式525216222(2)22n n n +++=⋅⋅-=-=-.2、已知2220x +=,求2x 的值.【思路点拨】同底数幂乘法的逆用:22222x x +=⋅ 【答案与解析】 解:由2220x +=得22220x ⋅=.∴ 25x=.【总结升华】(1)本题逆用了同底数幂的乘法法则,培养了逆向思维能力.(2)同底数幂的乘法法则的逆运用:m nm n a a a +=⋅.类型二、幂的乘方法则3、计算:(1)2()m a ;(2)34[()]m -;(3)32()m a -. 【思路点拨】此题是幂的乘方运算,(1)题中的底数是a ,(2)题中的底数是m -,(3)题中的底数a 的指数是3m -,乘方以后的指数应是2(3)62m m -=-. 【答案与解析】解:(1)2()m a 2ma=.(2)34[()]m -1212()m m =-=.(3)32()m a -2(3)62m ma a --==. 【总结升华】运用幂的乘方法则进行计算时要注意符号的计算及处理,一定不要将幂的乘方与同底数幂的乘法混淆.幂的乘方法则中的底数仍可以为单个数字、字母,也可以是单项式或多项式.4、(2016春•湘潭期末)已知a x =3,a y =2,求a x+2y 的值.【思路点拨】 直接利用同底数幂的乘法运算法则将原式变形进而将已知代入求出答案. 【答案与解析】 解:∵a x =3,a y =2, ∴a x+2y =a x ×a 2y =3×22=12.【总结升华】本题考查同底数幂的乘法,幂的乘方,解题时记准法则是关键. 举一反三:【变式1】已知2ax =,3bx =.求32a bx+的值.【答案】 解:32323232()()238972a b a b a b x x x x x +===⨯=⨯=. 【变式2】已知84=m ,85=n ,求328+m n的值.【答案】解:因为3338(8)464===m m , 2228(8)525===n n .所以323288864251600+=⨯=⨯=m n m n.类型三、积的乘方法则5、指出下列各题计算是否正确,指出错误并说明原因:(1)22()ab ab =; (2)333(4)64ab a b =; (3)326(3)9x x -=-. 【答案与解析】解:(1)错,这是积的乘方,应为:222()ab a b =. (2)对.(3)错,系数应为9,应为:326(3)9x x -=. 【总结升华】(1)应用积的乘方时,特别注意观察底数含有几个因式,每个因式都分别乘方. (2)注意系数及系数符号,对系数-1不可忽略. 举一反三:【变式】(2015春•铜山县校级月考)(﹣8)57×0.12555. 【答案】解:(﹣8)57×0.12555=(﹣8)2×[(﹣8)55×]=﹣64.北师大版七年级下册数学重难点突破知识点梳理及重点题型巩固练习【巩固练习】 一.选择题1.(2015•杭州模拟)计算的x 3×x 2结果是( ) A .x 6 B .6xC . x 5D . 5x2.2nn a a+⋅的值是( ).A. 3n a + B. ()2n n a + C. 22n a+D. 8a3.(2016•淮安)下列运算正确的是( )A .a 2•a 3=a 6B .(ab )2=a 2b 2C .(a 2)3=a 5D .a 2+a 2=a 44.下列各题中,计算结果写成10的幂的形式,其中正确的是( ).A. 100×210=310 B. 1000×1010=3010 C. 100×310=510 D. 100×1000=4105.下列计算正确的是( ). A.()33xy xy =B.()222455xyx y -=- C.()22439xx -=-D.()323628xy x y -=-6.若()391528m n a b a b=成立,则( ). A. m =6,n =12 B. m =3,n =12 C. m =3,n =5D. m =6,n =5二.填空题 7.(2016•大庆)若a m =2,a n =8,则a m+n = .8. 若()319x aa a ⋅=,则x =_______.9. 已知35na=,那么6n a =______. 10.若38m a a a ⋅=,则m =______;若31381x +=,则x =______. 11. ()322⎡⎤-=⎣⎦______; ()33n ⎡⎤-=⎣⎦______; ()523-=______.12.若n 是正整数,且210na =,则3222()8()n n a a --=__________.三.解答题13.(2015春•莱芜校级期中)计算:(﹣x )3•x 2n ﹣1+x 2n •(﹣x )2.14.(1) 3843()()x x x ⋅-⋅-; (2)2333221()()3a b a b -+-;(3)3510(0.310)(0.410)-⨯-⨯⨯⨯; (4)()()3522b a a b --;(5)()()2363353a a a -+-⋅;15.(1)若3335nn x x x +⋅=,求n 的值.(2)若()3915n ma b b a b ⋅⋅=,求m 、n 的值.【答案与解析】 一.选择题1. 【答案】C ;【解析】解:原式=x 3+2=x 5,故选C . 2. 【答案】C ; 【解析】2222nn n n n a a a a ++++⋅==.3. 【答案】B ;【解析】解:A 、a 2•a 3=a 2+3=a 5,故本选项错误;B 、(ab )2=a 2b 2,故本选项正确;C 、(a 2)3=a 2×3=a 6,故本选项错误;D 、a 2+a 2=2a 2,故本选项错误.故选B .4. 【答案】C ;【解析】100×210=410;1000×1010=1310;100×1000=510.5. 【答案】D ;【解析】()333xy x y =;()2224525xyx y -=;()22439x x -=.6. 【答案】C ; 【解析】()333915288,39,315m n m n a b a b a b m n ====,解得m =3,n =5.二.填空题7. 【答案】16;【解析】解:∵a m =2,a n =8,∴a m+n =a m •a n =16,故答案为:16. 8. 【答案】6;【解析】3119,3119,6x a a x x +=+==. 9. 【答案】25; 【解析】()2632525nn aa ===.10.【答案】5;1;【解析】338,38,5m m a a a a m m +⋅==+==;3143813,314,1x x x +==+==. 11.【答案】64;9n -;103-; 12.【答案】200;【解析】()()32322222()8()81000800200n nn n a a a a --=-=-=.三.解答题 13.【解析】解:(﹣x )3•x 2n ﹣1+x 2n •(﹣x )2 =﹣x 2n+2+x 2n+2 =0. 14.【解析】解:(1)3843241237()()x x x x x x x ⋅-⋅-=-⋅⋅=-;(2)233322696411()()327a b a b a b a b -+-=-+;(3)3535810(0.310)(0.410)0.30.4101010 1.210-⨯-⨯⨯⨯=⨯⨯⨯⨯=⨯;(4)()()()()()3535822222b a a b a b a b a b --=---=--;(5)()()236331293125325272a a a a a a a -+-⋅=-⋅=-.15.【解析】 解:(1)∵3335nn x x x +⋅= ∴ 4335n xx +=∴4n +3=35 ∴n =8(2)m =4,n =3解:∵()3915n ma b ba b ⋅⋅=∴ 333333915nmnm a b b a b a b +⋅⋅=⋅=∴3n =9且3m +3=15 ∴n =3且m =4北师大版七年级下册数学重难点突破知识点梳理及重点题型巩固练习同底数幂的除法【学习目标】1. 会用同底数幂的除法性质进行计算.2. 掌握零指数幂和负整数指数幂的意义. 3.掌握科学记数法. 【要点梳理】要点一、同底数幂的除法法则同底数幂相除,底数不变,指数相减,即mnm na a a -÷=(a ≠0,m n 、都是正整数,并且m n >)要点诠释:(1)同底数幂乘法与同底数幂的除法是互逆运算.(2)被除式、除式的底数相同,被除式的指数大于除式指数,0不能作除式. (3)当三个或三个以上同底数幂相除时,也具有这一性质. (4)底数可以是一个数,也可以是单项式或多项式. 要点二、零指数幂任何不等于0的数的0次幂都等于1.即01a =(a ≠0)要点诠释:底数a 不能为0,00无意义.任何一个常数都可以看作与字母0次方的积.因此常数项也叫0次单项式. 要点三、负整数指数幂任何不等于零的数的n -(n 为正整数)次幂,等于这个数的n 次幂的倒数,即1nnaa -=(a ≠0,n 是正整数).引进了零指数幂和负整数指数幂后,指数的范围已经扩大到了全体整数,以前所学的幂的运算性质仍然成立.m n m n a a a +=(m 、n 为整数,0a ≠);()mm m ab a b =(m 为整数,0a ≠,0b ≠)()nm mn a a =(m 、n 为整数,0a ≠).要点诠释:()0n a a -≠是na 的倒数,a 可以是不等于0的数,也可以是不等于0的代数式.例如()1122xy xy -=(0xy ≠),()()551a b a b -+=+(0a b +≠). 要点四、科学记数法的一般形式(1)把一个绝对值大于10的数表示成10na ⨯的形式,其中n 是正整数,1||10a ≤<(2)利用10的负整数次幂表示一些绝对值较小的数,即10na -⨯的形式,其中n 是正整数,1||10a ≤<.用以上两种形式表示数的方法,叫做科学记数法. 【典型例题】类型一、同底数幂的除法1、计算:(1)83x x ÷;(2)3()a a -÷;(3)52(2)(2)xy xy ÷;(4)531133⎛⎫⎛⎫-÷- ⎪ ⎪⎝⎭⎝⎭.【思路点拨】利用同底数幂相除的法则计算.(2)、(4)两小题要注意符号. 【答案与解析】 解:(1)83835x x xx -÷==.(2)3312()a a a a --÷=-=-.(3)5252333(2)(2)(2)(2)8xy xy xy xy x y -÷===.(4)535321111133339-⎛⎫⎛⎫⎛⎫⎛⎫-÷-=-=-= ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭. 【总结升华】(1)运用法则进行计算的关键是看底数是否相同.(2)运算中单项式的系数包括它前面的符号.2、计算下列各题:(1)5()()x y x y -÷- (2)125(52)(25)a b b a -÷- (3)6462(310)(310)⨯÷⨯ (4)3324[(2)][(2)]x y y x -÷-【思路点拨】(1)若被除式、除式的底数互为相反数时,先将底数变为相同底数再计算,尽可能地去变偶次幂的底数,如1212(52)(25)a b b a -=-.(2)注意指数为1的多项式.如x y -的指数为1,而不是0. 【答案与解析】解:(1)5514()()()()x y x y x y x y --÷-=-=-.(2)1251257(52)(25)(25)(25)(25)a b b a b a b a b a -÷-=-÷-=-(3)64626426212(310)(310)(310)(310)910-⨯÷⨯=⨯=⨯=⨯.(4)3324[(2)][(2)]x y y x -÷-9898(2)(2)(2)2x y x y x y x y -=-÷-=-=-.【总结升华】底数都是单项式或多项式,把底数作一个整体利用同底数幂的除法法则进行计算.3、已知32m=,34n=,求129m n+-的值.【答案与解析】解: 121222222221222244449(3)33333(3)399(3)33(3)(3)m m m m m m m nn n n n n n ++++-======. 当32m =,34n=时,原式224239464⨯==. 【总结升华】逆用同底数除法公式,设法把所求式转化成只含3m,3n 的式子,再代入求值.本题是把除式写成了分数的形式,为了便于观察和计算,我们可以把它再写成除式的形式. 举一反三:【变式】(2015春•苏州)已知以ma =2,na =4,ka =32.则32m n ka +-的值为 .【答案】解:3ma=32=8,2n a =24=16,32m n k a +-=3m a •2n a ÷k a =8×16÷32=4,故答案为:4.类型二、负整数次幂的运算4、计算:(1)223-⎛⎫- ⎪⎝⎭;(2)23131()()a b a b ab ---÷.【答案与解析】解:(1)222119434293-⎛⎫-=== ⎪⎝⎭⎛⎫- ⎪⎝⎭; (2)2313123330()()a b a b ab a b a b ab a b b -----÷===.【总结升华】要正确理解负整数指数幂的意义. 举一反三:【变式】计算:4513012222( 3.14)2π----⎛⎫++⨯⨯+- ⎪⎝⎭.【答案】解: 4513012222( 3.14)2π----⎛⎫++⨯⨯+- ⎪⎝⎭45311111122116212223228=++⨯⨯+=++⨯⨯+ 1151611732832=+++= 5、 已知1327m=,1162n⎛⎫= ⎪⎝⎭,则n m 的值=________.【答案与解析】 解: ∵ 331133273m-===,∴ 3m =-. ∵ 122n n -⎛⎫= ⎪⎝⎭,4162=,∴ 422n -=,4n =-.∴ 4411(3)(3)81n m -=-==-. 【总结升华】先将127变形为底数为3的幂,122nn -⎛⎫= ⎪⎝⎭,4162=,然后确定m 、n 的值,最后代值求nm . 举一反三:【变式】计算:(1)1232()a b c --;(2)3232312b c b c ---⎛⎫⨯ ⎪⎝⎭;【答案】解:(1)原式424626b a b c a c--==.(2)原式8236981212888b b c b c b cc---=⨯==. 类型三、科学记数法6、(2014秋•福州)观察下列计算过程:(1)∵33÷53=332231333=⨯,33÷53=353-=23-,∴23-=(2)当a≠0时,∵2a ÷7a =27a a=225a a a ⨯=51a ,2a ÷7a =27a -=5a -,5a -=51a ,由此可归纳出规律是:pa -=1p a(a≠0,P 为正整数)请运用上述规律解决下列问题: (1)填空:103-= ;259x x x ⨯÷= .(2)用科学记数法:3×410-= .(写成小数形式)(3)把0.00000002写成如(2)的科学记数法10na ⨯的形式是: . 【答案与解析】 解:(1)103-=1013; 259x x x ⨯÷ =259x +-=221x x -=; (2)3×410-=0.0003, (3)0.00000002=2×810-.【总结升华】本题考查用科学记数法表示较小的数,一般形式为10na ⨯,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.北师大版七年级下册数学重难点突破知识点梳理及重点题型巩固练习【巩固练习】一.选择题1. (2015•桂林)下列计算正确的是( )A .()25a=10a B .16x ÷4x =4x C .22a +23a =46a D .3b •3b =32b2.下列计算中正确的是( ).A.212a a xx x ++÷=B.()()6322xy xy x y ÷= C.()12529x x x x ÷÷=D.()42332n nn n x xx x +÷= 3.近似数0.33万表示为( )A .3.3×210-B .3.3000×310C .3.3×310D .0.33×410 4.020122012(1)(0.125)8π-+⨯的结果是( )A .3B .23-C .2D .05..将201)3(,)2(,)61(---这三个数按从小到大的顺序排列为()A .21)3()61()2(-<<-- B .201)3()2()61(-<-<-C .12)61()2()3(-<-<- D .12)61()3()2(-<-<-6.下列各式中正确的有( )①21()9;3-=②224-=-;③01a =;④()111--=;⑤()2336-=.A .2个B .3个C .4个D .1个二.填空题7. =-+-01)π()21(______,()011 3.142--++=______.8. ()()532aa -÷-=__________,201079273÷÷=__________,02139⎛⎫+= ⎪⎝⎭______.9. ()3223a b-=______,()22a b---=______.10.一种细菌的半径为0.0004m ,用科学记数法表示为______m .11.“神威一号”计算机运算速度为每秒384000000000次,其运算速度用科学记数法表示,为______次/秒.12(2015春•江西)若m a =-2, na =-12-,则23m na -= . 三.解答题13.(2015春•吉州)已知2x=3,2y=5.求:(1)2x y+的值;(2)32x的值; (3)212x y +-的值.14.用小数表示下列各数:(1)8.5×310-(2)2.25×810-(3)9.03×510-15. 先化简,后求值:()()23424211212a b a b a b ----⎛⎫--÷ ⎪⎝⎭,其中23a b ==-,.【答案与解析】一.选择题1. 【答案】A ; 【解析】A 、()25a=10a ,正确; B 、16x ÷4x =12x ,错误;C 、22a +23a =25a ,错误;D 、3b •3b =6b b 3•b 3=b 6,错误;故选A.2. 【答案】C ; 【解析】21a a xx x ++÷=;()()6333xy xy x y ÷= ;()4235n n n n x x x x ÷= .3. 【答案】C ;【解析】0.33万=3300=3.3×310. 4. 【答案】C ;【解析】2012020*******(1)(0.125)8181128π⎛⎫-+⨯=+⨯=+= ⎪⎝⎭.5. 【答案】A ; 【解析】1021()6,(2)1,(3)96-=-=-=,所以210)3()61()2(-<<--.6. 【答案】D ;【解析】只有①正确;2124-=;()010a a =≠;()111--=-;()239-=. 二.填空题 7. 【答案】3;12; 【解析】()01111 3.1421122--++=-++=. 8. 【答案】7;27;10a ;【解析】201074030739273333327÷÷=÷÷==.9.【答案】6627a b ;42a b【解析】()632266627327a a ba b b --==;()422422a a b a b b----==.10.【答案】4410-⨯; 11.【答案】113.8410⨯;12.【答案】-32; 【解析】解:()224mm a a ,==()3318n n a a ==-,23m n a -=4=﹣32.三.解答题 13.【解析】 解:(1)2x y+=2x•2y=3×5=15;(2)32x=()32x =33=27;(3)212x y +-=()22x •2y÷2=23×5÷2=.14.【解析】解:(1)8.5×310-=0.0085 (2)2.25×810-=0.0000000225(3)9.03×510-=0.0000903 15.【解析】 解:原式4863482323444a ba b a b a b a b ------=-÷=-=-当23a b ==-,时,原式23412(3)27=-=-.北师大版七年级下册数学重难点突破知识点梳理及重点题型巩固练习整式的乘法(基础)【学习目标】1. 会进行单项式的乘法,单项式与多项式的乘法,多项式的乘法计算.2. 掌握整式的加、减、乘、乘方的较简单的混合运算,并能灵活地运用运算律简化运算. 【要点梳理】要点一、单项式的乘法法则单项式与单项式相乘,把它们的系数,相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它们的指数作为积的一个因式.要点诠释:(1)单项式的乘法法则的实质是乘法的交换律和同底数幂的乘法法则的综合应用.(2)单项式的乘法方法步骤:积的系数等于各系数的积,是把各单项式的系数交换到一起进行有理数的乘法计算,先确定符号,再计算绝对值;相同字母相乘,是同底数幂的乘法,按照“底数不变,指数相加”进行计算;只在一个单项式里含有的字母,要连同它的指数写在积里作为积的一个因式.(3)运算的结果仍为单项式,也是由系数、字母、字母的指数这三部分组成. (4)三个或三个以上的单项式相乘同样适用以上法则. 要点二、单项式与多项式相乘的运算法则单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加. 即()m a b c ma mb mc ++=++. 要点诠释:(1)单项式与多项式相乘的计算方法,实质是利用乘法的分配律将其转化为多个单项式乘单项式的问题.(2)单项式与多项式的乘积仍是一个多项式,项数与原多项式的项数相同. (3)计算的过程中要注意符号问题,多项式中的每一项包括它前面的符号,同时还要注意单项式的符号.(4)对混合运算,应注意运算顺序,最后有同类项时,必须合并,从而得到最简的结果.要点三、多项式与多项式相乘的运算法则多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.即()()a b m n am an bm bn ++=+++.要点诠释:多项式与多项式相乘,仍得多项式.在合并同类项之前,积的项数应该等于两个多项式的项数之积.多项式与多项式相乘的最后结果需化简,有同类项的要合并.特殊的二项式相乘:()()()2x a x b x a b x ab ++=+++. 【典型例题】类型一、单项式与单项式相乘1、计算:(1)221323ab a b abc ⎛⎫⋅-⋅ ⎪⎝⎭; (2)121(2)(3)2n n x y xy x z +⎛⎫-⋅-⋅-⎪⎝⎭; (3)232216()()3m n x y mn y x -⋅-⋅⋅-.【思路点拨】前两个题只要按单项式乘法法则运算即可,第(3)题应把x y -与y x -分别看作一个整体,那么此题也属于单项式乘法,可以按单项式乘法法则计算. 【答案与解析】解: (1)221323ab a b abc ⎛⎫⋅-⋅ ⎪⎝⎭22132()()3a a a b b b c ⎡⎤⎛⎫=⨯-⨯⋅⋅⋅⋅ ⎪⎢⎥⎝⎭⎣⎦ 442a b c =-.(2)121(2)(3)2n nx y xy x z +⎛⎫-⋅-⋅- ⎪⎝⎭121(2)(3)()()2n n x x x y y z +⎡⎤⎛⎫=-⨯-⨯-⋅⋅⋅ ⎪⎢⎥⎝⎭⎣⎦413n n x y z ++=-.(3)232216()()3m n x y mn y x -⋅-⋅⋅- 232216()()3m n x y mn x y =-⋅-⋅⋅- 22321(6)()()[()()]3m m n n x y x y ⎡⎤=-⨯⋅⋅-⋅-⎢⎥⎣⎦3352()m n x y =--.【总结升华】凡是在单项式里出现过的字母,在其结果里也应全都有,不能漏掉. 举一反三:【变式】(2014•甘肃模拟)计算:2m 2•(﹣2mn )•(﹣m 2n 3). 【答案】解:2m 2•(﹣2mn )•(﹣m 2n 3)=[2×(﹣2)×(﹣)](m 2×mn×m 2n 3) =2m 5n 4.类型二、单项式与多项式相乘2、 计算:(1)21242233ab ab ab b ⎛⎫⎛⎫--+ ⎪⎪⎝⎭⎝⎭;(2)22213(6)32xy y x xy ⎛⎫-+-- ⎪⎝⎭;(3)2222340.623a ab b a b ⎛⎫⎛⎫+-- ⎪⎪⎝⎭⎝⎭;【答案与解析】 解:(1)21242233ab ab ab b ⎛⎫⎛⎫--+ ⎪⎪⎝⎭⎝⎭212114(2)23223ab ab ab ab ab b ⎛⎫⎛⎫⎛⎫=-⋅+--+-⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 232221233a b a b ab =-+-.(2)22213(6)32xy y x xy ⎛⎫-+-- ⎪⎝⎭2222213(6)(6)()(6)32xy xy y xy x xy ⎛⎫=--+-+-- ⎪⎝⎭23432296x y xy x y =-+.(3)2222340.623a ab b a b ⎛⎫⎛⎫+-- ⎪⎪⎝⎭⎝⎭2222334253a ab b a b ⎛⎫⎛⎫=+-- ⎪⎪⎝⎭⎝⎭222222223443423353a a b ab a b b a b ⎛⎫⎛⎫⎛⎫⎛⎫=⋅-+⋅-+-- ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭42332444235a b a b a b =--+.【总结升华】计算时,符号的确定是关键,可把单项式前和多项式前的“+”或“-”号看作性质符号,把单项式乘以多项式的结果用“+”号连结,最后写成省略加号的代数和. 举一反三:【变式1】224312(6)2m n m n m n ⎛⎫-+- ⎪⎝⎭.【答案】解:原式2224232211222m n m n m n +⨯⎛⎫=-+-⋅ ⎪⎝⎭26262262171221244m n m n m n m n m n =-+=-.【变式2】若n 为自然数,试说明整式()()2121n n n n +--的值一定是3的倍数. 【答案】解:()()2121n n n n +--=222223n n n n n +-+=因为3n 能被3整除,所以整式()()2121n n n n +--的值一定是3的倍数.类型三、多项式与多项式相乘3、计算:(1)(32)(45)a b a b +-; (2)2(1)(1)(1)x x x -++;(3)()(2)(2)()a b a b a b a b +--+-;(4)25(21)(23)(5)x x x x x ++-+-.【答案与解析】 解:(1)(32)(45)a b a b +-221215810a ab ab b =-+-2212710a ab b =--.(2)2(1)(1)(1)x x x -++22(1)(1)x x x x =+--+41x =-.(3)()(2)(2)()a b a b a b a b +--+-2222(2)(2)a ab b a ab b =---+-222222a ab b a ab b =----+2ab =-.(4)25(21)(23)(5)x x x x x ++-+-322(5105)(2715)x x x x x =++---32251052715x x x x x =++-++ 32581215x x x =+++.【总结升华】多项式乘以多项式时须把一个多项式中的每一项乘以另一个多项式的每一项,刚开始时要严格按法则写出全部过程,以熟悉解题步骤,计算时要注意的是:(1)每一项的符号不能弄错;(2)不能漏乘任何一项.4、(2016春•长春校级期末)若(x+a )(x+2)=x 2﹣5x+b ,则a+b 的值是多少? 【思路点拨】根据多项式与多项式相乘的法则把等式的左边展开,根据题意列出算式,求出a 、b 的值,计算即可. 【答案与解析】解:(x+a )(x+2)=x 2+(a+2)x+2a , 则a+2=﹣5,2a=b , 解得,a=﹣7,b=﹣14, 则a+b=﹣21.【总结升华】本题考查的是多项式乘多项式,多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加. 举一反三:【变式】求出使(32)(34)9(2)(3)x x x x +->-+成立的非负整数解. 【答案】不等式两边分别相乘后,再移项、合并、求解. 解:22912689(6)x x x x x -+->+-,229689954x x x x -->+-, 229699854x x x x --->-, 1546x ->-,4615x <.∴ x 取非负整数为0,1,2,3.北师大版七年级下册数学重难点突破知识点梳理及重点题型巩固练习【巩固练习】一.选择题1.下列算式中正确的是( ). A.326326a a a⋅=B.358248x x x ⋅= C.44339x x x ⋅=D.77145510y y y ⋅= 2.(2016•毕节市)下列运算正确的是( ) A .﹣2(a+b )=﹣2a+2b B .(a 2)3=a 5C .a 3+4a=a 3D .3a 2•2a 3=6a 53.(2014秋•白云区期末)下列计算正确的是( )A .x (x 2﹣x ﹣1)=x 3﹣x ﹣1B .ab (a+b )=a 2+b 2C .3x (x 2﹣2x ﹣1)=3x 3﹣6x 2﹣3xD .﹣2x (x 2﹣x ﹣1)=﹣2x 3﹣2x 2+2x 4.已知()()221323x x x mx +-=--,那么m 的值为( ). A.-2B.2C.-5D.55. 要使()23254x x a x b x x ++-=++成立,则a ,b 的值分别是( ).A. 22a b =-=-,B. 22a b ==,C. 22a b ==-,D. 22a b =-=,6.设M =()()37x x --,N =()()28x x --,则M 与N 的关系为( ). A.M <N B.M >N C.M =N D.不能确定 二.填空题7. 已知三角形的底边为(62)a b -,高是(26)b a -+,则三角形的面积是_________. 8. 计算:①()()23x x ++=________;②()()37x x ++=______;③()()710x x +-=_______;④()()56x x --=______.9.(2016•瑶海区一模)计算:x 2y (2x+4y )= .10. ()()()_______x y z y x z z x y ---+-=. 11.(2015•江都市模拟)若化简(ax+3y )(x ﹣y )的结果中不含xy 项,则a 的值为 . 12. 若2xy =,3x y +=,则()()11x y ++=____________.三.解答题13.(2015春•邳州市期末)当我们利用2种不同的方法计算同一图形的面积时,可以得到一个等式.例如,由图1,可得等式:(a+2b )(a+b )=a 2+3ab+2b 2. (1)由图2,可得等式: . (2)利用(1)中所得到的结论,解决下面的问题: 已知 a+b+c=11,ab+bc+ac=38,求a 2+b 2+c 2的值;(3)利用图3中的纸片(足够多),画出一种拼图,使该拼图可用来验证等式:2a 2+5ab+2b 2=(2a+b )(a+2b );(4)小明用2 张边长为a 的正方形,3 张边长为b 的正方形,5 张边长分别为a 、b 的长方形纸片重新拼出一个长方形,那么该长方形较长的一条边长为 .14. 解下列各方程.(1)222(1)(32)22y y y y y y +--+=- (2)25(3)4(6)(4)0x x x x x x +--++-+= 15. 化简求值:(1)11112323x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭,其中4x =-.(2)22323(21)(342)x x x x x x x -+--+,其中1x =-.【答案与解析】 一.选择题1. 【答案】B ;【解析】325326a a a ⋅=;45339x x x ⋅=;77145525y y y ⋅=. 2. 【答案】D ;【解析】A 、原式=﹣2a ﹣2b ,错误;B 、原式=a 6,错误;C 、原式不能合并,错误;D 、原式=6a 5,正确.3. 【答案】C ;【解析】解:A 、x (x 2﹣x ﹣1)=x 3﹣x 2﹣x ,故此选项错误;B 、ab (a+b )=a 2b+ab 2,故此选项错误;C 、3x (x 2﹣2x ﹣1)=3x 3﹣6x 2﹣3x ,故此选项正确;D 、﹣2x (x 2﹣x ﹣1)=﹣2x 3+2x 2+2x ,故此选项错误;故选:C .4. 【答案】D ;【解析】()()2221325323x x x x x mx +-=--=--,所以5m =. 5. 【答案】C ;【解析】由题意3524a b +=-=,,所以22a b ==-,.6. 【答案】B ;【解析】M =21021x x -+,N =21016x x -+,所以M >N. 二.填空题7. 【答案】2212182-++ab a b ;8. 【答案】222256;1021;370;1130x x x x x x x x ++++---+. 9. 【答案】x 3y+2x 2y 2;10.【答案】0;【解析】原式=0xy xz xy yz xz yz --++-=. 11.【答案】3;【解析】解:(ax+3y )(x ﹣y )=ax 2+(3﹣a )xy ﹣3y 2, 含xy 的项系数是3﹣a ,∵展开式中不含xy 的项, ∴3﹣a=0, 解得a=3. 故答案为:3.12.【答案】6;【解析】原式=12316xy x y +++=++=. 三.解答题 13.【解析】解:(1)(a+b+c )2=a 2+b 2+c 2+2ab+2ac+2bc ; (2)∵a+b+c=11,ab+bc+ac=38,∴a 2+b 2+c 2=(a+b+c )2﹣2(ab+ac+bc )=121﹣76=45; (3)如图所示:(4)根据题意得:2a 2+5ab+3b 2=(2a+3b )(a+b ), 则较长的一边为2a+3b . 14.【解析】解:(1)2222223222y y y y y y +-++=-.42y =-,12y =-. (2)222551524440x x x x x x +----+=.1515x -=, 1x =-.15.【解析】解:(1)原式2111111111111222332334669x x x x x x x ⎛⎫=⋅-⋅+⋅+-=-+- ⎪⎝⎭ 21149x =-. 当4x =-时,原式21118(4)434999=⨯--=-=.(2)原式4324324326333423x x x x x x x x x =-+-+-=++当1x =-时,原式4323(1)(1)(1)3113=⨯-+-+-=-+=.北师大版七年级下册数学重难点突破知识点梳理及重点题型巩固练习乘法公式(基础)【学习目标】1. 掌握平方差公式、完全平方公式的结构特征,并能从广义上理解公式中字母的含义;2. 学会运用平方差公式、完全平方公式进行计算.了解公式的几何意义,能利用公式进行乘法运算;3. 能灵活地运用运算律与乘法公式简化运算. 【要点梳理】要点一、平方差公式平方差公式:22()()a b a b a b +-=-两个数的和与这两个数的差的积,等于这两个数的平方差.要点诠释:在这里,b a ,既可以是具体数字,也可以是单项式或多项式.抓住公式的几个变形形式利于理解公式.但是关键仍然是把握平方差公式的典型特征:既有相同项,又有“相反项”,而结果是“相同项”的平方减去“相反项”的平方.常见的变式有以下类型:(1)位置变化:如()()a b b a +-+利用加法交换律可以转化为公式的标准型 (2)系数变化:如(35)(35)x y x y +- (3)指数变化:如3232()()m n m n +- (4)符号变化:如()()a b a b --- (5)增项变化:如()()m n p m n p ++-+(6)增因式变化:如2244()()()()a b a b a b a b -+++ 要点二、完全平方公式完全平方公式:()2222a b a ab b +=++2222)(b ab a b a +-=-两数和 (差)的平方等于这两数的平方和加上(减去)这两数乘积的两倍.要点诠释:公式特点:左边是两数的和(或差)的平方,右边是二次三项式,是这两数的平方和加(或减)这两数之积的2倍.以下是常见的变形:()2222a b a b ab +=+-()22a b ab =-+()()224a b a b ab +=-+要点三、添括号法则添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号.要点诠释:添括号与去括号是互逆的,符号的变化也是一致的,可以用去括号法则检查添括号是否正确. 要点四、补充公式2()()()x p x q x p q x pq ++=+++;2233()()a b a ab b a b ±+=±;33223()33a b a a b ab b ±=±+±;2222()222a b c a b c ab ac bc ++=+++++. 【典型例题】类型一、平方差公式的应用1、下列两个多项式相乘,哪些可用平方差公式,哪些不能?能用平方差公式计算的,写出计算结果.(1)()()2332a b b a --; (2) ()()2323a b a b -++; (3) ()()2323a b a b ---+; (4) ()()2323a b a b +-; (5) ()()2323a b a b ---; (6) ()()2323a b a b +--.【思路点拨】两个多项式因式中,如果一项相同,另一项互为相反数就可以用平方差公式. 【答案与解析】解:(2)、(3)、(4)、(5)可以用平方差公式计算,(1)、(6)不能用平方差公式计算. (2) ()()2323a b a b -++=()23b -()22a =2294b a -.(3) ()()2323a b a b ---+=()22a - -()23b =2249a b -.(4) ()()2323a b a b +-=()22a -()23b =2249a b -.(5) ()()2323a b a b ---=()23b --()22a =2294b a -.【总结升华】利用平方差公式进行乘法运算,一定要注意找准相同项和相反项(系数为相反数的同类项). 举一反三:【变式】计算:(1)332222x x y y ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭; (2)(2)(2)x x -+--; (3)(32)(23)x y y x ---.【答案】解:(1)原式2222392244x x y y ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭.(2)原式222(2)4x x =--=-.(3)原式22(32)(23)(32)(32)94x y y x x y x y x y =-+-=+-=-. 2、计算:(1)59.9×60.1; (2)102×98. 【答案与解析】解:(1)59.9×60.1=(60-0.1)×(60+0.1)=22600.1-=3600-0.01=3599.99(2)102×98=(100+2)(100-2)=221002-=10000-4=9996. 【总结升华】用构造平方差公式计算的方法是快速计算有些有理数乘法的好方法,构造时可利用两数的平均数,通过两式(两数)的平均值,可以把原式写成两数和差之积的形式.这样可顺利地利用平方差公式来计算.举一反三: 【变式】(2015春•莱芜校级期中)怎样简便就怎样计算: (1)1232﹣124×122 (2)(2a+b )(4a 2+b 2)(2a ﹣b ) 【答案】解:(1)1232﹣124×122 =1232﹣(123+1)(123﹣1) =1232﹣(1232﹣1) =1232﹣1232+1 =1;(2)(2a+b )(4a 2+b 2)(2a ﹣b ) =(2a+b )(2a ﹣b )(4a 2+b 2) =(4a 2﹣b 2)(4a 2+b 2) =(4a 2)2﹣(b 2)2 =16a 4﹣b 4.类型二、完全平方公式的应用3、计算:(1)()23a b +; (2)()232a -+; (3)()22x y -; (4)()223x y --.【思路点拨】此题都可以用完全平方公式计算,区别在于是选“和”还是“差”的完全平方公式.【答案与解析】解:(1) ()()22222332396a b a a b b a ab b +=+⨯⋅+=++.(2) ()()()222223223222334129a a a a a a -+=-=-⨯⨯+=-+.(3) ()()22222222244x y x x y y x xy y -=-⋅⋅+=-+ .(4) ()()()()2222222323222334129x y x y x x y y x xy y --=+=+⨯⨯+=++.【总结升华】(1)在运用完全平方公式时要注意运用以下规律:当所给的二项式符号相同时,结果中三项的符号都为正,当所给的二项式符号相反时,结果中两平方项为正,乘积项的符号为负.(2)注意()()22a b a b --=+之间的转化.4、(2015春•吉安校级期中)图a 是由4个长为m ,宽为n 的长方形拼成的,图b 是由这四个长方形拼成的正方形,中间的空隙,恰好是一个小正方形. (1)用m 、n 表示图b 中小正方形的边长为 . (2)用两种不同方法表示出图b 中阴影部分的面积;(3)观察图b ,利用(2)中的结论,写出下列三个代数式之间的等量关系,代数式(m+n )2,(m ﹣n )2,mn ;(4)根据(3)中的等量关系,解决如下问题:已知a+b=7,ab=5,求(a ﹣b )2的值.【答案与解析】解:(1)图b 中小正方形的边长为m ﹣n .故答案为m ﹣n ; (2)方法①:(m ﹣n )(m ﹣n )=(m ﹣n )2;方法②:(m+n )2﹣4mn ;(3)因为图中阴影部分的面积不变,所以(m ﹣n )2=(m+n )2﹣4mn ; (4)由(3)得:(a ﹣b )2=(a+b )2﹣4ab ,∵a+b=7,ab=5, ∴(a ﹣b )2=72﹣4×5=49﹣20=29.【总结升华】本题考查了完全平方公式的应用,列代数式,可以根据题中的已知数量利用代数式表示其他相关的量.5、已知7a b +=,ab =12.求下列各式的值: (1) 22a ab b -+;(2) 2()a b -.【答案与解析】解:(1)∵ 22a ab b -+=22a b +-ab =()2a b +-3ab =27-3×12=13.(2)∵ ()2a b -=()2a b +-4ab =27-4×12=1.【总结升华】由乘方公式常见的变形:①()2a b +-()2a b -=4ab ;②22a b +=()2a b +-2ab =()2a b -+2ab .解答本题关键是不求出,a b 的值,主要利用完全平方公式的整体变换求代数式的值. 举一反三:【变式】已知2()7a b +=,2()4a b -=,求22a b +和ab 的值.【答案】解:由2()7a b +=,得2227a ab b ++=; ①由2()4a b -=,得2224a ab b -+=. ② ①+②得222()11a b +=,∴ 22112a b +=. ①-②得43ab =,∴ 34ab =. 北师大版七年级下册数学重难点突破知识点梳理及重点题型巩固练习【巩固练习】一.选择题1. 在下列计算中,不能用平方差公式计算的是( )A.))((n m n m +--B.()()3333x yx y -+ C.))((b a b a --- D.()()2222cd d c -+2.若x y +=6,x y -=5,则22x y -等于( ). A.11 B.15 C.30 D.603.下列计算正确的是( ). A.()()55m m -+=225m -B. ()()1313m m -+=213m -C.()()24343916n n n ---+=-+D.( 2ab n -)(2ab n +)=224ab n -4.下列多项式不是完全平方式的是( ). A.244x x -- B.m m ++241C.2296a ab b ++D.24129t t ++5.(2015春•重庆校级期中)已知关于x 的二次三项式4x 2﹣mx+25是完全平方式,则常数m 的值为( ) A .10 B .±10 C .﹣20 D .±20 6.下列等式不能恒成立的是( ).A.()222396x y x xy y -=-+B.()()22a b c c a b +-=--C.22241)21(n m n m n m +-=- D.()()()2244x y x y x y x y -+-=-二.填空题7.若2216x ax ++是一个完全平方式,则a =______. 8. 若2294x y +=()232x y M ++,则M =______. 9. 若x y +=3,xy =1,则22x y +=_______.10.(2015春•陕西校级期末)(1+x )(1﹣x )(1+x 2)(1+x 4)= . 11. ()25(2)(2)21x x x -+--=___________.12.若()212x -=,则代数式225x x -+的值为________.三.解答题13.(2015春•兴平市期中)用平方差公式或完全平方公式计算(必须写出运算过程). (1)69×71; (2)992.14.先化简,再求值:22)1(2)1)(1(5)1(3-+-+-+a a a a ,其中3=a .15.已知:2225,7x y x y +=+=,且,x y >求x y -的值. 【答案与解析】 一.选择题1. 【答案】A ;【解析】A 中m 和m -符号相反,n 和n -符号相反,而平方差公式中需要有一项是符号相同的,另一项互为相反数.2. 【答案】C ;【解析】()()22x y x y x y -=+-=6×5=30.3. 【答案】C ;【解析】()()55m m -+=225m -;()()1313m m -+=219m -;(2ab n -)(2ab n +)=2224a b n -.4. 【答案】A ;【解析】2211()42m m m ++=+;22296(3)a ab b a b ++=+;224129(23)t t t ++=+. 5. 【答案】D ;【解析】解:∵关于x 的二次三项式4x 2﹣mx+25是完全平方式, ∴﹣m =±20,即m=±20. 故选:D .6. 【答案】D ;【解析】()()()()22222x y x y x yxy-+-=-.二.填空题7. 【答案】±4;【解析】222216244x ax x x ++=±⨯+,所以4a =±. 8. 【答案】12xy -;【解析】2294x y +=()23212x y xy +-. 9. 【答案】7;【解析】()2222x y x y xy +=++,22927x y +=-=.10.【答案】1﹣x 8;【解析】解:(1+x )(1﹣x )(1+x 2)(1+x 4)=(1﹣x 2)(1+x 2)(1+x 4) =(1﹣x 4)(1+x 4) =1﹣x 8, 故答案为:1﹣x 811.【答案】2421x x +-;【解析】()()()22225(2)(2)2154441421x x x x x x x x -+--=---+=+-.12.【答案】6;【解析】因为()212x -=,所以2221,256x x x x -=-+=.三.解答题 13.【解析】 解:(1)原式=(70﹣1)×(70+1)=4900﹣1=4899; (2)原式=(100﹣1)2=10000﹣200+1=9801. 14.【解析】解:223(1)5(1)(1)2(1)a a a a +-+-+-()()()22232151221210a a a a a a =++--+-+=+当3,=231016a =⨯+=时原式.15.【解析】解:∵()2222x y x y xy +=++,且2225,7x y x y +=+=∴27252xy =+,∴12xy =,∵()2222252121x y x y xy -=+-=-⨯=∴1x y -=±∵,x y >即0x y -> ∴1x y -=.北师大版七年级下册数学重难点突破知识点梳理及重点题型巩固练习整式的除法(基础)【学习目标】1. 会进行单项式除以单项式的计算.2. 会进行多项式除以单项式的计算. 【要点梳理】要点一、单项式除以单项式法则单项式相除,把系数与同底数幂分别相除作为商的因式,对于只有被除式里含有的字母,则连同它的指数作为商的一个因式.要点诠释:(1)法则包括三个方面:①系数相除;②同底数幂相除;③只在被除式里出现的字母,连同它的指数作为商的一个因式.(2)单项式除法的实质即有理数的除法(系数部分)和同底数幂的除法的组合,单项式除以单项式的结果仍为单项式.要点二、多项式除以单项式法则多项式除以单项式:先把多项式的每一项除以这个单项式,再把所得的商相加.即()am bm cm m am m bm m cm m a b c ++÷=÷+÷+÷=++要点诠释:(1)由法则可知,多项式除以单项式转化为单项式除以单项式来解决,其实质是将它分解成多个单项式除以单项式.(2)利用法则计算时,多项式的各项要包括它前面的符号,要注意符号的变化.【典型例题】类型一、单项式除以单项式1、计算:(1)342222(4)(2)x y x y ÷;(2)2137323m n m m n xy z x y x y z +⎛⎫÷÷- ⎪⎝⎭;(3)22[()()]()()x y x y x y x y +-÷+÷-;(4)2[12()()][4()()]a b b c a b b c ++÷++. 【思路点拨】(1)先乘方,再进行除法计算.(2)、(3)三个单项式连除按顺序计算.(3)、(4)中多项式因式当做一个整体参与计算. 【答案与解析】解:(1)342222684424(4)(2)1644x y x y x y x y x y ÷=÷=. (2)2137323m n m m n xy z x y x y z +⎛⎫÷÷- ⎪⎝⎭。
最新北师大版七年级数学下册总复习课件

►考点一 幂的运算 例 1 2a9-a9=___a_9____=(___a_3____)3=a7·___a_2____=
___a_1_2___÷a3. [解析] 本题涉及整式的加减、幂的乘方、同底数幂的乘
法、同底数幂的除法等运算,要准确把握各种运算的区别.
数学·新课标(BS)
第一章复习
方法技巧 计算前要先判断是哪一种运算,再确定应用什么法则 或公式.
数学·新课标(BS)
第二章复习
易错警示 要能够准确判断同位角、内错角、同旁内角等各种位 置关系.
数学·新课标(BS)
第二章复习
►考点三 平行的性质
例 3 如图 2-3 所示,AB∥CD,∠1=105°,∠EAB=65°,
则∠E 的度数是
(B )
图 2-3 A.30° B.40° C.50° D.60°
数学·新课标(BS)
已知(m-n)2=8,(m+n)2=2,则 m2+n2= A.10 B.6 C.5 D.3
(C )
数学·新课标(BS)
如图 YK-1-1,图中最大的正方形的面积是
( C)
A.a2 C.a2+2ab+b2
图 YK-1-1 B.a2+b2 D.a2+ab+b2
数学·新课标(BS)
数学·新课标(BS)
第一章复习
(3)多项式与多项式相乘: ①法则:多项式与多项式相乘,先用一个多项式的每一项乘 另一个多项式的每一项,再把所得的积 相加 . ②平方差公式:两个数的和与这两个数的差的乘积,等于这 两个数的 平方差 ,公式表示为(a+b)(a-b)= a2-b2 . ③完全平方公式:两个数和(或差)的平方,等于它们的 平方和 加上(或减去)它们的积的 2 倍,公式表示为(a+b)2 =a2+2ab+b2或(a-b)2= a2-2ab+b2 .
七年级数学北师大版总复习资料.doc

七年级数学北师大版总复习资料七年级数学北师大版总复习资料一第一章有理数一、知识要点本章的主要内容可以概括为有理数的概念与有理数的运算两部分。
有理数的概念可以利用数轴来认识、理解,同时,利用数轴又可以把这些概念串在一起。
有理数的运算是全章的重点。
在具体运算时,要注意四个方面,一是运算法则,二是运算律,三是运算顺序,四是近似计算。
基础知识:1、正数(position number):大于0的数叫做正数。
2、负数(negation number):在正数前面加上负号“-”的数叫做负数。
3、0既不是正数也不是负数。
4、有理数(rational number):正整数、负整数、0、正分数、负分数都可以写成分数的形式,这样的数称为有理数。
5、数轴(number axis):通常,用一条直线上的点表示数,这条直线叫做数轴。
数轴满足以下要求:在直线上任取一个点表示数0,这个点叫做原点(origin);通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;选取适当的长度为单位长度。
6、相反数(opposite number):绝对值相等,只有负号不同的两个数叫做互为相反数。
7、绝对值(absolute value)一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值。
记做|a|。
由绝对值的定义可得:|a-b|表示数轴上a点到b点的距离。
一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小。
8、有理数加法法则(1)同号两数相加,取相同的符号,并把绝对值相加。
(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
互为相反数的两个数相加得0.(3)一个数同0相加,仍得这个数。
加法交换律:有理数的加法中,两个数相加,交换加数的位置,和不变。
表达式:a+b=b+a。
加法结合律:有理数的加法中,三个数相加,先把前两个数相加或者先把后两个数相加,和不变。
2024年北师大版七年级上册数学复习专项突破练1 正方体的展开与折叠

图是一个正方体的平面展开图,把展开图折叠成正方体
后,“城”字对面的字是( B )
A. 文
B. 明
C. 典
D. 范
12345678
6. 【2024咸阳月考】如图,给正方体的各个侧面分别标上字 母 a , b , c , d , e , f ,其中 a 在后面, b 在下面, c 在 左面,则下列结论错误的是( D )
12345678
题型2 找正方体展开图的相对面 4. 【新趋势·跨学科】诸葛亮的《诫子书》中有言“非学无
以广才”,将这六个字写在一个正方体的六个面上,如图
是该正方体的一种表面展开图,则原正方体中与“学”字
所在的面相对的面上的汉字是( B )
A. 非
B. 以
C. 广
D. 才
12345678
5. 【立德树人·创建文明城市】“争创全国文明典范城市, 让文明成为宜昌人民的内在气质和城市的亮丽名片”.如
北师陕西 七年级上册
第一章 丰富的图形世界 专项突破练1 正方体的展开与折叠
3星题 发展素养
题型1 判断正方体的展开图 1. 下列各图中,可以是一个正方体的平面展开图的是
(C)
A
B
C
D
12345678
2. 【2024咸阳实验中学月考】如图是一个没有完全剪开的正 方体,若再剪开一条棱,则得到的平面展开图不可能是 (B)
A
B
C
D
12345678
3. 【陕西人文信息·旅游】2024年3月2日,陕西“三秦 四 季 ·汉 中 有 约 ” 最 美 油 菜 花 海 汉 中 旅 游 文 化 节 推 介 发 布会在西安大唐不夜城举行.志愿者为会场设计了一些 正方体抽纸盒.如图所示,将写有“汉”字的正方形添 加到图中,使它们构成抽纸盒的展开图,则添加方式 共有 4 种.
(完整版)北师大版七年级下册数学各章知识点总结(最新整理)

北师大版《数学》(七年级下册)知识点总结第一章整式的运算单项式式多项式同底数幂的乘法幂的乘方积的乘方同底数幂的除法零指数幂负指数幂整式的加减单项式与单项式相乘单项式与多项式相乘整式的乘法多项式与多项式相乘 整式运算平方差公式完全平方公式单项式除以单项式整式的除法多项式除以单项式一、单项式、单项式的次数:只含有数字与字母的积的代数式叫做单项式。
单独的一个数或一个字母也是单项式。
一个单项式中,所有字母的指数的和叫做这个单项式的次数。
二、多项式1、多项式、多项式的次数、项几个单项式的和叫做多项式。
其中每个单项式叫做这个多项式的项。
多项式中不含字母的项叫做常数项。
多项式中次数最高的项的次数,叫做这个多项式的次数。
三、整式:单项式和多项式统称为整式。
四、整式的加减法: 整式加减法的一般步骤:(1)去括号;(2)合并同类项。
五、幂的运算性质:1、同底数幂的乘法:a m ﹒a n =a m+n (m,n 都是正整数);2、幂的乘方:(a m )n =a mn (m,n 都是正整数);3、积的乘方:(ab )n =a n b n (n 都是正整数);4、同底数幂的除法:a m ÷a n =a m-n (m,n 都是正整数,a≠0) ;六、零指数幂和负整数指数幂:1、零指数幂:a 0=1(a≠0);2、负整数指数幂:1(0)ppa aa -=≠p 是正整数。
七、整式的乘除法: 1、单项式乘以单项式:法则:单项式与单项式相乘,把它们的系数、p 是正整数相同字母的幂分别相乘,其余的字母连同它的指数不变,作为积的因式。
2、单项式乘以多项式:法则:单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加。
3、多项式乘以多项式:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加。
4、单项式除以单项式:单项式相除,把系数、同底数幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同它的指数一起作为商的一个因式。
2022-2023学年北师大版七年级下学期期末数学复习题1(含答案)

2022-2023学年北师大版七年级下学期期末数学复习题1一、选择题(本大题共10小题,每小题3分,共30分.每小题给出四个选项中只有一个是正确的,请把答题卡上对应题目所选的选项涂黑)1.(3分)计算a6•a2的结果是( )A.a3B.a4C.a8D.a122.(3分)人体中红细胞的直径约为0.0000077米,将0.0000077用科学记数法表示为( )A.7.7×10﹣6B.7.7×10﹣5C.0.77×10﹣6D.0.77×10﹣5 3.(3分)下列几何图形不一定是轴对称图形的是( )A.等边三角形B.平行四边形C.角D.圆4.(3分)王老师的讲义夹里放了大小相同的试卷12张,其中语文5张,数学4张,外语3张,他随机从讲义夹中抽出1张,抽出的试卷恰好是数学试卷的概率是( )A.14B.13C.512D.125.(3分)下列事件中,是不确定事件的是( )A.三条线段可以组成一个三角形B.内错角相等,两条直线平行C.对顶角相等D.平行于同一条直线的两条直线平行6.(3分)如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )A.两点之间线段最短B.点到直线的距离C.两点确定一条直线D.垂线段最短7.(3分)如图所示,AB∥CD,EF⊥BD,垂足为E,∠1=50°,则∠2的度数为( )A.50°B.40°C.45°D.25°8.(3分)如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需( )A.AB=DC B.OB=OC C.∠C=∠D D.∠AOB=∠DOC 9.(3分)下列各式不能用平方差公式计算的是( )A.(a﹣1)(a+1)B.(3+a)(a﹣3)C.(﹣2a+b)(2a﹣b)D.(﹣2a+b)(﹣2a﹣b)10.(3分)如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果P也是图中的格点,且使得△ABP为等腰三角形,则点P的个数是( )A.5B.6C.7D.8二、填空题(本大题共7小题,每小题4分,共28分.请把答案填写在答题卡的横线上)11.(4分)计算:3a•(2a﹣5)= .12.(4分)若∠A=67°,则∠A的余角= .13.(4分)在一个不透明的盒子中装有a个除颜色外完全相同的球,其中只有6个白球.若每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子,通过大量重复试验后,发现摸到白球的频率稳定在20%左右,则a的值约为 .14.(4分)如图,A、B两点分别位于一个池塘的两端,点C是AD的中点,也是BE的中点,若DE=15米,则AB= 米.15.(4分)图书馆现有4000本图书供学生借阅,如果每个学生一次借5本,则剩下的书y (本)和借书学生人数x(人)之间的函数关系式是 .16.(4分)如图在△ABC中,BC=8,AB、AC的垂直平分线与BC分别交于E、F两点,则△AEF的周长为 .17.(4分)如果定义一种新运算,规定|a b c d|=ad﹣bc,请化简:|x―1x+2x x+3| = .三、解答题(一)(本大题3小题,每小题6分,共18分)18.(6分)计算:(1)(12)﹣1+(π﹣2020)0﹣(﹣1)2020;(2)(3xy3)2•(﹣xy).19.(6分)如图,如果AD∥BC,∠B=∠C,那么AD是∠EAC的平分线吗?请说明你判别的理由.20.(6分)如图,转盘被等分成六个扇形,并在上面依次写上数字1、2、3、4、5、6.(1)若自由转动转盘,当它停止转动时,指针指向偶数区域的概率是多少?(2)请你用这个转盘设计一个游戏,当自由转动的转盘停止时,指针指向区域的概率为13.四.解答题(本大题3小题,每小题8分,满分24分)21.(8分)先化简,再求值:[(x+2y)2﹣(x+y)(x﹣y)]÷2y,其中x=12,y=﹣2.22.(8分)如图,在正方形网格上的一个△ABC,且每个小正方形的边长为1(其中点A,B,C均在网格上).(1)作△ABC关于直线MN的轴对称图形△A′B′C′;(2)在MN上画出点P,使得PA+PC最小;(3)求出△ABC的面积.23.(8分)如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.(1)求证:△ABE≌△DCE;(2)当∠AEB=60°,求∠EBC的度数.五.解答题(本大题2小题,每小题10分,满分20分)24.(10分)小王周末骑电动车从家里出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离(米)与时间(分钟)之间的关系示意图,请根据图中提供的信息回答下列问题:(1)在此变化过程中,自变量是 ,因变量是 .(2)小王在新华书店停留了多长时间?(3)买到书后,小王从新华书店到商场的骑车速度是多少?25.(10分)如图,在等边三角形ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过t分钟后,它们分别爬行到了D、E处,设DC与BE的交点为F.(1)BE与CD有何数量关系?为什么?(2)问蜗牛在爬行过程中,DC与BE所成的∠BFC的大小有无变化?若有变化,请说明理由;若没有变化,求出∠BFC的大小.2019-2020学年广东省清远市阳山县七年级(下)期末数学试卷参考答案与试题解析一、选择题(本大题共10小题,每小题3分,共30分.每小题给出四个选项中只有一个是正确的,请把答题卡上对应题目所选的选项涂黑)1.(3分)计算a6•a2的结果是( )A.a3B.a4C.a8D.a12【解答】解:a6•a2=a8,故选:C.2.(3分)人体中红细胞的直径约为0.0000077米,将0.0000077用科学记数法表示为( )A.7.7×10﹣6B.7.7×10﹣5C.0.77×10﹣6D.0.77×10﹣5【解答】解:0.0000077=7.7×10﹣6.故选:A.3.(3分)下列几何图形不一定是轴对称图形的是( )A.等边三角形B.平行四边形C.角D.圆【解答】解:A、是轴对称图形,故本选项不符合题意;B、不是轴对称图形,故本选项符合题意;C、是轴对称图形,故本选项不符合题意;D、是轴对称图形,故本选项不符合题意.故选:B.4.(3分)王老师的讲义夹里放了大小相同的试卷12张,其中语文5张,数学4张,外语3张,他随机从讲义夹中抽出1张,抽出的试卷恰好是数学试卷的概率是( )A.14B.13C.512D.12【解答】解:∵王老师的讲义夹里放了大小相同的试卷共12页,数学4页,∴他随机地从讲义夹中抽出1页,抽出的试卷恰好是数学试卷的概率为412=13.故选:B.5.(3分)下列事件中,是不确定事件的是( )A.三条线段可以组成一个三角形B.内错角相等,两条直线平行C.对顶角相等D.平行于同一条直线的两条直线平行【解答】解:A、三条线段可以组成一个三角形,属于随机事件,符合题意;B、内错角相等,两条直线平行,是一定发生的事件,属于必然事件,不符合题意;C、对顶角相等,属于必然事件,不符合题意;D、在平面内,平行于同一条直线的两条直线平行,属于必然事件,不符合题意;故选:A.6.(3分)如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )A.两点之间线段最短B.点到直线的距离C.两点确定一条直线D.垂线段最短【解答】解:要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是:垂线段最短,故选:D.7.(3分)如图所示,AB∥CD,EF⊥BD,垂足为E,∠1=50°,则∠2的度数为( )A.50°B.40°C.45°D.25°【解答】解:在△DEF中,∠1=50°,∠DEF=90°,∴∠D=180°﹣∠DEF﹣∠1=40°.∵AB∥CD,∴∠2=∠D=40°.故选:B.8.(3分)如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需( )A.AB=DC B.OB=OC C.∠C=∠D D.∠AOB=∠DOC 【解答】解:A、AB=DC,不能根据SAS证两三角形全等,故本选项错误;B、∵在△AOB和△DOC中OA=OD∠AOB=∠COD,OB=OC∴△AOB≌△DOC(SAS),故本选项正确;C、两三角形相等的条件只有OA=OD和∠AOB=∠DOC,不能证两三角形全等,故本选项错误;D、根据∠AOB=∠DOC和OA=OD,不能证两三角形全等,故本选项错误;故选:B.9.(3分)下列各式不能用平方差公式计算的是( )A.(a﹣1)(a+1)B.(3+a)(a﹣3)C.(﹣2a+b)(2a﹣b)D.(﹣2a+b)(﹣2a﹣b)【解答】解:A、原式能用平方差公式计算,不合题意;B、原式能用平方差公式计算,不合题意;C、原式可化为﹣(2a﹣b)(2a﹣b),不能用平方差公式计算,符合题意;D、原式能用平方差公式计算,不合题意;故选:C.10.(3分)如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果P也是图中的格点,且使得△ABP为等腰三角形,则点P的个数是( )A.5B.6C.7D.8【解答】解:如图,分情况讨论:①AB为等腰△ABP的底边时,符合条件的P点有4个;②AB为等腰△ABP其中的一条腰时,符合条件的P点有4个.故选:D.二、填空题(本大题共7小题,每小题4分,共28分.请把答案填写在答题卡的横线上)11.(4分)计算:3a•(2a﹣5)= 6a2﹣15a .【解答】解:3a•(2a﹣5)=6a2﹣15a.故答案为:6a2﹣15a.12.(4分)若∠A=67°,则∠A的余角= 23° .【解答】解:∵∠A=67°,∴∠A的余角=90°﹣67°=23°.故答案为:23°.13.(4分)在一个不透明的盒子中装有a个除颜色外完全相同的球,其中只有6个白球.若每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子,通过大量重复试验后,发现摸到白球的频率稳定在20%左右,则a的值约为 30 .【解答】解:由题意可得,6a×100%=20%,解得,a=30.故答案为:30.14.(4分)如图,A、B两点分别位于一个池塘的两端,点C是AD的中点,也是BE的中点,若DE=15米,则AB= 15 米.【解答】解:∵点C是AD的中点,也是BE的中点,∴AC=DC,BC=EC,在△ACB和△DCE中,AC=DC∠ACB=∠DCE,BC=EC∴△ACB≌△DCE(SAS),∴DE=AB,∵DE=15米,∴AB=15米,故答案为:15.15.(4分)图书馆现有4000本图书供学生借阅,如果每个学生一次借5本,则剩下的书y (本)和借书学生人数x(人)之间的函数关系式是 y=4000﹣5x .【解答】解:由题意可得:y=4000﹣5x,故答案为y=4000﹣5x.16.(4分)如图在△ABC中,BC=8,AB、AC的垂直平分线与BC分别交于E、F两点,则△AEF的周长为 8 .【解答】解:∵AB、AC的垂直平分线与BC分别交于E、F两点,∴AE=BE,AF=CF,∴△AEF的周长=AE+EF+AF=BE+EF+CF=BC=8,故答案为:8.17.(4分)如果定义一种新运算,规定|a b c d|=ad﹣bc,请化简:|x―1x+2x x+3|= ﹣3 .【解答】解:根据题意得:|x―1x+2x x+3|=(x﹣1)(x+3)﹣x(x+2)=x2+3x﹣x﹣3﹣x2﹣2x=﹣3,故答案为:﹣3.三、解答题(一)(本大题3小题,每小题6分,共18分)18.(6分)计算:(1)(12)﹣1+(π﹣2020)0﹣(﹣1)2020;(2)(3xy3)2•(﹣xy).【解答】解:(1)(12)﹣1+(π﹣2020)0﹣(﹣1)2020=2+1﹣1=2.(2)(3xy3)2•(﹣xy)=9x2y6•(﹣xy)=﹣9x3y7.19.(6分)如图,如果AD∥BC,∠B=∠C,那么AD是∠EAC的平分线吗?请说明你判别的理由.【解答】解:∵AD∥BC,∴∠EAD=∠B,∠DAC=∠C,又∵∠B=∠C,∴∠EAD=∠DAC,∴AD是∠EAC的平分线.20.(6分)如图,转盘被等分成六个扇形,并在上面依次写上数字1、2、3、4、5、6.(1)若自由转动转盘,当它停止转动时,指针指向偶数区域的概率是多少?(2)请你用这个转盘设计一个游戏,当自由转动的转盘停止时,指针指向区域的概率为13.【解答】解:(1)P(指针指向偶数区域)=36=12;(2)方法一:如图,自由转动转盘,当转盘停止时,指针指向数字5或6所在的区域时则游戏者获胜.方法二:自由转动转盘,当它停止时,指针指向数字大于4的区域时,游戏者获胜.四.解答题(本大题3小题,每小题8分,满分24分)21.(8分)先化简,再求值:[(x+2y)2﹣(x+y)(x﹣y)]÷2y,其中x=12,y=﹣2.【解答】解:原式=(x2+4xy+4y2﹣x2+y2)÷2y =(5y2+4xy)÷2y=52y+2x,当x=12,y=﹣2时,原式=1﹣5=﹣4.22.(8分)如图,在正方形网格上的一个△ABC,且每个小正方形的边长为1(其中点A,B,C均在网格上).(1)作△ABC关于直线MN的轴对称图形△A′B′C′;(2)在MN上画出点P,使得PA+PC最小;(3)求出△ABC的面积.【解答】解:(1)如图,△A′B′C′为所作;(2)如图,点P为所作;(3)△ABC的面积=3×4―12×1×3―12×3×2―12×4×1=112.23.(8分)如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.(1)求证:△ABE≌△DCE;(2)当∠AEB=60°,求∠EBC的度数.【解答】解:(1)在△ABE和△DCE中,∠A=∠D∠AEB=∠DECAB=DC,∴△ABE≌△DCE(AAS);(2)∵△ABE≌△DCE,∴BE=EC,∴∠EBC=∠ECB,∵∠EBC+∠ECB=∠AEB=60°,∴∠EBC=30°.五.解答题(本大题2小题,每小题10分,满分20分)24.(10分)小王周末骑电动车从家里出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离(米)与时间(分钟)之间的关系示意图,请根据图中提供的信息回答下列问题:(1)在此变化过程中,自变量是 时间 ,因变量是 距离 .(2)小王在新华书店停留了多长时间?(3)买到书后,小王从新华书店到商场的骑车速度是多少?【解答】解:(1)在此变化过程中,自变量是时间,因变量是距离.故答案为:时间;距离;(2)30﹣20=10(分钟).所以小王在新华书店停留了10分钟;(3)小王从新华书店到商场的路程为6250﹣4000=2250米,所用时间为35﹣30=5分钟,小王从新华书店到商场的骑车速度是:2250÷5=450(米/分).25.(10分)如图,在等边三角形ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过t分钟后,它们分别爬行到了D、E处,设DC与BE的交点为F.(1)BE与CD有何数量关系?为什么?(2)问蜗牛在爬行过程中,DC与BE所成的∠BFC的大小有无变化?若有变化,请说明理由;若没有变化,求出∠BFC的大小.【解答】解:(1)BE=CD,理由如下:∵AB=BC=CA,两只蜗牛速度相同,且同时出发,∴CE=AD;∠A=∠BCE=60°,在△ACD和△CBE中,AC=BC∠A=∠BCE,AD=CE∴△ACD≌△CBE(SAS),∴BE=CD;(2)DC和BE所成的∠BFC的大小不变.理由如下:∵△ACD≌△CBE,∴∠FBC=∠ACD,∴∠BFC=180°﹣∠FBC﹣∠BCD=180°﹣∠ACD﹣∠BCD=180°﹣∠ACB=120°,∴∠BFC的大小不变,∠BFC=120°.。
北师大版七年级数学下册《同步考点解读-专题训练》专题1.2幂的除法运算(知识解读)(原卷版+解析)

专题1.2 幂的除法运算(知识解读)【学习目标】1. 掌握正整数幂的除法运算性质,能用文字和符号语言正确地表述这些性质,并能运用它们熟练地进行运算.2. 运用同底数幂的除法法则解决一下实际问题.3.理解零次幂的性质及有关综合运算。
4.掌握用科学计数法表示较小的数。
5.了解负整数指数幂的意义,并进行有关的运算。
【知识点梳理】知识点1:幂的除法运算口诀:同底数幂相除,底数不变,指数相减。
a m÷a n=a(m-n)(a≠0,m,n均为正整数,并且m>n)知识点2:零指数a0=1 (a≠0)知识3:科学记数法科学记数法:有了负指数幂后,绝对值小于 1 的数,也能写成a⨯10-n 的形式,其中n是正整数,1≤ a <10 ,这叫科学记数法.注:对于一个绝对值小于 1 的数,如果小数点后至第一个非0 数字前有m 个0,则10d 的指数n=m+1.知识点4:负整数幂当n 是正整数时,1nnaa-=(0a≠,n是正整数)【典例分析】【考点1 幂的除法运算】【典例1】计算a6÷a3,正确的结果是()A.3B.a3C.a2D.3a 【变式1-1】计算m3÷m3结果是()A.m6B.m C.0D.1【变式1-2】计算(﹣a)12÷(﹣a)3的结果为()A.a4B.﹣a4C.a9D.﹣a9【典例2】已知x a=3,x b=5,则x a﹣b=()A.B.C.D.15【变式2-1】已知3m=12,3n=4,则3m﹣n的值为()A.3B.4C.6D.8【变式2-2】若5a=3,5b=12,则5b﹣a=.【典例3】已知3m=6,9n=2,求32m﹣4n的值.【变式3-1】已知a m=4,a n=8,求a3m﹣2n的值.【变式3-2】(1)已知3a=4,3b=5,求32a﹣3b的值;(2)若3x+2y﹣3=0,求8x•4y.【典例4】计算:a2•(﹣a4)3÷(a3)2.【变式4-1】计算:(1)a•a2•a3;(2)(﹣2ab)2;(3)(a3)5;(4)(﹣a)6÷(﹣a)2÷(﹣a)2.【变式4-2】计算:(x2)3•x3﹣(﹣x)2•x9÷x2.【变式4-3】计算题:(1)(a2)3•(a2)4÷(a2)5;(2)(5a2+2a)﹣4(2+2a2).【考点2 零指数】【典例5】(一1)0等于()A.﹣1B.0C.1D.无意义【变式5-1】若(x﹣1)0有意义,那么x的取值范围是()A.x>1B.x<1C.x≠1D.x为任意数【变式5-2】计算(﹣5)0的结果是()A.1B.﹣5C.0D.﹣【考点3:科学计数法】【典例6】(2022•海曙区校级模拟)我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片,该芯片的制造工艺达到了0.000000022米.用科学记数法表示0.000000022为()A.22×10﹣10B.2.2×10﹣10C.2.2×10﹣9D.2.2×10﹣8【变式6-1】(2019•烟台一模)碳纳米管的硬度与金刚石相当,却拥有良好的柔韧性,可以拉伸,我国某物理所研究组已研制出直径为0.5纳米的碳纳米管,1纳米=0.000000001米,则0.5纳米用科学记数法表示为()A.0.5×10﹣9米B.5×10﹣8米C.5×10﹣9米D.5×10﹣10米【变式6-2】(2020•汇川区模拟)世界上最小的鸟是生活在古巴的吸蜜蜂鸟,它的质量约为0.056盎司.将0.056用科学记数法表示为()A.5.6×10﹣1B.5.6×10﹣2C.5.6×10﹣3D.0.56×10﹣1【考点4:负指数整数幂】【典例7】(2022春•元宝区校级期末)计算()﹣2的结果是()A.﹣9B.9C.D.﹣【变式7-1】(2022春•北碚区校级期末)()﹣2值为()A.B.﹣C.D.﹣【典例8】(2022•南陵县自主招生)计算.【变式8-1】(2022春•兰州期末)计算:()﹣1﹣(﹣3﹣3.14)0+(﹣)﹣2.【变式8-2】(2022春•城固县期末)计算:(﹣)﹣3+(﹣3)0﹣(﹣1)﹣2.【变式8-3】(2022春•西安期末)计算:﹣(﹣1)﹣1.专题1.2 幂的除法运算(知识解读)【学习目标】1. 掌握正整数幂的除法运算性质,能用文字和符号语言正确地表述这些性质,并能运用它们熟练地进行运算.2. 运用同底数幂的除法法则解决一下实际问题.3.理解零次幂的性质及有关综合运算。
北师大新版数学七年级上册期末复习知识点

北师大新版数学七年级上册期末复习知识点XXX新版《数学》(七年级上册)期末复知识点第一章丰富的图形世界1.几何图形包括立体图形和平面图形。
立体图形的各个部分不都在同一平面内,而平面图形的各个部分都在同一平面内。
2.几何图形由点、线、面和体组成。
点是几何图形中最基本的图形,线分为直线和曲线,面分为平面和曲面,而几何体也简称体。
同时,点可以形成线,线可以形成面,面可以形成体。
3.生活中常见的立体图形有圆柱、柱体、棱柱(如三棱柱、四棱柱(长方体、正方体)、五棱柱等)、圆锥、锥体、棱锥和球体。
需要注意的是,棱柱侧面的个数、侧棱条数与底面的边数相等。
4.棱柱有关概念:在棱柱中,任何相邻两个面的交线都叫做棱,相邻两个侧面的交线叫做侧棱。
n棱柱有两个底面,n个侧面,共(n+2)个面,3n条棱,n条侧棱和2n个顶点。
5.正方体有11种平面展开图。
6.截一个正方体:用一个平面去截一个正方体,截出的面可能是三角形、四边形、五边形或六边形。
7.物体的三视图指主视图、俯视图和左视图。
主视图是从正面看到的图,左视图是从左面看到的图,俯视图是从上面看到的图。
8.多边形是由一些不在同一条直线上的线段依次首尾相连组成的封闭平面图形。
从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,可以把这个n边形分割成(n-2)个三角形。
弧是圆上A、B两点之间的部分,扇形是由一条弧和经过这条弧的端点的两条半径所组成的图形。
第二章有理数及其运算1.有理数包括正有理数、有理数零、负有理数、整数和分数(有限小数和无限循环小数也属于分数)。
2.相反数指只有符号不同的两个数,它们互为相反数,零的相反数是零。
3.数轴的三要素是原点、正方向和单位长度。
4.倒数指如果a与b互为倒数,则有ab=1,反之亦成立。
倒数等于本身的数是1和-1,而零没有倒数。
5.绝对值是一个数所对应的点与原点的距离,叫做该数的绝对值,记作|a|。
零的绝对值是它本身,也可看成它的相反数。
北师大版 七年级数学第一章复习资料
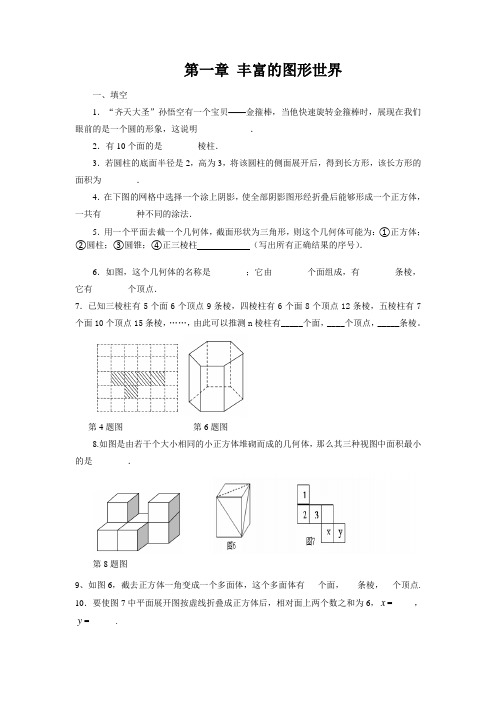
第一章丰富的图形世界一、填空1.“齐天大圣”孙悟空有一个宝贝——金箍棒,当他快速旋转金箍棒时,展现在我们眼前的是一个圆的形象,这说明____________.2.有10个面的是________棱柱.3.若圆柱的底面半径是2,高为3,将该圆柱的侧面展开后,得到长方形,该长方形的面积为________.4.在下图的网格中选择一个涂上阴影,使全部阴影图形经折叠后能够形成一个正方体,一共有________种不同的涂法.5.用一个平面去截一个几何体,截面形状为三角形,则这个几何体可能为:①正方体;②圆柱;③圆锥;④正三棱柱(写出所有正确结果的序号).6.如图,这个几何体的名称是________;它由________个面组成,有________条棱,它有________个顶点.7.已知三棱柱有5个面6个顶点9条棱,四棱柱有6个面8个顶点12条棱,五棱柱有7个面10个顶点15条棱,……,由此可以推测n棱柱有_____个面,____个顶点,_____条棱。
第4题图第6题图8.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是________.第8题图9、如图6,截去正方体一角变成一个多面体,这个多面体有___个面,___条棱,__个顶点. 10.要使图7中平面展开图按虚线折叠成正方体后,相对面上两个数之和为6,x=_____,y=______.11、点动成_____,线动成_____,_____动成体。
比如:(1)圆规在纸上划过会留下一个封闭的痕迹,这种现象说明_________。
(2)冬天环卫工人使用下部是长方形的木锨推雪时,木锨过处,雪就没了,这种现象说明________。
(3)一个人手里拿着一个绑在一根棍上的半圆面,当这个人把这个半圆面绕着这根棍飞快地旋转起来时就会看到一个球,这种现象说明______________。
二、选择题14、某物体的三视图是如图所示的三个图形,那么该物体的形状是()(A)长方体( B)圆锥体(C)立方体(D)圆柱体15.下列各个平面图形中,属于圆锥的表面展开图的是( ))16.下面每个图形都是由6个全等的正方形组成的,其中是正方体的展开图的是()A B C D17..一个正方体的表面展开图可以是下列图形中的( ).18. 下列图形中,不是三棱柱的表面展开图的是()19.如图,是一个正方体纸盒展开图,按虚线折成正方体后,若使相对面上的两数互为相反数,则A、B、C表示的数依次是()(A )235、、π-- (B)235、、π- (C )π、、235- (D)235-、、π 20、如图所示的立方体,如果把它展开,可以得到( )三.解答题(共6小题)19.画出下面几何体的主视图、左视图与俯视图.(6分)20. 如图所示是由几个小立方体所组成几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体的主视图、左视图。
北师大版七年级数学全册(上下册)知识点整理

北师大版七年级全册数学定理知识点汇总北师大数学七年级上册第一章丰富的图形世界单元备注:学生易错点:1、图形的展开与折叠2、“三视图”判断图形个数1、几何图形1.1从实物中抽象出来的各种图形,包括立体图形和平面图形。
1.2立体图形:有些几何图形的各个部分不都在同一平面内,它们是立体图形。
1.3平面图形:有些几何图形的各个部分都在同一平面内,它们是平面图形。
2、点、线、面、体2.1几何图形的组成➢点:线和线相交的地方是点,它是几何图形中最基本的图形。
➢线:面和面相交的地方是线,分为直线和曲线。
➢面:包围着体的是面,分为平面和曲面。
➢体:几何体也简称体。
2.2点动成线,线动成面,面动成体。
3、生活中的立体图形圆柱柱生活中的立体图形球棱柱:三棱柱、四棱柱(长方体、正方体)、五棱柱、……(按名称分) 锥圆锥棱锥4、棱柱及其有关概念4.1棱:在棱柱中,任何相邻两个面的交线,都叫做棱。
侧棱:相邻两个侧面的交线叫做侧棱。
4.2n棱柱有两个底面,n个侧面,共(n+2)个面;3n条棱,n条侧棱;2n个顶点。
5、正方体的平面展开图:11种侧面是曲面底面是圆面圆柱,:⎩⎨⎧侧面是正方形或长方形底面是多边形棱体柱体,:侧面是曲面底面是圆面圆锥,:⎩⎨⎧侧面都是三角形底面是多边形棱锥锥体,:6、截一个正方体用一个平面去截一个正方体,截出的面可能是三角形,四边形,五边形,六边形。
7、三视图物体的三视图指主视图、俯视图、左视图。
➢ 主视图:从正面看到的图,叫做主视图。
➢ 左视图:从左面看到的图,叫做左视图。
➢ 俯视图:从上面看到的图,叫做俯视图。
8、多边形8.1 由一些不在同一条直线上的线段依次首尾相连组成的封闭平面图形,叫做多边形。
8.2 从一个n 边形的同一个顶点出发,分别连接这个顶点与其余各顶点,可以把这个n边形分割成(n-2)个三角形。
8.3 弧:圆上A 、B 两点之间的部分叫做弧。
8.4 扇形:由一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形。
北师大版七年级下册数学总复习一整式的乘除

知识要点一、概念 1、代数式:2、单项式:由数字与字母的乘积的代数式叫做单项式。
单项式不含加减运算,分母中不含字母。
3、多项式:几个单项式的和叫做多项式。
多项式含加减运算。
4、整式:单项式和多项式统称为整式。
二、公式、法则:(1)同底数幂的乘法:a m﹒a n=a m+n(同底,幂乘,指加)逆用: a m+n=a m﹒a n(指加,幂乘,同底)(2)同底数幂的除法:a m÷a n=a m-n(a ≠0)。
(同底,幂除,指减)逆用:a m-n= a m÷a n(a ≠0)(指减,幂除,同底)(3)幂的乘方:(a m)n=a mn(底数不变,指数相乘)逆用:a mn=(a m)n(4)积的乘方:(ab )n=a n b n推广:逆用, a n b n=(ab )n(当ab=1或-1时常逆用)(5)零指数幂:a 0=1(注意考底数范围a ≠0)。
(6)负指数幂:11()(0)ppp a a a a-==≠(底倒,指反)(7)单项式与多项式相乘:m(a+b+c)=ma+mb+mc 。
(8)多项式与多项式相乘:(m+n)(a+b)=ma+mb+na+nb 。
(9)平方差公式:(a+b )(a-b)=a 2-b2公式特点:(有一项完全相同,另一项只有符号不同,结果=22()-相同)(不同 推广(项数变化):连用变化:(10)完全平方公式: 222222()2,()2,a b a ab b a b a ab b +=++-=-+逆用:2222222(),2().a ab b a b a ab b a b ++=+-+=-完全平方公式变形(知二求一):222()2a b a b ab+=-+222()2a b a b ab+=+-222212[()()]a b a b a b +=++-22222212()2()2[()()]a b a b ab a b ab a b a b +=+-=-+=++-22()()4a b a b ab +=-+ 2214[()()]ab a b a b =+-- 完全平方和公式中间项= 完全平方差公式中间项= 完全平方公式中间项= 例如:229x+mxy+4y 是一个完全平方和公式,则m = ;是一个完全平方差公式,则m = ;是一个完全平方公式,则m = ;(11)多项式除以单项式的法则:().a b c m a m b m c m ++÷=÷+÷+÷ (12)常用变形:221((n n x y x y +--2n 2n+1)=(y-x), )=-(y-x)练习。
北师大版七年级数学上册第一章知识点整理

北师大版七年级数学上册第一章知识点整理北师大版七年级数学上册第一章知识点整理七上第一章丰富的图形世界1.生活中常见的立体图形:圆柱、圆锥、棱柱、棱锥、球1)圆柱与棱柱相同点:圆柱和棱柱都有两个底面且两个底面的形状、大小完全相同。
不同点:①圆柱的底面是圆,棱柱的底面是多边形。
②圆柱的侧面是一个曲面,棱柱的侧面是由几个平面围成的,且每个平面都是平行四边形,棱柱的底面是多边形,而圆柱的底面是圆。
2)棱柱的有关概念及特点(1)棱柱的有关概念:在棱柱中相邻两个面的交线叫做棱,相邻两个侧面的交线叫做侧棱。
(2)棱柱的三个特征:一是棱柱的所有侧棱长都相等;二是棱柱的上、下底面的形状相同,并且都是多边形;三是侧面的形状都是平行四边形。
(3)棱柱的分类:棱柱可分为直棱柱和斜棱柱。
本书只讨论直棱柱(简称棱柱),直棱柱的侧面是长方形。
人们通常根据底面图形的边数将棱柱分为三棱柱、四棱柱、五棱柱……它们的底面图形的形状分别是三角形、四边形、五边形……(4)棱柱中的点、棱、面之间的关系:底面多边形的边数n确定该棱柱是n棱柱,它有2n个顶点,3n条棱,其中有n条侧棱,有(n+2)个面,n个侧面。
3)点、线、面构成立体图形(图形的构成元素)图形是由点、线、面构成的,其中面有平面,也有曲面;线有直线也有曲线。
点、线、面、体之间的关系是:点动成线,线动成面、面动成体,面与面相交得到线,线与线相交得到点。
2.展开与折叠1)棱柱的表面展开图是由两个相同的多边形和一些长方形组成的。
沿棱柱表面不同的棱剪开,可得到不同组合方式的表面展开图。
2)圆柱的表面展开图是由两个大小相同的圆(底面)和一个长方形(侧面)组成,其中侧面展开图长方形的一边的长是底面圆的周长,另一边的长是圆柱的高。
3)圆锥的表面展开图是由一个扇形(侧面)和一个圆(底面)组成,其中扇形的半径长是圆锥母线的长,而扇形的弧长则是圆锥底面圆的周长。
4)正方体是特殊的棱柱,它的六个面都是大小相同的正方形,将一个正方形的表面展开,可得到11个不同的展开图。
2024年北师大版七年级数学下册知识点总结(二篇)

2024年北师大版七年级数学下册知识点总结第一章:方程与不等式1.方程的概念:包含未知数的等式称为方程。
方程的解是使得方程成立的数。
2.解方程:通过变量的运算和移项,求出方程的解。
3.解一元一次方程:如ax+b=0,解得x=-b/a。
4.方程的证明:通过逆向思维,将给定的解代入方程,验证等式是否成立。
5.不等式的概念:含有不等于号的等式称为不等式,如ax>b。
6.解不等式:通过移项,求出不等式的解的范围。
7.不等式的证明:将给定的解代入不等式,验证不等式是否成立。
第二章:数据的收集和整理1.数据的表示:通过表格、图表和线段、折线图等图示进行数据的表示,便于观察和分析。
2.数据的整理:对收集到的数据进行整理,包括分类、排序、求最大值、最小值、众数、中位数等。
3.统计的总体与样本:通过抽取一部分数据作为样本,对总体数据进行概括和判断。
第三章:图形的认识1.点、线、面的概念:几何图形由点、线、面组成。
2.平行线与垂直线:平行线的特点是永不相交,垂直线的特点是相交成直角。
3.多边形:具有多个边的几何图形称为多边形,如三角形、四边形、五边形等。
4.正多边形:具有相等边长和相等内角的多边形。
5.对称图形:具有对称性的图形,可以通过某一条线进行折叠重合。
6.图形的相似性:具有相等比例关系的图形称为相似图形。
7.平移、旋转和翻折:运用平移、旋转和翻折等操作,使得图形位置和形态发生变化。
第四章:四边形1.四边形的概念:具有四个边的图形称为四边形,包括梯形、平行四边形、矩形、菱形、正方形等。
2.梯形:有两个底边,两个腰。
3.平行四边形:具有相对边平行的四边形。
4.矩形:具有四个直角的四边形,对角线相等。
5.菱形:具有四个相等边的四边形,对角线互相垂直。
6.正方形:具有四个相等边且具有对称性的四边形。
第五章:比例与相似1.比例的概念:比例是指两个或多个量之间的比值关系。
比值相等时称为成比例。
2.比例的性质:比例的性质包括交换律、放大和缩小、分配律等。
北师大版七年级数学下册第一章 整式的乘除 小结与复习

方法总结
在本章中应用幂的运算法则、乘法公式时,可以 将一个代数式看做一个字母,这就是整体思想,应用 这种思想方法解题,可以简化计算过程,且不易出错.
针对训练
8. 若 xn = 5,则 (x3n)2-5(x2)2n = 12500 .
9. 若 x + y = 2,则 1 x2 xy 1 y2 = 2 .
方法总结
幂的乘法运算包括同底数幂的乘法、幂的乘方、 积的乘方.这三种运算性质贯穿全章,是整式乘法的基 础.其逆向运用可将问题化繁为简,负数乘方结果的符 号,奇次方得负,偶次方得正.
针对训练
1. 下列计算不正确的是 ( D )
A. 2a3 ·a = 2a4
B. (-a3)2 = a6
C. a4 ·a3 = a7
针对训练
5. 求方程 (x-1)2-(x-1)(x + 1) + 3(1-x) = 0 的解.
解:原方程可化为-5x + 5 = 0,解得 x = 1.
6. 已知 x2 + 9y2 + 4x-6y + 5 = 0,求 xy 的值. 解:∵ x2 + 9y2 + 4x-6y + 5 = 0,
∴ (x2 + 4x + 4) + (9y2-6y + 1)=0. ∴(x + 2)2 + (3y-1)2 = 0.
(ab)n= anbn (n 为正整数)
[注意] (1) 其中的 a、b 可以是单独的数、单独
的字母,还可以是一个任意的代数式; (2) 这几个法则容易混淆,计算时必须先搞清楚
该不该用法则、该用哪个法则.
2.同底数幂的除法法则 (1) 任何不等于零的数的零次幂都等于 1.
北师大版七年级数学下册第一章整式的运算复习及其整理(带练习)

第一章 整式的运算第一节 整式1.整式的有关概念:(1)单项式的定义:像1.5V ,28n π,h r 231π等,都是数与字母的乘积,这样的代数式叫做单项式.(2)单项式的次数:一个单项式中,所有字母的指数和叫做这个单项式的次数.(3)多项式的概念:几个单项式的和叫做多项式.(4)多项式的次数:一个多项式中,次数最高项的次数,叫做这个多项式的次数.(5)整式的概念:单项式和多项式统称为整式.2.定义的补充: (1)单项式的系数:单项式中的数字因数叫做单项式的系数.(2)多项式的项数:多项式中单项式的个数叫做多项式的项数.(3)区别是否是整式:关键:分母中是否含有字母?分母有字母的为分式,如a 分之3是分式。
3.例题讲解:例1:下列代数式中,哪些是整式?单项式?多项式?并指出它们的系数和次数? (!)ab +c (2)ax 2+bx +c (3)-5(4)π.2y x - (5)12-x x 例2:求多项式363222+--b ab a 的各项系数之和?第二节 整式的加减一、 知识点复习:1、填空:整式包括单项式和多项式.2、整式的加减实质上就是去括号后,合并同类项,运算结果是一个多项式或是单项式.3、所含字母相同,并且相同字母的指数也分别相同的项叫做同类项。
4、括号前面是“-”号,去括号时,括号内各项要变号,一个数与多项式相乘时,这个数与括号内各项都要相乘。
二、练习: 例1:下列各式,是同类项的一组是( ) (A )y x 222与231yx (B )n m 22与22m n 例2、计算:(1))134()73(22+-++k k k k (2))2()2123(22x xy x x xy x +---+例3:先化简,再求值:()[],673235222x x x x x x +++--其中x=21 例4、已知:A=x 3-x 2-1,B=x 2-2,计算:(1)B -A (2)A -3B第三节 同底数幂的乘法一、复习提问2.指出下列各式的底数与指数:(1)34;(2)a 3;(3)(a+b)2;(4)(-2)3;(5)-23.3、同底数幂的乘法法则: m n m n a a a += (,m n 都是正数)是幂的运算中最基本的法则,在应用法则运算时,要注意以下几点:①法则使用的前提条件是:幂的底数相同而且是相乘时,底数a 可以是一个具体的数字式字母,也可以是一个单项或多项式;②指数是1时,不要误以为没有指数;③不要将同底数幂的乘法与整式的加法相混淆,对乘法,只要底数相同指数就可以相加;而对于加法,不仅底数相同,还要求指数相同才能相加;④当三个或三个以上同底数幂相乘时,法则可推广为 m n p m n p a a a a++=(其中m 、n 、p 均为正数);⑤公式还可以逆用: m n m n aa a +=(m 、n 均为正整数)二、巩固练习(1)107×104; (2)x 2·x 5;(3)10·102·104;(4)-a ·(-a)3;(5)(-a)2·(-a)3三、小结1.同底数幂相乘,底数不变,指数相加,对这个法则要注重理解“同底、相乘、不变、相加”这八个字.2.解题时要注意a 的指数是1.3.解题时,是什么运算就应用什么法则.同底数幂相乘,就应用同底数幂的乘法法则;整式加减就要合并同类项,不能混淆.4.-a 2的底数a ,不是-a .计算-a 2·a 2的结果是-(a 2·a 2)=-a 4,而不是(-a)2+2=a 4.5.若底数是多项式时,要把底数看成一个整体进行计算第四节 幂的乘方与积的乘方一、知识点复习:1. 幂的乘方法则:()m n mn a a =(,m n 都是正整数)幂的乘方,底数不变,指数相乘。
精编北师大版(BS)七年级数学上册第一和第二章知识点复习小结

北师大版(BS)七年级数学上册第一和第二章复习小结第一章丰富的图形世界一、教学目标:1、会辨认基本几何体(直棱柱、圆柱、圆锥、球等)2、了解直棱柱、圆柱、圆锥的侧面展开图,能根据展开图判断和制作立体模型;3、能想象基本几何体的截面形状;4、会画基本几何体的三视图,会判断简单物体的三视图,能根据三视图描述几何体或实物原型;5、能从丰富的现实背景中抽象出空间几何体和基本平面图形,进一步认识点、线、面。
6、获得一些研究问题的方法和经验,发展思维能力,加深理解相关的数学知识。
7、体验数学知识之间的内在联系,初步形成对数学整体性的认识。
教学重点:在具体的情境中,认识一些基本的几何体,并能描述这些几何体的特征。
教学难点:是描述几何体的特征,对几何体进行分类。
二、设疑自探1、梳理本章知识(一)生活中有哪些你熟悉的图形?举例说明.(二)你喜欢哪些几何体?举出一个生活中的物体,使它尽可能地包含不同的几何体.(三)用自己的语言说一说棱柱的特征?(直棱柱)如图是六棱柱模型,观察交流回答棱柱有以下特征:①棱柱上有_________底面,它们形状大小_______;②棱柱的侧面都是________;③侧棱的长度都__________;④侧面的个数与底面多边形边数________;⑤有__个顶点,有___条棱,有___条侧棱;⑥截面形状可以是___________________________________三、解疑合探1、利用棱柱的特征我们可以解决哪些问题?2、能根据下列给出的正方体平面展开图指出正方体中相对的面吗?BC(标出A、B、C的对面),发现了什么规律?3、画出若干个具有代表性的正方体平面展开图,4、找出两种几何体,使得分别用一个平面去截它们,可以得到三角形的截面.5、以正方体为例:A 、截下的几何体与剩余几何体分别是什么立体图形?B 、每个几何体的顶点数(v ),面数(f ),棱数(e )分别有什么关系?(f +v –e =2) 6、举出一种几何体,使得它的主视图,左视图和俯视图都一样,你能举出几种?与同伴进行交流.教师引导:7、想一想:三视图相同,立体物体的形状是否唯一确定(下图呢?)四、质疑再探说说你还有什么疑惑或问题(由学生或老师来解答所提出的问题) 五、运用拓展1、如下图中为棱柱的是( )2、如图绕虚线旋转得到的几何体是( ).俯视图左视图主视图(D)(B)(C)(A)3、用平面截几何体可得到平面图形,在表示几何体的字母后填上它可截出的平面图形的号码。
新北师大版七年级数学第一章复习辅导讲义

第一章复习1.立体图形(1)柱体①圆柱:两个底面是大小相等的______,侧面是一个___面.②棱柱:棱柱的底面是多边形,侧面是______________.(2)锥体①圆锥:由两个面围成,有一个顶点,底面是______,侧面是_________面.②棱锥:底面是多边形,侧面是________.(3)球体:只有一个____面.2.图形的构成点动成____,线动成____,面动成____.3.棱柱(1)棱柱的有关概念:在棱柱中,任何相邻两个面的交线都叫做_____,其中相邻两个侧面的交线叫做_______.(2)棱柱的特征:①棱柱的所有侧棱长都______;②棱柱的两个底面形状________,都是多边形;③棱柱的侧面都是____________. (3)棱柱的分类:根据底面多边形的边数,棱柱可以分为三棱柱、四棱柱、五棱柱、…,它们的底面分别是__________、_________、__________、…(4)棱柱各元素之间的关系:n棱柱的底面是____边形,它有______个顶点,_____条棱,其中有____条侧棱,有______个面,_______个侧面.4.正方体的展开图正方体的展开图有如下的11种情形:5.从三个方向看图形的形状(1)从正面看;(2)从左面看;(3)从上面看.6.多边形从n边形的一个顶点出发,有________条对角线,将n边形分成了_________个三角形.参考答案:1.(1):①圆面曲②平行四边形(2):①圆形曲②三角形 (3):曲2.线面体3.(1)棱侧棱 (2)相等相同平行四边形(3)三角形四边形五边形 (4)n 2n 3n n (n+2) n 6.(n-3) (n-2)►考点一立体图形的认识将如图1-2所示几何体分类,并说明理由.[解析]对几何体分类要按照一定的标准,根据不同的标准可以进行相应的分类,一般地可以根据柱体、锥体、球体和构成的面是平面还是曲面两个标准进行分类。
