七年级数学第二学期期中考试题用

合集下载

人教版数学七年级下学期《期中考试题》有答案解析

人教版数学七年级下学期期中测试卷学校________ 班级________ 姓名________ 成绩________一．选择题(每小题 3 分,共计 36 分)1. 一本笔记本5元,买x 本共付y 元,则5和y 分别是( )A. 常量,常量B. 变量,变量C. 常量,变量D. 变量,常量 2. 某种植物细胞的直径约为0.00012mm ,用科学计数法表示这个数为( )mmA. 41.210⨯B. 31210-⨯C. 31.210-⨯D. 41.210-⨯ 3. 下列各运算中,正确的是( )A. 3a+2a=5a 2B. (﹣3a 3)2=9a 6C. a 4÷a 2=a 3D. (a+2)2=a 2+4 4. 在弹性限度内,弹簧挂上物体后会伸长,测得弹簧的长度 y (cm )与所挂物体的质量 x (kg )之间有如下表关系：下列说法不正确的是( )A. y 随 x 的增大而增大B. 所挂物体质量每增加 1kg 弹簧长度增加 0.5cmC. 所挂物体为 7kg 时,弹簧长度为 13.5cmD. 不挂重物时弹簧的长度为 0cm5. 下列各式中不能用平方差公式计算的是( )A. ()()x y x y --+B. ()()x y x y -+--C. ()()x y x y ---D. ()()x y x y +-+ 6. 如图,直线a∥b ,点B 在直线b 上,且AB⊥BC ,∠1=55°,那么∠2度数是( )A. 20°B. 30°C. 35°D. 50°7. 若多项式29+x kx +是一个完全平方式,则常数的值是( )A. 6B. 3C. 6±D. 3±8. 如图,边长为a 的大正方形剪去一个边长为b 的小正方形后,将剩余部分通过割补拼成新的图形.根据图形能验证的等式为( )A. ()222a b a b -=-B. ()()22a b a b a b -=+-C. ()2222a b a ab b -=-+D. ()2222a b a ab b +=++ 9. 如图,已知点E 在BC 的延长线上,则下列条件中不能判断AB ∥CD 的是( )A. ∠B ＝∠DCEB. ∠BAD +∠D ＝180°C. ∠1＝∠4D. ∠2＝∠310. 一水池放水,先用一台抽水机工作一段时间后停止,然后再调来一台同型号抽水机,两台抽水机同时工作直到抽干．设从开始工作的时间为,剩下的水量为．下面能反映与之间的关系的大致图象是( ) A B. C. D. 11. 下列说法：①相等的角是对顶角；②同位角相等；③过一点有且只有一条直线与已知直线平行；④直线外一点到这条直线的垂线段的长度,叫做点到直线的距离；其中正确的有( )个．A. 0B. 1C. 2D. 312. 观察下列各式及其展开式()2a b +＝2a +2ab+2b()3a b +＝3a +32a b+3a 2b +3b ()4a b +＝+43a b+62a 2b +4a 3b +4b()5a b +＝5a +5b+103a 2b +102a 3b +5a 4b +5b …… 请你猜想()821x -的展开式中含2x 项的系数是( )A. 224B. 180C. 112D. 48二．填空题(每小题 3 分,共计 12 分)13. 如果一个角是120°,那么这个角的补角度数是___．14. 若()23a ＝m a •a ,则 m ＝____15. 已知长方形的周长为 16cm ,其中一边长为 xcm ,面积为 y 2cm ,则这个长方形的面积 y 与 x 之间的关系可表示为 ______16. 把一张长方形纸片 ABCD 沿 EF 折叠后 ED 与 BC 的交点为 G ,D 、C 分别在M 、N 的位置上,若∠EFG ＝40°,则∠2＝____．三、解答题(本题共 9 小题,其中第 17 题 16 分,第 18 题 5 分,第 19 题 6 分,第 20 题 5 分,第 21 题 6 分,第 22 题 6 分,第 23 题 8 分)17. 计算：(1) 2a (3a + 2)(2) ()()32422m m m -÷-(3) 22018011(3.14)2π-⎛⎫---- ⎪⎝⎭(4)用乘法公式计算：219818. 先化简,再求值：()()()2282x y y x y xy x ⎡⎤+-+-÷⎣⎦,其中12,2x y ==- 19. 列推理过程：如图,EF ∥AD ,∠1＝∠2,∠BAC ＝80°．求∠AGD 的度数．∵ EF ∥AD (已知)∴∠2＝()又∵∠1＝∠2 (已知)∴∠1＝∠3(等量代换)∴ AB∥()∴∠BAC+ ＝180°(两直线平行,同旁内角互补)∵∠BAC＝80°(已知)∴∠AGD＝20. (1)ma 的值a=2, =5,求2m n(2)(x+1)(x-p)=2x+qx-3,求q p的值．21. 小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校．以下是他本次上学所用的时间与路程的关系示意图．根据图中提供的信息回答下列问题：(1)小明家到学校的路程是米．(2)小明在书店停留了分钟．(3)本次上学途中,小明一共行驶了米．一共用了分钟．(4)我们认为骑单车的速度超过300 米/分就超过了安全限度．问：在整个上学途中哪个时间段小明的骑车速度最快,最快速度为多少,在安全限度内吗?22. 已知：如图,点E 直线DF 上,点B 在直线AC 上,∠1＝∠2,∠3＝∠4．①求证：BD∥CE②若∠A＝40°,求∠F 值．23. AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在的直线交于点E．∠ADC＝70°．(1)求∠EDC 的度数；(2)若∠ABC＝30°,求∠BED 的度数；(3)将线段BC沿DC方向移动,使得点B在点A的右侧,其他条件不变,若∠ABC＝n°,请直接写出∠BED 的度数(用含n的代数式表示)．答案与解析一．选择题(每小题3 分,共计36 分)1. 一本笔记本5元,买x本共付y元,则5和y分别是()A. 常量,常量B. 变量,变量C. 常量,变量D. 变量,常量[答案]C[解析][分析]根据变量,常量的定义即可判断.[详解]5为已知数,为常量,y为未知数,y随x的变化而变化,故为变量,故选C.[点睛]此题主要考查变量,常量的定义,解题的关键是熟知其定义方可判断.2. 某种植物细胞的直径约为0.00012mm,用科学计数法表示这个数为()mmA. 41.210⨯ B. 31.210-⨯ D. 4⨯1.210-1210-⨯ C. 3[答案]D[解析][分析]根据科学计数法的定义即可表示求解.[详解]0.00012=4⨯1.210-故选D.[点睛]此题主要考查科学计数法,解题的关键是熟知科学计数法的表示方法.3. 下列各运算中,正确的是( )A. 3a+2a=5a2B. (﹣3a3)2=9a6C. a4÷a2=a3D. (a+2)2=a2+4[答案]B[解析]根据合并同类项,幂的乘方与积的乘方,同底数幂的除法运算法则和完全平方公式,分别进行各选项的判断即可：A、3a+2a=5a,原式计算错误,故本选项错误；B、(﹣3a3)2=9a6,原式计算正确,故本选项正确；C、a4÷a2=a2,原式计算错误,故本选项错误；D、(a+2)2=a2+2a+4,原式计算错误,故本选项错误．故选B．4. 在弹性限度内,弹簧挂上物体后会伸长,测得弹簧的长度 y (cm )与所挂物体的质量 x (kg )之间有如下表关系：下列说法不正确的是( )A. y 随 x 的增大而增大B. 所挂物体质量每增加 1kg 弹簧长度增加 0.5cmC. 所挂物体为 7kg 时,弹簧长度为 13.5cmD. 不挂重物时弹簧的长度为 0cm[答案]D[解析][分析]根据表格中的数据先得到函数关系式,然后再根据一次函数图像的性质进行判断即可得解．[详解]解：由表格可得,弹簧的长度 y (cm )与所挂物体的质量 x (kg )之间的函数关系式为：0.510y x =+A. 0.50k =>,故随的增大而增大,故本选项不符合题意；B.当1x x =时,110.510y x =+；当211x x x ==+时,()2110.51100.511.5y x x =++=+,此时()()21110.511.50.5100.5y y x x -=+-+=,故本选项不符合题意；C.当7x =时,0.571013.5y =⨯+=,故本选项不符合题意；D.当0x =时,0.501010y =⨯+=,故本选项符合题意．故选：D[点睛]本题考查了函数关系式、一次函数图象的性质、,用挂重物与弹簧伸长的长度得出函数关系式是解题关键．5. 下列各式中不能用平方差公式计算的是( )A. ()()x y x y --+B. ()()x y x y -+--C. ()()x y x y ---D. ()()x y x y +-+[答案]A[解析][分析]根据平方差公式的特点：两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数,对各选项分析判断后利用排除法求解．[详解]A ．()()x y x y --+,含y 项符号相反,含x 的项符号相反,不能用平方差公式计算,故本选项符合题意； B ．()()x y x y -+--,含x 的项符号相同,含y 的项符号相反,能用平方差公式计算,故本选项不符合题意； C ．()()x y x y ---,含y 的项符号相同,含x 的项符号相反,能用平方差公式计算,故本选项不符合题意； D ．()()x y x y +-+,含y 的项符号相同,含x 的项符号相反,能用平方差公式计算．故本选项不符合题意．[点睛]本题考查了平方差公式,两个数的和与这两个数的差的积等于这两个数的平方差,用字母表示为：22()()a b a b a b +-=-6. 如图,直线a∥b ,点B 在直线b 上,且AB⊥BC ,∠1=55°,那么∠2的度数是( )A. 20°B. 30°C. 35°D. 50°[答案]C[解析][分析] 由垂线的性质可得∠ABC=90°,所以∠3=180°﹣90°﹣∠1=35°,再由平行线的性质可得到∠2的度数.[详解]解：由垂线的性质可得∠ABC=90°,所以∠3=180°﹣90°﹣∠1=35°,又∵a ∥b ,所以∠2=∠3=35°．故选C ．[点睛]本题主要考查了平行线性质.7. 若多项式29+x kx +是一个完全平方式,则常数的值是( )A. 6B. 3C. 6±D. 3±[答案]C[解析][分析]先根据两平方项确定出这两个数是x 和3,再根据完全平方式的结构特征求解即可．[详解]解：∵多项式29+x kx +是一个完全平方式,∴kx=±2×x×3, ∴k=±6, 故选：C ．[点睛]本题考查完全平方式,两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式．解题的关键是利用平方项来确定这两个数．8. 如图,边长为a 的大正方形剪去一个边长为b 的小正方形后,将剩余部分通过割补拼成新的图形.根据图形能验证的等式为( )A. ()222a b a b -=-B. ()()22a b a b a b -=+-C. ()2222a b a ab b -=-+D. ()2222a b a ab b +=++ [答案]B[解析][分析] 边长为a 的大正方形剪去一个边长为b 的小正方形后的面积=a 2-b 2,新的图形面积等于(a+b )(a-b ),由于两图中阴影部分面积相等,即可得到结论．[详解]图中阴影部分的面积等于两个正方形的面积之差,即为a 2-b 2；通过割补拼成的平行四边形的面积为(a+b )(a-b ),∵前后两个图形中阴影部分的面积相等,∴a 2-b 2=(a+b )(a-b )．故选B ．[点睛]考查了利用几何方法验证平方差公式,解决问题的关键是根据拼接前后的面积不变得到等量关系． 9. 如图,已知点E 在BC 的延长线上,则下列条件中不能判断AB ∥CD 的是( )A. ∠B＝∠DCEB. ∠BAD+∠D＝180°C. ∠1＝∠4D. ∠2＝∠3[答案]D[解析][分析]根据平行线的判定定理即可直接作出判断．[详解]A、根据同位角相等,两直线平行即可证得,故选项错误；B、根据同旁内角互补,两直线平行,即可证得,故选项错误；C、根据内错角相等,两直线平行即可证得,故选项错误；D、∠2和∠3是AD和BC被AC所截形成的角,因而不能证明AB∥CD,故选项正确．故选D．[点睛]本题考查了平行线判定定理,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行．10. 一水池放水,先用一台抽水机工作一段时间后停止,然后再调来一台同型号抽水机,两台抽水机同时工作直到抽干．设从开始工作的时间为,剩下的水量为．下面能反映与之间的关系的大致图象是()A. B. C. D.[答案]D[解析][分析]根据s随t的增大而减小,即可判断选项A、B错误；根据先用一台抽水机工作一段时间后停止,再调来一台同型号抽水机,两台抽水机同时工作直到抽干得出s随t的增大减小得比开始的快,即可判断选项C、D的正误．[详解]解：∵s随t的增大而减小,∴选项A、B错误；∵先用一台抽水机工作一段时间后停止,再调来一台同型号抽水机,两台抽水机同时工作直到抽干得出s 随t 的增大减小得比开始的快,∴s 随t 的增大减小得比开始的快,∴选项C 错误；选项D 正确；故选：D ．[点睛]本题主要考查对函数图象的理解和掌握,能根据实际问题所反映的内容来观察与理解图象是解答此题的关键11. 下列说法：①相等的角是对顶角；②同位角相等；③过一点有且只有一条直线与已知直线平行；④直线外一点到这条直线的垂线段的长度,叫做点到直线的距离；其中正确的有( )个．A. 0B. 1C. 2D. 3[答案]B[解析][分析]根据对顶角的性质即可判断①；根据同位角的定义和平行线的性质即可判断②；根据平行公理即可判断③；根据点到直线的距离的定义即可判断④．[详解]解：①对顶角相等,但相等的角不一定是对顶角,故①错误；②两直线平行,同位角相等,故②错误；③过直线外一点有且只有一条直线与已知直线平行,故③错误；④直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,故④正确．故选：B[点睛]本题考查了对顶角的性质、同位角的定义、平行线的性质、平行公理、点到直线的距离的定义,是基础题目,熟练掌握相关知识点是解题的关键．12. 观察下列各式及其展开式 ()2a b +＝2a +2ab+2b()3a b +＝3a +32a b+3a 2b +3b ()4a b +＝+43a b+62a 2b +4a 3b +4b()5a b +＝5a +5b+103a 2b +102a 3b +5a 4b +5b …… 请你猜想()821x -的展开式中含2x 项的系数是( )A. 224B. 180C. 112D. 48[答案]C[解析][分析] 归纳总结出()n a b +的展开式中含2x 项的系数是()12n n -,进而得出当8n =时,()8a b +展开式中含2x 项的系数是()1282n n -=,然后得到()8a b +展开式中含2x 项为2628a b ,最后将2a x =、1b =-代入式子2628a b 即可得到答案．[详解]解：∵()2222a b a ab b +=++,故展开式中含2x 项的系数是； ()3322333a b a a b ab b +=+++,故展开式中含2x 项的系数是； ()4432234464a b a a b a b ab b +=++++,故展开式中含2x 项的系数是；()543225345510105a a b a b a a a b b b b =++++++,故展开式中含2x 项的系数是；()11n n n n n a b a na b nab b --+=+++,故展开式中含2x 项的系数是()()112312n n n -++++-=∴当8n =时,()8a b +展开式中含2x 项的系数是()()18812822n n -⨯-== ∴()8a b +展开式中含2x 项2628a b ∴当2a x =、1b =-时,()()26262282821112a b x x =⋅⋅-=∴()821x -的展开式中含2x 项的系数是112．故选：C[点睛]本题考查了多项式乘以多项式中的规律问题,涉及到了完全平方公式、代数求值、多项式的项以及单项式的系数等,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力．二．填空题(每小题 3 分,共计 12 分)13. 如果一个角是120°,那么这个角的补角度数是___．[答案]60︒[解析][分析]根据互为补角的定义进行计算即可得解．[详解]解：∵一个角是120︒∴这个角的补角度数是18012600︒-︒=︒．故答案是：60︒[点睛]本题考查了互补的概念,和为180︒的两个角互为补角,属于基础题型、难度不大．14. 若()23a ＝m a •a ,则 m ＝____ [答案][解析][分析]根据幂的乘方运算、同底数幂的乘法运算先求得关于的方程,解方程即可得解．[详解]解：∵()23m a a a =⋅∴16m a a +=∴16m +=∴5m =．故答案是：[点睛]本题考查了幂的乘方运算法则、同底数幂的乘法运算法则以及简单的一元一次方程,体现了数学运算和逻辑运算的核心素养,熟练掌握相关知识点是解决问题的关键．15. 已知长方形的周长为 16cm ,其中一边长为 xcm ,面积为 y 2cm ,则这个长方形的面积 y 与 x 之间的关系可表示为 ______[答案]28y x x =-+[解析][分析]矩形周长为16cm ,则两邻边之和为8cm ,一边长为xcm ,另一边长为()8x cm -,根据矩形的面积公式即可列出函数关系式．[详解]解：∵矩形周长为16cm∴两邻边之和为8cm∴若一边长为xcm ,则另一边长为()8x cm -；面积为2ycm∴()8y x x =-即28y x x =-+．故答案是：28y x x =-+[点睛]本题考查了用长方形边长表示长方面积,列函数式的方法,能根据实际问题中的等量关系列二次函数关系式是解题的关键．16. 把一张长方形纸片 ABCD 沿 EF 折叠后 ED 与 BC 的交点为 G ,D 、C 分别在M 、N 的位置上,若∠EFG ＝40°,则∠2＝____．[答案]80︒[解析][分析]由长方形的性质可得40DEF ∠=︒,再由翻折的性质可得40MEF ∠=︒,两角相加可得80DEM ∠=︒,再根据平行线的性质即可得到答案．[详解]解：∵四边形ABCD是长方形∴//AD BC∴40DEF EFG ∠=∠=︒∵长方形纸片ABCD 沿 EF 折叠后ED 与BC 的交点为 ,、分别在M 、的位置上∴40MEF DEF ∠=∠=︒∴80DEM DEF MEF ∠=∠+∠=︒∴280DEM ∠=∠=︒．故答案是：80︒[点睛]本题考查了长方形的性质、翻折的性质、角的和差、平行线的性质等知识点,体现了逻辑推理的核心素养,难度不大,利用翻折的性质求得40MEF ∠=︒是解题的关键．三、解答题(本题共 9 小题,其中第 17 题 16 分,第 18 题 5 分,第 19 题 6 分,第 20 题 5 分,第 21 题 6 分,第 22 题 6 分,第 23 题 8 分)17. 计算：(1) 2a (3a + 2)(2) ()()32422m m m -÷-(3) 22018011(3.14)2π-⎛⎫---- ⎪⎝⎭(4)用乘法公式计算：2198[答案](1)264a a +(2)22m m -+(3)6-(4)39204[解析][分析](1)根据单项式乘以多项式法则进行计算即可得解；(2)根据多项式除以单项式法则进行计算即可得解；(3)根据实数的正整数指数幂法则、负整数指数幂法则、零次幂法则以及实数的加减运算法则进行计算即可得解；(4)先将2198改写成()22002-,然后根据完全平方差公式进行计算即可得解．[详解]解：(1)()232a a + 264a a =+；(2)()()32422m m m -÷-22m m =-+；(3)()20201811 3.142π-⎛⎫---- ⎪⎝⎭141=---6=-；(4)2198()22002=- 22200220022=-⨯⨯+400008004=-+39204=．故答案是：(1)264a a +(2)22m m -+(3)6-(4)39204[点睛]本题考查了单项式乘以多项式法则、多项式除以单项式法则、正整数指数幂法则、负整数指数幂法则、零次幂法则、实数的加减运算法则、完全平方差公式等知识点,体现了数学运算的核心素养,难度不大,认真计算是解题的关键．18. 先化简,再求值：()()()2282x y y x y xy x ⎡⎤+-+-÷⎣⎦,其中12,2x y ==- [答案]3[解析][分析]先根据整式混合运算顺序和运算法则化简原式,再将x 、y 代入计算可得．[详解]解：原式=()()2222282x xy y xy y xy x ++---÷ =()()218242x xy x x y -÷=-, 当12,2x y ==-时, 原式=112412322⎛⎫⨯-⨯-=+= ⎪⎝⎭． [点睛]考查整式的混合运算-化简求值,解题的关键是熟练掌握整式的混合运算顺序和运算法则． 19. 列推理过程：如图,EF ∥AD ,∠1＝∠2,∠BAC ＝80°．求∠AGD 的度数．∵ EF ∥AD (已知)∴∠2＝ ( )又∵∠1＝∠2 (已知)∴∠1＝∠3(等量代换)∴ AB ∥ ( )∴∠BAC+ ＝180°(两直线平行 ,同旁内角互补)∵∠BAC ＝80°(已知)∴∠AGD ＝[答案]3∠；两直线平行,同位角相等；DG ；内错角相等,两直线平行；AGD ∠；100︒[解析][分析]根据平行线性质推出2∠=3∠,根据等量代换推出13∠=∠,根据平行线的判定推出//AB DG ,根据平行线的性质得出BAC ∠+AGD ∠180=︒,将80BAC ∠=︒代入求出即可．[详解]解：∵//EF AD∴2∠=3∠(两直线平行,同位角相等)又∵12∠=∠(已知)∴13∠=∠(等量代换)∴//AB DG (内错角相等,两直线平行)∴BAC ∠+AGD ∠180=︒(两直线平行 ,同旁内角互补)∵80BAC ∠=︒(已知)∴AGD ∠=100︒．故答案是：3∠；两直线平行,同位角相等；DG ；内错角相等,两直线平行；AGD ∠；100︒[点睛]本题考查了平行线的性质和判定的应用,体现了逻辑推理的核心素养．注意：平行线的性质是：①两直线平行,同位角相等；②两直线平行,内错角相等；③两直线平行,同旁内角互补,反之亦然． 20. (1)m a =2, =5,求2m n a -的值(2)(x+1)(x-p)=2x +qx-3,求q p 的值．[答案](1)45(2)19 [解析][分析](1)先逆用同底数幂的除法法则、幂的乘方法则,将2m n a-转化为()2m n a a ÷,再把2m a =、5n a =代入计算即可得解；(2)根据多项式的乘法法则,可得一个多项式,再根据多项式相等,可得对应项系数相等,即1p q -+=、3p -=-,解方程组求得、的值,然后代入所求式子即可得解．[详解]解：(1)∵2m a =,5n a =∴2m n a -2m n a a =÷()2m n a a =÷225=÷45=； (2)∵()()213x x p x qx +-=+-∴223x px x p x qx -+-=+-∴()2213x p x p x qx +-+-=+- ∴13p q p -+=⎧⎨-=-⎩∴32p q =⎧⎨=-⎩∴2139q p -==．故答案：(1)45(2)19[点睛]本题考查了同底数幂的除法法则的逆用、幂的乘方法则的逆用、多项式乘以多项式法则、多项式等于多项式即各项对应相等原则、解二元一次方程组、代数求值等知识点,难度不大,体现了数学运算、逻辑推理的核心素养．21. 小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校．以下是他本次上学所用的时间与路程的关系示意图．根据图中提供的信息回答下列问题：(1)小明家到学校的路程是米．(2)小明在书店停留了分钟．(3)本次上学途中,小明一共行驶了米．一共用了分钟．(4)我们认为骑单车的速度超过 300 米/分就超过了安全限度．问：在整个上学途中哪个时间段小明的骑车速度最快,最快速度为多少,在安全限度内吗?[答案](1)1500(2)(3)2700；(4)小明在1214x ≤≤时间段速度最快,最快速度为450米/分；小明在1214x ≤≤时间段,行驶速度没有在安全限度内[解析][分析](1)根据图象,观察学校与小明家的纵坐标,可得答案；(2)读图,对应题意找到其在书店停留的时间段,进而可得其在书店停留的时间；(3)读图,计算可得答案,注意要计算路程；(4)分析图象,找函数变化最快的一段,可得小明骑车速度最快的时间段,进而可得其速度,再与安全限度值进行比较即可得出结论．[详解]解：(1)∵根据图象可知学校的纵坐标为1500,小明家的纵坐标为∴小明家到学校的距离为1500米；(2)∵根据图象可得小明在书店停留的时间为从到分∴小明在书店停留了分钟；(3)根据图像可得：小明共行驶了12006009002700++=米,共用了分钟；(4)∵根据图象可知：当1214x ≤≤时,直线最陡∴小明在1214x ≤≤时间段速度最快,最快速度为15006004501412-=-米/分 ∵450300>∴小明在1214x ≤≤时间段,行驶速度没有在安全限度内．故答案是：(1)1500(2)(3)2700；(4)小明在1214x ≤≤时间段速度最快,最快速度为450米/分；小明在1214x ≤≤时间段,行驶速度没有在安全限度内[点睛]本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决．需注意计算单位的统一,体现了数学建模的核心素养． 22. 已知：如图,点 E 在直线 DF 上,点 B 在直线 AC 上,∠1＝∠2,∠3＝∠4．①求证：BD ∥CE②若∠A ＝40°,求∠F 的值．[答案](1)证明见详解(2)40︒[解析][分析](1)结合已知条件根据对顶角相等可得2AHC ∠=∠,再根据平行线的判定即可得到结论；(2)由(1)结论与以及等量代换可得4180C ∠+∠=︒,进而可推出//AC DF ,再根据平行线的性质即可求解．[详解]解：(1)证明：∵12∠=∠(已知),1AHC ∠=∠(对顶角相等)∴2AHC ∠=∠(等量代换)∴//BD CE (同位角相等,两直线平行)(2)∵//BD CE (已证)∴3180C ∠+∠=︒(两直线平行,同旁内角互补)∵34∠=∠∴4180C ∠+∠=︒∴//AC DF (同旁内角互补,两直线平行)∵40A ∠=︒(已知)∴40F A ∠=∠=︒(两直线平行,内错角相等)．故答案是：(1)证明见详解(2)40︒[点睛]本题考查了平行线的判定与性质、对顶角相等的性质；熟练掌握平行线的判定与性质是解决问题的关键,注意两者的区别,体现了逻辑推理的核心素养．23. AB ∥CD ,C 在 D 的右侧,BE 平分∠ABC ,DE 平分∠ADC ,BE 、DE 所在的直线交于点 E ．∠ADC ＝70°．(1)求∠EDC 的度数；(2)若∠ABC ＝30°,求∠BED 的度数；(3)将线段 BC 沿 DC 方向移动,使得点 B 在点 A 的右侧,其他条件不变,若∠ABC ＝n°,请直接写出∠BED的度数(用含 n 的代数式表示)．[答案](1)35︒(2)50︒(3)12152n ︒-︒ [解析][分析](1)根据角平分线定义即可得到答案；(2)过点作//EF AB ,然后根据角平分线的定义、平行线的判定和性质以及角的和差进行推导即可得解；(3)过点作//EF AB ,然后根据角平分线的定义、平行线的判定和性质以及角的和差进行推导即可得解． [详解]解：(1)∵DE 平分ADC ∠,70ADC ∠=︒∴1352EDC ADC ∠=∠=︒； (2)过点作//EF AB ,如图：∵DE 平分ADC ∠,70ADC ∠=︒；BE 平分ABC ∠,30ABC ∠=︒∴1352EDC ADC ∠=∠=︒,1152ABE ABC ∠=∠=︒ ∵//AB CD ,//EF AB∴////AB EF CD∴35FED CDE ∠=∠=︒,15FEB ABE ∠=∠=︒∴50BED FED FEB ∠=∠+∠=︒；(3)过点作//EF AB ,如图：∵DE 平分ADC ∠,70ADC ∠=︒；BE 平分ABC ∠,ABC n ∠=︒ ∴1352EDC ADC ∠=∠=︒,1122ABE ABC n ∠=∠=︒ ∵//AB CD ,//EF AB∴////AB EF CD∴35FED CDE ∠=∠=︒,11801802FEB ABE n ∠=︒-∠=︒-︒ ∴113518021522BED FED FEB n n ∠=∠+∠=︒+︒-︒=︒-︒．故答案是：(1)35︒(2)50︒(3)12152n ︒-︒ [点睛]本题考查了角平分线的定义、平行线的判定和性质以及角的和差,解答本题的关键是作出辅助线,要求同学们掌握平行线的性质,难度中等．。

【人教版】七年级下册数学《期中考试题》(附答案)

A. B. C. D.
【答案】B
【解析】
【分析】
如果一个非负数x的平方等于a，那么x是a的算术平方根，根据此定义即可求出结果．
【详解】解：A、，故本选项错误；
B、，故本选项正确；
C、，故本选项错误；
D、，故本选项错误；
故选B．
【点睛】本题考查算术平方根的定义，主要考查学生的理解能力和计算能力．
答案与解析
一、选择题（共10题，每小题3分，共30分）
1.下列各数中，，无理数的个数有
A. 1个B. 2个C. 3个D. 4个
【答案】B
【解析】
试题分析：无限不循环小数为无理数，由此可得出无理数的个数，因此，由定义可知无理数有：0.131131113…，﹣π，共两个．故选B．
2.下列各式中，正确的是( )
3.立方根等于它本身的有( )
A.0,1B.-1,0,1C.0,D.1
【答案】B
【解析】
【分析】
根据立方根性质可知，立方根等于它本身的实数0、1或-1．
【详解】解：∵立方根等于它本身的实数0、1或-1．
故选B．
【点睛】本题考查立方根：如果一个数x的立方等于a，那么这个数x就称为a的立方根，例如：x3=a，x就是a的立方根；任意一个数都有立方根，正数的立方根是正数，负数的立方根是负数，0的立方根是0．
【答案】D
【解析】
【分析】
根据非负数的性质得到x﹣2＝0，y+1＝0，则可确定点P（x，y）的坐标为（2，﹣1），然后根据象限内点的坐标特点即可得到答案．
【详解】∵（x﹣2）2 0，∴x﹣2＝0，y+1＝0，∴x＝2，y＝﹣1，∴点P（x，y）的坐标为（2，﹣1），在第四象限．

【人教版】七年级下册数学《期中考试题》附答案解析

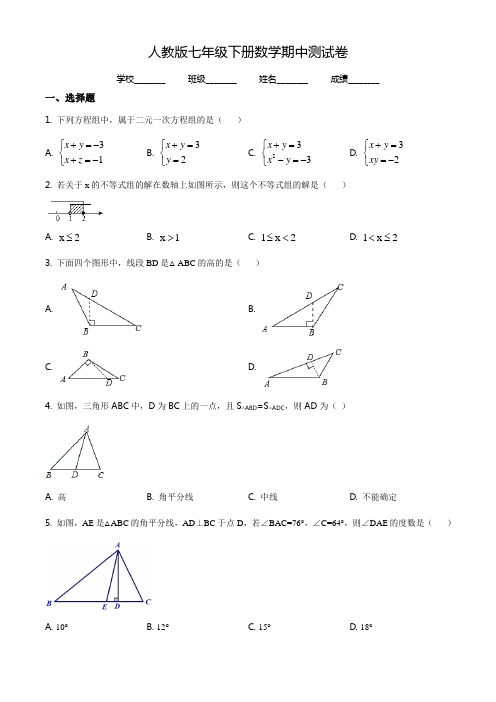
人教版七年级下册数学期中测试卷学校________ 班级________ 姓名________ 成绩________一、选择题1. 下列方程组中，属于二元一次方程组的是（）A. 31x y x z +=-⎧⎨+=-⎩B. 32x y y +=⎧⎨=⎩ C. 233x y x y +=⎧⎨-=-⎩ D. 32x y xy +=⎧⎨=-⎩2. 若关于x 的不等式组的解在数轴上如图所示，则这个不等式组的解是（）A. x 2≤B. x 1>C. 1x 2≤<D. 1x 2<≤ 3. 下面四个图形中，线段BD 是△ABC 的高的是（） A. B. C. D.4. 如图，三角形ABC 中，D 为BC 上的一点，且S △ABD =S △ADC ，则AD 为（）A. 高B. 角平分线C. 中线D. 不能确定 5. 如图，AE 是△ABC 的角平分线，AD ⊥BC 于点D ，若∠BAC=76°，∠C=64°，则∠DAE 的度数是（）A. 10°B. 12°C. 15°D. 18°6. 如图，已知点A 、D 、C 、F 在同一条直线上，AB=DE ，BC=EF ，要使△ABC≌△DEF，还需要添加一个条件是（）A . ∠BCA=∠F；B. ∠B=∠E；C. BC∥EF ；D. ∠A=∠EDF 7. 如图，在△ABC 和△CDE 中，若∠ACB＝∠CED＝90°，AB ＝CD ，BC ＝DE ，则下列结论中不正确的是( )A. △ABC≌△CDEB. CE ＝ACC. AB⊥CDD. E 为BC 的中点 8. 如图，在三角形模板ABC 中，∠A=60°，D 、E 分别为AB 、AC 上的点，则∠1+∠2的度数为（） A . 180°B. 200°C. 220°D. 240° 9. 若从一多边形的一个顶点出发，最多可引10条对角线，则它是（）A 十三边形 B. 十二边形 C. 十一边形 D. 十边形10. 如图，BE 和CE 分别为△ABC 的内角平分线和外角平分线，BE ⊥AC 于点H ，CF 平分∠ACB 交BE 于点F 连接AE ．则下列结论:①∠ECF=90°；②AE=CE ；③1902BFC BAC ∠=︒+∠；④∠BAC=2∠BEC ；⑤∠AEH=∠BCF ，正确的个数为（）A 2个 B. 3个 C. 4个 D. 5个二、填空题11. 已知12xy=⎧⎨=⎩是关于x、y的二元一次方程3210mx y--=的解，则m=__________．12. 不等式2x﹣1＞3的解集为_____．13. A、B两个码头相距140千米，一艘轮船在其间航行，顺流用了7小时，逆流用了10小时，则这艘轮船在静水中的速度是每小时__________千米．14. 把一些书分给几名同学，如果每人分3本，那么余8本，如果前面的每名同学分5本，那么最后一人分不到3本，那么这些书共有____本．15. 如图，在△ABC中，点D在AC上，点E在BD上，若∠A=70°，∠ABD=22°，∠DCE=25°，则∠BEC 的度数为__________．16. 一个多边形的内角和是1440°，则这个多边形是__________边形．17. 如图，在Rt三角形ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D，若AD=8cm，BE=3cm，则DE=__________cm．18. 如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于点E，DF⊥AC于点F，若△ABC的面积为21cm2，AB=8cm，AC=6cm，则DE的长为__________cm．19. 已知△ABC中，∠B=40°，AD是△ABC的高，且∠CAD=10°，则∠BAC的度数为__________．20. 如图，在Rt△ABC中，∠ACB=90°，AC=BC，CH为△ABC斜边上的中线，点F为CH上一点，连接BF并延长交AC于点D，过点A作AE⊥AC，连接CE和DE，若∠ACE=2∠ABF，CE=13，CD=8，则△CDE 的面积为__________．三、解答题21. 解方程组及不等式组（1）25 437 x yx y+=-⎧⎨+=-⎩（2）211841x xx x->+⎧⎨+<-⎩22. 正方形网格中，小格的顶点叫做格点．小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点，使其中任意两点不在同一条实线上；②连结三个格点，使之构成直角三角形．小华在左边的正方形网格中作出了Rt⊿ABC．请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等．23. 四川雅安发生地震后，某校学生会向全校1900名学生发起了”心系雅安”捐款活动，为了解捐款情况，学会生随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图①和图②，请根据相关信息，解答下列是问题:（1）本次接受随机抽样调查的学生人数为，图①中m的值是；（2）求本次调查获取的样本数据的平均数、众数和中位数；（3）根据样本数据，估计该校本次活动捐款金额为10元的学生人数．24. 如图，在△ABC中，BD，CE分别是AC，AB边上的高，在BD上截取BF=AC，延长CE至点G使CG=AB，连接AF，AG．（1）如图1，求证:AG=AF；（2）如图2，若BD恰好平分∠ABC，过点G作GH⊥AC交CA的延长线于点H，请直接写出图中所有的全等三角形并用全等符号连接．25. “双11”期间，某个体户在淘宝网上购买某品牌A、B两款羽绒服来销售，若购买3件A，4件B需支付2400元，若购买2件A，2件B，则需支付1400元．（1）求A、B两款羽绒服在网上的售价分别是多少元？（2）若个体户从淘宝网上购买A、B两款羽绒服各10件，均按每件600元进行零售，销售一段时间后，把剩下的羽绒服全部6折销售完，若总获利不低于3800元，求个体户让利销售的羽绒服最多是多少件？26. 如图，△ABC中，点E和点F在边BC上，连接AE，AF，使得∠EAC=∠ECA，∠BAE=2∠CAF．（1）如图1，求证:∠BAF=∠BFA；（2）如图2，在过点C且与AE平行的射线上取一点D，连接DE，若∠AED=∠B，求证:BE=CD；27. 如图，在平面直角坐标系中，点A 在第一象限，点B(a ，0)，点C(0，b)分别在x 轴，y 轴上，其中a ，b 是二元一次方程534a b -=的解，且a 为不等式312133a a -+≤的最大整数解．（1）证明:OB=OC ；（2）如图1，连接AB ，过点A 作AD ⊥AB 交y 轴于点D ，在射线AD 上截取AE=AB ，连接CE ，取CE 的中点F ，连接AF 并延长至点G ，使FG=AF ，连接CG ，OA ．当点A 在第一象限内运动（AD 不经过点C ）时，证明:∠OAF 的大小不变；答案与解析一、选择题1. 下列方程组中，属于二元一次方程组的是（）A. 31x y x z +=-⎧⎨+=-⎩B. 32x y y +=⎧⎨=⎩C. 233x y x y +=⎧⎨-=-⎩D. 32x y xy +=⎧⎨=-⎩【答案】B【解析】【分析】根据二元一次方程组的定义判断即可．【详解】A.31x y x z ，方程组中有三个未知数，不是二元一次方程组； B. 32x y y ，是二元一次方程组；C.233x y x y ，方程组中未知数的最高次是2，不是二元一次方程组；D. 32x y xy ，方程组中2xy =-不是二元一次方程，所以原方程组不是二元一次方程组；故选:B ．【点睛】本题考查的是二元一次方程组的判别，熟悉二元一次方程的定义是解题的关键．2. 若关于x 的不等式组的解在数轴上如图所示，则这个不等式组的解是（）A. x 2≤B. x 1>C. 1x 2≤<D. 1x 2<≤【答案】D【解析】【分析】不等式组的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．【详解】解:在表示解集时”≥”，”≤”要用实心圆点表示；”＜”，”＞”要用空心圆点表示．因此，这个不等式<≤．组的解是1x2故选D．3. 下面四个图形中，线段BD是△ABC的高的是（）A. B.C. D.【答案】D【解析】【分析】根据三角形高的定义，过点B向AC边作垂线，点B和垂足D之间的线段是△ABC的高，逐项判断即可．【详解】∵由三角形的高线定义可知:过点B作BD⊥AC，垂足为D，则线段BD为△ABC的高；∴选项A、B、C图形中垂足不正确，都不符合题意，只有选项D符合题意．故选:D．【点睛】本题考查三角形的高线，正确理解三角形的高线是解题关键．4. 如图，三角形ABC中，D为BC上的一点，且S△ABD=S△ADC，则AD为（）A. 高B. 角平分线C. 中线D. 不能确定【答案】C【解析】试题分析:三角形ABD和三角形ACD共用一条高，再根据S△ABD=S△ADC，列出面积公式，可得出BD=CD．解:设BC边上的高为h，∵S△ABD=S△ADC，∴，故BD=CD ，即AD 是中线．故选C ．考点:三角形的面积；三角形的角平分线、中线和高．5. 如图，AE 是△ABC 的角平分线，AD ⊥BC 于点D ，若∠BAC=76°，∠C=64°，则∠DAE 的度数是（）A. 10°B. 12°C. 15°D. 18°【答案】B【解析】【分析】根据直角三角形两锐角互余求出CAD ∠，再根据角平分线定义求出CAE ∠，然后根据DAE CAE CAD ∠=∠-∠，代入数据进行计算即可得解．【详解】解:AD BC ⊥，64C ∠=︒， 906426CAD ，AE ∵是ABC ∆的角平分线，76BAC， 11763822CAE BAC ，382612DAE CAE CAD ．故选:B ．【点睛】本题考查了三角形的内角和定理，三角形的角平分线，高线的定义，准确识图，找出各角度之间的关系并求出度数是解题的关键．6. 如图，已知点A 、D 、C 、F 在同一条直线上，AB=DE ，BC=EF ，要使△ABC≌△DEF，还需要添加一个条件是（）A. ∠BCA=∠F；B. ∠B=∠E；C. BC∥EF ；D. ∠A=∠EDF【答案】B【解析】全等三角形的判定方法SAS 是指有两边对应相等，且这两边的夹角相等的两三角形全等，已知AB=DE ，BC=EF ，其两边的夹角是∠B 和∠E，只要求出∠B=∠E 即可．解:A 、根据AB=DE ，BC=EF 和∠BCA=∠F 不能推出△ABC≌△DEF，故本选项错误；B 、∵在△ABC 和△DEF 中，AB=DE ，∠B=∠E，BC=EF ，∴△ABC≌△DEF（SAS ），故本选项正确；C 、∵BC∥EF，∴∠F=∠BCA，根据AB=DE ，BC=EF 和∠F=∠BCA 不能推出△ABC≌△DEF，故本选项错误；D 、根据AB=DE ，BC=EF 和∠A=∠EDF 不能推出△ABC≌△DEF，故本选项错误．故选B ．7. 如图，在△ABC 和△CDE 中，若∠ACB＝∠CED＝90°，AB ＝CD ，BC ＝DE ，则下列结论中不正确的是( )A. △ABC≌△CDEB. CE ＝ACC. AB⊥CDD. E 为BC 的中点【答案】D【解析】【分析】首先证明△ABC ≌△CDE ，推出CE=AC ，∠D=∠B ，由∠D+∠DCE=90°，推出∠B+∠DCE=90°，推出CD ⊥AB ，即可一一判断．【详解】在Rt △ABC 和Rt △CDE 中，AB CD BC DE =⎧⎨=⎩， ∴△ABC ≌△CDE ，∴CE =AC ，∠D =∠B ，90D DCE ∠+∠=，90B DCE ∴∠+∠=，∴CD ⊥AB ，D :E 为BC 的中点无法证明故A 、B 、C.正确，故选. D【点睛】本题考查全等三角形的判定和性质、解题的关键是熟练掌握全等三角形的判定和性质，属于基础题．8. 如图，在三角形模板ABC 中，∠A=60°，D 、E 分别为AB 、AC 上的点，则∠1+∠2的度数为（）A. 180°B. 200°C. 220°D. 240°【答案】D 【解析】【分析】根据三角形内角和定理求出B C ∠+∠，根据多边形内角和定理求出即可．【详解】解:60A ∠=︒，180120B C A ， 12360360120240BC，故选:D ．【点睛】本题考查了三角形内角和定理和多边形内角和定理，能熟记知识点的内容是解此题的关键，注意:三角形的内角和等于180︒，四边形的内角和等于360︒．9. 若从一多边形的一个顶点出发，最多可引10条对角线，则它是（） A. 十三边形 B. 十二边形C. 十一边形D. 十边形【答案】A 【解析】试题分析:根据多边形的对角线的定义可知，从n 边形的一个顶点出发，可以引（n ﹣3）条对角线，由此可得到答案．解:设这个多边形是n 边形．依题意，得n ﹣3=10， ∴n=13．故这个多边形是13边形．故选A ．考点:多边形的对角线．10. 如图，BE 和CE 分别为△ABC 的内角平分线和外角平分线，BE ⊥AC 于点H ，CF 平分∠ACB 交BE 于点F 连接AE ．则下列结论:①∠ECF=90°；②AE=CE ；③1902BFC BAC ∠=︒+∠；④∠BAC=2∠BEC ；⑤∠AEH=∠BCF ，正确的个数为（）A. 2个B. 3个C. 4个D. 5个【答案】D 【解析】【分析】根据AE 平分ACD ∠，CF 平分ACB ∠，可得12ACEECDACD ，12ACF BCFACB 则易证90ECF ∠=，可判断①正确；根据BE 平分ABC ∠，BE AC ⊥于点H ，可证()ABHHBC ASA ，得到AH CH =，可证()AHE CHE SAS ，则有AE CE =，可判断②正确；根据BE 平分ABC ∠，CF 平分ACB∠，得到12ABHHBCABC ，12ACF BCFACB ，则利用BFCFHCACFABH BAC ACF 可以判断③；根据90FCHHCE，90HECHCE，得到FCHHEC ，利用ABHHBC ，CF 平分ACB ∠，得22BAC BCA FCH HEC ，可以判断④正确；根据AHECHE ，CF 平分ACB ∠，得到AHEHEC ，BCF FCH ，FCHHEC ，AEHBCF ，故可以判断⑤正确；【详解】解:∵AE 平分ACD ∠，CF 平分ACB ∠，∴12ACE ECD ACD ，12ACF BCF ACB ∴1111180902222ECF ACFACEACB ACD ACBACD，故①正确；∵BE 平分ABC ∠，BE AC ⊥于点H ， ∴ABH HBC ，90AHB CHB，∴()ABHHBC ASA ，∴AH CH =， ∵90AHE CHE，HEHE ，∴()AHECHE SAS ，∴AE CE =，故②正确；∵BE 平分ABC ∠，CF 平分ACB ∠， ∴12ABH HBCABC ，12ACF BCFACB 又∵BFC FHCACFABH BAC ACF即有:1122BFCABC BAC ACB 12ABCACB BAC 11802BACBAC1902BAC ，故③正确； ∵90FCH HCE，90HECHCE∴FCH HEC ，又∵ABHHBC ，CF 平分ACB ∠，∴AB BC =， ∴22BAC BCAFCHHEC即:2BAC BEC ，故④正确；∵AHE CHE，CF平分ACB∠，∴AHE HEC，BCF FCH，FCH HEC，∴AEH BCF，故⑤正确；综上所述，正确的有:①②③④⑤，共5个，故选:D．【点睛】本题主要考查了全等三角形、角平分线的性质，能熟练应用相关性质是解题的关键．二、填空题11. 已知12xy=⎧⎨=⎩是关于x、y的二元一次方程3210mx y--=的解，则m=__________．【答案】5 3【解析】【分析】把x与y的值代入方程计算即可求出m的值．【详解】解:把12xy=⎧⎨=⎩代入二元一次方程3210mx y--=，得:32210m，解得:53 m=．故答案为:5 3【点睛】此题考查了二元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值．12. 不等式2x﹣1＞3的解集为_____．【答案】x＞2 【解析】【分析】【详解】解:移项得:2x＞3+1，合并同类项得:2x＞4，不等式的两边都除以2得x＞2，∴不等式2x﹣1＞3的解集为x＞2．13. A、B两个码头相距140千米，一艘轮船在其间航行，顺流用了7小时，逆流用了10小时，则这艘轮船在静水中的速度是每小时__________千米．【答案】17【解析】【分析】设这艘船在静水中的速度和水流速度分别为x千米/小时，y千米/小时，由于A、B两个码头相距140千米，一艘轮船在其间航行，顺流用了7小时，逆流用了10小时，由此即可方程组解决问题．【详解】解:设这艘船在静水中的速度和水流速度分别为x千米/小时，y千米/小时，依题意得771401010140x yx y，解之得:173xy=⎧⎨=⎩，∴这艘船在静水中的速度和水流速度分别为17千米/小时，3千米/小时，故答案为:17．【点睛】此题是一个行程问题，关键是知道如何求顺流和逆流的速度，如何根据速度、路程、时间即可列出方程组解决问题．14. 把一些书分给几名同学，如果每人分3本，那么余8本，如果前面的每名同学分5本，那么最后一人分不到3本，那么这些书共有____本．【答案】26【解析】【分析】设共有x名学生，根据每人分3本，那么余8本，可得图书共有（3x＋8）本，再由每名同学分5本，那么最后一人就分不到3本，可得出不等式，解出即可．【详解】解:设共有x名学生，则图书共有（3x＋8）本，由题意得，0＜3x＋8−5（x−1）＜3，解得:5＜x＜6.5，∵x为非负整数，∴x＝6．∴书的数量为:3×6＋8＝26．故答案为26．【点睛】本题考查了列一元一次不等式组解实际问题的运用，一元一次不等式组的解法的运用，解答时根据题意中的不相等关系建立不等式组是关键．15. 如图，在△ABC 中，点D 在AC 上，点E 在BD 上，若∠A=70°，∠ABD=22°，∠DCE=25°，则∠BEC 的度数为__________．【答案】117︒ 【解析】【分析】两次利用三角形的一个外角等于与它不相邻的两个内角的和，列式进行计算即可得解．【详解】解:在ABD ∆中，70A ∠=︒，22ABD ∠=︒，702292CDE A ABD， 2592117BECDCECDE．故答案为:117︒．【点睛】本题主要考查了三角形的外角性质，三角形的一个外角等于与它不相邻的两个内角的和，两次利用性质是解题的关键．16. 一个多边形的内角和是 1440°，则这个多边形是__________边形．【答案】十【解析】【分析】利用多边形的内角和定理:n 边形的内角和为()2180n -⨯︒ 便可得. 【详解】∵n 边形的内角和为()2180n -⨯︒ ∴()21801440n -⨯︒=，28,10n n -==. 故答案为:十边形.【点睛】本题考查多边形的内角和公式，掌握n 边形内角和定理为本题的关键.17. 如图，在Rt 三角形ABC 中，∠ACB=90°，AC=BC ，BE ⊥CE 于点E ，AD ⊥CE 于点D ，若AD=8cm ，BE=3cm ，则DE=__________cm ．【答案】4 【解析】【分析】易证CAD BCE ∠=∠，即可证明CDA BEC ，可得CD BE =，CE AD =，根据DE CE CD =-，即可解题．【详解】解:90ACB ∠=︒，BE CE ⊥于点E ，AD CE ⊥于点D ，90ACD BCE ∴∠+∠=︒，90ACD CAD ∠+∠=︒， CAD BCE ∴∠=∠，在CDA ∆和BEC ∆中， 90CDA BEC CAD BCEACBC，()CDA BEC AAS ，CD BE ∴=，AD CE =，DECE CD ，DE AD BE ∴=-，7AD cm ，3BE cm =， 734DEcm cmcm ．故答案为:4．【点睛】本题主要考查全等三角形的判定和性质，掌握全等三角形的判定方法和性质（全等三角形的对应边、对应角相等）是解题的关键．18. 如图，在△ABC 中，AD 为∠BAC 的平分线，DE ⊥AB 于点E ，DF ⊥AC 于点F ，若△ABC 的面积为21cm 2，AB=8cm ，AC=6cm ，则DE 的长为__________cm ．【答案】3 【解析】【分析】根据角平分线上的点到角的两边的距离相等可得DE DF =，再根据三角形的面积公式列式计算即可得解．【详解】解:AD 为BAC ∠的平分线，DE AB ⊥，DF AC ⊥，DE DF ∴=，ABC ∆面积112122AB DEAC DF，即11862122DE DE ，解得3DE =．故答案为:3．【点睛】本题考查了角平分线上的点到角的两边的距离相等的性质，根据三角形的面积公式列出方程是解题的关键．19. 已知△ABC 中，∠B=40°，AD 是△ABC 的高，且∠CAD=10°，则∠BAC 的度数为__________．【答案】40︒或60︒．【解析】【分析】在Rt ABD ∆中，B 与BAD ∠互余，而20CAD ∠=︒，故有BAC BADCAD ．【详解】解:90D ∠=︒，40B ∠=︒，50BAD ∴∠=︒，10CAD ，当△ABC 如图一所示时:501060BAC BAD CAD ，当△ABC 如图二所示时:501040BAC BAD CAD ，故答案为:40︒或60︒．【点睛】本题考查了直角三角形的性质和三角形的内角和，熟悉相关性质是解题的关键．20. 如图，在Rt △ABC 中，∠ACB=90°，AC=BC ，CH 为△ABC 斜边上的中线，点F 为CH 上一点，连接BF 并延长交AC 于点D ，过点A 作AE ⊥AC ，连接CE 和DE ，若∠ACE=2∠ABF ，CE=13，CD=8，则△CDE 的面积为__________．【答案】20 【解析】【分析】延长BD 交CE 于G 点，作AKGD 交CE 于K ，交GD 于O ，设ABF α∠=，则2ACE，根据90ACB ∠=︒，AC BC =，可得45CBG ,902BCG ，可证CBG CGB ∠=∠，则CGCBCA，根据ASA 易证明CAKCGD，利用CK CD ,9045135CKACDG DCB CBD ，可证EK EA ，可得5EA =，再利用三角形的面积公式即可求解．【详解】解:如图示:延长BD 交CE 于G 点，作AKGD 交CE 于K ，交GD 于O ，设ABF α∠=，则2ACE，∵90ACB ∠=︒，AC BC =， ∴45ABC ∠=︒， ∴45CBG CBA ABF , 902BCGACB ACE ∴1801809024545CGB BCGCBG,∴CBG CGB ∠=∠ ∴CGCBCA在Rt△ADO 和Rt△BDC 中， ADOBDC ，90AODBCD，∴DAO DBC ，则有CAK CGD在△CAK 和△CGD 中， CAKCGD ,CA CG =,ACK GCD∴()CAK CGD ASA∴CK CD ,9045135CKACDG DCB CBD∴18018013545EKACKA又∵904545EAKEAC CAK 即有EK EA ， ∴1385EAEK CE CK CE CD ∴11852022CDE S CD EA , 故答案为:20．【点睛】本题考查等腰直角三角形的性质，全等三角形的判定，解题的关键是正确寻找全等三角形解决问题．三、解答题21. 解方程组及不等式组（1）25437x y x y +=-⎧⎨+=-⎩ （2）211841x x x x ->+⎧⎨+<-⎩【答案】（1）43x y =-⎧⎨=⎩；（2）3x >．【解析】【分析】（1）把第一个方程乘以2然后和第二个方程进行计算，利用加减消元法求解即可；（2）先求出两个不等式的解集，再求其公共解．【详解】解:（1）25437x y x y ①②，将2①得:4210x y③，将②-③得:3y = 把3y =代入①得，235x +=-，解之得:4x =-所以，方程组的解是43x y =-⎧⎨=⎩；（2）211841x xx x①②，由①得，2x>，由②得，3x>，所以，不等式组的解集是3x>．【点睛】本题考查的是二元一次方程组的解法，一元一次不等式组解集的解集，熟悉相关解法是解题得关键．22. 正方形网格中，小格的顶点叫做格点．小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点，使其中任意两点不在同一条实线上；②连结三个格点，使之构成直角三角形．小华在左边的正方形网格中作出了Rt⊿ABC．请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等．【答案】可以是:【解析】【分析】画的直角三角形的三边应符合两直角边的平方和等于斜边的平方．第一个图形和第二个图形的面积可让两条直角边的积÷2即可．【详解】解:画图如下:易得图1三边长为10、10、20=25，符合两边和的平方等于第三边的平方，图2中三边长分别为2、18=32、20=25符合两边和的平方等于第三边的平方，第三个图中，三边长分别为8=22、8=22、16=4符合两边和的平方等于第三边的平方，【点睛】本题考查直角三角形的格点画法需满足的条件；直角三角形的三边应符合两直角边的平方和等于斜边的平方．23. 四川雅安发生地震后，某校学生会向全校1900名学生发起了”心系雅安”捐款活动，为了解捐款情况，学会生随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图①和图②，请根据相关信息，解答下列是问题:（1）本次接受随机抽样调查的学生人数为，图①中m的值是；（2）求本次调查获取的样本数据的平均数、众数和中位数；（3）根据样本数据，估计该校本次活动捐款金额为10元的学生人数．【答案】（1）50；32；（2）16；10；15；（3）608人．【解析】【分析】（1）根据条形统计图即可得出样本容量:4+16+12+10+8=50（人）；根据扇形统计图得出m的=----=；值:m100202416832（2）利用平均数、中位数、众数的定义分别求出即可．（3）根据样本中捐款10元的百分比，从而得出该校本次活动捐款金额为10元的学生人数．【详解】解:（1）根据条形图4+16+12+10+8=50（人），m=100-20-24-16-8=32；故答案为:50； 32．（2）∵1x 541016151220103081650=⨯+⨯+⨯+⨯+⨯=（）， ∴这组数据的平均数为:16．∵在这组样本数据中，10出现次数最多为16次，∴这组数据的众数为:10．∵将这组样本数据按从小到大的顺序排列，其中处于中间的两个数都是15，∴这组数据的中位数为:()11515152+=，（3）∵在50名学生中，捐款金额为10元的学生人数比例为32%，∴由样本数据，估计该校1900名学生中捐款金额为10元的学生人数有1900×32%=608人．∴该校本次活动捐款金额为10元的学生约有608人．【点睛】此题主要考查了平均数、众数、中位数的统计意义以及利用样本估计总体等知识．找中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数；众数是一组数据中出现次数最多的数据，注意众数可以不止一个；平均数是指在一组数据中所有数据之和再除以数据的个数．24. 如图，在△ABC 中，BD ，CE 分别是AC ，AB 边上的高，在BD 上截取BF=AC ，延长CE 至点G 使CG=AB ，连接AF ，AG ．（1）如图1，求证:AG=AF ；（2）如图2，若BD 恰好平分∠ABC ，过点G 作GH ⊥AC 交CA 的延长线于点H ，请直接写出图中所有的全等三角形并用全等符号连接．【答案】（1）证明见解析；（2）ABD CBD ∆≅∆，AGC FAB ∆≅∆，HGA DAF ∆≅∆．【解析】【分析】（1）根据BD 、CE 分别是AC 、AB 两条边上的高，BF=AC ，CG=AB ，利用SAS 可证AGC FAB ∆≅∆，则可证AG AF =；（2）利用等腰三角形的对称性，可得ABD CBD ∆≅∆；根据AGC FAB ∆≅∆易证90GAF ∠=︒，则可得90HAG FAD ，即有HGA DAF ，利用AAS 可证HGA DAF ∆≅∆．【详解】（1）证明:∵BD 、CE 分别是AC 、AB 两条边上的高，90ADB AEC ∴∠=∠=︒，90ABDBAD ACE CAE ，ABD ACG ，在AGC ∆与FAB ∆中，CABF GCAABF GC AB ， ()AGC FAB SAS ，∴AG AF =；（2）∵BD 平分∠ABC ，BD 是AC 边上的高，则BD 为△ABC 中三线合一的线，即△ABC 为等腰三角形，BD 为△ABC 的对称轴，根据对称性，有ABD CBD ∆≅∆AGC FAB ；AG AF ∴=，G BAF ∠=∠，90G GAE ， 90BAF GAE ，90GAF ∴∠=︒，∴90HAG FAD∵GH AC ⊥，∴90HAG HGA∴HGA DAF 在HGA 与DAF ∆中，90GHAADF HGADAFGA AF ，()HGA DAF AAS ，综上所述，全等三角形有ABD CBD ∆≅∆，AGC FAB ∆≅∆，HGA DAF ∆≅∆．【点睛】本题考查了全等三角形的判定和性质，等腰三角形的性质和判定和对称的性质，正确的识别图形是解题的关键．25. “双11”期间，某个体户在淘宝网上购买某品牌A 、B 两款羽绒服来销售，若购买3件A ，4件B 需支付2400元，若购买2件A ，2件B ，则需支付1400元．（1）求A 、B 两款羽绒服在网上的售价分别是多少元？（2）若个体户从淘宝网上购买A 、B 两款羽绒服各10件，均按每件600元进行零售，销售一段时间后，把剩下的羽绒服全部6折销售完，若总获利不低于3800元，求个体户让利销售的羽绒服最多是多少件？【答案】最多让利5件．【解析】【分析】（1）设设A 款a 元，B 款b 元，根据题意列方程组求解；（2）设让利的羽绒服有x 件，总获利不低于3800元，列不等式，求出最大整数解．【详解】解:（1）设A 款a 元，B 款b 元，可得:342400221400a b a b +=⎧⎨+=⎩，解得:400300a b =⎧⎨=⎩，答:A 款400元，B 款300元．（2）设让利的羽绒服有x 件，则已售出的有（20﹣x ）件600 （20﹣x ）+600×60% x ﹣400×10﹣30×10≥3800，解得x≤5，答:最多让利5件．考点:一元一次不等式的应用；二元一次方程组的应用．26. 如图，在△ABC 中，点E 和点F 在边BC 上，连接AE ，AF ，使得∠EAC=∠ECA ，∠BAE=2∠CAF ．（1）如图1，求证:∠BAF=∠BFA ；（2）如图2，在过点C 且与AE 平行的射线上取一点D ，连接DE ，若∠AED=∠B ，求证:BE=CD ；【答案】（1）证明见解析；（2）证明见解析．【解析】【分析】（1）设CAF α∠=，则2BAE α∠=，可得EAF EAC ，EFA EAC ，易证BAF BFA ∠=∠；（2）根据//AE CD ，EAC ECA ∠=∠，则有AED D ，AEB DCE ，AE EC =，利用AAS 可证AEB ECD ，则有BE DC =．【详解】解:（1）设CAF α∠=，则2BAE α∠=，∴EAF EAC ，EFA ECA EAC ， 22BAF EAF EAC EAC∴BAF BFA ∠=∠；（2）//AE CD ，EAC ECA ∠=∠∴AED D ，AEB DCE ，AE EC =又∵AED B ∠=∠，∴D B ∠=∠，∴()AEB ECD AAS ，∴BE DC =；【点睛】本题考查了三角形的外角，平行线的性质和三角形全等的证明，熟悉相关性质是解题的关键． 27. 如图，在平面直角坐标系中，点A 在第一象限，点B(a ，0)，点C(0，b)分别在x 轴，y 轴上，其中a ，b 是二元一次方程534a b -=的解，且a 为不等式312133a a -+≤的最大整数解．（1）证明:OB=OC ；（2）如图1，连接AB ，过点A 作AD ⊥AB 交y 轴于点D ，在射线AD 上截取AE=AB ，连接CE ，取CE 的中点F ，连接AF 并延长至点G ，使FG=AF ，连接CG ，OA ．当点A 在第一象限内运动（AD 不经过点C ）时，证明:∠OAF 的大小不变；【答案】（1）证明见解析；（2）证明见解析．【解析】【分析】（1）根据a 为不等式312133a a -+≤的最大整数解，求解不等式，利用534ab -=推出a b =即可；（2）求出TAO 为等腰直角三角形即可；【详解】（1）解:解不等式312133a a -+≤得2a ≤ ∵a 为不等式312133a a -+≤的最大整数解 2a ∴=，将2a =代入方程534a b -=得2b =， a b ∴=，OB OC ∴=；（2）证明:连接GO ，F 为CE 中点，CF EF ∴=，在GCF ∆和AEF ∆中CF EFCFG FEAFG FAGCF AEF SAS，()CG EA，GCF AEF，GC AD，//GCD CDA，=，AB AEGC AB，⊥，⊥，OB OCAD ABCOB BAD，90ABO ADO，180ADO ADC，180ADC ABO，GCD CDA，GCD ABO，∆中在GCO和ABOGC ABGCO ABOOC OBGCO ABO SAS，()GO AO，GOC AOB，AOB AOC，90GOC AOC，90GAO为等腰直角三角形，∠的大小不变；OAF，即OAF45【点睛】本题是三角形综合题，主要考查了解不等式，全等三角形判定和性质，等腰三角形的判定和性质，添加恰当的辅助线构造全等三角形是本题的关键．。

人教版七年级下册数学《期中考试题》(含答案)

人教版数学七年级下学期期中测试卷学校________ 班级________ 姓名________ 成绩________一、选择题1.下列各图中,∠1和∠2是对顶角的是( ) A. B. C. D.2.4的算术平方根是( )A. -2B. 2C. 2±D. 23.甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,能用其中一部分平移得到的是() A. B.C. D.4.如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段( )的长．A. BCB. BQC. APD. CP5.已知1∠与2∠互为补角,1120∠=︒,则2∠的余角的度数为( )A. 30B. 40︒C. 60︒D. 120︒6.在722,3.33,2π,122-,0.04445555⋯,0.9-1273127,无理数个数有( )A. 2个B. 3个C. 4个D. 5个7.如图,点E 在AD 的延长线上,下列条件中能判断BC ∥AD 的是( )A. ∠3=∠4B. ∠A +∠ADC =180°C. ∠1=∠2D. ∠A ＝∠58.平面直角坐标系内有一点P(-2020,-2020),则点P 在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限9.如图,三角板的直角顶点放在直线上,已知a b ∥,128∠=︒,则2∠的度数为( )A. 28︒B. 56︒C. 62︒D. 152︒10.如图,E,F 分别是AB,CD 上的点,G 是BC 的延长线上一点,且∠B＝∠DCG＝∠D ,则下列结论不一定成立的是( )A. ∠AEF＝∠EFCB. ∠A＝∠BCFC. ∠AEF＝∠EBCD. ∠BEF＋∠E FC ＝180°二、填空题11.如图直线AB 、CD 相交于点O ,OE ⊥AB ,O 为垂足,如果∠EOD=38°,则∠COB=_______．12.一个小区大门的栏杆如图所示,BA 垂直地面AE 于,CD 平行于地面AE ,那么ABC BCD ∠+∠=_________．13.把命题“对顶角相等”改写成“如果…那么…”的形式是__________________.14.某宾馆在重新装修后,准备在大厅的楼梯上铺上某种规格的红色地毯,其侧面如图,则至少需要购买地毯____米．15.49的平方根是_______；-125的立方根是_______；81的值是_______． 16.已知 a , b 为两个连续整数,且a<15 <b ,则 a+b 的值为______．17.平面直角坐标系内,点P(3,﹣4)到y 轴的距离是_____．18.已知点A(a ,0)和点B(0,5)两点,且直线AB 与坐标轴围成的三角形的面积等于10,则a 的值是______.三、解答题19.计算：(1)(6+3)-3(2)37+2720.利用平方根(或立方根)的概念解下列方程:(1)9(x-3)2=64;(2)(2x-1)3=-8.21.如图,直线CD 与直线AB 相交于C ,根据下列语句画图、解答．(1)过点P 作PQ ∥CD ,交AB 于点Q ；(2)过点P 作PR ⊥CD ,垂足R ；(3)若∠DCB=120°,猜想∠PQC 是多少度?并说明理由22.已知7a -和24a +是某正数的两个平方根,7b -的立方根是1．(1)求a b 、值；(2)求+a b 的算术平方根．23.如图,AD ⊥BC ,垂足为D ,点E 、F 分别在线段AB 、BC 上,EF ⊥BC ,∠CAD ＝∠DEF ,(1)求证：EF∥AD；(2)判断ED与AC的位置关系,并证明你的猜想．24.如图是某校的平面示意图,已知图书馆、行政楼的坐标分别为(－3,2),(2,3)．完成以下问题：(1)请根据题意在图上建立直角坐标系；(2)写出图上其他四个地点实验楼、校门口、综合楼、信息楼的坐标；(3)在图中用点P表示体育馆(－1,－3)的位置．25.把一张长方形纸片ABCD沿EF折叠后ED与BC交点为G,D、C分别在M、N的位置上,若∠EFG＝55°,求∠1和∠2的度数．26.如图AB∥CD．∠1=∠2,∠3=∠4,试说明AD∥BE．解：∵AB∥CD(已知)∴∠4=∠()∵∠3=∠4(已知)∴∠3=∠()∵∠1=∠2(已知)∴∠1+∠CAF=∠2+∠CAF(即∠=∠() ∴∠3=∠∴AD∥BE()答案与解析一、选择题1.下列各图中,∠1和∠2是对顶角的是()A. B. C. D.[答案]D[解析][分析]根据对顶角的两边互为反向延长线对各图形分析判断后进行解答．[详解]解：根据对顶角的定义可得,D是对顶角,故选D．[点睛]本题主要考查了对顶角的定义,熟记对顶角的定义是解决本题的关键．2.4的算术平方根是( )± D. 2A. -2B. 2C. 2[答案]B[解析]试题分析：因224=,根据算术平方根的定义即可得4的算术平方根是2．故答案选B．考点：算术平方根的定义．3.甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,能用其中一部分平移得到的是( )A. B.C. D.[答案]D[解析][分析]根据图形平移与翻折变换的性质解答即可．[详解]解：由图可知,A 、B 、C 利用图形的翻折变换得到,D 利用图形的平移得到．故选：D ．[点睛]此题考查的是翻折和平移的判断,掌握图形平移与翻折变换的性质是解决此题的关键．4.如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段( )的长．A. BCB. BQC. APD. CP[答案]C[解析]分析]根据垂线段最短解答． [详解]解：依据垂线段最短,他的跳远成绩是线段起跳线AP 的长,故选：C ．[点睛]本题考查了垂线段最短性质的运用,解答此题的关键是熟练掌握由点到直线的距离的定义． 5.已知1∠与2∠互为补角,1120∠=︒,则2∠的余角的度数为( )A. 30B. 40︒C. 60︒D. 120︒ [答案]A[解析][分析]根据互为邻补角的两个角的和等于180°求出∠2,再根据互为余角的两个角的和等于90°列式计算即可得解．[详解]∵∠1与∠2互为邻补角,∠1=120°,∴∠2=180°-∠1=180°-120°=60°,∴∠2的余角的度数为90°-60°=30°．故选：A ．[点睛]此题考查邻补角和余角的定义,是基础题,熟记概念是解题的关键．6.在722,3.33,2π,122-,0.04445555⋯,0.9-1273127,无理数的个数有( ) A. 2个B. 3个C. 4个D. 5个[答案]B[解析][分析]根据无理数的定义求解即可．[详解]解：2π,0.04445555⋯,0.9-共3个无理数故选B.[点睛]此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数．如π,2,0.8080080008…(每两个8之间依次多1个0)等形式．7.如图,点E 在AD 的延长线上,下列条件中能判断BC ∥AD 的是( )A. ∠3=∠4B. ∠A +∠ADC =180°C. ∠1=∠2D. ∠A ＝∠5[答案]C[解析]A. ∵∠3=∠4 ,∴ AB ∥CD (内错角相等,两直线平行),故不正确；B. ∵∠A+∠ADC=180°,∴ AB ∥CD (同旁内角互补,两直线平行),故不正确；C. ∵∠1=∠2,∴ AB ∥CD (内错角相等,两直线平行),故正确；D. ∵∠A=∠5,∴ AB ∥CD (同位角相等,两直线平行),故不正确；故选C.8.平面直角坐标系内有一点P(-2020,-2020),则点P 在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限 [答案]C[解析][分析]根据平面直角坐标系内各象限内点的坐标符号特征判定即可．[详解]点P(-2020,-2020)在第三象限内,故选：C ．[点睛]本题考查平面直角坐标系内象限及点的坐标符号,熟练掌握各象限内点的坐标符号特征是解答的关键．9.如图,三角板的直角顶点放在直线上,已知a b ∥,128∠=︒,则2∠的度数为( )A. 28︒B. 56︒C. 62︒D. 152︒[答案]C[解析][分析] 根据平行线的性质,可得：∠3=∠1=28°,结合∠4=90°,即可求解．[详解]∵三角板的直角顶点放在直线上,a b ∥,∴∠3=∠1=28°,∵∠4=90°,∴∠5=180°-90°-28°=62°,∴∠2=∠5=62°．故选C ．[点睛]本题主要考查平行线的性质定理,掌握两直线平行,同位角相等,是解题的关键．10.如图,E,F 分别是AB,CD 上的点,G 是BC 的延长线上一点,且∠B＝∠DCG＝∠D ,则下列结论不一定成立的是( )A. ∠AEF＝∠EFCB. ∠A＝∠BCFC. ∠AEF＝∠EBCD. ∠BEF＋∠EFC＝180° [答案]C[解析][分析]先根据平行线的判定得到AD∥BG,AB∥DC,再利用平行线的性质对各个选项进行判断即可. [详解]解：∵∠B＝∠DCG＝∠D,∴AB∥DC(同位角相等,两直线平行),AD∥BG(内错角相等,两直线平行),∴∠AEF＝∠EFC(两直线平行,内错角相等),∠BEF＋∠EFC＝180°(两直线平行,同旁内角互补),∠A+∠B=180°,∠B+∠BCF=180°(两直线平行,同旁内角互补),∴∠A＝∠BCF(等量代换),∵EF与BC不一定平行,∴无法证明∠AEF＝∠EBC.故选C.[点睛]本题主要考查平行线的判定与性质,解此题的关键在于熟练掌握其知识点.二、填空题11.如图直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠COB=_______．[答案]128°[解析][分析]根据垂直的定义得出∠AOE＝90°,最后根据∠COB＝∠AOD＝∠AOE +∠EOD进行求解．[详解]∵OE⊥AB,∠EOD=38°,∴∠AOE＝90°,∴∠COB＝∠AOD＝∠AOE +∠EOD＝90°+38°＝128°,故答案为：128°．[点睛]本题考查垂直的定义,对顶角的性质,熟练掌握对顶角相等是解题的关键．12.一个小区大门的栏杆如图所示,BA垂直地面AE于,CD平行于地面AE,那么∠+∠=_________．ABC BCD[答案]270[解析][分析]作CH⊥AE于H,如图,根据平行线的性质得∠ABC+∠BCH=180°,∠DCH+∠CHE=180°,则∠DCH=90°,于是可得到∠ABC+∠BCD=270°．[详解]解：作CH⊥AE于H,如图,∵AB⊥AE,CH⊥AE,∴AB∥CH,∴∠ABC+∠BCH=180°,∵CD∥AE,∴∠DCH+∠CHE=180°,而∠CHE=90°,∴∠DCH=90°,∴∠ABC+∠BCD=180°+90°=270°．故答案为270°．点睛]本题考查了平行线性质：两直线平行,同位角相等；两直线平行,同旁内角互补；两直线平行,内错角相等．13.把命题“对顶角相等”改写成“如果…那么…”的形式是__________________.[答案]如果两个角是对顶角,那么这两个角相等[解析][分析]命题中的条件是两个角是对顶角,放在“如果”的后面,结论是这两个角相等,应放在“那么”的后面．[详解]解：题设为：两个角是对顶角,结论为：这两个角相等,故写成“如果…那么…”的形式是：如果两个角是对顶角,那么这两个角相等,故答案为：如果两个角是对顶角,那么这两个角相等．[点睛]本题主要考查了将原命题写成条件与结论的形式,“如果”后面是命题的条件,“那么”后面是条件的结论,解决本题的关键是找到相应的条件和结论,比较简单．14.某宾馆在重新装修后,准备在大厅的楼梯上铺上某种规格的红色地毯,其侧面如图,则至少需要购买地毯____米．[答案]8.4[解析][分析]根据题意,结合图形,先把楼梯的横竖向上向右平移,构成一个长方形,据此计算即可．[详解]解：如图,利用平移把楼梯的横竖向上向右平移,构成一个长、宽分别为5.8米、2.6米的长方形,∴地毯的长度为2.6+5.8=8.4(米)．故答案为：8.4．[点睛]本题主要考查了平移的性质,掌握基本性质是解题的关键．15.49的平方根是_______；-125的立方根是_______81_______．[答案](1). 23(2). -5 (3). 9[解析][分析]根据平方根、立方根、算术平方根的定义,即可解答．[详解]49的平方根是23,-125的立方根是-5819,故答案为：23；-5；9．[点睛]本题考查了平方根、立方根、算术平方根,熟练掌握它们的定义及运算方法是解答的关键．16.已知 a , b 为两个连续整数,且<b ,则 a+b 的值为______．[答案]7[解析]<<,由此可确定a 和b 的值,进而可得出a+b 的值．本题解析: 根据a b, a 、b 为两个连续整数,又因为34,得a=3,b=4将a=3,b=4代入a+b,得a+b=7.故答案为7.点睛：此题考查的是如何根据无理数的范围确定两个有理数的值,,可以很容易得到其相邻两个整数,再结合已知条件即可确定a 、b 的值.17.平面直角坐标系内,点P(3,﹣4)到y 轴的距离是_____．[答案]3[解析]根据平面直角坐标系的特点,可知到y 轴的距离为横坐标的绝对值,因此可知P 点到y 轴的距离为3. 故答案为3.18.已知点A(a ,0)和点B(0,5)两点,且直线AB 与坐标轴围成的三角形的面积等于10,则a 的值是______.[答案]±4[解析]试题分析：根据坐标与图形得到三角形OAB 的两边分别为|a|与5,然后根据三角形面积公式有：15102a ⋅⋅=, 解得a=4或a=-4,即a 的值为±4．考点：1.三角形的面积；2.坐标与图形性质．三、解答题19.计算：(1(2)[答案](1；(2)[解析][分析](1)先去括号,再根据二次根式的加减运算法则即可解答；(2)直接利用二次根式的加法法则合并即可解答．[详解](1)(6+3)-3=6+3-3=6；(2)37+27=(3+2)7=57．[点睛]本题考查了二次根式的加减法运算,熟练掌握二次根式的加减法运算法则是解答的关键．20.利用平方根(或立方根)的概念解下列方程:(1)9(x-3)2=64;(2)(2x-1)3=-8.[答案](1)x=173或x=13；(2)x=-12. [解析][分析](1)先化简,再根据平方根的概念进行计算(2)根据立方根的概念直接开立方,再计算求值. [详解]解：(1)(x-3)2=649,则x-3=±83. ∴x=±83+3,即x=173,或x=13. (2)2x-1=-2,∴x=-12. [点睛]此题重点考察学生对平方根,立方根的理解,掌握平方根,立方根的计算方法是解题的关键.21.如图,直线CD 与直线AB 相交于C ,根据下列语句画图、解答．(1)过点P 作PQ ∥CD ,交AB 于点Q ；(2)过点P 作PR ⊥CD ,垂足为R ；(3)若∠DCB=120°,猜想∠PQC 是多少度?并说明理由[答案](1)见解析；(2)见解析；(3)∠PQC=60°,理由见解析[解析]详解]解：如图所示：(1)画出如图直线PQ(2)画出如图直线PR(3)∠PQC=60°理由是：因为PQ ∥CD所以∠DCB+∠PQC=180°又因为∠DCB=120°所以∠PQC=180°－120°=60° 22.已知7a -和24a +是某正数的两个平方根,7b -的立方根是1．(1)求a b 、的值；(2)求+a b 算术平方根．[答案](1)a=1,b=8；(2)a+b 的算数平方根为3[解析][分析](1)根据平方根的性质一个正数有两个平方根,它们互为相反数列出算式,求出a 的值,再根据立方根的定义求出b 的值即可；(2)求出a+b 的值,根据算数平方根的概念求出答案即可．[详解]解：(1)∵7a -和24a +是某正数的两个平方根,∴7a -+24a + =0,∴a=1,∵7b -的立方根是1,∴71b -=∴b=8；(2)∵a=1,b=8；∴a+b=9,∴a+b 的算数平方根为3[点睛]本题考查了平方根和立方根的概念．注意一个正数有两个平方根,它们互为相反数；0的平方根是0；负数没有平方根．立方根的性质：一个正数的立方根是正数,一个负数的立方根是负数,0的立方根是0．23.如图,AD⊥BC,垂足为D,点E、F分别在线段AB、BC上,EF⊥BC,∠CAD＝∠DEF,(1)求证：EF∥AD；(2)判断ED与AC的位置关系,并证明你的猜想．[答案](1)见解析；(2)ED与AC平行,见解析[解析]分析](1)先由AD⊥BC,EF⊥BC证得∠ADB=∠EFB=90°,再根据平行线的判定即可证得结论；(2)由EF∥AD得∠DEF=∠EDA,进而证得∠EDA=∠CAD,即可得出结论．[详解](1)∵ AD⊥BC,EF⊥BC,∴∠ADB=∠EFB=90°,∴ EF∥AD(2)ED与AC平行,理由为：∵EF∥AD,∴∠DEF=∠EDA,∵∠CAD＝∠DEF,∴∠EDA=∠CAD,∴ED∥AC．即ED与AC平行．[点睛]本题考查了平行线的判定与性质、垂直定义,掌握平行线的判定与性质并能熟练运用是解答的关键．24.如图是某校的平面示意图,已知图书馆、行政楼的坐标分别为(－3,2),(2,3)．完成以下问题：(1)请根据题意在图上建立直角坐标系；(2)写出图上其他四个地点实验楼、校门口、综合楼、信息楼的坐标；(3)在图中用点P表示体育馆(－1,－3)的位置．[答案](1)见解析；(2)实验楼(-4,0)；校门口(1,0)；综合楼(-5,-3)；信息楼(1,-2)；(3)见解析[解析][分析](1)根据图书馆、行政楼的坐标信息,建立合适的平面直角坐标系；(2)根据上题中建立的平面直角坐标系可以写出其他四个地点的坐标；(3)根据P点坐标可以直接在平面直角坐标系中表示出来．[详解](1)由图书馆、行政楼的坐标分别为(－3,2),(2,3)可找到O(0,0)点,从而建立平面直角坐标系,如下图；(2)根据(1)中的平面直角坐标系,可得其他四个地点的坐标．故实验楼(-4,0)；校门口(1,0)；综合楼(-5,-3)；信息楼(1,-2)；(3)根据平面直角坐标系,P(－1,－3)的位置如下图,[点睛]本题主要考查平面直角坐标系,根据题中所给的坐标信息确认O(0,0)的位置,从而建立平面直角坐标系是解答本题的关键．25.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG＝55°,求∠1和∠2的度数．[答案]∠1＝70°,∠2＝110°[解析][分析]由平行线的性质知∠DEF=∠EFG=55°,由折叠的性质知∠DEF=∠GEF=55°,则可求得∠2=∠GED=110°,进而可求得∠1的值.[详解]∵AD∥BC,∴∠DEF=∠EFG=55°.由对称性知∠GEF=∠DEF∠GEF=55°,∴∠GED=110°.∵AD∥BC,∴∠2=∠GED=110°.∴∠1=180°-110°=70°,[点睛]本题考查了翻折的性质及平行线的性质,平行线的性质：①两直线平行同位角相等；②两直线平行内错角相等；③两直线平行同旁内角互补；④夹在两平行线间的平行线段相等.在运用平行线的性质定理时,一定要找准同位角,内错角和同旁内角.26.如图AB∥CD．∠1=∠2,∠3=∠4,试说明AD∥BE．解：∵AB∥CD(已知)∴∠4=∠()∵∠3=∠4(已知)∴∠3=∠()∵∠1=∠2(已知)∴∠1+∠CAF=∠2+∠CAF(即∠=∠()∴∠3=∠∴AD∥BE()[答案]BAF；两直线平行,同位角相等；BAF；等量代换；等式的性质；角的和差；CAD；内错角相等,两直线平行．[解析][详解]解：∵AB∥CD(已知),∴∠4=∠BAE(两直线平行,同位角相等)；∵∠3=∠4(已知),∴∠3=∠BAE(等量代换)；∵∠1=∠2(已知),∴∠1+∠CAF=∠2+∠CAF(等式的性质),即∠BAE=∠DAC,∴∠3=∠DAC(等量代换),∴AD∥BE(内错角相等,两直线平行)．。

人教版数学七年级下册《期中考试题》及答案解析

人教版数学七年级下学期期中测试卷学校________ 班级________ 姓名________ 成绩________一、选择题(共10小题)1. 方程3x ﹣1＝5的解是( ) A. 43x = B. 53x = C. x ＝18 D. x ＝2 2. 下列方程变形中属于移项的是( ) A 由2x ＝﹣1得x ＝﹣12 B. 由2x ＝2得x ＝4 C. 由5x +b ＝0得5x ＝﹣b D. 由4﹣3x ＝0得﹣3x +4＝03. 由132x y -=,可以得到用表示的式子( ) A 223x y =- B. 2133x y =- C. 223x y -= D. 223x y =- 4. 解方程2x ＝3x 时,两边都除以x ,得2＝3,其错误原因是( )A. 方程本身是错的B. 方程无解C. 两边都除以了0D. 2x 小于3x 5. 下列说法正确的是( )A. 方程4+x ＝8和不等式4+x ＞8的解是一样的B. x ＝2不是不等式4x ＞5的解C. x ＝2是不等式4x ＞15的一个解D. 不等式x ﹣2＜6的两边都减去3,则此不等式仍成立6. 把方程0.10.20.510.30.4x x ---=的分母化成整数后,可得方程( ) A. 0.10.20.5134x x ---= B. 12510134x x ---= C. 125101034x x ---= D.120.5134x x ---= 7. 不等式325132x x ++≤-的解集表示在数轴上是( )A. B. C. D.8. 每瓶A 种饮料比每瓶B 种饮料少元,小峰买了2瓶A 种饮料和3瓶B 种饮料,一共花了13元,如果设每瓶A 种饮料为x 元,那么下面所列方程正确的是( )A. ()21313x x -+=B. ()21313x x ++=C. ()23113x x ++=D. ()23113x x +-=9. 如图,射线OC 的端点O 在直线AB 上,∠AOC 的度数比∠BOC 的2倍多10度．设∠AOC 和∠BOC 的度数分别为x ,y ,则下列正确的方程组为( )A. 18010x y x y +=⎧⎨=+⎩B. 180210x y x y +=⎧⎨=+⎩C. 180102x y x y +=⎧⎨=-⎩D. 180210x y y x +=⎧⎨=-⎩ 10. 小华在某月的日历上圈出相邻的四个数,算出这四个数的和是36,那么这个数阵的形式可能是( ) A. B. C. D.二、填空题(每小题3分,共15分)11. 若2x ﹣3与1互为相反数,则x ＝_____．12. 在公式S ＝12n (a +b )中,已知S ＝5,n ＝2,a ＝3,那么b 的值是_____． 13. 一个两位数,两个数位上数字一个是另一个的2倍,若把此两位数的两个数字对调,所得新数比原数大27,则此两位数是_____．14. 对有理数a ,b 规定运算“*”的意义为a *b ＝a +2b ,比如：5*7＝5+2×7,则方程3x *14＝2﹣x 的解为_____． 15. 如图,足球的表面是有一些黑颜色五边形和白颜色六边形的皮块缝合而成的,共计有32块,请观察图形,根据黑块五边形和白块六边形的边数之间的关系计算黑颜色五边形和白颜色六边形的皮块数分别是_____．三、解答题(本大题有8个小题,满分55分)16. 解方程：3(2x﹣1)﹣2(1﹣x)＝0．17. 解不等式52x+﹣1＜322x+,小兵的解答过程是这样的．解：去分母,得x+5﹣1＜3x+2①．移项,得x﹣3x＜2﹣5+1②．合并同类项,得﹣2x＜﹣2③．系数化1,得x＜1④．(1)请问：小兵同学的解答是否正确?如果错误,请指出错误步骤的标号,简述原因?(2)给出正确的解答过程．18. 用加减消元法解方程组：433 3215x yx y+=⎧⎨-=⎩．19. 已知关于x的方程a﹣5x＝﹣6与方程3x﹣6＝4x﹣5有相同的解,求a的值．20. 如图1,在边长为a的大正方形中剪去一个边长为b的小正方形,再将图中的阴影剪拼成一个长方形,如图2,这个拼成的长方形的长为30,宽为20．求图2中第Ⅱ部分的面积．21. 小明在解方程21134x x m-+=-,方程两边都乘以各分母的最小公倍数去分母时,漏乘了不含分母的项﹣1,得到方程的解是x＝3,请你帮助小明求出m的值和原方程正确的解．22. 阅读以下例题：解方程：|3x|＝1,解：①当3x≥0时,原方程可化为一元一次方程3x＝1,解这个方程得x＝13；②当3x＜0时,原方程可化一元一次方程﹣3x＝1,解这个方程得x＝﹣13．所以原方程的解是x＝13或x＝﹣13．(1)仿照例题解方程：|2x+1|＝3．(2)探究：当b为何值时,方程|x﹣2|＝b+1满足：①无解；②只有一个解；③有两个解．23. 某家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙单独做12天可以完成,需付费用3480元．(1)甲、乙两组工作一天,商店各应付多少钱?(2)已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所付费用较少?(3)在(2)的条件下,现有三种施工方案：①单独请甲组装修；②单独请乙组装修；③请甲、乙两组合做．若装修过程中,商店不但要支付装修费用,而且每天因装修损失收入200元,你认为如何安排施工更有利于商店?请你帮助商店决策．(可用(1)(2)问的条件及结论)答案与解析一、选择题(共10小题)1. 方程3x ﹣1＝5的解是( ) A. 43x = B. 53x = C. x ＝18 D. x ＝2[答案]D[解析][分析]先移项,再合并同类项,最后系数化为1即可得出答案.[详解]3x -1=5,移项得,3x =5+1,合并同类项得,3x =6,系数化为1得,x =2.故选D.[点睛]本题考查了一元一次方程的解法.熟练掌握解一元一次方程的步骤是解题的关键.2. 下列方程变形中属于移项的是( )A. 由2x ＝﹣1得x ＝﹣12B. 由2x ＝2得x ＝4 C. 由5x +b ＝0得5x ＝﹣bD. 由4﹣3x ＝0得﹣3x +4＝0 [答案]C[解析][分析]根据一元一次方程的解法直接进行排除选项即可．[详解]A 、由2x ＝﹣1得：x ＝12-,不符合题意； B 、由2x ＝2得：x ＝4,不符合题意； C 、由5x +b ＝0得5x ＝﹣b ,符合题意；D 、由4﹣3x ＝0得﹣3x +4＝0,不符合题意．故选：C ．[点睛]本题主要考查一元一次方程的解法,熟练掌握一元一次方程的解法是解题的关键．3. 由132x y -=,可以得到用表示的式子( ) A. 223x y =- B. 2133x y =- C. 223x y -= D. 223x y =- [答案]A[解析][分析] 只需把含有y 的项移到方程的左边,其它的项移到另一边,然后合并同类项、系数化为1就可用含x 的式子表示y ．[详解]解：移项,得123y x =-, 系数化为1,得223x y =-．故选：A ．[点睛]本题考查的是方程的基本运算技能,移项、合并同类项、系数化为1等．4. 解方程2x ＝3x 时,两边都除以x ,得2＝3,其错误原因是( )A. 方程本身是错的B. 方程无解C. 两边都除以了0D. 2x 小于3x[答案]C[解析][分析]出错的地方为：方程两边除以x ,没有考虑x 为0的情况,据此判断即可．[详解]解：错误的地方为：方程两边都除以x ,没有考虑x 是否为0,正确解法为：移项得：2x ﹣3x ＝0,合并得：﹣x ＝0,系数化为1得：x ＝0．故选：C ．[点睛]本题考查了解一元一次方程,熟练掌握运算法则是解题的关键．5. 下列说法正确的是( )A. 方程4+x ＝8和不等式4+x ＞8的解是一样的B. x ＝2不是不等式4x ＞5的解C. x＝2是不等式4x＞15的一个解D. 不等式x﹣2＜6的两边都减去3,则此不等式仍成立[答案]D[解析][分析]根据不等式的解法及不等式解集的概念直接进行排除选项即可．[详解]A、方程的解只有一个,而不等式的解有无数个；故本选项不合题意．B、不等式4x＞5的解集是x＞54,故本选项不合题意．C、不等式4x＞15的解集是x＞154不包括2,故本选项不合题意．D、不等式x﹣2＜6的两边都减去3,则此不等式仍成立,正确,依据是不等式的基本性质．故选：D．[点睛]本题主要考查一元一次不等式的解集及解法,熟练掌握一元一次不等式的解集及解法是解题的关键．6. 把方程0.10.20.510.30.4x x---=的分母化成整数后,可得方程( )A. 0.10.20.5134x x---= B.12510134x x---=C. 125101034x x---= D.120.5134x x---=[答案]B[解析][分析]本题方程两边都含有分数系数,在变形的过程中,利用分数的性质将分数的分子、分母同时扩大或缩小相同的倍数,将小数方程变为整数方程,把含分母的项的分子与分母都扩大原来的10倍．[详解]解：把原方程的分母化为整数得,12510134x x ---=故选B．[点睛]分母化成整数的过程的依据是分数的性质,掌握相关知识是解题的关键．7. 不等式325132x x++≤-的解集表示在数轴上是( )A. B.C.D.[答案]B[解析][分析] 根据一元一次不等式的解法,去分母,去括号,移项,合并同类项,系数化为1即可得解．[详解]解：去分母,得,2(3x +2)≤3(x +5)﹣6,去括号,得6x +4≤3x +15﹣6,移项、合并同类项,得3x ≤5,系数化为1,得,x ≤53, 在数轴上表示为：故选：B ．[点睛]本题考查了解一元一次不等式,以及在数轴上表示不等式的解集,＞向右画,＜向左画,≤与≥用实心圆点,＜与＞用空心圆圈．8. 每瓶A 种饮料比每瓶B 种饮料少元,小峰买了2瓶A 种饮料和3瓶B 种饮料,一共花了13元,如果设每瓶A 种饮料为x 元,那么下面所列方程正确的是( )A. ()21313x x -+=B. ()21313x x ++=C. ()23113x x ++=D. ()23113x x +-=[答案]C[解析][分析]设每瓶A 种饮料为x 元,则每瓶B 种饮料为()1x +元,由买了2瓶A 种饮料和3瓶B 种饮料,一共花了13元,列方程即可得到答案．[详解]解：设每瓶A 种饮料为x 元,则每瓶B 种饮料为()1x +元,所以：()23113x x ++=,故选C ．[点睛]本题考查的是一元一次方程的应用,掌握利用相等关系列一元一次方程是解题的关键．9. 如图,射线OC 端点O 在直线AB 上,∠AOC 的度数比∠BOC 的2倍多10度．设∠AOC 和∠BOC 的度数分别为x ,y ,则下列正确的方程组为( )A. 18010x y x y +=⎧⎨=+⎩B. 180210x y x y +=⎧⎨=+⎩C. 180102x y x y +=⎧⎨=-⎩D. 180210x y y x +=⎧⎨=-⎩[答案]B[解析][分析]根据∠AOC 的度数比∠BOC 的2倍多10°,得方程x ＝2y +10；然后由平角可建立方程组,则问题得解．[详解]解：根据∠AOC 的度数比∠BOC 的2倍多10°,得方程x ＝2y +10；根据∠AOC 和∠BOC 组成了平角,得方程x +y ＝180．列方程组为180210x y x y +=⎧⎨=+⎩．故选：B ．[点睛]本题主要考查二元一次方程组的应用,熟练掌握二元一次方程组的应用是解题的关键．10. 小华在某月的日历上圈出相邻的四个数,算出这四个数的和是36,那么这个数阵的形式可能是( ) A.B. C. D. [答案]C[解析][分析]可设第一个数为x ,根据已知对每个选项计算讨论得出．[详解]设第一个数为x,根据已知：A：得x+x+6+x+7+x+8=36,则x=6.25不是整数,故本选项不可能．B：得x+x+1+x+8+x+9=36,则x=4.5不是整数,故本选项不可能．C：得x+x+1+x+7+x+8=36,则x=5,为正数符合题意．D：得x+x+1+x+6+x+7=36,则x=5.5不是整数,故本选项不可能．故选C．[点睛]此题考查的是一元一次方程的应用,关键是根据题意对每个选项列出方程求解论证．二、填空题(每小题3分,共15分)11. 若2x﹣3与1互为相反数,则x＝_____．[答案]1．[解析][分析]根据互为相反数的关系直接进行求解即可．[详解]解：根据题意得：2x﹣3+1＝0,移项合并得：2x＝2,解得：x＝1．故答案：1．[点睛]本题主要考查相反数的定义,熟练掌握相反数的定义是解题的关键．12. 在公式S＝12n(a+b)中,已知S＝5,n＝2,a＝3,那么b的值是_____．[答案]2．[解析][分析]求公式中的一个字母ｂ的值,把已知其它字母的值代入,转化为关于b大的方程,解之即可．[详解]∵S＝12n(a+b)中,且S＝5,n＝2,a＝3,∴5＝12×2×(3+b),解得：b＝2．故答案为：2．[点睛]本题考查从公式中求某个字母值问题,关键是把给的已知字母的值代入,转化为某字母为未知数的方程．13. 一个两位数,两个数位上的数字一个是另一个的2倍,若把此两位数的两个数字对调,所得新数比原数大27,则此两位数是_____．[答案]36[解析][分析]设十位数字为x ,个位数字为y ,由题意可进行列方程组进行求解即可．[详解]解：设十位数字为x ,个位数字为y ,由题意得：2101027y x y x x y =⎧⎨+=++⎩, 解得：36x y =⎧⎨=⎩, 原两位数是36,即：原两位数是36．故答案是：36．[点睛]本题主要考查二元一次方程组的应用,熟练掌握二元一次方程组的应用是解题的关键．14. 对有理数a ,b 规定运算“*”的意义为a *b ＝a +2b ,比如：5*7＝5+2×7,则方程3x *14＝2﹣x 的解为_____． [答案]38． [解析][分析]已知等式利用题中的新定义化简,计算即可求出解．[详解]解：根据题中的新定义化简得：3x +12＝2﹣x , 去分母得：6x +1＝4﹣2x ,解得：x ＝38．故答案为：38． [点睛]本题考查了解一元一次方程,以及有理数的混合运算,弄清题中的新定义是解题的关键．15. 如图,足球的表面是有一些黑颜色五边形和白颜色六边形的皮块缝合而成的,共计有32块,请观察图形,根据黑块五边形和白块六边形的边数之间的关系计算黑颜色五边形和白颜色六边形的皮块数分别是_____．[答案]12和20[解析][分析]足球缝合规律：五边形的5条边都与六边形缝合,六边形只有3条边与五边形缝合,所以五边形的个数乘以5应该等于六边形的个数乘以3,据此设足球有黑色五边形皮块x 个,列方程求解即可[详解]设足球有黑色五边形皮块x 个,则有白色六边形皮块(32-x)个,由题意得,5x=3(32-x)解得：x=12所以白色皮块数为20,黑色皮块数为12．故答案为：12和20．[点睛]本题主要考查一元一次方程应用,熟练掌握一元一次方程的应用是解题的关键．三、解答题(本大题有8个小题,满分55分)16. 解方程：3(2x ﹣1)﹣2(1﹣x )＝0．[答案]x ＝58 [解析][分析]先去括号合并同类项,然后直接解一元一次方程即可．[详解]解：()()321210x x ---=去括号,得6x ﹣3﹣2+2x ＝0,移项,得6x +2x ＝3+2,合并同类项,得8x ＝5,系数化为1,得x ＝58． [点睛]本题主要考查一元一次方程的解法,熟练掌握一元一次方程的解法是解题的关键．17. 解不等式52x +﹣1＜322x +,小兵的解答过程是这样的．解：去分母,得x +5﹣1＜3x +2①．移项,得x ﹣3x ＜2﹣5+1②．合并同类项,得﹣2x ＜﹣2③．系数化为1,得x＜1④．(1)请问：小兵同学的解答是否正确?如果错误,请指出错误步骤的标号,简述原因?(2)给出正确的解答过程．[答案](1)解法错误,①去分母时,漏乘了没有分母的项,④系数化为1时不等号的方向没有改变,(2)正确的解答过程见解析,x＞12．[解析][分析](1)根据解一元一次不等式的步骤,逐一判断即可得出结论；(2)根据解一元一次不等式的步骤,解不等式即可．[详解](1)解法错误,①去分母时,漏乘了没有分母的项,④系数化为1时不等号的方向没有改变,(2)正确的解答是：去分母得(x+5)﹣2＜3x+2,移项,得x﹣3x＜2+2﹣5,合并同类项,得﹣2x＜﹣1,系数化为1,得x＞12．[点睛]此题考查的是解一元一次不等式,掌握解一元一次不等式的步骤是解题关键．18. 用加减消元法解方程组：433 3215x yx y+=⎧⎨-=⎩．[答案]33 xy=⎧⎨=-⎩．[解析][分析]先把方程组标号①②,把两个方程同一未知数的系数变绝对值相等的数,同号两式相减,异号两式相加,消去一个未知数,转化为一元一次方程,得解后再代入①或②,求另一未知数,把两个解联立起来即可．[详解]433 3315x yx y+=⎧⎨-=⎩①②,①×2得：8x+6y＝6③,②×3得：9x﹣6y＝45④,③+④得：17x＝51,解得：x＝3,把x＝3代入①,得4×3+3y＝3, 解得：y＝﹣3,所以原方程组的解是33 xy=⎧⎨=-⎩．[点睛]本题考查加减消元法解方程组,关键是要变方程一未知数系数绝对值相等,同号两式相减,异号两式相加．19. 已知关于x的方程a﹣5x＝﹣6与方程3x﹣6＝4x﹣5有相同的解,求a的值．[答案]a＝﹣11．[解析][分析]两个方程中,有一个只有一个未知数,先解这个方程,求出后,代入第二个方程解之即可．[详解]解方程.3x﹣6＝4x﹣5,移项,得3x﹣4x＝﹣5+6,合并同类项,得﹣x＝1,系数化为1得：x＝﹣1,把x＝﹣1代入方程a﹣5x＝﹣6,得a﹣5×(﹣1)＝﹣6．解得a＝﹣11．[点睛]本题考查用方程确定参数问题,关键是观察两个方程中有一个方程直接求解．20. 如图1,在边长为a大正方形中剪去一个边长为b的小正方形,再将图中的阴影剪拼成一个长方形,如图2,这个拼成的长方形的长为30,宽为20．求图2中第Ⅱ部分的面积．[答案]图2中第Ⅱ部分的面积为100．[解析][分析]根据在边长为a的大正方形中剪去一个边长为b的小正方形,以及长方形的长为30,宽为20,得出a+b=30,a-b=20,进而得出答案．[详解]解：根据题意得出：3020b a a b +=⎧⎨-=⎩, 解得：255a b =⎧⎨=⎩, 故图2中Ⅱ部分的面积是：5×20＝100, 答：第Ⅱ部分的面积为100．[点睛]本题考查了正方形的性质以及二元一次方程组的应用,根据已知得出a+b=30,a-b=20是解题的关键． 21. 小明在解方程21134x x m -+=-,方程两边都乘以各分母的最小公倍数去分母时,漏乘了不含分母的项﹣1,得到方程的解是x ＝3,请你帮助小明求出m 的值和原方程正确的解．[答案]m ＝4,x ＝45 [解析][分析]根据题意进行“将错就错”,即把方程的解是x ＝3代入()()42131x x m -=+-中求解m 的值,最后代入原方程进行求解即可．[详解]解：根据题意,x ＝3是方程()()42131x x m -=+-的解,将x ＝3代入得4×(2×3﹣1)＝3(3+m )﹣1,解得m ＝4, 所以原方程为214134x x -+=-, 解方程得x ＝45． [点睛]本题主要考查分式方程的解及分式方程的解法,熟练掌握分式方程的解及分式方程的解法是解题的关键．22. 阅读以下例题：解方程：|3x |＝1,解：①当3x ≥0时,原方程可化一元一次方程3x ＝1,解这个方程得x ＝13；②当3x＜0时,原方程可化为一元一次方程﹣3x＝1,解这个方程得x＝﹣13．所以原方程的解是x＝13或x＝﹣13．(1)仿照例题解方程：|2x+1|＝3．(2)探究：当b为何值时,方程|x﹣2|＝b+1满足：①无解；②只有一个解；③有两个解．[答案](1)x＝1或x＝﹣2；(2)当b＜﹣1时,方程无解；当b＝﹣1时,方程只有一个解；当b＞﹣1时,方程有两个解．[解析][分析](1)仿照例题分情况讨论：①当2x+1≥0时,②当2x+1＜0时,化简绝对值,解关于x的一元一次方程即可求解；(2)|x﹣2|≥0恒成立,①若无解,则b+1＜0,解不等式即可求解；②若只有一个解,则b+1＝0,求解即可；③若有两个解,则b+1＞0,解不等式即可求解．[详解]解：(1)①当2x+1≥0时,原方程可化为一元一次方程2x+1＝3,解这个方程得x＝1；②当2x+1＜0时,原方程可化为一元一次方程﹣2x﹣1＝3,解这个方程得x＝﹣2；所以原方程的解是x＝1或x＝﹣2；(2)因为|x﹣2|≥0,所以①当b+1＜0,即b＜﹣1时,方程无解；②当b+1＝0,即b＝﹣1时,方程只有一个解；③当b+1＞0,即b＞﹣1时,方程有两个解．[点睛]本题考查解绝对值方程,理解题意是解题的关键．23. 某家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙单独做12天可以完成,需付费用3480元．(1)甲、乙两组工作一天,商店各应付多少钱?(2)已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所付费用较少?(3)在(2)的条件下,现有三种施工方案：①单独请甲组装修；②单独请乙组装修；③请甲、乙两组合做．若装修过程中,商店不但要支付装修费用,而且每天因装修损失收入200元,你认为如何安排施工更有利于商店?请你帮助商店决策．(可用(1)(2)问的条件及结论)[答案](1)甲组工作一天商店应付300元,乙组工作一天商店应付140元；(2)单独请乙组,商店所付费用较少；(3)安排甲、乙两个装修组同时施工更有利于商店．[解析][分析](1)设甲组工作一天商店应付元,乙组工作一天商店应付元,根据“若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙单独做12天可以完成,需付费用3480元”,即可得出关于,的二元一次方程组,解之即可得出结论；(2)根据总费用每天需支付的费用工作时间,可分别求出单独请甲组和单独请乙组施工所需费用,比较后即可得出结论；(3)分单独请甲组施工、单独请乙组施工和请甲、乙两组合做施工三种情况考虑,利用损失的总钱数施工费用因装修损失收入,分别求出三种情况下损失的钱数,比较后即可得出结论．[详解](1)设甲组工作一天商店应付x元,乙组工作一天商店应付y元,依题意,得：883520 6123480x yx y+=⎧⎨+=⎩,解得：300140xy=⎧⎨=⎩．答：甲组工作一天商店应付300元,乙组工作一天商店应付140元．(2)单独请甲组需要的费用为300×12＝3600(元)；单独请乙组需要的费用为140×24＝3360(元)．∵3600＞3360,∴单独请乙组,商店所付费用较少．(3)单独请甲组施工,需费用3600元,少盈利200×12＝2400(元),相当于损失6000元；单独请乙组施工,需费用3360元,少盈利200×24＝4800(元),相当于损失8160元；请甲、乙两组合做施工,需费用3520元,少盈利200×8＝1600(元),相当于损失5120元．∵5120＜6000＜8160,∴甲、乙合做损失费用最少．答：安排甲、乙两个装修组同时施工更有利于商店．[点睛]本题考查了二元一次方程组的应用,解题的关键是找准等量关系,正确列出二元一次方程组．。

安徽省宣城市第六中学2023-2024学年七年级下学期期中数学试题

2023—2024学年度第二学期期中考试七年级数学试卷命题人：王勇审核人：谭建国一、选择题（本大题共10小题，共30.0分）1．下列各式正确的为（） A 164=±B ．3279--=-C ．819=D 9342= 2．下列各数：333,9,121,0.3,0.10100122π--⋅⋅⋅（每两个1之间的0增加一个）中，无理数有（） A ．1个B ．2个C ．3个D ．4个3．某种细胞的直径是0.00059毫米，0.00059这个数用科学记数法可表示为（） A ．45.910-⨯B ．55910-⨯C ．55.910-⨯D ．30.5910-⨯4．若a b <，则下列不等式正确的为（） A ．3131a b -->--B ．22a b> C ．11a b -+<-+D ．a x b x +>+5．不等式266x -+>的正整数解有（） A ．无数个B ．0个C ．1个D ．2个6．在代数式()()x a x b +-的积中不含x 的一次项，则a 、b 一定满足（） A ．互为倒数B ．互为相反数C ．相等D ．0ab =7．下列计算正确的是（） A ．()325a a =B ．23aa a ⋅=C ．933aa a ÷=D ．01a=8．计算：2023202420242(1.5)(1)3⎛⎫-⨯⨯- ⎪⎝⎭的结果为（） A ．23B ．23-C ．32D ．32-9．已知13x x -=，则221x x+的值为（） A ．2B ．4C ．6D ．1110．某商品进价为900元，出售时标价为1100元，后由于商品积压，商店准备打折销售，但要保证利润率不低于10%，则至多可打（） A ．六折B ．七折C ．八折D ．九折二、填空题（本大题共5小题，共15.0分）119______． 12．若多项式216xkx -+是一个完全平方式，则常数k =______．13．一个正数的平方根是2a +和217a -，那么这个数是______． 14．已知不等式组321x x a +≥⎧⎨-<⎩无解，则a 的取值范围是______．15．若22330,1030xy ==，则11x y+=______．三、计算题（本大题共2小题，共8．0分）16．计算22011(3)23-⎛⎫⎛⎫-+-- ⎪ ⎪⎝⎭⎝⎭17．计算()()235423x y x x ⎡⎤+-÷-⎢⎥⎣⎦四、解答题（本大题共6小题，共47.0分）18．（7分）先化简，再求值222()2()4xy x y x x y x ⎡⎤+-++-÷⎣⎦，其中2,2x y =-=19．（7分）解不等式组：3(2)4(1)113x x x x +≥+⎧⎪-⎨->⎪⎩，并把解集在数轴上表示出来． 20．（7分）在计算()()x a x b ++时，甲错把b 看成了4，得到结果是：2816x x ++，乙错把a 看成a -，得到结果：220xx +-（1）求出a ，b 的值（2）在（1）的条件下，计算()()x a x b ++的结果21．（8分）（1）如图是用4个全等的长方形拼成的一个“回形”正方形，图中阴影部分面积用2种方法表示可得一个等式，这个等式为_______．（2）若22(4)9,(4)169x y x y -=+=，求xy 的值．22．（8分）学校近期举办了一年一度的经典诵读比赛．某班级因节目需要，须购买A 、B 两种道具．已知购买1件A 道具比购买1件B 道具多10元，购买2件A 道具和3件B 道具共需要45元．（1）购买一件A 道具和一件B 道具各需要多少元？（2）根据班级情况，需要这两种道具共50件，且购买两种道具的总费用不超过620元．请问道具A 最多购买多少件？23．（10分）分别计算下列各式的值（1）填空：(1)(1)x x -+=______；()2(1)1x x x -++=______；()32(1)1x xx x -+++=______……由此可得()9872(1)1x x x x x x -+++⋅⋅⋅+++=______; （2）求：23910111222222++++⋅⋅⋅+++的值（3）根据以上结论：计算：234748491333333++++⋅⋅⋅+++的值2023-2024学年度第二学期期中考试七年级数学参考答案一、选择题（每小题3分，共30分）题号 1 2 3 4 5 6 7 8 9 10 答案DCAABCBDDD二、填空题（每小题3分，共15分） 11．3±12．8±13．4914．1a ≤-15．2三、计算题（本大题共2小题，共8.0分）16．解：原式1194=+-374=-．17．解：原式()()35829x yx x =+÷-569xy x =--四、解答题（本大题共8小题，共47.0分）18．解：原式222222224xy x xy y x xy x ⎡⎤=+---+-÷⎣⎦()2244x xy x =-÷12x y =-，当2,2x y =-=时，原式1(2)232=⨯--=-． 19．解()324113x x x +≥⎧⎪⎨-->⎪⎩①②解不等式①，得2x ≤，解不等式②，得1x >，所以原不等式组的解集是12x <≤．将其解集表示在数轴上如图所示：（箭头未标扣1分）20．（1）22()(4)(4)4816x a x x a x x x x ++=+++=++22()()()20x a x b x a b x ab x x -+=+-+-=+-所以48,1a a b +=-+=，解得：4,5a b == （2）2()()920x a x b x x ++=++ 21．（1）22()()4b a b a ab +--=（2）22(4)(4)16160x y x y xy +--==，10xy ∴=．22．（1）解：设购买一件A 道具需要x 元，购买一件B 道具需要y 元，依题意，得：102345x y x y -=⎧⎨+=⎩，解得：155x y =⎧⎨=⎩．答：购买一件A 道具需要15元，购买一件B 道具需要5元．（2）设购买A 道具m 件，则购买B 道具(50)m -件．依题意，得：155(50)620m m +-≤，解得：37m ≤．答：A 道具最多购买37件 23．（1）234101,1,1,1x x x x ---- （2）原式1221=-（3）原式50312-=。

人教版数学七年级下学期《期中考试题》带答案

人教版数学七年级下学期期中测试卷学校________ 班级________ 姓名________ 成绩________一、选择题1. 下列方程中,是一元一次方程的是( ) A. 2x ＝1B.120x-= C. 2x －y ＝5D. 2x ＋1＝2x2. 下列不是二元一次方程组是( )A. 14x y =⎧⎨=-⎩B. 35x y y =-⎧⎨=⎩C. 2215x y x ⎧=⎨+=⎩ D. 27x y =⎧⎨=-⎩3. 已知a<b ,则下列各式中正确的是( ) A. a<-b B. a-3<a-8C. a 2<b 2D. -3a>-3b4. 解方程1123x x --=时,去分母正确的是( ) A. 3322x x -=-B. 3622x x -=-C. 3621x x -=-D. 3321x x -=-5. 如果方程组864x y y z z x +=⎧⎪+=⎨⎪+=⎩的解使代数式kx +2y ﹣3z 的值为8,则k ＝( )A.13B. ﹣13C. 3D. ﹣36. 关于x 的不等式2x －10＞－5的最小整数解为( ) A. 3B. 2C. －2D. －37. 在数轴上表示不等式x －1＜0的解集,正确的是() AB.C.D.8. 若不等式组 x ax b ≥⎧⎨<⎩无解,则有( )A. b ＞aB. b ＜aC. b=aD. b ≤a9. 若方程组35223x y kx y k+=+⎧⎨+=⎩的解x与y的和为8,则k的值为()A. k=-2B. k=10C. k=4D. k=210. 在“五·一”黄金周期间,某超市推出如下购物优惠方案：(1)一次性购物在100元(不含100元)以内的,不享受优惠；(2)一次性购物在100元(含100元)以上,300元(不含300元)以内的,一律享受九折的优惠；(3)一次性购物在300元(含300元)以上时,一律享受八折的优惠．王茜在本超市两次购物分别付款80元、252元．如果王茜改成在本超市一次性购买与上两次完全相同商品,则应付款( )A. 332元B. 316元或332元C. 288元D. 288元或316元二、填空题11. 已知2x－3y =6,用含x代数式表示y =__________12. 已知二元一次方程组2728x yx y+=⎧⎨+=⎩,则x﹣y＝_____,x+y＝_____．13. 如果4x－5y＝0,且x≠0,那么12x5y12x5y-+的值是______.14. 如图,10块相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为x厘米和y厘米,则列出的方程组为________．15. 若不等式组12xx m<⎧⎨>-⎩恰有两个整数解,则的取值范围是__________．16. 对非负实数x“四舍五入”到个位的值记为<x>,即当n为非负整数时,若11n x<n22,则<x>＝n,如<0.46>=0,<3.67>=4．给出下列关于<x>的结论：①<1.493>=1；②<2x>=2<x>；③若1x1=42〈-〉,则实数x的取值范围是9x11≤<；④当x≥0,m为非负整数时,有m2013x=m2013x〈+〉+〈〉；⑤x y=x y〈+〉〈〉+〈〉．其中,正确结论有____(填写所有正确的序号)．三、解答题17. 计算：(1)5x﹣2＝3x+8(2)2151136 x x+--=(3)2 347 x yx y+=⎧⎨+=⎩(4)2362125x y zx y zx y z++=⎧⎪-+=-⎨⎪+-=⎩18. 解不等式(组),并将每道题的解集都在数轴上表示出来(1)5x﹣3≥13﹣3x；(2)212 324x x x x->-+⎧⎨+>⎩.19. 已知方程组x+y=3a+9?x-y=5a+1⎧⎨⎩的解为正数,求(1)a的取值范围；(2)化简|4a+5|－|a-4|.20. 已知方程组435215x ymx ny-=⎧⎨+=⎩与31153mx nyy x-=⎧⎨-=⎩有相同的解,求m、n的值．21. 一条河流上下游分别坐落A、B两个港口,一艘游轮从A港用了3小时到达B港,然后按原路返回至A 港用了4小时,已知游轮在静水中的航速为28千米/小时,求水流速度和A、B两个港口的距离22. 机械厂加工车间有27名工人,平均每人每天加工小齿轮12个或大齿轮10个,2个大齿轮和3个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大小齿轮刚好配套?23. 甲、乙两人想共同承包一项工程,甲单独做30天完成,乙单独做20天完成,合同规定15天完成,否则每超过1天罚款1 000元,甲、乙两人经商量后签订了该合同．(1)正常情况下,甲、乙两人能否履行该合同?为什么?(2)现两人合作了这项工程的75%,因别处有急事,必须调走1人,问调走谁更合适些?为什么?24. 为了更好地保护环境,某市污水处理厂决定先购买A,B两型污水处理设备共20台,对周边污水进行处理,每台A型污水处理设备12万元,每台B型污水处理设备10万元．已知2台A型污水处理设备和1台B型污水处理设备每周可以处理污水680吨,4台A型污水处理设备和3台B型污水处理设备每周可以处理污水1560吨．(1)求A、B两型污水处理设备每周每台分别可以处理污水多少吨?(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4500吨,请你列举出所有购买方案．(3)如果你是厂长,从节约资金的角度来谈谈你会选择哪种方案并说明理由?答案与解析一、选择题1. 下列方程中,是一元一次方程的是( )A. 2x＝1B. 120x-= C. 2x－y＝5 D. 2x＋1＝2x[答案]A[解析][分析]依据一元一次方程的定义解答即可．[详解]解：A、2x＝1是一元一次方程,故A正确；B、120x-=不是整式方程,故B错误；C、2x－y＝5是二元一次方程,故C错误；D、2x＋1＝2x是一元二次方程,故D错误；故选：A．[点睛]本题主要考查的是一元一次方程的定义,熟练掌握一元一次方程的概念是解题的关键．2. 下列不是二元一次方程组的是()A.14xy=⎧⎨=-⎩B.35x yy=-⎧⎨=⎩C.2215xy x⎧=⎨+=⎩D.27xy=⎧⎨=-⎩[答案]C[解析][分析]根据二元一次方程组的定义,含有两个未知数,含有每个未知数的项的次数都是1,并且一共有两个方程,像这样的方程组叫做二元一次方程组．据此对每个选项进行判断即可．[详解]A．14xy=⎧⎨=-⎩,满足二元一次方程组的定义,是二元一次方程组,故A不符合题意B．35x yy=-⎧⎨=⎩,满足二元一次方程组的定义,是二元一次方程组,故B不符合题意C ．2215x y x ⎧=⎨+=⎩,x 的次数是2,不满足二元一次方程组的定义,不是二元一次方程组,故C 符合题意 D ．27x y =⎧⎨=-⎩,满足二元一次方程组的定义,是二元一次方程组,故D 不符合题意故选：C[点睛]本题考查了二元一次方程组定义,判断一个方程组是不是二元一次方程组,必须满足方程组的每个方程都是整式方程,方程组共含有两个未知数,每个方程都是一次方程． 3. 已知a<b ,则下列各式中正确的是( ) A. a<-b B. a-3<a-8C. a 2<b 2D. -3a>-3b[答案]D [解析] [分析]根据不等式的性质,依次对每个选项进行判断．[详解]A.a<-b ,在不等式a<b 两边乘以不同的数,无法确定不等号的方向,故A 错误 B.a-3<a-8,在不等式两边减去不同的数,不等号方向无法确定,故B 错误 C.a 2<b 2,若a=-2,b=-1,a 2>b 2,故C 错误D.-3a>-3b ,在不等式a<b 两边乘以一个负数-3,不等号方向改变,故D 正确故选：D[点睛]本题考查了不等式的性质,不等式两边加(或减)同一个数(或式子),不等号的方向不变；不等式两边乘(或除以)同一个负数,不等号的方向改变． 4. 解方程1123x x --=时,去分母正确的是( ) A. 3322x x -=- B. 3622x x -=-C. 3621x x -=-D. 3321x x -=-[答案]B [解析] [分析]方程两边同时乘以各分母的最小公倍数即可去分母． [详解]解：去分母得：3x−6＝2(x−1)=2x-2, 故选B ．[点睛]本题考查解一元一次方程,在去分母时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号．5. 如果方程组864x y y z z x +=⎧⎪+=⎨⎪+=⎩的解使代数式kx +2y ﹣3z 的值为8,则k ＝( )A.13B. ﹣13C. 3D. ﹣3[答案]A [解析] [分析]解方程组,求出x ,y ,z 的值,将x ,y ,z 的值代入kx +2y ﹣3z =8中,即可求出k 的值．[详解]864x y y z z x +=⎧⎪+=⎨⎪+=⎩①②③①﹣②,得 x ﹣z ＝2④ ③+④,得 2x ＝6, 解得,x ＝3 将x ＝3代入①,得 y ＝5,将x ＝3代入③,得 z ＝1,故原方程组的解是351x y z ===，，,又∵方程组864x y y z z x +=⎧⎪+=⎨⎪+=⎩的解使代数式kx +2y ﹣3z 的值为8,∴3k +2×5﹣3×1＝8, 解得,k ＝13, 故选：A ．[点睛]本题考查了解方程组的问题,掌握解方程组的方法是解题的关键． 6. 关于x 的不等式2x －10＞－5的最小整数解为( ) A. 3 B. 2C. －2D. －3[答案]A[解析][分析]先移项合并,再系数化为1得到不等式的解,再取最小整数解即可得到答案；[详解]解：2x－10＞－5移项得：2x＞－5+10,合并得：2x＞5,系数化为1得：52 x> ,故最小的正数解为：3,故选：A；[点睛]本题主要考查了不等式的解集,并在不等式的解集里取最小整数解,熟练掌握解不等式的步骤是解题的关键；7. 在数轴上表示不等式x－1＜0的解集,正确的是()A. B. C. D.[答案]B[解析][分析][详解]解：x－1＜0的解集为x＜1,它在数轴上表示正确的是B．故选B．8. 若不等式组x ax b≥⎧⎨<⎩无解,则有()A. b＞aB. b＜aC. b=aD. b≤a [答案]D[解析]根据“同大取大；同小取小；大小小大中间找；大大小小找不到”可得：∵不等式组x ax b≥⎧⎨<⎩无解,∴b≤a, 故选D．9. 若方程组35223x y kx y k+=+⎧⎨+=⎩的解x与y的和为8,则k的值为()A. k=-2B. k=10C. k=4D. k=2 [答案]B[解析][分析]先根据方程组35223x y kx y k+=+⎧⎨+=⎩以及x与y的和为8,求解出x、y的值,再代入方程352x y k+=+求解即可得到答案．[详解]解：把方程组35223x y kx y k+=+⎧⎨+=⎩的两个方程相减得到：22x y+=,又∵x与y的和为8,∴得到方程组228x yx y+=⎧⎨+=⎩,解得：146 xy=⎧⎨=-⎩,把146xy=⎧⎨=-⎩代入方程352x y k+=+,解得：10k=,故选：B．[点睛]本题考查了二元一次方程组的解,利用方程组以及x、y的关系把x、y的值求解出来是解题的关键,在做题的过程中要灵活运用所学知识．10. 在“五·一”黄金周期间,某超市推出如下购物优惠方案：(1)一次性购物在100元(不含100元)以内,不享受优惠；(2)一次性购物在100元(含100元)以上,300元(不含300元)以内的,一律享受九折的优惠；(3)一次性购物在300元(含300元)以上时,一律享受八折的优惠．王茜在本超市两次购物分别付款80元、252元．如果王茜改成在本超市一次性购买与上两次完全相同的商品,则应付款( )A. 332元B. 316元或332元C. 288元D. 288元或316元[答案]D[解析]第二次付款252元的商品的标价为x元根据题意得：0.9x=252或0.8x=252,解得：x=280或315,∴两次所购商品总价为360元或395元,∴360×0.8=288,395×0.8=316．故选D．二、填空题11. 已知2x－3y =6,用含x的代数式表示y =__________[答案]26 3 x-[解析][分析]先移项,再化系数为1即可．[详解]解：移项得,-3y=6-2x,系数化为1得,y =26 3x-.故答案为26 3x-.[点睛]本题考查的是解二元一次方程,根据题意把原式化为y=263x-的形式是解答此题的关键．12. 已知二元一次方程组2728x yx y+=⎧⎨+=⎩,则x﹣y＝_____,x+y＝_____．[答案](1). -1 (2). 5[解析][分析]利用加减法①-②,再①+②即可得出结论[详解]解：2728 x yx y+=⎧⎨+=⎩①②①-②得x﹣y＝-1①+②得3(x+y)＝15,则x+y＝5故答案为：-1,5[点睛]本题考查了加减法解二元一次方程组,熟练掌握方法是解题的关键13. 如果4x －5y ＝0,且x≠0,那么12x 5y 12x 5y -+的值是______. [答案]12 [解析][分析]由4x-5y=0,可得5y=4x ,然后将4x 代换5y ,即可求得答案．[详解]∵4x-5y=0,∴5y=4x ,∴125125x y x y -+=124124x x x x -+=816x x =12, 故答案为12 [点睛]此题考查了分式的化简求值问题．注意整体思想的应用是关键．14. 如图,10块相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为x 厘米和y 厘米,则列出的方程组为________．[答案]2753x y x y +=⎧⎨=⎩[解析][分析]根据图示可得：大长方形的长可以表示为x+2y ,长又是75厘米,故x+2y=75,长方形的宽可以表示为2x ,或x+3y ,故2x=3y+x ,整理得x=3y ,联立两个方程即可．[详解]解：根据图示可得大长方形的长可以表示为x+2y ,长又是75厘米,故x+2y=75,长方形的宽可以表示为2x ,或x+3y ,故2x=3y+x ,整理得x=3y ,联立两个方程得到：2753x y x y +=⎧⎨=⎩, 故答案为：2753x y x y +=⎧⎨=⎩[点睛]此题主要考查了由实际问题抽象出二元一次方程组,关键是看懂图示,分别表示出长方形的长和宽．15. 若不等式组12x x m <⎧⎨>-⎩恰有两个整数解,则的取值范围是__________． [答案]01m ≤<[解析][分析]先求出不等式的解集,根据题意得出关于m 的不等式组,求出关于m 的不等式组的解集即可.[详解]解得不等式组12x x m <⎧⎨>-⎩的解集为21m x , 又∵不等式组12x x m <⎧⎨>-⎩恰有两个整数解, ∴221m ,解得：01m ≤<故答案为01m ≤<[点睛]本题主要考查对不等式组求解知识点的掌握,通过原不等式组有两个整数解,得出关于m 的不等式组为解题关键.16. 对非负实数x“四舍五入”到个位的值记为<x>,即当n 为非负整数时,若11nx <n 22,则<x>＝n ,如<0.46>=0,<3.67>=4．给出下列关于<x>的结论：①<1.493>=1；②<2x>=2<x>； ③若1x 1=42〈-〉,则实数x 的取值范围是9x 11≤<；④当x≥0,m 为非负整数时,有m 2013x =m 2013x 〈+〉+〈〉；⑤x y =x y 〈+〉〈〉+〈〉．其中,正确的结论有____(填写所有正确的序号)．[答案]①③④．[解析]①根据定义,∵0.5 1.493 1.5≤<,∴<1.493>=1．结论正确．②用特例反证：∵<1.3>=1,<2×1.3>=<2.6>=3,∴<2×1.3>≠2<1.3>．∴<2x>=2<x>不一定成立．结论错误．③若1x 1=42〈-〉,则11191114x 14x 9x 11222222-≤-<+⇒≤<⇒≤<． ∴实数x 的取值范围是9x 11≤<．结论正确．④设2013x＝k＋b,k为2013x的整数部分,b为其小数部分,1)当0≤b＜12时,<2013x>＝k,m＋2013x＝(m＋k)＋b,m＋k为m＋2013x的整数部分,b为其小数部分,< m＋2013x>＝m＋k, ∴< m＋2013x >＝m＋<2013x>．2)当b≥12时,<2013x>＝k＋1,则m＋2013x＝(m＋k)＋b,m＋k为m＋2013x的整数部分,b为其小数部分,< m＋2013x >＝m＋k＋1, ∴< m＋2013x >＝m＋<2013x>综上：当x≥0,m为非负整数时,< m＋2013x >＝m＋<2013x>成立．结论正确．⑤用特例反证：：<0.6>＋<0.7>＝1＋1＝2,而<0.6＋0.7>＝<1.3>＝1,∴<0.6>＋<0.7>≠<0.6＋0.7>．∴x y=x y〈+〉〈〉+〈〉不一定成立．结论错误．综上所述,正确的结论有①③④．三、解答题17. 计算：(1)5x﹣2＝3x+8(2)2151136 x x+--=(3)2 347 x yx y+=⎧⎨+=⎩(4)2362125x y zx y zx y z++=⎧⎪-+=-⎨⎪+-=⎩[答案](1)x=5；(2)x＝﹣3；(3)11xy=⎧⎨=⎩；(4)211xyz=⎧⎪=⎨⎪=-⎩[解析][分析](1)先移项合并,再系数化为1即可得到答案；(2)先去分母,再取括号移项,合并同类项后系数化为一即可得到答案；(3先把不等式组的第一个式子×3,再用第二个式子－第一个式子,即可求解；(4)先把不等式组的第一第三个式子相加,消去z,再消去x,系数化为1得到y的值,再分别求解x、z即可得到答案；[详解]解：(1)5x﹣2＝3x+8, 移项得：5x﹣3x＝8+2,合并同类项得：2x＝10,系数化为1得：x＝5；(2)2151136x x+--=,去分母,方程的两边同时乘以6得：2(2x+1)﹣6＝5x﹣1, 去括号得：4x+2﹣6＝5x﹣1,移项得：4x﹣5x＝﹣1+6﹣2,合并同类项得：﹣x＝3,系数化为1得：x＝﹣3；(3)2 347 x yx y+=⎧⎨+=⎩①②①×3得:3x+3y=6③②-3得：y=1把y=1代入①得x=1即不等式组的解为：11 xy=⎧⎨=⎩(4)2362125x y zx y zx y z++=⎧⎪-+=-⎨⎪+-=⎩①②③③+①得,3x+5y=11④,③×2+②得,3x+3y=9⑤,④﹣⑤得2y=2,y=1,将y=1代入⑤得,3x=6,解得：x=2,将x=2,y=1代入①得,z=6﹣2×2﹣3×1=﹣1,∴方程组的解为211 xyz=⎧⎪=⎨⎪=-⎩；[点睛]本题主要考查了解方程、分式方程、二元一次方程组、三元一次方程组,学会通分是解分式方程的关键,学会消元是解二元一次方程组以及三元一次方程组的关键；18. 解不等式(组),并将每道题的解集都在数轴上表示出来(1)5x﹣3≥13﹣3x；(2)212 324x x x x->-+⎧⎨+>⎩.[答案](1)x≥2,数轴表示见解析；(2)﹣1＜x＜2,数轴表示见解析．[解析][分析]1通过移项、合并同类项、系数化为1,求出其解；(2)把不等式组中的两个不等式分别通过移项、合并同类项、系数化为1,求出不等式的解,再根据不等式组解集的口诀：大小小大中间找,来求出不等式组的解,并把它表示在数轴上．[详解](1)5x﹣3≥13﹣3x,5x+3x≥13+3,8x≥16,x≥2,解集在数轴上如下图：(2)212324x xx x->-+⎧⎨+>⎩①②,解不等式①得：x＞﹣1,解不等式②得：x＜2,故原不等式组的解集为﹣1＜x＜2．解集在数轴上如下图：点睛]主要考查了一元一次不等式组解集的求法,利用不等式组解集的口诀：同大取大,同小取小,大小小大中间找,大大小小找不到(无解),来求不等式组的解；另外还考查了不等式的解集在数轴上表示出来的方法(＞,≥向右画；＜,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集．19. 已知方程组x+y=3a+9?x-y=5a+1⎧⎨⎩的解为正数,求(1)a的取值范围；(2)化简|4a+5|－|a-4|[答案](1)544a-<<；(2)5a+1．[解析][分析](1)首先解方程组求得方程组的解,在根据条件得到不等式组,即可求得a的范围；(2)根据正数的绝对值是正数,负数的绝对值是它的相反数即可去掉绝对值符号,化简．[详解]解：(1)解方程组得：454x ay a+⎧⎨-⎩＝＝,根据题意得：450 40aa+⎧⎨-⎩＞＞,解得：54 4a-<<.(2)4a+5＞0,a-4＜0,∴|4a+5|-|a-4|=4a+5-(4-a)=5a+1．[点睛]本题主要考查解二元一次方程组和一元一次不等式及绝对值的性质,根据题意列出关于a的不等式组是解题的关键．20. 已知方程组435215x ymx ny-=⎧⎨+=⎩与31153mx nyy x-=⎧⎨-=⎩有相同的解,求m、n的值．[答案]41 mn=⎧⎨=-⎩[解析][分析]根据方程组解相同,先重新联立关于x、y的方程组,解得x、y的值,进而可得关于m,n的方程组,根据解方程组可得答案．[详解]解：由题意,得435 53x yy x-=⎧⎨-=⎩,解得21 xy=⎧⎨=⎩,把21xy=⎧⎨=⎩代入215311mx nymx ny+=⎧⎨-=⎩,得4152311m n m n +=⎧⎨-=⎩, 解得41m n =⎧⎨=-⎩,答：m 的值为4,n 的值为-1．[点睛]本题考查了二元一次方程组的解,利用方程组的解相同得出关于m ,n 的方程组是解题关键． 21. 一条河流上下游分别坐落A 、B 两个港口,一艘游轮从A 港用了3小时到达B 港,然后按原路返回至A 港用了4小时,已知游轮在静水中的航速为28千米/小时,求水流速度和A 、B 两个港口的距离[答案]水流速度4千米/小时距离为96千米[解析][分析]设水流的速度为x 千米/小时,A 、B 两个港口的距离为y 千米,则顺流速度为(28+x )千米/小时,逆流的速度为(28-x )千米/小时,根据顺流3小时的行程等于A 、B 两港口的距离和逆流4小时的行程等于A 、B 两港口的距离列出方程组求解即可．[详解]解：设水流的速度为x 千米/小时,A 、B 两个港口的距离为y 千米,根据题意得：3(28)4(28)x y x y+=⎧⎨-=⎩, 解得：496x y =⎧⎨=⎩．答：水流速度4千米/小时 A 、B 两港口的距离为96千米．[点睛]本题考查了二元一次方程组的应用,根据题意找出相等关系列出方程组是解决此题的关键． 22. 机械厂加工车间有27名工人,平均每人每天加工小齿轮12个或大齿轮10个,2个大齿轮和3个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大小齿轮刚好配套?[答案]安排12名工人加工大齿轮,安排15名工人加工小齿轮．[解析][分析]设生产大齿轮的人数为x ,则生产小齿轮的人数为27-x ,再由两个大齿轮与三个小齿轮配成一套列出比例式,求出x 的值即可．[详解]设需安排x 名工人加工大齿轮,安排(27﹣x)名工人加工小齿轮,依题意得：12272103x x ⨯⨯=⨯（﹣）解得x=12,则27-x=15．答：安排12名工人加工大齿轮,安排15名工人加工小齿轮．[点睛]本题考查的知识点是简单的工程问题,解题关键是根据所给条件列出关于x的关系式,求出未知数的值．23. 甲、乙两人想共同承包一项工程,甲单独做30天完成,乙单独做20天完成,合同规定15天完成,否则每超过1天罚款1 000元,甲、乙两人经商量后签订了该合同．(1)正常情况下,甲、乙两人能否履行该合同?为什么?(2)现两人合作了这项工程的75%,因别处有急事,必须调走1人,问调走谁更合适些?为什么?[答案](1) 两人能履行合同．(2) 调走甲合适．[解析]试题分析：(1)设甲乙合作需要x天完成,建立方程求出合作时间,再与15进行比较可以得出结论；(2)先求出完成75%需要的时间,再求出完成剩余工作量所用的时间及完成剩余工作量的工作效率,然后与甲、乙独自完成这项工作的工作效率进行比较,可以求出结论．试题解析：(1)能履行合同．设甲、乙合作x天完成,则有(＋)x＝1,解得x＝12＜15.因此两人能履行合同．(2)由(1)知,二人合作完成这项工程的75%需要的时间为12×75%＝9(天)．剩下6天必须由某人做完余下的工程,故他的工作效率为25%÷6＝,因为＜＜,故调走甲合适．24. 为了更好地保护环境,某市污水处理厂决定先购买A,B两型污水处理设备共20台,对周边污水进行处理,每台A型污水处理设备12万元,每台B型污水处理设备10万元．已知2台A型污水处理设备和1台B型污水处理设备每周可以处理污水680吨,4台A型污水处理设备和3台B型污水处理设备每周可以处理污水1560吨．(1)求A、B两型污水处理设备每周每台分别可以处理污水多少吨?(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4500吨,请你列举出所有购买方案．(3)如果你是厂长,从节约资金的角度来谈谈你会选择哪种方案并说明理由?[答案](1)A型污水处理设备每周每台可以处理污水240吨,B型污水处理设备每周每台可以处理污水200吨；(2)第一种方案：当a=13时,20-a=7,即购买A型污水处理设备13台,购买B型污水处理设备7台；第二种方案：当a=14时,20-a=6,即购买A型污水处理设备14台,购买B型污水处理设备6台；第三种方案；当a=15时,20-a=5,即购买A型污水处理设备15台,购买B型污水处理设备5台；(3)选择第一种方案所需资金最少,最少是226万元．[解析][分析](1)根据2台A 型污水处理设备和1台B 型污水处理设备每周可以处理污水680吨,4台A 型污水处理设备和3台B 型污水处理设备每周可以处理污水1560吨,可以列出相应的二元一次方程组,从而解答本题；(2)、(3)根据题意可以列出相应的不等式组,从而可以得到购买方案,从而可以算出每种方案购买资金,从而可以解答本题．[详解](1)设A 型污水处理设备每周每台可以处理污水x 吨,B 型污水处理设备每周每台可以处理污水y 吨,由题意,得2x y 6804x 3y 1560+=⎧+=⎨⎩, 解得,{x 240y 200==即A 型污水处理设备每周每台可以处理污水240吨,B 型污水处理设备每周每台可以处理污水200吨；(2)设购买A 型污水处理设备a 台,则购买B 型污水处理设备(20-a )台,则()()12a 1020a 230240a 20020a 4500+-≤⎧⎪+-≥⎨⎪⎩, 解得,12.5≤x≤15,第一种方案：当a=13时,20-a=7,即购买A 型污水处理设备13台,购买B 型污水处理设备7台；第二种方案：当a=14时,20-a=6,即购买A 型污水处理设备14台,购买B 型污水处理设备6台；第三种方案；当a=15时,20-a=5,即购买A 型污水处理设备15台,购买B 型污水处理设备5台；(3)如果我是厂长,从节约资金的角度考虑,我会选择第一种方案,即购买A 型污水处理设备13台,购买B 型污水处理设备7台；因为第一种方案所需资金：13×12+7×10=226万元；第二种方案所需资金：14×12+6×10=228万元；第三种方案所需资金：15×12+5×10=230万元； ∵226＜228＜230,∴选择第一种方案所需资金最少,最少是226万元．[点睛]本题考查一元一次不等式组的应用、二元一次方程组的应用,解题的关键是明确题意,找出所求问题需要的条件．。

七年级数学下册期中考试题【含答案】

七年级数学下册期中考试题【含答案】班级：姓名：一、选择题（本大题共10小题，每题3分，共30分）1．方程13153520052007x x x x ++++=⨯的解是x ＝（） A ．20062007 B ．20072006 C ．20071003D ．10032007 2．如图，将长方形纸片ABCD 折叠，使边DC 落在对角线AC 上，折痕为CE ，且D 点落在对角线D ′处．若AB=3，AD=4，则ED 的长为A ．32B ．3C ．1D ．433．若整数x 满足5+19≤x ≤45+2，则x 的值是（）A ．8B ．9C ．10D ．114．若关于x 的方程230m mx m --+=是一元一次方程，则这个方程的解是（）A ．0x =B ．3x =C ．3x =-D ．2x =5．如图，四边形ABCD 内接于⊙O ，点I 是△ABC 的内心，∠AIC=124°，点E 在AD 的延长线上，则∠CDE 的度数为（）A ．56°B ．62°C ．68°D ．78°6．实数a ，b 在数轴上的对应点的位置如图所示，把﹣a ，﹣b ，0按照从小到大的顺序排列，正确的是（）A ．﹣a ＜0＜﹣bB ．0＜﹣a ＜﹣bC ．﹣b ＜0＜﹣aD ．0＜﹣b ＜﹣a7．如图，下列各三角形中的三个数之间均具有相同的规律，根据此规律，最后一个三角形中y 与n 之间的关系是（）A ．y=2n+1B ．y=2n +nC ．y=2n+1+nD ．y=2n +n+18．若0ab <且a b >，则函数y ax b =+的图象可能是（）A ．B ．C ．D ．9．设42-的整数部分为a ，小数部分为b ，则1a b-的值为（） A ．2- B ．2 C ．212+ D ．212- 10．下列四个不等式组中，解集在数轴上表示如图所示的是（）A ．23x x ≥⎧⎨>-⎩B ．23x x ≤⎧⎨<-⎩C ．23x x ≥⎧⎨<-⎩D ．23x x ≤⎧⎨>-⎩二、填空题（本大题共6小题，每小题3分，共18分）1．已知直角三角形的两边长分别为3、4．则第三边长为________．2．如果22(1)4x m x +-+是一个完全平方式，则m =__________．3．如图所示，在等腰△ABC 中，AB=AC ，∠A=36°，将△ABC 中的∠A 沿DE 向下翻折，使点A 落在点C 处．若3BC 的长是________．4．若216x mx++是一个完全平方式，则m=________5．有三个互不相等的整数a,b,c，如果abc=4，那么a+b+c=__________ 6．如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法，其理由是__________．三、解答题（本大题共6小题，共72分）1．解方程：53211 64x x---=2．已知关于x、y的二元一次方程组352{2718 x y a x y a-=+=-（1）若x，y的值互为相反数，求a的值；（2）若2x＋y＋35＝0，解这个方程组．3．如图，ABC中，点E在BC边上，AE AB=，将线段AC绕点A旋转到AF 的位置，使得CAF BAE∠=∠，连接EF，EF与AC交于点G(1)求证：EF BC=；(2)若65ABC∠=︒，28ACB∠=︒，求FGC∠的度数.4．如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC 边上，且BE=BD，连结AE、DE、DC①求证：△ABE≌△CBD；②若∠CAE=30°，求∠BDC的度数．5．为了解某市市民“绿色出行”方式的情况，某校数学兴趣小组以问卷调查的形式，随机调查了某市部分出行市民的主要出行方式（参与问卷调查的市民都只从以下五个种类中选择一类），并将调查结果绘制成如下不完整的统计图．种类 A B C D E出行方式共享单车步行公交车的士私家车根据以上信息，回答下列问题：（1）参与本次问卷调查的市民共有人，其中选择B类的人数有人；（2）在扇形统计图中，求A类对应扇形圆心角α的度数，并补全条形统计图；（3）该市约有12万人出行，若将A，B，C这三类出行方式均视为“绿色出行”方式，请估计该市“绿色出行”方式的人数．6．食品安全是老百姓关注的话题，在食品中添加过量的添加剂对人体有害，但适量的添加剂对人体无害且有利于食品的储存和运输．某饮料加工厂生产的A，B两种饮料均需加入同种添加剂，A饮料每瓶需加该添加剂2克，B饮料每瓶需加该添加剂3克，已知270克该添加剂恰好生产了A，B两种饮料共100瓶，问A，B两种饮料各生产了多少别瓶？参考答案一、选择题（本大题共10小题，每题3分，共30分）1、C2、A3、C4、A5、C6、C7、B8、A9、D10、D二、填空题（本大题共6小题，每小题3分，共18分）1、52、-1或334、±85、-1或-46、同位角相等，两直线平行．三、解答题（本大题共6小题，共72分）1、154x=．2、（1）a的值是8；（2）这个方程组的解是17 {1xy=-=-．3、(1)略；(2)78°.4、①略；②∠BDC＝75°．5、（1）800，240；（2）补图见解析；（3）9.6万人．6、A饮料生产了30瓶，B饮料生产了70瓶.。

陕西省西安未央区经开第一学校2023-2024学年七年级下学期期中数学试题(含解析)

2023-2024学年度第二学期期中质量检测七年级数学试卷（考试时间：100分钟分值：120分）一、选择题（共10小题，每小题3分，计30分．每小题只有一个选项是符合题意的）1．下列计算中，正确的是（）A ．326a a a ⋅=B ．22122a a -=C ．633422a a a ÷=D ．224a a a +=2．下列不能用平方差公式计算的是（）A ．()()x y x y +-B ．()()x y x y -+-C ．()()x y x y -+--D ．()()x y x y -++3．俗话说：“水滴石穿”，水滴不断地落在一块石头的同一个位置，经过几年后，石头上形成了一个深度为0.0039的小洞，数据0.0039用科学记数法表示为（）A ．33.910-⨯B ．33910-⨯C ．20.3910-⨯D ．23910-⨯4．如图，直线a ∥b ，直角三角板ABC 的直角顶点C 在直线b 上，若∠1＝55°，则∠2＝( )A ．55°B ．45°C ．35°D ．25°5．如图在边长为a 的正方形中挖掉一个边长为b 的小正方形(a ＞b )．把余下的部分剪拼成一个长方形，通过计算阴影部分的面积，验证了一个等式，则这个等式是( )A ．a 2﹣2ab +b 2＝(a ﹣b )2B ．a 2﹣ab ＝a (a ﹣b )C ．a 2﹣b 2＝(a ﹣b )2D ．a 2﹣b 2＝(a +b )(a ﹣b )6．如果一盒圆珠笔有12支，售价18元，用y （元）表示圆珠笔的售价，x 表示圆珠笔的支数，那么y 与x 之间的解析式为（）.A ．32y x =B ．23y x =C ．12y x =D ．18=y x7．车库的电动门栏杆如图所示，BA 垂直于地面AE 于A ，CD 平行于地面AE ，则∠ABC +∠BCD 的大小是（）A ．150︒B ．180︒C ．270︒D ．360︒8．小明一家自驾车到离家500km 的某景点旅游，出发前将油箱加满油．下表记录了行驶路程()km x 与油箱余油量()L y 之间的部分数据：行驶路程()km x 050100150200…油箱余油量()L y 4541373329…下列说法不正确的是（）A ．该车的油箱容量为45LB ．该车每行驶100km 耗油8LC ．油箱余油量()L y 与行驶路程()km x 之间的关系式为458y x=-D ．当小明一家到达景点时，油箱中剩余5L 油9．（x －m ）2＝x 2＋nx ＋36，则n 的值为（）A ．12B ．－12C ．－6D ．±1210．如图，两个正方形的边长分别为a ，b ，且满足10a b +=，12ab =，图中阴影部分的面积为（）A ．100B ．32C ．144D ．36二、填空题（共6小题，每小题3分，计18分）11．比较大小：334 443．12．如图，直线AB 与直线EF 相交于点O ，CD AB OG ⊥，平分EOB ∠，若60AOF ∠=︒，则DOG ∠的度数为．13．在三角形ABC 中，90BAC ∠=︒，AD BC ⊥垂足为D ，则有=B CAD ∠∠，其理由是．14．若()()23x m x x n +-+的展开式中不含x 项、2x 项（,m n 为常数），则m n ⋅= ．15．一个角的补角比它的余角的3倍少20︒，这个角的度数是度．16．南宋数学家杨辉在其著作《详解九章算法》中揭示了()n a b +（n 为非负整数）展开式的项数及各项系数的有关规律如下，后人也将右表称为“杨辉三角”．当代数式43242644816a a a a +⨯+⨯+⨯+的值为1时，则a 的值为．三、解答题（共8小题，计72分）17．计算下列各题：(1)20211( 2.74)()3π--+-+；(2)23332(3)(4)a a a a --⋅+；(3)2(5)(2)(3)x x x ----；(4)()()a b c a b c +-++．18．利用整式乘法公式计算(1)3994011⨯+(2)210319．如图，已知三角形ABC ，点P 是AB 边上一点，利用尺规在AC 上求作一点Q ，使PQ BC ∥（不写作法，保留作图痕迹）．20．先化简，再求值：()()()()222222x y x y x y y y ⎡⎤---+-÷-⎣⎦；其中2x =-，1y =．21．如图，若AB DE ∥，180A D ∠+∠=︒，求证：AC DF ∥．（请补全下面的解答过程，括号内填写依据）证明：∵AB DE ∥，A ∴∠= ① （ ② ）180A D ∠+∠=︒ （ ③ ）D ∴∠+ ④ 180=︒（ ⑤ ）AC DF ∴∥（ ⑥ ）22．动点H 以每秒1cm 的速度沿图1中的长方形ABCD 按从A B C D ---的路径匀速运动，相应的三角形HAD 的面积()2cm S 与时间()s t 的关系图象如图2，已知4cm AD =，设点H 的运动时间为t 秒．(1)AB =______，=a ______，b =______；(2)当三角形HAD 的面积为28cm 时，求点H 的运动时间t 的值．23．“数形结合”是一种非常重要的研究数学问题的思想方法．结合图形我们可以通过两种不同的方法计算面积，从而可以得到一个数学等式．(1)如图1，用两种不同的方法计算阴影部分的面积，可以得到的数学等式是______．(2)我们可以利用（1）中的关系进行求值，则3a b +=-．则227a b +=，ab =______；(3)小玲想利用图2中x 张A 纸片，y 张B 纸片，z 张C 纸片拼出一个面积为()()3a b a b ++的大长方形，则x y z ++=______；(4)如图3，已知正方形ABCD 的边长为x ，,E F 分别是AD DC 、上的点，且1AE =，3CF =，长方形EMFD 的面积是24，分别以MF DF 、为边作正方形，求阴影部分的面积．24．如图，已知AB CD ∥，E F 、分别在AB CD 、上，点P 在AB CD 、之间，连接PE PF 、．(1)如图1，若50AEP ∠=︒，20CFP ∠=︒，则EPF ∠=______；(2)如图2，点G 是AB CD 、之间另外一点，40BEG ∠=︒且EP 平分BEG ∠，FP 平分DFG ∠：①若GE GF ⊥，求P ∠的度数；②如图3，在CD 的下方有一点,Q EG 平分BEQ ∠，FD 平分GFQ ∠，求2Q P ∠+∠的度数．参考答案与解析1．C【分析】本题考查了同底数幂的乘法，负整数指数幂，单项式除以单项式，合并同类项．根据同底数幂的乘法，负整数指数幂，单项式除以单项式，合并同类项法则分别计算判断即可．【详解】解：A 、3256a a a a ⋅=≠，故此选项不符合题意；B 、2222122a a a-=≠，故此选项不符合题意；C 、633422a a a ÷=，故此选项符合题意；D 、22242a a a a +=≠，故此选项不符合题意；故选：C ．2．B【分析】本题考查平方差公式：()()22a b a b a b +-=-，解题的关键是掌握平方差公式的结构特征：左边是两个二项式相乘，且两个二项式中有一项相同，另一项互为相反数；右边是两项的平方差（相同项的平方减去相反项的平方）；公式中的a 和b 可以是单项式，也可以是多项式．据此依次对各选项逐一分析即可作出判断．【详解】解：A ．()()22x y x y x y +-=-，能用平方差公式计算，故此选项不符合题意；B ．()()()()222x y x y x y x y x xy y -+-=---=-+-，不能用平方差公式计算，故此选项符合题意；C ．()()()2222x y x y x y x y -+--=--=-，能用平方差公式计算，故此选项不符合题意；D ．()()()()22x y x y y x x y y x -++=-+=-，能用平方差公式计算，故此选项不符合题意．故选：B ．3．A【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为10n a -⨯，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数n 由原数左边起第一个不为零的数字前面的0的个数所决定．【详解】解：30.0039 3.910-=⨯，故选：A ．【点睛】本题考查了用科学记数法表示较小的数，一般形式为10n a -⨯，其中110a ≤<，n 为由原数左边起第一个不为零的数字前面的0的个数所决定．4．C【分析】先由平行线的性质求出∠3，再由直角和角的和差关系求出∠2．【详解】解：∵a ∥b ，∴∠1=∠3．∵∠1=55°，∴∠3=55°．∵∠2+∠3=∠ACB =90°，∴∠2=90°-∠3=35°．故选：C ．【点睛】本题主要考查了平行线的性质，掌握“两直线平行，同位角相等”是解决本题的关键．5．D【分析】这个图形变换可以用来证明平方差公式：已知在左图中，大正方形减小正方形剩下的部分面积为a 2﹣b 2；因为拼成的长方形的长为(a +b )，宽为(a ﹣b )，根据“长方形的面积＝长×宽”代入为：(a +b )×(a ﹣b )，因为面积相等，进而得出结论．【详解】解：由图可知，大正方形减小正方形剩下的部分面积为：a 2﹣b 2；拼成的长方形的面积为：(a+b)×(a﹣b)，所以得出：a2﹣b2＝(a+b)(a﹣b)，故选：D．【点睛】此题主要考查了平方差公式的几何背景，解题的关键是求出第一个图的阴影部分面积，进而根据长方形的面积计算公式求出拼成的长方形的面积，根据面积不变得出结论．6．A【分析】首先求出每支平均售价，即可得出y与x之间的关系．【详解】∵每盒圆珠笔有12支，售价18元，∴每只平均售价为：1812=1.5（元），∴y与x之间的关系是：32y x ，故选：A．【点睛】此题主要考查了列函数关系式，求出圆珠笔的平均售价是解题关键．7．C【分析】过B作BF∥AE，则CD∥BF∥AE．根据平行线的性质即可求解．【详解】解：过B作BF∥AE，则CD∥BF∥AE．∴∠BCD+∠1=180°；又∵AB⊥AE，∴AB⊥BF．∴∠ABF=90°．∴∠ABC+∠BCD=90°+180°=270°故选C．【点睛】本题主要考查了平行线的性质，两直线平行，同旁内角互补．正确作出辅助线是解题的关键．8．C【分析】根据表格中信息逐一判断即可．【详解】解：A、由表格知：行驶路程为0km时，油箱余油量为45L，故A正确，不符合题意；B 、0——100km 时，耗油量为45378L -= ；100——200km 时，耗油量为37298L -= ；故B 正确，不符合题意；C 、有表格知：该车每行驶50km 耗油4L ，则∴44550y x =-，故C 错误，符合题意；D 、当500x = 时，44454550055050y x L =-=-⨯=，故D 正确，不符合题意，故选：C ．【点睛】本题主要考查了函数的表示方法，明确题意，弄懂表格中的信息是解题的关键．9．D【详解】222()2x m x mx m -=-+ ，（x －m ）2＝x 2＋nx ＋36，222236x mx m x nx ∴-+=++，2236,m n m -=⎧∴⎨=⎩解得：121266,1212.m m n n ==-⎧⎧⎨⎨=-=⎩⎩ 故选D.10．B【分析】用含有a 、b 的代数式表示阴影部分的面积，再根据完全平方公式进行代数式的变形，进而求出答案．【详解】解：∵两个正方形的边长分别为a ，b ，∴()2221122S a b a a b b =+--+⋅阴影2222111222a b a ab b =+---22111222a ab b =-+()2212a ab b =-+()221232a ab b ab =++-()2132a b ab ⎡⎤=+-⎣⎦，∵10a b +=，12ab =，∴原式()2110312322=⨯-⨯=．故选：B ．【点睛】本题考查完全平方公式的应用，求代数式的值．正确的表示阴影部分的面积和适当的变形，是得到正确答案的关键．11．<##小于【分析】本题主要考查了幂的乘方的逆运算，根据幂的乘方的逆运算法则得到()11333114464==，()11444113381==，据此可得答案．【详解】解；()11333114464==，()11444113381==，∵11116481<，∴334443<，故答案为：<．12．120°##120度【分析】首先垂直的定义可得90BOD ∠=︒，根据对顶角相等可得60BOE AOF ∠=∠=︒, 再根据角平分线的定义以及角的和差关系算出DOG ∠的度数.【详解】∵CD AB ⊥,∴∠90BOD =︒,∵60AOF ∠=︒,∴60BOE AOF ∠=∠=︒,∵OG 平分BOE ∠,1302BOG BOE ∴∠=∠=︒，∴3090120DOG BOG BOD ∠=∠+∠=︒+︒=︒ ，故答案为:120︒.【点睛】此题主要考查了角平分线的定义，垂线和对顶角，关键是掌握对顶角相等，垂直定义，角平分线的性质.13．同角的余角相等【分析】此题考查了直角三角形的性质．根据直角三角形的性质得出90B C ∠+∠=︒，90C CAD ∠+∠=︒，再根据同角的余角相等求解即可．【详解】解：90BAC ∠=︒ ，90B C ∴∠+∠=︒，AD BC ⊥ ，90C CAD ∴∠+∠=︒，B CAD ∴∠=∠（同角的余角相等），故答案为：同角的余角相等．14．27【分析】利用多项式乘多项式的法则对式子进行运算，再结合条件进行求解即可．【详解】解：()()23x m x x n +-+32233x x nx mx mx mn=-++-+()()3233x m x n m x mn=+-++-+∵展开式中不含x 项，2x 项，∴30n m -=，30m -+=，解得：3m =，9n =，∴3927m n ⋅=⨯=．故答案为：27．【点睛】本题主要考查多项式乘多项式，解答的关键是对相应的运算法则的掌握．15．35【分析】设这个角为x 度．根据一个角的补角比它的余角的3倍少20°，构建方程即可解决问题．【详解】解：设这个角为x 度．则180°-x=3（90°-x ）-20°，解得：x=35°．答：这个角的度数是35°．故答案为：35．【点睛】本题考查余角、补角的定义，一元一次方程等知识，解题的关键是学会用方程分思想思考问题，属于中考常考题型．16．1-或3-【分析】本题考查了多项式乘法中的规律问题．当2b =时，4432(2)426448161a a a a a +=+⨯+⨯+⨯+=，再计算求值即可．【详解】解：根据有关规律，可得，4322344()464a b a a b a b ab b +=++++，当2b =时，++++432234a 4ab 6a b 4ab b 43242644816a a a a =+⨯+⨯+⨯+4(2)a =+，43242644816a a a a +⨯+⨯+⨯+ 的值为1，4(2)1a ∴+=，即21a +=±，1a ∴=-或3-．故答案为：1-或3-．17．(1)9(2)6411a a --(3)519x -+(4)2222a b ab c ++-【分析】（1）根据乘方运算法则、零指数幂运算法则以及负整数指数幂运算法则求解，再相加减即可；（2）根据积的乘方法则、同底数幂乘法法则进行运算，再合并同类项即可；（3）根据完全平方公式以及多项式乘以多项式法则求解，再合并同类项即可；（4）根据平方差公式和完全平方公式求解即可．【详解】（1）解：原式1199=-++=；（2）解：原式64664271611a a a a a =--+=--；（3）解：原式22221025(56)102556519x x x x x x x x x =-+--+==-+-+-=-+；（4）解：原式22222()2a b c a b ab c =+-=++-．【点睛】本题主要考查了实数运算和整式运算，熟练掌握相关运算法则是解题关键．18．(1)160000(2)10609【分析】本题考查了平方差公式，完全平方公式．（1）利用平方差公式进行计算，即可解答；（2）利用完全平方公式进行计算，即可解答．【详解】（1）解：3994011⨯+(4001)(4001)1=-⨯++240011=-+160000=；（2）解：21032(1003)+=10000210039=+⨯⨯+10609=．19．见解析【分析】本题考查了尺规作图能力—过直线外一点作已知直线的平行线．过点P 作APQ B ∠=∠，与AC 交于点Q ，即可．【详解】解：如图，点Q 即为所求．．20．522x y -，7-【分析】本题考查了整式的化简求值．先根据完全平方公式，多项式乘多项式法则进行计算，再合并同类项，算除法，最后代入求出答案即可．【详解】解：()()()()222222x y x y x y y y ⎡⎤---+-÷-⎣⎦()()22222442222x xy y x xy xy y y y =-+--++-÷-()()2542xy y y =-+÷-522x y =-，当2x =-，1y =时，原式5(2)212=⨯--⨯52=--7=-．21．DPC ∠；两直线平行，同位角相等；已知；DPC ∠；等量代换；同旁内角互补，两直线平行【分析】此题考查了平行线的判定与性质．根据平行线的判定与性质求解即可．【详解】证明：∵AB DE ∥，A DPC ∴∠=∠（两直线平行，同位角相等），180A D ∠+∠=︒ （已知），180D DPC ∴∠+∠=︒（等量代换），∴AC DF ∥（同旁内角互补，两直线平行），故答案为：DPC ∠；两直线平行，同位角相等；已知；DPC ∠；等量代换；同旁内角互补，两直线平行．22．(1)5cm ，14，10(2)点H 的运动时间为4s 或10s ．【分析】本题考查了动点问题的函数图象，能结合图象得到有用条件，利用动点的运动求出相关线段是本题的解题关键．（1）根据图2函数分别分析出当点H 运动到点B 、C 、D 处的路程，求出AB ，再求出当点H 在BC 上时的面积即可；（2）当三角形HAD 的面积为28cm 时，点H 在AB 或CD 上，分别计算求出高，再依题意求出路程即可．【详解】（1）解：由图2得，当05t <≤时，S 随t 的增大而增大，∴当点H 运动到点B 时，5s =t ，5cm AB ∴=，当59<≤t 时，S 的值不变，∴当点H 运动到点C 时，9t s =，此时三角形HAD 的面积为长方形面积的一半，2110cm 2S AD AB ∴=⋅=，即10b =，当点H 运动到点D 处时，0S =，9514cm a ∴=+=，故答案为：5cm ，14，10；（2）解：当点H 在AB 上时，三角形HAD 的面积12AD AH =⋅，当28cm S =时，182AD AH ⋅=，4cm AH ∴=，4t s ∴=，当点H 在CD 上时，三角形HAD 的面积12AD DH =⋅，当28cm S =时，182AD DH ⋅=，4cm DH ∴=，1cm CH =，()10cm AB BC CH ++=10s t ∴=，综上，点H 的运动时间为4s 或10s ．23．(1)()2222a b a b ab+=+-(2)1(3)8(4)阴影部分的面积为20．【分析】（1）方法一是直接将两个正方形的面积相加，方法二是用大的正方形面积减去两个长方形的面积，即可得到等式；（2）根据（1）中得到的关系式直接代入即可得到结果；（3）根据得到的大长方形的面积展开，可以得到一个关系式，由关系式中可知道用的纸张分别是多少，计算其和即可；（4）先根据阴影部分构造出来等式，然后根据两次完全平方公式得到结果．【详解】（1）解：方法一：阴影部分是两个正方形的面积和，即22a b +；方法二：阴影部分也可以看作边长为()a b +的面积减去两个长为a ，宽为b 的长方形面积，即()22a b ab +-，两种方法可得出：()2222a b a b ab +=+-；故答案为：()2222a b a b ab +=+-；（2）解：由（1）可得()2222a b a b ab +=+-，∵3a b +=-，227a b +=，∴()2732ab =--，∴1ab =；故答案为：1；（3）解：()()222233334a b a b a ab ab b a ab b ++=+++=++，A 纸片的面积为2a ，B 纸片面积为2b ，C 纸片面积为ab ，根据2234a ab b ++可知要拼出一个面积为()()3a b a b ++的大长方形，需要3张A 纸片，1张B 纸片，4张C 纸片，则3148x y z ++=++=；故答案为：8；（4）解：由图知1ED x =-，3DF x =-，∴()()2213S x x =---阴影，∵长方形EMFD 的面积是24，∴()()1324x x --=，设1x a -=，3x b -=，则2a b -=，24ab =，由()()224a b a b ab +=-+，得()222424100a b +=+⨯=，∴10a b +=，∴()()2210220a b a b a b -=+-=⨯=，即()()221320x x ---=，∴阴影部分的面积为20．【点睛】本题考查了完全平方公式在几何图形中的应用、多项式乘多项式、完全平方公式的变形适用，熟练掌握完全平方公式是解题的关键．24．(1)70︒(2)①45︒；②120︒【分析】本题考查了平行线的性质与判定，角平分线的定义，掌握平行线的性质与判定是解题的关键．（1）作PM AB ∥，根据平行线的性质与判定，以及角平分线的定义，即可求解；（2）①作GN AB ∥，PM AB ∥，根据平行线的性质与判定，以及角平分线的定义，可得()1122EPE BEG GFD EGF ∠=∠+∠=∠，根据垂直的定义可得90EGF ∠=︒，进而即可求解；②过点Q 作QK CD ∥，设GFD QFD αÐ=Ð=，根据平行线的性质以及角平分线的定义，可得80FQE αÐ=°-，由（1）可知，240G P BEG GFD α∠=∠=∠+∠=︒+，即可求解．【详解】（1）解：作PM AB ∥，∵AB CD ∥，∴AB CD PM ∥∥，∴AEP EPM CFP FPM ∠=∠∠=∠，，∵50AEP ∠=︒，20CFP ∠=︒，∴502070EPF EPM FPM ∠=∠+∠=︒+︒=︒，故答案为：70︒；（2）解：①如图，分别过点G ，P 作GN AB ∥，PM AB ∥，∵AB CD ∥，∴AB CD GN PM ∥∥∥，∴BEG EGN BEP EPM ∠=∠∠=∠，，NGF GFD MPF PFD ∠=∠∠=∠，，EGF EGN NGF BEG GFD ∠=∠+∠=∠+∠，EPF EPM MPF BEP PFD ∠=∠+∠=∠+∠，∵EG FG ⊥，∴90EGF ∠=︒，∵EP 平分BEG ∠，FP 平分DFG ∠，∴1122BEP BEG PFD DFG ∠=∠∠=∠，，∴()114522EPE BEG GFD EGF ∠=∠+∠=∠=︒；②如图，分别过点G ，P 作GN AB ∥，PM AB ∥，过点Q 作QK CD ∥，∵AB CD ∥，∴AB CD GN PM ∥∥∥，∴,BEG EGN BEP EPM ∠=∠∠=∠，,NGF GFD MPF PFD ∠=∠∠=∠，∴EGF EGN NGF BEG GFD ∠=∠+∠=∠+∠，EPF EPM MPF BEP PFD ∠=∠+∠=∠+∠，∵EP 平分BEG ∠，FP 平分DFG ∠，∴1122BEP BEG PFD DFG ∠=∠∠=∠，，∴()1122EPF BEG GFD EGF ∠=∠+∠=∠，∵40BEG ∠=︒，EG 平分BEQ ∠，FD 平分GFQ ∠，∴40,GEQ BEG GFD QFD ∠=∠=︒∠=∠，设GFD QFD αÐ=Ð=，∵,QK CD AB CD ∥∥，∴QK AB ∥，∴280EQK BEQ BEG ∠=∠=∠=︒，FQK QFD Ð=Ð，设FQK QFD αÐ=Ð=，∴80FQE αÐ=°-，∵12EPF EGF ∠=∠，∴240EGF EPF BEG GFD α∠=∠=∠+∠=︒+，∴28040120FQE P αα∠+∠=︒-+︒+=︒．。

人教版七年级下册数学《期中考试试题》含答案解析

人教版数学七年级下学期期中测试卷学校________ 班级________ 姓名________ 成绩________一、选择题(每小题3分,共30分)1. 下列各项中,是一元一次方程的是( )A. x ﹣2y=4B. xy=4C. 3y ﹣1=4D. 144x - 2. 已知x y >,则下列不等式成立的是( ) A. 11x y -<- B. 33x y < C. x y -<- D.22x y < 3. 用“加减法”将方程组325353x y x y -=⎧⎨+=-⎩中的x 消去后得到的方程是() A. 32y = B. 78y = C. 72y -= D. 78y -= 4. 不等式组12x ≤<的解集在数轴上可表示为() A.B. C. D.5. 不等式组 26x m x x >⎧⎨-+<-⎩的解集是x 4>,那么m 的取值范围是 A. m 4≤B. m 4≥C. m 4<D. m 4= 6. 方程组23x y x y +=⎧⎨+=⎩■的解为2x y =⎧⎨=⎩■,则被遮盖的前后两个数分别为( ) A. 1、2 B. 1、5 C. 5、1 D. 2、47. 下列变形正确的是( )A 若m ＞n ,则mc ＞ncB. 若m ＞n ,则mc 2＞nc 2C. 若m ＞b ,b ＜c ,则m ＞cD. 若m+c 2＞n+c 2,则m ＞n8. 不等式组211112x x -≤⎧⎪⎨-<⎪⎩的整数解的个数为( ) A 0个 B. 2个 C. 3个 D. 无数个 9. 一件羽绒服先按成本提高50%标价,再以8折(标价的80%)出售,结果获利250元. 若设这件羽绒服的成本是x 元,根据题意,可得到的方程是A x(1+50%) 80%=x-250B. x(1+50%) 80%=x+250C. (1+50%x) 80%=x-250D. (1+50%x) 80%=250-x10. 某人要完成2.1千米的路程,并要在不超过18分钟的时间内到达,已知他每分钟走90米．若跑步每分钟可跑210米,问这人完成这段路程,至少要跑( )A. 3分钟B. 4分钟C. 4.5分钟D. 5分钟二填空题( 每小题3分,共15分)11. 把二元一次方程2x+y —3=0化成用x 表示y 的形式,则y=_____．12. x 3倍与5的和大于8,用不等式表示为________________ ．13. 已知：237x y y z x z +=⎧⎪+=⎨⎪+=⎩,则x y z ++=__________．14. 不等式1﹣2x ＜6的负整数解是___________．15. 如图,由八块相同的长方形地砖拼成一个大长方形,则每块小长方形地砖的面积是_____．三.解答题(共8小题,共75分)16. 解下列方程：(1)2(x +3)=5(x -3)2123x -（）=435x --x 17. 解二元一次方程组：27{320x y x y -=+=． 18. 解不等式223x x -≤+,并把它的解集表示在数轴上． 19. 解不等式组：{3(x 2)x 42x 13>x 1-≥-+-①②并写出它的所有的整数解．20. 已知23x y =-⎧⎨=-⎩和41x y =⎧⎨=⎩是二元一次方程35mx ny -=的两个解. (1)求、的值；(2)若x＜-2,求的取值范围.21. 已知方程组331x y ax y a+=+⎧⎨-=-⎩的解是一对正数,求的取值范围．22. 一项工程,甲队单独完成需40天,乙队单独完成需50天,现甲队单独做4天后两队合作．()1求甲、乙合作多少天才能把该工程完成．()2在()1条件下,甲队每天的施工费用为2500元,乙队每天的施工费用为3000元,求完成此项工程需付给甲、乙两队共多少元．23. 某商店需要购进甲、乙两种商品共160件,其进价和售价如下表：(注：获利＝售价－进价)(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案．答案与解析一、选择题(每小题3分,共30分)1. 下列各项中,是一元一次方程的是( )A. x ﹣2y=4B. xy=4C. 3y ﹣1=4D. 144x - [答案]C[解析][分析]根据一元一次方程的定义进行分析判断即可.[详解]A 选项中的方程24x y -=中有两个未知数,所以不是一元一次方程；B 选项中的方程4xy =中有两个未知数,所以不是一元一次方程；C 选项中的方程314y -=是一元一次方程,所以可以选C ；D 选项中的式子144x -不是方程,所以不能选D. 故选C.[点睛]熟知“一元一次方程的定义：含有一个未知数,且含未知数的项的次数都是1的整式方程叫做一元一次方程”是解答本题的关键.2. 已知x y >,则下列不等式成立的是( )A. 11x y -<-B. 33x y <C. x y -<-D. 22x y < [答案]C[解析][分析]根据不等式的性质逐项分析.[详解]A 在不等式的两边同时减去1,不等号的方向不变11x y ->-,故A 错误；B 在不等式的两边同时乘以3,不等号的方向不变33x y >,故B 错误；C 在不等式的两边同时乘以-1,不等号的方向改变,故C 正确；D 在不等式的两边同时乘以12,不等号的方向不变22x y >,故D 错误. [点睛]本题主要考查不等式的性质,(1)在不等式的两边同时加上或减去同一个数,不等号的方向不变；(2)在不等式的两边同时乘以或除以(不为零的数)同一个正数,不等号的方向不变；(3)在不等式的两边同时乘以或除以(不为零的数)同一个负数,不等号的方向改变.3. 用“加减法”将方程组325353x y x y -=⎧⎨+=-⎩中的x 消去后得到的方程是() A. 32y =B. 78y =C. 72y -=D. 78y -= [答案]D[解析][分析]根据方程组中每一个方程中未知数x 的系数可知,两方程相减即可消去x ,据此即可得.[详解]325353x y x y -=⎧⎨+=-⎩①②, ①-②,得：-7y=8,故选D.[点睛]本题考查了二元一次方程组的解法——加减法,根据方程组的特点灵活选用加减法或代入法进行求解是关键.4. 不等式组12x ≤<的解集在数轴上可表示为() A.B. C.D.[答案]C[解析] [分析]先在数轴上表示出不等式组的解集,然后再根据选项选出即可.[详解]不等式组1≤x<2的解集在数轴上可表示为：,故选C.[点睛]本题考查了在数轴上表示不等式的解集,能把不等式组的解集要数轴上表示出来是解此题的关键.5. 不等式组 26x m x x >⎧⎨-+<-⎩的解集是x 4>,那么m 的取值范围是 A. m 4≤B. m 4≥C. m 4<D. m 4=[答案]A[解析][分析]先求出不等式的解集,再根据不等式组的解集得出答案即可．[详解]解：26x m x x >⎧⎨-+<-⎩①②,解不等式②,得：x 4>,∵不等式组 26x m x x >⎧⎨-+<-⎩的解集是x 4>, ∴m 4≤故选择：A[点睛]本题考查了解一元一次不等式组,能根据不等式的解集和不等式组的解集得出关于m 的不等式是解此题的关键．6. 方程组23x y x y +=⎧⎨+=⎩■的解为2x y =⎧⎨=⎩■,则被遮盖的前后两个数分别为( ) A. 1、2B. 1、5C. 5、1D. 2、4 [答案]C[解析][分析]把x =2代入x+y=3求出y,再将x,y 代入2x+y 即可求解.[详解]根据 {x 2y ==,把x=2代入x+y=3.解得y=1.把x=2,y=1代入二元一次方程组中2x+y=5故被遮盖的两个数分别为5和1.故选C .[点睛]主要考查学生对二元一次方程组知识点的掌握．将已知解代入其中x+y=3求出y 值为解题关键. 7. 下列变形正确的是( )A. 若m ＞n ,则mc ＞ncB. 若m ＞n ,则mc 2＞nc 2C. 若m ＞b ,b ＜c ,则m ＞cD. 若m+c 2＞n+c 2,则m ＞n[答案]D[解析][分析]直接利用不等式的基本性质分别判断得出答案．[详解]A 、若m ＞n ,则mc ＞nc ,只有c 为正数时成立,故此选项错误；B 、若m ＞n ,则mc ²＞nc ²,只有c 不等于0时成立,故此选项错误；C 、若m ＞b ,b ＜c ,则m ＞c ,不一定成立,故此选项错误；D 、若m ＋c ²＞n ＋c ²,则m ＞n ,故此选项正确．故选：D ．[点睛]此题主要考查了命题与定理,正确把握不等式的基本性质是解题关键．8. 不等式组211112x x -≤⎧⎪⎨-<⎪⎩的整数解的个数为( ) A. 0个B. 2个C. 3个D. 无数个[答案]C[解析][详解]可把不等式组化为 211112x x -≤⎧⎪⎨-<⎪⎩,即21x -<≤,整数为：－1,0,1, 故答案选C.考点：不等式组的整数解.9. 一件羽绒服先按成本提高50%标价,再以8折(标价的80%)出售,结果获利250元. 若设这件羽绒服的成本是x 元,根据题意,可得到的方程是A. x(1+50%) 80%=x-250B. x(1+50%) 80%=x+250C. (1+50%x) 80%=x-250D. (1+50%x) 80%=250-x[答案]B[解析]标价为：x(1+50%),八折出售的价格为：(1+50%)x×80%, 则可列方程为：(1+50%)x×80%=x+250, 故选B ．10. 某人要完成2.1千米的路程,并要在不超过18分钟的时间内到达,已知他每分钟走90米．若跑步每分钟可跑210米,问这人完成这段路程,至少要跑( )A. 3分钟B. 4分钟C. 4.5分钟D. 5分钟[答案]B[解析][分析]设这人跑了x分钟,则走了(18-x)分钟,根据速度×时间=路程结合要在18分钟内到达,即可得出关于x的一元一次不等式,解之即可得出x的取值范围,取其中的最小值即可得出结论．[详解]解：设这人跑了x分钟,则走了(18-x)分钟,根据题意得：210x+90(18-x)≥2100,解得：x≥4,答：这人完成这段路程,至少要跑4分钟．故选：B．[点睛]本题考查了一元一次不等式的应用,根据各数量之间的关系,正确列出一元一次不等式是解题的关键．二填空题( 每小题3分,共15分)11. 把二元一次方程2x+y—3=0化成用x表示y的形式,则y=_____．[答案]3-2x．[解析][分析]题意得将原式表示成y＝ax＋b的形式．[详解]∵2x+y＝3,∴y＝3-2x,故答案为：y＝3-2x．[点睛]此题考查了解二元一次方程,解题的关键是将x看做已知数,y看做未知数.12. x的3倍与5的和大于8,用不等式表示为________________ ．x+>[答案]358[解析][分析]先表示出x的3倍,再表示出与5的和,最后根据大于8即可得不等式.[详解]x的3倍为3x,x的3倍与5的和为3x+5,所以x的3倍与5的和大于8为：3x+5>8,故答案为3x+5>8.[点睛]本题考查由实际问题抽象出一元一次不等式,根据关键语句,弄清运算的先后顺序和不等关系,从而得出不等式是关键.13. 已知：237x yy zx z+=⎧⎪+=⎨⎪+=⎩,则x y z++=__________．[答案]6[解析][分析]根据方程组的特点,三个方程相加即可求出x+y+z的值.[详解]237x yy zx z+=⎧⎪+=⎨⎪+=⎩①②③,(①+②+③)÷2,得x+y+z=6,故答案为6.[点睛]本题考查了三元一次方程组的特殊解法,根据方程组中每一个方程的系数特点确定合适的解法是关键.14. 不等式1﹣2x＜6的负整数解是___________．[答案]﹣2,﹣1[解析]试题分析：根据不等式的性质求出不等式的解集,找出不等式的整数解即可．解：1﹣2x＜6,移项得：﹣2x＜6﹣1,合并同类项得：﹣2x＜5,不等式的两边都除以﹣2得：x ＞﹣,∴不等式的负整数解是﹣2,﹣1,故答案为﹣2,﹣1．点评：本题主要考查对解一元一次不等式,一元一次不等式的整数解,不等式的性质等知识点的理解和掌握,能根据不等式的性质求出不等式的解集是解此题的关键．15. 如图,由八块相同的长方形地砖拼成一个大长方形,则每块小长方形地砖的面积是_____．[答案]675cm 2[解析][分析]假设小长方形的长、宽分别为a 、b ,通过图形中大长方形的边长关系,可列出二元一次方程组,求得a 、b 的值,进而求得面积.[详解]设小长方形的长、宽分别为acm 、bcm.由题意可列方程组：a+b=602a=a+3b ⎧⎨⎩, 解得：a=45b=15⎧⎨⎩, 每块小长方形地砖的面积：45×15＝675(cm 2), 故填：675cm 2.[点睛]本题考查二元一次方程组在几何问题中的应用,结合图形找到两组等量关系是关键.三.解答题(共8小题,共75分)16. 解下列方程：(1)2(x +3)=5(x -3)2123x -（）=435x --x [答案](1)x=7;(2)x=12. [解析][分析]按：去分母,去括号,移项,合并同类项,系数化为1等步骤解方程.[详解]解：(1)去括号,得 2x+6=5x-15移项,得2x-5x=-6-15合并同类项,得-3x=-21系数化为1,得x=7(2)去分母,得 5(2x-1) =3(4-3x) – 15x去括号,得10x – 5=12-9x-15x移项,合并同类项,得34x=17 ,系数化为1,得 x=12[点睛]本题考核知识点：解一元一次方程.解题关键点：理解解方程的一般步骤.17. 解二元一次方程组：27{320x y x y -=+=． [答案]2{3x y ==-．[解析][分析] 解此方程组利用加减消元法求出解即可．详解]解：27{320x y x y -=+=①②①×2+②得：7x=14,即x=2,把x=2代入①得：y=-3,则方程组的解为2{3x y ==-．[点睛]本题考查解二元一次方程组．18. 解不等式223x x -≤+,并把它的解集表示在数轴上． [答案]1x ≥-,数轴见解析[解析][分析]按照去分母,去括号,移项,合并同类项,系数化为1的步骤解不等式即可,然后按照大于向右画,小于向左画,有等号是实心圆点,没有等号是空心圆点即可在数轴上表示出解集．[详解]去分母得,23(2)x x -≤+,去括号得,263x x -≤+,移项得,362x x --≤-,合并同类项得,44x -≤,系数化为1得,1x≥-,数轴如图：[点睛]本题主要考查解一元一次不等式,掌握不等式的解法及用数轴表示不等式解集的方法是解题的关键．19. 解不等式组：{3(x2)x42x13>x1-≥-+-①②并写出它的所有的整数解．[答案]1、2、3[解析][分析]解一元一次不等式组,先求出不等式组中每一个不等式的解集,再利用口诀求出这些解集的公共部分：同大取大,同小取小,大小小大中间找,大大小小解不了(无解)．最后求出整数解即可．[详解]解：解不等式①得,x≥1,解不等式②得,x＜4,∴不等式组的解集是1≤x＜4．∴不等式组的所有整数解是1、2、3．[点睛]解一元一次不等式组,一元一次不等式组的整数解．20. 已知23xy=-⎧⎨=-⎩和41xy=⎧⎨=⎩是二元一次方程35mx ny-=的两个解.(1)求、的值；(2)若x＜-2,求的取值范围.[答案](1)21mn=⎧⎨=⎩(2)y<-3[解析]分析：(1)把x与y的两对值代入方程计算求出m与n的值即可；(2)由方程求出x的表达式,解不等式即可．详解：(1)把23xy=-⎧⎨=-⎩和41xy=⎧⎨=⎩代入方程得：295435m nm n-+=⎧⎨-=⎩,解得：21mn=⎧⎨=⎩；(2)当21m n =⎧⎨=⎩时,原方程变为：2x -3y =5,解得：x =532y +． ∵x ＜-2,∴532y +＜-2,解得：y ＜－3．点睛：本题考查了二元一次方程组的解,以及解一元一次不等式,熟练掌握运算法则是解答本题的关键．21. 已知方程组331x y a x y a +=+⎧⎨-=-⎩的解是一对正数,求的取值范围． [答案]1 2.2a -＜＜[解析][分析]先解方程组,再由题意列不等式组可得答案．详解]解：331x y a x y a +=+⎧⎨-=-⎩①② ①＋②得：242,x a =+21,x a ∴=+把21x a =+代入①得：2,y a =-+21,2x a y a =+⎧∴⎨=-+⎩0,0x y ⎧⎨⎩＞＞ 21020a a +⎧∴⎨-+⎩＞＞ ③④ 解③得：1,2a -＞解④得：2,a ＜不等式组的解是12.2a -＜＜ a ∴的取值范围是1 2.2a -＜＜． [点睛]本题考查的是二元一次方程组与一元一次不等式组联系,掌握其解法是解题关键．22. 一项工程,甲队单独完成需40天,乙队单独完成需50天,现甲队单独做4天后两队合作．()1求甲、乙合作多少天才能把该工程完成．()2在()1的条件下,甲队每天的施工费用为2500元,乙队每天的施工费用为3000元,求完成此项工程需付给甲、乙两队共多少元．[答案](1)甲、乙合作20天才能把该工程完成；(2)完成此项工程需付给甲、乙两队共120000元．[解析][分析](1)设甲、乙合作x天才能把该工程完成,由题意一项工程甲单独做要40天完成,乙单独做需要50天完成,可以得出甲每天做整个工程的140,乙每天做整个工程的150,根据文字表述得到题目中的相等关系是：甲完成的部分+两人共同完成的部分=1,根据等量关系列出方程,然后求解即可；(2)根据甲、乙两队工作天数以及每个队每天的施工费用,每天的施工费用×施工天数即可求得. [详解]()1设甲、乙合作x天才能把该工程完成,根据题意得：1114x1 404050⎛⎫⨯++=⎪⎝⎭,解得：x20=．答：甲、乙合作20天才能把该工程完成；()2甲队的费用为()250020460000(⨯+=元),乙队的费用为30002060000(⨯=元),6000060000120000(+=元)．答：完成此项工程需付给甲、乙两队共120000元．[点睛]本题考查了一元一次方程的应用,弄清题意,找到等量关系是解题的关键.23. 某商店需要购进甲、乙两种商品共160件,其进价和售价如下表：(注：获利＝售价－进价)(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案．[答案](1)甲种商品购进100件,乙种商品购进60件.(2)有两种购货方案,方案一:甲种商品购进66件,乙种商品购进94件;方案二:甲种商品购进67件,乙种商品购进93件.其中获利最大的是方案一.[解析][分析](1)设甲种商品购进x件,乙种商品购进y件,根据题意列出二元一次方程组即可求解；(2)设甲种商品购进a件,则乙种商品购进(160-a)件,根据题意列出不等式组,再根据实际情况进行求解.[详解]解:(1)设甲种商品购进x件,乙种商品购进y件.根据题意,得1605101100x yx y+=⎧⎨+=⎩解得100,60.xy=⎧⎨=⎩答:甲种商品购进100件,乙种商品购进60件. (2)设甲种商品购进a件,则乙种商品购进(160-a)件.根据题意,得1535(160-)4?300, 510(160-)1?260.a aa a+<⎧⎨+>⎩解不等式组,得65<a<68.∵a为非负整数,∴a取66,67.∴ 160-a相应取94,93.所以有两种购货方案,方案一:甲种商品购进66件,乙种商品购进94件;方案二:甲种商品购进67件,乙种商品购进93件.其中获利最大的是方案一.[点睛]此题主要考查不等式组的应用,解题的关键是根据题意列出方程组或不等式组进行求解.。

七年级第二学期数学期中考试试题含答案

七年级第二学期数学期中考试（考试总分：100 分）一、单选题（本题共计10小题，总分30分）1.（3分）1．医学研究发现一种新病毒的直径约为0.000043毫米，则这个数用科学记数法表示为（）A．0.43×10﹣4B．0.43×104C．4.3×10﹣5D．0.43×1052.（3分）2．观察下面图案，在（A）（B）（C）（D）四幅图案中，能通过图案（1）平移得到的是（）A．B．C．D．3.（3分）3．下列运算正确的是（）A．a4•a2＝a8B．a6÷a2＝a3C．（2ab2）2＝4a2b⁴D．（a3）2＝a54.（3分）4．下列各题可以用平方差公式计算的是（）A．（2x+y）（y﹣2x）B．（x+2）（2+x）C．（x﹣y）（﹣x+y）D．（x﹣2）（x+1）5.（3分）5．下列分解因式中，正确的是（）A．3m2﹣6m＝3m（m﹣3）B．a2b+ab+a＝a（ab+b）C．x2+y2＝（x+y）2D．﹣x2+2xy﹣y2＝﹣（x﹣y）26.（3分）6．二元一次方程5x﹣y＝2的一个解为（）A．B．C．D．7.（3分）7．如图所示，将含有30°角的三角板（∠A＝30°）的直角顶点放在相互平行的两条直线其中一条上，若∠1＝38°，则∠2的度数（）A．28°B．22°C．32°D．38°8.（3分）8．已知3a＝10，9b＝5，则3a﹣2b的值为（）A．5 B．C．D．29.（3分）9．小明到药店购买了一次性医用口罩和N95口罩共40个，其中一次性医用口罩数量比N95口罩数量的3倍多4个，设购买一次性医用口罩x个，N95口罩y个，根据题意可得方程组（）A．B．C．D．10.（3分）10．如图，从边长为（a+4）的正方形纸片中剪去一个边长为（a+1）的正方形（a＞0），剩余部分沿虚线又剪拼成一个长方形（不重叠、无缝隙），若拼成的长方形一边的长为3，则另一边的长为（）A．2a+5B．2a+8C．2a+3D．2a+2二、填空题（本题共计6小题，总分18分）11.（3分）11．计算：x（x﹣2y）＝．12.（3分）12．如图，直线a∥b，直线c与直线a、b相交，∠1＝135°，∠2＝．13.（3分）13．已知是二元一次方程7x+2y＝10的一组解，则m的值是．14.（3分）14．若关于x，y的二元一次方程组，则x+y＝．15.（3分）15．如图，将△ABC沿BC方向平移至△DEF处，若EC＝2BE＝4，则CF的长为．16.（3分）16．（x﹣a）（x2+ x +b）的结果中不含x的一次项，则a-b的值是．三、解答题（本题共计8小题，总分52分）17.（6分）17．（6分）计算：（1）（﹣2）2﹣20200+3﹣2；（2）2x3y2•（﹣9x2）÷（6x4y）．18.（6分）18．（6分）如图所示，已知AD∥BC，BE平分∠ABC，∠A＝110°．求∠ADB的度数．19.（6分）19．（6分）如图，点M是△ABC外的一点，请你在网格内完成作图：（1）作过点M且平行于BC的直线．（2）画出△ABC先向左平移2个单位，再向上平移1个单位后的△A'B'C'．20.（6分）20．（6分）解方程：（1）（2）21.（6分）21．（6分）先化简再求值：[（2x+y）（2x﹣y）﹣（2x﹣3y）2]÷（﹣2y），其中x＝1，y＝﹣2．22.（6分）22．（6分）“脐橙结硕果，香飘引客来”，赣南脐橙以其“外表光洁美观，肉质脆嫩，风味浓甜芳香”的特点饮誉中外．现欲将一批脐橙运往外地销售，若用2辆A 型车和1辆B型车载满脐橙一次可运走10吨；用1辆A型车和2辆B型车载满脐橙一次可运走11吨．现有脐橙31吨，计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都载满脐橙．根据以上信息，解答下列问题：（1）1辆A型车和1辆B型车都载满脐橙一次可分别运送多少吨？（2）请你帮该物流公司设计租车方案；（3）若1辆A型车需租金100元/次，1辆B型车需租金120元/次．请选出费用最少的租车方案，并求出最少租车费．23.（6分）23．（6分）教科书中这样写道：“我们把多项式a2+2ab+b2及a2﹣2ab+b2叫做完全平方式”，如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式最大值，最小值等．例如：分解因式x2+2x﹣3＝（x2+2x+1）﹣4＝（x+1）2﹣4＝（x+1+2）（x+1﹣2）＝（x+3）（x﹣1）；例如求代数式2x2+4x﹣6的最小值.2x2+4x﹣6＝2（x2+2x﹣3）＝2（x+1）2﹣8．可知当x＝﹣1时，2x2+4x﹣6有最小值，最小值是﹣8，根据阅读材料用配方法解决下列问题：（1）分解因式：m2﹣4m + 4＝．（2）分解因式：x2+6x﹣7＝．（3）当a，b为何值时，多项式a2+b2﹣4a+6b+18有最小值，并求出这个最小值．24.（10分）24．（10分）已知：直线EF分别与直线AB，CD相交于点G，H，并且∠AGE+∠DHE＝180°．（1）如图1，求证：AB∥CD；（2）如图2，点M在直线AB，CD之间，连接GM，HM，求证：∠M＝∠AGM+∠CHM；（3）如图3，在（2）的条件下，射线GH是∠BGM的平分线，在MH的延长线上取点N，连接GN，若∠N＝∠AGM，∠M＝∠N+∠FGN，求∠MHG的度数．答案一、单选题（本题共计10小题，总分30分）1.（3分）1．【解答】解：将0.000 043用科学记数法表示为4.3×10﹣5．故选：C．2.（3分）2．【解答】解：因为平移不改变图形的形状和大小，只改变图形的位置，所以在（A）（B）（C）（D）四幅图案中，能通过图案（1）平移得到的是C选项的图案，故选：C．3.（3分）3．【解答】解：A．a4•a2＝a6，故本选项不合题意；B．a6÷a2＝a4，故本选项不合题意；C．（2ab2）2＝4a2b4，正确；D．（a3）2＝a6，故本选项不合题意；故选：C．4.（3分）4．【解答】解：由平方差公式判断：A答案：（2x+y）（y﹣2x）＝y2﹣（2x）2＝y2﹣4x2，满足条件；B答案：（x+2）（2+x）不满足条件；C答案：（x﹣y）（﹣x+y）＝﹣（x﹣y）（x﹣y）不满足条件；D答案：（x﹣2）（x+1）不满足条件；故选：A．5.（3分）5．【解答】解：A、3m2﹣6m＝3m（m﹣2），故此选项错误；B、a2b+ab+a＝a（ab+b+1），故此选项错误；C、x2+y2，无法分解因式，不合题意；D、﹣x2+2xy﹣y2＝﹣（x﹣y）2，正确．故选：D．6.（3分）6．【解答】解：是方程5x﹣y＝2的一个解，故选：D．7.（3分）7．【解答】解：如图，延长AB交CF于E，∵∠ACB＝90°，∠A＝30°，∴∠ABC＝60°，∵∠1＝38°，∴∠AEC＝∠ABC﹣∠1＝22°，∵GH∥EF，∴∠2＝∠AEC＝22°，故选：B．8.（3分）8．【解答】解：∵9b＝5，∴32b＝5，又∵3a＝10，∴3a﹣2b＝3a÷32b＝10÷5＝2．故选：D．9.（3分）9．【解答】解：依题意，得：．故选：D．10.（3分）10．【解答】解：如图所示：由题意可得：拼成的长方形一边的长为3，另一边的长为：AB+AC＝a+4+a+1＝2a+5．故选：A．二、填空题（本题共计6小题，总分18分）11.（3分）11．【解答】解：x（x﹣2y）＝x2﹣2xy．故答案为：x2﹣2xy．12.（3分）12．【解答】解：∵直线a∥b，∴∠2+∠3＝180°，而∠3＝∠1＝135°，∴∠2＝180°﹣135°＝45°．故答案为45°．13.（3分）13．【解答】解：把代入方程7x+2y＝10，得，28+2m＝10，解得m＝﹣9，故答案为：﹣9．14.（3分）14．【解答】解：，①+②，得3x+3y＝6，∴3（x+y）＝6，∴x+y＝2，故答案为：2．15.（3分）15．【解答】解：∵△ABC沿BC方向平移至△DEF处．∴BE＝CF，∵EC＝2BE＝4，∴BE＝2，∴CF＝2．故答案为：2．16.（3分）16．【解答】解：（x﹣a）（x2+ x +b）＝x3+ x2+bx- ax2﹣ax-ab ＝x3+(1+a) x2 -(a-b）x﹣ab，∵（结果中不含x的一次项，∴a﹣b＝0，故答案为：0．三、解答题（本题共计8小题，总分52分）17.（6分）17．【解答】解：（1）（﹣2）2﹣20200+3﹣2＝4﹣1+＝3；（2）2x3y2•（﹣9x2）÷（6x4y）＝﹣18x5y2÷6x4y＝﹣3xy．18.（6分）18．【解答】解：如图所示：∵AD∥BC，∴∠A+∠ABC＝180°，∠ADB＝∠CBD，又∵∠A＝110°，∴∠ABC＝180°﹣110°＝70°，又∵BE平分∠ABC，∴∠CBD＝∴∠CBD＝×70°＝35°∴∠ADB＝35°．19.（6分）19．【解答】解：（1）如图，直线l即为所求；（2）如图，△A'B'C'即为所求．20.（6分）20．【解答】解：方程组的解为{x=2y=1；（2）方程组的解为{x=32y=−1．21.（6分）21．【解答】解：原式＝（4x2﹣y2﹣4x2+12xy﹣9y2）÷（﹣2y）＝（12xy﹣10y2）÷（﹣2y）＝﹣6x+5y，当x＝1，y＝﹣2时，原式＝﹣6﹣10＝﹣16．22.（6分）22．【解答】解：（1）设1辆A型车载满脐橙一次可运送x吨，1辆B型车载满脐橙一次可运送y吨，依题意，得：，解得：．答：1辆A型车载满脐橙一次可运送3吨，1辆B型车载满脐橙一次可运送4吨．（2）依题意，得：3a+4b＝31，∵a，b均为正整数，∴或或．∴一共有3种租车方案，方案一：租A型车1辆，B型车7辆；方案二：租A型车5辆，B型车4辆；方案三：租A型车9辆，B型车1辆．（3）方案一所需租金为100×1+120×7＝940（元）；方案二所需租金为100×5+120×4＝980（元）；方案三所需租金为100×9+120×1＝1020（元）．∵940＜980＜1020，∴最省钱的租车方案是方案一，即租A型车1辆，B型车7辆，最少租车费为940元．23.（6分）23．【解答】解：（1）m2﹣4m+4＝（m﹣2）2故答案为（m﹣2）2(2)分解因式：x2+6x﹣7＝(x+7) ( x—1) ．（3）∵a2+b2﹣4a+6b+18＝（a﹣2）2+（b+3）2+5，∴当a＝2，b＝﹣3时，多项式a2+b2﹣4a+6b+18有最小值5；24.（10分）24．【解答】（1）证明：如图1，∵∠AGE+∠DHE＝180°，∠AGE＝∠BGF．∴∠BGF+∠DHE＝180°，∴AB∥CD；（2）证明：如图2，过点M作MR∥AB，又∵AB∥CD，∴AB∥CD∥MR．∴∠GMR＝∠AGM，∠HMR＝∠CHM．∴∠GMH＝∠GMR+∠RMH＝∠AGM+∠CHM．（3）解：如图3，令∠AGM＝2α，∠CHM＝β，则∠N＝2α，∠M＝2α+β，∵射线GH是∠BGM的平分线，∴，∴∠AGH＝∠AGM+∠FGM＝2α+90°﹣α＝90°+α，∵，∴，∴∠FGN＝2β，过点H作HT∥GN，则∠MHT＝∠N＝2α，∠GHT＝∠FGN＝2β，∴∠GHM＝∠MHT+∠GHT＝2α+2β，∠CHG＝∠CHM+∠MHT+∠GHT＝β+2α+2β＝2α+3β，∵AB∥CD，∴∠AGH+∠CHG＝180°，∴90°+α+2α+3β＝180°，∴α+β＝30°，∴∠GHM＝2（α+β）＝60°．。

人教版数学七年级下册《期中考试题》附答案解析

人教版数学七年级下学期期中测试卷学校________ 班级________ 姓名________ 成绩________一、选择题：本大题共12个小题1.在实数2π, 无理数有( )个 A. 1 B. 2 C. 3 D. 42. 在平面直角坐标系中,将点()2,6P 向下平移3个单位长度,得到点的坐标为( )A ()2,3 B. ()2,9 C. ()1,6- D. ()5,6 3. 下列等式：① 2x + y = 4；② 3xy = 7；③220x y +=；④12y x -=；⑤ 2x + y + z = 1二元一次方程的个数是( )A. 1B. 2C. 3D. 44. 点P 是第二象限的点且到x 轴的距离为3、到y 轴的距离为4,则点P 的坐标是( )A. (﹣3,4)B. ( 3,﹣4)C. (﹣4,3)D. ( 4,﹣3) 5. 不等式组31027x x +>⎧⎨<⎩的整数解的个数是( ) A. 1个 B. 2个 C. 3个 D. 4个6. 在下列条件中：①∠A+∠B=∠C ,②∠A ∶∠B ∶∠C=1∶5∶6,③∠A=90°－∠B ,④∠A=∠B=12∠C 中,能确定△ABC 是直角三角形的条件有 ( )A. 1个B. 2个C. 3个D. 4个 7. 我国古代《四元玉鉴》中记载“二果问价”问题,其内容如下：九百九十九文钱,甜果苦果买一千,甜果九个十一文,苦果七个四文钱,试问甜苦果几个,又问各该几个钱?若设买甜果x 个,买苦果y 个,则下列关于x ,y 的二元一次方程组中符合题意的是( ) A. 999114100097x y x y +=⎧⎪⎨+=⎪⎩ B. 100097999114x y x y +=⎧⎪⎨+=⎪⎩ C. 10009928999,x y x y +=⎧⎨+=⎩ D. 100011499997x y x y +=⎧⎪⎨+=⎪⎩8. 下列说法不一定成立的是( )A. 若a b >,则a c b c +>+B. 若a c b c +>+,则a b >C. 若a b >,则22ac bc >D. 若22ac bc >,则a b >9. 为了解中学生获取资讯的主要渠道,随机抽取50名中学生进行问卷调查,调查问卷设置了“A.报纸,B.电视,C.网络,D.身边的人,E.其他”五个选项(五项中必选且只能选一项),根据调查结果绘制了如下的条形图．该调查的调查方式及图中a 的值分别是( )A. 全面调查；26B. 全面调查；24C. 抽样调查；26D. 抽样调查；2410. 若一个多边形的内角和与外角和之和是1800°,则此多边形是( )边形．A. 八B. 十C. 十二D. 十四11. 根据下列已知条件,不能唯一画出ABC 的是( )A. AB = 5, BC = 3, AC = 6B. AB = 4, BC = 3, ∠A = 50︒C. ∠A = 50︒, ∠B = 60︒, AB = 4D. AB = 10, BC = 20, ∠B = 80︒12. 如图,ABC 中, ∠A = 20︒,沿 BE 将此三角形对折,又沿BA '再一次对折,点C 落在BE 上的处,此时74C DB '∠=︒,则原三角形的∠C 的度数为( )A. 74︒B. 76︒ X. 79︒ ∆. 83︒二、填空题(本大题共6个小题) 13. 16 ⎽⎽⎽⎽⎽．14. 已知关于x ,y 的二元一次方程组2321x y k x y +=⎧⎨+=-⎩的解互为相反数,则k 的值是_________． 15. 若一个三角形的两边长分别为5和8,则下列长度：①14；②10；③3；④2．其中,可以作为第三边长的是_____(填序号)16. 某种商品的进价为每件100元,商场按进价提高50%后标价,为增加销量,准备打折销售,但要保证利润率不低于20%,则至多可以打_______折．17. 已知点(1,0)A 、(0,2)B ,点P 在轴上,且PAB △的面积为5,则点P 的坐标为__________． 18. 如图,已知 CB ⊥AD ,AE ⊥CD ,垂足分别为 B 、E ,AE 、BC 相交于点 F ,AB=BC ,若 AB=8,CF=2,则 BD=______.三、解答题：本大题共8个小题.19. 计算：23(2)9813---． 20. (1)解方程组：217126x y x y x y -=⎧⎪+-⎨+=⎪⎩； (2)解不等式组：2(2)3321123x x x x +≥+⎧⎪+-⎨->⎪⎩； 21. 由于新型冠状病毒的袭击,2020 春季各个学校不得不推迟开学,但停课不停学．各地都展开了网络学习,我校为了解七年级学生上网课的情况,开学后从该年级学生中随机抽取了部分学生进行数学科目的测试(把测试结果分为四个等级： A 级：优秀； B 级：良好； C 级：合格； D 级：不合格),并将测试记录绘成如下两幅完全不同的统计图,请根据统计图中的信息解答下列问题：(1)参加本次抽样测试的学生数是多少?(2)求图1 中A级扇形的圆心角∠a的度数,并把图2 中的条形统计图补充完整；(3)我校七年级共有1700 名学生,如果全部参加这次数学科目测试,请估计不合格的人数.22. 如图,△ADC中,DB是高,点E是DB上一点,AB＝DB,EB＝CB,M,N分别是AE,CD上点,且AM＝DN．(1)求证：△ABE≌△DBC．(2)探索BM和BN的关系,并证明你的结论．23. 某市环保局决定购买A、B两种型号的扫地车共40辆,对城区所有公路地面进行清扫．已知1辆A型扫地车和2辆B型扫地车每周可以处理地面垃圾100吨,2辆A型扫地车和1辆B型扫地车每周可以处理垃圾110吨．(1)求A、B两种型号的扫地车每辆每周分别可以处理垃圾多少吨?(2)已知A型扫地车每辆价格为25万元,B型扫地车每辆价格为20万元,要想使环保局购买扫地车的资金不超过910万元,但每周处理垃圾的量又不低于1400吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少资金是多少?24. 如图,AD为ABC的高,AE,BF为ABC的角平分线,若∠CBF = 32︒,∠AFB = 72︒.(1)∠BAD =︒；(2)求∠DAE的度数；(3)若点G为线段BC上任意一点,当GFC为直角三角形时,则求∠BFG的度数.25. (1)在关于x,y的二元一次方程组中2x yx y a-=⎧⎨+=⎩中,x >1,y < 0,求a的取值范围.(2)已知x - 2 y = 4,且x > 8,y < 4,求3x + 2 y的取值范围.(3)已知a -b =m,在关于x,y二元一次方程组21258x yx y a-=-⎧⎨+=-⎩中,x < 0,y > 0,化简含有绝对值的式子2334a b m m a b+-++-++(结果用含的式子表示)26. 同学们应该都见过光线照射在平面镜上出现反射光线的现象。

人教版数学七年级下学期《期中考试题》有答案

人教版数学七年级下学期期中测试卷学校________ 班级________ 姓名________ 成绩________一、选择题(本题12小题,每题中只有一个答案符合要求,每小题4分,共48分)1. 要调查下列问题,你认为哪些适合抽样调查[ ]①市场上某种食品的某种添加剂的含量是否符合国家标准②检测某地区空气质量③调查全市中学生一天的学习时间．A. ①②B. ①③C. ②③D. ①②③2.下列条件中不能判定AB∥CD的是()A. ∠1＝∠4B. ∠2＝∠3C. ∠5＝∠BD. ∠BAD+∠D＝180°3.下列图形中,可以由其中一个图形通过平移得到的是()A. B. C. D.4.下列说法：①()2-=-；1010②数轴上的点与实数成一一对应关系；③﹣216④任何实数不是有理数就是无理数；⑤两个无理数和还是无理数；⑥无理数都是无限小数,其中正确的个数有( )A. 2个B. 3个C. 4个D. 5个5.下列说法正确的个数有( )⑴过一点有且只有一条直线与已知直线平行⑵一条直线有且只有一条垂线⑶不相交的两条直线叫做平行线⑷直线外一点到这条直线的垂线段叫做这点到这条直线的距离A. 0个B. 1个C. 2个D. 3个6.在平面直角坐标系xOy中,线段AB两个端点坐标分别为A(-1,-1),B(1,2),平移线段AB得到线段A’B’(点A与A’对应),已知A’的坐标为(3,-1),则点B’的坐标为( )A. (4,2)B. (5,2)C. (6,2)D. (5,3)7.如图,把长方形ABCD沿EF按图那样折叠后,A、B分别落在点G、H处,若∠1=50°,则∠AEF=( )A. 110°B. 115°C. 120°D. 125°8.如果一元一次不等式组3xx a>⎧⎨>⎩的解集为＞3,则的取值范围是( )A. ＞3B. ≥3C. ≤3D. ＜39.如果方程组134541ax byx y-=⎧⎨-=⎩与3237ax byx y+=⎧⎨+=-⎩有相同解,则a,b的值是()A.21ab=⎧⎨=⎩B.23ab=⎧⎨=-⎩C.521ab⎧=⎪⎨⎪=⎩D.45ab=⎧⎨=-⎩10.某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则至多可打( )A. 6折B. 7折C. 8折D. 9折11.对于非零的两个实数a,b,规定a⊕b=am﹣bn,若3⊕(﹣5)=15,4⊕(﹣7)=28,则(﹣1)⊕2的值为()A. ﹣13B. 13C. 2D. ﹣212.运行程序如图所示,规定：从“输入一个值x”到“结果是否＞95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是( )A. x≥11B. 11≤x ＜23C. 11＜x≤23D. x≤23二、境空题(本题6个小题,每小题4分,共24分)13.已知一组数据有40个,把它分成六组,第一组到第四组的频数分别是10,5,7,6,第五组的频率是0.2,则第六组的频率是_____．14.将点P 向下平移3个单位,向左平移2个单位后得到点Q (3,-1),则点P 坐标为______． 15.若是64的立方根,则3m +=___________．16.如果一个角的两边与另一个角的两边分别平行,那么这两个角的数量关系是_____.17.如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B 到点C 的方向平移到△DEF 的位置,AB ＝10,DH ＝4,平移距离为6,则阴影部分面积是_____18.如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆1O 、2O 、3O ,组成一条平滑的曲线,点从原点出发,沿这条曲线向右运动,速度为每秒2π个单位长度,则第2019秒时,点的坐标是____．三、解答题(本题7个小题,共78分)19.计算：(1)(－2)2－95)4＋2×(327； (2)|12|381274-2； 20.求下列各式中x 的值：(1)4(x ＋1)2－9＝0； (2)(3x ＋2)3－1＝6164. 21.解方程组或不等式(组)(1)2520x y x y +=⎧⎨-=⎩ (2)2353212x y x y -=-⎧⎨+=⎩(3)334642x x ---＜； (4)()513112 1.3x x x x ⎧->+⎪⎨+>-⎪⎩，22.中央电视台举办的“中国汉字听写大会”节目受到中学生的广泛关注．某中学为了了解学生对观看“中国汉字听写大会”节目的喜爱程度,对该校部分学生进行了随机抽样调查,并绘制出如图所示的两幅统计图．在条形图中,从左向右依次为A 类(非常喜欢),B 类(较喜欢),C 类(一般),D 类(不喜欢)．已知A 类和B 类所占人数的比是5：9,请结合两幅统计图,回答下列问题：(1)写出本次抽样调查样本容量； (2)请补全两幅统计图；(3)若该校有2000名学生．请你估计观看“中国汉字听写大会”节目不喜欢的学生人数． 23.如图．将ABC 向右平移4个单位得到A B C '''．(1)写出A B C ，，的坐标； (2)画出A B C '''； (3)求ABC 的面积．24.已知：如图,点C 在AOB ∠的一边OA 上,过点C 的直线DE //OB ,CF 平分ACD ∠,CG CF ⊥于C ．()1若O 40∠=,求ECF ∠的度数； ()2求证：CG 平分OCD ∠；()3当O ∠为多少度时,CD 平分OCF ∠,并说明理由．25.为了更好的治理西流湖水质,保护环境,市治污公司决定购买10 台污水处理设备．现有A、B 两种型号的设备,其中每台的价格,月处理污水量如下表：A 型B 型价格(万元/台) a b处理污水量(吨／月) 240 200经调查：购买一台A 型设备比购买一台B 型设备多2 万元,购买2 台A 型设备比购买3 台B 型设备少6 万元．(1)求a,b 的值；(2)经预算：市治污公司购买污水处理设备的资金不超过105 万元,你认为该公司有哪几种购买方案；(3)在(2)问的条件下,若每月要求处理西流湖的污水量不低于2040 吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案．答案与解析一、选择题(本题12小题,每题中只有一个答案符合要求,每小题4分,共48分)1. 要调查下列问题,你认为哪些适合抽样调查[ ]①市场上某种食品的某种添加剂的含量是否符合国家标准②检测某地区空气质量③调查全市中学生一天的学习时间．A. ①②B. ①③C. ②③D. ①②③[答案]D[解析][详解]解：根据抽样调查的适用情况可得：①、②和③都适合抽样调查.故应选D考点：调查方法的选择2.下列条件中不能判定AB∥CD的是()A. ∠1＝∠4B. ∠2＝∠3C. ∠5＝∠BD. ∠BAD+∠D＝180°[答案]B[解析]解：A．∵∠1=∠4,∴AB∥CD(内错角相等,两直线平行),故本选项错误；B．∵∠2=∠3,∴AD∥BC(内错角相等,两直线平行),判定的不是AB∥CD,故本选项正确；C．∵∠5=∠B,∴AB∥CD(同位角相等,两直线平行),故本选项错误；D．∵∠BAD+∠D=180°,∴AB∥CD(同旁内角互补,两直线平行),故本选项错误．故选B．3.下列图形中,可以由其中一个图形通过平移得到的是()A. B. C. D.[答案]B[解析][分析]根据平移的定义直接判断即可．[详解]解：由其中一个图形平移得到整个图形的是B,故选B．[点睛]此题主要考查了图形的平移,把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同,图形的这种移动叫做平移．注意平移是图形整体沿某一直线方向移动．4.下列说法：①10=-；②数轴上的点与实数成一一对应关系；③﹣2④任何实数不是有理数就是无理数；⑤两个无理数的和还是无理数；⑥无理数都是无限小数,其中正确的个数有( )A 2个 B. 3个 C. 4个 D. 5个[答案]C[解析][分析]根据平方根,数轴,有理数的分类逐一分析即可.[详解]10=-是错误的；=,10②数轴上的点与实数成一一对应关系,故说法正确；4,故-2的平方根,故说法正确；④任何实数不是有理数就是无理数,故说法正确；⑤两个无理数的和还是无理数,和是错误的；⑥无理数都是无限小数,故说法正确；故正确是②③④⑥共4个；故选C.[点睛]本题考查了有理数的分类,数轴及平方根的概念,有理数都可以化为小数,其中整数可以看作小数点后面是零的小数,分数可以化为有限小数或无限循环小数；无理数是无限不循环小数,其中有开方开不尽的数,等,也有π这样的数.5.下列说法正确的个数有( )⑴过一点有且只有一条直线与已知直线平行⑵一条直线有且只有一条垂线⑶不相交的两条直线叫做平行线⑷直线外一点到这条直线的垂线段叫做这点到这条直线的距离A. 0个B. 1个C. 2个D. 3个[答案]A[解析]解：(1)过直线外一点有且只有一条直线与已知直线平行,故(1)错误；(2)一条直线无数条垂线,故(2)错误；(3)平面内,不相交的两条直线叫做平行线,故(3)错误；(4)直线外一点到这条直线的垂线段的长度叫做这点到这条直线的距离,故(4)错误．故正确的有0个．故选A．6.在平面直角坐标系xOy中,线段AB的两个端点坐标分别为A(-1,-1),B(1,2),平移线段AB得到线段A’B’(点A与A’对应),已知A’的坐标为(3,-1),则点B’的坐标为( )A. (4,2)B. (5,2)C. (6,2)D. (5,3)[答案]B[解析]试题解析：根据A点的坐标及对应点的坐标可得线段AB向右平移4个单位,然后可得B′点的坐标．∵A(﹣1,﹣1)平移后得到点A′的坐标为(3,﹣1),∴向右平移4个单位,∴B(1,2)的对应点坐标为(1+4,2),即(5,2)．故选B．7.如图,把长方形ABCD沿EF按图那样折叠后,A、B分别落在点G、H处,若∠1=50°,则∠AEF=( )A. 110°B. 115°C. 120°D. 125°[答案]B[解析]解：∵四边形ABCD为长方形,∴AE∥BF,∠AEF+∠BFE=180°；由折叠变换的性质得：∠BFE=∠HFE,而∠1=50°,∴∠BFE=(180°﹣50°)÷2=65°,∴∠AEF=180°﹣65°=115°．故选B．点睛：该题主要考查了翻折变换的性质、矩形的性质、平行线的性质及其应用问题；应牢固掌握矩形的性质、平行线的性质等几何知识点．8.如果一元一次不等式组3xx a>⎧⎨>⎩的解集为＞3,则的取值范围是( )A. ＞3B. ≥3C. ≤3D. ＜3[答案]C[解析][分析]由题意不等式组中的不等式分别解出来为x＞3,x＞a,已知不等式解集为x＞3,再根据不等式组解集的口诀：同大取大,得到a的范围．[详解]由题意x＞3,x＞a,∵一元一次不等式组3xx a>⎧⎨>⎩的解集为x＞3,∴a≤3．故选：C．[点睛]主要考查了一元一次不等式组解集的求法,将不等式组解集的口诀：同大取大,同小取小,大小小大中间找,大大小小找不到(无解)逆用,已知不等式解集反过来求a的范围．9.如果方程组134541ax byx y-=⎧⎨-=⎩与3237ax byx y+=⎧⎨+=-⎩有相同的解,则a,b的值是()A.21ab=⎧⎨=⎩B.23ab=⎧⎨=-⎩C.521ab⎧=⎪⎨⎪=⎩D.45ab=⎧⎨=-⎩[答案]A[解析][分析]因为两个方程组有相同的解,故只需把两个方程组中不含未知数和含未知数的方程分别组成方程组,求出未知数的值,再代入另一组方程组即可．[详解]由已知得方程组4541 237x yx y-⎧⎨+-⎩＝＝,解得45x y ⎧⎨-⎩＝＝, 代入133ax by ax by -⎧⎨+⎩＝＝,得到4513453a b a b +⎧⎨-⎩＝＝, 解得21a b =⎧⎨=⎩．故选A.[点睛]此题比较复杂,考查了学生对方程组有公共解定义的理解能力及应用能力,是一道好题．10. 某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则至多可打( ) A. 6折 B. 7折 C. 8折 D. 9折[答案]B [解析][详解]设可打x 折,则有1200×10x-800≥800×5%, 解得x≥7．即最多打7折．故选B ． [点睛]本题考查的是一元一次不等式的应用,解此类题目时注意利润和折数,计算折数时注意要除以10．解答本题的关键是读懂题意,求出打折之后的利润,根据利润率不低于5%,列不等式求解．11.对于非零的两个实数a ,b ,规定a ⊕b=am ﹣bn ,若3⊕(﹣5)=15,4⊕(﹣7)=28,则(﹣1)⊕2的值为( ) A. ﹣13 B. 13C. 2D. ﹣2[答案]A [解析][详解]解：根据题意得:3⊕(5)3515m n -=+=, 4⊕(7)4728m n -=+=35154728m n m n +=⎧∴⎨+=⎩,解得：3524m n =-⎧⎨=⎩∴(-1)⊕2=-m-2n=35-48=-13故选A12.运行程序如图所示,规定：从“输入一个值x”到“结果是否＞95”为一次程序操作,如果程序操作进行了三次才停止,那么x 的取值范围是( )A. x≥11B. 11≤x ＜23C. 11＜x≤23D. x≤23[答案]C[解析] [详解]解：根据运算程序,前两次运算结果小于等于95,第三次运算结果大于95可得不等式组()()219522119522211195x x x ⎧+≤⎪⎪++≤⎨⎪⎡⎤+++>⎪⎣⎦⎩①②③,解不等式①得,x ≤47；解不等式②得,x ≤23；解不等式③得,x >11,所以不等式组的解集为11<x ≤23,即x 的取值范围是11<x ≤23．故选C ．点睛：本题考查了一元一次不等式组的应用,根据题目所给的信息,并运用运输程序并列出不等式组是解题的关键．二、境空题(本题6个小题,每小题4分,共24分)13.已知一组数据有40个,把它分成六组,第一组到第四组的频数分别是10,5,7,6,第五组的频率是0.2,则第六组的频率是_____．[答案]0.1．[解析][分析]根据频率=频数÷总数,以及第五组的频率是0.2,可以求得第五组的频数；再根据各组的频数和等于1,求得第六组的频数,从而求得其频率．[详解]解：根据第五组的频率是0.2,其频数是40×0.2=8；则第六组的频数是40﹣(10+5+7+6+8)=4．故第六组的频率是440,即0.1．14.将点P向下平移3个单位,向左平移2个单位后得到点Q(3,-1),则点P坐标为______．[答案](5,2)[解析][分析]设点P的坐标为(x,y),然后根据向左平移,横坐标减,向下平移,纵坐标减,列式进行计算即可得解．[详解]设点P的坐标为(x,y),根据题意,x-2=3,y-3=-1,解得x=5,y=2,则点P的坐标为(5,2)．故答案是：(5,2)．[点睛]考查了平移与坐标与图形的变化,平移中点的变化规律是：横坐标右移加,左移减；纵坐标上移加,下移减．15.,则3m+=___________．[答案]5[解析][分析]根据立方根的定义进行计算即可．[详解]又∵m,∴m=2,则m+3=5,故答案为5．[点睛]本题考查了立方根,算术平方根,掌握立方根以及算术平方根的定义是解题的关键．16.如果一个角两边与另一个角的两边分别平行,那么这两个角的数量关系是_____.[答案]相等或互补[解析][分析]根据题意画出图形进行分析即可.[详解]如图所示：∵AB∥CD,∴∠1=∠3,∵BE∥DF,∴∠2=∠3,∴∠1=∠2；(2)如图所示：∵AB∥CD,∴∠1=∠3,∵BE∥DF,∴∠2+∠3=180°,∴∠1+∠2=180°；综合上述可得：如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补；故答案是：相等或互补．[点睛]考查了平行线性质：两直线平行,同位角相等；两直线平行,同旁内角互补；两直线平行,内错角相等．17.如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB＝10,DH＝4,平移距离为6,则阴影部分面积是_____[答案]48[解析][分析]根据平移的性质可知：AB =DE ,BE =CF ；由此可求出EH 和CF 的长．由于CH ∥DF ,根据成比例线段,可求出EC 的长．由EH 、EC ,DE 、EF 的长,即可求出△ECH 和△EFD 的面积,进而可求出阴影部分的面积．[详解]根据题意得：DE =AB =10；BE =CF =6；CH ∥DF ,∴EH =10﹣4=6；EH ：HD =EC ：CF ,即6：4=EC ：6,∴EC =9,∴S △EFD =12×10×(9+6)=75；S △ECH =12×9×6=27,∴S 阴影部分=75﹣27=48．故答案为48． [点睛]本题考查了平移的性质、由平行判断成比例线段及有关图形的面积计算,有一定的综合性．18.如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆1O 、2O 、3O ,组成一条平滑的曲线,点从原点出发,沿这条曲线向右运动,速度为每秒2π个单位长度,则第2019秒时,点的坐标是____．[答案](2019,-1)[解析][分析]根据速度及半圆的周长可知点P 每秒走12个半圆,分别求出第2、3、4、5、6秒时点P 的坐标,可得图象纵坐标4秒一循环,横坐标与移动的时间相同,即可得答案．[详解]∵半圆额半径为1,∴半圆的周长为12×2×1=, ∵点P 运动速度为每秒2π个单位长度, ∴点P 每秒走12个半圆, ∵点P 从原点O 出发,沿这条曲线向右运动,∴运动时间为1秒时,点P 的坐标为(1,1),运动时间为2秒时,点P 的坐标为(2,0),运动时间为3秒时,点P 的坐标为(3,-1),运动时间为4秒时,点P 的坐标为(4,0),运动时间为5秒时,点P 的坐标为(5,1),运动时间为6秒时,点P 的坐标为(6,0),…,∴纵坐标4秒一循环,横坐标与移动的时间相同,∵2019÷4=504……3,∴点P 2019的坐标为(2019,-1),故答案为：(2019,-1)[点睛]本题考查了点的规律变化,仔细观察图象,得到点的变化规律是解题关键．三、解答题(本题7个小题,共78分)19.计算：(1)(－2)2－5)＋2×(；(2)|1|； [答案](1)-2；(2)43-[解析][分析](1)原式先进行乘方与开方运算,再进行乘法运算,最后进行加减运算即可得到结果；(2)原式先进行开方运算,再进行乘法和化简绝对值,然后再进行合并即可得到结果．[详解](1)(－2)2－5)＋2×(＝4－3＋5－2＋2×(－3)＝4－3＋5－2－6＝－2(2)|1|21132-⨯ ＝113--＝43 -．[点睛]此题主要考查了实数的混合运算,熟练掌握运算法则和运算顺序是解答此题的关键．20.求下列各式中x的值：(1)4(x＋1)2－9＝0；(2)(3x＋2)3－1＝61 64.[答案](1)x＝12或x＝52-；(2)x＝14-[解析] [分析](1)通过移项得到(x＋1)2＝94,利用平方根的性质求解即可；(2)化简得到(3x＋2)3＝12564,可利用立方根的性质求解即可；[详解]解：(1)4(x＋1)2－9＝0, 4(x＋1)2＝9,(x＋1)2＝94,x＋1＝±32,x＝12或x＝－52．(2)(3x＋2)3－1＝61 64,(3x＋2)3＝125 64,3x＋2＝54,x＝－14．[点睛]本题主要考查了利用平方根和立方根的性质进行方程求解,求解过程中准确理解平方数和立方数是解题的关键．21.解方程组或不等式(组)(1)2520x yx y+=⎧⎨-=⎩(2)2353212x yx y-=-⎧⎨+=⎩(3)334642x x ---＜； (4)()513112 1.3x x x x ⎧->+⎪⎨+>-⎪⎩， [答案](1)21x y =⎧⎨=⎩；(2)23x y =⎧⎨=⎩；(3)x ＞-3；(4)2＜x ＜4． [解析][分析](1)化简之后用加减消元法求解；(2)化简之后用加减消元法求解；(2)去分母,化成整式,解一元一次不等式即可；(4)分别求出两个一元一次不等式,即可得到解集．[详解](1)2520x y x y +=⎧⎨-=⎩, 整理得：25240+=⎧⎨-=⎩x y x y , 两式相减得：1y =,把1y =代入20x y -=得：2x =,所以方程组的解是21x y =⎧⎨=⎩． (2)2353212x y x y -=-⎧⎨+=⎩ 整理得：69156424-=-⎧⎨+=⎩x y x y , 两式相减得：3y =,把3y =代入23-5x y -=得：2x =,所以方程组的解是23x y =⎧⎨=⎩． (3)334642x x ---＜化简得：()3234＜24---x x ,整理得：-721＜x ,解得：-3x ＞．(4)()51311213⎧->+⎪⎨+>-⎪⎩x x x x ,整理不等式组得：51331233->+⎧⎨+>-⎩x x x x , 化简得：244>⎧⎨->-⎩x x , 解得：24＜>⎧⎨⎩x x , ∴不等式的解集为：2＜x ＜4．[点睛]本题主要考查了二元一次方程组和一元一次不等式组的解法,准确的进行化简计算是解题的关键． 22.中央电视台举办的“中国汉字听写大会”节目受到中学生的广泛关注．某中学为了了解学生对观看“中国汉字听写大会”节目的喜爱程度,对该校部分学生进行了随机抽样调查,并绘制出如图所示的两幅统计图．在条形图中,从左向右依次为A 类(非常喜欢),B 类(较喜欢),C 类(一般),D 类(不喜欢)．已知A 类和B 类所占人数的比是5：9,请结合两幅统计图,回答下列问题：(1)写出本次抽样调查的样本容量；(2)请补全两幅统计图；(3)若该校有2000名学生．请你估计观看“中国汉字听写大会”节目不喜欢的学生人数．[答案](1)本次抽样调查的样本容量为100；(2)图形见解析；(3)估计观看“中国汉字听写大会”节目不喜欢的学生人数为520人．[解析][分析](1)用A 类的人数除以它所占的百分比,即可得样本容量；(2)分别计算出D类的人数为：100﹣20﹣35﹣100×19%=26(人),D类所占的百分比为：26÷100×100%=26%,B 类所占的百分比为：35÷100×100%=35%,即可补全统计图；(3)用2000乘以26%,即可解答．[详解]解：(1)20÷20%=100,∴本次抽样调查的样本容量为100．(2)D类的人数为：100﹣20﹣35﹣100×19%=26(人),D类所占的百分比为：26÷100×100%=26%,B类所占的百分比为：35÷100×100%=35%,如图所示：(3)2000×26%=520(人)．故若该校有2000名学生．估计观看“中国汉字听写大会”节目不喜欢的学生人数为520人．考点：1.条形统计图；2.用样本估计总体；3.扇形统计图．23.如图．将ABC向右平移4个单位得到A B C'''．(1)写出A B C，，的坐标；(2)画出A B C'''；(3)求ABC的面积．[答案](1)A(-4,1)、B(-2,0)、C(-1,3)；(2)见解析；(3)72．[解析] [分析](1)根据各点在坐标系中的位置写出各点坐标即可；(2)根据图形平移的性质画出△A′B′C′即可；(3)利用正方形的面积减去三个顶点上三角形的面积即可．[详解](1)由图可知,A (-4,1)、B (-2,0)、C (-1,3)；(2)如图,△A′B′C′即为所求；(3)S △ABC =3×3-12×2×1-12×3×1-12×2×3=9-1-32-3=72． [点睛]本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键．24.已知：如图,点C 在AOB ∠的一边OA 上,过点C 的直线DE //OB ,CF 平分ACD ∠,CG CF ⊥于C ． ()1若O 40∠=,求ECF ∠的度数；()2求证：CG 平分OCD ∠；()3当O ∠为多少度时,CD 平分OCF ∠,并说明理由．[答案](1) ∠ECF ＝110°;(2)答案见解析;(3) ∠O ＝60°.[解析]试题分析：由两直线平行,同位角相等得∠ACE =40︒,由平角定义得∠ACD=140︒,再由角平分线定义得70ACF ∠=︒,由邻补角定义得到∠ECF=110︒；(2)由垂直的定义得90FCG ∠=︒,由平角定义得90GCO FCA ∠+∠=︒,由等角的余角相等可证；(3)由两直线平行,同位角相等得∠DCO=∠O=60︒,由角平分线性质得∠DCF=60︒,由等量代换得DCO DCF ∠=∠即可得证.试题解析：(1)∵DE//OB ,∴∠O=∠ACE ,(两直线平行,同位角相等)∵∠O =40︒,∴∠ACE =40︒,∵∠ACD+∠ACE=180︒ (平角定义)∴ ∠ACD=140︒又 ∵CF 平分∠ACD ,∴ 70ACF DCF ∠=∠=︒ (角平分线定义)∴ ∠ECF=110︒(2)证明：∵CG ⊥ CF,∴90FCG ∠=︒ .∴ 90DCF DCG ∠+∠=︒又 ∵180GCO GCD FCA FCD ∠+∠+∠+∠=︒ (平角定义)∴ 90GCO FCA ∠+∠=︒∵ACF FDC ∠=∠∴GCO DCG ∠=∠(等角的余角相等)即CG 平分∠OCD ．(3)结论：当∠O=60︒时 ,CD 平分∠OCF ．当∠O=60︒时∵DE//OB,∴ ∠DCO=∠O=60︒.∴ ∠ACD=120︒.又 ∵CF 平分∠ACD∴ ∠DCF=60︒,∴DCO DCF ∠=∠即CD 平分∠OCF ．点睛：本题主要考查平行线的判定与性质,掌握平行线的性质和判定是解题的关键,即两直线平行⇔同位角相等；两直线平行⇔内错角相等；两直线平行⇔同旁内角互补；a ∥b,b ∥ca ∥c.25.为了更好的治理西流湖水质,保护环境,市治污公司决定购买 10 台污水处理设备．现有 A 、B 两种型号的设备,其中每台的价格,月处理污水量如下表：经调查：购买一台A 型设备比购买一台B 型设备多2 万元,购买2 台A 型设备比购买3 台B 型设备少6 万元．(1)求a,b 的值；(2)经预算：市治污公司购买污水处理设备的资金不超过105 万元,你认为该公司有哪几种购买方案；(3)在(2)问的条件下,若每月要求处理西流湖的污水量不低于2040 吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案．[答案](1)1210ab==⎧⎨⎩；(2)①A型设备0台,B型设备10台；②A型设备1台,B型设备9台；③A型设备2台,B型设备8台. ；(3)了节约资金,应选购A型设备1台,B型设备9台.[解析][分析](1)根据“购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元”即可列出方程组,继而进行求解；(2)可设购买污水处理设备A型设备x台,B型设备(10-x)台,则有12x+10(10-x)≤105,解之确定x的值,即可确定方案；(3)因为每月要求处理流溪河两岸的污水量不低于2040吨,所以有240x+200(10-x)≥2040,解之即可由x的值确定方案,然后进行比较,作出选择．[详解](1)根据题意得：2326a bb a-=-=⎧⎨⎩,∴1210ab==⎧⎨⎩；(2)设购买污水处理设备A型设备x台,B型设备(10−x)台, 则：12x+10(10−x)⩽105,∴x⩽2.5,∵x取非负整数,∴x=0,1,2,∴有三种购买方案：①A型设备0台,B型设备10台；②A型设备1台,B型设备9台；③A型设备2台,B型设备8台.(3)由题意：240x+200(10−x)⩾2040,∴x⩾1,又∵x⩽2.5,x取非负整数,∴x为1,2.当x=1时,购买资金为：12×1+10×9=102(万元),当x=2时,购买资金为：12×2+10×8=104(万元),∴为了节约资金,应选购A型设备1台,B型设备9台.[点睛]此题考查一元一次不等式应用,二元一次方程组的应用,解题关键在于理解题意列出方程.。

人教版数学七年级下册《期中考试试题》及答案

人教版数学七年级下学期期中测试卷学校________ 班级________ 姓名________ 成绩________一、选择题：(每小题3分,共30分)1.有理数223-的倒数是( )． A. 43 B. 94- C. 34- D. 942.在有理数：23,0.25,27--,12⎛⎫-- ⎪⎝⎭中,是正分数的有( )个． A. 1 B. 2 C. 3 D. 43.从金花中学驾车到天府广场大约有13千米的路程,如果用科学记数法来表示13千米则可以表示成( )米．A. 31310⨯B. 41.310⨯C. 21310⨯D. 31.310⨯ 4.下列说法中,正确的是( )．A. 有理数可分为：正整数、负整数、正分数以及负分数．B. 绝对值最小的数与任何有理数相加答案都不变．C. 两个有理数相加,和一定大于或等于这两个加数．D. 两个有理数相乘的积为正数,说明这两个数同号．5.下列计算正确是( )． A. 12()33m n m n m n ⎛⎫---=+ ⎪⎝⎭ B. 32a a -= C. 235x y xy += D.()a b c a b c --=--6.有一款服装原价元,悦悦百货商店先按原价上涨20%后标价,再按标价降价20%售出,那么最终商店卖出一件这样的服装( )．A. 赚了125a 元B. 亏了125a 元 C. 既不赚也不亏D. 无法判断是赚钱还是亏损,这和值有关 7.下列式子中,和3232x yz -次数相同的是( )．A. 64abB. 328a b π-C. 25367a b ab -+-D.8.如图是一个正方体的表面展开图,如果原正方体的相对两个面上的数和相等,那么m n +=( )．A. 4B. 3C. 2D. 19.在一次考试中,某班17名男生的平均分为分,19名女生的平均分为分,那么这个班的全体同学的平均分为( )． A. 2a b + B. 36a b + C. 17192a b + D. 171936a b + 10.根据如图所示的流程图中的程序,当输入数据为3-时,输出数值为( )．A. 0B. 2C. 4D. 6二、填空题：(每小题4分,共20分)11.若22a a -=-,且29a =,则a =__________．12.一个棱柱有12个面,它有__________个顶点,___________条棱．13.若在数轴上对应点到表示的点的距离为3,则x =__________．14.如果关于,的单项式23m n x y -与2axy -可合并为单项式0,则a m n -+的值为 _________．15.如图,正方形ABCD 的边长为2,以B 为圆心,AB 为半径在正方形内作14圆,再以CD 为直径在正方形内作半圆,得图中阴影部分,面积分别表示为1S 、2S ,则12S S -=__________．三、解答题：(共50分)16.计算(1)24111341323⎡⎤⎛⎫-+-+⨯-÷⨯⎢⎥ ⎪⎝⎭⎢⎥⎣⎦ (2)225(2)3(0.2)013317---⨯-+÷⨯ 17.化简(1)()()332332223234x y x y x y x y -----(2)22()()3()()a b a b b a b a ---+-+-18.已知：有理数,,在数轴上的位置如图,化简：|||||||3|a c b a b c a a +---+-+．19.下图是一个由若干棱长都为2cm 的小立方块搭成的几何体,求这个几何体的表面积．20.已知2333A x xy y =--+,2343B x xy y =+-,且112x =-,537y =,求：4(2)(23)A A B A B -+--的值．21.用简便方法计算下列各式的值：(1)()151 2.7 1.5 4.8 1.522⎛⎫-⨯+-⨯+⨯- ⎪⎝⎭(2)12345678979899100--++--+++--+…22.在数轴上有点,,,它们表示的数分别为,,,且满足：()24980a b c -+-++=；,,三点同时出发沿数轴向右运动,它们的速度分别为：1A V =(单位/秒),2B V =(单位/秒),3C V =(单位/秒)．(1)求,,的值；(2)运动时间等于多少时,点与点、点距离相等?23.成都市的水费实行下表的收费方式：每月用水量单价不超出310m (包括310m )2元/3m 超出310m 但不超出320m (包括320m )的部分 3元/3m(1)周老师家九月份用了316m 的水,应付多少水费? (2)如果李老师家九月份的用水量为3xm ,那么应付的水费为多少元?(3)如果曹老师家九月和十月一共用了328m 的水,且已知九月比十月少,设九月用水量为3xm ,那么曹老师这两个月一共要交多少钱的水费?(可用含的代数式表示)答案与解析一、选择题：(每小题3分,共30分)1.有理数223-的倒数是()．A. 43B.94- C.34- D.94[答案]C[解析][分析]先计算原式的值,再根据倒数的定义解答即可．[详解]解：22433-=-,43-的倒数是34-．故选：C．[点睛]本题考查了有理数的乘方运算和倒数的定义,属于基础题型,熟练掌握基本知识是关键．2.在有理数：23,0.25,27--,12⎛⎫-- ⎪⎝⎭中,是正分数的有()个．A. 1B. 2C. 3D. 4 [答案]B[解析][分析]先化简27--与12⎛⎫-- ⎪⎝⎭,再找出其中的正分数即可．[详解]解：2277=---,11=22,所以在有理数：23,0.25,27--,12⎛⎫-- ⎪⎝⎭中,是正分数的有：0.25,12⎛⎫-- ⎪⎝⎭共2个．故选：B．[点睛]本题考查了有理数的分类以及有理数的绝对值等知识,属于应知应会题型,熟练掌握有理数的概念是关键．3.从金花中学驾车到天府广场大约有13千米的路程,如果用科学记数法来表示13千米则可以表示成()米．A. 31310⨯B. 41.310⨯C. 21310⨯D. 31.310⨯[答案]B[解析][分析] 先换算单位,再根据科学记数法的表示方法解答即可．[详解]解：13千米=13000米=41.310⨯米．故选：B ．[点睛]此题考查了科学记数法的表示方法,科学记数法的表示形式为a ×10n 的形式,其中1≤|a |＜10,n 为整数,表示时关键要正确确定a 的值以及n 的值．4.下列说法中,正确的是( )．A. 有理数可分为：正整数、负整数、正分数以及负分数．B. 绝对值最小的数与任何有理数相加答案都不变．C. 两个有理数相加,和一定大于或等于这两个加数．D. 两个有理数相乘的积为正数,说明这两个数同号．[答案]D[解析][分析]分别根据有理数的定义、绝对值的意义、有理数的加法法则和有理数的乘法法则逐项判断即可．[详解]解：A 、有理数可分为：正整数、负整数、0、正分数以及负分数,所以本选项说法错误,不符合题意； B 、绝对值最小的数是0,0与任何有理数相加都得这个数,所以本选项说法错误,不符合题意；C 、两个有理数相加,和不一定大于或等于这两个加数,所以本选项说法错误,不符合题意；D 、两个有理数相乘的积为正数,说明这两个数同号,所以本选项说法正确,符合题意．故选：D ．[点睛]本题考查了有理数的定义、有理数绝对值的意义、有理数的加法法则和有理数的乘法法则等知识,属于基础题目,熟练掌握基本知识是解题关键．5.下列计算正确的是( )． A. 12()33m n m n m n ⎛⎫---=+ ⎪⎝⎭ B. 32a a -= C. 235x y xy += D.()a b c a b c --=--[答案]A根据整式的加减运算法则计算可判断A ,根据合并同类项的法则可判断B ,根据同类项的定义可判断C ,根据去括号法则可判断D ,进而可得答案．[详解]解：A 、12()32233m n m n m n m n m n ⎛⎫---=--+=+ ⎪⎝⎭,所以本选项计算正确；B 、32a a a -=,所以本选项计算错误；C 、2x 与3y 不是同类项,不能合并,所以本选项计算错误；D 、()a b c a b c --=-+,所以本选项计算错误．故选：A ．[点睛]本题考查了整式的加减运算,属于基础题型,熟练掌握去括号的法则和合并同类项的法则是解题关键． 6.有一款服装原价元,悦悦百货商店先按原价上涨20%后标价,再按标价降价20%售出,那么最终商店卖出一件这样的服装( )．A. 赚了125a 元B. 亏了125a 元 C. 既不赚也不亏D. 无法判断是赚钱还是亏损,这和的值有关[答案]B[解析][分析] 先用含a 的代数式表示出最终该服装的售价,再减去原价a 即可进行判断．[详解]解：根据题意可得：该服装的标价为()120%a +元,降价20%后售价为()()120%120%a +-元, 所以该商店卖出一件这样的服装盈利为()()1120%120%0.960.0425a a a a a a +--=-=-=-元．即最终该商店卖出一件这样的服装亏了125a 元．故选：B ．[点睛]本题考查了列代数式的知识和整式的加减运算,解题的关键是明确题意、正确表示出该服装的最终售价．7.下列式子中,和3232x yz -次数相同的是( )．A. 64abB. 328a b π-C. 25367a b ab -+-D. [答案]C先根据单项式次数的定义判断已知单项式的次数,再逐项判断即可．[详解]解：单项式3232x yz -的次数是6次．A 、64ab 的次数是7次,与已知式子的次数不相同,所以本选项不符合题意；B 、328a b π-的次数是5次,与已知式子的次数不相同,所以本选项不符合题意；C 、多项式25367a b ab -+-的次数是6次,与已知式子的次数相同,所以本选项符合题意；D 、的次数是0次,与已知式子的次数不相同,所以本选项不符合题意．故选：C ．[点睛]本题考查了单项式和多项式的次数,属于基础概念题型,熟练掌握二者的概念是关键．8.如图是一个正方体的表面展开图,如果原正方体的相对两个面上的数和相等,那么m n +=( )．A. 4B. 3C. 2D. 1[答案]A[解析][分析] 先根据原正方体的相对两个面上的数之和相等求出m 、n 的值,再代入所求式子计算即可．[详解]解：由题意,得：()()13743m n +-=+=+-=,所以m =4,n =0,所以404m n +=+=．故选：A ．[点睛]本题考查了正方体的表面展开图和有理数的加减运算,属于基本题型,解题的关键是根据题意正确确定m 、n 的值．9.在一次考试中,某班的17名男生的平均分为分,19名女生的平均分为分,那么这个班的全体同学的平均分为( )． A. 2a b + B. 36a b + C. 17192a b + D. 171936a b + [答案]D根据平均数的定义解答即可．[详解]解：由题意得：这个班的全体同学的平均分=17191719171936a b a b +++=．故选：D ．[点睛]本题考查了平均数的定义,属于基础题型,熟练掌握平均数的计算方法是解题关键．10.根据如图所示的流程图中的程序,当输入数据为3-时,输出数值为( )．A. 0B. 2C. 4D. 6[答案]A[解析][分析] 把x =﹣3代入所给出的流程图,按照程序计算即可．[详解]解：当x =﹣3时,﹣3+2=﹣1,﹣1×2=﹣2,﹣2＜0；当x =﹣2时,﹣2+2=0,0×2=0,0=0；所以输出的数值y =0．故选：A ．[点睛]本题主要考查了代数式求值,属于常见题型,弄懂所给出的流程图、按照程序准确计算是解题关键．二、填空题：(每小题4分,共20分)11.若22a a -=-,且29a =,则a =__________．[答案]﹣3[解析][分析]由29a =可确定a 的值,再根据绝对值的意义确定a －2的取值范围,进而可得答案．[详解]解：因为29a =,所以3a =±, 因为22a a -=-,所以20a -≤,所以3a =-．故答案为：﹣3．[点睛]本题考查了有理数的乘方和有理数的绝对值,属于常考题型,熟练掌握基本知识是关键．12.一个棱柱有12个面,它有__________个顶点,___________条棱．[答案] (1). 20 (2). 30[解析][详解]解：一个棱柱有12个面,除上下两个底面后还有10个侧面,所以这个棱柱为10棱柱,它有20个顶点,30条棱故答案：20；30．[点睛]本题考查立体图形的认识.．13.若在数轴上对应的点到表示的点的距离为3,则x =__________．[答案]﹣5或1[解析][分析]分表示数x 点在表示的点的左边和右边两种情况解答即可．[详解]解：当表示数x 的点在的点的左边时,x =﹣2－3=﹣5,当表示数x 的点在的点的右边时,x =﹣2+3=1,所以x =﹣5或1．故答案为：﹣5或1．[点睛]本题考查了数轴的有关知识,属于基本题型,正确理解数轴上两点间的距离是解题关键．14.如果关于,的单项式23m n x y -与2axy -可合并为单项式0,则a m n -+的值为 _________．[答案]2[解析][分析]由题意可得题目所给出的两项是同类项,再根据同类项的定义可得关于a 和m －n 的等式,然后把求得的a 的值和m －n 的值整体代入所求式子计算即可．[详解]解：根据题意,得：30a -=,1m n -=,所以a =3,所以()312a m n a m n -+=--=-=．故答案为：2．[点睛]本题考查了同类项的定义和合并同类项的法则,属于基础题目,熟练掌握基本知识是解题关键． 15.如图,正方形ABCD 的边长为2,以B 为圆心,AB 为半径在正方形内作14圆,再以CD 为直径在正方形内作半圆,得图中阴影部分,面积分别表示为1S 、2S ,则12S S -=__________．[答案]342π-[解析][分析]如图,可先计算13S S +,即为半圆CD 的面积,再计算23S S +,即为正方形的面积减去以AB 为半径的14圆的面积,然后再计算()13S S +与()23S S +的差即可．[详解]解：如图,记右边的空白部分的面积为S 3,则由题意得：21311112222CD S S πππ⎛⎫+=⋅=⨯= ⎪⎝⎭,2222311242444S S AB πππ+=-⋅=-⨯=-；所以()()()121323134422S S S S S S πππ-=+-+=--=-．故答案为：342π-．[点睛]本题考查了列代数式和阴影面积的计算等知识,弄清题意、明确()()121323S S S S S S -=+-+是解题关键．三、解答题：(共50分)16.计算(1)24111341323⎡⎤⎛⎫-+-+⨯-÷⨯⎢⎥ ⎪⎝⎭⎢⎥⎣⎦ (2)225(2)3(0.2)013317---⨯-+÷⨯[答案](1)13-；(2)1．[解析][分析](1)先计算乘方,同时把除法转化为乘法,再计算乘法,最后计算加减；(2)前一项绝对值内先计算乘方,同时后一项计算乘除,再计算乘法即可．[详解]解：(1)24111341323⎡⎤⎛⎫-+-+⨯-÷⨯⎢⎥ ⎪⎝⎭⎢⎥⎣⎦ =911134433⎛⎫-+-+⨯⨯⨯ ⎪⎝⎭ =()11399-+-+⨯=1169-+⨯=213-+ =13-；(2)原式=49(0.2)0--⨯-+=5(0.2)-⨯-=1．[点睛]本题考查了有理数的混合运算,属于基本题型,熟练掌握有理数的混合运算法则是解题关键． 17.化简(1)()()332332223234x y x y x y x y -----(2)22()()3()()a b a b b a b a ---+-+-[答案](1)322y x y --；(2)()()242a b a b ---．[解析][分析](1)先去括号,再合并同类项即可；(2)把a －b 看作一个整体,然后根据合并同类项的法则化简即可．[详解]解：(1)原式=332332246234x y x y x y x y ---++=322y x y --；(2)原式=()()()()223a b a b a b a b -+-----=()()242a b a b ---．[点睛]本题考查了整式的加减运算,属于基本题型,熟练掌握整式的加减运算法则是解题关键．18.已知：有理数,,在数轴上的位置如图,化简：|||||||3|a c b a b c a a +---+-+．[答案]2b ．[解析][分析]先由a 、b 、c 在数轴上的位置可确定a ＞0,c ＜b ＜0,b a c <<,进而可确定,,,3a c b a b c a a +-+-的符号,再根据绝对值的性质去掉绝对值符号,然后根据整式的加减运算法则计算即可．[详解]解：由题意得：a ＞0,c ＜b ＜0,b a c <<,所以0,0,0,30a c b a b c a a +<-<+-<>,所以原式=()()()3a c b a b c a a -+-----+-+⎡⎤⎡⎤⎣⎦⎣⎦=3a c b a b c a a --+-++-+=2b ．[点睛]本题主要考查了数轴、有理数的绝对值和整式的加减运算等知识,属于常考题型,根据点在数轴上的位置确定相关式子的符号、熟练进行绝对值的化简和整式的加减运算是解题的关键．19.下图是一个由若干棱长都为2cm 的小立方块搭成的几何体,求这个几何体的表面积．[答案]120cm 2．[解析][分析]先计算需要求的正方形的个数：可看作三个方向(正面、左面、上面)上的正方形的个数之和乘以2再加上挡住的2个正方形,所求得的结果再乘以一个正方形的面积即可．[详解]解：几何体的表面积=()425632=120⨯⨯+++⎡⎤⎣⎦cm 2．答：这个几何体的表面积是120cm 2．[点睛]本题考查了几何体的视图和表面积的计算,属于常见题型,掌握求解的方法是关键．20.已知2333A x xy y =--+,2343B x xy y =+-,且112x =-,537y =,求：4(2)(23)A A B A B -+--的值．[答案]94． [解析][分析] 先根据整式的加减运算法则化简原式,再把x 、y 的值代入化简后的式子计算即可．[详解]解：原式=4223A A B A B ---+=A B +()()23233343x xy y x xy y +=--++-23233343x xy y x xy y +=--++-2x =；当112x =-,537y =,原式=219124⎛⎫-= ⎪⎝⎭． [点睛]本题考查了整式的加减运算与代数式求值,属于常考题型,熟练掌握整式的加减运算法则是解题的关键．21.用简便方法计算下列各式值：(1)()151 2.7 1.5 4.8 1.522⎛⎫-⨯+-⨯+⨯- ⎪⎝⎭(2)12345678979899100--++--+++--+…[答案](1)-15；(2)0．[解析][分析](1)可把原式变形为()()1.5 2.7 1.5 4.8 1.5 2.5-⨯+-⨯+-⨯,再逆用乘法分配律计算；(2)可将原式变形为()()()12345678979899100--++--+++--+…,进一步即可求出结果．[详解]解：()151 2.7 1.5 4.8 1.522⎛⎫-⨯+-⨯+⨯-⎪⎝⎭=()()1.5 2.7 1.5 4.8 1.5 2.5-⨯+-⨯+-⨯=()1.5 2.7 4.8 2.5-⨯++= 1.510-⨯=-15；(2)12345678979899100--++--+++--+…=()()()12345678979899100--++--+++--+…=000+++=0．[点睛]本题考查了有理数的加法和乘法运算律,属于常见题型,熟练掌握有理数的运算律和混合运算法则是解题关键．22.在数轴上有点,,,它们表示的数分别为,,,且满足：()24980a b c -+-++=；,,三点同时出发沿数轴向右运动,它们的速度分别为：1A V =(单位/秒),2B V =(单位/秒),3C V =(单位/秒)．(1)求,,的值；(2)运动时间等于多少时,点与点、点的距离相等?[答案](1)a =4,b =9,c =﹣8；(2)6t =．[解析][分析](1)根据非负数的性质可得关于a 、b 、c 的方程,解方程即得答案；(2)先根据数轴上两点间的距离的表示方法得出点与点、点的距离,进而可得关于t 的方程,解方程即可求出结果．[详解]解：(1)根据题意,得：a －4=0,b －9=0,c +8=0,解得a =4,b =9,c =﹣8；(2)运动t 秒时,A 、B 、C 三点运动的路程分别为：t 、2t 、3t ,此时,点与点距离为：2945t t t -+-=+,点与C 点的距离为：()239817t t t -+--=-,由题意,得：517t t +=-,所以517t t +=-,解得：6t =；或()517t t +=--,此时t 的值不存在．所以当6t =时,点与点、点的距离相等．[点睛]本题主要考查了数轴上两点间的距离和一元一次方程的知识,属于常考题型,正确理解题意、准确用含t 的关系式表示点与点、点的距离是解题的关键．23.成都市的水费实行下表的收费方式：(1)周老师家九月份用了316m 的水,应付多少水费?(2)如果李老师家九月份的用水量为3xm ,那么应付的水费为多少元?(3)如果曹老师家九月和十月一共用了328m 的水,且已知九月比十月少,设九月用水量为3xm ,那么曹老师这两个月一共要交多少钱的水费?(可用含的代数式表示)[答案](1)38元；(2)当010x <≤时,应付水费10x 元；当1020x <≤时,应付水费310x -(元)；当20x >时,应付水费为430x -(元)；(3)若08x <<,要交水费822x -(元)；若810x ≤≤,要交水费为74x -(元)；若1014x <<,要交水费为64元．[解析][分析](1)根据不超310m 的按照2元/3m 计算,超出310m 的63m 按照3元/3m 计算,据此解答即可；(2)分用水量不超出310m (包括310m )、超出310m 但不超出320m (包括320m )、超出320m 三种情况,按照应付水费的计算方法解答即可；(3)先根据九月比十月用水量少确定x 的范围是014x <<,然后分08x <<、810x ≤≤、1014x <<三种情况,再根据(2)题中的结论和计费方法解答即可．[详解]解：(1)10263=38⨯+⨯元,答：周老师家九月份应付水费38元；(2)当用水量不超出310m (包括310m )即010x <≤时,应付水费为10x 元；当用水量超出310m 但不超出320m (包括320m )即1020x <≤时,应付水费为()102310310x x ⨯+⨯-=-(元)；当用水量超出320m 即20x >时,应付水费为()102103420430x x ⨯+⨯+⨯-=-(元)；答：当010x <≤时,应付水费10x 元；当1020x <≤时,应付水费310x -(元)；当20x >时,应付水费430x -(元)；(3)因为九月比十月用水量少,所以014x <<,若08x <<,则202828x <-<,所以曹老师这两个月一共要交水费为()242830822x x x +--=-(元)；若810x ≤≤,则182820x ≤-≤,所以曹老师这两个月一共要交水费为()23281074x x x +--=-(元)；若1014x <<,则142818x <-<,所以曹老师这两个月一共要交水费为()3103281064x x -+--=元．答：若08x <<,要交水费822x -(元)；若810x ≤≤,要交水费为74x -(元)；若1014x <<,要交水费为64元．[点睛]本题考查的是列出实际问题中的代数式,属于常考题型,正确理解题意、灵活应用分类思想是解题的关键．。

人教版数学七年级下册《期中考试题》含答案解析

人教版数学七年级下学期期中测试卷学校________ 班级________ 姓名________ 成绩________一．选择题(每小题3分,共24分)1.下列调查中,最适宜采用普查方式是( )A. 对全国初中学生视力状况的调査B. 对“十一国庆”期间全国居民旅游出行方式的调查C. 旅客上飞机前的安全检查D. 了解某种品牌手机电池的使用寿命2.如图,下列结论中错误的是( )A. 1∠与2∠同旁内角B. 1∠与6∠是内错角C. 2∠与5∠是内错角D. 3∠与5∠是同位角3.下列方程组中是二元一次方程组的是( ) A. 346564x y z y +=⎧⎨-=⎩B. 3112x y x y +=⎧⎪⎨-=⎪⎩C. 2228x y x y +=⎧⎨-=⎩D. 2.54x y x y +=⎧⎨-=⎩4.如图,OA OB ⊥,若3420BOC '∠=︒,则AOC ∠的度数是( )A. 5520'︒B. 5540'︒C. 5560'︒D. 5580'︒ 5.某县为了传承中华优秀传统文化,组织了一次全县600名学生参加的“中华经典诵读”大赛．为了解本次大赛的选手成绩,随机抽取了其中50名选手的成绩进行统计分析．在这个问题中,下列说法：①这600名学生的“中华经典诵读”大赛成绩的全体是总体．②每个学生个体．③50名学生是总体的一个样本．④样本容量是50名．其中说法正确的有()A. 1个B. 2个C. 3个D. 4个6.某公司的生产量在1－7月份的增长变化情况如图所示,从图上看,下列结论正确的是()A. 2－6月生产量逐月减少B. 1月份生产量最大C. 这七个月中,每月生产量不断增加D. 这七个月中,生产量有增加有减少7.二元一次方程3x+2y＝15正整数解有( )组．A. 1B. 2C. 3D. 无数组8.某公司有学徒工和熟练工两个工种的工人,已知一个学徒工每天制造的零件比一个熟练少20个,一个学徒工与两个熟练工每天共可制造220个零件,求一个学徒工与一个熟练工每天各能制造多少个零件?设一个学徒工每天能制造个零件,一个熟练工每天能制造个零件,根据题意可列方程组为( )A.202220y xx y-=⎧⎨+=⎩B.202220x yx y-=⎧⎨+=⎩C.202220y xx y-=⎧⎨+=⎩D.202220x yx y-=⎧⎨+=⎩二．填空题(共6小题,每小题3分,满分18分)9.如图,从点P向直线l所画的4条线段中,线段__最短,理由是__．10.如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD＝80°,则∠BOM的度数是__．11.已知方程组|a|-(-1)5y (-5)3y a x b xy =⎧⎨+=⎩是关于x,y 的二元一次方程组,则a b 的值是____. 12.对某中学同年级70名男生的身高进行了测量,得到一组数据,其中最大值是183cm ,最小值是146cm ,对这组数据进行整理时,确定它的组距为5cm ,则至少应分__________组.13.六一儿童节将至,孩子王儿童商店推出甲、乙、丙三种特价玩具,若购甲3件,乙2件,丙1件需要400元；购甲1件,乙2件,丙3件需要440元,则购买甲乙丙三种玩具各一件需要_________元.14.对于X ,Y 定义一种新运算“*”：X *Y ＝aX ＋bY ,其中a ,b 为常数,等式右边是通常的加法和乘法运算．已知：3*5＝15,4*7＝28,那么2*3＝________．三．解答题(共58分)15.先化简,再求值：()22223m mn m mn +--,其中1m =-,2n =．16.解下列方程组：(1)312236x y x y +=⎧⎨-=⎩； (2)2(1)54(1)2(5)x y y x -=+⎧⎨-=+⎩． 17.请在图中,过P 点分别画OA 、OB 的垂线．18.网络时代新兴词汇层出不穷．为了解大众对网络词汇的理解,某兴趣小组举行了一个调查活动：选取四个热词A ：“硬核人生”,B ：“好嗨哦”,C ：“双击666”,D ：“杠精时代”在街道上对流动人群进行了抽样调查,要求被调查的每位只能勾选一个最熟悉的热词,根据调查结果,该小组绘制了如下的两幅不完整的统计图,请你根据统计图提供的信息,解答下列问题：(1)本次调查中,一共调查了多少名路人?(2)补全条形统计图,并求出a 的值；(3)请算出扇形图中的b 的值．19.列方程组解应用题某校组织“大手拉小手,义卖献爱心”活动,计划购买黑、白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子．已知该学校从批发市场花2400元购买了黑、白两种颜色的文化衫100件,每件文化衫的批发价及手绘后的零售价如表：批发价(元) 零售价(元) 黑色文化衫25 45 白色文化衫20 35(1)学校购进黑、白文化衫各几件?(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润．20.如图,直线AB ,CD ,EF 相交于点O .(1)请写出,AOC ∠,AOE ∠EOC ∠的对顶角；(2)若50AOC ︒∠=,求,BOD ∠BOC ∠的度数.21.在等式y ＝ax 2+bx +c 中,当x ＝﹣1时,y ＝3；当x ＝0时,y ＝1,当x ＝1时,y ＝1,求这个等式中a 、b 、c 的值． 22.九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理．请解答以下问题：(1)把上面的频数分布表和频数分布直方图补充完整；(2)若该小区用水量不超过15t 的家庭占被调查家庭总数的百分比；(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t 的家庭大约有多少户?23.若规定a c b d ＝ad ﹣bc ,如2130-＝2×0﹣3×(﹣1)＝3 (1)计算：2531-； (2)计算：35x y-； (3)解方程组：321325y x x y ⎧-=⎪⎪⎨⎪=-⎪⎩．24.“利海”通讯器材商场,计划用60000元从厂家购进若干部新型手机,出厂价分别为甲种型号手机每部1800元,乙种型号手机每部600元,丙种型号手机每部1200元．若商场同时购进其中两种不同型号的手机共40部,并将60000元恰好用完,请你帮助商场计算一下如何购买．25.如图,∠1=28°,AB⊥CD ,垂足为O,EF 经过点O ．求∠2、∠3的度数．答案与解析一．选择题(每小题3分,共24分)1.下列调查中,最适宜采用普查方式的是( )A. 对全国初中学生视力状况的调査B. 对“十一国庆”期间全国居民旅游出行方式的调查C. 旅客上飞机前的安全检查D. 了解某种品牌手机电池的使用寿命[答案]C[解析][分析]由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似．[详解]A ．对全国初中学生视力状况的调査,范围广,适合抽样调查,故A 错误；B ．对“十一国庆”期间全国居民旅游出行方式的调查范围广,适合抽样调查,故B 错误；C ．旅客上飞机前的安全检查,适合普查,故C 正确；D ．了解某种品牌手机电池的使用寿命,适合抽样调查,故D 错误．故选：C ．[点睛]本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查．2.如图,下列结论中错误的是( )A. 1∠与2∠同旁内角B. 1∠与6∠是内错角C. 2∠与5∠是内错角D. 3∠与5∠是同位角[答案]C[解析][分析]利用同位角、内错角、同旁内角的定义判断即可.[详解]解；A ．1∠与2∠是同旁内角,所以此选项正确；B ．1∠与6∠是内错角,所以此选项正确；C ．∠2、∠5既不是同位角、不是内错角,也不是同旁内角,所以此选项错误；D ．3∠与5∠是同位角,所以此选项正确,故选：C ．[点睛]考查了同位角、内错角、同旁内角,三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定．在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线．同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形．3.下列方程组中是二元一次方程组的是( )A. 346564x y z y +=⎧⎨-=⎩ B. 3112x y x y +=⎧⎪⎨-=⎪⎩ C. 2228x y x y +=⎧⎨-=⎩D. 2.54x y x y +=⎧⎨-=⎩[答案]D[解析][分析] 由二元一次方程组的定义：两个方程都为整式方程；一共含有2个未知数；最高次项的次数是1；从而可得到答案．[详解]解：A 、该方程组中含有三个未知数,属于三元一次方程组,故本选项不符合题意；B 、第二个方程不是整式方程,不符合二元一次方程组的定义,故本选项不符合题意；C 、第二个方程中未知数的最高次数是2,该方程组属于二元二次方程组,故本选项不符合题意；D 、符合二元一次方程组的定义,故本选项符合题意．故选：D ．[点睛]本题考查的是二元一次方程组的定义,掌握定义是解题的关键．4.如图,OA OB ⊥,若3420BOC '∠=︒,则AOC ∠的度数是( )A. 5520'︒B. 5540'︒C. 5560'︒D. 5580'︒[答案]B[解析][分析] 因为OA OB ⊥,所以90AOB ∠=︒,再利用AOC AOB BOC ∠=∠-∠即可得出答案.[详解]∵OA OB ⊥∴90AOB ∠=︒∴903420'5540'AOC AOB BOC ∠=∠-∠=︒-︒=︒故选B[点睛]本题主要考查角和与差,掌握角的运算是解题的关键.5.某县为了传承中华优秀传统文化,组织了一次全县600名学生参加的“中华经典诵读”大赛．为了解本次大赛的选手成绩,随机抽取了其中50名选手的成绩进行统计分析．在这个问题中,下列说法：①这600名学生的“中华经典诵读”大赛成绩的全体是总体．②每个学生是个体．③50名学生是总体的一个样本．④样本容量是50名．其中说法正确的有( )A. 1个B. 2个C. 3个D. 4个[答案]A[解析][分析]”我们在区分总体、个体、样本、样本容量这四个概念时,首先找出考查的对象,考查对象是组织了一次全县600名学生参加的“中华经典诵读”大赛的成绩,再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量．[详解]①这600名学生的“中华经典诵读”大赛成绩的全体是总体,正确；②每个学生的成绩是个体,故原说法错误；③50名学生的成绩是总体的一个样本,故原说法错误；④样本容量是50,故原说法错误．所以说法正确有①,1个．故选：A．[点睛]考查统计知识的总体,样本,个体,等相关知识点,要明确其定义．易错易混点：学生易对总体和个体的意义理解不清而错选．6.某公司的生产量在1－7月份的增长变化情况如图所示,从图上看,下列结论正确的是()A. 2－6月生产量逐月减少B. 1月份生产量最大C. 这七个月中,每月的生产量不断增加D. 这七个月中,生产量有增加有减少[答案]C[解析][分析]根据增长率均为正数,即后边的月份与前面的月份相比是增加的,据此即可求出答案．[详解]图示为增长率的折线图,读图可得：这七个月中,增长率为正,故每月生产量不断上涨,故A,B,D均错误；故选C．[点睛]本题考查折线统计图的运用,折线统计图表示的是事物的变化情况,如增长率．7.二元一次方程3x+2y＝15的正整数解有( )组．A. 1B. 2C. 3D. 无数组[答案]B[解析][分析]把方程变形为：25,3x y=-由是3的倍数直接写出方程的正整数解即可．[详解]解：3x+2y＝15,25,3x y =- ,x y 为正整数,方程在正整数解为：31,.36x x y y ==⎧⎧⎨⎨==⎩⎩则方程的正整数解有2组．故选：B ．[点睛]本题考查的是二元一次方程的正整数解,掌握求二元一次方程的正整数解的方法是解题的关键． 8.某公司有学徒工和熟练工两个工种的工人,已知一个学徒工每天制造的零件比一个熟练少20个,一个学徒工与两个熟练工每天共可制造220个零件,求一个学徒工与一个熟练工每天各能制造多少个零件?设一个学徒工每天能制造个零件,一个熟练工每天能制造个零件,根据题意可列方程组为( )A. 202220y x x y -=⎧⎨+=⎩B. 202220x y x y -=⎧⎨+=⎩C. 202220y x x y -=⎧⎨+=⎩D. 202220x y x y -=⎧⎨+=⎩[答案]A[解析][分析]根据题意找到两个等量关系列出方程组即可． [详解]解：一个学徒工每天能制造个零件,一个熟练工每天能制造个零件,根据题中：一个学徒工每天制造的零件比一个熟练少20个,以及一个学徒工与两个熟练工每天共可制造220个零件可得方程组：202220y x x y -=⎧⎨+=⎩. 故选A.[点睛]本题考查了由实际问题抽象出二元一次方程组的知识,解题的关键是能够根据题意找到两个等量关系,这是列方程的依据．二．填空题(共6小题,每小题3分,满分18分)9.如图,从点P 向直线l 所画的4条线段中,线段__最短,理由是__．[答案] (1). PB (2). 从直线外一点,到直线上各点所连的线段中,垂线段最短[解析][分析]根据“从直线外一点,到直线上各点所连的线段中,垂线段最短”,进行判断即可．[详解]解：根据“垂线段最短”可知,PB 最短,理由是从直线外一点,到直线上各点所连的线段中,垂线段最短,故答案为：PB ,从直线外一点,到直线上各点所连的线段中,垂线段最短．[点睛]本题考查的是“直线外一点与直线上各点所连的线段中,垂线段最短”,掌握这个基本事实是解题的关键．10.如图,两条直线AB ,CD 交于点O ,射线OM 是∠AOC 的平分线,若∠BOD ＝80°,则∠BOM 的度数是__．[答案]140°[解析][分析]先根据对顶角相等得出∠AOC ＝80°,再根据角平分线的定义得出∠COM ,最后解答即可．[详解]解：∵∠BOD ＝80°,∴∠AOC ＝80°,∠COB ＝100°,∵射线OM 是∠AOC 的平分线,∴∠COM ＝40°,∴∠BOM ＝40°+100°＝140°,故答案为：140°．[点睛]此题考查对顶角和角平分线的定义,关键是得出对顶角相等．11.已知方程组|a|-(-1)5y (-5)3y a x b xy =⎧⎨+=⎩是关于x,y 的二元一次方程组,则a b 的值是____.[答案]-1[解析][分析]利用二元一次方程组的定义确定出a与b的值,代入原式计算即可得到结果．[详解]解：由题意得：|a|＝1,b－5＝0,a－1≠0,解得：a＝－1,b＝5,则原式＝(－1)5＝－1．故答案为－1．[点睛]此题考查了二元一次方程组的定义,熟练掌握二元一次方程组的定义是解本题的关键．12.对某中学同年级70名男生的身高进行了测量,得到一组数据,其中最大值是183cm,最小值是146cm,对这组数据进行整理时,确定它的组距为5cm,则至少应分__________组.[答案]8[解析][分析]根据组数的计算公式即可得出答案.组数=(最大值-最小值)组距,计算结果为小数或分数时,用进一法来确定组数.[详解]解：∵1831467.45-=∵计算结果为小数,我们利用进一法来确定组数,因此组数为8.故答案为：8.[点睛]本题考查的知识点是组数的计算,此类题目要根据题意找出样本数据的最大值和最小值,结合组距,利用公式来求解.13.六一儿童节将至,孩子王儿童商店推出甲、乙、丙三种特价玩具,若购甲3件,乙2件,丙1件需要400元；购甲1件,乙2件,丙3件需要440元,则购买甲乙丙三种玩具各一件需要_________元.[答案]210[解析][分析]设甲玩具的单价为x元,乙玩具的单价为y元,丙玩具的单价为z元,根据“购甲3件,乙2件,丙1件需400元：购甲1件,乙2件,丙3件需440元”,即可得出关于x,y,z的三元一次方程组,再利用(①+②)÷4,即可求出结论．[详解]设甲玩具的单价为x元,乙玩具的单价为y元,丙玩具的单价为z元,依题意,得：32=40023=440x y z x y z ++⎧⎨++⎩①② , (①+②)÷4,得：x+y+z=210．故答案为：210．[点睛]此题考查三元一次方程组的应用,找准等量关系,正确列出三元一次方程组是解题的关键． 14.对于X ,Y 定义一种新运算“*”：X *Y ＝aX ＋bY ,其中a ,b 为常数,等式右边是通常的加法和乘法运算．已知：3*5＝15,4*7＝28,那么2*3＝________．[答案]2[解析][分析]利用题中的新定义列出方程组,求出方程组的解得到a 与b 的值,代回到新定义的式子中,然后再根据新定义计算2*3即可．[详解]∵X*Y=aX+bY , 3*5=15,4*7=28,∴35154728a b a b +=⎧⎨+=⎩, 解得3524a b =-⎧⎨=⎩, ∴X*Y=-35X+24Y ,∴2*3=-35×2+24×3=2, 故答案为2.[点睛]本题考查了新定义运算与解二元一次方程组,求出a 、b 的值是解题的关键.三．解答题(共58分)15.先化简,再求值：()22223m mn m mn +--,其中1m =-,2n =．[答案]254m mn -+；13-[解析][分析]根据整式的加减法则进行化简,再代数求值即可.[详解]原式=22262m mn m mn +-+=254m mn -+当1m =-,2n =时,原式= ()()251412-⨯-+⨯-⨯ 5813=--=-.[点睛]本题以代数求值方式考查整式的加减与代数计算,熟练掌握整式加减运算是解答关键.16.解下列方程组：(1)312236x y x y +=⎧⎨-=⎩； (2)2(1)54(1)2(5)x y y x -=+⎧⎨-=+⎩． [答案](1)62x y =⎧⎨=⎩；(2)77x y =⎧⎨=⎩[解析][分析](1)方程组利用加减消元法求出解即可；(2)方程组整理后,利用加减消元法求出解即可．[详解]解：(1)312236x y x y +=⎧⎨-=⎩①②, ①+②得：3x ＝18,解得：x ＝6,把x ＝6代入①得：y ＝2,则方程组的解为62x y =⎧⎨=⎩； (2)方程组整理得：272414x y x y -=⎧⎨-=-⎩①②, ①﹣②得：3y ＝21,解得：y ＝7,把y ＝7代入①得：x ＝7,则方程组的解为77x y =⎧⎨=⎩． [点睛]此题考查了解二元一次方程组,利用了消元的思想,消元的方法有：代入消元法与加减消元法． 17.请在图中,过P 点分别画OA 、OB 的垂线．[答案]详见解析[解析][分析]根据垂线的定义利用尺规即可过P点分别画OA、OB的垂线．[详解]解：如图,PC和PD即为所求．[点睛]本题考查了作图-基本作图,解决本题的关键是掌握基本作图过程．18.网络时代新兴词汇层出不穷．为了解大众对网络词汇的理解,某兴趣小组举行了一个调查活动：选取四个热词A：“硬核人生”,B：“好嗨哦”,C：“双击666”,D：“杠精时代”在街道上对流动人群进行了抽样调查,要求被调查的每位只能勾选一个最熟悉的热词,根据调查结果,该小组绘制了如下的两幅不完整的统计图,请你根据统计图提供的信息,解答下列问题：(1)本次调查中,一共调查了多少名路人?(2)补全条形统计图,并求出a的值；(3)请算出扇形图中的b的值．[答案](1)300名；(2)图见解析,a＝90；(3)b＝90[解析](1)根据选择A的人数和扇形统计图中所对的圆心角的度数,可以求得本次调查了多少名路人；(2)根据扇形统计图中的数据可以求得选择C和选择D的人数,从而补全统计图；(3)根据条形统计图中的数据可以求得b的值．[详解]解：(1)本次调查中,一共调查了：120÷144360︒＝300(名)；(2)选D的有：a＝300×108360︒︒＝90(名)选C的有300﹣120﹣75﹣90＝15(名), 补全的条形统计图如下图所示：(3)b°＝360°×75300＝90°,则b＝90．[点睛]本题考查条形统计图、扇形统计图,解答本题的关键是明确题意,利用数形结合的思想解答．19.列方程组解应用题某校组织“大手拉小手,义卖献爱心”活动,计划购买黑、白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子．已知该学校从批发市场花2400元购买了黑、白两种颜色的文化衫100件,每件文化衫的批发价及手绘后的零售价如表：批发价(元) 零售价(元)黑色文化衫25 45白色文化衫20 35(1)学校购进黑、白文化衫各几件?(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润．[答案](1)学校购进黑文化衫80件,白文化衫20件；(2)该校这次义卖活动共获得1900元利润．[分析](1)设学校购进黑文化衫x 件,白文化衫y 件,根据两种文化衫100件共花费2400元,即可得出关于x ,y 的二元一次方程组,解之即可得出结论；(2)根据总利润=每件利润×数量,即可求出结论．[详解]解：(1)设学校购进黑文化衫x 件,白文化衫y 件,依题意,得：10025202400x y x y +=⎧⎨+=⎩；解得： 8020x y =⎧⎨=⎩答：学校购进黑文化衫80件,白文化衫20件．(2)(45-25)×80+(35-20)×20=1900(元)．答：该校这次义卖活动共获得1900元利润．[点睛]本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键． 20.如图,直线AB ,CD ,EF 相交于点O .(1)请写出,AOC ∠,AOE ∠EOC ∠的对顶角；(2)若50AOC ︒∠=,求,BOD ∠BOC ∠的度数.[答案](1)AOC ∠的对顶角是BOD ∠,AOE ∠的对顶角是BOF ∠,EOC ∠的对顶角是DOF ∠；(2)50BOD ︒∠=,130BOC ︒∠=[解析][分析](1)根据对顶角的定义写出对顶角即可；(2)根据对顶角的性质和邻补角的性质即可得出结论.[详解](1)AOC ∠的对顶角是BOD ∠,AOE ∠的对顶角是BOF ∠,EOC ∠的对顶角是DOF ∠.(2)因为AOC ∠的对顶角是BOD ∠,50AOC ︒∠=,所以50BOD ︒∠=.因为BOC ∠是BOD ∠的邻补角,所以18050130BOC ︒︒︒∠=-=.[点睛]此题考查的是对顶角的定义及性质和邻补角的性质,掌握对顶角的定义、对顶角相等和邻补角互补是解决此题的关键.21.在等式y ＝ax 2+bx +c 中,当x ＝﹣1时,y ＝3；当x ＝0时,y ＝1,当x ＝1时,y ＝1,求这个等式中a 、b 、c 的值．[答案]a ＝1,b ＝﹣1,c ＝1．[解析][分析]根据题意列出三元一次方程组,解方程组即可．[详解]由题意得,311a b c c a b c -+=⎧⎪=⎨⎪++=⎩,解得,a ＝1,b ＝﹣1,c ＝1．[点睛]本题考查的是三元一次方程组的解法,解三元一次方程组的一般步骤：①首先利用代入法或加减法,把方程组中一个方程与另两个方程分别组成两组,消去两组中的同一个未知数,得到关于另外两个未知数的二元一次方程组．②然后解这个二元一次方程组,求出这两个未知数的值．③再把求得的两个未知数的值代入原方程组中的一个系数比较简单的方程,得到一个关于第三个未知数的一元一次方程．④解这个一元一次方程,求出第三个未知数的值,得到方程组的解．22.九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理．请解答以下问题：(1)把上面的频数分布表和频数分布直方图补充完整；(2)若该小区用水量不超过15t 的家庭占被调查家庭总数的百分比；(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t 家庭大约有多少户?[答案](1)12户和0.08；补图见解析；(2)68%；(3)120户．[解析][分析](1)根据0＜x≤5中频数为6,频率为0.12,则调查总户数为6÷0.12=50,进而得出在5＜x≤10范围内的频数以及在20＜x≤25范围内的频率；(2)根据(1)中所求即可得出不超过15t 的家庭总数即可求出,不超过15t 的家庭占被调查家庭总数的百分比；(3)根据样本数据中超过20t 的家庭数,即可得出1000户家庭超过20t 的家庭数．[详解](1)如图所示：根据0＜x≤5中频数为6,频率为0.12,则6÷0.12=50,50×0.24=12户,4÷50=0.08, 故表格从上往下依次是：12户和0.08；(2)6121650++×100%=68%； (3)1000×(0.08+0.04)=120户,答：该小区月均用水量超过20t 的家庭大约有120户．考点：1.频数(率)分布直方图；2.用样本估计总体；3.频数(率)分布表．23.若规定a cb d ＝ad ﹣bc ,如2130-＝2×0﹣3×(﹣1)＝3 (1)计算：2531-； (2)计算：35x y -；(3)解方程组：321325 y xx y⎧-=⎪⎪⎨⎪=-⎪⎩．[答案](1)﹣17；(2) 5x+3y；(3)11 xy=⎧⎨=-⎩[解析][分析](1)根据所给的式子求出代数式的值即可；(2)根据所给的式子得出关于x、y的方程即可；(3)先根据题意得出关于x、y的二元一次方程组,求出x、y的值即可．[详解]解：(1)∵a bb c＝ad﹣bc,∴原式＝﹣2﹣15 ＝﹣17；(2)原式＝5x+3y；(3)由题意可得321 325 x yy x+=⎧⎨-=-⎩,解得11 xy=⎧⎨=-⎩．[点睛]本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键．24.“利海”通讯器材商场,计划用60000元从厂家购进若干部新型手机,出厂价分别为甲种型号手机每部1800元,乙种型号手机每部600元,丙种型号手机每部1200元．若商场同时购进其中两种不同型号的手机共40部,并将60000元恰好用完,请你帮助商场计算一下如何购买．[答案]两种购买方法：甲种型号手机购买30部,乙种型号手机购买10部；或甲种型号手机购买20部,丙种型号手机购买20部[解析]分析]分三种情况：①设分别购进甲乙两种手机为x、y部,根据两种不同型号的手机共40部,并将60000元恰好用完可以列出方程组,解方程组即可解决问题；②设分别购进甲丙两种手机为x、z部,根据两种不同型号的手机共40部,并将60000元恰好用完可以列出方程组,解方程组即可解决问题；③设分别购进乙丙两种手机为y、z部,根据两种不同型号的手机共40部,并将60000元恰好用完可以列出方程组,解方程组即可解决问题．[详解]解：分三种情况：①设分别购进甲乙两种手机为x、y部,依题意得,40 180060060000 x yx y+=⎧⎨+=⎩,解得：3010 xy=⎧⎨=⎩,即可以购进甲乙两种手机分别是30部、10部；②设分别购进甲丙两种手机为x、z部,依题意得,40 1800120060000 x zx z+=⎧⎨+=⎩,解得：2020 xz=⎧⎨=⎩,即可以购进甲丙两种手机分别是20部、20部；③设分别购进乙丙两种手机为y、z部,依题意得,40 600120060000 y zy z+=⎧⎨+=⎩,解得：2060yz=-⎧⎨=⎩(不合题意,舍去),答：有两种购买方法：甲种型号手机购买30部,乙种型号手机购买10部；或甲种型号手机购买20部,丙种型号手机购买20部；[点评]本题考查了二元一次方程组的应用,比较复杂,解题的关键是根据已知条件分类讨论,然后在可能的情况下分别列出方程组,解方程组根据解的情况就可以确定购买方案．25.如图,∠1=28°,AB⊥CD,垂足为O,EF经过点O．求∠2、∠3的度数．[答案]62°[解析][分析]利用余角和对顶角的关系,即可求得角的度数．[详解]解：∵直线AB、EF相交于O点,∠1=28°,∴∠3=∠1=28°(对顶角相等),又∵AB⊥CD,∴∠2=90°-∠3=62°,[点睛]本题考查了垂线,对顶角、邻补角．注意：当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直．。

北京市顺义区仁和中学2023-2024学年七年级下学期期中数学试题(解析版)

仁和中学2023-2024学年度第二学期期中考试初一年级数学试卷一、选择题（每题2分，共20分）1. 不等式的解集在数轴上表示正确的是（）A. B.C.D.【答案】D【解析】【分析】本题主要考查了一元一次不等式的求解，在数轴上表示不等式解集；解不等式，即可得出合适的选项．【详解】解：解不等式，可得，故不等式解集在数轴上表示为：故选：D ．2. 下列命题中，假命题是（）A. 同角的补角相等B. 同一平面内，过一点有且只有一条直线与已知直线垂直C. 如果，，那么D. 两条直线被第三条直线所截，同旁内角互补【答案】D【解析】【分析】利用同角的补角的性质、垂直的定义、平行线的性质等知识分别判断后即可．【详解】解：A 、同角的补角相等，是真命题，故本选项不符合题意；B 、同一平面内，过一点有且只有一条直线与已知直线垂直，是真命题，故本选项不符合题意；C 、如果，，那么，是真命题，故本选项不符合题意；D、两条平行直线被第三条直线所截，同旁内角互补，故原命题是假命题，故本选项符合题意；的10x +<10x +<10x +<1x <-10x +<a b =b c =a c=a b =b c =a c =【点睛】考查了命题与定理的知识，解题的关键是了解同角的补角的性质、垂直的定义、平行线的性质等知识，难度不大．3. 下列各组数值中，哪个是方程的解（）A. B. C. D. 【答案】B【解析】【分析】将四个选项分别代入原方程，能使方程左右两边相等的未知数的值是方程的解．【详解】解：将代入原方程，左边右边，选项不符合题意；将代入原方程，左边右边，选项符合题意；将代入原方程，左边右边，选项不符合题意；将代入原方程，左边右边，选项不符合题意．故选：．【点睛】本题主要考查了二元一次方程的解．正确利用二元一次方程的解的意义是解题的关键．4. 如图，，射线在内部，下列说法一定成立的是（）A. 和互余B. 和互补C. 和互为对顶角D. 和相等21x y +=21x y =⎧⎨=⎩13x y =-⎧⎨=⎩13x y =⎧⎨=-⎩22x y =⎧⎨=-⎩ 21x y =⎧⎨=⎩5=≠A ∴ 13x y =-⎧⎨=⎩1==B ∴13x y =⎧⎨=-⎩1=-≠C ∴ 22x y =⎧⎨=-⎩2=≠D ∴B AO OB ⊥OC AOB ∠1∠2∠1∠2∠1∠2∠1∠2∠【解析】【分析】本题考查了角的互余概念、对顶角的定义，准确理解角的互余概念，对顶角的定义是解题的关键．【详解】解：∵，∴，又∵射线在内部，∴，∴和互余，故选A5. 如图，下列条件中，能判断的是（）A. B. C. D. 【答案】A【解析】【分析】由平行线的判定方法，即可判断．【详解】解：A.，由内错角相等，两直线平行，能判断，故A 符合题意；B.不是被截成的内错角，不能判断，故B 不符合题意；C. 不是被截成的内错角，不能判断，故C 不符合题意；D.不是被截成的同旁内角，不能判断，故D 不符合题意；故选：A ．【点睛】本题考查平行线的判定，熟练掌握：①内错角相等，两直线平行；②同位角相等，两直线平行；③同旁内角互补，两直线平行，是解题的关键．6. 如图，由可以得到的结论是（）AO OB ⊥90AOB ∠=︒OC AOB ∠1290∠∠+=︒1∠2∠AB CD 12∠=∠13∠=∠14∠=∠13180∠+∠=︒12∠=∠AB CD 13∠∠、AB CD 、()AD BC AB CD 14∠∠、AB CD 、()AD BC AB CD 13∠∠、AB CD 、()AD BC AB CD AB CD ∥A. B. C. D. 【答案】B【解析】【分析】由平行线的性质，角平分线的定义逐项判断可求解【详解】解：A ．当平分时，，故此选项不符合题意；B ．当时，，故此选项符合题意；C ．当时，，故此选项不符合题意；D ．当平分时，，故此选项不符合题意．故选：B ．【点睛】本题考查平行线的性质：两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．掌握平行线的性质是解题的关键．也考查了角平分线的定义．7. 将一个长方形的长减少，宽变成现在的2倍，设这个长方形的长为，宽为，则下列方程中正确的是（）A. B. C. D. 【答案】C【解析】【分析】根据长方形的长减少宽变成现在的2倍，列出方程即可．【详解】解：设这个长方形的长为，宽为，根据题意得：，故C 正确．故选：C ．【点睛】本题主要考查了列二元一次方程，解题的关键是找出题目中的等量关系．8. 实数，对应的位置如图所示，下列式子正确的是（）A. B. C. D. 【答案】D【解析】【分析】根据数轴得出a 和b 的范围，进而得出，，根据有理数运算法则逐一判断即可．【详解】解：由数轴可得：，，∴，，12∠=∠14∠=∠23∠∠=34∠∠=AC BAD ∠12∠=∠AB CD ∥14∠=∠AD BC ∥23∠∠=AC BCD ∠34∠∠=5cm cm x cm y 52x y+=52x y +=+52x y -=52x y -=+5cm=cm x cm y 52x y -=a b 22a b <22a b -<-50a +<44a b +<+a b <a b >54a -<<-3<<4b a b <a b >∴，，，，故A 、B 、C 错误，D 正确，故选：D ．【点睛】本题考查了利用数轴判断式子的正负，有理数运算和符号之间的关系，乘、除法注意：同号得正，异号得负．9. 如图为小丽和小欧依次进入电梯时，电梯因超重而警示音响起的过程，且过程中没有其他人进出．已知当电梯乘载的重量超过400千克时警示音响起，且小丽、小欧的重量分别为50千克、70千克．若小丽进入电梯前，电梯内已乘载的重量为千克，则的取值范围是（）A. B. C. D. 【答案】A【解析】【分析】由图可得，小丽的重量为50千克，且进入电梯后，警示音没有响起，小欧的重量分别为70千克．且进入电梯后，警示音响起，分别列出不等式即可求解．【详解】由题意可知：当电梯乘载的重量超过400千克时警示音响起，小丽进入电梯前，电梯内已乘载的重量为x 千克，由图可知：小丽的重量为50千克，且进入电梯后，警示音没有响起，所以此时电梯乘载的重量，解得因为小欧的重量为70千克．且进入电梯后，警示音响起，所以此时电梯乘载的重量，解得因此的取值范围是故选：A【点睛】本题考查了一元一次不等式组的应用，解决本题的关键是根据题意找到不等关系．22a b >22a b ->-50a +>44a b +<+x x 280350x <≤280400x <≤330350x <≤330400x <≤50400x +≤350x ≤5070400x ++>280x >x 280350x <≤10. 已知关于的不等式组有以下说法：①当时，则不等式组的解集是；②若不等式组的解集是，则；③若不等式组无解，则；④若不等式组的整数解只有，0，1，2，则．其中正确的说法有（）A. ①③B. ②④C. ①②③D. ①②③④【答案】C【解析】【分析】先求出各不等式的解集，再根据各小题的结论解答即可．【详解】解：关于的不等式组，①当时，则不等式组的解集是，故本小题正确，符合题意；②若不等式组的解集是，则，故本小题正确，符合题意；③若不等式组无解，则，故本小题正确，符合题意；④若不等式组的整数解只有，0，1，2，则，故本小题错误，不符合题意；故选：C ．【点睛】本题考查的是由不等式组的解集情况求参数，熟知解一元一次不等式组的基本步骤是解题的关键．二、填空题（每题2分，共20分）11. 用不等式表示“的3倍与7的差小于11”为______．【答案】【解析】【分析】首先表示“的3倍”为，再表示“与7的差”为，最后再表示“小于11”为．【详解】解：∵“的3倍”为，再表示“与7的差”为，∴用不等式表示“的3倍与7的差小于11”为：，故答案为：．【点睛】本题考查由实际问题抽象出一元一次不等式，用不等式表示不等关系时，要抓住题目中的关键词，如“大于（小于）、不超过（不低于）、是正数（负数）”、“至少”、“最多”等等，正确选择不等号．x 2x x m >-⎧⎨≤⎩1m =21x -<≤20x -<≤0m =2m ≤-1-2m =x 2x x m >-⎧⎨≤⎩1m =21x -<≤20x -<≤0m =2m ≤-1-23m ＜≤m 3711m -<m 3m 37m -3711m -<m 3m 37m -m 3711m -<3711m -<12. 已知方程的三个解为方程的三个解为则方程组的解为______．【答案】【解析】【分析】根据方程组解的定义，能够同时满足方程组中的两个方程的解是方程组的解观察得出两个方程的解中相同的解为方程组的解．【详解】解：根据方程组的解的定义，能够同时满足方程组中的两个方程的解是方程组的解，可知是这两个方程中所有的解中能同时满足两个方程的解，∴方程组的解为，故答案为：．【点睛】此题主要是考查了方程组的解的定义，能够熟练掌握同时满足方程组中的两个方程的解是方程组的解是解答此题的关键．13. 如图，利用工具测量角，则的大小为______．【答案】##30度【解析】【分析】根据对顶角的性质解答即可.【详解】解：量角器测量的度数为，根据对顶角相等的性质，可得，故答案为：.【点睛】本题考查量角器的使用和对顶角的性质，掌握对顶角相等是解题的关键.的24x y -+=1,2;x y =-⎧⎨=⎩0,4;x y =⎧⎨=⎩1,6,x y =⎧⎨=⎩1x y +=2,3;x y =-⎧⎨=⎩1,2;x y =-⎧⎨=⎩0,1.x y =⎧⎨=⎩24,1x y x y -+=⎧⎨+=⎩12x y =-⎧⎨=⎩12x y =-⎧⎨=⎩24,1x y x y -+=⎧⎨+=⎩12x y =-⎧⎨=⎩12x y =-⎧⎨=⎩1∠30︒30︒130∠=︒30︒14. 如图，将含有的直角三角板的两个顶点分别放在直尺的一组对边上，如果，那么______°．【答案】40【解析】【分析】首先根据题意求出，然后根据平行线的性质求解即可．【详解】解：如图，∵∴ ∵∴．故答案为：40．【点睛】本题主要考查了平行线的性质，解题时注意：两直线平行，内错角相等．15. 下列命题中，①对顶角相等；②内错角相等；③平行于同一条直线的两条直线平行；④若，则.是真命题的是______．【答案】①③【解析】【分析】根据对顶角的性质判断①；根据平行线的性质判断②；根据平行公理的推论判断③；根据平方根定义判断④．【详解】解：①对顶角相等，是真命题；②内错角不一定相等，是假命题；③平行于同一条直线的两条直线互相平行，是真命题；60︒120∠=︒2∠=140EBC ABC ∠=∠-∠=︒120∠=︒140EBC ABC ∠=∠-∠=︒EB CD∥240EBC ∠=∠=︒22a b >a b >④若，则a 不一定大于b ，是假命题；故答案为：①③．【点睛】本题考查的是命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．16. 如果关于的不等式的解集为，则的值是___________．【答案】1【解析】【分析】解不等式得，结合关于的不等式的解集为，得出，解之可得答案．详解】解：∵，∴，则， ∵关于的不等式的解集为，∴，解得，故答案为：1．【点睛】本题主要考查解一元一次不等式的基本能力，严格遵循解不等式的基本步骤是关键，尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变．17. 在一本书上写着方程组的解是，其中的值被墨渍盖住了，但我们可解得的值为___________．【答案】【解析】【分析】根据，代入中，解得；把，代入中，即可求出的值．【22a b >x 3223x a a +≤-1x ≤-a 253x a ≤-x 3223x a a +≤-1x ≤-2153a -=-3223x a a +≤-325x a ≤-253x a ≤-x 3223x a a +≤-1x ≤-2153a -=-1a =43x py x y +=⎧⎨+=⎩1x y =⎧⎨=⎩y p 321x =3x y +=2y =1x =2y =4x py +=p【详解】解：∵方程组的解是，∴代入中，解得，把，代入，得解得．故答案为：．【点睛】本题考查二元一次方程组的知识，解题的关键是代入中，求出．18. 如图，一条公路两次转弯后，和原来的方向相同.如果第一次的拐角∠A 是135°，则第二次的拐角∠B 是________，根据是________________.【答案】①. 135° ②. 两直线平行，内错角相等【解析】【分析】由两次转弯后，和原来的方向相同可知拐弯前、后的两条路平行，可考虑用平行线的性质解答．【详解】解：如图：∵两次转弯后，和原来的方向相同，∴AC∥BD，∴∠B=∠A=135°（两直线平行，内错角相等）．故答案为135°；两直线平行，内错角相等．【点睛】本题考查了平行线性质的应用，解答此题的关键是将实际问题转化为几何问题，利用平行线的性质求解．19. 如图，四边形纸片，．折叠纸片，使点D 落在上的点处，点C 落在点处，折痕为．若，则______．43x py x y +=⎧⎨+=⎩1x y =⎧⎨=⎩1x =3x y +=2y =1x =2y =4x py +=124p +=32p =321x =3x y +=2y =ABCD AD BC ∥ABCD AB 1D 1C EF 102EFC ∠=︒1AED ∠=︒【答案】24【解析】【分析】根据平行线的性质可得，再根据折叠的性质可得，然后利用平角的定义求解即可．【详解】∵，∴，∵，∴，∵折叠纸片，使点D 落在上的点处，∴，∴，故答案为：24．【点睛】本题考查了折叠的性质，平行线的性质，平角的定义等知识点，熟练掌握其性质是解决此题的关键．20. 某快递公司的快递件分为甲类件和乙类件，快递员送甲类件每件收入1元，送乙类件每件收入2元．累计工作1小时，只送甲类件，最多可送30件，只送乙类件，最多可送10件；累计工作2小时，只送甲类件，最多可送55件，只送乙类件，最多可送20件；…，经整理形成统计表如表：累计工作时长最多件数（时）种类（件）12345678甲类件305580100115125135145乙类件1020304050607080（1）如果快递员一天工作8小时，且只送某一类件，那么他一天的最大收入为_____元；180EFC DEF ∠+∠=︒178DEF D EF ∠=∠=︒AD BC ∥180EFC DEF ∠+∠=︒102EFC ∠=︒18010278DEF ∠=︒-︒=︒ABCD AB 1D 178DEF D EF ∠=∠=︒1180787824AED ∠=︒-︒-︒=︒（2）如果快递员一天累计送x小时甲类件，y小时乙类件，且x+y＝8，x，y均为正整数，那么他一天的最大收入为_____元．【答案】①. 160②. 180【解析】【分析】（1）根据表格数据得出答案即可；（2）根据x+y＝8，x，y均为正整数，把所有收入可能都计算出，即可得出最大收入．【详解】解：(1)由统计表可知:如果该快递员一天工作8小时只送甲类件，则他的收入是1×145=145(元)如果该快递员一天工作8小时只送乙类件，则他的收入是2 × 80= 160 (元)∴他一天的最大收入是160元;(2)依题意可知：x和y均正整数，且x+y= 8①当x=1时，则y=7∴该快递员一天的收入是1 ×30+2×70=30+ 140= 170 (元)；②当x=2时，则y=6∴该快递员-天的收入是1×55+2×60=55+120=175(元)；③当x=3时，则y=5∴该快递员一天的收入是1× 80+2×50= 80+ 100= 180 (元)；④当x=4时，则y=4∴该快递员一天的收入是1×100+2×40= 100+80 = 180 (元)；⑤当x=5时，则y=3∴该快递员一天的收入是1×115+2×30=115十60 = 175 (元)；⑥当x=6时，则y=2∴该快递员一天的收入是1 × 125+ 2× 20= 125+40 = 165 (元)；⑦当x=7时，则y=1∴该快递员一天的收入是1×135+2×10=135+20= 155 (元)综上讨论可知：他一天的最大收入为180元.故填：160；180.【点睛】本题主要考查二元一次方程的应用，在给定的“x+y＝8，x，y均为正整数”的条件下，分情况讨论出最大收入即可.三、解答题（共60分，第21-24题，每题3分，第25题5分，第26-27题，每题4分，第28题6分，第29-31题，每题5分，第32-33题7分）21. 解方程组【答案】【解析】【分析】利用加减消元法求解可得；【详解】解：，得∴把代入①，得∴所以，原方程组的解为【点睛】此题考查了解二元一次方程组，利用了消元的思想，解决本题的关键是要掌握消元的方法，即代入消元法与加减消元法．22. 解方程组：【答案】【解析】【分析】方程组整理后，方程组利用加减消元法求解即可．【详解】整理得，得，解得，将代入①得：342,328.x y x y +=⎧⎨-=⎩21x y =⎧⎨=-⎩342,328.x y x y +=⎧⎨-=⎩①②-①②66y =-1y =-1y =-()3412x +⨯-=2x =2,1.x y =⎧⎨=-⎩2,232 1.y x x y ⎧+=⎪⎨⎪-=-⎩12x y =⎧⎨=⎩2,232 1.y x x y ⎧+=⎪⎨⎪-=-⎩24321x y x y +=⎧⎨-=-⎩①②2⨯+①②77x =1x =1x =214y ⨯+=∴方程组的解为：．【点睛】此题考查了解二元一次方程组，利用了消元的思想，解题的关键是利用代入消元法或加减消元法消去一个未知数．23. 解不等式，并把解集在数轴上表示出来．【答案】，图见解析【解析】【分析】先去括号，再移项、合并同类项、最后系数化为1即可，再在数轴上把解集表示出来．【详解】解：去括号得，，去括号得，，合并同类项得，，系数化为1得，，解集在数轴上表示为：【点睛】本题考查了解一元一次不等式以及在数轴上表示不等式的解集，是基础知识要熟练掌握．24. 解不式组：并求出它的整数解．【答案】，整数解为3或4【解析】【分析】本题考查了解一元一次不等式组，不等式组的整数解．熟练掌握解一元一次不等式组，不等式组的整数解是解题的关键．先分别求出两个不等式的解集，进而可得不等式组的解集，最后求整数解即可．【详解】解：，，，12x y =⎧⎨=⎩()3157x x +-≤2x ≥-3357x x +-≤3573x x -≤-24x -≤2x ≥-()2241213x x x x ⎧-->⎪⎨+≥-⎪⎩24x <≤()2241213x x x x ⎧-->⎪⎨+≥-⎪⎩()224x x -->224x x -+>，，，，解得，，∴不等式组的解集为，整数解为3或4．25. 完成下列计算，并在括号内填写推理依据．如图，，直线分别交、于点E 和点F ，过点E 作交直线于点G ．若，计算的度数．解：∵，∴ （）．∵，∴ （）．∴ ．【答案】；两直线平行，内错角相等；垂直定义；；；【解析】【分析】由平行线的性质得，由垂直的定义得，进而可求的度数．【详解】解：∵，∴（两直线平行，内错角相等）．∵，∴（垂直定义）．∴．1213x x +≥-()1231x x +≥-1233x x +≥-4x -≥-4x ≤24x <≤AB CD MN AB CD EG MN ⊥CD 60EGF ∠=︒MEB ∠AB CD 60EGF ︒=∠=EG MN ⊥90MEG ∠=︒MEB ∠=-906030=︒-︒=︒BEG ∠MEG ∠BEG ∠60BEG EGF ︒∠=∠=90MEG ∠=︒MEB ∠AB CD 60BEG EGF ︒∠=∠=EG MN ⊥90MEG ∠=︒906030MEB MEG BEG ︒︒︒∠=∠-∠=-=故答案为：；两直线平行，内错角相等；垂直定义；；．【点睛】本题考查了平行线的性质，垂直的定义，数形结合是解答本题的关键．26. 如图，在三角形中，平分，求的度数．【答案】【解析】【分析】根据平行线的性质可得，根据角平分线的性质可得，则，最后根据三角形的一个外角定于与它不相邻两个内角之和，即可解答．【详解】解：∵，∴，∵平分，∴，∴，∵，∴．【点睛】本题主要考查了平行线的性质，角平分线的定义，三角形的外角定理，解题的关键是掌握两直线平行，内错角相等；三角形的一个外角定于与它不相邻两个内角之和．27. 如图，点B 、C 在线段异侧，E 、F 分别是线段、上的点，和分别交于点G 和点H ．已知，，．求证：．BEG ∠MEG ∠BEG ∠ABC CD ,,80ACB DE BC AED ∠∠=︒∥EDC ∠40︒BCD EDC ∠=∠ECD BCD ∠=∠ECD EDC ∠=∠DE BC ∥BCD EDC ∠=∠CD ACB ∠ECD BCD ∠=∠ECD EDC ∠=∠80AED ∠=︒180402EDC ∠=⨯︒=︒AD AB CD EC BF AD AEG AGE ∠=∠DGC C ∠=∠180BEC BFD ∠+∠=︒EC BF ∥【答案】见解析【解析】【分析】先证明出，从而得到，得到，再根据条件，得出，再根据平行线的判定求解即可．【详解】证明：证明：∵，，又∵∴，∴∴∵∴∴．【点睛】此题考查了平行线的判定与性质，熟记平行线的判定定理与性质定理是解题的关键．28. 围棋，起源于中国，古代称为“弈”，是棋类鼻祖，距今已有4000多年的历史．某商家销售A 、B 两种材质的围棋，每套进价分别为200元、170元，下表是近两个月的销售情况：销售数量销售时段A 种材质B 种材质销售收入第一个月3套5套1800元第二个月4套10套3100元（1）求A 、B 两种材质的围棋每套的售价．（2）若商家准备用不多于5400元的金额再采购A 、B 两种材质的围棋共30套，求A 种材质的围棋最多能采购多少套？（3）在（2）的条件下，商店销售完这30套围棋能否实现利润为1300元的目标？请说明理由．【答案】（1）A 种材质的围棋每套的售价为250元，B 种材质的围棋每套的售价为210元；（2）A 种材质的围棋最多能采购10套；（3）商店销售完这30套围棋能实现利润为1300元的目标；理由见解析．【解析】AEG C ∠=∠AB CD ∥180BEC C ∠+∠=︒180BEC BFD ∠+∠=︒C BFD ∠=∠AEG AGE ∠=∠DGC C ∠=∠DGC AGE∠=∠AEG C ∠=∠AB CD∥180BEC C ∠+∠=︒180BEC BFD ∠+∠=︒C BFD∠=∠EC BF ∥【分析】（1）设A 种材质的围棋每套的售价为x 元，B 种材质的围棋每套的售价为y 元，根据表格中的销量和收入列方程组求解即可；（2）设A 种材质的围棋采购a 套，则B 种材质的围棋采购套，根据“用不多于5400元的金额再采购A 、B 两种材质的围棋共30套”列不等式求解即可；（3）设销售利润为w ，根据题意列出一次函数解析式，然后利用一次函数的性质求解．【小问1详解】解：设A 种材质的围棋每套的售价为x 元，B 种材质的围棋每套的售价为y 元，由题意得：，解得：，答：A 种材质的围棋每套的售价为250元，B 种材质的围棋每套的售价为210元；【小问2详解】解：设A 种材质的围棋采购a 套，则B 种材质的围棋采购套，由题意得：，解得：，所以a 的最大值为10，答：A 种材质的围棋最多能采购10套；【小问3详解】解：商店销售完这30套围棋能实现利润为1300元的目标；理由：设销售利润为w ，由题意得：，∵，∴w 随a 的增大而增大，∵a 的最大值为10，∴当时，w 取最大值1300，即商店销售完这30套围棋能实现利润为1300元的目标．【点睛】本题考查了二元一次方程组的应用，一元一次不等式的应用以及一次函数的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系和不等关系，列出方程组、不等式以及一次函数解析()30a -3518004103100x y x y +=⎧⎨+=⎩250210x y =⎧⎨=⎩()30a -()200170305400a a +-≤10a ≤()()()25020021017030101200w a a a =-+--=+100>10a =式．29. 已知：如图，点D 在线段上，过点D 作交线段于点E ，连接，过点D 作于点F ，过点F 作交线段于点G ．（1）依题意补全图形；（2）用等式表示与的数量关系，并证明．【答案】（1）见解析；（2），证明见解析．【解析】【分析】（1）根据题意画出图形即可；（2）根据平行线的性质得出，，等量代换得出，根据，可知，进而可得出结论．【小问1详解】解：图形如下：【小问2详解】解：，证明：∵，∴，∵，∴，∴，∵，∴，∴，AB DE BC ∥AC CD DF BC ⊥FG CD ∥AB CDE ∠DFG ∠90CDE DFG ∠+∠=︒12∠=∠23∠∠=13∠=∠DF BC ⊥3490∠+∠=°90CDE DFG ∠+∠=︒DE BC ∥12∠=∠CD FG ∥23∠∠=13∠=∠DF BC ⊥3490∠+∠=°1490∠+∠=︒即．【点睛】本题考查平行线的性质，掌握平行线的性质是解题的关键．30. 解答题：解方程组时，由于，的系数及常数项的数值较大，如果用常规的代入消元法、加减消元法来解，不仅计算量大，而且易出现运算错误，而采用下面的解法则比较简单：①②得，所以③，③①得，解得，从而，所以原方程组的解是．请你运用上述方法解方程组：．【答案】【解析】【分析】仿照例子，利用加减消元法可解方程组求解．【详解】解：，得：，∴③，③①得：，解得：，将代入③得：，∴原方程组的解为．90CDE DFG ∠+∠=︒323538303336x y x y +=⎧⎨+=⎩①②x y -222x y +=1x y +=35⨯-33x =-=1x -2y =12x y =-⎧⎨=⎩201620182020201920212023x y x y +=⎧⎨+=⎩12x y =-⎧⎨=⎩201620182020201920212023x y x y +=⎧⎨+=⎩①②-②①333x y +=1x y +=2018⨯-22x =-=1x -=1x -2y =12x y =-⎧⎨=⎩【点睛】本题主要考查二元一次方程组解法，解二元一次方程组由代入消元法和加减消元法．31. 先阅读绝对值不等式和的解法，再解答问题：①因为，从数轴上（如图1）可以看出只有大于而小于6的数的绝对值小于6，所以的解集为．②因为，从数轴上（如图2）可以看出只有小于的数和大于6的数的绝对值大于6，所以的解集为或．（1）的解集为_________，的解集为_________；（2）已知关于x ，y 的二元一次方程组的解满足，其中m 是负整数，求m 的值．【答案】（1），或（2）【解析】【分析】本题考查了绝对值的意义，不等式组的解集，加减消元法解二元一次方程组等知识．理解题意是解题的关键．（1）根据题意求解集即可；（2）加减消元法解二元一次方程组得，由题意知，，即，，可求，然后作答即可．【小问1详解】解：由题意知，的解集为，的解集为或；故答案为：，或；【小问2详解】解：，的||6x <||6x >||6x <6-||6x <66x -<<||6x >6-||6x >6x <-6x >||2x <||5x >254482x y m x y m -=+⎧⎨+=-+⎩||3x y +≤22x -<<5x <-5x >1-42373x m y m ⎧=+⎪⎪⎨⎪=-⎪⎩472333m m +-≤23m -≤323m -≤-≤15m -≤≤||2x <22x -<<||5x >5x <-5x >22x -<<5x <-5x >254482x y m x y m -=+⎧⎨+=-+⎩①②得，，解得，，将代入①得，，解得，，∴，∵，∴，即，∴，解得，，∵m 是负整数，∴m 的值为．32. 已知：如图，直线，点A 、B 在直线a 上（点A 在点B 左侧），点C 、D 在直线b 上（点C 在点D 左侧），和相交于点E ．（1）求证：；（2）分别作和的角平分线相交于点F ．① 结合题意，补全图形；② 用等式表示和的数量关系，并证明．【答案】（1）见解析（2）①见解析；②；见解析【解析】【分析】（1）过点E 作，证明，，可得，从而可得答案；2⨯-②①921y m =-73y m =-73y m =-72543x m m ⎛⎫--=+ ⎪⎝⎭423x m =+42373x m y m ⎧=+⎪⎪⎨⎪=-⎪⎩||3x y +≤472333m m +-≤23m -≤323m -≤-≤15m -≤≤1-a b ∥AD BC BED BAD BCD ∠=∠+∠BAD ∠BCD ∠AFC ∠BED ∠12AFC BED ∠=∠EM AB ∥BAD AEM ∠=∠BCD MEC ∠=∠AEC BAD BCD ∠=∠+∠（2）①根据题意补全图形即可；②过点F 作，可得，证明，可得，结合、分别平分和，可得，结合，从而可得答案．【小问1详解】过点E 作，∴ ，∵，∴，∴，∵，∴，∵，∴．【小问2详解】①补全图形如图所示：②；证明：过点F 作，∴∵，∴，FN AB ∥AFN BAF ∠=∠NFC FCD ∠=∠AFC BAF FCD ∠=∠+∠AF CF BAD ∠BCD ∠()12AFC BAD BCD ∠=∠+∠BED BAD BCD ∠=∠+∠EM AB ∥BAD AEM ∠=∠AB CD ∥EM CD ∥BCD MEC ∠=∠AEC AEM MEC ∠=∠+∠AEC BAD BCD ∠=∠+∠AEC BED ∠=∠BED BAD BCD ∠=∠+∠12AFC BED ∠=∠FN AB ∥AFN BAF ∠=∠AB CD ∥FN CD ∥∴，∵，∴，∵、分别平分和，∴，∵，∴．【点睛】本题考查的是平行公理的应用，平行线的性质，角平分线的定义，熟练的利用平行线的性质进行证明是解本题的关键．33. 给出如下定义：如果一个未知数的值使得方程和不等式（组）同时成立，那么这个未知数的值称为该方程与不等式（组）的“关联解”．例如：已知方程和不等式，对于未知数，当时，使得，同时成立，则称是方程与不等式的“关联解”．（1）判断是否是方程与不等式的“关联解”_____（填是或否）；判断是方程与不等式（组）①，②，③中_______的“关联解”；（只填序号）（2）如果是关于的方程与关于的不等式组的“关联解”，那么____，的取值范围是_______；（3）如果是关于方程与关于的不等式组的“关联解”，求的取值范围．【答案】（1）否；①；（2）；；（3）．【解析】的NFC FCD ∠=∠AFC AFN NFC ∠=∠+∠AFC BAF FCD ∠=∠+∠AF CF BAD ∠BCD ∠()12AFC BAD BCD ∠=∠+∠BED BAD BCD ∠=∠+∠12AFC BED ∠=∠321x -=40x +>x 1x =3121⨯-=41450x +=+=>1x =321x -=40x +>3x =260x -=()234x +<=1x -231x +=1322x -<132x ->2050x x ->⎧⎨-<⎩2x =x 20x a -=x ()11212x x a b +⎧>-⎪⎨⎪+-≤⎩=a b x m =x 24x n -=x 121n m x m n x ⎧-+>-⎪⎨⎪-->-⎩m 4a =3b ≥-36m <<【分析】（1）根据“关联解”的定义求解即可；（2）根据“关联解”的定义，将代入方程即可求出，再解不等式得：，即可得出答案；（3）根据“关联解”的定义得出不等式组，求解即可【小问1详解】解：当时，使得成立，不成立，则不是方程与不等式的“关联解”；当时，使得成立，成立，则是方程与不等式的“关联解”；当时，使得成立，不成立，则不是方程与不等式的“关联解”；当时，使得成立，不成立，则不是方程与不等式组的“关联解”；故答案为：否；①；【小问2详解】解：根据题意可得：，解得：，不等式组解不等式得：，即，解得：；故答案为：；；【小问3详解】2x =4a =②8122b +-≥4122412m m -⎧>-⎪⎪⎨-⎪>-⎪⎩3x =2360⨯-=()2334+<3x =260x -=()234x +<=1x -()2131⨯-+=13122--<=1x -231x +=1322x -<=1x -()2131⨯-+=1132-->=1x -231x +=132x ->=1x -()2131⨯-+=120150-->⎧⎨--<⎩=1x -231x +=2050x x ->⎧⎨-<⎩220a ⨯-=4a =()11212x x a b +⎧>-⎪⎨⎪+-≤⎩①②②212b a x +-≤8122b +-≥3b ≥-4a =3b ≥-解：根据题意可得：，∴，不等式组为，化简得：，解不等式组得：．【点睛】本题考查解一元一次不等式组，方程的解，正确理解新定义是解题的关键．24m n -=42-=m n 4122412m m m m m m -⎧-+>-⎪⎪⎨-⎪-->-⎪⎩4122412m m -⎧>-⎪⎪⎨-⎪>-⎪⎩36m <<。

人教版数学七年级下册期中考试试题含答案

人教版数学七年级下册期中考试试卷一、选择题：（本大题共12个小题，每小题3分，共36分）1．在下列四个汽车标志图案中，能用平移变换来分析其形成过程的图案是（）2.已知是二元一次方程组的解，则a﹣b 的值为（）A．3B．2C．1D．﹣13.下列说法正确的是（）A .相等的两个角是对顶角B .和等于180度的两个角互为邻补角C .若两直线相交，则它们互相垂直D .两条直线相交所形成的四个角都相等，则这两条直线互相垂直4．下列命题中，属于真命题的是（）A．两个锐角的和是锐角B．在同一平面内，如果a⊥b，b⊥c，则a⊥cC．同位角相等D．在同一平面内，如果a//b，b//c，则a//c5.如图,已知b a //,直角三角板的直角顶点在直线a 上,若︒=∠301,则2∠等于：A.︒30B.︒40C.︒50D.︒606.如图,在数轴上表示实数7的可能是：A.点PB.点QC.点MD.点N7.若点P ),(y x 在第四象限,且3||,2||==y x ,则y x +等于:A.1-B.1C.5D.5-8.已知⎩⎨⎧-==11y x 是方程组⎩⎨⎧=-=+21by cx cyax 的解,则b a ,间的关系是：A.3=+b aB.1-=-b aC.0=+b aD.3-=-b a 9.两条直线最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点,……,那么7条直线最多有：A.28个交点B.24个交点C.21个交点D.15个交点10.下列四个数:31,,3,3----π,其中最大的数是（）A.3-B.3-C π- D.31-11.如右图,线段AB 经过平移得到线段CD,其中A、B 的对应点分别是C、D,这四个点都在格点上,若线段AB 上有一点P ),(b a ,则点P 在CD 上的对应点P'的坐标为：A.)2,4(+-b a B.)2,4(--b a C )2,4(++b a D.)2,4(-+b a 12.张小花家去年节余50000元,今年可节余95000元,并且今年收入比去年高15%,支出比去年低10%,今年的收入与支出各是多少?设去年的收入为x 元,支出为y 元,则可列方程为:A.⎩⎨⎧=++-=+95000%)101(%)151(50000y x y x B.⎩⎨⎧=--+=-95000%)101(%)151(50000y x y x C.⎩⎨⎧=+--=+95000%)101(%)151(50000y x y x D.⎩⎨⎧=+--=-95000%)101(%)151(50000y x y x 二、填空题：（本大题共6个小题，每小题3分，共18分）13.如图,要使BF AD //,则需要添加的条件是_____________(写一个即可).14.已知一个正数的两个平方根分别是62-m 和m +3,则2)(m -的值为____________.15.平面直角坐标系中,点A )7,5(-到x 轴的距离是__________.16.要把一张面值为10元的人民币换成零钱,如果现有足够的面值为2元、1元的人民币,那么有_____种换法.17.请将命题"等腰三角形的底角相等"改写为"如果……,那么……"的形式:____________________________________.18.如图,已知BE AD //,点C 是直线FG 上的动点,若在点C 的移动过程中,存在某时刻使得︒=∠︒=∠22,45DAC ACB ,则EBC ∠的度数为________.三、解答题：（本大题共7个小题，共46分）19.（本小题满分5分）计算:|21|27)4(3(322-+---+-20.（本小题满分5分）一个正方形鱼池的边长是xm ,当边长增加m 3后,这个鱼池的面积变为281m ,求x .21.（每小题4分,共计8分）按要求解下列方程组:(1)用代入法解方程组：⎩⎨⎧=-=+102322y x y x (2)用加减法解方程组：⎩⎨⎧=+=-8251153y x y x 22.（本小题满分5分）如图,已知CD AB //,C A ∠=∠.求证:BCAD //23.（本小题满分7分）甲乙两位同学在解方程组⎩⎨⎧=-=+1413y bx y ax 时,甲把字母a 看错了得到方程组的解为⎪⎩⎪⎨⎧-==472y x ;乙把字母b 看错了得到方程组的解为⎩⎨⎧-==12y x .求原方程组正确的解.24.（本小题满分8分）如图,︒=∠+∠180BCF ADE ,BE 平分ABC ∠,E ABC ∠=∠2.（1）AD 与BC 平行吗?请说明理由;（2）AB 与EF 的位置关系如何?为什么?（3）若AF 平分BAD ∠,试说明:︒=∠+∠90F E .(注:本题第(1)(2)小题在下面的解答过程的空格内填写理由或数学式;第(3)小题要写出解题过程)解:(1)BC AD //,理由如下:∵︒=∠+∠180BCF ADE (已知)︒=∠+∠180ADF ADE (平角的定义)∴=∠ADF __________(______________________)∴BC AD //(__________________________)(2)AB 与EF 的位置关系是:互相平行∵BE 平分ABC ∠(已知)∴ABE ABC ∠=∠2(角平分线定义)又∵E ABC ∠=∠2(已知)∴ABE E ∠=∠22(____________________)∴ABE E ∠=∠(____________________)∴______//_______(________________________)25.（本小题满分8分）如图平面直角坐标系内,已知点A 的坐标是)0,3(-.（1）点B 的坐标为_______,点C 的坐标为_____,=∠BAC ______;（2）求ABC ∆的面积;（3）点P 是y 轴负半轴上的一个动点,连接BP 交x 轴于点D,是否存在点P 使得ADP ∆与BDC ∆的面积相等?若存在,请直接写出点P 的坐标;若不存在,请说明理由.参考答案一.选择题题号123456789101112答案B D D D B C C A C D A B二.填空题13.︒=∠+∠180ABC A 或︒=∠+∠180DCB D 或EBF A ∠=∠或DCF D ∠=∠(任意写一个即可,不必写全)14.115.716.617.如果一个三角形是等腰三角形,那么它的两个底角相等18.︒︒6723或(第18题仅填一种情况并且正确的给2分,填了两种情况但其中有一种错误的不给分)三.解答题19.解:原式=12343-+++......................................3分=29+....................................................5分20.解:由题意得81)3(2=+x ...................................................................3分解得126-==x x 或(不合题意,舍去)..........................................4分答:该鱼池的边长x 等于m 6..........................................................5分21.解:(1)由①,得x y 22-=③..................................................1分将③代入②,得10)22(23=--x x 解这个方程,得2=x ...................................................2分将2=x 代入③,得2-=y ..........................................3分所以原方程组的解是⎩⎨⎧-==22y x ...................................................4分(2)①5⨯得,552515=-y x ③..........................................................5分②3⨯得,24615=+y x ④④－③,得3131-=y 1-=y .....................................................................6分将1-=y 代入①,得2=x ...........................................................7分所以原方程组的解是⎩⎨⎧-==12y x ....................................................8分22.证明:∵CDAB //∴︒=∠+∠180C B ....................................2分又∵C A ∠=∠................................................3分∴︒=∠+∠180A B ....................................4分∴BC AD //.................................................5分解:∵甲看错了字母a 但没有看错b ∴将⎪⎩⎪⎨⎧-==472y x 代入14=-y bx 得,147(42=-⨯-b ................................2分∴3-=b ....................................................................................................3分同理可求得2=a ......................................................................................4分将3,2-==b a 代入原方程组,得⎩⎨⎧=--=+143132y x y x ......................................5分解得⎩⎨⎧=-=57y x ..............................................................................................6分∴原方程组正确的解是⎩⎨⎧=-=57y x .................................................................7分解:(1)∠BCF 同角的补角相等同位角相等,两直线平行...............................1.5分等量代换等式性质AB EF 内错角相等,两直线平行...........................4分(每空0.5分,八个空共计4分)证明:由(1)知BCAD //∴︒=∠+∠180ABC DAB ...............................................................5分∵BE 平分ABC ∠,AF 平分DAB∠∴DABBAF ABC ABE ∠=∠∠=∠21,21∴︒=︒⨯=∠+∠=∠+∠90180212121DAB ABC BAF ABE ......6分由(2)知EFAB //∴F BAF E ABE ∠=∠∠=∠,.........................................................7分∴︒=∠+∠180F E ...........................................................................8分解:(1))5,2()0,5(︒45....................................................3分(2)过点B 作x BE ⊥轴于E∵点A,B,C 的坐标分别为)0,5(),5,2(),0,3(-∴5,835==+=+=BE OC OA AC ........................................5分∴20582121=⨯⨯=⋅=∆BE AC S ABC .........................................6分(3)存在点P 使得ADP ∆与的BDC ∆的面积相等........................................7分此时点P 的坐标为)5,0(-.........................................................................8分。

山东省潍坊市潍城区2023-2024学年七年级下学期期中数学试题(含答案)

试卷类型：A2023—2024学年度第二学期期中质量检测七年级数学试题注意事项：1．考试时间120分钟，试卷满分150分；2．答卷前，请将试卷密封线内和答题纸上的项目填涂清楚；3．请在答题纸相应位置作答，不要超出答题区域，不要答错位置．第Ⅰ卷（选择题共52分）一、单选题（本大题共8小题，共32分．在每个小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来，每小题选对得4分，错选、不选均记0分）1．巨噬细胞是人体的“清道夫”，它是由单核细胞演变而来，一直在为我们的身体做清洁工作，其直径可达0.00008米．将0.00008用科学记数法可表示为（）A ．B ．C ．D ．2．如图，已知OB 是内部的一条射线，下列说法一定正确的是（）A ．B ．C ．可以用表示D ．与表示同一个角3．下列方程是二元一次方程的是（）A ．B ．C ．D ．4．如图，从旗杆AB 的顶端A 处向地面拉一条绳子，绳子底端恰好在地面P 处，若旗杆的高度为13.8米，则绳子AP的长度不可能是（）40.810-⨯50.810-⨯4810-⨯5810-⨯AOC ∠2AOC BOC ∠=∠BOC AOB∠<∠AOC ∠O ∠1∠AOB ∠20x y -=10xy +=223x x +=8y x=A ．16米B ．15米C ．14米D ．13米5．光在不同介质中的传播速度是不同的，因此光从水中射向空气时，要发生折射．已知在水中平行的光线射向空气中时也是平行的．如图，，则的值为（）A ．B ．C ．D ．6．小亮在做“化简，并求时的值”一题时，错将看成了，但结果却和正确答案一样．由此可知k 的值是（）A ．2B ．3C ．4D ．57．某校预安排若干间宿舍给七年级男寄宿生住，若每间宿舍住6人，则有4人住不下，若每间住7人，则有1间只住2人且空余8间宿舍．设该校七年级男寄宿生有x 人，预安排给七年级男寄宿生的宿舍有y 间，则下列方程组正确的是（）A ．B ．C ．D ．8．如图，将一条对边互相平行的纸带进行两次折叠，折痕分别为AB 、CD ，若，且，则的度数是（）A ．B ．C ．D ．二、多选题（本大题共4小题，共20分．在每个小题给出的四个选项中，有多项符合题目要求，全部选对得5分，部分选对得3分，错选、多选均记0分）9．如图，下列说法正确的是（）140,2120∠=︒∠=︒34∠+∠160︒150︒100︒90︒()()()23263516x k x x x x +⋅+-⋅+++6x =6x =6x =-()647812y x y x +=⎧⎪⎨--+=⎪⎩()64782y x y x -=⎧⎪⎨-+=⎪⎩()64782y x y x +=⎧⎪⎨-+=⎪⎩()647812y x y x-=⎧⎪⎨---=⎪⎩CD BE ∥125∠=︒2∠60︒75︒80︒85︒A ．与是对顶角B ．与是内错角C ．与是同位角D ．与是同旁内角10．下列运算正确的是（）A ．B ．C ．D ．11．解方程组时，下列消元方法正确的是（）A ．②×3-①，消去xB ．①×3+②×2，消去yC ．②×2-①×3，消去yD ．由②得：，然后代入①中消去x12．如图，的平分线BE 交AC 于点E ，的平分线CD 交AB 于点D ，BE ，CD 相交于点F ，，且于点G ，下列结论中正确的是（）A ．B ．CA 平分C ．D ．第Ⅱ卷（非选择题共98分）三、填空题（本大题共6小题，共24分．只要求填写最后结果，每小题填对得4分）13．计算：________．14．如图，点O 在直线AB 上，，OE 平分，则的度数为_____°．1∠2∠1∠4∠1∠B ∠4∠D ∠2327a a a a -⋅÷=22(2)(2)222b a b a b ab a ---⋅+=2336(3)27ab a b ---=()122112323nn n n n n a a aa a a a --+⋅-+=-+3216331x y x y +=⎧⎨-=⎩①②313x y =+ABC ∠ACB ∠90,A EG BC ∠=︒∥CG EG ⊥2CEG DCB ∠=∠BCG ∠ADC GCD ∠=∠45DFB ∠=︒109287031︒'-︒'=118,AOC OC OD ∠=︒⊥BOC ∠DOE ∠15．对任意有理数x ，等式总成立，那么________．16．如图，直线，一块三角板ABC （）按如图所示放置．若，则的度数为________°．17．如图，在四边形ABCD 中，，对角线AC ，BD 交于点O ，若三角形AOB 的面积为6，且，则三角形AOD 的面积是_________．18．如图，将一个大长方形ABCD 分割成5个正方形①②③④⑤和1个小长方形⑥，若，则大长方形ABCD 的面积是_______．()()236x x n x mx -+=+-m n =a b ∥60,90A C ∠=︒∠=︒150∠=︒2∠AD BC ∥:1:2AO OC =3,4GF EF ==四、解答题（本题共7小题，满分74分．解答应写出文字说明、证明过程或推演步骤）19．（本题满分8分）计算下列各题：（1）；（2）．20．（本题满分8分）解下列方程组：（1），（2）21．（本题满分9分）按下列要求画图并填空．如图，P 是的边OB 上一点，（1）过点P 作射线OA 的垂线，垂足为H ；（2）过点P 作射线OB 的垂线，交OA 于点C ；（3）过点P 作直线（点D 在点P 的右侧）；（4）与的数量关系是_________．（5）线段PC ，PH ，OC 这三条线段大小关系是________（用“<”号连接），依据是________．22．（本题满分10分）我们知道，一般的数学公式，法则、定义可以正向运用，也可以逆向运用．例如，“同底数幂的乘法”“幂的乘方”“积的乘方”这几个法则的逆向运用表现为：；；；其中m ，n 为正整数．结合以上材料解决下列问题．（1）已知，请把a ，b ，c 用“<”连接起来；（2）若，求的值；（3）化简：．23．（本题满分12分）如图，已知射线，连接AB ，点P 是射线AM 上的一个动点（与点A 不重合），BC ，BD 分别平分和，分别交射线AM 于点C ，D．()23155a a b ⎛⎫-⋅- ⎪⎝⎭()()21241x x x -⋅-+-21327x y x y -=⎧⎨+=⎩()111231211x y x y ⎧+=-⎪⎨⎪+-=⎩AOB ∠PD OA ∥HPC ∠DPC ∠m n m n a a a +=⋅()nmn m a a =()m mm a b ab =5544332,3,4a b c ===2,5a b x x ==32a b x +1031001021384⎛⎫⨯⨯ ⎪⎝⎭AM BN ∥ABP ∠PBN ∠（1）当时，求的度数；（2）试判断与之间的数量关系，并说明理由．24．（本题满分13分）已知用2辆A 型车和1辆B 型车载满货物—次可运货10吨；用3辆A 型车和2辆B 型车载满货物一次可运货17吨．某物流公司现有货物35吨，计划同时租用A 型车a 辆，B 型车b 辆，一次运完，且恰好每辆车都载满货物．根据以上信息，解答下列问题：（1）1辆A 型车和1辆B 型车都载满货物一次可分别运货多少吨?（2）请你帮该物流公司设计租车方案；（3）若A 型车每辆需租金100元/次，B 型车每辆需租金130元/次，请选出最省钱的租车方案，并求出最少租车费．25．（本题满分14分）已知，直线，点P 为平面上一点，连接AP 与CP ．（1）如图1，点P 在直线AB ，CD 之间，当时，求的度数；（2）如图2，点P 在直线AB ，CD 之间，与的角平分线相交于点K ，写出与之间的数量关系，并说明理由；（3）如图3，点P 落在直线CD 的下方，与的角平分线相交于点K ，与有何数量关系?请说明理由．40A ∠=︒CBD ∠APB ∠ADB ∠AB CD ∥56,24BAP DCP ∠=︒∠=︒APC ∠BAP ∠DCP ∠AKC ∠APC ∠BAP ∠DCP ∠AKC ∠APC ∠2023-2024学年度第二学期期中学情诊断七年级数学试题参考答案及评分标准一、单选题（本大题共8小题，每小题4分，共32分．在每小题给出的四个选项中只有一项是正确的，请把正确的选项选出来每小题选对得4分，错选、不选均记0分）题号12345678答案DDADCBAC二、多项选择题（共4小题，每小题5分，共20分．每小题的四个选项中，有多项正确，全部选对得5分，部分选对得3分，错选、多选均记0分）题号9101112答案ADADABDACD三、填空题（本大题共6小题，每小题4分，共24分．只填写最后结果）13．14．15．16．17．318．99四、解答题（本题共6小题，共74分．请写出必要的文字说明、证明过程或演算步骤）19．解：（本题8分，1、2小题每题4分）（1） 4分（2）6分8分20．解：（本题8分，1、2小题每题4分）（1）①+②得：1分解得：2分将代入①得：3分解得：，所以4分（4）化简方程组得：①×2得：③③-②得： 6分将代入①得：3857︒'59︒12110︒()()23627211525555a a b a a b a b ⎛⎫⎛⎫-⋅-=-⋅=- ⎪ ⎪⎝⎭⎝⎭()()2322124124241x x x x x x x x --+-=-+-+-+⋅322651x x x =-+-+48x =2x =2x =221y -=12y =212x y =⎧⎪⎨=⎪⎩24328x y x y -=-⎧⎨-=⎩①②428x y -=-16x =-16x =-()2164y ⨯--=-解得：7分所以 8分21．解：（本题9分）（1）如图所示 1分（2）如图所示 2分（3）如图所示3分（4）互余5分（5），垂线段最短9分22．解：（本题10分）（1）∵3分∴ 4分（2 6分∵∴原式7分（3）10分23．解：（本题12分）（1）∵∴，1分28y =-6281x y =-=-⎧⎨⎩PH PC OC <<()55511112232a ===44411113(3)81b ===()13331114464c ===a c b <<()()323232a baba b xx x xx +=⋅=⋅2,5a b x x ==3225200=⨯=1031003100102100100211138388444⎛⎫⎛⎫⎛⎫⨯⨯=⨯⨯⨯⨯ ⎪⎪⎪⎝⎭⎝⎭⎝⎭100310010010021001113883816444⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫=⨯⨯⨯⨯=⨯⨯⨯=⎢⎥⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦,40AM BN A ∠=︒∥180140ABN A ∠=︒-∠=︒∵BC ，BD 分别平分和，∴，3分∴5分（2），7分∵BD 平分，∴，9分∵，∴，∴．12分24．解：（本题13分）（1）设每辆A 型车、B 型车都载满货物一次可以分别运货x 吨、y 吨，根据题意，得，2分解得，3分经检验，方程组的解符合题意．答：1辆A 型车载满货物一次可运3吨，1辆B 型车载满货物一次可运4吨．（2）由（1），得，5分∴，∵a ，b 都是正整数，∴，或，或，∴有3种租车方案：方案一：A 型车9辆，B 型车2辆；方案二：A 型车5辆，B 型车5辆：8分方案三：A 型车1辆，B 型车8辆．（3）∵A 型车每辆需租金100元/次，B 型车每辆需租金130元/次，∴方案一需租金：（元）；方案二需租金：（元）；方案三需租金：（元）． 11分∵12分∴最省钱的租车方案是方案三答：租A 型车1辆，B 型车8辆，最少租车费为1140元．25．解：（本题14分）（1）如图1，过P 作，ABP ∠PBN ∠11,22CBP ABP DBP PBN ∠=∠∠=∠1111140702222CBD CBP DBP ABP PBN ABN ∠=∠+∠=∠+∠=∠=⨯︒=︒2APB ADB ∠=∠PBN ∠2PBN DBN ∠=∠AM BN ∥,APB PBN BDP DBN ∠=∠∠=∠2APB ADB ∠=∠2103217x y x y +=⎧⎨+=⎩34x y =⎧⎨=⎩3435a b +=3543ba -=92a b =⎧⎨=⎩55a b =⎧⎨=⎩ 1 8a b =⎧⎨=⎩910021301160⨯+⨯=510051301150⨯+⨯=110081301140⨯+⨯=116011501140>>PE AB ∥∵，∴，∴， 2分∵∴4分（2）．理由如下： 5分如图2，过K 作，∵，∴，∴，∴，过P 作，同理可得，，∵与的角平分线相交于点K ，∴， 8分∴，∴；9分（3）．理由如下：10分如图3，过K 作，AB CD ∥PE AB CD ∥∥,APE BAP CPE DCP ∠=∠∠=∠56,24BAP DCP ∠=︒∠=︒562480APC APE CPE BAP DCP ∠=∠+∠=∠+∠=︒+︒=︒2AKC APC ∠=∠KE AB ∥AB CD ∥KE AB CD ∥∥,AKE BAK CKE DCK ∠=∠∠=∠AKC AKE CKE BAK DCK ∠=∠+∠=∠+∠PF AB ∥APC BAP DCP ∠=∠+∠BAP ∠DCP ∠11,22DCK DCP BAK BAP ∠=∠∠=∠11112222()BAK DCK BAP DCP BAP DCP APC ∠+∠=∠+∠=∠+∠=∠2AKC APC ∠=∠2AKC APC ∠=∠KE AB ∥∵，∴，∴，∴，…分过P 作同理可得，，12分∵与的角平分线相交于点K ，∴，3分∴，∴．14分AB CD ∥KE AB CD ∥∥,BAK AKE DCK CKE ∠=∠∠=∠AKC AKE CKE BAK DCK ∠=∠-∠=∠-∠PF AB∥APC BAP DCP ∠=∠-∠BAP ∠DCP ∠11,22BAK BAP DCK DCP ∠=∠∠=∠()11112222BAK DCK BAP DCP BAP DCP APC ∠-∠=∠-∠=∠-∠=∠2AKC APC ∠=∠。

东北师范大学附属中学2023-2024学年七年级下学期期中数学试题(解析版)

2023-2024学年东北师大附中初中部初一年级数学学科试卷第二学期期中考试考试时长：120分钟试卷分值：120分一、选择题（共8小题，每题3分，共24分）1. 如图，下列四种通信标志中，其图案是轴对称图形的是（）A. B. C. D.【答案】C【解析】【分析】本题主要考查了轴对称图形的识别，根据轴对称图形的定义进行逐一判断即可：如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形，这条直线就叫做对称轴．【详解】解：A 、不是轴对称图形，故此选项不符合题意；B 、不是轴对称图形，故此选项不符合题意；C 、是轴对称图形，故此选项符合题意；D 、不是轴对称图形，故此选项不符合题意；故选：C ．2. 已知a b >，下列不等式成立的是（）A. a b −>−B. 22a b −<−C. 22a b <D. 0a b −<【答案】B【解析】【分析】本题考查了不等式的基本性质，易错在不等式的基本性质3，不等式两边同时乘以或除以同一个负数，不等号的方向改变．不等式性质：基本性质1．不等式两边同时加上或减去同一个整式，不等号的方向不变．基本性质2．不等式两边同时乘以或除以同一个正数，不等号的方向不变．基本性质3．不等式两边同时乘以或除以同一个负数，不等号的方向改变．根据性质逐一分析即可．【详解】解：A ．∵a b >，∴a b −<−，故不符合题意；B ． ∵a b >，∴a b −<−，∴22a b −<−，故符合题意；C ．∵a b >，∴22a b >，故不符合题意；D ． ∵a b >，∴0a b −>，故不符合题意．故选：B ．3. 一副三角板，按如图所示叠放在一起，则图中α∠的度数为（）A. 60°B. 65°C. 75°D. 85°【答案】C【解析】【分析】本题考查了与三角板有关的运算以及三角形内角和性质，先得出115ABD ABC ∠=∠−∠=°，再运用三角形内角和进行列式，计算即可作答．【详解】解：如图所示：由题意得出6045ABD ABC ∠=°∠=°，，∴1604515ABD ABC ∠=∠−∠=°−°=°，∵90D ∠=︒，∴180901575α∠=°−°−°=°，故选：C ．4. 下列多边形材料中，不能单独用来铺满地面的是（）A. 三角形B. 四边形C. 正五边形D. 正六边形【答案】C【解析】【分析】一个多边形的镶嵌应该符合其内角度数可以整除360°【详解】A 、三角形内角和为180°，能整除360°，能密铺，故此选项不合题意；B 、四边形内角和为360°，能整除360°，能密铺，故此选项不合题意；C 、正五边形每个内角是180°﹣360°÷5＝108°，不能整除360°，不能密铺，故此选项合题意；D 、正六边形每个内角为180°﹣360°÷6＝120°，能整除360°，能密铺，故此选项不合题意；故选C ．【点睛】本题主要考查图形的镶嵌问题，重点是掌握多边形镶嵌的原理．5. 已知12x y = =是关于x ，y 的方程，x ＋ky ＝3的一个解，则k 的值为（） A. －1B. 1C. 2D. 3 【答案】B【解析】【分析】把x 与y 的值代入方程计算即可求出k 的值．【详解】解：∵12x y = =是关于x 、y 的方程x +ky ＝3的一个解， ∴把12x y = =代入到原方程，得1+2k ＝3，解得k ＝1，故选：B ．【点睛】本题主要考查了二元一次方程的解的定义，解一元一次方程，熟知方程的解是使方程两边相等的未知数的值是解题的关键．6. 一个三角形两边的长分别是3和5，则这个三角形第三边的长可能是（）A. 1B. 1.5C. 2D. 4【答案】D【解析】【分析】本题主要考查了三角形的三边关系，即任意两边之和大于第三边，任意两边之差小于第三边．先根据三角形的三边关系求出x 的取值范围，再求出符合条件的x 的值即可．【详解】解：设三角形第三边的长为x ，则 5353x −<<+，即28x <<，只有选项D 符合题意．故选D ．7. 不等式53x −≥的解集在数轴上表示正确的是（）A.B.C.D.【答案】A【解析】【分析】本题考查的是解一元一次不等式，利用数轴表示不等式的解集．先求出不等式的解集，再在数轴上表示出来不等式的解集即可，注意大于小于用空心，大于等于小于等于用实心，大于大于等于开口向右，小于小于等于开口向左．【详解】解：53x −≥，∴2x ≤，数轴上表示：，故选：A ．8. 某学校为学生配备物理电学实验器材，一个电表包内装有1个电压表和2个电流表．某生产线共60名工人，每名工人每天可生产14个电压表或20个电流表．若分配x 名工人生产电压表，y 名工人生产电流） A. 6022014x y y x += ×=B. 6014202x y x y += =C. 601420x y x y += =D. 6021420x y x y += ×=【答案】D【解析】【分析】本题考查了由实际问题抽象出二元一次方程组，解决本题的关键是得到电压表数量和电流表数量的等量关系．【详解】解：若分配x 名工人生产电压表，y 名工人生产电流表，由题意，得6021420x y y y += ×=．故选：D ．二、填空题（共6小题，每小题3分，共18分）9. 已知二元一次方程327x y +=，用含x 的代数式表示y ，则y =______．为【答案】7322x − 【解析】【分析】本题考查了解二元一次方程，根据327x y +=，将x 看成已知数，进行移项，再系数化1，即可作答．【详解】解：∵327x y +=∴273y x =−7322y x =− 故答案为：7322x − 10. 在通过桥洞时，往往会看到如图所示标志：这是限制车高的标志，表示车辆高度不能超过5m ，通过桥洞的车高m x 应满足的不等式为_____________．【答案】5x ≤##5x ≥【解析】【分析】根据不等式的定义列不等式即可．5m ，∴5x ≤．故答案为5x ≤．【点睛】本题主要考查列不等式，掌握不等式的定义是解答本题的关键．11. 不等式组10{212x x −<−≥的最小整数解为_________. 【答案】2【解析】【分析】本题考查的是一元一次不等式组的整数解，正确求出每一个不等式解集，根据“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．【详解】解：解不等式组10{212x x −<−≥得：32x ≥， ∴最小整数解为2，故答案为：2．的12. 如图，正五边形ABCDE 和正六边形EFGHMN 的边CD 、FG 在直线l 上，正五边形在正六边形左侧，两个正多边形均在l 的同侧，则DEF ∠的大小是___度．【答案】48【解析】【分析】利用正多边形的内角和，求出其中一个角的度数，进一步求出三角形DEF 的两个内角，最后由三角形内角和定理来求解．【详解】解：正五边形内角和为540°且CD 在直线l 上，5401085EDC °∴∠==°，正六边形内角和为720°且FG 在直线l 上， 7201206EFG °∴∠==°，在EDF 中，180DEF EDF EFD ∠=°−∠−∠，18010872EDF ∠=°−°=° ，18012060EFD ∠=°−°=°，48DEF ∴∠=°，故答案是：48．【点睛】本题考查了正多边形的内角、三角形的内角和定理，解题的关键是：掌握正多边形内角和的求法．13. 我国传统数学名著《九章算术》记载：“今有牛五、羊二，直金十九两；牛二、羊五，直金十六两.问牛、羊各一直金几何？”译文问题：“假设有5头牛、2只羊，值19两银子；2头牛、5只羊，值16两银子，问一头牛、一只羊一共值多少两银子？”则1头牛、1只羊一共值 ______ 两银子．【答案】5【解析】【分析】设每头牛值x 两银子，每只羊值y 两银子，根据“5头牛、2只羊，值19两银子；2头牛、5只羊，值16两银子”，可得出关于x ，y 的二元一次方程组，利用()7+÷①②，即可求出结论．【详解】解：设每头牛值x 两银子，每只羊值y 两银子，根据题意得：52192516x y x y += +=①②， ()7+÷①②得：5x y +=， ∴1头牛、1只羊一共值5两银子，故答案为：5．【点睛】本题考查了二元一次方程组的应用以及数学文化，找准等量关系，正确列出二元一次方程组是解题的关键．14. 为了更好的开展大课间活动，某班级计划购买跳绳和呼啦圈两种体育用品，已知一个跳绳8元，一个呼啦圈12元．准备用120元钱全部用于购买这两种体育用品（两种都要买且钱全部用完），则该班级的购买方案有______种．【答案】4【解析】【分析】设购买x 个跳绳，y 个呼啦圈，利用总价=单价×数量，即可得出关于x ，y 的二元一次方程，结合x ，y 均为正整数，即可得出购买方案的数量．本题考查了二元一次方程的应用，找准等量关系，正确列出二元一次方程是解题的关键．【详解】解：设购买x 个跳绳，y 个呼啦圈，依题意得：812120x y +=， 2103y x ∴=−． x ，y 均为正整数，x ∴为3的倍数，∴38x y = = 或66x y = =或94x y = = 或122x y = = ， ∴该班级共有4种购买方案．故答案为：4．三、解答题（共10小题，共78分）15. 解方程组：（1）23328y x x y =− +=（2）28452x y x y += −=【答案】（1）21x y = =（2）32x y = =【解析】【分析】本题主要考查了解二元一次方程组：（1）利用代入消元法解方程组即可；（2）利用加减消元法解方程组即可．【小问1详解】解：23328y x x y =− +=①② 把①代入②得：()32238x x +−=，解得2x =，把2x =代入①得2231y =×−=，∴方程组的解为21x y = =；小问2详解】解：28452x y x y += −=①② 2×−①②得：714y =，解得2y =，把2y =代入①得：228x +=，解得3x =， ∴方程组解为32x y = = ． 16. 解下列不等式（组）：（1）()32723x +≥；（2）()313122x x x x −> −−≥【的【答案】（1）13x ≥（2）无解【解析】【分析】本题考查了解一元一次不等式以及解一元一次不等式组，正确掌握相关性质内容是解题的关键．（1）先去括号，再移项合并同类项，系数化1，即可作答．（2）分别算出每个不等式组的解集，再取公共部分的解集，即可作答．【小问1详解】解：()32723x +≥，62123x +≥，62x ≥，13x ≥；【小问2详解】解：()313122x x x x −> −−≥，由()31x x −>，得33x x −>，解得32x >，由3122x x −−≥，得243x x −≥−1x ≤，此时不等式组无解．17. 如图，在由边长为1个单位长度的小正方形组成的网格中，给出了以格点（网格线的交点）为顶点的ABC ，线段MN 在网格线上．（1）画出AB 边上的高线CD ；（2）画出BC 边上的中线AE ；（3）在线段MN 上任取一点P ，则ABP 的面积是______．【答案】（1）见详解（2）见详解（3）5【解析】【分析】本题考查了三角形的高，中线的定义，运用网格求面积，正确掌握相关性质内容是解题的关键．（1）过点C作CD垂直于BA的延长线，交点为点D，即可作答．（2）根据网格特征以及中线定义，进行作图即可；（3）根据平行线之间的距离处处相等的性质，得出MN与AB的距离为5，再结合三角形面积公式进行计算，即可作答．【小问1详解】解：AB边上的高线CD如图所示：【小问2详解】解：BC边上的中线AE如图所示：【小问3详解】解：如图所示：∴ABP 的面积12552=××=． 18. 如图，在ABC 中，AN 是ABC 的角平分线，50B ∠=°，80ANC ∠=°，求C ∠的度数．【答案】70° 【解析】【分析】根据三角形外角的性质，角平分线的定义以及三角形的内角和定理即可得到结论．此题主要考查了三角形外角的性质，角平分线的定义，关键是掌握三角形的一个外角等于和它不相邻的两个内角的和．【详解】解：∵5080ANC B BAN B ANC ∠=∠+∠∠=°∠=°，，． ∴805030BAN ANC B ∠∠∠=−=°−°=°，∵AN 是BAC ∠角平分线，∴223060BAC BAN ∠∠×°°，在ABC 中，180180506070C B BAC ∠=°−∠−∠=°−°−°=°． 19. 若一个多边形的内角和的14比它的外角和多90°，那么这个多边形的边数是多少？【答案】12 【解析】【分析】设这个多边形的边数是n ，根据题意,列方程1(2)180360904n −×°=°+°求解即可．【详解】解：设这个多边形的边数是n ，由题意得：1(2)180360904n −×°=°+°，解得：12n =，答：这个多边形的边数是12．【点睛】本题考查了多边形的内角和和外角和定理，熟练掌握两个定理是解题的关键． 20. 在长方形ABCD 中，放入5个形状大小相同的小长方形（空白部分），其中8cm AB =，12cm BC =，求图中阴影部分图形的面积．【答案】236cm 【解析】【分析】设小长方形的长为xcm ，宽为ycm ，根据图形中大长方形的长和宽列二元一次方程组，求出x 和y 的值，即可解决问题．本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键．【详解】解：设小长方形的长为xcm ，宽为ycm ，根据题意，得：3128x y x y +=+=，解得：62x y ==， ∴每个小长方形的面积为()22612cm ×=， ∴阴影部分的面积()281251236cm =×−×=．21. 阅读下列材料：解方程组23237432323832x y x yx y x y +− +=+− += ．小明发现，如果用代入消元法或加减消元法求解，运算量比较大，容易出错．如果把方程组中的()23x y +看成一个整体，把()23x y −看成一个整体，通过换元，可以解决问题．以下是他的解题过程：令23mx y =+，23n x y =−．原方程组化为743832m nm n += += ，解得6024m n = =− ，把6024m n = =− 代入23m x y =+，23n x y =−，得23602324x y x y +=−=− ，解得914x y = = ，∴原方程组的解为914x y ==．（1）学以致用：运用上述方法解方程组：()()()()213211224x y x y ++−=+−−=（2）拓展提升：已知关于x ，y 的方程组111222a x b y c a x b y c +=+=的解为34x y = = ，请直接写出关于m 、n 的方程组()()1112222323a m b n c a m b n c +−=+−= 的解是______．【答案】（1）11x y == （2）143m n = =−【解析】【分析】本题主要考查了换元法解二元一次方程组：（1）结合题意，利用整体代入法求解，令1m x =+，2n y =−得23124m n m n +=−=，解得21m n = =− 即1221x y +=−=− 即可求解；（2）结合题意，利用整体代入法求解，令2x m =+，3y n =−，则()()1212222323a m b n c a m b n c +−=+−= 可化为121222a x b y c a x b y c +=+= ，且解为34x y = = 则有2334m n +=−= ，求解即可．【小问1详解】解：令1m x =+，2ny =−，原方程组化为23124m n m n += −=，解得21m n ==− ，1221x y +=∴ −=−，解得：11x y ==， ∴原方程组的解为 11x y = =；【小问2详解】解：在()()1212222323a m b n c a m b n c +−=+−= 中，令2x m =+，3y n =−，则()()1212222323a m b n c a m b n c +−=+−= 可化为121222a x b y c a x b y c += += ， ∵方程组121222a x b y c a x b y c +=+= 解为34x y = = ，∴2334m n +=−=， 143m n = ∴ =−，故答案为：143m n ==−．22. “粮食生产根本在耕地、出路在科技”．为提高农田耕种效率，今年开春某农村合作社计划投入资金购进甲、乙两种农耕设备，已知购进2台甲种农耕设备和1台乙种农耕设备共需4.2万元；购进1台甲种农耕设备和3台乙种农耕设备共需5.1万元．（1）求甲种农耕设备和乙种农耕设备单价各是多少万元；（2）若该合作社决定购买甲、乙两种农耕设备共7台，且购进甲、乙两种农耕设备总资金不超过10万元，求最多可以购进甲种农耕设备多少台．【答案】（1）1台甲种农耕设备需1.5万元，1台乙种农耕设备需1.2万元；（2）5台【解析】【分析】（1）设购进1台甲种农耕设备需x 万元，1台乙种农耕设备需y 万元，根据“购进2台甲种农耕设备和1台乙种农耕设备共需4.2万元；购进1台甲种农耕设备和3台乙种农耕设备共需5.1万元”，可得出关于x ，y 的二元一次方程组，解之即可得出结论；（2）设购进甲种农耕设备m 台，则购进乙种农耕设备()7m −台，利用总价=单价×数量，结合总价不超过10万元，可得出关于m 的一元一次不等式，解之可得出m 的取值范围，再取其中的最大整数值，即可得出结论．本题考查了二元一次方程组的应用以及一元一次不等式的应用，解题的关键是：（1）找准等量关系，正确列出二元一次方程组；（2）根据各数量之间的关系，正确列出一元一次不等式．【小问1详解】解：设购进1台甲种农耕设备需x 万元，1台乙种农耕设备需y 万元，根据题意得：2 4.23 5.1x y x y += +=，解得： 1.51.2x y ==．答：购进1台甲种农耕设备需1.5万元，1台乙种农耕设备需1.2万元；【小问2详解】解：设购进甲种农耕设备m 台，则购进乙种农耕设备()7m −台，根据题意得：()1.5 1.2710m m +−，解得：153m ≤，又m 为正整数，m ∴的最大值为5．答：最多可以购进甲种农耕设备5台．23. 【探究】如图①，在ABC 中，点D 是BC 延长线上一点，ABC ∠的平分线BP 与ACD ∠的平分线CP 相交于点P ．则有12P A ∠=∠，请补全下面证明过程：证明：BP 平分ABC ∠，CP 平分ACD ∠， 2ABC PBC ∴∠=∠，2ACD ∠=∠______（______）． ACD A ∠=∠+∠ ______（三角形的一个外角等于与它不相邻的两个内角的和）， 22PCD A PBC ∴∠=∠+∠．_____PCD PBC ∠=∠+∠ （三角形的一个外角等于与它不相邻的两个内角的和），12P A ∴∠=∠．【应用】如图②，在四边形MNCB 中，设M α∠=，N β∠=，若180αβ+>°，四边形的内角MBC ∠与外角NCD ∠的角平分线BP CP ，相交于点P ．为了探究P ∠的度数与α和β的关系，小明同学想到将这个问题转化图①的模型，因此，延长了边BM 与CN 交于点A ．如图③，若106BMN∠=°，124MNC ∠=°，则______A ∠=°，因此______P ∠=°．【拓展】如图④，在四边形MNCB 中，设M α∠=，N β∠=，若180αβ+<°，四边形的内角MBC ∠与外角NCD ∠的角平分线所在的直线相交于点P ，请直接写出P ∠=______．（用含有α和β的代数式表示）【答案】探究：PCD ；角平分线的定义；PBC ；P ；应用：50°；25°；拓展：121902αβ°−− 【解析】【分析】本题主要考查了三角形内角和定理，三角形外角的性质，角平分线的定义：探究：根据三角形外角的性质和角平分线的定义结合已给推理过程求解即可；应用：先利用平角的定义和三角形内角和定理求出A ∠的度数，再有探究的结论即可得到答案；拓展：延长MB 交NC 的延长线于A ，则由三角形内角和定理可得180A αβ=°−−∠；再由题意可得PB PC ，分别平分ABH ACB ∠，∠，则11190222PA αβ==°−−∠∠．【详解】解：探究：证明：BP 平分ABC ∠，CP 平分ACD ∠， 2ABC PBC ∴∠=∠，2ACD PCD ∠=∠（角平分线的定义）． ACD A ABC ∠=∠+∠ （三角形的一个外角等于与它不相邻的两个内角的和）， 22PCD A PBC ∴∠=∠+∠．PCD P PBC ∠=∠+∠ （三角形的一个外角等于与它不相邻的两个内角的和）， 12P A ∴∠=∠，故答案为：PCD ；角平分线的定义；PBC ；P ；应用：延长了边BM 与CN 交于点A ．如图③， ∵106BMN∠=°，124MNC ∠=°，∴1807418056AMN BMN ANM MNC =°−=°=°−=°∠∠，∠∠， ∴18050A AMN ANM =°−−=°∠∠∠， ∴1252P A ∠=∠=°，故答案：50°；25°．拓展：如图，延长MB 交NC 的延长线于A ，∵M α∠=，N β∠=， ∴180180A M N αβ=°−−=°−−∠∠∠； ∵四边形的内角MBC ∠与外角NCD ∠的角平分线所在的直线相交于点P ， ∴PB PC ，分别平分ABH ACB ∠，∠，∴11190222PA αβ==°−−∠∠，故答案为：121902αβ°−−．24. 如图①，点O 为数轴原点，3OA =，正方形ABCD 的边长为6，点P 从点O 出发，沿射线OA 方向运动，速度为每秒2个单位长度，设运动时间为t 秒，请回答下列问题．为（1）点A 表示的数为______，点D 表示的数为______．（2）APC △的面积为6时，求t 的值．（3）如图②，当点P 运动至D 点时，立即以原速返回，到O 点后停止．在点P 运动过程中，作线段3PE =，点E 在数轴上点P 右侧，以PE 为边向上作正方形PEFG ，当DPF 与ABG 面积和为16时，直接写出t 的值．【答案】（1）3，9 （2）t 的值为12秒或52秒（3）1318t =或236或316或14918．【解析】【分析】（1）根据线段OA 的长和正方形的边长可以求解．（2）根据P 点的运动速度与运动时间得出运动路程，对应数数轴得出结论．（3）根据P 点运动确定正方形的位置再去讨论DPF 与ABG 面积和为16时的t 值．本题考查了数轴与动点的结合，表示出P 点的运动距离是本题的解题关键．【小问1详解】解： 3OA = ，且O 为数轴原点，在O 的右侧，A ∴表示的数为3，正方形的边长为6，639OD ∴=+=，D ∴表示的数为9．故答案是3，9；【小问2详解】解：∵APC △的面积为6， ∴116622APC S AP CD AP =×=××=△，解得2AP =，P 点从O 点开始运动且速度为每秒2个单位长度，2OP t ∴=，∵3OA =，∴当点P 在AO 之间时，则3322AP OP t =−=−=，解得12t =， ∴当点P 在OA 的延长线上时，则3232AP OP t =−=−=，解得52t =， ∴APC △的面积为6时，t 的值为12秒或52秒；【小问3详解】解：①当P 点在A 点左侧时，2OP t =，由题意得：连接BG AG PF FD ，，，，如图所示：∵36OA AD ==，， ∴9OD =，∵速度为每秒2个单位长度，设运动时间为t 秒， ∴902t ≤≤， ∴32PA OA OP t =−=−， ∴()11279233222DPF S PD EF t t =××=−×=− ， ()116329622ABGS AB AP t t =××=××−=− ， ∵DPF 与ABG 面积和为16， ∴27396162DPF ABG S S t t +=−+−= ，解得1318t =，当P 点在A 点右侧时，连接BG AG PF FD ，，，，如图所示：同理得()11279233222DPF S PD EF t t =××=−×=− ， ()116236922ABGS AB AP t t =××=××−=− ， ∵DPF 与ABG 面积和为16， ∴27369162DPF ABG S S t t +=−+−= ，解得236t =， ②点P 从D 向O 运动时，则9999222t <≤+=，连接BG AG PF FD ，，，，如图所示：∴9926222PD t AP AD PD t=×−=−=−−，此时119272332222DPF S PD EF t t =××=×−×=− ， 119662456222ABG S AB AP t t=××=××−−=−， ∵DPF 与ABG 面积和为16， ∴273456162DPF ABG S S t t +=−+−= ，第21页/共21页解得316t =，当P 点在A 点左侧时，由题意得：连接BG AG PF FD ，，，，如图所示：∴92292962152PD t t AP PD AD t t=×−=−=−=−−=−，，此时119272332222DPF S PD EF t t =××=×−×=− ， ()11621564522ABG S AB AP t t =××=××−=− ， ∵DPF 与ABG 面积和为16， ∴273645162DPF ABG S S t t +=−+−= ，解得14918t =，综上：1318t =或236或316或14918．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

七年级数学期中检测试题
一、选择题(请将正确答案填入答题卡中，每题3分，共36分) 1、点P （1，-5）所在的象限是（）
Ａ、第一象限Ｂ、第二象限Ｃ、第三象限Ｄ、第四象限 2、下面四个图形中，∠1与∠2是对顶角的图形（）
A 、1个
B 、2个
C 、3个
D 、4个
3、如图，直线a ∥b ，直线c 是截线，如果∠1=50°，那么∠2等于( )
A 、50°
B 、150°
C 、140°
D 、130°
4、如图，PO ⊥OR ，OQ ⊥PR ，则点O 到PR 所
在的直线的距离是线段（）
A 、PO
B 、RO
C 、OQ
D 、PQ
5、用一批完全相同的多边形地砖铺地面，不能进行镶嵌的是（） A 、正八边形 B 、正六边形 C 、正方形 D 、正三角形
6、现有两根木棒，它们长分别是40㎝和50㎝，若要钉成一个三角形木架，则下列四根木棒应选取（）
A 、10㎝的木棒
B 、40㎝的木棒
C 、90㎝的木棒
D 、100㎝的木棒
7、点P 是△ABC 内一点，连结BP 并延长交AC 于D ，连结PC ，则图中∠1、∠2、∠A 的大小关系是（） A 、∠A ＞∠2＞∠1 B 、∠A ＞∠2＞∠1
C 、∠2＞∠1＞∠A
D 、∠1＞∠2＞∠A
8、若x 轴上的点P 到y 轴的距离为3，则点P 的坐标为（）
A 、(0,3)
B 、(0,3)或(0,-3)
C 、(3,0)
D 、(3,0)或(-3,0)
9、一个正方形在平面直角坐标系中三个顶点的坐标为（－2，－3），（－2，1），（2，1），则第四个顶点的坐标为（）
A 、（2，2）；
B 、（3，2）；
C 、（2，－3）；
D 、（2，3）
10、下列语句中，假命题的是（）
O P
A
B
C
D
P
1
2第7题
A 、如果A(a ，b)在x 轴上，那么
B （b ，a ）在y 轴上 B 、如果直线a 、b 、c 满足a ∥b ，b ∥c 那么a ∥c
C 、两直线平行，同旁内角互补
D 、相等的两个角是对顶角
11、已知有两边相等的三角形两边长分别为6cm 、3cm,则该三角形的周长是( •) A 、12cm 或15cm B 、12cm C 、15cm D 、10cm 12、如图所示，在△ABC 中，CD 、BE 分别是AB 、AC 边上的高，并且
CD 、BE 交于点P ，若∠A=50°，则 ∠BPC 等于（）
A 、90°
B 、130°
C 、100°
D 、150°
二、填空题（每题3分，共21
分）
13、如图，∠AOB=90°，∠MON=60°，OM 平分∠AOB ，
ON 平分∠BOC ，则∠AOC ＝________ 14、边长为3cm,xcm,5cm 的三条线段首尾顺次相接组成三角形, •若x 为奇数,
则组成三角形的周长是___________cm.
15、如图,∠A+∠B+∠C+∠D+∠E+∠F 的
和为度
16、如果p （a+b,ab ）在第二象限，那么点Q 在第象限.
17、如图是小刚画的一张脸，他对妹妹说“如果我用（1，3）
表示左眼，用（3，3）表示右眼，那么嘴的位置可以表
示成
18．如图，一条公路修到湖边，需拐弯绕湖而过，如果第一次拐的角∠Ａ是120°，第二次拐的角∠Ｂ是150°，第三次拐的角是∠Ｃ，这时的道路恰好和第一次拐弯之前的道路平行，则∠Ｃ是（）度。

19、已知a,b,c 是△ABC 的三条边，化简下列式子
︱a-b-c ︱-︱a+b-c ︱+︱a-b+c ︱=
B
C
D
F D C B A
三、解答题（共43分）
20、已知：如图，AB ⊥CD ，垂足为O ，EF 经过点O ，∠1＝25°，
求∠2，∠3的度数。

（6分）
21、完成下列推理说明。

（4分）
如图，已知AB ∥DE ，且有∠1＝∠2，∠3＝∠4，试说明BC ∥EF 。

∵AB ∥DE （已知）
∴∠1＝（__________________________） ∵∠1＝∠2，∠3＝∠4(已知) ∴∠2＝（等量代换）
∴BC ∥EF （___________________________）
22、如图，AF 是△ABC 的高，AD 是△ABC 的角平分线，且∠B ＝36°，∠C ＝76°，求∠DAF 的度数。

（6分）
23、多多和爸爸、妈妈周末到动物园游玩，回到家后，她利用平面直角坐标系画出了动物园的景区地图，如图所示。

可是她忘记了在图中标出原点和x 轴、y 轴。

只知道马场的坐标为（-3，-3），你能帮她建立平面直角坐标系并求出其他各景点的坐标？（6分）
F
E
O
D
C
B
A 3
21
马
南门
两栖动物
飞禽
24、如图，一轮船由B 处向C 处航行，在B 处测得C 处在B 的北偏东75°方向上，在海岛上的观察所A 测得B 在A 的南偏西30°方向上，C 在A 的南偏东25°方向。

若轮船行驶到C 处，那么从C 处看A ，B 两处的视角∠ACB 是多少度？（7分）
25
．有一块三角形优良品种试验基地，如图所示，
•
由于引进四个优良品种进行对比试验，需将这块土地分成面积相等的四块，请你制定出三种划分方案供选择（画图说明）．（6分）
26、如图，CD ⊥AB 于D ，点F 是BC 上任意一点，FE ⊥AB 于E ，且∠1=∠
2，
C
北
∠3=80°．
（1）试证明∠B=∠ADG
（2）求∠BCA的度数．（8分）
28、如图，在△ ABC中，∠ ABC、∠ ACB的平分线交于点O。

(1)若∠ ABC=40，∠ ACB=50°，则∠ BOC=_______
(2)若∠ ABC+∠ ACB=lO0°，则∠ BOC=________ 。

(3)若∠ A=70°，则∠ BOC=_________。

(4)若∠ BOC=140°，则∠ A=________。

(5)你能发现∠ BOC与∠ A之间有什么数量关系吗?写出并说明理由。

（12分）
2010-2011学年第二学期期中考试
七年级数学试题答案
一、1.D 2.A 3.D 4.C 5.A 6.B 7.D 8.D 9.C 10.D 11.C 12.B
二、13.120° 14.11或13或15 15.360° 16.二 17.（2,1）
18.3c-a-b 19. 150°
三、20. ∠ 2=65°，∠ 3=25°21. ∠ 3 两直线平行，同位角相等
∠ 4 同位角相等，两直线平行 22.AB CD EF 3cm²
23. 20° 24. 南门（0,0），狮子（-4,5），飞禽（3,4）两栖动物（4,1）
25. 80°
26. 方案1：如图（1），在BC上取D、E、F，使BD=ED=EF=FC，连接AE、ED、•AF．
(1) (2) (3)
方案2：如答图2，分别取AB、BC、CA的中点D、E、F，连接DE、EF、DF．
方案3：如答图3，分别取BC、CD、AB的中点，的中点D、E、F，连接AD、AE、DF．
27.（2）80°28.（1）135（2）130°（3）125°（4）100°
（5）90°+1/2∠ A。