2018数学何红卫
全国初中数学联赛北京赛区获奖名单.docx
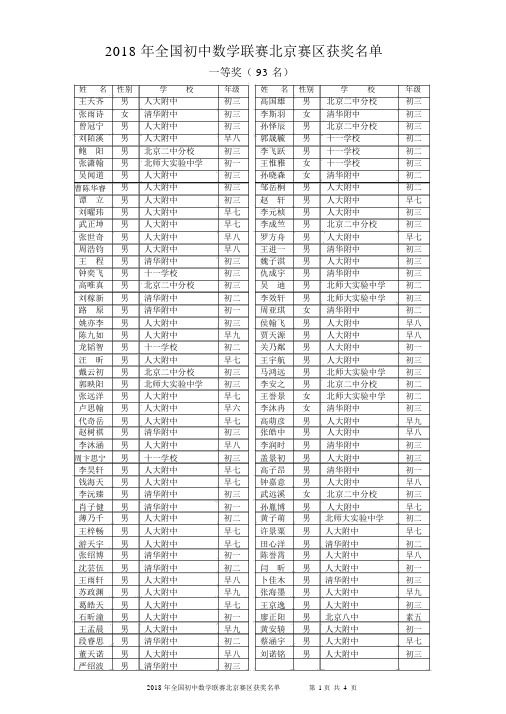
2018 年全国初中数学联赛北京赛区获奖名单一等奖( 93 名)姓名性别学校年级姓名性别学校年级王天齐男人大附中初三高国雄男北京二中分校初三张雨诗女清华附中初三李斯羽女清华附中初三曾冠宁男人大附中初三孙怿辰男北京二中分校初三刘陌溪男人大附中早八郭晟毓男十一学校初二鲍阳男北京二中分校初三李飞跃男十一学校初二张潇翰男北师大实验中学初一王惟雅女十一学校初三吴闻道男人大附中初三孙晓森女清华附中初二曹陈华睿男人大附中初三邹岳桐男人大附中初二谭立男人大附中初三赵轩男人大附中早七刘曜玮男人大附中早七李元桢男人大附中初三武正坤男人大附中早七李成竺男北京二中分校初三张世奇男人大附中早八罗方舟男人大附中早七周浩钧男人大附中早八王进一男清华附中初三王程男清华附中初三魏子淇男人大附中初三钟奕飞男十一学校初三仇成宇男清华附中初三高唯真男北京二中分校初三吴迪男北师大实验中学初二刘稼新男清华附中初二李效轩男北师大实验中学初三路原男清华附中初一周亚琪女清华附中初二姚亦李男人大附中初三侯翰飞男人大附中早八陈九如男人大附中早九贾天源男人大附中早八龙韬智男十一学校初二关乃粼男人大附中初一汪昕男人大附中早七王宇航男人大附中初三戴云初男北京二中分校初三马鸿远男北师大实验中学初三郭映阳男北师大实验中学初三李安之男北京二中分校初二张远洋男人大附中早七王誉景女北师大实验中学初二卢思翰男人大附中早六李沐冉女清华附中初三代奇岳男人大附中早七高萌彦男人大附中早九赵树祺男清华附中初三张皓中男人大附中早八李沐涵男人大附中早八李润时男清华附中初三周卞思宁男十一学校初三盖景初男人大附中初三李昊轩男人大附中早七高子昂男清华附中初一钱海天男人大附中早七钟嘉意男人大附中早八李沅臻男清华附中初三武远溪女北京二中分校初三肖子健男清华附中初一孙胤博男人大附中早七薄乃千男人大附中初二黄子萌男北师大实验中学初二王梓畅男人大附中早七许景粟男人大附中早七游天宇男人大附中早七田心洋男清华附中初二张绍博男清华附中初一陈誉霄男人大附中早八沈芸伍男清华附中初二闫昕男人大附中初一王雨轩男人大附中早八卜佳木男清华附中初三苏政渊男人大附中早九张海墨男人大附中早九葛皓天男人大附中早七王京逸男人大附中初三石昕潼男人大附中初一廖正阳男北京八中素五王孟晨男人大附中早九黄安辀男人大附中初一段睿思男清华附中初二蔡涵宇男人大附中早七董天诺男人大附中早八刘诺铭男人大附中初三严绍波男清华附中初三二等奖( 140 名)姓名性别学校年级姓名性别学校年级阎禹辰男北京二中分校初三魏闻达男北师大实验中学初三谈亮男人大附中初二高翔男人大附中初二陈竞帆男人大附中早八袁浩然男人大附中早八杨家宁男人大附中早九郭佳祺女十一学校初三王之略男人大附中早六史澍庚男清华附中初三李佳栩男人大附中早八赵可彤云女北京二中分校初三许昊翔男人大附中早六董亦麟女人大附中早八杨振男北大附中初三姚盛迪男清华附中初三马天佑男人大附中早七李永一男人大附中早七张致远男北京二中分校初二戴大伟男人大附中初三唐颂恩男人大附中初一邓宇晨男人大附中早七王心睿男人大附中早八李思学女北大附中初二李梦喆男北京一零一中初三胡梁栋男人大附中早九徐文昕男人大附中早七陶羽翘女人大附中早七林雨晨男人大附中早九纪明悦女清华附中初二王星瀚男人大附中早九马帅男清华附中初三邱子墨男清华附中初三吴梦涵女清华附中初二赵芳宸男人大附中早九顾笑恺男北师大实验中学初三陈容乾男人大附中早六郝宇衡男北京八中初二赵亦阳男十一学校初二杨博昌男北京十二中初三李悦旻男清华附中初三赵佳滢女北师大实验中学初三权尚浩然男北京一零一中初三陆霆松男人大附中初二崔焱扬男北京二中分校初二滕家齐男清华附中初三李亦之女人大附中早九褚天骏男人大附中早九李天骥男人大附中初三刘弘瑞女北大附中初三王安睿男清华附中初三陈智谦男人大附中早八姚冠名男清华附中初三罗奕翔男清华附中初三李昕孜女人大附中早九王翼飞男清华附中初三刘涵祚男人大附中早六任弈海男人大附中早七安庭毅男北师大实验中学初三武逸文男清华附中初三张释瑄男北京二中分校初三赵培源男清华附中初二张博阳男人大附中初三王子来男人大附中初三李丁一城男北师大实验中学初三陈国凯男北师大实验中学初三徐子健男十一学校初一向宇扬男人大附中初三赵秦怡女北师大实验中学初三邹晨男人大附中早八虞明达男清华附中初一马牧洲男清华附中初三苗硕男人大附中早八李天皓男人大附中早九王慕涵男人大附中早八吕博延男首师大附中初三斯文男人大附中早八高祎晨男人大附中初三万林普男北师大实验中学初三闫昕宇男清华附中初三郑承远男十一学校初三石羽女北京二中分校初三徐金女人大附中初二钟沐阳男人大附中初二张蕙心女人大附中早九范天舒男人大附中早八叶方舟男人大附中早七杨钧天男人大附中早七廖昱博男人大附中早七金雨晨男清华附中初三尚子衿男人大附中早七罗天择男人大附中初二杨泽畅男人大附中早八吴雨轩男人大附中早八宋驰男人大附中早九冯奕棠男人大附中初三邢博轩男人大附中早八魏川男北师大实验中学初三吴亚珩男人大附中初三陈羽翔男北师大实验中学初三王子兮女清华附中初二洪伊婷女北京一零一中初三李骏潇男北师大实验中学初三刘天睿男北师大实验中学初三李凯阳男人大附中初三胡蝶沐歌女人大附中早七卢远男人大附中初一黄嘉萌女北京一零一中初三马景伦男人大附中早九王照峰男人大附中早九肖天睿男清华附中初三宋知雨男人大附中分校初二王以翔男北师大实验中学初三国奕扬男清华附中初三王雍湉女北师大实验中学初三刘嘉祺男人大附中早七王中祺男北京二中分校初三黄鹤鸣男人大附中早七於嘉鹏男北大附中初三郑家怡女清华附中初三苏禹畅男清华附中初三吴宇桐男北京二中分校初三张英杰男十一学校初三刘程程女人大附中早八王凤仪女人大附中早八姜雅楠女清华附中初三弓佳彤女清华附中初三东紫昭女十一学校初二晁一沣男人大附中初二孟晙阳男北京二中分校初二李宗润男北师大实验中学初二郑良飞男人大附中初二简宇卿男人大附中初三陈平男北京二中分校初二张昊田男人大附中早九赵天珺男十一学校初二潘佳骐男人大附中早九李飞阳男北大附中初三孙嘉阳女清华附中初一马昊宇男十一学校初二三等奖( 107名)姓名性别学校年级姓名性别学校年级陈佳妤女清华附中初一李东宇男首师大附中初三汪泰宇男人大附中初三李天圣男北大附中初一解相儒男北京十二中初三罗翔天男清华附中初二张锴睿男北京八中初三王宸熙男人大附中初三杨家齐男人大附中早八刘立今男人大附中初三傅大韦男人大附中初二吴青阳男人大附中早八李子豪男清华附中初一王程禹男北京一零一中初三关涛男人大附中早八高梓博男人大附中早八耿玥峰男人大附中初三戴其铭男人大附中初三梅自涵男十一学校初三张书豪男十一学校初二蒋沅健男中美力迈国际学校初三宋德霖男清华附中初三刘卜文男人大附中早九陈家祺男清华附中初三陈吉轲男人大附中早八张雪桢女北京二中分校初二汲绍达男清华附中初三李钟辰女北京一零一中初三王菁女清华附中初三唐汪宇达男清华附中初三周尚男北师大实验中学初三李行初男北京二中分校初二秦禹洲男北师大实验中学初三黄佳惠女人大附中初二郭俊游男人大附中早六李俊驰男北京四中初三魏歆哲男十一学校初三石峰宇男北京二中分校初三彭文钰女北京五中分校初三严鼎华男十一学校初三黄小棋男北京十二中初三温雪岭女人大附中早八王雨晗男十一学校初二胡沛骅男北师大实验中学初三刘馨阳男人大附中早七张章男北京一零一中初二王嘉硕男北京一零一中初三李秉伦男人大附中初三穆华林男人大附中初一张许瞰女清华附中初三王世屹男清华附中初二顾斌瑞男人大附中早八王溪斌男人大附中早八吕承融男北京二中分校初三汪锦程男北师大实验中学初三何欣悦女人大附中早八徐岫旸女北师大实验中学初三王未然女北京十二中初三王众一女人大附中初二张冰喆男人大附中早七杨书泰男十一学校初二黄子宽男北师大实验中学初三陈宇驰男清华附中初三杨嘉彦男人大附中早八王梓荃男十一学校初三郑思瑜男清华附属实验学校初三余欣锴男人大附中早八赵韵博女北京八中初三衣威旭男人大附中早七刘一晨男北京一零一中初二陈柯学男清华附中初三樊峻一男人大附中早七贾博暄男人大附中初二饶邦略男十一学校初三史奕然男人大附中初三晋康玮男十一学校初三王箫男清华附中初三杨淏天男十一学校初二张俊哲男北大附中初三张添淇男清华附中初三魏士尧男北京十二中初三赵天健男北师大实验中学初三肖翊宸男人大附中早七刘海丰男清华附中初三白宇繁男十一学校初三洪嘉阳男北京五中分校初三肖鉴洲男人大附中早八徐启鑫男清华附中初一刘文岳男十一学校初三邹听雨男十一学校初一宋加宸男人大附中初三李海峰男清华附中初一陈桢懿男北大附中初二浦皓天男十一学校初三高钰翔男人大附中早七张博信男人大附中早九赵大为男人大附中早九万宇泽男清华附中初三周以端女十一学校初二付浩辰男十一学校初二张韩乐男北京二中分校初三王剑超男北京十二中初三蒋佳宏男人大附中初三李冠葳男首师大附中初三赵晨迪男人大附中初三王序书男人大附中初三刘皓达男人大附中初一。
2018年高考“圆锥曲线与方程”专题解题分析

二、解法分析
1. 强调数学运算,利用“直译法”进行求解 近几年的高考数学试卷,对本专题的考查中,重
点考查学生的运算能力. 尤其是考查学生对含字母的 代数式的化简变形的能力,在2018年的高考数学试卷 中得到了很好的体现.
“直译法”就是在解决圆锥曲线试题的过程中,利
用数学运算程序,将条件中的文字描述都转化为数学
-
3 2
ö2 ø
+
æ ç è
3+
3 2
ö2 ÷ ø
关键词:圆锥曲线;几何特征;平面向量;试题综合;复习建议
2018年高考数学试卷中,圆锥曲线试题位置前移 是数学试卷结构上的重大调整,这种调整,在适当降 低圆锥曲线试题难度的同时仍然保证了对圆锥曲线主 干知识的考查,在强调通性、通法的基础上重视对数 学学科思想与核心素养的考查,重视对圆锥曲线核心 思想的考查.
8
=
0. 解得
y1
=
2,y2=
4
.
不妨令 M(1,2),N(4,4),所
以 FM = (0,2) , FN = (3,4) . 所以 FM · FN = 8 . 故
答案选D.
【评析】 该题直接求出点 M,N 的坐标,然后利用
向量的基本概念及其运算进行求解.
得 yN =
y1 + y2 2
=1.
故k=
y1 - y2 x1 - x2
=
4 y1 + y2
=2.
y
A1
A
M
N
O
x
B1
B
图1
【评析】 该题主要考查圆锥曲线与平面几何图形的
联系. 数形结合,利用直角三角形的几何性质,问题
2018求实杯数学竞赛考场监考安排4.10
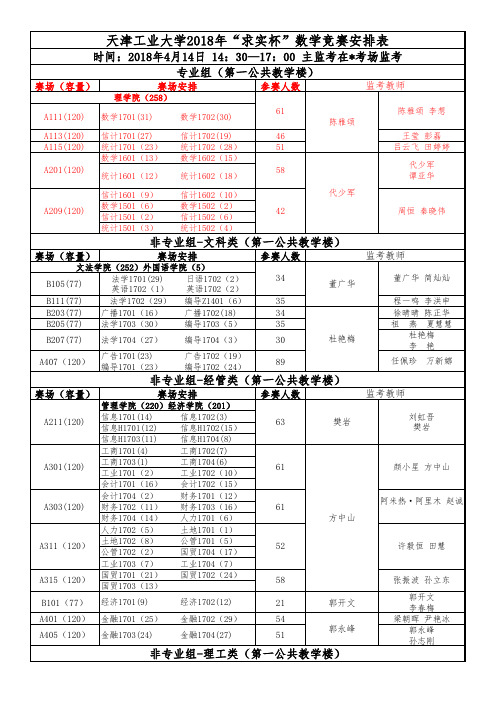
应化1702(22)
46
吴永军
监考教师
郭云莲 王慧敏 张毅 何洋 张霞 王梅
张莘苑 于春萍
宿方萍 任欢 谭勇 章珂菲
孔庆军 焦翠姣
监考教师
李庚雷 周强
权全 曲鸽
赵军建 史晓腾
牛自委 赵慧娟
马晓燕 崔凤烨
李孟芹
杜建华
任连飞 陈虹
刘明
侯小露
王明霞 魏成彪
岳程飞 纪艳红
李天旭
郑佳
刘秀芳
于鸿彬
李国兴 肖新华
49
B118(180)
机械学院(408人) 机械Z1701(30)
机械1702(27)
57
刘明
B120(180) 机械1701(26)
机自1703(29)
55
刘秀芳
B224(180) 机电1701(25)
机自1704(26)
51
D103(250)
工设1701(27) 测控1701(30)
建筑1702(23) 机电1702(27)
38
光信1604(2)物理1501(8)
物理1502(2)物理1601(4)
物理1602(3)
经济学院(162)
国贸1603(10)国贸1604(13)
A411(120) 金创1501(30)金融1501(3)
83
金融1505(1)金融1601(7)
经济1602(19)
金融1602(8)金融1603(22)
高年级组(第二公共教学楼)
赛场(容量)
赛场安排
纺织学院(45人)
参赛 人数
材料1501(3) 材料1502(2) 材料1602(1)
纺织1501(3) 纺织1502(4)
数学学院2018年硕士研究生招生复试工作方案

数学学院2018年硕士研究生招生复试工作方案一、招生单位复试工作领导小组名单组长:郭真华组员:刘阿丽邵勇张瑞康静桂贵龙张海袁敏二、复试分数线二级学科招生计划参加复试人数复试分数线备注基础数学应用数学计算数学38 45 329统计学9 9 281科学技术史 1 1 350注:招生计划中包含推免研究生6人。
三、达到复试线的考生名单(分学科专业)数学:报考专业总分政治外语业务一业务二姓名考生编号备注应用数学393 67 61 133 132 张学耀106978611603340 储才计划应用数学392 73 57 121 141 李一帆106978414008371 基础数学391 71 67 117 136 赵晓璐106978412308362 基础数学389 70 58 123 138 张佳凡106978611603289 应用数学387 67 64 116 140 程雅楠106978611603321 储才计划应用数学379 75 47 113 144 刘孟珂106978414108375 应用数学376 72 52 114 138 王琪106978140908320 应用数学373 62 63 125 123 唐洁106978370608357 基础数学367 66 58 126 117 杨琪琪106978614108386 应用数学366 71 51 115 129 刘艳娇106978410708359 基础数学365 69 60 113 123 张珮瑜106978140908314 应用数学365 73 61 109 122 姜自文106978371308358 基础数学363 63 51 111 138 刘靖子喆106978611603295 应用数学358 73 63 100 122 潘敏106978611603323 储才计划基础数学355 73 58 116 108 汤鼎玄106978611603290 应用数学355 60 60 121 114 杨银银106978611603339 基础数学354 78 67 89 120 武利利106978611603292 储才计划应用数学353 69 47 120 117 李迎106978370608356 基础数学351 69 45 126 111 荆晓燕106978611603300 基础数学350 65 58 119 108 刘静106978611603305 计算数学348 73 47 105 123 程彦亮106978620208402 应用数学348 70 58 106 114 朱孟孟106978413208366 应用数学348 65 55 106 122 姬儒雅106978414108376 基础数学347 63 39 105 140 郝倩106978611603284 应用数学344 63 53 106 122 宋倩106978140608312 基础数学343 66 47 112 118 樊丹106978140908323 计算数学343 58 52 114 119 刘锐斐106978611603313 计算数学343 64 55 116 108 孙小梅106978360808355 应用数学343 73 50 124 96 杨静106978140608308 应用数学342 63 52 102 125 刘雅楠106978152608349 基础数学341 62 42 118 119 陈嘉浩106978330508351 应用数学337 67 48 99 123 林妍106978614408393 基础数学335 65 59 106 105 张瑜106978141108330 应用数学335 55 42 120 118 李存吉106978611603344 应用数学335 61 58 108 108 祁雪萍106978621308404 基础数学334 70 55 106 103 孙青青106978140908322 应用数学334 65 56 95 118 史婷婷106978611603335 基础数学333 63 55 114 101 顼霞106978142008344 基础数学332 57 38 104 133 曹苗106978141208334 基础数学332 69 42 118 103 刘艺明106978141508340 应用数学332 61 58 99 114 王增学106978330608352 应用数学331 65 43 107 116 张月慧106978140908317 应用数学331 64 53 109 105 张研106978614408397 计算数学329 58 44 104 123 马春洁106978611603318 应用数学329 63 64 94 108 郭宁106978141108328统计学:报考专业总分政治外语业务一业务二姓名考生编号备注统计学379 66 63 132 118 陈金灵106978611603359 统计学349 67 61 105 116 杜琦106978611603351 储才计划统计学344 69 48 102 125 许筱敏106978614408398 统计学324 63 53 86 122 李子涵106978611603354 储才计划统计学323 69 52 79 123 李晓达106978611603358统计学306 69 62 68 107 田苗106978611603361 储才计划统计学300 62 53 90 95 陈伟杰106978611603360 储才计划统计学300 72 57 91 80 魏松106978340108354 统计学281 64 56 83 78 白娟娟106978611603353 储才计划科学技术史:报考专业总分政治外语业务一业务二姓名考生编号备注科学技术史350 72 58 105 115 倪佳106978614308388四、复试工作流程及原则;严格按照学校要求,制定复试工作方案,按照复试工作时间表有条不紊进行。
浙教数学八下《6.3反比例函数的应用》[何老师]【市一等奖】优质课
![浙教数学八下《6.3反比例函数的应用》[何老师]【市一等奖】优质课](https://img.taocdn.com/s3/m/e777d7ce0242a8956bece497.png)
6.3反比例函数的应用的教学设计教学目标知识与技能目标 1.经历通过实验获得数据,然后根据数据建立反比例函数模型的一般过程. 2.会综合运用反比例函数的表达式,函数图象及性质解决实际问题. 过程与方法目标培养学生分析问题和解决问题的能力,增强学生用函数思想分析、解决问题的意识. 情感与态度目标 1.通过对实际问题的分析,培养学生关注生活,感受函数的应用价值,体会数学建模的思想。
2.通过应用函数的性质和利用图象解决问题,体验数形结合的思想. 学情分析学生已经掌握了方程,不等式的解法,掌握了用待定系数法求反比例函数的表达式,学习了反比例函数的图象和性质。
学生已经有了用反比例函数解决实际问题的知识储备.在应用的过程中能更好地巩固反比例函数的图象和性质. 学时重点用反比例函数的表达式和图象表示问题情境中成反比例的量之间的关系,进而利用反比例函数的图象和性质解决问题. 学时难点应用一中变量的反比例函数关系的确定建立在对实验数据进行有效的分析、整合的基础之上,过程较为复杂,学生理解有一定难度. 教学方法与教学手段 1.通过创设问题情境, 体会到反比例函数来自于现实生活实际,是解决实际问题的需要. 2.通过观察、思考、交流等活动,激发学习情绪,营造学习气氛. 3.通过学练结合,师生之间,学生之间相互交流、讨论的形式让学生及时巩固所学知识. 教学活动活动1【导入】6.3.1创设情境导入新课随着经济和科技的发展,人们的生活水平日益提高.汽车这个现代化的交通工具也走近了千家万户!这是汽车发动机的汽缸。
活塞在不断地往复运动,汽缸内气体的压强和体积发生变化.科学家们通过实验发现:当汽缸内气体的压强和体积达到一定值时,柴油就会燃烧,产生动力。
科学家们是怎么研究的呢?同学们想知道吗?今天这节课,我们就来学习反比例函数在一些实际问题中的应用.(板书:6.3反比例函数的应用)活动2【观察、思考、回答、交流、归纳】6.3.2师生互动探索新知 1.例1(反比例函数的应用一)教学设△ABC 中BC 边的长为x(cm),BC上的高线AD为y(cm),△ABC的面积为常数.已知y关于x的函数图象过点(3,4). (1)求y关于x的函数表达式和△ABC的面积. (2)画出函数的图象,并利用图象,求当2<x<8时y的取值范围. 条件变式:当三角形BC边的长不小于5cm时,高线AD的范围. 给学生充分的时间,让学生积极主动地思考,师生之间一起交流、分享、归纳方法:(1)根据三角形的面积公式找到了变量x和y之间的等量关系,求出函数表达式。
从“旋转”角度认识“倒序相加”

这样一道作 图题, 考虑用直尺和圆规准确作 图, 其中包 含了很多知识, 涉及到椭 圆的参数方 程, 坐标变换 的几何解释, 圆的光学性质等, 椭 竟
蕴含着如此丰富的内容. 几何作图与代数研究性 质结 合 , 示 了圆锥 曲线 中深刻 的几 何联 系, 揭 高
P1
考试题给 我们提供 了研究学习的素材.类似 的 作 图是否适用于双 曲线和抛物线? 如何仅用尺 规求作圆锥 曲线的中心、焦点等, 还有更多有趣 的问题值得广大师生继续探讨.
构造如下所示 的正方形数阵 () 1。
竹
f
2 礼
f
3 n
f
● ● ●
的值是否也能通过旋转后对应项相加求解? 为 此, 构造三角形数 阵 ① :
I
惫 —2 — 3 — — — —… — —
礼
l
● ●
I
n —— 2 — — 3 —— .. n 礼 .— — 礼 — — … —— n2
把“ 序 相 加, 成 是 所 求 和 式 “ 心 旋 转 了 倒 , 看 中
10 8 后和原式对应项相加, 在这种认识背景下,
解析:
S
n
=
n
+
= 1 +3 +2 +… +n … … …() , 1 n - i +( ) n一2 +… + ‘2 ) ,() 。 (
‘ )。
f 、+ r 1 得 】 9
21年第 1期 00 2
数 学教 学
1-9 2 1
从“ 旋转" 角度认识 “ 倒序相加’ ’
21 0 江苏省盱眙中学 周志国 10 7
“ 序 相 加” 是 等差 数 列 求 和 公 式 的推 导 倒 法 方法 , 实质 上 来看 是 应 用 了对 称 的 思想 . 若 从 倘 1 .旋转 1 0 模 型 8。 求 1+2+ 3+ … +
最新2018届高考数学第二轮专题教案7

《方程的根与函数的零点》教学反思本节课的教学重点有两个,一个是函数的零点、方程的根以及函数图象与x轴交点的横坐标三者的关系,另一个中心就是函数零点存在性定理。
在教学设计上,我采用自习时间以问题引导的形式让学生先学习新知,然后完成我设计的重点典型题目。
课堂上,和学生一起探讨自习给学生的问题,使学生进一步理解并掌握所学新知。
然后再给学生时间让学生以小组为单位讨论交流晚自习的典型题目。
我在教室进行巡视,了解学生的自主完成情况,哪些题型会了,哪些部分会了,哪些需要点拨,哪些根本没思路,无法下手,需要老师的讲解。
对于学生都会的就不讲了,部分学生会的让学生讲解。
没办法下手去做,我给学生点思路,留时间让学生试着完成,最后再讲解,点评。
例如:类型一利用解方程的方法求零点,学生没问题,就不讲了;类型二的第一题有部分学生会,我就让姚佳舟进行讲解,然后我再加一点评,类型二的第二题学生给了一种数形结合的方法处理,我在给学生介绍了一种利用函数的单调性处理的方法。
类型三的第二题好多学生不会,但我在巡视时发现王佳乐会,就让她上黑板讲解,其实学生就是变型不到位,当佳乐一给学生变型到位后,学生瞬间就明白了。
类型三的第二题很难,学生几乎没办法下手,我就提示学生用整体的思想换元法,慢慢就有人会做了。
不过我还是很惊喜的发现我班的刘二林在我提示之前就把这道题做对了,虽然在后面的处理是用解方程的方法,但成功的完成了此题。
我在点评他这道题时,又引导学生采用数形结合的思想,利用图像法让学生掌握了此类题目的处理方法。
在课堂教学中,主要体现了以下几个亮点:一是问题引导,激发学生的求知欲,调动学生参与课堂的积极性,提高热情。
二是数形结合和转化与化归思想在整个课堂中恰到好处的应用,对突破知识的难点非常有用,使教学效果明显提高;三是多媒体的使用,课件和投影是使用,为展示提供了方便。
三是小组讨论,充分调动了学生的积极性,不但能让学困生能掌握基本方法,而且也为学优生提供的平台,使他们更熟练的掌握了所学知识和所学方法。
支架式问题在小学几何概念教学中的应用——兼评《平稳与旋转》教学设计

上, 结合我国小学数学新课程标准中 对
几 何教学 的要求以及小 学生的认 知特
黪 目前在小学生学习几何概念
中所存在的问题
点, 我们认为小学生的几何学习发展水
平划分为以下几个水 平 ( 如图) :
新课程标准强调素质教育, 特别
是各 种能力的培养。 作为数 学教 师, 在 教学 中培 养 学 生各 方 面的 能 力, 是提 高学生 数学 素质 的关 踟 键 。 间想 象能 力是指人 们对 空
客 观 事 物 的空 间形式 进 行 观 察、 分析和抽象的能力, 是逻辑 思维 与几何 知识及 相关技 能、
任 何 事物 都既有 本 质属性 , 也有 非 本质 属 性 。 谓 掌 握几 何 概 念 , 所 就
是 掌 握 几 何 中同类 事 物 共 同的 本 质
属性 , 关键是 必须 把几 何 概 念的特 殊 ( 非共有 ) 因素和一般 ( ) 共有 因素区分 开来 , 如果 找不 出一类 事 物所 共 有的
这 种识别活动常常依赖于具体的佯板, 如
学 生说 所给的图形是长方形 , ‘ 看 因为 它
起来像是门”这时他们并不关一 种图 , 婚
形的特征陛凰 也未自 孰 姒 识各科图
形盼 陛质, 仅仅是建立—种直观感知, 在 头脑 啪 相关物 表象信
体思维向抽象 思维 过渡的时期, 抽象概 括 能力比较弱。 支架 式问题在小 学几何 概念
何思维主要存在5 个水平: 直观、 分析、
推理 、 绎以及严谨 。 演 这五个 水平 并不
容 。 究学 生在 学 习几 何 概 念 过程 中 研 产生思维 障碍 的原 因, 讨 排除思维障 探 碍的方法, 对于改进和加强几何 概念的 教学 , 提高学生运用几何概念分析 和解
2018命题研讨会材料汇总(修订)

2018命题研讨会材料汇总(修订)2018年全国数学竞赛命题研讨会试题汇编2018年6⽉⽬录代数代数1 不等式…………………………………………………⼈⼤附中张端阳1 代数2 不等式…………………………………………………⼈⼤附中张端阳1 代数3 不等式……………………………复旦附中李朝晖、施柯杰、肖恩利3 代数4 不等式……………………………复旦附中李朝晖、施柯杰、肖恩利4 代数5 不等式……………………………复旦附中李朝晖、施柯杰、肖恩利7 代数6 不等式…………………………………………华东师⼤⼆附中唐⽴华8 代数7 不等式……………………………………………湖南师⼤附中张湘君9 代数8 不等式……………………………………………湖南师⼤附中张湘君10 代数9 不等式……………………………………………湖南师⼤附中汤礼达11 代数10 不等式……………………………………………湖南师⼤附中汤礼达12 代数11 不等式………………………………………吉⼤附中⽯泽晖、王庶赫13 代数12 不等式…………………………………绵阳东⾠学校袁万伦、姚先伟14 代数13 不等式……………………………………………绵阳东⾠学校袁万伦15 代数14 三⾓不等式……………………………………………⼴州⼆中程汉波16 代数15 不等式……………………………………………⼤连⼆⼗四中邰海峰17 代数16 数列…………………………………………………东北育才学校张雷18 代数17 不等式………………………………………………东北育才学校张雷19 代数18 不等式………………………………………………⼤连⼆⼗四中李响23 代数19 多项式……………………………………学⽽思培优苏州分校李家夫24 代数20 不等式…………………………………………………华东师⼤张丽⽟24 代数21 不等式……………………………………………………杭州⼆中赵斌25⼏何⼏何1……………………………………复旦附中李朝晖、施柯杰、肖恩利28⼏何2………………………………………………………湖南师⼤附中苏林29 ⼏何3………………………………………………………湖南师⼤附中苏林30 ⼏何4……………………………………………………………郑州⼀中张甲31 ⼏何5………………………………………………………西安铁-中杨运新32 ⼏何6………………………………………………………西安交⼤附中⾦磊33 ⼏何7………………………………………………………西安交⼤附中⾦磊34 ⼏何8………………………………………………………西安交⼤附中⾦磊35 ⼏何9………………………………………………………西安交⼤附中⾦磊36 ⼏何10………………………………………………………西安交⼤附中⾦磊36 ⼏何11………………………………………………………西安交⼤附中⾦磊37 ⼏何12……………………………………………………东北育才学校缠祥瑞38 ⼏何13………………………………………………学⽽思培优北京分校陈楷39 ⼏何14………………………………………………学⽽思培优北京分校陈楷40 ⼏何15 ……………………………………………学⽽思培优北京分校杨溢⾮41 ⼏何16 ……………………………………………………………北京四中侯彬42 ⼏何17………………………………………………………西安交⼤附中⾦磊43数论数论1…………………………………………………………东北育才学校张雷45 数论2………………………………………………………………杭州⼆中赵斌45 数论3………………………………………复旦附中李朝晖、施柯杰、肖恩利47 数论4………………………………………………………东北育才学校缠祥瑞48 数论5……………………………………………………………杭州⼆中胡克元50 数论6………………………………………………学⽽思培优杭州分校李卓伦52 数论7………………………………………………学⽽思培优杭州分校李卓伦54 数论8………………………………………………学⽽思培优武汉分校巩鸿⽂55 数论9………………………………………………学⽽思培优武汉分校巩鸿⽂55 数论10……………………………………………学⽽思培优深圳分校涂⼩林58 数论11……………………………………………学⽽思培优深圳分校涂⼩林60。
云南省富源县胜境中学2018届高三第一次仿真高考试题
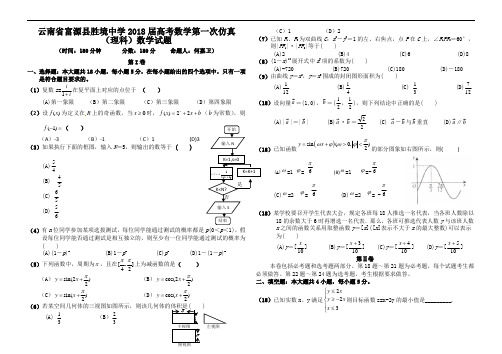
云南省富源县胜境中学2018届高考数学第一次仿真(理科)数学试题(时间:180分钟 分数:180分 命题人:何嘉卫)第I 卷一、选择题:本大题共18小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)复数z =1ii+在复平面上对应的点位于 ( )(A)第一象限 (B )第二象限 (C )第三象限 (D )第四象限 (2)设()f x 为定义在R 上的奇函数,当0x ≥时,()22x f x x b =++(b 为常数),则(1)f -=( )(A )-3 (B )-1 (C )1 (D)3 (3)如果执行下面的框图,输入N =5,则输出的数等于 ( )(A)45(B) 54(C) 56 (D) 65(4)有n 位同学参加某项选拔测试,每位同学能通过测试的概率都是p (0<p <1),假设每位同学能否通过测试是相互独立的,则至少有一位同学能通过测试的概率为( ) (A)(1-p )n (B)1-p n (C)p n (D)1-(1-p )n(5)下列函数中,周期为π,且在[,]42ππ上为减函数的是( ) (A )sin(2)2y x π=+ (B )cos(2)2y x π=+ (C )sin(2y x π=+ (D )cos()2y x π=+ (6))(A) 31 (B )32 (C )1 (D )2(7)已知F 1、F 2为双曲线C :x 2-y2=1的左、右焦点,点P 在C 上,∠F 1PF 2=60°,则|PF 1|²|PF 2|等于( )(A)2 (B)4 (C)6 (D)8 (8)(1-x )18展开式中x 3项的系数为( )(A)-720 (B)720 (C)180 (D)-180 (9)由曲线y =x 2,y =x 3围成的封闭图形面积为( )(A)121 (B)41 (C) 31(D)127(18)设向量=(1,0),=(21,21),则下列结论中正确的是( )(A)||=|| (B)²=22(C) -与垂直 (D)∥)已知函数()sin (0,)2y x πωϕωϕ=+><的部分图象如右图所示,则( ) (A)ω=1 ϕ= 6π (B)ω=1 ϕ=-6π (C)ω=2 ϕ= 6π (D)ω=2 ϕ= -6π)某学校要召开学生代表大会,规定各班每18人推选一名代表,当各班人数除以18的余数大于6时再增选一名代表.那么,各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数y =[x ]([x ]表示不大于x 的最大整数)可以表示为( ) (A)y =[10x ] (B)y =[103+x ] (C)y =[104+x ] (D)y =[105+x ]第Ⅱ卷 本卷包括必考题和选考题两部分。
翻转课堂理念下高中数学教学效率方面探究

探索篇•教学研究翻转课堂这种教学模式把更多的教学时间交给学生,这样一来,可以促使教学效率的有效提升。
然而,如果教师无法对翻转课堂这种教学模式加以恰当运用,反而会对教学效果产生影响。
所以,怎样在高中阶段的数学教学之中对翻转课堂这种教学模式加以运用,需要教师不断进行探讨以及总结。
由此可见,对翻转课堂这一理念之下高中阶段数学教学整体效率展开有关探究意义重大。
一、关于翻转课堂的概述实际上,翻转课堂这种教学模式早已产生,并且在国内多数学科教学中已有广泛渗透,并且取得良好效果。
在翻转课堂这种教学理念之下,学生具有学习的主动权,可以对一些数学知识进行自主学习,之后由教师在课堂之上对知识加以讲解。
这样一来,教师可以对课堂时间加以有效利用,有针对性地对数学知识加以讲解,这对提升课堂教学实际效率十分有利。
在课前,数学教师把有关知识设计成相应的数学问题,然后让学生在课前通过自主学习寻找答案。
在课堂之上,高中生可带着问题进行学习,这样可以提升其课堂之上的学习效果[1]。
如此一来,不仅能够完成相应的教学任务,同时还能对学生素养以及学生能力加以有效培养。
二、高中数学当中翻转课堂的应用(一)设计课前的预习问题在翻转课堂这一理念之下开展高中阶段的数学教学,教师首先应对教学重点加以梳理,并且设计一些针对性较强的问题,以此来引导高中生对数学公式、定理以及有关概念具体形成机制进行思考,给翻转课堂这种教学方法开辟相应的学习路径。
例如,进行“余弦二倍角公式”教学期间,函数的表达式是:cos2θ=cos2θ-sin2θ=1-2sin2θ=2cos2θ-1。
但在实际运算中,所得结果比较复杂,高中生是否可以对其中包含的知识点加以理解十分关键。
所以,在教学之前,数学教师需围绕有关知识点来设计问题。
比如,把cos2θ转化成sinθ或cosθ的方法有哪些?再消去题中数字1,其运算结果会发生哪些变化。
类似问题是高中阶段数学考试当中的常见题型,高中生只有对关键知识加以熟练掌握,才可提升自身的解题能力。
顺势而为,把探究引向深入

顺势而为,把探究引向深入
葛文君
【期刊名称】《教育研究与评论(小学教育教学版)》
【年(卷),期】2010(000)010
【摘要】@@ 引导学生探索多边形内角和的一般计算方法时,教师依次出示一个任意四边形、一个任意五边形和一个任意六边形,启发他们联系三角形内角和是1800的已有知识,把四边形分成2个三角形、把五边形分成3个三角形、把六边形分成4个三角形……由此分别得到四边形的内角和是1800X2、五边形的内角和是1800X3、六边形的内角和是1800X4……再通过进一步的观察和比较,帮助他们逐步归纳出:多边形的内角和=(边数-2)X180°.
【总页数】2页(P89-90)
【作者】葛文君
【作者单位】南京市鼓楼区教师进修学校,210009
【正文语种】中文
【相关文献】
1.在探究教学中把学生思考引向深入——一道课本习题的探究过程及其反思 [J], 漆光宗
2.探究无涯“乐”作舟——浅谈如何将小学生的科学探究引向深入 [J], 叶水明;杨邦清
3.借“直”之妙境顺势而为——对一类解析几何问题的解法探究 [J], 洪新华
4.顺势而为·展开探究·提升素养
——抛物线"距离和"最值问题引发的探究与思考 [J], 张琦;高慧明
5.顺势而为,合理建构,打造生长型活力课堂——由"矩形中的折叠问题"引发的探究与思考 [J], 汤忠芳
因版权原因,仅展示原文概要,查看原文内容请购买。
生活,有多重——对于小学数学实践性作业的思考

课程教育研究Course Education Research2018年第22期质量,虽是对客观事物轻重的一种描述,与现实世界中所有物体息息相关,但不能简洁明了的通过观察获得感受。
质量单位看似非常贴近学生生活,但学起来并不容易。
于是,克与千克的两节课上设计了丰富的体验活动。
但课后练习中,出错率达59.5%。
三年级学生思维发展处在具体形象思维为主的阶段,学生对质量单位的感知,仅靠课堂中一些体验活动明显不够。
数学知识来源于生活,生活才是学习数学更宽阔的课堂。
如果能引导学生在生活中多关注常见物品的质量,并积累下来,相信对质量单位的认识会更清晰,感受也会更深刻。
于是笔者尝试设计了一份作业:生活,有多重?1.称出1千克下列食品,数数大约有多少个,结果填在表里。
2.到超市或者商店进行调查,完成下面的填空。
写出两种净含量是100克的物品:写出两种净含量是200克的物品:写出两种净含量是500克的物品:3.到超市找一找,哪些袋装食品是用“克”作单位的,各是多少克?哪些是用“千克”作单位的,各是多少千克?学生们利用假期带着自己的秤到附近的超市称一称,并记录下来再在课上进行交流分享。
交流后再次完成上一次题型的题目,全对人数提高了30%。
看来,当学生对常见物品的轻重有了越来越多的直接感受后,脑中建立的质量单位的表象也越来越清晰。
通过实践作业,将学科知识和实际生活、课内学习和课外活动紧密相连。
那么如何有效得设计一份实践性作业,《新课标》指明了方向:内容有利于学生主动地观察、猜测、实验、判断、推理与交流,多利用各种形式,关心学生在学习中的自主性的落实。
这样才能提高孩子学习的积极性,才能使他们感到学习是有用的、有效的。
这不仅有利于学生的学习,还有利于他们的思考和创新。
一、来源生活的数学知识的学习,只有与生活结合,才能真正做到培养学生独立工作的能力,有利于发展学生的创造才能,提高学生创新思维。
教学苏教版三年级下册年月日这一单元时,学生对24时记时法和年月日的内容不能充分感受。
向量问题的几何解法

向量问题的几何解法
葛卫国
【期刊名称】《新高考(高一语文、数学、英语)》
【年(卷),期】2009(000)002
【摘要】向量是既有大小又有方向的量,它可以用有向线段表示,也可以用坐标
表示.因此,向量既有形的特征,也有数的特征,堪称数与形的完美结合.在解决有关向量问题时,我们更多倾向于从代数(即坐标运算)角度人手,不过有趣的是,有些向量问题从几何角度求解也让人耳目一新.
【总页数】2页(P33,41)
【作者】葛卫国
【作者单位】无
【正文语种】中文
【中图分类】G633.6
【相关文献】
1.平面向量问题的几何解法和几何问题的平面向量解法 [J], 黄鸿义
2.基于数学核心素养视角下的立体几何解法赏析——以2019年全国高考Ⅲ卷文科数学第19题为例 [J], 唐敏; 严忠权
3.圆锥曲线中的平面几何解法分析圆锥曲线中的平面几何解法分析 --2019年高考数学试题圆锥曲线部分求解为例 [J], 吴作成
4.注重模型意识回归数学本质——2020年新高考全国Ⅰ卷20题立体几何解法赏
析 [J], 安学保
5.一道优化题的几何解法 [J], 陈思齐
因版权原因,仅展示原文概要,查看原文内容请购买。
谈初中数学教学中的逆向思维

谈初中数学教学中的逆向思维罗彦勋【期刊名称】《数学教学研究》【年(卷),期】2007(000)011【摘要】如果说分析问题时,人们的习惯性思维叫正向思维,那么从习惯性思维的反面进行的思维叫做逆向思维.学生在数学学习中习惯于正向思维,久而久之形成思维定势,造成思维的单调性和理解的片面性,这有碍于思维的发展.因此教师在教学中,要根据教学内容和学生的认识水平,引导学生进行逆向思维,广开学生的思路,促进其思维能力的提高.在数学教学中,教师如何引导学生进行逆向思维呢?下面结合教学实践谈谈自己的点滴作法.1在概念教学中重视可逆联想,培养学生的逆向思维意识数学中有许多概念是互逆的,对于这些互逆概念的教学,可采取先正向,后逆向,再正逆联用的办法,这样不仅可使学生对概念辨析得清楚,理解得更透彻,而且能养成双向考虑问题的良好习惯,培养学生逆向思维的意识.如在学生学习锐角三角函数一章时,我们知道若∠A+∠B=90°时,则sinA=cosB(或cosA=sinB),反过来若sinA=cosB时,∠A+∠B=90°是否还成立,进一步追问:当∠A+∠B>90°时,sinA与cosB有什么关系呢?当∠A+∠B<90°时呢?又有怎样的结论呢?通过上述过程,总结得出以下结论:在锐角△ABC中,∠A+∠B=90°sinA=cosB;∠A+∠B>90°...【总页数】2页(P24-25)【作者】罗彦勋【作者单位】河南省临颖县三家店镇一中,462621【正文语种】中文【中图分类】G63【相关文献】1.谈初中数学教学中学生逆向思维能力的培养 [J], 白莹;2.谈初中数学教学中学生逆向思维能力的培养 [J], 王秋桂3.谈初中数学教学中学生逆向思维能力的培养 [J], 王万银[1]4.谈初中数学教学中学生逆向思维能力的培养 [J], 田彦鸿5.谈初中数学教学中学生逆向思维能力的培养 [J], 格桑因版权原因,仅展示原文概要,查看原文内容请购买。
以课本为本 显探究为真——2018年南通市数学中考一道压轴题的探究过程

以课本为本显探究为真——2018年南通市数学中考一道压
轴题的探究过程
杨卫东
【期刊名称】《数理化解题研究》
【年(卷),期】2018(000)023
【摘要】遵循课标、紧扣课本、重视能力是全国各地数学中考命题的必备原则,立德树人、减负增效、学会学习是命题组精心给予考生未来可持续发展的科学方向,同时也对当地初中数学教师的日常教学有着很好的导向与指导作用.不言而喻,如何明扣教材、暗扣探究、命制好题、值得回味正是追求数学本真境界的充分体现,也是命题组所有成员努力奋斗的目标所在.
【总页数】3页(P22-24)
【作者】杨卫东
【作者单位】江苏省海门市悦来初级中学,226100
【正文语种】中文
【中图分类】G632
【相关文献】
1.南通市中考数学“压轴题”之探究与思考——2016年8月暑期能仁教育集团研训中考试题分析 [J], 仇建新;
2.以课本为本显探究为真\r——2018年南通市数学中考一道压轴题的探究过程[J], 杨卫东
3.立足数学核心素养,培养几何探究能力--剖析2018年广州市中考数学几何压轴题[J], 张河源;
4.对一道中考题的模式、策略、本质的探究——基于贵阳市2019年中考几何压轴题的探究 [J], 邓清; 陈丽
5.对一道中考题的模式、策略、本质的探究——基于贵阳市2019年中考几何压轴题的探究 [J], 邓清; 陈丽
因版权原因,仅展示原文概要,查看原文内容请购买。
一道课后习题的多种解法与思考

一道课后习题的多种解法与思考
王永利
【期刊名称】《数学学习与研究:教研版》
【年(卷),期】2015(000)002
【摘要】一道普通的课后习题,只要我们深入研究,往往会发现多种解法."已知⊙O 外一点P,你能用尺规过点P作⊙O的切线吗?你有几种方法?"对于这道课后习题,我们可以利用直径所对的圆周角是直角作图;也可以利用等腰三角形的"三线合一"作图;可以通过构造全等的直角三角形作图:(1)利用圆中的条件构造全等的直角三角形;(2)借助圆外任意直角构造全等的直角三角形.以上解法,丰富多彩,细细品味,每一种解法都有它的独到之处.
【总页数】1页(P110-110)
【作者】王永利
【作者单位】西北工业大学附属中学,710072
【正文语种】中文
【中图分类】G633.6
【相关文献】
1.一道课后习题的多种解法
2.一道课后练习题的多种解法
3.一道课后练习题的多种解法
4.一道课后习题的多种解法
5.一道数学分析课后习题的解法研究
因版权原因,仅展示原文概要,查看原文内容请购买。
一道全国初中数学竞赛题的简单解法

一道全国初中数学竞赛题的简单解法
范晖
【期刊名称】《中学数学月刊》
【年(卷),期】1998(000)0Z1
【摘要】1998年全国初中数学竞赛第12题是: 设抛物线y=x<sup>2</sup>+(2a+1)x+2a+5/4的图象与x轴只有一个交点. (1)求a的值; (2)求
a<sup>18</sup>+323a<sup>-6</sup>的值. 本文目的是对(2)给出两种较简单解法: 解(1)据题设知,方程y=x<sup>2</sup>+(2a+ 1)
x+2a+5/4=0有两个相等实根,所以△=(2a+1)<sup>2</sup>-4(2a+5/4)=0,即
【总页数】2页(P72-73)
【作者】范晖
【作者单位】江苏省启东中学 226200
【正文语种】中文
【中图分类】G634.605
【相关文献】
1.一道2015年全国初中数学竞赛题的推广 [J], 李远翠;彭文强;潘亦宁;
2.一道全国初中数学联合竞赛题的多种解法 [J], 刘仁
3.对一道全国初中数学竞赛题的探究 [J], 许峰
4.对一道2013年全国初中数学竞赛题的剖析 [J], 章礼抗
5.一道2013年全国初中数学竞赛题的再研究 [J], 周慧鸽
因版权原因,仅展示原文概要,查看原文内容请购买。
高考解析几何题中的数学思想应用

高考解析几何题中的数学思想应用作者:韦敏
来源:《中学教学参考·理科版》2018年第12期
[摘; ;要]从近年来全国高考数学试卷的分析入手,针对高考解析几何题中所主要考查的数学思想进行探讨,并通过具体实例对数形结合思想、坐标思想、分类讨论思想、化归思想等数学思想的应用进行详细的论述,以促进学生有效解决解析几何问题,提高学生解决问题的能力和數学核心素养.
[关键词]高考;解析几何;数学思想
[中图分类号]; ; G633.6; ; ; ; [文献标识码]; ; A; ; ; ; [文章编号]; ; 1674-6058(2018)35-0025-03
解析几何是高中数学教学的重要内容,同时也是历年高考数学考查的重点内容之一.高考数学全国卷对于解析几何知识的考查一般都是两个小题目和一个大题目,解答题一般都是放在最后压轴,其中包含巨大的计算量和缜密的思维逻辑,而图形和坐标系是解题过程中必备的辅助工具,使用的目的在于找到解析几何问题的突破口,从而顺利解题.在这过程中,涉及多种数学思想方法.如代数方法,它是解决解析几何问题常用到的数学方法,同时也是研究几何问题的重要思考方向.又如坐标思想,它同样是研究平面图形必不可少的数学思想方法.解决解析几何问题时需要适当建立平面直角坐标系来列出圆锥曲线的方程关系,研究得到曲线位置的内在联系,实现在坐标系和圆锥曲线方程中找到几何性质的目标.因此,掌握多种数学思想方法有利于学生有效解决解析几何问题.本文从分析近年来的全国高考数学试卷入手,对解析几析问题中主要应用的数学思想进行开分析与探讨.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三年级数学渗透环保教案
《吨的认识》教案
湛江市第十小学何卫
教学目标:
1.知道1吨=1000千克,能进行吨和千克间的简单换算。
2.借助生活中的具体物体,感知和了解吨的含义,通过想像和推理初步建立1吨的质量观念,培养学生初步的观察能力、想像能力、推理能力和估计重量的能力。
3.学生能在数学实践活动中,积极主动地与同学合作交流,体会数学与生活的密切联系,增强学习数学的兴趣和学好数学
教学目标:
1.知道1吨=1000千克,能进行吨和千克间的简单换算。
2.借助生活中的具体物体,感知和了解吨的含义,通过想像和推理初步建立1吨的质量观念,培养学生初步的观察能力、想像能力、推理能力和估计重量的能力。
3.学生能在数学实践活动中,积极主动地与同学合作交流,体会数学与生活的密切联系,增强学习数学的兴趣和学好数学的信心,获得学习成功的体验。
并通过学习渗透节约用水的环保意识。
教学重点:
建立1吨的质量观念。
知道1吨=1000千克,会对吨和千克进行单位间的简单换算。
教学准备:
教学课件、若干只装有10千克水的塑料桶。
课前让学生了解自己的体重,并组织每个学生提一提装有10千克水的塑料桶。
教学过程:
(一)引入:
1.创设情境:出示4个动物过桥图:小熊、小马、小牛和小鹿是好朋友,一天,他们来到一条小河边,发现小桥边有一个标志,是什么呀?(限重1吨)
师:“限重1吨”表示什么意思?
师:你对“吨”有什么了解?
2.同学们说得对不对呢,今天这节课我们就一起来学习“吨的认识”(出示课题,板书)
(二)新授:
1.直观感受一吨水的重量
(1)估计:刚才每个同学都提了这样的一桶水,你估计这桶水有多重?为什么?(10千克)
(2)经历:现在我把这样的4桶水倒入这只桶内,这只桶中的水大约有多少千克?谁认为自己能提起这40千克的水?
(3)学生排队尝试
(4)这样的一桶水是10千克,4桶这样的水是40千克,100桶这样的水是1000千克,也就是1吨。
(5)谁听清楚了1吨就是()千克?(板书1吨=1000千克)
(6)想象一下,如果装了1吨的一桶水让你提,你能提得起来吗?
2.直观感受学生体重,加深对1吨的印象。
(1)找个喜欢的同学相互做背一背的游戏,了解对方有多重。
(2)汇报:你背的是谁?有多重?
(3)如果按每个同学25千克计算,4个同学有()千克,()个同学就有1000千克重,也就是1吨。
(4)让26个学生站立,相互观望,感受26名学生的群体。
3.联系生活,强化对“吨”的认识
(1)生活中有很多物体的重量用“吨“作单位。
下面这些物体的重量都是1吨,你能用吨来说一句话吗?
一头牛重500千克,2头牛重1000千克,也就是1吨。
一袋水泥重50千克,20袋水泥重1000千克,也就是1吨。
一桶油重200千克,5桶油重1000千克,就是1吨。
一头猪重100千克,10头猪重1000千克,也就是1吨。
(2)想想,生活中还有哪些物体的重量用吨来作单位?
(3)老师也搜集了一些用吨作单位的东西。
课件出示:
蓝鲸大象大型机床
万吨货轮一车皮的煤一大堆木材
出示:计量较重或大宗物品的重量时,一般用吨来作单位名称。
4.在具体情景中进行单位化聚(注意让学生说出推理过程)
(1)常见的拖拉机载重2吨,也就是()千克。
(2)T是“吨”的国际单位制符号。
有段路路口有一个限载重5T的标志,这个路口最多能让一辆载重()千克的车通过。
(3)当年曹冲称得大象是6000千克,也就是()吨。
(4)(课件出示地磅、车辆衡图片)由于科学技术的发达,我们现在可以用地磅、车辆衡直接称出一些很重的或大宗物品的重量。
再也不用向曹冲当年那么麻烦了。
(三)解决问题
1.我们一共学了几个质量单位?他们分别怎样使用?填上合适的单位名称:(1)一块橡皮重约10()
(2)1头猪重约120()
(3)1袋水泥重约50(),1拖拉机水泥约重2()
(4)中国举重运动员张国政在雅典奥运会上将160()的杠铃举过了头顶。
2.课件出示情境图:“还记得熊老弟、牛大哥、小鹿和小马一同来到了一座小桥边想过桥的事吗?他们能同时过桥吗?怎么过桥?”
3.课堂小结:今天你有什么收获?
4.如果我们全班同学每人每天节约1千克水,大约多少天就能节约1吨水?
5.节水教育:在我国西北地区,是严重缺水的地区,出示图片。
倡导学生“节约用水。
”
(四)课堂作业。
