中考数学复习专题三:代数、三角、几何综合问题
中考数学专题练习 综合问题(含解析)-人教版初中九年级全册数学试题

综合题综合题是初中数学中涵盖广、综合性最强的题型,它可以包含初中阶段所学的代数、平面几何、解析几何、统计概率的若干知识点和各种数学思想方法,还能有机结合探索性、开放性等有关问题;它既突出考查了初中数学的主干知识,又突出了与高中衔接的重要内容,如函数、方程、不等式、三角形、四边形、相似形、圆等.它不但考查学生数学基础知识和灵活运用知识的能力还可以考查学生对数学知识迁移整合能力;既考查学生对几何与代数之间的内在联系,多角度、多层面综合运用数学知识、数学思想方法分析问题和解决问题的能力,还考查学生知识网络化、创新意识和实践能力。
前面专题已对代数之方程和不等式综合问题、函数之一次函数和反比例函数综合问题、函数之一次函数、反比例函数和二次函数综合问题、代数和函数综合问题、静态几何之综合问题等有过介绍,本专题主要原创编写代数和平面几何的综合问题、代数和统计概率的综合问题、平面几何和统计概率的综合问题、解析几何和统计概率的综合问题、平面几何和解析几何的综合问题模拟题。
1.已知一元二次方程x2-11x+30=0 的两个解恰好分别是等腰△ABC的底边长和腰长,则△ABC底边上的高为。
【答案】4或1192。
【考点】因式分解法解一元二次方程,等腰三角形的性质,三角形三边关系,勾股定理,分类思想的应用。
1. 已知关于x 的方程x 2-(m +2)x +(2m -1)=0的一个根是2,请求出方程的另一个根,并求以此两根为边长的直角三角形的面积。
【答案】解:∵此方程的一个根是1,∴12-1×(m +2)+(2m -1)=0,解得,m=2, 则方程的另一根为:m +2-1=2+1=3。
①该直角三角形的两直角边是1、3时,该直角三角形的面积为131322⋅⋅=。
②当该直角三角形的直角边和斜边分别是1、3时,由勾股定理得该直角三角形的另一直角边为22;则该直角三角形的面积为112222⋅⋅=。
综上所述,该直角三角形的面积为32或2。
中考数学 考点系统复习 第三章 函数 第九节 二次函数与几何综合题 类型三:二次函数与特殊三角形问题

求点的坐标: 1.分别表示出点 A,B,P 的坐标,再表示出线段 AB,BP,AP 的长度, 由①AB=AP,②AB=BP,③AP=BP 分别列方程求解即可. 2.作等腰三角形底边上的高,用勾股定理或相似建立等量关系. 3.以 AB 为底边时,可用解析法,先求中垂线的解析式,再联立方程组 求交点.
此时点 C 的坐标为21,1+32
5
或2 1,13-2
5
.
综上可知,当△ABC 是直角三角形时,点 C 的坐标共有 4 个为((1 1,,33)),
((1,1,- -2)
2),21,1+23
5
或21,1-23
5
.
问题:已知线段 AB 和直线 l,在 l 上求点 P,使△PAB 为直角三角形.
【分层分析】 点 P 在线段 BC 的中垂线与抛物线的交点处.求中垂线的解析式,联立方 程组求解.
解:存在.由题意得 B(3,0),C(0,-3),由点 B,C 的坐标求得直线
BC 的解析式为 y=x-3,线段 BC 的中点为32,-32,设线段 BC 的中垂线 的解析式为 y=-x+b,代入23,-32,得 b=0. ∴线段 BC 的中垂线的解析式为 y=-x,
【分层分析】 利用两圆一中垂的方法在直线 l上找出点 P,共有 5 个,并注意检验点 P 是否满足条件,当点 P,A,C 共线时,不符合题意.
解:存在.设 P(1,p),AC2=10, PA2=(1+1)2+(p-0)2=p2+4, PC2=(1-0)2+(p+3)2=p2+6p+10. 分三种情况讨论: ①当 PA=PC 时,p2+4=p2+6p+10, 解得 p=-1,∴P1(1,-1); ②当 AC=PC 时,p2+6p+10=10,解得 p1=0,p2=-6, 当 p=-6 时,显然 A,C,P 三点在一条直线上不能构成三角形,舍去, ∴P2(1,0);
【复习专题】中考数学复习:几何综合题

几何综合题(旋转为主的题型)一、知识梳理二、教学重、难点三、作业完成情况四、典题探究例1 已知:如图,点P 是线段AB 上的动点,分别以AP 、BP 为边向线段AB 的同侧作正△APC和正△BPD ,AD 和BC 交于点M.(1)当△APC 和△BPD 面积之和最小时,直接写出AP : PB 的值和∠AMC 的度数; (2)将点P 在线段AB 上随意固定,再把△BPD 按顺时针方向绕点P 旋转一个角度α,当α<60°时,旋转过程中,∠AMC 的度数是否发生变化?证明你的结论.(3)在第(2)小题给出的旋转过程中,若限定60°<α<120°,∠AMC 的大小是否会发生变化?若变化,请写出∠AMC 的度数变化范围;若不变化,请写出∠AMC 的度数.例2 探究:(1)如图1,在正方形ABCD 中,E 、F 分别是BC 、CD 上的点,且∠EAF =45°,试判断BE 、DF 与EF 三条线段之间的数量关系,直接写出判断结果: ;(2)如图2,若把(1)问中的条件变为“在四边形ABCD 中,AB =AD ,∠B +∠D =180°,E 、F 分别是边BC 、CD 上的点,且∠EAF=21∠BAD ”,则(1)问中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由;(3)在(2)问中,若将△AEF 绕点A 逆时针旋转,当点分别E 、F 运动到BC 、CD 延长线上时, 如图3所示,其它条件不变,则(1)问中的结论是否发生变化?若变化,请给出结论并予以证明..例3 已知:△ABC 和△ADE 是两个不全等的等腰直角三角形,其中BA =BC ,DA =DE ,联结EC ,取EC 的中点M ,联结BM 和DM .(1)如图1,如果点D 、E 分别在边AC 、AB 上,那么BM 、DM 的数量关系与位置关系是 ;(2)将图1中的△ADE 绕点A 旋转到图2的位置时,判断(1)中的结论是否仍然成立,并说明理由.DCB AEMMEABCD图1 图2例4 在ABCD 中,A DBC ∠=∠,过点D 作DE DF =,且EDF ABD =∠,连接EF ,EC ,N 、P 分别为EC ,BC 的中点,连接NP . (1)如图1,若点E 在DP 上,EF 与DC 交于点M ,试探究线段NP 与线段NM 的数量关系及ABD ∠与MNP ∠满足的等量关系,请直接写出你的结论;(2)如图2,若点M 在线段EF 上,当点M 在何位置时,你在(1)中得到的结论仍然成立,写出你确定的点M 的位置,并证明(1)中的结论.五、演练方阵A 档(巩固专练)1.(1)如图1,△ABC 和△CDE 都是等边三角形,且B 、C 、D 三点共线,联结AD 、BE相交于点P ,求证: BE = AD .(2)如图2,在△BCD 中,∠BCD <120°,分别以BC 、CD 和BD 为边在△BCD 外部作等边三角形ABC 、等边三角形CDE 和等边三角形BDF ,联结AD 、BE 和CF 交于点P ,下列结论中正确的是 (只填序号即可)①AD=BE=CF ;②∠BEC=∠ADC ;③∠DPE=∠EPC=∠CPA =60°; (3)如图2,在(2)的条件下,求证:PB+PC+PD=BE .2. 已知:2AD =,4BD =,以AB 为一边作等边三角形ABC .使C 、D 两点落在直线AB 的两侧. (1)如图,当∠ADB=60°时,求AB 及CD 的长;(2)当∠ADB 变化,且其它条件不变时,求CD 的 最大值,及相应∠ADB 的大小.3. 如图,△ABC 中,∠ACB=90°,AD=AC,AB=AN,连结CD 、BN,CD 的延长线交BN 于点F . (1)当∠ADN 等于多少度时,∠ACE=∠EBF,并说明理由;(2)在(1)的条件下,设∠ABC=α,∠CAD =β,试探索α、β满足什么关系时,△ACE ≌△FBE ,并说明理由.4. 在△ABC 中,AB =4,BC =6,∠ACB =30°,将△ABC 绕点B 按逆时针方向旋转,得到△A 1BC 1. (1)如图1,当点C 1在线段CA 的延长线上时,求∠CC 1A 1的度数; (2)如图2,连接AA 1,CC 1.若△CBC 1的面积为3,求△ABA 1的面积;(3)如图3,点E 为线段AB 中点,点P 是线段AC 上的动点,在△ABC 绕点B 按逆时针方向旋转的过程中,点P 的对应点是点P 1,直接写出线段EP 1长度的最大值与最小值.图2AFAB 图1C 1C BA 1A图2A 1C 1ABC图1图3A5. 问题1:如图1,在等腰梯形ABCD 中,AD ∥BC ,AB =BC =CD ,点M ,N 分别在AD ,CD 上,若∠MBN =12∠ABC ,试探究线段MN ,AM ,CN 有怎样的数量关系?请直接写出你的猜想,不用证明;问题2:如图2,在四边形ABCD 中,AB =BC ,∠ABC +∠ADC =180°,点M ,N 分别在DA ,CD 的延长线上,若∠MBN =12∠ABC 仍然成立,请你进一步探究线段MN ,AM ,CN 又有怎样的数量关系?写出你的猜想,并给予证明.6. 如图,四边形ABCD 、1111A B C D 是两个边长分别为5和1且中心重合的正方形.其中,正方形1111A B C D 可以绕中心O 旋转,正方形ABCD 静止不动.(1)如图1,当11D D B B 、、、四点共线时,四边形11DCC D 的面积为 __; (2)如图2,当11D D A 、、三点共线时,请直接写出11CD DD = _________; (3)在正方形1111A B C D 绕中心O 旋转的过程中,直线1CC 与直线1DD 的位置关系是______________,请借助图3证明你的猜想.B 档(提升精练)1. 如图,△ABC 中,∠90ACB =︒, 2=AC ,以AC 为边向右侧作等边三角形ACD . (1)如图24-1,将线段AB 绕点A 逆时针旋转︒60,得到线段1AB ,联结1DB ,则与1DB 长度相等的线段为 (直接写出结论);(2)如图24-2,若P 是线段BC 上任意一点(不与点C 重合),点P 绕点A 逆时针旋转︒60得到点Q ,求ADQ ∠的度数; (3)画图并探究:若P 是直线BC 上任意一点(不与点C 重合),点P 绕点A 逆时针旋转︒60得到点Q ,是否存在点P ,使得以 A 、 C 、 Q 、 D 为顶点的四边形是梯形,若存在,请指出点P 的位置,并求出PC 的长;若不存在,请说明理由.2. 如图1,△ABC 是等腰直角三角形,四边形ADEF 是正方形,D 、F 分别在AB 、AC 边上,此时BD=CF ,BD ⊥CF 成立.(1)当正方形ADEF 绕点A 逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF 成立吗? 若成立,请证明;若不成立,请说明理由.(2)当正方形ADEF 绕点A 逆时针旋转45°时,如图3,延长BD 交CF 于点G . ①求证:BD ⊥CF ; ②当AB=4,AD=时,求线段BG 的长.3. 已知:在△AOB 与△COD 中,OA =OB ,OC =OD ,︒=∠=∠90COD AOB .(1)如图1,点C 、D 分别在边OA 、OB 上,连结AD 、BC ,点M 为线段BC 的中点,连结OM ,则线段AD 与OM 之间的数量关系是 ,位置关系是 ; (2)如图2,将图1中的△COD 绕点O 逆时针旋转,旋转角为α (︒<<︒900α).连结AD 、BC ,点M 为线段BC 的中点,连结OM .请你判断(1)中的两个结论是否仍然成立.若成立,请证明;若不成立,请说明理由;(3)如图3,将图1中的 △COD 绕点 O 逆时针旋转到使 △COD 的一边OD 恰好与△AOB 的边OA 在同一条直线上时,点C 落在OB 上,点M 为线段BC 的中点.请你判断(1)中线段AD 与OM 之间的数量关系是否发生变化,写出你的猜想,并加以证明.4. 在Rt △ABC 中,AB =BC ,∠B =90°,将一块等腰直角三角板的直角顶点O 放在斜边AC 上,将三角板绕点O 旋转. (1)当点O 为AC 中点时,①如图1, 三角板的两直角边分别交AB ,BC 于E 、F 两点,连接EF ,猜想线段AE 、CF 与EF 之间存在的等量关系(无需证明);②如图2, 三角板的两直角边分别交AB ,BC 延长线于E 、F 两点,连接EF ,判断①中的猜想是否成立.若成立,请证明;若不成立,请说明理由;(2)当点O 不是AC 中点时,如图3,,三角板的两直角边分别交AB ,BC 于E 、F 两点,若14AO AC ,求OE OF的值.5. 如图1,四边形ABCD ,将顶点为A 的角绕着顶点A 顺时针旋转,若角的一条边与DC 的延长线交于点F ,角的另一条边与CB 的延长线交于点E ,连接EF . (1)若四边形ABCD 为正方形,当∠EAF=45°时,有EF=DF -BE .请你思考如何证明这个结论(只思考,不必写出证明过程);(2)如图2,如果在四边形ABCD 中,AB=AD ,∠ABC=∠ADC=90°,当∠EAF=21∠BAD 时,EF 与DF 、BE 之间有怎样的数量关系?请写出它们之间的关系式(只需写出结论); (3)如图3,如果四边形ABCD 中,AB=AD ,∠ABC 与∠ADC 互补,当∠EAF=21∠BAD 时,EF 与DF 、BE 之间有怎样的数量关系?请写出它们之间的关系式并给予证明.(4)在(3)中,若BC=4,DC=7,CF=2,求△CEF 的周长(直接写出结果即可).C 档(跨越导练)1. 已知:正方形ABCD 中,45MAN ∠=,绕点A 顺时针旋转,它的两边分别交CB 、DC (或它们的延长线)于点M 、N . (1)如图1,当M A N ∠绕点A 旋转到BM DN =时,有BM DN MN +=.当M A N ∠ 绕点A 旋转到BM DN ≠时,如图2,请问图1中的结论还是否成立?如果成立,请给予证明,如果不成立,请说明理由;(2)当MAN ∠绕点A 旋转到如图3的位置时,线段BM DN ,和MN 之间有怎样的等量关系?请写出你的猜想,并证明.2. 如图,已知四边形ABCD 是正方形,对角线ACBD 相交于O .(1) 如图1,设 E 、F 分别是AD 、AB 上的点,且∠EOF =90°,线段AF 、BF 和EF 之间存在一定的数量关系.请你用等式直接写出这个数量关系;(2)如图2,设 E 、F 分别是AB 上不同的两个点,且∠EOF =45°,请你用等式表示线段AE 、BF 和EF 之间的数量关系,并证明.3. 问题:如图1, 在Rt △ABC 中,90C ∠=︒,30ABC ∠=︒,点D 是射线CB 上任意一点,△ADE 是等边三角形,且点D 在ACB ∠的内部,连接BE .探究线段BE 与DE 之间的数量关系. 请你完成下列探究过程:先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明.(1) 当点D 与点C 重合时(如图2),请你补全图形.由BAC ∠的度数为 ,点E落在 ,容易得出BE 与DE 之间的数量关系为 ;(2) 当点D 在如图3的位置时,请你画出图形,研究线段BE 与DE 之间的数量关系是否与(1)中的结论相同,写出你的猜想并加以证明.4. 在△ABC 中,AB=AC ,∠BAC=α(︒<<︒600α),将线段BC 绕点B 逆时针旋转60°得到线段BD 。
中考数学复习:专题3-7 例析一次函数图象截出的等腰三角形问题

例析一次函数图象截出的等腰三角形【专题综述】当一次函数图象与坐标轴围成的三角形是一个等腰直角三角形时,不仅仅考查一次函数的图象和性质,还会涉及等腰三角形一系列性质,的这个特殊的三角形能给我们解题带来许多的精彩. 【方法解读】例1 如图1,直线4y x =-+与两坐标轴分别相交于A 、B 两点,点M 是线段AB 上任意一点(A 、B 两点除外),过点M 分别作MC OA ⊥于点C ,MD OB ⊥于点D .(1)当点M 在AB 上运动时,你认为四边形OCMD 的周长是否发生变化?并说明理由; (2)当点M 运动到什么位置时,四边形OCMD 的面积有最大值?最大值是多少?(3)如图2,3当四边形OCMD 为正方形时,将四边形OCMD 沿着x 轴的正方向移动,设平移的距离为(04)a a <<,正方形OCMD 与AOB ∆重叠部分的面积为S .试求S 与a 的函数关系式,并画出该函数的图象.分析 第(1)问,要想确定四边形的周长在点的运动过程是如何变化的,首先要解决的就是结合图形表示出四边形的周长.根据矩形的性质,已知这里四边形的周长是2()OC MC +,四边形周长的变化规律就取决于线段和OC MC +的变化规律.结合题目条件,我们会有两种基本的思路:一是坐标法表示线段,线段OC 的长恰好是点M 的横坐标的绝对值,MC 的长恰好是点M 的纵坐标的绝对值,这是这一方法的精髓;二是转化线段和法,根据条件知道OAB ∆是一个等腰直角三角形,且腰4OA OB ==,因此MC CA =,所以线段MC OC +就转化成了OC AC OA +=,从而也能将所求化解.第(2)问,在探求周长的基础上,进一步探求四边形的面积变化规律.借鉴第(1)问的思路,解题的关键是先表示出四边形的面积,即OC MC ⨯,利用坐标法就可以将四边形的面积转化成二次函数的,最值自然就可以确定.第(3)问,解答时体现两种数学思想的灵活应用:一是数形结合的思想,初步判定重合部分图形的形状,确定面积的分割法表示;二是分类的思想,抓住a 的变化规律,立足正方形成立的条件,给出a 的正确分类也是解题的重要因素.解 (1)因为直线4y x =-+与两坐标轴分别相交于A 、B 两点,所以点A 的坐标为(4,0),点B 的坐标为(0,4).所以4OA =,4OB =,所以ABO ∆是等腰直角三角形.因为MC OA ⊥,MD OB ⊥,所以四边形OCMD 是矩形,且MCA ∆是等腰直角三角形,所以MC AC =.因为矩形OCMD 的周长为2()2()28OC MC OC CA OA +=+==,所以四边形OCMD 的周长是定值,且为8;(2)设四边形OCMD 的面积为S ,根据题意,得22(4)4(2)4S MC MD x x x x x ==-+=-+=--+所以四边形OCMD 的面积是关于点M 的横坐标(04)x x <<的二次函数,并且当2x =,即当点M 运动到线段AB 的中点时,四边形OCMD 的面积最大且最大面积为4;(3)设两个图形重合部分的面积为S ,正方形OCMD 与直线的交点Q ,如图2,当02a <≤时,2142S a =-. 如图3,当24a <<时,此时a 为正方形的边与直线交点的横坐标,所以交点的纵坐标为4a -+;纵坐标的绝对值恰好是重叠图形的等腰直角三角形的腰长,所以21(4)2s a =-;所以S 与a 函数的图象如图4所示.点评 这道题是知识与方法的盛宴.涉及的知识点广,有几何知识,一次函数知识,二次函数知识等;涉及的数学思想多,有数形结合的思想,转化的思想,分类的思想,平移的思想等,可谓是包罗万象,值得深思与探究.例2 (2013年长沙中考题)如图5,在平面直角坐标系中,直线2y x =-+与x 轴,y 轴分别交于点A ,点B ,动点(,)P a b 在第一象限,由点P 向x 轴,y 轴所作的垂线PM ,PN (垂足为M ,N )分别与直线AB 相交于点E ,点F ,当点(,)P a b 运动时,矩形PMON 的面积为定值2.(1)求OAB ∠的度数; (2)求证AOF ∆∽BEO ∆;(3)当点E ,F 都在线段AB 上时,由三条线段AE ,EF ,BF 组成一个三角形,记此三角形的外接圆面积为1S ,OEF ∆的面积为2S ,试探究:12S S +是否存在最小值?若存在,请求出该最小值;若不存在,请说明理由.分析 第(1)问的证明是比较容易的;第(2)问的证明抓住一个关键点:两边对应成比例且夹角相等的两个三角形相似;第(3)问的关键在判定三条线段组成的三角形的形状.解 (1)当0x =时,2y =,当0y =时,2x =,所以点A 坐标为(2,0),点B 坐标为(0,2),OA OB =,所以45OAB ∠=︒ ;(2)法 1 因为矩形OMPN 的面积是2,所以点P 坐标为2(,)a a,点E 坐标为(,2)a a -+,点F 坐标为222(,)a a a-22AF a=,2BE a =222OA BE a a==,2222AF a OB ==OA AFBE OB∴= 45OAF EBO ∠=∠=︒∴AOF ∆∽BEO ∆法2:(2,0)A ,(0,2)B2OA OB ∴== 4OA OB ∴=点P 的坐标为(,)a b(,2)E a a ∴-,(2,)F b b -,如图5在等腰直角三角形AFD 中,得2AF b =,在等腰直角三角形BEP 中,2BE a =,222AF BE b a ab ∴==因为矩形的面积是定值2,2ab ∴=4AF BE ∴=AF BE OA OB ∴=OA AFBE OB∴= 45OAF EBO ∠=∠=︒AOF ∴∆∽BEO ∆(3)根据(2)知,以BF EF AE ,,为边的三角形是直角三角形,且斜边是2(2)EF a b =+-,所以三角形的外接圆面积为212(2)(a b S π+-=2(2)2a b π=+-过点O 作EF 边上的高OD ,易求得高为2OD =,2122(2)2S a b ∴=+-2a b =+-212(2)(2)2S S a b a b π∴+=+-++-所以关于2a b +-的二次函数的开口向上,所以12S S +有最小值,当12a b π+-=-时,函数有最小值,但是此值不在取值范围内,因此取不到.因为a ,b 都是正数,222a b ab ∴+≥=12222a b π∴+-≥->-∴当2222a b +-=-时,12S S +的值最小,最小值为2(222)2222π-+-反思 此题可以引申出如下几个独立的新结论:结论1 如图5,在平面直角坐标系中,直线2y x =-+与x 轴,y 轴分别交于点A ,点B ,动点(,)P a b 在第一象限,由点P 向x 轴,y 轴所作的垂线PM ,PN (垂足为M ,N )分别与直线AB 相交于点E ,点F ,当点(,)P a b 运动时,矩形PMON 的面积为定值2,若E ,F 都在直线AB 上,求证:EOF ∠是一个定值.第(2)问的三种证明方法都可以帮助你实现证明.结论2 如图5,在平面直角坐标系中,直线2y x =-+与x 轴,y 轴分别交于点A ,点B ,动点(,)P a b 在第一象限,由点P 向x 轴,y 轴所作的垂线PM ,PN (垂足为M ,N )分别与直线AB 相交于点E ,点F ,当点(,)P a b 运动时,矩形PMON 的面积为定值2,若E ,F 都在直线AB 上,试判断以BF EF AE ,,为边的三角形的形状,并证明你的猜想.相信读者也会轻松解决.结论3 如图5,在平面直角坐标系中,直线2y x =-+与x 轴,y 轴分别交于点A ,点B ,动点(,)P a b 在第一象限,由点P 向x 轴,y 轴所作的垂线PM ,PN (垂足为M ,N )分别与直线AB 相交于点E ,点F ,当点(,)P a b 运动时,矩形PMON 的面积为定值2,若E ,F 都在直线AB 上,设OBF ∆面积为1S ,OEF ∆的面积为2S ,OEA ∆的面积为3S ,试判断1S ,2S ,3S 之间的关系,并证明你的猜想.根据结论2,你同样能轻松解决.结论4 如图5,在平面直角坐标系中,直线2y x =-+与x 轴,y 轴分别交于点A ,点B ,动点(,)P a b 在第一象限,由点P 向x 轴,y 轴所作的垂线PM ,PN (垂足为M ,N )分别与直线AB 相交于点E ,点F ,当点(,)P a b 运动时,矩形PMON 的面积为定值2,若E ,F 都在直线AB 上,设BNF ∆面积为1S ,PEF ∆的面积为2S ,MEA ∆的面积为3S ,试判断1S ,2S ,3S 之间的关系,并证明你的猜想.结论5 如图5,在平面直角坐标系中,直线2y x =-+与x 轴,y 轴分别交于点A ,点B ,动点(,)P a b 在第一象限,由点P 向x 轴,y 轴所作的垂线PM ,PN (垂足为M ,N )分别与直线AB 相交于点E ,点F ,当点(,)P a b 运动时,矩形PMON 的面积为定值2,确定点P 所在函数的解析式. 上述结论的答案分别是: 结论1:45EOF ∠=︒. 结论2:直角三角形.结论3:222213S S S =+.结论4:213S S S =+. 结论5:2y x=. 【强化训练】1.(2016浙江省温州市)如图,一直线与两坐标轴的正半轴分别交于A ,B 两点,P 是线段AB 上任意一点(不包括端点),过P 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是( )A .y =x +5B .y =x +10C .y =﹣x +5D .y =﹣x +102.(2016四川省内江市)如图所示,已知点C (1,0),直线y =﹣x +7与两坐标轴分别交于A ,B 两点,D ,E 分别是AB ,OA 上的动点,则△CDE 周长的最小值是 .3.(2017丽水)如图,在平面直角坐标系x Oy中,直线y=﹣x+m分别交x轴,y轴于A,B两点,已知点C (2,0).(1)当直线AB经过点C时,点O到直线AB的距离是;(2)设点P为线段OB的中点,连结P A,PC,若∠CP A=∠ABO,则m的值是.4.如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上,C、D两点不重合,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是()A. (A)B. (B)C. (C)D. (D)5.如图,直线l:y=x+1交y轴于点A1,在x轴正方向上取点B1,使OB1=OA1;过点B1作A2B1⊥x轴,交l 于点A2,在x轴正方向上取点B2,使B1B2=B1A2;过点B2作A3B2⊥x轴,交l于点A3,在x轴正方向上取点B3,使B2B3=B2A3;…记△OA1B1面积为S1,△B1A2B2面积为S2,△B2A3B3面积为S3,…则S2017等于()A. 24030B. 24031C. 24032D. 240336.正方形OABC的边长为2,其中OA、OC分别在x轴和y轴上,如图①所示,直线l经过A、C两点.(1)若点P是直线l上的一点,当△OP A的面积是3时,请求出点P的坐标;(2)如图②,坐标系xOy内有一点D(-1,2),点E是直线l上的一个动点.①请求出|BE+DE|的最小值和此时点E的坐标;②若将点D沿x轴翻折到x轴下方,直接写出|BE-DE|的最大值,并写出此时点E的坐标.7.一次函数y=kx+b(k≠0)的图象由直线y=3x向下平移得到,且过点A(1,2).(1)求一次函数的解析式;(2)求直线y=kx+b与x轴的交点B的坐标;(3)设坐标原点为O,一条直线过点B,且与两条坐标轴围成的三角形的面积是12,这条直线与y轴交于点C,求直线AC对应的一次函数的解析式.8.如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b)(1)求b,m的值(2)垂直于x轴的直线x=a与直线l1,l2分别相交于C,D,若线段CD长为2,求a的值9.如图,在平面直角坐标系中,已知直线2y x =+和6y x =-+与x 轴分别相交于点A 和点B ,设两直线相交于点C ,点D 为AB 的中点,点E 是线段AC 上一个动点(不与点A 和C 重合),连结DE ,并过点D 作DF DE ⊥交BC 于点F . (1)判断ABC 的形状,并说明理由.(2)当点E 在线段AC 上运动时,四边形CEDF 的面积是否为定值?若是,请求出这个定值;若不是,请说明理由.(3)当点E 的横坐标为12-时,在x 轴上找到一点P 使得PEF 的周长最小,请直接写出点P 的坐标.10.如图,在平面直角坐标系xOy 中,点A 的坐标为(5,0),点B 的坐标为(3,2),直线111l y k x =:经过原点和点B ,直线222l y k x b =+:经过点A 和点B .(1)求直线1l , 2l 的函数关系式;(2)根据函数图像回答:不等式120y y ⋅<的解集为 ;(3)若点P 是x 轴上的一动点,经过点P 作直线m ∥y 轴,交直线1l 于点C ,交直线2l 于点D ,分别经过点C ,D 向y 轴作垂线,垂足分别为点E , F ,得长方形CDFE .①若设点P 的横坐标为m ,则点C 的坐标为(m , ),点D 的坐标为(m , );(用含字母m 的式子表示)②若长方形CDFE 的周长为26,求m 的值.。
2019年中考数学复习专题《代数综合、代数几何综合》(有答案)

代数综合题一:对于实数a,b,我们用符号min{a,b}表示a,b两数中较小的数,如min{3,5}=3,因此,min{-1,-2}=________;若{}22min(1),4+=,则x=___________.x x题二:对于实数c,d,我们用符号max{c,d}表示c,d两数中较大的数,如max{3,5}=5,因此,题四:在平面直角坐标系中,点P(0,m2)(m>0)在y轴正半轴上,过点P作平行于x轴的直线,分别交抛物线C1:y A、B,交抛物线C2:y于点C、D.(1)如图①,原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC 和QD,求△AOB与△CQD面积比为_______.(2)如图②过点A作y轴的平行线交抛物线C2于点E,过点D作y轴的平行线交抛物线C1于点F,在y轴上任取一点M,连接MA、ME、MD和MF,则△MAE与△MDF面积的比值为_______.题七: 设函数y =⎩⎨⎧<+≥+-0130242x x x x x , ,,若互不相等的实数x 1,x 2,x 3,满足y 1=y 2=y 3, 求x 1+x 2+x 3的取值范围.题八: 在平面直角坐标系xOy 中,抛物线y =243x x ++与x 轴交于点A 、B (点A 在点B 的左侧),与y 轴交于点C . (1)求直线AC 的表达式;(2)在x 轴下方且垂直于y 轴的直线l 与抛物线交于点P (x 1,y 1),Q (x 2,y 2),与直线AC 交于点N (x 3,y 3),若x 1>x 2>x 3,结合函数的图象,求x 1+x 2+x 3的取值范围.参考答案题一:-2,-3或2.详解:∵-2<-1,∴min{-1,-2}=-2,∵{}22+=,x xmin(1),4当(x+1)2=x2时,解得:x=-0.5,(x+1)2=x2=0.25,这时不可能得出最小值为4,当x>-0.5,(x+1)2>x2,则x2=4,解得x1=2或x2=-2(舍去),当x<-0.5,(x+1)2<x2,则(x+1)2=4,解得x1=-3或x2=1(舍去),∴x=-3或x=2.题二:∵{}22++=,max22,2x x x当x2+2x+2=x2时,解得:x=-1,x2+2x+2=x2=1,这时不可能得出最大值为2,当x>-1,x2+2x+2>x2,则x2+2x+2=2,解得x1=0或x2=-2(舍去),∴x=0.题三:∴C (-3m ,m 2),D (3m ,m 2),∴CD =6m ,∵O 、Q 关于直线CD 对称, ∴PQ =OP ,∵CD ∥x 轴,∴∠DPQ =∠DPO =90°,∴△AOB 与△CQD 的高相等, PQ CD PO AB ⋅⋅2121=mm 64=32.AEM DFMS S=∵S △OEF +S △OFD =S △OEC +S 梯形ECDF ,而S △OFD =S △OEC =2, 2详解:先作出函数y =⎩⎨⎧<+≥+-0130242x x x x x , ,的图象,如图,不妨设x 1<x 2<x 3,∵y =242x x -+(x ≥0)的对称轴为x =2,y 1=y 2,∴x 2+x 3=4, ∵y =242x x -+(x ≥0)的顶点坐标为(2,-2),令y =-2,代入y =3x +1,解得:x =-1,∴-1<x 1<0,则x 1+x 2+x 3的取值范围是:-1+4<x 1+x 2+x 3<0+4,∴3<x 1+x 2+x 3<4.题八: (1)y =x +3;(2)-8<x 1+x 2+x 3<-7.详解:(1)由y =243x x ++得到:y =(x +3)(x +1),C,∴A (-3,0),B (-1,0),设直线AC 的表达式为:y =kx +b (k ≠0), ∴⎩⎨⎧==+303-b b k ,解得:⎩⎨⎧==31b k ,所以直线AC 的表达式为y =x +3,(2)由y =243x x ++得到:y =(x +2)2-1,∴抛物线y =243x x ++的对称轴是x =-2, 顶点坐标是(-2,-1),∵y 1=y 2,∴x 1+x 2=-4,令y =-1,代入y =x +3,解得:x =-4,∵x 1>x 2>x 3,∴-4<x 3<-3,∴-4-4<x 1+x 2+x 3<-3-4,∴-8<x 1+x 2+x 3<-7.代数几何综合题一:如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).(1)求抛物线的解析式及顶点M坐标;(2)在抛物线的对称轴上找到点P,使得△P AC的周长最小,并求出点P 的坐标.题二:如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-4,0),B(1,0),与y轴交于点D(0,4),点C(-2,n)也在此抛物线上.(1)求此抛物线的解析式及点C的坐标;(2)设BC交y轴于点E,连接AE,AC请判断△ACE的形状,并说明理由.题三:在平面直角坐标系xOy中,给出如下定义:若点P在图形M上,点Q在图形N上,称线段PQ长度的最小值为图形M,N的密距,记为d(M,N).特别地,若图形M,N有公共点,规定d(M,N)=0.(1)如图1,⊙O的半径为2,①点A(0,1),B(4,3),则d(A,⊙O)=,d(B,⊙O)=.是⊙O的关联点,求m的取值范围;(2)若线段EF上的所有点都是某个圆的关联点,求这个圆的半径r的取值范围.参考答案题一: (1)y =214x --+(),M (1,4);(2)P (1,2). 详解:(1)∵抛物线y =ax 2+bx +c (a ≠0)过A (-1,0)、B (3,0),C (0,3)三点,∴93003a b c a b c c ++=⎧⎪-+=⎨⎪=⎩,解得12c=3a b =-⎧⎪=⎨⎪⎩.故抛物线的解析式为222314y x x x =-++=--+(),故顶点M 为(1,4); (2)如图1,∵点A 、B 关于抛物线的对称轴对称,∴连接BC与抛物线对称轴交于一点,即为所求点P .设对称轴与x 轴交于点H ,题二: (1)y =-x 2-3x +4,C (-2,6);(2)△ACE 为等腰直角三角形.详解:(1)∵抛物线经过A 、B 、D 三点,∴代入抛物线解析式可得164004a b c a b c c -+⎧⎪++⎨⎪⎩===,解得134a b c -⎧⎪-⎨⎪⎩===,∴抛物线的解析式为 y =-x 2-3x +4, ∵点C (-2,n )也在此抛物线上,∴n =-4+6+4=6,∴C 点坐标为(-2,6);∴AE2+CE2=20+20=40=AC2,且AE=CE,∴△ACE为等腰直角三角形.。
中考数学复习知识点归纳总结6篇

中考数学复习知识点归纳总结6篇篇1一、数与代数1. 数的基本概念:整数、分数、小数、百分数、比例、方程等。
2. 数的运算:加减乘除四则运算,乘方、开方运算,分数运算,小数运算等。
3. 代数表达式:用字母表示数,表达数量关系和变化规律。
4. 方程与不等式:解一元一次方程,解一元一次不等式,理解函数的概念。
二、几何与图形1. 几何概念:点、线、面、体,角、度数,平行、垂直等基本几何概念。
2. 图形与变换:平移、旋转、对称等图形变换,相似图形,全等图形。
3. 面积与体积:计算平面图形的面积,计算立体图形的体积。
4. 解析几何:理解直线的方程,理解圆及其方程。
三、函数与图像1. 函数的概念:理解变量间的关系,用解析式表示函数关系。
2. 函数的运算:函数的加减法,函数的乘法,复合函数。
3. 函数的图像:理解函数的图像及其变换,根据图像理解函数的性质。
4. 反函数与对称函数:理解反函数的概念,理解对称函数的概念。
四、数据与概率1. 数据收集与整理:理解数据收集的方法,会用统计图表表示数据。
2. 数据的计算:平均数、中位数、众数等统计量的计算,方差和标准差的计算。
3. 概率的概念:理解概率的基本概念,会计算事件的概率。
4. 概率的应用:理解概率在生活中的应用,会解决与概率相关的问题。
五、综合与实践1. 图形的变换与对称:运用几何知识解决实际问题,理解图形的变换和对称。
2. 函数的实际应用:理解函数在实际问题中的应用,如利润、成本等问题。
3. 数据的分析与决策:运用统计知识解决实际问题,理解数据的分析与决策。
4. 课题学习与研究性学习:理解课题学习与研究性学习的意义和方法。
在中考数学复习过程中,我们需要对以上知识点进行全面的梳理和总结,形成系统的知识框架。
同时,我们需要关注考试动态和命题趋势,结合历年真题进行有针对性的练习和巩固。
此外,我们还要注重解题技巧和策略的学习和应用,提高解题效率和准确性。
希望同学们能够认真复习备考,取得优异的成绩!篇2一、数与代数(一)数的认识复习要点:整数、小数、分数、百分数的认识及其关系,数的运算规则和运算性质。
中考数学几何压轴题(有关三角形、四边形)的综合专题(含答案解析)
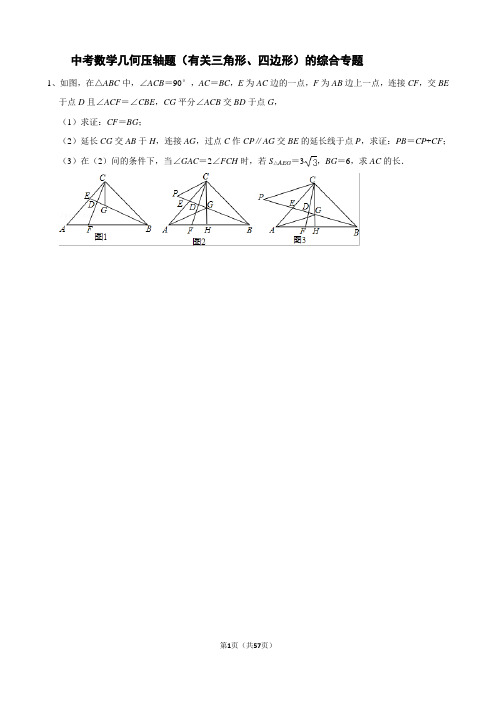
中考数学几何压轴题(有关三角形、四边形)的综合专题1、如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G,(1)求证:CF=BG;(2)延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)在(2)问的条件下,当∠GAC=2∠FCH时,若S△AEG=3,BG=6,求AC的长.2、[问题背景]如图1所示,在△ABC中,AB=BC,∠ABC=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.[问题初探]如果点D在线段BC上运动,通过观察、交流,小明形成了以下的解题思路:过点E作EF⊥BC 交直线BC于F,如图2所示,通过证明△DEF≌△,可推证△CEF是三角形,从而求得∠DCE=.[继续探究]如果点D在线段CB的延长线上运动,如图3所示,求出∠DCE的度数.[拓展延伸]连接BE,当点D在直线BC上运动时,若AB=,请直接写出BE的最小值.3、(2019秋•锦江区校级期末)在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线.(1)如图1,求证:AD=2DC.(2)如图2,作∠CBD的角平分线交线段CD于点M,若CM=1,求△DBM的面积;(3)如图3,过点D作DE⊥AB于点E,点N是线段AC上一点(不与C、D重合),以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,试探究线段ND,DG与AD之间的数量关系,并说明理由.4、(2019•镇平县三模)如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.(1)发现问题:线段EF,CF之间的数量关系为;∠EFC的度数为;(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.5、(2017春•西城区校级期末)如图1,在等腰△ABC中,AB=AC,∠BAC=a,点P是线段AB的中点,点E是线段CB延长线上一点,且PE=PC,将线段PC绕点P顺时针旋转α得到PD,连接BD.(1)如图2,若α=60°,其他条件不变,先补全图形,然后探究线段BD和BC之间的数量关系,并说明理由.(2)如图3,若α=90°,其他条件不变,探究线段BP、BD和BC之间的等量关系,并说明理由.6、【发现问题】如图1,已知△ABC,以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE.请你以A为直角顶点、AC为腰,向△ABC外作等腰直角△ACD(不写作法,保留作图痕迹).连接BD、CE.那么BD与CE的数量关系是BD=CE.【拓展探究】如图2,已知△ABC,以AB、AC为边向外作正方形AEFB和正方形ACGD,连接BD、CE,试判断BD与CE之间的数量关系,并说明理由.【解决问题】如图3,有一个四边形场地ABCD,∠ADC=60°,BC=15,AB=8,AD=CD,求BD的最大值.7、(1)如图1,点C为线段AB外一个动点,已知AB=a,AC=b.当点C位于BA的延长线上时,线段BC取得最大值,则最大值为(用含a,b的式子表示);(2)如图2,点C为线段AB外一个动点,若AB=10,AC=3,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接AE,DB.①求证:AE=DB;②请直接写出线段AE的最大值;(3)如图3,AB=6,点M为线段AB外一个动点,且AM=2,MB=MN,∠BMN=90°,请直接写出线段AN的最大值.8、【初步探索】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF =BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;【灵活运用】(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.9、(2018•大东区一模)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P逆时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P在BC延长线上时,若∠BPO=45°,AC=,请直接写出BQ的长.10、模型发现:同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C的位置的不同而发生变化.因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.特别的,当点C位于时,线段BC的长取得最大值,且最大值为(用含b,c的式子表示)(直接填空).模型应用:点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD 和等边三角形BCE,连接BD,AE.(1)求证:BD=AE.(2)线段AE长的最大值为.模型拓展:如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB =8.若AC⊥AB,AC=3,试求OC长的最大值.11、已知:△ABC中,∠ACB=90°,AC=BC.(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC =3MC,请直接写出的值.12、已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:∠1=∠2;②如图2,若BF=2AF,连接CF,求证:BF⊥CF;(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求的值.13、已知,△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE.(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;(2)如图2,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC于点D,连接DF交BE于点G,连接AG;①若AG平分∠CAD,求证:AH=AC;②如图3,当G落在△ABC外时,若将△EFG沿EF边翻折,点G刚好落在AB边上点P,直接写出AG与EF的数量关系.14、如图所示,Rt△ABC中,∠ACB=90°,E为AC中点,作ED⊥AC交AB于D,连接CD;(1)如图1,求证:AB=2CD;(2)如图2,作CF⊥AB交AB于F,点G为CF上一点,点H为DE延长线上一点,分别连接AH、GH,若∠AHG=2∠B,求证:AH=GH;(3)如图3,在(2)的条件下,连接DG,且有DE=BF,∠EDG=90°,若AC=6,求AH的长度.15、【问题情境】一节数学课后,老师布置了一道课后练习题:如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.(1)阅读理解,完成解答本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写这道练习题的证明过程;(2)特殊位置,证明结论若CE平分∠ACD,其余条件不变,求证:AE=BF;(3)知识迁移,探究发现如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)16、在正方形ABCD和等腰直角△BGF中,∠BGF=90°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,延长GP交DC于点E.求证:PG=PC;(2)如图2,当点F在AB的延长线上时,(1)中的结论是否成立?请证明你的结论;(3)如图3,若四边形ABCD为菱形,且∠ABC=60°,△BGF为等边三角形,点F在CB的延长线上时,线段PC、PG又有怎样的数量关系,请直接写出你的结论,并画出论证过程中需要添加的辅助线.17、在△ABC中,∠BAC=60°,点D、E分别在边AC、AB上,AD=AE,连接CE、BD相交于点F,且∠BEC=∠ADF,连接AF.(1)如图1,连接ED,求证:∠ABD=∠CED;(2)如图2,求证:EF+FD=AF;(3)如图3,取BC的中点G,连接AG交BD于点H,若∠GAC=3∠ABD,BH=7,求△ABH的面积.18、点D,E分别在△ABC的边AC,BD上,BD,CE交于点F,连接AF,∠F AE=∠F AD,FE=FD.(1)如图1,若∠AEF=∠ADF,求证:AE=AD;(2)如图2,若∠AEF≠∠ADF,FB平分∠ABC,求∠BAC的度数;(3)在(2)的条件下,如图3,点G在BE上,∠CFG=∠AFB若AG=6,△ABC的周长为20,求BC长.中考数学几何压轴题(有关三角形、四边形)的综合专题参考答案1、如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G,(1)求证:CF=BG;(2)延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)在(2)问的条件下,当∠GAC=2∠FCH时,若S△AEG=3,BG=6,求AC的长.证明:(1)如图1,∵∠ACB=90°,AC=BC,∴∠A=45°,∵CG平分∠ACB,∴∠ACG=∠BCG=45°,∴∠A=∠BCG,在△BCG和△CAF中,∵,∴△BCG≌△CAF(ASA),∴CF=BG;(2)如图2,∵PC∥AG,∴∠PCA=∠CAG,∵AC=BC,∠ACG=∠BCG,CG=CG,∴△ACG≌△BCG,∴∠CAG=∠CBE,∵∠PCG=∠PCA+∠ACG=∠CAG+45°=∠CBE+45°,∠PGC=∠GCB+∠CBE=∠CBE+45°,∴∠PCG=∠PGC,∴PC=PG,∵PB=BG+PG,BG=CF,∴PB=CF+CP;(3)解法一:如图3,过E作EM⊥AG,交AG于M,∵S△AEG=AG•EM=3,由(2)得:△ACG≌△BCG,∴BG=AG=6,∴×6×EM=3,EM=,设∠FCH=x°,则∠GAC=2x°,∴∠ACF=∠EBC=∠GAC=2x°,∵∠ACH=45°,∴2x+x=45,x=15,∴∠ACF=∠GAC=30°,在Rt△AEM中,AE=2EM=2,AM==3,∴M是AG的中点,∴AE=EG=2,∴BE=BG+EG=6+2,在Rt△ECB中,∠EBC=30°,∴CE=BE=3+,∴AC=AE+EC=2+3+=3+3.解法二:同理得:∠CAG=30°,AG=BG=6,如图4,过G作GM⊥AC于M,在Rt△AGM中,GM=3,AM===3,∵∠ACG=45°,∠MGC=90°,∴GM=CM=3,∴AC=AM+CM=3+3.2、[问题背景]如图1所示,在△ABC中,AB=BC,∠ABC=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.[问题初探]如果点D在线段BC上运动,通过观察、交流,小明形成了以下的解题思路:过点E作EF⊥BC 交直线BC于F,如图2所示,通过证明△DEF≌△ADB,可推证△CEF是等腰直角三角形,从而求得∠DCE=135°.[继续探究]如果点D在线段CB的延长线上运动,如图3所示,求出∠DCE的度数.[拓展延伸]连接BE,当点D在直线BC上运动时,若AB=,请直接写出BE的最小值.解:[问题初探]如图2,过点E作EF⊥BC交直线BC于F,∴∠DFE=90°=∠ABD,∴∠EDF+∠DEF=90°,由旋转知,AD=DE,∠ADE=90°,∴∠ADB+∠EDF=90°,∴∠ADB=∠DEF,∴△ABD≌△DFE(AAS),∴BD=EF,DF=AB,∵AB=BC,∴BC=DF,∴BD=CF,∴EF=CF,∴△CEG是等腰直角三角形,∴∠ECF=45°,∴∠DCE=135°,故答案为:ADB,等腰直角,135;[继续探究]如图3,过点E作EF⊥BC于F,∴∠DFE=90°=∠ABD,∴∠EDF+∠DEF=90°,由旋转知,AD=DE,∠ADE=90°,∴∠ADB+∠EDF=90°,∴∠ADB=∠DEF,∴△ABD≌△DFE(AAS),∴BD=EF,DF=AB,∵AB=BC,∴BC=DF,∴BD=CF,∴EF=CF,∴△CEG是等腰直角三角形,∴∠ECF=45°,∴∠DCE=45°;[拓展延伸]如图4,在△ABC中,∠ABC=90°,AB=BC=,∴∠ACB=45°当点D在射线BC上时,由[问题初探]知,∠BCM=135°,∴∠ACM=∠BCM﹣∠ACB=90°,当点D在线段CB的延长线上时,由[继续探究]知,∠BCE=45°,∴∠ACN=∠ACB+∠BCM=90°,∴点E是过点C垂直于AC的直线上的点,∴当BE⊥MN时,BE最小,∵∠BCE=45°,∴∠CBE=45°=∠BCE,∴BE=CE,∴BE最小=BC=,即:BE的最小值为.3、在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线.(1)如图1,求证:AD=2DC.(2)如图2,作∠CBD的角平分线交线段CD于点M,若CM=1,求△DBM的面积;(3)如图3,过点D作DE⊥AB于点E,点N是线段AC上一点(不与C、D重合),以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,试探究线段ND,DG与AD之间的数量关系,并说明理由.证明:(1)如图1,过点D作DE⊥AB,∵BD是△ABC的角平分线,DE⊥AB,∠ACB=90°,∴DC=DE,∵∠A=30°,DE⊥AB,∴AD=2DE,∴AD=2DC;(2)如图2,过点M作ME∥BD,∵∠ACB=90°,∠A=30°,∴∠ABC=60°,∵BD是△ABC的角平分线,∴∠ABD=∠DBC=30°,∵BM平分∠CBD,∴∠CBM=15°=∠DBM,∵ME∥BD,∴∠MEC=∠CBD=30°,∠EMB=∠DBM=∠MBE,∴ME=BE,∵∠MEC=30°,∠C=90°∴CE=MC=,ME=2MC=2=BE,∴BC=+2,∵∠CBD=30°,∠C=90°,∴BC=CD,∴CD=1+,∴DM=,∴△DBM的面积=××(+2)=1+;(3)若点N在CD上时,AD=DG+DN,理由如下:如图3所示:延长ED使得DW=DN,连接NW,∵∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E,∴∠ADE=∠BDE=60°,AD=BD,∵DN=DW,且∠WDN=60°∴△WDN是等边三角形,∴NW=DN,∠W=∠WND=∠BNG=∠BDN=60°,∴∠WNG=∠BND,在△WGN和△DBN中,∴△WGN≌△DBN(SAS),∴BD=WG=DG+DN,∴AD=DG+DN.(3)若点N在AD上时,AD=DG﹣DN,理由如下:如图4,延长BD至H,使得DH=DN,连接HN,由(1)得DA=DB,∠A=30°.∵DE⊥AB于点E.∴∠2=∠3=60°.∴∠4=∠5=60°.∴△NDH是等边三角形.∴NH=ND,∠H=∠6=60°.∴∠H=∠2.∵∠BNG=60°,∴∠BNG+∠7=∠6+∠7.即∠DNG=∠HNB.在△DNG和△HNB中,∴△DNG≌△HNB(ASA).∴DG=HB.∵HB=HD+DB=ND+AD,∴DG=ND+AD.∴AD=DG﹣ND.4、如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.(1)发现问题:线段EF,CF之间的数量关系为EF=CF;∠EFC的度数为120°;(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.解:(1)如图1中,∵DE⊥AB,∴∠BED=90°,∵∠BCD=90°,BF=DF,∴FE=FB=FD=CF,∴∠FBE=∠FEB,∠FBC=∠FCB,∴∠EFC=∠EFD+∠CFD=∠FBE+∠FEB+∠FBC+∠FCB=2(∠FBE+∠FBC)=2∠ABC=120°,故答案为:EF=CF,120°.(2)结论成立.理由:如图2中,取AB的中点M,AD的中点N,连接MC,MF,ED,EN,FN.∵BM=MA,BF=FD,∴MF∥AD,MF=AD,∵AN=ND,∴MF=AN,MF∥AN,∴四边形MFNA是平行四边形,∴NF=AM,∠FMA=∠ANF,在Rt△ADE中,∵AN=ND,∠AED=90°,∴EN=AD=AN=ND,同理CM=AB=AM=MB,在△AEN和△ACM中,∠AEN=∠EAN,∠MCA=∠MAC,∵∠MAC=∠EAN,∴∠AMC=∠ANE,又∵∠FMA=∠ANF,∴∠ENF=∠FMC,在△MFC和△NEF中,,∴△MFC≌△NEF(SAS),∴FE=FC,∠NFE=∠MCF,∵NF∥AB,∴∠NFD=∠ABD,∵∠ACB=90°,∠BAC=30°,∴∠ABC=60°,△BMC是等边三角形,∠MCB=60°∴∠EFC=∠EFN+∠NFD+∠DFC=∠MCF+∠ABD+∠FBC+∠FCB=∠ABC+∠MCB=60°+60°=120°.(3)如图3中,作EH⊥AB于H.在Rt△ABC中,∵∠BAC=30°,BC=3,∴AB=2BC=6,在Rt△AED中,∠DAE=30°,AD=2,∴DE=AD=1,在Rt△DEH中,∵∠EDH=60°,DE=1,∴EH=ED•sin60°=,DH=ED•cos60°=,在Rt△EHG中,EG==.5、如图1,在等腰△ABC中,AB=AC,∠BAC=a,点P是线段AB的中点,点E是线段CB延长线上一点,且PE=PC,将线段PC绕点P顺时针旋转α得到PD,连接BD.(1)如图2,若α=60°,其他条件不变,先补全图形,然后探究线段BD和BC之间的数量关系,并说明理由.(2)如图3,若α=90°,其他条件不变,探究线段BP、BD和BC之间的等量关系,并说明理由.解:(1)BC=2BD,理由:如图2,连接CD,由旋转可得,CP=DP,∠CPD=60°,∴△CDP是等边三角形,∴∠CDP=60°=∠PCD,又∵P是AB的中点,AB=AC,∠A=60°,∴等边三角形ABC中,∠PCB=30°,CP⊥AB,∴∠BCD=30°,即BC平分∠PCD,∴BC垂直平分PD,∴∠BDC=∠BPC=90°,∴Rt△BCD中,BC=2BD.(2)如图3,取BC中点F,连接PF,∵∠A=90°,AB=AC,∴△ABC是等腰直角三角形,∵P是AB的中点,F是BC的中点,∴PF是△ABC的中位线,∴PF∥AC,∴∠PFB=∠ACB=45°,∠BPF=∠A=90°,∴△BPF是等腰直角三角形,∴BF=BP,BP=PF,∵∠DPC=∠BPF=90°,∴∠BPD=∠FPC,又∵PD=PC,∴△BDP≌△FCP,∴BD=CF,∵BC=BF+FC,∴BC=BD+BP.6、【发现问题】如图1,已知△ABC,以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE.请你以A为直角顶点、AC为腰,向△ABC外作等腰直角△ACD(不写作法,保留作图痕迹).连接BD、CE.那么BD与CE的数量关系是BD=CE.【拓展探究】如图2,已知△ABC,以AB、AC为边向外作正方形AEFB和正方形ACGD,连接BD、CE,试判断BD与CE之间的数量关系,并说明理由.【解决问题】如图3,有一个四边形场地ABCD,∠ADC=60°,BC=15,AB=8,AD=CD,求BD的最大值.【发现问题】解:延长CA到M,作∠MAC的平分线AN,在AN上截取AD=AC,连接CD,即可得到等腰直角△ACD;连接BD、CE,如图1所示:∵△ABE与△ACD都是等腰直角三角形,∴AB=AE,AD=AC,∠BAE=∠CAD=90°,∴∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE,【拓展探究】解:BD=CE;理由如下:∵四边形AEFB与四边形ACGD都是正方形,∴AB=AE,AD=AC,∠BAE=∠CAD=90°,∴∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE;【解决问题】解:以AB为边向外作等边三角形ABE,连接CE,如图3所示:则∠BAE=60°,BE=AB=AE=8,∵AD=CD,∠ADC=60°,∴△ACD是等边三角形,∴∠CAD=60°,AC=AD,∴∠CAD+∠BAC=∠BAE+∠BAC,即∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE;当C、B、E三点共线时,CE最大=BC+BE=15+8=23,∴BD的最大值为23.7、如图1,点C为线段AB外一个动点,已知AB=a,AC=b.当点C位于BA的延长线上时,线段BC取得最大值,则最大值为a+b(用含a,b的式子表示);(2)如图2,点C为线段AB外一个动点,若AB=10,AC=3,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接AE,DB.①求证:AE=DB;②请直接写出线段AE的最大值;(3)如图3,AB=6,点M为线段AB外一个动点,且AM=2,MB=MN,∠BMN=90°,请直接写出线段AN的最大值.(1)解:∵点C为线段AB外一动点,且AC=b,AB=a,∴当点C位于BA的延长线上时,线段BC的长取得最大值,且最大值为AC+AB=a+b,(2)①证明:如图2中,∵△ACD与△BCE是等边三角形,∴CD=AC,CB=CE,∠ACD=∠BCE=60°,∴∠DCB=∠ACE,在△CAD与△EAB中,,∴△CAD≌△EAB(SAS),∴AE=BD.②∵线段AE长的最大值=线段BD的最大值,由(1)知,当线段BD的长取得最大值时,点D在BA的延长线上,∴最大值为AD+AB=3+10=13;(3)如图3中,连接BN,∵将△AMN绕着点M顺时针旋转90°得到△PBM,连接AP,则△APM是等腰直角三角形,∴MA=MP=2,BP=AN,∴P A=2,∵AB=6,∴线段AN长的最大值=线段BP长的最大值,∴当P在线段BA的延长线时,线段BP取得最大值最大值=AB+AP=6+2.8、【初步探索】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF =BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是∠BAE+∠F AD=∠EAF;【灵活运用】(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.解:(1)∠BAE+∠F AD=∠EAF.理由:如图1,延长FD到点G,使DG=BE,连接AG,根据SAS可判定△ABE≌△ADG,进而得出∠BAE=∠DAG,AE=AG,再根据SSS可判定△AEF≌△AGF,可得出∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF.故答案为:∠BAE+∠F AD=∠EAF;(2)仍成立,理由:如图2,延长FD到点G,使DG=BE,连接AG,∵∠B+∠ADF=180°,∠ADG+∠ADF=180°,∴∠B=∠ADG,又∵AB=AD,∴△ABE≌△ADG(SAS),∴∠BAE=∠DAG,AE=AG,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF;(3)∠EAF=180°﹣∠DAB.证明:如图3,在DC延长线上取一点G,使得DG=BE,连接AG,∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,∴∠ADC=∠ABE,又∵AB=AD,∴△ADG≌△ABE(SAS),∴AG=AE,∠DAG=∠BAE,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠F AE=∠F AG,∵∠F AE+∠F AG+∠GAE=360°,∴2∠F AE+(∠GAB+∠BAE)=360°,∴2∠F AE+(∠GAB+∠DAG)=360°,即2∠F AE+∠DAB=360°,∴∠EAF=180°﹣∠DAB.9、如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P逆时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P在BC延长线上时,若∠BPO=45°,AC=,请直接写出BQ的长.解:(1)CP=BQ,理由:如图1,连接OQ,由旋转知,PQ=OP,∠OPQ=60°⊅∴△POQ是等边三角形,∴OP=OQ,∠POQ=60°,在Rt△ABC中,O是AB中点,∴OC=OA=OB,∴∠BOC=2∠A=60°=∠POQ,∴∠COP=∠BOQ,在△COP和△BOQ中,,∴△COP≌△BOQ(SAS),∴CP=BQ,(2)CP=BQ,理由:如图2,连接OQ,由旋转知,PQ=OP,∠OPQ=60°∴△POQ是等边三角形,∴OP=OQ,∠POQ=60°,在Rt△ABC中,O是AB中点,∴OC=OA=OB,∴∠BOC=2∠A=60°=∠POQ,∴∠COP=∠BOQ,在△COP和△BOQ中,,∴△COP≌△BOQ(SAS),∴CP=BQ,(3)如图3,在Rt△ABC中,∠A=30°,AC=,∴BC=AC•tan∠A=,过点O作OH⊥BC,∴∠OHB=90°=∠BCA,∴OH∥AB,∵O是AB中点,∴CH=BC=,OH=AC=,∵∠BPQ=45°,∠OHP=90°,∴∠BPQ=∠PQH,∴PH=OH=,∴CP=PH﹣CH=﹣=,连接BQ,同(1)的方法得,BQ=CP=.10、模型发现:同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C的位置的不同而发生变化.因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.特别的,当点C位于线段BA的延长线上时,线段BC的长取得最大值,且最大值为b+c(用含b,c的式子表示)(直接填空)模型应用:点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD 和等边三角形BCE,连接BD,AE.(1)求证:BD=AE.(2)线段AE长的最大值为5.模型拓展:如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB =8.若AC⊥AB,AC=3,试求OC长的最大值.解:当点C位于线段BA的延长线上时,线段BC的长取得最大值,最大值为b+c,故答案为:线段BA的延长线上;b+c;模型应用:(1)证明:∵△ACD、△BCE都是等边三角形,∴CD=CA=AD,CB=CE,∠ACD=60°,∠BCE=60°,∴∠DCB=∠ACE,在△DCB和△ACE中,,∴△DCB≌△ACE(SAS)∴BD=AE;(2)当点D位于线段BA的延长线上时,线段BD的长取得最大值,最大值为AB+AD=AB+AC=3+2=5,∵AE=BD,∴线段AE长的最大值为5,模型拓展:取AB的中点G,连接OG、CG,在Rt△AOB中,G为AB的中点,∴OG=AB=4,在Rt△CAG中,CG===5,当点O、G、C在同一条直线上时,OC最大,最大值为4+5=9.11、已知:△ABC中,∠ACB=90°,AC=BC.(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC =3MC,请直接写出的值.(1)证明:如图1中,∵BE⊥AD于E,∴∠AEF=∠BCF=90°,∵∠AFE=∠CFB,∴∠DAC=∠CBF,∵BC=CA,∴△BCF≌△ACD,∴BF=AD.(2)结论:BD=2CF.理由:如图2中,作EH⊥AC于H.∵∠AHE=∠ACD=∠DAE=90°,∴∠DAC+∠ADC=90°,∠DAC+∠EAH=90°,∴∠DAC=∠AEH,∵AD=AE,∴△ACD≌△EHA,∴CD=AH,EH=AC=BC,∵CB=CA,∴BD=CH,∵∠EHF=∠BCF=90°,∠EFH=∠BFC,EH=BC,∴△EHF≌△BCF,∴FH=CF,∴BD=CH=2CF.(3)如图3中,同法可证BD=2CM.∵AC=3CM,设CM=a,则AC=CB=3a,BD=2a,∴==.12、已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:∠1=∠2;②如图2,若BF=2AF,连接CF,求证:BF⊥CF;(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求的值.(1)①证明:如图1中,∵AB=AC,∠ABC=60°∴△ABC是等边三角形,∴∠BAC=60°,∵AD⊥BN,∴∠ADB=90°,∵∠MBN=30°,∠BFD=60°=∠1+∠BAF=∠2+∠BAF,∴∠1=∠2②证明:如图2中,在Rt△BFD中,∵∠FBD=30°,∴BF=2DF,∵BF=2AF,∴BF=AD,∵∠BAE=∠FBC,AB=BC,∴△BFC≌△ADB,∴∠BFC=∠ADB=90°,∴BF⊥CF(2)在BF上截取BK=AF,连接AK.∵∠BFE=∠2+∠BAF,∠CFE=∠4+∠1,∴∠CFB=∠2+∠4+∠BAC,∵∠BFE=∠BAC=2∠EFC,∴∠1+∠4=∠2+∠4∴∠1=∠2,∵AB=AC,∴△ABK≌CAF,∴∠3=∠4,S△ABK=S△AFC,∵∠1+∠3=∠2+∠3=∠CFE=∠AKB,∠BAC=2∠CEF,∴∠KAF=∠1+∠3=∠AKF,∴AF=FK=BK,∴S△ABK=S△AFK,∴=2.13、已知,△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE.(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;(2)如图2,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC于点D,连接DF交BE于点G,连接AG;①若AG平分∠CAD,求证:AH=AC;②如图3,当G落在△ABC外时,若将△EFG沿EF边翻折,点G刚好落在AB边上点P,直接写出AG与EF的数量关系.(1)解:如图1中,在AB上取一点M,使得BM=ME,连接ME.在Rt△ABE中,∵OB=OE,∴BE=2OA=2,∵MB=ME,∴∠MBE=∠MEB=15°,∴∠AME=∠MBE+∠MEB=30°,设AE=x,则ME=BM=2x,AM=x,∵AB2+AE2=BE2,∴(2x+x)2+x2=22,∴x=(负根已经舍弃),∴AB=AC=(2+)•,∴BC=AB=+1.方法二:作EH⊥BC于H,求出BH,CH即可解决问题.(2)证明:如图2中,作CP⊥AC,交AD的延长线于P,GM⊥AC于M.∵BE⊥AP,∴∠AHB=90°,∴∠ABH+∠BAH=90°,∵∠BAH+∠P AC=90°,∴∠ABE=∠P AC,在△ABE和△CAP中,,∴△ABE≌△CAP,∴AE=CP=CF,∠AEB=∠P,在△DCF和△DCP中,,∴△DCF≌△DCP,∴∠DFC=∠P,∴∠GFE=∠GEF,∴GE=GF,∵GM⊥EF,∴FM=ME,∵AE=CF,∴AF=CE,∴AM=CM,在△GAH和△GAM中,,∴△AGH≌△AGM,∴AH=AM=CM=AC(3)解:结论:AG=EF.理由:如图3中,作CM⊥AC交AD的延长线于M,连接PG交AC于点O.由(2)可知△ACM≌△BAE,△CDF≌△CDM,∴∠AEB=∠M=∠GEF,∠M=∠CFD=∠GFE,AE=CM=CF,∴∠GEF=∠GFE,∴GE=GF,∵△EFP是由△EFG翻折得到,∴EG=EP=GF=PF,∴四边形EGFP是菱形,∴PG⊥AC,OE=OF,∵AE=CF,∴AO=OC,∵AB∥OP,∴BP=PC,∵PF∥BE,∴EF=CF=AE,∵PB=PC,AO=OC,∴PO=OG=AB,∴AB=PG,AB∥PG,∴四边形ABPG是平行四边形,∴AG∥BC,∴∠GAO=∠ACB=45°,设EO=OF=a,则OA=OG=3a,AG=3a,∴==,∴AG=EF14、如图所示,Rt△ABC中,∠ACB=90°,E为AC中点,作ED⊥AC交AB于D,连接CD;(1)如图1,求证:AB=2CD;(2)如图2,作CF⊥AB交AB于F,点G为CF上一点,点H为DE延长线上一点,分别连接AH、GH,若∠AHG=2∠B,求证:AH=GH;(3)如图3,在(2)的条件下,连接DG,且有DE=BF,∠EDG=90°,若AC=6,求AH的长度.解:(1)∵E为AC中点,作ED⊥AC交AB于D,∴AD=CD,∵∠ACB=90°,∴BC∥DE,∴AD=BD,∴CD=BD,∴AB=2CD;(2)如图2,连接CH,∵点E是AC的中点,∴AE=CE,∵DE⊥AC,∴CH=AH,∴∠ACH=∠CAH,∵∠ACB=90°,∴∠B+∠BAC=90°,∵CF⊥AB,∴∠BAC+∠ACF=90°,∴∠ACF=∠B,∴∠HCG=∠ACH+∠ACF=∠CAH+∠B,∠AHG=2∠B∴在四边形AHGF中,∠AFG+∠FGH+∠AHG+∠F AH=360°,∴∠FGH=360°﹣(∠AFG+∠AHG+∠F AH)=360°﹣(90°+2∠B+∠CAH+∠BAC)=360°﹣(90°+2∠B+∠CAH+90°﹣∠B)=360°﹣(180°+∠B+∠CAH)=180°﹣(∠B+∠CAH),∵∠CGH=180°﹣∠FGH=∠B+∠CAH=∠HCG,∴CH=GH,∵CH=AH,∴AH=GH;(3)如图3,由(1)知,DE∥BC,∴∠B=∠ADE,在△BFC和△DEA中,,∴△BFC≌△DEA,∴BC=AD,∵AD=BD=CD,∴BC=BD=CD,∴△BCD是等边三角形,∴∠B=60°,在Rt△ABC中,AC=6,∴BC=2,AB=4,∵CF⊥BD,∴DF=,CF=3,∵∠BAC=30°,∴∠ADE=60°,∵∠EDG=90°,∠FDG=30°,在Rt△DFG中,DF=,∴FG=1,DG=2,∴CG=CF﹣FG=2过点H作HN⊥CF,由(2)知,CH=GH,∴NG=CG=1,∴FN=NG+FG=2,过点H作HM⊥AB,∴∠FMH=∠NFM=∠HNF=90°,∴四边形NFMH是矩形,∴HM=FN=2,在Rt△DMH中,∠ADE=60°,HM=2,∴DH=,在Rt△HDG中,根据勾股定理得,HG==.15、【问题情境】一节数学课后,老师布置了一道课后练习题:如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.(1)阅读理解,完成解答本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写这道练习题的证明过程;(2)特殊位置,证明结论若CE平分∠ACD,其余条件不变,求证:AE=BF;(3)知识迁移,探究发现如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)(1)证明:∵AC=BC,∠ACB=90°,∴∠A=∠B=45°,∵CD⊥AB,∴∠CDB=90°,∴∠DCB=45°,∵∠ECF=∠DCB+∠1=45°+∠1,∠EFC=∠B+∠2=45°+∠2,∠1=∠2,∴∠ECF=∠EFC,∴CE=EF,∵CD⊥AB,FG⊥AB,∴∠CDE=∠EGF=90°,在△CDE和△EGF中,,∴△CDE≌△EGF(AAS);(2)证明:由(1)得:CE=EF,∠A=∠B,∵CE平分∠ACD,∴∠ACE=∠1,∵∠1=∠2,∴∠ACE=∠2,在△ACE和△BEF中,,∴△ACE≌△BEF(AAS),∴AE=BF;(3)AE=BF,作EH⊥BC与H,如图3所示:设DE=x,根据题意得:BE=DE=x,AD=BD=2x,CD=AD=2x,AE=3x,根据勾股定理得:BC=AC=2x,∵∠ABC=45°,EH⊥BC,∴BH=x,∴CH=BC﹣BH=x,∵EC=EF,∴FH=CH=x,∴BF=x﹣x=x,∴=,∴AE=.16、在正方形ABCD和等腰直角△BGF中,∠BGF=90°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,延长GP交DC于点E.求证:PG=PC;(2)如图2,当点F在AB的延长线上时,(1)中的结论是否成立?请证明你的结论;(3)如图3,若四边形ABCD为菱形,且∠ABC=60°,△BGF为等边三角形,点F在CB的延长线。
2020年数学中考复习,几何代数综合压轴题解析(三)

2020年数学中考复习,几代综合压轴题解析(三)1.(2019.眉山)如图,在平面直角坐标系中,抛物线y=-94x 2+bx+c 经过点A(-5,0)和点B (1,0).(1)求抛物线的解析式及顶点D 的坐标;(2)点P 是抛物线上A 、D 之间的一点,过点P 作PE ⊥x 轴于点F ,当矩形PEFG 的周长最大时,求点P 的横坐标;(3)如图连接AD 、BD ,点M 在线段AB 上(不与A 、B 重合),作∠DMN=∠DBA ,MN 交线段AD 于点N ,是否存在这样点M ,使得△DMN 为等腰三角形?若存在,求AN 的长;若不存在,请说明理由。
解析:(1)将A(-5,0)和点B (1,0)代入y=-94x 2+bx+c ,可得b=-916,c=920∴抛物线的解析式:y=-94x 2-916x+920,D (-2,4).(2)设P (m,-94m 2-916m+920),根据对称性可得GP=-4-2m 。
矩形PEFG 的周长=2(PE+PG )=2(-94m 2-916m+920-4-2m )=-98(m+417)2+18225 当m=-417时,矩形PEFG 的周长有最大值,即P 的点的横坐标为m=-417。
(3)由A(-5,0)和点B (1,0),D (-2,4)可求得AB=6,AD=DB=5。
①当MD=MN 时,由∠DBA=∠MAB,∠BDM=∠AMN.可证得△MBD ≌△NAM, ∴AN=MB.又∠DMN=∠DBA=∠DAB ,∠MDN=∠ADM,∴∠DNM=∠AMD ∴△ADM 是等腰三角形,即AM=AD=5,∴AN=MB=6-5=1②当ND=MN 时,∠NDM=∠DMN=∠DBA,又∠DAM 是公共角, ∴△ADM ∽△ABD ,∴AD 2=AM ·AB,可求得AM=625,BM=611 又△ANM ∽△BMD,∴DBAM=MB AN , 可得AN=3655。
③当ND=MD 时,可得∠DNM=∠DMN,又知∠DMN=∠DBA=∠DAB ,而发生了∠PNM=∠PAM,显然 这种情况不成立。
中考数学复习考点知识专题讲解10---三角形的综合问题

中考数学复习考点知识专题讲解中考数学复习考点知识专题讲解三角形的综合问题专题10三角形的综合问题】方法指导】【方法指导1.全等三角形解决问题的常见技巧:(1)全等三角形的判定方法有SSS、SAS、ASA、AAS、HL(适用于直角三角形).(2)作辅助线构造全等三角形①把三角形一边的中线延长,把分散条件集中到同一个三角形中是解决中线问题的基本规律.②证明一条线段等于两条线段的和,可采用“截长法”或“补短法”,这些问题经常用到全等三角形来证明.2.等腰三角形解题技巧:(1)等腰三角形提供了好多相等的线段和相等的角,判定三角形是等腰三角形是证明线段相等、角相等的重要手段.(2)在等腰三角形有关问题中,会遇到一些添加辅助线的问题,其顶角平分线、底边上的高、底边上的中线是常见的辅助线,虽然“三线合一”,但添加辅助线时,有时作哪条线都可以,有时不同的做法引起解决问题的复杂程度不同,需要具体问题具体分析.3.等边三角形常用方法与思路:(1)等边三角形是一个非常特殊的几何图形,它的角的特殊性给有关角的计算奠定了基础,它的边角性质为证明线段、角相等提供了便利条件.同是等边三角形又是特殊的等腰三角形,同样具备三线合一的性质,解题时要善于挖掘图形中的隐含条件广泛应用.(2)等边三角形的特性如:三边相等、有三条对称轴、一边上的高可以把等边三角形分成含有30°角的直角三角形、连接三边中点可以把等边三角形分成四个全等的小等边三角形等.(3)等边三角形判定最复杂,在应用时要抓住已知条件的特点,选取恰当的判定方法,一般地,若从一般三角形出发可以通过三条边相等判定、通过三个角相等判定;若从等腰三角形出发,则想法获取一个60°的角判定.【题型剖析题型剖析】】【类型1】三角形有关角的综合计算三角形有关角的综合计算【例1】(2019•泉山区模拟)如图,点A 、B 分别在射线OM 、ON 上运动(不与点O 重合).(1)如图1,若90MON ∠=°,OBA ∠、OAB ∠的平分线交于点C ,则ACB ∠= °;(2)如图2,若MON n ∠=°,OBA ∠、OAB ∠的平分线交于点C ,求ACB ∠的度数;(3)如图2,若MON n ∠=°,AOB ∆的外角ABN ∠、BAM ∠的平分线交于点D ,求ACB ∠与ADB ∠之间的数量关系,并求出ADB ∠的度数;(4)如图3,若80MON ∠=°,BC 是ABN ∠的平分线,BC 的反向延长线与OAB ∠的平分线交于点E .试问:随着点A 、B 的运动,E ∠的大小会变吗?如果不会,求E ∠的度数;如果会,请说明理由.【变式1-1】(2019•沭阳县模拟)探究与发现: 如图1所示的图形,像我们常见的学习用品−−圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:(1)观察“规形图”,试探究BDC ∠与A ∠、B ∠、C ∠之间的关系,并说明理由;(2)请你直接利用以上结论,解决以下三个问题:①如图2,把一块三角尺XYZ 放置在ABC ∆上,使三角尺的两条直角边XY 、XZ 恰好经过点B 、C ,若50A ∠=°,则ABX ACX ∠+∠= 40 °;②如图3,DC 平分ADB ∠,EC 平分AEB ∠,若50DAE ∠=°,130DBE ∠=°,求DCE ∠的度数; ③如图4,ABD ∠,ACD ∠的10等分线相交于点1G 、2G …、9G ,若140BDC ∠=°,177BG C ∠=°,求A ∠的度数.【变式1-2】(2019春•海安市期末)如图,已知BE 是ABC ∆的角平分线,CP 是ABC ∆的外角ACD ∠的平分线.延长BE ,BA 分别交CP 于点F ,P(1)求证:12BFC BAC ∠=∠;(2)小智同学探究后提出等式:BAC ABC P ∠=∠+∠.请通过推理演算判断“小智发现”是否正确?(3)若2180BEC P ∠−∠=°,求ACB ∠的度数.【变式1-3】(2019春•高淳区校级模拟)ABC ∆中,三个内角的平分线交于点O ,过点O 作OD OB ⊥,交边AB 于点D .(1)如图1,①若40ABC ∠=°,则AOC ∠= ,ADO ∠= ;②猜想AOC ∠与ADO ∠的关系,并说明你的理由;(2)如图2,作ABC ∠外角ABE ∠的平分线交CO 的延长线于点F .若105AOC ∠=°,32F ∠=°,则AOD ∠= _______°.【类型2】全等三角形的判定与性质全等三角形的判定与性质【例2】(2019•如皋市一模)如图,A 、B 、C 是直线l 上的三个点,DAB DBE ECB a ∠=∠=∠=,且BD BE =.(1)求证:AC AD CE =+;(2)若120a =°,点F 在直线l 的上方,BEF ∆为等边三角形,补全图形,请判断ACF ∆的形状,并说明理由.【变式2-1】(2019•碑林区校级模拟)如图,四边形ABCD 中,//AD BC ,90A ∠=°,CE BD ⊥,垂足为E ,BE DA =.(1)求证:ABD ECB ∆≅∆;(2)若45DBC ∠=°,1BE =,求DE 的长(结果精确到0.01, 1.414≈ 1.732)≈【变式2-2】(2019•灌南县校级模拟)如图,在四边形ABCD 中,//AD BC ,AD BC =,点F 是AB 的中点,点E 是BC 边上的点,DE AD BE =+,DEF ∆的周长为l .(1)求证:DF 平分ADE ∠;(2)若FD FC =,2AB =,3AD =,求l 的值.【类型3】等腰三角形的有关计算与证明等腰三角形的有关计算与证明【例3】(2018秋•灌云县期末)如图,已知D 是ABC ∆的边BC 上的一点,CD AB =,(1)若BDA BAD ∠=∠,60B ∠=°,求C ∠的大小;(2)若AE 既是ABD ∆的高又是角平分线,54B ∠=°,求C ∠的大小.【变式3-1】(2018秋•泗阳县期末)已知,在ABC ∆中,点D 在BC 上,点E 在BC 的延长线上,且BD BA =,CE CA =.(1)如图1,若90BAC ∠=°,45B ∠=°,试求DAE ∠的度数;(2)若90BAC ∠=°,60B ∠=°,则DAE ∠的度数为 (直接写出结果);(3)如图2,若90BAC ∠>°,其余条件不变,探究DAE ∠与BAC ∠之间有怎样的数量关系?【变式3-2】(2018秋•秦淮区期末)如图,在ABC ∆中,AB AD =,CB CE =.(1)当90ABC ∠=°时(如图①),EBD ∠= °;(2)当(90)ABC n n ∠=°≠时(如图②),求EBD ∠的度数(用含n 的式子表示).【类型4】等边三角形的有关计算与证明等边三角形的有关计算与证明【例4】(2019春•鼓楼区校级模拟)已知,ABC ∆为等边三角形,点D 为AC 上的一个动点,点E 为BC 延长线上一点,且BD DE =.(1)如图1,若点D 在边AC 上,猜想线段AD 与CE 之间的关系,并说明理由;(2)如图2,若点D 在AC 的延长线上,(1)中的结论是否成立,请说明理由.【变式4-1】(2018秋•泰兴市月考)如图,ABC ∆是等边三角形,BD 是中线,延长BC 至点E ,使CE CD =.取BE 中点F ,连接DF .(1)求证:BD DE =;(2)延长ED 交边AB 于点G ,试说明:DG DF =.【变式4-2】(2019•淮阴区模拟)如图,ABC ∆中,90ACB ∠=°,以AC 为边在ABC ∆外作等边三角形ACD ,过点D 作AC 的垂线,垂足为F ,与AB 相交于点E ,连接CE .(1)说明:AE CE BE ==;(2)若15AB cm =,P 是直线DE 上的一点.则当P 在何处时,PB PC +最小,并求出此时PB PC +的值.【类型5】直角三角形的综合问题直角三角形的综合问题【例5】(2019 •溧水校级模拟)已知ABC ∆中,90A ∠=°,AB AC =,D 为BC 的中点. (1)如图,若E 、F 分别是AB 、AC 上的点,且BE AF =.求证:DEF ∆为等腰直角三角形;(2)若E ,F 分别为AB ,CA 延长线上的点,仍有BE AF =,其他条件不变,那么DEF ∆是否仍为等腰直角三角形?证明你的结论.【变式5-1】(2018秋•常熟市期末)如图,在Rt ABC ∆中,90ACB ∠=°,AC BC =.点D 是边AC 上一点,DE AB ⊥,垂足为E .点F 是BD 的中点,连接CF ,EF .(1)求证:CF EF =;(2)判断CF 与EF 的位置关系,并说明理由;(3)若30DBE ∠=°,连接AF ,求AFE ∠的度数.【变式5-2】(2019•江都区校级模拟)如图所示,已知ABC ∆是等腰直角三角形,90ABC ∠=°,10AB =,D 为ABC ∆外的一点,连结AD 、BD ,过D 作DH AB ⊥,垂足为H ,DH 的延长线交AC 于E .(1)如图1,若BD AB =,且34HB HD =,求AD 的长; (2)如图2,若ABD ∆是等边三角形,求DE 的长.【达标检测达标检测】】一.选择题选择题((共4小题小题))1.(2019•徐州)下列长度的三条线段,能组成三角形的是( )A.2,2,4 B.5,6,12 C.5,7,2 D.6,8,102.(2019•扬州)已知n是正整数,若一个三角形的3边长分别是n+2、n+8、3n,则满足条件的n的值有( )A.4个B.5个C.6个D.7个3.(2019•盐城)如图,点D、E分别是△ABC边BA、BC的中点,AC=3,则DE的长为( )A.2 B.C.3 D.4.(2018•南通)如图,Rt△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,按下列步骤作图:步骤1:分别以点C和点D为圆心,大于CD的长为半径作弧,两弧相交于M,N两点;步骤2:作直线MN,分别交AC,BC于点E,F;步骤3:连接DE,DF.若AC=4,BC=2,则线段DE的长为( )A.B.C.D.)小题)二.填空题(共4小题填空题(5.(2019•南通)如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E 在BC上,且AE=CF,若∠BAE=25°,则∠ACF= 度.6.(2019•苏州)如图,扇形OAB中,∠AOB=90°.P为弧AB上的一点,过点P作PC⊥OA,垂足为C,PC与AB交于点D.若PD=2,CD=1,则该扇形的半径长为 .7.(2019•南京)在△ABC中,AB=4,∠C=60°,∠A>∠B,则BC的长的取值范围是 .8.(2019•南京)无盖圆柱形杯子的展开图如图所示.将一根长为20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有 cm.)小题)(共8小题三.解答题解答题(9.(2019•南通)如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC 并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离.为什么?10.(2019•镇江)如图,四边形ABCD中,AD∥BC,点E、F分别在AD、BC上,AE=CF,过点A、C分别作EF的垂线,垂足为G、H.(1)求证:△AGE≌△CHF;(2)连接AC,线段GH与AC是否互相平分?请说明理由.11.(2019•无锡)如图,在△ABC中,AB=AC,点D、E分别在AB、AC上,BD=CE,BE、CD相交于点O.(1)求证:△DBC≌△ECB;(2)求证:OB=OC.12.(2018•无锡)如图,在△ABC中,∠ACB=90°,AC=m,BC=n,m>n,点P是边AB上一点,连结CP,将△ACP沿CP翻折得到△QCP.(1)若m=4,n=3,且PQ⊥AB,求BP的长;(2)连结BQ,若四边形BCPQ是平行四边形,求m与n之间的关系式.13.(2018•徐州)如图,将等腰直角三角形纸片ABC对折,折痕为CD.展平后,再将点B 折叠在边AC上(不与A、C重合),折痕为EF,点B在AC上的对应点为M,设CD与EM交于点P,连接PF.已知BC=4.(1)若M为AC的中点,求CF的长;(2)随着点M在边AC上取不同的位置,①△PFM的形状是否发生变化?请说明理由;②求△PFM的周长的取值范围.14.(2019•扬州)如图,平面内的两条直线l1、l2,点A,B在直线l1上,点C、D在直线l2上,过A、B两点分别作直线l2的垂线,垂足分別为A1,B1,我们把线段A1B1叫做线段AB在直线l 2上的正投影,其长度可记作T(AB,CD)或T,特别地线段AC在直线l2上的正投影就是线段A1C.请依据上述定义解决如下问题:=3,则T(BC,AB)= ;(1)如图1,在锐角△ABC中,AB=5,T(AC,AB)=4,T(BC,AB)═9,求△ABC的面(2)如图2,在Rt△ABC中,∠ACB=90°,T(AC,AB)积;(3)如图3,在钝角△ABC中,∠A=60°,点D在AB边上,∠ACD=90°,T(AD,AC)=6,求T(BC,CD),=2,T(BC,AB)。
中考数学专题复习:几何综合题

【考点总结】四、全等三角形的性质与判定
1.概念:能够完全重合的两个三角形叫做全等三角形. 2.性质:全等三角形的对应边、对应角分别相等. 3.判定:(1)有三边对应相等的两个三角形全等,简记为(SSS); (2)有两边和它们的夹角对应相等的两个三角形全等,简记为(SAS); (3)有两角和它们的夹边对应相等的两个三角形全等,简记为(ASA); (4)有两角和其中一角的对边对应相等的两个三角形全等,简记为(AAS); (5)有斜边和一条直角边对应相等的两个直角三角形全等,简记为(HL).
三角形专题
1,掌握三角形相关基础知识(2课时)
目标
2,掌握三角形有关模型的全等或相似证明(3课时) 3,完成三角形有关模型的全等或相似证明(3课时)
三角形
模型
手拉手模型
三垂直模型
相似模型
三角形有关的知识
【考点总结】一、三角形中的重要线段 1.三角形的高线:从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做 三角形的高线,简称高. 特性:三角形的三条高线相交于一点. 2.三角形的中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.特性:三角 形的三条中线交于一点. 3.三角形的中位线:连接三角形两边中点的线段叫做三角形的中位线. 定理:三角形的中位线平行于第三边,且等于它的一半 4.三角形的角平分线:三角形一个角的平分线和这个角的对边相交,这个角的顶点和交点之间的线 段叫做三角形的角平分线. 特性:三角形的三条角平分线交于一点,这点叫做三角形的内心. 性质:角平分线上的点到角的两边的距离相等.
小组合作
1.在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.
(1)如图1,点M,N分别在AD,AB上,且∠BMN=90°,当∠AMN=30°,AB=2时,求线段
2021年九年级数学中考复习——几何小专题:三角形综合之解答题专项(三)

2021年九年级数学中考复习——几何小专题:三角形综合之解答题专项(三)练习一1.在△ABC中,AB=AC,点D是直线BC上一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=度;(2)如图2,如果∠BAC=60°,则∠BCE=度;(3)设∠BAC=α,∠BCE=β.①如图3,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;②当点D在直线BC上移动,请直接写出α,β之样的数量关系,不用证明.2.在△ABC中,∠ACB=90°,AC=BC.点D是直线AB上一点(点D与点A、B不重合),以CD为直角边作等腰直角三角形DCE,使∠DCE=90°,连结AE.(1)如图①,当点D在线段AB上,点E与点A在CD同侧.求证:AE=BD.(2)如图②,当点D在AB的延长线上,点E与点A在CD同侧.若AE=1,AB=4,则AD=.(3)如图③,当点D在BA的延长线上,点E与点A在CD的两侧时,直接写出线段AB、AD、AE三者之间的数量关系:.3.如图,在Rt△ABC中,∠ACB=90°,AC=20,BC=15,动点P从点A出发(动点P不与△ABC的顶点重合),沿折线AC﹣CB以每秒5个单位的速度向终点B运动,过点P作PD⊥AB于点D,以点P为直角顶点作Rt△PDE,使DE与点P所在的直角边平行,设点P的运动时间为t(秒).(1)求AB的长;(2)当点E落在△ABC的直角边上时,求t的值;(3)当△PDE的两条直角边所在的直线截△ABC所得的三角形全等时,求△PDE与△ABC重叠部分图形的周长;(4)设Q为边DE的中点,作射线CQ,当CQ将△PDE分成面积比为1:3两部分时,直接写出t的值.4.如图,在△ABC中,AB=AC=3,∠B=50°,点D在线段BC上运动(不与B、C 重合),连接AD,作∠ADE=50°,DE交线段AC于E.(1)当∠BDA=105°时,∠BAD=°,∠DEC=°;(2)若DC=AB,求证:△ABD≌△DCE;(3)在点D的运动过程中,是否存在△ADE是等腰三角形?若存在,请直接写出此时∠BDA的度数;若不存在,请说明理由.5.已知△ABC是等边三角形,点P,Q分别为边AB,BC上的动点(端点除外)点P,Q 以相同的速度,同时从点A,点B出发,直线AQ,CP相交于点M.(Ⅰ)如图①,求证:△ABQ≌△CAP;(Ⅱ)如图①,当点P,Q分别在AB,BC边上运动时,∠QMC的大小是否变化?若变化,请说明理由;若不变,求出它的大小;(Ⅲ)如图②,当点P,Q分别在AB,BC的延长线上运动时,∠QMC的大小是否变化?若变化,请说明理由;若不变,求出它的度数.练习二6.在Rt△ABC中,∠ACB=90°,AC=BC,点D、F是线段AB上两点,连结CD,过A作AE⊥CD于点E,过点F作FM⊥CD于点M.(1)如图1,若点E是CD的中点,求∠CAE的大小;(2)如图2,若点D是线段BF的中点,求证:CE=FM;(3)如图3,若点F是线段AB的中点,AE=,CE=1,求FM的值.7.在△ABC中,∠A=90°,AB=AC=+1.且AD=AE=1.(1)如图1,点D,E分别在边AB,AC上,连接DE.直接写出DE的值,BC的值;(2)现将△ADE如图2放置,连接CE,BE,CD,求证:CD=BE;(3)现将△ADE如图3放置,使C,A,E三点共线,延长CD交BE于点F,求证:CF垂直平分BE.8.在等腰直角△ABC中,AB=AC,∠A=90°,过点B作BC的垂线l.点P为直线AB上的一个动点(不与点A,B重合),将射线PC绕点P顺时针旋转90°交直线l 于点D.(1)如图l,点P在线段AB上,依题意补全图形.①求证:∠BDP=∠PCB;②用等式表示线段BC,BD,BP之间的数量关系,并证明.(2)点P在线段AB的延长线上,直接写出线段BC,BD,BP之间的数量关系.9.定义:点P是△ABC内部的一点,若经过点P和△ABC中的一个顶点的直线把△ABC 平分成两个面积相等的图形,则称点P是△ABC关于这个顶点的均分点,例如图1中,点P是△ABC关于顶点A的均分点.(1)下列图形中,点D一定是△ABC关于顶点B的均分点的是;(填序号)(2)在△ABC中,BC=2,AB=AC且AB>BC,点P是△ABC关于顶点A的均分点,且≤BP≤2,直接写出∠BPC的范围;(3)如图2,在△ABC中,∠BAC=90°,BC=10,点P是△ABC关于顶点A的均分点,直线AP与BC交于点D,当BP⊥AD时,BP=4,求CP的长.10.在△ABC和△DBE中,CA=CB,EB=ED,点D在AC上.(1)如图1,若∠ABC=∠DBE=60°,求证:∠ECB=∠A;(2)如图2,设BC与DE交于点F.当∠ABC=∠DBE=45°时,求证:CE∥AB;(3)在(2)的条件下,若tan∠DEC=时,求的值.练习三11.如图,△AOB是等边三角形,以直线OA为x轴建立平面直角坐标系,若B(a,b)且a、b满足+(b﹣5)2=0,D为y轴上一动点,以AD为边作等边△ADC,CB交y轴于E.(1)如图1,求A点坐标;(2)如图2,D为y正半轴上一点,C在第二象限,CE的延长线交x轴于M,当D 点在y轴正半轴上运动时,M点坐标是否变化,若不变,求M点的坐标,若变化,说明理由;(3)如图3,D在y轴负半轴上,以DA为边向右构造等边△DAC,CB交y轴于E 点,如果D点在y轴负半轴上运动时,仍保持△DAC为等边三角形,连BE,试求CE,OD,AE三者的数量关系,并证明你的结论.12.【教材呈现】数学课上,胡老师用无刻度的直尺和圆规按照华师版教材八年级上册87页完成角平分线的作法,方法如下:【试一试】如图1,∠AOB为已知角,试按下列步骤用直尺和圆规准确地作出∠AOB的平分线.第一步:在射线OA、OB上,分别截取OD、OE,使OD=OE;第二步:分别以点D和点E为圆心、适当长(大于线段DE长的一半)为半径作圆弧,在∠AOB内,两弧交于点C;第三步:作射线OC.射线OC就是所要求作的∠AOB的平分线.【问题1】胡老师用尺规作角平分线时,用到的三角形全等的判定方法是.【问题2】小萱同学发现只利用直角三角板也可以作∠AOB的角平分线,方法如下(如图2):步骤:①利用三角板上的刻度,在OA、OB上分别截取OM、ON,使OM=ON.②分别过点M、N作OM、ON的垂线,交于点P.③作射线OP,则OP为∠AOB的平分线.(1)请写出小萱同学作法的完整证明过程.(2)当∠MON=60°时,量得MN=4cm,则△MON的面积是cm2.13.某校组织数学兴趣探究活动,爱思考的小实同学在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中,AF、BE是△ABC的中线,AF⊥BE于点P,像△ABC这样的三角形均称为“中垂三角形”.【特例探究】(1)如图1,当∠PAB=45°,AB=6时,AC=,BC=;如图2,当sin∠PAB=,AB=4时,AC=,BC=;【归纳证明】(2)请你观察(1)中的计算结果,猜想AB2、BC2、AC2三者之间的关系,用等式表示出来,并利用图3证明你的结论.【拓展证明】(3)如图4,在△ABC中,AB=4,BC=2,D、E、F分别是边AB、AC、BC的中点,连结DE并延长至G,使得GE=DE,连结BG,当BG⊥AC于点M时,求GF的长.14.如图,△ABC为等边三角形,直线l经过点C,在l上位于C点右侧的点D满足∠BDC =60°.(1)如图1,在l上位于C点左侧取一点E,使∠AEC=60°,求证:△AEC≌△CDB;(2)如图2,点F、G在直线l上,连AF,在l上方作∠AFH=120°,且AF=HF,∠HGF=120°,求证:HG+BD=CF;(3)在(2)的条件下,当A、B位于直线l两侧,其余条件不变时(如图3),线段HG、CF、BD的数量关系为.15.阅读材料:小明遇到这样一个问题:如图1,在△AC中,∠A=2∠B,CD平分∠ACB,AD=2.2,AC=3.6,求BC的长.小明的想法:因为CD平分∠ACB,所以可利用“翻折”来解决该问题.即在BC边上取点E,使EC=AC,并连接DE(如图2).(1)如图2,根据小明的想法,回答下面问题:①△DEC和△DAC的关系是,判断的依据是;②△BDE是三角形;③BC的长为.(2)参考小明的想法,解决下面问题:已知:如图3,在△ABC中,AB=AC,∠A=20°,BD平分∠ABC,BD=2.3,BC =2,求AD的长.参考答案1.解:(1)∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,∵∠DAE=∠BAC,∴∠BAD=∠CAE,且AB=AC,AD=AE,∴△BAD≌△CAE(SAS)∴∠ABC=∠ACE=45°,∴∠BCE=∠ACB+∠ACE=90°,故答案为:90;(2)∵∠BAC=60°,AB=AC,∴△ABC为等边三角形,∴∠ABD=∠ACB=60°,∵∠BAC=∠DAE,∴∠BAD=∠CAE,在△ABD和△ACE中,∵∠BAD=∠CAE,且AB=AC,AD=AE,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE=60°,∴∠BCE=∠ACE+∠ACB=60°+60°=120°,故答案为:120.(3)①α+β=180°,理由:∵∠BAC=∠DAE,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC.即∠BAD=∠CAE.在△ABD与△ACE中,,∴△ABD≌△ACE(SAS),∴∠B=∠ACE.∴∠B+∠ACB=∠ACE+∠ACB.∵∠ACE+∠ACB=β,∴∠B+∠ACB=β,∵α+∠B+∠ACB=180°,∴α+β=180°.②如图1:当点D在射线BC上时,α+β=180°,连接CE,∵∠BAC=∠DAE,∴∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,在△ABC中,∠BAC+∠B+∠ACB=180°,∴∠BAC+∠ACE+∠ACB=∠BAC+∠BCE=180°,即:∠BCE+∠BAC=180°,∴α+β=180°,如图2:当点D在射线BC的反向延长线上时,α=β.连接BE,∵∠BAC=∠DAE,∴∠BAD=∠CAE,且AB=AC,AD=AE,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∴∠ABD=∠ACE=∠ACB+∠BCE,∴∠ABD+∠ABC=∠ACE+∠ABC=∠ACB+∠BCE+∠ABC=180°,∵∠BAC=180°﹣∠ABC﹣∠ACB,∴∠BAC=∠BCE.∴α=β;综上所述:点D在直线BC上移动,α+β=180°或α=β.2.(1)证明:如图①,∵∠ACB=90°,∠DCE=90°,∴∠BCD+∠ACD=90°,∠ACE+∠ACD=90°,∴∠BCD=∠ACE,在△BCD和△ACE中,,∴△BCD≌△ACE(SAS),∴AE=BD;(2)解:如图②,∵∠ACB=90°,∠DCE=90°,∴∠BCD+∠BCE=90°,∠ACE+∠BCE=90°,∴∠BCD=∠ACE,在△BCD和△ACE中,,∴△BCD≌△ACE(SAS),∴AE=BD,∴AD=AB+BD=AB+AE=5,故答案为:5;(3)解:同(2)的证明方法可得,△BCD≌△ACE(SAS),∴AE=BD,∴AB+BD=BD=AE,故答案为:AB+AD=AE.3.解:(1)在Rt△ABC中,∠ACB=90°,AC=20,BC=15,∴AB===25;(2)如图1,P在AC上时,点E在BC上,DE∥AC,∵DE∥AC,∴∠CPE=∠DEP,∵PD⊥AB,∴∠ADP=90°,由题意得:AP=5t,sin A=,即,∴PD=3t,∴AD=4t,BD=25﹣4t,∵∠DPE=90°,∴∠APD+∠CPE=90°=∠APD+∠A,∴∠CPE=∠A=∠DEP,∴sin∠DEP=,∴DE=5t,∵DE∥AC,∴,即,解得:t=;如图2,P在BC上时,点E在AC上,DE∥BC,由题意得:CP=5t﹣20,PB=15﹣(5t﹣20)=35﹣5t,∵∠EPD=∠PDB=90°,∴EP∥AB,∵DE∥BC,∴四边形EPBD是平行四边形,∴DE=PB=35﹣5t,∵∠CEP=∠A=∠PDE,∴sin∠CEP=sin∠PDE,∴=,即,∴EP=,∴=,解得:t=;综上,t的值是或;(3)如图3,P在AC上,△PDE与△ABC重叠部分图形是△PDE,设直线PE与BC 交于点F,∵AP∥DE,AD∥PE,∴四边形APED是平行四边形,∴DE=AP=5t,AD=PE=4t,∵△ADP≌△PCF,∴PC=AD=4t,∵AC=AP+CP,即20=5t+4t,∴t=,∴△PDE的周长=PD+PE+DE=3t+4t+5t=12t=12×=,即△PDE与△ABC重叠部分图形的周长是;如图4,P在BC上,△PDE与△ABC重叠部分的图形是△PDE,设直线PE与AC交于点G,同理得:四边形DEPB是平行四边形,∴DE=PB,∵△GCP≌△PDB,∴PC=BD=5t﹣20,Rt△PDB中,cos B==,∴=,解得:t=,∴PB=35﹣5×=,∵∠C=∠PDB=90°,∠B=∠B,∴△PDB∽△ACB,∴=,∴△PDB的周长=×(15+20+25)=,∴△PDE的周长=,即△PDE与△ABC重叠部分图形的周长是;综上,△PDE与△ABC重叠部分图形的周长为或;(4)分两种情况:①如图5,P在AC上,设PE与CQ交于点O,连接PQ,∵Q是DE的中点,∴DQ=EQ=t,∴S△PDQ=S△PQE,Rt△PDE中,PD=3t,PE=4t,DE=5t,∵==,∴=,∴=,∴=1,∵DE∥CP,∴,即=1,解得:t=;②如图6,P在BC上,=,同理得:=1,∵CP=5t﹣20,PB=35﹣5t,由上题知:四边形DEPB是平行四边形,∴DE=PB=35﹣5t,∴EQ=,∵ED∥PC,∴=1,∴EQ=CP,∴=5t﹣20,解得:t=5;综上,t的值是或5.4.解:(1)∵在△BAD中,∠B=∠50°,∠BDA=105°,∴∠BAD=180°﹣∠B﹣∠BDA=180°﹣50°﹣105°=25°;∵AB=AC,∴∠B=∠C=50°,∴∠DEC=180°﹣∠C﹣∠EDC=180°﹣50°﹣25°=105°,故答案为:25,105;(2)∵∠B=∠C=50°,∴∠DEC+∠EDC=130°,又∵∠ADE=50°,∴∠ADB+∠EDC=130°,∴∠ADB=∠DEC,在△ABD和△DCE中,,∴△ABD≌△DCE(AAS).(3)当∠BDA的度数为100°或115°时,△ADE的形状是等腰三角形,①∠BDA=100°时,则∠ADC=80°,∵∠C=50°,∴∠DAC=50°,∴∠DAC=∠ADE,∴△ADE的形状是等腰三角形;②∠BDA=115°时,则∠ADC=65°,∵∠C=50°,∴∠DAC=65°,∵∠ADE=50°,∴∠AED=65°,∴∠DAC=∠AED,∴△ADE的形状是等腰三角形.5.解:(1)证明:如图1,∵△ABC是等边三角形∴∠ABQ=∠CAP=60°,AB=CA,又∵点P、Q运动速度相同,∴AP=BQ,在△ABQ与△CAP中,,∴△ABQ≌△CAP(SAS);(2)点P、Q在AB、BC边上运动的过程中,∠QMC不变.理由:∵△ABQ≌△CAP,∴∠BAQ=∠ACP,∵∠QMC是△ACM的外角,∴∠QMC=∠ACP+∠MAC=∠BAQ+∠MAC=∠BAC,∵∠BAC=60°,∴∠QMC=60°;(3)如图2,点P、Q在运动到终点后继续在射线AB、BC上运动时,∠QMC不变.理由:同理可得,△ABQ≌△CAP,∴∠BAQ=∠ACP,∵∠QMC是△APM的外角,∴∠QMC=∠BAQ+∠APM,∴∠QMC=∠ACP+∠APM=180°﹣∠PAC=180°﹣60°=120°,即若点P、Q在运动到终点后继续在射线AB、BC上运动,∠QMC的度数为120°.6.(1)解:∵AC=BC,∠ACB=90°,∴∠CAB=∠B=45°,∵AE⊥CD,EC=ED,∴AC=AD,∴∠CAE=∠DAE=22.5°,∴∠CAE=22.5°.(2)证明:过点B作BN⊥CD交CD的延长线于点N.∴∠BNC=90°,∵AE⊥CD,∴∠CEA=∠BNC=90°,∴∠CAE+∠ACD=90°,∵∠ACB=90°,∴∠ACD+∠BCN=90°,∴∠CAE=∠BCN,在△AEC和△CNB中,,∴△AEC≌△CNB(AAS),∴CE=BN,∵FM⊥CD,BN⊥CD,∴∠FMD=∠BND=90°,∵点D是线段BF的中点,∴FD=BD,在△FMD和△BND中,,∴△FMD≌△BND(AAS),∴FM=BN,∴CE=FM.(3)解:在线段AE上取点G,使得AG=CE,连结CF、EF,如图3所示:∵AF=FB,AC=BC,∠ACB=90°,∴CF⊥AB,CF=AF,∵∠FAG+∠ADE=90°,∠ADE+∠FCE=90°,∴∠GAF=∠ECF,在△AGF和△CEF中,,∴△AGF≌△CEF(SAS),∴FG=EF,∠AFG=∠CFE,∴∠EFG=∠AFC=90°∴△EFG是等腰直角三角形,∴EG=EF,∠GEF=45°,∴∠MEF=90°﹣45°=45°,∴△EFM是等腰直角三角形,∴EF=FM,∴AE﹣CE=AE﹣AG=EG=EF=2FM=﹣1,∴FM=.7.(1)解:在Rt△ADE中,∠A=90°,AD=AE=1,∴DE===,同理,BC==2+,故答案为:;2+;(2)证明:∵∠CAB=∠DAE=90°,∴∠CAB﹣∠DAB=∠DAE﹣∠DAB,即∠CAD=∠BAE,在△CAD和△BAE中,,∴△CAD≌△BAE(SAS),∴CD=BE;(3)证明:∵C,A,E三点共线,∴CE=CA+AE=+2,∴CE=CB,∴点C在线段BE的垂直平分线上,∵BD=AB﹣AD=,DE=,∴BD=DE,∴点D在线段BE的垂直平分线上,∴CF垂直平分BE.8.解:(1)①补全图形如图1,证明:如图1,设PD与BC的交点为点E,根据题意可知,∠CPD=90°,∵BC⊥l,∴∠DBC=90°,∴∠BDP+∠BED=∠PCB+∠PEC=90°,∴∠BDP=∠PCB;②BC﹣BD=BP.证明:如图2,过点P作PF⊥BP交BC于点F,∵AB=AC,∠A=90°,∴∠ABC=45°,∴BP=BF,∠PFB=45°,∴∠PBD=∠PFC=135°,又∵∠BDP=∠PCF,∴△BPD≌△FPC(AAS),∴BD=FC,在等腰直角△BPF中,BF=BP,∴BC﹣BD=BP.(2)BD﹣BC=BP.证明:如图3,过点P作PM⊥PB交BD于点M,由(1)可知∠ABC=∠PBM=45°,∴∠PBM=∠PMB=45°,∴PB=PM,∠PBC=∠PCB=135°,同(1)可得∠PDB=∠PCB,∴△PMD≌△PBC(AAS),∴DM=BC,∵PB=PM,∠BPM=90°,∴BM=PB,∴BD﹣DM=BM=BD﹣BC=PB.9.解:(1)在图①中,∵∠BAE=∠CAE,∴点D不一定是△ABC关于顶点B的均分点;在图②中,∵BE=CE,∴点D一定是△ABC关于顶点A的均分点,但点D不一定是△ABC关于顶点B的均分点.在③中,∵∠ABE=∠CBE,AB≠BC,∴点D不一定是△ABC关于顶点B的均分点;④∵AE=CE,∴点D一定是△ABC关于顶点B的均分点.故答案为:④.(2)60°≤∠BPC≤90°.如图1,点P是△ABC关于顶点A的均分点,∵AB=AC,点P是△ABC关于顶点A的均分点,∴BD=CD,∴AD⊥BC,∵BC=2,∴BD=1,∴当∠BED=45°时,BE=,当∠BFD=30°时,BF=2BD=2,∵点P在AD上运动,且≤BP≤2,∴60°≤∠BPC≤90°.(3)解:如图2,过C点作CE⊥AP,交直线AP于点E.∵点P是△ABC关于顶点A的均分点,BC=10,∴BD=CD=5.在Rt△BPD中,∵∠BPD=90°,∴BP2+PD2=BD2.∵BP=4,BD=5,∴PD=3.∵BP⊥AP,CE⊥AP,∴∠BPD=∠CED=90°.∵∠BDP=∠CDE,∴△BPD≌△CDE(AAS).∴PD=DE,PB=CE=4.∴PE=2PD=6.在Rt△PEC中,∵∠PEC=90°,∴PE2+CE2=CP2.∴CP===.10.(1)证明:∵CA=CB,EB=ED,∠ABC=∠DBE=60°,∴△ABC和△DBE都是等边三角形,∴AB=BC,DB=BE,∠A=60°.∵∠ABC=∠DBE=60°,∴∠ABD=∠CBE,∴△ABD≌△CBE(SAS).∴∠A=∠ECB;(2)证明:∵∠ABC=∠DBE=45°,CA=CB,EB=ED,∴△ABC和△DBE都是等腰直角三角形,∴∠CAB=45°,∴,∴,∵∠ABC=∠DBE,∴∠ABD=∠CBE,∴△ABD∽△CBE,∴∠BAD=∠BCE=45°,∵∠ABC=45°,∴∠ABC=∠BCE,∴CE∥AB;(3)解:过点D作DM⊥CE于点M,过点D作DN∥AB交CB于点N,∵∠ACB=90°,∠BCE=45°,∴∠DCM=45°,∴∠MDC=∠DCM=45°,∴DM=MC,设DM=MC=a,∴a,∵DN∥AB,∴△DCN为等腰直角三角形,∴DN=DC=2a,∵tan∠DEC=,∴ME=2DM,∴CE=a,∴,∵CE∥DN,∴△CEF∽△NDF,∴.11.解:(1)如图1中,作BF⊥AO于F.∵+(b﹣5)2=0,∴a=﹣5,b=5,∴B(﹣5,5),∵BA=BO,BF⊥OA,∴FA=FO=5,∴OA=10,∴A(﹣10,0).(2)点M的坐标不发生变化.理由:如图2中,∵△ABO,△ADC都是等边三角形,∴∠OAB=∠DAC,OA=OB,AD=AC,∴∠OAD=∠BAC,∴△OAD≌△BAC,∴∠AOD=∠CBA=90°,在Rt△ABM中,∵∠ABM=90°,AB=OA=10,∠BAM=60°,∴AM=2AB=20,∴OM=AM﹣OA=10,∴M(10,0).(3)结论:OD=CE+AE.理由:如图3中,取AE的中点R,连接BR、OR.∵∠ABE=∠AOE=90°,AR=ER,∴BR=AR=RE=OR,∴A、B、E、O四点共圆,∴∠BAE=∠BOE=90°﹣60°=30°,∴BE=AE,∵△ABO,△ADC都是等边三角形,∴∠OAB=∠DAC,OA=OB,AD=AC,∴∠OAD=∠BAC,∴△OAD≌△BAC,∴OD=BC=CE+BE=CE+AE.即OD=CE+AE.12.解:【问题1】胡老师用尺规作角平分线时,用到的三角形全等的判定方法是SSS,故答案为:SSS;【问题2】(1)在Rt△OPN和Rt△OPM中,,∴Rt△OPN≌Rt△OPM(HL),∴∠NOP=∠MOP,∴OP为∠AOB的平分线;(2)∵∠MON=60°,OM=ON,∴△MON为等边三角形,∴OM=ON=MN=4(cm),∵OM=ON,OP为∠AOB的平分线,∴NH=HM=MN=2(cm),由勾股定理得,OH===2(cm),∴△MON的面积=×MN×OH=×4×2=4(cm2),故答案为:4.13.(1)解:如图1,∵AF⊥BE,∴∠APB=∠APE=∠BPF=90°,∵∠PAB=45°,AB=6,∴AP=PB=6,如图1,连接EF,∵AF,BE是△ABC的中线,∴EF是△ABC的中位线,∴EF∥AB.且EF=AB,∴,∴PE=PF=3,由勾股定理得:AE=BF===3,∴AC=BC=2AE=6,如图2,∵sin∠PAB=,AB=4,AF⊥BE,∴∠PAB=30°,∴BP=AB=2,AP=2,∵AF、BE是△ABC的中线,∴PE=PB=1,PF=AP=,由勾股定理得:AE===,BF===,∴AC=2AE=2,BC=2BF=2,故答案为:6,6,2,2;(2)解:猜想:AB2、BC2、AC2三者之间的关系是:AC2+BC2=5AB2,证明:如图3,设PF=m,PE=n则AP=2m,PB=2n,在Rt△APB中,(2m)2+(2n)2=AB2①,在Rt△APE中,(2m)2+n2=()2②,在Rt△BPF中,m2+(2n)2=()2③,由①得:m2+n2=,由②+③得:5(m2+n2)=,∴AC2+BC2=5AB2;(3)解:如图4,连接CG,EF,过点F作FN∥BG交CG于点N,FG与AC交于点Q,∵FN∥BG,BG⊥AC,∴FN⊥AC,∵F是BC的中点,∴N是CG的中点,∵D、E分别是AB、AC的中点,∴DE=FC,DE∥FC,∵ED=EG,∴EG=FC,EG∥FC,∴四边形EFCG是平行四边形,∴Q是FG的中点,∴△FCG是中垂三角形,∵AB=4,BC=2,∴CG=EF=BD=2,FC=,由(2)中结论可知:5FC2=CG2+FG2,即5×5=(2)2+FG2,∴GF=.14.(1)证明:如图1,∵△ABC是等边三角形,∴AC=BC,∠ACB=60°,∴∠BCD+∠ACE=120°,∵∠AEC=60°,∴∠ACE+∠EAC=120°,∴∠BCD=∠EAC,∵∠AEC=∠BDC=60°,∴△AEC≌△CDB(AAS);(2)证明:如图2,在l上位于C点左侧取一点E,使∠AEC=60°,连接AE,由(1)知:△AEC≌△CDB,∴BD=CE,∵∠AEF=∠AFH=60°,∴∠AFE+∠FAE=∠AFE+∠GFH=60°,∴∠FAE=∠GFH,∵∠HGF=∠AEF=120°,AF=FH,∴∠HGF≌△FEA(AAS),∴GH=EF,∴CF=EF+CE=HG+BD;(3)解:HG=CF+BD,理由是:如图3,在l上位于C点右侧取一点E,使∠AED=60°,连接AE,在l上取一点M,使BM=BD,∵∠BDC=60°,∴△BDM是等边三角形,∴∠DBM=60°,∴∠CBM+∠ABM=∠ABM+∠ABD,∴∠ABD=∠CBM,∵∠CAB=∠BDC=60°,∠ANC=∠DNB,∴∠ACE=∠ABD=∠CBM,∵∠ACE+∠BCE=∠ACE+∠CAE=60°,∴∠CAE=∠BCE,∵AC=BC,∴△ACE≌△CBM(ASA),∴CE=BM=BD,∵∠AFH=120°,∴∠AFC+∠GFH=∠AFC+∠FAE=60°,∴∠GFH=∠FAE,∵∠HGF=∠AEF=120°,AF=FH,∴△HGF≌△FEA(AAS),∴GH=FE,∵EF=CF+CE∴HG=CF+BD.故答案为:HG=CF+BD.15.解:(1)如答图1,①在△ACD与△ECD中,,∴△ACD≌△ECD(SAS);②由①知,△ACD≌△ECD,∴AD=DE,∠A=∠DEC,∵∠A=2∠B,∴∠DEC=2∠B,∴∠B=∠EDB,∴BE=DE,∴△BDE是等腰三角形;③由①知,△ACD≌△ECD,则EC=AC=3.6,DE=AD=2.2.又∵BE=DE,∴BE=AD=2.2.∴BC=BE+EC=2.2+3.6=5.8.故答案是:①△ACD≌△ECD;SAS;②等腰;③5.8;(2)∵△ABC中,AB=AC,∠A=20°,∴∠ABC=∠C=80°,∵BD平分∠B,∴∠1=∠2=40°∠BDC=60°,如答图2,在BA边上取点E,使BE=BC=2,连接DE,则△DEB≌△DBC,∴∠BED=∠C=80°,∴∠4=60°,∴∠3=60°,在DA边上取点F,使DF=DB,连接FE,则△BDE≌△FDE,∴∠5=∠1=40°,BE=EF=2,∵∠A=20°,∴∠6=20°,∴AF=EF=2,∵BD=DF=2.3,∴AD=BD+BC=4.3.。
2023年九年级数学中考压轴复习专题几何综合——添加辅助线

1
(2)若弦MN垂直于AB,垂足为G, = ,MN= 3,求⊙O的半径;
4
(3)在(2)的条件下,当∠BAC=36°时,求线段CE的长
【详解】
(3) 作∠ABC的平分线BF交AC于F,连接AD
∵∠BNC=36°,AB=AC
∴∠ABC=∠ACB=72°
∵BF平分∠ABC
∴∠ABF=∠CBP=36°
∴∠BFC=72°即∠BAF=∠ABF、
∠BFC=∠ACB
∴BC=BF=AF
∵∠CBF=∠BAC,∠C=∠C
∴△CBF∽△CAB
∴BC²=CF·AC
设BC=x则AF=x
∴CF=2-x
∴x²=2(2-x)解得:x=± 5 − 1
∴BC= 5 − 1
∴AB是⊙O的直径
∴∠ADB=90°
∵AB=AC
1
∴CD=BD= BC
【分析】①由旋转性质证明△ABD∽△ACE即可判断;
②由①的结论可得,∠ABD=∠ACE,进而得到∠BOC=∠CAB=45°,即可判断∠COD;
③证明△ABD为等腰三角形即可判断;
④由题意直线BD、CE相交于点O,当AD⊥AC时,△AOC的面积最大,通过勾股定理计
算求出最大值,进而进行判断
试炼场:
从而得出∠ODE=90°,即可得证DE是CO的切线;
3
1
(2)连接OM,先求出MG= ,得出OG= OM,最后用勾股定理求解,即可得
2
2
出结论;
(3)作∠ABC的平分线交AC于F,判断出△BCF∽△ACB,得出比例式求成
BC= 5 − 1,连接AD,再求出CD=
例式求解,即可得出结论
5−1
,再判断出△DEC∽△ADC,得出比
2019届中考数学(通用版)复习专题学案:几何综合题

几何综合题【题型特征】以几何知识为主体的综合题,简称几何综合题,主要研究图形中点与线之间的位置关系、数量关系,以及特定图形的判定和性质.一般以相似为中心,以圆为重点,常常是圆与三角形、四边形、相似三角形、锐角三角函数等知识的综合运用.【解题策略】解答几何综合题应注意:(1)注意观察、分析图形,把复杂的图形分解成几个基本图形,通过添加辅助线补全或构造基本图形.(2)掌握常规的证题方法和思路;(3)运用转化的思想解决几何证明问题,运用方程的思想解决几何计算问题.还要灵活运用其他的数学思想方法等.【小结】几何计算型综合问题,是以计算为主线综合各种几何知识的问题.这类问题的主要特点是包含知识点多、覆盖面广、逻辑关系复杂、解法灵活.解题时必须在充分利用几何图形的性质及题设的基础上挖掘几何图形中隐含的数量关系和位置关系,在复杂的“背景”下辨认、分解基本图形,或通过添加辅助线补全或构造基本图形,并善于联想所学知识,突破思维障碍,合理运用方程等各种数学思想才能解决.【提醒】几何论证型综合题以知识上的综合性引人注目.值得一提的是,在近年各地的中考试题中,几何论证型综合题的难度普遍下降,出现了一大批探索性试题,根据新课标的要求,减少几何中推理论证的难度,加强探索性训练,将成为几何论证型综合题命题的新趋势.为了复习方便,我们将几何综合题分为:以三角形为背景的综合题;以四边形为背景的综合题;以圆为背景的综合题.类型一以三角形为背景的综合题典例1(2019·江苏泰州)如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,EF∥AC.(1)求证:BE=AF;(2)若∠ABC=60°,BD=6,求四边形ADEF的面积.【技法梳理】(1)由DE∥AB,EF∥AC,可证得四边形ADEF是平行四边形,∠ABD=∠BDE,又由BD是△ABC的角平分线,易得△BDE是等腰三角形,即可证得结论;(2)首先过点D作DG⊥AB于点G,过点E作EH⊥BD于点H,易求得DG与DE的长,继而求得答案.【解析】(1)∵DE∥AB,EF∥AC,∴四边形ADEF是平行四边形,∠ABD=∠BDE.∴AF=DE.∵BD是△ABC的角平分线,∴∠ABD=∠DBE.∴∠DBE=∠BDE.∴BE=DE.∴BE=AF.(2)过点D作DG⊥AB于点G,过点E作EH⊥BD于点H,∵∠ABC=60°,BD是∠ABC的平分线,∴∠ABD=∠EBD=30°.∴DE=BE=2.∴四边形ADEF的面积为DE·DG=6.举一反三1. (2019·湖北武汉)如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm 的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.(1)若△BPQ与△ABC相似,求t的值;(2)连接AQ,CP,若AQ⊥CP,求t的值;(3)试证明:PQ的中点在△ABC的一条中位线上.(1)(2)(第1题)【小结】此类题考查了平行四边形的判定与性质、等腰三角形的判定与性质以及三角函数等知识.注意掌握辅助线的作法,注意掌握数形结合思想的应用.类型二以四边形为背景的综合题典例2(2019·安徽)如图(1),正六边形ABCDEF的边长为a,P是BC边上一动点,过P作PM∥AB交AF于M,作PN∥CD交DE于点N.(1)①∠MPN=;②求证:PM+PN=3a;(2)如图(2),点O是AD的中点,连接OM,ON,求证:OM=ON;(3)如图(3),点O是AD的中点,OG平分∠MON,判断四边形OMGN是否为特殊四边形?并说明理由.(1)(2)(3)【全解】(1)①∵四边形ABCDEF是正六边形,∴∠A=∠B=∠C=∠D=∠E=∠F=120°.∵PM∥AB,PN∥CD,∴∠BPM=60°,∠NPC=60°.∴∠MPN=180°-∠BPM-∠NPC=180°-60°-60°=60°.故答案为60°.②如图(1),作AG⊥MP交MP于点G,BH⊥MP于点H,CL⊥PN于点L,DK⊥PN于点K,(1)(2)如图(2),连接OE.(2)∵四边形ABCDEF是正六边形,AB∥MP,PN∥DC, ∴AM=BP=EN.又∠MAO=∠NOE=60°,OA=OE,在△ONE和△OMA中,∴△OMA≌△ONE(SAS).(3)如图(3),连接OE.(3)由(2)得,△OMA≌△ONE,∴∠MOA=∠EON.∵EF∥AO,AF∥OE,∴四边形AOEF是平行四边形.∴∠AFE=∠AOE=120°.∴∠MON=120°.∴∠GON=60°.∵∠GON=60°-∠EON,∠DON=60°-∠EON,∴∠GOE=∠DON.∵OD=OE,∠ODN=∠OEG,在△GOE和∠DON中,∴△GOE≌△NOD(ASA).又∠GON=60°,∴△ONG是等边三角形.∴ON=NG.∵OM=ON,∠MOG=60°,∴△MOG是等边三角形.∴MG=GO=MO.∴MO=ON=NG=MG.∴四边形MONG是菱形.【技法梳理】(1)①运用∠MPN=180°-∠BPM-∠NPC求解,②作AG⊥MP交MP于点G,BH⊥MP于点H,CL⊥PN于点L,DK⊥PN于点K,利用MP+PN=MG+GH+HP+PL+LK+KN求解;(2)连接OE,由△OMA≌△ONE证明;(3)连接OE,由△OMA≌△ONE,再证出△GOE≌△NOD,由△ONG是等边三角形和△MOG是等边三角形求出四边形MONG是菱形.举一反三2. (2019·山东烟台)在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.(1)如图(1),当点E自D向C,点F自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的位置关系,并说明理由.(2)如图(2),当E,F分别移动到边DC,CB的延长线上时,连接AE和DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不需证明)(3)如图(3),当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?请说明理由.(4)如图(4),当E,F分别在边DC,CB上移动时,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP的最小值.(1)(2)(3)(4)(第2题)【小结】主要考查了四边形的综合题,解题的关键是恰当的作出辅助线,根据三角形全等找出相等的线段.类型三以圆为背景的综合题典例3(2019·江苏苏州)如图,已知l1⊥l2,☉O与l1,l2都相切,☉O的半径为2cm,矩形ABCD的边AD,AB分别与l1,l2重合,AB=4cm,AD=4cm,若☉O与矩形ABCD沿l1同时向右移动,☉O的移动速度为3cm,矩形ABCD的移动速度为4cm/s,设移动时间为t(s),(1)如图,连接OA,AC,则∠OAC的度数为°;(2)如图,两个图形移动一段时间后,☉O到达☉O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1,A1,C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);(3)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm),当d<2时,求t的取值范围(解答时可以利用备用图画出相关示意图).【全解】(1)∵l1⊥l2,☉O与l1,l2都相切,∴∠OAD=45°.∵AB=4cm,AD=4cm,∴CD=4cm,AD=4cm.∴∠DAC=60°.∴∠OAC的度数为∠OAD+∠DAC=105°.(2)如图位置二,当O1,A1,C1恰好在同一直线上时,设☉O1与l1的切点为点E, 连接O1E,可得O1E=2,O1E⊥l1,在Rt△A1D1C1中,∵A1D1=4,C1D1=4,∴tan∠C1A1D1=.∴∠C1A1D1=60°.∴OO1=3t=2+6.(3)①当直线AC与☉O第一次相切时,设移动时间为t1,如图,此时☉O移动到☉O2的位置,矩形ABCD移动到A2B2C2D2的位置,设☉O2与直线l1,A2C2分别相切于点F,G,连接O2F,O2G,O2A2,∴O2F⊥l1,O2G⊥A2G2.由(2)得,∠C2A2D2=60°,∴∠GA2F=120°.∴∠O2A2F=60°.在Rt△A2O2F中,O2F=2,②当直线AC与☉O第二次相切时,设移动时间为t2,记第一次相切时为位置一,点O1,A1,C1共线时为位置二,第二次相切时为位置三, 由题意知,从位置一到位置二所用时间与位置二到位置三所用时间相等,【提醒】本题主要考查了切线的性质以及锐角三角函数关系等知识,利用分类讨论以及数形结合t的值是解题关键.【技法梳理】(1)利用切线的性质以及锐角三角函数关系分别求出∠OAD=45°,∠DAC=60°,进而得出答案;(2)首先得出,∠C1A1D1=60°,再利用A1E=AA1-OO1-2=t-2,求出t的值,进而得出OO1=3t得出答案即可;(3)①当直线AC与☉O第一次相切时,设移动时间为t1,②当直线AC与☉O第二次相切时,设移动时间为t2,分别求出即可.举一反三3. (2019·浙江宁波)木匠黄师傅用长AB=3,宽BC=2的矩形木板做一个尽可能大的圆形桌面,他设计了四种方案:方案一:直接锯一个半径最大的圆;方案二:圆心O1,O2分别在CD,AB上,半径分别是O1C,O2A,锯两个外切的半圆拼成一个圆;方案三:沿对角线AC将矩形锯成两个三角形,适当平移三角形并锯一个最大的圆;方案四:锯一块小矩形BCEF拼到矩形AFED下面,利用拼成的木板锯一个尽可能大的圆.(1)写出方案一中圆的半径.(2)通过计算说明方案二和方案三中,哪个圆的半径较大?(3)在方案四中,设CE=x(0<x<1),圆的半径为y.①求y关于x的函数表达式;②当x取何值时圆的半径最大,最大半径为多少?并说明四种方案中哪一个圆形桌面的半径最大.方案一方案二方案三方案四方案备用图方案备用图(第3题)【小结】本题考查了圆的基本性质及通过勾股定理、三角形相似等性质求解边长及分段函数的表示与性质讨论等内容,题目虽看似新颖不易找到思路,但仔细观察每一小问都是常规的基础考点,所以总体来说是一道质量很高的题目,值得认真练习.类型一2. (2019·浙江嘉兴)如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB 上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为2;③当AD=2时,EF与半圆相切;④若点F恰好落在上,则AD=2;⑤当点D从点A运动到点B时,线段EF扫过的面积是16.其中正确结论的序号是.(第2题)类型二3. (2019·广东珠海)如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连接EF与边CD相交于点G,连接BE与对角线AC相交于点H,AE=CF,BE=EG.(1)求证:EF∥AC;(2)求∠BEF大小;.(第3题)4. (2019·浙江温州)如图,在平面直角坐标系中,点A,B的坐标分别为(-3,0),(0,6).动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造▱PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.(1)当点C运动到线段OB的中点时,求t的值及点E的坐标.(2)当点C在线段OB上时,求证:四边形ADEC为平行四边形.(3)在线段PE上取点F,使PF=1,过点F作MN⊥PE,截取FM=2,FN=1,且点M,N分别在一,四象限,在运动过程中▱PCOD的面积为S.①当点M,N中有一点落在四边形ADEC的边上时,求出所有满足条件的t的值;②若点M,N中恰好只有一个点落在四边形ADEC的内部(不包括边界)时,直接写出S的取值范围.(第4题)类型三5. (2019·湖南怀化)如图,E是长方形ABCD的边AB上的点,EF⊥DE交BC于点F.(1)求证:△ADE∽△BEF;(2)设H是ED上一点,以EH为直径作☉O,DF与☉O相切于点G,若DH=OH=3,求图中阴影部分的面积(结果保留到小数点后面第一位,≈1.73,π≈3.14).(第5题)6. (2019·黑龙江大庆)如图(1),已知等腰梯形ABCD的周长为48,面积为S,AB∥CD,∠ADC=60°,设AB=3x.(1)用x表示AD和CD;(2)用x表示S,并求S的最大值;(3)如图(2),当S取最大值时,等腰梯形ABCD的四个顶点都在☉O上,点E和点F分别是AB 和CD的中点,求☉O的半径R的值.(1)(2)(第6题)参考答案【真题精讲】(2)如图(1),过P作PM⊥BC于点M,AQ,CP交于点N,则有PB=5t,PM=3t,MC=8-4t,(第1题(1))∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,∴∠NAC=∠PCM且∠ACQ=∠PMC=90°.∴△ACQ∽△CMP.(3)如图(2),仍有PM⊥BC于点M,PQ的中点设为点D,再作PE⊥AC于点E,DF⊥AC于点F,(第1题(2))∵∠ACB=90°,∴DF为梯形PECQ的中位线.∵BC=8,过BC的中点R作直线平行于AC,∴RC=DF=4成立.∴D在过R的中位线上.∴PQ的中点在△ABC的一条中位线上.2. (1)AE=DF,AE⊥DF.理由:∵四边形ABCD是正方形,∴AD=DC,∠ADC=∠C=90°.∵DE=CF,∴△ADE≌△DCF.∴AE=DF,∠DAE=∠CDF.由于∠CDF+∠ADF=90°.∴∠DAE+∠ADF=90°.∴AE⊥DF;(2)是.(3)成立.理由如下:由(1)同理可证AE=DF,∠DAE=∠CDF,如图(1),延长FD交AE于点G,(第2题(1))则∠CDF+∠ADG=90°,∴∠ADG+∠DAE=90°.∴AE⊥DF;(4)如图(2):(第2题(2)) 由于点P在运动中保持∠APD=90°,∴点P的路径是一段以AD为直径的弧,设AD的中点为O,连接OC交弧于点P,此时CP的长度最小,在Rt△ODC中,OC===,∴CP=OC-OP=-1.3. (1)方案一中的最大半径为1.分析如下:因为长方形的长宽分别为3,2,那么直接取圆直径最大为2,则半径最大为1.(2)如图(1),方案二中连接O1,O2,过O1作O1E⊥AB于E,方案三中,过点O分别作AB,BF的垂线,交于M,N,此时M,N恰为☉O与AB,BF的切点.方案二方案三(第3题)方案二:设半径为r.在Rt△O1O2E中,∵O1O2=2r,O1E=BC=2,O2E=AB-AO1-CO2=3-2r,∴(2r)2=22+(3-2r)2,比较知,方案三半径较大.(3)①∵EC=x,∴新拼图形水平方向跨度为3-x,竖直方向跨度为2+x.类似题(1),所截出圆的直径最大为3-x或2+x较小的.∴方案四时可取的圆桌面积最大.【课后精练】1.①②③④解析:①∵AB=AC,∴∠B=∠C.∵∠ADE=∠B,∴∠ADE=∠C.∴△ADE∽△ACD.故①结论正确.故③正确.④易证得△CDE∽△BAD,由②可知BC=16, 设BD=y,CE=x,整理,得y2-16y+64=64-10x,即(y-8)2=64-10x,∴0<y<8,0<x<6.4.故④正确.2.①③⑤解析:①连接CD,如图(1)所示.(第2题(1))∵点E与点D关于AC对称,∴CE=CD.∴∠E=∠CDE.∵DF⊥DE,∴∠EDF=90°.∴∠E+∠F=90°,∠CDE+∠CDF=90°.∴∠F=∠CDF.∴CD=CF.∴CE=CD=CF.∴结论“CE=CF”正确.②当CD⊥AB时,如图(2)所示.(第2题(2))∵AB是半圆的直径,∴∠ACB=90°.∵AB=8,∠CBA=30°,∴∠CAB=60°,AC=4,BC=4.∵CD⊥AB,∠CBA=30°,根据“点到直线之间,垂线段最短”可得:点D在线段AB上运动时,CD的最小值为2.∵CE=CD=CF,∴EF=2CD.∴线段EF的最小值为4.∴结论“线段EF的最小值为2”错误.③当AD=2时,连接OC,如图(3)所示.(第2题(3))∵OA=OC,∠CAB=60°,∴△OAC是等边三角形.∴CA=CO,∠ACO=60°.∵AO=4,AD=2,∴DO=2.∴AD=DO.∴∠ACD=∠OCD=30°.∵点E与点D关于AC对称,∴∠ECA=∠DCA.∴∠ECA=30°.∴∠ECO=90°.∴OC⊥EF.∵EF经过半径OC的外端,且OC⊥EF,∴EF与半圆相切.∴结论“EF与半圆相切”正确.④当点F恰好落在上时,连接FB,AF,如图(4)所示.(第2题(4))∵点E与点D关于AC对称,∴ED⊥AC.∴∠AGD=90°.∴∠AGD=∠ACB.∴ED∥BC.∴△FHC∽△FDE.∴DB=4.∴AD=AB-DB=4.∴结论“AD=2”错误.⑤∵点D与点E关于AC对称,点D与点F关于BC对称,∴当点D从点A运动到点B时,点E的运动路径AM与AB关于AC对称,点F的运动路径NB与AB关于BC对称.∴EF扫过的图形就是图(5)中阴影部分.(第2题(5))∴EF扫过的面积为16.∴结论“EF扫过的面积为16”正确.3. (1)∵四边形ABCD是正方形,∴AD∥BF.∵AE=CF,∴四边形ACFE是平行四边形.∴EF∥AC.(2)连接BG,(第3题)∵EF∥AC,∴∠F=∠ACB=45°.∵∠GCF=90°,∴∠CGF=∠F=45°.∴CG=CF.∵AE=CF,∴AE=CG.在△BAE与△BCG中,∴△BAE≌△BCG(SAS).∴BE=BG.∵BE=EG,∴△BEG是等边三角形.∴∠BEF=60°.(3)∵△BAE≌△BCG,∴∠ABE=∠CBG.∵∠BAC=∠F=45°,∴△AHB∽△FGB.(2)如图(1),连接CD交OP于点G,(第4题(1))在▱PCOD中,CG=DG,OG=PG,∵AO=PO,∴AG=EG.∴四边形ADEC是平行四边形.(3)①(Ⅰ)当点C在BO上时,第一种情况:如图(2),当点M在CE边上时,(第4题(2))∵MF∥OC,∴△EMF∽△ECO.∴t=1.第二种情况:如图(3),当点N在DE边(第4题(3))∵NF∥PD,∴△EFN∽△EPD.(Ⅱ)当点C在BO的延长线上时,第一种情况:如图(4),当点M在DE边上时,(第4题(4))∵MF∥PD,∴EMF∽△EDP.第二种情况:如图(5),当点N在CE边上时,(第4题(5))∵NF∥OC,∴△EFN∽△EOC.5. (1)∵四边形ABCD是矩形, ∴∠A=∠B=90°.∵EF⊥DE,∴∠DEF=90°.∴∠AED=90°-∠BEF=∠EFB.∵∠A=∠B,∠AED=∠EFB,∴△ADE∽△BEF.(2)∵DF与☉O相切于点G, ∴OG⊥DG.∴∠DGO=90°.∵DH=OH=OG,∴∴图中阴影部分的面积约为6.2.6. (1)作AH⊥CD于点H,BG⊥CD于点G,如图(1),(第6题(1))则四边形AHGB为矩形,∴HG=AB=3x.∵四边形ABCD为等腰梯形,∴AD=BC,DH=CG.在Rt△ADH中,设DH=t,∵∠ADC=60°,∴∠DAH=30°.∴AD=2t,AH=t.∴BC=2t,CG=t.∵等腰梯形ABCD的周长为48,∴3x+2t+t+3x+t+2t=48,解得t=8-x.∴AD=2(8-x)=16-2x,CD=8-x+3x+8-x=16+x.(3)连接OA,OD,如图(2),(第6题(2))当x=2时,AB=6,CD=16+2=18,等腰梯形的高为(8-2)=6, 则AE=3,DF=9,∵点E和点F分别是AB和CD的中点,∴直线EF为等腰梯形ABCD的对称轴.∴EF垂直平分AB和CD,EF为等腰梯形ABCD的高,即EF=6.∴等腰梯形ABCD的外接圆的圆心O在EF上.设OE=a,则OF=6-a.在Rt△AOE中,∵OE2+AE2=OA2,∴a2+32=R2.在Rt△ODF中,∵OF2+DF2=OD2,∴(6-a)2+92=R2.∴a2+32=(6-a)2+92,解得a=5.∴R2=(5)2+32=84.∴R=2.。
【北师大版2020中考数学专项复习】:几何综合题

【北师大版2020中考数学专项复习】:几何综合问题【中考展望】几何综合题是中考试卷中常见的题型,大致可分为几何计算型综合题与几何论证型综合题,它主要考查学生综合运用几何知识的能力.这类题型在近几年全国各地中考试卷中占有相当的分量,不仅有选择题、填空题、几何推理计算题以及代数与几何的综合计算题,还有更注重考查学生分析问题和解决问题能力的探究性的问题、方案设计的问题等等.主要特点是图形较复杂,覆盖面广、涉及的知识点较多,题设和结论之间的关系较隐蔽,常常需要添加辅助线来解答.几何综合题的呈现形式多样,如折叠类型、探究型、开放型、运动型、情景型等,背景鲜活,具有实用性和创造性,考查方式偏重于考查考生分析问题、探究问题、综合应用数学知识解决实际问题的能力.以几何为主的综合题常常在一定的图形背景下研究以下几个方面的问题:1、证明线段、角的数量关系(包括相等、和、差、倍、分及比例关系等);2、证明图形的位置关系(如点与线、线与线、线与圆、圆与圆的位置关系等);3、几何计算问题;4、动态几何问题等.【方法点拨】一、几何计算型综合问题,常常涉及到以下各部分的知识:1、与三角形有关的知识;2、等腰三角形,等腰梯形的性质;3、直角三角形的性质与三角函数;4、平行四边形的性质;5、全等三角形,相似三角形的性质;6、垂径定理,切线的性质,与正多边形有关的计算;7、弧长公式与扇形面积公式.二、几何论证型综合题的解答过程,要注意以下几个方面:1、注意图形的直观提示,注意观察、分析图形,把复杂的图形分解成几个基本图形,通过添加辅助线补全或构造基本图形;2、注意分析挖掘题目的隐含条件、发展条件,为解题创造条件打好基础,要由已知联想经验,由未知联想需要,不断转化条件和结论来探求思路,找到解决问题的突破点;3、要运用转化的思想解决几何证明问题,运用方程的思想解决几何计算问题,还要灵活运用 数学思想方法如数形结合、分类讨论、转化、方程等思想来解决问题.【典型例题】类型一、动态几何型问题1.已知正方形中,为对角线上一点,过点作交于,连接,为中点,连接.(1)直接写出线段与的数量关系;(2)将图1中绕点逆时针旋转,如图2所示,取中点,连接,你在(1)中得到的结论是否发生变化?写出你的猜想并加以证明.(3)将图1中绕点旋转任意角度,如图3所示,再连接相应的线段,问(1)中的结论是否仍然成立?(不要求证明)【思路点拨】本题的核心条件就是G 是中点,中点往往暗示很多的全等关系,如何构建一对我们想要的全等三角形就成为了分析的关键所在.连接AG 之后,抛开其他条件,单看G 点所在的四边形ADFE ,我们会发现这是一个梯形,于是根据我们在第一讲专题中所讨论的方法,自然想到过G 点做AD,EF 的垂线.于是两个全等的三角形出现了.第三问在△BEF 的旋转过程中,始终不变的依然是G 点是FD 的中点.可以延长一倍EG 到H ,从而构造一个和EFG 全等的三角形,利用BE=EF 这一条件将全等过渡.要想办法证明三角形ECH 是一个等腰直角三角形,就需要证明三角形EBC 和三角形CGH 全等,利用角度变换关系就可以得证了.【答案与解析】ABCD E BD E EF BD ⊥BC F DF G DF EG CG ,EG CG BEF ∆B 45︒DF G EG CG ,BEF ∆B 图3图2 图1F EA B C D A B C D E FG GF E DC BA(1)(2)(1)中结论没有发生变化,即.证明:连接,过点作于,与的延长线交于点.在与中,∵,∴.∴.在与中,∵, ∴.∴在矩形中,在与中,∵, ∴.∴.∴(3)(1)中的结论仍然成立.CG EG =CG EG =AG G MN AD ⊥M EF N DAG ∆DCG ∆AD CD ADG CDG DG DG =∠=∠=,,DAG DCG ∆∆≌AG CG =DMG ∆FNG ∆DGM FGN FG DG MDG NFG ∠=∠=∠=∠,,DMG FNG ∆∆≌MG NG =AENM AM EN =Rt AMG ∆Rt ENG ∆AM EN MG NG ==,AMG ENG ∆∆≌AG EG =EG CG =MN图2A BC D E F G【总结升华】本题是一道典型的从特殊到一般的图形旋转题.从旋转45°到旋转任意角度,要求讨论其中的不变关系.举一反三:【变式】已知:如图(1),射线射线,是它们的公垂线,点、分别在、 上运动(点与点不重合、点与点不重合),是边上的动点(点与、不重合), 在运动过程中始终保持,且.(1)求证:∽;(2)如图(2),当点为边的中点时,求证:;(3)设,请探究:的周长是否与值有关?若有关,请用含有的代数式表示 的周长;若无关,请说明理由.【答案】 (1)证明:∵,∴.∴.又∵,∴.∴.∴∽.(2)证明:如图,过点作,交于点,G图3F E ABCD//AM BN AB D C AM BN D A C B E AB E A B EC DE ⊥a AB DE AD ==+ADE ∆BEC ∆E AB CD BC AD =+m AE =BEC ∆m m BEC∆EC DE ⊥︒=∠90DEC ︒=∠+∠90BEC AED ︒=∠=∠90B A ︒=∠+∠90EDA AED EDA BEC ∠=∠ADE ∆BEC ∆E EF BC //CD F∵是的中点,容易证明. 在中,∵ ,∴ . ∴ . ∴ .(3)解:的周长,.设,则.∵ ,∴ .即.∴ . 由(1)知∽,∴ . ∴ 的周长的周长. ∴ 的周长与值无关.2.在△ABC 中,∠ACB=45º.点D (与点B 、C 不重合)为射线BC 上一动点,连接AD ,以AD为一E AB )(21BC AD EF +=DEC Rt ∆CF DF =CD EF 21=)(21BC AD +CD 21=CD BC AD =+AED ∆DE AD AE ++=m a +=m a BE -=x AD =x a DE -=︒=∠90A 222AD AE DE +=22222x m x ax a +=+-am a x 222-=ADE ∆BEC ∆的周长的周长BEC ∆∆ADE BEAD =m a a m a --=222a m a 2+=BEC ∆⋅+=m a a 2ADE ∆a 2=BEC ∆m边且在AD 的右侧作正方形ADEF .(1)如果AB=AC .如图①,且点D 在线段BC 上运动.试判断线段CF 与BD 之间的位置关系,并证明你的结论.(2)如果AB ≠AC ,如图②,且点D 在线段BC 上运动.(1)中结论是否成立,为什么?(3)若正方形ADEF 的边DE 所在直线与线段CF 所在直线相交于点P ,设AC =,,CD=,求线段CP 的长.(用含的式子表示)【思路点拨】(1)由题干可以发现,正方形中四条边的垂直关系是不动的,于是利用角度的互余关系进行传递,就可以得解.(2)是典型的从特殊到一般的问法,那么思路很简单,就是从一般中构筑一个特殊的条件就行,和上题一样找AC 的垂线,就可以变成第一问的条件,然后一样求解.(3)D 在BC 之间运动和它在BC 延长线上运动时的位置是不一样的,所以已给的线段长度就需要分情况去考虑到底是4+X 还是4-X.分类讨论之后利用相似三角形的比例关系即可求出CP.【答案与解析】(1)结论:CF ⊥BD ;证明如下:AB=AC ,∠ACB =45º,∴∠ABC=45º.由正方形ADEF 得 AD=AF ,∵∠DAF=∠BAC =90º,∴∠DAB=∠FAC ,∴△DAB ≌△FAC , ∴∠ACF=∠ABD .∴∠BCF=∠ACB+∠ACF= 90º.即 CF ⊥BD .(2)CF ⊥BD .(1)中结论仍成立.理由是:过点A 作AG ⊥AC 交BC 于点G ,∴AC=AG可证:△GAD ≌△CAF ∴∠ACF=∠AGD=45º∠BCF=∠ACB+∠ACF= 90º. 即CF ⊥BD3 BC xx(3)过点A 作AQ ⊥BC 交CB 的延长线于点Q ,①点D 在线段BC 上运动时,∵∠BCA=45º,可求出AQ= CQ=4.∴DQ=4-x ,易证△AQD ∽△DCP ,∴ ,∴, .②点D 在线段BC 延长线上运动时,∵∠BCA=45°,∴AQ=CQ=4,∴DQ=4+x .过A 作AQ ⊥BC ,∴∠Q=∠FQC=90°,∠ADQ=∠AFC ,则△AQD ∽△ACF .∴CF ⊥BD ,∴△AQD ∽△DCP ,∴, ∴, CP CD DQ AQ =44CP x x =-24x CP x ∴=-+CD DQ AQ 4+4x x =. 【总结升华】此题综合性强,需要综合运用全等、相似、正方形等知识点,属能力拔高性的题目.3.已知正方形ABCD 的边长为6cm ,点E 是射线BC 上的一个动点,连接AE 交射线DC 于点F ,将△ABE 沿直线AE 翻折,点B 落在点B′ 处.(1)当=1 时,CF=______cm , (2)当=2 时,求sin∠DAB′ 的值; (3)当= x 时(点C 与点E 不重合),请写出△ABE 翻折后与正方形ABCD 公共部分的面积y 与x 的关系式,(只要写出结论,不要解题过程).【思路点拨】动态问题未必只有点的平移、图形的旋转,翻折(即轴对称)也是一大热点.(1)给出比例为1,(2)比例为2,(3)比例任意,所以也是一道很明显的从一般到特殊的递进式题目.需要仔细把握翻折过程中哪些条件发生了变化,哪些条件没有发生变化.一般说来,翻折中,角,边都是不变的,所以轴对称图形也意味着大量全等或者相似关系,所以要利用这些来获得线段之间的比例关系.尤其要注意的是,本题中给定的比例都是有两种情况的,E 在BC 上和E 在延长线上都是可能的,所以需要分类讨论,不要遗漏.【答案与解析】(1)CF=6cm ;(2)① 如图1,当点E 在BC 上时,延长AB ′交DC 于点M ,24x CP x ∴=+CE BE CE BE CEBE 图1∵ AB ∥CF ,∴ △ABE ∽△FCE ,∴ . ∵ =2, ∴ CF=3. ∵ AB ∥CF ,∴∠BAE=∠F .又∠BAE=∠B ′ AE , ∴ ∠B ′ AE=∠F .∴ MA=MF .设MA=MF=k ,则MC=k -3,DM=9-k .在Rt △ADM 中,由勾股定理得:k 2=(9-k)2+62, 解得 k=MA=. ∴ DM=. ∴ sin ∠DAB ′=; ②如图2,当点E 在BC 延长线上时,延长AD 交B ′ E 于点N ,FCAB CE BE =CE BE 13252135=AM DM图2同①可得NA=NE .设NA=NE=m ,则B ′ N=12-m .在Rt △AB ′ N 中,由勾股定理,得m 2=(12-m)2+62, 解得 m=AN=. ∴ B ′N=. ∴ sin ∠DAB ′=. (3)①当点E 在BC 上时,y=; ②当点E 在BC 延长线上时,y=. 【总结升华】动态几何问题当中有点动,线动,乃至整体图形动几种可能的方式,动态几何问题往往作为压轴题出现,所以难度不言而喻,但是拿到题后不要慌张,因为无论是题目以哪种形式出现,始终把握的都是在变化过程中那些不变的量.只要一个个将条件抽出来,将大问题化成若干个小问题去解决,就很轻松了.类型二、几何计算型问题4.已知如图,在梯形中,点是的中点,是等边三角形.(1)求证:梯形是等腰梯形;(2)动点、分别在线段和上运动,且保持不变.设 求与的函数关系式;(3)在(2)中,当取最小值时,判断的形状,并说明理由.【思路点拨】(1)属于纯静态问题,只要证两边的三角形全等就可以了.(2)是双动点问题,所以就需要研究在P,Q 运动过程中什么东西是不变的.题目给定∠MPQ=60°,其实就1529253='AN N B 18x x 1+18x 18x -ABCD 24AD BC AD BC ==∥,,,M AD MBC △ABCD P Q BC MC 60MPQ =︒∠PC x MQ y ==,,y x y PQC△是将静态的那个等边三角形与动态条件联系了起来.因为最终求两条线段的关系,所以很自然想到要通过相似三角形找比例关系.(3)条件又回归了当动点静止时的问题,由第二问所得的二次函数,很轻易就可以求出当x 取对称轴的值时y 有最小值,接下来就变成了“给定PC=2,求△PQC 形状”的问题了,由已知的BC=4,自然看出P 是中点,于是问题轻松求解.【答案与解析】(1)证明:∵是等边三角形∴∵是中点∴∵∴∴∴∴梯形是等腰梯形.(2)解:在等边中, ∴ ∴∴∴ ∵ ∴∴ ∴MBC △60MB MC MBC MCB ===︒,∠∠M AD AM MD =AD BC ∥60AMB MBC ==︒∠∠,60DMC MCB ==︒∠∠AMB DMC △≌△AB DC =ABCD MBC △4MB MC BC ===,60MBC MCB ==︒∠∠,60MPQ =︒∠120BMP BPM BPM QPC +=+=︒∠∠∠∠BMP QPC =∠∠BMP CQP △∽△PC CQ BM BP=PC x MQ y ==,44BP x QC y =-=-,444x y x -=-2144y x x =-+(3)解:为直角三角形,∵ ∴当取最小值时,∴是的中点,而∴∴∴为直角三角形.【总结升华】以上题目是动点问题,这一类问题的关键就在于当动点移动中出现特殊条件,例如某边相等,某角固定时,将动态问题化为静态问题去求解.如果没有特殊条件,那么就需要研究在动点移动中哪些条件是保持不变的.举一反三:【高清课堂:几何综合问题 例3】【变式】已知:如图,N 、M 是以O 为圆心,1为半径的圆上的两点,B 是上一动点(B 不与点M 、N 重合),∠MON=90°,BA ⊥OM 于点A ,BC ⊥ON 于点C ,点D 、E 、F 、G 分别是线段OA 、AB 、BC 、CO 的中点,GF 与CE 相交于点P ,DE 与AG 相交于点Q .(1)四边形EPGQ (填“是”或者“不是”)平行四边形;(2)若四边形EPGQ 是矩形,求OA 的值.PQC △()21234y x =-+y 2x PC ==P BC MP BC ⊥,60MPQ =︒∠,30CPQ =︒∠,90PQC =︒∠PQC △MN【答案】(1)是.证明:连接OB,如图①,∵BA⊥OM,BC⊥ON,∴∠BAO=∠BCO=90°,∵∠AOC=90°,∴四边形OABC是矩形.∴AB∥OC,AB=OC,∵E、G分别是AB、CO的中点,∴AE∥GC,AE=GC,∴四边形AECG为平行四边形.∴CE∥AG,∵点D、E、F、G分别是线段OA、AB、BC、CO的中点,∴GF∥OB,DE∥OB,∴PG∥EQ,∴四边形EPGQ是平行四边形;(2)解:如图②,∵口EPGQ 是矩形. ∴∠AED+∠CEB=90°.又∵∠DAE=∠EBC=90°,∴∠AED=∠BCE .∴△AED ∽△BCE ,∴, 设OA=x ,AB=y ,则 得y 2=2x 2,又∵OA 2+AB 2=OB 2, 即x 2+y 2=12.∴x 2+2x 2=1,解得:x=. 即当四边形EPGQ 是矩形时,OA 的长度为. 5.在中,过点C 作CE ⊥CD 交AD 于点E,将线段EC 绕点E 逆时针旋转得到线段EF (如图1)(1)在图1中画图探究:①当P 为射线CD 上任意一点(P 1不与C 重合)时,连结EP 1绕点E 逆时针旋转 得到线段EC 1.判断直线FC 1与直线CD 的位置关系,并加以证明;②当P 2为线段DC 的延长线上任意一点时,连结EP 2,将线段EP 2绕点E 逆时针旋转得到线段EC 2.判断直线C 1C 2与直线CD 的位置关系,画出图形并直接写出你的结论.AD AE BE BC=::222x y y x =3333ABCD 909090(2)若AD=6,tanB=,AE=1,在①的条件下,设CP 1=,S =,求与之间的函数关系式,并写出自变量的取值范围.图1 备用图【思路点拨】(1)本题在于如何把握这个旋转90°的条件.旋转90°自然就是垂直关系,于是出现了一系列直角三角形,于是证角、证线就手到擒来了.(2)是利用平行关系建立函数式,但是不要忘记分类讨论.【答案与解析】(1)①直线与直线的位置关系为互相垂直.证明:如图1,设直线与直线的交点为.∵线段分别绕点逆时针旋转90°依次得到线段,∴.∵,, ∴. 43x 11P FC y y xx 1FG CD 1FG CD H 1EC EP 、E 1EF EG 、111190PEG CEF EG EP EF EC ∠=∠===°,,1190G EF PEF ∠=-∠°1190PEC PEF ∠=-∠°11G EF PEC ∠=∠FDC BAE 图1 G 2 G 1P 1 H P 2∴. ∴. ∵,∴, ∴.∴.∴.∴.②按题目要求所画图形见图1,直线与直线的位置关系为互相垂直.(2)∵四边形是平行四边形,∴.∵, ∴. 可得.由(1)可得四边形为正方形.∴.①如图2,当点在线段的延长线上时,11G EF PEC △≌△11G FE PCE ∠=∠EC CD ⊥190PCE ∠=°190G FE ∠=°90EFH ∠=°90FHC ∠=°1FG CD ⊥12G G CD ABCD B ADC ∠=∠461tan 3AD AE B ===,,45tan tan 3DE EBC B =∠==,4CE =EFCH 4CH CE ==1P CH∵, ∴. ∴. ②如图3,当点在线段上(不与两点重合)时,∵, ∴. ∴. ③当点与点重合时,即时,不存在.1114FG CP x PH x ===-,11111(4)22P FG x x S FG PH -=⨯⨯=△212(4)2y x x x =->1P CH C H 、1114FG CP x PH x ===-,11111(4)22P FG x x S FG PH -=⨯=△212(04)2y x x x =-+<<1P H 4x =11PFG △综上所述,与之间的函数关系式及自变量的取值范围是或. 【总结升华】本题着重考查了二次函数的解析式、图形的旋转变换、三角形全等、探究垂直的构成情况等重要知识点,综合性强,能力要求较高.考查学生分类讨论,数形结合的数学思想方法. 举一反三:【变式】已知,点P 是∠MON 的平分线上的一动点,射线PA 交射线OM 于点A ,将射线PA 绕点P 逆时针旋转交射线ON 于点B ,且使∠APB+∠MON=180°.(1)利用图1,求证:PA=PB ;(2)如图2,若点C 是AB 与OP 的交点,当S △POB =3S △PCB 时,求PB 与PC 的比值;(3)若∠MON=60°,OB=2,射线AP 交ON 于点D ,且满足且∠PBD=∠ABO ,请借助图3补全图形,并求OP 的长.【答案】(1)作PE ⊥OM,PF ⊥ON ,垂足为E 、F∵四边形OEPF 中,∠OEP=∠OFP=90°,∴∠EPF+∠MON=180°,已知∠APB+∠MON=180°,∴∠EPF=∠APB ,即∠EPA+∠APF=∠APF+∠FPB ,∴∠EPA=∠FPB ,由角平分线的性质,得PE=PF ,∴△EPA ≌△FPB ,即PA=PB ;y x x 212(4)2y x x x =->212(04)2y x x x =-+<<(2)∵S △POB =3S △PCB ,∴PO=3PC ,又∵∠BPC=∠OPB (公共角),∴△PBC ∽△POB ,即PB 2=PO •PC=3PC 2,(3)作BH ⊥OT ,垂足为H ,当∠MON=60°时,∠APB=120°,又∵∠PBD=∠ABO ,∠PBD+∠PBA+∠ABO=180°,在△OBP 中,∵∠BOP=30°,∴∠BPO=45°,在Rt △PBH 中,PH=BH=1,中考冲刺:几何综合问题—巩固练习(提高)【巩固练习】一、选择题1.如图,直角三角板ABC 的斜边AB=12cm ,∠A=30°,将三角板ABC 绕C 顺时针旋转90°至三角板A ′B ′C ′的位置后,再沿CB 方向向左平移,使点B ′落在原三角板ABC 的斜边AB 上,则三角板A ′B ′C ′平移的距离为( )A.6cmB.4cmC.cmD.cm2.如图,△ABC 和△DEF 是等腰直角三角形,∠C=∠F=90°,AB=2,DE=4.点B 与点D 重合,点A ,B (D ),E 在同一条直线上,将△ABC 沿DE 方向平移,至点A 与点E 重合时停止.设点B ,D 之间的距离为x ,△ABC 与△DEF 重叠部分的面积为y ,则准确反映y 与x 之间对应关系的图象是( )A B C D二、填空题3.如图,将两块直角三角板的斜边重合,E 是两直角三角形公共斜边AC 的中点.D 、B 分别为直角顶点,连接DE 、BE 、DB ,∠DAC=60°,∠BAC=45°.则∠EDB 的度数为_______.4.如图,一块直角三角形木板△ABC ,将其在水平面上沿斜边AB 所在直线按顺时针方向翻滚,使它滚动(6-()6cm .三、解答题5.如图,在正方形ABCD 中,对角线AC 与BD 相交于点E ,AF 平分∠BAC ,交BD 于点F.(1)EF+AC =AB ; (2)点C 1从点C 出发,沿着线段CB 向点B 运动(不与点B 重合),同时点A 1从点A 出发,沿着BA 的延长线运动,点C 1与点A 1运动速度相同,当动点C 1停止运动时,另一动点A 1也随之停止运动.如图,AF 1平分∠B A 1 C 1,交BD 于F 1,过F 1作F 1E 1⊥A 1 C 1,垂足为E 1,试猜想F 1E 1,A 1 C 1与AB 之间的数量关系,并证明你的猜想.(3)在(2)的条件下,当A 1 E 1=3,C 1 E 1=2时,求BD 的长.21216.如图,等腰Rt△ABC 中,∠C=90°,AC=6,动点P 、Q 分别从A 、B 两点同时以每秒1个单位长的速度按顺时针方向沿△ABC 的边运动,当Q 运动到A 点时,P 、Q 停止运动.设Q 点运动时间为t 秒,点P 运动的轨迹与PQ 、AQ 围成图形的面积为S.求S 关于t 的函数解析式.7.正方形ABCD中,点F 为正方形ABCD 内的点,△BFC 绕着点B 按逆时针方向旋转90°后与△BEA 重合.(1)如图1,若正方形ABCD 的边长为2,BE=1,FC=,求证:AE ∥BF ;(2)如图2,若点F 为正方形ABCD 对角线AC 上的点,且AF :FC=3:1,BC=2,求BF 的长.8.将正方形ABCD 和正方形BEFG 如图1摆放,连DF .3∠DMC=_____;∠DMC的值,并证明你的结论;∠DMC=_________.请画出图形,并直接写出你的结论(不用证明).9.已知△ABC≌△ADE,∠BAC=∠DAE=90°.(1)如图(1)当C、A、D在同一直线上时,连CE、BD,判断CE和BD位置关系,填空:CE_____BD.(2)如图(2)把△ADE绕点A旋转到如图所示的位置,试问(1)中的结论是否仍然成立,写出你的结论,并说明理由.(3)如图(3)在图2的基础上,将△ACE绕点A旋转一个角度到如图所示的△AC′E′的位置,连接10.将正方形ABCD 和正方形CGEF 如图1摆放,使D 点在CF 边上,M 为AE 中点,(1)连接MD 、MF ,则容易发现MD 、MF 间的关系是______________(2)操作:把正方形CGEF 绕C 点旋转,使对角线CE 放在正方形ABCD 的边BC 的延长线上(CG >BC ),取线段AE 的中点M ,探究线段MD 、MF 的关系,并加以说明;(3)将正方形CGEF 绕点C 旋转任意角度后(如图3),其他条件不变,(2)中的结论是否仍成立?直接写出猜想,不需要证明.图3D E C F GM B A 图2CF MA B D E G 图1A B G MF ED C【答案与解析】一、选择题1.【答案】C.2.【答案】B.二、填空题3.【答案】15°.4.三、解答题5.【答案与解析】 (1)证明:如图1,过点F 作FM ⊥AB于点M ,在正方形ABCD 中,AC ⊥BD 于点E . ∴AE=AC ,∠ABD=∠CBD=45°, ∵AF 平分∠BAC ,∴EF=MF ,又∵AF=AF ,∴Rt △AMF ≌Rt △AEF ,∴AE=AM ,∵∠MFB=∠ABF=45°,∴MF=MB ,MB=EF ,∴EF+AC=MB+AE=MB+AM=AB .1212证明:如图2,连接F1C1,过点F1作F1P⊥A1B于点P,F1Q⊥BC于点Q,∵A1F1平分∠BA1C1,∴E1F1=PF1;同理QF1=PF1,∴E1F1=PF1=QF1,又∵A1F1=A1F1,∴Rt△A1E1F1≌Rt△A1PF1,∴A1E1=A1P,同理Rt△QF1C1≌Rt△E1F1C1,∴C1Q=C1E1,由题意:A1A=C1C,∴A1B+BC1=AB+A1A+BC-C1C=AB+BC=2AB,∵PB=PF1=QF1=QB,∴A1B+BC1=A1P+PB+QB+C1Q=A1P+C1Q+2E1F1,即2AB=A1E1+C1E1+2E1F1=A1C1+2E1F1,(3)解:设PB=x,则QB=x,∵A1E1=3,QC1=C1E1=2,Rt△A1BC1中,A1B2+BC12=A1C12,即(3+x)2+(2+x)2=52,∴x1=1,x2=-6(舍去),∴PB=1,∴E1F1=1,又∵A1C1=5,6.【答案与解析】当P运动到C点时:t=6当Q运动到A点:t=∴分两种情况讨论(1)当0≤t≤6时,如图:作PH⊥AB于H,则△APH为等腰直角三角形此时AP=t,BQ=t,则AQ=-tPH=APsin45°=t∴S△AQP=AQ·PH=·(-t)·t=t2+3t(2)当6<t≤时,如图:过P过PH⊥AB于H,此时△PBH为等腰直角三角形AC+CP=t,BQ=t∴BP=AC+CB-(AC+CP)=12-t∴PH=BPsin45°=(12-t)∴S四边形AQPC=S△ABC-S△BPQ=AC·BC-BQ·PH=·6·6-·t·(12-t)=18-t+t 2=t 2-t+18.综上,.7.【答案与解析】(1)证明:∵△BFC 绕着点B 按逆时针方向旋转90°后与△BEA 重合∴BE=BF=1,∠EBF=∠ABC=90°,∠AEB=∠BFC在△BFC 中,BC2=22=4∴BF 2+FC 2=BC 2∴∠BFC=90°…(3分)∴∠AEB+∠EBF=180°∴AE ∥BF …(4分)(2)解:∵Rt △ABC 中,AB=BC=2,由勾股定理,得∵AF :FC=3:1,∵△BFC 绕着点B 按逆时针方向旋转90°后与△BEA 重合∵四边形ABCD 是正方形∴∠ABC=90°∴∠BAC+∠ACB=90°∴∠EAB+∠BAC=90°即∠EAF=90°在Rt△EBF中,EF2=BE2+BF2∵BE=BF8.【答案与解析】(1)如图2,连接BF,∵四边形ABCD、四边形BEFG是正方形,∴∠FBC=∠CBD=45°,∴∠CBD=∠GBC=90°,而BF=BG,BD=BC,∴△BFD∽△BGC,∴∠BCG=∠BDF,=而∠DMC=180°-∠BCG-∠BCD-∠CDF=180°-∠BDF-∠BCD-∠CDF=180-45°-90°=45°,∴=,∠DMC=45°;(2)如图3,∵将图1中的正方形BEFG绕B点顺时针旋转45°,DF的延长线交CG于M,∴B、E、D三点在同一条直线上,22DFCGBFBGDFCG2而四边形ABCD 、四边形BEFG 是正方形,∴△BFD ∽△BGC, 而∠DMC=180°-∠BCG-∠BCD-∠CDF=180°-∠BDF-∠BCD-∠CDF=180-45°-90° =45°,即∠DMC=45°;9.【答案与解析】(1)CE ⊥BD .(2)延长CE 交BD 于M ,设AB 与EM 交于点F .∵∠BAC=∠DAE=90°,∴∠CAE=∠BAD .又∵△ABC ≌△ADE ,∴AC=AE ,AB=AD ,∴∠ACE=,∠ABD=, ∴∠ACE=∠ABD .又∵∠AFC=∠BFM ,∠AFC+∠ACE=90°, ∴∠ABD+∠BFM=90°,∴∠BMC=90°,∴CE ⊥BD .(3)过C ′作C ′G ⊥AM 于G ,过D 作DH ⊥AM 交延长线于点H . 01802CAE -∠01802BAD -∠∵∠∠E ′NA=∠AGC ′=90°,∴∠NE ′A+∠NAE ′=90°,∠NAE ′+∠C ′AG=90°,∴∠NE ′A=∠C ′AG , ∵AE ′=AC ′∴△ANE ′≌△C ′GA (AAS ),∴AN=C ′G .同理可证△BNA ≌△AHD ,AN=DH .∴C ′G=DH .在△C ′GM 与△DHM 中,∠C ′GM=∠DHM=90°,∠C ′MG=∠DMH ,C ′G=DH ,∴△C ′GM ≌△DHM ,∴C ′M=DM ,∴. 10.【答案与解析】如图1,延长DM 交FE 于N ,图1∵正方形ABCD 、CGEF ,∴CF=EF ,AD=DC ,∠CFE=90°,AD ∥FE ,∴∠1=∠2,又∵MA=ME ,∠3=∠4,∴△AMD ≌△EMN ,∴MD=MN ,AD=EN .∵AD=DC ,12DM DC ='∴DC=NE.又∵FC=FE,∴FD=FN.又∵∠DFN=90°,∴FM⊥MD,MF=MD;(2)MD=MF,MD⊥MF.如图2,延长DM交CE于N,连接FD、FN.∵正方形ABCD,∴AD∥BE,AD=DC,∴∠1=∠2.又∵AM=EM,∠3=∠4,∴△ADM≌△ENM,∴AD=EN,MD=MN.∵AD=DC,∴DC=NE.又∵正方形CGEF,∴∠FCE=∠NEF=45°,FC=FE,∠CFE=90°.又∵正方形ABCD,∴∠BCD=90°,∴∠DCF=∠NEF=45°,∴△FDC≌△FNE,∴FD=FN,∠5=∠6,∠DFN=∠5+∠CFN=∠6+∠CFN=90°,∴△DFN为等腰直角三角形,且FM为斜边DN上的中线,∴MD=MF,MD⊥MF;(3)FM⊥MD,MF=MD.如图3,过点E作AD的平行线分别交DM、DC的延长线于N、H,连接DF、FN.∴∠ADC=∠H,AD∥EH,∴∠3=∠4.∵AM=ME,∠1=∠2,∴△AMD≌△EMN,∴DM=NM,AD=EN.∵正方形ABCD、CGEF,∴AD=DC,FC=FE,∠ADC=∠FCG=∠CFE=90°.∴∠H=90°,∠5=∠NEF,DC=NE.∴∠DCF+∠7=∠5+∠7=90°,∴∠DCF=∠5=∠NEF.∵FC=FE,∴△DCF≌△NEF.∴FD=FN,∠DFC=∠NFE.∵∠CFE=90°,∴∠DFN=90°.∴FM⊥MD,MF=MD.。
2018年中考数学选择填空压轴题专题3函数的几何综合问题

专题03函数的几何综合问题例1.如图,在平面直角坐标系中,直线 l : y= W3x — #与x 轴交于点B i ,以OB 为边长作等边三角 形A l OB |,过点A i 作A i B 2平行于x 轴,交直线l 于点B2 ,以A i B 2为边长作等边三角形 A 2A 1B 2,过点A 2 作A 2B 3平行于x 轴,交直线l 于点B 3 ,以A 2B 3为边长作等边三角形 A3A2B3 ,…,则点A 2017的横坐标同类题型1.1如图,直线l : y= x+1交y 轴-于点A i ,在x 轴正方向上取点B i ,使OB = OA ;过点B i 作A 2B i ,x 轴,交l 于点A 2 ,在x 轴正方向上取点B 2 ,使B i B 2=B 1A 2 ;过点 也彳^。
改,x 轴,交l 于点A 3 ,在 x 轴正方向上取点B 3 ,使B 2B3=E 2A 3 ;…记△ 0AB i 面积为S 1, △ B]A 2B 2面积为S 2 ,△ B 2A 3B 3面积为S3 ,…则S 2017等于 ( )同类题型1.2如图,已知直线| : y= W3 x,过点A (0, 1)作y 轴的垂线交直线l 于点B,过点B 作直 3 线l 的垂线交y 轴于点A 1 ;过点A 1作y 轴的垂线交直线l 于点B 1 ,过点B 1作直线l 的垂线交y 轴于点 A2 ;…;按此作法继续下去,则点 A 4的坐标为( )A. (0, 128)B. (0, 256)C. (0, 512)D. (0, 1024)八 c4030 A. 24031B. 2C. 240324033D. 2同类题型1.3如图,在平面直角坐标系中,直线 l : y= g 3 x+1交x 轴于点B,交y 轴于点A,过点A 作AB1 LAB 交x 轴于点M ,过点'彳^B1A 1,x 轴交直线l 于点A 2…依次作下去,则点 牛 的横坐标为例2.高速公路上依次有 3个标志点A 、R C,甲、乙两车分别从 A C 两点同时出发,匀速行驶,甲车从-B-C,乙车从 OB-A,甲、乙两车离 B 的距离y 1、V2 (千米)与行驶时间 x (小时)之间的函数关 系图象如图所示.观察图象,给出下列结论:① A C 之间的路程为690千米;②乙车比甲车每小时快30千米;③4.5小时两车相遇;④点 E 的坐标为(7, 180),「其中正确的有 号都填在横线上).2「千羽450同类题型2.1甲、乙两辆汽车沿同一路线从 A 地前往B 地,甲车以a 千米/时的速度匀速行驶,途中出现 故障后停车维修,修好后以 2a 千米/时的速度继续行驶;乙车在甲车出发 2小时后匀速前往 B 地,比甲车 早30分钟到达.到达 B 地后,乙车按原速度返回 A 地,甲车以2a 千米/时的速度返回 A 地.设甲、乙两 车与A 地相距s (千米),甲车离开 A 地的时间为t (小时),s 与t 之间的函数图象如图所示.下列说法:①a=40;②甲车维修所用时间为 1小时;③两车在途中第二次相遇时 相距40千米,其中不正确的个数为一…一、- 7 . 一、,(1) a=40, n^ 1; (2)乙的速度是 80km/h ; (3)甲比乙迟-h 到达B 地;240t 的值为5.25 ;④当t = 3时,两车 ( ) C. 2个D. 3个甲车比乙车早行驶 2h,并且甲车的函数图象.则下列结论:(把所有正确结论的序并以各自的速度匀速行驶, y (km)与时间x (h)50km.正确的个数是C. 3D. 4同类题型2.3甲、乙两人从科技馆出发, 沿相同的路线分别以不同的速度匀速跑向极地馆, 程后,乙开始出发,当乙超出甲 150米时,乙停在此地等候甲,两人相遇后乙又继续以原来的速度跑向极1例3.如图,已知动点P 在函数y= — (x>0)的图象上运动,PML x 轴于点 MPN! y 轴于点N,线段2xPM PN 分别与直线 AB : y=—x+ 1交于点E, F,则AF. BE 的值为6,,点D 在AB 的右侧,△ OA 丽△BCDTB 是等腰直角三角形,/ OAB= / BCD= 90 ,若函数y= - (x>0)的 x甲先跑一段路 地馆.如图是甲、乙两人在跑步的全过程中经过的路程下列四种说法:①甲的速度为 1.5米/秒;②a=750; 相遇时乙跑了 375米.其中正确的个数是 y (米)与甲出发的时间 x (秒)的函数图象.则 ③乙在途中等候甲 100秒;④乙出发后第一次与甲 疝眯900C.D.「4 个A. 4B. 2C. 1同类题型3.1如图,,一 一 一一 3 ,,一 ,,,, ,」在反比例函数y=法的图象上有一动点A,连接 AO 并延长交图象的另一支于点 B,在第二象限内有一点 C,满足AC= BC 当点A 运动时,点C 始终在函数 k ....... ................... y=x 的图象上运动,若tan/CABC. — 9D. — 12A 在x 轴的正半轴上,点B 在第一象限,点C 在线段AB 上,A. 1个B. 2个150A=2,则k 的值为同类题型3.2如图,在平面直角坐标系中,点一 6图象经过点 D,则^ OABW △ BCD 勺面积之差为( A. 12 B . 6 C. 3 D . 2一 .一 ................. .. ................ ......................... . . 1 一 9同类题型3.3如图,在平面直角坐标系 xOy 中,已知直线y = kx (k>0)分别交反比例函数y= -和丫= - x x在第一象限的图象于点 A, B,过点B 作BDLx 轴于点D,交y=1的图象于点C,连结AC.若△ABB 等x例4.如图,一次函,数y = x+b 的图象与反比例函数y= k 的图象交于点 A (3, 6)与点B,且与 x.... ___ k ............. ................................... ...............................................点C,右点P 是反比例函数y= -图象上的一个动点,作直线 AP 与x 轴、y 轴分别交于点 M N,x2同类题型4.2方程x 2 +3x —1 = 0的根可视为函数y=x+3的图象与函数....... 一 .、一一 2 .......... ............ ........ ....那么用此方法可推断出方程 x 2 +2x- 1=0的实数根x o 所在的范围是( )2 2例5.在平面直角坐标系 xOy 中,抛物线y= —x +2mx- m - 1父y 轴于点为A,顶点为D,对称轴与 x 轴交于点H.当抛物线顶点 D 在第二象限时,如果/ ADH / AHO 则m=.y 轴交于连结BNA. b> 2 2 , 9B. bv 2C. b<3D. 2 V2<b<1 . ................... ...... y=;的图象交点的横坐标,A. - 1<x 0 <0B. 0<xo <1C. 1<xo <2D. 2<xo <3A取值范围为AP1 ,点在函数y= x 的图象下万,同类题型5.1已知抛物线y= 4x 2 +1具有如下性质:该抛物线上任意一点到定点 F (0, 2)的距离与到12x 轴的距离始终相等,如图,点M 的坐标为(木,3), P 是抛物线丫= 4x 2 +1上一个动点,则4 PMF周长的最小值是()A. 3B. 4C. 5D. 6同类题型5.2抛物线y=ax2+bx+3 (aw0)经过点A(—1, 0), B( 2 , 0),且与y 轴相交于点C.设点D 是所求抛物线第一象限上一点,且在对称轴的右侧,点AOCf 似时,求点 D 的坐标.同类题型5.3小明家的洗手盆上装有一种抬启式水龙头(如图 1),完全开启后,水流路线呈抛物线,把手端点A,出水口 B 和落水点C 恰好在同一直线上,点 A 至出水管BD 的距离为12cm,洗手盆及水龙头的相 关数据如图2所示,现用高10.2cm 的圆柱型水杯去接水,若水流所在抛物线经过点 D 和杯子上底面中心 E, 则点E 到洗手盆内侧的距离 EH 为 cm.E 在线段 AC 上,且 DEL AG 当△ DCE^A图1图2参考答案例1 .如图,在平面直角坐标系中,直线l :y= W3x—率与x轴交于点B i ,以OB为边长作等边三角形々0耳,过点A1作A1B2平行于x轴,交直线l于点B2 ,以A1B2为边长作等边三角形A2A l B2,过点为作A2B3平行于x轴,交直线l于点B3 ,以A2B3为边长作等边三角形A3A2B3 ,…,则点A2017的横坐标是.Bi ,可得Bi (1, 0), D (0,—・•.OB =1, / OB D= 30 ,1一1如图所不,过A1作A1Al OB于A,则OA= 2。
中考数学压轴试题复习 第三部分 专题一 代数计算及通过代数计算进行说理问题-人教版初中九年级全册数学

§3.1 代数计算及通过代数计算进行说理问题课前导学计算说理是通过计算得到结论;说理计算侧重说理,说理之后进行代入求值.压轴题中的代数计算题,主要是函数类题.函数计算题必考的是待定系数法求函数的解析式,按照设、列、解、验、答五步完成,一般来说,解析式中待定几个字母,就要代入几个点的坐标.还有一类计算题,就是从特殊到一般,通过计算寻找规律.代数计算和说理较多的一类题目,是确定直线与抛物线的交点个数.联立直线和抛物线的解析式组成方程组,消去y ,得到关于x 的一元二次方程,然后根据∆确定交点的个数.我们介绍一下求函数图像交点坐标的几何方法.如图1,已知直线y =x +1与x 轴交于点A ,抛物线y =x 2-2x -3与直线y =x +1交于A 、B 两点,求点B 的坐标的代数方法,就是联立方程组,方程组的一个解是点A 的坐标,另一个解计算点的坐标.几何法是这样的:设直线AB 与y 轴分别交于C ,那么tan ∠AOC =1.作BE ⊥x 轴于E ,那么1BE AE=.设B(x , x 2-2x -3),于是22311x x x --=+. 请注意,这个分式的分子因式分解后,(1)(3)11x x x +-=+.这个分式能不能约分,为什么?因为x =-1的几何意义是点A ,由于点B 与点A 不重合,所以x ≠-1,因此约分以后就是x -3=1.这样的题目一般都是这样,已知一个交点求另一个交点,经过约分,直接化为一元一次方程,很简便.图1例 1 2014年某某省某某市中考第25题在平面直角坐标系中,我们不妨把横坐标和纵坐标相等的点叫“梦之点”,例如点(1,1),(-2,-2),,…,都是“梦之点”,显然“梦之点”有无数个.(1)若点P(2, m)是反比例函数nyx=(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;(2)函数y=3kx+s-1(k、s为常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标,若不存在,说明理由;(3)若二次函数y=ax2+bx+1(a、b是常数,a>0)的图象上存在两个“梦之点”A(x1, x1)、B(x2, x2),且满足-2<x1<2,| x1-x2|=2,令2157 248t b b=-+,试求t的取值X围.动感体验请打开几何画板文件名“14某某25”,拖动y轴正半轴上表示实数a的点,可以体验到,A、B两点位于y轴同侧,A、B两点间的水平距离、竖直距离都是2,并且对于同一个a,有两个对应的b和b′,但是t随b、t随b′变化时对应的t的值保持相等.思路点拨1.“梦之点”都在直线y=x上.2.第(2)题就是讨论两条直线的位置关系,分重合、平行和相交三种情况.3.第(3)题放弃了也是明智的选择.求t关于b的二次函数的最值,b的取值X围由“梦之点”、-2<x1<2和| x1-x2|=2三个条件决定,而且-2<x1<2还要分两段讨论.图文解析(1)因为点P(2, m)是“梦之点”,所以P(2, 2).所以4yx =.(2)“梦之点”一定在直线y=x上,直线y=3kx+s-1与直线y=x的位置关系有重合、平行、相交.图1 图2 图3①如图1,当直线y =3kx +s -1与直线y =x 重合时,有无数个“梦之点”.此时k =13,s =1.②如图2,当直线y =3kx +s -1与直线y =x 平行时,没有“梦之点”.此时k =13,s ≠1.③如图3,当直线y =3kx +s -1与直线y =x 相交时,有1个“梦之点”.此时k ≠13,“梦之点”的坐标为11(,)3131s s k k ----. (3)因为A (x 1,x 1)、B (x 2,x 2)两点是抛物线与直线y =x 的交点,联立y =ax 2+bx +1和y =x ,消去y ,整理,得ax 2+(b -1)x +1=0.所以x 1x 2=1a>0.所以A 、B 两点在y 轴的同侧. 如图4,由| x 1-x 2|=2,可知A 、B 两点间的水平距离、竖直距离都是2.已知-2<x 1<2,我们分两种情况来探求a 的取值X 围:①当A 、B 两点在y 轴右侧时,0<x 1<2,2<x 2<4.所以0<x 1x 2<8.②当A 、B 两点在y 轴左侧时,-2<x 1<0,-4<x 2<-2.所以0<x 1x 2<8. 综合①、②,不论0<x 1<2或-2<x 1<0,都有0<x 1x 2<8.所以0<1a <8.所以a >18. 由ax 2+(b -1)x +1=0,得x 1+x 2=1b a -,x 1x 2=1a. 由| x 1-x 2|=2,得(x 1-x 2)2=4.所以(x 1+x 2)2-4x 1x 2=4.所以22(1)44b a a--=.整理,得22(1)44b a a -=+. 所以2157248t b b =-+=2109(1)48b -+=21094448a a ++=261(21)48a ++.如图5,这条抛物线的开口向上,对称轴是直线12a =-,在对称轴右侧,t 随a 的增大而增大.因此当18a =时,t 取得最小值,t =2161(1)448++=176. 所以t 的取值X 围是t >176.图4 图5考点伸展第(3)题我们也可以这样来讨论:一方面,由| x 1-x 2|=2,得(x 1-x 2)2=4.所以(x 1+x 2)2-4x 1x 2=4. 所以22(1)44b a a--=.整理,得22(1)44b a a -=+. 另一方面,由f (2)>0,f (-2)<0,得f (2)f (-2)<0. 所以[42(1)1][42(1)1]a b a b +-+--+<0.所以22(41)4(1)a b +--=22(41)4(44)a a a +-+=18a -<0.所以a >18.例 2 2014年某某省某某市中考第23题设m 是不小于-1的实数,使得关于x 的方程x 2+2(m -2)x +m 2-3m +3=0有两个不相等的实数根x 1,x 2.(1)若12111x x +=,求132m-的值; (2)求2121211mx mx m x x +---的最大值. 动感体验请打开几何画板文件名“14某某23”,拖动x 轴上表示实数m 的点运动,可以体验到,当m 小于1时,抛物线与x 轴有两点交点A 、B .观察点D 随m 运动变化的图像,可以体验到,当m =-1时,点D 到达最高点.思路点拨1.先确定m 的取值X 围,由两个条件决定.2.由根与系数的关系,把第(1)题的已知条件转化为关于m 的方程.3.第(2)题首先是繁琐的式子变形,把m 提取出来,可以使得过程简便一点. 图文解析(1)因为方程x 2+2(m -2)x +m 2-3m +3=0有两个不相等的实数根,所以∆>0. 由∆=4(m -2)2-4(m 2-3m +3)=-4m +4>0,得m <1.又已知m 是不小于-1的实数,所以-1≤m <1.由根与系数的关系,得122(2)24x x m m +=--=-+,21233x x m m ⋅=-+. 若12111x x +=,那么1212x x x x +=⋅.所以22433m m m -+=-+. 整理,得210m m --=.解得m =m =.所以323(12m -=-=.所以132m -2. (2)2121211mx mx m x x +---=121211x x m m x x ⎡⎤+-⎢⎥--⎣⎦=122112(1)(1)(1)(1)x x x x m m x x ⎡⎤-+--⎢⎥--⎣⎦=12121212()21()x x x x m m x x x x ⎡⎤+--⎢⎥-++⎣⎦=22(24)2(33)1(24)33m m m m m m m m ⎡⎤-+--+-⎢⎥--++-+⎣⎦ =222+42m m m m m m ⎡⎤---⎢⎥-⎣⎦=22(1)(1)m m m m m ⎡⎤---⎢⎥-⎣⎦=222m m -+-=2(1)3m -++.所以当m =-1时,它有最大值,最大值为3(如图1所示).图1考点伸展当m变化时,抛物线y=x2+2(m-2)x+m2-3m+3=0的顶点的运动轨迹是什么?因为抛物线的对称轴是直线x=-(m-2),所以抛物线的顶点的纵坐标y=(m-2)2-2(m-2)2+m2-3m+3=m-1.因为x+y=-(m-2)+m-1=1为定值,所以y=-x+1.也就是说,抛物线的顶点(x, y)的运动轨迹是直线y=-x+1(如图2所示).图2例 3 2014年某某省某某市中考第26题如图1,已知二次函数y=-x2+bx+c的对称轴为x=2,且经过原点,直线AC的解析式为y=kx+4,直线AC与y轴交于点A,与二次函数的图象交于B、C两点.(1)求二次函数解析式; (2)若1=3AOB BOC S S △△,求k 的值; (3)若以BC 为直径的圆经过原点,求k 的值.图1动感体验请打开几何画板文件名“14某某26”,拖动点C 在抛物线上运动,可以体验到,当以BC 为直径的圆经过原点时,△BMO ∽△ONC .思路点拨1.第(2)题先将面积比转化为AB 与BC 的比,进而转化为B 、C 两点的横坐标的比.2.第(2)题可以用直线的解析式表示B 、C 两点的坐标,再代入抛物线的解析式列方程组;也可以用抛物线的解析式表示B 、C 两点的坐标,再代入直线的解析式列方程组.3.第(3)题先联立抛物线与直线,根据一元二次方程根与系数的关系,得到B 、C 两点的横坐标的和与积,再构造相似三角形列方程.图文解析(1)因为原点O 关于直线x =2的对称点为(4, 0),所以抛物线y =-x 2+bx +c 的解析式为y =-x (x -4)=-x 2+4x .(2)如图2,因为1==3AOB BOC S AB S BC △△,所以1=4B C x x .设x B =m ,那么x C =4m . 将点B (m , km +4)、C (4m , 4km +4)分别代入y =-x (x -4),得4(4),444(44).km m m km m m +=--⎧⎨+=--⎩①② ①-②÷4,整理,得m 2=1.所以m =1.将m =1代入①,得k +4=3.解得k =-1.此时点C 落在x 轴上(如图3).(3)因为B 、C 是直线y =kx +4与抛物线的交点,设B (x 1,kx 1+4),C (x 2,kx 2+4). 联立y =-x 2+4x 和y =kx +4,消去y ,整理,得x 2+(k -4)x +4=0.所以x 1+x 2=4-k ,x 1x 2=4.如图5,若以BC 为直径的圆经过原点,那么∠BOC =90°.作BM ⊥y 轴,⊥y 轴,垂足分别为M 、N ,那么△BMO ∽△ONC .根据BM ON MO NC=,得1212(4)4x kx kx x -+=+. 所以212121212(4)(4)[4()16]x x kx kx k x x k x x =-++=-+++.将x 1+x 2=4-k ,x 1x 2=4代入,得24[44(4)16]k k k =-+-+.解得54k =-.图2 图3 图4考点伸展第(2)题也可以先用抛物线的解析式设点B 、C 的坐标,再代入直线的解析式列方程组. 将点B (m ,-m 2+4m )、C (4m ,-16m 2+16m )分别代入y =kx +4,得 2244,16164 4.m m km m m km ⎧-+=+⎪⎨-+=+⎪⎩①②①×4-②,得12m 2=12.所以m =1.将m =1代入①,得3=k +4.解得k =-1.例 4 2014年某某省株洲市中考第24题已知抛物线252(2)4k y x k x +=-++和直线2(1)(1)y k x k =+++. (1)求证:无论k 取何实数值,抛物线与x 轴有两个不同的交点;(2)抛物线与x 轴交于A 、B 两点,直线与x 轴交于点C ,设A 、B 、C 三点的横坐标分别是x 1、x 2、x 3,求x 1·x 2·x 3的最大值;(3)如果抛物线与x 轴的两个交点A 、B 在原点的右边,直线与x 轴的交点C 在原点的左边,又抛物线、直线分别交y 轴于点D 、E ,直线AD 交直线CE 于点G (如图1),且CA ·GE =CG ·AB ,求抛物线的解析式.图1动感体验请打开几何画板文件名“14株洲24”,拖动y 轴上表示实数k 的点运动,可以体验到,抛物线与x 轴总是有两个交点.观察x 1·x 2·x 3随k 变化的函数图像,可以体验到,x 1·x 2·x 3是k 的二次函数.还可以体验到,存在一个正数k ,使得AD 与BE 平行.思路点拨1.两个解析式像庞然大物,其实第(1)题的语境非常熟悉,走走看,豁然开朗.2.第(2)题x 1·x 2·x 3的最小值由哪个自变量决定呢?当然是k 了.所以先求x 1·x 2·x 3关于k 的函数关系式,就明白下一步该怎么办了.x 1·x 2由根与系数的关系得到,x 3就是点C 的横坐标.3.第(3)题的等积式转化为比例式,就得到AD //BE .由此根据OD ∶OA =OE ∶OB 列方程,再结合根与系数的关系化简.还是走走看,柳暗花明.图文解析(1)因为222(52)17(2)42()424k k k k k +∆=+-⨯=-+=-+>0,所以无论k 取何实数值,抛物线与x 轴有两个不同的交点.(2)由2(1)(1)y k x k =+++,得C (-(k +1), 0).所以x 3=-(k +1).由根与系数的关系,得x 1·x 2=(52)4k +. 所以x 1·x 2·x 3=1(52)(1)4k k -++=21(572)4k k -++. 因此710x =-当时,x 1·x 2·x 3取得最大值,最大值=14949(52)410010-⨯-+=980. (3)如图2,由CA ·GE =CG ·AB ,得CA CG AB GE =. 所以AG //BE ,即AD //BE .所以OD OE OA OB =,即212(52)(1)4k k x x ++=.所以22122(52)(1)4k k x x x ++=⋅.所以222(1)1k x +=. 所以x 2=k +1,或-k -1(舍).又因为x 1+x 2=k +2,所以x 1=1,即A (1, 0).再将点A (1, 0)代入252(2)4k y x k x +=-++,得5201(2)4k k +=-++. 解得k =2.所以抛物线的解析式为y =x 2-4x +3.图2 图3考点伸展把第(3)题中的条件“CA ·GE =CG ·AB ”改为“EC =EB ”,其他条件不变,那么抛物线的解析式是怎样的呢?如图3,因为点E 在y 轴上,当EC =EB 时,B 、C 两点关于y 轴对称,所以B (k +1, 0). 将点B (k +1, 0)代入252(2)4k y x k x +=-++,得252(1)(2)(1)04k k k k ++-+++=. 解得k =2.所以抛物线的解析式为y =x 2-4x +3.。
中考数学复习专题三:代数、三角、几何综合问题

中考数学复习专题3 代数、三角、几何综合问题概述:代数、三角与几何综合题是较复杂与难度较大的问题,其中包括方程、函数、三角与几何等,内容基本上包含所有的初中数学知识,必须把以前的函数观念、方程思想、数形结合思想、转化与化归思想进行综合来解题.典型例题精析例1.有一根直尺的短边长2cm ,长边长10cm ,还有一块锐角为45°的直角三角形纸板,它的斜边长12cm ,如图1,将直尺的矩边DE 放置与直角三角形纸板的斜边AB 重合,且点D 与点A 重合,将直尺沿AB 方向平移如图2,设平移的长度为xcm (•0≤x ≤10),直尺和三角形纸板的重叠部分(图中阴影部分)的面积为Scm 2.(1)当x=0时(如图),S=________;当x=10时,S=___________; (2)当0<x ≤4时(如图2),求S 关于x 的函数关系式;(3)当4<x<10时,求S 关于x 的函数关系式,并求出S 的最大值(同学可在图3、•图4中画草图)解析:(1)2;2.(2)在Rt △ADG 中,∠A=45°, ∴DG=AD=x .同理EF=AE=x+2,∴S 梯形DEGF =12(x+x+2)×2=2x+2, ∴S=2x+2.(3)①当4<x<6时,(如图5) GD=AD=x ,EF=EB=12-(x+2)=10-x , 则S △ADG =12x -2,S △BEF =12(10-x )2, 而S △ABC =12×12×6=36,∴S=36-12x 2-12(10-x )2=-x 2+10x-14,S=-x 2+10x-14=-(x-5)2+11,∴当x=5(4<5<6)时,S 最大值=11.②当6≤x<10时(如图6), BD=BG=12-x ,BE=EF=10-x ,S=12(12-x+10-x )×2=22-2x , S 随x 的增大而减小,所以S ≤10.由①、②可得,当4<x<10时,S 最大值=11.例2.如图所示,点O 2是⊙O 1上一点,⊙O 2与⊙O 1相交于A 、D 两点,BC⊥AD,垂足为D ,分别交⊙O 1、⊙O 2于B 、C 两点,延长DO 2交⊙O 2于E ,交BA 的延长线于F ,BO 2交AD 于G ,连结AG .• (1)求证:∠BGD=∠C ;(2)若∠DO 2C=45°,求证:AD=AF ;(3)若BF=6CD ,且线段BD 、BF 的长是关于x 的方程x 2-(4m+2)x+4m 2+8=0•的两个实数根,求BD 、BF 的长.解析:(1)∵BC ⊥AD 于D ,∴∠BDA=∠CDA=90°,∴AB 、AC 分别为⊙O 1、⊙O 2的直径.∵∠2=∠3,∠BGD+∠2=90°,∠C+∠3=90°, ∴∠BGD=∠C .(2)∵∠DO 2C=45°,∴∠ABD=45°,∵O 2D=O 2C ,∴∠C=∠O 2DC=12(180°-∠DO 2C )=67.5°, ∴∠4=22.5°, ∵∠O 2DC=∠ABD+∠F , ∴∠F=∠4=22.5°,∴AD=AF .(3)∵BF=6CD ,∴设CD=k ,则BF=6k . 连结AE ,则AE ⊥AD ,∴AE ∥BC ,∴AE AFBD BF∴AE ·BF=BD ·AF . 又∵在△AO 2E 和△DO 2C 中,AO 2=DO 2 ∠AO 2E=∠DO 2C , O 2E=O 2C ,∴△AO 2E≌△DO 2C ,∴AE=CD=k,∴6k 2=BD·AF=(BC-CD )(BF-AB ). ∵∠BO 2A=90°,O 2A=O 2C ,∴BC=AB.∴6k 2=(BC-k )(6k-BC ).∴BC 2-7kBC+12k 2=0, 解得:BC=3k 或BC=4k . 当BC=3k ,BD=2k .∵BD 、BF 的长是关于x 的方程x 2-(4m+2)x+4m 2+8=0的两个实数根. ∴由根与系数的关系知:BD+BF=2k+6k=8k=4m+2.整理,得:4m 2-12m+29=0.∵△=(-12)2-4×4×29=-320<0,此方程无实数根. ∴BC=3k (舍). 当BC=4k 时,BD=3k .∴3k+6k=4m+2,18k 2=4m 2+8,整理,得:m 2-8m+16=0, 解得:m 1=m 2=4,∴原方程可化为x 2-18x+72=0,解得:x 1=6,x 2=12, ∴BD=6,BF=12.中考样题训练1.已知抛物线y=-x 2+(k+1)x+3,当x<1时,y 随着x 的增大而增大,当x>1时,y 随x 的增大而减小.(1)求k 的值及抛物线的解析式;(2)设抛物线与x 轴交于A 、B 两点(A 在B 的左边),抛物线的顶点为P ,试求出A 、•B 、P 三点的坐标,并在直角坐标系中画出这条抛物线;(3)求经过P 、A 、B 三点的圆的圆心O ′的坐标; (4)设点G (0,m )是y 轴上的动点.①当点G 运动到何处时,直线BG 是⊙O ′的切线?并求出此时直线BG 的解析式.②若直线BG 与⊙O 相交,且另一个交点为D ,当m 满足什么条件时,点D 在x 轴的下方?2.如图,已知圆心A (0,3),⊙A 与x 轴相切,⊙B 的圆心在x 轴的正半轴上,且⊙B 与⊙A 外切于点P ,两圆的公切线MP 交y 轴于点M ,交x 轴于点N .(1)若sin ∠OAB=45,求直线MP 的解析式及经过M 、N 、B 三点的抛物线的解析式; (2)若⊙A 的位置大小不变,⊙B 的圆心在x 轴的正半轴上移动,并使⊙B 与⊙A 始终外切,过M 作⊙B 的切线MC ,切点为C ,在此变化过程中探究:①四边形OMCB 是什么四边形,对你的结论加以证明;②经过M 、N 、B 三点的抛物线内是否存在以BN 为腰的等腰三角形?若存在,•表示出来;若不存在,说明理由.yMCBA xPO N3.如图,已知直线L与⊙O相交于点A,直径AB=6,点P在L•上移动,连结OP交⊙O于点C,连结BC并延长BC交直线L于点D.(1)若AP=4,求线段PC的长;的面积.(•答案要求保留根号)LA考前热身训练1.如图,已知A 为∠POQ 的边OQ 上一点,以A 为顶点的∠MAN 的两边分别交射线OP 于M 、N 两点,且∠MAN=∠POQ=α(α为锐角),当∠MAN 为以点A 为旋转中心,AM 边从与AO•重合的位置开始,按逆时针方向旋转(∠MAN 保持不变)时,M 、N 两点在射线OP•上同时以不同的速度向右平行移动.设OM=x ,ON=y(y>x ≥0),△AOM 的面积为S ,若cos α、OA•是方程2z 2-5z+2=0的两个根. (1)当∠MAN 旋转30°(即∠OAM=30°)时,求点N 移动的距离; (2)求证:AN 2=ON ·MN ;(3)求y 与x 之间的函数关系式及自变量量x 的取值范围;(4)试写出S 随x 变化的函数关系式,并确定S 的取值范围.2.如图,已知P 、A 、B 是x 轴上的三点,点A 的坐标为(-1,0),点B 的坐标为(3,0),•且PA :AB=1:2,以AB 为直径画⊙M 交y 轴的正半轴于点C . (1)求证:PC 是⊙M 的切线;(2)在x 轴上是否存在这样的点Q ,使得直线QC 与过A 、C 、B•三点的抛物线只有一个交点?若存在,求点Q 的坐标,若不存在,请说明理由;(3)画⊙N ,使得圆心N 在x 轴的负半轴上,⊙N 与⊙M 外切,且与直线PC 相切于D ,•问将过A 、C 、B 三点的抛物线平移后,能否同时经过P 、D 、A 三点?为什么?答案:中考样题看台1.(1)k=1,抛物线解析式y=-x 2+2x+3(2)A (-1,0),B (3,0),C (1,4)M AQP O N(3)∵⊙O′过A、B两点,∴O′在AB的垂直平分线上,即在抛物线的对称轴上,设抛物线的对称轴交x轴于M,交⊙O′于N,则有MP×MN=MA×MB,4MN=2×2,∴MN=1,•PN=5,O′P=52<PM,∴O′点在x轴上方,∴O′M=32,∴O′(1,32).(4)①过B点作⊙O′的切线交y轴于点G,直线BO′交y轴于点E,可求出直线BO•′的解析式为,y=-34x+94,∴E(0,94),∵BG是⊙O′的切线,BO⊥EG,∴BO=OE×OG,∴OG=4,•∴G(0,-4),求出直线BG的解析式为y=43x-4.②-4<m<0.2.(1)在Rt△AOB中,∵OA=3,sin∠OAB=45,cos∠OAB=35,∴AB=5,OB=4,BP=5-3=2.•在Rt△APM中,APAM=cos∠OAB=35,∴AM=5,OM=2,∴点M(0,-2),又△NPB∽△AOB,∴BN AB BP OB,∴BN=52,•∴ON=32,∴点B(32,0),设MP的解析式为y=kx+b,∵MP经过M、N两点,∴MP的解析式为y=43x-2,设过M、N、B的抛物线解析式为y=a(x-32)(x-4)且点M(0,-2)在其上,可得a=-13,即y=-13x2+116x-2.(2)①四边形OMCB是矩形.证明:在⊙A不动,⊙B运动变化过程中,恒有∠BAO=∠MAP,OA=AP,∠AOB=∠APM=90°,∴△AOB≌△APM,∴OB=PM,AB=AM,∴PB=OM,而PB=BC,∴OM=BC,由切线长定理知MC=MP,∴MC=OB,∴四边形MOBC是平行四边形,又∵∠MOB=90°,∴四边形MOBC是矩形.②存在,由上证明可知,Rt△MON≌Rt△BPN,∴BN=MN .因此在过M 、N 、B 三点的抛物线内有以BN 为腰的等腰三角形MNB 存在,• 由抛物线的轴对称性可知,在抛物线上必有一点M ′与M 关于其对称轴对称, ∴BN=BM ′,这样得到满足条件的三角形有两个,△MNB 和△M ′NB . 3.(1)∵L 与⊙O 相切于点A ,∴∠4=90°,∴OP 2=OA 2+AP 2, ∵OB=OC=12AB=3,AP=4, ∴OP 2=32+42,∴OP=5, ∴PC=5-3=2.(2)∵△PAO ∽△BAD ,且∠1>∠2,∠4=90°, ∴∠2=∠APO ,∴OB=OC ,∴∠2=∠3 ∵∠1=∠2+∠3,∴∠2=2∠2=2∠APO ∴∠4=90°,∴∠1+∠APO=90° ∴3∠APO=90°,∴∠APO=30°. 在Rt △BAD 中,∠2=∠APO=30°.∴AD=6sin30°=6 过点O 作OE ⊥BC 于点E ∵∠2=30°,BO=3,∴OE=32,BE=3×cos30°∴∴S 四边形OADC =S △BAD -S △BOC =12AB ·AD=12BC ·OE=12×6×12×3294154.考前热身训练1.(1)易知OA=2,cos α=12,∠POQ=∠MAN=60°, ∴初始状态时,△AON 为等边三角形,•∴ON=OA=2,当AM 旋转到AM ′时,点N 移动到N ′, ∵∠OAM ′=30°,∠POQ=∠M ′AN•′=60°,∴∠M ′N ′A=30°,在Rt △OAN 中,ON ′=2AO=4, ∴NN ′=ON ′-ON=2,∴点N 移动的距离为2.(2)易知△OAN ∽△AMN ,∴AN 2=ON ·MN .(3)∵MN=y-x ,∴AN 2=y 2-xy ,过A 点作AD ⊥OP ,垂足为D ,可得OD=1, ∴DN=ON-OD=y-1,在Rt △AND 中,AN 2=AD 2+DN 2=y 2-2y+4,∴y 2-xy=y 2-2y+4,即y=42x-. ∴y>0,∴2-x>0,即x<2,又∵x ≥0,∴x 的取值范围是:0≤x<2.(4)S=12·OM ·,∵S 是x ,∴0≤S<2·2.即0≤2.(1)易知⊙M 半径为2,设PA=x ,则x :4=1:2⇒x=2,由相交弦定理推论得OC=OA .OB=1×3,2=PO 2+OC 2=32+2=12,PM 2=42=16,MC 2=22=4,∴PM 2=PC 2+MC 2,∴∠PCM=90°.(2)易知过A 、C 、B 三点的抛物线的解析式为(x+1)(x-3),•假设满足条件的Q 点存在,坐标为(m ,0),直线QC 的解析式为 ∵直线QC 与抛物线只有一个公共点,∴方程x+1)(x-3)∴(2+3m)2=0,∴m=-32,即满足条件的Q 点存在,•坐标为(-32,0);(3)连结DN ,作DH ⊥PN ,垂足为H ,设⊙N 的半径为r ,则∵ND ⊥PC , ∴ND ∥MC ,∴DN PN MC PM =,∴224r r -=, ∴r=23,∵DN 2=NH ·NP , ∴(23)2=NH ·(2-23),∴NH=13,∴3,∴D (-2,3).∵抛物线(x+1)(x-3)平移,使其经过P 、A 两点的抛物线的解析式为x+•1)(x+3)又经验证D是该抛物线上的点,∴将过A、C、B三点的抛物线平移后能同时经过P、D、A三点.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学复习专题3 代数、三角、几何综合问题概述:代数、三角与几何综合题是较复杂与难度较大的问题,其中包括方程、函数、三角与几何等,内容基本上包含所有的初中数学知识,必须把以前的函数观念、方程思想、数形结合思想、转化与化归思想进行综合来解题.典型例题精析 例1.有一根直尺的短边长2cm ,长边长10cm ,还有一块锐角为45°的直角三角形纸板,它的斜边长12cm ,如图1,将直尺的矩边DE 放置与直角三角形纸板的斜边AB 重合,且点D 与点A 重合,将直尺沿AB 方向平移如图2,设平移的长度为xcm (•0≤x ≤10),直尺和三角形纸板的重叠部分(图中阴影部分)的面积为Scm 2.(1)当x=0时(如图),S=________;当x=10时,S=___________; (2)当0<x ≤4时(如图2),求S 关于x 的函数关系式;(3)当4<x<10时,求S 关于x 的函数关系式,并求出S 的最大值(同学可在图3、•图4中画草图)解析:(1)2;2.(2)在Rt △ADG 中,∠A=45°, ∴DG=AD=x .同理EF=AE=x+2,∴S 梯形DEGF =12(x+x+2)×2=2x+2, ∴S=2x+2.(3)①当4<x<6时,(如图5) GD=AD=x ,EF=EB=12-(x+2)=10-x , 则S △ADG =12x -2,S △BEF =12(10-x )2, 而S △ABC =12×12×6=36,∴S=36-12x 2-12(10-x )2=-x 2+10x-14,S=-x 2+10x-14=-(x-5)2+11,∴当x=5(4<5<6)时,S 最大值=11.②当6≤x<10时(如图6), BD=BG=12-x ,BE=EF=10-x ,S=12(12-x+10-x )×2=22-2x , S 随x 的增大而减小,所以S ≤10.由①、②可得,当4<x<10时,S 最大值=11.例2.如图所示,点O 2是⊙O 1上一点,⊙O 2与⊙O 1相交于A 、D 两点,BC⊥AD,垂足为D ,分别交⊙O 1、⊙O 2于B 、C 两点,延长DO 2交⊙O 2于E ,交BA 的延长线于F ,BO 2交AD 于G ,连结AG .•(1)求证:∠BGD=∠C ;(2)若∠DO 2C=45°,求证:AD=AF ;(3)若BF=6CD ,且线段BD 、BF 的长是关于x 的方程x 2-(4m+2)x+4m 2+8=0•的两个实数根,求BD 、BF 的长.解析:(1)∵BC ⊥AD 于D , ∴∠BDA=∠CDA=90°,∴AB 、AC 分别为⊙O 1、⊙O 2的直径.∵∠2=∠3,∠BGD+∠2=90°,∠C+∠3=90°, ∴∠BGD=∠C .(2)∵∠DO 2C=45°,∴∠ABD=45°,∵O 2D=O 2C ,∴∠C=∠O 2DC=12(180°-∠DO 2C )=67.5°, ∴∠4=22.5°, ∵∠O 2DC=∠ABD+∠F , ∴∠F=∠4=22.5°,∴AD=AF .(3)∵BF=6CD ,∴设CD=k ,则BF=6k . 连结AE ,则AE ⊥AD ,∴AE ∥BC ,∴AE AFBD BF∴AE ·BF=BD ·AF . 又∵在△AO 2E 和△DO 2C 中,AO 2=DO 2 ∠AO 2E=∠DO 2C , O 2E=O 2C ,∴△AO 2E≌△DO 2C ,∴AE=CD=k,∴6k2=BD·AF=(BC-CD)(BF-AB).∵∠BO2A=90°,O2A=O2C,∴BC=AB.∴6k2=(BC-k)(6k-BC).∴BC2-7kBC+12k2=0,解得:BC=3k或BC=4k.当BC=3k,BD=2k.∵BD、BF的长是关于x的方程x2-(4m+2)x+4m2+8=0的两个实数根.∴由根与系数的关系知:BD+BF=2k+6k=8k=4m+2.整理,得:4m2-12m+29=0.∵△=(-12)2-4×4×29=-320<0,此方程无实数根.∴BC=3k(舍).当BC=4k时,BD=3k.∴3k+6k=4m+2,18k2=4m2+8,整理,得:m2-8m+16=0,解得:m1=m2=4,∴原方程可化为x2-18x+72=0,解得:x1=6,x2=12,∴BD=6,BF=12.中考样题训练1.已知抛物线y=-x2+(k+1)x+3,当x<1时,y随着x的增大而增大,当x>1时,y 随x的增大而减小.(1)求k的值及抛物线的解析式;(2)设抛物线与x轴交于A、B两点(A在B的左边),抛物线的顶点为P,试求出A、•B、P三点的坐标,并在直角坐标系中画出这条抛物线;(3)求经过P、A、B三点的圆的圆心O′的坐标;(4)设点G(0,m)是y轴上的动点.①当点G运动到何处时,直线BG是⊙O′的切线?并求出此时直线BG的解析式.②若直线BG与⊙O相交,且另一个交点为D,当m满足什么条件时,点D在x轴的下方?2.如图,已知圆心A(0,3),⊙A与x轴相切,⊙B的圆心在x轴的正半轴上,且⊙B与⊙A外切于点P,两圆的公切线MP交y轴于点M,交x轴于点N.(1)若sin ∠OAB=45,求直线MP 的解析式及经过M 、N 、B 三点的抛物线的解析式; (2)若⊙A 的位置大小不变,⊙B 的圆心在x 轴的正半轴上移动,并使⊙B 与⊙A 始终外切,过M 作⊙B 的切线MC ,切点为C ,在此变化过程中探究: ①四边形OMCB 是什么四边形,对你的结论加以证明;②经过M 、N 、B 三点的抛物线内是否存在以BN 为腰的等腰三角形?若存在,•表示出来;若不存在,说明理由.3.如图,已知直线L 与⊙O 相交于点A ,直径AB=6,点P 在L•上移动,连结OP 交⊙O 于点C ,连结BC 并延长BC 交直线L 于点D .(1)若AP=4,求线段PC 的长;(2)若△PAO 与△BAD 相似,求∠APO 的度数和四边形OADC 的面积.(•答案要求保留根号)LyM CBA xPO N考前热身训练1.如图,已知A 为∠POQ 的边OQ 上一点,以A 为顶点的∠MAN 的两边分别交射线OP 于M 、N 两点,且∠MAN=∠POQ=α(α为锐角),当∠MAN 为以点A 为旋转中心,AM 边从与AO•重合的位置开始,按逆时针方向旋转(∠MAN 保持不变)时,M 、N 两点在射线OP•上同时以不同的速度向右平行移动.设OM=x ,ON=y (y>x ≥0),△AOM 的面积为S ,若cos α、OA•是方程2z 2-5z+2=0的两个根.(1)当∠MAN 旋转30°(即∠OAM=30°)时,求点N 移动的距离;(2)求证:AN 2=ON ·MN ; (3)求y 与x 之间的函数关系式及自变量量x 的取值范围;(4)试写出S 随x 变化的函数关系式,并确定S 的取值范围.2.如图,已知P 、A 、B 是x 轴上的三点,点A 的坐标为(-1,0),点B 的坐标为(3,0),•且PA :AB=1:2,以AB 为直径画⊙M 交y 轴的正半轴于点C . (1)求证:PC 是⊙M 的切线;(2)在x 轴上是否存在这样的点Q ,使得直线QC 与过A 、C 、B•三点的抛物线只有一个交点?若存在,求点Q 的坐标,若不存在,请说明理由;(3)画⊙N ,使得圆心N 在x 轴的负半轴上,⊙N 与⊙M 外切,且与直线PC 相切于D ,•问将过A 、C 、B 三点的抛物线平移后,能否同时经过P 、D 、A 三点?为什么?M A Q P O N答案:中考样题看台1.(1)k=1,抛物线解析式y=-x2+2x+3(2)A(-1,0),B(3,0),C(1,4)(3)∵⊙O′过A、B两点,∴O′在AB的垂直平分线上,即在抛物线的对称轴上,设抛物线的对称轴交x轴于M,交⊙O′于N,则有MP×MN=MA×MB,4MN=2×2,∴MN=1,•PN=5,O′P=52<PM,∴O′点在x轴上方,∴O′M=32,∴O′(1,32).(4)①过B点作⊙O′的切线交y轴于点G,直线BO′交y轴于点E,可求出直线BO•′的解析式为,y=-34x+94,∴E(0,94),∵BG是⊙O′的切线,BO⊥EG,∴BO=OE×OG,∴OG=4,•∴G(0,-4),求出直线BG的解析式为y=43x-4.②-4<m<0.2.(1)在Rt△AOB中,∵OA=3,sin∠OAB=45,cos∠OAB=35,∴AB=5,OB=4,BP=5-3=2.•在Rt△APM中,APAM=cos∠OAB=35,∴AM=5,OM=2,∴点M(0,-2),又△NPB∽△AOB,∴BN AB BP OB,∴BN=52,•∴ON=32,∴点B(32,0),设MP的解析式为y=kx+b,∵MP经过M、N两点,∴MP的解析式为y=43x-2,设过M、N、B的抛物线解析式为y=a(x-32)(x-4)且点M(0,-2)在其上,可得a=-13,即y=-13x2+116x-2.(2)①四边形OMCB是矩形.证明:在⊙A不动,⊙B运动变化过程中,恒有∠BAO=∠MAP,OA=AP,∠AOB=∠APM=90°,∴△AOB≌△APM,∴OB=PM,AB=AM,∴PB=OM ,而PB=BC ,∴OM=BC ,由切线长定理知MC=MP ,∴MC=OB , ∴四边形MOBC 是平行四边形, 又∵∠MOB=90°,∴四边形MOBC 是矩形.②存在,由上证明可知,Rt △MON ≌Rt △BPN , ∴BN=MN .因此在过M 、N 、B 三点的抛物线内有以BN 为腰的等腰三角形MNB 存在,• 由抛物线的轴对称性可知,在抛物线上必有一点M ′与M 关于其对称轴对称, ∴BN=BM ′,这样得到满足条件的三角形有两个,△MNB 和△M ′NB . 3.(1)∵L 与⊙O 相切于点A ,∴∠4=90°,∴OP 2=OA 2+AP 2, ∵OB=OC=12AB=3,AP=4, ∴OP 2=32+42,∴OP=5, ∴PC=5-3=2.(2)∵△PAO ∽△BAD ,且∠1>∠2,∠4=90°, ∴∠2=∠APO ,∴OB=OC ,∴∠2=∠3 ∵∠1=∠2+∠3,∴∠2=2∠2=2∠APO ∴∠4=90°,∴∠1+∠APO=90° ∴3∠APO=90°,∴∠APO=30°. 在Rt △BAD 中,∠2=∠APO=30°.∴AD=6sin30°=6×3. 过点O 作OE ⊥BC 于点E ∵∠2=30°,BO=3,∴OE=32,BE=3×cos30°=2,∴,∴S 四边形OADC =S △BAD -S △BOC =12AB ·AD=12BC ·OE=12×6×12××3294154.考前热身训练1.(1)易知OA=2,cos α=12,∠POQ=∠MAN=60°, ∴初始状态时,△AON 为等边三角形,•∴ON=OA=2,当AM 旋转到AM ′时,点N 移动到N ′, ∵∠OAM ′=30°,∠POQ=∠M ′AN•′=60°,∴∠M ′N ′A=30°,在Rt △OAN 中,ON ′=2AO=4, ∴NN ′=ON ′-ON=2,∴点N 移动的距离为2.(2)易知△OAN ∽△AMN ,∴AN 2=ON ·MN .(3)∵MN=y-x ,∴AN 2=y 2-xy ,过A 点作AD ⊥OP ,垂足为D ,可得OD=1, ∴DN=ON-OD=y-1,在Rt △AND 中,AN 2=AD 2+DN 2=y 2-2y+4, ∴y 2-xy=y 2-2y+4,即y=42x-. ∴y>0,∴2-x>0,即x<2,又∵x ≥0,∴x 的取值范围是:0≤x<2.(4)S=12·OM ·,∵S 是x ,∴0≤S<2·2.即0≤ 2.(1)易知⊙M 半径为2,设PA=x ,则x :4=1:2⇒x=2,由相交弦定理推论得OC=OA .OB=1×3,2=PO 2+OC 2=32+2=12,PM 2=42=16,MC 2=22=4,∴PM 2=PC 2+MC 2,∴∠PCM=90°.(2)易知过A 、C 、B 三点的抛物线的解析式为(x+1)(x-3),•假设满足条件的Q 点存在,坐标为(m ,0),直线QC 的解析式为, ∵直线QC 与抛物线只有一个公共点,∴方程-3(x+1)(x-3)=-m∴(2+3m)2=0,∴m=-32,即满足条件的Q 点存在,•坐标为(-32,0);(3)连结DN ,作DH ⊥PN ,垂足为H ,设⊙N 的半径为r ,则∵ND ⊥PC , ∴ND ∥MC ,∴DN PN MC PM =,∴224r r -=, ∴r=23,∵DN 2=NH ·NP ,∴(23)2=NH·(2-23),∴NH=13,∴D(-2∵抛物线(x+1)(x-3)平移,使其经过P、A两点的抛物线的解析式为y=-3(x+•1)(x+3)又经验证D是该抛物线上的点,∴将过A、C、B三点的抛物线平移后能同时经过P、D、A三点.。
