2017-2018学年七年级数学上册3.1从算式到方程
七年级上册数学第三章 3.1 从算式到方程人教版

七年级上册数学第三章 3.1 从算式到方程(人教版)第三章一元一次方程3.1 从算式到方程3.1.1 一元一次方程1.能根据题意用字母表示未知数,然后分析出等量关系,再根据等量关系列出方程.2.理解方程、一元一次方程的定义及解的概念.3.掌握检验某个数值是不是方程的解的方法.阅读教材P78~80,思考下列问题.什么是方程、一元一次方程及它们的解?怎样列方程?知识探究1.含有未知数的等式叫方程.只含有一个未知数,未知数的次数是1,这样的方程叫做一元一次方程.2.解方程就是求出使方程中等号左右两边相等的未知数的值,这个值就是方程的解.自学反馈根据下面实际问题中的数量关系,设未知数列出方程:1.用一根长为2 4 cm的铁丝围成一个正方形,正方形的边长为多少?解:设正方形的边长为x cm,列方程得:4x=24.2.某校女生人数占全体学生数的52%,比男生多80人,这个学校有多少学生?解:设这个学校的学生数为x,则女生数为52%x,男生数为52%x-80,依题意得方程:52%x+52%x-80=x.3.练习本每本0.8元,小明拿了10元钱买了若干本,还找回4.4元.问:小明买了几本练习本?解:设小明买了x本,列方程得:0.8x=10-4.4. 4.长方形的周长为24 cm,长比宽多2 cm,求长和宽分别是多少.解:设长为xcm,则宽为(x-2)cm,依题意得方程:2(x+x-2)=24.先设未知数,再找相等关系,列方程.[来源:学+科+网Z+X+X+K]活动1 小组讨论例 1 判断下列是不是一元一次方程,是打“√”,不是打“×”.①x+3=4;(√)②-2x+3=1;(√)③2x+13=6-y;(×)④1x=6;(×)⑤2x-8-10;(×)⑥3+4x=7x.(√)例2 检验2和-3是否为方程x-52-1=x-2的解.解:-3是,2不是.带入方程中左右两边相等的值就是方程的解.例3 设未知数列出方程:(1)用一根长为100 cm的铁丝围成一个正方形,正方形的边长为多少?(2)长方形的周长为40 cm,长比宽多3 cm,求长和宽分别是多少.(3)某校女生人数占全体学生数的55%,比男生多50人,这个学校有多少学生?(4)A、B两地相距200千米,一辆小车从A地开往B 地,3小时后离B地还有20千米,求小车的平均速度.解:略.设未知数,找等量关系,用方程表示简单实际问题中的相等关系.活动2 跟踪训练1.下列方程的解为x=2的是(C)A.5-x=2B.3x-1=4-2xC.3-(x-1)=2x-2D.x-4=5x-22.在2+1=3,4+x=1,y2-2y=3x,x2-2x+1中,一元一次方程有(A)A.1个B.2个C.3个D.4个3.老师要求把一篇有2 000字的文章输入电脑,小明输入了700字,剩下的让小华输入,小华平均每分钟能输入50个字,问:小华要多少分钟才能完成?(请设未知数列出方程,并尝试求出方程的解)解:设小华要x分钟完成,由题意,得50x+700=2 000,x=26.活动3 课堂小结1.方程及一元一次方程的定义.2.如何列方程,什么是方程的解.3.1.2 等式的性质1.了解等式的两条性质.2.会用等式的性质解简单的一元一次方程.阅读教材P81~82,思考下列问题.1.等式的性质有哪几条?用字母怎样表示?字母代表什么?2.解方程的依据是什么?知识探究1.如果a=b,那么a±c=b±c(字母a、b、c可以表示具体的数,也可以表示一个式子).2.如果a=b,那么ac=b.如果a=b(c≠0),那么ac=bc.自学反馈1.已知a=b,请用“=”或“≠”填空:(1)3a=3b;(2)a4=b4;(3)-5a=-5b.2.利用等式的性质解下列方程:(1)x+7=26;(2)- 5x=20;(3)-2(x+1)=10.解:(1)x=19.(2)x=-4.(3)x=-6.[来源:学_科_网]注意用等式的性质对方程进行逐步变形,最终可变形为“x=a”的形式.活动1 小组讨论例利用等式的性质解下列方程并检验:(1)x-9 =6;(2)-0.2x=10;(3)3-13x=2;(4)-2x+1=0;(5)4(x+1)=-20.解:(1)x=15.(2)x=-50.(3)x=3.(4)x=12.(5)x =-6.运用等式的性质解方程不能漏掉某一边或某一项.活动2 跟踪训练利用等式的性质解下列方程并检验:(1)x+5=8;[来源:学|科|网Z|X|X|K](2)-x-1=0;[来源:学+科+网Z+X+X+K](3)-2-14x=2;(4)6x-2=0.解:(1)x=3.(2)x=-1.(3)=-16.(4)x=活动3 课堂小结1.等式有哪些性质?2.在用等式的性质解方程时要注意什么?会从实际问题中抽象出数学模型,会用一元一次方程解决电话计费等有关方案决策的问题.阅读教材P104~105探究3的内容,思考题中所提出的问题.知识探究方案决策问题解题的基本方法是求得每种方案的结果,再结合结果做出判断.[来源:学科网]自学反馈某市乘公交车(非空调)每次需投币1.5元或者购买IC卡,每次刷卡扣款1.35元,但办理IC卡时需付工本费15元.问需乘坐公交车多少次时两种收费方式的收费一样?当超过这个次数后哪种收费方式较合算?[来源:]解:100次,购买IC卡合算.活动1 小组讨论例(教材P104探究3)电话计费问题下表中有两种移动电话计费方式.月使用费/元主叫限定时间/min主叫超时费/(元/min)被叫方式一581500.25免费方式二883500.19免费考虑下列问题:(1)设一个月用移动电话主叫为t min(t是正整数).根据上表,列表说明:当t在不同时间范围内取值时,按方式一和方式二如何计费;(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.活动2 跟踪训练某厂招聘运输工,有两种方法来结算工资,一种是每月基本工资300元,每运1吨货给15元;另一种是没有基本工资,每运1吨货给20元.问每月运多少吨货时两种结算方法给的工资一样多?如果某工人每月可运货70吨,那么用哪种结算方法可多拿工资?解:60吨,用第二种结算方法可多拿工资.活动3 课堂小结电话计费等有关的方案决策问题.。
人教版数学七年级上册3.1从算式到方程(第1课时)教案

3.1从算式到方程第1课时教学目标:1、通过处理实际问题,让学生体验从算术方法到代数方法是一种进步;2、初步学会如何寻找问题中的相等关系,列出方程,了解方程的概念;3、培养学生获取信息,分析问题,处理问题的能力。
教学重难点:重点:从实际问题中寻找相等关系难点:从实际问题中寻找相等关系教学过程:一、情境引入教师提出课本问题问题1:从上图中你能获得哪些信息?(必要时可以提示学生从时间、路程、速度、四地的排列顺序等方面去考虑。
)教师可以在学生回答的基础上做回顾小结。
问题2:你会用算术方法求出王家庄到翠湖的距离吗?(当学生列出不同算式时,应让他们说明每个式子的含义)教师可以在学生回答的基础上做回顾小结:1、问题涉及的三个基本物理量及其关系;2、从知的信息中可以求出汽车的速度;3、从路程的角度可以列出不同的算式 问题3:能否用方程的知识来解决这个问题呢?二、讲解新课1、教师引导学生设未知数,并用含未知数的字母表示有关的数量如果设王家庄到翠湖的路程为x 千米,那么王家庄距青山 千米,王家庄距秀水 千米。
2、教师引导学生寻找相等关系,列出方程.问题1:题目中的“汽车匀速行驶”是什么意思?问题2:汽车在王家庄至青山这段路上行驶的速度该怎样表示?你能表示其他各段路程的车速吗? 问题3:根据车速相等,你能列出方程吗?教师根据学生的回答情况进行分析,如:依据“王家庄至青山路段的车速=王家庄至秀水路段的车速”可列方程:x -503 =x+70 5,依据“王家庄至青山路段的车速=青山至秀水路段的车速”可列方程:x -503 =50+70 23、给出方程的概念,介绍等式、等式的左边、等式的右边等概念.4、归纳列方程解决实际问题的两个步骤: (1)用字母表示问题中的未知数(通常用x,y,z 等字母); (2)根据问题中的相等关系,列出方程. 渗透列方程解决实际问题的思考程序。
5、比较列算式和列方程两种方法的特点.建议用小组讨论的方式进行,可以把学生分成两部分分别归纳两种方法的优缺点,也可以每个小组同时讨论两种方法的优缺点,然后向全班汇报。
七年级数学上册 3.1 从算式到方程 3.1.1 一元一次方程

课题:3.1.1一元一次方程教学目标:1.理解方程、一元一次方程、方程的解的概念;2.并掌握检验某个值是不是方程的解的方法.重点:寻找等量关系,列出方程.难点:对于复杂一点的方程,用估算的方法寻求方程的解,需要多次的尝试,也需要一定的估计能力.教学流程:一、情境引入一辆客车和一辆卡车同时从A 地出发沿同一公路同方向行驶,客车的行驶速度是70 km/h ,卡车的行驶速度是60 km/h ,客车比卡车早1 h 经过B 地. A ,B 两地间的路程是多少? 问题引入:你会用算术方法解决这个问题吗?解:60÷(70-60)×7二、探究1问题1:一辆客车和一辆卡车同时从A 地出发沿同一公路同方向行驶,客车的行驶速度是70 km/h ,卡车的行驶速度是60 km/h ,客车比卡车早1 h 经过B 地. A ,B 两地间的路程是多少?追问1:时间和路程、速度有什么关系呢? 答案:路程时间=速度追问2:“客车比卡车早1 h 经过B 地. A ,B 两地间的路程是多少?”这句话中包含的相等关系是什么呢?答案:卡车所用时间-客车所用时间=1追问3:设A ,B 两地间的路程是x km .你能用式子分别表示两车所用的时间吗? 答案:卡车所用时间60x h ,客车所用时间70x h 解:设A ,B 两地间的路程是x km .则客车从A 地到B 地所用时间为:70x h ,卡车从A 地到B 地所用时间为:60x h ,则16070x x -= 归纳:含有未知数的等式,叫做方程.例:根据下列问题,设未知数并列出方程:(1)用一根长24 cm 的铁丝围成一个正方形,正方形的边长是多少?分析:相等关系:正方形的边长×4=24解:(1)设正方形的边长为x cm .根据题意可列方程4x =24(2)一台计算机已使用1700 h ,预计每月再使用150 h ,经过多少月这台计算机的使用时间达到规定的检修时间2450 h ?分析:相等关系:已使用时间+预计再使用时间=2450解: (2)设x 月后这台计算机的使用时间达到2450 h ,那么在x 月里这台计算机使用了150x h.根据题意可列方程1700+150x =2450(3)某校女生占全体学生数的52%,比男生多80人,这个学校有多少学生?分析:相等关系:女生人数-男生人数=80解: (3)设这个学校的学生数为x ,那么女生数为0.52x ,男生数为(1-0.52)x . 根据题意可列方程0.52x -(1-0.52)x =80问题2:想一想:这三个方程有什么共同的特征呢?4x =241700+150x =24500.52x -(1-0.52)x =80答案:1.只含有一个未知数x2.未知数x 的次数都是13.整式方程归纳:只含有一个未知数(元),未知数的次数都是1,等式两边都是整式,这样的方程叫做一元一次方程.练习1:1.下列式子:①x +y =1;②x -1=0;③8-6=2;④2x -1;⑤x 2=4;⑥1x=5.其中是方程的有( )A.1个B.2个C.3个D.4个答案:D2.下列方程中是一元一次方程的是( )A.x +3=y +2B.x +3=3-xC.x -1=1xD.x 2=1 答案:B三、探究2问题3:结合前面的例子,说一说如何利用一元一次方程解决实际问题?练习2:根据下列问题,设未知数,列出方程.(1)环形跑道一周长400 m ,沿跑道跑多少周,可以跑3 000 m ?解:设沿跑道跑x 周,可以跑3 000 m ,根据题意可列方程:400x =3 000(2)甲种铅笔每支0.3 元,乙种铅笔每支0.6 元,用9 元钱买了两种铅笔共20 支,两种铅笔各买了多少支?解:设甲种铅笔买了x 支,乙种铅笔习了(20-x )支,根据题意可列方程:0.3x +0.6 (20-x )=9四、探究3问题4:估算:用一些具体的数值代入方程,看方程是否成立.(1)4x =24解:当x =6时,4x 的值是24,方程4x =24等号左右两边相等.x =6叫做方程 4x =24的解.即:方程4x =24的未知数x 的值应该是6.(2)1700+150x =2450当x =5时,1700+150x 的值是24,方程1700+150x =2450等号左右两边相等. x =5叫做方程1700+150x =2450的解.即:方程1700+150x =2450的未知数x 的值应该是5.归纳:解方程就是求出使方程中等号左右两边相等的未知数的值,这个值就是方程的解. 练习3:x =1 000和x =2 000中哪一个是方程0.52x -(1-0.52)x =80的解? 解:当x =1 000时, 0.52x -(1-0.52)x =40 ,所以,x =1 000不是方程的解.当x =2 000时,0.52x -(1-0.52)x =80 ,所以,x =2 000是方程的解.归纳:一般地,要检验某个值是不是方程的解,就是用这个值代替方程中的未知数,看方程左右两边的值是否相等.五、巩固提高若方程(|m |-2)x 2-(m +2)x -6=0是关于x 的一元一次方程.(1)求m 的值;(2)判断x =3,x =-32,x =23是否是方程的解 解:(1)由题意知|m |-2=0,且m +2≠0,所以m =2(2)x =-32是方程的解,x =3,x =23不是方程的解 六、体验收获今天我们学习了哪些知识?1.什么是方程?什么是一元一次方程?2.从实际问题中列出方程的关键是什么?3.什么是方程的解,如何验证一个数值是不是这个方程的解?七、达标检测1.下列各式:①5x =0;②1+3x ;③y ²=4+y ;④x +y =5;⑤3m +2=1-m ;⑥y =3x -5-3x ⑦110x+= 是一元一次方程的有_____________(只填写序号)答案:①⑤⑥2. 方程2x -1=3的解是( )A.-1B. 12C.1D.2 答案:D3.已知3是关于x 的方程2x -a =1的解,则a 的值是( )A.-5B.5C.7D.2答案:B4.请写出一个解为x =2的一元一次方程:________________________.答案:x -2=0 注意:答案不唯一5.根据下列问题,设未知数,列出方程.(1)一个梯形的下底比上底多2 cm ,高是5 cm ,面积是40 cm 2,求上底.解:设上底长xcm ,根据题意可列方程: 5(2)402x x ++= (2)用买10 个大水杯的钱,可以买15 个小水杯,大水杯比小水杯的单价多5 元,两种水杯的单价各是多少元?解:设大水杯的单价为x 元,小水杯的单价为(x -5)元,根据题意可列方程: 1015(5)x x =-八、布置作业教材83页习题3.1第3、5题.。
七年级上学期数学 3.1 从算式到方程

七年级上学期数学中,第三章第一节“从算式到方程”主要介绍的是如何将实际问题抽象成数学算式,并进一步转化为方程的过程。
这一部分内容对于建立和理解方程的概念非常重要,是学习代数的基础。
核心内容包括:
1.算式与方程的概念:
●算式:表示数的运算过程,如(3+5)、(2\times4)等。
●方程:含有未知数的等式,目的是找到未知数的值,使等式成立,如
(x+5=10)。
2.方程的构成:
●方程通常包含未知数(如x、y)、常数、运算符(加、减、乘、除)以及等
号“=”。
3.建立方程:
●通过分析实际问题,确定未知数,根据问题中的条件关系,用代数表达式表示
这些关系,从而建立方程。
●例如,如果一个数加上3等于7,可以写成方程\(x+3=7\)。
4.解方程:
●学习基本的解方程方法,如加减法、乘除法,逐步求解未知数。
●对于简单的一元一次方程,目标是通过等式的性质,将未知数单独留在方程的
一边,求出其值。
5.应用题:
●结合生活实际,通过设定未知数,将文字问题转换为方程问题,解决诸如购物
找零、行程问题、工作量分配等问题。
学习重点:
●理解并区分算式与方程的含义。
●掌握将实际问题抽象成方程的能力。
●学会基本的方程解法,特别是解一元一次方程。
通过这部分的学习,学生能够初步掌握利用方程解决实际问题的方法,为后续更复杂的代数学习打下坚实的基础。
新人教版七年级数学上册3.1《从算式到方程》教学设计

新人教版七年级数学上册3.1《从算式到方程》教学设计一. 教材分析新人教版七年级数学上册3.1《从算式到方程》是学生在学习了整数和分数的基础上,开始接触代数的知识。
本节课主要让学生了解方程的概念,学会将实际问题转化为方程,从而解决实际问题。
教材通过丰富的实例,引导学生认识方程,理解方程的含义,并掌握方程的解法。
二. 学情分析七年级的学生已经具备了一定的数学基础,对整数和分数有了深入的理解。
但是,对于代数知识,尤其是方程,可能还比较陌生。
因此,在教学过程中,需要注重引导学生从实际问题中发现方程,理解方程,并掌握解方程的方法。
三. 教学目标1.让学生了解方程的概念,理解方程的含义。
2.培养学生将实际问题转化为方程,并解决实际问题的能力。
3.引导学生掌握方程的解法,提高学生的数学素养。
四. 教学重难点1.重点:方程的概念,方程的解法。
2.难点:将实际问题转化为方程,并解决实际问题。
五. 教学方法1.情境教学法:通过丰富的实例,引导学生认识方程,理解方程。
2.启发式教学法:在教学过程中,引导学生主动思考,发现规律,掌握方法。
3.合作学习法:鼓励学生之间相互讨论,共同解决问题。
六. 教学准备1.准备相关实例,用于引导学生认识方程。
2.准备练习题,用于巩固学生对方程的理解。
3.准备课件,用于辅助教学。
七. 教学过程1.导入(5分钟)通过一个实际问题,引导学生认识方程。
例如:小明有2个苹果,小红的苹果数是小明的3倍,请问小红有多少个苹果?让学生尝试用数学语言表述这个问题,从而引出方程的概念。
2.呈现(15分钟)呈现一组实际问题,让学生尝试用方程来解决。
例如:甲车和乙车同时出发,甲车每小时行驶60公里,乙车每小时行驶80公里,请问甲车追上乙车需要多少时间?引导学生发现实际问题中存在的等量关系,并将其转化为方程。
3.操练(15分钟)让学生分组讨论,尝试解决呈现的实际问题。
教师巡回指导,解答学生的疑问。
在这个环节中,重点让学生掌握方程的解法,并能够将实际问题转化为方程。
最新人教版2018-2019学年数学七年级上册:3.1从算式到方程(1)教学设计-优质课教案

初中数学七年级上册教案教学内容 3.1.1 从算式到方程(1)教学目标(一)知识与技能:(1)通过观察,归纳一元一次方程的概念.(2)根据方程解的概念,会估算出简单的一元一次方程的解.(二)数学思考:通过对多种实际问题的分析,感受方程作为刻画现实世界有效模型的意义.(三)问题解决:会解一元一次方程。
(四)情感态度:鼓励学生进行观察思考,发展合作交流的意识和能力。
教学重点:了解一元一次方程的有关概念教学难点:找出问题中的相等关系,列出一元一次方程以及估计方程的解.教具准备:多媒体课件制作。
教学时数:1课时。
教学过程:一、基本训练,激趣导入。
在小学里,我们已学习了像2x=50,3x+1=4等简单方程,那么什么叫方程呢?什么叫方程的解和解方程呢?方程是应用广泛的数学工具,把问题中未知数与已知数的联系用等式形式表示出来.在研究问题时,要分析数量关系,用字母表示未知数,列出方程,然后求出未知数.二、认准目标,指导自学。
怎样根据问题中的数量关系列出方程?怎样解方程?这是本章研究的问题.通过本章中丰富多彩的问题,你将进一步感受到方程的作用,并学习利用一地一次方程解决问题的方法.三、合作学习,引导发现。
1.怎样列方程?让学生观察章前图表,根据图表中给出的信息,回答以下问题.(1)根据图中的汽车匀速行驶途经王家庄、青山、秀水三地的时间表,•你知道,汽车从王家庄行驶到青山用了多少时间?青山到秀水呢?(2)青山与翠湖、秀水到翠湖的距离分别是多少?(3)本问题要求什么?(4)你会用算术方法解决这个实际问题呢?不妨试试列算式.(5)如果设王家庄到翠湖的路程为x(千米),你能列出方程吗?解:(1)汽车从王家庄行驶到青山用了3小时,青山到秀水用了2小时.(2)青山与翠湖的距离为50千米,秀水与翠湖的距离为70千米.(3)王家庄到翠湖的距离是多少千米?(4)分析:要求王家庄到翠湖的距离,只要求出王家庄到青山的距离,•而王家庄到青山的时间为3小时,所以必需求汽车的速度.如何求汽车的速度呢?这里青山到秀水的时间为2小时,路程为(50+70)千米,因此可求的汽车的平均速度为(50+70)÷2=60(千米/时)王家庄到青山的路程为:60×3=180(千米)所以王家庄到翠湖的路程为:180+50=230(千米)列综合算式为:50702+×3+50(5)分析:先画出示意图,示意图往往有助于分析问题.从上图中可以用含x的式子表示关于路程的数量:王家庄距青山(x-50)千米,王家庄距秀水(x+70)千米.从章前图表中可以得出关于时间的数量:从王家庄到青山行车3小时,从王家庄到秀水行车5小时.由路程数量和行车时间的数量,可以得到行车速度的表达式.汽车从王家庄开往青山时的速度为503x-千米/时,汽车从王家庄开往秀水的速度为705x+千米/时.要列出方程,必需找出“相等关系”,题目中还有哪些相等关系吗?根据汽车是匀速行驶的,可知各段路程的车速相等.于是列出方程:503x-=70 5 x+以后我们将学习如何解这个方程,求出未知数x的值,•从而得出王家庄到翠湖的路程.思考:对于以上的问题,你还能列出其他方程吗?如果能,你依据的是哪个相等关系?根据汽车匀速行驶,可知各段路程的车速相等.所以还可以列方程:503x -=50702+或705x +=50702+ (前者是汽车从王家庄到青山与从青山到秀水,这两段路程的车速相等,后者是汽车从王家庄到翠湖与从青山到秀水,这两段路程的车速相等)四、变式训练,反馈调节。
七年级数学上册-算式到方程3.1.1从算式到方程教案新版新人教版

第三章一元一次方程3.1 从算式到方程3.1.1 一元一次方程【知识与技能】(1)理解方程、一元一次方程、解方程、方程的解的含义,会检验一个数是否为某个一元一次方程的解.(2)初步学会如何寻找问题中的相等关系,列出方程.【过程与方法】通过解决实际问题,让学生体验从算术方法到代数方法是一种进步,体会方程思想.【情感态度与价值观】培养学生获取信息,分析问题,处理问题的能力.了解一元一次方程及其相关概念.寻找问题中的相等关系,列方程.多媒体课件教师提问:你知道什么叫方程吗?学生回答:含有未知数的等式叫作方程.教师:你能举出一些方程的例子吗?由学生举例,教师总结、板书课题.一、思考探究,获取新知教师利用多媒体展示图片,出示以下问题:某校初中一年级328名师生乘车外出春游,已有2辆校车可以乘坐64人,还需租用44座的客车多少辆?教师提问:你能解决这个问题吗?有哪些方法?学生小组内讨论,看能否用算术方法解,然后考虑用方程如何解决,教师可以参与到学生中去,关注学生解决问题的思路.教师总结:(方法一)算术法:(328-64)÷44=264÷44=6(辆).(方法二)列方程法:设需要租用x辆客车,那么这些客车共可乘坐44x人,加上乘坐校车的64人,就是全体师生共328人,可得44x+64=328.在这一教学过程中,教师不仅要使学生掌握此问题的解决方法,而且要让学生通过对比算术法与方程法,去体会列方程过程中的一般思路和方法.针对以上方程,教师提问:像上面这样的方程,你能给它起一个名字吗?学生阅读教材,体验方程的表达方式,并说说什么是一元一次方程.教师进一步提出问题:结合算术法,你能试着解出这个方程吗?得到的结果对所列的方程来说具有什么特点?学生可能利用逆运算求解,得出所求的结果使方程左右两边的值相等的特点,教师加以肯定,教师归纳总结有关方程的概念:①含有未知数的等式叫作方程.(44x+64=328,44,64,328为已知数,x为未知数)②只含有一个未知数(元),未知数的次数都是1,等号两边都是整式,这样的方程叫作一元一次方程.③解方程就是求出使方程中等号左右两边相等的未知数的值,这个值就是方程的解.教师:想一想,你是怎样列出方程的?找学生代表回答解题思路.教师归纳:分析实际问题中的数量关系,利用其中的相等关系列出方程,是用数学解决实际问题的一种方法.二、典例精析,掌握新知例1判断下列各式是不是方程,如果是,指出已知数和未知数,并说明哪些是一元一次方程;如果不是,说明理由.①5-2x=1;②y2+2=4y-1;③x-2y=6;④2x2+5x-8;⑤3×2=1;⑥(x-1)·(x+2)(x+1)=0;⑦1+x=x+1;⑧|x|=-2【解】①是一元一次方程,5,-2,1是已知数,x是未知数;②是方程,2,4,-1是已知数,y 是未知数;③是方程,-2,6是已知数,x,y是未知数;④不是方程,因为不是等式;⑤不是方程,因为不含有未知数;⑥是方程,-1,2,1,0是已知数,x是未知数;⑦是一元一次方程,1是已知数,x是未知数;⑧是方程,-2是已知数,x是未知数.例2在课外活动中,张老师发现同学们的年龄大多是13岁,就问同学:“我今年45岁,几年以后你们的年龄是我年龄的三分之一?”赵敏同学很快说出了答案为3年.她是这样算的:1年后,老师46岁,同学们的年龄是14岁,不是老师年龄的三分之一;2年后,老师47岁,同学们的年龄是15岁,也不是老师年龄的三分之一;3年后,老师48岁,同学们的年龄是16岁,恰好是老师年龄的三分之一.你能否用方程的方法来解答呢?(只列方程即可)【建议】学生独立完成,小组内交流,教师巡视,引导学生说一说这两种方法各自的特点,只要学生能谈出一两点体会,教师都应当加以鼓励.最后,教师给出总结:(用算术方法解)未知数不参加列式,表示计算过程,根据题里已知数和未知数间的关系,确定解题步骤,再列式计算;(用方程解)未知数用x表示,x参加列式,表示相等关系,根据题意找出数量间的相等关系,列出含有x的等式.【解】赵敏同学的方法是算术方法,用方程的方法解答如下:设x年后学生的年龄是老师年龄的三分之一,则可列方程为13+x=13(45+x).例3检验下列各数是不是方程4x-3=2x+3的解.(1)x=3;(2)x=8.【解】(1)把x=3分别代入方程等号的左边和右边,得左边=4×3-3=9,右边=2×3+3=9.左边=右边.所以x=3是方程4x-3=2x+3的解.(2)把x=8分别代入方程等号的左边和右边,得左边=4×8-3=29,右边=2×8+3=19.左边≠右边.所以x=8不是方程4x-3=2x+3的解.1.引出方程、一元一次方程等基本概念,并且对“根据实际问题中的数量关系,设未知数,列出一元一次方程”的分析问题的过程进行了归纳.2.通过现实生活中的例子,体会方程的意义,领悟一元一次方程的定义,会进行简单的辨别.教材P83习题3.1,第1,3,6,7题。
人教版七年级数学上:3.1《从算式到方程》(共3课时)

活动:拓广探索
训练提升
练习 根据下列问题,设 未知数并列出方程:
(1) 一台计算机已使用1 700小 时,预计每月再使用150小时, 经过多少月这台计算机的使用 时间达到规定的修检时间2 450 小时? 解: 设x月后这台计算机的使用时间达到2 450小
时, 那么在x月后使用了(1 700+150x)小时.
X千米
50 王家庄 10:00 青山 13:00 翠湖 70 秀水 15:00
若设王家庄到翠湖的路程为X千米,那么: 王家庄距青山 (X-50) 千米,从王家庄到青山时间 速度 速度
x 50 3 千米/小时
3 5
小时, 小时,
王家庄距秀水(x+70) 千米,从王家庄到秀水时间
x
1 700+150x
1
1 850
2
2 000
3
2 150
4 5
2 300 2 450
6
2 600
… …
当x=5时,1 700+150x的值是2 450,方程1 700+150=2 450中的未知数的值应是5.
活动:归纳总结 巩固发展
本 节 课 学 了 哪 些 内 容? 哪 些 方 法?
小结
内容 方程 列方程 解决实际问题的方法 含有未知数的等式.
分析:若知道王家庄到翠湖的路程(比如x千米), 用含 x的式子表示关于路程的数量: ( x+70) x-50) 王家庄距青山( _______ 千米,王家庄距秀水 _______ 千米. 有关时间的数量: 从王家庄到青山行车___ 3 小时,王家庄到秀水行车____ 5 小时. 有关速度的数量: x 50
2017-2018学年人教版七年级数学教案:3.1从算式到方程

4.掌握方程的解的概念,并能够根据实际问题列出相应的一元一次方程。
本节课旨在帮助学生建立方程的概念,培养他们解决实际问题的能力。教学内容与教材紧密相关,确保学生在掌握知识的同时,能够将所学应用于实际生活中。
直接输出:
二、核心素养目标
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了方程的基本概念、重要性和应用。同时,我们也通过实践活动和小组讨论加深了对方程的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
1.培养学生的逻辑推理能力:通过等式性质和方程解法的探究,让学生理解数学知识之间的内在联系,提高他们的逻辑推理能力。
2.提升问题解决能力:使学生能够从实际问题中抽象出一元一次方程,学会运用方程方法解决生活中的问题,增强问题解决能力。
3.增强数学建模素养:让学生在实际问题中建立数学模型,体验数学建模的过程,培养他们的数学建模素养。
-方程在解决实际问题中的应用:通过具体问题,让学生学会从实际情境中抽象出方程,体会方程在解决实际问题中的价值。
举例:在教学等式性质时,重点讲解等式两边同时加减或乘除同一个数后,等式依然成立的性质,并通过示例让学生进行验证。
2.教学难点
-未知数的引入与理解:学生刚开始接触方程时,对未知数的概念理解可能存在困难,需要通过具体实例和引导,帮助学生理解未知数的作用和意义。
2017年秋季学期新版新人教版七年级数学上学期3.1、从算式到方程课件11

个图形由2×3+1=7个棋子构成, 第2个图形由2×4+1=9个棋子构 成,第3个图形由2×5+1=11个棋 子构成,因此,第5个图形由 2×7+1=15个棋子构成,可见第n 个图形棋子的总个数为 Sn=2(n+2)+1=2n+5. (2)要判断2013个棋子能否摆成 “广”字,只需令2n+5=2013,解 这个方程,若有整数解,则能摆成 “广”字,否则不能.
2 3
【解题归纳】 此类题是中考中的常见题型, 其方法是将方程的解代入原方程,转化为另一 字母的方程,再进一步解方程.
1.若x=1是方程2x - a=0的解,则a的值为 ( C )
A.1
C.2
B. - 1
D. - 2
一元一次方程的有关概念 考查角度2 一元一次方程成立的条件 例2 若(a - 1)x+3=0是关于x的一元一次方程,则 a ≠1 . 〔解析〕一元一次方程的一般形式是ax+b=0,其 中a,b是常数,且a≠0,据此得出a - 1≠0,即a≠1. 故填≠1. 【解题归纳】 本题主要考查了一元一次方程 的一般形式,ax+b=0,必须强调a≠0.
2.若(k - 2)x+3=0是关于x的一元一次方程,则 ≠2 k .
等式性质的运用 例3 ▲●■分别表示三种不同的物体,如 图3 - 1所示,前两架天平保持平衡,如果要使第三 架天平也平衡,那么“?”处应放“■”的个数为 ( )B A.2个 B.3个 图3 - 1 C.4个 D.5个
〔解析〕 从第一个天平可以看出一个●相当于一个■的质量. 从第二个天平可以看出一个▲相当于两个■的质量,所以在第三 个天平的右边应放三个■.故选B.
人教版七年级数学上册:3.1 从算式到方程 教案

教学准备1. 教学目标1、了解一元一次方程的概念,能利用一元一次方程的概念解决简单问题通过列方程的过程,初步感受到方程作为刻画现实世界的数学模型的意义,体会由算式到方程是数的进步,从而初步体会方程思想如何检验一个方程的解是否正确?2、代入法作为一个非常重要的数学方法和数学思想,其直接作用就是验证方程的解的正确性,用来检验一个答案是否正确.本节可加强代入法的学习.3、在学习中,体会方程的便捷.2. 教学重点/难点教学重点:会列一元一次方程解决一些简单的应用题.教学难点:弄清题意,找出“相等关系”.3. 教学用具PPT课件4. 标签教学过程一.引入小学里已经学过列方程解简单的应用题,让我们回顾一下,如何列方程解应用题?例如:一本笔记本1.2元.小红有6元钱,那么她最多能买到几本这样的笔记本呢?解:设小红能买到工本笔记本,那么根据题意,得1.2x=6因为1.2×5=6,所以小红能买到5本笔记本.二.新课教学我们再来看下面一个例子:问题1:某校初中一年级328名师生乘车外出春游,已有2辆校车可以乘坐64人,还需租用44座的客车多少辆?问:你能解决这个问题吗?有哪些方法?(让学生思考后,回答,教师再作讲评)算术法:(328-64)÷44=264÷44=6(辆)列方程解应用题:设需要租用x辆客车,那么这些客车共可乘44x人,加上乘坐校车的64人,就是全体师生328人,可得.44x+64=328 (1)解这个方程,就能得到所求的结果.问:你会解这个方程吗?试试看?问题2:在课外活动中,张老师发现同学们的年龄大多是13岁,就问同学:“我今年45岁,几年以后你们的年龄是我年龄的三分之一?”小敏同学很快说出了答案.“三年”.他是这样算的:1年后,老师46岁,同学们的年龄是14岁,不是老师的三分之一.2年后,老师47岁,同学们的年龄是15岁,也不是老师的三分之一.3年后,老师48岁,同学们的年龄是16岁,恰好是老师的三分之一.你能否用方程的方法来解呢?通过分析,列出方程:13+x=(45+x)问:你会解这个方程吗?你能否从小敏同学的解法中得到启发?这个方程不像例l中的方程(1)那样容易求出它的解,小敏同学的方法启发了我们,可以用尝试,检验的方法找出方程(2)的解.也就是只要将x=1,2,3,4,……代人方程(2)的两边,看哪个数能使两边的值相等,这个数就是这个方程的解.把x=3代人方程(2),左边=13+3=16,右边=(45+3)=×48=16,问:若把例2中的“三分之一”改为“二分之一”,那么答案是多少?同学们动手试一试,大家发现了什么问题?同样,用检验的方法也很难得到方程的解,因为这里x的值很大.另外,有的方程的解不一定是整数,该从何试起?如何试验根本无法人手,又该怎么办?这正是我们本章要解决的问题.课堂小结小结:本节主要是学习分析问题列方程的三个步骤:1、确定未知量;2、找相等关系;3、列方程.还学习了通过尝试、代入寻找方程的解.这是一个很重要的思想和方法,要记住如何尝试以及如何代入.作业:第3页,习题6.1第1、3题课后习题1.第3页练习1、2.2.补充练习:检验下列各括号内的数是不是它前面方程的解.(1)x-3(x+2)=6+x (x=3,x=-4)(2)2y(y-1)=3 (y=-1,y=3/2 )(3)5(x-1)(x-2)=0 (x=0,x=1,x=2)板书从实际问题到方程1、如何确定未知量x;问题问什么,就设什么为未知数x.2、一定要根据相等关系列方程尝试法、代入法是很重要的数学方法.。
【人教版】2018年秋七年级上册数学:从算式到方程

3.1从算式到方程(第1课时)教学目标:1.了解方程、一元一次方程、方程的解等概念,会估算方程的解,会检验一个数是否是方程的解.2.根据实际问题中的数量关系,列出相等关系,列出方程,体会数学建模思想.3.让学生体会我们的生活处处有数学,对数学产生亲近感,提高学生学习数学的兴趣.教学重点:方程、一元一次方程和方程的解的概念.教学难点:从实际问题中找出相等关系,列出方程.教法:指导法学法:小组研讨法教学过程:一、情境引入问题1:一辆客车和一辆卡车同时从A 地出发沿同一公路同方向行驶,客车的行驶速度是车70km/h,卡车的行驶速度是60km/h,客车比卡车早1h 经过B 地,A,B 两地间的路程是多少?学生合作探究:小组讨论各个数量之间的运算关系,尝试列出算式.教师总结:由于客车比卡车早1h 经过B 地,则可计算出卡车行驶的时间:()76070170=-÷⨯(h),则A,B 两地的路程:420607=⨯(km)上述计算过程中的数量关系不是特别明显,我们是否能找到一种更加直接的求解方法呢?问题2:如果设A、B 两地的路程是x km,你能分别列出表示客车和卡车从A 地到B 地的行驶时间吗?从两车的时间相差1h,你能列出关于x 的方程吗?学生活动:小组合作探究,确定各个量之间的运算关系.师生合作探究:我们可知两车的时间相等关系:卡车行驶时间-客车行驶时间=1h 教师总结:本题主要数量关系是速度路程时间÷=.可列出方程:17060=-x x ①问题3:你还能列出其他方程吗?如果能,你依据的是哪个相等关系?学生活动:小组合作探究.师生合作探究:能否利用路程相等列出方程?教师总结:客车行驶路程=卡车行驶路程可以设客车行驶时间为x h,则卡车行驶时间为(x +1)h,则()16070+=x x .也可以设卡车行驶的时间为x h,则客车行驶的时间为(x -1)h.则()x x 60170=-.以上的利用列方程的解题过程告诉我们:列方程时,要先设字母表示未知数,然后根。
人教版七年级数学上第3章:3.1.1从算式到方程教学设计

《3.1.1从算式到方程》一、内容和内容分析1.内容:方程的概念,能根据具体问题中的数量关系列出方程,体会方程是刻画现实世界的数量关系的有效模型2.内容解析:方程是链接代数式和函数的桥梁,是初等代数学的核心内容,是解决实际问题的一种重要的数学模型,,方程的出现是从算术发展到代数方法的一个重要标志,这种以方程为工具的解决问题的思想在本章占有重要的地位。
本节是方程的起点,学生在小学数学学习过程中已经接触过,学生对此内容并不陌生。
关键是要让学生清楚为什么要用方程来解决问题。
基于以上分析,可以确定本节课的重点是:体验方程是刻画现实世界的一种有效的数学模型,经历探索数量关系列出方程的过程。
二、目标和目标解析1.目标(1)探究鸡兔同笼问题(2)设计研学旅行(3)通过问题情境让学生认识数学来源于生活2.目标解析达成目标(1)知道了方程是含有未知数的等式达成目标(2)感受方程达成目标(3)的标志是:学生通过实际问题情境体会到数学来源于生活,同时又作用于生活,体会用数学的意识基于以上分析:确定本节课的教学难点:(1)从列算式到列方程的思维习惯的转变(2)分析确定问题中的等量关系,能用方程来描述和刻画事物之间的等量关系三、学情分析在小学学段,学生已经习惯了用数学方法解决实际问题,而对于如何用设未知数的方法解决问题由一定难度,不够熟练。
四、教学策略分析回顾方程----感受方程---体会方程---品味方程五、教学过程设计(一)研学旅行——回顾方程:鸡兔同笼问题“鸡兔同笼问题是我国古代著名的趣题的问题之一,大约在1500多年前,我国古代一部较为普及的算书:今有鸡兔同笼问题,上有三十五头,下有九十四足,问:鸡兔各几何?问题1:请同学们回忆一下,小学里是怎样解决这个问题的?问题2:“猜年龄”我是9月份出生的,我的年龄的2倍加上6正好是我出生那个月的总天数的2倍。
猜猜我的年龄。
(二)研学旅行——感悟方程:问:1:冯老师外出学习一周,她回来的那天九十我们研学旅行出发的日子,这一周各天的日期和是84,问冯老师是几号回来的?问题2:小明、小强、小杰汉子听写大赛,规定每人听写20次,小强写对10个字,小杰比小明多写对2个字,三人平均每人写对14个字,问:小明、小杰各写对多少汉字?(三)研学旅行——体会方程问题:学校组织学生290人研学旅行,共使用8两客车,其中每辆大客车可以载40人,每辆小客车可以载30人,需要大小客车多少?(四)研学旅行——品味方程问题1:一辆大客车和一辆小客车从学校出发同时沿着相同方向的公路行驶,小车速度是每小时70千米,大车速速是每小时60千米,小车比大车早了1小时就到达目的地。
人教版七年级数学上册:3.1 从算式到方程 教案

教学准备1. 教学目标1、了解一元一次方程的概念,能利用一元一次方程的概念解决简单问题通过列方程的过程,初步感受到方程作为刻画现实世界的数学模型的意义,体会由算式到方程是数的进步,从而初步体会方程思想如何检验一个方程的解是否正确?2、代入法作为一个非常重要的数学方法和数学思想,其直接作用就是验证方程的解的正确性,用来检验一个答案是否正确.本节可加强代入法的学习.3、在学习中,体会方程的便捷.2. 教学重点/难点教学重点:会列一元一次方程解决一些简单的应用题.教学难点:弄清题意,找出“相等关系”.3. 教学用具PPT课件4. 标签教学过程一.引入小学里已经学过列方程解简单的应用题,让我们回顾一下,如何列方程解应用题?例如:一本笔记本1.2元.小红有6元钱,那么她最多能买到几本这样的笔记本呢?解:设小红能买到工本笔记本,那么根据题意,得1.2x=6因为1.2×5=6,所以小红能买到5本笔记本.二.新课教学我们再来看下面一个例子:问题1:某校初中一年级328名师生乘车外出春游,已有2辆校车可以乘坐64人,还需租用44座的客车多少辆?问:你能解决这个问题吗?有哪些方法?(让学生思考后,回答,教师再作讲评)算术法:(328-64)÷44=264÷44=6(辆)列方程解应用题:设需要租用x辆客车,那么这些客车共可乘44x人,加上乘坐校车的64人,就是全体师生328人,可得.44x+64=328 (1)解这个方程,就能得到所求的结果.问:你会解这个方程吗?试试看?问题2:在课外活动中,张老师发现同学们的年龄大多是13岁,就问同学:“我今年45岁,几年以后你们的年龄是我年龄的三分之一?”小敏同学很快说出了答案.“三年”.他是这样算的:1年后,老师46岁,同学们的年龄是14岁,不是老师的三分之一.2年后,老师47岁,同学们的年龄是15岁,也不是老师的三分之一.3年后,老师48岁,同学们的年龄是16岁,恰好是老师的三分之一.你能否用方程的方法来解呢?通过分析,列出方程:13+x=(45+x)问:你会解这个方程吗?你能否从小敏同学的解法中得到启发?这个方程不像例l中的方程(1)那样容易求出它的解,小敏同学的方法启发了我们,可以用尝试,检验的方法找出方程(2)的解.也就是只要将x=1,2,3,4,……代人方程(2)的两边,看哪个数能使两边的值相等,这个数就是这个方程的解.把x=3代人方程(2),左边=13+3=16,右边=(45+3)=×48=16,问:若把例2中的“三分之一”改为“二分之一”,那么答案是多少?同学们动手试一试,大家发现了什么问题?同样,用检验的方法也很难得到方程的解,因为这里x的值很大.另外,有的方程的解不一定是整数,该从何试起?如何试验根本无法人手,又该怎么办?这正是我们本章要解决的问题.课堂小结小结:本节主要是学习分析问题列方程的三个步骤:1、确定未知量;2、找相等关系;3、列方程.还学习了通过尝试、代入寻找方程的解.这是一个很重要的思想和方法,要记住如何尝试以及如何代入.作业:第3页,习题6.1第1、3题课后习题1.第3页练习1、2.2.补充练习:检验下列各括号内的数是不是它前面方程的解.(1)x-3(x+2)=6+x (x=3,x=-4)(2)2y(y-1)=3 (y=-1,y=3/2 )(3)5(x-1)(x-2)=0 (x=0,x=1,x=2)板书从实际问题到方程1、如何确定未知量x;问题问什么,就设什么为未知数x.2、一定要根据相等关系列方程尝试法、代入法是很重要的数学方法.。
七上3.1.1 从算式到方程
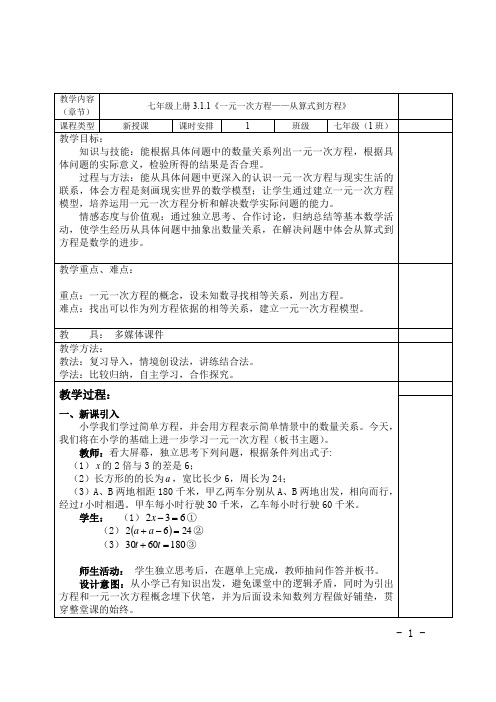
2、方程① ,② ,③ ,④ ,⑤ 中一元一次方程有②③⑤;
3、根据题意,列方程:
(1)小明买4本笔记本和3支圆珠笔一共用了7.8元,已知笔记本每本1.2元,圆珠笔每支多少元?
(2) 的3倍比它的2倍多12;
(3)校图书馆的图书被学生借出25%后,还剩15万册,则学校图书馆共有图书多少万册?(4)甲、乙两名同学练习百米赛跑,甲每秒跑7米,乙每秒跑6.5米,如果甲让乙先跑1秒,那么甲经过几秒可以追上乙?
(1)某校女生占全校学生人数的52%,比男生多80人,这个学校有多少名学生?
解:设这个学生有 名学生。
分析:女生人数 名,男生人数 名
相等关系:女生人数-男生人数=80
由题意得
解法2:设这个学生有 名学生。
分析:女生人数 名,男生人数 名
相等关系:女生人数+男生人数=全校学生人数
由题意得
(2)一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70km/h,卡车的速度是60km/h。客车比卡车早1h经过B地,A、B两地间的路程是多少?
情感态度与价值观:通过独立思考、合作讨论,归纳总结等基本数学活动,使学生经历从具体问题中抽象出数量关系,在解决问题中体会从算式到方程是数学的进步。
教学重、难点:
重点:一元一次方程的概念,设未知数寻找相等关系,列出方程。
难点:找出可以作为列方程依据的相等关系,建立一元一次方程模型。
教具:多媒体课件
教学方法:
(3)A、B两地相距180千米,甲乙两车分别从A、B两地出发,相向而行,经过 小时相遇。甲车每小时行驶30千米,乙车每小时行驶60千米。
学生:(1) ①
(2) ②
(3) ③
