本表格为计算(圆缓--缓直段)即第一段缓和曲线上 任意点路线边缘标高
曲线道路坐标计算(Excel)

曲线道路坐标计算§1 曲线要素计算缓和曲线是在不改变直线段方向和保持圆曲线半径不变的条件下,插入到直线段和圆曲线之间的。
其曲率半径ρ从直线的曲率半径∞(无穷大)逐渐变化到圆曲线的半径R ,在缓和曲线上任意一点的曲率半径ρ与缓和曲线的长度l 成反比,以公式表示为:l1∝ρ 或 C l =⋅ρ(C 为常数,称曲线半径变更率)。
当o l l =时,R =ρ,应有o l R l C ⋅=⋅=ρ以上几式是缓和曲线必要的前提条件。
在实际应用中,可采取符合这一前提条件的曲线作为缓和曲线。
常用的有辐射螺旋线及三次抛物线,我国采用辐射螺旋线。
为了在圆曲线与直线之间加入一段缓和曲线o l ,原来的圆曲线需要在垂直于其切线的方向移动一段距离p ,因而圆心就由'O 移到O ,而原来的半径R 保持不变,如图。
由图中可看出,缓和曲线约有一半的长度是靠近原来的直线部分,而另一半是靠近原来的圆曲线部分,原来圆曲线的两端其圆心角o β相对应的那部分圆弧,现在由缓和曲线所代替,因而圆曲线只剩下缓圆点(HY )到圆缓点(YH )这段长度即y l 。
o β为缓和曲线的切线角,即缓圆点或圆缓点切线与直缓点或缓直点切线的交角,亦即圆曲线HY→YH 两端各延长2ol 部分所对应的圆心角。
γ为缓和曲线总偏角,即从直缓点(ZH )测设缓圆点(HY )或从缓直点(HZ )测设圆缓点(YH )的偏角。
q 为切线增量(切垂距),即ZH (或HZ )到从圆心O 向ZH (或HZ )的切线作垂线垂足的距离。
p 为圆曲线内移值,即垂线(从圆心O 向ZH (或HZ )的切线作垂线)长与圆曲线半径R 之差。
§1.1 不等长缓和曲线要素计算:在铁路曲线测设中,线路曲线一般是由相等的两条缓和曲线中间加一个圆曲线构成,有时还会出现由两个不等长的缓和曲线中间加一个圆曲线构成的特殊情况,如图:缓和曲线长分别为1o l 、2o l , 切线长分别为1T 、2T ,曲线偏角(线路转角)为α,圆曲线半径为R ,圆曲线长为y l ,曲线长为L ,外矢距为E ,切曲差为J ,(缓和曲线后)圆曲线内移值分别为1p 、2p ,(缓和曲线)切线增量分别为1q 、2q ,缓和曲线偏角分别为1o β、2o β , 回旋线参数分别为121o Rl A =、222o Rl A =各曲线要素计算公式如下:231112402R ll q o o -=232222402Rll q o o -=341211268824R lR l p o o -=342222268824RlR l p o o -=ααsin )(2)(12111p p tgp R q T -+++=ααsin )(2)(21222p p tgp R q T -+++=Rl R l o o o ππβ111901802=⋅=Rl R l o o o ππβ222901802=⋅=︒--++=180)(2121Rl l L o o o o πββα从以上公式可以看出,当21o o l l =时,就是等长(对称)缓和曲线的情况。
道路曲线高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
道路曲线高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
道路曲线高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式

高速公正路路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式未知2021-12-27 21:40:34 本站高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,那么:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,那么:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度〔或缓曲上任意点到缓曲起点的长度〕l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算:①第一坡度:i1(上坡为“+〞,下坡为“-〞)②第二坡度:i2(上坡为“+〞,下坡为“-〞)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点〔过渡段终点〕的间隔:x求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-〞,右转为“+〞)⑦曲线终点处曲率:P1(左转为“-〞,右转为“+〞) 求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
道路曲线计算公式

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式时间:2009-12-27 21:40:34 来源:本站作者:未知我要投稿我要收藏投稿指南高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
关于连接两圆曲线的缓和曲线任意点坐标计算方法

关于连接两圆曲线的缓和曲线任意点坐标计算方法朱志全(中国水利水电第七工程局勘测队,四川成都 611730)[摘 要] 本文主要阐述连接两圆曲线的缓和曲线任意点坐标计算方法及实例计算。
[关键词] 圆曲线; 缓和曲线; 回旋曲线; 基本特征; 坐标计算[中图分类号]T B22 [文献标识码] B [文章编号]1001-8379(2001)04-0181-02收稿日期:1999-07-07THE METHOD T O CA LCU LATE COORDINATES OFANY POINT ON CURVE LINE JOINTING TWOCIRC LE LINESZH U Zhi 2quan1 前言由直线—缓和曲线—圆曲线所构成的缓和曲线任意点坐标计算公式[1],仅提及当相邻两圆曲线半径差超过一定值时,两圆曲线必须通过缓和曲线连接的平面曲线。
而对于高等级公路,特别是高速公路为保证汽车在转弯时的安全、稳定、消除曲率突变以及增加线形美观,此种平面曲线的设计显得极其重要。
这也使得曲线的计算和测设更为复杂。
本文就此类缓和曲线任意点坐标计算公式进行推导。
2 缓和曲线的基本特征在直线与圆曲线间嵌入缓和曲线后,其曲率半径由无穷大(与直线连接处)逐渐变化到圆曲线半径R (与圆曲线连接处)。
缓和曲线上任一点的曲率半径R ′与该点至曲线起点曲线长l i 成反比,即:R ′=C/l i (C 为常数,称曲线半径变化率)。
当l i 等于所采用的缓和曲线长度L O 时,曲率半径R ′等于R ,故C =R ×L O 。
如图1所示,建立以直缓点ZH 为原点,过ZH 点的缓和曲线的切线为X 轴的直角坐标系。
文献[1]中推导了缓和曲线任意点坐标计算公式:x i =l i -l 5i /(40R 2L 2O )+……(1)y i =l 3i /(6R L O )-L 7i /(336R 3L 3O )+……(2)当曲线左旋时,x 为正、y 为负,如图1;曲线右旋时,x 、y 均为正,如图2。
道路曲线高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
缓和曲线)计算公式
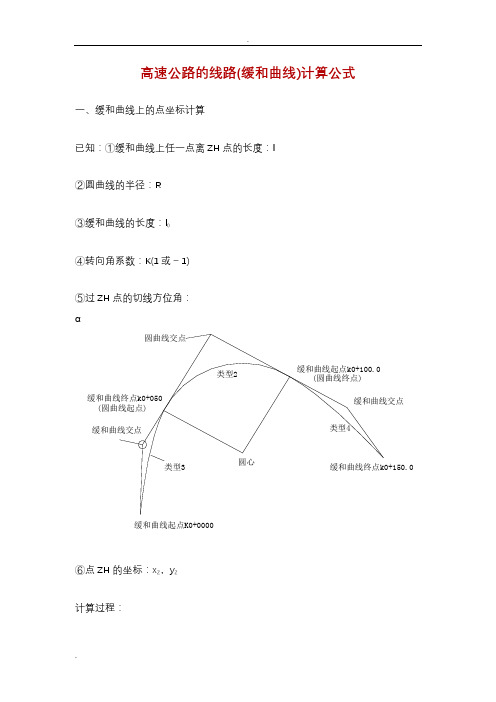
高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R 2——曲线终点处的半径P——曲线起点处的曲率1——曲线终点处的曲率P2α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i(上坡为“+”,下坡为“-”)1(上坡为“+”,下坡为“-”)②第二坡度:i2③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K③曲线终点桩号:K1④曲线起点坐标:x0,y⑤曲线起点切线方位角:α⑥曲线起点处曲率:P(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
公路缓和曲线段原理及缓和曲线计算公式Word版

公路缓和曲线段原理及缓和曲线计算公式一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车4)与圆曲线配合得当,增加线形美观2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A2/ρ(A:与汽车有关的参数)ρ=C/sC=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R,l h=s 则 l h=A2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ρ,a s=Δa/t≤0.62)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
4)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
公路、铁路曲线分段计算( 左右转通用)

0.004167
原始角 0.002753 0.011857 0.027327 0.049163 0.077365 0.079577 0.000048 0.000207 0.000477 0.000858 0.001350 0.001389
可用角度(1) 可用角度(2) 可用角度(y2) 1.000000 0.659605 -0.751612 1.000000 0.659486 -0.751717 1.000000 0.659283 -0.751895 1.000000 0.658996 -0.752146 1.000001 0.658626 -0.752471 1.000001 0.658597 -0.752496
0.000176 0.000429 0.000793 0.001268 0.001389
可用角1 可用角2 可用角y2 1.000000 -0.639876 0.768478 1.000000 -0.640070 0.768316 1.000000 -0.640350 0.768083 1.000001 -0.640715 0.767779 1.000001 -0.640808 0.767701
段计算
第二段缓和曲线
里 程 21537.780 21520.000 21510.000 21500.000 21490.000 21487.780 x 4625014.894 4625003.517 4624997.113 4624990.702 4624984.281 4624982.853 y 度 419210.445 1.5 0.02618 距离缓和曲线一 419224.1085 311.2725 5.43273 9.300000 419231.7888 309.7725 5.40655 19.299999 419239.4632 3.141593 29.299994 419247.1294 39.299974 419248.8303 49.299919 49.999913
缓和曲线五大要素计算表

注:1、表中蓝色部分为需要对照设计院给的参数表填写。 2、表中绿色部分为计算器程序所需的线元参数。
平曲线要素 缓和曲线长l0
曲线半径R 曲线长Lc 交点前直线切线角A
计算结果 180 800
341.3608756 3.308498635
设有缓和曲线的要素计算公式 计算公式
转向角α
0.651701095
曲线半径R 转向角α 曲线方向判别 Q 内移距p 前缓和曲线长l1 后缓和曲线长l2 切线长T1 切线长T2 切垂距m 外视距E 切曲差q 曲线长L 交点里程JD 直缓点ZH 缓圆点HY 曲中QZ 圆缓点YH 缓直点HZ
ZH(x) ZH(y) HZ(X) HZ(Y) HY(X) HY(Y)
θ YH(X) YH(Y)
和) 缓和曲线
缓和曲线(弧度制)
分
缓和曲线计算表

坐标计算第一章缓和曲线的坐标公式如图1-1所示,其坐标系是以缓和曲线起点ZH为原点O,以切线为x轴,以过原点的曲线半径为y 轴。
若原点O至P点的缓和曲线长度为,过P点切线与x轴的交角为β(即半径由∞变至的中心角)。
若P有微小变化至P′时,则增长,(x,y)增长(),则有以下关系,图1-1得,(2-1)由公式(常数)得知,故有则将上式代入(1-1)式中,得即(2-2)以及的关系代入上式得即以代入上式得(2-3)上式即为缓和曲线上任一点直角坐标(x,y)的计算公式。
缓和曲线上任一点P的切线与x轴的交角,称为缓和曲线螺旋角,或称缓和曲线角。
其计算可由前面公式得(弧度)(2-4)若将代入(2-4)及(2-3)式中,则有以下结果:(2-5)上式即为缓和曲线终点HZ(ZH)的坐标及螺旋角的计算公式。
第二章圆曲线要素及计算公式如图2-1所示,两相邻直线偏角(线路转向角)为,选定其图2-1连接曲线圆曲线的半径为R,这样,圆曲线和两直线段的切点位置ZY点、YZ点便被确定下来,我们称为对圆曲线相对位置起控制作用的直圆点ZY、圆直点YZ和曲中点QZ为圆曲线三主要点。
我们称R、α以及具体体现三主要点几何位置的切线长T、曲线长L、外矢距E和切曲差(切线长和曲线长之差)D为曲线6要素。
只要知道了曲线6要素,便可于实地测放出圆曲线。
现将圆曲线的元素列下::转向角(实地测出)R:曲率半径(设计给出)T:切线长(计算得出)L:曲线长(计算得出)D:切曲差(计算得出)偏角是在线路祥测时测放出的,圆曲线半径R是在设计中根据线路的等级以及现场地形条件等因素选定的,其余要素可根据以下公式计算:第三章偏角法测设介绍偏角法是一种极坐标标定点位的方法,它是用偏角和弦长来测设圆曲线细部。
如图3-1所示,1,2…,,…,n为设计之详测点,邻点间距均为c,弦长c所对应的圆心角为。
当放样至详测点时,可在ZY点置镜,后视JD方向,拨出偏角,再自-1点量距C和拨出的视线方向交会,即得出点。
三无曲线(有缓)绳正法拨道自动计算表

三无曲线(有缓)绳正法拨道自动计算表预览说明:预览图片所展示的格式为文档的源格式展示,下载源文件没有水印,内容可编辑和复制直缓点位置(X ZH )缓圆点位置(X HY )曲中点位置(X QZ )始端缓和曲线正矢递增率始端缓和曲线长度(m)终端缓和曲线长度(m)1.0157.01511.92021.006060圆缓点位置(X YH )缓直点位置(X HZ )圆曲线正矢终端缓和曲线正矢递增率曲线外轨全长(m)曲线线路中心全长(m)16.82522.825126.00021.00218.095217.809桩位a b 直缓点0.0150.985224936缓圆点0.9850.01522.8266385649.5983134835.89880884圆缓点0.8250.175曲线半径(m)缓直点0.1750.825396.83点号计划正矢(mm)计划正矢取整(mm)点号计划正矢(mm)计划正矢取整(mm)1F3.3316F 126.01262F20.72117F 120.41203F41.74218F 101.31014F62.76319F 80.3805F83.78420F 59.3596F104.710521F 38.338888F888F 888F888F 888F888F 888F888F 888F888F 888F888F 888F888F 888F888F 888F888F 7F122.312222F 17.3178F126.012623F 2.02正矢合计:1991566+882+543三无曲线(有缓)绳正法拨道正矢计算表(20米弦,10米点)始端缓和曲线始端缓和曲线请注意“a”表示缓和曲线以外和圆曲线以内分段数,“b”表示缓和曲线以内的分数段,请参考下面图示。
曲线转角(°′″)。
缓和曲线超高段计算

缓和曲线超高段计算
超高横坡计算公式:
公式(一):I=Abs(B-A) ×(E+D)/C-E
公式(二):I=Abs(B-A)×2E/Q-E ①
I=(Abs(B-A)-Q)(D-E)/(C-Q)+E ②
I———缓和曲线内任一横断面超高横坡度(I的正负,抬高边为正,降低边为负);
B———缓和曲线超高段内任一点里程桩号;
A———缓和曲线起点直缓(ZH)或终点缓直(HZ)的里程桩号;E———直线段路拱横坡度,输入时不考虑符号取正值;C———缓和曲线长度(M);
D———全超高段设定的最大超高横坡度,取正值;Abs———绝对值符号;
Q———缓和曲线起点(或终点)至超高变坡临界面距离,
Q=2E/(E+D)*C所谓临界面即抬高边I=+坡比,降低边I=-坡比。
即抬高值=降低值处,但符号相反。
程序清单:CGHP(文件名)
Lb1 0:E:D:C:A:L:{BH}:B≤0=> Goto 2⊿Q=2E/(E+D)*C:Abs(B-A)> Q=> Goto 1⊿
I=Abs(B-A)*2E/Q-E◢F=H+LI◢T=H-EL ◢Goto 0⊿(计算ZH或HZ至Q之间缓和曲线上任一点超高横坡度及左右边桩F、T之高程,注意须输入与边桩同横断面的中桩高程-中桩高程另算)
Lb1 1:I=(Abs(B-A)-Q)(D-E)/(C-Q)+E◢F=H+LI◢T=H-IL ◢Goto 0⊿(计算Q至HY或YH之间缓和曲线上任意一点超高横坡度及左右边桩之高程,L为半幅路宽,单位为M)
Lb1 2:{EDCAL}:Goto 0 注:输入B≤0重新开始。
道路曲线高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
道路曲线高程计算公式

道路曲线高程计算公式 Final revision by standardization team on December 10, 2020.高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
