竖曲线设计标高计算
公路设计 纵断面设计 坡度、坡长的应用及竖曲线半径的选取及设计高程的计算

五、纵坡设计的一般要求(P139)
1、纵坡设计必须满足《公路工程技术标准》中的各项 规定。
2、为保证汽车能以一定的车速安全舒顺地行驶,纵坡 应具有一定的平顺性,起伏不宜过大及过于频繁。 尽量避免采用极限纵坡值,合理安排缓和坡段,不 宜连续采用极限长度的陡坡夹最短长度的缓和坡段。 连续上坡或下坡路段,应避免设置反坡段。越岭线 垭口附近的纵坡应尽量放缓一些。
(一)坡长限制 坡长--指变坡点与变坡点之间的水平长度。
坡长
➢坡长限制,主要是对较陡纵坡的最大长度和一 般纵坡的最小长度加以限制。
最小坡长限制:任何路段 最大坡长限制:陡坡路段
1.最小坡长限制 :
(1)规定最小坡长的原因
①纵断面上若变坡点过多,纵向起伏变化频繁影响了行车的 舒适和安全;
②相邻变坡点之间的距离不宜过短,以便插入适当的竖曲线 来缓和纵坡的要求,同时也便于平、纵面线形的合理组合与 布置。
最大纵坡(%)
3
456 7 8
9
➢ 设计速度为120km/h、100km/h、80km/h的高速公路受地 形条件或其他特殊情况限制时,经技术经济论证合理,最大纵 坡可增加1%。
➢ 公路改建中,设计速度为40km/h、30km/h、20km/h的利 用原有公路的改建路段,经技术经济论证合理,最大纵坡可增 加1%。
(3) 自然因素:海拔高程、气候(积雪寒冷等)。 ➢ 纵坡度大小的优劣: 坡度大,行车困难,上坡速度低,下坡较危险。 山区公路可缩短里程,降低造价。
2.最大纵坡的确定
我国《公路工程技术标准》规定各级公路的最大纵坡 规定如表3-9所示。
最大纵坡
表3-9
纵断面设计——竖曲线设计

纵断面设计——竖曲线设计纵断面上相邻两条纵坡线相交的转折处,为了行车平顺用一段曲线来缓和,这条连接两纵坡线的曲线叫竖曲线。
竖曲线的形状,通常采用平曲线或二次抛物线两种。
在设计和计算上为方便一般采用二次抛物线形式。
纵断面上相邻两条纵坡线相交形成转坡点,其相交角用转坡角表示。
当竖曲线转坡点在曲线上方时为凸形竖曲线,反之为凹形竖曲线。
一、竖曲线如图所示,设相邻两纵坡坡度分别为i1 和i2,则相邻两坡度的代数差即转坡角为ω= i1-i2 ,其中i1、i2为本身之值,当上坡时取正值,下坡时取负值。
当i1- i2为正值时,则为凸形竖曲线。
当i1 - i2 为负值时,则为凹形竖曲线。
(一)竖曲线基本方程式我国采用的是二次抛物线形作为竖曲线的常用形式。
其基本方程为:若取抛物线参数为竖曲线的半径,则有:(二)竖曲线要素计算公式竖曲线计算图示1、切线上任意点与竖曲线间的竖距通过推导可得:2、竖曲线曲线长:L = Rω3、竖曲线切线长:T= TA =TB ≈ L/2 =4、竖曲线的外距:E =⑤竖曲线上任意点至相应切线的距离:式中:x —为竖曲任意点至竖曲线起点(终点)的距离, m;R—为竖曲线的半径,m。
二、竖曲线的最小半径(一)竖曲线最小半径的确定1.凸形竖曲线极限最小半径确定考虑因素(1)缓和冲击汽车行驶在竖曲线上时,产生径向离心力,使汽车在凸形竖曲线上重量减小,所以确定竖曲线半径时,对离心力要加以控制。
(2)经行时间不宜过短当竖曲线两端直线坡段的坡度差很小时,即使竖曲线半径较大,竖曲线长度也有可能较短,此时汽车在竖曲线段倏忽而过,冲击增大,乘客不适;从视觉上考虑也会感到线形突然转折。
因此,汽车在凸形竖曲线上行驶的时间不能太短,通常控制汽车在凸形竖曲线上行驶时间不得小于3秒钟。
(3)满足视距的要求汽车行驶在凸形竖曲线上,如果竖曲线半径太小,会阻挡司机的视线。
为了行车安全,对凸形竖曲线的最小半径和最小长度应加以限制。
学习之竖曲线

隧道内竖曲线计算当正线相邻坡段坡度差≥1‰,应设置竖曲线,竖曲线形式为圆曲线。
竖曲线计算公式如下:L=Rsh×λ/2000(L为竖曲线全长的一半,单位:m)y=x2/2R(y为竖曲线高度,单位:m)其中:Rsh—竖曲线半径(m),10000~20000m;x—竖曲线始点至计算纵距之距离,单位m;λ—为相邻竖曲线的代数差。
在设计图中,竖曲线的位置的标高应表示为:括号内的标高为未考虑竖曲线影响的标高,括号外的标高为已考虑竖曲线影响的标高。
一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1 ω为正时,是凹曲线;ω为负,是凸曲线。
1.二次抛物线基本方程:或ω:坡度差(%);L:竖曲线长度;R:竖曲线半径2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: (前提:ω很小)L=Rω竖曲线切线长:T=L/2=Rω/2竖曲线上任一点竖距h:竖曲线外距:例题4-3ω=-0.09 凸形;L=Rω=2000*0.09=180mT=L/2=90mE=T2/2R=2.03m起点桩号=k5+030 - T =K4+940起始高程=427.68 - 5%*90=423.18m=k5+000-k4+940=60m 桩号k5+000处:x1切线高程=423.18+60*0.05=426.18m 2/2R=602/2*2000=0.90mh1=x1设计高程=426.18 - 0.90=425.28m=k5+100-k4+940=160m 桩号k5+100处:x2切线高程=423.18+160*0.05=431.18m 2/2R=1602/2*2000=6.40mh2=x2设计高程=431.18 - 6.40=424.78m。
纵断面设计竖曲线

0.90
切线高程 HT = H1 + i1( Lcz - BPD) = 427.68 + 0.05×(5000.00 - 5030.00)
= 426.18m 设计高程 HS = HT - y1 = 426.18 - 0.90=425.18m (凸竖曲线应减去改正值)
K5+100.00:位于下半支
①按竖曲线终点分界计算:
横距x2= Lcz – QD = 5100.00 – 4940.00=160m
竖距
y2
x22 2R
1602 6.40 2 2000
切线高程 HT = H1 + i1( Lcz - BPD)
= 427.68 + 0.05×(5100.00 - 5030.00)
= 431.18m 设计高程 HS = HT – y2 = 431.18 – 6.40 = 424.78m
设3、计。坡长限制
大于i1为陡坡,汽车减速行驶,初速为V1,终速不低于V2,大于i2 的纵坡要限制其长度。 (1)最小坡长的限制
小坡长限制主要是指从汽车行驶平顺陛、路容美观、相邻竖曲线 设置、纵面视距等考虑.通常以计算行车速度9~15s的行程作为规 定值。《标准》规定值见表
(2)最大坡长限制 当汽车在坡道上行驶,车速下降到最低容许速度时所行驶的距离
路线纵断面图构成:
地面线:根据中桩点的高程绘的一条折线; 设计线:路线上各点路基设计高程的连线。 变坡导线:变坡点间的连线
一、纵断面设计的一般要求
1、满足设计标准 2、尽量避免使用极限值 3、纵断面和地形协调 4、填挖平衡 5、满足最小填土高度和排水要求 6、桥头和交叉口处应该平缓 7、考虑通道和农田的要求
K5+100.00:位于下半支
竖曲线

竖曲线是在变坡点处,为了行车平顺的需要而设置的一段曲线。
竖曲线的形状,通常采用圆曲线或二次抛物线两种。
在设计和计算上抛物线比圆曲线更为方便,故一般采用二次抛物线。
在纵坡设计时,由于纵断面上只反映水平距离和竖直高度,因此竖曲线的切线长与弧长是其在水平面上的投影,切线支距是竖直的高程差,相邻两条纵坡线相交角用坡度差表示。
一、竖曲线要素计算如图3-3所示,设变坡处相邻两纵坡度分别为i1和i2,坡度差以ω表示,则坡度差ω为i1和i2的代数差,即ω= i1-i2:当ω>0时,则为凸形竖曲线;当ω<0时,则为凹形竖曲线。
图3-3竖曲线示意图1、竖曲线的基本方程二次抛物线作为竖曲线的基本形式是我国目前常用的一种形式。
如图3-4所示,用二次抛物线作为竖曲线的基本方程:3-4 竖曲线要素示意图竖曲线上任意一点的斜率为:当x=0时:k= i1,则b= i1;当x=L,r=R时:,则:因此,竖曲线的基本方程式为:或 (3-19)2、竖曲线的要素计算曲线长:(3-20)切线长:(3-21)外距:(3-22)曲线上任意一点的竖距(改正值):(3-23)二、竖曲线设计标准竖曲线的设计标准包括竖曲线的最小半径和最小长度。
1、竖曲线设计的限制因素(1)缓和冲击汽车在竖曲线上行驶时会产生径向离心力,在凸形竖曲线上行驶会减重,在凹形竖曲线上行驶会增重,如果这种离心力达到某种程度时,乘客就会有不舒适的感觉,同时对汽车的悬挂系统也有不利影响,故应对径向离心力加速度加以控制。
根据试验得知,离心加速度a限制在0.5~0.7m/s2比较合适。
汽车在竖曲线上行驶时其离心加速度为:(3-24)《标准》中确定竖曲线半径时取a=0.278 m/s2。
或(3-25)(2)行程时间不宜过短汽车从直坡段驶入竖曲线时,如果其竖曲线长度过短,汽车倏忽而过,冲击力大,旅客会感到不舒适,太短的竖曲线长度从视觉上也会感到线形突然转折。
因此,应限制汽车在竖曲线上的行程时间,一般不宜小于3s。
竖曲线高程计算公式推导过程及计算流程

竖曲线⾼程计算公式推导过程及计算流程竖曲线⾼程计算公式推导及计算流程1. 竖曲线介绍竖曲线是指在纵断⾯内,两个坡线之间为了延长⾏车视距或者减⼩⾏车的冲击⼒,⽽设计的⼀段曲线。
⼀般可以⽤圆曲线和抛物线来充当竖曲线。
由于圆曲线的计算量较⼤,所以,通常采⽤抛物线作为竖曲线,以减少计算量。
2. 竖曲线⾼程计算流程竖曲线计算的⽬的是确定设计纵坡上指定桩号的路基设计标⾼,其计算步骤如下:a. 计算竖曲线的基本要素:竖曲线长L ;切线长T ;外失距Eb. 计算竖曲线起终点的桩号:竖曲线起点的桩号=变坡点的桩号-Tc. 计算竖曲线上任意点切线标⾼及改正值:切线标⾼=变坡点的标⾼±(x T -)?i 改正值:221x Ry =d. 计算竖曲线上任意点设计标⾼某桩号在凹形竖曲线的设计标⾼ = 该桩号在切线上的设计标⾼+ y 某桩号在凸形竖曲线的设计标⾼ = 该桩号在切线上的设计标⾼-y3. 竖曲线⾼程计算公式推导已知条件:第⼀条直线的坡度为1i ,下坡为负值,第⼀条直线的坡度为2i ,上坡为正值,变坡点的⾥程为K ,⾼程为H ,竖曲线的切线长为B A T T T ==, 待求点的⾥程为X K 曲线半径R竖曲线特点:抛物线的对称轴始终保持竖直,即:X 轴沿⽔平⽅向,Y 轴沿竖直⽅向,从⽽保证了X 代表平距,Y 代表⾼程。
抛物线与相邻两条坡度线相切,抛物线变坡点两侧⼀般不对称,但两切线长相等。
竖曲线⾼程改正数计算公式推导设抛物线⽅程为:()021≠++=a c bx ax y设直线⽅程为:()02≠+=k b kx y由图可知,抛物线与直线都经过坐标系222Y O X 的原点2O ,所以可得:00==b c ;分别对21y y 、求导可得:b ax y +=2'1k y ='2当0=x 时,由图可得:b i y ==1'1k i y ==1'2当L x =时,由图可得:12'12i aL i y +==由上式可得:RL L i i a 212212==-=ω所以抛物线⽅程为:x i x Ry 12121+=直线⽅程为:x i y 12=对于竖曲线上任意⼀点P ,到其切线上Q 点处的竖直距离,即⾼程改正数y 为:21122121X RX i X i X R y y y P Q =-+=-= 竖曲线曲线元素推导竖曲线元素有切线长T 、外失距E 和竖曲线长L 三个元素,推导过程如下:由图可知:2tan ω=R T 由于转⾓ω很⼩,所以可近似认为22tan ωω=,因此可得:2ωR T = 由图易得:ωR L =将切线长T 带⼊到221x Ry =中可得外失距RT E 22=4. 曲线⾼程计算⽰例已知:某条道路变坡点桩号为K25+460.00,⾼程为780.72.m ,i1=0.8%,i2=5%,竖曲线半径为5000m 。
高程的计算

学习情景一高程计算的专业知识 学习情景二Excel编写超高计算 实践教学情景Excel工程应用三
学习情景一高程计算的专业知识
一、竖曲线的测设
在路线纵坡变更处,为了行车平稳和视距要求,在竖直面内应以 曲线衔接,这种曲线称为竖曲线。竖曲线有凸形和凹形两种,如图1 一4一1所示
竖曲线一般采用二次抛物线,因为在一般情况下,相邻坡度差都 很小,而选用的竖曲线半径都很大,因此即使采用圆曲线等其他曲线, 所得到的结果也与二次抛物线相同。
根据△ACO与△ACF相似,可得 外距
同理,可导出竖曲线上任一点尸距切线的纵距(亦称高程改正值) 计算公式为
上一页 下一页 返回
学习情景一高程计算的专业知识
二、超高的计算
为抵消车辆在平曲线路段上行驶时所产生的离心力,将路面做成 外侧高内侧低的单向横坡形式,称为平曲线超高
为了便于施工,需要计算道路中线和内、外侧边线与设计标高之 差,从而进行施下放样。
本次以不设中间带的公路、绕内边轴旋转计算为例,具体计算 公式见表1 -4一1。
上一页 返回
学习情景二Excel编写超高计算
一、编制表格
根据上述理论内容编写计算表格,如图1一4一3所示
二、计算过程编写
1. ZH起点超高过渡段 2. HZ起点超高过渡段 计算结果如图1一4一4所示 根据以上计算表格,即可轻松计算出在曲线超高过渡段相应的高程
返回
图1一4一2竖返回
图1一4一4超高计算结果表
返回
图1一4一5超高计算表
返回
返回
实践教学情景Excel工程应用三
一、已知条件
见表1一4一2
二、计算
桩距为5 m的逐桩高程变化
三、参考计算结果
毕业设计---道路工程设计

毕业设计---道路工程设计目录一、概述 (1)1.1工程概况 (1)1.2道路结构工程: (1)二、设计的主要技术指标 (1)2.1道路等级 (2)2.2设计主要技术指标 (2)三、路线设计 (2)3.1确定导向线 (2)3.2修正导向线,确定设计路线 (3)四、平曲线设计 (3)4.1平面线形设计的一般原则 (3)4.2计算各点的主点桩号 (3)五、纵断面设计 (4)5.1纵断面地面线资料 (22)5.2纵断面线形设计的一般原则 (24)15.3纵坡的设计 (25)5.4平纵组合设计 (25)5.5设计标高的计算 (25)六、超高加宽计算 (27)6.1加宽 (27)6.2超高 (28)七、横断面设计计算 (34)7.1横断面地面资料 (34)7.2标准横断面图的形式与尺寸 (54)7.3横断面图的绘制(见横断面图).. 54 7.4横断面面积的计算 (54)7.5土石方的计算 (54)八、道路路面结构(水泥混凝土路面设计) (55)8.1交通分析 (55)8.2初拟路面结构 (55)18.3路面材料参数确定 (55)8.4荷载疲劳应力 (56)8.5温度疲劳应力计算 (56)8.6板厚验算 (56)九、结语 (57)参考文献: (57)1一、概述1.1工程概况本设计题目是:道路工程设计(子题目:毕业设计设计题二方案七),起点设计高程:2299.05m,终点设计高程:2439.8m。
道路等级是某山岭区三级公路,三级公路一般能适应按各种车辆折合成中型载重汽车的远景设计年限年平均昼夜量为1000~4000辆。
此次设计为期12周,指导教师是刘颖和谢石连等老师。
在设计工程中会运用到道路勘测设计、路基路面工程等知识,对规定道路进行选线、定线、平面、纵断面、横断面、路基路面等的计算。
这个设计的初步步骤如下:定线。
对于要设计得平面图纸,比例是1:2000,先要对规定道路进行选线、在以平面图所得的资料进行平面设计,包括超高1(缓和段)和加宽值的计算,平面视距的保证,绘出平面线形图。
竖曲线高程计算表格
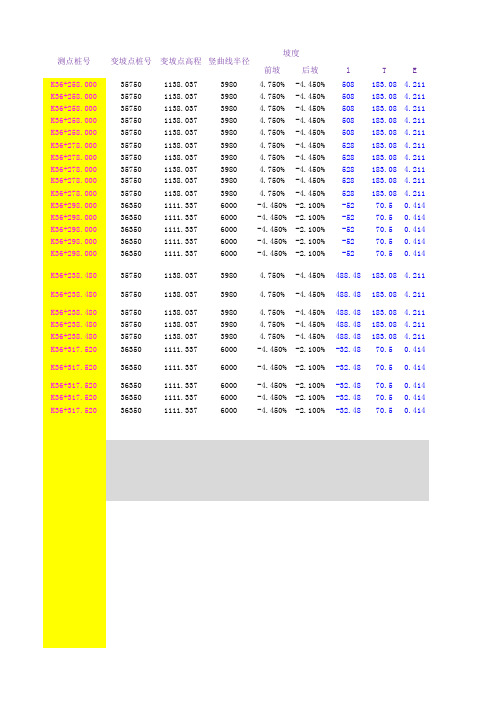
1114.4770
1114.5270 1114.4770 1114.4270 1111.3235
1111.2448
1111.1660 1111.0873 1111.0085
实测值
1113.622 1113.672 1113.722 1113.672 1113.622 1112.789 1112.811 1112.832 1112.782 1112.732 1112.026 1111.998 1111.971 1111.921 1111.871
误差
1号
实测值
误差
0.003 1113.06 1113.06 0.00
2号
实测值
1113.06 1113.06
误差 0.003
桥台左侧横 坡 0.02
0.035 1109.87 1109.84 0.03
1109.65
1109.61
0.04312
K36+238.480
K36+238.480
K36+238.480 K36+238.480 K36+238.480 K36+317.520
K36+317.520
K36+317.520 K36+317.520 K36+317.520
35750
35750
35750 35750 35750 36350
36350
3980 3980 3980 3980 3980 3980 3980 3980 3980 3980 6000 6000 6000 6000 6000
4.750% -4.450% 508 183.08 4.211 4.750% -4.450% 508 183.08 4.211 4.750% -4.450% 508 183.08 4.211 4.750% -4.450% 508 183.08 4.211 4.750% -4.450% 508 183.08 4.211 4.750% -4.450% 528 183.08 4.211 4.750% -4.450% 528 183.08 4.211 4.750% -4.450% 528 183.08 4.211 4.750% -4.450% 528 183.08 4.211 4.750% -4.450% 528 183.08 4.211 -4.450% -2.100% -52 70.5 0.414 -4.450% -2.100% -52 70.5 0.414 -4.450% -2.100% -52 70.5 0.414 -4.450% -2.100% -52 70.5 0.414 -4.450% -2.100% -52 70.5 0.414
竖曲线的计算方法

竖曲线铁路线路的纵断面最理想的当然是平道,然而事实上是不可能的,为了适应地形的起伏,以减少工程量,纵断面必须用各种不同的坡面连接而成。
两相邻坡段的连续点谓之变坡点。
相邻坡段的坡度差是两相邻坡段的坡度代数差。
当相邻坡段的坡度差超过允许值时,为了保证行车平顺和安全,应在变坡点处用竖曲线连接起来。
允许不设竖曲线的坡度差允许值是根据车轮不脱轨、车钩不脱钩、列车不撞车和行车平稳等要求进行分析确定的。
一般情况下,竖曲线采用圆曲线,也可以采用抛物线,个别情况下,还可以采用连续短坡曲线。
竖曲线的计算一、圆曲线形竖曲线圆曲线形竖曲线的几何要素和各点设计标高,可按下列公式计算,如图。
R α x T TyRCα/2 BAi1i21、竖曲线的切线长度TT=R·tan(α/2)=R/2·tanα=R/2·△i‰=R/2000·△i(m) (5-1)式中 R-竖曲线半径(m);α-竖曲线转角(度);△i-相邻坡段的坡度代数差(‰)。
R=5000m时, T=2.5△i(m)R=10000m时,T=5.0△i(m)R=15000m时,T=7.5△i(m)R=20000m时,T=10.0△i(m)R=25000m时,T=12.5△i(m)2、竖曲线长度CC≈2T=R/1000·△i(m) (5-2)3、竖曲线纵距yy=x2/2R (m) (5-3)式中 x-竖曲线上计算点至竖曲线起(终)点的横距(m)。
当x=T时,变坡点的纵距Y即为竖曲线的外矢距E。
Y=E=T2/2R=1/2R(C/2)2=C2/8R (5-3.1)4、竖曲线上各点的设计标高H设h为计算点的坡度标高,则H=h±y (5-4)式中的y值,凹形取“+”,凸形取“-”。
【算例一】一凹形竖曲线i1=-4‰,i2=+2‰,△i=6‰,变坡点的里程为K235+165,标高为54.60m,R=15000m,计算竖曲线上各20m点的设计标高。
第二章 平、纵、横三维断面设计

第二章平、纵、横三维断面设计第二章 平、纵、横三维断面设计2.1 道路等级的确定2.1.1交通量换算已知预算十年末交通量(年平均增长率Y=10%)为2500辆/日“公路工程技术标准—2.0.2”各种车型的折算系数为小客车1.0中型车1.5大型车2.0拖挂车3.0。
依据“国内外汽车参数”得知:东风EQ140载重5.21t 黄河,JN —150载重8.06t,解放CA10B 载重4.00t,跃进NJ130载重2.5t 。
十年末小客车标准车型交通量 表2-1 车型 交通组成量 实际交通量 折算系数 换成小客车交通量 解放CA10B 65% 2500×65%=1625 1.5 2437.5 进NJ130 15% 2500×15%=375 1.5 562.5 黄河JN150 10% 2500×10%=250 2.0 500 东风EQ14010% 2500×10%=2501.5 375∑=3875辆/日依据“道路勘察设计”交通辆换算公式为1d0(1)n NN r -=+式中:d N —规划交通量(辆/日);0N —起始年平均日交通量(辆/日);γ—年平均增长率(%); n —预测年限(年) 换算十五年初平均日交通量:用式(2—1)计算3875)1(10=+=-n d r N N 辆/日据服务对象,假设本条公路为三级公路。
“公路沥青路面设计规范JTG D50—2006”选三级公路路面为沥青表面处治时设计年限为八年。
日辆/4.5673)1.01(3875)1(1510=+=+=--n d r N N2.1.2道路等级确定地区的地形为重丘山岭区,公路使用性质任务是为沿线工农业服务,是沟通县乡村的支线公路,并小客车标准车型交通量为“公路工程技术标准JTG B01—2003”规定的三级公路小客车年平均日交通量2000—6000辆中间。
该公路为三级公路。
假设成立。
2.1.3道路技术标准的确定(重丘区三级公路)依据“公路工程技术标准JTG B01—2003”该公路的各项设计值取如下:设计速度30(㎞/h)单车道宽度3.25m土路肩宽度0.5m路基宽度7.5m停车视距30m会车视距60m超车视距150m“公路工程技术标准JTG B01—2003”规定半径﹑坡度调整的范围如下:圆曲线最小半径(m):一般值:65 极限值:30 不设超高最小半径:350 最大纵坡:8%当路拱≤2.00%时为350;当路拱>2%时为45同向曲线曲线间最短直线长度满足v6≥≥反向曲线间最短线长度满足v2越岭路线连续上坡(或下坡)路段,相对高差为200—500m时,平均纵坡不应大于5.5%;相对高差大于500m时,平均纵坡不应大于5%,任意连续3km路段的平均纵坡不应大于5.5%,最小坡长:100m。
第五章:竖曲线设计介绍

8000
60
9000
6000
40
3000
2000Βιβλιοθήκη (2)半径的选择选择竖曲线半径主要应考虑以下因素: 1)选择半径应符合表所规定的竖曲线的最小半径和最小长度 的要求。 2)在不过分增加土石方工程量的情况下,为使行车舒适,宜 采用较大的竖曲线半径。 3)结合纵断面起伏情况和标高控制要求,确定合适的外距值 ,按外距控制选择半径:
1. 竖曲线的计算
(1) 用二次抛物线作为竖曲线的基本方程式 二次抛物线一般方程为
y 1 x 2 ix 2k
i dy x i dx k
当x 0时,
i i1;
x L时,
i
L k i1
i2 ,
则
k L L
i2 i1
抛物线上任一点的曲率半径为
R
ω为正,变坡点在曲线下方,竖曲线开口向上,为凹形竖曲 线;ω为负,变坡点在曲线上方,竖曲线开口向下,为凸形 竖曲线。
各级道路在变坡点处均应设置竖曲线。 竖曲线的线形采用二次抛物线。由于在其应用范围内,圆
曲线与抛物线几乎没有差别,因此,竖曲线通常表示成圆 曲线的形式,用圆曲线半径R来表示竖曲线的曲率半径。
(3)
将(2)式和(3)式代入(1)式,得二次抛物线竖曲线基本
方程式为
y
2L
x2
i1x
或
y
1 2R
x2
i1x
式中:ω ——坡差 (%);
L——竖曲线长度 (m);
R——竖曲线半径 (m)。
(2) 竖曲线几何要素计算 竖曲线的几何要素主要有:竖曲线切线长T、曲线长L和外距E。
城市道路设计竖曲线计算例题

某交叉口的竖向设计,已知相交道路的路中心 线、街沟纵坡i 1=i 3=0.03,路面横坡i 2=0.02, 车行道宽度B = 15m ,缘石半径R = 10m,交 叉口中心标高为2.05m,等高线间距釆用 0.10m,试绘制交叉口的竖向设计图。
本例题所釆用的竖向设计方法足画方格线网,并把缘石曲线上的标点平均分配。
交叉口的竖向设计图町按卜•列步骤绘制(见图11-85):1・画路段上的设计等高线X 芥钛= 3.335) 2.画交叉口上的设计等高线(1)根据交叉口中心标离,求岀尸“出三 点标高。
=徐-AVx 八=2.05 - 17.5x0.03 =1 ・ 52(m)怏(或 = A jV x -=1.52-4f x0.02= l ・37(m)同理■可求出 理(或h E ) = 2.43m,好(或 好)二2.43m, h E (或h E ) = 1.37mI I 2 2(2)根据4,F 4>£4点的标高,求交叉口范围内等高点的变化c=5.00( in) 图11・85单向倾斜的竖向设计图式 15x0.02 2x0.03(2)根据A 9F 49E 4点的标高,求交叉口范围内等髙点的变化°(h F +g ) +(你-gV J ________ 4 〈1.37+ 10x()・03) + (2,43- 10x0.03)2= 2.05- 乂 礬 x 14.76 = 1.84(m) 血=he = 1.90m h c =1.67m h c =: = /i D = 1 .84m (3) 根据匕,。
4我4各点标高,求出缘石曲线上的各个等高点。
几久,。
4& 的弧长 L =J (2TT /?) = j (2x 3.1416 x 10) = 7.85(m )F4Q 间应有设计等高线为气二讣也&5(根) 等髙线的平均间距为7^ = 1.57(m ) 同理,Q 民间应有设计等高线为瞬=評*6(根〉 尊高线的平均间距为爹 i.31(m ) 厲6,66间应有设计等髙线为丄箸評"(根) 等高线的平均间距为警 = 3.93(m ) E l D i ,D l F l 间应有设计等高线为气j 严^3(根) 等高线的平均间距为 ¥*2・62(m )(4) 根据A,M,K,G,N 各点标高,分别求出路脊线儿“,狀的等髙点(计算从(5)根据以上求出的各点标高绘出等高线,经合理调软后即得如图H-86所示的竖向 设计图。
各级公路的竖曲线最小长度和半径规定表6

第一节 纵坡及坡长设计
合成坡度
合成坡度是指由路线纵坡与弯道超高 横坡或路拱横坡组合而成的坡度,其 方向即流水线方向。
ib
i
i合
合成坡度可按矢量关系或勾股定理关 系导出:
i合 i2 ib2
式中: i合—合成坡度(%);i —公路平曲线处的纵坡(%); ib —公路平曲线处的超高横坡度(%)。
第二节 竖曲线设计
竖曲线
如图所示,设相邻两纵坡坡度分别为i1 和i2,则相 邻两坡度的代数差即转坡角为ω= i1-i2 ,其中i1、 i2为本身之值,当上坡时取正值,下坡时取负值。
当 i1- i2为正值时,则为凸形竖曲线。当 i1 - i2 为负值时,则为凹形竖曲线。
第二节 竖曲线设计
的竖曲线半径的最小值,该值只有在地形受限制迫不得已时 采用。
通常为了使行车有较好的舒适条件,设计时多采用大于极限 最小半径1.5~2.0倍,该值为竖曲线一般最小值。我国按照 汽车在竖曲线上以设计速度行驶3s行程时间控制竖曲线最小 长度。
各级公路的竖曲线最小长度和半径规定表3-6所列,在竖曲 线设计时,不但保证竖曲线半径要求,还必须满足竖曲线最
改正值: y x2 2R
第二节 竖曲线设计
计算竖曲线上任意点设计标高: 某桩号在凸形竖曲线的设计标高 =该桩号在切线上的设计标高-y 某桩号在凹形竖曲线的设计标高 =该桩号在切线上的设计标高+y
第三节 爬坡车道
爬坡车道:是陡坡路段正线行车道外侧增设的供载重车行
驶的专用车道。
设置爬坡车道的条件
第二节竖曲线设计竖曲线的最小半径竖曲线最小半径的确定凸形竖曲线极限最小半径确定考虑因素缓和冲击经行时间不宜过短满足视距的要求第二节竖曲线设计凹形竖曲线极限最小半径确定考虑因素缓和冲击前灯照射距离要求跨线桥下视距要求经行时间不宜过短第二节竖曲线设计凸凹形竖曲线都要受到上述缓和冲击视距及行驶时间三种因素控制
竖曲线的形式及高程计算

一、设置竖曲线的要求铁路线路所包含的坡度除平坡外,有上坡、下坡。
所谓坡度,即铁路线路的高程变化率,用千分率表示,就是每1000m水平距离高程上升或下降的数值,通常用符号“+、-、0”依次表示上坡、下坡或平坡。
在进行纵断面设计时,相邻两坡段的交点叫变坡点,两变坡点之间的水平距离叫坡段长度。
《铁路线路设计规范》规定:工、Ⅱ级铁路相邻坡段坡度的代数差大于3%0和Ⅲ级铁路相邻坡段坡度的代数差大于4‰时,需用竖曲线连接。
竖曲线的形状主要分为圆曲线形和抛物线形两种。
《新建客货共线铁路设计暂行规定》规定:纵断面宜设计为较长的坡段,相邻坡段的连接宜设计为较小的坡度差。
旅客列车设计行车速度为200 km/h的路段,最小坡段长度不宜小于600m,困难条件下最小坡段长度不应小于400m,且最小坡段长度不得连续使用2个以上。
旅客列车设计行车速度为160km/h的路段,最小坡段长度不宜小于400m,且最小坡段长度不宜连续使用2个以上。
竖曲线不得与缓和曲线、相邻竖曲线重叠设置,也不得设在明桥面和正线道岔内。
二、竖曲线的计算方法1.圆曲线形竖曲线计算《铁路线路设计规范》规定:Ⅰ、Ⅱ级铁路竖曲线半径为10000m Tv=5 X △i ,Ⅲ级铁路竖曲线半径为5000m。
Tv=2.5 X △i(1)竖曲线的切线长Tv=Rv ×tan a/2 = Rv/2 ×tan a= Rv/2000 × △i △i=△i2-△i1 的绝对值Tv-竖曲线的切线长(m);Rv--竖曲线半径,a----竖曲线转角,△i-相邻坡段坡度的代数差(‰)。
(2)竖曲线的曲线长C≈2T。
(3)竖曲线的纵距竖曲线的纵距即竖曲线上任意点与切线上相邻点的标高差,用y表示,即y=x2/2Rv式中Y-竖曲线的纵距(m);x-竖曲线上任意点距竖曲线始点或终点的距离(m);(4)竖曲线标高H=Hp±y 式中H-竖曲线标高(m);Hp-计算点坡度线标高,【例题】某一级铁路,有一圆曲线形竖曲线(如图3-20所示),竖曲线中点里程为K24+400,标高为65.7 m,上坡i1=+2‰,下坡i2=-4‰,试计算竖曲线上每20 m点的标高。
