超高段横坡及竖曲线计算公式
道路曲线高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
高速公路的一些线路坐标、高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
横坡计算公式

横坡计算公式
横坡度计算公式:横坡度=2(中桩高程-边桩高程)/的路面实测宽度*100%,其中:中桩高程是指在线路施工测量中,作为定测的中桩的高程。
边桩高程=中桩标高±横坡×半幅道路宽度。
横坡一般有这样几个数据:坡长、水平长度、坡度、高差.它们之间的关系为:高差=坡度×水平长度一般坡度不大的时候,坡长≈水平长度,工程上可以用近似值,即:高差=坡度×坡长。
道路横坡坡率就是横坡度。
计算公式:(中心点标高-边线点标高)/(中心点到边线点的距离)。
路基的主要作用是为轨道或者路面铺设及列车或行车运营提供必要条件,并承受轨道及机车车辆或者路面及交通荷载的静荷载和动荷载,同时将荷载向地基深处传递与扩散。
横坡度是路基(路面)横断方向的坡度,一般的为2%,是为了便于排水,特别是在纵向坡度较小时就显得尤其重要了在弯道上,为了抵消离心力,需要设超高,即内弯低,外弯高。
纵坡度是路基(路面)纵向的坡度,也即平常我们所说的路线的坡度,坡度不宜太小(不利于排水),不宜过陡(不利于
行车及安全),同时对其坡长还有一定的限制。
平曲线、超高、竖曲线、超高

平曲线、超高、竖曲线、超高在线形设计时,各级公路(高速公路和一级公路除外)的视距应不小于两倍停车视距;并应根据需要,结合地形设置保证超车视距的路段。
平曲线半径:当汽车在平曲线上行驶时,所产生的横向力应不超过轮胎与路面摩阻力所允许的界限,并使驾驶员无不顺适感觉。
平曲线半径、行车速度、路面超高和横向摩阻系数[kg2]的关系式为[147-01],[kg2]其中(+)直接关系到汽车在平曲线上行驶时的安全和顺适感。
极限最小半径:是公路受到地形或地物等限制所允许采用的最小半径。
其计算的条件是:为0.10(=120公里/小时)~0.15(=40公里/小时),这时驾驶员仍感顺适;是路面超高允许最大值,一般用6%,个别用8%,特殊情况下用10%。
一般最小半径:为使公路平面线型在整体组合上不致不协调,驾驶员感到较为顺适的常用的最小半径。
这时,为0.05~0.06;为6%~8%,不用10%。
不设超高的最小半径公路的平曲线保持直线上的路拱(即不设超高),驾驶员不感到有弯道的最小半径,这时,为0.035;为-2%或-1.5%。
回头曲线:当公路需要展线以争取高程,而又受地形限制不能继续前进而须折返展线时,在折返处设转角一般大于180°的平曲线,称为回头曲线。
回头曲线因受地形限制,常采用极限甚至小于极限的最小半径。
超高:汽车在平曲线上行驶时产生离心力,设置超高,可抵消其部分离心力,使汽车不致向外倾覆。
超高值过大不利于驾驶操作和行车安全,也不利于公路养护、施工;过小则不利于排水。
专供汽车行驶的高速公路,一级公路的超高横坡度不超过10%,其他各级公路不超过8%。
在积雪寒冷地区,最大超高横坡度不超过6%。
平曲线加宽:汽车在平曲线上行驶时,后轮的轨迹在前轮的内侧,其车轮所占有宽度比在直线上的要宽,因此车道内侧应予加宽。
加宽值视车型和平曲线半径()而定,[kg2]一般可按/2计算。
式中为汽车前后轴距;如为半挂车时,可分别按牵引车和挂车的前后轴距[kg2],计算。
【高速公路】第四章-4-5曲线上的超高与加宽解析
<3240 <1940 <1710 <1550 <1240 <1130 <810 <720 <1710 <1550 <810 <720 <1210 <1130 <390 <360 <780 <720 <230 <210 <390 <360 <105 <95
3
~ 2160 ~ 1290 ~ 1220 ~ 1050 ~ 830 ~ 750 ~ 570 ~ 460 ~ 1220 ~ 1050 ~ 570 ~ 460 ~ 840 ~ 750 ~ 270 ~ 230 ~ 530 ~ 460 ~ 150 ~ 130 ~ 270 ~ 230 ~ 70 ~ 60
<1620 <970 <950 <760 <620 <520 <430 <300 <950 <760 <430 <300 <630 <520 <200 <150 <390 <300 <110 <80 <200 <150 <55 <40
5
~ 1300 ~ 780 ~ 770 ~ 550 ~ 500 ~ 360 ~ 340 ~ 190 ~ 770 ~ 550 ~ 340 ~ 190 ~ 500 ~ 360 ~ 150 ~ 90 ~ 300 ~ 190 ~ 80 ~ 50 ~ 150 ~ 90 40 ~ 25
4-5 弯道的超高与加宽
一、超高 1.定义
为抵消车辆在曲线路段 上行驶时所产生的离心 力,在该路段横断面上 设置的外侧高于内侧的 单向横坡,称之为超高。 当汽车行驶在设有超高 的弯道上时,汽车自重 分力将抵消一部分离心 力,从而提高行车的安 全性和舒适性。超高的 布置如图所示。
道路的横坡和纵坡计算公式

道路的横坡和纵坡计算公式道路的横坡和纵坡是道路设计和施工中非常重要的参数,它们直接影响着道路的安全性和舒适性。
横坡是指道路横向的坡度,纵坡是指道路纵向的坡度。
在道路设计和施工中,需要对道路的横坡和纵坡进行精确的计算,以确保道路的安全和舒适性。
横坡计算公式。
道路的横坡通常用百分比或度数来表示,它是指道路横向的坡度。
在道路设计中,横坡的计算是非常重要的,它直接影响着道路的排水和车辆行驶的舒适性。
横坡的计算公式如下:横坡(%) = (横向高差 / 道路宽度) × 100。
其中,横向高差是指道路两侧的高度差,道路宽度是指道路的横向宽度。
通过这个公式可以计算出道路的横坡百分比,从而确定道路的横向坡度。
纵坡计算公式。
道路的纵坡是指道路纵向的坡度,它直接影响着道路的爬坡能力和车辆行驶的舒适性。
在道路设计中,纵坡的计算是非常重要的,它需要根据道路的设计要求和地形条件来确定。
纵坡的计算公式如下:纵坡(%) = (纵向高差 / 道路长度) × 100。
其中,纵向高差是指道路两点之间的高度差,道路长度是指两点之间的距离。
通过这个公式可以计算出道路的纵坡百分比,从而确定道路的纵向坡度。
应用。
横坡和纵坡的计算在道路设计和施工中有着广泛的应用。
在道路设计中,需要根据道路的使用要求和地形条件来确定道路的横坡和纵坡。
通过精确的计算,可以确保道路的安全性和舒适性,提高道路的使用效率和寿命。
在道路施工中,横坡和纵坡的计算也是非常重要的。
施工人员需要根据设计要求和地形条件来进行道路的平整和坡度调整,以确保道路的质量和使用性能。
总结。
道路的横坡和纵坡是道路设计和施工中非常重要的参数,它们直接影响着道路的安全性和舒适性。
通过精确的计算,可以确保道路的安全性和舒适性,提高道路的使用效率和寿命。
因此,在道路设计和施工中,需要对道路的横坡和纵坡进行精确的计算,以确保道路的安全和舒适性。
高速公路边轴旋转超高方式横坡计算
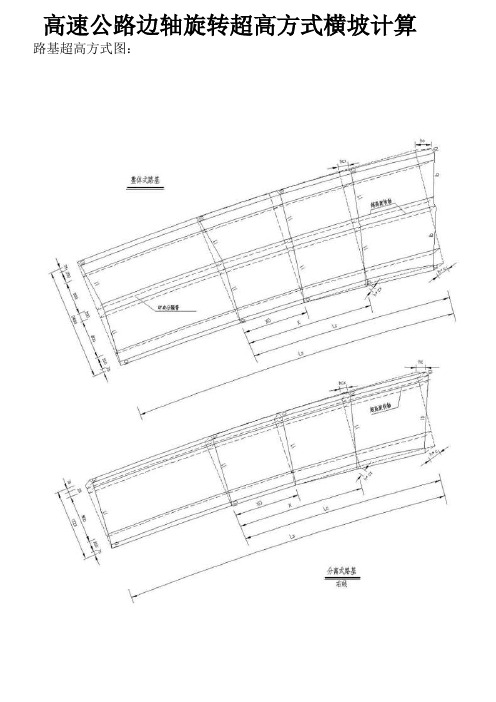
高速公路边轴旋转超高方式横坡计算路基超高方式图:说明∶1.路基超高采用边轴旋转,整体式路基旋转轴为中央分隔带边缘线;分离式路基为行车道前进方向左侧路基边缘内侧1.0米处。
2.行车道和硬路肩超高,土路肩不超高。
3.图中所示符号∶Ls--缓和曲线长,Lc--超高过渡段长;X0--与路拱同坡的单向超高点至超高过渡段起点的距离,I1--路拱横坡度;X--过渡段上任意点至超高过渡段起点的距离,I0--路肩横坡度;Ib--弯道超高横坡度,hc--路基外缘最大抬高值,h″c--路基内缘最大降低值;h″cx--x点路基内缘降低值,hcx--x点路基外缘抬高值.4.超高方式:圆曲线为全超高路段,超高过渡段长度(LC)从缓圆点(HY)往直缓点(ZH)或从圆缓点(YH)往缓直点(HZ)点计算。
先按超高渐变率p=1/330算出超高过渡段长度Lc,若Lc<Ls,则超高渐变率p=1/330。
若算出的Lc>Ls,则取Lc=Ls,超高过渡段长度等于缓和曲线长度。
5.图中尺寸均以厘米为单位,适用于设计时速V=80Km/h。
备注:正常路拱横坡(即直线段)为-2%;横坡计算按硬路肩比路缘带低为负。
一、整体式路基:图上为一左转直线到圆曲线的超高方式图。
半径为800m,缓和曲线长250m。
读图可得:R=800m,所以Ib弯道超高横坡度=4%;左转曲线,则黑线表示右幅,红线表示左幅;红点为直缓点;黑点为右幅超高起点;黄点为左幅超高起点;蓝点为缓圆点。
R=800,那么Lc=205<Ls=250.则:红点与黑点距离为:Ls-Lc=45m;黄点到蓝点距离为TX:(lb-|i左|)/(lb+|i右|)*Lc=(4-2)/(4+2)*205=68.333m; 黑点到黄点距离(与路拱同坡的单向超高点至超高过渡段起点):X0=Lc-68.333=136.667m 。
由此可得:1.直线段左右幅横坡都为-2%;2.圆曲线上分2种情况:曲线左转则:左幅横坡为-lb;右幅横坡为lb;曲线右转则:左幅横坡为lb;右幅横坡为-lb;3缓和曲线分为4种情况设桩号K:曲线左转:第一缓和曲线上则:左幅横坡= -2% -(K - (HY - TX)) / TX * (lb - 2%)右幅横坡= -2% +(K - (HY - Lc)) / lc * (lb + 2%)第二缓和曲线上则:左幅横坡= -lb + (K - YH) / TX * (lb - 2%)右幅横坡= lb - (K - YH) / lc * (lb + 2%)曲线右转:第一缓和曲线上则:左幅横坡= -2% +(K - (HY - Lc)) / Lc * (lb +2%)右幅横坡= -2% -(K - (HY - TX)) / TX * (lb -2%)第二缓和曲线上则:左幅横坡= lb - (K - YH) / Lc * (lb + 2%)右幅横坡=-lb + (K - YH) / TX * (lb - 2%)将缓和曲线公式汇总:设转向ZX,左转为-1,右转为1;设路幅A,左幅为-1,右幅为1;设与路拱同坡的过渡长TX,左转左幅或右转右幅Lc=TX,,即当ZX*A=1时,Lc=TX;公式为:第一缓和曲线:HP = -2% - ZX * A * (K - (HY - lc)) / lc * (lb - A * ZX * lz)第二缓和曲线:HP = -ZX * A * lb + ZX * A * (K - YH) / lc * (lb - ZX * A * lz)附:整体式路基excel VBA公式宏。
竖曲线高程计算公式

竖曲线上点的高程计算公式
1. 字母所代表的意义:
R:曲线半径
i1:ZY~JD方向的坡度
i2:JD~YZ方向的坡度
T:曲线的切线长
E:外失距
x:竖曲线上的点到直圆或圆直的距离
y:竖曲线上点的高程修正值
2. 计算公式:
超高计算公式
1. 字母所代表的意义:
i0:路拱坡度
i b:超高坡度
L s:缓和曲线长
b1:所求点~路中线距离
x0:从直缓开始,到路左右坡度一致的距离,即图中C---C
x:所求点~直缓或缓直的距离
h b:超高值
2. 计算公式公式1:绕中线旋转
1当x ≤x 0时
行车道外侧边缘:()0101i b L x
i i b h s
b b -+=
行车道内侧边缘:()01i b b h x b +-= 2当x ≥x0时
行车道外侧边缘:()0101i b L x
i i b h s b b -+= 行车道内侧边缘:()b s
x b i L x
b b h +-=
1 3. 计算公式公式2:
行车道外侧边缘:()100b L x i i i h s
b b ⎪⎪
⎭
⎫
⎝⎛
++
-= 行车道内侧边缘:()100b L x i i i h s
b b ⎪⎪
⎭
⎫
⎝⎛--
-=。
