前沿数学专题讨论班(08-09秋冬)
数学读书讨论主题

数学读书讨论主题2021年5月20日下午,区初中数学“爱阅读乐探究善表达”主题研讨活动在龙湾区实验中学教育集团学文校区举行。
这次莅临活动现场的专家有温州大学数学与信息科学专业教授方均斌老师,他带领了温大数理学院19数本(1)(2)班的同学们和20级教育硕士一起参加这次活动,出席活动还有龙湾区教研员省特级教师郑银凤老师,区初中数学名师工作室学员,区七八年级数学老师以及数学教研组长。
此次活动分课堂展示、学生展示、专家讲座和专家指导四部分。
课堂展示第一节课是由龙湾区实验中学教育集团学文校区的张小钗老师和七(6)班的同学们为大家带来的《图说因式分解》。
张老师通过图形的拼接“玩”转纸片,将“式”与“形”相结合帮助学生更好地理解因式分解,让学生在玩中合作,在玩中探究,在玩中体验与感悟数学学习,精彩纷呈。
第二节课《“剪﹒拼”拼图》由龙湾区实验中学教育集团学文校区的柳文瑞老师带领他的学生共同呈现。
柳老师组织学生“剪﹒拼”图形,让学生们在“剪”与“拼”中理解平行四边形和特殊平行四边形的联系,从而归纳“剪”与“拼”的方法,在活动中让学生感悟到“剪”与“拼”都要遵循所学的数学原理。
这是一个有趣的探索,为我们的数学教学提供了一个非常好的思路。
两节课的素材均选自教材中的设计题和阅读材料栏目,凸显课标关于“综合与实践”的理念,也是对数学学科立足教材开展“项目化”学习的初步探索!两节课的内容扎实丰富,既有代数模块又有几何模板,但都指向“拼图”,让学生在动手拼的过程中感受到数学好玩,同时又都突出通过“面积”将“数”与“形”结合在一起。
我们不禁感叹到,原来数学可以这么“玩”。
接下来是学生展示环节,先是由龙湾区实验中学教育集团学文校区八(8)班的项一帆同学进行说题展示《将“简”进行到底》(指导老师叶丹),项一帆同学充分运用了图形裁剪拼接技巧,通过数形结合思想和整体代入思想,对勾股定理的使用进行了生动诠释,把她隐性的探究思维显性地表达出来,非常精彩。
2024年秋季数学教研组工作计划(4篇)

秋季数学教研组工作计划一、教研组基本情况本组有____名教师,组员中,有主管学校教科研并兼市教科员的方校长,五十岁以上教师共七人。
二、指导思想及工作目标指导思想:在市教研室和学校教务处、教科处的指导下,以提高课堂教学的有效性为目标,以落实教学常规为重点,积极配合班级加强互助合作学习小组建设,精心营造有利于学生健康成长的学习环境,不断提高教师的专业水平、教学能力、科研水平。
工作目标:加强学习,落实常规,优化课堂,有效加强备课组建设;加强课件资源的共享;促进新教师的成长;提高教师的研究水平,形成我校数学课堂教学的特色。
三、具体措施1.指导本组成员认真研读数学新课程标准。
2.有计划进行专题理论学习,用新课程的思想指导自己的教学实践,不断提高本组成员的教育教学技能。
3.认真组织并督促好本教研组各年级备课组的活动,探索注重实效的备课组活动方法。
4.积极参与学校课题研究,不断地搞高本组教师的教研的能力。
5.创设条件,提供机会促进新教师的迅速成长。
6.通过互相听课、评课等活动加强提高课堂效益研究。
7.认真组织期中期末考试和进行考试的质量分析、总结经验、制定改进措施。
8.指导本组教师积极撰写教育教学论文。
四、活动内容如下:第____周:制定教研组、备课组工作计划、第____周:1.探讨教学案在使用过程中的出现的问题和解决的对策2.评议组内教研课;第____周:探讨如何指导学生自主学习系列活动一。
第____周:1.专题理论学习;____组内教师教研课研讨。
第____周:1.备课组交流集体备课中存在问题商讨解决方法;____组内教师教研课研讨;第____周:1.搞好期中考试复习、完成期中考试命题工作;____组内教师教研课研讨;第____周:____期中考试总结。
2.认真完成期中考试质量分析,培养学生良好的学习习惯。
第____周:1.专题理论学习研讨;____组内教师教研课研讨;第____周:1.探讨如何指导学生自主学习系列活动二;____组内教师教研课研讨;第____周:1.搞好期末考试复习;2.撰写总结、论文秋季数学教研组工作计划(二)指导思想以新区教研室数学学科教研工作计划和学校教师岗位规范为指导,以教育的____为核心,以加强理论学习更新教学理念、改善备课方法提高备课质量、进一步提高毕业班复习效率、加速培养青年教师的步伐为主要工作,继续发扬苦干精神,全身心投入到教育教学工作中去,为把我校建成镇江市一流名校做出我们应有的贡献。
秋季数学教研活动方案(3篇)

第1篇一、活动背景随着新学期的开始,教师们对教育教学工作有了新的思考和规划。
为了提高数学教学质量,加强教师之间的交流与合作,促进教师专业成长,特举办秋季数学教研活动。
本次活动旨在通过研讨、交流和实践,提升教师的教学水平和专业素养,为学生的全面发展奠定坚实基础。
二、活动目标1. 提高数学教师的教学设计能力,优化课堂教学。
2. 加强教师之间的沟通与协作,形成良好的教研氛围。
3. 增强教师对教材、教法和学法的认识,提高教学质量。
4. 培养教师的创新意识,促进教师专业成长。
三、活动时间2022年9月15日至10月15日四、活动地点学校多功能厅五、活动对象全校数学教师六、活动内容1. 教学研讨(1)主题:如何提高小学数学课堂教学效率(2)时间:2022年9月20日(3)内容:教师们结合自身教学经验,围绕提高小学数学课堂教学效率这一主题进行研讨,分享教学心得和教学方法。
(4)形式:分组讨论、经验分享、互动交流2. 教学观摩(1)主题:观摩优秀数学课堂教学(2)时间:2022年9月27日(3)内容:组织教师观摩优秀数学课堂教学,学习优秀教师的课堂教学方法和技巧。
(4)形式:现场观摩、课后研讨3. 教学设计比赛(1)主题:小学数学教学设计比赛(2)时间:2022年10月5日(3)内容:教师们根据指定的教学内容,进行教学设计,评选出优秀教学设计。
(4)形式:提交教学设计、评选优秀设计、交流心得4. 教学反思(1)主题:如何进行有效的教学反思(2)时间:2022年10月10日(3)内容:教师们结合自己的教学实践,探讨如何进行有效的教学反思,提高教学质量。
(4)形式:分组讨论、经验分享、互动交流5. 教学研究(1)主题:小学数学教材、教法与学法研究(2)时间:2022年10月15日(3)内容:教师们对小学数学教材、教法和学法进行深入研究,提出改进建议。
(4)形式:分组讨论、成果展示、交流心得七、活动组织1. 成立活动筹备组,负责活动的组织、协调和实施。
数学学科发展前沿完整版

数学学科发展前沿 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】数学学科发展前沿调研报告145407 徐珺,是研究、、、以及等的一门学科,从某种角度看属于形式的一种。
而在人类发展和生活中,数学发挥着不可替代的作用,也是学习和研究现代科学技术必不可少的基本工具。
近半个多世纪以来,随着计算机技术的迅速发展,数学的应用不仅在工程技术、自然科学等领域发挥着越来越重要的作用,而且以空前的广度和深度向经济、金融、生物、医学、环境、地质、人口、交通等新的领域渗透,所谓数学技术已经成为当代高新技术的重要组成部分。
一、数学学科的意义数学在人类文明的进步和发展中一直发挥着重要的作用。
过去,人们习惯把科学分为自然科学、社会科学两大类,数、理、化、天、地、生都归属于自然科学。
但是,现在科学家更倾向于把自然科学界定为以研究物质的某一运动形态为特征的科学,如物理学、化学、生物学。
数学是忽略了物质的具体运动形态和属性,纯粹从数量关系和空间形式的角度来研究现实世界的,具有超越具体科学和普遍适用的特征,具有公共基础的地位。
数学的许多高深理论与方法正广泛深入地渗透到自然科学的各个领域中去。
数学在当代科技、文化、社会、经济和国防等诸多领域中的特殊地位是不可忽视的。
发展数学科学,是推进我国科学研究和技术发展,保障我国在各个重要领域中可持续发展的战略需要。
由于数学的性质及其应用途径不断发生变化,新的数学领域不断涌现,数学的应用范围的不断扩充,加之计算机的发展和应用爆炸性的增长,都要求发展新的数学。
数学是打开科学大门的钥匙,数学在科学理论成就中的重要性。
早在古希腊的毕达哥拉斯学派就把数学看作万物之本源;享有“近代科学之父”尊称的伽利略认为,宇宙像一本用数学语言写成的大书,如不掌握数学的符号语言,就像在黑暗的迷宫里游荡,什么也认识不清。
第一位诺贝尔物理奖获得者伦琴在问道科学家需要什么样的修养时,他的回答是:第一是数学,第二是数学,第三是数学。
浙江省名校联盟2024届高三上学期9月新高考研究卷(全国I卷)数学试题(二)

浙江省名校联盟2024届高三上学期9月新高考研究卷(全国I卷)数学试题(二)学校:___________姓名:___________班级:___________考号:___________四、解答题分为以下两类情况:第一类:,,A C D 三个区域涂三种不同的颜色,第一步涂,,A C D 区域,从5种不同的颜色中选3种按序涂在不同的3个区域上,则有35A 种方法,第二步涂B 区域,由于,A C 颜色不同,有3种方法,第三步涂E 区域,由于,A D 颜色不同,则有3种方法,由分步计数原理,则共有3533A 540´=种方法;第二类:,,A C D 三个区域涂两种不同的颜色,由于,C D 不能涂同一色,则,A C 涂一色,或,A D 涂同一色,两种情况方法数相同.若,A C 涂一色,第一步涂,,A C D 区域,,A C 可看成同一区域,且,A D 区域不同色,即涂2个区域不同色,从5种不同的颜色中选2种按序涂在不同的2个区域上,则有25A 种方法,第二步涂B 区域,由于,AC 颜色相同,则有4种方法,第三步涂E 区域,由于,AD 颜色不同,则有3种方法,由分步计数原理,则共有2543A 240´=种方法;【点睛】直线与抛物线的位置关系和直线与椭圆、双曲线的位置与系数的关系;有关直线与抛物线的弦长问题,要注意直线是物线的焦点,可直接使用公式A B B x p A x ++=,若不过焦点,则用一解析几何简化运算的常见方法:(1)正确画出图形,利用平面几何知识简化运算;(2)坐标化,把几何关系转化为坐标运算;(3)巧用定义,简化运算.由题意知,直线l 的斜率存在且不为22(,)x y ,设圆N 的半径为r ,2222(21)4184y kx mk x kmx x y =+Þ++++=。
数学研讨交流会发言稿三年级

大家好!今天,我非常荣幸能够在这里参加数学研讨交流会,与大家共同探讨数学教育的话题。
首先,请允许我代表三年级数学组,向各位领导、老师的到来表示热烈的欢迎和衷心的感谢!数学是一门基础学科,对于培养孩子们的逻辑思维能力、解决问题的能力以及创新精神具有重要意义。
在新的教育形势下,我们三年级数学组一直在努力探索,以提高数学教学质量。
下面,我将从以下几个方面谈谈我们的做法和体会。
一、关注学生个体差异,因材施教每个学生都有自己的特点和优势,因此在教学过程中,我们要关注学生的个体差异,因材施教。
具体做法如下:1. 了解学生:通过观察、谈话等方式,了解学生的兴趣爱好、学习习惯、思维方式等,为教学提供依据。
2. 分层教学:根据学生的学习情况,将学生分为A、B、C三个层次,针对不同层次的学生制定相应的教学目标和方法。
3. 个性化辅导:针对学生在学习过程中遇到的问题,给予个别辅导,帮助他们克服困难,提高学习成绩。
二、创设情境,激发学生学习兴趣兴趣是最好的老师。
为了激发学生的学习兴趣,我们采取以下措施:1. 贴近生活:将数学知识与学生的日常生活紧密联系,让学生在熟悉的环境中学习数学。
2. 创设情境:通过游戏、故事、实验等方式,创设生动有趣的情境,激发学生的学习兴趣。
3. 多元评价:采用多样化的评价方式,关注学生在学习过程中的表现,激发他们的学习动力。
三、注重学生思维能力的培养数学教学不仅要传授知识,更要培养学生的思维能力。
以下是我们在培养学生思维能力方面的做法:1. 鼓励学生提问:鼓励学生在课堂上积极提问,培养学生的质疑精神。
2. 引导学生思考:在教学过程中,引导学生进行思考,培养学生的逻辑思维能力。
3. 强化练习:通过多样化的练习,巩固学生的知识点,提高他们的解题能力。
四、加强家校合作,共同促进学生成长家校合作是提高数学教学质量的重要途径。
我们采取以下措施加强家校合作:1. 定期召开家长会:向家长汇报学生在校的学习情况,听取家长意见和建议。
《数学物理前沿研究》国际学术研讨会邀请函-Zhejiang

“图像处理中的数学理论与方法”高级研讨班通知2009年5月11-22日我们在浙江大学数学科学研究中心举办了“Summer School on Medical Image Analysis”,该次暑期班邀请了图像处理方面国际著名专家、美国Florida大学陈韵梅教授主讲,加拿大Alberta大学贾荣庆教授、华东师范大学沈纯理教授、浙一医院影像中心主任、浙江大学医学院教授张敏鸣、浙江大学现代光学仪器国家重点实验室刘华锋教授等人也作了专题报告。
这次暑期班共有近百名全国各高校师生前来参加,规模大、效果佳、影响广。
为了能够让国内各高校青年师生进一步深入学习图像处理(尤其是医学图像处理)方面的知识,提高我国在该领域的实力与影响力,浙江大学数学科学研究中心将于2010年5月10—21日举办“图像处理中的数学理论与方法”高级研讨班。
本次研讨班的主要内容是图像处理中的数学理论与方法(特别是医学图像处理中的数学理论与方法等方面),届时我们将特别邀请陈韵梅教授及其研究团队进行授课并主持讨论班,同时我们也将邀请一些国际知名专家、学者作专题报告。
一、课程主讲人陈韵梅教授、叶筱倞博士(美国Florida大学)二、部分专题报告陈韵梅教授(美国Florida大学)R. Deriche教授(法国INRIA、待确定)贾荣庆教授(加拿大Alberta大学)刘华锋教授(浙江大学)彭志毅主任医师(浙一医院)唐孝威院士(中国科学院院士、浙江大学)叶筱倞博士(美国Florida大学)张敏鸣教授、主任医师(浙江大学医学院、浙二医院)郑树森院士(中国工程院院士、浙江大学医学院、浙一医院)三、专题讨论班1、医学图像处理主讲:陈韵梅教授、施江立(美国Florida大学)2、图像处理与编程主讲:陈韵梅教授、叶筱倞(美国Florida大学)3、题目待定主讲:董芳芳(浙江大学数学科学研究中心)4、双曲方程与图像处理主讲:刘春晓(浙江大学数学科学研究中心)5、自由讨论三、日程安排研讨班地点:浙江大学数学科学研究中心五楼会议室具体日程安排见浙江大学数学科学研究中心网页/conference/2010/ImageProcess/四、其它事项1、报到时间:2010.5.9;报到地点:浙江大学数学科学研究中心(浙江大学玉泉校区永谦数学大楼,邵逸夫科技馆旁)。
数学专业的研究方向与前沿问题

数学专业的研究方向与前沿问题数学是一门探索现实世界的抽象科学,广泛应用于自然科学、社会科学以及工程技术等领域。
作为数学专业的学生,深入研究数学的发展方向和前沿问题是必不可少的。
本文将介绍数学专业目前研究的主要方向以及一些引人注目的前沿问题。
一、代数与代数几何代数与代数几何是数学中重要的分支之一。
研究对象包括群论、环论、域论、模论等。
在代数几何领域,关注的是代数方程的解集,研究代数方程的几何性质。
在代数方向的研究中,一个重要的前沿问题是素数问题。
这个问题旨在解答素数的分布规律以及素数之间的联系。
目前,研究者已经取得了一些重要进展,但仍然存在许多难题等待解决。
二、微分方程与动力系统微分方程是数学中的一种基本工具,广泛应用于物理学、工程学和经济学等领域。
微分方程与动力系统的研究重点在于描述和分析系统的演化行为。
非线性偏微分方程是当前研究的热点之一。
这类方程具有复杂的数学结构和丰富的物理现象,对于许多实际问题的建模和求解具有重要意义。
研究者们致力于发展新的数学理论和数值方法,以解决非线性偏微分方程的一系列挑战。
三、概率论与数理统计概率论与数理统计是数学中的一门应用科学,用于研究随机现象和不确定性问题。
在现代科学和工程领域,概率论与数理统计的应用非常广泛。
在概率论与数理统计的研究中,机器学习是一个备受关注的前沿问题。
随着大数据时代的到来,机器学习成为了一种重要的数据分析方法。
研究者们致力于开发新的机器学习算法和模型,以提高数据处理的准确性和效率。
四、数值分析与科学计算数值分析与科学计算是数学中的一门应用科学,旨在研究数学问题的计算方法和计算结果的误差分析。
数值分析与科学计算在科学研究和工程设计中具有重要意义。
在数值分析与科学计算领域,高性能计算是目前的研究热点之一。
高性能计算通过利用大规模并行计算系统,加速计算过程,提高计算效率。
研究者们致力于开发高效的数值算法和优化策略,以满足不断增长的计算需求。
五、离散数学与组合优化离散数学与组合优化是数学的一个重要分支,涉及离散结构、图论、组合设计等方面的研究。
立秋数学用数学解读秋季的变化规律

立秋数学用数学解读秋季的变化规律立秋数学:用数学解读秋季的变化规律立秋,是二十四节气中的一个重要节气,标志着季节的转折。
在这个时刻,数学或许是我们理解秋季变化规律的一把钥匙。
本文将利用数学的分析方法,解读秋季的变化规律。
一、气温的变化规律秋季的气温变化常常让人感到神秘莫测,但数学却可以帮我们揭示其中的规律。
以某地秋季每日最高气温为例,可以将其抽象为一个函数f(x),其中x代表日期。
通过数学建模,我们可以使用曲线拟合方法来研究气温的变化趋势。
常见的拟合方法包括线性拟合、多项式拟合、指数拟合等。
以多项式拟合为例,可以得到一个多项式函数来描述气温的变化规律。
在此基础上,我们可以利用微积分等数学工具,求解函数的导数和极值点,从而确定秋季气温变化的关键节点。
二、降水量的变化规律秋季的降水量常常体现为规律性的周期性变化。
数学中的统计方法可以帮助我们揭示这种变化规律。
以某地区秋季每日降水量为例,可以将其抽象为一个随机变量序列。
通过统计方法,我们可以计算出降水量的平均值、方差、分布等参数,从而描述降水量的变化规律。
此外,我们还可以利用时间序列分析方法,判断降水量序列是否存在趋势、周期性等特征。
通过数学建模和预测,我们可以更好地理解和应对秋季降水的变化。
三、植物的生长规律秋季是植物的成熟季节,而植物的生长规律也可以通过数学公式进行描述。
以某种作物的生长过程为例,可以将其抽象为一个动力学系统。
通过数学模型,我们可以探究生长速率、生长周期、收获量等因素之间的关系。
在此基础上,可以运用微分方程等数学工具,解决植物生长过程中的优化问题,如最佳施肥量、最佳收割时机等。
数学帮助我们预测植物的生长状态,进而实现对农作物的合理管理和利用。
四、太阳高度角的变化规律秋天的太阳高度角发生变化,这一规律对人类的生活和工作有着重要影响。
以太阳高度角为例,可以通过几何学和三角学知识,计算出太阳光的投射角度。
通过数学分析,可以得出太阳高度角随日期变化的规律。
华中科技大学数学与统计学院研究生

数学与统计学院华中科技大学数学与统计学院始建于1953年,经历了由数学教研室、数学系到数学与统计学院的发展历程。
上世纪50年代初,著名数理统计学家林少宫先生从美国Illinois大学归来与熊庆来先生的弟子戴良谟等数学界老前辈一起主持了本学科的初创工作。
上世纪70年代末,徐利治教授亲任系主任主持了数学系的创建工作,并于1981年获得应用数学硕士点,随后形成了应用数学、计算数学与运筹学协调发展的良好局面,在全国率先举办了数理逻辑、模糊数学等专题讨论班,创建了《数学评论与研究》和《模糊数学》学术期刊,并培养了国际著名数理经济学家田国强、艾春荣,美国Purdue大学教授蔡智强等一批杰出学者。
八十年代中期,陈庆益教授加盟我校进一步推动和加速了本学科的发展,其主持创建了《应用数学》杂志,并培养了长江特聘教授方复全等一大批数学人才。
九十年代初,黄志远教授调来我校创建了随机分析研究中心,其与杰出青年基金获得者、长江特聘教授任佳刚一起推动了我校在概率统计领域的研究,并使我校获得了概率论与数理统计博士点。
经过几十年的艰苦努力,目前数学与统计学院拥有数学博士后流动站、数学一级学科博士点和数学一级学科硕士点、统计学一级学科博士点,以及应用统计专业硕士点。
在学位授权点建设的同时,数学与统计学院也先后建立了数学与应用数学、信息与计算科学、统计学三个本科专业。
学院现有在校学生648人,其中本科生446人、硕士生156人、博士生46人、硕博连读生所占比例为60%左右。
数学与统计学院现有教职工103人,在编教师87人,其中博士生导师13人,教授19人,副教授37人,教师中有博士学位者占61%,有“长江讲座教授”1名、“新世纪百千万人才工程”入选者1名、教育部“(跨)新世纪优秀人才支持计划”入选者5名、“高校青年教师奖”获得者1名、“湖北省有突出贡献的中青年专家”3名、“湖北省楚天学者”1名以及“宝钢优秀教师奖”获得者4名。
近五年来,数学与统计学院的学术团队共获科研经费890万元,其中国家自然科学基金27项,联合获批国家自然科学基金重大、重点项目2项,;发表SCI收录论文260余篇;出版各类专著、教材30余本。
专题04分类讨论型【讲】【通用版】
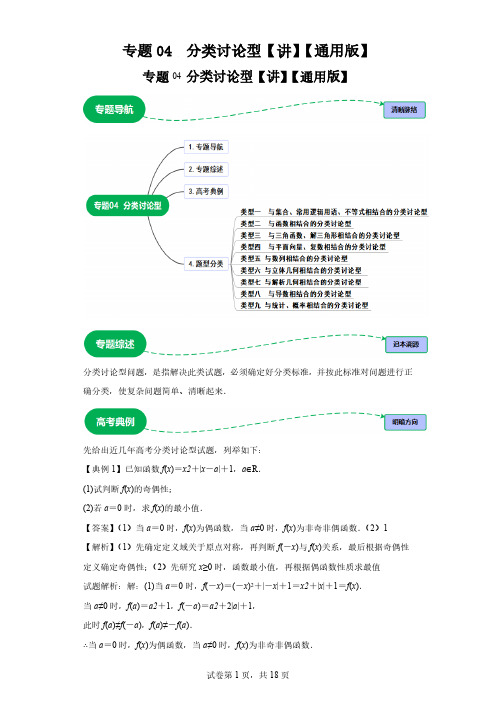
专题04 分类讨论型【讲】【通用版】专题04分类讨论型【讲】【通用版】分类讨论型问题,是指解决此类试题,必须确定好分类标准,并按此标准对问题进行正确分类,使复杂问题简单、清晰起来.先给出近几年高考分类讨论型试题,列举如下:【典例1】已知函数f(x)=x2+|x-a|+1,a∈R.(1)试判断f(x)的奇偶性;(2)若a=0时,求f(x)的最小值.【答案】(1)当a=0时,f(x)为偶函数,当a≠0时,f(x)为非奇非偶函数.(2)1【解析】(1)先确定定义域关于原点对称,再判断f(-x)与f(x)关系,最后根据奇偶性定义确定奇偶性;(2)先研究x≥0时,函数最小值,再根据偶函数性质求最值试题解析:解:(1)当a=0时,f(-x)=(-x)2+|-x|+1=x2+|x|+1=f(x).当a≠0时,f(a)=a2+1,f(-a)=a2+2|a|+1,此时f(a)≠f(-a),f(a)≠-f(a).∴当a=0时,f(x)为偶函数,当a≠0时,f(x)为非奇非偶函数.方法二(分类讨论)由题设知,求OMN 的面积S ,并观察S 最大值时l 的位置特点.类型三 与三角函数、解三角形相结合的分类讨论型【典例3-1】已知方程22sin cos 1x y αα+=,其中[0,α∈曲线?απ类型六 与立体几何相结合的分类讨论型【典例6-1】六盒磁带按“规则方式”打包.所谓“规则方式”,是指每相邻两盒必须是以全等的面积对接,最后得到的包装形状是一个长方体.若磁带盒长、宽、高的尺寸分别为,,a b c ,且a b c >>,请你给出一种使表面积最小的打包方式,予以证明,并画出其示意图.【解析】如果不考虑磁带盒之间的空隙,那么就要考虑长方体表面积可能的值.因为62316=⨯=⨯,所以“规则打包”只有两种类型.设磁带盒过同一顶点的三个面的面积为、、A B C .(1)若“16⨯”类型,表面积21212S A B C =++.要使S 取值最小,由于磁带盒三边长为a b c >>,从而令A a b =⋅,,B a c C b c =⋅=⋅,则121212S ab ac bc =++;(2)若“23⨯”类型,表面积4612S A B C =++.要S 最小,应为24612S ab ac bc =++.比较两种方式,即()126223S S ac ab a c b -=-=-.当3c b >时,2S 小,故采用“23⨯”打包类型;当3c b <时,1S 小,故采用“16⨯”打包类型;当3c b =时,两种类型都可以.示意图如图所示.【举一反三】7.在长方体1111ABCD A B C D -中,()2,0AB BC a a ==>,12AA =.(1)在BC 边上是否存在点Q ,使得1A Q QD ⊥,为什么?(2)当存在点Q ,使1A Q QD ⊥时,求a 的最小值,并求出此时二面角1A A D Q --的正弦值.类型七 与解析几何相结合的分类讨论型证明:(1)当2AB p ≥时,如图,记综上所述,满足条件的正整数(1)求315C -的值.(2)组合数的两个性质:①C C m n m n n -=;②11C C C m m m n n n -++=是否都能推广到C mx (x ∈R ,m 是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由;(3)已知组合数C m n 是正整数,证明:当x ∈Z ,m 是正整数时,C mx ∈Z .参考答案:)BC 上存在点Q ,且1A Q QD ⊥,且11,A Q A A ⊂平面1A AQ ,∴))知a 的最小值是4;4时,2x =,即Q 是BC 的中点,作作1PF A D ⊥,连结QF .∵QP对上面a 的各种取值范围,作出这两条曲线只有一个公共点的证明如下:上述探究中的方程()214ay a y +-若0a >,则210y a =-<,从而x。
数学讲座教研活动主题(3篇)

第1篇一、活动背景随着新课程改革的不断深入,数学教育逐渐从传统的知识传授转向关注学生的核心素养培养。
为了提高数学教学质量,促进学生全面发展,我校特举办此次数学讲座教研活动。
本次活动的主题为“创新思维与核心素养——构建高效数学课堂”,旨在通过讲座和研讨,激发教师的创新思维,提升教师的专业素养,探索构建高效数学课堂的有效途径。
二、活动目标1. 提高教师对创新思维与核心素养的认识,明确其在数学教育中的重要性。
2. 培养教师的创新意识和实践能力,提升教师的专业素养。
3. 探讨构建高效数学课堂的策略和方法,促进教师教学水平的提升。
4. 加强教师之间的交流与合作,形成良好的教研氛围。
三、活动内容1. 开幕式及领导致辞(1)主持人介绍活动背景和目的;(2)学校领导致辞,对数学教育的重要性进行强调,对教师提出期望;(3)宣布活动正式开始。
2. 主题讲座(1)创新思维在数学教育中的应用讲座内容:从创新思维的定义、特点、作用等方面展开,结合数学教育实例,探讨创新思维在数学教育中的应用策略。
(2)核心素养培养在数学教育中的实践讲座内容:解读核心素养的内涵,分析核心素养在数学教育中的具体体现,分享核心素养培养的实践经验。
(3)构建高效数学课堂的策略与方法讲座内容:从教学目标、教学内容、教学方法、教学评价等方面,探讨构建高效数学课堂的策略与方法。
3. 分组研讨(1)分组讨论:教师根据讲座内容,结合自身教学实际,分组进行讨论,分享教学经验和心得。
(2)成果展示:各小组派代表进行成果展示,分享研讨成果,促进教师之间的交流与学习。
4. 互动环节(1)教师提问:针对讲座内容,教师提出疑问,邀请主讲人进行解答。
(2)专家点评:邀请数学教育专家对讲座内容进行点评,对教师提出的问题进行解答。
5. 总结与闭幕式(1)总结活动成果,肯定教师在活动中的表现;(2)颁发优秀研讨小组、优秀论文等奖项;(3)宣布活动圆满结束。
四、活动预期效果1. 教师对创新思维与核心素养的认识得到提高,能够在教学中更好地培养学生的核心素养。
华东师范大学数学系研究生课程表
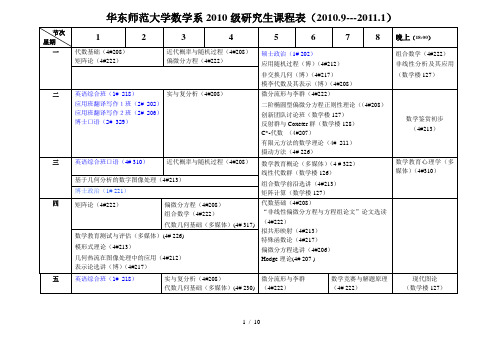
华东师范大学数学系2010级研究生课程表(2010.9---2011.1)
1 / 10
注:1.“数学鉴赏初步”不记学分,仅供有兴趣的同学参加!
2.“数学竞赛与解题原理”下午2:40开始上课!
2 / 10
华东师范大学数学系09级研究生课程表(2010.9---2011.1)
3 / 10
4 / 10
注:“数学鉴赏初步”不记学分,仅供有兴趣的同学参加!
5 / 10
华东师范大学数学系08级研究生课程表(2010.9---2011.1)
6 / 10
7 / 10
注:“数学鉴赏初步”不记学分,仅供有兴趣的同学参加!
华东师范大学数学系全日制教育硕士课程表(2010.9---2011.1)
8 / 10
注:“数学竞赛与解题原理”下午2:40开始上课!
华东师范大学数学系教育硕士双名班课程表(2010.9---2011.1)
9 / 10
注:专业课9月16日(星期四)开始上课,公共课9月9日(星期四)开始上课!
中午从数统楼出发坐12:45 的班车到中山北路校区!
10 / 10。
数学教研主题讨论发言稿范文

大家好!今天我非常荣幸能在这里就数学教研主题与大家进行讨论。
数学作为一门基础学科,在我国的教育体系中占有重要地位。
为了提高数学教学质量,激发学生的学习兴趣,我们有必要深入开展数学教研工作。
以下是我对数学教研的一些思考,希望能引起大家的共鸣。
一、加强数学教研队伍建设1. 提高教师的专业素养。
教师是教研工作的主体,教师的专业素养直接影响到教研工作的成效。
因此,我们要通过培训、学习等方式,不断提高教师的专业素养,使他们在教学过程中能够运用先进的教育理念和方法。
2. 建立健全教研制度。
学校应制定合理的教研制度,确保教研活动有序开展。
如:定期开展教研活动、组织教师参加各类学术交流、鼓励教师撰写论文等。
3. 营造良好的教研氛围。
学校要为教师创造一个宽松、和谐、民主的教研环境,使教师在教研活动中能够畅所欲言,充分展示自己的才华。
二、深化数学教学改革1. 优化教学内容。
教师应根据学生的实际情况,合理调整教学内容,注重培养学生的数学思维能力和创新能力。
2. 改进教学方法。
教师应积极探索有效的教学方法,如:探究式学习、合作学习、案例教学等,激发学生的学习兴趣,提高教学效果。
3. 加强实践教学。
实践教学是提高学生数学素养的重要途径。
学校应为学生提供丰富的实践机会,如:参观数学博物馆、参加数学竞赛等。
三、关注学生个体差异1. 因材施教。
教师应根据学生的个体差异,制定不同的教学策略,使每个学生都能在数学学习中获得成功。
2. 鼓励学生自主学习。
教师应引导学生主动探究数学问题,培养学生的自主学习能力。
3. 关注学生心理健康。
教师应关注学生的心理健康,及时发现和解决学生在数学学习过程中遇到的心理问题。
四、加强家校合作1. 加强家校沟通。
学校应定期与家长沟通,了解学生在家的学习情况,共同为学生创造良好的学习环境。
2. 开展家庭教育指导。
学校可以邀请专家为家长开展家庭教育讲座,提高家长的教育水平。
3. 共同关注学生的全面发展。
学校和家庭应共同努力,关注学生的德、智、体、美全面发展。
数学交流研讨发言稿题目

尊敬的各位领导、各位专家、各位同仁:大家好!今天,我很荣幸能站在这里,与大家共同探讨数学这一古老而充满活力的学科。
数学,作为人类智慧的结晶,不仅在科学技术的发展中扮演着至关重要的角色,更在日常生活中无处不在。
在此,我将以“探索数学之美,共筑智慧未来”为题,分享一些个人的思考与感悟。
一、数学之美,无处不在数学之美,在于其简洁、严谨、逻辑性。
从古至今,无数数学家为探寻数学之美付出了艰辛的努力。
正如我国古代数学家华罗庚所说:“数学是自然科学的皇后,哲学的皇后,又是艺术的皇后。
”数学之美,体现在以下几个方面:1. 逻辑之美:数学是一门逻辑性极强的学科,其推理过程严谨、条理清晰。
通过逻辑推理,我们能够从已知的事实中推导出未知的结论,这是数学的魅力所在。
2. 结构之美:数学是一门具有高度抽象性的学科,其研究对象是抽象的数学结构。
这些结构不仅具有内在的美感,而且能够揭示自然界和人类社会的规律。
3. 应用之美:数学在各个领域都有广泛的应用,如物理学、生物学、经济学等。
数学的应用之美,体现在其解决实际问题的能力上。
二、探索数学之美,助力人才培养数学之美,是培养人才的重要途径。
在探索数学之美的过程中,我们能够培养以下几方面的能力:1. 逻辑思维能力:数学要求我们具备严密的逻辑思维能力,这种能力在今后的学习和工作中都具有重要作用。
2. 创新能力:数学研究需要不断地探索和突破,这种精神有助于培养我们的创新能力。
3. 团队协作能力:数学研究往往需要多人合作,这种合作精神有助于培养我们的团队协作能力。
三、共筑智慧未来,推动数学发展面对新时代的挑战,我们应携手共筑智慧未来,推动数学的发展。
以下是一些建议:1. 加强数学教育:从基础教育阶段开始,注重培养学生的数学素养,提高全民数学水平。
2. 深化数学研究:鼓励数学家开展创新性研究,推动数学理论的突破和发展。
3. 促进数学应用:推动数学在各个领域的应用,为我国经济社会发展提供有力支撑。
冬天进行教研活动开场白(3篇)

第1篇大家好!在这寒冷的冬日里,我们欢聚一堂,共同开展教研活动。
首先,请允许我代表本次教研活动的组织者,向各位领导、同事们的到来表示热烈的欢迎和衷心的感谢!冬天,虽然寒冷,但正是我们思考和总结的黄金季节。
正如古人所说:“冬天到了,春天还会远吗?”在这个美好的时刻,我们开展教研活动,旨在进一步提高教育教学质量,激发教师的专业成长,共同为学生的全面发展贡献力量。
本次教研活动的主题是“深化课程改革,提高教学质量”。
在此,我想结合本次活动的主题,谈几点意见:一、提高认识,明确教研活动的意义教研活动是教师专业成长的重要途径,是提高教育教学质量的关键环节。
开展教研活动,有助于我们:1. 深入理解课程改革精神,把握教育教学方向。
2. 交流教育教学经验,取长补短,共同提高。
3. 提升教师的专业素养,为学生的全面发展奠定基础。
4. 促进教师之间的沟通与合作,形成良好的团队氛围。
二、明确目标,把握教研活动的重点本次教研活动,我们将围绕以下重点展开:1. 深入研究课程改革,探讨如何在教学中贯彻落实新课改理念。
2. 分析教育教学中的问题,寻找解决策略,提高教学质量。
3. 探索创新教学方法,激发学生的学习兴趣,培养学生的创新精神。
4. 加强教师队伍建设,提升教师的专业素养和教学能力。
三、精心组织,确保教研活动取得实效为确保本次教研活动取得实效,我们将:1. 制定详细的教研活动方案,明确活动目标、内容、时间和责任人。
2. 邀请专家进行专题讲座,为大家提供理论指导和实践经验。
3. 组织教师开展分组讨论,深入剖析教育教学中的问题,共同寻找解决方案。
4. 鼓励教师撰写教学心得和反思,分享教育教学经验,促进教师之间的交流与合作。
5. 对教研活动进行总结和评估,及时发现问题,不断改进和完善。
四、积极参与,共同推动教育教学改革本次教研活动,希望全体教师能够积极参与,做到以下几点:1. 认真聆听专家讲座,做好笔记,积极思考。
2. 积极参与分组讨论,踊跃发言,分享教育教学经验。
中学数学教研论坛(3篇)

第1篇一、前言随着教育改革的不断深入,中学数学教学面临着前所未有的挑战。
为了提高中学数学教学质量,推动数学教育事业的健康发展,全国各地中学数学教师纷纷积极参加教研活动,以提升自身教学水平和专业素养。
本论坛旨在为广大中学数学教师提供一个交流、学习、分享的平台,共同探讨中学数学教学中的热点问题,推动中学数学教学的创新与发展。
二、论坛主题1. 新课程背景下中学数学教学策略研究2. 中学数学课堂教学的有效性探讨3. 中学数学教师专业发展路径研究4. 中学数学教育评价改革与创新5. 中学数学信息技术与教学融合的研究三、论坛内容1. 新课程背景下中学数学教学策略研究(1)新课程理念下中学数学教学目标的确立(2)新课程背景下中学数学教学内容的选择与处理(3)新课程背景下中学数学教学方法的创新与应用(4)新课程背景下中学数学教学评价的改革与实践2. 中学数学课堂教学的有效性探讨(1)激发学生学习兴趣的策略与方法(2)提高课堂效率的教学技巧(3)培养学生的数学思维能力(4)课堂教学中如何实现师生互动3. 中学数学教师专业发展路径研究(1)中学数学教师专业素养的提升(2)中学数学教师教学能力的培养(3)中学数学教师科研能力的提高(4)中学数学教师职业生涯规划与成长4. 中学数学教育评价改革与创新(1)中学数学教育评价体系的构建(2)中学数学教育评价方法的创新(3)中学数学教育评价结果的应用(4)中学数学教育评价改革的实践与反思5. 中学数学信息技术与教学融合的研究(1)信息技术在中学数学教学中的应用(2)信息技术与中学数学教学的融合策略(3)信息技术对中学数学教师专业发展的影响(4)信息技术与中学数学教学评价的融合四、论坛形式1. 主题报告:邀请知名中学数学教育专家进行主题报告,分享他们在中学数学教学、教育评价、信息技术等方面的研究成果和实践经验。
2. 分组讨论:将参会教师分为若干小组,针对论坛主题进行深入探讨,分享教学经验,提出创新观点。
数学教研组发言主题八字

尊敬的校领导、各位老师、亲爱的同事们:大家好!今天,我非常荣幸能够代表数学教研组,就我们组的工作和未来规划进行一次发言。
在此,我将以“创新驱动,协同发展”为题,与大家分享我们的工作思路和目标。
一、创新驱动1. 引言创新是引领发展的第一动力,也是数学教研组不断前进的动力源泉。
在新时代背景下,数学教育面临着前所未有的挑战和机遇。
为了适应时代发展的需要,我们必须坚持创新驱动,不断提升教育教学质量。
2. 创新理念(1)树立以学生为中心的教学理念。
关注学生的个性差异,激发学生的学习兴趣,培养学生的创新思维和综合能力。
(2)倡导启发式教学。
注重培养学生的探究精神和自主学习能力,让学生在探索中发现知识,在实践中学以致用。
(3)加强课程整合。
将数学与其他学科知识相结合,拓展学生的知识视野,提高学生的综合素质。
3. 创新实践(1)开展课题研究。
围绕数学教学中的热点、难点问题,开展课题研究,推动教育教学改革。
(2)组织教学研讨。
定期开展教学研讨活动,分享教学经验,促进教师间的交流与合作。
(3)探索教学方法。
结合教学实际,探索新的教学方法,提高课堂教学效果。
二、协同发展1. 引言协同发展是数学教研组实现共同进步的关键。
在教育教学过程中,我们要加强团队合作,共同推动数学教育事业的繁荣。
2. 协同机制(1)建立教研组内部交流机制。
定期召开教研组会议,分享教学心得,交流教学经验,共同提高。
(2)加强与兄弟学校的合作。
通过开展校际交流活动,借鉴先进经验,拓宽教育教学思路。
(3)加强与社会各界的联系。
邀请企业、科研机构等参与数学教育,为学生提供更多实践机会。
3. 协同实践(1)开展跨学科教学。
结合其他学科知识,开展跨学科教学,提高学生的综合素养。
(2)组织学生参加各类数学竞赛。
通过竞赛,激发学生的学习兴趣,提高学生的数学素养。
(3)开展社会实践活动。
组织学生参观科技馆、企业等,让学生在实践中感受数学的魅力。
三、总结总之,数学教研组将以“创新驱动,协同发展”为工作主题,紧紧围绕教育教学这一中心任务,努力提高教育教学质量,为我国数学教育事业的发展贡献力量。
小学数学秋季教研工作计划博客

小学数学秋季教研工作计划博客尊敬的老师、亲爱的家长和同学们:大家好!我是某小学数学组组长。
在这个秋季学期,我为数学教研工作做出了详细的计划。
接下来,我将向大家介绍这个计划。
一、教学目标1. 提高学生的数学基础知识。
通过系统、全面的复习,夯实学生的基础知识,为后续的学习打下坚实的基础。
2. 培养学生的数学思维能力。
通过多种教学方法和教学手段,引导学生积极思考、独立解决问题,培养学生的逻辑思维、创造力和解决问题的能力。
3. 帮助学生建立数学学科的兴趣。
通过形象化、趣味化的教学方式,激发学生的兴趣,提高学生对数学学科的喜爱程度。
二、教研内容1. 教材分析和课堂设计。
对当前小学数学教材进行详细的分析,结合教学大纲和教学要求,设计出符合学生认知规律的课堂教学内容,保障教学的质量和有效性。
2. 课堂教学方式的探索和创新。
研究并运用新的教学方式和方法,如教学游戏、小组合作学习、教学演示等,提高教学的趣味性和参与性。
3. 教学资源的整理和开发。
整理和开发适合小学数学教学的教学资源,包括PPT、练习题、教学视频等,方便教师使用和学生复习。
三、教研活动1. 教研组会议。
每月举行一次教研组会议,共同研究教学难点和问题,分享教学经验和教学资源。
2. 教研交流。
与其他学校、其他年级的教师进行教研交流,借鉴其成功经验,互相学习和进步。
3. 教研展示。
每学期末举行一次教研展示,由教师们展示自己的教学成果和教研成果,互相学习和借鉴。
四、教学评估1. 学生评价。
通过课堂作业、考试成绩、学生反馈等方式,对学生的学习情况和成绩进行评估,及时发现和解决问题。
2. 教师评价。
教师互评、督导评价等方式,对教师的教学质量进行评估和反馈,帮助教师提高教学能力和教学水平。
以上就是我的小学数学秋季教研工作计划。
我相信,通过认真执行这个计划,我们的数学教学质量和效果一定会得到有效提升。
让我们一起努力,共同进步!谢谢大家!。
数学科学研究的前沿领域探讨

数学科学研究的前沿领域探讨数学科学始终是人类思维的重要部分,其涵盖面极广,涵盖物理、经济、生物等多个领域,成为这些领域的基石。
今天,本文将着重探讨数学科学的前沿领域,其中包括拓扑、代数、微积分等多个领域。
一. 拓扑学拓扑学是数学科学中的一个基本分支,研究的是空间与形状的一些基本性质。
在近年来,拓扑学的研究领域逐渐拓宽。
比如,纳米领域、生物领域等,都逐渐成为学者们研究的领域。
此外,拓扑学也成为了量子信息通信领域的关键部分。
二. 代数学代数学是在数学中研究代数结构的一个科目,主要研究群、环、域等代数结构,并探寻代数结构之间运算的本质。
在现代数学中,代数学更是扮演着眼下的基础角色。
近年来,随着数据及其应用的飞速发展,代数学及其在计算机科学中的应用逐渐受到关注。
聚类分析、污染检测等应用涉及了大量的代数学理论。
三. 微积分学微积分学在数学科学的发展史上有着极为重要的地位。
在各种工程、自然科学领域等都能够大量运用到微积分学的理论。
近年来,微积分学的研究领域也在逐渐增大。
比如,混沌动力学领域、生物科学领域等,都在某种程度上依赖于微积分学的理论支持。
四. 计算机科学计算机科学可以说是数学科学中的一个关键领域。
在如今已走进信息时代的今天,计算机科学更是成为人类思维重要的组成部分。
静态和动态的性质、算法,数据结构等,继续推动我们思考着如何落实这些计算机程序到不同领域的实际实施中去。
五. 统计学统计学是数学科学的一个非常实用的分支。
在各种领域,比如物理、经济、生物领域等,统计学理论的应用都是不可或缺的。
近年来,统计学的研究领域逐渐趋于了生物科学领域。
如何更好的推断population evolution等问题,在统计学真的达到这一目标之前,母亲自然是难以被设计为planned experiment的,这就调动了统计分析领域人才的积极性。
六. 量子计算和量子信息量子计算和量子信息是数学科学中的一个前沿领域。
量子计算机的出现可以说将会改变整个计算技术的构架。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
张彩伢
计算机图形与图像处理算法
吴庆标
围绕计算机图形与图像处理中曲线和曲面生成算法、图形填充算法、裁剪算法、真实感图形生成算法、图像增强算法等内容,通过文献查阅,报告讨论等形式,熟悉和掌握计算机图形与图像处理的前发技术
徐林荣
网络数据库开发技术是数据库技术与Web开发技术的结合,随着Internet技术的飞速发展,网络数据库及其开发技术成为新的热点。本讨论专题以SQL Server 2000作为后台数据库,以作为Web开发开发工具,以C#和作为编程语言,以常用的应用为实例展开讨论,系统掌握网络数据库的开发技术和发展趋势
2.以讲课者与其博士生近年来发明的发表在国际期刊上的曲线曲面等距逼近、区间逼近、细分逼近、降阶逼近、有理形式多项式逼近等最新算法为主干,讲解并讨论几何图形逼近的国际最新成果,进一步上机编程实现,制作工程中适用的造型曲面,引领学生进入计算机辅助设计前沿领域的研究与探索,并把大学基础课中所学的函数逼近方法拓展到几何逼近方法.
老师
主要内容
博弈论的数学基础与应用
谈之奕
讨论博弈论涉及的数学基础,及其在计算机、经济、管理等领域中的若干应用
几何插值与几何逼近:计算机动画与曲面造型的研究及实践
王国瑾
1.以讲课者与国际著名专家十年来合作发明的基于几何内在量的关键帧动画算法为主干,延伸到今年兴起的基于圆域参数曲线及球域参数曲线的几何插值方法,讲解并讨论关键帧动画的国际最新成果,进一步上机编程实现,制作计算机动画,引领学生进入计算机图形学的一个前沿分支领域的研究与探索,从数模推导与上机能力两方面培养学生.
A无穷代数基础
卢涤明
A无穷代数的概念起源于代数拓扑中“群状”拓扑空间的研究.之后,A无穷代数在代数拓扑、特别是同伦论等领域有很多应用.近年来,A无穷代数在数学物理、代数几何、代数表示论及非交换代数几何等领域扮演了愈来愈重要的角色.本课程主要讨论A无穷代数的基本理论,以及在非交换代数中的若干应用.
题目
前沿数学专题讨论班(08-09秋冬)
题目
老师
主要内容
微积分基本定理的高维推广
陈杰诚
交换代数
黄兆镇
与代数几何相关的初等交换代数
Fourier级数的收敛性
贾厚玉
Fourier级数的各种收敛性问题—点态收敛、一致收敛以及平均收敛。
金融数学
李胜宏
金融数学是一门交叉学科,应用数学,计算机等工具解决金融中问题,同时研究金融理论和实践
离散微分几何与图形学
杨勋年
离散微分几何以经典微分几何为基础,结合离散几何处理、计算机图形学和图象处理而成为数学与计算机科学结合而成的新的研究分支,在理论和应用中都有着广阔前景。学习离散微分几何的基本原理和方法,研究其在几何建模和计算机图形学中的应用。
博弈论及其应用(暂定)
张国川
金融时间序列分析
张立新,黄炜
遗传算法及其应用
毕惟红
主要学习遗传算法的基本思想、基本操作及基本理论,以及遗传算法在数值优化、组合优化、图像处理和图像识别等领域的应用情况。
数值计算方法和计算机模拟
梁克维
微分方程数值解的并行计算
陈明飞
目前,求微分方程数值解的并行计算方法有二类。一类是区域分解算法,该算法把求解区域分解为若干个形状容易计算的子区域,于是对原问题的求解转化为在子区域上求解。另一类是先把微分方程化为离散方程,再把传统的求解离散方程的方法改造为并行计算方法。
计算物理中的数学方法和进展
朱建新
本专题介绍现代计算物理中常用的数学处理方法和某些领域的最新研究进展。
金融投资管理中的数据分析和决策优化问题
刘康生
数论中的若干新问题
蔡天新
