辽宁省沈阳铁路实验中学2017-2018学年高一下学期期末考试数学试题 Word版含答案
辽宁省2017—2018学年高一数学下学期期末考试试卷(一)

辽宁省2017—2018学年高一数学下学期期末考试试卷(一)(文科)(考试时间120分钟满分150分)一.单项选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求.1.向量,且∥,则锐角α的余弦值为()A.B.C.D.2.=()A.﹣B.﹣C.D.3.函数f(x)=sin2x﹣4sin3xcosx(x∈R)的最小正周期为()A.B.π4C.π8D.π4.在△ABC中,acos2+ccos2=b,则()A.a,b,c依次成等差数列B.b,a,c依次成等差数列C.a,c,b依次成等差数列D.a,b,c既成等差数列,也成等比数列5.已知{a n}为等差数列,若a1+a5+a9=8π,则cos(a3+a7)的值为()A.B.C.D.6.函数y=log2x+log x2x的值域为()A.(﹣∞,﹣1]B.[3,+∞)C.[﹣1,3] D.(﹣∞,﹣1]∪[3,+∞)7.函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图示,则将y=f(x)的图象向右平移个单位后,得到的图象解析式为()A.y=sin2x B.y=cos2x C.y=sin(2x+)D.y=sin(2x﹣)8.《张丘建算经》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女不善织,日减功迟,初日织五尺,末日织一尺,今三十织迄,问织几何.”其意思为:有个女子不善于织布,每天比前一天少织同样多的布,第一天织五尺,最后一天织一尺,三十天织完,问三十天共织布()A.30尺B.90尺C.150尺D.180尺9.在平面直角坐标系xOy中,过定点Q(1,1)的直线l与曲线C:y=交于点M,N,则•﹣•=()A.2 B. C.4 D.10.已知、为平面向量,若+与的夹角为, +与的夹角为,则=()A.B.C.D.11.在斜三角形ABC中,sinA=﹣cosBcosC且tanB•tanC=1﹣,则∠A的值为()A.B.C.D.12.已知不等式组,表示的平面区域为D,点O(0,0),A(1,0).若点M 是D上的动点,则的最小值是()A.B.C.D.二.填空题:本大题共4小题,每小题5分,共20分13.已知向量夹角为45°,且,则=.14.在由正数组成的等比数列{a n}中,若a3a4a5=3π,则sin(log3a1+log3a2+…+log3a7)的值为.15.已知等差数列{a n}的前n项和为S n,a2=4,S10=110,则的最小值为.16.己知a(3﹣a)>0,那么的最小值是.三.解答题:共70分,解答应写出文字说明,证明过程或演算步骤.17.如图,平面四边形ABCD中,AB=,AD=2,CD=,∠CBD=30°,∠BCD=120°,求(Ⅰ)∠ADB;(Ⅱ)△ADC的面积S.18.在△ABC中,角A,B,C所对的边分别是a,b,c,且+=.(Ⅰ)证明:sinAsinB=sinC;(Ⅱ)若b2+c2﹣a2=bc,求tanB.19.某同学用“五点法”画函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<)在某一l23(Ⅱ)将f(x)的图象沿x釉向右平移个单位得到函数g(x),若函数g(x)在x∈[0,m](其中m∈(2,4))上的值域为[﹣,],且此时其图象的最高点和最低点分别为P,Q,求与夹角θ的大小.20.已知函数f(x)=sin(x﹣)+.(1)若x∈[0,],f(x)=,求cosx的值;(2)在△ABC中,角A、B、C的对边分别是a、b、c,且满足2bcosA≤2c﹣a,求f(B)的取值范围.21.已知等比数列{a n}的首项a1=8,公比为q(q≠1),S n是数列{a n}的前n项和.(1)若S3,2S4,3S5成等差数列,求{a n}的通项公式a n;(2)令b n=log2a n,T n是数列{b n}的前n项和,若T3是数列{T n}中的唯一最大项,求的q的取值范围.22.已知数列{b n}是首项b1=1,b4=10的等差数列,设b n+2=3log a n(n∈n*).(1)求证:{a n}是等比数列;(2)记c n=,求数列{c n}的前n项和S n;(3)记d n=(3n+1)•S n,若对任意正整数n,不等式++…+>恒成立,求整数m的最大值.参考答案一.单项选择题:1.D 2.D.3.A.4.A.5.A.6.D.7.D.8.B.9.C.10.D.11.A.12.A.二.填空题:13.答案为:314.答案是:.15.答案为:.16.答案为:.三.解答题:17.解:(Ⅰ)在△BCD中,由正弦定理得:,即,解得BD=3.在△ABD中,由余弦定理得:cos∠ADB===.∴∠ADB=45°.(Ⅱ)∵∠CBD=30°,∠BCD=120°,∴∠CDB=30°.∴sin∠ADC=sin(45°+30°)=,=•CDsin∠ADC==.∴S△ACD18.(Ⅰ)证明:在△ABC中,∵+=,∴由正弦定理得:,∴=,∵sin(A+B)=sinC.∴整理可得:sinAsinB=sinC,(Ⅱ)解:b2+c2﹣a2=bc,由余弦定理可得cosA=.sinA=,=+==1,=,tanB=4.19.解:(Ⅰ)由题意可得ω•+φ=,ω•+φ=,∴ω=,φ=,再结合表格中的数据,可得函数f(x)=sin(x+).再根据x1+=0,x2+=π,x3+=2π,求得x l =﹣,x2 =,x3,=;(Ⅱ)将f(x)的图象沿x釉向右平移个单位得到函数g(x)=sin[(x﹣)+]= sin x的图象,若函数g(x)在x∈[0,m](其中m∈(2,4))上的值域为[﹣,],且此时其图象的最高点和最低点分别为P(1,)、Q(3,﹣),∴=(3,﹣)、=(﹣2,2).设与夹角θ的大小为θ,则cosθ===﹣,∴θ=.20.解:(1)函数f(x)=sin(x﹣)+,由f(x)=,即sin(x﹣)=,由于x∈[0,],则x﹣∈[﹣],即有cos(x﹣)=,则cosx=cos(x﹣)=cos(x﹣)cos﹣sin(x﹣)sin=﹣=;(2)由于2bcosA≤2c﹣a,则由正弦定理得,2sinBcosA≤2sinC﹣sinA=2sin(A+B)﹣sinA=2sinAcosB+2cosAsinB﹣sinA,则有2cosB≥,B为三角形的内角,则0<B≤,由于f(B)=sin(B﹣),而﹣<B﹣,sin(B﹣)∈(﹣,],则有f(B)的取值范围是(0,1].21.解:(1)∵S3,2S4,3S5成等差数列,∴S3+3S5=2•2S4,∴3(a4+a5)=4a4,∴=,故等比数列{a n}的首项为8,公比为,故a n=8•=;(2)b n=log2a n=log2(8•q n﹣1)=3﹣log2q+nlog2q,∵T3是数列{T n}中的唯一最大项,∴b3=3﹣log2q+3log2q>0,b4=3﹣log2q+4log2q<0,∴﹣<log2q<﹣1,∴<q<.22.解:(1)证明:b1=1,b4=10,可得公差d==3,b n=1+3(n﹣1)=3n﹣2;b n+2=3log a n=3n,则a n =()n ,由=,可得数列{a n }是首项为,公比为的等比数列;(2)c n ===(﹣),则前n 项和S n =(1﹣+﹣+…+﹣)=(1﹣)=;(3)d n =(3n +1)•S n =(3n +1)•=n .则问题转化为对任意正整数n 使不等式++…+>恒成立.设,则f (n +1)﹣f (n )=[++…+]﹣(++…+)=+﹣=>0所以f (n +1)>f (n ),故f (n )的最小值是f (1)=,由<恒成立,即m <12,知整数m 可取最大值为11.。
2017-2018学年(新课标)最新辽宁省沈阳高一下学期期末考试数学试题及答案-精品试题

2017-2018学年辽宁省沈阳市下学期期末测试题高一数学时间:120分钟满分:150分一、选择题(共12小题,每小题5分,共计60分)1、设3(,sin )2a α= ,1(cos ,)3b α= ,且//a b,则锐角α为( )A .030 B .060 C .075 D .045 2、在正方形内任取一点,则该点在正方形的内切圆内的概率为 ( ) (A)12π (B) 4π (C) 3π (D) 2π 3、函数)62sin(π+-=x y 的单调递减区间是( )A .)](23,26[Z k k k ∈++-ππππB .)](265,26[Z k k k ∈++ππππC .)](3,6[Z k k k ∈++-ππππD .)](65,6[Z k k k ∈++ππππ4、数列815241,,,,579--的一个通项公式是( ) A 、2(1)21nn n -+ B 、(2)(1)1n n n n +-+C 、2(2)1(1)2(1)nn n +--+D 、(2)(1)21n n n n +-+ 5、执行右面的程序框图,若输出的结果是60,则输入的P 值是(A.52 B.1C.12D.1126、在函数cos y x =、tan y x =、)322sin(π+=x y 、 )322cos(π+=x y 中,最小正周期为π的函数的个数为( ) A .1个 B .2个 C .3个 D .4个7、函数)(x f y =的图象如图所示,则)(x f y =的解析式为( )A.sin 22y x =-B.13cos 2-=x yC.1)52sin(--=πx y D. )52sin(1π--=x y8、在等差数列}{n a 中,48)(2)(31310753=++++a a a a a ,则等差数列}{n a 的前13项的和为( )A 、24B 、39C 、52D 、10 49、将函数cos()3y x π=-的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向左平移6π个单位,所得函数图象的一条对称轴为( )A .9x π=B .8x π=C .2x π=D .x π=10、设向量()()cos 25sin 25sin 20cos 20a b =︒︒=︒︒r r ,,,若()c a tb t R =+∈r r r ,则||c uu r的最小值为( )AB 、1C 、2D 、1212、已知点P 是△ABC 的内心(三个内角平分线交点)、外心(三条边的中垂线交点)、重心(三条中线交点)、垂心(三个高的交点)之一,且满足2AP ·22BC AC AB =- ,则点P 一定是△ABC 的( ) A .内心B .外心C .重心D .垂心二、填空题(共4小题,每小题5分,共计20分)13、若||1,||2,a b c a b ===+,且c a ⊥ ,则向量a 与b 的夹角为 .14、设扇形的周长为8cm ,面积为24cm ,则扇形的圆心角的弧度数是 .15、如图,以摩天轮中心为原点,水平方向为x 轴建立平面直角坐标系,第18题图动点初始位于点()04,3P -处,现将其绕原点O 逆时针旋转120°角到达点P 处,则此时点P 的纵坐标为 .(15题 ) (16题)16、如图所示,要在山坡上A 、B 两点处测量与地面垂直的塔楼CD 的高. 如果从A 、B 两处测得塔顶的俯角分别为30和15,AB 的距离是30米,斜坡AD 与水平面成45 角,A 、B 、D 三点共线,则塔楼CD 的高度为 _米.三、解答题17、(本题满分10分)(1)数列{}n a 满足112,2n n a a a +-==,求数列{}n a 的通项公式。
2017-2018学年辽宁省五校高一下学期期末联考数学试题Word版含答案

2017-2018学年辽宁省五校下学期期末联考高一数学试题一、选择题(本大题共12小题,每小题5分,满分60分,每题四个选项中只有一项符合题目要求)1.sin1470︒=( )A .2 B .12 C .12- D .2-2.设向量a 与b 的夹角为θ,且(2,1)a =-,2(2,3)a b +=,则cos θ=( )A .35-B .35C .5D .5- 3.某校为了解1000名高一新生的身体生长状况,用系统抽样法(按等距的规则)抽取40名同学进行检查,将学生从1~1000进行编号,现已知第18组抽取的号码为443,则第一组用简单随机抽样抽取的号码为( )A .16B .17C .18D .194.已知2cos()423πθ-=,则sin θ=( ) A .79 B .19 C.19- D .79-5.已知下列命题:( )①向量a ,b 不共线,则向量a b +与向量a b -一定不共线 ②对任意向量a ,b ,则||||||||a b a b -≥-恒成立③在同一平面内,对两两均不共线的向量a ,b ,c ,若给定单位向量b 和正数λ,总存在单位向量c 和实数μ,使得a c b λμ=+ 则正确的序号为( )A .①②③B .①③ C. ②③ D .①②6.已知O ,A ,B 三地在同一水平面内,A 地在O 地正东方向2km 处,B 地在O 地正北方向2km 处,某测绘队员在A 、B 之间的直线公路上任选一点C 作为测绘点,用测绘仪进行测绘,O 地为一磁场,在其不的范围内会对测绘仪等电子形成干扰,使测绘结果不准确,则该测绘队员能够得到准确数据的概率是( )A .12-B .2 C. 12- D .127.如图所示的茎叶图为高一某班50名学生的化学考试成绩,算法框图中输入的i a 为茎叶图中的学生成绩,则输出的m ,n 分别是( )A .38m =,12n =B .26m =,12n = C.12m =,12n = D .24m =,10n = 8.在ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c .已知a b >,5a =,6c =,3sin 5B =,则sin()2A π+=( )A B .459.若将函数8sin 2y x =的图象向左平移(0)ϕϕ>个单位长度,得到的函数图象关于原点对称,则44cos sin ϕϕ+=( )A .1B .12 C.14 D .1810.有一块半径为R (R 是正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池ABCD 和其附属设施,附属设施占地形状是等腰CDE ∆,其中O 为圆心,A ,B 在圆的直径上,C ,D ,E 在半圆周上,如图.设BOC θ∠=,征地面积为()f θ,当θ满足2()()sin g f R θθθ=+取得最大值时,开发效果最佳,开发效果最佳的角θ和()g θ的最大值分别为( )A.21,(32R π+ B.21,(42R πC.2,(14R π+ D.2,(16R π+ 11.已知向量a ,b ,c 满足||2a =,||3b a b =⋅=,若2(2)()03c a c b -⋅-=,则||b c -的最小值是( )A.22+12.设ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c ,且3c os c os 5a Bb Ac -=,则ta n()A B-的最大值为( ) A.35 B.13 C.38 D.34第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题中,每小题5分,共20分)13.三个数390,455,546的最大公约数为 . 14.已知12,x x 是函数()2sin 2cos 2f x x x m =+-在[0,]2π内的两个零点,则12sin()x x += .15.已知点O 为ABC ∆的外心,外接圆半径为1,且满足2340OA OB OC ++=,则ABC ∆的面积为 .16.对于函数sin ,[0,2]()1(2),(2,)2x x f x f x x π∈⎧⎪=⎨-∈+∞⎪⎩,有下列3个命题:①任取12,[0,)x x ∈+∞,都有12|()()|2f x f x -≤恒成立; ②*()2(2)()f x kf x k k N =+∈,对于一切[0,)x ∈+∞恒成立; ③函数()ln(1)y f x x =--在(1,)+∞上有3个零点; 则其中所有真命题的序号是 .三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.下表提供了某厂节能降耗技术改造后生产甲产品过程记录的产量x (吨)与相应的生产能耗y (吨标准煤)的几组对照数据:(1)已知产量x 和能耗y 呈线性关系,请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程^^^y b x a =+;(2)已知该厂技改前100吨甲产品的生产耗能为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?参考公式:^1122211()()()ˆˆn ni i i i i i nn ii i i x y nx y x x y y b x nx x x a y bx ====⎧---⎪⎪==⎪⎨--⎪⎪=-⎪⎩∑∑∑∑18.在ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知2a =,3A π=.(1sin()sin 2B C B --=时,求ABC ∆的面积; (2)求ABC ∆周长的最大值.19.在ABC ∆中,a ,b ,c 分别为内角A ,B ,C 所对的边,S 为ABC ∆的面积,且222)4S a b c =--. (1)求角A 的大小;(2)若a =b c >,D 为BC 的中点,且AD =,求sin C 的值.20.某市为了解各校《国学》课程的教学效果,组织全市各学校高二年级全体学生参加了国学知识水平测试,测试成绩从高到低依次分为A 、B 、C 、D 四个等级.随机调阅了甲、乙两所学校各60名学生的成绩,得到如下的分布图:(1)试确定图中a 与b 的值;(2)若将等级A 、B 、C 、D 依次按照90分、80分、60分、50分转换成分数,试分别估计两校学生国学成绩的均值;(3)从两校获得A 等级的同学中按比例抽取5人参加集训,集训后由于成绩相当,决定从中随机选2人代表本市参加省级比赛,求两人来自同一学校的概率.21.已知函数23()cos cos 2f x x x x =++. (1)当[,]63x ππ∈-时,求函数()y f x =的单调区间; (2)已知0ω>,函数()()212x g x f ωπ=+,若函数()g x 在区间2[,]36x ππ∈-上是增函数,求ω的最大值.22.已知向量33(cos,sin )22x x a =,(cos ,sin )22x xb =-,函数()||1f x a b m a b =⋅-++,[,],34x m R ππ∈-∈.(1)若()f x 的最小值为-1,求实数m 的值; (2)是否存在实数m ,使函数224()()49g x f x m =+,[,]34x ππ∈-有四个不同的零点?若存在,求出m 的取值范围;若不存在,请说明理由.2017-2018学年辽宁省五校高一下学期期末联考数学试题参考答案一、选择题:1-5:BACCD6-10:ADAAB11、12:AD二、填空题:13.1314.515.3216.①③三、解答题:17.解:(1)由对照数据,计算得:4166.5i ii x y==∑,42186i i x ==∑,4.5x =, 3.5y =,∴ˆˆˆ0.7,0.35ba y bx ==-=, 所以回归方程为ˆ0.70.35yx =+. (2)当100x =时,1000.70.3570.35y =⨯+=(吨标准煤),预测生产100吨甲产品的生产能耗比技改前降低9070.3519.65-=(吨标准煤).18.解:(1)由条件得:sin sin()sin 2A B C B --=,∴sin()sin()sin 2B C B C B +--=, ∴2cos sin 2sin cos B C B B =.①cos 0B =时,2B π=,3c =,∴1122233S ac ==⋅⋅=②cos 0B ≠时,2sin 2sin C B =,∴3B C A π===,2a b c ===,∴1sin 2S bc A ==∴S =(2)设ABC ∆的外接圆半径为R ,∴由正弦定理得:2sin sin sin a b cR A B C===,∴22sin sin 3a R A π===∴周长l a b c =++=22sin 2sin R B R C ++=2sin )B C +. ∵3A π=,∴23B C π+=,∴23C B π=-,∴2(0,)3B π∈,∴22sin()]3l B B π=+-32(sin )2B B =+, 24sin()6B π=++,∵2(0,)3B π∈,∴5(,)666B πππ+∈∴1sin()(,1]62B π+∈,∴max 6l =. 19.解:(1)由已知得2221sin )2bc A a b c =--∴sin A =,∴sin A A =,∴tan A =(0,)A π∈∴23A π=. (2)由cos cos ADB ADC ∠=-∠,由余弦定理得:2222AD BD AB AD BD +-=⋅2222AD DC AC AD DC+--⋅,∵D 中点BC 中点,∴BD DC ==AD =2220AB AC +=,即2220b c +=,∵2cos cos 3A π==2228122b c bc +-=-∴8bc =, ∵b c >∴4b =,2c =.∴2sin sin c A C a ===20.解:(1)由频数分布条形图得:633660a +++=∴15a =, 由频率分布条形图得:0.150.20.151b +++=∴0.5b =. (2)906801560335066760x ⨯+⨯+⨯+⨯==甲,900.15800.5600.2500.1573x =⨯+⨯+⨯+⨯=乙.(3)由样本数据可知集训的5人中甲校抽2人,分别记作E ,F ;乙校抽3人,分别记作M ,N ,Q ;所以从5人中任选2人一共有10个基本事件;,,,,,,,,,EF EM EN EQ FM FN FQ MN MQ NQ ,其中2人来自同一学校包含的基本事件为:,,,EF MN MQ NQ , 所以所求的概率为:40.410P ==. 21.解:(1)1cos 23()222x f x x +=++sin(2)26x π=++,∵[,]63x ππ∈-∴单调递增区间为[,]66ππ-单调递减区间为[,]63ππ.(2)()()212x g x f ωπ=+=sin()23x πω++, 当2[,]36x ππ∈-,3x πω+∈2[,]3363ωππωππ-++, ∵()g x 在2[,]36ππ-上是增函数,且0ω>, ∴2[,]3363ωππωππ-++⊆[2,2]22k k ππππ-++,k Z ∈, ∴223322632k k ωππππωππππ⎧-+≥-+⎪⎪⎨⎪+≤+⎪⎩∴534112k k ωω⎧≤-⎪⎨⎪≤+⎩∵0ω>∴151212k -<<,k Z ∈∴0k =, ∴1ω≤∴ω的最大值为1. 22.解:(1)∵33coscos sin (sin )cos 22222x x x xa b x ⋅=⋅+⋅-=, 33(cos cos ,sin sin )2222x x x xa b +=+-,∴||(cosa b += ∵[,]34x ππ∈-∴||4cos 2cos a b x +==,()cos 22cos 1f x x m x =-+22cos 2cos x m x =-,令1cos [,1]2t x =∈,∴222y t mt =-∵min 1y =-,对称轴为2m t =,①当122m <即1m <时,当12t =时,min 112y m =-=-∴32m =舍,②当112m ≤≤即12m ≤≤时,当2m t =时,2min 12m y =-=-∴m =,③当12m >即2m >是,当1t =时,min 221y m =-=-∴32m =舍,综上,m =.(2)令224()()049m g x f x =+=,即22242cos 2cos 049m x m x -+=, ∴3cos 7m x =或47m ,∵()y g x =,[,]34x ππ∈-有四个不同的零点, ∴方程3cos 7m x =和4cos 7m x =在[,]34x ππ∈-上共有四个不同的实根,∴31274173477m m m m ≤<≤<⎪⎪≠⎪⎪⎩∴763740m m m ⎧≤<⎪≤<⎪≠⎪⎪⎪⎩∴764m ≤<.。
辽宁省沈阳铁路实验中学2017-2018学年高一下学期第二次月考数学试题 Word版含答案
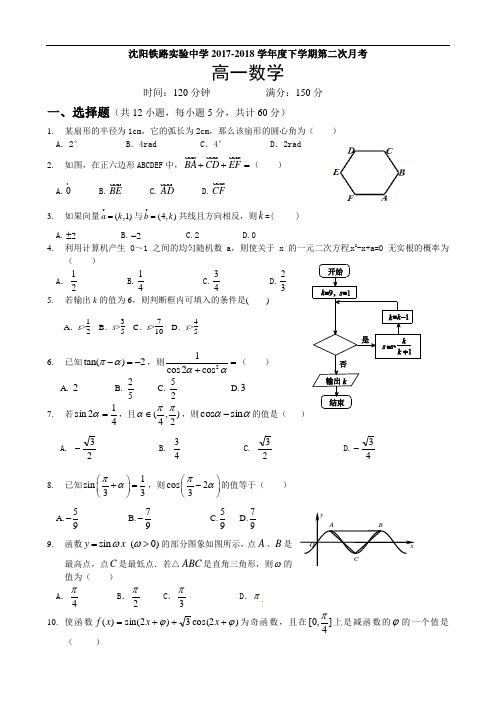
沈阳铁路实验中学2017-2018学年度下学期第二次月考高一数学时间:120分钟 满分:150分一、选择题(共12小题,每小题5分,共计60分)1. 某扇形的半径为1cm ,它的弧长为2cm ,那么该扇形的圆心角为( ) A .2° B .4rad C .4° D .2rad2. 如图,在正六边形ABCDEF 中,BA CD EF ++=( ) A.0 B.BE C.AD D.CF3. 如果向量(,1)a k =与(4,)b k =共线且方向相反,则k =( )A.2±B.2-C.2D.04. 利用计算机产生0~1之间的均匀随机数a ,则使关于x 的一元二次方程x 2-x+a=0无实根的概率为( ) A .12 B.14 C.34 D.235. 若输出k 的值为6,则判断框内可填入的条件是( )A .s >12B .s >35C .s >710D .s >456. 已知tan()2πα-=- )A.-2B.-25C.-2D.37. 若412sin =α,且)2,4(ππα∈,则ααsin cos -的值是( )A. 23-B. 43C.23 D.43-8.) A.59-B.79-C.59D.799. 函数sin (0)y x ωω=>的部分图象如图所示,点A 、B 是最高点,点C 是最低点.若△ABC 是直角三角形,则ω的 ) ABC D .π10.ϕ的一个值是( )11. 如图AB 是半圆O 的直径,D C ,是弧AB 的三等分点,N M ,是线段AB 的三等分点,若6=OA ,则MC ND ⋅= .A. 18B.8C. 32D. 3512. 已知,,A B C 为平面上不共线的三点,O 是△ABC 的垂心,动点P 满足1(2)OP OA OB OC =++,则点P 一定为△ABC 的( )A.AB 边中线的中点B. AB 边的中线的四等分点(非中点)C. 重心D. AB 边中线的三等分点(非重心)二、填空题(共4小题,每小题5分,共计20分)13. 一个样本方差是2s =120()()()22212333n x x x ⎡⎤-+-++-⎣⎦, 则这组数据的总和等于______14. 若α为锐角,且sin 6πα⎛⎫-⎪⎝⎭=13,则sin α的值为________. 15. 已知||1a =,||2b =,,60a b <>=,则a 在2a b +方向上的正射影的数量是 . 16. 设x ,y 具有线性相关关系的两个变量,它们的六组数据如下表:学生甲和乙分别从中选出4组数据计算回归直线方程分别为y=2x+1和55y x =+,且学生甲和乙所计算的x 的平均值分别为x 甲=9, x 乙=232,则n-m=三、解答题(共6题,17题10分,18~22每题12分,总计70分)17. 某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300] ,绘制成如图所示的频率分布直方图.(1)求直方图中x 的值;(2)求续驶里程在[200,300]的车辆数;(3)若从续驶里程在第二组与第五组的车辆中随机抽取2辆车,求两车的续驶里程差大于50公里概率.18. 已知关于x 的方程2x 2-1)x +2m =0的两根为sin θ和cos θ,且θ∈(0,2π).(1)求21()4sin cos tan θθπθθ+--的值;(2)求m 的值;(3)求方程的两根及此时θ的值.19. 设 ()()()1,1,4,3,5,2a b c =-==- (1)若()a tb c +⊥,求实数t 的值; (2)试用,a b 表示;c(3)若,a OA b OB ==,求OAB ∆的面积;20. 已知函数x x x x f 22cos sin )32cos()(-+-=π(1)求)(x f 的对称轴方程;(2)用“五点法”画出函数)(x f 在x ∈[]0,π的简图; (3)若⎥⎦⎤⎢⎣⎡-∈2,12ππx ,设函数[])()()(2x f x f x g +=,求)(x g 的值域。
辽宁省沈阳铁路实验中学207-2018学年高一6月月考数学试题 Word版含答案

沈阳铁路实验中学2017—2018学年度下学期6月月考试题高一数学 第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.某公司在甲、乙、丙、丁四个地区分别有150分、120个、180个、150个销售点,公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查 为(1);在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为(2)。
则完成(1)、(2)这两项调查宜采用的抽样方法依次是 ( ) A 、分层抽样法,系统抽样法 B 、简单随机抽样法,分层抽样法C 、系统抽样法,分层抽样法D 、分层抽样法,简单随机抽样法2.某程序框图如图所示,若输出的S=57,则判断框内为( )(A ) k >4? (B ) k >5? (C ) k >6? (D ) k >7?3. 若样本数据1x ,2x ,⋅⋅⋅,10x 的标准差为8,则数据121x -,221x -,⋅⋅⋅,1021x -的标准差为 ( )(A )8 (B )15 (C )16 (D )324.已知1sin cos ,8θθ=且42ππα<<,则cos sin θθ-的值( )A .34 D. 34± 5.已知扇形面积为,半径是1,则扇形的圆心角是 ( ) A .B .C .D .6.已知()2tan =-απ,则ααααcos sin cos sin +-的值为 ( )(A )3 (B )2 (C )3- (D )317.甲、乙两位同学在高一年级的5次考试中,数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是12,x x ,则下列叙述正确的是( )A .12>x x ,乙比甲成绩稳定B .12>x x ,甲比乙成绩稳定C .12<x x ,乙比甲成绩稳定D .12<x x ,甲比乙成绩稳定8.在△ABC 中,M 是BC 的中点,1=AM ,点P 在AM 上,且满足2-=,则()PA PB PC ⋅+=( ) A.49 B. 43- C. 43 D. 49- 9.已知函数()()sin f x x ωϕ=A +(A ,ω,ϕ均为正的常数)的最小正周期为π,当23x π=时,函数()f x 取得最小值,则下列结论正确的是 ( ) (A )⎪⎭⎫⎝⎛2πf <⎪⎭⎫ ⎝⎛6πf <()0f (B )()0f <⎪⎭⎫ ⎝⎛2πf <⎪⎭⎫⎝⎛6πf (C )⎪⎭⎫⎝⎛6πf <()0f <⎪⎭⎫ ⎝⎛2πf (D )⎪⎭⎫ ⎝⎛2πf <()0f <⎪⎭⎫ ⎝⎛6πf 10.要得到函数)42cos(π-=x y 的图象,只需要将2sin xy =的图象 ( )A.向右平移2π个单位 B.向右平移4π个单位 C.向左平移2π个单位 D.向左平移4π个单位11.ABC ∆中,AB 边的高为CD ,若C B a =,CA b =,0a b ⋅=,||1a =,||2b =,则AD =(第9题图)( )(A )1133a b - (B )2233a b - (C )3355a b - (D )4455a b - 12.将函数()sin 2f x x =的图像向右平移(0)2πϕϕ<<个单位后得到函数()g x 的图像,若对满足12()()2f x g x -=的1x , 2x ,有12min3x x π-=,则ϕ=( ) (A )512π (B )3π (C )4π (D )6π第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.设x R ∈ ,向量(,1),(1,2),a x b ==-且a b ⊥ ,则=x .14.ABC △的内角A B C ,,的对边分别为a b c ,,,若120c b B ===,则a 等于15.若动直线x=a 与函数f (x )=sin (x+)+sin (x﹣)和g (x )=cosx 的图象分别交于M ,N 两点,则||的最大值为 .16.、如图所示,要在山坡上A 、B 两点处测量与地面垂直的塔楼CD 的高. 如果从A 、B 两处测得塔顶的俯角分别为30和15,AB 的距离是30米,斜坡AD 与水平面成45角,A 、B 、D 三点共线,则塔楼CD 的高度为 _米.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分10分) 已知两向量,a b 的夹角为0120,1,3a b ==,(Ⅰ)求b a -5的值(Ⅱ)求向量a b a 与-5夹角的余弦值。
辽宁省实验中学分校2017-2018学年高一下学期期末考试数学试题 Word版含答案

辽宁省实验中学分校2017-2018学年度下学期期末测试数学学科 高一年级 第Ⅰ卷 (选择题 共60分)一、选择题(本大题共12小题,每小题5分,满分60分,每题四个选项中只有一项是符合题目要求的)1.若样本数据1x ,2x ,⋅⋅⋅,10x 的标准差为8,则数据121x -,221x -,⋅⋅⋅,1021x -的标准差为( )(A )8 (B )15 (C )16 (D )32 2.某程序框图如图所示,若输出的S=57,则判断框内为( )(A ) k >4? (B ) k >5?(C ) k >6? (D ) k >7?3.设R d c b a ∈,,,且d c b a >>,,则下列结论中正确的是( ) (A )d b c a +>+ (B )d b c a ->- (C )bd ac > (D )cb d a > 4.某地区2007年至2013年农村居民家庭人均纯收入y (单位:千元)的数据如下表:年份 2007 2008 2009 2010 2011 2012 2013 年份代号t 1 2 3 4 5 6 7 人均纯收入y2.93.33.64.44.85.25.9若y 关于t 的线性回归方程为y ^=0.5t +a,则据此该地区2015年农村居民家庭人均纯收入约为( )(A )6.6千元(B )6.5千元(C )6.7千元(D )6.8千元5.若,x y 满足约束条件10040x x y x y -≥⎧⎪-≤⎨⎪+-≤⎩则y x 的最大值为( )(A )1 (B )2 (C )3 (D )236.已知()2tan =-απ,则ααααcos sin cos sin +-的值为( )(A )3 (B )2 (C )3- (D )31 7.不等式252(1)x x +-≥的解集是( )(A )132⎡⎤-⎢⎥⎣⎦,(B )132⎡⎤-⎢⎥⎣⎦,(C )(]11132⎡⎫⎪⎢⎣⎭,,(D )(]11132⎡⎫-⎪⎢⎣⎭,,8.某公司的班车在7:30,8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是( ) (A )13 (B )12 (C )23 (D )349.已知函数()()sin f x x ωϕ=A +(A ,ω,ϕ均为正的常数)的最小正周期为π,当23x π=时,函数()f x 取得最小值,则下列结论正确的是( ) (A )⎪⎭⎫⎝⎛2πf <⎪⎭⎫ ⎝⎛6πf <()0f (B )()0f <⎪⎭⎫ ⎝⎛2πf <⎪⎭⎫ ⎝⎛6πf (C )⎪⎭⎫⎝⎛6πf <()0f <⎪⎭⎫⎝⎛2πf (D )⎪⎭⎫⎝⎛2πf <()0f <⎪⎭⎫ ⎝⎛6πf 10.从区间[]0,1随机抽取2n 个数1x ,2x ,…,n x ,1y ,2y ,…,n y ,构成n 个数对()11,x y ,()22,x y ,…,(),n n x y ,其中两数的平方和小于1的数对共有m 个,则用随机模拟的方法得到的圆周率π的近似值为( )(A )4n m (B )2n m (C )4m n (D )2m n11.ABC ∆中,AB 边的高为CD ,若C B a =,CA b =,0a b ⋅=,||1a =,||2b =,则AD =( )(A )1133a b - (B )2233a b - (C )3355a b - (D )4455a b - 12.将函数()sin 2f x x =的图像向右平移(0)2πϕϕ<<个单位后得到函数()g x 的图像,若对满足12()()2f x g x -=的1x ,2x ,有12min 3x x π-=,则ϕ=( )(A )512π (B )3π (C )4π (D )6π第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题5分,共20分。
2017-2018学年(新课标)最新辽宁省高一下学期期末考试数学试题及答案-精品试题

2017-2018学年辽宁省高一数学下学期期末综合测试第Ⅰ卷 (选择题,共60分)一.选择题 (本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.下列四个函数中,以π为最小正周期,且在区间),2(ππ上为减函数的是( )A.x y sin =B.x y sin 2=C.2cosxy = D.x y tan = 2.某初级中学领导采用系统抽样方法,从该校800名学生中抽50名学生做牙齿健康检查。
现将800名学生从1到800进行编号,求得间隔数k 80050==16,即每16人抽取一个人。
在1~16中随机抽取一个数,如果抽到的是7,则从33~48这16个数中应取的数是( )A .39B . 40C .37D . 38 3.已知2)tan(-=-απ,则αα22cos 2sin 1-=( ) A .2 B .52 C .25D .3 4.设向量(cos 25,sin 25),(sin 20,cos 20)a b →→==,若()c a t b t R →→→=+∈,则2()c 的最小值为 A .2 B.1 C.22 D.215.函数()cos 22sin f x x x =+的最小值和最大值分别为( ) A . 3,1- B . 2,2- C. 33,2- D. 32,2- 6.下图为某算法的程序框图,则程序运行后输出的结果是( ).A .2B .1C .3D .4 7.已知31)6sin(=+απ,则)232cos(απ-的值等于( ) A .-59 B .-79 C .59D .798.一张方桌的图案如图所示,将一颗豆子随机地扔到桌面上,假设豆子不落在线上,下列事件的概率:(1)豆子落在红色区域概率为49; (2)豆子落在黄色区域概率为13;(3)豆子落在绿色区域概率为29; (4)豆子落在红色或绿色区域概率为13;(5)豆子落在黄色或绿色区域概率为49.其中正确的结论有( ) A .2个B .3个C .4个D .5个9.若函数R x x x x f ∈+=,cos 3sin )(ωω,又0)(,2)(=-=βαf f ,且βα-的最小值为43π,则正数ω的值是( ) A.31 B. 23 C.34 D.32. 10.设函数()sin+4f x x πωω=()(>0)与函数()cos(2)(||)2g x x πφφ=+≤的对称轴完全相同,则φ的值为 A .4π B .4π- C .2π D .2π-11. 在ABC ∆中,点P 是AB 上一点,且2133CP CA CB =+, Q 是BC 中点,AQ 与CP 交点为M ,又CP t CM =,则t 的值为( )A .21 B .32 C .54 D .4312. 在ABC ∆中,若23()5CA CB AB AB +⋅=,则tan tan AB的值( )A.4B.2 D. 第Ⅱ卷 (主观题,共90分)二.填空题:(本大题共4小题,每小题5分,共 20分)13.已知,2.1cos cos ,4.0sin sin =+=+y x y x 则cos()x y -=14. 在2012~2013赛季NBA 季后赛中,当一个球队进行完7场比赛被淘汰后,某个篮球爱好者对该队的7场比赛得分情况进行统计,如下表:4为了对这个队的情况进行分析,此人设计计算σ的算法流程图如图所示(其中x 是这7场比赛的平均得分),输出的σ的值 = .15.在ABC ∆中,2cos 22A b c c +=(c b a ,,分别为角C B A ,,的对边),则cos 2A B+= 16.在ABC ∆中,①若A B >,则cos 2cos 2A B <;②tan tan tan 0A B C ++>,则ABC ∆是锐角三角形; ③若ABC ∆是锐角三角形,则cos sin A B <; ④若,2)tan 1)(tan 1(=++B A 则42ππ+=+k B A .以上命题的正确的是__________________.三.解答题:(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17. (本题满分10分)甲有大小相同的两张卡片,标有数字2,3;乙有大小相同的卡片四张,分别标有1,2,3,4; (1)求乙随机抽取的两张卡片的数字之和为奇数的概率:(2)甲乙分别取出一张卡,比较数字,数字大者获胜,求乙获胜的概率。
辽宁省2017-2018学年高一下学期期末考试数学(理)试题+答案

2017-2018学年度高一(下)期末考试数学(理)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 在中,已知,则的形状是( )A. 等腰三角形B. 直角三角形C. 等腰直角三角形D. 等腰三角形或直角三角形2. 两个相关变量满足如下关系:根据表格已得回归方程:,表中有一数据模糊不清,请推算该数据是( )A. 37B.C. 39D.3. 某单位有老年人27人,中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为42的样本,则老年人、中年人、青年人分别应抽取的人数是( )A. 7,11,18B. 6,12,18C. 6,13,17D. 7,14,214. 函数的单调递增区间是( )A. B.C. D.5. 盒中共有形状大小完全相同的5个球,其中有2个红球和3个白球,若从中随机取2个球,则概率为的事件是( )A. 都不是红球B. 恰有1个红球C. 至少有1个红球D. 至多有1个红球6. 如图圆内切于扇形,,若在扇形内任取一点,则该点在圆内的概率为( )A. B. C. D.7. 在中,分别为三个内角所对的边,设向量,,若,则角的大小为( )A. B. C. D.8. 下列命题中,假命题是( )A. 若且,则B. 若,则恒成立C. 的最小值是D. ,9. 在中,为的四分之一等分点(靠近点),点在线段上,若,则实数的值为( )A. B. C. 1 D.10. 已知圆,圆与圆关于直线对称,则圆的方程为( )A. B.C. D.11. 函数的图象与函数的图象所有交点的横坐标之和等于( )A. 12B. 14C. 16D. 1812. 如图,是同一平面内的三条平行的直线,与间的距离是1,与间的距离是2,正三角形的三顶点分别在上,则的边长是( )A. B. C. D.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 某四棱柱的三视图如图所示,则该四棱柱的体积为__________.14. 已知,则的值为__________.15. 已知圆的圆心是直线与直线的交点,直线与圆相交于,两点,且,则圆的方程为__________.16. 等腰的顶角,,以为圆心,1为半径作圆,为该圆的一条直径,则的最大值为__________.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 已知函数.(1)求的最小正周期;(2)求在区间上的最大值和最小值.18. 一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.(1)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;(2)先从袋中随机取一个球,该球的编号为,将球放回袋中,然后再从袋中随机取一个球,该球的编号为,求的概率.19. 在三角形中,角及其对边满足:.(1)求角的大小;(2)求函数的值域.20. 在中,分别为角的对边,设.(1)若,且,求角的大小;(2)若,求角的取值范围.21. 已知圆,直线.(1)求直线所过定点的坐标;(2)求直线被圆所截得的弦长最短时的值及最短弦长.(3)已知点,在直线上(为圆心),存在定点(异于点),满足:对于圆上任一点,都有为一常数,试求所有满足条件的点的坐标及该常数.22. 已知向量,,且向量.(1)求函数的解析式及函数的定义域;(2)若函数,存在,对任意,总存在唯一,使得成立,求实数的取值范围.一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 在中,已知,则的形状是( )A. 等腰三角形B. 直角三角形C. 等腰直角三角形D. 等腰三角形或直角三角形【答案】D【解析】根据正弦定理可知∵a cos A=b cos B,∴sin A cos A=sin B cos B,∴sin2A=sin2B,∴A=B,或2A+2B=180∘即A+B=90∘,所以△ABC为等腰或直角三角形。
辽宁省沈阳市铁路实验中学2017-2018学年高一下学期期末数学试卷 Word版含解析

辽宁省沈阳市铁路实验中学2017-2018学年高一下学期期末数学试卷一、选择题(共12小题,每小题5分,共计60分)1.sin480°等于()A.B.C.D.2.某大学数学系共有本科生1000人,其中一、二、三、四年级的人数比为4:3:2:1,要用分层抽样的方法从所有本科生中抽取一个容量为200的样本,则应抽取三年级的学生人数为()A.80 B.40 C.60 D.203.在区间上随机取一个x,sinx的值介于与之间的概率为()A.B.C.D.4.已知向量=(8,x),=(x,1),x>0,若﹣2与2+共线,则x的值为()A.4B.8C.0D.25.一次选拔运动员,测得7名选手的身高(单位cm)分布茎叶图如图,记录的平均身高为177cm,有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为()A.5B.6C.7D.86.设D,E,F分别为△ABC的三边BC,CA,AB的中点,则+=()A.B.C.D.7.要得到的图象,只需将y=3sin2x的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位8.已知f(x)=sin(x﹣φ)+cos(x﹣φ)为奇函数,则φ的一个取值()A.0B.πC.D.9.根据下表所示的统计资料,求出了y关于x的线性回归方程为=1.23x+0.08,则统计表中t的值为()x 2 3 4 5 6y 2.2 3.8 t 6.5 7.0A.5.5 B.5.0 C.4.5 D.4.810.若某程序框图如图所示,则该程序运行后输出的值是()A.B.C.D.11.已知cos(α﹣β)=,sinβ=﹣,且α∈(0,),β∈(﹣,0),则sinα=()A.B.C.﹣D.﹣12.已知函数f(x)=asinx﹣bcosx(a,b为常数,a≠0,x∈R)的图象关于直线对称,则函数是()A.偶函数且它的图象关于点(π,0)对称B.偶函数且它的图象关于点对称C.奇函数且它的图象关于点对称D.奇函数且它的图象关于点(π,0)对称二、填空题(共4小题,每小题5分,共计20分)13.用辗转相除法求两个数102、238的最大公约数是.14.在△ABC中,角A,B,C所对的边分别为a,b,c,满足=则角C=.15.设,则a,b,c的大小关系为.16.给出下列:①存在实数α,使sinα•cosα=1②函数是偶函数③是函数的一条对称轴方程④若α、β是第一象限的角,且α>β,则sinα>sinβ其中正确的序号是.三、解答题(共6题,17题10分,18~22每题12分,总计70分)17.为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:(Ⅰ)估计该校学生身高在170~185cm之间的概率;(Ⅱ)从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm 之间的概率.18.已知||=4,||=3,(2﹣3)•(2+)=61,(1)求的值;(2)求与的夹角θ;(3)求||的值.19.直角坐标系xOy中,锐角α的终边与单位圆的交点为P,将OP绕O逆时针旋转到OQ,使∠POQ=α,其中Q是OQ与单位圆的交点,设Q的坐标为(x,y).(Ⅰ)若P的横坐标为,求;(Ⅱ)求x+y的取值范围.20.已知函数.(1)求函数f(x)的最小正周期及单调增区间;(2)在△ABC中,A、B、C所对的边分别为a,b,c,若,f(A)=1,求b+c的最大值.21.如图△ABC中,已知点D在BC边上,满足•=0.sin∠BAC=,AB=3,BD=.(Ⅰ)求AD的长;(Ⅱ)求cosC.22.如图所示,扇形AOB,圆心角AOB的大小等于,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.(1)若C是半径OA的中点,求线段PC的大小;(2)设∠COP=θ,求△POC面积的最大值及此时θ的值.辽宁省沈阳市铁路实验中学2014-2015学年高一下学期期末数学试卷一、选择题(共12小题,每小题5分,共计60分)1.sin480°等于()A.B.C.D.考点:运用诱导公式化简求值.专题:计算题.分析:把所求式子的角度480°变为360°+120°后,利用诱导公式化简后,把120°变为180°﹣60°,再利用诱导公式及特殊角的三角函数值化简,即可求出值.解答:解:sin480°=sin(360°+120°)=sin120°=sin(180°﹣60°)=sin60=.故选D点评:此题考查了运用诱导公式化简求值,灵活变换角度及熟练掌握诱导公式是解本题的关键.2.某大学数学系共有本科生1000人,其中一、二、三、四年级的人数比为4:3:2:1,要用分层抽样的方法从所有本科生中抽取一个容量为200的样本,则应抽取三年级的学生人数为()A.80 B.40 C.60 D.20考点:分层抽样方法.专题:概率与统计.分析:要用分层抽样的方法从该系所有本科生中抽取一个容量为200的样本,根据一、二、三、四年级的学生比为4:3:2:1,利用三年级的所占的比例数除以所有比例数的和再乘以样本容量即得抽取三年级的学生人数.解答:解:∵要用分层抽样的方法从该系所有本科生中抽取一个容量为200的样本,一、二、三、四年级的学生比为4:3:2:1,∴三年级要抽取的学生是×200=40,故选:B.点评:本题考查分层抽样方法,本题解题的关键是看出三年级学生所占的比例,本题也可以先做出三年级学生数和每个个体被抽到的概率,得到结果.3.在区间上随机取一个x,sinx的值介于与之间的概率为()A.B.C.D.考点:几何概型.分析:解出关于三角函数的不等式,使得sinx的值介于到之间,在所给的范围中,求出符合条件的角的范围,根据几何概型公式用角度之比求解概率.解答:解:∵<sinx ,当x∈[﹣,]时,x∈(﹣,)∴在区间上随机取一个数x,sinx的值介于到之间的概率P==,故选A.点评:本题是一个几何概型,古典概型和几何概型是我们学习的两大概型,在解题过程中不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、和体积的比值得到.4.已知向量=(8,x),=(x,1),x>0,若﹣2与2+共线,则x的值为()A.4B.8C.0D.2考点:平行向量与共线向量;平面向量的坐标运算.专题:平面向量及应用.分析:由题意和向量的坐标运算求出和的坐标,再代入向量共线的坐标条件列出方程求解.解答:解:由题意得,=(8,)﹣2(x,1)=(8﹣2x,﹣2),=2(8,)+(x,1)=(16+x,x+1),∵与共线,∴(8﹣2x)(x+1)﹣(﹣2)(16+x)=0,解得x2=16,即x=±4,∵x>0,∴x=4,故选A.点评:本题考查向量共线的坐标表示,属基础题.5.一次选拔运动员,测得7名选手的身高(单位cm)分布茎叶图如图,记录的平均身高为177cm,有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为()A.5B.6C.7D.8考点:众数、中位数、平均数;茎叶图.专题:计算题.分析:求这7组数的平均数,列出方程,即可解题解答:解:解得x=8故选D点评:本题以茎叶图为载体,考查平均数,要求会读图.属简单题6.设D,E,F分别为△ABC的三边BC,CA,AB的中点,则+=()A.B.C.D.考点:向量在几何中的应用.专题:平面向量及应用.分析:利用向量加法的三角形法则,将,分解为+和+的形式,进而根据D,E,F分别为△ABC的三边BC,CA,AB的中点,结合数乘向量及向量加法的平行四边形法则得到答案.解答:解:∵D,E,F分别为△ABC的三边BC,CA,AB的中点,∴+=(+)+(+)=+=(+)=,故选:A点评:本题考查的知识点是向量在几何中的应用,熟练掌握向量加法的三角形法则和平行四边形法则是解答的关键.7.要得到的图象,只需将y=3sin2x的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位考点:函数y=Asin(ωx+φ)的图象变换.专题:计算题.分析:根据左加右减的原则进行左右平移即可.解答:解:∵,∴只需将y=3sin2x的图象向左平移个单位故选C.点评:本题主要考查三角函数的平移.三角函数进行平移时的原则是左加右减上加下减.8.已知f(x)=sin(x﹣φ)+cos(x﹣φ)为奇函数,则φ的一个取值()A.0B.πC.D.考点:三角函数中的恒等变换应用.专题:计算题.分析:首先通过两角和公式对函数表达式进行化简得f(x)=,要使f(x)为奇函数,则需φ﹣=kπ.解答:解:∵f(x)=sin(x﹣φ)+cos(x﹣φ)为奇函数而f(x)=sin(x﹣φ)+cos(x﹣φ)=∴φ的一个取值为故选:D点评:本题主要考查了三角函数中的奇偶性和两角和公式.属基础题.9.根据下表所示的统计资料,求出了y关于x的线性回归方程为=1.23x+0.08,则统计表中t的值为()x 2 3 4 5 6y 2.2 3.8 t 6.5 7.0A.5.5 B.5.0 C.4.5 D.4.8考点:线性回归方程.专题:应用题.分析:计算样本中心点,根据线性回归方程恒过样本中心点,即可得到结论.解答:解:由题意,==4,==3.9+,∵y关于x的线性回归方程为=1.23x+0.08,∴3.9+=1.23×4+0.08,∴t=5.5.故选A.点评:本题考查线性回归方程的运用,解题的关键是利用线性回归方程恒过样本中心点.10.若某程序框图如图所示,则该程序运行后输出的值是()A.B.C.D.考点:程序框图.专题:算法和程序框图.分析:根据框图的流程知:算法的功能是求S=sin+sin+sinπ+sin+…+sin+sin的值,根据sin,n∈N*的值的周期性变化规律求解可得答案.解答:解:由程序框图知:算法的功能是求S=sin+sin+sinπ+sin+…+sin+的值,∵sin,n∈N*的值是以6为周期变化,且sin+sin+sinπ+sin+sin+sin2π=0,2014=6×335+4,∴S=sin+sin+sinπ+sin=++0﹣=.故选:D.点评:本题考查了循环结构的程序框图,根据框图的流程判断算法的功能是解答本题的关键.11.已知cos(α﹣β)=,sinβ=﹣,且α∈(0,),β∈(﹣,0),则sinα=()A.B.C.﹣D.﹣考点:两角和与差的正弦函数;同角三角函数间的基本关系;两角和与差的余弦函数.专题:计算题.分析:由α和β的范围求出α﹣β的范围,然后由cos(α﹣β)及sinβ的值,分别利用同角三角函数间的基本关系求出sin(α﹣β)及cosβ的值,最后把所求式子中的角α变形为(α﹣β)+β,利用两角和与差的正弦函数公式化简后,将各自的值代入即可求出值.解答:解:∵α∈(0,),β∈(﹣,0),∴α﹣β∈(0,π),又cos(α﹣β)=,sinβ=﹣,∴sin(α﹣β)==,cosβ==,则sinα=sin[(α﹣β)+β]=sin(α﹣β)cosβ+cos(α﹣β)sinβ=×+×(﹣)=.故选A点评:此题考查了两角和与差的正弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键,同时注意角度的范围.12.已知函数f(x)=asinx﹣bcosx(a,b为常数,a≠0,x∈R)的图象关于直线对称,则函数是()A.偶函数且它的图象关于点(π,0)对称B.偶函数且它的图象关于点对称C.奇函数且它的图象关于点对称D.奇函数且它的图象关于点(π,0)对称考点:两角和与差的正弦函数;正弦函数的图象.专题:三角函数的图像与性质.分析:根据函数f(x)的对称性求出b=﹣a,然后求出函数的解析式,根据三角函数的性质进行判断即可.解答:解:∵函数f(x)的图象关于直线对称,∴f()=(a﹣b)=,平方得a2+2ab+b2=0,即(a+b)2=0,则a+b=0,b=﹣a,则f(x)=asinx+acosx=sin(x+),又a≠0,则=sin(﹣x+)=sin(π﹣x)=sinx为奇函数,且图象关于点(π,0)对称,故选:D.点评:本题主要考查三角函数的性质的应用,根据函数的对称性求出b=﹣a是解决本题的关键.二、填空题(共4小题,每小题5分,共计20分)13.用辗转相除法求两个数102、238的最大公约数是34.考点:辗转相除法.专题:计算题.分析:本题考查的知识点是辗转相除法,根据辗转相除法的步骤,将288与123代入易得到答案.解答:解:∵238=2×102+34102=3×34故两个数102、238的最大公约数是34故答案为:34点评:对任意整数a,b,b>0,存在唯一的整数q,r,使a=bq+r,其中0≤r<b,这个事实称为带余除法定理,若c|a,c|b,则称c是a,b的公因数.若d是a,b的公因数,且d 可被a,b的任意公因数整除则称d是a,b的最大公因数.当d≥0时,d是a,b公因数中最大者.若a,b的最大公因数等于1,则称a,b互素.累次利用带余除法可以求出a,b的最大公因数,这种方法常称为辗转相除法.14.在△ABC中,角A,B,C所对的边分别为a,b,c,满足=则角C=.考点:余弦定理的应用;正弦定理.专题:解三角形.分析:利用正弦定理化简已知的等式,再利用余弦定理表示出cosC,将得出的关系式变形后代入求出cosC的值,由C为三角形的内角,利用特殊角的三角函数值即可求出C的度数;解答:解:利用正弦定理化简已知等式得:,化简得a2+b2﹣ab=c2,即a2+b2﹣c2=ab,∴cosC==,∵C为三角形的内角,∴C=.故答案为:.点评:此题考查了正弦、余弦定理,正弦函数的定义域与值域,熟练掌握定理是解本题的关键,属于基础题.15.设,则a,b,c的大小关系为a<c<b.考点:三角函数的恒等变换及化简求值.专题:计算题.分析:利用两角和的余弦公式及诱导公式,我们可得a=sin22°,由二倍角的正切公式,可得b=tan26°,由半角公式,可得c=sin26°,再结合正弦函数的单调性和同角三角函数关系,即可得到a,b,c的大小关系.解答:解:∵=cos60°•cos8°﹣sin60°•sin8°=cos68°=sin22°,=tan26°=sin26°∵sin22°<sin26°<tan26°∴a<c<b故答案为:a<c<b点评:本题考查的知识点是三角函数的恒等变换及化简求值,其中根据两角和余弦公式、诱导公式、二倍角的正切公式、半角公式,求出a,b,c的值,是解答本题的关键.16.给出下列:①存在实数α,使sinα•cosα=1②函数是偶函数③是函数的一条对称轴方程④若α、β是第一象限的角,且α>β,则sinα>sinβ其中正确的序号是②③.考点:的真假判断与应用.专题:阅读型.分析:对于①,利用二倍角的正弦公式变形,可得sinα•cosα的最大值为;对于②,利用诱导公式化简为y=﹣cosx,该函数是偶函数;对于③,把代入,看y能否取得最值,若能取得最值,正确,否则,不正确;对于④举反例加以说明.通过以上分析即可得到正确答案.解答:解:由,∴sinα•cosα的最大值为,∴①错误;由,而y=﹣cosx是偶函数,∴②正确;∵,∴是函数的一条对称轴方程,∴③正确;取,,α、β是第一象限的角,且α>β,但sinα<sinβ,∴④错误.所以正确的是②③.故答案为②③.点评:本题考查了的真假判断与应用,考查了三角函数的被角公式、诱导公式及三角函数的性质,考查了举反例法在判断真假中的应用,此题是基础题.三、解答题(共6题,17题10分,18~22每题12分,总计70分)17.为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:(Ⅰ)估计该校学生身高在170~185cm之间的概率;(Ⅱ)从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm 之间的概率.考点:古典概型及其概率计算公式;频率分布直方图.专题:概率与统计.分析:(1)由图可知样本中身高在170~185cm之间的学生有14+13+4+3+1,样本容量为70,得到样本中学生身高在170~185cm之间的频率.用样本的频率来估计总体中学生身高在170~180cm之间的概率.(2)由题意知本题是一个古典概型,通过列举法看出试验发生包含的所有事件数,再从这些事件中找出满足条件的事件数,根据古典概型公式,得到结果.解答:解:(1)∵样本中身高在170~185cm之间的学生有14+13+4+3+1=35人,样本容量为700×10%=70,∴样本中学生身高在170~185cm之间的频率f=,故可估计该校学生身高在170~180cm之间的概率p=0.5;(2)样本中身高在180~185cm之间的男生有4人,设其编号为①,②,③,④,样本中身高在185~190cm之间的男生有2人,设其编号为⑤,⑥,从上述6人中任取2人的树状图为:∴从样本中身高在180~190cm之间的男生中任选2人得所有可能结果数为15,求至少有1人身高在185~190cm之间的可能结果数为9,∴所求概率p2=.点评:抽样过程中每个个体被抽到的可能性相同,这是解决一部分抽样问题的依据,样本容量、总体个数、每个个体被抽到的概率,这三者可以知二求一.18.已知||=4,||=3,(2﹣3)•(2+)=61,(1)求的值;(2)求与的夹角θ;(3)求||的值.考点:平面向量数量积的运算.专题:平面向量及应用.分析:(1)由(2﹣3)•(2+)=61,利用向量的运算法则,计算化简即可.(2)利用向量夹角公式计算.(3)利用(2)的结论和数量积运算性质即可得出.解答:解:(1)由(2﹣3)•(2+)=61,得4﹣4﹣3=61将||=4,||=3,代入,整理得=﹣6(2)cosθ===﹣,又0≤θ≤π,所以θ=.(3)|+|===.点评:本题主要考查两个向量的数量积的定义,两个向量夹角的范围,根据三角函数的值求角,属于基础题.19.直角坐标系xOy中,锐角α的终边与单位圆的交点为P,将OP绕O逆时针旋转到OQ,使∠POQ=α,其中Q是OQ与单位圆的交点,设Q的坐标为(x,y).(Ⅰ)若P的横坐标为,求;(Ⅱ)求x+y的取值范围.考点:任意角的三角函数的定义;二倍角的正切.专题:三角函数的求值.分析:(Ⅰ)利用三角函数的定义,求出sinα,转化为正切函数的形式,求解即可;(Ⅱ)表示出x+y的三角函数的形式,然后求解取值范围.解答:解:直角坐标系xOy中,锐角α的终边与单位圆的交点为P,将OP绕O逆时针旋转到OQ,使∠POQ=α,其中Q是OQ与单位圆的交点,设Q的坐标为(x,y).(Ⅰ)若P的横坐标为,则sinα=,cosα=,tanα=,=tan2α===﹣;(Ⅱ)x+y=cos2α+sin2α=sin(2),,∴,sin(2)∈(﹣1,]x+y的取值范围(﹣1,].点评:本题考查三角函数的定义,二倍角公式的应用,三角函数的化简求值.20.已知函数.(1)求函数f(x)的最小正周期及单调增区间;(2)在△ABC中,A、B、C所对的边分别为a,b,c,若,f(A)=1,求b+c的最大值.考点:解三角形;三角函数中的恒等变换应用.专题:解三角形.分析:(1)将f(x)解析式第一、三项结合,利用二倍角的余弦函数公式化简,第二项利用二倍角的正弦函数公式化简,再利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,找出ω的值,代入周期公式即可求出函数的最小正周期;由正弦函数的递增区间为[2kπ﹣,2kπ+](k∈Z),列出关于x的不等式,求出不等式的解集即可得到函数的递增区间;(2)由(1)确定的函数解析式,及f(A)=1,利用特殊角的三角函数值求出A的度数,确定出sinA的值,及B+C的度数,用B表示出C,由a与sinA的值,利用正弦定理表示出b与c,代入b+c中,将表示出的C代入,利用两角和与差的正弦函数公式及特殊角的三角函数值化简,整理后再利用两角和与差的正弦函数公式化为一个角的正弦函数,由正弦函数的值域即可求出正弦函数的最大值,即为b+c的最大值.解答:解:(1)f(x)=cos2x﹣sin2x+2sinxcosx=cos2x+sin2x=2sin(2x+),∵ω=2,∴f(x)的最小正周期为T=π,令2kπ﹣≤2x+≤2kπ+(k∈Z),解得:kπ﹣≤x≤π+,k∈Z,则f(x)的单调增区间为[kπ﹣,π+],k∈Z;(2)∵f(A)=2sin(2A+)=1,∴sin(2A+)=,∴2A+=,∴A=,∴B+C=,∵a=,sinA=,∴由正弦定理得:====2,∴b+c=2(sinB+sinC)=2[sinB+sin(﹣B)]=2(sinB+cosB+sinB)=2(sinB+cosB)=2sin(B+)≤2,∴当B=时,b+c最大为2.点评:此题属于解三角形的题型,涉及的知识有:正弦定理,两角和与差的正弦函数公式,二倍角的正弦、余弦函数公式,三角函数的周期性及其求法,以及正弦函数的单调性,熟练掌握定理及公式是解本题的关键.21.如图△ABC中,已知点D在BC边上,满足•=0.sin∠BAC=,AB=3,BD=.(Ⅰ)求AD的长;(Ⅱ)求cosC.考点:余弦定理的应用;正弦定理.专题:计算题;解三角形.分析:(I)通过向量的数量积,判断垂直关系,求出cos∠BAD的值,在△ABD中,由余弦定理求AD的长;(Ⅱ)在△ABD中,由正弦定理,求出sin∠ADB,通过三角形是直角三角形,即可求cosC.解答:解:(Ⅰ)∵•=0,∴AD⊥AC,∴,∵sin∠BAC=,∴….在△ABD中,由余弦定理可知BD2=AB2+AD2﹣2AB•ADcos∠BAD,即AD2﹣8AD+15=0,解之得AD=5或AD=3 ….由于AB>AD,∴AD=3…..(Ⅱ)在△ABD中,由正弦定理可知,又由,可知,∴=,∵∠ADB=∠DAC+∠C,∠DAC=,∴.…点评:本题考查解三角形,余弦定理以及正弦定理的应用,考查计算能力.22.如图所示,扇形AOB,圆心角AOB的大小等于,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.(1)若C是半径OA的中点,求线段PC的大小;(2)设∠COP=θ,求△POC面积的最大值及此时θ的值.考点:余弦定理;两角和与差的正弦函数.专题:解三角形.分析:(1)在△POC中,根据,OP=2,OC=1,利用余弦定理求得PC的值.(2)解法一:利用正弦定理求得CP和OC的值,记△POC的面积为S(θ),则,利用两角和差的正弦公式化为,可得时,S(θ)取得最大值为.解法二:利用余弦定理求得OC2+PC2+OC•PC=4,再利用基本不等式求得3OC•PC≤4,所以,再根据OC=PC 求得△POC面积的最大值时θ的值.解答:解:(1)在△POC中,,OP=2,OC=1,由得PC2+PC﹣3=0,解得.(2)解法一:∵CP∥OB,∴,在△POC中,由正弦定理得,即,∴.又,∴.记△POC的面积为S(θ),则======,∴时,S(θ)取得最大值为.解法二:,即OC2+PC2+OC•PC=4.又OC2+PC2+OC•PC≥3OC•PC,即3OC•PC≤4,当且仅当OC=PC时等号成立,所以,∵OC=PC,∴时,S(θ)取得最大值为.点评:本题主要考查两角和差的正弦公式,正弦定理、余弦定理、基本不等式的,属于中档题.。
【全国市级联考】辽宁省2017-2018学年高一下学期期末考试数学试题+答案

2017-2018下学期高一期末考试数学试卷本试卷分第I卷(选择题)和第II卷(非选择题)两部分,满分150分,考试时间为120分钟。
第I卷(60分)选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 的值是()A. B. C. D.2. 一段圆弧的长度等于其圆内接正三角形的边长,则其圆心角的弧度数为( )A. B. C. D.3. 2014年3月,为了调查教师对第十二届全国人民代表大会第二次会议的了解程度,抚顺市拟采用分层抽样的方法从三所不同的中学抽取60名教师进行调查。
已知学校中分别有180、270、90名教师,则从学校中应抽取的人数为()A. 10B. 12C. 18D. 244. 已知变量与正相关,且由观测数据算得样本平均数,则由该观测的数据算得的线性回归方程可能是()A. B. C. D.5. 某中学高三年级从甲、乙两个班级各选出8名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的平均分是86,乙班学生成绩的中位数是83,则的值为( )A. 9B. 10C. 11D. 136. 某学校为了解高一年级l203 名学生对某项教改试验的意见,打算从中抽取一个容量为40 的样本,考虑用系统抽样,则分段的间隔k为 ( )A. 40B. 30.1C. 30D. 127. 阅读如图所示的程序框图,输出结果s 的值为A. B. C. D.8. 从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是( )A. B. C. D.9. 若|a|=2sin 15°,|b|=4cos 15°,向量a与b的夹角为30°,则a·b的值是()A. B. C. 2 D.10. 已知则的值为()A. B. C. D.11. 已知函数的最大值为3,的图像在轴上的截距为2,其相邻两对称轴间的距离为1,则()A. 0B. 100C. 150D. 20012. ∆ABC的外接圆的圆心为O,半径为1,若,且,则向量在向量方向上的射影的数量为()A. B. C. 3 D.第II卷(非选择题)二.填空题:本大题共4小题,每小题5分,共20分.13. 已知向量=(2,1),=(x,-2),若,则=_______.14. 用秦九韶算法计算f(x)=x6-12x5+60x4-160x3+240x2-192x+64当x=2时的值时,的值为_____.15. 在边长为2的正三角形ABC内任取一点P,则使点P到三个顶点的距离至少有一个小于1的概率是________.16. 三角形ABC是锐角三角形,若角θ终边上一点P的坐标为(sin A-cos B,cos A-sin B),则++的值是________.三.解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17. 已知角为第三象限角,,若,求的值.18. 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准0〜3.5,用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图. (1)由于某种原因频率分布直方图部分数据丢失,请在图中将其补充完整;(2)用样本估计总体,如果希望80%的居民每月的用水量不超出标准0〜3.5,则月均用水量的最低标准定为多少吨,请说明理由;(3)从频率分布直方图中估计该100位居民月均用水量的平均数(同一组中的数据用该区间的中点值代表).19. 已知以点为圆心的圆与直线相切,过点的动直线与圆相交于两点.(1)求圆的方程;(2)当时,求直线的方程.20. 一个包装箱内有6件产品,其中4件正品,2件次品。
2017-2018学年辽宁省沈阳市重点高中高一下学期期末联考数学试题Word版含答案

2017-2018学年辽宁省沈阳市重点高中下学期期末联考高一数学试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.10sin 3π⎛⎫- ⎪⎝⎭的值等于( )A .B .C . 12D .12- 2.某公司生产三种型号的轿车,产量分别为1600辆、6000辆和2000辆,为检验公司的产品质量,现从这三种型号的轿车中抽取48辆进行检验,这三种型号的轿车依次应抽取 ( )A .16,16,16B .12,27,9C .8,30,10D .4,33,113.若sin cos 0,cos tan 0αααα><,则α的终边落在 ( )A .第一象限B .第二象限C .第三象限D .第四象限4.下列说法中正确的个数是 ( )①事件,A B 中至少有一个发生的概率一定比,A B 中恰有一个发生的概率大;②事件,A B 同时发生的概率一定比,A B 恰有一个发生的概率小;③互斥事件一定是对立事件,对立事件并不一定是互斥事件;④互斥事件不一定是对立事件,对立事件一定是互斥事件.A .0B .1 C. 2 D .35. 某程序框图如图所示,若输出的57S =,则判断框内为( )A .4k >B .5k > C.6k > D .7k >6.在区间,22ππ⎡⎤-⎢⎥⎣⎦上随机取一个x ,则sin x 的值介于12-与12之间的概率为 ( ) A .2π B .13 C. 12 D .23 7. 从随机编号为0001,0002,,1500的1500名参加某次沈阳市四校联考期末测试的学生中,用系统抽样的方法抽取一个样本进行成绩分析,已知样本中编号最小的两个编号分别为0018,0068,则样本中最大的编号应该是( )A .1466B .1467 C.1468 D .14698.若样本1231,1,1,,1n x x x x ++++的平均数是10,方差为2,则对于样本122,2,,2n x x x +++,下列结论正确的是 ( )A .平均数为10,方差为2B .平均数为11,方差为3C. 平均数为11,方差为2 D .平均数为12,方差为49.如图是函数()()sin 20,0,y A x A ωϕωϕπ=++>><的图象的一部分,则它的振幅、周期、初相分别是 ( )A .43,,36A T ππϕ===- B .433,,34A T ππϕ===- C. 41,,36A T ππϕ===- D .431,,34A T ππϕ===- 10.设sin 33,cos55,tan 35a b c =︒=︒=︒,则 ( )A .c b a >>B .b c a >> C.a b c >> D .c a b >>11.若22sin cos x x >,则x 的取值范围是 ( )A .322,44x k x k k Z ππππ⎧⎫-<<+∈⎨⎬⎩⎭B .522,44x k x k k Z ππππ⎧⎫+<<+∈⎨⎬⎩⎭C. ,44x k x k k Z ππππ⎧⎫-<<+∈⎨⎬⎩⎭ D .3,44x k x k k Z ππππ⎧⎫+<<+∈⎨⎬⎩⎭12.已知0ω>,函数()sin 4f x x πω⎛⎫=+ ⎪⎝⎭在,2ππ⎛⎫ ⎪⎝⎭上单调递减,则ω的取值范围是 ( )A .15,24⎡⎤⎢⎥⎣⎦B .13,24⎡⎤⎢⎥⎣⎦ C. 10,2⎛⎤ ⎥⎝⎦D .(]0,2 第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知扇形的周长等于它所在圆的周长的一半,则这个扇形的圆心角是 .14.已知函数()5432235f x x x x x x =++-+-,用秦九韶算法计算()5f = .15.已知角α的终边经过点()4,3P -,则2sin 3cos αα+= .16.下面四个命题:①tan y x =在定义域上单调递增;②若锐角,αβ满足cos sin αβ>,则2παβ+<;③()f x 是定义在[]1,1-上的偶函数,且在[]1,0-上是增函数,若0,4πθ⎛⎤∈ ⎥⎝⎦,则()()sin cos f f θθ>; ④函数4sin 23y x π⎛⎫=- ⎪⎝⎭的一个对称中心是,06π⎛⎫ ⎪⎝⎭; 其中真命题的序号为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 已知tan 2α=,求下列代数式的值:(1)4sin 2cos 5cos 3sin αααα-+;(2)22111sin sin cos cos 432αααα++.18. 在某次期末考试中,从高一年级中抽取60名学生的数学成绩(均为整数)分段为[)[)[)90,100,100,110,,140,150后,部分频率分布直方图如图.观察图形,回答下列问题:(1)求分数在[)120,130内的频率,并补全这个频率分布直方图;(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试中全年级数学成绩的平均分.19.在人流量较大的的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完全相同),旁边立着一块小黑板写道:摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱.(1)摸出的3个球为白球的概率是多少?(2)摸出的3个球为2个黄球1个白球的概率是多少?(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?20.为了研究某种细菌在特定条件下随时间变化的繁殖情况,得到如下所示实验数据,若t 与y 线性相关.(1)求y 关于x 的回归直线方程;(2)预测8t =时细菌繁殖的个数. (参考公式:1221n ii i n ii x y nx yb x nx ==-=-∑∑,,a y bx y bx a =-=+)21. 已知函数()()sin ,f x A x x R ωϕ=+∈,(其中0,0,02A πωϕ>><<)的图象与x 轴的交点中,相邻两个交点之间的距离为2π,且图象上一个最低点为2,23M π⎛⎫- ⎪⎝⎭. (1)求函数()f x 的解析式;(2)当12,2x ππ⎡⎤∈⎢⎥⎣⎦时,求函数()f x 的值域.22.已知函数()()2sin 0,06f x x πωϕϕπω⎛⎫=+-<<> ⎪⎝⎭为偶函数,且函数()y f x =图象的两相邻对称轴间的距离为2π. (1)求8f π⎛⎫ ⎪⎝⎭的值; (2)函数()y f x =的图象向右平移6π个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数()y g x =的图象,求()g x 的单调递减区间.2017-2018学年辽宁省沈阳市重点高中高一下学期期末联考数学试题答案一、选择题1-5: ACCBA 6-10: BCCDA 11、12:DA二、填空题13. ()2rad π- 14. 4485 15. 6516.②③④ 三、解答题17.解:(1)原式4tan 263tan 511αα-==+.(2)原式2222111sin sin cos cos 432sin cos αααααα++=+ 22111111tan tan 4213432432tan 1530ααα++⨯+⨯+===+ 18. 解:(1)分数在[)120,130内的频率为()10.010.0150.0150.0250.0051010.70.3-++++⨯=-=, 0.30.0310==频率组距. 直方图略.(2)平均分的估计值为950.11050.151150.31350.251450.05121=⨯+⨯+⨯+⨯+⨯=19.解: 把3只黄色乒乓球标记为A B C 、、,3只白色的乒乓球标记为1、2、3. 从6个球中随机摸出3个的基本事件为:123123121323ABC AB AB AB AC AC AC A A A 、、、、、、、、、、 123121323121323123BC BC BC B B B C C C 、、、、、、、、、,共20个(1)事件{E =摸出的3个球为白球},事件E 包含的基本事件有1个,即摸出123号3个球,()=1/20=0.05P E(2)事件{F =摸出的3个球为2个黄球1个白球},事件F 包含的基本事件有9个,()9/200.45P F ==(3)事件{G =摸出的3个球为同一颜色}={摸出的3个球为白球或摸出的3个球为黄球},()2/200.1P G ==,假定一天中100人次摸奖,由摸出的3个球为同一颜色的概率可估计事件G 发生有10次,不发生90次.则一天可赚90110540⨯-⨯=,每月可赚1200元.20. 解:(1)由已知5,8t y ==,则25200,5125t y t ==, 217200 1.7135125b -==- 所以,0.5a =-所以y 关于t 的回归直线方程 1.70.5y t =-(2)当8t =时, 1.780.513.1y =⨯-=(千个)21. 解:(1)由最低点为2,23M π⎛⎫- ⎪⎝⎭得2A = 由x 轴上相邻两个交点之间的距离为2π, 得22T π=,即T π=,∴222T ππωπ=== 由点2,23M π⎛⎫- ⎪⎝⎭在图象上得22sin 223πϕ⎛⎫⨯+=- ⎪⎝⎭,即4sin 13πϕ⎛⎫+=- ⎪⎝⎭故()42,32k k Z ππϕπ+=-∈, ∴()1126k k Z πϕπ=-∈. 又0,2πϕ⎡⎤∈⎢⎥⎣⎦,∴=6πϕ 故()f 2sin 26x x π⎛⎫=+ ⎪⎝⎭ (2)∵,122x ππ⎡⎤∈⎢⎥⎣⎦,∴72,636x πππ⎡⎤+∈⎢⎥⎣⎦当,即时,取得最大值2; 当262x ππ+=,即6x π=时,()f x 取得最小值; 当7266x ππ+=,即2x π=时,()f x 取得最小值1-. 故()f x 的值域为[]1,2-22. 解:(1)∵()2sin 6f x x πωϕ⎛⎫=+- ⎪⎝⎭为偶函数, ∴对()(),x R f x f x ∈-=恒成立,∴sin sin 66x x ππωϕωϕ⎛⎫⎛⎫-+-=+- ⎪ ⎪⎝⎭⎝⎭. 即:266x k x ππωϕππωϕ⎛⎫-+-=+-+- ⎪⎝⎭ 又∵0ϕπ<<,故62ππϕ-=.∴()2sin 2cos 2f x x x πωω⎛⎫=+= ⎪⎝⎭ 由题意得2=22ππω⋅,所以=2ω故()2cos2f x x =,∴2cos 84f ππ⎛⎫== ⎪⎝⎭(2)将()f x 的图象向右平移6π个单位后,得到6f x π⎛⎫- ⎪⎝⎭的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到()y g x =的图象.∴()2cos 22cos 4623x x g x ππ⎡⎤⎛⎫⎛⎫=-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦. 当()2223x k k k Z ππππ≤-≤+∈, 即()284433k x k k Z ππππ+≤≤+∈时,()g x 单调递减,因此()g x 的单调递减区间为()284,433k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦.。
全国百强校:辽宁省2017-2018学年高一下学期期末考试数学试卷+答案

2017~2018学年度第二学期期末考试试卷高一数学第Ⅰ卷选择题(共60分)一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求)1.等于( )A. B. C. D.2.已知角的终边落在直线上,则的值为( )A. B. C. D.3.用系统抽样的方法从个体数为1003的总体中抽取一个容量为50的样本,在整个抽样过程中每个个体被抽到的概率为 ( )A. B. C. D.4.已知,则的值为 ( )A. B. C. D.5.已知向量,,则向量在向量方向上的正射影的数量为()A. B. C. 1 D.6.阅读右边的程序框图,运行相应的程序,则输出s的值为( )A. -1B. 0C. 1D. 37.为了得到函数的图象,只需把函数的图象上所有的点()A. 向左平移个单位长度B. 向右平移个单位长度C. 向左平移个单位长度D. 向右平移个单位长度8.设的内角所对的边分别为,若,则的形状为()A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不确定9.甲、乙两位同学在高一年级的5次考试中,数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是,则下列叙述正确的是()A. ,乙比甲成绩稳定B. ,甲比乙成绩稳定C. ,乙比甲成绩稳定D. ,甲比乙成绩稳定10.某船开始看见灯塔时,灯塔在船南偏东方向,后来船沿南偏东的方向航行后,看见灯塔在船正西方向,则这时船与灯塔的距离是()A. B. C. D.11.如图,在中,已知,,,,则()A. -45B. 13C. -13D. -3712.在中,角所对的边分别为,若,,则周长的取值范围是()A. B. C. D.第Ⅱ卷非选择题(共90分)二.填空题(本大题共4小题,每小题5分,共20分,把答案填在答卷卡的相应位置上)13.已知点,向量,则点的坐标为__________14.已知,,则的值为__________15.某公司的班车在8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是__________16.若平面向量两两所成的角相等,且,则等于_____三.解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.已知向量,,满足.(Ⅰ)求的值;(Ⅱ)求向量与向量夹角的余弦值.18.已知.(Ⅰ)求的值;(Ⅱ)求的值.19.某校从参加高三模拟考试的学生中随机抽取60名学生,按其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图中的信息,回答下列问题:(Ⅰ)补全频率分布直方图;(Ⅱ)估计本次考试的数学平均成绩(同一组中的数据用该组区间的中点值作代表);(Ⅲ)用分层抽样的方法在分数段为[110,130)的学生成绩中抽取一个容量为6的样本,再从这6个样本中任取2人成绩,求至多有1人成绩在分数段[120,130)内的概率.20.设函数(,)的两个相邻的对称中心分别为,.(Ⅰ)求的解析式及其对称轴方程;(Ⅱ)利用五点法画出函数在上的简图.21.如图,是一块半径为1,圆心角为的扇形空地.现决定在此空地上修建一个矩形的花坛,其中动点在扇形的弧AB上,记.(Ⅰ)写出矩形的面积与角之间的函数关系式;(Ⅱ)当角取何值时,矩形的面积最大?并求出这个最大面积.22.已知函数,其中,.(Ⅰ)求函数的单调递减区间;(Ⅱ)在中,角所对的边分别为,,,且向量与向量共线,求的面积.第Ⅰ卷选择题(共60分)一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求)1.等于( )A. B. C. D.【答案】A【解析】【分析】利用诱导公式和特殊角的三角函数值进行化简.【详解】故选A.【点睛】本题考查诱导公式和特殊角的三角函数值,属基础题.2.已知角的终边落在直线上,则的值为( )A. B. C. D.【答案】B【解析】【分析】由条件利用任意角的三角函数的定义,求得的值.【详解】角的终边落在直线上,在直线上任意取一点,,则由任意角的三角函数的定义可得故选:B.【点睛】本题主要考查任意角的三角函数的定义,属于基础题.3.用系统抽样的方法从个体数为1003的总体中抽取一个容量为50的样本,在整个抽样过程中每个个体被抽到的概率为 ( )A. B. C. D.【答案】D【解析】【分析】根据统抽样方法的公平性即抽样过程中每个个体被抽到的概率是相等的,分析题意,可得答案.【详解】根据题意,抽样过程中每个个体被抽到的概率是相等的,即为,故选:D.【点睛】本题考查系统抽样方法,注意抽样中的公平性即可.4.已知,则的值为 ( )A. B. C. D.【答案】C【解析】【分析】两边平方解得,由此可求的值【详解】由已知已知,两边平方得可得即即故选C.【点睛】本题主要考查了二倍角公式,同角三角函数关系式的应用,属于基础题.5.已知向量,,则向量在向量方向上的正射影的数量为()A. B. C. 1 D.【答案】A【解析】【分析】根据向量数量积的关系进行化简,结合向量投影的定义进行求解即可.【详解】:∵向量∴∴向量在向量方向上的正射影为,故选:A.【点睛】本题主要考查向量数量积的应用,利用向量投影的定义是解决本题的关键.6.阅读右边的程序框图,运行相应的程序,则输出s的值为( )A. -1B. 0C. 1D. 3【答案】B【解析】经过第一次循环得到不满足执行第二次循环得到不满足,执行第三次循环得到s=1,i=4,不满足,经过第四次循环得到满足判断框的条件执行“是”输出故选B.视频7.为了得到函数的图象,只需把函数的图象上所有的点()A. 向左平移个单位长度B. 向右平移个单位长度C. 向左平移个单位长度D. 向右平移个单位长度【答案】D【解析】【分析】由于函数,再根据函数的图象变换规律,得出结论.【详解】由于函数,故把函数的图象上所有的点向右平移个单位长度,即可得到函数的图象,故选:D.【点睛】本题主要考查函数的图象变换规律,属于中档题.8.设的内角所对的边分别为,若,则的形状为()A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不确定【答案】B【解析】【分析】由条件利用正弦定理可得,再由两角和的正弦公式、诱导公式求得,可得由此可得的形状.【详解】的内角所对的边分别为,∵,则由正弦定理可得,即,可得,故,故为直角三角形,故选:B.【点睛】本题主要考查正弦定理以及两角和的正弦公式、诱导公式的应用,根据三角函数的值求角,属于中档题.9.甲、乙两位同学在高一年级的5次考试中,数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是,则下列叙述正确的是()A. ,乙比甲成绩稳定B. ,甲比乙成绩稳定C. ,乙比甲成绩稳定D. ,甲比乙成绩稳定【答案】C【解析】甲的平均成绩,甲的成绩的方差;乙的平均成绩,乙的成绩的方差.∴,乙比甲成绩稳定.故选C.10.某船开始看见灯塔时,灯塔在船南偏东方向,后来船沿南偏东的方向航行后,看见灯塔在船正西方向,则这时船与灯塔的距离是()A. B. C. D.【答案】D【解析】【分析】如图所示,设灯塔位于处,船开始的位置为,船行后处于,根据题意求出与的大小,在三角形中,利用正弦定理算出的长,可得该时刻船与灯塔的距离。
辽宁省实验中学2017-2018学年高一下学期期末考试数学试卷

2017-2018学年度下学期期末考试高一年级数学科试卷命题学校:辽宁省实验中学 命题人:刘铭 毕晓昕第I 卷一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)执行如右图所示的程序框图,若输入2x =-,( )则输出的y = (A )8- (B )4- (C )4 (D )8(2)已知角α的终边经过点(3,4)--,则 ( )(A )4sin 5α= (B )3cos 5α= (C )4tan 3α= (D )3cot 4α=-(3)cos(2040)-︒= ( )(A (B )12 (C )- (D )12-(4)在50瓶牛奶中,有5瓶已经过了保质期.从中任取一瓶,取到已经过保质期的牛奶的概率是 ( )(A )0.02 (B )0.05 (C )0.1 (D )0.9(5)已知(1,3)=a ,=b (,2)x ,(1,2)=-c ,若()+⊥a b c ,则x = ( ) (A )9- (B )9 (C )11- (D )11(6)已知平面向量||1=a ,||2=b ,且1⋅=-a b ,则|2|+a b 的值是 ( )(A )1 (B )2 (C )3 (D )4(7)tan10tan50tan50︒+︒︒= ( )(A )2 (B (C (D )1 (8)将函数3sin(2)4y x π=-的图象向左平移16个周期(即最小正周期)后,所得图象对应的函数为( )(A )3sin(2)12y x π=+(B )73sin(2)12y x π=+(C )3sin(2)12y x π=- (D )73sin(2)12y x π=-(9)函数()2sin()f x x ωϕ=+(0ω>,πϕπ-<<)的部分图像如图所示,点P 5(,2)3是该图像的一个最高点,点Q 4(,0)3-是该图像与x 轴交点,则 ( )(A )()2sin()3f x x ππ=-(B )2()2sin()3f x x ππ=- (C )()2sin()23f x x ππ=- (D )2()2sin()23f x x ππ=-(10)已知函数()f x 满足(1)(1)f x f x +=-,且(2)(2)0f x f x ++-=,当[0,1]x ∈时2()f x x =,则(2018.7)f = ( ) (A )0.09 (B )0.09- (C )0.49 (D )0.49-(11)已知,AB AC 不共线,AM m AB =,AN nAC =,其中1mn ≠.设点P 是直线,BN CM 的交点,则 ( ) (A )11mn m mn n AP AB AC mn mn --=+-- (B )11mn m mn nAP AB AC mn mn ++=+-- (C )11mn n mn m AP AB AC mn mn --=+-- (D )11mn n mn mAP AB AC mn mn ++=+-- (12)下列四个函数中,图象可能是下图的是 ( )(A )sin sin 2y x x =+ (B )sin sin 2y x x =-(C )sin sin3y x x =+ (D )sin 2sin3y x x =+第Ⅱ卷二.填空题:本大题共4小题,每小题5分。
2017-2018学年辽宁省实验中学分校高一(下)期末数学模拟试卷 Word版含解析

2017-2018学年辽宁省实验中学分校高一(下)期末数学模拟试卷一、选择题:本大题共12小题,每题5分,在每小题给出的四个选项中,只有一个是符合题目要求的.1.sin2cos3tan4的值()A.小于0 B.大于0 C.等于0 D.不存在2.已知样本9,10,11,x,y的平均数是10,标准差是,则xy=()A.98 B.88 C.76 D.963.在正方体内任取一点,则该点在正方体的内切球内的概率为()A.B.C.D.4.某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍.为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为()A.9 B.18 C.27 D.365.天气预报报导在今后的三天中,每一天下雨的概率均为60%,这三天中恰有两天下雨的概率是()A.0.432 B.0.6 C.0.8 D.0.2886.已知与为互相垂直的单位向量,,且与的夹角为锐角,则实数λ的取值范围是()A.(﹣∞,﹣2)B.(,+∞)C.(﹣2,)D.(﹣)7.如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为()A.锐角三角形B.直角三角形C.钝角三角形D.由增加的长度决定8.如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是()A.65 B.64 C.63 D.629.已知,则cosβ的值为()A.﹣1 B.﹣1或C.D.10.图是一算法的程序框图,若输出结果为S=5040,则在判断框中应填入的条件是()A.k≤9 B.k≤8 C.k≤7 D.k≤611.已知P是单位正方体ABCD﹣A1B1C1D1中异于A的一个顶点,则的值为()A.0 B.1 C.0或1 D.任意实数12.已知函数f(x)=Acos2(ωx+φ)+1(A>0,ω>0)的最大值为3,f(x)的图象在y 轴上的截距为2,其相邻两对称轴间的距离为1,则f(1)+f(2)+f(3)+…+f(100)=()A.0 B.100 C.150 D.200二、填空题:本大题共4小题,每小题5分.13.下列是某厂1~4月份用水量(单位:百吨)的一组数据,由其散点图可知,用水量y 与月份x之间有较好的线性相关关系,其线性回归方程是=﹣0.7x+,则=.月份x 1 2 3 4用水量y 4.5 4 3 2.514.△ABC的外接圆的圆心为O,两条边上的高的交点为H,,则实数m=.15.程序框图(如图所示),则该程序框图表示的算法的功能是:.16.△ABC中,a,b,c分别是角A,B,C的对边,且a2+b2=mc2(m为常数),若=2012,则m=.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.已知A(﹣1,2),B(2,8),(1)若=,=﹣,求的坐标;(2)设G(0,5),若⊥,∥,求E点坐标.18.从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件A:“取出的2件产品中至多有1件是二等品”的概率P(A)=0.96.(1)求从该批产品中任取1件是二等品的概率p;(2)若该批产品共100件,从中任意抽取2件,求事件B:“取出的2件产品中至少有一件二等品”的概率P(B).19.已知向量=(sin,1),=(cos,cos2),f(x)=•.(1)若f(x)=1,求cos(x+)的值;(2)在△ABC中,角A,B,C的对边分别是a,b,c且满足acosC+c=b,求函数f(B)的取值范围.20.某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了x•46%=230人,回答问题统计结果如图表所示.组号分组回答正确的人数回答正确的人数占本组的概率第1组[15,25) 5 0.5第2组[25,35) a 0.9第3组[35,45)27 x第4组[45,55) B 0.36第5组[55,65) 3 y(Ⅰ)分别求出a,b,x,y的值;(Ⅱ)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?(Ⅲ)在(Ⅱ)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.21.ABC中,a、b、c分别是角A、B、C的对边,<C<,且.(1)判断△ABC的形状(2)若,求的取值范围、22.定义在区间[﹣π,π]上的函数y=f(x)的图象关于直线x=﹣对称,当x∈[﹣,π]时,函数f(x)=Asin(ωx+φ),(A>0,ω>0,﹣<φ<),其图象如图.(Ⅰ)求函数y=f(x)在[﹣π,π]上的表达式;(Ⅱ)求方程f(x)=的解集.2017-2018学年辽宁省实验中学分校高一(下)期末数学模拟试卷参考答案与试题解析一、选择题:本大题共12小题,每题5分,在每小题给出的四个选项中,只有一个是符合题目要求的.1.sin2cos3tan4的值()A.小于0 B.大于0 C.等于0 D.不存在考点:三角函数值的符号.分析:根据2弧度、3弧度、4弧度所在象限分析三角函数值的正负,最后得出答案.解答:解:∵1弧度大约等于57度,2弧度等于114度,∴sin2>0∵3弧度小于π弧度,在第二象限∴cos3<0∵4弧度小于弧度,大于π弧度,在第三象限∴tan4>0∴sin2cos3tan4<0故答案选A点评:本题主要考查三角函数值的符号问题.常常根据角所在的象限来判断函数值的正负.2.已知样本9,10,11,x,y的平均数是10,标准差是,则xy=()A.98 B.88 C.76 D.96考点:极差、方差与标准差.专题:概率与统计.分析:先由平均数的公式列出x+y=20,然后根据方差的公式列方程,求出x和y的值即可求出xy的值.解答:解:根据平均数及方差公式,可得:9+10+11+x+y=10×5,即x+y=20,∵标准差是,∴方差为2.∴[(9﹣10)2+(10﹣10)2+(11﹣10)2+(x﹣10)2+(y﹣10)2]=2,即(x﹣10)2+(y﹣10)2=8,∴解得x=8,y=12或x=12,y=8,则xy=96,故选:D点评:本题主要考查了平均数和方差等概念,以及解方程组,考查学生的计算能力.3.在正方体内任取一点,则该点在正方体的内切球内的概率为()A.B.C.D.考点:几何概型.专题:概率与统计.分析:根据题意,求出正方体的体积,进而可得其内切球的直径,可得其内切球的体积,由几何概型的公式,计算可得答案.解答:解:不妨设正方体棱长为2,根据题意,棱长为2的正方体,其体积为8,而其内切球的直径就是正方体的棱长,所以球的半径为1,则这一点在球内的概率为:==;故选B.点评:本题考查几何概型的应用,解题的关键在于根据正方体及其内切球的位置关系,找到其内切球的直径半径,进而得到体积.4.某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍.为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为()A.9 B.18 C.27 D.36考点:分层抽样方法.专题:计算题.分析:根据条件中职工总数和青年职工人数,以及中年和老年职工的关系列出方程,解出老年职工的人数,根据青年职工在样本中的个数,算出每个个体被抽到的概率,用概率乘以老年职工的个数,得到结果.解答:解:设老年职工有x人,中年职工人数是老年职工人数的2倍,则中年职工有2x,∵x+2x+160=430,∴x=90,即由比例可得该单位老年职工共有90人,∵在抽取的样本中有青年职工32人,∴每个个体被抽到的概率是=,用分层抽样的比例应抽取×90=18人.故选B.点评:本题是一个分层抽样问题,容易出错的是不理解分层抽样的含义或与其它混淆.抽样方法是数学中的一个小知识点,但一般不难,故也是一个重要的得分点,不容错过.5.天气预报报导在今后的三天中,每一天下雨的概率均为60%,这三天中恰有两天下雨的概率是()A.0.432 B.0.6 C.0.8 D.0.288考点:n次独立重复试验中恰好发生k次的概率.专题:概率与统计.分析:由条件利用n次独立重复实验中恰好发生k次的概率计算公式,求得这三天中恰有两天下雨的概率.解答:解:每一天下雨的概率均为60%,这三天中恰有两天下雨的概率是•0.62×0.4=0.432,故选:A.点评:本题主要考查n次独立重复实验中恰好发生k次的概率计算公式,属于基础题.6.已知与为互相垂直的单位向量,,且与的夹角为锐角,则实数λ的取值范围是()A.(﹣∞,﹣2)B.(,+∞)C.(﹣2,)D.(﹣)考点:平面向量数量积的运算;数量积表示两个向量的夹角.分析:本题考查的知识点是平面向量数量积的运算,由与为互相垂直的单位向量,我们易得,,代入,可求出•,又由与的夹角为锐角,故•>0,由此得到一个关于λ的不等式,解不等式即可得到实数λ的取值范围,但要注意,与同向的排除.解答:解:∵与为互相垂直的单位向量∴,,又∵,且与的夹角为锐角,∴,但当λ=﹣2时,,不满足要求故满足条件的实数λ的取值范围是(﹣∞,﹣2)故选A点评:两个向量夹角为锐角,则两个向量的数量积为正;两个向量夹角为钝角,则两个向量的数量积为负;两个向量夹角为直角,则两个向量的数量积为零;7.如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为()A.锐角三角形B.直角三角形C.钝角三角形D.由增加的长度决定考点:余弦定理.专题:计算题.分析:先设出原来的三边为a、b、c且c2=a2+b2,以及增加同样的长度为x,得到新的三角形的三边为a+x、b+x、c+x,知c+x为最大边,所以所对的角最大,然后根据余弦定理判断出余弦值为正数,所以最大角为锐角,得到三角形为锐角三角形.解答:解:设增加同样的长度为x,原三边长为a、b、c,且c2=a2+b2,c为最大边;新的三角形的三边长为a+x、b+x、c+x,知c+x为最大边,其对应角最大.而(a+x)2+(b+x)2﹣(c+x)2=x2+2(a+b﹣c)x>0,由余弦定理知新的三角形的最大角的余弦=>0,则为锐角,那么它为锐角三角形.故选A点评:考查学生灵活运用余弦定理解决实际问题的能力,以及掌握三角形一些基本性质的能力.8.如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是()A.65 B.64 C.63 D.62考点:众数、中位数、平均数;茎叶图.专题:计算题.分析:由茎叶图分别看出两个运动员的得分,把这两组数据按照从小到大排列以后,因为两组数据都是有奇数个数字,最中间一个数字是中位数,得到两个中位数之和.解答:解:∵由茎叶图知甲运动员的得分是:13,15,23,26,28,34,37,39,41把这组数据按照从小到大排列以后,最中间一个数字是28,∴甲运动员得分的中位数是28,∵由茎叶图知乙运动员的得分是24,25,32,33,36,37,38,45,47把这组数据按照从小到大排列以后,最中间一个数字是36,∴乙运动员得分的中位数是36,∴两个中位数的和是28+36=64故选B . 点评: 本题考查茎叶图和中位数,是一个基础题,这种题目也可以从茎叶图中直接看出中位数,而不用把这组数据写下来,但是若茎叶图中所给的数字没有按照大小顺序时,容易弄错. 9.已知,则cos β的值为( )A . ﹣1B . ﹣1或C .D .考点: 两角和与差的正弦函数;两角和与差的余弦函数. 专题: 三角函数的求值. 分析: 先求出,,再利用cos β=cos[(α+β)﹣α],即可得出结论. 解答: 解:∵,∴,∴cos β=cos[(α+β)﹣α]==故选C . 点评: 本题考查三角函数的求值,考查角的变换,考查学生的计算能力,属于中档题.10.图是一算法的程序框图,若输出结果为S=5040,则在判断框中应填入的条件是( )A . k ≤9B . k ≤8C . k ≤7D . k ≤6考点: 程序框图. 专题: 算法和程序框图. 分析: 模拟程序的运行结果,分析不满足输出条件继续循环和满足输出条件退出循环时,变量k 值所要满足的要求,即可得到结论. 解答: 解:当k=10,S=1,不满足条件; 有S=10,k=9,不满足条件; 有S=10×9,k=8,不满足条件; 有S=10×9×8,k=7,不满足条件;有S=10×9×8×7=5040,k=6,满足输出条件;即当k=7时不满足条件,k=6时,满足条件,故k≤6,故选:D点评:本题主要考查程序框图的识别和判断,根据条件进行模拟是解决程序框图的基本方法.11.已知P是单位正方体ABCD﹣A1B1C1D1中异于A的一个顶点,则的值为()A.0 B.1 C.0或1 D.任意实数考点:平面向量数量积的运算.专题:平面向量及应用.分析:利用正方体的性质和数量积的定义即可得出.解答:解:如图所示,当点P取顶点D或A1或D1时,由AB⊥平面ADD1A1,可得=0.当点P取顶点B或B1或C或C1时,P取点B1时,====1;同理点P取点B或C时,可得;P取点C1时,===1×1=1.综上可知:=0或1.故选:C.点评:本题考查了正方体的性质和数量积的定义,属于基础题.12.已知函数f(x)=Acos2(ωx+φ)+1(A>0,ω>0)的最大值为3,f(x)的图象在y 轴上的截距为2,其相邻两对称轴间的距离为1,则f(1)+f(2)+f(3)+…+f(100)=()A.0 B.100 C.150 D.200考点:余弦函数的图象;二倍角的余弦.专题:三角函数的图像与性质.分析:由函数的最大值求出A,由周期求出ω,由图象在y轴上的截距为2求出φ的值,再利用函数的周期性求出所给式子的值.解答:解:∵函数f(x)=Acos2(ωx+φ)+1=A•+1=cos(2ωx+2φ)+的最大值为3,∴+=3,∴A=2.f(x)的图象在y轴上的截距为2,可得cos2φ+2=2,即cos2φ=0,∴可取φ=.再根据它的图象相邻两对称轴间的距离为1,可得它的周期为=2,求得ω=,∴f(x)=cos(πx+)+2=sinπx+2,故f(1)=2,f(2)=2,f(3)=2,…,(100)=2,故f(1)+f(2)+f(3)+…+f(100)=200,故选:D.点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的最大值求出A,由周期求出ω,由图象在y轴上的截距为2求出φ的值,利用函数的周期性求式子的值,属于基础题.二、填空题:本大题共4小题,每小题5分.13.下列是某厂1~4月份用水量(单位:百吨)的一组数据,由其散点图可知,用水量y 与月份x之间有较好的线性相关关系,其线性回归方程是=﹣0.7x+,则= 5.25.月份x 1 2 3 4用水量y 4.5 4 3 2.5考点:线性回归方程.专题:计算题;应用题.分析:根据所给的数据,做出x,y的平均数,即得到样本中心点,根据所给的线性回归方程,把样本中心点代入,只有a一个变量,解方程得到结果.解答:解:∵=3.5∴=﹣=3.5+0.7×2.5=5.25.故答案为:5.25点评:本题考查线性回归方程,考查样本中心点的性质,考查线性回归方程系数的求法,是一个基础题,本题运算量不大,是这一部分的简单题目.14.△ABC的外接圆的圆心为O,两条边上的高的交点为H,,则实数m=1.考点:向量的加法及其几何意义;三角形五心.专题:压轴题;数形结合.分析:根据题意作出图形,由外心和垂心的性质证明四边形AHCD是平行四边形,由向量加法的三角形法则得=+,由向量相等和向量的减法运算进行转化,直到用、和表示出来为止.解答:解:如图:作直径BD,连接DA、DC,由图得,=﹣,∵H为△ABC的垂心,∴CH⊥AB,AH⊥BC,∵BD为直径,∴DA⊥AB,DC⊥BC∴CH∥AD,AH∥CD,故四边形AHCD是平行四边形,∴=又∵=﹣=+,∴=+=+=++,对比系数得到m=1.故答案为:1.点评:本题考查了向量的线性运算的应用,一般的做法是根据图形找一个封闭的图形,利用向量的加法表示出来,再根据题意进行转化到用已知向量来表示,考查了转化思想.15.程序框图(如图所示),则该程序框图表示的算法的功能是:计算并输出使1×3×5×7×…>10000成立的最小整数.考点:循环结构.专题:图表型.分析:写出经过几次循环得到的结果,得到求的s的形式,判断出框图的功能.解答:解:经过第一次循环得到s=1×3,i=5经过第二次循环得到s=1×3×5,i=7经过第三次循环得到s=1×3×5×7,i=8…s=1×3×5×7×…>10000该程序框图表示算法的功能是求计算并输出使1×3×5×7×…>10000成立的最小整数故答案为计算并输出使1×3×5×7×…>10000成立的最小整数点评:本题考查程序框图,考查了循环体以及循环次数两个具体问题,常采用写出前几次循环的结果,找规律.属于基础题.16.△ABC中,a,b,c分别是角A,B,C的对边,且a2+b2=mc2(m为常数),若=2012,则m=4025.考点:余弦定理;同角三角函数间的基本关系;正弦定理.专题:解三角形.分析:先根据余弦定理表示出cosC,进而对题设条件化简,把切转换成弦,利用两角和公式化简整理后,进而利用正弦定理把角的正弦转化成边整理求得=2012,则m的值可求.解答:解:由余弦定理可知cosC=(a2+b2﹣c2)====•=2012,由正弦定理可知,∴=2012,∴m=4025.故答案为:4025点评:本题主要考查了正弦定理和余弦定理的应用.考查了考生对基础知识的理解和灵活利用.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.已知A(﹣1,2),B(2,8),(1)若=,=﹣,求的坐标;(2)设G(0,5),若⊥,∥,求E点坐标.考点:平面向量数量积的运算.专题:平面向量及应用.分析:(1)利用向量的数乘运算、坐标运算、三角形法则即可得出.(2)利用向量的共线定理、向量垂直与数量积的关系即可得出.解答:解:(1)∵=(3,6),∴==(1,2),=﹣=(﹣2,﹣4),∴==(2,4)﹣(1,2)=(1,2).(2)设E(x,y),则=(x+1,y﹣2),=(x﹣2,y﹣8),∵=(﹣2,﹣3),⊥,∥,∴,解得.∴E点坐标(﹣,).点评:本题考查了向量的数乘运算、坐标运算、三角形法则、向量的共线定理、向量垂直与数量积的关系,考查了计算能力,属于基础题.18.从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件A:“取出的2件产品中至多有1件是二等品”的概率P(A)=0.96.(1)求从该批产品中任取1件是二等品的概率p;(2)若该批产品共100件,从中任意抽取2件,求事件B:“取出的2件产品中至少有一件二等品”的概率P(B).考点:互斥事件的概率加法公式;等可能事件的概率.分析:(1)有放回地抽取产品二次,每次随机抽取1件,取出的2件产品中至多有1件是二等品包括无二等品和恰有一件是二等品两种情况,设出概率,列出等式,解出结果.(2)由上面可以知道其中二等品有100×0.2=20件取出的2件产品中至少有一件二等品的对立事件是没有二等品,用组合数列出结果.解答:解:(1)记A0表示事件“取出的2件产品中无二等品”,A1表示事件“取出的2件产品中恰有1件二等品”.则A0,A1互斥,且A=A0+A1,故P(A)=P(A0+A1)=P(A0)+P(A1)=(1﹣p)2+C21p(1﹣p)=1﹣p2于是0.96=1﹣p2.解得p1=0.2,p2=﹣0.2(舍去).(2)记B0表示事件“取出的2件产品中无二等品”,则.若该批产品共100件,由(1)知其中二等品有100×0.2=20件,故.点评:问题所涉及的是生活中常见的一种现象,问题的生活化可激发学生的兴趣和求知欲望,同样这样的问题也影响学生的思维方式,学会用数学的视野关注身边的数学.19.已知向量=(sin,1),=(cos,cos2),f(x)=•.(1)若f(x)=1,求cos(x+)的值;(2)在△ABC中,角A,B,C的对边分别是a,b,c且满足acosC+c=b,求函数f(B)的取值范围.考点:余弦定理;平面向量数量积的运算;三角函数的化简求值.专题:计算题.分析:(1)由两向量的坐标,利用平面向量的数量积运算法则列出f(x)的解析式,再利用二倍角的正弦、余弦函数公式及两角和与差的正弦函数公式化为一个角的正弦函数,由f(x)=1,得出sin(+)的值,最后将所求的式子中的角提取2,利用二倍角的余弦函数公式化简后,将sin(+)的值代入即可求出值;(2)利用余弦定理表示出cosC,代入已知的等式,整理后代入利用余弦定理表示出的cosA 中,得出cosA的值,由A为三角形的内角,利用特殊角的三角函数值求出A的度数,进而确定出B的范围,得出+的范围,利用正弦函数的图象与性质得出此时正弦函数的值域,即为f(B)的范围.解答:解:(1)∵=(sin,1),=(cos,cos2),∴f(x)=•=sin cos+cos2=sin+cos+=sin(+)+,又f(x)=1,∴sin(+)=,(4分)∴cos(x+)=cos2(+)=1﹣2sin2(+)=;(6分)(2)∵cosC=,acosC+c=b,∴a•+c=b,即b2+c2﹣a2=bc,∴cosA==,又∵A∈(0,π),∴A=,(10分)又∵0<B<,∴<+<,∴f(B)∈(1,).(12分)点评:此题考查了余弦定理,平面向量的数量积运算,二倍角的正弦、余弦函数公式,两角和与差的正弦函数公式,以及正弦函数的定义域与值域,熟练掌握定理及公式是解本题的关键.20.某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了x•46%=230人,回答问题统计结果如图表所示.组号分组回答正确的人数回答正确的人数占本组的概率第1组[15,25) 5 0.5第2组[25,35) a 0.9第3组[35,45)27 x第4组[45,55) B 0.36第5组[55,65) 3 y(Ⅰ)分别求出a,b,x,y的值;(Ⅱ)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?(Ⅲ)在(Ⅱ)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.考点:列举法计算基本事件数及事件发生的概率;频率分布直方图;用样本的频率分布估计总体分布.专题:概率与统计.分析:(Ⅰ)由回答对的人数:每组的人数=回答正确的概率,分别可求得要求的值;(Ⅱ)由分层抽样按比例抽取的特点可得各组的人数;(Ⅲ)记抽取的6人中,第2组的记为a1,a2,第3组的记为b1,b2,b3,第4组的记为c,列举可得从6名学生中任取2名的所有可能的情况,以及其中第2组至少有1人的情况种数,由古典概型可得概率.解答:解:(Ⅰ)第1组人数5÷0.5=10,所以n=10÷0.1=100,…(1分)第2组人数100×0.2=20,所以a=20×0.9=18,…(2分)第3组人数100×0.3=30,所以x=27÷30=0.9,…(3分)第4组人数100×0.25=25,所以b=25×0.36=9…(4分)第5组人数100×0.15=15,所以y=3÷15=0.2.…(5分)(Ⅱ)第2,3,4组回答正确的人的比为18:27:9=2:3:1,所以第2,3,4组每组应各依次抽取2人,3人,1人.…(8分)(Ⅲ)记抽取的6人中,第2组的记为a1,a2,第3组的记为b1,b2,b3,第4组的记为c,则从6名学生中任取2名的所有可能的情况有15种,它们是:(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,c),(a2,b1),(a2,b2),(a2,b3),(a2,c),(b1,b2),(b1,b3),(b1,c),(b2,b3),(b2,c),(b3,c).…(10分)其中第2组至少有1人的情况有9种,它们是:(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,c),(a2,b1),(a2,b2),(a2,b3),(a2,c).…(12分)故所求概率为.…(13分)点评:本题考查列举法求解古典概型的概率,涉及频率分布表的应用和分层抽样的特点,属基础题.21.ABC中,a、b、c分别是角A、B、C的对边,<C<,且.(1)判断△ABC的形状(2)若,求的取值范围、考点:平面向量数量积的运算;向量的模;三角函数中的恒等变换应用.专题:计算题.分析:本题考查的知识点是两角和与差的正弦公式,倍角公式,解三角形,平面向量的数量积运算,向量的模等知识点.(1)要判断△ABC的形状,我们可由,结论正弦定理边角互化的原则,将式子中边全部化为对应角的正弦值,然后根据两角和与差的正弦公式,倍角公式,得到sinB=sin2C,又由因为,我们易判断三角形的形状.(2)由,两边平方后,根据(1)的结论,我们可求出B的表达式及取值范围,进而求出的取值范围.解答:解:(1)⇒sinBsinA﹣sinBsin2C=sinAsin2C﹣sinBsin2C⇒sinB=sin2C,因为,所以B=π﹣2C⇒B+C=π﹣C⇒π﹣A=π﹣C⇒A=C即△ABC为等腰三角形.(2)因为所以,而所以,点评:要根据某个恒成立的三角函数关系式,判断三角形的形状,一般的思路是分析角与角的关系,如果有三个角相等,则为等边三角形;如果只能得到两个角相等,则为普通的等腰三角形;如果两个角和为90°,或一个角为90°,则为直角三角形.22.定义在区间[﹣π,π]上的函数y=f(x)的图象关于直线x=﹣对称,当x∈[﹣,π]时,函数f(x)=Asin(ωx+φ),(A>0,ω>0,﹣<φ<),其图象如图.(Ⅰ)求函数y=f(x)在[﹣π,π]上的表达式;(Ⅱ)求方程f(x)=的解集.考点:由y=Asin(ωx+φ)的部分图象确定其解析式;两角和与差的正弦函数.专题:综合题;数形结合;分类讨论.分析:(1)观察图象易得当时,:,再由函数y=f(x)的图象关于直线对称求出上的解析式,即可得到函数y=f(x)在的表达式;(2)由(1)函数的解析式是一个分段函数,故分段解方程求方程的解.解答:解:(1)当时,函数,观察图象易得:A=1,周期为2π,可得ω=1,再将点代入,结合题设可得φ=,即函数,由函数y=f(x)的图象关于直线对称得,时,函数f(x)=﹣sinx.∴.(2)当时,由得,;当时,由得,.∴方程的解集为点评:本题考查由函数的部分图象求函数的解析式,解题的关键是熟练掌握三角函数图象的特征,根据这些特征求出解析式中的系数,得出函数的解析式,本题涉及到函数的对称性求解析式,以及解三角方程,运算量较大,易因运算导致错误,解题时要谨慎.。
辽宁省沈阳市2017-2018学年高一数学下学期期末考试试题理

辽宁省沈阳市2017-2018学年高一数学下学期期末考试试题 理第Ⅰ卷(选择题,共60分)一.选择题(共12小题,每小题5分,共60分) 1.sin(225)-的值是( )122.在ABC ∆中,()2,4AB =,()1,3AC =,则CB =( ) A. ()3,7 B. ()3,5 C. ()1,1 D. ()1,1- 3.为了得到函数sin()3y x π=-的图像,只需把函数sin()6y x π=+的图像( )A. 向左平移4π个长度单位 B. 向右平移4π个长度单位 C. 向左平移2π个长度单位 D. 向右平移2π个长度单位4.已知4sin 65πα⎛⎫+= ⎪⎝⎭,则cos 3πα⎛⎫- ⎪⎝⎭的值为( )A.35 B. 45 C. 45- D. 35- 5.如图,在ABC ∆中,1,32BD DC AE ED ==,若=AB a ,AC b =,则BE 等于( )A. 11+33a b B .11+24a b -C. 11+24a b D .11+33a b -6.若()()2cos f x x k ωϕ=++的图像关于直线3x π=对称,且13f π⎛⎫=-⎪⎝⎭,则实数k 的值等于( )A. -3或1B. 1C. -1或3D. -37.已知23cos tan 3θθ=+,且()k k Z θπ≠∈,则sin 2θ等于( )A. 13-B. 13C. 23D. 23- 8.在以下关于向量的命题中,不正确的是( ) A. 若向量(,)a x y =,向量(,)(0)b y x xy =-≠,则a b ⊥. B. 若四边形ABCD 为菱形,则AB DC =且AB AD =. C. 点G 是ABC ∆的重心,则0GA GB GC ++= D. ABC ∆中,AB 和CA 的夹角等于A 9.如图,函数3cos tan (0,)22y x x x x ππ=≤<≠的图像是( ) A . B. C . D.10.已知在矩形ABCD 中,AB =, 3BC =,点E 满足13BE BC =,点F 在边CD 上,若1AB AF ⋅=,则AE BF ⋅=( )11.已知函数()()2cos 1(0,0,0)2f x A wx A w πϕϕ=++>><<的最大值为()3,f x 的图象与轴的交点坐标为()0,2,其相邻两条对称轴间的距离为2,则()()()()1232016f f f f ++++的值为( ) A. 2458 B. 3501 C. 4032 D. 573912.如图2,“六芒星”是由两个全等正三角形组成,中心重合于点O 且三组对边分别平行.点A ,B 是“六芒星”(如图1)的两个顶点,动点P 在“六芒星”上(内部以及边界),若OP xOA yOB =+, 则x y +的取值范围是A. []4,4- B. ⎡⎣ C. []5,5- D. []6,6-第Ⅱ卷(非选择题,共90分)二.填空题(共4小题,每小题5分,共20分) 13.函数sin()4y x π=-的单调递增区间是_____________________.14.已知向量(3,2)a =, (,4)b x =,且a ∥b ,则x 的值是 _______________.15.在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,且满足s i nc o s a B b A =,则i n c o s B C -的最大值是__________. 16.在下列结论中:①函数sin()()y k x k Z π=-∈为奇函数; ②函数tan(2)6y x π=+的图像关于点(,0)12π对称;③函数cos(2)3y x π=+的图像的一条对称轴为23x π=-; ④若tan()2x π-=,则21cos 5x =. 其中正确结论的序号为_________(把所有正确结论的序号都.填上). 三.解答题(共6小题) 17.(本小题10分) 已知tan()34πα+=-,求22sin cos sin sin cos 1ααααα-+的值.18. (本小题12分) 若平面向量,a b 满足()2,2,a b a b a ==-⊥(1)求a 与b 的夹角; (2)求2a b +.19.(本小题12分) 在ABC ∆中,角,,A B C 的对边分别为a ,b ,c, 22sin 3cos C C =,c =7,又ABC ∆的面积为332,求:(1)角C 的大小; (2)a b +的值.20.(本小题12分) 已知函数2()cos cos 1f x x x x =++.(1)求()f x 的最小正周期及单调递减区间;(2)在ABC ∆中,,,a b c 分别是角,,A B C 的对边,若()2f C =,4a b +=,且ABC ∆的ABC ∆外接圆的半径. 21.(本小题12分) 如图,在ABC ∆中,D 为AB 边上一点,DA DC =,已知4B π=,1BC =.(1)若ABC ∆是锐角三角形,DC =A 的大小; (2)若BCD ∆的面积为16,求边AB 的长. 22. 已知向量()()23sin ,cos ,cos ,1,(0)m tx tx n tx t =-=> ,把函数()12f x m n =⋅+化简为()()sin f x A x B ωφ=++的形式后,利用“五点法”画()y f x =在某一个周期内的图象时,列表并填入的部分数据如下表所示:(1)请直接写出处应填的值,并求的值及函数()y f x =在区间ππ,26⎡⎤-⎢⎥⎣⎦ 上的单增区间、单减区间;(2)设ABC ∆的内角,,A B C 所对的边分别为,,a b c ,已知π1,2726A f c a ⎛⎫+=== ⎪⎝⎭求BA BC ⋅辽宁省实验中学分校2016—2017学年下学期期末测试理科数学参考答案一.选择题(共12小题)1-5 ACDBB 6-10 ADDCB 11-12 CC 二.填空题(共4小题)13. 3(2,2)44k k ππππ-+14. 6 15. 1 16. ①③④ 三.解答题(共6小题) 17 解:4718解:(1),4a b π=(2)19.解(1)2π3(2)620.(1);(2)2.21.(1);(2).22.(1)①处应填入 5π6. 1t =,单减区间,26ππ⎡⎤--⎢⎥⎣⎦,单增区间,66ππ⎡⎤-⎢⎥⎣⎦ (2)1。
2017-2018学年辽宁省实验中学分校高一下学期期末数学试卷(文科)

2.已知平面向量 A. 1
=( 1, 2) , =(﹣ 2, m) ,且 ∥ ,则 m 的值为( D.﹣ 4
)
B.﹣ 1 C .4
【考点】 96:平行向量与共线向量. 【分析】 由 ∥ ,根据 1× m=2×(﹣ 2 )可得答案. 【解答】 解:∵ ∥ ∴ 1× m=2×(﹣ 2)∴ m=﹣ 4 故选 D.
2017-2018 学年度 辽宁省实验中学分校高一(下)期末数学试
卷(文科)
一、选择题:在每小题给出的四个选项中,只有一项符合题目要求(本大题共 12 小题,每小题 5 分,共 60 分) . 1.计算 sin43 cos13 ° ° ﹣cos43 ° sin13 的结果等于( ° A. B. C . D. ) )
3.给出下面四个命题:① 的个数为( )
+
= ;②
+
=பைடு நூலகம்
;③
﹣
=
;其中正确
A. 1 个 B .2 个 C . 3 个 D. 0 个 【考点】 99:向量的减法及其几何意义; 98:向量的加法及其几何意义. 【分析】 由向量加法的三角形法则和向量加减的几何意义即可判断 【解答】 解: :① ② ③ + ﹣ = = + = 正确,
5.在△ ABC中, A=60° , b=1,面积为 A. 1 B. 2 C . D.
6.已知 α ,β为锐角,且 cos α= A. B. C . D.
, cos β= ,则 α +β的值是(
)
7.在△ ABC中,若 lgsinA﹣ lgcosB ﹣ lgsinC=lg2 ,则△ ABC的形状是( A.直角三角形 B.等边三角形 8. tan 36 +tan ° 84 ﹣ ° A.﹣ B. C .不能确定 ) D.等腰三角形
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
沈阳铁路实验中学2017-2018学年度下学期期末考试
高一数学
时间:120分钟 满分:150分
一、选择题(共12小题,每小题5分,共计60分) 1.sin 480°等于( ) A .21-
B .21
C .23-
D .2
3
2.某大学数学系共有本科生1000人,其中一、二、三、四年级的人数比为4∶3∶2∶1,要用分层
抽样的方法从所有本科生中抽取一个容量为200的样本,则应抽取三年级的学生人数为( ) A .80 B .40 C .60 D .20 3.在区间,22ππ⎡⎤
-⎢⎥⎣⎦
上随机取一个x ,sin x 的值介于12-与12之间的概率为( )
(A)
13 (B)2π
(C)12 (D)2
3 4.已知向量=(8,x ),=(x ,1),x >0,若﹣2与2+共线,则x 的值为( ) A .
4 B .8 C .0 D .2
5.一次选拔运动员,测得7名选手的身高(单位:cm )分布茎叶图为
记录的平均身高为177 cm ,有一名选手的身高记录不清楚,其末位数记为x ,那么x 的值为 A .5 B .6 C .7 D .8
6.如图,F E D ,,分别为ABC ∆的三边AB CA BC ,,的中点, 则=+( )
A .AD
B .12AD
C .1
2
BC D .BC 7.要得到)4
2sin(3π
+=x y 的图象只需将y=3sin2x 的图象( )
A .向左平移4
π
个单位 B .向右平移
4
π
个单位 C .向左平移
8
π
个单位 D .向右平移
8
π
个单位
8.已知()sin()cos()f x x x ϕϕ=-+-为奇函数,则ϕ的一个取值为( ) A .0 B .π C .
2π D .4
π
9.根据下表所示的统计资料,求出了y 关于x 的线性回归方程为=1.23x+0.08,则统计表中t 的
值为( )
A .5.0
B .5.5
C .4.5
D .4.8
10.某程序框图如图所示,则该程序运行后输出的值是( )
A .. C D 11.已知cos (α-β)=53,sin β=135-,且α∈)2
,0(π
,β∈)0,2
(π
-,则sin α=
A .
6533 B .65
63 C .6533- D .6563
-
12.已知函数()sin cos f x a x b x =-(a b ,为常数,0a x ≠∈R ,)的图象关于直线4
π
=x 对称,
则函数)4
3(
x f y -=π
是( ) A .偶函数且它的图象关于点)0,(π对称 B .偶函数且它的图象关于点)0,23(π
对称 C .奇函数且它的图象关于点)0,(π对称 D .奇函数且它的图象关于点)0,2
3(π
对称 二、填空题(共4小题,每小题5分,共计20分)
13.用辗转相除法求两个数102、238的最大公约数是 _________ . 14.在△ABC 中,角,,A B C 所对的边分别为,,a b c ,满足
sin sin sin sin a c A B
b A C
+-=-则角C = .
15.设000
20
12tan13a cos8,,21tan 13b c ===-,则a ,b ,c 的大小关系为 _________ .
16.给出下列命题:
①存在实数α,使sin α•c os α=1 ②函数是偶函数
③
是函数
的一条对称轴方程
④若α、β是第一象限的角,且α>β,则sin α>sin β 其中正确命题的序号是 _________ .
三、解答题(共6题,17题10分,18~22每题12分,总计70分) 17. 为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:
(1)估计该校学生身高在170~185 cm 之间的概率;
(2)从样本中身高在180~190 cm 之间的男生中任选2人,
求至少有1人身高在185~190 cm 之间的概率.
18.已知向量满足:
a 4,|b|3,(2a 3b)(2a b)61==⋅+=||-, (1)求a
b ⋅的值; (2)求a b 与的夹角θ; (3)求a b +||的值;
19. 直角坐标系xoy 中,锐角α的终边与单位圆的交点为P ,将OP 绕O 逆时针旋转到OQ , 使α=∠POQ ,其中Q 是OQ 与单位圆的交点,设Q 的坐标为),(y x .
(Ⅰ)若P 的横坐标为5
3
,求x y ;
(Ⅱ)求
y x +的取值范围.
20
.已知函数22()cos cos sin f x x x x x =+-
(1)求函数()f x 的最小正周期及单调递增区间;
(2)在A B C ∆中,A 、B 、C 分别为三边a b c 、、
所对的角,若(A)1a f ==,求b c +的最大值.
21. 如图△ABC 中,已知点D 在BC 边上,且0=⋅AC AD
,sin BAC ∠=
,AB =
BD
(1)求AD 的长;
(2)求cosC .
22.如图所示,扇形AOB ,圆心角AOB 的大小等于,半径为2,在半径OA 上有一动点C ,过
点C 作平行于OB 的直线交弧AB 于点P .
(1)若C 是半径OA 的中点,求线段PC 的大小;
(2)设θ=∠COP ,求△POC 面积的最大值及此时θ的值.
参考答案
1.D .2.B.3.A .4.A .5.D .6. A7.C .8.D .9. B10.C .11. A .12. C
13.34 14.
3
π
15.a <c <b 16.②③ 17. 解(1)p 1=0.5;(2)p 2=
5
3159=. 18.解:(1)2
2
(23)(2)6144361a b a b a a b b ⋅+=-⋅-=由-得 又由a 4,|b|3==||得2
2169a b ==,
代入上式得6442761a b -⋅-=,∴6a b ⋅=- (2)61
cos 43
2||||a b a b θ⋅-=
==-⨯, 故23πθ= (3)2
2
2
||2162(6)913a b a a b b +=+⋅+=+⨯-+=故||13a b +=
19. 解:(Ⅰ)∵P 的横坐标为35, ∴34cos ,sin 55αα==, ∴4tan 3α= ∴22422tan 243tan 241tan 7
1()3
y x ααα⨯
====--- (Ⅱ)cos 2sin 2x y αα+=+),(0,)42
ππ
αα=
+∈,
∴ 52(0,),2(
,)444π
ππαπα∈+
∈,
∴
sin(2)(42
πα+∈-,
)(4
π
α+∈-, ∴x
y +
的取值范围是(-
20. 解:(1)
22
()cos cos sin 2cos 2f x x x x x x x =+-=+
2sin(2)6x π
=+
, 所以函数的最小正周期为
22T π
π=
=.
由
222()
2
6
2
k x k k Z π
π
π
ππ-
+<+
<
+∈得
()
3
6
k x k k Z π
π
ππ-
+<<
+∈
所以函数的单调递增区间为
(,
)()
3
6
k k k Z π
π
ππ-
++∈. 6分
(2)由(A)1f =可得
2sin(2)1
6
A π
+
=,又0A π<<,所以
3A π
=。
由余弦定理可得222
2cos a b c bc A =+-,即22
2
3()3b c bc b c bc =+-=+-又
2
(
)2b c bc +≤,
所以
222
3()3()3(
)2b c b c bc b c +=+-≥+-
,故b c +≤
当且仅当22,
3b c b c bc ⎧=⎪⎨+-=⎪⎩
,即b c ==时等号成立
因此b c +
的最大值为 12分
21. 解:(1)由AD AC ⊥
知,sin sin()cos 2BAC DAB DAB π∠=∠+=∠=
在△ABD 中,由余弦定理知2222cos BD AD AB AB AD BAD =+-⋅∠
即28150AD AD -+=,解得3AD =或5AD = 显然AB AD >,故3AD =.
(2
)由cos DAB ∠=
1
sin 3
BAD ∠= 在△ABD 中,由正弦定理知
sin sin BD AB
BAD ADB
=
∠∠
,故sin ADB ∠=
cos cos()sin 2C ADB ADB π=∠-=∠=.
22.解:(1
时,)(θS 取。
