层次分析法的不同标度word版本解析
层次分析法(详解)
第六章层次分析法决策是人们选择或进行判断的一种思维活动,在人们的实践活动中,常常要对某些系统的重要性作出恰当的评价,以便列出它们的轻重缓急,从而集中解决重要的问题。
有些决策是简单易断的,而有些决策则是复杂困难的,因此常常先把复杂问题分解成因素,然后把这些因素按支配关系分组形成有序的递阶层次结构,并衡量各方面的影响,最后综合人的判断,以决定决策诸因素相对重要性的先后优劣次序,这就是层次分析法的基本思路。
层次分析法的(Analytic Hierarchy Process 简记为AHP)是美国著名的运筹学家T.L.Saaty 教授于70年代初首先提出的一种定性与定量分析相结合的多准则决策方法。
该方法是社会、经济系统决策的有效工具,目前在工程计划、资源分配、方案排序、政策制定、冲突问题、性能评价等方面都有广泛的应用。
6.1 层次分析法的基本原理层次分析法的核心问题是排序,包括递阶层次结构原理、测度原理和排序原理。
下面分别予以介绍。
1.递阶层次结构原理。
一个复杂的结构问题可分解为它的组成部分或因素,即目标、准则、方案等。
每一个因素称为元素。
按照属性的不同把这些元素分组形成互不相交的层次,上一层次的元素对相邻的下一层次的全部或部分元素起支配作用,形成按层次自上而下的逐层支配关系。
具有这种性质的层次称为递阶层次。
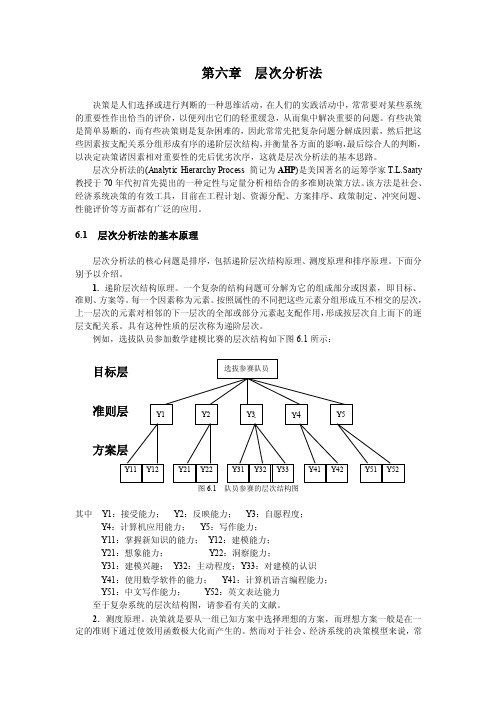
例如,选拔队员参加数学建模比赛的层次结构如下图6.1所示:图6.1 队员参赛的层次结构图其中Y1:接受能力;Y2:反映能力;Y3:自愿程度;Y4:计算机应用能力;Y5:写作能力;Y11:掌握新知识的能力;Y12:建模能力;Y21:想象能力;Y22:洞察能力;Y31:建模兴趣;Y32:主动程度;Y33:对建模的认识Y41:使用数学软件的能力;Y41:计算机语言编程能力;Y51:中文写作能力;Y52:英文表达能力至于复杂系统的层次结构图,请参看有关的文献。
2.测度原理。
决策就是要从一组已知方案中选择理想的方案,而理想方案一般是在一定的准则下通过使效用函数极大化而产生的。
9层次分析法

同样,我们可以通过计算“居住环境”、“结构布局和设施”、 “每平米单价”以及四个标准的两两比较矩阵的一致性检验率CI值, 可知他们都小于等于0.10,这些比较矩阵满足一致性要求,即相应 的特征向量都有效。
①能发挥自己才干作出较好贡献(即工作岗位适合发挥自 己的专长);
②工作收入较好(待遇好); ③生活环境好(大城市、气候等工作条件等); ④单位名声好(声誉等); ⑤工作环境好(人际关系和谐等) ⑥发展晋升机会多(如新单位或前景好)等。
目标层 准则层 方案层
工作选择
贡收 发 声 工 生 作活 环环
献入 展 誉 境 境
• 层次分析法是社会、经济系统决策中的有效工具。其特征是合理地将 定性与定量的决策结合起来,按照思维、心理的规律把决策过程层次 化、数量化。是系统科学中常用的一种系统分析方法。
• 该方法自1982年被介绍到我国以来,以其定性与定量相结合地处理各 种决策因素的特点,以及其系统灵活简洁的优点,迅速地在我国社会 经济各个领域内,如工程计划、资源分配、方案排序、政策制定、冲 突问题、性能评价、能源系统分析、城市规划、经济管理、科研评价 等,得到了广泛的重视和应用。
0.297
0.341
0.396
1.034
0.074 0.057 0.066 0.197
第二步:每个赋权和向量的分量分别除以对应的特征向 量的分量,即第i个赋权和向量的分量除以第i个特征向量
层次分析法详解

构建风险层次结构通过选取的指标可以看出这是一个多目标的且问题涉及到许多因素,各种因素的作用相互,情况复杂。
依据层次分析法处理这类复杂的问题就需要对所涉及的因素指标进行分析:哪些是需相互比较的;哪些是需相互影响的。
把那些需相互比较的因素归成同一类,构造出一个各因素类之间相互联结的层次结构模型。
各因素类的层次级别由其与目标的关系而定:第一层是目标层,也就是国家风险的评价排序第二层是准则层,这一层中是国家风险排序所涉及的国家风险类型,即政治风险、经济风险、社会风险。
第三层是子准则层,这一层是评价衡量准则层中各要素的影响因素及评价指标,即政权凝聚力、腐败状况、相关法律政策、国际关系、官僚主义、经济政策、汇率稳定性、金融环境、内部冲突、外部冲突、民族差异等。
第四层也就是我们要选择的方案即所要选择的并购方案国家。
图5.1风险层次结构模型Fig.5.1 The hierarchical structure model of country risk为了方便计算以及模型的理解,层次结构中各层次均用字母代替,目标层为iA ,准则层为B i ,子准则层为C i ,方案层为D i 。
5.2.2 重要性程度描述为了将上述复杂的多因素综合比较问题转化为简单的两因素相对比较问题。
首先找出所有两两比较的结果,并且把它们定量化;然后再运用适当的数学方法从所有两两相对比较的结果之中求出多因素综合比较的结果。
进行定性的成对比较时,我们将比较结果分为5种等级:相同、稍强、强、明显强、绝对强并将我们所做出的比较结果应用1~9个数字尺度来进行定量化,比较具体含义及相应数字对应如下表:表5.2 AHP重要程度描述表Table 5.2 Described table of AHP important degree 定性比较结果数字定量因素1相较于因素2具有相同的重要性 1因素1与因素2相比,前者重要性稍强 3因素1与因素2相比,前者重要性强 5因素1与因素2相比,前者重要性明显强7因素1与因素2相比,前者重要性绝对强9因素1与因素2相比,相对重要性处于上述等级之间2、4、6、8(续表5.2)定性比较结果数字定量因素1与因素2相比,后者的重要性要稍强、强、明显强、绝对强于前者1/3、1/5、1/7、1/9例如:在准则层中有三个因素政治风险B1、经济风险B2以及社会风险B3,假设如果政治风险B1相较于经济风险B2在风险中的重要性稍强那么就是B1:B2=3:1也就是3。
层次分析法

《运筹学》
例1
大学毕业生就业选择问题 获得大学毕业学位的毕业生,在“双向选择” 时,用人单位与毕业生都有各自的选择标准和要求。 就毕业生来说选择单位的标准和要求是多方面的, 例如: ①能发挥自己才干作出较好贡献(即工作岗位适 合发挥自己的专长); ②工作收入较好(待遇好); ③生活环境好(大城市、气候等工作条件等); ④单位名声好(声誉等); ⑤工作环境好(人际关系和谐等) ⑥发展晋升机会多(如新单位或前景好)等。
允许不一致,但要确定不一致的允许范围
2010年6月
管理工程学院
《运筹学》
w1 考察完全一致的情况 w 1 W ( 1) w1 , w2 ,wn 可作为一个排序向量 w2 w A 成对比较 1 令aij wi / w j 满足 aij a jk aik , i, j, k 1,2,, n wn 的正互反阵A称一致阵。 w1
它是用一定标度把人的主观判断进行客观量化,是将决策有关的元素分解 成目标、准则、方案等层次,在此基础之上进行定性和定量分析的分析方法。
2010年6月
管理工程学院
《运筹学》
层次分析法的特点: 在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基 础上,利用较少的定量信息使决策的思维过程数学化,从而为多目标、多准则
1 A (aij ) nn , aij 0, a ji aij
C2 C3 C4 C5
C3
C4 C5
1/ 2 4 3 3 1 2 1 7 5 5 A 1/ 4 1/ 7 1 1 / 2 1 / 3 1 / 3 1 / 5 2 1 1 3 1 1 1/ 3 1/ 5 要由A确定C1,… , Cn对O的权向量
层次分析法(详细)

1
1/5 1/3 2 6.53
5
1 3 3 20
3
1/3 1 1 7.33
1/2
1/3 1 1 3.83
B
p1 p2
p1
p2
p3
p4
p5
p6
0.16 0.17 0.15 0.20 0.14 0.13 0.16 0.17 0.30 0.20 0.14 0.13
p3
p4 p5 p6
0.16 0.09 0.15 0.25 0.42 0.13
3
1
1
和积法具体计算步骤:
o将判断矩阵的每一列元素作归一 化处理,其元素的一般项为:
bij= bij 1nbij
(i,j=1,2,….n)
B
p1 p2
p1 1 1
p2 1 1
p3 1 2
p4 4 4
p5 1 1
p6 1/2 1/2
p3
p4 p5 p6
1
1/4 1 2 6.25
1/2
1/4 1 2 5.75
层次分析法(AHP)特点: 分析思路清楚,可将系统分析人 员的思维过程系统化、数学化和模 型化; 分析时需要的定量数据不多,但 要求对问题所包含的因素及其关系 具体而明确;
层次分析法(AHP)特点: 这种方法适用于多准则、多目标 的复杂问题的决策分析,广泛用于 物流系统规划与评价、地区经济发 展方案比较、科学技术成果评比、 资源规划和分析以及企业人员素质 测评。
层次分析法(AHP)具体步骤: 建立两两比较的判断矩阵 判断矩阵表示针对上一层次 某单元(元素),本层次与它有关 单元之间相对重要性的比较。一般 取如下形式:
Cs
p1 b11 b21 … … bn1
层次分析法

对于不一致(但在允许范围内)的成对比较阵
A, Saaty等人建议用对应于最大特征根
的特征向量作为权向量w ,即
但允许范围是 多大?如何界 定?
Aw w
3. 层次单排序及其一致性检验
对应于判断矩阵最大特征根λmax的特征向量,经 归一化(使向量中各元素之和等于1)后记为W。
层次分析法应用实例
某单位拟从3名干部中选拔一名领导,选拔的标准 有政策水平、工作作风、业务知识、口才、写作能力 和健康状况。下面用AHP方法对3人综合评估、量化 排序。
⑴建立层次结构模型
目标层
选一领导干部
准则层
健业 康务 状知 况识
写口政工
作才 策作
能
水作
力
平风
方案层
P1
P2
P3
⑵构造成对比较矩阵及 层次单排序
层次分析法(AHP法)建模
• 决策是指在面临多种方案时需要依据一定的标准选 择某一种方案。日常生活中有许多决策问题。举例
• 1. 在海尔、新飞、容声和雪花四个牌号的电冰 箱中选购一种。要考虑品牌的信誉、冰箱的功能、 价格和耗电量。
• 2. 在泰山、杭州和承德三处选择一个旅游点。 要考虑景点的景色、居住的环境、饮食的特色、交 通便利和旅游的费用。
心理学家认为成对比较的因素不宜超过9个,即每层 不要超过9个因素。
判断矩阵元素aij的标度方法
标度 1 3 5 7 9
2,4,6,8 倒数
含义 表示两个因素相比,具有同样重要性 表示两个因素相比,一个因素比另一个因素稍微重要 表示两个因素相比,一个因素比另一个因素明显重要 表示两个因素相比,一个因素比另一个因素强烈重要 表示两个因素相比,一个因素比另一个因素极端重要
3.3 层次分析法

§3.3 层次分析法层次分析法(Analytic Hierarchy Process ,简称AHP ),又称为多层次权重解析方法,是20世纪70年代由美国著名运筹学家、匹兹堡大学T.L.Saaty 教授提出的一种系统分析方法。
该方法将定性分析和定量分析相结合,能够有效分析目标准则体系层次间的非序列关系,对综合测度决策者的判断和比较带来极大的方便,因此在社会经济管理许多方面得到越来越广泛的应用[1-2]。
3.3.1 层次分析法的基本原理层次分析法的基本思路是通过分析复杂系统所包含的因素及相关关系,把一个复杂的问题分解成各个组成因素,并将这些因素按支配关系分组,从而客观上形成多层次的有序的递阶层次结构。
下面以一个例子来说明。
例3.3.1[3] 某城市市中心有一座商场,由于街道狭窄,人员车辆流量过大,经常造成交通堵塞。
市政府决定要改善此处的交通环境,并经过有关专家会商研究,制定出三个可行方案:1P :在商场附近修建一座环形天桥; 2P :在商场附近修建地下人行通道; 3P :搬迁商场。
根据当地的具体条件和有关情况,需要考虑通车能力(1C )、群众方便(2C )、基建费用(3C )、交通安全(4C )和市容美观(5C )等一些准则,通过比较3个候选方案,从中选出最优的方案。
首先考虑这5个准则的重要性。
从缓解交通压力角度来考虑首选通车能力,从市政工程建设角度考虑又得兼顾市容美观,从关注国计民生角度考虑必须考虑群众方便,从公共安全角度思考又得强调交通安全,而如果市政建设费用有限,则必须重点考虑基建费用。
其次,需要就每一个准则对3个方案进行比较。
比如,就基建费用而言,3P 代价最高,2P 次之,1P 最小;就群众方便而言,1P 最佳,2P 次之,3P 最差,等等。
最后,需要将两个层次的判断结果进行综合,在1P 、2P 、3P 中选择最优方案。
上述过程可以归结为以下几步:1.该决策问题可以分为3个层次,最上层为目标层,即改善此处交通环境,选择一个最优方案,最下层为方案层,即包含1P 、2P 、3P 这3个可行方案,中间层为准则层,包含通车能力、群众方便、基建费用、交通安全和市容美观5个准则,每层之间的联系可以用相连的直线表示(如图3.3.1所示)。
层次分析法

层次分析法(Analytic Hierarchy Process,简称AHP)是将与决策总是有关的元素分解成目标、准则、方案等层次,在此基础之上进行定性和定量分析的决策方法。
该方法是美国运筹学家匹茨堡大学教授萨蒂于20世纪70年代初,在为美国国防部研究"根据各个工业部门对国家福利的贡献大小而进行电力分配"课题时,应用网络系统理论和多目标综合评价方法,提出的一种层次权重决策分析方法。
层次分析法的特点是在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上,利用较少的定量信息使决策的思维过程数学化,从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。
尤其适合于对决策结果难于直接准确计量的场合。
选择。
比如选择一个旅游景点时,你可以从宁波、普陀山、浙西大峡谷、雁荡山和楠溪江中选择一个作为自己的旅游目的地,在进行选择时,你所考虑的因素有旅游的费用、旅游的景色、景点的居住条件和饮食状况以及交通状况等等。
这些因素是相互制约、相互影响的。
我们将这样的复杂系统称为一个决策系统。
这些决策系统中很多因素之间的比较往往无法用定量的方式描述,此时需要将半定性、半定量的问题转化为定量计算问题。
层次分析法是解决这类问题的行之有效的方法。
层次分析法将复杂的决策系统层次化,通过逐层比较各种关联因素的重要性来为分析以及最终的决策提供定量的依据。
所谓层次分析法,是指将一个复杂的多目标决策问题作为一个系统,将目标分解为多个目标或准则,进而分解为多指标(或准则、约束)的若干层次,通过定性指标模糊量化方法算出层次单排序(权数)和总排序,以作为目标(多指标)、多方案优化决策的系统方法。
层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体的备投方案的顺序分解为不同的层次结构,然后得用求解判断矩阵特征向量的办法,求得每一层次的各元素对上一层次某元素的优先权重,最后再加权和的方法递阶归并各备择方案对总目标的最终权重,此最终权重最大者即为最优方案。
层次分析法

11.3层次分析法11.3.1方法的由来层次分析法是建立在系统理论基础上的一种解决实际问题的方法。
系统理论认为,世界万物皆系统,而系统是由两个以上的相互联系、相互作用的部分(要素)所组成的具有一定功能的有机整体。
所以在对事物的处理方法上也必然是从整体出发,辨证地处理整体与部分、结构与功能、系统与环境、功能与目标的关系,找到整体最优又不使部分损失过大的方案,以作为决策的依据,实现整体最优化。
现在,人们把系统方法运用在不同的领域内,由于目的的不同,使系统方法获得了不同的名称。
用系统的概念和观点去分析和处理各种与系统有关问题的思考方法称为系统思路、系统思维或系统性原则;以系统的组织建立和经营为特定目的的方法称为系统工程;以系统的总体最优为目标对系统的各个方面进行定性和定量分析,给决策者提供最优系统方案的方法称为系统分析,等等。
可见,系统方法实际上是各种研究系统方法和技术的混合物,是把事物作为系统来研究和处理的各种方法形态、类型及其特殊变种的总称。
系统方法具有3个特征。
(1)整体性系统是由诸多部分或要素组成的有机整体。
系统的整体性质和规律只存在于组成诸要素的相互联系和作用之中,并不等于各组成部分或要素的孤立的性质和活动规律的总和。
(2)综合性就是把任何整体都视为以要素为特定目的而组成的综合体,要求研究任一对象都必须从它的成分、结构、功能、相互联系方式、历史发展等方面进行综合考察,它是把分析与综合有机地结合起来,并从综合出发,在综合的指导下进行分析,然后在回到综合。
(3)优化性通过研究系统的要素,结构及环境的关系,经过科学的计算,预测,作出系统目标的多种方案,从中选择最佳的设计和实施方案以及所能达到的最佳功能目标,同时还要制定最佳控制和进行最优管理。
定性与定量结合是系统方法优化性的保证,而层次分析法恰恰符合上述这些特征。
但这里必须指出的是,人们应用系统方法总希望实现目标最优化,但在通常的情况下完全达到“最优化”是不可能的。
层次分析法

2. 构造判断(成对比较)矩阵
在确定各层次各因素之间的权重时,如果只是定性的结 果,则常常不容易被别人接受,因而Santy等人提出: 一致矩阵法,即: 1. 不把所有因素放在一起比较,而是两两相互比较。 2. 对此时采用相对尺度,以尽可能减少性质不同的诸因
最大特征根=5.073
准则层对目标的成对比较阵
1 1/ 2
2
1
A 1/ 4 1/ 7
1/ 3
1/ 5
1/ 3 1/ 5
4 3 3
7
5
5
1 1/ 2 1/ 3
2
1
1
3 1 1
权向量(特征向量)w =(0.263,0.475,0.055,0.090,0.110)T
一致性指标 CI 5.073 5 0.018 5 1
随机一致性指标 RI=1.12 (查表)
通过一致
一致性比率CR=0.018/1.12=0.016<0.1
性检验
正互反阵最大特征根和特征向量的简化计算
• 精确计算的复杂和不必要
• 简化计算的思路——一致阵的任一列向量都是特征向量,
一致性尚好的正互反阵的列向量都应近似特征向量,可取
其某种意义下的平均。
上述两相邻判断的中值
因素i与j比较的判断aij,则因素j与i比较的判断aji=1/aij
目标层
O(选择旅游地)
准则层
C1 景色
C2 费用
C3 居住
C4 饮食
C5 旅途
设要比较各准则C1,C2,… , Cn对目标O的重要性
层次分析法(AHP)解析

层次分析法(AHP)对于草地农业生态系统这个涉及复杂的社会、经济、生态问题的系统,过去的系统分析与设计常常凭经验,靠主观判断进行,缺乏应有的科学性,因而往往造成重大失误。
层次分析法是一种新的定性分析与定量分析相结合的系统分析方法,是将人的主观判断用数量形式表达和处理的方法,简称AHP(The Analytic Hierarchy Process)法。
近年来,层次分析法在草地农业生态系统的系统分析、设计与决策中日益受到重视。
1层次分析法的基本方法和步骤层次分析法是把复杂问题分解成各个组成因素,又将这些因素按支配关系分组形成递阶层次结构。
通过两两比较的方式确定各个因素相对重要性,然后综合决策者的判断,确定决策方案相对重要性的总排序。
运用层次分析法进行系统分析、设计、决策时,可分为4个步骤进行;(1)分析系统中各因素之间的关系,建立系统的递阶层次结构;(2)对同一层次的各元素关于上一层中某一准则的重要性进行两两比较,构造两两比较的判断矩阵;(3)由判断矩阵计算被比较元素对于该准则的相对权重;(4)计算各层元素对系统目标的合成权重,并进行排序,2递阶层次结构的建立首先把系统问题条理化、层次化,构造出一个层次分析的结构模型。
在模型中,复杂问题被分解,分解后各组成部分称为元素,这些元素又按属性分成若干组,形成不同层次。
同一层次的元素作为准则对下一层的某些元素起支配作用,同时它又受上面层次元素的支配。
层次可分为三类;(1)最高层:这一层次中只有一个元素,它是问题的预定目标或理想结果,因此也叫目标层;(2)中间层:这一层次包括要实现目标所涉及的中间环节中需要考虑的准则。
该层可由若干层次组成,因而有准则和子准则之分,这一层也叫准则层;(3)最底层:这一层次包括为实现目标可供选择的各种措施、决策方案等,因此也称为措施层或方案层。
上层元素对下层元素的支配关系所形成的层次结构被称为递阶层次结构。
当然,上一层元素可以支配下层的所有元素,但也可只支配其中部分元素。
层次分析法的计算步骤(可编辑修改word版)

8.3.2 层次分析法的计算步骤一、建立层次结构模型运用AHP 进行系统分析,首先要将所包含的因素分组,每一组作为一个层次,把问题条理化、层次化,构造层次分析的结构模型。
这些层次大体上可分为3 类1、最高层:在这一层次中只有一个元素,一般是分析问题的预定目标或理想结果,因此又称目标层;2、中间层:这一层次包括了为实现目标所涉及的中间环节,它可由若干个层次组成,包括所需要考虑的准则,子准则,因此又称为准则层;3、最底层:表示为实现目标可供选择的各种措施、决策、方案等,因此又称为措施层或方案层。
层次分析结构中各项称为此结构模型中的元素,这里要注意,层次之间的支配关系不一定是完全的,即可以有元素(非底层元素)并不支配下一层次的所有元素而只支配其中部分元素。
这种自上而下的支配关系所形成的层次结构,我们称之为递阶层次结构。
递阶层次结构中的层次数与问题的复杂程度及分析的详尽程度有关,一般可不受限制。
为了避免由于支配的元素过多而给两两比较判断带来困难,每层次中各元素所支配的元素一般地不要超过9 个,若多于9 个时,可将该层次再划分为若干子层。
例如,大学毕业的选择问题,毕业生需要从收入、社会地位及发展机会方面考虑是否留校工作、读研究生、到某公司或当公务员,这些关系可以将其划分为如图8.1 所示的层次结构模型。
图8.1再如,国家综合实力比较的层次结构模型如图6 .2:图 6 .2图中,最高层表示解决问题的目的,即应用AHP 所要达到的目标;中间层表示采用某种措施和政策来实现预定目标所涉及的中间环节,一般又分为策略层、约束层、准则层等;最低层表示解决问题的措施或政策(即方案)。
然后,用连线表明上一层因素与下一层的联系。
如果某个因素与下一层所有因素均有联系,那么称这个因素与下一层存在完全层次关系。
有时存在不完全层次关系,即某个因素只与下一层次的部分因素有联系。
层次之间可以建立子层次。
子层次从属于主层次的某个因素。
它的因素与下一层次的因素有联系,但不形成独立层次,层次结构模型往往有结构模型表示。
层次分析法

层次分析法(AHP)对于草地农业生态系统这个涉及复杂的社会、经济、生态问题的系统,过去的系统分析与设计常常凭经验,靠主观判断进行,缺乏应有的科学性,因而往往造成重大失误。
层次分析法是一种新的定性分析与定量分析相结合的系统分析方法,是将人的主观判断用数量形式表达和处理的方法,简称AHP(The Analytic Hierarchy Process)法。
近年来,层次分析法在草地农业生态系统的系统分析、设计与决策中日益受到重视。
1层次分析法的基本方法和步骤层次分析法是把复杂问题分解成各个组成因素,又将这些因素按支配关系分组形成递阶层次结构。
通过两两比较的方式确定各个因素相对重要性,然后综合决策者的判断,确定决策方案相对重要性的总排序。
运用层次分析法进行系统分析、设计、决策时,可分为4个步骤进行;(1)分析系统中各因素之间的关系,建立系统的递阶层次结构;(2)对同一层次的各元素关于上一层中某一准则的重要性进行两两比较,构造两两比较的判断矩阵;(3)由判断矩阵计算被比较元素对于该准则的相对权重;(4)计算各层元素对系统目标的合成权重,并进行排序,2递阶层次结构的建立首先把系统问题条理化、层次化,构造出一个层次分析的结构模型。
在模型中,复杂问题被分解,分解后各组成部分称为元素,这些元素又按属性分成若干组,形成不同层次。
同一层次的元素作为准则对下一层的某些元素起支配作用,同时它又受上面层次元素的支配。
层次可分为三类;(1)最高层:这一层次中只有一个元素,它是问题的预定目标或理想结果,因此也叫目标层;(2)中间层:这一层次包括要实现目标所涉及的中间环节中需要考虑的准则。
该层可由若干层次组成,因而有准则和子准则之分,这一层也叫准则层;(3)最底层:这一层次包括为实现目标可供选择的各种措施、决策方案等,因此也称为措施层或方案层。
上层元素对下层元素的支配关系所形成的层次结构被称为递阶层次结构。
当然,上一层元素可以支配下层的所有元素,但也可只支配其中部分元素。
层次分析法详解

构建风险层次结构通过选取的指标可以看出这是一个多目标的且问题涉及到许多因素,各种因素的作用相互,情况复杂。
依据层次分析法处理这类复杂的问题就需要对所涉及的因素指标进行分析:哪些是需相互比较的;哪些是需相互影响的。
把那些需相互比较的因素归成同一类,构造出一个各因素类之间相互联结的层次结构模型。
各因素类的层次级别由其与目标的关系而定:第一层是目标层,也就是国家风险的评价排序第二层是准则层,这一层中是国家风险排序所涉及的国家风险类型,即政治风险、经济风险、社会风险。
第三层是子准则层,这一层是评价衡量准则层中各要素的影响因素及评价指标,即政权凝聚力、腐败状况、相关法律政策、国际关系、官僚主义、经济政策、汇率稳定性、金融环境、内部冲突、外部冲突、民族差异等。
第四层也就是我们要选择的方案即所要选择的并购方案国家。
图5.1风险层次结构模型Fig.5.1 The hierarchical structure model of country risk为了方便计算以及模型的理解,层次结构中各层次均用字母代替,目标层为iA ,准则层为B i ,子准则层为C i ,方案层为D i 。
5.2.2 重要性程度描述为了将上述复杂的多因素综合比较问题转化为简单的两因素相对比较问题。
首先找出所有两两比较的结果,并且把它们定量化;然后再运用适当的数学方法从所有两两相对比较的结果之中求出多因素综合比较的结果。
进行定性的成对比较时,我们将比较结果分为5种等级:相同、稍强、强、明显强、绝对强并将我们所做出的比较结果应用1~9个数字尺度来进行定量化,比较具体含义及相应数字对应如下表:表5.2 AHP重要程度描述表Table 5.2 Described table of AHP important degree 定性比较结果数字定量因素1相较于因素2具有相同的重要性 1因素1与因素2相比,前者重要性稍强 3因素1与因素2相比,前者重要性强 5因素1与因素2相比,前者重要性明显强7因素1与因素2相比,前者重要性绝对强9因素1与因素2相比,相对重要性处于上述等级之间2、4、6、8(续表5.2)定性比较结果数字定量因素1与因素2相比,后者的重要性要稍强、强、明显强、绝对强于前者1/3、1/5、1/7、1/9例如:在准则层中有三个因素政治风险B1、经济风险B2以及社会风险B3,假设如果政治风险B1相较于经济风险B2在风险中的重要性稍强那么就是B1:B2=3:1也就是3。
层次分析法

由以上步骤求得一级(大类)指标 相对于目标G的权重为 ,则一级(大类)指标的权重分配向量 。二级指标 相对于一级指标 的相对权重为 ,则所属指标 的二级评价指标的相对权重分配向量 。
两个指标其中一个稍微重要
5
两个指标其中一个明显重要
7
两个指标其中一个强烈重要
9
两个指标其中一个极端重要
2,4,6,8
介于以上两相邻判断的中值
倒数
指标 与 相次单排序主要内容是指根据上层指标是否对本层指标有支配关系,并对本层指标按其被上层指标支配关系的紧密程度确定其本层次指标判断矩阵,并依此矩阵计算特征值和特征向量。如对航道整治工程项目管理绩效评价的准则层 的判断矩阵的计算应满足公式 的条件下,根据计算公式可求得矩阵的最大特征值 以及与之相对应的进行归一化处理过的特征向量 ,则求得的特征向量即为 对于上一层次元素G的单排序的权值。
表4-3 9阶判断矩阵值
矩阵阶数
1
2
3
4
5
6
7
8
9
0.00
0.00
0.58
0.90
1.12
1.24
1.32
1.41
1.45
如若判断矩阵是一阶、二阶时,数理上已经证明其总是一致的,因此不需要一致性检验。当判断矩阵为三阶及以上时需要选取 的值表示判断矩阵的随机一致性程度。当求得的值 就认为矩阵一致性可接受,此时 的大小即为 的重要性程度,如若 的值不满足上述条件,则需要调整判断矩阵,再进行检验。调整判断矩阵即重新估计 。同样的方法也可得到V层相对于U层元素 的单排序权值为 。
1、构造判断矩阵
通过判断相邻层次的指标即下层指标对于上层指标的相对重要程度,建立指标权重的判断矩阵。对于本文建立的指标体系而言,G层的指标G与下一层次U中的 具有相关性,则将构造的判断矩阵如下:
层次分析法中几种标度的比较

了自己的 t 的值 5 _ 关于标度问题研究 . 国内学者所做的工作基本上沿着以下两条路 线 % 一种方 法是 通过给 出新标 度 . 力 图 使决策者 + 专家 , 能够容易地填写比 较矩 阵 . 然 后 利用 某种 变换 . 将比 较矩阵 变换成 B 2 $标 度 < < > E的 & 法下的判断矩阵 . 如三标度法和五标度法 1 另一种方法是利用给出的新标度 . 直接构造判断矩阵 + 无需再转 换成 B 以 期 改 善 判 断 矩 阵 的 一 致 性. 如各种指数标度法和分数标度 2 $标 度 法 下 的 判 断 矩 阵 , . < < > E的 &
万方数据
D < 法!
系统工程理论与实践
< : : >年 .月
然而" 随着众多新标度的出现 " 给 #$%法的应用也带来一些困难 ! 这是因为 " 面对各种标度 " 人们 一 般并不知道哪一种标度孰优孰劣 ! 令人更为烦恼的是 " 对于某一排序问题 " 采用的标度不同 " 不仅会得到 甚至会得出不同的排序 ! 由此可见 " 建立一套行之有效的标度评价标准 " 已经成为当前 #$% 不同的权重 " 法研究的一项紧迫任务 !目前关于标度的评价 " 主要是利用一致性指标作为主要依据 !但仅用一致性作为 评价标准 " 似乎尚不足以说明某种标度优劣 ! 基于此 " 本文将提出一套标准 " 如保序性 & 判断一致性 & 标度均 匀性 & 标度可记忆性 " 标度可感知性 ’ 标度易操作性 ( 标度权重拟合性等 " 并对各种标度进行了评价 ! &
