第十章补充计算题及参考答案

合集下载

《结构力学》习题集及答案（下册）第十章结构弹性稳定计算

第十章结构弹性稳定计算一、判断题：1、稳定方程即是根据稳定平衡状态建立的平衡方程。

2、压弯杆件和承受非结点荷载作用的刚架丧失稳定都属于第一类失稳。

3、在稳定分析中，有n 个稳定自由度的结构具有n 个临界荷载。

4、两类稳定问题的主要区别是：荷载—位移曲线上是否出现分支点。

5、静力法确定临界荷载的依据是结构失稳时的静力平衡条件。

6、能量法确定临界荷载的依据是势能驻值原理。

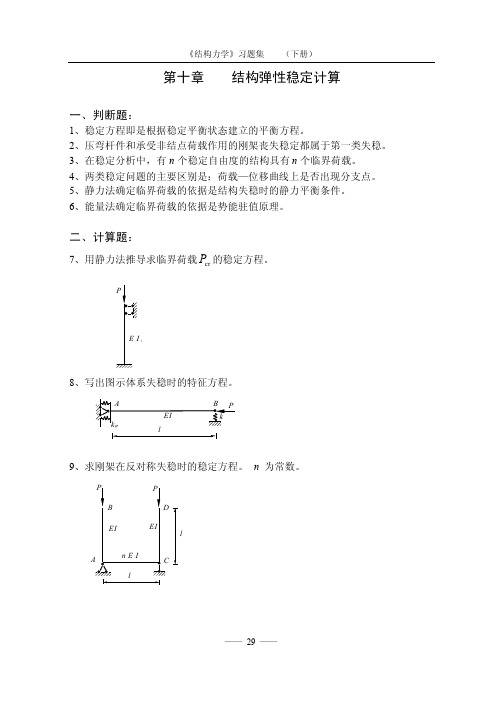
二、计算题：7、用静力法推导求临界荷载cr P 的稳定方程。

PE I ,l8、写出图示体系失稳时的特征方程。

k lEIk AB P9、求刚架在反对称失稳时的稳定方程。

n 为常数。

l Pl P n E IEIEI A C BD10、求图示完善体系的临界荷载cr P 。

转动刚度kl k r 2=，k 为弹簧刚度。

P l k r kl kEIO O EI O O11、求图示刚架的临界荷载cr P 。

已知弹簧刚度l EI k 33= 。

PEIlA BC lO O 0EI k12、求图示中心受压杆的临界荷载cr P 。

PEI l13、用静力法求图示结构的临界荷载cr P ，欲使B 铰不发生水平移动，求弹性支承的最小刚度k 值。

PlEI A Bk14、用静力法确定图示具有下端固定铰，上端滑动支承压杆的临界荷载crP。

P PEI yxδly15、用能量法求图示结构的临界荷载参数crP。

设失稳时两柱的变形曲线均为余弦曲线：yxh=-δπ(cos).12提示：cos d sin22u u u uabab⎰=+⎡⎣⎢⎤⎦⎥214。

PEIP2EI h3EA16、用能量法求中心受压杆的临界荷载crP与计算长度,BC段为刚性杆，AB段失稳时变形曲线设为：()y x a xxl=-().32EIPllEIABCyx→∞17、用能量法求图示体系的临界荷载cr P 。

l PEIEI 1=H18、用能量法求图示中心压杆的临界荷载cr P ，设变形曲线为正弦曲线。

高二物理第十章练习题及答案

高二物理第十章练习题及答案第一节选择题1. 下列选项中，不属于物理学家提出的克服摩擦阻力的方法的是：A. 使用滑润剂B. 降低物体表面的蓄热系数C. 增大物体和地面的接触面积D. 使用滑轮组答案：B2. 一块质量为1kg的木块，静止不动地放在水平地面上。

现有一个100N的平行于地面的力作用于木块上，木块开始滑动。

摩擦系数为0.2，计算摩擦力的大小是多少？A. 5NB. 10NC. 15ND. 20N答案：B3. 有一物体沿着水平方向运动，速度由v1增加到v2，则物体所受到的摩擦力：A. 增大B. 减少C. 不变D. 无法确定答案：A第二节填空题1. 摩擦力的方向是__________运动方向的__________方向。

答案：相反；正2. 一个质量为500 g的木块在水平地面上受到的摩擦力是20 N，计算摩擦系数的大小。

答案：0.43. 若物体受到的摩擦力与物体所受的压力成正比，比例系数为0.2，则当物体受到100 N的压力时，摩擦力的大小为__________。

答案：20 N第三节计算题1. 一质量为2 kg的物体在水平地面上受到20 N的外力作用下静止不动，求物体与地面之间的摩擦力大小。

答案：20 N2.以水平地面为参考系，一质量为3 kg的物体受到12 N的外力作用下保持匀速运动，摩擦系数为0.4，求物体的加速度。

答案：0 m/s^23. 一个质量为5 kg的箱子放在水平地面上，初速度为0 m/s，受到20 N的外力作用下匀加速运动，求箱子移动5 m所需的时间。

答案：1 s第四节解答题1. 什么是摩擦力？摩擦力有哪些特点？答案：摩擦力是指物体相对运动或者相对静止的两个接触面之间产生的阻碍运动的力。

摩擦力的特点包括：与物体所受压力成正比；与物体间的接触面积有关；与物体表面的粗糙程度有关；与速度无关（对于低速运动）。

2. 摩擦力可以有哪些应用？请举例说明。

答案：摩擦力可以有以下应用：a. 制动器的工作原理：汽车、自行车等的制动器利用摩擦力将运动的车轮减速或停止。

大学无机化学第十章试题及答案完整版

大学无机化学第十章试题及答案Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】第十章配位化合物本章总目标：1：掌握配合物的基本概念和配位键的本质2：掌握配合物的价键理论的主要论点，并能用此解释一些实例3：配离子稳定常数的意义和应用4：配合物形成时性质的变化。

各小节目标：第一节：配位化合物的基本概念1：掌握中心原子、配体、配位原子、配位键、配位数、螯合物等概念，○1配位单元：由中心原子（或离子）和几个配位分子（或离子）以配位键向结合而形成的复杂分子或离子。

○2配位化合物：含有配位单元的化合物。

○3配位原子：配体中给出孤电子对与中心直接形成配位键的原子。

○4配位数：配位单元中与中心直接成键的配位原子的个数。

2：学会命名部分配合物，重点掌握命名配体的先后顺序：（1）先无机配体后有机配体（2）先阴离子配体，后分子类配体（3）同类配体中，先后顺序按配位原子的元素符号在英文字母表中的次序（4）配位原子相同时，配体中原子个数少的在前（5）配体中原子个数相同，则按和配位原子直接相连的其它原子的元素符号的英文字母表次序；3：了解配合物的结构异构和立体异构现象第二节：配位化合物的价键理论1：熟悉直线形、三角形、正方形、四面体、三角双锥、正八面体构型的中心杂化类型。

2：会分辨内轨型和外轨型配合物。

可以通过测定物质的磁矩来计算单电子数μ=。

3：通过学习羰基配合物、氰配合物以及烯烃配合物的d pπ-配键来熟悉价键理论中的能量问题。

第三节：配合物的晶体场理论1：掌握配合物的分裂能、稳定化能概念 2：掌握配合物的晶体场理论。

3;了解影响分裂能大小的因素 ○1）晶体场的对称性0pt ∆>∆>∆○2中心离子的电荷数，中心离子的电荷高，与配体作用强，∆大。

○3中心原子所在的周期数，对于相同的配体，作为中心的过渡元素所在的周期数大，∆相对大些。

（4）配体的影响，配体中配位原子的电负性越小，给电子能力强，配体的配位能力强，分裂能大。

第十章企业所得税作业及参考答案

第十章企业所得税作业及参考答案第十章企业所得税作业与答案一、单项选择题1．下列单位不属于企业所得税纳税人的是( )。

A．股份制企业 B．合伙企业 C．外商投资企业 D．有经营所得的其他组织2．依据企业所得税法的规定，下列各项所得中，按负担、支付所得的企业或机构、场所所在地或者个人的住所所在地确定所得来源地的是( )。

A．提供劳务所得 B．转让房屋所得 C．权益性投资所得 D．特许权使用费所得3．根据企业所得税的相关规定，纳税人的下列收入中，按照公允价值确定收入的是 ( )。

A．债务的豁免C．应收票据B．准备持有到期的债券投资D．不准备持有到期的债券投资4．以下关于企业所得税收入确认时间的表述正确是( )。

A．股息、红利等权益性投资收益，以投资方收到分配金额作为收入的实现B．利息收入，按照合同约定的债务人应付利息的日期确认收入的实现C．租金收入，在实际收到租金收入时确认收入的实现D．特许权使用费收入，在实际收到使用费收入时确认收入的实现5．按照企业所得税的相关规定，下列关于商品销售收入的确认正确的是( )。

A．销售商品采用托收承付方式的，在发出商品时确认收入B．销售商品采取预收款方式的，在收到预收款时确认收入C．销售商品采用支付手续费方式委托代销的，在收到代销清单时确认收入D．企业以买一赠一方式组合销售本企业商品的，对赠品按照捐赠行为进行税务处理6．纳税人在计算企业所得税应纳税所得额时，以下项目中，不超过规定比例的准予在税前扣除，超过部分，准予在以后纳税年度结转扣除的是( )。

A．职工福利费 B．工会经费 C．职工教育经费 D．社会保险费7．某公司2011年度“财务费用”账户中利息金额，含有以年利率8％向银行借入的9个月期的生产用200万元贷款的借款利息；也包括12万元的向本企业职工借入与银行同期的生产用100万元资金的借款利息。

假设向企业职工的借款，双方签订了借款合同，也取得了相关合法票据。

该公司2011年度在计算应纳税所得额时允许扣除的利息费用是( ) 万元。

高等数学课后习题及参考答案(第十章)

高等数学课后习题及参考答案（第十章）习题 10-11. 设在xOy 面内有一分布着质量的曲线弧L , 在点(x , y )处它的线密度为μ(x , y ), 用对弧长的曲线积分分别表达:(1)这曲线弧对x 轴、对y 轴的转动惯量I x , I y ; (2)这曲线弧的重心坐标x , y .解在曲线弧L 上任取一长度很短的小弧段ds (它的长度也记做ds ), 设(x , y )为小弧段ds 上任一点.曲线L 对于x 轴和y 轴的转动惯量元素分别为 dI x =y 2μ(x , y )ds , dI y =x 2μ(x , y )ds . 曲线L 对于x 轴和y 轴的转动惯量分别为 ⎰=Lx ds y x y I ),(2μ, ⎰=Ly ds y x x I ),(2μ.曲线L 对于x 轴和y 轴的静矩元素分别为 dM x =y μ(x , y )ds , dM y =x μ(x , y )ds . 曲线L 的重心坐标为⎰⎰==L L y dsy x ds y x x M M x ),(),(μμ, ⎰⎰==LL x ds y x dsy x y M M y ),(),(μμ. 2. 利用对弧长的曲线积分的定义证明: 如果曲线弧L 分为两段光滑曲线L 1和L 2, 则⎰⎰⎰+=12),(),(),(LL L ds y x f ds y x f ds y x f .证明划分L , 使得L 1和L 2的连接点永远作为一个分点, 则∑∑∑+===∆+∆=∆111111),(),(),(n n i i i i ni n i i i i i i i s f s f s f ηξηξηξ.令λ=max{∆s i }→0, 上式两边同时取极限∑∑∑+=→=→=→∆+∆=∆nn i i i i n i i i i ni i i i s f s f s f 111011),(lim),(lim ),(lim ηξηξηξλλλ,即得⎰⎰⎰+=12),(),(),(LL L ds y x f ds y x f ds y x f .3. 计算下列对弧长的曲线积分:(1)⎰+Ln ds y x )(22, 其中L 为圆周x =a cos t , y =a sin t (0≤t ≤2π);解⎰+L nds y x)(22⎰+-+=π20222222)cos ()sin ()sin cos (dt t a t a t a t a n=⎰+-+π20222222)cos ()sin ()sin cos (dt t a t a t a t a n ⎰++==ππ2012122n n a dt a .(2)⎰+Lds y x )(, 其中L 为连接(1, 0)及(0, 1)两点的直线段;解 L 的方程为y =1-x (0≤x ≤1);⎰⎰'-+-+=+102])1[(1)1()(dx x x x ds y x L22)1(1=-+=⎰dx x x .(3)xdx L⎰, 其中L 为由直线y =x 及抛物线y =x 2所围成的区域的整个边界; 解 L 1: y =x 2(0≤x ≤1), L 2: y =x (0≤x ≤1) .xdx L ⎰xdx xdx LL ⎰⎰+=21⎰⎰'++'+=102122)(1])[(1dx x x dx x x⎰⎰++=10102241xdx dx x x )12655(121-+=.(4)ds ey x L22+⎰, 其中L 为圆周x 2+y 2=a 2, 直线y =x 及x 轴在第一象限内所围成的扇形的整个边界; 解 L =L 1+L 2+L 3, 其中 L 1: x =x , y =0(0≤x ≤a ),L 2: x =a cos t , y =a sin t )40(π≤≤t ,L 3: x =x , y =x )220(a x ≤≤,因而ds eds eds eds ey x L y x L y x L y x L22322222122++++⎰⎰⎰⎰++=,⎰⎰⎰+++-++=axa ax dx e dt t a t a e dx e 220222402202211)cos ()sin (01π2)42(-+=a e a π.(5)⎰Γ++ds z y x 2221, 其中Γ为曲线x =e t cos t , y =e t sin t , z =e t 上相应于t 从0变到2的这段弧;解 dt dtdz dt dydt dx ds 222)()()(++=dt e t e t e t e t e t t t t t 222)cos sin ()sin cos (+++-=dt e t 3=,⎰⎰++=++Γ20222222223sin cos 11dt e et e t e ds z y x t t t t ⎰----=-==2220)1(23]23[23e e dt e t t .(6)⎰Γyzds x 2, 其中Γ为折线ABCD , 这里A 、B 、C 、D 依次为点(0, 0, 0)、 (0, 0, 2)、(1, 0, 2)、(1, 3, 2); 解 Γ=AB +BC +CD , 其中 AB : x =0, y =0, z =t (0≤t ≤1), BC : x =t , y =0, z =2(0≤t ≤3), CD : x =1, y =t , z =2(0≤t ≤3), 故yzds x yzds x yzds x yzds x CD BC AB 2222⎰⎰⎰⎰++=Γ9010200322231=++++=⎰⎰⎰dt t dt dt .(7)⎰Lds y 2, 其中L 为摆线的一拱x =a (t -sin t ), y =a (1-cos t )(0≤t ≤2π);解⎰⎰'+'--=L dt t a t t a t a ds y π2022222])(cos [])sin ([)cos 1(⎰--=π2023cos 1)cos 1(2dt t t a 315256a =.(8)⎰+Lds y x )(22, 其中L 为曲线x =a (cos t +t sin t ), y =a (sin t -t cos t )(0≤t ≤2π).解 dt dtdydt dx ds 22)()(+=atdt dt t at t at =+=22)sin ()cos (atdt t t t a t t t a ds y x L ])cos (sin )sin (cos [)(22202222-++=+⎰⎰π⎰+=+=πππ2023223)21(2)1(a tdt t a .4. 求半径为a , 中心角为2ϕ的均匀圆弧(线密度μ=1)的重心. 解建立坐标系如图10-4所示, 由对称性可知0=y , 又 ⎰==L x xds a M M x ϕ21⎰-⋅=ϕϕθθϕad a a cos 21ϕϕsin a =, 所以圆弧的重心为)0 ,sin (ϕϕa5. 设螺旋形弹簧一圈的方程为x =a cos t , y =a sin t , z =kt , 其中0≤1≤2π, 它的线密度ρ(x , y , z )=x 2+y 2+z 2, 求:(1)它关于z 轴的转动惯量I z ; (2)它的重心. 解 dt t z t y t x ds )()()(222'+'+'=dt k a 22+=. (1)⎰+=Lz ds z y x y x I ),,()(22ρds z y x y x L))((22222+++=⎰dt k a t k a a ⎰++=π20222222)()43(32222222k a k a a ππ++=. (2)⎰⎰++==LLds z y x ds z y x M )(),,(222ρ⎰++=π2022222)(dt k a t k a)43(3222222k a k a ππ++=, ds z y x x M x L)(1222⎰++=⎰++=π2022222)(cos 1dt k a t k a t a M2222436k a ak ππ+=, ds z y x y M y L)(1222⎰++=⎰++=π2022222)(sin 1dt k a t k a t a M2222436k a ak ππ+-=, ds z y x z M z L)(1222⎰++=⎰++=π2022222)(1dt k a t k a kt M22222243)2(3k a k a k πππ++=,故重心坐标为)43)2(3 ,436 ,436(22222222222222k a k a k k a ak k a ak πππππππ+++-+.习题 10-21. 设L 为xOy 面内直线x =a 上的一段, 证明:⎰=L dx y x P 0),(.证明设L 是直线x =a 上由(a , b 1)到(a , b 2)的一段, 则L : x =a , y =t , t 从b 1变到b 2. 于是00) ,())( ,(),(2121⎰⎰⎰=⋅==b b b b L dt t a P dt dtda t a P dx y x P . 2. 设L 为xOy 面内x 轴上从点(a , 0)到(b , 0)的一段直线, 证明⎰⎰=Lbadx x P dx y x P )0 ,(),(.证明L : x =x , y =0, t 从a 变到b , 所以⎰⎰⎰='=baL b adx x P dx x x P dx y x P )0 ,())(0 ,(),(.3. 计算下列对坐标的曲线积分:(1)⎰-Ldx y x )(22, 其中L 是抛物线y =x 2上从点(0, 0)到点(2, 4)的一段弧;解 L : y =x 2, x 从0变到2, 所以⎰⎰-=-=-L dx x x dx y x2042221556)()(.(2)⎰Lxydx , 其中L 为圆周(x -a )2+y 2=a 2(a >0)及x 轴所围成的在第一象限内的区域的整个边界(按逆时针方向绕行); 解 L =L 1+L 2, 其中L 1: x =a +a cos t , y =a sin t , t 从0变到π, L 2: x =x , y =0, x 从0变到2a , 因此⎰⎰⎰+=21L L L xydx xydx xydx⎰⎰+'++=adx dt t a a t a t a 200)cos (sin )cos 1(π3020232)sin sin sin (a t td tdt a πππ-=+-=⎰⎰.(3)⎰+Lxdy ydx , 其中L 为圆周x =R cos t , y =R sin t 上对应t 从0到2π的一段弧;解 ⎰⎰+-=+L dt t tR R t R t R xdy ydx ]cos cos )sin (sin [20π⎰==20202cos πtdt R .(4)⎰+--+L y x dy y x dx y x 22)()(, 其中L 为圆周x 2+y 2=a 2(按逆时针方向绕行);解圆周的参数方程为: x =a cos t , y =a sin t , t 从0变到2π, 所以⎰+--+L yx dyy x dx y x 22)()( ⎰---+=π202)]cos )(sin cos ()sin )(sin cos [(1dt t a t a t a t a t a t a a ⎰-=-=ππ202221dt a a .(5)ydz zdy dx x -+⎰Γ2, 其中Γ为曲线x =k θ, y =a cos θ, z =a sin θ上对应θ从0到π的一段弧; 解⎰⎰--+=-+Γπθθθθθθ022]cos cos )sin (sin )[(d a a a a k k ydz zdy dx x233220331)(a k d a k ππθθπ-=-=⎰.(6)dz y x ydy xdx )1(-+++⎰Γ, 其中Γ是从点(1, 1, 1)到点(2, 3, 4)的一段直线;解 Γ的参数方程为x =1+t , y =1+2t , z =1+3t , t 从0变到1.⎰Γ-+++dz y x ydy xdx )1(⎰-+++++++=1)]1211(3)21(2)1[(dt t t t t⎰=+=1013)146(dt t .(7)⎰Γ+-ydz dy dx , 其中Γ为有向闭折线ABCA , 这里的A , B , C依次为点(1, 0, 0), (0, 1, 0), (0, 0, 1); 解 Γ=AB +BC +CA , 其中AB : x =x , y =1-x , z =0, x 从1变到0, BC : x =0, y =1-z , z =z , z 从0变到1, CA : x =x , y =0, z =1-x , x 从0变到1, 故ydz dy dx ydz dy dx ydz dy dx ydz dy dx CA BC AB +-++-++-=+-⎰⎰⎰⎰Γ⎰⎰⎰+-+'--+'--=101010)]1()1([])1(1[dx dt z z dx x 21=.(8)dy xy y dx xy x L)2()2(22-+-⎰, 其中L 是抛物线y =x 2上从(-1, 1)到(1, 1)的一段弧.解 L : x =x , y =x 2, x 从-1变到1, 故⎰-+-L dy xy y dx xy x )2()2(22⎰--+-=113432]2)2()2[(dx x x x x x 1514)4(21042-=-=⎰dx x x 4. 计算⎰-++Ldy x y dx y x )()(, 其中L 是:(1)抛物线y =x 2上从点(1, 1)到点(4, 2)的一段弧; 解 L : x =y 2, y =y , y 从1变到2, 故⎰-++L dy x y dx y x )()(⎰=⋅-+⋅+=2122334]1)(2)[(dy y y y y y . (2)从点(1, 1)到点(4, 2)的直线段; 解 L : x =3y -2, y =y , y 从1变到2, 故⎰-++L dy x y dx y x )()(11]1)23()23[(21=⋅+-+⋅+-=⎰dy y y y y y(3)先沿直线从点(1, 1)到(1, 2), 然后再沿直线到点(4, 2)的折线; 解 L =L 1+L 2, 其中L 1: x =1, y =y , y 从1变到2, L 2: x =x , y =2, x 从1变到4, 故⎰-++L dy x y dx y x )()(dy x y dx y x dy x y dx y x L L )()()()(21-+++-++=⎰⎰14)2()1(4121=++-=⎰⎰dx x dy y .(4)沿曲线x =2t 2+t +1, y =t 2+1上从点(1, 1)到(4, 2)的一段弧. 解 L : x =2t 2+t +1, y =t 2+1, t 从0变到1, 故⎰-++L dy x y dx y x )()(332]2)()14)(23[(1022=⋅--++++=⎰dt t t t t t t .5. 一力场由沿横轴正方向的常力F 所构成, 试求当一质量为m 的质点沿圆周x 2+y 2=R 2按逆时针方向移过位于第一象限的那一段时场力所作的功.解已知场力为F =(|F |, 0), 曲线L 的参数方程为 x =R cos θ, y =R sin θ,θ从0变到2π, 于是场力所作的功为R F d R F dx F d W LL||)sin (||||20-=-⋅==⋅=⎰⎰⎰πθθr F .6. 设z 轴与力方向一致, 求质量为m 的质点从位置(x 1, y 1, z 1) 沿直线移到(x 2, y 2, z 2)时重力作的功.解已知F =(0, 0, mg ). 设Γ为从(x 1, y 1, z 1)到(x 2, y 2, z 2)的直线, 则重力所作的功为⎰⎰⎰ΓΓ-==++=⋅=21)(0012z z z z mg dz mg mgdz dy dx d W r F .7. 把对坐标的曲线积分⎰+Ldy y x Q dx y x P ),(),(化成对弧长的曲线积分, 其中L 为:(1)在xOy 面内沿直线从点(0, 0)到(1, 1); 解 L 的方向余弦214cos cos cos ===πβα,故⎰+L dy y x Q dx y x P ),(),(ds y x Q y x P L]cos ),(cos ),([βα+=⎰⎰+=L ds y x Q y x P 2),(),(.(2)沿抛物线y =x 2从点(0, 0)到(1, 1);解曲线L 上点(x , y )处的切向量为τ=(1, 2x ), 单位切向量为 )412,411()cos ,(cos 22x x x ++==τβαe ,故⎰+L dy y x Q dx y x P ),(),(ds y x Q y x P L ]cos ),(cos ),([βα+=⎰⎰++=L ds xy x xQ y x P 241),(2),(. (3)沿上半圆周x 2+y 2=2x 从点(0, 0)到(1, 1). 解 L 的方程为22x x y -=, 其上任一点的切向量为 )21 ,1(2x x x --=τ, 单位切向量为)1 ,2()cos ,(cos 2x x x --==τβαe ,故⎰+L dy y x Q dx y x P ),(),(ds y x Q y x P L ]cos ),(cos ),([βα+=⎰⎰-+-=Lds y x Q x y x P x x )],()1(),(2[2.8. 设Γ为曲线x =t , y =t 2, z =t 3上相应于t 从0变到1的曲线弧,把对坐标的曲线积分⎰Γ++Rdz Qdy Pdx 化成对弧长的曲线积分.解曲线Γ上任一点的切向量为 τ=(1, 2t , 3t 2)=(1, 2x , 3y ), 单位切向量为)3 ,2 ,1(9211)cos ,cos ,(cos 22y x yx ++==τγβαe ,ds R Q P Rdz Qdy Pdx L ]cos cos cos [γβα++=++⎰⎰Γ⎰++++=L ds y x yRxQ P 2294132.习题 10-31. 计算下列曲线积分, 并验证格林公式的正确性:(1)⎰++-ldy y x dx x xy )()2(22, 其中L 是由抛物线y =x 2及y 2=x 所围成的区域的正向边界曲线; 解 L =L 1+L 2, 故⎰++-L dy y x dx x xy )()2(22⎰⎰++-+++-=21)()2()()2(2222L L dy y x dx x xy dy y x dx x xy⎰⎰++-+++-=112243423)](2)2[(]2)()2[(dy y y y y y dx x x x x x301)242()22(1010245235=++--++=⎰⎰dy y y y dx x x x ,而dxdy x dxdy yPx Q DD)21()(-=∂∂-∂∂⎰⎰⎰⎰⎰⎰-=102)21(y y dx x dy301)(42121=+--=⎰dy y y y y , 所以⎰⎰⎰+=∂∂-∂∂l DQdy Pdx dxdy yPx Q )(.(2)⎰-+-ldy xy y dx xy x )2()(232, 其中L 是四个顶点分别为(0, 0)、 (2, 0)、(2, 2)、和(0, 2)的正方形区域的正向边界.解 L =L 1+L 2+L 3+L 4, 故⎰-+-L dy xy y dx xy x )2()(232dy xy y dx xy x L L L L )2())((2324321-+-+++=⎰⎰⎰⎰ ⎰⎰⎰⎰+-+-+=202002022222)8()4(dy y dx x x dy y y dx x 8482020=-+=⎰⎰ydy xdx , 而 dxdy xy y dxdy y P x Q DD )32()(2+-=∂∂-∂∂⎰⎰⎰⎰ ⎰⎰+-=20220)32(dy xy y dx 8)48(20=-=⎰dx x , 所以 ⎰⎰⎰+=∂∂-∂∂l D Qdy Pdx dxdy yP x Q )(. 2. 利用曲线积分, 求下列曲线所围成的图形的面积:(1)星形线x =a cos 3t , y =a sin 3t ;解 ⎰⎰-⋅⋅-=-=L dt t t a t a ydx A π2023)sin (cos 3sin ⎰==ππ20224283cos sin 3a tdt t a . (2)椭圆9x 2+16y 2=144;解椭圆9x 2+16y 2 =144的参数方程为x =4cos θ, y =3sin θ, 0≤θ≤2π, 故⎰-=Lydx xdy A 21 ⎰-⋅-⋅=πθθθθθ20)]sin 4(sin 3cos 3cos 4[21d ⎰==ππθ20126d . (3)圆x 2+y 2=2ax .解圆x 2+y 2=2ax 的参数方程为x =a +a cos θ, y =a sin θ, 0≤θ≤2π,故 ⎰-=Lydx xdy A 21 ⎰-⋅-⋅+=πθθθθθ20)]sin (sin cos )cos 1([21d a a a a 2202)cos 1(2a d a ⎰=+=ππθθ.3. 计算曲线积分⎰+-L y x xdy ydx )(222, 其中L 为圆周(x -1)2+y 2=2, L 的方向为逆时针方向.解 )(222y x y P +=, )(222y x x Q +-=. 当x 2+y 2≠0时 y P x Q ∂∂=∂∂0)(2)(22222222222=+--+-=y x y x y x y x . 在L 内作逆时针方向的ε小圆周l : x =εcos θ, y =εsin θ(0≤θ≤2π),在以L 和l 为边界的闭区域D ε上利用格林公式得0)(=∂∂-∂∂=+⎰⎰⎰-+dxdy y P x Q Qdy Pdx D l L ε, 即 ⎰⎰⎰+=+-=+-lL l dy Pdx Qdy Pdx Qdy Pdx . 因此 ⎰⎰+-=+-l L y x xdy ydx y x xdy ydx )(2)(22222⎰--=πθεθεθε20222222cos sin d ⎰-=-=ππθ2021d .4. 证明下列曲线积分在整个xOy 面内与路径无关, 并计算积分值:(1)⎰-++)3 ,2()1 ,1()()(dy y x dx y x ;解 P =x +y , Q =x -y , 显然P 、Q 在整个xOy 面内具有一阶连续偏导数, 而且1=∂∂=∂∂xQ y P , 故在整个xOy 面内, 积分与路径无关.取L 为点(1, 1)到(2, 3)的直线y =2x -1, x 从1变到2, 则⎰⎰-+-=-++)3 ,2()1 ,1(21)]1(2)13[()()(dx x x dy y x dx y x ⎰=+=2125)1(dx x . (2)⎰-+-)4 ,3()2 ,1(2232)36()6(dy xy y x dx y xy ;解 P =6xy 2-y 3, Q =6x 2y -3xy 2, 显然P 、Q 在整个xOy 面内具有一阶连续偏导数, 并且2312y xy xQ y P -=∂∂=∂∂, 故积分与路径无关, 取路径 (1, 2)→(1, 4)→(3, 4)的折线, 则⎰-+-)4 ,3()2 ,1(2232)36()6(dy xy y x dx y xy236)6496()3642312=-+-=⎰⎰dx x dy y y .(3)⎰-++-)1 ,2()0 ,1(324)4()32(dy xy x dx y xy .解 P =2xy -y 4+3, Q =x 2-4xy 3, 显然P 、Q 在整个xOy 面内具有一阶连续偏导数, 并且342y x xQ y P -=∂∂=∂∂, 所以在整个xOy 面内积分与路径无关, 选取路径为从(1, 0)→(1, 2)→(2, 1)的折线, 则⎰-++-)1 ,2()0 ,1(324)4()32(dy xy x dx y xy⎰⎰=++-=102135)1(2)41(dx x dy y .5. 利用格林公式, 计算下列曲线积分:(1)⎰-+++-Ldy x y dx y x )635()42(, 其中L 为三顶点分别为(0, 0)、 (3, 0)和(3, 2)的三角形正向边界;解 L 所围区域D 如图所示, P =2x -y +4, Q =5y +3x -6,4)1(3=--=∂∂-∂∂yP x Q , 故由格林公式,得⎰-+++-L dy x y dx y x )6315()42(dxdy y P x Q D)(∂∂-∂∂=⎰⎰ 124==⎰⎰dxdy D.(2)⎰-+-+Lx x dy ye x x dx e y x xy x y x )2sin ()sin 2cos (222, 其中L 为正向星形线323232a y x =+(a >0);解 x e y x xy x y x P 22sin 2cos -+=, x ye x x Q 2sin 2-=,0)2cos sin 2()2cos sin 2(22=-+--+=∂∂-∂∂x x ye x x x x ye x x x x yP x Q , 由格林公式⎰-+-+L x x dy ye x x dx e y x xy x y x )2sin ()sin 2cos (2220)(=∂∂-∂∂=⎰⎰dxdy yP x Q D . (3)⎰+-+-Ldy y x x y dx x y xy )3sin 21()cos 2(2223, 其中L 为在抛物线 2x =πy 2上由点(0, 0)到)1 ,2(π的一段弧; 解 x y xy P cos 223-=, 223sin 21y x x y Q +-=,0)cos 26()6cos 2(22=--+-=∂∂-∂∂x y xy xy x y yP x Q , 所以由格林公式0)(=∂∂-∂∂=+⎰⎰⎰++-dxdy yP x Q Qdy Pdx D OB OA L , 其中L 、OA 、OB 、及D 如图所示.故 ⎰⎰++=+AB OA L Qdy Pdx Qdy Pdx4)4321(02201022πππ=+-+=⎰⎰dy y y dx . (4)⎰+--L dy y x dx y x )sin ()(22, 其中L 是在圆周22x x y -=上由点(0, 0)到点(1, 1)的一段弧.解 P =x 2-y , Q =-x -sin 2y ,0)1(1=---=∂∂-∂∂y P x Q , 由格林公式有0)(=∂∂-∂∂-=+⎰⎰⎰++dxdy y P x Q Qdy Pdx DBO AB L , 其中L 、AB 、BO 及D 如图所示.故 ⎰⎰++--=+--L OB BA dy y x dx y x dy y x dx y x )sin ()()sin ()(22222sin 4167)sin 1(102102+-=++-=⎰⎰dx x dy y .6. 验证下列P (x , y )dx +Q (x , y )dy 在整个xOy 平面内是某一函数u (x , y )的全微分, 并求这样的一个u (x , y ):(1)(x +2y )dx +(2x +y )dy ;证明因为yP x Q ∂∂==∂∂2, 所以P (x , y )dx +Q (x , y )dy 是某个定义在整个xOy 面内的函数u (x , y )的全微分.⎰++++=),()0,0()2()2(),(y x C dy y x dx y x y x u C y xy x +++=22222. (2)2xydx +x 2dy ;解因为y P x x Q ∂∂==∂∂2, 所以P (x , y )dx +Q (x , y )dy 是某个定义在整个 xOy 面内的函数u (x , y )的全微分.⎰++=),()0,0(22),(y x C dy x xydx y x u ⎰⎰+=++=y yC y x C xydx dy 00220. (3)4sin x sin3y cos xdx –3cos3y cos2xdy解因为yP x y x Q ∂∂==∂∂2sin 3cos 6, 所以P (x , y )dx +Q (x , y )dy 是某个定义在整个xOy 平面内的函数u (x , y )的全微分.⎰+-=),()0,0(2cos 3cos 3cos 3sin sin 4),(y x C xdy y xdx y x y x u C y x C xdy y dx xy +-=+-+=⎰⎰3sin 2cos 2cos 3cos 3000. (4)dy ye y x x dx xy y x y )128()83(2322++++解因为yP xy x x Q ∂∂=+=∂∂1632, 所以P (x , y )dx +Q (x , y )dy 是某个定义在整个xOy 平面内的函数u (x , y )的全微分. ⎰+++++=),()0,0(232)128()823(),(y x y C dy ye y x x dx xy iy xh y x u C dx xy y x dy ye yx y +++=⎰⎰0022)83(12C e ye y x y x y y +-++=)(124223.(5)dy y x x y dx x y y x )sin sin 2()cos cos 2(22-++解因为yP y x x y x Q ∂∂=-=∂∂sin 2cos 2, 所以P (x , y )dx +Q (x , y )dy 是某个函数u (x , y )的全微分 ⎰⎰+-+=x y C dy y x x y xdx y x u 002)sin sin 2(2),( C y x x y ++=cos sin 22.7. 设有一变力在坐标轴上的投影为X =x +y 2, Y =2xy -8, 这变力确定了一个力场, 证明质点在此场内移动时, 场力所做的功与路径无关. 解场力所作的功为⎰Γ-++=dy xy dx y x W )82()(2. 由于yX y x Y ∂∂==∂∂2, 故以上曲线积分与路径无关, 即场力所作的功与路径无关.习题10-41. 设有一分布着质量的曲面∑, 在点(x , y , z )处它的面密度为μ(x , y , z ), 用对面积的曲面积分表达这曲面对于x 轴的转动惯量.解. 假设μ(x , y , z )在曲面∑上连续, 应用元素法, 在曲面∑上任意一点(x , y , z )处取包含该点的一直径很小的曲面块dS (它的面积也记做dS ), 则对于x 轴的转动惯量元素为dI x =(y 2+z 2)μ(x , y , z )dS ,对于x 轴的转动惯量为dS z y x z y I x ),,()(22μ+=∑⎰⎰.2. 按对面积的曲面积分的定义证明公式dS z y x f dS z y x f dS z y x f ),,(),,(),,(21∑∑∑⎰⎰⎰⎰⎰⎰+=,其中∑是由∑1和∑2组成的.证明划分∑1为m 部分, ∆S 1, ∆S 2, ⋅⋅⋅, ∆S m ;划分∑2为n 部分, ∆S m +1, ∆S m +2, ⋅⋅⋅, ∆S m +n ,则∆S 1, ⋅⋅⋅, ∆S m , ∆S m +1, ⋅⋅⋅, ∆S m +n 为∑的一个划分, 并且i i i i nm m i i i i i m i i i i i n m i S f S f S f ∆∑+∆∑=∆∑++==+=),,(),,(),,(111ζηξζηξζηξ. 令}{max 11i mi S ∆=≤≤λ, }{max 12i n m i m S ∆=+≤≤+λ, } ,max{21λλλ=, 则当 λ→0时, 有dS z y x f dS z y x f dS z y x f ),,(),,(),,(21∑∑∑⎰⎰⎰⎰⎰⎰+=.3. 当∑是xOy 面内的一个闭区域时, 曲面积分dSz y x f ),,(∑⎰⎰与二重积分有什么关系？解 ∑的方程为z =0, (x , y )∈D ,dxdy dxdy z z dS y x=++=221, 故 dxdy z y x f dS z y x f D),,(),,(⎰⎰⎰⎰=∑.4. 计算曲面积分dS z y x f ),,(∑⎰⎰, 其中∑为抛物面z =2-(x 2+y 2)在xOy 面上方的部分, f (x , y , z )分别如下:(1) f (x , y , z )=1;解 ∑: z =2-(x 2+y 2), D xy : x 2+y 2≤2,dxdy y x dxdy z z dS y x22224411++=++=. 因此 dxdy y x dS z y x f xyD 22441),,(++=⎰⎰⎰⎰∑ ⎰⎰+=πθ2020241rdr r d ππ313])41(121[2202/32=+=r . (2) f (x , y , z )=x 2+y 2;解 ∑: z =2-(x 2+y 2), D xy : x 2+y 2≤2, dxdy y x dxdy z z dS y x22224411++=++=. 因此 dxdy y x y x dS z y x f xyD 2222441)(),,(+++=⎰⎰⎰⎰∑ ⎰⎰+=πθ2020241rdr r d ππ301494122022=+=⎰rdr r r . (3) f (x , y , z )=3z .解 ∑: z =2-(x 2+y 2), D xy : x 2+y 2≤2,dxdy y x dxdy z z dS y x22224411++=++=. 因此 dS z y x f ),,(∑⎰⎰dxdy y x y x xyD 2222441)](2[3+++-=⎰⎰⎰⎰+-=πθ20202241)2(3rdr r r d ππ1011141)2(62022=+-=⎰rdr r r . 5. 计算dS y x )(22+∑⎰⎰, 其中∑是: (1)锥面22y x z +=及平面z =1所围成的区域的整个边界曲面;解将∑分解为∑=∑1+∑2, 其中∑1: z =1 , D 1: x 2+y 2≤1, dS =dxdy ;∑1:22y x z +=, D 2: x 2+y 2≤1, dxdy dxdy z z dS y x2122=++=. dS y x dS y x dS y x )()()(22222221+++=+∑∑∑⎰⎰⎰⎰⎰⎰ dxdy y x dxdy y x D D )()(222221+++=⎰⎰⎰⎰⎰⎰=πθ20103dr r d +⎰⎰πθ201032dr r d πππ221222+=+=. 提示: dxdy dxdy yx y y x x dS 21222222=++++=.(2)锥面z 2=3(x 2+y 2)被平面z =0及z =3所截得的部分. 解 ∑:223y x z +=, D xy : x 2+y 2≤3,dxdy dxdy z z dS y x2122=++=, 因而 πθπ922)()(302202222==+=+⎰⎰⎰⎰⎰⎰∑rdr r d dxdy y x dS y x xy D . 提示: dxdy dxdy y x y y x x dS 2])(326[])(326[1222222=++++=.6. 计算下面对面积的曲面积分:(1)dS y x z )342(++∑⎰⎰, 其中∑为平面1432=++z y x 在第一象限中的部分;解 y x z 3424:--=∑, x y x D xy 2310 ,20 :-≤≤≤≤, dxdy z z dS y x 221++=dxdy 361=, 61436143614)342(==⋅=++⎰⎰⎰⎰⎰⎰∑dxdy dxdy dS y x z xy xyD D . (2)dS z x x xy )22(2+--∑⎰⎰, 其中∑为平面2x +2y +z =6在第一象限中的部分;解 ∑: z =6-2x -2y , D xy : 0≤y ≤3-x , 0≤x ≤3,dxdy dxdy z z dS y x3122=++=, dS z x x xy )22(2+--∑⎰⎰ dxdy y x x x xy xyD 3)22622(2--+--=⎰⎰⎰⎰--+--=x dy y xy x x dx 30230)22236(3 427)9103(33023-=+-=⎰dx x x . (3)dS z y x )(++∑⎰⎰, 其中∑为球面x 2+y 2+z 2=a 2上z ≥h (0<h <a )的部分;解 ∑:222y x a z --=, D xy : x 2+y 2≤a 2-h 2,dxdy z z dS y x 221++=dxdy y x a a 222--=,dxdy yx a a y x a y x dS z y x xy D 222222)()(----++=++⎰⎰⎰⎰∑ )(||22h a a D a adxdy xy D xy-===⎰⎰π(根据区域的对称性及函数的奇偶性).提示: dxdy yx a y y x a x dS 22222222)()(1+--++--+=dxdy y x a a 222--=, (4)dS zx yz xy )(++∑⎰⎰, 其中∑为锥面22y x z +=被x 2+y 2=2ax所截得的有限部分.解 ∑: 22y x z +=, D xy : x 2+y 2≤2ax ,dxdy dxdy z z dS y x2122=++=, dxdy y x y x xy dS zx yz xy xyD ])([2)(22+++=++⎰⎰⎰⎰∑ ⎰⎰++=-θππθθθθcos 202222)]sin (cos cos sin [2a rdr q r r dθθθθθθππd a )cos sin cos cos (sin 24422554⎰-++= 421564a =. 提示: dxdy yx y y x x dS 2222221++++=. 7. 求抛物面壳)10)((2122≤≤+=z y x z 的质量, 此壳的面密度为μ=z .解 ∑: )(2122y x z +=, D xy : x 2+y 2≤2, dxdy y x dxdy z z dS y x222211++=++=.故 dxdy y x y x zdS M xyD 22221)(21+++==⎰⎰⎰⎰∑ ⎰⎰+=πθ202022121rdr r r d )136(152+=π. 8. 求面密度为μ0的均匀半球壳x 2+y 2+z 2=a 2(z ≥0)对于z 轴的转动惯量. 解 ∑: 222y x a z --=, D xy : x 2+y 2≤a 2,dxdy z z dS y x 221++=dxdy yx a a 222--=, dxdy y x a a y x dS y x I z 222022022)()(--+=+=∑∑⎰⎰⎰⎰μμ ⎰⎰-=a dr ya r d a 0223200πθμ 4034a πμ=.提示:dxdy yx a y y x a x dS 22222222)()(1---+---+=dxdy y x a a 222--=.习题10-51. 按对坐标的曲面积分的定义证明公式:dydz z y x P z y x P )],,(),,([21±∑⎰⎰dydz z y x P dydz z y x P )],,(),,(21∑∑⎰⎰⎰⎰±=.解证明把∑分成n 块小曲面∆S i (∆S i 同时又表示第i 块小曲面的面积), ∆S i 在yOz 面上的投影为(∆S i )yz , (ξi , ηi ,ζi )是∆S i 上任意取定的一点, λ是各小块曲面的直径的最大值, 则dydzz y x P z y x P )],,(),,([21±∑⎰⎰ yz i i i i i i i n i S P P ))](,(),([lim ,2,110∆±==→∑ζηξζηξλyz i i i i ni yz i i i i n i S P S P ))(,(lim ))(,(lim ,210,110∆±∆==→=→∑∑ζηξζηξλλ dydz z y x P dydz z y x P )],,(),,(21∑∑⎰⎰⎰⎰±=.2. 当∑为xOy 面内的一个闭区域时, 曲面积分dxdy z y x R ),,(∑⎰⎰与二重积分有什么关系？解因为∑: z =0, (x , y )∈D xy , 故dxdy z y x R dxdy z y x R xyD ),,(),,(⎰⎰⎰⎰±=∑,当∑取的是上侧时为正号, ∑取的是下侧时为负号.3. 计算下列对坐标的曲面积分:(1)zdxdy y x 22∑⎰⎰其中∑是球面x 2+y 2+z 2=R 2的下半部分的下侧;解 ∑的方程为222y x R z ---=, D xy : x 2+y 2≤R , 于是zdxdy y x 22∑⎰⎰dxdy y x R y x xyD )(22222----=⎰⎰ ⎰⎰⋅-⋅⋅=πθθθ20222202sin cos rdr r R r r d R⎰⎰-=πθθ20052222sin 41R dr r r R d 71052R π=. (2)ydzdx xdydz zdxdy ++∑⎰⎰, 其中z 是柱面x 2+y 2=1被平面z =0及z =3所截得的第一卦限内的部分的前侧;解 ∑在xOy 面的投影为零, 故0=∑⎰⎰zdxdy .∑可表示为21y x -=, (y , z )∈D yz ={(y , z )|0≤y ≤1, 0≤z ≤3}, 故 ⎰⎰⎰⎰⎰⎰⎰-=-=-=∑3010102221311dy y dy y dz dydz y xdyz yz D ∑可表示为21x y -=, (z , x )∈D zx ={(z , x )|0≤z ≤3, 0≤x ≤1}, 故dzdx x ydzdx zx D 21-=⎰⎰⎰⎰∑⎰⎰⎰-=-=30101022131dx x dx x dz . 因此 ydzdx xdydz zdxdy ++∑⎰⎰)13(2102dx x ⎰-=ππ2346=⨯=. 解法二 ∑前侧的法向量为n =(2x , 2y , 0), 单位法向量为)0 , ,(1)cos ,cos ,(cos 22y x y x +=γβα, 由两种曲面积分之间的关系,dS z y x ydzdx xdydz zdxdy )cos cos cos (γβα++=++∑∑⎰⎰⎰⎰π23)(222222==+=+⋅++⋅=∑∑∑⎰⎰⎰⎰⎰⎰dS dS y x dS y x y y y x x x . 提示: dS ∑⎰⎰表示曲面的面积.(3)dxdy z z y x f dzdx y z y x f dydz x z y x f ]),,([]),,(2[]),,([+++++∑⎰⎰, 其中f (x , y , z )为连续函数, ∑是平面x -y +z =1在第四卦限部分的上侧; 解曲面∑可表示为z =1-x +y , (x , y )∈D xy ={(x , y )|0≤x ≤1, 0≤y ≤x -1}, ∑上侧的法向量为n =(1, -1, 1), 单位法向量为)31 ,31 ,31()cos ,cos ,(cos -=γβα, 由两类曲面积分之间的联系可得dxdy z z y x f dzdx y z y x f dydz x z y x f ]),,([]),,(2[]),,([+++++∑⎰⎰dS z f y f x f ]cos )(cos )2(cos )[(γβα+++++=∑⎰⎰dS z f y f x f ]31)()31()2(31)(⋅++-⋅++⋅+=∑⎰⎰ 2131)(31===+-=⎰⎰⎰⎰⎰⎰∑∑dxdy dS dS z y x xyD .(4)⎰⎰∑++yzdzdx xydydz xzdxdy , 其中∑是平面x =0, y =0, z =0, x +y +z =1所围成的空间区域的整个边界曲面的外侧.解 ∑=∑1+∑2+∑3+∑4, 其中∑1: x =0, D yz : 0≤y ≤1, 0≤z ≤1-y ,∑2: y =0, D zx : 0≤z 1, 0≤x ≤1-z ,∑3: z =0, D xy : 0≤x ≤1, 0≤y ≤1-x ,∑4: z =1-x -y , D xy : 0≤x ≤1, 0≤y ≤1-x ,于是 ⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰∑∑∑∑∑+++=4321xzdxdy xzdxdy 4000∑⎰⎰+++= dxdy y x x xy D )1(--=⎰⎰⎰⎰-=--=1010241)1(x dy y x xdx . 由积分变元的轮换对称性可知241⎰⎰⎰⎰∑∑==yzdzdx xydydz . 因此⎰⎰∑=⨯=++812413yzdzdx xydydz xzdxdy .解 ∑=∑1+∑2+∑3+∑4, 其中∑1、∑2、∑3是位于坐标面上的三块; ∑4: z =1-x -y , D xy : 0≤x ≤1, 0≤y ≤1-x .显然在∑1、∑2、∑3上的曲面积分均为零, 于是⎰⎰∑++yzdzdx xydydz xzdxdyyzdzdx xydydz xzdxdy ++=∑⎰⎰4dS xz yz xy )cos cos cos (4γβα++=∑⎰⎰dS xz yz xy )(34++=∑⎰⎰81)]1)(([3=--++=⎰⎰dxdy y x y x xy xyD . 4. 把对坐标的曲面积分dxdy z y x R dzdx z y x Q dydz z y x P ),,(),,(),,(++∑⎰⎰化成对面积的曲面积分:(1)∑为平面63223=++z y x 在第一卦限的部分的上侧;解令63223),,(-++=z y x z y x F , ∑上侧的法向量为:)32 ,2 ,3(),,(==z y x F F F n ,单位法向量为)32 ,2 ,3(51)cos ,cos ,(cos =γβα, 于是 Rdxdy Qdzdx Pdydz ++∑⎰⎰dS R Q P )cos cos cos (γβα++=∑⎰⎰dS R Q P )3223(51++=∑⎰⎰. (2)∑是抛物面z =8-(x 2+y 2)在xOy 面上方的部分的上侧.解令F (x , y , z )=z +x 2+y 2-8, ∑上侧的法向量n =(F x , F y , F z )=(2x , 2y , 1),单位法向量为)1 ,2 ,2(4411)cos ,cos ,(cos 22y x y x ++=γβα, 于是 Rdxdy Qdzdx Pdydz ++∑⎰⎰dS R Q P )cos cos cos (γβα++=∑⎰⎰dS R yQ xP yx )22(441122++++=∑⎰⎰.10-61. 利用高斯公式计算曲面积分:(1)⎰⎰∑++dxdy z dzdx y dydz x 222, 其中∑为平面x =0, y =0, z =0, x =a ,y =a , z =a 所围成的立体的表面的外侧;解由高斯公式原式dv z y x dv z R y Q x P )(2)(++=∂∂+∂∂+∂∂=ΩΩ⎰⎰⎰⎰⎰⎰ ⎰⎰⎰⎰⎰⎰===Ωaa a a dz dy xdx xdv 0400366(这里用了对称性).(2)⎰⎰∑++dxdy z dzdx y dydz x 333, 其中∑为球面x 2+y 2+z 2=a 2的外侧;解由高斯公式原式dv z y x dv z R y Q x P )(3)(222++=∂∂+∂∂+∂∂=ΩΩ⎰⎰⎰⎰⎰⎰ ⎰⎰⎰=ππϕϕθ20004sin 3a dr r d d 5512a π=. (3)⎰⎰∑++-+dxdy z y xy dzdx z y x dydz xz )2()(2322, 其中∑为上半球体 x 2+y 2≤a 2, 2220y x a z --≤≤的表面外侧;解由高斯公式原式dv y x z d z R y Q x P )()(222++=∂∂+∂∂+∂∂=ΩΩ⎰⎰⎰⎰⎰⎰ ⎰⎰⎰=ππϕϕθ2020022sin a dr r r d d 552a π=. (4)⎰⎰∑++zdxdy ydzdx xdydz 其中∑界于z =0和z =3之间的圆柱体x 2+y 2≤9的整个表面的外侧;解由高斯公式原式π813)(==∂∂+∂∂+∂∂=ΩΩ⎰⎰⎰⎰⎰⎰dv dv z R y Q x P . (5)⎰⎰∑+-yzdxdy dzdx y xzdydz 24,其中∑为平面x =0, y =0, z =0, x =1,y =1, z =1所围成的立体的全表面的外侧.解由高斯公式原式dv y y z dv z R y Q x P )24()(+-=∂∂+∂∂+∂∂=ΩΩ⎰⎰⎰⎰⎰⎰ ⎰⎰⎰=-=10101023)4(dz y z dy dx . 2. 求下列向量A 穿过曲面∑流向指定侧的通量: (1)A =yz i +xz j +xy k , ∑为圆柱x +y 2≤a 2(0≤z ≤h )的全表面, 流向外侧; 解 P =yz , Q =xz , R =xy ,⎰⎰∑++=Φxydxdy xzdzdx yzdydzdv z xy y xz x yz ))()()((∂∂+∂∂+∂∂=Ω⎰⎰⎰00==Ω⎰⎰⎰dv . (2)A =(2x -z )i +x 2y j - xz 2k , ∑为立方体0≤x ≤a , 0≤y ≤a , 0≤z ≤a ,的全表面, 流向外侧;解 P =2x -z , Q =x 2y , R =-xz 2,⎰⎰∑++=ΦRdxdy Qdzdx Pdydzdv xz x dv z r y Q x P )22()(2-+=∂∂+∂∂+∂∂=ΩΩ⎰⎰⎰⎰⎰⎰ ⎰⎰⎰-=-+=a a a a a dz xz x dy dx 023200)62()22(. (3)A =(2x +3z )i -(xz +y )j +(y 2+2z )k , ∑是以点(3, -1, 2)为球心, 半径R =3的球面, 流向外侧.解 P =2x +3z , Q =-(xz +y ), R =y 2+2z ,⎰⎰∑++=ΦRdxdy Qdzdx Pdydzdv dv z R y Q x P )212()(+-=∂∂+∂∂+∂∂=ΩΩ⎰⎰⎰⎰⎰⎰π1083==Ω⎰⎰⎰dv . 3. 求下列向量A 的散度:(1)A =(x 2+yz )i +(y 2+xz )j +(z 2+xy )k ;解 P =x 2+yz , Q =y 2+xz , R =-z 2+xy ,)(2222div z y x z y x zR y Q x P ++=++=∂∂+∂∂+∂∂=A . (2)A =e xy i +cos(xy )j +cos(xz 2)k ;解 P =e xy , Q =cos(xy ), R =cos(xz 2),)sin(2sin div 2xz xz xy x ye zR y Q x P xy --=∂∂+∂∂+∂∂=A . (3)A =y 2z i +xy j +xz k ;解 P =y 2, Q =xy , R =xz ,x x x zR y Q x P 20div =++=∂∂+∂∂+∂∂=A . 4. 设u (x , y , z )、v (x , y , z )是两个定义在闭区域Ω上的具有二阶连续偏导数的函数, n u ∂∂, nv ∂∂依次表示u (x , y , z )、v (x , y , z )沿∑的外法线方向的方向导数. 证明dS n u v n v u dxdydz u v v u )()∂∂-∂∂=∆-∆⎰⎰⎰⎰⎰∑Ω, 其中∑是空间闭区间Ω的整个边界曲面, 这个公式叫作林第二公式. 证明由第一格林公式(见书中例3)知dxdydz z v y v x v u )(222222∂∂+∂∂+∂∂Ω⎰⎰⎰ dxdydz z v z u y v y u x v x u dS n v u )(∂∂∂∂+∂∂∂∂+∂∂∂∂-∂∂=⎰⎰⎰⎰⎰∑Ω, dxdydz z u y u x u v )(222222∂∂+∂∂+∂∂Ω⎰⎰⎰dxdydz z v z u y v y u x v x u dS n u v )(∂∂∂∂+∂∂∂∂+∂∂∂∂-∂∂=⎰⎰⎰⎰⎰∑Ω. 将上面两个式子相减, 即得dxdyd z u y u x u v z v y v x v u )]()([222222222222∂∂+∂∂+∂∂-∂∂+∂∂+∂∂Ω⎰⎰⎰ ⎰⎰∑∂∂-∂∂=dS n u v n v u )(. 5. 利用高斯公式推证阿基米德原理: 浸没在液体中所受液体的压力的合力(即浮力)的方向铅直向上, 大小等于这物体所排开的液体的重力. 证明取液面为xOy 面, z 轴沿铅直向下, 设液体的密度为ρ, 在物体表面∑上取元素dS 上一点, 并设∑在点(x , y , z )处的外法线的方向余弦为cos α, cos β, cos γ, 则dS 所受液体的压力在坐标轴x , y , z 上的分量分别为-ρz cos αdS , -ρz cos β dS , -ρz cos γ dS ,∑所受的压力利用高斯公式进行计算得00cos ==-=Ω∑⎰⎰⎰⎰⎰dv dS z F x αρ,00cos ==-=Ω∑⎰⎰⎰⎰⎰dv dS z F y βρ,||cos Ω-=-=-=-=ΩΩ∑⎰⎰⎰⎰⎰⎰⎰⎰ρρργρdv dv dS z F z ,其中|Ω|为物体的体积. 因此在液体中的物体所受液体的压力的合力, 其方向铅直向上, 大小等于这物体所排开的液体所受的重力, 即阿基米德原理得证.习题10-71. 利用斯托克斯公式, 计算下列曲线积分:(1)⎰Γ++xdz zdy ydx , 其中Γ为圆周x 2+y 2+z 2=a 2, , 若从z 轴的正向看去, 这圆周取逆时针方向;解设∑为平面x +y +z =0上Γ所围成的部分, 则∑上侧的单位法向量为)31,31,31()cos ,cos ,(cos ==γβαn .于是 ⎰Γ++xdz zdy ydx dS x z y zy x ∂∂∂∂∂∂=∑⎰⎰γβαcos cos cos 2333)cos cos cos (a dS dS πγβα-=-=---=∑∑⎰⎰⎰⎰.提示:dS ∑⎰⎰表示∑的面积, ∑是半径为a 的圆.(2)⎰Γ-+-+-dz y x dy x z dz z y )()()(, 其中Γ为椭圆x 2+y 2=a 2, 1=+b z a x(a >0, b >0), 若从x 轴正向看去, 这椭圆取逆时针方向;解设∑为平面1=+b z a x 上Γ所围成的部分, 则∑上侧的单位法向量为) ,0 ,()cos ,cos ,(cos 2222b a b b a b ++==γβαn . 于是 ⎰Γ-+-+-dz y x dy x z dx z y )()()(dS y x x z z y zy x ---∂∂∂∂∂∂=∑⎰⎰γβαcos cos cos dS b a b a dS ∑∑⎰⎰⎰⎰++-=---=22)(2)cos 2cos 2cos 2(γβα)(2)(2)(22222b a a dxdy a b a dxdy a b a b a b a xyxyD D +-=+-=+++-=⎰⎰⎰⎰π.提示: ∑(即x ab b z -=)的面积元素为dxdy a b a dxdy a b dS 222)(1+=+=.(3)⎰Γ+-dz yz xzdy ydx 23, 其中Γ为圆周x 2+y 2=2z , z =2, 若从z 轴的正向看去, 这圆周是取逆时针方向;解设∑为平面z =2上Γ所围成的部分的上侧, 则⎰Γ+-dz yz xzdy ydx 2323yz xz y zy x dxdydzdx dydz -∂∂∂∂∂∂=∑⎰⎰ ππ2025)3()(22-=⨯-=+-+=∑⎰⎰dxdy z dydz x z .(4)⎰Γ-+dz z xdy ydx 232, 其中Γ为圆周x 2+y 2+z 2=9, z =0, 若从z 轴的正向看去, 这圆周是取逆时针方向.解设∑为xOy 面上的圆x 2+y 2≤9的上侧, 则⎰Γ-+dz z xdy ydx 232232z x y zy x dxdydzdx dydz -∂∂∂∂∂∂=∑⎰⎰ π9===⎰⎰⎰⎰∑dxdy dxdy xyD .2. 求下列向量场A 的旋度: (1)A =(2z -3y )i +(3x -z )j +(-2x )k ;解 k j i kj i A 6422332++=---∂∂∂∂∂∂=x y z x y z z y x rot . (2)A =(sin y )i -(z -x cos y )k ;解 j i kji A +=--+∂∂∂∂∂∂=0)cos (sin y x z y z z yx rot . (3)A =x 2sin y i +y 2sin(xz )j +xy sin(cos z )k .解 )sin(cos )sin(sin 22z xy xz y y x z y x ∂∂∂∂∂∂=kj i A rot=[x sin(cos z )-xy 2cos(xz )]i -y sin(cos z )j +[y 2z cos(xz )-x 2cos y ]k . 3. 利用斯托克斯公式把曲面积分dS n A ⋅∑⎰⎰rot 化为曲线积分, 并计算积分值,其中A 、∑及n 分别如下:(1)A =y 2i +xy j +xz k , ∑为上半球面221y x z --=, 的上侧, n 是∑的单位法向量;解设∑的边界Γ : x 2+y 2=1, z =0, 取逆时针方向, 其参数方程为 x =cos θ, y =sin θ, z =0(0≤θ≤2π, 由托斯公式dS n A ⋅∑⎰⎰rot ⎰Γ++=Rdz Qdy Pdx ⎰Γ++=xzdz xydy dx y 2⎰=+-=πθθθθθ20220]sin cos )sin ([sin d .(2)A =(y -z )i +yz j -xz k , ∑为立方体0≤x ≤2, 0≤y ≤2, 0≤z ≤2的表面外侧去掉xOy 面上的那个底面, n 是∑的单位法向量. 解dS n A ⋅∑⎰⎰rot ⎰Γ++=Rdz Qdy Pdx⎰Γ-++-=dz xz yzdy dx x y )()(⎰⎰Γ-===0242dx ydx .4. 求下列向量场A 沿闭曲线Γ(从z 轴正向看依逆时针方向)的环流量: (1)A =-y i +x j +c k (c 为常量), Γ为圆周x 2+y 2=1, z =0; 解θθθθθπd cdz xdy ydx L ]cos cos )sin ()(sin [(20+--=++-⎰⎰⎰==ππθ202d .(2)A =(x -z )i +(x 3+yz )j -3xy 2k , 其中Γ为圆周222y x z +-=, z =0. 解有向闭曲线Γ的参数方程为x =2cos θ, y =2sin θ, z =0(0≤π≤2π). 向量场A 沿闭曲线Γ的环流量为⎰⎰-++-=++LL dz xy dy yz x dx z x Rdz Qdy Pdx 223)()(。

《大学物理》第十章气体动理论习题参考答案

第十章气体动理论一、选择题参考答案1． (B) ；2． (B )；3． (C) ；4． (A) ；5． (C) ；6． (B )；7． (C )； 8． (C) ；9． (D) ；10． (D) ；11． (C) ；12． (B) ；13． (B) ；14． (C) ；15． (B) ；16．(D) ；17． (C) ；18． (C) ；19． (B) ；20． (B) ；二、填空题参考答案1、体积、温度和压强，分子的运动速度（或分子的动量、分子的动能）2、一个点；一条曲线；一条封闭曲线。

3. kT 21 4、1:1；4:1 5、kT 23；kT 25；mol /25M MRT 6、12.5J ；20.8J ；24.9J 。

7、1:1；2:1；10:3。

8、241092.3⨯9、3m kg 04.1-⋅10、（1）⎰∞0d )(v v v Nf ；（2）⎰∞0d )(v v v f ；（3）⎰21d )(212v v v v v Nf m 11、氩；氦12、1000m/s ； 21000m/s13、1.514、215、12M M三、计算题参考答案1．解：氧气的使用过程中，氧气瓶的容积不变，压强减小，因此可由气体状态方程得到使用前后的氧气质量，进而将总的消耗量和每小时的消耗量比较求解。

已知atm 1301=p ，atm 102=p ，atm 13=p ；L 3221===V V V ，L 4003=V 。

质量分布为1m ，2m ，3m ，由题意可得RT Mm V p 11=RT Mm V p 22= RT M m V p 333=所以该瓶氧气使用的时间为h)(6.94000.132)10130(3321321=⨯⨯-=-=-=V p V p V p m m m t 2．解：设管内总分子数为N ，由V NkT nkT p ==有 1210611)(⨯==.kT pV N （个）空气分子的平均平动动能的总和= J 10238-=NkT 空气分子的平均转动动能的总和 = J 106670228-⨯=.NkT 空气分子的平均动能的总和 = J 10671258-⨯=.NkT3．解：（1）根据状态方程RT MRT MV m p RT M m pV ρ==⇒=得 ρp M RT = ，pRT M ρ= 气体分子的方均根速率为1-2s m 49533⋅===ρp M RT v （2）气体的摩尔质量为1-2m ol kg 108.2⋅⨯==-p RTM ρ所以气体为N 2或CO 。

第十章所有者权益习题及答案

第十章所有者权益一、单项选择题1. 发行混合工具发生的交易费用，应当()。

A.计入负债B.在负债成份和权益成份之间按照各自的相对公允价值进行分摊C.计入财务费用D.计入权益2. 在接受投资时，非股份有限公司应通过()科目核算。

A.未分配利润B.盈余公积C.股本D.实收资本3. 甲股份有限公司委托A证券公司发行普通股1000万股，每股面值1元，每股发行价格为4元。

根据约定，股票发行成功后，甲股份有限公司应按发行收入的2%向A证券公司支付发行费。

如果不考虑其他因素，股票发行成功后，甲股份有限公司计入“资本公积”科目的金额应为()万元。

A.20B.80C.2920D.30004. 有限责任公司在增资扩股时，如有新投资者介入，新介入的投资者缴纳的出资额大于其按约定比例计算的其在注册资本中所占的份额部分的差额，应计入()。

A. 盈余公积B.资本公积C.未分配利润D.营业外收入5. 下列有关资本公积的会计处理，不正确的是()A.自用房地产转换为采用公允价值模式计量的投资性房地产，其公允价值大于账面价值的差额应调整资本公积B.持有至到期投资重分类为可供出售金融资产，并以公允价值进行后续计量的，重分类日，该投资的账面价值与公允价值的差额应计入“资本公积——其他资本公积”C.权益结算的股份支付，应在行权日根据行权情况，确认股本和股本溢价，同时结转等待期内确认的资本公积(其他资本公积)D.资产负债表日，投资性房地产以公允价值计量的，公允价值变动计入资本公积6. 下列各项中，会引起留存收益总额发生增减变动的是()。

A.用税后利润补亏B.盈余公积补亏C.资本公积转增资本D.发放股票股利7. 某企业经营第一年亏损100万元，第二年实现税前利润300万元，所得税税率为25%，法定盈余公积的提取比例是10%，则该企业当年应提取的法定盈余公积为()万元。

A.30B.22.5C.15D.15.58. 某企业年初未分配利润借方余额40万元(弥补期限已超过5年)，本年度税后利润1 00万元，法定盈余公积和任意盈余公积的提取比例分别为10%。

水力学第十章课后题答案

h1 h0
h0为均匀流正常水深，代入得
is
h2
h1
2.3h0
lg
h2 h1
h0 h0
即
h0
lg
h2 h1
h0 h0
1 2.3
is
h2
h1
1 2.3
0.0025
500
4
3
0.1087
由试算得h0 0.695m
河道单宽流量q=Kih0 0.005 0.0025 0.695 0.868cm2 / s m
*
*
*
思考题
10.4 何谓渗透系数？它的物理意义是什么？怎么确定渗透系数值？答：渗透系数为反应土的透水性质的比例系数，渗透系数K是综合反映土体渗透能力的一个指标，其数值的正确确定对渗透计算有着非常重要的意义。影响渗透系数大小的因素很多,主要取决于土体颗粒的形状、大小、不均匀系数和水的粘滞性等，要建立计算渗透系数K的精确理论公式比较困难，通常可通过试验方法 (包括实验室测定法和现场测定法)或经验估算法来确定K值。
代入题给已知数据
R=3000(H h0 ) K 3000(8 3) 0.00001 56.92
Q=K H2 h02 56.92
=0.000298m3
/
s
r0
0.1
井水水位与出水量关系，可按上边计算式列表计算于下。
h0 R
3 47.43
10.5 什么叫浸润线，浸润线的基本微分方程形式是什么？答：地下河槽水流的自由表面称为浸润面，其非均匀流动的水面曲线称为浸润线。 10.22。
10.3 什么叫普通完全井，什么叫不完全井？写出普通井浸润曲线方程。答：在地表的无压透水层中所开掘的井为普通井，若井底直达不透水层称为普通完全井，若未达不透水层则为不完全井。10.38。

注会财管第十章长期筹资习题及答案

C.不利于稳定公司股价
D.尽管可转换债券的票面利率比普通债券低，但是加入转股成本之后的总筹资成本比普通债券要高
9.下列关于可转换债券与附认股权证债券区别的表述中，正确的有（）。
A.附认股权证债券在认购股份时给公司带来新的权益资本，而可转换债券转换时没有增加新的资本
B.可转换债券相比附认股权证债券，灵活性较差
9.可转换债券设置合理的回售条款的目的是（）。
A.保护债券投资人的利益
B.保护发行公司的利益
C.促使债券持有人转换股份
D.实现发行公司扩大权益筹资的目的
10.出租人既是资产的出租者，又是款项的借入者的租赁方式是（）。
A.直接租赁
B.售后租回
C.杠杆租赁
D.经营租赁
二、多项选择题
1.下列属于公开发行股票的优点的是（）。
3.
【答案】D
【解析】非公开发行股票的发行价格应不低于定价基准日前20个交易日股票均价的80%。
4.
【答案】A
【解析】若预测市场利率将下降，企业应与银行签订浮动利率借款合同，此时对企业有利。
5.
【答案】A
【解析】长期债券筹资的优点包括筹资规模较大、具有长期性和稳定性和有利于资源优化配置。长期债券筹资的缺点包括发行成本高、信息披露成本高和限制条件多。
C.附认股权证债券发行者，主要目的是发行债券而不是股票，可转换债券的发行者主要目的是发行股票而不是债券
D.可转换债券的承销费用与普通债券类似，而附认股权证债券的承销费用介于债务融资和普通股融资之间
10.下列关于租赁分析的折现率的相关表述中，错误的有（）。
A.租赁费定期支付，类似债券的还本付息，折现率应采用类似债务的利率
债券发行公司
上市债券到期日

《第10章资本结构》习题(含答案)

《第十章资本结构》习题一、单项选择题1、根据财务分析师对某公司的分析，该公司无负债企业的价值为2000万元，利息抵税可以为公司带来100万元的额外收益现值，财务困境成本现值为50万元，债务的代理成本现值和代理收益现值分别为20万元和30万元，那么，根据资本结构的权衡理论，该公司有负债企业的价值为（）万元。

A、2050B、2000C、2130D、20602、某公司年营业收入为500万元，变动成本率为40%，经营杠杆系数为1.5，财务杠杆系数为2。

企业原来的利息费用为100万元。

如果利息增加20万元，总杠杆系数将变为（）。

A、3.75B、3.6C、3D、43、某公司经营杠杆系数为1.5，财务杠杆系数为2，该公司目前每股收益为1元，若使营业收入增加10%，则下列说法不正确的是（）。

A、息税前利润增长15%B、每股收益增长30%C、息税前利润增长6.67%D、每股收益增长到1.3元4、某公司预计明年产生的自由现金流量为350万元，此后自由现金流量每年按照5%的比率增长。

公司的无税股权资本成本为18%，债务税前资本成本为8%，公司的所得税税率为25%。

如果公司维持1.5的目标债务与股权比率，则债务利息抵税的价值为（）万元。

A、1134.48B、1730.77C、1234.48D、934.485、某公司年固定成本为100万元，经营杠杆系数为1.5，财务杠杆系数为2.如果年利息增加50万元，那么，总杠杆系数将变为（）。

A、3B、6C、5D、46、甲公司设立于上年年末，预计今年年底投产。

假定目前的证券市场属于成熟市场，根据优序融资理论的基本观点，甲公司在确定今年筹资顺序时，应当优先考虑的筹资方式是（）。

A、内部筹资B、发行可转换债券C、增发股票D、发行普通债券7、某公司息税前利润为500万元，债务资金200万元，无优先股，债务资本成本为7%，所得税税率为30%，权益资金2000万元，普通股的成本为15%，则企业价值比较法下，公司此时股票的市场价值为（）万元。

第十章_资本结构-计算题参考答案

第十章资本结构计算题：要求列出计算步骤，除非有特殊要求，每步骤运算得数精确到小数点后两位。

1、某企业只生产和销售A产品，其总成本习性模型为Y＝10000＋3X。

假定该企业2010年度A产品销售量为10000件，每件售价为5元；按市场预测2011年A产品的销售数量将增长10%。

要求：（1）计算2010年该企业的边际贡献总额。

（2）计算2010年该企业的息税前利润。

（3）计算销售量为10000件时的经营杠杆系数。

（4）计算2011年息税前利润增长率。

（5）假定企业2010年发生负债利息5000元，且无优先股股息，计算总杠杆系数。

〔参考答案〕（1）2010企业的边际贡献总额＝S－V＝10000×5－10000×3＝20000（元）（2）2010年企业的息税前利润＝边际贡献总额－固定成本＝20000－10000＝10000（元）（3）销售量为10000件时的经营杠杆系数＝边际贡献总额/息税前利润总额＝20000/10000＝2（4）2011年息税前利润增长率＝2×10%＝20%（5）总杠杆系数＝[（5－3）×10000]/[（5－3）×10000－10000－5000]＝4 或：2011年企业财务杠杆系数＝EBIT/（EBIT－I）＝10000/（10000－5000）＝2总杠杆系数＝财务杠杆系数×经营杠杆系数＝2×2＝42、某公司原有资本700万元，其中债务资本200万元（每年负担利息24万元），普通股资本500万元（发行普通股10万股，每股面值50元）。

由于扩大业务，需追加筹资300万元，假设没有筹资费用。

其筹资方式有三个：方案一：全部按面值发行普通股：增发6万股，每股发行价50元；方案二：全部增加长期借款：借款利率仍为12%，利息36万元；方案三：增发新股4万股，每股发行价47.5元；剩余部分用发行债券筹集，债券按10%溢价发行，票面利率为10%；公司的变动成本率为60%，固定成本为180万元，所得税税率为25%。

财务与成本管理第十章练习及答案

2014年注会《财务成本管理》第10章练习及答案一、单项选择题1.下列各项中，比率最大的是（）。

A．边际贡献与息税前利润之比B．净利润与息税前利润之比C．每股收益变化率与息税前利润变化率之比D．每股收益变化率与销售额变化率之比2.若经营风险和财务风险均存在且已知，在销售额下降时( )。

A．息税前利润下降最快B．产品成本下降最快C．单位变动成本下降最快D．每股利润下降最快3.某公司销售收入为500万元，变动成本率为40%，经营杠杆系数为1.5，财务杠杆系数为2。

如果固定成本增加50万元，则复合杠杆系数将变为（）。

A. 2B. 4C. 6D. 84.某企业借入资本和权益资本的比例为1:1，则该企业（）。

A. 既有经营风险又有财务风险B. 只有经营风险C. 只有财务风险D. 没有风险，因为经营风险和财务风险可以相互抵消5.甲公司目前存在融资需求。

如果采用优序融资理论，管理层应当选择的融资顺序是（）。

A.内部留存收益、公开增发新股、发行公司债券、发行可转换债券B.内部留存收益、公开增发新股、发行可转换债券、发行公司债券C.内部留存收益、发行公司债券、发行可转换债券、公开增发新股D.内部留存收益、发行可转换债券、发行公司债券、公开增发新股6.某公司全部资本为100万元，负债比率为40%，负债利率10%，息税前利润为14万元，则该公司的财务杠杆系数为（）。

A. 1.4B. 1C. 1.2D. 1.37.下列关于经营杠杆的说法中，错误的是（）。

A.经营杠杆反映的是营业收入的变化对每股收益的影响程度B.如果没有固定性经营成本，则不存在经营杠杆效应C.经营杠杆的大小是由固定性经营成本和息税前利润共同决定的D.如果经营杠杆系数为1，表示不存在经营杠杆效应8.下列关于资本结构的说法中，错误的是（）。

A.迄今为止，仍难以准确地揭示出资本结构与企业价值之间的关系B.能够使企业预期价值提高的资本结构，不一定是预期每股收益最大的资本结构C.在进行融资决策时，不可避免地要依赖人的经验和主观判断D.一般而言，盈利能力强的企业要比盈利能力弱的类似企业的负债水平高9.已知经营杠杆系数为4，每年的固定成本为9万元，利息费用为1万元，则利息保障倍数为（）。

分析化学第十章习题答案

第十章习题参考答案15.计算BaSO 4的溶解度。

（1）在纯水中；（2）考虑同离子效应，在0.10mol/LBaCl 2溶液中。

解：(1)设BaSO 4在纯水中的溶解度为S 1所以S 1=[Ba 2+]=[ SO 42-]=10101.1-⨯=sp K =1.0×10-5mol/L（2）设BaSO 4在0.10mol/L BaCl 2溶液中之溶解度为S 2.则[SO 42-]= S 2 mol/L [Ba 2+]=0.10+S 2≈0.10 mol/LS 2=[SO 42-]= K sp /[Ba 2+]=K sp /0.10=(1.1×10-10)/0.10=1.1×10-9mol/L16.计算在pH=2.00时的CaF 2溶解度。

解：设CaF 2的溶解度为S ，由于CaF 2在水中存在下列平衡：CaF 2=Ca 2++2F -H +HF HF= H + + F - K a =7.2×10-4F - + H +=HF β1=K 1=1/K a =1/(7.2×10-4)=1.4×103∴ αF(H)=1+β1[H +]=1+1.4×103×10-2=1513321132)(312101.1415107.2412---⋅⨯=⨯⨯=⋅=⋅'=L mol K K S H F SP SP α17.Ag 2CrO 4沉淀在（1）0.0010mol/L AgNO 3溶液中，（2）0.0010mol/L K 2CrO 4溶液中，溶解度何者为大？解：设Ag 2CrO 4沉淀在0.0010mol/L AgNO 3溶液中的溶解度为S 1，则：[Ag +]=2S 1+0.0010≈0.0010 mol/L ，[CrO 42-]= S 1 mol/L∴ S 1= [CrO 42-]= K sp /[ Ag +]2=2.0×10-12/(0.0010)2=2.0×10-6 mol/L设Ag 2CrO 4沉淀在0.0010mol/L K 2CrO 4溶液中的溶解度为S 2，则：[Ag +]=2S 2 mol/L ，[CrO 42-]= S 2+0.0010≈0.0010 mol/L∴ 1512242102.20010.0100.221][21][21----+⋅⨯=⨯===L mol O C K Ag S r SP 可见，Ag 2CrO 4沉淀在0.0010mol/LK 2CrO 4溶液中的溶解度大。

无机及分析化学课后习题第十章答案

无机及分析化学课后习题第十章答案Company number：【WTUT-WT88Y-W8BBGB-BWYTT-19998】一、选择题在给出的4个选项中，请选出1个正确答案。

1. 水溶液中不能大量共存的一组物质为( D )A. Mn 2+ ， Fe 3+B. CrO 42- ， Cl -C. MnO 4- ， MnO 2D. Sn 2+ ， Fe 3+2. 298K ，p (O 2)=100kPa 条件下，O 2+4H ++4e －=2H 2O 的电极电势为( D )A. /V =/V +/VB. /V =/ V – pH)/VC. /V =/V + pH)/VD. /V =/V – pH)/V3. 电极电势与溶液的酸度无关的电对为（ B ）A. O 2/H 2OB. Fe(OH)3/ Fe(OH)2C. MnO 4- /MnO 42-D. Cr 2O 72- /Cr 3+4. 根据(Cu 2Cu) = , (Zn 2Zn) = ，可知反应Cu+Zn 2(1105molL 1) = Cu 2 ( molL -1 )+Zn 在298 K 时平衡常数约为( A )A. 1037B. 1037C. 1042D. 10425. 已知K sp (CuI)< K sp (CuBr)< K sp (CuCl)，则 (Cu 2+/ CuI)， (Cu 2+/ CuBr)， (Cu 2+/ CuCl)由低到高的顺序为( D )A. (Cu 2+/ CuI) < (Cu 2+/ CuBr) < (Cu 2+/ CuCl)B. (Cu 2+/ CuBr)< (Cu 2+/ CuI) < (Cu 2+/ CuCl)C. (Cu 2+/ CuCl)< (Cu 2+/ CuI) < (Cu 2+/ CuBr)D. (Cu 2+/ CuCl) < (Cu 2+/ CuBr) < (Cu 2+/ CuI)6. 根据V 77.0,V 34.0θ/FeFe θ/Cu Cu 232==+++ϕϕ，标准态下能将Cu 氧化为Cu 2+、但不能氧化Fe 2+的氧化剂对应电对的值应是( C )A. <B. >C. < <D. <, >7. 铜元素的标准电势图为则下面说法正确的是( C )A. Cu + 在水溶液中能稳定存在B. 水溶液中Cu 2+与Cu 不能共存C. Cu + 在水溶液中会发生歧化反应D. Cu +的歧化产物是Cu 2+8. 在硫酸一磷酸介质中，用K 2Cr 2O 7标准溶液滴定Fe 2+试样时，其化学计量点电势为，则应选择的指示剂为( B )A. 次甲级蓝（ =）B. 二苯胺磺酸钠（ =）C. 邻二氮菲亚铁（ =）D. 二苯胺（ =）9. 某氧化还原指示剂， =,对应的半反应为Ox+2e -↔Red,则其理论变色范围为( A )A. ～B. ～C. V ～D. ～10. 测定维生素C 可采用的分析方法是( C )A. EDTA 法B. 酸碱滴定法C. 重铬酸钾法D. 碘量法二、填空题1．标出带*元素的氧化数：Na 2*S 4O 6 +，(NH 4)2*S 2O 8+7，K 2*Cr 2O 7+6。

第十章紫外-可见吸光光度法习题及答案

第十章紫外-可见吸光光度法习题1.是非判断题1-1物质的颜色是由于选择性地吸收了白光中的某些波长所致，VitB12溶液呈现红色是由于它吸收了白光中是红色光波。

1-2因为透射光和吸收光按一定比例混合而成白光，故称这两种光为互补色光。

1-3有色物质溶液只能对可见光范围内的某段波长的光有吸收。

1-4符合朗伯-比耳定律的某有色溶液的浓度越低，其透光率越小。

1-5符合比耳定律的有色溶液稀释时，其最大吸收峰的波长位置不移动，但吸收峰降低。

1-6朗伯-比耳定律的物理意义是：当一束平行单色光通过均匀的有色溶液时，溶液是吸光度与吸光物质是浓度和液层厚度的乘积成正比。

1-7在吸光光度法中，摩尔吸光系数的值随入射光的波长增加而减小。

1-8吸光系数与入射光波长及溶液浓度有关。

1-9有色溶液的透光度随着溶液浓度的增大而减小,所以透光度与溶液的浓度成反比关系。

1-10在吸光光度测定时，根据在测定条件下吸光度与浓度成正比的比耳定律的结论，被测溶液浓度越大，吸光度也越大，测定结果也就越准确。

1-11进行吸光光度法测定时，必须选择最大吸收波长的光作入射光。

1-12朗伯-比耳定律只适用于单色光，入射光的波长范围越狭窄，吸光光度测定的准确度越高。

1-13吸光光度法中所用的参比溶液总是采用不含被测物质和显色剂的空白溶液.1-14在实际测定中，应根据光吸收定律，通过改变比色皿厚度或待测溶液浓度，使吸光度的读数处于0.2～0.7之间，以减小测定的相对误差。

1-15在吸光光度法测定时，被测物质浓度相对误差的大小只有透光度为15%～65% 的范围内才是最小的。

2.选择题2-1分光光度法与普通比色法的不同点是A.工作范围不同B.光源不同C.检测器不同D.检流计不同E.获得单色光方法不同2-2 Zn2+的双硫腙-CCl4萃取吸光光度法中，已知萃取液为紫红色络合物，其吸收最大光的颜色为A.红B.橙C.黄D.绿2-3有色络合物的摩尔吸光系数，与下列因素中有关系的是A.比色皿的厚度B.有色络合物浓度C.吸收池材料D.入射光波长2-4透光率与吸光度的关系是A.1T =A B.㏒1T=A C.㏒T=A D.T=㏒1A2-5某物质的摩尔吸光系数（ε）较大，说明A.光通过该物质溶液的厚度厚B.该物质溶液的浓度大C.该物质对某波长的光吸收能力很强D.测定该物质的灵敏度高E.测定该物质的灵敏度低2-6朗伯-比耳定律说明，当一束单色光通过均匀有色溶液中，有色溶液的吸光度正比例于A.溶液的温度B.溶液的酸度C.液层的厚度D.有色配合物稳定性E.溶液的浓度和溶液厚度的乘积2-7符合比耳定律的有色溶液稀释时，其最大吸收峰的波长位置A.向长波方向移动B.向短波方向移动C.不移动，但高峰值降低D.不移动，但高峰值增大2-8已知磷钼杂多酸络合物的透光率为10%，而它与硅钼杂多酸络合物的吸光度差为0.699，那么，硅钼杂多酸络合物的透光率为A. 50%B. 20%C. 30%D. 40%2-9进行光度分析时，误将标准系列的某溶液作为参比溶液调透光率100％，在此条件下，测得有色溶液的透光率为85％。

高等数学第10章课后习题答案(科学出版社)

第十章曲线积分与曲面积分习题详解习题10—11 计算下列对弧长的曲线积分：（1）LI xds =⎰，其中L 是圆221x y +=中(0,1)A到B 之间的一段劣弧；解: L AB =的参数方程为：cos ,sin x y θθ==()42ππθ-≤≤，于是2cos I ππθ-=⎰4cos (1d ππθθ-==+⎰．（2）(1)Lx y ds ++⎰ ，其中L 是顶点为(0,0),(1,0)O A 及(0,1)B 所成三角形的边界；解: L 是分段光滑的闭曲线，如图9－2所示，根据积分的可加性，则有(1)Lx y ds ++⎰(1)OAx y ds =++⎰(1)ABx y ds +++⎰ (1)BOx y ds +++⎰，由于OA :0y =，01x ≤≤，于是ds dx ===，故 103(1)(01)2x y ds x dx ++=++=⎰⎰OA，而:AB 1y x =-,01x ≤≤，于是ds ==．故10(1)[(1)ABx y ds x x ++=+-+=⎰⎰，同理可知:BO 0x =（01y ≤≤），0d s =，则13(1)[01]2BOx y ds y dy ++=++=⎰⎰． xyoABC综上所述33(1)322Lx y ds -+=+=+⎰ （3）⎰，其中L 为圆周22x y x +=；解直接化为定积分．1L 的参数方程为11cos 22x θ=+,1sin 2y θ=（02θπ≤≤）, 且12ds d θθ==．于是201cos222d πθθ=⋅=⎰⎰．（4）2 Lx yzds ⎰，其中L 为折线段ABCD ，这里(0,0,0)A ，(0,0,2),B (1,0,2),C(1,2,3)D ；解如图所示， 2222 LABBCCDx yzds x yzds x yzds x yzds =++⎰⎰⎰⎰．线段AB 的参数方程为 0,0,2(01)x y z t t ===≤≤，则ds =2dt ==，故02200 12=⋅⋅⋅=⎰⎰dt t yzds x AB．线段BC 的参数方程为,0,2(01)x t y z t ===≤≤，则,ds dt ==故122 0020BCx yzds t dt =⋅⋅⋅=⎰⎰，线段CD 的参数方程为1,2,2x y t z t===+)10(≤≤t ，则ds ==，故1122012(2))x yzds t t t t dt =⋅⋅+=+=⎰⎰ 2 (2所以2222LBB CC Dx y z d s x y z d sx y z d sd s =++⎰⎰⎰⎰2 求八分之一球面2221(0,0,0)x y z x y z ++=≥≥≥的边界曲线的重心，设曲线的密度1ρ=。

八年级物理《第十章从粒子到宇宙》补充习题及解答

《第十章从粒子到宇宙》补充习题及解答一、选择题（每小题2分，共44分）1.下列现象中，可以说明分子在不停地做热运动的是（）A．水从高处向低处流B．风吹树叶动C．尘土飞扬D．公园里花香四溢2.下列关于分子的说法中，正确的是（）A．分子虽小，但可以用肉眼看见B．扩散现象证明分子不停地做无规则运动C．气体容易被压缩，说明分子作用力很大D．分子作用力即分子引力3.稻草一拉就断，而铁丝不易拉断。

按照分子动理论的观点，这是因为（）A．稻草的分子间没有引力，铁丝的分子间有引力B．稻草、铁丝的分子间都存在着引力，但稻草分子的引力远小于铁丝分子间的引力C．稻草的分子间存在斥力，铁丝的分子间没有斥力D．稻草具有“一拉就断”的性质4.把两块光滑的玻璃贴紧，它们不能吸引在一起，原因是（）A．两块玻璃分子间存在斥力B．两块玻璃的分子间距离太大，没有分子作用力C．玻璃分子间隔太小，不能形成扩散D．玻璃分子运动缓慢5.将一滴墨汁滴入一杯清水中，过一会儿，整杯水都变黑了，下面说法正确的是（）A.如果水的温度越低，整杯水变黑所需要的时间越短B.如果水的温度为0℃，则不会发生这种现象C.这是一种扩散现象，说明物质分子是不停地运动的D.这是一种扩散现象，说明物质的分子发生了变化，水分子变黑了6.图10-5所示是教材上的一个实验。

这个实验说明了（）A．分子间存在引力B．物质是由大量分子组成的C．分子间有空隙D．组成物质的分子在永不停息地做无规则运动图10－57.下列关于原子核的描述：①通常是由中子和电子构成；②通常是由质子和中子构成；③带正电荷；④不显电性；⑤不能再分；⑥跟原子比较体积很小，但却几乎集中了原子的全部质量。

其中正确的是（）A．②④⑥B．②③⑥C．①③⑤D．①④⑤8.关于原子核中的质子、中子，下列说法正确的是（）A．质子和中子不可再分了B．质子可再分，中子不可分C．质子不可再分，中子可再分D．质子和中子都可再分9.有四种物质：①细胞，②电子，③原子，④质子，按从大到小排列的顺序是（）A．①②③④B．①③④②C．②①④③D．②④③①10.下列说法中，正确的是（）A ．原子是保持物质性质不变的最小微粒B ．空气中细小的灰尘就是分子C ．原子的核式模型是由汤姆生提出的D ．原子核是由质子和中子组成的11. 氢原子只由1个质子和1个电子组成，在图10－6所示氢原子模型图中，正确的是（）12. 对于分子或原子的认识，你认为下面哪句话较准确？（）A ．没有生命的物质是由分子或原子组成的，有生命的物质则不是由分子或原子组成的B ．既然分子和原子都是构成物质的微粒，因此分子和原子没什么区别C ．一般显微镜就能观察到分子，但观察不到原子D ．分子很小，用一般显微镜观察不到13. 使人们确信原子有复杂结构的事实是（）A ．电子的发现B ．原子核的发现C ．质子的发现D ．中子的发现14. 卢瑟福在研究原子结构时做了如下实验：取一极薄的金箔，用一高速运动的氦核射击它，发现大多数氦核通过了金箔，极少数氦核发生偏转或被金箔弹回，根据上述现象得出以下结论，其中正确的是（）A ．金原子是实心球体，紧密结合排列B ．相对金原子而言原子核体积小质量大C ．金原子核带负电D ．金原子质量与氦核质量相当15. 原子能不能再分呢？1897年，英国科学家汤姆生进行了认真实验，发现了人们观察到的阴极射线是由原子内部发出的一种带负电的微粒组成的，并把这种微粒命名为电子，从而证明了原子是可分的。

第十章计算题参考答案

第十章计算题参考答案9. 在涤纶树脂生产中，已知缩聚温度为280℃(此温度下的酯化平衡常数K=4.9)，欲制得数均分子量为20000的涤纶树脂，试求反应釜内所允许的乙二醇的最大蒸气压（280℃，乙二醇的饱和蒸气压P0＝5.776mmHg)。

答案：涤纶树脂即聚对苯二甲酸乙二醇酯，其结构单元的分子量为：192/2=96故20000/96 = 208由公式:得 n w = 1.13×10-4 mol/L即釜内允许的乙二醇最大蒸气压为P s=0.65mmHg = 86.66Pa10. 聚酯化反应280℃时的平衡常数K＝4.9，聚酰胺化反应260℃时平衡常数K＝305，试作出水含量（摩尔分数表示）与数均聚合度的关系图，并讨论分析其结果。

答案：根据和联立求解得：（负值已经舍去）所以对聚酯化反应有对聚酰胺反应有对水含量赋值作图得：从图上可知，缩聚反应中水含量对数均分子量影响很大，特别是当平衡常数较小时，水含量对聚合度影响非常严重。

要想获得较高的聚合度，例如200左右，就必须使残存的小分子副产物极低。

而对于平衡常数较大的缩聚反应，要达到同样的聚合度，小分子副产物含量可适当高一些，亦即，对小分子副产物的排除可适当放宽。

11. 制造尼龙-66时，为了保持己二酸和己二胺的等摩尔比，通常先使二者成盐，然后于254℃(K=300)进行缩聚。

若反应在密闭容器中进行，当反应进行t小时后，测得体系中残留水为0.25mol/L。

试写出成盐方程式，并计算所得缩聚物的平均聚合度。

答案：尼龙-66盐的形成：假设起始氨基、羧基的摩尔浓度均为1mol/L，成盐后在密闭容器中缩聚，达平衡时, 氨基及羧基的量为c mol/L则生成聚合物为（1－c）mol/L，与残留水的量n a相同，均为0.25mol/L，则依照平衡反应式得到：，K ＝（1－c）2/c2依据平均聚合度和 P＝ 1－c 代入得：故，缩聚物得平均聚合度为6912. 从对苯二甲酸(1mol)和乙二醇(1mol)聚酯化反应体系中，共分出水18克，求产物的平均分子量和反应程度，设平衡常数K＝4。

数学分析课本(华师大三版)-习题及答案第十章

第十章定积分的应用一、填空题1．求曲线8,2222=+=y x x y 所围成图形面积A （上半平面部分），则A = 2．曲线xxey e y -==,及1=x 所围面积A =3．曲线θθcos 1,cos 3+==r r 所围面积A = 4．曲线)0(>=λλθaer 从0=θ到αθ=一段弧长S =5．曲线 ⎩⎨⎧-=+=)cos (sin )sin (cos t t t a y t t t a x 从0=t 到π=t 一段弧长S =6．均匀摆线)0(cos 1sin π≤≤⎩⎨⎧-=-=t ty tt x ，弧长4=S ，则其重心坐标是7．曲线0,0),0(==≤=y x x e y x所围图形绕Ox 轴旋转所得旋转体的体积为；而绕Oy 轴旋转所得旋转体的体积为 8．抛物线)(a x x y -=与直线x y =所围图形的面积为9．在抛物线24x y =上有一点P ，已知该点的法线与抛物线所围成的弓形面积为最小，则P 点的坐标是10．设有一内壁形状为抛物面22y x z +=的容器，原来盛有)(83cm π的水，后来又入注)(643cm π的水，设此时水面比原来提高了hcm ，则h = 11．由曲线,2,1=+=x xx y 及2=y 所围图形的面积S = 曲线x x x y 223++-=与x 轴所围成的图形的面积A = 二、选择填空题1．曲线)0(ln ,ln b a a y x y <<==与y 轴所围成图形的面积为A ，则A =（）（A ）⎰ba xdx ln ln ln （B ）⎰ba e ex dx e（C ）⎰baydy e ln ln （D ）⎰ba e exdx ln2．曲线x y xy ==,1，2=x 所围成的图形面积为A ，则A =（）（A ）dx x x )1(21-⎰（B ）dx xx )1(21-⎰（C ）⎰⎰-+-2121)2()12(dy y dy y （D ）⎰⎰-+-2121)2()12(dx x dx x3．曲线xe y =下方与该曲线过原点的切线左方及y 轴右方所围成的图形面积A =（）（A ）dx ex ex)(1-⎰ （B ）dy y y y e)ln (ln 1-⎰（C ）dx xe e ex x )(1⎰- （D ）dy y y y )ln (ln 1-⎰4．曲线)0(cos 2>=a a r θ所围图形面积A =（）（A ）()θθπd a 220cos 221⎰ （B ）θθππd a ⎰-2cos 221 （C ）()θθπd a 220cos 221⎰（D ）()θθπd a 220cos 2212⎰ 5．曲线πθπθθ=-==,,ae r 所围图形面积A =（）（A ）⎰πθθ02221d e a （B ）⎰πθθ20222d e a （C ）⎰-ππθθd e a22（D ）⎰-ππθθd e a 2226．曲线θθ2cos ,sin 22==r r 所围图形面积A =（）（A ）()()⎰⎰+-222121212cos 2sin 2θθθθd d（B ）()()⎰⎰+462602cos sin 2πππθθθθd d（C ）()()⎰⎰+46262cos 21sin 221πππθθθθd d（D ）()()⎰⎰+462602cos sin 22πππθθθθd d7．曲线()21ln xy -=上210≤≤x 一段弧长S =（）（A ）dx x ⎰⎪⎭⎫ ⎝⎛-+2102111 （B ）⎰-+2102211dx x x （C ）dx x x ⎰⎪⎭⎫ ⎝⎛--+212121 （D ）dx x ⎰-+21022])1[ln(1 8．摆线)0()cos 1()sin (>⎩⎨⎧-=-=a t a y t t a x 一拱与x 轴所围图形绕x 轴旋转，所得旋转体的体积=V （）（A ）()⎰-ππ2022cos 1dt t a（B ）())]sin ([cos 12202t t a d t a a--⎰ππ（C ）()⎰--ππ2022)]sin ([cos 1t t a d t a （D ）()⎰-adt t a ππ2022cos 19．星形线⎪⎩⎪⎨⎧==ta y ta x 33sin cos 的全长S =（）（A ）⎰-⋅202)sin (cos 3sec 4πdt t t a t（B ）⎰-⋅022)sin (cos 3sec 4πdt t t a t （C ）⎰-⋅π02)sin (cos 3sec 2dt t t a t（D ）⎰-⋅02)sin (cos 3sec 2πdt t t a t10．心形线)cos 1(4θ+=r 与直线2,0πθθ==围成图形绕极轴旋转的旋转体体积=V （）（A ）⎰+202)cos 1(16πθθπd （B ）⎰+2022sin )cos 1(16πθθθπd（C ）⎰++2022]cos )cos 1(4[sin )cos 1(16πθθθθπd（D ）⎰++0222]cos )cos 1(4[sin )cos 1(16πθθθθπd11．两个半径为a 的直交圆柱体所围的体积为V =（）（A ）⎰-adx x a 022)(4（B ）⎰-adx x a 022)(8（C ）⎰-a dx x a 022)(16 （D ）⎰-adx x a 022)(212．矩形闸门宽a 米，高h 米，垂直放在水中，上沿与水面齐，则闸门压力p =（）（A ）⎰hahdh 0（B ）⎰aahdh 0（C ）⎰hahdh 021（D ）⎰h ahdh 02 13．横截面为S ，深为h 的水池装满水，把水全部抽到高为H 的水塔上，所作功=W （）（A ）⎰-+hdy y h H S 0)( （B ）⎰-+Hdy y h H S 0)(（C ）⎰-hdy y H S 0)( （D ）⎰+-+Hh dy y h H S 0)(14．半径为a 的半球形容器，每秒灌水b ，水深)0(a h h <<，则水面上升速度是（）（A ）⎰h dy y dh d 02π （B ）⎰--h dy a y a dhd 022])([π （C ）⎰h dy y dhd b 02π （D ）⎰-h dy y ay dh d b 02)2( 15．设)(),(x g x f 在区间[]b a ,上连续，且m x g x f <<)()(（m 为常数），则曲线b x a x x f y x g y ====,),(),(所围平面图形绕直线m y =旋转而成的旋转体体积为（）（A ）⎰-+-badx x g x f x g x f m )]()()][()(2[π（B ）⎰---badx x g x f x g x f m )]()()][()(2[π（C ）⎰-+-badx x g x f x g x f m )]()()][()([π（D ）⎰---badx x g x f x g x f m )]()()][()([π三、计算题1．求抛物线2x y =与2x 2y -=所围图形的面积。