集合问题(容斥原理)2丨两者集合问题表格法
容斥原理万能解法之图示法

容斥原理之图示法济南华图杨东时为了使广大考生更好的准备2015年山东省公务员考试,我们为大家准备了数学运算中的一些解题技巧。
数学运算作为行测中的重要模块,数学运算中涉及到多种题型,但每种题型的出现频率有所差异,其中容斥原理相对来说出现的频率还是比较高的,但容斥原理中会出现各种不同的公式,不仅增加了学习的负担,更重要的是如果不能透彻的理解公式的适用条件,很可能用错,费时费力。
所以容斥原理,重在理解!容斥原理其实就是我们中学时所学的集合问题。
主要包括两集合问题和三集合问题。
容斥原理理解到位的话必须借助图示,并且我们所推导出来的公式也是来源于图示所以容斥原理的理解关键在于图示的理解!一、两集合问题:公式:满足条件A+满足条件B-两者都满足=总个数-两者都不满足两集合的问题公式就是通过上图得到的:A,B所覆盖的面积=集合A+集合B-两集合重复的部分(即两者都满足的)=总个数-A,B都不满足【真题】某科研单位共有68名科研人员,其中45人具有硕士以上学历,30人具有高级职称,12人兼而有之。
没有高级职称也没有硕士以上学历的科研人员是多少人?()A. 13B. 10C. 8D. 5【解析】首先判定这是关于学历和职称的两集合问题。
解法1:这道题给出的量完全符合两集合的公式,所以可以直接代入公式计算即:45+30-12=68-x解出x=5。
解法2:图示法,根据图示A,B 对应的数值分别为45,30,重复的部分为12,则AB 都不满足的为68-(45+30-12)=5二、三集合问题:三集合问题较两集合的问题复杂,所以理解更为重要!对应的标准公式:公式对应的意义为ABC 所覆盖的面积为A,B,C3个面积和-重复部分(A ∩B,B ∩C,A ∩C )这时最中间的部分多减了1次,再加上即为ABC 所覆盖的面积。
【真题】某专业有学生50人,现开设有甲、乙、丙三门选修课。
有40人选修甲课程,36人选修乙课程,30人选修丙课程,兼选甲、乙两门课程的有28人,兼选甲、丙两门课程的有26人,兼选乙、丙两门课程的有24人,甲、乙、丙三门课程均选的有20人,问三门课程均未选的有多少人?( )A.1人B.2人C.3人D.4人【解析】这个题目为三集合问题,通过分析题目给出的条件和问题都符合公式所以可以直接代入公式:40+36+30-28-26-24+20=50-x 解得x=2这里需要注意的是满足条件AB 和只满足条件AB 的区别。
两集合容斥标准公式

两集合容斥标准公式在咱们学习数学的这个奇妙旅程中,有一个叫做“两集合容斥标准公式”的小家伙,可别小瞧它,它在解决很多问题的时候都能派上大用场呢!先来说说什么是两集合容斥。
比如说,咱们班有喜欢语文的同学,有喜欢数学的同学。
那既喜欢语文又喜欢数学的同学,还有只喜欢语文或者只喜欢数学的同学,把这些人数关系弄清楚,就是两集合容斥要做的事儿。
两集合容斥标准公式就像是一把神奇的钥匙,能帮咱们打开这扇复杂的人数关系之门。
这个公式是:A∪B = A + B - A∩B 。
这里的 A 和B 呢,就分别代表两个集合。
我给您举个例子哈。
假设学校组织了一场知识竞赛,参加语文竞赛的有 30 个同学,参加数学竞赛的有 25 个同学,其中有 10 个同学既参加了语文竞赛又参加了数学竞赛。
那咱们来算算,参加竞赛的同学总共有多少人?按照公式,A 就是参加语文竞赛的 30 人,B 就是参加数学竞赛的25 人,A∩B 就是既参加语文又参加数学竞赛的 10 人。
咱们来算算,30 + 25 - 10 = 45(人),所以参加竞赛的同学总共有45 人。
再比如说,咱们学校组织了运动会,报名跑步项目的有40 个同学,报名跳远项目的有 35 个同学,其中有 15 个同学既报名了跑步又报名了跳远。
那用两集合容斥标准公式就能轻松算出参加这两个项目的同学总数:40 + 35 - 15 = 60(人)您看,这个公式是不是特别好用!其实啊,在生活中也有很多类似两集合容斥的情况。
就像我上次去超市买水果,我想买苹果和香蕉。
超市里一共有 50 种水果,其中苹果有 20 种,香蕉有 18 种,而既属于苹果又属于香蕉的水果,比如说苹果香蕉混合果干,有 8 种。
那我能选择的苹果或者香蕉的种类,用这个公式就能算出来:20 + 18 - 8 = 30(种)所以说,两集合容斥标准公式不仅在数学题里有用,在咱们的日常生活中也能帮咱们理清很多复杂的关系呢。
咱们再深入地想一想,这个公式背后反映的其实是一种分类和整合的思想。
两个集合的容斥关系公式

两个集合的容斥关系公式
容斥公式又称为全恒等式或容斥定律,基本定义是:如果从给定集合
中选择元素的总数超过集合的总数,那么所有元素的总和与集合的总数的
差值等于所有包含两个或更多集合元素的交集的总数,即:
设有第一组元素(A1,A2,A3,...,An),第二组元素(B1,B2,B3,...,Bn),则它们的容斥关系式:
N1+N2-N3=N4
其中:
N1=,A1∪A2∪...∪An,为第一组元素的总数
N2=,B1∪B2∪...∪Bn,为第二组元素的总数
N3=,A1∪A2∪...∪An∩B1∪B2∪...∪Bn,为两组元素的交集的总
数
N4=∑N4i为交集的子集的元素总数,即:
N4i=,Ai∩B1∪B2∪...∪Bn
即:
N1-N3+N4=N2
根据以上定义,可以将两个集合的容斥关系写成一个公式,即:
A1∪A2∪...∪An,-,A1∪A2∪...∪An∩B1∪B2∪...∪Bn,+,
A1∩B1∪B2∪...∪Bn,+,A2∩B1∪B2∪...∪Bn,+...+,
An∩B1∪B2∪...∪Bn,=,B1∪B2∪...∪Bn
或者简写为:
A1∪A2∪...∪An,-,A1∪A2∪...∪An∩B1∪B2∪...∪Bn,+∑,Ai∩B1∪B2∪...∪Bn,=,B1∪B2∪...∪Bn
它可以表示两个集合中的元素总和之间的关系,它表明两个集合的交集的容量可以用计算机编程来实现。
容斥关系是一个简单的但却极其强大的公式,它可以帮助我们更深入地理解和探索两个集合之间的关系。
容斥原理二集合公式

容斥原理二集合公式一、基本概念容斥原理是一种计数方法,用于解决多个集合的元素个数之和的问题。
假设有n个集合A1,A2,...,An,定义函数f(S)表示满足条件S的元素个数。
那么容斥原理的二集合公式可以表示为:f(A1∪A2) = f(A1) + f(A2) - f(A1∩A2)二、应用场景容斥原理广泛应用于概率论、组合数学和计算几何等领域,特别适用于求解满足多个条件的元素个数问题。
1. 求解不同条件下元素个数的问题容斥原理可以用来求解满足多个条件的元素个数问题。
例如,假设有一个集合S,它包含了所有既是A的子集又是B的子集的元素。
那么可以通过容斥原理计算出S的元素个数。
2. 求解排斥条件下元素个数的问题容斥原理还可以用来求解排斥条件下元素个数的问题。
例如,假设有一个集合S,它包含了所有既不是A的子集又不是B的子集的元素。
那么可以通过容斥原理计算出S的元素个数。
三、示例分析下面通过一个具体的示例来说明容斥原理的应用。
假设有一个由1到100的整数构成的集合S,现在要求满足以下条件的元素个数:1. 能被2整除的元素个数;2. 能被3整除的元素个数;3. 能被5整除的元素个数。
根据容斥原理的二集合公式,我们可以得到:f(S) = f(A) + f(B) + f(C) - f(A∩B) - f(A∩C) - f(B∩C) + f(A∩B∩C)其中,A表示满足条件1的元素,B表示满足条件2的元素,C表示满足条件3的元素。
根据条件,我们可以计算出:f(A) = 100 / 2 = 50f(B) = 100 / 3 = 33f(C) = 100 / 5 = 20f(A∩B) = 100 / (2*3) = 16f(A∩C) = 100 / (2*5) = 10f(B∩C) = 100 / (3*5) = 6f(A∩B∩C) = 100 / (2*3*5) = 3将这些值代入容斥原理的公式中,就可以求解出满足条件的元素个数。
公务员行测考试容斥问题速解宝典题集

公务员行测考试容斥问题速解宝典题集一、两集合类型1.解题技巧题目中所涉及事物属于两集合时,容斥原理适用于条件与问题都可以直接带入公式题目,如下:A∪B=A+B-A∩B快速解题:总数=两集合之和+两集合之外数-两集合公共数。
2.真题示例【例1】现有50名学生都做物理,化学实验,如果物理实验做正确的有40人,化学实验做正确的有31人,两种实验都错的有4人,则两种实验都做对有:A27人B25人C19人D10人【解析】B。
50=31+40+4-A∩B,得A∩B=25。
二、三集合类型1.解题步骤解题步骤分三步:①画文氏图;②弄清图形中每一部分所代表含义;③代入公式(A∪B∪C=A+B+C-A∩B-A ∩C-B∩C+A∩B∩C)进行求解。
2.解题技巧解题技巧主要包括一个计算公式和文氏图。
总数=各集合数之和-两集合数之和+三集合公共数+三集合之外数3.真题示例【例2】某高校对一些学生进行问卷调查。
在接受调查的学生中,准备参加会计师考试的有63人,准备参加英语六级考试的有89人,准备参加计算机考试的有47人,三种考试都准备参加的有24人,准备只选择两种考试都参加的有46人,不参加任何一种考试的有15人。
问接受调查问卷的学生共有多少人?A.120B.144C.177D.192【解析】A。
填充三个集合公共部分数字24;根据每个区域含义应用公式:总数=各集合之和-两两集合数之和+三集合公共数+三集合之外数=63+89+47-{(x+24)+(z+24)+(y+24)}+24+15=199-{(x+y+z)+24+24+24}+24+15。
x+y+z只属于两集合数之和,该题所讲只选择两种考试参加人数,所以x+y+z值为46人;得本题答案为120。
【例3】对某单位的100名员工进行调查,结果发现他们喜欢看球赛和电影、戏剧。
其中58人喜欢看球赛,38人喜欢看戏剧,52人喜欢看电影,既喜欢看球赛又喜欢看戏剧的有18人,既喜欢看电影又喜欢看戏剧的有16人,三种都喜欢看的有12人,则只喜欢看电影的有多少人?A.22人B.28人C.30人D.36人【解析】A。
容斥问题两个集合的公式

容斥问题两个集合的公式容斥问题在我们的数学学习中可算是个有趣但又有点小“调皮”的家伙。
咱们今天就来好好聊聊容斥问题中两个集合的公式。
先给大家举个小例子哈。
比如说,在一个班级里,喜欢数学的同学有 20 个,喜欢语文的同学有 15 个,但是呢,其中有 5 个同学既喜欢数学又喜欢语文。
那到底喜欢数学或者喜欢语文的同学一共有多少个呢?这时候,咱们的容斥问题两个集合的公式就派上用场啦!这个公式就是:A∪B = A + B - A∩B 。
这里的 A 就好比是喜欢数学的同学的集合,B 就是喜欢语文的同学的集合,A∪B 表示喜欢数学或者喜欢语文的同学的集合,A∩B 就是既喜欢数学又喜欢语文的同学的集合。
把咱们刚才班级里的数字带进去算算,喜欢数学的同学(A)有 20 个,喜欢语文的同学(B)有 15 个,既喜欢数学又喜欢语文的同学(A∩B)有 5 个。
那喜欢数学或者喜欢语文的同学(A∪B)就等于 20 + 15 - 5 = 30 个。
是不是一下子就清楚啦!我之前在给学生们讲这个知识点的时候,有个小家伙特别可爱。
他一直皱着眉头,嘴里还嘟囔着:“老师,这也太复杂啦,我脑袋都要转不过来了!”我就笑着跟他说:“别着急,咱们慢慢来。
”然后我又给他举了个例子,比如说学校组织运动会,参加跑步比赛的同学有 18 个,参加跳远比赛的同学有 12 个,其中有 3 个同学既参加了跑步又参加了跳远。
那参加跑步或者跳远比赛的同学一共有多少个呢?我带着他一步步地用公式去计算,先确定 A 是参加跑步比赛的同学集合,有 18 个;B 是参加跳远比赛的同学集合,有 12 个;A∩B 是既参加跑步又参加跳远的同学集合,有 3 个。
然后用公式 A∪B = A + B - A∩B ,算出 18 + 12 - 3 = 27 个。
这小家伙眼睛一下子亮了,兴奋地说:“老师,我懂啦!原来这么简单!”其实啊,容斥问题的两个集合公式在生活中也有很多用处呢。
比如说,咱们去超市买水果,喜欢吃苹果的有 30 个人,喜欢吃香蕉的有 25 个人,两种都喜欢的有 10 个人。
数量关系之容斥问题解题原理及方法

数量关系之容斥问题解题原理及⽅法 ⼀、知识点 1、集合与元素:把⼀类事物的全体放在⼀起就形成⼀个集合。
每个集合总是由⼀些成员组成的,集合的这些成员,叫做这个集合的元素。
如:集合A={0,1,2,3,……,9},其中0,1,2,…9为A的元素。
2、并集:由所有属于集合A或集合B的元素所组成的集合,叫做A,B的并集,记作A∪B,记号“∪”读作“并”。
A∪B读作“A 并B”,⽤图表⽰为图中阴影部分表⽰集合A,B的并集A∪B。
例:已知6的约数集合为A={1,2,3,6},10的约数集合为B={1,2,5,10},则A∪B={1,2,3,5,6,10} 3、交集:A、B两个集合公共的元素,也就是那些既属于A,⼜属于B的元素,它们组成的集合叫做A和B的交集,记作“A∩B”,读作“A交B”,如图阴影表⽰: 例:已知6的约数集合A={1,2,3,6},10的约数集合B={1,2,5,10},则A∩B={1,2}。
4、容斥原理(包含与排除原理): (⽤|A|表⽰集合A中元素的个数,如A={1,2,3},则|A|=3) 原理⼀:给定两个集合A和B,要计算A∪B中元素的个数,可以分成两步进⾏: 第⼀步:先求出∣A∣+∣B∣(或者说把A,B的⼀切元素都“包含”进来,加在⼀起); 第⼆步:减去∣A∩B∣(即“排除”加了两次的元素) 总结为公式:|A∪B|=∣A∣+∣B∣-∣A∩B∣ 原理⼆:给定三个集合A,B,C。
要计算A∪B∪C中元素的个数,可以分三步进⾏: 第⼀步:先求∣A∣+∣B∣+∣C∣; 第⼆步:减去∣A∩B∣,∣B∩C∣,∣C∩A∣; 第三步:再加上∣A∩B∩C∣。
即有以下公式: ∣A∪B∪C∣=∣A∣+∣B∣+∣C∣-∣A∩B∣-∣B∩C∣- |C∩A|+|A∩B∩C∣ ⼆、例题分析: 例1 求不超过20的正整数中是2的倍数或3的倍数的数共有多少个。
分析:设A={20以内2的倍数},B={20以内3的倍数},显然,要求计算2或3的倍数个数,即求∣A∪B∣。
二集合容斥问题公式

二集合容斥问题公式关于二集合容斥问题,我们可以通过以下公式来描述:设 A、B 两个集合,|A| 表示集合 A 的元素个数(即 A 的大小),|B| 同理。
则 A、B 两个集合的交集表示为A∩B,交集的大小为|A∩B|。
则 A、B 两个集合的并集表示为A∪B,并集的大小为|A∪B|。
则二集合容斥问题可以表述为:|A∪B| = |A| + |B| - |A∩B|这个公式表明,如果要求 A、B 两个集合的并集的大小,我们需要将A、B 两个集合的大小加起来,但是这样会重复计算A∩B 的部分,因此我们需要减去A∩B 的大小,才能得到正确的结果。
这个公式实际上是一个非常通用的公式,可以用来解决很多问题,比如三集合容斥问题、多集合容斥问题等等。
而且这个公式的证明非常简单,可以用一个 Venn 图来说明。
Venn 图是一种图形化表示集合和它们之间关系的方法。
它将集合表示为圆形区域,交集表示为圆形区域重叠的部分,如下图所示:[插入一张 Venn 图]在这个 Venn 图中,A、B 两个集合的交集用红色区域表示,而它们的并集用蓝色区域表示。
我们可以看到,A、B 两个集合的并集由四个部分组成:A、B 自身的部分,以及它们的交集部分。
而A∩B 的大小等于红色区域的大小。
因此,我们可以通过这个 Venn 图来解释上述公式的含义。
首先,我们将 A、B 两个集合的大小加起来,得到 |A|+|B|;这样会将A∩B 的大小重复算了一次,因此需要减去|A∩B|,得到正确的结果。
二集合容斥问题是一个非常基础的数学问题,但它却在很多领域得到了广泛的应用。
比如在概率论、组合数学、计算机科学等领域,都可以看到它的身影。
因此我们需要深入理解这个公式,并掌握它的应用方法,才能更好地应对各种数学问题。
容斥原理及公式的证明
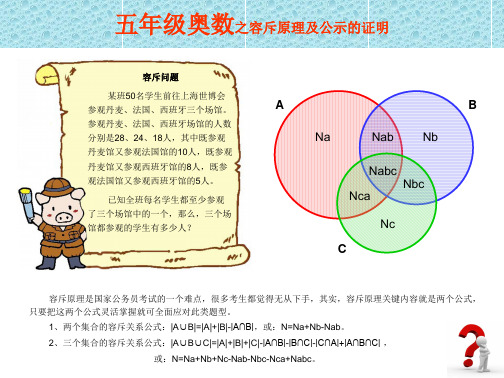
=50-(28+24+18)+(10+8+5) =3(人) 答:三个场馆都参观的有3人。
或:N=Na+Nb+Nc-Nab-Nbc-Nca+Nabc。
四年级奥数之容斥原理及公示的证明
பைடு நூலகம்
A
B
N1 Na
N4
N2
Nab Nb
Nabc
Nca N6
N7
Nbc N5
Nc
N3 C
定理: |A∪B∪C|=|A|+|B|+|C|-|A∩B|-|B∩C|-|C∩A|+|A∩B∩C| 或:N=(Na+Nb+Nc)-(Nab+Nbc+Nca)+Nabc
证明:设Na、Nb、Nc分别表示图A、B、C覆盖的 面积;Nab、Nbc、Nca分别表示图A和B、B和C、C和 A共同覆盖的面积;Nabc表示图A、B、C共同覆盖的面 积。再设N1、N2、N3、N4、N5、N6、N7分别表示7个 互不覆盖区域的面积;N表示7个互不覆盖区域的面积 总和。
则:N1=Na-Nab-Nca+Nabc, N2=Nb-Nab-Nbc+Nabc, N3=Nc-Nbc-Nca+Nabc N4=Nab-Nabc N5=Nbc-Nabc N6=Nca-Nabc N7=Nabc
五年级奥数之容斥原理及公示的证明
容斥问题
某班50名学生前往上海世博会 参观丹麦、法国、西班牙三个场馆。 参观丹麦、法国、西班牙场馆的人数 分别是28、24、18人,其中既参观 丹麦馆又参观法国馆的10人,既参观 丹麦馆又参观西班牙馆的8人,既参 观法国馆又参观西班牙馆的5人。
容斥原理总结

容斥原理习题总结首先讲一下有关这个问题的核心公式:(1)两个集合的容斥关系公式:A+B=A∪B+A∩B(2)三个集合的容斥关系公式:A+B+C=A∪B∪C+A∩B+B∩C+C∩A-A∩B∩C题型一:逆向思维题1、在一次展览会上展品中有366部手机不是A公司的,有276部手机不是B公司的,两公司的展品共有378部,问B公司有多少部手机参展?2、学校展览每个年级的书画作品,其中28副不是五年级的,24副不是六年级的,五六年级的展览作品共有20副。
一二年级的参展作品比三四年级总数少4副。
问一二年级的参赛作品有几幅?解:第一题中问B公司的手机有几部,设为X部。
X+276即为所有展品的数量。
X+276=366+378-X。
(等式右边是以A公司的展品表示的所有展品数量)第二题中设五年级的作品有X副,X+28=24+20-X,求得X=6.则共有作品8+28=36副。
一二三四年级加起来有16副。
X+Y=16X-Y=4 因此一二年级有展品6副。
题型二:需要列表的题(较复杂)1、某班有少先队员35人,这个班有男生23人,问女生少先队员比男生非少先队员多几人。
少先队员非少先队员男X 23-X 23女35-X容易得到答案为12.2、某校参加数学奖赛的有男生120人,女生80人,而参加语文竞赛的男生有80人,女生有120人。
已知共有260人参赛了,75名男生两科都参加了,问只参加数学竞赛而没参加语文竞赛的女生有几人?解:语文数学男120 80 200女80 120 200200 200400=260+75+X,求得参加两科的女生有65人。
80-65=15人。
题型三:分数题结合整除特性来做1、一次数学考试,小王做对的题占全部题目的2/3,小李做错了5道题,两人都做错的占全部的1/4,问小王做对了几道题?解:全部题目能被12整除,两人都做错的题目数≤5,全部题目数≤20,在≤20范围内能被12整除的只有12.所以8道题为答案。
集合之四:容斥原理

集合之四:容斥原理问题两个集合容斥问题容斥原理一:如果被计数的事物有A、B两类,那么,A类元素个数+B 类元素个数=既是A类又是B类的元素个数+A类或B类元素个数。
写成公式形式即:|A U B|=|A|+|B|一|A∩B|韦恩图:解决简单的两类或三类被计数事物之间的重叠问题时采用韦恩图会更加便捷、直接。
【例】1四年级一班有54人,定阅《小学生优秀作文》和《数学大世界》两种读物的有13人,订阅《小学生优秀作文》的有45人每人至少订阅一种读物,订阅《数学大世界》的有多少人?()A.13 B.22 C.33 D.41【例】2五年级有122名同学参加语文、数学考试,每个至少有一门功课取得优秀成绩,其中语文成绩优秀的有65人,数学成绩优秀的有87人。
语文、数学都优秀的有多少人?()A.30 B.35 C.57 D.65【例】3学校文艺组每人至少会演奏一种乐器,已知会拉手提琴的有24人,会弹电子琴的有17人,其中两样都会的有8人。
这个文艺组共有多少人?()A.25 B.32 C.33 D.41【例】4某班有36个同学在一项测试中,答对第一题的有25人,答对第二题的人有23人,两题都答对的有15人,问多少个同学两道题都没有答对?()A.1 B.2 C.3 D.4三个集合容斥问题容斥原理二:如果被计数的事物有A、B、C三类,那么,A类元素个数+B 类元素个数+C类元素个数=A类或B类或C类元素个数+既是A类义是B类的元素个数+既是A类又是B类的元素个数+既是B类又是C类元素个数—既是A 类又是B类而且是C类的元素个数。
写成公式形式即:|A U B U C|=|A|+|B|+|C|—|A∩B|—|B∩C|—|C∩A|+|A∩B∩C|【例】5某大学有外语教师120名,其中教英语的有50名,教日语的有45名,教法语的有40名,有15名既教英语又教日语,有10名既教英语又教法语,有8名既日语又教法语,有4名教英语、日语和法语三门课,则不教三门课的外语教师有多少名?()A.12 B.14 C.16 D.18【例】6对厦门大学计算机系100名学生进行调查,结果发现他们喜欢看NBA 和足球、赛车。
容斥原理题再也不用怕,两个万能公式

容斥原理题再也不用怕,两个万能公式容斥原理题再也不用怕,两个万能公式1.关键提示:容斥原理是2004年、2005年中央国家公务员考试的一个难点,很多考生都觉得无从下手,其实,容斥原理关键内容就是两个公式,考生只要把这两个公式灵活掌握就可全面应对此类题型。
另外在练习及真考的过程中,请借助图例将更有助于解题。
2.核心公式:(1)两个集合的容斥关系公式:A +B=A∪B+A∩B(2)三个集合的容斥关系公式:A +B+C=A∪B∪C+A∩B+B∩C+C∩A-A∩B∩C例题1:2004年中央A类真题某大学某班学生总数为32人,在第一次考试中有26人及格,在第二次考试中有24人及格,若两次考试中,都没有及格的有4人,那么两次考试都及格的人数是( )。
A.22 B.18 C.28 D.26解析:设A=第一次考试中及格的人(26),B=第二次考试中及格的人(24)显然,A+B=26+24=50;A∪B=32-4=28,则根据公式A∩B=A+B-A∪B=50-28=22所以,答案为A。
例题2:2004年山东真题某单位有青年员工85人,其中68人会骑自行车,62人会游泳,既不会骑车又不会游泳的有12人,则既会骑车又会游泳的有()人 A.57 B.73 C.130 D.69解析:设A=会骑自行车的人(68),B=会游泳的人(62)显然,A+B=68+62=130;A∪B=85-12=73,则根据公式A∩B=A+B-A∪B=130-73=57所以,答案为A。
例题3:电视台向100人调查前一天收看电视的情况,有62人看过2频道,34人看过8频道,11人两个频道都看过。
两个频道都没看过的有多少人?解析:设A=看过2频道的人(62),B=看过8频道的人(34)显然,A+B=62+34=96;A∩B=两个频道都看过的人(11)则根据公式A∪B=A+B-A∩B=96-11=85所以,两个频道都没有看过的人数=100-85=15所以,答案为15。
辽宁省政法干警考试备考技巧:容斥原理两集合例题精解

辽宁省政法干警考试备考技巧:容斥原理两集合例题精解在政法干警考试中,数量关系中一个典型的模块容斥原理要引起大家注意,但是考生们并不用担心,只要掌握好容斥原理的解题方法,充分利用公式,那么容斥原理自然会迎刃而解了。
在容斥原理中,大体分为两集合、三集合两个题型,那么下面我们就看看对于两集合容斥原理我们该如何去解决。
题型类型:两集合标准型解题方法:满足条件1个数+满足条件2个数-两者都满足的个数=总个数- 两者都不满足的个数例题详解:【例1】电视台向100人调查昨天收看电视的情况,有62人看过2频道,34人看过8频道,11人两个频道都看过。
问,两个频道都没看过的有多少人?A. 4B. 15C. 17D. 28【答案】B【解析】根据两集合公式:满足条件1的个数+满足条件2的个数-两者都满足的个数=总数-两者都不满足的个数。
条件1为看过2频道有62人,条件2为看过8频道有34人,两者都满足为两个频道都看过有11人,代入公式解得两者都不满足的也就是两个频道都没看过为15人。
因此,本题答案为B选项。
【例2】旅行社对120人的调查显示,喜欢爬山的与不喜欢爬山的人数比为5:3;喜欢游泳的与不喜欢游泳的人数比为7:5;两种活动都喜欢的有43人。
对这两种活动都不喜欢的人数是( )。
A. 18B. 27C. 28D. 32【答案】A辽宁公务员 | 国家公务员 | 事业单位 | 政法干警 | 公安招警 | 村官三支一扶 | 党政公选 |【解析】设两种活动都不喜欢的人数有x,依题意有,喜欢爬山的有120×5/8=75人,喜欢游泳的有120×7/120=70人,根据二集合容斥原理公式,75+70-43=120-x,解得x=18,因此,本题答案为A。
【例3】一名外国游客到北京旅游,他要么上午出去游玩,下午在旅馆休息,要么上午休息,下午出去游玩,而下雨天他只能一天都呆在屋里。
在此期间,不下雨的天数是12天,他上午呆在旅馆的天数为8天,下午呆在旅馆的天数为12天,他在北京共呆了( )。
容斥原理四集合公式

容斥问题公式,四个集合的容斥原理公式怎么解决技术容斥问题公式,四个集合的容斥原理公式怎么解决用|A|表示集合A的基数,也即集合A中元素的个数。
则有|A∪B∪C∪D|=|A|+|B|+|C|+|D|-|A∩B|-|A∩C|-|A∩D|-|B∩C|-|B∩D|-|C∩用|A|表示集合A的基数,即集合A中的元素个数,然后| Abcd |=| A | | b | | c | | d |-| Ab |-| Ac |-| Ad |-| b。
计数时,一定要注意不重复,不遗漏。
为了防止重复计算重叠部分,人们开发了一种新的计数方法。
这种方法的基本思想是包含和排除问题的公式:首先计算某一内容中包含的所有对象的数量,不考虑重叠,然后排除重复计算的数量,使计算结果既不遗漏也不重复。
这种计数方法称为包含和排除原理。
扩展数据:包含和排除原则中经常使用以下两个公式:1.两个集合之间包含关系的公式:aB=a B- aB.如果有两种东西要计算:a和b。
那么属于a类或b类的所有元素之和=属于a类的元素数属于b类的元素数-属于a类和b类的元素数。
2.三个集合的公式:ABC=a b c-aB- AC-bC ABC .如果要统计的东西有三种:A、B、C,那么属于A、B或C的元素总数=A B C元素-a、B两个元素-B、C两个元素-A、C两个元素-A、B、C两个元素。
二集排除原理的公式为:| AB |=| A | | B |-| AduB |。
三集排除原理的本质与二集排除原理相同,只是多了一集,公式和图形描述变得更加复杂。
其中A和b是两个集合,|A|代表集合A中的元素个数,当我们理解包含和排除的原理时,我们可以将元素个数与一个图形的面积进行比较。
三套包含排除原则这类问题主要出现在近几年的省考中,主要有三个独立的个体。
做这类题的主要方法是公式和作图。
配方应用:【示例】某专业50人,必修课A、B、C三门.课程A有40人,课程B有36人,课程C有30人,课程A和课程B都有28人,课程A和课程C都有26人,课程B和课程C都有24人,课程A、课程B和课程C都有20人,有多少人没有修完这三门课程?()C.3人D.4人。
列表法与容斥原理

列表法与容斥原理列表法与容斥原理是概率论与组合数学中常用的计数方法。
它们可以帮助我们解决各种排列组合的计数问题,包括但不限于二项式系数、集合的交并补运算、事件的概率计算等等。
本文将分别介绍列表法与容斥原理的定义、应用以及优缺点,并通过实际例子展示它们在解决问题时的具体步骤和技巧。
一、列表法列表法又称为穷举法,它通过列举所有可能的情况,逐个判断其是否满足要求,最后计数满足要求的情况的个数。
列表法可以用来求解排列组合问题、二项式系数等。
在使用列表法解决问题时,我们需要明确问题的要求,确定可能的情况,并将其列成一个简明的列表。
然后,我们逐个判断列表中的情况是否满足要求,并计数满足要求的情况的个数。
最后,得到的计数结果即为问题的解答。
例如,我们有5个球,其中3个红球,2个蓝球,要求从中选出两个球,至少选择一个红球。
我们可以使用列表法解决这个问题。
可能情况列表如下:1. 选出一个红球,一个蓝球2. 选出两个红球根据要求,我们可以判断上述两种情况都满足要求。
因此,满足要求的情况共有2种,即答案为2。
列表法的优点是直观、容易理解,并且适用于简单的计数问题。
但当问题规模较大时,列表法可能会变得繁琐且耗时。
此时,我们可以使用容斥原理来简化计算。
二、容斥原理容斥原理是一种用于计算多重集合交、并、补运算问题的方法。
它通过对包含或排除某些情况进行计数,来得到最终的计数结果。
容斥原理的核心思想是利用原问题与互斥事件之间的关系,求解它们的交、并、补运算。
在求解过程中,我们需要明确事件的概念、定义互斥事件的具体条件,并利用容斥原理进行计数。
例如,假设集合A表示能被3整除的数,集合B表示能被5整除的数。
我们要求集合A与B的交集,即同时能被3和5整除的数。
我们可以使用容斥原理来解决这个问题。
根据容斥原理的计数公式:|A ∩ B| = |A| + |B| - |A ∪ B|其中,|A|代表集合A的计数个数,|B|代表集合B的计数个数,|A ∪ B|代表集合A与B的并集的计数个数。
第12讲 容斥原理

第12讲容斥原理解题思路:熟悉集合的概念,多画示意图。
我们称一些事物的全体为一个集合。
集合通常用大写的英文字母A、B、C、…表示.构成这个集合的事物称为这个集合的元素例1 B={全体自然数}={1,2,3,4,…}是一个具体有无限多个元素的集合。
例2 C={在1,2,3,…,100中能被3整除的数}={3,6,9,12,…,99}是一个具有有限多个元素的集合。
记号A∪B表示所有属于集合A或属于集合B的元素所组成的集合.就是下图a中两个圆所覆盖的部分.集合A∪B 叫做集合A与集合B的并集.“∪”读作“并”,“A∪B”读作“A并B”。
记号A∩B表示所有既属于集合A也属于集合B中的元素的全体.就是下图a中阴影部分所表示的集合.即是由集合A、B的公共元素所组成的集合.它称为集合A、B的交集.符号“∩”读作“交”,“A∩B”读作“A交B”.如例3中的集合A、B,则A∩B={2,4}。
图a 图b例3 设集合A={1,2,3,4},集合B={2,4,6,8},则A∪B={1,2,3,4,6,8}.元素2、4在集合A、B中都有,在并集中只写一个。
例4 设集合I={1,3,5,7,9},集合A={3,5,7}。
A={属于集合I,但不属于集合A的全体元素}={1,9}我们称属于集合I,但不属于集合A的元素的集合为集合A在集合I中的补集(或余集),如上图b中阴影部分表示的集合(整个长方形表示集合I).常记作A。
A∪B=A+B-A∩B这就是关于两个集合的容斥原理:集合A与B的并的元素个数,等于集合A的元素个数与集合B的元素个数的和,减去集合A与B的交的元素个数。
例5 桌上有两张圆纸片A、B.假设圆纸片A的面积为30平方厘米,圆纸片B的面积为20平方厘米.这两张圆纸片重叠部分的面积为10平方厘米.求这两张圆纸片覆盖桌面的面积例6 求在1至100的自然数中能被3或7整除的数的个数。
例7 求在1~100的自然数中不是5的倍数也不是6的倍数的数有多少个?例8 设下面图中正方形的边长为1厘米,半圆均以正方形的边为直径,求图中阴影部分的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
14
26
合计
31
29
60
2010
31.某部门共有82人,其中男பைடு நூலகம்52人;本省籍42人,不是本省籍的女性11人,则本省籍的男性人数有
A.23 B.33 C.21 D.22
【解析】A。常见的集合问题。可以利用表格来枚举。
本省
外省
总数
男
23
29
52
女
19
11
30
总数
42
40
82
2011
65.今年某高校数学系毕业生为60名,其中70%是男生,男生中有1 /3选择继续攻读硕士学位,女生选择攻读硕士学位的人数比例是男生选择攻读硕士学位人数比例的一半.那么该系选择攻读硕士学位的毕业生共有:
A.15位B.19位C.17位D.21位
【解析】C。
男
女
合计
硕
14
3(比例六分之一)
17
非硕
28
15
43
合计
42
18
60
2016
54.有64%的教师发表了核心期刊论文,有40%的教师承担了科研项目,这其中有90%的公开发表了论文,这些论文均发表在核心期刊上,那么发表核心期刊论文但没有承担科研项目的教师是承担了科研项目但没发表核心前论文的教师人数的()倍。
集合问题(容斥原理)
7.某服装厂生产出来的一批衬衫中大号和小号各占一半。其中25%是白色的,75%是蓝色的。如果这批衬衫总共有100件,其中大号白色衬衫有10件,问小号蓝色衬衫有多少件?( )。
A.15 B.25 C.35 D.40
【解析】C。两者集合问题。匹配类表格最清晰。
白色
蓝色
合计
大
10
40
50
2008
14.某单位有60名运动员参加运动会开幕式,他们着装白色或黑色上衣,黑色或蓝色裤子。其中有12人穿白上衣蓝裤子,有34人穿黑裤子,29人穿黑上衣,那么穿黑上衣黑裤子的有多少人?( )
A.12 B.14 C.15 D.19
【解析】C。两者集合问题。表格法最清晰。
白上
黑上
合计
黑裤
19
15
34
蓝裤
小
15
35
50
合计
25
75
100
2007
113.调查发现,男女生各半的一个100人的班,20%患有色盲症,其余正常;如果女生有色盲5人,则正常男生的人数是( )。
A.15 B.30 C.35 D.40
【解析】C。两者集合问题。匹配类表格最清晰。
男
女
合计
色盲
15
5
20
非色盲
35
45
80
合计
50
50
100
A. 6 B. 7 C. 9 D. 10
【解析】C。两者集合问题。可以利用表格或者画图。
科研
非科研
核心论文
36
28
64
非核心论文
4
32
36
