matlab与分布拟合
正态分布拟合matlab

正态分布拟合matlab在MATLAB中,可以使用 normfit 函数来拟合一组数据到一个正态分布。
normfit 函数会提供正态分布的参数估计,包括均值(mean)和标准差(standard deviation)。
以下是一个使用normfit函数的简单例子:假设有一组数据datadata = randn(1000,1);这会生成一个标准正态分布的随机样本数据使用normfit函数拟合正态分布[mu, sigma] = normfit(data);显示拟合得到的均值和标准差disp(['均值 = ', num2str(mu)]);disp(['标准差 = ', num2str(sigma)]);可以使用normpdf函数生成拟合的正态分布的概率密度函数(PDF)值x = linspace(min(data), max(data), 100);pdf_fitted = normpdf(x, mu, sigma);绘制原始数据的直方图和拟合得到的正态分布曲线histogram(data, 30, 'Normalization', 'pdf');数据的PDF直方图hold on;保持图像,以便在同一图上绘制plot(x, pdf_fitted, 'r', 'LineWidth', 2); 绘制拟合的正态分布曲线hold off; 释放图像在上述代码中,randn 函数生成了一个标准正态分布的随机样本。
在实际操作中,可以使用自己的数据集替换data变量。
normfit函数返回数据集的均值mu和标准差sigma,是正态分布的参数。
我们可以用normpdf函数和这些参数来生成拟合的正态分布的PDF,并将其与原始数据的直方图一起绘制出来。
需要注意的是,确保在使用这些函数之前,的MATLAB环境中已经安装了统计和机器学习工具箱,因为normfit函数是这个工具箱的一部分。
matlab正态分布拟合曲线

matlab正态分布拟合曲线
本篇文章将介绍如何使用MATLAB对一组数据进行正态分布拟合,并绘制出拟合曲线。
正态分布是一种常见的概率分布,它在统计学中有着广泛的应用。
我们将通过以下步骤来实现正态分布拟合曲线:
1. 导入数据:我们首先需要将数据导入到 MATLAB 中。
可以使
用 MATLAB 中的“readtable”函数来读取数据文件,并将数据存储
到表格中。
2. 统计数据:在拟合曲线前,我们需要对数据进行一些统计分析。
可以使用 MATLAB 中的“mean”和“std”函数来计算样本均值
和样本标准差。
3. 计算概率密度函数:根据正态分布的定义,我们可以使用计
算公式计算概率密度函数。
可以使用 MATLAB 中的“normpdf”函数
来计算。
4. 拟合曲线:使用 MATLAB 中的“fit”函数可以对数据进行正态分布拟合。
该函数将返回一个包含拟合参数的结构体。
5. 绘制拟合曲线:使用 MATLAB 中的“plot”函数将拟合曲线
绘制出来。
通过以上步骤,我们可以很容易地在 MATLAB 中实现正态分布拟合曲线。
这对于进行统计分析和数据可视化是非常有帮助的。
- 1 -。
Matlab曲线拟合(cftool)分布拟合(dfittool)

、单一变量的曲线逼近Matlab有一个功能强大的曲线拟合工具箱cftool,使用方便,能实现多种类型的线性、非线性曲线拟合。
下面结合我使用的Matlab R2009b来简单介绍如何使用这个工具箱。
假设我们要拟合的函数形式是y=A*x*x + B*x,且A>0,B>0。
1、在命令行输入数据:》x=[110.3323 148.7328 178.064 202.8258033 224.7105 244.5711 262.908 280.0447 296.204 311.5475];》y=[5 10 15 20 25 30 35 40 45 50];2、启动曲线拟合工具箱》cftool3、进入曲线拟合工具箱界面“Curve Fitting tool”(1)点击“Data”按钮,弹出“Data”窗口;(2)利用X data和Y data的下拉菜单读入数据x,y,可修改数据集名“Data set name”,然后点击“Create data set”按钮,退出“Data”窗口,返回工具箱界面,这时会自动画出数据集的曲线图;(3)点击“Fitting”按钮,弹出“Fitting”窗口;(4)点击“New fit”按钮,可修改拟合项目名称“Fit name”,通过“Data set”下拉菜单选择数据集,然后通过下拉菜单“Type of fit”选择拟合曲线的类型,工具箱提供的拟合类型有:∙Custom Equations:用户自定义的函数类型∙Exponential:指数逼近,有2种类型,a*exp(b*x)、a*exp(b*x) + c*exp(d*x)∙Fourier:傅立叶逼近,有7种类型,基础型是a0 + a1*cos(x*w) + b1*sin(x*w)∙Gaussian:高斯逼近,有8种类型,基础型是a1*exp(-((x-b1)/c1)^2)∙Interpolant:插值逼近,有4种类型,linear、nearest neighbor、cubic spline、shape-preserving∙Polynomial:多形式逼近,有9种类型,linear ~、quadratic ~、cubic ~、4-9th degree ~∙Power:幂逼近,有2种类型,a*x^b、a*x^b + c∙Rational:有理数逼近,分子、分母共有的类型是linear ~、quadratic ~、cubic ~、4-5th degree ~;此外,分子还包括constant型∙Smoothing Spline:平滑逼近(翻译的不大恰当,不好意思)∙Sum of Sin Functions:正弦曲线逼近,有8种类型,基础型是a1*sin(b1*x + c1)∙Weibull:只有一种,a*b*x^(b-1)*exp(-a*x^b)选择好所需的拟合曲线类型及其子类型,并进行相关设置:——如果是非自定义的类型,根据实际需要点击“Fit options”按钮,设置拟合算法、修改待估计参数的上下限等参数;——如果选Custom Equations,点击“New”按钮,弹出自定义函数等式窗口,有“Linear Equations线性等式”和“General Equations构造等式”两种标签。
matlab拟合正态分布曲线

matlab拟合正态分布曲线在统计学和数据分析领域中,正态分布是一种非常重要的概率分布。
而在处理数据以及进行模拟和预测时,拟合正态分布曲线是一项常见的任务。
MATLAB作为一款强大的数学软件,提供了丰富的工具和函数,可以方便地进行正态分布曲线的拟合。
首先,在使用MATLAB进行正态分布拟合之前,我们需要先了解正态分布的特点和参数。
正态分布的概率密度函数可以用如下的数学表达式表示:f(x; μ, σ) = (1 / (σ * sqrt(2π))) * exp(-((x - μ)² / (2 * σ²)))其中,μ为均值,σ为标准差。
均值决定了正态分布的中心位置,标准差则决定了分布的幅度和变化程度。
接下来,我们将具体介绍一下MATLAB中常用的正态分布拟合函数和方法。
1. histfit函数histfit函数是MATLAB中用于拟合数据并显示拟合结果的函数之一。
它可以绘制数据的直方图,并拟合正态分布曲线,并将曲线添加到直方图上。
使用histfit函数非常简单,只需要将数据作为输入参数传入即可。
```matlabdata = [1.2, 2.3, 3.4, 4.5, 5.6, 6.7, 7.8, 8.9, 9.0];histfit(data)```上述代码将给定的数据data进行正态分布拟合,并绘制直方图和拟合曲线。
2. fitdist函数fitdist函数是MATLAB中用于对一组数据进行分布拟合的函数。
通过fitdist函数可以选择不同的分布族进行拟合,包括正态分布、指数分布、伽玛分布等。
对于正态分布的拟合,只需要指定分布类型为'Normal'即可。
```matlabdata = [1.2, 2.3, 3.4, 4.5, 5.6, 6.7, 7.8, 8.9, 9.0];pd = fitdist(data, 'Normal')```上述代码将给定的数据data拟合为正态分布,并将结果存储在pd 对象中。
matlab学生t分布拟合

matlab学生t分布拟合
在Matlab中,可以使用自带的曲线拟合工具去拟合学生t分布。
下面是一般步骤:
1. 准备数据:将数据整理成适合混合效应逻辑回归模型的格式。
确保数据包括一个二分类的因变量和一个或多个自变量。
2. 导入工具箱:在Matlab命令窗口中输入"toolbox",然后选择并导入统计和机器学习工具箱。
3. 拟合模型:使用`fitglme`函数来拟合混合效应逻辑回归模型。
该函数的语法如下:`mdl = fitglme(data, formula, 'Distribution', 'binomial', 'Link', 'logit')`,其中,`data`是包含因变量和自变量的数据表或数据集,`formula`是描述模型的公式,`'Distribution'`参数指定分布为二项分布,`'Link'`参数指定链接函数为对数函数。
拟合学生t分布需要一定的数学和统计学知识,如果你需要更详细的指导或有特定的问题,请提供更多信息,以便我能更好地帮助你。
matlab拟合正态分布

matlab拟合正态分布在Matlab中,拟合正态分布可以使用正态拟合函数normfit(),该函数可以帮助我们对数据进行正态分布拟合并返回其均值和标准差。
此外,还可以使用拟合工具箱中的拟合函数fitdist()来拟合正态分布。
下面我将详细介绍如何使用这两种拟合方法。
1. normfit()函数这个函数主要用于对已有数据进行正态拟合。
假设我们有一组数据如下:x = [1.2, 2.9, 3.5, 4.2, 5.1, 6.7, 8.3, 9.9];接着,我们可以调用normfit()函数来进行拟合:[mu, sigma] = normfit(x)拟合结果会被保存在mu和sigma变量中。
其中,mu表示拟合得到的正态分布的均值,sigma表示标准差。
如果需要自定义置信度,可以通过增加第三个参数来实现:[mu, sigma, muci, sigmaci] = normfit(x, alpha)其中,muci和sigmaci分别是均值和标准差的置信区间。
另外,如果需要查看拟合后的正态分布在数据中的图像,可以使用如下代码:histfit(x)其中,histfit()函数默认使用normfit()函数拟合数据。
2. fitdist()函数该函数可用于拟合多种分布,包括正态分布。
与normfit()函数不同,fitdist()函数需要先选择分布类型,之后再进行拟合。
例如,要使用正态分布拟合上文中的数据,可以使用如下代码:pd = fitdist(x, 'Normal')这里pd表示已经得到的正态分布对象。
如果需要查看拟合效果,可以使用如下代码:histfit(x)hold onx_values = -5:0.1:15;y = pdf(pd, x_values);plot(x_values, y, 'r')hold off其中,pdf()函数是用于计算概率密度函数的函数。
在这段代码中,我们对数据进行了绘图,并在上面叠加了拟合后的正态分布曲线。
正态分布拟合matlab

正态分布拟合matlab
在MATLAB中,可以使用normfit函数对数据进行正态分布拟合。
该函数返回给定数据的正态分布拟合参数,包括均值、标准差和拟合优度。
以下是一个简单的示例:
matlab% 生成一些随机数据data = randn(1000,1);% 进行正态分布拟合params = normfit(data);% 输出拟合参数mean =
params(1);stddev = params(2);gof = params(3);disp(['均值:', num2str(mean)]);disp(['标准差:', num2str(stddev)]);disp(['拟合优度:', num2str(gof)]);
在上面的示例中,randn函数用于生成1000个标准正态分布的随机数。
然后,使用normfit函数对这些数据进行正态分布拟合,并将返回的拟合参数存储在params变量中。
最后,通过索引将拟合参数的均值、标准差和拟合优度提取出来,并使用disp函数将其输出到命令窗口。
除了normfit函数,还有其他一些函数可以用于正态分布拟合,例如fitdist和pdfndist。
这些函数的使用方法可能会有所不同,但它们的基本原理都是通过对数据进行最小二乘拟合来计算正态分
布的参数。
需要注意的是,正态分布拟合并不一定能够完全拟合数据,因为数据通常不是完全符合正态分布的。
因此,在进行正态分布拟合时,
需要谨慎评估数据的拟合程度,并使用适当的的方法对数据进行处理和分析。
matlab 对数正态分布拟合

matlab 对数正态分布拟合
对数正态分布是概率统计中的一种重要分布,它具有许多的应用。
在 MATLAB 中我们可以使用拟合工具箱中的 lognfit 函数来对样本数
据进行对数正态分布拟合。
具体操作步骤如下:
首先,我们需要准备一个样本数据。
假设我们有一个数据集 x,
我们可以使用 lognfit 函数来对其进行拟合,代码如下:
```
% 准备样本数据
x = [0.2587 0.6065 0.4711 1.3658 0.0054 0.5037 3.0179 0.1664 0.1144 2.3894];
% 对数正态分布拟合
[mu, sigma] = lognfit(x);
```
运行上述代码后,我们可以得到对数正态分布的两个参数 mu 和sigma。
其中,mu 代表对数正态分布的期望值,sigma 代表对数正态
分布的标准差。
如果我们想要绘制对数正态分布的概率密度函数,可以使用lognpdf 函数,代码如下:
```
% 绘制对数正态分布的概率密度函数
x_values = 0:0.1:4;
y_values = lognpdf(x_values, mu, sigma);
plot(x_values, y_values);
```
上述代码中,我们使用 lognpdf 函数来计算对数正态分布在给
定值处的概率密度值,然后使用 plot 函数来绘制概率密度函数图形。
在 MATLAB 中,对数正态分布拟合和绘制概率密度函数都非常简
单。
通过上述步骤,我们可以快速地对样本数据进行拟合,并且可视化结果,帮助我们更好地理解对数正态分布的特性。
matlab 正态分布拟合

matlab 正态分布拟合MATLAB 正态分布拟合是一种基于数学统计理论,用来估计实际数据与理想正态分布之间的相似度,从而量化描述一组数据的分布特征。
MATLAB 可以使用 fitdist 函数来实现正态分布拟合。
正态分布拟合是基于几何概率理论的,假设一个变量的概率密度函数(PDF)是正态分布的,我们可以使用拟合方法来找到该变量的平均值和标准差。
在 MATLAB 中,fitdist 函数可以用于拟合正态分布,它接受一组数据x,然后返回拟合正态分布的参数 mu 和 sigma,mu 是均值,sigma 是标准差。
如果我们有一组数据x,第一步就是对其进行排序,这样可以确保有序数据的准确性。
接下来,我们可以使用MATLAB 的 fitdist 函数来拟合正态分布。
fitdist 函数接受一个参数,即拟合的分布类型,比如 normal、lognormal、weibull 等。
最后,函数会计算出拟合的参数,并将其作为输出参数返回。
此外,MATLAB 还提供了一种统计检验方法,即 chi-square 测试,它可以用于检验拟合结果是否有效。
chi-square 测试要求检验样本的大小至少是 5 个,并且模型和数据必须是独立的,即模型不能影响数据,而数据也不能影响模型。
如果拟合结果有效,则 chi-square 检验的结果将为 0,如果拟合结果无效,则 chi-square 检验的结果将大于 0。
总的来说,MATLAB 正态分布拟合可以用于估计实际数据与理想正态分布之间的相似度,从而量化描述一组数据的分布特征。
它可以帮助我们更好地分析和研究数据。
MATLAB 的 fitdist 函数可以用于拟合正态分布,并且可以使用 chi-square 测试来检验拟合结果的有效性。
matlab用weibull分布函数拟合曲线

matlab用weibull分布函数拟合曲线Weibull分布函数是一种常用于可靠性分析的概率分布函数,可以用来估计产品的平均故障时间。
在MATLAB中,我们可以使用curve fitting toolbox工具箱中的weibull分布函数进行曲线拟合。
具体步骤如下:1. 导入数据:将需要拟合的数据导入MATLAB中,可以使用xlsread函数读取Excel文件,也可以手动输入数据。
2. 创建拟合曲线对象:可以使用cftool命令打开curvefitting toolbox,选择Weibull分布函数进行拟合,也可以在代码中使用cfit函数创建一个Weibull对象。
3. 设置拟合参数:使用setoptions函数设置拟合参数,包括起点、终点、步长等。
4. 拟合曲线:使用fit函数进行曲线拟合,得到拟合结果。
5. 绘制拟合曲线:使用plot函数绘制拟合曲线,并将图表美化。
下面是MATLAB代码示例:% 导入数据data = xlsread('data.xlsx');% 创建拟合曲线对象weibull_fit = cfit('a*x^b*exp(-x^b/a)', 'a', 'b', 'x');% 设置拟合参数options = fitoptions('Method','NonlinearLeastSquares',...'StartPoint',[1 1],...'Lower',[0 0],...'Upper',[Inf Inf]);% 拟合曲线weibull_result = fit(data(:,1), data(:,2), weibull_fit, options);% 绘制拟合曲线plot(weibull_result, data(:,1), data(:,2)); xlabel('时间');ylabel('概率密度');title('Weibull分布函数拟合曲线');。
Matlab中的随机数生成与分布拟合技巧

Matlab中的随机数生成与分布拟合技巧在科学研究和工程应用中,我们常常需要使用随机数生成和分布拟合技巧来解决各种问题。
Matlab作为一款强大的科学计算软件,提供了一系列方便的函数和工具,可以帮助我们快速、准确地处理随机数和分布相关的任务。
本文将介绍一些常用的Matlab函数和技巧,以及它们在随机数生成和分布拟合中的应用。
一、随机数生成在Matlab中,我们可以使用rand和randn函数快速生成服从均匀分布和正态分布的随机数序列。
rand函数可以生成0到1之间的均匀分布的随机数,例如:```matlabrandom_numbers = rand(100,1);```上述代码将生成一个100行1列的随机数矩阵。
如果我们需要生成服从其他均匀分布的随机数,可以利用rand函数生成0到1之间的随机数,然后利用线性变换将其映射到目标分布区间。
例如,如果我们需要生成一个在区间[2,5]上均匀分布的随机数,可以使用如下代码:```matlaba = 2;b = 5;random_numbers = a + (b-a)*rand(100,1);```其中a和b分别为所需区间的上下界。
同样,randn函数可以生成服从均值为0、标准差为1的正态分布的随机数序列。
例如:```matlabrandom_numbers = randn(100,1);```与均匀分布类似,如果我们需要生成服从其他正态分布的随机数,也可以通过线性变换来实现。
假设我们需要生成一个均值为m,标准差为s的正态分布随机数,可以使用如下代码:```matlabm = 10;s = 2;random_numbers = m + s*randn(100,1);```其中m和s分别为所需正态分布的均值和标准差。
二、分布拟合在实际问题中,我们经常需要将一组实验数据与某种理论概率分布进行拟合,以揭示数据背后的规律。
在Matlab中,可以利用hist函数快速绘制直方图,并借助一些函数进行分布拟合。
matlab 分布拟合器 概率

标题:探讨MATLAB分布拟合器在概率领域的应用在统计学和概率论中,分布函数扮演着至关重要的角色。
分布函数描述了随机变量的取值概率分布规律,是统计推断和概率分析的基本工具之一。
而MATLAB作为一款强大的数学建模和计算软件,其分布拟合器功能可以帮助我们更好地理解概率分布并进行数据分析。
本文将深入探讨MATLAB分布拟合器在概率领域的应用,希望能为读者提供一些有价值的观点和方法。
1. MATLAB分布拟合器简介MATLAB提供了丰富的统计工具箱,其中包括了分布拟合器功能,可以自动拟合数学模型到样本数据以估计概率密度函数。
在MATLAB中,可以使用fitdist函数进行分布拟合,该函数支持包括正态分布、指数分布、泊松分布、beta分布等多种分布类型的拟合。
通过分布拟合器,我们可以分析样本数据的分布规律,进行概率密度函数的估计和拟合,从而更好地理解数据的特性和分布情况。
2. 概率概念概率是描述随机现象结果的可能性大小的数学工具。
在概率论中,概率分布描述了随机变量的取值和其对应的概率,是概率论和统计学中的核心概念。
常见的概率分布包括离散分布(如伯努利分布、泊松分布)和连续分布(如正态分布、指数分布),它们被广泛应用于风险评估、市场预测、财务分析等领域,具有重要的理论和实际意义。
3. MATLAB分布拟合器在概率分布分析中的应用MATLAB的分布拟合器功能为我们提供了便利的工具,可以对样本数据进行分布拟合,并且根据拟合结果进行概率分布的分析和推断。
通过使用MATLAB分布拟合器,我们可以实现以下应用:3.1 分布拟合通过fitdist函数,我们可以对样本数据进行分布拟合,得到某一特定类型分布的参数估计。
这使我们能够更好地了解样本数据的特性和分布类型,为后续的概率分析和建模提供重要参考。
3.2 概率密度函数估计通过分布拟合器,我们可以估计得到概率密度函数,从而分析随机变量的取值概率分布规律。
这对于理解样本数据的分布情况、评估风险和进行预测具有重要意义。
matlab拟合正态分布曲线

正态分布曲线是统计学中常用的一种分布模型,也叫高斯分布曲线,它是以高斯函数为基础的一种连续分布函数。
在实际的统计分析中,经常需要对数据进行拟合,使得数据分布符合正态分布曲线。
而MATLAB作为一个强大的数学计算工具,提供了丰富的函数和工具箱,可以用来进行正态分布曲线的拟合。
本文将介绍MATLAB中拟合正态分布曲线的方法和步骤,以及一些实际案例的应用。
一、MATLAB拟合正态分布曲线的方法1. 数据准备在进行正态分布曲线拟合之前,首先需要准备好数据。
这些数据可以是实验测量得到的,也可以是从其他来源获取的。
在MATLAB中,可以将这些数据存储在一个向量或矩阵中,以便后续进行处理。
2. 正态分布曲线拟合函数MATLAB提供了normfit函数来进行正态分布曲线的拟合。
normfit函数的基本语法是:[mu, sigma] = normfit(X)其中,X是输入的数据向量,mu和sigma分别是拟合得到的正态分布曲线的均值和标准差。
利用这些参数,可以画出拟合得到的正态分布曲线。
3. 绘制正态分布曲线一旦得到了拟合的参数mu和sigma,就可以利用normpdf函数绘制出拟合得到的正态分布曲线。
normpdf函数的基本语法是:Y = normpdf(X, mu, sigma)其中,X是自变量的取值,mu和sigma是拟合得到的均值和标准差,Y是对应的概率密度函数值。
将X和Y绘制在图上,就可以得到拟合的正态分布曲线了。
4. 拟合效果评估拟合得到的正态分布曲线与原始数据的分布进行比较,一般采用残差分析、拟合优度检验等方法来评估拟合的效果。
MATLAB提供了相应的函数和工具,可以进行这些评估。
二、实际案例应用以下是一个简单的实际案例,演示了如何利用MATLAB进行正态分布曲线的拟合。
假设有一组实验测量数据X,需要对其进行正态分布曲线的拟合。
% 生成实验数据X = randn(1, 1000);% 进行正态分布曲线的拟合[mu, sigma] = normfit(X);% 绘制拟合得到的正态分布曲线x = -4:0.1:4;y = normpdf(x, mu, sigma);plot(x, y, 'r', X, zeros(1, 1000), 'o');在这个案例中,首先生成了一组标准正态分布的随机数据X。
matlab 曲线 正态分布拟合

matlab 曲线正态分布拟合摘要:本文将介绍如何使用MATLAB曲线拟合工具箱进行正态分布拟合。
正文:正态分布是一种非常常见的概率分布,广泛应用于各个领域,如统计分析、质量控制、金融分析等。
在MATLAB中,我们可以使用曲线拟合工具箱来拟合正态分布。
本文将介绍如何使用MATLAB进行正态分布拟合,并通过一个实例来说明其应用。
一、正态分布的基本概念正态分布,也被称为高斯分布,其概率密度函数为:f(x) = (1 / sqrt(2 * pi * sigma^2)) * exp(-(x - mu)^2 / (2 * sigma^2))其中,μ是分布的均值,σ是分布的标准差。
正态分布的形状由均值和标准差决定,其概率密度函数在均值两侧对称,且随着与均值的距离增加而递减。
二、使用MATLAB进行正态分布拟合在MATLAB中,我们可以使用曲线拟合工具箱来进行正态分布拟合。
以下是步骤:1. 导入数据:首先,我们需要将数据导入MATLAB。
可以使用load命令导入数据文件,或者使用MATLAB的数据导入功能。
2. 数据预处理:在进行拟合之前,我们需要对数据进行预处理,如去除异常值、对数变换等。
这可以使用MATLAB的统计和数学函数来完成。
3. 正态性检验:在拟合之前,我们需要检验数据是否满足正态分布。
可以使用Kolmogorov-Smirnov检验或者Shapiro-Wilk检验等方法。
如果数据不满足正态分布,我们需要进行数据的转换或者选择其他分布进行拟合。
4. 正态分布拟合:使用MATLAB的fitlm函数进行线性最小二乘法拟合。
fitlm函数会自动选择合适的分布类型,如果数据满足正态分布,则拟合结果为正态分布。
5. 模型评估:评估拟合模型的性能,可以使用R-squared、AIC等指标。
如果模型的性能不佳,可以尝试更换其他分布进行拟合,或者调整数据的预处理方法。
三、实例分析以下是一个使用MA TLAB进行正态分布拟合的实例:1. 导入数据:假设我们有一个数据文件名为"data.txt",内容如下:1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.92.02.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.93.0...可以使用以下命令导入数据:load data.txt2. 数据预处理:对数据进行排序和计算均值和标准差:sort data ; mu = mean(data) ; sigma = std(data) ;3. 正态性检验:我们可以使用Kolmogorov-Smirnov检验来检验数据是否满足正态分布。
Matlab中的正态分布拟合技术介绍

Matlab中的正态分布拟合技术介绍正态分布(Normal Distribution)作为统计学中最为重要的概率分布之一,被广泛运用于各类数据的分析与建模中。
而在Matlab中,我们可以利用其强大的数学计算和图形展示功能,实现对数据的正态分布拟合。
本文将介绍Matlab中的正态分布拟合技术,从理论基础、计算方法、示例应用等方面进行详细阐述。
一、理论基础1.1 正态分布概念正态分布,又称高斯分布(Gaussian Distribution),是指随机变量在一定范围内服从的概率分布模式。
其概率密度函数呈钟形曲线,对称分布于平均值处,并由均值mu和标准差sigma两个参数来完全描述。
在Matlab中,我们可以通过命令normpdf(x,mu,sigma)计算给定x处概率密度函数的值。
1.2 正态分布拟合正态分布拟合是指通过一组给定的数据,利用最大似然估计等方法,确定数据的均值和标准差,进而构建满足数据分布的正态分布模型。
拟合过程中,可以使用均方误差(MSE)等指标评估拟合效果。
在Matlab中,我们可以使用命令fitdist(data,'Normal')实现对给定数据的正态分布拟合。
二、计算方法2.1 最大似然估计最大似然估计是一种常用的参数估计方法,其基本思想是寻找一组使得给定数据样本的概率最大化的参数。
在正态分布拟合中,最大似然估计的目标是找到使得样本数据与正态分布之间的差异最小化的参数组合。
Matlab中的fitdist函数采用了最大似然估计的方法进行拟合。
2.2 拟合效果评估拟合效果的评估常常使用均方误差(MSE)来进行度量。
MSE是指拟合模型预测值与实际观测值之间差异的平方平均值。
在Matlab中,可以使用命令mse = immse(data,fitdata)计算给定数据data与拟合数据fitdata之间的均方误差。
三、示例应用我们以某市居民月收入数据为例,展示Matlab中正态分布拟合技术的应用。
matlab 拟合数据的分布函数

matlab 拟合数据的分布函数Matlab是一种强大的数值计算和数据分析软件,它不仅能够进行各种数值计算和数据处理,还可以进行数据拟合和分布函数的估计。
本文将介绍如何使用Matlab拟合数据的分布函数。
我们需要准备一组数据,这组数据应该是符合某个特定分布的样本数据。
例如,我们可以使用正态分布生成一组样本数据。
假设我们需要生成1000个符合正态分布的随机数,均值为0,标准差为1,可以使用如下代码:```matlabdata = normrnd(0, 1, 1000, 1);```接下来,我们需要选择一个合适的分布函数来拟合这组数据。
Matlab提供了多种分布函数的拟合方法,包括正态分布、指数分布、伽马分布等。
在这里,我们选择正态分布作为例子。
使用Matlab拟合数据的分布函数,可以使用`fitdist`函数。
`fitdist`函数的第一个参数是数据,第二个参数是分布函数的名称。
例如,如果我们要拟合正态分布,可以使用如下代码:```matlabpd = fitdist(data, 'Normal');```这样,我们就得到了拟合后的分布函数对象`pd`。
通过这个对象,我们可以获取拟合后的参数,如均值和标准差,以及进行其他分析。
例如,我们可以使用`pd`对象的`mean`方法获取拟合后的均值,使用`pd`对象的`std`方法获取拟合后的标准差。
代码如下:```matlabmu = pd.mean;sigma = pd.std;```除了均值和标准差,我们还可以使用`pd`对象的其他方法获取更多拟合后的参数信息,例如中位数、偏度、峰度等。
除了获取参数信息外,我们还可以使用`pd`对象进行其他分析。
例如,我们可以使用`pd`对象的`pdf`方法计算拟合后的概率密度函数值。
代码如下:```matlabx = -3:0.1:3;y = pdf(pd, x);```这样,我们就得到了在区间`[-3, 3]`上的概率密度函数值。
Matlab中的核密度估计与参数分布拟合技巧

Matlab中的核密度估计与参数分布拟合技巧近年来,数据分析与模型拟合在各个领域中都有着广泛的应用。
其中,核密度估计与参数分布拟合技巧是数据分析与模型拟合中的重要环节之一。
Matlab作为一种功能强大的数据分析工具,为用户提供了丰富的工具箱和函数,使得核密度估计和参数分布拟合变得更加高效和便捷。
一、核密度估计核密度估计是一种非参数方法,用于估计数据的概率密度函数。
在Matlab中,可以使用kde函数进行核密度估计。
kde函数基于样本数据,通过选择合适的核函数和核宽度参数,计算每个数据点的概率密度,并对结果进行平滑。
在进行核密度估计时,用户需要根据数据的特征选择适当的核函数和核宽度参数。
Matlab提供了多种核函数选择,如高斯核函数、Epanechnikov核函数等。
用户可以根据实际情况选择合适的核函数。
同时,核宽度参数的选择也十分重要,过小的核宽度会导致过拟合,过大的核宽度会导致估计结果平滑。
用户可以通过交叉验证等方法选择合适的核宽度参数。
核密度估计的结果可以通过图表展示。
在Matlab中,可以使用plot函数将概率密度曲线绘制出来。
通过观察概率密度曲线,用户可以对数据的整体分布情况有一个直观的了解。
二、参数分布拟合除了核密度估计外,参数分布拟合也是一种常用的数据分析方法。
参数分布拟合的目标是找到最适合数据的概率分布函数,并估计其参数。
在Matlab中,可以使用fitdist函数进行参数分布拟合。
使用fitdist函数进行参数分布拟合时,用户需要选择一个合适的概率分布函数。
Matlab提供了多种常见的概率分布函数,如正态分布、指数分布、伽玛分布等。
用户可以根据数据的特征选择合适的概率分布函数。
fitdist函数会根据所选的概率分布函数,利用最大似然估计方法估计参数,并返回拟合后的参数估计结果。
拟合后的参数可以用于进一步的数据分析与模型建立。
比如,可以使用参数分布函数生成随机数,用于模拟实验数据;可以计算分布函数的累积分布函数值,用于计算概率和置信区间。
正态分布拟合matlab

正态分布拟合 MATLAB介绍正态分布(也称为高斯分布)是统计学中最重要的概率分布之一。
它在自然界和社会科学中广泛应用,因为许多现象都服从正态分布。
在某些情况下,我们可能需要将一组数据与正态分布进行拟合,以便更好地理解和分析数据。
MATLAB是一种功能强大的数值计算和科学编程工具,它提供了各种函数和工具箱来处理和拟合数据。
在本文中,我们将介绍如何使用MATLAB来拟合正态分布。
步骤数据准备首先,我们需要准备一组数据来进行正态分布的拟合。
可以通过以下方式生成一个符合正态分布的随机数向量:mu = 0; % 均值sigma = 1; % 标准差n = 1000; % 数据点数量data = mu + sigma * randn(n, 1);上述代码将生成一个包含1000个符合标准正态分布(均值为0,标准差为1)的随机数的向量。
根据需要,您可以调整均值、标准差和数据点数量。
拟合正态分布接下来,我们使用MATLAB的fitdist函数来拟合正态分布。
这个函数可以根据给定的数据点估计出最佳的正态分布参数。
pd = fitdist(data, 'Normal');上述代码将使用给定的数据点data来拟合一个正态分布,并将结果存储在一个概率分布对象(ProbabilityDistribution object)中。
可视化拟合结果一旦我们拟合了正态分布,我们可以使用MATLAB的pdf函数来计算并可视化该分布的概率密度函数。
x = -4:0.1:4; % x轴范围y = pdf(pd, x); % 计算概率密度plot(x, y);title('正态分布拟合');xlabel('x');ylabel('概率密度');上述代码将在x轴范围内计算并绘制出正态分布的概率密度函数。
您可以根据需要调整x轴范围。
拟合质量评估除了可视化拟合结果,我们还可以使用一些指标来评估拟合质量。
分布的拟合与检验的matlab实现

%--------------------------------------------------------------------------% 分布的拟合与检验%--------------------------------------------------------------------------%--------------------------------------------------------------------------% 描述性统计量和统计图%--------------------------------------------------------------------------%读取文件中数据% 读取文件examp02_14.xls的第1个工作表中的G2G52中的数据,即总成绩数据score = xlsread('examp02_14.xls','Sheet1','G2G52';% 去掉总成绩中的0,即缺考成绩score = score(score 0;%计算描述性统计量score_mean = mean(score % 计算平均成绩s1 = std(score % 计算(5.1式的标准差s1 = std(score,0 % 也是计算(5.1式的标准差s2 = std(score,1 % 计算(5.2式的标准差score_max = max(score % 计算样本最大值score_min = min(score % 计算样本最小值score_range = range(score % 计算样本极差score_median = median(score % 计算样本中位数score_mode = mode(score % 计算样本众数score_cvar = std(scoremean(score % 计算变异系数score_skewness = skewness(score % 计算样本偏度score_kurtosis = kurtosis(score % 计算样本峰度%绘制箱线图figure; % 新建图形窗口boxlabel = {'考试成绩箱线图'}; % 箱线图的标签% 绘制带有刻槽的水平箱线图boxplot(score,boxlabel,'notch','on','orientation','horizontal' xlabel('考试成绩'; % 为X轴加标签%绘制频率直方图% 调用ecdf函数计算xc处的经验分布函数值f[f, xc] = ecdf(score;figure; % 新建图形窗口% 绘制频率直方图ecdfhist(f, xc, 7;xlabel('考试成绩'; % 为X轴加标签ylabel('f(x'; % 为Y轴加标签%绘制理论正态分布密度函数图% 产生一个新的横坐标向量xx = 400.5100;% 计算均值为mean(score,标准差为std(score的正态分布在向量x处的密度函数值y = normpdf(x,mean(score,std(score;hold onplot(x,y,'k','LineWidth',2 % 绘制正态分布的密度函数曲线,并设置线条为黑色实线,线宽为2% 添加标注框,并设置标注框的位置在图形窗口的左上角legend('频率直方图','正态分布密度曲线','Location','NorthWest';%绘制经验分布函数图figure; % 新建图形窗口% 绘制经验分布函数图,并返回图形句柄h和结构体变量stats,% 结构体变量stats有5个字段,分别对应最小值、最大值、平均值、中位数和标准差[h,stats] = cdfplot(scoreset(h,'color','k','LineWidth',2; % 设置线条颜色为黑色,线宽为2%绘制理论正态分布函数图x = 400.5100; % 产生一个新的横坐标向量x% 计算均值为stats.mean,标准差为stats.std的正态分布在向量x处的分布函数值y = normcdf(x,stats.mean,stats.std;hold on% 绘制正态分布的分布函数曲线,并设置线条为品红色虚线,线宽为2plot(x,y,'k','LineWidth',2;% 添加标注框,并设置标注框的位置在图形窗口的左上角legend('经验分布函数','理论正态分布','Location','NorthWest';%绘制正态概率图figure; % 新建图形窗口normplot(score; % 绘制正态概率图%--------------------------------------------------------------------------% 分布的检验%--------------------------------------------------------------------------%读取文件中数据% 读取文件examp02_14.xls的第1个工作表中的G2G52中的数据,即总成绩数据score = xlsread('examp02_14.xls','Sheet1','G2G52';% 去掉总成绩中的0,即缺考成绩score = score(score 0;%调用chi2gof函数进行卡方拟合优度检验% 进行卡方拟合优度检验[h,p,stats] = chi2gof(score% 指定各初始小区间的中点ctrs = [50 60 70 78 85 94];% 指定'ctrs'参数,进行卡方拟合优度检验[h,p,stats] = chi2gof(score,'ctrs',ctrs[h,p,stats] = chi2gof(score,'nbins',6 % 指定'nbins'参数,进行卡方拟合优度检验% 指定分布为默认的正态分布,分布参数由x进行估计[h,p,stats] = chi2gof(score,'nbins',6;% 求平均成绩ms和标准差ssms = mean(score;ss = std(score;% 参数'cdf'的值是由函数名字符串与函数中所含参数的参数值构成的元胞数组[h,p,stats] = chi2gof(score,'nbins',6,'cdf',{'normcdf', ms, ss};% 参数'cdf'的值是由函数句柄与函数中所含参数的参数值构成的元胞数组[h,p,stats] = chi2gof(score,'nbins',6,'cdf',{@normcdf, ms, ss};% 同时指定'cdf'和'nparams'参数[h,p,stats] = chi2gof(score,'nbins',6,'cdf',{@normcdf,ms,ss},'nparams',2[h,p] = chi2gof(score,'cdf',@normcdf % 调用chi2gof函数检验数据是否服从标准正态分布% 指定初始分组数为6,检验总成绩数据是否服从参数为ms = 79的泊松分布[h,p] = chi2gof(score,'nbins',6,'cdf',{@poisscdf, ms}% 指定初始分组数为6,最小理论频数为3,检验总成绩数据是否服从正态分布h = chi2gof(score,'nbins',6,'cdf',{@normcdf, ms, ss},'emin',3%调用jbtest函数进行正态性检验randn('seed',0 % 指定随机数生成器的初始种子为0x = randn(10000,1; % 生成10000个服从标准正态分布的随机数h = jbtest(x % 调用jbtest函数进行正态性检验x(end = 5; % 将向量x的最后一个元素改为5h = jbtest(x % 再次调用jbtest函数进行正态性检验% 调用jbtest函数进行Jarque-Bera检验[h,p,jbstat,critval] = jbtest(score%调用kstest函数进行正态性检验% 生成cdf矩阵,用来指定分布:均值为79,标准差为10.1489的正态分布cdf = [score, normcdf(score, 79, 10.1489];% 调用kstest函数,检验总成绩是否服从由cdf指定的分布[h,p,ksstat,cv] = kstest(score,cdf%调用kstest2函数检验两个班的总成绩是否服从相同的分布% 读取文件examp02_14.xls的第1个工作表中的B2B52中的数据,即班级数据banji = xlsread('examp02_14.xls','Sheet1','B2B52';% 读取文件examp02_14.xls的第1个工作表中的G2G52中的数据,即总成绩数据score = xlsread('examp02_14.xls','Sheet1','G2G52';% 去除缺考数据score = score(score 0;banji = banji(score 0;% 分别提取60101和60102班的总成绩score1 = score(banji == 60101;score2 = score(banji == 60102;% 调用kstest2函数检验两个班的总成绩是否服从相同的分布[h,p,ks2stat] = kstest2(score1,score2%分别绘制两个班的总成绩的经验分布图figure; % 新建图形窗口% 绘制60101班总成绩的经验分布函数图F1 = cdfplot(score1;% 设置线宽为2,颜色为红色set(F1,'LineWidth',2,'Color','r'hold on% 绘制60102班总成绩的经验分布函数图F2 = cdfplot(score2;% 设置线型为点划线,线宽为2,颜色为黑色set(F2,'LineStyle','-.','LineWidth',2,'Color','k'% 为图形加标注框,标注框的位置在坐标系的左上角legend('60101班总成绩的经验分布函数','60102班总成绩的经验分布函数',...'Location','NorthWest'%调用kstest2函数进行正态性检验randn('seed',0 % 指定随机数生成器的初始种子为0% 产生10000个服从均值为79,标准差为10.1489的正态分布的随机数,构成一个列向量xx = normrnd(mean(score,std(score,10000,1;% 调用kstest2函数检验总成绩数据score与随机数向量x是否服从相同的分布[h,p] = kstest2(score,x,0.05%调用lillietest函数进行分布的检验% 调用lillietest函数进行Lilliefors检验,检验总成绩数据是否服从正态分布[h,p,kstat,critval] = lillietest(score% 调用lillietest函数进行Lilliefors检验,检验总成绩数据是否服从指数分布[h, p] = lillietest(score,0.05,'exp'。
MATLAB分布拟合工具箱distributionFitter
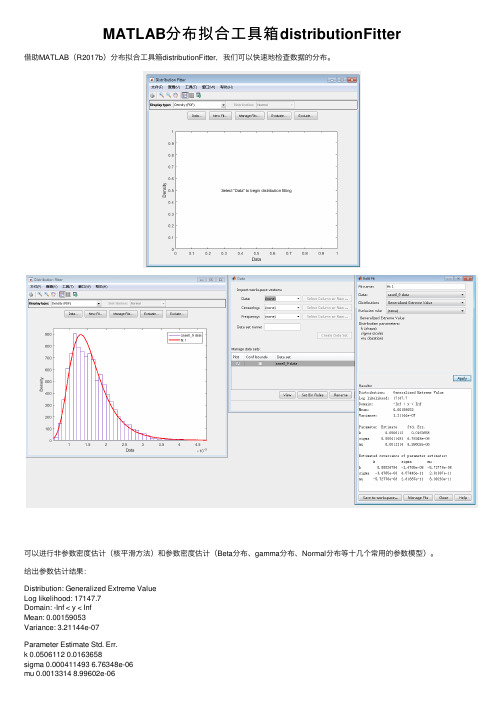
MATLAB分布拟合工具箱 distributionFitter
借助MATLAB(R2017b)分布拟合工具箱distributionFitter,我们可以快速地检查数据的分布。
可以进行非参数密度估计(核平滑方法)和参数密度估计(Beta分布、gamma分布、Normal分布等十几个常用的参数模型)。 给出参数估计结果: Distribution: Generalized Extreme Value Log likelihood: 17147.7 Domain: -Inf < y < Inf Mean: 0.00159053 Variance: 3.21144e-07 Parameter Estimate Std. Err. k 0.0506112 0.0163658 sigma 0.000411493 6.76348e-06 mu 0.0013314 8.99602e-06
cdf
inverse cdf
pp图 Survivor func(互补累积分布函数(complementary cumulative distribution function, CCDF))
Cumulted covariance of parameter estimates: k sigma mu k 0.00026784 -3.4765e-08 -5.72776e-08 sigma -3.4765e-08 4.57446e-11 2.81887e-11 mu -5.72776e-08 2.81887e-11 8.09283e-11 可视化pdf、cdf、inverse cdf、概率图(PP图)、Survivor func(互补累积分布函数(complementary cumulative distribution function, CCDF))、Cumulative hazard
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
……
……
概率密度函数
表 概率密度函数(pdf) 函数名称 normpdf chi2pdf tpdf fpdf 函数说明 正态分布 调用格式 Y=normpdf (X, MU, SIGMA) Y=chi2pdf (X, N) Y=tpdf (X, N) Y=fpdf (X, N1, N2)
2
2 分布
Matlab相关命令
数据统计处理基本命令
– 相关系数
MATLAB提供了corrcoef函数,可以求出数据的相关系数矩阵。 corrcoef函数的调用格式为: • corrcoef(X):返回从矩阵X形成的一个相关系数矩阵。此相关系数矩 阵的大小与矩阵X一样。它把矩阵X的每列作为一个变量,然后求它 们的相关系数。 • corrcoef(X,Y):在这里,X,Y是向量,它们与corrcoef([X,Y])的作用一 样。
1 偏度: g1 3 s
(Xi X )
i 1
n
3
1 峰度: g 2 4 s
(X i X )4
i 1
n
偏度反映分布的对称性,g1 >0 称为右偏态,此时数据位于均值 右边的比位于左边的多;g1 <0 称为左偏态,情况相反;而 g1 接近 0 则可认为分布是对称的. 峰度是分布形状的另一种度量,正态分布的峰度为 3,若 g2 比 3 大很多,表示分布有沉重的尾巴,说明样本中含有较多远离均值的数 据,因而峰度可用作衡量偏离正态分布的尺度之一.
Matlab相关命令
数据统计处理基本命令
– 排序
MATLAB中对向量X是排序函数是sort(X),函数返回一个对X中的元素 按升序排列的新向量。
sort函数也可以对矩阵A的各列或各行重新排序,其调用 格式为: [Y,I]=sort(A,dim)
其中dim指明对A的列还是行进行排序。若dim=1,则按列排;若dim=2, 则按行排。Y是排序后的矩阵,而I记录Y中的元素在A中位置。
t 分布
F 分布
【例】 求服从标准正态分布的随机变量落在区间[-2, 2]上的概率. >> P=normcdf ([-2, 2]) ans = 0.0228 0.9772
>> P(2)-P(1) ans = 0.9545
累积分布函数(cdf)
表 逆累积分布函数(icdf) 函数名称 norminv chi2inv tinv finv 函数说明 正态分布 调用格式 X=norminv (P, MU, SIGMA) X=chi2inv (P, N) X=tinv (P, N) X=finv (P, N1, N2)
0.4 0.35 0.3 0.25 0.2 0.15 0.1 0.05 0 -8
-6
-4
-2
0
2
4
6
8
连续分布:均匀分布
均匀分布(连续分布)
如果随机变量 X 的密度函数为:
1 , a xb f ( x) b a 0, 其他
上面的数据能否证实X 具有 泊松分布的假设是正确的?
又如,某钟表厂对生产的钟进行精确性检 查,抽取100个钟作试验,拨准后隔24小时 以后进行检查,将每个钟的误差(快或慢) 按秒记录下来.
问该厂生产的钟的误差是否服从正态 分布?
再如,某工厂制造一批骰子, 声称它是均匀的.
也就是说,在投掷中,出 现1点,2点,…,6点的概 率都应是1/6.
累积分布函数(cdf)
表 累积分布函数(cdf) 函数名称 normcdf chi2cdf tcdf fcdf 函数说明 正态分布 调用格式 P=normcdf (X, MU, SIGMA) P=chi2cdf (X, N) P=tcdf (X, N) P=fcdf (X, N1, N2)
2 分布
内容提纲
1.Matlab相关命令介绍 2.常见概率分布 3.频数直方图与频数表 4.参数估计 5.假设检验
Matlab相关命令
数据统计处理基本命令
– 最值:max(x), min(x)
• (1) max(X):返回向量X的最大值,如果X中包含复数元素, 则按模取最大值。
• (2) max(A):返回一个行向量,向量的第i个元素是矩阵A 的第i列上的最大值。 • (3) [Y,U]=max(A):返回行向量Y和U,Y向量记录A的每列 的最大值,U向量记录每列最大值的行号。 • (4) max(A,[],dim):dim取1或2。dim取1时,该函数和 max(A)完全相同;dim取2时,该函数返回一个列向量,其 第i个元素是A矩阵的第i行上的最大值。
Matlab相关命令
数据统计处理基本命令
类似的用法,请自己借助matlab在线帮 助功能自己了解:
– 中位数:median(x) – 标准差:std(x) – 方差:var(x) – 偏度:skewness(x) – 峰度:kurtosis(x)
偏度和峰度的说明
表示分布形状的统计量—偏度和峰度
Matlab相关命令介绍
例: x=-8:0.1:8;
y=pdf('norm',x,0,1); y1=pdf('norm',x,1,2); plot(x,y,x,y1,':') 注: y=pdf('norm',x,0,1) 相类似地, y=pdf('beta',x,A,B) y=pdf('bino,x,N,p) y=betapdf(x,A,B) y=binopdf(x,N,p) y=normpdf(x,0,1)
常见的概率分布
二项式分布 卡方分布 指数分布 F分布 几何分布 正态分布 泊松分布 T分布 均匀分布 离散均匀分布 Binomial Chisquare Exponential F Geometric Normal Poisson T Uniform
Discrete Uniform
bino chi2 exp f geo norm poiss t unif unid
正态分布也称高斯分布,是概率论中最重要的一个分布。 如果一个变量是大量微小、独立的随机因素的叠加,那么 它一定满足正态分布。如测量误差、产品质量、月降雨量等
正态分布举例
例:标准正态分布和非标准正态分布密度函数图形
x=-8:0.1:8; y=normpdf(x,0,1); y1=normpdf(x,1,2); plot(x,y,x,y1,':')
2 分布
t 分布
F 分布
【例】求下列分位数:
(i)
>> >> >> >>
u0.9 ;
(ii)
t0.25 (4) ;
(iii)
F0.1 (14,10) ;
(iv)
2 0.025 (50)
u_alpha=norminv(0.9,0,1) t_alpha=tinv(0.25,4) F_alpha=finv(0.1,14,10) X2_alpha=chi2inv(0.025,50)
从2009国赛B题
眼科病床的合理安排
说起。。。
从1500到1931年的432年间,每年爆发战争的 次数可以看作一个随机变量,椐统计,这432 年间共爆发了299次战争,具体数据如下:
战争次数X 发生 X次战争的年数 223 0 142 1 48 2 15 3 4 4
在概率论中,大家对泊松分布产生的一 般条件已有所了解,容易想到,每年爆发战 争的次数,可以用一个泊松随机变量来近似 描述 . 也就是说,我们可以假设每年爆发战 争次数分布X近似泊松分布. 现在的问题是:
Matlab相关命令
数据统计处理基本命令
–例
生成满足正态分布的10000×5随机矩阵,然后求各列元 素的均值和标准方差,再求这5列随机数据的相关系数矩阵。 命令如下: X=sqrt(3)*randn(10000,5)+4; M=mean(X) D=std(X) R=corrcoef(X)
Matlab相关命令介绍
Matlab相关命令
数据统计处理基本命令
– 求和: • (1) sum(X),返回向量X各元素的和。 • (2) sum(A) ,返回一个行向量,其第i个元素是 A的第i列的元素和。 • (3)sum(A,dim) ,当dim为1时,该函数等同于sum(A);当dim为2 时,返回一个列向量,其第i个元素是A的第i行的各元素之和。 – 乘积: • (1) prod(X) ,返回向量X各元素的乘积。 • (2) prod (A) , 返回一个行向量,其第i个元素是A的第i列元素的乘 积。 • (3) prod(A,dim) ,当dim为1时,该函数等同于prod(A);当dim为2 时,返回一个列向量,其第i个元素是A的第i行的各元素之乘积。
pdf 概率密度函数
y=pdf(name,x,A) 返回由 name 指定的单参数分布的概率密度,x为样本数据 y=pdf(name,x,A,B) 或 y=pdf(name,x,A,B,C) 返回由 name 指定的双参数或三参数分布的概率密度 name 用来指定分布类型,其取值可以是: 'beta'、'bino'、'chi2'、'exp'、'ev'、'f' 、 'gam'、'gev'、'gp'、'geo'、'hyge'、'logn'、 'nbin'、'ncf'、'nct'、'ncx2'、'norm'、 'poiss'、'rayl'、't'、'unif'、'unid'、'wbl'。
