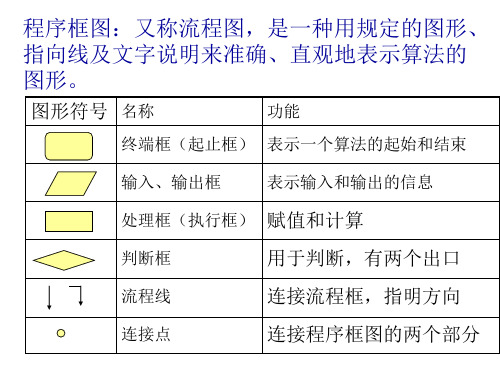
程序法知识脉络图片
人教B版高中数学必修三课件:1.1.2 程序框图 1.1.3 算法的三种基本逻辑结构和框图表示

首页
自主预习
合作学习
当堂检测
探究一
探究二
探究三
探究二
易错辨析
顺序结构框图
【例2】 给出如图所示的程序框图,根据该图回答以下问题:
(1)该程序框图表示的算法的功能是什么? (2)若输入a=-2,则输出结果是什么? 解:(1)该程序框图表示的算法的功能是求二次函数y=-x2+4x的函 数值.
(2)若输入a=-2,则x=-2,此时y=-(-2)2+4×(-2)=-12,因此输出结果
1.1.2 程序框图 1.1.3 算法的三种基本逻辑结构和框图表示
第1课时 顺序结构、条件分支结构
-1-
首页
自主预习
合作学习 当堂检测
课标阐释
思维脉络
1.了解程序框图的概念,掌握各种程序
框和流程线的功能,掌握画程序框图
的基本规则. 2.理解算法中的顺序结构、条件分支
结构,并能选用这两种结构解决有关
合作学习
当堂检测
A.4 B.5 C.6 D.13 解析:在所给的程序框图中,使用了变量的赋值,先给x赋初始值2,再 把2x+1的结果赋给变量y,又把3y-2的结果赋给变量b,最后输出b的 值.所以最后结果为13. 答案:D
首页
自主预习
12345
2.如图所示的程序框图表示的算法的功能是
合作学习
.
当堂检测
答案:A
首页
自主预习
合作学习 当堂检测
二、画程序框图的规则 【问题思考】 1.填空: (1)使用标准的框图的符号. (2)框图一般按从上到下、从左到右的方向画. (3)除判断框外,其他框图符号只有一个进入点和一个退出点.判 断框是具有超过一个退出点的唯一符号. (4)一种判断框是二择一形式的判断,有且仅有两个可能结果;另 一种是多分支判断,可能有几种不同的结果. (5)在图形符号内描述的语言要非常简练清楚. 2.判断框有两个退出点是否表示同时执行? 提示:不是.退出点是根据条件去执行其中的一种结果,而不是同 时执行,这样保障算法过程中每一步是确定的、有序的.
程序框图、顺序结构 课件

[思路分析] 解题的关键是理解程序框图的含义. 解 (1)该程序框图解决的是求二次函数 f(x)=-x2+mx的函数值的问题. (2)当输入的x的值为0和4时,输出的值相等, 即f(0)=f(4). 因为f(0)=0,f(4)=-16+4m, 所以-16+4m=0, 所以m=4.所以f(x)=-x2+4x. 因为f(3)=-32+4×3=3, 所以当输入的x的值为3时,输出的f(x)的值为3. (3)因为f(x)=-x2+4x=-(x-2)2+4, 当x=2时,f(x)max=4, 所以要想使输出的值最大,输入的x的值应为2.
题型一 程序框图的认识和理解
【例1】下列关于程序框图的理解,正确的有
( ).
①任何一个程序框图都必须有起、止框;②输入框只能放
在开始框后,输出框只能放在结束框前;③判断框是唯一
具有超过一个退出点的图形符号;④对于一个程序而言,
判断框内的条件是唯一的.
A.1个
B.2个
C.3个
D.4个
[思路探索] 根据各程序框图的意义判断.
(3)常见的程序框、流程线及各自功能.
:用程序框图表示算法,相对于自然语言描述的算法 有什么优点? 提示 程序框图相对于自然语言表述算法,看起来更清 晰,更明确,也更接近于计算机的程序设计.
2.顺序结构 顺序结构是由若干个依次执行的_步__骤__组成的,这是任何
一个算法都离不开的基本结构.用程源自框图表示如图.方法技巧 算法中的函数与方程思想
【示例】如图所示的程序框图,当输入的x的值为0和4时,输 出的值相等,根据该图和下列各小题的条件回答下面几个 问题. (1)该程序框图解决的是一个什么问题? (2)当输入的x的值为3时,输出的f(x)的值为 多大? (3)要想使输出的值最大,输入的x的值应为 多大? (4)按照这个程序框图输出的f(x)值,当x的 值大于2时,x值大的输出的f(x)值反而小,为什么? (5)要想使输出的值等于3,输入的x的值应为多大? (6)要想使输入的值与输出的值相等,输入的x的值应为多大?
程序框图及算法的基本逻辑结构

程序框图与算法的根本逻辑构造教学目标能够正确说出各种程序框图及流程线的功能与作用能够画出顺序构造、条件构造、循环构造的流程图能够设计简单问题的流程图教学重点程序框图的画法.教学难点程序框图的画法.课时安排4课时教学过程 第1课时 程序框图及顺序构造图形符号名称 功能终端框〔起止框〕 表示一个算法的起始和完毕输入、输出框 表示一个算法输入和输出的信息处理框〔执行框〕 赋值、计算 判断框 判断*一条件是否成立,成立时在出口处标明“是〞或“Y 〞;不成立时标明“否〞或“N 〞流程线连接程序框 连接点 连接程序框图的两局部三种逻辑构造可以用如下程序框图表示:顺序构造 条件构造 循环构造应用例如例1 请用程序框图表示前面讲过的“判断整数n(n>2)是否为质数〞的算法.解:程序框图如下:变式训练观察下面的程序框图,指出该算法解决的问题.解:这是一个累加求和问题,共99项相加,该算法是求100991431321211⨯++⨯+⨯+⨯ 的值.例2 一个三角形三条边的边长分别为a ,b ,c ,利用海伦—秦九韶公式设计一个计算三角形面积的算法,并画出程序框图表示.〔三角形三边边长分别为a,b,c ,则三角形的面积为S=))()((c p b p a p p ---〕,其中p=2c b a ++.这个公式被称为海伦—秦九韶公式〕 算法步骤如下:第一步,输入三角形三条边的边长a,b,c.第二步,计算p=2c b a ++.第三步,计算S=))()((c p b p a p p ---.第四步,输出S.程序框图如下:点评:很明显,顺序构造是由假设干个依次执行的步骤组成的,它是最简单的逻辑构造,它是任何一个算法都离不开的根本构造.顺序构造可以用程序框图表示为变式训练 下列图所示的是一个算法的流程图,a 1=3,输出的b=7,求a 2的值.解:根据题意221a a +=7, ∵a 1=3,∴a 2=11.即a 2的值为11.随堂练习 如下给出的是计算201614121++++ 的值的一个流程图,其中判断框内应填入的条件是______________.答案:i>10.第2课时 条件构造 教学目标1、认识条件构造2、能独立画出两种条件构造图示教学重点: 直到型构造、当型构造教学难点: 直到型构造、当型构造互化学习对象条件构造:先根据条件作出判断,再决定执行哪一种操作的构造就称为条件构造〔或分支构造〕,如图1所示.执行过程如下:条件成立,则执行A 框;不成立,则执行B 框.图1 图2应用例如例1 任意给定3个正实数,设计一个算法,判断以这3个正实数为三边边长的三角形是否存在,并画出这个算法的程序框图.算法步骤如下:第一步,输入3个正实数a ,b ,c.第二步,判断a+b>c ,b+c>a ,c+a>b 是否同时成立.假设是,则存在这样的三角形;否则,不存在这样的三角形.程序框图如右图:例2 设计一个求解一元二次方程a*2+b*+c=0的算法,并画出程序框图表示.解决这一问题的算法步骤如下:第一步,输入3个系数a ,b ,c.第二步,计算Δ=b 2-4ac.第三步,判断Δ≥0是否成立.假设是,则计算p=ab 2-,q=a 2∆;否则,输出“方程没有实数根〞,完毕算法.第四步,判断Δ=0是否成立.假设是,则输出*1=*2=p;否则,计算*1=p+q,*2=p-q,并输出*1,*2.程序框图如下:随堂练习1、设计算法判断一元二次方程a*2+b*+c=0是否有实数根,并画出相应的程序框图.相应的程序框图如右:2、〔1〕设计算法,求a*+b=0的解,并画出流程图.程序框图如下:作业:设计算法,找出输入的三个不相等实数a、b、c中的最大值,并画出流程图.解:算法步骤:第一步,输入a,b,c的值.第二步,判断a>b是否成立,假设成立,则执行第三步;否则执行第四步.第三步,判断a>c是否成立,假设成立,则输出a,并完毕;否则输出c,并完毕.第四步,判断b>c是否成立,假设成立,则输出b,并完毕;否则输出c,并完毕.程序框图如下:第3课时循环构造教学目标1、认识循环构造2、能独立画出两种循环构造图示3、能把直到型循环改写成当型构造,反之亦然教学重点: 直到型构造、当型构造教学难点: 直到型构造、当型构造互化学习对象在一些算法中,经常会出现从*处开场,按照一定的条件反复执行*些步骤的情况,这就是循环构造.反复执行的步骤称为循环体.循环构造有两种形式:当型循环构造和直到型循环构造.当型循环构造直到型循环构造直到型循环构造是程序先进入循环体,然后对条件进展判断,如果条件不满足,就继续执行循环体,直到条件满足时终止循环.当型循环构造是在每次执行循环体前,先对条件进展判断,当条件满足时,执行循环体,否则终止循环.应用例如例1 设计一个计算1+2+……+100的值的算法,并画出程序框图.第一步,令i=1,S=0.第二步,假设i≤100成立,则执行第三步;否则,输出S,完毕算法.第三步,S=S+i.第四步,i=i+1,返回第二步.当型循环直到型循环变式训练例1 设计框图实现1+3+5+7+…+131的算法.第一步,赋初值i=1,sum=0.第二步,sum=sum+i ,i=i+2.第三步,如果i ≤131,则反复执第二步;否则,执行下一步.第四步,输出sum.第五步,完毕.程序框图如右图知能训练设计一个算法,求1+2+4+…+249的值,并画出程序框图.第4课时 程序框图的画法应用例如例1 结合前面学过的算法步骤,利用三种根本逻辑构造画出程序框图,表示用“二分法〞求方程*2-2=0〔*>0〕的近似解的算法.算法分析:〔1〕算法步骤中的“第一步〞“第二步〞和“第三步〞可以用顺序构造来表示〔如下列图〕:〔2〕算法步骤中的“第四步〞可以用条件构造来表示〔如下列图〕.在这个条件构造中,“否〞分支用“a=m 〞表示含零点的区间为[m ,b ],并把这个区间仍记成[a ,b ];“是〞分支用“b=m 〞表示含零点的区间为[a,m ],同样把这个区间仍记成[a ,b ].〔3〕算法步骤中的“第五步〞包含一个条件构造,这个条件构造与“第三步〞“第四步〞构成一个循环构造,循环体由“第三步〞和“第四步〞组成,终止循环的条件是“|a-b|<d 或f(m)=0”.在“第五步〞中,还包含由循环构造与“输出m 〞组成的顺序构造〔如下列图〕. 〔4〕将各步骤的程序框图连接起来,并画出“开场〞与“完毕〞两个终端框,就得到了表示整个算法的程序框图〔如下列图〕.解:将实际问题转化为数学模型,该问题就是要求1+2+4+……+263的和.程序框图如下:点评:对于开放式探究问题,我们可以建立数学模型〔上面的题目可以与等比数列的定义、性质和公式联系起来〕和过程模型来分析算法,通过设计算法以及语言的描述选择一些成熟的方法进展处理.例3 乘坐火车时,可以托运货物.从甲地到乙地,规定每*火车客票托运费计算方法是:行李质量不超过50 kg 时按0.25元/kg ;超过50 kg 而不超过100 kg 时,其超过局部按0.35元/kg ;超过100 kg 时,其超过局部按0.45元/kg .编写程序,输入行李质量,计算出托运的费用.分析:此题主要考察条件语句及其应用.先解决数学问题,列出托运的费用关于行李质量的函数关系式.设行李质量为* kg ,应付运费为y 元,则运费公式为: y=⎪⎩⎪⎨⎧>-+⨯+⨯≤<-+⨯≤<,100),100(45.05035.05025.0,10050),50(35.05025.0,500,25.0x x x x x x整理得y=⎪⎩⎪⎨⎧>-≤<-≤<.100,1545.0,10050,535.0,500,25.0x x x x x x要计算托运的费用必须对行李质量分类讨论,因此要用条件语句来实现.解:算法分析:第一步,输入行李质量*.第二步,当*≤50时,计算y=0.25*,否则,执行下一步.第三步,当*≤100,计算y=0.35*-5,否则,计算y=0.45*-15.第四步,输出y.程序框图如下:课堂小节〔1〕进一步熟悉三种逻辑构造的应用,理解算法与程序框图的关系.〔2〕根据算法步骤画出程序框图.作业习题1.1B组1、2.设计感想本节是前面内容的概括和总结,在回忆前面内容的根底上,选择经典的例题,进展了详尽的剖析,这样降低了学生学习的难度.另外,本节的练习难度适中,并且多为学生感兴趣的问题,这样为学生学好本节内容作好充分准备,希望大家喜欢这一节课.。
1.1.2.1 程序框图与顺序结构(共32张PPT)

4.已知梯形的上底为 3,下底为 7,高为 6,计算此梯形的面积,试设计该 问题的算法,并画出程序框图. 分析:先输入梯形的上底 a、 下底 b 及高 h,再利用公式 S=2(a+b)h 求 得梯形的面积.
1
解:算法如下: 第一步,输入上底 a,下底 b,高 h, 第二步,S=2(a+b)h, 第三步,输出 S. 程序框图如图:
题型二
易错辨析
【例题 2】设计程序框图,求半径为 10 的圆的面积. 错解:程序框图如下:
错因分析:错解中的程序框图中缺少终端框,不是完整的. 正解:程序框图如下:
1 如图,程序框图表示的算法的运行结果是
.
(第 1 题图)
解析:第一步,p=
5+6+7 =9. 2
第二步,执行 S= ������(������-5)(������-6)(������-7) = 9 × (9-5) × (9-6) × (9-7)=6 6. 第三步,输出 S. 答案:6 6
(2)程序框: 图形符 名称 号 终端 框 (起止 框) 输入、 输出 框 处理 框 (执行 框) 判断 框 流程 线 连接 点
功能
表示一个算法的起始和结束
表示一个算法输入和输出的信息
赋值、计算 判断某一条件是否成立,成立时在出口处标明 “是”或“Y”;不成立时标明“否”或“N” 连接程序框 连接程序框图的两部分
【做一做 1-1】下列关于流程线的说法,不正确的是( ) A.流程线表示算法步骤执行的顺序,用来连接程序框 B.流程线只要是上下方向就表示自上向下执行可以不要箭头 C.流程线无论什么方向,总要按箭头的指向执行 D.流程线是带有箭头的线,它可以画成折线 答案:B 【做一做 1-2】具有判断条件是否成立的程序框是( ) 答案:C
人教A版高中数学必修3:1.1.2 程序框图与算法的基本逻辑结构

b = 10
30
b < 60
Y
b =1b0+ 20
N
30
输出b
结束
50<60
回血(多次)程序框图
开始
b = 10
50
b < 60
Y
b =3b0+ 20
N
50
输出b
结束
70>60
回血(多次)程序框图
开始
b = 10
70
b < 60
Y
b =5b0 + 20
N
70
输出b
结束
我们一起来分析一下这个程序框图
程序框图的基本逻辑结构(1)—顺序结构
回血(多次)程序框图
开始
b = 10
b < 60
Y
b = b + 20
顺序结构
N
输出b
结束
程序框图的基本逻辑结构(2)—条件分支结构
回血(多次)程序框图
开始
b = 10
b < 60
Y
b = b + 20
条件结构
N
输出b
结束
程序框图的基本逻辑结构(2)—条件分支结构
条件算法需要进行逻辑判断, 当P成立(记作“Y”)时执 行语句A,当P不成立(记作 “N”)时执行语句B,条件 分支结构是一种有条件的二 选的操作结构.
程序框图的基本逻辑结构(3)—循环结构
回血(多次)程序框图
开始
b = 10
b < 60
Y
b = b + 20
循环结构
N
输出b
结束
程序框图的基本逻辑结构(3)—循环结构
高中数学必修三课件-1.1.2 程序框图与算法的基本逻辑结构4-人教A版

程序框图的基本逻辑结构(1)—顺序结构
回血(一次)程序框图
开始
b = 10
一个人血量为10, 用b来代表
b = b + 20 输出b
结束
让血量在原有值 上增加20
用平行四边形表
示输入、输出 框
为了便于理解,我们借 助动画小人帮忙演示
程序框图的基本逻辑结构(1)—顺序结构
回血(一次)程序框图
回血视频
我们假定回血的步 骤分为如下几步:
试一试!
走进回血区 增加血量 停止回血
走进回血区 增加血量 停止回血
试一试!
先在步骤外面加上处理框 再加上表示顺序的流程线
开始 走进回血区 增加血量 停止回血
结束
试一试!
不要忘记加上表示 开始结束的起止框!
程序框图的基本逻辑结构(1)—顺序结构
顺序结构的语句与语句 之间,框与框之间是按照从 上到下的顺序进行.
开始
b = 10 b = b + 20
输出b
结束
执行第一步时,按照框图 中的指令b=10,小人身上
的牌子就会显示10
程序框图的基本逻辑结构(1)—顺序结构
回血(一次)程序框图
开始
b = 10 10 b = b + 20
输出b
结束
程序框图的基本逻辑结构(1)—顺序结构
回血(一次)程序框图
开始
b = 10
必须要使用起止框!
把冰箱门带上
结束
麦兜,你喜欢玩网络游戏吗?
喜欢!我可喜欢了!
那你最喜欢什么游戏呢?
你知道程序员叔叔 是怎么编程的吗?
对,写代码!
一个游戏包含上百万行 代码,怎么能想清楚、 不出错呢?
程序框图ppt课件

m
a
2
b
顺序结构 条件结构
第四步:若 f (a) f (m) 0,则含零点的区间为[a, m]; 否则,
含零点的区间为 [m, b].将新得到的含零点的区间仍记为 [a, b].
第五步:判断 [a, b] 的长度是否小于d或f(m)是否等于0. 若是,则m是方程的近似值;否则,返回第三步.
循环结构
是
小结
顺序结构的程序框图的基本特征: (1)必须有两个起止框,穿插输入、输出框和处理框,没有判断 框. (2)各程序框从上到下用流程线依次连接.
条件结构的程序框图的基本特征: (1)程序框图中必须有两个起止框,穿插输入、输出框和处理框, 一定有判断框. (2)条件结构的程序框图各有两种形式.
循环结构的程序框图的基本特征: (1)循环结构中包含条件结构,条件结构中不含循环结构. (2)循环结构的程序框图各有两种形式.
设有x只鸡,y只兔.则
x y H, 2x 4 y F .
解方程组,得
x (4H F ) / 2,
y
(F
2H
)
/
2.
解:算 法
第一步:输入总头 数H,总脚数F 第二步:计算鸡的 个数x=(4H-F)/2 第三步:计算兔的 个数y=(F-2H)/2 第四步:输出x,y
程序框图 开始
输入H和F x=(4H-F)/2 y=(F-2H)/2
2.算法的基本逻辑结构
顺序结构
开始 输入n
i=2
求n除以i的余数r
i=i+1
①
r =0?
条件结构
否
是
n不是质数 n是质数
否
i>n-1 或r=0?
结束
是循环结构
程序流程图基础知识

程序流程图基础知识一、什么是程序流程图“程序流程图”常简称为“流程图”,是一种传统的算法表示法,程序流程图是人们对解决问题的方法、思路或算法的一种描述。
它利用图形化的符号框来代表各种不同性质的操作,并用流程线来连接这些操作。
在程序的设计(在编码之前)阶段,通过画流程图,可以帮助我们理清程序思路。
下图是一个简单的流程图,描述求两个数的最大公约数的算法(辗转相除法)。
流程图中常用的符号见图,在前述求最大公约数的流程图中找出对应的部分。
二、三种控制结构的流程图表示三、练习题目(各部分分别至少选两个画一画,注意用一张质量好一些纸,书写整齐,确保越画越高兴)1、热身(1)将英尺转换为米(2)输入两个点的坐标,求两点之间的距离并输出2、分支程序(1)描述一下今晚的计划:如果下雪,校园内玩雪;否则,在103上机(怀念)(2)丢硬币决定今晚:正面,K歌;反面:逛街;立起来,学C++(3)输入一元二次方程ax^2+bx+c=0的各项系数,并根据各系数的值的情况,分别进行求解(考虑对系数的各种可能太复杂时,给自己降低些难度,先从不考虑系统直接求解开始)(4)输入个人月收入总额,计算出他本月应缴税款和税后收入(税率等参考第9周任务)3、循环结构(1)求1+2+3+...+100(三种循环结构都画一画)(2)输出1/3-3/5+5/7-7/9…+19/21的结果(3)一个数如果恰好等于它的因子之和,这个数就称为“完数”。
找出1000内的所有完数。
(4)输出1000以内的所有回文数(5)鸡翁一,值钱五,鸡母一,值钱三,鸡雏三,值钱一,百钱买百鸡,如何买?4、复杂结构的程序在解决问题中,利用函数可以让我们利用更“有序”的思维去想问题,“自顶向下,逐步求精”,真理。
例:下面的流程图用于输出星号图,体现的是这种思维,右边的图可以嵌入到左边中,替代“输出第i行”的框子,也可以指导我们专门编成一个函数。
任务:(1)输出10000以内的所有回文素数。
程序框图(PPT)4-3
【最全PPT】程序框图及基本逻辑结构

2公里的里程每公里收元,
另每车次超过2公里收燃油
附加费1元(其他因素不考虑).
y 5
相应收费系统的流程图如图
所示,则①处应填(
)
A.y=5+x
B.y=6+x
C.y=5+2.6(x-2)
D.y=6+2.6(x-2)
跟踪练习1 (1)如下图是求实数x的绝对值的算法程序框图,则判断框①中 可填___X_>_0_?__.
有一个进入点和一个退出点.判断框 是具有超过一个退出点的惟一符号 (4)在图形符号内描述的语言要简练清楚
注:每一个程序框图必须要有起止框
跟踪练习2.1、已知圆的半径,设计一个 算法求圆的周长和面积的近似值,并用程序框 图表示.
解析:算法设计:
第一步,输入圆的半径R.
第二步,计算L=2πR.
第三步,计算S=πR2.
循环结构按条件出现位置可分为:
1)当型循环结构(也称“前测试型”循环)如图(1
如图(1)
如图(2)
2)直到型循环结构(也称“后测试型”循环) 如图(2)
如图(1)
如图(2)
如图(3)
二、典例讲练
题型一:完善程序框图内容及求输入输出值或范围等
例1、县内打的士收费办法如下: 不超过2公里收5元,超过
从某处开始,按照一定条
显然,循环结构中一定包含条件结构。
计算1×2×3×4×…×100的值 另每车次超过2公里收燃油
注:每一个程序框图必须要有起止框
.
(3)除判断框外,大多数框图符号只
C.圆形框
D.椭圆形框
3、下面哪个是处理框(
)
所示,则①处应填(
)
自测自评
1.算法的三种基本结构是( A )
