共点力平衡典型例题练习
共点力的平衡经典题型汇总

B.OC绳所受拉力先减小后增大
C.轻杆AO所受弹力逐渐增大
D.轻杆AO所受弹力不变
7.一名杂技演员在两幢高10m的楼之间表演“高空走钢丝”。当他缓慢经过钢丝的中点时,钢丝与水平方向的夹角为10°。已知演员及横杆的总质量为60kg,钢丝重量不计。重力加速度取10m/s2, ,下列说法正确的有( )
D.增大F,木块有可能沿墙壁向上做匀速直线运动
13.如图,A、B是两个长方体物块,水平力F作用在物块A上,下列说法正确的是( )
A.若A、B一起向右匀速运动,则B对A的摩擦力方向向右
B.若A、B一起向右匀速运动,则B对地面的摩擦力方向向右
C.若A、B均相对于地面静止,则B受到6个力
D.若A、B均相对于地面静止,则A受到4个力
请根据上述数据在坐标纸上(图c)作出摩擦力f和砝码对木块的压力F的关系图象(以F为横坐标)____.并分析图象不过原点的原因是_____.求木块间的滑动摩擦因数为_____.
四、解答题
18.长为20cm的轻绳BC两端靠在一起固定在天花板上,在中点A系上一重60N的重物(可视为质点),如图所示:
(1)AB段绳上拉力大小;
三、实验题
16.建筑、桥梁工程中所用的金属材料(如钢筋钢梁等)在外力作用下会伸长,其伸长量不仅与和拉力的大小有关,还和金属材料的横截面积有关。人们发现对同一种金属,其所受的拉力与其横截面积的比值跟金属材料的伸长量与原长的比值的比是一个常数,这个常数叫做杨氏模量。用E表示,即∶E= ;某同学为探究其是否正确,根据下面提供的器材∶不同粗细不同长度的同种金属丝;不同质量的重物;螺旋测微器;游标卡尺;米尺;天平;固定装置等。设计的实验如图所示。
18.(1)30N;(2)20 N;(3)10 cm
共点力平衡练习题(有答案)

1. 如图所示,在一细绳B 点系住一重物,细绳AB 、BC 两端分别固定在竖直墙面上,使得AB 保持水平,BC 与水平方向成30º角,已知三段细绳最多都只能承受200N 的拉力;那么为使三段细绳都不断裂,BD 段最多能悬挂多重的物体? 1.100N2.甲、乙两球的半径均为R ,质量相等,用轻绳悬挂起来,如图所示,已知AB 段绳的拉力为F=120N ,绳BD=BC=R ,求:(1)绳BD 和BC 受到的拉力T 。
(2) 甲、乙两球间的相互作用力N 的大小。
69.28N 34.643.如图所示,A 、B 都是重物,A 被绕过小滑轮P 的细线所悬挂,B 放在粗糙的水平桌面上.滑轮P 被一根斜短线系于天花板上的O 点,O ′是三根细线的结点,细线bO ′水平拉着物体B ,cO ′沿竖直方向拉着弹簧.弹簧、细线、小滑轮的重力不计,细线与滑轮之间的摩擦力可忽略,整个装置处于静止状态.若悬挂小滑轮的斜线中的拉力是F =203N ,∠cO′a=120°,重力加速度g 取10m/s2,则下列说法正确的是 (BC ) A .弹簧的弹力为20N B .重物A 的质量为2kgC .桌面对物体B 的摩擦力为103ND .细线OP 与竖直方向的夹角为60°4.如图所示,石拱桥的正中央有一质量为m 的对称楔形石块,侧面与竖直方向的夹角为α,重力加速度为g 。
若接触面间的摩擦力忽略不计,求石块侧面所受弹力的大小为多少?解:楔形石块受力如图,根据力的合成可得:2cos(90)mg F α=⨯-,所以02cos(90)2sin mg mgF αα==-5、质量为kg m 4=的物体放置在粗糙的水平面上,如图在水平向右的N F 201=的作用下使其向右匀速运动。
当改为斜向下的2F 作用时仍然可以使物体向右匀速运动,已知2F 与水平方向之间的夹角为037=α。
(COS37°=0.8, Sin37°=0.6,g=10m/s2)试求: (1)2F 的大小?(2)在第(1)问的前提下,若该物体匀速运动的初速度是10 m/s,要使物体不撞到前方30m 处的障碍物,力2F 最多作用多长的时间?(若物体在水平面上运动,只受滑动摩擦阻力时,其加速度大小为5 m/s2)(1)以物体为研究对象,受力分析建立如图直角坐标系,根据平衡条件,得N f mg N f F μ==-=-001 联立①②③代入数据 解得,5.0=μ 当施加2F 力时,对30A C B D ααmfxα 2FNy Gv v1F2F α物体受力分析如图所示Nf mg F N f F μαα==--=-0sin 0cos 22 联立⑤⑥⑦代入数据 解得 N F 402=(2) 要求物体不撞到障碍物上力2F 最多作用的时间,即力2F 作用t 时间后,撤去2F 物体减速至障碍物处刚好静止.撤去2F 前物体运动距离 x1=vt=10t 撤去2F 后物体运动距离 ma v x 1010100222===又 x1 + x2 = x, 即 10t + 10 =30, 所以t=2s 6.如图所示,物体m 与天花板间的动摩擦因数为μ,当力F 与水平方向夹角为θ时,物体沿天花板匀速运动. 画出物体的受力图,并求力F 的大小. FCos θ=FfFSin θ=FN+GF=μmg/(μSin θ-Cos θ)7.如图所示, 质量为m 的物块在质量为M 的木板上滑行, 木板与地面间摩擦系数为μ1, 物块与木板间摩擦系数为μ2, 已知木板处于静止状态, 那么木板所受地面摩擦力的大小是A .μ1Mg B. μ2mg C .μ1(m+M )g D .μ1Mg+μ2mgB 10.如图所示装置,两物体质量分别为m1、m2,悬点A 、B 间的距离远大于滑轮的直径(即滑轮的大小可忽略不计),不计一切摩擦及滑轮的重力,装置处于静止状态,则A .m2可能大于m1B .m2一定大于m1/2C .m2可能等于m1D .θ1一定等于θ2 ABCD8.所受重力G1=8 N 的砝码悬挂在绳PA 和PB 的结点上.PA 偏离竖直方向37°角,PB 在水平方向,且连在所受重力为G2=100 N 的木块上,木块静止于倾角为37°的斜面上,如图12所示,试求: (1)木块与斜面间的摩擦力;(2)木块所受斜面的弹力. 解析:如图甲所示分析P 点受力,由平衡条件可得: FA cos37°=G 1FA sin37°=FB 可解得:FB =6 N再分析G2的受力情况如图乙所示.由物体的平衡条件可得: Ff =G2 sin37°+FB ′cos37°FN+FB′ sin37°=G2 cos37° FB′=FB 可求得:Ff =64.8 N FN =76.4 N.答案:(1)64.8 N ,方向沿斜面向上 (2)76.4 N ,垂直斜面向上 θ F F f θ F F N G θ1 θ2m 1m 2A B9、质量m =15kg 的光滑球A 悬空靠在墙和木块B 之间,木块B 的质量为M =150kg ,且静止在水平地板上,如图所示,取g =10m/s2,求:⑴墙和木块B 受到的球的压力各为多少?⑵水平地板所受的压力和木块B 所受的摩擦力各为多少?⑴小球A 和木块B 受力分析如图所示,用N1、N2、N3、N1/分别表示木块对A 的弹力、墙壁对A 的支持力、地面对木块的支持力以及球A 对木块B 的压力。
共点力平衡习题

1、如图所示,用弹簧测力计称物块时,静止时弹簧测力计读数是F1=7.5 N.用弹簧测力计拉着物块沿着倾角为θ=37°的斜面向上匀速滑动时,弹簧测力计读数是F2=6 N,弹簧测力计的拉力方向与斜面平行.求物块与斜面间的动摩擦因数.(sin 37°=0.6,cos 37°=0.8)2.如下图所示,灯重G=20N,绳AO与天花板的夹角α=30°,绳BO与墙面垂直,试求AO、BO两绳所受的拉力各为多大?3.质量为11kg的物块放在水平地面上,在大小为55N水平向右拉力F1作用下恰好沿水平地面匀速滑动.若改用与水平方向成37°角斜向右上方的拉力F2作用,该物块在水平地面上仍匀速滑动.(g取10m/s2,sin37°=0.6,cos37°=0.8)求:(1)物块与地面间的动摩擦因数μ.(2)拉力F2的大小.4.所受重力G 1=8 N 的物块悬挂在绳PA 和PB 的结点上。
PA 偏离竖直方向37°角,PB 在水平方向,且连在所受重力为G 2=100 N 的木块上,木块静止于倾角为37°的斜面上,如图所示,试求:(sin 37°=0.6,cos 37°=0.8,重力加速度g 取10 m/s 2)(1)木块与斜面间的摩擦力大小;(2)木块所受斜面的弹力大小。
5.如图所示,三根轻质绳子OA 、OB 与OC 将一质量为10 kg 的重物悬挂空中而处于静止状态,其中OB 与天花板夹角为30°,OA 与天花板夹角为60°,要求画出结点O 的受力分析图,标出对应的力及角度.(g 取10 m/s 2)(1)求绳子OA 、OB 对应的拉力大小FA 、FB ;(2)若保持O 、B 点位置不变,改变OA 绳长度,将A 点移动到D 点,使得OD =OB ,求此时绳子OD 对应的拉力大小FD .6.如图所示,轻杆上端可绕固定的光滑轴O 转动,下端固定一质量为m 的小球,小球搁在质量为2m 的木板M 上,木板置于光滑的水平地面上。
共点力作用下物体的平衡(经典例题推荐)

解析
对悬挂的物体由力的平衡条
件可知绳子的拉力等于其重力,绳子 拉O点的力也等于重力.求OA和OB的 弹力,选择的研究对象为作用点O,受力分析如右图所 示,由平衡条件可知,F1和F2的合力与FT等大反向,由
mg 平行四边形定则和几何关系得:F1=mgtan θ ,F2= , cos 则D正确.
答案 D
共点力作用下物体的平衡(经典例题)
1.如图所示,光滑半球形容器固定
在水平面上,O 止于P点.设滑块 为球心,一质量为 所受支持力为FN. ( ) B.F=mgtan θ D.FN=mgtan θ m的小滑块,在水 平力F的作用下静 OP与水平方向的夹角为θ .下列关系正确的是 A. C.
mg F tan mg FN tan
答案
D
10.如图所示是给墙壁粉刷涂料用的“涂料滚”的示意图. 使用时,用撑竿推着粘有涂料的涂料滚沿墙壁上下缓缓滚
动,把涂料均匀地粉刷到墙上.撑竿的重力和墙壁的摩擦均
不计,且撑竿足够长.粉刷工人站在离墙壁一定距离处缓缓 上推涂料滚,设该过程中撑竿对涂料滚的推力为F1,涂料滚 对墙壁的压力为F2,则( A.F1增大,F2减小 )
所示,在此过程中 (
)
A.F1保持不变,F3缓慢增大 B.F1缓慢增大,F3保持不变
C.F2缓慢增大,F3缓慢增大
D.F2缓慢增大,F3保持不变
解析
B的受力如下图甲所示,因为F和G的方向始终
沿竖直方向,当F增大时,F1′、F2′都缓慢增大, F1′=F1,F2′=F2,所以F1、F2都缓慢增大.A物体受力 如图乙所示.由图乙知F2 sin θ =F3,所以F3缓慢增大.
解析
小滑块受力分析如右图所示,
根据平衡条件得 FNsin θ =mg
高中物理 专题 共点力平衡的几类典型问题 习题

小专题(二) 共点力平衡的几类典型问题1.(人教版必修第一册第77页第2题改编)如图甲,一台空调外机用两个三角形支架固定在外墙上,空调外机的重心恰好在支架水平横梁OA 和斜梁OB的连接点O的上方,图乙为示意图。
如果把斜梁加长一点,仍保持连接点O的位置不变,横梁仍然水平,这时OA对O点的作用力F1和OB对O点的作用力F2的变化是( )A.F1变大,F2变大B.F1变小,F2变小C.F1变大,F2变小D.F1变小,F2变大2.(2020·全国Ⅲ卷,17)如图,悬挂甲物体的细线拴牢在一不可伸长的轻质细绳上O点处;绳的一端固定在墙上,另一端通过光滑定滑轮与物体乙相连。
甲、乙两物体质量相等。
系统平衡时,O点两侧绳与竖直方向的夹角分别为α和β。
若α=70°,则β等于( )A.45°B.55°C.60°D.70°3.如图甲所示, 两小球通过两根轻绳连接并悬挂于O点,已知两轻绳OA和AB的长度之比为√3∶1,A、B处两小球质量分别为2m和m。
现对A、B处两小球分别施加水平向右的力F1和水平向左的力F2,两球恰好处于如图乙的位置静止,此时B处小球恰好在悬点O的正下方,轻绳OA与竖直方向成30°角,则( )A.F1=F2B.F1=√3F2C.F1=2F2D.F1=3F24.(粤教版必修第一册第91页第4题改编)如图所示,一根粗糙的水平横杆上套有甲、乙两个轻环,系在两环上的等长细绳拴住的书本处于静止状态。
现将两环距离变小后书本仍处于静止状态,则( )A.杆对甲环的支持力变大B.乙环对杆的摩擦力变小C.杆对甲环的力不变D.与乙环相连的细绳对书本的拉力变大5.飞艇常常用于执行扫雷、空中预警、电子干扰等多项作战任务。
如图所示为飞艇拖拽扫雷具扫除水雷的模拟图。
当飞艇匀速飞行时,绳子与竖直方向恒成θ角。
已知扫雷具质量为m,重力加速度为g,扫雷具所受浮力不能忽略,下列说法正确的是( )A.扫雷具受3个力作用B.绳子拉力大小为mg cosθC.海水对扫雷具作用力的水平分力小于绳子拉力D.绳子拉力一定大于mg6.重力都为G 的两个小球A 和B 用三段轻绳连接后悬挂在O 点(如图所示),O 、B 间的绳子长度是A 、B 间的绳子长度的2倍,将一个拉力F 作用到小球B 上,使三段轻绳都伸直,且O 、A 间和A 、B 间的两段绳子分别处于竖直和水平方向上,则拉力F 的最小值为( )A.12GB.√33G C.G D.2√33G 7.如图所示,竖直放置的光滑圆环,顶端D 点处固定一定滑轮(大小忽略),圆环两侧套着质量分别为m 1、m 2的两小球甲、乙,两小球用轻绳绕过定滑轮相连,并处于静止状态,甲、乙连线过圆心O 点,且与右侧绳的夹角为θ。
专题--共点力平衡
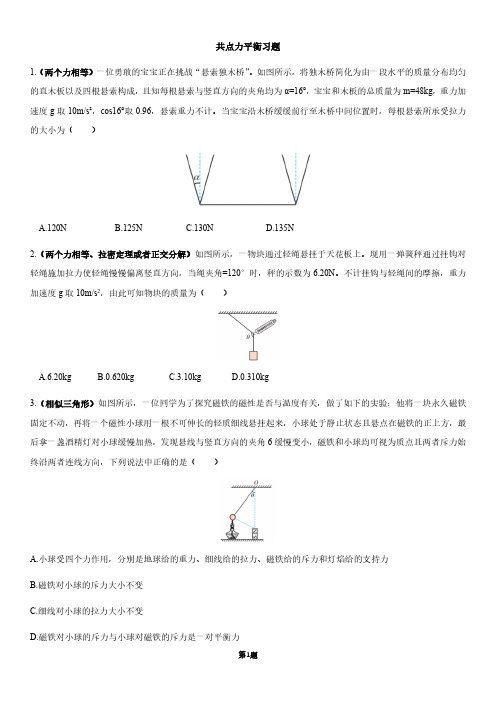
共点力平衡习题1.(两个力相等)一位勇敢的宝宝正在挑战“悬索独木桥”。
如图所示,将独木桥简化为由一段水平的质量分布均匀的直木板以及四根悬索构成,且知每根悬索与竖直方向的夹角均为α=16°,宝宝和木板的总质量为m=48kg,重力加速度g取10m/s²,cos16°取0.96,悬索重力不计。
当宝宝沿木桥缓缓前行至木桥中间位置时,每根悬索所承受拉力的大小为()A.120NB.125NC.130ND.135N2.(两个力相等、拉密定理或者正交分解)如图所示,一物块通过轻绳悬挂于天花板上。
现用一弹簧秤通过挂钩对轻绳施加拉力使轻绳慢慢偏离竖直方向,当绳夹角=120°时,秤的示数为6.20N。
不计挂钩与轻绳间的摩擦,重力加速度g取10m/s2,由此可知物块的质量为()A.6.20kgB.0.620kgC.3.10kgD.0.310kg3.(相似三角形)如图所示,一位同学为了探究磁铁的磁性是否与温度有关,做了如下的实验:他将一块永久磁铁固定不动,再将一个磁性小球用一根不可伸长的轻质细线悬挂起来,小球处于静止状态且悬点在磁铁的正上方,最后拿一盏酒精灯对小球缓慢加热,发现悬线与竖直方向的夹角6缓慢变小,磁铁和小球均可视为质点且两者斥力始终沿两者连线方向,下列说法中正确的是()A.小球受四个力作用,分别是地球给的重力、细线给的拉力、磁铁给的斥力和灯焰给的支持力B.磁铁对小球的斥力大小不变C.细线对小球的拉力大小不变D.磁铁对小球的斥力与小球对磁铁的斥力是一对平衡力4.(动态分析)如图所示,O点为半径为R的半圆形碗的圆心,质量相同的a、b两小球用一长为R的轻质细杆相连,a球表面粗糙,b球表面光滑。
现将a、b两小球及杆放入碗内,系统处于静止状态,细杆水平。
现将碗绕O点在纸面内逆时针缓慢旋转30°,此过程a、b两球始终相对碗静止。
在旋转过程中,下列说法正确的是()A.细杆对b球的弹力逐渐增大B.碗壁对b球的弹力逐渐增大C.a球受到碗壁的摩擦力最大值为其重力的√3倍 D.a球受到碗壁的支持力最大值为其重力的√3倍26.(正交分解)某创新实验小组制作一个半径为12.00cm的圆盘,将3个相同的弹簧的一端均匀固定在圆环上,另外一端固定打结,结点恰好在圆心○处,如图所示,已知弹簧(质量不计)的自然长度均为9.00cm,弹簧的劲度系数k=32.5N/m。
共点力的平衡 经典小练习

共点力的平衡 小练习1.如图所示,物体在水平外力作用下处于静止状态,当外力F 由图示位置逆时针转到竖直位置的过程中,物体仍保持静止,则在此过程中静摩擦力可能为( )A .0B .FC .F 2D .2F 【答案】ABC【解析】由于物体不动,当F 逆时针转动时,静摩擦力与F 的水平分力平衡,当F 水平时,F f =F ,当F 竖直时,F f =0,所以静摩擦力的变化范围是0≤F f ≤F ,故A 、B 、C 正确.2.如图所示,物体M 在竖直向上的拉力F 作用下静止在一固定的粗糙斜面上,则物体M 受力的个数可能为( )A .2个B .3个C .4个D .5个【答案】AC【解析】当F =mg 时,物体只受到重力和拉力F 的作用;当F <mg 时,物体还受到斜面弹力和摩擦力的作用,故本题选A 、C .3.“阶下儿童仰面时,清明妆点正堪宜.游丝一断浑无力,莫向东风怨别离.”这是《红楼梦》中咏风筝的诗,风筝在风力F 、线的拉力F T 以及重力G 的作用下,能够高高地飞在蓝天上.关于风筝在空中的受力可能正确的是( )【答案】A【解析】在B 、C 、D 三个图中,合力不可能为零,不能处于平衡状态,只有A 图,在三个力的作用下能处于平衡,故A 正确,B 、C 、D 错误.4.重力为G 的两个完全相同的小球,与水平面的动摩擦因数均为μ.竖直向上的较小的力F 作用在连接两球轻绳的中点,绳间的夹角α=60°,如图所示.缓慢增大F ,到两球刚要运动的过程中,下列说法正确的是( )A.地面对球的支持力变大,摩擦力变大B.地面对球的支持力变小,摩擦力变小C.球刚开始运动时,地面对球没有支持力D.球刚开始运动时,球受到的摩擦力最大【答案】D【解析】先用整体法,将两小球看成一整体,F增大,则地面对小球的支持力变小,但不会变为零,A、C 错误.再用隔离法,取左边的小球为研究对象,因为F增大,绳子的拉力F T增大,那么F T在水平面上的分量增大,所以地面对小球的摩擦力变大,B错误,D正确.5.如图所示,一个半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的.一根细线跨在碗口上,线的两端分别系有质量为m1和m2的小球.当它们处于平衡状态时,质量为m1的小球与O点的连线与水平线的夹角为α=90°,质量为m2的小球位于水平地面上,设此时质量为m2的小球对地面压力大小为F N,细线的拉力大小为F T,则()A.F N=(m2-m1)g B.F N=m2g C.F T=22m1g D.F T=(m2-22m1)g【答案】B【解析】分析小球m1的受力情况,由物体的平衡条件可得,绳的拉力F T=0,故C、D均错误;分析m2受力,由平衡条件可得:F N=m2g,故A错误,B正确.6.如图所示,有一质量不计的杆AO,长为R,可绕A自由转动.用轻绳在O点悬挂一个重为G的物体,另一根轻绳一端系在O点,O点为圆弧的圆心,另一端系在圆弧形墙壁上的C点.当该轻绳端点由点C逐渐沿圆弧CB向上移动的过程中(保持OA与地面夹角θ不变),OC绳拉力的大小变化情况是()A.逐渐减小B.逐渐增大C.先减小后增大D.先增大后减小【答案】C【解析】对物体分析,物体受力平衡,则竖直绳的拉力等于物体的重力,故竖直绳的拉力不变;再对O点分析,O受竖直绳的拉力、OA的支持力F及OC绳的拉力而处于平衡状态,受力分析如图所示.F和OC 绳的拉力的合力与G大小相等,方向相反,则在OC绳端点上移的过程中,平行四边形的对角线保持不变,由图可知OC绳的拉力先减小后增大,故C正确.7.如图,一不可伸长的光滑轻绳,其左端固定于O点,右端跨过位于O′点的固定光滑轴悬挂一质量为M 的物体;OO′段水平,长度为L;绳上套一可沿绳滑动的轻环.现在轻环上悬挂一钩码,平衡后,物体上升L.则钩码的质量为()A.22M B.32M C.2M D.3M【答案】D【解析】如图所示,轻环上挂钩码后,物体上升L,则根据几何关系可知,三角形OO′A为等边三角形,根据物体的平衡条件可知,2Mg cos 30°=mg,求得m=3M,D项正确.8.一铁球悬挂在OB绳的下端,轻绳OA、OB、OC的结点为O,轻绳OA悬挂在天花板上的A点,轻绳OC拴接在轻质弹簧测力计上.第一次,保持结点O位置不变,某人拉着轻质弹簧测力计从竖直位置缓慢转动到水平位置,如图中的甲所示,弹簧测力计的示数记为F1.第二次,保持轻绳OC垂直于OA,缓慢释放轻绳,使轻绳OA转动到竖直位置,如图中的乙所示,弹簧测力计的示数记为F2.则()A.F1恒定不变,F2逐渐增大B.F1、F2均逐渐增大C.F1先减小后增大,F2逐渐减小D.F1逐渐增大,F2先减小后增大【答案】C【解析】题图甲中,OA 与OC 的合力与重力等大反向,且保持不变,OA 的方向不变,通过画平行四边形可知,当OC 顺时针转动到水平位置时,F 1先减小后增大.题图乙中,设OA 绳与竖直方向的夹角为θ,因为OA 与OC 垂直,且合力与重力等大反向,故F 2=mg sin θ,根据题意,随着θ的减小,F 2逐渐减小,故选项C 正确.9.如图所示,两根轻弹簧a 、b 的上端固定在竖直墙壁上,下端连接在小球上.当小球静止时,弹簧a 、b与竖直方向的夹角分别为53°和37°.已知a 、b 的劲度系数分别为k 1、k 2,sin 53°=0.8,则a 、b 两弹簧的伸长量之比为( )A .4k 23k 1B .3k 24k 1C .3k 14k 2D .4k 13k 2【答案】B 【解析】作出小球的受力分析图如图所示,根据平衡条件有F =mg ,弹簧a 的弹力F 1=F cos 53°=35mg ,弹簧b 的弹力F 2=F sin 53°=45mg ,根据胡克定律有x =F k ,则a 、b 两弹簧的伸长量之比为x 1x 2=F 1k 1F 2k 2=3k 24k 1.故选项B 正确.10.如图所示,a 、b 两个质量相同的球用线连接,a 球用线挂在天花板上,b 球放在光滑斜面上,系统保持静止,以下图示中正确的是( )【答案】B【解析】对b 球受力分析,受重力、垂直斜面向上的支持力和细线的拉力,由于三力平衡时三个力中任意两个力的合力与第三个力等值、反向、共线,故细线拉力向右上方,故A 图错误;再对a 、b 两个球整体受力分析,受总重力、垂直斜面向上的支持力和上面细线的拉力,再次根据共点力平衡条件判断上面的细线的拉力方向斜向右上方,故C 、D 图均错误.11. 如图所示,光滑半球形容器固定在水平面上,O 为球心.一质量为m 的小滑块,在水平力F 的作用下静止于P 点,设滑块所受支持力为F N ,OP 与水平方向的夹角为θ.下列关系正确的是( )A .F =mg tan θB .F =mg tan θC .F N =mg tan θD .F N =mg tan θ【答案】A【解析】法一:合成法滑块受力如图甲,由平衡条件知:mg F =tan θ,mg F N =sin θ⇒F =mg tan θ,F N =mg sin θ.法二:效果分解法将重力按产生的效果分解,如图乙所示,F =G 2=mg tan θ,F N =G 1=mg sin θ.法三:正交分解法将滑块受的力水平、竖直分解,如图丙所示,mg =F N sin θ,F =F N cos θ,联立解得:F =mg tan θ,F N =mg sin θ.法四:封闭三角形法如图丁所示,滑块受的三个力组成封闭三角形,解直角三角形得:F =mg tan θ,F N =mg sin θ.12. 如图,一不可伸长的光滑轻绳,其左端固定于O 点,右端跨过位于O ′点的固定光滑轴悬挂一质量为M 的物体;OO ′段水平,长度为L ;绳子上套一可沿绳滑动的轻环.现在轻环上悬挂一钩码,平衡后,物体上升L ,则钩码的质量为( )A .22MB .32MC .2MD .3M【解析】重新平衡后,绳子形状如图,由几何关系知:绳子与竖直方向夹角为30°,则环两边绳子的夹角为60°,根据平行四边形定则,环两边绳子拉力的合力为3Mg,根据平衡条件,则钩码的质量为3M,故选项D正确.13. 如图所示,用完全相同的轻弹簧A、B、C将两个相同的小球连接并悬挂,小球处于静止状态,弹簧A 与竖直方向的夹角为30°,弹簧C水平,则弹簧A、C的伸长量之比为()A.3∶4B.4∶ 3 C.1∶2 D.2∶1【答案】D【解析】法一:隔离法分别对两小球受力分析,如图甲所示F A sin 30°-F B sin α=0F′B sin α-F C=0,F B=F′B得F A=2F C,即弹簧A、C的伸长量之比为2∶1,选项D正确.法二:整体法将两球作为一个整体,进行受力分析,如图乙所示由平衡条件知:F C =sin 30°,即F ′A =2F C 又F ′A =F A ,则F A =2F C ,即弹簧A 、C 的伸长量之比为2∶1,故选项D 正确.14.如图所示,小球用细绳系住,绳的另一端固定于O 点.现用水平力F 缓慢推动斜面体,小球在斜面体上无摩擦地滑动,细绳始终处于直线状态,当小球升到接近斜面顶端时细绳接近水平,此过程中斜面对小球的支持力F N 以及绳对小球的拉力F T 的变化情况是( )A .F N 保持不变,F T 不断增大B .F N 不断增大,F T 不断减小C .F N 保持不变,F T 先增大后减小D .F N 不断增大,F T 先减小后增大【答案】D【解析】选小球为研究对象,其受力情况如图所示,用平行四边形定则作出相应的“力三角形O ′AB ”,其中O ′A 的大小、方向均不变,AB 的方向不变,推动斜面时,F T 逐渐趋于水平,B 点向下移动,根据动态平衡,F T 先减小后增大,F N 不断增大,选项D 正确.15.如图所示,物体A 、B 跨过定滑轮并用轻绳连接起来,物体A 放在倾角为θ的固定粗糙斜面上,滑轮左边的轻绳平行斜面.已知物体A 的质量为m ,物体A 与斜面的动摩擦因数为μ(μ<tan θ<1),不计滑轮与绳之间的摩擦,要使物体A 能在斜面上滑动,物体B 的质量可能为( )A .m (1-μ)sin θB .m (1+μ)cos θC .m (1-μ)cos θ D.m (sin θ-μcos θ)2【答案】BD【解析】当物体A恰好下滑时有mg sin θ=μmg cos θ+m B g,得m B=m(sin θ-μcos θ),当物体A恰好上滑时有mg sin θ+μmg cos θ=m B g,得m B=m(sin θ+μcos θ),即B的质量只要小于m(sin θ-μcos θ)或者大于m(sin θ+μcos θ)即可,D正确;又由题意tan θ<1,所以θ<45°即sin θ+μcos θ小于(1+μ)cos θ,所以B正确,A、C错误.16.质量均匀分布的光滑球A与B通过轻绳连接,悬挂于平台两侧,初始状态A球与地面和平台侧面接触且有挤压,B球悬于空中,如图所示.不计轻绳摩擦,若A发生均匀的少量膨胀后,两球仍能保持静止状态.则()A.两球的质量可能相等B.地面对平台一定有静摩擦力C.膨胀后平台侧面对A弹力变小D.膨胀后A对地面压力会变大【答案】D【解析】因初始状态A球与地面接触且有挤压,可知B的质量小于A的质量,选项A错误;对平台及A、B的整体受力分析,水平方向不受力,则地面对平台无静摩擦力作用,选项B错误;膨胀后拉A的细线与竖直方向的夹角θ变大,由平衡知识可知平台侧面对A弹力F N=T sin θ=m B g sin θ,可知平台侧面对A弹力变大,选项C错误;地面对A的支持力F′N=m A g-T cos θ,可知膨胀后F′N变大,即A对地面压力会变大,选项D正确.17.如图所示,小球a的质量为小球b质量的一半,分别与轻弹簧A、B和轻绳相连接并处于平衡状态.轻弹簧A与竖直方向夹角为60°,轻弹簧A、B伸长量刚好相同,则下列说法正确的是()A.轻弹簧A、B的劲度系数之比为3∶1B.轻弹簧A、B的劲度系数之比为2∶1C.轻绳上拉力与轻弹簧A上拉力的大小之比为2∶1D.轻绳上拉力与轻弹簧A上拉力的大小之比为3∶2【答案】AD【解析】设轻弹簧A、B伸长量都为x,小球a的质量为m,则小球b的质量为2m.对小球b,由平衡条件,弹簧B中弹力为k B x=2mg;对小球a,由平衡条件,竖直方向k B x+mg=k A x cos60°,联立解得:k A=3k B,选项A正确,B错误;水平方向,轻绳上拉力F=k A x sin 60°,选项C错误,D正确.18.轻绳一端系在质量为m的物块A上,另一端系在一个套在粗糙竖直杆MN的圆环上.现用水平力F拉住绳子上一点O,使物块A从图中实线位置缓慢下降到虚线位置,但圆环仍保持在原来位置不动,在这一过程中,环对杆的摩擦力F1和环对杆的压力F2的变化情况是()A.F1保持不变,F2逐渐增大B.F1保持不变,F2逐渐减小C.F1逐渐增大,F2保持不变D.F1逐渐减小,F2保持不变【答案】B【解析】以圆环、物块A及轻绳整体为研究对象,受力情况如图甲所示,根据平衡条件得,杆对环的摩擦力F1′=G,保持不变,杆对环的弹力F2′=F;以结点O为研究对象,受力情况如图乙所示,由平衡条件得,F=mg tanθ,物块A从图中实线位置缓慢下降到虚线位置过程中,θ逐渐减小,则F逐渐减小,F2′逐渐减小.所以F1′保持不变,F2′逐渐减小,由牛顿第三定律知F1不变,F2减小,选项B正确.19.如图所示,顶端附有光滑定滑轮的斜面体静止在粗糙水平地面上,三条细绳结于O点.一条绳跨过定滑轮平行于斜面连接物块P,一条绳连接小球Q,P、Q两物体处于静止状态,另一条绳OA在外力F的作用下,处于水平方向,现缓慢改变绳OA的方向至θ<90°,且保持结点O位置不变,整个装置始终处于静止状态.下列说法正确的是()A.绳OA的拉力先减小后增大B.绳OB的拉力一直增大C.地面对斜面体有向右的摩擦力D.地面对斜面体的支持力不断减小【答案】AD【解析】缓慢改变绳OA的方向至θ<90°的过程,OA拉力的方向变化如图所示,从3位置到2位置到1位置可见OA的拉力先减小后增大,OB的拉力一直减小,故A正确,B错误;以斜面和P、Q整体为研究对象受力分析,根据平衡条件可知斜面受地面的摩擦力与OA绳水平方向的分力等大、反向,故摩擦力方向向左,C错误;以斜面体和P整体为研究对象受力分析,绳OB对其竖直向下的分力减小,则地面对斜面的支持力减小,故D 正确.20.将轻绳和轻弹簧的一端分别固定在圆弧上的A 、B 两点,另一端固定在小球a 上,静止时,小球a 恰好处于圆心O 处,如图甲所示,此时绳与水平方向夹角为30°,弹簧恰好水平,现将轻弹簧与轻绳对调,将a 球换成b 球后,小球仍位于O 点,如图乙所示,则a 、b 两个小球的质量之比为( )A .1∶1B .3∶1C .2∶3D .3∶2【答案】C 【解析】在甲图和乙图中,由于弹簧的长度是相等的,所以两种情况下的弹簧的弹力是相等的.甲图中:m 1g F =tan 30°=33乙图中:m 2g F =sin 30°=12所以:m 1g m 2g =33F 12F =233=2∶ 3.。
共点力的平衡练习题

一、选择题1.如图所示,在倾角为θ的斜面上,放着一个质量为m 的光滑小球,小球被竖直的木板挡住,则小球对木板的压力大小为( )A .mg cos θB .mg tan θC .mg cos θD .mg tan θ 2.如图2所示,一个半球形的碗放在桌面上,碗口水平,O 点为其球心,碗的内表面及碗 口是光滑的.一根细线跨在碗口上,线的两端分别系有质量为m 1和m 2的小球,当它们处于平衡状态时,质量为m 1的小球与O 点的连线与水平线的夹角为α=60°.两小球的质量比m2m1为A.33B.23C.32D.223.一只蚂蚁从半球形小碗内的最低点沿碗壁向上缓慢爬行,在其滑落之前的爬行过程中受力情况是( )A .弹力逐渐增大B .摩擦力逐渐增大C .摩擦力逐渐减小D .碗对蚂蚁的作用力逐渐增大4.如图所示,一箱苹果沿着倾角为θ的斜面,以速度v 匀速下滑,在箱子中夹有一只质量为m 的苹果,它受到周围苹果对它作用力的方向是( )A .沿斜面向上B .沿斜面向下C .竖直向上D .垂直斜面向上5.如图所示,质量m 1=10 kg 和m 2=30 kg 的两物体,叠放在动摩擦因数为0.50的粗糙水平地面上,一处于水平位置的轻弹簧,劲度系数为k =250 N/m ,一端固定于墙壁,另一端与质量为m 1的物体相连,弹簧处于自然状态,现用一水平推力F 作用于质量为m 2的物体上,使它缓慢地向墙壁一侧移动,当移动0.40 m 时,两物体间开始相对滑动,这时水平推力F 的大小为( )A .100 NB .300 NC .200 ND .250 N6.如图5所示,在水平面上有三个质量分别为m 1、m 2、m 3的木块,木块1和2、2和3间分别用一原长为L 、劲度系数为k 的轻弹簧连接起来,木块1、2与水平面间的动摩擦因数为μ,木块3和水平面之间无摩擦力.现用一水平恒力向右拉木块3,当木块一起匀速运动时,1和3两木块间的距离为(木块大小不计)( )A .L +μm2g kB .L +μm1+m2g kC .2L +μ2m1+m2g kD .2L +2μm1+m2g k7.如图6所示,a 、b 是两个位于固定斜面上的完全相同的正方形物块,它们在水平方向的外力F 的作用下处于静止状态.已知a 、b 与斜面的接触面都是光滑的,则下列说法正确的是( )A .物块a 所受的合外力大于物块b 所受的合外力B .物块a 对斜面的压力大于物块b 对斜面的压力C .物块a 、b 间的相互作用力等于FD .物块a 对斜面的压力等于物块b 对斜面的压力8.如图所示,斜面倾角为θ(θ为锐角)两个物体A 和B 相接触放在粗糙的斜面上,当他们加速下滑时,下面对A 、B 之间相互作用力的析正确的是( )A .当mB >m A 时,A 、B 之间有相互作用力;当m B ≤m A 时,A 、B 之 图6间无相互作用力B .设两物体与斜面的动摩擦因数分别为μA 、μB ,当μA >μB 时,A 、B 之间有相互作用力;当μA ≤μB 时,A 、B 之间没有相互作用力C .设A 、B 与斜面摩擦力分别为F f A 、F f B ,当F f A >F f B 时,A 、B 间有相互作用力;当F f A ≤F F b时,A 、B 之间没有相互作用力D .A 、B 间是否有相互作用力跟斜面倾角θ无关9.(哈尔滨第学)如图所示,在水平力F 作用下,木块A 、B 均保持静止.若木块A 与B 的接触面是水平的,且F ≠0.则关于木块B 的受力个数可能为( )A .3个或4个B .3个或5个C .4个或5个D .4个或6个10.如图所示,竖直放置的轻弹簧一端固定在地面上,另一端与斜面体P 连接,P 的斜面与固定挡板MN 接触且处于静止状态,则斜面体P 此刻所受的外力个数有可能为( )A .2个 B.3个C .4个 D.5个11.(2010·淄博模拟)如图所示,物块A 放在倾斜的木板上,已知木板的倾角α分别为30°和45°时物块所受摩擦力的大小恰好相同,则物块和木板间的动摩擦因数为( ) A.12 B.32C.22 D.5212.(2010·黄冈月考)如图5所示,质量为m 的两个球A 、B 固定在杆的两端,将其放入光滑的半圆形碗中,杆的长度等于碗的半径,当杆与碗的竖直半径垂直时,两球刚好能平衡,则杆对小球的作用力为( )A.33mg B.233mgC.32mg D.2mg 13.(2010·湖南师大附中模拟)如图所示,A 、B 两木块放在水平面上,它们之间用细线相连,两次连接情况中细线倾斜方向不同但倾角一样,两木块与水平面间的动摩擦因数相同.先后用水平力F 1和F 2拉着A 、B 一起匀速运动,则( )A.F 1≠F 2B.F 1=F 2C.F T1>F T2D.F T1=F T214.(2010·三十二校联考)如图所示,质量为m 的物体用细绳栓住放在水平粗糙传送带上,物体距传送带左端距离为L ,稳定时绳与水平方向的夹角为θ,当传送带分别以v 1、v 2的速度做逆时针转动时(v 1<v 2),绳中的拉力分别为F 1、F 2;若剪断细绳时,物体到达左端的时间分别为t 1、t 2,则下列说法正确的是( )A.F 1<F 2B.F 1=F 2C.t 1>t 2D.t 1<t 215.如图所示,固定在水平面上的斜面倾角为θ,长方体木块A 的质量为M ,其PQ 面上钉着一枚小钉子,质量为m 的小球B 通过一细线与小钉子相连接,细线与斜面垂直,以下说法正确的是( )A.若木块匀速下滑,则小球对木块的压力为零B.若木块匀速下滑,则小球对木块的压力为mg sin θC.若木块匀加速自由下滑,则小球对木块的压力为零D.若木块匀加速自由下滑,则小球对木块的压力为mg sin θ16.(2009·北京高考)如图所示,将质量为m 的滑块放在倾角为θ的固定斜面上.滑块与斜面之间的动摩擦因数为μ.若滑块与斜面之间的最大静摩擦力和滑动摩擦力大小相等,重力加速度为g ,则( )A.将滑块由静止释放,如果μ>tan θ,滑块将下滑B.给滑块沿斜面向下的初速度,如果μ<tanθ,滑块将减速下滑C.用平行于斜面向上的力拉滑块向上匀速滑动,如果μ=tanθ,拉力大小应是2mg sinθD.用平行于斜面向下的力拉滑块向下匀速滑动,如果μ=tanθ,拉力大小应是mg sinθ17.质细线把两个质量未知的小球悬挂起来,如图2-3-17(甲)所示,今对小球a持续施加一个向左偏下30°的恒力,并对小球b持续施加一个向右偏上30°的同样大的恒力,最后达到平衡,表示平衡状态的图可能是图中的18.如图所示,A、B两球用劲度系数为k1的轻弹簧相连,B球用长为L的细线悬于O点,A球固定在O点正下方,且O、A间的距离恰为L,此时绳子所受的拉力为F1,现把A、B间的弹簧换成劲度系数为k2的轻弹簧,仍使系统平衡,此时绳子所受的拉力为F2,则F1与F2的大小关系为A.F1<F2B.F1>F2C.F1=F2D.因k1、k2大小关系未知,故无法确定19.(2010·安徽合肥一模)如图所示,在粗糙水平地面上放着一个截面为四分之一圆弧的柱状物体A,A的左端紧靠竖直墙,A与竖直墙之间放一光滑圆球B,整个装置处于静止状态,若把A向右移动少许后,它们仍处于静止状态,则A.B对墙的压力增大B.A与B之间的作用力增大C.地面对A的摩擦力减小D.A对地面的压力减小20.(2009·江苏高考)用一根长 1 m的轻质细绳将一幅质量为 1 kg的画框对称悬挂在墙壁上(如图.已知绳能承受的最大张力为10 N.为使绳不断裂,画框上两个挂钉的间距最大为(g取10 m/s2)A.32mB.22mC.12mD.34m22.(长春二模)如图所示,质量为m的正方体和质量为M的正方体放在两竖直墙和水平面间,处于静止状态.m与M 相接触面与竖直方向的夹角为α,若不计一切摩擦,下列说法正确的是( )A.水平面对正方体M的弹力大小大于(M+m)gB.水平面对正方体M的弹力大小为(M+m)g·cot αC.墙面对正方体M的弹力大小为mg cot αD.墙面对正方体M的弹力大小为mg tan α23.(不定项选择)如图所示,质量为m的质点,与三根相同的螺旋形轻弹簧相连.静止时,弹簧c沿竖直方向,相邻两弹簧间的夹角均为120°.已知弹簧a、b对质点的作用力大小均为F,则弹簧c对质点的作用力大小可能为( )A.F B.F+mgC.F-mg D.mg-F24.如图所示,在倾角为θ的粗糙斜面上,有一个质量为m的物体被水平力F推着静止于斜面上,已知物体与斜面间的动摩擦因数为μ,且μ<tanθ,若物体恰好不下滑,则推力F为多少?若物体恰好不上滑,则推力F为多少?(最大静摩擦力等于滑动摩擦力)25.(2010·齐河月考)所受重力G1=8 N的砝码悬挂在绳PA和PB的结点上.PA偏离竖直方向37°角,PB在水平方向,且连在所受重力为G2=100 N的木块上,木块静止于倾角为37°的斜面上,如图所示,试求:(1)木块与斜面间的摩擦力;(2)木块所受斜面的弹力.26.如图所示,板A的质量为m,滑块B的质量为2m,板A用绳拴住,绳与斜面平行,滑块B沿倾角为α的斜面在A板的中间一段匀速下滑,若A、B之间以及B与斜面间的动摩擦因数相同,求动摩擦因数μ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§课题《共点力的平衡》
【班级
姓名 】
高一物理学案 第1页 共2页 高一物理学案 第2页 共2页 请参考例题,认真画图,规范认真写清解题步骤!!!
1.如图,重为200N 的重物由ON 、OM 绳悬挂在天花板上,已知∠ONM=60°,∠OMN=30°,
请画出受力分析图并求绳ON 和绳OM 受到的拉力的大小?
2、如图所示,在倾角为θ的斜面上,放着一个质量为m 的光滑小球,小球被竖直的木
板挡住,求小球对木板的压力和小球对斜面的压力。
3、如图所示,灯重G=20 N ,绳AO 与天花板的夹角α=30°,绳BO 与墙面垂直,试求
AO 、BO 两绳的拉力各为多大?
4.在固定的斜面上有一质量为m =2kg 的物体,如图所示,当用水平力F =20N 推物体时,物体沿斜面匀速上升,若 30=α,求物体与斜面间动摩擦因数。
(g 取10m/s 2) 解析:受力分析,建立直角坐标系如图所示, 物体做匀速运动,由平衡条件得 x 轴方向:f G F +α=αsin cos ① y 轴方向:α+α=sin cos F G N ② 又因μN f = ③ 由以上三式可解得:27.0≈μ。
5.将一个质量为m 的木块放在倾角为θ的斜面上,木块恰好可以沿斜面匀速下滑,求: ⑴木块与斜面间的动摩擦因数 ⑵要使该物块沿斜面匀速上滑,沿斜面向上施加的推力的大小 6.如图所示,物体A 重10 N ,与竖直墙面间的动摩擦因数为0.5,受与水平方向成45°角的力F 作用,沿墙向上匀速运动,求F 的大小。
