中考一轮复习专题2 整式(含答案)

合集下载

(中考复习)第2节代数式与整式(含答案)

第2节代数式与整式(建议答题时间：45分钟)命题点一列代数式及求值1. (2017海南)已知a＝－2，则代数式a＋1的值为()A. －3B. －2C. －1D. 12. (2017重庆巴蜀模拟)若m＝－1，n＝2，则n2－2mn－1的值是()A. 1B. 7C. 9D. －43. (2017重庆西大附中模拟)已知2a－b＝3，则2b－4a＋3的值为()A. －6B. 9C. －3D. 64. (2017淄博)若a＋b＝3，a2＋b2＝7，则ab等于()A. 2B. 1C. －2D. －15. (2017宁夏)如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成右边的矩形．根据图形的变化过程写出的一个正确的等式是()第5题图A. (a－b)2＝a2－2ab＋b2B. a(a－b)＝a2－abC. (a－b)2＝a2－b2D. a2－b2＝(a＋b)(a－b)6. (2017丽水)已知a2＋a＝1，则代数式3－a－a2的值为________．第7题图7. (2017山西)某商店经销一种品牌的洗衣机，其中某一型号的洗衣机每台进价为a元，商店将进价提高20%后作为零售价进行销售，一段时间后，商店又以9折优惠价促销，这时该型号洗衣机的零售价为________元．命题点二整式的相关概念8. (2017济宁)单项式9x m y 3与单项式4x 2y n 是同类项，则m ＋n 的值是( )A. 2B. 3C. 4D. 59. (2017河北)＝( )A. 2m 3nB. 2m 3nC. 2m n 3D. m 23n命题点三整式的运算10. (2017安徽)计算(－a 3)2的结果是( )A. a 6B. －a 6C. －a 5D. a 511. (2017乌鲁木齐)计算(ab 2)3的结果是( )A . 3ab 2B . ab 2C . a 3b 5D . a 3b 612. (2017武汉)下列计算的结果是x 5的为( )A. x 10÷x 2B. x 6－xC. x 2·x 3D. (x 2)313. (2017江西)下列运算正确的是( )A. (－a 5)2＝a 10B. 2a ·3a 2＝6a 2C. －2a ＋a ＝－3aD. －6a 6÷2a 2＝－3a 314. (2017郴州改编)下列运算错误的是( )A. (a 2)3＝a 6B. a 2·a 3＝a 5C. a －1＝1aD. (a ＋b )(a －b )＝a 2＋b 215. (2017黄冈)下列计算正确的是( )A. 2x ＋3y ＝5xyB. (m ＋3)2＝m 2＋9C. (xy 2)3＝xy 6D. a 10÷a 5＝a 516. (2017天津)计算x 7÷x 4的结果等于________．17. (2017眉山)先化简，再求值：(a ＋3)2－2(3a ＋4)，其中a ＝－2.18. (2017重庆西大附中模拟)化简：(b＋2a)(2a－b)－3(2a－b)219. (2017重庆八中模拟)化简：(2x＋1)(2x－1)－(x＋1)(3x－2)．20. (2017河南改编)计算：(2x＋y)2＋(x－y)(x＋y)－5x(x－y)．21. 先化简，再求值：m(m－1)＋(m＋1)(m－2)，其中m2－m－2＝0.22. 已知b＝－2a，求a(a－2b)＋2(a＋b)(a－b)－(a－b)2的值．命题点四因式分解23. (2017常德)下列各式由左到右的变形中，属于分解因式的是()A. a(m＋n)＝am＋anB. a2－b2－c2＝(a－b)(a＋b)－c2C. 10x2－5x＝5x(2x－1)D. x2－16＋6x＝(x＋4)(x－4)＋6x24. (2017甘肃)分解因式：x2－2x＋1＝________.25. (2017安徽)因式分解：a2b－4ab＋4b＝________.命题点五图形规律探索26. (2017烟台) 用棋子摆出下列一组图形：第26题图按照这种规律摆下去，第n个图形用的棋子个数为()A. 3nB. 6nC. 3n＋6D. 3n＋327. (2017随州)在公园内，牡丹按正方形种植，在它的周围种植芍药，下图反映了牡丹的列数(n)和芍药的数量规律，那么当n＝11时，芍药的数量为()第27题图A. 84株B. 88株C. 92株D.121株28. (2017娄底)刘莎同学用火柴棒依图中的规律摆六边形图案，用10086根火柴棒摆出的图案应是第________个．第28题图答案1. C2. B3. C4. B5.D【解析】第一个图形的阴影部分的面积为两个正方形的面积差：a2－b2，第二个图形是长方形，长为(a＋b)，宽为(a－b)，∴面积为(a＋b)(a－b)．6. 27. 1.08a【解析】洗衣机每台进价为a元，商店将进价提高20%后零售价为a(1＋20%)＝1.2a元，又九折促销为 1.2a·0.9＝1.08a，则该型号洗衣机的零售价为1.08a元.8. D9. B10. A11. D12. C13. A14. D15. D16. x317.解：原式＝a2＋6a＋9－6a－8＝a2＋1，当a＝－2时，原式＝(－2)2＋1＝5.18. 解：原式＝4a2－b2－3(4a2－4ab＋b2) ＝4a2－b2－12a2＋12ab－3b2＝－8a2＋12ab－4b2.19.解：原式＝4x2－1－(3x2－2x＋3x－2) ＝x2－x＋1.20.解：原式＝4x2＋4xy＋y2＋x2－y2－5x2＋5xy＝9xy.21.解：原式＝m2－m＋m2－m－2＝2m2－2m－2＝2(m2－m)－2，∵m2－m－2＝0，∴m2－m＝2，∴原式＝2×2－2＝2.22. 解：原式＝a2－2ab＋2(a2－b2)－(a2＋b2－2ab)＝a2－2ab＋2a2－2b2－a2－b2＋2ab＝2a2－3b2.将b＝－2a代入得，原式＝2a2－3(－2a)2＝2a2－12a2＝－10a2.23. C24. (x－1)225.b(a－2)226. D【解析】第1个图形，棋子个数：3×1＋3；第2个图形，棋子个数：3×2＋3；第3个图形，棋子个数3×3＋3；…；因此，第n个图形棋子的个数等于3·n ＋3＝3n＋3.27.B【解析】当n＝1时，芍药的数量为8；当n＝2时，芍药的数量为16；当n＝3时，芍药的数量为24；当n＝4时，芍药的数量为32，由此可发现规律，芍药的数量是n的8倍，所以芍药的数量为：8n株，所以当n＝11时，芍药的数量为8×11＝88株.28. 2017【解析】由图可以找出规律：第n个图形需要5n＋1(其中n是正整数)个火柴棒，设5n＋1＝10086，解得n＝2017.。

中考数学一轮复习第2讲《整式》试题(2021学年)

江苏省苏州市2０１７年中考数学一轮复习第2讲《整式》试题编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望(江苏省苏州市２０17年中考数学一轮复习第2讲《整式》试题)的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉，前进的动力。

本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步,以下为江苏省苏州市201７年中考数学一轮复习第2讲《整式》试题的全部内容。

2017年中考数学一轮复习第2讲《整式》【考点解析】１. 代数式及相关问题【例题】. (2０16·重庆市A卷）若a=２，b=﹣1,则a+2b＋3的值为( )A．﹣1ﻩB．3 C．６ﻩD.５【分析】把a与b代入原式计算即可得到结果.【解答】解：当a=2,b=﹣1时,原式=2﹣2+３=３，故选B ﻩﻩ【点评】此题考查了代数式求值,熟练掌握运算法则是解本题的关键．【变式】(２015·湖州市）当ｘ=1时,代数式4−３x的值是( ）A. １B。

2 ﻩC. 3 D. 4【分析】把x的值代入代数式进行计算即可得解。

【解析】把x＝1代入代数式４−3x即可得原式＝4－3=１.故选A。

【点评】代入正确计算即可．２。

幂的运算【例题】（20１６海南）下列计算中，正确的是( ）A.(a３）4=ａ12Ｂ．a3•a5=a１５Ｃ．a２＋ａ2=a4D.a6÷ａ2=a3【考点】同底数幂的除法;合并同类项；同底数幂的乘法；幂的乘方与积的乘方.【分析】根据合并同类项法则，同底数幂相乘，底数不变指数相加;幂的乘方,底数不变指数相乘;同底数幂相除,底数不变指数相减,对各选项分析判断后利用排除法求解．【解答】解:A、(ａ３）4＝a3×4=a1２,故A正确;B、ａ3•a5=a３+5=a8,故B错误；C、a2+a2=2a２,故C错误;D、a6÷a2=a6﹣2=a4,故D错误；故选：Ａ．【点评】本题考查合并同类项、同底数幂的乘法、幂的乘方、同底数幂的除法,熟练掌握运算性质和法则是解题的关键．【变式】（2016·重庆市B卷)计算（x2ｙ)3的结果是（)A.ｘ6y３B.ｘ5ｙ３C.ｘ５yD.x２y3【考点】幂的乘方与积的乘方．【分析】根据积的乘方和幂的乘方法则求解.【解答】(x２y）3=（x2)３y3=x6y3，故选A．【点评】本题考查了积的乘方和幂的乘方，熟练掌握运算法则是解题的关键.3。

中考数学一轮复习讲义2__整式

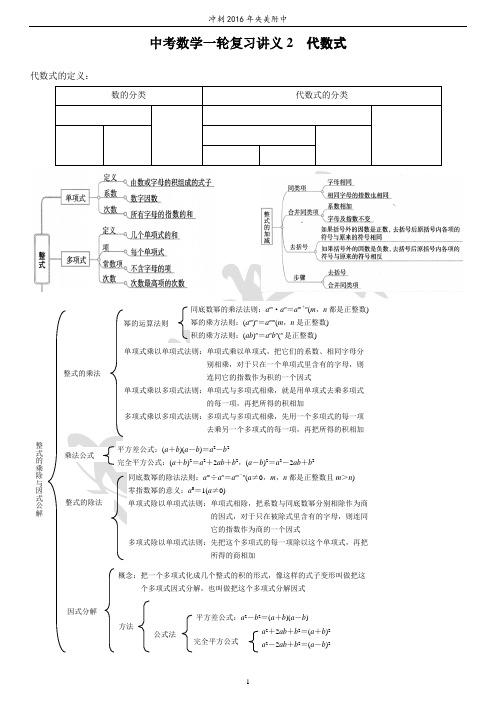
中考数学一轮复习讲义2 代数式代数式的定义：整式的乘法整式的乘除与因式公解幂的运算法则同底数幂的乘法法则：a m·a n＝a m＋n(m，n都是正整数)幂的乘方法则：(a m)n＝a mn(m，n是正整数)积的乘方法则：(ab)n＝a n b n(n是正整数)单项式乘以单项式法则：单项式乘以单项式，把它们的系数、相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式单项式乘以多项式法则：单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加多项式乘以多项式法则：多项式与多项式相乘，先用一个多项式的每一项去乘另一个多项式的每一项，再把所得的积相加同底数幂的除法法则：a m÷a n＝a m－n(a≠0，m，n都是正整数且m＞n)零指数幂的意义：a0＝1(a≠0)单项式除以单项式法则：单项式相除，把系数与同底数幂分别相除作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式多项式除以单项式法则：先把这个多项式的每一项除以这个单项式，再把所得的商相加乘法公式平方差公式：(a＋b)(a－b)＝a2－b2完全平方公式：(a＋b)2＝a2＋2ab＋b2，(a－b)2＝a2－2ab＋b2整式的除法因式分解概念：把一个多项式化成几个整式的积的形式，像这样的式子变形叫做把这个多项式因式分解，也叫做把这个多项式分解因式方法公式法平方差公式：a2－b2＝(a＋b)(a－b)完全平方公式a2＋2ab＋b2＝(a＋b)2a2－2ab＋b2＝(a－b)2题型一整式的加减运算例1 已知与是同类项，则a b 的值为. 例2 计算：（7x 2＋5x －3）－（5x 2－3x ＋2）．题型二整式的求值例3 已知（a ＋2）2＋|b ＋5|＝0，求3a 2b 一[2a 2b －（2ab －a 2b ）－4a 2]－ab 的值．例例5例例7例8例9A.解析：第二个图案中正三角形的个数为：第三个图案中正三角形的个数为：．．，；第n 个图案中正三角形的个数为：题型四：幂的运算法则及其逆运用例1 计算2x 3·(－3x )２＝．例2 计算[a 4(a 4－4a )－(－3a 5)2÷(a 2)3]÷(－2a 2)2．3313a x y --533b y x -85a +题型五：整式的混合运算与因式分解例3 计算[(a －2b )(2a －b )－(2a ＋b )2＋(a ＋b )(a －b )－(3a )2]÷(－2a )．例4 分解因式． (1)m 3－m ； (2)(x ＋2)(x ＋3)＋x 2－4．例5 分解因式a 2－2ab ＋b 2－c 2．例6 (1)已知x ＋y ＝7，xy ＝12，求(x －y )2； (2)已知a ＋b ＝8，a －b ＝2，求ab 的值．15.（2011•临沂，2，3分）下列运算中正确的是（） A 、（﹣ab ）2=2a 2b 2B 、（a+b ）2=a 2+1C 、a 6÷a 2=a 3D 、2a 3+a 3=3a 316.（2011泰安，2，3分）下列运算正确的是（） A ．3a 2＋4a 2＝7a 4B ．3a 2－4a 2＝－a 2C ．3a ×4a 2＝12a 2D ．2222434)3(a a a -=÷17.（2011四川眉山，2，3分）下列运箅正确的是（） A ．2a 2﹣a=aB ．（a+2）2=a 2+4C ．（a 2）3=a 6D ．3)3(2-=-19.（2011•南充，11，3分）计算（π﹣3）0=．20.（2011四川攀枝花，3，3分）下列运算中，正确的是（） A 、2+3=5 B 、a 2•a=a 3C 、（a 3）3=a 6D 、327=－3中考真题精选21.（2011泰安，5，3分）下列等式不成立的是（） A ．m 2－16＝（m －4）（m ＋4）B ．m 2＋4m ＝m （m ＋4）C ．m 2－8m ＋16＝（m －4）2D ．m 2＋3m ＋9＝（m ＋3）22.（2011•丹东，4，3分）将多项式x 3﹣xy 2分解因式，结果正确的是（） A 、x （x 2﹣y 2）B 、x （x ﹣y ）2C 、x （x+y ）2D 、x （x+y ）（x ﹣y ）4.（2011天水，4，4）多项式2a 2﹣4ab +2b 2分解因式的结果正确的是（） A 、2（a 2﹣2ab +b 2）B 、2a （a ﹣2b ）+2b 2C 、2（a ﹣b ）2D 、（2a ﹣2b ）25.（2011江苏无锡，3，3分）分解因式2x 2﹣4x+2的最终结果是（） A ．2x （x ﹣2）B ．2（x 2﹣2x+1） C ．2（x ﹣1）2D ．（2x ﹣2）26.（2011•台湾5，4分）下列四个多项式，哪一个是2x 2+5x ﹣3的因式（） A 、2x ﹣1B 、2x ﹣3C 、x ﹣1D 、x ﹣37.（2011台湾，24，4分）下列四个多项式，哪一个是33x ＋7的倍式（） A ．33x 2－49B ．332x 2＋49C ．33x 2＋7xD ．33x 2＋14x10.（2011梧州，6，3分）因式分解x 2y ﹣4y 的正确结果是（） A 、y （x+2）（x ﹣2）B 、y （x+4）（x ﹣4）C 、y （x 2﹣4）D 、y （x ﹣2）211.（2011河北，3，2分）下列分解因式正确的是（） A ．－a ＋a 3＝－a （1＋a 2） B ．2a －4b ＋2＝2（a －2b ）C ．a 2－4＝（a －2）2D ．a 2－2a ＋1＝（a －1）213.（2011，台湾省，25,5分）若多项式33x 2﹣17x ﹣26可因式分解成（ax+b ）（cx+d ），其中a 、b 、c 、d 均为整数，则|a+b+c+d|之值为何？（） A 、3B 、10C 、25D 、2914.（2011浙江金华，3，3分）下列各式能用完全平方式进行分解因式的是（） A ．x 2 +1 B.x 2+2x －1 C.x 2+x +1 D.x 2+4x +415.（2011浙江丽水，3，3分）下列各式能用完全平方公式进行分解因式的是（） A 、x 2+1 B 、x 2+2x ﹣1 C 、x 2+x +1D 、x 2+4x +4综合验收评估测试题1一、选择题l. 在代数式－2x 2，3xy ，，，0，mx －ny 中，整式的个数为（） A ．2 B ．3 C ．4 D. 5 2. 二下列语句正确的是（）A ．x 的次数是0B ．x 的系数是0 C. －1是一次单项式 D ．－1是单项式 3.4.5. 6. 7. 8. C ．m ≠－1，n 为大于3的整数 D ．m ≠－1，n ＝5二、填空题9. －mx n y 是关于x ，y 的一个单项式，且系数是3，次数是4，则m ＝，n ＝． 10. 多项式ab 3－3a 2b 2－a 3b －3按字母a 的降幂排列是．按字母b 的升幂排列是． 11. 当b ＝时，式子2a ＋ab －5的值与a 无关． 12. 若－7xy n ＋1 3x m y 4是同类项，则m ＋n ．13．多项式2ab －5a 2＋7b 2加上等于a 2－5ab ．b a 3xy -三、解答题14．先化简，再求值：，其中m ＝－l ，n ＝.综合验收评估测试题2一、选择题(每小题3分，共30分) 1．计算(a 3)2的结果是 ( ) A ．a 5 B ．a 6 C ．a 8 D ．a 9 2．下列运算正确的是 ( )A ．a 2·a 3＝a 4B ．(－a )4＝a 4C ．a 2＋a 3＝a 5D ．(a 2)3＝a 5 3．已知x －3y ＝－3，则5－x ＋3y 的值是 ( ) A ．0 B ．2 C ．5 D ．8 4．若m ＋n ＝3，则2m 2＋4mn ＋2n 2－6的值为 ( ) A ．12 B ．6 C ．3 D ．05．如图15－4所示，在边长为a 的正方形中挖去一个边长为b 的小正方形(a ＞b )，把余下的部分拼成一个矩形，根据两个图形中阴影部分的面积相等，可以验证 ( )A ．(a ＋b )2＝a 2＋2ab ＋b 2B ．(a －b )2＝a 2－2ab ＋b 2C ．a 2－b 2＝(a ＋b )(a －b )D ．(a ＋2b )(a －b )＝a 2＋ab －2b 2 6．下列各式中，与(a －b )2一定相等的是 ( )A ．a 2＋2ab ＋b 2B ．a 2－b 2C ．a 2＋b 2D ．a 2－2ab ＋b 0 7．已知x ＋y ＝－5，xy ＝6，则x 2＋y 2的值为 ( ) A ．1 B ．13 C ．17 D ．25 8．下列从左到右的变形是因式分解的是 ( )A ．ma ＋mb －c ＝m (a ＋b )－cB ．(a －b )(a 2＋ab ＋b 2)＝a 3－b 3C ．a 2－4ab ＋4b 2－1＝a (a －4b )＋(2b ＋1)(2b －1)D ．4x 2－25y 2＝(2x ＋5y )(2x －5y ) 9．下列各式中，能用平方差公式分解因式的是 ( ) A ．－a 2＋b 2 B ．－a 2－b 2 C ．a 2＋b 2 D ．a 3－b 3 10．如果(x －2)(x －3)＝x 2＋px ＋q ，那么p ，q 的值是 ( )A ．p ＝－5，q ＝6B ．p ＝1，q ＝－6C ．p ＝1，q ＝6D ．p ＝5，q ＝－622222212(52)3(2)2m n mn m n mn mn m n ⎛⎫+---- ⎪⎝⎭13二、填空题(每小题3分，共30分) 11．已知10m ＝2，10n ＝3，则103m＋2n＝．12．当x ＝3，y ＝1时，代数式(x ＋y )(x －y )＋y 2的值是． 13．若a －b ＝1，ab ＝－2，则(a ＋1)(b －1)＝． 14．分解因式：2m 3－8m ＝． 15．已知y ＝31x －1，那么31x 2－2xy ＋3y 2－2的值为． 16．计算：5752×12－4252×12＝．17 18192021 22(1)m 2n (m23．已知a ，b 是有理数，试说明a 2＋b 2－2a －4b ＋8的值是正数．24．先化简，再求值：(a ＋b )(a －b )＋(4ab 3－8a 2b 2)÷4ab ，其中a ＝2，b ＝1．25．(1)计算．①(a －1)(a ＋1)；②(a －1)(a 2＋a ＋1)；③(a －1)(a 3＋a 2＋a ＋1)；④(a －1)(a 4＋a 3＋a 2＋a ＋1)． (2)根据(1)中的计算，你发现了什么规律?用字母表示出来． (3)根据(2)中的结论，直接写出下题的结果． ①(a －1)(a 9＋a 8＋a 7＋a 6＋a 5＋a 4＋a 3＋a 2＋a ＋1)＝； ②若(a －1)·M ＝a 15－1，则M ＝； ③(a －b④(226(1) (2) (3) (4)(5)答案：1．D 解析：不是整式，故选D ． 2．D 解析：x 的次数是1，系数是1；－1是单项式．故选D ．3．C 解析：所含字母相同，并且相同字母的指数也相同的项叫做同类项．故选C ：4．D 解析：如果括号外的因数是正数，去括号后原括号内各项的符号与原来的符号相同；如果括号外的因数是负数，去括号后原括号内各项的符号与原来的符号相反．故选D ．5．6．B ． 7．2n ＋38．910 1112137b 2． 142×＝1．15 50πa 2＋100ab ．答：美化这块空地共需资金（50πa 2＋100ab ）元．点拨：根据题意，可以先求出建造花台及种花所需费用，再求出种草的费用，两者相加即为美化这块空地共需的资金．ba1314π4a ⨯参考答案1．B2．B[提示：选项A ：a 2·a 3＝a 5；选项C ：a 2和a 3不能合并；选项D ：(a 2)3＝a 6．] 3．D[提示：5－x ＋3y ＝5－(x －3y )＝5－(－3)＝8．]4．A ［提示：2m 2＋4mn ＋2n 2－6＝2(m ＋n )2－6＝2×32－6＝12．]5．6．7．8．9．10111213141531(x －3y )2－216] 17181920] 21＋1)(2x －1)－＝20002－(200022(x ＋y －8)2．232)2≥0，∴(a －1)＝a 2－b 2＋b 2－25n －2＋…＋a 3＋a 2＋a ＋1)＝a n ＋1－1． (3)①a 10－1 ②a 14＋a 13＋a 12＋a 11＋…＋a 3＋a 2＋a ＋1 ③a 6－b 6④32x 5－126．解：(1)各层对应的点数依次为：4，8．12，16，20，24；所有层的总点数依次为：4，12，24，40，60．84． (2)4n ． (3)2n (n ＋1)． (4)第24层． (5)有，第25层．。

中考第一轮复习讲义第二讲代数式与整式

第二讲代数式与整式一.考点分析考点一.列代数式（含规律探索）例题1.一次知识竞赛共有20道选择题，规定答对一题得5分，不答或答错扣1分，如果某学生答对题数为x ，用代数式表示该学生的得分为（）A.5x-(20-x)B.100-(20-x)C.5xD.5x-5(20-x)-(20-x)例题2.某商店经销一种品牌的洗衣机，其中某一型号的洗衣机每台进价为a 元，商店将进价提高20%后作为零售价进行销售，一段时间后，商店又以9折优惠价促销，这时该型号洗衣机的零售价为元.例题3.观察下列数据：3579,,,,, (357911)x x x x x 它们是按一定规律排列的，依照此规律，第n 个数据是（用含n 的式子表示）.例题4.如图，观察各图中小圆点的摆放规律，并按这样的规律摆放下去，则第10个图形中小圆点的个数为 .考点二.代数式求值例题1.已知4a+3b=1，则整式8a+6b-3的值为 . 例题2.已知3,6x y xy +==，则22x y xy +的值为 .例题3.如果x=1时，代数式3234ax bx ++的值是5，那么x=-1时，代数式3234ax bx ++的值是 .例题4.一组“数值转换机”按下面的程序计算，如果输入的数是36，则输出的结果为106，要使输出的结果为127，则输入的最小正整数是 .考点三.非负数的性质例题1.120x y ++-=，那么xy= .例题2.若25(3)0a b -++=，则a-2b= .例题3.若21(2)3322102x y z -++-=，则式子2x yz 的值为 .考点四.整式的相关概念例题1.若单项式22m x y 与41-3n x y 可以合并成一项，则m n = . 例题2.在代数式21215,5,,,,,233x y z x y a x y xyz y π+---+-中有（） A.5个整式 B.4个单项，3个多项式 C.6个整式，4个单项式 D.6个整式，单项式与多项式个数相同例题3.（1）单项式－22xy π的系数是，次数是；（2）多项式125323+--xy y x 的次数 . 考点五.整式的运算例题1.下列计算正确的是（）A.325(3)6a a a -=B.331a a a a÷= C.22(-21)441a a a -=++ D.235235a a a += 例题2.4张长为a ，宽为b （a ＞b ）的长方形纸片，按如图的方式拼成一个边长为（a+b ）的正方形，图中空白部分的面积为S 1，阴影部分的面积为S 2，若S 1=2S 2，则a ，b 满足（）A.2a=5bB.2a=3bC.a=3bD.a=2b例题3.先化简，再求值：2(2)(43)a b a a b +-+，其中1,2a b ==.例题4.先化简，再求值：23(21)(21)(1)(2)(8)m m m m m +---+÷-，其中m 是方程220x x +-=的根.考点六.因式分解例题1.分解因式：44ax ay -= .例题2.下列等式从左到右的变形，属于因式分解的是（）A.2221(1)x x x +-=-B.22()()a b a b a b +-=-C.2244(2)x x x ++=+D.22(1)ax a a x -=-例题3.分解因式：22(2)(2)y x x y +-+= .例题4.若21x x +=，则433331x x x +++的值为 .例题5.把下列各式分解因式（1）)()()(y x c x y b y x a -+---；（2）2296y xy x +-；（3）y x y x 2222-+-；（4）22216)4(x x -+.二.同步练习 1.4y x 33-它的系数为，次数为 . 2.多项式4423x xy 2y y 5x +--是次项式,它的最高次项是，二次项系数为，把这个多项式按y 降幂排列得 .3.若m 10y x 41与4n 13y x 31+是同类项，则m n ＝ . 4.若05a a 2=-+，则20082a 2a 2++的值为 .5.计算：_______43=⋅-a a , 2a a a +⋅= , (a+2)(a-1)= .3条2条1条图66.若3,5==nm aa，则___________32=+nma.7.在多项式142+x中，添加一个单项式使其成为一个完全平方式，则添加的单项式是（只写出一个即可）.8.把下列各式分解因式：（1）x2－xy＝；（2）4x2－16＝；（3）2x2＋4x＋2＝；（4）x2－6x－7＝；（5）a3－a2＋a－1＝．9.已知1)1(+-=nna,当1=n时,01=a；当2=n时,22=a；当3=n时,03=a…则654321aaaaaa+++++= .10.如图是小亮用8根，14根，20根火柴搭的1条，2条，3条“金鱼”，按此方法搭n条“金鱼”需要火柴根.(用含n的代数式表示)11.已知5,3a b ab-==，则代数式32232a b a b ab-+的值为 .12.观察下列各等式的数字特征：85358535⨯=-，1192911929⨯=-，17107101710710⨯=-……，将你所发现的规律用含字母a，b的等式表示出来： .13.下列运算正确的是（）A.12-=÷xxx B. 33332244)2(yxxyx-=⋅-C.653)()(xxx-=-⋅-- D.22941)321)(321(yxyxyx-=+--14.下列从左到右的变形，属于因式分解的是（）A.(x＋2)(x＋3)＝x2＋x＋6B.ax－ay＋1＝a(x－y)＋1C.8a2b3＝2a2·4b3D.x2－4＝(x＋2)(x－2)15.计算：(1)22462(32)2m m m m⎡⎤--+-⎣⎦； (2)223()(3)(7)4a bc ab ac-÷-•-.16.先化简,再求值:(1),3)12(2)12(2++-+a a 其中2=a ； (2)2()()()x y x y x y x ⎡⎤-++-÷⎣⎦,其中11,2x y =-=.17.把下列各式因式分解：（1）x 3－4x ；（2）x 2－3xy －10y 2； (3) x 2－y 2－4x ＋4；（4）x 4－5x 2＋4.18.对于实数a ，b ，c ，d 规定一种运算bc ad d c b a -=，如220)2(12201-=⨯--⨯=-，那么当255)3(42=--x 时，求x 的值.三.拓展练习1.某商店压了一批商品，为尽快售出，该商店采取如下销售方案：将原来每件m 元，加价50%，再做两次降价处理，第一次降价30%，第二次降价10%，经过两次降价后的价格为元（结果用含m 的代数式表示）.2.7张如图1的长为a ，宽为b （a ＞b ）的小长方形纸片，按图2的方式不重叠地放在矩形ABCD 内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S ，当BC 的长度变化时，按照同样的放置方式，S 始终保持不变，则a ，b 满足（）A. 52a b =B.a=3bC.72a b = D.a=4b3.如图，小聪用一张面积为1的正方形纸片，按如下方式操作：①将正方形纸片四角向内折叠，使四个顶点重合，展开后沿折痕剪开，把四个等腰直角三角形扔掉；②在余下纸片上依次重复以上操作，当完成第2019次操作时，余下纸片的面积为（）A. 20192B.201812C.201912D.2020124.代数式2221126,4,,,2,5x y xy z y xy x x a b +-+-+-+ 中，不是整式的有个.5.化简222222123323a b ab a b ab a b +-+--并按字母a 的降幂排列为 .6.若823x y a b +-与234y x y a b -的和是单项式，则x y += . 7.12x n a b -与223m a b -是同类项，则()2xm n -= .8.单项式0.25b c x y 与单项式1210.125m n x y ---的和是0.625n m ax y ，则abc = .9.若249x mx ++是一个完全平方式，则m 的值为 .10.已知22412x x m -+是一个完全平方式，则m 的值为 .11.计算2200120002002-⨯的结果是 .12.计算：（1）2200920072008⨯-；（2）22007200720082006-⨯；（3）22003451()(2)542x π--⎛⎫⎛⎫⎛⎫÷-+---÷- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭；（4）24643(21)(21)(21)1++++；（5）22222111111)(1)(1)(1)(1)234910-----（；（6）12345678921234567890123456789112345678902⨯-.13.求24832(21)(21)(21)(21)(21)(21)1-++++++的个位数字.14. 已知5m a =，3n a =，求23m n a +的值.15. 已知5m a =，275m n a +=，求n a 的值.16. 已知33m a =，32n b =，求233242()()m n m n m n a b a b a b +-⋅⋅⋅的值.17. △ABC 中，a b c 、、为其三边长，且222a b c ab bc ac ++=++，试判断△ABC 的形状.18. 若20002001a x =+，20002002b x =+，20002003c x =+，求222a b c ab bc ac ++---的值.19.已知15a a +=，则221a a += ；21()a a-= . 20.若244210x x x-+=，则的值为 . 21.化简：（1）221111())2525a b a b ---（；（2）231)(231)a b a b -++-（；（3）222(9)(3)(3)(9)a a a a +-+-+.22. 已知()()31222a b ab a b +==--，，化简的结果是 . 23. 已知2012x xy xy y x y -=-=-，，则的值为 .24.若22ab =，则代数式()253ab a b ab b ---的值为 .25.若22011x y xy x xy y +==--+，，则的值为 .26.已知2()4x y -=，2()64x y +=，求①22x y +；②xy 的值.27. 已知：212x xy +=，215xy y +=，求()2x y +－()()x y x y +-的值．28. 已知：2(1)()5a a a b ---=-求代数式222a b ab +-的值．29. 已知2226100a b a b +-++=，求20061a b-的值.30. 先化简，再求值：2(23)(23)(3)a b a b a b +-+-，其中15,3a b =-=.31. 已知2215,31,3A x x B x x =-+=-+ 当23x =时，求2A B -的值.32.若()()2210231a b b ab ab ab +++=---⎡⎤⎣⎦，则的值是 .33.已知()()()()312m x y x y x y x y -⋅-⋅-=-，求()()22421225m m m m ++---的值.34.若0a b c ++=，则()()()a b b c c a abc ++++= .35.若2,3,5a b b c c d -=-=--=，则 ()()()a c b d a d --÷-= .36.已知3a b a b-=+，则()()()243a b a b a b a b +--=-+ . 37.若210m m +-=，则3222010m m +-= .38.若3220x x x ---= ，则4322451x x x x +---= .39.若2310x x x +++= ，则2320111x x x x +++++= .40.已知多项式731ax bx cx +++，当2x =-时，多项式的值为2010，则当2x =时，这个多项式的值为 .41.已知等式()()()221111x x ax x b x c x ++=+++++是关于x 的恒等式，则a= ，b= ，c= .42.如果2231x x +-与()()211a x b x c -+-+是同一个多项式，则a b c += . 43.已知()6212111021211102101x x a x a x a x a x a x a -+=++++++则01212a a a a ++++= ，12312a a a a ++++= ，02412a a a a ++++= ，121110921a a a a a a -+-++-= . 44.若a ，b ，c ，d 是整数，b 是正整数，且满,,a b c b c d c d a +=+=+=，则a b c d +++的最大值是 .45.已知0a b c d +++=，则()()()()()()333333a b a c b c b d a d c d +++++++++++= .46.已知等式()()222121k x k y k k z +-+--=与k 值无关，则x = ；y = ；z = .47.若()()2283a pa a a q ++-+中不含有32a a 和项，则p = ，q = .48.当x = ，y = 时，多项式22494121x y x y +-+-有最小值，此时这个最小值是 .49.若()()023236x x ----有意义，则x 的取值范围是 .50.若代数式2214250x y x y +-++的值为0，则x = ，y = .51.已知23a =，26b =，272c =，试问a b c 、、之间有什么关系？请说明理由.52.已知552a =，443b =，334c =，比较a b c 、、的大小.。

【一轮复习】2023年中考数真题分点透练-2 整式及其运算

第二讲整式及其运算【命题1 列代数式及代数式求值】类型一列代数式1．（2022•长沙）为落实“双减”政策，某校利用课后服务开展了主题为“书香满校园”的读书活动．现需购买甲，乙两种读本共100本供学生阅读，其中甲种读本的单价为10元/本，乙种读本的单价为8元/本，设购买甲种读本x本，则购买乙种读本的费用为（）A．8x元B．10（100﹣x）元C．8（100﹣x）元D．（100﹣8x）元2．（2022•杭州）某体育比赛的门票分A票和B票两种，A票每张x元，B票每张y元．已知10张A票的总价与19张B票的总价相差320元，则（）A．||＝320 B．||＝320C．|10x﹣19y|＝320 D．|19x﹣10y|＝3203．（2022•舟山）某动物园利用杠杆原理称象：如图，在点P处挂一根质地均匀且足够长的钢梁（呈水平状态），将装有大象的铁笼和弹簧秤（秤的重力忽略不计）分别悬挂在钢梁的点A，B处，当钢梁保持水平时，弹簧秤读数为k（N）．若铁笼固定不动，移动弹簧秤使BP扩大到原来的n（n＞1）倍，且钢梁保持水平，则弹簧秤读数为（N）（用含n，k的代数式表示）．类型二列代数式求值4．（2022•北碚区自主招生）已知x﹣y＝1，则代数式3x﹣3y+1的值是（）A．2 B．﹣2 C．4 D．﹣4 5．（2022•六盘水）已知（x+y）4＝a1x4+a2x3y+a3x2y2+a4xy3+a5y4，则a1+a2+a3+a4+a5的值是（）A．4 B．8 C．16 D．32 6．（2022•郴州）若＝，则＝．7.（2022•广西）阅读材料：整体代值是数学中常用的方法．例如“已知3a﹣b＝2，求代数式6a﹣2b﹣1的值．”可以这样解：6a﹣2b﹣1＝2（3a﹣b）﹣1＝2×2﹣1＝3．根据阅读材料，解决问题：若x＝2是关于x的一元一次方程ax+b＝3的解，则代数式4a2+4ab+b2+4a+2b﹣1的值是．8．（2022•岳阳）已知a2﹣2a+1＝0，求代数式a（a﹣4）+（a+1）（a﹣1）+1的值．9．（2022•苏州）已知3x2﹣2x﹣3＝0，求（x﹣1）2+x（x+）的值．【命题点2 整式的有关概念及运算】类型一整式的有关概念10．（2022•攀枝花）下列各式不是单项式的为（）A．3 B．a C．D．x2y 11．（2022•广东）单项式3xy的系数为．类型二整式的运算12．（2022•淮安）计算a2•a3的结果是（）A．a2B．a3C．a5D．a6 13．（2022•镇江）下列运算中，结果正确的是（）A．3a2+2a2＝5a4B．a3﹣2a3＝a3C．a2•a3＝a5D．（a2）3＝a514．（2022•淄博）计算（﹣2a3b）2﹣3a6b2的结果是（）A．﹣7a6b2B．﹣5a6b2C．a6b2D．7a6b2 15．（2022•毕节市）计算（2x2）3的结果，正确的是（）A．8x5B．6x5C．6x6D．8x616．（2022•河北）计算a3÷a得a？，则“？”是（）A．0 B．1 C．2 D．317．（2022•包头）若24×22＝2m，则m的值为（）A．8 B．6 C．5 D．2 18．（2022•黔西南州）计算（﹣3x）2•2x正确的是（）A．6x3B．12x3C．18x3D．﹣12x3 19．（2022•临沂）计算a（a+1）﹣a的结果是（）A．1 B．a2C．a2+2a D．a2﹣a+1 20．（2022•南通）已知实数m，n满足m2+n2＝2+mn，则（2m﹣3n）2+（m+2n）（m﹣2n）的最大值为（）A．24 B．C．D．﹣4 21．（2022•甘肃）计算：3a3•a2＝．22．（2022•常州）计算：m4÷m2＝．23．（2022•包头）若一个多项式加上3xy+2y2﹣8，结果得2xy+3y2﹣5，则这个多项式为．类型三乘法公式的应用及几何背景24．（2022•兰州）计算：（x+2y）2＝（）A．x2+4xy+4y2B．x2+2xy+4y2C．x2+4xy+2y2D．x2+4y2 25．（2022•百色）如图，是利用割补法求图形面积的示意图，下列公式中与之相对应的是（）A．（a+b）2＝a2+2ab+b2B．（a﹣b）2＝a2﹣2ab+b2C．（a+b）（a﹣b）＝a2﹣b2D．（ab）2＝a2b226．（2022•滨州）若m+n＝10，mn＝5，则m2+n2的值为．27．（2022•德阳）已知（x+y）2＝25，（x﹣y）2＝9，则xy＝．28．（2022•大庆）已知代数式a2+（2t﹣1）ab+4b2是一个完全平方式，则实数t的值为．29．（2022•益阳）已知m，n同时满足2m+n＝3与2m﹣n＝1，则4m2﹣n2的值是．30．（2022•遵义）已知a+b＝4，a﹣b＝2，则a2﹣b2的值为．31．（2022•六盘水）如图，学校劳动实践基地有两块边长分别为a，b的正方形秧田A，B，其中不能使用的面积为M．（1）用含a，M的代数式表示A中能使用的面积；（2）若a+b＝10，a﹣b＝5，求A比B多出的使用面积．32．（2022•荆门）已知x+＝3，求下列各式的值：（1）（x﹣）2 （2）x4+．33．（2022•河北）发现两个已知正整数之和与这两个正整数之差的平方和一定是偶数，且该偶数的一半也可以表示为两个正整数的平方和．验证如，（2+1）2+（2﹣1）2＝10为偶数．请把10的一半表示为两个正整数的平方和；探究设“发现”中的两个已知正整数为m，n，请论证“发现”中的结论正确．类型四整式的化简及求值考向1 整式的化简34.（2022•安顺）先化简，再求值：（x+3）2+（x+3）（x﹣3）﹣2x（x+1），考向2 整式的化简求值35.（2022•湖北）先化简，再求值：4xy﹣2xy﹣（﹣3xy），其中x＝2，y＝﹣1．36．（2022•盐城）先化简，再求值：（x+4）（x﹣4）+（x﹣3）2，其中x2﹣3x+1＝0．37．（2022•长春）先化简，再求值：（2+a）（2﹣a）+a（a+1），其中a＝﹣4．38．（2022•北京）已知x2+2x﹣2＝0，求代数式x（x+2）+（x+1）2的值．39．（2022•广西）先化简，再求值：（x+y）（x﹣y）+（xy2﹣2xy）÷x，其中x＝1，y＝．40.（2022•南充）先化简，再求值：（x+2）（3x﹣2）﹣2x（x+2），其中x＝﹣1．41．（2022•衡阳）先化简，再求值．（a+b）（a﹣b）+b（2a+b），其中a＝1，b＝﹣2．命题点3 因式分解及其应用42．（2022•济宁）下面各式从左到右的变形，属于因式分解的是（）A．x2﹣x﹣1＝x（x﹣1）﹣1 B．x2﹣1＝（x﹣1）2C．x2﹣x﹣6＝（x﹣3）（x+2）D．x（x﹣1）＝x2﹣x 43．（2022•柳州）把多项式a2+2a分解因式得（）A．a（a+2）B．a（a﹣2）C．（a+2）2D．（a+2）（a﹣2）44．（2022•广州）分解因式：3a2﹣21ab＝．45．（2022•常州）分解因式：x2y+xy2＝．46．（2022•河池）多项式x2﹣4x+4因式分解的结果是（）A．x（x﹣4）+4 B．（x+2）（x﹣2）C．（x+2）2D．（x﹣2）2 47．（2022•菏泽）分解因式：x2﹣9y2＝．48．（2022•绥化）因式分解：（m+n）2﹣6（m+n）+9＝．49．（2022•绵阳）因式分解：3x3﹣12xy2＝．50．（2022•丹东）因式分解：2a2+4a+2＝．51．（2022•巴中）因式分解：﹣a3+2a2﹣a＝．【命题点4 规律套索题】类型一数式规律52．（2022•西藏）按一定规律排列的一组数据：，﹣，，﹣，，﹣，…．则按此规律排列的第10个数是（）A．﹣B．C．﹣D．53．（2022•新疆）将全体正偶数排成一个三角形数阵：按照以上排列的规律，第10行第5个数是（）A．98 B．100 C．102 D．104 54．（2022•云南）按一定规律排列的单项式：x，3x2，5x3，7x4，9x5，……，第n个单项式是（）A．（2n﹣1）x n B．（2n+1）x n C．（n﹣1）x n D．（n+1）x n 55．（2022•徐汇区校级自主招生）设x1，x2，x3，…，x100是整数，且满足下列条件：①﹣1≤x i≤2，i＝1，2，3， (100)②x1+x2+x3+…+x100＝20；③x12+x22+x32+…+x1002＝100，则x13+x23+x33+…+x1003的最小值和最大值的和为．56．（2022•恩施州）观察下列一组数：2，，，…，它们按一定规律排列，第n个数记为a n，且满足+＝．则a4＝，a2022＝．57．（2022•泰安）将从1开始的连续自然数按以下规律排列：若有序数对（n，m）表示第n行，从左到右第m个数，如（3，2）表示6，则表示99的有序数对是．类型二图形规律58．（2022•济宁）如图，用相同的圆点按照一定的规律拼出图形．第一幅图4个圆点，第二幅图7个圆点，第三幅图10个圆点，第四幅图13个圆点……按照此规律，第一百幅图中圆点的个数是（）A．297 B．301 C．303 D．400 59．（2022•广州）如图，用若干根相同的小木棒拼成图形，拼第1个图形需要6根小木棒，拼第2个图形需要14根小木棒，拼第3个图形需要22根小木棒……若按照这样的方法拼成的第n个图形需要2022根小木棒，则n的值为（）A．252 B．253 C．336 D．337 60．（2022•江西）将字母“C”，“H”按照如图所示的规律摆放，依次下去，则第4个图形中字母“H”的个数是（）A．9 B．10 C．11 D．12 61．（2022•重庆）用正方形按如图所示的规律拼图案，其中第①个图案中有5个正方形，第②个图案中有9个正方形，第③个图案中有13个正方形，第④个图案中有17个正方形，此规律排列下去，则第⑨个图案中正方形的个数为（）A．32 B．34 C．37 D．4162.（2022•黑龙江）如图所示，以O为端点画六条射线OA，OB，OC，OD，OE，OF，再从射线OA上某点开始按逆时针方向依次在射线上描点并连线，若将各条射线所描的点依次记为1，2，3，4，5，6，7，8…后，那么所描的第2013个点在射线上．答案与解析【命题1 列代数式及代数式求值】类型一列代数式1．（2022•长沙）为落实“双减”政策，某校利用课后服务开展了主题为“书香满校园”的读书活动．现需购买甲，乙两种读本共100本供学生阅读，其中甲种读本的单价为10元/本，乙种读本的单价为8元/本，设购买甲种读本x本，则购买乙种读本的费用为（）A．8x元B．10（100﹣x）元C．8（100﹣x）元D．（100﹣8x）元【答案】C【解答】解：设购买甲种读本x本，则购买乙种读本的费用为：8（100﹣x）元．故选：C．2．（2022•杭州）某体育比赛的门票分A票和B票两种，A票每张x元，B票每张y元．已知10张A票的总价与19张B票的总价相差320元，则（）A．||＝320 B．||＝320C．|10x﹣19y|＝320 D．|19x﹣10y|＝320【答案】C【解答】解：由题意可得：|10x﹣19y|＝320．故选：C．3．（2022•舟山）某动物园利用杠杆原理称象：如图，在点P处挂一根质地均匀且足够长的钢梁（呈水平状态），将装有大象的铁笼和弹簧秤（秤的重力忽略不计）分别悬挂在钢梁的点A，B处，当钢梁保持水平时，弹簧秤读数为k（N）．若铁笼固定不动，移动弹簧秤使BP扩大到原来的n（n＞1）倍，且钢梁保持水平，则弹簧秤读数为（N）（用含n，k的代数式表示）．【答案】【解答】解：如图，设装有大象的铁笼重力为aN，将弹簧秤移动到B′的位置时，弹簧秤的度数为k′，由题意可得BP•k＝PA•a，B′P•k′＝PA•a，∴BP•k＝B′P•k′，又∵B′P＝nBP，∴k′＝＝，故答案为：．类型二列代数式求值4．（2022•北碚区自主招生）已知x﹣y＝1，则代数式3x﹣3y+1的值是（）A．2 B．﹣2 C．4 D．﹣4【答案】C【解答】解：∵x﹣y＝1，∴3x﹣3y+1＝3（x﹣y）+1＝3×1+1＝4．故选：C．5．（2022•六盘水）已知（x+y）4＝a1x4+a2x3y+a3x2y2+a4xy3+a5y4，则a1+a2+a3+a4+a5的值是（）A．4 B．8 C．16 D．32【答案】C【解答】解：∵（x+y）4＝x4+4x3y+6x2y2+4xy3+y4，∴a1+a2+a3+a4+a5＝1+4+6+4+1＝16，故选：C．6．（2022•郴州）若＝，则＝．【答案】【解答】解：根据＝得3a＝5b，则＝．故答案为：．7.（2022•广西）阅读材料：整体代值是数学中常用的方法．例如“已知3a﹣b＝2，求代数式6a﹣2b﹣1的值．”可以这样解：6a﹣2b﹣1＝2（3a﹣b）﹣1＝2×2﹣1＝3．根据阅读材料，解决问题：若x＝2是关于x的一元一次方程ax+b＝3的解，则代数式4a2+4ab+b2+4a+2b﹣1的值是．【答案】14【解答】解：∵x＝2是关于x的一元一次方程ax+b＝3的解，∴2a+b＝3，∴b＝3﹣2a，∴4a2+4ab+b2+4a+2b﹣1＝4a2+4a（3﹣2a）+（3﹣2a）2+4a+2（3﹣2a）﹣1＝4a2+12a﹣8a2+9﹣12a+4a2+4a+6﹣4a﹣1＝14．解法二：原式＝（2a+b）2+2（2a+b）﹣1＝32+2×3﹣1＝14，故答案为：14．8．（2022•岳阳）已知a2﹣2a+1＝0，求代数式a（a﹣4）+（a+1）（a﹣1）+1的值．【解答】解：a（a﹣4）+（a+1）（a﹣1）+1＝a2﹣4a+a2﹣1+1＝2a2﹣4a＝2（a2﹣2a），∵a2﹣2a+1＝0，∴a2﹣2a＝﹣1，∴原式＝2×（﹣1）＝﹣2．9．（2022•苏州）已知3x2﹣2x﹣3＝0，求（x﹣1）2+x（x+）的值．【解答】解：原式＝x2﹣2x+1+x2+x＝2x2﹣x+1，∵3x2﹣2x﹣3＝0，∴x2﹣x＝1，∴原式＝2（x2﹣x）+1＝2×1+1＝3．【命题点2 整式的有关概念及运算】类型一整式的有关概念10．（2022•攀枝花）下列各式不是单项式的为（）A．3 B．a C．D．x2y 【答案】C【解答】解：A、3是单项式，故本选项不符合题意；B、a是单项式，故本选项不符合题意；C、不是单项式，故本选项符合题意；D、x2y是单项式，故本选项不符合题意；故选：C．11．（2022•广东）单项式3xy的系数为．【答案】3【解答】解：单项式3xy的系数为3．故答案为：3．类型二整式的运算12．（2022•淮安）计算a2•a3的结果是（）A．a2B．a3C．a5D．a6【答案】C【解答】解：a2•a3＝a5．13．（2022•镇江）下列运算中，结果正确的是（）A．3a2+2a2＝5a4B．a3﹣2a3＝a3C．a2•a3＝a5D．（a2）3＝a5【答案】C【解答】解：A.3a2+2a2＝5a2，故此选项不合题意；B．a3﹣2a3＝﹣a3，故此选项不合题意；C．a2•a3＝a5，故此选项符合题意；D．（a2）3＝a6，故此选项不合题意；故选：C．14．（2022•淄博）计算（﹣2a3b）2﹣3a6b2的结果是（）A．﹣7a6b2B．﹣5a6b2C．a6b2D．7a6b2【答案】C【解答】解：原式＝4a6b2﹣3a6b2＝a6b2，故选：C．15．（2022•毕节市）计算（2x2）3的结果，正确的是（）A．8x5B．6x5C．6x6D．8x6【答案】D【解答】解：（2x2）3＝8x6．故选：D．16．（2022•河北）计算a3÷a得a？，则“？”是（）A．0 B．1 C．2 D．3 【答案】C【解答】解：根据同底数幂的除法可得：a3÷a＝a2，∴？＝2，故选：C．17．（2022•包头）若24×22＝2m，则m的值为（）A．8 B．6 C．5 D．2 【答案】B【解答】解：∵24×22＝24+2＝26＝2m，故选：B．18．（2022•黔西南州）计算（﹣3x）2•2x正确的是（）A．6x3B．12x3C．18x3D．﹣12x3【答案】C【解答】解：（﹣3x）2•2x＝9x2•2x＝18x3．故选：C．19．（2022•临沂）计算a（a+1）﹣a的结果是（）A．1 B．a2C．a2+2a D．a2﹣a+1【答案】B【解答】解：a（a+1）﹣a＝a2+a﹣a＝a2，故选：B20．（2022•南通）已知实数m，n满足m2+n2＝2+mn，则（2m﹣3n）2+（m+2n）（m﹣2n）的最大值为（）A．24 B．C．D．﹣4【答案】B【解答】解：方法1、∵m2+n2＝2+mn，∴（2m﹣3n）2+（m+2n）（m﹣2n）＝4m2+9n2﹣12mn+m2﹣4n2＝5m2+5n2﹣12mn＝5（mn+2）﹣12mn＝10﹣7mn，∵m2+n2＝2+mn，∴（m+n）2＝2+3mn≥0（当m+n＝0时，取等号），∴mn≥﹣，∴（m﹣n）2＝2﹣mn≥0（当m﹣n＝0时，取等号），∴mn≤2，∴﹣≤mn≤2，∴﹣14≤﹣7mn≤，∴﹣4≤10﹣7mn≤，即（2m﹣3n）2+（m+2n）（m﹣2n）的最大值为，故选：B．方法2、设m+n＝k，则m2+2mn+n2＝k2，∴mn+2+2mn＝k2，∴mn＝k2﹣，∴原式＝10﹣7mn＝﹣k2+≤，故选：B．21．（2022•甘肃）计算：3a3•a2＝．【答案】3a5【解答】解：原式＝3a3+2＝3a5．故答案为：3a5．22．（2022•常州）计算：m4÷m2＝．【答案】m2【解答】解：m4÷m2＝m4﹣2＝m2．故答案为：m223．（2022•包头）若一个多项式加上3xy+2y2﹣8，结果得2xy+3y2﹣5，则这个多项式为．【答案】y2﹣xy+3【解答】解：由题意得，这个多项式为：（2xy+3y2﹣5）﹣（3xy+2y2﹣8）＝2xy+3y2﹣5﹣3xy﹣2y2+8＝y2﹣xy+3．故答案为：y2﹣xy+3．类型三乘法公式的应用及几何背景24．（2022•兰州）计算：（x+2y）2＝（）A．x2+4xy+4y2B．x2+2xy+4y2C．x2+4xy+2y2D．x2+4y2【答案】A【解答】解：（x+2y）2＝x2+4xy+4y2．故选：A．25．（2022•百色）如图，是利用割补法求图形面积的示意图，下列公式中与之相对应的是（）A．（a+b）2＝a2+2ab+b2B．（a﹣b）2＝a2﹣2ab+b2C．（a+b）（a﹣b）＝a2﹣b2D．（ab）2＝a2b2【答案】A【解答】解：根据题意，大正方形的边长为a+b，面积为（a+b）2，由边长为a的正方形，2个长为a宽为b的长方形，边长为b的正方形组成，所以（a+b）2＝a2+2ab+b2．故选：A．26．（2022•滨州）若m+n＝10，mn＝5，则m2+n2的值为．【答案】90【解答】解：∵m+n＝10，mn＝5，∴m2+n2＝（m+n）2﹣2mn＝102﹣2×5＝100﹣10＝90．故答案为：90．27．（2022•德阳）已知（x+y）2＝25，（x﹣y）2＝9，则xy＝．【答案】4【解答】解：∵（x+y）2＝x2+y2+2xy＝25，（x﹣y）2＝x2+y2﹣2xy＝9，∴两式相减得：4xy＝16，则xy＝4．故答案为：428．（2022•大庆）已知代数式a2+（2t﹣1）ab+4b2是一个完全平方式，则实数t的值为．【答案】或﹣．【解答】解：根据题意可得，（2t﹣1）ab＝±（2×2）ab，即2t﹣1＝±4，解得：t＝或t＝．故答案为：或﹣．29．（2022•益阳）已知m，n同时满足2m+n＝3与2m﹣n＝1，则4m2﹣n2的值是．【答案】3【解答】解：∵2m+n＝3，2m﹣n＝1，∴4m2﹣n2＝（2m+n）（2m﹣n）＝3×1＝3．故答案为：3．30．（2022•遵义）已知a+b＝4，a﹣b＝2，则a2﹣b2的值为．【答案】8【解答】解：∵a+b＝4，a﹣b＝2，∴a2﹣b2＝（a+b）（a﹣b）＝4×2＝8，故答案为：8．31．（2022•六盘水）如图，学校劳动实践基地有两块边长分别为a，b的正方形秧田A，B，其中不能使用的面积为M．（1）用含a，M的代数式表示A中能使用的面积；（2）若a+b＝10，a﹣b＝5，求A比B多出的使用面积．【解答】解：（1）A中能使用的面积＝大正方形的面积﹣不能使用的面积，即a2﹣M，故答案为：a2﹣M；（2）A比B多出的使用面积为：（a2﹣M）﹣（b2﹣M）＝a2﹣b2＝（a+b）（a﹣b）＝10×5＝50，答：A比B多出的使用面积为50．32．（2022•荆门）已知x+＝3，求下列各式的值：（1）（x﹣）2；（2）x4+．【解答】解：（1）∵＝，∴＝＝＝﹣4x•＝32﹣4＝5；（2）∵＝，∴＝+2＝5+2＝7，∵＝，∴＝﹣2＝49﹣2＝47．33．（2022•河北）发现两个已知正整数之和与这两个正整数之差的平方和一定是偶数，且该偶数的一半也可以表示为两个正整数的平方和．验证如，（2+1）2+（2﹣1）2＝10为偶数．请把10的一半表示为两个正整数的平方和；探究设“发现”中的两个已知正整数为m，n，请论证“发现”中的结论正确．【解答】解：验证：10的一半为5，5＝1+4＝12+22，探究：两个已知正整数之和与这两个正整数之差的平方和一定是偶数，且该偶数的一半也可以表示为两个正整数的平方和．理由如下：（m+n）2+（m﹣n）2＝m2+2mn+n2+m2﹣2mn+n2＝2m2+2n2＝2（m2+n2），故两个已知正整数之和与这两个正整数之差的平方和一定是偶数，且该偶数的一半也可以表示为两个正整数的平方和．类型四整式的化简及求值考向1 整式的化简34.（2022•安顺）先化简，再求值：（x+3）2+（x+3）（x﹣3）﹣2x（x+1），【解答】解：（x+3）2+（x+3）（x﹣3）﹣2x（x+1）＝x2+6x+9+x2﹣9﹣2x2﹣2x考向2 整式的化简求值35.（2022•湖北）先化简，再求值：4xy﹣2xy﹣（﹣3xy），其中x＝2，y＝﹣1．【解答】解：4xy﹣2xy﹣（﹣3xy）＝4xy﹣2xy+3xy＝5xy，当x＝2，y＝﹣1时，原式＝5×2×（﹣1）＝﹣10．36．（2022•盐城）先化简，再求值：（x+4）（x﹣4）+（x﹣3）2，其中x2﹣3x+1＝0．【解答】解：原式＝x2﹣16+x2﹣6x+9＝2x2﹣6x﹣7，∵x2﹣3x+1＝0，∴x2﹣3x＝﹣1，∴2x2﹣6x＝﹣2，∴原式＝﹣2﹣7＝﹣9．37．（2022•长春）先化简，再求值：（2+a）（2﹣a）+a（a+1），其中a＝﹣4．【解答】解：（2+a）（2﹣a）+a（a+1）＝4﹣a2+a2+a＝4+a，当a＝﹣4时，原式＝4+﹣4＝．38．（2022•北京）已知x2+2x﹣2＝0，求代数式x（x+2）+（x+1）2的值．【解答】解：x（x+2）+（x+1）2＝x2+2x+x2+2x+1＝2x2+4x+1，∵x2+2x﹣2＝0，∴x2+2x＝2，∴当x2+2x＝2时，原式＝2（x2+2x）+1＝2×2+1＝4+139．（2022•广西）先化简，再求值：（x+y）（x﹣y）+（xy2﹣2xy）÷x，其中x＝1，y＝．【解答】解：（x+y）（x﹣y）+（xy2﹣2xy）÷x＝x2﹣y2+y2﹣2y＝x2﹣2y，当x＝1，y＝时，原式＝12﹣2×＝0．40.（2022•南充）先化简，再求值：（x+2）（3x﹣2）﹣2x（x+2），其中x＝﹣1．【解答】解：原式＝（x+2）（3x﹣2﹣2x）＝（x+2）（x﹣2）＝x2﹣4，当x＝﹣1时，原式＝（﹣1）2﹣4＝﹣2．41．（2022•衡阳）先化简，再求值．（a+b）（a﹣b）+b（2a+b），其中a＝1，b＝﹣2．【解答】解：（a+b）（a﹣b）+b（2a+b）＝a2﹣b2+2ab+b2＝a2+2ab，将a＝1，b＝﹣2代入上式得：原式＝12+2×1×（﹣2）＝1﹣4＝﹣3．命题点3 因式分解及其应用42．（2022•济宁）下面各式从左到右的变形，属于因式分解的是（）A．x2﹣x﹣1＝x（x﹣1）﹣1 B．x2﹣1＝（x﹣1）2C．x2﹣x﹣6＝（x﹣3）（x+2）D．x（x﹣1）＝x2﹣x【答案】C【解答】解：A选项不是因式分解，故不符合题意；B选项计算错误，故不符合题意；C选项是因式分解，故符合题意；D选项不是因式分解，故不符合题意；故选：C．43．（2022•柳州）把多项式a2+2a分解因式得（）A．a（a+2）B．a（a﹣2）C．（a+2）2D．（a+2）（a﹣2）【答案】A【解答】解：a2+2a＝a（a+2）．故选：A．44．（2022•广州）分解因式：3a2﹣21ab＝．【答案】3a（a﹣7b）【解答】解：3a2﹣21ab＝3a（a﹣7b）．故答案为：3a（a﹣7b）．45．（2022•常州）分解因式：x2y+xy2＝．【答案】xy（x+y）【解答】解：x2y+xy2＝xy（x+y）．故答案为：xy（x+y）．46．（2022•河池）多项式x2﹣4x+4因式分解的结果是（）A．x（x﹣4）+4 B．（x+2）（x﹣2）C．（x+2）2D．（x﹣2）2【答案】D【解答】解：原式＝（x﹣2）2．故选：D．47．（2022•菏泽）分解因式：x2﹣9y2＝．【答案】（x﹣3y）（x+3y）【解答】解：原式＝（x﹣3y）（x+3y）．故答案为：（x﹣3y）（x+3y）．48．（2022•绥化）因式分解：（m+n）2﹣6（m+n）+9＝．【答案】（m+n﹣3）2【解答】解：原式＝（m+n）2﹣2•（m+n）•3+32＝（m+n﹣3）2．故答案为：（m+n﹣3）2．49．（2022•绵阳）因式分解：3x3﹣12xy2＝．【答案】3x（x+2y）（x﹣2y）【解答】解：原式＝3x（x2﹣4y2）＝3x（x+2y）（x﹣2y）．故答案为：3x（x+2y）（x﹣2y）．50．（2022•丹东）因式分解：2a2+4a+2＝．【答案】2（a+1）2【解答】解：原式＝2（a2+2a+1）＝2（a+1）2．故答案为：2（a+1）2．51．（2022•巴中）因式分解：﹣a3+2a2﹣a＝．【答案】﹣a（a﹣1）2【解答】解：原式＝﹣a（a2﹣2a+1）＝﹣a（a﹣1）2．故答案为：﹣a（a﹣1）2．【命题点4 规律套索题】类型一数式规律52．（2022•西藏）按一定规律排列的一组数据：，﹣，，﹣，，﹣，…．则按此规律排列的第10个数是（）A．﹣B．C．﹣D．【答案】A【解答】解：原数据可转化为：，﹣，，﹣，，﹣，…，∴＝（﹣1）1+1×，﹣＝（﹣1）2+1×，＝（﹣1）3+1×，..．∴第n个数为：（﹣1）n+1，∴第10个数为：（﹣1）10+1×＝﹣．故选：A．53．（2022•新疆）将全体正偶数排成一个三角形数阵：按照以上排列的规律，第10行第5个数是（）A．98 B．100 C．102 D．104【答案】B【解答】解：由三角形的数阵知，第n行有n个偶数，则得出前9行有1+2+3+4+5+6+7+8+9＝45个偶数，∴第9行最后一个数为90，∴第10行第5个数是90+2×5＝100，故选：B．54．（2022•云南）按一定规律排列的单项式：x，3x2，5x3，7x4，9x5，……，第n个单项式是（）A．（2n﹣1）x n B．（2n+1）x n C．（n﹣1）x n D．（n+1）x n【答案】A【解答】解：∵单项式：x，3x2，5x3，7x4，9x5，…，∴第n个单项式为（2n﹣1）x n，故选：A．55．（2022•徐汇区校级自主招生）设x1，x2，x3，…，x100是整数，且满足下列条件：①﹣1≤x i≤2，i＝1，2，3， (100)②x1+x2+x3+…+x100＝20；③x12+x22+x32+…+x1002＝100，则x13+x23+x33+…+x1003的最小值和最大值的和为．【答案】160【解答】解：由题意可设x1，x2，x3，…，x100中有a个﹣1，b个0，c个1，d个2，则a+b+c+d＝100，﹣a+c+2d＝20，a+c+4d＝100，可得a＝40﹣d，b＝3d，c＝60﹣3d，∴x13+x23+x33+…+x1003＝﹣a+c+8d＝20+6d，由，解得：0≤d≤20，∴当d＝0时，x13+x23+x33+…+x1003的最小值为20，当d＝20时，x13+x23+x33+…+x1003的最大值为140．∴x13+x23+x33+…+x1003的最小值和最大值的和为160．故答案为：160．56．（2022•恩施州）观察下列一组数：2，，，…，它们按一定规律排列，第n个数记为a n，且满足+＝．则a4＝，a2022＝．【答案】【解答】解：由题意可得：a1＝2＝，a2＝＝，a3＝，∵+＝，∴2+＝7，∴a4＝＝，∵＝，∴a5＝，同理可求a6＝＝，•∴a n＝，∴a2022＝，故答案为：，．57．（2022•泰安）将从1开始的连续自然数按以下规律排列：若有序数对（n，m）表示第n行，从左到右第m个数，如（3，2）表示6，则表示99的有序数对是．【答案】（10，18）【解答】解：∵第n行的最后一个数是n2，第n行有（2n﹣1）个数，∴99＝102﹣1在第10行倒数第二个，第10行有：2×10﹣1＝19个数，∴99的有序数对是（10，18）．故答案为：（10，18）．类型二图形规律58．（2022•济宁）如图，用相同的圆点按照一定的规律拼出图形．第一幅图4个圆点，第二幅图7个圆点，第三幅图10个圆点，第四幅图13个圆点……按照此规律，第一百幅图中圆点的个数是（）A．297 B．301 C．303 D．400【答案】B【解答】解：观察图形可知：摆第1个图案需要4个圆点，即4+3×0；摆第2个图案需要7个圆点，即4+3＝4+3×1；摆第3个图案需要10个圆点，即4+3+3＝4+3×2；摆第4个图案需要13个圆点，即4+3+3+3＝4+3×3；…第n个图摆放圆点的个数为：4+3（n﹣1）＝3n+1，∴第100个图放圆点的个数为：3×100+1＝301．故选：B59．（2022•广州）如图，用若干根相同的小木棒拼成图形，拼第1个图形需要6根小木棒，拼第2个图形需要14根小木棒，拼第3个图形需要22根小木棒……若按照这样的方法拼成的第n个图形需要2022根小木棒，则n的值为（）A．252 B．253 C．336 D．337【答案】B【解答】解：由题意知，第1个图形需要6根小木棒，第2个图形需要6×2+2＝14根小木棒，第3个图形需要6×3+2×2＝22根小木棒，按此规律，第n个图形需要6n+2（n﹣1）＝（8n﹣2）根小木棒，当8n﹣2＝2022时，解得n＝253，故选：B．60．（2022•江西）将字母“C”，“H”按照如图所示的规律摆放，依次下去，则第4个图形中字母“H”的个数是（）A．9 B．10 C．11 D．12【答案】B【解答】解：第1个图中H的个数为4，第2个图中H的个数为4+2，第3个图中H的个数为4+2×2，第4个图中H的个数为4+2×3＝10，故选：B．61．（2022•重庆）用正方形按如图所示的规律拼图案，其中第①个图案中有5个正方形，第②个图案中有9个正方形，第③个图案中有13个正方形，第④个图案中有17个正方形，此规律排列下去，则第⑨个图案中正方形的个数为（）A．32 B．34 C．37 D．41【答案】C【解答】解：由题知，第①个图案中有5个正方形，第②个图案中有9个正方形，第③个图案中有13个正方形，第④个图案中有17个正方形，…，第n个图案中有4n+1个正方形，∴第⑨个图案中正方形的个数为4×9+1＝37，故选：C．62.（2022•黑龙江）如图所示，以O为端点画六条射线OA，OB，OC，OD，OE，OF，再从射线OA上某点开始按逆时针方向依次在射线上描点并连线，若将各条射线所描的点依次记为1，2，3，4，5，6，7，8…后，那么所描的第2013个点在射线上．【答案】OC【解答】解：∵1在射线OA上，2在射线OB上，3在射线OC上，4在射线OD上，5在射线OE上，6在射线OF上，7在射线OA上，…每六个一循环，2013÷6＝335…3，∴所描的第2013个点在射线和3所在射线一样，∴所描的第2013个点在射线OC上．故答案为：OC．。

2023年江苏中考数学一轮复习专题训练第2讲整式与因式分解

第2讲整式与因式分解 2023年中考数学一轮复习专题训练（江苏专用）一、单选题1．（2022·徐州）下列计算正确的是（）A．a2⋅a6=a8B．a8÷a4=a2C．2a2+3a2=6a4D．(−3a)2=−9a22．（2022·镇江）下列运算中，结果正确的是（）A．3a2+2a2=5a4B．a3−2a3=a3C．a2⋅a3=a5D．(a2)3=a5 3．（2022·南通）已知实数m，n满足m2+n2=2+mn，则(2m−3n)2+(m+2n)(m−2n)的最大值为（）A．24B．443C．163D．-4 4．（2022·南通模拟）如果多项式x2+2x+k是完全平方式，则常数k的值为（）A．1B．-1C．4D．-45．（2022·海陵模拟）已知3x﹣y＝3a2﹣6a+9，x+y＝a2+6a﹣10，当实数a变化时，x与y的大小关系是（）A．x＞y B．x＝yC．x＜y D．x＞y、x＝y、x＜y都有可能6．（2022·沭阳模拟）下列计算正确的是（）A．−3a+4a=a2B．a2⋅a3=a6C．a3+a6=a3D．(a3)2=a6 7．（2022·建湖模拟）2、6、m是某三角形三边的长，则√(m−4)2−√(m−8)2等于（）.A．2m−12B．12−2m C．12D．−4 8．（2022·南通模拟）计算(√2+√3)2021(√2−√3)2020的结果是（）A．√2+√3B．−√2−√3C．−√2+√3D．√2−√3 9．（2021·丰县模拟）下列运算正确的是（）A．3x3−x3=3B．a4÷a4=1(a≠0)C．(−2m)2=−4m2n4D．a2b3÷(−ab2)=ab10．（2021·阜宁模拟）分解因式4x2﹣y2的结果是（）A．（4x+y）（4x﹣y）B．4（x+y）（x﹣y）C．（2x+y）（2x﹣y）D．2（x+y）（x﹣y）二、填空题11．（2022·南通模拟）单项式−5πa3b4的次数是．12．（2022·常州）计算：m4÷m2=.13．（2022·苏州）已知x+y=4，x−y=6，则x2−y2=.14．（2022·苏州）定义：一个三角形的一边长是另一边长的2倍，这样的三角形叫做“倍长三角形”.若等腰△ABC是“倍长三角形”，底边BC的长为3，则腰AB的长为.15．（2022·扬州）掌握地震知识，提升防震意识.根据里氏震级的定义，地震所释放出的能量E与震级n 的关系为E=k×101.5n（其中k为大于0的常数），那么震级为8级的地震所释放的能量是震级为6级的地震所释放能量的倍.16．（2022·沭阳模拟）已知：a m=10，a n=2，则a m+n=.17．（2022·泗洪模拟）已知x＝﹣2时，二次三项式x2﹣2mx+4的值等于﹣4，当x＝时，这个二次三项式的值等于﹣1.18．（2022·锡山模拟）如果代数式x2+3x+1的值是5，那么代数式3﹣2x2﹣6x的值等于19．（2022·江苏模拟）若x+y=5，2x－3y=10，则x－4y的值为.20．（2021·常州模拟）观察下列等式：2+22=23﹣2；2+22+23=24﹣2；2+22+23+24=25﹣2；2+22+23+24+25=26﹣2；…已知按一定规律排列的一组数：220，221，222，223，224，…，238，239，240，若220=m，则220+221+222+223+224+…+238+239+240=(结果用含m的代数式表示).21．（2021·丰县模拟）把多项式9x2y−y3分解因式的结果是. 22．（2022·徐州模拟）分解因式：3a2+12a+12=．23．（2021·南通模拟）将3x2y−27y因式分解为.24．（2021·连云港）分解因式：9x2+6x+1=.三、解答题25．（2022·盐城）先化简，再求值：(x+4)(x−4)+(x−3)2，其中x2−3x+1=0．26．（2022·苏州）已知3x2−2x−3=0，求(x−1)2+x(x+23)的值.27．（2021·大丰模拟）先化简，再求值：(x+1)(x-1)+x(3-x)，其中x=2．28．（2021·射阳模拟）已知a=12014x+2013，b=12014x+2014，c=12014x+2015，求代数式2(a2+b2+c2−ab−bc−ac)的值.答案解析部分1．【答案】A【解析】【解答】解：A、a2⋅a6=a8，故该选项正确，符合题意；B、a8÷a4=a4，故该选项不正确，不符合题意；C、2a2+3a2=5a2，故该选项不正确，不符合题意；D、(−3a)2=9a2，故该选项不正确，不符合题意.故答案为：A.【分析】同底数幂相乘，底数不变，指数相加，据此判断A；同底数幂相除，底数不变，指数相减，据此判断B；合并同类项法则：同类项的系数相加减，所得的结果作为系数，字母和字母的指数不变，据此判断C；积的乘方，先对每一个因式进行乘方，然后将所得的幂相乘，据此判断D. 2．【答案】C【解析】【解答】解：A、3a2+2a2=5a2，故A计算错误，不符合题意；B、a3−2a3=−a3，故B计算错误，不符合题意；C、a2⋅a3=a5，故C计算正确，符合题意；D、(a2)3=a6，故D计算错误，不符合题意．故答案为：C.【分析】合并同类项法则：同类项的系数相加减，所得的结果作为系数，字母和字母的指数不变，据此判断A、B；同底数幂相乘，底数不变，指数相加，据此判断C；幂的乘方，底数不变，指数相乘，据此判断D.3．【答案】B【解析】【解答】解：∵m2＋n2＝2＋mn，∴（2m−3n）2＋（m＋2n）（m−2n）＝4m2＋9n2−12mn＋m2−4n2＝5m2＋5n2−12mn＝5（mn＋2）−12mn＝10−7mn，∵m2＋n2＝2＋mn，∴（m＋n）2＝2＋3mn≥0（当m＋n＝0时，取等号），∴mn≥−2 3，∴（m−n）2＝2−mn≥0（当m−n＝0时，取等号），∴mn≤2，∴−23≤mn≤2，∴−14≤−7mn ≤143， ∴−4≤10−7mn ≤443，即（2m−3n ）2＋（m ＋2n ）（m−2n ）的最大值为443，故答案为：B.【分析】将代数式利用平方差公式和完全平方公式先去括号，再合并同类项，结合已知可转化为10−7mn ；将m 2＋n 2＝2＋mn 进行配方，可得到关于mn 的不等式，求出mn 的取值范围为−23≤mn ≤2，利用不等式的性质可得到10−7mn 的取值范围，即可求出已知代数式的最大值.4．【答案】A【解析】【解答】解： ∵2x =2×1⋅x ，∴k =12=1 ，故答案为：A ．【分析】根据完全平方式的特点可得2=2√k ，求解可得k 的值.5．【答案】A【解析】【解答】解：∵3x ﹣y ＝3a 2﹣6a+9，x+y ＝a 2+6a ﹣10，∴3x −y −(x +y)=(3a 2−6a +9)−(a 2+6a −10)，∴2x −2y =2a 2−12a +19=2(a 2−6a +9)+1=2(a −3)2+1， ∵不论a 为何值，2(a −3)2+1≥1， ∴2x −2y ＞0， ∴2x ＞2y ， ∴x ＞y ．故答案为：A ．【分析】先求出2x −2y =2a 2−12a +19=2(a 2−6a +9)+1=2(a −3)2+1，再求出2x −2y ＞0，最后求解即可。

专题2代数式与整式含答案解析2023年湖南省中考数学一轮复习专题训练

专题2 代数式与整式一、单选题1．下列运算正确的是（）A．3a﹣2a＝a B．（a3）2＝a5C．2√5﹣√5＝2D．（a﹣1）2＝a2﹣12．下列整式与ab2为同类项的是（）A．a2b B．﹣2ab2C．ab D．ab2c3．下列运算正确的是（）A．a2+a3=a5B．a3⋅a4=a12C．(a3)4=a7D．a3÷a2=a 4．（2022·长沙）下列计算正确的是（）A．a7÷a5=a2B．5a−4a=1C．3a2⋅2a3=6a6D．(a−b)2=a2−b25．（2022·永州）下列各式正确的是（）.A．√4=2√2B．20=0C．3a−2a=1D．2−(−2)=4 6．（2022·娄底）下列式子正确的是（）A．a3⋅a2=a5B．(a2)3=a5C．(ab)2=ab2D．a3+a2=a5 7．（2022·长沙）为落实“双减”政策，某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲，乙两种读本共100本供学生阅读，其中甲种读本的单价为10元/本，乙种读本的单价为8元/本，设购买甲种读本x本，则购买乙种读本的费用为（）A．8x元B．10(100−x)元C．8(100−x)元D．(100−8x)元8．（2022·娄底）若10x=N，则称x是以10为底N的对数.记作：x=lgN.例如：102=100，则2=lg100；100=1，则0=lg1.对数运算满足：当M>0，N>0时，lgM+lgN=lg(MN)，例如：lg3+lg5=lg15，则(lg5)2+lg5×lg2+lg2的值为（）A．5B．2C．1D．09．（2022·怀化）下列计算正确的是（）A．（2a2）3＝6a6B．a8÷a2＝a4C．√(−2)2＝2D．（x﹣y）2＝x2﹣y210．（2022·常德）计算x4⋅4x3的结果是（）A．x B．4x C．4x7D．x11二、填空题11．（2022·邵阳）已知x2−3x+1=0，则3x2−9x+5=.12．（2022·长沙）当今大数据时代，“二维码”具有存储量大.保密性强、追踪性高等特点，它己被广泛应用于我们的日常生活中，尤其在全球“新冠”疫情防控期间，区区“二维码”已经展现出无穷威力.看似“码码相同”，实则“码码不同”.通常，一个“二维码”由1000个大大小小的黑白小方格组成，其中小方格专门用做纠错码和其他用途的编码，这相当于1000个方格只有200个方格作为数据码.根据相关数学知识，这200个方格可以生成2200个不同的数据二维码，现有四名网友对2200的理解如下：YYDS（永远的神）：2200就是200个2相乘，它是一个非常非常大的数；DDDD（懂的都懂）：2200等于2002；JXND（觉醒年代）：2200的个位数字是6；QGYW（强国有我）：我知道210=1024，103=1000，所以我估计2200比1060大.其中对2200的理解错误的网友是（填写网名字母代号）.13．（2022·怀化）正偶数2，4，6，8，10，…，按如下规律排列，则第27行的第21个数是.14．（2022·永州）若单项式3x m y的与−2x6y是同类项，则m=.15．（2021·株洲）计算：2a2⋅a3=.16．（2021·岳阳）已知x+1x=√2，则代数式x+1x−√2=.17．（2021·怀化）观察等式：2+22=23−2，2+22+23=24−2，2+22+23+24=25−2，……，已知按一定规律排列的一组数：2100，2101，2102，……，2199，若2100=m，用含m的代数式表示这组数的和是.18．（2021·岳阳模拟）若7a x b2与−3a3b y的和为单项式，则x y=.19．（2021·娄底模拟）观察下列图形：它们是按一定规律排列的，依照此规律，用6064个五角星摆出的图案应该是第个图形. 20．（2021·新化模拟）已知a²+2a−5=0，则代数式2a2+4a−1的值是.三、计算题21．（2021·衡阳）计算：(x+2y)2+(x−2y)(x+2y)+x(x−4y).22．（2021·长沙）先化简，再求值：(x−3)2+(x+3)(x−3)+2x(2−x)，其中x=−12. 23．（2021·新化模拟）先化简，再求值：(a+b)(a−b)+(a−b)2−(2a2−ab)，其中a，b是一元二次方程x2+x−2=0的两个实数根. 24．（2021·永州）先化简，再求值：（x+1）2+（2+x）（2﹣x），其中x＝1.25．（2021·永州模拟）先化简，再求值：（a＋b）（a－b）＋（a＋b）2，其中a＝－1，b＝12答案解析部分1．【答案】A【解析】【解答】解：A、3a﹣2a＝a，故A符合题意；B、（a3）2＝a6，故B不符合题意；C、2√5﹣√5＝√5，故C不符合题意；D、（a﹣1）2＝a2-2a+1，故D不符合题意；故答案为：A.【分析】利用合并同类项是把同类项的系数相加，字母和字母的指数不变，可对A作出判断；利用幂的乘方，底数不变，指数相乘，可对B作出判断；再利用合并同类二次根式的法则，可对C作出判断；然后根据（a-b）2=a2-2ab+b2，可对D作出判断.2．【答案】B【解析】【解答】解：∵ab2和﹣2ab2所含的字母相同，相同的字母系数也相同，∴ab2和﹣2ab2是同类项.故答案为：B.【分析】所谓同类项就是所含字母相同，而且相同字母的指数也分别相同的单项式，根据定义分别判断即可.3．【答案】D【解析】【解答】解：A、a2+a3不能合并，故A不符合题意；B、a3·a4=a7，故B不符合题意；C、（a3）4=a12，故C不符合题意；D、a3÷a2=a，故D符合题意；故答案为：D.【分析】只有同类项才能合并，可对A作出判断；利用同底数幂相乘，底数不变，指数相加，可对B 作出判断；利用幂的乘方，底数不变，指数相乘，可对C作出判断；利用同底数幂相除，底数不变，指数相减，可对D作出判断.4．【答案】A【解析】【解答】解：A、a7÷a5=a2，故该选项正确，符合题意；B、5a−4a=a，故该选项不正确，不符合题意；C、3a2⋅2a3=6a5，故该选项不正确，不符合题意；D、(a−b)2=a2−2ab+b2，故该选项不正确，不符合题意.故答案为：A.【分析】同底数幂相除，底数不变，指数相减，据此判断A；合并同类项法则：同类项的系数相加减，所得的结果作为系数，字母和字母的指数不变，据此判断B；根据单项式与单项式的乘法法则“把系数与同底数幂分别相乘，对于只在某一个单项式中含有的字母，则连同指数作为积的一个因式”可判断C；根据完全平方公式的展开式是一个三项式可判断D.5．【答案】D【解析】【解答】解：A、√4=2，故A不符合题意；B、20=1，故B不符合题意；C、3a-2a=a，故C不符合题意；D、2-（-2）=2+2=4，故D符合题意；故答案为：D.【分析】利用正数的算术平方根只有一个，可对A作出判断；利用任何不等于0的数的0次幂为1，可对B作出判断；合并同类项是把同类项的系数相加，字母和字母的指数不变，可对C作出判断；利用减去一个数等于加上这个数的相反数，可对D作出判断.6．【答案】A【解析】【解答】解：a3⋅a2=a5，故A选项符合题意；(a2)3=a6，故B不符合题意；(ab)2=a2b2，故C不符合题意；a3，a2不是同类项，不能合并，故D不符合题意.故答案为：A.【分析】同底数幂相乘，底数不变，指数相加，据此判断A；幂的乘方，底数不变，指数相乘，据此判断B；积的乘方，先将每一个因式进行乘方，然后将所得的幂相乘，据此判断C；整式加法的实质就是合并同类项，所谓同类项就是所含字母相同，而且相同字母的指数也分别相同的项，同类项与字母的顺序及系数没有关系，合并同类项的时候，只需要将系数相加减，字母和字母的指数都不变，但不是同类项的不能合并，据此可判断D.7．【答案】C【解析】【解答】解：设购买甲种读本x本，则购买乙种读本（100-x）本，乙种读本的单价为8元/本，则购买乙种读本的费用为8（100-x）元故答案为：C.【分析】设购买甲种读本x本，则购买乙种读本(100-x)本，根据乙种读本的单价×本数可得购买乙种读本的费用，据此解答.8．【答案】C【解析】【解答】解：∵lgM+lgN=lg(MN)，∴(lg5)2+lg5×lg2+lg2=lg5(lg5+lg2)+lg2=lg5·lg10+lg2=lg5+lg2=lg10=1.故答案为：C.【分析】原式可边形为lg5(lg5+lg2)+lg2，然后结合lgM+LGN=lg(MN)进行计算.9．【答案】C【解析】【解答】解：A、（2a2）3=8a6≠6a6，故此选项错误，不符合题意；B、a8÷a2=a6≠a4，故此选项错误，不符合题意；C、√(−2)2=2，故此选项正确，符合题意；D、（x﹣y）2=x2﹣2xy+y2≠x2﹣y2，故此选项错误，不符合题意.故答案为：C.【分析】积的乘方，先对每一个因式分别进行乘方，然后将所得的幂相乘；幂的乘方，底数不变，指数相乘，据此判断A；同底数幂相除，底数不变，指数相减，据此判断B；根据二次根式的性质“√a2=|a|”可判断C；根据完全平方公式的展开式是一个三项式，可判断D.10．【答案】C【解析】【解答】解：x4⋅4x3=4x4+3=4x7，故C正确.故答案为：C.【分析】单项式乘以单项式，积的系数等于原来两个单项式的系数的积，它的各个变数字母的幂指数，等于在原来两个单项式中相应的变数字母的幂指数的和，据此计算.11．【答案】2【解析】【解答】解：3x2−9x+5=3x2−9x+3+2=3(x2−3x+1)+2∵x2−3x+1=0∴3x2−9x+5=0+2=2故答案为：2.【分析】待求式可变形为3(x2-3x+1)+2，然后将已知条件代入进行计算.12．【答案】DDDD【解析】【解答】解：2200是200个2相乘，YYDS（永远的神）的理解是正确的；2200=(2100)2≠2002，DDDD（懂的都懂）的理解是错误的；∵21=2，22=4，23=8，24=16，25=32⋯，∴2的乘方的个位数字4个一循环，∵200÷4=50，∴2200的个位数字是6，JXND（觉醒年代）的理解是正确的；∵2200=(210)20，1060=(103)20，210=1024，103=1000，且210>103∴2200>1060，故QGYW（强国有我）的理解是正确的；故答案为：DDDD.【分析】根据乘方的意义可得DDDD的理解是错误的，观察发现：2的乘方的个位数字4个一循环，据此判断JXND；根据幂的乘方法则可得2200=(210)20，1060=(103)20，且210>103，据此判断QGYW. 13．【答案】744【解析】【解答】解：由题意知，第n行有n个数，第n行的最后一个偶数为n（n+1），∴第27行的最后一个数，即第27个数为27×28=756，∴第27行的第21个数与第27个数差6位数，即756−2×6=744，故答案为：744.【分析】由题意知，第n行有n个数，第n行的最后一个偶数为n(n+1)，求出第27行的最后一个数，据此解答.14．【答案】6【解析】【解答】解：∵单项式3x m y的与−2x6y是同类项∴m=6.故答案为：6.【分析】利用同类项中相同字母的指数相等，可求出m的值.15．【答案】2a5【解析】【解答】解：2a2⋅a3=2a2+3=2a5.故答案：2a5.【分析】根据单项式乘单项式法则"单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，其余字母连同它的指数不变，作为积的因式."可求解.16．【答案】0【解析】【解答】x+1x−√2=√2−√2=0故答案为：0.【分析】直接代入计算即可.17．【答案】(2100−1)m【解析】【解答】由题意规律可得：2+22+23+⋯+299=2100−2.∵2100=m∴2+22+23+⋯+299+2=2100=m=20m，∵2+22+22+⋯+299+2100=2101−2，∴2101=2+22+23+⋯+299+2100+2=m+m=2m=21m.2102=2+22+23+⋯+299+2100+2101+2=m+m+2m=4m=22m.2103=2+22+23+⋯+299+2100+2101+2102+2=m+m+2m+4m=8m=23m.……∴2199=299m.故2100+2101+2101+⋯+2199=20m+21m+⋯+299m.令20+21+22+⋯+299=S①21+22+23+⋯+2100=2S②②-①，得2100−1=S∴2100+2101+2101+⋯+2199=20m+21m+⋯+299m= (2100−1)m故答案为：(2100−1)m.【分析】利用已知等式可得到数字的变化规律，再根据2100=m，由此可求出这组数据的和. 18．【答案】9【解析】【解答】解：∵7a x b2与−3a3b y的和为单项式，∴7a x b2与−3a3b y是同类项，∴x=3，y=2，∴x y=32=9，故答案为：9.【分析】根据题意7a x b2与−3a3b y是同类项，所谓同类项就是所含字母相同，而且相同字母的指数也分别相同，由此求出x、y的值，进而可求得x y的值.19．【答案】2021【解析】【解答】解：观察发现，第1个图形五角星的个数是：1+3＝4，第2个图形五角星的个数是：1+3×2＝7，第3个图形五角星的个数是：1+3×3＝10，第4个图形五角星的个数是：1+3×4＝13，⋯第n个图形五角星的个数是：1+3•n＝1+3n，∵6064−13=2021，∴用6064个五角星摆出的图案应该是第2021个图形，故答案为：2021.【分析】把每个图案分成两部分，最下面位置处的一个不变，其它的分三条线，每一条线上后一个图形比前一个图形多一个，据此规律找出第n个图形五角星的个数为：1+3n，据此求解即可.20．【答案】9【解析】【解答】解：∵a2+2a-5=0，∴a2+2a=5，∴a2+2a-1=2(a2+2a)-1=2×5-1=10-1=9.故答案为：9.【分析】将a2+2a-5=0变形为a2+2a=5，然后将代数式含字母的部分提取公因式2后整体代入所求的代数式进行化简求值.21．【答案】解：(x+2y)2+(x−2y)(x+2y)+x(x−4y)=x2+4xy+4y2+x2−4y2+x2−4xy=3x2【解析】【分析】利用完全平方公式、平方差公式、单项式乘以多项式将原式展开，然后去括号、合并即可.22．【答案】解：原式=x2−6x+9+x2−9+4x−2x2，=−2x，将x=−12代入得：原式=−2x=−2×(−12)=1【解析】【分析】根据平方差公式“（a+b）（a-b）=a2-b2”、完全平方公式“（a-b）2=a2-2ab+b2”和根据单项式与多项式的乘法法则“单项式与多项式相乘，就是依据分配律用单项式去乘多项式的每一项，再把所得的积相加”可去括号，再根据合并同类项法则“把同类项的系数相加，字母和字母的指数不变”可将多项式化简，然后把x的值代入化简后的代数式计算即可求解.23．【答案】解：原式= a2−b2+a2−2ab+b2−2a2+ab=﹣ab∵a，b是一元二次方程x2+x−2=0的两个实数根，∴ab=﹣2，则原式=﹣ab=2【解析】【分析】根据平方差公式、完全平方公式及去括号法则分别去括号，再合并同类项化为最简形式，进而根据根与系数的关系可得ab=﹣2，即可得出答案.24．【答案】解：（x+1）2+（2+x）（2﹣x）＝x2+2x+1+4﹣x2＝2x+5，当x＝1时，原式＝2+5＝7.【解析】【分析】根据完全平方公式、平方差公式以及合并同类项法则可将原式化简为2x+5，然后将x 的值代入计算.25．【答案】解：原式＝a2−b2+a2+2ab+b2＝2a2+2ab当a＝﹣1 ，b= 12时，原式＝2a2+2ab=2×(−1)2+2×(−1)×1 2=1【解析】【分析】利用平方差公式和完全平方公式先去括号，再合并同类项化为最简形式，然后将a，b 的值代入代数式进行计算。

备战九年级中考数学一轮复习第2课整式(含因式分解)(全国通用)

13.(202X·哈尔滨)把多项式m2n＋6mn＋9n分解因式的结果是_____n_(m__＋__3_)2_____.
14.(202X·重庆)已知a＋b＝4，则代数式1＋ a ＋b 的值 22
为( A )
A.3
B．1
C．0
D．－1
考点3 求代数式的值
15.【例3】(202X·广东)已知x＝5－y，xy＝2，计算代数式 3x＋3y－4xy＝____7____.
第2课整式(含因式分解)
1．(1)单项式：数与字母的积所表示的代数式叫做单项式，单独一个数或者一个字母也是单项式． (2)多项式：几个单项式的和叫做多项式． (3)整式：单项式与多项式统称为整式.
1．(1)单项式－3xy2的系数是__－__3____，次数是____3____； (2)多项式2x－5xy3－1是____4____次____三____项式，其中一次项为____2_x___，一次项系数为____2____．
23．(202X·天水)分解因式：m3n－mn＝ mn(m＋1)(m－1) .
24．(海南中考)某工厂去年的产值是a万元，今年比去年增加10%，今年的产值是__1_._1_a___万元．
25．(广东中考)下列计算正确的是( C )
A．b6＋b3＝b2
B．b3·b3＝b9
C．a2＋a2＝2a2
C．2kk
D．k2＋k
31.(202X·苏州)若单项式2xm－1y2与单项式1 x2yn＋1是同类项， 3
则m＋n＝___4_____.
32．(202X·枣庄)若a＋b＝3，a2＋b2＝7，则ab＝___1_____.
C组 33．(202X·聊城)因式分解：x(x－2)－x＋2＝ (x－1)(x－2) .

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

中考复习之整式知识考点：整式是初中代数的基础知识，也是学习分式、根式的基础；去添括号法则，合并同类项、乘法公式及幂的运算法则是本节的重点。

在运算中根据题目特征，灵活运用公式是本节知识的关键。

精典例题：【例1】填空：1、单项式z y x 32的系数是，次数是。

2、若1)1(3+--x m x n 为三次二项式，则2n m +-＝。

3、计算：a a a ⋅÷343)(＝；)4(2232y x y x -⋅＝；)3()3(2332y x y x ÷-＝；)1)(22(+-x x ＝。

4、已知3y xm与4x y n -是同类项，则m ＝，n ＝。

5、如果2=xa ，3=ya，则yx a32+＝。

6、当m ＝时，25)3(22+-+x m x 是完全平方式。

7、计算：()()()22423432c b b c c b --+-+-＝。

答案：1、1，6；2、8；3、10a ，358y x -，849y x -，22x ，－2；4、4±=m ，3=n ；5、108；6、8或－2；7、161611622++--bc c b 【例1】选择题：1、下列计算正确的是（）A 、()()9323323=--- B 、()222b a b a +=+C 、()3322)2(b a b ab a b a +=+-+ D 、()()54512-+=+-a a a a2、如果长方形的周长为m 4，一边长为n m -，则另一边长为（）A 、n m +3B 、n m 22+C 、n m +D 、n m 3+ 3、如果多项式n mnx mx +-2与m mnx nx ++2的和是单项式，下列m 与n 的正确关系为（）4、化简()()()()131********++++得（） A 、()2813+ B 、()2813- C 、1316- D 、()132116-分析：3题求得两个多项式的和为()n m x n m +++2，要使这个二次二项式为单项式，令0=+n m 即可；4题将式子前面变形为()1321221-=⨯，使()13-乘入后，能连锁反应地使用平方差公式，这种技巧比较有代表性。

答案：1、D ；2、C ；3、B ；4、D 【例3】列代数式填空：1、某校学生给“希望小学”邮寄每册a 元的图书240册，若每册图书的邮费为书价的5％，则共需邮费元。

2、托运行李p 公斤（p 为整数），的费用为C 元，现托运第一个1公斤需付2元，以后每增加1公斤（不足1公斤按1公斤计算）需增加5角，则托运行李的费用C ＝。

3、如图：在△ABC 中，∠A 、∠B 的对边分别为a 、b ，且∠C ＝900，分别以AC 、BC 为直径作半圆，则图中阴影部分的面积为。

例3第3题图bCBA问题一图1 问题一图2答案：1、240%5⋅⋅a ；2、)1(5.02-+p ；3、()ab ba21822-+π探索与创新：【问题一】某公司计划砌一个形状如图1所示的喷水池，经人建议改为如图2所示的形状，且外圆半径不变，只是担心原来准备好的材料不够。

请你比较两种方案，哪一种需要的材料多？分析：比较两种方案的材料，就是比较两个图形的周长。

解：设大圆直径为d ，周长为 l ，4个小圆直径分别为1d 、2d 、3d 、4d ，周长分别为1l 、2l 、3l 、4l ，则)(4321d d d d d l +++==ππ＝4321d d d d ππππ+++＝4321l l l l +++，所以大圆周长与4个小圆周长之和相等，即两种方案用料一样多。

个成品，且每个车间每天都生产b （b ＞0）个成品，质检科派出若干名质检员星期一、星期二检查其中两个车间原有和这两天生产的所有成品，然后星期三至星期五检查另两个车间原有的和本周生产的所有成品。

假定每个检验员每天检查的成品数相同。

（1）这若干名检验员1天检验多少个成品？（用含a 、b 的代数式表示）（2）试求用b 表示a 的关系式；（3）若1名质检员1天能检验b 54个成品，则质检科至少要派出多少名检验员？解：（1）这若干名检验员1天能检验()b a b a 2222+=+或()352b a +或23⨯b ＝()()b a b a 2252+-+。

（2）依题意得：()222b a +＝()352b a +，化简得：b a 4=另解：()222b a +＝23⨯b ，化简得：b a 4=（3）()b b a 54222÷+＝7.5（名）另解：()b b 5423÷⨯＝7.5（名）答：质检科至少要派出8名检验员。

跟踪训练：一、填空题：1、多项式5545y y x x n+-是五次三项式，则正整数n 可以取值为。

2、()()-=-=+-x x x 4223423、计算：a a a 43223÷⋅＝；()()()y x y x y x -+-+2＝；()2c b a -+＝；()()++=-22b a b a ＝++22b a ；4、如果m x x ++542是完全平方式，则m ＝。

5、若y xm2-与x ymn31是同类项，则n m +-2＝。

6、若()()622+-=--mx x n x x ，则m ＝，n ＝。

7、五个连续奇数中间一个是n ，则这五个连续奇数的和为。

8、某城市一年漏掉的水，相当于新建一个自来水厂，据不完全统计，全市至少有5106⨯个水龙头、5102⨯个抽水马桶漏水。

如果一个关不紧的水龙头一个月漏掉a 立方米水，一个抽水马桶一个月漏掉b 立方米水，那么一个月造成的水流失量至少是立方米。

二、选择题：1、如果n 32732=⨯，则n 的值为（）A 、6B 、1C 、5D 、8 2、下列计算正确的是（）A 、422642a a a =+ B 、()53282a a =C 、()53222a a a -=-⋅D 、33236a aamm=÷3、已知532++x x 的值为3，则代数式1932-+x x 的值为（）A 、0B 、－7C 、－9D 、34、受季节影响，某种商品每年按原售价降低10％后，又降价a 元，现在每件售价b 元，那么该商品每件的原售价为（） A 、%101-+b a B 、()()b a +-%101C 、%101--a b D 、()()b a --%1015、如图：正六边形ABCDEF 的边长为a ，分别以C 、F 为圆心，a 为半径画弧，则图中阴影部分的面积是（）A 、261a π B 、231a π C 、232a π D 、234a π三、计算题：1、()()()()223232422ab ab b a -÷÷-⋅-第5题图CB2、()()()()()232211221------+-a a a a a3、()()()()2164242+++-a a a a4、()()53253222-++-a a a a四、解答题： 1、已知231+=-y x ，231-=-y z ，求xz yz xy z y x ---++222的值。

2、（1）观察下列各式：121= 422=823= 1624= 3225=6426=12827=25628=……通过观察，用你发现的规律写出98的末位数字是。

（2）观察下列各式：()()1112-=+-x x x()()11132-=++-x x x x()()111423-=+++-x x x x x()()1115234-=++++-x x x x x x ……由规律可得()()111++⋅⋅⋅++--x xx x n n＝。

3、当5-=x 时，6199920012003+--cxbxax 的值为－2，求当5=x 时，这个代数式的值。

4、本市出租车的收费标准为：3千米以内（含3千米）收费5元，超过3千米的部分每千米收费1.20元（不足1千米按1千米计算），另加收0.60元的返空费。

（1）设行驶路程为x千米（x≥3且取整数），用x表示出应收费y元的代数式；（2）当收费为10.40元时，该车行驶路程不超过多少千米？路程数在哪个范围内？参考答案一、填空题：1、1，2，3，4；2、234x x +-，232-x ；3、423a ，222y xy +，ac bc abc b a 222222--+++，ab 4-，ab 2-4、1625；5、1；6、5=m ，3=n ；7、n 5；8、b a 55102106⨯+⨯二、选择题：CCBAC 三、计算题：1、ab 41-；2、12132-+a a ；3、2568-a ；4、25309424-+-a a a四、解答题：1、2.5；2、8，11-+n x；3、14；4、（1）()()36.02.15-++=x y （x ≥3），（2）x ＝6，5＜x ≤6。