暂态第四章
合集下载
第四章电路的暂态响应
uL(0+) i1(0+)
i2(0+)
Us
12V
R1 4Ω
R2 6Ω
i1(0 )R1 Us uL (0 ) 0
uL (0 ) 4.8V
2）求S闭合后的各稳态值
S闭合达到稳态时，电感相当 于短路，其等效电路图如图所 示
uL() 0V
i1()
US R1
3A
i2 ()
US R2
2A
iL() i1() i2() 5A
R2 6Ω
iL
i1
Us
12V
R1 4Ω
1）求S闭合后的各初始值 由换路定律可得： il (0 ) il (0 ) 3A
L iL
S
uL
i1
i2
Us
12V
R1 4Ω
R2 6Ω
等效一个电流源，等效电路图如下图
i1(0 )
R2 R1 R2
iL (0 )
6 4
6
3
1.8A
iL(0+)
i2 (0 ) 1.2A 由KVL，可知
+ uL – R
iC
+ R IS –
0+电路
uL(0+)= - RIS
iC ( 0
)
Is
RI S R
0
例4
S闭合前电路已处于稳态，试确定S
闭合后电压uL和电流iL、 i1 、 i2的初始值和稳态值。
【解】开关S闭合之前
il
(0
)
US R1
12V 4
3A
L iL
S
uL
i1
i2
Us
12V
R1 4Ω
第4章 电路的暂态分析-习题解答
4.7 在题 4.7 图所示电路中，开关 S 闭合前电路已处于稳态，试确定 S 闭合后电
4
压 uL 和电流 iL、i1、i2 的初始值和稳态值。 【解】由于 i L (0 ) i L (0 )
uS 6 3A ，则 R1 2
i1 (0 )
R2 4 iL (0 ) 3 2A 24 R1 R2
6
【解】该电容电压的初始值为 20000V，放电的起始瞬间的冲击电流达到最 大值，冲击电流的峰值大小为 流。 这种情况下不会造成触电事故是由于放电时间极短，等效电路的时间常数为
20000 V 200 A ，远远超过了人体允许的致命电 100
RC 100 50 1012 5 109 s 5ns
u c (0 ) u c (0 ) R1i1 (0 ) 6V i1 (0 )
u c (0 ) 1A R1
i2 (0 ) 0 ic (0 ) I S i1 (0 ) 3 1 2A
1
②
） 。
① 立即亮 ③ 由亮逐渐变为不亮
② 逐渐变亮 ④ 由不亮逐渐变亮，再逐渐变为不亮 ① )。
（7）R、C 电路在零状态条件下，时间常数的意义是( ① 响应由零值增长到稳态值的 0.632 倍时所需时间 ② 响应由零值增长到稳态值的 0.368 倍时所需时间 ③ 过渡过程所需的时间 ④ 响应由稳态值下降到零值的 0.632 倍时所需时间 （8）一阶线性电路时间常数的数值取决于( ① 电路的结构形式 ③ )。
因此该电容的初始电压将在 5 25ns 时间内释放完毕，虽然冲击电流很大，但 是作用时间极短，对人体而言最多感觉到颤抖，不会造成致命伤害。
第4章 电路的暂态分析
换路定则公式 电感电路： L (0 ) L (0) 电容电路： uC (0 ) uC (0)
注：换路定则仅用于换路瞬间来确定暂态过程中 uC、 iL初始值。
4.1.2 换路定则
2. 初始值的确定
暂态过程期间，电路中电压、电流的变化开 始于换路后瞬间的初始值，即t=0+时刻的值，终 止于达到新稳态时的稳定值。因此分析电压、电 流的初始值是必要的。确定电路中电压、电流的 初始值，换路定则是重要依据。电路中各处的电 压和电流的初始值记为 f (0+)。
4.1 暂态过程与换路定则
电路的暂态过程一般比较短暂，但它的作用和影响却十分 重要。
一方面，我们要充分利用电路的暂态过程来实现振荡信号 的产生、信号波形的改善和变换、电子继电器的延时动作等；
另一方面，又要防止电路在暂态过程中可能产生的比稳态 时大得多的电压或电流(即所谓的过电压或过电流)现象。
过电压可能会击穿电气设备的绝缘，从而影响到设备的安 全运行；过电流可能会产生过大的机械力或引起电气设备和器 件的局部过热，从而使其遭受机械损坏或热损坏，甚至产生人 身安全事故。
开关S断开，试求换路后电路中各电量的初始值 。
(b) t= 0-时的等效电路 (a)
解：因为t=0-时电路已处于稳态，则电感元 件已储满能量，即uL(0-)= 0 V，电容元件被 开关S短接而未储能，即uC(0-)= 0 V。作出t= 0-时的等效电路如图 (b)所示。
例： 电路如图(a)所示，换路前电路已处于稳态。在t=0时
4.1 暂态过程与换路定则
前面各章讨论的线性电路中，当电源电压（激 励）为恒定值或作周期性变化时，电路中各部分电 压或电流（响应）也是恒定或按周期性规律变化， 即电路中响应与激励的变化规律完全相同，称电路 所处的这种工作状态为稳定状态，简称稳态。
注：换路定则仅用于换路瞬间来确定暂态过程中 uC、 iL初始值。
4.1.2 换路定则
2. 初始值的确定
暂态过程期间，电路中电压、电流的变化开 始于换路后瞬间的初始值，即t=0+时刻的值，终 止于达到新稳态时的稳定值。因此分析电压、电 流的初始值是必要的。确定电路中电压、电流的 初始值，换路定则是重要依据。电路中各处的电 压和电流的初始值记为 f (0+)。
4.1 暂态过程与换路定则
电路的暂态过程一般比较短暂，但它的作用和影响却十分 重要。
一方面，我们要充分利用电路的暂态过程来实现振荡信号 的产生、信号波形的改善和变换、电子继电器的延时动作等；
另一方面，又要防止电路在暂态过程中可能产生的比稳态 时大得多的电压或电流(即所谓的过电压或过电流)现象。
过电压可能会击穿电气设备的绝缘，从而影响到设备的安 全运行；过电流可能会产生过大的机械力或引起电气设备和器 件的局部过热，从而使其遭受机械损坏或热损坏，甚至产生人 身安全事故。
开关S断开，试求换路后电路中各电量的初始值 。
(b) t= 0-时的等效电路 (a)
解：因为t=0-时电路已处于稳态，则电感元 件已储满能量，即uL(0-)= 0 V，电容元件被 开关S短接而未储能，即uC(0-)= 0 V。作出t= 0-时的等效电路如图 (b)所示。
例： 电路如图(a)所示，换路前电路已处于稳态。在t=0时
4.1 暂态过程与换路定则
前面各章讨论的线性电路中，当电源电压（激 励）为恒定值或作周期性变化时，电路中各部分电 压或电流（响应）也是恒定或按周期性规律变化， 即电路中响应与激励的变化规律完全相同，称电路 所处的这种工作状态为稳定状态，简称稳态。
电工学-第四章 电路的暂态分析
2 u c (0 ) 10 4V 3 2 10 i L (0 ) 2A 3 2
（2）由换路定理得： uc (0 ) uc (0 ) 4V
iL (0 ) iL (0 ) 2 A
因此，在t=0+ 瞬间，电容元件相当于一个4V 的电压源，电感元件相当于一个2A的电流源。据 此画出t=0+ 时刻的等效电路，如图3-3 (C) 所示。
可见τ等于电压uc衰减到初始值36.8%的时间 从理论上讲,电路只有经过t=∞的时间,才能达到稳定; 实际上经过5 τ就认为达到稳定. 另外,RL电路的时间常数 L / R
画出uc及i的波形如图所示。
RC 电路零输入响应 电压电流波形图
在激励作用之前，电路的初始储能为零仅由激励引起 的响应叫零状态响应。
（3）在t=0+ 电路中，应用直流电阻电路的分析方 法，可求出电路中其他电流、电压的初始值，即
4 i1 (0 ) 2 A 2 4 i 2 (0 ) 1 A 4
iC(0+)=2-2-1=-1A uL(0+)=10-3×2-4=0
例2: 电路如图3-4 (a)所示，开关S闭合前电路无储能，开 关S在 t=0时闭合，试求 i1 、i2 、i3、 uc、uL的初始值。
uC uC ()(1 e
t RC
)
t≥0
2式
由2式可知，当t=0时，uc(0)=0，当 t=τ时， uc(τ) =US（1-e–1）=63.2%US，即在零状态响应中，电容电压 上升到稳态值uc=(∞)=US的63.2%所需的时间是τ。而当t=4~5τ 时，u c上升到其稳态值US的98.17%~99.3%，一般认为充电过 程即告结束。电路中其他响应分别为
（2）由换路定理得： uc (0 ) uc (0 ) 4V
iL (0 ) iL (0 ) 2 A
因此，在t=0+ 瞬间，电容元件相当于一个4V 的电压源，电感元件相当于一个2A的电流源。据 此画出t=0+ 时刻的等效电路，如图3-3 (C) 所示。
可见τ等于电压uc衰减到初始值36.8%的时间 从理论上讲,电路只有经过t=∞的时间,才能达到稳定; 实际上经过5 τ就认为达到稳定. 另外,RL电路的时间常数 L / R
画出uc及i的波形如图所示。
RC 电路零输入响应 电压电流波形图
在激励作用之前，电路的初始储能为零仅由激励引起 的响应叫零状态响应。
（3）在t=0+ 电路中，应用直流电阻电路的分析方 法，可求出电路中其他电流、电压的初始值，即
4 i1 (0 ) 2 A 2 4 i 2 (0 ) 1 A 4
iC(0+)=2-2-1=-1A uL(0+)=10-3×2-4=0
例2: 电路如图3-4 (a)所示，开关S闭合前电路无储能，开 关S在 t=0时闭合，试求 i1 、i2 、i3、 uc、uL的初始值。
uC uC ()(1 e
t RC
)
t≥0
2式
由2式可知，当t=0时，uc(0)=0，当 t=τ时， uc(τ) =US（1-e–1）=63.2%US，即在零状态响应中，电容电压 上升到稳态值uc=(∞)=US的63.2%所需的时间是τ。而当t=4~5τ 时，u c上升到其稳态值US的98.17%~99.3%，一般认为充电过 程即告结束。电路中其他响应分别为
第四章电路的暂态分析
设：t＝0 时换路
0
− --- 换路前瞬间
则：
0 --- 换路后瞬间 + − u C (0 ) = u C (0 )
+
iL (0 ) = iL (0 )
2011-6-17 15
+
−
换路瞬间，电容上的电压、 换路瞬间，电容上的电压、电感中的电流不能 突变的原因解释如下： 突变的原因解释如下： 自然界物体所具有的能量不能突变， 自然界物体所具有的能量不能突变，能量的积累 或释放需要一定的时间。所以： 或释放需要一定的时间。所以：
2011-6-17
R C
i
uC
24
一阶电路过渡过程的求解方法
(一). 经典法: 用数学方法求解微分方程； 一 用数学方法求解微分方程； 微分方程
∗
(二). 三要素法: 求 二
初始值 稳态值 时间常数
……………...
2011-6-17
25
(一) 经典法
K + _E C R
例
i
一阶常系数 线性微分方程
ui
τ<<T/2
T/2 T C R 2T
E t E T 2T t
ui
uo
uo uC
E
2011-6-17 34
t
作业: 作业 P49-50
2-1
2011-6-17
35
结束
END
2011-6-17 36
19
2011-6-17
电路的响应
♣ 零输入响应： 零输入响应：
在零输入的条件下，由非零初始态引起的响 在零输入的条件下， 为零输入响应； 此时， 应，为零输入响应； 此时， u c ( 0 + ) 或 iL (0+ ) 被视为一种输入信号。 被视为一种输入信号。
0
− --- 换路前瞬间
则：
0 --- 换路后瞬间 + − u C (0 ) = u C (0 )
+
iL (0 ) = iL (0 )
2011-6-17 15
+
−
换路瞬间，电容上的电压、 换路瞬间，电容上的电压、电感中的电流不能 突变的原因解释如下： 突变的原因解释如下： 自然界物体所具有的能量不能突变， 自然界物体所具有的能量不能突变，能量的积累 或释放需要一定的时间。所以： 或释放需要一定的时间。所以：
2011-6-17
R C
i
uC
24
一阶电路过渡过程的求解方法
(一). 经典法: 用数学方法求解微分方程； 一 用数学方法求解微分方程； 微分方程
∗
(二). 三要素法: 求 二
初始值 稳态值 时间常数
……………...
2011-6-17
25
(一) 经典法
K + _E C R
例
i
一阶常系数 线性微分方程
ui
τ<<T/2
T/2 T C R 2T
E t E T 2T t
ui
uo
uo uC
E
2011-6-17 34
t
作业: 作业 P49-50
2-1
2011-6-17
35
结束
END
2011-6-17 36
19
2011-6-17
电路的响应
♣ 零输入响应： 零输入响应：
在零输入的条件下，由非零初始态引起的响 在零输入的条件下， 为零输入响应； 此时， 应，为零输入响应； 此时， u c ( 0 + ) 或 iL (0+ ) 被视为一种输入信号。 被视为一种输入信号。
电力系统暂态分析(第四章习题答案)
za + zb + zc Z2 Z1
Z1 za + zb + zc
Z2
Z2 Z1 za + zb + zc
其中: Z1 = za + a2zb + azc; Z2 = za + azb + a2zc
1) 当 za = zb = zc 时 ， 非 对 角 元 素 Z1 = za 1 + a2 +
a = Z2 = 0，则三序分量可以解藕。
33 13 (6 + 6 ) − j(6 + 6 )
=
33
13
6 − 6 + j(− 6 + 6 )
1 j3
②各序分量解藕单独作用分别求解序电流
正序电流：
I1
=
E1 j2
=
(−
1 12
−
3 12)
−
3 j(12
+
3 12)
负序电流：
I2
=
E2 j2
=
(−
1 12
+
3 12)
−
3 j(12
−
3 12)
零序电压标幺值：
10
U(0) = 220/
= 0.0797 3
按等值电路可求得各側电流：
0.0787 I1 = −0.12＋(−0.014)//0.244） = 0.748
0.244 I2 = I1 × （ − 0.014 + 0.244） = 0.794
I3 = I1 − I2 = −0.0455 电流有名值：
障时的正序、负序、零序等效电路； 解：正序： 负序：
零序：
电子电工技术第四章 电路的暂态过程分析
设一阶线性电路中所求变量为 f (t) ，变量的初始值为 f (0 ) ，变量在过渡过程结束后的稳态值为 f () ，时间常
数为 ，则我们可直接写出全响应的表达式为
f (t)
f ' (t)
f "(t)
f () [ f (0 )
t
f ()]e
式中，f '(t) 和 f "(t) 分别表示全响应中对应齐次方程的解和对 应非齐次方程的特解。
uC
t
E(1 e
)
3(1
t
e 2106
)
3(1
e5105 t
)
三、RC电路的全响应
由电容元件的初始储能和外接激励共同作用所产生的电路
响应，称为RC电路的全响应。
在图示电路中，电容元件
已具有初始储能 uC (0 ) U0 ＜U S
当开关S在 t 0 时刻合向电路 ，根据KVL，列出t ≥ 0 的电路
0
从理论上讲电容二端的电压经过无限长时间才能衰减至零
，但在工程上一般认为换路后，经过4 ~ 5 时间过渡过程即结
束。如图所示曲线分别为 uC 、i 、uR 随时间变化的曲线。
uC,uR
i
U
uC
t
t
uR
-U
US R
例 4-3 在图中，开关S长期合在位置1上，当t 0 时把它
合在位置2上，求换路后电容元件上电压uC和放电电流 i 。
第一节 储能元件和换路定则
由于电路结构（例如电路的接通、断开、短路等）或参
数的变化而引起电路从一种状态转变到另一种状态称之为换路
。
当初始时刻无储能，电容、电感中储存的能量与任一时刻
电压与电流的关系为
第四章暂态基础与暂态技术
根据电化学极化方程式
正，所以dη=-dφ
( ( ) ( )) ρ σ
i = i −i = i0
exp COs
αnFη
CO0
RT
− exp CRs
−βnFη
CR0
RT
( ) di
=
ρ di −
σ di =
dCOs COs
ρ i−
dC
s R
CRs
σ i+
nF RT
ρσ αi + βi dη
( ) R = = − = dηa r di
1、液相传质的三种方式：
• ③、电迁移 • 带电微粒在电场作用下的定向运动： Πx,电= ±ExuoC • （1）淌度uo：单位电场强度作用下带电微
粒的运动速度 • （2）电场强度Ex：
4.2 暂态扩散过程
• 2、浓差极化： –①、浓差极化的含义： –②、研究浓差极化的意义：
•（1）寻求克服浓差极化的方法： •（2）了解浓差极化的作用： •（3）研究电极过程的机理。
4、 暂态研究方法的特点：
• n 研究方法的多样性： • o 结果解析的复杂性： • p 获得信息的全面性： • q 实验时间的短暂性：有利于：
– c 降低甚至消除浓差极化； – d 研究快速进行的电极过程； – e 研究性质相对较不稳定，易于变化的体系； – f 消除干扰效应，
• r 实验结果的重现性： • s 仪器设备的高要求：
c dt
dt
( ) = Cd
+ d (η −iRl ) dt
η
− iRl
dCd dt
d.暂态电化学极化物理模型的数学表示
在使用微扰技术即激励信号的幅度不太大
电力系统暂态分析第四章-PPT精选文档
《电力系统分析》
2019/3/8
a2 5.78 150 I b1 I a1 a 5 . 78 150 b2 I a2 I 0 I I b 0 a 0
a 5.7890 I c1 I a1 2 c2 a I a2 5.78 90 I 0 I I a0 c0
（4－8）
如图所示。零序电流必须以中性线为通路。
《电力系统分析》
2019/3/8
有零序
无零序
无零序
《电力系统分析》
2019/3/8
例：
a
b c
10 0 I
a
10 180 0 I Ic
b
请分解成对称相量。
《电力系统分析》
2019/3/8
解：
I 1 a a(1) 1 2 I 1 a a(2) 3 a(0) I a 1
（4－1）
《电力系统分析》
2019/3/8
由于每一组是对称的，故有下列关系：
F b ( 1 ) e j 240 F a ( 1 ) a 2 F a ( 1 ) j 120 F c ( 1 ) e F a ( 1 ) a F a ( 1 ) j 120 Fb(2) e F a(2) a F a(2) j 240 2 Fc(2) e F a(2) a F a(2) F b (0) F c(0) F a (0)
Fb(1)
正序
(a)
Fc(2)
负序
(b)
《电力系统分析》
2019/3/8
《电力系统暂态分析》第四章提纲
第四章 对称分量法及电力系统元件的各序等值电路三相短路属对称短路，短路电流交流分量是对称的。
在对称三相电路中，三相阻抗相同，三相电压、电流有效值相等。
因此对称三相系统三相短路的分析与计算，可只分析和计算其中一相。
单相接地短路、两相短路、两相接地短路以及单相断线、两相断线属不对称故障故障。
不对称故障时，三相阻抗不同，三相电压、电流的有效值不等，相与相之间相位差也不相等。
因此不对称故障的分析与计算，就不能只分析其中一相。
通常采用对称分量法。
第一节 对称分量法适用于线性电路：可应用叠加原理。
一、对称分量法的基本思想1918年，美国学者C.L.Fortescue 提出：n 相的不对称分量，可以分解为n 组的对称分量。
应用于三相交流电力系统，对称分量法的基本思想是：任意3个不对称相量，可以分解为3组对称分量。
即(1)a F 、(1)b F 、(1)c F ——称为正序分量 a F 、b F 、c F (2)a F 、(2)b F 、(2)c F ——称为负序分量 (0)a F、(0)b F 、(0)c F ——称为零序分量 这3组对称分量具有不同的相序。
然后对3组对称分量系统分别进行求解，求得3组对称分量，最后在进行叠加，求得3个不对称分量。
相量F可以是：电流、电压、电势或磁链等电路学中的相量。
二、基本公式1．正序分量：(1)a F 、(1)b F 、(1)c F )1(c F三相分量大小：相等；相位：互差120°电角度；相序：b 相超前a 相240°电角度，c 相超前a 相120°电角度。
因此，有如下关系)1(2)1(240)1(0a a j b F a F e F == )1()1(120)1(0a a j c F a F e F == 式中2321120101200jea j +-=∠==； 2321240102402jea j --=∠==。
2．负序分量：(2)a F 、(2)b F 、(2)c F)2F三相分量大小：相等；相位：互差120°电角度；相序：b 相超前a 相120°电角度，c 相超前a 相240°电角度。
电力系统暂态分析 第四章 习题
试计算发电机按偏移量调节和按导数调节的静态稳定极限和储备系数。
图习题 4-21 4-22 两个有限容量发电厂的电力系统，其等值电路如图习题 4-22 所示。
系统有关参数为：
X1 2.49 ； X 2 0.506 E1 2.39 ； E2 2.52 ；Uk 10 Sk 3.66 j2.27 ； S1 0.583 j0.362 ； S2 3.08 j1.91
4-27 如何用小干扰分析判断简单电力系统的静态稳定性? 4-28 如何利用复平面法判断电力系统的静态稳定性? 4-29 提高电力系统的静态稳定性的措施有哪些?理论根据是什么？
习题
4-1 如图习题 4-1 所示电力系统，参数标幺值如下：
网络参数 X d 1.21 ， X d 0.4 ， XT1 0.169 ， XT 2 0.14 ， Xl / 2 0.373 。 运行参数Uc 1，发电机向受端输送功率 P0 0.8 ， cos0 0.98 。 试计算当 Eq 、 E 及UG 常数时，此系统的静态稳定功率极限及静态稳定储备系数 KP 。
E
'
q
2.05
2.81
3.61
cos 2
-0.5
0
0.5
P
1.31
1.74
2.01
(提示：用近似分析法计算，利用判据 S'Eq 0 判断系统稳定与否。)
图习题 4-14
4-15 一台同步发电机经输电线连接到无限大功率母线上运行。其接线图和参数如图习题 4-15 所示。若用手 动调节励磁维持机端电压不变。试问： (1) 用什么判据判断同步电机的静态稳定？
图习题 4-3 4-4 某一输电系统图及参数如图习题 4-4 所示，发电机给定电抗的数值已计及电机的饱和，传输给受端的
图习题 4-21 4-22 两个有限容量发电厂的电力系统，其等值电路如图习题 4-22 所示。
系统有关参数为：
X1 2.49 ； X 2 0.506 E1 2.39 ； E2 2.52 ；Uk 10 Sk 3.66 j2.27 ； S1 0.583 j0.362 ； S2 3.08 j1.91
4-27 如何用小干扰分析判断简单电力系统的静态稳定性? 4-28 如何利用复平面法判断电力系统的静态稳定性? 4-29 提高电力系统的静态稳定性的措施有哪些?理论根据是什么？
习题
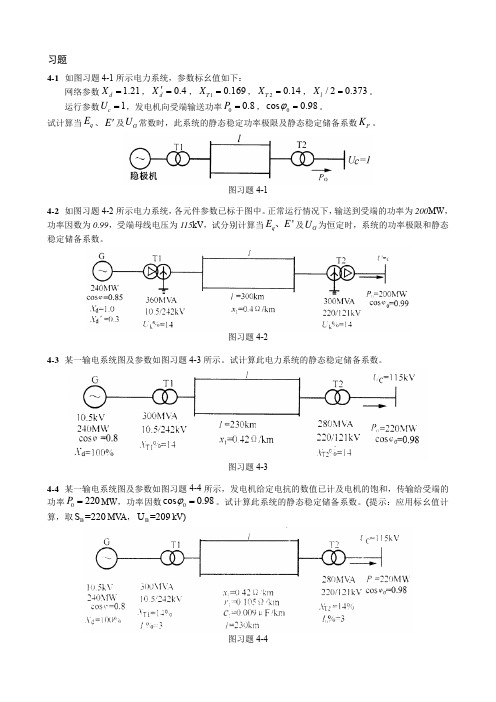
4-1 如图习题 4-1 所示电力系统，参数标幺值如下：
网络参数 X d 1.21 ， X d 0.4 ， XT1 0.169 ， XT 2 0.14 ， Xl / 2 0.373 。 运行参数Uc 1，发电机向受端输送功率 P0 0.8 ， cos0 0.98 。 试计算当 Eq 、 E 及UG 常数时，此系统的静态稳定功率极限及静态稳定储备系数 KP 。
E
'
q
2.05
2.81
3.61
cos 2
-0.5
0
0.5
P
1.31
1.74
2.01
(提示：用近似分析法计算，利用判据 S'Eq 0 判断系统稳定与否。)
图习题 4-14
4-15 一台同步发电机经输电线连接到无限大功率母线上运行。其接线图和参数如图习题 4-15 所示。若用手 动调节励磁维持机端电压不变。试问： (1) 用什么判据判断同步电机的静态稳定？
图习题 4-3 4-4 某一输电系统图及参数如图习题 4-4 所示，发电机给定电抗的数值已计及电机的饱和，传输给受端的
电化学测量第4章暂态ppt课件
• 电极的极化分为哪几种？各种极化有何特 点？他们分别受哪些因素影响？
• 请以图示的方法给出由稳态极化曲线求解 电化学动力学参数的原理，并说明其注意 事项。
4.3 电化学等效电路
• 4.3.1 电路模型的建立
4.3.2 电化学反应电阻
• 电化学反应电阻Rr，用以表示Faraday电流对电化 学极化过电势的关系
ic：由双电层的电荷改变引起 Non-Faradaic Current ir：由电极界面的电化学反应所产生 Faradaic Current
ic
dQ dt
d(Cd )
dt
Cd
d
dt
dCd dt
电化学反应迟缓； 反应物、产物在电极附 近的扩散迟缓
活性物质在电 极/溶液界面的 吸脱附
4.1 暂态与暂态电流－特点
• 定解的边界条件
假定扩散系数不变，即Di＝常数
开始极化的瞬间（初始条件）
半无限扩散条件
ci (x, 0)=ciB ci (, t)=ciB
4.2.1 电势阶跃下的非稳态扩散电流
• 小幅度电势阶跃（未破坏平衡）
c0, t cS=const
• 大的电势阶跃（达完全浓度极化）
c0, t 0
解Fick第二定律，得反应粒子浓度
• 可用来研究快速电极过程，测定快速电极反应的 动力学参数；
• 有利于研究界面结构和吸附现象。也有利于研究 电极反应的中间产物及复杂的电极过程；
• 适合于那些表面状态变化较大的体系 。
4.5 电流阶跃法（Current Step）
• 4.5.1 电流阶跃下的电极响应特点
• 4.5.2 小幅度电流阶跃测量法 极限简化法、方程解析法
Rr
de
• 请以图示的方法给出由稳态极化曲线求解 电化学动力学参数的原理，并说明其注意 事项。
4.3 电化学等效电路
• 4.3.1 电路模型的建立
4.3.2 电化学反应电阻
• 电化学反应电阻Rr，用以表示Faraday电流对电化 学极化过电势的关系
ic：由双电层的电荷改变引起 Non-Faradaic Current ir：由电极界面的电化学反应所产生 Faradaic Current
ic
dQ dt
d(Cd )
dt
Cd
d
dt
dCd dt
电化学反应迟缓； 反应物、产物在电极附 近的扩散迟缓
活性物质在电 极/溶液界面的 吸脱附
4.1 暂态与暂态电流－特点
• 定解的边界条件
假定扩散系数不变，即Di＝常数
开始极化的瞬间（初始条件）
半无限扩散条件
ci (x, 0)=ciB ci (, t)=ciB
4.2.1 电势阶跃下的非稳态扩散电流
• 小幅度电势阶跃（未破坏平衡）
c0, t cS=const
• 大的电势阶跃（达完全浓度极化）
c0, t 0
解Fick第二定律，得反应粒子浓度
• 可用来研究快速电极过程，测定快速电极反应的 动力学参数；
• 有利于研究界面结构和吸附现象。也有利于研究 电极反应的中间产物及复杂的电极过程；
• 适合于那些表面状态变化较大的体系 。
4.5 电流阶跃法（Current Step）
• 4.5.1 电流阶跃下的电极响应特点
• 4.5.2 小幅度电流阶跃测量法 极限简化法、方程解析法
Rr
de
第4章 一阶线性电路的暂态分析
表示换路后的初始瞬间。 换路定律：在 t 0 到 t 0 的换路瞬间，电容元件的 电压和电感元件的电流不能突变。即
uC (0 ) uC (0 ) iL (0 ) iL (0 )
含有储能元件的电路在换路时产生过渡过程的根本原因 是能量不能突变。由于电阻不是储能元件，因而纯电阻电路 不存在过渡过程。
US U 0 US 式中 L iL (t ) iL () [iL (0 ) iL ()]e （ ）e R R R R （3）时间常数 （秒），或 L（秒） RC R 时间常数 影响动态电路的变化过程，反间越长，τ小则过渡过程时间越 短。
（1）直流电源激励的RC电路
图示电路，开关S原处于a端且已 稳定。在t=0时发生换路，开关S从a 端切换到b端。 由换路定律，有初始值
uC (0 ) uC (0 ) U 0
4(12)
第4章
一阶线性电路的暂态分析
当电路达到新的稳定状态时，有稳态值
uC () US
通过定性分析可知，当初始值大于稳 态值（U0>US）时，电容发生放电，如图 (b)；当初始值小于稳态值（U0<US）时， 电容发生充电，如图(c)。电容电压uC(t)按
4(4)
第4章
一阶线性电路的暂态分析
4.1.2 动态电路初始值的确定 分析暂态过程的变化规律，首先要确定电路中待求量的 初始值。电路初始值的确定可按照以下步骤进行。
（1）由t=0-时的电路求uC(0-)或iL(0-)。
（2）由换路定律，有uC(0+)=uC(0-)、iL(0+)=iL(0-)。 （3）由t=0+的电路及uC(0+)或iL(0+)求其他待求电压、电流 的初始值。 注意：在换路瞬间， uC或iL不能突变，但电路中其他电
uC (0 ) uC (0 ) iL (0 ) iL (0 )
含有储能元件的电路在换路时产生过渡过程的根本原因 是能量不能突变。由于电阻不是储能元件，因而纯电阻电路 不存在过渡过程。
US U 0 US 式中 L iL (t ) iL () [iL (0 ) iL ()]e （ ）e R R R R （3）时间常数 （秒），或 L（秒） RC R 时间常数 影响动态电路的变化过程，反间越长，τ小则过渡过程时间越 短。
（1）直流电源激励的RC电路
图示电路，开关S原处于a端且已 稳定。在t=0时发生换路，开关S从a 端切换到b端。 由换路定律，有初始值
uC (0 ) uC (0 ) U 0
4(12)
第4章
一阶线性电路的暂态分析
当电路达到新的稳定状态时，有稳态值
uC () US
通过定性分析可知，当初始值大于稳 态值（U0>US）时，电容发生放电，如图 (b)；当初始值小于稳态值（U0<US）时， 电容发生充电，如图(c)。电容电压uC(t)按
4(4)
第4章
一阶线性电路的暂态分析
4.1.2 动态电路初始值的确定 分析暂态过程的变化规律，首先要确定电路中待求量的 初始值。电路初始值的确定可按照以下步骤进行。
（1）由t=0-时的电路求uC(0-)或iL(0-)。
（2）由换路定律，有uC(0+)=uC(0-)、iL(0+)=iL(0-)。 （3）由t=0+的电路及uC(0+)或iL(0+)求其他待求电压、电流 的初始值。 注意：在换路瞬间， uC或iL不能突变，但电路中其他电
暂态分析第四章第五章
arc
s
in
I
q
xd
x' d
E'
δ
arcsin
U E'
1
x' d
xd
sinδ
第二节 同步发电机组的机电特性
（3）发电机端电压为常数
PUG
U GU xe
s inδ G
xe xT xL
δG
δ
arc s in
U
U G
1
xe xd
sinδ
2.凸极式发电机的功—角特性 （1）以空载电动势和 同步电抗表示发电机
dEq' dt
Eqe
E' q
Id
xd
x' d
第三节 发电机励磁系统与原动 机系统的数学模型
一、发电机励磁系统及其数学模型
自动调节励磁系统 发电机主励磁系统和自动调节励磁装置的合称。
主励磁系统 是从励磁电源到发电机励磁绕组的励磁主回路
自动调节励磁装置 根据发电机的运行参数，如端电压、电流等自动地调节主励磁 系统的励磁电压。
•
•
YG 0Y001Y0G U G YGG U G
•
(YG 0Y001Y0G YGG )U G
。
。
I YU
。
。
I YU
.
n
.
I i E j Yij
j 1
Pei
Re
Ei
Ii
Re
Ei
n
j 1
Ei
Yij
n
Ei E j (Gij cosδij j 1
Bijsinδij )
n
Pei Ei2Gii Ei E j (Gij cosδij Bijsinδij ) j 1 ji
《电力系统暂态分析》书稿(第四章)(杨耿杰,定稿版20200215)(再修改)
第四章对称分量法及电力系统元件的各序等值电路电力系统正常运行时可以认为是三相对称的，即各元件三相阻抗相同，三相电压、电流大小相等，相与相之间的相位差也相等，且具有正弦波形和正常相序。
对称的三相交流系统，可以用单相电路来计算。
只要计算出一相的量值，其他两相就可以推算出来，因为其他两相的模值与所计算相相等，相位相差o 120±。
三相对称短路或三相断线时，交流分量三相是对称的，因此，可以利用系统固有的对称性，只需分析其中一相，避免逐相进行计算的复杂性。
但是，电力系统发生单相接地短路、两相短路和两相接地短路，以及单相断线和两相断线等不对称故障时，三相阻抗不同，三相电压、电流大小不相等，相与相之间的相位差也不相等。
对这样的三相系统不能只分析其中一相，通常采用对称分量法进行分析。
对称分量法是分析不对称故障的常用方法，其目的是将一组不对称的abc 三相相量，变换为三组各自对称的abc 三相相量，分别称为正序、负序和零序三序量。
与各序电压、电流量对应，电力系统也分为正序、负序和零序网络。
电力系统发生不对称故障后产生的不对称电压、电流三相相量，通过应用对称分量法，可以将其分解到三个序网，在各序网内按照序电压、电流对称的方式进行分析，之后再合成为实际的abc 三相相量，从而使得不对称故障计算大为简化。
第一节对称分量法假设电力网络是线性网络，即网络各元件参数与通过它的电流、电压的大小无关，是恒定的。
线性网络可以应用叠加原理进行分析计算。
通常情况下，电力系统都是三相并列运行，各相之间存在有互感。
对于图4-1所示的任一静止三相交流系统元件，可以用下式简单表示其各相电流、电压之间的关系⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∆∆∆c b a cc bc ac bc bbabac ab aa c b a I I I Z Z Z Z Z Z Z Z Z U U U （4-1）式中：aa Z 、bb Z 和cc Z 为各相自阻抗，其余为相间互阻抗。
第四章_暂态测量方法
第二节 暂态过程的等效电路
等效电路： 用电阻、电容元件所构成的电路来模拟电极／溶液 界面上所发生的过程。 每个电极基本过程 等效电路元件
抽象的电化学反应
模拟电子电路
优点：利用电极基本过程对时间的不同响应，可以使复杂 的等效电路得以简化或进行解析，从而简化问题的分析和 计算。
一、 各种极化下的等效电路
a. 控制电流法暂态测量 b. 控制电位法暂态测量
②按极化波形方式分；
a. 阶跃法 b. 方波法
c. 线性扫描法
d. 交流阻抗法
③ 按极化或控制的幅度分(幅度：电极极化的幅度， 界面电位变化量)；
a. 大幅度暂态测量(研究电极过程) |Δφ|>10 mV (大幅度)
浓差极化不可忽略，方程解析的研究方法。 b. 小幅度暂态测量(用于测定参数Rr、RL、Cd) |Δφ|<10 mV (小幅度)，电极过程处于传荷控制，采用等效电路的研究方 法。
2/3双电层 充电电流
1/3双电层 充电电流
双电层充电 电流为零
电极电势改变时引起双 电层充电电流
双电层电容改变时引起 的双电层充电电流
当表面活性物质在电极界面吸脱附时，双电层电容Cd有剧 烈的变化。 ic是暂态电流，因为达到稳态后的电极电势和吸脱附状态不
变（即）E和Cd不变，ic=0.
2. 电极表面上反应物、生成物浓度不仅与位置有关， 还与时间有关。
Zw：扩散传质过程／步骤，浓差极化；
Ru：离子导电过程／步骤，欧姆极化（溶液完成导电所产生 的极化过程）。
第三节 等效电路的简化
一、传荷过程控制下的电极极化
1、浓差极化忽略的条件
① 适于小幅度暂态测量（ 10mV ）； ② 单向持续时间短。 ③ 电极体系i0比较小。
暂态电路分析PPT课件
0
0.2
i2 (t) 0 .2 (1 e 1 0 t)m At 0
0
目录
上一页
下一页
返回
退出
4.4一阶线性电路暂态过程的三要素分析法
线性直流或无源一阶电路的方程：
u(t)du(t) u()
或
i(t) di(t) i()
dt
其中，时间常数
RC 或 L
dt
R
R为与储能元件相接的线性电路的戴维宁等效电阻。
上一页下一页目录返回退出41换路定律与电压电流初始值的确定42rc电路的暂态过程43rl电路的暂态过程44一阶线性电路暂态过程的三要素分析法45矩形脉冲作用于一阶电路46rlc串联电路的零输入响应上一页下一页目录返回退出前面讨论电路的响应时都没有考虑所讨论的电路是什么时刻开始工作的事实上我们默认所分析的电路包括组成电路的各元件参数和它们之间的连接方式已经工作了足够长时间电路进入了稳态状态电路响应不再随时间变化例如直流稳态时响应为恒定值或随时间按某一规律周期性变化如正弦稳态时响应为与激励同频率的正弦量
dt
dt
其中，所求电压、电流可为电路中任意一条支路上的响 应，方程右边的符号表示该响应在直流稳态时的值。
由于在直流稳态时，所有电压电流都为直流，电容电流 和电感电压必为0，因此，直流稳态时，电容将等效为开路、 电感将等效为短路。
目录
上一页
下一页
返回
退出
4.2.3 RC/RL电路的暂态过程（续3）
零输入响应和零状态响应
电路与模拟电子技术
第4章 暂态电路分析
本章教学内容
4.1 换路定律与电压电流初始值的确定 4.2 RC电路的暂态过程 4.3 RL电路的暂态过程 4.4 一阶线性电路暂态过程的三要素分析法 4.5 矩形脉冲作用于一阶电路 4.6 RLC串联电路的零输入响应
0.2
i2 (t) 0 .2 (1 e 1 0 t)m At 0
0
目录
上一页
下一页
返回
退出
4.4一阶线性电路暂态过程的三要素分析法
线性直流或无源一阶电路的方程：
u(t)du(t) u()
或
i(t) di(t) i()
dt
其中，时间常数
RC 或 L
dt
R
R为与储能元件相接的线性电路的戴维宁等效电阻。
上一页下一页目录返回退出41换路定律与电压电流初始值的确定42rc电路的暂态过程43rl电路的暂态过程44一阶线性电路暂态过程的三要素分析法45矩形脉冲作用于一阶电路46rlc串联电路的零输入响应上一页下一页目录返回退出前面讨论电路的响应时都没有考虑所讨论的电路是什么时刻开始工作的事实上我们默认所分析的电路包括组成电路的各元件参数和它们之间的连接方式已经工作了足够长时间电路进入了稳态状态电路响应不再随时间变化例如直流稳态时响应为恒定值或随时间按某一规律周期性变化如正弦稳态时响应为与激励同频率的正弦量
dt
dt
其中，所求电压、电流可为电路中任意一条支路上的响 应，方程右边的符号表示该响应在直流稳态时的值。
由于在直流稳态时，所有电压电流都为直流，电容电流 和电感电压必为0，因此，直流稳态时，电容将等效为开路、 电感将等效为短路。
目录
上一页
下一页
返回
退出
4.2.3 RC/RL电路的暂态过程（续3）
零输入响应和零状态响应
电路与模拟电子技术
第4章 暂态电路分析
本章教学内容
4.1 换路定律与电压电流初始值的确定 4.2 RC电路的暂态过程 4.3 RL电路的暂态过程 4.4 一阶线性电路暂态过程的三要素分析法 4.5 矩形脉冲作用于一阶电路 4.6 RLC串联电路的零输入响应
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
0 0
•
IIaa((12))
Ua(0) 0
0 zs 2zm Ia(0) 0 0 z(0) Ia(0)
三相对称系统对称分量变换为三个互不耦合的 正、负、零序系统。
式中z(1)、z(2)、z(0)分别称为线路的正序、负序、零序阻抗。 对于静止元件，如线路、变压器等，正序和负序阻抗是相等 的。对于旋转的电机，正序和负序阻抗不相等。
a2I&fa(1) aI&fa(1) a2I&fa(2) aI&fa(2) a2 a I&fa(1) a2 a I&fa(2)
I&fa(1) I&fa(2)
1
aI&fa(1) a2I&fa(2) I&fa(0) 0 a a2 I&fa(1) I&fa(0) 0
根据施加电压、注入电流及不同的短路情况，可有
x(2)
1 2
(
xd
xq )
x(2)
2xd xq xd xq
x(2) xd xq
计及远离机端的短路，因与外部电抗串联，以上三式的结果接近。
实用计算中，取
x(2)
1 2
(
xd
xq )
19
同步发电机的零序电抗
零序电流只产生漏磁通，由于迭绕线圈，零序漏 磁通 小于正序漏磁通。
0
X ms
rms
X mN
rmN
rms rmN
rs jX s jX r rr s
X ms X mN
s 2－ N
s
1
2
异步电动机等值电抗、电阻与转差率关系曲线
异步电动机的负序参数可以按转差率为2—s来确定
当转差率增加到一定值，特别在转差率为1~2之间时，曲线变化很缓慢。
因此，异步电动机的负序参数可用s=1，即转子制动情况下的参数来代替，
jxI
jx II
U(0)
jxm(0)
负 载
25
其他接线形式下对应的等值电路
零序励磁电抗xm(0)
对于由三个单相变压器组成的三相变压器组，每相的零序主磁通与
正序主磁通一样，都有独立的铁芯磁路，因此，零序励磁电抗与正
序的相等。对于三相四柱式（或五柱式）变压器，零序主磁通也能在
铁芯中形成回路，磁阻很小，即零序励磁电抗的数值很大（也即励
对称 系统
思想： 把不对称的三相系统分解为相序分别为正 、负、零的三个独立的对称系统的叠加
4
• 三个不对称相量可以分解为三组对称相量
FFaa((12)) Fa(0)
1 3
1 1 1
a a2
1
a2 a
•
FFba
1
Fc
FS T 1 • FP
若F为电流I，则：
&I = 1
3 a(0)
I&fa(1) I&fa(0)
2
序分量关系： I&fa(1) I&fa(2) I&fa(0)
12
序电压方程和边界条件联立求解
Ufa(1) Ea Ifa(1) z(1)
Ufa(2) Ifa(2) z(2)
Ufa(0) Ifa(0) z(0)
Ufa(1) Ufa(2) Ufa(0) 0
15
§4-3 同步发电机的负序和零序电抗
同步发电机对称运行
只有正序电流存在，电机的参数为正序参数，稳态时同步电抗为
等是正序电抗 ；暂态过程 xd xd xq 都属于正序电抗。
x
d
xq
一.同步发电机不对称短路时的高次谐波（负序电流的影响）
短路电流 iabc 中包含周期分量和非周期分量，因不对称短路, Iω不对称。
序电压方程 边界条件
Ifa (1)
z (1)
Ufa 0 z(2)
z(0)
14
求解不对称故障中短路电压和电流的计算步骤
1.针对短路情况，列出边界条件 2.根据边界条件，推导出序分量关系 3.结合序分量关系和三序电压方程，画出复合序网图 4.结合复合序网图，求解电流和电压的序分量值 5.根据求出的电压、电流序分量值，带入P87公式4-4 中求解短路点处对应的电压和电流值（边界条件值除 外）
子
I4
f
f
脉动磁场
转
子
If
f
_ f 2
f 3
f 3
If 3
f 3
这些高次谐波分量与定子直流分量一样衰减，最后衰减为零。
①不对称短路时，输电线路中出现强大的高次谐波干扰； ②施加负序电流（压），机端不仅仅出现负序电压（流）。
18
同步发电机的负序电抗
定义:
x(2)
U(2) I (2)
磁电流很小）。以上两种变压器，在短路计算中都可以当作xm0=∞，
即忽略励磁电流，认为励磁支路断开。
I0
I0
I0
I0
I0
I0
30
3I0
三个单相变压器组成的三相变压器组
3I0
三相四柱式变压器
27
对于三相三柱式变压器，由于三相零序磁通大小相等，相位相同，
主磁通不能在铁芯中构成回路，而必须经过气隙由油箱壁中返回，
z(0)
Ifa(0) Ufa ( 0)
正序序网图
负序序网图
零序序网图
9
z (1)
Ifa(1)
Ea
Ufa (1)
正序序网图
z(2)
Ifa(2)
Ufa ( 2)
负序序网图
z(0)
Ifa(0) Ufa ( 0)
零序序网图
故障点的序电压方程
Ufa(1) Ea Ifa(1) z(1) Ufa(2) Ifa(2) z(2) Ufa(0) Ifa(0) z(0)
I5
2 f
2 f
3
3
4 f 4 f
脉动磁场
转 子
If 2
f 2
If 4
f 4
这些高次谐波均由定子电流基频负序分量所派生，而后者又与基频 正序分量密切相关。所以，在暂态过程中，这些高次谐波分量和基频正 序分量一样衰减，至稳态时仍存在。
17
定子直流分量iα引起的高次谐波
定
I
I2 I2 (1) I2 (2)
即 x2 x
21
§4-5 变压器的零序电抗和等值电路
变压器的正序电抗为两个绕组漏抗之和（双绕组变压器），即稳态运 行时的电抗（电力系统稳态分析中），负序电抗和正序相同。
对于零序电抗，当在变压器端点施加零序电压时，其绕组中有无零序 电流，以及零序电流的大小与变压器三相绕组的接线方式和变压器的结 构密切相关。
Ia Ib Ic
由上式可得，三相系统为三角形接法和没有中性线 的星型接法时，三相电流之和为0，零序电流不存在 ；只有在有中性线的星型接法中才存在零序电流
5
§4-2 对称分量法在不对称故障分析中的应用
一. 三相阻抗的对称分量
对于三相对称元件，各序分量是独立的。
正序电流
三序分量
负序电流
零序电流
三相静止对称元件：
要遇到很大的磁阻，这时的励磁电抗比正、负序等值电路中的励
磁电抗小得多，在短路计算中，应视为有限值，其值一般由实验
方法确定，大致取xm0=0.3~1.0。
I(0) I(0) I(0)
(0) (0) (0)
三相三柱式变压器
28
二、三绕组变压器
三绕组变压器中，总有一个绕组结成三角形， 可不计零序励磁电抗。（YNdyn， YNdy ， YNdd）
正序压降 负序压降 零序压降
zab zbc zac zm
zaa
zaa zbb zcc zs
zab zbb
zac
zcc
zbc
6
U a
zaa
z ab
z
ac
I a
zs
z m
z
m
I a
Ub
z ba
z bb
z bc
Ib
z m
z s
z
m
Ib
Uc
z ca
z cb
z cc
Ic
是表征了网络结构和故障前 运行方式的序电压方程
10
单相短路接地分析计算
单相接地短路故障的相分量边界条件： Ufa 0 Ifb Ifc 0
用序分量表示为：Ufa Ufa(1) Ufa(2) Ufa(0) 0
？ I&fb a2I&fa(1) aI&fa(2) I&fa(0) 0 I&fc aI&fa(1) a2I&fa(2) I&fa(0) 0
序分量关系： Ifa(1) Ifa(2) Ifa(0)
11
用序分量表示为：Ufa Ufa(1) Ufa(2) Ufa(0) 0
I&fb a2I&fa(1) aI&fa(2) I&fa(0) 0 I&fc aI&fa(1) a2I&fa(2) I&fa(0) 0
a2 I&fa(1) aI&fa(2) I&fa(0) aI&fa(1) a2I&fa(2) I&fa(0) 1 aI&fa(1) a2I&fa(2) I&II
U(0)
jx II
jxI
jxIII
U(0)
jx II
Ndyn
YNdy
分析方法与双绕组变压器相同
29
§4-6 输电线路的零序阻抗和电纳
一、双绕组变压器
零序电压施加在Y、d侧
U(0)
因在三相绕组端并联施加零序电压，端点
等电位，故I(0) 0 ， 用阻抗表示为：x(0) 即开路。