第六章树和二叉树
合集下载
第6章 树和二叉树

1) 若 i=1,则该结点是二叉树的根,无双亲,否则,编号 为 i/2 的结点为其双亲结点; 2) 若 2i > n,则该结点无左孩子,否则,编号为 2i 的结 点为其左孩子结点; 3) 若 2i+1 > n,则该结点无右孩子结点,否则,编号为 2i+1 的结点为其右孩子结点。
二叉树的存储结构
1. 二叉树的顺序存储表示
DeleteChild( T, p, LR ); 初始条件:二叉树 T 存在。 操作结果:根据LR的值,删除结点p的子树。
✓ 加工型操作(续)
Assign( T, &e, value ) 初始条件:二叉树 T 存在。 操作结果:用 value 给当前结点 e 赋值。
ClearBiTree( &T ) 初始条件:二叉树 T 存在。 操作结果:清空二叉树中的所有结点。
Value( T, cur_e ) 初始条件:树 T 存在。 操作结果:用 cur_e 返回当前结点的元素值。
Parent( T, cur_e ) 初始条件:树 T 存在。 操作结果:用 cur_e 返回当前结点双亲的元素值。
✓ 引用型操作(续)
LeftSibling( T, cur_e ) 初始条件:树 T 存在。 操作结果:用 cur_e 返回当前结点左兄弟的元素值。
证明:
设二叉树上结点总数 n = n0 + n1 + n2,二叉树上分支总数 (总度数) b = n1+2n2,而 b = n-1 = n0 + n1 + n2 – 1,由此, n0 = n2 + 1。
除根结点外,每个结 点指向双亲结点的分
支只有一条。
两类特殊的二叉树:
满二叉树(Full Binary Tree) :指的是深度为 k 且含有 2k-1 个结点的二 叉树。
二叉树的存储结构
1. 二叉树的顺序存储表示
DeleteChild( T, p, LR ); 初始条件:二叉树 T 存在。 操作结果:根据LR的值,删除结点p的子树。
✓ 加工型操作(续)
Assign( T, &e, value ) 初始条件:二叉树 T 存在。 操作结果:用 value 给当前结点 e 赋值。
ClearBiTree( &T ) 初始条件:二叉树 T 存在。 操作结果:清空二叉树中的所有结点。
Value( T, cur_e ) 初始条件:树 T 存在。 操作结果:用 cur_e 返回当前结点的元素值。
Parent( T, cur_e ) 初始条件:树 T 存在。 操作结果:用 cur_e 返回当前结点双亲的元素值。
✓ 引用型操作(续)
LeftSibling( T, cur_e ) 初始条件:树 T 存在。 操作结果:用 cur_e 返回当前结点左兄弟的元素值。
证明:
设二叉树上结点总数 n = n0 + n1 + n2,二叉树上分支总数 (总度数) b = n1+2n2,而 b = n-1 = n0 + n1 + n2 – 1,由此, n0 = n2 + 1。
除根结点外,每个结 点指向双亲结点的分
支只有一条。
两类特殊的二叉树:
满二叉树(Full Binary Tree) :指的是深度为 k 且含有 2k-1 个结点的二 叉树。
大学数据结构课件6.树和二叉树

H I J K L MN O
AB C D E F GHI J KLMNO 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Байду номын сангаас
结点:i=5
父结点:i/2=5/2=2 左孩子:2i=2*5=10 右孩子:2i+1=2*5+1=11
完全二叉树:
1A
2
3
4 B5 6 C7
D
EF
G
8
1 0…0 0 0 k
证明三:
等比数列前n项和的计算公式:
Sn
a1(1 qn ) 1 q
n=k a1=1 q=2
性质3 对于一棵非空的二叉树,如果叶结点个数为n0, 度为2的结点数为n2,则有n0= n2+1。
A
证明:设n为二叉树的结点总数,n1为二叉树
中度为1的结点个数,则有:
B
C
n = n0 + n1 + n2 …… (1)
6.1.2 若干术语
(从结构上分)
B
E
F
B
F
E
K
L
K
L
无序树:树中任意一个结点的各孩子结点之间的次序构成 无关紧要的树
有序树:树中任意一个结点的各孩子结点有严格排列次序的树
6.1.3 树的表示形式
(1)倒悬树法(直观表示) (2)集合包含关系图法 (3)凹入表示法
B
E
F
KL
A
H
M
D J
I
CG
A
BC
child next
1 3 6∧
2∧ 4
7
8∧
B
D
E
第6章树和二叉树

2.孩子表示法 孩子表示法 在结点中设置指向每个孩子的指针域, 在结点中设置指向每个孩子的指针域,利用指针 指向该结点的所有孩子结点。 指向该结点的所有孩子结点。 大多采用按树的度设置结点的指针域的个数。 大多采用按树的度设置结点的指针域的个数。
9
6.1.4 树的存储结构
3.孩子兄弟表示法 孩子兄弟表示法 在结点中设置两个指针域, 在结点中设置两个指针域,一个指针域指向该结 点的第一个孩子,另一个指针域指向其右兄弟。 点的第一个孩子,另一个指针域指向其右兄弟。
2
6.1.1树的定义 树的定义
结点的度:结点所拥有子树的个数称为结点的度。 结点的度:结点所拥有子树的个数称为结点的度。 子树 称为结点的度 树的度:树中所有结点的度的最大值称为树的度。 最大值称为树的度 树的度:树中所有结点的度的最大值称为树的度。 叶结点:度为零的结点称为叶结点。也称终端结点 终端结点或 叶结点:度为零的结点称为叶结点。也称终端结点或叶 子 分支结点:度不为零的结点称为分支结点。也称非终端 分支结点:度不为零的结点称为分支结点。也称非终端 结点。除根结点以外,分支结点也称为内部结点。 结点。除根结点以外,分支结点也称为内部结点。 孩子结点和双亲结点: 孩子结点和双亲结点:树中一个结点的子树的根结点称 为孩子结点。该结点就称为孩子结点的双亲结点。 为孩子结点。该结点就称为孩子结点的双亲结点。 兄弟结点:具有同一双亲的孩子结点互为兄弟结点。 兄弟结点:具有同一双亲的孩子结点互为兄弟结点。 结点的祖先:从根到该结点所经分支上的所有结点, 结点的祖先:从根到该结点所经分支上的所有结点,称 为结点的祖先。 为结点的祖先。
17
6.2.2 二叉树的性质
性质4 具有n( 性质 具有 (n>0)个结点的完全二叉树的深度 )个结点的完全二叉树的深度h= log 2 n + 1 证明: 证明: 根据完全二叉树的定义可知深度为h-1层及以上的结点构成 根据完全二叉树的定义可知深度为 层及以上的结点构成 满二叉树,因此由性质2得深度为 得深度为h的完全二叉树满足 满二叉树,因此由性质 得深度为 的完全二叉树满足 n>2h-1-1和n≤2h-1 和 整理后得到 2h-1≤n<2h 不等式两边取对数, 不等式两边取对数,得 h-1≤log2n<h 由于h为正整数 为正整数, 由于 为正整数,因此 h= log 2 n + 1
9
6.1.4 树的存储结构
3.孩子兄弟表示法 孩子兄弟表示法 在结点中设置两个指针域, 在结点中设置两个指针域,一个指针域指向该结 点的第一个孩子,另一个指针域指向其右兄弟。 点的第一个孩子,另一个指针域指向其右兄弟。
2
6.1.1树的定义 树的定义
结点的度:结点所拥有子树的个数称为结点的度。 结点的度:结点所拥有子树的个数称为结点的度。 子树 称为结点的度 树的度:树中所有结点的度的最大值称为树的度。 最大值称为树的度 树的度:树中所有结点的度的最大值称为树的度。 叶结点:度为零的结点称为叶结点。也称终端结点 终端结点或 叶结点:度为零的结点称为叶结点。也称终端结点或叶 子 分支结点:度不为零的结点称为分支结点。也称非终端 分支结点:度不为零的结点称为分支结点。也称非终端 结点。除根结点以外,分支结点也称为内部结点。 结点。除根结点以外,分支结点也称为内部结点。 孩子结点和双亲结点: 孩子结点和双亲结点:树中一个结点的子树的根结点称 为孩子结点。该结点就称为孩子结点的双亲结点。 为孩子结点。该结点就称为孩子结点的双亲结点。 兄弟结点:具有同一双亲的孩子结点互为兄弟结点。 兄弟结点:具有同一双亲的孩子结点互为兄弟结点。 结点的祖先:从根到该结点所经分支上的所有结点, 结点的祖先:从根到该结点所经分支上的所有结点,称 为结点的祖先。 为结点的祖先。
17
6.2.2 二叉树的性质
性质4 具有n( 性质 具有 (n>0)个结点的完全二叉树的深度 )个结点的完全二叉树的深度h= log 2 n + 1 证明: 证明: 根据完全二叉树的定义可知深度为h-1层及以上的结点构成 根据完全二叉树的定义可知深度为 层及以上的结点构成 满二叉树,因此由性质2得深度为 得深度为h的完全二叉树满足 满二叉树,因此由性质 得深度为 的完全二叉树满足 n>2h-1-1和n≤2h-1 和 整理后得到 2h-1≤n<2h 不等式两边取对数, 不等式两边取对数,得 h-1≤log2n<h 由于h为正整数 为正整数, 由于 为正整数,因此 h= log 2 n + 1
第六章-树和二叉树

之
树 和 二 叉 树 13
1 2 3 A B C
4 5 6 7 0 D E F
8 0
9 10 0 G
¾ 二叉树顺序存储的算法描述
数 据 结 构
¾ 初始化二叉树
之
树 和 二 叉 树 14
#define Max_Size 100 typedef int TElemType; typedef TElemType SqBT[Max_Size+1]; void InitBT(SqBT bt){//设置空树 int i; for(i=1;i<=Max_Size;i++) bt[i]=0; }
数 据 结 构
之
树 和 二 叉 树 19
¾ 后序遍历顺序二叉树算法 void PostBT(SqBT bt,int i){ if(i>Max_Size||!bt[i]) return; PostBT(bt,2*i); PostBT(bt,2*i+1); printf("%3d ",bt[i]); }
数 据 结 构
之
树 和 二 叉 树 4
5. 孩子结点、双亲结点、兄弟结点、堂兄弟 结点、祖先结点、子孙结点…… 6. 结点的层次从根开始,根为第一层,根的 孩子为第二层;若某结点在第L层,则其 子树的根就在第L+1层。 7. 树的深度或高度:树中结点的最大层次。 8. 有序树:如果将树中结点的各子树看成是 从左至右有次序的;反之,则是无序树。 9. 森林:是m棵互不相交的树的集合。
数 据 结 构
之
树 和 二 叉 树 25
¾ 打印一维数组 void printSq(SqBT bt){ int i; printf("\nSeqArray:"); for(i=1;i<=Max_Size;i++) printf("%3d ",bt[i]); }
第六章树和二叉树

6.2 二叉树
二叉树的定义
定义
二叉树是n(n0)个结点的有限集合,它或为空 树(n=0),或由一个根结点和两棵互不相交的左 子树和右子树的二叉树组成。
二叉树的特点:
定义是递归的; 0结点的度2; 是有序树。
二叉树(续)
二叉树的五种基本形态
两种特殊的二叉树
满二叉树:每一层上的结点数都是最大结点数。
树的表示方法
A
B
C
D
EF G
HI
1层 特点:除根结点外, 每个结点都仅有一 个前趋(父)结点。
2层 其它表示方法:
嵌套集合表示法
凹入表表示法
3层
参见教材120页
J
4层
树的一些基本术语
结点的度(degree)
结点所拥有的子树的数目。
叶子结点(leaf--又称终端结点 terminal node)
} }
利用遍历结果确定二叉树问题
利用遍历结果确定二叉树问题
先序序列+中序序列 中序序列+后序序列 先序序列+后序序列 (x)
A
B
F
C
G
先序序列: ABCDEFGH 中序序列: BDCEAFHG
DE H
思考:层序+先序/中序/后序, 能否确定?如何做?
例如:层序ABCDEFGHIJ,中序DBGEHJACIF
} }
void Inorder(BiTree t) {
if (t) { Inorder(t->lchild); visit(t); Inorder(t->rchild);
} }
void Postorder(BiTree t) {
if (t) { Postorder(t->lchild); Postorder(t ->rchild); visit( t );
第6章树和二叉树

23
§6.3 遍历二叉树
• 遍历二叉树 • 遍历二叉树的递归与非递归算法 • 表达式求值 • 二叉树的运算举例 • 层序遍历二叉树
计算机科学与技术学院——数据结构
24
§6.3 遍历二叉树
§6.3.2 遍历二叉树的递归与非递归算法(1)
先序遍历二叉树
若二叉树为空,则空操作;否则
根
访问根;
先序遍历左子树;
具有三个结点的树与二叉树
A、三个结点的树有两种不同的形态
B、三个结点的二叉树有五种不同的形态
树型结构的共同特征:层次性、分支性
计算机科学与技术学院——数据结构
10
§6.2 二叉树
§6.2.1 二叉树的定义(3)
二叉树的基本操作
初始化空二叉树 销毁二叉树 创建二叉树 清空二叉树 判断空二叉树 求二叉树深度 求双亲 求左孩子 求右孩子 求左兄弟 求右兄弟 插入子树 删除子树 先序遍历二叉树 中序遍历二叉树 后序遍历二叉树 按层次遍历
InitTree(&T); DestroyTree(&T); CreateTree(&T, definition); ClearTree(&T); TreeEmpty(T); TreeDepth(T); parent(T, cur_e); LeftChild(T, cur_e); RightSibling(T, cur_e); InsertChild(&T, &p, i, c); DeleteChild(&T, &p, i); TraverseTree(T, visite());
∧G ∧
三叉链表表示
计算机科学与技术学院——数据结构
数据结构第六章:树和二叉树

性质2:深度为 的二叉树至多有 个结点(k≥ 性质 :深度为k的二叉树至多有2 k 1 个结点 ≥1)
证明:由性质 ,可得深度为k 证明:由性质1,可得深度为 的二叉树最大结点数是
(第i层的最大结点数 ) = ∑ 2 i 1 = 2 k 1 ∑
i =1 i =1
k
k
10
性质3:对任何一棵二叉树 ,如果其终端结点数(即 性质 :对任何一棵二叉树T,如果其终端结点数 即 叶节点)为 度为2的结点数为 的结点数为n 叶节点 为n0,度为 的结点数为 2,则n0=n2+1 证明: 为二叉树 中度为1的结点数 为二叉树T中度为 证明:n1为二叉树 中度为 的结点数 因为:二叉树中所有结点的度均小于或等于2 因为:二叉树中所有结点的度均小于或等于 所以:其结点总数n=n0+n1+n2 所以:其结点总数 又二叉树中,除根结点外, 又二叉树中,除根结点外,其余结点都只有一个 分支进入; 分支进入; 为分支总数, 设B为分支总数,则n=B+1 为分支总数 又:分支由度为1和度为 的结点射出,∴B=n1+2n2 分支由度为 和度为2的结点射出, 和度为 的结点射出 于是, 于是,n=B+1=n1+2n2+1=n0+n1+n2 ∴n0=n2+1
7
结点A的度:3 结点 的度: 的度 结点B的度:2 结点 的度: 的度 结点M的度:0 结点 的度: 的度 结点A的孩子: , , 结点 的孩子:B,C,D 的孩子 结点B的孩子 的孩子: , 结点 的孩子:E,F 树的度: 树的度:3 E K 结点A的层次: 结点 的层次:1 的层次 结点M的层次 的层次: 结点 的层次:4 L B F A C G H M
数据结构 第六章 树和二叉树

F
G
H
M
I
J
结点F,G为堂兄弟 结点A是结点F,G的祖先
5
树的基本操作
树的应用很广,应用不同基本操作也不同。下面列举了树的一些基本操作: 1)InitTree(&T); 2)DestroyTree(&T); 3)CreateTree(&T, definition); 4)ClearTree(&T); 5)TreeEmpty(T); 6)TreeDepth(T); 7) Root(T); 8) Value(T, &cur_e); 9) Assign(T, cur_e, value); 10)Paret(T, cur_e); 11)LeftChild(T, cur_e); 12)RightSibling(T, cur_e); 13)InsertChild(&T, &p, i, c); 14)DeleteChild(&T,&p, i); 15)TraverseTree(T, Visit( ));
1
2 4 8 9 10 5 11 12 6 13 14 3 7 15 4 6 2
1
3
5 7
证明:设二叉树中度为1的结点个数为n1 根据二叉树的定义可知,该二叉树的结点数n=n0+n1+n2
又因为在二叉树中,度为0的结点没有孩子,度为1的结点有1 个孩子,度为2的结点有2个结孩子,故该二叉树的孩子结点 数为 n0*0+n1*1+n2*2(分支数) 而一棵二叉树中,除根结点外所有都为孩子结点,故该二叉 树的结点数应为孩子结点数加1即:n=n0*0+n1*1+n2*2+1
文件夹1
文件夹n
第六章 树与二叉树

44
森林的遍历
(4) 广度优先遍历(层次序 遍历) :
数据结构
若森林F为空,返回; 否则 依次遍历各棵树的根 结点; 依次遍历各棵树根结 点的所有子女; 依次遍历这些子女结 森林的二叉树表示 点的子女结点。
45
二叉树的计数 由二叉树的前序序列和中序序列可唯 一地确定一棵二叉树。例, 前序序列 { ABHFDECKG } 和中序序列 { HBDFAEKCG }, 构造二叉树过程如 下:
三个结点构成的不同的二叉树
8
用二 叉 树 表达实际问题
例2 双人比赛的所有可能的结局
开始
甲
开局连赢两局 或五局三胜
乙
甲
甲 甲 乙
乙
乙 甲 乙 甲 甲 乙
甲
乙 甲
乙
乙
甲
乙甲
乙
甲
乙 甲 乙
二叉树的性质
数据结构
性质1 若二叉树的层次从1开始, 则在二叉树的 第 i 层最多有 2i -1个结点。(i 1) [证明用数学归纳法] 性质2 高度为k的二叉树最多有 2k-1个结点。 (k 0) [证明用求等比级数前k项和的公式]
前序遍历二叉树算法的框架是 若二叉树为空,则空操作; 否则 – 访问根结点 (V); – 前序遍历左子树 (L); – 前序遍历右子树 (R)。
遍历结果 -+a*b-cd/ef
27
数据结构
后序遍历 (Postorder Traversal)
后序遍历二叉树算法的框架是 若二叉树为空,则空操作; 否则 – 后序遍历左子树 (L); – 后序遍历右子树 (R); – 访问根结点 (V)。
数据结构
36
左子女-右兄弟表示法 第一种解决方案
森林的遍历
(4) 广度优先遍历(层次序 遍历) :
数据结构
若森林F为空,返回; 否则 依次遍历各棵树的根 结点; 依次遍历各棵树根结 点的所有子女; 依次遍历这些子女结 森林的二叉树表示 点的子女结点。
45
二叉树的计数 由二叉树的前序序列和中序序列可唯 一地确定一棵二叉树。例, 前序序列 { ABHFDECKG } 和中序序列 { HBDFAEKCG }, 构造二叉树过程如 下:
三个结点构成的不同的二叉树
8
用二 叉 树 表达实际问题
例2 双人比赛的所有可能的结局
开始
甲
开局连赢两局 或五局三胜
乙
甲
甲 甲 乙
乙
乙 甲 乙 甲 甲 乙
甲
乙 甲
乙
乙
甲
乙甲
乙
甲
乙 甲 乙
二叉树的性质
数据结构
性质1 若二叉树的层次从1开始, 则在二叉树的 第 i 层最多有 2i -1个结点。(i 1) [证明用数学归纳法] 性质2 高度为k的二叉树最多有 2k-1个结点。 (k 0) [证明用求等比级数前k项和的公式]
前序遍历二叉树算法的框架是 若二叉树为空,则空操作; 否则 – 访问根结点 (V); – 前序遍历左子树 (L); – 前序遍历右子树 (R)。
遍历结果 -+a*b-cd/ef
27
数据结构
后序遍历 (Postorder Traversal)
后序遍历二叉树算法的框架是 若二叉树为空,则空操作; 否则 – 后序遍历左子树 (L); – 后序遍历右子树 (R); – 访问根结点 (V)。
数据结构
36
左子女-右兄弟表示法 第一种解决方案
第六章树和二叉树

k
k
(第 i层的最大 )结2i点 12数 k 1
i1
i1
❖性质3:对任何一棵二叉树T,如果其终端结点数为n0, 度为2的结点数为n2,则n0=n2+1
证明:n1为二叉树T中度为1的结点数 因为:二叉树中所有结点的度均小于或等于2 所以:其结点总数n=n0+n1+n2 又二叉树中,除根结点外,其余结点都只有一个 分支进入 设B为分支总数,则n=B+1 又:这些分支是由度为1和度为2的结点射出, B=n1+2n2 于是,n=B+1=n1+2n2+1=n0+n1+n2 n0=n2+1
f
gh
4. 嵌套括号表示
a ( b ( d, e ( i, j ),f), c ( g, h ) )
★树的存储结构
※ 1. 双亲表示法
实现:结构数组存放树的结点,每个结点含两个域 数据域:存放结点本身信息 双亲域:指示本结点的双亲结点在数组中位置
特点:找双亲容易,找孩子难
typedef struct node { datatype data;
int parent; }JD; JD t[M];
a
b
c
d
e
f
gh i
如何找孩子结点
0号单元不用或
存结点个数
data
parent
00
9
1
a
0
2
b
1
3
c
1
4
d
2
5
e
2
6f
3
7g
5
8h
5
9i
5
※ 2. 孩子表示法
第6章树与二叉树
Q3: 设一棵完全二叉树具有1000个结点,则它有 489 个叶 子结点,有 488 个度为2的结点,有 1 个结点只有非空左子 树,有 0 个结点只有非空右子树。
A3:易求出总层数和末层叶子数。总层数k=log2n+1 =10; 且前9层总结点数为29-1=511 (完全二叉树的前k-1层肯定是满的) 所以末层叶子数为1000-511=489个。
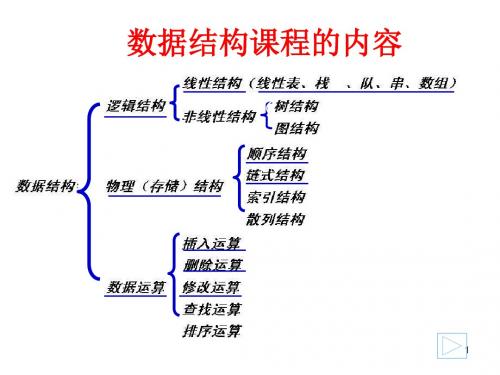
数据结构课程的内容
1
第6章 树和二叉树( Tree & Binary Tree )
特点:非线性结构,一个直接前驱,但可能有多个 直接后继(1:n)
6.1 树的基本概念 6.2 二叉树 6.3 遍历二叉树和线索二叉树 6.4 树和森林 6.5 赫夫曼树及其应用
2
6.1 树的基本概念
1. 树的定义 2 若干术语 3. 逻辑结构 4. 存储结构 5. 树的运算
所以, 全部叶子数=489(末层)+11(k-1层)=500个。 度为2的结点=叶子总数-1=499个。
第i层上的满 结点数为2i-1
另一法:可先求2度结点数,再由此得到叶子总数。 首先,k-2层的28-1(255)个结点肯定都是2度的(完全二叉) 另外,末层叶子(刚才已求出为489)所对应的双亲也是度=2, (共有489/2=244个)。 所以,全部2度结点数为255(k-2层)+244(k-1层)=499个; 总叶子数=2度结点数+1=500个。
3
1. 树的定义 由一个或多个(n≥0)结点组成的有限集合T,有
且仅有一个结点称为根(root),当n>1时,其余的 结点分为m(m≥0)个互不相交的有限集合T1,T2,…, Tm。每个集合本身又是棵树,被称作这个根的子树 。
注1:过去许多书籍中都定义树为n≥1,曾经有“空树不是 树”的说法,但现在树的定义已修改。
A3:易求出总层数和末层叶子数。总层数k=log2n+1 =10; 且前9层总结点数为29-1=511 (完全二叉树的前k-1层肯定是满的) 所以末层叶子数为1000-511=489个。
数据结构课程的内容
1
第6章 树和二叉树( Tree & Binary Tree )
特点:非线性结构,一个直接前驱,但可能有多个 直接后继(1:n)
6.1 树的基本概念 6.2 二叉树 6.3 遍历二叉树和线索二叉树 6.4 树和森林 6.5 赫夫曼树及其应用
2
6.1 树的基本概念
1. 树的定义 2 若干术语 3. 逻辑结构 4. 存储结构 5. 树的运算
所以, 全部叶子数=489(末层)+11(k-1层)=500个。 度为2的结点=叶子总数-1=499个。
第i层上的满 结点数为2i-1
另一法:可先求2度结点数,再由此得到叶子总数。 首先,k-2层的28-1(255)个结点肯定都是2度的(完全二叉) 另外,末层叶子(刚才已求出为489)所对应的双亲也是度=2, (共有489/2=244个)。 所以,全部2度结点数为255(k-2层)+244(k-1层)=499个; 总叶子数=2度结点数+1=500个。
3
1. 树的定义 由一个或多个(n≥0)结点组成的有限集合T,有
且仅有一个结点称为根(root),当n>1时,其余的 结点分为m(m≥0)个互不相交的有限集合T1,T2,…, Tm。每个集合本身又是棵树,被称作这个根的子树 。
注1:过去许多书籍中都定义树为n≥1,曾经有“空树不是 树”的说法,但现在树的定义已修改。
第6章(树和二叉树)

A B C E D F B A
^ ^
^
C
^ ^
E
D
G
24/106
在n个结点的 三叉链表 中,有n+2个 空指针域
^ ^
G
F
^
^
用链表表示的二叉树中也会存在许多空链域。例如在含有n个 结点的二叉链表中,共有2n个链域,实际用n-1链域(仅有n-1 个分支),还有n+1个空链域。 可以利用这些空链域存储其它有用信息,从而得到另一种链式 存储结构——线索链表。
B=n1+2n2
因此,N=B+1=n1+2n2+1
(6-2)
由式(6-1)和(6-2)得到:
n0+n1+n2=n1+2n2+1
可得 n0=n2+1
性质3: 对任何一棵二叉树T,如果其终端结点数为n0,度为2的 结点数为n2,则n0=n2+1。
11/106
下面介绍两种特殊形态的二叉树: 满二叉树和完全二叉树。
假设此二叉树的深度为k,则根据性质2及完全二叉树的定义得:
2k-1-1<n≤2k-1 或 2k-1≤n<2k
取对数得到: k-1≤ log2n < k ,又因为k是整数,所以有: k= log2n +1
14/106
性质5: 如果对一棵有n个结点的完全二叉树的结点按层序 编号(从第1层到第log2n +1层,每层从左到右),则对任 一结点i(1≤i≤n),有: (1)如果i=1,则结点i无双亲,是二叉树的根;如果i>1, 则其双亲是结点i/2 。 (2)如果2i>n,则结点i为叶子结点,无左孩子;否则,其 左孩子是结点2i。 (3)如果2i+1>n,则结点i无右孩子;否则,其右孩子是 结点2i+1。
^ ^
^
C
^ ^
E
D
G
24/106
在n个结点的 三叉链表 中,有n+2个 空指针域
^ ^
G
F
^
^
用链表表示的二叉树中也会存在许多空链域。例如在含有n个 结点的二叉链表中,共有2n个链域,实际用n-1链域(仅有n-1 个分支),还有n+1个空链域。 可以利用这些空链域存储其它有用信息,从而得到另一种链式 存储结构——线索链表。
B=n1+2n2
因此,N=B+1=n1+2n2+1
(6-2)
由式(6-1)和(6-2)得到:
n0+n1+n2=n1+2n2+1
可得 n0=n2+1
性质3: 对任何一棵二叉树T,如果其终端结点数为n0,度为2的 结点数为n2,则n0=n2+1。
11/106
下面介绍两种特殊形态的二叉树: 满二叉树和完全二叉树。
假设此二叉树的深度为k,则根据性质2及完全二叉树的定义得:
2k-1-1<n≤2k-1 或 2k-1≤n<2k
取对数得到: k-1≤ log2n < k ,又因为k是整数,所以有: k= log2n +1
14/106
性质5: 如果对一棵有n个结点的完全二叉树的结点按层序 编号(从第1层到第log2n +1层,每层从左到右),则对任 一结点i(1≤i≤n),有: (1)如果i=1,则结点i无双亲,是二叉树的根;如果i>1, 则其双亲是结点i/2 。 (2)如果2i>n,则结点i为叶子结点,无左孩子;否则,其 左孩子是结点2i。 (3)如果2i+1>n,则结点i无右孩子;否则,其右孩子是 结点2i+1。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5
树的基本概念
结点
度不为0的结点 根结点 结点
分支结点
叶子结点
内部结点
B E F
A C G H D I J
度为0的结点
K
L
M
6
树的基本概念
结点的度和树的度
•结点的度即结点拥有的子树个数。
•树的度是树内各结点的度的最大值。
2 B 2 E 0 F 0 A 3 C G 0 0 1 H 1 D 3 I 0 0
32
自测题
一棵完全二叉树有1000个结点,则它必 有 (1000+1)/2 =500 个叶子结点;
有 叶子总数-1=499 个度为2的结点;
有
有
1
个结点只有非空左子树;
个结点只有非空右子树。
0
因为最后一个结点坐标是偶数,所以必为左子树。有1个结点只有非 空左子树,有0个结点只有非空右子树。
33
凹入表示
广义表
14
2.二叉树
• 为何要重点研究每结点最多只有两个“叉” 的树?
– 树太一般,子树的个数无限制,表示困难 – 二叉树的结构最简单,规律性最强 – 可以证明,所有树都能转为唯一对应的二叉树,不失 一般性。
15
二叉树的基本定义
• 二叉树的定义 – 是n≥0个结点的有穷集合 – 该集合或者为空、或者由一个根结点和两个分别称为左 子树和右子树的互不相交的二叉树组成。
I
J
10
树的基本概念
• 森林:m(m>=0)棵互不相交的树的集合
A B C D
E
K L
F
G
H
M
I
J B C D H
E
K L
F
G
I
J
M
11
树的基本概念
– 树的有序性:若树中结点的子树的相对位置不能随意 改变,则称该树为有序树,否则称该树为无序树。
有序树 无序树
A B C D
=
A C D B
12
树的基本概念
31
完全二叉树性质的推论
• n个结点的完全二叉树中:
– 度为1的结点数为(n+1)%2
– 度为0的结点数为(n+1)/2 – 度为2的结点数为(n+1)/2-1
– 编号最大的分支结点是n/2
– 编号最小的叶子结点是n/2+1 • 具有n0个叶子结点的完全二叉树中共有2n0个结点或2n0-1个 结点。
n0=1+n2+2n3+…+(m-1)nm
24
特殊形态的二叉树
• 满二叉树(Full Binary Tree)
– 深度为k,结点数为2k-1
8 2 4 9 5 6 1 3 7
– 即结点数达到最大值
10 11 12 13 14 15
• 完全二叉树(Complete Binary Tree)
– 树中每个结点的编号(从上到下,从左到右)都与一个同 深度的满二叉树的结点一一对应 – 叶子结点只可能在层次最大的两层上出现
提问:第i层上至少有 1 个结点?
21
二叉树的性质
• 性质2: – 深度为k的二叉树最多有2k-1个结点(k>=1)
– 证明: • 由性质1可知:第i层最多有2i-1个结点 • 所以总的结点数最多为
1 2 3 4
k=4
22
二叉树的性质
4
1 2 5 9 10 11 12 6 3 7
• 性质3:
8
– 对任何一棵二叉树T,若叶子结点数(即度为0的结点数) 为n0,度为2的结点数为n2,则n0=n2+1
1 2 4 5 9 6 3 7
23-1 24-1
– 证明:
• 由此推出:2k-1 <= n <2k
8
10 11 12 13 14 15
• 设深度为k,则:2k-1-1< n <=2k-1
• 两边求对数:k-1 <= log2n < k
• 所以:
27
1
二叉树的性质
4
2 5 9 10 6
3 7
• 性质5:
7 8
8
9
10
9 10
10 11 12 13 14 15
BT[3]的双亲为3/2=1,即在BT[1]中; 其左孩子在BT[2i]=BT[6]中; 其右孩子在BT[2i+1]=BT[7]中。
38
一般二叉树的顺序存储结构
1 2 4 7 8 9 5 3 6 10
1 1
2 2
3 3
4 4
5 5
6 6
7 7
– 当集合为空时,称该二叉树为空二叉树。
– 逻辑结构:一对二(1:2) – 基本特征:
树的一种 每个结点最多有2棵子树(即度<=2)
D
A
B
E
C
16
二叉树与树的区别
• 树至少应有一个结点,而二叉树可以为空;
• 树的孩子结点没有限制,而二叉树中的每个结点最多有2个 孩子结点;
• 树的子树没有顺序,但如果二叉树的根结点只有一棵子树, 必须明确区分它是左子树还是右子树,因为两者将构成不同 形态的二叉树。
– 证明: • 总结点数n=n0+n1+n2
结点无外乎度为0、1、2三种情况 • 解方程组: • ”五个手指四个叉”
• 设分支数为B,则n=B+1
• 又B=n1+2n2
n n 0 n 1 n 2 • 除了树根,其余每个结 n B 1 点”上方”都有一个分 B n 1 2n 2 支 • 度为2的结点“下方”有2个分支 得:n0=n2+1 • 度为1的结点“下方”有1个分支
39
1 2 4 8 9 5 6 3 7
10 11 12 3
4 4
5 0
6 6
7 7
8 8
9 10 11 12 13 14 15 9 0 0 12 0 0 15
BT[6]的双亲为6/2=3,即在BT[3]中!
其左孩子在BT[2i]=BT[12]中;
其右孩子在BT[2i+1]=BT[13]中,而BT[13]=0,表示无右孩子。
有序树的第一个孩子和最后一个孩子
有序树中最左边的子树的根称其第一个孩子,最右边的 子树的根称其最后一个孩子。 A
B
老大
C
D 老三
13
老二
树的常用表示法
A
E F B A D J G C A B C D
B E F
C G J
D H I
E F G H I
H
I
J
嵌套集合
A(B(E,F),C,D(G(J),H,I))
• n个结点的树:高最多为n,最低为2。
• n个结点的二叉树: – 高最多为n(单支树),最低为log2n+1(完全二叉树)。
30
自测题
3.有关二叉树下列说法正确的是( ) A.二叉树的度为2
B.一棵二叉树的度可以小于2
C.二叉树中至少有一个结点的度为2 D.二叉树中任何一个结点的度都为2 4.已知一棵完全二叉树的第6层(设根是第1层)有8个叶结点, 则该完全二叉树的结点个数最多是( ) A. 39 B. 52 C. 111 D. 119
1种
20
二叉树的性质
• 性质1: – 在二叉树的第i层最多有2i-1个结点(i>=1)
– 证明: • 当i=1时,显然成立 • 假设当i=k时,也成立,即第k层最多2k-1个结点
• 当i=k+1时,由于二叉树的每个结点最多有2个孩子,所 以第k+1层最多有2*2k-1=2(k+1)-1个结点
• 故对于任意i(i>=1),二叉树的第i层最多有2i-1个结点
•结点的子树的根称为结点的孩子。 •该结点称为其孩子的双亲。 •同一双亲的孩子间互称兄弟。
双亲
B E K L F
A C G H M D I J
孩子
9
树的基本概念
祖先、子孙
结点的祖先是从根到该结点所经分支上的所有结点; 以某结点为根的子树中的任一结点都称该结点的子孙。
A
B C D
E
K L
F
G
H
M
1
完全二叉树和和满二叉树相比,就是最 底层最右边连续缺少一些结点
2 4 8 9 5 6
3 7
10 11 12 13 14 15
25
特殊形态的二叉树
思考:深度为h的完全二叉树至少有多少个结点? 2h1
结论: 深度为h且具有2h-1个结点的二叉树为满二叉树。
26
二叉树的性质
• 性质4:
– 具有n个结点的非空完全二叉树的深度为
17
二叉树的五种基本形态
A
1.空树Φ
3.只有左子树
D
B E A
4.只有右子树 2.只有树根
A
B D
E A B D E
18
5.左右子树都有
C
二叉树的基本形态
Φ
问:具有3个结点的二叉树可能有几种不同形态?
有5种
19
1.度为2的树是二叉树。 2.度为2的有序树是二叉树。
3.具有三个结点的树可以有以下五种形态:
8.已知一棵度为3的树有2个度为1的结点,3个度为2的结点, 4个度为3的结点,则该树有______ 个叶子结点。 12
35
二叉树
• 本节小结
– 二叉树的概念和类型定义
• 注意和树的类型定义的对比 – 二叉树的性质 • 要求自己能推导、应用、推广
36
3.二叉树的存储结构
• 二叉树的顺序存储结构 – 用一维数组来表示 #define MAX_TREE_SIZE 100 typedef datatype SqBiTree[MAX_TREE_SIZE]; SqBiTree Bt; – 按照满二叉树的顺序存放
树的基本概念
结点
度不为0的结点 根结点 结点
分支结点
叶子结点
内部结点
B E F
A C G H D I J
度为0的结点
K
L
M
6
树的基本概念
结点的度和树的度
•结点的度即结点拥有的子树个数。
•树的度是树内各结点的度的最大值。
2 B 2 E 0 F 0 A 3 C G 0 0 1 H 1 D 3 I 0 0
32
自测题
一棵完全二叉树有1000个结点,则它必 有 (1000+1)/2 =500 个叶子结点;
有 叶子总数-1=499 个度为2的结点;
有
有
1
个结点只有非空左子树;
个结点只有非空右子树。
0
因为最后一个结点坐标是偶数,所以必为左子树。有1个结点只有非 空左子树,有0个结点只有非空右子树。
33
凹入表示
广义表
14
2.二叉树
• 为何要重点研究每结点最多只有两个“叉” 的树?
– 树太一般,子树的个数无限制,表示困难 – 二叉树的结构最简单,规律性最强 – 可以证明,所有树都能转为唯一对应的二叉树,不失 一般性。
15
二叉树的基本定义
• 二叉树的定义 – 是n≥0个结点的有穷集合 – 该集合或者为空、或者由一个根结点和两个分别称为左 子树和右子树的互不相交的二叉树组成。
I
J
10
树的基本概念
• 森林:m(m>=0)棵互不相交的树的集合
A B C D
E
K L
F
G
H
M
I
J B C D H
E
K L
F
G
I
J
M
11
树的基本概念
– 树的有序性:若树中结点的子树的相对位置不能随意 改变,则称该树为有序树,否则称该树为无序树。
有序树 无序树
A B C D
=
A C D B
12
树的基本概念
31
完全二叉树性质的推论
• n个结点的完全二叉树中:
– 度为1的结点数为(n+1)%2
– 度为0的结点数为(n+1)/2 – 度为2的结点数为(n+1)/2-1
– 编号最大的分支结点是n/2
– 编号最小的叶子结点是n/2+1 • 具有n0个叶子结点的完全二叉树中共有2n0个结点或2n0-1个 结点。
n0=1+n2+2n3+…+(m-1)nm
24
特殊形态的二叉树
• 满二叉树(Full Binary Tree)
– 深度为k,结点数为2k-1
8 2 4 9 5 6 1 3 7
– 即结点数达到最大值
10 11 12 13 14 15
• 完全二叉树(Complete Binary Tree)
– 树中每个结点的编号(从上到下,从左到右)都与一个同 深度的满二叉树的结点一一对应 – 叶子结点只可能在层次最大的两层上出现
提问:第i层上至少有 1 个结点?
21
二叉树的性质
• 性质2: – 深度为k的二叉树最多有2k-1个结点(k>=1)
– 证明: • 由性质1可知:第i层最多有2i-1个结点 • 所以总的结点数最多为
1 2 3 4
k=4
22
二叉树的性质
4
1 2 5 9 10 11 12 6 3 7
• 性质3:
8
– 对任何一棵二叉树T,若叶子结点数(即度为0的结点数) 为n0,度为2的结点数为n2,则n0=n2+1
1 2 4 5 9 6 3 7
23-1 24-1
– 证明:
• 由此推出:2k-1 <= n <2k
8
10 11 12 13 14 15
• 设深度为k,则:2k-1-1< n <=2k-1
• 两边求对数:k-1 <= log2n < k
• 所以:
27
1
二叉树的性质
4
2 5 9 10 6
3 7
• 性质5:
7 8
8
9
10
9 10
10 11 12 13 14 15
BT[3]的双亲为3/2=1,即在BT[1]中; 其左孩子在BT[2i]=BT[6]中; 其右孩子在BT[2i+1]=BT[7]中。
38
一般二叉树的顺序存储结构
1 2 4 7 8 9 5 3 6 10
1 1
2 2
3 3
4 4
5 5
6 6
7 7
– 当集合为空时,称该二叉树为空二叉树。
– 逻辑结构:一对二(1:2) – 基本特征:
树的一种 每个结点最多有2棵子树(即度<=2)
D
A
B
E
C
16
二叉树与树的区别
• 树至少应有一个结点,而二叉树可以为空;
• 树的孩子结点没有限制,而二叉树中的每个结点最多有2个 孩子结点;
• 树的子树没有顺序,但如果二叉树的根结点只有一棵子树, 必须明确区分它是左子树还是右子树,因为两者将构成不同 形态的二叉树。
– 证明: • 总结点数n=n0+n1+n2
结点无外乎度为0、1、2三种情况 • 解方程组: • ”五个手指四个叉”
• 设分支数为B,则n=B+1
• 又B=n1+2n2
n n 0 n 1 n 2 • 除了树根,其余每个结 n B 1 点”上方”都有一个分 B n 1 2n 2 支 • 度为2的结点“下方”有2个分支 得:n0=n2+1 • 度为1的结点“下方”有1个分支
39
1 2 4 8 9 5 6 3 7
10 11 12 3
4 4
5 0
6 6
7 7
8 8
9 10 11 12 13 14 15 9 0 0 12 0 0 15
BT[6]的双亲为6/2=3,即在BT[3]中!
其左孩子在BT[2i]=BT[12]中;
其右孩子在BT[2i+1]=BT[13]中,而BT[13]=0,表示无右孩子。
有序树的第一个孩子和最后一个孩子
有序树中最左边的子树的根称其第一个孩子,最右边的 子树的根称其最后一个孩子。 A
B
老大
C
D 老三
13
老二
树的常用表示法
A
E F B A D J G C A B C D
B E F
C G J
D H I
E F G H I
H
I
J
嵌套集合
A(B(E,F),C,D(G(J),H,I))
• n个结点的树:高最多为n,最低为2。
• n个结点的二叉树: – 高最多为n(单支树),最低为log2n+1(完全二叉树)。
30
自测题
3.有关二叉树下列说法正确的是( ) A.二叉树的度为2
B.一棵二叉树的度可以小于2
C.二叉树中至少有一个结点的度为2 D.二叉树中任何一个结点的度都为2 4.已知一棵完全二叉树的第6层(设根是第1层)有8个叶结点, 则该完全二叉树的结点个数最多是( ) A. 39 B. 52 C. 111 D. 119
1种
20
二叉树的性质
• 性质1: – 在二叉树的第i层最多有2i-1个结点(i>=1)
– 证明: • 当i=1时,显然成立 • 假设当i=k时,也成立,即第k层最多2k-1个结点
• 当i=k+1时,由于二叉树的每个结点最多有2个孩子,所 以第k+1层最多有2*2k-1=2(k+1)-1个结点
• 故对于任意i(i>=1),二叉树的第i层最多有2i-1个结点
•结点的子树的根称为结点的孩子。 •该结点称为其孩子的双亲。 •同一双亲的孩子间互称兄弟。
双亲
B E K L F
A C G H M D I J
孩子
9
树的基本概念
祖先、子孙
结点的祖先是从根到该结点所经分支上的所有结点; 以某结点为根的子树中的任一结点都称该结点的子孙。
A
B C D
E
K L
F
G
H
M
1
完全二叉树和和满二叉树相比,就是最 底层最右边连续缺少一些结点
2 4 8 9 5 6
3 7
10 11 12 13 14 15
25
特殊形态的二叉树
思考:深度为h的完全二叉树至少有多少个结点? 2h1
结论: 深度为h且具有2h-1个结点的二叉树为满二叉树。
26
二叉树的性质
• 性质4:
– 具有n个结点的非空完全二叉树的深度为
17
二叉树的五种基本形态
A
1.空树Φ
3.只有左子树
D
B E A
4.只有右子树 2.只有树根
A
B D
E A B D E
18
5.左右子树都有
C
二叉树的基本形态
Φ
问:具有3个结点的二叉树可能有几种不同形态?
有5种
19
1.度为2的树是二叉树。 2.度为2的有序树是二叉树。
3.具有三个结点的树可以有以下五种形态:
8.已知一棵度为3的树有2个度为1的结点,3个度为2的结点, 4个度为3的结点,则该树有______ 个叶子结点。 12
35
二叉树
• 本节小结
– 二叉树的概念和类型定义
• 注意和树的类型定义的对比 – 二叉树的性质 • 要求自己能推导、应用、推广
36
3.二叉树的存储结构
• 二叉树的顺序存储结构 – 用一维数组来表示 #define MAX_TREE_SIZE 100 typedef datatype SqBiTree[MAX_TREE_SIZE]; SqBiTree Bt; – 按照满二叉树的顺序存放
