2刚体的转动惯量(大学物理---刚体部分)
大学物理实验报告测量刚体的转动惯量

大学物理实验报告测量刚体的转动惯量.doc“大学物理实验报告测量刚体的转动惯量.doc”是一份关于大学物理实验,它的目的是测量刚体的转动惯量。
本文将详细介绍这次实验的基本步骤、原理以及实验的结果。
一、实验的基本步骤1.准备实验仪器:本次实验使用的仪器包括:示波器、图形表、旋转惯量测试仪、调速装置、力传感器及其他部件。
2.组装实验装置:将准备好的实验仪器组装成实验装置,并将刚体放入实验装置内,使之受到示波器的旋转作用。
3.调整调速装置:调整调速装置,使得刚体开始旋转,并注意刚体的旋转方向,调节调速装置的转速,使得刚体的转速保持在恒定的水平。
4.记录数据:用示波器记录旋转角度随时间的变化,并同时记录力传感器所测量的旋转惯量。
5.分析实验结果:根据记录下来的数据,分析实验结果,计算出刚体的转动惯量。
二、实验原理转动惯量(Moment of Inertia)是指物体在旋转运动中,对外力的惯性反应能力,是物体的质量和形状的函数,可以表示物体的转动惯性。
转动惯量可以用符号I表示,它的单位是公斤·米²/秒²。
根据牛顿的第二定律,可以知道,物体受到外力的作用时,它的转动惯量会发生变化。
即:F=ma= dI/dt (F 为外力,m为物体的质量,a为物体的转动加速度,I为物体的转动惯量)。
因此,可以通过测量刚体受到外力作用时,它的转动惯量的变化来获得刚体的转动惯量。
三、实验结果本次实验结果显示,所测量刚体的转动惯量为I=3.7 kg·m²/s²。
因此,我们可以得出结论:当刚体受到外力作用时,它的转动惯量会发生变化,且转动惯量的变化量与外力的大小成正比。
总结本次实验的目的是测量刚体的转动惯量。
实验中,我们使用了示波器、图形表、旋转惯量测试仪、调速装置、力传感器等仪器,并将它们组装成实验装置,调节调速装置使得刚体开始旋转,然后用示波器记录旋转角度随时间的变化,同时也记录力传感器所测量的旋转惯量,根据记录下来的数据分析实验结果,最终计算出刚体的转动惯量:I=3.7 kg·m²/s²。
大学物理.第三章.刚体的转动

和角速度 .
解 细杆受重力和
铰链对细杆的约束力
FN
作用 3g sin
2l
3g (1 cos )
l
§3-4 力矩的功 定轴转动的动能定理
一、力矩的功
z
O
d r
速度ω 绕端点转动,摩擦系数为μ 求M摩擦力。
ω
解: 质量线密度:
m L
dm
r dr
质量元:
r dm dr
所受摩擦力为:
dF gdm gdr
例3-5 现有一圆盘在平面内以角速度ω 转动,求 摩擦力产生的力矩(μ 、m、R)。
dr
ωr
解:
dm ds rdrd dF gdm grdrd dM1 rdF r2gdrd
I mi ri2 -质量不连续分布
i
r 2dm -质量连续分布
d -线分布λ=m/ι 质量元: dm ds -面分布σ=m/S
dV -体分布ρ=m/V
二、决定转动惯量的三因素
1)刚体的质量; 2)刚体的质量分布; (如圆 环与圆盘的不同);
3)刚体转轴的位置。 (如细棒绕中心、绕一端)
运动。 一、何谓刚体
在任何情况下形状和大小都不发生变化的
物体。即每个质元之间的距离无论运动或
受外力时都保持不变。
理想模型
ri j c mj
二、刚体运动的两种基本形式 mi
平动----刚体运动时,刚体内任一直线恒保 持平行的运动(即该直线方向保持不变)
刚体的平动过程
c a b
刚体的平动过程
能运用以上规律分析和解决包括 质点和刚体的简单系统的力学问题.
大学物理刚体的转动惯量的研究实验报告

大学物理仿真实验报告电子 3班实验名称:刚体的转动惯量的研究实验简介在研究摆的重心升降问题时,惠更斯发现了物体系的重心与后来欧勒称之为转动惯量的量。
转动惯量是表征刚体转动惯性大小的物理量,它与刚体的质量、质量相对于转轴的分布有关。
本实验将学习测量刚体转动惯量的基本方法,目的如下:1.用实验方法验证刚体转动定律,并求其转动惯量;2.观察刚体的转动惯量与质量分布的关系3.学习作图的曲线改直法,并由作图法处理实验数据。
实验原理1.刚体的转动定律具有确定转轴的刚体,在外力矩的作用下,将获得角加速度β ,其值与外力矩成正比,与刚体的转动惯量成反比,即有刚体的转动定律:M = I β(1)利用转动定律,通过实验的方法,可求得难以用计算方法得到的转动惯量。
2.应用转动定律求转动惯量如图所示,待测刚体由塔轮,伸杆及杆上的配重物组成。
刚体将在砝码的拖动下绕竖直轴转动。
设细线不可伸长,砝码受到重力和细线的张力作用,从静止开始以加速度 a 下落,其运动方程为 mg – t=ma ,在 t 时间内下落的高度为 h=at 2/2 。
刚体受到张力的力矩为T r和轴摩擦力力矩 M。
由转动定律可得到刚体的转动运动方程:T - Mf = I β 。
绳与塔轮间f r无相对滑动时有 a = r β,上述四个方程得到:m(g - a)r - M f = 2hI/rt2(2)M f与张力矩相比可以忽略,砝码质量m比刚体的质量小的多时有a<<g,所以可得到近似表达式:mgr = 2hI/ rt 2(3)式中 r 、h、t 可直接测量到, m是试验中任意选定的。
因此可根据( 3)用实验的方法求得转动惯量 I 。
3.验证转动定律,求转动惯量从( 3)出发,考虑用以下两种方法:A.作 m – 1/t 2图法:伸杆上配重物位置不变,即选定一个刚体,取固定力臂r 和砝码下落高度 h,( 3)式变为:M = K 1/ t 2(4)式中 K1 = 2hI/ gr 2 为常量。
大学物理实验报告-刚体转动定律

大学物理实验报告-刚体转动定律
实验目的:探究刚体转动的基本定律。
实验仪器:转动台、刚体转轴、刚体、刻度盘、秤、细线、阻尼器。
实验原理:刚体转动的基本定律包括:1)转动定律:刚体受
外力矩的作用产生角加速度,且角加速度与作用力矩成正比,与物体的转动惯量成反比;2)动量定理:刚体的角动量在无
外力矩作用下保持守恒。
实验步骤:
1. 将转动台放在水平桌面上,并调整水平度。
2. 将刚体转轴安装在转动台上,保证转轴能够自由转动。
3. 在转轴上放置刚体,并固定好。
4. 将刻度盘压在转轴上,确保盘面与刚体转动面平行,并零位对准。
5. 在刚体上绑上细线,另一端挂上适量的重物。
6. 调整阻尼器,使刚体转动不受外界干扰。
7. 按下计时器,同时放开刚体。
8. 记录刚体的转动时间,并测量刚体转过的角度。
9. 重复实验多次,取平均值。
实验数据处理:
1. 根据实验数据计算刚体的转动惯量,转动惯量的计算公式为:
I = m * g * R * T^2 / (2 * π^2 * θ),其中m为挂在细线末端的
重物质量,g为重力加速度,R为细线长度,T为转动时间,θ
为刚体转过的角度。
2. 将实验得到的转动惯量与刚体的几何结构进行比较,检验是
否符合刚体转动定律。
3. 计算实验误差,评估实验结果的可靠性。
实验注意事项:
1. 安全操作,避免伤害自己和他人。
2. 实验时要保持转动台的稳定,阻尼器的正确调整。
3. 实验时要注意量具的准确读数和记录。
4. 实验结束后,保持实验环境整洁,归还实验器材。
大学物理—刚体的动轴转动

F
(3) F1 对转轴的力矩为零,
在定轴转动中不予考虑。
转动 平面
r
F2
(4)在转轴方向确定后,力对 转轴的力矩方向可用+、-号表示。
2. 刚体定轴转动定律 对刚体中任一质量元mi
O’
f i -内力
-外力
ω
Fi
ri
mi
fi
i i
Fi
应用牛顿第二定律,可得: O
v v r sin r sin 900
和 构成的平面,如 图所示相应的切向加速度和向心加速度分别为
v 的方向垂直于
2
r 78.5m / s
r
at ar 3.14m / s
3
2
2
an r 6.16 10 m / s 边缘上该点的加速度 a an al 其中 a l 的方向 与 v 的方向相反,a n 的方向指向轴心,a 的大小
1 m1 2m 2 m g M / r 2 T1 m1 g a 1 m 2 m1 m 2
22
1 m2 2m1 m g+M / r 2 T2 m1 g-a 1 m 2 m1 m 2
§4- 1 刚体的平动、转动和定轴转动
1. 刚体 刚体是一种特殊的质点系,无论它在多大外力 作用下,系统内任意两质点间的距离恒保持不变。 2.平动和转动 刚体最简单的运动形式是平动和转动。 当刚体运动时,如果刚体内任何一条给定的直 线,在运动中始终保持平行,这种运动叫平动。 刚体平动时,在任意一段时间内,刚体中各质 点的位移相同。且在任何时刻,各质点的速度和加 速度都相同。
常见刚体的转动惯量

常见刚体的转动惯量
刚体是指在运动过程中形状和大小不变的物体。
在物理学中,常见的刚体有球体、圆盘、长方体等。
这些刚体在绕某一轴旋转时,会具有不同的转动惯量。
转动惯量是描述刚体在转动过程中惯性特征的物理量。
它与刚体的形状、质量分布以及绕轴旋转的位置有关。
对于球体来说,转动惯量与球的半径和质量有关。
球体的转动惯量是一个常量,与绕轴旋转的位置无关。
而对于长方体来说,转动惯量则与长方体的质量分布有关,不同位置的转动惯量也会有所不同。
转动惯量的大小决定了刚体在转动过程中的惯性。
转动惯量越大,刚体的转动越困难,需要更大的力来改变其转动状态。
而转动惯量越小,刚体的转动越容易,需要较小的力就可以改变其转动状态。
在日常生活中,我们可以观察到转动惯量的一些实际应用。
比如,当我们骑自行车时,如果车轮的转动惯量较大,那么在起步或者停车时会感到较大的阻力。
而如果车轮的转动惯量较小,那么起步和停车的时候则会感到比较轻松。
转动惯量还可以影响到一些运动的稳定性。
例如,当我们骑自行车或者滑冰时,如果身体的转动惯量较大,那么在转弯或者改变方向时会感到不稳定,容易失去平衡。
而如果身体的转动惯量较小,那么在转弯或者改变方向时会感到相对稳定。
转动惯量是刚体在转动过程中的一个重要物理量。
它与刚体的形状、质量分布以及绕轴旋转的位置有关。
转动惯量的大小决定了刚体转动的惯性特征,影响着刚体在转动过程中所受力的大小和方向。
通过研究转动惯量,我们可以更好地理解刚体的转动行为,并且应用到日常生活和工程实践中。
大学物理实验报告-刚体转动定律

(4)在同一张坐标纸上,分别准确作出空载时的 — 直线和载荷时的 — 直线,从图上准备读出 、 和 、 (这是关键,对计算结果的误差影响很大);
(5)由公式再分别算出 、 、 、 、 ;
(6)算出理论值 ,将理论值与实验值比较,算出 和 的相对误差,作实验讨论,进行误差分析。
可见: 和 呈线性关系,以 为纵坐标,以 为横坐标,作出 — 曲线(这种处理数据的方法称为曲线改直法),如果各点的连线是一条直线,就验证了转动定律,并可由直线的斜率 和在纵坐标轴上的截距C分别求出转动惯量和摩擦力矩为:
, 。为求出 ,必须在同一张坐标纸上,分别作出空载时的 — 直线和载荷时的 — 直线,由图上分别准备读出 、 和 、 ,再分别算出 、 和 、 ,则算出 ,并与 的理论值进行比较,已知圆盘转动惯量的理论值为: 。式中: 为圆盘的质量, 为圆盘的半径。
在外力矩 和摩擦力矩 的共同作用下,由转动定律得知: — =
式中: 是转动体系的转动惯量, 是角加速度, 是下落砝码的质量, 是绕线轮的半径。由式看出:测定转动惯量的关键是角加速度 ,这可由下述方法确定:
1.单角度设置法( =0)求出刚体的转动惯量和摩擦力矩
在恒力矩作用下,转动体系将作均匀变速转动,故有下列公式:
方法、步骤:
1.单角度设置法( =0)
(1)调节实验装置。用水准仪器调节承物台水平,使转轴垂直于底座,尽量减少摩擦。选用合适的塔轮半径。调整塔轮和定滑轮之间的拉线呈水平状态,并保持定滑轮的滑槽与所选用的塔轮半径垂直。
(2)承物台空载。接通毫秒计电源,预置数N,毫秒计复零准备记录,将遮光细棒紧靠光电门,轻轻放手,使( =0),使塔轮在砝码作用下,从静止开始转动,记下时间t,以后每次增加砝码5g,重复测时3次,从5g一直增加到55g,记入表5-9;
刚体转动惯量的测定

刚体转动惯量的测定转动惯量是描述刚体转动惯性大小的物理量,是研究和描述刚体转动规律的一个重要物理量,它不仅取决于刚体的总质量,而且与刚体的形状、质量分布以及转轴位置有关。
对于质量分布均匀、具有规则几何形状的刚体,可以通过数学方法计算出它绕给定转动轴的转动惯量。
对于质量分布不均匀、没有规则几何形状的刚体,用数学方法计算其转动惯量是相当困难的,通常要用实验的方法来测定其转动惯量。
因此,学会用实验的方法测定刚体的转动惯量具有重要的实际意义。
实验上测定刚体的转动惯量,一般都是使刚体以某一形式运动,通过描述这种运动的特定物理量与转动惯量的关系来间接地测定刚体的转动惯量。
测定转动惯量的实验方法较多,如拉伸法、扭摆法、三线摆法等,本实验是利用“刚体转动惯量实验仪”来测定刚体的转动惯量。
为了便于与理论计算比较,实验中仍采用形状规则的刚体。
【实验目的】1. 学习用转动惯量仪测定物体的转动惯量。
2. 研究作用在刚体上的外力矩与刚体角加速度的关系,验证刚体转动定律和平行轴定理。
3. 观测转动惯量随质量、质量分布及转动轴线的不同而改变的状况。
【实验仪器】ZKY-ZS 转动惯量实验仪及其附件(砝码,金属圆柱、圆盘及圆柱), ZKY-J1通用电脑计时器.图1 转动惯量测定装置实物图【实验原理】根据刚体的定轴转动定律dtd JJ M ωβ==, 只要测定刚体转动时所受的合外力矩及该力矩作用下刚体转动的角加速度β,则可计算出该刚体的转动惯量,这是恒力矩转动法测定转动惯量的基本原理和设计思路。
一、转动惯量J 的测量原理砝码盘及其砝码是系统转动的动力。
分析转动系统受力如图2所示:当砝码钩上放置一定的砝码时,若松开手,则在重力的作用下,砝码就会通过细绳带动塔轮加速转动。
当砝码绳脱离塔轮后,系统将只在摩擦力矩的作用下转动。
图2 转动系统受力图本实验中待测试件放在实验台上,随同实验台一起做定轴转动。
设空实验台(未加试件)转动时,其转动惯量为0J ,加上被测刚体后的转动惯量为J ,由转动惯量的叠加原理可知,则被测试件的转动惯量被测J 为0J J J -=被测 或 被测物J J J +=0实验时,先测出系统支架(空实验台)的转动惯量0J ,然后将待测物放在支架上,测量出转动惯量为J ,利用上式可计算出待测物的转动惯量。
大学刚体知识点总结

大学刚体知识点总结一、刚体的概念和基本性质1. 刚体的基本概念刚体是指在运动或受力作用时,其内部各个部分之间的相对位置保持不变的物体。
刚体的定义包括两个方面:一是刚体的形状和大小在所讨论的现象中不发生改变;二是刚体内各点的相对位置在所讨论的现象中也不发生改变。
这意味着刚体是刚性的,并且不会发生形变。
2. 刚体的基本性质(1)刚性:刚体的所有部分在相互作用下保持相对位置不变,不发生相对位移或形变,这就是刚体的基本性质之一。
(2)刚体的自由度:刚体的自由度是指刚体可以自由运动的最少独立坐标数。
刚体的自由度可以通过不同类型的运动来描述,包括平动、转动和复合运动。
(3)刚体的质心:刚体的质心是指一个质点,它等效于整个刚体对于外力的作用。
在某些情况下,刚体可以看作是一个质点,其运动和受力可以通过质心来描述。
二、刚体的平动1. 刚体的平动运动在刚体的平动运动中,刚体上的各个点都以相同的速度和方向移动。
平动运动可以通过刚体的速度和加速度来描述,它是刚体运动的一种常见形式。
2. 刚体的平动运动描述(1)刚体的平动速度:刚体上的各个点的速度大小和方向相同,这就是刚体的平动速度。
刚体的平动速度可以通过质点运动方程或者质心运动方程来描述。
(2)刚体的平动加速度:刚体上的各个点的加速度大小和方向相同,这就是刚体的平动加速度。
刚体的平动加速度可以通过质点加速度方程或者质心加速度方程来描述。
(3)刚体的平动运动学问题:刚体的平动运动学问题包括刚体的位移、速度、加速度等相关内容,它们可以通过运动学方法来解决。
三、刚体的转动1. 刚体的转动运动在刚体的转动运动中,刚体围绕固定轴旋转。
转动运动是刚体运动的另一种常见形式,它可以通过角度和角速度来描述。
2. 刚体的转动运动描述(1)刚体的角度和角速度:刚体围绕固定轴旋转时,可以通过角度和角速度来描述。
角度是指刚体围绕轴线旋转的角度,角速度是指刚体围绕轴线旋转的角度变化率。
(2)刚体的转动惯量:刚体围绕轴线旋转时,需要通过转动惯量来描述其转动惯性。
大学物理4-2刚体的角动量 转动动能 转动惯量

刚体绕定轴的角动量表达式:
Lz J
刚体的转动动能
2. 刚体的转动动能
刚体的转动动能应该是组成刚体的各个质点
的动能之设和刚。体中第i个质点的质量为 , mi
速度为 v,i 则该质点的动能为:
1 2
mivi2
刚体做定轴转动时,各质点的角速度相同。
设质点
mi
离轴的垂直距离为
vi ri
ri ,则它的线速度
因此整个刚体的动能
EK
12mivi2
1 2
ri2mi 2
刚体的转动动能
式中 式写为
是m刚iri体2 对转轴的转动惯量
EK
1 2
J 2
,所J以上
上式中的动能是刚体因转动而具有的动能,因 此叫刚体的转动动能。
转动惯量的计算
3. 转动惯量的计算
按转动惯量的定义: J ri2mi
刚体的质量可认为是连续分布的,所以上式可 写成积分形式
J r2dm 要求: 细棒、薄圆盘、圆环
dl 其中质元dm可表示为 dm ds
dv
r —为质元到转轴的距离
转动惯量的计算
刚体运动:
平动: 平动动能 1 mv2 线动量 mv
2
定轴转动:转动动能 1 J 2 角动量 J
2
质量是刚体平动时惯性大小的量度。 转动惯量是刚体转动时惯性大小的量度。 补:平行轴定理、垂直轴定理(适用于薄平面刚体)。
Li Ri pi Ri mivi
因 vi Ri ,所以 L的i 大小为
Li mi Rivi
方向如图所示。
z
L
Li Liz
ri
O Ri mi
刚体的角动量
大学物理实验刚体转动惯量

大学物理实验刚体转动惯量【预习要求】1.参见大学物理刚体一章,导出规则物体:圆柱、圆筒和圆球过几何轴,圆柱、圆筒和细杆对过中心、垂直于几何轴的转动惯量的计算公式。
2.根据实验内容,在预习报告上自行设计、准备好数据记录表格。
【实验目的】1.了解扭摆测量转动惯量的原理和方法。
2.用扭摆测定弹簧的扭转常数及几种不同形状刚体的转动惯量。
3.验证刚体转动的平行轴定理。
【实验原理】1.扭摆测量物体转动惯量、弹簧的扭转常数图10-1扭摆扭摆的构造如图10-1所示。
在垂直轴1上装有一根薄片状的螺旋弹簧2,用以产生恢复力矩。
在轴的上方可以装上各种待测物体。
垂直轴与支座间装有轴承,以降低摩擦力矩。
3为水平仪,用来调整仪器转轴成铅直。
将物体在水平面内转过角,在弹簧的恢复力矩作用下,物体就开始绕垂直轴作往返扭转运动。
根据虎克定律,弹簧受扭转而产生的恢复力矩M与所转过的角度成正比,即MK(10-1)式中,K为弹簧的扭转常数,根据转动定律MI式中,I为物体绕转轴的转动惯量,为角加速度,由上式得令2M(10-2)IKI,忽略轴承的摩擦阻力矩,由(10-1)、(10-2)得ddt22KI2上述微分方程表示扭摆运动具有角谐振动的特性,即角加速度与角位移成正比,并且方向相反。
此微分方程的解为Acot式中,A为谐振动的角振幅,为角位移,为初相位角,为角频率。
此谐振动的周期为2IKT2(10-3)由式(10-3)可知,只要实验测得物体扭摆的摆动周期T,并在I和K中任何一个量已知时,即可计算出另一个量。
-1-本实验利用测量一个形状规则物体(圆柱体)在扭摆上的摆动周期来测量弹簧K值。
圆柱体的转动惯量I1'可根据它的质量和几何尺寸用理论公式直接计算得到,从而可算出本仪器弹簧的K值。
因圆柱是放在金属载物盘上测量,须考虑载物盘的转动惯量I盘,所以有K422I1T1T盘2'和I盘I1T盘T1T盘22'2(10-4)式中T盘和T1分别为只有金属载物盘和载有圆柱体时测出的摆动周期。
实验2 刚体转动惯量的测定
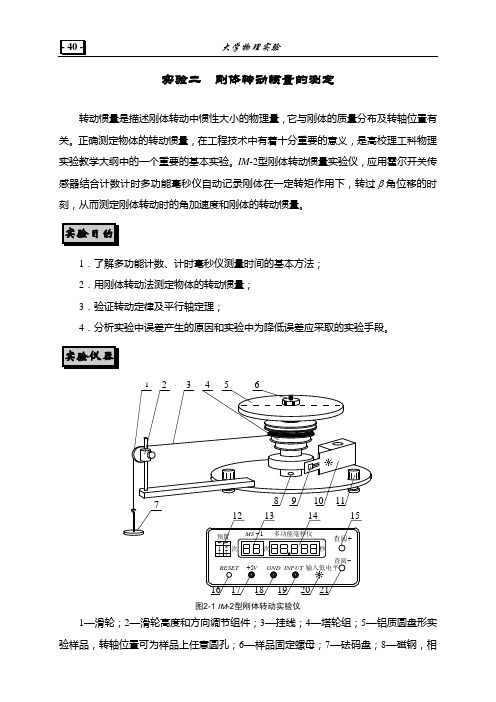
实验二刚体转动惯量的测定转动惯量是描述刚体转动中惯性大小的物理量,它与刚体的质量分布及转轴位置有关。
正确测定物体的转动惯量,在工程技术中有着十分重要的意义,是高校理工科物理实验教学大纲中的一个重要的基本实验。
IM-2型刚体转动惯量实验仪,应用霍尔开关传感器结合计数计时多功能毫秒仪自动记录刚体在一定转矩作用下,转过β角位移的时刻,从而测定刚体转动时的角加速度和刚体的转动惯量。
1.了解多功能计数、计时毫秒仪测量时间的基本方法;2.用刚体转动法测定物体的转动惯量;3.验证转动定律及平行轴定理;4.分析实验中误差产生的原因和实验中为降低误差应采取的实验手段。
图2-1IM-2型刚体转动实验仪1—滑轮;2—滑轮高度和方向调节组件;3—挂线;4—塔轮组;5—铝质圆盘形实验样品,转轴位置可为样品上任意圆孔;6—样品固定螺母;7—砝码盘;8—磁钢,相对霍尔开关传感器时,传感器输出低电平;9—霍尔开关传感器,红线接毫秒仪V5+接线柱,黑线接GND接线柱,黄线接INPUT接线柱;10—传感器固定架,装有磁钢,可任意放置于铁质底盘上;11—实验样品水平调节旋钮;12—毫秒仪次数预置拔码开关,可预设641-次;13—次数显示,00为开始计数、计时;14—时间显示,与次数相对应,时间为开始计时的累计时间;15—计时结束后,用手按+1查阅键,查阅对应次数的时间;16—毫秒仪复位键,测量前和重新测量时可按该键;17—V 5+电源接线柱;18—电源GND 接线柱;19—INPUT 输入接线柱;20—输入低电平指示;21—计时结束后,用手按次数1-查阅键,查阅对应次数的时间。
一、转动力矩、转动惯量和角加速度的关系当系统受外力作用时,系统作匀加速转动。
系统所受的外力矩有二个,一个为绳子张力T 产生的力矩r T M ⋅=,r 为塔轮上绕线轮的半径;一个是摩擦力矩μM 。
所以,2βμJ MM =+,即2βμJ Mr T =+⋅ ------------------------------------ (2-1)式中2β为系统的角加速度,此时为正值,J 为转动系统的转动惯量,μM 为摩擦力矩,数值为负。
2刚体的转动惯量(大学物理 - 刚体部分)

刚体的转动惯量与哪些物理量有关? ①.与刚体质量有关。 ②.与质量对轴的分布有关。
③.与轴的位置有关。
二.质量连续分布刚体的转动惯量计算
1.计算公式
2 i i
J m r
i 1
n
ri
mi
r
dm
J r dm
2
§4.刚体的转动惯量/ 二、转动惯量的计算
例2:长为 l、质量为 m 的匀质细杆,绕 与杆垂直的质心轴转动,求转动惯量 J。
J r dm
2
m l
l 2
dm
细杆为线质量分布,单位长 度的质量为:
xБайду номын сангаас
l 2
m l 建立坐标系,坐标原点选在质心处。 分割质量元 dm ,长度为 dx ,
dm dx
§4.刚体的转动惯量/ 二、转动惯量的计算
§4.刚体的转动惯量/ 四、平行轴定理
2
r l
r l 圆柱体转轴通过 中心与几何轴垂直
圆柱体转轴沿几何轴
1 2 J mr 2
mr ml J 4 12
2
2
§4.刚体的转动惯量/ 三、典型刚体的转动惯量
l 细棒转轴通过 中心与棒垂直
l 细棒转轴通过 端点与棒垂直
ml J 12
2
ml2 J 3
§4.刚体的转动惯量/ 三、典型刚体的转动惯量
o x dx
J r dm
2
J x dm x dx
2 2 l / 2 l / 2
l/2
l/2
1 3 x l 3 12 m l 1 2 J ml 12
3 l/2 l / 2
大学物理03-刚体力学基础

J
r
m
2
dm
• 刚体的形状(质量分布)
16
J
注 意
r
m
2
dm
只有对于几何形状规则、质量连续且均匀分布 的刚体,才能用积分计算出刚体的转动惯量
例3-2 一均匀细棒,质量为 m ,长为 l 。求该棒对下列转轴 的转动惯量:(1)通过棒中心且与棒垂直的轴;(2)通过 棒的一端且与棒垂直的轴。 解:取如图坐标,在棒上任取质元,到转轴的垂直距离为x, 长度为 d x,该质元的质量为 dm = (m/l )dx (质量为线分布)。 A L/2 C
S
O
Mz r d
P
F
M r F
O r
F
P
F
F //
大小: M rF sin Fd 方向: 由右手螺旋法则确定
转动平面
F 应该理解为外力在转动平面内的 分力F//
转动平面
在定轴转动中,M 的方向只有两种可能指向。若先选 定了转轴的正方向,则 M 与转轴方向一致时取正 值,反之为负值
11
(3) 如果有几个外力矩作用在刚体上,则合力矩等 于各个力矩的代数和
M
i i i
ri Fi
12
2
二 刚体绕定轴的转动定律
刚体可视为由许多质点组成的,而每一个质点都遵从质点力学 的规律。刚体转动定律可由牛顿第二定律直接导出。
Fi f i mi ai mi ri
一、力对转轴的力矩
力是引起质点运动状态变化的原因,而力 矩是引起转动物体运动状态变化的原因
(2) 外力F 不在转动平面内(任意力) 可将 F 分解为转动平面内的分力 F// 和垂直于转动平面的分力F F不能引起刚体转动状态的变化 力矩:
刚体转动惯量计算方法

刚体绕轴转动惯性的度量。
其数值为J=∑ mi*ri^2,式中mi表示刚体的某个质点的质量,ri表示该质点到转轴的垂直距离。
;求和号(或积分号)遍及整个刚体。
转动惯量只决定于刚体的形状、质量分布和转轴的位置,而同刚体绕轴的转动状态(如角速度的大小)无关。
规则形状的均质刚体,其转动惯量可直接计得。
不规则刚体或非均质刚体的转动惯量,一般用实验法测定。
转动惯量应用于刚体各种运动的动力学计算中。
描述刚体绕互相平行诸转轴的转动惯量之间的关系,有如下的平行轴定理:刚体对一轴的转动惯量,等于该刚体对同此轴平行并通过质心之轴的转动惯量加上该刚体的质量同两轴间距离平方的乘积。
由于和式的第二项恒大于零,因此刚体绕过质量中心之轴的转动惯量是绕该束平行轴诸转动惯量中的最小者。
还有垂直轴定理:垂直轴定理一个平面刚体薄板对于垂直它的平面轴的转动惯量,等于绕平面内与垂直轴相交的任意两正交轴的转动惯量之和。
表达式:Iz=Ix+Iy刚体对一轴的转动惯量,可折算成质量等于刚体质量的单个质点对该轴所形成的转动惯量。
由此折算所得的质点到转轴的距离,称为刚体绕该轴的回转半径κ,其公式为_____,式中M为刚体质量;I为转动惯量。
转动惯量的量纲为L^2M,在SI单位制中,它的单位是kg·m^2。
刚体绕某一点转动的惯性由更普遍的惯量张量描述。
惯量张量是二阶对称张量,它完整地刻画出刚体绕通过该点任一轴的转动惯量的大小。
补充对转动惯量的详细解释及其物理意义:先说转动惯量的由来,先从动能说起大家都知道动能E=(1/2)mv^2,而且动能的实际物理意义是:物体相对某个系统(选定一个参考系)运动的实际能量,(P势能实际意义则是物体相对某个系统运动的可能转化为运动的实际能量的大小)。
E=(1/2)mv^2 (v^2为v的2次方)把v=wr代入上式(w是角速度,r是半径,在这里对任何物体来说是把物体微分化分为无数个质点,质点与运动整体的重心的距离为r,而再把不同质点积分化得到实际等效的r)得到E=(1/2)m(wr)^2由于某一个对象物体在运动当中的本身属性m和r都是不变的,所以把关于m、r的变量用一个变量K代替,K=mr^2得到E=(1/2)Kw^2K就是转动惯量,分析实际情况中的作用相当于牛顿运动平动分析中的质量的作用,都是一般不轻易变的量。
刚体转动惯量及其计算方法

刚体转动惯量及其计算方法刚体转动惯量,又称为转动惯性矩或转动惯量,是刚体在绕一些轴旋转时所表现出的惯性特性,表示刚体的转动惯性大小。
刚体转动惯量的计算方法取决于刚体的形状和绕轴的方向。
以下将介绍一些常见的刚体形状及其转动惯量的计算方法。
1.点质量对于一个具有质量m的质点,其转动惯量I可以简化为I=m*r^2,其中r是质点到旋转轴的距离。
2.细长棒对于一个质量为m、长度为L且绕其一端点O转动的细长棒,其转动惯量I=(1/3)*m*L^23.圆盘对于一个质量为m、半径为R的圆盘绕其垂直于圆盘平面的轴转动,其转动惯量I=(1/2)*m*R^24.球体对于一个质量为m、半径为R的球体绕其直径转动,其转动惯量I=(2/5)*m*R^25.长方体对于一个质量为m、边长分别为a、b、c的长方体绕其长边转动,其转动惯量I=(1/12)*m*(a^2+b^2)+(1/3)*m*c^26.圆环对于一个质量为m、外半径为R、内半径为r的圆环绕其中心垂直于环面的轴转动,其转动惯量I=m*(R^2+r^2)/2以上是一些简单常见形状刚体的转动惯量计算公式,实际上,对于更复杂的刚体形状,计算其转动惯量可能需要使用积分方法。
这涉及到刚体的质量分布情况以及积分计算的具体步骤,在毕业论文中可以详细描述。
此外,当刚体绕不通过其质心的轴转动时,其转动惯量的计算需要利用平行轴定理或垂直轴定理。
平行轴定理认为,刚体绕任意平行于通过其质心的轴转动的转动惯量等于其绕通过质心的轴转动惯量加上刚体质量乘以轴与质心之间的距离的平方。
垂直轴定理认为,刚体绕通过其质心的垂直轴转动的转动惯量等于其绕通过质心的任意轴转动的转动惯量减去刚体质量乘以质心到垂直轴的距离的平方。
总结起来,刚体转动惯量的计算方法依赖于刚体的形状和绕轴的方向。
对于简单形状的刚体,可以使用已知的转动惯量公式进行计算。
对于复杂形状的刚体,可能需要使用积分方法来计算转动惯量。
在计算转动惯量时,还需要考虑平行轴定理和垂直轴定理。
实验2刚体转动惯量的测定

实验2 刚体转动惯量的测量[预习思考题]1.实验中的刚体转动惯量实验仪是由哪几部分组成的?2.实验中可以通过什么方法改变转动力矩?3.实验中刚体转动过程的角加速度如何测得?转动惯量是描述刚体转动中惯性大小的物理量,对于绕定轴转动的刚体,它为一恒量,以J表示,即式中,mi为刚体上各个质点的质量,ri为各个质点至转轴的距离。
由此可见,物体的转动惯量J与刚体的总质量、质量分布及转轴的位置有关。
对于几何形状规则、对称和质量分布均匀的刚体,可以通过积分直接计算出它绕某定轴的转动惯量。
对于形状复杂或非匀质的任意物体,则一般要通过实验来测定,例如,机械零件、电机的转子、炮弹等。
测定物体的转动惯量有多种实验方法,主要分为扭摆法和恒力矩转动法两类。
本实验介绍用塔轮式转动惯量仪测定的方法,是使塔轮以一定形式旋转,通过表征这种运动特征的物理量与转动惯量的关系,进行转换测量。
该方法属于恒力矩转动法。
转动惯量是研究、设计、控制转动物体运动规律的重要参数,实验测定刚体的转动惯量具有十分重要的意义,是高校理工科物理实验教学大纲中的一个重要基本实验。
一、实验目的1.学习用转动惯量仪测定刚体的转动惯量。
2.研究作用于刚体上的外力矩与角加速度的关系。
3.验证转动定律及平行轴定理。
二、实验仪器IM-2刚体转动惯量实验仪及其附件(霍尔开关传感器、砝码等)和MS-1型多功能数字毫秒仪。
三、仪器介绍1.滑轮2.滑轮高度和方向调节组件3.挂线 4.塔轮组5.铝质圆盘承物台6.样品固定螺母7.砝码 8.磁钢9.霍尔开关传感器10.传感器固定架11.实验样品水平调节旋钮(共3个)12.毫秒仪次数预置拨码开关,可预设1-64次13.次数显示屏14.时间显示屏 l5.次数+1查阅键 16.毫秒仪复位键17.+5V电源接线柱18.电源GND(地)接线柱 19.INPUT输入接线柱 20.输入低电平指示 21.次数-1查阅键图4-3-1 IM-2刚体转动惯量实验仪和MS-1型多功能数字毫秒仪结构示意图IM-2刚体转动惯量实验仪主要由绕竖直轴转动的铝质圆盘承物台、绕线塔轮、霍尔开关传感器、磁钢、滑轮组件、砝码等组成。
常见刚体转动惯量

常见刚体转动惯量
刚体转动惯量是描述刚体绕某个轴旋转时,对绕轴的旋转惯性的度量。
它反映了刚体的形状和质量分布对转动的影响程度,是刚体运动学和动力学研究中的重要参数之一。
刚体转动惯量可以用一个标量来表示,通常用大写字母I表示。
对于一个质量均匀分布的刚体,其转动惯量可以通过几何形状和质量分布的特征来计算。
例如,对于一个球体,其转动惯量可由球体的质量和半径来确定。
对于一个长方体,则可以由长方体的质量、长度、宽度和高度来计算。
在刚体转动惯量的计算中,形状对结果有很大的影响。
例如,一个绕自身对称轴旋转的物体,其转动惯量通常较小,因为质量分布相对均匀;而一个不规则形状的物体,其转动惯量可能较大,因为质量分布不均匀。
刚体转动惯量在物理学和工程学中具有广泛的应用。
在机械工程中,它是设计和分析旋转机械系统的重要参数。
在物理学中,它是解释刚体旋转和角动量守恒定律的基础。
在天体物理学中,它用于描述行星、恒星等天体的旋转。
刚体转动惯量是描述刚体绕轴旋转时的旋转惯性的度量。
它是由刚体的形状和质量分布决定的,对于不同形状的刚体有不同的计算方法。
刚体转动惯量在物理学和工程学中具有广泛的应用,是研究刚
体运动和旋转的重要参数之一。
刚体的转动惯量公式

刚体的转动惯量公式
刚体的转动惯量是描述刚体在转动过程中抵抗改变转动状态的物理量。
转动惯量的大小与刚体的形状和质量分布有关,可以通过转动惯量公式来计算。
对于一个刚体围绕某个轴转动,其转动惯量可以表示为I,根据刚体的形状和质量分布的不同,转动惯量公式也会有所不同。
以下是一些常见形状的刚体转动惯量公式:
1. 杆状刚体绕其一端的转动惯量:
对于一个质量为m、长度为L的细长杆,其绕一端的转动惯量可以表示为I=1/3 * m * L^2。
2. 球状刚体绕其直径轴的转动惯量:
对于一个质量为m、半径为R的均匀球体,其绕直径轴的转动惯量可以表示为I=2/5 * m * R^2。
3. 圆环状刚体绕其对称轴的转动惯量:
对于一个质量为m、半径为R的圆环,其绕对称轴的转动惯量可以表示为I=m * R^2。
需要注意的是,上述公式仅适用于均匀分布质量的刚体。
对于非均匀分布的刚体,转动惯量公式需要根据具体的质量分布情况进行积分计算。
转动惯量公式在物理学中有着广泛的应用,例如在刚体的转动运动方程中,转动惯量是一个重要的物理量。
通过转动惯量的计算,我们可以了解刚体在转动过程中的惯性特性,进而分析和预测其转动运动的行为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、典型的几种刚体的转动惯量
r2 r1
薄圆盘转轴通过 中心与盘面垂直
J 1mr2 2
圆筒转轴沿几何轴
J 12m(r12r22)
§4.刚体的转动惯量/ 三、典型刚体的转动惯量
r
l
圆柱体转轴沿几何轴
J 1mr2 2
r
l 圆柱体转轴通过中 心与几何轴垂直
J mr2 ml2 4 12
§4.刚体的转动惯量/ 三、典型刚体的转动惯量
解:细杆为线质量 分布,单位长度的 质量为:
m
l
ml
dm x
o xdx l
建立坐标系,坐标原点选在边缘处。分 割质量元 dm ,长度为 dx ,
dm dx
§4.刚体的转动惯量/ 二、转动惯量的计算
J r2dm
l
l
J x2dm x2dx
0
0
x3 3
l 0
1 l3
3
m l
ml
dm x
1 3
ml
2
结果与前相同。
§4.刚体的转动惯量/ 四、平行轴定理
l
细棒转轴通过中 心与棒垂直
J ml 2 12
l
细棒转轴通过端 点与棒垂直
J ml 2 3
§4.刚体的转动惯量/ 三、典型刚体的转动惯量
2r
2r
球体转轴沿直径
J 2mr2 5
球壳转轴沿直径
J 2mr2 3
§4.刚体的转动惯量/ 三、典型刚体的转动惯量
四、平行轴定理
定理表述:刚体绕平行于质心轴的转动惯 量 J,等于绕质心轴的转动惯量 JC 加上刚 体质量与两轴间的距离平方的乘积。
JJCm2 d
J
JC
d Cm
§4.刚体的转动惯量/ 四、平行轴定理
例1:再以绕长为 l、质量为 m 的匀质细
杆,绕细杆一端轴转动为例,利用平行轴
定理计算转动惯量 J 。 J
解:绕细杆质心的
ml
JC
转动惯量为:
JC
1 ml2 12
o
C
l/2
绕杆的一端转动惯量为 JJCm2 d
J
112m2lm2l2
二.质量连续分布刚体的转动惯量计算
1.计算公式
J
n
miri2
i1
J r2dm
ri r
mi
dm
§4.刚体的转动惯量/ 二、转动惯量的计算
例1:在无质轻杆的 b 处 3b 处各系质量 为 2m 和 m 的质点,可绕 o 轴转动,求: 质点系的转动惯量J。
解:由转动惯量的定义
2m m
J
2
miri2
o b 3b
i1
m 1 r 1 2m 2 r2 2
2m2b m(3b)2
11mb2
§4.刚体的转动惯量/ 二、转动惯量的计算
例2:长为 l、质量为 m 的匀质细杆,绕 与杆垂直的质心轴转动,求转动惯量 J。
J r2dm
细杆为线质量分布,单位长
ml
dm x
度的质量为:
m
l
l
o xdx l
2
2
建立坐标系,坐标原点选在质心处。 分割质量元 dm ,长度为 dx ,
dm dx
§4.刚体的转动惯量/ 二、转动惯量的计算
J r2dm
l/2
l/2
J x2dm x2dx
l /2
l /2
x3 3
l/2 l /2
1 l3
12
m l
J 1 ml2 12
ml
dm x
l
o xdx l
2
2
§4.刚体的转动惯量/ 二、转动惯量的计算
例3:长为 l、质量为 m 的匀质细杆,绕 细杆一端轴转动,求转动惯量 J。
Ek
1mv2 2
n
miri2
相当于描写转动惯性的物理量
i1
转动惯量的定义:
J
n
miri2
i1
单位:千克·米2
§4.刚体的转动惯量/ 一、转动惯量
转动惯量
§4.刚体的转动惯量/ 二、转动惯量的计算
刚体的转动惯量与哪些物理量有关?
①.与刚体质量有关。 ②.与质量对轴的分布有关。 ③.与轴的位置有关。
第二节 转动惯量
一、转动惯量
刚体的动能等于各 质点动能之和。
mn m1
rn r1
r2 m2
Ek
12m1v12
1 2
m2v22
12mnvn2
n
i1
12mivi2
i n 1 1 2mi(ri)2
1 2(i n 1 miri2) 2
刚体的动能 Ek1 2(i n 1 miri2) 2
与平动动能比较
o xdx l
J 1ml2 3
§4.刚体的转动惯量/ 二、转动惯量的计算
例4:半径为 R 质量为 M 的圆环,绕垂直 于圆环平面的质心轴转动,求转动惯量J。
解: 分割质量元 dm
圆环上各质量元到 轴的距离相等,
M
J R2dm
0
M o R dm
R20M dmMR2
§4.刚体的转动惯量/ 二、转动惯量的计算
