2017二次根式导学案.doc
第十六章-二次根式导学案 Microsoft Word 文档

二次根式的概念 (第1课时) 学生姓名:学习目标:理解二次根式的概念,并利用a (a ≥0)的意义解答具体题目重点:形如a (a ≥0)的式子叫做二次根式的概念;难点:利用“a (a ≥0)”解决具体问题.学习过程 一、知识准备平方根的性质:正数有 个平方根,它们 ;0的平方根是 ;负数 平方根。
思考:用带有根号的式子填空,看看写出的结果有什么特点:(1)面积为5的正方形的边长为 ;(2)要修建一个面积为3的圆形喷水池,它的半径为 m ;(3)一个位图从高处自由落下,落到地面所用的时间t (单位:s )与开始落下时的高度h(单位:m)满足关系h=t 2 如果用含有h 的式子表示t,则t= 。
(4)6的算术平方根的相反数为 ;(5)0的算术平方根为 。
(用表示)二、探究在上面的问题中,结果分别是 ,它们都表示一些正数的算术平方根。
一般地,我们把形如 ( )的式子叫做二次根式,“”称为(二次)根号.注:开平方时,被开方数a 的取值范围 (为什么?) 例1.当x 是多少时,2-x 在实数范围内有意义?例2、当x 是多少时,23x ++11x +在实数范围内有意义?例3若1a ++1b -=0,求a 2004+b2004的值.三、练习(1)下列式子,哪些是二次根式,哪些不是二次根式:2、33、1x、x (x>0)、0、-2、1x y +、x y +(x ≥0,y•≥0)是二次根式的有: 不是二次根式的有: (2)当a 是怎样的实数时,下列各式在实数范围内有意义?32+a a -3 a 5a - 2a 12+a 四、课堂小结二次根式的概念需注意:五、课后作业1、形如________ 的式子叫做二次根式.2、若3x -+3x -有意义,则x =_______.3、下列式子中,是二次根式的是( )A .-7B .37C .xD .x 4、已知一个正方形的面积是5,那么它的边长是( ) A .5 B .5 C .15D .以上皆不对 5、当x 是多少时,23x x+在实数范围内有意义?6、已知a 、b 为实数,且满足021=-++b a ,求b a的值.六、课后反思二次根式的性质(第2课时) 学生姓名:教学目标1、理解a (a ≥0)是一个非负数2、理解二次根式的两个性质(a )2=a (a ≥0)和2a =a (a ≥0)。
二次根式优秀导学案

22ba >2231+35-32+1>b a1<b a 第16章 二次根式复习课导学案一、复习目标1.进一步了解二次根式的有关概念,加深理解其基本性质,并能熟练地化简二次根式。
2.熟练地进行二次根式的加、减、乘、除混合运算。
3.准确地进行二次根式与分式的化简求值。
4. 通过例题的讨论,学会综合、灵活运用二次根式的意义、基本性质和法则解答有关含二次根式的式子的化简、计算及求值等问题. 二、考点聚焦:考点1 二次根式的有关概念考点2 二次根式的性质考点3 二次根式的运算考点4 二次根式的分母有理化二次根式的有关计算要求:结果要化为最简二次根式,并且分母中不含根号,这就要求分母要进行有理化。
在分子和分母同时乘以分母的有理化因式(不为0)。
考点5 二次根式的大小比较常见的有4种方法:1、平方法;2、作差法;3、作商法;4倒数法。
1、平方法:性质:当a>0, b>0时, 如果 , 那么a>b 。
例1.比较 和 的大小。
2、作差法:性质:如果a-b>0, 那么a>b; 如果a-b<0, 那么a<b. 例2.比较 和 的大小。
3、作商法:性质:当a>0, b>0时,如果 ,那么 a>b ;如果 ,那么 a<b 。
二次根式的除法二次根式的乘法 先化为最简二次根式,再将被开方数相同的二次根式进行合并 二次根式的加减 a ·b =ab (a ________,b ________) b a =ba (a ________,b ________)b a 11<371+261+(2-3)2012·(2+3)2013-2⎪⎪⎪⎪⎪⎪-32-(-2)0. (a -2a 2+2a -a -1a 2+4a +4)÷a -4a +2,其中a =2- 1.100991431321211++++++++ 例3.比较 和 的大小。
二次根式全章导学案

h 的意义。 s
2 x
针对问题 2 教师 可点拨学生被开 方数非负性。帮 助学生理解二次 根式定义。
x8 x4
5、思考:当 x 是怎样的实数时,
x 2 , x 3 在实数范围内有意义?
三、自我提高,拓展新知(比一比,看谁表现的最好)
(一)强化练习,提高能力 1、当 x 是怎样的实数时,下列各式在实数范围内有意义? ⑴ 5 3x ⑸ ( x 2) 2 ⑵ 教师引导学生总 结求字母范围的 方法。
198767936.doc
先学后教
师生合作
训练拓展
九
课题:二次根式(1)
年级 上
学期
数学
审核人:
教学案
( 1理解掌握二次根式的概念;2、利用二次根式意义解决问题。
学习重点:理解二次根式的概念。 学习难点:灵活运用二次根式有意义的条件解决问题 教 学 流 程: 学生活动 感受新知
198767936.doc
先学后教
师生合作
训练拓展
2、被开方数必须是
。
二、自信展示、合作交流(下列问题先在组内交流,再由小组
代表向全班交流) 1、组内交流自主学习部分思考问题中的答案。 2、说明式子 65 、 S 、 2 、 3、你怎样理解二次根式的定义? 4、 例题尝试: x 是怎样的实数时, 当 下列式子在实数范围内有意义? (分组展示过程、结果) (1) x 2 (4) (2) 2 x 1 (3)
2
教师巡回观察看 学生有无疑问。
⑵面积为 S 的正方形的边长为 m(π 取 3.14);
⑶ 要 修 建 一 个 面 积 为 6.28m 的 圆 形 喷 水 池 , 它 的 半 径 为 ⑷一个物体从高处自由下落,落到地面所用的时间为 t, (单位:s) 与开始下落的高度 h(单位:米)满足关系 h=5t 。如果用含有 h 的式子 表示 t, 则 t= . , 它们都是表 . ;0 的平方根 在上面的问题中, 结果分别是 示分别表示 65,S,2,
16章 二次根式全章导学案

16.1二次根式(1)学习目标:1、了解二次根式的概念,能判断一个式子是不是二次根式,掌握二次根式有意义的条件。
2、掌握二次根式的基本性质:)0(0≥≥a a 和)0()(2≥=a a a· ·预 习 案(一)复习回顾:(1)已知a x =2,那么a 是x 的_ ____;x 是a 的___ _, 记为_ ___,a 一定是__ __数。
(2)4的算术平方根为2,用式子表示为 =______;正数a 的算术平方根为_____, 0的算术平方根为____;式子)0(0≥≥a a 的意义是 。
思考:16 ,πs,3-b 等式子.说一说他们的共同特征.定义: 一般地我们把形如a (0≥a )叫做二次根式,a 叫做______。
“”称为 。
1、判断下列各式,哪些是二次根式在后面“√”,哪些不是在后面“×”?为什么?3( ),16-( ),34( ) ),)0(3≥a a ( ),12+x ( ) 2、当a 为正数时a 指a 的 ,而0的算术平方根是 ,负数 ,只有非负数a 才有算术平方根。
所以,在二次根式a 中,字母a 必须满足 , a 才有意义。
3、根据算术平方根意义计算 :(1) 2)4( = (2) = (3)2)5.0( = (4)2)31(=根据计算结果,你能得出结论:(0≥a ) 4、由公式)0()(2≥=a a a ,我们可以得到公式a =2)(a ,利用此公式可以把任意一个非负数写成一个数的平方的形式。
如(5)2=5或5=(5)2.练习:(1)把下列非负数写成一个数的平方的形式:6= 0.35=合 作 探 究________)(2=a 42)3(例1:当x 是怎样的实数时,2-x 在实数范围内有意义?练习1:x 取何值时,下列各二次根式有意义?①②③ 2例2:在式子xx+-121中,x 的取值范围是什么?练习2:x 取何值时,下列各二次根式有意义?① ② ③训练案1、计算: 2)3(= 2)5.0(= 2= 2= 2、二次根式1-a 中,字母a 的取值范围是( )A 、 a <lB 、a ≤1C 、a ≥1D 、a >1 3、已知03=+x 则x 的值为( )A 、 x >-3B 、x <-3C 、x =-3D 、 x 的值不能确定4有意义,则a 的值为_______.若xx+-121有意义,x 的取值范围是________.5、当x = 时,代数式有最小值,其最小值是 。
(完整word版)新人教版八年级数学二次根式导学案

第十六章 二次根式 16.1 《 二次根式(1)》学案课型: 新授课 上课时间: 课时: 1学习内容:二次根式的概念及其运用 学习目标:1(a ≥0)的意义解答具体题目.2、提出问题,根据问题给出概念,应用概念解决实际问题.学习过程一、自主学习 (一)、复习引入(学生活动)请同学们独立完成下列三个问题: 问题1:面积为3的正方形的边长为_____ ,面积为S 的正方形的边长为___________..问题2:一个长方形的围栏,长是宽的2 倍,面积为130㎡,则它的宽为_________.问题3; 一个物体从高处自由落下,落到地面所用的时间t (单位:S )与开始下落时离地面的高度h(单位;m)满足关系式h=5t 2..如果用含有h 的式子表示t,那么t 为 . (二)学生学习课本知识(三)、探索新知1、知识:像这样一些正数的算术平方根的式子,我们就把它称二次根式.因此,一般地,我们把形如 •的式子叫”称为 .例如:形如 、 、 是二次根式。
形如 、 、 不是二次根式。
2、应用举例例1.下列式子,哪些是二次根式,x>0)、、(x ≥0,y•≥0). 解:二次根式有: ;不是二次根式的有: 。
例2.当x 在实数范围内有意义? 解:由 得: 。
当 时,在实数范围内有意义.1x1x y+(3)注意:1(a ≥0)的式子叫做二次根式的概念;2(a ≥0)”解决具体问题3、要使二次根式在实数范围内有意义,必须满足被开方数是非负数。
二、学生小组交流解疑,教师点拨、拓展 例3.当x +在实数范围内有意义? 例4(1)已知,求的值.(答案:2) (2),求a 2004+b 2004的值.(答案:) 三、巩固练习 教材练习.四、课堂检测 (1)、简答题1.下列式子中,哪些是二次根式那些不是二次根式?(2)、填空题1.形如________的式子叫做二次根式. 2.面积为5的正方形的边长为________. (3)、综合提高题1.某工厂要制作一批体积为1m 3的产品包装盒,其高为0.2m ,按设计需要,•底面应做成正方形,试问底面边长应是多少? 2=_______.3.有意义的未知数x 有( )个.A .0B .1C .2D .无数4.已知a 、b =b+4,求a 、b 的值.11x +xy251x16.1 《 二次根式(2)》学案课型: 新授课 上课时间: 课时: 2 学习内容:1(a ≥0)是一个非负数; 2)2=a(a ≥0).学习目标:1(a≥0)2=a(a ≥0),并利用它进行计算和化简.2(a ≥0)是一个非负数,用具)2=a (a ≥0);最后运用结论严谨解题.教学过程 一、自主学习 (一)复习引入1.什么叫二次根式?2.当a ≥0叫什么?当a<0有意义吗? (二)学生学习课本知识 (三)、探究新知1(a ≥0)是一个 数。
二次根式导学案(人教版全章)

二次根式(1)主备人______ 审核人:______ 审核时间:一、学习目标1、了解二次根式的概念,能判断一个式子是不是二次根式。
2、掌握二次根式有意义的条件。
3、掌握二次根式的基本性质:)0(0≥≥a a 和)0()(2≥=a a a二、学习重点、难点重点:二次根式有意义的条件;二次根式的性质.难点:综合运用性质)0(0≥≥a a 和)0()(2≥=a a a 。
三、学习过程 (一)复习回顾:(1)已知a x =2,那么a 是x 的______;x 是a 的_____, 记为___,a 一定是___数。
(2)4的算术平方根为2,用式子表示为 =__________;正数a 的算术平方根为_______,0的算术平方根为_______;式子)0(0≥≥a a 的意义是 。
(二)自主学习(1)16的平方根是 ;(2)圆的面积为S ,则圆的半径是 ; (3)正方形的面积为3-b ,则边长为 。
思考:16 ,πs,3-b 等式子的实际意义.说一说他们的共同特征.定义: 一般地我们把形如a (0≥a )叫做二次根式,a 叫做_____________。
1、试一试:判断下列各式,哪些是二次根式?哪些不是?为什么?3,16-,34,)0(3≥a a ,12+x2、根据算术平方根意义计算 :(1) 2)4( (2)2)5.0( (3)2)31(43、根据计算结果,你能得出结论: ,其中0≥a , (三)合作探究练习:1、(1有意义,则a 的值为___________.(2)若在实数范围内有意义,则x 为( )。
A.正数 B.负数 C.非负数D.非正数2、(1)在式子xx+-121中,x 的取值范围是____________.(2)已知42-x +y x +2=0,则=-y x _____________.(3)已知233--+-=x x y ,则x y = _____________。
(四)达标测试 (一)填空题:1、若0112=-+-y x ,那么x = ,y = 。
6、《二次根式》导学案.doc
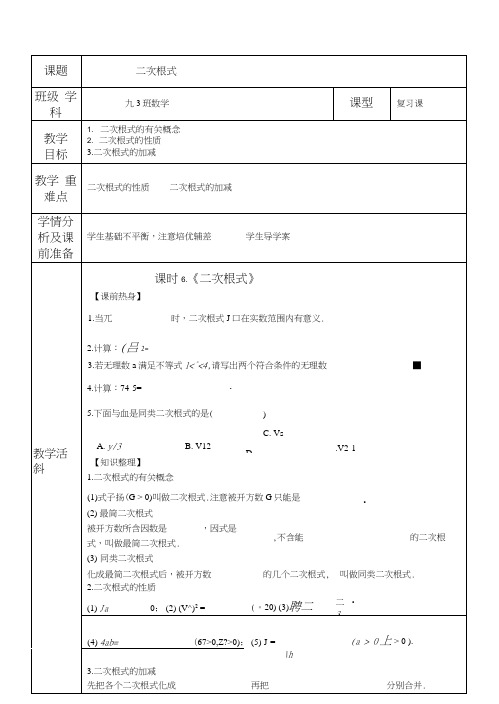
C.(2)估计辰 XJ-+V20的运算结果应在(A. 6到7之间B. 7到8之间C. 例2下列根式屮属最简二次根式的是(8到9之间)D. 9到10之间A. Ja 1 +1B. D. V27例3计算:(1)(7t + l)°-V12+ -V3V8 + (-1)3-2X —24.易错知识辨析:二次根式四则运算最后结杲若有根式,必须是最简二次根式. 【例题讲解】例1 (1)二次根式yj\-a 中,字母G 的収值范围是( )【中考演练】 1. 计算:屁一 3的=X2.式了 -/ ----- 有意义的兀取值范围是y/2-X 3.当 0W/W1 时,化简\[x^ + \x-\\= .4.汁算:J1 —兀 + A /X —1+f —1 二 •5.计算:(亦—彳严9 (亦+ 2严。
二 .6.已知 Jo —2 + Jb + 3 =0,则(a~b)1-7.请你观察思考下列计算过程:V 112=121, A 712? =11;同样:V 1112=12321,712321=111;….由此猜想 J12345678987654321 二 _______________________________ .规律用含正整数n 的等式表示出來 _______________________________ 9. 下列根式中能与V3合并的二次根式为()A. J#B. >/2410.下列计算正确的是()A. y/s — \p2 — >/2 C. (2-A /5)(2 + A /5) = 1C. V12D. V18B 呵-屁二迥一灵“3D.匚迄=3血(3) V12-V0^5-8.观察下列各式:…请你将猜想到的这种说明问题点B 关于B. 2丽 C. a + bD. a-b1. 8的立方根是A. 2B. )-2C. 3D. 4化简后(11. 数轴上的点并不都表示有理数,如图小数轴上的点P 所表示的数是辺”, 的方式体现的数学思想方法叫做( ) 八 A.代入法 B.换元法 y \c.数形结合 n.分类讨论r —r —12. 如图,数轴上表示1、血的对应点分别为A 、B, 点A 的对称点为C,则点C 所表示的数是( )A. ^/2 —1B. 1 —>/2 ,9 4 3*、 ~0~? 1 逅 2 /C. 2 —D. >/2 — 213.若 x = 4a- 4b, y = 4a+4b ,则小的值为()14. 在数轴上与表示亦的点的距离最近的整数点所表示的数是 15. (1)计算:—(兀―J^)° + tan45。
二次根式的意义导学案.doc

姓名: 班级: 课题:22.1二次根式(1)主备人:牛晓云课型:新课 授课时间: 课时数:1 学习目标九年级上册数学导学案1、 了解二次根式的意义;2、 掌握二次根式的基本性质,并会用二次根式的性质进行简单的二次根式的化简;3、 会判断二次根式,能求简单的二次根式中字母的取值范围。
学习重点二次根式的概念及意义。
学习难点二次根式的判断与字母取值范围的确定。
学习过程一、知识衔接1 .什么叫平方根、算术平方根?2. 说出下列各式的意义,并计算:观察上面儿个式子的特点,总结它们的被平方数都二、自主学习感受新知【思考】用带根号的式子填空,看看写出的结果有什 么特点?⑴如图,要做—个两条直角边的长分别是7cm 和\cm 的三角尺,斜边的长应为 cm ;⑵面积为S 的正方形的边长为;⑶要修建一个面积为6. 28〃/的圆形喷水池,它的半径为 〃z ( JT 取3. 14);⑷一个物体从高处自山下落,落到地面所用的时间为,(单位:s )与开始下落 的高度(单位:米)满足关系h=5f o 如果用含有力的式子表示,,则户.在上面的问题中,结果分别是,它们都是表示分别表一 h “Tie _屈 To 士 7C T4zjx 65, S, 2, — fi'J.5我们知道:一个正数有四个平方根,它们;。
的平方根是—;在实数范围内,数没有平方根。
因此,开平方时,被开方数只能是。
【归纳】一•般地,我们把形如的式子叫做二次根式,“丁”称为二次根号.【注意】二次根式应满足两个条件:1、形式上必须是插的形式;2、被开方• •数必须是一。
例l:a为实数时,下列各式中哪些是二次根式?+ 10, - 1’ J决 + 1,J(a - I)?.例2:当x是怎样的实数时,在实数范围内有意义?三、自主应用巩固新知【例1】下列式子,哪些是二次根式,哪些不是二次根式:也、抠、£ X(x>0)、Vo > 扼、-A/2>—!—、Jx+ y (xNO, y NO).x+y【例2】当x是多少时,V2x + 3 + —在实数范围内有意义?x + 1【例3】⑴己知y= j2-x +Jx-2+5,求三的值.y⑵若亦TT+VF二1=0,求ti201W012的值.(3)已知:Jx + 2 + (x+y)2 =0,则x2 -X)7 =四、知识集锦1.式子叫做二次根式,实际上是一个非负的实数a的算术平方根的表达式.2.式子中,被开方数(式)必须.无、检测1、下列各式是否是二次根式⑴如;⑵右^ ;⑶一 &Ul ;⑷班;(5)J(P ;(6)/1⑺Vx2+2r+32、当字母取何值时,下列各式为二次根式:(])+»'⑵J-3x⑶梧(4)^^7X-2 (5) 1 ----V2A-4(6)』2x + 3 + Jx + \X(7)心一1 (8)十1一4x -3(9)』2々+ 3(10) 丫3 々-1 (11)3、(1)若 0日-JJ二有意义,则a的值为(2)若C在实数范围内有意义,则x为()oA.正数B.负数C.非负数D.非正数六、中考连接1、下列各式中,-2 JW+2 , , J二打(a<0) , & , Vtz + 1是二次根式的是o2、当x是怎样的实数时,下列各式在实数范围内有意义?(D A/5-3X⑵卜三7 (3)7?+ 1 (4)J|-1 (5)扁2)2 (6)^^3、已知“、b为实数,且y/a—5 +2V10 — 2tz =b+4,求白、8的值.Vl-2x4、(1)在式子 --------- 中,工的取值范围是______________ .1 + X(2)已知& -4 +J2牙+ y =0,则尤一),=.(3)已知y = J3-尤 + J JC-3 一2,则y x=(4)若』2x-\ + y - 1 = 0 ,那么工二, y =。
二次根式导学案(人教版全章)

第十六章 二次根式第一课时 二次根式一、学习目标1、了解二次根式的概念,能判断一个式子是不是二次根式。
2、掌握二次根式有意义的条件。
3、掌握二次根式的基本性质:)0(0≥≥a a 和)0()(2≥=a a a二、学习重点、难点重点:二次根式有意义的条件;二次根式的性质. 难点:综合运用性质)0(0≥≥a a 和)0()(2≥=a a a 。
三、学习过程(一)复习回顾:(1)已知a x =2,那么a 是x 的______;x 是a 的________ 记为______,a 一定是_______数。
(2)4的算术平方根为2,用式子表示为 =__________;正数a 的算术平方根为_______,0的算术平方根为_______;式子)0(0≥≥a a 的意义是 。
(二)自主学习(1)16的平方根是 ;(2)一个物体从高处自由落下,落到地面的时间是t (单位:秒)与开始下落时的高度h (单位:米)满足关系式25t h =。
如果用含h 的式子表示t ,则t = ;(3)圆的面积为S ,则圆的半径是 ;(4)正方形的面积为3-b ,则边长为 。
思考:16,5h ,πs ,3-b 等式子的实际意义.说一说他们的共同特征. 4定义: 一般地我们把形如a (0≥a )叫做二次根式,a 叫做_____________1、试一试:判断下列各式,哪些是二次根式?哪些不是?为什么? 3,16-,34)0(3≥a a ,12+x 2、当a 为正数时a 指a 的 ,而0的算术平方根是 ,负数 ,只有非负数a 才有算术平方根。
所以,在二次根式a 中,字母a 必须满足 , a 才有意义。
3、根据算术平方根意义计算 : (1) 2)4((2) (3)2)5.0( (4)2)31( 根据计算结果,你能得出结论: ,其中0≥a , 4、由公式)0()(2≥=a a a ,我们可以得到公式a =2)(a ,利用此公式可以把任意一个非负数写成一个数的平方的形式。
二次根式导学案

二次根式导学案《二次根式》复习1一、学习目标1、了解二次根式的定义,掌握二次根式有意义的条件和性质。
2、熟练进行二次根式的乘除法运算。
3、理解同类二次根式的定义,熟练进行二次根式的加减法运算。
4、了解最简二次根式的定义,能运用相关性质进行化简二次根式。
二、学习重点、难点重点:二次根式的计算和化简。
难点:二次根式的混合运算,正确依据相关性质化简二次根式。
三、复习过程 (一)知识体系请写出框中数字处的内容:① ; ① ; ① ; ① ; ① ; ① ; ① ; (二)归纳考点考点1:二次根式成立的条件及性质 1、 二次根式成立的条件:被开方数0≥a 。
2、 二次根式的性质:(1))0(≥a a 是一个非负数。
(2))0()(2≥=a a a 。
(3))0(2≥=a a a 【例1】(2013.凉州)如果代数式1-x x有意义,那么x 的取值范围是( ) A.0≥x B.1≠x C.0>x D.10≠≥x x 且【思路点拨】要使代数式有意义,应同时满足分式和二次根式都有意义。
分式有意义的条件是分母不为零,二次根式有意义的条件是被开方数为非负数,二者缺一不可。
【中考在线】1、(2012.株洲)要使二次根式42-x 有意义,那么x 的取值范围是( ) A.2>x B.2<x C.2≥x D.2≤x2、(2012.大庆)代数式12-x x有意义,那么x 的取值范围是( ) A.21>x B.21<x C.21≥x D.21≠x 3、(2013.曲靖)下列等式成立的是( ) A.1052a a a =⋅ B.b a b a +=+ C.1863)(a a =- D.a a =24、(2013.永州)已知0y 2)3(2=+++-x y x ,则y x +的值为( ) A.0 B.1- C.1 D.5 5、(2013.襄阳)使代数式xx --312有意义的x 的取值范围是 。
6、(2011.黔东)若2>m ,化简=-2)2(m 。
二次根式导学案(一)

达标测评
课海拾贝
反思纠错
课海拾贝
反思纠错
课海拾贝
反思纠错
三、检测反馈
1、师生共同解决“自学指导”中的问题。
2、找同学演板3页练习1、2.
四、课堂小结:
本节课你有哪些收获?
(1)什么叫二次根式?
(2)二次根式在实数范围内有、无意义的条件是什么?
五、布置作业:
1、正式作业:课本第5页 习题 第1题
2、课外延伸
1.下列式子一定是二次根式的是()
A. B. C. D.
2.在 , , , , , 中,一定是二次根式的有:。
3.若 为二次根式,则m的取值为()
A.m≤2B.m<2C.m≥2D.m>2
4.使式子 无意义的x的取值范围是______________________。
5.当x________时,式子 有意义。
6.求使下列各式有意义的字母的取值范围:
(1) (2) (3)
学习过程
一、引入新课:
提问:(1)、 3的算术平方根是多少?
(2)、面积为a的正方形的边长是多少?
(3)、直角三角形的两直角边是1和2,则斜边是多少?
大家很容易知道答案分别是 、 和 ,像这样的式子就是我们本章要学习的二次根式。今天我们先来认识一下什么是二次根式。
二、展示目标,自主学习:
自学指导认真阅读课本第2页——3页内容,完成下列任务:
1、用带有根号的式子完成第2页“思考”填空,看看写出的结果有什么特点。
2、开平方时,被开方数只能是和,为什么?
3、一般的,我们把形如( )的式子叫做二次根式,叫做二次根号。
4、结合例1回答:
二次根式在实数范围内有意义的条件是。
二次根式导学案

7.1二次根式导学案班级:__________姓名:_________【学习目标】1. 理解二次根式的概念,会判断一个式子是否为二次根式,明确被开方数必须是非负数,能找出使二次根式有意义的条件,会判断二次根式是否有意义。
2、理解一个非负数的算术平方根是一个非负数。
即a 0≥ )0(≥a ;一个二次根式的平方等于它的被开放式。
即(a )2 =a (0≥a )。
并会正确应用。
【知识准备】算术平方根:_____________________________________________注意:负数没有..算术平方根。
【自学提示】预习课本第32-33页的内容,完成以下知识:1. 二次根式:__________________________________________其中a 叫做____________.2. 二次根式的性质(1)a 0≥ )0(≥a ,即一个非负数的算术平方根是一个________________。
(2)(a )2 =a (0≥a ),即一个二次根式的平方等于它的_________________。
我的学习困惑是:____________________________________________________________-。
【共同释疑】1. 例1 x 取什么实数时,下列二次根式在实数范围内有意义?a 312-对应练习 当a 取什么实数时,下列各式有意义?21+a ; 12+a 。
例2计算: (15)2 ; (—83.0)2 ; (—32)2对应练习 计算: (—41)2 (23)2 ; (—552)2【当堂测试】1.a 取什么实数时,下列各式在实数范围内有意义? 341+a ; 21a ; a 22、 计算:(1)2 (2)2(-3、数学理解(1)(2(0)a ≥ (2)21()5b ≥-4、若x -5 +2-x 有意义,则x 的取值范围是什么?。
二次根式全章导学案

§16.1.1《二次根式》导学案【学习目标】1、了解二次根式的概念,能判断一个式子是不是二次根式。
2、掌握二次根式有意义的条件。
【学习重点】二次根式有意义的条件. 【学习过程】【活动一】知识链接(5分钟)这些知识你还记得吗(先独立完成1分钟,后同桌互查1分钟。
)1、如果对于任意数x ,有x 2= a ,那么x 叫a 的________, 记为______,其中 a 是x 的______;所以a 一定是_______数。
2、如果对于一个正数x ,有x 2= a ,那么x 叫a 的________, 记为______,其中 a 仍是x 的______;所以a 一定是_______数。
3、正数a 的算术平方根为_______,0的算术平方根为_______;式子)0(0≥≥a a 的意义是 。
4的算术平方根为2,用式子表示为 =__________; 【活动二】自主交流 探究新知(25分钟) 1、二次根式定义的学习:(12分钟)完成P2—思考中的内容,阅读例1以上的内容,尝试完成下面的问题: 1) 思考:如何判定一个式子是否是二次根式23,16-,34,12+x 3)已知一个正方形的面积是5,那么它的边长是 。
4)下列各式一定是二次根式的是( )A 、12+xB 、12-xC 、1--xD 、x总结:二次根式应满足的条件: 。
2、 二次根式有意义的条件的学习:(13分钟)自学课本P--2页例1后,模仿例题的解答过程合作完成练习 : 1)x 取何值时,下列各二次根式有意义①43-x ③x--212)(1有意义,则a 的值为___________.(2)若在实数范围内有意义,则x 为( )。
B.负数C.非负数D.非正数总结:二次根式有意义的条件是: 【活动三】课内小结 (学生归纳总结) (3分钟)1.非负数a 的算术平方根a (a ≥0)叫做二次根式.二次根式的概念有两个要点:一是从形式上看,应含有二次根号;二是被开方数的取值范围有限制:被开方数a 必须是非负数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第22章 二次根式导学案22.1 二次根式(1)一、学习目标1、了解二次根式的概念,能判断一个式子是不是二次根式。
2、掌握二次根式有意义的条件。
3、掌握二次根式的基本性质:)0(0≥≥a a 和)0()(2≥=a a a二、学习重点、难点重点:二次根式有意义的条件;二次根式的性质. 难点:综合运用性质)0(0≥≥a a 和)0()(2≥=a a a 。
三、学习过程(一)复习引入:(1)已知x 2 = a ,那么a 是x 的______; x 是a 的________, 记为______,a 一定是_______数。
(2)4的算术平方根为2,用式子表示为 =__________; 正数a 的算术平方根为_______,0的算术平方根为_______; 式子)0(0≥≥a a 的意义是 。
(二)提出问题1、式子a 表示什么意义?2、什么叫做二次根式?3、式子)0(0≥≥a a 的意义是什么?4、)0()(2≥=a a a 的意义是什么?5、如何确定一个二次根式有无意义?(三)自主学习自学课本第2页例前的内容,完成下面的问题:1、试一试:判断下列各式,哪些是二次根式?哪些不是?为什么?43,16-,34,5-,)0(3≥a a ,12+x 2、计算 : (1) 2)4( (2)(3)2)5.0( (4)2)31( 根据计算结果,你能得出结论: ,其中0≥a ,)0()(2≥=a a a 的意义是 。
3、当a 为正数时指a 的 ,而0的算术平方根是 ,负数 ,只有非负数a 才有算术平方根。
所以,在二次根式中,字母a 必须满足 , 才有意义。
(四)合作探究1、学生自学课本第2页例题后,模仿例题的解答过程合作完成练习 :x 取何值时,下列各二次根式有意义?①43-x 223x + ③ 2、(133a a --有意义,则a 的值为___________.(2 在实数范围内有意义,则x 为( )。
A.正数B.负数C.非负数D.非正数(五)展示反馈 (学生归纳总结)1.非负数a 的算术平方根a (a ≥0)叫做二次根式.二次根式的概念有两个要点:一是从形式上看,应含有二次根号;二是被开方数的取值范围有限制:被开方数a 必须是非负数。
2.式子)0(≥a a 的取值是非负数。
(六)精讲点拨1、二次根式的基本性质(a )2=a 成立的条件是a ≥0,利用这个性质可以求二次根式的平方,如2)3(________)(2=a x--21x -(5)2=5;也可以把一个非负数写成一个数的平方形式,如5=(5)2.2、讨论二次根式的被开方数中字母的取值,实际上是解所含字母的不等式。
(七)拓展延伸1、(1)在式子xx +-121中,x 的取值范围是____________. (2)已知42-x +y x +2=0,则x-y = _____________.(3)已知y =x -3+23--x ,则x y = _____________。
2、由公式)0()(2≥=a a a ,我们可以得到公式a=2)(a ,利用此公式可以把任意一个非负数写成一个数的平方的形式。
(1)把下列非负数写成一个数的平方的形式:5 0.35(2)在实数范围内因式分解72-x 4a-11(八)达标测试A 组(一)填空题:1、 =________;2、 在实数范围内因式分解:(1)x 2-9= x 2 - ( )2= (x+ ____)(x-____)(2) x 2 - 3 = x 2 - ( ) 2 = (x+ _____) (x- _____)(二)选择题: 1、计算 ( )253⎪⎪⎭⎫ ⎝⎛的值为2)13(-A. 169B.-13 C±13 D.132A. x>-3B. x<-3C.x=-3 D x 的值不能确定3、下列计算中,不正确的是 ( )。
A. 3= 2)3( B 0.5=2)5.0( C .2)3.0(=0.3 D 2)75(=35B 组(一)选择题:1、下列各式中,正确的是( )。
A. = BC D2、 如果等式2)(x -= x 成立,那么x 为( )。
A x ≤0; B.x=0 ; C.x<0; D.x ≥0(二)填空题:1、 若20a -=,则 2a b -= 。
2、分解因式:x 4 - 4X 2 + 4= ________.3、当x= 时,代数式其最小值是 。
22.1二次根式(2)一、学习目标1、掌握二次根式的基本性质:a a =22、能利用上述性质对二次根式进行化简.二、学习重点、难点0,x =则为( )4949+=+4994⨯=⨯2424-=-653625=重点:二次根式的性质a a =2. 难点:综合运用性质a a =2进行化简和计算。
三、学习过程(一)复习引入:(1)什么是二次根式,它有哪些性质?(2x 。
(3)在实数范围内因式分解:x 2-6= x 2 - ( )2= (x+ ____)(x-____)(二)提出问题1、式子a a =2表示什么意义?2、如何用aa =2来化简二次根式? 3、在化简过程中运用了哪些数学思想?(三)自主学习自学课本第3页的内容,完成下面的题目:1、计算:=24 =22.0 =2)54( =220观察其结果与根号内幂底数的关系,归纳得到: 当=>a a ,0时2、计算:=-2)4( =-2)2.0( =-2)54(=-2)20( 观察其结果与根号内幂底数的关系,归纳得到:当=<a a ,0时3、计算:=20 当==a a ,0时(四)合作交流1、归纳总结将上面做题过程中得到的结论综合起来,得到二次根式的又一条非常重要的性质:⎪⎩⎪⎨⎧<-=>==0a a 0a 00a a 2 a a2、化简下列各式:______=______=_______=_____a 0=(<)3、请大家思考、讨论二次根式的性质)0()(2≥=a a a 与a a =2有什么区别与联系。
(五)展示反馈1、化简下列各式 (1))0(42≥x x (2) 4x2、化简下列各式 (1))3()3(2≥-a a (2)()232+x (x <-2)(六)精讲点拨 利用a a =2可将二次根式被开方数中的完全平方式“开方”出来,达到化简的目的,进行化简的关键是准确确定“a ”的取值。
(七)拓展延伸(1)a 、b 、c 为三角形的三条边,则=--+-+c a b c b a 2)(____________.(2) 把(2-x)21-x 的根号外的(2-x )适当变形后移入根号内,得( ) A 、x -2B 、2-x C 、x --2 D 、2--x(3) x-4│-│7-x │。
(八)达标测试: A 组 1、填空:(1)、2)12(-x -2)32(-x )2(≥x =_________.(2)、2)4(-π=2、已知2<x <3,化简:3)2(2-+-x xB 组1、 已知0 <x <1,化简:4)1(2+-x x -4)1(2-+xx2、 边长为a 的正方形桌面,正中间有一个边长为3a 的正方形方孔.若沿图中虚线锯开,可以拼成一个新的正方形桌面.你会拼吗?试求出新的正方形边长.22.2二次根式的乘除法二次根式的乘法一、学习目标1、掌握二次根式的乘法法则和积的算术平方根的性质。
2、熟练进行二次根式的乘法运算及化简。
二、学习重点、难点重点:掌握和应用二次根式的乘法法则和积的算术平方根的性质。
难点:正确依据二次根式的乘法法则和积的算术平方根的性质进行二次根式的化简。
三、学习过程(一)复习回顾1、计算:(1)4×9=______ 94⨯=_______16⨯=_______(2)16×25 =_______ 25100⨯=_______(3)100×36 =_______ 362、根据上题计算结果,用“>”、“<”或“=”填空:4⨯(1)4×9_____916⨯(2)16×25____25(3) 100×36__36100(二)提出问题1、二次根式的乘法法则是什么?如何归纳出这一法则的?2、如何二次根式的乘法法则进行计算?3、积的算术平方根有什么性质?4、如何运用积的算术平方根的性质进行二次根式的化简。
(三)自主学习自学课本第5—6页“积的算术平方根”前的内容,完成下面的题目:1、用计算器填空:(1)2×3____6 (2)5×6____30(3)2×5____10 (4)4×5____202、由上题并结合知识回顾中的结论,你发现了什么规律?能用数学表达式表示发现的规律吗?3、二次根式的乘法法则是:(四)合作交流1、自学课本6页例1后,依照例题进行计算:(1)9×27 (2)25×32(3)a 5·ab 51 (4)5·a 3·b 312、自学课本第6—7页内容,完成下列问题:(1)用式子表示积的算术平方根的性质:。
(2)化简: ①54 ②2212b a③4925⨯ ④64100⨯(五)展示反馈 展示学习成果后,请大家讨论:对于9×27的运算中不必把它变成243后再进行计算,你有什么好办法?(六)精讲点拨1、当二次根式前面有系数时,可类比单项式乘以单项式法则进行计算:即系数之积作为积的系数,被开方数之积为被开方数。
2、化简二次根式达到的要求:(1)被开方数进行因数或因式分解。
(2)分解后把能开尽方的开出来。
(七)拓展延伸1、判断下列各式是否正确并说明理由。
(1))9()4(-⨯-=94-⨯-(2)323b a =ab b 3(3)=68)2(6⨯-⨯=4812-(4)161694⨯ =161694⨯⨯=34⨯=12 2、不改变式子的值,把根号外的非负因式适当变形后移入根号内。
(1) -332 (2) a a 212-(八)达标测试:A 组1、选择题(1)等式1112-=-•+x x x 成立的条件是( )A .x ≥1B .x ≥-1C .-1≤x ≤1D .x ≥1或x ≤-1(2)下列各等式成立的是( ).A .45×25=85B .53×42=205C .43×32=75D .53×42=206(3)二次根式6)2(2⨯-的计算结果是( )A .26B .-26C .6D .122、化简:(1)360; (2)432x ;3、计算:(1)3018⨯; (2)7523⨯;B 组1、选择题(1)若04144222=+-++++-c c b b a ,则c a b ••2=()A .4B .2C .-2D .1(2)下列各式的计算中,不正确的是( )A .64)6()4(-⨯-=-⨯-=(-2)×(-4)=8B .2222442)(244a a a a =⨯=⨯=C .5251694322==+=+D .12512131213)1213)(1213(121322⨯=-⨯+=-+=-2、计算:(1)68×(-26); (2;二次根式的除法一、学习目标1、掌握二次根式的除法法则和商的算术平方根的性质。
