第2讲 Mathematics入门
Mathematica教程-2常用的数学函数

。
Round[x]: 最接近x的整数 Floor[x]: 不大于x的最大整数 Ceiling[x]: 不小于x的最小整数 Abs[x]: x的绝对值或复数的摸 x+Iy : 复数x+iy;Re[z]: 复数z的实部 Im[z]: 复数z的虚部;Arg[z]: 复数z的幅角 Divisors[n]: 能整除n的所有整数组成的表 Mod[m,n]: m被n除的正余数 Quotient[m,n]: m/n的整数部分 GCD[n1,n2……]: 求n1,n1,……的最大公因数 LCM[n1,n2……]: 求n1,n2,……的最小公倍数
函数的立即定义
立即定义函数的语法如下f[x_]=expr函数名为f, 自变量为x,expr是表达式。在执行时会把expr 中的x都换为f的自变量x(不是x_)。函数的自变 量具有局部性,只对所在的函数起作用。函数 执行结束后也就没有了,不会改变其它全局定 义的同名变量的值。例: 定义函数f(x)=x*Sinx+x2, 对定义的函数求函数 值,并绘制它的图形。
当然使用If命令也可以定义上面的函数
表
将一些相互关联的元素放在一起,使它们成 为一个整体。既可以对整体操作,也可以对 整体中的一个元素单独进行操作。在 Mathematica中这样的数据结构就称作表 (List)。表主要有三个用法:表{a,b,c} 可以表示一个向量;表{{a,b},{c,d}}可表示一 个矩阵。
常用函数的命令格式
三角函数 :Sin[x],Cos[x] ,Tan[x] ,Cot[x] 等
反三角函数 :ArcSin[x] ,ArcCos[x] ,ArcTan[x]等 双曲函数与反双曲函数 :Sinh[x] ,Cosh[x] ,Tanh[x], ArcSinh[x],ArcCosh[x],ArcTanh[x] 指数函数E^x(或Exp[x]),指数函数a^x
Mathematica快速入门

Mathematica 快速入门倪 致 祥一、引言Mathematica 是美国Wolfram Research 公司开发的数学软件,主要用途是科学研究与工程技术中的计算。
由于它的功能十分强大,使用非常简便,现在已成为理工科师生进行科学研究和教学改革的有力工具。
它的主要特点有:1、既可以进行程序运行,又可以进行交互式运行。
一句简单的Mathematic 命令常常可以完成普通的c 语言几十甚至几百个语句的工作。
例如解方程:x 4 + x 3 + 3x -5 = 0只要运行下面的命令 Solve[x^4 +x^3 + 3x -5==0, x ]2、既可以进行任意高精度的数值计算,又可以进行各种复杂的符号演算,如函数的微分、积分、幂级数展开、矩阵求逆等等。
它使许多以前只能靠纸和笔解决的推理工作可以用计算机处理。
例如求不定积分:⎰ x 4 e -2x dx 只要运行下面的命令:Integrate[x^4*Exp[-2x], x ]3、既可以进行科学计算,又可以很方便地画出用各种方式表示的函数图形,使人能够直观地把握住函数的特性。
例如绘制函数图形:y = e -x /2 cos x , x ∈ [0, π],只要运行下面的命令Plot [ Exp[-x/2]*Cos[x], {x, 0, Pi} ]4、Mathematica 把各种功能有机地结合在一个集成环境里,可以根据需要做不同的操作,给使用者带来极大的方便。
二、Mathematica 的使用1、 基本运算及其对象Mathematica 的基本数值运算有加法、减法、乘法、除法和乘(开)方,分别用运算符“+”、“-”、“*”、“/”和“^”来表示(在不引起误解的情况下,乘号可以省略或用空格代替),例如2.4*3^2 -(5/(6+3))^(1/3)表示3236534.2)(+÷-⨯。
小括号“(”和“)”作为表示运算优先顺序的符号,用于组合运算;中括号用于命令和函数,大括号用于集合和列表。
第2讲 Mathematics入门

(6) sin 290
4.近似值、赋值、引用符
(1)若想获得计算结果的近似值,可按如下格式输入: 表达式//N(N[表达式]) 例如求近似值 In[5]:= 1/3+2/7 //N Out[5]= 0.619048 In[6]:= N[1/3+2/7] Out[6]= 0.619048 该格式的输出结果, 自 动保 留六位 有 效数 字 , 如何获得更加满意的结 果呢?
(2)Range[n] 生成前n个相邻整数组成的列表
Range[10] {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(3)Range[m,n] 生成由m到n个相邻整数组成的列表
Range[10,20] {10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}
f ( x) = x2
f[x_]:=x^2
g[x_,y_]:=(x-y)^2/y
( x − y)2 g( x, y) = y
注 意
1.自定义函数表达式左边的自变量要写在[ ]号内,且 后面跟随“—”(空格), 右边则不需要。 2.所使用的函数名尽量以小写字母口头,从而避免与 Mathematica内部函数名发生冲突。 3.所定义的函数名应与前面所用过的其它函数不重复.
初等数值计算
Mathematica可以看作是一个功能齐全的计算器, 但它的功能又绝非计算器所能比拟.这里我们仅简单 介绍其基本功能。 利用Mathematica完成某一代数运算, 关键在于 正确输入Mathematica能够接受的代数的表达式。 要点: Mathematica代数符的规定 各种操作符的运算顺序
第二讲
Mathematica入门 入门
Mathematica软件使用入门

Mathematica软件使用入门目录第一章基本知识与基本操作 (3)1.1 Mathematica的基本语法特征 (3)1.2 Mathematica的启动、基本操作 (5)1.3 操作小技巧 (7)1.4 数值计算 (8)1.5 赋值与替换 (9)1.6 自定义函数 (10)1.7 方程与方程组解 (11)1.8 解不等式与不等式组 (12)1.9 由递推式求数列的通项公式 (14)1.10 作函数图像 (15)页脚内容1第二章运用Mathematica实现高等数学中的基本运算 (17)2.1 求极限运算 (17)2.2 求导数与微分 (20)2.3 求不定积分 (28)2.4 求定积分 (29)第三章实验练习题 (32)Mathematica是当今世界上最为流行的计算机代数系统之一.Mathematica系统是美国物理学家Stephen.Wolfram领导的一个小组开发的,后来他们成立了Wolfram研究公司.1987年推出了系统的1.0版;现在的最新版本是8.0版.页脚内容2Mathematica可以做:符号计算和数值计算问题,如:能做多项式的计算、因式分解和展开等;做各种有理式计算,求多项式、有理式方程和超越方程的精确解和近似解;做向量、矩阵的各种计算;求极限、导数、积分,做幂级数展开,求解某些微分方程等;做任意位数的整数或分子分母为任意大整数的有理数的精确计算,做具有任意位精度的数值(实、复数值)的计算.可以很方便地画出用各种方式表示的一元和二元函数的图形,通过图形,可以立即形象地掌握函数的某些特性,而这些特性一般是很难从函数的符号表达式中看清楚.第一章基本知识与基本操作1.1 Mathematica的基本语法特征使用Mathematica,一定要牢牢记住:Mathematica中大写小写是有区别的,如Name、name、NAME等是不同的变量名或函数名;系统所提供的功能大部分以系统函数的形式给出,内部函数一般写全称,而且一定是以大写英文字母开头,如Sin[x],Cos[z]等;页脚内容3页脚内容4乘法即可以用*,又可以用空格表示,如 2 3=2*3=6 , 2 Sin[x]=2* Sin[x]乘幂可以用“^”表示,如x^0.5 表示: Tan[x]^y 表示:自定义的变量可以取几乎任意的名称,长度不限,但不可以数字开头.当你赋予变量任何一个值,除非你: 明显地改变该值或 使用Clear[变量名] 或 使用“变量名=.”取消该值,否则它将始终保持原值不变.一定要注意四种括号的用法:( ): 表示项的结合顺序,如: (x+(y^x+1/(2x))); [ ]: 表示函数,如:Log[x], Sin[x];{ }: 表示一个“表”(即是一组数字、或任意表达式、或函数等的一个有序集合),如:{2x,Sin[12 Pi],A ,1}, {1+A,y*x ,1,2};[[ ]]: 双方括号表示“表”或“表达式”的下标,如: a[[2,3]]表示:23a ; {3,5,7}[[2]]=5.Mathematica 的语句书写十分方便,一个语句可以分为多行写,同一行可以写多个语句(但要以分号间隔).当语句以分号结束时,语句计算后不做输出(输出语句除外),否则将输出计算的结果.0.5xyTan[x]Mathematica命令中的标点符号必须是英文的.1.2 Mathematica的启动、基本操作1.2.1 启动“Mathematica”:在windows操作系统中安装了Mathematica后,与其他的常用软件一样,可从“开始”→“程序”→“Mathematica5”Mathematica的主窗口并出现第一个notebook窗口(Untitled-1):1.2.2 简单使用:例1.1 计算+33的值①在“Untitled-1”窗口中输入:329/412+3^3②按下“Shift+Enter”(或数字键盘上的Enter键),就得到计算结果:页脚内容5其中“In[1]:=”是Mathematica自动加上的,表示第一个输入;“Out[1]:=”表示第一个输出.一般地:In[n]:= 表示第n个输入Out[n]:=表示第n个输出.注意:“In[n]:=”自动加上的,不能人工输入!1.2.3 保存结果:保存方法同一般的Windows软件:“文件”→“保存”“另存为”窗口→在“查找范围”内找到目标文件夹→输入文件名(比如输入“1”)→“”.Mathematica 4或Mathematica 5的文件的后缀是“nb”,当输入“1”时,即产生文件“1.nb”.1.2.4打开文件1.nb启动Mathematica →“文件”→“打开”打开”窗口:→在“查找范围”内找到文件“1.nb”→“”即可.页脚内容61.2.5 退出Mathematica:与一般应用软件一样,单击右上方的“”按钮(或用菜单:“文件”→“退出”).1.3 操作小技巧1.3.1Ctrl+K的用途如果只知道命令的首写字母,可在输入该首写字母(要大写),再按下“Ctrl+K”组合键,则所有以该字母为首的命令都列出来,只要用鼠标双击命令名就输入了该命令.1.3.2使用前面已有的结果举例如下:例1.2 做如下操作:①输入:Integrate[x^2*(11-Sin[x]),{x,-1,1}]按:“Shift+Enter”;②输入:%+1,按:“Shift+Enter”;③输入:%+1,按:“Shift+Enter”;④输入:%1+1,按:“Shift+Enter”;Integrate[f,x]是求:()f x dxIntegrate[f,{x,xmin,xmax}]是求:页脚内容7⑤输入:%3+1,按:“Shift+Enter”,计算结果如下:可见,“%”表示前一个计算结果;“%n”表示第n个计算结果.1.3.3 删除行:见下图示1.4 数值计算请看下例:只要选定且删1.5 赋值与替换X=. 或Clear[x] 清除赋给x的值expr/.{x->xval,y->yval} 用xval、yval分别替换expr中的x、y.例1.3输入:x=3;y=4;w=x+y 计算清除变量的定义和值输入:Clear[x,y];计算输入:z=(x+y)^2 计算将(x+y)^2赋给z页脚内容9页脚内容10输入:z/.x->5 计算输入:Clear[x,y]; 计算 输入:u=x+y 计算 输入:u/.{x->5,y->6} 计算 计算结果如下:1.6 自定义函数用户可以自行定义函数,一个函数一旦被定义好之后就可以象系的内部函数一样使用. 例1.4 如要定义函数 f(x)=x 2+3x-2变量替换:变量替换:分别用5、6代替表达式u 中的“:=”是定义符.左边f 是函数名,方括号内x 是自变量,其页脚内容11只要键入: f[x_]:=x^2+3x-2即可.又如要定义分段函数2+1 < 0()= 2sin 0x x g x x x ⎧⎨≥⎩可键入:g[x_]:= Which[x<0,x^2+1,x>=0,2Sin[x]] 或g[x_]:=If[x<0,x^2+1,2Sin[x]] 请见以下计算结果:1.7 方程与方程组解 例1.5 ① 解方程:0652=+-x x输入:Solve[x^2-5x+6==0,x]Solve 是解方程或方程组的函数.其格式为:Solve[eqns,vars] 其中方程用exp==0的形式(其中页脚内容12即可.② 解方程组输入:Solve[{x+y==1,3x^2-y^2==0},{x,y}] 即可(结果见下图).1.8 解不等式与不等式组 例1.6 ① 解不等式组2213x y x y +=⎧⎨-=⎩加载解不等式的程序包,这是必须的,可谓是固定的格式, “< ”为键盘上的小于号, “`”为数字键1的左侧的 Algebra —— 代数类页脚内容13⎪⎩⎪⎨⎧>-<--0101222x x x输入: <<Algebra`InequalitySolve` InequalitySolve[{x^2-5x-6<0,x^2-1>0}, x] 即可. ② 解不等式3)3(12>--x x输入: <<Algebra`InequalitySolve` InequalitySolve[Abs[x-1](x^2-3) > 3, x] 即可(结果见下图)注: Mathematica 系统有内部函数.还有一些系统扩展的功能但不是作为内部函数的、以文件的形式存页脚内容14储在磁盘上的文件,要使用它们,必须用一定的方式来调用这些文件,这些文件我们称之为程序包. 调用方式之一如上所述: <<Algebra`InequalitySolve` 或用:Needs["Algebra`InequalitySolve`"] 1.9 由递推式求数列的通项公式例1.7 设 求数列的通项公式 只要输入:<<DiscreteMath`RSolve`RSolve[{a[n]==n *a[n-1], a[1]==1}, a[n], n] 即可(结果见下图)11,1,nn a na a -==1.10 作函数图像例1.8在同一坐标系中作出2-1y x 和y=sinx在[-2,2]内的图像.输入:Plot[{x^2-1,Sin[x]},{x,-2,2}]结果见下图例1.9作出sinxcosy的三维图形输入:Plot3D[Sin[x]*Cos[y],{x,-2Pi,2Pi},{y,-2Pi,2Pi},PlotPoints->100]即可(结果见下图)增加取样点提高光滑度页脚内容15页脚内容16页脚内容17第二章 运用Mathematica 实现高等数学中的基本运算极限、导数和积分是高等数学中的主要概念和基本运算,如果你在科研中遇到较复杂的求极限、求导数或求积分问题,Mathematica 可以帮你快速解决这些问题。
mathematics-课件学习

10/51
5. 数学常数
最常见的数学常数有:
Pi
圆周率, = 3.14159…
E
自然对数的底e,e=2.71828…
Degree
角度1度,1度 = 1 /180
I
虚数单位i,i =
Infinity
无穷大,即
Indeterminate 不定值,即0/0,/
此外,还有欧拉常数、黄金分割常数、光速常数、万有
15
16/51
2.2.2 变量命名
变量命名即用标识符给变量命名,给变量用标识符命 名时必须严格依照标识符的有关规定进行。
给函数命名时,除了要遵守标识符的规定外,还要 遵守函数命名的一些规则,这将在下一节作介绍。
标识符除了可给变量命名和给函数命名外,还可有 别的用途,例如可以用它来表示计算中的单位:
1.5Kg + 2.3Kg 3.8Kg
16
17/51
2.2.3 变量赋值
在Mathematica中运算符“=”的作用是赋值。常常 用它来给变量赋一个值,这个值可以是一个数值、一个 数组、一个表达式,甚至一个图形。例如
如果其中有一些是近似数,那么运算的结果也只能 是近似数,但保持尽可能高的精度,仍然不轻易丢失 信息。
注:(*…*)为Mathematica系统的注释符号,两个*号 之间为注释内容,注释部分可以放在程序的任何位置。
8
9/51
4. 复数 同数学中的复数表示法一样,在Mathematica里的每
一个复数也表示为z=x+Iy,其中x与y为实数,I为虚数 单位,即,运算规则与数学中的规则一样。
软件介绍
第2讲 Mathematica的基本量
1
2/51
1.2Mathematica的入门

Mathematica是1988年美国WR公司开发的数学软件,它是第一个将数值 计算、符号运算和图形显示结合在一起的数学软件,具有高精度的数值计 算功能和强大的图形功能。
一、Mathematica的主要特点和功能
特点:Mathematica系统是用C语言编写的,它吸取了不同类型软件的特点 (1)具有类似于Basic语言那样简单易学的交互式操作方式 (2)具有MathCAD,Matlab那样强大的数值计算功能 (3)具有Macsyma,Maple,Reduce和SMP那样的符号计算功能 (4)具有APL和Lisp那样的人工智能列表处理功能 (5)具有C和Pascal那样的结构化程序设计语言
select、 全选All以及取消Undo等
(3)Cell为“单元”菜单,“单元”是指工作窗输入的一组命令及其输出的一组结 (4)Format是格式菜单. Mathematica支持多种输入格式,如支持汉字输入
(5)Kernel是执行计算菜单.当输入完表达式后,选取kernel菜单中的Evaluate cells 项,就可对鼠标所停留处的“单元”执行计算任务.通常使用快捷方式Shift + Enter
(2)注释语句要放在(* *)中间,在运行时系统不执行这部分内容
(3)变量名最好小写,以避免与系统变量冲突,比如大写C和D都不能用做变量名 (4) 若输入键盘上没有的字符或数学符号,可以单击File菜单中Palettes项里的 “Basic Input”(如图1),以打开特殊符号表单
(5) 乘法记号“*”,两个式子相乘中间要键入“*”,Basic Input模板上有“×”
(6) Mathematica的标点符号必须是在英文状态下输入.在一行指令后加上“;”,标 识指令执行但不显示结果.“( )”仅用来改变运算次序.“{ }”则用于命令中的选项 表示集合
《Mathematica》使用手册

《Mathematica》使用手册Mathematica使用手册=========================第一章:介绍Mathematica-------------------------------------1.1 Mathematica的概述Mathematica是一种强大的数学计算和数据处理软件,广泛应用于科学、工程、计算机科学等领域。
1.2 安装和启动本节介绍如何安装Mathematica软件并启动它。
1.3 界面和基本操作介绍Mathematica的界面和基本操作,包括工具栏、菜单、笔记本等。
第二章:基本语法和数据类型-------------------------------------2.1 表达式和运算符讲解Mathematica的表达式和运算符,包括数值运算、符号运算、逻辑运算等。
2.2 变量和函数介绍Mathematica中的变量和函数的定义和使用方法。
2.3 数据类型讲解Mathematica中的基本数据类型,包括数值类型、字符串类型、列表类型等。
第三章:图形绘制-------------------------------------3.1 绘制函数图像介绍使用Mathematica绘制函数图像的方法和技巧。
3.2 绘制二维图形讲解Mathematica中绘制二维图形的常用函数和参数设置。
3.3 绘制三维图形介绍Mathematica中绘制三维图形的方法,包括绘制曲面、绘制立体图形等。
第四章:方程求解和数值计算4.1 方程求解讲解Mathematica中方程求解的方法和技巧。
4.2 数值计算介绍Mathematica中数值计算的函数和用法。
4.3 微分方程求解讲解Mathematica中求解微分方程的方法和技巧。
第五章:数据分析和统计-------------------------------------5.1 数据导入和导出介绍Mathematica中的数据导入和导出方法。
Mathematica使用入门数学软件Mathematica课件

16
内置函数
Mathematica 具有超过 3000 个内置函数,具体见 “帮助” “参考资料中心” 的左下角处的 “函数索引”
Mathematica 函数命名规则 ① 第一个字母大写,后面跟小写字母,如 Sin[x], Log[x] ② 大多数函数名与数学中的名称相同 ③ 当函数名分为几段时,每一段的头一个字母大写,后面 的用小写字母,如:ArcSin[x]
In[1]:= Clear[x,y]; In[2]:= f=2*x+y; In[3]:= f./{x->2,y->3} (* f(2,3) 的值 *) In[3]:= f./{2->5} (*把 2 替换成 5*)
14
数的基本运算
Mathematica 中的实数分精确数和双精度数
N[x,n] N[x] IntegerPart[x]
可以运行单个命令或语句 也可以运行多个语句:输入全部语句后再按执行键 命令(语句)分隔符:回车或分号 如果不需要显示运行结果:在语句后面加分号
输入和输出标识符:In[n]: 和 Out[n]
In[1]:= Sin[Pi/4]+Cos[Pi/4]
Out[1]= 2
8
数学公式的输入
数学公式的输入
lim(1 1
n
2
黄金分割数:1 1 5 2
虚部单位
1 ln n) 0.577215 n
无穷大
圆周率
11
基本运算符
基本运算:
算术运算 +-*/ ^ !
加减乘除 幂 阶乘(运算级别比加减乘除和幂运算高)
比较运算与逻辑运算 == > < >= <= != && || ! Xor
Mathematica软件使用入门讲解

Mathematica软件使用入门目录第一章基本知识与基本操作 (3)1.1 Mathematica的基本语法特征 (3)1.2 Mathematica的启动、基本操作 (4)1.3 操作小技巧 (7)1.4 数值计算 (8)1.5 赋值与替换 (9)1.6 自定义函数 (10)1.7 方程与方程组解 (11)1.8 解不等式与不等式组 (12)1.9 由递推式求数列的通项公式 (13)1.10 作函数图像 (14)第二章运用Mathematica实现高等数学中的基本运算 (16)2.1 求极限运算 (16)2.2 求导数与微分 (18)2.3 求不定积分 (25)2.4 求定积分 (25)第三章实验练习题 (28)Mathematica是当今世界上最为流行的计算机代数系统之一.Mathematica系统是美国物理学家Stephen.Wolfram领导的一个小组开发的,后来他们成立了Wolfram研究公司.1987年推出了系统的1.0版;现在的最新版本是8.0版.Mathematica可以做:●符号计算和数值计算问题,如:能做多项式的计算、因式分解和展开等;●做各种有理式计算,求多项式、有理式方程和超越方程的精确解和近似解;●做向量、矩阵的各种计算;●求极限、导数、积分,做幂级数展开,求解某些微分方程等;●做任意位数的整数或分子分母为任意大整数的有理数的精确计算,做具有任意位精度的数值(实、复数值)的计算.●可以很方便地画出用各种方式表示的一元和二元函数的图形,通过图形,可以立即形象地掌握函数的某些特性,而这些特性一般是很难从函数的符号表达式中看清楚.第一章 基本知识与基本操作1.1 Mathematica 的基本语法特征使用Mathematica ,一定要牢牢记住:● Mathematica 中大写小写是有区别的,如Name 、name 、NAME 等是不同的变量名或函数名;● 系统所提供的功能大部分以系统函数的形式给出, 内部函数一般写全称, 而且一定是以大写英文字母开头, 如Sin[x], Cos[z]等;● 乘法即可以用*,又可以用空格表示,如2 3=2*3=6 , 2 Sin[x]=2* Sin[x] ● 乘幂可以用“^”表示,如x^0.5 表示: Tan[x]^y 表示: ● 自定义的变量可以取几乎任意的名称,长度不限,但不可以数字开头. ● 当你赋予变量任何一个值,除非你:明显地改变该值或 使用Clear[变量名] 或 使用“变量名=.”取消该值,否则它将始终保持原值不变.● 一定要注意四种括号的用法:0.5x yTan[x]( ):表示项的结合顺序,如: (x+(y^x+1/(2x)));[ ]:表示函数,如:Log[x], Sin[x];{ }:表示一个“表”(即是一组数字、或任意表达式、或函数等的一个有序集合),如:{2x,Sin[12 Pi],A,1}, {1+A,y*x,1,2};[[ ]]:双方括号表示“表”或“表达式”的下标,如:a; {3,5,7}[[2]]=5.a[[2,3]]表示:23●Mathematica的语句书写十分方便,一个语句可以分为多行写,同一行可以写多个语句(但要以分号间隔).●当语句以分号结束时,语句计算后不做输出(输出语句除外),否则将输出计算的结果.●Mathematica命令中的标点符号必须是英文的.1.2 Mathematica的启动、基本操作1.2.1 启动“Mathematica”:在windows操作系统中安装了Mathematica后,与其他的常用软件一样,可从“开始”→“程序”→“Mathematica5” Mathematica的主窗口并出现第一个notebook窗口(Untitled-1):1.2.2 简单使用:例1.1 计算+33的值①在“Untitled-1”窗口中输入:329/412+3^3②按下“Shift+Enter”(或数字键盘上的Enter键),就得到计算结果:其中“In[1]:=”是Mathematica自动加上的,表示第一个输入;“Out[1]:=”表示第一个输出.一般地:In[n]:= 表示第n个输入Out[n]:=表示第n个输出.注意:“In[n]:=”自动加上的,不能人工输入!1.2.3 保存结果:保存方法同一般的Windows软件:“文件”→“保存”⇒“另存为”窗口→在“查找范围”内找到目标文件夹→输入文件名(比如输入“1”)→“”.Mathematica 4或Mathematica 5的文件的后缀是“nb”,当输入“1”时,即产生文件“1.nb”.1.2.4打开文件1.nb启动Mathematica →“文件”→“打开”⇒打开”窗口:→在“查找范围”内找到文件“1.nb”→“”即可.1.2.5 退出Mathematica :与一般应用软件一样,单击右上方的“ ”按钮(或用菜单:“文件”→“退出”).1.3 操作小技巧1.3.1 Ctrl+K 的用途如果只知道命令的首写字母, 可在输入该首写字母(要大写),再按下“Ctrl+K ”组合键, 则所有以该字母为首的命令都列出来,只要用鼠标双击命令名就输入了该命令. 1.3.2 使用前面已有的结果 举例如下:例1.2 做如下操作:① 输入:Integrate[x^2*(11-Sin[x]),{x,-1,1}]按:“Shift +Enter ”; ② 输入:%+1,按:“Shift +Enter ”; ③ 输入:%+1,按:“Shift +Enter ”; ④ 输入:%1+1,按:“Shift +Enter ”; ⑤ 输入:%3+1,按:“Shift +Enter ”, 计算结果如下:Integrate[f,x]是求:()f x dx ⎰ Integrate[f,{x,xmin,xmax}]是求:maxmin()x x f x dx ⎰可见,“%”表示前一个计算结果;“%n”表示第n个计算结果.1.3.3删除行:见下图示1.4 数值计算请看下例:只要选定且删除此即可系统默认的计算结果,是精确的.N[],取近似值函数,默认输出6位有效数字.N[],取近似值函数,指定输出3位有效数字.1.5 赋值与替换X=. 或Clear[x] 清除赋给x的值expr/.{x->xval,y->yval} 用xval、yval分别替换expr中的x、y.例1.3输入:x=3;y=4;w=x+y 计算输入:Clear[x,y];计算输入:z=(x+y)^2 计算输入:z/.x->5 计算输入:Clear[x,y];计算输入:u=x+y 计算将(x+y)^2赋给z清除变量的定义和值变量替换:用5代替表达式z中的变量变量替换:输入:u/.{x->5,y->6} 计算 计算结果如下:1.6 自定义函数用户可以自行定义函数,一个函数一旦被定义好之后就可以象系的内部函数一样使用.例1.4 如要定义函数f(x)=x 2+3x-2只要键入:f[x_]:=x^2+3x-2即可.又如要定义分段函数2+1 < 0()= 2sin 0x x g x x x ⎧⎨≥⎩“:=”是定义符.左边f 是函数名,方括号内x 是自变量,其后的下划线“_”不能少.右边是函数的表达式.可键入:g[x_]:= Which[x<0,x^2+1,x>=0,2Sin[x]]或g[x_]:=If[x<0,x^2+1,2Sin[x]]请见以下计算结果:1.7 方程与方程组解例1.5 ① 解方程:0652=+-x x输入:Solve[x^2-5x+6==0,x]即可.② 解方程组 输入:Solve[{x+y==1,3x^2-y^2==0},{x,y}] 即可(结果见下图).Solve 是解方程或方程组的函数.其格式为:Solve[eqns,vars]其中方程用exp==0的形式(其中exp 为未知元的表达式,“= =”必须是2个等号);方程列表 2213x y x y +=⎧⎨-=⎩未知数列表1.8 解不等式与不等式组例1.6 ① 解不等式组⎪⎩⎪⎨⎧>-<--0101222x x x输入: <<Algebra`InequalitySolve`InequalitySolve[{x^2-5x-6<0,x^2-1>0}, x]即可.② 解不等式3)3(12>--x x输入: <<Algebra`InequalitySolve`即可(结果见下图)不等式列表 变量列表加载解不等式的程序包,这是必须的,可谓是固定的格式, “< ”为键盘上的小于号, “`”为数字键1的左侧的Algebra —— 代数类InequalitySolve —— 解不等式程序包绝对值函数注: Mathematica 系统有内部函数.还有一些系统扩展的功能但不是作为内部函数的、以文件的形式存储在磁盘上的文件,要使用它们,必须用一定的方式来调用这些文件,这些文件我们称之为程序包. 调用方式之一如上所述:<<Algebra`InequalitySolve`或用:Needs["Algebra`InequalitySolve`"]1.9 由递推式求数列的通项公式例1.7 设 求数列的通项公式只要输入:<<DiscreteMath`RSolve` RSolve[{a[n]==n *a[n-1], a[1]==1}, a[n], n]即可(结果见下图)11,1,n n a na a -==函数名 递推关系 初始条件调用程序包 类名,此处是函数类 函数类中的这个函数离散类 离散类中的这个函数1.10 作函数图像例1.8在同一坐标系中作出2-1y x 和y=sinx在[-2,2]内的图像.输入: Plot[{x^2-1,Sin[x]},{x,-2,2}] 结果见下图例1.9作出sinxcosy的三维图形输入:Plot3D[Sin[x]*Cos[y],{x,-2Pi,2Pi},{y,-即可(结果见下图)增加取样点提高光滑度第二章 运用Mathematica 实现高等数学中的基本运算极限、导数和积分是高等数学中的主要概念和基本运算,如果你在科研中遇到较复杂的求极限、求导数或求积分问题,Mathematica 可以帮你快速解决这些问题。
mathematical教程 第二讲

求定积分命令
例:(1) 求下列函数的原函数:
ln(x 1) x 1
(1 cos x ) 2
(2) 判断下列广义积分的敛散性
1
1 dx p x
x ln xdx
0
1
2
0
1 dx 2 (1 x)
(3)原函数无法用初等函数表示的积分
sin x x dx
导数的应用
可导函数的单调性及凹凸性
二元函数作图
一元显函数作图
格式:
Plot[函数f,{x,xmin, xmax}, 选项] 在区间{xmin, xmax}上,按选项的要求画出函数f的图形.
功能:
注:
1) 选项可有可无, 可有多个依次排列,中间用逗号隔开. 2) 选项的格式: 选项名 —> 选项值 Plot[Sin[x]* x, {x, 0, 2Pi}, PlotStyle -> {RGBColor[1, 0, 0]}, Axes -> False]
点的表示:{x,y} 点的集合:{{x1,y1},{x2,y2},{x3,y3}…} 数据点作图的stPlot[{{x1,y1},{x2,y2},…}] 功能:画出数据点{x1,y1},{x2,y2},… ListPlot[{y1,y2,…yn}] 功能:画出数据点{{1,y1},{2,y2},…{n,yn}} ListPlot[数据,PlotJoined—>True] 功能:画一条通过数据点的光滑曲线
方法:先求驻点再画图确定 例:考察如下三个函数的单调区间: y=x3-3x2-9x+14 y=sinx+x2
Mathematica简易教程

Page 21
使用条件运算符,基本格式为:f[x_]:=expr/;condition,当condition条件满足 时才把expr赋给f(x)。
Page 22
当然,使用If命令也可以定义上面的函数,If语句的格式为If[条件,值1,值 2],如果条件成立取“值1”,否则取“值2”,用If语句定义如下:
mathematicapage目录第一章mathematica简介第二章mathematica的基本量第三章mathematica的基本运算第四章函数作图第五章微积分的基本操作page第一章mathematica简介mathematica由美国物理学家stephenwolfram领导开发的他们组建wolfram研究公司mathematica是一个计算机代数系统把符号运算数值计算与图形显示集一体可以完成上述三项功能更重要的是它把这些功能融合在一个系统里使它们成为一个整体
3.2.4 解条件方程
在作方程计算时,可以把一个方程看做你要处理的主要方程,而把其 他方程作为必须满足的辅助条件,你就会发现这样处理很方便。 在Mathematica中,我们通常是首先命名辅助条件组,然后用名字把辅 助条件包含在你要用函数Solve[]求解的方程组中。
Page 40
3.3 求和与求积
Mathematica简介与入门
目录
第一章 Mathematica简介 第二章 Mathematica的基本量
第三章 Mathematica的基本运算
第四章 函数作图 第五章 微积分的基本操作
Page 2
第一章 Mathematica简介
Mathematica由美国物理学家Stephen Wolfram领导开发的,他们组建Wolfram 研究公司 Mathematica是一个计算机代数系统,把 符号运算、数值计算与图形显示集一体, 可以完成上述三项功能,更重要的是它把 这些功能融合在一个系统里,使它们成为 一个整体.此外,Mathematica还是一个 易于扩充的系统,即实际上提供了功能强 大的程序设计语言,可以定义用户需要的 各种函数,完成用户需要的各种工作,系 统本身还提供了一大批用这个语言写出的 专门程序或软件包 Mathematica的发布标志着现代科技计算 的开始。Mathematica是世界上通用计算 系统中最强大的系统。自从1988发布以来, 它已经对如何在科技和其它领域运用计算 机产生了深刻的影响
Mathematica培训教程

蒋晓云主编2005年3月第二章 Mathematica4基础2.1 Mathematica4.0简介Mathematica 是由位于美国伊利州的伊利诺大学Champaign 分校附近的WolframResearch 公司开发的一套专门进行数学计算的软件。
从1988年问世至今,已广泛地应用到工程、应用数学、计算机科学、生物、药学、教育学等领域,深受科学家、学生、教师、研究人员的广泛喜爱。
早在1995年发表的Mathematica3.0版,可以说是数学计算软件史上的一个大创新。
而1999年发表的Mathematica4.0版则在到了这类软件的顶峰。
Mathematica 除了提供数值处理与绘图的功能之外还具有符号计算能力。
能使您轻松地进行各种运算、函数的图像的绘画、解方程等。
对中学数学教学而言:可以通过Mathematica 进行函数性质的研究、处理多项式的各种运算提供很好的工具。
要安装Mathematica4.0建议你的计算机配置要达到如下的要求: 1、 操作系统: Windows95或Windows NT3.51以上的版本。
2、 CPU 处理器:Intel 、Cyrix 或ADM586级以上的CPU 。
3、 硬盘空间: 具备有200MB 以上的硬盘空间才能使Mathematica 能正常地运算。
4、 内存空间: 至少具备32MB 内存空间,建议使用64MB 以上的内存空间。
2.2 Mathematica4.0的启动与退出Mathematica4.0的启动有两种:1、 双击Windows 桌面上的快捷方式可启动Mathematica4.0;单击:开始→程序→Mathematica4→Mathematica4可以启动Mathematica4;启动Mathematica4后主程序会打开一个新的工作窗口,如下图所示:Mathematica4的退出:1、 单击标题栏右边的关闭按钮;2、 单击:File 菜单下的Exit 也可退出Mathematica4;2.3 Mathematica4的基本操作本节我们将对Mathematica4的基本运算、输入/输出等操作进行介绍。
mathematica经典教程

M athematica是美国Wolfram研究公司生产的一种数学分析型的软件,以符号计算见长,也具有高精度的数值计算功能和强大的图形功能。
假设在Windows环境下已安装好Mathematica4.0,启动Windows后,在“开始”菜单的“程序”中单击,就启动了Mathematica4.0,在屏幕上显示如图的Notebook 窗口,系统暂时取名Untitled-1,直到用户保存时重新命名为止输入1+1,然后按下Shif+Enter键,这时系统开始计算并输出计算结果,并给输入和输出附上次序标识In[1]和Out[1],注意In[1]是计算后才出现的;再输入第二个表达式,要求系统将一个二项式展开,按Shift+Enter输出计算结果后,系统分别将其标识为In[2]和Out[2].如图在Mathematica的Notebook界面下,可以用这种交互方式完成各种运算,如函数作图,求极限、解方程等,也可以用它编写像C那样的结构化程序。
在Mathematica系统中定义了许多功能强大的函数,我们称之为内建函数(built-in function), 直接调用这些函数可以取到事半功倍的效果。
这些函数分为两类,一类是数学意义上的函数,如:绝对值函数Abs[x],正弦函数Sin[x],余弦函数Cos[x],以e为底的对数函数Log[x],以a为底的对数函数Log[a,x]等;第二类是命令意义上的函数,如作函数图形的函数Plot[f[x],{x,xmin,xmax}],解方程函数Solve[eqn,x],求导函数D[f[x],x]等。
必须注意的是:如果输入了不合语法规则的表达式,系统会显示出错信息,并且不给出计算结果,例如:要画正弦函数在区间[-10,10]上的图形,输入plot[Sin[x],{x,-10,10}],则系统提示“可能有拼写错误,新符号‘plot’ 很像已经存在的符号‘Plot’”,实际上,系统作图命令“Plot”第一个字母必须大写,一般地,系统内建函数首写字母都要大写。
Mathematica数学入门教程【2】-分数和小数

Mathematica数学入门教程【2】-分数和小数
译自: FAST INTRODUCTION FOR MATH STUDENTS 英文教程在本教程中可以学会在 Mathematica 下怎样用 Wolfram 语言来解决典型的数学问题, 从基本的算术计算到微积分, 涵盖了从 K12 到大学及其以后科学研究各个阶段内容.
通过学习本教程, 学生在数学的各个层次都可以掌握相关如何用Wolfram 语言进行计算, 绘制图形和制作演示文档, 以此来锻炼在未来职场中所需的计算思维和能力.
好了, 现在让我们在下一篇的Mathematica快速数学入门课堂再见. 这里感谢各位每一位看到这里的老师和朋友!
Thank You, Everyone!
本入门教程全部内容:
指令的输入
分数与小数
变量和函数
代数
2D绘图
几何
三角学
极坐标
指数函数和对数
极限
微分
积分
序列, 求和, 级数
更多2D绘图
3D绘图
多元微积分
矢量分析和可视化
微分方程
复分析
矩阵和线性代数
离散数学
概率
统计
数据图和最佳拟合曲线群论
数学智力题
互动模式
数学排版
笔记本文档
云部署。
数学建模首选软件Mathematica画图专讲(很全)省名师优质课赛课获奖课件市赛课一等奖课件

GrayLevel[t] 曲线灰度描述函数,自变量t旳取值范围为闭区间[0, 1],t取0值为白色,t取1值为黑色。
• 举例:
n=4; r=5Cos[nt]+2Sin[5nt]; tu2=ParametricPlot[{rCos[t],rSin[t]},{t,0,2Pi},PlotStyle->{RGBColor[0,0,1],
Thickness[0.01]},AspectRatio->1];
6 4 2
-6 -4 -2 -2 -4 -6
例:AxesLabel-> None, 表达显示旳图形坐标轴没有标识;
AxesLabel->{"time" , "speed"}, 表达平面图形旳横坐标轴标识 显示为time 纵坐标轴标识显示为speed;
AxesLabel->{“时间”,“速度”,“高度”}, 表达空间图形旳 横坐标轴标识设置为时间, 纵坐标轴标识设置为速度, 竖坐标轴 标识设置为高度。
1.5 1
0.5
-2 -1 0 1
2 1 0 -1
2 -2
返回
• 例3:
n=5; r=5Cos[nt]+Sin[5nt]; tu1=Parametricplot[{rCos[t],rSin[t]},{t,0,2pi},AspectRatio->1,
Axes->False,PlotStyle->{RGBColor[1,0,0],Thickness[0.01]}];
Mathematic教程

(2)求微分:dy=f(x)dx
命令形式:Dt[f]
功能: 对函数f(x)求微分df
例 求y=sinx2的微分dy.
In[20]:=Dt[Sin[x^2]]
Out[20]=2xCos[x2]Dt[x]
3、求不定积分与定积分
(1)求不定积分 命令形式:Integrate[f, x] 1 dx 例 计算 2 2 sin xcos x In[21]:=Integrate[1/(Sin[x]^2 Cos[x]^2),x] Out[21]=-Cot[x]+Tan[x] (2)计算定积分 命令形式1: Integrate[f[x],{x,xmin,xmax}] 功能:计算定积分 xmin,xmax表示积分下限和上限。 命令形式2: NIntegrate[f[x],{x,xmin,xmax}] 功能: 计算定积分的数值积分,xmin,xmax必须 是数字,不能是字母。
7、初等代数运算
(1)多项式运算与因式分解 Expand[多项式] 将多项式按升幂展开 Factor[多项式] 将多项式进行因式分解 Simplify[多项式] 将多项式化为最简形式 Collect[多项式,x] 将多项式按x的同次幂合并形式展开
例1 设q=(1+2x-y)2,将q展开. In[6]:=q=Expand[(1+2*x-y)^2] Out[6]=1+4x+4x2-2y-4xy+y2 例2 将多项式120-46x-19x2+4x3+x4分解因式. In[7]:=Factor[120-46*x-19*x^2+4*x^3+x^4] Out[7]=(-3+x)(-2+x)(4+x)(5+x)
Mathematica 教程 2

Mathematica 教程 2第二章列表在上节课中我们已经用过Mathematica中的列表。
在这一章中我们将学习列表的许多不同方式。
用户将发现列表是Mathematica 中最灵活和最强有力的对象之一,将看到Mathematica 列表是数学和计算机科学中一些标准概念的一般化。
Mathematica列表通常是提供一种将一些相互关联的元素放在一起的方法,使他们成为一个整体。
这样一来,既可以对整体操作,也可以对整体中的一个元素进行单独的操作。
在Mathematica 中这样的数据结构被称为表(List)。
在Mathematica中表主要有三个用法,在后续的课程中会分别学习。
注:在Mathematica中,表是用{}来表示,表中元素用“,”隔开。
多维列表中每一维用{}分隔。
如表{a,b,c}可以表示一个一维列表, 表{{a,b},{c,d}}可以表示二维列表。
2.1 表的生成在表中的元素较少时,可以采取直接列表的方式列出表中的元素,如{1,2,3}如果列表元素较多时,可以通过建表函数进行建表,见下表:生成列表的函数*:f表示一个表达式或者函数如:上面的例子都是通过变化单个参数而得到的,用户也可以使用多个参数产生列表。
这些例子表示的都是一个列表的列表,其中外层列表的元素对应于i的值,内层列表的元素相应于j的值。
2.2获取列表的部分元素对于列表,我们可以象普通数值给予变量名。
当ABC表示一个列表时,我们可以对列表也可以对列表中的元素进行操作。
在Mathematica 中提取部分元素的方法如下。
提取列表中的部分元素的方法产生三维列表t提取t的i=2的部分提取t的i=2,i=1部分提取t的i=2,j=1的部分提取t的i=2,j=1,k=1的部分注:用户可以将Mathematica列表看作“数组”,那么列表的列表可以看作二维数组,当把列表显示为表格形式时,每个元素的两个下标如x和y坐标一样。
2.3 检测和搜索列表元素上一节讨论的是根据元素的位置或标号提取列表的元素。
mathematic使用说明第二讲
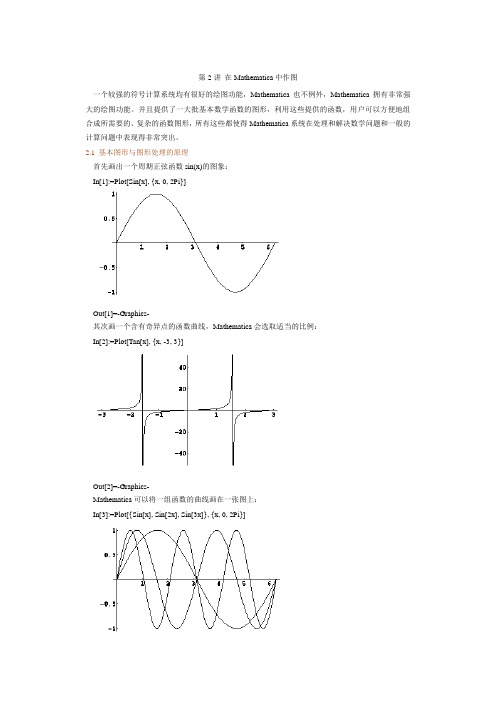
第2讲在Mathematica中作图一个较强的符号计算系统均有很好的绘图功能,Mathematica也不例外,Mathematica拥有非常强大的绘图功能。
并且提供了一大批基本数学函数的图形,利用这些提供的函数,用户可以方便地组合成所需要的、复杂的函数图形,所有这些都使得Mathematica系统在处理和解决数学问题和一般的计算问题中表现得非常突出。
2.1 基本图形与图形处理的原理首先画出一个周期正弦函数sin(x)的图象:In[1]:=Plot[Sin[x], {x, 0, 2Pi}]Out[1]=-Graphics-其次画一个含有奇异点的函数曲线,Mathematica会选取适当的比例:In[2]:=Plot[Tan[x], {x, -3, 3}]Out[2]=-Graphics-Mathematica可以将一组函数的曲线画在一张图上:In[3]:=Plot[{Sin[x], Sin[2x], Sin[3x]}, {x, 0, 2Pi}]Out[3]=-Graphics-当Mathematica去画函数f的图象时,为了得到光滑的曲线,系统需要计算许多点的函数值。
Mathematica中存在两种可能的方法解决这个问题。
第一种方法是先设法求出函数f关于x的大致的表达式,然后按顺序计算出相应的x处的函数表达式的值。
另一方法就是,先写出各点的x值,然后顺序算出相应点x的函数值f。
如果输入Plot[Sin[x], {x, 0, 2Pi}],Mathematica使用了上面所述的第二种方法。
使用这种方法的好处在于,Mathematica只需要去计算对应的x的函数值,这样它就不需要去关注当x为符号的时候所对应的函数表达式。
在有些情况下,在画出该函数的曲线之前,计算出函数f的表达式还是非常有用的,一个典型的实例是,当f是生成一个函数表的命令,此时系统先要生成一个表,然后计算函数值。
可用绘图格式Plot[Evaluate[f],{x,xmin,xmax}]来实现。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
cos x x = 0.5,1.5,2 在
的精确到50位的值。
f[x_]:=Exp[-x^2]*Cos[x] N[{f[0.5],f[1.5],f[2]},50]; TableForm[%] 0.6834619864100321 0.007455646203452103 -0.007621995182886547555251812613108957106093655\ 021473
2 2 例如 z = sin( x + y )
f[x_,y_]:=Sin[x^2+y^2] f[x,y] Plot3D[%,{x,-3,3},{y,-3,3}]
Mathematica的怪癖
Mathematica 严格区分大小写
(所有用户定义符号最好用小写字母开头)
不同的括号有不同的用途
Mathematica 中的四种括号 ( ),[ ],{ },[ [ ] ]。 应用如下: 小括号( ) 中括号 [ ] 大括号{ } 双括号[ [ ] ] 表示分组,主要用于输入的算式中 用于函数,指明自变量。 用于表示集合。 表示目录索引,用于集合元素的处理
例 如
A={1,2,3,4,5,6,7,8,9,10} A^2 1/A A! {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} {1, 4, 9, 16, 25, 36, 49, 64, 81, 100}
1 1 1 1 1 1 1 1 1 {1, , , , , , , , , } 2 3 4 5 6 7 8 9 10
f ( x) = x2
f[x_]:=x^2
g[x_,y_]:=(x-y)^2/y
( x − y)2 g( x, y) = y
注 意
1.自定义函数表达式左边的自变量要写在[ ]号内,且 后面跟随“—”(空格), 右边则不需要。 2.所使用的函数名尽量以小写字母口头,从而避免与 Mathematica内部函数名发生冲突。 3.所定义的函数名应与前面所用过的其它函数不重复.
(2)要求符合任意精度要求的结果,其格式如下: N[表达式,n] (结果保留n位精度) 例如
[In7]: N[Pi,25] [Out7]:3.1415926535897932384626434 115/496 N[115/496,10] 0.2318548387
115 496
比较下面两个输入的输出结果
(2)Range[n] 生成前n个相邻整数组成的列表
Range[10] {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(3)Range[m,n] 生成由m到n个相邻整数组成的列表
Range[10,20] {10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}
第二讲
Mathematica入门 入门
河北理工大学轻工学院
--基础教学部 --基础教学部
jc@
Mathematica界面简介 界面简介
软 件 入 门
初等数值计算 自定义函数 表的构造与计算
y 30 20 10 x -2 -10 -20 2 4 6
前
言
当今时代,数学已渗透到各个领域,大量的公式 推导、计算数据、画图等,要花费掉很多宝贵的时间和 精力,而其中绝大多数是按照固定的法则进行的繁琐和 重复的劳动,电子计算机的普及和应用为我们从上述枯 燥的工作中解脱出来提供了可能,许多绘图软件及符号 运算系统的问世终于使人们可以比以往更加迅速有效 地工作。
3.常用数学常数
Pi
E
I Infinity
注
意
(1)Mathematica函数的自变量都在[ ]内。 (2)Mathematica中的函数都以大写字母开头。
代数运算
Mathematica 的一个重要的功能是进行代数公式演算,即符号 运算.
例 3 设有多项式 3x2+2 x-1 和 x2-1,(1) 求二者的和、差、积、 商;(2) 将二者的积展开成单项式之和; (3) 将二者的积进行分解 因式. 解 In[1]:=p1=3*x^2+2x-1 Out[5]=(-1+x2)(-1+2x+3x2)
赋给列表一个符号 名称,方便引用和 运算
{1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800}
例如 当列表的元素复合集合运算规则时可以运算
A={1,3,5,7,9} B={2,4,6,8,10} A+B A.B B^A
{1, 3, 5, 7, 9} {2, 4, 6, 8, 10} {3, 7, 11, 15, 19} 190 {2, 64, 7776, 2097152, 1000000000}
请同学们练习:
(1) 321 ^ 4
1 (7) arcsin 3
(8) tan 0.54
( 2)
π 2 +1
264
( 3) log 3
(9) arctan eπ
10 ( )17.2 × 16.3 + 4.8 ( )
( ) 2 x + 3 + ( 5 x + 9) × ( 4 x + 2) 11 ( )
例:问 3100是多少位数?
3^100 ScientificForm[%]
5.15378×1047
ii
例:求 i 精确到20位的值?
N[I^(I^I),20] 0.94715899807237838065 + 0.32076444997930853466 I
例:在围棋盘的第一位位置放1粒米,第二位置放 2粒米,第三位置放 22粒米,第四位置放 23 粒米… 摆完整个棋盘一共要放多少粒米?如40000粒米的 体积是一升,这些米有多少升? 能充满多大一个 球形容器? 程序如下
(4)Range[m,n,d] 生成由m到步长为d的整数组成的列表
Range[10,50,5] {10, 15, 20, 25, 30, 35, 40, 45, 50}
(5)Table[f[n],{n}] f[n_]:=n^3 Table[f[n],{n,1,10}] {1, 8, 27, 64, 125, 216, 343, 512, 729, 1000} g[n_]:=1/n Table[g[n],{n,1,10}] (6)Array [f[n],{n}] f[x_]:=x^2+x+1 Array[f,10] {3, 7, 13, 21, 31, 43, 57, 73, 91, 111}
2.常用数学函数
Sqrt[x] Exp[x] Log[x] Sin[x] ArcSin[x] Abs[x] Sign[x] Random[ ] n! Max[x,y…] Min[x,y…] Log[a,x] Cos[x] ArcCos[x] Tan[x] ArcTan[x] 三角函数 反三角函数 取x的绝对值 取x的符号 产生[0,1]上的随机数 n的阶乘 取最值 开方 ex
g1=Sum[2.^n,{n,0,360}]; 米粒数 = 4.69709×10108 ScientificForm[%] 104 米升数 =1.17427×10 %/40000 (3.%/(4Pi))^(1/3)//N 球形容器半径 = 3.03781×1034
表的构造和运算
列表有广泛的应用, Mathematica提供了一大类列表 命令。 常用命令如下: (1) A={a,b,c,d} List[a,b,c,d] {a, b, c, d}
全局赋值 局部赋值
7 1537
7 18 -89
(4)引用符 “ % ”
在利用Mathematica计算时,你往往要使用你已得 到的精确结果。如下的使用方法非常方便: % %% %。。。%(k个) %n 最后计算结果 倒数第二个计算结果 倒数第k个计算结果 第Out[n]行结果
例如 计算 π + π + π 精确到20位的近似值
Sqrt[Pi+Sqrt[Pi+Sqrt[Pi]]]//N 2.31481 Sqrt[Pi]; Sqrt[Pi+%]; Sqrt[Pi+%]//N 2.31481
1 计算 1+ 1 1+ 1 1+ 1 1+ 2
程序
1+1/2; 1+1/%; 1+1/%; 1+1/%
13 8
自定义函数
虽然Mathematica内部提纲了大量函数,但在 很多应用中还远远不能满足需要,用户可以自己定 义新的函数。定义方式如下:
1. 表达式的输入
x+y 表示 x+y x-y 表示 x-y x/y 表示 x÷y x*y 表示 x×y x^y 表示 x 的y次方 Sqrt〔x〕 (加) (减) (除) (乘) (乘方) (开方)
这是根据国际数学标准来确定的,另外表达式中也允许而且 只允许出现小括号“( )”,表达式的运算顺序也与我们熟知的一 样:先乘除后加减,有括号的先算括号中的。
Mathematica的界面简介
1.安装、退出 2.界面简介
双击 Mathematica 之图标 ,启动 Mathematica 系 统,计算机屏幕出现 Mathematica 的工作窗口(见下图) , 此时可以通过键盘输入要计算的表达式.
例 1 计算 100!
解
在主工作窗口用户区 (见下页图) 输入 100! 中,
前
言(续)
Mathematica是美国WolframResearch公司开发的一 套专门用于进行数学计算的软件。 1988年问世, 1995年Mathematica3.0版是数学软件史上的一大创 新 2004年的Mathematica4.1版达到这类软件的顶峰
