中考数学压轴题7(90--119)
中考数学几何压轴题及答案及答案

中考数学几何压轴题及答案一、解答题(共30小题)1.观察猜想(1)如图①,在Rt△ABC中,∠BAC=90°,AB=AC=3,点D与点A重合,点E在边BC上,连接DE,将线段DE绕点D顺时针旋转90°得到线段DF,连接BF,BE与BF的位置关系是,BE+BF=;探究证明(2)在(1)中,如果将点D沿AB方向移动,使AD=1,其余条件不变,如图②,判断BE与BF的位置关系,并求BE+BF的值,请写出你的理由或计算过程;拓展延伸(3)如图③,在△ABC中,AB=AC,∠BAC=α,点D在边BA的延长线上,BD=n,连接DE,将线段DE绕着点D顺时针旋转,旋转角∠EDF=α,连接BF,则BE+BF的值是多少?请用含有n,α的式子直接写出结论2.在△ABC的边BC上取B′、C′两点,使∠AB′B=∠AC′C=∠BAC(1)如图1中∠BAC为直角,∠BAC=∠AB′B=∠AC′C=90°(点B′与点C′重合),则△ABC∽△B'BA∽△C'AC,,,进而可得AB2+AC2=;(2)如图2中当∠BAC为锐角,图3中∠BAC为钝角时(1)中的结论还成立吗?若不成立,则AB2+AC2等于什么(用含用BC和B′C′的式子表示)?并说明理由(3)若在△ABC中,AB=5,AC=6,BC=9,请你先判断出△ABC的类型,再求出B′C′的长3.(1)问题发现如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D是线段AB上一动点,连接BE填空:①的值为;②∠DBE的度数为.(2)类比探究如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D是线段AB上一动点,连接BE.请判断的值及∠DBE的度数,并说明理由;(3)拓展延伸如图3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE 的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.4.(1)问题发现:如图①,在△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,以点D为顶点作正方形DFGE,使点A、C分别在DE和DF上,连接BE、AF.则线段BE 和AF数量关系.(2)类比探究:如图②,保持△ABC固定不动,将正方形DFGE绕点D旋转α(0°<α≤360°),则(1)中的结论是否成立?如果成立,请证明;如果不成立,请说明理由.(3)解决问题:若BC=DF=2,在(2)的旋转过程中,连接AE,请直接写出AE的最大值.5.如图,在平行四边形ABCD中,AC与BD交于点O,以点O为顶点的∠EOF的两边分别与边AB、AD交于点E、F,且∠EOF与∠BAD互补.(1)若四边形ABCD是正方形,则线段OE与OF有何数量关系?请直接写出结论;(2)若四边形ABCD是菱形,那么(1)中的结论是否成立?若成立,请画出图形并给出证明;若不成立,请说明理由;(3)若AB:AD=m:n,探索线段OE与OF的数量关系,并证明你的结论.6.如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.(1)证明与推断:①求证:四边形CEGF是正方形;②推断:的值为:(2)探究与证明:将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由;(3)拓展与运用:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2,则BC=.7.如图1,在△ABC中,AB=AC=2,∠BAC=120°,点D、E分别是AC、BC的中点,连接DE.定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.探索发现:图1中,的值为;的值为.(2)拓展探完若将△CDE绕点C逆时针方向旋转一周,在旋转过程中的大小有无变化?请仅就图2的情形给出证明.(3)问题解决当△CDE旋转至A,D,E三点共线时,直接写出线段BE的长.8.已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D是射线OM上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE,设OD=m.(1)问题发现如图1,△CDE的形状是三角形.(2)探究证明如图2,当6<m<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.(3)解决问题是否存在m的值,使△DEB是直角三角形?若存在,请直接写出m的值;若不存在,请说明理由.9.等腰直角三角形ABC和等腰直角三角形ADE中,∠BAC=∠DAE=90°,AB=4,AE=2,其中△ABC固定,△ADE绕点A作360°旋转,点F、M、N分别为线段BE、BC、CD 的中点,连接MN、NF.问题提出:(1)如图1,当AD在线段AC上时,则∠MNF的度数为,线段MN 和线段NF的数量关系为;深入讨论:(2)如图2,当AD不在线段AC上时,请求出∠MNF的度数及线段MN和线段NF的数量关系;拓展延伸:(3)如图3,△ADE持续旋转过程中,若CE与BD交点为P,则△BCP面积的最小值为.10.四边形是我们在学习和生活中常见的图形,而对角线互相垂直的四边形也比较常见,比如筝形、菱形、图1中的四边形ABCD等.它们给我们的学习和生活带来了很多的乐趣和美感.(1)如图2,在四边形ABCD中,AB=AD,CB=CD,则AC与BD的位置关系是,请说明理由.(2)试探究图1中四边形ABCD的两组对边AB,CD与BC,AD之间的数量关系,请写出证明过程.(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE的长.11.问题发现:如图(1)在Rt△ABC和Rt△BDE中,∠A=∠DEB=30°,BC=BE=6,Rt△BDE绕点B逆时针旋转,H为CD的中点,当点C与点E重合时,BH与AE的位置关系为,BH与AE的数量关系为;问题证明:在Rt△BDE绕点B旋转的过程中,(1)中的结论是否仍然成立?若成立,请就图(2)的情形给出证明若不成立,请说明理由;拓展应用:在Rt△BDE绕点B旋转的过程中,当DE∥BC时,请直接写出BH2的长.12.如图1,菱形ABCD与菱形GECF的顶点C重合,点G在对角线AC上,且∠BCD=∠ECF=60°,(1)问题发现的值为;(2)探究与证明将菱形GECF绕点C按顺时针方向旋转α角(0°<α<60°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;(3)拓展与运用:菱形GECF在旋转过程中,当点A,G,F三点在一条直线上时,如图3所示连接CG并延长,交AD于点H,若CE=2,GH=,则AH的长为.13.如图,在Rt△ABC中,∠ACB=90°,=,CD⊥AB于点D,点E是直线AC上一动点,连接DE,过点D作FD⊥ED,交直线BC于点F.(1)探究发现:如图1,若m=n,点E在线段AC上,则=;(2)数学思考:①如图2,若点E在线段AC上,则=(用含m,n的代数式表示);②当点E在直线AC上运动时,①中的结论是否仍然成立?请仅就图3的情形给出证明;(3)拓展应用:若AC=,BC=2,DF=4,请直接写出CE的长.14.如图,已知点E是射线BC上的一点,以BC、CE为边作正方形ABCD和正方形CEFG,连接AF,取AF的中点M,连接DM、MG(1)如图1,判断线段DM和GM的数量关系是,位置关系是;(2)如图2,在图中的正方形CEFG绕点C逆时针旋转的过程中,其他条件不变,(1)中的结论是否成立?说明理由;(3)已知BC=10,CE=2,正方形CEFG绕点C旋转的过程中,当A、F、E共线时,直接写出△DMG的面积.15.在Rt△ABC中,∠ACB=90°,AB=,AC=2,过点B作直线m∥AC,将△ABC绕点C顺时针旋转得到△A′B′C(点A,B的对应点分别为A',B′),射线CA′,CB′分别交直线m于点P,Q.(1)如图1,当P与A′重合时,求∠ACA′的度数;(2)如图2,设A′B′与BC的交点为M,当M为A′B′的中点时,求线段PQ的长;(3)在旋转过程中,当点P,Q分别在CA′,CB′的延长线上时,试探究四边形P A'B′Q的面积是否存在最小值.若存在,求出四边形P A′B′Q的最小面积;若不存在,请说明理由.16.如图(1),在等边三角形ABC中,点D,E分别在边AB,AC上,AD=AE,连接BE,CD,点M,N,P分别是BE,CD,BC的中点,连接DE,PM,PN,MN.(1)观察猜想,图(1)中△PMN是(填特殊三角形的名称)(2)探究证明,如图(2),△ADE绕点A按逆时针方向旋转,则△PMN的形状是否发生改变?并就图(2)说明理由.(3)拓展延伸,若△ADE绕点A在平面内自由旋转,AD=2,AB=6,请直接写出△PMN 的周长的最大值.17.已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β,(1)如图1,若点D在线段BC上,点E在线段AC上.∠ABC=60°,∠ADE=70°,则α=°;β=°.(2)如图2,若点D在线段BC上,点E在线段AC上,则α,β之间有什么关系式?说明理由.(3)是否存在不同于(2)中的α,β之间的关系式?若存在,请写出这个关系式(写出一种即可),说明理由;若不存在,请说明理由.18.问题提出:(1)如图1,在四边形ABCD中,连接AC、BD,AB=AD,∠BAD=∠BCD=90°,将△ABC绕点A逆时针旋转90°,得到△ADE,点B的对应点落在点D,点C的对应点为点E,可知点C、D、E在一条直线上,则△ACE为三角形,BC、CD、AC的数量关系为;探究发现:(2)如图2,在⊙O中,AB为直径,点C为的中点,点D为圆上一个点,连接AD、CD、AC、BC、BD,且AD<BD,请求出CD、AD、BD间的数量关系.拓展延伸:(3)如图3,在等腰直角三角形ABC中,点P为AB的中点,若AC=13,平面内存在一点E,且AE=10,CE=13,当点Q为AE中点时,PQ=.19.已知△ABC中,CA=CB,0°<∠ACB≤90°,点M、N分别在边CA,CB上(不与端点重合),BN=AM,射线AG∥BC交BM延长线于点D,点E在直线AN上,EA=ED.(1)【观察猜想】如图1,点E在射线NA上,当∠ACB=45°时,①线段BM与AN的数量关系是;②∠BDE的度数是;(2)【探究证明】如图2点E在射线AN上,当∠ACB=30°时,判断并证明线段BM与AN的数量关系,求∠BDE的度数;(3)【拓展延伸】如图3,点E在直线AN上,当∠ACB=60°时,AB=3,点N是BC 边上的三等分点,直线ED与直线BC交于点F,请直接写出线段CF的长.20.如图①,在正方形ABCD和正方形AB'C'D'中,AB=2,AB'=,连接CC’(1)问题发现:.(2)拓展探究:将正方形AB'C'D'绕点A逆时针旋转,记旋转角为θ,连接BB',试判断:当0°≤θ<360°时,的值有无变化?请仅就图②中的情形给出你的证明;(3)问题解决:请直接写出在旋转过程中,当C,C′,D'三点共线时BB′的长.21.如图1,在正方形ABCD中,点O是对角线BD的中点.(1)观察猜想将图1中的△BCD绕点O逆时针旋转至图2中△ECF的位置,连接AC,DE,则线段AC与DE的数量关系是,直线AC与DE的位置关系是.(2)类比探究将图2中的△ECF绕点O逆时针旋转至图3的位置,(1)中的结论是否成立?并说明理由.(3)拓展延伸将图2中的△ECF在平面内旋转,设直线AC与DE的交点为M,若AB=4,请直接写出BM的最大值与最小值.22.如图1,点B在直线l上,过点B构建等腰直角三角形ABC,使∠BAC=90°,且AB=AC,过点C作CD⊥直线l于点D,连接AD.(1)小亮在研究这个图形时发现,∠BAC=∠BDC=90°,点A,D应该在以BC为直径的圆上,则∠ADB的度数为°,将射线AD顺时针旋转90°交直线l于点E,可求出线段AD,BD,CD的数量关系为;(2)小亮将等腰直角三角形ABC绕点B在平面内旋转,当旋转到图2位置时,线段AD,BD,CD的数量关系是否变化,请说明理由;(3)在旋转过程中,若CD长为1,当△ABD面积取得最大值时,请直接写AD的长.23.如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F.另一边交CB的延长线于点G.(1)观察猜想:线段EF与线段EG的数量关系是;(2)探究证明:如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:(3)拓展延伸:如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a、BC=b,求的值.24.如图1,在Rt△ABC中,∠B=90°,AB=2,BC=1,点D,E分别是边BC,AC的中点,连接DE.将△EDC绕点C按顺时针方向旋转,记旋转角为α.(1)问题发现①当α=0°时,=;②当α=180°时,=.(2)拓展探究试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情况给出证明.(3)问题解决当△EDC旋转至A、B、E三点共线时,直接写出线段BD的长.25.在△ABC中,AD为BC边上的中线,E为AD上一动点,设DE=nEA,连接CE并延长,交AB于点F.(1)尝试探究如图(1),当∠BAC=90°,∠B=30°,DE=EA时,BF,BA之间的数量关系是;(2)类比延伸如图(2),当△ABC为锐角三角形,DE=EA时,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;(3)拓展迁移如图(3),当△ABC为锐角三角形,DE=nEA时,请直接写出BF,BA之间的数量关系.26.古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”.请研究如下美丽的圆.如图,线段AB是⊙O的直径,延长AB至点C,使BC=OB,点E是线段OB的中点,DE ⊥AB交⊙O于点D,点P是⊙O上一动点(不与点A,B重合),连接CD,PE,PC.(1)求证:CD是⊙O的切线;(2)小明在研究的过程中发现是一个确定的值.回答这个确定的值是多少?并对小明发现的结论加以证明.27.定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.(1)如图1,∠E是△ABC中∠A的遥望角,若∠A=α,请用含α的代数式表示∠E.(2)如图2,四边形ABCD内接于⊙O,=,四边形ABCD的外角平分线DF交⊙O 于点F,连结BF并延长交CD的延长线于点E.求证:∠BEC是△ABC中∠BAC的遥望角.(3)如图3,在(2)的条件下,连结AE,AF,若AC是⊙O的直径.①求∠AED的度数;②若AB=8,CD=5,求△DEF的面积.28.【性质探究】如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E.作DF⊥AE于点H,分别交AB,AC于点F,G.(1)判断△AFG的形状并说明理由.(2)求证:BF=2OG.【迁移应用】(3)记△DGO的面积为S1,△DBF的面积为S2,当=时,求的值.【拓展延伸】(4)若DF交射线AB于点F,【性质探究】中的其余条件不变,连结EF,当△BEF的面积为矩形ABCD面积的时,请直接写出tan∠BAE的值.29.如图,已知AC为正方形ABCD的对角线,点P是平面内不与点A,B重合的任意一点,连接AP,将线段AP绕点P顺时针旋转90°得到线段PE,连接AE,BP,CE.(1)求证:△APE∽△ABC;(2)当线段BP与CE相交时,设交点为M,求的值以及∠BMC的度数;(3)若正方形ABCD的边长为3,AP=1,当点P,C,E在同一直线上时,求线段BP 的长.30.如图1和图2,在△ABC中,AB=AC,BC=8,tan C=.点K在AC边上,点M,N 分别在AB,BC上,且AM=CN=2.点P从点M出发沿折线MB﹣BN匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持∠APQ=∠B.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当0≤x≤3及3<x≤9时,分别求点P到直线AC的距离(用含x的式子表示);(4)在点P处设计并安装一扫描器,按定角∠APQ扫描△APQ区域(含边界),扫描器随点P从M到B再到N共用时36秒.若AK=,请直接写出点K被扫描到的总时长.参考答案与试题解析一.解答题(共30小题)1.【解答】解:(1)如图①中,∵∠EAF=∠BAC=90°,∴∠BAF=∠CAE,∵AF=AE,AB=AC,∴△BAF≌△CAE,∴∠ABF=∠C,BF=CE,∵AB=AC,∠BAC=90°,∴∠ABC=∠C=45°,∴∠FBE=∠ABF+∠ABC=90°,BC=BE+EC=BE+BF,故答案为:BF⊥BE,BC.(2)如图②中,作DH∥AC交BC于H.∵DH∥AC,∴∠BDH=∠A=90°,△DBH是等腰直角三角形,由(1)可知,BF⊥BE,BF+BE=BH,∵AB=AC=3,AD=1,∴BD=DH=2,∴BH=2,∴BF+BE=BH=2;(3)如图③中,作DH∥AC交BC的延长线于H,作DM⊥BC于M.∵AC∥DH,∴∠ACB=∠H,∠BDH=∠BAC=α,∵AB=AC,∴∠ABC=∠ACB∴∠DBH=∠H,∴DB=DH,∵∠EDF=∠BDH=α,∴∠BDF=∠HDE,∵DF=DE,DB=DH,∴△BDF≌△HDE,∴BF=EH,∴BF+BE=EH+BE=BH,∵DB=DH,DM⊥BH,∴BM=MH,∠BDM=∠HDM,∴BM=MH=BD•sin.∴BF+BE=BH=2n•sin.2.【解答】解:(1)如图1中,∵△ABC∽△B'BA∽△C'AC,∴=,=,∴AB2=BB′×BC,AC2=CC′×BC,∴AB2+AC2=BC(BB′+CC′)=BC×BC=BC2,故答案为BC2.(2)不成立.理由:如图2中当∠BAC为锐角时,BB′+CC′﹣B′C′=BC,且△ABC∽△B'BA∽△C'AC,∴∴=,=,∴AB2=BB′×BC,AC2=CC′×BC,∴AB2+AC2=BC(BB′+CC′)=BC2+BC•B′C′.图3中∠BAC为钝角时,BB′+CC′+B′C′=BC.AB2+AC2=BC(BB′+CC′)=BC2﹣BC•B′C′.(3)当AB=5,AC=6,BC=9时,则AB2+AC2<BC2,可知△ABC为钝角三角形,由图3可知:AB2+AC2=BC2﹣BC•B′C′,∴52+62=92﹣9B′C′,∴B′C′=.3.【解答】解:(1)∵∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,∴∠ABC=∠CAB=45°=∠CDE=∠CED,∴AC=BC,CD=CE,∵∠ACB=∠DCE=90°,∴∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴BE=AD,∠CAB=∠CBE=45°,∴∠DBE=∠ABC+∠CBE=90°,=1,故答案为:1,90°(2),∠DBE=90°理由如下:∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,∴∠ACD=∠BCE,∠CED=∠ABC=30°∴tan∠ABC=tan30°==∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,∴Rt△ACB∽Rt△DCE∴∴,且∠ACD=∠BCE∴△ACD∽△BCE∴=,∠CBE=∠CAD=60°∴∠DBE=∠ABC+∠CBE=90°(3)若点D在线段AB上,如图,由(2)知:=,∠ABE=90°∴BE=AD∵AC=2,∠ACB=90°,∠CAB=90°∴AB=4,BC=2∵∠ECD=∠ABE=90°,且点M是DE中点,∴CM=BM=DE,∵△CBM是直角三角形∴CM2+BM2=BC2=(2)2,∴BM=CM=∴DE=2∵DB2+BE2=DE2,∴(4﹣AD)2+(AD)2=24∴AD=+1∴BE=AD=3+若点D在线段BA延长线上,如图同理可得:DE=2,BE=AD∵BD2+BE2=DE2,∴(4+AD)2+(AD)2=24,∴AD=﹣1∴BE=AD=3﹣综上所述:BE的长为3+或3﹣4.【解答】解:(1)∵△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,∴AD=BD=DC,∠BDA=90°,∵四边形DFGE是正方形,∴DE=DF,∠EDF=90°,∴∠BDE=∠ADF=90°,在△BDE和△ADF中,,∴△BDE≌△ADF(SAS),∴BE=AF故答案为:BE=AF;(2)成立;理由如下:当正方形DFGE在BC的上方时,如图②所示,连接AD,∵在Rt△ABC中,AB=AC,D为斜边BC的中点,∴AD=BD,AD⊥BC,∴∠ADE+∠EDB=90°,∵四边形DFGE为正方形,∴DE=DF,且∠EDF=90°,∴∠ADE+∠ADF=90°,∴∠BDE=∠ADF,在△BDE和△ADF中,,∴△BDE≌△ADF(SAS),∴BE=AF;当正方形DFGE在BC的下方时,连接AD,如图③所示:∵∠BDE=∠BDF+90°,∠ADF=∠BDF+90°,∴∠BDE=∠ADF,在△BDE和△ADF中,,∴△BDE≌△ADF(SAS),∴BE=AF;综上所述,(1)中的结论BE=AF成立;(3)在△ADE中,∵AE<AD+DE,∴当点A、D、E共线时,AE取得最大值,最大值为AD+DE.如图④所示:则AD=BC=1,DE=DF=2,∴AE=AD+DE=3,即AE的最大值为3.5.【解答】解:(1)如图1,过点O作OM⊥AB于M,ON⊥AD于N,∴∠OME=∠ONF=90°,∴∠BAD+∠MON=180°,∵∠BAD+∠EOF=180°,∴∠MON=∠EOF,∴∠EOM=∠FON,∵O是正方形ABCD的对角线的交点,∴∠BAO=∠DAO,∵OM⊥AB,ON⊥AD,∴OM=ON,∴△OME≌△ONF(AAS)∴OE=OF;(2)(1)的结论成立;理由:如图2,过点O作OM⊥AB于M,ON⊥AD于N,∴∠OME=∠ONF=90°,∴∠BAD+∠MON=180°,∵∠BAD+∠EOF=180°,∴∠MON=∠EOF,∴∠EOM=∠FON,∵O是菱形ABCD的对角线的交点,∴∠BAO=∠DAO,∵OM⊥AB,ON⊥AD,∴OM=ON,∴△OME≌△ONF(AAS)∴OE=OF;(3)如图3,过点O作OG⊥AB于G,OH⊥AD于H,∴∠OGE=∠OHF=90°,∴∠BAD+∠GOH=180°,∵∠BAD+∠EOF=180°,∴∠GOH=∠EOF,∴△EOG∽△FOH,∴,∵O是▱ABCD的对角线的交点,∴S△AOB=S△AOD,∵S△AOB=AB•OG,S△AOD=AD•OH,∴AB•OG=AD•OH,∴=,∴.6.【解答】解:(1)①∵四边形ABCD是正方形,∴∠BCD=90°,∠BCA=45°,∵GE⊥BC、GF⊥CD,∴∠CEG=∠CFG=∠ECF=90°,∴四边形CEGF是矩形,∠CGE=∠ECG=45°,∴EG=EC,∴四边形CEGF是正方形;②由①知四边形CEGF是正方形,∴∠CEG=∠B=90°,∠ECG=45°,∴=,GE∥AB,∴==,故答案为:;(2)连接CG,由旋转性质知∠BCE=∠ACG=α,在Rt△CEG和Rt△CBA中,=cos45°=、=cos45°=,∴==,∴△ACG∽△BCE,∴==,∴线段AG与BE之间的数量关系为AG=BE;(3)∵∠CEF=45°,点B、E、F三点共线,∴∠BEC=135°,∵△ACG∽△BCE,∴∠AGC=∠BEC=135°,∴∠AGH=∠CAH=45°,∵∠CHA=∠AHG,∴△AHG∽△CHA,∴==,设BC=CD=AD=a,则AC=a,则由=得=,∴AH=a,则DH=AD﹣AH=a,CH==a,∴=得=,解得:a=3,即BC=3,故答案为:3.7.【解答】解:(1)如图1,连接AE,∵AB=AC=2,点E分别是BC的中点,∴AE⊥BC,∴∠BEC=90°,∵AB=AC=2,∠BAC=120°,∴∠B=∠C=30°,在Rt△ABE中,AE=AB=1,根据勾股定理得,BE=∵点E是BC的中点,∴BC=2BE=2,∴==,∵点D是AC的中点,∴AD=CD=AC=1,∴==,故答案为:,;(2)无变化,理由:由(1)知,CD=1,CE=BE=,∴=,,∴=,由(1)知,∠ACB=∠DCE=30°,∴∠ACD=∠BCE,∴△ACD∽△BCE,∴,(3)当点D在线段AE上时,如图2,过点C作CF⊥AE于F,∠CDF=180°﹣∠CDE=60°,∴∠DCF=30°,∴DF=CD=,∴CF=DF=,在Rt△AFC中,AC=2,根据勾股定理得,AF==,∴AD=AF+DF=,由(2)知,,∴BE=AD=当点D在线段AE的延长线上时,如图3,过点C作CG⊥AD交AD的延长线于G,∵∠CDG=60°,∴∠DCG=30°,∴DG=CD=,∴CG=DG=,在Rt△ACG中,根据勾股定理得,AG=,∴AD=AG﹣DG=,由(2)知,,∴BE=AD=即:线段BE的长为或.8.【解答】解:(1)证明:∵将△ACD绕点C逆时针方向旋转60°得到△BCE,∴∠DCE=60°,DC=EC,∴△CDE是等边三角形;故答案为:等边;(2)存在,当6<t<10时,由旋转的性质得,BE=AD,∴C△DBE=BE+DB+DE=AB+DE=4+DE,由(1)知,△CDE是等边三角形,∴DE=CD,∴C△DBE=CD+4,由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,此时,CD=2,∴△BDE的最小周长=CD+4=2+4;(3)存在,①∵当点D与点B重合时,D,B,E不能构成三角形,∴当点D与点B重合时,不符合题意,②当0≤m<6时,由旋转可知,∠ABE=60°,∠BDE<60°,∴∠BED=90°,由(1)可知,△CDE是等边三角形,∴∠DEB=60°,∴∠CEB=30°,∵∠CEB=∠CDA,∴∠CDA=30°,∵∠CAB=60°,∴∠ACD=∠ADC=30°,∴DA=CA=4,∴OD=OA﹣DA=6﹣4=2,∴m=2;③当6<m<10时,由∠DBE=120°>90°,∴此时不存在;④当m>10时,由旋转的性质可知,∠DBE=60°,又由(1)知∠CDE=60°,∴∠BDE=∠CDE+∠BDC=60°+∠BDC,而∠BDC>0°,∴∠BDE>60°,∴只能∠BDE=90°,从而∠BCD=30°,∴BD=BC=4,∴OD=14,∴m=14,综上所述:当m=2或14时,以D、E、B为顶点的三角形是直角三角形.9.【解答】解:(1)如图1中,连接DB,MF,CE,延长BD交EC于H.∵AC=AB,AE=AD,∠BAD=∠CAE=90°,∴△BAD≌△CAE(SAS),∴BD=EC,∠ACE=∠ABD,∵∠ABD+∠ADB=90°,∠ADB=∠CDH,∴∠ADH+∠DCH=90°,∴∠CHD=90°,∴EC⊥BH,∵BM=MC,BF=FE,∴MF∥EC,MF=EC,∵CM=MB,CN=ND,∴MN∥BD,MN=BD,∴MN=MF,MN⊥MF,∴∠NMF=90°,∴∠MNF=45°,NF=MN.故答案为:45°(2):如图2中,连接MF,EC,BD.设EC交AB于O,BD交EC于H.∵AC=AB,AE=AD,∠BAD=∠CAE=90°,∴∠BAD=∠CAE,∴△BAD≌△CAE(SAS),∴BD=EC,∠ACE=∠ABD,∵∠AOC+∠ACO=90°,∠AOC=∠BOH,∴∠OBH+∠BOH=90°,∴∠BHO=90°,∴EC⊥BD,∵BM=MC,BF=FE,∴MF∥EC,MF=EC,∵CM=MB,CN=ND,∴MN∥BD,MN=BD,∴MN=MF,MN⊥MF,∴∠NMF=90°,∴∠MNF=45°,NF=MN.(3):如图3中,如图以A为圆心AD为半径作⊙A.当直线PB与⊙A相切时,此时∠CBP的值最小,点P到BC的距离最小,即△BCP的面积最小,∵AD=AE,AB=AC,∠BAC=∠DAE=90°,∴∠BAD=∠CAE,∴△BAD≌△CAE(SAS),∴∠ACE=∠ABD,BD=EC,∵∠ABD+∠AOB=90°,∠AOB=∠CPO,∴∠CPB=90°,∵PB是⊙A的切线,∴∠ADP=90°,∵∠DPE=∠ADP=∠DAE=90°,∴四边形ADPE是矩形,∵AE=AD,∴四边形ADPE是正方形,∴AD=AE=PD=PE=2,BD=EC==2,∴PC=2﹣2,PB=2+2,∴S△BCP的最小值=×PC×PB=(2﹣2)(2+2)=4.10.【解答】(1)解:AC⊥BD,理由如下:连接AC、BD,如图2所示:∵AB=AD,∴点A在线段BD的垂直平分线上,∵CB=CD,∴点C在线段BD的垂直平分线上,∴直线AC是线段BD的垂直平分线,∴AC⊥BD,故答案为:AC⊥BD;(2)解:AD2+BC2=AB2+CD2;理由如下:如图1,已知四边形ABCD中,AC⊥BD,设BD、AC相交于E,∵AC⊥BD,∴∠AED=∠AEB=∠BEC=∠CED=90°,由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,AB2+CD2=AE2+BE2+CE2+DE2,∴AD2+BC2=AB2+CD2;(3)解:如图3,连接CG、BE,∵四边形ACFG和四边形ABDE是正方形,∴AC=AG,AB=AE,∠CAG=∠BAE=90°,∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,在△GAB和△CAE中,,∴△GAB≌△CAE(SAS),∴∠ABG=∠AEC,又∠AEC+∠AME=90°,∴∠ABG+∠AME=90°,即CE⊥BG,由(2)得,CG2+BE2=CB2+GE2,在Rt△ABC中,AC=4,AB=5,根据勾股定理得,BC2=52﹣42=9,∵CG和BE分别是正方形ACFG和正方形ABDG的对角线,∴CG2=42+42=32,BE2=52+52=50,∴GE2=CG2+BE2﹣CB2=32+50﹣9=73,∴GE=.11.【解答】解:问题发现:如图1中,结论:AE=2BH,AE⊥BH.理由:在Rt△ABC中,∵BC=6,∠A=30°,∴AE=2BC=12,在Rt△CDB中,∵∠DCB=30°,∴CD==4,∵CH=DH,∴BH=CD=2,∴==2,∴AE=2BH.故答案为AE⊥BH,AE=2BH.问题证明:如图2中,(1)中结论成立.理由:延长BH到F使得HF=BH,连接CF.设AE交BF于O.∵CH=DH,BH=HF,∠CHF=∠BHD,∴△CHF≌△DHB(SAS),∴BD=CF,∠F=∠DBH,∴CF∥BD,∵AB=BC,BE=BD,∴BE=CF,∴==,∵CF∥BD,∴∠BCF+∠CBD=180°,∵∠ABC+∠DBE=∠ABD+∠CBD+∠CBD+∠CBE=∠CBD+∠ABE=180°,∴∠BCF=∠ABE,∴△ABE∽△BCF,∴∠CBF=∠BAE,==,∴AE=BF=2BH,∵∠CBF+∠ABF=90°,∴∠ABF+∠BAE=90°,∴∠AOB=90°,∴BH⊥AE.拓展应用:如图3﹣1中,当DE在BC的下方时,延长AB交DE于F.∵DE∥BC∴∠ABC=∠BFD=90°,由题意BC=BE=6,AB=6,BD=2,DE=4,∵•BD•BE=•DE•BF,∴BF==3,∴EF=BF=3,∴AF=6+3,∴AE2=AF2+EF2=(6+3)2+(3)2=144+36.∵AE=2BH,∴AE2=12BH2,∴BH2=12+3如图3﹣2中,当DE在BC的上方时,同法可得AF=6﹣3,EF=3,∴BH2==(=12﹣3.12.【解答】解:(1)如图1中,作EH⊥CG于H.∵四边形ECFG是菱形,∠ECF=60°,∴∠ECH=∠ECF=30°,EC=EG,∵EH⊥CG,∴GH=CG,∴=cos30°=,∴=2•=,∵EG∥CD,AB∥CD,∴GE∥AB,∴==.故答案为.(2)结论:AG=BE.理由:如图2中,连接CG.∵四边形ABCD,四边形ECFG都是菱形,∠ECF=∠DCB=60°,∴∠ECG=∠EGC=∠BCA=∠BAC=30°,∴△ECG∽△BCE,∴=,∵∠ECB=∠GCA,∴△ECB∽△GCA,∴==,∴AG=BE.(3)如图3中,∵∠AGH=∠CGF=30°.∠AGH=∠GAC+∠GCA,又∵∠DAC=∠HAG+∠GAC=30°,∴∠HAG=∠ACH,∵∠AHG=∠AHC,∴△HAG∽△HCA,∴HA:HC=GH:HA,∴AH2=HG•HC,∴FC=2,CG=CF,∴GC=2,∵HG=,∴AH2=HG•HC=•3=9,∵AH>0,∴AH=3.故答案为3.13.【解答】解:(1)当m=n时,即:BC=AC,∵∠ACB=90°,∴∠A+∠ABC=90°,∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE﹣∠CDE=∠ADC﹣∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴=1,∴=1(2)①∵∠ACB=90°,∴∠A+∠ABC=90°,∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE﹣∠CDE=∠ADC﹣∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴,∴②成立.如图,∵∠ACB=90°,∴∠A+∠ABC=90°,又∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE+∠CDE=∠ADC+∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴,∴.(3)由(2)有,△ADE∽△CDF,∵=,∴=,∴CF=2AE,在Rt△DEF中,DE=2,DF=4,∴EF=2,①当E在线段AC上时,在Rt△CEF中,CF=2AE=2(AC﹣CE)=2(﹣CE),EF=2,根据勾股定理得,CE2+CF2=EF2,∴CE2+[2(﹣CE)]2=40∴CE=2,或CE=﹣(舍)而AC=<CE,∴此种情况不存在,②当E在AC延长线上时,在Rt△CEF中,CF=2AE=2(AC+CE)=2(+CE),EF=2,根据勾股定理得,CE2+CF2=EF2,∴CE2+[2(+CE)]2=40,∴CE=,或CE=﹣2(舍),③如图1,当点E在CA延长线上时,CF=2AE=2(CE﹣AC)=2(CE﹣),EF=2,根据勾股定理得,CE2+CF2=EF2,∴CE2+[2(CE﹣)]2=40,∴CE=2,或CE=﹣(舍)即:CE=2或CE=.14.【解答】解:(1)如图1,延长GM交AD于H,∵AD∥GF,∴∠GFM=∠HAM,在△FMG和△AMH中,,∴△FMG≌△AMH(ASA),∴HM=GM,AH=FG,∵AD=CD,AH=FG=CG,∴DH=DG,∵∠HDG=90°,HM=GM,∴DM=MG,DM⊥MG,故答案为DM=MG,DM⊥MG.(2)结论成立:DM=MG,DM⊥MG,理由:如图2中,延长GM使得MH=GM,连接AH、DH、DG,延长AD交GF的延长线于N,交CD于O.∵AM=MF,∠AMH=∠FMG,MH=MG,∴△AMH≌△FMG(SAS),∴AH=GF=CG,∠AHM=∠FGM,∴AH∥GN,∴∠HAD=∠N,∵∠ODN=∠OGC=90°,∠DON=∠GOC,∴∠N=∠OCG,∴∠HAD=∠DCG,∵AH=CG,AD=CD,∴△HAD≌△GCD(SAS),∴DH=DG,∠HDA=∠CDG,∴∠HDG=∠ADC=90°,∴△HDG是等腰直角三角形,∵MH=MG,∴DM⊥GH,DM=MH=MG,(3)①如图3﹣1中,连接AC.在Rt△ABC中,AC==10,在Rt△ACE中,AE==14,∴AF=AE=EF=14﹣2=12,∴FM=AM=AF=6,在Rt△MGF中,MG==2,∴S△DMG=×2×2=20,②如图3﹣2中,连接AC.同法可得AE=14,AF=16,FM=8,MG==2,∴S△DMG=×2×2=34,综上所述,满足条件的△DMG的面积为20或34.15.【解答】解:(1)由旋转可得:AC=A'C=2,∵∠ACB=90°,AB=,AC=2,∴BC=,∵∠ACB=90°,m∥AC,∴∠A'BC=90°,∴cos∠A'CB==,∴∠A'CB=30°,∴∠ACA'=60°;(2)∵M为A'B'的中点,∴∠A'CM=∠MA'C,由旋转可得,∠MA'C=∠A,∴∠A=∠A'CM,∴tan∠PCB=tan∠A=,∴PB=BC=,∵∠PCQ=∠PBC=90°,∴∠BQC+∠BPC=∠BCP+∠BPC=90°,∴∠BQC=∠BCP=∠A,∴tan∠BQC=tan∠A=,∴BQ=BC×=2,∴PQ=PB+BQ=;(3)∵S四边形P A'B′Q=S△PCQ﹣S△A'CB'=S△PCQ﹣,∴S四边形P A'B′Q最小,即S△PCQ最小,∴S△PCQ=PQ×BC=PQ,法一:(几何法)取PQ的中点G,∵∠PCQ=90°,∴CG=PQ,即PQ=2CG,当CG最小时,PQ最小,∴CG⊥PQ,即CG与CB重合时,CG最小,∴CG min=,PQ min=2,∴S△PCQ的最小值=3,S四边形P A'B′Q=3﹣;法二(代数法)设PB=x,BQ=y,由射影定理得:xy=3,∴当PQ最小时,x+y最小,∴(x+y)2=x2+2xy+y2=x2+6+y2≥2xy+6=12,当x=y=时,“=”成立,∴PQ=+=2,∴S△PCQ的最小值=3,S四边形P A'B′Q=3﹣.16.【解答】解:(1)结论:△PMN是等边三角形.理由:如图1中,∵△ABC是等边三角形,∴AB=AC,∠ABC=∠ACB=60°,∵AD=AE,∴BD=EC,∵PB=PC,CN=ND,BM=EM,∴PN∥BD,PM∥EC,PN=BD,PM=EC,∴PM=PN,∠NPC=∠ABC=60°,∠MPB=∠ACB=60°,∴∠MPN=60°,∴△PMN是等边三角形,故答案为等边三角形.(2)△PMN的形状不发生改变,仍为等边三角形,理由如下:如图2中,连接BD,CE.由旋转可得∠BAD=∠CAE,∵△ABC是等边三角形,∴AB=AC,∠ACB=∠ABC=60°又∵AD=AE,∴△ABD≌△ACE(SAS),∴BD=CE,∠ABD=∠ACE,∵M是BE的中点,P是BC的中点,∴PM是△BCE的中位线,∴PM=,且PM∥CE.同理可证PN=BD且PN∥BD,∴PM=PN,∠MPB=∠ECB,∠NPC=∠DBC,∴∠MPB+∠NPC=∠ECB+∠DBC=(∠ACB+∠ACE)+(∠ABC﹣∠ABD)=∠ACB+∠ABC=120°,∴∠MPN=60°,∴△PMN是等边三角形.(3)∵PM=EC,∴当EC最大时,等边△PMN的周长最大,∵EC≤AE+AC,∴EC≤8,∴PM≤4,∴PM的最大值为4,∴△PMN的周长的最大值为12.17.【解答】解:(1)∵AB=AC,∠ABC=60°,∴∠BAC=60°,∵AD=AE,∠ADE=70°,∴∠DAE=180°﹣2∠ADE=40°,∴α=∠BAD=60°﹣40°=20°,∴∠ADC=∠BAD+∠ABD=60°+20°=80°,∴β=∠CDE=∠ADC﹣∠ADE=10°,故答案为:20,10;(2)设∠ABC=x,∠AED=y,∴∠ACB=x,∠AED=y,在△DEC中,y=β+x,在△ABD中,α+x=y+β=β+x+β,∴α=2β;(3)①当点E在CA的延长线上,点D在线段BC上,如图1设∠ABC=x,∠ADE=y,∴∠ACB=x,∠ACE=y,在△ABD中,x+α=β﹣y,在△DEC中,x+y+β=180°,∴α=2β﹣180°,②当点E在CA的延长线上,点D在CB的延长线上,如图2,同①的方法可得α=180°﹣2β.18.【解答】解:(1)由旋转变换的性质可知,∠CAE=90°,AC=AE,∴△ACE为等腰直角三角形,∴CE=AC,∵CE=CD+DE=CD+BC,∴BC+CD=AC,故答案为:等腰直角;BC+CD=AC;(2)延长CO交⊙O于E,连接AE、BE、DE,则∠CDE=90°,∵点C为的中点,∴点E为的中点,∴EA=EB,∵AB为⊙O的直径,∴∠ADB=90°,由(1)得,DE=(AD+BD),由勾股定理得,CD2=CE2﹣DE2=AD2+BD2﹣(AD+BD)2=(AD﹣BD)2,∴CD=(BD﹣AD);(3)如图3,当点E在直线AC的左侧时,连接CQ、PC,∵CA=CB,点P为AB的中点,∴CP⊥AB,∵CA=CE,点Q为AE中点,∴CQ⊥AE,AQ=QE=AE=5,∴由勾股定理得,CQ==12,由(1)得,AQ+CQ=PQ,。
全国各地中考数学压轴题精选(含详细答案)

12.(黄冈)已知:如图,在直角梯形COAB中,OC∥AB,以O为原点建立平面直角坐标系 ,A,B,C三点的坐标分别为A(8,0),B(8,10),C(0,4),点D为线段BC的中点, 动点P从点O出发,以每秒1个单位的速度,沿折线OABD的路线移动,移动的时间为t秒. (1)求直线BC的解析式; (2)若动点P在线段OA上移动,当t为何值时,四边形OPDC的面积是梯形COAB面积的 ; (3)动点P从点O出发,沿折线OABD的路线移动过程中,设△OPD的面积为S,请直接写出S 与t的函数关系式,并指出自变量t的取值范围;
8
点F重合时,梯形ABCD停止移动.观察得知:在梯形ABCD移动过程中,其腰BC始终经过坐 标原点O.(如图2) ①设点A的坐标为(a,b),梯形ABCD与梯形OEFG重合部分的面积为S,试求a与何值时, S的值恰好等于梯形OEFG面积的 ;
②当点A在EF上滑动时,设AD与x轴的交点为M,试问:在y轴上是否存在点P,使得△PAM 是底角为30°的等腰三角形?如果存在,请求出所有符合条件的点P的坐标;如果不存在, 请说明理由.(利用图3进行探索)
中考数学压轴题十大类型经典题目

中考数学压轴题十大类型目录第一讲 中考压轴题十大类型之动点问题 1 第二讲 中考压轴题十大类型之函数类问题 7 第三讲 中考压轴题十大类型之面积问题 13 第四讲 中考压轴题十大类型之三角形存在性问题 19 第五讲 中考压轴题十大类型之四边形存在性问题 25 第六讲 中考压轴题十大类型之线段之间的关系 31 第七讲 中考压轴题十大类型之定值问题 38 第八讲 中考压轴题十大类型之几何三大变换问题 44 第九讲 中考压轴题十大类型之实践操作、问题探究 50 第十讲 中考压轴题十大类型之圆 56 第十一讲 中考压轴题综合训练一 62 第十二讲 中考压轴题综合训练二 68第一讲 中考压轴题十大类型之动点问题1.2011吉林如图,梯形ABCD 中,AD ∥BC ,∠BAD =90°,CE ⊥AD 于点E ,AD =8cm,BC =4cm,AB =5cm .从初始时刻开始,动点P ,Q 分别从点A ,B 同时出发,运动速度均为1cm/s,动点P 沿A -B -C -E 方向运动,到点E 停止;动点Q 沿B -C -E -D 方向运动,到点D 停止,设运动时间为x s,△PAQ 的面积为y cm 2,这里规定:线段是面积为0的三角形解答下列问题:1 当x =2s 时,y =_____ cm 2;当x =92s 时,y =_______ cm 2. 2当5 ≤ x ≤ 14时,求y 与x 之间的函数关系式.3当动点P 在线段BC 上运动时,求出154 y S 梯形ABCD 时x 的值. 4直接写出在整个..运动过程中,使PQ 与四边形ABCE 的对角线平行的所有x 的值.D C BA 2.2007河北如图,在等腰梯形ABCD 中,AD ∥BC ,AB =DC =50,AD =75,BC =135.点P 从点B 出发沿折线段BA -AD -DC 以每秒5个单位长的速度向点C 匀速运动;点Q 从点C 出发沿线段CB 方向以每秒3个单位长的速度匀速运动,过点Q 向上作射线QK ⊥BC ,交折线段CD -DA -AB 于点E .点P 、Q 同时开始运动,当点P 与点C 重合时停止运动,点Q 也随之停止.设点P 、Q 运动的时间是t 秒t >0.1当点P 到达终点C 时,求t 的值,并指出此时BQ 的长;2当点P 运动到AD 上时,t 为何值能使PQ ∥DC3设射线QK 扫过梯形ABCD 的面积为S ,分别求出点E 运动到CD 、DA 上时,S 与t 的关系式;,写出t 的取值范围;若不能,请说明理由. 备用图3.2008河北如图,在Rt ABC △中,∠C=90°,AB =50,AC =30,D ,E ,F 分别是AC ,AB ,B C 的中点.点P 从点D 出发沿折线DE -EF -FC -CD 以每秒7个单位长的速度匀速运动;点Q 从点B 出发沿BA 方向以每秒4个单位长的速度匀速运动,过点Q 作射线QK AB ⊥,交折线BC -CA 于点G .点P Q ,同时出发,当点P 绕行一周回到点D 时停止运动,点Q 也随之停止.设点P Q ,运动的时间是t 秒0t >.1D F ,两点间的距离是 ;2射线QK 能否把四边形CDEF 分成面积相等的两部分若能,求出t 的值.若不能,说明理由;3当点P 运动到折线EF FC -上,且点P 又恰好落在射线QK 上时,求t 的值; 4连结PG ,当PG AB ∥时,请直接..写出t 的值. 4.2011山西太原如图,在平面直角坐标系中,四边形OABC 是平行四边形.直线l 经过O 、C 两点.点A 的坐标为8,0,点B 的坐标为11,4,动点P 在线段OA 上从点O 出发以每秒1个单位的速度向点A 运动,同时动点Q 从点A 出发以每秒2个单位的速度沿A →B →C 的方向向点C 运动,过点P 作PM 垂直于x 轴,与折线O -C -B 相交于点M .当P 、Q 两点中有一点到达终点时,另一点也随之停止运动,设点P 、Q 运动的时间为t秒0t>,△MPQ的面积为S.1点C的坐标为________,直线l的解析式为__________.2试求点Q与点M相遇前S与t的函数关系式,并写出相应的t的取值范围.3试求题2中当t为何值时,S的值最大,并求出S的最大值.4随着P、Q两点的运动,当点M在线段CB上运动时,设PM的延长线与直线l相交于点N.试探究:当t为何值时,△QMN为等腰三角形请直接写出t的值.5.2011四川重庆如图,矩形ABCD中,AB=6,BC=2错误!,点O是AB的中点,点P在AB的延长线上,且BP=3个单位长度的速度沿OA匀速运动,到达A点后,F从P点出发,以每秒1个单位长度的速度沿射线当两点相遇时停止运动.在点E、F的运动过程中,以和矩形ABCD在射线PA的同侧,设运动的时间为t秒1当等边△EFG的边FG恰好经过点C时,求运动时间t的值;2在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积为S,请直接写出S 与t之间的函数关系式和相应的自变量t的取值范围;3设EG与矩形ABCD的对角线AC的交点为H,是否存在这样的t,使△AOH是等腰三角形若存在,求出对应的t的值;若不存在,请说明理由.备用图1备用图2三、测试提高1.2011山东烟台如图,在直角坐标系中,梯形ABCD的底边AB在x轴上,底边CD的端点D在y轴上.直线CB的表达式为41633y x=-+,点A、D的坐标分别为-4,0,0,4.动点P自A点出发,在AB上匀速运动.动点Q自点B出发,在折线BCD 上匀速运动,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P运动t秒时,△OPQ的面积为S不能构成△OPQ的动点除外.1求出点B、C的坐标;2求S随t变化的函数关系式;3当t为何值时S有最大值并求出最大值.备用图第二讲中考压轴题十大类型之函数类问题12011浙江温州如图,在平面直角坐标系中,O是坐标原点,点A的坐标为-4,0,点B的坐标为0,bb>0.P是直线AB上的一个动点,作PC⊥x轴,垂足为C,记点P 关于y轴的对称点为P′ 点P′不在y轴上,连结P P′,P′A,P′C,设点P的横坐标为a.(1) 当b =3时,①直线AB 的解析式;②若点P ′的坐标是-1,m ,求m 的值;2若点P 在第一象限,记直线AB 与P ′C 的交点为D .当P ′D :DC =1:3时,求a 的值; 3是否同时存在a ,b ,使△P ′CA 为等腰直角三角形若存在,请求出所有满足要求的a ,b 的值;若不存在,请说明理由.2. 2010武汉如图,抛物线212y ax ax b=-+经过A -1,0,C 2,32两点,与x 轴交于另一点B . 1求此抛物线的解析式; 2若抛物线的顶点为M ,点P 为线段OB 上一动点 不与点B 重合,点Q 在线段MB 上移动,且∠MPQ =45°,设线段OP =x ,MQ=22y ,求y 2与x 的函数关系式,并直接写出自变量x 的取值范围; 3在同一平面直角坐标系中,两条直线x =m ,x =n 分别与抛物线交于点E ,G ,与2中的函数图象交于点F ,H .问四边形EFHG 能否为平行四边形 若能,求m ,n 之间的数量关系;若不能,请说明理由.备用图3. 2011江苏镇江在平面直角坐标系xOy 中,直线1l 过点A 1,0且与y 轴平行,直线2l 过点B 0,2且与x 轴平行,直线1l 与2l 相交于点P .点E 为直线2l 上一点,反比例函数k y x=k >0的图象过点E 且与直线1l 相交于点F . 1若点E 与点P 重合,求k 的值; 2连接OE 、OF 、EF .若k >2,且△OEF 的面积为△PEF 的面积2倍,求点E 的坐标; 3是否存在点E 及y 轴上的点M ,使得以点M 、E 、F 为顶点的三角形与△PEF 全等若存在,求E 点坐标;若不存在,请说明理由.4. 2010浙江舟山△ABC 中,∠A =∠B =30°,AB=ABC 放在平面直角坐标系中,使AB 的中点位于坐标原点O 如图,△ABC 可以绕点O 作任意角度的旋转.1当点B 在第一象限,,求点B 的横坐标; x y P'DO C B A P2如果抛物线2y ax bx c =++a ≠0的对称轴经过点C ,请你探究:①当a =,12b =-,c =,A ,B 两点是否都在这条抛物线上并说明理由; ②设b =-2am ,是否存在这样的m 值,使A ,B 两点不可能同时在这条抛物线上若存在,直接写出m 的值;若不存在,请说明理由.5.12若点N 为线段BMQ .当点N 在线段BM 上运动时点N 不与点B ,点M 面积为S ,求S 与t 之间的函数关系式及自变量3,求出所有符合条件的点P 4将△OAC 补成矩形,使得△,第三个顶点落在矩形这一边的对边上,试直接写出矩形的未知的顶点坐标不需要计算过程. 三、测试提高1. 2011山东东营如图所示,四边形OABC 是矩形,点A 、C 的坐标分别为30-,,0,1,点D是线段BC 上的动点与端点B 、C 不重合,过点D 作直线12y x b =+交折线OAB 于点E . 1记△ODE 的面积为S .求S 与b 的函数关系式;2当点E 在线段OA 上时,且tan ∠DEO =12.若矩形OABC 关于直线DE 的对称图形为四边形1111O A B C .试探究四边形1111O A B C 与矩形OABC 的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由. 第三讲 中考压轴题十大类型之面积问题1. 2011辽宁大连如图,抛物线y =ax 2+bx +c 经过A -1,0、B 3,0、C 0,3三点,对称轴与抛物线相交于点P 、与直线BC 相交于点M ,连接PB .1求该抛物线的解析式;2抛物线上是否存在一点Q ,使△QMB 与△PMB 的面积相等,若存在,求点Q 的坐标;若不存在,说明理由;3在第一象限、对称轴右侧的抛物线上是否存在一点R ,使△RPM 与△RMB 的面积相等,若存在,直接写出点R 的坐标;若不存在,说明理由.2. 2011湖北十堰如图,和点 B ,与y 轴交于点C 0,-3.1求抛物线的解析式;2如图1,己知点H 0,-1.问在抛物线上是否存在点G 点G 在y 轴的左侧,使得S △GHC =S △GHA 若存在,求出点G 的坐标,若不存在,请说明理由:3如图2,抛物线上点D 在x 轴上的正投影为点E ﹣2,0,F 是OC 的中点,连接DF ,P 为线段BD 上的一点,若∠EPF =∠BDF ,求线段PE 的长.3. 2010天津在平面直角坐标系中,已知抛物线2y x bx =-+c +与x 轴交于点A 、B 点A 在点B 的左侧,与y 轴的正半轴交于点C ,顶点为E . Ⅰ若2b =,3c =,求此时抛物线顶点E 的坐标;Ⅱ将Ⅰ中的抛物线向下平移,若平移后,在四边形ABEC 中满足S △BCE = S △ABC ,求此时直线BC 的解析式;Ⅲ将Ⅰ中的抛物线作适当的平移,若平移后,在四边形ABEC 中满足S △BCE =2S △AOC ,且顶点E 恰好落在直线43y x =-+上,求此时抛物线的解析式.4. 2011山东聊城如图,在矩形ABCD 中,AB =12cm,BC =8cm .点E 、F 、G 分别从点A 、B 、C 同时出发,沿矩形的边按逆时针方向移动,点E 、G 的速度均为2cm/s,点F 的速度为4cm/s,当点F 追上点G 即点F 与点G 重合时,三个点随之停止移动.设移动开始后第t s 时,△EFG 的面积为S cm 2.1当t =1s 时,S 的值是多少2写出S 与t 之间的函数解析式,并指出自变量t 的取值范围;3若点F 在矩形的边BC 上移动,当t 为何值时,以点B 、E 、F 为顶点的三角形与以C 、F 、G 为顶点的三角形相似请说明理由.5. 2011江苏淮安如图,在Rt△ABC中,∠C =90°,AC =8,BC =6,点P 在AB 上,AP =2,点E 、F 同时从点P 出发,分别沿PA 、PB 以每秒1个单位长度的速度向点A 、B 匀速运动,点E 到达点A 后立刻以原速度沿AB 向点B 运动,点F 运动到点B 时停止,点E 也随之停止.在点E 、F 运动过程中,以EF 为边作正方形EFGH ,使它与△ABC 在线段AB 的同侧.设E 、F 运动的时间为t 秒t >0,正方形EFGH 与△ABC 重叠部分面积为S .1当t =1时,正方形EFGH 的边长是 .当t =3时,正方形EFGH 的边长是 . 2当0<t ≤2时,求S 与t 的函数关系式;3直接答出:在整个运动过程中,当t 为何值时,S 最大最大面积是多少A EB FC GDA 备用图三、测试提高1. 2010山东东营如图,在锐角三角形ABC 中,BC =12,△ABC 的面积为48,D ,E 分别是边AB ,AC 上的两个动点D 不与A ,B 重合,且保持DE ∥BC ,以DE 为边,在点A 的异侧作正方形DEFG .1当正方形DEFG 的边GF 在BC 上时,求正方形DEFG 的边长;2设DE = x ,△ABC 与正方形DEFG 重叠部分的面积为y ,试求y 关于x 的函数关系式,写出x 的取值范围,并求出y 的最大值.第四讲 中考压轴题十大类型之 三角形存在性问题板块一、等腰三角形存在性1. 2011江苏盐城如图,已知一次函数7y x =-+与正比例函数34y x =的图象交于点A ,且与x 轴交于点B .1求点A 和点B 的坐标;2过点A 作AC ⊥y 轴于点C ,过点B 作直线l ∥y 轴.动点P 从点O 出发,以每秒1个单位长的速度,沿O —C —A 的路线向点A 运动;同时直线l 从点B 出发,以相同速度向左平移,在平移过程中,直线l 交x 轴于点R ,交线段BA 或线段AO 于点Q .当点P 到达点A 时,点P 和直线l 都停止运动.在运动过程中,设动点P 运动的时间为t 秒.是否存在以A 、P 、Q 为顶点的三角形是等腰三角形若存在,求t 的值;若不存在,请说明理由.备用图2. 2009湖北黄冈如图,在平面直角坐标系xOy 中,抛物线21410189y x x =--与x 轴的交点为点A ,与y 轴的交点为点B ,过点B 作x 轴的平行线BC ,交抛物线于点C ,连结AC .现有两动点P ,Q 分别从O ,C 两点同时出发,点P 以每秒4个单位的速度沿OA 向终点A 移动,点Q 以每秒1个单位的速度沿CB 向点B 移动,点P 停止运动时,点Q 也同时停止运动,线段OC ,PQ 相交于点D ,过点D 作DE ∥OA ,交CA 于点E ,射线QE 交x 轴于点F .设动点P ,Q 移动的时间为t 单位:秒B AD E F G C B 备用图1 A C B 备用图2 A C1求A ,B ,C 三点的坐标和抛物线的顶点的坐标;2当t 为何值时,四边形PQCA 为平行四边形请写出计算过程;3当902t <<时,△PQF 的面积是否总为定值若是,求出此定值,若不是,请说明理由;4当t 为何值时,△PQF 为等腰三角形请写出解答过程.板块二、直角三角形3. 2009四川眉山如图,已知直线112y x =+与y 轴交于点A ,与x 轴交于点D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为 1,0. 1求该抛物线的解析式;2动点P 在x 轴上移动,当△PAE 是直角三角形时,求点P 的坐标.4. 2010广东中山如图所示,矩形ABCD 的边长AB =6,BC =4,点F 在DC 上,DF =2.动点M 、N 分别从点D 、B 同时出发,沿射线DA 、线段BA 向点A 的方向运动点M 可运动到DA 的延长线上,当动点N 运动到点A 时,M 、N 两点同时停止运动.连接FM 、FN ,当F 、N 、M 不在同一直线上时,可得△FMN ,过△FMN 三边的中点作△PWQ .设动点M 、N 的速度都是1个单位/秒,M 、N 运动的时间为x 秒.试解答下列问题:1说明△FMN ∽△QWP ;2设04x ≤≤即M 从D 到A 运动的时间段.试问x 为何值时,△PWQ 为直角三角形当x 在何范围时,△PQW 不为直角三角形3问当x 为何值时,线段MN 最短求此时MN 的值.板块三、相似三角形存在性 5. 2011湖北天门在平面直角坐标系中,抛物线2y ax bx =+ 3+与x 轴的两个交点分别为-3,0、B 1,0,过顶点C 作CH ⊥x 轴于点. 1直接填写:a = ,b = ,顶点C 的坐标为 ;2在y 轴上是否存在点D ,使得△ACD 是以AC 为斜边的直角三角形若存在,求出点D 的坐标;若不存在,说明理由; 3若点P 为x 轴上方的抛物线上一动点点P 与顶点C 不重合,PQ ⊥AC 于点Q ,当△PCQ 与△ACH 相似时,求点P 的坐标. W QPNM F D CB A备用图三、测试提高1. 2009广西钦州如图,已知抛物线234y x bx c =++与坐标轴交于A 、B 、C 三点, A 点的坐标为-1,0,过点C 的直线334y x t=-与x 轴交于点Q ,点P 是线段BC 上的一个动点,过P 作PH ⊥OB 于点H .若PB =5t ,且01t <<.1填空:点C 的坐标是_____,b =_____,c =_____;2求线段QH 的长用含t 的式子表示;3依点P 的变化,是否存在t 的值,使以P 、H 、Q 为顶点的三角形与△COQ 相似若存在,求出所有t 的值;若不存在,说明理由.第五讲 中考压轴题十大类型之四边形存在性问题1. 2009黑龙江齐齐哈尔直线364y x =-+与坐标轴分别交于A 、B 两点,动点P 、Q 同时从O 点出发,同时到达A 点,运动停止.点Q 沿线段OA 运动,速度为每秒1个单位长度,点P 沿路线O →B →A 运动.1直接写出A 、B 两点的坐标;2设点Q 的运动时间为t 秒,△OPQ 的面积为S ,求出S 与t 之间的函数关系式;3当485S =时,求出点P 的坐标,并直接写出以点O 、P 、Q 为顶点的平行四边形的第四个顶点M 的坐标.2. 2010河南在平面直角坐标系中,已知抛物线经过A (40),-,B (04),-,C (20),三点.1求抛物线的解析式;2若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S .求S 关于m 的函数关系式,并求出S 的最大值.3若点P 是抛物线上的动点,点Q 是直线x y -=上的动点,判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.3. 2011黑龙江鸡西已知直线y =+与x 轴、y 轴分别交于A 、B 两点,∠ABC =60°,BC 与x 轴交于点C .1试确定直线BC 的解析式;2若动点P 从A 点出发沿AC 向点C 运动不与A 、C 重合,同时动点Q 从C 点出发沿CBA 向点A 运动不与C 、A 重合,动点P 的运动速度是每秒1个单位长度,动点Q 的运动速度是每秒2个单位长度.设△APQ 的面积为S ,P 点的运动时间为t 秒,求S 与t 的函数关系式,并写出自变量的取值范围;3在2的条件下,当△APQ 的面积最大时,y 轴上有一点M ,平面内是否存在一点N ,使以A 、Q 、M 、N 为顶点的四边形为菱形若存在,请直接写出N 点的坐标;若不存在,请说明理由.4. 2007河南如图,对称轴为直线x =27的抛物线经过点A 6,0和B0,4.1求抛物线解析式及顶点坐标;2设点Ex ,y 是抛物线上一动点,且位于第四象限,四边形OEAF 是以OA 为对角线的平行四边形,求四边形OEAF 的面积S 与x 之间的函数关系式,并写出自变量x 的取值范围;3①当四边形OEAF 的面积为24时,请判断OEAF 是否为菱形②是否存在点E ,使四边形OEAF 为正方形若存在,求出点E 的坐标;若不存在,请说明理由.5. 2010黑龙江大兴安岭如图,在平面直角坐标系中,函数2y x =+12的图象分别交x轴、y 轴于A 、B 两点.过点A 的直线交y 轴正半轴于点M,且点M 为线段OB 的中点. 1求直线AM 的解析式;2试在直线AM 上找一点P ,使得S △ABP =S △AOB ,请直接写出点P 的坐标;3若点H 为坐标平面内任意一点,在坐标平面内是否存在这样的点H ,使以A 、B 、M 、H 为顶点的四边形是等腰梯形若存在,请直接写出点H 的坐标;若不存在,请说明理由.三、测试提高 1. 2009辽宁抚顺已知:如图所示2=++y ax x c a ≠0与x C .1求出此抛物线的解析式,2在抛物线上有一点D ,D 的坐标,并求出直线AD 的解析式;3在2中的直线AD P ,x 轴上有一动点Q .是否存在以A 、M 、P 、Q 为顶点的平行四边形如果存在,请直接写出点Q 的坐标;如果不存在,请说明理由.第六讲 中考压轴题十大类型之线段之间的关系1. 2010天津在平面直角坐标系中,矩形OACB 的顶点O 在坐标原点,顶点A 、B 分别在x 轴、y 轴的正半轴上,3OA =,4OB =,D 为边OB 的中点.Ⅰ若E 为边OA 上的一个动点,当△CDE 的周长最小时,求点E 的坐标;Ⅱ若E 、F 为边OA 上的两个动点,且2EF =,当四边形CDEF 的周长最小时,求点E 、F 的坐标.2. 2011四川广安四边形ABCD 是直角梯形,BC ∥AD ,∠=90°,BC 与y 轴相交于点M ,且M 是BC 的中点,A 、B 、D 三点的坐标分别是A 1 0-,,B 1 2-,,D 3,0.连接DM ,并把线段DM 沿DA 方向平移到ON .若抛物线2y ax bx c =++经过点D 、M 、N .1求抛物线的解析式;2抛物线上是否存在点P ,使得PA =PC ,若存在,求出点P 的坐标;若不存在,请说明理由;3设抛物线与x 轴的另一个交点为E ,点Q 是抛物线的对称轴上的一个动点,当点Q 在什么位置时有|QE -QC |最大并求出最大值.3. 2011四川眉山如图,在直角坐标系中,已知点A 0,1,B 4-,4,将点B 绕点A 顺时针方向旋转90°得到点C ,顶点在坐标原点的抛物线经过点B . 1 求抛物线的解析式和点C 的坐标;2 抛物线上有一动点P ,设点P 到x 轴的距离为1d ,点P 到点A 的距离为2d ,试说明211d d =+;3 在2的条件下,请探究当点P 位于何处时,△PAC 的周长有最小值,并求出△PAC 的周长的最小值.4. 2011福建福州已知,如图,二次函数223y ax ax a =+-(0)a ≠图象的顶点为H ,与x轴交于A 、B 两点B 在A 点右侧,点H 、B 关于直线3:33l y x =+ 1求A 、B 两点坐标,并证明点A 在直线l 上; 2求二次函数解析式;3过点B 作直线BK ∥AH 交直线l 于K 点,M 、N 分别为直线AH 和直线l 上的两个动点,连接HN 、NM 、MK ,求HN +NM +MK 和的最小值.5. 2009湖南郴州 如图1,已知正比例函数和反比例函数的图象都经过点M -2,-1,且y B O D C A xEyB O DC A x温馨提示:如图,可以作点D 关于x 轴的对称点D ',连接CD '与xP -1,-2为双曲线上的一点,Q 为坐标平面上一动点,PA 垂直于x 轴,QB 垂直于y 轴,垂足分别是A 、B .1写出正比例函数和反比例函数的关系式;2当点Q 在直线MO 上运动时,直线MO 上是否存在这样的点Q ,使得△OBQ 与△OAP 面积相等如果存在,请求出点Q 的坐标,如果不存在,请说明理由;3如图2,当点Q 在第一象限中的双曲线上运动时,作以OP 、OQ 为邻边的平行四边形OPCQ ,求平行四边形OPCQ 周长的最小值. 图1 图26. 2010江苏苏州如图,以A 为顶点的抛物线与y 轴交于点B .已知A 、B 两点的坐标分别为3,0、0,4. 1求抛物线的解析式;2设()M m n ,M B O A 、、、,求点M 的坐标; 3在2的条件下,试问:22228PA PB PM ++>是否总成立请说明理由.三、测试提高1. 2009浙江舟山如图,已知点A -4,8和点B 2,n 在抛物线2=y ax 上.1求a 的值及点B 关于x 轴对称点P 的坐标,并在x 轴上找一点Q ,使得AQ +QB 最短,求出点Q 的坐标;2平移抛物线2=y ax ,记平移后点A 的对应点为A ′,点B 的对应点为B ′,点C -2,0和点D -4,0是x 轴上的两个定点.①当抛物线向左平移到某个位置时,A ′C +CB ′ 最短,求此时抛物线的函数解析式;②当抛物线向左或向右平移时,是否存在某个位置,使四边形A ′B ′CD 的周长最短若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.第七讲 中考压轴题十大类型之定值问题1. 2011天津已知抛物线1C :21112y x x =-+,点F 1,1. Ⅰ求抛物线1C 的顶点坐标;Ⅱ①若抛物线1C 与y 轴的交点为A ,连接AF ,并延长交抛物线1C 于点B ,求证:112AF BF +=;②抛物线1C 上任意一点P P P x y ,01P x <<,连接PF ,并延长交抛物线1C 于点Q Q Q x y ,,试判断112PF QF+=是否成立请说明理由; Ⅲ将抛物线1C 作适当的平移,得抛物线2C :221()2y x h =-,若2x m <≤时,2y x ≤恒成立,求m 的最大值.2. 2009湖南株洲如图,已知△ABC 为直角三角形,90ACB ∠=︒,AC BC =,点A 、C 在x轴上,点B 坐标为3,m 0m >,线段AB 与y 轴相交于点D ,以P 1,0为顶点的抛物线过点B 、D .1求点A 的坐标用m 表示; 2求抛物线的解析式;3设点Q 为抛物线上点P 至点B 之间的一动点,连结PQ 并延长交BC 于点E ,连结BQ 并延长交AC 于点F ,试证明:()FC AC EC +为定值.3. 2008山东济南已知:抛物线2y ax bx c =++a ≠0,顶点C1,3-,与x 轴交于A 、B 两点,(10)A -,. 1求这条抛物线的解析式; 2如图,以AB 为直径作圆,与抛物线交于点D ,与抛物线对称轴交于点E ,依次连接A 、D 、B 、E ,点P 为线段AB 上一个动点P 与A 、B 两点不重合,过点P 作断PM PNBE AD+是否为PM ⊥AE 于M ,PN ⊥DB 于N ,请判定值 若是,请求出此定值;若不是,请说明理由;3在2的条件下,若点S 是线段EP 上一点,过点S 作FG ⊥EP ,FG 分别与边.AE 、BE相交于点F 、GF 与A 、E 不重合,G 与E 、B 不重合,请判断PA EFPB EG=是否成立.若成立,请给出证明;若不成立,请说明理由.4. 2011湖南株洲孔明是一个喜欢探究钻研的同学,他在和同学们一起研究某条抛物线2(0)y ax a =<的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点O ,两直角边与该抛物线交于A 、B 两点,请解答以下问题: 1若测得OA OB ==如图1,求a 的值;2对同一条抛物线,孔明将三角板绕点O 旋转到如图2所示位置时,过B 作BF x ⊥轴于点F ,测得1OF =,写出此时点B 的坐标,并求点A 的横坐标...; 3对该抛物线,孔明将三角板绕点O 旋转任意角度时惊奇地发现,交点A 、B 的连线段总经过一个固定的点,试说明理由并求出该点的坐标.5. 2009湖北武汉如图,抛物线24y ax bx a =+-经过()10A -,、()04C ,两点,与x 轴交于另一点B .1求抛物线的解析式;2已知点(),1D m m +在第一象限的抛物线上,求点D 关于直线BC 对称的点的坐标; 3在2的条件下,连接BD ,点P 为抛物线上一点,且45DBP ∠=︒,求点P 的坐标.三、测试提高1. 2009湖南湘西在直角坐标系xOy与x 轴交于两点A 、B ,与y 的坐标是3,0.将直线y kx =沿y 轴向上平移3(1) 求k 的值;(2) 求直线BC 和抛物线的解析式; (3) 求△ABC 的面积;(4) 设抛物线顶点为D ,点P 在抛物线的对称轴上,且∠APD =∠ACB ,求点P 的坐标.、第八讲 中考压轴题十大类型之 几何三大变换问题1. 2009山西太原问题解决:如图1,将正方形纸片ABCD 折叠,使点B 落在CD 边上一方法指导:图1 图2 图3 图4αθ4HB 2B 3A 3A 222B 1A 1A 011点E 不与点C ,D 重合,压平后得到折痕MN .当12CE CD =时,求AMBN 的值. 类比归纳:在图1中,若13CE CD =,则AMBN 的值等于 ;若14CE CD =,则AMBN的值等于 ;若1CE CD n=n 为整数,则AMBN 的值等于 .用含n 的式子表示 联系拓广: 如图2,将矩形纸片ABCD 折叠,使点B 落在CD 边上一点E 不与点C D ,重合,压平后得到折痕MN ,设()111AB CE m BC m CD n=>=,,则AMBN 的值等于 .用含m n ,的式子表示 2. 2011陕西如图①,在矩形ABCD 中,将矩形折叠,使B落在边AD 含端点上,落点记为E ,这时折痕与边BC 或边CD 含端点交于点F ,然后再展开铺平,则以B 、E 、F 为顶点的△BEF 称为矩形ABCD 的“折痕三角形”.1由“折痕三角形”的定义可知,矩形ABCD 的任意一个“折痕△BEF ”是一个_________三角形;2如图②,在矩形ABCD 中,AB =2,BC =4.当它的“折痕△BEF ”的顶点E 位于边AD 的中点时,画出这个“折痕△BEF ”,并求出点F 的坐标;3如图③,在矩形ABCD 中, AB =2,BC =4,该矩形是否存在面积最大的“折痕△BEF ”若存在,说明理由,并求出此时点E 的坐标;若不存在,为什么图① 图② 图③3. 2010江西南昌课题:两个重叠的正多边形,其中的一个绕某一个顶点旋转所形成的有关问题. 实验与论证设旋转角∠A 1A 0B 1=αα<∠A 1A 0A 2,θ1,θ2,θ3,θ4,θ5,θ6所表示的角如图所示. 1用含α的式子表示:θ3=_________,θ4=_________,θ5=_________;图1-图4中,连接A 0H 时,在不添加其他辅助线的情况下,是否存在与直线0H 垂直且被它平分的线段若存在,请选择其中的一个图给出证明;若不存在,请说明理由;归纳与猜想图2NA B CD E F M图1A BCDE FM N设正n 边形A 0A 1A 2…A n -1与正n 边形A 0B 1B 2…B n -1重合其中,A 1与B 1重合,现将正n 边形A 0B 1B 2…B n -1绕顶点A 0逆时针旋转αn1800<<α. 3设θn 与上述“θ3,θ4,…”的意义一样,请直接写出θn 的度数;4试猜想在n 边形且不添加其他辅助线的情形下,是否存在与直线A 0H 垂直且被它平分的线段若存在,请将这条线段用相应的顶点字母表示出来不要求证明;若不存在,请说明理由.4. 2009山东德州已知正方形ABCD 中,E 为对角线BD 上一点,过E 点作EF ⊥BD 交BC于F ,连接DF ,G 为DF 中点,连接EG ,CG . 1求证:EG =CG ;2将图①中△BEF 绕B 点逆时针旋转45o,如图②所示,取DF 中点G ,连接EG ,CG .问1中的结论是否仍然成立若成立,请给出证明;若不成立,请说明理由. 3将图①中△BEF 绕B 点旋转任意角度,如图③所示,再连接相应的线段,问1中的结论是否仍然成立通过观察你还能得出什么结论均不要求证明5. 2010江苏苏州刘卫同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.图①中,90°,B ∠=306cm °,;A BC ∠==图②中,90D =°,45E ∠=°, 4cm DE =.图③是刘卫同学所做的一个实验:他将DEF △的直角边DE 与△ABC 的斜边AC 重合在一起,并将DEF △沿AC 方向移动.在移动过程中,D 、E 两点始终在AC 边上移动开始时点与点重合. 1在DEF △沿AC 方向移动的过程中,刘卫同学发现:F C 、两点间的距离逐渐_________.填“不变”、“变大”或“变小” 2刘卫同学经过进一步地研究,编制了如下问题:问题①:当DEF △移动至什么位置,即AD 的长为多少时,F C 、的连线与AB 平行 问题②:当DEF △移动至什么位置,即AD 的长为多少时,以线段AD FC BC 、、的长度为三边长的三角形是直角三角形问题③:在DEF △的移动过程中,是否存在某个位置,使得15FCD ∠=°?如果存在,求出AD 的长度;如果不存在,请说明理由. 请你分别完成上述三个问题的解答过程.三、测试提高1. 2009湖南常德如图1,若△ABC 和△ADE 为等边三角形,M ,N 分别EB ,CD 的中点,易证:F BA D E G图①F A D G图② F A E 图③ ①图②F ED AB图③D。
中考数学压轴题提升训练一次函数与反比例函数综合题含解析

一次函数与反比例函数综合题【例1】。
如图,直线l:y=ax+b交x轴于点A(3,0),交y于第一象限的点P,点P的轴于点B(0,-3),交反比例函数y kx横坐标为4.的解析式;(1)求反比例函数y kx(2)过点P作直线l的垂线l1,交反比例函数y k的图象于x点C,求△OPC的面积.【答案】见解析。
【解析】解:(1)∵y=ax+b交x轴于点A(3,0),交y轴于点B(0,-3),∴3a+b=0,b=-3,解得:a=1,即l1的解析式为:y=x-3,当x=4时,y=1,即P(4,1),将P点坐标代入y k得:k=4,x;即反比函数的解析式为:y4x(2)设直线l1与x轴、y轴分别交于点E,D,∵OA=OB=3,∴∠OAB=∠OBA=45°,∵l⊥l1,∴∠DPB=90°,∴∠ODP=45°,设直线l1的解析式为:y=-x+b,将点P(4,1)代入得:b=5,联立:y=-x+5,y4x,解得:x=1,y=4或x=4,y=1,即C(1,4),∴S△OPC=S△ODE-S△OCD-S△OPE=12×5×5-12×5×1-12×5×1=152.【变式1—1】.如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=–12x+3交AB,BC于点M,N,反比例函数kyx的图象经过点M,N.(1)求反比例函数的解析式;(2)若点P在x轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.【答案】见解析.【解析】解:(1)∵B(4,2),四边形OABC为矩形,∴OA=BC=2,在y=–12x+3中,y=2时,x=2,即M(2,2),将M(2,2)代入kyx=得:k=4,∴反比例函数的解析式为:4yx=.(2)在4yx=中,当x=4时,y=1,即CN=1,∵S四边形BMON=S矩形OABC-S△AOM-S△CON=4×2-12×2×2-12×4×1=4,∴S△OPM=4,即12·OP·OA=4,∵OA=2,∴OP=4,∴点P 的坐标为(4,0)或(-4,0)。
2022年中考数学压轴题(含答案)

一、解答题1.如图,四边形ABCD 和四边形GHIJ 都是正方形,点E 同时是边BC 和HI 的中点,点F 是边AD 的中点,点K 是边GJ 的中点,连接BH ,FK .(1)如图1,当HI 与BC 在同一条直线上时,直接写出BH 与FK 的数量关系和位置关系;(2)正方形ABCD 固定不动,将图1中的正方形GHIJ 绕点E 顺时针旋转角,如图2所示,判断(1)中的结论是否仍然成立,若成立,请加以证明:若不成立,说明理由;(3)正方形ABCD 固定不动,将图1中的正方形GHIJ 绕点E 旋转角,作于点L .设,线段AB ,BH ,HG ,GK ,KF ,FA 所围成的图形面积为S .当6AB =,时,求S 关于x 的函数关系式,并写出相应的x 的取值范围. 2.问题发现如图1,在Rt ABC △和Rt CDE △中,90ACB DCE ∠=∠=︒,45CAB CDE ∠=∠=︒,点D 是线段AB 上一动点,连接BE .(1)填空: ①BE AD的值为______; ②DBE ∠的度数为______.(2)类比探究如图2,在Rt ABC △和Rt CDE △中,90ACB DCE ∠=∠=︒,60CAB CDE ∠=∠=︒,点D 是线段AB 上一动点,连接BE .请求出BE AD 的值及DBE ∠的度数,并说明理由; (3)拓展延伸如图3,在Rt ABC △和Rt CDE △中,90ACB DCE ∠=∠=︒,CAB CDE ∠=∠,点D 是线段AB 上一动点,连接BE ,M 为DE 中点.若4BC =,3AC =,在点D 从A 点运动到B 点的过程中,请直接写出M 点经过的路径长.3.如图1,在菱形ABCD 中,对角线AC 、BD 相交于点O ,过点B 作BE CD ⊥,交AC 于点H ,交CD 于点E .过点C 作//CF BD ,交BE 的延长线于点F ,过点F 作//FG BC ,交BD 的延长线于点G .(1)若8AC =,6BD =,求BE 的长;(2)如图2,连接AF ,交BG 于点K ,若GFA BFC ∠=∠,求证:2BF BC CD -.(3)如图3,当点D 与点G 重合时,若9AB =,将BOH 沿射线BC 方向平移,当点B 到达点C 时停止平移.当平移结束后(即点B 到达点C 时),将BOH 绕点B 顺时针旋转一个角度()0360αα<<︒,O 的对应点'O ,H 的对应点'H ,直线'CH 与直线BF 的交点为M ,直线''O H 与直线BF 的交点为N ,在旋转过程中,当'MNH △是直角三角形,且'90MNH ∠=︒时,直接写出'MNH △的面积.4.已知:抛物线l 1:y =—x 2+bx +3交x 轴于点A 、B ,(点A 在点B 的左侧),交y 轴于点C ,其对称轴为直线x =1,抛物线l 2经过点A ,与x 轴的另一个交点为E (5,0),交y轴于点D (0,5—2) (1)求抛物线2l 的函数表达式;(2)P 为直线1x =上一动点,连接PA ,PC ,当PA PC =时,求点P 的坐标;(3)M 为抛物线2l 上一动点,过点M 作直线//MN y 轴,交抛物线1l 于点N ,求点M 自点A 运动至点E 的过程中,线段MN 长度的最大值.5.在△ABC中,AB=BC=5,AD⊥BC于D,AD=4.动点P从点B出发,沿折线BA→AC运动(点P不与B、C重合),点P在边BA上运动的速度为2.5个单位长度,在个单位长度,过P作PQ⊥BC于点Q,以PQ为边向右作矩形边AC上的运动速度为52PQFE,使PQ=2PE,点F在线段BC上,设点P运动的时间为t.(1)点P在BA上时,则PQ=;(用含t代数式表示)(2)点P在AC上时,则PQ=;(用含t代数式表示)(3)连结DE,当△DEF与△ADC相似时,求t的值.(4)设矩形PQFE的对角线相交于点O,当点O在△ACD边上时,直接写出t的取值范围.6.如图,在平面直角坐标系中,已知点A(a,0)、B(0,b)分别为x轴和y轴上一点,且a,b满足22260+-+=,过点B作BE⊥AC于点E,延长BE至点D,使得BD=AC,连a b ab b接OC、OD.(1)A点的坐标为;∠OAB的度数为.(2)如图1,若点C在第四象限,试判断OC与OD的数量关系与位置关系,并说明理由.(3)如图2,连接CD,若点C的坐标为(4,3),CE平分∠OCD,AC与OD交于点F.①求D点的坐标;②试判断DE与CF的数量关系,并说明理由.7.如图1,在平面直角坐标系中,直线y=2x+8与x轴交于点A,与y轴交于点B,过点B的另一条直线483y x=-+交x轴正半轴于点C.(1)写出C点坐标;(2)若M为线段BC上一点,且满足S△AMB=S△AOB,请求出点M的坐标;(3)如图2,设点F为线段AB中点,点G为y轴正半轴上一动点,连接FG,以FG为边向FG右侧作正方形FGQP,在G点的运动过程中,当顶点Q落在直线BC上时,求出点G 的坐标.8.如图1,在平面直角坐标系中,抛物线y=ax2+154x+c与x轴负半轴相交于点A(﹣20,0),与y轴相交于点B(0,﹣15).(1)求抛物线的函数表达式及直线AB的函数表达式;(2)如图2,点C是第三象限内抛物线上的一个动点,连接AC、BC,直线OC与直线AB 相交于点D,当△ABC的面积最大时,求此时△ABC面积的最大值及点C的坐标;(3)在(2)的条件下,点E为线段OD上的一个动点,点E从点O开始沿OD以每秒10D运动(运动到点D时停止),以OE为边,在OD的左侧做正方形OEFG,设正方形OEFG与△OAD重叠的面积为S,运动时间为t秒.当t>3时,请直接写出S 与t 之间的函数关系式为 (不必写出t 的取值范围).9.二次函数y =ax 2﹣4ax +2的图象与y 轴交于点A ,且过点B (3,6).(1)试求二次函数的解析式及点A 的坐标;(2)若点B 关于二次函数对称轴的对称点为点C ,设点D 在直线AB 上方的抛物线上,当∠CBD =∠ABC 时,求出点D 的坐标;(3)若在抛物线的对称轴上有一点P ,使得△ABP 是以AB 为腰的等腰三角形,试直接写出符合题意的所有的点P 的坐标.10.如图,已知抛物线23y ax bx =++(a 、b 为常数,且a ≠0)与x 轴交于点A (-1,0)和点B ,与y 轴交于点C ,其对称轴是直线x =1,顶点为P ,连接BP ,CP .(1)求抛物线的表达式;(2)判断△BCP 的形状,并说明理由;(3)该抛物线上是否存在点Q ,使得∠QBC=∠ACO ?若存在,请直接写出满足条件的所有点Q 是坐标;若不存在,请说明理由.11.如图,抛物线与x 轴交于A 、B 两点( 点A 在点B 的左侧),点B 坐标()3,0,抛物线与y 轴交于点()0,3C -,点D 为抛物线顶点,对称轴1x =与x 轴交于点E ,连接BC 、EC .(1)求抛物线的解析式;(2)点P 是BC 下方异于点D 的抛物线上一动点,若PBC EBC SS =,求此时点P 的坐标; (3)点Q 是抛物线上一动点,点M 是平面上一点,若以点B 、C 、Q 、M 为顶点的四边形为矩形,直接写出满足条件的点Q 的横坐标.12.如图,已知抛物线2y ax bx c =++与x 轴交于点(1,0)A -,点(3,0)B ,与y 轴交于点(0,3)C ,顶点为点D .(1)求抛物线的解析式;(2)若过点C 的直线交线段AB 于点E ,且,求的正切值; (3)若点P 在抛物线上,点Q 在x 轴上,当以点D 、C 、P 、Q 为顶点的四边形是平行四边形时,直接写出点P 的坐标.13.如图1,在平面直角坐标系中,已知△ABC 中,∠ABC =90°,B (4,0),C (8,0),tan∠ACB =2,抛物线y =ax 2+bx 经过A ,C 两点.(1)求点A 的坐标及抛物线的解析式;(2)如图2,过点A 作AD ⊥AB 交BC 的垂线于点D ,动点P 从点A 出发,沿线段AB 向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E.①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG取得最大值?最大值是多少?②连接EQ,在点P,Q运动过程中,t为何值时,使得△CEQ与△ABC相似?14.如图,在平面直角坐标系中,抛物线y=ax2+bx+2与直线y=x﹣2交于点A(m,0)和点B(﹣2,n),与y轴交于点C.(1)求抛物线的解析式及顶点D的坐标;(2)若向下平移抛物线,使顶点D落在x轴上,原来的抛物线上的点P平移后的对应点为P',若,求点P的坐标;(3)在抛物线上是否存在点Q,使△QAB的面积是△ABC面积的一半?若存在,直接写出点Q的坐标;若不存在,请说明理由.15.如图,在平面直角坐标系中,四边形AOBC是矩形,OB=4,OA=3,F是BC边上一个动点(不与B、C重合),过点F的反比例函数y=kx(k>0)的图象与边AC交于点E.(1)当BF=13BC时,求点E的坐标;(2)连接EF,求∠EFC的正切值;(3)将△EFC沿EF折叠,得到△EFG,当点G恰好落在矩形AOBC的对角线上时,求k的值.16.如图,在长方形ABCD中,10AB=,9BC=,点E在AB上,点G在AD上,AEFG 为正方形.点M,N分别为BC,CD上的动点,MO BC⊥,NO CD⊥,且点O始终在正方形AEFG的内部,MO交EF于点P,NO交FG于点Q.(1)设CM AE a ==,①用含a 的代数式表示四边形EBMP 的周长;②若四边形OPFQ ,GQND 的周长之和恰好为四边形EBMP 周长的两倍,求a 的值.(2)设3CM x =,2CN x =,AE n CN =,是否存在正整数x ,n ,使得EBMP GQND S S =四边形四边形若存在,求出x ,n 的值;若不存在,请说明理由.17.如图,在平面直角坐标系中,ABC 是等腰直角三角形,90ACB ∠=︒,AC BC =,1OA =,4OC =,抛物线,2y x bx c =++经过A ,B 两点,抛物线的顶点为D .(1)求抛物线的解析式;(2)点E 是Rt ABC 斜边AB 上一动点(点A 、B 除外),过点E 作x 轴的垂线交抛物线于点F ,当线段EF 的长度最大时,求点E 的坐标;(3)若在抛物线的对称轴上恰好存在唯一的点P ,使EFP △是以EF 为直角边的直角三角形?若存在,求出所有点P 的坐标;请确定此时点E 的坐标.18.如图1,在直角坐标系中,O 是坐标原点,点A 在y 轴正半轴上,二次函数y =ax 2+16x +c 的图象F 交x 轴于B 、C 两点,交y 轴于M 点,其中B (﹣3,0),M (0,﹣1).已知AM =BC .(1)求二次函数的解析式;(2)证明:在抛物线F上存在点D,使A、B、C、D四点连接而成的四边形恰好是平行四边形,并请求出直线BD的解析式;(3)在(2)的条件下,设直线l过D且l⊥BD,分别交直线BA、BC于不同的P、Q两点,AC、BD相交于N,求11BP BQ+的值;19.如图1,过点C(0,5)的抛物线y=ax2+bx+c与直线y=21033x-+相交于B(5,0)、D(﹣1,4)两点,点E为线段BD上一动点(不与点B、D重合),连接AE并将其延长交抛物线于点F,过点F作FG∥y轴,交BD于点G.(1)求抛物线的表达式;(2)求线段FG的最大值,并求出此时点E的坐标;(3)在(2)的条件下,把抛物线y=ax2+bx+c先向左平移1个单位,再向下平移53个单位得到新抛物线,点P是新抛物线与原抛物线的交点,点Q为射线BA上一动点,连接CQ,将△CQB沿直线BC翻折到△CNB,连接NQ,交直线BC于点M,R为平面直角坐标系中一点,直接写出所有使得以M、P、F、R为顶点的四边形是菱形的点R的坐标,并把求其中一个点R的坐标的过程写出来.20.如图①,在平面直角坐标系中,点A、B的坐标分别为A(4,0)、B(0,3),连结AB.抛物线经过点B,且对称轴是直线.(1)求抛物线的函数关系式.(2)将图①中的△ABO沿x轴向左平移得到△DCE(如图②),当四边形ABCD是菱形时,说明点C和点D都在该抛物线上.(3)在(2)中,若点M是抛物线上的一个动点(点M不与点C、D重合),过点M作MN∥y轴交直线CD于点N.设点M的横坐标为m,线段MN的长为l.求l与m之间的函数关系式.(4)在(3)的条件下,直接写出m为何值时,以M、N、C、E为顶点的四边形是平行四边形.【参考答案】**科目模拟测试一、解答题1.(1)BH与FK的数量关系为FK=2BH,位置关系为FK⊥BH(2)仍然成立,BH与FK的数量关系不变,FK=2BH,位置关系不变FK⊥BH,证明见解析(3),变量x的取值范围是【解析】【分析】(1),根据正方形的性质和中点定义,可知AB=BC,GH=HI,BE=EC,EH=EI,进而得出BH=IC,再根据FK=AB-GH,可得答案.(2),先连接FE,KE,再根据两边成比例且夹角相等的两个三角形形似,得,进而得出,即可得出数量关系.再延长FK,交BC于M,延长BH,交FM于N,由①可得∠HBE=∠KFE,进而得出∠BNM=90°,即可得出位置关系.(3),分两种情况:第一:当正方形GHIJ绕点E顺时针旋转α时,表示EL,再求出,,表示,再根据,得出,最后根据列出关系式,并求出取值范围.第二:当正方形GHIJ绕点E逆时针旋转α时,与第一类似,再根据列出关系式,并求出自变量取值范围,最后确定答案即可.(1)解:BH与FK的数量关系为FK=2BH,位置关系为FK⊥BH.根据题意可知AB=BC,GH=HI,BE=EC,EH=EI,∴BH=BE-HE,IC=EC-EI,即BH=IC.∴FK=AB-GH=BC-HI=BH+IC=2BH.(2)当正方形GHIJ绕点E旋转α()角时,其数量和位置关系不变先证FK=2BH连接FE,KE由题意可得到,∠FEB=∠KEH=90°可得∠HEB+∠FEH=∠KEF+∠FEH∴∠HEB=∠KEF∴∴即FK=2BH②再证FK⊥BH延长FK,交BC于M,延长BH,交FM于N由①可得∠HBE=∠KFE∴∠HBE+∠FMB=∠KFE+∠FMB=90°∴∠BNM=90°即FK⊥BH∴BH与FK的数量关系不变,FK=2BH,位置关系不变FK⊥BH (3)正方形GHIJ绕点E旋转α(0°≤α≤90°),有以下两种情况:当正方形GHIJ绕点E顺时针旋转α时,EL=x-3.如图,,∵,∴∴又∵因此自变量x的取值范围是当正方形GHIJ绕点E逆时针旋转α时,EL=3-x.如图,, ∵, ∴∴又∵因此自变量x 的取值范围是. 综上所述,.【点睛】 这是一道关于正方形的综合问题,考查了正方形的性质,相似三角形的性质和判定,旋转的性质,求一次函数的关系式及自变量取值范围等.2.(1)①1;②90°;(2)3BE AD =90DBE ∠=︒,理由见解析;(3)256 【解析】【分析】(1)①证明ACD △≌BCE 即可求得BE AD的值;②由①的结论,可得DBE ABC CBE ∠=∠+∠,进而可得DBE ∠的度数; (2)由已知条件证明Rt ACB △∽Rt DCE ,可得AC CD BC CE =,又ACD BCE ∠=∠,可得ACD △∽BCE ,进而根据3AC BC =3BE BC AD AC ==1)可得DBE ABC CBE ∠=∠+∠,进而可得DBE ∠的度数;(3)设AB 的中点为P ,BE 的中点为Q ,由题意M 的路径长为PQ 的长,根据(2)的结论可得ACD △∽BCE ,进而求得CE 的长,根据中位线定理即可求得PQ ,即M 点经过的路径长.【详解】(1)∵90ACB DCE ∠=∠=︒,45CAB CDE ∠=∠=︒,∴45ABC CAB CDE CED ∠=∠=︒=∠=∠,∴AC BC =,CD CE =,∵90ACB DCE ∠=∠=︒,∴ACD BCE ∠=∠,在ACD △和BCE 中,AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩, ∴ACD △≌BCE (S A S ),∴BE AD =,45CAB CBE ∠=∠=︒,∴90DBE ABC CBE ∠=∠+∠=︒,1BE AD=. 故答案为:1,90°.(2)BE AD =90DBE ∠=︒. 理由如下:∵90ACB DCE ∠=∠=︒,60CAB CDE ∠=∠=︒,∴30CED ABC ∠=∠=︒,ACB DCB DCE DCB ∴∠-∠=∠-∠,即ACD BCE ∠=∠,∴tan tan 30AC ABC BC ∠=︒== ∵90ACB DCE ∠=∠=︒,60CAB CDE ∠=∠=︒,∴Rt ACB △∽Rt DCE , ∴AC CD BC CE =, ∴AC BC CD CE=,且ACD BCE ∠=∠, ∴ACD △∽BCE ,∴BE BC AD AC =60CBE CAD ∠=∠=︒, ∴90DBE ABC CBE ∠=∠+∠=︒.(3)如图,设AB 的中点为P ,BE 的中点为Q ,点D 是线段AB 上一动点, M 为DE 中点,在点D 从A 点运动到B 点的过程中,M 点从AB 的中点P 运动到BE 的中点Q ,当D 点与B 点重合时,M 点与Q 点重合,此时如图,则M 点的运动路径长为PQ 的长,由(2)可得ACD △∽BCE ,4BC =,3AC =,90ACB ∠=︒,∴43BE BC EC AD AC CD ===,225AB AC BC +=, 4CD BC ==,163EC ∴=, 1625333AE AC EC ∴=+=+=, ,P Q 分别为,AD BE 的中点,则256PQ =, ∴M 点的运动路径长为256. 【点睛】本题考查了三角形全等的性质与判定,相似三角形的性质与判定,解直角三角形,综合运用以上知识是解题的关键.3.(1)245;(2)见解析;(3)815434+或543814- 【解析】【分析】(1)由菱形的对角线互相垂直平分,得到直角三角形及其两条直角边的长,再由勾股定理求出边CD 的长,利用菱形的面积列方程即可求解;(2)延长AD 交BF 于点L ,根据平行四边形的判定和性质及直角三角形斜边上的中线等于斜边的一半、菱形的每条对角线平分一组对角等,可得:45BLA BAL ∠=∠=︒,进而得出2BF BC CD -=;(3)在0360α<<︒范围内,O H BF ''⊥即90MNH ∠='︒的情况有两种,准确的画出相应图形进行求解即可.【详解】解:(1)如图1,∵四边形ABCD 是菱形,∴90COD ∠=︒,118422OC AC ==⨯=,116322OD BD ==⨯=, ∴22435CD =+=,∴15862BE =⨯⨯, 解得245BE =.(2)如图2,延长AD 交BF 于点L .∵//CF BD ,//FG BC ,∴四边形BCFG 是平行四边形,∵90ABF DEF ∠=∠=︒,90AOB ∠=︒,∴90GBF ABO BAC DAC ∠=︒-∠=∠=∠,∵////FG BC AD ,GFA BFC ∠=∠,∴LAF GFA BFC ∠=∠=∠,∵BFC GBF ∠=∠,∴GFA BFC LAF BAC DAC ∠=∠=∠=∠=∠,设GFA BFC LAF BAC DAC β∠=∠=∠=∠=∠=,∵AKD FKG ∠=∠,DAK GFK ∠=∠,FG AD =,∴()AKD FKG AAS ≅△△,∴AK FK =, ∴12BK AF AK ==, ∴3KAB KBA GBC GFC β∠=∠=∠=∠=,∴LFA LAF β∠==∠,∵90LFA LAF BAC DAC ∠+∠+∠+∠=︒, ∴45LFA LAF BAC DAC ∠=∠=∠=∠=︒,∴LF LA =,45BLA BAL ∠=∠=︒,∴22LA AB LB ==,∵BC AB BL ==,∴2BF BC BF BL LF LA AB -=-===,∵AB CD =,∴2BF BC CD -=.(3)当点D 与点G 重合时,则四边形ABCD 和四边形BCFD 都是菱形,∴60ADB BDC CDF ∠=∠=∠=︒,30DAO ∠=︒,∵9AD AB ==,∴1922BO DO AD ===,933AO CO DO ===. 当0180α<≤︒,且'90MNH ∠=︒时,如图3,∵9'2EN CO BO ===,932ME CO ==, ∴993993222MN +=+=, ∵'30NMH ∠=︒,∴9933339'tan 30232NH MN ++=⋅︒=⨯=, ∴'1993339815432224MNH S +++=⨯⨯=△.当180360α︒<<︒,且'90MNH ∠=︒时,如图4,则939939222MN -=-=, 9393933'tan 30232NH MN --=⋅︒=⨯=, ∴'1939933543812224MNH S ---=⨯⨯=△.综上所述,'MNH △.【点睛】 题目主要考查平行四边形的判定和性质、直角三角形斜边上的中线等于斜边的一半以及全等三角形的性质和判定、二次根式和化简等知识点,综合运用这些知识点是解题关键.4.(1)215222y x x =--;(2)(1,1);(3)12 【解析】【分析】(1)由对称轴可求得b ,可求得1l 的解析式,令0y =可求得A 点坐标,再利用待定系数法可求得2l 的表达式;(2)设P 点坐标为(1,)y ,由勾股定理可表示出2PC 和2PA ,由条件可得到关于y 的方程可求得y ,可求得P 点坐标;(3)可分别设出M 、N 的坐标,可表示出MN ,再根据函数的性质可求得MN 的最大值.【详解】解:(1)抛物线21:3l y x bx =-++的对称轴为1x =,12b ∴-=-,解得2b =, ∴抛物线1l 的解析式为2y x 2x 3=-++,令0y =,可得2230x x -++=,解得1x =-或3x =,A ∴点坐标为(1,0)-,抛物线2l 经过点A 、E 两点,∴可设抛物线2l 解析式为(1)(5)y a x x =+-, 又抛物线2l 交y 轴于点(20,5)D -, 552a ∴-=-,解得12a =, 2115(1)(5)2222y x x x x ∴=+-=--, ∴抛物线2l 的函数表达式为215222y x x =--; (2)设P 点坐标为(1,)y ,由(1)可得C 点坐标为(0,3),22221(3)610PC y y y ∴=+-=-+,2222[1(1)]4PA y y =--+=+,PC PA =,226104y y y ∴-+=+,解得1y =,P ∴点坐标为(1,1);(3)由题意可设215(,2)22M x x x --, //MN y 轴,2(,23)N x x x ∴-++, 令221523222x x x x -++=--,可解得1x =-或113x =, ①当1113x -<时,2222153113449(23)(2)4()2222236MN x x x x x x x =-++---=-++=--+, 显然411133-<,∴当43x =时,MN 有最大值496; ②当1153x <时,2222153113449(2)(23)4()2222236MN x x x x x x x =----++=--=--, 显然当43x >时,MN 随x 的增大而增大, ∴当5x =时,MN 有最大值,23449(5)12236⨯--=; 综上可知在点M 自点A 运动至点E 的过程中,线段MN 长度的最大值为12.【点睛】本题主要考查二次函数的综合应用,涉及待定系数法、二次函数的性质、勾股定理等知识点,在(1)中求得A 点的坐标是解题的关键,在(2)中用P 点的坐标分别表示出PA 、PC 是解题的关键,在(3)中用M 、N 的坐标分别表示出MN 的长是解题的关键,注意分类讨论.5.(1)2t ;(2)6﹣t ;(3)67或613或2或5;(4)t =32或2≤t <6 【解析】【分析】(1)由四边形PQFE 是矩形,可得PQ ⊥QF ,进而推出PQ ∥AD ,可得△BPQ ∽△BAD ,得出BP PQ AB AD=,即可求出PQ 的长; (2)由勾股定理得出BD 、AC 的长度,表示出AP 的长,CP 的长,利用△CPQ ∽△CAD ,得出PQ CP AD AC=,即可求出PQ 的长; (3)分两种情况:①当点P 在边BA 上运动时,由四边形PQFE 是矩形,可得QF =PE =t ,EF =PQ =2t ,当△EFD ∽△ADC 时,DF CD EF DA = , 求得t =67,当△DFE ∽△ADC 时, DF AD EF CD =,求得t =613,②如图4,当点P 在边AC 上运动时,当△EFD ∽△ADC 时,则DF DC EF AD =,求得t =2,当△DFE ∽△ADC 时,DF AD EF CD =,求得t =5,综上所述,t 的值为67或613或2或5; (4)分三种情况讨论:①当矩形PQFE 的对角线交点O 在AD 上,②当矩形PQFE 的对角线交点O 在AC 上,③当矩形PQFE 的对角线交点O 在CD 上,即可得到t 的取值范围.【详解】解:(1)点P 在BA 上时,点P 在边BA 上运动的速度为2.5个单位长度,BP =2.5t , ∵四边形PQFE 是矩形,∴PQ ⊥QF ,∵点F 在线段BC 上,∴PQ ⊥BC ,∵AD ⊥BC ,∴PQ ∥AD ,∴∠BPQ =∠BAD ,∵∠B =∠B ,∴△BPQ ∽△BAD ,∴BP PQ AB AD=, ∵BP =2.5t ,AB =5,AD =4, ∴2.554t PQ =, ∴PQ =2t ,故答案为:2t ;(2)如图2,点P 在AC 5个单位长度, 由题意得:AP 5(t ﹣2), ∵AD ⊥BC ,AB =5,AD =4,∴BD 2222543AB AD -=-=,∴CD =BC ﹣BD =5﹣3=2,∴AC 22224225AD CD ++∴CP =AC ﹣AP =)5525235t -=,∵PQ∥AD,∴∠QPC=∠DAC,∠PQC=∠ADC,∴△CPQ∽△CAD,∴PQ CPAD AC=,即5352425tPQ-=,∴PQ=6﹣t,故答案为:6﹣t;(3)分两种情况:①如图3,当点P在边BA上运动时,∵四边形PQFE是矩形,∴QF=PE=t,EF=PQ=2t,在Rt△BPQ中,BQ=BP•cos∠B=BP×32.5 1.55BDt t AB=⨯=,∴DF=3﹣2.5t,当△EFD∽△ADC时,DF CD EF DA=∴3 2.52 24tt-=,∴t=67,经检验符合题意,当△DFE∽△ADC时,DF AD EF CD=,∴3 2.54 22tt-=,∴t=6 13,经检验符合题意,②如图4,当点P在边AC上运动时,∵四边形PQFE是矩形,∴QF=PE=t,EF=PQ=6﹣t,∴DF=DC=2,当△EFD∽△ADC时,则DF DC EF AD=,即22 64t=-,∴t=2,经检验符合题意,当△DFE∽△ADC时,DF AD EF CD=,∴24 62t=-,∴t=5,经检验符合题意,综上所述,t的值为67或613或2或5;(4)分三种情况讨论:①当矩形PQFE的对角线交点O在AD上时,如图5,∴QD=12QF=0.5t,∵BQ =1.5t ,BQ +QD =BD =3,∴1.5t +0.5t =3,∴t =32, ②当矩形PQFE 的对角线交点O 在AC 上时,∵点F 始终与点C 重合,点P 从点A 运动到点C ,4AC = ∴点P 在AC 上运动时间为2≤t <6,∴当2≤t <6时,矩形PQFE 的对角线交点O 在AC 上;③由题意知,矩形PQFE 的对角线交点O 不可能在CD 上;综上所述,t 的取值范围t =32或2≤t <6. 【点睛】本题考查锐角三角函数,勾股定理,等腰三角形性质,三角形相似判定与性质,可化为一元一次方程的分式方程,矩形性质,动点动图形问题,分类讨思想的运用,掌握锐角三角函数,勾股定理,等腰三角形性质,三角形相似判定与性质,可化为一元一次方程的分式方程,矩形性质,动点动图形问题,分类讨思想的运用,本题难度大,涉及知识多,是中考压轴题.6.(1)(6,0)-,45︒;(2)OC OD =,OC OD ⊥;理由见解析;(3)①(3,4)D -;②12DE CF = 【解析】【分析】(1)直接根据完全平方式的非负性,二次根式有意义的条件得出,a b 的值即可得出答案;(2)根据题意证明()OAC OBD SAS △≌△,根据全等三角形的性质以及三角形内角和定理可得结论;(3)①作DG x ⊥轴交x 轴于点G ,⊥CH x 轴交x 轴于点H ,证明()OGD CHO AAS ≌,即可得到答案;②延长CO 交BD 于点M ,根据题意证明COF DOM ≌,然后证明DCE MCE ≌,可得结论.【详解】解:(1)∵2220a b ab +-=,即2()0a b -+,∴6b =-,6a b ==-,∴A 点的坐标为(6,0)-,点(0,6)B -∴6OA OB ,∵90AOB ∠=︒,∴45OAB ∠=︒,故答案为:(6,0)-,45︒;(2)设AC 与y 轴交于点F ,BD 与OC 交于点G ,∵BE ⊥AC ,∴90BEF ∠=︒,在AOF 和BEF 中,90AOF BEF ∠=∠=︒,AFO BFE =∠∠,∴FAO FBE ∠=∠,即OAC OBD ∠=∠,在OAC 和OBD 中,OA OB OAC OBD AC BD =⎧⎪∠=∠⎨⎪=⎩, ∴()OAC OBD SAS △≌△,∴OC OD =,C D ∠=∠,在OGD 和EGC 中,C D ∠=∠,OGD EGC ∠=∠,∴90DOC GEC ∠=∠=︒,∴OC OD ⊥,∴OC OD =,OC OD ⊥;(3)①作DG x ⊥轴交x 轴于点G ,⊥CH x 轴交x 轴于点H ,∵点C的坐标为(4,3),∴4,3OH CH==,由(2)知,90OC OD COD=∠=︒,∵90DOG COH∠+∠=︒,90COH OCH∠+∠=︒,∴DOG OCH∠=∠,∵90OGD CHO∠=∠=︒,∴()OGD CHO AAS≌,∴3OG CH==,4GD HO==,∴(3,4)D-;②延长CO交BD于点M,∵ODB OCA∠=∠,90COD DOM∠=∠=︒,OC OD=,∴COF DOM≌,∴CF DM=,∵CE平分∠OCD,∴DCA OCA∠=∠,∵,90CE CE DEC MEC=∠=∠=︒,∴DCE MCE≌,∴12DE ME DM==,∴12DE CF=.【点睛】本题考查了完全平方式的非负性,二次根式有意义的条件,坐标与图形,全等三角形的判定与性质,正确作出辅助线,熟练掌握全等三角形的判定定理以及性质定理是解本题的关键.7.(1)点C (6,0);(2)点1224(,)55M ;(3)满足条件的点G 坐标为34(0,)7或(0,-2).【解析】【分析】(1)直接利用直线483y x =-+,令y=0,解方程即可; (2)结合图形,由S △AMB =S △AOB 分析出直线OM 平行于直线AB ,再利用两直线相交建立方程组2483y x y x =⎧⎪⎨=-+⎪⎩,解方程组求得交点M 的坐标; (3)分两种情形:①当n >4时,如图2-1中,点Q 落在BC 上时,点Q 落在BC 上时,过G 作MN 平行于x 轴,过点F ,Q 作该直线的垂线,分别交于M ,N .求出Q (n-4,n-2).②当n <4时,如图2-2中,同法可得Q (4-n ,n +2),代入直线BC 的解析式解方程即可解决问题.【详解】解:(1)∵直线483y x =-+交x 轴正半轴于点C . ∴当y =0时,48=03x -+, 解得x =6∴点C (6,0)故答案为(6,0);(2)连接OM 并双向延长,∵S △AMB =S △AOB ,∴点O 到AB 与点M 到AB 的距离相等,∴直线OM 平行于直线AB ,∵AB 解析式为y =2x +8,故设直线OM 解析式为:2y x =,将直线OM 的解析式与直线BC 的解析式联立得方程组得:2483y x y x =⎧⎪⎨=-+⎪⎩, 解得:125245x y ⎧=⎪⎪⎨⎪=⎪⎩故点1224(,)55M ; (3)∵直线y =2x +8与x 轴交于点A ,与y 轴交于点B ,∴令y=0,2x +8=0,解得x =-4,∴A (-4,0),令x =0,则y =8∴B (0,8),∵点F 为AB 中点,点F 横坐标为()1-4+0=-22,纵坐标为()10+8=42∴F (-2,4),设G (0,n ),①当n >4时,如图2-1中,点Q 落在BC 上时,过G 作MN 平行于x 轴,过点F ,Q 作该直线的垂线,分别交于M ,N .∵四边形FGQP 是正方形,∴FG =QG ,∠FGQ =90°,∴∠MGF +∠NGQ =180°-∠FGQ=180°-90°=90°,∵FM ⊥MN ,QN ⊥MN ,∴∠M =∠N =90°,∴∠MFG +∠MGF =90°,∴∠MFG =∠NGQ ,在△FMG 和△GNQ 中,M N MFG NGQ FG GQ ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△FMG ≌△GNQ ,∴MG =NQ =2,FM =GN =n -4,∴Q (n -4,n -2),∵点Q 在直线483y x =-+上, ∴42(4)43n n -=--+, ∴34=7n , ∴34(0,)7G . ②当n <4时,如图2-2中,点Q 落在BC 上时,过G 作MN 平行于x 轴,过点F ,Q 作该直线的垂线,分别交于M ,N .∵四边形FGQP 是正方形,∴FG =QG ,∠FGQ =90°,∴∠MGF +∠NGQ =180°-∠FGQ=180°-90°=90°,∵FM ⊥MN ,QN ⊥MN ,∴∠M =∠N =90°,∴∠MFG +∠MGF =90°,∴∠MFG =∠NGQ ,在△FMG 和△GNQ 中,M N MFG NGQ FG GQ ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△FMG ≌△GNQ ,∴MG =NQ =2,FM =GN = 4-n ,∴Q (4- n , n +2),∵点Q 在直线483y x =-+上, ∴42(4)83n n +=--+,∴n =-2,∴(0,-2)G .综上所述,满足条件的点G 坐标为34(0,)7或(0,-2). 【点睛】本题属于一次函数综合题,考查了一次函数与坐标轴的交点,平行线性质,两直线联立解方程组,全等三角形的判定和性质,正方形的性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.8.(1)291515404y x x =+-,y =﹣34x ﹣15;(2)面积最大值225,C (﹣10,﹣30);(3)S =﹣2553t +160t ﹣240. 【解析】【分析】(1)利用待定系数法将点A (﹣20,0),B (0,﹣15)代入抛物线y =ax 2+154x +c 即可求出抛物线的函数表达式;设AB 的函数表达式是y =kx +b ,然后利用待定系数法将点A (﹣20,0),B (0,﹣15)代入y =kx +b 即可求出直线AB 的函数表达式;(2)作CE ⊥OA 于E ,交AB 于F ,设C (a ,940a 2+154a ﹣15),F (a ,﹣34a ﹣15),根据题意表示出CF 的长度,进而表示出ABC S ∆,然后利用二次函数的性质求解即可;(3)作AN ⊥OD 于N ,AD 与FG 交于点I ,首先根据题意求出OC 的解析式,然后联立33154y x y x =⎧⎪⎨=--⎪⎩求出点D 的坐标,然后求出AD OD =,利用等腰三角形三线合一性质求出ON 的长度,进而利用勾股定理求出AN 的长度,表示出S △AON ,然后证明出△GFI ∽△OGH ∽△ANO ,利用相似三角形的性质表示出S △IJF =803(t ﹣3)2,S △GOH =253t ,最后利用面积之间的关系即可求出S 与t 之间的函数关系式.【详解】解:(1)由题意得,将点A (﹣20,0),B (0,﹣15)代入抛物线y =ax 2+154x +c 得, 21515(20)(20)04c a c =-⎧⎪⎨-+⨯-+=⎪⎩, ∴15940c a =-⎧⎪⎨=⎪⎩, ∴291515404y x x =+-, 设AB 的函数表达式是y =kx +b ,将点A (﹣20,0),B (0,﹣15)代入y =kx +b 得,∴15200b k b =-⎧⎨-+=⎩, ∴1534b k =-⎧⎪⎨=-⎪⎩, ∴y =﹣34x ﹣15; (2)如图1,作CE ⊥OA 于E ,交AB 于F ,设C (a ,940a 2+154a ﹣15),F (a ,﹣34a ﹣15), ∴FC =(﹣315)4a -﹣(2940a +154a ﹣15)=﹣2940a ﹣92a , ∴ABC S ∆=12CF •AO =12(﹣2940a ﹣92a )×20=﹣94(a +10)2+225, ∴当a =﹣10时,ABC S ∆=225,当a =﹣10时,y =29(10)40⨯-+()15104⨯-﹣15=﹣30, ∴C (﹣10,﹣30); (3)如图2,作AN ⊥OD 于N ,∵C (﹣10,﹣30),∴OC 的解析式是:y =3x ,由33154y x y x =⎧⎪⎨=--⎪⎩得, 412x y =-⎧⎨=-⎩, ∴D (﹣4,﹣12),∵A (﹣20,0),OD 22412+10 ∴AD ()2220412-++=20, ∴AD OD =,又∵AN ⊥OD ,∴ON =12OD =1022610AN AO ON -= S △AON =116102106022AN ON =⨯=, ∵OE 10,OD =10, ∴DE =1010,∴JE =3(1010),∴FJ =EF ﹣JE 10t ﹣3(1010t )=10(t ﹣3),∵OG AN FJ ∥∥, ∴GOH OAN DAN AJF ∠=∠=∠=∠,又∵90G ANO F ∠=∠=∠=︒,∴△GFI ∽△OGH ∽△ANO , ∴IJF AON S S ∆∆=(FJ AN )2=410(3)610t -2,GOH AON S S ∆∆=(OG AN )210610t )2,∴S △IJF =803(t ﹣3)2,S △GOH =253t , ∴S =S 正方形OEFG ﹣S △IJF ﹣S △GOH=10t 2﹣53t 2﹣803(t ﹣3)2 =﹣2553t +160t ﹣240, 故答案是:S =﹣2553t +160t ﹣240. 【点睛】此题考查了待定系数法求二次函数和一次函数表达式,二次函数与一次函数综合问题,相似三角形的性质和判定,二次函数中最大面积问题等知识,解题的关键是正确分析题目中的条件,设出点的坐标,根据相似三角形的性质以及勾股定理表示出相应的线段和面积.9.(1)二次函数的解析式为2416233y x x =-++;A (0,2);(2)D (2,223);(3)点P 的坐标为(2,22,22,6-2,6+【解析】【分析】(1)把B (3,6)代入y =ax 2﹣4ax +2,列方程求a 的值,求出二次函数的解析式,再令x =0,求出点A 的纵坐标;(2)先作点A 关于直线BC 的对称点E ,交抛物线于点D ,得到∠CBD =∠ABC ,求直线BD 的解析式且与二次函数的解析式组成方程组,解方程组求出点D 的坐标;(3)以AB 为腰的等腰三角形PAB ,可按以BP 为底边或以AP 为底边两种情况分类讨论,由AP 2=AB 2或PB 2=AB 2列方程,分别求出相应的点P 的坐标.【详解】解:(1)把B (3,6)代入y =ax 2﹣4ax +2,得9a ﹣12a +2=6,解得,a =43-, ∴二次函数的解析式为2416233y x x =-++; 当x =0时,24162233y x x =-++=, ∴A (0,2).(2)如图1,∵()22416422223333y x x x =-++=--+, ∴抛物线的对称轴为直线x =2,∵点C 与点B (3,6)关于直线x =2对称,∴C (1,6),∴BC ∥x 轴,作点A (0,2)关于直线BC 的对称点E ,交抛物线于点D ,则E (0,10), ∵BC 垂直平分AE ,∴AB =AE ,∴∠CBD =∠ABC ,设直线BD 的解析式为y =kx +10,则3k +10=6, 解得,43k =-, ∴y =43-x +10, 由24103416233y x y x ⎧=-+⎪⎪⎨⎪=-++⎪⎩, 得112223x y =⎧⎪⎨=⎪⎩,2336x y =⎧⎨=⎩, ∴D (2,223); (3)设P (2,m ),∵A (0,2),B (3,6),∴AB 2=32+(6﹣2)2=25,当AP =AB 时,如图2,由AP2=AB2得,22+(m﹣2)2=25,整理得,m2﹣4m﹣17=0,解得,m1=221-,+,m2=221∴P(2,221-),+)或P′(2,221当PB=AB时,如图3,由PB2=AB2,得(3﹣2)2+(6﹣m)2=25,整理得,m2﹣12m+12=0,解得,m1=66+-m2=66∴P(2,626-P′(2,626+综上所述,点P的坐标为(2,2212,221-2,-2,626626+【点睛】本题考查二次函数的图象与性质、一次函数的图象与性质、用待定系数法求函数解析式、等腰三角形的性质、解一元二次方程、二次根式的化简及分类讨论数学思想的运用等知识与方法,熟练掌握相关知识是解题关键10.(1)2y x2x3=-++(2)直角三角形,理由见解析(3)Q (1,4)或Q【解析】【分析】 (1)将A (-1,0)代入解析式得到,结合对称轴12b x a=-=解出,a b 即可; (2)求出顶点P 坐标,分别计算出CP 、BC 、BP 的长度,得到CP 2+BC 2=BP 2,进而得到△BCP 为直角三角形;(3)分Q 点在直线BC 上方和下方结合相似三角形分类讨论即可.(1)解:∵抛物线23y ax bx =++经过A (-1,0),其对称轴是直线x =1,∴,解出12a b =-⎧⎨=⎩, ∴抛物线的解析式为:2y x 2x 3=-++.(2)解:当x =1时代入抛物线解析式中得, ∴抛物线的顶点坐标P (1,4),令2y x 2x 3=-++中0y =得到C (0,3),令2y x 2x 3=-++中0x =得到B (3,0),∴PC 2=(1-0)2+(4-3)2=2,PB 2=(1-3)2+(4-0)2=20,BC 2=(3-0)2+(0-3)2=18,∵PC 2+BC 2=2+18=20=PB 2,∴△PBC 为直角三角形,且∠PCB =90°.(3)解:分类讨论:情况一:当Q 点在直线BC 上方时,如下图所示:,由(2)中可知,△PBC为直角三角形,∴,∴,此时只要Q点与P点重合,必有,故Q点坐标为(1,4);情况二:当Q点在直线BC下方时,如下图所示:由情况一可知,∠CBQ=∠ACO,故只要将直线BQ沿BC对折,Q点落在M处,此时∠CBM=∠CBQ=∠ACO,且△CBQ≌△CBM,CQ=CM,分别过Q、M作QE⊥y轴于E,作MF⊥y轴于F,∵CQ=CM,∠QEC=∠MFC=90°,∠MCF=∠QCE,∴△QCE≌△MCF(AAS),∴MF=QE=1,CF=EC=4-3=1,∴M(-1,2),设直线MB解析式为:y=mx+n,代入B(3,0)和M(-1,2),得到,解出,∴MB解析式为:,与抛物线联立,即,解得:(为上述图中Q 1点坐标,符合题意),(为B 点坐标,舍去), 综上所述, Q 坐标存在,为(1,4)或.【点睛】 本题考查二次函数综合知识,准确把握二次函数相关性质,学会数形结合,分类讨论思想在抛物线中的应用是解题关键,本题属于中考常考压轴题型.11.(1)223y x x =---(2)点P 的坐标为()2,3-(3)点Q 的横坐标为1m =或2-【解析】【分析】(1)用待定系数法即可求解;(2)在x 轴上取点H ,使BH =BE =2,过点H (5,0)作BC 的平行线交抛物线于点P ,则点P 为所求点,进而求解;(3)分BC 是边、BC 是对角线两种情况,利用图形平移、中点公式和矩形的性质,分别求解即可.(1) 解:由题意得:123930b x a c a b c ⎧=-=⎪⎪=-⎨⎪++=⎪⎩, 解得123a b c =⎧⎪=-⎨⎪=-⎩, 故抛物线的表达式为223y x x =---①;(2)解:在x 轴上取点H ,使2BH BE ==,过点()5,0H 作BC 的平行线交抛物线于点P ,则点P 为所求点,。
中考数学压轴题集锦精选100题(含答案)

中考数学压轴题集锦精选100题(含答案)一、中考压轴题1.如图,在△ABC中,∠BAC=30°,以AB为直径的⊙O经过点C.过点C作⊙O的切线交AB的延长线于点P.点D为圆上一点,且=,弦AD的延长线交切线PC于点E,连接BC.(1)判断OB和BP的数量关系,并说明理由;(2)若⊙O的半径为2,求AE的长.【分析】(1)首先连接OC,由PC切⊙O于点C,可得∠OCP=90°,又由∠BAC=30°,即可求得∠COP=60°,∠P=30°,然后根据直角三角形中30°角所对的直角边等于斜边的一半,证得OB=BP;(2)由(1)可得OB=OP,即可求得AP的长,又由=,即可得∠CAD=∠BAC=30°,继而求得∠E=90°,继而在Rt△AEP中求得答案.【解答】解:(1)OB=BP.理由:连接OC,∵PC切⊙O于点C,∴∠OCP=90°,∵OA=OC,∠OAC=30°,∴∠OAC=∠OCA=30°,∴∠COP=60°,∴∠P=30°,在Rt△OCP中,OC=OP=OB=BP;(2)由(1)得OB=OP,∵⊙O的半径是2,∴AP=3OB=3×2=6,∵=,∴∠CAD=∠BAC=30°,∴∠BAD=60°,∵∠P=30°,∴∠E=90°,在Rt△AEP中,AE=AP=×6=3.【点评】此题考查了切线的性质、直角三角形的性质以及圆周角定理.此题难度适中,注意掌握数形结合思想的应用,注意掌握辅助线的作法.2.如图,在矩形ABCD中,AB=8,AD=6,点P、Q分别是AB边和CD边上的动点,点P从点A向点B运动,点Q从点C向点D运动,且保持AP=CQ.设AP=x.(1)当PQ∥AD时,求x的值;(2)当线段PQ的垂直平分线与BC边相交时,求x的取值范围;(3)当线段PQ的垂直平分线与BC相交时,设交点为E,连接EP、EQ,设△EPQ的面积为S,求S关于x的函数关系式,并写出S的取值范围.【分析】(1)根据已知条件,证明四边形APQD是矩形,再根据矩形的性质和AP=CQ 求x即可;(2)连接EP、EQ,则EP=EQ,设BE=y,列出等式(8﹣x)2+y2=(6﹣y)2+x2然后根据函数的性质来求x的取值范围;(3)由图形的等量关系列出方程,再根据函数的性质来求最值.【解答】解:(1)当PQ∥AD时,则∠A=∠APQ=90°,∠D=∠DQP=90°,又∵AB∥CD,∴四边形APQD是矩形,∴AP=QD,∵AP=CQ,AP=CD=,∴x=4.(2)如图,连接EP、EQ,则EP=EQ,设BE=y.∴(8﹣x)2+y2=(6﹣y)2+x2,∴y=.∵0≤y≤6,∴0≤≤6,∴≤x≤.(3)S△BPE=•BE•BP=••(8﹣x)=,S△ECQ==•(6﹣)•x=,∵AP=CQ,∴S BPQC=,∴S=S BPQC﹣S△BPE﹣S△ECQ=24﹣﹣,整理得:S==(x﹣4)2+12(),∴当x=4时,S有最小值12,当x=或x=时,S有最大值.∴12≤S≤.【点评】解答本题时,涉及到了矩形的判定、矩形的性质、勾股定理以及二次函数的最值等知识点,这是一道综合性比较强的题目,所以在解答题目时,一定要把各个知识点融会贯通,这样解题时才会少走弯路.3.汽车产业的发展,有效促进我国现代化建设.某汽车销售公司2005年盈利1500万元,到2007年盈利2160万元,且从2005年到2007年,每年盈利的年增长率相同.(1)该公司2006年盈利多少万元?(2)若该公司盈利的年增长率继续保持不变,预计2008年盈利多少万元?【分析】(1)需先算出从2005年到2007年,每年盈利的年增长率,然后根据2005年的盈利,算出2006年的利润;(2)相等关系是:2008年盈利=2007年盈利×每年盈利的年增长率.【解答】解:(1)设每年盈利的年增长率为x,根据题意得1500(1+x)2=2160解得x1=0.2,x2=﹣2.2(不合题意,舍去)∴1500(1+x)=1500(1+0.2)=1800答:2006年该公司盈利1800万元.(2)2160(1+0.2)=2592答:预计2008年该公司盈利2592万元.【点评】本题的关键是需求出从2005年到2007年,每年盈利的年增长率.等量关系为:2005年盈利×(1+年增长率)2=2160.4.如图,已知直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,连接PC并延长PC交y轴于点D(0,3).(1)求证:△POD≌△ABO;(2)若直线l:y=kx+b经过圆心P和D,求直线l的解析式.【分析】(1)首先连接PB,由直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,可求得∠APB=∠DPO=60°,∠ABO=∠POD=90°,即可得△P AB是等边三角形,可得AB=OP,然后由ASA,即可判定:△POD≌△ABO;(2)易求得∠PDO=30°,由OP=OD•tan30°,即可求得点P的坐标,然后利用待定系数法,即可求得直线l的解析式.【解答】(1)证明:连接PB,∵直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,∴∠APB=∠DPO=×180°=60°,∠ABO=∠POD=90°,∵P A=PB,∴△P AB是等边三角形,∴AB=P A,∠BAO=60°,∴AB=OP,∠BAO=∠OPD,在△POD和△ABO中,∴△POD≌△ABO(ASA);(2)解:由(1)得△POD≌△ABO,∴∠PDO=∠AOB,∵∠AOB=∠APB=×60°=30°,∴∠PDO=30°,∴OP=OD•tan30°=3×=,∴点P的坐标为:(﹣,0)∴,解得:,∴直线l的解析式为:y=x+3.【点评】此题考查了圆周角定理、全等三角形的判定与性质、直角三角形的性质、等边三角形的判定与性质以及待定系数法求一次函数的解析式.此题综合性较强,难度适中,注意准确作出辅助线,注意数形结合思想的应用.5.广安市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.(1)求平均每次下调的百分率.(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?【分析】(1)根据题意设平均每次下调的百分率为x,列出一元二次方程,解方程即可得出答案;(2)分别计算两种方案的优惠价格,比较后发现方案①更优惠.【解答】解:(1)设平均每次下调的百分率为x,则6000(1﹣x)2=4860,解得:x1=0.1=10%,x2=1.9(舍去),故平均每次下调的百分率为10%;(2)方案①购房优惠:4860×100×(1﹣0.98)=9720(元);方案②可优惠:80×100=8000(元).故选择方案①更优惠.【点评】本题主要考查一元二次方程的实际应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解,属于中档题.6.用两种方法解答:已知m、n是关于x的方程x2+(p﹣2)x+1=0两个实数根,求代数式(m2+mp+1)(n2+np+1)的值.【分析】本题主要是利用韦达定理来计算.已知m、n是关于x的方程x2+(p﹣2)x+1=0两个实数根,有四个等式可供使用:m+n=2﹣p①,mn=1②,m2+(p﹣2)m+1=0③,n2+(p﹣2)n+1=0④.通过变形方法,合理地选择解题方法.【解答】解:∵m、n是x2+(p﹣2)x+1=0的根,∴m+n=2﹣p,mn=1.方法一:m2+(p﹣2)m+1=0,n2+(p﹣2)n+1=0.即m2+pm+1=2m,n2+pn+1=2n.原式=2m×2n=4mn=4.方法二:(m2+mp+1)(n2+np+1)=(m2+mp)(n2+np)+m2+mp+n2+np+1=m2n2+m2np+mpn2+mnp2+m2+mp+n2+np+1=1+mp+np+p2+m2+n2+mp+np+1=2+p2+m2+n2+2(m+n)p=2+p2+m2+n2+2(2﹣p)p=2+p2+m2+n2+4p﹣2p2=2+(m+n)2﹣2mn+4p﹣2p2+p2=2+(2﹣p)2﹣2+4p﹣2p2+p2=4﹣4p+p2+4p﹣p2=4.【点评】本题主要是通过根与系数的关系来求值.注意把所求的代数式转化成m+n=2﹣p,mn=1的形式,正确对所求式子进行变形是解题的关键.7.如图,⊙O是等边△ABC的外接圆,AB=2,M、N分别是边AB、AC的中点,直线MN交⊙O于E、F两点,BD∥AC交直线MN于点D.求出图中线段DM上已有的一条线段的长.【分析】连接OA交MN于点G,则OA⊥BC,由三角形的中位线的性质可得MN的长,易证得△BMD≌△AMN,有DM=MN,由相交弦定理得ME•MF=MA•MB,就可求得EM,DE的值.【解答】解:∵M,N分别是边AB,AC的中点∴MN∥BC,MN=BC=1又∵BD∥AC∴∠DBA=∠A=60°∵BM=AM,∠BMD=∠AMN∴△BMD≌△AMN∴DM=MN=1连接OA交MN于点G,则OA⊥BC∴OA⊥EF∴EG=FG,MG=FN由相交弦定理得:ME•MF=MA•MB∴EM(EM+1)=1解得EM=(EM=不合题意,舍去)∴DE=DM﹣EM=∴DE(3﹣DE)=1解得DE=(DE=不合题意,舍去).【点评】本题利用了三角形的中位线的性质,等边三角形的性质,全等三角形的判定和性质,一元二次方程的解法求解.8.如图,已知△BEC是等边三角形,∠AEB=∠DEC=90°,AE=DE,AC,BD的交点为O.(1)求证:△AEC≌△DEB;(2)若∠ABC=∠DCB=90°,AB=2 cm,求图中阴影部分的面积.【分析】(1)在△AEC和△DEB中,已知AE=DE,BE=CE,且夹角相等,根据边角边可证全等.(2)由图可知,在连接EO并延长EO交BC于点F,连接AD之后,整个图形是一个以EF所在直线对称的图形.即△AEO和△DEO面积相等,只要求出其中一个即可,而三角形AEO面积=•OE•FB,所以解题中心即为求出OE和FB,有(1)中结论和已知条件即可求解.【解答】(1)证明:∵∠AEB=∠DEC=90°,∴∠AEB+∠BEC=∠DEC+∠BEC,即∠AEC=∠DEB,∵△BEC是等边三角形,∴CE=BE,又AE=DE,∴△AEC≌△DEB.(2)解:连接EO并延长EO交BC于点F,连接AD.由(1)知AC=BD.∵∠ABC=∠DCB=90°,∴∠ABC+∠DCB=180°,∴AB∥DC,AB==CD,∴四边形ABCD为平行四边形且是矩形,∴OA=OB=OC=OD,又∵BE=CE,∴OE所在直线垂直平分线段BC,∴BF=FC,∠EFB=90°.∴OF=AB=×2=1,∵△BEC是等边三角形,∴∠EBC=60°.在Rt△AEB中,∠AEB=90°,∠ABE=∠ABC﹣∠EBC=90°﹣60°=30°,∴BE=AB•cos30°=,在Rt△BFE中,∠BFE=90°,∠EBF=60°,∴BF=BE•cos60°=,EF=BE•sin60°=,∴OE=EF﹣OF==,∵AE=ED,OE=OE,AO=DO,∴△AOE≌△DOE.∴S△AOE=S△DOE∴S阴影=2S△AOE=2וEO•BF=2×××=(cm2).【点评】考查综合应用等边三角形、等腰三角形、解直角三角形、直角三角形性质,进行逻辑推理能力和运算能力.9.如图,有一直径MN=4的半圆形纸片,其圆心为点P,从初始位置Ⅰ开始,在无滑动的情况下沿数轴向右翻滚至位置Ⅴ,其中,位置Ⅰ中的MN平行于数轴,且半⊙P与数轴相切于原点O;位置Ⅱ和位置Ⅳ中的MN垂直于数轴;位置Ⅲ中的MN在数轴上;位置Ⅴ中的点N到数轴的距离为3,且半⊙P与数轴相切于点A.解答下列问题:(1)位置Ⅰ中的MN与数轴之间的距离为2;位置Ⅱ中的半⊙P与数轴的位置关系是相切;(2)求位置Ⅲ中的圆心P在数轴上表示的数;(3)纸片半⊙P从位置Ⅲ翻滚到位置Ⅳ时,求点N所经过路径长及该纸片所扫过图形的面积;(4)求OA的长.[(2),(3),(4)中的结果保留π].【分析】(1)先求出圆的半径,再根据切线的性质进行解答;(2)根据位置Ⅰ中的长与数轴上线段ON相等求出的长,再根据弧长公式求出的长,进而可得出结论;(3)作NC垂直数轴于点C,作PH⊥NC于点H,连接P A,则四边形PHCA为矩形,在Rt△NPH中,根据sin∠NPH==即可∠NPH、∠MP A的度数,进而可得出的长,【解答】解:(1)∵⊙P的直径=4,∴⊙P的半径=2,∵⊙P与直线有一个交点,∴位置Ⅰ中的MN与数轴之间的距离为2;位置Ⅱ中的半⊙P与数轴的位置关系是相切;故答案为:2,相切;(2)位置Ⅰ中的长与数轴上线段ON相等,∵的长为=π,NP=2,∴位置Ⅲ中的圆心P在数轴上表示的数为π+2.(3)点N所经过路径长为=2π,S半圆==2π,S扇形==4π,半⊙P所扫过图形的面积为2π+4π=6π.(4)如图,作NC垂直数轴于点C,作PH⊥NC于点H,连接P A,则四边形PHCA为矩形.在Rt△NPH中,PN=2,NH=NC﹣HC=NC﹣P A=1,于是sin∠NPH==,∴∠NPH=30°.∴∠MP A=60°.从而的长为=,于是OA的长为π+4+π=π+4.【点评】本题考查的是直线与圆的关系、弧长的计算、扇形的面积公式,在解答此题时要注意Ⅰ中的长与数轴上线段ON相等的数量关系.10.如图,△ABC内接于⊙O,AB=6,AC=4,D是AB边上一点,P是优弧BAC的中点,连接P A、PB、PC、PD.(1)当BD的长度为多少时,△P AD是以AD为底边的等腰三角形?并证明;(2)在(1)的条件下,若cos∠PCB=,求P A的长.【分析】(1)根据等弧对等弦以及全等三角形的判定和性质进行求解;(2)过点P作PE⊥AD于E.根据锐角三角函数的知识和垂径定理进行求解.【解答】解:(1)当BD=AC=4时,△P AD是以AD为底边的等腰三角形.∵P是优弧BAC的中点,∴=.∴PB=PC.又∵∠PBD=∠PCA(圆周角定理),∴当BD=AC=4,△PBD≌△PCA.∴P A=PD,即△P AD是以AD为底边的等腰三角形.(2)过点P作PE⊥AD于E,由(1)可知,当BD=4时,PD=P A,AD=AB﹣BD=6﹣4=2,则AE=AD=1.∵∠PCB=∠P AD(在同圆或等圆中,同弧所对的圆周角相等),∴cos∠P AD=cos∠PCB=,∴P A=.【点评】综合运用了等弧对等弦的性质、全等三角形的判定和性质、锐角三角函数的知识以及垂径定理.11.在△ABC中,AB=BC,将△ABC绕点A沿顺时针方向旋转得△A1B1C1,使点C1落在直线BC上(点C1与点C不重合),(1)如图,当∠C>60°时,写出边AB1与边CB的位置关系,并加以证明;(2)当∠C=60°时,写出边AB1与边CB的位置关系(不要求证明);(3)当∠C<60°时,请你在如图中用尺规作图法作出△AB1C1(保留作图痕迹,不写作法),再猜想你在(1)、(2)中得出的结论是否还成立并说明理由.【分析】(1)AB1∥BC.因为等腰三角形,两底角相等,再根据平行线的判定,内错角相等两直线平行,可证明两直线平行.(2)当∠C=60°时,写出边AB1与边CB的位置关系也是平行,证明方法同(1)题.(3)成立,根据旋转变换的性质画出图形.利用三角形全等即可证明.【解答】解:(1)AB1∥BC.证明:由已知得△ABC≌△AB1C1,∴∠BAC=∠B1AC1,∠B1AB=∠C1AC,∵AC1=AC,∴∠AC1C=∠ACC1,∵∠C1AC+∠AC1C+∠ACC1=180°,∴∠C1AC=180°﹣2∠ACC1,同理,在△ABC中,∵BA=BC,∴∠ABC=180°﹣2∠ACC1,∴∠ABC=∠C1AC=∠B1AB,∴AB1∥BC.(5分)(2)如图1,∠C=60°时,AB1∥BC.(7分)(3)如图,当∠C<60°时,(1)、(2)中的结论还成立.证明:显然△ABC≌△AB1C1,∴∠BAC=∠B1AC1,∴∠B1AB=∠C1AC,∵AC1=AC,∴∠AC1C=∠ACC1,∵∠C1AC+∠AC1C+∠ACC1=180°,∴∠C1AC=180°﹣2∠ACC1,同理,在△ABC中,∵BA=BC,∴∠ABC=180°﹣2∠ACC1,∴∠ABC=∠C1AC=∠B1AB,∴AB1∥BC.(13分)【点评】考查图形的旋转,等腰三角形的性质,平行线的判定.本题实质是考查对图形旋转特征的理解,旋转前后的图形是全等的.12.九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,求旗杆AB的高度.【分析】利用三角形相似中的比例关系,首先由题目和图形可看出,求AB的长度分成了2个部分,AH和HB部分,其中HB=EF=1.6m,剩下的问题就是求AH的长度,利用△CGE∽△AHE,得出,把相关条件代入即可求得AH=11.9,所以AB=AH+HB=AH+EF=13.5m.【解答】解:∵CD⊥FB,AB⊥FB,∴CD∥AB∴△CGE∽△AHE∴即:∴∴AH=11.9∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m).【点评】主要用到的解题思想是把梯形问题转化成三角形问题,利用三角形相似比列方程来求未知线段的长度.13.一个不透明的口袋里有红、黄、绿三种颜色的球(除颜色外其余都相同),其中红球有2个,黄球有1个,任意摸出一个黄球的概率为.(1)试求口袋里绿球的个数;(2)若第一次从口袋中任意摸出一球(不放回),第二次任意摸出一球,请你用树状图或列表法,求出两次都摸到红球的概率.【分析】(1)根据概率的求解方法,利用方程求得绿球个数;(2)此题需要两步完成,所以采用树状图法或者列表法都比较简单,解题时要注意是放回实验还是不放回实验,此题为不放回实验.【解答】解:(1)设口袋里绿球有x个,则,解得x=1.故口袋里绿球有1个.(2)红一红二黄绿红一红二,红一黄,红一绿,红一红二红一,红二黄,红一绿,红二黄红一,黄红二,黄绿,黄绿红一,绿红二,绿黄,绿故,P(两次都摸到红球)=.【点评】(1)解题时要注意应用方程思想;(2)列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.14.已知:y关于x的函数y=(k﹣1)x2﹣2kx+k+2的图象与x轴有交点.(1)求k的取值范围;(2)若x1,x2是函数图象与x轴两个交点的横坐标,且满足(k﹣1)x12+2kx2+k+2=4x1x2.①求k的值;②当k≤x≤k+2时,请结合函数图象确定y的最大值和最小值.【分析】(1)分两种情况讨论,当k=1时,可求出函数为一次函数,必与x轴有一交点;当k≠1时,函数为二次函数,若与x轴有交点,则△≥0.(2)①根据(k﹣1)x12+2kx2+k+2=4x1x2及根与系数的关系,建立关于k的方程,求出k 的值;②充分利用图象,直接得出y的最大值和最小值.【解答】解:(1)当k=1时,函数为一次函数y=﹣2x+3,其图象与x轴有一个交点.当k≠1时,函数为二次函数,其图象与x轴有一个或两个交点,令y=0得(k﹣1)x2﹣2kx+k+2=0.△=(﹣2k)2﹣4(k﹣1)(k+2)≥0,解得k≤2.即k≤2且k≠1.综上所述,k的取值范围是k≤2.(2)①∵x1≠x2,由(1)知k<2且k≠1,函数图象与x轴两个交点,∴k<2,且k≠1.由题意得(k﹣1)x12+(k+2)=2kx1①,将①代入(k﹣1)x12+2kx2+k+2=4x1x2中得:2k(x1+x2)=4x1x2.又∵x1+x2=,x1x2=,∴2k•=4•.解得:k1=﹣1,k2=2(不合题意,舍去).∴所求k值为﹣1.②如图,∵k1=﹣1,y=﹣2x2+2x+1=﹣2(x﹣)2+.且﹣1≤x≤1.由图象知:当x=﹣1时,y最小=﹣3;当x=时,y最大=.∴y的最大值为,最小值为﹣3.【点评】本题考查了抛物线与x轴的交点、一次函数的定义、二次函数的最值,充分利用图象是解题的关键.15.如图①,有四张编号为1、2、3、4的卡片,卡片的背面完全相同.现将它们搅匀并正面朝下放置在桌面上.(1)从中随机抽取一张,抽到的卡片是眼睛的概率是多少?(2)从四张卡片中随机抽取一张贴在如图②所示的大头娃娃的左眼处,然后再随机抽取一张贴在大头娃娃的右眼处,用树状图或列表法求贴法正确的概率.【分析】根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.【解答】解:(1)所求概率为;(2)方法①(树状图法)共有12种可能的结果:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)∵其中有两种结果(1,2),(2,1)是符合条件的,∴贴法正确的概率为,方法②(列表法)1 2 3 4第一次抽取第二次抽取1(2,1)(3,1)(4,1)2(1,2)(3,2)(4,2)3(1,3)(2,3)(4,3)4(1,4)(2,4)(3,4)共有12种可能的结果:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3),∵其中有两种结果(1,2),(2,1)是符合条件的,∴贴法正确的概率为.【点评】此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.16.经统计分析,某市跨河大桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为80千米/小时,研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.(1)求大桥上车流密度为100辆/千米时的车流速度;(2)在交通高峰时段,为使大桥上的车流速度大于40千米/小时且小于60千米/小时,应控制大桥上的车流密度在什么范围内?(3)车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.求大桥上车流量y的最大值.【分析】(1)当20≤x≤220时,设车流速度v与车流密度x的函数关系式为v=kx+b,根据题意的数量关系建立方程组求出其解即可;(2)由(1)的解析式建立不等式组求出其解即可;(3)设车流量y与x之间的关系式为y=vx,当x<20和20≤x≤220时分别表示出函数关系由函数的性质就可以求出结论.【解答】解:(1)设车流速度v与车流密度x的函数关系式为v=kx+b,由题意,得,解得:,∴当20≤x≤220时,v=﹣x+88,当x=100时,v=﹣×100+88=48(千米/小时);(2)由题意,得,解得:70<x<120.∴应控制大桥上的车流密度在70<x<120范围内;(3)设车流量y与x之间的关系式为y=vx,当0≤x≤20时y=80x,∴k=80>0,∴y随x的增大而增大,∴x=20时,y最大=1600;当20≤x≤220时y=(﹣x+88)x=﹣(x﹣110)2+4840,∴当x=110时,y最大=4840.∵4840>1600,∴当车流密度是110辆/千米,车流量y取得最大值是每小时4840辆.【点评】本题考查了车流量=车流速度×车流密度的运用,一次函数的解析式的运用,一元一次不等式组的运用,二次函数的性质的运用,解答时求出函数的解析式是关键.17.如图,反比例函数的图象经过点A(4,b),过点A作AB⊥x轴于点B,△AOB 的面积为2.(1)求k和b的值;(2)若一次函数y=ax﹣3的图象经过点A,求这个一次函数的解析式.【分析】(1)由△AOB的面积为2,根据反比例函数的比例系数k的几何意义,可知k的值,得出反比例函数的解析式,然后把x=4代入,即可求出b的值;(2)把点A的坐标代入y=ax﹣3,即可求出这个一次函数的解析式.【解答】解:(1)∵反比例函数的图象经过点A,AB⊥x轴于点B,△AOB的面积为2,A(4,b),∴OB×AB=2,×4×b=2,∴AB=b=1,∴A(4,1),∴k=xy=4,∴反比例函数的解析式为y=,即k=4,b=1.(2)∵A(4,1)在一次函数y=ax﹣3的图象上,∴1=4a﹣3,∴a=1.∴这个一次函数的解析式为y=x﹣3.【点评】本题主要考查了待定系数法求一次函数的解析式和反比例函数中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.18.图(1)是一个10×10格点正方形组成的网格.△ABC是格点三角形(顶点在网格交点处),请你完成下面的两个问题:(1)在图(1)中画出与△ABC相似的格点△A1B1C1和△A2B2C2,且△A1B1C1与△ABC的相似比是2,△A2B2C2与△ABC的相似比是;(2)在图(2)中用与△ABC,△A1B1C1,△A2B2C2全等的格点三角形(每个三角形至少使用一次),拼出一个你熟悉的图案,并为你设计的图案配一句贴切的解说词.【分析】(1)△A1B1C1与△ABC的相似比是2,则让△ABC的各边都扩大2倍就可.△A2B2C2与△ABC的相似比是;△ABC的直角边是2,所以△A2B2C2与的直角边是即一个对角线的长度.斜边为2.依此画图即可;(2)拼图有审美意义即可,答案不唯一.【解答】解:【点评】本题主要考查了相似图形的画法,做这类题时根据的是相似图形的性质,即相似比相等.对应角相等.19.如图,矩形ABCD的边AD、AB分别与⊙O相切于点E、F,(1)求的长;(2)若,直线MN分别交射线DA、DC于点M、N,∠DMN=60°,将直线MN沿射线DA方向平移,设点D到直线的距离为d,当时1≤d≤4,请判断直线MN与⊙O的位置关系,并说明理由.【分析】(1)连接OE、OF,利用相切证明四边形AFOE是正方形,再根据弧长公式求弧长;(2)先求出直线M1N1与圆相切时d的值,结合1≤d≤4,划分d的范围,分类讨论.【解答】解:(1)连接OE、OF,∵矩形ABCD的边AD、AB分别与⊙O相切于点E、F,∴∠A=90°,∠OEA=∠OF A=90°∴四边形AFOE是正方形∴∠EOF=90°,OE=AE=∴的长==π.(2)如图,将直线MN沿射线DA方向平移,当其与⊙O相切时,记为M1N1,切点为R,交AD于M1,交BC于N1,连接OM1、OR,∵M1N1∥MN∴∠DM1N1=∠DMN=60°∴∠EM1N1=120°∵MA、M1N1切⊙O于点E、R∴∠EM1O=∠EM1N1=60°在Rt△EM1O中,EM1===1∴DM1=AD﹣AE﹣EM1=+5﹣﹣1=4.过点D作DK⊥M1N1于K在Rt△DM1K中DK=DM1×sin∠DM1K=4×sin∠60°=2即d=2,∴当d=2时,直线MN与⊙O相切,当1≤d<2时,直线MN与⊙O相离,当直线MN平移到过圆心O时,记为M2N2,点D到M2N2的距离d=DK+OR=2+=3>4,∴当2<d≤4时,MN直线与⊙O相交.【点评】本题考查的是直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d 与圆半径大小关系完成判定.20.如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连接ED、BE.(1)试判断DE与BD是否相等,并说明理由;(2)如果BC=6,AB=5,求BE的长.【分析】(1)可通过连接AD,AD就是等腰三角形ABC底边上的高,根据等腰三角形三线合一的特点,可得出∠CAD=∠BAD,根据圆周角定理即可得出∠DEB=∠DBE,便可证得DE=DB.(2)本题中由于BE⊥AC,那么BE就是三角形ABC中AC边上的高,可用面积的不同表示方法得出AC•BE=CB•AD.进而求出BE的长.【解答】解:(1)DE=BD证明:连接AD,则AD⊥BC,在等腰三角形ABC中,AD⊥BC,∴∠CAD=∠BAD(等腰三角形三线合一),∴=,∴DE=BD;(2)∵AB=5,BD=BC=3,∴AD=4,∴S△ABC=•AC•BE=•CB•AD,∴BE=4.8.【点评】本题主要考查了等腰三角形的性质,圆周角定理等知识点的运用,用等腰三角形三线合一的特点得出圆周角相等是解题的关键.21.如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.(1)求证:AP=AO;(2)求证:PE⊥AO;(3)当AE=AC,AB=10时,求线段BO的长度.【分析】(1)根据等角的余角相等证明即可;(2)过点O作OD⊥AB于D,根据角平分线上的点到角的两边的距离相等可得CO=DO,利用“SAS”证明△APE和△OAD全等,根据全等三角形对应角相等可得∠AEP=∠ADO=90°,从而得证;(3)设C0=3k,AC=8k,表示出AE=CO=3k,AO=AP=5k,然后利用勾股定理列式求出PE=4k,BC=BD=10﹣4k,再根据相似三角形对应边成比例列式求出k=1然后在Rt △BDO中,利用勾股定理列式求解即可.【解答】(1)证明:∵∠C=90°,∠BAP=90°∴∠CBO+∠BOC=90°,∠ABP+∠APB=90°,又∵∠CBO=∠ABP,∴∠BOC=∠APB,∵∠BOC=∠AOP,∴∠AOP=∠APB,∴AP=AO;(2)证明:如图,过点O作OD⊥AB于D,∵∠CBO=∠ABP,∵AE=OC,∴AE=OD,∵∠AOD+∠OAD=90°,∠P AE+∠OAD=90°,∴∠AOD=∠P AE,在△AOD和△P AE中,,∴△AOD≌△P AE(SAS),∴∠AEP=∠ADO=90°∴PE⊥AO;(3)解:设AE=OC=3k,∵AE=AC,∴AC=8k,∴OE=AC﹣AE﹣OC=2k,∴OA=OE+AE=5k.由(1)可知,AP=AO=5k.如图,过点O作OD⊥AB于点D,∵∠CBO=∠ABP,∴OD=OC=3k.在Rt△AOD中,AD===4k.∴BD=AB﹣AD=10﹣4k.∵OD∥AP,∴,即解得k=1,∵AB=10,PE=AD,∴PE=AD=4K,BD=AB﹣AD=10﹣4k=6,OD=3在Rt△BDO中,由勾股定理得:BO===3.【点评】本题考查了全等三角形的判定与性质,角平分线上的点到角的两边的距离相等的性质,勾股定理,相似三角形的判定与性质,(2)作辅助线构造出过渡线段DO并得到全等三角形是解题的关键,(3)利用相似三角形对应边成比例求出k=1是解题的关键.22.如图,AD是⊙O的直径.(1)如图①,垂直于AD的两条弦B1C1,B2C2把圆周4等分,则∠B1的度数是22.5°,∠B2的度数是67.5°;(2)如图②,垂直于AD的三条弦B1C1,B2C2,B3C3把圆周6等分,分别求∠B1,∠B2,∠B3的度数;(3)如图③,垂直于AD的n条弦B1C1,B2C2,B3C3,…,B n∁n把圆周2n等分,请你用含n的代数式表示∠B n的度数(只需直接写出答案).【分析】根据条件可以先求出圆的各段弧的度数,根据圆周角等于所对弧的度数的一半,就可以求出圆周角的度数.【解答】解:(1)垂直于AD的两条弦B1C1,B2C2把圆周4等分,则是圆的,因而度数是45°,因而∠B1的度数是22.5°,同理的度数是135度,因而,∠B2的度数是67.5°;(2)∵圆周被6等分∴===360°÷6=60°∵直径AD⊥B1C1∴==30°,∴∠B1==15°∠B2==×(30°+60°)=45°∠B3==×(30°+60°+60°)=75°;(3)B n∁n把圆周2n等分,则弧BnD的度数是:,则∠B n AD=,在直角△AB n D中,.【点评】本题是把求圆周角的度数的问题转化为求弧的度数的问题,依据是圆周角等于所对弧的度数的一半.23.今年,我国政府为减轻农民负担,决定在5年内免去农业税.某乡今年人均上缴农业税25元,若两年后人均上缴农业税为16元,假设这两年降低的百分率相同.(1)求降低的百分率;(2)若小红家有4人,明年小红家减少多少农业税?(3)小红所在的乡约有16000农民,问该乡农民明年减少多少农业税?【分析】(1)设降低的百分率为x,则降低一次后的数额是25(1﹣x),再在这个数的基础上降低x,则变成25(1﹣x)(1﹣x)即25(1﹣x)2,据此即可列方程求解;(2)每人减少的税额是25x,则4个人的就是4×25x,代入(1)中求得的x的值,即可求解;(3)每个人减少的税额是25x,乘以总人数16000即可求解.【解答】解:(1)设降低的百分率为x,依题意有,25(1﹣x)2=16,解得,x1=0.2=20%,x2=1.8(舍去);(2)小红全家少上缴税25×20%×4=20(元);(3)全乡少上缴税16000×25×20%=80 000(元).答:降低的增长率是20%,明年小红家减少的农业税是20元,该乡农民明年减少的农业税是80 000元.【点评】本题考查求平均变化率的方法.若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.24.在△ABC中,AB=AC,D为BC上一点,由D分别作DE⊥AB于E,DF⊥AC于F.设DE=a,DF=b,且实数a,b满足9a2﹣24ab+16b2=0,并有=2566,∠A使得方程x2﹣x•sin A+sin A﹣=0有两个相等的实数根.(1)试求实数a,b的值;(2)试求线段BC的长.【分析】(1)由题意可知:2a2b=2566,则2a2b=248,则a2b=48.化简9a2﹣24ab+16b2=0得:(3a﹣4b)2=0,则3a﹣4b=0,即3a=4b,则根据,可求得a与b的值;(2)要求BC的长需求出BD和CD的长,知BD、CD分别是直角三角形BDE和直角三角形CDF中的斜边.又知在△ABC中,AB=AC,则∠B=∠C,则根据三角函数只要知道∠B或∠C的读数即可,要求∠B或∠C的读数需求的∠A的读数,根据判别式可以求得∠A的读数.【解答】解:(1)由条件有,解得;(2)又由关于x的方程的判别式△=sin2A﹣sin A+=(sin A﹣)2=0,则sin A=,而∠A为三角形的一个内角,所以∠A1=60°或∠A2=120° 2分当∠A=60°时,△ABC为正三角形,∠B=∠C=60°于是分别在Rt△BDE和Rt△CDF中有BD=,CD=所以BC=BD+DC=.当∠A=120°时,△ABC为等腰三角形,∠B=∠C=30°同上方法可得BC=14. 3分所以线段BC的长应为或14.【点评】考查了解直角三角形以及判别式的应用.25.某市城建部门经过长期市场调查发现,该市年新建商品房面积P(万平方米)与市场新房均价x(千元/平方米)存在函数关系P=25x;年新房销售面积Q(万平方米)与市场新房均价x(千元/平方米)的函数关系为Q=﹣10;(1)如果年新建商品房的面积与年新房销售面积相等,求市场新房均价和年新房销售总额;(2)在(1)的基础上,如果市场新房均价上涨1千元,那么该市年新房销售总额是增加还是减少?变化了多少?结合年新房销售总额和积压面积的变化情况,请你提出一条合理。
压轴题27选择压轴题(几何篇)-2023年中考数学压轴题专项训练(全国通用)(原卷版)

2023年中考数学压轴题专项训练压轴题27选择压轴题(几何篇)一.选择题(共40小题)1.(2023•朝阳区校级三模)如图,AB是⊙O的直径,将OB绕着点O逆时针旋转40°得到OC,P是⊙O 上一点,且与点C在AB的异侧,连结P A、PC、AC,若P A=PC,则∠P AB的大小是()A.20°B.35°C.40°D.70°2.(2023•河北区二模)如图,在平面直角坐标系中,菱形OABC的顶点A在x轴上,且∠COA=45°,OA =4,则点B的坐标为()A.(4+2√2,2√2)B.(2√2,2√2)C.(2+2√2,2)D.(√2,2)3.(2023•奉贤区二模)如图,矩形ABCD中,AB=1,∠ABD=60°,点O在对角线BD上,圆O经过点C.如果矩形ABCD有2个顶点在圆O内,那么圆O的半径长r的取值范围是()A.0<r≤1B.1<r≤√3C.1<r≤2D.√3<r≤24.(2023•广灵县模拟)如图,在Rt△ABC中,∠C=90°,BC=3,AC=6,点O,D,E是AB边上的点,以点O为圆心,DE长为直径的半圆O与AC相切于点M,与BC相切于点N,则图中阴影部分的面积为()A .5B .9﹣2πC .9﹣πD .5﹣π5.(2023•普陀区二模)如图,△ABC 中,∠BAC =60°,BO 、CO 分别平分∠ABC 、∠ACB ,AO =2,下面结论中不一定正确的是( )A .∠BOC =120°B .∠BAO =30°C .OB =3D .点O 到直线BC 的距离是16.(2023•瓯海区模拟)如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD 与正方形EFGH ,连结DH 并延长交AB 于点K ,若DF 平分∠CDK ,则DH HK =( )A .2√33B .65C .√5−1D .4√577.(2023•花溪区模拟)勾股定理是人类数学文化的一颗璀璨明珠,是用代数思想解决几何问题的最重要工具也是数形结合的组带之一,如图,秋千静止时,踏板离地的垂直高度BE =1m ,将它往前推6m 至C 处时(即水平距离CD =6m ),踏板离地的垂直高度CF =4m ,它的绳索始终拉直,则绳索AC 的长是( )A .152mB .92mC .6mD .212m8.(2023•承德一模)如图,在菱形ABCD 中,AC 、BD (AC >BD )相交于点O ,E 、F 分别为OA 和OC 上的点(不与点A 、O 、C 重合).其中AE =OF .过点E 作GH ⊥AC ,分别交AD 、AB 于点G 、H ;过点F 作IJ ⊥AC 分别交CD 、CB 于点J 、I ;连接GJ 、HI ,甲、乙、丙三个同学给出了三个结论:甲:随着AE 长度的变化,GH +IJ =BD 始终成立.乙:随着AE 长度的变化,四边形GHIJ 可能为正方形.丙:随着AE 长度的变化,四边形GHIJ 的面积始终不变,都是菱形ABCD 面积的一半.下列选项正确的是( )A .甲、乙、丙都对B .甲、乙对,丙不对C .甲、丙对,乙不对D .甲不对,乙、丙对 9.(2023•石家庄二模)如图,在平行四边形ABCD 中,对角线AC ,BD 交于点O ,E ,F 分别是OB 与OD 的中点,依连接点A ,E ,C ,F ,A ,当四边形AECF 是矩形时,与线段BE 相等的线段有( )A .4条B .5条C .6条D .7条10.(2023•青山区二模)如图,边长为2的正方形ABCD 的对角线AC 与BD 相交于点O ,E 是BC 边上一点,F 是BD 上一点,连接DE ,EF .若△DEF 与△DEC 关于直线DE 对称,则OF 的长为( )A .√22B .2√2−2C .2−√2D .√2−111.(2023•柳城县一模)七巧板是我国古代劳动人民的发明之一,被誉为“东方魔板”,它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.(清)陆以活《冷庐杂识》卷中写道:近又有七巧图,其式五,其数七,其变化之式多至千余,体物肖形,随手变幻,盖游戏之具,足以排闷破寂,故世俗皆喜为之.如图,是一个用七巧板拼成的装饰图,放入长方形ABCD 内,装饰图中的三角形顶点E ,F 分别在边AB ,BC 上,三角形①的边GD 在边AD 上,则BF BE 的值为( )A .1+√22B .√22C .2+√24D .2+√2212.(2023•泉州模拟)如图,在矩形ABCD 中,AB =2,BC =4,将△ABC 沿BC 的方向平移至△A 'B 'C ',使得A ′E =A ′F ,其中E 是A ′B ′与AC 的交点,F 是A ′C ′与CD 的交点,则CC ′的长为( )A .52−√52B .112−√5C .5−√5D .92−√5 13.(2023•定远县二模)如图,在Rt △ABC 中,∠BAC =90°,AB =3,BC =5,点P 为BC 边上任意一点,连接P A ,以P A ,PC 为邻边作平行四边形P AQC ,连接PQ ,则PQ 长度的最小值为( )A .3B .2.5C .2.4D .214.(2023•烟台一模)如图,在矩形ABCD 中,AB =12,AD =10,点E 在AD 上,点F 在BC 上,且AE =CF ,连结CE ,DF ,则CE +DF 的最小值为( )A .26B .25C .24D .2215.(2023•郯城县一模)如图,在Rt △ABC 中,∠BAC =90°,AB =6,BC =10,点P 为BC 边上任意一点,连接P A ,以P A ,PC 为邻边作平行四边形P AQC ,连接PQ ,则PQ 长度的最小值为( )A .4.8B .5C .2.4D .416.(2023•白云区一模)如图,正方形ABCD 的面积为3,点E 在边CD 上,且CE =1,∠ABE 的平分线交AD 于点F ,点M ,N 分别是BE ,BF 的中点,则下列结论错误的是( )A .FD =√2MNB .△DEF 是等腰直角三角形C .BN =1D .tan ∠FBE =√317.(2023•九龙坡区校级模拟)如图,在正方形ABCD 中,O 为AC 、BD 的交点,△DCE 为直角三角形,∠CED =90°,OE =3√2,若CE •DE =6,则正方形的面积为( )A .20B .22C .24D .2618.(2023•杭州一模)如图,有两张矩形纸片ABCD 和EFGH ,AB =EF =2cm ,BC =FG =8cm .把纸片ABCD 交叉叠放在纸片EFGH 上,使重叠部分为平行四边形,且B 点D 与点G 重合,当两张纸片交叉所成的角α最小时,tan α等于( )A .14B .815C .12D .81719.(2023•高明区二模)矩形ABCD 和直角三角形EFG 的位置如图所示,点A 在EG 上,点D 在EF 上,若∠2=55°,则∠1等于( )A.155°B.135°C.125°D.105°20.(2023•余姚市一模)如图,由两个正三角形组成的菱形内放入标记为①,②,③,④的四种不同大小的小正三角形5个,其中编号①的有2个.设未被覆盖的浅色阴影部分的周长为C1,深色阴影部分的周长为C2,若要求出C1﹣C2的值,只需知道其中两个小正三角形的边长,则这两个小三角形的编号为()A.①②B.②③C.①③D.②④21.(2023•衡水二模)如图,点P是正方形ABCD的边BC上一点,点M是对角线BD上一点,连接PM 并延长交BA的延长线于点Q,交AD于点G,取PQ的中点N.连接AN.若AQ=PC,有下面两个结论:①DM=DG,②AN⊥BD,则这两个结论中,正确的是()A.①对B.②对C.①②都对D.①②都不对22.(2023•新乡二模)如图,在矩形ABCD中,点B(0,4),点C(2,0),BC=2CD,先将矩形ABCD 沿y轴向下平移至点B与点O重合,再将平移后的矩形ABCD绕点O逆时针旋转90°得到矩形EOMN,则点D的对应点N的坐标为()A.(3,3)B.(4,4)C.(3,4)D.(4,3)23.(2023•荆门一模)如图,菱形ABCD各边的中点分别是E、F、G、H,若EH=2EF,则下列结论错误的是()A.EH⊥EF B.EH=AC C.∠B=60°D.AB=√5EF24.(2023•中原区校级二模)如图,在Rt△ABO中,AB=OB,顶点A的坐标为(2,0),以AB为边向△ABO的外侧作正方形ABCD,将组成的图形绕点O逆时针旋转,每次旋转45°,则第98次旋转结束时,点D的坐标为()A.(1,﹣3)B.(﹣1,3)C.(﹣1,2+√2)D.(1,3)25.(2023•中原区模拟)如图,▱ABCD的边BC在x轴的负半轴上,点B与原点O重合,DE⊥AB,交BA 的延长线于点E,已知∠ABC=60°,AB=4,BC=6,则点E的坐标为()A.(﹣2,﹣,2√3)B.(﹣3,3√3)C.(−72,72√3)D.(−52√3,52)26.(2023•武邑县二模)如图,N是正六边形ABCDEF对角线CF上一点,延长FE,CD相交于点M,若S△ABN=2,则S五边形ABCMF=()A.10B.12C.14D.1627.(2023•承德一模)如图,正六边形的两条对角线AE、BE把它分成Ⅰ、Ⅱ、Ⅲ三部分,则该三部分的面积比为()A.1:2:3B.2:2:4C.1:2:4D.2:3:528.(2023•罗湖区二模)如图,AB为圆O的直径,C为圆O上一点,过点C作圆O的切线交AB的延长线于点D,DB=13AD,连接AC,若AB=8,则AC的长度为()A.2√3B.2√5C.4√3D.4√529.(2023•杭州一模)如图,过⊙O外一点A作⊙O的切线AD,点D是切点,连结OA交⊙O于点B,点C是⊙O上不与点B,D重合的点.若∠A=α°,则∠C的度数为()A.(45−12α)°B.12α°C.2α°D.(45+12α)°30.(2023•西宁一模)如图,扇形纸片AOB的半径为3,沿AB所在直线折叠扇形纸片,圆心D恰好落在AB̂上的点C处,则阴影部分的面积是()A.3π−9√32B.3π−3√32C.2π−3√32D.2π−9√3231.(2023•太原一模)如图,在扇形纸片OAB 中,∠AOB =105°,OA =6、点C 是半径OA 上的点、沿直线BC 折叠△OBC 得到△DBC ,点O 的对应点D 落在AB̂上,图中阴影部分的面积为( )A .9π−92B .9π−182C .9π﹣18D .12π﹣1832.(2023•西山区校级模拟)如图,分别以等边△ABC 的三个顶点为圆心,边长为半径画弧,得到的封闭图形是莱洛三角形,若AB 为6,则图中阴影部分的面积为( )A .18π−27√3B .6π−9√3C .12π−9√3D .18π−18√333.(2023•莆田模拟)如图,在⊙O 中,∠AOB =120°,点C 在AB̂上,连接AC ,BC ,过点B 作BD ⊥AC 的延长线于点D ,当点C 从点A 运动到点B 的过程中,∠CBD 的度数( )A .先增大后减小B .先减小后增大C .保持不变D .一直减小 34.(2023•蚌埠二模)如图是某芯片公司的图标示意图,其设计灵感源于传统照相机快门的机械结构,圆O 中的阴影部分是一个正六边形,其中心与圆心O 重合,且AB =BC ,则阴影部分面积与圆的面积之比为( )A .3√38πB .√32πC .√3πD .2√39π35.(2023•鄞州区校级模拟)如图,AB 为⊙O 的直径,将弧BC 沿BC 翻折,翻折后的弧交AB 于D .若BC =4√5,sin ∠ABC =√55,则图中阴影部分的面积为( )A .256πB .253πC .8D .1036.(2023•九龙坡区模拟)如图,在⊙O 中,AB 是圆的直径,过点B 作⊙O 的切线BC ,连接AC 交⊙O 于点D ,点E 为弧AD 中点,连接AE ,若AE =AO ,AB =6,则CD 的长为( )A .2B .3√32C .√3D .3√337.(2023•宁德模拟)“莱洛三角形”是工业生产中加工零件时广泛使用的一种图形.如图,以等边三角形ABC 的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的图形就是“莱洛三角形”.若等边三角形ABC 的边长为2,则该“莱洛三角形”的周长等于( )A .2πB .2π−√3C .23πD .2π+√338.(2023•虹口区二模)如图,在矩形ABCD 中,对角线AC 与BD 相交于点O ,AB =5,BC =12.分别以点O 、D 为圆心画圆,如果⊙O 与直线AD 相交、与直线CD 相离,且⊙D 与⊙O 内切,那么⊙D 的半径长r 的取值范围是( )A .12<r <4B .52<r <6C .9<r <252D .9<r <1339.(2023•苏州一模)东南环立交是苏州中心城区城市快速内环道路系统的重要节点,也是江苏省最大规模的城市立交.左图是该立交桥的部分道路示意图(道路宽度忽略不计),A 为立交桥入口,D 、G 为出口,其中直行道为AB 、CD 、FG ,且AB =CD =FG ;弯道是以点O 为圆心的一段弧,且BC 、CE 、EF 所在的圆心角均为90°.甲、乙两车由A 口同时驶入立交桥,均以16m /s 的速度行驶,从不同出口驶出,其间两车到点O 的距离y (m )与时间x (s )的对应关系如右图所示.结合题目信息,下列说法错误的是( )A .该段立交桥总长为672mB .从G 口出比从D 口出多行驶192mC .甲车在立交桥上共行驶22sD .甲车从G 口出,乙车从D 口出40.(2023•滨城区一模)如图,点A ,B 是半径为2的⊙O 上的两点,且AB =2√3,则下列说法正确的是( )A .圆心O 到AB 的距离为√3B .在圆上取异于A ,B 的一点C ,则△ABC 面积的最大值为3√3C .以AB 为边向上作正方形,与⊙O 的公共部分的面积为3+√34πD .取AB 的中点C ,当AB 绕点O 旋转一周时,点C 运动的路线长为3π。
中考数学压轴题100 (1)

中考数学压轴题100题精选【含答案】【001】如图,已知抛物线2(1)y a x =-+a ≠0)经过点(2)A -,0,抛物线的顶点为D ,过O 作射线OM AD ∥.过顶点D 平行于x 轴的直线交射线OM 于点C ,B 在x 轴正半轴上,连结BC . (1)求该抛物线的解析式;(2)若动点P 从点O 出发,以每秒1个长度单位的速度沿射线OM 运动,设点P 运动的时间为()t s .问当t 为何值时,四边形DAOP 分别为平行四边形?直角梯形?等腰梯形? (3)若OC OB =,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t ()s ,连接PQ ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长.【002】如图16,在Rt △ABC 中,∠C=90°,AC = 3,AB = 5.点P 从点C 出发沿CA 以每秒1个单位长的速度向点A 匀速运动,到达点A 后立刻以原来的速度沿AC 返回;点Q 从点A 出发沿AB 以每秒1个单位长的速度向点B 匀速运动.伴随着P 、Q 的运动,DE 保持垂直平分PQ ,且交PQ 于点D ,交折线QB-BC-CP 于点E .点P 、Q 同时出发,当点Q 到达点B 时停止运动,点P 也随之停止.设点P 、Q 运动的时间是t 秒(t >0). (1)当t = 2时,AP = ,点Q 到AC 的距离是 ; (2)在点P 从C 向A 运动的过程中,求△APQ 的面积S 与t 的函数关系式;(不必写出t 的取值范围)(3)在点E 从B 向C 运动的过程中,四边形QBED 能否成 为直角梯形?若能,求t 的值.若不能,请说明理由; (4)当DE 经过点C 时,请直接写出t 的值.【003】如图,在平面直角坐标系中,已知矩形ABCD 的三个顶点B (4,0)、C (8,0)、D (8,8).抛物线y=ax2+bx 过A 、C 两点. (1)直接写出点A 的坐标,并求出抛物线的解析式;(2)动点P 从点A 出发.沿线段AB 向终点B 运动,同时点Q 从点C 出发,沿线段CD 向终点D 运动.速度均为每秒1个单位长度,运动时间为t 秒.过点P 作PE ⊥AB 交AC 于点E ,①过点E 作EF ⊥AD 于点F ,交抛物线于点G .当t 为何值时,线段EG 最长? ②连接EQ .在点P 、Q 运动的过程中,判断有几个时刻使得△CEQ 是等腰三角形? 请直接写出相应的t 值。
中考数学压轴题100题及答案

中考数学压轴题100题精选【001】如图,已知抛物线2(1)y a x =-+a ≠0)经过点(2)A -,0,抛物线的顶点为D ,过O 作射线OM AD ∥.过顶点D 平行于x 轴的直线交射线OM 于点C ,B 在x 轴正半轴上,连结BC . (1)求该抛物线的解析式;(2)若动点P 从点O 出发,以每秒1个长度单位的速度沿射线OM 运动,设点P 运动的时间为()t s .问当t 为何值时,四边形DAOP 分别为平行四边形?直角梯形?等腰梯形? (3)若OC OB =,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t ()s ,连接PQ ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长.【C=90°,AC = 3,AB = 5.点P 从点C 出发沿CA 以每秒1个单位长的速度向点A 匀速运动,到达点A 后立刻以原来的速度沿AC 返回;点Q 从点A 出发沿AB 以每秒1个单位长的速度向点B 匀速运动.伴随着P 、Q 的运动,DE 保持垂直平分PQ ,且交PQ 于点D ,交折线QB-BC-CP 于点E .点P 、Q 同时出发,当点Q 到达点B 时停止运动,点P 也随之停止.设点P 、Q 运动的时间是t 秒(t >0). (1)当t = 2时,AP = ,点Q 到AC 的距离是 ; (2)在点P 从C 向A 运动的过程中,求△APQ 的面积S 与 t 的函数关系式;(不必写出t 的取值范围)(3)在点E 从B 向C 运动的过程中,四边形QBED 能否成 为直角梯形?若能,求t 的值.若不能,请说明理由; (4)当DE 经过点C 时,请直接写出t 的值.【003】如图,在平面直角坐标系中,已知矩形ABCD 的三个顶点B (4,0)、C (8,0)、D (8,8).抛物线y=ax2+bx 过A 、C 两点. (1)直接写出点A 的坐标,并求出抛物线的解析式;A P 图16(2)动点P 从点A 出发.沿线段AB 向终点B 运动,同时点Q 从点C 出发,沿线段CD 向终点D 运动.速度均为每秒1个单位长度,运动时间为t 秒.过点P 作PE ⊥AB 交AC 于点E ,①过点E 作EF ⊥AD 于点F ,交抛物线于点G .当t 为何值时,线段EG 最长? ②连接EQ .在点P 、Q 运动的过程中,判断有几个时刻使得△CEQ 是等腰三角形? 请直接写出相应的t 值。
最新九年级中考数学复习:几何探究压轴题(面积问题)

(2)如图2,在等腰三角形ABC中,∠C=120°,点O为AB的中点,点M为AC上一点,将射线OM绕点O顺时针旋转60°交BC于点N,则OM与ON的数量关系是否改变,请说明理由;
9.在△ABC中,CA=CB,∠ACB=a,将△CAD绕点C按逆时针方向旋转角a得到△CBE,点A,D的对应点分别为点B,E.
(1)如图1,若A,D,E三点在同一直线上,则∠CDE=(用含a的代数式表示);
(2)如图2,若A,D,E三点在同一直线上,a=60°,过点C作CF⊥AE于点F,然后探究线段CF,AE,BE之间的数量关系,并证明你的结论;
(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=3,AB=7,请直接写出△PMN面积的最大值.
18.如图1,在等腰三角形ABC中,∠A=120°,AB=AC,点D、E分别在边AB、AC上,AD=AE,连接BE,点M、N、P分别为DE、BE、BC的中点.
(1)观察猜想:图1中,线段NM、NP的数量关系是,∠MNP的大小为;
(2)在三角板旋转的过程中,边 与AB所在直线交于点D,过点D作DE∥ 交 边于点E,连接BE.
①当 时,设AD= ,BE= ,求 与 之间的函数解析式及自变量 的取值范围;
②当 时,求AD的长.
13.在中 中. , ,点E在射线CB上运动.连接AE,将线段AE绕点E顺时针旋转90°得到EF,连接CF.
②如图3,连接AF,若AC=3,CD=1,求S△ADF的取值范围.
2.如图,矩形 中, 为等边三角形.点E,F分别为 边上的动点,且 ,P为 上一动点,连接 ,将线段 绕点B顺时针旋转 至 ,连接 .
中考数学压轴题---《与折叠有关的计算》题型讲解

中考数学压轴题---《与折叠有关的计算》题型讲解1、(2020•青岛)如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF,EF与AC交于点O.若AE=5,BF=3,则AO的长为()A.B.C.2D.4【答案】C【解答】解:∵矩形ABCD,∴AD∥BC,AD=BC,AB=CD,∴∠EFC=∠AEF,由折叠得,∠EFC=∠AFE,∴∠AFE=∠AEF,∴AE=AF=5,由折叠得,FC=AF,OA=OC,∴BC=3+5=8,在Rt△ABF中,AB==4,在Rt△ABC中,AC==4,∴OA=OC=2,故选:C.2、如图,在△ABC纸片中,∠B=30°,AB=AC=,点D在AB上运动,将纸片沿CD折叠,得到点B的对应点B′(D在A点时,点D的对应点是本身),则折叠过程对应点B′的路径长是()A.3B.6C.πD.2π【答案】C【解答】解:过点A作AE⊥BC于点E,∵∠B=30°,AB=AC=,∴BE=AB cos∠B=,∴BC=2BE=3,由折叠的性质可得:∠BCB''=2∠ACB=60°,∴B′的路径长==π.故选:C.3、(2022•宜宾)如图,在矩形纸片ABCD中,AB=5,BC=3,将△BCD沿BD折叠到△BED位置,DE交AB于点F,则cos∠ADF的值为()A.B.C.D.【答案】C【解答】解:∵四边形ABCD是矩形,∴∠A=90°,AB∥CD,AD=BC=3,AB=CD=5,∴∠BDC=∠DBF,由折叠的性质可得∠BDC=∠BDF,∴∠BDF=∠DBF,∴BF=DF,设BF=x,则DF=x,AF=5﹣x,在Rt△ADF中,32+(5﹣x)2=x2,∴x=,∴cos∠ADF=,故选:C.4、(2022•毕节市)矩形纸片ABCD中,E为BC的中点,连接AE,将△ABE沿AE折叠得到△AFE,连接CF.若AB=4,BC=6,则CF的长是()A.3B.C.D.【答案】D【解答】解:连接BF,交AE于O点,∵将△ABE沿AE折叠得到△AFE,∴BE=EF,∠AEB=∠AEF,AE垂直平分BF,∵点E为BC的中点,∴BE=CE=EF=3,∴∠EFC=∠ECF,∵∠BEF=∠ECF+∠EFC,∴∠AEB=∠ECF,∴AE∥CF,∴∠BFC=∠BOE=90°,在Rt△ABE中,由勾股定理得,AE==,∴BO==,∴BF=2BO=,在Rt△BCF中,由勾股定理得,CF===,故选:D.5、(2022•湖州)如图,已知BD是矩形ABCD的对角线,AB=6,BC=8,点E,F分别在边AD,BC上,连结BE,DF.将△ABE沿BE翻折,将△DCF沿DF翻折,若翻折后,点A,C分别落在对角线BD上的点G,H处,连结GF.则下列结论不正确的是()A.BD=10B.HG=2C.EG∥FH D.GF⊥BC 【答案】D【解答】解:∵四边形ABCD是矩形,∴∠A=90°,BC=AD,∵AB=6,BC=8,∴BD===10,故A选项不符合题意;∵将△ABE沿BE翻折,将△DCF沿DF翻折,点A,C分别落在对角线BD上的点G,H处,∴AB=BG=6,CD=DH=6,∴GH=BG+DH﹣BD=6+6﹣10=2,故B选项不符合题意;∵四边形ABCD是矩形,∴∠A=∠C=90°,∵将△ABE沿BE翻折,将△DCF沿DF翻折,点A,C分别落在对角线BD上的点G,H处,∴∠A=∠BGE=∠C=∠DHF=90°,∴EG∥FH.故C选项不符合题意;∵GH=2,∴BH=DG=BG﹣GH=6﹣2=4,设FC=HF=x,则BF=8﹣x,∴x2+42=(8﹣x)2,∴x=3,∴CF=3,∴,又∵,∴,若GF⊥BC,则GF∥CD,∴,故D选项符合题意.故选:D.6、(2021•天津)如图,在△ABC中,∠BAC=120°,将△ABC绕点C逆时针旋转得到△DEC,点A,B的对应点分别为D,E,连接AD.当点A,D,E在同一条直线上时,下列结论一定正确的是()A.∠ABC=∠ADC B.CB=CD C.DE+DC=BC D.AB∥CD【答案】D【解答】解:由旋转的性质得出CD=CA,∠EDC=∠BAC=120°,∵点A,D,E在同一条直线上,∴∠ADC=60°,∴△ADC为等边三角形,∴∠DAC=60°,∴∠BAD=60°=∠ADC,∴AB∥CD,故选:D.7、(2022•滨州)正方形ABCD的对角线相交于点O(如图1),如果∠BOC绕点O按顺时针方向旋转,其两边分别与边AB、BC相交于点E、F(如图2),连接EF,那么在点E由B到A的过程中,线段EF的中点G经过的路线是()A.线段B.圆弧C.折线D.波浪线【答案】A【解答】解:建立如图平面直角坐标系,设正方形ABCD的边长为1,∵四边形ABCD是正方形,∴∠OAE=∠OBF=45°,OA=OB,∵∠AOB=∠EOF=90°,∴∠AOE=∠BOF,∴△AOE≌△BOF(ASA),∴AE=BF,设AE=BF=a,则F(a,0),E(0,1﹣a),∵EG=FG,∴G(a,﹣a),∴点G在直线y=﹣x+上运动,∴点G的运动轨迹是线段,故选:A.8、(2022•眉山)如图,四边形ABCD为正方形,将△EDC绕点C逆时针旋转90°至△HBC,点D,B,H在同一直线上,HE与AB交于点G,延长HE与CD的延长线交于点F,HB=2,HG=3.以下结论:①∠EDC=135°;②EC2=CD•CF;③HG=EF;④sin∠CED=.其中正确结论的个数为()A.1个B.2个C.3个D.4个【答案】D【解答】解:∵△EDC旋转得到△HBC,∴∠EDC=∠HBC,∵ABCD为正方形,D,B,H在同一直线上,∴∠HBC=180°﹣45°=135°,∴∠EDC=135°,故①正确;∵△EDC旋转得到△HBC,∴EC=HC,∠ECH=90°,∴∠HEC=45°,∴∠FEC=180°﹣45°=135°,∵∠ECD=∠ECF,∴△EFC∽△DEC,∴,∴EC2=CD•CF,故②正确;设正方形边长为a,∵∠GHB+∠BHC=45°,∠GHB+∠HGB=45°,∴∠BHC=∠HGB=∠DEC,∵∠GBH=∠EDC=135°,∴△GBH∽△EDC,∴,即,∵△HEC是等腰直角三角形,∴,∵∠GHB=∠FHD,∠GBH=∠HDF=135°,∴△HBG∽△HDF,∴,即,解得:EF=3,∵HG=3,∴HG=EF,故③正确;过点E作EM⊥FD交FD于点M,∴∠EDM=45°,∵ED=HB=2,∴,∴,∵∠DEC+∠DCE=45°,∠EFC+∠DCE=45°,∴∠DEC=∠EFC,∴,故④正确综上所述:正确结论有4个,故选:D.9、(2022•单县一模)如图,将边长为8cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG 的周长是cm.【答案】16【解答】解:设EF=x,∵EF=DF,∴DF=x,则AF=8﹣x;而AE=4,由勾股定理得:x2=42+(8﹣x)2,解得:x=5;AF=8﹣5=3;∠GEF=∠D=90°,∠A=∠B=90°,∴∠AEF+∠AFE=∠AEF+∠BEG,∴∠AFE=∠BEG;∴△AEF∽△BGE,∴==,∴EG==,BG==,∴△EBG的周长=++4=16.故答案为16.10、如图,在矩形ABCD中,AB=3,BC=5,点P在CD边上,联结AP.如果将△ADP沿直线AP翻折,点D恰好落在线段BC上,那么的值为.【答案】【解答】解:如图:∵将△ADP沿直线AP翻折,点D恰好落在线段BC上的D',∴AD'=AD=5,PD=PD',∠AD'P=∠D=90°,在Rt△ABD'中,BD'===4,∴CD'=BC﹣BD'=5﹣4=1,设CP=x,则PD=PD'=3﹣x,在Rt△CPD'中,CD'2+CP2=PD'2,∴12+x2=(3﹣x)2,解得x=,∴CP=,PD=,∴S△ADP=AD•PD=×5×=,S四边形ABCP=S矩形ABCD﹣S△ADP=3×5﹣=,∴==,故答案为:.11、(2022•铜仁市)如图,在边长为2的正方形ABCD中,点E为AD的中点,将△CDE沿CE翻折得△CME,点M落在四边形ABCE内.点N为线段CE 上的动点,过点N作NP∥EM交MC于点P,则MN+NP的最小值为.【答案】【解答】解:作点P关于CE的对称点P′,由折叠的性质知CE是∠DCM的平分线,∴点P′在CD上,过点M作MF⊥CD于F,交CE于点G,∵MN+NP=MN+NP′≥MF,∴MN+NP的最小值为MF的长,连接DG,DM,由折叠的性质知CE为线段DM的垂直平分线,∵AD=CD=2,DE=1,∴CE==,∵CE×DO=CD×DE,∴DO=,∴EO=,∵MF⊥CD,∠EDC=90°,∴DE∥MF,∴∠EDO=∠GMO,∵CE为线段DM的垂直平分线,∴DO=OM,∠DOE=∠MOG=90°,∴△DOE≌△MOG,∴DE=GM,∴四边形DEMG为平行四边形,∵∠MOG=90°,∴四边形DEMG为菱形,∴EG=2OE=,GM=DE=1,∴CG=,∵DE∥MF,即DE∥GF,∴△CFG∽△CDE,∴,即,∴FG=,∴MF=1+=,∴MN+NP的最小值为;方法二:同理方法一得出MN+NP的最小值为MF的长,DO=,∴OC==,DM=2DO=,∵S△CDM=DM•OC=CD•MF,即×=2×MF,∴MF=,∴MN+NP的最小值为;故答案为:。
中考数学压轴题专题训练-----方程、不等式中的含参问题

中考数学压轴题专题训练-----方程、不等式中的含参问题例1.已知三个非负实数a ,b ,c 满足:3a +2b +c =5和2a +b -3c =1,若m =3a +b -7c ,则m 的最小值为__________.同类题型1.1 已知x +2y -3z =0,2x +3y +5z =0,则=________.x +y +z x -y +z同类题型 1.2 方程组的解x ,y 满足x >y ,则m 的取值范围是{4x +3m =28x -3y =m )( )A .B .C .D .m > 910m > 109m > 1910m > 1019例2.关于x 的方程+mx -9=0和+6m =0有公共根,则m 的值为________.x x -3x +m 同类题型2.1 已知a 是一元二次方程-2018x +1=0的一个根,则代数式的值是___.x a -2017a + 2018a +1同类题型2.2 已知关于x 的方程+(2k -1)x +1=0有两个不相等的实数根,那么实数k 的取值(k -1)x 范围为_____________.同类题型2.3 已知α、β是方程-2x -4=0的两个实数根,则+8β+6的值为( )x αA .-1 B .2 C .22 D .30例3.已知方程的两根分别为a ,,则方程的根是( )x + 1x =a + 1a 1a x + 1x -1=a + 1a -1A .a ,B .,a -1C .,a -1D .a ,1a -11a -11a a a -1同类题型3.1 若关于x 的方程=3的解是非负数,则b 的取值范围是________.2x -b x -1同类题型3.2 观察分析下列方程:①=3;②=5;③=7.请利用它们所蕴含的规律,求x + 2x x + 6x x + 12x关于x 的方程=2n +5(n 为正整数)的根,你的答案是_________________.x + n +n x -4同类题型 3.3 已知关于x 的方程只有整数解,则整数a 的值为2x -1- a +1x +2= 3a (x -1)(x +2)_____________.例4.[x ]表示不超过x 的最大整数.如,[π]=3,[2]=2,[-2.1]=-3.则下列结论:①[-x ]=-[x ];②若[x ]=n ,则x 的取值范围是n ≤x <n +1;③当-1<x <1时,[1+x ]+[1-x ]的值为1或2;④x =-2.75是方程4x -2[x ]+5=0的唯一一个解.其中正确的结论有_________(写出所有正确结论的序号).同类题型4.1 设[x ]表示不大于x 的最大整数,{x }表示不小于x 的最小整数,(x )表示最接近x 的整数(x ≠n +0.5,n 为整数).例如[3.4]=3,{3.4}=4,(3.4)=3.则不等式8≤2x +[x ]+3{x }+4(x )≤14的解为( )A .0.5≤x ≤2B .0.5<x <1.5或1.5<x <2C .0.5<x <1.5D .1.5<x <2同类题型4.2规定:[x ]表示不大于x 的最大整数,(x )表示不小于x 的最小整数,[x )表示最接近x 的整数(x ≠n +0.5,n 为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.则下列说法正确的是___________.(写出所有正确说法的序号)①当x =1.7时,[x ]+(x )+[x )=6;②当x =-2.1时,[x ]+(x )+[x )=-7;③方程4[x ]+3(x )+[x )=11的解为1<x <1.5;④当-1<x <1时,函数y =[x ]+(x )+x 的图象与正比例函数y =4x 的图象有两个交点.同类题型4.3 如果关于x 的不等式(a +b )x +2a -b >0的解集是,那么关于x 的不等式(b -a )x x < 52+a +2b ≤0的解集是____________.同类题型4.4 若关于x 的不等式组解集为x <2,则a 的取值范围是___________.{x +43> x 2+1x -a <0)同类题型4.5 按如图的程序计算,若开始输入的值x 为正数,最后输出的结果为656,则满足条件的x 的不同值最多有___________.参考答案例1.已知三个非负实数a ,b ,c 满足:3a +2b +c =5和2a +b -3c =1,若m =3a +b -7c ,则m 的最小值为__________.解:由题意可得,{3a +2b +c =52a +b -3c =1m =3a +b -7c )解得-3,,,a =7﹒(m +2)3b =7-11﹒(m +2)3c =m +23由于a ,b ,c 是三个非负实数,∴a ≥0,b ≥0,c ≥0,∴.-111≥m ≥-57所以m _(最小值)=.-57故本题答案为:-.57同类题型1.1 已知x +2y -3z =0,2x +3y +5z =0,则=________.x +y +z x -y +z解:由题意得:,{x +2y -3z =0①2x +3y +5z =0②)①×2-②得y =11z ,代入①得x =-19z ,原式.=x +y +z x -y +z =-19z +11z +z -19z -11z +z =729同类题型1.2 方程组的解x ,y 满足x >y ,则m 的取值范围是( ){4x +3m =28x -3y =m )A .B .C .D .m > 910m > 109m > 1910m > 1019解:{4x +3m =2①8x -3y =m ②)由①得,代入②得,-3y =m ,.x =2-3m 48×2-3m 4y =4-7m 3∵x >y ,即,解得.2-3m 4>4-7m 3m >1019选D .例2.关于x 的方程+mx -9=0和+6m =0有公共根,则m 的值为________.x x -3x +m 解:设这个公共根为α.则方程+mx -9=0的两根为α、-m -α;方程+6m =0的两根为α、3-α,x x -3x +m 由根与系数的关系有:α(-m -α)=-9,+6m ,α(3-α)=m 整理得,+mα=9①,+6m =0②,αα-3α+m ②-①得,+6m -3α-mα=-9,m 即-α(m +3)=0,(m +3)(m +3)(m +3-α)=0,所以m +3=0或m +3-α=0,解得m =-3或α=m +3,把α=m +3代入①得,+m (m +3)=9,(m +3)+3m =9,m +6m +9+m m (2m +9)=0,所以m =0或2m +9=0,解得m =0或m =-4.5,综上所述,m 的值为-3,0,-4.5.同类题型2.1 已知a 是一元二次方程-2018x +1=0的一个根,则代数式的值是___.x a -2017a +2018a +1解:由题意,把根a 代入-2018x +1=0,可得:-2018a +1=0,x a ∴-2017a -a +1=0,+1=2018a ;a a ∴-2017a =a -1,a ∴-1a -2017a +2018a +1=a -1+20182018a =a +1a-1=a +1a -1=2018a a=2018-1,=2017.同类题型2.2 已知关于x 的方程+(2k -1)x +1=0有两个不相等的实数根,那么实数k 的取值(k -1)x 范围为_____________.解:由题意知,k ≠±1,-1)=5-4k >0△=(2k -1)-4(k ∴且k ≠±1.k <54同类题型2.3 已知α、β是方程-2x -4=0的两个实数根,则+8β+6的值为( )x αA .-1 B .2 C .22 D .30解:∵α、β是方程-2x -4=0的两个实数根,x ∴α+β=2,-2α-4=0,α∴=2α+4α∴+8β+6α+8β+6=α﹒α=α﹒(2α+4)+8β+6+4α+8β+6=2α=2(2α+4)+4α+8β+6=8α+8β+14=8(α+β)+14=30,故选D .例3.已知方程的两根分别为a ,,则方程的根是( )x + 1x =a + 1a 1a x + 1x -1=a + 1a -1A .a ,B .,a -1C .,a -1D .a ,1a -11a -11a a a -1解:方程可以写成的形式,x +1x -1=a +1a -1x -1+1x -1=a -1+1a -1∵方程的两根分别为a ,,x +1x =a +1a 1a∴方程的两根的关系式为x -1=a -1,,即方程的根为x =a 或x -1+1x -1=a -1+1a -1x -1=1a -1a a -1,∴方程的根是a ,.x +1x -1=a +1a -1a a -1选D .同类题型3.1 若关于x 的方程=3的解是非负数,则b 的取值范围是________.2x -b x -1解:去分母得,2x -b =3x -3∴x =3-b∵x ≥0∴3-b ≥0解得,b ≤3又∵x -1≠0∴x ≠1即3-b ≠1,b ≠2则b 的取值范围是b ≤3且b ≠2.同类题型3.2 观察分析下列方程:①=3;②=5;③=7.请利用它们所蕴含的规律,求x + 2x x + 6x x + 12x关于x 的方程=2n +5(n 为正整数)的根,你的答案是_________________.x + n +n x -4解:=3,解得:x =2或x =1;x +1×2x=5,解得:x =2或x =3;x +2×3x=7,解得:x =3或x =4,x +3×4x得到规律=m +n 的解为:x =m 或x =n ,x +mn x所求方程整理得:=2n +1,x -4+n (n +1)x -4根据规律得:x -4=n 或x -4=n +1,解得:x =n +4或x =n +5.同类题型 3.3 已知关于x 的方程只有整数解,则整数a 的值为2x -1- a +1x +2= 3a (x -1)(x +2)_____________.解:方程两边同乘以(x -1)(x +2),得:2(x +2)-(a +1)(x -1)=3a ,解得:,x =2a -51-a =-2-31-a∵方程只有整数解,∴1-a =3或1或-3或-1,当1-a =3,即a =-2时,x =-2-1=-3,检验,将x =-3代入(x -1)(x +2)=4≠0,故x =-3是原分式方程的解;当1-a =1,即a =0时,x =-2-3=-5,检验,将x =-5代入(x -1)(x +2)=18≠0,故x =-7是原分式方程的解;当1-a =-3,即a =4时,x =-2+1=-1,检验,将x =-1代入(x -1)(x +2)=-2≠0,故x =-1是原分式方程的解;当1-a =-1,即a =2时,x =1,检验,将x =1代入(x -1)(x +2)=0,故x =1不是原分式方程的解;∴整数a 的值为:-2,0或4.例4.[x ]表示不超过x 的最大整数.如,[π]=3,[2]=2,[-2.1]=-3.则下列结论:①[-x ]=-[x ];②若[x ]=n ,则x 的取值范围是n ≤x <n +1;③当-1<x <1时,[1+x ]+[1-x ]的值为1或2;④x =-2.75是方程4x -2[x ]+5=0的唯一一个解.其中正确的结论有_________(写出所有正确结论的序号).解:①当x =-3.5时,[-3.5]=-4,-[x ]=-3,不相等,故原来的说法错误;②若[x ]=n ,则x 的取值范围是n ≤x <n +1是正确的;③当-1<x <0时,[1+x ]+[1-x ]=0+1=1;当x =0时,[1+x ]+[1-x ]=1+1=2;当0<x <1时,[1+x ]+[1-x ]=1+0=1;故当-1<x <1时,[1+x ]+[1-x ]的值为1或2是正确的;④x -[x ]的范围为0~1,4x -2[x ]+5=0,-5≤2x <-7,即-2.5≤x <-3.5,x =-2.75或x =-3.25都是方程4x -2[x ]+5=0,故原来的说法错误.故答案为:②③.同类题型4.1 设[x ]表示不大于x 的最大整数,{x }表示不小于x 的最小整数,(x )表示最接近x 的整数(x ≠n +0.5,n 为整数).例如[3.4]=3,{3.4}=4,(3.4)=3.则不等式8≤2x +[x ]+3{x }+4(x )≤14的解为( )A .0.5≤x ≤2B .0.5<x <1.5或1.5<x <2C .0.5<x <1.5D .1.5<x <2解:根据题意得:x >0,若x ≥2,则2x ≥4,[x ]≥2,3{x }≥6,4(x )≥8,不等式不成立.故只需分析0<x <2时的情形即可,①0<x ≤0.5时,不等式可化为:8≤2x +0+3+0≤14,解得:2.5≤x ≤5.5,不符合不等式;②当0.5<x ≤1时,不等式可化为:8≤2x +0+3+4≤14,解得:0.5≤x ≤3,因此0.5<x ≤1,符合不等式;③当1<x <1.5时,不等式可化为:8≤2x +1+6+4≤14,解得:-1.5≤x ≤1.5,因此1<x <1.5,符合不等式;④当1.5<x <2时,不等式可化为:8≤2x +1+6+8≤14,解得:-3.5≤x ≤-0.5,不符合不等式.故原不等式的解集为:0.5<x <1.5.故选C .同类题型4.2规定:[x ]表示不大于x 的最大整数,(x )表示不小于x 的最小整数,[x )表示最接近x 的整数(x ≠n +0.5,n 为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.则下列说法正确的是___________.(写出所有正确说法的序号)①当x =1.7时,[x ]+(x )+[x )=6;②当x =-2.1时,[x ]+(x )+[x )=-7;③方程4[x ]+3(x )+[x )=11的解为1<x <1.5;④当-1<x <1时,函数y =[x ]+(x )+x 的图象与正比例函数y =4x 的图象有两个交点.解:①当x =1.7时,[x ]+(x )+[x )=[1.7]+(1.7)+[1.7)=1+2+2=5,故①错误;②当x =-2.1时,[x ]+(x )+[x )=[-2.1]+(-2.1)+[-2.1)=(-3)+(-2)+(-2)=-7,故②正确;③4[x ]+3(x )+[x )=11,7[x ]+3+[x )=11,7[x ]+[x )=8,1<x <1.5,故③正确;④∵-1<x <1时,∴当-1<x <-0.5时,y =[x ]+(x )+x =-1+0+x =x -1,当-0.5<x <0时,y =[x ]+(x )+x =-1+0+x =x -1,当x =0时,y =[x ]+(x )+x =0+0+0=0,当0<x <0.5时,y =[x ]+(x )+x =0+1+x =x +1,当0.5<x <1时,y =[x ]+(x )+x =0+1+x =x +1,∵y =4x ,则x -1=4x 时,得;x +1=4x 时,得;当x =0时,y =4x =0,x =-13x =13∴当-1<x <1时,函数y =[x ]+(x )+x 的图象与正比例函数y =4x 的图象有三个交点,故④错误,故答案为:②③.同类题型4.3 如果关于x 的不等式(a +b )x +2a -b >0的解集是,那么关于x 的不等式(b -a )x x < 52+a +2b ≤0的解集是____________.解:∵关于x 的不等式(a +b )x +2a -b >0的解集是,x <52∴,x <b -2a a +b∴,且a +b <0,b -2a a +b =52即b =-3a ,a +b <0,∴a -3a <0,即a >0,∴b -a =-4a <0,∴关于x 的不等式(b -a )x +a +2b ≤0的解集是,x ≥-a -2b b -a∵,-a -2b b -a =-a +6a -3a -a =-54∴关于x 的不等式(b -a )x +a +2b ≤0的解集是.x ≥-54同类题型4.4 若关于x 的不等式组解集为x <2,则a 的取值范围是___________.{x +43> x 2+1x -a <0)解:由+1,得x +43>x 22x +8>3x +6,解得x <2,由x -a <0,得x <a ,又因关于x 的不等式组解集为x <2,{x +43>x 2+1x -a <0)所以a ≥2.同类题型4.5 按如图的程序计算,若开始输入的值x 为正数,最后输出的结果为656,则满足条件的x 的不同值最多有___________.解:∵最后输出的数为656,∴5x +1=656,得:x =131>0,∴5x +1=131,得:x =26>0,∴5x +1=26,得:x =5>0,∴5x +1=5,得:x =0.8>0;∴5x +1=0.8,得:x =-0.04<0,不符合题意,故x 的值可取131,26,5,0.8共4个.。
2020中考数学压轴题专项突破训练

中考数学压轴题专项突破训练一、几何压轴题专题突破1、如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G,(1)求证:CF=BG;(2)延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)在(2)问的条件下,当∠GAC=2∠FCH时,若S△AEG=3,BG=6,求AC的长.2、[问题背景]如图1所示,在△ABC中,AB=BC,∠ABC=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.[问题初探]如果点D在线段BC上运动,通过观察、交流,小明形成了以下的解题思路:过点E作EF⊥BC交直线BC于F,如图2所示,通过证明△DEF≌△ADB,可推证△CEF是等腰直角三角形,从而求得∠DCE=135°.[继续探究]如果点D在线段CB的延长线上运动,如图3所示,求出∠DCE的度数.[拓展延伸]连接BE,当点D在直线BC上运动时,若AB,请直接写出BE的最小值.3、在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线.(1)如图1,求证:AD=2DC.(2)如图2,作∠CBD的角平分线交线段CD于点M,若CM=1,求△DBM的面积;(3)如图3,过点D作DE⊥AB于点E,点N是线段AC上一点(不与C、D重合),以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,试探究线段ND,DG与AD之间的数量关系,并说明理由.4、如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.(1)发现问题:线段EF,CF之间的数量关系为EF=CF;∠EFC的度数为120°;(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.5、如图1,在等腰△ABC中,AB=AC,∠BAC=a,点P是线段AB的中点,点E是线段CB延长线上一点,且PE=PC,将线段PC绕点P顺时针旋转α得到PD,连接BD.(1)如图2,若α=60°,其他条件不变,先补全图形,然后探究线段BD和BC之间的数量关系,并说明理由.(2)如图3,若α=90°,其他条件不变,探究线段BP、BD和BC之间的等量关系,并说明理由.6、【发现问题】如图1,已知△ABC,以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE.请你以A为直角顶点、AC为腰,向△ABC外作等腰直角△ACD(不写作法,保留作图痕迹).连接BD、CE.那么BD与CE的数量关系是BD=CE.【拓展探究】如图2,已知△ABC,以AB、AC为边向外作正方形AEFB和正方形ACGD,连接BD、CE,试判断BD与CE之间的数量关系,并说明理由.【解决问题】如图3,有一个四边形场地ABCD,∠ADC=60°,BC=15,AB=8,AD=CD,求BD的最大值.7、(1)如图1,点C为线段AB外一个动点,已知AB=a,AC=b.当点C位于BA的延长线上时,线段BC取得最大值,则最大值为a+b(用含a,b的式子表示);(2)如图2,点C为线段AB外一个动点,若AB=10,AC=3,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接AE,DB.①求证:AE=DB;②请直接写出线段AE的最大值;8、【初步探索】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF=BE+FD,探究图中∠BAE、∠FAD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是∠BAE+∠FAD=∠EAF;【灵活运用】(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.9、如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P逆时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P在BC延长线上时,若∠BPO=45°,AC=,请直接写出BQ的长.10、模型发现:同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C 的位置的不同而发生变化.因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.特别的,当点C位于线段BA的延长线上时,线段BC的长取得最大值,且最大值为b+c(用含b,c的式子表示)(直接填空)模型应用:点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接BD,AE.(1)求证:BD=AE.(2)线段AE长的最大值为5.模型拓展:如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB=8.若AC⊥AB,AC=3,试求OC长的最大值.11、已知:△ABC中,∠ACB=90°,AC=BC.(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC=3MC,请直接写出DBBC的值.12、已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:∠1=∠2;②如图2,若BF=2AF,连接CF,求证:BF⊥CF;(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求ABFACF △△的值.13、已知,△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE.(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;(2)如图2,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC于点D,连接DF交BE于点G,连接AG;①若AG平分∠CAD,求证:AH=12AC;②如图3,当G落在△ABC外时,若将△EFG沿EF边翻折,点G刚好落在AB边上点P,直接写出AG与EF的数量关系.14、如图所示,Rt△ABC中,∠ACB=90°,E为AC中点,作ED⊥AC交AB于D,连接CD;(1)如图1,求证:AB=2CD;(2)如图2,作CF⊥AB交AB于F,点G为CF上一点,点H为DE延长线上一点,分别连接AH、GH,若∠AHG=2∠B,求证:AH=GH;(3)如图3,在(2)的条件下,连接DG,且有DE=BF,∠EDG=90°,若AC=6,求AH的长度.15、【问题情境】一节数学课后,老师布置了一道课后练习题:如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC 上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.(1)阅读理解,完成解答. 本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写这道练习题的证明过程;(2)特殊位置,证明结论若CE平分∠ACD,其余条件不变,求证:AE=BF;(3)知识迁移,探究发现如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)16、在正方形ABCD和等腰直角△BGF中,∠BGF=90°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,延长GP交DC于点E.求证:PG=PC;(2)如图2,当点F在AB的延长线上时,(1)中的结论是否成立?请证明你的结论;(3)如图3,若四边形ABCD为菱形,且∠ABC=60°,△BGF为等边三角形,点F在CB的延长线上时,线段PC、PG又有怎样的数量关系,请直接写出你的结论,并画出论证过程中需要添加的辅助线.17、在△ABC中,∠BAC=60°,点D、E分别在边AC、AB上,AD=AE,连接CE、BD相交于点F,且∠BEC=∠ADF,连接AF.(1)如图1,连接ED,求证:∠ABD=∠CED;(2)如图2,求证:EF+FD=AF;(3)如图3,取BC的中点G,连接AG交BD于点H,若∠GAC=3∠ABD,BH=7,求△ABH的面积.18.点D,E分别在△ABC的边AC,BD上,BD,CE交于点F,连接AF,∠FAE=∠FAD,FE=FD.(1)如图1,若∠AEF=∠ADF,求证:AE=AD;(2)如图2,若∠AEF≠∠ADF,FB平分∠ABC,求∠BAC的度数;(3)在(2)的条件下,如图3,点G在BE上,∠CFG=∠AFB若AG=6,△ABC的周长为20,求BC长.二、二次函数压轴题专题突破1.如图,对称轴为x=1的抛物线经过A(﹣1,0),B(2,﹣3)两点.(1)求抛物线的解析式;(2)P是抛物线上的动点,连接PO交直线AB于点Q,当Q是OP中点时,求点P的坐标;(3)C在直线AB上,D在抛物线上,E在坐标平面内,以B,C,D,E为顶点的四边形为正方形,直接写出点E的坐标.2.如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,﹣2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=﹣1.(1)求抛物线的函数表达式;(2)若点P在第二象限内,且PE=OD,求△PBE的面积.(3)在(2)的条件下,若M为直线BC上一点,在x轴的上方,是否存在点M,使△BDM是以BD为腰的等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.3.在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点B,抛物线y=ax2+bx+c(a <0)经过点A、B.(1)求a、b满足的关系式及c的值.(2)当x<0时,若y=ax2+bx+c(a<0)的函数值随x的增大而增大,求a的取值范围.(3)如图,当a=﹣1时,在抛物线上是否存在点P,使△PAB的面积为1?若存在,请求出符合条件的所有点P的坐标;若不存在,请说明理由.4.如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,直线y=x+经过点A,与抛物线的另一个交点为点C(3,m),线段PQ在线段AB上移动,PQ=1,分别过点P、Q作x轴的垂线,交抛物线于E、F,交直线于D、G.(1)求抛物线的解析式;(2)设四边形DEFG的面积为S,求S的最大值;(3)在线段PQ的移动过程中,以D,E,F,G为顶点的四边形是平行四边形时,求点P的坐标.5.抛物线y=ax2﹣4ax+3a交x轴于点B、C两点,交y轴于点A,点D为抛物线的顶点,连接AB、AC,已知△ABC的面积为3.(1)求抛物线的解析式;(2)点P为抛物线对称轴右侧一点,点P的横坐标为m,过点P作PQ∥AC交y轴于点Q,AQ的长度为d,求d与m的函数关系式;(3)在(2)的条件下,当d=4时,作DN⊥y轴于点N,点G为抛物线上一点,AG交线段PD于点M,连接MN,若△AMN是以MN为底的等腰三角形,求点G的坐标.6.已知直线l:y=kx+4与抛物线y=x2交于点A(x1,y1),B(x2,y2).(1)求:x1•x2;y1•y2的值.(2)过点(0,﹣4)作直线PQ∥x轴,且过点A、B分别作AM⊥PQ于点M,BN⊥PQ于点N,设直线l:y=kx+4交y轴于点F,求证:AF=AM=4+y1.(3)证明:+为定值,并求出该值.7.如图,已知抛物线y=x2+bx+c与x轴相交于点A(1,0)和点B,与y轴交于点C(0,﹣3)顶点为D(1)求抛物线的函数关系式;(2)判断△BCD的形状,并说明理由;(3)点P在抛物线上,点Q在直线y=x上,是否存在点P、Q使以点P、Q、C、O为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.8.抛物线y=﹣x2+2x+3与y轴交于B,与x轴交于点D、A,点A在点D的右边,顶点为F,C(0,1)(1)直接写出点B、A、F的坐标;(2)设Q在该抛物线上,且S△BAF=S△BAQ,求点Q的坐标;(3)对大于1常数m,在x轴上是否存在点M,使得sin∠BMC=?若存在,求出点M坐标;若不存在,说明理由?9.抛物线C1经过A(﹣3,0)、B(1,0)、C(0,﹣3)三点.(1)求抛物线的解析式.(2)抛物线的对称轴交x轴于D,过D的直线交抛物线于P、Q(P在Q左边),且S△APD=2S△BQD,求l的解析式.(3)点E是抛物线C1的顶点,将C1沿着lEC的方向平移至C2.当C2与y=2x﹣5只有一个公共点时:①求C2的解析式.②P(xP,yP)是C2上一点,若﹣6≤xP≤2且yP为整数,满足条件的P点共有51个.10.如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,点P是线段AB 上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.(1)若抛物线的解析式为y=﹣2x2+2x+4,设其顶点为M,其对称轴交AB于点N.①求点M和点N的坐标;②在抛物线的对称轴上找一点Q,使|AQ﹣BQ|的值最大,请直接写出点Q的坐标;③是否存在点P,使四边形MNPD为菱形?并说明理由;(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB 相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.11.已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B 左侧.点B的坐标为(2,0).OC=3OB.(1)求抛物线的解析式;(2)若点P是线段AC下方抛物线上的动点,求三角形PAC面积的最大值.(3)在(2)的条件下,△PAC的面积为S,其中S为整数的点P作“好点”,则存在多个“好点”,则所有“好点”的个数为9(4)在(2)的条件下,以PA为边向直线AC右上侧作正方形APHG,随着点P的运动,正方形的大小、位置也随之改变,当顶点H或G恰好落在y轴上时,直接写出对应的点P的坐标.12.已知抛物线y=x2﹣mx+m2+m+1的顶点为A,交y轴于点B.(1)求证:抛物线的顶点A在定直线l上,并求定值线l的解析式;(2)当m=1时,直线l交抛物线于另一点M,交x轴于点C,N为抛物线上一点,且∠NMC=2∠ACO,求点N的坐标;(3)如图2,当m=2时,过点A作直线l1(不经过点O),分别交x轴,y轴于点E,F,点P为对称轴右侧抛物线上的动点(点P、A、O不共线),直线PA分别交x轴,y轴于点G、H,过点P 作PK∥y轴交直线l1于点K,若AE•AF=AG•AH,求点K的纵坐标.13.已知:如图1,抛物线y=mx2+nx﹣3m,其中m>0,抛物线交x轴负半轴于点A(﹣1,0),交x轴正半轴于点B.(1)求点B的坐标;(2)若抛物线的顶点为点D,且∠ACB=∠DCB,求m的值;(3)如图,若点P为抛物线在第四象限的一个动点,直线PA、PB分别交y轴于点M、N,试猜想的值时否发生变化?并证明你的结论.14.如图1,已知抛物线y=ax2+(1﹣3a)x﹣3(a>0)与x轴交于A、B两点,与y轴交于C点,直线y=﹣x+5与抛物线交于点D、E,与直线BC交于点P.(1)求点P的坐标;(2)求PD×EP的值;(3)如图2,若二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点为A(x1,0)、B(x2,0),定点为C,若∠CAB=30°,则b2﹣4ac的值是否发生变化?若不变,求其值.15.已知抛物线C1:y=(x﹣1)2+1与y轴交于点A,过点A与点(1,3)的直线与C1交于点B.(1)求直线AB的函数表达式;(2)如图1,若点P为直线AB下方的C1上一点,求点P到直线AB的距离的最大值;(3)如图2,将直线AB绕点A顺时针旋转90°后恰好经过C1的顶点C,沿射线AC的方向平移抛物线C1得到抛物线C2,C2的顶点为D,两抛物线相交于点E.设交点E的横坐标为m.若∠AED =90°,求m的值.参考答案一、几何1、如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G,(1)求证:CF=BG;(2)延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)在(2)问的条件下,当∠GAC=2∠FCH时,若S△AEG=3,BG=6,求AC的长.证明:(1)如图1,∵∠ACB=90°,AC=BC,∴∠A=45°,∵CG平分∠ACB,∴∠ACG=∠BCG=45°,∴∠A=∠BCG,在△BCG和△CAF中,∵AC BC∠A∠BCG∠ACF∠CBE ⎧===⎪⎨⎪⎩,∴△BCG≌△CAF(ASA),∴CF=BG;(2)如图2,∵PC∥AG,∴∠PCA=∠CAG,∵AC=BC,∠ACG=∠BCG,CG=CG,∴△ACG≌△BCG,∴∠CAG=∠CBE,∵∠PCG=∠PCA+∠ACG=∠CAG+45°=∠CBE+45°,∠PGC=∠GCB+∠CBE=∠CBE+45°,∴∠PCG=∠PGC,∴PC=PG,∵PB=BG+PG,BG=CF,∴PB=CF+CP;(3)解:如图,过E作EM⊥AG,交AG于M,∵S△AEG=12AG•EM=由(2)得:△ACG≌△BCG,∴BG=AG=6,∴12×6×EM=EM设∠FCH=x°,则∠GAC=2x°,∴∠ACF=∠EBC=∠GAC=2x°,∵∠ACH=45°,∴2x+x=45,x=15,∴∠ACF=∠GAC=30°,在Rt△AEM中,AE=2EM=,AM3,∴M是AG的中点,∴AE=EG=∴BE=BG+EG=,在Rt△ECB中,∠EBC=30°,∴CE=12BE=∴AC=AE+EC==.2、[问题背景]如图1所示,在△ABC中,AB=BC,∠ABC=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.[问题初探]如果点D在线段BC上运动,通过观察、交流,小明形成了以下的解题思路:过点E作EF⊥BC交直线BC于F,如图2所示,通过证明△DEF≌△ADB,可推证△CEF是等腰直角三角形,从而求得∠DCE=135°.[继续探究]如果点D在线段CB的延长线上运动,如图3所示,求出∠DCE的度数.[拓展延伸]连接BE,当点D在直线BC上运动时,若AB,请直接写出BE的最小值.解:[问题初探]如图2,过点E作EF⊥BC交直线BC于F,∴∠DFE=90°=∠ABD,∴∠EDF+∠DEF=90°,由旋转知,AD=DE,∠ADE=90°,∴∠ADB+∠EDF=90°,∴∠ADB=∠DEF,∴△ABD≌△DFE(AAS),∴BD=EF,DF=AB,∵AB=BC,∴BC=DF,∴BD=CF,∴EF=CF,∴△CEG是等腰直角三角形,∴∠ECF=45°,∴∠DCE=135°,故答案为:ADB,等腰直角,135;[继续探究]如图,过点E作EF⊥BC于F,∴∠DFE=90°=∠ABD,∴∠EDF+∠DEF=90°,由旋转知,AD=DE,∠ADE=90°,∴∠ADB+∠EDF=90°,∴∠ADB=∠DEF,∴△ABD≌△DFE(AAS),∴BD=EF,DF=AB,∵AB=BC,∴BC=DF,∴BD=CF,∴EF=CF,∴△CEG是等腰直角三角形,∴∠ECF=45°,∴∠DCE=45°;[拓展延伸] 如图,在△ABC中,∠ABC=90°,AB=BC,∴∠ACB=45°当点D在射线BC上时,由[问题初探]知,∠BCM=135°,∴∠ACM=∠BCM﹣∠ACB=90°,当点D在线段CB的延长线上时,由[继续探究]知,∠BCE=45°,∴∠ACN=∠ACB+∠BCM=90°,∴点E是过点C垂直于AC的直线上的点,∴当BE⊥MN时,BE最小,∵∠BCE=45°,∴∠CBE=45°=∠BCE,∴BE=CE,∴BE最小=2BCBE3、在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线.(1)如图1,求证:AD=2DC.(2)如图2,作∠CBD的角平分线交线段CD于点M,若CM=1,求△DBM的面积;(3)如图3,过点D作DE⊥AB于点E,点N是线段AC上一点(不与C、D重合),以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,试探究线段ND,DG与AD之间的数量关系,并说明理由.证明:(1)如图,过点D作DE⊥AB,∵BD是△ABC的角平分线,DE⊥AB,∠ACB=90°,∴DC=DE,∵∠A=30°,DE⊥AB,∴AD=2DE,∴AD=2DC;(2)如图2,过点M作ME∥BD,∵∠ACB=90°,∠A=30°,∴∠ABC=60°,∵BD是△ABC的角平分线,∴∠ABD=∠DBC=30°,∵BM平分∠CBD,∴∠CBM=15°=∠DBM,∵ME∥BD,∴∠MEC=∠CBD=30°,∠EMB=∠DBM=∠MBE,∴ME=BE,∵∠MEC=30°,∠C=90°∴CEMCME=2MC=2=BE,∴BC,∵∠CBD=30°,∠C=90°,∴BC,∴CD=1+3,∴DM=3,∴△DBM的面积=12×+2)=1+;(3)若点N在CD上时,AD=DG+DN,理由如下:如图3所示:延长ED 使得DW =DN ,连接NW ,∵∠ACB =90°,∠A =30°,BD 是△ABC 的角平分线,DE ⊥AB 于点E , ∴∠ADE =∠BDE =60°,AD =BD ,∵DN =DW ,且∠WDN =60°∴△WDN 是等边三角形,∴NW =DN ,∠W =∠WND =∠BNG =∠BDN =60°,∴∠WNG =∠BND ,在△WGN 和△DBN 中,60WN DN°∠W ∠NDB ∠WNG ∠DNB ⎧====⎪⎨⎪⎩∴△WGN ≌△DBN (SAS ),∴BD =WG =DG+DN ,∴AD =DG+DN .(3)若点N 在AD 上时,AD =DG ﹣DN ,理由如下:如图4,延长BD 至H ,使得DH =DN ,连接HN ,由(1)得DA =DB ,∠A =30°.∵DE ⊥AB 于点E .∴∠2=∠3=60°.∴∠4=∠5=60°.∴△NDH 是等边三角形.∴NH =ND ,∠H =∠6=60°.∴∠H =∠2.∵∠BNG =60°,∴∠BNG+∠7=∠6+∠7.即∠DNG =∠HNB .在△DNG 和△HNB 中,DN HN∠DNG ∠HNB ∠H ∠2===⎧⎪⎨⎪⎩∴△DNG ≌△HNB (ASA ).∴DG =HB .∵HB =HD+DB =ND+AD ,∴DG =ND+AD .∴AD =DG ﹣ND .4、如图1,已知直角三角形ABC ,∠ACB =90°,∠BAC =30°,点D 是AC 边上一点,过D 作DE ⊥AB 于点E ,连接BD ,点F 是BD 中点,连接EF ,CF .(1)发现问题:线段EF ,CF 之间的数量关系为 EF =CF ;∠EFC 的度数为 120° ;(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.解:(1)如图1中,∵DE⊥AB,∴∠BED=90°,∵∠BCD=90°,BF=DF,∴FE=FB=FD=CF,∴∠FBE=∠FEB,∠FBC=∠FCB,∴∠EFC=∠EFD+∠CFD=∠FBE+∠FEB+∠FBC+∠FCB=2(∠FBE+∠FBC)=2∠ABC=120°,故答案为:EF=CF,120°.(2)结论成立.理由:如图2中,取AB的中点M,AD的中点N,连接MC,MF,ED,EN,FN.∵BM=MA,BF=FD,∴MF∥AD,MF=12AD,∵AN=ND,∴MF=AN,MF∥AN,∴四边形MFNA是平行四边形,∴NF=AM,∠FMA=∠ANF,在Rt△ADE中,∵AN=ND,∠AED=90°,∴EN=12AD=AN=ND,同理CM=12AB=AM=MB,在△AEN和△ACM中,∠AEN=∠EAN,∠MCA=∠MAC,∵∠MAC=∠EAN,∴∠AMC=∠ANE,又∵∠FMA=∠ANF,∴∠ENF=∠FMC,在△MFC和△NEF中,MF NE MC NF ∠FMC ∠ENF⎧===⎪⎨⎪⎩,∴△MFC ≌△NEF (SAS ),∴FE =FC ,∠NFE =∠MCF ,∵NF ∥AB ,∴∠NFD =∠ABD ,∵∠ACB =90°,∠BAC =30°,∴∠ABC =60°,△BMC 是等边三角形,∠MCB =60°∴∠EFC =∠EFN+∠NFD+∠DFC =∠MCF+∠ABD+∠FBC+∠FCB =∠ABC+∠MCB =60°+60°=120°.(3)如图3中,作EH ⊥AB 于H .在Rt △ABC 中,∵∠BAC =30°,BC =3,∴AB =2BC =6,在Rt △AED 中,∠DAE =30°,AD =2,∴DE =12AD =1,在Rt △DEH 中,∵∠EDH =60°,DE =1,∴EH =ED •sin60°=,DH=ED•cos60°=1 2,在Rt△EHG中,EG.5、如图1,在等腰△ABC中,AB=AC,∠BAC=a,点P是线段AB的中点,点E是线段CB延长线上一点,且PE=PC,将线段PC绕点P顺时针旋转α得到PD,连接BD.(1)如图2,若α=60°,其他条件不变,先补全图形,然后探究线段BD和BC之间的数量关系,并说明理由.(2)如图3,若α=90°,其他条件不变,探究线段BP、BD和BC之间的等量关系,并说明理由.解:(1)BC=2BD,理由:如图2,连接CD,由旋转可得,CP=DP,∠CPD=60°,∴△CDP是等边三角形,∴∠CDP=60°=∠PCD,又∵P是AB的中点,AB=AC,∠A=60°,∴等边三角形ABC中,∠PCB=30°,CP⊥AB,∴∠BCD=30°,即BC平分∠PCD,∴BC垂直平分PD,∴∠BDC=∠BPC=90°,∴Rt△BCD中,BC=2BD.(2)如图3,取BC中点F,连接PF,∵∠A=90°,AB=AC,∴△ABC是等腰直角三角形,∵P是AB的中点,F是BC的中点,∴PF是△ABC的中位线,∴PF∥AC,∴∠PFB=∠ACB=45°,∠BPF=∠A=90°,∴△BPF是等腰直角三角形,∴BF=BP,BP=PF,∵∠DPC=∠BPF=90°,∴∠BPD=∠FPC,又∵PD=PC,∴△BDP≌△FCP,∴BD=CF,∵BC=BF+FC,∴BC=2BP.6、【发现问题】如图1,已知△ABC,以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE.请你以A为直角顶点、AC为腰,向△ABC外作等腰直角△ACD(不写作法,保留作图痕迹).连接BD、CE.那么BD与CE的数量关系是BD=CE.【拓展探究】如图2,已知△ABC,以AB、AC为边向外作正方形AEFB和正方形ACGD,连接BD、CE,试判断BD与CE之间的数量关系,并说明理由.【解决问题】如图3,有一个四边形场地ABCD,∠ADC=60°,BC=15,AB=8,AD=CD,求BD的最大值.【发现问题】解:延长CA到M,作∠MAC的平分线AN,在AN上截取AD=AC,连接CD,即可得到等腰直角△ACD;连接BD、CE,如图1所示:∵△ABE与△ACD都是等腰直角三角形,∴AB=AE,AD=AC,∠BAE=∠CAD=90°,∴∠BAD=∠EAC,在△BAD和△EAC中,AB AEAD AC∠BAD∠EAC ⎧===⎪⎨⎪⎩,∴△BAD≌△EAC(SAS),∴BD=CE,【拓展探究】解:BD=CE;理由如下:∵四边形AEFB与四边形ACGD都是正方形,∴AB=AE,AD=AC,∠BAE=∠CAD=90°,∴∠BAD=∠EAC,在△BAD和△EAC中,AB AEAD AC∠BAD∠EAC ⎧===⎪⎨⎪⎩,∴△BAD≌△EAC(SAS),∴BD=CE;【解决问题】解:以AB为边向外作等边三角形ABE,连接CE,如图3所示:则∠BAE=60°,BE=AB=AE=8,∵AD=CD,∠ADC=60°,∴△ACD是等边三角形,∴∠CAD=60°,AC=AD,∴∠CAD+∠BAC=∠BAE+∠BAC,即∠BAD=∠EAC,在△BAD和△EAC中,AB AEAD AC∠BAD∠EAC ⎧===⎪⎨⎪⎩,∴△BAD≌△EAC(SAS),∴BD=CE;当C、B、E三点共线时,CE最大=BC+BE=15+8=23,∴BD的最大值为23.7、(1)如图1,点C为线段AB外一个动点,已知AB=a,AC=b.当点C位于BA的延长线上时,线段BC取得最大值,则最大值为a+b(用含a,b的式子表示);(2)如图2,点C为线段AB外一个动点,若AB=10,AC=3,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接AE,DB.①求证:AE=DB;②请直接写出线段AE的最大值;(1)解:∵点C为线段AB外一动点,且AC=b,AB=a,∴当点C位于BA的延长线上时,线段BC的长取得最大值,且最大值为AC+AB=a+b,(2)①证明:如图2中,∵△ACD与△BCE是等边三角形,∴CD=AC,CB=CE,∠ACD=∠BCE=60°,∴∠DCB=∠ACE,在△CAD与△EAB中,CD CACB CE∠DCB∠ACE ⎧===⎪⎨⎪⎩,∴△CAD≌△EAB(SAS),∴AE=BD.②∵线段AE长的最大值=线段BD的最大值,由(1)知,当线段BD的长取得最大值时,点D在BA的延长线上,∴最大值为AD+AB=3+10=13;8、【初步探索】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF=BE+FD,探究图中∠BAE、∠FAD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是∠BAE+∠FAD=∠EAF;【灵活运用】(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.解:(1)∠BAE+∠FAD=∠EAF.理由:如图1,延长FD到点G,使DG=BE,连接AG,根据SAS可判定△ABE≌△ADG,进而得出∠BAE=∠DAG,AE=AG,再根据SSS可判定△AEF≌△AGF,可得出∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF.故答案为:∠BAE+∠FAD=∠EAF;(2)仍成立,理由:如图2,延长FD到点G,使DG=BE,连接AG,∵∠B+∠ADF=180°,∠ADG+∠ADF=180°,∴∠B=∠ADG,又∵AB=AD,∴△ABE≌△ADG(SAS),∴∠BAE=∠DAG,AE=AG,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF;(3)∠EAF=180°﹣12∠DAB.证明:如图3,在DC延长线上取一点G,使得DG=BE,连接AG,∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,∴∠ADC=∠ABE,又∵AB=AD,∴△ADG≌△ABE(SAS),∴AG=AE,∠DAG=∠BAE,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠FAE=∠FAG,∵∠FAE+∠FAG+∠GAE=360°,∴2∠FAE+(∠GAB+∠BAE)=360°,∴2∠FAE+(∠GAB+∠DAG)=360°,即2∠FAE+∠DAB=360°,∴∠EAF=180°﹣12∠DAB.9、如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P逆时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P在BC延长线上时,若∠BPO=45°,AC=,请直接写出BQ的长.解:(1)CP=BQ,理由:如图1,连接OQ,由旋转知,PQ=OP,∠OPQ=60°⊅∴△POQ是等边三角形,∴OP=OQ,∠POQ=60°,在Rt△ABC中,O是AB中点,∴OC=OA=OB,∴∠BOC=2∠A=60°=∠POQ,∴∠COP=∠BOQ,在△COP和△BOQ中,OC OBOP OQ∠COP∠BOQ ⎧===⎪⎨⎪⎩,∴△COP≌△BOQ(SAS),∴CP=BQ,(2)CP=BQ,理由:如图2,连接OQ,由旋转知,PQ=OP,∠OPQ=60°∴△POQ是等边三角形,∴OP=OQ,∠POQ=60°,在Rt△ABC中,O是AB中点,∴OC=OA=OB,∴∠BOC=2∠A=60°=∠POQ,∴∠COP=∠BOQ,在△COP和△BOQ中,OC OBOP OQ∠COP∠BOQ ⎧===⎪⎨⎪⎩,∴△COP≌△BOQ(SAS),∴CP=BQ,(3)如图3,在Rt△ABC中,∠A=30°,AC,∴BC=AC•tan∠A,过点O作OH⊥BC,∴∠OHB=90°=∠BCA,∴OH∥AB,∵O是AB中点,∴CH=12BC=2,OH=12AC=2,∵∠BPQ=45°,∠OHP=90°,∴∠BPQ=∠PQH,∴PH=OH=,∴CP=PH﹣CH=﹣2=,连接BQ,同(1)的方法得,BQ=CP=.10、模型发现:同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C的位置的不同而发生变化.因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.特别的,当点C位于线段BA的延长线上时,线段BC的长取得最大值,且最大值为b+c(用含b,c的式子表示)(直接填空)模型应用:点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接BD,AE.(1)求证:BD=AE.(2)线段AE长的最大值为5.模型拓展:如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB=8.若AC⊥AB,AC=3,试求OC长的最大值.解:当点C位于线段BA的延长线上时,线段BC的长取得最大值,最大值为b+c,故答案为:线段BA的延长线上;b+c;模型应用:(1)证明:∵△ACD、△BCE都是等边三角形,∴CD=CA=AD,CB=CE,∠ACD=60°,∠BCE=60°,∴∠DCB=∠ACE,在△DCB和△ACE中,CD CA∠DCB∠ACECB CE⎧===⎪⎨⎪⎩,∴△DCB≌△ACE(SAS)∴BD=AE;(2)当点D位于线段BA的延长线上时,线段BD的长取得最大值,最大值为AB+AD=AB+AC=3+2=5,∵AE=BD,∴线段AE长的最大值为5,模型拓展:取AB的中点G,连接OG、CG,在Rt△AOB中,G为AB的中点,∴OG=12AB=4,在Rt△CAG中,CG=5,当点O、G、C在同一条直线上时,OC最大,最大值为4+5=9.11、已知:△ABC中,∠ACB=90°,AC=BC.(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC=3MC,请直接写出DBBC的值.(1)证明:如图1中,∵BE⊥AD于E,∴∠AEF=∠BCF=90°,∵∠AFE=∠CFB,∴∠DAC=∠CBF,∵BC=CA,∴△BCF≌△ACD,∴BF=AD.(2)结论:BD=2CF.理由:如图2中,作EH⊥AC于H.∵∠AHE=∠ACD=∠DAE=90°,∴∠DAC+∠ADC=90°,∠DAC+∠EAH=90°,∴∠DAC=∠AEH,∵AD=AE,∴△ACD≌△EHA,∴CD=AH,EH=AC=BC,∵CB=CA,∴BD=CH,∵∠EHF=∠BCF=90°,∠EFH=∠BFC,EH=BC,∴△EHF≌△BCF,∴FH=CF,∴BD=CH=2CF.(3)如图3中,同法可证BD=2CM.∵AC=3CM,设CM=a,则AC=CB=3a,BD=2a,∴DB BC=2a3a=23.12、已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:∠1=∠2;②如图2,若BF=2AF,连接CF,求证:BF⊥CF;(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求ABFACF △△的值.(1)①证明:如图1中,。
中考数学选择填空压轴题汇编 最值问题(含解析)-人教版初中九年级全册数学试题

2020年中考数学选择填空压轴题汇编:最值问题1.(2020•某某)有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图,∠ABC =90°,点M,N分别在射线BA,BC上,MN长度始终保持不变,MN=4,E为MN的中点,点D到BA,BC 的距离分别为4和2.在此滑动过程中,猫与老鼠的距离DE的最小值为2√5−2 .【解答】解:如图,连接BE,BD.由题意BD=√22+42=2√5,∵∠MBN=90°,MN=4,EM=NE,MN=2,∴BE=12∴点E的运动轨迹是以B为圆心,2为半径的弧,∴当点E落在线段BD上时,DE的值最小,∴DE的最小值为2√5−2.故答案为2√5−2.2.(2020•某某)把二次函数y=ax2+bx+c(a>0)的图象作关于x轴的对称变换,所得图象的解析式为y=﹣a(x﹣1)2+4a,若(m﹣1)a+b+c≤0,则m的最大值是()A.﹣4B.0C.2D.6【解答】解:∵把二次函数y=ax2+bx+c(a>0)的图象作关于x轴的对称变换,所得图象的解析式为y =﹣a(x﹣1)2+4a,∴原二次函数的顶点为(1,﹣4a),∴原二次函数为y=a(x﹣1)2﹣4a=ax2﹣2ax﹣3a,∴b=﹣2a,c=﹣3a,∵(m﹣1)a+b+c≤0,∴(m﹣1)a﹣2a﹣3a≤0,∵a>0,∴m﹣1﹣2﹣3≤0,即m≤6,∴m的最大值为6,故选:D.3.(2020•某某)如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交BB̂于点D,点E为半径OB上一动点.若OB=2,则阴影部分周长的最小值为6√2+B3.【解答】解:如图,作点D关于OB的对称点D′,连接D′C交OB于点E′,连接E′D、OD′,此时E′C+E′C最小,即:E′C+E′C=CD′,由题意得,∠COD=∠DOB=∠BOD′=30°,∴∠COD′=90°,∴CD′=√BB2+BB′2=√22+22=2√2,BB̂的长l=30B×2180=B3,∴阴影部分周长的最小值为2√2+B3=6√2+B3.故答案为:6√2+B3.4.(2020•某某)如图,已知直线y=−√3x+4与x、y轴交于A、B两点,⊙O的半径为1,P为AB上一动点,PQ切⊙O于Q点.当线段PQ长取最小值时,直线PQ交y轴于M点,a为过点M的一条直线,则点P到直线a的距离的最大值为2√3.【解答】解:如图,在直线y=−√3x+4上,x=0时,y=4,当y=0时,x=4√33,∴OB=4,OA=4√33,∴tan∠OBA=BBBB =√33,∴∠OBA=30°,由PQ切⊙O于Q点可知:OQ⊥PQ,∴PQ=√BB2−BB2,由于OQ=1,因此当OP最小时PQ长取最小值,此时OP⊥AB,∴OP=12OB=2,此时PQ=√22−12=√3,BP=√42−22=2√3,∴OQ=12OP,即∠OPQ=30°,若使点P到直线a的距离最大,则最大值为PM,且M位于x轴下方,过点P作PE⊥y轴于点E,∴EP=12BP=√3,∴BE=√(2√3)2−(√3)2=3,∴OE=4﹣3=1,OP,∵OE=12∴∠OPE=30°,∴∠EPM=30°+30°=60°,即∠EMP=30°,∴PM=2EP=2√3.故答案为:2√3.5.(2020•某某)在平面直角坐标系中,长为2的线段CD(点D在点C右侧)在x轴上移动,A(0,2),B(0,4),连接AC,BD,则AC+BD的最小值为()A.2√5B.2√10C.6√2D.3√5【解答】解:设C(m,0),∵CD=2,∴D(m+2,0),∵A(0,2),B(0,4),∴AC+BD=√B2+22+√(B+2)2+42,∴要求AC+BD的最小值,相当于在x轴上找一点P(m,0),使得点P到M(0,2)和N(﹣2,4)的距离和最小,(PM+PN=√B2+22+√(B+2)2+42),如图1中,作点M关于原点O的对称点Q,连接NQ交x轴于P′,连接MP′,此时P′M+P′N的值最小,∵N(﹣2,4),Q(0,﹣2)P′M+P′N的最小值=P′N+P′M=P′N+P′Q=NQ=√22+62=2√10,∴AC+BD的最小值为2√10.故选:B.6.(2020•某某)如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上x﹣3与x轴、y轴分别交于点D、E,则△CDE面积的最小值为 2 .一动点,点C为弦AB的中点,直线y=34【解答】解:如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.∵AC=CB,AM=OM,∴MC=12OB=1,∴点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.∵直线y=34x﹣3与x轴、y轴分别交于点D、E,∴D(4,0),E(0,﹣3),∴OD=4,OE=3,∴DE=√32+42=5,∵∠MDN=∠ODE,∠MND=∠DOE,∴△DNM∽△DOE,∴BBBB =BBBB,∴BB3=35,∴MN=95,当点C与C′重合时,△C′DE的面积最小,最小值=12×5×(95−1)=2,故答案为2.7.(2020•某某)在△ABC中,若AB=6,∠ACB=45°.则△ABC的面积的最大值为9√2+9 .【解答】解:作△ABC的外接圆⊙O,过C作CM⊥AB于M,∵弦AB已确定,∴要使△ABC的面积最大,只要CM取最大值即可,如图所示,当CM过圆心O时,CM最大,∵CM⊥AB,CM过O,∴AM=BM(垂径定理),∴AC=BC,∵∠AOB=2∠ACB=2×45°=90°,∴OM=AM=12AB=12×6=3,∴OA=√BB2+BB2=3√2,∴CM=OC+OM=3√2+3,∴S△ABC=12AB•CM=12×6×(3√2+3)=9√2+9.故答案为:9√2+9.8.(2020•某某)如图,在▱ABCD中,∠B=60°,AB=10,BC=8,点E为边AB上的一个动点,连接ED并延长至点F,使得DF=14DE,以EC、EF为邻边构造▱EFGC,连接EG,则EG的最小值为9√3.【解答】解:作CH⊥AB于点H,∵在▱ABCD中,∠B=60°,BC=8,∴CH=4√3,∵四边形ECGF是平行四边形,∴EF∥CG,∴△EOD∽△GOC,∴BBBB =BBBB=BBBB,∵DF=14DE,∴BBBB =45,∴BBBB =45,∴BBBB =45,∴当EO取得最小值时,EG即可取得最小值,当EO⊥CD时,EO取得最小值,∴CH=EO,∴EO=4√3,∴GO=5√3,∴EG的最小值是9√3,故答案为:9√3.9.(2020•聊城)如图,在直角坐标系中,点A(1,1),B(3,3)是第一象限角平分线上的两点,点C的纵坐标为1,且CA=CB,在y轴上取一点D,连接AC,BC,AD,BD,使得四边形ACBD的周长最小,这个最小周长的值为4+2√5.【解答】解:∵点A(1,1),点C的纵坐标为1,∴AC∥x轴,∴∠BAC=45°,∵CA=CB,∴∠ABC=∠BAC=45°,∴∠C=90°,∵B(3,3)∴C(3,1),∴AC=BC=2,作B关于y轴的对称点E,连接AE交y轴于D,则此时,四边形ACBD的周长最小,这个最小周长的值=AC+BC+AE,过E作EF⊥AC交CA的延长线于F,则EF=BC=2,AF=6﹣2=4,∴AE=√BB2+BB2=√22+42=2√5,∴最小周长的值=AC+BC+AE=4+2√5,故答案为:4+2√5.10.(2020•某某)如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为()A.√2+1B.√2+12C.2√2+1D.2√2−12【解答】解:如图,∵点C为坐标平面内一点,BC=1,∴C在⊙B的圆上,且半径为1,取OD=OA=2,连接CD,∵AM=CM,OD=OA,∴OM是△ACD的中位线,∴OM=12CD,当OM最大时,即CD最大,而D,B,C三点共线时,当C在DB的延长线上时,OM最大,∵OB=OD=2,∠BOD=90°,∴BD=2√2,∴CD=2√2+1,∴OM=12CD=√2+12,即OM的最大值为√2+12;故选:B.11.(2020•某某)如图,在平面直角坐标系中,直线y =﹣x 与双曲线y =B B交于A 、B 两点,P 是以点C (2,2)为圆心,半径长1的圆上一动点,连结AP ,Q 为AP 的中点.若线段OQ 长度的最大值为2,则k 的值为( )A .−12B .−32C .﹣2D .−14【解答】解:点O 是AB 的中点,则OQ 是△ABP 的中位线,当B 、C 、P 三点共线时,PB 最大,则OQ =12BP 最大,而OQ 的最大值为2,故BP 的最大值为4,则BC =BP ﹣PC =4﹣1=3,设点B (m ,﹣m ),则(m ﹣2)2+(﹣m ﹣2)2=32,解得:m 2=12,∴k =m (﹣m )=−12,故选:A .12.(2020•内江)如图,在矩形ABCD 中,BC =10,∠ABD =30°,若点M 、N 分别是线段DB 、AB 上的两个动点,则AM+MN的最小值为15 .【解答】解:作点A关于BD的对称点A′,连接MA′,BA′,过点A′H⊥AB于H.∵BA=BA′,∠ABD=∠DBA′=30°,∴∠ABA′=60°,∴△ABA′是等边三角形,∵四边形ABCD是矩形,∴AD=BC=10,=10√3,在Rt△ABD中,AB=BBBBB30°∵A′H⊥AB,∴AH=HB=5√3,∴A′H=√3AH=15,∵AM+MN=A′M+MN≥A′H,∴AM+MN≥15,∴AM+MN的最小值为15.故答案为15.13.(2020•某某)如图,在△ABC中,∠A=90°,∠B=60°,AB=2,若D是BC边上的动点,则2AD+DC的最小值为 6 .【解答】解:如图所示,作点A关于BC的对称点A',连接AA',A'D,过D作DE⊥AC于E,∵△ABC中,∠BAC=90°,∠B=60°,AB=2,∴BH=1,AH=√3,AA'=2√3,∠C=30°,CD,即2DE=CD,∴Rt△CDE中,DE=12∵A与A'关于BC对称,∴AD=A'D,∴AD+DE=A'D+DE,∴当A',D,E在同一直线上时,AD+DE的最小值等于A'E的长,×2√3=3,此时,Rt△AA'E中,A'E=sin60°×AA'=√32∴AD+DE的最小值为3,即2AD+CD的最小值为6,故答案为:6.。
2023年中考数学高频压轴题突破——二次函数与一次函数(含解析)
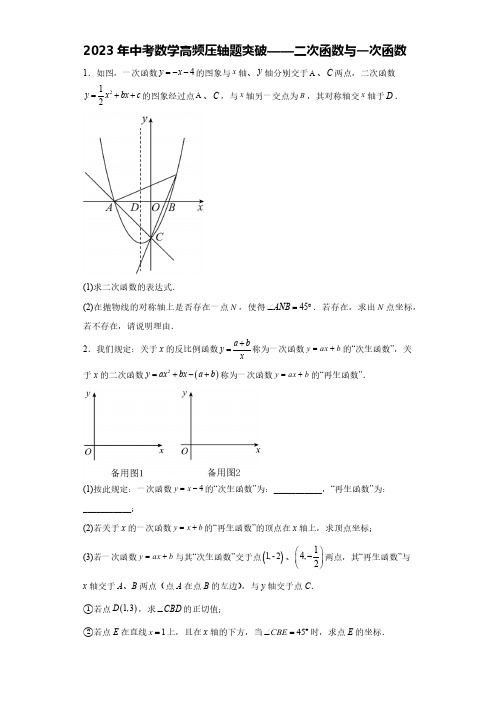
(3)若一次函数
y
ax
b
与其“次生函数”交于点
(1,
-
2)
、
4,
1 2
两点,其“再生函数”与
x 轴交于 A、B 两点(点 A 在点 B 的左边),与 y 轴交于点 C.
①若点 D 1,3 ,求 CBD 的正切值;
②若点 E 在直线 x 1 上,且在 x 轴的下方,当 CBE 45 时,求点 E 的坐标.
10.如图,直线 y 1 x 1 与 x 轴交于点 A,与 y 轴交于点 C,抛物线 y a x 12 2
22 过点 A.
(1)求出抛物线解析式的一般式; (2)抛物线上的动点 D 在一次函数的图象下方,求 VACD 面积的最大值,并求出此时点 D 的坐标; (3)若点 P 为 x 轴上任意一点,在(2)的结论下,求 PD 3 PA 的最小值.
A1,0,B 4,0,C 0,2 ,点 D 是点 C 关于原点的对称点,连接 BD,点 E 是 x 轴上
的一个动点,设点 E 的坐标为 m,0 ,过点 E 作 x 轴的垂线 l 交抛物线于点 P.
(1)求这个二次函数的解析式; (2)当点 E 在线段 OB 上运动时,直线 l 交 BD于点 Q,当四边形 CDQP 是平行四边形时, 求 m 的值; (3)是否存在点 P,使△BDP 是不以 BD为斜边的直角三角形?如果存在请直接写出点 P 的坐标;如果不存在,请说明理由.
2
(1)求二次函数解析式和一次函数解析式; (2)已知点 C 与点 F 关于抛物线的对称轴对称,求点 F 的坐标;
(3)记抛物线点 A 与点 C 之间的图象为 U(不包括点 A 和点 C),若将直线 BE 向上平移 h(h >0)个单位,与图象 U 恰有一个公共点,求 h 的取值范围.
2024哈尔滨中考数学压轴题

在平面直角坐标系中,点A(3, -2)关于x轴对称的点的坐标是:A. (-3, 2)B. (3, 2)(正确答案)C. (-3, -2)D. (2, 3)已知二次函数y = ax2 + bx + c的图像经过点(1,0),(0,3),且对称轴为直线x = 1,则a的值为:A. 1B. -1C. 3(正确答案)D. -3若正n边形的一个内角等于与其相邻外角的2倍,则n的值为:A. 4B. 5C. 6(正确答案)D. 7已知圆O的半径为5,圆心O到直线l的距离为4,则直线l与圆O的位置关系是:A. 相离B. 相切C. 相交(正确答案)D. 无法确定在△ABC中,AB = AC,AD是BC边上的中线,若△ABD的周长为34,△ACD的周长为28,则AB的长度为:A. 12B. 10C. 8(正确答案)D. 6若关于x的一元二次方程kx2 - 6x + 9 = 0有两个不相等的实数根,则k的取值范围为:A. k < 1B. k < 1且k ≠ 0(正确答案)C. k ≤ 1D. k ≤ 1且k ≠ 0已知点P(m, n)和直线y = kx + b,若点P到直线的距离d满足d = |km - n + b| / √(1 + k2) = 3,且点P在直线y = -x + 5上,当k = 2时,b的值为:A. 1或-7B. -1或7(正确答案)C. 2或-8在平行四边形ABCD中,AB = 4,BC = 5,△ABC = 60°,E是边BC上的动点,不与B、C重合,过点E作EF△AB,交AB于点F,连接DE,则△BDE面积的最大值为:A. 10√3B. 8√3C. 6√3(正确答案)D. 4√3已知函数y = (x - 1)2 + k的图像上有三个点(x1, y1),(x2, y2),(x3, y3),若x1 < x2 < x3,且y1 = y2 = y3,则x1 + x3的值为:A. 4B. 3C. 2(正确答案)D. 1。
压轴题17与圆有关的阴影部分面积的计算-2023年中考数学压轴题专项训练(全国通用)(原卷

2023年中考数学压轴题专项训练压轴题17与圆有关的阴影部分面积的计算例1.(2023•长沙模拟)如图,已知AB为⊙O的直径,CD是弦,AB⊥CD,垂足为点E,OF⊥AC,垂足为点F,BE=OF.(1)求证:AC=CD;(2)若BE=4,CD=8√3,求阴影部分的面积.例2.(2022•益阳)如图,C是圆O被直径AB分成的半圆上一点,过点C的圆O的切线交AB的延长线于点P,连接CA,CO,CB.(1)求证:∠ACO=∠BCP;(2)若∠ABC=2∠BCP,求∠P的度数;(3)在(2)的条件下,若AB=4,求图中阴影部分的面积(结果保留π和根号).例3.(2023•武安市一模)如图、点P是△ABC内一点,PD⊥BC,垂足为点D,将线段PD绕点P顺时针̂交于点F,过点P作PN⊥旋转90°得到扇形DPE,过点E作EM⊥PE交AB于点M、连接PM,与DEPM交BC于点N.(1)求证:△PEM≌△PDN;(2)已知PD=3,EM=√3;̂哪个长度更长;①通过计算比较线段PN和DF②计算图中阴影部分的面积(结果保留π).1.(2023•青山区模拟)如图,已知AB是⊙O的直径,E为弦CD的中点.(1)求证:∠BOD=2∠BAC;(2)若CD=AC=4,求阴影部分的面积.2.(2023•黄浦区二模)已知,如图,⊙O的半径为2,半径OP被弦AB垂直平分,交点为Q,点C在圆上,̂=BP̂.且BC(1)求弦AB的长;(2)求图中阴影部分面积(结果保留π).3.(2023•庐阳区校级一模)如图,AB是半圆O的直径,点C在半圆上,点D在AB上,且AC=AD,OC =8,弧BC的度数是60°.(1)求线段OD的长;(2)求图中阴影部分的面积(结果保留根号和π).4.(2022秋•青山湖区校级期末)如图,在矩形ABCD中,AB=10,AD=6,以点A为圆心,AB长为半径画弧,交AD的延长线于点E,以点C为圆心,CB长为半径画弧,交CD于点F.(1)求证:E、F、B在同一条直线上;(2)求阴影部分的面积(结果保留π).̂的度数为60°.5.(2022秋•上城区期末)已知AB是圆O的直径,半径OD⊥BC于点E,BD(1)求证:OE=DE;(2)若OE=1,求图中阴影部分的面积.̂=BĈ.6.(2022秋•嘉兴期末)已知:如图,弦AB,CD相交于⊙O内一点P的直径,AD (1)求证:AB=CD.(2)连接OP,求证:线段OP平分∠BPD.(3)若CP:DP=1:3,OP=√7,AP=√3,求阴影部分面积.7.(2023•武汉模拟)如图,AB,CD是⊙O的两条弦,∠AOB+∠COD=180°.(1)在图(1)中,∠AOB=120°,CD=6,直接写出图中阴影部分的面积;(2)在图(2)中,E是AB的中点,判断OE与CD的数量关系,并证明你的结论.8.(2022•临沭县二模)如图,在⊙O中,AC为⊙O的直径,AB为⊙O的弦,点E是AĈ的中点,过点E 作AB的垂线,交AB于点M,交⊙O于点N,分别连接EB,CN.(1)EM与BE的数量关系是;̂=CN̂;(2)求证:EB(3)若AM=2√3,MB=2,求阴影部分图形的面积.9.(2022•海陵区二模)如图,已知AD是⊙O的直径,B、C为圆上的点,OE⊥AB、BC⊥AD,垂足分别为E、F.(1)求证:2OE=CD;(2)若∠BAD+∠EOF=150°,AD=4,求阴影部分的面积.10.(2022•荆门)如图,已知扇形AOB中,∠AOB=60°,半径R=3.(1)求扇形AOB的面积S及图中阴影部分的面积S阴;̂只有一个交点C,此时我们称⊙O1为扇形(2)在扇形AOB的内部,⊙O1与OA,OB都相切,且与ABAOB的内切圆,试求⊙O1的面积S1.11.(2022•息烽县二模)如图,已知AB是⊙O的直径,点C,D在⊙O上,∠D=60°且AB=6,过O点作OE⊥AC,垂足为E.(1)填空:∠CAB=度;(2)求OE的长;(3)若OE的延长线交⊙O于点F,求弦AF,AC和弧FC围成的图形(阴影部分)的面积S.12.(2022•南漳县模拟)如图,AB为⊙O的直径,弦CD垂直平分半径OA,垂足为E,弦CF交直径AB于点G,连接DF,∠CDF=75°,CD=2√3.(1)求⊙O的半径;̂围成的阴影部分的面积.(2)求线段GB,GF与BF13.(2022•石家庄模拟)如图,Rt△ABC中∠ACB=90°,AC=4,且BC>AC,以边AC为直径的⊙O交斜边AB于D,AD=2,点E为AC左侧半圆上一点,连接AE,DE,CD.(1)求∠AED的度数.(2)求DB的长.(3)求图中阴影部分的面积.14.(2022•高唐县二模)如图,在菱形ABCD中,对角线AC,BD交于点O,∠BAO=30°,AC=8.过点O作OH⊥AB于点H,以点O为圆心,OH为半径的半圆交AC于点M.(1)求图中阴影部分的面积;(2)点P是BD上的一个动点(点P不与点B,D重合),当PH+PM的值最小时,求PD的长度.15.(2021•高港区校级三模)如图,在△ABC中,∠C=90°,以点C为圆心,CA长为半径的圆交AB于点D.̂的度数;(1)若∠B=24°,求AD(2)若D是AB的中点,AB=3,求阴影部分的面积;(3)若AD•AB=12,求AC的值.16.(2021•开平区一模)如图,∠AOB 内有一点P ,PC ⊥OA ,垂足为C ,以P 为圆心PC 为半径画14⊙P ,与OB 交于点E ,(1)过点D 作PD 的垂线与OB 交于点M ,连接PM ,过圆心P 作PN ⊥PM 交OA 于点N ,求证△PMN 是等腰直角三角形.(2)若PC =2,∠DPE =15°,计算扇形PEC 的面积(结果保留π).17.(2022•柯城区二模)如图,在⊙O 中,AC 为⊙O 的直径,AB 为⊙O 的弦,点E 是AĈ的中点,过点E 作AB 的垂线,交AB 于点M ,交⊙O 于点N ,分别连接EB ,CN .(1)EM 与BE 的数量关系是 ;(2)求证:EB̂=CN ̂; (3)若AM =√3,MB =1,求阴影部分图形的面积.18.(2022•龙岗区模拟)如图,四边形ABCD 中,AD ∥BC ,∠BAD =90°,CB =CD ,连接BD ,以点B 为圆心,BA 长为半径作⊙B ,交BD 于点E .(1)试判断CD 与⊙B 的位置关系,并说明理由;(2)若AB =2√3,∠BCD =60°,求图中阴影部分的面积.19.(2021•南昌模拟)如图,在Rt△ABC中,∠ACB=90°,O在斜边AB上,且AO=AC,连接CO,并延长至D,使∠D=∠OCB,以O为圆心,OD为半径画圆,交DB延长线于E点.(1)求证:BD=BE;(2)已知AC=1cm,BC=√3cm.①连接CE,过B作BF⊥EC于F点,求线段BF的长;②求图中阴影部分面积.20.(2022•衢州)如图,C,D是以AB为直径的半圆上的两点,∠CAB=∠DBA,连结BC,CD.(1)求证:CD∥AB.(2)若AB=4,∠ACD=30°,求阴影部分的面积.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年7月施王金羽的初中数学组卷2013年7月施王金羽的初中数学组卷一.解答题(共30小题)1.(2013•郑州模拟)如图1所示,已知二次函数y=ax2﹣6ax+c与x轴分别交于点A(2,0)、B(4,0),与y轴交于点C(0,﹣8t)(t>0).(1)求a、c的值及抛物线顶点D的坐标(用含t的代数式表示);(2)如图1,连接AC,将△OAC沿直线AC翻折,若点O的对应点O′恰好落在该抛物线的对称轴上,求实数t的值;(3)如图2,在正方形EFGH中,点E、F的坐标分别是(4,﹣4)、(4,﹣3),边HG位于边EF的右侧.若点P 是边EF或边FG上的任意一点(不与E、F、G重合),请你说明以PA、PB、PC、PD的长度为边长不能构成平行四边形;(4)将(3)中的正方形EFGH水平移动,若点P是正方形边FG或EH上任意一点,在水平移动过程中,是否存在点P,使以PA、PB、PC、PD的长度为边长构成平行四边形,其中PA、PB为对边.若存在,请直接写出t的值;若不存在,请说明理由.2.(2013•郑州模拟)如图,抛物线与直线AB交于点A(﹣1,0),B(4,).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.(1)求抛物线的解析式;(2)设点D的横坐标为m,△ADB的面积为S,求S关于m的函数关系式,并求出当S取最大值时的点C的坐标;(3)当点D为抛物线的顶点时,若点P是抛物线上的动点,点Q是直线AB上的动点,判断有几个位置能使以点P,Q,C,D为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.3.(2013•舟山)如图,在平面直角坐标系xOy中,抛物线y=(x﹣m)2﹣m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.(1)当m=2时,求点B的坐标;(2)求DE的长?(3)①设点D的坐标为(x,y),求y关于x的函数关系式?②过点D作AB的平行线,与第(3)①题确定的函数图象的另一个交点为P,当m为何值时,以,A,B,D,P为顶点的四边形是平行四边形?4.(2013•闸北区一模)已知:如图,二次函数的图象与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为Q,直线QB与y轴交于点E.(1)求点E的坐标;(2)在x轴上方找一点C,使以点C、O、B为顶点的三角形与△BOE相似,请直接写出点C的坐标.5.(2013•益阳)阅读材料:如图1,在平面直角坐标系中,A、B两点的坐标分别为A(x1,y1),B(x2,y2),AB 中点P的坐标为(x p,y p).由x p﹣x1=x2﹣x p,得x p=,同理,所以AB的中点坐标为.由勾股定理得AB2=,所以A、B两点间的距离公式为.注:上述公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:如图2,直线l:y=2x+2与抛物线y=2x2交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.(1)求A、B两点的坐标及C点的坐标;(2)连结AB、AC,求证△ABC为直角三角形;(3)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.6.(2013•宜昌模拟)抛物线y=ax2+bx+c中,b,c是非零常数,无论a为何值(0除外),其顶点M一定在直线y=kx+1上,这条直线和x轴,y轴分别交于点E,A,且OA=OE.(1)求k的值;(2)求证:这条抛物线经过点A;(3)经过点A的另一条直线y=mx+n和这条抛物线只有一个公共点,经过点M作x轴的平行线和直线y=mx+n交于点B,经过点B作x轴的垂线和这条抛物线交于点C,和直线y=kx+1交于点D,探索CD和BC的数量关系.7.(2013•宜昌)如图1,平面之间坐标系中,等腰直角三角形的直角边BC在x轴正半轴上滑动,点C的坐标为(t,0),直角边AC=4,经过O,C两点做抛物线y1=ax(x﹣t)(a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)(1)填空:用含t的代数式表示点A的坐标及k的值:A_________,k=_________;(2)随着三角板的滑动,当a=时:①请你验证:抛物线y1=ax(x﹣t)的顶点在函数y=的图象上;②当三角板滑至点E为AB的中点时,求t的值;(3)直线OA与抛物线的另一个交点为点D,当t≤x≤t+4,|y2﹣y1|的值随x的增大而减小,当x≥t+4时,|y2﹣y1|的值随x的增大而增大,求a与t的关系式及t的取值范围.8.(2013•燕山区一模)己知二次函数(t>1)的图象为抛物线C1.(1)求证:无论t取何值,抛物线C1与y轴总有两个交点;(2)已知抛物线C1与x轴交于A、B两点(A在B的左侧),将抛物线C1作适当的平移,得抛物线C2:,平移后A、B的对应点分别为D(m,n),E(m+2,n),求n的值.(3)在(2)的条件下,将抛物线C2位于直线DE下方的部分沿直线DE向上翻折后,连同C2在DE上方的部分组成一个新图形,记为图形G,若直线(b<3)与图形G有且只有两个公共点,请结合图象求b的取值范围.9.(2013•盐都区一模)已知二次函数y=ax2+bx﹣2的图象与x轴交于A、B两点,与y轴交于点C,点A的坐标为(4,0),且当x=﹣2和x=5时二次函数的函数值y相等.(1)求实数a、b的值;(2)如图1,动点E、F同时从A点出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.①是否存在某一时刻t,使得△DCF为直角三角形?若存在,求出t的值;若不存在,请说明理由.②设△DEF与△ABC重叠部分的面积为S,求S关于t的函数关系式;10.(2013•玄武区一模)在函数中,我们规定:当自变量增加一个单位时,因变量的增加量称为函数的平均变化率.例如,对于函数y=3x+1,当自变量x增加1时,因变量y=3(x+1)+1=3x+4,较之前增加3,故函数y=3x+1的平均变化率为3.(1)①列车已行驶的路程s(km)与行驶的时间t(h)的函数关系式是s=300t,该函数的平均变化率是_________;其蕴含的实际意义是_________;②飞机着陆后滑行的距离y(m)与滑行的时间x(s)的函数关系式是y=﹣1.5x+60x,求该函数的平均变化率;(2)通过比较(1)中不同函数的平均变化率,你有什么发现;(3)如图,二次函数y=ax2+bx+c的图象经过第一象限内的三点A、B、C,过点A、B、C作x轴的垂线,垂足分别为D、E、F,AM⊥BE,垂足为M,BN⊥CF,垂足为N,DE=EF,试探究△AMB与△BNC面积的大小关系,并说明理由.11.(2013•相城区模拟)如图,已知二次函数y=x2+bx+c的图象与x轴交于A,B两点,交y轴于点C,过点C作CD⊥y轴交该抛物线于点D,且AB=2,CD=4.(1)该抛物线的对称轴为_________,B点坐标为(_________),CO=_________;(2)若P为线段OC上的一个动点,四边形PBQD是平行四边形,连接PQ.试探究:①是否存在这样的点P,使得PQ2=PB2+PD2?若存在,求出此时点P的坐标;若不存在,请说明理由.②当PQ长度最小时,求出此时点Q的坐标.12.(2013•咸宁)如图,已知直线y=x+1与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.(1)点C的坐标是_________线段AD的长等于_________;(2)点M在CD上,且CM=OM,抛物线y=x2+bx+c经过点C,M,求抛物线的解析式;(3)如果点E在y轴上,且位于点C的下方,点F在直线AC上,那么在(2)中的抛物线上是否存在点P,使得以C,E,F,P为顶点的四边形是菱形?若存在,请求出该菱形的周长l;若不存在,请说明理由.13.(2013•武汉模拟)已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2,以O 为原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.(1)求点C的坐标和过O、C、A三点的抛物线的解析式;(2)P是此抛物线的对称轴上一动点,当以P、O、C为顶点的三角形是等腰三角形时,请直接写出点P的坐标;(3)M(x,y)是此抛物线上一个动点,当△MOB的面积等于△OAB面积时,求M的坐标.14.(2013•泰州一模)如图,在平面直角坐标系中,O是坐标原点,直线y=3x+9与x轴、y轴分别交于A、C两点,抛物线经过A、C两点,与x轴的另一个交点为点B,动点P从点A出发沿AB以每秒3个单位长度的速度向点B运动,动点Q从点B出发沿BC以每秒3个单位长度的速度向点C运动,动点N从点C出发沿CA以每秒个单位长度的速度向点A运动,点P、Q、N同时出发、同时停止,设运动时间为t(0<t<5)秒.(1)求抛物线的解析式;(2)判断△ABC的形状;(3)以OC为直径的⊙O′与BC交于点M,求当t为何值时,PM与⊙O′相切?请说明理由;(4)在点P、Q、N运动的过程中,是否存在△NCQ为直角三角形的情形?若存在,求出相应的t值;若不存在,请说明理由.15.(2013•威海)如图,在平面直角坐标系中,直线y=x+与直线y=x交于点A,点B在直线y=x+上,∠BOA=90°.抛物线y=ax2+bx+c过点A,O,B,顶点为点E.(1)求点A,B的坐标;(2)求抛物线的函数表达式及顶点E的坐标;(3)设直线y=x与抛物线的对称轴交于点C,直线BC交抛物线于点D,过点E作FE∥x轴,交直线AB于点F,连接OD,CF,CF交x轴于点M.试判断OD与CF是否平行,并说明理由.16.(2013•咸宁)阅读理解:如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;拓展探究:(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.17.(2011•衡阳)如图,在矩形ABCD中,AD=4cm,AB=m(m>4),点P是AB边上的任意一点(不与点A、B 重合),连接PD,过点P作PQ⊥PD,交直线BC于点Q.(1)当m=10时,是否存在点P使得点Q与点C重合?若存在,求出此时AP的长;若不存在,说明理由;(2)连接AC,若PQ∥AC,求线段BQ的长(用含m的代数式表示);(3)若△PQD为等腰三角形,求以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式,并写出m的取值范围.18.(2011•常州)在平面直角坐标系XOY中,直线l1过点A(1,0)且与y轴平行,直线l2过点B(0,2)且与x轴平行,直线l1与直线l2相交于点P.点E为直线l2上一点,反比例函数(k>0)的图象过点E与直线l1相交于点F.(1)若点E与点P重合,求k的值;(2)连接OE、OF、EF.若k>2,且△OEF的面积为△PEF的面积的2倍,求E点的坐标;(3)是否存在点E及y轴上的点M,使得以点M、E、F为顶点的三角形与△PEF全等?若存在,求E点坐标;若不存在,请说明理由.19.(2013•桥东区二模)如图,Rt△ABC在平面直角坐标系中,BC在x轴上,B(﹣1,0)、A(0,2),AC⊥AB.(1)求线段OC的长.(2)点P从B点出发以每秒4个单位的速度沿x轴正半轴运动,点Q从A点出发沿线段AC以个单位每秒速度向点C运动,当一点停止运动,另一点也随之停止,设△CPQ的面积为S,两点同时运动,运动的时间为t秒,求S与t之间关系式,并写出自变量取值范围.(3)Q点沿射线AC按原速度运动,⊙G过A、B、Q三点,是否有这样的t值使点P在⊙G上?如果有求t值,如果没有说明理由.20.(2013•济南一模)如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.(1)求AC、BC的长;(2)设点P的运动时间为x(秒),△PBQ的面积为y(cm2),当△PBQ存在时,求y与x的函数关系式;(3)当点Q在CA上运动,使PQ⊥AB时,以点B、P、Q为顶点的三角形与△ABC是否相似,请说明理由.21.(2011•江西模拟)某班甲、乙、丙三位同学进行了一次用正方形纸片折叠探究相关数学问题的课题学习活动.活动情境:如图2,将边长为8cm的正方形纸片ABCD沿EG折叠(折痕EG分别与AB、DC交于点E、G),使点B落在AD 边上的点F处,FN与DC交于点M处,连接BF与EG交于点P.所得结论:当点F与AD的中点重合时:(如图1)甲、乙、丙三位同学各得到如下一个正确结论(或结果):甲:△AEF的边AE=_________cm,EF=_________cm;乙:△FDM的周长为16cm;丙:EG=BF.你的任务:(1)填充甲同学所得结果中的数据;(2)写出在乙同学所得结果的求解过程;(3)当点F在AD边上除点A、D外的任何一处(如图2)时:①试问乙同学的结果是否发生变化?请证明你的结论;②丙同学的结论还成立吗?若不成立,请说明理由,若你认为成立,先证明EG=BF,再求出S(S为四边形AEGD 的面积)与x(AF=x)的函数关系式,并问当x为何值时,S最大?最大值是多少?22.(2009•白下区一模)如图①,已知平面内一点P与一直线l,如果过点P作直线l′⊥l,垂足为P′,那么垂足P′叫做点P在直线l上的射影;如果线段PQ的两个端点P和Q在直线l上的射影分别为点P′和Q′,那么线段P′Q′叫做线段PQ在直线l上的射影.(1)如图②,E、F为线段AD外两点,EB⊥AD,FC⊥AD,垂足分别为B、C.则E点在AD上的射影是_________点,A点在AD上的射影是_________点,线段EF在AD上的射影是_________,线段AE在AD上的射影是_________;(2)根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)23.(2010•石家庄二模)如图所示,在菱形ABCD中,对角线AC、BD相交于点O,AC=8,BD=6.现有两动点P、Q分别从A、C两点同时出发,点P以每秒1个单位长的速度由点A向点D做匀速运动,点Q沿折线CB﹣BA向点A做匀速运动.(1)菱形ABCD的边长为_________;(2)若点Q的速度为每秒2个单位长,设运动时间为t秒.①求△APQ的面积S关于t的函数关系式;②当t为何值时,S有最大值,最大值是多少?(3)若点Q的速度为每秒a个单位长(a≤),当t=4秒时,△APQ是等腰三角形,请直接写出a的值.24.(2010•双鸭山)已知在Rt△ABC中,∠ABC=90°,∠A=30°,点P在AC上,且∠MPN=90°.当点P为线段AC的中点,点M、N分别在线段AB、BC上时(如图1),过点P作PE⊥AB于点E,PF⊥BC于点F,可证Rt△PME∽Rt△PNF,得出PN=PM.(不需证明)当PC=PA,点M、N分别在线段AB、BC或其延长线上,如图2、图3这两种情况时,请写出线段PN、PM之间的数量关系,并任选取一给予证明.25.(2009•襄阳)如图,已知:在⊙O中,直径AB=4,点E是OA上任意一点,过E作弦CD⊥AB,点F是上一点,连接AF交CE于H,连接AC、CF、BD、OD.(1)求证:△ACH∽△AFC;(2)猜想:AH•AF与AE•AB的数量关系,并说明你的猜想;(3)探究:当点E位于何处时,S△AEC:S△BOD=1:4,并加以说明.26.(2013•自贡)将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;(2)在图②中,若AP1=2,则CQ等于多少?(3)如图③,在B1C上取一点E,连接BE、P1E,设BC=1,当BE⊥P1B时,求△P1BE面积的最大值.27.(2013•温州)如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0.8),点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴上的一动点,连接CD,DE,以CD,DE为边作▱CDEF.(1)当0<m<8时,求CE的长(用含m的代数式表示);(2)当m=3时,是否存在点D,使▱CDEF的顶点F恰好落在y轴上?若存在,求出点D的坐标;若不存在,请说明理由;(3)点D在整个运动过程中,若存在唯一的位置,使得▱CDEF为矩形,请求出所有满足条件的m的值.28.(2013•衢州)【提出问题】(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.【类比探究】(1)中结论∠ABC=∠ACN (2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,还成立吗?请说明理由.【拓展延伸】(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.29.(2013•遵义)如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm 的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.30.(2013•苏州)如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm,点E、F、G分别从A、B、C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为1.5cm/s,当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB′F.设点E、F、G运动的时间为t(单位:s).(1)当t=_________s时,四边形EBFB′为正方形;(2)若以点E、B、F为顶点的三角形与以点F,C,G为顶点的三角形相似,求t的值;(3)是否存在实数t,使得点B′与点O重合?若存在,求出t的值;若不存在,请说明理由.2013年7月施王金羽的初中数学组卷参考答案与试题解析一.解答题(共30小题)1.(2013•郑州模拟)如图1所示,已知二次函数y=ax2﹣6ax+c与x轴分别交于点A(2,0)、B(4,0),与y轴交于点C(0,﹣8t)(t>0).(1)求a、c的值及抛物线顶点D的坐标(用含t的代数式表示);(2)如图1,连接AC,将△OAC沿直线AC翻折,若点O的对应点O′恰好落在该抛物线的对称轴上,求实数t的值;(3)如图2,在正方形EFGH中,点E、F的坐标分别是(4,﹣4)、(4,﹣3),边HG位于边EF的右侧.若点P 是边EF或边FG上的任意一点(不与E、F、G重合),请你说明以PA、PB、PC、PD的长度为边长不能构成平行四边形;(4)将(3)中的正方形EFGH水平移动,若点P是正方形边FG或EH上任意一点,在水平移动过程中,是否存在点P,使以PA、PB、PC、PD的长度为边长构成平行四边形,其中PA、PB为对边.若存在,请直接写出t的值;若不存在,请说明理由.得,OC=,∴,.t=或或t=或2.(2013•郑州模拟)如图,抛物线与直线AB交于点A(﹣1,0),B(4,).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.(1)求抛物线的解析式;(2)设点D的横坐标为m,△ADB的面积为S,求S关于m的函数关系式,并求出当S取最大值时的点C的坐标;(3)当点D为抛物线的顶点时,若点P是抛物线上的动点,点Q是直线AB上的动点,判断有几个位置能使以点P,Q,C,D为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.CD﹣﹣+时,取最大值抛物线与直线)∴x)y=.,)的纵坐标是(﹣m)﹣m+2S=CD×(﹣m+2()(﹣取最大值,此时,))),﹣x)x+﹣﹣x=3,﹣x)x+∴x+x,﹣),﹣x),﹣+2x+)﹣x﹣﹣(﹣+2x+)﹣,)3.(2013•舟山)如图,在平面直角坐标系xOy中,抛物线y=(x﹣m)2﹣m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.(1)当m=2时,求点B的坐标;(2)求DE的长?(3)①设点D的坐标为(x,y),求y关于x的函数关系式?②过点D作AB的平行线,与第(3)①题确定的函数图象的另一个交点为P,当m为何值时,以,A,B,D,P为顶点的四边形是平行四边形?m代入﹣y=(m﹣(﹣m∴,即:,,﹣m﹣•+4x x+4(﹣m m m,﹣x x+4﹣×(﹣m mx x+4m m+44.(2013•闸北区一模)已知:如图,二次函数的图象与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为Q,直线QB与y轴交于点E.(1)求点E的坐标;(2)在x轴上方找一点C,使以点C、O、B为顶点的三角形与△BOE相似,请直接写出点C的坐标.,得,时,=1时,,即=,则时,,即=,解得,时,=1=,即=,或=OC=.∵y=y=,x=,即(,,)(,()5.(2013•益阳)阅读材料:如图1,在平面直角坐标系中,A、B两点的坐标分别为A(x1,y1),B(x2,y2),AB 中点P的坐标为(x p,y p).由x p﹣x1=x2﹣x p,得x p=,同理,所以AB的中点坐标为.由勾股定理得AB2=,所以A、B两点间的距离公式为.注:上述公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:如图2,直线l:y=2x+2与抛物线y=2x2交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.(1)求A、B两点的坐标及C点的坐标;(2)连结AB、AC,求证△ABC为直角三角形;(3)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.)解:由,)(3+,,,)|=点的坐标为(,)=CG=CG=AH=||=..6.(2013•宜昌模拟)抛物线y=ax2+bx+c中,b,c是非零常数,无论a为何值(0除外),其顶点M一定在直线y=kx+1上,这条直线和x轴,y轴分别交于点E,A,且OA=OE.(1)求k的值;(2)求证:这条抛物线经过点A;(3)经过点A的另一条直线y=mx+n和这条抛物线只有一个公共点,经过点M作x轴的平行线和直线y=mx+n交于点B,经过点B作x轴的垂线和这条抛物线交于点C,和直线y=kx+1交于点D,探索CD和BC的数量关系.,)代入,),),)BC=CD=|7.(2013•宜昌)如图1,平面之间坐标系中,等腰直角三角形的直角边BC在x轴正半轴上滑动,点C的坐标为(t,0),直角边AC=4,经过O,C两点做抛物线y1=ax(x﹣t)(a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)(1)填空:用含t的代数式表示点A的坐标及k的值:A(t,4),k=(k>0);(2)随着三角板的滑动,当a=时:①请你验证:抛物线y1=ax(x﹣t)的顶点在函数y=的图象上;②当三角板滑至点E为AB的中点时,求t的值;(3)直线OA与抛物线的另一个交点为点D,当t≤x≤t+4,|y2﹣y1|的值随x的增大而减小,当x≥t+4时,|y2﹣y1|的值随x的增大而增大,求a与t的关系式及t的取值范围.y=y=y==横坐标是+4(a=x,其顶点坐标为(,﹣)x=×﹣,即点(,﹣y=时,抛物线y=EK=BC=2∴,则x=ax+4+t+t(8.(2013•燕山区一模)己知二次函数(t>1)的图象为抛物线C1.(1)求证:无论t取何值,抛物线C1与y轴总有两个交点;(2)已知抛物线C1与x轴交于A、B两点(A在B的左侧),将抛物线C1作适当的平移,得抛物线C2:,平移后A、B的对应点分别为D(m,n),E(m+2,n),求n的值.(3)在(2)的条件下,将抛物线C2位于直线DE下方的部分沿直线DE向上翻折后,连同C2在DE上方的部分组成一个新图形,记为图形G,若直线(b<3)与图形G有且只有两个公共点,请结合图象求b的取值范围.二次函数为:,图形,此时,图形:的取值范围是9.(2013•盐都区一模)已知二次函数y=ax2+bx﹣2的图象与x轴交于A、B两点,与y轴交于点C,点A的坐标为(4,0),且当x=﹣2和x=5时二次函数的函数值y相等.(1)求实数a、b的值;(2)如图1,动点E、F同时从A点出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.①是否存在某一时刻t,使得△DCF为直角三角形?若存在,求出t的值;若不存在,请说明理由.②设△DEF与△ABC重叠部分的面积为S,求S关于t的函数关系式;)由题意得,﹣y=x xAC=2,∴==EF=AE=AB=÷;t=;t=或t=时,重叠部分为S=×)当<,∴((×t+;时,重叠部分为S=×10.(2013•玄武区一模)在函数中,我们规定:当自变量增加一个单位时,因变量的增加量称为函数的平均变化率.例如,对于函数y=3x+1,当自变量x增加1时,因变量y=3(x+1)+1=3x+4,较之前增加3,故函数y=3x+1的平均变化率为3.(1)①列车已行驶的路程s(km)与行驶的时间t(h)的函数关系式是s=300t,该函数的平均变化率是300;其蕴含的实际意义是列车的速度;②飞机着陆后滑行的距离y(m)与滑行的时间x(s)的函数关系式是y=﹣1.5x2+60x,求该函数的平均变化率;(2)通过比较(1)中不同函数的平均变化率,你有什么发现;(3)如图,二次函数y=ax2+bx+c的图象经过第一象限内的三点A、B、C,过点A、B、C作x轴的垂线,垂足分别为D、E、F,AM⊥BE,垂足为M,BN⊥CF,垂足为N,DE=EF,试探究△AMB与△BNC面积的大小关系,并说明理由.=BN11.(2013•相城区模拟)如图,已知二次函数y=x2+bx+c的图象与x轴交于A,B两点,交y轴于点C,过点C作CD⊥y轴交该抛物线于点D,且AB=2,CD=4.(1)该抛物线的对称轴为直线x=2,B点坐标为(3,0),CO=3;(2)若P为线段OC上的一个动点,四边形PBQD是平行四边形,连接PQ.试探究:①是否存在这样的点P,使得PQ2=PB2+PD2?若存在,求出此时点P的坐标;若不存在,请说明理由.②当PQ长度最小时,求出此时点Q的坐标.=2=3﹣∴,=,×=×=7)12.(2013•咸宁)如图,已知直线y=x+1与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.(1)点C的坐标是(0,3)线段AD的长等于4;(2)点M在CD上,且CM=OM,抛物线y=x2+bx+c经过点C,M,求抛物线的解析式;(3)如果点E在y轴上,且位于点C的下方,点F在直线AC上,那么在(2)中的抛物线上是否存在点P,使得以C,E,F,P为顶点的四边形是菱形?若存在,请求出该菱形的周长l;若不存在,请说明理由.x+1,),∴﹣CP=CH=PH﹣x+3﹣x=CP=CH=×=为:.﹣x﹣+∴xx=﹣x=(4=18或﹣13.(2013•武汉模拟)已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2,以O 为原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.(1)求点C的坐标和过O、C、A三点的抛物线的解析式;(2)P是此抛物线的对称轴上一动点,当以P、O、C为顶点的三角形是等腰三角形时,请直接写出点P的坐标;(3)M(x,y)是此抛物线上一个动点,当△MOB的面积等于△OAB面积时,求M的坐标.的距离等于OC=OA==2点的坐标为(,解得,,)或()或()或(,3+2OA=2,AR=2的距离等于ON=xy=,,,()2(﹣)14.(2013•泰州一模)如图,在平面直角坐标系中,O是坐标原点,直线y=3x+9与x轴、y轴分别交于A、C两点,抛物线经过A、C两点,与x轴的另一个交点为点B,动点P从点A出发沿AB以每秒3个单位长度的速度向点B运动,动点Q从点B出发沿BC以每秒3个单位长度的速度向点C运动,动点N从点C出发沿CA以每秒个单位长度的速度向点A运动,点P、Q、N同时出发、同时停止,设运动时间为t(0<t<5)秒.(1)求抛物线的解析式;(2)判断△ABC的形状;(3)以OC为直径的⊙O′与BC交于点M,求当t为何值时,PM与⊙O′相切?请说明理由;(4)在点P、Q、N运动的过程中,是否存在△NCQ为直角三角形的情形?若存在,求出相应的t值;若不存在,请说明理由.,则﹣+OB=×t=.AC=,∴,,t=∴,,t=t=或,使15.(2013•威海)如图,在平面直角坐标系中,直线y=x+与直线y=x交于点A,点B在直线y=x+上,∠BOA=90°.抛物线y=ax2+bx+c过点A,O,B,顶点为点E.(1)求点A,B的坐标;(2)求抛物线的函数表达式及顶点E的坐标;(3)设直线y=x与抛物线的对称轴交于点C,直线BC交抛物线于点D,过点E作FE∥x轴,交直线AB于点F,连接OD,CF,CF交x轴于点M.试判断OD与CF是否平行,并说明理由.x+与直线列出方程组,则y=与直线,,y=x+∴,∴x x y=).,﹣).,)()代入,得x+.﹣x+=﹣=代入x+,,DON=.,﹣)的纵坐标是﹣代入y=x+,的坐标是(﹣,﹣)EF=+=CE==,CFE=,16.(2013•咸宁)阅读理解:如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;拓展探究:(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.。
