Ch120603e2数学分析
数学分析与高等代数考研真题详解--中科院卷

∫∫∫ 算积分 I = ex+y+zdxdydz . D
4.(15
⎛ 分)定义向量场 F (x, y) = ⎜⎜⎝
xe x2 + y2 ,
x2 + y2
ye
x2 + y2
⎞ ⎟, x2 + y2 > 0
x2 + y2 ⎟⎠
证明 F (x, y) 是有势
场, 并求出 F (x, y) 的一个势函数.
∑ 5.(25
博士家园考研丛书 (2010 版)
全国重点名校数学专业考研真题及解答
数学分析与高等代数 考研真题详解
中国科学院数学专卷 博士家园 编著
博士家园系列内部资料
《 博士家园数学专业考研丛书》
编委会
这是一本很多数学考研人期待已久的参考书,对于任何一个想通过考取重点院校的研究
生来进一步深造的同学来说,历年的各个院校的真题的重要性是显而易见的。为了帮助广大
多更新的信息与资源建立了专业网站——博士家园网站。本站力图成为综合性全国数学信息
交换的门户网站,旨在为科研人员和数学教师服务,提供与数学研究和数学教学有关的一切
有价值的信息和国内外优秀数学资源检索,经过几年的不懈努力,成为国内领先、国际一流
的数学科学信息交流中心之一。由于一般的院校可能提供一些往年试题,但是往往陈旧或者
2
博士家园系列内部资料
数学分析与高等代数考研真题详解
中国科学院考研数学专卷
目录
中国科学院考研数学专卷...............................................................................................................3 2000 年招收硕士研究生入学考试《数学分析》试题 ..................................................................3 2000 年招收硕士研究生入学考试《数学分析》试题解答 ..........................................................4 2000 年招收硕士研究生入学考试《线代解几》试题 ..................................................................6 2000 年招收硕士研究生入学考试《线代解几》解答 ..................................................................7 2001 年中科院数学与系统科学研究所《高等代数》试题及解答 ............................................10 2002 年招收硕士研究生入学考试《高等代数》试题 ................................................................16 2003 年招收硕士研究生入学考试《数学分析》试题 ................................................................17 2003 年招收硕士研究生入学考试《数学分析》试题解答 ........................................................18 2003 年招收硕士研究生入学考试《高等代数》试题 ................................................................24 2003 年招收硕士研究生入学考试《高等代数》试题解答 ........................................................25 2004 年招收硕士研究生入学考试《数学分析》试题 ................................................................28 2004 年招收硕士研究生入学考试《数学分析》试题解答 ........................................................29 2004 年招收硕士研究生入学考试《高等代数》试题 ................................................................32 2004 年招收硕士研究生入学考试《高等代数》试题解答 ........................................................33 2005 年招收硕士研究生入学考试《数学分析》试题及解答 ....................................................37 2005 年招收硕士研究生入学考试《高等代数》试题 ................................................................41 2005 年招收硕士研究生入学考试《高等代数》试题解答 ........................................................43 2006 年招收硕士研究生入学考试《数学分析》试题 ................................................................51 2006 年招收硕士研究生入学考试《数学分析》试题解答 ........................................................52 2006 年招收硕士研究生入学考试《高等代数》试题 ................................................................55 2006 年招收硕士研究生入学考试《高等代数》试题解答 ........................................................57 2007 年招收硕士研究生入学考试《数学分析》试题及解答 ....................................................64 2007 年招收硕士研究生入学考试《高等代数》试题及解答 ....................................................69 2008 年招收硕士研究生入学考试《数学分析》部分试题及解答 ............................................75 2009 年招收硕士研究生入学考试《高等代数》两试题及解答 ................................................78 2010 年招收硕士研究生入学考试《高等代数》试题及解答 ....................................................80 2010 年招收硕士研究生入学考试《数学分析》试题及解答 ....................................................86 中科院数学所复试时遇到的题目.................................................................................................96
数学分析选讲习题答案。我们学校自己编的《数学分析选讲》讲义习题解答,不要乱评论。OK?

27. 28. 29. 30. 31. 32. 33. 34. 35.
Burkill, J.C., and Burkill,H., A Second Course in Mathematical Analysis, London, Cambridge, 1970. Gelbaum, B., Problems in Analysis, New York, Springer-Verlag, 1982. Klambauer, G., Problems and Propositions in Analysis, New York, Marcel Dekker, 1979. Lang, S., Undergraduate Analysis, New York, Springer-Verlag, 1983. Pö lya, G. and Szegö , G., Problems and Theorems in Analysis, Vol.1, Berlin, Springer-Verlag, 1972. Smith, K. T., Primer of Modern Analysis, New York, Springer-Verlag, 1983. Stromberg, K.R., An Introduction to Classical Analysis, Belmont, Wadsworth, 1981. Van Rooij, A. C. M., and Schikhof, W. H. A Second Course on Real Functions, London, Cambridge, 1982. Lewin, J. W., Amer. Math. Monthly, 93(1986), 395 397.
< 1 (x12 + x1+ 1) | x n 1 | ,极限为 1. 7 n n n 14. 由平均不等式, 1 kak n !( ak )1 / n . n k 1 k 1 15. 由 F (1, y) = ½ f (y 1) = ½ y2 y + 5 得 f (t ) = t + 9, 故 xn+1 =
数学分析C(2)课程教学大纲

学时 0 6 6 14 10 14 12 10 8 8 8
教学方式 自学 面授 面授 面授 面授 面授 面授 面授 面授 面授 面授
作业及要求 习题 习题 习题 习题 习题 习题 习题 习题 习题 习题 习题
基本要求 完成要求 完成要求 完成要求 完成要求 完成要求 完成要求 完成要求 完成要求 完成要求 完成要求 完成要求
数学分析 C(2)课程教学大纲
课程基本信息(Course Information) 课程代码 (Course Code) *课程名称 (Course Name) 课程性质 (Course Type) 授课对象 (Audience) 授课语言 (Language of Instruction) *开课院系 (School) 先修课程 (Prerequisite) 授课教师 (Instructor) MA0012/MA043 *学时 (Credit Hours) 96 *学分 (Credits) 6
考查方式 单元测验 书面作业 书面作业 书面作业 书面作业 书面作业 书面作业 书面作业 书面作业 书面作业 书面作业
*考核方式 (Grading)
本课程的考试,注重对学生掌握知识以及运用所学知识解决问题能 力的考核,考试成绩包括四个方面: (1)期中考试,占总成绩的 30%。 (2)期末考试,占总成绩的 40%。 (3)测验成绩,占 10%。 (4)作业成绩(课堂表现+出勤),占 20%。
7-04-014364-X
2. 数学分析学习指导, 裘兆泰等, 科学出版社, 2004, ISBN: 7-03-012219-4
3.
数学分析试题分析与解答,上海交通大学数学系著,上海交通大学
出版社,2015,ISBN:978-7-313-12311-4
数学分析推荐书目

费定晖,周学圣
1
17
б.п.吉米多维奇数学分析习题集题解6(第4版)
山东科学技术出版社
费定晖,周学圣
1
18
吉米多维奇数学分析习题集学习指引(第1册)
高等教育出版社
沐定夷,谢惠民
1
19
吉米多维奇数学分析习题集学习指引(第2册)
高等教育出版社
沐定夷,谢惠民
1
20
吉米多维奇数学分析习题集学习指引(第3册)
25
数学分析全程辅导及习题精解(下册)
中国水利水电出版社
焦艳芳,李光敏
1
26
数学分析讲义全程导学及习题全解(上册)
中国时代经济出版社
马訾伟闫晓红
1
27
数学分析讲义全程导学及习题全解(下册)
中国时代经济出版社
马訾伟闫晓红
1
28
数学分析原理
机械工业出版社
(美)卢丁著赵慈庚蒋铎译
1
29
数学分析原理(英文版)
高等教育出版社
沐定夷,谢惠民
1
21
数学分析(第1册)
北京师范大学出版社
北京师范大学数学科学学院
1
22
数学分析(第2册)
北京师范大学出版社
北京师范大学数学科学学院
1
23
数学分析(第3册)
北京师范大学出版社
北京师范大学数学科学学院
1
24
数学分析全程辅导及习题精解(上册)
中国水利水电出版社
焦艳芳,李光敏
1
数学系书目推荐表
序号
书 名
出版社
作 者
购数
1
微积分学教程(第一卷)
2003年考研数学(二)真题评注

2003年考研数学(二)真题评注一、填空题(本题共6小题,每小题4分,满分24分. 把答案填在题中横线上)(1) 若0→x 时,1)1(412--ax 与x x sin 是等价无穷小,则a= .(2) 设函数y=f(x)由方程4ln 2y x xy =+所确定,则曲线y=f(x)在点(1,1)处的切线方程是 .(3) xy 2=的麦克劳林公式中nx 项的系数是 .(4) 设曲线的极坐标方程为)0(>=a e a θρ ,则该曲线上相应于θ从0变到π2的一段弧与极轴所围成的图形的面积为 .(5) 设α为3维列向量,Tα是α的转置. 若⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=111111111T αα,则ααT = .(6) 设三阶方阵A,B 满足E B A B A =--2,其中E 为三阶单位矩阵,若⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=102020101A ,则=B .二、选择题(本题共6小题,每小题4分,满分24分. 每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内)(1)设}{},{},{n n n c b a 均为非负数列,且0lim =∞→n n a ,1lim =∞→n n b ,∞=∞→n n c lim ,则必有(A) n n b a <对任意n 成立. (B) n n c b <对任意n 成立.(C) 极限n n n c a ∞→lim 不存在. (D) 极限n n n c b ∞→lim 不存在. [ ](2)设dx x xa n n nn n +=⎰+-123101, 则极限n n na ∞→lim 等于 (A) 1)1(23++e . (B) 1)1(231-+-e .(C) 1)1(231++-e . (D) 1)1(23-+e . [ ](3)已知xxy ln =是微分方程)(y x x y y ϕ+='的解,则)(y x ϕ的表达式为(A ) .22xy - (B) .22x y(C) .22yx - (D) .22y x [ ](4)设函数f(x)在),(+∞-∞内连续,其导函数的图形如图所示,则f(x)有(A) 一个极小值点和两个极大值点.(B) 两个极小值点和一个极大值点. (C) 两个极小值点和两个极大值点.(D) 三个极小值点和一个极大值点. [ ](5)设⎰=401tan πdx xx I ,dx x xI ⎰=402tan π, 则(A) .121>>I I (B) .121I I >>(C) .112>>I I (D) .112I I >> [ ] (6)设向量组I :r ααα,,,21Λ可由向量组II :s βββ,,,21Λ线性表示,则 (A) 当s r <时,向量组II 必线性相关. (B) 当s r >时,向量组II 必线性相关.(C) 当s r <时,向量组I 必线性相关. (D) 当s r >时,向量组I 必线性相关. [ ]三 、(本题满分10分)设函数 ,0,0,0,4sin1,6,arcsin )1ln()(23>=<⎪⎪⎪⎩⎪⎪⎪⎨⎧--+-+=x x x xx ax x e x x ax x f ax问a 为何值时,f(x)在x=0处连续;a 为何值时,x=0是f(x)的可去间断点?四 、(本题满分9分)设函数y=y(x)由参数方程)1(,21ln 2112>⎪⎩⎪⎨⎧=+=⎰+t du u e y t x t u所确定,求.922=x dx y d五 、(本题满分9分) 计算不定积分.)1(232arctan dx x xe x ⎰+六 、(本题满分12分)设函数y=y(x)在),(+∞-∞内具有二阶导数,且)(,0y x x y =≠'是y=y(x)的反函数.(1) 试将x=x(y)所满足的微分方程0))(sin (322=++dy dx x y dyx d 变换为y=y(x)满足的微分方程;(2) 求变换后的微分方程满足初始条件23)0(,0)0(='=y y 的解. 七 、(本题满分12分)讨论曲线k x y +=ln 4与x x y 4ln 4+=的交点个数. 八 、(本题满分12分)设位于第一象限的曲线y=f(x)过点)21,22(,其上任一点P(x,y)处的法线与y 轴的交点为Q ,且线段PQ 被x 轴平分.(1) 求曲线 y=f(x)的方程;(2) 已知曲线y=sinx 在],0[π上的弧长为l ,试用l 表示曲线y=f(x)的弧长s. 九 、(本题满分10分)有一平底容器,其内侧壁是由曲线)0)((≥=y y x ϕ绕y 轴旋转而成的旋转曲面(如图),容器的底面圆的半径为2 m. 根据设计要求,当以min /33m 的速率向容器内注入液体时,液面的面积将以min /2m π的速率均匀扩大(假设注入液体前, 容器内无液体).(1) 根据t 时刻液面的面积,写出t 与)(y ϕ之间的关系式; (2) 求曲线)(y x ϕ=的方程.(注:m 表示长度单位米,min 表示时间单位分.) 十 、(本题满分10分)设函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且.0)(>'x f 若极限ax a x f ax --+→)2(lim 存在,证明:(1) 在(a,b)内f(x)>0; (2) 在(a,b)内存在点ξ,使)(2)(22ξξf dxx f a b ba=-⎰; (3) 在(a,b) 内存在与(2)中ξ相异的点η,使 ⎰-=-'ba dx x f aa b f .)(2))((22ξξη 十 一、(本题满分10分)若矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=60028022a A 相似于对角阵Λ,试确定常数a 的值;并求可逆矩阵P 使.1Λ=-AP P十二 、(本题满分8分)已知平面上三条不同直线的方程分别为 :1l 032=++c by ax , :2l 032=++a cy bx , :3l 032=++b ay cx .试证这三条直线交于一点的充分必要条件为.0=++c b a真题答案解析1. 【分析】 根据等价无穷小量的定义,相当于已知1sin )1(lim4120=-→xx ax x ,反过来求a. 注意在计算过程中应尽可能地应用无穷小量的等价代换进行化简.【详解】 当0→x 时,241241~1)1(ax ax ---,2~sin x x x . 于是,根据题设有 14141lim sin )1(lim 2204120=-=-=-→→a xaxx x ax x x ,故a=-4.【评注】 本题属常规题型,完全类似例题见《数学复习指南》P.38 【例1.62】.2.. 【分析】 先求出在点(1,1)处的导数,然后利用点斜式写出切线方程即可. 【详解】 等式4ln 2y x xy =+两边直接对x 求导,得 y y xy x y '=+'+342, 将x=1,y=1代入上式,有 .1)1(='y 故过点(1,1)处的切线方程为 )1(11-⋅=-x y ,即 .0=-y x【评注】 本题属常规题型,综合考查了隐函数求导与求切线方程两个知识点,类似例题见《数学复习指南》P.55 【例2.13】和【例2.14】.3.. 【分析】 本题相当于先求y=f(x)在点x=0处的n 阶导数值)0()(n f,则麦克劳林公式中nx 项的系数是.!)0()(n fn 【详解】 因为 2ln 2xy =',2)2(ln 2xy ='',n x x y )2(ln 2,)(=Λ,于是有nn y )2(ln )0()(=,故麦克劳林公式中nx 项的系数是.!)2(ln !)0()(n n y nn = 【评注】 本题属常规题型,在一般教材中都可找到答案. 4.. 【分析】 利用极坐标下的面积计算公式θθρβαd S ⎰=)(212即可. 【详解】 所求面积为θθθρπθπd e d S a ⎰⎰==20220221)(21==πθ20241a e a )1(414-ae aπ. 【评注】 本题考查极坐标下平面图形的面积计算,也可化为参数方程求面积,但计算过程比较复杂. 完全类似例题见《数学复习指南》P.200 【例7.38】.5.. 【分析】 本题的关键是矩阵Tαα的秩为1,必可分解为一列乘一行的形式,而行向量一般可选第一行(或任一非零行),列向量的元素则为各行与选定行的倍数构成.【详解】 由⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=111111111Tαα=[]111111-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-,知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=111α,于是[].3111111=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=ααT【评注】 一般地,若n 阶矩阵A 的秩为1,则必有[].2121n n b b b a a a A ΛM ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=完全类似例题见《数学复习指南》P.389 【例2.11】和《考研数学大串讲》P.162 【例13】.6.. 【分析】 先化简分解出矩阵B ,再取行列式即可.【详解】 由E B A B A =--2知,E A B E A +=-)(2,即 E A B E A E A +=-+))((,易知矩阵A+E 可逆,于是有 .)(E B E A =- 再两边取行列式,得 1=-B E A ,因为 2002010100=-=-E A , 所以 =B 21.【评注】 本题属基本题型,综合考查了矩阵运算与方阵的行列式,此类问题一般都应先化简再计算. 完全类似例题见《考研数学大串讲》P.160 【例11】.二、选择题(本题共6小题,每小题4分,满分24分. 每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内)7. 【分析】 本题考查极限概念,极限值与数列前面有限项的大小无关,可立即排除(A),(B); 而极限n n n c a ∞→lim 是∞⋅0型未定式,可能存在也可能不存在,举反例说明即可;极限n n n c b ∞→lim 属∞⋅1型,必为无穷大量,即不存在.【详解】 用举反例法,取n a n 2=,1=n b ,),2,1(21Λ==n n c n ,则可立即排除(A),(B),(C),因此正确选项为(D).【评注】 对于不便直接证明的问题,经常可考虑用反例,通过排除法找到正确选项. 完全类似方法见《数学最后冲刺》P.179.8.. 【分析】 先用换元法计算积分,再求极限. 【详解】 因为dx x x a n n n n n +=⎰+-123101=)1(12310n n nn x d x n ++⎰+=}1])1(1{[1)1(1231023-++=++n n n nn n n x n, 可见 n n na ∞→lim =.1)1(}1])1(1{[lim 23123-+=-++-∞→e n n n n 【评注】 本题属常规题型,综合考查了定积分计算与求数列的极限两个知识点,但定积分和数列极限的计算均是最基础的问题,一般教材中均可找到其计算方法.9.. 【分析】 将xxy ln =代入微分方程,再令ϕ的中间变量为u ,求出)(u ϕ的表达式,进而可计算出)(yx ϕ.【详解】将xxy ln =代入微分方程)(y x x y y ϕ+=',得)(ln ln 1ln 1ln 2x x x x ϕ+=-,即 xx 2ln 1)(ln -=ϕ. 令 lnx=u ,有 21)(uu -=ϕ,故 )(y x ϕ=.22x y - 应选(A).【评注】 本题巧妙地将微分方程的解与求函数关系结合起来,具有一定的综合性,但问题本身并不复杂,只要仔细计算应该可以找到正确选项.10.. 【分析】 答案与极值点个数有关,而可能的极值点应是导数为零或导数不存在的点,共4个,是极大值点还是极小值可进一步由取极值的第一或第二充分条件判定.【详解】 根据导函数的图形可知,一阶导数为零的点有3个,而 x=0 则是导数不存在的点. 三个一阶导数为零的点左右两侧导数符号不一致,必为极值点,且两个极小值点,一个极大值点;在x=0左侧一阶导数为正,右侧一阶导数为负,可见x=0为极大值点,故f(x)共有两个极小值点和两个极大值点,应选(C).【评注】 本题属新题型,类似考题2001年数学一、二中曾出现过,当时考查的是已知f(x)的图象去推导)(x f '的图象,本题是其逆问题. 完全类似例题在文登学校经济类串讲班上介绍过.11.. 【分析】 直接计算21,I I 是困难的,可应用不等式tanx>x, x>0. 【详解】 因为当 x>0 时,有tanx>x ,于是1tan >x x ,1tan <xx,从而有 4tan 41ππ>=⎰dx x x I , 4tan 402ππ<=⎰dx x x I ,可见有 21I I >且42π<I ,可排除(A),(C),(D),故应选(B).【评注】 本题没有必要去证明11<I ,因为用排除法,(A),(C),(D)均不正确,剩下的(B) 一定为正确选项.12.. 【分析】 本题为一般教材上均有的比较两组向量个数的定理:若向量组I :r ααα,,,21Λ可由向量组II :s βββ,,,21Λ线性表示,则当s r >时,向量组I 必线性相关.或其逆否命题:若向量组I :r ααα,,,21Λ可由向量组II :s βββ,,,21Λ线性表示,且向量组I 线性无关,则必有s r ≤. 可见正确选项为(D). 本题也可通过举反例用排除法找到答案.【详解】 用排除法:如⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=10,01,00211ββα,则21100ββα⋅+⋅=,但21,ββ线性无关,排除(A);⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=01,01,00121βαα,则21,αα可由1β线性表示,但1β线性无关,排除(B);⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=10,01,01211ββα,1α可由21,ββ线性表示,但1α线性无关,排除(C). 故正确选项为(D).【评注】 本题将一已知定理改造成选择题,如果考生熟知此定理应该可直接找到答案,若记不清楚,也可通过构造适当的反例找到正确选项。
数学分析课后习题答案--高教第二版(陈纪修)--2章

数列极限
1. 按定义证明下列数列是无穷小量: ⑴ ⎨
⎧ n +1 ⎫ ⎬; 2 ⎩ n + 1⎭ 1 ⎩n
⑵ { ( −1) n (0.99) n }; ⑷ ⎨
⎧1 + 2 + 3 + n3 ⎩ + n⎫ ⎬; ⎭
⎧ −n ⎫ ⑶ ⎨ + 5 ⎬; ⎭
⑺ ⎨
⎧ n! ⎫ ; n ⎬ ⎩n ⎭ 2
⎧ ⑻ ⎨ − 1 ⎩n
hd
(2) ∀ε (0 < ε < 1) ,取 N = ⎢
n n
⎡ lg ε ⎤ ⎥ ,当 n > N 时,成立 ⎣ lg 0.99 ⎦
lg ε lg 0.99
案 网
(−1) (0.99) < (0.99)
后 答
2⎤ 2⎤ 1 ε ⎡ n > N 取 N1 = ⎡ , 当 时, 成立 ; 取 (3) = ∀ε (0 < ε < 2) , N log < 1 2 5 ⎢ ⎥ ⎢ ⎥, ⎣ε ⎦ n 2 ⎣
α
2
案 网
(1)的结论矛盾。
ww w
9
3+ 2 =
m2 m2 5 m ,于是 3 + 2 6 + 2 = 2 , 6 = 2 − ,即 6 是有理数,与 2 n n 2n
.k
hd
aw .c om
max C 与 min C 都不存在,因为 ∀
n n n +1 ,所以 max C 与 min C 都不存在。 < < m +1 m m +1
n n n +1 ∈ C ,有 ∈C , ∈C , m m +1 m +1
Ch120503

展开成 x 的幂级数, 则这个幂级数就是 f ( x )的麦
克劳林级数. 但是, 反过来如果 f ( x ) 的麦克劳林级
数在点 x0 0 的某领域内收敛, 它却不一定收敛于
一点处具有任意阶的导数. 即没有任意阶导数的函
数是不可能展开成幂级数的. 函数的麦克劳林级数 是 x 的幂级数, 可以证明, 如果 f ( x ) 能展开成 x 的
麦克劳林级数
是 x 的幂级数, 可以证明, 如果 f ( x ) 能展开成 x 的
麦克劳林级数
是 x 的幂级数, 可以证明, 如果 f ( x ) 能展开成 x 的
麦克劳林级数
x0 0 时的泰勒级数
(n) f ( 0) 2 f ( 0) n f ( 0 ) f ( 0 ) x x x (5.3) 2! n! 称为 f ( x ) 的麦克劳林级数.
注: 由上节定理 3( 3)可知, 如果函数 f ( x ) 能在某个 区间内展开成幂级数, 则它必定在这个区间内的每
12 e x , x 0 f ( x ). 例如, 函数 f ( x ) 0, x 0
麦克劳林级数
12 e x , x 0 f ( x ). 例如, 函数 f ( x ) 0, x 0
麦克劳林级数
12 e x , x 0 f ( x ). 例如, 函数 f ( x ) 0, x 0 在 x0 0 点任意阶可导, 且
麦克劳林级数
因此,当 f ( x ) 在 x0 0 处具有各阶导数时, 虽然
数学分析上册chp11习题解答
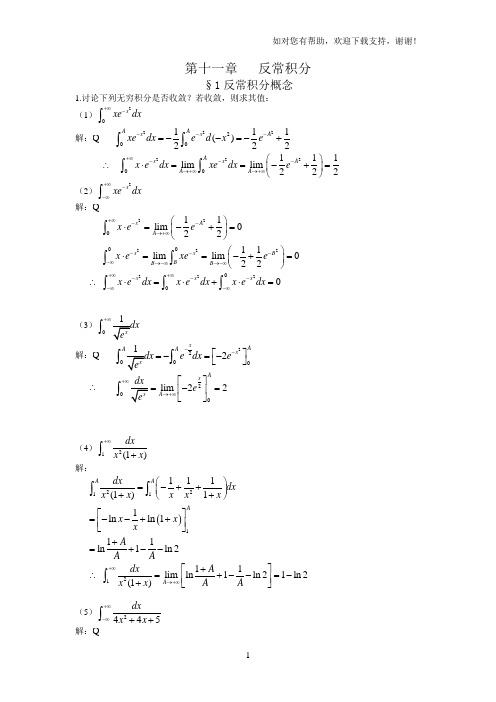
第十一章 反常积分§1反常积分概念1.讨论下列无穷积分是否收敛?若收敛,则求其值: (1)2x xe dx +∞-⎰解:222200111()222AA x x A xe dx e d x e ---=--=-+⎰⎰ ∴ 22200111lim lim 222A x x A A A x e dx xe dx e+∞---→+∞→+∞⎛⎫⋅==-+= ⎪⎝⎭⎰⎰ (2)2x xe dx +∞--∞⎰解:2222200011lim 02211lim lim 022x A A x x B B B B x e e x e xe e +∞--→+∞----∞→-∞→-∞⎛⎫⋅=-+= ⎪⎝⎭⎛⎫⋅==-+= ⎪⎝⎭⎰⎰⎰ ∴ 2220x x x x e dx x e dx x e dx +∞+∞----∞-∞⋅=⋅+⋅=⎰⎰⎰(3)0+∞⎰解:22002xAAA x e dx e --⎡⎤=-=-⎣⎦⎰⎰∴2l i m 22AxA e →+∞+∞⎡⎤-=⎢⎥⎣⎦=⎰(4)21(1)dxx x +∞+⎰解:()22111111(1)11ln ln 111ln 1ln 2AA Adx dx x x x x x x x x A A A ⎛⎫=-++ ⎪++⎝⎭⎡⎤=--++⎢⎥⎣⎦+=+--⎰⎰ ∴ 21lim 11ln 1ln 21ln 2(1)A dx A x x A A →+∞+∞+⎡⎤=⎢⎥=+--⎣-⎦+⎰ (5)2445dxx x +∞-∞++⎰解:2202001445(21)lim lim 1lim arcta 2(2n 1)82AA A A AA dx x x x x π→+∞→+∞→+∞==+++++=⎰⎰2220001445(21)2(21)l i m l i m 1l i m a r c t a n 41l i m a r c t a 1)48n(2B B B B B B Bdx dx x x x x B π→-∞→-∞→-∞→-∞=+++++=+=⎡⎤-=⎢⎥⎣⎦⎰⎰ ∴ 002224454454l i m l m 4i 5884A B A B dx dx dxx x x x x x πππ→++∞-→∞∞-∞=+++++=+=++⎰⎰⎰(6)0sin x e xdx +∞-⎰解:()0sin sin 1sin co limim s l 22AxA x x A A e xdx e xdxe x x →+∞→++---∞∞==--=⎰⎰(7)sin x e xdx +∞--∞⎰解:limsin sin AA x x e xdx e xdx →++∞∞=⎰⎰0sin limcos 2AA x x →+∞-= ()1sin lim cos 12A A A →+∞=-+发散 而limsin sin B xx Be xdx e xdx →∞--∞⋅=⎰⎰0sin limcos 2BB x x →-∞-=发散∴sin x e xdx +∞--∞⎰发散(8)+∞⎰解:0limli m A A A A →+∞→+∞=⎰发散故+∞⎰2. 讨论下列瑕积分是否收敛?若收敛,则求其值:(1)()bp a dxx a -⎰解:()21()f x x a =-在(,]a b 上连续, 从而在(,]a b 上可积,x a =为其瑕点由瑕积分定义,知111lim()()lim ()()1lim ()11lim ()()1bb p pau u a bp uu a p bu u a p pu a dx dx x a x a x a d x a x a pb a u a p →-→-→--→=--=--=--⎡⎤=---⎣⎦-⎰⎰⎰显然当1p <时,上式收敛于1()1pb a p---,其瑕积分也收敛,其值为1()1pb a p---若1p ≥,则上式发散,其瑕积分也发散(2)1201dx x -⎰解:122001010010011lim 11111lim 211111lim 21111lim ln 1ln 12211lim ln 1ln 122u u u u u u u u u u u dxdx x x dx x x dx dx x x x x u u →→→→→=--⎛⎫=+ ⎪-+⎝⎭⎡⎤=+⎢⎥-+⎣⎦⎧⎫=-⎡-⎤+⎡+⎤⎨⎬⎣⎦⎣⎦⎩⎭⎡⎤=--++⎢⎥⎣⎦⎰⎰⎰⎰⎰ 上式的极限不存在,故瑕积分1201dxx -⎰发散(3)2⎰解:()()()()()()212001112221111222011112211lim 1lim 1lim 21lim 21lim 212lim 2214uuu u u uu u u u x dx x dxx x u u --→→--→→--→→=+=-+-⎡⎤=--+-⎢⎥⎣⎦⎡⎤⎡⎤=--++--⎢⎥⎢⎥⎣⎦⎣⎦=⎰⎰⎰⎰⎰故瑕积分收敛,其值为4 (4)1⎰解:()()()()())11122201222112201111121lim 1121lim 12lim11u u uu u x d x x d x x --→-→→=---=---=--=-=⎰⎰⎰ 故瑕积分收敛,其值为1 (5)1ln xdx ⎰解:()111100ln lim ln lim ln lim ln 11u u u u u u xdx xdxx x dx u u u +++→→→=⎡⎤=-⎢⎥⎣⎦=--+=-⎰⎰⎰故瑕积分收敛,其值为-1(6)⎰解:令21xt x=-,则()20200020202lim 1lim 21lim arctan 12tdt t t t t t εεεπ+++→→→=+⎡⎢=⎢+⎣⎦⎛=- +⎝=⎰故瑕积分收敛,其值为2π(7)1⎰解:()()()()1111121211210200lim lim lim arcsin 21lim arcsin 21lim arcsin 21lim arcsin 21122x x εεεεεεεεεεεεπππ++++++-→→-→→→→==+=-+-=--+---⎡⎤⎡⎤⎣⎦⎣⎦=+=⎰⎰⎰⎰故瑕积分收敛,其值为π (8)10ln (ln )p d x x ⎰解:()()1112100211210211112100211100ln (ln )ln (ln )ln (ln )lim (ln 2)ln lim (ln )ln 11lim (ln )lim (ln )11111lim ln ln lim ln 1121p p p p p p p p p d x x d x x d x x d x x d xx x ppp p εεεεεεεεεεεε++++++-----→→---→→---→→=+=+=+--⎡⎤⎛⎫=-+-⎢⎥ ⎪--⎝⎭⎢⎥⎣⎦⎰⎰⎰⎰⎰11ln 2pp -⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦上面极限式发散,故瑕积分发散3. 举例说明:瑕积分⎰badx x f )(收敛时,⎰badx x f )(2不一定收敛。
数学分析上册chp03习题解答

第三章 函数极限§1函数极限概念1.按定义证明下列极限:⑴ 656lim=++∞→xx x证 0>∀ε,要ε<=-+xx x 5|656|,只需ε5>x ,于是0>∀ε,取ε5=N ,N x >∀,有ε<=-+x x x 5|656|,所以656lim =++∞→xx x⑵ 2)106(lim 22=+-→x x x证 |4||2||2106|2-⋅-=-+-x x x x ,因为2→x ,不妨设1|2|<-x ,于是31<<x ,从而|2|3|4||2||2106|2-<-⋅-=-+-x x x x x . 所以0>∀ε,取}3,1m i n {εδ=,δ<-<∀|2|0:x x ,有ε<-<-+-|2|3|2106|2x x x所以2)106(lim 22=+-→x x x⑶ 115lim 22=--∞→x x x 证 0>∀ε,设1||>x ,要ε<-≤+-≤-=---1||4)1|)(|1|(|414|115|222x x x x x x ,只需ε41||+>x ,于是0>∀ε,取ε41+=N ,N x >∀||,有ε<-≤---1||4|115|22x x x ,所以115lim 22=--∞→x x x ⑷ 04lim 22=--→x x证 因为2||≤x ,于是x x x x -<+-=-22)2)(2(42. 从而0>∀ε,取42εδ=,δ<-<∀x x 20:,有εεδ=⋅≤<-<-22222|4|2x x ,所以04lim 22=--→x x⑸ 0cos cos lim 0x x x x =→证 因为|2sin |2|2sin ||2sin|2|cos cos |0000x x x x x x x x -≤-⋅+=- |||2|200x x x x -=-≤. 所以0>∀ε,取εδ=,δ<-<∀||0:0x x x ,有ε<-≤-|||c o s c o s |00x x x x ,所以0cos cos lim 0x x x x =→2.根据定义2叙述A x f x x ≠→)(lim 0解 00>∃ε,0>∀δ,δ<-'<'∃||0:0x x x ,0|)(|ε≥-'A x f3.设A x f x x =→)(lim 0,证明A h x f h =+→)(lim 00证 因为A x f x x =→)(lim 0,所以0>∀ε,0>∃δ,δ<-<∀||0:0x x x ,有ε<-|)(|A x f .当δ<<||0h 时,必有δ<-+<|)(|000x h x ,从而ε<-+|)(|0A h x f ,所以A h x f h =+→)(lim 004.证明:若A x f x x =→)(lim 0,则|||)(|lim 0A x f x x =→. 当且仅当A 为何值时反之也成立?证 因为A x f x x =→)(l i m 0,所以0>∀ε,0>∃δ,δ<-<∀||0:0x x x ,有ε<-|)(|A x f . 而ε<-≤-|)(|||||)(||A x f A x f ,所以|||)(|lim 0A x f x x =→.当且仅当A 为零时反之也成立.5.证明:A x f x f A x f x x x x x x ==⇔=-+→→→)(lim )(lim )(lim 0证 ⇒)因为A x f x x =→)(lim 0,所以0>∀ε,0>∃δ,δ<-<∀||0:0x x x ,有ε<-|)(|A x f . 于是当δ<-<00x x ,也有ε<-|)(|A x f ,从而A x f x x =+→)(lim 0. 同样,当δ<-<x x 00,有ε<-|)(|A x f ,从而也有A x f x x =-→)(lim 0.⇐)设A x f x f x x x x ==-+→→)(lim )(lim 0,于是0>∀ε,0>∃δ,当δ<-<00x x ,有ε<-|)(|A x f ,当δ<-<x x 00,也有ε<-|)(|A x f ,从而当δ<-<||00x x 时,有ε<-|)(|A x f .6.讨论下列函数在0→x 时的极限或左、右极限:⑴ xx x f ||)(=解 1lim ||lim )(lim 00===+++→→→x x x x x f x x x ,1lim )(lim 00-=-=--→→xxx f x x ,所以)(lim 0x f x →不存在.⑵ ][)(x x f =解 00lim ][lim )(lim 0===+++→→→x x x x x f ,11lim ][lim )(lim 0-=-==---→→→x x x x x f ,所以)(l i m 0x f x →不存在.⑶ ⎪⎩⎪⎨⎧<+=>=010002)(2x x x x x f x解 12lim )(lim 0==++→→x x x x f ,1)1(lim )(lim 20=+=--→→x x f x x ,所以1)(lim 0=→x f x .7.设A x f x =+∞→)(lim ,证明A xf x =+→)1(lim 0.证 ⇒)因为A x f x =+∞→)(lim ,所以0>∀ε,0>∃N ,N x >∀,有ε<-|)(|A x f .现在取N 1=δ,当δ<<x 0时,有N x =>δ11,于是ε<-|)1(|A x f ,所以A xf x =+→)1(lim 0.8.证明:对Riemann 函数)(x R 有0)(lim 0=→x R x x ,]1,0[0∈x证 若q p x ≠,即x 为无理数时,那末由于此时0)(=x f ,所以有ε<-|0)(|x f . 若px q=,那么由于q 是正整数,所以对于任意的0ε>,使11()q q εε><即的q 值只可 能是有限个,设为m 个,同时因为1<q p ,从而以小于ε1的正整数q 为分母的有理点q p 也只可能是有限个,设为k x x x ,,,21 . 于是在]1,0[中除了这有限个点之外,都使ε<=qx f 1)(,从而对于]1,0[中的任一点0x ,任给的0>ε,取 |}|,|,||,m in{|00201x x x x x x k ---= δ,那么由上面的讨论可知,当δ<-||0x x 时,就有ε<-|0)(|x f .§2 函数极限的性质1. 求下列极限:(1)22lim 2(sin cos )x x x x π→--;解:22lim 2(sin cos )x x x x π→--22222lim 2(lim sin lim cos lim lim )x x x x x x x x x πππππ→→→→→=--222sin cos212224ππππ⎡⎤⎛⎫⎛⎫=--=-⎢⎥ ⎪ ⎪⎝⎭⎢⎥⎝⎭⎣⎦(2)2201lim 21x x x x →---;解:220101lim 121001x x x x →--==---- (3)2211lim 21x x x x →---;解:32)12()1(lim )1)(12()1)(1(lim 121lim 11221=++=-+-+=---→→→x x x x x x x x x x x x(4)3230(1)(13)lim 2x x x x x→-+-+; 解:3213lim 23lim 2)31()1(lim 0322303230-=+-=+-=+-+-→→→x x x x x x x x x x x x x(5)11lim 1n m x x x →--(m,n 为正整数)解:mnx x x x x x x x x x x x x x x x m m n n x m m n n x m n x =++++++++=++++-++++-=------→----→→11lim )1)(1()1)(1(lim 11lim 21211212111(6)x →解:34321)2(2lim )321)(4()2)(921(lim)321)(2)(2()2)(321)(321(lim 2321lim4444=+++=++-+-+=+++-+++-+=--+→→→→x x x x x x x x x x x x x x x x x x(7)00)x a →>; 解:a a x a a x a x a x a x a x a x x x 211lim )()(lim lim 20222020=++=++-+=-+→→→ (8)702090(36)(85)lim (51)x x x x →+∞+--.解:902070902070902070583155863lim )15()58()63(lim ⋅=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+=--++∞→+∞→x x x x x x x x2. 用迫敛性求极限:(1)cos limx x xx→-∞-;解 因为)0(,11cos 11<-≤-≤+x x x x x x ,并且1)11(lim )11(lim =-=+-∞→-∞→x x x x ,所以1cos lim =--∞→x x x x(2)2sin lim 4x x xx →+∞-.解 因为)0(,44sin 4222>-≤-≤--x x x x x x x x ,并且04lim 4lim 22=-=--+∞→+∞→x xx x x x 所以,04sin lim 2=-+∞→x x x x 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
其截断误差为
故取近似式为
5
1 | r2 | . 20000 1 1 240 3 1 4 . 5 3
为了使舍入误差与截断误差之和不超过 104 , 计算 时应取五位小数, 然后再四舍五入. 因此最后得
5
240 2.9926.
完
5
似值, 其截断误差为
1 4 1 1 4 9 1 | r2 | 3 2 8 3 12 5 2! 3 5 3! 3 1 4 9 14 1 16 4 5 4! 3
例2 计算 5 240 的近似值, 要求误差不好过 0.0001. 解
例2 计算 5 240 的近似值, 要求误差不好过 0.0001. 解
5
1 1 1 4 1 1 4 9 1 8 3 240 3 1 4 2 12 . 5 3 5 2! 3 5 3! 3
其截断误差为
| r2 |
1 . 20000
5
1 1 1 4 1 1 4 9 1 8 3 240 3 1 4 2 . 12 5 3 5 2! 3 5 3! 3
其截断误差为
1 4 1 1 4 9 1 | r2 | 3 2 8 3 12 5 2! 3 5 3! 3 1 4 9 14 1 16 4 5 4! 3
例2 计算 5 240 的近似值, 要求误差不好过 0.0001. 5 解 240 5 243 3 3(1 1 / 34 )1 / 5 , 利用二项展开式, 并取 m 1 / 5, x 1 / 34 , 即得
1 1 1 4 1 1 4 9 1 8 3 240 3 1 4 2 . 12 5 3 5 2! 3 5 3! 3 这个级数收敛很快. 取前两项的和作为 5 240 的近
2 1 4 1 1 1 3 2 8 1 5 2! 3 81 81
例2 计算 5 240 的近似值, 要求误差不好过 0.0001. 解
5
1 1 1 4 1 1 4 9 1 8 3 240 3 1 4 2 12 . 5 3 5 2! 3 5 3! 3
其截断误差为
2 1 4 1 1 1 | r2 | 3 2 8 1 5 2! 3 81 81 1 1 1 6 18 . 25 3 1 1 / 81 25 27 40 20000 1 1 故取近似式为 5 240 3 1 4 . 5 3 为了使舍入误差与截断误差之和不超过 104 ,
例2 计算 5 240 的近似值, 要求误差不好过 0.0001. 解
5
1 1 1 4 1 1 4 9 1 8 3 240 3 1 4 2 12 . 5 3 5 2! 3 5 3! 3
其截断误差为
1 4 1 1 4 9 1 | r2 | 3 2 8 3 12 5 2! 3 5 3! 3 1 44 9 14 1 16 5 4! 3
故取近似式为
5
1 1 240 3 1 4 . 5 3
为了使舍入误差与截断误差之和不超过 104 ,
例2 计算 5 240 的近似值, 要求误差不好过 0.0001. 解
5
1 1 1 4 1 1 4 9 1 8 3 240 3 1 4 2 12 . 5 3 5 2! 3 5 3! 3
其截断1 3 2 8 1 5 2! 3 81 81
例2 计算 5 240 的近似值, 要求误差不好过 0.0001. 解
5
1 1 1 4 1 1 4 9 1 8 3 240 3 1 4 2 12 . 5 3 5 2! 3 5 3! 3
