18容斥原理(二)(含答案)-

合集下载

奥数四年级--容斥问题(二)

练 1.有30名运动员，其中18人会三级跳，16人习会撑杆跳高，10人三级跳远、撑杆跳高均不
会。既会三级跳远又会撑杆跳高的运动员有多少名？
14名
练 2、操场上的学生排成10路纵队做操，毎路习纵队人数同样多，小明站在第四纵队，从排
头数他是第13个，从后往前数他是第8人。操场上有多少人在做操？
200人
练 3、一个年级有120人爱好数学，100人爱好习语文，85人爱好美术，30人既爱好数学又爱
好语文，20人既爱好语文又爱好美术，35人既爱好美术又爱好数学，有18人三门学科都爱好。请问:这个年级中数学、语文、美术三门学科中至少爱好一门学科的学生有多少人？
238人
练 4、某班全体学生进行了数学、语文、英语习三个科目的测试，有8名学生在这三个科目
球、蓝球的学生人数分别为10人，10人，6 人，其中手中既有红球又有黄球的有3人，既有黄球又有蓝球的有2人，既有蓝球又有红球的有4人。已知全队每人手中都至少有一种颜色的球，那么，手中三种颜色的球都有的多少人？
3人
练 6、某班50名同学全部参加数学、语文、美习术三个课外兴趣小组，参加数学小组的有29
17人
18人
15人
求全班人数。
这道题目条件比较复杂，可以根据题意画出示意图，以便形象直观地显示他们之间的关系。全班人数=至少有一个项目达到优秀的人数+三个项目上都没有达到优秀的人数
篮球15人 6人短跑 17人
篮球游泳短跑 2人
6人游泳 18人
6人
经典题型
运用容斥定理至少有一个项目达到优秀的人数=（短跑达到优秀人数+游泳达到优秀人数+篮球达到优秀人数）-（短跑、游泳达到优秀人数+ 游泳、篮球达到优秀人数+篮球、短跑达到优秀人数）+短跑、游泳、篮球都达到优秀的人数

完整版容斥原理习题加答案

1. 现有50名学生都做物理、化学实验，如果物理实验做正确的有40人，化学实验做正确的有31人，两种实验都错的有4人，则两种实验都做对的有（）【答案】B【解析】直接代入公式为：50=31+40+4- A H B得A H B=25,所以答案为B。

2. 某服装厂生产出来的一批衬衫大号和小号各占一半。

其中25%是白色的, 75%是蓝色的。

如果这批衬衫共有100件，其中大号白色衬衫有10件，小号蓝色衬衫有多少件？（）A 、15B、25C 、35D40【答案】C【解析】这是一种新题型，该种题型直接从求解出发，将所求答案设为A H B,本题设小号和蓝色分别为两个事件A和B,小号占50%蓝色占75%直接代入公式为：100=50+75+10- A H B，得：A H B=353. 某高校对一些学生进行问卷调查。

在接受调查的学生中，准备参加注册会计师考试的有63人，准备参加英语六级考试的有89人，准备参加计算机考试的有47人，三种考试都准备参加的有24人，准备只选择两种考试都参加的有46人,【解析】本题画图按中路突破原则，先填充三集合公共部分数字 24,再推其他部分数字：根据每个区域含义应用公式得到：总数=各集合数之和-两两集合数之和+三集合公共数+三集合之外数=63+89+47— {(x+24)+(z+24)+(y+24)}+24+15=199— { (x+z+y ) +24+24+24}+24+15根据上述含义分析得到：x+z+y 只属于两集合数之和，也就是该题所讲的只选择两种考试都参加的人数，所以 x+z+y 的值为46人；得本题答案为120.4. 对某单位的100名员工进行调查，结果发现他们喜欢看球赛和电影、戏剧。

其中58人喜欢看球赛，38人喜欢看戏剧，52人喜欢看电影，既喜欢看球赛又喜欢看戏剧的有18人，既喜欢看电影又喜欢看戏剧的有16人，三种都喜欢看的有 12人，则只喜欢看电影的有多少人( )A.22 人B.28 人C.30 人D.36 人【答案】A【解析】本题画图按中路突破原则，先填充三集合公共部分数字 12,再推其他部分数字：根据各区域含义及应用公式得到：总数=各集合数之和-两两集合数之和+三集合公共数+三集合之外数100= 58+38+52- {18+16+ (12+ x ) }+12+0,因为该题中，没有三种都不喜欢的人，所以三集合之外数为 0,解方程得到：x = 14。

(完整版)容斥原理习题加答案

1.现有50名学生都做物理、化学实验，如果物理实验做正确的有40人，化学实验做正确的有31人，两种实验都错的有4人，则两种实验都做对的有( )A、27人B、25人C、19人D、10人【答案】B【解析】直接代入公式为：50=31+40+4－A∩B得A∩B=25，所以答案为B。

2.某服装厂生产出来的一批衬衫大号和小号各占一半。

其中25％是白色的，75％是蓝色的。

如果这批衬衫共有100件，其中大号白色衬衫有10件，小号蓝色衬衫有多少件？（）A、15B、25C、35D、40【答案】C【解析】这是一种新题型，该种题型直接从求解出发，将所求答案设为A∩B，本题设小号和蓝色分别为两个事件A和B，小号占50%，蓝色占75%，直接代入公式为：100=50+75+10－A∩B，得：A∩B=35。

3.某高校对一些学生进行问卷调查。

在接受调查的学生中，准备参加注册会计师考试的有63人，准备参加英语六级考试的有89人，准备参加计算机考试的有47人，三种考试都准备参加的有24人，准备只选择两种考试都参加的有46人，不参加其中任何一种考试的都15人。

问接受调查的学生共有多少人？（）A．120B．144C．177D．192【答案】A【解析】本题画图按中路突破原则，先填充三集合公共部分数字24，再推其他部分数字：根据每个区域含义应用公式得到：总数=各集合数之和－两两集合数之和＋三集合公共数＋三集合之外数＝63+89+47－{(x+24)+(z+24)+(y+24)}+24+15＝199－{（x+z+y）+24+24+24}+24+15根据上述含义分析得到：x+z+y只属于两集合数之和，也就是该题所讲的只选择两种考试都参加的人数，所以x+z+y的值为46人；得本题答案为120.4.对某单位的100名员工进行调查，结果发现他们喜欢看球赛和电影、戏剧。

其中58人喜欢看球赛，38人喜欢看戏剧，52人喜欢看电影，既喜欢看球赛又喜欢看戏剧的有18人，既喜欢看电影又喜欢看戏剧的有16人，三种都喜欢看的有12人，则只喜欢看电影的有多少人（）A.22人B.28人C.30人D.36人【答案】A【解析】本题画图按中路突破原则，先填充三集合公共部分数字12，再推其他部分数字：根据各区域含义及应用公式得到：总数=各集合数之和－两两集合数之和＋三集合公共数＋三集合之外数100＝58+38+52－{18+16+（12+ x）}+12+0,因为该题中，没有三种都不喜欢的人，所以三集合之外数为0，解方程得到：x＝14。

5.3 容斥原理(二)

博易新思维数学
五年级秋季拓展版
5.3 容斥原理（二）
容斥原理一：
如果被计数的事物有A、B两类，那么，A类或B类元素个数
=A类元素个数＋B类元素个数－既是A类又是B类的元素个数。
A
B
C
A或B的个数=A＋B－C
准备题1：一次期末考试，某班有15人数学得满分，有 12人语文得满分，并且有4人语、数都是满分，那么这个班至少有一门得满分的同学有多少人？
128＋145＋136－75－56－82＋13 =209（个）
答：六年级一共有209个学生。
例2：某校六(1)班有学生44人，每人在暑假里都参加体育训练队，其中参加足球队的有25人，参加排球队的有22人，参加游泳队的有 34人，足球、排球都参加的有12人，足球、游泳都参加的有18人，排球、游泳都参加的有14人，问：三项都参加的有多少人?
红色白色黑色红、白色红、黑色白、黑色红白黑三色
95 102 89
34
42
54
21
求活动现场的观众有多少？
喜欢3种颜色的人：95＋102＋89－34－42－54＋21 =177(人) 现场的观众：177＋35=212(人)
答：活动现场的观众有212人。
例5：在1到100的自然数中：（1）是3的倍数或是5的倍数的数共有多少个？
数学得满分 15人
4人
语文得满分 12人
语数都得满分
15＋12－4=23(人)
答：这个班至少有一门得满分的同学有23人。
准备题2：有一根180厘米长的绳子，从一端开始，每3厘米作一记号，每4厘米也作一记号，然后将作有记号的地方剪断，绳子共被剪成多少段？
3厘米作记号 60段
4厘米作记号 45段

容斥原理

容斥原理（二）效能训练：姓名：1、13．65扩大（）倍是1365；6.8缩小（）倍是0.0682、把7.4343434343……用简便方法写出来是（），保留两位小数是（）。

3、把7.1687保留整数约是（），精确到千分位约是（）.4、4.09×0.05的积有（）小数，5.2×4.76的积有（）位小数。

5、根据13×28=364，很快地写出下面各式的积。

1.3×2.8= 0.13×0.28= 13×2.8=0.013×28= 0.13×2.8= 1.3×0.028=6、在（）里填上>、<或=163×0.8（）16336×2.8（）367、判断题（正确的打√，错误的打×）①、0.03与0.04的积是0.12。

（）②、一个数的1.65倍一定大于这个数。

（）③、53.78保留一位小数是53.8。

（）④、一个数乘小数，积一定小于这个数。

（）8、选择（把正确答案的序号填入括号里）①、一个小数的小数点右移动2位，再向左移动3位，这个小数（）。

A、扩大了10倍B、缩小10倍C、扩大100倍D、缩小1000倍②、下面各式得数小于0.85的是（）。

A、0.85×1.01B、0.85×0.99C、 0.85×19、直接写出得数。

0.6×0.83×0.9 2.5×0.4 3.6×0.412.5×8 50×0.04 80×0.3 1.1×910、脱式计算（能简算的要用简算）12.5×0.4×2.5×89.5×101 4.2×7.8+2.2×4.211、列式计算：1、 25乘4.8减5，差是多少？2、比4.7的1.5倍多3.05的数是多少？典型例题1、在参加数学竞赛的46人中，做第一题的有32人，做对第二题的有24人，两道题都做对的有20人，两道题都没有做对的有几人？开心一练：全班46名同学，仅会乒乓球的有28人，即会打乒乓球又会打羽毛球的有10人，不会打乒乓球又不会打羽毛球的有6人，仅会打羽毛球的有多少人？典型例题2、一个单位有70个职工，其中有的职工会打网球，有的会打乒乓球，有的两样都会，现在知道会打网球的48人，会打网球又会打乒乓球的有24人，问会打乒乓球的有多少人？典型例题3、一次数学小测验只有两道题，结果全班有10人全对，第一题有25人做对，第二题有18人做错，那么两题都做错的有多少人？（1）两道题全对的有人。

容斥原理（2）

容斥原理例1一个班有55名学生，订阅《小学生数学报》的有12人，订阅《今日少年报》的有9人，两种报纸都订阅的有5人。

(1)订阅报纸的总人数是多少？(2)两种报纸都没订阅的有多少人？例2有62名学生，其中会弹钢琴的有1 1人，会吹竖笛的有56人，两样都不会的有4人，两样都会的有多少人？例3艺术节那天，学校的画廊里展出了每个年级学生的图画作品，其中有23幅不是五年级的，有21幅画不是六年级的，五、六年级参展的画共有8幅。

其他年级参展的画共有多少幅？例4五(1)班的全体学生进行了短跑、游泳、篮球三个项目的测试，有4名学生在这三个项目上都没有达到优秀，其余每人至少有一个项目达到优秀，这部分学生达到优秀的项目和人数如下表：例5某班有60名同学参加乒乓球、羽毛球和足球三个兴趣小组，参加乒乓球兴趣小组的有32人，参加羽毛球兴趣小组的有22人，参加足球兴趣小组的有28人，有20人既参加乒乓球兴趣小组又参加羽毛球兴趣小组，有18人既参加乒乓球兴趣小组又参加足球兴趣小组，有16人既参加羽毛球兴趣小组又参加足球兴趣小组。

已知全班每人都至少参加了以上三个小组中的某一个，那么，三个兴趣小组都参加的学生有多少人？例6某外语学习班有40名学员，规定他们至少学习英语、日语、德语中的一种。

结果学习英语的有20人，学习日语的有12人，学习德语的有18人，其中有5人既学了英语又学了日语，有2人既学了日语又学了德语，没有人同时学习三种语言。

那么，既学英语又学德语的有多少人？例7松山小学45名学生参加数学、作文、美术竞赛。

有21人参加数学竞赛，15人参加作文竞赛，其中7人既参加作文竞赛又参加数学竞赛，3人既参加作文竞赛又参加美术竞赛，但没有一人既参加数学竞赛又参加美术竞赛。

求：(1)只参加数学竞赛的有多少人？(2)只参加作文竞赛的有多少人？(3)只参加美术竞赛的有多少人？练习与思考：1．四(2)班有50名学生，下课后每人都至少做完了一门作业，其中做完语文作业的有35人，做完数学作业的有40人。

四年级数学思维能力拓展专题突破系列(十八)容斥原理讲义(含答案)

四年级数学思维能力拓展专题突破系列（十八）容斥原理------容斥原理基础（1）1、了解容斥原理二量重叠和三量重叠的内容。

2、掌握容斥原理在组合计数等各个方面的应用。

1、掌握容斥原理的概念。

2、熟记二元容斥原理。

例题1：实验小学四年级二班，参加语文兴趣小组的有28人，参加数学兴趣小组的有29人，有12人两个小组都参加。

这个班有多少个人参加了语文或数学兴趣小组？例题2：某班共有46人，参加美术小组的有12人，参加音乐小组的有23人，有5人两个小组都参加了。

这个班既没参加美术小组也没参加音乐小组的有多少个人？例题3：某次英语考试由两部分组成，结果全班有12人得满分，第一部分有25人做对，第二部分有19人有错，问两部分都有错的有多少个人？例题4：在一根长30厘米的木棍上，从它的两端开始做标记，从左端开始每隔3厘米做一个标记，从右端开始每隔5厘米做一个标记。

那么木棍上共有多少个标记？例题5：某校参加数学竞赛有120名男生，80名女生。

参加语文竞赛有120名女生，80名男生。

已知该校总共有260名学生参加了竞赛，其中有75名男生两科竞赛都参加了，那么只参加数学竞赛而没有参加语文竞赛的女生人数是多少名？（即是该课程的课后测试）练习1：芳草地小学四年级有58人学钢琴，43人学画画，37人既学钢琴又学画画，问只学钢琴和只学画画的分别有多少人？练习2：四(二)班有48名学生，在一节自习课上，写完语文作业的有30人，写完数学作业的有20人，语文数学都没写完的有6人。

⑴问语文数学都写完的有多少人？⑵只写完语文作业的有多少人？练习3：四年级一班有45人，其中26人参加了数学竞赛，22人参加了作文比赛，12人两项比赛都参加了．一班有多少人两项比赛都没有参加？练习4：实验二校一个歌舞表演队里，能表演独唱的有10人，能表演跳舞的有18人，两种都能表演的有7人．这个表演队共有多少人能登台表演歌舞?练习5：对全班同学调查发现，会游泳的有20人，会打篮球的有25人．两项都会的有10人，两项都不会的有9人．这个班一共有多少人？练习1：解析：如图，C BAA圆表示学画画的人，B圆表示学钢琴的人，C表示既学钢琴又学画画的人，图中A圆不含阴影的部分表示只学画画的人，有：43376-=(人)，图中B圆不含阴影的部分表示只学钢琴的人，有：583721-=(人)。

容斥原理(数学技巧点拨系列)

容斥原理【知识点讲解】1、原理容斥原理指把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。

2、解释由图可以直接看出各部分之间的关系由Venn图可知：（A∪B=A+B-A∩B)由Venn图可知：（A∪B∪C=A+B+C-A∩B-B∩C-C∩A+A∩B∩C）3、应用两类如果被计数的事物有A、B两类，那么，A类B类元素个数总和=属于A类元素个数+属于B类元素个数—既是A类又是B类的元素个数。

三类如果被计数的事物有A、B、C三类，那么，A类和B类和C类元素个数总和=A类元素个数+B类元素个数+C类元素个数—既是A类又是B类的元素个数—既是A类又是C类的元素个数—既是B类又是C类的元素个数+既是A类又是B类而且是C类的元素个数。

4、解题导语使用容斥原理一般用于集合相关问题中，但是此类思想在数学学习中仍有巨大作用。

例如在计数原理中使用间接法等等。

因此学习此类问题对数学能力的提升是有很大帮助的，它可以帮助你换一个角度看数学题，从而找到更简单的办法。

【例题详析】例1、（2020宁夏）《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝，并称为中国古典小说四大名著，六盘水市第七中学为了解我校学生阅读四大名著的情况，随机调查了100位学生，其中阅读过《西游记》或《红楼梦》的学生共有90位，阅读过《红楼梦》的学生共有80位，阅读过《西游记》且阅读过《红楼梦》的学生共有60位，则在调查的100位同学中阅读过《西游记》的学生人数为（）A ．80B ．70C ．60D ．50【参考答案】B【详解】因为阅读过《西游记》或《红楼梦》的学生共有90位，阅读过《西游记》且阅读过《红楼梦》的学生共有60位，所以《西游记》与《红楼梦》两本书中只阅读了一本的学生共有90-60=30位，因为阅读过《红楼梦》的学生共有80位，所以只阅读过《红楼梦》的学生共有80-60=20位，所以只阅读过《西游记》的学生共有30-20=10位，故阅读过《西游记》的学生人数为10+60=70位，【方法解析】由两类的容斥原理得：总人数=阅读过《西游记》+阅读过《红楼梦》-阅读过《红楼梦》和《西游记》的，由此得阅读过《西游记》的学生人数=90+60-80=70（位）例2：某中学的学生积极参加体育锻炼，其中有96名学生喜欢足球或游泳，60名学生喜欢足球，82名学生喜欢游泳，则该中学既喜欢足球又喜欢游泳的学生有（）名．A ．62B ．56C ．46D ．42【参考答案】C【详解】喜欢足球的学生、喜欢游泳的学生形成的集合分别记为A ，B ，依题意，集合A ，B ，A B 中元素个数分别为：()60,()82,()96n A n B n A B ==⋃=，则()()()()60829646n A B n A n B n A B ⋂=+-⋃=+-=，所以中学既喜欢足球又喜欢游泳的学生有46名.例3．某小学对小学生的课外活动进行了调查.调查结果显示：参加舞蹈课外活动的有63人，参加唱歌课外活动的有89人，参加体育课外活动的有47人，三种课外活动都参加的有24人，只选择两种课外活动参加的有46人，不参加其中任何一种课外活动的有15人.问接受调查的小学生共有多少人？（）A ．120B ．144C ．177D ．192【参考答案】A 【详解】如图所示，用韦恩图表示题设中的集合关系，不妨将参加舞蹈、唱歌、体育课外活动的小学生分别用集合,,A B C 表示，则()63,()89,()47,()24card A card B card C card A B C ===⋂⋂=不妨设总人数为n ，韦恩图中三块区域的人数分别为,,x y z即()24,()24,()24card A B x card A C y card B C z ⋂=+⋂=+⋂=+46x y z ++=，由容斥原理：15()()()()()()()n card A card B card C card A B card A C card B C card A B C -=++-⋂-⋂-⋂+⋂⋂638947(24)(24)(24)24x y z =++-+-+-++解得：120n =【跟踪训练】一、单选题1．某校高三（1）班有50名学生，春季运动会上，有15名学生参加了田赛项目，有20名学生参加了径赛项目，已知田赛和径赛都参加的有8名同学，则该班学生中田赛和径赛都没有参加的人数为（）A ．27B ．23C ．15D ．72．某网店统计了连续三天售出商品的种类情况：第一天售出19种商品，第二天售出13种商品，第三天售出18种商品；前两天都售出的商品有3种，后两天都售出的商品有4种．则该网店这三天售出的商品最少有（）．A．25种B．27种C．29种D．31种3．为了丰富同学们的课外生活，某班58名同学在选课外兴趣小组时，选择篮球小组的有28人，选择乒乓球小组的有36人，既没有选择篮球小组又没有选择乒乓球小组的有12人，那么选择篮球小组但没有选择乒乓球小组的人数为（）A．8B．10C．18D．204．某班有50名同学，有20名同学既不选修足球课程也不选修篮球课程，有18名同学选修了足球课程，28名同学选修了篮球课程，则既选修了足球课程也选修了篮球课程的同学有（）名A．10B．12C．14D．165．中共一大会址、江西井冈山、贵州遵义、陕西延安是中学生的几个重要的研学旅行地.某中学在校学生3000人，学校团委为了了解本校学生到上述红色基地研学旅行的情况，随机调查了500名学生，其中到过中共一大会址或井冈山研学旅行的共有40人，到过井冈山研学旅行的20人，到过中共一大会址并且到过井冈山研学旅行的恰有10人，根据这项调查，估计该学校到过中共一大会址研学旅行的学生大约有（）人A．240B．180C．120D．606．某班45名学生参加“3·12”植树节活动，每位学生都参加除草､植树两项劳动.依据劳动表现，评定为“优秀”､“合格”2个等级，结果如下表：等级优秀合格合计项目除草301545植树202545若在两个项目中都“合格”的学生最多有10人，则在两个项目中都“优秀”的人数最多为（）A．5B．10C．15D．207．高考“33 ”模式指考生总成绩由语文、数学、外语3个科目成绩和高中学业水平考试3个科目成绩组成．计入总成绩的高中学业水平考试科目，由考生根据报考高校要求和自身特长，在思想政治、历史、地理、物理、化学、生物6个科目中自主选择．某中学为了解本校学生的选择情况，随机调查了100位学生的选择意向，其中选择物理或化学的学生共有40位，选择化学的学生共有30位，选择物理也选择化学的学生共有10位，则该校选择物理的学生人数与该校学生总人数比值的估计值为（）A．0.1B．0.2C．0.3D．0.48．移动支付、高铁、网购与共享单车被称为中国的新“四大发明”，某中学为了解本校学生中新“四大发明”的普及情况，随机调查了100位学生，共中使用过移动支付或共享单车的学生共90位，使用过移动支付的学生共有80位，使用过共享单车的学生且使用过移动支付的学生共有60位，则该校使用共享单车的学生人数与该校学生总数比值的估计值为（）A．0.5B．0.6C．0.7D．0.89．某地对农户抽样调查，结果如下：电冰箱拥有率为45％，电视机拥有率为55％，洗衣机拥有率为65％，拥有上述三种电器的任意两种的占35％，三种电器齐全的为25％，那么一种电器也没有的农户所占比例是（）A．20％B．10％C．15％D．12％10．某学校高三教师周一、周二、周三开车上班的人数分别是8，10，14，若这三天中至少有一天开车上班的职工人数是20，则这三天都开车上班的职工人数至多是（）A．8B．7C．6D．5二、填空题11．学校运动会，某班所有同学都参加了羽毛球或乒乓球比赛，已知该班共有23人参加羽毛球赛，35人参加乒乓球赛，既参加羽毛球又参加乒乓球赛有6人，则该班学生数为______．12．某校高三（1）班有50名学生，春季运动会上，有15名学生参加了田赛项目，有20名学生参加了径赛项目，已知田赛和径赛都参加的有8名同学，则该班学生中田赛和径赛都没有参加的人数为__________．13．某单位共有员工85人，其中68人会骑车，62人会驾车，既会骑车也会驾车的人有57人，则既不会骑车也不会驾车的人有___________人.14．高一某班有学生45人，其中参加数学竞赛的有32人，参加物理竞赛的有28人，另外有5人两项竞赛均不参加，则该班既参加数学竞赛又参加物理竞赛的有___.人．15．某班有学生48人，经调查发现，喜欢打羽毛球的学生有35人，喜欢打篮球的学生有20人.设既喜欢打羽毛球，又喜欢打篮球的学生的人数为x，则x的最小值是_________.16．网络流行词“新四大发明’’是指移动支付､高铁､网购与共享单车.某中学为了解本校学生中“新四大发明”的普及情况，随机调查了100名学生，其中使用过移动支付或共享单车的学生共90名，使用过移动支付的学生共有80名，使用过共享单车的学生且使用过移动支付的学生共有60名，则该校使用共享单车的学生人数与该校学生总数比值的估计值为___________. 17．某班有39名同学参加数学、物理、化学课外研究小组，每名同学至多参加两个小组.已知参加数学、物理、化学小组的人数分别为26，15，13，同时参加数学和物理小组的有6人，同时参加物理和化学小组的有4人，则同时参见数学和化学小组有多少人__________. 18．某班共40人，其中24人喜欢篮球运动，16人喜欢乒乓球运动，6人这两项运动都不喜欢，则只喜欢其中一项运动的人数为________19．某班有45名同学参加语文、数学、英语兴趣小组.已知仅参加一个兴趣小组的同学有20人，同时参加语文和数学兴趣小组的同学有9人，同时参加数学和英语兴趣小组的同学有15人，同时参加语文和英语兴趣小组的同学有11人，则同时参加这三个兴趣小组的同学有人___________.20．某班进行集体活动，为活跃气氛，班主任要求班上60名同学从唱歌、跳舞、讲故事三个节目中至少选择一个节目、至多选两个节目为大家表演，已知报名参加唱歌、跳舞、讲故事的人数分别为40，20,30，同时参加唱歌和讲故事的有15人，同时参加唱歌和跳舞的有10人，则同时只参加跳舞和讲故事的人数为__________．21．对班级40名学生调查对A、B两事件的态度，有如下结果：赞成A的人数是全体的五分之三，其余的不赞成，赞成B的比赞成A的多3人，其余的不赞成，另外，对A、B都不赞成的学生数比对A、B都赞成的学生数的三分之一多1人，问对A、B都赞成的学生有________人. 22．2021年是中国共产党成立100周年，电影频道推出“经典频传：看电影，学党史”系列短视频，传扬中国共产党的伟大精神，为广大青年群体带来精神感召.现有《青春之歌》《建党伟业》《开国大典》三支短视频，某大学社团有50人，观看了《青春之歌》的有21人，观看了《建党伟业》的有23人，观看了《开国大典》的有26人.其中，只观看了《青春之歌》和《建党伟业》的有4人，只观看了《建党伟业》和《开国大典》的有7人，只观看了《青春之歌》和《开国大典》的有6人，三支短视频全观看了的有3人，则没有观看任何一支短视频的人数为________【参考答案】1．B【详解】设高三（1）班有50名学生组成的集合为U ,参加田赛项目的学生组成的集合为A ，参加径赛项目的学生组成的集合为B由题意集合A 有15个元素，B 有20个元素，A B 中有8个元素所以A B 有15+20827-=个元素.所以该班学生中田赛和径赛都没有参加的人数为5027=23-故选：B2．C【详解】解：因为前两天都售出的商品有3种，因此第一天售出且第二天没有售出的商品有19316-=（种)；同理第三天售出的商品中有14种第二天未售出，有1种商品第一天未售出；所以三天商品种数最少时，是第三天中14种第二天未售出的商品都是第一天售出过的，此时商品总数是1416129+-=（种)；分别用集合A 、B 、C 表示第一、第二和第三天售出的商品，则商品数最少时，如图所示．故选：C ．3．B【详解】设既选择篮球小组又选择乒乓球小组的有x 人，则选择篮球小组但没有选择乒乓球小组的有()28x -人，选择乒乓球小组但没有选择篮球小组的有()36x -人.由题意可得()()12283658x x x +-+-+=，解得18x =，所以选择篮球小组但没有选择乒乓球小组的人数为2810x -=.【详解】设既选修了足球课程也选修了篮球课程的同学有x 名，由容斥原理得20182850x ++-=，解得16x =.故选：D.5．B【详解】如下图所示，设调查的学生中去过中共一大会址研学旅行的学生人数为x ，由题意可得()102040x -+=，解的30x =，因此，该学校到过中共一大会址研学旅行的学生的人数为303000180500⨯=.6．C【详解】用集合A 表示除草优秀的学生，B 表示植树优秀的学生，全班学生用全集U 表示，则U A ð表示除草合格的学生，则U B ð表示植树合格的学生，作出Venn 图，如图，设两个项目都优秀的人数为x ，两个项目都是合格的人数为y ，由图可得203045x x x y -++-+=，5x y =+，因为max 10y =，所以max 10515x =+=．故选：C ．【详解】选择物理的学生人数为40301020-+=，即该校选择物理的学生人数与该校学生总人数比值的估计值为200.2100=．故选：B8．C【详解】根据题意使用过移动支付、共享单车的人数用韦恩图表示如下图，因此，该校使用共享单车的学生人数与该校学生总数比值的估计值700.7100=，故选C.9．A【详解】解：设农户总共为100家，则有55家农户有电视机，45家农户有电冰箱，65家农户有洗衣机，有25家农户同时拥有这三种电器，另外75家只有其中两种或一种或没有电器．设只有电冰箱和电视机的农户有a 家，只有电冰箱和洗衣机的农户有b 家，只有洗衣机和电视机的农户有c 家，只有电视机、电冰箱、洗衣机的分别有d 、e 、f 家，没有任何电器的农户有x 家．那么对于拥有电冰箱的农户可得出：2545a b e +++=①那么对于拥有电视机的农户可得出：2555a c d +++=②那么对于拥有洗衣机的农户可得出：2565b c f +++=③把上面三个式子相加可得：()290a b c d e f +++++=④对于拥有上述三种电器的任意两种的占35%，得到：35a b c ++=⑤把⑤代入④可得到20d e f ++=⑥因为农户共有100家，所以25100a b c d e f x +++++++=，把⑤和⑥代入上式得到20x =，即一种电器也没有的农户所占比例为20%，10．C【详解】解：设周三，周二，周一开车上班的职工组成的集合分别为A ，B ，C ，集合A ，B ，C 中元素个数分别为n A ．，n B ．，n C ．，则n A ．14=，n B ．10=，n C ．8=，()20n A B C ⋃⋃=，因为()n A B C n ⋃⋃=A ．n +B ．n +C ．()()()()n A B n A C n B C n A B C -⋂-⋂-⋂+⋂⋂，且()()n A B n A B C ⋂⋂⋂ ，()()n A C n A B C ⋂⋂⋂ ，()()n B C n A B C ⋂⋂⋂ ，所以1410820()3()n A B C n A B C ++-+⋂⋂⋂⋂ ，即1410820()62n A B C ++-⋂⋂= ．故选：C ．11．52【详解】解：设参加羽毛球赛为集合A ，参加乒乓球赛为集合B ，依题意可得如下韦恩图：所以该班一共有1762952++=人；故答案为：5212．23【详解】由题意，15名参加田赛的同学中有7名没有参加径赛，20名参加径赛的同学中有12名没有参加田赛，所以参加田赛和径赛的同学共有781227++=人，综上，该班学生中田赛和径赛都没有参加的人数为502723-=人.13．12【详解】设会骑车的人组合的集合为A ，会驾车的人组成的集合为B ，既会骑车也会驾车的人组成的集合为集合C ,易知A B C = ，记card()A 表示集合A 中的元素个数，则有()()()()68625773card A B card A card B card A B =+-=+-= ，所以既不会骑车也不会驾车的人为857312-=.故答案为：1214．20【详解】设该班既参加数学竞赛又参加物理竞赛的学生人数为x ，以集合U 表示该班集体，集合A 表示参加数学竞赛的学生组成的集合，集合B 表示参加物理竞赛的学生组成的集合，如下图所示：由题意可得()()322856545x x x x -++-+=-=，解得20x =.故答案为：20.15．7【详解】设既不喜欢打羽毛球，又不喜欢打篮球的学生的人数为y ，则352048x y +-+=，即7x y -=，因为0y，所以7x .因为20x ，所以720x .故答案为：7.16．710##0.7【详解】根据题意，将使用过移动支付､共享单车的人数用如图所示的韦恩图表示，所以该校使用共享单车的学生人数与该校学生总数比值的估计值为6010710010+=.故答案为：710.17．5【详解】设参加数学、物理、化学小组的同学组成的集合分别为A ，B 、C ，同时参加数学和化学小组的人数为x ，因为每名同学至多参加两个小组，所以同时参加三个小组的同学的人数为0，如图所示：由图可知：20654939x x x -+++++-=，解得5x =，所以同时参加数学和化学小组有5人.故答案为：5.18．28【详解】6 人这两项运动都不喜欢，∴喜欢一项或两项运动的人数为40634-=人；∴喜欢两项运动的人数为：2416346+-=人，∴喜欢篮球的人数为24618-=人；喜欢乒乓球的人数为16610-=人；∴只喜欢其中一项运动的人数为181028+=人.故答案为：28.19．5【详解】以集合A 、B 、C 表示分别参加语文、数学、英语兴趣小组的学生，如下图所示：设同时参加这三个兴趣小组的同学有x 人，由图可得()()()209111555245x x x x x +-+-+-+=-=，解得5x =.故答案为：5.20．5【详解】参加唱歌、跳舞、讲故事的人分别用集合,,A B C 表示，作出Venn 图，如图，图中字母表示相应区域人数，则0n =，又40a b m ++=，20b c d ++=，30d e m ++=，15m =，10b =，60a b c d e m +++++=，则()()()a b m b c d d e m b m ++++++++--2a b c d e m =+++++，∴4020301510605d =++---=，∴同时只参加跳舞和讲故事的人数为5人．故答案为：5．21．18【详解】赞成A 的人数为340245⨯=，赞成B 的人数为24327+=，设对A 、B 都赞成的学生有x ，则112724403x x x x ++-++-=，解得18x =.故答案为：18.22．3【详解】把大学社团50人形成的集合记为全集U ，观看了《青春之歌》《建党伟业》《开国大典》三支短视频的人形成的集合分别记为A，B，C，依题意，作出韦恩图，如图，观察韦恩图：因观看了《青春之歌》的有21人，则只看了《青春之歌》的有214638---=(人)，因观看了《建党伟业》的有23人，则只看了《建党伟业》的有234739---=(人)，因观看了《开国大典》的有26人，则只看了《开国大典》的有2667310---=(人)，因此，至少看了一支短视频的有3467891047++++++=(人)，-=所以没有观看任何一支短视频的人数为50473。

【精品】通用版2022年六年级奥数精品讲义易错专项高频计算题-容斥原理(含答案)

通用版六年级奥数专项精品讲义及常考易错题汇编计数问题:容斥原理【知识点归纳】在日常生活中，人们常常需要统计一些数量，在统计的过程中，往往会发现有些数量重复出现，为了使重复出现的部分不致被重复计算，人们研究出一种新的计数方法，既先不考虑重复的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排除出去，使计算的结果既无遗漏又无重复．这种计数方法称为包含排除法，也叫做容斥原理或重叠问题．一般方法：在解答有关包含排除问题时，我们常常利用圆圈图（韦恩图）来帮助分析思考．容斥原理1：两量重叠问题A类与B类元素个数的总和=A类元素的个数+B类元素个数-既是A类又是B类的元素个数用符号可表示成：A∪B=A+B-A∩B （其中符号“∪”读作“并”，相当于中文“和”或者“或”的意思，符号“∩”读作“交”，相当于中文“且”的意思）．容斥原理2：三量重叠问题A类、B类与C类元素个数的总和=A类元素的个数+B类元素个数+C类元素个数-既是A类又是B类的元素个数-既是B类又是C类的元素个数-既是A类又是C类的元素个数+同时是A类、B类、C类的元素个数．用符号表示为：A∪B∪C=A+B+C-A∩B-B∩C-A∩C+A∩B∩C【经典例题】例1：聚会时，有5人喝可乐，有6人喝果汁，有4人喝茶水，其中有3人既喝果汁又喝茶水，有（）人参加聚会．A、18B、12C、10分析：由题意可知，聚会人数=喝可乐的人数+喝果汁的人数+喝茶水的人数-既喝果汁又喝茶水的人数即可．解：5+6+4-3=12（人）答：共有12人参加聚会．故选：B点评：此题考查利用容斥原理解决实际问题的灵活应用，可借助图形解决问题一．选择题1．三（1）班有30人，订阅《少儿书画》的有20人，订阅《少年博览》的有25人，每人至少订阅一种刊物，两种刊物都订阅的有()人．2．某班同学积极参加跳绳比赛，参加集体比赛的有10人、参加个人比赛的有19人，两项都参加的有8人，这个班共有()人参加跳绳比赛．A．21B．27C．29D．373．同学们去秋游，休息时玩了2个游戏．玩贴鼻子的有27人，玩抢椅子的有34人，两个游戏都玩的有11人，参加秋游的同学共()人．A．72B．61C．504．一班进行语文、数学测试，得优的共30人．其中语文得优的有18人，两科全得优的有9人，数学得优的有()人．A．3B．12C．215．某单位职工24人中，有女性11人，已婚的16人．在已婚的16人中有女性6人．问这个单位的未婚男性有多少人？()A．1B．3C．9D．126．小强和小刚经常向王爷爷借书来读．已知王爷爷有100本书，其中小强读过的书有60本，小刚读过的书有50本，两人都读过的书有20本，那么() A．两人都没读过的书有20本B．小强读过但小刚没读过的书有30本C．小刚读过但小强没读过的书有40本D．只有一人读过的书有70本7．同学们去动物园游玩，参观猴馆的有31人，参观孔雀馆的有26人，参观两个馆的有20人．每位同学至少参观这两馆中的一个，则去动物园的一共有( )人8．三（1）班喜欢读书的有28人，喜欢运动的有31人，既喜欢读书又喜欢运动的有12人，三（1）班共有()人．（每人至少选一项喜欢的）A．59B．35C．479．三（1）班有学生45人，喜欢喜羊羊的有38人，喜欢美羊羊的有36人，每个学生至少喜欢喜羊羊和美羊羊中的一个，既喜欢喜羊羊又喜欢美羊羊的有( )人．A．12B．29C．3310．下列4句话中正确的说法是哪些？()（1）步测一段距离，每步的平均长度和走的步数成反比例．（2）用4个圆心角是90 的扇形肯定可以拼成一个圆．（3）将形状、大小一样的红、白两种颜色的小球各5个，放在一个不透明的袋子里，任意摸出1个球，摸到红球和白球的可能性相等．（4）一个班有40名学生，其中有18人参加美术组，15人参加数学组，有10人这两个小组都参加，那么这两个小组都没参加的有17人．A．（1）（2）（3）B．（1）（3）（4）C．（2）（3）（4）D．（1）（2）（4）二．填空题11．三（1）班有32人订阅了《小学科学》，有24人订阅了《纸上天文馆》，有12人两种刊物都订阅了，每人至少订阅了其中的一种刊物，三（1）班共有人。

(完整版)容斥原理例题

学科：奥数教学内容：第四讲容斥原理（二）上一讲我们已经初步研究了简单的容斥原理，今天我们继续研究较复杂的容斥问题。

例1五年级一班有45名同学，每人都积极报名参加暑假体育训练班，其中报足球班的有25人，报篮球班的有20人，报游泳班的有30人，足球、篮球都报者有10人，足球、游泳都报者有10人，足球、篮球都报者有12人。

请问：三项都报的有多少人？分析：由于问题比较复杂，我们把它简化成下图.要计算阴影部分的面积，我们记A∩B 为圆A与圆B公共部分的面积，B∩C为圆B与圆C公共部分的面积，A∩C表示圆A与圆C 的公共部分的面积，x为阴影部分的面积则图形盖住的面积为：A+B+C-A∩B-B∩C-A∩C+X。

请同学们注意：阴影部分的面积先加了3次，然后又被减了3次，最后又加了1次。

解答：设三项都报的有x人，由容斥原理有30+25+20-10-10-12+x=45解得 x=2。

答：三项都报名的有2人。

说明：在“A+B+C-A∩B-B∩C-A∩C+X”式中，A，B，C，A∩B，B∩C，A∩C，x和总量这8个数中，只要知道了7个数，就可通过列方程求出第8个数。

例2从1至1000这1000个自然数中，不能被3、5、7中任何一个自然数整除的数一共有多少个？分析：第一步先求出：能被3、5、7中任何一个自然数整除的数一共有多少个？第二步再求出：不能被3、5、7中任何一个自然数整除的数一共有多少个？能被3整除的自然数的个数+能被5整除的自然数的个数+能被7整除的自然数的个数－（既能被3整除又能被5整除的自然数的个数+既能被3整除又能被7整除的自然数的个数+既能被5整除又能被7整除的自然数的个数）+能同时被3、5、7整除的自然数的个数=能被3、5、7中任何一个自然数整除的数的个数。

解答：能被3整除的自然数有多少个？1000÷3=333……1 有333个。

能被5整除的自然数有多少个？1000÷5=200 有200个。

小学数学六年级奥数《容斥原理(2)》练习题(含答案)

小学数学六年级奥数《容斥原理(2)》练习题（含答案）一、填空题1.某校有500名学生报名参加学科竞赛,数学竞赛参加者共312名,作文竞赛参加者共353名,其中这两科都参加的有292名,那么这两科都没有参加的人数为人.2.某门诊部统计某一天挂号的病人,内科150人,外科92人,其中内、外两科都求诊的18人，这一天共来了个病人.3.两个正方形的纸片盖在桌面上,位置与尺寸如图所示,则它们盖住 (平方厘米).4.不超过30的正整数中,是3的倍数或4的倍数的数有个.5.在一次运动会中,甲班参加田赛的有15人,参加径赛的有12人,参加田赛又参加径赛的有7人,没有参加比赛的有21人.那么甲班共有人.6.在桌面上放置着三个两两重叠的圆纸片(如图),它们的面积都是100(cm 2)并知A 、B 两圆重叠的面积是20(cm 2),A 、C 两圆重叠的面积为45(cm 2),B 、C 两圆重叠面积为31(cm 2),三个圆共同重叠的面积为15(cm 2),求盖住桌子的总面积是平方厘米.7.在一次考试中,某班数学得100分的有17人,语文得100分的有13人,两科都得100分的有7人,那么两科中至少有一科得100分的共有人.全班45人中两科都不得100分的有人.8.在1,2,3,…,1000这1000个自然数中,既不是2的倍数,又不是3的倍数的数共有个.9.小于1000的自然数中,是完全平方数而不是完全立方数的数有个.10.某校有学生960人,其中有510人订阅“作文报”,有330人订阅“数学报”,有120人订阅“科学爱好者”,全校学生中有270人订阅两种报刊,有58人三种报刊都订,那么这学校中没有订阅任何报刊的有人.2 AB C二、解答题11.70名学生参加体育比赛,短跑得奖的31人,投掷得奖的36人,弹跳得奖的29人,短跑与投掷二项均得奖的12人,跑、跳、投三项均得奖的有5人,只得弹跳奖的有7人,只得投掷奖的有15人.求(1)只得短跑奖的人数;(2)得二项奖的总人数;(3)一项奖均未得的人数.12.64人订A 、B 、C 三种杂志.订A 种杂志的28人,订B 种杂志的有41人,订C 种杂志的有20人, 订A 、B 两种杂志的有10人,订B 、C 两种杂志的有12人,订A 、C 两种杂志的有12人,问三种杂志都订的有多少人?13.求从1到1994中不能被5整除,也不能被6或7整除的自然数的个数.14.夏日的一天,有十个同学去吃冷饮.向服务员交出需要冷饮的统计,数字如下,有6个人要可可,有5个人要咖啡,有5个人要果汁,有3个人既要可可又要果汁,有一个人既要可可、咖啡又要了果汁.求证其中一定有一个人什么冷饮也没有要.———————————————答案——————————————————————1. 127从图中可以看出:参加数学、作文竞赛的总人数为312+353-292=373(人) 从而可知这两科都没有参加的人数为500-373=127(人).2. 224从图可以看出,来诊病人总数为150+92-18=224(人).3. 10.75把两个正方形面积加起来得22+32=13,但其中多算了一块阴影部分的面积,这部分面积为 1.52=2.25(平方厘米),故两个正方形盖住的总面积是22+32-1.52=13-2.25=10.75(cm 2)4. 15内科 150人外科92人18 人不超过30的3的倍数有10330=⎥⎦⎤⎢⎣⎡(个),不超过30的4的倍数有7430=⎥⎦⎤⎢⎣⎡-(个);不超过30的3⨯4=12的倍数有24330=⎥⎦⎤⎢⎣⎡⨯(个),因此不超过30的正整数中是3的倍数,或是4的倍数的数共有10+7-2=15(个).5. 41如图所示,易知总人数为(15+12-7)+21=41(人).6. 219由容斥原理知,盖住桌面的总面积为100+100+100-(20+45+31)+15=219(平方厘米).7. 23;22至少一科得100分的有17+13-7=23(人),两科都不得100分的有45-23=22(人).8. 333在1~1000的自然数中,2的倍数有50021000=⎥⎦⎤⎢⎣⎡(个),3的倍数有33331000=⎥⎦⎤⎢⎣⎡(个),2⨯3=6的倍数共有166321000=⎥⎦⎤⎢⎣⎡⨯(个),故是2或是3的倍数共有500+333-166=667(个),从而既不是2的倍数,又不是3的倍数的数共有1000-667=333(个).9. 28小于1000的自然数中,是完全平方数的有12、22、…,312共31个.其中12=13,82=43,272=93.又是完全立方数,故符合条件的数有31-3=28(个)10. 121由容斥原理知,或订“作文报”或订“数学报”或订“科学爱好者”的总人数为510+330+120-270+58=748(人)故三种报刊都没有订的人数为960-748=212(人).11. (1)如图,用矩形表示参赛的70个学生,而用三个圆表示分别在跑、跳、投中得奖的人.数学语文 7 17 13设x 为只得短跑奖的人数,y 为只在短跑和弹跳两项得奖的人数,z 为只在弹跑与投掷两项得奖的人数,u 为只在投掷和短跑两项得奖的人数.则有u =12-5=7(人),z =36-15-12=9(人),y =29-5-7=8(人),x =31-12-8=11(人).即只得短跑奖的有11人.(2)得二次奖的人数为y +z +u =8+9+7=24(人).(3)因至少得一次奖的人数为x +y +z +u +5+7+15=62(人),故一项奖均未得的人数为70-62=8(人).12. 设三种杂志均订的人数为x ,则有28+41+20-10-12-12+x =64,解得x =9,即三种杂志都订的有9人.13. 在1~1994中,能被5整除的个数为39851994=⎥⎦⎤⎢⎣⎡;能被6整除的个数为33261994=⎥⎦⎤⎢⎣⎡;能被7整除的个数为28471994=⎥⎦⎤⎢⎣⎡;能被5⨯6=30整除的个数为66301994=⎥⎦⎤⎢⎣⎡;能被5⨯7=35整除的数为56351994=⎥⎦⎤⎢⎣⎡;能被6⨯7=42整除的个数为47421994=⎥⎦⎤⎢⎣⎡;能被5⨯6⨯7=210整除的个数为92101994=⎥⎦⎤⎢⎣⎡. 根据容斥原理,1~1994中或能被5,或能被6,或能被7整除的数的个数为:(398+332+284)-(66+54+47)+9=854,从而不能被5整除,也不能被6或7整除的自然数的个数为1994-854=1140(个).14. 要了冷饮的总人数为6+5+5-3-2-3+1=9(人),但总人数为10人,故一定有一个人什么冷饮也没有要.AB C x。

小学数学奥林匹克竞赛容斥原理(二)(含答案)

容斥原理（二）【例题分析】例1. 有25人参加跳远达标赛，每人跳三次，每人至少有一次达到优秀。

第一次达到优秀的有10人，第二次达到优秀的有13人，第三次达到优秀的有15人，三次都达到优秀的只有1人。

只有两次达到优秀的有多少人？分析与解：“每人至少有一次达到优秀”说明没有三次都没达到优秀的。

要求只有两次达到优秀的人数，就是求重叠两层的部分（图中阴影部分）。

答：只有两次达到优秀的有11人。

例2. 在一个炎热的夏日，几个小朋友去冷饮店，每人至少要了一样冷饮，其中有6人要了冰棍，6人要了汽水，4人要了雪碧，只要冰棍和汽水的有3人，只要冰棍和雪碧的没有，只要汽水和雪碧的有1人；三样都要的有1人。

问：共有几个小朋友去了冷饮店？分析与解：根据题意画图。

答：共有10个小朋友去了冷饮店。

例3. 有28人参加田径运动会，每人至少参加两项比赛。

已知有8人没参加跑的项目，参加投掷项目的人数与参加跑和跳两项的人数都是17人。

问：只参加跑和投掷两项的有多少人？分析与解：“每人至少参加两项比赛”说明没有不参加的，也没有参加一项比赛的，我们可以在下图中参加一项的区域用0表示。

答：只参加跑和投掷两项的有3人。

例4. 某校六年级二班有49人参加了数学、英语、语文学习小组，其中数学有30人参加，英语有20人参加，语文小组有10人。

老师告诉同学既参加数学小组又参加语文小组的有3人，既参加数学又参加英语和既参加英语又参加语文的人数均为质数，而三种全参加的只有1人，求既参加英语又参加数学小组的人数。

分析与解：根据已知条件画出图。

三圆盖住的总体为49人，假设既参加数学又参加英语的有x人，既参加语文又参加英语的有y由于x、y均为质数，因而这两个质数中必有一个偶质数2，另一个质数为7。

答：既参加英语又参加数学小组的为2人或7人。

例5. 某班同学参加升学考试，得满分的人数如下：数学20人，语文20人，英语20人，数学、英语两科满分者8人，数学、语文两科满分者7人，语文、英语两科满分者9人，三科都没得满分者3人。

小学尖子生训练之-容斥原理之重叠问题(二)模块练习(含答案)

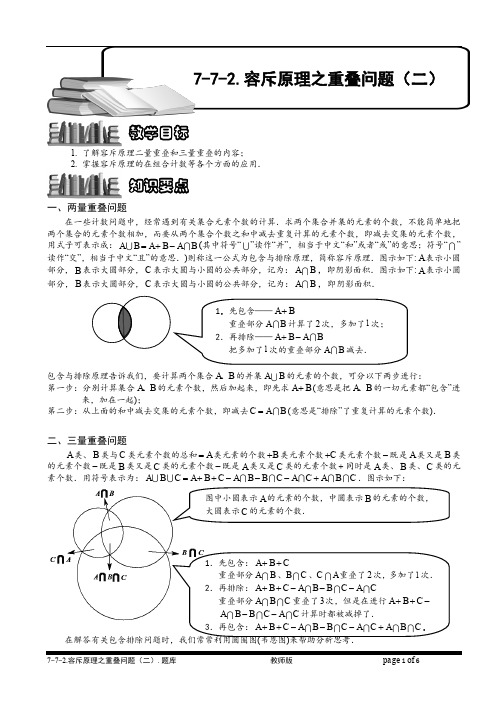
1. 了解容斥原理二量重叠和三量重叠的内容；2. 掌握容斥原理的在组合计数等各个方面的应用．一、两量重叠问题在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，用式子可表示成：A B A B A B =+-(其中符号“”读作“并”，相当于中文“和”或者“或”的意思；符号“”读作“交”，相当于中文“且”的意思．)则称这一公式为包含与排除原理，简称容斥原理．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B ，即阴影面积．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B ，即阴影面积．包含与排除原理告诉我们，要计算两个集合A B 、的并集A B 的元素的个数，可分以下两步进行：第一步：分别计算集合A B 、的元素个数，然后加起来，即先求A B +(意思是把A B 、的一切元素都“包含”进来，加在一起)；第二步：从上面的和中减去交集的元素个数，即减去C A B =(意思是“排除”了重复计算的元素个数)．二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数．用符号表示为：A B C A B C A B B C A C A B C =++---+．图示如下：在解答有关包含排除问题时，我们常常利用圆圈图(韦恩图)来帮助分析思考．教学目标知识要点7-7-2.容斥原理之重叠问题（二）1．先包含——A B + 重叠部分A B 计算了2次，多加了1次； 2．再排除——A B A B +- 把多加了1次的重叠部分A B 减去．图中小圆表示A 的元素的个数，中圆表示B 的元素的个数，大圆表示C 的元素的个数．1．先包含：A B C ++ 重叠部分A B 、B C 、C A 重叠了2次，多加了1次． 2．再排除：A B C A B B C A C ++--- 重叠部分A B C 重叠了3次，但是在进行A B C ++- A B B C A C --计算时都被减掉了． 3．再包含：A B C A B B C A C A B C ++---+．模块一、三量重叠问题【例1】一栋居民楼里的住户每户都订了2份不同的报纸。

容斥原理(二)(含答案)-

容斥原理（二）【例题分析】例1. 有25人参加跳远达标赛，每人跳三次，每人至少有一次达到优秀。

第一次达到优秀的有10人，第二次达到优秀的有13人，第三次达到优秀的有15人，三次都达到优秀的只有1人。

只有两次达到优秀的有多少人？分析与解：“每人至少有一次达到优秀”说明没有三次都没达到优秀的。

要求只有两次达到优秀的人数，就是求重叠两层的部分（图中阴影部分）。

101315251211++--⨯=（人）答：只有两次达到优秀的有11人。

问：共有几个小朋友去了冷饮店？分析与解：根据题意画图。

方法一：664310111110++-+-+-++=()()()（人）方法二：664311210++---⨯=（人）答：共有10个小朋友去了冷饮店。

例3. 有28人参加田径运动会，每人至少参加两项比赛。

已知有8人没参加跑的项目，参加投掷项目的人数与参加跑和跳两项的人数都是17人。

--=（人）281783答：只参加跑和投掷两项的有3人。

例4. 某校六年级二班有49人参加了数学、英语、语文学习小组，其中数学有30人参加，英语有20人参加，语文小组有10人。

分析与解：根据已知条件画出图。

三圆盖住的总体为49人，假设既参加数学又参加英语的有x 人，既参加语文又参加英语的有y 人，可以列出这样的方程：3020103149++---+=x y 整理后得：x y +=9由于x 、y 均为质数，因而这两个质数中必有一个偶质数2，另一个质数为7。

行测理-容斥原理(标准含讲解过程)

2.图解法求只A/只B，在公式中没有——>画图（从里向外、注意去重）
......
容斥原理
x = 34
容斥原理
◆例题5◆
某研究室有 12 人，其中 7 人会英语，7 人会德语，6 人会法语，4 人既会英语又
会德语，3 人既会英语又会法语，2 人既会德语又会法语，1 人三种语言都会。会且只
会一种语言的有多少人？
A.8
B.4
√C.5
D.6
A+B+C -A∩B-B∩C-A∩C +A∩B∩C=全-都不 A+B+C-满足两项 - 满足三项×2=全-都不
B.15
C.5
100
√D.3
A + B- A∩B = 全 - 都不
15 73 ？
图解法：
都=88-15 =73
?=76-73 =3
求只A/只B，在公式中没有——>画图
容斥原理
2.三集合
标准型公式：A+B+C-A∩B-B∩C-A∩C+A∩B∩C=全-都不
B
A
+2 -1
+3 -1
-1 -1
+2 -1
+2 -1
2.三集合
非标准型公式：A+B+C-满足两项 - 满足三项×2=全-都不
B
满足两项：只具有其中两个属性（灰色区域）
A
+2
+3
+2
+2
A+B+C - 满足两项 - 满足三项×2 +都不 = 全 A+B+C-满足两项 - 满足三项×2=全-都不
C
都不

5.3 容斥原理(二)(教案教学设计导学案)

5.3 容斥原理（二）学习目标:1.理解容斥原理（一）（二），会画韦恩图分析其中关系，正确找出答案；2.培养学生的逻辑思维和数学思考能力；3.培养学生良好的书写习惯。

教学重点:理解容斥原理（二），会画韦恩图分析。

教学难点：容斥原理的一些变式题的分析理解教学过程：一、情境体验展示图片师：还记得图中这家人吗？这里有几对父子呢？学生回答，师用韦恩图表示出来。

师：有两对父子，因为爸爸既是爷爷的儿子，又是儿子的爸爸，所以只有爷爷、爸爸、儿子三个人，爸爸重复计算了一次。

那么图中有几对母女呢？学生回答师：这是三年级学习的简单的重叠问题，其实呢还可以称之为容斥原理（一），是指如果被计数的事物有A、B两类，那么，A类或B类元素个数=A类元素个数＋B类元素个数－既是A类又是B类的元素个数。

（师画出韦恩图，进行讲解）师：如果被计数的事物有三类，又该怎么解决呢？今天我们重点来学习容斥原理（二）（板书课题：容斥原理二）师：首先我们来看两道准备题复习回顾有关容斥原理（一）的相关知识。

师和学生一起完成准备题1、2师：结合韦恩图可以发现，容斥原理（一）A或B的个数=A＋B－C是两个圆圈代表的数量之和减去两两重叠部分。

那么大家看书本上写的容斥原理（2）的文字和图形，很明显，就应该是三个圆圈代表的数量之和减去它们两两重叠部分，即为A＋B＋C－A∩B－A∩C－B∩C。

最后的三者重叠部分怎么办呢？学生思考师引导学生画韦恩图分析，发现减去两两重叠部分的时候，已经把三者重叠部分都减掉了，所以最后应该加上一个三者重叠部分。

即A或B或C的个数= A＋B＋C－A∩B－A∩C－B∩C＋A∩B∩C二、思维探索展示例1例1：五年级学生在一次春游中每个人都带了饮料，其中有51人带了汽水，有48人带了可乐，有32人带了果汁，有16人带了汽水、可乐两种饮料，有11人带了可乐、果汁两种饮料，有13人带了汽水、果汁两种饮料，另外还有7人带了汽水、可乐和果汁三种饮料。

四年级数学思维能力拓展专题突破系列(十八)容斥原理

四年级数学思维能力拓展专题突破系列（十八）容斥原理------容斥原理基础（1）温馨提示：该文档包含本课程的讲义和课后测试题，课后测试题即每一部分内容对应的“课后练习”。

1、了解容斥原理二量重叠和三量重叠的内容。

2、掌握容斥原理在组合计数等各个方面的应用。

1、掌握容斥原理的概念。

2、熟记二元容斥原理。

例题1：实验小学四年级二班，参加语文兴趣小组的有28人，参加数学兴趣小组的有29人，有12人两个小组都参加。

这个班有多少个人参加了语文或数学兴趣小组？例题2：某班共有46人，参加美术小组的有12人，参加音乐小组的有23人，有5人两个小组都参加了。

那么木棍上共有多少个标记？例题5：某校参加数学竞赛有120名男生，80名女生。

参加语文竞赛有120名女生，80名男生。

⑴问语文数学都写完的有多少人？⑵只写完语文作业的有多少人？练习3：四年级一班有45人，其中26人参加了数学竞赛，22人参加了作文比赛，12人两项比赛都参加了．一班有多少人两项比赛都没有参加？练习4：实验二校一个歌舞表演队里，能表演独唱的有10人，能表演跳舞的有18人，两种都能表演的有7人．这个表演队共有多少人能登台表演歌舞?练习5：对全班同学调查发现，会游泳的有20人，会打篮球的有25人．两项都会的有10人，两项都不会的有9人．这个班一共有多少人？练习1：解析：如图，A 圆表示学画画的人，B 圆表示学钢琴的人，C 表示既学钢琴又学画画的人，图中A 圆不含阴影的部分表示只学画画的人，有：43376-=(人)，图中B 圆不含阴影的部分表示只学钢琴的人，有：583721-=(人)。

容斥原理习题加答案

1.现有50名学生都做物理、名学生都做物理、化学实验，化学实验，化学实验，如果物理实验做正确的有如果物理实验做正确的有40人，化学实验做正确的有31人，两种实验都错的有4人，则两种实验都做对的有人，则两种实验都做对的有( ()A 、27人B 、25人C 、19人D 、10人【答案】【答案】B B 【解析】直接代入公式为：【解析】直接代入公式为：50=31+40+450=31+40+450=31+40+4－－A ∩B得A ∩B=25B=25，所以答案为，所以答案为B 。

2.2.某服装厂生产出来的一批衬衫大号和小号各占一半。

某服装厂生产出来的一批衬衫大号和小号各占一半。

其中其中2525％是白色的，％是白色的，7575％是蓝色的。

如果这批衬衫共有％是蓝色的。

如果这批衬衫共有100件，其中大号白色衬衫有10件，小号蓝色衬衫有多少件？（）A 、15B 、25C 、35D 、40【答案】【答案】C C 【解析】这是一种新题型，该种题型直接从求解出发，将所求答案设为A ∩B ，本题设小号和蓝色分别为两个事件A 和B ，小号占50%50%，蓝色占，蓝色占75%75%，直接代，直接代入公式为：入公式为：100=50+75+10100=50+75+10100=50+75+10－－A ∩B ，得：，得：A A ∩B=35B=35。

3.3.某高校对一些学生进行问卷调查。

某高校对一些学生进行问卷调查。

问接受调查的学生共有多少人？（人。

问接受调查的学生共有多少人？（）A ．120B ．144C ．177D ．192【答案】【答案】A A【解析】本题画图按中路突破原则，先填充三集合公共部分数字2424，再推，再推其他部分数字：其他部分数字：根据每个区域含义应用公式得到：根据每个区域含义应用公式得到：总数总数==各集合数之和－两两集合数之和＋三集合公共数＋三集合之外数各集合数之和－两两集合数之和＋三集合公共数＋三集合之外数＝63+89+4763+89+47－－{(x+24)+(z+24)+(y+24)}+24+15＝199199－－{（x+z+y x+z+y））+24+24+24}+24+15根据上述含义分析得到：根据上述含义分析得到：x+z+y x+z+y 只属于两集合数之和，也就是该题所讲的只选择两种考试都参加的人数，所以x+z+y 的值为46人；得本题答案为120.4.4.对某单位的对某单位的100名员工进行调查，结果发现他们喜欢看球赛和电影、戏剧。