2018苏科版八年级下《9.5三角形中位线》同步测试精选有答案
八年级数学下册9、5三角形的中位线习题新版苏科版

6 【2021·十堰】如图,O是矩形ABCD的对角线AC的中 点,M是AD的中点,若AB=5,AD=12,则四边形 ABOM的周长为____2_0___.
7 如图,在△ABC(纸片)中,AB=BC>AC,点D是AB边 的中点,点E在AC边上,将纸片沿DE折叠,使点A落 在BC边上的点F处,则下列结论成立的个数有( B ) ①△BDF是等腰直角三角形; ②∠DFE=∠CFE; ③DE是△ABC的中位线; ④BF+CE=DF+DE. A.1个 B.2个 C.3个 D.4个
苏科版 八年级下
第9章 中心对称图形——平行四边形
9.5 三角形的中位线
习题链接
温馨提示:点击 进入讲评
1B 2D 3A 4B
58 6 20 7B 8答来自呈现9 10 111 【中考·广州】在△ABC中,点D,E分别是△ABC的边
AB,AC的中点,连接DE.若∠C=68°,则∠AED=
(B) A.22°
8 如图,M是△ABC的边BC的中点,AN平分∠BAC, BN⊥AN于点N,延长BN交AC于点D.已知AB=10, AC=16. (1)求证:BN=DN;
证明:∵AN 平分∠BAC,∴∠BAN=∠DAN, ∵BN⊥AN,∴∠ANB=∠AND=90°.
∠BAN=∠DAN, 在△ABN 和△ADN 中,AN=AN,
【点拨】 本题容易因得不出中位线而给解题造成困难, 由折叠可得AD=FD,∠ADE=∠FDE, ∴∠ADF=2∠FDE. ∵AD=BD,∴BD=FD.∴∠DBF=∠DFB. ∴∠ADF=∠DBF+∠DFB=2∠DFB, ∴∠FDE=∠DFB.∴DE∥BC. 不难得出DE是△ABC的中位线,进而判断出②③正确.
【点拨】 (1)中欲证相等的两个角所在三角形不全等,考虑到E,
2018苏科版八年级下《9.5三角形中位线》同步测试精选有答案

《9.5三角形中位线》同步测试精选有难度一、选择题1、如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )A.AB=24m B.MN∥AB C.△CMN∽△CABD.CM:MA=1:22、如图,⊙O的半径为5,弦AB=8,点C在弦AB上,且AC=6,过点C作CD⊥AB交OB于点D,则CD的长为( )A.1B.2C.1.5D.2.5第1题图第2题图第4题图3、梯形ABCD中,AD∥BC,AD=3,BC=5,MN是梯形的中位线,则MN的长是( )A.1B.2C.3D.44、如图,为测量池塘边A、B两点的距离,小明在池塘的一侧选取一点O,测得OA、OB的中点分别是点D、E,且DE=14米,则A、B间的距离是( )A.18米B.24米 C.28米D.30米5、如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为( )A.50° B.60° C.70°D.80°6、如图,在△ABC中,∠ACB=90°,AC=BC=4,M是CB中点,P、N分别在AC、AB上,若△APN的面积与△ANM的面积相等,则AP长为( )A.3B.2C.D.2第5题图第6题图第7题图7、如图,△ABC中,AB=AC=6,BC=8,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的周长是( )A.7+B.10 C.4+2D.128、如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为( )A.4B.8C.2D.49、如图,△ABC中,AB=8cm,AC=5cm,AD平分∠BAC,且AD⊥CD,E 为BC中点,则DE=( )A.3B.5C.2.5D.1.5第8题图第9题图第10题图10、如图,△ABC中,D为BC中点,E为AD的中点,BE的延长线交AC 于F,则为( )A. 1:5B.1:4C.1:3D.1:2二、填空题11、三角形的三边长分别是3cm,5cm,6cm,则连结三边中点所围成的三角形的周长是_________cm.12、在Rt△ABC中,∠C=90°,AC= 5, BC= 12, 则连结两条直角边中点的线段长为_______.13、如图,△ABC的面积为12cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为 cm2.第13题图第15题图第16题图14、在△ABC中,点D、E分别是边AB、AC的中点,那么△ADE的面积与△ABC的面积的比是 .15、如图,在△ABC中,点D、E、F分别是边AB、BC、CA上的中点,且AB=6cm,AC=8cm,则四边形ADEF的周长等于 cm.16、如图,EF为△ABC的中位线,△AEF的周长为6cm,则△ABC的周长为 cm.17、如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是 .三、解答题18、如图,在梯形ABCD中,AD∥BC,AB=DC,过点D作DE⊥BC,垂足为E,并延长DE至F,使EF=DE.连接BF、CF、AC.求证:四边形ABFC是平行四边形.19、如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3(1)求证:BN=DN;(2)求△ABC的周长.20、已知:如图,在□ABCD中,E是CD的中点,F是AE的中点,FC与BE交于G.求证:GF=GC.21、已知:如图,在四边形ABCD中,AD=BC,E、F分别是DC、AB边的中点,FE的延长线分别与AD、BC的延长线交于H、G点.求证:∠AHF=∠BGF.22、如图1,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).(温馨提示:在图1中,连接BD,取BD的中点H,连接HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE.)问题一:如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连接EF,分别交DC、AB于点M、N,判断△OMN的形状,请直接写出结论;问题二:如图3,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,与BA的延长线交于点G,若∠EFC=60°,连接GD,判断△AGD的形状并证明.23、如图,已知AD与BC相交于E,∠1=∠2=∠3,BD=CD ,∠ADB=90°,CH ⊥AB 于H ,CH 交AD 于F .(1)求证:CD ∥AB ;(2)求证:△BDE ≌△ACE ;(3)若O 为AB 中点,求证:OF=BE .24、某厂有一块如图所示的△ABC 铁板,根据需要,现要把它加工成一个平行四边形铁板.要把材料完全利用起来,可怎样加工? 请你利用学过的知识帮助工人师傅把切割的线用虚线画出来,并指出加工后的平行四边形.能否将此三角形铁板加工成长方形?请予以探索.C A C A CA答案1、D2、C3、D4、C5、C6、B7、B8、D9、D 10、D11、 7 12、 6.5 13、9 14、 15、14. 16、12. 17、或.18、证明:等腰梯形ABCD 中,AB=DC ,∴∠ABC=∠DCB ,∵DE ⊥BC ,DE=EF ,∴△DFC 是等腰三角形,∴∠DCB=∠FCE ,DC=CF ,∴∠ABC=∠FCE ,∴AB ∥CF ,∵AB=CD=CF ,∴四边形ABFC 是平行四边形19、(1)证明:在△ABN和△ADN中,∵,∴△ABN≌△ADN,∴BN=DN.(2)解:∵△ABN≌△ADN,∴AD=AB=10,DN=NB,又∵点M是BC中点,∴MN是△BDC的中位线,∴CD=2MN=6,故△ABC的周长=AB+BC+CD+AD=10+15+6+10=41.20、取BE的中点H,连接FH、CH∵F、G分别是AE、BE的中点∴FH是△ABE的中位线∴FH∥AB FH=1/2*AB∵四边形ABCD是平行四边形∴CD∥AB CD=AB∵E是CD的中点∴CE=1/2*AB∵CE=1/2*AB FH=1/2*AB21、证明:连接AC,取AC的中点M,连接ME、MF ∵M是AC的中点,E是DC的中点∴ME是△ACD的中位线∴ME=AD/2,PE∥AH∴∠MEF=∠AHF (同位角相等)同理可证:MF=BC/2, ∠MFE=∠BGF (内错角相等)∵AD=BC∴ME=MF∴∠MFE=∠MEF∴∠AHF=∠BGF22、解:(1)取AC中点P,连接PF,PE,可知PE=,PE∥AB,∴∠PEF=∠ANF,同理PF=,PF∥CD,∴∠PFE=∠CME,又PE=PF,∴∠PFE=∠PEF,∴∠OMN=∠ONM,∴△OMN为等腰三角形.(2)判断出△AGD是直角三角形.证明:如图连接BD,取BD的中点H,连接HF、HE,∵F是AD的中点,∴HF∥AB,HF=AB,同理,HE∥CD,HE=CD,∵AB=CD∴HF=HE,∵∠EFC=60°,∴∠HEF=60°,∴∠HEF=∠HFE=60°,∴△EHF是等边三角形,∴∠3=∠EFC=∠AFG=60°,∴△AGF是等边三角形.∵AF=FD,∴GF=FD,∴∠FGD=∠FDG=30°∴∠AGD=90°即△AGD是直角三角形.23、证明:(1)∵BD=CD,∴∠BCD=∠1;∵∠1=∠2,∴∠BCD=∠2;∴CD∥AB.(2)∵CD∥AB,∴∠CDA=∠3.∵∠BCD=∠2=∠3,∴BE=AE.且∠CDA=∠BCD,∴DE=CE.在△BDE和△ACE中,∵.∴△BDE≌△ACE(SAS);(3)∵△BDE≌△ACE,∴∠4=∠1,∠ACE=∠BDE=90°∴∠ACH=90°﹣∠BCH;又∵CH⊥AB,∴∠2=90°﹣∠BCH;∴∠ACH=∠2=∠1=∠4,∴AF=CF;∵∠AEC=90°﹣∠4,∠ECF=90°﹣∠ACH,又∵∠ACH=∠4,∴∠AEC=∠ECF24、参照图形:。
9.4矩形、菱形、正方形9.5三角形的中位线同步练习含答案苏科版数学八年级下试卷分析
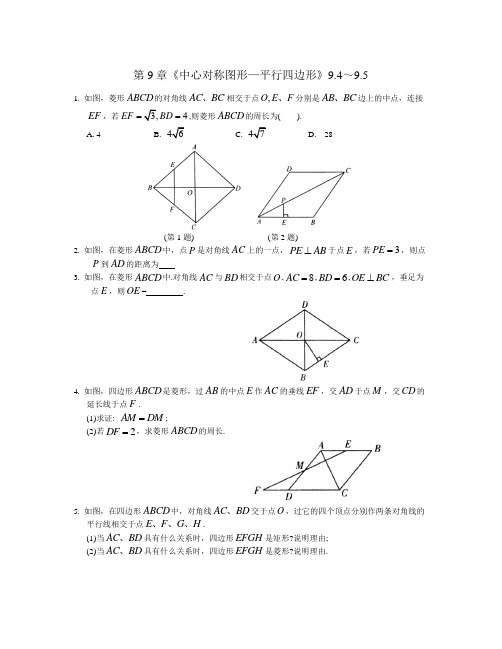
第9章《中心对称图形—平行四边形》9.4~9.51. 如图,菱形ABCD 的对角线AC BC 、相交于点,O E F 、分别是AB BC 、边上的中点,连接EF ,若4EF BD ==,则菱形ABCD 的周长为( ).A. 4B.C. D. 28(第1题) (第2题)2. 如图,在菱形ABCD 中,点P 是对角线AC 上的一点,PE AB ⊥于点E ,若3PE =,则点P 到AD 的距离为3. 如图,在菱形ABCD 中.对角线AC 与BD 相交于点O ,8AC =,6BD =,OE BC ⊥,垂足为点E ,则OE = .4. 如图,四边形ABCD 是菱形,过AB 的中点E 作AC 的垂线EF ,交AD 于点M ,交CD 的延长线于点F . (1)求证: AM DM =;(2)若2DF =,求菱形ABCD 的周长.5. 如图,在四边形ABCD 中,对角线AC BD 、交于点O ,过它的四个顶点分别作两条对角线的平行线相交于点E F G H 、、、.(1)当AC BD 、具有什么关系时,四边形EFGH 是矩形?说明理由; (2)当AC BD 、具有什么关系时,四边形EFGH 是菱形?说明理由.6. 如图,E F G H 、、、是菱形ABCD 的边AB BC CD DA 、、、上的点,且AE CF CG AH ===. 求证: EG FH =.7. 如图,四边形ABCD 是菱形,DE AB ⊥交BA 的延长线于点E ,DF BC ⊥交BC 的延长线于点F .请你猜想DE 与DF 的大小有什么关系?并证明你的猜想.8. 如图,已知矩形ABCD , E F G H 、、、分别为AB BC CD DA 、、、的中点,若2AB =,4AD =,则图中阴影部分的面积为 .9. 如图,在ABC ∆中,,AB AC M =是BC 的中点,MD AB ⊥,ME AC ⊥,DF AC ⊥,EG AB ⊥,垂足分别为D E F G 、、、,DF EG 、相交于点P ,四边形MDPE 是菱形吗?为什么?10. 如图,在ABC ∆中,AC 的垂直平分线MN 交AB 于点D ,交AC 于点O , //CE AB 交MN 于点E ,连接AE CD 、. (1)求证: AD CE =;(2)四边形ADCE 的形状是 .11. 如图,在ABC ∆中,90,ACB BC ∠=︒的垂直平分线DE 交BC 于点D ,交AB 于点E ,点F 在DE 的延长线上,并且AF CE =. (1)说明:四边形ACEF 是平行四边形;(2)当B ∠的大小满足什么条件时,四边形ACEF 是菱形?并证明你的结论.12. 如图,在ABCD 中,AE 是边BC 上的高,将ABE ∆沿BC 方向平移,使点E 与点C 重合,得GFC ∆. (1)求证: BE DG =;(2)若60B ∠=︒.当AB 与BC 满足什么数量关系时,四边形ABFG 是菱形?证明你的结论.13. 如图,在四边形ABCD 中,点E F 、分别是AD BC 、的中点,G H 、分别是BD AC 、 的中点,AB CD 、满足什么条件时,四边形EGFH 是菱形?请证明你的结论.14. 如图,在平行四边形ABCD 中,点E F G H 、、、分别在边AB BC 、、CD 、DA 上,AE CG =,AH CF =,且EG 平分HEF ∠.求证:(1) AEH ∆≌CGF ∆; (2)四边形EFGH 是菱形.15. 如图,正方形ABCD 的对角线BD长为l 满足:(1)点D 到直线lA C 、两点到直线l 的距离相等.则符合题意的直线l 的条数为( ).A. 1B. 2C. 3D. 4(第15题) (第16题)16. 如图,在正方形ABCD 的外侧,作等边三角形,ADE AC BE 、相交于点F ,则BFC ∠ 为( ).A. 45°B. 55°C. 60°D. 75°17. 如图,在正方形ABCD 中,G 是CD 上一点,延长BC 到点E ,使CE CG =,连接BG并延长交DE 于点F .(1)说明BCG ∆≌DCE ∆的理由;(2)将DCE ∆绕点D 顺时针旋转90°得到DAE '∆,判断四边形E BGD '是什么特殊四边 形?并说明理由.18. 如图,有两个正方形ABCD 与OPQS ,正方形OPQS 的顶点O 是正方形ABCD 对角线的交点,若正方形OPQS 绕点O 任意旋转.(1)当两正方形的边长相等时,AP 与BS 的大小有何关系?简述你的理由;(2)若两正方形的边长不相等,正方形ABCD 的边长为a ,正方形OPQS 的边长为b ,且a b <,上述结论是否仍然成立?简述你的理由.19. 如图,在Rt ABC ∆与Rt ABD ∆中,90ABC BAD ∠=∠=︒ , AD BC =, AC 、BD 相交于点G ,过点A 作//AE DB 交CB 的延长线于点E ,过点B 作//BF CA 交DA 的延 长线于点F ,AE BF 、相交于点H .(1)图中有若干对三角形是全等的,请你任选一对进行证明;(不添加任何辅助线) (2)说明四边形AHBG 是菱形的理由; (3)若使四边形AHBG 是正方形,还需在Rt ABC ∆的边长之间再添加一个什么条件?请你写出这个条件.(不必证明)20. 如图,四边形ABCD 是正方形,E F 、是AD DC 、上的点,且45EBF ∠=︒,则EF 与CF AE +相等吗?说明理由.21. 如图,在ABCD 中,E F 、是AD BC 、上的点,且AE BF =,G 是AF 与BE 的交点,H 是CE 与DF 的交点.求证: //GH AD .22. 如图,在ABC ∆中,D 是边AB 上一点,且,AD AC AE CD =⊥于点E F 、是BC 的中点.求证: 2BD EF =.23. 如图,在四边形ABCD 中,,AD BC E F G =、、分别是AB CD AC 、、的中点,试说明:EFG ∆是等腰三角形.24. 如图,E F 、分别是四边形ABCD 的边AB CD 、的中点,G H 、分别是对角线AC BD 、的中点,试说明EF 与GH 互相平分.25. 已知E F G H 、、、是四边形ABCD 各边的中点,连接EF FG GH EH 、、、.(1)如图(1),试判断四边形EFGH 的形状;(2)如图(2),若四边形ABCD 是梯形,上述结论还成立吗?(3)如图(3),若四边形ABCD 是等腰梯形呢?判断四边形EFGH 的形状.26. 若ABC ∆的周长为1,它的3条中位线组成一个新的三角形,记作111A B C ∆,111A B C ∆的3条中位线又组成一个新的三角形,记作222A B C ∆ (如图所示),…,以此类推,求201720172017A B C ∆的周长.参考答案1. C2. 33.1254. (1)Q 四边形是菱形,//,.AB CD AB AD ∴=,AC EF ⊥Q .AM AE ∴=1,2AE AB =Q1.2AM AD ∴=.AM DM ∴=(2)提示:证明AEM ∆≌. 2.DMF DF AE ∆==菱形ABCD 的周长为16.5.(1)当AC BD ⊥时,四边形EFGH 是矩形.理由如下://,//,AO EB AE BO Q∴四边形AEBO 是平行四边形. 又90AOB ∠=︒,∴四边形AEBO 是矩形.90E ∴∠=︒ 同理四边形EFGH 是平行四边形. ∴四边形EFGH 是矩形. (2).AC BD =理由如下: AC BD =Q , .EF FG ∴=EFGH ∴Y 是菱形.6. 连接EH 、EF 、FG 、GH .,AE AH =Q1(180)2AEH A ∴∠=︒-∠. Q 在菱形ABCD 中,,AB BC = 又,AE CF =1.(180)2BE BF BEF B ∴=∴∠=︒-∠.11(180)(180)9022AEH BEF A B ∴∠+∠=︒-∠+︒-∠=︒,90HEF ∴∠=︒.同理90EFG FGH ∠=∠=︒.90HEF EFG FGH ∴∠=∠=∠=︒. ∴四边形EFGH 是矩形.EG FH ∴= 7. DE DF =.理由如下:连接BD .Q 四边形ABCD 是菱形. .CBD ABD ∴∠=∠,,DF BC DE AB ⊥⊥Q .DE DF ∴=8. 49. 是.理由如下:,,DM AB EG AB ⊥⊥Q //.DM GE ∴,,ME AC DF AC ⊥⊥Q //.ME DF ∴∴四边形DMEP 是平行四边形. M Q 是BC 的中点,,AB AC =,,90.B C BM CM BDM CEM ∴∠=∠=∠=∠=︒BDM ∴∆≌CEM ∆..DM ME ∴= ∴四边形MDPE 是菱形.10. (1)MN Q 是AC 的垂直平分线,,90.OA OC AOD EOC ∴=∠=∠=︒//,CE AB Q.DAO ECO ADO ∴∠=∠∴∆≌CEO ∆..AD CE ∴=(2)菱形11. (1)90,ACB DE ∠=︒Q 垂直平分BC ,.EC AE ∴= ,AF CE =Q.AF AE CE ∴==.EAC ACE FEA EFA ∴∠=∠=∠=∠ AFE ∴∆≌..ECA EF AC ∆∴= ∴四边形是ACEF 平行四边形.(2)当30B ∠=︒时,四边形ACEF 是菱形.理由如下: 90,30,ACB B ∠=︒∠=︒Q60EAC ∴∠=︒. 又AE CE =,AEC ∴∆是等边三角形. .CE AC ∴= ACEF ∴Y 是菱形.12. (1)Q 四边形ABCD 是平行四边形..AB CD ∴=AE Q 是边BC 上的高,且CG 是由AE 沿BC 方向平移而成, .90.CG AD AEB CGD ∴⊥∴∠=∠=︒ ,AE CG =QRt ABE ∴∆≌Rt CDG ∆..BE DG ∴=(2)当32BC AB =时,四边形ABFC 是菱形.//,//,AB GF AG BF Q∴四边形ABFG 是平行四边形.在Rt ABE ∆中,60B ∠=︒Q ,130..2BAE BE AB ∴∠=︒∴=3,,2BE CF BC AB ==Q 1..2EF AB AB BF ∴=∴= ∴四边形ABFG 是菱形.13. AB CD =提示:利用“一组邻边相等的平行四边形是菱形”. 14. (1)ABCD Y 中, ,A C ∠=∠Q又,,AE CG AH CF ==AEH ∴∆≌CGF ∆. (2)在ABCD Y 中,,,,B D AB CD AD BC ∠=∠==Q 又,,AE CG AH CF ==,.BE DG DH BF DHG ∴==∴∆≌..BFE HG EF ∆∴=又,HE GF =∴四边形是EFGH 平行四边形. EG Q 平分HEF ∠,1 2.∴∠=∠ //,HG EF Q2 3.1 3..HE HG ∴∠=∠∴∠=∠∴= EFGH ∴Y 是菱形.15. B 16. C17. (1)提示:SAS. (2)平行四边形.18. (1)AP BS =.理由如下:Q 正方形ABCD 、OPQS , ,.OA OB OP OS ∴==90,AOP POB SOB POB ∠+∠=∠+∠=︒Q.AOP SOB AOP ∴∠=∠∴∆≌..BOS AP BS ∆∴=(2)仍然成立,理由同上. 19. (1)略(2)//,//,AH GB BH GA Q∴四边形AHBG 为平行四边形. ABC ∆Q ≌,BAD ∆..ABD BAC GA GB ∴∠=∠∴= ∴平行四边形AHBG 是菱形. (3)AB BC =20. 延长FC 到点P ,使CP AE =,连接BP ,Q 四边形ABCD 是正方形,,90AB BC A BCD BCP ∴=∠=∠=∠=︒.,AE CP =QABE ∴∆≌CBP ∆.,.BE BP ABE CBP ∴=∠=∠ 90ABC ABE EBC ∠=∠+∠=︒Q ,90CBP EBC ∴∠+∠=︒,即90.EBP ∠=︒45,904545.EBF PBF EBP EBF ∠=︒∠=∠-∠=︒-︒=︒Q 45.EBF PBF ∴∠=∠=︒,,BE BP BF BF ==QEBF ∴∆≌PBF ∆,.EF PF ∴=,,PF PC CF CP AE =+=Q.EF CF AE ∴=+21. AE BF = ,四边形ABCD 是平行四边形,//AD BC ∴.£¬.EAF AFB AEB FBE ∴∠=∠∠=∠ AE BF = ,AGE ∴∆≌FGB ∆.AG GF ∴=. 同理1.2DH HF GH AD =∴=. 22. ,,AD AC AE CD =⊥ .CE DE ∴=F 是BC 的中点,EF ∴是BCD ∆的中位线.2.BD EF ∴=23. FG 是ADC ∆的中位线,12GF AD ∴=, GE 是ABC ∆的中位线,12GE BC ∴=..GF GE ∴= EFG ∴∆是等腰三角形.24. 连接EG 、EH 、FG 、FH ..E 、F 、G 、H 分别是AB 、CD 、AC 、BD 的中点, FG ∴、EH 分别是CAD ∆、BAD ∆的中位线.11,22FG AD EH AD ∴==..FG EH ∴= ∴四边形EGFH 是平行四边形.EF ∴与GH 互相平分.25. (1)四边形EFGH 是平行四边形.理由如下:连接BD .EF 是ABD ∆的中位线,1.2EF BD ∴= GH 是BCD ∆的中位线,1.2GH BD ∴=.EF GH ∴= ∴四边形EFGH 是平行四边形.(2)成立.(3)是菱形.理由如下:连接AC 与BD .,AC BD = 又EF 是ABD ∆的中位线, 1.2EF BD = EH ∴是ADC ∆的中位线,1.2EH AC ∴=.EF EH ∴= EFGH ∴ 是菱形. 26.201612。
完整版三角形的中位线经典练习题及其答案
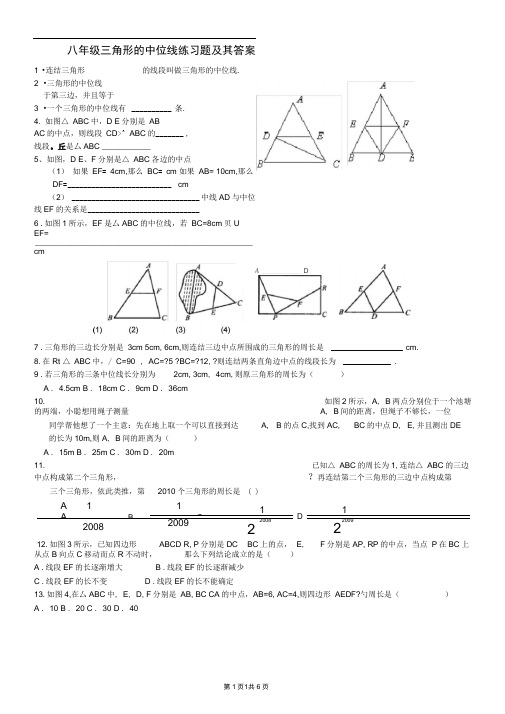
八年级三角形的中位线练习题及其答案1 •连结三角形2 •三角形的中位线于第三边,并且等于3 •一个三角形的中位线有__________ 条.4. 如图△ ABC中,D E分别是ABAC的中点,则线段CD>^ ABC的_______ ,线段。
丘是厶ABC ___________5、如图,D E、F分别是△ ABC各边的中点(1)如果EF= 4cm,那么BC= cm 如果AB= 10cm,那么DF= __________________________ cm(2) ________________________________ 中线AD与中位线EF的关系是____________________________6 .如图1所示,EF是厶ABC的中位线,若BC=8cm贝UEF=_________________________________________________cm7 .三角形的三边长分别是3cm 5cm, 6cm,则连结三边中点所围成的三角形的周长是 __________________ cm.8.在Rt △ ABC中,/ C=90°, AC=?5 ?BC=?12, ?则连结两条直角边中点的线段长为 ____________ .9 .若三角形的三条中位线长分别为2cm, 3cm, 4cm,则原三角形的周长为()A . 4.5cmB . 18cmC . 9cmD . 36cm10. 如图2所示,A, B两点分别位于一个池塘的两端,小聪想用绳子测量A, B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A, B的点C,找到AC, BC的中点D, E,并且测出DE 的长为10m,则A, B间的距离为()A . 15mB . 25mC . 30mD . 20m11. 已知△ ABC的周长为1,连结△ ABC的三边中点构成第二个三角形,?再连结第二个三角形的三边中点构成第三个三角形,依此类推,第2010个三角形的周长是( )A 1 1 1 1A、 B C D、2008 2009 20082 2009212.如图3所示,已知四边形ABCD R, P分别是DC BC上的点,E,F分别是AP, RP的中点,当点P在BC上从点B向点C移动而点R不动时,那么下列结论成立的是()A .线段EF的长逐渐增大B .线段EF的长逐渐减少C .线段EF的长不变D .线段EF的长不能确定13.如图4,在厶ABC中, E, D, F分别是AB, BC CA的中点,AB=6, AC=4,则四边形AEDF?勺周长是()A . 10B . 20C . 30D . 40A__________ D的线段叫做三角形的中位线.14. 如图所示,口ABCD的对角线AC, BD相交于点O, AE=EB求证:OE// BC.15. 已知矩形ABCD中,AB=4cm, AD=10cm,点P在边BC上移动,点E、F、G、H 分别是AB、AP、DP、DC的中点.求证:EF+GH=5cm;16 .如图所示,在△ ABC中,点D在BC上且CD=CA CF平分/ ACB AE=EB求证:EF=1BD.217.如图所示,已知在口ABCD中, E, F分别是AD, BC的中点,求证:MN/ BC.18.已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、arc CD、DA的中点.求证:四边形EFGH是平行四边形.19.如图,点E, F, G, H分别是CD, BC, AB , DA的中点。
八年级数学下册同步训练:必刷基础题9.5 三角形的中位线(含答案及解析)(苏科版)

2019-2020学年八年级数学下册同步闯关练(苏科版)第九章《中心对称图形——平行四边形》9.5 三角形的中位线知识点1:三角形中位线定理【例1】(2019秋•苏州期末)如图,在ABC ∆中,D ,E 分别是AB ,AC 边的中点,若2DE =,则BC 的长度是( )A .6B .5C .4D .3【解析】在ABC ∆中,D ,E 分别是AB ,AC 边的中点,DE ∴是ABC ∆的中位线,2DE =,BC ∴的长度是:4.故选:C .【变式1-1】(2019春•西湖区校级月考)如图所示,在ABC ∆中,AB AC =,D ,E 分别是AB ,AC 的中点,F ,G 为BC 上的点,连接DG 、EF ,若5AB cm =,8BC cm =,4FG cm =,则HFG ∆的面积为( )A .21cmB .21.5cmC .22cmD .23cm【解析】连接,作AK BC ⊥于K .AB AC =,118422BK CK BC ∴===⨯=, 在Rt ABK ∆中,2222543AK AB BK =-=-=, D 、E 分别是AB ,AC 的中点,DE ∴是中位线,即平分三角形的高且824DE =÷=,12DE BC FG ∴==, DEH GFH ∴∆≅∆,H 也是DG ,EF 的中点,HFG ∴∆的高是12 1.520.752AK ÷=÷=, 40.752 1.5HFG S ∆∴=⨯÷=.故选:B .【变式1-2】(2019•铜仁市)如图,D 是ABC ∆内一点,BD CD ⊥,7AD =,4BD =,3CD =,E 、F 、G 、H 分别是AB 、BD 、CD 、AC 的中点,则四边形EFGH 的周长为( )A .12B .14C .24D .21【解析】BD CD ⊥,4BD =,3CD =, 2222435BC BD CD ∴=+=+=, E 、F 、G 、H 分别是AB 、AC 、CD 、BD 的中点,12EH FG BC ∴==,12EF GH AD ==, ∴四边形EFGH 的周长EH GH FG EF AD BC =+++=+,又7AD =,∴四边形EFGH 的周长7512=+=.故选:A .【变式1-3】(2020春•丽水期中)如图,在三角形ABC 中,90ACB ∠=︒,M ,N 分别是AB 、AC 的中点,延长BC 至点D ,使13CD BD =,连结DM 、DN 、MN ,若5AB =,则DN = .【解析】连接CM ,在Rt ACB ∆中,90ACB ∠=︒,M 是AB 的中点,1522CM AB ∴==, M ,N 分别是AB 、AC 的中点,MN ∴是ABC ∆的中位线,12MN BC ∴=,//MN BC , 13CD BD =, MN CD ∴=,又//MN BC , ∴四边形NDCM 为平行四边形,52DN CM ∴==, 故答案为:52.【变式1-4】(2019秋•五华区期末)如图(1)是一个三角形,分别连接这个三角形三边中点得到图(2),图(2)中共有5个三角形:再分别连接图(2)的中间小三角形三边的中点,得到图(3).按上面的方法继续下去,第20个图形中共有 个三角形.【解析】第1个图形中共有1个三角形,第2个图形中共有5个三角形,第3个图形中共有9个三角形,则第n 个图形中共有(43)n -个三角形,∴第20个图形中共有77个三角形,故答案为:77.【变式1-5】(2019•西宁)如图,ABC ∆中,点D ,E 分别是AB ,AC 的中点,连接DE 并延长交ABC ∆的外角ACM ∠的角平分线于点F ,若6BC =,10AC =,则线段DF 的长为 .【解析】点D ,E 分别是AB ,AC 的中点,132DE BC ∴==,152EC AC ==,//DE BC , F FCM ∴∠=∠, CF 是ACM ∠的角平分线,FCE FCM ∴∠=∠,F FCE ∴∠=∠,5EF EC ∴==,8DF DE EF ∴=+=,故答案为:8.【变式1-6】(2019秋•安丘市期末)如图,在等边ABC ∆中,D ,E 分别为AB ,AC 的中点,延长BC 至点F ,使12CF BC =,连结CD 和EF . (1)求证:CD EF =;(2)猜想:ABC ∆的面积与四边形BDEF 的面积的关系,并说明理由.【解析】(1)D 、E 分别为AB 、AC 的中点,DE ∴为ABC ∆的中位线,//DE BC ∴,12DE BC =, 12CF BC =, DE FC ∴=,//DE FC ,∴四边形DCFE 是平行四边形,CD EF ∴=;(2)猜想:ABC ∆的面积=四边形BDEF 的面积,理由如下:DE 为ABC ∆的中位线,//DE BC ∴,12DE BC = ADE ∴∆的面积DEC =∆的面积,∴四边形DCFE 是平行四边形,DEC ∴∆的面积ECF =∆的面积,ADE ∴∆的面积ECF =∆的面积,ABC ∴∆的面积=四边形BDEF 的面积.【变式1-7】(2019春•新乐市期末)已知:如图,在四边形ABCD 中,AD BC =,P 为对角线BD 的中点,M 为AB 的中点,N 为DC 的中点.求证:PMN PNM ∠=∠.【解析】在四边形ABCD 中,P 是对角线BD 的中点,M ,N 分别是AB ,CD 的中点, NP ∴,PM 分别是CDB ∆与DAB ∆的中位线,12PN BC ∴=,12PM AD =,//PN BC ,//PM AD , NPD DBC ∴∠=∠,MPB ADB ∠=∠,AD BC =,PN PM ∴=,故NMP ∆是等腰三角形.PMN PNM ∴∠=∠.【变式1-8】(2019•丰南区一模)如图,在四边形ABCD 中,AC 平分BAD ∠,90ABC ∠=︒,2AC AD ==,M 、N 分别为AC 、CD 的中点,连接BM 、MN 、BN .(1)求证:BM MA =;(2)若60BAD ∠=︒,求BN 的长;(3)当BAD ∠= ︒时,1BN =.(直接填空)【解析】(1)证明:在CAD ∆中,90ABC ∠=︒,M 是AC 的中点,12BM MA AC ∴==; (2)60BAD ∠=︒,AC 平分BAD ∠,30BAC DAC ∴∠=∠=︒,由(1)可知,12BM AC AM MC ===, 260BMC BAM ABM BAM ∴∠=∠+∠=∠=︒,//MN AD ,30NMC DAC ∴∠=∠=︒,90BMN BMC NMC ∴∠=∠+∠=︒222BN BM MN ∴=+,由(1)可知1MN BM ==,2BN ∴=;(3)40BAD ∠=︒,AC 平分BAD ∠,20BAC DAC ∴∠=∠=︒,由(1)可知,12BM AC AM MC ===, 240BMC BAM ABM BAM ∴∠=∠+∠=∠=︒,//MN AD ,20NMC DAC ∴∠=∠=︒,60BMN BMC NMC ∴∠=∠+∠=︒由(1)可知1MN BM ==,1BN ∴=.故答案为:40︒.【变式1-9】(2019春•天心区校级期中)如图,在ABC ∆中,AE 平分BAC ∠,BE AE ⊥于点E ,点F 是BC 的中点.(1)如图1,BE 的延长线与AC 边相交于点D ,求证:1()2EF AC AB =-;(2)如图2,写出线段AB 、AC 、EF 的数量关系,并证明你的结论.【解析】(1)证明:如图1中,AE BD ⊥,90AED AEB ∴∠=∠=︒,90BAE ABE ∴∠+∠=︒,90DAE ADE ∠+∠=︒,BAE DAE ∠=∠,ABE ADE ∴∠=∠,AB AD ∴=,AE BD ⊥,BE DE ∴=,BF FC =,111()()222EF DC AC AD AC AB ∴==-=-.(2)结论:1()2EF AB AC =-, 理由:如图2中,延长AC 交BE 的延长线于P .AE BP ⊥,90AEP AEB ∴∠=∠=︒,90BAE ABE ∴∠+∠=︒,90PAE APE ∠+∠=︒,BAE PAE ∠=∠,ABE APE ∴∠=∠,AB AP ∴=,AE BD ⊥,BE PE ∴=,BF FC =,111()()222EF PC AP AC AB AC ∴==-=-. 知识点2:梯形中位线定理【例2】(2017秋•利川市校级期中)如图,已知//AD BC ,AP 平分DAB ∠,BP 平分ABC ∠,点P 恰好在CD 上,则PD 与PC 的大小关系是( )A .PD PC >B .PD PC = C .PD PC < D .无法判断【解析】作//PE AD ,交AB 于点E .//AD BC ,//PE BC ∴DAP EPA ∴∠=∠ AP 平分DAB ∠,DAP BAP ∴∠=∠,EAP EPA ∴∠=∠,AE EP ∴=,同理可证EP EB =,E ∴为BA 的中点,P ∴为DC 的中点,PD PC ∴=,故选:B .【变式2-1】(2015•召陵区一模)如图,2AB a =,点C 是线段AB 上的一个动点,ACD ∆和BCE ∆是在AB 同侧的两个等边三角形,DM ,EN 分别是ACD ∆和BCE ∆的高,点C 在线段AB 上沿着点A 向点B 的方向移动(不与点A 、B 重合),连接DE ,得到四边形DMNE .这个四边形的面积为( )A .2aB .232aC .234aD .不能确定【解析】ADC ∆是等边三角形,DM 是ADC ∆的高,DC AC ∴=,60DCM ∠=︒,90DMC ∠=︒,3sin 2DM CD DCM AC ∴=∠=,12CM AC =. 同理,32EN BC =,12CN BC =, 223333311122(2)22224282DMNE AC BC DM EN S MN AC BC AB AB a a ++⎛⎫∴=⋅=⋅+=⨯=⨯= ⎪⎝⎭梯形. 故选:B .【变式2-2】(2013秋•沙湾区期末)如图,梯形ABCD 中,//AD BC ,EF 是梯形的中位线,对角线AC 交EF 于P ,若10BC =,8EF =,则(PF = )A .2B .5C .3D .4 【解析】梯形ABCD 中,//AD BC ,EF 是梯形的中位线,1()2EF AD BC ∴=+,PF 是ADC ∆的中位线, 10BC =,8EF =,∴解得:6AD =,132PF AD ∴==. 故选:C .【变式2-3】(2018秋•沙坪坝区校级期中)如图,在梯形ABCD 中,//AD BC ,O 为CD 中点,6OA =,10AD BC AB +==,则OB 长为 .【解析】如图,过点O 作//OE AD , O 为CD 中点,OE ∴是梯形ABCD 的中位线,2AD BC OE ∴+=,AD BC AB +=,2AB OE ∴=,90AOB ∴∠=︒,6OA =,10AB =,22221068OB AB OA ∴=-=-=.故答案为:8.【变式2-4】(2014秋•沙坪坝区校级期末)如图,梯形ABCD 中,ABC ∠和DCB ∠的平分线相交于梯形中位线EF 上的一点P ,PH AB ⊥于H .若3EF =,1PH =,2AD =,则BPC ∆的面积为 .【解析】如图,过点P 作PQ BC ⊥于点Q ; BP 平分ABC ∠,且PH AB ⊥于点H ,1PQ PH ∴==;设BC λ=,由题意得:232λ+=,解得:4λ=; ∴14122BPC S ∆=⨯⨯=, 故答案为2.【变式2-5】(2014•徐州一模)如图,在梯形ABCD 中,//AD BC ,点E 在AB 上,点F 在CD 上,EF 为中位线,EF 与BD 交于点O ,若5FO EO -=,则BC AD -= .【解析】//AD BC ,中位线EF 交BD 于点O ,EO ∴,FO 分别为ABD ∆,BDC ∆的中位线,2BC FO ∴=,2AD EO =,2()10BC AD FO EO ∴-=-=.故答案为:10.【变式2-6】(2015•凉山州一模)梯形ABCD 中,//AD BC ,E 、F 分别是AB 、CD 的中点,连接AF 并延长并BC 延长线于点G .求证:////EF AD BC ,1()2EF AD BC =+.【解析】证明://AD BC ,ADF GCF ∴∠=∠,DAF CGF ∠=∠, F 为CD 的中点,DF CF ∴=,在ADF ∆和GCF ∆中,DAF CGF ADF GCF DF CF ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ADF GCF AAS ∴∆≅∆,AD CG ∴=, E 是AB 的中点,EF ∴为ABG ∆的中位线,//EF BG ∴,12EF BG =, ////EF AD BC ∴,11()()22EF BC CG AD BC =+=+. 【变式2-7】(2011春•闵行区期末)已知:如图,在梯形ABCD 中,//AD BC ,8AB DC ==,对角线AC AB ⊥,60B ∠=︒,M 、N 分别是边AB 、DC 的中点,连接MN ,求线段MN 的长.【解析】AC AB ⊥,90BAC ∴∠=︒.在Rt ABC ∆中,由60B ∠=︒,得30BCA ∠=︒.又8AB =,216BC AB ∴==.//AD BC ,AB DC =,60BCD B ∴∠=∠=︒.即得30ACD ACB ∠=∠=︒.又由//AD BC ,得30DAC ACB ∠=∠=︒.DAC ACD ∴∠=∠,即得 8AD CD ==. M 、N 分别是边AB 、DC 的中点,MN ∴是梯形ABCD 的中位线.即得 11()(816)1222MN AD BC =+=+=. 【变式2-8】(2008秋•淮安区期末)如图,在梯形ABCD 中,E 、F 分别为AD 、BC 的中点,G 、H 分别为BD 、AC 的中点,且E 、F 、G 、H 四点在一条直线上,6AB =,10CD =. 求:(1)EF 、EG 的长;(2)试说明GH 与AB 的位置关系;(3)你能计算GH 的长吗?请写出你的算法并求出结果.【解析】①、因为E 、F 分别为AD 、BC 的中点,则EF 为梯形ABCD 的中位线,所以//EF AB ,0.5()8EF AB CD =+=;因为E 、G 分别为AD 、BD 的中点,所以EG 为三角形ABD 的中位线,3EG =;②、由①知://GH AB ;③、GH EH EG =-.因为E 、H 分别为AD 、AC 的中点,EH 为三角形ADC 的中位线,5EH =,3EG =, 2GH =.【变式2-9】如图,在梯形ABCD 中,//AD BC ,E 、F 分别是对角线BD 、AC 的中点.若6AD cm =,18BC cm =,求EF 的长.【解析】如图,取AB 的中点G ,连接EG , E 、F 分别是对角线BD 、AC 的中点,//EG AD ∴,116322EG AD cm ==⨯=,//GF BC ,1118922GF BC cm ==⨯=, 又//AD BC ,∴点G 、E 、F 三点共线,936EF GF EG cm ∴=-=-=.。
(完整版)三角形的中位线经典练习题及其答案

八年级三角形的中位线练习题及其答案1.连结三角形___________的线段叫做三角形的中位线. 2.三角形的中位线______于第三边,并且等于_______. 3.一个三角形的中位线有_________条. 4。
如图△ABC 中,D 、E 分别是AB 、AC 的中点,则线段CD 是△ABC 的___, 线段DE 是△ABC _______5、如图,D 、E 、F 分别是△ABC 各边的中点 (1)如果EF =4cm ,那么BC =__cm 如果AB =10cm ,那么DF =___cm(2)中线AD 与中位线EF 的关系是___6.如图1所示,EF 是△ABC 的中位线,若BC=8cm ,则EF=_______cm .(1) (2) (3) (4)7.三角形的三边长分别是3cm ,5cm ,6cm ,则连结三边中点所围成的三角形的周长是_________cm . 8.在Rt △ABC 中,∠C=90°,AC=•5,•BC=•12,•则连结两条直角边中点的线段长为_______. 9.若三角形的三条中位线长分别为2cm ,3cm,4cm,则原三角形的周长为( ) A .4。
5cm B .18cm C .9cm D .36cm10.如图2所示,A ,B 两点分别位于一个池塘的两端,小聪想用绳子测量A ,B 间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A ,B 的点C ,找到AC ,BC 的中点D,E ,并且测出DE 的长为10m ,则A ,B 间的距离为( )A .15mB .25mC .30mD .20m11.已知△ABC 的周长为1,连结△ABC 的三边中点构成第二个三角形,•再连结第二个三角形的三边中点构成第三个三角形,依此类推,第2010个三角形的周长是( ) A 、20081 B 、20091 C 、220081 D 、22009112.如图3所示,已知四边形ABCD ,R ,P 分别是DC ,BC 上的点,E ,F 分别是AP ,RP 的中点,当点P 在BC上从点B 向点C 移动而点R 不动时, 那么下列结论成立的是( ) A .线段EF 的长逐渐增大 B .线段EF 的长逐渐减少 C .线段EF 的长不变 D .线段EF 的长不能确定13.如图4,在△ABC 中,E ,D ,F 分别是AB ,BC ,CA 的中点,AB=6,AC=4,则四边形AEDF•的周长是( ) A .10 B .20 C .30 D .4014.如图所示,□ ABCD 的对角线AC ,BD 相交于点O ,AE=EB ,求证:OE ∥BC .15.已知矩形ABCD 中,AB =4cm ,AD =10cm ,点P 在边BC 上移动,点E 、F 、G 、H 分别是AB 、AP 、DP 、DC 的中点。
初中数学苏科版八年级下册9.5 三角形的中位线 同步练习A卷

初中数学苏科版八年级下册9.5 三角形的中位线同步练习A卷姓名:________ 班级:________ 成绩:________一、选择题(每小题5分,共20分) (共4题;共17分)1. (5分)等边三角形的一条中位线长为2,则此等边三角形的周长为()A . 12B . 6C . 8D . 102. (5分)如图所示,A,B两点分别位于一个池塘的两端,小聪想用绳子测量A,B 间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为10m,则A,B间的距离为()A . 15mB . 25mC . 30mD . 20m3. (5分) (2015八下·鄂城期中) 已知:如图,在矩形ABCD中,DE⊥AC,∠ADE=∠CDE,那么∠BDC等于()A . 60°B . 45°C . 30°D . 22.5°4. (2分) (2019九上·定安期末) 如图,在中,分别是边上的中点,则()A . 1B .C .D .二、填空题(每小题5分,共30分) (共6题;共24分)5. (2分)(2019·卫东模拟) 如图,折叠长方形纸片ABCD,先折出对角线BD,再将AD折叠到BD上,得到折痕DE,点A的对应点是点F,若AB=8,BC=6,则AE的长为________.6. (5分) (2018九上·阜宁期末) 若分别为各边的中点,且的周长为9,则的周长为________7. (2分)(2017·雁江模拟) 如图,在平面直角坐标系中,A、B两点分别在x轴和y轴上,OA=1,OB= ,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1 ,连接A1B1 ,再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为________.8. (5分)①如图1,在等腰梯形ABCD中,AD∥BC,AB=AD=CD.若∠ABC=60°,BC=12,则梯形ABCD的周长为________.②如图2,在梯形ABCD中,AB∥DC,DB⊥AD,AD=DC=BC=2cm,那么梯形ABCD的面积是________.③如图3,在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°.则∠ABD的度数为________;若AD=2,则对角线BD的长为________.9. (5分)如图:在中,AB=6,BC=7,AC=10.点 D、E、F 分别是相应边上的中点,则四边形 DEBF的周长等于________10. (5分) (2016九下·十堰期末) 木工做一个长方形桌面,量得桌面的长为45cm,宽为28cm,对角线为53cm,这个桌面________.(填“合格”或“不合格”).三、解答题(共50分) (共4题;共38分)11. (12分) (2017八下·萧山期中) 将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2 ,P 是AC上的一个动点.(1)当点P运动到∠ABC的平分线上时,连接DP、BP,求CP、DP的长;(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;(3)当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC 上?求出此时平行四边形的面积.12. (12分)如图,在△ABC中,点D是AB边的中点,点E在AC边上(不与端点重合).(1)若AB=BC,且BD=DE,求证:DE是△ABC的中位线;(2)若DE=BC,则结论“DE一定是△ABC的中位线”是否正确?若正确请证明;若不正确,请举出反例.13. (12分)如图所示,在锐角△ABC中,AB<AC,AD⊥BC,交BC于点D,E,F,G 分别是BC,CA,AB的中点,求证:四边形DEFG是等腰梯形.14. (2分) (2019八下·海口期中) 如图,四边形ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.(1)求∠APB的度数;(2)如果AD=5cm,AP=8cm,求△APB的周长.四、能力挑战(满分:30 分) (共4题;共29分)15. (5分)(2017·成华模拟) 如图,在菱形ABCD中,AC、BD相交于点O,E为AB 的中点,若OE=2,则菱形ABCD的周长是________.16. (5分) 6、如图,在▱ABCD中,AD=8 cm,点E,F分别从点A,B同时出发,沿AD,BC方向以相同的速度运动(分别运动到点D,C即停止),AF与BE相交于点G,CE与DF相交于点H. 则在此运动过程中,线段GH 的长始终等于________cm17. (5分)如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点O,点F、G分别是BO、CO的中点,连接AO.若AO=6cm,BC=8cm,则四边形DEFG的周长是()A . 14cmB . 18 cmC . 24cmD . 28cm18. (14分) (2019八下·博罗期中) 如图,点D在△ABC的边AB上,点E为AC的中点,过点C作CF∥AB交DE的延长线于点F,连接AF.(1)求证:CD=AF;(2)若∠AED=2∠ECD,求证:四边形ADCF是矩形.参考答案一、选择题(每小题5分,共20分) (共4题;共17分)1、答案:略2、答案:略3、答案:略4、答案:略二、填空题(每小题5分,共30分) (共6题;共24分)5、答案:略6、答案:略7、答案:略8、答案:略9、答案:略10、答案:略三、解答题(共50分) (共4题;共38分)11、答案:略12、答案:略13、答案:略14、答案:略四、能力挑战(满分:30 分) (共4题;共29分)15、答案:略16、答案:略17、答案:略18、答案:略。
苏科版八年级数学下册三角形的中位线同步练习

9.5 三角形的中位线知识点三角形中位线定理1.如图9- 5- 1,在△ ABC 中,E , D 分别是边 AB , AC 的中点,若 BC = 3,贝U DE 的 长为() 3 A.2B . 1C . 2D . 32. 如图9- 5-2,在厶ABC 中,D , E 分别是 AB , AC 的中点,/ A = 50°,/ ADE =60°,则/ C 的度数为() A . 50° B . 60° C . 70° D . 80°3.三角形三条中位线的长分别为 3 cm , 4 cm , 5 cm ,则此三角形的周长为( )A . 48 cmB . 24 cmC . 12 cmD . 10 cm4. 如图 9- 5-3 所示,在△ ABC 中,AB = AC , / A v 90°,边 BC , CA , AB 的中点分 别是D , E , F ,则四边形AFDE 是()A .菱形B .正方形C .矩形D .梯形5. 如图9- 5- 4,为测量位于一水塘旁的两点―图 9- 5- 1 .图 9 —5-2 图 9- 5- 4A, B间的距离,在地面上确定点O,分别取OA, OB的中点C, D,量得CD = 20 m,则A, B两点之间的距离是_____________ m.6. 2017 淮安 如图 9-5- 5,在 Rt △ ABC 中,/ ACB = 90° , D , E 分别是 AB , AC 的中点,F 是AD 的中点.若 AB = 8,贝U EF = __________________ .如图9- 5-6,在菱形 ABCD 中,对角线 AC , BD 相交于点 O , AB = 8, E 是BC 的 中点,贝U OE 的长为 ______________ .10. 如图9 — 5-9,在四边形 ABCD 中,E , F , G , H 分别是 AB , BC , CD , DA 的中 占八、、♦⑴判断四边形EFGH 的形状;(2)当四边形ABCD 的对角线满足条件 __________ 时,四边形EFGH 是正方形;⑶在⑵的条件下,说明四边形 EFGH 是正方形.7.&如图9-5-7,在厶ABC 中,D , 点H , FD= 8,贝U EH 等于 __________________ .9.如图 9- 5-8,在△ ABC 中,D , 「口 1一点,且CF =尹C ,连接CD , EF.求证: E , F 分别为BC , AC , AB 边的中点,AH 丄BC 于E 分别是边AB , AC 的中点,F 是BC 的延长线上CD = EF.【能力提升】11. 如图 9-5 — 10,在 Rt △ ABC 中,/ A = 30°, BC = 1 , D , E 分别是直角边 BC ,12.如图9 — 5 — 11,四边形 ABCD 的两条对角线 AC , BD 互相垂直,四边形 A 1B 1C 1D 1 是四边形ABCD 的中点四边形,如果AC = 8, BD = 10,那么四边形 A 1B 1C 1D 1的面积为() A . 10 B . 20 C . 36 D . 408 D E C图 9— 5— 1213. 2017 达州 如图 9— 5 — 12,A ABC 的周长为 19,点D , E 在边BC 上,/ ABC 的 平分线垂直于 AE , 垂足为 N ,/ ACB 的平分线垂直于 AD ,垂足为 M ,若 BC = 7,贝U MN 的长为( )35 A.2 B .2 C.2 D .3 14. 2017射阳校级月考 已知:如图9— 5 — 13,在?ABCD 中,E 是CD 的中点,F 是 AE 的中点,G 是BE 的中点.求证:四边形CEFG 是平行四边形.AC 的中点,则 A . 1 DE 的长为()图9-5- 1315. 如图9 —5- 14, ?ABCD的对角线AC与BD相交于点O, AC = 2AD , E, F, G分别是AB, OC , OD的中点.试判断厶EFG的形状,并说明理由.A E B图9-5- 1416. 如图9- 5- 15,在厶ABC中,BD , CE分别为边AC和AB上的中线,且相交于点O, F, G分别是OB, OC的中点.⑴求证:四边形EFGD是平行四边形;(2)当AB = AC时,判断四边形EFGD的形状,并证明你的结论;⑶连接OA,当OA= BC时,判断四边形EFGD的形状,并证明你的结论.图9-5- 151. A2. C[解析]由题意,得/ AED = 180°—/ A -Z ADE = 70° . •/ D, E 分别是AB , AC 的中点,••• DE 是厶ABC 的中位线,••• DE // BC ,A / C=/ AED = 70° .故选 C.3. B4. A [解析]•••边BC, CA的中点分别是D, E,•线段DE是厶ABC的中位线,1•DE = 2AB , DE // AB.1同理,DF = 2AC , DF // AC.又••• AB = AC,/ A V 90°,•DE // AF , DF // AE , DE = DF,•四边形AFDE是菱形.故选 A.5. 40 [解析]T C, D分别是OA , OB的中点,•CD是厶OAB的中位线.•/ CD = 20 m,•AB = 2CD = 2X 20= 40(m).6. 2 [解析]在Rt A ABC中,T D是AB的中点,1--CD = 2AB = 4.T F, E分别是AD , AC的中点,1•EF= ^CD = 2.7. 4 [解析]T四边形ABCD是菱形,•OA = OC.1又T E是BC的中点,• OE= 2AB.•/ AB = 8, • OE = 4.8. 8 [解析]T D, F分别是BC , AB的中点,1•DF是厶ABC的中位线,• FD = ^AC.又T E是线段AC的中点,AH丄BC,1•EH = pc , • EH = FD = 8.9. 证明:T D, E分别是边AB , AC的中点,1•DE // BC , DE = ^BC.1T CF= ^BC ,• DE = CF.又T DE // BC ,•四边形DEFC是平行四边形,•CD = EF.10. 解:(1)如图,连接AC, BD.理由:••• E, F分别是AB , BC的中点,1••• EF// AC, EF= 2AC.1同理,GH // AC , GH = 2AC.•EF / GH, EF = GH ,•四边形EFGH是平行四边形.(2) AC = BD 且AC 丄BD(3) •/ AC = BD ,•结合⑴可得EF= FG = GH = EH ,•四边形EFGH是菱形.又AC丄BD ,•结合(1)可得/ HEF = 90°,•四边形EFGH是正方形.11. A [解析]•••在Rt A ABC 中,/ C= 90°,/ A = 30° ,• AB = 2BC = 2•又T D, E 分别是BC , AC的中点,• DE是厶ABC的中位线,• DE = 1.12. B13. C [解析]由题意易证△ BAE和厶CAD都是等腰三角形,•N是AE的中点,M是AD的中点,•MN是厶ADE的中位线.•/ BE + CD = AB + AC = 19- BC = 19-7= 12,•DE = BE + CD —BC = 5,1 5• MN= 1DE=2.14. 证明:依题意得FG是厶EAB的中位线,1• FG / AB,且FG= 2AB.又•••四边形ABCD是平行四边形,E是CD的中点,1•CE/ AB , 且CE= 2AB ,•CE / FG,且CE = FG,•四边形CEFG是平行四边形.15. 解:△ EFG是等腰三角形.理由如下: 连接AG.••• G, F分别是OD , OC的中点,1• GF= 2CD.在?ABCD 中,AC = 2OA , AB = CD.又••• AC = 2AD , • OA = AD.•/ G是0D的中点,••• AG丄OD,•••/ AGB = 90° .••• E是AB的中点,1 1…EG= 2AB = 2CD ,•EG= GF,•△ EFG是等腰三角形.16. 解:⑴证明:T D , E分别为边AC和AB上的中点,1•ED // BC,且ED = qBC.1同理,FG // BC,且FG=尹C.• ED // FG,且ED = FG ,•四边形EFGD是平行四边形.⑵当AB = AC时,四边形EFGD为矩形.图◎证明:如图①,连接AO并延长交BC于点M.•••三角形的三条中线相交于同一点,△ABC的中线BD , CE交于点0, •M为BC的中点.当AB = AC 时,AM 丄BC.••• E, F, G分别是AB , OB , 0C的中点,•EF // AO , FG // BC ,•EF丄FG.又•••四边形EFGD是平行四边形,•四边形EFGD是矩形.(3)当0A = BC时,四边形EFGD是菱形.证明:如图②,••• D , G分别是AC , 0C的中点,• “ 1--DG = ?0A.1又T FG = 2BC , 0A = BC,• DG = FG.又•••四边形EFGD是平行四边形,•••四边形EFGD是菱形.。
苏教科版初中数学八年级下册9.5 三角形的中位线

在上一题的 手让学生自己完 助于知识的进一
在课堂上要 生的学习积极性 课堂,积极思 言,锻炼思维能 好数学非常有帮
及时有效地
苏科版初中数学
的评价,有助于 自信心.
相信自己,就能走向成功的第一步 教师不光要传授知识,还要告诉学生学会生活。数学思维
可以让他们更理性地看待人生
TB:小初高题库
能运用三角 性质进行推理.
教师的板书
△EFG 是等腰三角形.
最后在黑板上写出详细的过程.
着关键的示范作 学生有条理的说
D A
E
F
C G 在△ABC 中 , AB=AC,D、E、 、BC、AC 的中点. 四边形 ADEF 的周长等于 2AB.
TB:小初高题库
根据题意,画出图形; 小组内讨论交流 3 分钟; 小组推荐代表阐述思路; 找两名学生到黑板前详细写出证明过程; 师生共同纠错; 教师及时评价(表扬激励为主),找出学生的闪光点.
与平行四边形建
的两部分能拼成一个平行四边
而发现三角形中
证明思路.
操作——观察——探索
互相讨论,踊跃回答.
此活动既是
张三角形纸片,记为△ABC;分
参考答案:四边形 BCFD 是平行四边形.
的三角形中位线
的中点 D、E,连接 DE;沿 DE
由题意知,点 A、E、C 在一条直线上,点 D、E、F 在一 铺垫,又渗透了
标
2.会利用三角形的中位线的性质解决有关问题;
3.经历探索三角形中位线性质的过程,体会转化的思想方法.
点
会利用三角形的中位线的性质解决有关问题.
点
经历探索三角形中位线性质的过程,体会转化的思想方法.
教学过程(教师)
学生活动
八年级数学苏科版下册随堂测试第9单元 《9.5三角形的中位线 》(含答案解析)

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!随堂测试9.5三角形的中位线一.选择题1.如图,在△ABC中,点D,E分别是边AB,BC的中点,若△DBE的周长是7,则△ABC 的周长是()A.8B.10C.12D.142.如图,EF是△ABC的中位线,BD平分∠ABC交EP于D,BE=3,DF=1,则BC的长为()A.2B.4C.6D.83.如图,在△ABC中,D是AC的中点,且BD⊥AC,DE∥BC,交AB于点E,BC=7cm,AC=6cm,则△AED的周长等于()A.12cm B.10cm C.7cm D.9cm4.如图,在Rt△ABC中,∠B=90°,BC=5,AB=12,点D,E分别是AB,AC的中点,CF平分Rt△ABC的一个外角∠ACM,交DE的延长线于点F,则DF的长为()A.5B.8.5C.9D.125.如图,△ABC是等边三角形,D、E、F分别是边AB、AC、BC的中点,若BC=4,则△DEF的周长等于()A.3B.6C.9D.126.如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E 作EF∥DC交BC的延长线于F.若四边形CDEF的周长是10cm,AC的长为4cm,则△ABC的周长是()A.28B.24C.14D.187.如图,BD、CE是△ABC的中线,P、Q分别是BD、CE的中点,则PQ:BC等于()A.1:4B.1:5C.1:6D.1:78.如图,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点,则下列结论错误的是()A.GF=AD B.EF=AC C.GE=BC D.GE=GF9.如图,△ABC周长20,D,E在边BC上,BN和CM分别是∠ABC和∠ACB的平分线,BN⊥AE,CM⊥AD,若BC=8,则MN的长为()A.1B.2C.3D.310.如图,△ABC中,∠ACB=90°,点D,E分别在BC,AC边上,且AE=4,BD=6,分别连接AD,BE,点M,N分别是AD,BE的中点,连接MN,则线段MN的长()A.B.3C.3D.二.填空题11.如图,在△ABC中,点D、E分别是边AB、AC的中点,连接DE,∠ABC的平分线BF 交DE于点F,若AB=4,BC=6,则EF的长为.12.如图,在△ABC中,点D,E,F分别是边AB,BC,CA上的中点,且AB=10cm,AC =16cm,则四边形ADEF的周长等于cm.13.如图,在Rt△ABC中,∠ACB=90°,D、E、F分别为AB、AC、AD的中点.若AB =6,则EF的长度为.14.如图,在Rt△ABC中,∠ACB=90°,点D、F分别为AC、BC边上的中点,CE是斜边上的中线,若DF=3,则CE=.15.如图,D是△ABC内一点,BD⊥CD,E,F,G,H分别是AB,BD,CD,AC的中点.若AD=5,BD=4,CD=3,则四边形EFGH的周长是.三.解答题16.如图,在△ABC中,AB=AC,D、E分别是AB、BC的中点,EF⊥AC,垂足F;(1)求证:AD=DE;(2)求证:DE⊥EF.17.在△ABC中,E是AC边上一点,线段BE垂直∠BAC的平分线于D点,点M为BC边的中点,连接DM.(1)求证:DM=CE;(2)若AD=6,BD=8,DM=2,求AC的长.18.如图,在四边形ABCD中,∠DAB=90°,DB=DC,点E、F分别为DB、BC的中点,连接AE、EF、AF.(1)求证:AE=EF;(2)当AF=AE时,设∠ADB=α,∠CDB=β,求α,β之间的数量关系.参考答案一.选择题1.D.2.D.3.B.4.C.5.B.6.C.7.A.8.B.9.B.10.D.二.填空题11.1.12.26.13..14.3.15.10.三.解答题16.解:(1)∵AB=AC,∴∠B=∠C,∵D、E分别是AB、BC的中点,∴AD=AB,DE=AC,∴AD=DE;(2)∵D、E分别是AB、BC的中点,∴DE∥AC,∵EF⊥AC,∴DE⊥EF.17.(1)证明:在△ADB和△ADE中,,∴△ADB≌△ADE(ASA)∴AE=AB,BD=DE,∵BD=DE,BM=MC,∴DM=CE;(2)解:在Rt△ADB中,AB==10,∴AE=10,由(1)得,CE=2DM=4,∴AC=CE+AE=14.18.(1)证明:∵点E、F分别为DB、BC的中点,∴EF是△BCD的中位线,∴EF=CD,在Rt△ABD中,点E为斜边DB的中点,∴AE=DB,∵DB=DC,∴AE=EF;(2)如图,由(1)知AE=EF,∵AF=AE,∴AE=EF=AF,∴△AEF是等边三角形,∴∠AEF=60°,∵EF是△BCD的中位线,∴EF∥CD,∴∠BEF=∠BDC=β,∴β+∠AEB=60°,又∵∠AEB=α+∠DAE,∴β+α+∠DAE=60°,∵∠DAB=90°,∴AE是斜边BD上的中线,∴AE=DE,∴∠DAE=α,∴β+α+α=60°,即2α+β=60°.。
苏科版八年级数学下册9.5 三角形的中位线 同步练习A卷

苏科版八年级下册9.5 三角形的中位线同步练习A卷姓名:________ 班级:________ 成绩:________考试须知:1、请首先按要求在本卷的指定位置填写您的姓名、班级等信息。
2、请仔细阅读各种题目的回答要求,在指定区域内答题,否则不予评分。
一、选择题(每小题5分,共20分) (共4题;共17分)1. (5分)如图,在▱ABCD中,AB=3,AD=5,AM平分∠BAD,交BC于点M,点E,F分别是AB,CD的中点,DM与EF交于点N,则NF的长等于()A . 0.5B . 1C .D . 22. (5分) (2017八下·广东期中) 如图,△ABC中,已知AB=8,∠C=90°,∠A=30°,DE是中位线,则DE 的长为()A . 4B . 3C .D . 23. (5分) (2015八下·武冈期中) 顺次连接矩形四边中点所得的四边形一定是()A . 正方形B . 矩形C . 菱形D . 等腰梯形4. (2分) (2019八下·慈溪期中) 如图,在平行四边形ABCD中,∠C=120°,AD=2AB=4,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF,则EF的最大值与最小值的差为()A . 1B .C .D .二、填空题(每小题5分,共30分) (共6题;共24分)5. (2分)(2019·江北模拟) 如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的点F处,若DE =5,AB=8,则S△ABF:S△FCE=________.6. (5分)(2012·抚顺) 如图,平行四边形ABCD的面积是16,对角线AC、BD相交于点O,点M1、N1、P1分别为线段OD、DC、CO的中点,顺次连接M1N1、N1 P1、P1M1得到第一个△P1M1N1 ,面积为S1 ,分别取M1N1、N1P1、P1M1三边的中点P2、M2、N2 ,得到第二个△P2M2N2 ,面积记为S2 ,如此继续下去得到第n个△PnMnNn ,面积记为Sn ,则Sn﹣Sn﹣1=________.(用含n的代数式表示,n≥2,n为整数)7. (2分)(2017·嘉兴模拟) 如图,点P(3,4),⊙P半径为2,A(2.8,0),B(5.6,0),点M是⊙P上的动点,点C是MB的中点,则AC的最小值是________.8. (5分)等腰梯形的两底和为20,差为8,且一个底角为60°,则梯形的面积为________.9. (5分)(2018·峨眉山模拟) 如图,中,等于,,,、分别是、的中点,连结,则的面积是________10. (5分)如图,平行四边形ABCD,请你添一个条件________,使四边形ABCD为矩形.三、解答题(共50分) (共4题;共38分)11. (12分)如图1,△ABC为等腰直角三角形,∠ACB=90°,F是AC边上的一个动点(点F与A、C不重合),以CF为一边在等腰直角三角形外作正方形CDEF,连接BF、AD.(1)①猜想图1中线段BF、AD的数量关系及所在直线的位置关系,直接写出结论;②将图1中的正方形CDEF,绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2、图3的情形.图2中BF交AC于点H,交AD于点O,请你判断①中得到的结论是否仍然成立,并选取图2证明你的判断.(2)将原题中的等腰直角三角形ABC改为直角三角形ABC,∠ACB=90°,正方形CDEF改为矩形CDEF,如图4,且AC=4,BC=3,CD=, CF=1,BF交AC于点H,交AD于点O,连接BD、AF,求BD2+AF2的值.12. (12分)如图所示,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点.求证:△EFG是等腰三角形.13. (12分)如图,在四边形ABCD中,AB=DC,E、F分别是AD、BC的中点,G、H分别是对角线BD、AC的中点.(1)求证:四边形EGFH是菱形;(2)若AB=,则当∠ABC+∠DCB=90°时,求四边形EGFH的面积.14. (2分)(2019·相城模拟) 已知平行四边形ABCD中,如图,对角线AC和BD相交于点O,AC=10,BD=8.(1)若AC⊥BD,试求四边形ABCD的面积;(2)若AC与BD的夹角∠AOD=60°,求四边形ABCD的面积.四、能力挑战(满分:30 分) (共4题;共29分)15. (5分)(2019·宝鸡模拟) 如图,在边长为4的菱形ABCD中,∠A=60°,点M、N是边AB、BC上的动点,若△DMN为等边三角形,点M、N不与点A、B、C重合,则△BMN面积的最大值是________.16. (5分)如图,在△ABC中,CD是高,CE是中线,CE=CB,点A、D关于点F对称,过点F作FG∥CD,交AC边于点G,连接GE.AC=18,BC=12,则△CEG的周长为________17. (5分)已知:菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=6cm,则OE的长为()A . 6cmB . 4cmC . 3cmD . 2cm18. (14分)综合题。
苏科版初中数学八年级下册《9.5 三角形的中位线》同步练习卷

苏科新版八年级下学期《9.5 三角形的中位线》同步练习卷一.选择题(共12小题)1.如图,△ABC中,点D、E分别在AB、AC边上,AD=BD,AE=EC,BC=6,则DE=()A.4B.3C.2D.52.如图,A、B两地被池塘隔开,小康通过下列方法测出了A、B间的距离:先在AB外选一他点C,然后测出AC,BC的中点M、N,并测量出MN的长为18m,由此他就知道了A、B间的距离.下列有关他这次探究活动的结论中,错误的是()A.AB=36m B.MN∥AB C.MN=CB D.CM=AC 3.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠FPE=136°,则∠PFE的度数是()A.15°B.20°C.22°D.44°4.点P是△ABC内一点,且P到△ABC的三边距离相等,则P是△ABC哪三条线的交点()A.边的垂直平分线B.角平分线C.高线D.中位线5.如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为()A.3cm B.6cm C.9cm D.12cm6.如图,△ABC中,BE平分∠ABC,AE⊥BE于点E,M为AB的中点,连接ME并延长交AC于点N.若AB=6,BC=12,则线段EN的长为()A.2B.3C.4D.57.如图,点D是△ABC内一点,BD⊥CD,AD=11,BD=8,CD=6,点E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是()A.14B.18C.21D.248.如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且DE=3cm,则AF=()cm.A.1B.2C.3D.49.如图,已知AB=8,P为线段AB上一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和PBFE,点P,C,E在一条直线上,∠DAP=60°,M,N分别是对角线AC,BE的中点,当点P在线段AB上移动时,点M,N之间的距离最短为()A.B.C.4D.310.如图,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD 的中点∠ABD=20°,∠BDC=70°,则∠NMP的度数为()A.50°B.25°C.15°D.2011.如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA延长线上,∠FDA=∠B,AC=3,AB=4,则四边形AEDF的周长为()A.8B.9C.10D.1112.如图,在▱ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF.若EF=3,则CD的长为()A.3B.6C.8D.12二.填空题(共11小题)13.直角△ABC中,∠BAC=90°,D、E、F分别为AB、BC、AC的中点,已知DF=3,则AE=.14.已知三角形的各边长分别是8cm、10cm和12cm,则以各边中点为顶点的三角形的周长为cm.15.如图,在▱ABCD中,AD=6,点E、F分别是BD、CD的中点,则EF=.16.如图,点A(0,4),点B(3,0),连接AB,点M、N分别是OA、AB的中点,在射线MN上有一动点P.当AP⊥PB时,点P的坐标是.17.如图,△ABC中,AB=7cm,BC=6cm,AC=5cm,D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长等于cm.18.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB =5,BC=7,则EF的长为.19.已知:如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE =2,则AC的长等于.20.观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,…将这种做法继续下去(如图2,图3…),则图5中挖去三角形的个数为21.在四边形ABCD中,对角线AC⊥BD且AC=4,BD=8,E、F分别是边AB、CD的中点,则EF=.22.如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE ∥DB,BE∥DC,AD=3,DF=1,四边形DBEC面积是23.如图,在R△ABC中,∠ACB=90°,BC=3,AC=4,点M为边AC的中点,点N为边BC上任意一点,若点C关于直线MN的对称点C′恰好落在△ABC的中位线上,则CN的长为.三.解答题(共17小题)24.如图,在△ABC中,AB=BC,∠ABC=84°,点D是AC的中点,DE∥BC.求∠EDB的度数.25.如图,在四边形ABCD中,AD=BC,E,F,G,H分别是AB,CD,AC,EF的中点,求证:GH⊥EF.26.如图,在△ABC中,已知AB=6,AC=10,AD平分∠BAC,BD⊥AD于点D,E为BC中点.求DE的长.27.如图,在等腰三角形ABC中,CA=CB=5,AB=6,D、E分别是AB、AC 的中点,延长BC至点F,使CF=BC,连接DE、CD和EF.(1)求证:DE=CF.(2)求EF的长.(3)求四边形DEFC的面积.28.如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.(1)求证:FG=FH;(2)若∠A=90°,求证:FG⊥FH;(3)若∠A=80°,求∠GFH的度数.29.如图、在△ABC中,AB=AC,M,N分别为AC,BC的中点,以AC为斜边在△ABC的外侧作Rt△ACD,且∠CAD=30°,连接MN,DM,DN.(1)求证:△DMN是等腰三角形;(2)若AC平分∠BAD,AB=6,求DN的长.30.如图,在△ABC中,点D,E,F分别是各边中点,AG是BC边上的高.求证:∠GDE=∠GFE.31.如图,在四边形ABCD中,∠ADC=90°,AB=AC,E,F分别为AC,BC 的中点,连接EF,ED,FD.(1)求证:ED=EF;(2)若∠BAD=60°,AC平分∠BAD,AC=6,求DF的长.32.如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA的延长线上,∠FDA=∠B,AC=6,AB=8,求四边形AEDF的周长P.33.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,AC=16.(1)求证:BN=DN;(2)求MN的长.34.如图所示,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC 的中点,N是AB的中点.请判断△PMN的形状,并说明理由.35.如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=12,CD=AC=16,M、N分别是对角线BD、AC的中点.(1)求证:MN⊥AC;(2)求MN的长.36.如图,在△ABC中,D、E、F分别是AB、BC、AC的中点,AH⊥BC,垂足为H.求证:(1)HD=EF.(2)∠DHF=∠DEF.37.已知:如图,在四边形ABCD中,对角线AC、BD相交于点O,AC=BD,E,F分别是四边形ABCD边AD、BC的中点,EF分别交AC,BD于G,H,求证:∠OGH=∠OHG.38.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,求∠PFE的度数.39.如图,在四边形ABCD中,∠ABC=90°,AC=AD,M、N分别为AC、CD 的中点,连接BM、MN、BN.(1)求证:BM=MN.(2)若∠BAD=60°,AC平分∠BAD,AC=4,①求∠BMN的度数;②求BN 的长.40.如图,△ABC中,AD平分∠BAC,AD⊥BD,E为BC的中点.(1)求证:DE∥AC;(2)若AB=4,AC=6,求DE的长.苏科新版八年级下学期《9.5 三角形的中位线》同步练习卷参考答案与试题解析一.选择题(共12小题)1.如图,△ABC中,点D、E分别在AB、AC边上,AD=BD,AE=EC,BC=6,则DE=()A.4B.3C.2D.5【分析】根据三角形的中位线的定理即可求出答案.【解答】解:∵AD=BD,AE=EC,∴DE是△ABC的中位线,∴BC=2DE,∴DE=3,故选:B.【点评】本题考查三角形的中位线,解题的关键是熟练运用三角形的中位线定理,本题属于基础题型.2.如图,A、B两地被池塘隔开,小康通过下列方法测出了A、B间的距离:先在AB外选一他点C,然后测出AC,BC的中点M、N,并测量出MN的长为18m,由此他就知道了A、B间的距离.下列有关他这次探究活动的结论中,错误的是()A.AB=36m B.MN∥AB C.MN=CB D.CM=AC 【分析】根据三角形的中位线定理即可判断;【解答】解:∵CM=MA,CNB,∴MN∥AB,MN=AB,∵MN=18m,∴AB=36m,故A、B、D正确,故选:C.【点评】本题考查的是三角形的中位线定理在实际生活中的运用,锻炼了学生利用几何知识解答实际问题的能力.3.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠FPE=136°,则∠PFE的度数是()A.15°B.20°C.22°D.44°【分析】根据三角形中位线定理得到EP=AD,FP=BC,得到PE=PF,根据等腰三角形的性质、三角形内角和定理计算即可.【解答】解:∵P是对角线BD的中点,E是AB的中点,∴EP=AD,同理,FP=BC,∵AD=BC,∴PE=PF,∵∠FPE=136°,∴∠PFE=∠PEF=22°,故选:C.【点评】本题考查的是三角形中位线定理的应用,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.也考查了等腰三角形的性质、三角形内角和定理.4.点P是△ABC内一点,且P到△ABC的三边距离相等,则P是△ABC哪三条线的交点()A.边的垂直平分线B.角平分线C.高线D.中位线【分析】根据到角的两边的距离相等的点在角的平分线上解答.【解答】解:∵P到△ABC的三边距离相等,∴点P在△ABC的三条角平分线上,∴P是△ABC三条角平分线的交点,故选:B.【点评】本题考查的是角平分线的性质,掌握到角的两边的距离相等的点在角的平分线上是解题的关键.5.如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为()A.3cm B.6cm C.9cm D.12cm【分析】因为四边形ABCD是平行四边形,所以OA=OC;又因为点E是BC的中点,所以OE是△ABC的中位线,由OE=3cm,即可求得AB=6cm.【解答】解:∵四边形ABCD是平行四边形,∴OA=OC;又∵点E是BC的中点,∴BE=CE,∴AB=2OE=2×3=6(cm)故选:B.【点评】此题考查了平行四边形的性质:平行四边形的对角线互相平分.还考查了三角形中位线的性质:三角形的中位线平行且等于三角形第三边的一半.6.如图,△ABC中,BE平分∠ABC,AE⊥BE于点E,M为AB的中点,连接ME并延长交AC于点N.若AB=6,BC=12,则线段EN的长为()A.2B.3C.4D.5【分析】延长AE交BC于H,根据等腰三角形的判定和性质得到AE=EH,BH =AB,求出HC,根据三角形中位线定理计算.【解答】解:延长AE交BC于H,∵BE平分∠ABC,AE⊥BE,∴AE=EH,BH=AB=6,∴HC=BC﹣BH=6,∵AE=EH,AN=NC,∴EN=HC=3,故选:B.【点评】本题考查的是三角形中位线定理、等腰三角形的判定和性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.7.如图,点D是△ABC内一点,BD⊥CD,AD=11,BD=8,CD=6,点E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是()A.14B.18C.21D.24【分析】利用勾股定理列式求出BC的长,再根据三角形的中位线平行于第三边并且等于第三边的一半求出EH=FG=AD,EF=GH=BC,然后代入数据进行计算即可得解.【解答】解:∵BD⊥CD,BD=8,CD=6,∴BC===10,∵E、F、G、H分别是AB、AC、CD、BD的中点,∴EH=FG=AD,EF=GH=BC,∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC,又∵AD=11,∴四边形EFGH的周长=11+10=21.故选:C.【点评】本题考查了三角形的中位线定理,勾股定理的应用,熟记三角形的中位线平行于第三边并且等于第三边的一半是解题的关键.8.如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且DE=3cm,则AF=()cm.A.1B.2C.3D.4【分析】由中位线性质得到BC,再由直角三角形斜边上中线等于斜边一半,可求得AF.【解答】解:由已知D、E分别为AB、AC中点∴DE∥BC,DE=∵DE=3∴BC=6∵∠BAC=90°,F为BC中点∴AF==3故选:C.【点评】本题考查三角形中位线和直角三角形斜边上中线等于斜边一半的性质,解答时注意数形结合即可.9.如图,已知AB=8,P为线段AB上一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和PBFE,点P,C,E在一条直线上,∠DAP=60°,M,N分别是对角线AC,BE的中点,当点P在线段AB上移动时,点M,N之间的距离最短为()A.B.C.4D.3【分析】连接PM、PN.首先证明∠MPN=90°,设P A=2a,则PB=8﹣2a,PM=a,PN=(4﹣a),构建二次函数,利用二次函数的性质即可解决问题.【解答】解:连接PM、PN.∵四边形APCD,四边形PBFE是菱形,∠DAP=60°,∴∠APC=120°,∠EPB=60°,∵M,N分别是对角线AC,BE的中点,∴∠CPM=∠APC=60°,∠EPN=∠EPB=30°,∴∠MPN=60°+30°=90°,设P A=2a,则PB=8﹣2a,PM=a,PN=(4﹣a),∴MN===,∴a=3时,MN有最小值,最小值为2,故选:A.【点评】本题考查菱形的性质、勾股定理、二次函数的性质等知识,解题的关键是学会添加常用辅助线,构建二次函数解决最值问题.10.如图,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD 的中点∠ABD=20°,∠BDC=70°,则∠NMP的度数为()A.50°B.25°C.15°D.20【分析】根据中位线定理和已知,易证明△PMN是等腰三角形,根据等腰三角形的性质和已知条件即可求出∠PMN的度数.【解答】解:∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,∴PN,PM分别是△CDB与△DAB的中位线,∴PM=AB,PN=DC,PM∥AB,PN∥DC,∵AB=CD,∴PM=PN,∴△PMN是等腰三角形,∵PM∥AB,PN∥DC,∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°,∴∠MPN=∠MPD+∠NPD=20°+(180﹣70)°=130°,∴∠PMN==25°.故选:B.【点评】本题考查了三角形中位线定理及等腰三角形的判定和性质,解题时要善于根据已知信息,确定应用的知识.11.如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA延长线上,∠FDA=∠B,AC=3,AB=4,则四边形AEDF的周长为()A.8B.9C.10D.11【分析】根据勾股定理先求出BC的长,再根据三角形中位线定理和直角三角形的性质求出DE和AE的长,进而由已知可判定四边形AEDF是平行四边形,从而求得其周长.【解答】解:在Rt△ABC中,∵AC=3,AB=4,∴BC=5,∵E是BC的中点,∴AE=BE=2.5,∴∠BAE=∠B,∵∠FDA=∠B,∴∠FDA=∠BAE,∴DF∥AE,∵D、E分别是AB、BC的中点,∴DE∥AC,DE=AC=1.5,∴四边形AEDF是平行四边形,∴四边形AEDF的周长=2×(1.5+2.5)=8.故选:A.【点评】本题主要考查了直角三角形的性质、等腰三角形的判定以及平行四边形的判定.熟练运用三角形的中位线定理和直角三角形的勾股定理是解题的关键.12.如图,在▱ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF.若EF=3,则CD的长为()A.3B.6C.8D.12【分析】根据平行四边形的对边相等、三角形的中位线定理“三角形的中位线等于第三边的一半”求解.【解答】解:∵四边形ABCD是平行四边形,∴AB=CD;又∵E、F分别是AD、BD的中点,∴EF是△DAB的中位线,∴EF=AB,∴EF=CD=3,∴CD=6;故选:B.【点评】本题考查了平行四边形的性质、三角形中位线定理的综合运用.中位线是三角形中的一条重要线段,由于它的性质与线段的中点及平行线紧密相连,因此,它在几何图形的计算及证明中有着广泛的应用.二.填空题(共11小题)13.直角△ABC中,∠BAC=90°,D、E、F分别为AB、BC、AC的中点,已知DF=3,则AE=3.【分析】由三角形中位线定理得到DF=BC;然后根据直角三角形斜边上的中线等于斜边的一半得到AE=BC,则DF=AE.【解答】解:如图,∵在直角△ABC中,∠BAC=90°,D、F分别为AB、AC 的中点,∴DF是△ABC的中位线,∴DF=BC.又∵点E是直角△ABC斜边BC的中点,∴AE=BC,∵DF=3,∴DF=AE.故填:3.【点评】本题考查了三角形中位线定理和直角三角形斜边上的中线.熟记定理是解题的关键.14.已知三角形的各边长分别是8cm、10cm和12cm,则以各边中点为顶点的三角形的周长为15cm.【分析】由中点和中位线定义可得新三角形的各边长为原三角形各边长的一半,即可求其周长.【解答】解:如图,D,E,F分别是△ABC的三边的中点,则DE=AC,DF=BC,EF=AB,∴△DEF的周长=DE+DF+EF=(AC+BC+AB)=×(8+10+12)cm=15cm.故答案为15.【点评】解决本题的关键是利用中点定义和中位线定理得到新三角形各边长与原三角形各边长的数量关系.15.如图,在▱ABCD中,AD=6,点E、F分别是BD、CD的中点,则EF=3.【分析】由四边形ABCD是平行四边形,根据平行四边形的对边相等,可得BC =AD=8,又由点E、F分别是BD、CD的中点,利用三角形中位线的性质,即可求得答案.【解答】解:∵四边形ABCD是平行四边形,∴BC=AD=6,∵点E、F分别是BD、CD的中点,∴EF=BC=×6=3.故答案为:3.【点评】此题考查了平行四边形的性质与三角形中位线的性质.此题比较简单,注意掌握数形结合思想的应用.16.如图,点A(0,4),点B(3,0),连接AB,点M、N分别是OA、AB的中点,在射线MN上有一动点P.当AP⊥PB时,点P的坐标是(4,2)..【分析】根据题意求出OM,根据勾股定理求出AB,根据三角形中位线定理求出MN,根据直角三角形的性质求出PN,根据坐标与图形性质解答.【解答】解:∵点A(0,4),点M是OA的中点,∴OM=2,∵点M、N分别是OA、AB的中点,∴MN∥OB,MN=OB=1.5,在Rt△AOB中,AB==5,∵∠APB=90°,点N是AB的中点,∴PN=AB=2.5,则PM=PN+MN=4,∴点P的坐标是(4,2),故答案为:(4,2).【点评】本题考查的是考查的是三角形中位线定理,直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.17.如图,△ABC中,AB=7cm,BC=6cm,AC=5cm,D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长等于12cm.【分析】根据三角形中位线定理得到DE∥AC,DE=AC,EF∥AB,EF=AB,得到四边形ADEF是平行四边形,计算即可.【解答】解:∵D,E分别是AB,BC的中点,∴DE∥AC,DE=AC=2.5cm,同理,EF∥AB,EF=AB=3.5cm,∴四边形ADEF是平行四边形,∴四边形ADEF的周长=2×(2.5+3.5)=12(cm),故答案为:12.【点评】本题考查的是三角形中位线定理、平行四边形的判定和性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.18.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB =5,BC=7,则EF的长为1.【分析】根据三角形中位线定理得到DE=BC=3.5,根据直角三角形的性质得到DF=AB=2.5,计算即可.【解答】解:∵DE是△ABC的中位线,∴DE=BC=3.5,DE∥BC,∵∠AFB=90°,D为AB的中点,∴DF=AB=2.5,∴EF=DE﹣DF=1,故答案为:1.【点评】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半和在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.19.已知:如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE =2,则AC的长等于.【分析】过D点作DF∥BE,则DF=BE=1,F为EC中点,在Rt△ADF中求出AF的长度,根据已知条件易知G为AD中点,因此E为AF中点,则AC=AF.【解答】解:过D点作DF∥BE,∵AD是△ABC的中线,AD⊥BE,∴F为EC中点,AD⊥DF,∵AD=BE=2,则DF=1,AF==,∵BE是△ABC的角平分线,AD⊥BE,∴△ABG≌△DBG,∴G为AD中点,∴E为AF中点,∴AE=EF=CF,∴AC=AF=.故答案为:.【点评】本题考查了三角形中线、三角形中位线定理和角平分线的性质以及勾股定理的应用,作出辅助线构建直角三角形是解题的关键.20.观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,…将这种做法继续下去(如图2,图3…),则图5中挖去三角形的个数为121【分析】根据题意找出图形的变化规律,根据规律计算即可.【解答】解:图1挖去中间的1个小三角形,图2挖去中间的(1+3)个小三角形,图3挖去中间的(1+3+32)个小三角形,…则图5挖去中间的(1+3+32+33+34)个小三角形,即图5挖去中间的121个小三角形,故答案为:121.【点评】本题考查的是图形的变化,掌握图形的变化规律是解题的关键.21.在四边形ABCD中,对角线AC⊥BD且AC=4,BD=8,E、F分别是边AB、CD的中点,则EF=2.【分析】取BC的中点G,连接EG、FG,根据三角形的中位线平行于第三边并且等于第三边的一半求出EG、FG,并求出EG⊥FG,然后利用勾股定理列式计算即可得解.【解答】解:如图,取BC的中点G,连接EG、FG,∵E、F分别是边AB、CD的中点,∴EG∥AC且EG=AC=×4=2,FG∥BD且FG=BD=×8=4,∵AC⊥BD,∴EG⊥FG,∴EF=.故答案为:2【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,勾股定理的应用,作辅助线构造出直角三角形是解题的关键.22.如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE ∥DB,BE∥DC,AD=3,DF=1,四边形DBEC面积是4【分析】根据平行四边形的判定定理首先推知四边形DBEC为平行四边形,然后由直角三角形斜边上的中线等于斜边的一半得到其邻边相等:CD =BD ,得出四边形DBEC 是菱形,由三角形中位线定理和勾股定理求得AB 边的长度,然后根据菱形的性质和三角形的面积公式进行解答.【解答】解:∵CE ∥DB ,BE ∥DC ,∴四边形DBEC 为平行四边形.又∵Rt △ABC 中,∠ABC =90°,点D 是AC 的中点,∴CD =BD =AC ,∴平行四边形DBEC 是菱形;∵点D ,F 分别是AC ,AB 的中点,AD =3,DF =1,∴DF 是△ABC 的中位线,AC =2AD =6,S △BCD =S △ABC∴BC =2DF =2.又∵∠ABC =90°,∴AB =. ∵平行四边形DBEC 是菱形,∴S 四边形DBEC =2S △BCD =S △ABC =AB •BC =×4×2=4,故答案为:4 【点评】考查了菱形的判定与性质,三角形中位线定理,直角三角形斜边上的中线以及勾股定理,熟练掌握相关的定理与性质即可解题,难度中等.23.如图,在R △ABC 中,∠ACB =90°,BC =3,AC =4,点M 为边AC 的中点,点N 为边BC 上任意一点,若点C 关于直线MN 的对称点C ′恰好落在△ABC 的中位线上,则CN 的长为 或 .【分析】取BC 、AB 的中点H 、G ,理解MH 、HG 、MG .分三种情形:①如图1中,当点C ′落在MH 上时;②如图2中,当点C ′落在GH 上时;③如图3中,当点C ′落在直线GM 上时,分别求解即可解决问题;【解答】解:取BC、AB的中点H、G,理解MH、HG、MG.如图1中,当点C′落在MH上时,设NC=NC′=x,由题意可知:MC=MC′=2,MH=,HC′=,HN=﹣x,在Rt△HNC中,∵HN2=HC′2+NC′2,∴(﹣x)2=x2+()2,解得x=.如图2中,当点C′落在GH上时,设NC=NC′=x,在Rt△GMC′中,MG=CH=,MC=MC′=2,∴GC′=,∵△HNC′∽△GC′M,∴=,∴=,∴x=.如图3中,当点C′落在直线GM上时,易证四边形MCNC′是正方形,可得CN=CM=2.此时点C′在中位线GM的延长线上,不符合题意舍弃.综上所述,满足条件的线段CN的长为或.故答案为为或.【点评】本题考查轴对称、三角形的中位线、勾股定理、相似三角形的判定和性质、正方形的判定和性质等知识,解题的关键是学会用分类讨论的扇形思考问题,属于中考常考题型.三.解答题(共17小题)24.如图,在△ABC中,AB=BC,∠ABC=84°,点D是AC的中点,DE∥BC.求∠EDB的度数.【分析】利用等腰三角形的三线合一结合∠ABC的度数,可求出∠DBC的度数,再利用“两直线平行,内错角相等”,即可求出∠EDB的度数.【解答】解:∵AB=BC,点D是AC的中点,∴∠DBC=∠ABC=42°.又∵DE∥BC,∴∠EDB=∠DBC=42°.【点评】本题考查了三角形中位线定理、平行线的性质以及等腰三角形的判定与性质,利用等腰三角形的三线合一求出∠DBC的度数是解题的关键.25.如图,在四边形ABCD中,AD=BC,E,F,G,H分别是AB,CD,AC,EF的中点,求证:GH⊥EF.【分析】根据三角形中位线的性质得到FG=AD,EG=BC,由AD=BC,于是得到FG=GE,根据等腰三角形的性质即可得到结论.【解答】证明:∵E,F,G分别是AB,CD,AC的中点,∴FG=AD,EG=BC,∵AD=BC,∴FG=GE,∵H是EF的中点,∴GH⊥EF.【点评】本题考查了三角形的中位线的性质,等腰三角形的判定和性质,少了掌握三角形的中位线的性质是解题的关键.26.如图,在△ABC中,已知AB=6,AC=10,AD平分∠BAC,BD⊥AD于点D,E为BC中点.求DE的长.【分析】延长BD与AC相交于点F,根据等腰三角形的性质可得BD=DF,再利用三角形的中位线平行于第三边并且等于第三边的一半可得DE=CF,然后求解即可.【解答】解:如图,延长BD与AC相交于点F,∵AD平分∠BAC,BD⊥AD,∴∠DAB=∠DAF,AD=AD,∠ADB=∠ADF,∴△ADB≌△ADF,∴AF=AB,BD=DF,∵AB=6,AC=10,∴CF=AC﹣AF=AC﹣AB=10﹣6=4,∵E为BC中点,∴DE是△BCF的中位线,∴DE=CF=×4=2.【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,等腰三角形的判定与性质,作辅助线构造出以DE为中位线的三角形是解题的关键.27.如图,在等腰三角形ABC中,CA=CB=5,AB=6,D、E分别是AB、AC 的中点,延长BC至点F,使CF=BC,连接DE、CD和EF.(1)求证:DE=CF.(2)求EF的长.(3)求四边形DEFC的面积.【分析】(1)直接利用三角形中位线定理分析得出答案;(2)首先利用勾股定理得出CD的长,再利用已知得出DE CF,进而得出答案;(3)过点D作HD⊥BC,垂足为点H,求出DH的长,再得出CF的长,进而得出答案.【解答】(1)证明:∵D、E分别是AB、AC的中点,∴DE是△ABC的中位线.∴DE=BC.又∵CF=BC∴DE=CF;(2)解:EF=4.理由如下:∵在等腰三角形ABC中,CA=CB=5,AB=6,点D是AB的中点,∴CD⊥AB,BD=AB=3,∴在Rt△BCD中,BD=3,CB=5,由勾股定理可得,CD===4,由(1)可知,DE是△ABC的中位线.∴DE∥CF,又∵DE=CF,∴四边形CDEF是平行四边形.∴CD=EF=4;(3)解:四边形DEFC的面积为6,理由如下:过点D作HD⊥BC,垂足为点H.∵S=BD•CD=BC•DH△BCD∴×3×4=×5×DH∴DH=,∵DE=BC=,∴DE=CF=,=CF•DH=×=6.∴S四边形DEFC【点评】此题主要考查了平行四边形的判定以及三角形的中位线定理,正确得出DH的长是解题关键.28.如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.(1)求证:FG=FH;(2)若∠A=90°,求证:FG⊥FH;(3)若∠A=80°,求∠GFH的度数.【分析】(1)由中点性质及AB=AC,得到BD=EC,再由中位线性质证明FG ∥BD,GF=,FH∥EC,FH=,从而得到FG=FH;(2)由(1)FG∥BD,FH∥EC,再由∠A=90°,可证FG⊥FH;(3)由(1)FG∥BD,∠A=80°,可求得∠FKC,再由FH∥EC,可求得∠GFH的度数.【解答】(1)证明:∵AB=AC,点D,E分别是边AB,AC的中点∴BD=EC∵点F,G,H分别为BE,DE,BC的中点∴FG∥BD,GF=FH∥EC,FH=∴FG=FH;(2)证明:由(1)FG∥BD又∵∠A=90°∴FG⊥AC∵FH∥EC∴FG⊥FH;(3)解:延长FG交AC于点K,∵FG∥BD,∠A=80°∴∠FKC=∠A=80°∵FH∥EC∴∠GFH=180°﹣∠FKC=100°【点评】本题是几何问题,考查了三角形中位线的有关性质,解答时应根据题意找到相应三角形的中位线.29.如图、在△ABC中,AB=AC,M,N分别为AC,BC的中点,以AC为斜边在△ABC的外侧作Rt△ACD,且∠CAD=30°,连接MN,DM,DN.(1)求证:△DMN是等腰三角形;(2)若AC平分∠BAD,AB=6,求DN的长.【分析】(1)依据三角形的中位线定理可得到MN=AB,由直角三角形斜边上中线的性质可得到DM=AM=AC,然后结合已知条件可得到DM=MN;(2)由AM=DM可得到∠CAD=∠ADM=30°,从而可得到∠DMC=60°,然后再证明∠CMN=30°,从而可得到∠DMN=90°,最后,依据勾股定理求解即可.【解答】解:(1)∵在△ABC中,M、N分别是AC、BC的中点,∴MN∥AB,MN=AB,AM=MC=AC.∵∠ADC=90°,DM为斜边上的中线,∴MD=AC.∵AC=AB,∴MN=DM.∴△DMN是等腰三角形.(2)∵∠CAD=30°,AC平分∠BAD,∴∠BAC=∠CAD=30°.∵MN∥AB,∴∠NMC=∠BAC=30°.由(1)DM=AM,∴∠DMC=60°.∴∠DMN=∠DMC+∠NMC=30°+60°=90°.在Rt△ABC中,DN2=DM2+MN2,DM=MN=AB=3,∴DN=3.【点评】本题主要考查的是三角形的中位线定理、勾股定理、等腰三角形的判断,熟练掌握相关知识是解题的关键.30.如图,在△ABC中,点D,E,F分别是各边中点,AG是BC边上的高.求证:∠GDE=∠GFE.【分析】根据三角形中位线定理得到DE∥AC,根据平行线的性质得到∠DEG=∠C,根据直角三角形的性质得到∠FGC=∠C,得到∠DEG=∠FGC,同理可证.【解答】证明:∵D,E分别是BA、BC中点,∴DE∥AC,∴∠DEG=∠C,∵AG⊥BC,F是AC的中点,∴FG=FC,∴∠FGC=∠C,∴∠DEG=∠FGC,同理∠BGD=∠FEC,∴∠DGH=∠FEH,∴∠GDE=∠GFE.【点评】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.31.如图,在四边形ABCD中,∠ADC=90°,AB=AC,E,F分别为AC,BC 的中点,连接EF,ED,FD.(1)求证:ED=EF;(2)若∠BAD=60°,AC平分∠BAD,AC=6,求DF的长.【分析】(1)利用直角三角形斜边上的中线等于斜边的一半及三角形中位线定理,可得出DE=AC、EF=AB,结合AB=AC,即可证出ED=EF;(2)由∠BAD的度数结合角平分线的定理可得出∠BAC=∠DAC=30°,利用平行线的性质及三角形外角的性质可得出∠FEC=30°、∠DEC=60°,进而可得出∠FED=90°,在Rt△DEF中利用勾股定理可求出DF的长.【解答】(1)证明:∵∠ADC=90°,E为AC的中点,∴DE=AE=AC.∵E、F分别为AC、BC的中点,∴EF为△ABC的中位线,∴EF=AB.∵AB=AC,∴DE=EF.(2)解:∵∠BAD=60°,AC平分∠BAD,∴∠BAC=∠DAC=∠BAD=30°.由(1)可知EF∥AB,AE=DE,∴∠FEC=∠BAC=30°,∠DEC=2∠DAC=60°,∴∠FED=90°.∵AC=6,∴DE=EF=3,∴DF==3.【点评】本题考查了三角形中位线定理、直角三角形斜边上的中线、平行线的性质、三角形外角的性质以及勾股定理,解题的关键是:(1)找出DE=AC、EF=AB;(2)通过角的计算找出∠FED=90°.32.如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA的延长线上,∠FDA=∠B,AC=6,AB=8,求四边形AEDF的周长P.【分析】根据勾股定理先求出BC的长,再根据三角形中位线定理和直角三角形的性质求出DE和AE的长,进而由已知可判定四边形AEDF是平行四边形,从而求得其周长.【解答】解:在Rt△ABC中,∵AC=6,AB=8,∴BC==10,∵E是BC的中点,∴AE=BE=5,∴∠BAE=∠B,∵∠FDA=∠B,∴∠FDA=∠BAE,∴DF∥AE,∵D、E分别是AB、BC的中点,∴DE∥AC,DE=AC=3,∴四边形AEDF是平行四边形∴四边形AEDF的周长=2×(3+5)=16.【点评】本题考查了三角形中位线定理的运用,熟悉直角三角形的性质、等腰三角形的判定以及平行四边形的判定.熟练运用三角形的中位线定理和直角三角形的勾股定理是解题的关键.。
新苏科版八年级数学下册《三角形的中位线》题及答案.docx

(新课标)苏科版八年级下册第11课时三角形的中位线1.如图,DE是△ABC的中位线,若BC的长为3 cm,则DE 的长是( )A.2 cm B.1.5 cm C.1.2 cm D.1cm2.如图,小区的一角有一块形状为等腰梯形的空地,为了美化小区,社区居委会计划在空地上建一个四边形的水池,使水池的四个顶点恰好在梯形各边的中点上,则水池的形状一定是( )A.梯形B.矩形C.菱形D.正方形3.如图,在△ABC中,点D、E、F分别是AB、BC、CA的中点,若△ABC的周长为10 cm,则△DEF的周长是_______cm.4.如图,为测量位于一水塘旁的两点A、B间的距离,在地面上确定点O,分别取OA、OB的中点C、D,量得CD=20 m,则A、B之间的距离是_______m.5.将一块直角三角形纸片ABC折叠,使点A与点C重合,展开后平铺在桌面上(如图所示).若∠C=90°,BC=8 cm,则折痕DE的长度是_______cm.6.如图,在四边形ABCD中,AD=BC,E、F、G分别是AB、CD、AC的中点,试说明△EFG的形状.7.一个三角形的周长是36 cm,则以这个三角形各边中点为顶点的三角形的周长是( )A.6 cm B.12 cm C.18 cm D.36 cm 8.如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )A.AB∥DC B.AB=DCC.AC⊥BD D.AC=BD9.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为_______.10.如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=5 cm,则EF=_______cm.11.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,连接DE、EF、FD,则图中平行四边形的个数为_______.12.如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN ⊥AN,垂足为N,且AB=6,BC=10,MN=1.5,求△ABC的周长.13.如图,在四边形ABCD中,AD∥BC,AB与CD不平行,H、G分别是两条对角线BD、AC的中点,求证:GH∥AD,且GH (BC-AD).=1214.如图,在四边形ABCD中,E为AB上一点,△ADE和△BCE 都是等边三角形,AB、BC、CD、DA的中点分别为P、Q、M、N,试判断四边形PQMN为怎样的四边形,并说明你的理由.参考答案1.B 2.C 3.5 4.40 5.4 6.略7.C 8.C 9.20 10.5 11.3 12.25 13.14.四边形PQMN为菱形.。
八下9.5三角形的中位线难题训练(有答案)

八下9.5三角形的中位线难题训练(有答案)八下9.5三角形的中位线难题训练姓名:___________班级:___________考号:___________一、选择题1.若顺次连结四边形四条边的中点,所得的四边形是菱形,则原四边形一定是()A. 平行四边形B. 矩形C. 对角线相等的四边形D. 对角线互相垂直的四边形2.如图,△ABC中,AB=15,AC=13,点D为BC上一点,且AD=12,BD=9,点E,F分别为AB,AC的中点,则△DEF的周长为()A. 25B. 24C. 26D. 213.如图,正方形ABCD和正方形DEFG的边长分别为5和3,点E,G分别为AD,CD边上的点,H为BF的中点,连接HG,则HG的长为A. 2√2B. 4C. √15D. √174.如图,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.过点D作DG//BE,交BC于点G,连接FG交BD于点O.若AB=3,AD=4,则FG的长为()A. 258B. 158C. 254D. 1545.如图,三角形ABC中,∠B,∠C的平分线BF,CE相交于O,AG⊥BF于G,AH⊥CE于H.其中AB=9cm,AC=14cm,BC=18cm,则GH的长为()A. 2cmB. 52cm C. 3cm D. 72cm6.如图,在平行四边形ABCD中,AD=2AB,CE⊥AB于点E,点F、G分别是AD、BC的中点,连接CF、EF、FG,下列结论:①CE⊥FG;②四边形ABGF是菱形;③EF=CF;④∠EFC=2∠CFD.其中正确的个数是()A. 1个B. 2个C. 3个D. 4个7.如图,AC,BD是四边形ABCD的对角线,点E,F分别是AD,BC的中点,点M,N分别是AC,BD的中点,连接EM,MF,FN,NE,要使四边形EMFN为正方形,则需添加的条件是()A. AB=CD,AB⊥CDB. AB=CD,AD=BCC. AB=CD,AC⊥BDD. AB=CD,AD//BC8.如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边中点得到第二个矩形,依次类推若第一格矩形的面积为1,则第n个矩形的面积为()A. 12n B. 14nC. 12n?1D. 14n?1二、填空题9.如图所示,?ABCD的对角线AC,BD相交于点O,AE=EB,OE=3,AB=5,?ABCD的周长________.10.如图,在梯形ABCD中,AD//BC,∠BCD=90°,BC=2AD,F、E分别是BA、BC的中点,现有四个结论:①△ABC 是等腰三角形②四边形EFAM是菱形③S△BEF=12S△ACD④DE平分∠CDF.则下列结论正确的是_______________ 11.如图,E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足________时,四边形EFGH是菱形.12.如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=13,AC=8,则DF的长为___________13.如图,△ABC中,BD平分∠ABC,AD⊥BD于D,F为AC中点,AB=5,BC=7,则DF=_________.14.如图,已知矩形ABCD的长和宽分别为16cm和12cm,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形l1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形l2;…如此操作下去,则l4的面积是______cm2.三、解答题15.类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.(1)概念理解:如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件,你添加的条件是.(2)问题探究:如图2,在“等邻边四边形”ABCD中,∠DAB=60°,∠ABC=∠ADC=90°,AB=AD=6,求对角线AC的长.(3)拓展应用:如图3,“等邻边四边形”ABCD中,AB=AD,∠BAD=60°,∠BCD=30°,AC为对角线,试探究AC,BC,DC的数量关系,并证明你的结论.16.在△ABC中,借助作图工具可以作出中位线EF,沿着中位线EF 一刀剪切后,用得到的△AEF和四边形EBCF可以拼成平行四边形EBCP,剪切线与拼图如图示1,仿上述的方法,按要求完成下列操作设计,并在规定位置画出图示,(1)在△ABC中,增加条件______ ,沿着______ 一刀剪切后可以拼成矩形,剪切线与拼图画在图示2的位置;(2)在△ABC中,增加条件______ ,沿着______ 一刀剪切后可以拼成菱形,剪切线与拼图画在图示3的位置;(3)在△ABC中,增加条件______ ,沿着______ 一刀剪切后可以拼成正方形,剪切线与拼图画在图示4的位置.17.阅读下面材料:子薇遇到这样一个问题:如图1,在正方形ABCD中,点E、F分别为DC、BC边上的点,∠EAF=45°,连接EF,求证:DE+BF=EF.子薇是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段集中到同一条线段上.她先后尝试了平移、翻折、旋转的方法,发现通过旋转可以解决此问题.她的方法是将△ADE绕点A顺时针旋转90°得到△ABG(如图2),此时GF即是DE+BF.请回答:在图2中,∠GAF的度数是_______.参考子薇得到的结论和思考问题的方法,解决下列问题:(1)如图3,在直角梯形ABCD中,AD//BC(AD>BC),∠D=90°,AD=CD=10,E是CD上一点,若∠BAE=45°,DE=4,求BE的长度.(2)如图4,在平面直角坐标系xOy中,点B是x轴上一动点,且点A(?3,2),连接AB和AO,并以AB为边向上作正方形ABCD,若C(x,y),求用含x的代数式表示y。
八年级数学下册第9章9.5三角形的中位线同步练习(含解析)苏科版

故选B.
【分析】本题依据三角形三边关系,可求第三边大于2小于10,原三角形的周长大于12小于20,连接中点的三角形周长是原三角形周长的一半,那么新三角形的周长应大于6而小于10,看哪个符合就可以了.
8、【答案】D
【考点】三角形中位线定理
【解析】【解答】解:∵O是AB的中点,OD垂直于地面,AC垂直于地面,∴OD是△ABC的中位线,
6、【答案】A
【考点】三角形中位线定理,平行四边形的判定
【解析】【解答】解:连接AC,BD.利用三角形的中位线定理可得EH∥FG,EH=FG.∴这块草地的形状是平行四边形.
故选A.
【分析】连接AC,BD,构造三角形的中位线.
7、【答案】B
【考点】三角形三边关系,三角形中位线定理
【解析】【解答】解:设三角形的三边分别是a、b、c,令a=4,b=6,则2<c<10,12<三角形的周长<20,
∵AH⊥BC,F是AC的中点,∴HF= AC,
∴ED=HF,
∵EF∥DH,ED=HF且ED不平行HF,
∴四边形EDHF是等腰梯形,
故选B.
【分析】根据三角形中位线定理及直角三角形中斜边上的中线为斜边的一半即可证明;
4、【答案】B
【考点】三角形中位线定理,梯形
【解析】【解答】解:∵M,N,P分别为AD、BC、BD的中点,∴MP∥AB,PN∥CD,MP= AB=3,PN= CD=4.
∴∠MPD=∠ABD,∠PNB=∠C.
又∠ABC+∠C=90°,∠DPN=∠PBN+∠PNB,
∴∠MPN=90°.
∴MN= =5.
故选B.
【分析】根据三角形的中位线定理,得MP∥AB,PN∥CD,MP= AB=3,PN= CD=4;再根据平行线的性质,得∠MPD=∠ABD,∠PNB=∠C;根据三角形的外角的性质和已知∠ABC+∠C=90°,得∠MPN=90°,进而根据勾股定理求解.
苏科版八年级下册9.5三角形的中位线训练(有答案)

八下9.5三角形的中位线训练学校:___________姓名:___________班级:___________考号:___________一、选择题1.在ΔABC中,D,E分别是边AB,AC的中点,已知BC=10,则DE的长为()A. 3B. 4C. 5D. 62.如图,在□ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF.若EF=3,则CD的长为()A. 3B. 6C. 8D. 123.如图,在四边形ABCD中,点E,F,G分别是边AB,AD,DC的中点,则EF=()A. 13BD B. 12BD C. 12BG D. BG4.如图,在菱形ABCD中,∠A=60°,AD=4,点P是AB边上的一个动点,点E、F分别是DP、BP的中点,则线段EF的长为()A. 2B. 4C. 2√2D. 2√35.如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且DE=3cm,则AF=()cmA. 1B. 2C. 3D. 46.如图,在Rt△ABC中,∠ACB=90∘,点D,E分别是边AB,AC的中点,延长BC至F,使CF=12BC,若AB=10,则EF 的长是()A. 5B. 4C. 3D. 27.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为()A.B.C. 3D. 48.如图,在△ABC中,D,E分别是AB,AC的中点,AC=10,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为()A. 10B. 12C. 14D. 16二、填空题9.如图,已知△ABC中,AB=AC,AD平分∠BAC,E是AC的中点,若AB=6,则DE的长为_________.10.如图,平行四边形ABCD的对角线AC、BD相交于点O,点E、F分别是线段AO、OB的中点,若AC+BD=24cm,△OAB的周长是18cm,则EF=___________cm.11.如图,在△ABC中,D、E、F分别是各边的中点,AH是高,∠DHF=50°,则∠DEF=______ °.12.如图,D,E,F分别为△ABC三边的中点,则图中平行四边形的个数为_________.13.如下图所示,AD//BC,∠1=∠2,∠3=∠4,AD=4,BC=2,则AB的值为________.14.如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠FPE=100°,则∠PFE的度数是________.三、解答题15.如图,在Rt△ABC中,∠ACB=90°,DE、DF是△ABC的中位线,连接EF、CD,求证:CD=EF.16.如图,在△ABC中,D、E分别是边AB、AC的中点,点F是BCBC,连结CD、EF,那么CD与EF延长线上一点,且CF=12相等吗?请证明你的结论.17.证明:三角形的一条中位线与第三边上的中线互相平分.已知:如图,DE是△ABC的中位线,AF是△ABC的中线,AF、DE交于点O.求证:.证明:.18.已知:如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E,F分别是线段BM,CM的中点.(1)求证:△ABM≌△DCM;(2)判断四边形MENF是什么特殊四边形,并证明你的结论;(3)当AD:AB=______时,四边形MENF是正方形.19.如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连接,得到四边形DEFG.(1)求证:四边形DEFG是平行四边形;(2)连接AO,当AO与BC满足什么位置关系时四边形DEFG是矩形?(不需要证明)20.如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH.求证:四边形EFGH是平行四边形.答案和解析1.C解:∵△ABC中,D,E分别是边AB,AC的中点,∴DE是△ABC的中位线,故DE=12BC=12×10=5.2.B解:∵EF是△ABD的中位线,EF=3,∴AB=2EF=6,又∵AB=CD,∴CD=6.3.B解:∵E,F分别是边AB,AD的中点,∴EF=12BD,且EF//BD.4.A解:如图连接BD.∵四边形ABCD是菱形,∴AD=AB=4,∵∠A=60°,∴△ABD是等边三角形,∴BA=AD=BD=4,∵点E、F分别是DP、BP的中点,∴EF是△BDP的中位线,∴EF=12BD=2.5.C解:由已知D、E分别为AB、AC中点,∴DE//BC,DE=12BC,∵DE=3cm,∴BC=6cm,∵∠BAC=90°,F为BC中点,∴AF=12BC=3cm.6.A解:∵点D,E分别是边AB,AC的中点,∴AD=DB,AE=EC,DE//BC,DE=12BC,∵CF=12BC,∴DE//CF,DE=CF,∴四边形DEFC是平行四边形,∴EF=CD,∵∠ACB=90°,AD=DB,AB=10,∴CD=12AB=5,∴EF=5.7.A解:∵四边形ABCD是正方形,∴∠DCE=90°,OD=OB,∵DF=FE,∴CF=FE=FD,∵EC+EF+CF=18,EC=5,∴EF+FC=13=DE,∴DC=√DE2−EC2=12,∴BC=CD=12,∴BE=BC−EC=7,∵OD=OB,DF=FE,∴OF=12BE=72,8.B解:如图,∵∠AFC=90°,AE=CE,∴EF=1AC=5,2∴DE=1+5=6;∵D,E分别是AB,AC的中点,∴DE为△ABC的中位线,∴BC=2DE=12,9.3解:∵△ABC中,AB=AC,AD平分∠BAC,∴BD=CD,又∵E是AC的中点,∴DE是△ABC的中位线,AB,∴DE=12又∵AB=6,∴DE=3.10.3解:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,又∵AC+BD=24(cm),∴OA+OB=12(cm),∵△OAB的周长是18cm,∴AB=6(cm),∵点E,F分别是线段AO,BO的中点,∴EF是△OAB的中位线,∴EF=1AB=3(cm).211.50解:∠DHF=∠DEF,如图.∵AH⊥BC于H,又∵D为AB的中点,∴DH=1AB=AD,2∴∠1=∠2,同理可证:∠3=∠4,∴∠1+∠3=∠2+∠4,即∠DHF=∠DAF,∵E、F分别为BC、AC的中点,AB,∴EF//AB且EF=12即EF//AD且EF=AD,∴四边形ADEF是平行四边形,∴∠DAF=∠DEF,∴∠DHF=∠DEF=50°.12.3解:∵D,E,F分别为△ABC三边的中点∴DE//AF,DF//EC,DF//BE且DE=AF,DF=EC,DF=BE ∴四边形ADEF、DECF、DFEB分别为平行四边形13.6解:延长AD,BE交于F.∵AD//BC,∠4=∠F=∠3,∴AB=AF,∵∠1=∠2,AE⊥BF,BE=EF,AD//BC,∴CE=DE,BC=DF,∴AF=AD+DF=AD+BC=6,AB=AF=6.14.40°解:∵在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,∴FP,PE分别是△CDB与△DAB的中位线∴PF=12BC,PE=12AD∵AD=BC∴PF=PE故△EPF是等腰三角形.∵∠FPE=100°∴∠PEF=∠PFE=40°15.证明:∵DE、DF是△ABC的中位线,∴DE//BC,DF//AC,∴四边形DECF是平行四边形,∵∠ACB=90°,∴平行四边形DECF是矩形,∴CD=EF.16.解:结论:CD=EF.理由::∵D、E分别是边AB、AC的中点,∴DE//BC,DE=12BC,∵CF=12BC,∴DE=CF,∴四边形DEFC是平行四边形,∴CD=EF.17.求证:AF、DE互相平分.证明:连结DF、EF,∵DE是△ABC的中位线,AF是△ABC的中线,∴D、E、F分别是各边的中点,∴DF//AE,EF//AD,∴四边形ADFE是平行四边形,∴AF、DE互相平分.18.证明:∵四边形ABCD是矩形,∴AB=CD,∠A=∠D=90°,又∵M是AD的中点,∴AM=DM.在△ABM和△DCM中,∴△ABM≌△DCM(SAS).(2)解:四边形MENF是菱形.证明如下:∵E,F,N分别是BM,CM,CB的中点,∴NE//MF,NE=MF,∴四边形MENF是平行四边形,由(1),得BM=CM,∴ME=MF,∴四边形MENF是菱形.(3)2:1.理由如下:∵M为AD中点,∴AD=2AM,∵AD:AB=2:1,∴AM=AB,∵∠A=90,∴∠ABM=∠AMB=45°,同理∠DMC=45°,∴∠EMF=180°−45°−45°=90°,由(2)可知四边形MENF是菱形,所以,四边形MENF是正方形.19.解:(1)四边形DEFG是平行四边形.理由如下:∵D、G分别是AB、AC的中点,∴DG是△ABC的中位线;BC;∴DG//BC,且DG=12BC;同理可证:EF//BC,且EF=12∴DG//EF,且DG=EF;故四边形DEFG是平行四边形;(2)当AO⊥BC时,四边形DEFG是矩形.(2)解:当AO⊥BC时,四边形DEFG是矩形.理由如下:连接OA;∵把AB、OB、OC、AC的中点D、E、F、G依次连接形成四边形DEFG.∴DE//OA//GF,EF//BC,∵AO⊥BC,∴AO⊥EF,∵DE//OA,∴DE⊥EF,∴四边形DEFG是矩形.20.证明:连接AC.∵G是DC的中点,H是AD的中点,AC,∴HG//AC,且HG=12AC,同理可知EF//AC,且EF=12∴EF//HG,且EF=HG,∴四边形EFGH是平行四边形.。
苏科版八年级下册9.5三角形的中位线提优训练(有答案)

八下9.5三角形的中位线提优训练姓名:___________班级:___________考号:___________一、选择题1.如图,在四边形ABCD中,AB//CD,∠C=90°,AB=8,AD=CD=5,点M、N分别为BC、AB上的动点(含端点),E、F分别为DM、MN的中点,则EF长度的最小值为()A. 3B. 2.5C. 2D. 12.如图,点D,E分别是AB,AC的中点,BE是∠ABC的平分线,对于下列结论:①BC=2DE;②DE//BC;③BD=DE;④BE⊥AC,其中正确的个数是()A. 1个B. 2个C. 3个D. 4个3.如图,AD,AE分别是△ABC的角平分线和中线,CG⊥AD于F,交AB于G,若AB=8,AC=6,则EF的长为()A. 2B. 32C. 1D. 124.如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为()A. 1cmB. 2cmC. 3cmD. 4cm5.如图所示,在△ABC中,M是BC的中点,AN平分∠BAC,BN⊥AN.若AB=10,AC=15,则MN的长为()A. 2B. 2.5C. 3D. 3.56.如图,矩形纸片ABCD中,AB=10,AD=5,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.当P落在矩形ABCD内部时,PD的最小值等于()B. 10−5√3C. 5√5−10D. 2A. 327.如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,与AB交于点N,连接OM,ON,MN.下列四个结论:①△CNB≌△DMC;②OM=ON;③△OMN∽△OAD;④AN2+CM2=MN2,其中正确结论的个数是()A. ①②③B. ②③④C. ①③④D. ①②③④8.如图,已知直线l//AB,l与AB之间的距离为2.C、D是直线l上两个动点(点C在D点的左侧),且AB=CD=5.连接AC、BC、BD,将△ABC沿BC折叠得到△A′BC.下列说法:①四边形ABCD的面积始终为10;②当A′与D重合时,四边形ABDC 是菱形;③当A′与D不重合时,连接A′、D,则∠CA′D+∠BCA′=180°;④若以A′、C、B、D为顶点的四边形为矩形,则此矩形相邻两边之和为3或7.其中正确的是()A. ①②④B. ①③C. ①②③D. ①②③④二、填空题9.如图:在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长是______.10.已知:△ABC中,AB=a.如图(1),若A1、B1分别是CA、CB的中点,则A1B1=a2;如图(2),若A1、A2、B1、B2分别是CA、CB的三等分点,则A1B1+A2B2=2+13a=a;如图(3),若A1、A2、A3、B1、B2、B3分别是CA、CB的四等分点,则A1B1+A2B2+A3B3=1+2+34a=32a;如图(4),若A1、A2、A3、…A9、B1、B2、B3、…B9分别是CA、CB的十等分点,则A1B1+A2B2+A3B3+⋯+A9B9=______ .11.如图,△ABC的面积为1,取△ABC各边的中点A1,B1,C1,作第二个△A1B1C1,再取△A1B1C1各边的中点A2,B2,C2,作第三个△A2B2C2,…,则▵A5B5C5的面积是________.12.如图,平行四边形ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,BC,连接OE,下列结论:④∠CAD=30°;S ABCD=AB⋅AC;且∠ADC=60°,AB=12BC.其中正确的结论的有_____________(只填序号).③OB=AB:④OE=1413.已知,在四边形ABCD中,AB=CD,E是BC的中点,G是AD的中点,EG交AC于点F,∠ACD=30°,∠CAB=70°,则∠AFG的度数是.三、解答题14.如图1,已知点E,F,G,H分别是四边形ABCD各边AB,BC,CD,DA的中点,若连接BD根据三角形中位线定理容易证明四边形EFGH是平行四边形:(1)如图2,将图1中的点C移动至与点E重合的位置,F,G,H仍是BC,CD,DA的中点,求证:四边形CFGH是平行四边形;(2)如图3,在边长为1的小正方形组成的5×5网格中,点A,C,B都在格点上,在格点上画出点D,使点C与BC,CD,DA的中点F,G,H组成正方形CFGH;(3)在(2)条件下求出正方形CFGH的边长.15.如图①,矩形ABCD中,AB=a,BC=6,E、F分别是AB、CD的中点.图①图②(1)求证:四边形AECF是平行四边形;(2)是否存在a的值使得四边形AECF为菱形,若存在求出a的值,若不存在说明理由;(3)如图②,点P是线段AF上一动点且∠APB=90∘.①求证:PC=BC;②直接写出a的取值范围.16.如图,在矩形ABCD中,Q是BC的中点,P是AD上一点,连接PB、PC,E、F分别是PB、PC的中点,连接QE、QF.(1)求证:四边形PEQF是平行四边形.(2)①当点P在什么位置时,四边形PEQF是菱形?证明你的结论;②矩形ABCD的边AB和AD满足什么条件时,①中的菱形PEQF是正方形?(直接写出结论,不需要说明理由)17.如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG,H为FG的中点,连接AF,DH.(1)求证:四边形AFHD为平行四边形;(2)若CB=CE,∠EBC=75°,∠DCE=10°,求∠DAB的度数.18.已知:如图,△ABC是锐角三角形,分别以AB,AC为边向外侧作等边三角形ABM和等边三角形CAN.D、E、F分别是MB、BC、CN的中点,连结DE、EF.求证DE=FE.答案和解析1.C解:如图所示:连接DN,过点D作DG⊥AB于点G,∵AB//CD,∠C=90°,DG⊥AB,∴∠B=∠DGB=90°,∴四边形DGBC是矩形,GB=CD=5,∴AG=AB−GB=3,在Rt△DGA中,AD=5,AG=3,∴DG=4,∵E、F分别为DM、MN的中点,DN=2.∴当N与点G重合时,DN最小,此时EF最小,EF=122.D解:∵点D,E分别是AB,AC的中点,∴DE//BC,BC=2DE,故①②正确;∵BE是∠ABC的平分线,∴∠DBE=∠CBE,∵DE//BC,∴∠DEB=∠CBE,∴∠DBE=∠DEB,∴BD=DE,故③正确;∵AD=BD=DE,∴△ABE是直角三角形,即BE⊥AC,故④正确.解:∵AE为△ABC的角平分线,CG⊥AD,∴△ACG是等腰三角形,∴AG=AC,∵AC=6,∴AG=AC=6,FG=CF,∵AE为△ABC的中线,∴EF是△BCG的中位线,∴EF=12BG,∵AB=8,∴BG=AB−AG=8−6=2.∴EF=1.4.C解:∵BQ平分∠ABC,BQ⊥AE,∴△BAE是等腰三角形,同理△CAD是等腰三角形,∴点Q是AE中点,点P是AD中点(三线合一),∴PQ是△ADE的中位线,∵BE+CD=AB+AC=26−BC=26−10=16,∴DE=BE+CD−BC=6,∴PQ=12DE=3.5 B解:延长BN交AC于E,在△ANB和△ANE中,{∠BAN=∠EAN AN=AN∠ANB=∠ANE,∴△ANB≌△ANE,∴AE=AB=10,BN=NE,又BM=MC,∴MN=12EC=2.5,解:如图,∵当点P落在矩形的内部时,∠P=∠A=90°,∴四边形PFAE是以EF为直径的圆内接四边形,∴只有当直径EF最大,且点A落在BD上时,PD最小,此时E与点B重合;由题意得:PE=AB=10,由勾股定理得:BD2=102+52=125,∴BD=5√5,∴PD=5√5−10.7.D解:∵正方形ABCD中,CD=BC,∠BCD=90°,∴∠BCN+∠DCN=90°,又∵CN⊥DM,∴∠CDM+∠DCN=90°,∴∠BCN=∠CDM,又∵∠CBN=∠DCM=90°,∴△CNB≌△DMC(ASA),故①正确;根据△CNB≌△DMC,可得CM=BN,又∵∠OCM=∠OBN=45°,OC=OB,∴△OCM≌△OBN(SAS),∴OM=ON,故②正确;∵∠BON+∠BOM=∠COM+∠BOM=90°,∴∠MON=90°,即△MON是等腰直角三角形,又∵△AOD是等腰直角三角形,∴△OMN∽△OAD,故③正确;∵AB=BC,CM=BN,∴BM=AN,又∵Rt△BMN中,BM2+BN2=MN2,∴AN2+CM2=MN2,故④正确;综上所述,正确结论的个数是4个,解:①∵AB=CD=5,AB//CD,∴四边形ABCD为平行四边形,∴四边形ABDC的面积=2×5=10;故①正确;②∵四边形ABDC是平行四边形,∵A′与D重合时,∴AC=CD,∵四边形ABDC是平行四边形,∴四边形ABDC是菱形;故②正确;③连结A′D,如图,∵△ABC沿BC折叠得到△A′BC,∴CA′=CA=BD,AB=CD=A′B,在△A′CD和△A′BD中{CA′=BD CD=BA′A′D=A′D,∴△A′CD≌△DBA′(SSS),∴∠3=∠4,又∵∠1=∠CBA=∠2,∴∠1+∠2=∠3+∠4,∴∠1=∠4,∴A′D//BC,∴∠CA′D+∠BCA′=180°;故③正确;④设矩形的边长分别为a,b,当∠CBD=90°,∵四边形ABDC是平行四边形,∴∠BCA=90°,∴S△A′CB=S△ABC=12×2×5=5,∴S矩形A′CBD=10,即ab=10,而BA′=BA=5,∴a2+b2=25,∴(a+b)2=a2+b2+2ab=45,∴a+b=3√5,当∠BCD=90°时,∵四边形ABDC是平行四边形,∴∠CBA=90°,∴BC=2,而CD=5,∴a+b=7,∴此矩形相邻两边之和为3√5或7.故④正确.9.18解:∵D,E分别是AB,BC的中点,∴AC=2DE=5,AC//DE,AC2+BC2=52+122=169,AB2=132=169,∴AC2+BC2=AB2,∴∠ACB=90°,∵AC//DE,∴∠DEB=90°,又∵E是BC的中点,∴直线DE是线段BC的垂直平分线,∴DC=BD,∴△ACD的周长=AC+AD+CD=AC+AD+BD=AC+AB=18,10.解:根据题意:图(1),有1条等分线,等分线的总长=a2;图(2),有2条等分线,等分线的总长=1+23a;图(3),有3条等分线,等分线的总长=1+2+34a;…图(4),有9条等分线,等分线的总长=1+2+⋯+910a=92a.11.145解:∵A 1,B 1,C 1是△ABC 三边的中点,∴A 1C 1,A 1B 1,B 1C 1为△ABC 的中位线,∴A 1C 1//AC ,A 1B 1//AB ,C 1B 1:BC =12,∴四边形AC 1A 1B 1为平行四边形,∴∠A =∠C 1A 1B 1,同理可得四边形BA 1B 1C 1为平行四边形,∴∠B =∠C 1B 1A 1,∴△A 1B 1C 1∽△ABC ,∴S △A 1B 1C 1S △ABC =(12)2,∴S △A 1B 1C 1=14×1=14, 同理可得:S △A 2B 2C 2S △A 1B 1C 1=(12)2, ∴S △A 2B 2C 2=14×14=(14)2,∴S △A 3B 3C 3=14×14×14=(14)3 ....∴S △A 5B 5C 5=14×14×14×14×14=(14)5=145,12. ①②④解:∵四边形ABCD 是平行四边形,∴∠ABC =∠ADC =60°,∠BAD =120°,∵AE 平分∠BAD ,∴∠BAE =∠EAD =60°∴△ABE 是等边三角形,∴AE =AB =BE ,∵AB =12BC , ∴AE =12BC ,∴∠BAC =90°,∴∠CAD =30°,故①正确;∵AC ⊥AB ,∴S ▵ABCD =AB ⋅AC ,故②正确,∵AB =12BC ,OB =12BD ,∵BD >BC ,∴AB≠OB,故③错误;∵∠CAD=30°,∠AEB=60°,AD//BC,∴∠EAC=∠ACE=30°,∴AE=CE,∴BE=CE,∵OA=OC,∴OE=12AB,∵AB=12BC,∴OE=14BC.故④正确.13.50°解:取AC的中点M,连接GM、EM,∵G是AD的中点,E是BC的中点,∴GM是△ADC的中位线,EM是△ABC的中位线,∴GM=12DC,EM=12AB,GM//CD,EM//AB,∵AB=CD,∴GM=EM,∴∠GEM=∠EGM,∵EM//AB,∴∠EMC=∠BAC=70°,∴∠AME=180°−70°=110°,∵GM//CD,∴∠AMG=∠ACD=30°,∴∠EMG=110°+30°=140°,∴∠EGM=180°−140°2=20°,∴∠AFG=∠EGM+∠AMG=20°+30°=50°,14.(1)证明:如图2,连接BD,∵C,H是AB,DA的中点,∴CH是△ABD的中位线,∴CH//BD,CH=12BD,同理FG//BD,FG=12BD,∴CH//FG,CH=FG,∴四边形CFGH是平行四边形;(2)如图3所示,(3)解:如图3,∵BD=√5,∴FG=12BD=√52,∴正方形CFGH的边长是√52.15.解:(1)因为ABCD是平行四边形,所以AB//CD,AB=CD,又因为E,F分别为AB,CD的中点,所以AE=CF,所以AECF是平行四边形,(2)不存在,为为AE=BE=12a,而CE直角三角形BCE的斜边,的以CE>BE=AE,即CE>AE,所以不存在a的值使得四边菜AECF是菱形,(3)①证明:连接PE.∵∠APB=90°,E是AB的中点,∴PE+BE.又四边形AECF是平行四边形,∴AF//EC.∴EC⊥BP.∴∠BEC=∠PEC.又EC=EC.∴△BEC≌△PEC(SAS),∴PC=BC.②0<a≤12.16.(1)证明:在△PBC中,E、F分别是PB、PC的中点,Q是BC的中点,∴QE、QF为△PBC的中位线,∴QE//PF,QF//PE,∴四边形PEQF是平行四边形;(2)解:①当点P为AD的中点时,四边形PEQF是菱形,理由是:当P为AD的中点时,AP=PD,由勾股定理得:PB=√AB2+AP2,PC=√CD2+PD2,∵四边形ABCD是矩形,∴AB=CD,∴PB=PC,∵E、F分别是PB、PC的中点,∴PE=PF,由(1)知:四边形PEQF是平行四边形,∴四边形PEQF是菱形;②矩形ABCD的边AB和AD满足AD=2AB时,①中的菱形PEQF是正方形.17.(1)证明:∵四边形ABCD为平行四边形,∴AD//BC,AD=BC,又∵BF=BE,CG=CE,∴BC为△EFG的中位线,FG,∴BC=12BC//FG,∵H为FG中点,FG,∴FH=12∴BC=FH,∴AD=FH,AD//FH,∴四边形AFHD为平行四边形;(2)解:∵CB=CE,∠EBC=75°,∴∠BEC=75°,∴∠BCE=30°,又∵∠DCE=10°,∴∠BCD=40°,∵四边形ABCD是平行四边形,∴∠DHB=40°.18.证明:连接MC、BN,∵△ABM和△CAN是等边三角形,∴∠BAM=∠CAN=60°,MA=BA,AN=AC ∴∠BAM+∠BAC=∠CAN+∠BAC,即∠MAC=∠BAN,在△MAC与△BAN中,{MA=BA∠MAC=∠BAN AN=AC,∴△MAC≌△BAN(SAS),∴MC=NB,∵D、E、F分别是MB,BC,CN的中点,∴DE=12MC,EF=12BN,∴DE=EF.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018苏科版八年级下《9.5三角形中位线》同步测试精选有答案
《9.5三角形中位线》同步测试精选有难度
一、选择题
1、如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是()A.AB=24m B.MN∥AB C.△CMN∽△CAB D.CM:MA=1:2
2、如图,⊙O的半径为5,弦AB=8,点C在弦AB上,且AC=6,过点C作CD⊥AB交OB于点D,则CD的长为()
A.1 B.2 C.1.5
D.2.5
第1题图第2题图第4题图
3、梯形ABCD中,AD∥BC,AD=3,BC=5,MN是梯形的中位线,则MN的长是()
A.1 B.2 C.3 D.4
4、如图,为测量池塘边A、B两点的距离,小明在池塘的一侧选取一点O,测得OA、OB的中点分别是点D、E,且DE=14米,则A、B间的距离是()A.18米B.24米C.28米D.30米
5、如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为()
A.50°B.60°C.70°D.80°
6、如图,在△ABC中,∠ACB=90°,AC=BC=4,M是CB中点,P、N分别在AC、AB上,若△APN的面积与△ANM的面积相等,则AP长为()
A.3 B.2 C.D.2
第5题图第6题图
第7题图
7、如图,△ABC中,AB=AC=6,BC=8,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的周长是()
A.7+B.10 C.4+2D.12
8、如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为()
A.4 B.8 C.2D.4
9、如图,△ABC中,AB=8cm,AC=5cm,AD平分∠BAC,且AD⊥CD,E为BC中点,则DE=()
A.3
B.5
C.2.5
D.1.5
第8题图第9题图
第10题图
10、如图,△ABC中,D为BC中点,E为AD的中点,BE的延长线交
AC于F,则为()
A. 1:5
B.1:4
C.1:3
D.1:2
二、填空题
11、三角形的三边长分别是3cm,5cm,6cm,则连结三边中点所围成的三角形的周长是_________cm.
12、在Rt△ABC中,∠C=90°,AC=•5,•BC=•12,•则连结两条直角边中点的线段长为_______.
13、如图,△ABC的面积为12cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为cm2.
第13题图第15题图第16题图
14、在△ABC中,点D、E分别是边AB、AC的中点,那么△ADE的面积与△ABC的面积的比是.
15、如图,在△ABC中,点D、E、F分别是边AB、BC、CA上的中点,且AB=6cm,AC=8cm,则四边形ADEF的周长等于cm.
16、如图,EF为△ABC的中位线,△AEF的周长为6cm,则△ABC的周长为cm.
17、如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是
△ABC的中位线,点M是边BC上一点,BM=3,点N是线段
MC上的一个动点,连接DN,ME,DN与ME相交于点O.若
△OMN是直角三角形,则DO的长是.
三、解答题
18、如图,在梯形ABCD中,AD∥BC,AB=DC,过点D作DE
⊥BC,垂足为E,并延长DE至F,使EF=DE.连接BF、CF、
AC.求证:四边形ABFC是平行四边形.
19、如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
(1)求证:BN=DN;
(2)求△ABC的周长.
20、已知:如图,在□ABCD中,E是CD的中点,F是AE的中点,FC与
BE交于G.求证:GF=GC.
21、已知:如图,在四边形ABCD中,AD=BC,E、F分别是DC、
AB边的中点,FE的延长线分别与AD、BC的延长线交于H、G
点.
求证:∠AHF=∠BGF.
22、如图1,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).
(温馨提示:在图1中,连接BD,取BD的中点H,连接HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE.)
问题一:如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连接EF,分别交DC、AB于点M、N,判断△OMN的形状,请直接写出结论;
问题二:如图3,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F 分别是BC、AD的中点,连接EF并延长,与BA的延长线交于点G,若∠EFC=60°,连接GD,判断△AGD的形状并证明.
23、如图,已知AD与BC相交于E,∠1=∠2=∠3,BD=CD,∠ADB=90°,CH⊥AB于H,CH交AD于F.
(1)求证:CD∥AB;
(2)求证:△BDE≌△ACE;
(3)若O为AB中点,求证:
OF=BE.
24、某厂有一块如图所示的△ABC铁板,根据需要,现要把它加工成一个平行四边形铁板.要把材料完全利用起来,可怎样加工?•请你利用学过的知识帮助工人师傅把切割的线用虚线画出来,并指出加工后的平行四边形.能否将此三角形铁板加工成长方形?请予以探索.
B A
B
A
B
A
答案
1、D
2、C
3、D
4、C
5、C
6、B
7、B
8、D
9、D 10、D
11、7 12、6.5 13、9 14、15、14.16、12.17、或.
18、证明:等腰梯形ABCD中,AB=DC,
∴∠ABC=∠DCB,
∵DE⊥BC,DE=EF,
∴△DFC是等腰三角形,
∴∠DCB=∠FCE,DC=CF,
∴∠ABC=∠FCE,
∴AB∥CF,
∵AB=CD=CF,
∴四边形ABFC是平行四边形
19、(1)证明:在△ABN和△ADN中,
∵,
∴△ABN≌△ADN,
∴BN=DN.
(2)解:∵△ABN≌△ADN,
∴AD=AB=10,DN=NB,
又∵点M是BC中点,
∴MN是△BDC的中位线,
∴CD=2MN=6,
故△ABC的周长=AB+BC+CD+AD=10+15+6+10=41.20、取BE的中点H,连接FH、CH
∵F、G分别是AE、BE的中点
∴FH是△ABE的中位线
∴FH∥AB FH=1/2*AB
∵四边形ABCD是平行四边形
∴CD∥AB CD=AB
∵E是CD的中点
∴CE=1/2*AB
∵CE=1/2*AB FH=1/2*AB
21、证明:连接AC,取AC的中点M,连接ME、MF ∵M是AC的中点,E是DC的中点
∴ME是△ACD的中位线
∴ME=AD/2,PE∥AH
∴∠MEF=∠AHF (同位角相等)
同理可证:MF=BC/2, ∠MFE=∠BGF (内错角相等)
∵AD=BC
∴ME=MF
∴∠MFE=∠MEF
∴∠AHF=∠BGF
22、解:(1)取AC中点P,连接PF,PE,
可知PE=,
PE∥AB,
∴∠PEF=∠ANF,
同理PF=,
PF∥CD,
∴∠PFE=∠CME,
又PE=PF,
∴∠PFE=∠PEF,
∴∠OMN=∠ONM,
∴△OMN为等腰三角形.
(2)判断出△AGD是直角三角形.
证明:如图连接BD,取BD的中点H,连接HF、HE,∵F是AD的中点,
∴HF∥AB,HF=AB,
同理,HE∥CD,HE=CD,
∵AB=CD
∴HF=HE,
∵∠EFC=60°,
∴∠HEF=60°,
∴∠HEF=∠HFE=60°,
∴△EHF是等边三角形,
∴∠3=∠EFC=∠AFG=60°,
∴△AGF是等边三角形.
∵AF=FD,
∴GF=FD,
∴∠FGD=∠FDG=30°
∴∠AGD=90°
即△AGD是直角三角形.
23、证明:(1)∵BD=CD,
∴∠BCD=∠1;
∵∠1=∠2,
∴∠BCD=∠2;
∴CD∥AB.
(2)∵CD∥AB,∴∠CDA=∠3.∵∠BCD=∠2=∠3,
∴BE=AE.
且∠CDA=∠BCD,
∴DE=CE.
在△BDE和△ACE中,
∵.
∴△BDE≌△ACE(SAS);
(3)∵△BDE≌△ACE,
∴∠4=∠1,∠ACE=∠BDE=90°
∴∠ACH=90°﹣∠BCH;
又∵CH⊥AB,
∴∠2=90°﹣∠BCH;
∴∠ACH=∠2=∠1=∠4,
∴AF=CF;
∵∠AEC=90°﹣∠4,∠ECF=90°﹣∠ACH,又∵∠ACH=∠4,
∴∠AEC=∠ECF
24、参照图形:。
