2016-2017年北京市东城区初三二模试卷及答案

合集下载

北京市东城区2016年中考物理二模试卷含答案解析

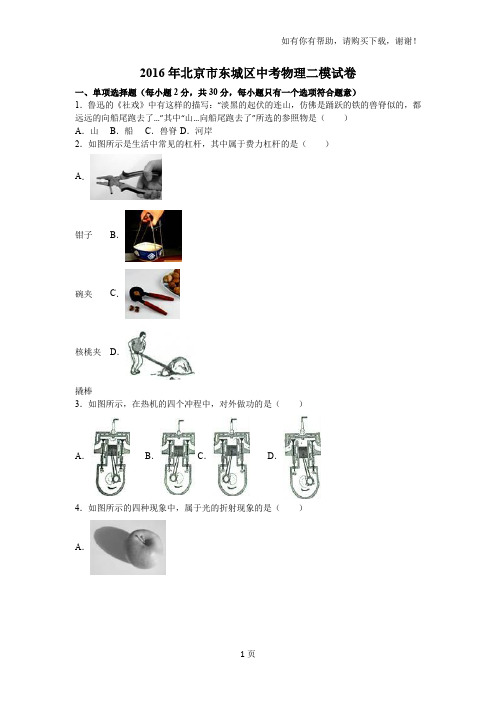
2016年北京市东城区中考物理二模试卷一、单项选择题（每小题2分，共30分，每小题只有一个选项符合题意）1．鲁迅的《社戏》中有这样的描写：“淡黑的起伏的连山，仿佛是踊跃的铁的兽脊似的，都远远的向船尾跑去了…”其中“山…向船尾跑去了”所选的参照物是（）A．山B．船C．兽脊 D．河岸2．如图所示是生活中常见的杠杆，其中属于费力杠杆的是（）A．钳子B．碗夹C．核桃夹D．撬棒3．如图所示，在热机的四个冲程中，对外做功的是（）A．B． C．D．4．如图所示的四种现象中，属于光的折射现象的是（）A．苹果在桌面上形成的影子B．叶子经露珠成放大的像C．铁罐在平面镜中形成的像D．日食5．估测在实际生活中应用十分广泛，下列所估测的数据中最接近实际的是（）A．初三体育测试中，男生完成一次标准的引体向上，头顶上升的最大高度约为150cm B．初三体育测试中，女生完成一次标准的仰卧起坐的最大高度约为150cmC．一般智能手机的质量约为1kgD．随着音乐做一套眼保健操用时约4min6．下列实例中，体现力改变物体运动状态的是（）A．用力拉弹簧，弹簧变长 B．把橡皮泥捏成不同造型C．滚动的足球受阻力缓缓停下 D．被拉弯的鱼竿7．下列关于家庭电路的说法正确的是（）A．我国照明电路的电压为220VB．家用空调不需要接地C．只要不接触高压带电体就会很安全D．更换灯泡的时候可以不用断开电源开关8．下列实例中，属于增大压强的是（）A．书包背带做得宽一些B．图钉尖进入墙时要用较大的力按C．骆驼长着宽大的脚掌D．载重汽车装有许多车轮9．有关大气压强下列说法正确的是（）A．在同一地点大气压强的值是固定不变的B．茶壶利用了连通器原理，茶壶盖上小孔的巧妙设计与大气压无关C．历史上是用马德堡半球实验首先测出了大气压强的值D．大气压强随海拔高度的增加而减小，水的沸点也随着降低10．如图所示的电路中，属于用电器串联的是（）A．B．C．D．11．下列关于浮力的说法正确的是（）A．漂浮的物体浮力大于重力B．钢铁比水的密度大，所以用钢铁做成的物体放入水中后最终一定处于沉底状态C．若气球里充满密度小于空气的气体，那么气球可以飘在空中D．悬浮在水中的潜水艇，若水舱中水位在上升，那么潜水艇一定上浮12．下列说法正确的是（）A．相邻的两个波峰（或波谷）的距离叫做波长B．声音的响度由频率决定C．声音的音调由振幅决定D．只有发声体在做无规则振动时，产生的声音才是噪声13．关于近视眼和远视眼及其矫正，下列说法正确的是（）A．形成远视眼的原因是晶状体太厚，折光能力太强B．远视眼成像于视网膜前C．近视眼用凹透镜进行矫正D．若把透镜焦距的倒数乘以100的值叫做镜片的度数，则200度的眼镜片焦距是2m 14．下列关于电阻的说法中正确的是（忽略温度对电阻的影响）（）A．导体的电阻与其两端的电压及通过的电流有关B．两根粗细一样的导体，长的一定比短的电阻大C．若导体不接入电路，其电阻为零D．电阻的大小由导体本身的材料、长度和横截面积决定15．2016年4月24日，被命名为首个“中华航天日”，是为了纪念1970年4月24日我国东方红一号卫星首次成功发射升空．近年来，我国的航空航天技术飞速发展．2013年12月2日发射的嫦娥三号探测器，开启了我国对月球的实地探索之旅．目前我国实地探测月球的主角是“玉兔号月球车”，其设计质量140kg，能源为太阳能，能够耐受月球表面真空、强辐射、零下180℃到零上150℃极限温度等极端环境．月球车具备20°爬坡、20cm越障能力，并配备有全景相机、红外成像光谱仪、测月雷达、粒子激发X射线谱仪等科学探测仪器．自发射升空至今，嫦娥三号月球探测器创造了全世界在月工作最长记录．嫦娥三号和玉兔月球车拍摄的迄今为止最清晰的月面高分辨率全彩照片不久前首次公布，让全世界看到了一个真实的月球，也给全世界科学家研究月球提供了第一手资料．依据对玉兔号月球车的介绍，下列说法正确的是（）A．玉兔号月球车所用到的太阳能为不可再生能源B．玉兔号月球车上配备的红外成像光谱仪中的红外线属于可见光。

北京市东城区2016-2017学年第二学期统一检测(一) 初三化学试卷

北京市东城区2016-2017学年第二学期统一检测（一）初三化学 2017.05可能用到的相对原子质量：H 1 C 12 N 14 O 16 Al 27 Fe 56第一部分选择题（共20分）（每小题只有1个选项符合题意。

每小题1分）1．我们每时每刻都离不开空气。

空气中含量最多的气体是 A ．O 2 B ．CO 2 C ．稀有气体 D ． N 22. 下列符号中，表示2个氮原子的是 A ．N 2B ．2N 2C ．2ND ．2NO3. “高钙奶”“加锌盐”里的“钙”“锌”指的是A. 元素 B ．原子 C. 分子 D. 单质 4. 下列粒子中，带正电的是A ．质子B ．中子C ．原子D ．电子 5.下列物品所使用的主要材料为金属材料的是A. 陶瓷花瓶B. 纯棉帽子C. 黄金首饰D. 塑料油瓶 6. 下列物质对应的化学式正确的是A ．氯化铜—CaCl 2B ．氧化汞—HgOC ．碳酸钾—KCO 3D ．硫酸锌—ZnSO 3 7．下列物质的性质中，属于化学性质的是A.硝酸钾易溶于水B. 二氧化碳能使澄清石灰水变浑浊C.金刚石硬度大D. 盐酸是无色液体 8.下列说法不正确．．．的是 A ．铜有良好的导电性，可用于制导线 B ．氮气的化学性质不活泼，可用作保护气 C ．氧气具有可燃性，可用于航天火箭燃料 D ．氢氧化钙溶液显碱性，可用来改良酸性土壤9. 采取正确的措施，能够避免火灾发生或减少灾害损失。

下列灭火方法不恰当．．．的是 A ．油锅起火——用锅盖盖灭 B ．酒精灯着火——用湿抹布盖灭C ．汽车油箱着火——用水浇灭D ．森林起火——砍伐树木形成隔离带10．阿司匹林的化学式为C 9H 8O 4。

下列关于阿司匹林的说法不．正确．．的是 A ．阿司匹林由碳、氢、氧三种元素组成B．1个阿司匹林分子由9个碳原子、8个氢原子、4个氧原子构成C．阿司匹林中氢、氧元素的质量比为1∶8D．阿司匹林中氧元素的质量分数最小11．倡导“低碳”生活，应从生活中的点滴做起。

2016-2017学年北京市东城区初三二模数学试卷(含答案)

2017年北京市东城区九年级中考二模数学试卷一、选择题（本题共30分，每小题3分）1．中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为440 000万人，将440 000用科学记数法表示为（）A．64.410⨯B．54.410⨯C．44410⨯D．60.4410⨯2．下列运算正确的是（）A．2a +3b=5ab B．a2•a3=a6C．（a2b）3=a6 b3D．(a＋2)2＝a2＋43．有5张看上去无差别的卡片，上面分别写着0，π，18，1.333．背面朝上放在不透明的桌子上，若随机抽取1张，则取出的卡片上的数是无理数的概率是（）A．15B．25C．35D．454．下列关于二次函数y=x2+2x+3的最值的描述正确的是（）A．有最小值是2 B．有最小值是3C．有最大值是2 D．有最大值是35. 学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛，各组的平时成绩的平均数（单位：分）及方差如表所示：如果要选出一个成绩较好且状态稳定的组去参赛，那么应选的组是（）A．甲B．乙C．丙D．丁6．如图，正五边形ABCDE放入某平面直角坐标系后，若顶点A，B，C，D的坐标分别是（0，a），（﹣3，2），（b，m），（- b，m），则点E的坐标是（）A．（2，﹣3）B．（2，3）C．（3，2）D．（3，﹣2）7．将一副直角三角板如图放置，使含30°角的三角板的直角边和含45°角的三角板一条直角边在同一条直线上，则∠1的度数为（）A．75°B．65°C．45°D．30°8. 关于x 的一元二次方程x 2+ax ﹣1=0的根的情况是（） A ．没有实数根 B ．只有一个实数根C ．有两个相等的实数根D ．有两个不相等的实数根9. 图1和图2中所有的正方形都全等，将图1的正方形放在图2中的①②③④某一位置，所组成的图形不能．．围成正方体的位置是（）A ．①B ．②C ．③D ．④10. 如右图，点E 为菱形ABCD 的BC 边的中点，动点F 在对角线AC 上运动，连接BF ，EF ．设AF =x ，△BEF 的周长为y ，那么能表示y 与x 的函数关系的大致图象是（）二、填空题（本题共18分，每小题3分） 11．若分式31x 在实数范围内有意义，则实数x 的取值范围是． 12．请你写出一个多项式，含有字母a ，并能够在有理数范围内用平方差公式进行因式分解. 此多项式可以是．13. 已知一次函数y 1=k 1x +5和y 2=k 2x +7，若k 1＞0且k 2＜0，则这两个一次函数的图象的交点在第象限．14. 如图，⊙O 的半径为4，△ABC 是⊙O 的内接三角形，连接OB ，OC ．若∠BAC 与∠BOC 互补，则弦BC 的长为．15. 如图，一扇形纸扇完全打开后，外侧两竹条AB 和AC 的夹角为120°，竹条AB 的长为25cm ，贴纸部分的宽BD 为15cm ，若纸扇两面贴纸，则一面贴纸的面积为 cm 2. （结果保留π）16．小明在他家里的时钟上安装了一个电脑软件，他设定当钟声在n 点钟响起后，下一次则在（3n -1）小时后响起，例如钟声第一次在3点钟响起，那么第2次在(3318)⨯-=小时后，也就是11点响起；第3次在(311132)⨯-=小时后，即7点响起，以此类推……；现在第1次钟声响起时为2点钟，那么第3次响起时为_____点，第2017次响起时为_____点.(如图钟表，时间为12小时制)三、解答题（本题共72分，第17—26题，每小题5分，第27题7分，第28题8分，第29题7分）17．计算：02(π2017)4cos60-+--18. 解不等式组32211,52x x x x -⎧⎪++⎨⎪⎩≤，＜并把解集在数轴上表示出来．19．小明化简 (21)(21)(5)x x x x +--+的过程如图. 请指出他化简过程中的错误，写出对应的序号，并写出正确的化简过程．20．如图，在Rt △ABC 中，∠C =90°. 以顶点A 为圆心，适当长为半径画弧，分别交AC ，AB 于点M ，N ，再分别以点M ，N 为圆心，大于21MN 的长为半径画弧，两弧交于点P ，作射线AP 交边BC 于点D . 若CD =4，AB =15，求△ABD 的面积.21．如图，在平面直角坐标系中，OA ⊥OB ，AB ⊥x 轴于点C ，点A ）在反比例函数(0)ky k x=≠的图象上.（1）求反比例函数(0)ky k x=≠的解析式和点B 的坐标；（2）若将△BOA 绕点B 按逆时针方向旋转 60º 得到△BDE （点O 与点D 是对应点），补全图形，直接写出点E 的坐标，并判断点E 是否在该反比例函数的图象上，说明理由.22．列方程或方程组解应用题：某校为美化校园，计划对一些区域进行绿化，安排了甲、乙两个工程队完成．已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且两队在独立完成面积为400m 2区域的绿化时，甲队比乙队少用4天．求甲、乙两工程队每天能完成绿化的面积分别是多少m 2？23．如图，BD是△AB C的角平分线，它的垂直平分线分别交AB，BD，BC于点E，F，G，连接ED，DG．（1）请判断四边形EBGD的形状，并说明理由；（2）若∠ABC=30°，∠C=45°，ED=2，求GC的长.24. 某市为提倡节约用水，准备实行自来水“阶梯计费”方式，用户用水不超出基本用水量的部分享受基本价格，超出基本用水量的部分实行加价收费. 为更好地决策，自来水公司随机抽取了部分用户的用水量数据，并绘制了如下不完整的统计图（每组数据包括右端点但不包括左端点）. 请你根据统计图解答下列问题：（1）此次抽样调查的样本容量是__________________；（2）补全频数分布直方图；（3）如果自来水公司将基本用水量定为每户25吨，那么该地区6万用户中约有多少用户的用水全部享受基本价格？25. 如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，CE⊥AD交AD的延长线于点E．（1）求证：∠BDC=∠A；（2）若CE=4，DE=2，求AD的长．26. 佳佳想探究一元三次方程32220x x x +--=的解的情况. 根据以往的学习经验，他想到了方程与函数的关系：一次函数(0)y kx b k =+≠的图象与x 轴交点的横坐标即为一次方程0(0)kx b k +=≠的解；二次函数2(0)y ax bx c a =++≠的图象与x 轴交点的横坐标即为一元二次方程20(0)ax bx c a ++=≠的解. 如：二次函数223y x x =--的图象与x 轴的交点为(1,0)-和(3,0)，交点的横坐标-1和3即为方程2230x x --=的解.根据以上方程与函数的关系，如果我们知道函数3222y x x x =+--的图象与x 轴交点的横坐标，即可知道方程32220x x x +--=的解.佳佳为了解函数3222y x x x =+--的图象，通过描点法画出函数的图象：（1）直接写出m 的值，并画出函数图象；（2）根据表格和图象可知，方程的解有_____个，分别为__________________；（3）借助函数的图象，直接写出不等式3222x x x +>+的解集.27.在平面直角坐标系xOy 中，抛物线2221y x mx m m =-+--+.（1）当抛物线的顶点在x 轴上时，求该抛物线的解析式；（2）不论m 取何值时，抛物线的顶点始终在一条直线上，求该直线的解析式；（3）若有两点()1,0A -，()1,0B ，且该抛物线与线段AB 始终有交点，请直接写出m 的取值范围.28. 取一张正方形的纸片进行折叠，具体操作过程如下：第一步：如图1，先把正方形ABCD 对折，折痕为MN ；第二步：点G 在线段MD 上，将△GCD 沿GC 翻折，点D 恰好落在MN 上，记为点P ，连接BP .（1）判断△PBC 的形状，并说明理由；（2）作点C 关于直线AP 的对称点C ′，连PC′，D C′， ①在图2中补全图形，并求出∠APC′的度数； ②猜想∠PC′D 的度数，并加以证明.（温馨提示：当你遇到困难时，不妨连接A C′，C C′，研究图形中特殊的三角形）29．在平面直角坐标系xOy中，点P与点Q不重合.错误！未找到引用源。

2016北京市东城区二模考试题及答案

北京市东城区2016年第二学期统一练习（二）一、选择题（本题共30分，每小题3分）1．我国最大的领海是南海，总面积有3 500 000平方公里，将数3 500 000用科学记数法表示应为A ．63.510⨯B ．73.510⨯C ．53510⨯D ． 80.3510⨯2．如图，已知数轴上的点A ，O ，B ，C ，D 分别表示数﹣2，0，1，2，3，则表示数2点P 应落在线段3．一个不透明的盒子中装有6个除颜色外完全相同的乒乓球，其中4个是黄球，2个是白球．从该盒子中任意摸出一个球，摸到黄球的概率是A ．13B ．25C ．12D ．234. 下列图案中，既是中心对称又是轴对称图形的是A B C D5．如图所示的几何体是由一些正方体组合而成的立体图形，则这个几何体的俯视图是6 如图，在等腰△ABC 中，AB =AC ，BD ⊥AC ，∠ABC =72°，则∠ABD 等于7．某小组5名同学在一周内参加家务劳动的时间如下表所示，关于“劳动时间”的这组数据，以下说法正确的是8．用一个圆心角为120°，半径为6的扇形作一个圆锥的侧面，这个圆锥的底面圆的半径是A ．4B ．3C ．2D ． 19. 如图所示，购买一种苹果，所付款金额y （元）与购买量x （千克）之间的函数图象由线段OA 和射线AB 组成，则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省 A ．1元 B ． 2元 C ．3元D ．4元10. 某班有20位同学参加乒乓球、羽毛球比赛，甲说：“只参加一项的人数大于14人.”乙说：“两项都参加的人数小于5人.”对于甲、乙两人的说法，有下列四个命题，其中真命题的是 A.若甲对，则乙对 B.若乙对，则甲对 C.若乙错，则甲错 D.若甲错，则乙对二、填空题（本题共18分，每小题3分）11．分解因式：2242ax ax a -+= ．12．关于x 的一元二次方程0122=-+x kx 有两个不相等的实数根，则k 的取值范围是．13. 如图，点P 在△ABC 的边AC 上，请你添加一个条件，使得△ABP ∽△ACB ，这个条件可以是．14. 九年级（3）班共有50名同学，如图是该班一次体育模拟测试成绩的频数分布直方图（满分为30分，成绩均为整数）．若将不低于23分的成绩评为合格，则该班此次成绩达到合格的同学占全班人数的百分比是．15．定义运算“*”，规定x*y=a （x+y ）+xy ，其中a 为常数，且1*2=5，则2*3= ．16．在平面直角坐标系中，小明玩走棋的游戏，其走法是：棋子从原点出发，第1步向右走1个单位，第2步向右走2个单位，第3步向上走1个单位，第4步向右走1个单位，…，依此类推，第n 步的走法是：当n 能被3整除时，则向上走1个单位；当n 被3除，余数为1时，则向右走1个单位；当n 被3除，余数为2时，则向右走2个单位，当走完第8步时，棋子所处位置的坐标是；当走完第2016步时，棋子所处位置的坐标是．三、解答题（本题共72分，第17—26题，每小题5分，第27题7分，第28题7分，第29题8分）17．计算：0112sin 60(3π)()4-︒-+.18．已知023a b =≠，求代数式22422a b a b a ab-++的值．19．如图，已知∠ABC =90°，分别以AB 和BC 为边向外作等边△ABD 和等边△BCE ，连接AE ，CD .求证：AE =CD ．20．列方程或方程组解应用题：为迎接“五一劳动节”，某超市开展促销活动，决定对A ，B 两种商品进行打折出售．打折前，买6件A 商品和3件B 商品需要108元，买3件A 商品和4件B 商品需要94元.问：打折后，若买5件A 商品和4件B 商品仅需86元，比打折前节省了多少元钱？21. 如图，在边长为4的正方形ABCD 中，请画出以A 为一个顶点，另外两个顶点在正方形ABCD 的边上，且含边长为3的等腰三角形．（要求：画出三个．．大小不同，符合题意的等腰三角形，只要画出示意图，并在所画等腰三角形长为3的边上标注数字3）DCBADCBADCBA22．如图，矩形ABCD 中，M 为BC 上一点，F 是AM 的中点，EF ⊥AM ，垂足为F ，交AD于点E ．（1）求证：∠BAM =∠AEF ；（2）若AB =4，AD =6，4cos 5BAM ∠=，求DE 的长.23.如图，四边形ABCD 是平行四边形，点(10)(31)(33)A B C ，，，，，．反比例函数(0)my x x=>的图象经过点D .（1）求反比例函数的解析式；（2）经过点C 的一次函数(0)y kx b k =+≠的图象与反比例函数的图象交于P 点，当k ＞0时，确定点P 横坐标的取值范围（不必写出过程）.2013年是北京市正式执行新《环境空气质量标准》的第一年.这一年，北京建立起35个覆盖全市的监测站点，正式对PM2.5、二氧化硫、二氧化氮等六项污染物开展监测.2013年全年,本市空气质量一级优的天数有41天；二级良天数135天.本市主要大气污染物PM2.5年均浓度为89.5微克/立方米，单就PM2.5的浓度而言，全年共有204天达到一级优或二级良水平.2014年全年，PM2.5年均浓度为85.9微克/立方米.，PM2.5优良天数总计204天，其中PM2.5一级优天数达到93天，比2013年的71天增加了22天.2015年全年，本市空气质量达标天数为186天，即空气质量优良的好天儿占了一半，比2014年增加了14天. 本市主要大气污染物PM2.5年均浓度为80.6微克/立方米，单就PM2.5的浓度而言，2015年PM2.5优良天数累计达到223天，其中一级优天数首次突破100达到105天，二级良天数累计为118天.根据以上材料解答下列问题：（1）北京市2014年空气质量达到优良的天数为天；单就PM2.5的浓度而言，北京市2013年全年达到二级良的天数为天；（2）选择统计表或统计图，将2013—2015年北京市PM2.5的年均浓度和PM2.5的优良天数表示出来.25. 如图，在△ABC中，BA=BC，以AB为直径的⊙O分别交AC，BC于点D，E，BC的延长线与⊙O的切线AF交于点F．（1）求证：∠ABC=2∠CAF；（2）若AC=，sin CAF∠=BE的长．在学习完锐角三角函数后，老师提出一个这样的问题：如图1，在Rt △ABC 中，∠ACB =90°， AB =1，∠A =α，求sin2α（用含sin α，cos α的式子表示）．聪明的小雯同学是这样考虑的：如图2，取AB 的中点O ，连接OC ，过点C 作CD ⊥AB 于点D ，则∠COB = 2α，然后利用锐角三角函数在Rt △ABC 中表示出AC ，BC ，在Rt △ACD 中表示出CD ，则可以求出sin 2α=CD OC=21sin AC ⋅α=21cos sin αα⋅=ααcos sin 2⋅．图1 图2阅读以上内容，回答下列问题：在Rt △ABC 中，∠C =90°，AB =1. (1)如图3，若BC =13，则 sin α= ， sin2α= ；图3(2)请你参考阅读材料中的推导思路，求出tan2α的表达式（用含sin α，cos α的式子表示）．27. 二次函数21:C y x bx c =++的图象过点A （-1,2），B （4,7）. （1）求二次函数1C 的解析式；（2）若二次函数2C 与1C 的图象关于x 轴对称，试判断二次函数2C 的顶点是否在直线AB 上；（3）若将1C 的图象位于A ，B 两点间的部分（含A ，B 两点）记为G ，则当二次函数221y x x m =-+++与G 有且只有一个交点时，直接写出m 满足的条件.28. 【问题】在△ABC 中，AC=BC ，∠ACB=90°，点E 在直线BC 上（B,C 除外），分别经过点E 和点B 做AE 和AB 的垂线，两条垂线交于点F ，研究AE 和EF 的数量关系. 【探究发现】某数学兴趣小组在探究AE ，EF 的关系时，运用“从特殊到一般”的数学思想，他们发现当点E 是BC 的中点时，只需要取AC 边的中点G （如右图），通过推理证明就可以得到AE 和EF 的数量关系，请你按照这种思路直接写出AE 和EF 的数量关系；【数学思考】那么当点E 是直线BC 上（B ，C 除外）（其它条件不变），上面得到的结论是否仍然成立呢？请你从“点E 在线段BC 上”；“点E 在线段BC 的延长线”；“点E 在线段BC 的反向延长线上”三种情况中，任选一种情况，在图2中画出图形，并证明你的结论；图2 备用图【拓展应用】当点E 在线段CB 的延长线上时，若BE =nBC （01n ＜＜），请直接写出ABC S △：AEF S △的值．29. 定义：y 是一个关于x 的函数，若对于每个实数x ，函数y 的值为三数2+x ，12+x ，205+-x 中的最小值，则函数y 叫做这三数的最小值函数.（1）画出这个最小值函数的图象，并判断点A （1， 3）是否为这个最小值函数图象上的点；（2）设这个最小值函数图象的最高点为B ，点A （1, 3），动点M （m ，m ）.①直接写出△ABM 的面积，其面积是； ②若以M 为圆心的圆经过B A ,两点，写出点M 的坐标；③以②中的点M 为圆心，以2为半径作圆. 在此圆上找一点P ，使2PA +的值最小，直接写出此最小值.北京市东城区2015-2016学年第二学期统一练习（二）初三数学参考答案及评分标准 2016.6一、选择题（本题共30分，每小题3分）二、填空题（本题共18分，每小题3分）三、解答题（本题共72分，第17—26题，每小题5分，第27题7分，第28题7分，第29题8分）17．计算：0112sin 60(3π)()4-︒-+.解：原式14+ …………4分=3. …………5分18. 解： 22422a b a b a ab-++ =224(2)(2)a b a a b a a b -++ =2a ba- …………3分∵a 2=b 3¹0 ∴设2,3.a k b k ==…………4分∴ 原式=-2 . …………5分 19. 证明：因为△ABD 和△BCE 为等边三角形，∴∠ABD =∠CBE =60°，BA=BD ，BC=BE. ……2分∴∠ABD+∠ABC =∠CBE+∠ABC ，即∠CBD =∠ABE.…3分∴△CBD ≌△EBA.（SAS ） ……4分∴AE=CD.……5分20.解：设打折前一件商品A 的价格为x 元，一件商品B 的价格为y 元.………1分依据题意，得631083494x y x y +=⎧⎨+=⎩. …………3分解得：1016x y =⎧⎨=⎩. …………4分所以5×10+4×16-86=28（元）答：比打折前节省了28元.…………5分21. 满足条件的所有图形如图所示：…………5分注意：画出一个给2分，二个给4分，三个给5分. 22.解：（1）∵矩形ABCD ，∴∠B =∠BAC =90°. ∵EF ⊥AM ，∴∠AFE =∠B =∠BAD =90°. ∴∠BAM +∠EAF =∠AEF+∠EAF =90°. ∴∠BAM =∠AEF . …………2分（2）在Rt △ABM 中，∠B =90°，AB =4，cos ∠BAM =45， ∴AM =5.∵F 为AM 中点， ∴AF =52.12 / 15∵∠BAM =∠AEF ，∴cos ∠BAM = cos ∠AEF =45.∴sin ∠AEF =35.在Rt △AEF 中， ∠AFE =90°，AF =52，sin ∠AEF =35， ∴AE =256. ∴DE=AC-AE =6-256=116. …………5分23.解：（1）∵四边形ABCD 是平行四边形，点(10)(31)(33)A B C ，，，，，，∴BC =2. ∴D （1,2）. ∵反比例函数my x=的图象经过点D ， ∴21m=. ∴2m =. ∴2y x=. …………3分（2）233p x <<. …………5分24.解：（1）172；133. …………2分（2）…………5分25.（1）证明：连结BD .∵AB 是O ∵的直径， ∴90ADB ∠=︒. ∴90DAB DBA ∠+∠=︒.∵AB AC =，∴2ABD ABC ∠=∠，12AD AC =. ∵AF 为⊙O 的切线， ∴∠F AB =90°. ∴90FAC CAB ∠+∠=︒. ∴FAC ABD ∠=∠.∴2.ABC CAF ∠=∠ …………2分⑵ 解：连接AE.∴∠AEB =∠AEC =90°.∵sin CAF ABD CAF CBD CAE ∠=∠=∠=∠=∠，∴sin sin ABD CAF ∠=∠=．∵90ABD AC ∠=︒=，∴AD =10sin ADAB ABD==∠=BC .∵90AEC AC ∠=︒=， ∴sin 2CE AC CAE =⋅∠=.∴1028BE BC CE =-=-=. …………5分26.解：（1）sin α=13， sin2α…………2分（2）∵AC = cos α，BC =sin α，∴CD =AC BCAB⨯=sin cos αα⋅. ∵∠DCB =∠A ，∴在Rt △BCD 中，BD =sin 2α. ∴OD =12- sin 2α.14 / 15∴tan2α=CD OD =22sin cos 2sin cos 112sin sin 2αααααα⋅⋅=--. …………5分 27.解：（1）∵21:C y x bx c =++的图象过点A （-1,2），B （4,7），∴217164.b c b c =-+⎧⎨=++⎩，∴21.b c =-⎧⎨=-⎩， ∴221y x x =--. …………2分（2）∵二次函数2C 与1C 的图象关于x 轴对称，∴22:21C y x x =-++. ∴2C 的顶点为（1,2）. ∵A （-1,2），B （4,7）,∴过A 、B 两点的直线的解析式：3y x =+. 令x =1，则y =4.∴2C 的顶点不在直线AB 上. …………4分（3）414m <≤或4m =-. …………7分28.解：【探究发现】：相等. …………1分【数学思考】证明：在AC 上截取CG=CE ，连接GE. ∵∠ACB =90°, ∴∠CGE =∠CEG =45°. ∵AE ⊥EF ，AB ⊥BF ， ∴∠AEF =∠ABF =∠ACB =90°,∴∠FEB +∠AEF =∠AEB =∠EAC +∠ACB. ∴∠FEB =∠EAC. ∵CA=CB ，∴AG=BE ，∠CBA =∠CAB =45°.∴∠AGE =∠EBF =135°. ∴△AGE ≌△EBF .∴AE=EF . …………5分【拓展应用】ABC S △：AEF S △=1：（222n n ++） …………7分29.解：（1）图象略；是.…………2分（2）①2.…………4分 ②M （3,3）. …………6分③…………8分。

北京市东城区2017届九年级6月综合测试(二模)语文试题(WORD版)

2016-2017学年北京市东城区初三年级综合能力测试（二）语文试卷一、基础·运用（共19分）2016年11月30日，我国申报的“二十四节气——中国人通过观察太阳周年运动而形成的时间知识体系及其实践”被列入联合国教科文组织人类非物质文化遗产代表作名录，这是我国继京剧、珠算等项目之后第三十一个被列入该名录的项目。

阅读下面的文字，完成1-5题。

（共12分）二十四节气是中华文明的独特贡献。

农民借助节气，将一年定格到耕种、施肥、灌溉、收割等农作物生长、收藏的循环体系之中，将时间和生产、生活定格到人与天道相印相应乃【甲】（致至）合一的状态。

“日出而作，日入而息□生产生活有时，人生社会有节，人身人性有气，节气不仅成为时间坐标，也①成气节，提醒人生百年，需要有精神，有守有为。

孔子像农民那样观察到，“岁寒，然后知松柏之后凋也”。

他为此引申：“三军可夺帅也，匹夫不可夺志也。

”可以说，中国源远流长的精神气节，源头正是时间中的节气。

从节气到气节，仍是今天人们生存的重要问题：我们是否把握了时间的节气？我们是否把握了人生的节点？我们是否为社会、技术一类的事物裹挟．，而对生物世界、天时地利等失去了感觉，以【乙】（至致）无知于道法自然的本质，从而失去先人那样的精神气节？节气不仅跟农民农业有关，不仅跟养生有关，也跟我们每个人对生命、自然、人生、宇宙的②有关。

普通人只有了解节气的诸多含义，才能理解天人关系，才能提升自己在人生百年中的地位。

在立秋时需要有谋划意识，在小寒时需要有经纶意识，在大寒时需要修省．自己……古人把五天称为微，把十五天称为著，五天又称为一候，十五天则是一节气，见微知著，跟观候知节一样，是先民立身处世的生活，也是他们安身立命的参照。

1.文中【甲】【乙】处选填的汉字和加点字的注音，全都正确的一项是（2分）A.【甲】致【乙】至裹挟．（xié）修省．（xǐng）B.【甲】至【乙】致裹挟．（jiā）修省．（shěng）C.【甲】致【乙】至裹挟．（jiā）修省．（shěng）D.【甲】至【乙】致裹挟．（xié）修省．（xǐng）2.文中“□”处使用的标点符号和画线字“远”的笔顺，全都正确的一项是（2分）A.”，“远”字的第三笔是B.，”“远”字的第三笔是C.。

5.北京2016初三中考二模数学word版答案-东城

5.北京2016初三中考二模数学试题及答案word 版答案-东城初三数学参考答案及评分标准 2016.6二、填空题（本题共18分，每小题3分）三、解答题（本题共72分，第17—26题，每小题5分，第27题7分，第28题7分，第29题8分） 17．计算：0112sin 60(3π)()4-︒-+.解：原式14+ …………4分 =3 …………5分18. 解： 22422a b a b a ab-++=224(2)(2)a b a a b a a b -++ =2a ba - …………3分 023a b=≠ ， ∴设2,3.a k b k == …………4分∴ 原式=-2 . …………5分 19. 证明： △ABD 和△BCE 为等边三角形， ∴∠ABD =∠CBE =60°，BA=BD ，BC=BE. …………2分∴∠ABD+∠ABC =∠CBE+∠ABC ，即∠CBD =∠ABE. …………3分∴△CBD ≌△EBA.（SAS ） …………4分∴AE=CD. …………5分20.解：设打折前一件商品A 的价格为x 元，一件商品B 的价格为y 元. …………1分依据题意，得631083494x y x y +=⎧⎨+=⎩. …………3分解得：1016x y =⎧⎨=⎩. …………4分所以5×10+4×16-86=28（元）答：比打折前节省了28元. …………5分 21. 满足条件的所有图形如图所示：…………5分注意：画出一个给2分，二个给4分，三个给5分. 22.解：（1）∵矩形ABCD ，∴∠B =∠BAC =90°.∵EF ⊥AM ，∴∠AFE =∠B =∠BAD =90°.∴∠BAM +∠EAF =∠AEF+∠EAF =90°. ∴∠BAM =∠AEF . …………2分（2）在Rt △ABM 中，∠B =90°，AB =4，cos ∠BAM =45， ∴AM =5.∵F 为AM 中点， ∴AF =52. ∵∠BAM =∠AEF ， ∴cos ∠BAM = cos ∠AEF =45. ∴sin ∠AEF =35.在Rt △AEF 中， ∠AFE =90°，AF =52，sin ∠AEF =35， ∴AE =256. ∴DE=AC-AE =6-256=116. …………5分 23.解：（1）∵四边形ABCD 是平行四边形，点(10)(31)(33)A B C ，，，，，，∴BC =2.∴D （1,2）. ∵反比例函数my x=的图象经过点D ， ∴21m =. ∴2m =.∴2y x=. …………3分（2）233p x <<. …………5分 24.解：（1）172；133. …………2分25.（1）证明：连结BD .∵AB 是O 的直径， ∴90ADB ∠=︒.∴90DAB DBA ∠+∠=︒. ∵AB AC =，∴2ABD ABC ∠=∠，12AD AC =. ∵AF 为⊙O 的切线， ∴∠F AB =90°.∴90FAC CAB ∠+∠=︒. ∴FAC ABD ∠=∠.∴2.ABC CAF ∠=∠ …………2分⑵ 解：连接AE.∴∠AEB =∠AEC =90°.∵sin CAF ABD CAF CBD CAE ∠=∠=∠=∠=∠，∴sin sin ABD CAF ∠=∠=．∵90ABD AC ∠=︒=，∴AD 10sin ADAB ABD==∠=BC .∵90AEC AC ∠=︒=， ∴sin 2CE AC CAE =⋅∠=.∴1028BE BC CE =-=-=. …………5分26.解：（1）sin α=13， sin2α…………2分（2）∵AC = cos α，BC =sin α，∴CD =AC BCAB⨯=sin cos αα⋅.∵∠DCB =∠A ，∴在Rt △BCD 中，BD =sin 2α.∴OD =12- sin 2α. ∴tan2α=CD OD =22sin cos 2sin cos 112sin sin 2αααααα⋅⋅=--. …………5分 27.解：（1）∵21:C y x bx c =++的图象过点A （-1,2），B （4,7），∴217164.b c b c =-+⎧⎨=++⎩，∴21.b c =-⎧⎨=-⎩，∴221y x x =--. …………2分（2）∵二次函数2C 与1C 的图象关于x 轴对称，∴22:21C y x x =-++. ∴2C 的顶点为（1,2）. ∵A （-1,2），B （4,7）,∴过A 、B 两点的直线的解析式：3y x =+. 令x =1，则y =4.∴2C 的顶点不在直线AB 上. …………4分（3）414m <≤或4m =-. …………7分28.解：【探究发现】：相等. …………1分【数学思考】证明：在AC 上截取CG=CE ，连接GE. ∵∠ACB =90°,∴∠CGE =∠CEG =45°.∵AE ⊥EF ，AB ⊥BF ，∴∠AEF =∠ABF =∠ACB =90°,∴∠FEB +∠AEF =∠AEB =∠EAC +∠ACB. ∴∠FEB =∠EAC. ∵CA=CB ，∴AG=BE ，∠CBA =∠CAB =45°. ∴∠AGE =∠EBF =135°. ∴△AGE ≌△EBF .∴AE=EF . …………5分【拓展应用】ABC S △：AEF S △=1：（222n n ++） …………7分29.解：（1）图象略；是. …………2分（2）①2. …………4分②M （3,3）. …………6分…………8分。

2017东城二模英语试卷参考答案评分标准北京市初三中考

2016-2017学年北京市东城区初三年级综合能力测试（二）英语试卷学校姓名考号听力理解（共30分）一、听对话，从下面各题所给的A、B、C三幅图片中选择与对话内容相符的图片。

每段对话你将听两遍。

（共5分，每小题1分）12.3.4.5.二、听对话或独白，根据对话或独白的内容，从下面各题所给的A、B、C三个选项中选择最佳选项。

每段对话或独白你将听两遍。

（共15分，每小题1.5分）请听一段对话，完成第6至第7小题。

6. Where will the speakers go?A. To a hospital.B. To a post office.C. To a restaurant.7. How will they get there?A. On foot.B. By bike.C. By bus.请听一段对话，完成第8至第9小题。

8. Who is the man looking for?A. His sister.B. His daughter.C. His friend.9. How long has the man looked for her?A. For about 6 hour.B. For about 20 minutes.C. For about half an hour.请听一段对话，完成第10至第11小题。

10. Who is Tom’s role model?A. His favorite teacher.B. A basketball player.C. His grandfather.11. What does Tom’s role model do every day?A. He runs for one hour.B. He writes stories on the Internet.C. He helps others with computer problems.请听一段对话，完成第12至第13小题。

北京市东城2016-2017学年第二学期统一练习(一)

北京市东城区2016-2017学年第二学期统一练习（一）初三数学参考答案及评分标准 2017.5题号 1 2 3 4 5 6 7 8 9 10 答案 A CB DC BB AC A二、填空题（本题共18分，每小题3分）题号1112 1314 15 16答案2(-1)a b答案不唯一如：21y x =+1k ＜6答案不唯一，合理就行垂直平分线的判定；垂直平分线的定义和圆的定义29题8分） 17011122sin 60(2π)()2-︒+-解：原式=23312- …………4分 31. …………5分 18. 解：去分母得：3（x +1）＞2（2x +2）﹣6， …………1分去括号得：3x +3＞4x +4﹣6， …………2分移项得：3x ﹣4x ＞4﹣6﹣3， …………3分合并同类项得：﹣x ＞﹣5，系数化为1得：x ＜5. …………4分故不等式的正整数解有1，2，3，4这4个. …………5分19. 解： 224122x x x x x -+⎛⎫-÷- ⎪++⎝⎭ =22422x x x x x x -++⋅--+ =242x x x x ++-+ =4(2)x x +. …………3分∵ 22410x x +-=. ∴ 2122x x +=. …………4分原式=8. …………5分20. 解：由题意可得：MN 是AC 的垂直平分线．F ECBAD则AD =DC ．故∠C =∠DAC ．…………2分 ∵ ∠C =30°， ∴ ∠DAC =30°． …………3分 ∵ ∠B =55°， ∴ ∠BAC =95°． …………4分 ∴ ∠BAD =∠BAC ﹣∠CAD =65°． …………5分21．解：（1）由题意可求：m =2，n =-1．将（2，3），B (-6，-1)带入y kx b =+，得32,16.k b k b =+⎧⎨-=-+⎩解得 1,22.k b ⎧=⎪⎨⎪=⎩∴ 直线的解析式为122y x =+. …………3分（2）（-2,0）或（-6,0）. …………5分22．解：设本场比赛中该运动员投中两分球x 个，三分球y 个. …………1分依题意有23633,11.x y x y ++=⎧⎨+=⎩. …………3分解得6,5.x y =⎧⎨=⎩…………4分答：设本场比赛中该运动员投中两分球6个，三分球5个． …………5分 23. 解：（1）证明：∵ 四边形ABCD 为平行四边形，∴ AB =CD ，∠F AD =∠AFB. 又∵ AF 平分∠BAD ， ∴ ∠F AD =∠F AB . ∴ ∠AFB =∠F AB . ∴ AB =BF .∴ BF =CD . …………3分（2）解：由题意可证△ABF 为等边三角形，点E 是AF 的中点.在Rt △BEF 中，∠BF A =60°，BE=可求EF=2，BF=4.∴平行四边形ABCD的周长为12.…………5分24. 解：（1）…………4分（2）答案不唯一．…………5分25. 解：（1）证明：连接OD.∵OD=CD，∴∠ODC=∠OCD.∵AC为⊙O的直径，∴∠ADC=∠EDC=90°.∵点F为CE的中点，∴DF=CF.∴∠FDC=∠FCD.∴∠FDO=∠FCO.又∵AC⊥CE，∴∠FDO=∠FCO=90°.∴DF是⊙O的切线. …………2分（2）○1由DB平分∠ADC，AC为⊙O的直径，证明△ABC是等腰直角三角形；○2由AB=a，求出AC2a；○3由∠ACE=∠ADC=90°，∠CAE是公共角，证明△ACD∽△AEC，得到2AC AD AE=⋅；○4设DE为x，由AD∶DE=4∶1，求出1010DE a=. …………5分26．解：（1）○2.…………1分（2）它是一个轴对称图形；两组邻边分别相等；一组对角相等；一条对角线所在的直线垂直平分另一条对角线等等. …………3分已知：如图，在凹四边形ABCD中，AB=AD，BC=DC.求证：∠B=∠D.证明：连接AC.,60. ..AD DE ADE ADE ABC EAB DAC AB AC AE AD EAB DAC CD BE =∠=︒∴∴∠=∠==∴∴=Q Q ，△为等边三角形.△为等边三角形,，，△≌△EE∵AB=AD,CB=CD,AC=AC ， ∴△ABC ≌△ADC.∴∠B =∠D. …………4分（3）燕尾四边形ABCD的面积为. …………5分 27.解：（1）对称轴方程：2(2)12(2)m x m -+=-=+. …………1分（2）①∵直线l 与抛物线只有一个公共点,∴23n m =-+. …………3分② 依题可知：当237m -+=-时，直线l 与新的图象恰好有三个公共点. ∴5m =. …………5分（3）抛物线2(2)2(2)5y m x m x m =+-+-+的顶点坐标是(1,23)m -+.依题可得 20,23 1.m m +>⎧⎨-+≥⎩解得2,1.m m >-⎧⎨≤⎩∴ m 的取值范围是21m -<≤. …………7分28.解：（1）30°； …………1分（2）思路1：如图，连接AE .…………5分思路2：过点D 作DF ∥AB ，交AC 于F .EDCBA…………5分思路3：延长CB 至G ，使BG =CD.…………5分（3）k (BE +BD )=AC . …………7分 29.解：（1）E ,F ; …………2分（2）①解：依题意A （0，2），M （32，0）.可求得直线AM 的解析式为233+-=x y . 经验证E 在直线AM 上.因为OE =OA =2，∠MAO =60°，所以△OAE 为等边三角形，所以AE 边上的高长为3. 当点P 在AE 上时，3≤OP ≤2.所以当点P 在AE 上时，点P 都是等边△ABC 的中心关联点. 所以0≤m ≤3; …………4分=60.,=60..===60,.,..ABC AC BC BAC DF AB DFC CDF AF BD ADE ACB ABC DAF EDB AD DE ADF DEB DF BE CD ∴=∠︒∴∠︒∴∴=∠∠∠︒∴∠=∠=∴∴==Q Q Q Q △为等边三角形，，∥△为等边三角形.又△≌△=60.,.===60,.,.,==60..ABC AC BC BAC CD BG DG AC ADE ACB ABC DAF EDB AD DE ADC DEG CD EG BG C G BGE BE BG CD ∴=∠︒=∴=∠∠∠︒∴∠=∠=∴∴==∠∠︒∴∴==Q Q Q Q △为等边三角形,，又△≌△△为等边三角形.②﹣334≤b ≤2; …………6分（3）t =25425-4 或 …………8分。

2016-2017北京东城二中初三下3月月考

北京二中教育集团2016—2017学年度第二学期初三数学阶段检测（一）第I 卷（选择题共30分）一、选择题（以下每题只有一个正确的选项，每小题3分，共30分）1．截止到2015年6月1日，北京市已建成34个地下调蓄设施，蓄水能力达到140000立方平米．将140000用科学记数法表示应为（） A ．41410⨯ B ．51.410⨯C ．61.410⨯D ．60.1410⨯【答案】B【解析】140000用科学计数法表示为51.410⨯．2．实数a ，b 在数轴上的对应点的位置如图所示，则正确的结论是（）A ．aB ．C ．D ．【答案】略（题干不全）【解析】略3．剪纸是我国传统的民间艺术，下列剪纸作品中，是轴对称图形的为（）A ．B ．C ．D ．【答案】D【解析】由轴对称图形的定义可知，选D ．4．如图，下面的几何体由三个大小相同的小立方块组成，则它的左视图是（）A ．B ．C ．D ．ba 320-3-2【答案】C（题干不全）【解析】根据题意得到几何体的左视图为，故选C．5．下列等式一定成立的是（）A．2510⨯=B C．3412a a a-=D a()a a【答案】C【解析】A．25710⨯=≠，所以A错误，a a a aB B错误，C．3412-=，所以C正确，()a aD||a=，所以D错误．6．如果一个多边形的内角是外角的3倍，那么这个多边形是（）A．五边形B．六边形C．七边形D．八边形【答案】D【解析】由题可知多边形内角与外角是互补的，设外角度数为x，则内角为3x，3180+=︒x xx=︒45︒÷︒，360458故选D．7．下列事件是随机事件的是（）A．购买一张彩票，中奖B．在一个标准大气压下，加热到100℃，水沸腾C．奥运会上，百米赛跑的成绩为5秒D．掷一枚普通骰子，朝上一面的点数是8【答案】A【解析】A．可能发生，也可能不发生，是随机事件，符合题意B．是确定事件中的不可能事件C．是确定事件中的不可能事件D．掷一枚普通骰子，朝上一面的点数是8，是不可能事件8．如图，一个量角器放在BAC ∠的上面，则BAC ∠=（）度A ．20B ．40C ．45D ．80【答案】A【解析】解：连接OB ，由题意，得：40BOC ∠=︒，∴1202BAC BOC ∠=∠=︒．9．【重测】某班体育委员统计了全班45名同学一周的体育锻炼时间，并绘制了如图所示的折线统计图，则在体育锻炼时间这组数据中，众数和中位数分别是（）A ．18，18B ．9，9C ．9，10D ．18，9【答案】B【解析】由图可知，把45个数据从小到大排列，中位数是第23位数，第23位是9，所以中位数是9，然后锻炼时间为9小时共有18人，人数最多，所以众数也是9．10．如图，正方形ABCD 中，4cm AB =，点E 、F 同时从C 点出发，以1cm /s的速度分别沿CB BA -、CD DA -运动，到点A 时停止运动．设运动时间为()t s ，AEF △的面积为2(cm )S ，则2(cm )S 与()t s 的函数关系可用图象表示为（）4090180O C BAFE DCBAA ．B ．C ．D ．【答案】D【解析】当4o t ≤≤时ADF ABE CEF ABCD S S S S S =---正方形△△△ 111444(4)4(4)222t t t t =⋅-⋅⋅--⋅⋅--⋅⋅2142t t =-+当48t <≤，2211(8)(8)22S t t =⋅-=-，故选D ．二、填空题（每小题3分，共18分） 11．分解因式：325105x x x -+=__________ 【答案】25(1)x x -【解析】原式25(21)x x x =-+ 25(1)x x =-．12．【重测】如图，小军、小珠之间的距离为2.7m ，他们在同一盏路灯下的影长分别为1.8m ，1.5m ，已知小军、小珠的身高分别为1.8m ，1.5m ，则路灯的高为__________m ．【答案】3【解析】如图：∵CD AB NW ∥∥， ∴ABE CDE ∽△△，ABF MNF ∽△△， ∴CD DE AB BE =，FN NW FB AB =，即1.8 1.81.8AB BD =+，1.5 1.51.50.7AB BD =+-，解得：3m AB =．13．【重测】《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．它的代数成就主要包括开放术、正负术和方程术．其中，方程术是《九章算术》最高的数学成就．《九章算术》中记载：“今有牛五、羊二，直金十两：牛二、羊五，直金八两．问牛、羊各直金几何？”译文：“假设有5头牛、2只羊，值金10两；2头牛、5只羊，值金8两．问每头牛、每只羊各值金多少两”设每头牛值金x ，每只羊各值金y 两，可列方程组为__________．【答案】5210258x y x y +=⎧⎨+=⎩【解析】由题可知5210258x y x y +=⎧⎨+=⎩14．抛物线25y x x =-当03x ≤≤时，对应的y 的取值范围是__________．【答案】2504y -≤≤ 【解析】∵二次函数25y x x =-中，对称轴52x =， ∴当52x =时y 最小， 255522y x ⎛⎫=- ⎪⎝⎭254=-，当0x =时，y 最大，MNFED CB A∴2504y -≤≤．15．如图，正方形ABCD 内接于⊙O ，⊙O 的半径为2，以圆心O 为顶点作MON ∠，使90MON ∠=︒，OM 、ON 分别与⊙O 交于点E 、F ，与正方形ABCD 的边交于点G 、H ，则由OE 、OF 、 EF及正方形ABCD 的边围成的图形（阴影部分）的面积S =__________．【答案】2π-【解析】由题意可知BDC S S S =-阴扇△211π22242=⋅⋅-⨯⨯， 2π=-．16．下面是“经过已知圆上一点作这个圆的切线”的作图过程已知：⊙O 及⊙O 上一点P求作：⊙O 的切线，使它经过P 点作法：如图（1）连结并延长OP ，在OP 的延长线上取点A ，使PA OP =．（2）分别以O ，A 为圆心，大于OP 长为半径画弧．两弧交于点C ．（3）作直线PC ．所以直线PC 就是所求的切线．请回答：该作图的依据是__________________________________________________．【答案】①与线段两端点距离相等的点，在这条线段的垂直平分线上 ②两点确定一条直线③过半径外端并且与半径垂直的直线为圆的切线【解析】①与线段两端点距离相等的点，在这条线段的垂直平分线上． ②两点确定一条直线．③过半径外端并且与半径垂直的直线为圆的切线．O N M O HGFE DCBA三、解答题（本题共72分，第17-26题，每小题5分，第27题7分，第28题7分，第29题8分） 17．(21π23tan 602-⎛⎫-+︒ ⎪⎝⎭【答案】5【解析】原式412=-+5．18．解不等式组4(1)710853x x x x ++⎧⎪⎨--<⎪⎩≤，并写出它的所有非负整数解．【答案】0,1,2,3【解析】4(1)710 85 3x x x x ++⎧⎪⎨--<⎪⎩≤①②，由①得2x -≥，由②得72x <， ∴解集为722x -≤≤，则不等式组的所有非负整数解为0,1,2,3．19．已知230x x +-=，求代数式221112112x x x x x x -+⋅+-+++的值．【答案】4【解析】由题可知230x x +-=，23x x +=，原式221112112x x x x x x -+=⋅+-+++ 2(1)(1)11(1)12x x x x x x +-+=⋅+-++1112x x x +=+-+ 2(1)(1)(1)(2)x x x x x +++-=-+2212x x x x ++=+- 3131+=-4=．20．如图，CE 平分ACB ∠且CE BD ⊥，DAB DBA ∠=∠，18AC =，8BD =，求BC 的长．【答案】10【解析】∵CE 平分ACB ∠且CE BD ⊥， ∴CD CB =（等腰三角形三线合一），又DAB DBA ∠=∠， ∴AD BD =， ∵18AC =8BD =， ∴BC AC AD =-AC BD =- 188=- 10=．21．已知关于x 的一元二次方程2(2)230m x mx m -+++=有两个不相等的实数根．（1）求m 的取值范围．（2）当m 取满足条件的最大整数时，求方程的根．【答案】（1）6m <且2m ≠（2）12x =-243x =-【解析】（1）由题意可得， 24b ac =-△2(2)4(2)(3)m m m =-⋅-+ 244m =-，∴2440m ->且20m -≠， ∴6m <且2m ≠-．（2）由（1）得符合条件的m 为5，故原方程为231080x x ++=，(2)(34)0x x ++=，EDCBA解得22x =-243x =-．22．【重测】如图，在ABC △中，90ABC ∠=︒，过点B 作AC 的平行线交CAB ∠的平分线于点D ，过点D 作AB 的平行线交AC 于点E ，交BC 于点F ，连接BE ，交AD 于点G ．（1）求证：四边形ABDE 是菱形；（2）若14BD =，7cos 8GBH ∠=，求GH 的长．【答案】（1）证明见解析（2）154【解析】（1）证明：∵ AC BD AB ED ∥∥， ∴四边形ABDE 是平行四边形， ∵AD 平分CAB ∠， ∴CAD BAD ∠=∠， ∵AC BD ∥， ∴CAD ADB ∠=∠，BAD ADB ∠=∠，∴AB BD =，∴四边形ABDE 是菱形．（2）解：∵90ABC ∠=︒， ∴90GBA ABG ∠+∠=︒， ∵AD BE ⊥，∴90GAB ABG ∠+∠=︒， ∴GAB GBH ∠=∠，∵7cos 8GBH ∠=， ∴7cos 8GAB ∠=，∴78AB AG AH AB ==， ∵四边形ABDE 是菱形，14BD =， ∴14AB BD ==，∴4916 4AH AG ==， ∴154GH AH AG =-=．ABCDEF GH23．【重测】已知反比例函数(0)ky k x=≠的图象经过点(1,4)A -．（1）k 的值为__________；（2）过点A 作直线AC 与函数ky x=的图象交于点B ，与x 轴交于点C ，且2AB BC =，求点B 的坐标．【答案】（1）4k =- （2）43,3⎛⎫- ⎪⎝⎭或(1,4)-【解析】解：由（1）可知4y x=-，①当直线AC 与图像交于第二象限时，如图(1,4)A -1112AB B C =，11AB N AC M ∽△△， 1112AB ANMN B C ==， ∴43MN =， ∴43,3B ⎛⎫- ⎪⎝⎭．②当直线AC 与图象交于第四象限时，如图可知2222AB B C =， ∴222A B C =， ∴1AON △≌2B OQ △， ∴24B Q =， ∴(1,4)B -，综上所述B 的坐标为43,3⎛⎫- ⎪⎝⎭或(1,4)-．24．阅读下列材料：中国是一个干旱缺水严重的国家．淡水资源总量为28000亿立方米，占全球水资源的6%，仅次于巴西、俄罗斯和加拿大，居世界第四位，但人均只有2200立方米，仅为世界平均水平的14、美国的15，在世界上名称121位，是全球13个人均水资源最贫乏的国家之一．扣除难以利用的洪水泾流和散布在偏远地区的地下水资源后，中国现实可利用的淡水资源量则更少，仅为11000亿立方米左右，人均可利用水资源量约为900立方米，并且其分布极不均衡．到20世纪末，全国600多座城市中，已有400多个城市存在供水不足问题，其中比较严重的缺水城市达110个，全国城市缺水总量为60亿立方米．我国的总用水量逐年增加，全国总用水量可分为农业用水量、工业用水量和生活用水量三部分．为了合理利用水资源，连续多年对水资源利用情况进行跟踪调查：2005年全年总用水量640亿3m ，其中3384m 为生活用水，20%为工业用水，其余为农业用水；2006年全年生活用水量为414亿3m ，占全年总用水量为60%，农业用水3103.5m ，其余为工业用水；2007年农业用水3108.5m ，工业用水点3182m ，生活用水3434.5m ；根据以上材料，回答下列问题：（1）2006年我国全年总用水量为__________3m ．（2）选择统计表或统计图，将2005年至2007年这三年的全国各部分用水量和用水总量表示出来．【答案】（1）690 （2）见解析【解析】（1）41460%690÷=．（2）2005年至2007年全国各部分用水量和总量单位（亿3m ）．25．如图，AB 是⊙O 的直径，PA ，PC 与⊙O 相切，切点分别为A 、C ，PC 的延长线与AB 的延长线相交与点D ．（1）求证：BC OP ∥；（2）若1OA =，2PA =，求BD 的长．【答案】（1）见解析（2）23【解析】（1）证明：连结OC ， ∵PA 、PC 与⊙O 相切， ∴OA PA ⊥，OC PC ⊥， ∴90PAO PCO ∠=∠=︒，在Rt PAO △和Rt PCO △中， OP OPOA OC =⎧⎨=⎩， ∴Rt PAO △≌Rt PCD △，∴12AOP COP AOC ∠=∠=∠，∴OC OB =，POE DCBAOBC OCB ∠=∠，∴OCB OBC AOC ∠+∠=∠，∴12OCB OBC AOC ∠=∠=∠，∴AOP OBC ∠=∠， ∴//BC OP ．（2）解：在Rt PAO △中，=90PAO ∠︒1OA =2PA =，由勾股定理得：PO 作OE BC ⊥，垂足为E ，则，190 2PAO OEB BE BC ∠=∠=︒=，∵AOP EBD ∠=∠，90PAO BEO ∠=∠=︒，∴OAP BEO ∽△△， ∴OA BEOP OB=，121BC =，解：BC =，由（1）知BC OP ∥， ∴DCB DPO ∽△△，∴OD BDOP BC =，=， ∴23BD =．26．对于钝角α，定义它的三角函数值如下：()sin sin 180αα=︒-，()cos cos 180αα=-︒-（1）求sin120︒，cos150︒的值；（2）若一个三角形的三个内角的比是1:1:4，A ，B 是这个三角形的两个顶点，sin A ，cos B 是方程2410x mx --=的两个不相等的实数报，求m 的值及A ∠和B ∠的大小．【答案】（1，（2）0 30 120m A B =∠=︒∠=︒【解析】（1）sin120sin(180120)sin 60︒=︒-︒=︒=，cos150cos(180150)cos30︒=︒-︒=-︒=．（2）∴三角形的三个内角的比是1:1:4， ∴三个内角分别为30︒，30︒，120︒， ①当30A ∠=︒，120B ∠=︒时方程的两根为12，12-，将12代入方程得， 21141022m ⎛⎫⨯-⨯-= ⎪⎝⎭，解得0m =，经检验12-是方程2410x -=的根：∴0m =符合题意．②当120A ∠=︒，30B ∠=︒③当30A ∠=︒，30B ∠=︒时，两根为12将12代入方程得：214(1)02m ⎛⎫⨯-⨯-= ⎪⎝⎭，解得0m =不是方程2410x -=的根，不符合题意， ∴综上所述0 30 120m A B =∠=︒∠=︒．27．在平面直角坐标系xOy 中，抛物线222(0)y mx mx m =--≠与y 轴交于点A ，其对称轴与x 轴交于点B ．（1）求点A ，B 的坐标；（2）设直线l 与直线AB 关于该抛物线的对称轴对称，求直线l的解析式；（3）若该抛物线在21x -<<-这一段位于直线l 的上方，并且在23x <<这一段位于直线AB 的下方，求该抛物线的解析式．【答案】（1）(0,2) (1,0)A B - （2）22y x =-+ （3）2242y x x =--【解析】（1）当0x =时，2y =-，∴(02)-，△，抛物线的对称轴为直线212mx m-=-=， ∴(1,0)B ．（2）易得A 点关于对称轴直线1x =的对称点(2,2)A '-，则直线l 经过A '、B ，设直线l 的解析式为()0y kx b k =+≠，则220k b k b +=-⎧⎨+=⎩，解得22k b =-⎧⎨=⎩，所以直线l 的解析式为22y x =-+．（3）∵抛物线的对称轴为直线1x =，∴抛物线在23x <<这一段与在10x -<<这一段，关于1x =对称结合图像可以观察到抛物，线在1x x -<<-这一段在直线l 的上方，在10x -<<这一段位于直线l 的下方， ∴抛物线与直线l 交点横坐标为1-，当1x =-时，2(1)24y x =--+=， ∴422m m =+-， ∴2m =，∴抛物线的解析式为2242y x x =--．28．已知MAN ∠，AC 平分MAN ∠．（1）在图1中，若120MAN ∠=︒，90ABC ADC ∠=∠=︒，AB AD +__________AC （填写>，<，=）；（2）在图2中，若120MAN ∠=︒，180ABC ADC ∠+∠=︒，则（1）中的结论是否仍然成立？若成立，请给出证明：若不成立，请说明理由；（3）在图3中：①60MAN ∠=︒，180ABC ADC ∠+∠=︒，判断AB AD +与AC 的数量关系，并说明理由；②若(0180)MAN αα∠=︒<<︒，180ABC ADC ∠+∠=︒，则A B A D +=_________AC （用含α的三角函数表喜洋洋，直接写出结果，不必证明）．【答案】（1）二（2）仍然成立，证明见解析（3）2cos2α⋅【解析】（1）二（2）如图，过C 作CE AM ⊥于E ，CF AN ⊥于F ，则90CEA CFA ∠==︒，∵AC 平分MAN ∠120MAN ∠=︒， ∴60MAC NAC ∠=∠=︒，又AC AC =， ∴ABC △≌AFC △， ∴AE AF =，CE CF =，在Rt CEA △中，60EAC ∠=︒， ∴30ECA ∠=︒， ∴2AC AE =，DE DA AE AC ++=，∵180ABC ADC ∠+∠=︒，180CDE ADC ∠+∠=︒，∴CDE CBF ∠=∠，又CE CF =，CED CFB ∠=∠，∴CED △≌CFB △， ∴ED FB =，∴FB DA AF AC ++=， ∴AB AD AC +=．（3）理由，如图（2）方法同（2）可证．AGC △≌AHC △，AB AD AH AB AD +=++AH DG AD =++ AH AG =+图3图2图1ABCD MN AB CD MNNMDCB AMNF E D CBAA2AH =，在Rt AHC △中，cos2AHACα=， cos2AH AC α=⋅，2cos2AB AD AC α+=⋅⋅，29．如图，在平面直角坐标系中，已知点(2,3)A 、(6,3)B ，连结AB ．若对于平面内一点P ，线段AB 上都在点Q ，使得 1PQ ≤，则称点P 是线段AB 的“邻近点”．（1）判断点719,55D ⎛⎫⎪⎝⎭，是否线段AB 的“邻近点”____________（填“是”或“否”）；（2）若点(,)H m n 在一次函数1y x =-的图象上，且是线段AB 的“邻近点”，求m 的取值范围．（3）若一次函数y x b =+的图象上至少存在一个邻近点，接写出b 的取值范围．【答案】（1）是（2）35m ≤≤（3）31b ≤【解析】（1）点D 是线段AB 的“邻近点”，∴1AD ==，∴719,55D ⎛⎫⎪⎝⎭是线段AB 的“邻近点”．（2）如图1：∵点(,)H m n 是线段AB 的“邻近点”，点(,)H m n 在直线1y x =-上，∴1n m =-，直线1y x =-与线段AB 交于(4,3)． ①当4m ≥时，有13n m =-≥，又∵AB x ∥轴，∴此时点(,)H m n 到线段AB 的距离是3n -， ∴31O n -≤≤， ∴45m ≤≤．③当4m ≤时，有1n m =--， ∴3n ≤，又∵//AB x 轴，∴此时点(,)H m n 到线段AB 的距离是3n -， ∴031n -≤≤， ∴34m ≤≤，综上所述，35m ≤≤．（3）①如图2，有直线y x b =+可知145AN H ∠=︒， ∵1PH = ，∴1AN ∴=∴(12,3N ∴+，把横坐标2，纵坐标3代入直线y x b =+，得32b ++，∴1b ∴．②如图3，同理可得(163N ⋅-，把2N 代入直线y x b =+中，得36b =+， ∴∴3b =，故b的取值范围为31b ≤．图2。

东城二模试题及答案

东城二模试题及答案———————————————————————————————— 作者： ———————————————————————————————— 日期：2东城区 2015-2016 学年第二学期初三统一练习（二）语文2016.6学校班级姓名考号1．本试卷共 11 页，共五道大题，24 道小题。

满分 120 分。

考试时间 150 分钟。

考2．在试卷和答题卡上准确填写学校名称、班级、姓名和准考证号。

生3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

须4．在答题卡上，第 1、3、4、8、11⑵、12⑵题选择的答案，大小作文选择的作答知题目必须用 2B 铅笔填涂，其他试题用黑色字迹签字笔作答。

5．考试结束，将本试卷、答题卡和草稿纸一并交回。

一、基础·运用。

（共 20 分）学生会是学生自我管理、自我服务的群众性组织，是帮助学生与学校保持有效沟通的桥梁和纽带。

现在，学校新一届学生代表大会即将举行，假如你是该会秘书处成员，请帮助完成如下任务：1.秘书处按姓氏笔画（由少到多）或音序排序法对学生名单进行排序，下列名单中排序有误的一项是（2 分）A.三好学生名单（按笔画）：冯嘉义、孙初、杨宇桐……B.优秀干部名单（按笔画）：陈雪、周悦言、赵璇……C.候选委员名单（按音序）：单世君、闫彤彤、臧新阳……D.学生代表名单（按音序）：郝一辰、计俊逸、耿子禾……2.下面是会务组将要张贴在礼堂门口的通知草稿，其中有两处需要修改。

请写出这两处序号，并进行修改。

(2 分)通知各位代表：①明天是我校新一届学生代表大会召开的日子，②欢迎各位莅临参加。

③为了代表大会顺利召开，④请各位先到接待处，⑤并于上午3 / 24九点到礼堂参加大会。

大会会务组×月×日修改 1：修改 2：3.大会重要议题之一是审议下一学年的学生活动计划，下列计划最恰当的一项是（2 分）A.公历一月十五日元宵节各社团花灯、灯谜设计比赛B.农历五月初五寒食节话剧《屈原》展演C.农历九月初九重阳节前往养老院慰问孤寡老人D.农历八月十五中秋节中国古代科学家事迹展览4.为庆祝大会的召开，学校图书馆打算开放科幻小说阅读区，供学生阅览。

7.东城2017二模答案.docx

2016-2017学年北京市东城区初三年级综合能力测试（二〉数学试卷参考答案及评分标准2017.6一、选择题（本题共30分，每小题3分）二、填空题（本题共18分，每小题3分）三、解答题（本题共72分，第17—26题，每小题5分，第27题7分，第28题8分，第29题7分）17・计算：-2 +（7T - 2017）° - 4 cos 60° + V27解：原式=2 + 1-2 + 3的 ....... 4分= 3^3 4-1・................ 5分18.解：解①得戏1,解②得x> -3. .............. 2分・•・不等式组的解集是：-3<x^l ................................. 4分将不等式组的解集表示在数轴上，_I_5_|_!_I_A_!_I_I_-5 -4 -3 -2 -1 0 1 2 3 4 5............... 5分19.解：错误的步骤是①和②........ 2分正确的化简过程：原式=4x2 -1-x(%+5)二4无2 — 1 —兀2 — 5x20•解：由题意得4P是ABAC的平分线，过点D作DE丄AB于E .................... 2分又V ZC=90°,・・.DE=CD・ .............. 3分・•・ /\ABD的面积15x4=30............... 5分21・解：(1)由题意可求反比例函数的解析式为由点A(V3,l), AB丄A•轴可知，Z・・・04丄08,・・・ZBOC=60°・・•・可求出BC=3・・••点〃的坐标为(能,一3) ............ 2分(2)点E的坐标为(-能1),在反比例函数y二逅的图象上.X理由：当x = _品时，代入y主,得到)=一1 ..................................... 5分22. 解：设乙工程队每天能完成绿化的面积是兀in?,甲工程队每天能完成绿化的面积是加!!？.根据题意得：--— = 4.x 2x解得：兀=50・经检验兀=50是原方程的解.则甲工程队每天能完成绿化的面积是50x2=100 (m2)・答：甲、乙两工程队每天能完成绿化的面积分别是100m2, 50m2.......................... 5分23. 解：(1)四边形EBGD是菱形.理由：TEG垂直平分BD,:・EB=ED, GB=GD.:.ZEBD=ZEDB・I ZEBD=ZDBC f・•・ ZEDF=ZGBF.又•：DF=BF, ZEFD=ZGFB f:・/\EFD 竺4GFB,：・ED=BG,:・BE=ED=DG=GB,・・・四边形EBGD是菱形. ...... 3分(2)过点D作DH丄BC于点H・・・・DG〃AB,A ZDGC=ZABC=30°・在Rt/\DGH中，可求D G =迟,GH = \.在RtADGH中，可求CH=乜.:.GC = 1 + V3 ・........... 5分24. 解:(1) 10010%二100・ .......... 1 分(2) 100-10-38-24-8=20；补充图如下：用户用水量频数分布直方團.......... 3分(3) 6X峠严二4. 08 (万)・答：该地区6万用户中约有4. 08万用户的用水全部享受基本价格...... 5分25. (1)证明：连接ODTCD是OO切线，・•・ ZODC=90°.即ZODB+ZBDC=90°.VAB为(DO的直径，・•・ ZADB=90°.即ZODB+ZADO=90°.:.ZBDC=ZADO.•・・OA=OD,・・・ZADO=ZA・・・・ZBDC=ZA・(2) TCE丄AE,:.ZE=ZADB=90°.:.DB//EC.:.ZDCE=ZBDC.VZBDC=ZA,・•・ ZA=ZDCE.I ZE=ZE,・•・ /\AEC^/\CED.:.Eg=DE・AE・:.16=2 (2+AD)・:.AD=6.26.解：(1)m = 0,画出函数的图象如下：.......... 2分.......... 4分.......... 5分（2）可求抛物线的顶点坐标为（加，■加+1）・不妨令加二0或1,得到两点坐标为（0,1）和（1,0）设直线解析式为y = kx + b,可求阡-1,[h = \.直线的解析式为j=-x+l. .......... 5分（3）m的取值范围是-3W加W1・ .......... 7分28. （1） APBC是等边三角形.证明：在正方形ABCD中，BC=CD, 又CD=CP,.・・ BC=CP,TP在MN上，・•・ PB=PC.・・・PB=BC=PC.:.APBC是等边三角形........... 2分（2）①补全图形如图所示.由B4=BP, ZCBP=60° ,可求得ZAPB=15°，又ZBPC=60° ,可得ZAPC=135°・根据对称性，ZAPC=ZAPC=135°・②证法一：连AC, CC・由①可得ZCPC=90°・由对称性可知PC=PC,从而可求得AC=AC=CC=42AB.从而△ACC为等边三角形；由AC=CC, DA=DC, CD=CD, 可证△ ACD 竺/\CCD,可得ZACD=ZCCD=30°・根据对称性 ZACC=ZACC 9 ZPCC=ZPCC f 从而 ZACP =ZACP 9 由△ABC 为等腰直角三角形，可得ZACB=45° , 由APBC 为等边三角形，可得ZBCP=60° , 从而ZACP=ZACP=15° ・所以ZPCD=ZACD- ZACP=i5° ・ .......... 8 分证法二：连AC, CC ・由 BA=BP 9 ZCBP=60° ,可求得ZAPB=75° , 又ZBAC=45° ,可得ZCAP=30° ・根据对称性，ZCAP=ZCAP=30°，从而ZCAC=60° ；由对称性可知 AC=AC 9从而△ACC 为等边三角形；以下同证法一. 29•解：（1）①PQ=逅点P, Q 的“相关圆”的面积5兀； ②依题可得12+«2=（A /5）2，解得〃 =±2・即点P 的坐标为（0, 1）,且PQ=l. 因为点。

2016年北京市东城区初三二模物理试卷和答案.

北京市东城区2016学年第二学期统一练初三物理2016.6一、单项选择题1.鲁迅的《社戏》中有这样的描写：“淡黑的起伏的连山，仿佛是踊跃的铁的兽脊似的，都远远的向船尾跑去了……”其中“山……向船尾跑去了”所选的参照物是A.山B.船C.兽脊D.河岸2.如图1所示是生活中常见的杠杆，其中属于费力杠杆的是A.钳子B.碗夹C.核桃夹D.撬棒图13.如图2所示，在热机的四个冲程中，对外做功的是A B C D图24.如图3所示的四种现象中，属于光的折射现象的是A.苹果在桌面上形成影子B.叶子经露珠成放大的像C.铁罐在平面镜中形成像D.日食图35.估测在实际生活中应用十分广泛，下列所估测的数据中最接近实际的是A.初三体育测试中，男生完成一次标准的引体向上，头顶上升的最大高度约为150cmB.初三体育测试中，女生完成一次标准的仰卧起坐，头顶上升的最大高度约为150cmC.一般智能手机的质量约为1kgD.随着音乐做一套眼保健操用时约为4min6.下列实例中，体现力改变物体运动状态的是A.用力拉弹簧，弹簧变长B.把橡皮泥捏成不同造型C.滚动的足球受阻力缓缓停下D.被拉弯的鱼竿7.下列关于家庭电路的说法正确的是A.我国照明电路的电压为220VB.家用空调不需要接地C.只要不接触高圧帯电体就会很安全D.更换灯泡的时候可以不用断开电源开关8.下列事例中，属于增大压强的是A.书包背带做得宽一些B.图钉尖进入墙时要用较大的力按C.骆驼长着宽大的脚掌D.载重汽车装有许多车轮9.大气压强下列说法正确的是A.在同一地点大气压强的值是固定不变的B.茶壶利用了连通器原理，茶壶盖上小孔的巧妙设计与大气压无关C.历史上是用马德堡半球实验首先测出了大气压强的值D.大气压强随海拔高度的增加而减小，水的沸点也随着降低10.如图4所示的电路中，属于用电器串联的是A B C D图411.下列关于浮力的说法正确的是A.漂浮的物体浮力大于重力B.钢铁比水的密度大，所以用钢铁做成的物体放入水中后最终一定处于沉底状态C.若气球里充满密度小于空气的气体，那么气球可以飘在空中D.悬浮在水中的潜水艇，若水舱中水位在上升，那么潜水艇一定上浮12.下列说法正确的是A.相邻的两个波峰（或波谷）的距离叫做波长B.声音的响度由频率决定C.声音的音调由振幅决定D.只有发声体在做无规则振动时，产生的声音才是噪声13.关于近视眼和远视眼及其矫正，下列说法正确的是A.形成远视眼的原因是晶状体太厚，折光能力太强B.远视眼成像于视网膜前C.近视眼用凹透镜进行矫正D.若把透镜焦距的倒数乘以100的值叫做眼镜片的度数，则200度的眼镜片焦距是2m14.下列关于电阻的说法中正确的是（忽略温度对电阻的影响）A.导体的电阻与其两端的电压及通过的电流有关B.两根粗细一样的导体，长的一定比短的电阻大C.若导体不接入电路，其电阻为零D.电阻的大小由导体本身的材料、长度和横截面积决定15.2016年4月24日，被命名为首个“中华航天日”，是为了纪念1970年4月24日我国东方红一号卫星首次成功发射升空。

东城区二模化学及答案

2016-2017学年北京市东城区初三年级综合能力测试（二）化学试卷 2017.6考生须知1．本试卷共10页，共39道小题，满分80分。

考试时间100分钟。

2．在试卷和答题卡上准确填写学校名称、姓名和准考证号。

3．试题答题一律填涂或书写在答题卡上，在试卷上作答无效。

4．在答题卡上，选择题用2B铅笔作答，其他试题用黑色字迹签字笔作答。

4．考试结束，将试卷、答题卡和草稿纸一并交回。

可能用到的相对原子质量H 1 C 12 N 14 O16Na23S 32 Cl 35.5 Ca40 Cu 64 Ag 108第一部分选择题（共20分）（每小题只有1个选项符合题意。

每小题1分）1．下列属于非金属元素的是A．硅B．铁C．铜D．金2．下列物质属于混合物的是A．水银B．液氮C．干冰D．盐水3．人体缺钙易引发的病症是A．贫血B．夜盲症C．骨质疏松D．甲状腺肿大4．下列我国古代生产工艺（或技术发明的使用）中主要体现物理变化的是5．青铜是一种常见合金，其主要成分是铜、镍。

下图为铜元素和镍元素在元素周期表中的部分信息。

下列有关说法不正确．．．的是A．镍的元素符号为NiB．铜原子核外电子数为29C．镍元素的原子序数为28D．铜的相对原子质量比镍的相对原子质量小6．某气体常温下不与空气中的成分反应，密度比空气小，极易溶于水，以下收集该气体的方法正确的是A．B．C．D．7．下列属于物理性质的是A．可燃性B．氧化性C．酸碱性D．延展性8．下列物品废弃后可能会带来“白色污染”的是A．塑料袋B．报纸C．玻璃瓶D．铝制易拉罐9．下列实验现象描述不正确．．．的是A．铁丝在氧气中剧烈燃烧、火星四射B．湿润的紫色石蕊纸花遇二氧化碳变红C．硫燃烧时生成有刺激性气味的气体D．氢氧化钠溶于水时溶液温度降低10．实验室配制一定质量分数的稀硫酸并用其除铁锈，部分操作如下图所示，其中正确的是A．B．C．D．A．读浓硫酸体积B．稀释浓硫酸C．装生锈铁钉D．倾倒稀硫酸11．下表列出了一些常见物质在常温下的pH范围，其中呈碱性的是物质名称液体肥皂菠萝汁柠檬汁牛奶pH范围9.5~10.5 3.3~5.2 2.0~3.0 6.3~6.6 A．液体肥皂B．菠萝汁C．柠檬汁D．牛奶12．下列对分子、原子、离子的认识，不正确．．．的是A．水是由水分子构成的B．分子和原子不带电，离子带电C．构成物质的粒子有分子、原子和离子D．氧气和臭氧的分子都是由氧原子构成，因此它们的化学性质相同13．下列有关空气的说法不正确．．．的是A．空气是一种资源B．空气中只含氧气和氮气C．酸雨的产生与空气污染有关D．空气中的CO2是植物光合作用的重要原料14．乙硫醇（化学式为C2H6S）易挥发，有蒜臭味，人对该气体极其敏感。

2017东城区初三化学二模答案

北京市东城区2016-2017学年第二学期统一检测（二）初三化学试卷参考答案第一部分选择题（共20分）每小题只有一个选项符合题意。

共20个小题，每小题1分。

第二部分非选择题（共60分）21．（1分）A22．（2分）（1）C 3H 3N （2）H 2O23．（1分）水洗（或晾晒等）24—A ．（2分）蔬菜（或水果）蛋白质24—B ．（2分）鸡肉糖类25．（1分）能溶于水，水溶液显酸性26．（2分）CH 4 + 2O 2点燃CO 2 + 2H 2O 甲烷不充分燃烧（或燃烧时氧气不充足）27.（2分）（1）元素（2）CaCO 3+ 2HCl = CaCl 2 + H 2O + CO 2↑28．（1分）一氧化碳（或氮的氧化物、含铅化合物、烟尘等）29．（3分）（1）C （或B 或BC ）（2）乙醇机械能（或动能）30．（3分）（3）+7 （4）吸收（5）65%31．（5分）（1）物理．．防晒是阻隔．．紫外线，化学．．防晒是吸收．．紫外线（2）二氧化钛、氧化锌（3）UVB （4）C（5）较短时间的室外活动，可以选择SPF 值低的防晒霜（或夏季海边游泳，最好选用SPF值高的防晒霜）32．（3分）（1）2N 2+ 6H 2O 4NH 3 + 3O 2置换反应（2）B33．（4分）（1）MnCO 3 + H 2SO 4 = MnSO 4+ H 2O + CO 2↑（2）Mn 、Fe 、O（3）氮（4）④⑤34．（5分）（1）纯碱（或苏打）（2）H 2O 2（3）Ca O+ H 2O =Ca(OH)2（4）Ca(OH)2 + Na 2CO 3 = CaCO 3↓+ 2NaOH Na 2CO 3、NaOH题号 1 2 3 4 5 6 7 8 9 10 答案 A D C B D B D A D B 题号11 12 13 14 15 16 17 18 19 20 答案 A D B C C D C B A C35．（4分）（1）A （2）18 （3）搅拌加速溶解36．（5分）（1）白磷燃烧，冒出大量白烟，水进入试管（2）探究同种溶质在不同溶剂中的溶解性（或探究碘在不同溶剂中的溶解性）（3）水（4）蜡烛自上而下依次熄灭（5）二氧化碳能与氢氧化钠溶液反应37．（4分）（1）⑨（2）温度越高，pH值越大（3）①④⑦（或③⑥⑨）在一定的质量分数范围内，温度一定时，溶质质量分数越大，溶液pH越大38．（4分）（1）盛有白磷的燃烧匙在水面上方（2）4P + 5O2点燃2P2O5（3）量筒内的水进入集气瓶（或水倒吸进入瓶中）×100% 39．（8分）【进行实验一】CuSO4 + 2NaOH = Na2SO4 +Cu(OH)2↓【解释与结论】（1）检验蓝绿色沉淀是否洗涤干净（2）不能（3）BaCl2溶液【反思与评价】（4）②CuSO4溶液③Cu(OH)2 + CuSO4 = Cu2(OH)2SO4（5）NaOH溶液（6）氢氧化钠溶液要足量（或过量）。

2017东城中考-二模物理

北京市东城区2016-2017学年第二学期综合练习(二)初三物理 2017.5学校班级姓名考号一、单项选择题（下列各小题均有四个选项，其中只有一个选项符合题意。

共30分，每小题2分）1．在国际单位制中，电功的单位是A ．瓦特B ．焦耳C ．安培D ．千克 2．下列物质中，通常情况下属于导体的是A ．盐水B ．空气C ．煤油D ．塑料 3．图1所示的四种现象中，属于光的反射现象的是4．下列四个物态变化的实例中，属于汽化的是A ．下雨天，车窗玻璃内侧“起雾”B ．冬天，树枝上出现“雾凇”C ．水烧开时，从壶嘴喷出“白气”D ．用手指蘸水在黑板上写字，字迹逐渐消失 5．下列家用电器中，利用电流热效应工作的是 A ．电磁炉 B ．电饭锅 C ．抽油烟机 D ．空气净化器6．图2所示的工具中，正常使用时属于费力杠杆的是D.核桃夹B.剥线钳A.瓶起子C.食品夹图2D.笔好像在水面处“折断”C.小朋友在哈哈镜中成了“小巨人” B.玻璃砖后面的吸管发生了“移位” A.太阳光经三棱镜后形成“彩色光带”图17．图3所示的实例中，属于增大压强的是8．在“中国梦想秀”的舞台上，一位模仿秀演员可以惟妙惟肖地模仿十多位明星的声音，观众要判断他所模仿的是哪位明星，主要依据的是A. 响度B. 音色C. 音调D. 波长9．物理课上，同学们将自带的普通指甲刀与一个光学器件进行组合，使其具有了放大功能。

则他们用到的这个光学器件是A ．凸面镜B ．平面镜C ．凸透镜D ．凹透镜10．下列估测的数据，符合实际的是A ．普通教室门的高度约为10mB ．初中生步行速度约为10m/sC ．今年北京5月份的平均气温约为10℃D ．一瓶380mL 塑料瓶装矿泉水的总质量约为400g11．图4所示的电路中，电源两端电压保持不变，当开关S 闭合时，LED 正常发光。

若将滑动变阻器的滑片向右滑动，则下列说法中正确的是 A ．LED 仍正常发光B ．电压表的示数变大C ．电流表的示数不变D ．滑动变阻器两端电压不变12．关于图5所示的四种仪器，下列说法中正确的是A ．B 超——利用超声波获取人体内部信息 B ．声呐——利用次声波探知海底深度C ．验钞机——红外线使钞票上的荧光物质发光D ．遥控器——靠紫外线实现对电视机的控制B 超声呐验钞机遥控器图 5 图3A.人民英雄纪念碑筑有宽大的底座C.滑雪杖的触地端较尖锐B.大型载重车装有很多车轮D.用拎带器提装有重物的塑料袋图R V S A13．甲、乙两个实心球的质量之比为3∶1、体积之比为1∶ 3，则它们的密度之比为A ．1∶1B ．2∶3C ．1∶9D ．9∶114．用手提着一根挂有重物的轻弹簧沿竖直方向匀速上升。