华南理工大学高等数学统考试卷上2007期中

合集下载

07年高等数学期中考试

高等数学II 2007期中试卷一、选择题（每小题3分，共计 15 分）1、下列微分方程中，通解是)sin cos (x C x C e y x2221+=的方程是。

(A )．032=-'-''y y y ； (B )．052=+'-''y y y ；(C )．02=-'+''y y y ； (D )．0136=+'+''y y y 。

2、微分方程x xe y y y 265=+'-''的特解形式是=*y 。

(A )．x xe b ax 2)(+；(B )．xe b ax 2)(+；(C )．b e ax x +22；(D )．b ae x+2。

3、设f 为可微函数，)(bz y f az x -=-，则=∂∂+∂∂y zb xz a。

(A )．1； (B )．a ； (C )．b ； (D )．b a +。

4、设D 是以原点为圆心，R 为半径的圆围成的闭区域，则 d Dxy σ=⎰⎰ 。

(A )．44R ； (B )．34R ； (C )．24R ； (D )．4R 。

5、设),(y x f 在10 10≤≤-≤≤x x y D ,:上连续，则二重积分⎰⎰Dy x f σd ),(表示成极坐标系下的二次积分的形式为。

(A)．12 0d (cos ,sin )d f r r r rπθθθ⎰⎰；(B )．cos sin 2 0 0d (cos ,sin )d f r r r rπθθθθθ+⎰⎰；(C)．1cos 2 0d (cos ,sin )d f r r r rπθθθθ-⎰⎰；(D )．12cos sin 0 0d (cos ,sin )d f r r r rπθθθθθ+⎰⎰。

二、填空题（每小题4分，共计24 分）1、设xy xy z )(=，则=z d ，在点),(2 1P 处的梯度=P z grad 。

华南理工大学高等数学统考试卷下07期中

2007-2008高等数学下册期中考试试卷姓名：班级：成绩单号：一、填空题（45⨯）1、[4分] 与直线112211-=+=+z y x 及112x y t z t =⎧⎪=+⎨⎪=+⎩都平行，且过原点的平面方程为。

2、[4分]设()()(),,sin ,arctan ,,z f u v u xy v y f u v ===可微，则,z z x y ∂∂∂∂各为。

3、[4分]设2x y u e =，则2u x y∂=∂∂ 。

4、[4分] 设函数u x xy xyz =++在点()1,2,0的所有方向导数中，最大的方向导数是沿方向。

5、[4分]曲面1xy yz zx ++=在点()3,1,2-处的切平面方程为，法线方程为。

二、（8分）设(,)f s t 具有连续的偏导数，且(,)0f s t ≠，方程(,)0y z f x x=确定了z 是,x y 的函数，试求z z x y x y∂∂+∂∂ 三、（8分）设arctan 1x y z xy-=+，求(dz 四、[8分] 求函数2223u x y z z =++-在点()01,1,2M -的梯度及沿梯度方向上函数的方向导数五、[8分]设直线0:30x y b L x ay z ++=⎧⎨+--=⎩在平面π上，而平面π与曲面22z x y =+相切于点()1,2,5-，求,a b 之值。

六、 [8分] 计算二重积分{}max ,1Dxy dxdy ⎰⎰，其中:02,02D x y ≤≤≤≤七、[8分] 计算10010x dx +⎰⎰八、[8分] 计算()22I x y dv Ω=+⎰⎰⎰，其中Ω为平面曲线220y z x ⎧=⎨=⎩ 绕z 轴旋转一周的曲面与平面8z =所围的区域。

九、 [8分] 设由曲面22z x y =+与2z =所围成的立体中每点的密度与该点到xoy 平面距离成正比，试求该立体的质量M十、计算()222357x y z dxdydz Ω++⎰⎰⎰，其中:0z Ω≤≤十一、 [8分]1=上求一点()0000,,M x y z ，使曲面上过点的切平面与三个坐标面所围成的四面体的体积为最大十二、 [附加题5分] 计算积分C⎰，式中曲线C 是y =在02x a ≤≤上的一段弧。

执信2007-2008学年度第一学期高三期中考试(理科基础)

2007-2008学年度第一学期高三级理科基础期中考试试卷本试卷分选择题和非选择题两部分，共10页，满分为150分。

考试用时120分钟. 注意事项：1、答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和学号填写在答题卡和答卷密封线内相应的位置上，用2B 铅笔将自己的学号填涂在答題卡上。

2、选择题每小题选出答案后，有2B 铅笔把答题卡上对应题目的答案标号涂黑：如需改动，用橡皮擦干净后，再选涂其他答案；不能答在试卷上。

3、非选择题必须用黑色字迹的钢笔或签字笔在答卷纸上作答，答案必须写在答卷纸各题目指定区域内的相应位置上，超出指定区域的答案无效；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4、考生必须保持答题卡的整洁和平整。

本试卷共75题，全部是单先择题，每题2分。

在每题的四个选项中，只有一项是符合题目要求的，多选、错选均不得分。

1．一辆汽车停在水平地面上，一个人用力水平推车，但车始终静止，以下说法正确的是：A. 推力与汽车所受的静摩擦力不是平衡力B ．椎力大小变化时，汽车所受的静摩擦力大小不变C ．推力越大，汽车所受的静摩擦力越大，椎力与静摩擦力平衡D.地面对汽车的支持力与汽车对地面的压力是一对平衡力2．一个物体以初速度v o 水平抛出，经t 秒其竖直方向速度大小与v o 相等,那么t 为A ．g 0νB ．g o 2ν C.g 20ν D ．g 02ν3．一物体m 受到一个撞击力后，沿斜面向上滑动，在向上滑动的过程中，物体m 受到的力是A.重力，沿斜面向上的冲力，斜面的支持力B.重力，沿斜面向上的冲力，沿斜面向下的滑动摩擦力C.重力，沿斜面向下的滑动摩擦力，斜面的支持力D.重力，沿斜面向上的冲力，沿斜面向下的滑动摩擦力，斜面的支持力4．如图是做直线运动的甲、乙物体的位移一时间图象，由图象可知，下列说法中错误的是A ．甲起动的时间比乙早t l 秒B ．当t=t 2时两物体相遇C ．当t=t 2时两物体相距最远D. 当t=t 3时两物体相距S o 米5．对静止在光滑水平面上的物体施加一水平拉力，当力刚开始作用的瞬间A.物体立即获得速度B. 物体立即获得加速度C ．物体同时获得速度和加速度D. 由于物体未来得及运动，所以速度和加速度都为零6．如图所示，物体在水平拉力F 作用下沿水平地面匀速直线运动，速度是v 。

华南理工大学高等数学统考试卷上2007期中答案.

姓名学号学院专业座位号( 密封线内不答题……………………………………………………密………………………………………………封………………………………………线……………………………………线………………………………………_____________ ________…华南理工大学期中考试2007-2008学年第一学期《高等数学》期中试卷简单答案一. 解答下列各题 (每小题6分,共36分1. 当时，无穷小量与是等价无穷小，求常数.解2.指出函数的间断点，并判断它们的类型.解为跳跃间断点.3. 求过坐标原点且与曲线相切的切线方程.解或4. 设函数, 求.解.5. 设函数由所确定，求.解.6. 设函数由方程确定，求在处的值.解在处的值为.二. 解答下列各题(每小题8分,共24分7. 求极限．解.８．（Ａ）求函数的极值．解极小值，极大值.（Ｂ）已知，求使成立的被积函数．解.９. 设，（１）讨论在处的可导性，（２）讨论在处的连续性．解在处的不连续.三. (本题１０分１０（Ａ）．当时，证明不等式成立．证明设，在连续，可导.，，于是在单调增加，，从而在单调增加，.１０（Ｂ）．设在上连续，证明：存在，使．证明设，在上连续，且，.由闭区间上连续函数的零值定理知存在，使.四. (本题１０分１１（Ａ）. 曲线在点处的切线和法线分别与轴交于点和点，求常数的值，使三角形的面积最小．解为最小.１１（Ｂ）设函数由方程所确定，求．解，.五. (本题１０分１２（Ａ）讨论曲线与的交点的个数．解设，当，无实根，没交点.当，有唯一实根，一个交点当，，有两个实根，两个交点１２（Ｂ）（1）设，求的表达式；解（2）求不定积分．解六. (本题10分１３（Ａ）设在上有界且可导，证明方程至少有一个实根．解设，在可导，.由在上有界知，.若在上，则，对任意的实数.若在上不恒等于零，不妨设，可知在上必有最大值，最大值点为.１３（Ｂ）设函数在上连续，且，证明存在一点，使．证明在上连续，有最值，，，，由介值定理知存在一点，使．。

华南理工2007高代

464
华南理工大学
2007年攻读硕士学位研究生入学考试试卷（试卷上做答无效，请在答题纸上做答，试后本卷必须与答题纸一同交回）
科目名称：高等代数
适用专业：基础数学计算数学概率论与数理统计应用数学
八、设 σ为数域P 上的n 维向量空间V 上的一个线性变换，为P 上的多项式，)(x f σ的最小多项式为，则)(x m )(σf 可逆⇔)(x m ，互素。

（20分）
)(x f 九、设为2n+1阶实对称矩阵，试求正交矩阵⎟⎟⎟⎟⎟
⎟⎠
⎞⎜⎜⎜⎜⎜⎜⎝⎛=0001001001001000""""""A P ，使得D AP P =−1为对角形矩阵，并求。

D （20分）
十、证明（1）n 阶实反对称矩阵的特征根为纯虚数或者为零；（2）n 阶
实反对称矩阵的行列式大于等于零。

（15分）。

《高等数学》(上理工) 试卷A

华南理工大学广州汽车学院 2008——2009学年度第一学期期末考试《高等数学》（上册•理工类）试卷A考生注意：1．考前请将密封线内各项填写清楚，“序号”即交作业的序号，勿写学号；2．本试卷共四个大题，满分100分，考试时间120分钟；3．所有答案应直接写在试卷上。

一．填空题（本大题共5小题，每小题3分，共15分。

将答案写在横线上）1．函数ln(1)y x =+的定义域是。

2．设0sin 2lim 3x kx x→=，则常数k = 。

3．设y =dy = 。

4．不定积分2x dx xe ⎰= 。

5．反常积分 (0)a pI a dxx +∞=>⎰，当1p >时，I = 。

二．单项选择题（本大题共5小题，每小题3分，共15分。

将正确选项的字母填在括号内）1．曲线ln y x x =在点(1,0)处的切线方程是（） A ．(ln 1)(1)y x x =+- B ．1y x -= C ．1y x =- D ．(1)y x =--2．设||,0;()1,0,x x f x x x ⎧≠⎪=⎨⎪=⎩，则()f x 在0x =处（）A ．0lim ()x f x →不存在 B ．'(0)f 存在C ．0lim ()x f x →存在，但()f x 在0x =处不连续D ．()f x 在0x =处连续，但不可导3．在区间[1,1] -上，不满足罗尔中值定理条件的是（） A ．2()1x f x e =- B ．2()ln(1)f x x =+ C．()f x = D ．21()1f x x=+ 4．下列等式中，正确的是（） A ．[()]()d f x dx f x =⎰ B ．[()]()df x dx f x dx dx=⎰ C ．()()df x f x =⎰ D ．' ()()f x dx f x C =+⎰5．设()f x 连续，且()sin xa f t dt x x =⎰，则()2f π= （）A ．sin cos x x x +B ．12π-C ．2πD ．1三．计算题（本大题共7小题，每小题7分，共49分） 1．求极限 22sin 1lim (2)x x x ππ→--。

华南理工大学2007~2010年概率论试卷答案

2007级概率论与数理统计试卷A 卷参考答案一、1. C注释：由“A ⊂B 成立”得P(A)=P(AB) ()()(|)()()P AB P A P A B P B P B ==故2. C3. B 注释：参考课本86页4.B 2sin 1A xdx π=⎰0注释： ?5.6. B A 项参见课本64页，D 项参见课本86页二、 1. 2 注释：若X 服从Poisson 分布，则EX=λ，DX=λ。

（课本84页） 2. 12 注释：cov(X,Y)= r X Y DX DY ⋅⋅。

（参考课本86页） 3. 1/5 注释：运用等比求和公式S=1(1)1na q q--4. 38.4 注释：22()(),(,),,E D E B n p E np D npq ξξξξξξ=+== 对于 5．p(x)=,00,0x e x x λλ-⎧>⎨≤⎩,211,E D ξξλλ==6. 0.2 注释：类似2006级试卷填空题第6题7.2/5三、（1）1/20; (2)14/15 注释：（1）P(A)=224431078910C C C，表示从、、、这四个数中选两个;（2）B =“三个号码中既含4又含6” 四、（1）C=4; (2)112()-2{1}41-3e ;xx y P dx edy ξη--++<==⎰⎰(3)222__02__0(),()0_____00_____0()()(,),x y e x e y p x p y x y p x p y p x y ξηξηξη--⎧⎧≥≥==⎨⎨<<⎩⎩⋅=因故与独立？(4)2222022112,2221()41124xxE x edx E x edx D E E E D ξηξηξξξξξηη+∞+∞--=⋅==⋅==-===⎰⎰与独立，所以cov(,)=0故同理，，五、 0.9979 注释：运用全概率公式，类似2006级试卷第三题六、0.9525100(100,0.9),))85{85)1)1( 1.67)(1.67)0.9525X X B P X ⨯⨯≈Φ-Φ≥≈-Φ=-Φ-=Φ=注释：设这个部件中没有损坏部件数为，则服从二项分布且有______EX=np=1000.9=90,DX=npq=900.1=9由拉普拉斯定理，b-EX a-EX P{a<X<b}((DXDX故至少须有个部件工作的概率为：85-90(9七、M=160,X ⨯⨯⨯≈⨯⨯≥≥≤≥≤注释：设出事人数为则有X B(5000000,0.0003)EX=50000000.0003=1500,DX=50000000.00030.99971500若要以99%的概率保证保险公司在此项保险中获得60万元以上的利润，则P{5000000M (1-40%)-X 300000600000}99%得P{X 10M-2}99%X-150010M-2-1500故需满足P{15001}99%99% 2.33159.22,160M M ≥Φ≥≈Φ≥=50010M-2-1500即（）（）1500解得故八、（1）课本98页辛欣大数定理（2）22222n 11221222211()0(1)()0()()[()]()211_____0(1)()()211,2,3,,()()0112)()2n n n n n n n kn kk k n n k k E n n nnn D E E E n n nnnk E E nn D n nnnξξξξξξξξξξξ++==+==⋅-+⋅+-⋅==-==⋅-+⋅+-⋅===⋅⋅⋅====⋅=∑∑∑由于令则______________________ D(由契比雪夫2n 0,2()|}1lim ()|}1}n n n n n E n E εξξεεξξεξ→∞>-<≥--<=不等式，对任意的有________________P{|故有P{|即{服从大数定律2008年概率论与数理统计试卷A 卷参考答案一、1.D 1(1)()X u u uP X u P σσ-+-≤+=≤注释：=1()σΦ2.C 注释：参考课本第8页3.A 注释：连续型随机变量在某一个点上的概率取值为零，故A 正确？B 项是否正确4.B 注释：参考课本86页5.A 二、 1. 1.33(或者填13591024) 2．25 注释：参考课本86页 3. 0.254. （X+Y ）～B(7,p)注释：E(X)=3p,E(Y)=4p,故E(X+Y)=E(X)+E(Y)=3p+4p=7p;D(X)=3p(1-p),D(Y)=4p(1-p)且X 、Y 独立，故D(X+Y)=D(X)+D(Y)= 3p(1-p)+ 4p(1-p) 设（X+Y ）～B(n,P),则有E (X +Y )=7p=nPD (X +Y )=3p(1-p)+4p(1-p)=nP(1-P)⎧⎨⎩解得n=7,P=p5. 2/52215041()5b 4(2)41(54)0,1 4.112555X f x ac X X X X P dx dx =∆=-=-⨯⨯-≥≤≥=+=⎰⎰的密度函数为方程有实根，则必须满足即或者故方程有实根的概率6. 0.3522(35)112(35),9322242{24}0.15,{}0.15333200.1532233202222}33333E X EX D X D X D X X P X P X σσσσσσσσσσσσσσ+==+===---<<=<<=ΦΦ=-ΦΦ----<=ΦΦΦ由得由得因故所以（）-（）所以（）-（）=0.3P{X<0}=P{（）=[1-（）-（）]/2______=[1-0.3]/2=0.35?7. 相关三、四、1__1___30.3_0.5_0.2(1)0.310.530.20.8X EX -⎛⎫⎪⎝⎭=-⨯+⨯+⨯=五、1022201____02(1)()1___021____02()11_0211(2)(510)1)(2211(322_____012xx xx xxxe xf x e x e x F x e x P X eex e dx x e dx EXx e dx x ---∞--∞-∞⎧≤⎪⎪=⎨⎪>⎪⎩⎧≤⎪⎪=⎨⎪->⎪⎩-<<=--⋅+⋅===⋅+⋅⎰⎰⎰0+0由题意故（）EX=221211___[22][22(2xxxxe dx x e xe e xD X EX ∞--∞=-++-=-=⎰+2EX)？六、2220001(0.005,0.035)0.0050.03510.02,(0.0350.005)0.000075212a 1(,),,())2120.0250.02520005020000{50}{i i i i i i i ii X i X U EX D X b X U a b EX D X b a Y X Y Y P Y P =+===-=+==-=<⨯=-⨯<=∑设为第台机床生产的次品率（注：对于均匀分布有设总次品率若要满足这批产品的平均次品率小于，则.025020000.02}(25.8)20000.00007520000.000075-⨯<=Φ⨯⨯A=B =B =B =B B B B (B )|)0.50.9|)0.540.83P A ⨯⨯⨯⋅⨯====甲乙丙乙甲丙甲甲甲甲设“取出的产品是正品”；取出的产品是甲厂生产的” 取出的产品是乙厂生产的” 取出的产品是丙厂生产的”则P(A)=P(A )+P(A )+P(A )=0.50.9+0.30.8+0.20.7=0.83P(A )P(A B P(B P(A)P(A)？试卷中没有给出(25.8)Φ的值，且直观上感觉(25.8)Φ的值太大了，故不能肯定题中的做法是否可行七、____,0_______2________()0__________2________()0__________22(2)0,0a b ababa x ab y b a x a x ab y b y bEX x dx EY y dy a bππππππ--=⎧-≤≤-≤≤⎪⎨⎪⎩⎧-≤≤⎪=⎨⎪⎩⎧-≤≤⎪=⎨⎪⎩=⋅==⋅=⎰⎰椭圆X Y (1)S 1故（x,y)的联合密度函数f(x,y)=ab其它X 的边缘密度函数f 其它Y 的边缘密度函数f 其它222222222222,2424,3344()25,()4335332(3),22()()ab aba b EXx dx EY y dy aba b D X EX EX D Y EY EY a b a x a b y b x y a bπππππππππππ--=⋅==⋅==-===-====-≤≤-≤≤⋅=⋅≠⎰⎰X Y 解得，时，1f f ，故X与Y不独立ab八、555511___________5()1(1)(xzzZ dx zedx eeF z z e ----≤⋅≤≤=-=-=--⋅-⎰⎰1z 1z的分布函数F(z)=P{Z z}=1-P(Z>z)=1-P{min(X,Y)>z}_______________=1-P(X>z,Y>z)=1-P(X>z)P(Y>z)当z 0时，P(X>z)=P(Y>z)=1故F(z)=1-1=0当0<z 1时，P(X>z)=P(Y>z)=故555555)z 1()1010__________________0()1(1)()__0_____________________0()65_______010_____________________1z z z e F z z F z z e e z f z e ze e z z ------>=-=≤⎧⎪=--⋅-≤⎨⎪⎩≤⎧⎪=--<≤⎨⎪>⎩当时，P(X>z)=0故所以0<z 11__________________z>12009年2学分参考答案一、解：设i A ＝｛第i 枚弹道导弹击沉航空母舰｝，i B ＝｛第i 枚弹道导弹击伤航空母舰｝i C ＝｛第i 枚弹道导弹没有击中航空母舰｝，i ＝1，2，3，4D ＝｛发射4枚弹道导弹能击沉航空母舰｝()31=i A P ，()21=i B P ，()61=i C P ，i ＝1，2，3，443214321432143214321B C C UC C B C UC C C B UC C C C UB C C C C D =()()()()()()434432143214321432143216132161461=⨯⎪⎭⎫⎝⎛⨯+⎪⎭⎫ ⎝⎛=++++=B C C C P C B C C P C C B C P C C C B P C C C C P D P()()461311-=-=D P D P = 0.99二、解：（1）A ＝｛同花顺（5张同一花色连续数字构成）｝()55255236)413(4C C A P =-⨯=（只要说明顺子的构成，分子40也算对）（2）A ＝｛3张带一对（3张数字相同、2张数字相同构成）｝()5522411234113CC C C C A P =（3）A ＝｛3张带2散牌（3张数字相同、2张数字不同构成）｝()552141421234113C C C C C C A P =三、解：（1）设A ＝｛被查后认为是非危险人物｝， B ＝｛过关的人是非危险人物｝，则()()()()()B A P B P B A P B P A P +=9428.005.004.098.096.0=⨯+⨯= ()()()()998.0==A PB A P B P A B P（2）设需要n 道卡，每道检查系统是相互独立的，则Ci={第i 关危险人物被误认为非危险人物}，{}n n C C P 05.01= ，所以999.005.01≥-n，05.0ln 0001.0ln ≥n ，即1005.0ln 0001.0ln +⎥⎦⎤⎢⎣⎡=n =[3.0745]+1 = 4 四、解：当1=a 时，1=Y ，则()⎩⎨⎧>≤=1110y y y F Y当10<<a 时，当0≤y 时，()()0=<=y Y P y F Y ，()()0==dyy dF y f Y Y当0>y 时，()()()y a X P y a P y F X Y ln ln <=<=()⎪⎭⎫ ⎝⎛>=a y X P y F Y ln ln ⎪⎭⎫⎝⎛Φ-=⎪⎭⎫ ⎝⎛≤-=a y a y X P ln ln 1ln ln 1()()222)ln ln (21ln 1σμπσ--⋅-==ay Y Y ea y dyy dF y f当1>a 时，当0≤y 时，()()0=<=y Y P y F Y ，()()0==dyy dF y f Y Y当0>y 时，()⎪⎭⎫ ⎝⎛<=a y X P y F Y ln ln ⎪⎭⎫⎝⎛Φ=a y ln ln ()()222)ln ln (21ln 1σμπσ--⋅==ay Y Y ea y dyy dF y f五、解：（1）E(X+Y)=6.0315.0314.0213.0103.0101.0114.023=+--=⨯+⨯+⨯+⨯+⨯--⨯--=b a b a174.015.014.013.012.003.002.001.014.0=++=+++++++++b a b a联立解得：17.0=a ，09.0=b （2）X 的概率分布函数：-2-110.17 0.23 0.060.54（3）E(XY)＝8.015.0214.0112.0114.0117.02=⨯+⨯+⨯-⨯+⨯六、解：95.01.0≥⎭⎬⎫⎩⎨⎧<-p n m P ，因()()1,0~1N np p pnm--()()95.011.01≥⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧-<--n p p np p pnm P ，()96.111.0975.0=≥-u np p()()p p n -≥16.192；因为()4/11≤-p p ，取()4/6.192≥n =96.04即97=n七、解：（1）二维随机变量(X,Y)的联合概率密度：⎩⎨⎧<<<<=othersby a x ab y x f ,00,0,/1),(边缘概率密度：⎩⎨⎧<<=othersa x a x f X ,00,/1)(，⎩⎨⎧<<=othersb y b y f Y ,00,/1)(（2）36)12/1(,12)12/1(22====b DY a DX ，312,12==b a （3）随机变量X 与Y 相互独立，因为)()(),(y f x f y x f Y X = 八、解： 333||33||33||||)(||)(||)()|(|tc tE x dF tx x dF tx x dF t P x t x tx ==≤≤=>⎰⎰⎰≥>>ξξ九、解：（1）dx Axydy dxdy y x f ⎰⎰⎰⎰⎪⎭⎫ ⎝⎛=+∞∞-+∞∞-1010),(4A =＝1，A ＝4 （2）P(X<0.4，Y<1.3)＝16.044.0010=⎪⎭⎫ ⎝⎛⎰⎰dx xydy （3）⎰⎰⎪⎭⎫ ⎝⎛=++1014dx xydy e Eesytx sYtX ⎰⎰⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫⎝⎛=101114dx dy e s s ye x e sysy txX⎪⎪⎭⎫⎝⎛+-⎪⎪⎭⎫ ⎝⎛+-=2222114t t e t e s s e s e tt s s （4）32410102=⎪⎭⎫ ⎝⎛=⎰⎰dx ydy x EX ，214101032=⎪⎭⎫ ⎝⎛=⎰⎰dx ydy x EX()91942122=-=-=EX EXDX ，()=XY E 944101022=⎪⎭⎫ ⎝⎛⎰⎰dx dy y x ()0323294,=⨯-=⋅-=EY EX EXY Y X Cov十、解：（1）设ξ表示该观众答对题数， ,2,1,0=ξ 则第ξ+1次解答答错（即首次出错）。

华南理工大学期中考试

华南理工大学线性代数与解析几何期中考试
一．选择题
1.设A 为n 阶对称矩阵, B 为n 阶反对称矩阵, 则下列矩阵中为反对称矩阵的是( ).
(A)BA AB -; (B)BA AB +; (C)2)(AB ; (D)BAB ;
2.均为n 阶方阵, 则下面结论正确的是( ).
(A)若A 或B 可逆, 则AB 必可逆; (B)若A 或B 不可逆, 则AB 必不可逆; (C)若B A 、均可逆, 则B A +必可逆; (D)若B A 、均不可逆, 则B A +必不可逆.
3.若n 阶方阵B A 、都可逆, 且BA AB =, 则下列( )结论错误.
(A)11--=BA B A ; (B)A B AB 11--=; (C)1111----=A B B A ; (D)11--=AB BA ;
4.设C B A 、、为同阶方阵, 且E ABC =, 则下列各式中不成立的是( ).
(A)E CAB =; (B)E C A B =---111; (C)E BCA =; (D)E B A C =---111.
二．填空题
2. 求此平面方程
3.设n i a i ,3,2,1,0=≠, 且⎥⎥⎥⎥⎥
⎥⎦
⎤
⎢⎢⎢⎢⎢
⎢⎣⎡=-00
000000000121
n
n a a a a A ,则1-A
=
三．解答题 1.设n 阶矩阵A 和B 满足:
AB B A =+.
(1)证明: E A -为可逆矩阵, 其中E n 阶单位矩阵; (2)证明: BA AB =
;
(3)已知⎥⎥
⎥⎦
⎤
⎢⎢⎢⎣⎡-=200012031B , 求矩阵A .
2.（附加题）计算下面行列式。

华南理工大学2009-2010高等数学下册期中考试试卷答案.

华南理工大学期中考试2009-2010学年第二学期《高等数学》期中考试试卷注意事项：1. 考试形式：闭卷；．本试卷满分100分，考试时间90分钟。

. 解答下列各题 (每小题5分,共20分)设函数由方程确定，其中F为可微函数，且，求z是由方程所确定的函数，其中具有二阶导数，且22求dz.对等式两端取微分得22，x在点处的梯度. yiP为椭球面上的一动点，若S在点P处的切平面与xoy面垂直，P的轨迹C。

椭球面S点处的法向量是，222《高等数学》试卷第 1 页共 6 页点P处的切平面与xoy面垂直的充要条件是n⋅{0,0,1}=2z-y=0⎧232⎧x2+y2+z2-yz=1⎪x+y=1所以点P的轨迹C的方程为：⎨，即⎨ 4⎩2z-y=0⎪⎩2z-y=0二. 解答下列各题 (每小题10分,共30分)５．求二元函数f(x,y)=x解 fx'(x,y)=2x2+y2(2+y)+ylny的极值 22y(2),f'(x,y)=2xy+lny+1令fx'(x,y)=0,fy'(x,y)=0，解得唯一驻点 0,⎪⎛⎝1⎫e⎭'' 0,⎪=2 2+由于A=fxx⎛⎝1⎫e⎭⎛⎝1⎫1⎛1⎫''>0,B=f0,=4⋅0⋅=0 xy⎪2⎪e⎭e⎝e⎭1⎫1⎫⎛22''⎛C=fyy0,=2⋅0+e=e,B-AC=-2e2+<0 ⎪ 2⎪ee⎝⎭⎝⎭从而f 0,⎪=-是f(x,y)的极小值⎛⎝1⎫e⎭1e∂2u∂2u∂2u+52=0。

确定的６．设函数u=f(x,y)具有二阶连续偏导数，且满足等式42+12∂x∂x∂y∂y∂2u=0 a,b值，使等式在变换ξ=x+ay,η=x+by下简化为∂ξ∂η2∂u∂u∂u∂2u∂2u∂u∂u2=+,=+2+解，∂x∂ξ∂η∂x2∂ξ2∂ξ∂η∂η222∂u∂u∂u∂2u∂2u∂2u∂2u∂2u∂2u2∂u2∂u=a+b,2=a+2ab+b=a2+(a+b)+b222∂y∂ξ∂η∂y∂ξ∂ξ∂η∂η∂x∂y∂ξ∂ξ∂η∂η将以上各式代入原等式，得∂2u∂2u∂2u2(a+12a+4)2+⎡⎣10ab+12(a+b)+8⎤⎦∂ξ∂η+(5b+12b+4)∂η2=0 ∂ξ2《高等数学》试卷第 2 页共 6 页由题意，令a+12a+4=0,10ab+12(a+b)+8≠0,5b+12b+4=0 22解得a=-2,b=-22，或a=-,b=-2 55⎧x2+y2-2z2=07．已知曲线C:⎨，求C上距离xOy面最远的点和最近的点。

华南理工大学2007线性代数期末试卷A

,考试作弊将带来严重后果！华南理工大学期末考试（A 卷）《 2007线性代数》试卷1. 考前请将密封线内各项信息填写清楚；所有答案请直接答在试卷上(或答题纸上)；．考试形式：闭卷；．设A 是n m ⨯矩阵，B 是m 维列向量，则方程组B AX =无解的充分必要条件是：．已知可逆矩阵P 使得1sin sin con P AP con θθθθ-⎛⎫=⎪-⎝⎭，则12007P A P -= ．若向量组α=（0，4，t ），β=（2，3，1），γ=（t ，2，3）的秩为2，则t= ．若A 为2n 阶正交矩阵，*A 为A 的伴随矩阵，则*A = ．设A 为n 阶方阵，12,,,n λλλ⋅⋅⋅⋅⋅⋅是A 的n 个特征根，则1ni i E A λ=-∑=选择题（共20分）．将矩阵n m A ⨯的第i 列乘C 加到第j 列相当于对A ：，左乘一个m 阶初等矩阵， B ，右乘一个m 阶初等矩阵，左乘一个n 阶初等矩阵， D ，右乘一个n 阶初等矩阵．若A 为m ×n 矩阵，B 是m 维非零列向量，()min{,}r A r m n =<。

集合{:,}n M X AX B X R ==∈则，M 是m 维向量空间， B ， M 是n-r 维向量空间，M 是m-r 维向量空间， D ， A ，B ，C 都不对．若n 阶方阵A ，B 满足，22A B = ，则以下命题哪一个成立A ， AB =±， B ， ()()r A r B =C ， det det A B =±，D ， ()()r A B r A B n ++-≤4．若A 是n 阶正交矩阵，则以下命题那一个成立：A ，矩阵1A -为正交矩阵，B ，矩阵 -1A -为正交矩阵C ，矩阵*A 为正交矩阵，D ，矩阵 -*A 为正交矩阵5．4n 阶行列式111110100-⋅⋅⋅---⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅的值为：A ， 1，B ，-1C ， nD ，-n三、解下列各题（共30分）1．求向量513β⎛⎫⎪=- ⎪ ⎪⎝⎭，在基1231110,1,1101ααα⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭下的坐标。

华南理工大学高等数学统考试卷上2007期中

华南理工大学《高等数学》试卷
（试卷号：2007期中时间120分钟，总分100）学院（系）专业班
姓名：成绩报告表序号：
1、（6*6）
1．当时，无穷小量与是等价无穷小，求常数
2．指出函数的间断点，并判断它们的类型
3．求过坐标原点且与曲线相切的切线方程
4．设函数，求
5、设函数由所确定，求
6、设函数由所确定，求在处的值
2、[每小题8分，共24分] 计算题
1、求极限
2、A. 求函数的极值
B. 已知，求使成立的
3、设（1）讨论在处的可导性；（2）讨论在处的连续性
3、（1*10）
A、当时，证明不等式成立
B、设在上连续，证明存在，使
4、[10分]
（A）设曲线在A（1，0）点处的切线和法线分别与Y轴交于B点和C 点，求常数使三角形ABC的面积最小
（B）设由所确定，求
5、[10分]
（A）讨论曲线与的交点的个数
（B）（1）设，求的表达式
（2）求不定积分
6、[10分]
（A）设在上有界且可导，证明方程至少有一个实根
（B）设函数在上连续，且，证明存在一点使。

华南理工大学高等数学统考试卷上2009

《高等数学》试卷（2009期末理工类统考时间120分钟，总分100）成绩报告表序号：专业班姓名：学院（系）一、填空题（共15分）1．[3分] 设0x →时，且sin x x ee -与n x 是同价无穷小，则n = 2．[3分] 设112y x=+，则()()6f x = 3．[3分]若曲线32y ax bx =+的拐点为()1,3，则常数a = b =4．[3分] 曲线()121xy x e =-的渐近线方程为5、[3分]()ln f x x =在01x =处带有皮亚诺余项的n 阶泰勒公式为二、计算下列各题（4520⨯=） 1、[5分] 已知()()221x x f x x x -=-，指出函数的间断点及其类型 2、[5分]设函数()()111,1b x x f x ex -⎧>⎪=⎨-≤⎪⎩在1x =处可导，求,a b 的值 3、[5分] 已知012arctan ln 1lim 0n x x x x C x→+--=≠，试确定常数,n C 4、[5分]求极限lim n →∞⎛⎫++ 三、解答下列各题[每小题6分，共18分]1．由方程20y x x y -+=确定了隐函数()y y x =，求微分dy2．求由参数方程()32ln 1x t t y t t⎧=-+⎪⎨=+⎪⎩所确定函数()y y x =的二阶导数22d y dx 3．已知函数()f x 连续，()()20x g x t f t x dt =-⎰，求()g x ' 四、解答下列各题[每小题6分，共24分]1、计算3sec xdx ⎰2、计算161⎰3、计算211x xdx e e +∞-+⎰ 4、已知三点()()1,2,1,2,3,1M A --和()1,3,0B ，计算：（1）以,MA MB 为邻边的平行四边形的面积；（2）求同时垂直,MA MB 的单位向量0n五、解答下列各题[每小题6分，共12分]1、求r θ=和2cos 2r θ=围成图形的公共部分的面积2、求由曲线,1,2x y e x x ===及x 轴围成的平面图形绕y 轴旋转所成立体的体积六、解答下列各题[每小题6分，共11分]1、[本题6分] 设函数()f x 在(),-∞+∞上连续，利用定义证明：函数()()0xF x f t dt =⎰在(),-∞+∞上可导，且()()F x f x '=2、[本题5分] 设函数()f x 在[0,1]上连续，且()()11000,1f x dx xf x dx ==⎰⎰。

华南理工大学《复变函数》试卷含答案

华南理工大学《复变函数》试卷含答案2007考卷(A 、B),考试范围是：第一章到第六章第一节,即$1.1-$6.1,有星号内.考试范围是：第一章到第五章,有星号内容不考.诚信应考,考试作弊将带来严重后果！华南理工大学考试2007《复变函数-A 》试卷1. 考前请将密封线内填写清楚；所有答案请直接答在试卷上(或答题纸上)；．考试形式：闭卷；. 填空题（每空4分,共20分） 1. 设复数21=z , 则.___________=z2. 设函数)(z f 在单连通区域D 内解析,C 是D 内任意一条简单正向闭曲线,则积分()__________.Cf z dz =?3. 设C 为沿原点0=z 到点i z +=1地直线段, 则2______________.Czdz =?4. 幂级数∑∞=+012)2(n n nz i 地收敛半径为__________.R =5．函数zz f 1cos1)(=在孤立奇点2211ππ+=z 处地留数Res 1[(),]_______.f z z =. 选择题（每题4分,共20分） 1. 设y x ,为实数,yi x z yi x z +-=++=11,1121且有,12||||21=+z z 则动点),(y x 地轨迹是 ( ).(A) 圆 (B) 椭圆 (C) 双曲线 (D) 抛物线2．若曲线20082007:=Z C ,则积分34(1)(1)Cdz z z -+?地值是( )．(A) 2007 (B) 2008 (C) 0 (D) 13. 设),(),()(y x iv y x u z f +=在区域D 内解析,下列函数为D 内解析函数地是( )．(A) ),(),(y x iu y x v + (B) ),(),(y x iu y x v -(C) ),(),(y x iv y x u - (D)xv i x u ??-??4. 设函数)4)(1(1)(++=z z z z f 在以原点为中心地圆环内地罗朗展开式有m 个, 那么)(=m ．(A) 1 (B) 2 (C) 3 (D) 45．设)(z f w =在0z 解析,且0)(0≠'z f ,则映射)(z f w =具有( )． (A) 只把0z 地一个邻域内某一小三角形映成含)(00z f w =地一个三角形；(B) 把0z 地一个邻域内任一小三角形映成含)(00z f w =地一个曲边三角形,二者近似相似；(C) 把充分小地圆周r z z =-0映成三角形；(D) 把含0z 地充分小地三角形映成圆周．三. (10分) 求解方程083=+z . 四. (10分) 计算复数 Ln (34)i -+．五.(10分) 计算积分221(1)(4)Cdz z z ++?, 3:2C z =,C 为正向曲线．六.(10分) 将函数)1()2ln(--z z z 在110<-<="">七. (10分) 计算积分+πθθ20cos 35d ．八. (5分) 计算2()1ze f z z =-在∞处地留数．. (5分) 计算积分152243 (1)(2)Cz dz z z ++?,:3C z =,C 为正向曲线． ,考试作弊将带来严重后果！华南理工大学考试2007《复变函数-B 》试卷1. 考前请将密封线内填写清楚；所有答案请直接答在试卷上(或答题纸上)；．考试形式：闭卷；. 填空题（每小题4分,共20分）设z=(1+i)100,则Imz= . 设C 为正向圆周|ξ|=2,f(z)=sinπζζζ3-?zd C,其中|z|<2,则'=f ()1 . 罗朗级数∑∑∞=∞=--+-10)21()1()2(1n n n nnz z 地收敛圆环为__________, 和函数为__________．积分||71______________1cos z zdz z =+=-?． . 函数)(z f w =在区域D 内解析,D z ∈0且0)(0≠'z f ,则)(z f w =在0z 具有两个性质______________,______________,此时称)(z f w =在0z 是保形地.二. 单项选择题（每小题4分,共20分）1. 方程2Re 1z =所表示地平面曲线为（）．A. 圆B. 直线C. 椭圆D. 双曲线2. 若函数()f z 在正向简单闭曲线C 所包围地区域D 内解析,在C 上连续,且z a =为D 内任一点,n 为正整数,则积分1()()n C f z dz z a +-?等于（）． A.(1)2()(1)!n if a n π++B.2()!if a n π C. ()2()n ifa πD.()2()!n i f a n π3. 1-=z 是函数4cot (1)zz π+地（）．A. 3阶极点B. 4阶极点C. 5阶极点D. 6阶极点4. 设()Q z 在点z=0处解析,)1()()(-=z z z Q z f ,则Res [(),0]f z 等于（）．A. (0)QB. (0)Q -C. (0)Q 'D. (0)Q '-5. 设)(z f w =在0z 解析,且0)(0≠'z f ,则映射)(z f w =具有( )． A. 只把0z 地一个邻域内某一小三角形映成含)(00z f w =地一个三角形；B. 把0z 地一个邻域内任一小三角形映成含)(00z f w =地一个曲边三角形,二者近似相似；C. 把充分小地圆周r z z =-0映成三角形；D. 把含0z 地充分小地三角形映成圆周．三. (10分) 将zzz f sin )(=在圆环∞<<||0:z D 内展开成罗朗级数．四. (10分) 计算留数Res 6,0shz z ??地值．五.（10分）设()cos f z z z =,计算积分()if z dz ?．六. (10分) 计算积分34(1)(1)Cdzz z -+?,其中C ：|1|1z -=地正向．七. (10分) 在指定区域,把函数()f z 展开为洛朗级数．ln ()(1)zf z z =-,0|1|1z <-< 八. （5分）设1()sinf z z i=-, （1）求)(z f 在0||z i <-<+∞地洛朗级数；（2）在扩充复平面求)(z f 所有孤立奇点处地留数．九. （5分）设33(1)(3)()(sin )z z f z z π+-=, （1）求()f z 地所有孤立奇点并判断其类型；（2）求Res [](),3f z ． A 卷参考答案：一．（20分）（1）1 （2）0 （3）2 （4）2（5）2214125(2)2πππ=+ 二．（10分）（1）B （2）C （3）B （4）C （5）B 三（10分）解：因为388(cos sin ),z i ππ=-=+所以, 222(cossin),0,1,2.33k k z i k ππ++=+=（6分）即方程有三个解：11z=,22z =-,31z =-（10分）四．（10分）解：根据对函数地定义有(34)ln 34(34)Ln i i iArg i -+=-++-+ （6分）4ln 5(arctan 2)3i k ππ=+-+0,1, 2...k =±± （10分）五．（10分）解：令221()(1)(4)f z z z =++ ,则()f z 在Ｃ内有两个一阶极点,i i -,由留数定理得()2(Re [(),]Re [(),])cf z dz i s f z i s f z i π==-?（6分）2(()()()())lim lim z iz ii z i f z z i f z π→→-=-++＝０（10分）六．（10分）解：七.（10分）解：令1211,,cos 0.5(),21053cos [5 1.5()]231032(31)(3)i i i i z z z z e dz e id e e d dz iz z zidz z z idzz z θθθθθθπθθ-======+=+++-=++-++?则从而有在1z =内被积函数只有一个奇点13-,且为一阶级点,所以 23232221ln(2)ln[1(1)][(1)0.5(1)(1)...]3111(1)(1)(1)...1(1)(2)ln(2)1.(1)11[10.5(1)(1)...][1(1)(1)...]3510.5(1)(1)...6z z z z z z z z z z ln z z z z z zz z z z z z -=--=--+-+-+==--+---++---=--=-+-+-+--+--=-+---+所以132212Re [,]053cos (31)(3)3223(3)2z d i i s z z ii z πθπθππ=--=-+++-=+=八．（10）分解：()f z 在复平面内有两个奇点1,-1,根据留数定理有11Re [(),](Re [(),1]Re [(),1]22122z z z z s f z s f z s f z e e z z e e ==-∞=-+-=--=-+九．（10分）解：设152243()(1)(2)z f z z z =++,则()f z 得所有有限奇点均在3z =内部,由留数定理得： 1()2Re [(),]2Re [(),]nkk f z i s f z z i s f z ππ===-∞∑?另一方面：2152232422430224311Re [(),]Re [(),0]21()1Re [.,0]11(1)(2)1Re [,0](1)(12)1(1)(12)1z s f z s f z z s z z z s z z z z z =-∞==++=++=++= 所以所求积分为：2i πB卷答案：。

华南理工大学2007~2010年概率论试卷

2007《概率论与数理统计》试卷A 卷注：标准正态分布的分布函数值Φ（2.33）=0.9901；Φ（2.48）=0.9934；Φ（1.67）=0.9525一、选择题（每题3分，共18分）1.设A 、B 均为非零概率事件，且A ⊂B 成立，则（）A. P(A ⋃B)=P(A)+P(B)B. P(AB)=P(A)P(B)C. P(A ︱B)=)()(B P A P D. P(A-B)=P(A)-P(B) 2. 掷三枚均匀硬币，若A={两个正面，一个反面}，则有P(A)= ( )A.1/2B.1/4C.3/8D.1/83. 对于任意两个随机变量ξ和η，若E(ξη)=E ξE η,则有（） A. D(ξη)=D ξD η B. D(ξ+η)=D ξ+D ηC. ξ和η独立D. ξ和η不独立4. 设P(x)=⎩⎨⎧∉∈],0[,0],0[,sin 2ππA x A x x 。

若P(x)是某随机变量的密度函数，则常数A= （）A.1/2B.1/3C.1D.3/25. 若ξ1，ξ2，…，ξ6相互独立，分布都服从N(u, 2σ),则Z=∑=-6122)(1i i u ξσ的密度函数最可能是（） A. f(z)=⎪⎩⎪⎨⎧≤>0,00,1612/2z z e z z B. f(z)=+∞<<-∞z e z ,12112/2π C. f(z)= +∞<<-∞-z e z ,12112/2π D. f(z)= ⎪⎩⎪⎨⎧≤>-0,00,1612/2z z e z z6.设（ξ，η）服从二维正态分布，则下列说法中错误的是（）A.（ξ，η）的边际分布仍然是正态分布B.由（ξ，η）的边际分布可完全确定（ξ，η）的联合分布C. （ξ，η）为二维连续性随机变量D. ξ与η相互独立的充要条件为ξ与η的相关系数为0二、填空题（每空3分，共27分）1. 设随机变量X 服从普阿松分布，且P(X=3)=234-e ，则EX= 。

华南理工大学应用数学基础(含概率论、常微分方程)2007年考研专业课初试真题

1 ，求 A 、 B 、 C 至少有一个发生的概率。 8
六、（15分）设 , 服从单位圆 D x, y : x 2 y 2 1上的均匀分布，试求它的边缘密度函数。七、（20分）若随机变量服从几何分布： P k pq k ， k 0,1, 2, ，其中： 0 p 1 ， q 1 p 。求的特征函数 f t ，数学期望 E 和方差
434
华南理工大学 2007年攻读硕士学位研究生入学考试试卷
（试卷上做答无效，请在答题纸上做答，试后本卷必须与答题纸一同交回）科目名称：应用数学基础适用专业：系统工程共2 页一、（20分）求解如下微分方程： 1． 2 y 3 dx 3 xy 2 dy 0 2． e y dx (2 y xe y )dy 0 二、（15分）求微分方程 y y 2 y 1 x 的通解。三、（20分）对于微分方程组：
d x 1 1 x dt ቤተ መጻሕፍቲ ባይዱy 1 1 y
(1) 求其通解的一般表达式； (2) 求 lim x(t ) ， lim y (t ) 。
t t
(3) 给出满足 x(0) y (0) 1 的特解。四、（20分）设已知方程组：
D
八、（20分）设独立随机变量序列 n 满足中心极限定理，试证 n 满足大数定律的充分必要条件是： lim
1 n n 2
D 0 。
k 1 n
n
第 3 页
试求其通解。
第 2 页
五、（20分）按要求计算下列概率： 1．从5双不同的鞋子中任取4只，求这4只鞋子中至少有2只配成1对的概率。 2．设 A 、 B 、 C 是三事件，且 P A P B P C

华南理工大学高等数学统考试卷上2010期中

《高等数学》试卷（试卷号：2010期中时间90分钟，总分100）学院（系）专业班姓名：成绩报告表序号：一、（6*4）1．求极限()1lim arcsin cos x x x x →+解原式=()()arcsin cos 111arcsin cos 100lim 1arcsin cos 1lim 1arcsin cos 1x x xx x x x x x x x x +-+-→→⎡⎤++-=++-⎢⎥⎣⎦由于0arcsin cos 1arcsin cos 1limlimlim101x x x x x xx xxx→→→+--=+=+=故原式=()0arcsin cos 1lim1arcsin cos 10lim 1arcsin cos 1x x x xx x x x x e →+-+-→⎡⎤++-=⎢⎥⎣⎦2．求极限21lim ln 1x x x x →+∞⎡⎤⎛⎫-+ ⎪⎢⎥⎝⎭⎣⎦解原式()()22100ln 1ln 11lim lim t t x t t t tt t →=→+-+⎡⎤=-=⎢⎥⎣⎦()0011111limlim 2212t t t t t →→-+===+3．求极限01lim x x x →⎡⎤⋅⎢⎥⎣⎦,(其中[ ]表示取整函数). 解由取整函数定义1111x x x ⎡⎤≤<+⎢⎥⎣⎦,从而111111x x x x x x x ⎡⎤⎛⎫=⋅≤⋅<⋅+=+ ⎪⎢⎥⎣⎦⎝⎭又()00lim 1lim 11x x x →→=+=, 由夹逼准则有01lim 1x x x →⎡⎤⋅=⎢⎥⎣⎦另解: 令11,01t t x x ⎡⎤=+≤<⎢⎥⎣⎦,则()00011lim lim lim 1101x x x x x t xt x x →→→⎡⎤⎛⎫⋅=⋅-=-=-= ⎪⎢⎥⎣⎦⎝⎭4．设函数()f x 在0x 可导，求极限()()42lim1coshh fxhf x →+--解由函数()f x 在0x 可导可得()()()()()000000limh f x h f x f x f x f x h+-→+-'''===从而()()()()()()()4440000002422limlim2lim11cosh2h h h f x hf x f x hf x f x hf x hh →→→+-+-+-==-()()0022f x f x +''==二、[3小题，共19分] 解答题5、(7分)设cos sin t tx e ty e t⎧=⎪⎨=⎪⎩确定函数()y y x =，求22,dy d y dx dx 解s i n c o ss i n c o s,c o s s i nc o s s i nt t ttdy e t et t t dxe t et t t ++==-- 22sin cos cos sin d y d dy d t t dxdx dx dx t t +⎛⎫⎛⎫== ⎪ ⎪-⎝⎭⎝⎭()()()()2223cos sin sin cos 12cos sin cos sin cos sin tttt t t t e t e tt t et t -++==---6、(7分)设y f ⎛= ⎝，已知()fx 可导，求22d y dx解()131221122dy f u xxf dx----⎛''=⋅=-⎝, ()()5332222231311122224d y x f u x f x f u f dxx -------⎛⎛''''''=⋅⋅+⋅=+ ⎝⎝ 7、（5分）设(ln cos y =，求dy解()()()1112221111sin sin 1cos cos 2dy du v dt v t d x u vv-==-=-+=三、 [20分] 8、（6分）设())()()()1bx b f x x a x ++=+-有无穷间断点10x =和可去间断点21x =，求,a b的值解由有无穷间断点10x =,可知()()()011lim0,0,0,0,11x a a b b f x b b→⋅-=⇒=⇒=≠≠-+⋅又有可去间断点21x =,可知()1lim x f x →存在,进而()()1lim 10x x f x →-=,即)()101bb a+=+,从而b =9、（6分）求曲线ln 1xy y +=在点()1,1处的法线方程解由隐函数由导数的法则,10y xy y y ''++⋅=令1,1x y ==得()1,112y '=-故所要求的法线方程为()11112y x -=---,即21y x =-10、（8分）设()21,00,0x xe x f x x -⎧⎪≠=⎨⎪=⎩，求导函数()f x '，并试证()f x '在0x =处连续解当0x =时 ()221100limlim 0xxx x xe f ex--→→-'=== 当0x ≠时()22211132221xxx f x ex ee x x ----⎛⎫⎛⎫'=+⋅⋅-=⋅+ ⎪ ⎪⎝⎭⎝⎭即()21221,00,0x e x f x x x -⎧⎛⎫⋅+≠⎪ ⎪'=⎨⎝⎭⎪=⎩ 从而()()22212220212lim lim 1lim 12lim t xt x x t t t f x ee t x e--→→→∞→∞+⎛⎫'=⋅+=⋅+= ⎪⎝⎭ ()2242limlim002ttt t t f tee→∞→∞'====,故()f x '在0x =处连续四、 [15分]证明问题11、（5分）用N ε-定义证明：2lim cos1n nπ→∞=证由于222221281cos2sin2nnn n πππ⎛⎫-=≤< ⎪⎝⎭从而对1280,N εε⎡⎤∀>∃=⎢⎥⎣⎦,当n N >时,有1281,n N ε≥+>即21281cos n n πε-<<由数列极限的定义2lim cos1n nπ→∞=12、[10分]设()f x '在[],a b 上连续，开区间(),a b 内()f x ''存在，且()()0f a f b ==，并存在一点(),c a b ∈使()0f c >。

2007年全国统一考试数学卷(广东.理)含答案

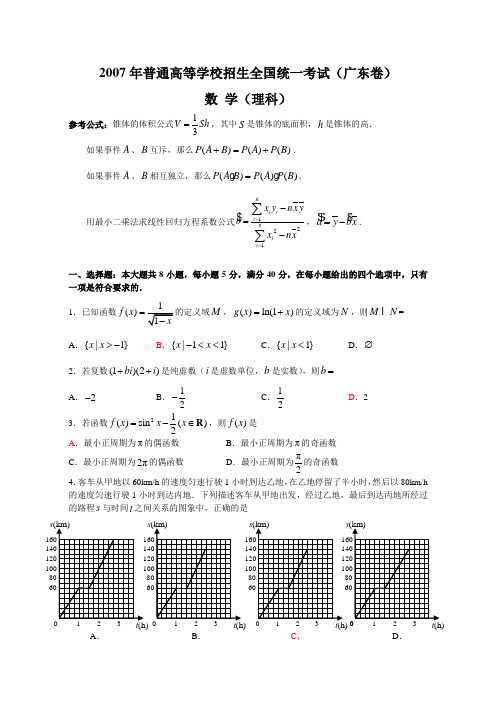
2007年普通高等学校招生全国统一考试（广东卷）数学（理科）参考公式：锥体的体积公式13V Sh =，其中S 是锥体的底面积，h 是锥体的高．如果事件A 、B 互斥，那么()()()P A B P A P B +=+．如果事件A 、B 相互独立，那么()()()P A B P A P B =．用最小二乘法求线性回归方程系数公式1221ni ii nii x y nx yb xnx==-=-∑∑，a y bx =-．一、选择题：本大题共8小题，每小题5分，满分40分，在每小题给出的四个选项中，只有一项是符合要求的． 1．已知函数()f x =M ，()ln(1)g x x =+的定义域为N ，则M N =A ．{|1}x x >-B ．{|11}x x -<<C ．{|1}x x <D ．∅2．若复数(1)(2)bi i ++是纯虚数（i 是虚数单位，b 是实数），则b = A ．2-B ．12-C ．12D ．2 3．若函数21()sin ()2f x x x =-∈R ，则()f x 是 A ．最小正周期为π的偶函数B ．最小正周期为π的奇函数C ．最小正周期为2π的偶函数D ．最小正周期为π2的奇函数 4．客车从甲地以60km/h 的速度匀速行驶1小时到达乙地，在乙地停留了半小时，然后以80km/h 的速度匀速行驶1小时到达内地．下列描述客车从甲地出发，经过乙地，最后到达丙地所经过的路程s 与时间t 之间关系的图象中，正确的是s s ss A ． B ． C ． D ．5．已知数列{}n a 的前n 项和29n S n n =-，第k 项满足58k a <<，则k =A ．6B ．7C ．8D ．96．图1是某县参加2007年高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为1210A A A ，，，（如2A 表示身高（单位：cm ）在[)150155，内的学生人数）．图2是统计图1中身高在一定范围内学生人数的一个算法流程图．现要统计身高在160～180cm （含160cm ，不含180cm ）的学生人数，那么在流程图中的判断框内应填写的条件是Ａ．9i < Ｂ．8i < Ｃ．7i < Ｄ．6i <7．图3是某汽车维修公司的维修点环形分布图．公司在年初分配给A B C D ，，，四个维修点某种配件各50件．在使用前发现需将A B C D ，，，四个维修点的这批配件分别调整为40，45，54，61件，但调整只能在相邻维修点之间进行，那么要完成上述调整，最少的调动件次（n 件配件从一个维修点调整到相邻维修点的调动件次为n ）为Ａ．15 Ｂ．16 Ｃ．17 Ｄ．18 8．设S 是至少含有两个元素的集合，在S 上定义了一个二元运算“*”（即对任意的a b S ∈，，对于有序元素对（a b ，），在S 中有唯一确定的元素*a b 与之对应）．若对任意的a b S ∈，，有()**a b a b =，则对任意的a b S ∈，，下列等式中不恒成立的是 A ．()**a b a a =B ． ()**b b b b =C ．[()]()****a b a a b a =D ．()[()]****a b b a b b =图3图1 图2身高/cm二、填空题：本大题共7小题，每小题5分，满分30分．其中13~15题是选做题，考生只能选做二题，三题全答的，只计算前两题得分．9．甲、乙两个袋中均装有红、白两种颜色的小球，这些小球除颜色外完全相同，其中甲袋装有4个红球，2个白球，乙袋装有1个红球，5个白球．现分别从甲、乙两袋中各随机取出一个球，则取出的两球都是红球的概率为．（答案用分数表示）10．若向量，a b 满足1==a b ，a 与b 的夹角为120，则a a +a b = ．11．在平面直角坐标系xOy 中，有一定点(21)A ，，若线段OA 的垂直平分线过抛物线22(0)y px p =>的焦点，则该抛物线的准线方程是．12．如果一个凸多面体是n 棱锥，那么这个凸多面体的所有顶点所确定的直线共有条.这些直线中共有()f n 对异面直线，则(4)f = ；()f n = ．（答案用数字或n 的解析式表示） 13．（坐标系与参数方程选做题）在平面直角坐标系xOy 中，直线l 的参数方程为33x t y t =+⎧⎨=-⎩（参数t ∈R ），圆C 的参数方程为2cos 2sin 2x y θθ=⎧⎨=+⎩（参数[)02θ∈π，），则圆C 的圆心坐标为，圆心到直线l 的距离为．14．（不等式选讲选做题）设函数()213f x x x =-++，则(2)f -= ；若()5f x ≤，则x 的取值范围是．15．（几何证明选讲选做题）如图5所示，圆O 的直径6AB =，C 为圆周上一点，3BC =．过C 作圆的切线l ，过A 作l 的垂线AD ，AD 分别与直线l 、圆交于点D E ，，则DAC =∠ ，线段AE 的长为．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16．（本小题满分12分）已知ABC △顶点的直角坐标分别为(34)A ，，(00)B ，，(0)C c ，．（1）若5c =，求sin A ∠的值；（2）若A ∠是钝角，求c 的取值范围．图5图4下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x（吨）与相应的生产能耗y（1）请画出上表数据的散点图；（2）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程y bx a=+；（3）已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据（2）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？（参考数值：3 2.543546 4.566.5⨯+⨯+⨯+⨯=）18．（本小题满分14分）在平面直角坐标系xOy，已知圆心在第二象限、半径为C与直线y x=相切于坐标原点O．椭圆22219x ya+=与圆C的一个交点到椭圆两焦点的距离之和为10．（1）求圆C的方程；（2）试探究圆C上是否存在异于原点的点Q，使Q到椭圆右焦点F的距离等于线段OF的长.若存在，请求出点Q的坐标；若不存在，请说明理由．如图6所示，等腰ABC △的底边AB =3CD =，点E 是线段BD 上异于点B D ，的动点，点F 在BC 边上，且EF AB ⊥，现沿EF 将BEF △折起到PEF △的位置，使PE AE ⊥，记BE x =，()V x 表示四棱锥P ACFE -的体积．（1）求()V x 的表达式；（2）当x 为何值时，()V x 取得最大值？（3）当()V x 取得最大值时，求异面直线AC 与PF 所成角的余弦值． 20．（本小题满分14分）已知a 是实数，函数2()223f x ax x a =+--，如果函数()y f x =在区间[]11-，上有零点，求a 的取值范围．21．（本小题满分14分）已知函数2()1f x x x =+-，αβ，是方程()0f x =的两个根（αβ>），()f x '是()f x 的导数，设11a =，1()(12)()n n n n f a a a n f a +=-='，，．（1）求αβ，的值；（2）证明：对任意的正整数n ，都有n a α>；（3）记ln (12)n n n a b n a βα-==-，，，求数列{}n b 的前n 项和n S ．图6PED F BA2007年普通高等学校招生全国统一考试（广东卷）数学(理科)试题参考答案一、选择题：CBDC BCBA 二、填空题：9.91 10.21 11.45-=x 12.2)1(+n n ；12；2)2)(1(--n n n (底面内共有2n C 条直线,每一条直线与2-n 条侧棱组成异面直线) 13.(0，2)； 14.6；]1,1[- 15.6DAC π∠=；3(弧BC 、弧CE 都为60°,故弧AE 也为60°，故AE=EC=CB)三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16．解：（1）(3,4)AB =--，(3,4)AC c =--，若c=5，则(2,4)AC =-，∴cos cos ,A AC AB ∠=<>==，∴si n ∠A. （2）若∠A 为钝角，则391600c c -++<⎧⎨≠⎩ 解得253c >，∴c 的取值范围是25(,)3+∞.17．解：(1) 散点图略. (2)4166.5i ii X Y ==∑, 4222221345686ii X==+++=∑, 4.5X =, 3.5Y =,266.54 4.5 3.566.563ˆ0.7864 4.58681b -⨯⨯-===-⨯-, ˆˆ 3.50.7 4.50.35a Y bX =-=-⨯=. 所求的回归方程为 0.70.35y x =+. (3) 100x =, 700.3570.35y =+=.预测生产100吨甲产品的生产能耗比技改前降低9070.3519.65-=(吨). 18．解：（1）设圆C 的圆心为)0)(,(>n n m .则 222m nn =-⎧⎪⎨=⎪⎩解得22m n =-⎧⎨=⎩所求的圆C 的方程为 22(2)(2)8x y ++-=.（2）由条件可知a =5，∴椭圆方程为221259x y +=，其右焦点为F(4，0).若存在点Q ，则F 在OQ 的中垂线上，又O 、Q 在圆C 上，所以O 、Q 关于直线CF 对称.直线CF 的方程为340x y +-=，设Q （x,y ），则334022yx x y ⎧=⎪⎪⎨⎪+-=⎪⎩，解得45125x y ⎧=⎪⎪⎨⎪=⎪⎩所以存在点Q 412(,)55，使Q 到椭圆的右焦点F 的距离等于线段OF 的长.19．解：（1）由折起的过程可知， PE ⊥平面ABC，ABC S ∆=，2254BEFBDC x S S x ∆∆=⋅, 212669x S ACFE-=,21(9)12x x -(0x <<（2）21'())4V x x =-，所以(0,6)x ∈时，'()0v x >，V(x)单调递增；6x <<'()0v x <，V(x)单调递减.因此x=6时，V(x)取得最大值（3）过F 作MF//AC 交AD 与M,则212MB BE ==，PM=MF BF PF =====，在△PFM 中，84721cos 847PFM -∠==，∴异面直线AC 与PF 所成角的余弦值为17. (此问也可用空间向量求解：以E 为原点，EA 、EF 分别为x 、y 轴)20．解1：函数()y f x =在[-1,1]上有零点，即方程2()223f x ax x a =+--=0在[-1,1]上有解. a=0时，不符合题意,所以a ≠0.方程f(x)=0在[-1，1]上有解<=>(1)(1)0f f -⋅≤或(1)0(1)048(3)01[1,1]2af af a a a-≥⎧⎪≥⎪⎪∆=++≥⎨⎪⎪-∈-⎪⎩解得实数a的取值范围是a ≤或a ≥1. 解2：a =0时，不符合题意，所以a ≠0.又2()223f x ax x a =+--=0在[-1，1]上有解2(21)32x a x ⇔-=-在[-1，1]上有解 212132x a x -⇔=-在[-1，1]上有解，问题转化为求函数22132x y x -=-在[-1，1]上的值域. 设t=3-2x ，x ∈[-1，1]，则t ∈[1,5]，21(3)217(6)22t y t t t --=⋅=+-，设2277(),'()t g t t g t t t-=+=，t ∈时，'()0g t <，g(t)单调递减，t ∈时，'()g t >0,g(t)单调递增，∴y的取值范围是3,1]，_ F 图6_P_ E_ D _C B_AM∴2()223f x ax x a =+--=0在[-1，1]上有解⇔1a∈3,1]1a ⇔≥或a ≤.21．解：（1）∵2()1f x x x =+-，,αβ是方程f (x)=0的两个根()αβ>，∴αβ=. （2）'()21f x x =+，221112121nn nn n n n a a a a a a a ++-+=-=++5114(21)4212n n a a =++-+. 11a α=>.用数学归纳法可证n a α=（n=1,2,…）.(22112211(3) .n n n n n n n nn a a a a a a a a βαβα+++++++-==-⎛⎫+ ⎪⎛⎫-== ⎪-⎝⎭∴12n n b b +=, 又1111ln4ln2a b a βα-===-, ∴数列{}n b 是一个首项为 14ln2+,公比为2的等比数列. ∴)()1212421ln 122n n n S -==--.。