初一上册几何证明题(多篇)
七年级数学典型几何证明50题

七年级数学典型几何证明50题初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)A BC DEF 21 ADBC∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF, ∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF,可得,∠EFD=CGD DE =DC∠FDE=∠GDC(对顶角)∴△EFD≌△CGD EF =CG ∠CGD=∠EFD又,EF∥AB ∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC4、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CBA CDF2 1 EA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB ≌△CEF ∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180° ∴∠D =∠CFA ∵AC 平分∠BAD ∴∠DAC =∠FAC ∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE6、如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
初一几何证明题及答案

初一几何证明题及答案【篇一:七年级数学几何证明题(典型)】3.已知,如图,在△ abc中,ad,ae分别是△ abc的高和角平分线,若∠b=30dc4、一个零件的形状如图,按规定∠a=90o ,∠c=25o,∠b=25o,检验已量得∠bdc=150o,就判断这个零件不合格,运用三角形的有关知识说明零件不合格的理由。
db5、如图,已知df∥ac,∠c=∠d,你能否判断ce∥bd?试说明你的理由 aebc8、如图,ad⊥bc于d,eg⊥bc于g,∠e =∠1,求证ad平分∠bac。
e3gdc10、如图,将一副三角板叠放在一起,使直角的顶点重合于o,则∠aoc+∠dob11、如图,将两块直角三角尺的直角顶点c叠放在一起. (1)若∠dce=35,求∠acb的度数;(2)若∠acb=140,求∠dce的度数;(3)猜想:∠acb与∠dce有怎样的数量关系,并说明理由12、已知:直线ab与直线cd相交于点o,∠boc=45,(1)如图1,若eo⊥ab,求∠doe的度数;(2)如图2,若eo平分∠aoc,求∠doe的度数.13、已知?aob,p为oa上一点.(1)过点p画一条直线pq,使pq∥ob;(2)过点p画一条直线pm,使pm⊥oa交ob于点m;(3)若?aob?40?,则?pmo? ?adecodbad cob16、已知:线段ab=5cm,延长ab到c,使ac=7cm,在ab的反向延长线上取点d,使bd=4bc,设线段cd的中点为e,问线段ae 是线段cd的几分之一?【篇二:初中数学几何证明经典试题(含答案)】题(一)1、已知:如图,o是半圆的圆心,c、e是圆上的两点,cd⊥ab,ef⊥ab,eg⊥co.求证:cd=gf.(初二).如下图做gh⊥ab,连接eo。
由于gofe四点共圆,所以∠gfh=∠oeg, 即△ghf∽△oge,可得eogf=gogh=cocd,又co=eo,所以cd=gf得证。
eadofb2、已知:如图,p是正方形abcd内点,∠pad=∠pda=150.求证:△pbc是正三角形.(初二) a.如下图做gh⊥ab,连接eo。
初一上册几何证明题(精选多篇)

初一上册几何证明题(精选多篇)初一上册几何证明题 1.在三角形abc中,∠acb=90°,ac=bc,e是bc边上的一点,连接ae,过c作cf⊥ae于f,过b作bd⊥bc交cf 的延长线于d,试说明:ae=cd。
满意回答因为ae⊥cf,bd⊥bc所以∠afc=90°,∠dbc=90°又∠acb=90°,所以∠ace=∠dbc因为∠cae+∠aec=90°∠ecf+∠aec=90°所以∠cae=∠ecf又ac=bc所以△ace全等于△cbd所以ae=cd像这类题目,一般用全等较好做些2.如图所示,已知ad、bc相交于o,∠a=∠d,试说明∠c=∠b.解:证1:∠a=∠d=====>ab∥cd=====>∠c=∠b证2:△abo角和180=△cdo角和180∠a=∠d∠aob=∠d0c∴∠c=∠b证明:显然有:∠aob=∠cod又∠a=∠d,且三角形三个角的和等于180º∴一定有∠c=∠b.3.d是三角形abc的bc边上的点且cd=ab,角adb=角bad,ae是三角形abd 的中线,求证ac=2ae。
在直角三角形abc中,角c=90度,bd是角b的平分线,交ac于d,ce 垂直ab于e,交bd于o,过o作fg平行ab,交bc于f,交ac于g。
求证cd=ga。
延长ae至f,使ae=ef。
be=ed,对顶角。
证明abe全等于def。
=》ab=df,角b=角edf角adb=角bad=》ab=bd,cd=ab=》cd=df。
角ade=bad+b=adb+edf。
ad=ad=》三角形adf全等于adc=》ac=af=2ae。
题干中可能有笔误地方:第一题右边的e点应为c点,第二题求证的cd 不可能等于ga,是否是求证cd=fa或cd=co。
如上猜测准确,证法如下:第一题证明:设f是ab边上中点,连接ef角adb=角bad,则三角形abd为等腰三角形,ab=bd;∵ae是三角形abd的中线,f是ab边上中点。
初中几何证明题(精选多篇)

初中几何证明题(精选多篇)第一篇:初中几何证明题初中几何证明题己知m是△abc边bc上的中点,,d,e分别为ab,ac上的点,且dm⊥em。
求证:bd+ce≥de。
1.延长em至f,使mf=em,连bf.∵bm=cm,∠bmf=∠cme,∴△bfm≌△cem(sas),∴bf=ce,又dm⊥em,mf=em,∴de=df而∠dbf=∠abc+∠mbf=∠abc+∠acb<180°,∴bd+bf>df,∴bd+ce>de。
2.己知m是△abc边bc上的中点,,d,e分别为ab,ac上的点,且dm⊥em。
求证:bd+ce≥de如图过点c作ab的平行线,交dm的延长线于点f;连接ef因为cf//ab所以,∠b=∠fcm已知m为bc中点,所以bm=cm又,∠bmd=∠cmf所以,△bmd≌△cmf(asa)所以,bd=cf那么,bd+ce=cf+ce (1)且,dm=fm而,em⊥dm所以,em为线段df的中垂线所以,de=ef在△cef中,很明显有ce+cf>ef (2)所以,bd+ce>de当点d与点b重合,或者点e与点c重合时,仍然采用上述方法,可以得到bd+ce=de综上就有:bd+ce≥de。
3.证明因为∠dme=90°,∠bmd<90°,过m作∠bmd=∠fmd,则∠cme=∠fme。
截取bf=bc/2=bm=cm。
连结df,ef。
易证△bmd≌△fmd,△cme≌△fme所以bd=df,ce=ef。
在△dfe中,df+ef≥de,即bd+ce≥de。
当f点落在de时取等号。
另证延长em到f使mf=me,连结df,bf。
∵mb=mc,∠bmf=∠cme,∴△mbf≌△mce,∴bf=ce,df=de,在三角形bdf中,bd+bf≥df,即bd+ce≥de。
分析已知、求证与图形,探索证明的思路。
对于证明题,有三种思考方式:(1)正向思维。
七年级数学典型几何证明50题
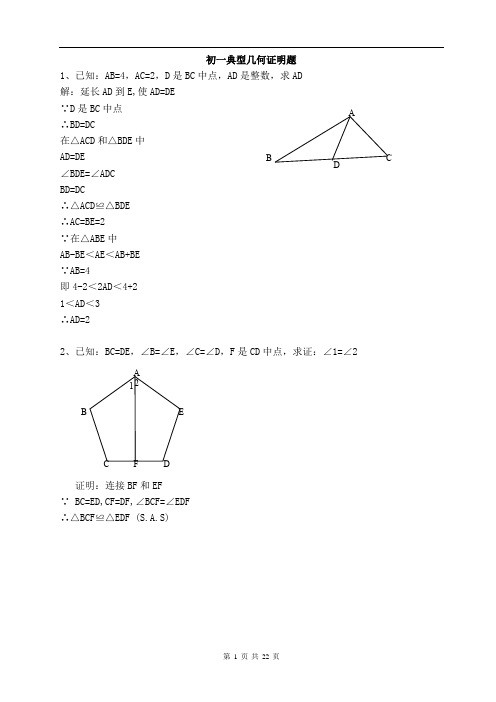
初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)ADBCA BC DEF 21∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF,可得,∠EFD=CGD DE =DC∠FDE=∠GDC(对顶角) ∴△EFD≌△CGD EF =CG ∠CGD=∠EFD 又,EF∥AB ∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC4、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CBA CDF2 1 EA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE6、如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
七年级上册几何证明题

七年级上册几何证明题引言在数学学科中,几何证明题是一种重要的题型。
通过解答几何证明题,不仅能够帮助学生提高对几何形状的理解,还能够培养学生的逻辑思维能力和推理能力。
本文将介绍七年级上册的一些典型的几何证明题,并提供相应的解答。
题目一:等腰三角形的性质证明题目描述:证明等腰三角形的两底角相等。
证明过程: 1. 假设三角形ABC是一个等腰三角形,其中AB=AC。
2. 根据等腰三角形的定义,我们知道AB=AC,即两边的长度相等。
3. 由于等腰三角形的两边相等,所以两个底角也一定相等。
4. 因此,我们可以得出结论:等腰三角形的两底角相等。
题目二:垂直线段的性质证明题目描述:证明垂直线段相互垂直。
证明过程: 1. 假设线段AB和线段CD是两条垂直线段。
2. 根据垂直线段的定义,我们知道线段AB和CD的斜率相乘等于-1。
3. 过点A和点C分别作AB所在直线和CD所在直线的垂线,设交点为E。
4. 根据直线的性质,垂直相交的两条直线所成的角度为90度,即角AED为直角。
5. 同理,过点B和点D分别作AB所在直线和CD所在直线的垂线,设交点为F。
6. 根据直线的性质,垂直相交的两条直线所成的角度为90度,即角BFD为直角。
7. 因此,我们可以得出结论:垂直线段相互垂直。
题目三:等边三角形的性质证明题目描述:证明等边三角形的三个内角都为60度。
证明过程: 1. 假设三角形ABC是一个等边三角形,其中AB=BC=AC。
2. 根据等边三角形的定义,我们知道AB=BC=AC,即三边的长度都相等。
3. 由于等边三角形的三边相等,所以三个角度也相等。
4. 假设角A的度数为x度,那么角B和角C的度数也分别为x度。
5. 根据角的性质,三个角的度数之和等于180度,所以x + x + x = 180。
6. 解以上方程,得到x = 60度。
7. 因此,我们可以得出结论:等边三角形的三个内角都为60度。
结论几何证明题是数学学科中的重要题型,通过解答这些题目,可以帮助学生加深对几何形状的理解。
初一几何证明题及答案

初一几何证明题及答案【篇一:七年级数学几何证明题(典型)】3.已知,如图,在△ abc中,ad,ae分别是△ abc的高和角平分线,若∠b=30dc4、一个零件的形状如图,按规定∠a=90o ,∠c=25o,∠b=25o,检验已量得∠bdc=150o,就判断这个零件不合格,运用三角形的有关知识说明零件不合格的理由。
db5、如图,已知df∥ac,∠c=∠d,你能否判断ce∥bd?试说明你的理由 aebc8、如图,ad⊥bc于d,eg⊥bc于g,∠e =∠1,求证ad平分∠bac。
e3gdc10、如图,将一副三角板叠放在一起,使直角的顶点重合于o,则∠aoc+∠dob11、如图,将两块直角三角尺的直角顶点c叠放在一起. (1)若∠dce=35,求∠acb的度数;(2)若∠acb=140,求∠dce的度数;(3)猜想:∠acb与∠dce有怎样的数量关系,并说明理由12、已知:直线ab与直线cd相交于点o,∠boc=45,(1)如图1,若eo⊥ab,求∠doe的度数;(2)如图2,若eo平分∠aoc,求∠doe的度数.13、已知?aob,p为oa上一点.(1)过点p画一条直线pq,使pq∥ob;(2)过点p画一条直线pm,使pm⊥oa交ob于点m;(3)若?aob?40?,则?pmo? ?adecodbad cob16、已知:线段ab=5cm,延长ab到c,使ac=7cm,在ab的反向延长线上取点d,使bd=4bc,设线段cd的中点为e,问线段ae 是线段cd的几分之一?【篇二:初中数学几何证明经典试题(含答案)】题(一)1、已知:如图,o是半圆的圆心,c、e是圆上的两点,cd⊥ab,ef⊥ab,eg⊥co.求证:cd=gf.(初二).如下图做gh⊥ab,连接eo。
由于gofe四点共圆,所以∠gfh=∠oeg, 即△ghf∽△oge,可得eogf=gogh=cocd,又co=eo,所以cd=gf得证。
eadofb2、已知:如图,p是正方形abcd内点,∠pad=∠pda=150.求证:△pbc是正三角形.(初二) a.如下图做gh⊥ab,连接eo。
华师大版七年级数学上册立体几何证明专题

华师大版七年级数学上册立体几何证明专题简介本文档介绍了华师大版七年级数学上册立体几何证明专题。
立体几何是数学中的一个重要分支,主要研究空间中的图形和对象。
本文档将涵盖常见的立体几何证明题目和解题方法,帮助读者提高解题能力。
目录1. 证明题目一: 零件的组合2. 证明题目二: 三棱柱的表面积3. 证明题目三: 平行四边形棱台的体积4. 证明题目四: 正方体的表面积和体积证明题目一: 零件的组合这个题目要求证明一个图形由几个零件组合而成。
我们需要分析每个零件的特征和位置,然后通过证明每个零件的特征是相等的,进而得出整个图形的特征是相等的。
具体的证明步骤和思路将在文中详细解释。
证明题目二: 三棱柱的表面积这个题目要求证明一个三棱柱的表面积的公式。
我们可以通过拆解三棱柱为几个简单的平面图形,然后计算每个平面图形的面积,最后将它们相加得出整个三棱柱的表面积。
在文中,将详细解释这个证明过程。
证明题目三: 平行四边形棱台的体积这个题目要求证明一个平行四边形棱台的体积的公式。
我们可以将平行四边形棱台拆解为两个三棱柱和一个平行四边形棱台,然后分别计算它们的体积并相加得出整个平行四边形棱台的体积公式。
具体的证明过程将在文中详细解释。
证明题目四: 正方体的表面积和体积这个题目要求证明一个正方体的表面积和体积的公式。
我们可以通过拆解正方体为六个面,然后计算每个面的面积和体积,最后将它们相加得出整个正方体的表面积和体积。
在文中,将详细解释这个证明过程。
总结立体几何证明题目需要通过分析和推理,来得出图形特征或公式的证明过程。
通过理解每个题目的要求,我们可以运用合适的解题方法,来解决立体几何证明题目。
本文档提供了一些常见题目的证明方法,希望读者能够在学习立体几何的过程中有所帮助。
初一上册几何证明题(精选多篇)

初一上册几何证明题(精选多篇)第一篇:初一上册几何证明题初一上册几何证明题1.在三角形abc中,∠acb=90°,ac=bc,e是bc边上的一点,连接ae,过c作cf ⊥ae于f,过b作bd⊥bc交cf的延长线于d,试说明:ae=cd。
满意回答因为ae⊥cf,bd⊥bc所以∠afc=90°,∠dbc=90°又∠acb=90°,所以∠ace=∠dbc因为∠cae+∠aec=90°∠ecf+∠aec=90°所以∠cae=∠ecf又ac=bc所以△ace全等于△cbd(asa)所以ae=cd像这类题目,一般用全等较好做些2.如图所示,已知ad、bc相交于o,∠a=∠d,试说明∠c=∠b.解:证1:∠a=∠d=====>ab∥cd=====>∠c=∠b(内错角相等)证2:△abo内角和180=△cdo内角和180∠a=∠d∠aob=∠d0c∴∠c=∠b证明:显然有:∠aob=∠cod(两直线相交,对顶角相等)又∠a=∠d,且三角形三个内角的和等于180º∴一定有∠c=∠b.3.(1)d是三角形abc的bc边上的点且cd=ab,角adb=角bad,ae是三角形abd的中线,求证ac=2ae。
(2)在直角三角形abc中,角c=90度,bd是角b的平分线,交ac于d,ce垂直ab于e,交bd于o,过o作fg平行ab,交bc于f,交ac于g。
求证cd=ga。
延长ae至f,使ae=ef。
be=ed,对顶角。
证明abe全等于def。
=》ab=df,角b=角edf角adb=角bad=》ab=bd,cd=ab=》cd=df。
角ade=bad+b=adb+edf。
ad=ad=》三角形adf全等于adc=》ac=af=2ae。
题干中可能有笔误地方:第一题右边的e点应为c点,第二题求证的cd不可能等于ga,是否是求证cd=fa或cd=co。
初一几何证明题

初一几何证明题1.已知AB∥CD,∠1=∠2,证明:∠XXX∠XXX。
根据平行线内角相等的性质,可得∠1=∠2=∠XXX。
同时,因为AB∥CD,所以∠BEF+∠EFC=180°,即∠BEF=180°-∠XXX。
代入前面的等式,可得∠XXX∠XXX。
2.如图2,AB∥CD,∠3∶∠2=3∶1,求∠1的度数。
根据平行线内角相等的性质,可得∠1=180°-∠2.又因为∠3∶∠2=3∶1,所以∠3=3x,∠2=x。
代入前面的等式,可得∠1=180°-x。
因此,∠1+∠2+∠3=180°,即4x=180°,x=45°。
代入前面的等式,可得∠1=135°。
3.如图3,C在AB的延长线上,CE⊥AF于E,交FB于D,若∠F=40°,∠C=20°,求∠XXX的度数。
根据直角三角形的性质,可得∠CEA=90°。
又因为CE⊥AF,所以∠EAF=90°-∠F=50°。
根据三角形内角和为180°的性质,可得∠EFA=180°-∠F-∠EAF=90°。
因为AB∥CD,所以∠XXX∠EFA=90°。
4.如图4,EF∥AD,∠1=∠2,∠BAC=80°。
求证:∠AGD=100°。
因为EF∥AD,所以∠AGD=∠AGE。
又因为∠BAC=80°,所以∠XXX°-∠BAC/2=50°。
因为∠1=∠2,所以∠DGE=∠AGE=180°-∠1-∠GAC=50°。
因此,∠AGD=∠AGE=50°+∠DGE=100°。
5.如图5,B处在A处的南偏西57°的方向,C处在A处的南偏东15°方向,C处在B处的XXX°方向。
求∠C的度数。
根据题意,可画出如图6所示的图形。
(完整word版)七年级数学几何证明题
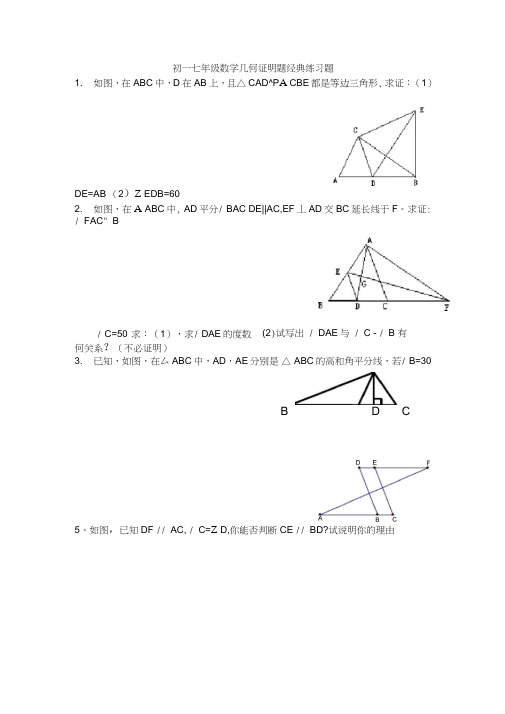
初一七年级数学几何证明题经典练习题1. 如图,在ABC 中,D 在AB 上,且△ CAD^P A CBE 都是等边三角形, 求证:(1)DE=AB (2)Z EDB=602. 如图,在A ABC 中, AD 平分/ BAC DE||AC,EF 丄AD 交BC 延长线于F 。
求证: / FAC " B3. 已知,如图,在厶ABC 中,AD ,AE 分别是 △ ABC 的高和角平分线,若/ B=30 B D C5、如图,已知DF // AC, / C=Z D,你能否判断CE // BD?试说明你的理由/ C=50°求:(1),求/ DAE 的度数 何关系?(不必证明)(2)试写出 / DAE 与 / C - / B 有6、如图,△ ABC中,D在BC的延长线上,过D作DE丄AB于E,交AC于F.已知/ A=30 ° ,Z FCD=80° ,求/D。
A87、如图,BE 平分/ ABD , CF 平分/ ACD , BE 、CF 交于 G , 若/ BDC = 140。
,/ BGC = 110。
,则 / A ?8、如图,AD 丄BC 于D , EG 丄BC 于G ,Z E =Z 1,求证 AD 平分/ BAC9、如图,直线。
丘交厶ABC 的边AB AC 于 D E,交BC 延长线于F , 若/ B = 67°,/ ACB= 74°,/ AED= 48°,求/ BDF 的度数•10、如图,将一副三角板叠放在一起,使直角的顶点重 合于O,贝U/ AOC / DOB11、如图,将两块直角三角尺的直角顶点C 叠放在一起 (1) 若/ DCE=3&求/ ACB 的度数;(2) 若/ ACB=140,求/ DCE 的度数; (3) 猜想:/ ACB 与/ DCE 有怎样的数量关系,并说明理由 AE12、已知:直线AB 与直线CD 相交于点O ,/ B0C= 45° ,(1) 如图1,若E0丄AB ,求/ D0E 的度数;(2) 如图2,若E0平分/ AOC ,求/ DOE 的度数.13、已知 AOB , P 为0A 上一点. (1)过点P 画一条直线PQ ,使PQ // 0B ;(2)过点P 画一条直线PM ,使PM 丄0A 交0B 于点M ;14、如图。
七年级数学典型几何证明50题

初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)ADBCA BC DEF 21∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF,可得,∠EFD=CGD DE =DC∠FDE=∠GDC(对顶角) ∴△EFD≌△CGD EF =CG ∠CGD=∠EFD 又,EF∥AB ∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC4、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CBA CDF2 1 EA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE6、如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
初中几何基础证明题初一
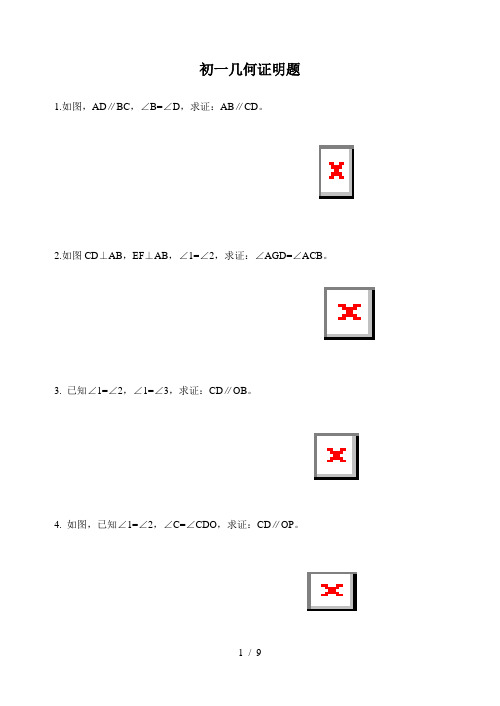
初一几何证明题1.如图,AD∥BC,∠B=∠D,求证:AB∥CD。
2.如图CD⊥AB,EF⊥AB,∠1=∠2,求证:∠AGD=∠ACB。
3. 已知∠1=∠2,∠1=∠3,求证:CD∥OB。
4. 如图,已知∠1=∠2,∠C=∠CDO,求证:CD∥OP。
5. 已知∠1=∠2,∠2=∠3,求证:CD∥EB。
6. 如图∠1=∠2,求证:∠3=∠4。
7. 已知∠A=∠E,FG∥DE,求证:∠CFG=∠B。
8.已知,如图,∠1=∠2,∠2+∠3=1800,求证:a∥b,c∥d。
9.如图,AC∥DE,DC∥EF,CD平分∠BCA,求证:EF平分∠BED。
10、已知,如图,∠1=450,∠2=1450,∠3=450,∠4=1350,求证:l1∥l2,l3∥l5,l2∥l4。
11、如图,∠1=∠2,∠3=∠4,∠E=900,求证:AB∥CD。
12、如图,∠A=2∠B,∠D=2∠C,求证:AB∥CD。
13、如图,EF∥GH,AB、AD、CB、CD是∠EAC、∠FAC、∠GCA、∠HCA平分线,求证:∠BAD=∠B=∠C=∠D。
14、已知,如图,B、E、C在同一直线上,∠A=∠DEC,∠D=∠BEA,∠A+∠D=900,求证:AE⊥DE,AB∥CD。
15、如图,已知,BE平分∠ABC,∠CBF=∠CFB=650,∠EDF=500,,求证:BC∥AE。
16、已知,∠D=900,∠1=∠2,EF⊥CD,求证:∠3=∠B。
17、如图,AB∥CD,∠1=∠2,∠B=∠3,AC∥DE,求证:AD∥BC。
对顶角相等:几何语言:∵∠1、∠2是对顶角∴∠1=∠2(对顶角相等)垂线:几何语言:正用反用:∵∠AOB=90°∵AB⊥CD∴AB⊥CD(垂直定义)∴∠AOB=90°(垂直定义)证明线平行方法:1、平行公理如果两条直线都与第三条直线平行,那么,这两条直线也平行。
简述为:平行于同一直线两直线平行。
几何语言叙述:如图:∵AB∥EF,CD∥EF∴AB∥CD(平行于同一直线两直线平行。
七年级数学证明题目5则范文

七年级数学证明题目5则范文第一篇:七年级数学证明题目七年级数学证明题目1、如图,EF//AD,∠1=∠2.说明:∠DGA+∠BAC=180°.请将说明过程填写完成.解:∵EF//AD,(已知)∴∠2=_____.(_____________________________).又∵∠1=∠2,(______)∴∠1=∠3,(________________________).∴AB//______,(____________________________)∴∠DGA+∠BAC=180°.(_____________________________)2、如图,AD为△ABC的中线,BE为△ABD的中线。
(8)(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;A3、在△ABC中,已知∠ABC=66°,∠ACB=54°,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,求∠ABE、∠ACF和∠BHC的度数.14、在△ABC中,∠A=(∠B+∠C)、∠B-∠C=20°,求∠A、∠B、∠C的度数。
25、如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=25°,∠CB=95°(1)求∠DCA的度数;(2)求∠DCE的度数。
6、如图所示,请填写下列证明中的推理依据证明:∵∠A=∠C (已知),∴AB∥CD(___________________)∴∠ABO=∠CDO (_________________________)又∵DF平分∠CDO,BE平分∠ABO(已知)1∴∠1=∠CDO,∠2=∠ABO(_________________________)2∴∠1=∠2,∴DF∥BE (_____________________________________________)7、如图∆ABC中,AD是BC上的中线,BE是∆ABD中AD边上的中线,若∆ABC的面积是24,则∆ABE的面积是__?B8、完成下列推理,并填写理由如图4,∵ ∠ACE=∠D(已知),∴∥().∴ ∠ACE=∠FEC(已知),∴∥().∵ ∠AEC=∠BOC(已知),∴∥().∵ ∠BFD+∠FOC=180°(已知),∴∥().AECD图49、已知,如图5,∠1+∠2=180°,∠3=108°,则∠4的度数是多少?10、如图6,AB∥CD,∠BAE=∠DCE=45°,求∠ED图411、如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数12、已知:AE平分△ABC的外角,且AE//BC,试判断∠B、∠C的大小关系,并说明理由13、已知:△ABC,射线BE、CF分别平分∠ABC和∠ACB,且BE、CF相交于点O。
初中数学的证明题(精选多篇)

初中数学的证明题(精选多篇)第一篇:初中数学的证明题初中数学的证明题在△abc中,ab=ac,d在ab上,e在ac的延长线上,且bd=ce,线段de交bc于点f,说明:df=ef。
对不起啊我不知道怎么把画的图弄上来所以可能麻烦大家了谢谢1.过d作dh∥ac交bc与h。
∵ab=ac,∴∠b=∠acb.∵dh∥ac,∴∠dhb=∠acb,∴∠b=∠dhb,∴db=dh.∵bd=ce,∴dh=ce.∵dh∥ac,∴∠hdf=∠fec.∵∠dfb=∠cfe,∴△dfh≌△efc,∴df=ef.2.证明:过e作eg∥ab交bc延长线于g则∠b=∠g又ab=ac有∠b=∠acb所以∠acb=∠g因∠acb=∠gce所以∠g=∠gce所以eg=ec因bd=ce所以bd=eg在△bdf和△gef中∠b=∠g,bd=ge,∠bfd=∠gfe则可视gef绕f旋转1800得△bdf故df=ef3.解:过e点作em∥ab,交bc的延长线于点m, 则∠b=∠bme,因为ab=ac,所以∠acb=∠bme因为∠acb=∠mce,所以∠mce=∠bme所以ec=em,因为bd=ec,所以bd=em在△bdf和△mef中∠b=∠bmebd=em∠bfd=∠mfe所以△bdf以点f为旋转中心,旋转180度后与△mef重合,所以df=ef4.已知:a、b、c是正数,且a>b。
求证:b/a要求至少用3种方法证明。
(1)a>b>0;c>01)(a+c)/(b+c)-a/b=/=(ab+ac-ab-bc}/(b^2+bc) =(ac-bc)/(b^2+bc)=c(a-b)/a>b--->a-b>0;a>0;b>0;c>0--->b(b+c)>0-->c(a-b)/>0--->(a+c)/(b+c)>a/b2)a>b>0;c>0--->bc---ab+bc--->a(b+c)--->a(b+c)/--->a/b<(a+c)/(b+c)3)a>b>0--->1/a<1/b;c>0--->c/a--->c/a+1--->(c+a)/a<(c+b)/b--->(a+c)/(b+c)>a/b(2)makeb/a=k<1b=kab+c=ka+c(b+c)/(a+c)=(ka+c)/(a+c)=(ka+kc-c)/(a+c)=k(a+c)/(a+c)-(k-1)c/(a+c)=k+(1-k)c/(a+c)>k=b/a。
七年级数学几何证明题(典型)

EDC BAEODCBA七年级数学几何证明题1.如图,在ABC 中,D 在AB 上,且ΔCAD 和ΔCBE 都是等边三角形, 求证:(1)DE=AB ,(2)∠EDB=60°2.如图,在ΔABC 中,AD 平分∠BAC ,DE||AC,EF ⊥AD 交BC 延长线于F 。
求证: ∠FAC=∠B3.已知,如图,在△ ABC 中,AD ,AE 分别是 △ ABC 的高和角平分线,若∠B=30∠C=50°求:(1),求∠DAE 的度数。
(2) 试写出 ∠DAE 与 ∠C - ∠B 有何关系?(不必证明) 4、一个零件的形状如图,按规定∠A=90o ,∠ C=25o,∠B=25o ,检验已量得∠BDC=150o ,就判断这个零件不合格,运用三角形的有关知识说明零件不合格的理由。
CDA B5、如图,已知DF ∥AC,∠C=∠D,你能否判断CE ∥BD?试说明你的理由6、如图,△ABC 中,D 在BC 的延长线上,过D 作DE ⊥AB 于E,交AC 于F. 已知∠A=30°,∠FCD=80°,求∠D 。
7、如图,BE 平分∠ABD ,CF 平分∠ACD ,BE 、CF 若∠BDC = 140°,∠BGC = 110°,则∠A ?8、如图,AD ⊥BC 于D ,EG ⊥BC 于G ,∠E =∠1,求证BAC 。
EB A 3219、如图,直线DE 交△ABC 的边AB 、AC 于D 、E ,交BC 延长线于F , 若∠B =67°,∠ACB =74°,∠AED =48°,求∠BDF 的度数. 10、如图,将一副三角板叠放在一起,使直角的顶点重合于O , 则∠AOC+∠DOB11、如图,将两块直角三角尺的直角顶点C 叠放在一起. (1)若∠DCE=350,求∠ACB 的度数; (2)若∠ACB=1400,求∠DCE 的度数;(3)猜想:∠ACB 与∠DCE 有怎样的数量关系,并说明理由 12、已知:直线AB 与直线CD 相交于点O ,∠BOC=45,(1)如图1,若EO ⊥AB ,求∠DOE 的度数; (2)如图2,若EO 平分∠AOC ,求∠DOE 的度数. 13、已知AOB ,P 为OA 上一点.(1)过点P 画一条直线PQ ,使PQ ∥OB ;(2)过点P 画一条直线PM ,使PM ⊥OA 交OB 于点M ;BA CD213FDCBH EG A(3)若︒=∠40AOB ,则=∠PMO ?14、如图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初一上册几何证明题初一上册几何证明题1.在三角形abc中,∠acb=90°,ac=bc,e是bc边上的一点,连接ae,过c作cf⊥ae于f,过b作bd⊥bc交cf的延长线于d,试说明:ae=cd。
满意回答因为ae⊥cf,bd⊥bc所以∠afc=90°,∠dbc=90°又∠acb=90°,所以∠ace=∠dbc因为∠cae+∠aec=90°∠ecf+∠aec=90°所以∠cae=∠ecf又ac=bc所以△ace全等于△cbd(asa)所以ae=cd像这类题目,一般用全等较好做些2.如图所示,已知ad、bc相交于o,∠a=∠d,试说明∠c=∠b.解:证1:∠a=∠d=====>ab∥cd=====>∠c=∠b(内错角相等)证2:△abo内角和180=△cdo内角和180∠a=∠d∠aob=∠d0c∴∠c=∠b证明:显然有:∠aob=∠cod(两直线相交,对顶角相等)又∠a=∠d,且三角形三个内角的和等于180º∴一定有∠c=∠b.3.(1)d是三角形abc的bc边上的点且cd=ab,角adb=角bad,ae是三角形abd的中线,求证ac=2ae。
(2)在直角三角形abc中,角c=90度,bd是角b的平分线,交ac 于d,ce垂直ab于e,交bd于o,过o作fg平行ab,交bc于f,交ac 于g。
求证cd=ga。
延长ae至f,使ae=ef。
be=ed,对顶角。
证明abe全等于def。
=》ab=df,角b=角edf角adb=角bad=》ab=bd,cd=ab=》cd=df。
角ade=bad+b=adb+edf。
ad=ad=》三角形adf全等于adc=》ac=af=2ae。
题干中可能有笔误地方:第一题右边的e点应为c点,第二题求证的cd不可能等于ga,是否是求证cd=fa或cd=co。
如上猜测准确,证法如下:第一题证明:设f是ab边上中点,连接ef角adb=角bad,则三角形abd为等腰三角形,ab=bd;∵ae是三角形abd的中线,f是ab边上中点。
∴ef为三角形abd对应da边的中位线,ef∥da,则∠fed=∠adc,且ef=1/2da。
∵∠fed=∠adc,且ef=1/2da,af=1/2ab=1/2cd∴△afe∽△cda∴ae:ca=fe:da=af:cd=1:2ac=2ae得证第二题:证明:过d点作dh⊥ab交ab于h,连接oh,则∠dhb=90°;∵∠acb=90°=∠dhb,且bd是角b的平分线,则∠dbc=∠dbh,直角△dbc与直角△dbh有公共边db;∴△dbc≌△dbh,得∠cdb=∠hdb,cd=hd;∵dh⊥ab,ce⊥ab;∴dh∥ce,得∠hdb=∠cod=∠cdb,△cdo为等腰三角形,cd=co=dh;四边形cdho中co与dh两边平行且相等,则四边形cdho为平行四边形,ho∥cd且ho=cd∵gf∥ab,四边形ahof中,ah∥of,ho∥af,则四边形ahof为平行四边形,ho=fa∴cd=fa得证。
第二篇:初一几何证明题初一《几何》复习题XX--6—29姓名:一.填空题1.过一点2.过一点,有且只有直线与这条直线平行;3.两条直线相交的,它们的交点叫做;4.直线外一点与直线上各点连接的中,最短;a b 5.如果c[图1]6.如图1,ab、cd相交于o 点,oe⊥cd,∠1和∠2叫做,∠1和∠3叫做,∠1和∠4叫做,∠2和∠3叫做;a7.如图2,ac⊥bc,cd⊥ab,b点到ac的距离是a点到bc的距离是,c点到ab的距离是d438.如图3,∠1=110°,∠2=75°,∠3=110°,∠4=;cb二.判断题[图2][图3] 1.有一条公共边的两个角是邻补角;()2.不相交的两条直线叫做平行线;()3.垂直于同一直线的两条直线平行;()4.命题都是正确的;()5.命题都是由题设和结论两部分组成()6.一个角的邻补角有两个;()三.选择题1.下列命题中是真命题的是()a、相等的角是对顶角b、如果a⊥b,a⊥c,那么b⊥cc、互为补角的两个角一定是邻补角d、如果a∥b,a⊥c,那么b⊥c 2.下列语句中不是命题的是()a、过直线ab外一点c作ab 的平行线cf b、任意两个奇数之和是偶数c、同旁内角互补,则两直线平行d、两个角互为补角,与这两个角所在位置无关a 3.如图4,已知∠1=∠2,若要∠3=∠4,则需()da、∠1=∠3b、∠2=∠3c、∠1=∠4d、ab∥cdc [图4] 4.将命题“同角的补角相等”改写成“如果??,那么??”的形式,正确的是()a.如果同角的补角,那么相等b.如果两个角是同一个角,那么它们的补角相等 c.如果有一个角,那么它们的补角相等d.如果两个角是同一个角的补角,那么它们相等四.解答下列各题:p 1. 如图5,能表示点到直线(或线段)的距离的线段qac 有、、;abf 2.如图6,直线ab、cd分别和ef相交,已知ab∥cd,orebba平分∠cbe,∠cbf=∠dfe,与∠d相等的角有∠[图5][图6]d∠、∠、∠、∠等五个。
c 五.证明题e[图8]如图7,已知:be平分∠abc,∠1=∠3。
求证:de∥bcb[图7]cadb六.填空题1.过一点可以画条直线,过两点可以画 2.在图8中,共有条线段,共有个锐角,个直角,∠a的余角是; 3.ab=3.8cm,延长线段ab 到c,使bc=1cm,再反向延长ab到d,使ad=3cm,e是ad中点,f是cd的中点,则ef=cm ;4.35.56°=度分秒;105°45′15″—48°37′26 ″ 5.如图9,三角形abc中,d是bc上一点,e是ac上一点,ad与be交于f点,则图中共有e 6.如图10,图中共有条射线,七.计算题bdc 1.互补的两个角的比是1:2,求这两个角各是多少度?[图9]a2.互余的两角的差为15°,小角的补角比大角的补角大多少?e bdc[图10] 1.如图11,aob是一条直线,od是∠boc的平分线,若∠aoc=34°56′求∠bod的度数;dc 八.画图题。
1 .已知∠α,画出它的余角和补角,并表示出来aob[图11]北 2.已知∠α和∠β,画一个角,使它等于2∠α—∠β北偏西20β 3.仿照图12,作出表示下列方向的射线:西东⑴北偏东43° ⑵南偏西37° ⑶东北方向⑷ 西北方向九.证明题[图12]南两直线平行,内错角的平分线平行(要求:画出图形,写出已知、(推荐访问:)求证,并进行证明)已知:求证:证明:第三篇:初一几何证明题初一几何证明题一、1)d是三角形abc的bc边上的点且cd=ab,角adb=角bad,ae是三角形abd的中线,求证ac=2ae。
(2)在直角三角形abc中,角c=90度,bd是角b的平分线,交ac 于d,ce垂直ab于e,交bd于o,过o作fg平行ab,交bc于f,交ac 于g。
求证cd=ga。
延长ae至f,使ae=ef。
be=ed,对顶角。
证明abe全等于def。
=》ab=df,角b=角edf角adb=角bad=》ab=bd,cd=ab=》cd=df。
角ade=bad+b=adb+edf。
ad=ad=》三角形adf全等于adc=》ac=af=2ae。
题干中可能有笔误地方:第一题右边的e点应为c点,第二题求证的cd不可能等于ga,是否是求证cd=fa或cd=co。
如上猜测准确,证法如下:第一题证明:设f是ab边上中点,连接ef角adb=角bad,则三角形abd为等腰三角形,ab=bd;∵ae是三角形abd的中线,f是ab边上中点。
∴ef为三角形abd对应da边的中位线,ef∥da,则∠fed=∠adc,且ef=1/2da。
∵∠fed=∠adc,且ef=1/2da,af=1/2ab=1/2cd∴△afe∽△cda∴ae:ca=fe:da=af:cd=1:2ac=2ae得证第二题:证明:过d点作dh⊥ab交ab于h,连接oh,则∠dhb=90°;∵∠acb=90°=∠dhb,且bd是角b的平分线,则∠dbc=∠dbh,直角△dbc与直角△dbh有公共边db;∴△dbc≌△dbh,得∠cdb=∠hdb,cd=hd;∵dh⊥ab,ce⊥ab;∴dh∥ce,得∠hdb=∠cod=∠cdb,△cdo为等腰三角形,cd=co=dh;四边形cdho中co与dh两边平行且相等,则四边形cdho为平行四边形,ho∥cd且ho=cd∵gf∥ab,四边形ahof中,ah∥of,ho∥af,则四边形ahof为平行四边形,ho=fa∴cd=fa得证有很多题1.已知在三角形abc中,be,cf分别是角平分线,d是ef中点,若d 到三角形三边bc,ab,ac的距离分别为x,y,z,求证:x=y+z证明;过e点分别作ab,bc上的高交ab,bc于m,n点.过f点分别作ac,bc上的高交于p,q点.根据角平分线上的点到角的2边距离相等可以知道fq=fp,em=en.过d点做bc上的高交bc于o点.过d点作ab上的高交ab于h点,过d点作ab上的高交ac于j点.则x=do,y=hy,z=dj.因为d是中点,角ane=角ahd=90度.所以hd平行me,me=2hd同理可证fp=2dj。
又因为fq=fp,em=en.fq=2dj,en=2hd。
又因为角fqc,doc,enc都是90度,所以四边形fqne是直角梯形,而d是中点,所以2do=fq+en又因为fq=2dj,en=2hd。
所以do=hd+jd。
因为x=do,y=hy,z=dj.所以x=y+z。
2.在正五边形abcde中,m、n分别是de、ea上的点,bm与cn相交于点o,若∠bon=108°,请问结论bm=cn是否成立?若成立,请给予证明;若不成立,请说明理由。
当∠bon=108°时。
bm=cn还成立证明;如图5连结bd、ce.在△bci)和△cde中∵bc=cd,∠bcd=∠cde=108°,cd=de∴δbcd≌δcde∴bd=ce,∠bdc=∠ced,∠dbc=∠cen∵∠cde=∠dec=108°,∴∠bdm=∠cen∵∠obc+∠ecd=108°,∠ocb+∠ocd=108°∴∠mbc=∠ncd又∵∠dbc=∠ecd=36°,∴∠dbm=∠ecn∴δbdm≌δcne∴bm=cn3.三角形abc中,ab=ac,角a=58°,ab的垂直平分线交ac与n,则角nbc=()3°因为ab=ac,∠a=58°,所以∠b=61°,∠c=61°。
