平面解析几何三角形与圆相关章节综合检测提升试卷(一)带答案新高考高中数学

合集下载

平面解析几何三角形与圆相关章节综合检测提升试卷(六)附答案新高考高中数学

高中数学专题复习
《平面解析几何三角形、圆相关》单元过关检测
经典荟萃，匠心巨制！独家原创，欢迎下载！
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息
2．请将答案正确填写在答题卡上评卷人
得分一、填空题
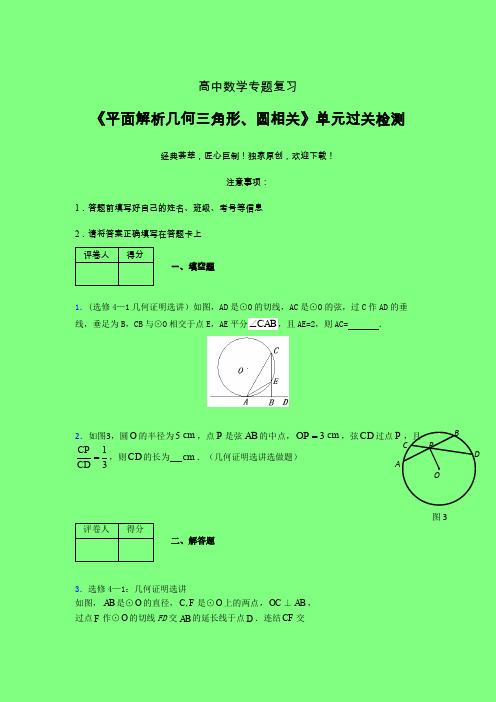
1．(选修4—1几何证明选讲）如图，
AD 是⊙O 的切线，AC 是⊙O 的弦，过C 作AD 的垂线，垂足为B ，CB 与⊙O 相交于点E ，AE 平分CAB ∠，且AE=2，则AC= ．
2．如图3，圆O 的半径为5cm ，点P 是弦AB 的中点，3OP =cm ，弦CD 过点P ，且13
CP CD =，则CD 的长为 cm ．（几何证明选讲选做题）
评卷人
得分二、解答题
3．选修4—1：几何证明选讲
如图，AB 是⊙O 的直径，,C F 是⊙O 上的两点，OC ⊥AB ，
过点F 作⊙O 的切线FD 交AB 的延长线于点D ．连结CF 交 P O A B C D 图3。

平面解析几何三角形与圆相关章节综合检测提升试卷(五)带答案人教版高中数学新高考指导

高中数学专题复习《平面解析几何三角形、圆相关》单元过关检测经典荟萃，匠心巨制！独家原创，欢迎下载！注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上评卷人得分一、填空题1．如图,AB 是圆O 的直径,点C 在圆O 上,延长BC 到D 使BC CD =,过C 作圆O 的切线交AD 于E .若6AB =,2ED =,则BC =_________.（汇编年普通高等学校招生统一考试广东省数学（理）卷（纯WORD 版））(几何证明选讲选做题)2．设12,,,n P P P 为平面α内的n 个点,在平面α内的所有点中,若点P 到12,,,n P P P 点的距离之和最小,则称点P 为12,,,n P P P 点的一个“中位点”.例如,线段AB 上的任意点都是端点,A B 的中位点.则有下列命题:①若,,A B C 三个点共线,C 在线AB 上,则C 是,,A B C 的中位点;②直角三角形斜边的点是该直角三角形三个顶点的中位点;③若四个点,,,A B C D 共线,则它们的中位点存在且唯一;④梯形对角线的交点是该梯形四个顶点的唯一中位点.其中的真命题是____________.(写出所有真命题的序号数学社区) （汇编年高考四川卷（理））.AE D CBO 第15题评卷人得分二、解答题3．如图,AB 和BC 分别与圆O 相切于点D ,,C AC 经过圆心O ,且2BC OC = 求证:2AC AD = （汇编年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD 版含附加题））A.[选修4-1:几何证明选讲]本小题满分10分.4．如图，AT 为单位圆O 的切线，过切点T 引OA 的垂线TH ，H 为垂足．求证：AO OH ⋅为定值．5．如图，自⊙O 外一点P 作⊙O 的切线PC 和割线PBA ，点C为切点，割线PBA 交⊙O 于A ，B 两点，点O 在AB 上.作AB CD ⊥，垂足为点.D求证：DCBD PA PC =.O A H T （第21—A 题）6．如图，圆O 的直径C AB ,4=为圆周上一点，2=BC ，过C 作圆O 的切线l ，过A 作l 的垂线AD AD ,分别与直线l 、圆O 交于点,,E D 求DAC ∠的度数与线段AE 的长．7．如图，圆1O 与圆2O 内切于点A ，其半径分别为1r 与212()r r r >，圆1O 的弦AB 交圆2O 于点C （1O 不在AB 上），求证：:AB AC 为定值。

平面解析几何三角形与圆相关章节综合检测专题练习(二)带答案新高考高中数学

高中数学专题复习《平面解析几何三角形、圆相关》单元过关检测经典荟萃，匠心巨制！独家原创，欢迎下载！注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上评卷人得分一、填空题1．(选修4—1几何证明选讲）如图，AD 是⊙O 的切线，AC 是⊙O 的弦，过C 作AD 的垂线，垂足为B ，CB 与⊙O 相交于点E ，AE 平分C A B ∠，且AE=2，则AC= ．2．如图2,在半径为7的O 中,弦,AB CD 相交于点,2P PA PB ==,1PD =,则圆心O 到弦CD 的距离为____________.（汇编年高考湖南卷（理））评卷人得分二、解答题3．选修4 1：几何证明选讲（本小题满分10分）如图，MN 为两圆的公共弦，一条直线与两圆及公共弦依次交于A ，B ，C ，D ，E ，求证：AB ·CD = BC ·DE ．4．选修4—1：几何证明选讲如图，等腰梯形ABCD 内接于⊙O ，AB ∥CD ．过点A 作⊙O 的切线交CD 的延长线于点E ．求证：∠DAE =∠BAC .（第21-A 题）AEOCDBGF EDCBAO5．如图，AB 、AC 切圆O 于点B 和点C ，直径BD 的延长线交AC 的延长线与E ，若ED=1，EC=2，求AB 的长．6．已知：如图，在RT ABC ∆中，90ACB ∠=︒，以AC 为直径的⊙O 交AB 于点D ，过点D 作⊙O 的切线DE 交BC 于点E ．求证：BE CE =．7．如图，AB 是⊙O 的一条切线，切点为B ，CGE CFD ADE ,,都是⊙O 的割线，已知AB AC =．(1）证明：2AC AE AD =⋅；(2）证明：AC FG //．ABCD EOABCMN 第21－A 题O8．在△ABC 中，已知CM 是∠ACB 的平分线，△AMC 的外接圆交BC 于点N ．若AC=12AB ，求证：BN=2AM ．【参考答案】***试卷处理标记，请不要删除评卷人得分一、填空题1．． 2．23评卷人得分二、解答题3．4．选修4—1：几何证明选讲证明：∵ABCD 是等腰梯形，AB ∥CD ， ∴AD =BC ．从而AD BC ．∴∠ACD =∠BAC . ……………………………………………………4分∵AE为圆的切线，∴∠EAD=∠ACD. …………………………………8分∴∠DAE=∠BAC. ……………………………………………………10分5．选修4－1：几何证明选讲解：由切割线定理 EC2=ED·EB，得EB=4，∴BD=3．连接OC，则32OC=，由ABE∆∽OCE∆，AB EBOC EC=,∴AB=3．……………10分6．7．8．A．选修4－1（几何证明选讲）证明：如图，在△ABC中，因为CM是∠ACM的平分线,所以AC AMBC BM=．又已知12AC AB=，所以2AB AMBC BM=…①…………… 4分又因为BA与BC是圆O过同一点B的弦，所以BM BA BN BC⋅=⋅，即BA BNBC BM=......② (8)分由①、②可知，2AM BNBM BM=，所以BN=2AM．……………………………………10分ABCD EO。

平面解析几何三角形与圆相关章节综合检测提升试卷(二)带答案人教版高中数学新高考指导

2．如图,AB为圆O的直径,PA为圆O的切线,PB与圆O相交于D.若PA=3, ,则PD=_________;AB=___________.（汇编年高考北京卷（理））
评卷人
得分
二、解答题
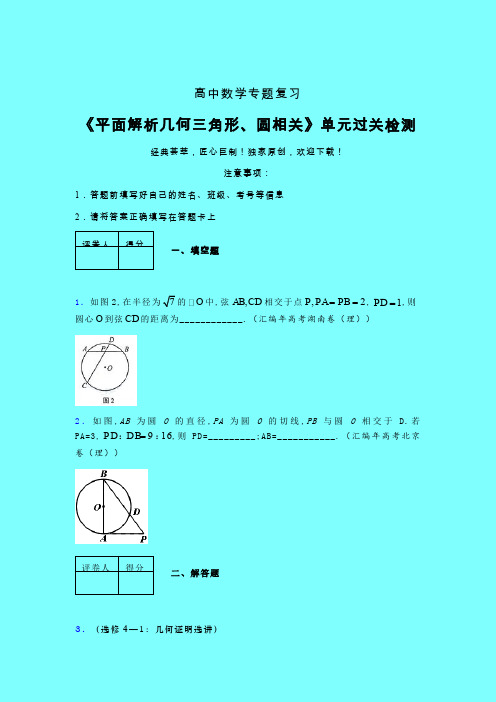
3．（选修4—1：几何证明选讲）
如图，是圆的直径，点在圆上，延长到使，过作圆的切线交于 .若，，求的长.
∴PA2= × ．∴PA= ．……………………10分
(Ⅰ)证明: 是△ 外接圆的直径;
(Ⅱ)若 ,求过四点的圆的面积与△ 外接圆面积的比值.（汇编年普通高等学校招生统一考试新课标Ⅱ卷数学（理）（纯WORD版含答案））选修4—1几何证明选讲:
6．如图, 垂直于于 ,垂直于 ,连接 .证明:
( ) ( ) （汇编年普通高等学校招生统一考试辽宁数学（理）试题（WORD版））选修4-1:几何证明选讲
4．【题文】几何证明选讲（本小题满分10分）
如图，设AB为⊙O的任一条不与直线l垂直的直径，P是⊙O与l的公共点，AC⊥l，BD⊥l，垂足分别为C，D，且PC=PD，求证：
（1）l是⊙O的切线；
（2）PB平分∠ABD.
【结束】
5．如图, 为△ 外接圆的切线, 的延长线交直线于点 , 分别为弦与弦上的点,且 , 四点共圆.
， .………………………………………………………………10分
4．
5．
6．
7．
8．解(1）∵DE2=EF·EC，
∴DECE=EFED．
∵DEF是公共角，
∴ΔDEF∽ΔCED．∴EDF=C．
∵CD∥AP，∴C=P．
∴P=EDF．……………………3分
(2）∵P=EDF，DEF=PEA，
∴ΔDEF∽ΔPEA．∴DEPE=EFEA．即EF·EP=DE·EA．

平面解析几何三角形与圆相关章节综合检测提升试卷(三)带答案新高考高中数学

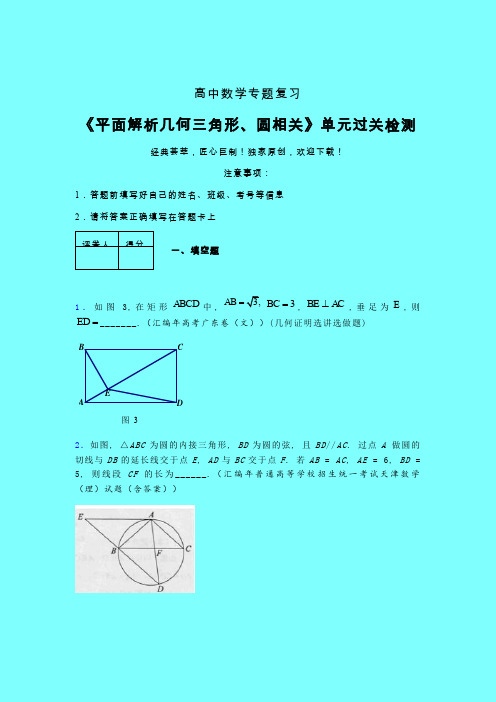
高中数学专题复习《平面解析几何三角形、圆相关》单元过关检测经典荟萃，匠心巨制！独家原创，欢迎下载！注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上评卷人得分一、填空题1．如图3,在矩形ABCD 中,3,AB =3BC =,BE AC ⊥,垂足为E ,则ED =_______.（汇编年高考广东卷（文））(几何证明选讲选做题)图 3ECBDA2．如图, △ABC 为圆的内接三角形, BD 为圆的弦, 且BD //AC . 过点A 做圆的切线与DB 的延长线交于点E , AD 与BC 交于点F . 若AB = AC , AE = 6, BD =5, 则线段CF 的长为______.（汇编年普通高等学校招生统一考试天津数学（理）试题（含答案））(第21-A 题图)A B PO EDC· 评卷人得分二、解答题3．选修4-1：几何证明选讲（本小题满分10分）如图，⊙O 的直径AB 的延长线与弦CD 的延长线相交于点P ，E 为⊙O 上一点，AE =AC ， DE 交AB 于点F ．求证：△PDF ∽△POC ．4．如图,直线AB 为圆的切线,切点为B,点C 在圆上,∠ABC 的角平分线BE 交圆于点E,DB 垂直BE 交圆于D. (Ⅰ)证明:DB=DC; (Ⅱ)设圆的半径为1,BC=,延长CE 交AB 于点F,求△BCF 外接圆的半径.（汇编年高考新课标1（理））选修4—1:几何证明选讲5．如图，⊙O 的直径AB 的延长线与弦CD 的延长线相交于点P ，E 为⊙O 上一点，AE =AC ，求证：∠PDE =∠POC ．证明：因AE =AC ，AB 为直径，故∠OAC =∠OAE ． ……………………………………………………………3分（第21-AA B PFO EDC ·F ED AB C所以∠POC =∠OAC+∠OCA=∠OAC+∠OAC=∠EAC ．又∠EAC =∠PDE ，所以，∠PDE =∠POC ．…………………………………………………………10分6．如图，已知梯形ABCD 为圆内接四边形，AD//BC ，过C 作该圆的切线，交AD 的延长线于E ，求证：ΔABC ∽ΔEDC 。

平面解析几何三角形与圆相关一轮复习专题练习(二)带答案新高考高中数学

高中数学专题复习《平面解析几何三角形、圆相关》单元过关检测经典荟萃，匠心巨制！独家原创，欢迎下载！注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上评卷人得分一、填空题1．如图,在ABC 中,090C ∠=, 060,20A AB ∠==,过C 作ABC 的外接圆的切线CD ,BD CD ⊥,BD 与外接圆交于点E ,则DE 的长为__________（汇编年普通高等学校招生统一考试重庆数学（理）试题（含答案））2．设12,,,n P P P 为平面α内的n 个点,在平面α内的所有点中,若点P 到12,,,n P P P 点的距离之和最小,则称点P 为12,,,n P P P 点的一个“中位点”.例如,线段AB 上的任意点都是端点,A B 的中位点.则有下列命题: ①若,,A B C 三个点共线,C 在线AB 上,则C 是,,A B C 的中位点; ②直角三角形斜边的点是该直角三角形三个顶点的中位点; ③若四个点,,,A B C D 共线,则它们的中位点存在且唯一; ④梯形对角线的交点是该梯形四个顶点的唯一中位点.其中的真命题是____________.(写出所有真命题的序号数学社区) （汇编年高考四川卷（理））（第21—A 题）A BCDPOEF 评卷人得分二、解答题3．如图，PA ，PB 是⊙O 的切线，切点分别为A ，B ，线段OP 交⊙O 于点C ．若PA ＝12，PC ＝6，求AB 的长．4．如图，⊙O 的半径为3，两条弦AB ，CD 交于点P ，且1AP =， 3CP =，6OP =．求证：△APC ≌△DPB ．证明：延长OP交⊙O 与点E ，F ， ………2分由相交弦定理得()()36363CP DP AP BP FP EP ⋅=⋅=⋅=-⨯+=， ………6分又1AP =，3CP =，故1DP =，3BP =， (8)分所以AP DP =，BP CP =，而APC DPB ∠=∠，ABPOC （第21题DCBA（第21—A 题）所以△APC ≌△DPB ． ………10分5．如图，圆O 的直径C AB ,4=为圆周上一点，2=BC ，过C 作圆O 的切线l ，过A 作l 的垂线AD AD ,分别与直线l 、圆O 交于点,,E D 求DAC ∠的度数与线段AE 的长．6．如图，已知AB 、CD 是圆O 的两条弦，且AB 是线段CD 的垂直平分线，已知6,25AB CD ==，求线段AC 的长度．7．如图,CD 为△ABC 外接圆的切线,AB 的延长线交直线CD 于点D ,,E F 分别为弦AB 与弦AC 上的点,且BC AE DC AF ⋅=⋅,,,,B E F C 四点共圆. (Ⅰ)证明:CA 是△ABC 外接圆的直径;(Ⅱ)若DB BE EA ==,求过,,,B E F C 四点的圆的面积与△ABC 外接圆面积的比值. （汇编年高考课标Ⅱ卷（文））选修4—1几何证明选讲:8．如图,四边形ABCD 内接于O ,BC 是圆的直径,两条对角线AC BD 与交于点CABDFEP ,P 是AC 的中点,2BP PD =,直线MN 切O 于A ,若30,8MAB BC ︒∠==,求(1)ADC ∠的大小;(2)对角线BD 的长．【参考答案】***试卷处理标记，请不要删除评卷人得分一、填空题1．5 2．①④ 评卷人得分二、解答题3．证明如图，延长PO 交⊙O 于D ，连结AO ，BO ．AB 交OP 于点E ．因为PA 与⊙O 相切，所以PA 2＝PC ·PD ．设⊙O 的半径为R ，因为PA ＝12，PC ＝6，所以122＝6(2R ＋6)，解得R ＝9． …………………… 4分因为PA ，PB 与⊙O 均相切，所以PA ＝PB ．又OA ＝OB ，所以OP 是线段AB 的垂直平分线． …………………… 7分O PCBDNMAABP OC （第21题DEADCBE即AB ⊥OP ，且AB ＝2AE ．在Rt △OAP 中，AE ＝OA ·PA OP ＝365．所以AB＝725． (10)分 4． 5．解：6．【选做题】连接BC 设,AB CD 相交于点E ，AE x =，∵AB 是线段CD 的垂直平分线，∴AB 是圆的直径，∠ACB ＝90°………………………2分则6EB x =-，5CE =．由射影定理得2CE AE EB =，即有(6)5x x -=，解得1x =（舍）或5x = …………8分∴ 25630AC AE AB ==⨯=，即30AC =．………10分7．8．解：(1) ∵MN O 为的切线，∴,BAM BDA CAM ADC ∠=∠∠=∠又∵30,MAB BCO ︒∠=为直径，∴90,120BAC CAM ︒︒∠=∠=．∴120ADC ︒∠=． ……………………4分(2)由相交弦定理知PB PD PC PA =．又∵P 是AC 中点,2PB PD =, ∴222PD PC =．∴2PC PD =．又∵30,BCA BAM OP AC ︒∠=∠=⊥,∴OCP ∆是直角三角形．又8BC =,∴4OC =,∴23PC =,∴6PD =,∴336BD PD ==． (10)分。

平面解析几何三角形与圆相关章节综合检测提升试卷(三)带答案人教版高中数学新高考指导

高中数学专题复习《平面解析几何三角形、圆相关》单元过关检测经典荟萃，匠心巨制！独家原创，欢迎下载！注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上评卷人得分一、填空题1．如图,AB 是圆O 的直径,点C 在圆O 上,延长BC 到D 使BC CD =,过C 作圆O 的切线交AD 于E .若6AB =,2ED =,则BC =_________.（汇编年普通高等学校招生统一考试广东省数学（理）卷（纯WORD 版））(几何证明选讲选做题)2．如图,在ABC 中,090C ∠=, 060,20A AB ∠==,过C 作ABC 的外接圆的切线CD ,BD CD ⊥,BD 与外接圆交于点E ,则DE 的长为__________（汇编年普通高等学校招生统一考试重庆数学（理）试题（含答案））. AEDC B O第15题评卷人得分二、解答题3．如图所示，已知PA 与O 相切，A 为切点，PBC 为割线，弦CD AP ∥，AD ，BC 相交于点E ，F 为CE 上一点，且P EDF ∠=∠．求证：2DE CE EF =⋅.4．如图，圆1O 与圆2O 内切于点A ，其半径分别为1r 与212()r r r >，圆1O 的弦AB 交圆2O 于点C （1O 不在AB 上），求证：:AB AC 为定值。

证明：由弦切角定理可得11212,O B r AB AO C AO B AC O C r∴== 5．如图，⊙O 的直径AB 的延长线与弦CD 的延长线相交于点P ，E 为⊙O 上一点，AE AC =,DE 交AB 于点F．求证：PF ·PO ＝PA ·PB ．F ABPD E C21-A 第图DCBA（第21—A 题）6．如图，已知AB 、CD 是圆O 的两条弦，且AB 是线段CD 的垂直平分线，已知6,25AB CD ==，求线段AC 的长度．7．如图,AB 为半圆直径,D 为AB 上一点,分别在半圆上取点E 、F ,使EA ＝DA ,FB ＝DB .过D 作AB 的垂线,交半圆于C .求证：CD 平分EF .8．如图,直线AB 为圆的切线,切点为B ,点C 在圆上,ABC ∠的角平分线BE 交圆于点E ,DB 垂直BE 交圆于点D . (Ⅰ)证明:DB DC =;(Ⅱ)设圆的半径为1,3BC =,延长CE 交AB 于点F ,求BCF ∆外接圆的半径.（汇编年高考课标Ⅰ卷（文））选修4—1:几何证明选讲【参考答案】***试卷处理标记，请不要删除评卷人得分一、填空题1．23 2．5 评卷人得分二、解答题3．证明：CD PA∥ P C ∴∠=∠ …………（2分）又P EDF ∠=∠C EDF ∴∠=∠ …………（4分）又CED DEF ∠=∠CED DEF ∴∆∆ …………（8分）ED CEEF DE∴=2DE EF EC ∴=⋅．…………（10分）F A BPDE CADCBE4． 5．6．【选做题】连接BC 设,AB CD 相交于点E ，AE x =，∵AB 是线段CD 的垂直平分线，∴AB 是圆的直径，∠ACB ＝90°………………………2分则6EB x =-，5CE =．由射影定理得2CE AE EB =，即有(6)5x x -=，解得1x =（舍）或5x = …………8分∴ 25630AC AE AB ==⨯=，即30AC =．………10分7．证明：如图,分别过点E 、F 作AB 的垂线,G 、H 为垂足,连FA 、EB .易知 DB 2＝FB 2＝AB ·HB , AD 2＝AE 2＝AG ·AB . 二式相减,得DB 2－AD 2＝AB ·(HB －AG ),或 (DB －AD )·AB ＝AB ·(HB －AG ). 于是,DB －AD ＝HB －AG , 或 DB －HB ＝AD －AG . 就是DH ＝GD . 显然,EG ∥CD ∥FH . 故CD 平分EF .2.8．解:(1)连接DE,交BC 为G,由弦切角定理得,ABE BCE ∠=∠,而,,ABE CBE CBE BCE BE CE ∠=∠∠=∠=故.又因为D B B E ⊥,所以DE 为直径,∠DCE=90°,由勾股定理可得DB=DC.A BECFD GH(II)由(1),CDE BDE ∠=∠,DB DC =,故DG 是BC 的中垂线,所以32BG =,圆心为O,连接BO,则060BOG ∠=,030ABE BCE CBE ∠=∠=∠=,所以CF BF ⊥,故外接圆半径为32.。

平面解析几何三角形与圆相关章节综合检测专题练习(三)带答案新高考高中数学

高中数学专题复习《平面解析几何三角形、圆相关》单元过关检测经典荟萃，匠心巨制！独家原创，欢迎下载！注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上评卷人得分一、填空题1．如图, △ABC 为圆的内接三角形, BD 为圆的弦, 且BD //AC . 过点A 做圆的切线与DB 的延长线交于点E , AD 与BC 交于点F . 若AB = AC , AE = 6, BD = 5, 则线段CF 的长为______.（汇编年普通高等学校招生统一考试天津数学（理）试题（含答案））2．设12,,,n P P P 为平面α内的n 个点,在平面α内的所有点中,若点P 到12,,,n P P P 点的距离之和最小,则称点P 为12,,,n P P P 点的一个“中位点”.例如,线段AB 上的任意点都是端点,A B 的中位点.则有下列命题: ①若,,A B C 三个点共线,C 在线AB 上,则C 是,,A B C 的中位点; ②直角三角形斜边的点是该直角三角形三个顶点的中位点; ③若四个点,,,A B C D 共线,则它们的中位点存在且唯一; ④梯形对角线的交点是该梯形四个顶点的唯一中位点.其中的真命题是____________.(写出所有真命题的序号数学社区) （汇编年高考四川卷（理））EODCBA评卷人得分二、解答题3．如图，⊙O 的直径AB 的延长线与弦CD 的延长线相交于点P ，E 为⊙O 上一点，AE =AC ， DE 交AB 于点F ．求证：△PDF ∽△POC ．证明：∵AE =AC ，∠CDE ＝∠AOC ，………………………3分又∠CDE ＝∠P +∠PDF ，∠AOC ＝∠P +∠OCP ，从而∠PDF ＝∠OCP ．………………………………8分在△PDF 与△POC 中， ∠P ＝∠P ，∠PDF ＝∠OCP ，故△PDF ∽△POC ．…………………………………10分 4．如图，半径分别为R ，r(R>r>0)的两圆1,O O 内切于点T ，P 是外圆O 上任意一点，连PT 交1O 于点M ，PN 与内圆1O 相切，切点为N 。

平面解析几何三角形与圆相关章节综合检测专题练习(二)含答案新教材高中数学

平面解析几何三角形与圆相关章节综合检测提升试卷(一)带答案新人教版高中数学名师一点通

高中数学专题复习《平面解析几何三角形、圆相关》单元过关检测经典荟萃，匠心巨制！独家原创，欢迎下载！注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上评卷人得分一、填空题1．如图，已知PE 是圆O 的切线，直线P B 交圆O 于A 、B两点，PA=4，AB=12，43AE =，则PE 的长为，ABE ∠的大小为。

2．如图3，圆O 的半径为5cm ，点P 是弦AB 的中点，3OP =cm ，弦CD 过点P ，且13CP CD =，则CD 的长为 cm ．（几何证明选讲选做题）评卷人得分二、解答题3．选修4—1：几何证明选讲P OAB C D图3如图，圆O 的两弦AB 和CD 交于点E ，//EF CB ，EF 交AD 的延长线于点F ．求证：△DEF ∽△EAF ．4．如图，已知CB 是⊙O 的一条弦，A 是⊙O 上任意一点，过点A 作⊙O 的切线交直线CB 于点P ，D 为⊙O 上一点，且ABD ABP ∠=∠．求证：2AB BP BD =⋅．5．已知 ABC ∆中，AC AB =,D 是ABC ∆外接圆劣弧AC 上的点（不与点C A ,重合），延长BD 至E . 求证：AD 的延长线平分CDE ∠.6．如图，ABC ∆的角平分线AD 的延长线交它的外接圆于点E 若ABC ∆的面积AE AD S ⋅=21，求BAC ∠的大小．（第21—A 题） FB CDAO E （第21-A· OA BPDC7．过平行四边形ABCD 的顶点B 、C 、D 的圆与直线AD 相切，与直线AB 相交于点E ，已知AD=4，CE=5。

(1)如图1，若点E 在线段AB 上，求AE 的长；(2)点E 能否在线段AB 的延长线上？(即图2的情形是否存在？)若能，求出AE 的长；若不能，请说明理由。

8．如图，ABC △是圆O 的内接三角形，AC BC =，D 为圆O 中AB 上一点，延长DA 至点E ，使得CE CD =．求证：AE BD =．【参考答案】***试卷处理标记，请不要删除评卷人得分一、填空题1． 2．62 评卷人得分二、解答题3．因为//EF CB ，所以BCE FED ∠=∠， ………………3分又BAD BCD ∠=∠，所以BAD FED ∠=∠， ………………6分又EFD EFD ∠=∠，所以△DEF ∽△EAF ． ………………10分 4．5．解（Ⅰ）设F 为AD 延长线上一点 ∵D C B A ,,,四点共圆， ∴CDF ABC ∠=∠3分又ACAB = ∴ACBABC ∠=∠,5分且ACBADB ∠=∠, ∴CDFADB ∠=∠,7分对顶角ADB EDF ∠=∠, 故CDF EDF ∠=∠, 即AD的延长线平分CDE∠.10分6．（选修4—1：几何证明选讲）科网由已知条件，可得∠BAE ＝∠CAD ．因为∠AEB 与∠ACB 是同弧上的圆周角，所以∠AEB ＝∠ACD ．故ABE ∆∽ADC ∆．所以AB ADAE AC=，即AB ·AC ＝AD ·AE ．又S ＝12AB ·ACsin ∠BAC ，且S ＝12AD ·AE ，故AB ·ACsin ∠BAC ＝AD ·AE ．则sin ∠BAC ＝1，又∠BAC 为三角形内角，所以∠BAC ＝90°． (10)7．A．解题探究：利用切割线定理解决第（1）题，而第（2）题是探究性问题，应假设其存在，再推出矛盾或符合题意。

平面解析几何三角形与圆相关章节综合检测提升试卷(五)带答案新教材高中数学

高中数学专题复习《平面解析几何三角形、圆相关》单元过关检测经典荟萃，匠心巨制！独家原创，欢迎下载！注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上评卷人得分一、填空题1．如图3，圆O 的半径为5cm ，点P 是弦AB 的中点，3OP =cm ，弦CD过点P ，且13CP CD =，则CD 的长为 cm ．（几何证明选讲选做题）2．如图，已知圆O 的弦AB 交半径OC 于点D ．若3=AD ，2=BD ，且D 为OC 的中点，则=CD ．P OAB C D图3评卷人得分二、解答题3．如图，以正方形ABCD 的顶点C 为圆心，CA 为半径的圆交BC 的延长线于点E 、F ，且点B 为线段CG 的中点．求证：2GE GF BE BF ⋅=⋅．4．如图，自⊙O 外一点P 作⊙O 的切线PC 和割线PBA ，点C 为切点，割线PBA交⊙O 于A ，B 两点，点O 在AB 上.作AB CD ⊥，垂足为点.D求证：DCBDPA PC =.5．如图，AB 为圆O 的切线，A 为切点，过线段AB 上一点C 作圆O 的割线，CED （E 在C 、D 之间），若∠ABE=∠BDE ，求证：C 为线段AB的中点。

AB DCE GF（第21 —A 题）F ED ABC6．过圆O 外一点A 作圆O 的两条切线AT 、AS ，切点分别为T 、S ，过点A 作圆O 的割线APN ，证明：22AT PT PSAN NT NS=．[来源:学科网ZXXK] (汇编年3月苏、锡、常、镇四市高三数学教学情况调查一) 证明：AT 是圆O 的切线，∠ATP =∠ANT ,又∠TAP =∠NAT ,∴三角形ATP 与三角形ANT ，∴AT PT AN TN =同理AS PSAN NS=两等式相乘222,AT AS PT PSAT PT PS AT AS AN NT NSAN NT NS∙∙∙==∴=∙∙. 7．如图，在△ABC 中，D 是AC 的中点，E 是BD 的中点，AE 的延长线交BC 于F . （1）求FCBF的值；（2）若△BEF 的面积为1S ，四边形CDEF 的面积为2S ，求21:S S 的值．8．如图，在△ABC中，∠C=900,BE是角平分线，D E⊥BE交AB于D，⊙O是△BDE的外接圆。