最新重庆市2018年中考数学一轮复习第七章图形的变化第1节图形的轴对称与中心对称练习册_41含答案

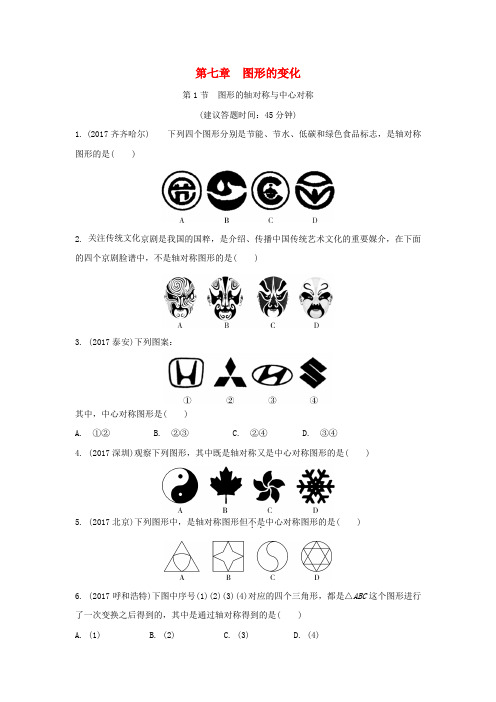
第七章图形的变化第1节图形的轴对称与中心对称(建议答题时间：45分钟)1. (2017齐齐哈尔) 下列四个图形分别是节能、节水、低碳和绿色食品标志，是轴对称图形的是( )2. 关注传统文化京剧是我国的国粹，是介绍、传播中国传统艺术文化的重要媒介，在下面的四个京剧脸谱中，不是轴对称图形的是( )3. (2017泰安)下列图案：其中，中心对称图形是( )A. ①②B. ②③C. ②④D. ③④4. (2017深圳)观察下列图形，其中既是轴对称又是中心对称图形的是( )5. (2017北京)下列图形中，是轴对称图形但不是．．中心对称图形的是( )6. (2017呼和浩特)下图中序号(1)(2)(3)(4)对应的四个三角形，都是△ABC这个图形进行了一次变换之后得到的，其中是通过轴对称得到的是( ) A. (1) B. (2) C. (3) D. (4)第6题图 第7题图 7. (2017河北)图①和图②中所有的小正方形都全等．将图①的正方形放在 图②中①②③④的某一位置，使它与原来7个小正方形组成的图形是中心对称图形，这个位置是( )A. ①B. ②C. ③D. ④8. (2017广州)如图，E ，F 分别是▱ABCD 的边AD ，BC 上的点，EF ＝6，∠DEF ＝60°，将四边形EFCD 沿EF 翻折，得到EFC ′D ′，ED ′交BC 于点G ，则△GEF 的周长为( ) A. 6 B. 12 C. 18 D. 24第8题图 第9题图 9. (2017内江)如图，在矩形AOBC 中，O 为坐标原点，OA 、OB 分别在x 轴、y 轴上，点B 的坐标为(0，33)，∠ABO ＝30°，将△ABC 沿AB 所在直线对折后，点C 落在点D 处，则点D 的坐标为( )A. (32，332)B. (2，332)C. (332，32)D. (32，3－332) 10. (2017安徽)如图，在矩形ABCD 中，AB ＝5，AD ＝3，动点P 满足S △PAB ＝13S 矩形ABCD ，则点P 到A ，B 两点距离之和PA ＋PB 的最小值为( )A. 29B. 34C. 5 2D. 41第10题图 第11题图11. (2017长沙)如图，将正方形ABCD 折叠，使顶点A 与CD 边上的一点H 重合(H 不与端点C ，D 重合)，折痕交AD 于点E ，交BC 于点F ，边AB 折叠后与边BC 交于点G ，设正方形ABCD 的周长为m ，△CHG 的周长为n ，则n m 的值为( ) A.22 B. 12 C. 5－12 D. 随H 点位置的变化而变化12. (2017宁夏)如图，将平行四边形ABCD 沿对角线BD 折叠，使点A 落在点A ′处．若∠1＝∠2＝50°，则∠A ′为________.第12题图 第13题图 13. (2017扬州)如图，把等边△ABC 沿着DE 折叠，使点A 恰好落在BC 边上的点P 处，且DP ⊥BC ，若BP ＝4 cm ，则EC ＝________cm.14. (2017重庆大渡口区模拟)如图，正方形ABCD 中，点P 是BC 的中点，把△PAB 沿PA 翻折得到△PAE ，过点C 作CF ⊥DE 于点F ，当CF ＝2时，四边形APED 的周长为________．第14题图 第15题图15. (2017重庆育才二模)在正方形ABCD 中，AB ＝25＋2，E 是边BC 的中点，F 是AB 上一点，线段AE 、CF 交于点G ，且CE ＝EG ，将△CBF 沿CF 翻折，使得点B 落在点M 处，连接GM 并延长交AD 于点N ，则△AGN 的面积为________．16. (2017衡阳)如图，方格图中每个小正方形的边长为1，点A 、B 、C 都是格点．(1)画出△ABC 关于直线BM 对称的△A 1B 1C 1；(2)写出AA 1的长度．第16题图17. (2017重庆一中一模)在等腰Rt △ABC 中，∠BAC ＝90°，AB ＝AC ，D 是斜边BC 的中点，连接AD .(1)如图①，E 是AC 的中点，连接DE ，将△CDE 沿CD 翻折到△CDE ′，连接AE ′，当AD ＝6时，求AE ′的值．(2)如图②，在AC 上取一点E ，使得CE ＝13AC ，连接DE ，将△CDE 沿CD 翻折到△CDE ′，连接AE ′交BC 于点F ，求证：DF ＝CF .第17题图答案1. D2. A3. D4. D5. A6. A7. C 【解析】将图形绕着某个点旋转180°后，能够与本身重合的图形就是中心对称图形，只有将小正方形放在③的位置才能使它与原来7个小正方形组成的图形是中心对称图形．8. C 【解析】由折叠的性质可知：∠FEG ＝∠DEF ＝60°，∵AD ∥BC ，∴∠EFG ＝∠DEF ＝60°，∴△EFG 是等边三角形，则△EFG 的周长为3×6＝18.第9题解图9. A 【解析】如解图，过D 作DE ⊥x 轴于点E.根据矩形和折叠的性质可得AD ＝AC ＝OB ＝33，∠BAD ＝∠CAB ＝∠ABO ＝30°，∴∠DAE ＝30°.在Rt △ADE 中，DE ＝AD ·sin ∠DAE ＝33·sin 30°＝332，AE ＝AD ·cos ∠DAE ＝33·cos 30°＝92.在Rt △ABO 中，AO ＝OB ·tan ∠ABO ＝33·33＝3，∴OE ＝AE －AO ＝92－3＝32，∴点D 的坐标是(32，332)． 10. D 【解析】如解图所示，设△PAB 底边AB 上的高为h ，∵S △PAB ＝13S 矩形ABCD ，∴12·AB ·h ＝13·AB ·AD ，∴h ＝2，第10题解图为定值，在AD 上截取AE ＝2，作EF ∥AB 交CB 于F ，故P 点在直线EF 上 ，作点A 关于直线EF 的对称点A ′，连接A ′B 交直线EF 于点P ，此时PA ＋PB 最小，且PA ＋PB ＝A ′B ＝AA ′2＋AB 2＝42＋52＝41.11. B 【解析】令DH ＝x ，DE ＝y ，∵正方形ABCD 周长为m ，∴边长为m 4，∴EH ＝AE ＝m 4－y ，HC ＝m 4－x.∠EHG ＝90°，∠DHE ＋∠CHG ＝90°，∠DHE ＋∠DEH ＝90°，∴∠DEH ＝∠CHG ，又∵∠D ＝∠C ＝90°，∴△DHE ∽△CGH ，∴DH CG ＝HE GH＝DE CH ，∴CG ＝x （m 4－x ）y ，GH ＝（m 4－x ）（m 4－y ）y ，∵n ＝CG ＋GH ＋CH ＝m 216－x 2y，∴在Rt △DHE 中，DE 2＋DH 2＝EH 2，即y 2＋x 2＝(m 4－y)2，∴n ＝m 2，即n m ＝12. 12. 105° 【解析】由折叠的性质知：∠DBA ′＝∠2＝50°，∠ADB ＝∠BDA ′，∵AD ∥BC ，∴∠ADB ＝∠DBG ，∴∠BDG ＝∠DBG ，又∵∠1＝∠BDG ＋∠DBG ，∠1＝∠2＝50°，∴∠BDG ＝25°，∴∠A ′＝180°－50°－25°＝105°.13. 2＋2 3 【解析】∵等边△ΑΒC 沿着D Ε折叠，使点Α恰好落在ΒC 边上的点Ρ处，且D Ρ⊥ΒC, ΒΡ＝4 cm ，∴∠BDP ＝30°，BD ＝2BP ＝2×4＝8 cm .∴AD ＝DP ＝82－42＝4 3 cm ，BC ＝AB ＝BD ＋AD ＝(8＋43)cm .在Rt △CPE中，∠EPC ＝30°，∴CE ＝12CP ＝12(BC －BP)＝12(8＋43－4)＝(2＋23)cm . 14. 52＋310＋4 【解析】如解图，过A 作AM ⊥ED ，第14题解图∵∠1＋∠3＝∠1＋∠4＝90°，∴∠4＝∠3，∵∠AMD ＝∠F ＝90°，∠4＝∠3，AD ＝DC ，∴△AMD ≌△DFC(AAS )，∴DM ＝FC ＝2，由折叠知AE ＝AB ＝AD ，∵AM ⊥ED ，∴∠1＝∠2，∵∠2＋∠5＝90°，∠DCF ＋∠6＝90°，∠DCF ＝∠2，∴∠5＝∠6，∵点P 为BC 中点，∴BP ＝PC ＝PE ，∴∠PEC ＝∠PCE ，∴∠FEC ＝∠FCE ，∴EF ＝FC ＝2，∴DF ＝6，∴DC ＝DF 2＋FC 2＝62＋22＝210，∴AP ＝AB 2＋BP 2＝（210）2＋（10）2＝52，∴四边形APED 周长为AP ＋PE ＋ED ＋AD ＝52＋10＋4＋210＝52＋310＋4.15. 1655 【解析】如解图，连接BG ，∵CB ＝CM ，∠BCG ＝∠MCG ，CG ＝CG ，∴△CBG ≌△CMG ，∴∠CGB ＝∠CGM ，∵CE ＝EB ＝EG ，∴∠CGB ＝90°，∴∠CGM ＝90°，∴B 、G 、M 共线，∴EA ＝BA 2＋BE 2＝（25＋2）2＋（5＋1）2＝5＋5，∴GA ＝EA －EG ＝5＋5－(5＋1)＝4，∵EB ＝EG ，∴∠EBG ＝∠EGB ，∵AD ∥BC ，∴∠EBG ＝∠GNA ，∵∠EGB ＝∠NGA ，∴AN ＝AG ＝4，过G 作GH ⊥AB 交AB 于点H ，∴GH ∶BE ＝AG ∶AE ，∴GH ∶(5＋1)＝4∶(5＋5)，∴GH ＝455∴S △AGN＝S △ABN －S △ABG ＝12×(25＋2)(4－455)＝1655.第15题解图 16. 解：(1) △A 1B 1C 1如解图所；第16题解图(2)由解图可得AA 1＝10.17. 解：(1)∵∠BAC ＝90°，AB ＝AC ，D 是斜边BC 的中点，∴∠ADC ＝90°，∠ACD ＝45°，在Rt △ADC 中，AC ＝AD sin 45°＝23， ∵E 是AC 的中点，∴CE ＝12AC ＝3， ∵将△CDE 沿CD 翻折到△CDE ′，∴CE ′＝CE ＝3，∠ACE ′＝90°，由勾股理得：AE ′＝CE ′2＋AC 2＝15；(2)证明：如解图，过B 作AE ′的垂线交AD 于点G ，交AC 于点H∵∠ABH ＋∠BAF ＝90°，∠CAF ＋∠BAF ＝90°，∴∠ABH ＝∠CAF ，又∵AB＝AC，∠BAH＝∠ACE′＝90°，∴△ABH≌△CAE′(ASA)，∴AH＝CE′＝CE，∵CE＝13 AC，∴AH＝HE＝CE，∵D是BC中点，∴DE∥BH，∴G是AD中点，在△ABG和△CAF中，AB＝AC，∠BAD＝∠ACD＝45°，∠ABH＝∠CAF，∴△ABG≌△CAF(ASA)，∴AG＝CF，∵AG＝12 AD，∴CF＝12AD＝12CD，∴DF＝CF.第17题解图。