深度优先搜索
离散数学有向图常用算法思路概述

离散数学有向图常用算法思路概述离散数学是数学的一个分支,研究离散对象及其性质。
在离散数学中,有向图是一种常见的离散结构,它由一组节点(顶点)和一组有向边(弧)组成。
有向图在计算机科学、网络分析和运筹学等领域中具有广泛的应用。
针对有向图,有许多常用的算法思路可以帮助解决各种问题。
在本文中,我们将概述离散数学中常用的有向图算法思路。
一、深度优先搜索(DFS)深度优先搜索是一种常见的图搜索算法,用于遍历有向图。
它从图中的一个节点开始,沿着路径一直前进,直到无法继续,然后回溯到前一个节点继续搜索。
深度优先搜索可以用于检测环路、寻找连通分量以及生成拓扑排序等。
该算法的思路可以用以下伪代码表示:```DFS(节点v):标记节点v为已访问对于v的每个邻接节点u:如果u未被访问:递归调用DFS(u)```二、广度优先搜索(BFS)广度优先搜索是另一种用于遍历有向图的常见算法。
与深度优先搜索不同,广度优先搜索从源节点开始,首先遍历源节点的邻接节点,然后依次遍历它们的邻接节点,直到遍历完所有可达节点。
广度优先搜索可以用于寻找最短路径、检测连通性以及解决迷宫问题等。
该算法的思路可以用以下伪代码表示:```BFS(源节点s):创建一个空队列Q标记源节点s为已访问并入队while Q非空:取出队首节点v对于v的每个未被访问的邻接节点u:标记u为已访问并入队```三、拓扑排序拓扑排序是一种特殊的有向图排序算法,用于将有向无环图(DAG)中的所有节点排序为线性序列。
拓扑排序的思想是通过不断删除图中入度为0的节点,并更新相关节点的入度值,直到所有节点都被排序。
拓扑排序可以用于任务调度、依赖关系分析等场景。
该算法的思路可以用以下伪代码表示:TopologicalSort(有向图G):创建一个空队列Q和空列表L初始化所有节点的入度将所有入度为0的节点入队while Q非空:取出队首节点v并加入Lfor v的每个邻接节点u:更新u的入度值if u的入度变为0:将u入队```四、最短路径算法最短路径算法用于找到两个节点之间的最短路径。
DFS和BFS算法比较

DFS和BFS算法比较深度优先搜索(Depth First Search,简称DFS)和广度优先搜索(Breadth First Search,简称BFS)是图遍历中常用的两种算法。
它们在问题求解、图搜索和路径查找等领域都有广泛的应用。
本文将对DFS和BFS算法进行比较,并讨论它们在不同场景中的适用性和特点。
一、DFS算法DFS是一种用于图遍历和搜索的算法,它从起始节点开始,递归地探索图中的每个可能的路径,直到不能再继续下去为止。
在DFS过程中,若遇到未被访问过的节点,则以该节点为起点开始另一轮的递归搜索。
DFS具有以下特点:1. 深度搜索:DFS以深度探索图中的路径,沿着每条路径尽可能深入搜索,直到无法继续为止。
2. 栈结构:DFS通常使用栈来保存待访问的节点,通过在栈中进行出栈和入栈操作来实现深度遍历。
3. 可能会陷入局部最优解:由于DFS的搜索策略,可能会陷入局部最优解而无法找到全局最优解。
4. 适合解决路径搜索问题:DFS在寻找图中的路径、回溯和连通性等问题上表现出色,特别适合解决有向无环图(DAG)和迷宫等问题。
二、BFS算法BFS是一种用于图遍历和搜索的算法,它从起始节点开始,按照广度顺序逐层扩展,直到遍历完整个图。
在BFS过程中,将当前节点的所有相邻节点加入到队列中,并按照入队的顺序进行遍历。
BFS具有以下特点:1. 广度搜索:BFS按照广度优先的原则进行遍历,先访问离起始节点最近的节点,然后再逐渐扩展到离起始节点更远的节点。
2. 队列结构:BFS通常使用队列来保存待访问的节点,通过在队列中进行出队和入队操作来实现广度遍历。
3. 保证最短路径:由于BFS的搜索策略,可以保证在无权图中找到的路径是最短路径。
4. 适合解决连通性和最短路径问题:BFS在寻找图中的连通性和最短路径等问题上表现出色,特别适合解决无权图中的路径查找问题。
三、比较与应用1. 时间复杂度:DFS和BFS在最坏情况下的时间复杂度都是O(V +E),其中V为顶点数,E为边数。
深度优先搜索和广度优先搜索

二、 重排九宫问题游戏
在一个 3 乘 3 的九宫中有 1-8 的 8 个数及一个空格随机摆放在其中的格子里。如下面 左图所示。现在要求实现这样的问题:将该九宫调整为如下图右图所示的形式。调整规则是: 每次只能将与空格(上,下或左,右)相临的一个数字平移到空格中。试编程实现。
|2|8 |3|
|1|2|3|
from = f; to = t; distance = d; skip = false; } } class Depth { final int MAX = 100; // This array holds the flight information. FlightInfo flights[] = new FlightInfo[MAX]; int numFlights = 0; // number of entries in flight array Stack btStack = new Stack(); // backtrack stack public static void main(String args[]) {
下面是用深度优先搜索求解的程序:
// Find connections using a depth-first search. import java.util.*; import java.io.*; // Flight information. class FlightInfo {
String from; String to; int distance; boolean skip; // used in backtracking FlightInfo(String f, String t, int d) {
int dist; FlightInfo f; // See if at destination. dist = match(from, to); if(dist != 0) {
dfs序列和bfs序列

dfs序列和bfs序列dfs序列和bfs序列是图遍历算法中的两种常见序列。
它们分别代表了深度优先搜索(Depth-First Search)和广度优先搜索(Breadth-First Search)在图中遍历节点的顺序。
1. DFS序列深度优先搜索是一种以深度为优先级的遍历算法。
它从图的起始节点开始,一直沿着一个分支遍历到底,然后回溯到前一个节点,再遍历下一个分支。
这样直到遍历完所有的节点。
DFS序列的生成是通过递归或栈的方式完成的。
在递归实现中,每次深入某个节点时,都对其邻接节点进行深度优先遍历,直到遍历完所有节点为止。
生成的DFS序列可以用一个数组来表示,序列中每个节点的顺序即为其被遍历到的顺序。
2. BFS序列广度优先搜索是一种以广度为优先级的遍历算法。
它从图的起始节点开始,首先遍历其所有的邻接节点,然后再逐层遍历下一个邻接节点的邻接节点。
这样依次遍历完所有的节点。
BFS序列的生成是通过队列的方式完成的。
首先将起始节点入队,然后从队列中依次取出节点,并将其所有未被访问的邻接节点入队,直到队列为空为止。
生成的BFS序列可以用一个数组来表示,序列中每个节点的顺序即为其被遍历到的顺序。
3. DFS序列和BFS序列的应用DFS序列和BFS序列在图遍历算法中具有不同的应用场景。
DFS适用于解决一些涉及路径搜索、连通性、拓扑排序等问题。
由于DFS的特点是往深层次搜索,因此在找到目标节点后可以停止搜索,适合在有限深度的图中应用。
而BFS适用于解决一些涉及最短路径、最小生成树、社交网络分析等问题。
由于BFS的特点是逐层遍历,因此可以保证找到的路径是最短路径,并且可以用于计算节点之间的距离。
总结:DFS序列和BFS序列是图遍历算法中常见的两种序列。
DFS以深度为优先级,递归或栈实现,适合解决路径搜索等问题。
BFS以广度为优先级,队列实现,适合解决最短路径等问题。
对于不同的应用场景,可以选择使用适合的算法序列来进行图遍历。
第9单元 基本算法 第 10 课 深度优先搜索

第9 单元基本算法作者:林厚从第10 课深度优先搜索学习目标1.掌握深度优先搜索的基本思想和算法框架。
2.熟练应用深度优先搜索求解一些实际问题。
3.初步了解深度优先搜索中的剪枝优化。
深度优先搜索深度优先搜索是将当前状态按照一定的规则顺序,先拓展一步得到一个新状态,再对这个新状态递归拓展下去。
如果无法拓展,则退回一步到上一个状态(回溯),再按照原先设定的规则顺序重新寻找一个状态拓展。
如此搜索,直至找到目标状态,或者遍历完所有状态。
所以,深度优先搜索也是一种“盲目”搜索。
深度优先搜索对于图9.10-1所示的一个“无向图”,从顶点V0开始进行深度优先搜索,得到的一个序列为:V0,V1,V2,V6,V5,V3,V4。
1. 深度优先搜索的算法框架深度优先搜索(Depth First Search,DFS),简称深搜,其状态“退回一步”的顺序符合“后进先出”的特点,所以采用“栈”存储状态。
深搜适用于要求所有解方案的题目。
深搜可以采用直接递归的方法实现,其算法框架如下:1. 深度优先搜索的算法框架void dfs(int dep, 参数表);{自定义参数;if( 当前是目标状态){输出解或者作计数、评价处理;}else for(i = 1; i <= 状态的拓展可能数; i++)if( 第i 种状态拓展可行){维护自定义参数;dfs(dep+1, 参数表);}}例1、体积【问题描述】给出n 件物品,每件物品有一个体积V i,求从中取出若干件物品能够组成的不同的体积和有多少种可能。
【输入格式】第1 行1 个正整数,表示n。
第2 行n 个正整数,表示V i,每两个数之间用一个空格隔开。
【输出格式】一行一个数,表示不同的体积和有多少种可能。
【输入样例】31 3 4【输出样例】6【数据规模】对于30% 的数据满足:n≤5,V i≤10。
对于60% 的数据满足:n≤10,V i≤20。
对于100% 的数据满足:n≤20,1≤V i≤50。
广度优先和深度优先的例子

广度优先和深度优先的例子广度优先搜索(BFS)和深度优先搜索(DFS)是图遍历中常用的两种算法。
它们在解决许多问题时都能提供有效的解决方案。
本文将分别介绍广度优先搜索和深度优先搜索,并给出各自的应用例子。
一、广度优先搜索(BFS)广度优先搜索是一种遍历或搜索图的算法,它从起始节点开始,逐层扩展,先访问起始节点的所有邻居节点,再依次访问其邻居节点的邻居节点,直到遍历完所有节点或找到目标节点。
例子1:迷宫问题假设有一个迷宫,迷宫中有多个房间,每个房间有四个相邻的房间:上、下、左、右。
现在我们需要找到从起始房间到目标房间的最短路径。
可以使用广度优先搜索算法来解决这个问题。
例子2:社交网络中的好友推荐在社交网络中,我们希望给用户推荐可能认识的新朋友。
可以使用广度优先搜索算法从用户的好友列表开始,逐层扩展,找到可能认识的新朋友。
例子3:网页爬虫网页爬虫是搜索引擎抓取网页的重要工具。
爬虫可以使用广度优先搜索算法从一个网页开始,逐层扩展,找到所有相关的网页并进行抓取。
例子4:图的最短路径在图中,我们希望找到两个节点之间的最短路径。
可以使用广度优先搜索算法从起始节点开始,逐层扩展,直到找到目标节点。
例子5:推荐系统在推荐系统中,我们希望给用户推荐可能感兴趣的物品。
可以使用广度优先搜索算法从用户喜欢的物品开始,逐层扩展,找到可能感兴趣的其他物品。
二、深度优先搜索(DFS)深度优先搜索是一种遍历或搜索图的算法,它从起始节点开始,沿着一条路径一直走到底,直到不能再继续下去为止,然后回溯到上一个节点,继续探索其他路径。
例子1:二叉树的遍历在二叉树中,深度优先搜索算法可以用来实现前序遍历、中序遍历和后序遍历。
通过深度优先搜索算法,我们可以按照不同的遍历顺序找到二叉树中所有节点。
例子2:回溯算法回溯算法是一种通过深度优先搜索的方式,在问题的解空间中搜索所有可能的解的算法。
回溯算法常用于解决组合问题、排列问题和子集问题。
例子3:拓扑排序拓扑排序是一种对有向无环图(DAG)进行排序的算法。
noi常用算法

noi常用算法NOI(National Olympiad in Informatics)是指全国青少年信息学奥林匹克竞赛,是我国高中阶段最高水平的信息学竞赛。
在NOI 竞赛中,常用的算法是指在解决问题时经常使用的算法,下面将介绍一些常用的NOI算法。
一、深度优先搜索(DFS)深度优先搜索是一种用于遍历或搜索树或图的算法。
它从一个顶点开始,沿着路径直到无法继续,然后返回到前一个节点,继续搜索其他路径。
DFS通常使用递归或栈来实现。
它常用于解决迷宫问题、连通性问题等。
二、广度优先搜索(BFS)广度优先搜索是一种用于遍历或搜索树或图的算法。
它从一个顶点开始,先访问其所有相邻节点,然后访问这些相邻节点的相邻节点,以此类推。
BFS通常使用队列来实现。
它常用于解决最短路径问题、连通性问题等。
三、动态规划(Dynamic Programming)动态规划是一种解决多阶段决策问题的算法。
它将问题划分为若干个子问题,并分别求解这些子问题的最优解,然后利用子问题的最优解来推导出原问题的最优解。
动态规划常用于解决最优路径问题、背包问题等。
四、贪心算法(Greedy Algorithm)贪心算法是一种在每一步选择中都采取当前状态下最优的选择,从而希望最终能得到全局最优解的算法。
贪心算法不一定能得到最优解,但在某些问题上表现出良好的效果。
贪心算法常用于解决最小生成树问题、哈夫曼编码问题等。
五、最短路径算法最短路径算法用于求解两个节点之间的最短路径。
常用的最短路径算法有Dijkstra算法、Floyd-Warshall算法和Bellman-Ford算法等。
这些算法可以求解有向图或无向图中的最短路径问题,用于解决网络路由问题、导航问题等。
六、最大流算法最大流算法用于求解网络中从源节点到汇节点的最大流量。
常用的最大流算法有Ford-Fulkerson算法、Edmonds-Karp算法和Dinic算法等。
最大流算法可以用于解决网络优化问题、流量分配问题等。
信息学竞赛中的深度优先搜索算法

信息学竞赛中的深度优先搜索算法深度优先搜索(Depth First Search, DFS)是一种经典的图遍历算法,在信息学竞赛中被广泛应用。
本文将介绍深度优先搜索算法的原理、应用场景以及相关的技巧与注意事项。
一、算法原理深度优先搜索通过递归或者栈的方式实现,主要思想是从图的一个节点开始,尽可能地沿着一条路径向下深入,直到无法继续深入,然后回溯到上一个节点,再选择其他未访问的节点进行探索,直到遍历完所有节点为止。
二、应用场景深度优先搜索算法在信息学竞赛中有广泛的应用,例如以下场景:1. 图的遍历:通过深度优先搜索可以遍历图中的所有节点,用于解决与图相关的问题,如寻找连通分量、判断是否存在路径等。
2. 剪枝搜索:在某些问题中,深度优先搜索可以用于剪枝搜索,即在搜索的过程中根据当前状态进行一定的剪枝操作,提高求解效率。
3. 拓扑排序:深度优先搜索还可以用于拓扑排序,即对有向无环图进行排序,用于解决任务调度、依赖关系等问题。
4. 迷宫求解:对于迷宫类的问题,深度优先搜索可以用于求解最短路径或者所有路径等。
三、算法实现技巧在实际应用深度优先搜索算法时,可以采用以下的一些技巧和优化,以提高算法效率:1. 记忆化搜索:通过记录已经计算过的状态或者路径,避免重复计算,提高搜索的效率。
2. 剪枝策略:通过某些条件判断,提前终止当前路径的搜索,从而避免无效的搜索过程。
3. 双向搜索:在某些情况下,可以同时从起点和终点进行深度优先搜索,当两者在某个节点相遇时,即可确定最短路径等。
四、注意事项在应用深度优先搜索算法时,需要注意以下几点:1. 图的表示:需要根据实际问题选择合适的图的表示方法,如邻接矩阵、邻接表等。
2. 访问标记:需要使用合适的方式标记已经访问过的节点,避免无限循环或者重复访问造成的错误。
3. 递归调用:在使用递归实现深度优先搜索时,需要注意递归的结束条件和过程中变量的传递。
4. 时间复杂度:深度优先搜索算法的时间复杂度一般为O(V+E),其中V为节点数,E为边数。
深度优先搜索算法

深度优先搜索算法深度优先搜索算法(Depth-First Search,DFS)是一种用于遍历或搜索树或图数据结构的算法。
在DFS中,我们会尽可能深地探索一个分支,直到无法继续为止,然后回溯到前一个节点,继续探索其他分支。
DFS通常使用递归或栈数据结构来实现。
在本文中,我们将深入探讨DFS的原理、实现方法、应用场景以及一些相关的扩展主题。
1.原理深度优先搜索算法的原理非常简单。
从图或树的一个起始节点开始,我们首先探索它的一个邻居节点,然后再探索这个邻居节点的一个邻居节点,依此类推。
每次都尽可能深地探索一个分支,直到无法继续为止,然后回溯到前一个节点,继续探索其他分支。
这个过程可以用递归或栈来实现。
2.实现方法在实现DFS时,我们可以使用递归或栈来维护待访问的节点。
下面分别介绍这两种实现方法。
2.1递归实现递归是实现DFS最直观的方法。
我们可以定义一个递归函数来表示探索节点的过程。
该函数接受当前节点作为参数,并在该节点上进行一些操作,然后递归地调用自身来探索当前节点的邻居节点。
这样就可以很容易地实现DFS。
```pythondef dfs(node, visited):visited.add(node)#对当前节点进行一些操作for neighbor in node.neighbors:if neighbor not in visited:dfs(neighbor, visited)```2.2栈实现除了递归,我们还可以使用栈来实现DFS。
我们首先将起始节点入栈,然后循环执行以下步骤:出栈一个节点,对该节点进行一些操作,将其未访问的邻居节点入栈。
这样就可以模拟递归的过程,实现DFS。
```pythondef dfs(start):stack = [start]visited = set()while stack:node = stack.pop()if node not in visited:visited.add(node)#对当前节点进行一些操作for neighbor in node.neighbors:if neighbor not in visited:stack.append(neighbor)```3.应用场景深度优先搜索算法在实际的软件开发中有着广泛的应用。
算法描述的三种方法

算法描述的三种方法
1. 深度优先搜索算法:
通过递归的方式遍历图或树的每个节点,先访问当前节点,然后依次递归访问当前节点的每个邻接节点。
该算法使用栈来记录遍历的节点顺序。
示例:
对于以下图结构,初始节点为A:
A ->
B -> D
| |
V V
C E
通过深度优先搜索算法的结果为:A -> B -> D -> E -> C
2. 广度优先搜索算法:
通过迭代的方式遍历图或树的每个节点,先访问当前节点的所有邻接节点,然后将邻接节点加入队列尾部,依次访问队列中的节点。
该算法使用队列来记录遍历的节点顺序。
示例:
对于以下图结构,初始节点为A:
A ->
B -> D
| |
V V
C E
通过广度优先搜索算法的结果为:A -> B -> C -> D -> E
3. 贪心算法:
在每一步选择中,贪心算法选择当前状态下最优的选择,不考虑未来的后果。
贪心算法通常用于求解最优解问题,但并不
能保证一定能得到全局最优解。
示例:
如果要在一组物品中选择总重量不超过背包容量的物品,可以用贪心算法选择具有最高价值重量比的物品放入背包,直到背包无法再放入物品为止。
但是这种选择方式并不一定能得到真正的最优解。
深度优先搜索算法利用深度优先搜索解决迷宫问题

深度优先搜索算法利用深度优先搜索解决迷宫问题深度优先搜索算法(Depth-First Search, DFS)是一种常用的图遍历算法,它通过优先遍历图中的深层节点来搜索目标节点。
在解决迷宫问题时,深度优先搜索算法可以帮助我们找到从起点到终点的路径。
一、深度优先搜索算法的实现原理深度优先搜索算法的实现原理相当简单直观。
它遵循以下步骤:1. 选择一个起始节点,并标记为已访问。
2. 递归地访问其相邻节点,若相邻节点未被访问,则标记为已访问,并继续访问其相邻节点。
3. 重复步骤2直到无法继续递归访问,则返回上一级节点,查找其他未被访问的相邻节点。
4. 重复步骤2和3,直到找到目标节点或者已经遍历所有节点。
二、利用深度优先搜索算法解决迷宫问题迷宫问题是一个经典的寻找路径问题,在一个二维的迷宫中,我们需要找到从起点到终点的路径。
利用深度优先搜索算法可以很好地解决这个问题。
以下是一种可能的解决方案:```1. 定义一个二维数组作为迷宫地图,其中0代表通路,1代表墙壁。
2. 定义一个和迷宫地图大小相同的二维数组visited,用于记录节点是否已经被访问过。
3. 定义一个存储路径的栈path,用于记录从起点到终点的路径。
4. 定义一个递归函数dfs,参数为当前节点的坐标(x, y)。
5. 在dfs函数中,首先判断当前节点是否为终点,如果是则返回True,表示找到了一条路径。
6. 然后判断当前节点是否越界或者已经访问过,如果是则返回False,表示该路径不可行。
7. 否则,将当前节点标记为已访问,并将其坐标添加到path路径中。
8. 依次递归访问当前节点的上、下、左、右四个相邻节点,如果其中任意一个节点返回True,则返回True。
9. 如果所有相邻节点都返回False,则将当前节点从path路径中删除,并返回False。
10. 最后,在主函数中调用dfs函数,并判断是否找到了一条路径。
```三、示例代码```pythondef dfs(x, y):if maze[x][y] == 1 or visited[x][y] == 1:return Falseif (x, y) == (end_x, end_y):return Truevisited[x][y] = 1path.append((x, y))if dfs(x+1, y) or dfs(x-1, y) or dfs(x, y+1) or dfs(x, y-1): return Truepath.pop()return Falseif __name__ == '__main__':maze = [[0, 1, 1, 0, 0],[0, 0, 0, 1, 0],[1, 1, 0, 0, 0],[1, 1, 1, 1, 0],[0, 0, 0, 1, 0]]visited = [[0] * 5 for _ in range(5)]path = []start_x, start_y = 0, 0end_x, end_y = 4, 4if dfs(start_x, start_y):print("Found path:")for x, y in path:print(f"({x}, {y}) ", end="")print(f"\nStart: ({start_x}, {start_y}), End: ({end_x}, {end_y})") else:print("No path found.")```四、总结深度优先搜索算法是一种有效解决迷宫问题的算法。
深度优先搜索

深度优先搜索所谓 " 深度 " 是对产生问题的状态结点而言的, " 深度优先 " 是一种控制结点扩展的策略,这种策略是优先扩展深度大的结点,把状态向纵深发展。
深度优先搜索也叫做 DFS法 (Depth First Search) 。
深度优先搜索的递归实现过程:procedure dfs(i);for j:=1 to r doif if 子结点子结点mr 符合条件 then产生的子结点mr 是目标结点 then输出mr 入栈;else dfs(i+1);栈顶元素出栈(即删去mr);endif;endfor;[ 例 1] 骑士游历 :设有一个 n*m 的棋盘,在棋盘上任一点有一个中国象棋马.马走的规则为 :1.马走日字2.马只能向右走。
当 N,M 输入之后 , 找出一条从左下角到右上角的路径。
例如:输入N=4,M=4,输出 : 路径的格式 :(1,1)->(2,3)->(4,4),若不存在路径,则输出"no"算法分析:我们以 4×4的棋盘为例进行分析,用树形结构表示马走的所有过程,求从起点到终点的路径 , 实际上就是从根结点开始深度优先搜索这棵树。
马从(1,1)开始,按深度优先搜索法,走一步到达(2,3),判断是否到达终点,若没有,则继续往前走,再走一步到达(4,4),然后判断是否到达终点,若到达则退出,搜索过程结束。
为了减少搜索次数,在马走的过程中,判断下一步所走的位置是否在棋盘上,如果不在棋盘上,则另选一条路径再走。
程序如下:constdx:array[1..4]of integer=(2,2,1,1);dy:array[1..4]of integer=(1,-1,2,-2);typemap=recordx,y:integer;end;vari,n,m:integer;a:array[0..50]of map;procedure dfs(i:integer);var j,k:integer;beginfor j:=1 to 4 doif(a[i-1].x+dx[j]>0)and(a[i-1].x+dx[j]<=n)and(a[i-1].y+dy[j]>0)and(a[i-1].y+dy[j]<=n) then{判断是否在棋盘上} begina[i].x:=a[i-1].x+dx[j];a[i].y:=a[i-1].y+dy[j];{入栈}if (a[i].x=n)and(a[i].y=m)thenbeginwrite('(',1,',',1,')');for k:=2 to i do write('->(',a[k].x,',',a[k].y,')');halt;{输出结果并退出程序 }end;dfs(i+1);{搜索下一步 }a[i].x:=0;a[i].y:=0;{出栈 }end;end;begina[1].x:=1;a[1].y:=1;readln(n,m);dfs(2);writeln('no');end.从上面的例子我们可以看出,深度优先搜索算法有两个特点:1、己产生的结点按深度排序,深度大的结点先得到扩展,即先产生它的子结点。
深度优先搜索和广度优先搜索

深度优先搜索和广度优先搜索深度优先搜索(DFS)和广度优先搜索(BFS)是图论中常用的两种搜索算法。
它们是解决许多与图相关的问题的重要工具。
本文将着重介绍深度优先搜索和广度优先搜索的原理、应用场景以及优缺点。
一、深度优先搜索(DFS)深度优先搜索是一种先序遍历二叉树的思想。
从图的一个顶点出发,递归地访问与该顶点相邻的顶点,直到无法再继续前进为止,然后回溯到前一个顶点,继续访问其未被访问的邻接顶点,直到遍历完整个图。
深度优先搜索的基本思想可用以下步骤总结:1. 选择一个初始顶点;2. 访问该顶点,并标记为已访问;3. 递归访问该顶点的邻接顶点,直到所有邻接顶点均被访问过。
深度优先搜索的应用场景较为广泛。
在寻找连通分量、解决迷宫问题、查找拓扑排序等问题中,深度优先搜索都能够发挥重要作用。
它的主要优点是容易实现,缺点是可能进入无限循环。
二、广度优先搜索(BFS)广度优先搜索是一种逐层访问的思想。
从图的一个顶点出发,先访问该顶点,然后依次访问与该顶点邻接且未被访问的顶点,直到遍历完整个图。
广度优先搜索的基本思想可用以下步骤总结:1. 选择一个初始顶点;2. 访问该顶点,并标记为已访问;3. 将该顶点的所有邻接顶点加入一个队列;4. 从队列中依次取出一个顶点,并访问该顶点的邻接顶点,标记为已访问;5. 重复步骤4,直到队列为空。
广度优先搜索的应用场景也非常广泛。
在求最短路径、社交网络分析、网络爬虫等方面都可以使用广度优先搜索算法。
它的主要优点是可以找到最短路径,缺点是需要使用队列数据结构。
三、DFS与BFS的比较深度优先搜索和广度优先搜索各自有着不同的优缺点,适用于不同的场景。
深度优先搜索的优点是在空间复杂度较低的情况下找到解,但可能陷入无限循环,搜索路径不一定是最短的。
广度优先搜索能找到最短路径,但需要保存所有搜索过的节点,空间复杂度较高。
需要根据实际问题选择合适的搜索算法,例如在求最短路径问题中,广度优先搜索更加合适;而在解决连通分量问题时,深度优先搜索更为适用。
《深度优先搜索》课件

04 重复步骤3,直到栈为空,表示所有节点都已访问过
单击此处输入你的项正文,文字是您思想的提炼,请尽量言简意 赅的阐述观点单击此处输入你的项正文
深度优先搜索中,栈用于存 储待访问的节点
栈是一种先进后出的数据结 构
不适用于大规模问题:深度优先搜索在处理大规模问题时,效率较低,不适用
深度优先搜索:适用于树形结构,能够找到最优解,但时间复杂度较高 广度优先搜索:适用于图结构,时间复杂度较低,但无法找到最优解 贪心算法:适用于最优化问题,但无法保证找到最优解 动态规划:适用于最优化问题,能够找到最优解,但时间复杂度较高
结果:通过深度 优先搜索,可以 找到所有可能的 八皇后解,并输 出结果
深度优先搜索的性 能优化
剪枝策略:根 据问题特性, 选择合适的剪
枝策略
剪枝方法:如 最小堆、最大 堆、贪心算法
等
剪枝效果:减 少搜索空间, 提高搜索效率
剪枝技巧:如 动态规划、启
发式搜索等
概念:将已经搜索过的状态记录下来,避免重复搜索 优点:减少重复搜索,提高搜索效率 实现方法:使用哈希表或数组存储已搜索过的状态 应用:广泛应用于各种搜索问题,如迷宫求解、最短路径等
剪枝优化:通过剪枝减少不必要的搜索 记忆化搜索:将已搜索过的状态存储起来,避免重复搜索 启发式搜索:根据问题特性选择合适的启发式函数,提高搜索效率 并行搜索:利用多核CPU进行并行搜索,提高搜索速度
动态规划是一种解决最优化问题的方法,通过将问题分解为更小的子问题来解决
动态规划可以用于优化深度优先搜索,提高搜索效率 动态规划可以避免重复计算,减少搜索时间 动态规划可以找到最优解,提高搜索质量
数据结构与算法(13):深度优先搜索和广度优先搜索
2.2.2 有向图的广广度优先搜索
下面面以“有向图”为例例,来对广广度优先搜索进行行行演示。还是以上面面的图G2为例例进行行行说明。
第1步:访问A。 第2步:访问B。 第3步:依次访问C,E,F。 在访问了了B之后,接下来访问B的出边的另一一个顶点,即C,E,F。前 面面已经说过,在本文文实现中,顶点ABCDEFG按照顺序存储的,因此会先访问C,再依次访 问E,F。 第4步:依次访问D,G。 在访问完C,E,F之后,再依次访问它们的出边的另一一个顶点。还是按 照C,E,F的顺序访问,C的已经全部访问过了了,那么就只剩下E,F;先访问E的邻接点D,再访 问F的邻接点G。
if(mVexs[i]==ch)
return i;
return -1;
}
/* * 读取一一个输入入字符
*/
private char readChar() {
char ch='0';
do {
try {
ch = (char)System.in.read();
} catch (IOException e) {
数据结构与算法(13):深度优先搜索和 广广度优先搜索
BFS和DFS是两种十十分重要的搜索算法,BFS适合查找最优解,DFS适合查找是否存在解(或者说 能找到任意一一个可行行行解)。用用这两种算法即可以解决大大部分树和图的问题。
一一、深度优先搜索(DFS)
1.1 介绍
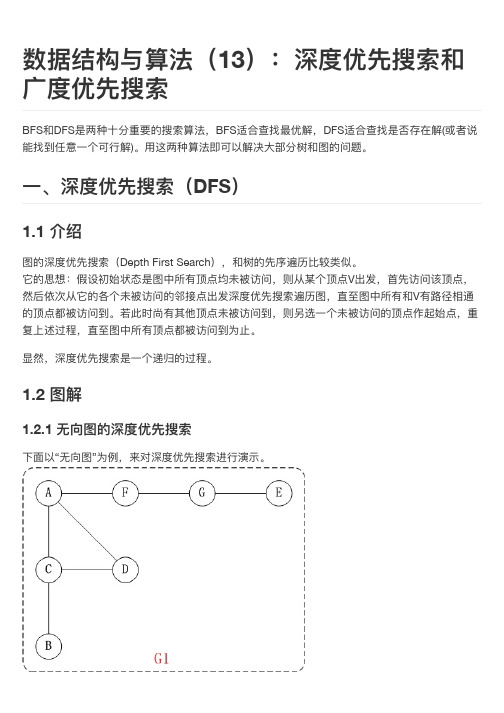
图的深度优先搜索(Depth First Search),和树的先序遍历比比较类似。 它的思想:假设初始状态是图中所有顶点均未被访问,则从某个顶点V出发,首首先访问该顶点, 然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至至图中所有和V有路路径相通 的顶点都被访问到。若此时尚有其他顶点未被访问到,则另选一一个未被访问的顶点作起始点,重 复上述过程,直至至图中所有顶点都被访问到为止止。 显然,深度优先搜索是一一个递归的过程。
bfs和dfs算法

bfs和dfs算法BFS(Breadth-First Search,广度优先搜索)和DFS (Depth-First Search,深度优先搜索)是两种常用的图搜索算法。
它们的主要区别在于访问节点的顺序不同。
BFS(广度优先搜索)BFS从图的某一节点(源节点)出发,首先访问该节点的所有未访问过的邻居节点,然后对每个邻居节点,再访问它们各自的未访问过的邻居节点,如此类推,直到所有的节点都被访问过。
BFS使用队列来保存待访问的节点,队列的先进先出(FIFO)特性保证了先访问的节点先被处理,后访问的节点后被处理,即按照广度优先的顺序进行搜索。
DFS(深度优先搜索)DFS也从图的某一节点(源节点)出发,但它首先访问该节点的任意一个未访问过的邻居节点,然后对这个邻居节点进行同样的操作,即再访问它的任意一个未访问过的邻居节点,如此类推,直到当前节点没有未访问过的邻居节点为止。
此时,DFS返回上一级节点,再尝试访问它的其他未访问过的邻居节点,直到所有节点都被访问过。
DFS使用栈来保存待访问的节点,栈的后进先出(LIFO)特性保证了先访问的节点后被处理,后访问的节点先被处理,即按照深度优先的顺序进行搜索。
应用BFS和DFS都有各自的应用场景。
例如,在解决图的连通性问题时,BFS和DFS都可以用来判断图是否是连通的。
在寻找最短路径时,BFS可以用来解决无权图的单源最短路径问题(例如,广度优先搜索算法可以用来实现图的Floyd-Warshall算法)。
DFS则可以用来解决树的深度、图的直径等问题。
此外,DFS还可以用于图的遍历、拓扑排序等任务。
总结BFS和DFS的主要区别在于访问节点的顺序不同,这导致它们在处理某些问题时具有不同的优势和劣势。
因此,在选择使用哪种算法时,需要根据具体问题的特点进行决策。
深度优先搜索和广度优先搜索的比较和应用场景

深度优先搜索和广度优先搜索的比较和应用场景在计算机科学中,深度优先搜索(DFS)和广度优先搜索(BFS)是两种常用的图搜索算法。
它们在解决许多问题时都能够发挥重要作用,但在不同的情况下具有不同的优势和适用性。
本文将对深度优先搜索和广度优先搜索进行比较和分析,并讨论它们在不同应用场景中的使用。
一、深度优先搜索(DFS)深度优先搜索是一种通过遍历图的深度节点来查找目标节点的算法。
它的基本思想是从起始节点开始,依次遍历该节点的相邻节点,直到到达目标节点或者无法继续搜索为止。
如果当前节点有未被访问的相邻节点,则选择其中一个作为下一个节点继续进行深度搜索;如果当前节点没有未被访问的相邻节点,则回溯到上一个节点,并选择其未被访问的相邻节点进行搜索。
深度优先搜索的主要优势是其在搜索树的深度方向上进行,能够快速达到目标节点。
它通常使用递归或栈数据结构来实现,代码实现相对简单。
深度优先搜索适用于以下情况:1. 图中的路径问题:深度优先搜索能够在图中找到一条路径是否存在。
2. 拓扑排序问题:深度优先搜索能够对有向无环图进行拓扑排序,找到图中节点的一个线性排序。
3. 连通性问题:深度优先搜索能够判断图中的连通分量数量以及它们的具体节点组合。
二、广度优先搜索(BFS)广度优先搜索是一种通过遍历图的广度节点来查找目标节点的算法。
它的基本思想是从起始节点开始,先遍历起始节点的所有相邻节点,然后再遍历相邻节点的相邻节点,以此类推,直到到达目标节点或者无法继续搜索为止。
广度优先搜索通常使用队列数据结构来实现。
广度优先搜索的主要优势是其在搜索树的广度方向上进行,能够逐层地搜索目标节点所在的路径。
它逐层扩展搜索,直到找到目标节点或者遍历完整个图。
广度优先搜索适用于以下情况:1. 最短路径问题:广度优先搜索能够在无权图中找到起始节点到目标节点的最短路径。
2. 网络分析问题:广度优先搜索能够在图中查找节点的邻居节点、度数或者群组。
三、深度优先搜索和广度优先搜索的比较深度优先搜索和广度优先搜索在以下方面有所不同:1. 搜索顺序:深度优先搜索按照深度优先的顺序进行搜索,而广度优先搜索按照广度优先的顺序进行搜索。
《深度优先搜索》课件

总结词
应用广泛,涉及图论和算法
要点二
详细描述
图的着色问题是一个经典的NP难问题,通过深度优先搜索 可以找到一种合适的颜色分配方案,使得相邻的顶点颜色 不同。在深度优先搜索过程中,我们可以使用回溯算法来 尝试不同的颜色分配方案,直到找到可行解或证明无解。
旅行商问题
总结词
组合优化问题,适合理解最短路径算法
详细描述
深度优先搜索、广度优先搜索和最佳优先搜索是常见的三种搜索算法。它们在处理问题的侧重点和适用场景上有 所不同。深度优先搜索更注重深度上的探索,而广度优先搜索则更注重广度上的探索。最佳优先搜索则是在启发 式搜索中常用的算法,它根据某种启发式信息来选择下一个要探索的节点。
02
深度优先搜索的基本原理
图的表示与遍历
图的表示
图是由节点和边组成的数据结构,可以用邻接矩阵或邻接表来表示。邻接矩阵是一种二 维矩阵,其中行和列都代表图中的节点,如果两个节点之间存在一条边,则矩阵中相应 的元素为1,否则为0。邻接表则是用链表来表示图中的边,每个节点包含一个链表,
链表中的元素是与该节点相邻的节点。
图的遍历
图的遍历是指按照某种顺序访问图中的所有节点。常见的图的遍历算法有深度优先搜索 (DFS)和广度优先搜索(BFS)。DFS是一种递归的算法,通过不断深入探索图的分 支,直到达到终点或无法再深入为止。BFS则是按照层次顺序访问图中的节点,从根节
05
深度优先搜索的案例分析
八皇后问题
总结词
经典问题,适合初学者理解深度优先搜索
详细描述
八皇后问题是一个经典的回溯算法问题,通过深度优先搜索 可以找出在8x8棋盘上放置8个皇后,使得它们互不攻击的方 案。在深度优先搜索过程中,我们可以使用递归和剪枝技巧 来减少搜索空间,提高搜索效率。
数据结构之的遍历深度优先搜索和广度优先搜索的实现和应用

数据结构之的遍历深度优先搜索和广度优先搜索的实现和应用深度优先搜索和广度优先搜索是数据结构中重要的遍历算法,它们在解决各种问题时起着关键作用。
本文将介绍深度优先搜索和广度优先搜索的实现方法以及它们的应用。
一、深度优先搜索的实现和应用深度优先搜索(Depth First Search,DFS)是一种用于图或树的遍历算法。
它的基本思想是从起始节点开始,一直沿着某一分支深入直到不能再深入为止,然后回溯到前一个节点,再沿另一分支深入,直到遍历完所有节点。
深度优先搜索可以通过递归或者栈来实现。
在实现深度优先搜索时,可以采用递归的方式。
具体的实现步骤如下:1. 创建一个访问数组,用于标记节点是否已经被访问过。
2. 从起始节点开始,将其标记为已访问。
3. 遍历当前节点的邻接节点,对于每个邻接节点,如果该节点未被访问过,则递归调用深度优先搜索函数。
4. 重复步骤3,直到所有节点都被访问过。
深度优先搜索的应用非常广泛,以下是几个常见的应用场景:1. 图的连通性判断:深度优先搜索可以用于判断图中的两个节点是否连通。
2. 拓扑排序:深度优先搜索可以用于对有向无环图进行拓扑排序,即按照一种特定的线性顺序对节点进行排序。
3. 岛屿数量计算:深度优先搜索可以用于计算给定矩阵中岛屿的数量,其中岛屿由相邻的陆地单元组成。
二、广度优先搜索的实现和应用广度优先搜索(Breadth First Search,BFS)是一种用于图或树的遍历算法。
它的基本思想是从起始节点开始,逐层遍历,先访问当前节点的所有邻接节点,然后再依次访问下一层的节点,直到遍历完所有节点。
广度优先搜索可以通过队列来实现。
在实现广度优先搜索时,可以采用队列的方式。
具体的实现步骤如下:1. 创建一个访问数组,用于标记节点是否已经被访问过。
2. 创建一个空队列,并将起始节点入队。
3. 当队列不为空时,取出队首节点,并标记为已访问。
4. 遍历当前节点的邻接节点,对于每个邻接节点,如果该节点未被访问过,则将其入队。
深度优先搜索与回溯算法

深度优先搜索与回溯算法深度优先(Depth First Search,简称DFS)和回溯算法是两种常见的算法,它们可以用来解决图和树相关的问题。
尽管它们在一些情况下可能无法找到最优解,但在许多实际应用中都有着广泛的应用。
深度优先是一种常用的遍历算法,其基本原理是从起始节点开始,沿着图的深度遍历到达最深处,然后回溯到上一层节点,继续遍历其他子节点直到所有节点都被访问过为止。
DFS可以用递归或者栈来实现。
在深度优先中,每个节点只能访问一次,避免陷入死循环。
通常,我们需要维护一个访问过的节点列表,以确保不会重复访问。
深度优先的时间复杂度为O(,V,+,E,),其中,V,表示图中节点的数量,E,表示边的数量。
在最坏的情况下,DFS需要遍历图中的所有节点和边。
深度优先的一个经典应用是在图中查找特定路径。
它也被广泛应用于迷宫问题、拓扑排序、连通性问题等。
回溯算法是一种通过枚举所有可能解的方法来解决问题的算法。
在过程中,如果当前路径无法达到目标,就返回上一层,寻找另一种可能的路径。
回溯算法通常使用递归来实现。
回溯算法通常包含三个步骤:1.选择:在当前节点选择一个可行的选项,并向前进入下一层节点。
2.约束:在进入下一层之前,检查当前节点的状态是否符合要求,即剪枝操作。
3.撤销选择:在下一层节点完毕后,返回上一层节点,撤销当前选择。
通过不断地进行选择、约束和撤销选择,回溯算法可以遍历所有可能的解空间,并找到满足条件的解。
回溯算法的时间复杂度取决于问题的规模和约束条件。
在最坏的情况下,回溯算法需要遍历所有的可能解,因此时间复杂度可以达到指数级。
回溯算法的一个经典应用是在数独游戏中寻找解。
它也被广泛应用于组合优化问题、八皇后问题、0-1背包问题等。
总结起来,深度优先和回溯算法是两种常用的算法,它们在图和树的遍历以及问题求解中有着广泛的应用。
深度优先通过遍历到达最深处再回溯,而回溯算法则是通过枚举所有可能解并进行剪枝来寻找解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安庆十四中胡锋
搜索问题着眼点
1)简化问题:突出问题的核心,用数学描述问题的状态空间—状态、状态转移;
2)问题的条件分析:显式条件、隐式条件、问题转化; 3)搜索策略:搜索对象、搜索顺序、结点扩展顺序; 4)剪技:可行性剪技、最优性剪技、充分抓住问题给予的条件剪技; 5)常数项优化:数据结构选择与利用,预处理,判重算法的选择,„„ 6)其他:细节处理、程序设计能力„„
问题4 AP数(ap.pas) 【问题描述】 正整数n是无穷的,但其中有些数有神奇的性质,我们给他个名字——AP数。 对于一个数字i他是AP数的充要条件是所有比他小的数的因数个数都没有i的因数个数 多。比如6的因数是1 2 3 6 共计有4个因数。他就是一个AP数(1-5的因数个数不是2就是 3)。我们题目的任务就是找到一个最大的,且不超过n的AP数。 【输入文件】 每个测试点可能拥有多组数据。请用seekeof来确认是否已读完 对于每一行有一个n,如题目所描述 【输出文件】 对于每一行输出最大的且不超过n的AP数 输入样例(ap.in) 1000 输出样例(ap.out) 840
【数据规模】 n<=15 0000 0000
【算法分析】 请先分析AP数有何特点? 首先定义一个函数f(x),f(x)表示x的约数的个数。题目中要求的最大的一个数m 满足下列条件:m≤n,且对于一切i<m,有f(i)<f(m)。 令x=p1x1*p2x2*„„*pnxn(p1,p2„„pn均为质数),则f(x)=(x1+1)*(x2+1) *„„*(xn+1)。 例:x=24=23*3 f(x)=(3+1)*(1+1)=8 约数为:1 2 3 4 6 8 12 24 性质一: 令A= p1x1*p2x2*„„*pnxn(p1,p2„„pn均为质数)。若A是AP数,那么p1, p2„„pn是相邻的质数,且p1=2。 这点很容易证明,若pi,pi+1不是相邻的质数或p1>2,则存在质数p,满足 p<pn,且p不是A的质因子。这时我们可将pn换成p,A变小了,但所含有的约数个数却没 变。这与A是AP矛盾。 性质二: 令A= p1x1*p2x2*„„*pnxn(p1,p2„„pn均为质数)。若A是AP数,那么 x1≥x2≥„„≥xn。 同样的,我们用反证法来证明,若xi<xj(i<j),我们可将xi与xj互换,A 变小了,但所含的约数个数没变,与A是AP矛盾。 请给出算法要点。 有了以上的两条结论我们可以知道AP数的质因子只能是由2开始的连续的质数, 而且质因子上的指数递减。题目中规定AP的上界为2*10^9,而 2*3*5*7*11*13*17*19*23*29>6*10^9,故我们只用考虑从2到29内的质数即可。这样, 确定了搜索对象,枚举2到29中质数上的因子就可以得到最大的反质数了。
引例1:分书(book.pas) 学校放暑假时,信息学辅导教师有n本书要分给参加培训的n个学生。如:A,B,C,D, E共5本书要分给参加培训的张、刘、王、李、孙5位学生,每人只能选1本。教师事先让每 个人将自己喜爱的书填写在如下的表中,然后根据他们填写的表来分配书本,希望设计一 个程序帮助教师求出可能的分配方案,使每个学生都满意。
3
【数据规模】 1<=N<=76
3 1 2 1 3 2
【算法分析】
1.状态空间及描述
(1)定义lin数组存放排列。 搜索对象:数字。 每个数字搜索的状态空间为lin数组序列的第1位至第2N位; (2)当在序列第i位和序列第i+t+1位上能够放入数字,则将第i位和第i+t+1位上放 置数字t,然后递归放置t+1。如果不符合放置条件则退回t重新搜索。当t=n时输出。 请考虑搜索序的选择,T值从小到大搜索还是从大到小搜索? 考查搜索树的形态: (1)T值从小到大: 第一层即T=1时,有2n-2分支选择。 (2)T值从大到小: 第一层即T=n时,有n-1分支选择。 相比较,(1)的搜索树形态要比(2)的搜索树形态宽得多。 因些直观分析倒序搜索能够更快得到解. 试验不同的搜索序程序得到解的效率. 结论:对搜索问题的解决,搜索序的选择将影响得到问题的解的效率. 2.无解判断 • • • • 最耗时的是无解状态,如果能时先将情况排除,程序的效率就快多了。 方法1: 打表发现规律 方法2: 数学方法分析,被夹住的数的个数分别为1,2,„n,被夹住的 数的总数为 (1+n)*n/2。如果这个数是奇数,无解。
【参考程序】line.pas
实例: <<CD>>(cd.pas) 【问题描述】 在Q迷的千呼万唤之下,N+Q终于推出了新专辑《My Cow Life》.其中一首《God is a cow》更是天籁之音,令Q迷们为之倾倒。可是,让Q迷们不爽的是,这张专辑是限量 发行的,并且价格„„.许多Q迷们在音像店前排起了长队,想要买到一张CD或者磁带。 SGaPb小店的店长SGaPb是个热心人。他看到这么多Q迷想要买专辑,就设计了一个小游 戏——抽奖。 规则是这样的:每位Q迷可以抽到一张奖券。奖券上写有1到M这M个自然数。Q迷可以在 这M个数中任意选取N个不同的数打圈。每个Q迷只能买一张奖券,不同的奖券上的选择 不同。每次抽奖将抽出两个自然数X和Y。如果某人拿到的奖券上,所选N个自然数的倒 数和,恰好等于X/Y,则他将免费获得一张CD《My Cow Life》。 现在,已知抽奖结果X 和Y。作为N+Q的fans,你的任务是:求出必须准备多少CD,才能保证支付所有获奖者。 且对于同一种选数, SGaPb只用支付一盘个整数N,M,X,Y。 【输出格式】 输出有且仅有一行,即所需准备的CD数量。 输入样例(cd.in) 输出样例(cd.out) 2 4 3 4 1 【数据规模】 对于30%的数据,1<=N<=M<=15 对于60%的数据,1<=N<=M<=20 对于100%的数据,1<=N<=M<=25,X<=25,Y<=25
实例:《Line》(line.pas) 【问题描述】 N+Q是班长。在校运动会上,N+Q班要进行队列表演。N+Q要选出2*N名同学编队,每 人都被编上一个号,每一个从1到N的自然数都被某2名同学佩戴,现在要求将他们排成 一列,使两个编号为1的同学中间恰好夹1名同学,两个编号为2的同学中间恰好夹2名同 学,„„,两个编号为N的同学中间恰好夹N名同学,N+Q希望知道这样的排法能否实现。 【输入格式】 输入文件仅包括一行,即要处理的N。 【输出格式】 输出文件有两种情况,如果这样的排法能实现,则输出排列顺序;如果这样的排法不能 实现,则输出“No Solution.”。格式如样例所示。 输入样例(line.in) 输出样例(line.out)
A
张 王 刘 孙 李 Y Y Y Y Y Y Y
B
C
Y
D
Y
E
【输入格式】第一行一个数n(学生的个数,书的数量) 以下共n行,每行n个0或1(由空格隔开),第I行数据表示第i个同学对所有书的喜爱 情况。0表示不喜欢该书,1表示喜欢该书。 【输出格式】依次输出每个学生分到的书号。 输入样例(book.in) 5 0 1 0 0 0 0 1 1 0 1 1 0 1 0 0 1 0 0 1 0 0 0 0 0 1 输出样例(book.out)
【算法设计】 1、搜索对象:2,3,5,7,11,13,17,19,23,29十个质数; 2、搜索状态:每个质数取多少个,最多为20个,根据性质2, 质数指数 x1≥x2≥„„≥xn,因些,每个质数的搜索状态为:1----i个(i为上一个质数 的个数); 3、搜索参数:k,now,m,lim 分别表示第k个质数,产生的乘积,约数的个数,下一 个质数搜索的个数范围; 4、判断条件:(1)质数乘积小于N;(2)约数的个数最多;(3)相同约数的个数 中的最小乘积为AP数。 本题分析特点:充分挖掘数据的特征性质,缩小了搜索范围,挖掘利用问题自身 的性质进行剪枝,达到了优化的目的。 【参考程序】ap.pas
【算法分析】
本题是组合数的问题,需要组合算法,利用dfs产生所有的字符串,一旦比较可 等于输入的字符串,那么就继续输出下五个字符串。当然本题也有更优秀的算法, 就是利用组合的数学特性产生字符串,这样可以从本身入手,速度更快。
【参考程序】count.pas
问题1:迷宫(maze.pas) 【问题描述】 给定一个N*M方格的迷宫,迷宫里有T处障碍,障碍处不可通过。给定起点坐标和 终点坐标,问每个方格最多经过1次,有多少种从起点坐标到终点坐标的方案。 在迷宫中移动有上下左右四种方式。保证起点上没有障碍。 【输入格式】 第一行N、M和T,N为行,M为列,T为障碍总数。 第二行起点坐标SX,SY,终点坐标FX,FY。 接下来T行,每行为障碍的坐标。 【输出格式】 给定起点坐标和终点坐标,问每个方格最多经过1次,从起点坐标到终点坐 标的方案总数。 【数据规模】 1<=N,M<=5。 输入样例(maze.in) 2 2 1 1 1 2 2 1 2 输出样例(maze.out) 1
【算法分析】 状态空间及描述
(1)搜索对象:迷宫,需要 表达每个位置, 方向,走到点的坐标: I,X,Y (2)状态转移: x:=x+dx[i]; y:=y+dy[i]; {const dx:array[1..4]of integer=(-1,0,1,0); dy:array[1..4]of integer=(0,1,0,-1);} (3)可行状态判定方法: map[x+dx[i],y+dy[i]]是否被访问过 【参考程序】maze.pas
【算法分析】 1、搜索对象:N个数 2、搜索状态:第1个数为1—M,第2个数为2—M,第i个数为上一个数T+1—M. 3、满足条件:从M个数中搜索选择N个数,当它们的倒数和与X/Y相等,组数 累加器SUM加1。 4、参数设置:(1)当前数;(2)搜索到了几个数;(3)累加的倒数和 2、剪枝处理 (1)搜索的起始值要比上一层搜索的起始值要大,这样既可以减少运行的时间,又 可以避免重复解; (2)可行性剪枝 在每一次搜索前,如果当前搜索到数的倒数和+接下去要搜索的所有数倒数和小 于X/Y,那就没有可能得出 一个解。我们可以中止它; 如果当前枚举值的倒数加上+上一层的和大于X/Y,也可以掐掉。 结论:可行性剪枝是常用的一种剪枝手法 REMARK 1、实数处理中的误差处理; 2、常数项优化,如:每处数倒数事先预处理好,避免在搜索过程中重复运算 【参考程序】cd.pas
