安徽省合肥市2012届高三第二次教学质量检测(理数)word版
合肥市2012年高三第二次教学质量检测

A. makes out B. turns out C. watches out D. checks out
25. It's reported that the future generations are going to live longer than we ______ now.
The American parenting style is characterized by an active interest and involvement in children's lives. Parents' 36 in their children' s lives have grown greatly, 37 a generation of emotionally healthy, capable and successful adults.
29. When choosing a university, don't just think about its reputation; ______ for the most suitable one for your goals.
A. to look B. looking some people claim they can predict the future, there is no scientific basis behind it.
A. As B. Once C. While D. Because
A. guide B. show C. act D. behave
23. ______ uality, technology and service, most Chinese ear makers are years behind their western competitors.
安徽省合肥市2012届高三第二次教学质量检测(合肥二模)理综(word版)

合肥市2012年高三第二次教学质量检测理科综合试题(考试时间:150分钟满分:300分)注意事项:1. 答题前,务必在答题卡和答题卷规定的地方填写自己的姓名、准考证号和座位号后两位。
2. 答第I卷时,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
3. 答第II卷时,必须使用O.5毫米的黑色墨水签字笔在答题卷上书写,要求字体工整、笔迹清晰。
作图题可先用铅笔在答题卷规定的位置绘出,确认后再用O.5毫米的黑色墨水签字笔描清楚。
4. 考试结束后,务必将答题卡和答题剪子一并上交第I卷选择题(本卷包括20小题,每小题只有一个选项符合题意,每小题6分,共120分)可能用到的相对原子质量H:1 0:16 S:32 Cu:64 I:1271.生物膜系统是细胞膜、细胞器膜和核膜等构成的整体。
生物膜系统与细胞代谢和细胞通讯密切相关。
下列有关说法错误的是A.细胞膜的成分有磷脂、蛋白质、糖蛋白和糖脂等B.细胞之间的信息交流均依赖于细胞膜上的特异性受体C.溶酶体和高尔基体在行使功能时可能伴随膜组分的更新D.内质网的膜上附着有多种酶,性腺细胞内质网丰富2.为研究酵母菌的发酵产物,某研究小组设计了如下图甲所示的装置,并将有关检测结果绘制成图乙。
①号、②号试管中均加入3mL蒸馏水和一定量的检验试剂。
据图分析下列说法正确的是A.检验发酵产物酒精需向①号试管中滴加含重铬酸钾的浓硫酸B.设②号试管对照组是为了排除无关变量温度对实验的干扰C.图乙曲线b表示①号试管内玻璃管口气泡释放速率变化D.图乙曲线a表示酵母菌培养液中酵母菌数量变化规律3.核酸是一切生物的遗传物质,下列有关核酸的说法正确的是A.使用盐酸能加速甲基绿进入细胞,并有利于甲基绿与DNA结合B.真核生物的遗传物质都是DNA,部分原核生物遗传物质是RNA C.DNA分子的每个脱氧核糖上均连接一个磷酸和一个含氮碱基D.RNA病毒的遗传物质均能在宿主细胞中反向转录生成DNA 4.下列关于人体内环境的叙述正确的是A.饮水不足,抗利尿激素增加会导致内环境稳态失调B.内环境是一个主要由H2PO4-/HPO42-构成的缓冲体系C.内环境中的血浆、淋巴、组织液等成分稳定时,机体达到稳态D.细胞内外液Na+、K+分布不均匀是神经纤维兴奋传导的基础5.科学家依据基因工程的原理最新研制的某种疫苗是用病原微生物中编码抗原的基因制成的,这个基因编码的产物能诱导机体产生免疫反应。
2012合肥二模理科数学试题及答案(免费WORD版)
【答案】D
10.定义域为R的偶函数f(x)满足对∀x∈R,有f(x+ 2) =f(x)-f(1),且当x∈[2,3]时f(x) =-2x2+ 12x-18,若函数y=f(x)-loga(x+ 1)在(0,+)上至少有三个零点,则a的取值范围为( )
(1)求证:PC⊥BD
(2)过直线BD且垂直于直线PC的平面交PC于点E,且三棱锥E-BCD的体积取到最大值
(i)求此时四棱锥E-ABCD的高;
(ii)求二面角A-DE-B的余弦值的大小。
解:(1)连接AC,则AC⊥BD
∵PA⊥平面ABCD.
∴PA⊥BD
∴BD⊥平面PAC
∴PC⊥BD
(2) (i)设AC与BD的交点M,连接EM,过点E作EN⊥AC于N,则EN⊥面ABCD,EN是三棱锥E-BCD的高
【答案】128
12.在极坐标系中,点(1,)到直线2cos-sin+2=0的距离为_____.
【答案】
13.若sin(+)=,则sin(+2)=__
【答案】-
14.设函数y=(x∈R,x≠,n∈N*)的最大值和最小值分别为an和bn,且cn=an+bn+anbn-15,Sn=|c1|+|c2|+|c3|+…+ |cn| = ______.
【答案】Sn=
15.函数y=f(x)的定义域为[-1,0)∪(0,1],其图像上任一点P(x,y)满足x2+y2= 1。
①函数y=f(x)一定是偶函数;
②函数y=f(x)可能既不是偶函数,也不是奇函数;
③函数y=f(x)可以是奇函数;
安徽省合肥市第六中学2012届高三第二次调研考试 数学理

…………………12 分
17.(本小题满分 12 分) 解:(1) 列联表补充如下:----------------------------------------3 分 喜爱打篮球 男生 女生 合计 (2)∵ K
2
不喜爱打篮球 5 15 20
合计 25 25 50
20 10 30
50 (20 15 10 5) 2 8.333 7.879 ------------------------5 分 30 20 25 25
A1
A D
19. (本小题满分 14 分) 列.
已知函数 f ( x) log m x ( m 为常数, 0 m 1 ) ,且数列 f ( a n ) 是首项为 2 ,公差为 2 的等差数
2 时,求数列 bn 的前 n 项和 Sn ; 2 (2)设 c n a n lg a n ,如果 c n 中的每一项恒小于它后面的项,求 m 的取值范围.
cos sin 7 0 的距离
C
B O
A
____________.
(第 15 小题) 三、解答题: 本大题共 6 小题,共 80 分.解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分 12 分) 已知函数 f ( x ) 2 cos (1)求 f ( ) 的值;
18.(本小题满分 14 分)三棱柱 ABC A1 B1C1 的直观图及三视图(主视图和俯视图是正方形,左侧 图是等腰直角三角形)如图, D 为 AC 的中点. (1)求证: AB1 // 平面 BDC1 ; (2)求证: A1C 平面 BDC1 ; (3)求二面角 A BC1 D 的正切值.
安徽省合肥市高三第二次教学质量检测数学理试题

安徽省合肥市届高三第二次教学质量检测数学理试题————————————————————————————————作者:————————————————————————————————日期:合肥市2019届高三第二次教学质量检测数学试题(理科)(考试时间:120分钟 满分:150分)第Ⅰ卷一、选择题:本大题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设复数z 满足41iz i=+,则z 在复平面内的对应点位于A.第一象限B.第二象限C.第三象限D.第四象限2.若集合201x A x x +⎧⎫=≤⎨⎬-⎩⎭,{}12B x x =-<<,则A B =A.[)22-,B.(]11-,C.(-1,1)D.(-1,2) 3.已知双曲线22221x y a b-=(00a b >>,)的一条渐近线方程为2y x =,且经过点P (6,4),则双曲线的方程是A.221432x y -=B.22134x y -=C.22128x y -=D.2214y x -= 4.在ABC ∆中,12BD DC =,则AD =A. 1344AB AC +B. 2133AB AC +C. 1233AB AC +D. 1233AB AC -5.下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:空调类 冰箱类 小家电类 其它类 营业收入占比90.10% 4.98% 3.82% 1.10% 净利润占比95.80%-0.48%3.82%0.86%则下列判断中不正确...的是 A.该公司2018年度冰箱类电器销售亏损B.该公司2018年度小家电类电器营业收入和净利润相同C.该公司2018年度净利润主要由空调类电器销售提供D.剔除冰箱类电器销售数据后,该公司2018年度空调类电器销售净利润占比将会降低6.将函数()2sin 16f x x π⎛⎫=+- ⎪⎝⎭的图象上各点横坐标缩短到原来的12(纵坐标不变)得到函数()g x 的图象,则下列说法正确的是A.函数()g x 的图象关于点 012π⎛⎫- ⎪⎝⎭,对称 B.函数()g x 的周期是2πC.函数()g x 在0 6π⎛⎫ ⎪⎝⎭,上单调递增D.函数()g x 在0 6π⎛⎫⎪⎝⎭,上最大值是17.已知椭圆22221x y a b+=(0a b >>)的左右焦点分别为12F F ,,右顶点为A ,上顶点为B ,以线段1F A 为直径的圆交线段1F B 的延长线于点P ,若2//F B AP ,则该椭圆离心率是A.33 B. 23 C. 32D. 228.某部队在一次军演中要先后执行六项不同的任务,要求是:任务A 必须排在前三项执行,且执行任务A之后需立即执行任务E ,任务B 、任务C 不能相邻,则不同的执行方案共有A.36种B.44种C.48种D.54种 9.函数()2sin f x x x x =+的图象大致为10.如图,正方形网格纸中的实线图形是一个多面体的三视图,则该多面体各表面所在平面互相垂直的有A.2对B.3对C.4对D.5对11.“垛积术”(隙积术)是由北宋科学家沈括在《梦溪笔谈》中首创,南宋数学家杨辉、元代数学家朱世杰丰富和发展的一类数列求和方法,有茭草垛、方垛、刍童垛、三角垛等等.某仓库中部分货物堆放成如图所示的“茭草垛”:自上而下,第一层1件,以后每一层比上一层多1件,最后一层是n 件.已知第一层货物单价1万元,从第二层起,货物的单价是上一层单价的910.若这堆货物总价是910020010n⎛⎫- ⎪⎝⎭万元,则n 的值为 A.7 B.8 C.9 D.1012.函数()121x x f x e e b x -=---在(0,1)内有两个零点,则实数b 的取值范围是A.()() 11 e ee e ---,,B.()()1 00 1e e --,,C.()()1 00 1e e --,, D.()()1 1e e e e ---,,第Ⅱ卷本卷包括必考题和选考题两部分.第13题—第21题为必考题,每个试题考生都必须作答.第22题、第23题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分.把答案填在答题卡上的相应位置.13.设等差数列{}n a 的前n 项和为n S ,若23a =,416S =, 则数列{}n a 的公差d =__________.14.若1sin 23πα⎛⎫+= ⎪⎝⎭,则cos2cos αα+=_____________.15.若0a b +≠,则()2221a b a b +++的最小值为_________.16.已知半径为4的球面上有两点A B ,,42AB =,球心为O ,若球面上的动点C 满足二面角C AB O --的大小为60o ,则四面体OABC 的外接球的半径为____________.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分) 在ABC ∆中,角A B C ,,所对的边分别为a b c ,,,22sin sin sin sin 2sin A B A B c C ++=,ABC ∆的面积S abc =.(Ⅰ)求角C ;(Ⅱ)求ABC ∆周长的取值范围.18.(本小题满分12分)如图,三棱台ABC EFG -的底面是正三角形,平面ABC ⊥平面BCGF ,2CB GF =,BF CF =.(Ⅰ)求证:AB CG ⊥;(Ⅱ)若BC CF =,求直线AE 与平面BEG 所成角的正弦值.19.(本小题满分12分)某种大型医疗检查机器生产商,对一次性购买2台机器的客户,推出两种超过质保期后两年内的延保维修优惠方案:方案一:交纳延保金7000元,在延保的两年内可免费维修2次,超过2次每次收取维修费2000元; 方案二:交纳延保金10000元,在延保的两年内可免费维修4次,超过4次每次收取维修费1000元. 某医院准备一次性购买2台这种机器。
安徽省示范高中2012届高三第二次大联考(数学理)word版

安徽省示范高中2012届高三第二次联考理科数学第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设全集U R =,集合2{|log }A x y x ==,2{|40}B x Z x =∈-≤,则下列结论正确的是( ) A .(0,)A B =+∞B .(](),0U C A B =-∞C .(){2,1,0}U A B =--ðD .(){1,2}U C A B =答案:C 解析:(0,),(,0],{2,1,0,1,2},U A A B =+∞=-∞=--ð所以(){2,1,0}U A B =--ð。
(2)若复数2(4)(2)z a a i =-++(其中a R ∈,21i =-)是纯虚数,则4log a 的值为( )A. 0B. 1C. 2D. 12答案:D解析:2(4)(2)z a a i =-++是纯虚数可得2a =,所以441log log 22a ==,选D 。
(3)下列命题中的真命题是 ( )A .x ∃∈R ,使得 sin cos 1.5x x += B.(0,),1xx e x ∀∈+∞>+ C .(,0),23x xx ∃∈-∞< D .(0,),sin cos x x xπ∀∈>答案:B解析:,sin cos x R x x ∀∈+≤(,0),23x xx ∀∈-∞>,sincos44ππ=,所以A 、C 、D是假命题。
令()1()10x x f x e x f x e '=--⇒=->对于(0,)x ∈+∞恒成立,故()f x 在(0,)x ∈+∞上单调增,()(0)01x f x f e x >=⇒>+,B 是真命题。
(4)30sin 105cos 30cos 15cos +的值是( )(A)2(B) (C)12 (D)1答案:A解析:2cos15cos30cos105sin 30=cos15cos30sin15sin 30cos 452+-==。
安徽省合肥市年高三第二次教学质量检测理数汇编

合肥市2017年高三第二次教学质量检测数学试题(理)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.i 为虚数单位,若复数()()12mi i ++是纯,则实数m =( ) A .1 B .1- C .12- D .22.已知[)1,A =+∞,1|212B x x a ⎧⎫=∈≤≤-⎨⎬⎩⎭R ,若A B φ≠I ,则实数a 的取值范围是( )A .[)1,+∞B .1,12⎡⎤⎢⎥⎣⎦C .2,3⎡⎫+∞⎪⎢⎣⎭D .()1,+∞3.已知变量x ,y 满足约束条件241x y x y y -≥⎧⎪+≤⎨⎪≥-⎩,则目标函数2z x y =-的最小值为( )A .1-B .1C .3D .74.若输入4n =,执行如图所示的程序框图,输出的s =( ) A .10 B .16 C.20 D .355.若中心在原点,焦点在y 轴上的双曲线离心率为3,则此双 曲线的渐近线方程为( )A .y x =±B .22y x =±C.2y x =± D .12y x =±6.等差数列{}n a 的前n 项和为n S ,且36S =,63S =,则10S =( ) A .110B .0 C.10- D .15- 7.一个几何体的三视图及其尺寸如图所示,则该几何体的体积为( )A .283B 28 D .22+8.对函数()f x ,如果存在00x ≠使得()()00f x f x =--,则称()()00,x f x 与()()00,x f x --为函数图像的一组奇对称点.若()x f x e a =-(e 为自然数的底数)存在奇对称点,则实数a 的取值范围是( )A .(),1-∞B .()1,+∞ C.()e,+∞ D .[)1,+∞9.若平面α截三棱锥所得截面为平行四边形,则该三棱锥与平面α平行的棱有( ) A .0条 B .1条 C.2条 D .1条或2条10.已知5件产品中有2件次品,现逐一检测,直至能确定...所有次品为止,记检测的次数为ξ,则E ξ=( )A .3B .72 C.185D .4 11.锐角..ABC ∆中,内角A ,B ,C 的对边分别为a ,b ,c ,且满足()()()sin sin sin a b A B c b C -+=-,若a =22b c +的取值范围是( )A .(]3,6B .()3,5 C.(]5,6 D .[]5,612.已知函数()ln xf x x x ae =-(e 为自然对数的底数)有两个极值点,则实数a 的取值范围是( ) A .10,e ⎛⎫ ⎪⎝⎭ B .()0,e C.1,e e ⎛⎫⎪⎝⎭D .(),e -∞第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.等比数列{}n a 满足0n a >,且284a a =,则21222329log log log log a a a a ++++=L . 14.不共线向量a r ,b r 满足a b =r r ,且()2a a b ⊥-r r r ,则a r 与b r的夹角为 .15.在411x x ⎛⎫-- ⎪⎝⎭的展开式中,常数项为 .16.已知关于x 的方程()1cos sin 2t x t x t +-=+在()0,π上有实根,则实数t 的最大值是 . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.已知()sin a =x x r ,()cos ,cos b x x =-r ,函数()f x a b =⋅r r .(Ⅰ)求函数()y f x =图像的对称轴方程; (Ⅱ)若方程()13f x =在()0,π上的解为1x ,2x ,求()12cos x x -的值.18. 某校计划面向高一年级1200名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了180名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有105人.在这180名学生中选择社会科学类的男生、女生均为45人.(Ⅰ)分别计算抽取的样本中男生及女生选择社会科学类的频率,并以统计的频率作为概率,估计实际选课中选择社会科学类学生数;(Ⅱ)根据抽取的180名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过0.025的前提下认为科类的选择与性别有关?附:()()()()()22n ab bc K a b c d a c b d -=++++,其中n a b c d =+++.19. 矩形ABCD 中,1AB =,2AD =,点E 为AD 中点,沿BE 将ABE ∆折起至PBE ∆,如右图所示,点P 在面BCDE 的射影O 落在BE 上.(Ⅰ)求证:BP CE ⊥;(Ⅱ)求二面角B PC D --的余弦值.20. 如图,抛物线E :()220y px p =>与圆O :228x y +=相交于A ,B 两点,且点A 的横坐标为2.过劣弧AB 上动点()00,P x y 作圆O 的切线交抛物线E 于C ,D 两点,分别以C ,D 为切点作抛物线E 的切线1l ,2l ,1l 与2l 相交于点M . (Ⅰ)求p 的值;(Ⅱ)求动点M 的轨迹方程.21. 已知()()ln f x x m mx =+-. (Ⅰ)求()f x 的单调区间;(Ⅱ)设1m >,1x ,2x 为函数()f x 的两个零点,求证:120x x +<.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程在直角坐标系xoy 中,以坐标原点为极点,x 轴的非负半轴为极轴建立极坐标系,圆C 的极坐标方程为4cos ρθ=.(Ⅰ)求出圆C 的直角坐标方程;(Ⅱ)已知圆C 与x 轴相交于A ,B 两点,直线l :2y x =关于点()()0,0M m m ≠对称的直线为'l .若直线'l 上存在点P 使得90APB ∠=o ,求实数m 的最大值.23.选修4-5:不等式选讲已知函数())0f x =≠. (Ⅰ)求函数()f x 的定义域;(Ⅱ)若当[]0,1x ∈时,不等式()1f x ≥恒成立,求实数a 的取值范围.试卷答案一、选择题1-5:DABCB 6-10:DABCB 11、12:CA二、填空题 13.9 14.3π15.5- 16.1-三、解答题17.解:(Ⅰ)()()()sin cos ,cos f x a b x x x x =⋅+=⋅-+r r21sin cos sin 22sin 223x x x x x x π⎛⎫=⋅-+=-=- ⎪⎝⎭ 令232x k πππ-=+,得()5122kx k Z ππ=+∈ 即()y f x =的对称轴方程为5122kx ππ=+,()k Z ∈ (Ⅱ)由条件知121sin 2sin 20333x x ππ⎛⎫⎛⎫-=-=> ⎪ ⎪⎝⎭⎝⎭,且12520123x x ππ<<<<易知()()11,x f x 与()()22,x f x 关于512x π=对称,则1256x x π+=()1211111551cos cos cos 2cos 2sin 2663233x x x x x x x πππππ⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫∴-=--=-=--=-=⎢⎥ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦18.(Ⅰ)由条件知,抽取的男生105人,女生18010575-=人。
安徽马鞍山市2012届高三第二次教学质量检测(理数,word版)【精品】

安徽省马鞍山市2012届高三第二次教学质量检测 数学理 2012.4第I 卷(选择题,共50分)一、透择月:本大题共10个小皿,每小班5分,共so 分.在每小月给出的四个选项中,只有-项是符合题目要求的. (1)在复平面内,复数201211i i++(i 是虚数单位)对应的点位于 A.第一象限 B.第二象限 C.第三象限 D.第四象限 (2)己知全集U =R ,函数y的定义域为集合A ,函数y =log 2(x+1)的定义域为B ,则集合()U A C B I =A. (2,-1)B. (-2,-1]C.(-∞,-2)D. [-1,+ ∞)(3)己知α、β为两个平面,l 为直线.若α⊥β,α∩β=l ,则 A.垂直于平面β的平面一定平行于平面α B.垂直于直线I 的直线一定垂直于平面α C.垂直于平面β的平面一定平行于直线lD.垂直于直线l 的平面一定与平面a ,β都垂直(4)为得到函数y=cos(x+3π)的图象,只需将函数y =sinx 的图象 A.向左平移6π个长度单位 B.向右平移6π个长度单位C.向左平移56π个长度单位D.向右平移6π个长度单位(5)以直角坐标系的原点为极点,x 轴正半轴为极轴,单位长度不变,建立极坐标系,则曲线C :2cos 22sin x y αα=⎧⎨=-⎩(α为参数)的极坐标方程是A.ρ=-4sin θ B. ρ=4sin θ C. ρ=-2sin θ D. ρ=2sin θ(6)某程序的框图如下图所示,若执行该程序,则输出的i 值为A. 5B. 6C.7D. 8(7)等差数列{n a }的前n 项和为Sn.,且a 1+a 2=l0,a 3+a 4=26,则过点P(n ,n a )和Q(n+2, 2n a +) (n ∈N +)的直线的一个方向向量是 A.、 (-12,-2) B.、 (-1,-1) C.、 (-12,-1) D.、 (2,12) (8)已知椭圆C 1:222x y m n ++=1与双曲线C 2:22x y m n-=1共焦点,则椭圆C 1的离心率e 的取值范围为A 、(2,1) B 、(0,2) C 、(0,1) D 、(0,12) (9)定义在R 上的函数f(x)满足f(x+32)+f(x)=0,且函数y=f (x -34)为奇函数,给出下列命题:①函数f (x)的最小正周期是32;②函数y=f(x)的图象关于点(-34,0)对称:③函数y=f(x)的图象关于y 轴对称.其中真命题的个数是A 、0B 、1C 、2D 、3(10)点M(x,y)满足:3cos cos ()3sin sin x R y θθθθθ≤≤⎧∈⎨≤≤⎩,点N (x,y )满足:(x -3)2+(y -3)2=1,则||MN uuu r 的最小值是-3 -4 C. 5 D. 4第II 卷(非选择题,共100分)二、填空题:共25分。
安徽省合肥届高三第二次教学质量检测(数学理)扫描版.pdf

20.3 电磁铁 电磁继电器 课 题课 型新授课授 课 时 间设 计 人教 学 目 标知 识 目 标 : 1、了解电能的各种来源与应用;体验电能可以转化其他形式的能量。
2、知道电能及电功的单位;会进行电能单位间的换算 3、会使用家庭电能表。
会正确读出电能表的示数,并能进行电能的简单计算。
能 力 目 标 : 1、通过调查、查阅资料收集电能的各种来源和各种应用的知识,学习收集和处理信息的方法; 2、通过小组的讨论与交流,课堂踊跃发言,了解电能对促进人类社会进步与发展的重要作用。
通过压强知识解决生活实际的应用培养学生分析问题和解决问题的能力 情 感 目标 :1、初步认识科学技术的进步对人类社会的发展具有巨大的促进作用; 2、培养学生对科学的求知欲,使学生乐于探究日常生产生活中所包含的物理学知识,提高学习物理的兴趣。
3、认识节约用电的重要性。
教学重点1、从电能的各种来源与各种应用来学习电能。
2、会使用家庭电能表。
教学难点1、电能的单位及单位间的换算。
2、功和电功的概念。
教 学 过 程 一、电磁铁的构造 电磁铁是利用电流的磁效应,使软铁具有磁性的装置。
将软铁棒插入一螺形线圈内部,则当线圈通有电流时,线圈内部的磁场使软铁棒磁化成磁铁;当电流切断时,则线圈及软铁棒的磁性随着消失。
软铁棒磁化后所产生的磁场,加上原有线圈内的磁场,使得总磁场强度大大增强,故电磁铁的磁力大于天然磁铁。
二、电磁铁的应用 1.电铃 工作原理:电路闭合,电磁铁具有磁性,吸引弹性片,使铁锤向铁铃方向运动,铁锤打击铁铃而发出声音,同时电路断开,电磁铁失去磁性,铁锤又被弹回,电路闭合。
上述过程不断重复,电铃发出了持续的铃声。
2.电磁选矿机和电磁起重机 探究 如图所示是电磁选矿机和电磁起重机,请你根据电磁铁 的原理,解释这两种机械的工作原理。
3.电磁继电器 说出电磁电器的作用和工作原理 (1)电磁继电器是由电磁铁控制的自动开关。
2012年合肥三模理科综合答案[1]
![2012年合肥三模理科综合答案[1]](https://img.taocdn.com/s3/m/ae98808e84868762caaed5ed.png)
合肥市2012年高三第三次教学质量检测数学试题(理)(考试时间:120分钟满分:150分)第I卷(满分50分)一.选择题(本大题共⑴小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若复数(i是虚数单位)为纯虚数,则实数a的值为()A. a = 1B. a = - 1C. a =0D. a = ± 12."m=2"是“f(x)=x”为(,)上的偶函数”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件3.R表示实数集,集合,则()A. B. C. D.4.双曲线(a>0,b>0)的一个焦点与抛物线的焦点重合,且双曲线上有一点到一个焦点的距离比到另一焦点的距离大4,则()A. b =4B.C.D.5.已知|a|=1,|b|=2,a与b的夹角为60°,则a+b在a方向上的投影为()A.2B.1C.D.6.极点与直角坐标系的原点重合,极轴与x轴非负半轴重合,曲线C的极坐标方程为,直线l的参数方程为(t为参数),直线l与曲线C交于A、B,则线段AB的长等于()A. 1/2B.C. 1D.7.巳知,若,对成立,则最小值为()A. B. C. D.8.已知梯形ABCD中,AB//CD,,DC=2AB=2BC = 2,以直线AD为旋转轴旋转一周得到的几何体的表面积为()A. B. C. D.9•设,则=( )A. B. C. D.10.函数y=f(x)定义域为,f(1) =f(3) =1 ,f(x)的导数.,其中a为常数且a>0,则不等式组所表示的平面区域的面积等于()A. B. C. D. 1第II卷(满分100分)二.填空题(本大题共5小题,每小题5分,共25分.把答案填在答题卡的相应位置)11.已知等差数列{a n}满足a2= -1,,S15=75 ,则a5=_____;12.先阅读第(1)题的解法,再解决第(2)题:(1)已知“a=(3,4),b= (x,y), a.b = 1,求x2+y2的最小值.解:由,故的最小值为.(2) 已知实数x、y,z z满足:2x+3y+z = 1,则的最小值为_____;13.如图所示,程序框图的输出结果S=________;14.先后掷骰子(骰子的六个面上分别标有1、2、3、4、5、6个点)两次,落在水平桌面后,记正面朝上的点数分别为x,y,设事件A为“x +y 为偶数”,事件B为“x ,y中有偶数且”,则概率P(B| A) =________;15.对于曲线y=f(x),若存在直线I使得曲线y=f(x)位于直线l的同一侧,则称曲线y =f(X) 为半面曲线.下列曲线中是半面曲线的序号为_______(填上所有正确的序号)①y=-②y=x3③Y=X4+X3④Y=X+-⑤y=ln|x| ⑥y=xsin三.解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤)16.(本小题满分12分)在ΔABC 中,AB=,BC=5,tan(C--) = -7.(1) 求ΔABC的面积;(2) 求的值.17.(本小题满分12分)某市对该市小微企业资金短缺情况统计如下表:(1) 试估计该市小微企业资金缺额的平均值;(2) 某银行为更好的支持小微企业健康发展,从其第一批注资的A行业4家小微企业和B行业的3家小微企业中随机选取4家小微企业,进行跟踪调研.设选取的4家小微企业中是B行业的小微企业的个数为随机变量,求的分布列.18.(本题满分13分)在菱形ABCD中AC= 2,BD = 4,将ΔACD沿着AC折起,使点D翻折到D'位置,连BD',直线BD'与平面ABC 所成的角为30°,如右图所示.(1) 求证AC BD’(2) 若E为A B中点,过C作平面ABC的垂线l,直线l上是否存在一点F, 使EF//平面AD’C?若存在,求出CF的长;若不存在,请说明理由.19.(本小题满分13分)已知a>0且,函数.(1) 求函数y=f(x)的极值点; (2) 对使恒成立,求a 的取值范围.20.(本小题满分12分)椭圆C :(a >b >0)的左、右焦点分别为F 1, F 2,左顶点为上顶点为B ,ΔBF 1F 2是等边三角形,椭圆C 上的点到F 1的距离的最大值为3. (1) 求椭圆C 的方程;(2) 过F 1任意作一条直线l 交椭圆C 于M 、N 两点(均不是椭圆的顶点),设直线AM 与直线l 0 x = -4交于P 点,直线AN 与l 0交于Q 点,请判断点F 1与以线段PQ 为直径的圆 的位置关系.21.(本小题满分13分)}满足,S n是数列{a n}的前n项和.已知数列{an(1) 若a1=1,求a2,a3,a4并推证数列{a n}的通项公式;(2) 若,求证:。
高考专题安徽省合肥市高三第二次教学质量检测数学理试题.docx

合肥市2015年高三第二次教学质量检测数学试卷(理科)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数3412i z i+=-(其中i 为虚数单位),则复数z 的共轭复数z 等于 A.12i -- B.12i -+ C.12i + D.12i -2.若集合1{|1}M x x=<,则R M ð等于 A.{|1}x x ≤ B.{|01}x x <≤ C.{|01}x x ≤≤ D.{|1}x x <3.双曲线2221x y -=的离心率是 A.32B.62C.3D.3 4.某空间几何体的三视图如图所示(其中俯视图的弧线为四分之一圆),则该几何体的表面积为A.54π+B.84π+C.512π+D.812π+5.“1a =”是“直线1:10l ax y +-=与直线2:4(3)50l x a y a ++++=平行”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分又不必要条件6.等差数列{}n a 的前n 项和为n S ,若3426235a a a +-=,则7S 等于A.28B.21C.14D.77.已知函数()sin cos f x x x ωω=+,如果存在实数1x ,使得对于任意的实数x ,都有11()()(2015)f x f x f x ≤≤+成立,则ω的最小正值是A.12015B.2015π C.14030 D.4030π 8.如图所示的程序框图的输出结果是A.7B.8C.9D.109.某校开设5门不同的数学选修科,每位同学可以从中任选1门或2门课学习,甲,乙,丙三位同学选择的课没有一门是相同的,则不同的选法共有A.330种B.420种C.510种D.600种10.已知ABC ∆的三边长分别为,,a b c ,且满足3b c a +≤,则c a的取值范围是 A.(1,)+∞ B.(0,2) C.(1,3) D.(0,3)二、本大题共5小题,每小题5分,共25分,请将答案填在答题卡的相应位置.11.甲,乙两位同学5次考试的数学成绩(单位:分)统计结果如下:学生 第一次 第二次 第三次 第四次 第五次甲77 81 83 80 79 乙89 90 92 91 88 则成绩较为稳定的那位同学成绩的方差为12.以平面直角坐标系的原点为极点,x 轴的非负半轴为极轴,建立极坐标系,两种坐标系取相同的长度单位,曲线1C 的参数方程为2(x t t y at =-+⎧⎨=⎩为参数),曲线2C 的极坐标方程为4cos ρθ=,若1C 与2C 有两个不同的交点,则实数a 的取值范围是 13.已知已知点O 是ABC ∆内一点,且OA OB OC λμ=+u u u r u u u r u u u r ,若ABC ∆与OBC ∆的面积之比为3:1,则 λμ+=14.已知,αβ为钝角,若sin()2sin()αβαβ+=-,则tan()αβ-的最小值是15.定义:1()()f x f x =,当2n ≥且*n N ∈时,1()(())n n f x f f x -=,对于函数()f x 定义域内的0x ,若存在正整数n 是使得00()n f x x =成立的最小正整数,则称n 是点0x 的最小正周期,0x 称为()f x 的n -周期点.已知定义在[0,1]上的函数()f x 的图象如图,对于函数()f x ,下列说法正确的是 (写出你认为正确的所有命题的序号)①0是函数()f x 的一个5-周期点;②3是点12的最小正周期; ③对于任意正整数n ,都有22()33n f =; ④若0x 是()f x 的一个2-周期点,则01(,1]2x ∈⑤若0x 是()f x 的一个2-周期点,则0()f x 一点是()f x 的2-周期点. 三、解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.16(本小题满分12分)锐角ABC ∆中,角,,A B C 的对边分别为,,a b c ,已知tan c B 是tan b A 和tan b B 的等差中项.(Ⅰ)求角A 的大小; (Ⅱ)若(sin ,sin ),(cos ,cos )m B C n B C ==r r ,求m n ⋅r r 的取值范围.17(本小题满分12分)某商场为回馈大客户,开展摸球中奖活动,规则如下:从一个装有质地和大小完全相同的4个白球和一个红球的摸奖箱中随机摸出一球,若摸出红球,则摸球结束,若摸出白球(不放回),则向摸奖箱中放入一个红球后继续进行下一轮摸球,直到摸出红球结束,若大客户在第n 轮*()n N ∈摸到红球,则可获得 1110000()2n -⋅的奖金(单位:元) (Ⅰ)求某位大客户在一次摸球中奖活动中至少获得2500元奖金的概率;(Ⅱ)设随机变量ξ为某位大客户所能获得的奖金,求随机变量ξ的概率分布列及数学期望.18(本小题满分12分)长方体1111ABCD A B C D -中,12,2,AA BC E ==为1CC 的中点. (Ⅰ)求证:平面1A BE ⊥平面1B CD ;(Ⅱ)平面1A BE 与底面1111A B C D 所成的锐二面角的大小为θ,当210225AB <<时,求θ的取值范围.19(本小题满分13分)已知函数12()(2)xf x e ax a -=-(其中0)a ≠.(Ⅰ)若函数()f x 在(2,)+∞上单调递减,求实数a 的取值范围;(Ⅱ)设函数()f x 的最大值为()g a ,当0a >时,求()g a 的最大值.20(本小题满分13分) 已知椭圆2222:1(0)x y E a b a b +=>>的焦距为23,且该椭圆经过点1(3,)2. (Ⅰ)求椭圆E 的方程;(Ⅱ)经过点(2,0)P -分别作斜率为12,k k 的两条直线,两直线分别与椭圆E 交于,M N 两点,当直线MN 与y 轴垂直时,求12k k ⋅的值.21(本小题满分13分) 记曲线*()()n n f x n N x=∈图象上任一点处的切线与两坐标轴围成的三角形的面积为n a . (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若数列1{}na 的前n 项和为n T , 求证:231212123232n n n T T T T T T T n n -+++<<++++L L (其中*n N ∈且2)n ≥.——————————新学期新成绩新目标新方向——————————桑水。
安徽省合肥市届高三第二次教学质量检测数学理试题

(考试时间: 120 分钟总分值: 150 分 )第一卷一、选择题:本大题共 12 小题,每题5 分 . 在每题给出的四个选项中,只有一项为哪一项切合题目要求的 .1. 设复数 z 知足 z4i,那么 z 在复平面内的对应点位于1 iA. 第一象限B. 第二象限C. 第三象限D.第四象限2. 假定会合 Ax 2 0 , B x 1 x 2,那么AI Bx 1xA. 2,2B. 1,1C.(-1 , 1)D.(-1 , 2)3.双曲线x 2y 21( a0,b0 ) 的一条渐近线方程为y2x ,且经过点 P (6 ,4) ,那么a 2b 2双曲线的方程是A. x 2y 2 1 B.x 2 y 2 1C.x 2 y 2 1D.x 2 y 214 323 42844. 在uuur 1 uuuruuurABC 中, BD 2 DC ,那么AD2 uuur 1 uuur1 uuur2 uuur1 uuur2 uuurA.1 uuur 3 uuurB. C.D.4 AB AC 3 AB 3 ACAB AC AB AC43 3 3 3 5. 下表是某电器销售企业 2021 年度各种电器营业收入占比和净收益占比统计表:空调类冰箱类小家电类其余类营业收入占比 %%% %净收益占比 % %%%那么以下判断中不正确 的是...A. 该企业 2021 年度冰箱类电器销售损失B. 该企业 2021 年度小家电类电器营业收入和净收益同样C. 该企业 2021 年度净收益主要由空调类电器销售供给D. 剔除冰箱类电器销售数据后,该企业 2021 年度空调类电器销售净收益占比将会降低6. 将函数 fx2sin x1 的图象上各点横坐标缩短到本来的 1( 纵坐标不变 ) 获得函数62g x 的图象,那么以下说法正确的选项是A. 函数 g x 的图象对于点,0 对称 B. 函数 gx 的周期是122C. 函数 g x 在 0, 上单一递加D. 函数 g x 在 0,上最大值是 1 6 62 27. 椭圆 xy 1( a b 0 ) 的左右焦点分别为 F 1,F 2 ,右极点为 A ,上极点为 B ,以线段a 2b 2F 1 A 为直径的圆交线段 F 1 B 的延伸线于点 P ,假定 F 2B // AP ,那么该椭圆离心率是 A. 3 B. 2 C. 3 D. 23 3 2 28. 某队伍在一次军演中要先后履行六项不一样的任务,要求是:任务 A 一定排在前三项履行,且履行任务 A 以后需立刻履行任务 E ,任务 B 、任务 C 不可以相邻,那么不一样的履行方案共有种 种 种 种9. 函数 f xx 2xsin x 的图象大概为10. 如图,正方形网格纸中的实线图形是一个多面体的三视图,那么该多面体各表面所在平面相互 垂直的有对对对对11. “垛积术〞 ( 隙积术 ) 是由北宋科学家沈括在 ?梦溪笔谈? 中开创,南宋数学家杨辉、元朝数学家朱世杰丰富和展开的一类数列乞降方法, 有茭草垛、 方垛、 刍童垛、 三角垛等等 . 某库房中局部货物堆放成以下列图的“茭草垛〞:自上而下,第一层1 件,此后每一层比上一层多 1 件,最后一层是 n 件.第一层货物单价1 万元,从第二层起, 货物的单价是上一层单价的9.假定这堆货物总价n109是 100 200万元,那么 n 的值为10.8 C12. 函数 f xe xe 1 xb 2x1 在 (0 , 1) 内有两个零点,那么实数 b 的取值范围是,1e U e 1, e B. 1 e ,0 U 0,e 1C. 1 e ,0 U 0, e 1D.1 e , e U e ,e 1第二卷本卷包含必考题和选考题两局部.第 13题—第 21 题为必考题, 每个试题考生都一定作答 . 第 22题、第 23 题为选考题,考生依据要求作答.二、填空题:本大题共 4 小题,每题5 分 . 把答案填在答题卡上的相应地点.13. 设等差数列 n 的前 n 项和为 n 2 4 a n的公差 d __________.a S ,假定 a 3 , S 16, 那么数列 14. 假定 sin1,那么cos2cos_____________.2315. 假定 a b 0,那么a 2b 2a1 2 的最小值为 _________.b16. 半径为4 的球面上有两点 A ,B , AB 4 2 ,球心为 O ,假定球面上的动点 C 知足二面角C AB O 的大小为 60o ,那么四周体 OABC 的外接球的半径为____________.三、解答题:解允许写出文字说明、证明过程或演算步骤.17.( 本小题总分值 12 分 )在 ABC 中,角 A ,B ,C 所对的边分别为 a ,b ,c , sin 2 A sin 2 B sin Asin B 2c sinC , ABC 的面积 Sabc .(Ⅰ)求角 C ; ( Ⅱ) 求 ABC 周长的取值范围 .18.(本小题总分值12 分 )如图,三棱台ABC EFG 的底面是正三角形,平面ABC平面 BCGF , CB2GF, BF CF .( Ⅰ) 求证:AB CG ;( Ⅱ) 假定 BC CF ,求直线AE与平面 BEG 所成角的正弦值.19.( 本小题总分值 12 分 )某种大型医疗检查机器生产商,对一次性购买 2 台机器的客户,推出两种超出质保期后两年内的延保维修优惠方案:方案一:缴纳延保金7000 元,在延保的两年内可免费维修 2 次,超出 2次每次收取维修费2000元;方案二:缴纳延保金10000 元,在延保的两年内可免费维修 4 次,超出 4次每次收取维修费1000元 .某医院准备一次性购买 2 台这类机器。
2012年合肥市二模

合肥2012年‚二模‛难度看齐高考[1]都说‚二模‛是高考的‚风向标‛,不仅因为今年全市模拟考的考试流程和形式首次模仿高考,更因为在内容、难度、知识点的跟进和补充上都比照高考。
4月7日上午,合肥市‚二模‛开考,第一天语文、数学两门课,学生最大的感受是难度比‚一模‛明显增加、内容上也有了比较‚偏‛的点。
一起来听听老师怎么说——语文篇(审题至上:这次作文要求‚选好角度‛)‚古往今来立志做一品大员和一品高官的很多,但著名教育家陶行知立志做人要做‘一品百姓’,请选好角度立意、写作。
‛十中语文老师高晓荣说,这次作文回归材料题,看似熟悉但请注意写作要求有变化,‚以往都是‘自选角度’,这次是‘选好角度’。
‛材料中对‚一品百姓‛是持赞赏态度,如果考生一不留神从中任选一个角度,结果就可能是偏离中心思想。
‚能紧扣材料的考生比较多,但立意较好的并不太多。
比如有考生说要做‘平凡人’,但还必须要是做好,不能丢了‘一品’。
‛高晓荣提醒考生,看卷、审题要惜字如金。
立竿见影:考纲变动、选修内容别落下‚新考试说明中的变动必须引起关注。
‛高晓荣说,比如默写内容变动,‚二模中已经有所体现,新增了4处,比如孟子的‘生于忧患,死于安乐’。
‛难度倒也不大,主要是给考生提个醒,考纲中的变动不容忽视,选修内容也别落下。
犄角旮旯:外国散文、文言小品亮相‚大阅读《我的梦中城市》有点看不懂,但有题目是要结合自身感受说一说认识,还是有话可讲。
‛考生有这种反应很正常,高晓荣说:‚这是篇美国散文,2007年以后的高考都没有考过这一题材,安徽考生平时也很少涉及。
‛‚这与现在大批农民想进城寻找新生活的现实紧扣,文中是对纽约的向往,合肥考生有没有对北上广的向往?‛高晓荣提醒考生,遇到此类试题,不妨做个思考者,把自己的生活体验带进文本,臵身其中谈想法。
‚文言文选了篇小品,不是传统的考人物传记和序言。
考生需要关注较多题材的文言文。
‛生活范儿:说说乔布斯和苹果的那些事‚香港理工大学学生在乔布斯逝世后,将咬了一口的苹果图标改动为乔布斯的头像标。
合肥市2012年高三第二次教学质量检测理科综合试题化学部分

合肥市2012年高三第二次教学质量检测理科综合试题(化学部分)第I 卷 选择题(7小题,小题,每小题只有一个选项符合题意,每小题每小题只有一个选项符合题意,每小题6分,共42分) 可能用到的相对原子质量H :1 O :16 S :32 Cu :64 I :127 7.下列说法不正确的是.下列说法不正确的是A .人造纤维、合成纤维和光导纤维都是有机高分子化合物B .太阳能电池可采用硅材料制作,其应用有利于节能环保C .“冰,水为之,而寒于水”,说明相同质量的水和冰,水的能量高D .锅炉中沉积的CaSO 4可用Na 2CO 3溶液浸泡后再用酸溶解去除溶液浸泡后再用酸溶解去除 8.下列溶液中离子一定能够大量共存的是A .加入铝粉能产生氢气的溶液中:NH 4+、Fe 2+、SO 42–、NO 3– B .无色透明的溶液中:Ba 2+、H +、MnO 4–、Br –C .使甲基橙变红的溶液中:NH 4+、NO 3–、Na +、SO 42–D .能使淀粉碘化钾试纸显蓝色的溶液中:K +、SO 42–、S 2–、SO 32–9.在一固定体积的密闭容器中,进行下列反应:CO 2(g) +H 2(g) CO(g)+H 2O(g) ∆H= akJ /mol 其化学平衡常数K 和温度T 的关系如下表所示:的关系如下表所示:T(℃) 700 800 830 1000 1200 K 0.6 0.9 1.0 1.7 2.6 则下列有关叙述正确的是则下列有关叙述正确的是A .a<0 B .可测量客器总压变化来判定化学反应是否达到平衡C .温度为830℃时,若c(CO 2)·c(H 2) > c(CO)·c(H 2O),此时v 正 > v 逆 D .平衡时,其它条件不变,使用催化剂有利于CO 2的转化的转化 10.下列实验操作正确且能达到预期目的的是实验目的实验目的操作操作A .确定碳和硅两元素非金属性强弱属性强弱 测同温同浓度Na 2CO 3和Na 2SiO 3水溶液的pH B . 除去苯中混有的苯酚除去苯中混有的苯酚 向混合液中加入浓溴水,充分反应后,过滤C . 证明SO 2具有漂白性具有漂白性 将SO 2通入酸性KMnO 4溶液中溶液中D . 证明氯乙烷中含氯元素证明氯乙烷中含氯元素 向氯乙烷中滴几滴AgNO 3溶液再滴加稀HNO 3 A .图①表示向AlCl 3溶液中滴人NaOH 溶液,沉淀质量变化溶液,沉淀质量变化B .图②表示25℃时,用0.0lmol ·L –1盐酸滴定20mL0.01 mol·L –1 NaOH 溶液,溶液的pH 随加入酸体积的变化随加入酸体积的变化C .图③表示向Na 2CO 3稀溶液中滴人稀HC1,产生气体的量随加入盐酸量的( aq) O(1) HC1溶液、③pH =12的量:② > ① > ③ > ① 放电放电①②③④⑤⑥⑦(用元素符号表示);元素⑦基态原子的外围电子排布式 。
安徽省合肥市届高三第二次教学质量检测数学理试题.docx

安徽省合肥市2016届高三第二次教学质量检测数学理试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项 是符合题目要求的.1.若集合20,1x M x R N x 禳+镲=危睚-镲铪为自然数集,则下列选项正确的是( )A .{}1M x x统 B .{}2M x x ?- C .{}0MN = D .MN N =2.若i 是虚数单位,复数z 满足()11i z -=,则23z -=( ) A .3 B .5 C .6 D .73.已知等差数列{}n a 的前n 项和为n S ,9181,=0a S =,当n S 取最大值时n 的值为( ) A .7 B .8 C .9 D .104.若,a b 都是正数,则411b a a b骣骣琪琪++琪琪桫桫的最小值为( ) A .7 B .8 C .9 D .105.已知抛物线()220y px p =>上一点M 到焦点F 的距离等于2p ,则直线MF 的斜率为( )A .3±B .1±C .34±D .33±7.由棱锥和棱柱组成的几何体的三视图如图所示,则该几何体的体积为( )A .14B .2132C .22D .27328.执行下面的程序框图,则输出的n 的值为( )A .10B .11C .1024D .20489.在三棱锥P ABC -中,PA ABC ^平面,=60=23,2BAC AB AC PA ?=,,则三棱锥P ABC -的外接球的表面积为( )A .20pB .24pC .28pD .32p10.已知实数,x y 满足103101x y x y x ì-+?ïï--?íï£ïî,若z kx y =-的最小值为-5,则实数k 的值为( )A .-3B .3或-5C .-3或-5D .3±11.某校组织由5名学生参加的演讲比赛,采用抽签法决定演讲顺序,在“学生A 和B 都不是第一个出场,B 不是最后一个出场”的前提下,学生C 第一个出场的概率为( )A .13 B .15 C .19 D .32012.定义在R 上的偶函数()f x 的导函数为()f x ¢,若对任意的实数x ,都有()()22f x xf x ¢+<恒成立,则使()()2211x f x f x -<-成立的实数x 的取值范围为( ) A .{}1x x 贡 B .()(),11,-?+? C .()1,1- D .()()1,00,1-第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.命题“20,1x x x ">+>”的否定是 .14.双曲线222:1y M x b-=的左,右焦点分别为12,F F ,记12=2F F c ,以坐标原点O 为圆心,c 为半径的圆与双曲线M 在第一象限的交点为P ,若1=2PF c +,则P 点的横坐标为 .15.已知各项均为正数的数列{}n a 前n 项和为n S ,若22111=2,32n n n n S S a S a ++-=,则n a = .16.若函数()()2221f x xx a x a =---+有4个零点,则a 的取值范围为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.在ABC D 中,三个内角,,A B C 所对的边分别为,,a b c ,已知函数()()()sin 23cos 2f x x B x B =+++为偶函数,12b f p骣琪=琪桫(1)求b ;(2)若3a =,求ABC D 的面积S18.某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(x 个月)和市场占有率(%y )的几组相关对应数据;x1 2 3 4 5 y0.020.050.10.150.18(1)根据上表中的数据,用最小二乘法求出y 关于x 的线性回归方程;(2)根据上述回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测自上市起经过多少个月,该款旗舰机型市场占有率能超过0.5%(精确到月)附:1221ˆˆˆ,ni i i ni i x y nx y bay bx x nx==-?==--åå19.如图,六面体ABCDHEFG 中,四边形ABCD 为菱形,,,,AE BF CG DH 都垂直于平面ABCD ,若4,3DA DH DB AE CG =====(1)求证:EG DF ^;(2)求BE 与平面EFGH 所成角的正弦值20.已知椭圆()2222:10x y E a b a b+=>>经过点()222,,且离心率为22,12,F F 是椭圆E 的左,右焦点(1)求椭圆E 的方程;(2)若点,A B 是椭圆上E 关于y 轴对称两点(,A B 不是长轴的端点),点P 是椭圆E 上异于,A B 的一点,且直线,PA PB 分别交y 轴于点,N M ,求证:直线1MF 与直线2NF 的交点G 在定圆上 21.已知函数()32g x ax x x =++(a 为实数) (1)试讨论函数()g x 的单调性; (2)若对()0,x "??恒有()1ln g x xx?,求实数a 的取值范围 请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.22.如图,PA 为四边形ABCD 外接圆的切线,CB 的延长线交PA 于点P ,AC 与BD 相交于点M ,PA BD(1)求证:ACB ACD ??;(2)若3,6,1PA PC AM ===,求AB 的长23.在直角坐标系xOy 中,曲线2cos 1:2sin 1x C y a a ì=+ïíï=+î(a 为参数),在以O 为极点,x 轴的非负半轴为极轴的极坐标系中,直线:sin cos l m r q r q += (1)若0m =,判断直线l 与曲线C 的位置关系; (2)若曲线C 上存在点P 到直线l 的距离为22,求实数m 的取值范围 24.已知函数()4f x x x a =-+-(a R Î)的最小值为a (1)求实数a 的值; (2)解不等式()5f x £合肥市2016届高三第二次教学质量检测 数学试题(理)参考答案及评分标准一、选择题题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 CBBCADACADAB二、填空题13. 20000,1x x x $>+? 14.312+ 15. 12,12,2n n n a n -ì=ï=í³ïî 16. 3210027a a a a 禳镲=--<<>睚镲铪或或三、解答题17.解:(1)()()()sin 23cos 22sin 23f x x B x B x B p骣琪=+++=++琪桫由()f x 为偶函数可知,32B k k Z p p p +=+?,所以,6B k k Z pp =+? 又0B p <<,故6B p =所以()2sin 2=2cos 2,3212f x x x b f pp 骣骣琪琪=+==琪琪桫桫……………6分当23A p=时,ABC D 的面积334S =……………12分 18.解:(1)经计算ˆˆ0.042,0.026ba ==-,所以线性回归方程为ˆ=0.0420.026y x -;……………6分 (2)由上面的回归方程可知,上市时间与市场占有率正相关,即上市时间每增加1个月,市场占有率都增加0.042个百分点;由ˆ=0.0420.0260.5yx ->,解得13x ³ 预计上市13个月时,市场占有率能超过0.5% ……………12分19.解:(1)连接AC ,由,AE CG AE CG =可得AEGC 为平行四边形,所以EG AC ,而,AC BD AC BF ^^,所以,EG BD EG BF ^^,因为BD BF B =,所以EG BDHF ^平面,又DF BDHF Í平面,EG DF \^ ……………5分 (2)设,ACBD O EG HF P ==,由已知可得:ADHE BCGF 平面平面,所以EH FG ,同理可得:EH HG ,所以EFGH 为平行四边形,所以P 为EG 的中点,O 为AC 的中点,所以,OP AE AE OP =,从而OP ABCD ^平面,又OA OB ^,所以,,OA OB OP 两两垂直,由平几知识,得2BF =如图,建立空间直角坐标系O xyz -,则()()()()0,2,0,23,0,3,0,2,2,0,0,3B E F P()()()23,2,3,23,0,0,0,2,1BE PE PF \=-==-设平面EFGH 的一个法向量为(),,z n x y =,由00PE n PF n ì?ïíï?î可得:020x y z ì=ïí-=ïî,令1y =,则2z =()0,1,2n \=设BE 与平面EFGH 所成角为q ,则45sin 25BE nBE nq ×==× ……………12分20.解:(1)由条件得4,22a b c ===,所以椭圆C 的方程221168x y += ……………5分 (2)解设()()0011,,P ,B x y x y ,则()00,A x y - 直线PA 的方程为()101110y y y y x x x x --=-+,令0x =,得100110x y x y y x x +=+ 故1001100,x y x y M x x 骣+琪琪+桫,同理可得1001100,x y x yN x x 骣-琪琪-桫1001100112101022,,22,x y x y x y x y F M F N x x x x 骣骣+-琪琪==-琪琪+-桫桫所以,22221001100110011210101022,22,8x y x y x y x y x y x y F M F Nx x x x x x 骣骣+--琪琪??=-+琪琪+--桫桫222201102210818116168880x x x x x x 骣骣琪琪?-?琪琪桫桫=-+=-+=- 所以,12F M F N ^,所以直线1F M 与直线2F N 交于点G 在以12F F 为直径的圆上 ……………12分 21.解:(1)()2321g x ax x ¢=++1)当0a =时,()g x 在1,2骣琪-?琪桫单调减和1,2骣琪-+?琪桫单调增;2)当0a ¹时,=412a D -当13a ³时,()23210g x ax x ¢=++?恒成立,此时()g x 在R 单调增; 当103a <<时,由()2321=0g x ax x ¢=++得,12113113,33a a x x a a ----+-==, ()g x 在()12,x x 单调减,在()()12,,x x -??和单调增; 当0a <时,()g x 在()21,x x 单调增,在()()21,,x x -??和单调减, ……………5分(2)令()1ln f x x x =+,则()211f x x x¢=- 因此,()f x 在()0,1单调减,在()1,+?单调增()()min 11f x f \==当1a >-时,()()1211g a f =+>=,显然,对()0,x "?? 不恒有()()f x g x ³; 当1a ?时,由(1)知,()g x 在()10,x 单调增,在()1,x +?单调减211321=0ax x ++,即()2111213ax x =-+ 所以,在()0,+?上,()()()2322max 1111111121113333g x g x ax x x x x x ==++=+=+- 又(]111310,13131a x a a ---==?--所以()()()2max 1min 1111=33g x x f x =+-?,即满足对()0,x "?? 恒有()()f x g x ³综上,实数(],1a ?? ……………12分22.解:(1)PA 为切线,PAB ACB \??,PA BD PAB ABD ACD \???ACB ACD \?? ……………5分(2)已知3,6,1PA PC AM ===,由切割线定理2PA PB PC =?得:39,B ,22PB C PA BD ==,得,3AM PBMC MC BC=\= 又知AMB ABC D D ,所以AB ACAM AB= 所以24AB AM AC=?,所以2AB = ……………10分23.解:(1)曲线C 的直角坐标方程为:()()22112x y -+-=,是一个圆;直线l 的直角坐标方程为:0x y +=圆心C 到直线l 的距离2211211d r +===+,所以直线l 与圆C 相切 ……………5分(2)由已知可得:圆心C 到直线l 的距离221132211m d +-=?+ 解得15m-# ……………10分24.解:(1)()44f x x x a a a =-+-?=,从而解得2a = ……………5分(2)由(1)知,()()()()26242224264x x f x x x x x x ì-+?ïï=-+-=<?íïï->î 综合函数()y f x =的图象知,解集为11122x x禳镲#睚镲铪……………10分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
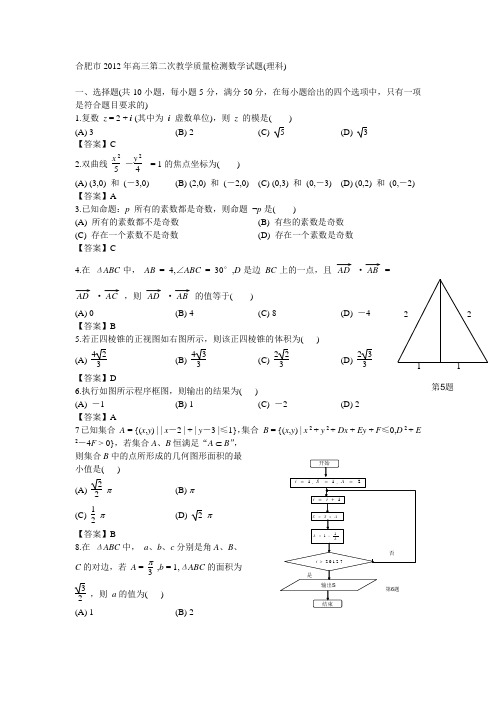
2 21 1 第5题合肥市2012年高三第二次教学质量检测数学试题(理科)一、选择题(共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.复数2z i =+(其中为i 虚数单位),则z 的模是( C )2.双曲线22154x y -=的焦点坐标为( A ) A. (3,0)和(3,0)- B. (2,0)和(2,0)- C. (0,3)和(0,3)- D. (0,2)和(0,2)-3.已知命题:p 所有的素数都是奇数,则命题p ⌝是( C )A. 所有的素数都不是奇数B. 有些的素数是奇数C.存在一个素数不是奇数D. 存在一个素数是奇数4.在ABC ∆中,4,30,AB ABC D =∠=︒是边BC 上的一点,且AD AB AD AC =,则AD AB的值等于( B )A.0B.4C.8D.-45.若正四棱锥的正视图如右图所示,则该正四棱锥的体积为( D )A.3B.3C.3D.36.执行如图所示程序框图,则输出的结果为( A ) A.-1 B.1 C.-2 D.27已知集合{(,)||2||3|1}A x y x y =-+-≤,集合()2222{,|y 0,4B x y x Dx Ey F D E F =++++≤+->若集合A 、B 恒满足“A ⊂B ”,则集合B 中的点所形成的几何 图形面积的最小值是( B ) A.2B.πC. 12π8.在ABC ∆中,a b c 、、分别是角A 、B 、C 的对边, 若,1,3A b ABC π==∆的面积为2,则a 的值为( D )A.1B.2C.29.中小学校车安全引起社会的关注,为了彻底消除校车安全隐患,某市购进了50台完全相同的校车,准备发放给10所学校,每所学校至少2台,则不同的发放方案的种数有(D )(提示:mn C 表示组合数)A. 941CB. 938CC. 940CD. 939C10.定义域为R 的偶函数()f x 满足对x R ∀∈,有(2)()(1)f x f x f +=-,且当[2,3]x ∈时2()21218f x x x =-+-,若函数()log (1)a y f x x =-+在0+∞(,)上至少有三个零点,则a 的取值范围为( A )A.(0,3 B.(0,2 C 。
(0,5. D. (0,6第二卷(满分100分)二、填空题(本大题共5小题,每小题5分,共25分。
把答案填在答题卡的相应的位置) 11.已知集合1234567{,,,,,,}A a a a a a a a =,1234567100{,,,,,,,,}A B a a a a a a a a = ,则所有满足题意的集合B 的个数有_____.12812.在极坐标系中,点(1,)2π到直线2cos sin 20ρθρθ-+=的距离为_____13.若1sin()33πα+=,则sin(2)__6πα+=79- 14.设函数2*222(,,)13x x n n y x R x n N x x -+-=∈≠∈++的最大值和最小值分别为n a 和n b ,且15n n n n n c a b a b =++-,n 123||||||||______.n S c c c c =++++= 2n 2102(3)=2102(4)n n n S n n n ⎧-≤⎪⎨-+≥⎪⎩ 15.函数()y f x =的定义域为[1,0)(0,1]-⋃,其图像上任一点(,)P x y 满足22y 1x +=。
①函数()y f x =一定是偶函数;②函数()y f x =可能既不是偶函数,也不是奇函数; ③函数()y f x =可以是奇函数;④函数()y f x =如果是偶函数,则值域是[1,0)(0,1]-或; ⑤函数()y f x =值域是(1,1)-,则一定是奇函数。
其中正确的命题的序号是_______③④⑤(填上所有正确的序号)三、解答题(本大题共6小题,共75分。
解答应写出文字说明、证明过程或演算步骤。
解答写在答题卡的指定区域) 16.(本题满分12分)将函数sin cos cos sin (0,0)y x x ωϕωϕωϕπ=-><<的图像上各点的横坐标伸长为原来的2倍(纵坐标不变),再向左平移6π个单位,得到函数()y f x =的图像。
若函数()y f x =的图像过点(,0)6π,且相邻两对称轴间的距离为2π。
(1)求,ωϕ值;(2)若锐角ABC ∆中 A B C 、、成等差数列,求()f A 的取值范围。
解:(1)由题得:1()sin()212f x x ωπωϕ=+-相邻两对称轴间的距离为2π T π∴=24Tπω∴==()sin(2)3f x x πϕ∴=+-又函数()y f x =的图像过点(,0)6π()06f π∴=2,3k k Z πϕπ∴-=∈又0ϕπ<<23πϕ∴=(2)由(1)知:()sin(2)3f x A π=-A B C 、、成等差数列3B π∴=又ABC ∆是锐角三角形62A ππ∴<<20233A ππ∴<-<0sin(2)13A π∴<-≤∴()f A 的取值范围为:(0,1]17. (本题满分12分)食品安全已引起社会的高度关注,卫生监督部门加大了对食品质量的监测。
已知某种食品的合格率为0.9.现有8盒该种食品,质监部门对其逐一检测。
(1) 求8盒中恰有4盒合格的概率(保留三位有效数字) (2) 设检测合格的盒数为随机变量ξ,求ξ的数学期望E ξ.解:(1)记“8盒中恰有4盒合格”为事件A ,则4448()0.9(10.9)0.00459P A C =⨯⨯-=(2)有题可知: 随机变量ξ(8,0.9)B 则ξ的数学期望80.97.2E ξ=⨯= 18. (本题满分12分)在四棱锥P-ABCD 中,底面ABCD 是边长为1的正方形。
且PA ⊥ 面ABCD.(1) 求证:PC ⊥BD(2) 过直线BD 且垂直于直线PC 的平面交PC 于点E ,且三棱锥E-BCD 的体积取到最大值()i 求此时四棱锥E-ABCD 的高; ()ii 求二面角A-DE-B 的余弦值的大小。
解:(1)连接AC ,则AC BD ⊥ PA ⊥ 面ABCD.PA BD ∴⊥BD PAC ∴⊥平面∴ PC ⊥BD(2) ()i 设,AC BD M 与的交点连接EM ,过点E 作EN AC ⊥于N ,则EN ABCD ⊥面,EN 是三棱锥E-BCD 的高由题知:CEM ∆是直角三角形,其中2CEM π∠=设CN x =,则MN x =-,从而在直角CEM ∆中有:2)EN x x =-∴当且仅当4x =时,EN 4,此时三棱锥E-BCD 的体积取到最大值∴此时四棱锥E-ABCD 的高为:4()ii 以A 为原点建立空间直角坐标系A xyz -,如图所示,则(0,0,0)A ;(1,0,0)B ;(1,1,0)C ;(0,1,0)D由()i 知:33(,44E P(1,1,PC ∴= ,(0,1,0)AD =,33(,,444AE = 设平面ADE 的法向量为:(,,)m x y z =,则00mA D mAE ⎧=⎪⎨=⎪⎩ ,即0330444y x y z =⎧⎪⎨++=⎪⎩,令:1z =则3x =-,0y = ∴平面ADE的一个法向量为:(3m =- (1,1,PC =是平面BDE 的一个法向量 cos ,11PC m ∴<>= A DE B ∴--二面角的余弦值的大小为:1119.(本小题满分13分)已知数列{}n a 满足121,5,2a a n ==≥时,1156n n n a a a +-=-(1)证明:数列1{3}n n a a +-为等比数列,并求数列{}n a 的通项公式 ; (2)试比较n a 与221n +的大小,并说明理由。
解:(1)证明: 当2n ≥时,1156n n n a a a +-=-1113262(3)n n n n n n a a a a a a +--∴-=-=-又121,5a a ==21320a a ∴-=≠∴数列1{3}n n a a +-是以2为首项以2为公比的等比数列 113222n n n n a a -+∴-=⨯=1131(1)222n nn n a a ++∴+=+ ∴数列12n na ⎧⎫+⎨⎬⎩⎭是以32为首项以32为公比的等比数列 ∴数列{}n a 的通项公式为:32n n n a =-(2)由(1)知:当1n =时211,213a n =+=221n a n ∴<+当2n =时225,219a n =+=221n a n ∴<+当3n =时2319,2119a n =+=221n a n ∴=+当4n ≥时011221222+12222212421n n n n n n n n n n n n n n a C C C C C C n --=-=++++->++=+ ()221n a n ∴>+综上:当12n =或时221n a n <+;当3n =时221n a n =+;当4n ≥时221n a n >+ 20. (本题满分12分)已知函数()y f x =的定义域为R ,其导数'()f x 满足'0()1f x <<,常数α为方程()f x x=的实数根。
(1)求证:当x α>时,总有()x f x >成立;(2)对任意12x x 、,若满足12||1,||1,x x αα-<-<求证:12|()()| 2.f x f x -<(1)证明:令()()g x x f x =-则''()1()g x f x =-'0()1f x << ∴''()1()0g x f x =->∴函数()()g x x f x =-为R 增函数∴当x α>时()()()0g x x f x f αα=->-= ∴当x α>时,总有()x f x >成立(2)证明:12||1,||1x x αα-<-<1211;11x x αααα∴-<<+-<<+又'0()1f x <<()f x ∴在R 是增函数12(1)()(1);(1)()(1)f f x f f f x f αααα∴-<<+-<<+ 12(1)(1)()()(1)(1)f f f x f x f f αααα∴--+<-<+-- 12|()()|(1)(1)f x f x f f αα∴-<+--由(1)知:(1)1f αα+<+ ;(1)(1)f αα--<--12|()()|(1)(1)2f x f x f f αα∴-<+--<∴12|()()| 2.f x f x -<21. (本题满分13分)已知ABC ∆的三边长|||4,||1,AB BC AC ===动点M 满足,CM CA CB λμ=+ 且14λμ=(1)求||CM最小值,并指出此时CM 与CA CB 、的夹角(2)是否存在两定点12F F 、使12||||||MF MF -恒为常数k ?若存在,指出常数k 的值,若不存在,说明理由。
