工程数学(本科)复习题
《工程数学(本)》期末综合练习

《工程数学(本)》期末综合练习一、单项选择题1.设B A ,均为n 阶可逆矩阵,则下列等式成立的是( ). A .()BAAB 11=- B .()111---+=+B A B A C .()111---=B A AB D .1111----+=+B A B A正确答案:A2.方程组⎪⎩⎪⎨⎧=+=+=-331232121a x xa x x a x x 相容的充分必要条件是( ),其中0≠i a ,)3,2,1(=i .A .0321=++a a aB .0321=-+a a aC .0321=+-a a aD .0321=++-a a a 正确答案:B3.设矩阵⎥⎦⎤⎢⎣⎡--=1111A 的特征值为0,2,则3A 的特征值为 ( ) .A .0,2B .0,6C .0,0D .2,6 正确答案:B4. 设A ,B 是两事件,则下列等式中( )是不正确的. A. )()()(B P A P AB P =,其中A ,B 相互独立 B. )()()(B A P B P AB P =,其中0)(≠B P C. )()()(B P A P AB P =,其中A ,B 互不相容 D. )()()(A B P A P AB P =,其中0)(≠A P 正确答案:C5.若随机变量X 与Y 相互独立,则方差)32(Y X D -=( ). A .)(3)(2Y D X D - B .)(3)(2Y D X D + C .)(9)(4Y D X D - D .)(9)(4Y D X D + 正确答案:D6.设A 是n m ⨯矩阵,B 是t s ⨯矩阵,且B C A '有意义,则C 是( )矩阵.A .s n ⨯B .n s ⨯C .t m ⨯D .m t ⨯ 正确答案:B7.若X 1、X 2是线性方程组AX =B 的解,而21ηη、是方程组AX = O 的解,则( )是AX =B 的解. A .213231X X + B .213231ηη+ C .21X X - D .21X X + 正确答案:A8.设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=211102113A ,则A 的对应于特征值2=λ的一个特征向量α=( ) . A .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡101 B .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-101 C .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡011 D .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100 正确答案:C9. 下列事件运算关系正确的是( ).A .AB BA B += B .A B BA B +=C .A B BA B +=D .B B -=1 正确答案:A10.若随机变量)1,0(~N X ,则随机变量~23-=X Y ( ). A .)3,2(-N B .)3,4(-N C .)3,4(2-N D .)3,2(2-N 正确答案:D11.设321,,x x x 是来自正态总体),(2σμN 的样本,则( )是μ的无偏估计. A .321525252x x x ++ B .321x x x ++ C .321535151x x x ++ D .321515151x x x ++ 正确答案:C12.对给定的正态总体),(2σμN 的一个样本),,,(21n x x x ,2σ未知,求μ的置信区间,选用的样本函数服从( ).A .χ2分布 B .t 分布 C .指数分布 D .正态分布 正确答案:B二、填空题1.设412211211)(22+-=x x x f ,则0)(=x f 的根是 .应该填写:2,2,1,1--2.设向量β可由向量组n ααα,,,21 线性表示,则表示方法唯一的充分必要条件是n ααα,,,21 .应该填写:线性无关3.若事件A ,B 满足B A ⊃,则 P (A - B )= . 应该填写:)()(B P A P -4..设随机变量的概率密度函数为⎪⎩⎪⎨⎧≤≤+=其它,010,1)(2x x kx f ,则常数k = .应该填写:π45.若样本n x x x ,,,21 来自总体)1,0(~N X ,且∑==ni i x n x 11,则~x .应该填写:)1,0(nN 6.行列式701215683的元素21a 的代数余子式21A 的值为= . 应该填写-567.设三阶矩阵A 的行列式21=A ,则1-A = . 应该填写:28.若向量组:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=2121α,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1302α,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=2003k α,能构成R 3一个基,则数k .应该填写:2≠9.设4元线性方程组AX =B 有解且r (A )=1,那么AX =B 的相应齐次方程组的基础解系含有 个解向量. 应该填写:310.设A B ,互不相容,且P A ()>0,则P B A ()= . 应该填写:011.若随机变量X ~ ]2,0[U ,则=)(X D . 应该填写:31 12.设θˆ是未知参数θ的一个估计,且满足θθ=)ˆ(E ,则θˆ称为θ的 估计. 应该填写:无偏三、计算题1.设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=210211321,100110132B A ,求:(1)AB ;(2)1-A . 解:(1)因为210110132-=--=A 12111210211110210211321-=-===B 所以2==B A AB .(2)因为 []⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=100100010110001132I A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--→10010011001012/32/1001100100110010101032所以 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=-10011012/32/11A .2.求齐次线性方程组 ⎪⎩⎪⎨⎧=++--=++++=++++0233035962023353215432154321x x x x x x x x x x x x x x 的通解.解: A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--326001130012331203313596212331⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡→100001130012331⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡→100000130001031 一般解为 ⎪⎪⎩⎪⎪⎨⎧=-=--=0313543421x x x x x x ,其中x 2,x 4 是自由元令x 2 = 1,x 4 = 0,得X 1 =)0,0,0,1,3('-; x 2 = 0,x 4 = 3,得X 2 =)0,3,1,0,3('--所以原方程组的一个基础解系为 { X 1,X 2 }.原方程组的通解为: 2211X k X k +,其中k 1,k 2 是任意常数.3.设随机变量)1,4(~N X .(1)求)24(>-X P ;(2)若9332.0)(=>k X P ,求k 的值. (已知9332.0)5.1(,8413.0)1(,9775.0)2(=Φ=Φ=Φ).解:(1))24(>-X P =1-)24(≤-X P= 1-)242(≤-≤-X P =1-()2()2(-Φ-Φ) = 2(1-)2(Φ)=0.045. (2))44()(->-=>k X P k X P =1-)44(-≤-k X P=1-)5.1(9332.0)4(Φ==-Φk )5.1()5.1(1)4(-Φ=Φ-=-Φk即 k -4 = -1.5, k =2.5.4.某切割机在正常工作时,切割的每段金属棒长服从正态分布,且其平均长度为10.5 cm ,标准差为0.15cm.从一批产品中随机地抽取4段进行测量,测得的结果如下:(单位:cm )10.4,10.6,10.1,10.4问:该机工作是否正常(05.0=α, 96.1975.0=u )?解:零假设5.10:0=μH .由于已知15.0=σ,故选取样本函数nx U σμ-=~)1,0(N经计算得375.10=x ,075.0415.0==nσ,67.1075.05.10375.10=-=-nx σμ由已知条件96.121=-αu,且2196.167.1αμσμ-=<=-nx故接受零假设,即该机工作正常.5.已知矩阵方程B AX X +=,其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=301111010A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=350211B ,求X . 解:因为B X A I =-)(,且⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=-101210011110001011100201010101001011)(I A I ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----→11100121010120001110100011110010101 即 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=--110121120)(1A I所以 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=-=-334231350211110121120)(1B A I X .6.设向量组)1,421(1'--=,,α,)4,1684(2'--=,,α,)2,513(3'--=,,α,)1,132(4'-=,,α,求这个向量组的秩以及它的一个极大线性无关组. 解:因为(1α 2α 3α 4α)=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-------12411516431822341 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----→1100770075002341⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---→0000200011002341 所以,r (4321,,,αααα) = 3.它的一个极大线性无关组是 431,,ααα(或432,,ααα).7.设齐次线性方程组⎪⎩⎪⎨⎧=+-=+-=+-0830352023321321321x x x x x x x x x λ,λ为何值时方程组有非零解?在有非零解时,求出通解. 解:因为A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---λ83352231⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---→610110231λ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---→500110101λ505==-λλ即当时,3)(<A r ,所以方程组有非零解.方程组的一般解为: ⎩⎨⎧==3231x x x x ,其中3x 为自由元.令3x =1得X 1=)1,1,1(',则方程组的基础解系为{X 1}. 通解为k 1X 1,其中k 1为任意常数.8.罐中有12颗围棋子,其中8颗白子,4颗黑子.若从中任取3颗,求:(1)取到3颗棋子中至少有一颗黑子的概率;(2)取到3颗棋子颜色相同的概率.解:设1A =“取到3颗棋子中至少有一颗黑子”,2A =“取到的都是白子”,3A =“取到的都是黑子”,B =“取到3颗棋子颜色相同”,则 (1))(1)(1)(211A P A P A P -=-=745.0255.01131238=-=-=C C .(2))()()()(3232A P A P A A P B P +=+=273.0018.0255.0255.031234=+=+C C .9.设随机变量X ~ N (3,4).求:(1)P (1< X < 7);(2)使P (X < a )=0.9成立的常数a . (8413.0)0.1(=Φ,9.0)28.1(=Φ,9973.0)0.2(=Φ). 解:(1)P (1< X < 7)=)23723231(-<-<-X P =)2231(<-<-X P =)1()2(-Φ-Φ = 0.9973 + 0.8413 – 1 = 0.8386 (2)因为 P (X < a )=)2323(-<-a X P =)23(-Φa = 0.9 所以28.123=-a ,a = 3 + 28.12⨯ = 5.56 10.从正态总体N (μ,9)中抽取容量为64的样本,计算样本均值得x = 21,求μ的置信度为95%的置信区间.(已知 96.1975.0=u ) 解:已知3=σ,n = 64,且nx u σμ-= ~ )1,0(N因为 x = 21,96.121=-αu,且735.064396.121=⨯=-nuσα所以,置信度为95%的μ的置信区间为: ]735.21,265.20[],[2121=+---nux nux σσαα.四、证明题1.设A 是n 阶矩阵,若3A = 0,则21)(A A I A I ++=--. 证明:因为 ))((2A A I A I ++-=322A A A A A I ---++ =3A I -= I所以 21)(A A I A I ++=--2.设n 阶矩阵A 满足0))((=+-I A I A ,则A 为可逆矩阵.证明: 因为 0))((2=-=+-I A I A I A ,即I A =2 所以,A 为可逆矩阵.3.设向量组321,,ααα线性无关,令2112ααβ+=,32223ααβ+=,1334ααβ-=,证明向量组321,,βββ线性无关。
工程数学复习题及答案

试卷代号:1008中央广播电视大学2005~2006学年度第一学期“开放本科”期末考试水利水电、土木工程专业工程数学(本)试题2006年1月一、单项选择题(每小题3分,共21分)1。
设均为3阶可逆矩阵,且k〉0,则下式()成立.A。
B。
C. D。
2。
下列命题正确的是().A.个维向量组成的向量组一定线性相关;B.向量组是线性相关的充分必要条件是以为系数的齐次线性方程组有解C.向量组,,0的秩至多是D.设是矩阵,且,则的行向量线性相关3.设,则A的特征值为().A.1,1 B.5,5 C.1,5 D.—4,64.掷两颗均匀的股子,事件“点数之和为3”的概率是()。
A.B.C.D.5.若事件与互斥,则下列等式中正确的是( )。
A. B.C. D.6.设是来自正态总体的样本,其中已知,未知,则下列()不是统计量.A.B.C.;D.7。
对正态总体的假设检验问题中,检验解决的问题是( ).A。
已知方差,检验均值 B.未知方差,检验均值C。
已知均值,检验方差 D。
未知均值,检验方差二、填空题(每小题3分,共15分)1.已知矩阵A,B,C=满足AC = CB,则A与B分别是__________________矩阵。
2.线性方程组一般解的自由未知量的个数为__________________。
3.设A,B为两个事件,若P (AB)=P(A)P(B),。
则称A与B__________________。
4.设随机变量,则E(X)= __________________。
5.矿砂的5个样本中,经测得其铜含量为(百分数),设铜含量服从未知,检验,则区统计量__________________.三、计算题(每小题10分,共60分)1.设矩阵,求(1);(2)2.设齐次线性方程组的系数矩阵经过初等行变换,得求此齐次线性方程组的一个基础解系和通解.3.用配方法将二次型化为标准型,并求出所作的满秩变换。
4.假设是两个随机事件,已知,求⑴;⑵5。
本科工程数学试题及答案

本科工程数学试题及答案一、选择题(每题2分,共10分)1. 下列哪个选项是微积分基本定理的一个表述?A. 导数的存在性B. 积分的可加性C. 牛顿-莱布尼茨公式D. 函数的连续性答案:C2. 在复数域中,以下哪个表达式表示复数的模?A. |z|B. z^2C. Re(z)D. Im(z)答案:A3. 线性代数中,一个矩阵A是可逆的,当且仅当:A. A的行列式不为零B. A的主对角线元素都不为零C. A的所有元素都不为零D. A的秩等于A的阶数答案:D4. 以下哪个函数是周期函数?A. f(x) = x^2B. f(x) = sin(x)C. f(x) = e^xD. f(x) = ln(x)答案:B5. 多元函数在某点连续的充分必要条件是:A. 该点的所有偏导数存在B. 该点的所有偏导数连续C. 该点的函数值由极限唯一确定D. 该点的函数值由路径无关答案:C二、填空题(每题3分,共15分)6. 如果函数f(x)在点x=a处可导,那么f'(a)等于______。
答案:函数在点x=a的导数7. 微分方程dy/dx = x^2 + y^2的通解是______。
答案:y^2 + x^2 = C(C为任意常数)8. 对于二阶常系数线性齐次微分方程ay'' + by' + cy = 0,其特征方程为______。
答案:ar^2 + br + c = 09. 在概率论中,随机变量X的概率密度函数f(x)满足的条件是______。
答案:非负且积分为110. 线性代数中,若向量v1和v2线性无关,则它们构成的矩阵的行列式______。
答案:不为零三、解答题(共75分)11. (15分)计算定积分∫[0,1] (2x^2 + 3x) dx,并给出其几何意义。
答案:首先计算原函数F(x) = (2/3)x^3 + (3/2)x^2 + C。
然后计算F(1) - F(0) = (2/3) + (3/2) = 7/6。
工程数学本科试题及答案

工程数学本科试题及答案一、选择题(每题2分,共20分)1. 下列哪个选项是微分方程 \( y'' - y' - 2y = e^{2x} \) 的一个解?A. \( y = e^{-x} \)B. \( y = e^{2x} \)C. \( y = e^{x} \)D. \( y = e^{3x} \)2. 在复数域中,下列哪个表达式是正确的?A. \( |z|^2 = z \cdot \bar{z} \)B. \( |z|^2 = z + \bar{z} \)C. \( |z|^2 = z - \bar{z} \)D. \( |z|^2 = z / \bar{z} \)3. 对于向量 \( \mathbf{A} = (2, -3, 4) \) 和 \( \mathbf{B} = (1, 2, -1) \),它们的点积 \( \mathbf{A} \cdot \mathbf{B} \) 等于:A. 1B. 2C. 3D. 54. 在 \( z = x^2 + y^2 \) 中,如果 \( \frac{\partialz}{\partial x} = 2x \),那么 \( \frac{\partial z}{\partial y} \) 等于:A. \( 2y \)B. \( -2y \)C. \( 2x \)D. \( -2x \)5. 一个函数 \( f(x) \) 在点 \( x = a \) 处连续的充分必要条件是:A. \( \lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) \)B. \( \lim_{x \to a} f(x) = f(a) \)C. \( f(a) \) 存在D. \( f(x) \) 在 \( x = a \) 处可导6. 微分方程 \( y' = y^2 \) 的解的形式是:A. \( y = Ce^x \)B. \( y = \frac{1}{Ce^x + 1} \)C. \( y = Ce^{-x} \)D. \( y = \frac{1}{Cx + 1} \)7. 傅里叶级数中的 \( a_n \) 系数是由以下哪个积分计算得出的?A. \( a_n = \frac{2}{L} \int_{-L}^{L} f(x) \cos(\frac{n\pi x}{L}) dx \)B. \( a_n = \frac{1}{L} \int_{-L}^{L} f(x) \cos(\frac{n\pi x}{L}) dx \)C. \( a_n = \frac{2}{L} \int_{0}^{L} f(x) \cos(\frac{n\pi x}{L}) dx \)D. \( a_n = \frac{1}{L} \int_{0}^{L} f(x) \cos(\frac{n\pi x}{L}) dx \)8. 矩阵 \( A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \) 的行列式 \( |A| \) 等于:A. 7B. 2C. 1D. -29. 函数 \( f(x) = x^3 - 6x^2 + 11x - 6 \) 的零点个数是:A. 1B. 2C. 3D. 410. 拉普拉斯变换 \( \mathcal{L} \{ f(t) \} \) 的定义是:A. \( \mathcal{L} \{ f(t) \} = \int_{0}^{\infty} e^{-st} f(t) dt \)B. \( \mathcal{L} \{ f(t) \} = \int_{-\infty}^{\infty} e^{-st} f(t) dt \)C. \( \mathcal。
工程数学复习题及答案.doc

工程数学(一)一、、计算下列行列式: 1、29092280923521534215 =100028092100034215 =10002809206123 =61230002、D n =n 333333333233331 解:D n =n 333333333233331 (把第三列的-1倍加到其余各列) =3n 3030003100302=3n 0030000100002=6(n -3)! (n 3) 二、已知X=AX+B ,其中A= 101111010, B=350211,求X解:(E -A)X=B X=(E -A)-1BE -A= 100010001- 101111010= 201101011,(E -A)-1= 11012312031X= 11012312031 350211=1102133133063931 三、求向量组 1=(1,-2,3,-1,2), 2=(3,-1,5,-3,-1), 3=(5,0,7,-5,-4), 4=(2,1,2,-2,-3)的一个极大线性无关组,并用该极大线性无关组线性表示出其它向量。
解:令A=( 1T , 2T , 3T , 4T )=~34122531275310122531~242000004840510502531000000000000121025311, 2,为一极大线性无关组,且 3= - 1+2 2, 4=- 1+ 2四、求方程组0x x 0x 0x x 41241的一个基础解系。
解:A= 100100101001~ 200000101001~100000100001 同解方程组是: 0x x x 0x 0x 43321 所以基础解系是:0100五、已知线性方程组 2x x 3x 3x 4x 5b x 6x 2x 2x 0x 3x x x 2x 3ax x x x x 5432154325432154321,问a,b 为何值时,方程组有解?并求其通解。
工程数学期末复习题库(111页)

电大工程数学复习题库工程数学复习题(一)2014年12月一、单项选择题(将正确答案的序号填入括号,每小题2分,共计30分二、填空题(每小题3分,共15分}三、计算题{每小题16分,共64分)四、证明题(本题6分}答案工程数学复习题(二)2014年12月一、单项选择题(将正确答案的序号填入括号,每小题2分,共计30分二、填空题(每小题3分,共15分)三、计算题{每小题16分,共64分)四、证明题(本题6分}答案工程数学复习题(三)2014年12月一、单项选择题(将正确答案的序号填入括号,每小题2分,共计30分二、填空题(每小题3分,共15分}三、计算题{每小题16分,共64分)四、证明题(本题6分}答案工程数学复习题(四)2014年12月一、单项选择题(将正确答案的序号填入括号,每小题2分,共计30分二、填空题(每小题3分,共15分}三、计算题{每小题16分,共64分)四、证明题(本题6分}答案电大工程数学试题及答案2018电大工程数学(本)期末复习辅导一、单项选择题1.若100100200001000=aa ,则=a (12).⒊乘积矩阵⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡1253014211中元素=23c (10). ⒋设A B ,均为n 阶可逆矩阵,则下列运算关系正确的是()AB B A --=11).⒌设A B ,均为n 阶方阵,k >0且k ≠1,则下列等式正确的是(D).D.-=-k A k An() ⒍下列结论正确的是(A. 若A 是正交矩阵则A -1也是正交矩阵). ⒎矩阵1325⎡⎣⎢⎤⎦⎥的伴随矩阵为( C.5321--⎡⎣⎢⎤⎦⎥ ). ⒏方阵A 可逆的充分必要条件是(A ≠0)⒐设A B C ,,均为n 阶可逆矩阵,则()A C B '=-1(D).D. ()B C A ---'111⒑设A B C ,,均为n 阶可逆矩阵,则下列等式成立的是(A).A.()A B A A B B+=++2222 ⒈用消元法得x x x x x x 12323324102+-=+=-=⎧⎨⎪⎩⎪的解x x x 123⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥为(C.[,,]--'1122 ). ⒉线性方程组x x x x x x x 12313232326334++=-=-+=⎧⎨⎪⎩⎪(有唯一解).⒊向量组100010001121304⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥,,,,的秩为( 3).⒋设向量组为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1111,0101,1100,00114321αααα,则(ααα123,, )是极大无关组.⒌A 与A 分别代表一个线性方程组的系数矩阵和增广矩阵,若这个方程组无解,则D. 秩()A =秩()A -1⒍若某个线性方程组相应的齐次线性方程组只有零解,则该线性方程组(A ). A. 可能无解 ⒎以下结论正确的是(D ).D. 齐次线性方程组一定有解 ⒏若向量组ααα12,,, s线性相关,则向量组内(A )可被该向量组内其余向量线性表出. A. 至少有一个向量9.设A ,B为n 阶矩阵,λ既是A又是B的特征值,x 既是A又是B的属于λ的特征向量,则结论( A )成立.A.λ是AB 的特征值10.设A,B,P为n 阶矩阵,若等式(C )成立,则称A和B相似.C.B PAP =-1⒈A B ,为两个事件,则( B )成立. B.()AB B A+-⊂ ⒉如果( C )成立,则事件A 与B 互为对立事件.C.A B =∅且A B U= ⒊10张奖券中含有3张中奖的奖券,每人购买1张,则前3个购买者中恰有1人中奖的概率为( D.307032⨯⨯..). 4. 对于事件A B ,,命题(C)是正确的. C. 如果A B ,对立,则A B,对立⒌某随机试验的成功率为)10(<<p p ,则在3次重复试验中至少失败1次的概率为(D.)1()1()1(223p p p p p -+-+-6.设随机变量X B n p ~(,),且E X D X ().,().==48096,则参数n 与p 分别是(6, 0.8). 7.设f x ()为连续型随机变量X 的密度函数,则对任意的ab a b ,()<,E X ()=(A ). A.xf x x ()d -∞+∞⎰8.在下列函数中可以作为分布密度函数的是(B ).B.f x x x ()s in ,,=<<⎧⎨⎪⎩⎪020π其它9.设连续型随机变量X 的密度函数为f x (),分布函数为F x (),则对任意的区间(,)a b ,则=<<)(b X a P D.f x x ab ()d ⎰). 10.设X 为随机变量,EX D X (),()==μσ2,当(C )时,有E Y D Y (),()==01.C. σμ-=X Y1.A 是34⨯矩阵,B 是52⨯矩阵,当C 为( B 24⨯)矩阵时,乘积AC B ''有意义。
工程数学复习题

工程数学复习题一、单项选择题1.设i z i z 26,2121+-=-=,,则21z z +的幅角为【D 】 A.2π-B.2πC.0D.π 2.常数1的傅氏变换为【C 】 A.)(ωδ B.)(ωπδ C.)(2ωπδ D.)(1ωπδω+j1是函数f 9.若函数)(z f 在0z 不连续,则【D 】A.)()(lim 00z f z f z z =→ B.[]0)()(lim 00=-→z f z f z zC.)()(lim 000z f z z f z =∆+→∆ D.[]0)()(lim 00≠-→z f z f z z10.幂级数∑∞=0)3(n nz 的收敛半径是【B 】A.1B.31C.0D.311.函数z e 在00=z 展开成的泰勒级数是【A 】A.∑∞=0!n n n z B.∑∞=++-011)1(n n n n zC.∑∞=++-012)!12()1(n n nn z D.∑∞=-02)!2()1(n n n n z 12.设0z 是)(z f 的孤立奇点,0z 是)(z f 的二级极点,则=]),([Re 0z z f s 【D 】d2=【A 】A.0B. C. D.18.函数),(),()(y x iv y x u z f +=在0z 点解析的充要条件是【C 】 A.),(),,(y x v y x u 在0z 点可微B.在0z 点xvy u y v x u ∂∂-=∂∂∂∂=∂∂, C.在0z 点),(),,(y x v y x u 可微且xv y u y v x u ∂∂-=∂∂∂∂=∂∂, D.)(z f 在0z 点可导 19.3)(z z f =在z 平面上【C 】A.可导不解析B.连续不可导C.处处解析D.有奇点20.设)(z f 在单连域G 内解析,C 为G 内任意一条正向简单闭曲线,0z 是C 内的一点,则积分()=-⎰C dz z z 501【B 】A.!42i π B.0 C.i π2 D.2iπ 21.若)(z f ,)(z g 在单连域G 内解析,C 为G 内任意一条闭曲线,则[]=⋅⎰Cdz z g z f )()(【A 】A.0B.)0()0(2g if π C.i π2 D.π2=dz 【B 】C.[])6()6(--+ωδωδπj D.[])6()6(-++ωδωδπj 29.函数)1ln(z +在00=z 展开成的泰勒级数是【B 】A.∑∞=0!n n n z B.∑∞=++-011)1(n n n n z C.∑∞=++-012)!12()1(n n nn z D.∑∞=-02)!2()1(n n n n z30.设)(z f 在单连域G 内解析,C 为G 内任意一条正向简单闭曲线,0z 是C 内的一点,则积分()=-⎰C dz z z z f 50)(【A 】A.!4)(20)4(z if π B.0 C.)(20z if π D.)0(2)4(if π31.常数10的傅氏变换为【B 】 A.)(20ωδ B.)(20ωπδ C.)(10ωπδ D.)(101ωπδω+j 32.A.-33.A.[πC.πj 34.z A.35.A.(u C.(u A.s1037.A.∑∞=0!n n B.∑=+-01)1(n n nC.∑∞=++-012)!12()1(n n nn z D.∑∞=-02)!2()1(n n n n z 38.te 5的拉氏变换为【A 】 A.51-s B.s 1C.252+s s D.2552+s 39.幂级数在收敛圆内【A 】A.可以微分任意次B.必发散C.可能收敛,可能发散D.非绝对收敛40.幂级数∑∞=+011n nzn 的收敛半径是【A 】A.1B.+∞C.0D.241.函数),(),()(y x iv y x u z f +=在区域D 内解析的条件是【C 】A.),(),,(y x v y x u 在区域D 内可微B.在区域D 内xv y u y v x u ∂∂-=∂∂∂∂=∂∂, C.在区域D 内),(),,(y x v y x u 可微且vu v u ∂-=∂∂=∂, D.以上都不对 42.A.(u C.z →43.z A.44.A.-45.46.A.若B.若C.若D.若)(z f 在0z 处连续,则)(z f 在0z 可导47.设0z 是)(z f 的孤立奇点,0z 是)(z f 的一级极点,则=]),([Re 0z z f s 【D 】 A.1c B.1 C.-1D.)()(lim 00z f z z z z -→48.1=z 是函数32)1(1)(-=z z z f 的【D 】A.可去奇点B.本性奇点C.二级极点D.三级极点 49.常数5的傅氏变换为【B 】A.)(10ωδB.)(10ωπδC.)(2ωπδD.)(51ωπδω+j 50.设)(z f 在单连域G 内解析,C 为G 内任意一条正向简单闭曲线,0z 是C 内的一点,则积分=-⎰Cdz z z z f 0)(【A 】A.)(20z if πB.0C.i π2D.)0(2if π 51.t e 3的拉氏变换为【A 】57.设)(z f 在区域G 内解析,C 为G 内任意一条正向简单闭曲线,0z 是C 内的一点,则积分()=-⎰C dz z z z 20)(【A 】A.)(20z f i 'πB.0C.i π2D.)0(2f i 'π 58.幂级数在收敛圆上【C 】A.必收敛B.必发散C.可能收敛,可能发散D.绝对收敛 59.幂级数在收敛圆内【D 】(A )收敛于非解析函数)(z f (B )必发散(C )可能收敛,可能发散(D)绝对收敛60.函数)(z f 在0z 的某个邻域内展开成泰勒级数的条件是【A 】 A.)(z f 在0z 的某个邻域内解析B.)(z f 在0z 的某个邻域内连续 C.)(z f 在0z 可导D.)(z f 在0z 连续且可导 61.函数z sin 在00=z 展开成的泰勒级数是【C 】A.∑∞=0!n n n z B.∑∞=++-011)1(n n n n zC.∑∞=0n 62.f A.63.A.6δ64.A.若B.若C.若D.若65.5A.s566.A.i 2B.2 C.i 22+ D.i 22-67.设0z 是)(z f 的孤立奇点,0z 是)(z f 的本性奇点,则=]),([Re 0z z f s 【D 】 A.1c B.1 C.-1D.1-c 68.t 0cos ω的傅氏变换为【B 】A.[])()(00ωωδωωδπ--+B.[])()(00ωωδωωδπ-++C.[])()(00ωωδωωδπ--+jD.[])()(00ωωδωωδπ-++j69.)(z f ,)(z g 在单连域G 内解析,C 为G 内任意一条闭曲线,则[]=+⎰Cdz z g z f )()(【A 】A.0B.)0(2if π C.i π2 D.π270.函数),(),()(y x iv y x u z f +=在000iy x z +=连续的条件是【C 】 A.),(y x u 在),(00y x 连续B.),(y x v 在),(00y x 连续C.),(y x u ,),(y x v 均在),(00y x 连续D.),(y x u ,),(y x v 均不在),(00y x 连续 71.t 3cos 的拉氏变换为【C 】4.⎰=310z z 【0】5.=⎰=31z dz z【i π2】6.级数∑∞=0)5(n nz 的收敛半径为【1/5】7.kt sin (k 为常数)的傅氏变换为()()()k k j --+ωδωδπ 8.10的幅角为【0】9.函数)(z f 在0z 点可导,)(z f 在0z 点必【连续】10.连续函数的和、差、积仍然是【连续函数】11.若函数)(z f 在10=z 处可导,则)()(02z f z z f '-在0z 点的导数为【)1(f '-】12.=⎰z z d 10【1/2】13.=⎰z z d cos 20π【1】14.设51)(z e z f z-=,则0=z 是)(z f 的【4级】极点15.t 16.117.⎰18.20.21.22.23.i 24.⎰25.26.27.28.=-⎰=151z dz z 【0】29.=]0,51[Re z s 【51】30.设3cos sin 2)(z zz z f -=,则0=z 是)(z f 的【3级】极点31.te 的拉氏变换为11-s32.级数∑∞=-0)2(n nz 的收敛半径为【1/2】33.)(t δ的拉氏变换为【1】 34.设 ,2,1,=+=n ib a n n n α,若∑∞=1n nα收敛,则∑∞=1n nα【收敛】35.1+2i 的模为536.1[37.t 38.39.40.C 41.42.43.44.δ45.46.47.级数∑=-0)(n nz 的收敛半径为【1】48.=]0,1[Re zs 1 49.1+i 的幅角为【4π】 50.设 ,2,1,=+=n ib a n n n α,则∑∞=1n nα收敛的必要条件是0lim =∞→n n α三:名词解释 1.调和函数如果二元实函数),(y x H 在区域D 内具有二阶连续的偏导数,并且满足拉普拉斯方程0=∆H ,则称),(y x H 为区域D 内的调和函数。
工程数学复习及答案

工程数学 复习题 填空题1.设A 是2阶矩阵,且9=A ,='-)(31A .2.已知齐次线性方程组0=AX 中A 为53⨯矩阵,且该方程组有非零解,则≤)(A r .3.2.0)(,5.0)(==A B P A P ,则=+)(B A P .4.若连续型随机变量X 的密度函数的是⎩⎨⎧≤≤=其它,010,2)(x x x f ,则=)(X E .5.若参数θ的两个无偏估计量1ˆθ和2ˆθ满足)ˆ()ˆ(21θθD D >,则称2ˆθ比1ˆθ更 .单项选择题1.设B A ,都是n 阶矩阵)1(>n ,则下列命题正确的是( ).A. 若AC AB =,且0≠A ,则C B =B. 2222)(B AB A B A ++=+C. A B B A '-'='-)(D. 0=AB ,且0≠A ,则0=B 2.在下列所指明的各向量组中,( )中的向量组是线性无关的.A. 向量组中含有零向量B. 任何一个向量都不能被其余的向量线性表出C. 存在一个向量可以被其余的向量线性表出D. 向量组的向量个数大于向量的维数3.设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=211102113A ,则A 的对应于特征值2=λ的一个特征向量α=( ) .A .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡101B .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-101C .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡011D .⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1004. 甲、乙二人射击,A B ,分别表示甲、乙射中目标,则AB 表示( )的事件.A. 至少有一人没射中B. 二人都没射中C. 至少有一人射中D. 两人都射中5.设)1,0(~N X ,)(x Φ是X 的分布函数,则下列式子不成立的是( ).A. 5.0)0(=ΦB. 1)()(=Φ+-Φx xC. )()(a a Φ=-ΦD. 1)(2)(-Φ=<a a x P6.设321,,x x x 是来自正态总体N (,)μσ2的样本,则( )是μ无偏估计. A. 321x x x ++ B. 321525252x x x ++ C.321515151x x x ++ D. 321535151x x x ++ 7.对正态总体),(2σμN 的假设检验问题中,U 检验解决的问题是( ).A. 已知方差,检验均值B. 未知方差,检验均值C. 已知均值,检验方差D. 未知均值,检验方差 计算题1.设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=500050002,322121011B A ,问:A 是否可逆?若A 可逆,求B A 1-.2.线性方程组的增广矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----1123132111511求此线性方程组的全部解.3.用配方法将二次型32212322213214242),,(x x x x x x x x x x f ++++=化为标准型,并求出所作的满秩变换.4.两台车床加工同样的零件,第一台废品率是1%,第二台废品率是2%,加工出来的零件放在一起。
2019-2020年电大考试《工程数学》历年期末考试题汇总

期末考试工程数学(本) 试题一、单项选择题(每小题3分,共15分)1. 设A ,B 为三阶可逆矩阵,且0k >,则下列( )成立. A . A B A B +=+B .AB A B '=C . 1AB A B -=D .kA k A =2. 设A 是n 阶方阵,当条件( )成立时,n 元线性方程组AX b =有惟一解.3.设矩阵1111A -⎡⎤=⎢⎥-⎣⎦的特征值为0,2,则3A 的特征值为( )。
A .0,2 B .0,6 C .0,0 D .2,64.若随机变量(0,1)X N ,则随机变量32Y X =- ( ).5. 对正态总体方差的检验用( ).二、填空题(每小题3分,共15分)6. 设,A B 均为二阶可逆矩阵,则111OA BO ---⎡⎤=⎢⎥⎣⎦.8. 设 A , B 为两个事件,若()()()P AB P A P B =,则称A 与B . 9.若随机变量[0,2]XU ,则()D X = .10.若12,θθ都是θ的无偏估计,且满足 ______ ,则称1θ比2θ更有效。
三、计算题(每小题16分,共64分)11. 设矩阵234123231A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,111111230B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,那么A B -可逆吗?若可逆,求逆矩阵1()A B --.12.在线性方程组123121232332351x x x x x x x x λλ++=⎧⎪-+=-⎨⎪++=⎩ 中λ取何值时,此方程组有解。
在有解的情况下,求出通解。
13. 设随机变量(8,4)XN ,求(81)P X -<和(12)P X ≤。
(已知(0.5)0.6915Φ=,(1.0)0.8413Φ=,(2.0)0.9773Φ=)14. 某切割机在正常工作时,切割的每段金属棒长服从正态分布,且其平均长度为10.5cm ,标准差为0.15cm 。
从一批产品中随机地抽取4段进行测量,测得的结果如下:(单位:cm )10.4, 10.6, 10.1, 10.4 问:该机工作是否正常(0.9750.05, 1.96u α==)? 四、证明题(本题6分)15. 设n 阶矩阵A 满足2,A I AA I '==,试证A 为对称矩阵。
工程数学专升本试题及答案

工程数学专升本试题及答案一、选择题(每题2分,共20分)1. 极限lim(x→0) (sin(x)/x) 的值是:A. 0B. 1C. 2D. 不存在2. 函数f(x) = x^2 + 3x - 2的导数是:A. 2x + 3B. 2x^2 + 3C. x^2 + 3D. x + 33. 微分方程dy/dx + 2y = 6x的解是:A. y = 3x^2 - x + CB. y = 3x^2 + x + CC. y = 3x^2 - 2x + CD. y = 3x^2 + 2x + C4. 级数∑(1/n^2)(n从1到∞)是:A. 1B. 2C. π^2/6D. 无穷大5. 矩阵A = [1 2; 3 4]的行列式det(A)是:A. 7B. -7C. 1D. 06. 线性方程组x + 2y + 3z = 6,2x - y + z = 1,3x + y - 2z = 4的解是:A. x=1, y=1, z=1B. x=2, y=1, z=1C. x=1, y=2, z=1D. x=1, y=1, z=27. 函数f(x) = e^x的泰勒展开式在x=0处的前三项是:A. 1 + x + x^2/2!B. 1 + x + x^2/3!C. 1 + x + x^2/4!D. 1 + x + x^2/5!8. 傅里叶级数中,周期函数f(x) = sin(x)的傅里叶系数an是:A. 0B. 1C. -1D. 29. 拉普拉斯变换F{sin(at)}是:A. a/(s^2 + a^2)B. s/(s^2 + a^2)C. 1/(s^2 + a^2)D. 1/(s + a^2)10. 线性代数中,向量空间的基是:A. 一组线性无关的向量B. 一组线性相关的向量C. 任意一组向量D. 只有一个向量的集合二、填空题(每空1分,共10分)11. 函数f(x) = ln(x)的原函数是________。
12. 微分方程dy/dx - y = x^2的特解是________。
自考工程数学试题及答案

自考工程数学试题及答案一、单项选择题(每题2分,共10分)1. 以下哪个选项是微分方程的解?A. y = 3x + 2B. y = x^2 + 3x + 2C. y = e^xD. y = ln(x)答案:A2. 定积分∫(0,1) x^2 dx的值是多少?A. 1/3B. 1/2C. 1D. 2答案:B3. 以下哪个函数是奇函数?A. f(x) = x^2B. f(x) = x^3C. f(x) = x^4D. f(x) = x^5答案:B4. 以下哪个选项是线性方程组的解?A. x = 1, y = 2B. x = 2, y = 4C. x = 3, y = 6D. x = 4, y = 8答案:A5. 以下哪个矩阵是可逆的?A. [1 2; 3 4]B. [2 0; 0 2]C. [1 0; 0 0]D. [0 1; 1 0]答案:B二、填空题(每题2分,共10分)1. 函数f(x) = x^3 - 3x + 2的导数是______。
答案:3x^2 - 32. 函数f(x) = e^x的不定积分是______。
答案:e^x + C3. 函数f(x) = sin(x)的原函数是______。
答案:-cos(x) + C4. 矩阵A = [1 2; 3 4]的行列式是______。
答案:-25. 函数f(x) = x^2在区间[0,1]上的定积分是______。
答案:1/3三、解答题(每题15分,共30分)1. 求函数f(x) = x^2 - 4x + 3的极值点,并说明极值类型。
答案:函数f(x) = x^2 - 4x + 3的导数为f'(x) = 2x - 4,令f'(x) = 0,得到x = 2。
将x = 2代入原函数,得到f(2) = -1,为极小值点。
2. 求解线性方程组:\begin{cases}x + y = 5 \\2x - y = 1\end{cases}答案:将方程组写成增广矩阵形式,通过行变换得到:\begin{bmatrix}1 & 1 & | & 5 \\0 & 1 & | & 3\end{bmatrix}由此可得y = 3,代入第一个方程得到x = 2,所以方程组的解为x = 2,y = 3。
工程数学自考试题及答案

工程数学自考试题及答案一、单项选择题(每题2分,共20分)1. 下列哪项是线性方程组的解?A. 解存在且唯一B. 解不存在C. 解有无穷多个D. 无解答案:A2. 矩阵的秩是指什么?A. 矩阵的行数B. 矩阵的列数C. 矩阵中线性无关的行数或列数D. 矩阵的元素个数答案:C3. 微分方程的解是下列哪一项?A. 函数B. 数值C. 矩阵D. 向量答案:A4. 泰勒级数展开的中心点是?A. 0B. 1C. 任意点D. 函数的零点答案:C5. 傅里叶级数是用于什么?A. 函数的近似B. 函数的精确表示C. 函数的积分D. 函数的微分答案:A6. 线性代数中,向量空间的基是什么?A. 一组线性无关的向量B. 一组线性相关的向量C. 一组向量D. 一组标量答案:A7. 拉普拉斯变换是用于解决什么问题?A. 微分方程B. 积分方程C. 代数方程D. 线性方程组答案:A8. 欧拉公式是用于解决什么问题?A. 微分方程B. 积分方程C. 代数方程D. 线性方程组答案:A9. 概率论中,随机变量的期望值是什么?A. 随机变量的平均值B. 随机变量的中位数C. 随机变量的众数D. 随机变量的方差答案:A10. 泊松分布适用于描述什么?A. 连续型随机变量B. 离散型随机变量C. 正态分布的随机变量D. 二项分布的随机变量答案:B二、填空题(每题2分,共20分)1. 如果一个线性方程组有唯一解,则该方程组是_________的。
答案:相容2. 矩阵的对角线元素之和称为矩阵的_________。
答案:迹3. 微分方程的通解是包含_________的解。
答案:任意常数4. 泰勒级数展开的公式是_________。
答案:f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^2/2! + ...5. 傅里叶级数的公式是_________。
答案:f(x) = a0/2 + Σ[an*cos(nπx/L) + bn*sin(nπx/L)]6. 向量空间的基有_________个向量。
《工程数学》复习题

)
4 7 1
A1
B2
C3
7、设 A, B 是 n 阶方阵,满足等式 AB 0 ,则必有( )
D4
A A0或B 0 B A B 0
C A 0或 B 0 D A B 0
8、设 Ann 是 n 阶可逆矩阵, A 是 A 伴随矩阵,则( )
A A A n1
B A A
)
A 0.16
B 0.2
C 0.28
D 0.32
23、掷一枚骰子,设 A {出现奇数点},B {出现 1 或 3 点},则下列说法正确的是( )。
A AB {出现奇数点} C B {出现 5 点}
B AB {出现 5 点} D AB
24、已知 P( A) 0.5 , P(B) 0.4 , P( A B) 0.6 ,则 P( A B) (
A (5)n A
B (5) A
C 5A
D 5n A
3、向量组1,2 , S ( s 2 ) 线性无关的充分必要条件是(
)
A 1,2 , S 均不为零向量
B 1,2 , S 中任意两个向量不成比例
C 1,2 , S 中任意 s 1个向量线性无关
D 1,2 , S 中任意一个向量均不能由其余的 s 1个向量线性表示
取 1 个球,放入乙盒中,再从乙盒中任取 2 个球,(1)求从乙盒中取出的是 2 个黑球的概率;
(2)己知从乙盒中取出的是 2 个黑球,问从甲盒中取出的是白球的概率。
10、某产品由三个不同的厂家生产,其中第一和第二个厂家生产的产品分别占产品总数的
1/5,第三个厂家生产的产品占产品总数的 3/5。已知第一和第二个厂家生产的产品分别有
D 若 P(B) P(B A) P(B A) 1,则 B 为不可能事件
电大本科 工程数学-期末复习试卷含答案

工程数学综合练习(一)一、单项选择题A. 1B. -1C. 0D. 24. A.B 都是〃阶矩阵(〃:>1),则下列命题正确的是(). A.AB=BAB,若AB = O ,则 A = 0或8 = 0C. (A-B)2 =A 2-2AB + B 2D.仇耳=凤同 5. 若A 是对称矩阵,则等式()成立. A. A -1 = A f B. A = —A C. A = A'D. A ,= -A1 2 6. 若 A = 3 5,则A. 0 9. 向量组a, =[1 2 3]',%=[2 2 4]',%=[1 极大无关组可取为().B. a,,a 2C.D. %,。
2,%,。
410. 向量组 %=[1,0,-2],%=[2,3,5],%=[1,2,1],则 2a,+a 2-3a 3 =b a 2 b 2a 3 a 2 3角-如C 2a 33%-打 C3B 是矩阵,则下列运算中有意义的是(). A'B D AB' 3. 己知A7.若人=2 2 2 23 3 3 3 44 4 4C. 2A. 4 2]',%= [2 3 5]'的一个 C 2 C 3C|设A 是〃xs 矩阵, AB B. BA C.2. A. 0 0 -a,若 AB = ,则。
=(8.向量组A. 1,-3,2B. 1,-3,-2]C. 1,3,-2]D. 1,3,2]11. 线性方程组」X,+X2=+X2=解的情况是(). x 2 + x 3 = 0A.无解 D.只有零解 C.有唯一非零解 D.有无穷多解12, 若线性方程组AX=O 只有零解,则线性方程组AX=b (). A.有唯一解 B.有无穷多解C.可能无解 D.无解 13. 若〃元线性方程组AX=O 有非零解,则()成立. A. r(A) < n B. r(A) = n C. |A| = 0D. A 不是行满秩矩阵14. 下列事件运算关系正确的是(). C. D. B = BA+BA15. 对于随机事件A,B.下列运算公式()成立. A. P(A + B) = P(A) + P(B) - P(AB) B. P(AB) = P(A)P(B) C. P(AB) = P(8)P(B|A) D. P(A + B) = P(A) + P(B)16. 袋中有3个红球,2个白球,第一次取出一球后放回,第二次再取一球,则两球都 是红球的概率是(). A. AB. Ac. AD .210 20 252517.若随机事件满足AB = 0,则结论()成立 A. A 与8是对立事件 B. A 与B 互不相容C. A 与B 相互独立D. 1与京互不相容 18.若A, B 满足() ,则A 与8是相互独立. A. P(A + B) = P(A) + P(B) B. P(A-B) = P(A)-P(B)Dpg端 中的数组可以作为离散型随机变量的概率分布.A. B = BA + BAB. A = BA + BAC. P(AB) = P(A)P(B) 19.下列数组中,(1 1 1 3 1 1 3 12 4 16 162 4 8 820. 设X123则 P(X <2)=0.1 0.3 0.4 0.2A. 0.1B. 0.4C. 0.3D. 0.221. 随机变量X 〜8(3,:), 则 P(X <2)=()A. 0B.C.1D782822.已知X 〜N(2,22),若aX+b~ N(O,1),那么(). A. a = 2,b = -2 B.。
工程数学复习题
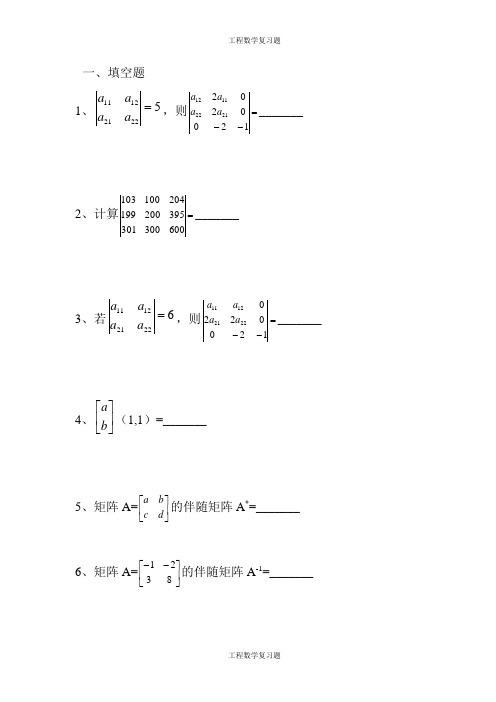
一、1、522211211=a a a a ,则=--120020221221112a a a a _______2、计算=600300301395200199204100103_______3、若622211211=a a a a ,则=--120022022211211a a a a _______4、⎥⎦⎤⎢⎣⎡b a (1,1)=_______5、矩阵A=⎥⎦⎤⎢⎣⎡d c b a 的伴随矩阵A *=_______6、矩阵A=⎥⎦⎤⎢⎣⎡--8321的伴随矩阵A -1=_______7、=--1300020001_______8、已知点P (x,y )的坐标满足⎪⎩⎪⎨⎧≥≥≤+14x x y y x ,点O 为坐标原点,则PO的最大值_______9、当x=_______时,齐次方程组⎩⎨⎧=+=+002121x x x x λ只有零解 10、向量组x 1=(1,2,-1),x 2=(2,-3,-1),x 3=(4,1,-1)的秩为_______11、已知x 1=(1,4,3)T ,x 2=(2,t ,-1)T ,x 3=(-2,3,1)T 线性相关,则t=_______12、向量组x 1=(1,2,-1,1),x 2=(2,0,3,0),x 3=(0,-4,5,-2)的秩为_______13、如果x 1,x 2都是方程组A x =b 的解,则x 1-x 2一定是方程_______的解14、设函数F (x )=⎩⎨⎧<≥--0002x x be a x ,为连续型随机变量x 的分布函数,则=+b a _______15、同时抛掷3枚均称的硬币,恰好两枚正面向上的概率为_______16、用"C"连接B A B A B ,,-⋃_,Ω,φ为_______17、一批电子元件共100个,次品率为0.05,连续两次不放回从中任取一个,则第二次才取到正品概率为_______18、设每次试验的成功率为P (0<P<1),独立进行几次重复试验,则恰好有r 次试验取得成功的概率为_______19、函数f (x)=sinwt 的拉普拉斯变换为_______20、同时掷两骰子,出现点数三和为10的概率为_______21、设x~z (0,1),φ(x )是x 的分布函数,则Φ(0)=_______22、设x 为连续型随机变量,则p {}100=x =_______二、选择题1、行列式453175934中,代数余子式A 21=( )A 、33B 、-33C 、5D 、-52、设A 为n 阶方阵,则det (KA )=( )A 、k n detAB 、kdetAC 、k detAD 、(kdetA)n3、若n 阶方阵A 与B 都可逆,则下列命题中错误的是( )A 、AB+3B=(A+3)B B 、(AB)T =B T A TC 、(AB)-1=B -1A -1D 、线性齐次方程(AB)x=0只有零解4、设A 是5×4的矩阵,A 的秩为3,则齐次线性方程组A x =0的一个基础解系含有的个数为( )A 、4B 、3C 、2D 、15、设A 是5×4的矩阵,A 的秩为3,则齐次线性方程组A x =0,下列说法正确的是( )A 、方程组A x =0的一个基础解系中含有解得个数为3B 、方程组A x =0的一个基础解系中含有解得个数为2C 、方程组A x =0的一个基础解系中含有解得个数为1D 、方程组A x =0不存在基础解系6、袋中油5个黑球,3个白球,从中任取4个,则所取4个中恰好有3个白球的概率为( )A 、83B 、81.)83(5C 、81.)83(548CD 、485C7、设x~n(0,1),F(x)是x 的分布函数,则F (0)=( )A 、1B 、0C 、π21D 、218、设x 为连续随机变量,则p {}100=x =( )A 、0B 、31C 、1D 、219、设x 与y 是任意两个相互独立的连续型随机变量,它们的概率密度分别为p 1(x)和p 2(y),分布函数分别为F 1(x)和F 2(y),则( )A 、p 1(x)+p 2(y)必为某一随机变量的概率密度B 、p 1(x)、p 2(y)必为某一随机变量的概率密度C 、F 1(x)+F 2(y)必为某一随机变量的分布函数D 、F 1(x)-F 2(y)必为某一随机变量的分布函数10、假设A 、B 为两个互斥事件,则下列关系中不一定正确的是( )A 、P(A+B)=P(A)+P(B)B 、P(A)=1-P(B)C 、P(AB)=0D 、P(A/B)=011、设Ex 与Dx 都存在,而Y=-x+Ex ,则下列结论错误的是( )A 、EY=0B 、E(x+Y)=Ex+EYC 、DY=-DxD 、 D(x+Y)=012、对于单正态总体的假设检验,方差σ2未知,检验假设H 0:0--=U U ,则( ) A 、若拒绝H 0,则总体的真实均值-U 不可能等于给定值0-U B 、若接受H 0,则总体的真实均值-U 恰好等于给定值0-U C 、应采用t 一检验法,选取统计量T=n sU x .0--- D 、应采用-U 一检验法,选取统计量U=n U x .0σ---13、设随机变量的分布函数F(y)=1100103>≤≤<⎪⎩⎪⎨⎧y y y y ,则E(Y)=( )A 、dy y 20⎰+∞B 、dy y 2103⎰C 、ydy dy y ⎰⎰∞+0410D 、dy y 3103⎰三、多项选择题1、若A 、B 、C 都是n 阶方阵,则下列命题错误的是( )A 、所有零矩阵都相等B 、若AB=E ,则AB 都可逆C 、AB+3A=A(B+3)D 、BA+CA=(B+C)A2、设A 、B 均为n 阶可逆矩阵,则下列错误的公式是( )A 、(A 2)-1=(A -1)2B 、(KA)-1=KA -1 (K ≠0)C 、(A+B)-1=A -1+B -1D 、(A+B)(A-B)=A 2-B 23、设A 、B 、C 是n 阶可逆矩阵,则下列命题正确的是( )A 、若AB=CB,则A=CB 、AB=BAC 、det(AB)=detA·detbD 、秩R(A)=R(B)=R(C)4、设A 、B 均为n 阶矩阵,且(AB)2=E ,则下列命题中正确的是( )A 、(BA)2=EB 、A -1=BC 、r(A)=r(B)D 、A -1=BAB5、若A 是4阶方阵,A*是A 得伴随矩阵,A 可逆且逆矩阵A -1,则下列命题中正确的是( )A 、detA -1=(detA)-1B 、detA*=(detA)3C 、A*=(detA)A -1D 、AA*=detA6、若n 元线性齐次方程组Ax=0只有唯一解,则下列命题中正确的是( )A 、R(A)=nB 、detA ≠0C 、R(A) <nD 、A 不可逆7、下列命题中错误的是( )A、若整个向量组线性相关,则必有部分组也线性相关B、若整个向量组线性相关,则其中必有零向量C、若有一部分向量组线性无关,则其整个向量组必线性无关D、若有一部分向量组线性相关,则其整个向量组必线性有关8、设n元齐次线性方程组Ax=0的系数矩阵A的秩为r,且Ax=0有非零解,则下列命题正确的是()A、r=nB、r<nC、A可逆D、detA=09、设线性方程组Ax=6有n个未知量,m个方程,且(A)=r,则对比方程组下列说法错误的是()A、r=m时,有解B、r=n时,有唯一解C、m=n时,有唯一解D、r<n时,有无穷多解四、判断题1、若A≠0,且AB=AC,则一定有B=C ( )2、若A可逆,数λ≠0,则又(λA)-1=λA-1()3、任何两个矩阵都能相乘()4、克拉默法则只适合系数矩阵A为方阵的线性方程组Ax=b的求解 ( )5、矩阵A通过有限次初等变换后,其秩一定不变()6、对向量组x1、x2……x n,若其中有一部分向量组线性相关,则整个向量组x1、x2……x n必线性相关()7、如果x1是线性方程组Ax=b的解,x2是线性组Ax=b对应的齐次方程组的解,则x1+x2一定是方程组Ax=b的解( )8、设A 是5×4矩阵,r(A)=4,则齐次线性方程组Ax=0不存在基础解系 ( )9、若K 1=K 2……=Kn=0,只K 1X 1+K 2X 2+……KnXn=0,则向量组X 1、X 2……Xn 线性无关 ( )10、互斥事件必为互逆事件 ( )11、在假设检验问题中,检验水平X 的意义是原假设H 0成立,经检验被拒绝的概率 ( )12、若P(A-B)=P(A)-P(B)成立,则A 、B 独立 ( )13、设A 、B 、C 为三个时间,则A 、B 、C 中至少有一个发生课表示为C B A ⋃⋃或---C B A 或Ω----C B A ( )14、若E(x)、D(x)都存在,且Y=-x+E(x),则D(Y)=-D(x) ( )15、A 与B 是两个相互独立事件,则-A 与-B 相互独立 ( )五、计算题1、解矩阵方程⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡243152X2、设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=161620101A 满足AX+E=A 2+X ,求矩阵X3、已知实数x 、y满足条件⎪⎩⎪⎨⎧≥≥≤--≥+-0,003304221x x y x y x ,求z=x+2y 的解4、求线性规划问题,maxs=x 1+2x 2,⎪⎩⎪⎨⎧≥≥≤+≤+0,012261553211121x x x x x x 的最大优解与最优值5、已知⎪⎩⎪⎨⎧≥≥-≤+00632y y x y x ,求z=3x+y 的最大值6、某公司有60万元资金,计划投资甲、乙两个项目,按需求对项目甲的投资不小于对项目乙投资的32倍,且对每个项目的投资不能低于5万元,对项目甲每投资1 万元可获得0.4万元利润,对项目乙每投资1万元可获得0.6万元的利润,求该公司正确理财后,在两个项目上共可获得的最大利润7、在约束条件⎪⎪⎩⎪⎪⎨⎧≤+≤+≥≥4200x y sy x y x ,当s=3与s=5时,求目标函数z=3x+2y 的最大值8、某公司计划2012年再甲乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲乙电视台的广告收费标准分别为500元/分钟和200万元/分钟,规定甲乙两个电视台为该公司做的每分钟广告能给公司带来的收益分别为0.3万元和0.2万元,问该公司如何分配在甲乙两个电视台的广告时间,才能使公司的收益最大,最大的利润是多少万?9、求齐次线性方程组⎪⎩⎪⎨⎧=++-=+--=++-010********2432143214321x x x x x x x x x x x x 的基础解系,并写出其通解10、求方程2x 1+x 2-2x 3+3x 4=1对应齐次方程组的基础解系,并写出该方程组的解11、求向量组x 1=(1,4,1,0)T ,x 2=(2,5,-1,-3)T ,x 3=(-1,2,5,6)T ,x 4=(0,2,2,-1)T 的秩,并指出一个极大无关组12、求方程组⎪⎩⎪⎨⎧=+++=-++=-++0243204202432143214321x x x x x x x x x x x x 的基础解系,并写出其通解13、求矩形脉冲函数f (t)=⎩⎨⎧≤≤其他O A τ10的傅里叶变换14、有3个参加考试抽签,共有10个签,其中有4个难,每人抽一个考签,甲先乙后,丙最后,试猜想3个人抽到难签的概率是否相等,并证明你的结论15、设随机变量x 的概率密度为P(x)=⎩⎨⎧<<其他0102x Ax 求:(1)常数A (2)P(21>x )(3)E D (4)E(10x+5) D(10x+5)16、四川省今年三诊数学测验平均分为68,现在从某中学随机抽取6份试卷,其分数如下:72、68、78、62、61、85试问该学校三诊平均成绩与全省是否一致(x=0.05)。
工程数学本 工程数学复习

(06春-12春)复习资料总结一、单项选择题(每小题3分,本题共15分)1. 若0351021011=---x ,则=x (A ). A. 3 B. 2 C. 3- D. 2-2. 已知2维向量组4321,,,αααα,则),,,(4321ααααr 至多是(B ). A 1 B 2 C 3 D 43. 设B A ,为n 阶矩阵,则下列等式成立的是(C )A.BA AB = B. B A AB ''=')( C. B A B A '+'='+)( D. AB AB =')(4. 若A B ,满足(B),则A 与B 是相互独立.A. )()()(A B P A P B P = B. )()()(B P A P AB P = C. )()()(B P A P B A P -=- D. )()()(B A P B P A P = 5. 若随机变量X 的期望和方差分别为)(X E 和)(X D ,则等式( D )成立.A. )]([)(X E X E X D -=B. 22)]([)()(X E X E X D +=C. )()(2X E X D =D. 22)]([)()(X E X E X D -=6.若A 是对称矩阵,则等式( B )成立. A. I AA =-1 B. A A =' C. 1-='A A D. A A =-17.=⎥⎦⎤⎢⎣⎡-15473(D ). A. ⎥⎦⎤⎢⎣⎡--3547 B. 7453-⎡⎤⎢⎥-⎣⎦ C. 7543-⎡⎤⎢⎥-⎣⎦ D. 7543-⎡⎤⎢⎥-⎣⎦8.若(A )成立,则n 元线性方程组AX O =有唯一解.A. r A n ()=B. A O ≠C. r A n ()<D. A 的行向量线性相关 4. 若条件( C )成立,则随机事件A ,B 互为对立事件.A. ∅=AB 或A B U +=B. 0)(=AB P 或()1P A B +=C. ∅=AB 且A B U +=D. 0)(=AB P 且1)(=+B A P9.对来自正态总体X N ~(,)μσ2(μ未知)的一个样本X X X 123,,,记∑==3131i iX X ,则下列各式中(C )不是统计量. A.XB.∑=31i iX C. ∑=-312)(31i i X μ D. ∑=-312)(31i i X X10.设B A ,都是n 阶方阵,则下列命题正确的是( A ).A .AB A B = B .222()2A B A AB B -=-+C .AB BA = D .若AB O =,则A O =或B O =11.向量组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡732,320,011,001的秩是( B ). A. 1 B. 3 C. 2 D. 4 12.n 元线性方程组AX b =有解的充分必要条件是( A ).A. )()(b A r A r M= B. A 不是行满秩矩阵 C. r A n ()< D. r A n ()= 13. 袋中有3个红球,2个白球,第一次取出一球后放回,第二次再取一球,则两球都是红球的概率是(D ).A.256 B. 103 C. 203 D. 25914.设x x x n 12,,,Λ是来自正态总体N (,)μσ2的样本,则(C )是μ无偏估计.A.321515151x x x ++ B. 321x x x ++ C. 321535151x x x ++ D. 321525252x x x ++15.设B A ,为n 阶矩阵,则下列等式成立的是( A).A .BA AB = B .B A B A +=+C .111)(---+=+B A B AD .111)(---=B A AB16.方程组⎪⎩⎪⎨⎧=+=+=-331232121a x xa x x a x x 相容的充分必要条件是( B ),其中0≠ia ,)3,2,1(=i .A .0321=++a a aB .0321=-+a a aC .0321=+-a a aD .0321=++-a a a17.下列命题中不正确的是( D ). A .A 与A '有相同的特征多项式B .若λ是A 的特征值,则O X A I=-)(λ的非零解向量必是A 对应于λ的特征向量C .若λ=0是A 的一个特征值,则O AX =必有非零解D .A 的特征向量的线性组合仍为A 的特征向量18.若事件A 与B 互斥,则下列等式中正确的是( A ).A .P AB P A P B ()()()+=+ B .P B P A ()()=-1C .P A P A B ()()=D .P AB P A P B ()()()=19.设n x x x ,,,21Λ是来自正态总体)1,5(N 的样本,则检验假设5:0=μH 采用统计量U =(C ).A .55-xB .5/15-x C .n x /15- D .15-x二、填空题(每小题3分,共15分) 1. 设B A ,均为n 阶可逆矩阵,逆矩阵分别为11,--B A ,则='--11)(A B B A )(1'-.2. 向量组),0,1(),1,1,0(),0,1,1(321k ===ααα线性相关,则_____=k -1.3. 已知2.0)(,8.0)(==AB P A P ,则=-)(B A P.0.64. 已知随机变量⎥⎦⎤⎢⎣⎡-5.01.01.03.0521~X ,那么=)(X E 2.4. 5. 设1021,,,x x x Λ是来自正态总体)4,(μN 的一个样本,则~101101∑=i ix )104,(μN .6.设B A ,均为3阶方阵,6,3A B =-=,则13()A B -'-=8.7.设A 为n 阶方阵,若存在数?和非零n 维向量X ,使得 AX X λ= ,则称X 为A 相应于特征值?的特征向量.8.若5.0)(,8.0)(==B A P A P ,则=)(AB P 0.3.9.如果随机变量X 的期望2)(=X E ,9)(2=X E ,那么=)2(X D 20.10.不含未知参数的样本函数称为 统计量 11.设B A ,均为3阶方阵,2,3A B ==,则13A B -'-=-18.12.设随机变量012~0.20.5X a ⎛⎫ ⎪⎝⎭,则a = 0.3.13.设X 为随机变量,已知3)(=X D ,此时D X ()32-=27 . 14.设θˆ是未知参数θ的一个无偏估计量,则有 ˆ()E θθ= .15.设22112112214A x x =-+,则0A =的根是1,-1,2,-2 .16.设4元线性方程组AX =B 有解且r (A )=1,那么AX =B 的相应齐次方程组的基础解系含有 3 个解向量. 17.设A B ,互不相容,且P A ()>0,则P B A ()=0.18.设随机变量X ~ B (n ,p ),则E (X )= np . 19.若样本n x x x ,,,21Λ来自总体)1,0(~N X ,且∑==n i i x n x 11,则~x )1,0(n N .三、计算题(每小题16分,共64分) 1设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=423532211A ,求(1)A ,(2)1-A .解: (1)1111021121110211423532211=---=---=---=A (2)利用初等行变换得→------⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥→-----⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥110922010721001511100201010721001511即 A -=-----⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥12017215112. 当λ取何值时,线性方程组⎪⎩⎪⎨⎧+=++-=++-=+-2532342243214321421λx x x x x x x x x x x 有解,在有解的情况下求方程组的全部解.解:将方程组的增广矩阵化为阶梯形 由此可知当λ≠3时,方程组无解。
工程数学(本)

一、单项选择题1. 设2321321321=c c c b b b a a a ,则=---321332211321333c c c b a b a b a a a a (A ). A . 2- 2. 设A 是n s ⨯矩阵,B 是m s ⨯矩阵,则下列运算中有意义的是( D ).D . AB '3. 已知⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡-=21101210,20101B a A ,若⎥⎦⎤⎢⎣⎡=1311AB ,则=a ( B ). B . 1- 4.B A ,都是n 阶矩阵()1>n ,则下列命题正确的是 ( D ) .D .B A AB = 5. 若A 是对称矩阵,则等式(C )成立. C . A A =' 6. 若⎥⎦⎤⎢⎣⎡=5321A ,则=*A (D ). D . ⎥⎦⎤⎢⎣⎡--1325 7. 若⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=4321432143214321A ,则秩=)(A (B ). B . 1 8. 向量组10001200123012341111⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥,,,,的秩是(A ). A . 49. 向量组]532[,]211[,]422[,]321[4321'='='='=αααα的一个极大无关组可取为(B ).B .21,αα10. 向量组[][][]1,2,1,5,3,2,2,0,1321==-=ααα,则=-+32132ααα(B ).[]2,3,1-- 11. 线性方程组⎩⎨⎧=+=+013221x x x x 解的情况是(D )D . 有无穷多解12. 若线性方程组AX =0只有零解,则线性方程组AX b =(C ).C . 可能无解13. 若n 元线性方程组AX =0有非零解,则( A )成立.A . r A n ()< 14. 下列事件运算关系正确的是( A ).A . BA A B B +=15. 对于随机事件A B ,,下列运算公式( A )成立.A . )()()()(AB P B P A P B A P -+=+16. 袋中有3个红球,2个白球,第一次取出一球后放回,第二次再取一球,则两球都是红球的概率是(D ).25917. 若随机事件A ,B 满足AB =∅,则结论(B )成立.A 与B 互不相容18. 若A B ,满足(C ),则A 与B 是相互独立.C . )()()(B P A P AB P = 19. 下列数组中,(C )中的数组可以作为离散型随机变量的概率分布.163161412120. 设⎥⎦⎤⎢⎣⎡2.04.03.01.03210~X ,则=<)2(X P (B ). B .0.4 21. 随机变量)21,3(~B X ,则=≤)2(X P (D ). D . 87 22. 已知)2,2(~2N X ,若)1,0(~N b aX +,那么(C ).1,21-==b a23. 若)4,2(~N X ,Y =(C ),则Y N ~(,)01. C . 22-X24. 设n x x x ,,,21 是来自正态总体22,)(,(σμσμN 均未知)的样本,则( A )是统计量.A . 1x 25. 设x x x n 12,,, 是来自正态总体N (,)μσ2的样本,则(D )是μ无偏估计.D .321535151x x x ++ ⒈设a a a b b b c c c 1231231232=,则a a a a b a b a b c c c 123112233123232323---=(D ).D. -6 ⒉若000100002001001a a=,则a =(A )⒊乘积矩阵1124103521-⎡⎣⎢⎤⎦⎥-⎡⎣⎢⎤⎦⎥中元素c 23=(C ).C. 10 ⒋设A B ,均为n 阶可逆矩阵,则下列运算关系正确的是( B )⒌设A B ,均为n 阶方阵,k >0且k ≠1,则下列等式正确的是(D )⒍下列结论正确的是( A ).若A 是正交矩阵,则A -1也是正交矩阵⒎矩阵1325⎡⎣⎢⎤⎦⎥的伴随矩阵为( C ).5321--⎡⎣⎢⎤⎦⎥⒏方阵A 可逆的充分必要条件是(B) ⒐设A B C ,,均为n 阶可逆矩阵,则()ACB '=-1(D ).()B C A ---'111⒑设A B C ,,均为n 阶可逆矩阵,则下列等式成立的是(A ).()A B A AB B +=++2222⒈用消元法得x x x x x x 12323324102+-=+=-=⎧⎨⎪⎩⎪的解x x x 123⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥为(C ).[,,]--'1122 ⒉线性方程组x x x x x x x 12313232326334++=-=-+=⎧⎨⎪⎩⎪(B ).有唯一解⒊向量组100010001121304⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥,,,,的秩为( A ).A. 3⒋设向量组为αααα12341100001110101111=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥,,,,则(B )⒌A 与A 分别代表一个线性方程组的系数矩阵和增广矩阵,若这个方程组无解,则(D ⒍若某个线性方程组相应的齐次线性方程组只有零解,则该线性方程组(A ).可能无解⒎以下结论正确的是(D ).齐次线性方程组一定有解⒏若向量组ααα12,,, s 线性相关,则向量组内(A )可被该向量组内其余向量线性表出.至少有一个向量 10.设A,B,P为n 阶矩阵,若等式(C )成立,则称A和B相似.B PAP =-1 ⒈A B ,为两个事件,则(B )成立.()A B B A +-⊂⒉如果(C )成立,则事件A 与B 互为对立事件.AB =∅且AB U =⒊10张奖券中含有3张中奖的奖券,每人购买1张,则前3个购买者中恰有1人中奖的概率为(D ).307032⨯⨯.. 4. 对于事件A B ,,命题(C )⒌某随机试验的成功率为)10(<<p p ,则在3次重复试验中至少失败1次的概率为(D ).)1()1()1(223p p p p p -+-+-6.设随机变量X B n p ~(,),且E X D X ().,().==48096,则参数n 与p 分别是(A ). A. 6, 0.87.设f x ()为连续型随机变量X 的密度函数,则对任意的a b a b ,()<,E X ()=(A ).xf x x ()d -∞+∞⎰8.在下列函数中可以作为分布密度函数的是(B )9.设连续型随机变量X 的密度函数为f x (),分布函数为F x (),则对任意的区间(,)a b ,则=<<)(b X a P ( D ).f x x ab()d ⎰10.设X 为随机变量,E X D X (),()==μσ2,当(C )时,有E Y D Y (),()==01.⒈设x x x n 12,,, 是来自正态总体N (,)μσ2(μσ,2均未知)的样本,则(A )是统计量.x 1⒉设x x x 123,,是来自正态总体N (,)μσ2(μσ,2均未知)的样本,则统计量(D )不是μ的无偏估计.x x x 123--1. 若0351021011=---x ,则=x (A ).A . 3 2. 已知2维向量组4321,,,αααα,则),,,(4321ααααr 至多是(B ). A 1 B 2 C 3 D 43. 设B A ,为n 阶矩阵,则下列等式成立的是(C ).B A B A '+'='+)(4. 若A B ,满足(B ),则A 与B 是相互独立.)()()(B P A P AB P =5. 若随机变量X 的期望和方差分别为)(X E 和)(X D ,则等式(D )成立.22)]([)()(X E X E X D -=1. 设A 为43⨯矩阵,B 为25⨯矩阵,当C 为(B )矩阵时,乘积B C A ''有意义.42⨯2. 向量组[][][][]αααα1234000*********====,,,,,,,,,,,的极大线性无关组是(A ).ααα234,, 3. 若线性方程组的增广矩阵为⎥⎦⎤⎢⎣⎡=41221λA ,则当λ=(D )时线性方程组有无穷多解.124. 掷两颗均匀的骰子,事件“点数之和为4”的概率是(C ). 1215. 在对单正态总体N (,)μσ2的假设检验问题中,T检验法解决的问题是(B ).未知方差,检验均值二、填空题1. 1111111---x x 是关于x 的一个多项式,该式中一次项x 系数是 2 .2. 设B A ,是3阶矩阵,其中2,3==B A ,则='-12B A 12 .3. 设D C B A ,,,均为n 阶矩阵,其中C B ,可逆,则矩阵方程D BXC A =+的解=X 11)(---C A D B .4. 若方阵A 满足A A '=,则A 是对称矩阵.5.设矩阵⎥⎦⎤⎢⎣⎡=1111A ,则r A ()= 1 . 6. =⎥⎦⎤⎢⎣⎡-12514⎥⎦⎤⎢⎣⎡--451231. 7. 向量组)01(),110(),011(321k ===ααα线性相关,则_____=k .1-8.含有零向量的向量组一定是线性 相关 的.9. 若n 元线性方程组0=AX 满足r A n ()<,则该线性方程组有非零解.10. 线性方程组b AX =中的一般解的自由元的个数是2,其中A 是54⨯矩阵,则方程组增广矩阵)(b A r = 3 . 11. 齐次线性方程组0=AX 的系数矩阵经初等行变换化为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--→→000020103211 A则方程组的一般解为 4342431,(22x x x x x x x ⎩⎨⎧=--= .是自由未知量)12. 当λ= 1 时,方程组⎩⎨⎧-=--=+112121x x x x λ有无穷多解.13. 若5.0)(,1.0)(,9.0)(===+B A P B A P B A P ,则)(AB P 3.0 . 14. 设A ,B 为两个事件,若)()()(B P A P AB P =,则称A 与B 相互独立 .15. 设随机变量⎥⎦⎤⎢⎣⎡-25.03.0101~a X ,则a =45.0.16. 设随机变量的概率密度函数为⎪⎩⎪⎨⎧≤≤+=其它,010,1)(2x x kx f ,则常数k =π4.17. 设随机变量⎥⎦⎤⎢⎣⎡5.02.03.0210~X ,则=≠)1(X P 8.0.18. 设随机变量X 的概率密度函数为⎩⎨⎧≤≤=其它103)(2x x x f , 则=<)21(X P 81.19. 已知随机变量⎥⎦⎤⎢⎣⎡-5.05.05.05.05201~X ,那么=)(X E 3 .20. 设随机变量)15.0,100(~B X ,则=)(X E 15 . 21. 设随机变量X 的期望存在,则E X E X (())-= 0 .22. 设随机变量X ,若5)(,2)(2==X E X D ,则=)(X E 3.23. 不含未知参数的样本函数称为统计量.24. 设1021,,,x x x 是来自正态总体)4,(μN 的一个样本,则~101101∑=i i x )104,(μN .25. 若参数θ的两个无偏估计量1ˆθ和2ˆθ满足)ˆ()ˆ(21θθD D >,则称2ˆθ比1ˆθ更 有效 .⒈210140001---= 7 .⒉---11111111x 是关于x 的一个一次多项式,则该多项式一次项的系数是 2 . ⒊若A 为34⨯矩阵,B 为25⨯矩阵,切乘积AC B ''有意义,则C 为 5×4 矩阵.⒋二阶矩阵A =⎡⎣⎢⎤⎦⎥=11015⎥⎦⎤⎢⎣⎡1051.⒌设A B =-⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥=--⎡⎣⎢⎤⎦⎥124034120314,,则()A B +''=⎥⎦⎤⎢⎣⎡--815360 ⒍设A B ,均为3阶矩阵,且A B ==-3,则-=2AB 72 .⒎设A B ,均为3阶矩阵,且A B =-=-13,,则-'=-312()A B -3 .⒏若A a =⎡⎣⎢⎤⎦⎥101为正交矩阵,则a = 0 .⒐矩阵212402033--⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥的秩为 2 .⒑设⒈当λ= 1 时,齐次线性方程组x x x x 12120+=+=⎧⎨⎩λ有非零解.⒉向量组[][]αα12000111==,,,,,线性 相关 .⒊向量组[][][][]123120100000,,,,,,,,,,,的秩是 3 . ⒋设齐次线性方程组ααα1122330x x x ++=的系数行列式ααα1230=,则这个方程组有 无穷多 解,且系数列向量ααα123,,是线性 相关 的.⒌向量组[][][]ααα123100100===,,,,,的极大线性无关组是21,αα. ⒍向量组ααα12,,, s 的秩与矩阵[]ααα12,,, s 的秩 相同 .⒎设线性方程组AX =0中有5个未知量,且秩()A =3,则其基础解系中线性无关的解向量有 2 个. ⒏设线性方程组AX b =有解,X 0是它的一个特解,且AX =0的基础解系为X X 12,,则AX b =的通解为22110X k X k X ++.9.若λ是A的特征值,则λ是方程0=-A I λ 的根.10.若矩阵A满足A A '=-1 ,则称A为正交矩阵.是两个可逆矩阵,则A O O A 121⎡⎣⎢⎤⎦⎥=-⎥⎦⎤⎢⎣⎡--1211A O O A . ⒈从数字1,2,3,4,5中任取3个,组成没有重复数字的三位数,则这个三位数是偶数的概率为52. 2.已知P A P B ().,().==0305,则当事件A B ,互不相容时,P A B ()+= 0.8 ,P AB ()= 0.3 . 3.A B ,为两个事件,且B A ⊂,则P A B ()+=()A P . 4. 已知P AB P AB P A p ()(),()==,则P B ()=P -1.5. 若事件A B ,相互独立,且P A p P B q (),()==,则P A B ()+=pq q p -+.6. 已知P A P B ().,().==0305,则当事件A B ,相互独立时,P A B ()+= 0.65 ,P A B ()= 0.3 . 7.设随机变量X U ~(,)01,则X 的分布函数F x ()=⎪⎩⎪⎨⎧≥<<≤111000x x x x .8.若X B ~(,.)2003,则E X ()= 6 .9.若X N ~(,)μσ2,则P X ()-≤=μσ3)3(2Φ.10.E X E X Y E Y [(())(())]--称为二维随机变量(,)X Y 的 协方差 .1.统计量就是 不含未知参数的样本函数 .2.参数估计的两种方法是 点估计 和 区间估计 .常用的参数点估计有 矩估计法 和 最大似然估计 两种方法.3.比较估计量好坏的两个重要标准是 无偏性 , 有效性 .4.设x x x n 12,,, 是来自正态总体N (,)μσ2(σ2已知)的样本值,按给定的显著性水平α检验H H 0010:;:μμμμ=≠,需选取统计量nx U /0σμ-=.5.假设检验中的显著性水平α为事件u x >-||0μ(u 为临界值)发生的概率.1. 设B A ,均为n 阶可逆矩阵,逆矩阵分别为11,--B A ,则='--11)(A BB A )(1'-2. 向量组),0,1(),1,1,0(),0,1,1(321k ===ααα线性相关,则_____=k .1-3. 已知2.0)(,8.0)(==AB P A P ,则=-)(B A P 6.0.4. 已知随机变量⎥⎦⎤⎢⎣⎡-5.01.01.03.05201~X ,那么=)(X E 4.2.5. 设1021,,,x x x 是来自正态总体)4,(μN 的一个样本,则~101101∑=i ix )104,(μN . 1. 设B A ,均为3阶矩阵,且3==B A ,则=--12AB 8-.2.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=070040111A ,则_________________)(=A r .2 3. 设A B C ,,是三个事件,那么A 发生,但C B ,至少有一个不发生的事件表示为)(C B A +.4. 设随机变量)15.0,100(~B X ,则=)(X E 15.5. 设n x x x ,,,21 是来自正态总体N (,)μσ2的一个样本,∑==ni ix n x 11,则=)(x D n2σ.三、计算题1. 已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=244213001,543322011B A ,证明B A -可逆,并求1)(--B A . 解: ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=-301111010B A , 因为023111301111010≠=---=--=-B A ,所以B A - 可逆 且⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡--=--212121001212323)(1B A 2. 设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=423532211A ,求(1)A ,(2)1-A .解: (1)1100110211210110211423532211=---=---=---=A (2)利用初等行变换得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---103210012110001211100423010532001211 →-----⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥→-----⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥112100011210001511112100011210001511→------⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥→-----⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥110922010721001511100201010721001511即 A -=-----⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥121721511 3. 设矩阵A B =--⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥101011111122212221,,求A -1及A BA -1.解: 利用初等行变换得101100011010111001101100011010012101--⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥→-⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥ →⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥→⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥10110001101000311110110011010001131313 →--⎡⎣⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥→----⎡⎣⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥101100010132313001131313100231313010132313001131313 即 A -=----⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥1132******** 由矩阵乘法得A BA -=----⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥--⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥1132111211111222122211010111114. 已知B AX X +=,其中02323347,5858901A B --⎡⎤⎡⎤⎢⎥⎢⎥=---=⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦,求X . 解:由方程B AX X +=,得()I A X B -=,且1233575810I A ⎡⎤⎢⎥-=⎢⎥⎢⎥⎣⎦利用初等行变换得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1055200132100013211001085010753001321 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---→121100255010364021121100013210001321 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----→121100255010146001 即 1()I A --=641552121--⎡⎤⎢⎥-⎢⎥⎢⎥--⎣⎦ 由矩阵乘法得164123813()55258152312101812X I A B ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-=-=--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦5. 设矩阵11512112353181913978A --⎡⎤⎢⎥-⎢⎥=⎢⎥-⎢⎥-⎣⎦,求矩阵A 的秩. 解:用初等行变换将矩阵化为阶梯形⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----→⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----68144034720347202151187931918135321121511 11512027430000000000--⎡⎤⎢⎥-⎢⎥→⎢⎥⎢⎥⎣⎦ 由此可知矩阵的秩为2.6. 求向量组[]11,3,2,1,1α=---,[]23,8,4,1,0α=---,[]32,1,4,2,1α=--,[]41,2,6,1,2α=---的秩,并求该向量组的一个极大无关组.解:将向量组组成的矩阵化为阶梯形1321138410214211261213211012230580305803-----------⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥→--------⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥1321101223002101200000---⎡⎤⎢⎥-⎢⎥→⎢⎥-⎢⎥⎣⎦ 由此可知该向量组的秩为3,且321,,ααα是一个极大无关组.7. 分别说明当a b ,取何值时,线性方程组x x x x x x x x x x x x x x x ax b12341234123412343127224321248-+-=-+-+=--++=-++=⎧⎨⎪⎪⎩⎪⎪无解、有唯一解、有无穷多解.在有无穷多解的情况下求出一般解. 解: 将方程组的增广矩阵化为阶梯形13111272121432124813111010100123002622-------⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥→----+-⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥a b a b →---+-⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥→-----⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥1311101010*******64213111010100022000022a b a b …当a b =≠22,时,方程组无解。
2021自考本科工程数学(线性代数、复变函数)习题习题

2021自考本科工程数学(线性代数、复变函数)习题一、单项选择题1.设行列式n a a a a a a a a a =333231232221131211,则=2-3+2-3+2-3+333233312322232113121311a a a a a a a a a a a a ( ) A. n 2- B. n 6 C. n 6-D. n 22.设矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛=1021400204022001A ,则()TA r =( ) A.1B.2C. 3D. 43.设矩阵333332⨯⨯⨯C B A 、、,下列哪一个运算是可行的( )A. BAB. ()B C A +C. TBCAD.BCA4.设A 和B 均为n 阶方阵,则下列结论成立的是( )A.0≠A 且0≠B 0≠⇔ABB. 00=⇔=A AC.00=⇔=A AB 或0=B D .E A A =⇔=15.设向量组1α,2α,3α线性无关,1α,2α,4α线性相关,则( )A.1α必可由2α,3α,4α线性表示B.1α必不可由2α,3α,4α线性表示C.4α必可由1α,2α,3α线性表示D.4α必不可由1α,2α,3α线性表示6.下列复数中,位于第二象限的复数是( )A.ii+12 B.ii -12 C.i+12 D.i-12 7.0z =是函数()z z f cos 1-=的( )A .一级零点B .二级零点C .一级极点D .二级极点8.设函数()f z 在区域D 内解析,且()z f 为实常数,则()f z 在区域D 必为( )A. zB.0C. 常数D.ze9.设()12+=⋅z e z f iz ,则[]Res (),f z i =( )A.i e i --2B.0C.121--e D.12--e i 10.满足11+=-z z 的点z 所组成的点集为( ) A.()0Im =z B.()0Re =z C.()0Im >zD.()0Re >z11.求排列32514的逆序数( ).A. 1B. 3C. 5D. 7 12.B A 、为n 阶方阵,则下列各式中成立的是( ).A.22A A =B.()()B A B A B A -+=-22C. ()AB A A B A -=-2D. ()T T TB A AB =13.21321ββααα,,,,都是四维列向量,则四阶行列式,1321m =βααα,,,,2321n =βααα,,,则行列式=-21321ββααα,,,( ).A. n m +B. n m -C. n m +-D.n m --14.线性方程组⎩⎨⎧=+=+012121x x x x ( ).A.无解B. 只有0解C.有唯一解 D .有无穷多解15.若向量组⎪⎪⎪⎭⎫ ⎝⎛=0011α,⎪⎪⎪⎭⎫ ⎝⎛=0112α,⎪⎪⎪⎭⎫ ⎝⎛=c b a 3α线性无关,则有( ).A.c b a ==B.0==c bC.0=cD.0≠c16.=-+ii23( ) A.i +1 B.i +2 C.i 32+D.i -117.()1-Ln 为( )A. 无定义B.0C.i πD.()i k π12+ (k 为整数)18.0z =是函数()4cos 1z zz f -=的( ) A .一级零点 B .二级零点C .一级极点D .二级极点19.设()122+=z z z f ,则[]Res (),f z i =( )A.2i - B.0 C.21 D.2i 20.满足232=-+i z 的点z 所组成的点集为( )A. 圆周B.直线C.双曲线D. 椭圆21.已知R k d c b a ∈,,,,,则以下等式正确的是( ).A.⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫⎝⎛d c b a k d kc b ka B.dc ba kkd kc kb ka = C.⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫⎝⎛++d c b a d cd b c a D.abcd dc b a = 22.设B A 、为n 阶方阵,则必有(). A.B A B A +=+ B.BA AB = C. BA AB =D. 22B A=23.设A 为n 阶方阵,且0=A ,则().A. A 中两行(列)对应元素成比例B.A 中任意一行为其它行的线性组合C. A 中至少有一行元素为零D. A 中必有一行为其它行的线性组合24.设21ββ,是b Ax =的两个不同的解,21αα,是0=Ax 的基础解系,21k k 与为任意常数,则b Ax =的通解是(). A.()()212121121ββααα++-+k k B.()()212121121ββααα-+++k k C.()()212121121ββββα-+++k k D. ()()212121121ββββα++-+k k 25.下列矩阵为初等矩阵的是( ).A.⎪⎪⎪⎭⎫ ⎝⎛002010100B.⎪⎪⎪⎭⎫ ⎝⎛-010100001 C.⎪⎪⎪⎪⎭⎫ ⎝⎛-1000210001 D. ⎪⎪⎪⎭⎫ ⎝⎛100020001 26.设i z 21+=,则()=2Re z ()A.1B.3C. 1-D.3- 27.()i Ln +1的主值是( ) A.i 42ln 21π+ B.i 42ln 21π- C.i 432ln 21π+ D. i 432ln 21π-28.以0z =是函数()2cos 1z zz f -=的( ) A .一级零点B .可去奇点C .本性奇点D .二级极点29.设()z z z f tan =,则()[]=0,s Re z f ( )A.2B.iC.1D. 0 30.满足1221<-<i z 的点z 所组成的点集为( ) A. 圆周 B.圆环 C.双曲线D. 椭圆31.若622211211=a a a a ,则12020221221112--a a a a 的值是(). A. 12 B. -12 C. 18 D.032.设A 是n m ⨯矩阵,B 是m n ⨯矩阵(n m ≠),则下列运算结果是m 阶方阵的是().A. ABB. TTB A C. BA D. ()TB A +33.21321ββααα,,,,都是四维列向量,则四阶行列式,1321m =βααα,,,,2321n =ααβα,,,则行列式=+21321ββααα,,,( ).A. n m +B. n m -C. n m +-D.n m -- 34.设A 为n 阶方阵,如果()1-=n A r ,则齐次线性方程组0=Ax 的基础解系所含向量的个数是().A. 0B.1C. 2D.n 35.下列矩阵中,是初等矩阵的是( ).A.⎪⎪⎭⎫⎝⎛0001 B.⎪⎪⎪⎭⎫ ⎝⎛101010001 C.⎪⎪⎪⎭⎫ ⎝⎛--100101110 D. ⎪⎪⎪⎭⎫⎝⎛001300010 36.=-=2,22z i z ()A.i 8B.i 88-C.i 8-D. i 88+ 37.设i y y ax xy x z f )(3)(3223-+-=在复平面上解析,则=a () A.3- B.1 C.2 D. 3 38.以0z =为本性奇点的函数( )A .z zsin B .()11-z zC .2cos 1z z- D .z1sin39.设()zz z z f 212-+=,则()[]=0,s Re z f ( )A.21B.iC.21-D. 040.满足)Im()Re(z z =的点z 所组成的点集为( ) A.圆周 B.椭圆 C.双曲线D.直线41.设行列式2333231232221131211=a a a a a a a a a ,则=------332332223121333231131211333a a a a a a a a a a a a ( ). A. -6 B. -3C. 3D. 6 42.设方阵C B A 、、满足AC AB =,当A 满足( )时,C B =.A. BA AB =B. 0≠AC. 方程组0=AX 有非零解D.C B 、可逆 43.n 阶方阵A 可逆的充分必要条件().A. ()n r A r <=B. A 列秩为nC. A 的每一个行向量都是非零向量D. A 的伴随矩阵存在44.设b Ax =是非齐次线性方程组,21αα,是其任意2个解,则下列结论错误的是( ).A. 21αα+是0=Ax 的一个解B.212121αα+是b Ax =的一个解 C. 21αα-是0=Ax 的一个解 D.212αα-是b Ax =的一个解45.设矩阵⎪⎪⎭⎫ ⎝⎛=22211211a a a a A ,⎪⎪⎭⎫ ⎝⎛++=121112221121a a a a a a B ,⎪⎪⎭⎫⎝⎛=01101P ,⎪⎪⎭⎫ ⎝⎛=11012P ,则必有().A.B A P P =21B.B A P P =12C.B P AP =21D. B P AP =12 46.设复数i z i z 64,2221-=-=,则=+21z z ().A. i 24+-B. i 86+C.i 42+D.i 86-47.若()),(,)(y x iv y x u z f +=在复平面上解析,()x y x y x u +-=22,,则()=y x v ,().A. y x 22+B. y xy +2C.x xy +D.y x +48. 以0z =是函数()zz z f )1ln(+=的( ) A .一级零点B .可去奇点C .本性奇点D .二级极点49.设()12-=z ze z f z,则()[]=-1,s Re z f ( )A.21 B.21-C.e 21D. e 21-50.满足522=++-z z 所表示的区域是( ). A. 圆周 B.双曲线C.椭圆D. 直线51.=0001001001001000( ). A. 0 B. -1 C. 1 D. 2 52.设B A 、为n 阶方阵,22B A =,则下列各式成立的是( ).A. B A =B. B A -=C.BA = D.22BA =53. 设n 阶方阵A 不可逆,则必有( ).A. ()n A r <B. ()1-=n A rC. 0=AD. 方程组0=AX 只有零解 54.设21ββ,是非齐次线性方程组b Ax =的两个解向量,则下列像两种仍为该方程组解的是( ).A. 21ββ+B.()21341ββ+ C.()21221ββ+ D. 21ββ- 55.下列矩阵是正交矩阵的是( ).A. ⎪⎪⎪⎭⎫ ⎝⎛--100010001B. ⎪⎪⎪⎭⎫⎝⎛11001110121 C. ⎪⎪⎭⎫⎝⎛--θθθθcos sin sin cos D. ⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--336102233660336122 56.i 是虚数单位,则复数=+ii22( ) A. i 5452+- B.i 5452+ C.i 5452- D.i 5452--57.()i Ln -的主值是( ) A.ik π⎪⎭⎫⎝⎛-212B.i π21-C.i k π⎪⎭⎫ ⎝⎛+212 D. i π21 58.以0z =是函数()()112-=z e z z f 的( )A .一级零点B .本性奇点C .三级极点D .二级极点59.设()14-=z zz f ,则()[]=-1,s Re z f ( ) A.e 41-B.41-C.e 41D. 4160.对于映射zi =ω,圆周()1122=-+y x 的曲线是( ) A. 圆周B.双曲线C.椭圆D. 直线61.若已知m a a a a =22211211,n a a a a =23211311,则行列式23222113121122a a a a a a--的值为( )A. n m 2+B. )2(n m +-C. n m 2-D. n m 4- 62.设n 阶方阵A 满足02=A ,则必有( )A. E A +不可逆B. E A -可逆C. A 可逆D. 0=A63.下列等式中正确的是( )A. 222)(B BA AB A B A +++=+ B. TTTB A AB =)( C. 22))((B A B A B A -=+- D. ()A A A A 332-=-64.设矩阵⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=100001010,,333111222333222111P c b a c b a c b a B c b a c b a c b a A ,则必有( )A. B PA =B. B A P =2C .B AP =D .B AP =265.设21,ββ是非齐次线性方程组b Ax =的两个解,则下列向量为方程组解的是( )A. 21ββ+B. 21ββ-C.2221ββ+D.52321ββ+ 66.设222iz -=,则z 的幅角主值为( ) A. 43π-B.43πC.4π D. 4π-67.下列函数中,以0=z 为一级极点的函数是( )A.)1(sin +z z zB.)1(1-z e zC. 3)1(2-z zD. )2sin(-z z68. 方程13z -=所表示的图形是( )A .圆B .椭圆C .线段D .双曲线69.下列函数中,在其定义域上不是调和函数的是 ( )A .22x y - B. 323y x y - C. cos xe yD. x ye-70. 若级数((1))nn n c z i ∞=-+∑在点0z =处收敛, 则该级数( )A .一定在1z =处发散B .一定在z i =处收敛C .一定在3z =处收敛D .一定在3z i =处发散71.若已知m b b a a =2121,n c c b b =2121,则行列式221121c a c a b b --的值为( )A. n m +B. n m -C. n m --D. m n -72.设n 阶方阵A 可逆,且其伴随矩阵*A 也是可逆的,则*A 的逆矩阵( )A.AA B.AA C. AD. A A73.下列等式中正确的是( )A. 222)(B A AB ⋅=B. TT T B A AB =)( C. BA AB = D. BA AB =74.已知n 元线性方程组0=AX ,其系数矩阵A 的秩为n r <,则下列说法正确的是( )A. 该方程组只有零解B. 该方程组有r 个线性无关的解 C .该方程组有r n -个线性无关的解D .该方程组有r n -个解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013 级工程数学(本科)复习题
4 1. 求行列式 D= 3 0 1 1 2 2 3 2 3 0 5 0 1 0 0 3 2 1 1 0 ,的秩,极大 1 4 3 −3 −1 2
2. 求向量组������1 =
1 1 2 ,������2= 2 1
−1
多解,并在无穷多解时求出通解; 5. 一袋麦种其中一等麦种占 80%,二等占 18%,三等占 2%,一等发芽率 为 0.8,二等发芽率为 0.5,三等发芽率为 0.2,现从袋中任取一粒,求 (1)此粒发芽的概率; (2)若已知此粒未发芽,求它是一等麦种的概 率。 0, ������ < −1 6. 连续随机变量 X 的分布函数 F ������ = ������ + ������������������������������������������ ������ , − 1 < x < 1, 1, ������ ≥ 1 (1)求常数 A,B; (2)求密度函数; (3)求 P(|X|<0.5) ������ 1 − ������ 2 , −1 < ������ < 1 7. 随机变量 X 的密度函数为 x = (1) 求常数 C; 0, 其他 (2)求分布函数; (3)求期望 Ex 8. 连续随机变量 X-U(0,5),求4������ 2 + 4������������ + ������ + 2 = 0有实根的概率
无关组 0 −2 2 3. 求正交矩阵Ρ ,使得Ρ AΡ 为对角矩阵其中 A= −2 −3 4 2 4 −3 2������1 + ������������2 − ������3 = 1 4. λ 为何值时,方程组 ������������1 − ������2 + ������3 = 2 有唯一解,无解,有无穷 4������1 + 5������2 − 5������3 = −1
复习提纲: 1. 行列式的计算,Laplace 展式 2. 矩阵的运算,逆矩阵,方阵的行列式,矩阵的秩 3. 线性方程组解的判别,解的求法(齐次和非齐次) 4. 向量组线性相关、无关的判别,向量组的秩 5. 特征值,特征向量的求取 scbmidt 正交化,矩阵对角化 6. 二次型的矩阵,正定矩阵的判别 7. 事件的运算,全概率公式,逆概率公式 8. 随机变量分布函数性质,离散随机变量分布律性质,连续随 机变量函数性质,均匀分布,正态分布 9. 随机变量联合分布函数性质,联合密度函数性质 10. 期望,方差的性质和计算,均匀分布,正态分布的期望和 方差
