由三视图还原成实物图
由三视图还原成实物图

由三视图还原成实物图
难点
由三视图还原成实物图
教法
学
法
教具
个人主页
教
学
过
程
一.知识回顾
回顾上节课知识内容—引出课题
二.研探新知
(一)本课学习目标解读
>学会由三视图还原成实物图.
>体验学习过程,提高自己的想象能力.
(二)自主学习点评
>练习册学案“预习自查”.
>活页学案“自主学习”部分.
1.下面给出的三视图表示的几何体是( )
富县高级中学高一年级数学科目集体备课教案
中心发言人:白治军授课人:
课题
§3.2由三视图还原成实物图
第课时
三
维
目
标
知识与技能
掌握由三视图还原成实物图的方法.
过程与方法
培养学生的空间概念,提高学生空间想象力,掌握画三视图的基本技能.
情感态度与价值观
认识到数学是解决实际问题和进行交流的重要工具,了解数学对促进社会进步的人类理性思考的作用,培养学生热爱数学的情感.
A、圆锥B、正三棱柱C、正三棱锥D、圆柱
2.一个几何体的三视图如下图所示,这个几何体是( )
A、球B、圆柱C、长方体D、圆锥
3.如图是一个几何体的三视图,则这个几何体是( )
A、圆锥B、圆柱C、长方体D、球体
(三)课堂互动探究
课本例6、例7
三.本课小结
四.课堂训练
五.布置作业与练习
教后反思
备课组长签字:
2012年月日
由三视图还原成实物图教学设计

《由三视图还原成实物图》教学设计一.教学理念设计新课程下教学的基本理念是倡导合作探究性学习,培养学生的创新精神和实践能力,更加贴近素质教育,更加人性化、信息化、多元化。
根据这一理念,本节是以实际问题的出现通过自主探究的方式掌握数学知识,以交流合作的模式发展数学能力,以理论是为实践服务的宗旨解决实际问题,最后升华为培养数学精神为理念。
“学起于思,思源于疑”。
学生有了疑问才会去进一步思考问题,才会有所发展,有所创造,二.教材分析本节是北师大版必修2第1章第3节的教学内容.在学完组合体的三视图后,教材从逆向思维的角度给出了本节内容.这两节内容的有机结合,使学生认图,识图的空间想象能力有了一定的提高, 为后面立体几何的学习做了一个很好的铺垫.同时它也是许多知识的载体,如计算几何体的体积或面积等。
从我们的教学经验可知:该节内容在整个立体几何中起到了承上启下的巨大作用,三.学情分析三视图是教材新增内容,在高考中一般总与几何体的体积(或面积)相结合来命题.但由于学生目前还没有学几何体的体积(或面积)内容,因此本节的教学只局限于如何由三视图还原成实物图. 但由于高一学生刚刚接触到立体几何,而立体几何则要求学生要有较强的空间想象能力,因此初学起来具有一定的难度,为了突破这个“瓶颈”,本节课特采用多媒体辅助教学,这既能充分发挥学生主观能动性,又能达到预期的教学目的.四.教学目标1. 知识目标①了解由实物图到三视图与由三视图还原成实物图之间的关系②掌握由三视图还原成实物图的方2. 教学重、难点教学重点:由三视图如何还原成实物图及其方法教学难点:复杂的组合体如何由三视图还原成实物图.3.能力目标①提高学生的空间想象能力和对所学知识的整合能力.②培养学生的动手动脑的习惯,培养学生的团队合作精神五.情感、态度与价值观通过师生共同探究,体会数学知识的形成过程,培养学生的空间想象能力,培养学生的团队合作精神,自觉养成动手、动脑及勤学严谨的良好学习习惯.六.教学方法探究式与启发式相结合.充分体现学生的主体地位和教师的主导作用七.授课类型:新授课( 1课时)八.教学过程设计一.教学程序与环节设计从教材的【思考交流】(奖杯的形状)引入新通过师生双边互动来组织课堂教学二.教学过程1.复习旧课此环节为两个部分:一部分是复习知识点,另一部分是一个及时巩固练习题设计的意图是:复习知识点是温故知新.加个习题一是为了及时巩固二是为了照顾基础弱的同学教学方法是:教师设问,学生齐答的形式.后再用多媒体给出答案2 课题提出为了表彰我校篮球赛中表现优秀的班级,学生会设计了一个如下图所示“大力神”奖杯.假设你是一个工艺加工店的老板, 你能生产出这种奖杯吗?这是教材上的一个素材.引用意图是:从实际问题出发激发学生的学习兴趣,同时也根据更好的处理了教材.3 例题讲解例题1下面是一些立体图形的三视图,请根据视图说出立体图形的名称.例题1由两个小题组成.此两题是基础题.设计意图是从基础入手,树立学生的信心.教学方法是:学生稍思考后提问例题2:根据三视图想像物体原形,并画出物体的实物草图?此题是个简单组合体的三视图.比上题稍难.设计意图是满足学生的挑战心教学方法是:师生共同探讨后得出结果.体现师生互动变式训练 根据三视图想像物体原形,并画出物体的实物草图此题与例2很相似,但不完全一样.设计意图:一是及时课堂反馈,二是锻炼学生的观察能力和类比能力.三是培养学生的语言表达能力和胆识.教学方法是:学生独立思考后提问,再让学生自己为同伴判断正误.针对学生的疑问再适当点评.体现学生是主体,老师是主导的教学理念.把课堂推向一个小高潮例题3:图1—33是4个三视图和4个实物图,请将三视图与实物图正确配对此例题为课本的例6.设计意图是:处理教材,利用好教材初步涉及到几何体的切和挖.教学方法是:把学生分成四组,每组派个同学来回答,后交互评价.这可以培养学生的团队合作精神,也可以再次推动课堂学习气氛.例题4根据三视图想像物体原形,并画出物体的实物草图此题也是课本上的例题.但和上题的区别在于现在要画出几何体.比上题要设计意图是锻炼学生的动手能力,培养学生的空间想象能力.教学方法是图1由学生独立思考完成,图2在教师的点评基础完成变式训练请由三视图画出实物图,此两题是中等题.难度大些.一个是组合体,一个是几何体的切与挖.设计意图是进一步由三视图还原成实物图该知识点,扩大学生的视野教学方法是,教师一边巡视,一边检查学生实际情况并以指导最后用动画演示验证.思维拓展已知一几何体的三视图如左图,主视图和左视图都是矩形,俯视图为正方形,在该几何体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是_________(写出所有正确结论的编号).①矩形;②不是矩形的平行四边形;③有三个面为直角三角形,有一个面为等腰三角形的四面体;④每个面都是等腰三角形的四面体;⑤每个面都是直角三角形的四面体.此题是个多选题,难度大,学生可能会做,但不一定选全.设计意图:一是巩固该节所学内容,二是锻炼学生的空间想象和逻辑推理能力,三是为学有余力的同学提供了舞台.教学方法是:小组讨论,多让学生回答.把这节课推向高潮.最后用动画演示各种情况.九. 板书设计十. 教学反思:本节课的主要任务是引导学生完由三视图想象立体图形的复杂过程。
三视图还原几何体的方法
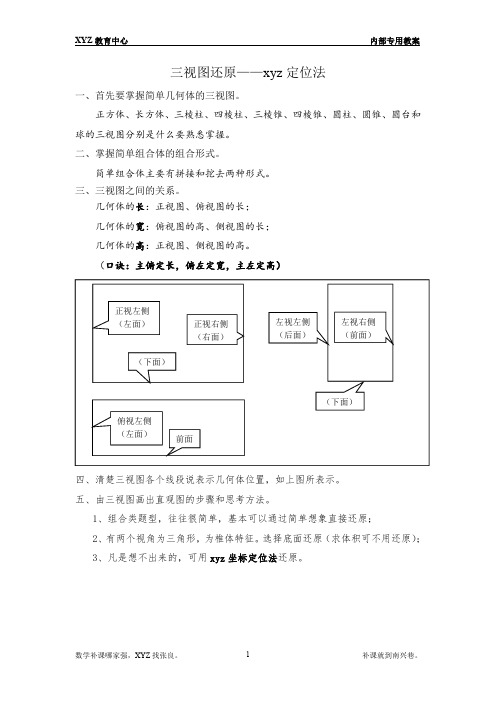
三视图还原——xyz 定位法一、首先要掌握简单几何体的三视图。
正方体、长方体、三棱柱、四棱柱、三棱锥、四棱锥、圆柱、圆锥、圆台和球的三视图分别是什么要熟悉掌握。
二、掌握简单组合体的组合形式。
简单组合体主要有拼接和挖去两种形式。
三、三视图之间的关系。
几何体的长:正视图、俯视图的长;几何体的宽:俯视图的高、侧视图的长;几何体的高:正视图、侧视图的高。
(口诀:主俯定长,俯左定宽,主左定高)(下面)左视左侧(后面)正视左侧(左面)正视右侧(右面)左视右侧(前面)(下面)四、清楚三视图各个线段说表示几何体位置,如上图所表示。
五、由三视图画出直观图的步骤和思考方法。
1、组合类题型,往往很简单,基本可以通过简单想象直接还原;2、有两个视角为三角形,为椎体特征。
选择底面还原(求体积可不用还原);3、凡是想不出来的,可用xyz 坐标定位法还原。
前面俯视左侧(左面)【类型一】:(三线交汇)例2:【类型二】:例3:连接这五个点的四棱锥,不满足俯视图。
而顶点又必须在这五点交点中,所以当点数超过4个,可能不需要全部连接,则这些点有所取舍。
第一法:俯视图看到的面不可以为上面四个点构成的整个四边形,而是中间有一条折痕,故只能说左半边三角形乡下折。
即舍弃前面左上方的点。
故得,第二:唯一法:正视图看,已标记下面的点必不可少;从俯视图看,上面有3个点必不可少;故只能舍弃前面左上方的点。
第三:口诀:实线两端的点保留,虚线两端的点待定。
从俯视图一看,便知道答案了。
取舍关键:墙角点是取舍的备选。
练习【类型三】:(八点齐飞,直观图不唯一)例4此题八点齐飞,通过类型二中的第三取舍法,我们很容易就能还原出来。
答案:然而,我们发现这个三视图也可以看成,是上图中的三棱锥与另外一个三棱锥组合而成。
如下图所示:M为顶点的三棱锥(四种)与上图的组合。
同理,还有其他两种形式,此处就不一一画图了。
由此得出,上题中的三视图至少有5种不同的直观图。
【三视图题目几点技巧】1,部分椎体求体积,直接用公式(可以不还原)2,斜二测画法与原图面积比例为定值(可以不还原)3,三视图中,和视线垂直的线段,长度不变。
高一数学空间几何体的三视图与直观图试题答案及解析
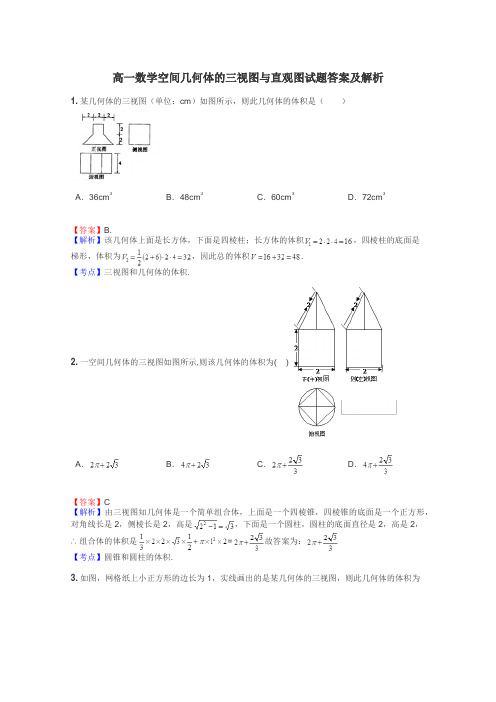
高一数学空间几何体的三视图与直观图试题答案及解析1.某几何体的三视图(单位:cm)如图所示,则此几何体的体积是()A.36cm3B.48cm3C.60cm3D.72cm3【答案】B.【解析】该几何体上面是长方体,下面是四棱柱;长方体的体积,四棱柱的底面是梯形,体积为,因此总的体积.【考点】三视图和几何体的体积.2.一空间几何体的三视图如图所示,则该几何体的体积为( )A.B.C.D.【答案】C【解析】由三视图知几何体是一个简单组合体,上面是一个四棱锥,四棱锥的底面是一个正方形,对角线长是2,侧棱长是2,高是,下面是一个圆柱,圆柱的底面直径是2,高是2,∴组合体的体积是=故答案为:【考点】圆锥和圆柱的体积.3.如图,网格纸上小正方形的边长为1,实线画出的是某几何体的三视图,则此几何体的体积为()A.6B.9C.12D.18【答案】C【解析】该几何体是三棱锥,底面是俯视图,三棱锥的高为4;底面三角形是斜边长为6,高为3的等腰直角三角形,此几何体的体积为.故选C.【考点】三视图与几何体的关系;几何体的体积的求法.4.某向何体的三视图如图所示,则该几何体的体积为()A.B.C.D.【答案】A【解析】由三视图可知,该几何体是一个长方体和一个半圆柱组成的几何体,所以体积为。
【考点】(1)根据三视图确定几何体的构成,(2)圆柱及长方体的体积公式的应用。
5.一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为 .【答案】11【解析】由图可知切去的是直淩柱的一角,先算直棱柱的体积,再算切去部分的体积,所以.【考点】1、立体图形的三视图;2、体积的计算.6.右图中的三个直角三角形是一个体积为的几何体的三视图,则()A.B.C.D.【答案】B【解析】由三视图可知该几何体为三棱锥,其中一侧棱垂直底面,且底面为直角三角形,∴三棱锥的体积为,解得,故选B.【考点】由几何体的三视图求体积.7.已知四棱锥的三视图如图所示,则四棱锥的四个侧面中面积最大的是()A.3B.C.6D.8【答案】C【解析】通过三视图可作出该几何体的直观图,如图所示.其中底面为矩形,面面,且,,.易得,,,故侧面中面积最大值为6.【考点】几何体的三视图与直观图.8.右图是水平放置的的直观图,轴,,则是()A.等边三角形B.等腰三角形C.直角三角形D.等腰直角三角形【答案】C【解析】直观图为斜二测画法,原图的画为,因此原为直角三角形.【考点】斜二测画法.9.如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是()A.B.C.D.【答案】D【解析】主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,本题求的是球和圆柱的表面积.三视图的投影规则是:“主视、俯视长对正;主视、左视高平齐,左视、俯视宽相等”.由三视图可知几何体是半径为1的球和底面半径为1,高为3的圆柱,故其表面积应为球的表面积与圆柱的表面积面积之和减去圆柱一个底面积,即.故选D.【考点】本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用10.如图是一个简单的组合体的直观图与三视图,一个棱长为4的正方体,正上面中心放一个球,且球的一部分嵌入正方体中,则球的半径是()A.B.1C.D.2【答案】B【解析】由已知题中三视图中的俯视图中圆上的点到正方形边长的最小距离为1,已知中的正方体的棱长为4,可得球的半径为1,故选B.【考点】由三视图还原实物图.11.一个几何体的三视图如图所示,则该几何体可以是()A.棱柱B.棱台C.圆柱D.圆台【答案】D【解析】由正视图和左视图可知此几何体为台体,结合俯视图可知此几何体为圆台。
由三视图还原立体图形

下面所给的三视图表示什么几何体?
下面所给的三视图表示什么几何体?
下面所给的三视图表示什么几何体?
这是一个立体图形的三视图,你能说出 它的名称
四棱锥
下列是一个物体的三视图,请描述出它的形状
主视图 左视图 俯视图
三棱锥
小结:1.三视图中有2个长方形的一定是:
柱体 2.三视图中有2个三角形的一定是:
解:物体是五棱柱形状的,如图所示.
练习 由三视图想象实物现状:
实
物
实
物
使用帮助
实
实
物
物
点击文字”实物”,回出现对应的实物
返回页面
合作学习
你能从下面 所给的三视图中推断出它们分别 表示什么几何体吗?
(1)
(2)
(3)
(4)
下面所给的三视图表示什么几何体? 直四棱柱
下面所给的三视图表示什么几何体? 直五棱柱
思考:狗蛋回家,只找到了主视图和俯视图, 仍然可以恢复狗蛋的积木原来的形状吗?如果 不能,那么按照这2个图,对应的立体图形最 少有几个正方体?最多有几个正方体?
主视图
俯视图
最少
最多
方法:从一张视图开始, 从另一张视图研究最少 或最多的情况
由三视图描述几何体(或实物原型), 一般先根据各视图想像从各个方向看到 的几何体形状, 然后综合起来确定几何 体(或实物原型)的形状, 再根据三视图 “长对正、高平齐、宽相等”的关系, 确定轮廓线的位置,以及各个方向的尺 寸.
解:由三视图可知,密封罐的现状是正六棱柱.
密封罐的高为50mm,店面正六边形的直径为100mm,边长为 50mm,图是它的展开图. 由展开图可知,制作一个密封罐所需钢板的面积为
65050 2 6 1 5050sin 60 2
押新高考第16题 空间几何体(新高考)(解析版)

押第16题 空间几何体空间几何体是高考全国卷每年必考知识点,作为客观题考查的空间几何体试题主要涉及三视图、几何体的表面积与体积、截面等内容,难度有容易题也有难度较大的题,求解本类问题的关键是空间想象能力及运算能力,预测2021年依然会有2道立体几何客观题.依然会遵循前几年的命题风格.1.空间几何的结构特征(1)关于空间几何体的结构特征辨析关键是紧扣各种空间几何体的概念,要善于通过举反例对概念进行辨析,即要说明一个命题是错误的,只需举一反例即可.(2)圆柱、圆锥、圆台的有关元素都集中在轴截面上,解题时要注意用好轴截面中各元素的关系.(3)既然棱(圆)台是由棱(圆)锥定义的,所以在解决棱(圆)台问题时,要注意“还台为锥”的解题策略.2.三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图.注意观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.(2)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.(3)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形状,然后再找其剩下部分三视图的可能形状.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.3.用斜二测画法画直观图的技巧(1)在原图形中与x 轴或y 轴平行的线段在直观图中与x ′轴或y ′轴平行,原图中不与坐标轴平行的直线段可以先画出线段的端点再连线,原图中的曲线段可以通过取一些关键点,作出在直观图中的相应点后,用平滑的曲线连接而画出.(2)注意斜二测画法中的“三变”与“三不变”“三变”⎩⎪⎨⎪⎧ 坐标轴的夹角改变与y 轴平行的线段的长度变为原来的一半图形改变“三不变”⎩⎪⎨⎪⎧ 平行性不改变与x ,z 轴平行的线段的长度不改变相对位置不改变4.空间几何体表面积的求法(1)以三视图为载体的几何体的表面积问题,关键是分析三视图确定几何体中各元素之间的位置关系及数量.(2)多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理.(3)旋转体的表面积问题注意其侧面展开图的应用.5.空间几何体体积问题的常见类型及解题策略(1)若所给定的几何体是可直接用公式求解的柱体、锥体或台体,则可直接利用公式进行求解.(2)若所给定的几何体的体积不能直接利用公式得出,则常用转换法、分割法、补形法等方法进行求解.(3)若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,然后根据条件求解.1.(2020年新高考全国卷Ⅰ数学高考试题(山东))已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2,∠BAD =60°.以1D 为球心,5为半径的球面与侧面BCC 1B 1的交线长为________.【答案】22π. 【详解】如图:取11B C 的中点为E ,1BB 的中点为F ,1CC 的中点为G ,因为BAD ∠=60°,直四棱柱1111ABCD A BC D -的棱长均为2,所以△111DB C 为等边三角形,所以1D E 3=111D E B C ⊥,又四棱柱1111ABCD A BC D -为直四棱柱,所以1BB ⊥平面1111D C B A ,所以111BBB C ⊥, 因为1111BB B C B =,所以1D E ⊥侧面11BC CB ,设P 为侧面11BC CB 与球面的交线上的点,则1DE EP ⊥, 因为球的半径为5,13D E =,所以2211||||||532EP D P D E =-=-=, 所以侧面11BC CB 与球面的交线上的点到E 的距离为2,因为||||2EF EG ==,所以侧面11BC CB 与球面的交线是扇形EFG 的弧FG ,因为114B EF C EG π∠=∠=,所以2FEG π∠=,所以根据弧长公式可得2222FG ππ=⨯=. 2.(2020年新高考全国卷Ⅱ数学考试题文档版(海南卷))已知正方体ABCD -A 1B 1C 1D 1的棱长为2,M 、N 分别为BB 1、AB 的中点,则三棱锥A -NMD 1的体积为____________【答案】13【详解】因为正方体ABCD -A 1B 1C 1D 1的棱长为2,M 、N 分别为BB 1、AB 的中点所以11111112323A NMD D AMN V V --==⨯⨯⨯⨯= 3.(2020年浙江省高考数学试卷)已知圆锥的侧面积(单位:2cm ) 为2π,且它的侧面积展开图是一个半圆,则这个圆锥的底面半径(单位:cm )是_______.【答案】1【详解】设圆锥底面半径为r ,母线长为l ,则21222r l r l ππππ⨯⨯=⎧⎪⎨⨯⨯=⨯⨯⨯⎪⎩,解得1,2r l ==. 4.(2020年全国统一高考数学试卷(理科)(新课标Ⅰ))如图,在三棱锥P –ABC 的平面展开图中,AC =1,3AB AD ==,AB ⊥AC ,AB ⊥AD ,∠CAE =30°,则cos ∠FCB =______________.【答案】14-【详解】 AB AC ⊥,3AB =1AC =, 由勾股定理得222BC AB AC =+=, 同理得6BD 6BF BD ∴==在ACE 中,1AC =,3AE AD =30CAE ∠=,由余弦定理得22232cos30132131CE AC AE AC AE =+-⋅=+-⨯=, 1CF CE ∴==,在BCF △中,2BC =,6BF =,1CF =,由余弦定理得2221461cos 22124CF BC BF FCB CF BC +-+-∠===-⋅⨯⨯. 5.(2020年全国统一高考数学试卷(理科)(新课标Ⅲ))已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_________.2 【详解】易知半径最大球为圆锥的内切球,球与圆锥内切时的轴截面如图所示,其中2,3BC AB AC ===,且点M 为BC 边上的中点,设内切圆的圆心为O ,由于223122AM =-=,故1222222S =⨯⨯=△ABC , 设内切圆半径为r ,则: ABC AOB BOC AOC S S S S =++△△△△111222AB r BC r AC r =⨯⨯+⨯⨯+⨯⨯ ()1332222r =⨯++⨯=, 解得:22r ,其体积:34233V r ππ==. 6.(2020年江苏省高考数学试卷)如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm ,高为2 cm ,内孔半径为0.5 cm ,则此六角螺帽毛坯的体积是____cm.【答案】32π【详解】 正六棱柱体积为23622=1234⨯⨯⨯圆柱体积为21()222ππ⋅=所求几何体体积为1232π-1.(2021·山东德州市·高三一模)已知三棱锥P ABC -中,AP 、AB 、AC 三条棱两两垂直,且长度均为23,以顶点P 为球心,4为半径作一个球,则该球面被三棱锥四个表面截得的所有弧长之和为______.【答案】3π【详解】 由题可知:AP 、AB 、AC 三条棱两两垂直,且长度均为23如图:所以()222326PC PB BC ====()224232AM AF ==-=, 所以3tan tan 323APF APM ∠=∠==,则6APF APM π∠=∠= 所以12EPF CPM π∠=∠=,则4123EF MN ππ==⨯=44,2332NE MF ππππ=⨯==⨯= 所以球面被三棱锥四个表面截得的所有弧长之和为42333ππππ⨯++= 2.(2021·山东烟台市·高三一模)已知正三棱锥 P ABC -的底面边长为2,13面,PAB PBC 分别切于点,M N ,则MN 的长度为___________.【答案】56【详解】如图,设正三棱锥内切球的半径为R ,M 为内切球与侧面PAB 的切点,Q 为侧面上切点所在小圆的圆心,半径为r , ABC 为等边三角形,223CD BC BD ∴=-=, 2233CH CD ==,133DH CD ==, 22121051393PH PC CH =-=-=, POM PDH △△, OM PO DH PD ∴=, .3PH R PD -= 13123PB PD ==-=1053323R -=,解得105R = 35sin sin PH OMQ PDH PD ∠=∠==, 35cos sin sin r MQ R OMQ R PMQ R PDH R ∴==∠=∠=∠=由正三棱锥的定义知,内切圆与三个侧面相切,切点构成的三角形为等边三角形,故120QMN ∠=︒,由余弦定理可得22222355252cos12033362136MN r r r r =+-︒==⨯⨯=, 所以56MN = 3.(2021·山东济宁市·高三一模)在长方体1111ABCD A BC D -中,3AB =,14A D A A ==,E ,F ,G 分别是棱AB ,BC ,1CC 的中点,P 是底面ABCD 内一动点,若直线1D P 与平面EFG 平行,当三角形1BB P 的面积最小时,三棱锥1A BB P -的外接球的体积是______.【答案】125π6【详解】补全截面EFG 为截面1EFGHQR 如图,设BR AC ⊥,直线1D P 与平面EFG 不存在公共点,1//D P ∴平面1EFGHQR ,易知平面1//ACD 平面1EFGHQR ,P AC ∴∈,且当P 与R 重合时,BP BR =最短,此时1PBB 的面积最小,由等面积法得1122BR AC AB BC ⨯=⨯,即2211343422BR ⨯+=⨯⨯,125BP ∴=, 1B B AP ⊥,BP AP ⊥,AP ∴⊥平面1B BP ,则1AP B P ⊥,又1AB B B ⊥,1AB ∴为三棱锥1A BB P -的外接球的直径,长度为22345+=.∴三棱锥1A BB P -的外接球的半径为52,体积为35125π2643V π⎛⎫= ⎪⎝⎭=⨯. 故答案为:125π6.4.(2020·山东高三其他模拟)将一个斜边长为4的等腰直角三角形以其一直角边所在直线为旋转轴旋转一周,所得几何体的表面积为_________. 【答案】(882)π+ 【详解】因为等腰直角三角形的斜边长为4,所以直角边长为22,由题意可知所得几何体是圆锥,其底面圆的半径22r =,母线长4l, 则其表面积为()2882r rl πππ+=+.5.(2020·山东高三专题练习)已知正方体棱长为2,以正方体的一个顶点为球心,以22为半径作球面,则该球面被正方体表面所截得的所有的弧长和为______________.【答案】3π【详解】如图所示,球面被正方体表面所截得3段相等的弧长,与上底面截得的弧长,是以1D 为圆心,以2为半径的四分之一的圆周,所以11111224A C AB BC ππ===⨯⨯= , 则所有弧长和为3π(限时:30分钟)1.如图,在矩形ABCD 中,22AB BC ==,22AB BC ==.将A ,C 分别沿BE ,DF 向上翻折至A ',C ',则A C ''取最小值时,二面角A EF C ''--的正切值是________.【答案】26 【详解】 分别取BE ,DF 中点为M 、N ,连接A M ',MF ,C N ',NE .四边形ABCD 为矩形,22AB BC ==,1AE CF ==,∴翻折前,四边形ABFE 和四边形CDEF 都是正方形,则1EF =,CE DF ∴⊥,AF BE ⊥,即NE DF ⊥,CN DF ⊥,AM BE ⊥,MF BE ⊥, ∴翻折后仍有A M BE '⊥,C N DF '⊥,NE DF ⊥,MF BE ⊥,又A M MF M '⋂=,且A M ',MF ⊂平面A MF ',BE ∴⊥平面A MF '; 同理可得:DF ⊥平面C NE ',又//DE BF ,且1DE BF ==,∴四边形BFDE 是平行四边形,则//BE DF , BE ∴、DF 都是平面A MF '与平面C NE '的公垂线,,BE DF ⊂平面BFDE , ∴平面A MF '⊥平面BFDE ,平面C NE '⊥平面BFDE .分别记1A ,1C 为点A ',C '在底面的投影,则点A '在底面的投影1A 落在直线MF 上,且沿MF 方向运动;点C '在底面的投影1C 落在直线NE 上,且沿NE 方向运动.当且仅当A C ''为平面A MF '与平面C NE '的公垂线段时长度最小,此时//A C ME '',故//A C ''平面MFNE ,则11A A C C ''=.又11//A A C C '',A '∴,1A ,1C ,C '共面,平面11A ACC ''⋂平面11MFNE AC =,11AC 也是平面A MF '与平面C NE '的公垂线,此时11Rt A A M Rt C C N ''≌,11MA NC ∴=,又11//AC ME ,11//MA EC ,∴四边形11MACE 为平行四边形, ∴11MA EC =,∴1C 为NE 的中点,1A 为MF 的中点,1124MA NC ∴==, 则11A A C C ''==126216-=,62216162A F C E ''∴==+=, 将二面角A EF C ''--单独画出如图.过点A '作AP EF '⊥于点P ,过点C '作E C Q F '⊥于点Q ,又1A E AE '==,1C F CF '==, 222122cos 24222A F EF A E A FE A F EF ''+-'∴∠==='⋅⨯, 则1cos 4FP A F A FE ''=∠=,117216A P '∴=-= 同理14EQ =,7C Q '=1141314FP FQ ==-, 过点P 作//PG C Q '交FC '于点G ,连接A G ',则GP EF ⊥,∴A PG '∠即为二面角A EF C ''--的平面角,则13FG PG FC QC =='',∴7PG=,13 FG=,又2A F A C'''==,1C F'=,则A FC''为等腰直角三角形,∴2cos A FC''∠=,2211212102cos45229232A F FG A F FGA G''=+-⋅⋅︒=+-⨯⨯⨯='∴,在A PG'中,22277103051614436144cos72777224A P PG A GA PGA P PG+-''+-'∠===='⋅⨯⨯,26tan A PG'∴∠=.2.如图,二面角A BD C--的平面角的大小为120︒,120BDA∠=︒,150BDC=∠︒,2AD BD==,3CD=,则四面体ABCD的外接球表面积为________.【答案】116π【详解】在BDA中,120BDA∠=︒,2AD BD==,所以222+cos23ADAB AD BD DBD B A-⋅∠=⋅设BDA的外接圆的半径为1r,则124sinABrBDA==∠,所以12r=,在BDC中,150BDC=∠︒,2BD=,3CD=222+cos13CDBC CD BD DBD B C-⋅∠=⋅,设BDC的外接圆的半径为2r,则22213sinBCrBDC==∠113r=又作12,OG BD O G BD⊥⊥,所以12O GO∠为二面角A BD C--的平面角,即12120OGO∠=,所以2211132O G r BD⎛⎫=-=⎪⎝⎭22221232O G r BD⎛⎫=-=⎪⎝⎭()()221223233+23cos12021O O -⨯==⨯,设四面体ABCD 的外接球的球心为O ,球半径为R ,则121227sin O O OG O MO ==∠, 所以2229R OG GD =+=,所以四面体ABCD 的外接球表面积为24429116R πππ=⨯=, 故答案为:116π.3.蹴鞠,又名“蹴球”“蹴圆”等,“蹴”有用脚蹴、踢的含义,鞠最早系外包皮革、内饰米糠的球,如图所示.因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动,类似今日的足球.现已知某“鞠”的表面上有四个点A ,B ,C ,D 满足10cm AB BC CD DA DB =====,15cm AC =,则该“鞠”的表面积为___________2cm .【答案】7003π 【详解】由已知得ABD △,CBD 均为等边三角形.如图所示,设球心为O ,BCD △的中心为O ',取BD 的中点F ,连接,,,,AF CF OO OB O B '',则AF BD ⊥,CF BD ⊥,得BD ⊥平面AFC , 且可求得53cm AF CF ==, 而15cm AC =,所以120AFC ∠=︒.在平面AFC 中过点A 作CF 的垂线,与CF 的延长线交于点E ,由BD ⊥平面AFC ,得BD AE ⊥,故AE ⊥平面BCD ,过点O 作OG AE ⊥于点G ,则四边形O EGO '是矩形,则()2103sin 60cm 3O B BC ︒'=⨯=,()153cm 2O F O B ''==, ()15sin 60cm 2AE AF =︒=,53sin 30EF AF =︒=. 设球的半径为R ,OO x '=,则由222OO O B OB ''+=,222OA AG GO =+,得221003x R +=,2225353152x R ⎛⎫⎛⎫++-= ⎪ ⎪ ⎪⎝⎭⎝⎭, 解得5cm x =,2175cm 3R = 故三棱锥A BCD -外接球的表面积()227004cm 3S R ππ== 4.如图,正方体ABCD ﹣A 1B 1C 1D 1的顶点C 在平面α上,若A 1B 和A 1D 与平面α都成60°角,则A 1C 与平面α所成角的余弦值为______.【答案】13【详解】设直线l 过点A 1且垂直于α,则A 1B 与A 1D 都与直线l 夹角为30°,连结BD ,由题意得△A 1BD 是等边三角形,取BD 中点E ,由题意得A 1E 可以承担直线l 的角色,但同时与直线A 1B 、A 1D 夹角为相等的直线,最小也要30°,∴此时直线l 是唯一的,由题意知A 1C 与直线l (直线A 1E )的余弦值恰为A 1C 与平面α所成角的正弦,设正方体ABCD ﹣A 1B 1C 1D 1的棱长为2,则A 1C =222222++=23,CE =221222+=2,A 1E =22(22)(2)-=6, ∴设A 1C 与平面α所成角为θ,则sin θ=22211112AC A E CE AC A E +-⨯⨯=2236⨯⨯=223, ∴A 1C 与平面α所成角的余弦值为:cos θ=2221()3-=13. 故答案为:13.5.如图,在棱长为1的正方体ABCD ﹣A 1B 1C 1D 1中,点M 是AD 的中点,动点P 在底面正方形ABCD 内(不包括边界),若B 1P //平面A 1BM ,则C 1P 长度的取值范围是____.【答案】30[,2) 【详解】 取BC 中点N ,连结B 1D,B 1N ,DN ,作CO ⊥DN ,连结C 1O ,因为平面B 1DN ∥平面A 1BM ,所以点P 在底面ABCD 内的轨迹是线段DN (动点P 在底面正方形ABCD 内,不包括边界,故不含点N 和点D ),在1C DN △中,2211152,1()2C D DN C N ===+=, 所以12215262()()222C DN S =⨯⨯-=, 过C 1O ⊥DN ,则当P 与O 重合时,C 1P 长度取最小值,所以C 1P 长度的最小值为1630415C O ==⨯, 当P 与D 重合时,C 1P 长度取最大值,∴C 1P 长度的最大值为C 1D =2,∵P 与D 不重合,∴C 1P 长度的取值范围是30[,2). 故答案为:30[,2) .6.鲁班锁是中国传统的智力玩具,起源于中国古代建筑中首创的榫卯结构,它的外观是如图所示的十字立方体,其上下、左右、前后完全对称,六根完全一样的正四棱柱体分成三组,经90榫卯起来.若正四棱柱的高为6,底面正方形的边长为1,现将该鲁班锁放进一个球形容器(容器壁的厚度忽略不计),则该球形容器表面积的最小值为_____.【答案】41π【详解】由题意,该球形容器的半径的最小值为并在一起的两个长方体体对角线的一半, 即为14136412⨯++=, ∴该球形容器体积的最小值为:4241()412ππ⨯=. 7.在三棱锥D ABC -中,ABC 是以A ∠为直角的等腰直角三角形,DBC △是边长为2的等边三角形,二面角A BC D --的余弦值为6-,则三棱锥D ABC -的外接球的表面积为______. 【答案】8π【详解】如图,设BC 的中点为E ,过点E 作平面ABC 的法线EO ,过BCD △的重心F 作平面DBC 的法线FO ,EO 与FO 交于点O ,则O 为三棱锥D ABC -的外接球的球心.又133EF DE==,6cosDEA∠=-,所以3cos FEO∠=.又3cosEFFEOOE∠==,所以1OE=,故外接球的半径为2,所以球的表面积为8π.8.已知球O的半径为10,以球心O为中心的正四面体Γ的各条棱均在球O的外部,若球O的球面被Γ的四个面截得的曲线的长度之和为8π,则正四面体Γ的体积为_________.【答案】182【详解】由题知,正四面体截球面所得曲线为四个半径相同的圆,每个圆的周长为2π,半径为1,故球心O到正四面体各面的距离为210612⎛⎫-=⎪⎝⎭,设正四面体棱长为a,如图所示,则斜高332AE EF a==,体高63=AF a,在Rt AEF和R t AGO中,13OG EFAO AE==,612366a=-,∴6a=,∴23136261823V===9.已知菱形ABCD的边长为4,对角线4BD=,将ABD△沿着BD折叠,使得二面角A BD C--为120︒,则三棱锥A BCD-的外接球的表面积为___________.【答案】1123π【详解】如图所示:将ABD △沿BD 折起后,取BD 中点为E ,连接AE ,CE ,则AE BD ⊥,CE BD ⊥,所以AEC ∠即为二面角A BD C --的平面角,所以120AEC ∠=︒;ABD △与BCD △是边长为4的等边三角形.分别记三角形ABD △与BCD △的重心为G 、F , 则1233EG EA ==1233EF EC ==;即EF EG =; 因为ABD △与BCD △都是边长为4的等边三角形,所以点G 是ABD △的外心,点F 是BCD △的外心;记该几何体ABCD 的外接球球心为O ,连接OF ,OG ,根据球的性质,可得OF ⊥平面BCD ,OG ⊥平面ABD , 所以OGE 与OFE △都是直角三角形,且OE 为公共边,所以Rt OGE △与Rt OFE 全等,因此1602OEG OEF AEC ∠=∠=∠=︒, 所以43OE = 因为AE BD ⊥,CE BD ⊥,AECE E =,且AE ⊂平面AEC ,CE ⊂平面AEC , 所以BD ⊥平面AEC ;又OE ⊂平面AEC ,所以BD OE ⊥,连接OB ,则外接球半径22221OB OE BE =+=, 所以外接球表面积为1123π. 10.三棱锥A BCD -的一条棱长为a ,其余棱长均为1,当三棱锥A BCD -的体积最大时,它的外接球的表面积为___________.【答案】53π 【详解】解:由题意画出三棱锥的图形,其中1AB BC CD BD AC =====,AD a =.取BC ,AD 的中点分别为E ,F ,可知AE BC ⊥,DE BC ⊥,且AEDE E =, ∴BC ⊥平面AED ,∴平面ABC ⊥平面BCD 时,三棱锥A BCD -的体积最大, 此时162214AD a AE ===-=设三棱锥外接球的球心为O ,半径为R ,由球体的对称性知, 球心O 在线段EF 上,∴OA OC R ==, 又2222366244EF AE AF ⎛⎫⎛⎫=-=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 设6OF x OE x ==-,, 在三角形AOF 中:2222216R ()x 2AD OF =+=+⎝⎭, 在三角形OEC 中:22222161R ()x 22OE BC ⎫⎛⎫=+=-+⎪ ⎪⎪⎝⎭⎝⎭ ∴22222661442R x x ⎛⎫⎛⎫⎛⎫=+=-+ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,解得6x =. ∴球的半径R 满足222665R 41212⎛⎫⎛⎫=+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, ∴三棱锥外接球的表面积为25544123R πππ=⨯=. 11.四面体ABCD 中,90ABC BCD ∠=∠=︒,2AB BC CD ===,23AD =,则该四面体的外接球表面积为__________.【答案】12π【详解】由题意90ABC BCD ∠=∠=︒,2AB BC CD ===,23AD =,则22AC BD ==, 所以222AB BD AD +=,AB BD ⊥,同理AC CD ⊥,取AD 中点O ,则O 到,,,A B C D 四点的距离相等,O 即为ABCD 外接球的球心, 所以球半径为32AD r ==,球表面积为2412ππ==S r . 故答案为:12π.12.如图所示,正方体1111ABCD A BC D -的棱长为2,,E F 为1,AA AB 的中点,M 点是正方形11ABB A 内的动点,若1//C M 平面1CD E ,则M 点的轨迹长度为______.【答案】2 【详解】如图所示,11A B 的中点H ,1BB 的中点G ,连接11,,,,GH C H C G EG HF .可得四边形11EGC D 是平行四边形,∴11//C G D E ,又1C G ⊄平面1CD E ,1D E ⊂平面1CD E ,可得1//C G 平面1CDE .同理可得1//C H CF ,1//C H 平面1CD E ,又111C H CG C =,∴平面1//C GH 平面1CD E . ∵M 点是正方形11ABB A 内的动点,1//C M 平面1CD E ,∴点M 在线段GH 上. ∴M 点的轨迹长度为22112GH =+=.故答案为:2.132ABCD A B C D ''''-中,点E 、F 、G 分别是棱A B ''、B C '、CD 的中点,则由点E 、F 、G 确定的平面截正方体所得的截面多边形的面积等于___________.【答案】33 【详解】分别取AD 中点P ,1CC 中点M ,1AA 中点N ,可得出过E ,F ,G 三点的平面截正方体所得截而为正六边形EFMGPN , 则正六边形的边长2211122MG CG CM =+=+=, 故截面多边形的面积等于233361S =⨯⨯=. 故答案为:33.14.球O 为正方体1111ABCD A BC D -的内切球,平面11AC B 截球O 的截面面积为π,则球的表面积为________.【答案】6π【详解】设内切球半径为R ,则正方体棱长为2R ,如图,平面11AC B 截球O 所得圆为正11AC B △的内切圆,而截面圆半径为1, 在正11AC B △中122A B R =,3221R =,6R = 故内切球的表面积为264(6ππ⋅⋅=. 故答案为:6π 15.某圆台下底半径为2,上底半径为1,母线长为2,则该圆台的表面积为________.【答案】11π【详解】由题意该圆台的表面积为2221(21)211S ππππ=⨯+⨯+⨯+⨯=.。
由三视图还原几何体

互动授课
(2)
(2)从正面、侧面看立体图形,图象都是等腰三角形; 从上面看,图象是圆;可以想象出:整体是圆锥,如图 所示
互动授课
分析:由主视图可知,物体正面是正五边形;由俯视图可知,由上向 下看物体是矩形的,且有一条棱(中间的实线)可见到,两条棱(虚 线)被遮挡;由左视图 可知,物体的侧面是矩形的,且有一条棱 (中间的实线)可见到.综合各视图可知,物体是五棱柱形状的. 解:物体是五棱柱形状的,如图所示.
随堂检测:
1.请找出下列三视图对应的几何体 第
一 组
a
b
c
A
B
C
第
二
俯
e
俯
f
俯
g
左 左 左
组
正三棱锥 长方体 正四棱 台
E
F
G
2、如图是一个物体的三视图,试说出物体 的形状。
正 视 图 侧 视 图
俯 视 图
正视图
侧视图
俯视图 A
B
4、下面所给的三视图表示什么几何体?
1、课本114页练习(1)(2) 116页4 1、2号学生加做118页8题
学以致用
变式训练1: 你可以出一道类似例1的题吗?(两人一组, 一人给出单个几何体的三视图,一人猜几何体。)
提示:正方体、圆柱、三棱柱、球、六棱柱、四棱锥等
例2 下面所给的三视图表示什么几何体?
主视图
左视图
俯视图
答案:一个四棱柱和 一个圆柱体组成的简 单组合体。
正视图
侧视图
俯视图
学以致用
变式训练2: 你可以出一道类似例2的题吗?(两人一组, 一人给出单个几何体的三视图,一人猜几 (1)正方体的三视图都是——— 长方形 (2)圆柱的三视图中有两个是——— 圆 另一个是—— 三角形 (3)圆锥的三视图中有两个是———,另 圆和一个点 一个是—————。 圆 (4)球的三视图都是——
三视图还原直观图教案

三视图还原直观图教案(实用版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的实用范文,如学习资料、英语资料、学生作文、教学资源、求职资料、创业资料、工作范文、条据文书、合同协议、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this shop provides various types of practical sample essays, such as learning materials, English materials, student essays, teaching resources, job search materials, entrepreneurial materials, work examples, documents, contracts, agreements, other essays, etc. Please pay attention to the different formats and writing methods of the model essay!三视图还原直观图教案本节课是“空间几何体的三视图和直观图”的第一课时,主要内容是投影和三视图,这部分知识是立体几何的基础之一,一起看看三视图还原直观图教案!欢迎查阅!三视图还原直观图教案1一、教材的地位和作用本节课是“空间几何体的三视图和直观图”的第一课时,主要内容是投影和三视图,这部分知识是立体几何的基础之一,一方面它是对上一节空间几何体结构特征的再一次强化,画出空间几何体的三视图并能将三视图还原为直观图,是建立空间概念的基础和训练学生几何直观能力的有效手段。
2019-2020学年北师大版高中数学必修二教师用书:1-3 三视图 Word版含答案

姓名,年级:时间:§3三视图1.由基本几何体形成的组合体有两种基本的组成形式:(1)将基本几何体拼接成组合体;(2)从基本几何体中切掉或挖掉部分构成组合体.2.绘制三视图时的注意点(1)主、俯视图长对正;主、左视图高平齐;俯、左视图宽相等,前后对应.(2)在三视图中,需要画出所有的轮廓线,其中,视线所见的轮廓线画实线,看不见的轮廓线画虚线.(3)同一物体放置的位置不同,所画的三视图可能不同.(4)清楚简单组合体是由哪几个基本几何体组成的,并注意它们的组成方式,特别是它们的交线位置.判断正误(正确的打“√”,错误的打“×”)(1)任何几何体的三视图都与其摆放的位置有关.( )(2)任何几何体的三视图都与其摆放的位置无关.()(3)有的几何体的三视图与其摆放的位置无关.()(4)正方体的三视图一定是三个全等的正方形.( )[答案] (1)×(2)×(3)√(4)×题型一简单几何体的三视图【典例1】画出如图所示几何体的三视图.[思路导引]图①为正六棱柱,可按棱柱的画法画出,图②为一个圆锥与一个圆台的组合体,按圆锥、圆台的三视图画出它们的组合形状.[解] 按正六棱柱、圆锥、圆台的三视图画法如图所示.(1)画三视图时,首先确定主视、左视、俯视的方向,同一物体放置的位置不同,所画的三视图可能不同.一般主视方向确定了,则左视与俯视的方向也就确定了,在有的问题里,直接给出主视图,也是确定主视方向的一个方法.(2)一个物体的三视图的排列规则是:俯视图放在主视图的下面,左视图放在主视图的右面.[针对训练1]如下图所示,图(1)是底面边长和侧棱长都是2 cm 的四棱锥,图(2)是上、下底面半径分别为1 cm,2 cm,高为2 cm的圆台,分别画出它们的三视图.[解](1)四棱锥的三视图如下图所示:(2)圆台的三视图如下图所示:题型二简单组合体的三视图【典例2】画出如图所示的几何体的三视图.[思路导引]画三视图之前,先把几何体的结构弄清楚,图为两个圆柱的组合体.[解] 如图所示.画简单组合体的三视图时要注意的问题(1)分清简单组合体是由哪些简单几何体组成的,是组合型还是切挖型.(2)先画主体部分,后画次要部分.(3)几个视图要配合着画.一般是先画主视图再确定左视图和俯视图.(4)组合体的各部分之间要画出分界线.[针对训练2]画出如图所示几何体的三视图.[解] 如图所示(1)(2)题型三由三视图还原成实物图【典例3】如图是一个物体的三视图,则此三视图所描述的物体是下列哪个几何体( )[思路导引](1)通过主视图和左视图确定是柱体、锥体还是台体.若主视图和左视图为矩形,则原几何体为柱体;若主视图和左视图为等腰三角形,则原几何体为锥体;若主视图和左视图为等腰梯形,则原几何体为台体.(2)通过俯视图确定是多面体还是旋转体,若俯视图为多边形,则原几何体为多面体;若俯视图为圆,则原几何体为旋转体.[解析] 由俯视图可知该几何体为旋转体,由主视图、左视图、俯视图可知该几何体是由圆锥、圆柱组合而成.[答案] D由三视图还原成实物图时,一般先由俯视图确定底面,由主视图与左视图确定几何体的高及位置,同时想象视图中每一部分对应实物部分的形状.[针对训练3]根据三视图(如图所示)想象物体原形,指出其结构特征,并画出物体的实物草图.[解]由俯视图知,该几何体的底面是一直角梯形;再由主视图和左视图知,该几何体是一四棱锥,且有一侧棱与底面垂直,所以该几何体如图所示.1.如图,甲、乙、丙是三个立体图形的三视图,与甲、乙、丙相对应的标号是()①长方体;②圆锥;③三棱锥;④圆柱.A.③①② B.①②③ C.③②④ D.④②③[答案] D2.已知三棱柱ABC—A1B1C1如右图所示,以BCC1B1的前面为正前方,画出的三视图正确的是( )[解析]主视图是矩形,左视图是三角形,俯视图是矩形,中间有一条线.[答案] A3.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的主视图的面积不可能等于()A.1 B. 2 C。
三视图还原实物图“五步走”

三视图还原直观图“五步走”石门县第一中学415300陈锦鑫三视图是高中立体几何中的一个重要知识点,也是今后进一步学习机械制图、建筑制图等的必修课,三视图也是近几年高考必考的知识点。
主要题型就是给出几何体的三视图,计算几何体的面积和体积等相关量。
学生丢分的主要原因是不能由三视图还原为几何体,画出相应的直观图。
本文通过一道例题介绍一种将三视图还原成实物图的方法。
如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,将该三视图还原成实物图第一步:根据三视图中三种视图的长与宽,作一个与正视图等长等高,与俯视图等宽的长方体。
例如本例中需要作一个边长为2的正方体ABCD-A’B’C’D’,如图。
第二步:根据三视图中的正视图对长方体切割。
例如本例中由正视图知道,原几何体只能在三棱柱ADD’-BCC’范围内,因此将三棱柱AA’D’-BB’C’部分截掉,如图。
第三步:根据三视图中的侧视图对剩余几何体切割。
例如本例中由侧视图知道,原几何体只能在四棱锥C’-ABCD范围内,因此将三棱锥D’-ADC’部分截掉,如图。
第四步:根据三视图中的俯视图对剩余几何体切割。
,同时结合三种视图需要将例如本例中由俯视图知道,原几何体在底面上的投影为BCD三棱锥C’-ABDC部分截掉,得到三棱锥C’-BCD,如图。
第五步:根据三种视图多边形内部的实线或虚线对剩余几何体切割。
例如本例中正视图、俯视图中均有一条虚线,三视图的虚线表示虚线所在的位置有立体图形的轮廓线,只是在观察者所在的位置看不到。
根据正视图、俯视图中知点E为三棱锥C’-BCD 中BC边的中点,连接ED、EC’,ED、EC’是立体图形的轮廓线,因此我们需要将截掉三棱锥C’-ECD,得到三棱锥C’-BDE即为三视图所对应的实物图。
知识卡片-由三视图判断几何体

由三视图判断几何体
能量储备
由几何体的三种视图想象其立体形状可以从如下途径进行分析:
(1)根据主视图想象物体的正面形状及上、下和左、右位置,根据俯视图想象物体上面形状及左、右和前、后位置,再结合左视图验证该物体的左侧面形状,并验证上、下和前、后位置;
(2)从实线和虚线想象几何体看得见部分和看不见部分的轮廓线。
通关宝典
★基础方法点
方法点1:由三种视图还原几何体时,要了解简单的、常见的规则物体的三种视图,还要善于分析和想象。
例:如图527所示,是某一物体的三种视图,请说明它是一个什么形状的物体。
解:该物体是圆锥和圆柱的组合体,如图528所示。
分析:由三种视图可知,该物体的上半部分是圆锥,下半部分是圆柱,所以该物体是圆锥和圆柱的组合体
方法点2:主视图能体现物体的左右长度、上下高度;俯视图能体现物体的左右长度、前后宽度;左视图能体现物体的上下高度、前后宽度.通过观察三种视图可以想象出几何体的立体图形.
例:已知一个几何体的三种视图如图5220所示,则该几何体是( )
解析:A图的主视图、左视图均为等腰三角形,B图的左视图、俯视图均为矩形,C图的俯视图的外轮廓线为四边形,由此可排除A,B,C选项.答案:D,
蓄势待发
考前攻略
中考题和教材习题都是考查根据视图判断几何体的形状,只不过教材习题是根据两种视图与画出的几何体进行对照,比较容易判断,而中考题是根据三种视图直接分析和想象出几何体,难度有所增加,通常采用排除法进行选择。
完胜关卡。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
俯 视 图
例2说出下面的三视图表示的几何体的结
构特征,并画出其示意图.
主视图
左视图
将一个长方体挖去两个
俯视图
小长方体后剩余的部分
例 3 一个几何体的三视图如图所示,其中正视
图和左视图是腰长为6的两个全等的等腰直角 三角形.用多少个这样的几何体可以拼成一个棱 长为6的正方体.
主视图
左视图
俯视图
该几何体为四棱锥D1—ABCD
如何把组合体的三视图还原成几何体的实形
1、把每个视图分解为基本图形(三角形,圆
等) 2、结合对应部分的三视图想象对应的基本几 何体 3、结合虚实线概括组合体
.
课外思考题
用小方块搭一个几何体,使得它的主视图和俯视图 如图所示,这样的几何体只有一种吗?它至少需要多 少个小立方块?最多需要多少个小立方块?分别画出 它们的几何体的左视图.
由三视图还原成实物图
设计制作:神木中学杨小玲
复习回顾:
一、三视图:
1、从正面看到的图形叫做主视图;从左面看到的图形 叫左视图;从上面看到的图形叫俯视图。这三张图, 称为三视图. 2、形体可见轮廓线画粗实线,不可见轮廓线画虚线
二、三视图的对应规律:
---高平齐
主视图
俯视图
主视图
俯视图
左视图
主视图
俯视图
左视图
主视图
俯视图
俯视图和左视图
----宽相等
请找出下列三视图对应的几何体 第
一 组
a
b
c
A
B
C
第
二
俯
e
俯
f
俯
g
左 左 左
组
正三棱锥 长方体 正四棱 台
E
F
G
一个几何体的三视图如下,你能说出它是什么 立体图形吗?
主视图 左视图
俯视图
与上一张三视图有何区别与联系?
思考1:下列图分别是简单组合体的三 视图,想象它们表示的组合体的结 构特征,并画出其示意图.
D1 D1 C1 A1
B1
D
D C A B B
C
A
正视图:等腰直角三角形; 左视图:等腰直角三角形; 俯视图:正方形(要加对角线BD哟) 要三个这样的几何体才能拼成正方体,分别 四棱锥 D ABCD 、四棱锥 D 1 ABB 1 A1 、 四棱锥 D BCC B
1
1 1 1
说出下面的三视图表示的几何体的结构特征
正视图
侧视图
俯视图
思考2:下列两图分别是两个简单组合体的三视 图,想象它们表示的组合体的结构特征,并 作适当描述.
主视图 主视图
左视图
左 视 图
六棱锥与六棱柱 的组合体
俯视图
举重杠铃
俯视图
变式训练一:
主视图
左视图
俯视图 A
B
2、如图是一个物体的三视图,试说出物体 的形状。
主 视 图 左 视 图
